点线面位置关系定理总结培训讲学
(完整版)点、直线、平面之间的位置关系知识点总结,推荐文档
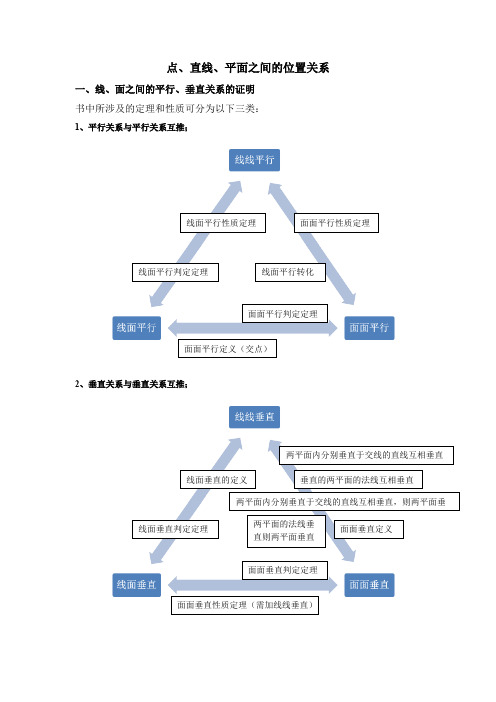
点、直线、平面之间的位置关系一、线、面之间的平行、垂直关系的证明书中所涉及的定理和性质可分为以下三类:1、平行关系与平行关系互推;2、垂直关系与垂直关系互推;线面垂直判定定理线面垂直的定义两平面的法线垂直则两平面垂直面面垂直判定定理线面平行判定定理线面平行性质定理线面平行转化面面平行判定定理面面平行性质定理3、平行关系与垂直关系互推。
以线或面为元素,互推的本质是以某一元素为中介,通过另外两元素与中介元素的垂直或平行关系,推导出该两元素的关系,总共有21种情况,能得出结论的有以下9种情况。
线线平行传递性:;b c c a b a //////⇒⎭⎬⎫面面平行传递性:;γαβγβα//////⇒⎭⎬⎫线面垂直、线面垂直线面平行:;⇒ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥线面垂直线线平行(线面垂直性质定理):;⇒b a b a //⇒⎭⎬⎫⊥⊥αα线面垂直面面平行:;⇒βαβα//⇒⎭⎬⎫⊥⊥a a 线面垂直、面面平行线面垂直:;⇒βαβα⊥⇒⎭⎬⎫⊥a a //线线平行、线面垂直线面垂直:;⇒αα⊥⇒⎭⎬⎫⊥b a b a //线面垂直、线面平行面面垂直:。
⇒βααβ⊥⇒⎭⎬⎫⊥a a //备注:另外证明平行关系时可以从最基本的定义交点入手,证明垂直关系时可以从最基本的定义角度入手。
符号化语言一览表①线面平行;;;ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂αββα////a a ⇒⎭⎬⎫⊂ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥②线线平行:;;;;////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ b a b a //⇒⎭⎬⎫⊥⊥αα////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭b c c a b a //////⇒⎭⎬⎫③面面平行:;;;,////,//a b a b O a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭βαβα//⇒⎭⎬⎫⊥⊥a a γαβγβα//////⇒⎭⎬⎫④线线垂直:;b a b a ⊥⇒⎭⎬⎫⊂⊥αα⑤线面垂直:;;,,a b a b O l l a l b ααα⊂⊂⎫⎪=⇒⊥⎬⎪⊥⊥⎭,l a a a l αβαββα⊥⎫⎪=⇒⊥⎬⎪⊂⊥⎭ ;;βαβα⊥⇒⎭⎬⎫⊥a a //αα⊥⇒⎭⎬⎫⊥b a b a //⑥面面垂直:二面角900; ;;βααβ⊥⇒⎭⎬⎫⊥⊂a a βααβ⊥⇒⎭⎬⎫⊥a a //二、立体几何中的重要方法1、求角:(步骤-------Ⅰ找或作角;Ⅱ求角)⑴异面直线所成角的求法:①平移法:平移直线,构造三角形;②补形法:补成正方体、平行六面体、长方体等,发现两条异面直线间的关系.注:还可用向量法,转化为两直线方向向量的夹角.⑵直线与平面所成的角:①直接法(利用线面角定义);②先求斜线上的点到平面距离h ,与斜线段长度作比,得sin ;③三线三角公式.θ12cos cos cos θθθ=注:还可用向量法,转化为直线的方向向量与平面法向量的夹角.⑶二面角的求法:①定义法:在二面角的棱上取一点(特殊点),作出平面角,再求解;②垂面法:作面与二面角的棱垂直; ③投影法(三垂线定理);④面积摄影法.注:对于没有给出棱的二面角,应先作出棱,然后再选用上述方法;还可用向量法,转化为两个班平面法向量的夹角.2、求距离:(步骤-------Ⅰ找或作垂线段;Ⅱ求距离)⑴两异面直线间的距离:一般先作出公垂线段,再进行计算;或转化为线面距离、点面距离;⑵点到直线的距离:一般用三垂线定理作出垂线段,再求解;⑶点到平面的距离:①垂面法:借助面面垂直的性质作垂线段(确定已知面的垂面是关键),再求解;②等体积法;还可用向量法:.||n d =3、证明平行、垂直的理论途径:①证明直线与直线的平行的思考途径:(1)转化为判定共面二直线无交点(定义);(2)转化为两直线同与第三条直线平行;(3)转化为线面平行;(4)转化为线面垂直;(5)转化为面面平行.②证明直线与平面的平行的思考途径:(1)转化为直线与平面无公共点(定义);(2)转化为线线平行;(3)转化为面面平行.③证明平面与平面平行的思考途径:(1)转化为判定两平面无公共点(定义);(2)转化为线面平行;(3)转化为线面垂直.④证明直线与直线的垂直的思考途径:(1)转化为相交垂直;(2)转化为线面垂直.⑤证明直线与平面垂直的思考途径:(1)转化为该直线与平面内任一直线垂直(定义);(2)转化为该直线与平面内相交的两条直线垂直;(3)转化为该直线与平面的一条垂线平行;(4)转化为该直线垂直于另一个平行平面;(5)转化为该直线与两个垂直平面交线垂直.⑥证明平面与平面的垂直的思考途径:(1)转化为判断二面角是直二面角;(2)转化为线面垂直.。
点线面间的位置关系知识点总结(含题)(

点线面间的位置关系知识点总结一、三个公理公理1如果一条直线上的两点在一个平面内,那么_________________________________________公理2:过________________________ 的三个点,有且只有一个平面公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________________二、空间两条直线间的位置关系分类为:______________ , ______________ ,_______________ ;其中__________ , _________ 合称为______________三、空间直线与平面间的位置关系分类为:__________________ ,____________ ,__________________ ;其中__________ , _________ 合称为______________四、空间平面与平面间的位置关系分类为:______________ ,当两个平面成90。
时,属于____________ 关系常用证明技巧一、线面平行列1 (2IH1年怀化楓蝌)如图所示*已知几0是单位止方WABCn-A^.C^的面A^BA和面』肮2>的中心*求证:卩总〃平面ncr^n.练习1. 正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q且AP = DQ. 求证:PQ//平面BCE.2・妇匿,四棱链/一乩噸一平面所裁*截面为平厅四边形吕他求证,m/zz面日捌3* (加10年彌考■陕丙雜)如图’在四棱饰P ABCD中.底血ABCD^矩形「只4 丄平SLUJC/h .lP-.Ltf, BP-IiC-1, E, F分别&l f B T PC 的中点.门)证明* EF//平血知";卩)求二棱锥E—.【号「的休枳匚(2)1/3二、线面垂直1、(2006年北京卷)如图,在底面为平行四边形的四棱锥P ABCD中,AB 点E是PD的中点•(I)求证:AC PB ; (n)求证:PB〃平面AEC ;2、( 2006年浙江卷)如图,在四棱锥P-ABCD中,底面为直角梯形BAD=90 ° ,PA丄底面ABCD,且PA= AD=AB=2BC,M、N 分别为PC、PB 求证:PB丄DM;3、(2006年福建卷)如图,四面体ABCD中,0、E分别是BD、BC的中点,CA(I)求证:AO 平面BCD;AC , PA 平面ABCD,且PA AB , CB CD BD 2, AB AD . 2.,AD // BC, /的中点•ADOE4、( 2006年重庆卷)如图,在四棱锥P—ABCD中,PA 底面ABCD, PC、DAB 为直角,AB II CD,AD=CD=24B,E、F 分另U为CD的中点.(I)试证:CD 平面BEF;5、(全国H ?理?9题)如图,在四棱锥SCS-ABCD中,底面ABCD为正方形,侧棱SD丄底面ABCD , E、F分别是AB、的中点。
(完整word版)点线面之间的位置关系的知识点总结,推荐文档

高中空间点线面之间位置关系知识点总结第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线 a ∥b 。
2 公理4:平行于 c ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;D CBAα LA ·α C ·B·A · α P· αLβ 共面直线=>a ∥c2⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
点线面位置关系定理总结

培优辅导,陪你更优秀!
//a b //a b
1.线面平行判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(简述为线线平行线面平行) 表述及图示
2.线面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
(简述为线面平行线线平行)
//a a b
α
β
αβ⊂⋂= 3.平面平行判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
////a b a b a b P
β
β
αα
⊂⊂⋂=//αβ
4.平面平行性质定理:如果两个平行平面都和第三个平面相交,那么它们的交线平行
//a b
αβ
γαγβ⋂=⋂=
5.线面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,那么这条直线就垂直于这个
平面。
a b
a c
b c A b c α
α
⊥⊥⋂=⊂⊂a α⊥
6.线面垂直性质定理:垂直于同一平面的两条直线平行。
a b α
α⊥⊥ 7.面面垂直判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
简述为“线面垂直,则面面垂直”。
a a αβ
⊂⊥αβ⊥ 8.面面垂直性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
l a a l αβ
αβα
⊥⋂=⊂⊥αβ⊥ //a b a b α
α⊄
⊂//a
α
//a
b。
点线面的位置关系总结

点线面的位置关系总结1. 引言在几何学中,点、线和面是最基本的几何图形。
它们之间的位置关系对于我们理解和描述物体的形状、空间关系以及解决几何问题非常重要。
本文将总结点、线和面之间的常见位置关系,帮助读者在几何学的学习和解题过程中更加清晰地理解这些关系。
2. 点与点之间的位置关系在二维空间中,两个点之间有三种基本的位置关系:•重合(Coincident):两个点的位置完全重合,表示它们的坐标值完全相同。
•相邻(Adjacent):两个点的位置非常接近,但它们的坐标值不完全相同。
•不重合(Non-coincident):两个点的位置完全不同,它们的坐标值没有任何相似之处。
在三维空间中,点与点之间的位置关系也有类似的定义。
3. 点与线之间的位置关系点与线之间的位置关系可以描述为:•在线上(On the line):一个点位于一条直线上。
•在线的延长线上(On the extension of the line):一个点位于一条直线的延长线上,但不在直线上。
•在线的两侧(On one side of the line):一个点与一条直线相交,但不在直线上。
4. 点与面之间的位置关系点与面之间的位置关系可以描述为:•在平面上(On the plane):一个点位于一个平面上。
•在平面的延伸方向上(On the extension of the plane):一个点位于一个平面的延伸方向上,但不在平面上。
•在平面的两侧(On one side of the plane):一个点与一个平面相交,但不在平面上。
5. 线与线之间的位置关系线与线之间的位置关系可以描述为:•相交(Intersecting):两条线在二维空间或三维空间中相交,即它们有一个或多个共同的点。
•平行(Parallel):两条线在二维空间或三维空间中永不相交,即它们没有共同的点。
•重合(Coincident):两条线在二维空间或三维空间中完全重合,表示它们是同一条线。
立体几何讲空间点线面的位置关系课件

线与面的关系
总结词
线与面的关系是空间几何中 复杂的关系之一
详细描述
线与面的关系有多种形式, 如线在面上、线与面相交、 线与面平行等。这些关系可 以通过几何定理进行证明和 推导,如线面平行的判定定 理和性质定理等。
总结词
线与面的关系是空间几何中 复杂的关系之一
详细描述
线与面的关系有多种形式, 如线在面上、线与面相交、 线与面平行等。这些关系可 以通过几何定理进行证明和 推导,如线面平行的判定定 理和性质定理等。
空间面的定义与性质
总结词
几何中的面是由一组线围成的闭合空间。
详细描述
面是由一组线围成的闭合空间,表示一个二维的空间区域。根据定义,面有一定的厚度和大小。面的性质包括封 闭性和延展性,即面是封闭的边界,可以延展成一定的大小和形状。同时,面也可以由三个不同的点确定一个唯 一的平面。
03
点线面的位置关系
点与面的关系
总结词
详细描述
总结词
详细描述
点与面的关系是决定面形状的 关键
一个点可以确定一个平面,当 这个点位于平面上时,它与平 面的关系是固定的。此外,当 多个点位于同一平面时,它们 共同确定了该平面的形状和大 小。
点与面的关系是决定面形状的 关键
一个点可以确定一个平面,当 这个点位于平面上时,它与平 面的关系是固定的。此外,当 多个点位于同一平面时,它们 共同确定了该平面的形状和大 小。
详细描述
在几何学中,点被视为最基本的元素,表示一个具体的空间 位置。它没有大小和形状,只有位置。点的性质包括唯一性 和无限可重复性,即任意两个不同的点都可以确定一条直线 ,且同一直线上可以有无数个点。
空间线的定义与性质
总结词
几何中的线是点的集合,表示一个连续的空间路径。
点线面之间的位置关系的知识点总结

点线面之间的位置关系的知识点总结-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN高中空间点线面之间位置关系知识点总结第二章 直线与平面的位置关系空间点、直线、平面之间的位置关系平面含义:平面是无限延展的 2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线 a ∥b 。
2 公理4:平行于c ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;D CBAα LA ·α C ·B·A·α P· αLβ 共面直线=>a ∥c2⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
点线面的位置关系和判定方法

点线面的位置关系和判定方法在几何学中,点、线段和平面是最基本的图形元素,它们之间的位置关系和判定方法对于几何问题的解决至关重要。
本文将探讨点线面的位置关系以及相应的判定方法。
一、点与线段的位置关系和判定方法1. 点在线段上的情况:一个点可以在线段的两端点之间,也可以在线段上,或者在线段外。
要判断一个点是否在线段上,可以使用如下方法:(1)距离判定法:计算点到线段两个端点的距离,如果两个距离之和等于线段长度,那么点就位于线段上。
(2)向量判定法:将线段的两个端点视为向量A和向量B,将点与线段的一个端点视为向量C。
如果向量C可以表示为向量A与向量B的线性组合,且系数的和等于1,那么点就位于线段上。
2. 点在线段的延长线上的情况:当一个点在线段的延长线上时,意味着可以无限延长线段,点位于线段的一侧。
判定方法如下:(1)向量判定法:同样将线段的两个端点视为向量A和向量B,将点与线段的一个端点视为向量C。
如果向量C可以表示为向量A与向量B的线性组合,且系数的和大于1,那么点在线段的延长线上。
3. 点在线段的左侧或右侧的情况:若点位于线段的左侧(或右侧),则该点与线段的两个端点所形成的线段组合为逆时针(或顺时针)方向。
判定方法如下:(1)向量叉积法:将线段的一个端点与点构成的向量记为向量A,将线段的一个端点与线段另一端点构成的向量记为向量B。
计算向量A和向量B的叉积,若叉积大于0,则点在线段的左侧;若叉积小于0,则点在线段的右侧;若叉积等于0,则点在线段上。
二、点与平面的位置关系和判定方法1. 点在平面上的情况:一个点可以位于平面上,也可以位于平面外部。
判定方法如下:(1)向量法:选择平面上的三个非共线点A、B、C,将点与这三个点分别构成向量。
如果点与向量A、B、C共面,那么点就位于平面上。
2. 点在平面的一侧或另一侧的情况:当一个点在平面的一侧时,意味着通过该点可以画出与平面垂直的直线。
判定方法如下:(1)点法向量法:选择平面上的一个点P,计算向量AP与平面的法向量N的点积。
第2讲 点、线、面的位置关系 (1)

第一讲 点、线、面的位置关系【知识梳理】1.平面的基本性质(平面是平的;无厚薄;可无限延展)公理1.如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
即:,,,A l B l A B l ααα∈∈∈∈⇒⊂公理2.过不在一条直线上的三点,有且只有一个平面。
(不共线三点确定一个平面)推论1:一条直线和直线外一点确定一个平面。
推论2:两条相交直线确定一个平面。
推论3:两条平行直线确定一个平面。
公理3.如果两个不重合的平面有一个公共点,那么它们有且只有一条经过该点的公共直线。
即: ,P P l P l αβαβ∈∈⇒=∈ 且且P l ∈2.空间两直线(1)位置关系:⎧⎧⎪⎨⎨⎩⎪⎩相交直线:在同一平面内,有且只有一个公共点共面直线平行直线:在同一平面内,没有公共点异面直线:不同在任何一个平面内,没有公共点(2)公理4:平行于同一条直线的两条直线互相平行(平行线的传递性)。
即://////a b a c b c ⎫⇒⎬⎭(3)等角定理:空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补。
(同向或反向时相等)(4)异面直线:不同在任何一个平面内的两条直线。
①异面直线的判定:定义法:反证法;结论法:平面内一点与平面外一点的连线与平面内不过该点的直线是异面直线。
②异面直线所成的角:设,a b 是两条异面直线,经过空间任一点O 作直线//a a ',//b b ',把,a b ''所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角)。
其范围是(0,]2π③两异面直线垂直:所成的角是直角的异面直线,a b ,记作a b ⊥。
3.直线与平面的位置关系: ⎧⎪⎨⎪⎩直线在平面内:直线与平面有无数个公共点直线与平面相交:直线与平面有且只有一个公共点直线与平面平行:直线与平面没有公共点4.平面与平面的位置关系:⎧⎨⎩两个平面平行:没有公共点两个平面相交:有一条公共直线5.共点(线,面)问题的证明方法(1)共点问题:证明123,,l l l 三线共点,一般先证12l l A = ,再证点3A l ∈即可。
点线面的位置关系知识点

点线面的位置关系知识点在几何学中,点、线和面是三个基本的几何概念,它们之间存在着一系列的位置关系。
这些位置关系的理解对于解决几何问题以及应用几何知识有着重要的意义。
本文将介绍点线面的位置关系的几个重要知识点。
一、点与直线的位置关系1. 在直线上:当一个点恰好位于一条直线上时,我们可以说这个点在直线上。
例如,点A在直线AB上。
2. 在直线的两侧:如果一个点既不在直线上,也不在直线的延长线上,我们可以说这个点在直线的两侧。
例如,点C在直线AB的两侧。
3. 在直线的延长线上:如果一个点不在直线上,但位于直线的延长线上,我们可以说这个点在直线的延长线上。
例如,点D在直线AB的延长线上。
4. 平行于直线:如果一条直线与给定直线没有任何交点,我们可以说这条直线平行于给定直线。
例如,直线CD平行于直线AB。
二、点与平面的位置关系1. 在平面上:当一个点位于一个平面内部时,我们可以说这个点在平面上。
例如,点A在平面P上。
2. 不在平面上:如果一个点既不在平面上,也不在平面的延长线上,我们可以说这个点不在平面上。
例如,点B不在平面P上。
3. 在平面的延长线上:如果一个点不在平面上,但位于平面的延长线上,我们可以说这个点在平面的延长线上。
例如,点C在平面P的延长线上。
4. 垂直于平面:如果一条直线与给定平面的任意一条线都垂直,我们可以说这条直线垂直于给定平面。
例如,直线EF垂直于平面P。
三、直线与平面的位置关系1. 相交于一点:当一条直线与平面有且仅有一个交点时,我们可以说这条直线与平面相交于一点。
例如,直线L与平面P相交于点A。
2. 平行于平面:如果一条直线与给定平面的任意一条线都平行,我们可以说这条直线平行于给定平面。
例如,直线M平行于平面P。
3. 包含于平面:当一条直线上的所有点都位于给定平面上时,我们可以说这条直线被包含于给定平面中。
例如,直线N被包含于平面P 中。
4. 相交于一条线:当一条直线与平面有无穷多个交点时,我们可以说这条直线与平面相交于一条线。
空间点线面的位置关系知识讲解共53页

1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
53
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
点线面位置关系总结

点线面位置关系总结在几何学中,点、线和面是最基本的几何图形。
它们之间的位置关系非常重要,可以帮助我们更好地理解和描述空间中的对象。
本文将对点线面位置关系进行总结,并探讨其应用。
一、点与线的位置关系1. 点在直线上:当一个点位于某条直线上时,我们可以说该点在直线上。
一个直线可以有无限个点。
2. 点在线段的内部:如果一个点位于一个线段的两个端点之间,我们可以说该点在线段的内部。
一个线段上可以有无限个点。
3. 点在线段的延长线上:如果一个点位于一个线段的延长线上,我们可以说该点在线段的延长线上。
延长线上也可以有无限个点。
4. 点在线段的外部:如果一个点既不在线段上,也不在线段的延长线上,我们可以说该点在线段的外部。
5. 点垂直于线:当一个点与一条直线垂直相交时,我们可以说该点垂直于线。
此时,点到直线的距离是最短的。
6. 点平行于线:当一个点与一条直线平行时,我们可以说该点平行于线。
此时,点到直线的距离是不变的。
二、点与面的位置关系1. 点在平面上:当一个点位于一个平面上时,我们可以说该点在平面上。
一个平面可以有无限个点。
2. 点在平面内部:如果一个点位于一个平面的边界之内,我们可以说该点在平面的内部。
一个平面内部可以有无限多个点。
3. 点在平面外部:如果一个点不在平面上,也不在平面的边界之内,我们可以说该点在平面的外部。
三、线与面的位置关系1. 线在平面上:当一条直线完全位于一个平面上时,我们可以说该线在平面上。
一条直线可以有无限个点。
2. 线与平面相交:当一条直线与一个平面相交时,我们可以说该线与平面相交。
相交点有可能是一个点、一条线或者空集。
3. 线平行于平面:当一条直线与一个平面平行时,我们可以说该线平行于平面。
此时,线上的所有点到平面的距离是相等的。
4. 线垂直于平面:当一条直线与一个平面垂直相交时,我们可以说该线垂直于平面。
此时,线上的所有点到平面的距离是最短的。
四、面与面的位置关系1. 平行面:当两个平面之间的夹角为0度时,我们可以说这两个平面是平行的。
点线面之间的位置关系——垂直关系-简单-讲义

点、线、面之间的位置关系——垂直关系知识讲解一、线面垂直1.定义:如果一条直线和一个平面相交于点0,并且和这个平面内过交点的任何直线都垂直,则称这条直线与这个平面互相垂直.1)这条直线叫做平面的垂线,这个平面叫做直线的垂面,交点叫垂足.2)垂线上任意一点到垂足间的线段,叫做这个点到这个平面的垂线段.垂线段的长度叫做这个点到平面的距离.3)如果一条直线垂直于一个平面,那么它就和平面内的任意一条直线垂直.4)画直线与平面垂直时,通常把直线画成和表示平面的平行四边形的一边垂直,如下图.直线l与平面a互相垂直,记作l ±a .2.线面垂直的判定定理:如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直.符号语言表述:l ±a,l ±b,a,b u a,a p|b = A n l ±a图像语言表述:l la3.线面垂直的性质定理:如果两条直线垂直于同一个平面,那么这两条直线平行.符号语言表述:a±a,b±a n a//b图像语言表述:4.线面垂直的性质(1)一条直线垂直于一个平面,则这条直线垂直于该平面内的所有直线(2 )推论1 :如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面;(3)推论2 :如果两条直线垂直于同一个平面,那么这两条直线平行;(4)垂直于同一直线的两个平面平行.5.证明线面垂直的方法(1)线面垂直的定义(2)线面垂直的判定定理(a± b, a± c, b u a, c u a, b^c = M n a±a )(3)平行线垂直平面的传递性(a g, b l a n a l a)(4)面面垂直的性质(a l。
, a Qp = l, a u p , a 11 n a l a)(5)面面平行的性质(a l a, a Q p n a 1p)(6)面面垂直的性质(a n P=l,a l y , p l y n l l y)二、面面垂直1.定义:如果两个相交平面的交线与第三个平面垂直,又这两个平面与第三个平面相交所得的两条交线互相垂直,则称这两个平面互相垂直.2.平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.符号语言表述:m l a, m u p n a l p图像语言表述:3.面面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.符号语言表述:a l p, aqp=l,m G P,m 11 n m l a图像语言表述:4.面面垂直的性质(1)两相交平面同时垂直于第三个平面,那么两相交平面的交线垂直于第三个平面(2)两平面互相垂直,过公共交线上一点做一个平面的垂线,则这条直线在第二个平面内5.证明面面垂直的方法(1)面面垂直的定义(2)面面垂直的判定定理(a l p, a u a n a l p )三、垂直模型总结1.勾股定理a2 + b2 = C2 n AC 1 CB2.等腰三角形三线合一AB = AC, D为BC重点n AD ± BC3,直径所对的圆周角为直角BD = CD = AD n BA ± AC4.菱形对角线垂直平分在菱形ABCD中n BD ± AC5.正方形、矩形临边垂直AB 1 BC, BC 1 CD6.正方形中点连线垂直在正方形ABCD中,E, F为CD, BC的中点n AE1DF7.直棱柱、正棱柱中侧棱垂直底面在直三棱柱中n AD ± 面ABC, AD 1 AB, AD 1BC, AD 1 AC典型例题一,选择题(共10小题)1 (2018•云南模拟)在正方体ABCD - A1B1c1D1中"点P是线段BC1上任意一点,则下列结论中正确的是()A- AD J DPB- AP±B1C C. AC J DP D• A i P,B i C2 . (2018春•武邑县校级月考)如图,四棱锥P - ABCD中,4PAB与^PBC是正三角形,平面PAB,平面PBC, AC X BD,则下列结论不一定成立的是()AA . PB±ACB . PD,平面ABCDC . AC±PD D .平面PBD,平面ABCDA . AE±CEB . BE±DEC . DE±CED .面ADE±® BCE4 (2016秋•杭州期末)如图所示,四边形ABCD中,AD〃BC ,AD=AB ,N BCD=45°,N BAD=90°,将△ABD沿BD折起,使面ABD,面BCD,连结AC ,则下列命题正确的是()A .面ABD±® ABCB .面ADC±® BDC C .面ABC±® BDCD .面ADC±® ABC 5 . (2017春•昆都仑区校级期中)如图,A ABC是直角三角形,N ABC=90°, PA ,平面ABC ,此图中直角三角形的个数为()BA . 1B . 2C . 3D . 46.( 2017•青州市模拟)如图,在三棱锥A - BCD中,AB,平面BCD , N ACB=45°, N ADB=30°, N BCD=120°, CD=40 视AB=( )A . 10B . 20C . 30D . 407(2017秋•赣州期中)设a邛为不重合的平面,m , n为不重合的直线,则下列命题正确的是()A .若m u a, n u 0, m〃n,则U a〃B B .若n±a , n±P , m,B,则U m±aC .若m〃a,n〃B,m,n,UU a±0D .若a±0 ,n,0,m,n,UU m±a8. (2015秋•临海市校级月考)在三棱锥A - BCD中,若AD±BC , BD1AD , △BCD是锐角三角形,那么必有()A .平面八8口,平面ADCB .平面八8口,平面ABCC .平面ADC,平面BCDD .平面ABC,平面BCD9. (2014秋•兴庆区校级期末)两个平面平行的条件是()A.一个平面内一条直线平行于另一个平面B.一个平面内两条直线平行于另一个平面C.一个平面内的无数条直线平行于另一个平面D.一个平面内的任意一条直线平行于另一个平面10(2015秋•东昌区校级期中)过^ABC所在平面a外一点P ,作PO,a ,垂足为O,若PA±PB,PB±PC,PC L PA,则点O 是 ^ABC 的()A .垂心B .重心C .内心D .外心二,填空题(共4小题)11.过平面外两点,可作个平面与已知平面平行.12. (2015春•上海校级期末)点P为^ABC所在平面外一点,PO,平面ABC , 垂足为。
点线面位置关系学习知识点梳理及经典例题带解析

【知识梳理】( 1)四个公义公义 1:假如一条直线上的两点在一个平面内,那么这条直线在此平面内。
符号语言: A l , B l ,且 A, B l。
公义 2:过不在一条直线上的三点,有且只有一个平面。
三个推论:①经过一条直线和这条直线外一点,有且只有一个平面② 经过两条订交直线,有且只有一个平面③ 经过两条平行直线,有且只有一个平面公义它给出了确立一个平面的依照。
3:假如两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)。
符号语言:P , 且 P l , P l 。
公义 4:(平行线的传达性)平行与同向来线的两条直线相互平行。
符号语言: a // l ,且 b // l a // b 。
( 2)空间中直线与直线之间的地点关系1.观点异面直线及夹角:把不在任何一个平面内的两条直线叫做异面直线。
已知两条异面直线a, b ,经过空间随意一点O 作直线a // a,b // b ,我们把 a 与 b 所成的角(或直角)叫异面直线 a,b 所成的夹角。
(易知:夹角范围0 90 )定理:空间中假如一个角的两边分别与另一个角的两边分别平行,那么这两个角相等或互补。
(注意:会画两个角互补的图形)共面直线订交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;2. 地点关系:异面直线:不一样在任何一个平面内,没有公共点( 3)空间中直线与平面之间的地点关系直线在平面内( l )有无数个公共点直线与平面的地点关系有三种:直线与平面订交(l A)有且只有一个公共点直线在平面外直线与平面平行(l / / )没有公共点( 4)空间中平面与平面之间的地点关系两个平面平行(/ / )没有公共点平面与平面之间的地点关系有两种:l)有一条公共直线两个平面订交(直线、平面平行的判断及其性质1.内容概括总结( 1)四个定理定理定理内容直线与平面平面外的一条直线与平面内的一条直线平行,则该直平行的判断线与此平面平行平面与平面一个平面内的两条订交直线与另一个平面平行,则这平行的判断两个平面平行一条直线与一个平面平行,符号表示a, b ,且 a // b a//a,b,a b P, a //, b ////剖析解决问题的常用方法在已知平面内“找出”一条直线与已知直线平行便可以判断直线与平面平行。
高中数学讲义微专题62 点线面位置关系

微专题62点线面位置关系的判定一、基础知识(一)直线与直线位置关系:1、线线平行的判定(1)平行公理:空间中平行于同一直线的两条直线平行(2)线面平行性质:如果一条直线与平面平行,则过这条直线的平面与已知平面的交线和该直线平行(3)面面平行性质:2、线线垂直的判定(1)两条平行直线,如果其中一条与某直线垂直,则另一条直线也与这条直线垂直直线与平面位置关系:(2)线面垂直的性质:如果一条直线与平面垂直,则该直线与平面上的所有直线均垂直(二)直线与平面的位置关系1、线面平行判定定理:∥(1)若平面外的一条直线l与平面α上的一条直线平行,则lα(2)若两个平面平行,则一个平面上的任一直线与另一平面平行2、线面垂直的判定:⊥(1)若直线l与平面α上的两条相交直线垂直,则lα(2)两条平行线中若其中一条与平面垂直,则另一条直线也与该平面垂直(3)如果两个平面垂直,则一个平面上垂直于交线的直线与另一平面垂直(三)平面与平面的位置关系1、平面与平面平行的判定:(1)如果一个平面上的两条相交直线均与另一个平面平行,则两个平面平行(2)平行于同一个平面的两个平面平行2、平面与平面垂直的判定如果一条直线与一个平面垂直,则过这条直线的所有平面均与这个平面垂直(四)利用空间向量判断线面位置关系1、刻画直线,平面位置的向量:直线:方向向量平面:法向量2、向量关系与线面关系的转化:设直线,a b 对应的法向量为,a b ,平面,αβ对应的法向量为,m n(其中,a b 在,αβ外)(1)a ∥b ⇔a ∥b(2)a b a b ⊥⇔⊥(3)a a α⊥⇔ ∥m(4)a a m α⇔⊥∥(5)m n αβ⇔∥∥(6)m nαβ⊥⇔⊥3、有关向量关系的结论(1)若,a b b c ∥∥,则a c∥平行+平行→平行(2)若,a b b c ⊥ ∥,则a c⊥平行+垂直→垂直(3)若,a b b c ⊥⊥ ,则,a c的位置关系不定。
空间几何中的点线面的位置关系

空间几何中的点线面的位置关系在空间几何学中,点、线和面是最基本的几何元素。
它们在空间中的位置关系对于理解和解决几何问题至关重要。
本文将讨论点线面在空间中的常见位置关系以及它们之间的相互作用。
一、点与线的位置关系1.1 点在直线上当一个点位于一条直线上时,称该点在直线上。
点在直线上的特点是它与直线上的任意两个点都在同一直线上。
1.2 点在直线上的延长线上当一个点位于直线的延长线上时,称该点在直线上的延长线上。
点在直线延长线上的特点是它与直线上的任意两个点都在同一直线上,包括线的两个端点。
1.3 点在线段上当一个点位于一条线段上时,称该点在线段上。
点在线段上的特点是它位于线段的两个端点之间。
1.4 点在线段的延长线上当一个点位于线段的延长线上时,称该点在线段的延长线上。
点在线段延长线上的特点是它位于线段的两个端点之外。
二、点与面的位置关系2.1 点在平面上当一个点位于一个平面上时,称该点在平面上。
点在平面上的特点是它与平面上的任意两个点都在同一平面上。
2.2 点在平面上的延长线上当一个点位于平面的延长线上时,称该点在平面上的延长线上。
点在平面延长线上的特点是它与平面上的任意两个点都在同一平面上,包括平面的边界和内部点。
2.3 点在平面外当一个点不在平面上时,称该点在平面外。
点在平面外的特点是它无法与平面上的任意两个点构成一条直线。
三、线与面的位置关系3.1 线在平面上当一条线位于平面内时,称该线在平面上。
线在平面上的特点是它与平面上的任意两个点都在同一平面上。
3.2 线平行于平面当一条线与平面上的所有点都不相交时,称该线平行于平面。
平行于平面的特点是线上的所有点与平面上的任意两个点的连线都平行。
3.3 线与平面相交于一点当一条线与平面上的某个点相交时,称该线与平面相交于一点。
线与平面相交于一点的特点是线上的所有点与平面上的任意两个点的连线都相交于同一点。
四、面与面的位置关系4.1 平行面当两个面的法向量平行时,称这两个面为平行面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点线面位置关系定理
总结
精品文档
收集于网络,如有侵权请联系管理员删除 //a b
//a b 1.线面平行判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(简述为线线平行线面平行) 表述及图示
2.线面平行性质定理: 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
(简述为线面平行线线平行)
//a a b α
βαβ⊂⋂= 3.平面平行判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
////a b a b a b P
β
β
α
α⊂⊂⋂=//αβ
4.平面平行性质定理:如果两个平行平面都和第三个平面相交,那么它们的交线平行
//a b
αβ
γαγβ⋂=⋂= 5.线面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,那么这条直线就垂直于这个
平面。
a b
a c
b c A b c α
α
⊥⊥⋂=⊂⊂ a α⊥6.线面垂直性质定理:垂直于同一平面的两条直线平行。
a b αα
⊥⊥ 7.面面垂直判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
简述为“线面垂直,则面面垂直”。
a a αβ
⊂⊥ αβ⊥ 8.面面垂直性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
l a a l
αβ
αβα
⊥⋂=⊂⊥ αβ⊥ //a b a b αα⊄⊂//a α//a b。
