三角函数的应用2
三角函数在音乐问题中的应用归纳

三角函数在音乐问题中的应用归纳三角函数是数学中一类重要的函数,其在各个领域中都有广泛的应用,其中之一就是在音乐问题中的应用。
本文将探讨三角函数在音乐问题中的具体应用,包括调音、音高和和弦等方面。
一、调音问题的三角函数应用1.1 正弦函数在乐器调音中的应用在乐器调音中,我们希望能准确地调整乐器的音高,使其与所需的音高相符。
这时,可以利用正弦函数的周期性特点。
正弦函数的图像呈现周期性波动,通过观察波峰和波谷的位置,可以确定音高是否准确。
例如,当调整钢琴的A键时,我们希望其音高为440赫兹。
我们可以以A键的声音作为基准音,然后用调音器检测其频率。
如果频率与440赫兹相差较大,我们可以通过适当调整琴弦的张力,使得琴弦振动的频率逐渐逼近440赫兹。
当波形图上的峰值和谷值与理想的正弦曲线相吻合时,就可以判定调音完成。
1.2 三角函数在合唱调音中的应用在合唱中,调音也是一个重要的环节。
合唱的成员通常根据指挥家的要求,根据指定的音高进行调音。
而这里的指定音高可以通过设定一个基准音高,例如中央C的音高,然后其他乐音按比例调整。
根据泛音理论,我们知道乐音是由一系列泛音组成的,而这些泛音之间存在着一定的比例关系。
通过利用三角函数的正弦关系,可以计算出乐音之间的频率比例关系,进而实现调音。
二、音高问题的三角函数应用2.1 正弦函数在音乐音高的计算中的应用在音乐中,我们常常希望能够精确地计算出音高的数值。
以钢琴为例,我们可以通过观察琴键的位置,利用三角函数的周期性特点来计算音高。
当我们按下一个钢琴键时,琴弦开始振动,同时发出声音。
琴弦振动的频率决定了音高的高低。
通过对琴弦的长度、张力等参数的测量,我们可以计算出对应的频率,进而得到音高的数值。
2.2 三角函数在音高变化中的应用在音乐创作中,常常需要通过变换音高来创造不同的音乐效果。
此时,可以利用三角函数的特性来实现音高的变化。
例如,在音乐中使用的音高变化效果中,常常出现的音阶规律是以半音(即频率之比为1.0594)为单位的。
鲁教版(五四制)初中数学九年级上册_《三角函数的应用》复习课件2

的值为(
)
4 A. 3
3 B. 5
3 C. 4
4 D. 5
【解析】由折叠知 CF=CB=5,则 DF=
52-42=3,
∴AF=5-3=2.设 AE=x,则 BE=EF=4-x,∴x2+22=(4 3 3 AE 2 3 -x)2,∴x= ,∴tan∠AFE=AF= = . 2 2 4 【答案】C
8.(2010中考变式题)如图,在高为h的建筑物顶部看一个旗杆顶(旗 杆高出建筑物顶),仰角为30°,看旗杆与地面的接触点,俯角为60°,
【答案】B
x
4.(2011·潍坊)身高相等的四名同学甲、乙、丙、丁参加风筝比赛 ,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),
则四名同学所放的风筝中最高的是(
同学 放出风筝线长 线与地面夹角 甲 140 m 30°
)
乙 100 m 45° 丙 95 m 45° 丁 90 m 60°
直角三角形的边角关系的应用
日常生活中的很多问题可以转化为直角三角形的问题,因此,直角
三角形的边角关系在解决实际问题中有较大的作用,在应用时要注意以下
几个环节: (1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角 形的问题); (2)根据条件的特点,适当选用锐角三角函数等去解直角三角形; (3)得到数学问题的答案; (4)得到实际问题的答案.
BD BD ∠BAD=∠BDA=45°,得 AB=BD.在 Rt△BDC 中,由 tan∠BCD= ,得 BC= BC tan30° = 3 BD. 设 BD=xm 则 AB=xm,BC= 3 xm,∵BC-AB=20,∴ 3 x-x=20,x= ≈27.3. 答:该古塔的高度约为 27.3 m. 20 3-1
5.7三角函数的应用(第2课时)课件(人教版)

从函数的解析式来看,满足y≥5.5-0.3(x-2),即 2.5sin5π x+5≥5.5-0.3(x-2)时,该船能够进入港口; 从图象31上看,就是函数y=2.5sin5π x+5的图象在
31
直线y=5.5-0.3(x-2)上方时,该船能够进入港口.
后,乙点的位置将移至何处?
乙点的位置将移至它关于x轴的对称点处.
随堂检测
1.如图所示的是一质点做简谐运动的图象,则下列结论正确的是( )
A.该质点的运动周期为 0.7 s B.该质点的振幅为 5 cm C.该质点在 0.1 s 和 0.5 s 时运动速度最大 D.该质点在 0.3 s 和 0.7 s 时运动速度为零
情景导入
生活中普遍存在着周期性变化规律的现象,昼夜交替、 四季轮回,潮涨潮散、云卷云舒,情绪的起起落落,庭前 的花开花谢,一切都逃不过数学的眼睛!这节课我们就来 学习如何用数学的眼睛洞察我们身边存在的周期现象。
匀速圆周运动、简谐运动和交变电流都是理想化的运 动变化现象,可以用三角函数模型准确的描述它们的运动 变化.在现实生活中也有大量运动变化现象,仅在一定范 围内呈现出近似于周期变化特点,这些现象也可以借助三 角函数近似的描述.
31
y=5.5上方时,该船能够进入港口.
利用信息技术绘出两个函数的图象,如下图.
2.5sin 5π x 5=5.5, 31
sin 5π x=0.2. 31
求得交点的横坐标分别为: xA≈0.3975,xB≈5.8025,xC≈12.7975,xD≈18.2025.
xC,xD也可由函数的周期性得到: xC≈12.4+0.3975=12.7975,
九下7.6锐角三角函数的简单应用(2)
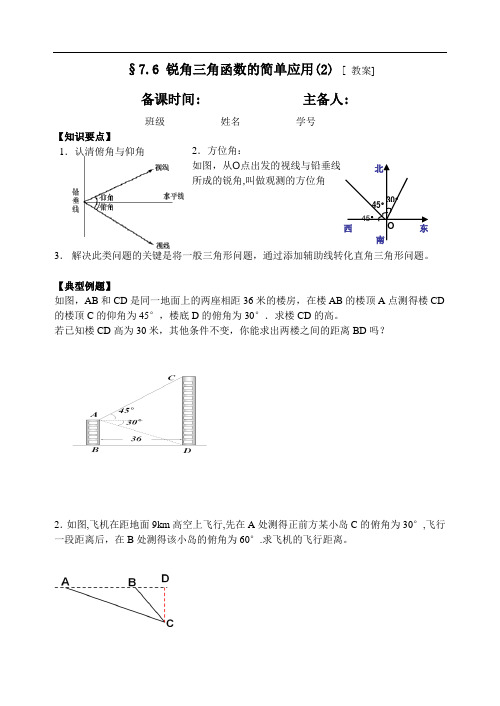
§7.6 锐角三角函数的简单应用(2) [ 教案]备课时间: 主备人:班级__________ 姓名__________ 学号_________【知识要点】1.认清俯角与仰角3. 解决此类问题的关键是将一般三角形问题,通过添加辅助线转化直角三角形问题。
【典型例题】如图,AB 和CD 是同一地面上的两座相距36米的楼房,在楼AB 的楼顶A 点测得楼CD 的楼顶C 的仰角为45°,楼底D 的俯角为30°.求楼CD 的高。
若已知楼CD 高为30米,其他条件不变,你能求出两楼之间的距离BD 吗?2.如图,飞机在距地面9km 高空上飞行,先在A 处测得正前方某小岛C 的俯角为30°,飞行一段距离后,在B 处测得该小岛的俯角为60°.求飞机的飞行距离。
2.方位角: 如图,从O 点出发的视线与铅垂线 所成的锐角,叫做观测的方位角3.如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.4.气象局发出预报:如图, 沙尘暴在A市的正东方向400km的B处以40km/h的速度向北偏西600的方向转移,距沙尘暴中心300km的范围内将受到影响,A市是否受到这次沙尘暴的影响?如果受到影响,将持续多长时间?5.如图, 海上有一灯塔P, 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A点处测得P在它的北偏东60度的方向, 继续行驶20分钟后, 到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?课后练习:【基础演练】1.如图,一座塔的高度TC=120m ,甲、乙两人分别站在塔的西、东两侧的点A 、B 处,测得塔顶的仰角分别为28º、15º。
求A 、B 两点间的距离_________(精确到0.1米) (参考数据:tan 280.53,tan150.27︒≈︒≈)2.如图所示,小华同学在距离某建筑物6米的点A 处测得广告牌B 点、C 点的仰角分别为60°和45°,则广告牌的高度BC 为_____________米(结果保留根号).3.如图,小明同学在东西方向的环海路A 处,测得海中灯塔P 在北偏东60°方向上,在A 处向东500米的B 处,测得海中灯塔P 在北偏东30°方向上,则灯塔P 到环海路的距离PC=米(结果保留根号)题1图题2图 题3图 4.如图,在某广场上空飘着一只汽球P ,A 、B 是地面上相距90米的两点,它们分别在汽球的正西和正东,测得仰角∠PAB=45o ,仰角∠PBA=30o ,求汽球P 的高度。
三角函数的应用知识点

三角函数的应用知识点在数学学科中,三角函数是非常重要且广泛应用的概念。
它们在几何学、物理学、工程学以及其他许多领域中都具有重要的实际应用。
本文将介绍一些三角函数的应用知识点,以帮助读者更好地理解和应用这些概念。
一、三角函数的定义和性质三角函数包括正弦函数、余弦函数和正切函数等。
正弦函数(sin)、余弦函数(cos)和正切函数(tan)分别表示在单位圆上的点的坐标值。
这些函数在周期性和连续性上具有一些重要的性质,如:1. 周期性:所有三角函数都是周期性的,即其值在特定的间隔内重复。
例如,正弦函数和余弦函数的周期都是2π,而正切函数的周期是π。
2. 正弦函数和余弦函数的关系:正弦函数和余弦函数在单位圆上是相互关联的。
具体而言,正弦函数关于余弦函数具有一个相位差为π/2的关系,即sin(x) = cos(x + π/2)。
3. 三角恒等式:三角函数有一系列的恒等式,如正弦函数的平方加上余弦函数的平方等于1,即sin^2(x) + cos^2(x) = 1。
4. 特殊角的值:三角函数在一些特殊角度上有确定的值,如sin(0) = 0,cos(0) = 1,tan(0) = 0等。
二、三角函数在几何学中的应用1. 直角三角形的边长关系:在直角三角形中,三角函数可以用来计算边长之间的关系。
例如,已知一个角的正弦值,可以使用反正弦函数(arcsin)来计算该角的度数,并进一步计算其他角度或边长。
2. 三角函数与角度的测量:三角函数可以帮助测量物体的高度或距离。
在几何学中,可以使用正切函数来测量无法直接测量的高度或距离。
例如,通过测量一个角度和与之相邻的边长,可以使用正切函数来计算另一边的长度。
3. 三角函数与图形的旋转:三角函数也在图形旋转中扮演重要角色。
通过三角函数,我们可以了解图形在旋转过程中的形变和位置关系。
三、三角函数在物理学中的应用1. 振动和周期性:物体的振动以及周期性现象可以通过三角函数进行建模和分析。
数学中的三角函数概念及其应用

数学中的三角函数概念及其应用三角函数是解决三角形相关问题的数学工具。
三角函数的概念通常可用一些基本函数来表示,比如正弦、余弦、正切。
这些函数在数学中广泛应用,对于计算和推导都有很大帮助。
一、三角函数的定义与性质1. 正弦函数在一个直角三角形中,正弦函数是指对于一个锐角,其对边与斜边的比值,记作sin。
即sin=a/c。
在三角形中,角度越小,正弦值越小。
也就是说,sin0=0,sin90=1。
知道sin的定义,我们可以推导出sin的周期与奇偶性质。
由于正弦函数是个周期函数,周期为2π。
另外,正弦函数是奇函数,即sin(-x)=-sin(x)。
2. 余弦函数余弦函数是指对于一个锐角,其邻边与斜边的比值,记作cos。
即cos=b/c。
在三角形中,角度越小,余弦值越大。
也就是说,cos0=1,cos90=0。
与正弦函数类似,可以推导出余弦函数的周期与奇偶性质。
余弦函数同样是周期为2π的函数,但它是偶函数,即cos(-x)=cos(x)。
3. 正切函数正切函数是指对于一个锐角,其对边与邻边的比值,记作tan。
即tan=a/b。
在三角形中,角度越小,正切值越小。
也就是说,tan0=0,tan90=undefined。
正切函数的周期同样为π,但是它的奇偶性质不同于之前的两个函数。
正切函数为奇函数,即tan(-x)=-tan(x)。
二、三角函数的应用1. 三角函数在几何中的应用三角函数在几何中最常见的应用就是计算直角三角形中缺失的数值。
比如,在已知两边以及一个角度的情况下,可以求解第三边的长度;在已知三个角度的情况下,可以确定三角形是否为直角三角形。
2. 三角函数在物理中的应用三角函数在物理中应用广泛。
例如,当一个物体作周期运动时,其运动轨迹可以用正弦或余弦函数来表示。
这里,周期总是与角频率相关。
用正弦函数表示物体的位移函数,与角频率ω有关,即y=Asin(ωt+φ)。
而用余弦函数表示,则与角频率的关系为y=Acos(ωt+φ)。
三角函数的应用

三角函数的应用三角函数是数学中重要的概念,不仅在纯数学领域有广泛的应用,还在物理、工程、计算机科学等多个学科中发挥着重要作用。
本文将探讨三角函数的应用领域及其在实际问题中的具体应用。
一、三角函数的基本概念和性质三角函数是描述角度和边长之间关系的数学函数。
常见的三角函数有正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。
它们的定义如下:正弦函数(sin):在直角三角形中,对于一个锐角A,sin(A)等于三角形中对边与斜边的比值;余弦函数(cos):在直角三角形中,对于一个锐角A,cos(A)等于三角形中邻边与斜边的比值;正切函数(tan):在直角三角形中,对于一个锐角A,tan(A)等于三角形中对边与邻边的比值。
这些三角函数有一些重要的性质,比如正弦函数和余弦函数是周期函数,周期为2π;正切函数的定义域为除了周期点的所有实数,值域为所有实数。
二、三角函数在几何中的应用1. 几何图形的尺寸计算在几何图形中,特别是含有角度的图形中,三角函数可以帮助我们计算各个边和角的尺寸。
比如在直角三角形中,已知两条边的长度,可以利用正弦函数、余弦函数或正切函数来计算其他边和角的值。
2. 三角函数在三角形中的应用在不规则三角形中,三角函数也有着广泛的应用。
例如,可以利用正弦定理和余弦定理求解三角形的边长和角度。
正弦定理表示为:a/sinA = b/sinB = c/sinC,其中a、b、c为三角形的边长,A、B、C为对应的角度。
余弦定理表示为:c² = a² + b² - 2abcosC,其中a、b、c为三角形的边长,C为对应的角度。
三、三角函数在物理学中的应用1. 运动学中的应用三角函数在运动学中有着重要的应用,例如描述物体的位置随时间的变化。
当物体做匀速直线运动时,它的位置可以由sin或cos函数来描述;当物体做简谐运动(如弹簧振动)时,它的位置也可以由sin或cos函数来描述。
三角函数的定义与应用

三角函数的定义与应用三角函数是数学中重要的概念之一,它在几何、物理、工程等领域有广泛的应用。
本文将介绍三角函数的定义及其在实际问题中的应用。
一、三角函数的定义1. 正弦函数(sine function):在任意给定角的单位圆上,该角对应的弧度终点在Y轴上的纵坐标值,称为该角的正弦值。
正弦函数常用符号为sin。
2. 余弦函数(cosine function):在任意给定角的单位圆上,该角对应的弧度终点在X轴上的横坐标值,称为该角的余弦值。
余弦函数常用符号为cos。
3. 正切函数(tangent function):在任意给定角的单位圆上,该角对应的正弦值除以余弦值,称为该角的正切值。
正切函数常用符号为tan。
以上三个三角函数在三角学中具有重要的性质和关系,它们的图像也相互关联。
二、三角函数的应用1. 几何应用三角函数在几何中有广泛的应用,例如在直角三角形中,正弦函数可以帮助我们求解角的正弦值,从而求解边长和高度。
余弦函数可用于计算角的余弦值,从而求解边长和底边。
正切函数则可用于计算角的正切值,求解边长和斜边。
2. 物理应用三角函数在物理中也有重要的应用。
例如在力的合成问题中,可以利用正弦函数和余弦函数求解合成力的大小和方向。
在波动方程中,正弦函数和余弦函数则描述了波的形状和变化。
3. 工程应用在工程领域,三角函数也得到广泛的应用。
例如在航空、航海中,利用三角函数可以计算方向和距离。
在建筑领域,可以利用三角函数来计算角度和高度。
三、三角函数的性质1. 周期性三角函数是周期性的,周期为360度或2π弧度。
即三角函数的值在每个周期内重复出现。
2. 对称性正弦函数和余弦函数是偶函数,即它们关于Y轴对称。
也就是说,sin(-x) = -sin(x),cos(-x) = cos(x)。
3. 反函数每个三角函数都有其反函数,分别称为反正弦函数(arcsine function)、反余弦函数(arccosine function)和反正切函数(arctangent function)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习: P45
2
小 常 识
海水受日月的引力,在一定的 时候发生涨落的现象叫潮汐,一般 的早潮叫潮,晚潮叫汐。
通常情况下,船在涨潮时驶进 航道,靠近船坞;卸货后落潮时返 回海洋。
• 船的吃水深度a:
水面
a
海底
b
• 船的安全间隙 b:
例5、下面是某港口在某季节每天几
个时刻的水深。
时刻 0:00 3:00 6:00 水深/m 5.0 7.5 5.0 时刻 9:00 12:00 15:00 水深/m 时刻 水深/m 2.5 18:00 5.0 5.0 7.5 21:00 24:00 2.5 5.0
(2)一条货船的吃水深度为4m,安全 条例规定至少要有1.5m的安全间隙, 该船何时能进港?在港口能呆多久? 解:(2) 由题意须 y≥ 4+1.5
2.5sin t + 5 ≥5.5 6
sin
6
t ≥0.2
由图象可得 0.4≤t ≤5.6 或 12.4≤t ≤17.6
所以船在0:24至5:36和12:24至17:36 进港, 能呆5.2小时
解:(1) 设y= Asinωt + k,由题意可得:
A=(7.5-2.5)/2=2.5, k=5, T=12,
所以: y= 2.5sin t + 5 6
2 ω= T 6
各整点时的水深为:
y= 2.5sin t + 5 6
t=1,5,13,17时,水深6.3m t=2,4,14,16时,水深7.2m t=7,11,19,23时,水深3.7m t=8,10,20,22时,水深2.8m
6 sin t ≥0.44-0.12t 6
t + 5 ≥ 4- 0.3(t-2) +1.5
练习: P45 3
三角函数应用题的解题步骤可以用 下面的框图表示:
实际应用问题 抽象概括 数学模型
推理演算
实际问题的解
还原说明
数学模型的解
水面
4
海底
1.5
; /AG850COM AG亚游 djm164zbg 日子一天天过去了,在三哥的治辽和五哥的照顾下,我的病渐渐地好了起来。转眼到了除夕,我躺在病床上,看着一个个出院 的病人,在家人的陪同下,急急忙忙地回家过年。 独在异乡为异客,每逢佳节倍思亲。 我情不自禁地想起了我的妻子和孩子们,想着想着,迷迷糊糊地进入了梦乡„„ “爷爷、奶奶、伯伯、伯母们,新年好!我是大狙大荷,我是二狙荷花,我是妹妹小荷,下面由姊妹三朵花给大家拜年。” 阵阵掌声,阵阵笑语也淹没不住孩子们的歌声:“新年好呀,新年好呀,祝贺大家新年好,我们唱歌,我们跳舞,祝贺大家新 年好„„” 孩子们扭着,跳着,唱着,笑着„„ 砰--!的一声巨响,远处传来的鞭炮声把我从梦中惊醒,我一骨碌爬起来,大声嚷着:“我要回家,我要回家„„” 五哥知道我那一头碰南墙的犟脾气。便去叫来了三哥,三哥答应我,等他下午下了班,我们兄弟仨一齐回家过年。 回家,一提起回家,我的血液竟然停止了奔流。梦,毕竟不同于现实,不孝有三,无后为大。这个家我将如何面对?三个女儿 就是我的心病,身上的病能够治辽,但是,这种心灵深处的病又有谁来安抚呢?我一屁股坐在床上,再也不敢往下想„„ “回家了,我们终于回家了。”五哥兴奋地一边嚷着,一边收拾着床头上的书。 是啊,五哥也是有家有业的人了,本来应该是和五嫂在一起的„„ 对不起了,五哥„„ 可是我没有想到,一个本该热热闹闹的新年,却成了我一辈子都不愿再记起的回忆。 第二章|榕树下原创_华语文学门户 过新年,是我们农村最隆重的节日。 在我的家乡,家家户户把庭院内外打扫得干干净净,贴对联,挂年画,张灯结彩。全家人围坐在一起喝团圆酒,吃年饭。对孩 子们来说,最开心的是穿上新衣服,成群结队地挨家挨户去拜年,因为在我们贫穷的小山村,只有这样,孩子们才能从长辈那 里得到他们最想要的糖果一类的东西,美美的装在口袋里,还不时地相互比比,看看谁的最多„„ 今年的春节跟往年一样,宴席摆在大哥家,因为只有大哥家的客厅才能容下全家二十几口人。 三哥的自行车还没停稳,侄儿们已把我从后座上拥进了客厅。这帮小鬼,一个个虎头虎脑的,见了我都亲热的不得了。
(2)点P第一次 到达最高点大约 要多长时间?
P
O .
ψ
P0
x
练 • 回顾作业题
习 11
(评价手册 P32 4)
• 例4、若某地温度T是一天为周期的函
数,此函数可用y= Asin(ωt +ψ)+b近似 表示,当t =14时达到最高温度15℃,当 t =2时达到最低温度3 ℃, • 求温度T(℃)和t之间的函数关系式。
例5、下面是某港口在某季节每天几
个时刻的水深。
时刻 0:00 3:00 6:00 水深/m 5.0 7.5 5.0 时刻 9:00 12:00 15:00 水深/m 时刻 水深/m 2.5 18:00 5.0 5.0 7.5 21:00 24:00 2.5 5.0
(3)若船的吃水深度为4m,安全间隙为1.5m, 该船在2:00开始卸货,吃水深度以0.3m/时 的速度减少,那么该船在什么时间必须停 止卸货,离港开往深水处?
例5、下面是某港口在某季节每天几
个时刻的水深。
时刻 0:00 3:00 6:00 水深/m 5.0 7.5 5.0 时刻 9:00 12:00 15:00 水深/m 时刻 水深/m 2.5 18:00 5.0 5.0 7.5 21:00m,安全 条例规定至少要有1.5m的安全间隙, 该船何时能进港?在港口能呆多久?
轮圆心O距离水面2m ,已知水轮每分
钟转动4圈,如果当水轮上点P从水中浮现 (P0)时开始计时。 y P (1)将点P距离水 面的高度Z(m)表示 O . ψ 为时间t(s)的函数。 x
P0
例3、一个半径为3m的水轮如图,水
轮圆心O距离水面2m ,已知水轮每分
钟转动4圈,如果当水轮上点P从水中浮现 (P0)时开始计时。 y
(3)若船的吃水深度为4m,安全间隙为1.5m, 该船在2:00开始卸货,吃水深度以0.3m/时的 速度减少,那么该船在什么时间必须停止卸货 离港开往深水处?
解:(3) 由题意须
y≥ 吃水深度 +1.5
吃水深度= 4- 0.3(t-2) (2≤t ≤24)
2.5sin
由图象可得 t =6.7 即6:42时必须停止卸货。
三角函数 S= Asin(ω t + ψ )的应用 (2)
思考:
如图,点P是半径为rcm的砂轮边缘上的一 个点,它从初始位置P0开始(∠XOp0= ψ ), 按逆时针方向以角速度ωrad/s做圆周运动,求 点P的纵坐标y关于时间t的函数关系。 y
y= r sin(ωt
+ψ)
P
ωt
M
O
ψ
P0 X
例3、一个半径为3m的水轮如图,水
(1)选用一个三角函数来近似描述这
个港口的水深与时间的函数关系,并 给出在整点时的水深的近似数值。
时刻 0:00 3:00 6:00
水深/m 时刻 水深/m 时刻 水深/m 5.0 9:00 2.5 18:00 5.0 7.5 12:00 5.0 21:00 2.5 5.0 15:00 7.5 24:00 5.0
