基于贝叶斯MSSV-ST金融波动模型的股市特征及机制转移性研究
金融资产波动率的持续性检验:基于厚尾贝叶斯随机波动模型

究受 到 了研 究 者 的重 视 。 基 于随机 波动模 型 ,s o和 L ( 99)首先 运用 贝叶 斯 因子检验 统计 量 i 19
是 波 动方 程 ,其形 式可 表 达为 :
Y =z p £,t x (t2 l t [, t t + t :eph/), ~N 0 、 l £ /, 1
h =/ (f 一 +o/ r ~N[,,:1 , r f - h一 ) v ,f +0 1 t/ 01 f , …, 】 2 / ( ) 1
的因素。 另外 , 从宏观经济政策层面上讲 , 政府对于股市调控 的一系列方针 、 政策是否有效果 ,也可以通过观察资产波动持续性来反 映。因此 ,如何检验
波 动是 否具 有持 续 性 引起 了研究 者 的广 泛注 意和 兴趣 。
现代资产定价理论 已经证明,波动持续性可以通过检验波动模型是否有 单位根来反映 ,详见 s o和 L ( 9 9 。然而 ,对于随机波动模型单位根检 i 19 ) 验问题来说 ,经典单位根检验统计量如 A F检验统计量应用非常困难 ,甚 D
布, 但是他们并没有调查基于 t 分布下贝叶斯因子的有限样本检验行为 ,另
外 ,他 们 在 随机 波 动 模 型指 定 中也 没有 考 虑 收益 测 量 方程 的协 变 量结 构 问
题。在实践中,协变量通常被用来解释资产收益 ,如三因子资产定价模型, 四因子资产定价模型等等。而且 ,对于单位根检验问题 ,s o和 L ( 9 9 i 19 )
( , ,) 丛 w z= J
Pr l J Y Z
o c (
贝叶斯决策理论在金融风险控制中的应用

贝叶斯决策理论在金融风险控制中的应用I. 引言随着金融市场的不断发展和日益复杂化,风险控制问题变得越来越重要。
如何在金融交易中合理评估风险,并采取有效的风险控制手段已成为金融业各个领域所关注的重要问题。
而贝叶斯决策理论作为一种有效的风险评估与判断工具,逐渐在金融领域得到应用。
II. 贝叶斯决策理论概述贝叶斯决策理论是在给定先验概率的条件下,根据实验结果来更新后验概率的理论。
换句话说,它是一种对不确定性进行量化的方法。
贝叶斯决策理论最早主要应用于统计学领域,但随着信息技术和计算能力的不断提升,它也逐渐运用到了金融领域。
III. 贝叶斯决策理论在金融风险评估中的应用在金融领域,贝叶斯决策理论可以用来估计资产收益率、评估信用风险、预测市场波动性等。
下面就以金融风险评估为例,介绍贝叶斯决策理论在金融领域的应用。
1. 贝叶斯网络模型贝叶斯网络模型是利用变量之间的依赖关系构建的一种概率性图。
在金融风险评估中,这种模型可以帮助分析家和其他投资者了解资产关联以及特定事件对这些资产的影响。
例如,在利用贝叶斯网络模型分析股票市场时,将价格乘以基本面变量(例如企业数据)之后,在使用模型之前,可以设定一个先验概率分布。
此时,可以使用历史数据训练模型,以优化先验分布并得到更准确的分析结果。
在股票市场风险评估中,贝叶斯网络模型可以帮助投资者根据不同的信息和事件来预测未来的风险。
2. 贝叶斯风险度量贝叶斯风险度量是另一种利用贝叶斯理论进行风险评估的方法。
它可以评估交易的风险、资产定价模型以及对波动性进行预测等。
例如,在股票市场中,如果一个交易员想要买进或卖出股票,他可以使用贝叶斯风险度量来预测这个决策的结果及其风险。
贝叶斯风险度量还可以去除市场噪音因素,形成更准确的市场风险评估。
3. 在投资组合中的应用通过将贝叶斯决策理论应用于投资组合中,可以计算不同的资产组合的期望收益和风险。
这种方法可以帮助投资者提高投资组合的效率和有效性。
贝叶斯统计在金融分析中的应用

贝叶斯统计在金融分析中的应用贝叶斯统计是一种基于贝叶斯定理的概率推断方法,具有广泛的应用范围,从医学、金融、环境等领域皆可涉及。
本文主要探讨贝叶斯统计在金融分析中的应用。
一、贝叶斯统计的基本原理首先,我们需要了解贝叶斯统计的基本原理。
在传统的机率统计中,我们通常先给定一个假设,然后利用数据来验证这个假设的可信度。
而贝叶斯统计则是从相反的角度考虑,即先利用数据来更新一个假设,根据新的数据调整假设的概率。
其中,贝叶斯定理是关键,它将一个先验概率与新的数据联合考虑,得到一个后验概率。
在贝叶斯统计中,我们通常要考虑两个问题:一个是先验概率,一个是似然函数。
先验概率是指在没有考虑数据之前,我们对某个假设可信程度的主观判断。
似然函数是指给定假设下的数据出现的概率。
贝叶斯定理将这两个因素结合起来,得到后验概率。
而利用贝叶斯统计,我们可以通过不断地利用新的数据来更新我们对假设的看法,这样我们的判断将越来越准确。
二、贝叶斯统计在金融分析中的应用贝叶斯统计在金融分析中的应用非常广泛。
举个例子来说,我们可以用贝叶斯统计来分析股票市场的波动情况。
在这种情况下,我们可以通过考虑历史数据来计算先验概率,然后再通过当前的股票数据来更新我们对股票走势的看法。
这样做的好处是,我们可以较为准确地预测股票价格的波动情况,从而做出明智的投资决策。
另一个例子是贝叶斯统计在风险评估中的应用。
在金融领域中,风险评估是非常重要的。
传统的方法是基于正态分布假设,但这种假设在许多情况下并不成立。
贝叶斯统计在这方面的应用可以有效地克服传统方法的缺陷,因为它可以基于不完全数据、不确定信息和非常态分布来估计不同的风险。
此外,贝叶斯统计在金融分析中的另一个应用是在金融工程和金融模型中。
我们可以利用贝叶斯统计来开发各种金融模型,从而预测未来的市场走势。
同时,我们可以基于不完全信息来估算各种金融模型的参数,这样我们的模型将更加准确。
三、结语总之,贝叶斯统计在金融分析中的应用非常广泛。
基于SMOTE—贝叶斯网络的商业银行风险评估模型研究

基于SMOTE—贝叶斯网络的商业银行风险评估模型研究摘要商业银行风险评估是银行业务中至关重要的一环,在现代化的金融风险管理中占据重要地位。
由于银行贷款业务存在风险,因此需要通过风险评估来衡量和控制风险水平。
本文基于SMOTE-贝叶斯网络算法,针对商业银行风险评估的问题进行了研究和探究,并提出了一种适用于商业银行风险评估的模型。
该模型考虑了信贷风险的多种因素,包括信用评级、利率、收入情况等,同时利用SMOTE算法对样本不平衡问题进行处理,提升了模型的准确性和可靠性。
通过对模型的实证分析发现,所提出的基于SMOTE-贝叶斯网络的商业银行风险评估模型相较于其他模型具有更高的预测准确率和有效性,具有一定的应用价值和推广意义。
关键词:商业银行;风险评估;SMOTE算法;贝叶斯网络;样本不平衡AbstractCommercial bank risk assessment is an essential part of banking business and occupies an important position in modern financial risk management. Due to the risks associated with bank lending business, risk assessment is necessary to measure and control risk levels. Based on the SMOTE-Bayesian network algorithm, this paperhas conducted research and exploration on the issue of commercial bank risk assessment and proposes a model suitable for commercial bank risk assessment. The model considers various factors of credit risk, including credit rating, interest rates, income situation, etc., and uses the SMOTE algorithm to address the problem of sample imbalance, which enhances the accuracy and reliability of the model. The empirical analysis of the model shows that the proposed SMOTE-Bayesian network-based commercial bank risk assessment model has a higher prediction accuracy and effectiveness than other models, and has a certain application value and promotion significance.Keywords: commercial bank; risk assessment; SMOTE algorithm; Bayesian network; sample imbalance一、绪论随着金融市场的不断发展和完善,商业银行作为重要的金融机构在经济发展中扮演着重要的角色。
贝叶斯统计模型在金融风险评估中的实证分析

贝叶斯统计模型在金融风险评估中的实证分析金融风险是指金融市场中可能出现的损失或不确定性,风险评估是金融机构必备的重要环节。
在近年来,贝叶斯统计模型在金融风险评估中得到了广泛的应用。
本文将就贝叶斯统计模型的基本原理、优势以及其在金融风险评估中的实证分析进行探讨。
首先,我们将介绍贝叶斯统计模型的基本原理。
贝叶斯统计模型是基于贝叶斯定理的一种统计推断方法。
其核心思想是将先验信息和观测数据结合起来,通过计算后验概率来进行推断。
与传统的频率统计方法相比,贝叶斯统计模型能够有效地利用样本数据的信息,增加模型的准确性和鲁棒性。
其次,贝叶斯统计模型在金融风险评估中具有诸多优势。
首先,贝叶斯统计模型能够较好地处理小样本问题。
在金融领域,由于金融市场的复杂性和不确定性,样本数据往往较为有限。
贝叶斯统计模型可以通过引入先验信息,对小样本数据进行合理推断,从而提高风险评估的准确性。
其次,贝叶斯统计模型具有较强的灵活性。
金融市场的风险因素往往繁多且复杂,传统统计模型可能无法很好地捕捉和建模这些因素之间的相互关系。
贝叶斯统计模型通过引入先验分布和模型参数的全概率分布,能够较好地对复杂的金融风险进行建模。
此外,贝叶斯统计模型还能够处理不确定性问题。
金融风险评估往往面临许多未知和难以测量的因素,贝叶斯统计模型通过引入先验分布和后验概率,可以对这些不确定性进行合理的估计。
基于贝叶斯统计模型的优势,许多研究者在金融风险评估中进行了实证分析。
例如,研究者可以利用贝叶斯线性回归模型对金融市场的风险进行预测。
通过引入先验信息和观测数据,可以更准确地对股票、债券等金融资产的回报率进行估计,从而对投资组合的风险进行评估。
此外,研究者还可以利用贝叶斯结构方程模型对金融市场中的因果关系进行建模。
通过对金融市场的多个因素进行联合建模,可以有效地分析和预测金融风险的传播和影响路径。
除了传统的线性模型和结构方程模型,贝叶斯统计模型还可以与机器学习方法相结合,进一步提高金融风险评估的准确性和鲁棒性。
基于贝叶斯判别的上市公司ST分析--北京市教委统计学特色专业项目资助

五 实证 分 析
将 19 年及2 0 年的观测值导入R软件 , 99 00 编程调用软件 自带的程序 包进行贝叶斯判别分析。 首先对数据作简要描述 以获得初步的认识。 在R软 件 中作 各 财 务 指 标 与 因变 量 ST 的 盒状 图 ,可 以得 出结 论 ,公 司规 模 ( S E 及资产周转率 ( A S T) ATO) 与公司是否被特殊处理没有 明显的关系 , 而公司是否被特殊处理在其余指标上均明显不 同。 例如被特殊处理的公司的 平均销售率 ( GROWTH) 盈利能力 ( , ROA) 第一大股东持股比例 , ( HAR 都 明显地 低于 没有被 特 殊处 理 的 公司 , 被特 殊 处理 的 公司 的应 S E) 而
较 多 的应 用 。 单变 量模 型 只是 利 用 个别 比率 指 标 预测 企 业财 务 失 败 , 而企业 的生 产 经营 活 动受 到许 多 因素 的 影响 , 单个 比率 反 映 的信 息往 往有 限 , 法 全面 故 无 显示 企业 的财务状 况。 多元判 别模 型要 求 自变量 呈 正态分 布且 两组 样本 等协
概 率 函数 的P 位数 可 以 用财 务 指标 线 性解 释 , 假设 不 算很 严 , 分 其 但计 算 过 程复 杂 , 有 较多 近 似处 理 , 测精 度较 高 。 且 其预 贝叶 斯判 别 模 型 虽计 算 过程
复杂 , 但不需要严格的假设条件 , 预测精度又较高 , 具有广泛的适用范围。 本 文 旨在运 用判 别分 析 方法 来进 行 我国上 市 公 司财务 危机 的预警 分析 。
用于度量资产利用效率。 GRO WTH: 销售收入增长率 , 用于反映公司的成
长 潜力 。 E 负债 资 产 比率 , 于 反映 债 务情 况 。 L V: 用 ROA: 资产 收 益率 , 用 于 度量 盈 利 能力 。 HA S RE: 大股 东 的持股 比例 , 于 反映 股 权结 构 。 最 用
基于贝叶斯网络的股市波动率混合预测模型研究

基于贝叶斯网络的股市波动率混合预测模型研究基于贝叶斯网络的股市波动率混合预测模型研究摘要:随着全球股市的不断发展,股市波动率的准确预测变得越来越重要。
本研究旨在应用贝叶斯网络构建股市波动率混合预测模型,并通过实证研究验证其预测能力。
首先,通过对股市波动率的特征进行分析,选择了包括历史波动率、成交量、市场情绪指标等因素作为贝叶斯网络的输入变量。
然后,利用历史数据构建贝叶斯网络结构,并通过贝叶斯推断法学习网络参数。
最后,使用实际的股市数据进行预测,并与其他传统预测模型进行比较。
关键词:贝叶斯网络;股市波动率;混合预测模型;贝叶斯推断1. 引言股市波动率是衡量股市风险的重要指标,对投资者的决策具有重要影响。
因此,正确预测股市波动率对于投资者制定有效投资策略至关重要。
然而,股市波动率的预测是一个复杂而不确定的问题,传统的统计模型在处理非线性和非正态分布数据时具有一定的局限性。
因此,寻找一种准确、可靠的股市波动率预测模型成为一个热门的研究领域。
2. 贝叶斯网络的基本原理贝叶斯网络是一种概率图模型,他可以用于表示变量之间的因果关系,并且能够通过观测数据进行参数估计和预测推理。
贝叶斯网络的基本原理是贝叶斯定理,通过建立一个有向无环图(DAG),将研究对象的变量建模为节点,节点之间的有向连接表示变量之间的依赖关系。
通过假设每个节点的条件概率分布,可以通过贝叶斯推断法推断出缺失节点的概率分布。
3. 模型构建基于股市波动率的特征分析,我们选择历史波动率、成交量和市场情绪指标作为贝叶斯网络的输入变量。
其中,历史波动率反映了股市的波动性,成交量反映了市场的活跃度,市场情绪指标反映了投资者的情绪波动。
我们通过构建一个三层的贝叶斯网络结构,其中输入层为历史波动率、成交量和市场情绪指标,中间层为隐藏节点,输出层为波动率。
使用贝叶斯推断法学习网络参数,通过最大后验概率估计方法进行参数估计。
4. 实证研究我们使用实际的股市数据进行实证研究,选取了某股票的历史数据作为样本数据。
基于贝叶斯因子模型金融高频波动率预测研究

基于贝叶斯因子模型金融高频波动率预测研究罗嘉雯;陈浪南【摘要】构建了包含时变系数和动态方差的贝叶斯HAR潜在因子模型(DMA(DMS)-FAHAR),并对我国金融期货(主要是股指期货和国债期货)的高频已实现波动率进行预测.通过构建贝叶斯动态潜在因子模型提取包含波动率变量、跳跃变量和考虑杠杆效应的符号跳跃变量等预测变量的重要信息.同时,在模型中加入了投机活动变量,以考察市场投机活动对中国金融期货市场波动率预测的影响.预测结果表明,时变贝叶斯潜在因子模型在所有参与比较的预测模型当中具有最优的短期、中期和长期预测效果.同时,具有时变参数和时变预测变量的贝叶斯HAR族模型在很大程度上提高了固定参数HAR族模型的预测能力.在股指期货和国债期货的预测模型中加入投机活动变量可以获得更好的预测效果.%The realized volatilities of China's financial futures is forecasted by constructing a Bayesian factor augmented heterogeneous autoregressive model (DMA (DMS)-FAHAR) with time-varying parameters and stochastic volatility.The Bayesian inference is employed to obtain the latent factors of the daily,weekly,and monthly predictor sets including the lagged volatility variables,jump variables,and signed jump variables.Speculation variables are used to investigate the impact of speculation activities on the volatilityforecast.The results suggest that the Bayesian factor augmented HAR model performs best for short-term,mid-term,and long-term forecasts among all candidate forecast models.Meanwhile,the time-varying Bayesian HAR models have superior forecast performances compared with the fixed parameter HAR models.In addition,better forecast performances areachieved after incorporating the speculation variables into the forecast models for both the stock index futures and the Treasury futures.【期刊名称】《管理科学学报》【年(卷),期】2017(020)008【总页数】14页(P13-26)【关键词】已实现波动率的预测;HAR模型;金融期货;时变性;潜在因子【作者】罗嘉雯;陈浪南【作者单位】华南理工大学工商管理学院,广州510006;中山大学岭南学院,广州510275【正文语种】中文【中图分类】F833-5中国的金融期货起步较晚. 2010年4月16日,中国首次推出融资融券业务和沪深300股指期货,双向交易在沪深股票市场成为可能. 2013年9月6日,停牌近18年的国债期货合约的上市交易宣告了中国国债市场重新进入双边市场时代. 金融期货市场的建立为投资者提供了规避市场风险的有效对冲场所. 然而,金融期货本身的稳定是其能够作为对冲场所的前提条件. 因此,准确预测金融期货的波动性(率)对于投资者从事资产定价、构建资产组合和进行风险管理是至关重要的.传统文献通常运用低频GARCH模型对低频波动率进行预测[1]. 随着金融高频/超高频数据的可获得程度的提高,利用基于日内高频金融数据估计的已实现波动率(realized volatility 或RV)进行建模逐步成为该领域研究的主导并得到广泛认可. 在RV的基础上,Corsi[2]提出异质自回归(heterogeneous autoregressive,HAR)模型,即在已实现波动率的自回归方程中引入日、周、月已实现波动率变量作为预测变量,对已实现波动率进行预测. 由于HAR模型具有灵活的线性模型结构,估计方法简单且获得更好的预测效果,不少学者在HAR模型的基础上作进一步的拓展. 例如, Corsi 等 [3,4]分别在HAR-CJ模型中考虑门限效应和波动率的杠杆效应,构建HAR-TCJ和LHAR-CJ模型对已实现波动率进行预测. Huang 等[5]结合已实现GARCH模型和HAR模型构建已实现HAR-GARCH模型. 部分国内学者也应用最新发展的HAR模型对我国金融市场的高频已实现波动率进行预测,如文凤华等[6]考虑波动率的杠杆效应和量价关系,建立了LHAR-RV-V模型并对波动率进行预测. 陈浪南等[7]在HAR-GARCH模型和HAR-CJ模型基础上建立了自适应的不对称的HAR-CJ-D-FIGARCH模型并对我国股票市场波动率进行预测. 吴恒煜等[8]构建包含跳跃和马尔可夫机制转换结构的HAR模型,并认为区分跳跃和结构转换特征的模型可以显著提高HAR模型预测能力. 从以上文献来看,大部分文献都假定系数和预测变量集不随时间变化, Liu等[9]及Choi 等[10]均认为假定预测模型的系数和预测变量集不随时间而变,不仅损失了模型的灵活性,也容易造成预测偏误. 尽管部分文献[8]在建模中加入马尔科夫机制转换结构消除结构断点的影响,但他们并未考虑不同预测变量的预测能力有可能会随着时间的变化而变化. 近年来发展的贝叶斯时变预测模型为解决此类问题提供了很好的思路和方法,如,Cogley等[11]及Primiceri[12]提出的基于状态空间模型建立参数随时间逐步演化的时变参数(time-varying parameter, TVP)模型. Raftery 等 [13]在TVP模型框架基础上提出运用动态模型平均(dynamic model averaging, DMA)和动态模型选择(dynamic model selection, DMS)的方法筛选有效的预测变量,并应用于工程学预测. Koop等[14]将DMA和DMS方法应用于宏观经济预测领域,并实证证明了DMA/DMS估计方法相对于TVP模型的优势. Groen 等[15]通过引入隐变量对模型的不确定性进行建模,即基于该隐变量对每一时期的预测变量进行筛选,并运用该模型对多个宏观变量进行预测. Koop等 [16]通过贝叶斯因子模型提取多个金融变量中的重要信息,并用以预测宏观经济变量. Kalli等 [17]提出贝叶斯时变稀疏性(TVS)模型,通过模型参数先验分布设定使得不重要的预测变量可以衰减为0. Audrino等[18]提出运用套索方法预测变量进行筛选. 从以上文献来看,大部分的贝叶斯时变模型方法均运用于宏观经济变量如通货膨胀率、GDP等的预测,但较少的文献将其运用于金融资产的高频波动率的预测当中.从现有文献来看,大部分基于HAR建模的已实现波动率模型均假定系数和预测变量集不随时间变化,然而,由于政策变动以及外部冲击等诸多因素的影响,金融市场收益的波动率在不同时期通常会呈现不同的特征,即存在结构断点. 运用定参数模型对已实现波动率进行预测容易造成预测偏误. 而从现有的贝叶斯时变方法来看,DMA方法和DMS方法基于最初的TVP方法进行建模,通过包含概率对预测变量进行筛选,并可以灵活嵌套于线性和非线性模型之中. 此外,相对于其他贝叶斯时变方法(如TVS和Lasso方法),DMA方法和DMS方法可以通过设置遗忘因子,结合卡尔曼滤波方法对时变参数进行估计,降低在贝叶斯MCMC推导中高维参数模型的运算量.因此,结合DMA方法和DMS方法建立具有时变参数和随机方差的贝叶斯动态潜在因子HAR模型(DMA-FAHAR模型和DMS-FAHAR模型),其中DMA方法是在每个时点根据不同预测模型的预测效果并计算不同模型的权重,再进一步通过加权平均获得预测结果,而DMS方法在每个时点选出最优的预测模型作为该时点的预测模型. 此外,市场的投机活动也是影响市场波动的主要要素,其中Lucia等[19]提出投机活动对期货市场波动率有重要影响,陈海强等[20]提出期货市场的投机活动活跃程度会对市场跳跃有影响. 因此,考虑市场的投机活动会对市场的未来波动行为产生影响,因此,首次在波动率预测模型中加入投机活动变量,以考察市场投机活动变量对高频波动率预测的影响.运用以上模型对中国期货市场(主要是股指期货和国债期货)的高频已实现波动率进行预测.主要贡献如下, 1)首次结合贝叶斯时变模型方法和高频波动率预测模型——HAR模型构建参数和预测变量均可时变的已实现波动率预测模型,模型具有更大的灵活性并可以消除潜在截断点对预测的影响,并可以获得更好的预测效果. 2)构建多个包含门限效应和杠杆效应的高频波动率和跳跃变量,并通过构建贝叶斯潜在动态因子模型提取预测变量集的主要信息,并引入预测模型,从而获取更好的预测效果并不会带来过度参数化的问题. 3)首次考虑市场投机活动对期货市场波动率预测的影响,以交易量和持仓量的比例作为投机活动的代理变量,利用时变包含概率和预测效果比较分析投机活动对期货市场高频波动率预测效果的影响.采用已实现波动率作为股指期货波动率的代理变量. 假设日内价格Pt的观测频率为δ,δ等于观测间隔(如5 min)与每日交易时间之比,1/δ表示每日价格的观测次数,可得日内收益率为rt=100×(ln Pt-ln Pt-δ),通过计算日内收益率的平方和即可得到每日的已实现波动率Barndorff-Nielsen等[21]通过建立已实现二次幂变差(realized bi-power variation)得到对跳跃稳健(jump-robust)的波动率变量,并获得跳跃的估计,已实现二次幂变差可以表示为当等[3]在BPV的基础上进一步提出门限二次幂变差 (threshold bipower variation,TBPV),从而消除小样本观测值在不连续状态下存在的正向误差对BPV收敛性的影响. TBPV的计算公式为ϑjδ}其中其中cϑ是校准门阀常数,是用于计算局部方差的非参迭代滤子. 依据Corsi等 [3]的论述,设定通过Barndorff-Nielsen等[21]和Corsi等 [3]提出的C_Zt和C_TZt统计量*其中,和ϑ(j-1+k)δ}.可以得到跳跃的一致估计,并计算出波动率的连续成分.C_Zt=C_TZt=从而可以分离出波动率的连续成分和跳跃连续成分Barndorff-Nielsen等 [22]提出的已实现半变差,将已实现波动率分解成正的收益波动成分和负的收益波动成分,从而在波动率预测中可以考虑到杠杆效应的影响. 已实现半变差的计算过程如下并有RV=RS-+RS+,且ΔJ=RS+-RS-表示符号跳跃变差(signed jump variation) 假设RM是已实现波动率的估计量,定义其中RMt,5表示已实现波动率的周估计量,RMt,22表示已实现波动率的月估计量. 主要采用Corsi[2]的标准HAR模型,Andersen 等 [23], Corsi 等 [3]提出的带跳跃成分HAR-CJ模型和门阀跳跃成分的和HAR-TCJ模型以及Patton等[24]的提出的加入符号跳跃变量和已实现半变差的HAR-ΔJ模型这四种具有代表性的HAR族模型对波动率进行预测(见式(6)).基于这四种模型,结合Raftery 等 [13]提出的DMA和DMS方法,Koop等 [16]提出的时变动态潜在因子模型,建立贝叶斯HAR潜在因子模型. 潜在因子根据贝叶斯推导确定,具体模型如下上述模型可以定义为DMA(DMS)-FAHAR模型,其中Xt为n×1维向量,包含了HAR模型,HAR-CJ模型,HAR-TCJ模型,以及HAR-ΔJ模型中所有可能的预测变量,即,Xt=(BPVt,TBPVt,Ct,TCt,Jt,TJt,ΔJt). Ft 为潜在因子变量,通过估计Ft 可以提取预测变量集中的主要信息.和为对应的滞后潜在因子.此外,考虑投机活动对期货市场波动率有重要影响. 根据Lucia等 [19],加入基于未平仓合约和交易量建立的投机活动衡量指标,即Xspec=.Xspec的值越大,说明市场的投机交易活动越活跃. 进一步构建包含投机活动变量的贝叶斯动态潜在因子模型DMA-FAHAR-spec,其中Xt=(BPVt,TBPVt,Ct,TCt,Jt,TJt,ΔJt,Xspec).假设为Xt包含不同预测变量情况下所有可能的子集,对于包含m个预测变量的模型,预测变量的子集个数有K=2m个(定义为M1,…,MK).是潜在因子模型中的因子载荷. ct为常数, B1,t,B5,t和B22,t分别对应日、周、月预测元(预测元包含滞后的RV和潜在因子)向量的系数矩阵,为因子模型方程的时变扰动项方差,为预测方程扰动项的时变方差.定义系数向量βt=(,vec(B1,t)′,vec(B5,t)′,vec(B22,t)′)′ ,根据状态空间模型定义系数的时变性,则有其中为因子载荷迭代方程中的扰动项方差,为系数向量迭代方程中的扰动项方差. 运用MCMC推导方法对模型参数和潜在因子进行估计,待估的时变参数为θt={βt,λt,Vt,Qt,Wt,Rt} . 具体的估计步骤为,1)设置所有模型参数的初始值,各参数的初始值设置如下.f0~N(0,4),λ0~N(0,4×IN),β0~N(0,Vmin),V0≡1×InQ0≡1×In, π0≡其中Vmin服从Minnesota先验分布,对于常数项,Vmin=4,对于日、周、月的变量,Vmin=4/r2, r=1, 5 or 22.2)在给定情况下,抽取时变参数θt.①根据指数加权平减法(EWMA)估计出时变方差矩阵Vt,Qt,Wt,Rt;②根据卡尔曼滤波方法估计时变系数βt,λt;③在给定时变参数θt情况下,抽取动态因子Ft.基于不同的预测变量集Xt的子集,可以建立不同的预测模型. 进一步运用DMA和DMS方法对不同预测模型进行筛选,其中DMA方法是在每个时点根据不同预测模型的预测效果并计算不同模型的权重,再进一步通过加权平均获得预测结果,而DMS方法在每个时点选出最优的预测模型作为该时点的预测模型.给定初始权重值等 [13]提出运用遗忘因子α推导出权重值的预测方程.概率的迭代更新方程为其中 pl(RVt|RVt-1)为第l个子模型的似然函数值. 因此,通过式(10)和式(11)的更新迭代方法可以计算出每个时期包含模型k的概率在DMA方法下,通过运用概率对不同预测模型的预测值进行加权平均获得已实现波动率的预测值,而在DMS方法下则通过选择在t时期时具有最大的概率的单个模型作为t时期的预测模型. 定义则已实现波动率在这两种方法下的h期预测值分别为where,{k∶πt|t-h,k=max{πt|t-h,1,…,πt|t-h,l,l=1,…,K}}采用中国沪深300股指期货和中国国债期货每5分钟的高频数据. 沪深300股指期货样本期包括从股指期货第一天上市交易(2010年4月16日)到2015年6月30日一共1 263个交易日,而中国国债期货的样本期包括从国债期货第一天上市交易(2013年9月6日)到2015年6月30日一共440个交易日. 数据来源为万得数据库. 股指期货和国债期货的日交易区间为9:15到15:15,每五分钟的日内数据为54个.表1列出所有变量的统计分析. 如表1所示,股指期货的波动率均值和标准差均比国债期货大,说明股指期货市场的交易波动比国债期货市场大. 同时根据投机活动指标来看,股指期货的投机活动更为活跃. JB统计量和峰度偏度统计量表示所有变量都不服从正态分布,显现出金融时间序列普遍的尖峰厚尾的特征. 同时Ljung-Box指数表示收益和波动率以及跳跃变量都有着较强的自相关性,显示出长记忆性的特征. 同时ADF统计量表示所有变量均是平稳序列.由于已实现波动率RV的估计是无模型形式,所以无法根据传统的数据生成过程(DGP)生成已实现波动率RV的模拟序列. 根据Audrino等 [18],根据以下数据生成过程进行蒙特卡罗模拟,从而对模型估计方法的稳健性进行验证. 运用最基本的HAR模型(Corsi[3])进行数据模拟,验证DMA方法和DMS估计方法对HAR族模型的参数估计的有效性. 以股指期货样本为例,蒙特卡罗模拟的步骤具体如下.1)基于股指期货全样本数据估计HAR模型(见式(6)的第一个模型)的参数.①运用OLS估计方法估计HAR模型得到估计系数模型可以写成带约束的VAR(22)模型,根据系数写成VAR(22)模型的系数②计算模型的非条件均值和非条件方差是滞后i阶的自方差2)利用HAR模型生成模特卡罗模拟样本.①从正态分布中抽取x1, (x22)②根据模型(6)通过迭代运算得到x23,…,x2 000,取后1 000个模拟数据进行模拟运算;③运用DMA方法估计出HAR模型中各预测变量的时变包含概率.通过对第二步重复1 000次,并获得1 000个蒙特卡罗模拟结果.图1显示蒙特卡罗模拟下HAR模型的滞后日、周和月波动率的时变包含概率. 其中中间的线是1 000次蒙特卡罗模拟的中位数值,而上下两条实线分别是75%和25%的区间线. 从结果来看,1 000次蒙特卡罗模拟下HAR模型的日、周和月滞后波动率变量的包含概率均在较小范围内浮动,证明运用DMA方法可以有效估计HAR模型的时变参数并筛选出合适的预测变量. 而DMS方法与DMA方法运用相同的包含概率,所以同理也可以证明DMS方法是有效的.对于DMA和DMS模型,对应m维的预测变量集的子集总个数为K = 2m. 根据模型设定,模型中的预测变量集为Xt=(BPVt,TBPVt,Ct,TCt,Jt,TJt,ΔJt,Xspec),因此,子模型的总个数为28=256. 结合两种贝叶斯时变模型方法(动态模型平均(DMA)和动态模型选择(DMS)),建立DMA-FAHAR-spec模型和DMS-FAHAR-spec模型. 根据模型设定,模型系数和预测变量集可以随着模型结构的变化而变化,从而消除未知截断点对预测效果的影响. 根据全样本分析预测变量集的时变规模和不同预测变量的时变包含概率. 计算DMA和DMS模型的时变包含概率是贝叶斯HAR族模型估计的关键,其中DMS模型与DMA模型具有相同的包含概率. 对于DMS模型,根据DMA模型计算的包含概率在每个时点选出最大包含概率的子模型进行预测. 对于DMA模型,第k个预测变量的包含概率(PIP)可以定义为其中为第k个子模型sub_Mk被包含在预测模型中的贝叶斯概率,可以根据第1部分中式(10)~式(11)的迭代计算得到,而I(·)是示性函数,当括号内的条件被满足时候取值为1,其余情况取值为0.图2显示股指期货(图2(a))和国债期货(图2(b))DMA-FAHAR-spec模型中不同预测变量的时变包含概率. 更大的包含概率值表示该变量具有更好的预测能力,即该变量包含了更有用的预测信息. 根据Koop等[14]的论述,当包含概率值大于0.5时,该预测变量可以认为是好的预测变量. 因此,可以根据每个预测变量的包含概率大于0.5的时期来判断好的预测变量. 如图2(a)所示,对于股指期货样本,各预测变量在不同时期表现出不同的预测能力,其中带门限效应的波动率变量和跳跃变量(包括TBPV、TC和TJ)在大部分时期内的包含概率大于0.5,表现出较强的预测能力,投机活动变量Xspec在股指期货推出初期以及2011年至2013年期间较长一段时期内的包含概率大于0.5,表现出较强的预测能力. 如图2(b)所示,对于国债期货样本,在国债期货推出后的初期,各预测变量的预测能力均衡,稳定在0.5. 而在随后的样本期内,各预测变量的包含概率的时变趋势表现出较大的起伏. 从整体来看,波动率变量(BPV和TC),跳跃变量(J和TJ)在较长一段时间内具有较大的包含概率,表现出较强的预测能力. 而投机活动变量在样本期末期表现出较强的预测能力.基于DMA和DMS方法构建了具有时变参数和时变预测变量集的贝叶斯HAR潜在因子模型,并利用贝叶斯潜在因子方法减少模型参数维度. 为了评价新创建模型的预测效果,同时建立了一系列的比较模型,如结合DMA和DMS方法和包含式(6)中的所有模型预测变量构建的贝叶斯HAR模型(DMA(DMS)-HAR模型)以及结合TVP方法的TVP-FAHAR族和TVP-HAR族模型. 同时,为了证明投机活动对期货市场波动率预测的影响,去除投机活动变量建立DMA(DMS)-FAHAR模型以及在基础的DMA(DMS)-HAR模型中加入日、周和月投机活动变量构建DMA(DMS)-HAR-spec模型. 此外,以经典文献中提到的标准HAR模型[2],HAR-CJ模型 [23]和HAR-TCJ模型 [3]以及HAR-ΔJ模型 [24]作为基准参考模型. 运用以上模型对我国股指期货和国债期货的已实现波动率进行短期、中期和长期预测,预测期包括向前1期(h=1),向前5期(h=5)和向前22期(h=22),分别对应一天、一周和一个月.把股指期货和国债期货的样本期分成两个部分,分别约占整个样本期的2/3和1/3. 其中股指期货的样本内时期(定义为T1)从2010 年4月16日~2013年10月14日一共863个样本值,样本外时期从2013年10月15日~2015年6月30日包含最后的400个样本值. 与之类似,国债期货的样本内时期(定义为T2)从2013 年9月6日~2014年11月24日一共290个样本数,样本外时期从2014年11月25日~2015年6月30日一共150个样本值. 先利用Patton[25]提出的稳健损失函数对不同预测模型的样本外预测表现进行比较. 根据Patton[25]的设定,选取四种不同的损失参数b=0,b=-2,b=-1和b=1,其中b=0,b=-2,分别代表传统的MSE和QLIKE损失函数,b=-1代表齐次损失函数,b=1代表正向损失函数. 表2和表3分别显示基于不同损失函数股指期货波动率的样本外预测结果和国债期货波动率的样本外预测结果,损失函数值越小表示模型的样本外精度越高. 本文对最优预测模型的结果进行加粗显示. 根据表2中损失函数的比较结果,从大部分的损失函数来看,对于股指期货波动率的预测, DMS-FAHAR-spec模型具有最优的短期、中期和长期预测效果. 根据表3中损失函数的比较结果,对于国债期货,所有损失函数显示DMA-FAHAR-spec模型具有最优的短期和中期预测效果,而DMS-FAHAR-spec具有最优的长期预测效果. 对比包含投机活动变量的贝叶斯潜在因子模型和不包含投机活动变量的贝叶斯潜在因子模型,投机活动变量的引入明显改善了股指期货和国债期货贝叶斯HAR潜在因子模型的短期、中期和长期的样本外预测效果. 进一步对比包含投机活动的贝叶斯HAR模型和不包含投机活动的贝叶斯HAR模型,发现投机活动变量的引入改善了股指期货贝叶斯HAR模型的短期样本外预测能力,并且改善了国债期货贝叶斯HAR模型的短期、中期和长期样本外预测能力. 因此,从整体来说,投机活动变量的引入改善了贝叶斯HAR时变模型的预测能力. 从结合DMA/DMS方法的HAR族模型和结合TVP方法的HAR族模型的比较来看,DMA(DMS)-HAR族模型比TVP-HAR族模型具有更优的样本外预测效果. 此外,比较贝叶斯时变模型和基础HAR模型的预测精度,发现结合贝叶斯时变参数方法建模在很大程度上提高了基础HAR模型的样本外预测精度.由于Patton[25]提出的损失函数法是基于样本外时期的所有损失函数值的平均值对不同预测模型进行预测精度比较,因此,该方法的缺陷是容易受到某些异常值的影响. Hansen 等[26]提出的模型置信区间法(MCS)通过假设检验方法选取最优模型集,并被广泛运用于波动率预测的检验之中[27]. 选取MSE和QLIKE损失函数作为MCS检验的损失函数,通过10 000次bootstrap抽样计算出拒绝原假设的p值,p值越大,代表该预测模型包含于最优预测模型集的概率越大. 表4和表5分别显示股指期货和国债期货基于TR 和TSQ统计量的MCS结果. 设立两种置信区间α=0.5和α=0.25,代表预测模型被包含于和之中,分别用**和*进行标记.如表4所示,对于股指期货,基于MSE和QLIKE损失函数的MCS检验结果均显示DMS-FAHAR-spec模型具有最优的短期和中期预测效果,对于长期预测模型,基于MSE损失函数的MCS检验结果显示DMA-FAHAR-spec模型具有最优的预测精度,而基于QLIKE损失函数的DMS-FAHAR模型具有最优的预测精度. 此外,从MSE损失函数的MCS检验结果来看,贝叶斯潜在因子模型模型基本都在50%或75%的置信区间内被包含入最优预测模型集. 从QLKE损失函数的MCS检验结果来看,短期预测模型中只有DMS-FAHAR族模型和DMS-HAR族模型被包含入最优预测模型集,而在中期预测模型和长期预测模型中,只有DMS-FAHAR族模型被包含入最优预测模型集. 因此,贝叶斯潜在因子模型在股指期货的中期和长期的预测显示出较大的比较优势.如表5所示,对于国债期货,基于MSE损失函数和QLIKE损失函数的MCS检验结果均显示DMA-FAHAR-spec模型具有最优的短期预测效果和DMS-FAHAR-spec最优的长期预测效果,而基于MSE损失函数的MCS检验结果显示DMA-FAHAR-spec模型具有最优的中期预测效果,而基于QLKE损失函数的MCS检验结果分别认为DMA-FAHAR模型具有最优的中期预测效果. 对于长期预测模型,只有贝叶斯因子模型在50%或25%的置信区间内被包含入MCS,这显示,贝叶斯因子模型具有较大的预测优势,而对于短期和中期模型,大部分的预测模型都被包含入MCS,显示这些模型具有较为相似的预测能力. 因此,贝叶斯潜在因子模型在国债期货的长期预测中显示出较大的比较优势.综上所述,根据四种稳健的损失函数判断和MCS方法判断,对于股指期货波动率,DMS-FAHAR-spec模型具有最优的短期、中期和长期样本外预测能力,而对于国。
基于分层动态贝叶斯网络的股市趋势扰动推理算法

精品文档供您编辑修改使用专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,希望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请根据实际需要进行调整和使用,谢谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、学习资料、课堂资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想学习、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestylematerials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!基于分层动态贝叶斯网络的股市趋势扰动推理算法一、引言股市的波动一直以来都是投资者关注的焦点。
贝叶斯网络在金融分析中的应用

贝叶斯网络在金融分析中的应用贝叶斯网络是一种常用于处理不确定性问题的概率图模型,其特殊的条件概率表达方式可以帮助研究者更清晰地理解个体间的依赖关系,并据此推断各因素之间潜在的因果关系。
贝叶斯网络既可用于建模,也可用于预测,在金融分析中也有着广泛的应用。
在本文中,作者将以此为主题探讨贝叶斯网络在金融领域的具体应用以及优势。
一、应用场景贝叶斯网络经常被用来模拟金融市场中的复杂因果关系,例如:1. 个股的推荐评级:该模型可以基于市场指标、公司财务等因素构建贝叶斯网络,预测一家公司股票会在未来几个月内的表现,并相应地进行推荐或反对等投资建议。
2. 风险评估:该模型可以帮助识别可能影响公司收益的风险因素,并通过各自的概率权重评估其影响力,以便进行投资风险评估和控制。
3. 资本结构分析:该模型可以确定资本结构的影响力,以便投资者评估公司的短期和长期收益。
4. 经济指标预测:贝叶斯网络也常被用于对宏观经济趋势的预测,例如通货膨胀率、失业率和利率等。
二、优势1. 显露变量之间的因果关系:贝叶斯网络可通过概率图表达变量之间的因果关系,让分析者更加清晰地了解变量之间的相互影响,以便进行更好的预测和决策。
2. 能够发现隐藏变量:隐藏变量是不能直接被观察到的变量,而是需要通过观察其他变量的关系来揭示其存在。
贝叶斯网络可以发现隐藏变量,这些变量与金融分析领域中的决策制定者和金融机构都有着密切联系。
3. 适用性广泛:贝叶斯模型不需要假定数学方程的形态,因此它适用于各种数据类型,包括财务、经济、社会以及环境数据。
这是贝叶斯网络在金融分析中得以广泛应用的理由之一。
4. 数据库可重复:贝叶斯网络需要经过训练以确定模型中变量之间的关系,这使得成果能够与金融领域内的其他研究相比较,从而得到更完善的结果。
模型的确定性还可以保证所得结论和推论的稳定性和精度。
三、局限性1. 数据量要求高:贝叶斯网络对大量数据的需求比较高,因此在数据不足或难以获取的情况下可能会存在一定的局限性。
随机波动模型贝叶斯估计效率研究

随机波动模型贝叶斯估计效率研究近年来,随机波动模型在金融经济学的研究中越来越受到关注,在经济领域已经成为一种基本的研究方法。
因为经济过程的不确定性,随机波动模型可以更好地反映经济系统的特性,更准确地模拟经济过程。
此外,随机波动模型可以更好地分析资产收益率之间的关联关系。
贝叶斯估计是一种具有统计学属性的数据处理方法,它考虑有关观测结果的预先认知和历史知识,以此来改善对模型参数的估计。
随机波动模型贝叶斯估计的研究,就是在给定的随机波动模型的条件下,借助贝叶斯估计的方法,对模型参数进行优化,优化后的模型可以更加准确的反映经济状况。
贝叶斯估计的技术在金融随机波动模型的研究中有着重要的应用价值,结合随机波动模型技术可以更好地表征金融市场数据。
贝叶斯估计技术能够更加有效地优化模型参数,避免由于参数选取不当而导致的模型不准确的情况。
随机波动模型技术可以提供更准确的表示资产收益率之间的关联,可以更好地考虑投资组合的风险以及对冲策略,以确保风险收益之间的最佳折衷结果。
此外,在做出金融决策时,可以利用贝叶斯估计技术,深入研究决策方面的可靠性。
随机波动模型贝叶斯估计的研究,结合随机波动模型技术和贝叶斯估计技术,可以更准确、可靠地模拟经济状况,提供更准确的资产收益率关联建模,创新投资组合的风险控制方法,准确分析决策的可靠性,从而有效地指导投资决策,实现经济系统的健康发展。
国内外已有学者就随机波动模型的贝叶斯估计效率展开研究,他们提出了提高模型估计效率的有效方法。
例如利用Markov Chain Monte Carlo算法优化随机波动模型参数;利用不确定标度准则更新模型参数;结合随机序列状态空间模型优化参数等等。
尽管随机波动模型贝叶斯估计已经有很多成果,但仍有许多内容尚待研究。
首先,仍有大量的模型参数需要优化,而这些参数的优化一般是非常耗时间且复杂的。
其次,随机波动模型的参数估计本身存在误差,如何有效消除这种误差也是未来发展的方向之一。
随机波动模型贝叶斯估计效率研究

随机波动模型贝叶斯估计效率研究随着社会经济发展的加速,经济活动的复杂性、频繁性、持续性也日益增强,经济体系的稳定性也日益突出,生产运行变得不可预测。
近年来,投资者日益重视风险的管理,并在经济领域中提出了新的经济理论随机波动模型。
由于这一理论的出现,人们开始探究市场变化背后的原因,并将贝叶斯定理与随机波动模型结合,运用贝叶斯估计的技术标准较高,有效地改善了投资者投资决策的效率。
贝叶斯定理是数学上一个非常重要的概念,它是指观测到了一些变量后,根据观测数据对原变量的概率进行估计。
它可以为投资者提供有价值的参考和决策,使投资者的投资行为更加合理和理性。
贝叶斯估计是一种根据贝叶斯定理,结合实际情况,计算出参数估计的方法。
它的优点在于,通过参数估计,已经观测到的信息可以用于未知信息的预测。
随机波动模型是指风险因素以不确定的方式出现,而且其出现的影响因素也是随机的,即,市场中存在着随机性,所以投资者在投资决策时会面临不确定性。
贝叶斯估计是把随机波动模型和贝叶斯定理结合起来,从而构建一种具有技术标准高的估计方法,以确定未来行为的可能性,对投资者提供科学合理的投资决策。
首先,贝叶斯估计的技术标准非常高,它将不同的因素综合考虑,它考虑多维度的时间序列,考虑多元回归模型,考虑负面自响应现象,考虑信息不对称等,将多种数据信息收集在一起,全面把握市场的变化动态。
此外,贝叶斯估计在投资决策中有着重要的作用,它可以更详细地分析市场的行为,考虑不同的投资机会,从而有效提高投资决策的效率。
其次,贝叶斯估计可以有效提高投资者的风险管理能力,投资者可以估算未来的收益,并对投资风险进行合理的调整,使投资组合更加稳健,降低风险。
同时,贝叶斯估计可以考虑负面自响应现象,即投资者投资行为会影响市场的变化,这样投资者就可以及时进行合理性评估,更好地控制投资风险。
最后,贝叶斯估计可以有效的提高投资者的决策效率,投资者可以以更高的技术标准和更精确的参数估计来分析市场,而且不仅可以估计已观测到的变量,还可以预测还未出现的变量,从而实现更加合理和全面的投资决策。
基于贝叶斯MSSV―ST金融波动模型的股市特征及机制转移性研究6200字

基于贝叶斯MSSV―ST金融波动模型的股市特征及机制转移性研究6200字摘要:针对有偏厚尾金融随机波动模型难以刻画参数的动态时变性及结构突变的问题,设置偏态参数服从Markov转换过程,采用贝叶斯方法,构建带机制转移的有偏厚尾金融随机波动模型,考量股市不同波动状态间的机制转移性,捕捉股市间多重波动特性。
通过设置先验分布,实现模型的贝叶斯推断,设计相应的马尔科夫链蒙特卡洛算法进行估计,并利用上证指数进行实证。
结果表明:模型不仅刻画了股市的尖峰厚尾、杠杆效应等特性,发现收益率条件分布的偏度参数具有动态时变性,股市波动呈现出显著的机制转移特性,而且证实了若模型考虑波动的不同阶段性状态后,将降低持续性参数向上偏倚幅度的结论。
关键词:机制转移;贝叶斯估计;金融波动;偏态;厚尾中图分类号:F224文献标识码:A文章编号:1003-7217(2015)02-0040-06一、引言波动率作为金融市场测度的重要指标,无论是对刻画金融资产分布的形态特征,还是对投资组合、期权定价和风险管理等问题都具有十分重要的现实指导意义。
因此,如何对金融市场的波动率建模日益成为金融经济学领域研究的热点问题之一。
SV模型作为模拟波动率建模的经典模型之一,已被广泛地应用于刻画时变方差、尖峰厚尾及突变跳跃行为等特征,如何建敏[1]利用带协变量的跳跃SV模型研究发现社保基金具有跳跃性,且跳跃概率较高。
近年来,诸多研究也表明资产收益分布存在有偏性,即厚尾分布的非对称性。
Chen和Liu[2]利用厚尾门限波动模型对HIS和Nikkei225收益率进行建模,研究发现这两大亚洲股票市场的收益分布均呈现出有偏性和尖峰厚尾性。
然而,已有研究对波动性建模存在两个不足点:(1)波动持续性参数估计值过高;(2)未能考虑外生冲击导致的模型结构突变问题。
Lamoureux和Lastrapes[3]研究指出:若忽视外生重大偶发事件导致的模型结构变化问题,则会导致持续性参数向上偏倚等估计偏差。
基于贝叶斯方法的高维因子模型在中国股市的应用

基于贝叶斯方法的高维因子模型在中国股市的应用廖春芳;刘金山【摘要】基于高维时间序列因子模型,分析了2008年金融危机前后中国股市的波动状况.利用高维因子模型分析的一种新方法,发现金融危机前的因子个数为4个,危机后因子个数为2个.通过对内在消极因子建立随机波动率模型,发现相对于金融危机后,危机前因子的波动性大而且具有很强的依赖性.对上证综合指数和主因子建立模型,发现两者具有很强的线性相关性,说明中国股市具有显著的因子效应.【期刊名称】《佛山科学技术学院学报(自然科学版)》【年(卷),期】2016(034)006【总页数】6页(P31-36)【关键词】因子模型;金融危机;中国股市;随机波动率;MCMC【作者】廖春芳;刘金山【作者单位】华南农业大学数学与信息学院,广东广州510642;华南农业大学数学与信息学院,广东广州510642【正文语种】中文【中图分类】F832.512007年美国次贷危机对全球金融市场产生巨大冲击,在这次金融危机中,中国股市受到了极大影响,如上证指数在2008年1月到2008年11月,股指从5000多点跌到1700多点[1],对中国股票市场的发展产生了严重的负面影响。
本文从计量经济的角度来研究这次金融危机对中国股市的影响,通过建立因子模型来找到金融危机前后中国股市的主要影响因子,从而做出相应的比较分析。
中国股市的上市公司一共有2 635家,其中上海证券交易所有1029家,深圳交易所有1606家,因此要分析中国股市的行情趋势,势必要接触大数据。
随着信息技术的发展,人们对于大数据的收集越来越多,社会对于大数据的研究需求越来越大。
然而对于这种高维度高样本大数据的研究,若用以往传统的高维方法来研究,比如多元ARIMA模型、多元GARCH模型等等,受到的挑战是过参数化的问题,继而引发“维数灾难”。
为了有效地避免“维数灾难”问题,利用因子模型来进行降维是一种简单而又行之有效的方法,进而达到利用少数维数的变量来解释高维变量的目的。
基于贝叶斯滤波的股指动态结构特征研究

基于贝叶斯滤波的股指动态结构特征研究郝立亚;朱慧明;虞克明【摘要】针对股指波动所具有的动态结构信息特征,在状态空间建模理论的框架下,将服从Markov过程的潜在波动状态变量引入状态方程,同时在观测方程中考虑极值点的影响,构造出一类非高斯Markov随机波动状态空间模型.针对传统的MCMC方法对该类模型估计时效率低下的缺陷,设计了基于序贯Monte Carlo方法的贝叶斯滤波算法进行仿真分析,并且从算法效率和准确性方面对两种方法进行了比较.通过对沪深300股指波动的实证研究表明:对于一类非线性非高斯状态空间模型,贝叶斯滤波算法在保证估计精度的同时较MCMC方法更加有效率,能够有效刻画股指波动的动态结构特征.%To demystify the regime-switching information hidden in the stock index, a kind of non-Gauss nonlinear state space model is brought forward to allow for fat-tails in the mean equation innovation to capture the changes in volatility caused by economic forces and for Markov switching process in the latent volatility equation. In the sequential Bayesian perspective we provide a Bayesian filtering algorithm for parameter learning and state filtering of the model. In empirical study, the regime-switching information based on the stochastic volatility model is demystified by using this algorithm on CSI300 index spots open price futures. In the applications, we compare the algorithm with MCMC method in both efficiency and accuracy. We find that the Bayesian filtering algorithm outperforms existing MCMC.【期刊名称】《运筹与管理》【年(卷),期】2011(000)006【总页数】10页(P147-156)【关键词】仿真分析;随机波动;贝叶斯方法;滤波【作者】郝立亚;朱慧明;虞克明【作者单位】湖南大学工商管理学院,湖南长沙410082;湖南大学工商管理学院,湖南长沙410082;Brunel大学数学系,英国伦敦UB83PH【正文语种】中文【中图分类】F830.91股指价格作为金融市场上的一类重要时间序列,具有波动时变性和聚集性等典型特征。
基于贝叶斯原理的随机波动率模型分析及其应用

基于贝叶斯原理的随机波动率模型分析及其应用
蒋祥林;王春峰
【期刊名称】《系统工程》
【年(卷),期】2005(23)10
【摘要】基于贝叶斯原理,对随机波动性模型进行研究,并将随机波动率模型应用股市风险价值V aR的估计与预测。
针对中国股市数据进行的实证结果表明,与GARCH模型相比,随机波动率模型能更好地描述股票市场回报的异方差和波动率的序列相关性;基于随机波动率的V aR较GARCH模型的V aR具有更高的精度。
【总页数】7页(P22-28)
【关键词】随机波动率模型;GARCH模型;风险价值;贝叶斯原理
【作者】蒋祥林;王春峰
【作者单位】复旦大学金融研究院;天津大学金融工程研究中心
【正文语种】中文
【中图分类】F830.91
【相关文献】
1.金融资产波动率的持续性检验:基于厚尾贝叶斯随机波动模型 [J], 王贵银;李勇
2.厚尾随机波动率模型的贝叶斯参数估计及实证研究 [J], 黄文礼;张睿轩
3.基于MCMC模拟的贝叶斯厚尾金融随机波动模型分析 [J], 朱慧明;李峰;杨锦明
4.基于Gibbs抽样的贝叶斯金融随机波动模型分析 [J], 朱慧明;李素芳;虞克明;曾
慧芳;林静
5.次贷危机背景下中美股市波动性研究——基于贝叶斯随机波动模型 [J], 刘峰因版权原因,仅展示原文概要,查看原文内容请购买。
基于贝叶斯分析框架下的VAR和DSGE模型

基于贝叶斯分析框架下的VAR和DSGE模型
阳晓明
【期刊名称】《当代教育理论与实践》
【年(卷),期】2014(000)004
【摘要】回顾应用宏观经济学的主要分析方法和最新进展,现有校准、向量自回归、一般矩方法和极大似然估计等方法都存在诸多缺点,而贝叶斯分析框架的引入能有效地应对这些问题。
贝叶斯分析方法能很好地将微观文献和宏观研究相结合,将经济理论、数据和政策分析融为一体,而且很适合进行模型比较和政策分析。
基于我国转轨经济和宏观数据的特点,贝叶斯方法将在我国宏观经济建模和预测,中央银行制定和执行货币政策中发挥重要作用。
【总页数】5页(P178-182)
【作者】阳晓明
【作者单位】湘潭大学商学院,湖南湘潭411105
【正文语种】中文
【中图分类】F062.4
【相关文献】
1.理解我国名义利率传导机制有效性的时变特征——基于DSGE模型的理论分析与TVP-VAR模型的实证检验
2.中国货币政策冲击预期效应的实证研究——基于贝叶斯推断的BVAR、BSVAR、BVECM和BDSGE模型
3.金融杠杆、利率市场化与宏观经济波动——基于金融加速器框架下的DSGE模型研究
4.国际收支结构与
中国低利率之谜--基于TVP-VAR和DSGE模型的双重检验5.国际收支结构与中国低利率之谜——基于TVP-VAR和DSGE模型的双重检验
因版权原因,仅展示原文概要,查看原文内容请购买。
基于动态贝叶斯网模型的股指收益率序列预测

基于动态贝叶斯网模型的股指收益率序列预测
席海涛;赵杰煜
【期刊名称】《计算机仿真》
【年(卷),期】2008(25)9
【摘要】证券市场预测,是当前研究的热点和难点.动态贝叶斯网(DBNs),能够学习变量间的概率依存关系及其随时间变化的规律,表达时间序列蕴含的潜在信息.利用DBNs方法,在证券心理分析技术的基础上.建立中国证券指数的日收益率预测模型.文中使用上海证券交易所综合指数日收益率数据对模型进行训练与预测.在离散量预测环境下,模型能达到80.12%预测命中率,在采用混合高斯(GMM)分布的连续量预测中,模型的平均绝对比例误差(MAPE)指标<1%.低于BP神经网络和GARCH-BP神经网络,而且累计误差增长稳定.说明:在市场高噪声的情况下,模型具有良好的稳定性和预测能力.
【总页数】5页(P275-279)
【作者】席海涛;赵杰煜
【作者单位】宁波大学计算机科学技术研究所,浙江宁波,315211;宁波大学计算机科学技术研究所,浙江宁波,315211
【正文语种】中文
【中图分类】O242.1
【相关文献】
1.基于DCC-GARCH模型的股指期货收益率r动态相关性和风险溢出效应研究 [J], 方杰
2.基于ARMA模型的沪深300股指期货高频数据收益率研究与预测 [J], 王苏生;王俊博;李光路
3.基于长短时记忆和动态贝叶斯网络的序列预测 [J], 司阳;肖秦琨
4.沪市股指收益率预测—基于ARCH模型 [J], 杨翻翻
5.基于TV-Copula-X模型的金砖国家股指收益率与波动率的动态相依关系 [J], 叶五一;丁雅霖;焦守坤
因版权原因,仅展示原文概要,查看原文内容请购买。
基于贝叶斯算法的上证指数择时研究
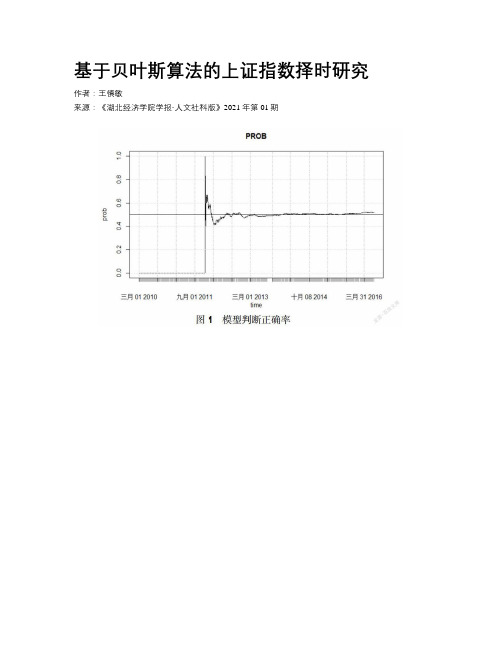
基于贝叶斯算法的上证指数择时研究作者:***来源:《湖北经济学院学报·人文社科版》2021年第01期摘要:本文根据贝叶斯算法构建了一套多因子择时模型,以上证综指为标的,使用了20多个技术因子和基本面因子,选取2008到2016年的数据,每天开盘前根据前两年的数据建模,预测当日标的指数的涨跌,并对比了朴素贝叶斯算法和基于爬山算法的贝叶斯网算法。
回测结果显示,贝叶斯网算法可以提供更稳定的收益和更高的正确率。
本文同时根据模型输出信号设计了一种仓位优化算法提升模型效果,在后续的模拟组合跟踪中,模型也持续有效。
关键词:朴素贝叶斯;贝叶斯网;指数择时一、引言股票市场的价格在表面上看杂乱无章,但众多学者的研究表明,众多因素都可以影响股票价格,股价并非完全随机的。
量化择时的目的就是通过各种指标来预测市场趋势,并在低位买入,高位卖出来获得超过市场的收益。
对量化择时的研究,在目前主要分为技术派和基本面派,前者主要通过研究各类技术指标和形态等,结合历史数据来对后市进行判断,后者主要通过基本面以及资金面等来研判后市。
而本文尝试使用贝叶斯算法,将技术面和基本面信息结合在一起,构建因子间的贝叶斯网络,對下一交易日的指数涨跌进行预测。
二、贝叶斯模型简介(一)朴素贝叶斯朴素贝叶斯分类(Nave Bayes Classifier)是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法,先通过已给定的训练集,以特征值之间独立作为前提假设,学习从输入到输出的联合概率分布,再基于学习到的模型,求出使得后验概率最大的输出。
(二)基于爬山算法的贝叶斯网朴素贝叶斯分类只能处理离散数据,需要将连续数据离散化。
对于连续数据,这里也使用了基于爬山算法的贝叶斯网。
爬山算法是一种搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
在一个贝叶斯网中,存在许多不同的父子级。
而每个子级都有其自己的区域联合概率密度函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p 1-p ( ) 6 1-q q 其 中, s s t =1表示高水平波动的潜在状态 , t =2 表示低水平波动的潜在状态 , s p 和q 则分别表示 t=
1] 为等特 征 , 如 何 建 敏[ 利用带协变量的跳跃 S V模
[] 动态 时 变 性 。 H a r v e i d d i u e4 在 股 市 收 益 率 y和 S q
分布中考虑条件偏态 情 况 , 在 GAR CH 模 型 中 构 建 偏度参数服从一阶自回归过程 , 结果表明美国 、 德国 和日本股市的偏态参数确实存在动态时变行为 。 因 在建模过程中 , 如 果 忽 视 突 发 大 事 件、 政策等外 此, 在冲击带来的结构 突 变 影 响 , 则可能会导致模型参 数估计的系统性偏 差 及 推 断 无 效 问 题 , 并降低波动 模型对收益率时序数据的拟合度 。 自H a m i l t o n 首 次 针 对 美 国 季 度 GN P 波动呈 现出的非线性动态性及非对称特征提出马尔科夫机 , 制转 移 模 型 ( 以 M a r k o v S w i t c h i n M o d e l MS M) g 它有效地解决了 传 统 波 动 性 建 模 未 能 考 虑 市 场 来, 冲击 、 国家政策等外 界 干 扰 因 素 带 来 的 结 构 性 突 变 问题 , 进而成为捕捉 市 场 事 件 或 经 济 力 量 突 变 性 行
) ; ) 基金项目 : 教育部博士点基金 ( 7 1 2 2 1 0 0 1、 7 1 0 3 1 0 0 4、 7 1 7 1 0 7 5、 7 1 4 3 1 0 0 8 2 0 1 1 0 1 6 1 1 1 0 0 2 5 国家自然科学基金 ( , 作者简介 : 男, 湖南湘潭人 , 湖南大学工商管理学院教授 、 博士生导师 , 研究方向 : 贝叶斯计量经济模型 。 1 9 6 6—) 朱慧明 (
( ) (() ( ))
I I D
ε t
~N
0
, 而是具有状态相依的参数值γ 假设模型有 M 个机 s t ) 制, 则需要进行估计的转移概率参数共有 M ( M -1 , , 个。 离散状态变量s 且s 1, 2, . . . . M} t ∈ { t 服从转 ) , , 移概率为p r( s s i 1, 2, | j∈ { i t =j t 1 =i - j =P …, 例如 M = 2, 则一阶两 M }的一阶 M a r k o v 过程 , 状态马尔科夫过程的转移概率矩阵 P 为 : )P ) P r( s s r( s s | | t =1 t =1 t =2 t =1 烄 烌 = ( ) ( ) P rs s P rs s | | t =1 t =2 t =2 t =2烎 烆
DOI:10.16339/ki.hdxbcjb.2015.02金 融 市 场 测 度 的 重 要 指 标 , 无论是 对刻画金融资产分布的形态特征 , 还是对投资组合 、 期权定价和风险管理等问题都具有十分重要的现实 指导意义 。 因此 , 如何对金融市场的波动率建模日 益成为金融 经 济 学 领 域 研 究 的 热 点 问 题 之 一 。S V 模型作为模拟波动 率 建 模 的 经 典 模 型 之 一 , 已被广 泛地应用于刻画时 变 方 差 、 尖峰厚尾及突变跳跃行
[] 题 。L 若忽视外 a m o u r e u x和 L a s t r a e s3 研究指出 : p
生重大偶发事件导 致 的 模 型 结 构 变 化 问 题 , 则会导 致持续性参数向上偏倚等估计偏差 。 现有文献中对 于收益率序列的研 究 大 都 从 静 态 角 度 进 行 建 模 , 然 而, 由于现实状态中 各 国 经 济 状 况 的 动 态 性 和 市 场 竞争者敏感度的差 异 , 收益率分布的偏态可能具有
[ 8]
)函数的峰度值增大 , · 形 态 参 数α 越 小 , 则分布 f z( 函数尾部形态越薄 , 有偏参数 β 越大 , 则收益分布 的偏态越显著 。 令λ=-0. 即可得 5 v, v, δ= 槡 γ =0,
[1] 到 Om 提出的 GH 偏态t 分布 , 测度方程中的 o r i1
随机变量ε t 用 GH 分布的变量 x t 表示为 : 0. 5 ) x 0, 1 γ λ λ ε t =u w + t+ t ε t, t ~ N(
{
x 0. 5 θ ε y p( t =e t) t ( +ω θ θ α) t 1 =α+φ t- t +
1τ ,ρ , 变量y y 1: T = ( 1, 2 0 ρ τ τ ω t ′ ′ …, …, θ θ θ y y 2, T ) 和潜在状态θ 1: T = ( 1, 2, T) 分别 为资产t 时刻可观测到的零均值化收益与服从高斯 其中
( ) 4
其中 参 数 λ t 服从形状参数和尺度参数均为 ( / )的逆伽玛分布 , / / ) , 即λ 定义位 2 G( v 2, v 2 ν t ~I / ( ) , 模型引 置参数 u u u =ν γ λ ν-2 w =- s, s ≡ E[ t] 入了 GH 分布 , 参数γ 和 ν 一同决定分布的厚尾和有 偏形态 , 此时模型称为 S V S K t模型 。 ( 二 )含马尔科夫机制转移的波动模型 由于现实经济状况的动态性和市场竞争者敏感 度差异可 能 导 致 收 益 率 分 布 的 偏 态 具 有 动 态 时 变 性, 为了捕捉波动过 程 中 潜 在 不 可 见 的 状 态 变 化 及
[] 为的 有 利 工 具 。 如 L a m5 在 波 动 截 距 项 中 嵌 入 ; M a r k o v 跳跃因子构建区制转换波动模型 ( MS S V) 6] 李想 [ 通过 G i b b s抽样并利用持续期依赖 MS 模型 对上证股市泡沫情 况 进 行 研 究 , 结果表明股市呈现 7] 出显 著 的 持 续 期 依 赖 性; 欧 阳 红 兵[ 通过在多元
第3 6卷 第1 9 4期 2 0 1 5年3月
财经理论与实践 ( 双月刊 ) THE THE O R Y AN D P RA C T I C E O F F I NAN C E AN D E C ONOM I C S
V o l .3 6 N o .1 9 4 M a r . 0 1 5 2
0 1 4-1 1-1 2 * 收稿日期 : 2
分析次贷 D C C CH 模型中引 入 隐 M a r k o v 链, -GAR 危机 和 欧 债 危 机 环 境 下 S Z、 F T S E、 H S、 N I KK 和 S P 5 0 0 五个证券市场间的传染性和机制转移性 。 可 见, 股市波动存在显著的结构突变 , 呈现出差异化的 波动状态过 程 , MS 模 型 非 常 适 合 对 结 构 突 变 问 题
[ 1 0] [ 9]
提出广义双曲线分布
( , 随后 , 高勇标 将 GH 分布应用到证券市场 GH) 中, 并采用 V a R、 E S 和 Om e a三个指标进行风险度 g 量和尾部特征分析 。 具体地 , 定义 R 为一个服从 GH 分布的变量 , 其形式为 : ) ( ) R = u+β K+槡 KZ, Z ~ N( 0, 1 2 此处 , 变量 K 服从 参 数 为λ, δ, γ 的广义逆高斯 , 分布即 : K ~G I G( K 与变量R 相互独立 , K λ, δ, γ) 的密度函数形式为 :
) 方程中引入 MS模型 , 假设式 ( 中偏态参数是状态 4 ( ) 1 相依的 , 则模型表示为如下对数波动形式 :
0. 5 ( ( ) e x 0. 5 5 +λ γ λ θ p( y t = { s t -u z) t ε t} t) t )中 的 偏 态 参 数 不 再 为 恒 定 数 值 γ, 可见 , 式( 5
总第 1 2 0 1 5 年第 2 期 ( 9 4期)
朱慧明 , 徐雅琴等 : 基于贝叶斯 M S S V- S T 金融波动模型的股市特征及机制转移性研究
4 1
进行建模 , 从而考察模型参数的动态时变性 。 目前 , 机制转移波动模型的参数估计方法主要 、 有广义矩 估 计 ( 近似滤波的伪极大似然法 GMM) ( ) 及多步移动( QML) m u l t i o v e MCMC 方 法 等 。 -m 由于 MCMC 算法将 M a r k o v 过程嵌入 M o n t e C a r l o 模拟当中 , 既克服了传统方法 “ 高维性 ” 的缺陷 , 又实 现了其动 态 性 。 同 时 , Y u 等 人 研 究 表 明: MCMC
[2] 在波动 刻画有偏参数的动态时变特性 , N a k a i m a1 j
方法估计的参数精度优于 GMM 和 QML 算法 。 因 此, 本文利 用 多 步 移 动 MCMC 算 法 对 潜 在 状 态 变 量进行分块抽取 , 成块更新 , 以解决抽样序列间高相 关性和 M a r k o v C h a i n 收敛缓慢的难题 。 二、 贝叶斯 M S S V S T 波动模型的构建 - ( 一) 波动模型结构分析 S V 模型的各类扩 展 形 式 已 被 广 泛 地 应 用 于 数 量经济学领域 , 其中 , 带“ 杠杆效应 ” 的随机波动模型 的数学表达式为 :
型研究发现社保基金具有跳跃性 , 且跳跃概率较高 。 近年来 , 诸多研究也表明资产收益分布存在有偏性 ,
[] 即厚 尾 分 布 的 非 对 称 性 。C h e n和 L i u2 利 用 厚 尾
门限 波 动 模 型 对 H I S和 N i k k e i 2 2 5收益率进行建 模, 研究发现这两大 亚 洲 股 票 市 场 的 收 益 分 布 均 呈 现出有偏性和尖 峰 厚 尾 性 。 然 而 , 已有研究对波动 ( ) 性建模存在两个不足点 : 波动持续性参数估计值 1 ( ) 过高 ; 未能考虑外生冲击导致的模型结构突变问 2
· 证券与投资 ·
基于贝叶斯 MS S V- S T 金融波动模型的 股市特征及机制转移性研究
