2018沪科版数学九年级下册247《弧长与扇形面积》练习题2
弧长与扇形面积经典习题(有难度)

弧长与扇形面积练习题1. 一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A.5πB. 4πC.3πD.2π2. 如图,如果从半径为9cm的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A.6cmB.35cm C.8cm D.53cm3.如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是()A.60° B.90° C.120° D.180°12cm 6cm7.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B’,则图中阴影部分的面积是().A. 3πB. 6πC. 5πD. 4π8.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC= 6cm,点P是母线BC上一点,且PC=23 BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A.(64π+)cm B.5cm C.35cm D.7cm9.如图,半径为1的小圆在半径为 9 的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为()A . 17πB . 32πC . 49πD . 80π10. 如图,AB切⊙O于点B,OA=23,AB=3,弦BC∥OA,则劣弧⌒BC的弧长为().A.33πB.32πC.πD.32π11. 在半径为4π的圆中,45°的圆心角所对的弧长等于.12. 已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是 m。
(结果用π表示)13.如图,圆锥的底面半径OB为10cm,它的展开图扇形的半径AB为30cm,则这个扇形的圆心角a的度数为____________.14. 如图,点A、B、C在直径为32的⊙O上,∠BAC=45º,则图中阴影的面积等于______________,(结果中保留π).2、如果一条弧长等于l,它的半径等于R,这条弧所对的圆心角增加1o,则它的弧长增加()A.lnB.180RπC.180lRπD.360l3、已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的面积为()A、18πcm2B、36πcm2C、12πcm2D、9πcm24、圆的半径增加一倍,那么圆的面积增加到()A、1倍B、2倍C、3倍D、4倍5、一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是()A、1.5cmB、7.5cmC、1.5cm或7.5cmD、3cm或15cm8、扇形的周长为16,圆心角为360πo,则扇形的面积是()A.16 B.32 C.64 D.16π10、如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB交⊙O于E,则图中与12∠BOC相等的角共有()A、2个B、3个C、4个D、5个15、如图,将三角尺ABC(其中∠B=60°,∠C=90°,AB=6)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,点A所经过的路程是()A、2πB、4πC、8πD、12π16、如图,圆锥的轴截面是边长为6cm 的正三角形ABC ,P 是母线AC 的中点.则在圆锥的侧面上从B 点到P 点的最短路线的长为( )13、如图,扇形OAB 的圆心角为90o,且半径为R ,分别以OA ,OB 为直径在扇形内作半圆,P 和Q 分别表示两个阴影部分的面积,那么P 和Q 的大小关系是()A.P Q = B.P Q > C.P Q <D.无法确定17、如图,在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻,当甲带球冲到A 点时,乙已跟随冲到B 点。
沪科版数学九年级下册《24.7 弧长与扇形面积》教学设计1

沪科版数学九年级下册《24.7 弧长与扇形面积》教学设计1一. 教材分析《24.7 弧长与扇形面积》是沪科版数学九年级下册的教学内容。
这部分内容主要包括弧长的计算公式、扇形面积的计算公式以及弧长和扇形面积在实际问题中的应用。
教材通过实例引入弧长和扇形面积的概念,然后引导学生通过观察、思考、探索,得出弧长和扇形面积的计算公式。
这部分内容是圆相关知识的重要组成部分,对于学生理解和掌握圆的相关概念和计算方法具有重要意义。
二. 学情分析九年级的学生已经学习了平面几何的基本知识,对图形的性质和计算方法有一定的了解。
但是,对于弧长和扇形面积的计算,学生可能还比较陌生。
因此,在教学过程中,需要引导学生通过观察、思考、探索,自己发现弧长和扇形面积的计算公式。
同时,学生需要具备一定的逻辑思维能力和空间想象力,能够将实际问题抽象为数学问题,并运用所学知识解决实际问题。
三. 教学目标1.理解弧长和扇形面积的概念,掌握弧长和扇形面积的计算公式。
2.能够将实际问题抽象为数学问题,运用弧长和扇形面积的计算公式解决实际问题。
3.培养学生的观察能力、思考能力和探索能力,提高学生的逻辑思维能力和空间想象力。
四. 教学重难点1.弧长和扇形面积的概念理解。
2.弧长和扇形面积的计算公式的推导和应用。
3.将实际问题抽象为数学问题,并运用所学知识解决实际问题。
五. 教学方法1.引导观察法:通过观察实例,引导学生发现弧长和扇形面积的计算规律。
2.探索法:引导学生通过思考、探索,自己得出弧长和扇形面积的计算公式。
3.实例教学法:通过实际问题,引导学生将所学知识应用于解决实际问题。
4.小组合作学习法:引导学生分组讨论,共同解决问题,提高学生的合作能力。
六. 教学准备1.教学课件:制作课件,展示实例和计算公式的推导过程。
2.教学素材:准备一些实际问题,用于引导学生运用所学知识解决实际问题。
3.计算器:为学生提供计算器,方便他们进行计算。
七. 教学过程1.导入(5分钟)通过展示一些与圆相关的实例,如自行车轮子、地球仪等,引导学生观察和思考这些实例中圆的弧长和面积的计算方法。
沪科版数学九年级下册24.7 弧长与扇形面积 同步练习(含解析)

24.7 弧长与扇形面积一.选择题(共20小题)1.(2019•济南)如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为()A.9﹣3πB.9﹣2πC.18﹣9πD.18﹣6π2.(2019•青海)如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为()A.B.C.2πD.2π3.(2019•遵义)圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是()A.5cm B.10cm C.6cm D.5cm 4.(2019•西藏)如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为()A.15cm B.12cm C.10cm D.20cm 5.(2019•大庆)如图,在正方形ABCD中,边长AB=1,将正方形ABCD绕点A按逆时针方向旋转180°至正方形AB1C1D1,则线段CD扫过的面积为()A.B.C.πD.2π6.(2019•云南)一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是()A.48πB.45πC.36πD.32π7.(2019•包头)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是()A.π﹣1 B.4﹣πC.D.2 8.(2019•荆州)如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O 恰好落在上的点D处,且l:l=1:3(l表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为()A.1:3 B.1:πC.1:4 D.2:9 9.(2019•山西)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为()A.﹣B.+C.2﹣πD.4﹣10.(2019•资阳)如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为()A.5πB.6πC.20πD.24π11.(2019•临沂)如图,⊙O中,=,∠ACB=75°,BC=2,则阴影部分的面积是()A.2+πB.2++πC.4+πD.2+π12.(2019•巴中)如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是()A.15πB.30πC.45πD.60π13.(2019•宁波)如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE 和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为()A.3.5cm B.4cm C.4.5cm D.5cm 14.(2019•长沙)一个扇形的半径为6,圆心角为120°,则该扇形的面积是()A.2πB.4πC.12πD.24π15.(2019•温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为()A.πB.2πC.3πD.6π16.(2019•金华)如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为()A.2 B.C.D.17.(2018•天水)已知圆锥的底面半径为2cm,母线长为10cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm2 18.(2018•巴彦淖尔)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA 交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为()A.+B.+2C.+D.2+ 19.(2018•黑龙江)如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为()A.π﹣6 B.πC.π﹣3 D.+π20.(2018•宁夏)用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是()A.10 B.20 C.10πD.20π二.填空题(共20小题)21.(2019•营口)圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为.22.(2019•鞍山)如图,AC是⊙O的直径,B,D是⊙O上的点,若⊙O的半径为3,∠ADB =30°,则的长为.23.(2019•青海)如图在正方形ABCD中,点E是以AB为直径的半圆与对角线AC的交点,若圆的半径等于1,则图中阴影部分的面积为.24.(2019•吉林)如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的▱ODCE的顶点C在上.若OD=8,OE=6,则阴影部分图形的面积是(结果保留π).25.(2019•十堰)如图,AB为半圆的直径,且AB=6,将半圆绕点A顺时针旋转60°,点B旋转到点C的位置,则图中阴影部分的面积为.26.(2019•福建)如图,边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合,E、F分别是AD、BA的延长线与⊙O的交点,则图中阴影部分的面积是.(结果保留π)27.(2019•河南)如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC ⊥OA.若OA=2,则阴影部分的面积为.28.(2019•黄冈)用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为.29.(2019•杭州)如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位).30.(2019•重庆)如图,四边形ABCD是矩形,AB=4,AD=2,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.31.(2019•天水)如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,2),OC与⊙D交于点C,∠OCA=30°,则图中阴影部分面积为.(结果保留根号和π)32.(2019•无锡)已知圆锥的母线长为5cm,侧面积为15πcm2,则这个圆锥的底面圆半径为cm.33.(2019•天门)75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是cm.34.(2019•徐州)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm.35.(2019•连云港)一圆锥的底面半径为2,母线长3,则这个圆锥的侧面积为.36.(2019•淮安)若圆锥的侧面积是15π,母线长是5,则该圆锥底面圆的半径是.37.(2019•安顺)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为.38.(2019•黄石)如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC 上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=,∠ADC=60°,则劣弧的长为.39.(2019•泰州)如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm.40.(2019•泰安)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB 于点A、点C,交OB于点D,若OA=3,则阴影部分的面积为.三.解答题(共10小题)41.(2019•长春)如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G.(1)求证:△ABE≌△BCG;(2)若∠AEB=55°,OA=3,求劣弧的长.(结果保留π)42.(2019•邵阳)如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.43.(2018•荆州)问题:已知α、β均为锐角,tanα=,tanβ=,求α+β的度数.探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求的弧长.44.(2018•湖州)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.45.(2017•贵阳)如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE ⊥AB,垂足为E,DE交AC于点F.(1)求∠AFE的度数;(2)求阴影部分的面积(结果保留π和根号).46.(2016•张家界)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).(1)△A1B1C1是△ABC绕点逆时针旋转度得到的,B1的坐标是;(2)求出线段AC旋转过程中所扫过的面积(结果保留π).47.(2016•攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE ⊥AF,垂足为点E(1)求证:DE=AB;(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)48.(2016•新疆)如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点.(1)求⊙O的半径OA的长;(2)计算阴影部分的面积.49.(2016•梅州)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.50.(2015•沈阳)如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.(1)求∠OCA的度数;(2)若∠COB=3∠AOB,OC=2,求图中阴影部分面积(结果保留π和根号)24.7 弧长与扇形面积参考答案与试题解析一.选择题(共20小题)1.(2019•济南)如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为()A.9﹣3πB.9﹣2πC.18﹣9πD.18﹣6π解:连接AC,∵四边形ABCD是菱形,∴AB=BC=6,∵∠B=60°,E为BC的中点,∴CE=BE=3=CF,△ABC是等边三角形,AB∥CD,∵∠B=60°,∴∠BCD=180°﹣∠B=120°,由勾股定理得AE==3,∴S△AEB=S△AEC=×6×3×=4.5=S△AFC,∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=4.5+4.5﹣=9﹣3π,故选A.2.(2019•青海)如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为()A.B.C.2πD.2π解:连接OC,∵OA=OC,∠CAO=60°,∴△AOC为等边三角形,∴∠AOC=60°,∴∠BOC=∠AOB﹣∠AOC=140°﹣60°=80°,则的长==,故选B.3.(2019•遵义)圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是()A.5cm B.10cm C.6cm D.5cm解:设圆锥的母线长为R,根据题意得2π•5=,解得R=10.即圆锥的母线长为10cm,∴圆锥的高为=5cm.故选A.4.(2019•西藏)如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为()A.15cm B.12cm C.10cm D.20cm解:过O作OE⊥AB于E,∵OA=OB=90cm,∠AOB=120°,∴∠A=∠B=30°,∴OE=OA=45cm,∴弧CD的长==30π,设圆锥的底面圆的半径为r,则2πr=30π,解得r=15.故选A.5.(2019•大庆)如图,在正方形ABCD中,边长AB=1,将正方形ABCD绕点A按逆时针方向旋转180°至正方形AB1C1D1,则线段CD扫过的面积为()A.B.C.πD.2π解:∵将正方形ABCD绕点A按逆时针方向旋转180°至正方形AB1C1D1,∴CC1=2AC=2×AB=2,∴线段CD扫过的面积=×()2•π﹣×π=,故选B.6.(2019•云南)一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是()A.48πB.45πC.36πD.32π解:侧面积是πr2=×π×82=32π,底面圆半径为,底面积=π×42=16π,故圆锥的全面积是32π+16π=48π.故选A.7.(2019•包头)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是()A.π﹣1 B.4﹣πC.D.2解:连接CD,∵BC是半圆的直径,∴CD⊥AB,∵在Rt△ABC中,∠ACB=90°,AC=BC=2,∴△ACB是等腰直角三角形,∴CD=BD,∴阴影部分的面积=×22=2,故选D.8.(2019•荆州)如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O 恰好落在上的点D处,且l:l=1:3(l表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为()A.1:3 B.1:πC.1:4 D.2:9解:连接OD交OC于M.由折叠的知识可得OM=OA,∠OMA=90°,∴∠OAM=30°,∴∠AOM=60°,∵且:=1:3,∴∠AOB=80°设圆锥的底面半径为r,母线长为l,=2πr,∴r:l=2:9.故选D.9.(2019•山西)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为()A.﹣B.+C.2﹣πD.4﹣解:∵在Rt△ABC中,∠ABC=90°,AB=2,BC=2,∴tan A=,∴∠A=30°,∴∠DOB=60°,∵OD=AB=,∴DE=,∴阴影部分的面积是=,故选A.10.(2019•资阳)如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为()A.5πB.6πC.20πD.24π解:圆所扫过的图形面积=π+2π×2=5π,故选A.11.(2019•临沂)如图,⊙O中,=,∠ACB=75°,BC=2,则阴影部分的面积是()A.2+πB.2++πC.4+πD.2+π解:作OD⊥BC,则BD=CD,连接OB,OC,∴OD是BC的垂直平分线,∵=,∴AB=AC,∴A在BC的垂直平分线上,∴A、O、D共线,∵∠ACB=75°,AB=AC,∴∠ABC=∠ACB=75°,∴∠BAC=30°,∴∠BOC=60°,∵OB=OC,∴△BOC是等边三角形,∴OA=OB=OC=BC=2,∵AD⊥BC,AB=AC,∴BD=CD,∴OD=OB=,∴AD=2+,∴S△ABC=BC•AD=2+,S△BOC=BC•OD=,∴S阴影=S△ABC+S扇形BOC﹣S△BOC=2++﹣=2+π,故选A.12.(2019•巴中)如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是()A.15πB.30πC.45πD.60π解:圆锥的母线l===10,∴圆锥的侧面积=π•10•6=60π,故选D.13.(2019•宁波)如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE 和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为()A.3.5cm B.4cm C.4.5cm D.5cm解:设AB=xcm,则DE=(6﹣x)cm,根据题意,得=π(6﹣x),解得x=4.故选B.14.(2019•长沙)一个扇形的半径为6,圆心角为120°,则该扇形的面积是()A.2πB.4πC.12πD.24π解:S==12π,故选C.15.(2019•温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为()A.πB.2πC.3πD.6π解:该扇形的弧长==3π.故选C.16.(2019•金华)如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为()A.2 B.C.D.解:∵∠A=90°,AB=AD,∴△ABD为等腰直角三角形,∴∠ABD=45°,BD=AB,∵∠ABC=105°,∴∠CBD=60°,而CB=CD,∴△CBD为等边三角形,∴BC=BD=AB,∵上面圆锥与下面圆锥的底面相同,∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,∴下面圆锥的侧面积=×1=.故选D.17.(2018•天水)已知圆锥的底面半径为2cm,母线长为10cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm2解:圆锥侧面积=π×2×10=20πcm2;故选A.18.(2018•巴彦淖尔)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA 交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为()A.+B.+2C.+D.2+解:连接OE、AE,∵点C为OA的中点,∴EO=2OC,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==,∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)=﹣﹣(﹣)=4π﹣π﹣+2=+2故选B.19.(2018•黑龙江)如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为()A.π﹣6 B.πC.π﹣3 D.+π解:∵AB=5,AC=3,BC=4,∴△ABC为直角三角形,由题意得,△AED的面积=△ABC的面积,由图形可知,阴影部分的面积=△AED的面积+扇形ADB的面积﹣△ABC的面积,∴阴影部分的面积=扇形ADB的面积==π,故选B.20.(2018•宁夏)用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是()A.10 B.20 C.10πD.20π解:设圆锥的底面圆半径为r,依题意,得2πr=,解得r=10.故小圆锥的底面半径为10.故选A.二.填空题(共20小题)21.(2019•营口)圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为3.解:设该圆锥的底面半径为r,根据题意得2πr=,解得r=3.故答案为3.22.(2019•鞍山)如图,AC是⊙O的直径,B,D是⊙O上的点,若⊙O的半径为3,∠ADB =30°,则的长为2π.解:由圆周角定理得,∠AOB=2∠ADB=60°,∴∠BOC=180°﹣60°=120°,∴的长==2π,故答案为2π.23.(2019•青海)如图在正方形ABCD中,点E是以AB为直径的半圆与对角线AC的交点,若圆的半径等于1,则图中阴影部分的面积为1.解:如图所示:连接BE,可得,AE=BE,∠AEB=90°,且阴影部分面积=S△CEB=S△ABC=S正方形ABCD=×2×2=1故答案为124.(2019•吉林)如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的▱ODCE的顶点C在上.若OD=8,OE=6,则阴影部分图形的面积是25π﹣48(结果保留π).解:连接OC,∵∠AOB=90°,四边形ODCE是平行四边形,∴▱ODCE是矩形,∴∠ODC=90°.∵OD=8,OE=6,∴OC=10,∴阴影部分图形的面积=﹣8×6=25π﹣48.故答案为25π﹣48.25.(2019•十堰)如图,AB为半圆的直径,且AB=6,将半圆绕点A顺时针旋转60°,点B旋转到点C的位置,则图中阴影部分的面积为6π.解:由图可得,图中阴影部分的面积为=6π,故答案为6π.26.(2019•福建)如图,边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合,E、F分别是AD、BA的延长线与⊙O的交点,则图中阴影部分的面积是π﹣1.(结果保留π)解:延长DC,CB交⊙O于M,N,则图中阴影部分的面积=×(S圆O﹣S正方形ABCD)=×(4π﹣4)=π﹣1,故答案为π﹣1.27.(2019•河南)如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为+π.解:作OE⊥AB于点F,∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,∴∠AOD=90°,∠BOC=30°,OA=OB,∴∠OAB=∠OBA=30°,∴OD=OA•tan30°=×=2,AD=4,AB=2AF=2×2×=6,OF=,∴BD=2,∴阴影部分的面积是S△AOD+S扇形OBC﹣S△BDO==+π,故答案为+π.28.(2019•黄冈)用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为4π.解:扇形的弧长==4π,∴圆锥的底面半径为4π÷2π=2.∴面积为4π,故答案为4π.29.(2019•杭州)如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于113cm2(结果精确到个位).解:这个冰淇淋外壳的侧面积=×2π×3×12=36π≈113(cm2).故答案为113.30.(2019•重庆)如图,四边形ABCD是矩形,AB=4,AD=2,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是8﹣8.解:连接AE,∵∠ADE=90°,AE=AB=4,AD=2,∴sin∠AED=,∴∠AED=45°,∴∠EAD=45°,∠EAB=45°,∴AD=DE=2,∴阴影部分的面积是(4×﹣)+()=8﹣8,故答案为8﹣8.31.(2019•天水)如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,2),OC与⊙D交于点C,∠OCA=30°,则图中阴影部分面积为2π﹣2.(结果保留根号和π)解:连接AB,∵∠AOB=90°,∴AB是直径,根据同弧对的圆周角相等得∠OBA=∠C=30°,∵OB=2,∴OA=OB tan∠ABO=OB tan30°=2×=2,AB=AO÷sin30°=4,即圆的半径为2,∴S阴影=S半圆﹣S△ABO=﹣×2×2=2π﹣2.故答案为2π﹣2.32.(2019•无锡)已知圆锥的母线长为5cm,侧面积为15πcm2,则这个圆锥的底面圆半径为3cm.解:∵圆锥的母线长是5cm,侧面积是15πcm2,∴圆锥的侧面展开扇形的弧长为l===6π,∵锥的侧面展开扇形的弧长等于圆锥的底面周长,∴r===3cm,故答案为3.33.(2019•天门)75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是6cm.解:由题意得圆的半径R=180×2.5π÷(75π)=6cm.故本题答案为6.34.(2019•徐州)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为6cm.解:圆锥的底面周长=2π×2=4πcm,设圆锥的母线长为R,则:=4π,解得R=6.故答案为6.35.(2019•连云港)一圆锥的底面半径为2,母线长3,则这个圆锥的侧面积为6π.解:该圆锥的侧面积=×2π×2×3=6π.故答案为6π.36.(2019•淮安)若圆锥的侧面积是15π,母线长是5,则该圆锥底面圆的半径是3.解:设该圆锥底面圆的半径是为r,根据题意得×2π×r×5=15π,解得r=3.即该圆锥底面圆的半径是3.故答案为3.37.(2019•安顺)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为6.解:根据题意得2π×2=,解得,l=6,即该圆锥母线l的长为6.故答案为6.38.(2019•黄石)如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC 上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=,∠ADC=60°,则劣弧的长为π.解:如图,连接DF,OD,∵CF是⊙O的直径,∴∠CDF=90°,∵∠ADC=60°,∠A=90°,∴∠ACD=30°,∵CD平分∠ACB交AB于点D,∴∠DCF=30°,∵OC=OD,∴∠OCD=∠ODC=30°,∴∠COD=120°,在Rt△CAD中,CD=2AD=2,在Rt△FCD中,CF===4,∴⊙O的半径=2,∴劣弧的长==π,故答案为π.39.(2019•泰州)如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为6πcm.解:该莱洛三角形的周长=3×=6π(cm).故答案为6π.40.(2019•泰安)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影部分的面积为π.解:连接OC,作CH⊥OB于H,∵∠AOB=90°,∠B=30°,∴∠OAB=60°,AB=2OA=6,由勾股定理得,OB==3,∵OA=OC,∠OAB=60°,∴△AOC为等边三角形,∴∠AOC=60°,∴∠COB=30°,∴CO=CB,CH=OC=,∴阴影部分的面积=﹣×3×3×+×3×﹣=π,故答案为π.三.解答题(共10小题)41.(2019•长春)如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G.(1)求证:△ABE≌△BCG;(2)若∠AEB=55°,OA=3,求劣弧的长.(结果保留π)(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,∴∠ABE=∠BCG=∠AFB=90°,∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,∴∠EBF=∠BAF,在△ABE与△BCG中,,∴△ABE≌△BCG(ASA);(2)解:连接OF,∵∠ABE=∠AFB=90°,∠AEB=55°,∴∠BAE=90°﹣55°=35°,∴∠BOF=2∠BAE=70°,∵OA=3,∴的长==.42.(2019•邵阳)如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.解:∵在等腰△ABC中,∠BAC=120°,∴∠B=30°,∵AD是∠BAC的角平分线,∴AD⊥BC,BD=CD,∴BC=2BD=12,∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC﹣S扇形EAF=×6×12﹣=36﹣12π;(2)设圆锥的底面圆的半径为r,根据题意得2πr=,解得r=2,这个圆锥的高h==4.43.(2018•荆州)问题:已知α、β均为锐角,tanα=,tanβ=,求α+β的度数.探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求的弧长.解:(1)连结AM、MH,则∠MHP=∠α.∵AD=MC,∠D=∠C,MD=HC,∴△ADM≌△MCH.∴AM=MH,∠DAM=∠HMC.∵∠AMD+∠DAM=90°,∴∠AMD+∠HMC=90°,∴∠AMH=90°,∴∠MHA=45°,即α+β=45°.方法二:连接P A.只要证明△P AQ∽△PHA,∵∠APG=45°,∠APG=α+β,∴α+β=45°.(2)由勾股定理可知MH==.∵∠MHR=45°,∴==.44.(2018•湖州)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,∵OC∥BD,∴∠AEO=∠ADB=90°,即OC⊥AD,∴AE=ED;(2)∵OC⊥AD,∴,∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°=72°,∴.45.(2017•贵阳)如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE ⊥AB,垂足为E,DE交AC于点F.(1)求∠AFE的度数;(2)求阴影部分的面积(结果保留π和根号).解:(1)连接OD,OC,∵C、D是半圆O上的三等分点,∴==,∴∠AOD=∠DOC=∠COB=60°,∴∠CAB=30°,∵DE⊥AB,∴∠AEF=90°,∴∠AFE=90°﹣30°=60°;(2)由(1)知,∠AOD=60°,∵OA=OD,AB=4,∴△AOD是等边三角形,OA=2,∵DE⊥AO,∴DE=,∴S阴影=S扇形AOD﹣S△AOD=﹣×=π﹣.46.(2016•张家界)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,B1的坐标是(1,﹣2);(2)求出线段AC旋转过程中所扫过的面积(结果保留π).解:(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,B1的坐标是(1,﹣2),故答案为C,90,(1,﹣2);(2)线段AC旋转过程中所扫过的面积为以点C为圆心,AC为半径的扇形的面积.∵AC==,∴面积为=,即线段AC旋转过程中所扫过的面积为.47.(2016•攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE ⊥AF,垂足为点E(1)求证:DE=AB;(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD=BC,AD∥BC,∴∠DAE=∠AFB,∵DE⊥AF,∴∠AED=90°=∠B,在△ABF和△DEA中,∴△ABF≌△DEA(AAS),∴DE=AB;(2)解:∵BC=AD,AD=AF,∴BC=AF,∵BF=1,∠ABF=90°,∴由勾股定理得AB==,∴∠BAF=30°,∴扇形ABG的面积==.48.(2016•新疆)如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点.(1)求⊙O的半径OA的长;(2)计算阴影部分的面积.解;(1)连接OD,∵OA⊥OB,∴∠AOB=90°,∵CD∥OB,∴∠OCD=90°,在RT△OCD中,∵C是AO中点,CD=,∴OD=2CO,设OC=x,∴x2+()2=(2x)2,∴x=1,∴OD=2,∴⊙O的半径为2.(2)∵sin∠CDO==,∴∠CDO=30°,∵FD∥OB,∴∠DOB=∠ODC=30°,∴S阴=S△CDO+S扇形OBD﹣S扇形OCE=×+﹣=+.49.(2016•梅州)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.(1)证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.∵OA=OC,∴∠2=∠A=30°.∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,∴CD是⊙O的切线.(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.在Rt△OCD中,∵,∴.∴.∴图中阴影部分的面积为.50.(2015•沈阳)如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.(1)求∠OCA的度数;(2)若∠COB=3∠AOB,OC=2,求图中阴影部分面积(结果保留π和根号)解:(1)∵四边形ABCD是⊙O的内接四边形,∴∠ABC+∠D=180°,∵∠ABC=2∠D,∴∠D+2∠D=180°,∴∠D=60°,∴∠AOC=2∠D=120°,∵OA=OC,∴∠OAC=∠OCA=30°;(2)∵∠COB=3∠AOB,∴∠AOC=∠AOB+3∠AOB=120°,∴∠AOB=30°,∴∠COB=∠AOC﹣∠AOB=90°,在Rt△OCE中,OC=2,∴OE=OC•tan∠OCE=2•tan30°=2×=2,∴S△OEC=OE•OC=×2×2=2,∴S扇形OBC==3π,∴S阴影=S扇形OBC﹣S△OEC=3π﹣2.。
【新】2018年秋九年级数学下册24.7弧长与扇形面积习题(新版)沪科版

24.7 弧长与扇形面积第1课时 弧长与扇形面积01 基础题知识点1 与弧长相关的计算(l =n πR180)1.钟表的轴心到分针针端的长为5 cm ,那么经过40分钟,分针针端转过的弧长是(B )A.10π3cm B.20π3 cmC.25π3cm D.50π3cm2.圆心角为120°,弧长为12π的扇形半径为(C )A .6B .9C .18D .363.(2017·台州)如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 的夹角为120°,AB 长为30厘米,则BC ︵的长为20π厘米.(结果保留π)第3题图 第4题图4.(2018·合肥名校一模)如图,点A ,B ,C 都在⊙O 上,∠ACB =60°,⊙O 的直径是6,则劣弧AB ︵的长是2π.5.如图,一根绳子与半径为30 cm 的滑轮的接触部分是CMD ︵,绳子AC 和BD 所在的直线成30°的角.请你测算一下接触部分CMD ︵的长.(精确到0.1 cm )解:连接OC ,OD , 则OC⊥AC,BD ⊥OD.又∵AC 与BD 夹角为30°, ∴∠COD =150°.∴lCMD ︵=150π×30180=25π≈78.5(cm ).知识点2 与扇形面积相关的计算(S =n πR 2360=12lR )6.如图,半径为1的圆中,圆心角为120°的扇形面积为(C )A.13B.12C.13πD.12π 7.一个扇形的圆心角是120°,面积是3π cm 2,那么这个扇形的半径是(B )A .1 cmB .3 cmC .6 cmD .9 cm8.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,那么半径为2的“等边扇形”的面积为(C )A .πB .1C .2D .23π9.已知扇形的面积为2π,半径为3,则该扇形的弧长为4π3.(结果保留π)10.(2018·蚌埠古镇县一模)如图,在⊙O 中,CD 是直径,弦AB⊥CD,垂足为E.若∠C=22.5°,AB =6 cm ,则阴影部分的面积为92π-9.第10题图 第11题图11.如图,反比例函数y =k x 与⊙O 的一个交点为P (2,1),则图中阴影部分的面积为5π4.12.如图,PA ,PB 分别与⊙O 相切于点A ,B ,∠APB =60°,连接AO ,BO.(1)AB ︵所对的圆心角∠AOB=120度; (2)若OA =3,求阴影部分的面积.解:连接OP ,则∠OPA=∠OPB=12∠APB=30°.在Rt △OAP 中,OA =3, ∴AP =3 3.∴S △OPA =12×3×33=932.∴S 阴影=2×932-120π×32360=93-3π.02 中档题13.(2018·合肥、安庆名校大联考模拟)一个扇形的半径等于一个圆的半径的2倍,且扇形面积是圆的面积的一半,则这个扇形的圆心角度数是(A )A .45°B .60°C .90°D .75°14.(2017·重庆)如图,在矩形ABCD 中,AB =4,AD =2,分别以A ,C 为圆心,AD ,CB 为半径画弧,交AB 于点E ,交CD 于点F ,则图中阴影部分的面积是(C )A .4-2πB .8-π2C .8-2πD .8-4π第14题图 第15题图15.如图,在Rt △ABC 中,∠C =90°,∠ABC =30°,AC =2,将Rt △ABC 绕点A 逆时针旋转45°后得到△AB′C′,点B 经过的路径为BB′︵,则图中阴影部分的面积是(A )A .2πB .2C .4πD .416.(2018·蚌埠怀远县模拟)如图,四边形ABCD 内接于半径为2的⊙O,E 为CD 延长线上一点.若∠ADE=120°,则劣弧AC ︵的长为43π.第16题图 第17题图17.(2018·白银)如图,分别以等边三角形的每个顶点以圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a ,则勒洛三角形的周长为πa .18.(2018·临沂)如图,△ABC 为等腰三角形,O 是底边BC 的中点,腰AB 与⊙O 相切于点D ,OB 与⊙O 相交于点E.(1)求证:AC 是⊙O 的切线;(2)若BD =3,BE =1.求阴影部分的面积.解:(1)证明:连接OD ,过点O 作OF⊥AC 于点F. ∵△ABC 为等腰三角形,O 是底边BC 的中点, ∴AO ⊥BC ,AO 平分∠BAC. ∵AB 与⊙O 相切于点D , ∴OD ⊥AB. ∵OF ⊥AC ,∴OF =OD ,即OF 为⊙O 的半径. ∴AC 是⊙O 的切线.(2)在Rt △BOD 中,设⊙O 的半径为r ,则OD =OE =r , ∴r 2+(3)2=(r +1)2,解得r =1. ∴OD =1,OB =2.∴∠B =30°,∠BOD =60°. ∴∠AOD =30°.∴∠DOF =60°. 在Rt △AOD 中,AD =33OD =33. ∴S 阴影=2S △AOD -S 扇形DOF =2×12×1×33-60×π×12360=33-π6.03 链接中考19.(2016·安徽)如图,已知⊙O 的半径为2,A 为⊙O 外一点,过点A 作⊙O 的一条切线AB ,切点为B ,AO 的延长线交⊙O 于点C.若∠BAC=30°,则劣弧BC ︵的长为4π3.第19题图 第20题图20.(2018·贵港)如图,在Rt △ABC 中,∠ACB =90°,AB =4,BC =2,将△ABC 绕点B 顺时针旋转到△A′BC′的位置,此时点A′恰好在CB 的延长线上,则图中阴影部分的面积为4π.(结果保留π)第2课时 圆锥的侧面展开图01 基础题知识点 与圆锥侧面展开图相关的计算(S 侧=πrl ,S 全=πrl +πr 2)1.如图,圆锥的底面半径r 为6 cm ,高h 为8 cm ,则圆锥的侧面积为(C )A .30π cm 2B .48π cm 2C .60π cm 2D .80π cm 2第1题图 第4题图2.(2017·宿迁)若将半径为12 cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是(D )A .2 cmB .3 cmC .4 cmD .6 cm3.(2018·仙桃)一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是(B )A .120°B .180°C .240°D .300°4.如图,把一个圆锥沿母线OA 剪开,展开后得到扇形AOC ,已知圆锥的高h 为12 cm ,OA =13 cm ,则扇形AOC 中AC ︵的长是10πcm .(结果保留π)5.一个几何体由圆锥和圆柱组成,其尺寸如图所示,求该几何体的全面积(即表面积).(结果保留π)解:圆锥的母线长是32+42=5. 圆锥的侧面积是π×4×5=20π, 圆柱的侧面积是8π×4=32π.几何体的下底面面积是π×42=16π.则该几何体的全面积(即表面积)为20π+32π+16π=68π.02 中档题6.(2018·衢州)如图,AB 是圆锥的母线,BC 为底面直径,已知BC =6 cm ,圆锥的侧面积为15π cm 2,则sin ∠ABC 的值为(C )A .34B .35C .45D .537.如图,将半径为3 cm 的圆弧形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为(A )A .2 2B . 2C .10D .32第7题图 第8题图8.一个圆锥形漏斗,某同学用三角板测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为15π__cm 2.9.如图,在Rt △ABC 中,∠ACB =90°,AC =BC =22,若把Rt △ABC 绕边AB 所在直线旋转一周,则所得几何体的表面积为π)03 链接中考10.(2018·通辽)如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的面积是(C )A.18πB.24πC.27πD.42π小中高精品教案试卷。
《弧长及扇形面积》练习题(含答案)

ED6题CBAC 71()题B AC 72()题B ACE D 8题BAEC D10题BA《弧长及扇形面积》练习题1.如图是排水管的横截面,此管道的半径为54㎝,水面以上部分的弓形的弧长为30π㎝,则这段弓形弧所对的圆心角度数为 。
2.阴影部分是某广告标志,已知两弧所在圆的半径为20cm 和10cm,∠AOB=120°,则S 阴= .3.某种商标图案如图所示(阴影部分),已知菱形ABCD 的边长为4,∠A=60°,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为 。
4.如图,四边形OABC 为菱形,点B ,C 在以O 为圆心的上,若OA=3,∠1=∠2,则S 扇形OEF = 。
5.如图,⊙O 2与⊙O 3外切于点C,⊙O 1分别与⊙O 2、⊙O 3内切于A 、B,若⊙O 1的半径为6,⊙O 2、⊙O 3的半径为2,则图中阴影部分的周界长为 ,阴影部分的面积为 。
6.如图,△ABC 中,∠C=90°,AB=12㎝,∠ABC=60°,将△ABC 以点B 为中心顺时针旋转,使点C 旋转到AB 边上的点D 处,则AC 边扫过的图形(阴影部分) 的面积为 。
7.如图,Rt △ABC 中,∠C=90°,AC=3,BC=4,①若⊙C 与AB 相切,则图中阴影部分的面积为 。
②若⊙O 与三角形的三边都相切,则图中阴影部分的面积为 。
8.如图,Rt △ABC 中,∠C=90°,∠A=30°,BC=4,分别以A 、B 为圆心,AC 、BC 长为半径画弧交AB 于D 、E ,则阴影部分的面积为 。
9.如图,矩形ABCD 中,AB=2,BC=2 3 ,以BC 中点E 为圆心,作 切AD 于点H ,与AB 、CD交于M 、N ,则阴影部分的面积为 。
10.如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE ,则五个扇形的面积之和为 。
沪科新版九年级下学期 中考题同步试卷:24.7 弧长与扇形面积(07)
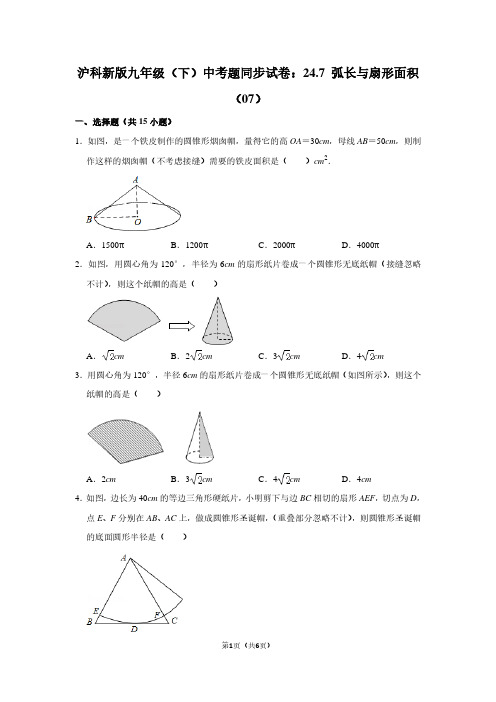
2.如图,用圆心角为 120°,半径为 6cm 的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略
不计),则这个纸帽的高是( )
A. cm
B.2 cm
C.3 cm
D.4 cm
3.用圆心角为 120°,半径 6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个
纸帽的高是( )
A.2cm
B.3 cm
C.4 cm
沪科新版九年级(下)中考题同步试卷:24.7 弧长与扇形面积 (07)
一、选择题(共 15 小题) 1.如图,是一个铁皮制作的圆锥形烟囱帽,量得它的高 OA=30cm,母线 AB=50cm,则制
作这样的烟囱帽(不考虑接缝)需要的铁皮面积是( )cm2.
A.1500π
B.1200π
C.2000π
D.4000π
旋转一周,则所形成的几何体的侧面积为
cm2(结果用含 π 的式子表示).
20.一个底面直径是 80cm,母线长为 90cm 的圆锥的侧面展开图的圆心角的度数为
.
21.圆锥的底面半径为 6cm,母线长为 10cm,则圆锥的侧面积为
cm2.
22.一个底面直径为 1角是
A.20πcm2
B.20cm2
C.40πcm2
D.40cm2
6.已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A.12πcm2
B.15πcm2
C.24πcm2
D.30πcm2
7.如果圆锥的母线长为 5cm,底面半径为 2cm,那么这个圆锥的侧面积为( )
A.10cm2
B.10πcm2
A.6π
B.8π
C.12π
D.16π
13.一个圆锥的侧面展开图是半径为 6 的半圆,则这个圆锥的底面半径为( )
沪科版数学 九年级下册 24.7 弧长与扇形面积 课后练习题

一、单选题1. 如图,在中,,点D、E分别是的中点.将绕点A顺时针旋转,射线与射线交于点P,在这个旋转过程中有下列结论:①;②存在最大值为;③存在最小值为;④点P运动的路径长为.其中,正确的是()A.①③④B.①②④C.①②③D.②③④2. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为()A.B.C.D.3. 若圆锥的底面直径为4cm,侧面展开图的面积为,则圆锥的母线长为()C.3cm D.2cmA.cm B.cm4. 若一个扇形的弧长l=,面积S=2π,则这个扇形的圆心角为()A.50°B.60°C.70°D.80°5. 如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则与的长度之和为()D.A.B.C.二、填空题6. 直线l与⊙O相切于点P,点A在直线l上,线段AO与⊙O相交于点B,若AB=2,∠OAP=30°,则劣弧PB的长为______.7. 正的边长为,边长为的正的顶点与点重合,点分别在,上,将沿边顺时针连续翻转(如图所示),直至点第一次回到原来的位置,则点运动路径的长为___________(结果保留)8. 如图,以A为圆心AB为半径作扇形ABC,线段AC交以AB为直径的半圆弧的中点D,若AB=4,则阴影部分图形的面积是_______(结果保留π).三、解答题9. 图中的小方格都是边长为1的正方形,△ABC的顶点都在正方形的顶点上.(1)在方格图中将△ABC先向上平移3格,再向右平移4格,画出平移后的△A1B1C1;再将△A1B1C1绕点A1顺时针旋转,画出旋转后的△A1B2C2;(2)求顶点C在整个运动过程中所经过的路径长.10. 如图是一段弯形管道,其中,,中心线的两条圆弧半径都为.求图中管道的展直长度.11. 如图,的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若绕点O逆时针旋转后,得到(A和是对应点)(1)画出;(2)点坐标为______,点坐标为______;(3)点A的运动路径长为______.。
沪科版九年级数学下册第24章24.7.1弧长与扇形面积

夯实基础
10.已知A︵B所对的圆周角为 30°,A︵B所在圆的半径为 30 cm, 求A︵B的长. 【点拨】在公式 C=n1π8R0 ,S 扇形=n3π6R02中,n°是圆心角 的度数,而题干给出的是圆周角的度数,不能直接代入 公式计算,要求出圆心角的度数后再代入公式计算.本
题易错解为A︵B的长=30×1π80×30=5π(cm).
A.2π B.4π C.12π D.24π
夯实基础
6.【中考·山西】如图,在 Rt△ ABC 中,∠ABC=90°,AB
=2 3,BC=2,以 AB 的中点 O 为圆心,OA 的长为半
径作半圆交 AC 于点 D,则图中阴影部分的面积为( )
5 A.
4
3-π2
C.2 3-π
B.5 4 3+π2 D.4 3-π2
整合方法
12.【中考·朝阳】如图,分别以五边形 ABCDE 的顶点为圆 心,1 为半径作五个圆,则图中阴影部分的面积之和为
() A.32π C.72π
B.3π D.2π
整合方法
【点拨】五边形 ABCDE 的内角和为 180°×(5-2)=540°. 则把阴影部分作为整体的周角和为 360°×5-540°=1 260°. ∵一个圆的面积是 π,∴1326600°°=3.5,面积是72π. 【答案】C
夯实基础
【点拨】作O点关于直线AB的对称点O′,连接O′A, O′B, 则OA=OB=O′A=O′B, ∴四边形OAO′B为菱形.
夯实基础
∵折叠后的A︵B与 OA,OB 相切, ∴O′A⊥OA,O′B⊥OB. ∴四边形 OAO′B 为正方形. ∴∠AOB=90°. ∴劣弧 AB 的长=901·8π0·5=52π. 【答案】B
3-π2.
九年数学下册第24章圆247弧长与扇形面积2471弧长与扇形面积习题课件新版沪科版2

径为 R,圆心角为 n°的扇形的面积为____3_6_0______;若已知 1
扇形的半径为 R,弧长为 C1,则扇形的面积为__2_C_1_R___.
1.如果一个扇形的半径是 1,弧长是π3,那么此扇形的圆心角的 大小为( C ) A.30° B.45° C.60° D.90°
【答案】B
4.[教材改编题]如图,用一个半径为 5 cm 的滑轮带动重物上升,
滑轮上一点 P 旋转了 108°,假设绳索(粗细不计)与滑轮之间
没有滑动,则重物上升了( C )
A.π cm
B.2π cm
C.3π cm
D.5π cm
5.[合肥肥东统考]75°的圆心角所对的弧长是 2.5π cm,则此弧所 在圆的半径是____6____cm.
∴OB 垂直平分 EF,∴PF=12EF=9 cm, ∴OP= 182-92=9 3(cm).
易知△PFB 为等腰直角三角形,∴PB=PF=9 cm,
∴OB=(9 3+9)cm,∴OC= 22OB=9
即正方形纸片的边长为9
6+9 2
2 cm.
6+9 2
2 cm,
线段 AB 绕点 O 顺时针旋转 120°到线段 A′B′的位置,则线段
AB 在旋转过程中扫过的图形的面积 10π
为____3____cm2.(结果保留 π)
11.如图,在 Rt△ABC 中,∠C=90°,AC= 5,BC=2AC,半 ︵
径为 2 的⊙C 分别交 AC,BC 于点 D,E,得到DE. (1)求证:AB 为⊙C 的切线;
8.[合肥北城新区月考]如果一个扇形的弧长和半径均为 2,则此
九年级数学下册第24章圆24.7弧长与扇形面积第1课时弧长与扇形面积同步练习含解析沪科版201811

24.7第1课时弧长与扇形面积]一、选择题1.已知扇形的圆心角为45°,半径为12,则该扇形的弧长为()3πA. B.2πC.3πD.12π4︵2.已知扇形OMN的半径为3,MN的长为6,则扇形OMN的面积是()A.6 B.7 C.8 D.9163.若一个扇形的半径为8 cm,弧长为πcm,则该扇形的圆心角为链接听课例1归纳总结3()A.60°B.120°C.150°D.180°4.若扇形的面积为3π,圆心角为60°,则该扇形的半径为()A.3 B.9 C.2 3 D.3 2︵5.2018·淄博如图K-15-1,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为()图K-15-18π3π4πA.2π B. C. D.3 4 36.一块等边三角形的木板,边长为1,现将木板沿水平线无滑动翻滚,如图K-15-2,那么点B从开始至结束所走过的路径长度为()图K-15-23π4πA. B.2 33πC.4 D.2+27.2017·重庆如图K-15-3,在矩形ABCD中,AB=4,AD=2,分别以A,C为圆心,AD,CB为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是链接听课例3归纳总结()图K-15-3πA.4-2πB.8-2C.8-2πD.8-4π8.2018·合肥模拟如图K-15-4,点O是半径为3的圆形纸片的圆心,将这个圆形纸片︵︵按下列顺序折叠,使AB和BC都经过圆心O,则阴影部分的面积为()图K-15-44π3πA.2πB.3π C. D.3 5二、填空题9.如图K-15-5,PA为⊙O的切线,A为切点,B是OP与⊙O的交点,若∠P=20°,OA ︵=3,则AB的长为________.(结果保留π)图K-15-510.2017·黄石如图K-15-6,已知扇形AOB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为________.链接听课例2归纳总结图K-15-611.如图K-15-7,已知正方形铁丝框ABCD的边长为10,现使其变形为以A为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为________.图K-15-712.如图K-15-8,⊙O的半径是2,弦AB和弦CD相交于点E,∠AEC=60°,则扇形AOC 和扇形BOD的面积(图中阴影部分)之和为________.图K-15-813.2018·白银如图K-15-9,分别以等边三角形的每个顶点为圆心、以边长为半径在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为________.图K-15-914.如图K-15-10所示,正方形ABCD的对角线AC所在直线上有一点O,OA=AC=2,将正方形绕点O顺时针旋转60°,在旋转过程中,正方形扫过的面积是________.(结果保留π)图K-15-10三、解答题︵15.如图K-15-11,在⊙O中,半径r=2,弦AB=2 3,求AB的长(结果保留π).链接听课例1归纳总结图K-15-1116.如图K-15-12,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).链接听课例3归纳总结图K-15-1217.如图K-15-13,曲线CD表示某条公路的一段,其中AmB是一段圆弧,AC,BD是线︵段,且AC,BD分别与圆弧AmB相切于点A,B,线段AB=180 m,∠ABD=150°.︵(1)画出圆弧AmB的圆心O;(2)求A到B这段弧形公路的长.图K-15-1318.如图K-15-14,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O 顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以点︵︵O,E为圆心,OA,ED长为半径画AF和DF,连接AD,求图中阴影部分的面积.图K-15-14规律探究如图K-15-15,矩形ABCD的长与宽分别是2 cm和1 cm,AB在直线l上.依次以点B,︵C′,D″为中心将矩形ABCD按顺时针方向旋转90°,这样点A走过的曲线依次为AA′,︵︵︵A′A″,A″A,其中AA′交CD于点P.(1)求矩形A′BC′D′的对角线A′C′的长;︵(2)求AA′的长;(3)求图中部分的面积S;(4)求图中部分的面积T.图K-15-15详解详析[课堂达标]nπr 45 ×π× 121.[解析] C根据弧长公式C=,可知C==3π.180 1802.[答案] Dn ×π× 8 163.[解析] B设该扇形的圆心角为n°,根据弧长公式可得=π,解得n180 3=120.4.[答案] D5.[解析] D连接OC.∵∠CAB=50°,∴∠COB=100°,∴∠AOC=80°. ∵⊙O的直径AB=6,∴⊙O的半径=3.︵80π× 3 4π∴AC的长==.180 36.[答案] B7.[解析] C∵四边形ABCD是矩形,∴AD=CB=2,∴S阴影=S矩形-S扇形DAE-S扇形BCF=1 12×4-π×22-π×22=8-2π.故选C.4 418.[解析] B过点O作OD⊥AB于点D,连接AO,BO,CO,如图,则OD=OB,∴∠ABO=230°,∴∠ABC=60°,∴∠AOC=120°.运用割补思想,图中阴影部分的面积为扇形AOC的面1积,即×π×32=3π.379.[答案] π6[解析] ∵PA切⊙O于点A,∴∠PAO=90°.∵∠P=20°,∴∠POA=70°,︵70π·37∴AB==π.180 67故答案为π.610.[答案] 2π60·π·r2[解析] 设扇形的半径是r,则=6π,解得r=6.3601设扇形的弧长是 l ,则 lr =6π,即 3l =6π,解得 l =2π.故答案是 2π.211.[答案] 1001[解析] 由题意可知扇形的半径为 10,弧长为 20,则 S 扇形 DAB = ×20×10=100.2 4 12.[答案] π 3[解析] 连接 BC.由圆周角定理,得∠AOC +∠BOD =2(∠CBE +∠ECB)=2∠AEC =120°,120 × π × 22 4 故 S 阴影=S 扇形 AOC +S 扇形 BOD == π. 360 313.[答案] πa︵[解析] 如图.∵△ABC 是等边三角形,∴∠A =∠B =∠C =60°,AB =BC =CA =a ,∴lAB ︵ ︵ 60 π π=lBC =lAC = πa = a.∴勒洛三角形的周长为 a×3=πa. 180 3 314.[答案] 2π+260[解析] 正方形扫过的面积即为阴影部分的面积.S 阴影=S 大扇形-S 小扇形+2S △ABC = π×36060 1 42- π×22+2× × 2× 2=2π+2. 360 215.解:过点 O 作 OC ⊥AB 于点 C ,1则 AC = AB = 3.2AC 3在 Rt △AOC 中,sin ∠AOC = = ,则∠AOC =60°, OA 2 ︵ 120π × 2 4 ∴∠AOB =120°,∴AB 的长为 = π. 180 316.解:∵AB 是⊙O 的直径,弦 CD ⊥AB 于点 E , ∴CE =DE ,∠CEO =∠DEB =90°. 又∵∠CDB =30°,∴∠COB =60°,∠OCE =∠CDB.∠OCE =∠BDE ,在△OCE 和△BDE 中,∠CE =D =E ,∴△OCE ≌△BDE ,60π × 22 2 ∴S 阴影=S 扇形 BOC == π. 360 317.解:(1)如图,过点 A 作 AO ⊥AC ,过点 B 作 BO ⊥BD ,AO 与 BO 相交于点 O ,点 O 即为 圆心.︵(2)∵AO ,BO 都是圆弧AmB 的半径,O 是其圆心, ∴∠OBA =∠OAB =150°-90°=60°. ∴△AOB 为等边三角形, ∴AO =BO =AB =180 m ,︵ 60 × π × 180 ∴AmB = =60π(m). 180∴A 到 B 这段弧形公路的长为 60π m. 18.解:过点 D 作 DH ⊥AE 于点 H.∵∠AOB =90°,OA =3,OB =2, ∴AB = OA 2+OB 2= 13.由旋转的性质可知,OE =OB =2,DE =EF =AB = 13,∴AE =OA +OE =5. ∵∠DEF =90°,即∠DEA +∠AEF =90°. 又∵∠AEF +∠EFO =90°, ∴∠DEA =∠EFO.在△DHE 和△EOF 中, ∠DHE =∠EOF =90°, ∠DEH =∠EFO ,{DE=EF ,)∴△DHE ≌△EOF , ∴DH =OE =OB =2,∴阴影部分面积=△ADE 的面积+△EOF 的面积+扇形 AOF 的面积-扇形 DEF 的面积=1 1 90 × π × 32 90 × π × ( 13)2 ×5×2+ ×2×3+ - =8-π. 2 2 360 360[素养提升]解:(1)由旋转得 A′C′=AC = AB 2+BC 2= 22+12= 5(cm).︵90π× 2(2)AA′的长为=π(cm).180(3)连接A″C′,由旋转的性质,得△A′D′C′≌△A″D″C′,故所求的面积S=S扇形90π(A′C′)2 1 5 A′C′A″==π×()2=π(cm2).5360 4 4(4)连接BP,在Rt△BCP中,BC=1,BP=BA=2.∴∠BPC=30°,CP=3,∴∠ABP=30°,30π× 22 1 π 3∴T=S扇形ABP+S△PBC=+×1×=cm2.3 ( +2)360 2 39。
上海市金山区山阳镇九年级数学下册 24.7 弧长与扇形的面积 24.7.2 弧长与扇形面积同步检测 (新版)沪科版

124.7.2 弧长与扇形面积同步检测一、选择题:1.圆锥的母线长为5cm,底面半径为3cm,那么它的侧面展开图的圆心角是( ).A.180°B.200°C.225°D.216°2.用一个半径长为 6cm 的半圆围成一个圆锥的侧面,则此圆锥的底面半径为( ).A. 2cmB. 3cmC. 4crnD. 6cm3.已知某个圆锥的侧面展开图是一个半圆,则它的母线与高的夹角为 ( ).A.15°B.30°C.45°D.60°4.沿着圆锥的轴剖开的剖面的等腰三角形的顶角为60°,这个圆锥的母线长为8cm ,则这个圆锥的高为( ). A.34cm B.38cm C.4cm D.8cm二、填空题:5.已知圆锥的底面半径为2cm ,母线长为5cm ,则它的侧面积是_______cm 2.6.已知圆锥的母线长是10cm ,侧面展开图的面积是60πcm 时,则这个圆锥的底面半径是 cm.7.已知圆锥的底面直径是10,高是10,则它的全面积为 .8.一个扇形的圆心角为120°,以这个扇形围成一个无底圆锥, 所得圆锥的底面半径为6cm,则这个扇形的半径是______cm.9.已知圆锥的底面直径是6,母线长6,求它的侧面展开图的圆心角与圆锥的全面积.10.在一边长为a 的正方形铁皮上剪下一块圆形和一块扇形铁皮(如图),使之恰好做成一个圆锥模型,求它的底面半径.11.已知扇形的圆心角为120°,面积为300 cm 2.(1)求扇形的弧长;(2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少?12.如图,一个圆锥的高为33 cm ,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)锥角的大小(锥角为过圆锥高的平面上两母线的夹角);2 (3)圆锥的侧面积.参考答案:1.D.提示:底面圆的周长为6π,根据弧长计算公式,得21656180180=⨯==πππR l n . 2.B.提示:底面圆的周长等于半圆的弧长,设圆锥的底面半径为r,则有2πr=6π,解得r=3.3.B.设半圆的半径为R,圆锥的底面半径为r,由2πr=πR,解得R=2r,因此母线与高的夹角为30°.4.A.提示:圆锥的高为8cos30°=34(cm).5.10π.提示:直接利用公式rl S π=圆锥侧计算.6.6.提示:根据公式rl S π=圆锥侧,61060===πππl S r 圆锥侧. 7.提示:先求得圆锥的母线长为55,则全面积为5π(5+55)=25(1+5)π.8.提示:圆锥的底面圆周长为12π,为展开图的扇形的弧长,由弧长公式,可得1812012180180=⨯==πππn l R . 9.圆锥展开图扇形的弧长为6π,由弧长公式,得rl n π180=,代入后求得展开图的圆心角为180°,全面积为3π(6+3)=27π.10.设圆的半径为r,扇形的半径为R,则1224R r ππ⨯⨯=⨯,故R=4r ,又,将R=4r 代入,3 可求得≈0.22a.11.解:(1)如图所示:∵300π=2120360R π∴R=30∴弧长L=12030180π⨯⨯=20π(cm )(2)如图所示:∵20π=20πr ,∴r=10,R=30∴S 轴截面=12×BC ×AD =12×2×10×(cm 2) 因此,扇形的弧长是20πcm 卷成圆锥的轴截面是cm 212.(1)设此圆锥高为h ,底面半径为r.∵2πr=π·AC , ∴r AC=2.(2)∵r AC=2, ∴圆锥高与母线的夹角为30°,则锥角为60°.(3)∵h=33 cm ,∴r=3 cm ,AC=6 cm.圆锥的侧面积=2πAC 2=18π cm 2.。
九年级数学下册 24.7 弧长与扇形面积课时训练2(无答案

第24章圆24.7弧长与扇形面积(2)填空题1.以直角三角形的一条______所在直线为旋转轴,其余各边旋转形成的曲面所围成的几何体叫做______.连结圆锥______和____________的线段叫做圆锥的母线,圆锥的顶点和底面圆心的距离是圆锥的______.2.沿一条母线将圆锥侧面剪开并展平,得到圆锥的侧面展开图是一个______.若设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为______,扇形的弧长为______,因此圆锥的侧面积为____,圆锥的全面积为_____.3.Rt△ABC中,∠C=90°,AB=5cm,BC=3cm,以直线BC为轴旋转一周所得圆锥的底面圆的周长是_____,这个圆锥的侧面积是______,圆锥的侧面展开图的圆心角是______.4.若把一个半径为12cm,圆心角为120°的扇形做成圆锥的侧面,则这个圆锥的底面圆的周长是______,半径是____,圆锥的高是______,侧面积是______.选择题5.若圆锥的底面半径为2cm,母线长为3cm,则它的侧面积为( ).A.2cm2B.3cm2C.6cm2D.12cm26.若圆锥的底面积为16cm2,母线长为12cm,则它的侧面展开图的圆心角为( ).A.240°B.120°C.180°D.90°7.底面直径为6cm的圆锥的侧面展开图的圆心角为216°,则这个圆锥的高为( ).A.5cm B.3cm C.8cm D.4cm8.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角为( ).A.120°B.1 80°C.240°D. 300°综合提高题9.如图,矩形ABCD中,AB=18cm,AD=12cm,以AB上一点O为圆心,OB长为半径画恰与DC边相切,交AD于F点,连结OF.若将这个扇形OBF围成一个圆锥,求这个圆锥的底面积S.。
【课课练】九年级数学下册 3.7.2 弧长及扇形的面积测试题(2)

第2课时㊀弧长及扇形的面积(2)㊀1.掌握弧长和扇形面积公式的变形.㊀2.在求阴影部分面积时,应学会转化成规则的图形(如扇形㊁三角形)的面积.㊀开心预习梳理,轻松搞定基础.1.若正方形与圆的周长相等,则正方形与圆的面积之比为(㊀㊀).A.4ʒπB .πʒ2C .πʒ4D.2ʒπ2.已知扇形的圆心角为120ʎ,弧长为20πc m ,则扇形的面积为㊀㊀㊀㊀c m 2.3.已知某段弧长为2πc m ,它所对的圆心角为60ʎ,则此弧的半径为㊀㊀㊀㊀.(第4题)4.如图,凸轮 的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于㊀㊀㊀㊀.㊀重难疑点,一网打尽.5.如图,两个同心圆被两条半径截得的A B ︵的长为10πc m ,C D ︵的长为6πc m ,且A C =12c m,则图中阴影部分的面积为(㊀㊀).(第5题)A.96πc m 2B .144πc m2C .20πc m 2D.192πc m 26.在下列命题中,真命题有(㊀㊀).①若圆周长为C ,圆面积为S ,则S =C 24π;②圆心角相等的两个扇形的面积比等于半径比;③若☉O 的面积为☉A 面积的一半,则☉O 的半径是☉A 的半径的一半.A.3个B .2个C .1个D.0个7.在平面内,将长度为4的线段A B 绕它的中点M ,按逆时针方向旋转30ʎ,则线段A B 扫过的面积为㊀㊀㊀㊀㊀.8.如图,在小正方形的边长都为1的方格纸中,әA B O 的顶点都在小正方形的顶点上,将әA B O 绕点O 顺时针方向旋转90ʎ得到әA 1B 1O ,则点A 运动的路径长为㊀㊀㊀㊀.(第8题)㊀㊀9.如图,在扇形O A B 中,øA O B =90ʎ,半径O A =6.将扇形O A B 沿过点B 的直线折叠.点O 恰好落在弧A B 上点D 处,折痕交O A 于点C ,求整个阴影部分的周长和面积.(第9题)10.某种商品的商标图案如图所示(阴影部分),已知菱形A B C D 的边长为4,øA =60ʎ,B D ︵是以点A 为圆心,A B 长为半径的弧,C D 是以点B 为圆心,B C 为半径的弧,则该商标图案的面积是多少?(第10题)㊀源于教材,宽于教材,举一反三显身手.11.如果一个扇形的弧长等于它的半径,那么此扇形称为 等边扇形 ,则半径为2的 等边扇形 的面积为(㊀㊀).A.πB .1C .2D.2π12.如图,一根5m 长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A (羊只能在草地上活动),那么小羊A 在草地上的最大活动区域面积是(㊀㊀).A.1712πm 2B .176πm 2C .254πm 2D.7712πm 2(第12题)㊀㊀㊀㊀(第13题)13.兰州市某中学的铅球场如图所示,已知扇形A O B 的面积是36m 2,弧A B 的长为9m ,那么半径O A =㊀㊀㊀㊀m .㊀㊀14.如图,在矩形A B C D中,B C=2A B,以点B为圆心,B C长为半径的圆交A D于点E,交B A的延长线于点F,设A B=1.求阴影部分的面积.(第14题)15.用48m长的篱笆材料,在空地上围成一个绿化场地,现有两种设计方案:一种是围成正方形的场地;另一种是围成圆形场地.试问选用哪一种方案,围成的场地面积较大?并说明理由.㊀瞧,中考曾经这么考!16.(2012 四川广安)如图,R tәA B C的边B C位于直线l上,A C=3,øA C B=90ʎ,øA=30ʎ,若әR t A B C由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为㊀㊀㊀㊀(结果用含π的式子表示).(第16题)17.(2012 江苏南京)某玩具由一个圆形区域和一个扇形区域组成,如图,在☉O1和扇形O2C D中,☉O1与O2C㊁O2D分别相切于点A㊁B,已知øC O2D=60ʎ,E㊁F是直线O1O2与☉O1㊁扇形O2C D的两个交点,且E F=24厘米,设☉O1的半径为x厘米.(1)用含x的代数式表示扇形O2C D的半径;(2)若☉O1㊁扇形O2C D两个区域的制作成本分别为0.45元/厘米2和0.06元/厘米2,当☉O1的半径为多少时,该玩具的制作成本最小?(第17题)第2课时㊀弧长及扇形的面积(2)1.C㊀2.300π㊀3.6c m㊀4.π㊀5.A6.C㊀7.23π㊀8.5π9.连接O D.(第9题)ȵ㊀O B=O D,O B=B D,ʑ㊀әO D B是等边三角形,øD B O=60ʎ.ʑ㊀øO B C=øC B D=30ʎ.在R tәO C B中,O C=O B t a n30ʎ=23.ʑ㊀SәO C B=12O C O B=12ˑ23ˑ6=63.ʑ㊀S阴影部分=S扇形A O B-2SәO B C=14π 36-2ˑ63=9π-123.由图可知,C D=O C,D B=O B,L阴影部分=弧A B+A C+C D+D B=2ˑ6+3π=12+3π.10.43㊀11.C㊀12.D㊀13.814.连接B E,S阴影=S扇形B C F+S矩形A B C D-2(SәA B E+S扇形B C E)=π3-3+2.15.应选圆形场地的方案,理由略.16.3π+3π17.(1)连接A O1,ȵ㊀☉O1与O2C㊁O2D分别相切于点A㊁B,ʑ㊀O1AʅO2A,øA O2E=øD O2E.ȵ㊀øC O2D=60ʎ,ʑ㊀øA O2O1=30ʎ.在R tәA O1O2中,O1E=O1A=x,ʑ㊀O1O2=24-3x.(2)费用y总=y圆+y扇y总=0.45πx2+0.06ˑ(360-60)π(24-3x2)360=0.9πx2-7.2πx+28.8π.ʑ㊀当x=--7.2π2ˑ0.9π=4时,该玩具的制作成本最小,最小值y=14.4π.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24、7 弧长与扇形面积
第2课时 圆锥的侧面展开图
一、课前预习 (5分钟训练)
1、圆锥的底面积为25π,母线长为13 cm ,这个圆锥的底面圆的半径为________ cm ,高为________ cm ,侧面积为________ cm
2、 2、圆锥的轴截面是一个边长为10 cm 的正三角形,则这个圆锥的侧面积为________ cm 2,锥角为_________,高为________ cm 、
3、已知Rt △ABC 的两直角边AC=5 cm ,BC=12 cm,则以BC 为轴旋转所得的圆锥的侧面积为_________ cm 2,这个圆锥的侧面展开图的弧长为_________ cm ,面积为_________ cm 2、
4、如图,已知圆锥的底面直径为4,母线长为6,则它的全面积为__________、
二、课中强化(10分钟训练)
1、粮仓的顶部是圆锥形,这个圆锥的底面直径是4 m,母线长为3 m,为防雨需在粮仓的顶部铺上油毡,那么这块油毡的面积至少为( )
A 、6 m 2
B 、6π m 2
C 、12 m 2
D 、12π m 2
2、若圆锥的侧面展开图是一个半径为a 的半圆,则圆锥的高为( )
A 、a
B 、 33a
C 、3a
D 、23a 3、用一张半径为9 cm 、圆心角为120°的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是_________ cm 、
4、如图,已知圆锥的母线长OA=8,地面圆的半径r=2、若一只小虫从A
点出发,绕圆锥的侧面爬行一周后又回到A 点,则小虫爬
行的最短路线的长是______(结果保留根式)、
5、一个圆锥的高为33 cm ,侧面展开图是半圆
求:(1)圆锥母线与底面半径的比;(2)锥角的大小;(3)圆锥的全面积、
三、课后巩固(30分钟训练)
1、已知圆锥的母线与高的夹角为30°,母线长为4 cm ,则它的侧面积为_________ cm 2(结果保留π)、
2、如图,有一圆锥形粮堆,其主视图是边长为6 m 的正三角形ABC ,母线AC 的中点P 处有一老鼠正在偷吃粮食,小猫从B 处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是
___________ m、(结果不取近似数)
第2题图第5题图
3、若圆锥的底面直径为6 cm,母线长为5 cm,则它的侧面积为___________、(结果保留π)
4、在Rt△ABC中,已知AB=6,AC=8,∠A=90°、如果把Rt△ABC绕直线AC旋转一周得到一个圆锥,其全面积为S1;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其全面积为S2、那么S1∶S2等于()
A、2∶3
B、3∶4
C、4∶9
D、5∶12
5、如图是小芳学习时使用的圆锥形台灯灯罩的示意图,则围成这个灯罩的铁皮的面积为
____________ cm2(不考虑接缝等因素,计算结果用π表示)、
6、制作一个底面直径为30 cm、高为40 cm的圆柱形无盖铁桶,所需铁皮至少为()
A、1 425π cm2
B、1 650π cm2
C、2 100π cm2
D、2 625π cm2
7、如图所示,在半径为27 m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°,求光源离地面的垂直高度SO、(精确到0、1 m;2=1、414,3=1、732,5=2、236,以上数据供参考)。
