2014年秋季学期九年级数学下第一二章测试题
九年级(下)数学第一、二章综合测试卷(含答案)
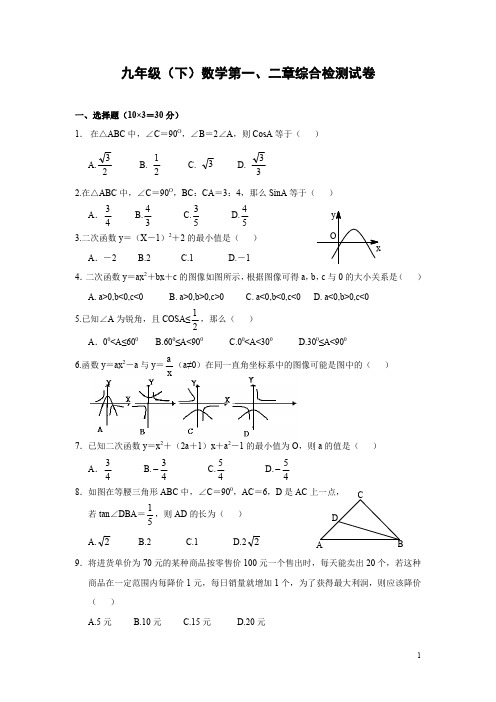
DCA九年级(下)数学第一、二章综合检测试卷一、选择题(10×3=30分)1. 在△ABC 中,∠C =90O ,∠B =2∠A ,则CosA 等于( ) A.23 B. 21C. 3D.332.在△ABC 中,∠C =90O ,BC :CA =3:4,那么SinA 等于( ) A .43 B.34 C.53 D.54 3.二次函数y =(X -1)2+2的最小值是( ) A .-2 B.2 C.1 D.-14.二次函数y =ax 2+bx +c 的图像如图所示,根据图像可得a ,b ,c 与0的大小关系是( ) A. a>0,b<0,c<0 B. a>0,b>0,c>0 C. a<0,b<0,c<0 D. a<0,b>0,c<0 5.已知∠A 为锐角,且COSA≤21,那么( ) A .00<A≤600 B.600≤A<900 C.00<A<300 D.300≤A<900 6.函数y =ax 2-a 与y =xa(a≠0)在同一直角坐标系中的图像可能是图中的( )7.已知二次函数y =x 2+(2a +1)x +a 2-1的最小值为O ,则a 的值是( ) A .43 B.43- C.45 D.45- 8.如图在等腰三角形ABC 中,∠C =900,AC =6,D 是AC 上一点, 若tan ∠DBA =51,则AD 的长为( ) A.2 B.2 C.1 D.229.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品在一定范围内每降价1元,每日销量就增加1个,为了获得最大利润,则应该降价( )A.5元B.10元C.15元D.20元10.某二元方程的解是21x m y m m =⎧⎨=++⎩,若把x 看作平面直角坐标系中点的横坐标,y 看作是纵坐标,下面说法正确的是( )A.点(x,y )一定不在第一象限B.点(x,y )一定不是坐标原点C.y 随x 的增大而增大D.y 随x 的增大而减小二、填空题:(8×3=24分)11.∠A 和∠B 是一直角三角形的两锐角,则tan2BA +=_________. 12.如图,某中学生推铅球,铅球在点A 处出手,在点B 处落地,它的运行路线满足y =-121x 2+32x +35,则这个学生推铅球的成绩是_______米.13.把抛物线y =ax 2+bx+c 的图像向右平移3个单位,再向下平移2个单位,得到图像解析式为y=x 2-4x+5,则有a=______ b=_______ c=_______.14.已知等腰三角形腰长为2cm ,面积为1cm ,则这个等腰三角形的顶角为_______度。
2014-2015学年度(下)初三数学科 试题附答案

ABC D2014-2015学年度(下)初三数学科 试题(本试卷满分120分,考试时间100分钟)一.选择题(每题3分,共30分)1.3的倒数是( )A .3B .3-C .13D .13-2.下图是由大小相同的5个小正方体搭成的几何体,则它的主视图是( )3.下列计算正确的是( )A.236a a a ⋅= B.623÷= C.21()22-=- D. 326()a a -=-4.某省各级各部门已筹集抗旱救灾救济资金32亿元,32亿元用科学记数法表示为( )A .83.210⨯元B .100.3210⨯元C .93.210⨯元 D .83210⨯元5.某外贸公司要出口一批规格为150g 的苹果,现有两个厂家提供货源,它们的价格相同,苹果的品质也相近. 质检员分别从甲、乙两厂的产品中随机抽取了50个苹果称重,并将所得数据处理后,制成如下表格. 根据表中信息判断,下列说法错误的是( ). A .本次的调查方式是抽样调查 B .甲、乙两厂被抽取苹果的平均质量相同C .被抽取的这100个苹果的质量是本次调查的样本D .甲厂苹果的质量比乙厂苹果的质量波动大6.某商场第一季度的利润是82.75万元,其中一月份的利润是25万元,若利润平均月增长率为x ,则依题意列方程为( )A .25(1+x )2=82.75B .25+50x=82.75C .25+75x=82.75D .25[1+(1+x )+(1+x )2]=82.757. 在反比例函数a y x=中,当0x >时,y 随x 的增大而减小,则二次函数2y ax ax =-的图象大致是下图中的( )8.如图,把矩形纸条ABCD 沿EF 、GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD 的边BC 长为( )A .20B .22C .24D .30个数平均质量(g ) 质量的方差 甲厂 50 150 2.6 乙厂 50 1503.1 xy O A .x yO B .x yOC .x y O D .xO yP 第16题9.如图,阴影部分组成的图案既是关于x 轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A 坐标是(1,3), 则点M 和N 的坐标分别是( )A . )(),,(3-1.-3-1N MB .)(),,( 1.3-3-1-N M C.)(),,(3-1.3-1-N M D .)(),,(3-1.31-N M10.如图,某渔船在海面上朝正东方向匀速航行,在A 处观测到灯塔M 在北偏东60º方向上,航行半小时后到达B 处,此时观测到灯塔M 在北偏东30º方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )A .10分钟B .15分钟C .20分钟D .25分钟二.填空题(每题4分,共24分)11.分解因式:4x 2-25=______________. 12 .化简:483-= .13.关于x 的一元二次方程210x x p -+-=有两个实数根12x x 、,则p 的取值范围是______________. 14. 若一个圆锥的侧面积是18π,侧面展开图是半圆,则该圆锥的底面圆半径是___________. 15.一个多边形的内角和与它的一个外角的和为570,那么这个多边形的边数为___________. 16.如图,点P (3a ,a )是反比例函y =kx(k >0)图像与⊙O 的一个交点,图中阴影部分的面积为10π, 则反比例函数的解析式为___________.三.解答题一(每题6分,共18分)17. 解不等式组:18.先化简,再求值:()2x 1x+1x 1x x ⎛⎫-÷ ⎪--⎝⎭,其中x=2.…………②…………① 30121123-⎧⎪--⎨->⎪⎩x x x ≤ ONMA yxA E PD GH FBA CD第8题第9题第10题19. 如图,在Rt △OAB 中,∠OAB =90º,且点B 的坐标为(4,2). (1)画出△OAB 绕点O 逆时针旋转90º后的△OA 1B 1; (2)以坐标原点O 为位似中心,按1:2的位似比在y 轴的右侧画出△OA 1B 1缩小后的△OA 2B 2.第19题图四.解答题二(本大题共3小题,每小题7分,共21分)20.已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上, AE = AF .(1)求证:BE = DF ;(2)连接AC 交EF 于点O ,延长OC 至点M , 使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.21. 某渔场计划购买甲、乙两种鱼苗共6000尾,甲种鱼苗每尾0.5元,乙种鱼苗每尾0.8元.相关资料表明:甲、乙两种鱼苗的成活率分别为90%和95%.(1)若购买这批鱼苗共用了3600元,求甲、乙两种鱼苗各购买了多少尾?(2)若要使这批鱼苗的成活率不低于93%,且购买鱼苗的总费用最低,应如何选购鱼苗?22.端午节吃粽子是中华民族的传统习俗,今年某商场销售甲厂家的高档、中档、低档三个品种及乙厂家的精装、简装两个品种的盒装粽子.现需要在甲、乙两个厂家中各选购一个品种. (1) 写出所有选购方案(利用树状图或列表方法求选购方案);(2) 如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的高档粽子被选中的概率是多少?AD BEF OCM 第20题图五、解答题三(本大题共3小题,每小题9分,共27分)23. 如图,小明在一次高尔夫球争霸赛中,从山坡下O 点打出一球向球洞A 点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度BD=12米时,球移动的水平距离为OD=9米 .已知山坡OA 与水平方向OC 的夹角为30o ,O 、A 两点相距OA=83米. (1)求出点A 的坐标及直线OA 的解析式; (2)求出球的飞行路线所在抛物线的解析式; (3)判断小明这一杆能否把高尔夫球从O 点直接打入球洞A 点 .第23题图24.如图,BD 为⊙O 的直径,点A 是弧BC 的中点,AD 交BC 于E 点,AE=2,ED=4. (1)求证: ABE ∆~△ADB ;(2) 求tan ADB ∠的值;(3)延长BC 至F ,连接FD ,使BDF ∆的面积 等于83,求证DF 与⊙O 相切。
花都区2014学年第二学期九年级综合练习(一)(答案)

PBEBDCA2014年九年级数学综合测试(一)答案及评分标准二、填空题(本大题共6小题,每小题3分,满分18分。
)11.x ≠2 ; 12. y((x+1)(x-1) ; 13. 0720 ; 14. -2 ; 15. 080 ; 16. 4028三、解答题(本大题共9小题,共102 分)17. (本小题满分9分)解:不等式①的解:x >1 …………(3分)不等式②的解:x ≤2…………(6分) ∴不等式组的解:1<x ≤2 …………(9分) 18. (本小题满分9分)解:(1)射线CP 为所求…………(3分)(2)证明:∵CP 是∠ACB 的平分线 ∴∠DCE =∠BCE …………(5分) ∵BC=CD CE=CE∴△DC E ≌△BCE …………(8分) ∴BE =DE …………(9分) 19. (本小题满分lO 分)解:原式=26939a a a -+--…………(4分) =29a a -…………(6分) ∵240a +=∴2a =-…………(7分)∴原式=2(2)9(2)--⨯-…………(8分)=22…………(10分) 20. (本小题满分10分)解: 在Rt △ABC 中 ∠ABC =0906030-= …………(1分)∵tanA=BCAC …………(3分) ∴AC=tan BCA=………(5分)∵∠ACB=090 点D 是斜边AB 的中点 ∴CD=BD …………(7分) ∵CD=BE∴BD=BE ……(8分)三等奖二等奖一等奖·(4,5,6)(5,6)(3,4,5,6)(4,5,6)(5,6)(3)(3,4)(2)(2,3)(2,3,4)(1,2)(1)∴∠E=∠BDE ……(9分) ∵∠CBD =∠E+∠BDE ∴∠E=01152ABC ∠= …………(10分)21. (本小题满分12分)解:设小明在跑前200米的速度为x 米/秒 …………(1分)20020080(110%)x x +=-…………(6分) 解得:x=5518…………(9分) 检验:把x=5518代入(1-10%)x ≠0∴x=5518是原方程的根 …………(10分)∴x ≈5.3 …………(11分)答:小明在跑前200米的速度是5.3米/秒 …………(12分)22. (本小题满分12分) 解:(1)极差=95-88=7众数=88 平均数=959491908888916+++++=…………(3分)(2)…………(8分)从树形图可知,有机会均等的5种情况,其中九(3)班获二等奖(记为A )有4种…………(10分) ∴ P(A)=45…………(12分) 23. (本小题满分12分) 解:(1)作BF ⊥y 轴,垂足为点F ,则四边形OABF 为矩形 ∴OF=AB=8, BF=OA=4…………(1分) ∴CF=OC-OF=11-8=3…………(2分) 在Rt △FBC 中5B C ==…………(5xCF(2)当x=0时,y=b∴D(0,b) OD= b …………(6分) 当x=4时,y=4+b∴E(4,4+b) AE =4+b …………(7分) OD+OA+AE=b+4+4+b=8+2b …………(8分)梯形OABC 的周长=OC+OA+AB+BC=11+4+8+5=28 …………(10分) ∵直线l 把梯形OABC 的周长分为3:4两部分∴OD+OA+AE=37×(梯形OABC 的周长) 或 OD+OA+AE=47×(梯形OABC 的周长) ∴8+2b=37×28 或 8+2b=47×28 …………(11分)∴b=2或4 …………(12分)24(本小题满分14分)解:(1)证明:∵E 是AD 的中点∴AE=DE∵ABE △沿BE 折叠后得到GBE △ ∴AE=EG …………1分 ∴AE=DE= EG …………2分∴三点A 、G 、D 在以点E 为圆心,EA 的长为半径的圆上…………3分 (2)连接EF ,则90EGF D ∠=∠=°,EG AE ED EF EF ===,.Rt Rt EGF EDF ∴△≌△ …………4分 GF DF ∴= …………5分设AB a =,DF b =,则有BC =,CF DC DF a b =-=-,由对称性有BG AB a ==,BF BG GF a b ∴=+=+.…………6分在Rt BCF △中,222BC CF BF +=,即222)()()a b a b +-=+,…………7分34a b ∴=,…………8分∴43a b =∴43DC a DF b == …………9分(3)由(2)知,GF DF =.设DF x BC y ==,,则有.GF x AD y ==, ∵DCk DF= DC k DF =∙,DC AB BG kx ∴===.…………10分 (1)1CF k x BF BG GF k x ∴=-=+=+,().…………11分在Rt BCF △中,222BC CF BF +=,即222[1][(1)]y k x k x +-=+().…………12分2y ∴=…………13分AD y AB kx k∴==…………14分25. (本小题满分14分)解:(1)∵y 2(1)4m x m =--是顶点式 ∴点D 的坐标为(14)m -,………(1分) 当x=0时,y= -3m 点C 的坐标为(03)C m -,………(2分)(2) 连接CD 、 BC ,过点D 作DE y ⊥轴于E∵BD 是⊙G 的直径 ∴∠DCB=090∴∠ECD+∠BCO=090 ∵∠ECD+∠EDC=090∴∠BCO=∠EDC∵∠DEC=∠BOC=090∴ DEC COB △∽△ ………(4分)DE ECCO OB=∴ ………(5分) 133mm -=-∴21m =∴ 1m =± ………(6分) ∵0m < ∴1m =-∴抛物线的解析式为223y x x =-++………(7分)(3)能在抛物线上找到一点Q ,使△BDQ 为直角三角形 很明显,点C 即在抛物线上,又在⊙G 上,90BCD ∠=°,这时Q 与C 点重合 点Q 坐标为(03)Q , ………(8分)如图②,若DBQ ∠为90°,作QF y ⊥轴于F ,DH x ⊥轴于H同理可证:Rt Rt DHB BFQ △∽△∴DH HBBF FQ= ∴DH FQ BF HB ∙=∙∵点Q 坐标2(23)k k k -++, ∴24(23)2(3)k k k --=- 化简得:22390k k --=解得:3k =(不合题意,舍去),32k =-由32k =-得Q 坐标: 3924Q ⎛⎫-- ⎪⎝⎭,………(10分) 若BDQ ∠为90°如图③,延长DQ 交y 轴于M , 作DE y ⊥轴于E ,DH x ⊥轴于H同理可证:DEM DHB △∽△ ∴DE EM DH HB= 则142EM = 得12EM =,点M 的坐标为702⎛⎫⎪⎝⎭, 设DM 所在的直线解析式为y=kx+b,把M 702⎛⎫⎪⎝⎭,和D (1,4)代入得:724b k b ⎧=⎪⎨⎪+=⎩ 解得:17,22k b == ∴直线DM 的解析式为1722y x =+ ………(11分)把1722y x =+代入223y x x =-++得:22310x x -+= 解为:1x =(不合题意,舍去),12x =, 把12x =代入1722y x =+ 得154y =点Q 的坐标为11524⎛⎫⎪⎝⎭, ………(12分)综合上述,满足题意的Q 点有三个:(03),、3924⎛⎫- ⎪⎝⎭,和11524⎛⎫⎪⎝⎭, ………(14分)。
2014下期末初三数学试题答案

2014-2015学年第一学期期末考试初三数学参考答案及评分标准一、选择题:每小题3分,共45分.1.C 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.A 10.D11.A 12.A 13.C 14.D 15.D二、填空题:每小题4分,共20分.16.2(41)(21)(21)a a a ++- 172 18.AE=CF (答案不唯一) 19.±6 20.2<m<3三、解答题:21、解:(1) 原式=534-515a b c a b…………………………………………………………………………1分 =(54)(31)13ab c --- ……………………………………………………………………………………3分 =213ab c -……………………………………………………………………………………………4分 (2) 原式=4x 221()x x x x÷-- ……………………………………………………………………1分 =4x 221x x x-÷- …………………………………………………………………………2分 =4x 2x 21x x ⨯-- …………………………………………………………………………3分 =2 …………………………………………………………………………………………4分(3)原式= ………………………………………………2分= ……………………………………………………………………………………4分(4) 原式=22(44)y x xy y --+ …………………………………………………………………2分 =2(2)y x y -- ………………………………………………………………………………4分22、解:方程两边都乘以2x 4-得:2(2)34x x x ++=- ………………………………1分 22234x x x ++=-27x =- ……………………………………………………………………………………………2分72x =- ……………………………………………………………………………………………3分检验:把72x =-代入240x ≠-…………………………………………………………………4分 所以72x =-是原方程的解 …………………………………………………………5分 23、解:根据题意,得12APB y S PB AC ==⋅⋅ …………………………………………1分 ∴16(8)2y x =⨯⨯- ……………………………………………………………………………2分 ∴243y x =- ………………………………………………………………………………3分 而且P 点不与B,C 重合,所以x 的值的取值范围只能在0到8之间,而取不到0或者8,所以x 0<<8……………………………………………………………………………………5分 ∴y 与x 的函数解析式:243y x =-自变量x 的取值范围:x 0<<8 ……………………………………………………………6分24、解:在Rt △ABC 中:BC 2=225030-=1600,∴BC =40,………………………………3分 小汽车速度为:40÷2=20米/秒=72千米/时>70千米/时.………………………………………5分 ∴这辆小汽车超速了 ………………………………………………………………………………6分25、证明:四边形ABCD 是平行四边形,∴AF ∥CD ,AB=CD ………………………1分 AB=BE ,∴四边形BECD 是平行四边形………………………………………………………2分 ∴BD ∥CE∴∠BDF=∠EMF=∠DMC ………………………………………………………………………3分 BF=BD ,∴∠BDF=∠F=∠FDC ………………………………………………………………4分 ∴∠DMC=∠MDC ………………………………………………………………………………5分 ∴CD=CM …………………………………………………………………………………………6分26、证明:∵AD 是∠CAB 的平分线,∠ACD=∠ AED=90°∴CD=DE …………………………………………………………………………………………1分 ∵∠ACD=∠ AED ,∠CAD=∠DAE ,AD=AD∴△ACD ≌△AED ,∴∠ADC=∠ADE …………………………………………………………2分 又∵CD=DE ,DF=DF∴△CDF ≌△EDF ………………………………………………………………………………3分 ∴CF=EF ……………………………………………………………………………………………4分 ∵∠CDF=∠B+12∠CAB ,∠CFD=∠ACH+12∠CAB. ∵∠B=90°-∠CAB ,∠ACH=90°-∠CAB ,∴∠ACH=∠B∴∠CDF=∠CFD …………………………………………………………………………………5分 ∴CF=CD. ……………………………………………………………………………………6分∴CF=CD=DE=EF.∴四边形CDEF 是菱形……………………………………………………………………7分27、解:(1)如图:; ………………2分(2)2次 …………………………………………………………………………………………3分(3)如图,设直线AB 的解析式为y=k 1x+b 1∵图象过A (4,0)B (6,150),1111406150k b k b +=⎧∴⎨+=⎩ 1175300k b =⎧∴⎨=-⎩ 则75300y x =-① ……………………………………………………………………………5分 设直线CD 的解析式为y=k 2x+b 2∵图象过C (7,0),D (5,150),2222705150k b k b +=⎧∴⎨+=⎩ 2275525k b =-⎧∴⎨=⎩ 则75525y x =-+②……………………………………………………………………………7分 解由①、②组成的方程组得 5.5112.5x y =⎧⎨=⎩ ∴最后一次相遇时距离乌鲁木齐市的距离为112.5千米……………………………………9分。
2014年秋季九年级期考数学科参考答案

2014年秋季九年级期考数学科参考答案一、选择题(每小题3分,共21分)1.A ;2.D ;3.C ;4.C ;5.D ;6.A ;7.B. 二、填空题(每小题4分,共40分)8.10;9.1x =0,2x =3;10.5;11. 略;12. 2;13.1000; 14.31;15. (3,6);16.-3,-2;17.(1)120 (2)1413. 三、解答题(89分)18.原式=4-33-6(8分)=-2-33(9分) 19.写出求根公式 (4分) 2133±=x (9分) 20. ∵ AD ∥BE ,∴ ∠AEB =∠FAD , 3分∵DF ⊥AE ∴∠AFD =∠B=90°, 6分∴ △ABE ∽△DFA 9分 21. 在Rt △AEC 中,Cos70°=AB BC 4分 ∴AB = 70cos BC≈5.3 (米) 8分 答:梯子AB 的长度为5.6米. 9分22.(1) 用列表或画树状图表示 6分 (2) P(在第二象限)=41. 9分 23.(1)(0,1) 3分(2)画出△A 1B 1C 1(画出一个点各2分 ) 9分 24.(1) 2 2+x 4分(2)根据题意,得 (2+x )(200-20x )=700. 6分整理,得x 2-8x +15=0, 7分解这个方程得x 1=3 x 2=5, 8分 答:售价应定为13元或15元. 9分25.(1)36 3分(2)①当P 点与D 点重合时,t =3 4分 ∴H 为AD 的中点,∵EF ⊥AD ,∴EF 为AD 的垂直平分线 ∴四边形AEDF 的对角线互相垂直平分A EHDF LCB图1∴四边形AEDF 为菱形 5分 ∵AD=BD=CD=6 ∴∠BAC=90° ∴四边形AEDF 为正方形 6分 ②∵ EF ∥BC , ∴△AEF ∽△ABC , 7分 ∴AD AH BC EF =,即6612tEF -=,解得:EF=2(6-t ). S △PEF =EF ·DH=×2(6-t )t =-(t ﹣3)2+9 8分 ∴当t =3秒时,S △PEF 的最大值为9. 9分 ③ 1)若点E 为直角顶点,如图所示, 此时PE ∥AD ,PE =t ,BP=2t . ∵PE ∥AD ,∴BD BP AD PE =,即626tt =,t =0, 与题设矛盾; 10分 2)若点F 为直角顶点,如图所示, 此时PF ∥AD ,PF=t ,BP=2t ,CP=12﹣2t . ∵PF ∥AD ,∴CD CP AD PF =,即62126tt -=, 解得t =4; 11分3)若点P 为直角顶点,如图所示.法1:四边形AEDF 为正方形 ∠EDF=90°当P 点与D 点重合时,△PEF 为直角三角形. ∴t =3 13分 法1:过点E 作EM ⊥BC 于点M ,过点F 作FN ⊥BC 于点N ,则EM=FN=DH=t ,EM ∥FN ∥AD .∵EM ∥AD ,∴BDBMAD EM =,解得BM=t , ∴PM=BP ﹣BM=t .在Rt △EMP 中,由勾股定理得:PE 2=EM 2+PM 2=2t 2. ∵FN ∥AD ,∴CDCN AD FN =,解得CN=t , ∴PN=BC ﹣BP ﹣CN=12﹣2t ﹣t =12﹣3t . 12分在Rt △FNP 中,由勾股定理得:PF 2=FN 2+PN 2=t 2+(12﹣3t )2=10t 2﹣72t +144.在Rt △PEF 中,由勾股定理得:EF 2=PE 2+PF 2,即:(12﹣2t )2=2t 2+10t 2﹣72t +144 化简得:t 2﹣3t =0,PA EHDF LCB图2P图3BCLF DHEAM N P 图4BCLF DHEA解得:t=3或t=0(舍去) 13分综上所述,当t=3秒或t=4秒时,△PEF为直角三角形.26.(1)b=-3;m=-2 3分(2)过点A作AC∥x轴,交抛物线于点C,可求得C(4,4)又B(2,-2)∴∠COB=90° 4分①若以O、B、C为顶点的三角形和以O、B、P为顶点的三角形相似,只能是△OBC∽△OCP 5分∴△OBC与△OPB的相似比为OC:OB=2:1; 6分②由①知CO=42,BO=22,BF=FC=10.1)若翻折后,点B′落在BC的右侧,BC与PB′的交点为M,如图.S△MFP =S△BCP =S△CPF =S△B′PF,∴M为FC、PB′的中点∴四边形B′FPC为平行四边形, 7分∴PC=10, PO=42-10 8分2)若翻折后,点B′落在BC上,则点B,D重合, S△MFP =S△BCP,不合题意,舍去. 10分3)若翻折后,点B落在OD的左侧,OC与FB′的交点为N,如图,S△NFP =S△BCP =S△BPF =S△CPF =S△B′PF∴N为PC、FB′的中点∴四边形B′PFC为平行四边形,11分B′P=FC=10∴BP= B′P=10 12分在直角三角形OPB中OP2+OB2=BP2,PO=2, 13分综上所述,PO=42-10或PO=2.B'MPFyxOCABBACO xyFPNB'。
2014北师大九年级下第一章直角三角形的边角关系达标测试卷及答案(pdf版)
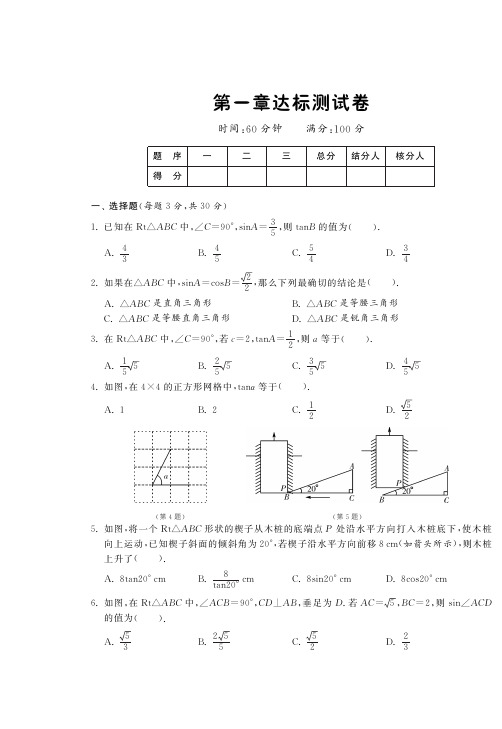
第一章达标测试卷时间:60分钟㊀㊀满分:100分题㊀序一二三总分结分人核分人得㊀分一㊁选择题(每题3分,共30分)1.已知在R tәA B C中,øC=90ʎ,s i n A=35,则t a n B的值为(㊀㊀).A.43B.45C.54D.342.如果在әA B C中,s i n A=c o s B=22,那么下列最确切的结论是(㊀㊀).A.әA B C是直角三角形B.әA B C是等腰三角形C.әA B C是等腰直角三角形D.әA B C是锐角三角形3.在R tәA B C中,øC=90ʎ,若c=2,t a n A=12,则a等于(㊀㊀).A.155B.255C.355D.4554.如图,在4ˑ4的正方形网格中,t a nα等于(㊀㊀).A.1B.2C.12D.52(第4题)㊀㊀㊀㊀(第5题)5.如图,将一个R tәA B C形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20ʎ,若楔子沿水平方向前移8c m(如箭头所示),则木桩上升了(㊀㊀).A.8t a n20ʎc m B.8t a n20ʎc m C.8s i n20ʎc m D.8c o s20ʎc m 6.如图,在R tәA B C中,øA C B=90ʎ,C DʅA B,垂足为D.若A C=5,B C=2,则s i nøA C D 的值为(㊀㊀).A.53B.255C.52D.23(第6题)㊀㊀㊀(第7题)㊀㊀㊀(第8题)7.河堤的横断面如图所示,堤高A B 为10m ,斜坡B C 的长为26m ,那么斜坡B C 的坡度是(㊀㊀).A.1ʒ3B .1ʒ2.6C .1ʒ2.4D.1ʒ28.如图,A ㊁B ㊁C 三点在正方形网格线的交点处,若将әA B C 绕着点A 逆时针旋转得到әA C ᶄB ᶄ,则t a n B ᶄ的值为(㊀㊀).A.12B .13C .14D.249.在әA B C 中,s i n B =c o s (90ʎ-C )=12,那么әA B C 是(㊀㊀).A.等腰三角形B .等边三角形C .直角三角形D.等腰直角三角形10.在平面直角坐标系中,设点P 到原点O 的距离为p ,O P 与x 轴正方向的夹角为α,则用[p ,α]表示点P 的极坐标,显然,点P 的极坐标与它的坐标存在一一对应关系.例如:点P 的坐标为(1,1),则其极坐标为[2,45ʎ].若点Q 的极坐标为[4,60ʎ],则点Q 的坐标为(㊀㊀).A.(2,23)B .(2,-23)C .(23,2)D.(2,2)二㊁填空题(第13㊁14题每题4分,其余每题3分,共29分)11.在R t әA B C 中,øC =90ʎ,øA =60ʎ,斜边上的高是3,则a =㊀㊀㊀㊀,b =㊀,c =㊀㊀㊀㊀.12.计算:c o s 245ʎ+t a n 30ʎ s i n 60ʎ=㊀㊀㊀㊀.13.如图,建筑物甲㊁乙两楼的高均为20m ,在某一时刻太阳光线与水平线的夹角为30ʎ,如果两楼间隔为18m ,那么楼甲的影子落在楼乙上的高度A B 等于㊀㊀㊀㊀m .(结果保留根号)(第13题)㊀㊀㊀(第14题)㊀㊀㊀(第17题)14.如图,øA C B =90ʎ,A B =13,A C =12,øB C M =øB A C ,则s i n øB A C =㊀㊀㊀㊀,点B 到直线M C 的距离为㊀㊀㊀㊀.15.在等腰三角形中,腰与底边之比为1ʒ2,则底角为㊀㊀㊀㊀.16.张华同学遇到了这样一道题:3t a n (β+20ʎ)=1,你猜想锐角β的度数应是㊀㊀㊀.17.如图,某公园入口处原有三级台阶,每级台阶高为18c m ,宽为30c m ,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡B C 的坡度i =1ʒ5,则A C 的长度是㊀㊀㊀㊀c m .18.某厂家新开发的一种电动车如图,它的大灯A 射出的光线A B ㊁A C 与地面MN 所夹的锐角分别为8ʎ和10ʎ,大灯A 与地面的距离为1m ,则该车大灯照亮地面的宽度B C 是㊀m .(参考数据:s i n 8ʎ=425,t a n 8ʎ=17,s i n 10ʎ=950,t a n 10ʎ=58)(第18题)㊀㊀㊀㊀(第19题)19.在207国道襄阳段改造工程中,需沿A C 方向开山修路(如图所示),为了加快施工进度,要在小山的另一边同时施工,从A C 上的一点B 取øA B D =140ʎ,B D =1000m ,øD =50ʎ,为了使开挖点E 在直线A C 上,那么D E =㊀㊀㊀㊀m .(供选用的三角函数值:s i n 50ʎ=0.7660,c o s 50ʎ=0.6428,t a n 50ʎ=1.192)三㊁解答题(第20题5分,第21㊁22题每题6分,第23㊁24题每题7分,第25题10分,共41分)20.计算:s i n 30ʎ-c o s 245ʎ+34t a n 230ʎ+s i n 260ʎ-c o s 60ʎ.21.如图,在әA B C 中,øA =30ʎ,t a n B =13,B C =10,则AB 的长是多少?(第21题)22.如图,水渠边有一棵大木瓜树,树干D O (不计粗细)上有两个木瓜A ㊁B (不计大小),树干垂直于地面,量得A B =2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45ʎ㊁木瓜B 的仰角为30ʎ.求C 处到树干D O 的距离C O .(结果精确到1米,参考数据:3ʈ1.73,2ʈ1.41)(第22题)23.如图所示,A㊁B两城市相距100k m.现计划在这两座城市间修筑一条高速公路(即线段A B),经测量,森林保护中心P在A城市的北偏东30ʎ和B城市的北偏西45ʎ的方向上.已知森林保护区的范围在以点P为圆心,50k m为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区?为什么?(参考数据:3ʈ1.732,2ʈ1.414)(第23题)24.如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,A B是A到l的小路.现新修一条路A C到公路l.小明测量出øA C D=30ʎ,øA B D=45ʎ,B C=50m.请你帮小明计算他家到公路l的距离A D的长度.(精确到0.1m,参考数据:2ʈ1.414,3ʈ1.732)(第24题)25.某市规划局计划在一坡角为16ʎ的斜坡A B上安装一球形雕塑,其横截面示意图如图所示.已知支架A C与斜坡A B的夹角为28ʎ,支架B DʅA B于点B,且A C㊁B D的延长线均过☉O的圆心,A B=12m,☉O的半径为1.5m,求雕塑最顶端到水平地面的垂直距离.(结果精确到0.01m,参考数据:c o s28ʎʈ0.9,s i n62ʎʈ0.9,s i n44ʎʈ0.7,c o s46ʎʈ0.7)(第25题)第一章达标测试卷1.A㊀2.C ㊀3.B ㊀4.B ㊀5.A㊀6.A7.C ㊀8.B ㊀9.A㊀10.A11.23㊀2㊀4㊀12.1㊀13.20-6314.513㊀2513㊀15.45ʎ㊀16.10ʎ㊀17.21018.75㊀19.642.820.原式=12-22()2+34ˑ33()2+32()2-12=12.21.3+322.设C O 为x 米.在R t әB C O 中,t a n 30ʎ=B OC O,则B O =33x .在R t әA C O 中,A O =C O ,则A O =x .即方程33x +2=x ,解得x ʈ5.故C O 长大约是5米.23.过点P 作P C ʅA B 于点C ,则P C =50(3-3)ʈ63.4>50,所以高速公路不会穿越保护区.24.因为在R t әA B D 中,øA B D =45ʎ,所以A D =D B ,设A D =x ,在R t әA C D 中,t a n 30ʎ=A D C D =x x +50,x =25(3+1)ʈ68.3.25.过点O 作水平地面的垂线,垂足为E .在R t әA O B 中,c o s øO A B =A B O A ,即c o s 28ʎ=A B O A =12O A,所以O A =12c o s 28ʎʈ120.9ʈ13.3333.因为øE A B =16ʎ,所以øO A E =28ʎ+16ʎ=44ʎ.在R t әA O E 中,s i n øO A E =O E O A,即s i n 44ʎʈO E 13.3333,所以O E ʈ13.3333ˑ0.7ʈ9.3333(m ).9.3333+1.5=10.83(m ).所以雕塑最顶端到水平地面的垂直距离约为10.83m .。
2014初三下册数学试卷及参考答案精编

2014初三下册数学试卷及参考答案精编一、选择题(本大题共10小题,每小题4分,共40分.)在每小题给出的四个选项中,只有一项是符合题意的,请把你认为正确的选项前字母填写在该题后面的括号中.1.下列几何图形中,一定是轴对称图形的有 ( )A.2个B.3个C.4个D.5个2.今年5月,随着第四条水泥熟料生产线的点火投产,芜湖海螺水泥熟料已达年产6000000吨,用科学记数法可记作()A.吨B.吨 C.吨 D.吨3.如果,则= ( )A.B.1C.D.24.下列计算中,正确的是()A. B. C.D.5.如图,在△ABC中ADperp;BC,CEperp;AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3、AE=4,则CH 的长是( )A.1B.2C.3D.46.已知关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )A.mgt;-1B.mlt;-2C.mge;0D.mlt;07.筹建中的安徽芜湖核电站芭茅山厂址位于长江南岸繁昌县狄港镇,距离繁昌县县城约17km,距离芜湖市区约35km,距离无为县城约18km,距离巢湖市区约50km,距离铜陵市区约36km,距离合肥市区约99km.以上这组数据17、35、18、50、36、99的中位数为().A.18B.50C.35D.35.58.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A 的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为()A.cm B.4cm C.cm D.3cm9.函数中自变量x的取值范围是()A.xge;B.xne;3C.xge;且xne;3 D.10.如图,Rt△ABC绕O点旋转90deg;得Rt△BDE,其中ang;ACB=ang;E= 90deg;,AC=3,DE=5,则OC的长为()A.B.C.D.二、填空题(本大题共6小题,每小题5分,共30分)11.已知是一元二次方程的一个根,则方程的另一个根是.12.在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,其图象如图所示,P(5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是米.13.据芜湖市环保局6月5日发布的2006年环境状况公报,去年我市城市空气质量符合国家二级标准.请根据图中数据计算出该年空气质量达到一级标准的天数是天.(结果四舍五入取整数).14.因式分解:.15.如图,,以为直径的圆与一个以5为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与CD 切于点Q.则.16.定义运算“@”的运算法则为:x@y=,则.三、解答题(本大题共8小题,共80分.)解答应写明文字说明和运算步骤.17.(本题共两小题,每小题6分,满分12分)(1)计算:deg;.(2)解不等式组芜湖供电公司分时电价执行时段分为平、谷两个时段,平段为8:00~22:00,14小时,谷段为22:00~次日8:00,10小时.平段用电价格在原销售电价基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元,小明家5月份实用平段电量40千瓦时,谷段电量60千瓦时,按分时电价付费42.73元.(1)问小明该月支付的平段、谷段电价每千瓦时各为多少元?(2)如不使用分时电价结算,5月份小明家将多支付电费多少元?19.(本小题满分8分)如图,在△ABC中,AD是BC上的高,,(1)求证:AC=BD;(2)若,BC=12,求AD的长.20.(本小题满分8分)已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.21.(本小题满分10分)如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形(要求与△ABC同在P点一侧);(2)求线段BC的对应线段所在直线的解析式.22.(本小题满分10分)一园林设计师要使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成,为使得绿化效果最佳,还须使得扇环面积最大.(1)求使图1花圃面积为最大时R-r的值及此时花圃面积,其中R、r分别为大圆和小圆的半径;(2)若L=160m,r=10m,求使图2面积为最大时的theta;值.23.(本小题满分12分)阅读以下材料,并解答以下问题.“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N= m + n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n 种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?24.(本小题满分12分)已知圆P的圆心在反比例函数图象上,并与x轴相交于A、B两点.且始终与y轴相切于定点C(0,1).(1)求经过A、B、C三点的二次函数图象的解析式;(2)若二次函数图象的顶点为D,问当k为何值时,四边形ADBP为菱形.参考答案一、选择题(本大题共10小题,每题4分,满分40分)题号1234567910答案BCCDAADACB二、填空题(本大题共6小题,每题5分,满分30分) 11.12.0.513.11714.15.616.6三、解答题(本大题共8小题,共80分)解答应写明文字说明和运算步骤.17.(本小题满分12分)(1)解:原式=,,4分==. ,,6分(2)解:解不等式①,得:xle;2. ,,2分解不等式②,得xgt;1. ,4分所以原不等式组的解集为 1。
2014年初三数学下期综合测试

2014年初三数学下期综合测试一、选择题:本大题共10个小题,每小题3分,共30分。
1、已知x =-1是关于x 的方程012=++mx x 的一个根,则m = ( )A .0B .1C .2D .-22、点(-sin60°,cos60°)关于y 轴对称的点的坐标是( ) A .(2,12) B .(-2,12) C .(-2,-12) D .(-12,-32) 3、一元二次方程2210x x --=的根的情况为( )A .有两个相等的实数根B .有两个不相等的实数根C .只有一个实数根D .没有实数根4、如图,⊙O 的直径CD =5cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,OM :OD =3:5 ,则AB 的长是( )A .2cmB .3cmC .4cmD .221cm5、如图,AC 是⊙O 的直径,弦AB ∥CD ,若∠BAC=32°,则∠AOD 等于( ).A .64°B .48°C .32°D .76°6、如图,AB 是⊙O 的直径,DB 、DC 分别切⊙O 于B 、C ,若∠ACE =250,则∠D 为( )A 、500B 、550C 、600D 、6507、如果把ABC V 各顶点的纵、横坐标都乘-1,得到111A B C V ,则这两个三角形在坐标系中的位置关系是( )A 、关于x 轴对称B 、关于y 轴对称C 、关于原点对称D 、无对称关系8、如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为CE ,且D 点落在对角线D ′处.若AB=3,AD=4,则ED 的长为( )A .32 B .3 C .1 D .439、如图,正方形ABCD 中,E F 、分别为AB BC 、的中点,AF 与DE 相交于点O ,则cot DAO Ð ( )第4题 第5题∙ 第 6 题图EO D CBA第15题第8题 第10题E F第9题A .31B .552 C .23D .2110、如图,△ABC 内接于⊙O ,∠A=50°,∠ABC=60°,BD 是⊙O 的直径,BD 交AC 于点E ,连结DC ,则∠AEB 等于( ). A .70° B .90° C .110° D .120°二、填空题:本大题共6个小题,每小题3分,共18分。
九年级数学下册第一章《直角三角形的边角关系》测试卷及答案

九年级数学下册第一章《直角三角形的边角关系》单元测试卷(满分150分)题号一二三四总分得分一、选择题(本大题共15小题,共45.0分)1.在直角三角形中sin A的值为12,则cos A的值等于()A. 12B. √22C. √32D. √32.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA=45,则BD的长度为()A. 94B. 125C. 154D. 43.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边AB=a,BC=b,∠DAO=x,则点C 到x轴的距离等于()A. acosx+bsinxB. acosx+bcosxC. asinx+bcosxD. asinx+bsinx4.已知α为锐角,且sinα=√32,则α的度数为()A. 30°B. 45°C. 60°D. 75°5.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. tanαtanβB. sinβsinαC. sinαsinβD. cosβcosα6.在Rt△ABC中,∠C=90°,若AB=2AC,则sin A的值是()A. √3B. 12C. √32D. √337.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为()A. 7sin35°B. 7cos35∘C. 7cos35°D. 7tan35°8.如图,在Rt△ACB中,∠C=90°,sinB=0.5,若AC=6,则BC的长为()A. 8B. 12C. 6√3D. 12√39.如图,∠C=90°,AB=10米,∠B=36°,则AC为()A. 10tan36°B. 10cos36°C. 10sin36°D. 10sin36∘10.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°=ACCD =2+√3=√3(2+√3)(2−√3)=2−√3.类比这种方法,计算tan22.5°的值为()A. √2+1B. √2−1C. √2D. 1211..如图,在△ABC中,sinB=13,tanC=2,AB=3,则AC的长为()A. √2B. √52C. √5D. 212.2cos30∘−tan45∘−√(1−tan60∘)2的值是()A. 2√3−2B. 0C. 2√3D. 213.如图,在△ABC中AB=2√5,将△ABC绕点A按逆时针方向旋转,使得点B恰好落在BC的中点B′处,得到△AB′C′.若tan∠CB′C′=43,则BC的长为()A. 4√5B. 6C. 8D. 1014.若sin(∠A+15°)=√32,则tan∠A的值为()A. .12B. √33C. 1D. √2215.中考结束后,小明和好朋友一起前往三亚旅游.他们租住的宾馆AB坐落在坡度为i=1:2.4的斜坡上.宾馆AB高为129米.某天,小明在宾馆顶楼的海景房A处向外看风景,发现宾馆前有一座雕像C(雕像的高度忽略不计),已知雕像C距离海岸线D的距离CD为260米,与宾馆AB的水平距离为36米,远处海面上一艘即将靠岸的轮船E的俯角为27°.则轮船E距离海岸线D的距离ED的长为()米(参考数据:tan27°≈0.5,sin27°≈0.45)A. 262B. 212C. 244D. 276二、填空题(本大题共5小题,共25.0分)16.将一副三角尺如图所示叠放在一起,则BE的值是________.EC17.如图,在△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cos C=________.18.如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是4,则sinα3的值为________.19.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD∠ACB,若AE=2,则上,且DE=CD,连接OE,∠ABE=12OE的长为______.20.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是______m(结果保留根号)三、计算题(本大题共3小题,共30.0分)21.下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=ℎ,太阳光线与水平线的夹角为α.(1)用含α的式子表示h;(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光?22. 先化简,再求值:(1−x +3x+1)÷x 2+4x+4x+1,其中x =tan45°+(12)−1.23. 计算:|2−tan60°|−(π−3.14)0+(−12)−2+12√12.四、解答题(本大题共4小题,共50.0分)24. 如图,在Rt △ABC 中,∠C =90°,M 是直角边AC 上一点,MN ⊥AB 于点N ,AN =3,AM =4,求cos B 的值.25. 对于钝角α,定义它的三角函数值如下:sinα=sin(180°−α),cosα=−cos(180°−α).(1)求sin120°,cos120°,sin150°的值;(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sin A,cos B是方程4x2−mx−1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.26.如图,矩形ABCD中,AB=6,∠ABD=60°,点E从点A出发,以每秒2个单位长度的速度沿边AB运动,到点B停止运动.过点E作EF//BD交AD于点F,将△AEF绕点E顺时针旋转得到△GEH,且点G落在线段EF上,设点E的运动时间为t(秒)(0<t<3).(1)若t=1,求△GEH的面积;(2)若点G在∠ABD的平分线上,求BE的长;(3)设△GEH与△ABD重叠部分的面积为T,用含t的式子表示T,并直接写出当0<t<3时T的取值范围.27.先化简,再求代数式x2−1x+2÷(1−3x+2)的值,其中x=4sin45°−2cos60°.答案1.C2.C3.A4.C5.B6.C7.C8.C9.C10.B11.B12.B13.C14.C15.B16.√3317.2318.4519.√1320.40√321.解:(1)过E作EF⊥AB,垂足为F,则∠BEF=α,在Rt△AFE中,FE=AC=30,AB=10×3=30,∴BF=AB−EC=30−ℎ,∵tanα=BF,FE∴BF=EF×tanα,即30−ℎ=30×tanα,ℎ=30−30tanα;(2)当α=30°时,ℎ=30−30tan30°≈12.68,∴甲楼顶B的影子落在第五层,不影响乙楼的采光时,AB的影子顶部应刚好落在C处,此时,AB=30,AC=30,∴∠BCA=45°,则∠α’=45°,∵角α每小时增加10度,∴应在1个半小时后,甲楼的影子刚好不影响乙楼的采光.22.解:原式=(1−x2x+1+3x+1)÷(x+2)2x+1=(2+x)(2−x)x+1⋅x+1(2+x)2=2−x2+x,当x=tan45°+(12)−1=1+2=3时,原式=2−32+3=−15.23.解:原式=|2−√3|−1+4+√3,=2−√3−1+4+√3,=5.24.解:∵∠C=90°,MN⊥AB,∴∠C=∠ANM=90°,又∵∠A=∠A,∴△AMN∽△ABC,∴ANAM =ACAB=34,设AC=3x,AB=4x,由勾股定理得BC=√AB2−AC2=√7x,∴在Rt△ABC中,cosB=BCAB =√7x4x=√74.25.解:(1)由题意得,;(2)∵三角形的三个内角的比是1:1:4,∴三个内角分别为30°,30°,120°,①当∠A =30°,∠B =120°时,方程的两根为12,−12, 将x =12代入方程得:4×(12)2−m ×12−1=0,解得:m =0,经检验x =−12是方程4x 2−1=0的根,∴m =0符合题意;②当∠A =120°,∠B =30°时,两根为√32,√32,不符合题意; ③当∠A =30°,∠B =30°时,两根为12,√32, 将x =12代入方程得:4×(12)2−m ×12−1=0,解得:m =0,经检验x =√32不是方程4x 2−1=0的根. 综上所述:m =0,∠A =30°,∠B =120°.26.解:(1)如图1中,∵四边形ABCD 是矩形,∴∠A =90°,∵EF//BD ,∴∠AEF =60°,∵AE =2,∴AF =AE ⋅tan60°=2√3,∴S △EGH =S △AEF =12⋅AE ⋅AF =12×2×2√3=2√3.(2)如图2中,由题意得,BG平分∠ABD,∠ABD=30°,∴∠EBG=12∵∠AEG=∠EBG+∠EGB=60°∴∠EBG=∠EGB=30°,∴BE=EG=AE=3.(3)如图1−1中,当点H落在BD上时,作EJ⊥BD于J.∵EF//BD,∴∠FEH=∠EHB=60°,∴△EBH是等边三角形,∴EH=EB=EF=2AE,∴AE=2,BE=4,∴t=1,×2t×2t×√3=2√3t2.如图3中,当0<t≤1时,重叠部分是△EGH,T=S△AEF=12如图4中,当1<t<3时,重叠部分是四边形MNGE,作EJ⊥BD于J.在Rt△EBJ中,∵BE=6−2t,∠EBJ=60°,∴BJ=12BE=3−t,EJ=√3BJ=3√3−√3t,∵△EBM是等边三角形,∴BJ=JM=3−t,∵四边形EGNJ是矩形,∴EG=NJ=2t,∴MN=NJ−MJ=3t−3,∴T=12⋅(MN+EG)⋅EJ=12⋅(3t−3+2t)⋅(3√3−√3t)=−5√32t2+9√3t−9√32.综上所述,T={2√3t2(0<t≤1)−5√32t2+9√3t−9√32(1<t<3).27.解:x2−1x+2÷(1−3x+2)=(x+1)(x−1)x+2÷x+2−3x+2=(x+1)(x−1)x+2⋅x+2x−1=x+1,∵x=4sin45°−2cos60°=2√2−1,∴原式=2√2.。
九年级数学下册第一章《直角三角形的边角关系》单元测试卷及答案

九年级数学下册第一章《直角三角形的边角关系》单元测试卷(满分150分)题号 一 二 三 四 总分 得分一、选择题(本大题共15小题,共45.0分)1. 在直角三角形中sin A 的值为12,则cos A 的值等于( )A. 12B. √22C. √32D. √32. 已知α为锐角,且sinα=√32,则α的度数为( )A. 30°B. 45°C. 60°D. 75°3. 若sin(∠A +15°)=√32,则tan∠A 的值为( )A. .12B. √33C. 1D. √224. 在0,−√273,sin45°,13这四个数中,无理数是( )A. 0B. −√273C. sin45°D. 135. 如图,Rt △ABC 中,∠C =90°,点D 在AC 上,∠DBC =∠A.若AC =4,cosA =45,则BD 的长度为( )A. 94 B. 125 C. 154 D. 46. 如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC =α,∠ADC =β,则竹竿AB 与AD 的长度之比为( )A. tanαtanβ B. sinβsinα C. sinαsinβ D. cosβcosα7.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为()A. 7sin35°B. 7cos35∘C. 7cos35°D. 7tan35°8.如图,在Rt△ACB中,∠C=90°,sinB=0.5,若AC=6,则BC的长为()A. 8B. 12C. 6√3D. 12√39.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边AB=a,BC=b,∠DAO=x,则点C 到x轴的距离等于()A. acosx+bsinxB. acosx+bcosxC. asinx+bcosxD. asinx+bsinx10.在Rt△ABC中,∠C=90°,若AB=2AC,则sin A的值是()A. √3B. 12C. √32D. √3311.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°=ACCD =12+√3=2−√3(2+√3)(2−√3)=2−√3.类比这种方法,计算tan22.5°的值为()A. √2+1B. √2−1C. √2D. 1212..如图,在△ABC中,sinB=13,tanC=2,AB=3,则AC的长为()A. √2B. √52C. √5D. 213.如图,在△ABC中,AB=10,AC=8,BC=6,直线l经过点A,且垂直于AB,分别与AB,AC相交于点M,N.直线l从点A出发,沿AB方向以1cm/s的速度向点B运动,当直线l经过点B时停止运动,若运动过程中△AMN的面积是y(cm2),直线l的运动时间是x(s),则y与x之间函数关系的图象大致是()A. B.C. D.14.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为()(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).A. 5.1米B. 6.3米C. 7.1米D. 9.2米15.如图,在矩形ABCD中,AB=4,对角线AC,BD交于点O,sin∠COD=√3,P为AD上一动点,PE⊥AC于点E,2PF⊥BD于点F,分别以PE,PF为边向外作正方形PEGH和PFMN,面积分别为S1,S2.则下列结论:①BD=8;②点P在运动过程中,PE+PF 的值始终保持不变,为2√3;③S1+S2的最小值为6;④当PH:PN=5:6时,则DM:AG=5:6.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共5小题,共25.0分)16.计算:−(5−π)0−2⋅sin45°=______.17.如图,在△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cos C=________.18.将一副三角尺如图所示叠放在一起,则BE的值是________.EC19.如图,在平面直角坐标系中,P是第一象限内的点,其坐标,则sinα是(3,m),且OP与x轴正半轴的夹角α的正切值是43的值为________.20.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD∠ACB,若AE=2,则上,且DE=CD,连接OE,∠ABE=12OE的长为______.三、计算题(本大题共3小题,共30.0分)21.共抓长江大保护,建设水墨丹青新岳阳,推进市中心城区污水系统综合治理项目,需要从如图A,B两地向C地新建AC,BC两条笔直的污水收集管道,现测得C地在A地北偏东45°方向上,在B地北偏西68°向上,AB的距离为7km,求新建管道的总长度.(结果精确到0.1km,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,√2≈1.41)22. 计算:|2−tan60°|−(π−3.14)0+(−12)−2+12√12.23. 小甬工作的办公楼(矩形ABCD)前有一旗杆MN ,MN ⊥DN ,旗杆高为12m ,在办公楼底A 处测得旗杆顶的仰角为30°,在办公楼天台B 处测旗杆顶的仰角为45°,在小甬所在办公室楼层E 处测得旗杆顶的俯角为15°. (1)办公楼的高度AB ;(2)求小甬所在办公室楼层的高度AE .四、解答题(本大题共4小题,共50.0分)24.图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE 落在AD′E′的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.(1)求点D′到BC的距离;(2)求E、E′两点的距离.25.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cos B的值.26.对于钝角α,定义它的三角函数值如下:sinα=sin(180°−α),cosα=−cos(180°−α).(1)求sin120°,cos120°,sin150°的值;(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sin A,cos B是方程4x2−mx−1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.27.如表是小菲填写的实践活动报告的部分内容.求铁塔的高度FE.(结果精确到1米)【参考数据:sin44°=0.69,cos44°=0.72,tan44°=0.97】答案1.C2.C3.C4.C5.C6.B7.C8.C9.A10.C11.B12.B13.B14.A15.C16.−1−√217.2318.√3319.4520.√1321.解:如图,过点C作CD⊥AB于点D,根据题意可知:AB=7,∠ACD=45°,∠CBD=90°−68°=22°,∴AD=CD,∴BD=AB−AD=7−CD,在Rt△BCD中,∵tan∠CBD=CDBD,∴CD7−CD≈0.40,∴CD=2,∴AD=CD=2,BD=7−2=5,∴AC=2√2≈2.83,BC=CDsin22∘≈20.37≈5.41,∴AC+BC≈2.83+5.41≈8.2(km).答:新建管道的总长度约为8.2km.22.解:原式=|2−√3|−1+4+√3,=2−√3−1+4+√3,=5.23.解:(1)如图,过点M作MH⊥AB于点H,∵MN⊥DN,∠BAN=90°,∴四边形MNAH是矩形,∴AH=MN=12,MH//AN//BC,∴∠AMH=∠MAN=30°,在Rt△AMH中,MH=AHtan30∘=12√3,∵∠BMH=45°,∴BH=MH=12√3,∴AB=AH+BH=12+12√3.答:办公楼的高度AB为(12+12√3)m.(2)过点E作EQ⊥AM于点Q,由(1)得,∠EAQ=60°,∴∠EMQ=180°−∠EAM−∠AEM=180°−60°−75°=45°,设AE=x,则AQ=x⋅cos60°=12x,MQ=EQ=x⋅sin60°=√32x,由AM=2MN=24,x 2+√32x=24,解得x=24√3−24(m).答:小甬所在办公室楼层的高度AE为(24√3−24)m.24.解:(1)过点D′作D′H⊥BC,垂足为点H,交AD于点F,如图3所示.由题意,得:AD′=AD=90厘米,∠DAD′=60°.∵四边形ABCD是矩形,∴AD//BC,∴∠AFD′=∠BHD′=90°.在Rt△AD′F中,D′F=AD′⋅sin∠DAD′=90×sin60°=45√3厘米.又∵CE=40厘米,DE=30厘米,∴FH=DC=DE+CE=70厘米,∴D′H=D′F+FH=(45√3+70)厘米.答:点D′到BC的距离为(45√3+70)厘米.(2)连接AE,AE′,EE′,如图4所示.由题意,得:AE′=AE,∠EAE′=60°,∴△AEE′是等边三角形,∴EE′=AE.∵四边形ABCD是矩形,∴∠ADE=90°.在Rt△ADE中,AD=90厘米,DE=30厘米,∴AE=√AD2+DE2=30√10厘米,∴EE′=30√10厘米.答:E、E′两点的距离是30√10厘米.25.解:∵∠C=90°,MN⊥AB,∴∠C=∠ANM=90°,又∵∠A =∠A ,∴△AMN∽△ABC , ∴AN AM =AC AB =34, 设AC =3x ,AB =4x , 由勾股定理得BC =√AB 2−AC 2=√7x , ∴在Rt △ABC 中,cosB =BC AB =√7x 4x =√74. 26.解:(1)由题意得,;(2)∵三角形的三个内角的比是1:1:4, ∴三个内角分别为30°,30°,120°, ①当∠A =30°,∠B =120°时,方程的两根为12,−12, 将x =12代入方程得:4×(12)2−m ×12−1=0, 解得:m =0,经检验x =−12是方程4x 2−1=0的根, ∴m =0符合题意;②当∠A =120°,∠B =30°时,两根为√32,√32,不符合题意; ③当∠A =30°,∠B =30°时,两根为12,√32, 将x =12代入方程得:4×(12)2−m ×12−1=0, 解得:m =0,经检验x =√32不是方程4x 2−1=0的根. 综上所述:m =0,∠A =30°,∠B =120°. 27.解:在Rt △DGF 中,∵FG =DG ×tan∠FDG ,=CE ×tan∠FDG=25×tan44°=24.25,∴FE=FG+GE=FG+CD,=24.25+10≈34(米)答:铁塔FE的高度约为34米.。
九年级下第一章直角三角形的边角关系全章综合测评题含答案

全章综合测评题一、选择题1.在Rt ABC △中,90C ∠=︒,若2AC BC =,则sin A 的值是( )A.12B.2 2.如图,ABC △的三个顶点分别在正方形网格的格点上,则tan A 的值是( )A.65B.563.在ABC △中,若cos A ,tan B = ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形4.如图,在平地上种树时,要求株距(相邻两树间的水平距离)为4m ,如果在坡度为0.5的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离约为( ) 2.24)A.4.5mB.4.6mC.6mD.8m5.在Rt ABC △中,90C ∠=︒,若4AB =,3sin 5A =,则斜边上的高等于( ) A.6425 B.4825C.165D.125 6.甲、乙、丙三个梯子斜靠在一堵墙上(梯子顶端靠谱),小明测得:甲与地面的夹角为60︒;乙的底3 )A.甲较陡B.乙较陡C.丙较陡D.一样陡7.如图,一艘海轮位于灯塔P 的南偏东70︒方向的M 处,它以每小时40海里的速度向正北方方向航行,2小时后到达位于灯塔P 的北偏东40︒方向的N 处,则N 处与灯塔P 的距离为( )A.40海里B.60海里C.70海里D.80海里8.小亮在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B 的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出67.5︒角的正切值是( )1 1 C.2.5二、填空题9.计算:()0212sin 45π 3.142-︒+-+=________. 10.周长为20的等腰三角形,一边长为6,则底角的余弦值为______.11.如图,小颖利用有一个锐角是30︒的三角板测量一棵树的高度,已知她与树之间的水平距离BE 为5m ,AB 为1.5m (即小颖的眼睛与地面的距离),那么这棵树高是______m .(结果保留根号)12.如图,一个小球由地面沿着坡度1:3i =的坡面向上前进了10m ,此时小球距离地面的高度为_____m .13.如图,某河道要建造一座公路桥,要求桥面离地面高度AC 为3米,引桥的坡角ABC ∠为15︒,则引桥的水平距离BC 的长是______米.(精确到0.1米,sin150.26︒≈,cos150.97︒≈,tan150.27︒≈)14.在平面直角坐标系中,已知()2,3P ,OP 与x 轴所夹锐角为α,则tan α=_____.15.将一副三角尺如图所示叠放在一起,若14cm AB =,则阴影部分的面积是______2cm .16.如图,已知直线1234l l l l ∥∥∥,相邻两条平行直线间的距离都是1,如果正方形ABCD 的四个顶点分别在四条直线上,则sin α=______.三、解答题17.水务部分为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD ,如图所示,已知迎水坡面AB 的长为16米,60B ∠=︒,背水坡面CD 的长为ABED ,CE 的长为8米.(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)求加固后大坝背水坡面DE 的坡度.18.如图所示,秋千链子的长度为3m ,静止时的秋千踏板(大小忽略不计)距地面0.5m ,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53︒,则秋千踏板与地面的最大距离约为多少?(参考数据:sin530.8︒≈,cos530.6︒≈)19.如图,某校教学楼AB 的后面有一建筑物CD ,当光线与地面的夹角是22︒是,教学楼在建筑物的墙上留下高2m 的影子CE ;而当光线与地面的夹角是45︒时,教学楼顶A 在地面上的影子F 与墙角C 有13m 的距离(B 、F 、C 在一条直线上).求教学楼AB 的高度. (参考数据:3sin228︒≈,15cos2216︒≈,2tan 225︒≈)20.小红家的阳台上放置了一个晒衣架,如图所示是晒衣架的侧面示意图,立杆AB 、CD 相交于点O ,B 、D 两点立于地面,经测量:136cm AB CD ==,51cm OA OC ==,34cm OE OF ==,现将晒衣架完全稳固张开,扣链EF 成一条线段,且32cm EF =.(1)求扣链EF 与立杆AB 的夹角OEF ∠的度数.(精确到0.1︒)(2)小红的连衣裙挂在衣架后的总长度达到122cm ,垂挂在晒衣架上是否拖落到地面?通过计算说明理由.(参考数据:sin 61.90.882︒≈,cos61.90.471︒≈,tan 28.10.533︒≈)聊旺角认识新朋友——正弦:小菱形面积的性质新朋友——正弦,它已帮我们解决了好几个题目,但我们对它了解得却并不多,现在就来熟悉一下它. 正弦性质1:sin 0sin1800︒=︒=,sin 901︒=.道理很简单:菱形的一个角为0︒或180︒时,菱形就退化为线段;面积当然是0,菱形的一个角为90︒时,菱形就是正方形,因此,sin 90︒就是单位正方形的面积,当然是1.(如图1-1)正弦性质2:()sin 180sin αα︒-=.这是因为,当菱形有一角为α时,必有另一个角等于180α︒-,因此,sin α和()sin 180α︒-按定义表示的是同一块面积.(如图1-2)当菱形一个角为0︒时,面积为0,这个角慢慢变大时,菱形面积也随着增大,直到变为正方形,这个角继续变大时,菱形面积又变小,直到变成0,这种性质也体现在正弦的性质上.在我们的书上,直接规定“直角三角形中锐角的正弦sin A 等于A ∠的对边与斜边之比”,这种用直角三角形的边长之比来定义正弦的方法,是18世纪的大数学家欧拉首先引进的,关于正弦的性质我们将在以后继续学习,有兴趣的同学可以试一试.创新寄语提出新的疑问,新的可能,从新的角度看老问题,需要创造性的想象力,并且标志着科学的真正进步. 答案一、1.C2.A3.A4.A5.B6.D7.D8.B二、 9.1410.23或373213.11.1 14.3215.49三、17.(1)(2 18.1.7m19.12m20.解:(1)如图,在OEF △中,34cm OE OF ==,32cm EF =,作OM EF ⊥于点M ,则16cm EM =,16cos 0.47134EM OEF OE ∠==≈∴, 61.9OEF ∠=︒∴(2)小红的连衣裙垂挂在晒衣架上会拖落到地面.理由:EF BD ∵∥,61.9ABD OEF ∠=∠=︒∴过点A 作AH BD ⊥于点H在Rt ABH △中,sin AH AND AB∠=∵,()sin 136sin61.91360.882120.0cm AH AB ABD ⋅=∠=⨯︒≈⨯≈∴ ∵小红的连衣裙挂在晒衣架后总长度122cm >晒衣架高度120.0cm , ∴会拖落到地面上.。
2014~2015学年第二学期九年级数学第1章 解直角三角形 单元测试卷

班级_____________________ 姓名____________________ 考场号____________ 考号___________----------------------------------------------------密--------------------------------封--------------------------------线------------------------------------------------ 2014~2015学年第二学期九年级数学第1章 解直角三角形一、选择题1.计算sin 245°+cos30°•tan60°,其结果是( ) A . 2B . 1C .112D .03. (2014 甘肃省兰州市) 如图,在Rt △ABC 中,∠C=90°,BC=3,AC=4,那么cosA 的值等于( )A.43 B.34 C.53 D.544. (2014 湖北省随州市)如图,要测量B 点到河岸AD 的距离,在A 点测得∠BAD=30°,在C 点测得∠BCD=60°,又测得AC=100米,则B 点到河岸AD 的距离为( )米米5. (2014 山东省泰安市) 如图(1)是直角三角形纸片,∠A=30°,BC=4cm ,将其折叠为BD ,如图(2),再将(2)沿DE 折叠,使点A 落在DC`的延长线上的点A`处,如图(3),则折痕DE 的长为( )(A )83cm (B )(C ) (D )3cm6. (2014 浙江省湖州市) 如图,已知Rt △ABC 中,∠C=90°,AC=4,tanA=,则BC 的长是( )A .2B . 8C .2 D.47. (2014 浙江省丽水市) 如图,河坝横断面迎水坡AB 的坡比BC 与水平宽度AC 之比),坝高BC=3m ,则坡面AB 的长度是( ) A .9m B .6m C . D .班级_____________________ 姓名____________________ 考场号____________ 考号___________----------------------------------------------------密--------------------------------封--------------------------------线------------------------------------------------ 8. (2014 四川省绵阳市) 如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,这时,海轮所在的B 处与灯塔P 的距离为( )A . 40海里B . 4海里C . 80海里D . 4海里9. (2014 四川省巴中市) 在Rt △ABC 中,∠C=90°,5sin 13A =,则tanB 的值为( ) A. 1213 B. 512 C. 1312 D. 12510. (2014 浙江省义乌市) 如图,点A (t,3)在第一象限,OA 与x 轴所夹的锐角为α,3tan =2α,则t 的值是( )A .1B .1.5C .2D .3二、填空题11. (2014 辽宁省锦州市) 计算:tan45°-)113=________.12. (2014 江苏省常州市) 若∠α=30°,则∠α的余角等于 度, sin α的值为 .13. (2014 广西南宁市) 如图,一渔船由西往东航行,在A 点测得海岛C 位于北偏东60°的方向,前进20海里到达B 点,此时,测得海岛C 位于北偏东30°的方向,则海岛C 到航线AB 的距离CD 等于 海里。
2014下期九年级数学试卷

学校: 姓名: 考场: 考号:☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼雨花区2014年下学期期末质量检测卷九 年 级 数 学注意事项:1、答题前,请考生先将自己的姓名、考号填写清楚,并认真核对答题卡的姓名、考号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3、答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;5、答题卡上不得使用涂改液、涂改胶和贴纸;6、本试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(本大题共12小题,每小题3分,满分36分) 1.“抛一枚硬币,正面向上”这一事件的概率为A .21B .-21C .0D .12.在一个直角三角形中,斜边为5,一条直角边为3,这条直角边所对锐角的正弦值为 A .43B .54C.35D .533.“明天下雨的概率为80%”这句话指的是A .明天一定下雨B .明天80%的地区下雨,20%的地区不下雨C .明天下雨的可能性是80%D .明天80%的时间下雨,20%的时间不下雨4.如图是由5个大小相同的正方体摆成的立体图形,它的俯视图是 A . B .C .D .5.若两圆的半径分别是1cm 和4cm ,圆心距为5cm ,则这两圆的位置关系是 A .内切 B .相交 C .外切D .外离6.在△ABC 中,∠A ,∠B 都是锐角,sinA =21,cosB =23,则△ABC 是 A .直角三角形B .钝角三角形C .锐角三角形D .不能确定7.△ABC 与△A′B′C′相似,相似比是1:2,已知△ABC的周长是3,则△A′B′C′的周长是 A .3B .6C .9D .12 8.如图,∠AOB 放置于正方形网格中,则sin ∠AOB =AB .C .12D .2(第8题)(第9题)9.如图,河堤横断面迎水坡AB 的坡角是30,堤高BC =10m ,则坡面AB 的长度是 A .15mB .C .20mD .10.如图,P 是反比例函数图象上第二象限内的一点,若矩形PEOF 的面积为3,则反比例函数的解析式是A .x y 3= B .x y 3-=C .3xy =D .3x y -=11.如图,已知AB 是⊙O 的直径,CD 是弦,AB ⊥CD 于点E ,若AB =10,CD =6,则BE 的长是A .4B .3C .2D .1(第10题)(第11题) (第12题)12.如图,在□ABCD 中,AB =5,BC =8,∠ABC ,∠BCD的角平分线分别交AD 于E 和F ,BE 与CF 交于点G ,则△EFG 与△BCG 面积之比是 A .5:8 B .25:64 C .1:4D .1:16二、填空题(本大题共6小题,每小题3分,满分18分) 13.tan 45︒ = . 14.反比例函数ky x=的图象经过点(1,2),则k = . 15.100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是 . 16.双曲线y =xk2的图象经过第二、四象限,则k 的取值范围是 .17.扇形的半径为8cm ,扇形圆心角为90︒,则弧长为 cm .18.如图,已知四边形ABCD 中,AB ∥CD ,△COD 与△AOB的周长比为1:2,则CDB COB SS ∆∆:= .三、解答题(本大题满分66分)19.(本题满分6分)计算: ()4160220152--++ tan .20.(本题满分6分)先化简,再求值:(第4题)ba b b a b ab a ++-+-22222,其中a =﹣2,b =230sin .21.(本题满分8分)某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A 、B 、C 、D 表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图.请根据以上信息回答:(1)本次参加抽样调查的居民有多少人? (2)将两幅不完整的图补充完整;(3)若有外型完全相同的A 、B 、C 、D 粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C 粽的概率.22.(本题满分8分)如图,已知△ABC 中,点D 在AC 上且∠ABD =∠C ,求证:AB 2=AD •AC .23.(本题满分9分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面时,面条的总长度y (m )是面条的粗细(横截面积)S (mm 2)的反比例函数,其图象如图所示. (1)求出y (m )与S (mm 2)的函数关系式并写出自变量的取值范围;(2)求当面条粗1.6 mm 2时,面条的总长度是多少米?24.(本题满分9分)在一次空中搜寻中,水平飞行的飞机观测到在点A 正前方俯角为30°方向的F 点处有疑似目标物体(该物体视为静止).飞机继续向前飞行了800米到达B 点,此时测得点F 在点B 俯角为45°的方向上,请你计算当飞机飞临F 点的正上方点C 时(点A 、B 、C 在同一直线上),竖直高度CF 约为多少米?(结果保留整数,参考数值:73213.≈)25.(本题满分10分)如图,AB 为⊙O 的直径,AE 平分∠BAF ,交⊙O 于点E ,过点E 作直线ED ⊥AF ,交AF 的延长线于点D ,交AB 的延长线于点C . (1)求证:CD 是⊙O 的切线(2)若CB =2,CE =4,求AB 的长26.(本题满分10分)规定对于平面直角坐标系 x Oy 中的点P(a ,b ),则称点P ´(kb a +,b ka +)为点P 的“k 型派生点”(其中k 为常数,且k ≠0)。
2014九级下册数学测试卷

2014年九年级下册数学测试卷二.填空题:(每题3分,共24分)11.一个点到圆的最小距离是,最大距离是,则该圆的直径为。
12.⊙O直径为10,弦AB为8,P是AB上的一个动点,则OP 的取值范围为。
13.中,,,以点C为圆心,CA为半径的圆交BA于D,交BC于E,则的度数为。
14.设AB是⊙O的一条弦,AB=1,C是圆周上一点,,则圆的半径是。
15.如图:一束光线从轴上的点A(0,1)出发,经轴上的点C反射后经过B(3,3),则光线从A到B所经过的路程是。
16.一次函数的图象经过点M(3,4)且于轴的负半轴、轴的正半轴分别交于A、B两点,当|OA|+|OB|=5时,此函数的解析式为。
17.函数是一次函数,此函数图象与两个坐标轴围成的三角形的面积为。
18.如图,已知:四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点是P,AB=BD,且PC=0.6,则四边形ABCD的周长是。
三.解答题:(19至25题每题8分,26题10分)19.已知:,其中与成正比例,与成正比例,且时,;当时,,求:与的函数关系式。
20.已知:一次函数的图象与轴、轴分别交于A、B两点,过C(4,0)作AB的垂线交AB于E,交轴于D,求点D、E的坐标。
21.直线与轴、轴分别交于A、B,以线段AB为直角边在第一象限作等腰直角三角形,使,如果第二象限内有一点P(),使,求的值。
22.如图,已知:AB是圆O的直径,CDAB于点D,AB=,CD=1()。
求BD的长。
23.设一圆的圆心为O,AB、CD是两条在点O两侧的平行弦,已知AB=40,CD=48,⊙O的半径为25,求AC的长。
24.如图,已知:⊙O中,M、N分别是两条不平行的弦AB、CD 的中点,且AB=CD,求证:。
25.如图,已知:点A、B、C、D顺次在⊙O上,,BMAC于点M,求证:AM=DC+CM。
26.已知:一次函数具有性质:随的增大而减小,又直线分别与直线,相交于A、D,且点A在第一象限内,直线,分别与轴相交于B、C。
九年级数学下册第一、二章综合检测题(含答案)-
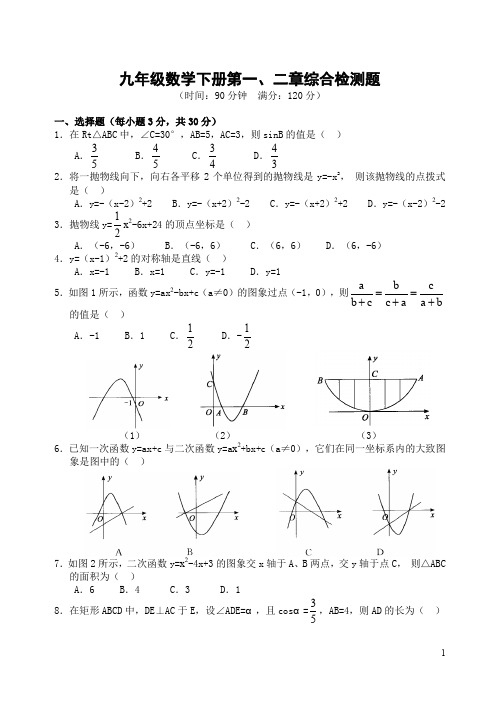
九年级数学下册第一、二章综合检测题(时间:90分钟 满分:120分)一、选择题(每小题3分,共30分)1.在Rt △ABC 中,∠C=30°,AB=5,AC=3,则sinB 的值是( ) A .35 B .45 C .34 D .432.将一抛物线向下,向右各平移2个单位得到的抛物线是y=-x 2,•则该抛物线的点拨式是( )A .y=-(x-2)2+2B .y=-(x+2)2-2C .y=-(x+2)2+2D .y=-(x-2)2-2 3.抛物线y=12x 2-6x+24的顶点坐标是( ) A .(-6,-6) B .(-6,6) C .(6,6) D .(6,-6) 4.y=(x-1)2+2的对称轴是直线( )A .x=-1B .x=1C .y=-1D .y=15.如图1所示,函数y=ax 2-bx+c (a ≠0)的图象过点(-1,0),则a b c b c c a a b==+++的值是( )A .-1B .1C .12 D .-12(1) (2) (3)6.已知一次函数y=ax+c 与二次函数y=a x 2+bx+c (a ≠0),它们在同一坐标系内的大致图象是图中的( )7.如图2所示,二次函数y=x 2-4x+3的图象交x 轴于A 、B 两点,交y 轴于点C ,•则△ABC 的面积为( )A .6B .4C .3D .1 8.在矩形ABCD 中,DE ⊥AC 于E ,设∠ADE=α,且cos α=35,AB=4,则AD 的长为( )A .3B .162016..335C D 9.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,•如图3所示,•栅栏的跨径AB 间,按相同的间距0.2米用5根立柱加固,拱高OC 为0.6米,以O 为原点,OC 所在的直线为y 轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )A .1.5米B .1.9米C .2.3米D .2.5米 10.如图所示,已知△ABC 中,BC=8,BC 上的高h=4,D 为BC 上一点,EF ∥BC ,交AB 于点E ,交AC 于点F (EF 不过A 、B ),设E 到BC 的距离为x .则△DEF 的面积y 关于x 的函数的图象大致为( )二、填空题(每空3分,共30分)11.已知α为等边三角形的一个内角,则cos α等于________. 12.已知α是锐角,sin α=23,则cos (90°-α)的值为_______. 13.已知tan α=23,则锐角α的取值范围是________. 14.已知点(1,3)是双曲线y=mx与抛物线y=x 2+(k+1)x+m 的交点,则k 的值等于_____.15.已知二次函数y=-4x 2-2mx +m 2与反比例函数y=24m x的图象在第二象限内的一个交点的横坐标是-2,则m 的值是_______.16.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,记第n 个图中小黑点的个数为________________.17.若抛物线y=ax 2+bx+c (a ≠0)的对称轴为直线x=2,最小值为-2,则关于x 的方程a x 2+b x+c=-2的根为______.18.抛物线y=(k+1)x 2+k 2-9开口向下,且经过原点,则k=______.19.如图4所示,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC•为2m,那么相邻两棵树的斜坡距离AB约为_______m.(结果精确到0.1m,≈1.732 1.414)(4) (5) (6)20.如图5所示,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知,AB=1,则点A1的坐标是________.三、解答题(共60分,写出必要的步骤,直接写出答案不得分)21.(本题16分)计算下列各题:(1(-2)2×4-1-4sin60°(2│+-1+2 005022.(本题10分)如图6所示,河对岸有古塔AB,小敏在C处测得塔顶A的仰角为α,•向塔前进s米到达D,在D处测得A的仰角为β,则塔高是多少米?23.(本题10分)某企业投资112万元引进一条农产品加工生产线,若不计维修、•保养等费用预计投产后每年可创利33万元,该生产线投产后从第一年到第x年的维修、保养费用累计为y万元,且y=a x2+bx,若第一年的维修、保养费用为2万元,第二年为4万元.(1)求y关于x的点拨式;(2)设x年后企业的纯利润为z万元(纯利润=创利-维修、保养费用),则投产后这个企业在第几年就能收回投资?24.(本题12分)已知抛物线y=x2+(n-3)x+n+1经过坐标原点O.(1)求这条抛物线的顶点P的坐标;(2)设这条抛物线与x轴的另一个交点为A,求以直线PA为图象的一次函数点拨式.25.(本题12分)某医药研究所进行某一治疗病毒新药的开发,经过大量的服用试验后知,成年人按规定的剂量服用后,每毫升血液中含药量y微克(1微克=10-3毫克)•随时间x小时的变化规律与某一个二次函数y=a x2+bx+c(a≠0)相吻合,并测得服用时(即时间为0时)每毫升血液中含药量为0微克;服用后2小时每毫升血液中含药量为6微克;服用后3小时,每毫升血液中含药量为7.5微克.(1)试求出含药量y(微克)与服药时间x(小时)的函数表达式,并画出0≤x≤8•内的函数图象的示意图;(2)求服药后几小时,才能使每毫升血液中含药量最大?•并求出血液中的最大含药量;(3)结合图象说明一次服药后的有效时间是多少小时?(•有效时间为血液中含药量不为0的总时间)答案:1.A 点拨:用三角函数的定义. 2.C 3.C 4.B5.A 点拨:将点(-1,0)代入y=a x 2-bx+c (a ≠0)中得a+b+c=0,而a ≠b ≠c ,所以a b cb c c a a b==+++=•-1. 6.C 7.C 8.B 9.C 10.D 11.12 12.2313.30°<α<45° 点拨:tan30°<tan α=23<tan45°. 14.-2 15.-7 16.y=n 2-n+1 17.x 1=x 2=2 18.-319.约为2.3 20.(2,32)21.点拨:(1)原式×14-4×2=1;(2)原式+3=3-23 22.点拨:在Rt △ABC 中,BC=tan ABα.在Rt △ABD 中,BD=tan ABβ∴tan ABα-tan AB β=s即tan tan tan tan tan tan tan tan AB AB s s AB βααβαββα-=∴=-23.点拨:(1)2,1,642,1a b a a b b =+=⎧⎧⎨⎨=+=⎩⎩解得 ∴y=x 2+x .(2)z=33x-x 2-x ,当z=112时,x 2-32x+112=0, x 1=4,x 2=28(舍去) ∴第四年就可收回投资.24.点拨:(1)∵抛物线y=x 2+(n-3)x+n-1经过原点,∴n+1=0,∴n=-1. 得y=x 2-4x ,即y =x 2-4x=(x-2)2-4.∴抛物线的顶点P 的坐标为(2,-4). (2)根据题意,得点A 的坐标为(4,0) 设所求的一次函数点拨式为y=kx+b .根据题意,得04,2,42.8k b k k b b =+=⎧⎧⎨⎨-=+=-⎩⎩解得 ∴所求的一次函数点拨式为y=2x-8.25.点拨:(1)由题意得2221,000,2226,4,0.337.5.a a b c a b c b c a b c ⎧=-⎧⎪++=⎪⎪++==⎨⎨⎪⎪=++=⎩⎪⎩解得所以y=-12x 2+4x . 示意图如图所示.(2)y=-12x 2+4x=-12(x-4)2+8,所以服药后4小时,才能使血液中含药量最大,•这时每毫升血液中含有药液8微克.(3)当y=0时,x 1=0,x 2=8,故一次服药后的有效时间为8小时.。
2014北师大初三下册数学第一、二单元综合练习(含答案)

2014北师大初三下册数学第一、二单元综合练习一.选择题(共15小题)2.m2m2Cm2D25.在平面直角坐标系中,抛物线关于x轴对称的抛物线的解析式为().C D.2.C D.7.(2008•达州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时,x的取值范围是()8.一名男同学推铅球时,铅球行进中离地的高度y(m)与水平距离x(m)之间的关系式是,.m.C D.11.(2003•广州)如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为().C D12.(2004•四川)如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于()C D:.:114.(2001•福州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)c<0;(2)b>0;(3)4a+2b+c >0;(4)(a+c)2<b2,其中正确的有()15.(2004•贵阳)已知抛物线y=(x﹣4)2﹣3的部分图象(如图),图象再次与x轴相交时的坐标是()二.填空题(共6小题)16.(2011•闸北区一模)已知抛物线y=ax2+bx+c有最大值﹣3,那么该抛物线的开口方向是_________.17.已知实数x、y满足x2﹣2x+4y=5,则x+2y的最大值为_________.18.若抛物线的对称轴是x=1,函数有最大值为4,且过点(0,3),则其解析式为_________.19.若函数的图象是抛物线,则m的值为_________,该抛物线开口向_________.20.函数的图象向左平移3个单位,再向下平移4个单位,可以得到二次函数_________的图象.21.若抛物线y=x2﹣6x+c的顶点在x轴,则c=_________.三.解答题(共3小题)22.如图所示,一块由篱笆围成的矩形绿地长x m,并且中间有一条与长边平行的篱笆,篱笆的总长为600m,求矩形绿地的最大面积.23.如图所示,已知△ABC的面积为2400cm2,底边BC长为80cm.若点D在BC边上,E在AC边上,F在AB 边上,且四边形BDEF为平行四边形,设BD=xcm,S平行四边形BDEF=ycm2,求:(1)y与x的函数关系式;(2)自变量x的取值范围;(3)当x为何值时,y有最值,最值是多少?24.(2007•广州)二次函数图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.(1)求C的坐标;(2)求二次函数的解析式,并求出函数最大值.2014北师大初三下册数学第一、二单元综合练习(打印版)参考答案与试题解析一.选择题(共15小题)2.m2m2Cm2D﹣+.25.在平面直角坐标系中,抛物线关于x轴对称的抛物线的解析式为().C D.抛物线,).2.C D.7.(2008•达州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时,x的取值范围是()8.一名男同学推铅球时,铅球行进中离地的高度y(m)与水平距离x(m)之间的关系式是,.m时,﹣+=0.C D.cosB==.11.(2003•广州)如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为().C DAC=2.12.(2004•四川)如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于()C D==2=.:.:1=.14.(2001•福州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)c<0;(2)b>0;(3)4a+2b+c >0;(4)(a+c)2<b2,其中正确的有()﹣﹣15.(2004•贵阳)已知抛物线y=(x﹣4)2﹣3的部分图象(如图),图象再次与x轴相交时的坐标是()二.填空题(共6小题)16.(2011•闸北区一模)已知抛物线y=ax2+bx+c有最大值﹣3,那么该抛物线的开口方向是向下.17.已知实数x、y满足x2﹣2x+4y=5,则x+2y的最大值为.y=×x最大值为.18.若抛物线的对称轴是x=1,函数有最大值为4,且过点(0,3),则其解析式为﹣x2+2x+3.19.若函数的图象是抛物线,则m的值为2,该抛物线开口向上.函数∴20.函数的图象向左平移3个单位,再向下平移4个单位,可以得到二次函数的图象.y=(y=+3x+.y=x.21.若抛物线y=x2﹣6x+c的顶点在x轴,则c=9.三.解答题(共3小题)22.如图所示,一块由篱笆围成的矩形绿地长x m,并且中间有一条与长边平行的篱笆,篱笆的总长为600m,求矩形绿地的最大面积.=x(﹣23.如图所示,已知△ABC的面积为2400cm2,底边BC长为80cm.若点D在BC边上,E在AC边上,F在AB 边上,且四边形BDEF为平行四边形,设BD=xcm,S平行四边形BDEF=ycm2,求:(1)y与x的函数关系式;(2)自变量x的取值范围;(3)当x为何值时,y有最值,最值是多少?BC2400=×∴h=.y=•x﹣24.(2007•广州)二次函数图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.(1)求C的坐标;(2)求二次函数的解析式,并求出函数最大值.x x+5<=有最大值=;,(的中点坐标为(,<时,=,.。
九年级数学下第一,二章测试卷(北师大版)

座位号古田十五中2013—2014学年度上学期初三第二次月考数 学 试 卷姓名___座号___成绩___一、选择题(本大题共10小题,每小题3分,共30分)每小题只有一个正确选项.1. 在△ABC 中,A ,B 为锐角,且有 B A cos sin =,则这个三角形是( ) A. 等腰三角形; B.直角三角形; C.钝角三角形; D. 锐角三角形2.sin70°、cos70°、tan70°的大小关系是( )A.sin70°>cos70°>tan70°;B. tan70°>cos70°>sin70°;C. cos70°> sin70º> tan70°;D. tan70º > sin70º >cos70º 3.已知△ABC 中,AD 是高,AD=2,DB=2,CD=23,则∠BAC= ( )A. 1050B. 150C.1050或150D. 6004. 下列四个函数图象中,当x<0时,函数值y 随自变量x 的增大而减小的是【 】5.直角坐标平面上将二次函数y =-2(x -1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0)B.(1,-2)C.(0,-1)D.(-2,1) 6.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )A .3<kB .03≠<k k 且C .3≤kD .03≠≤k k 且6、如图,已知四边形ABCD 中,R ,P 分别是BC ,CD 上的点,E ,F 分别是AP ,RP 的中点,当点P 在CD 上从C 向D 移动而点R 不动时,那么下列结论成立的是【 】 A 、线段EF 的长逐渐增大 B 、线段EF 的长逐渐减少C 、线段EF 的长不变D 、线段EF 的长与点P 的位置有关7、某几何体的三视图如下所示,则该几何体可以是【 】8、如图,四边形ABCD 中,∠BAD =∠ACB =90°,AB =AD ,AC =4BC ,设CD 的长为x ,四边形ABCD 的面积为y ,则y 与x 之间的函数关系式是【 】 A .2252x y =B . 2254x y =C .252x y =D .254x y =9、在一幅长60cm ,宽40cm 的矩形风景画的四周镶 一条金色纸边,制成一幅矩形挂图,如图所示,如果 要使整个挂图的面积是2816cm 2,设金色纸边的宽为 xcm ,那么x 满足的方程是【 】 A 、(60+x )(40+2x )=2816 B 、(60+x )(40+x )=2816 C 、(60+2x )(40+x )=2816 D 、(60+2x )(40+2x )=281610.直线)0(≠+=ab b ax y 不经过第三象限, 那么bx ax y +=2+3的图象大致为( )y y y yO x O x O x O x A B C D二、填空题(本大题共8小题,每空2分,共28分)1.在Rt ⊿ABC 中,∠C =90°,BC =10,AC =4,则cosB= ,tanA= ;2.等腰三角形的腰长为3,底边长为2,则底角的余弦值为 ;3. 若∠A 为锐角,且03tan 2tan 2=-+A A ,则∠A = ; 4抛物线m x x y +--=22,若其顶点在x 轴上,则=m .5.已知二次函数232)1(2-++-=m mx x m y ,则当=m 时,其最大值为0.6. 锐角A 满足cosA=21,利用计算器求∠A 时,依次按键,则计算器上显示的结果是________ 7.如果抛物线2y ax =和直线y x b =+都经过点P(2,6),则a _______,b =_______,直线不经过第_______象限,抛物线不经过第_______象限.8.如图,是以直角坐标原点O 为圆心的两个同心圆,则其阴影部分的面积之和为 ;(结果保留π)9、如图,在正方形网格中,∠AOB 的正切值是=______.y x O Ay xO By x O CDy x O俯视图主视图 左视图 ABCDABC DE F RP ABC D40cmx x x60cmx=2ndf cos 1 ÷ 2 )10、二次函数cbxxy++-=2的图象如图所示,下列几个结论:①对称轴为x=2;②当y≤0时,x<0或x>4;③函数解析式为)4(--=xxy;④当x≤0时,y随x的增大而增大. 其中正确的结论有_________﹙错填的得0分,少填的酌情给分).第九题图三、(本大题共3小题,每小题6分,共18分,写出必要的步骤,直接写出答案不得分)1.计算:cos2300-sin300tan600+sin600.2. 已知反比例函数y=xk的图象与二次函数y=ax2+x-1的图象相交于点(2,2)(1)求a和k的值;(2)反比例函数的图象是否经过二次函数图象的顶点,为什么?3.如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1) 求∠ABD的度数;(2)求线段BE的长.四.解答题(每题8分共24分,写出必要的步骤,直接写出答案不得分)1.如图,已知二次函数y=ax2+bx+c的图象的形状与抛物线y=21x2+1的形状相同,且经过A(2,0)、B(0,-6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.2.某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.3.如图,某船由西向东航行,在点A测得小岛O在北偏东60°,船行了10海里后到达点B,这时测得小岛O在北偏东45°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学下册(第一、二章)测试题
(总分100分,考试时间120分钟)
一、选择题(每题3分,共24分)
1、在正方形网格中,∠α的位置如图,则Sin α的值为( )
A 、12
B
2、某市为改善交通状况,修建了大量的高架桥,一汽车在坡度为300
的笔直高架桥点A 开始爬行,行驶了150米到达B 点,这时汽车离地面高度为( )米.
A 、300
B 、150
C 、75
D 、50
3、把Rt △ABC 的各边都扩大3倍得Rt △A /B /C /,那么锐角A 、A / 的余弦值的关系是( ).
A 、cosA = cosA /
B 、cosA = 3cosA /
C 、3cosA = cosA /
D 、不能确定 4、下列各式中,y 是x 的二次函数的是 ………… ( )
A . 21xy x +=
B . 220x y +-=
C . 22y ax -=-
D . 2210x y -+= 5、把抛物线2
3x y =向上平移2个单位,再向右平移3个单位,则所得的抛物线是( ) A.2)3(32
-+=x y B. 2)3(32
++=x y C. 2)3(32
--=x y D. 2)3(32
+-=x y 6、若二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值必为 ( ) A . 0或2 B . 0 C . 2 D . 无法确定 7、在同一直角坐标系中,函数b ax y -=2与)0(≠+=ab b ax y 的图象大致如图 ( )
8
、已知二次函数c bx ax y ++
=2
的图象如图,下列结论:(
)
①0<++c b a ;② 0>+-c b a ; ③0<abc ; ④a b 2=;⑤,△0< 正确的个数是
A 4 个
B 3个
C 2 个
D 1个
二、填空题(每题3分,共18分)
9、一辆汽车沿30°角的山坡从山底开到山顶,共走了4000米,那么这座山的高度为 米.
10、在Rt △ABC 中,∠C = 900,sinA = 1213
,则sinB = .
11、等边三角形的边长为2cm ,则它的面积是 cm 2.
12、当_____=m 时,函数2
1(1)m y m x +=-是二次函数;
13、写出一个开口向上,顶点坐标是(2,-3)的函数解析式 ;
14、如果抛物线b ax y +=2和直线y x b =+都经过点P(2,6),则a _______,
b =_______,抛物线不经过第_______象限
15、把二次函数y=-2x 2+4x+3化成y=a (x+h )2+k 的形式是 其开口方向是 三、解答题(共58分)
16、(6分)计算0000230tan 6)20103(60cos 2745sin +-+-
17、(8分)△ABC 中,∠ACB = 900,高BCD
的正弦值、余弦
值、正切值。
A
B
C
D
年级 班级 姓名
18、(8分)在新平县举行30周年县庆时,某建筑物AC上挂着“和谐新平崛起新平”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为300,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为600,求宣传条幅BC的长. (小明的身高不计,结果精确到O.1米)
19、(8分)已知抛物线与x轴交于点M(-1,0)、N(2,0),且经过点(1,2),
求这个函数的表达式;
20、(8分)求直线y=3与抛物线y=-x2+8x-12的两个交点坐标;若抛物线y=-x2+8x -12的顶点是P,与X轴的两个交点是A、B两点,求△PAB的面积。
21、(10分)已知二次函数的图象的顶点坐标为(3,-2)且与y轴交与(0,
2
5
)(1)求函数的解析式;
(2)当x为何值时,y随x增大而增大。
22、(10分)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价一元,日销售量将减少20千克。
(1)现要保证每天盈利6000元,同时又要让顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多。
C
E
F。
