河北省邯郸市重点中学高三数学规范性课时作业(十四)(学生版)
河北省邯郸市重点中学高三数学规范性课时作业(五十五)(学生版)

课时作业(五十五)一、选择题1.现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众.报告会结束后,为了听取意见,需要请32名听众进行座谈.③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是()A.①简单随机抽样,②系统抽样,③分层抽样B.①简单随机抽样,②分层抽样,③系统抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①分层抽样,②系统抽样,③简单随机抽样2.某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是()A.8,8 B.10,6C.9,7 D.12,43.某班共有学生54人,学号分别为1~54号,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号的同学在样本中,那么样本中还有一个同学的学号是()A.10 B.16 C.53 D.324.某校要从高一、高二、高三共2 012名学生中选取50名组成志愿团,若采用下面的方法选取,先用简单随机抽样的方法从2 012人中剔除12人,剩下的2 000人再按分层抽样的方法进行,则每人入选的概率()A.都相等且为502 012B.都相等且为140C.不会相等D.均不相等5.当前,某城市正分批修建经济适用房以解决低收入家庭住房紧张问题.已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户,若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题,现采用分层抽样的方法决定各社区户数,则应从乙社区中抽取低收入家庭的户数为()A.40 B.36C.30 D.206.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系数抽样三种方案.使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有如下四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,195,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中,正确的是()A.②③都不能为系统抽样B.②④都不能为分层抽样C.①④都可能为系统抽样D.①③都可能为分层抽样二、填空题7.某商场有来自三个国家的进口奶制品,其中A国、B国、C国的奶制品分别有40种、10种、30种,现从中抽取一个容量为16的样本进行三聚氰胺检测,若采用分层抽样的方法抽取样本,则抽取来自B国的奶制品________种.8.某地有居民100 000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取100户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收入家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________.9.某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是________.若用分层抽样方法,则40岁以下年龄段应抽取________人.10.一个总体中的80个个体编号为0,1,2,…,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本.即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数字为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码是________.三、解答题11.某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:(1)(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?(3)若要抽20人调查对2016年巴黎奥运会筹备情况的了解,则应怎样抽样?12.某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体.求样本容量n.[热点预测]13.(1)某校高一(4)班有男生28人,女生21人,用分层抽样的方法从全体学生中抽取一个调查小组,调查该校学生对2013年元月1日起执行的新交规的知晓情况,已知某男生被抽中的概率为17,则抽取的女生人数为( )A .1B .3C .4D .7(2)某市为增强市民的节约粮食意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加10月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为________人.。
邯郸市重点中学2024年高三3月高考考前仿真数学试题

邯郸市重点中学2024年高三3月高考考前仿真数学试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,在平面四边形ABCD 中,满足,AB BC CD AD ==,且10,8AB AD BD +==,沿着BD 把ABD 折起,使点A 到达点P 的位置,且使2PC =,则三棱锥P BCD -体积的最大值为( )A .12B .122C .1623D .1632.函数()()()sin 0,0f x x ωϕωϕπ=+><<的图象如图所示,为了得到()cos g x x ω=的图象,可将()f x 的图象( )A .向右平移6π个单位 B .向右平移12π个单位C .向左平移12π个单位D .向左平移6π个单位 3.已知集合{}}242{60M x x N x x x =-<<=--<,,则M N ⋂=A .}{43x x -<<B .}{42x x -<<-C .}{22x x -<<D .}{23x x <<4.复数()1z i i -=(i 为虚数单位),则z 的共轭复数在复平面上对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限5.已知21,0(),0x x f x x x ⎧-≥=⎨-<⎩,则21log 3f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( )A .2B .23 C .23-D .36.已知双曲线2222:1(0,0)x y C a b a b -=>>的一条渐近线的倾斜角为θ,且5cos 5θ=,则该双曲线的离心率为( )A .5B .52C .2D .47.若某几何体的三视图如图所示,则该几何体的表面积为( )A .240B .264C .274D .2828.从5名学生中选出4名分别参加数学,物理,化学,生物四科竞赛,其中甲不能参加生物竞赛,则不同的参赛方案种数为 A .48B .72C .90D .969.设()y f x =是定义域为R 的偶函数,且在[)0,+∞单调递增,0.22log 0.3,log 0.3a b ==,则( ) A .()()(0)f a b f ab f +>> B .()(0)()f a b f f ab +>> C .()()(0)f ab f a b f >+>D .()(0)()f ab f f a b >>+10.若复数2(2)(32)m m m m i -+-+是纯虚数,则实数m 的值为( ) A .0或2B .2C .0D .1或211.定义在R 上的偶函数()f x ,对1x ∀,()2,0x ∈-∞,且12x x ≠,有()()21210f x f x x x ->-成立,已知()ln a f π=,12b f e -⎛⎫= ⎪⎝⎭,21log 6c f ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系为( )A .b a c >>B .b c a >>C .c b a >>D .c a b >>12.记M 的最大值和最小值分别为max M 和min M .若平面向量a 、b 、c ,满足()22a b a b c a b c ==⋅=⋅+-=,则( )A .max372a c+-=B .max372a c-+=C .min372a c+-= D .min372a c-+=二、填空题:本题共4小题,每小题5分,共20分。
河北省邯郸市重点中学高三数学规范性课时作业(六十三)(学生版)

课时作业(六十三)一、选择题1.在⎝⎛⎭⎪⎫x 3-3x 6的二项展开式中,x 2的系数为( ) A .-427 B .-227 C. 227 D.4272.若(1-x )n =1+a 1x +a 2x 2+a 3x 3+…+a n x n (n ∈N *),且a 1∶a 3=1∶7,则n =( )A .8B .9C .7D .103.设a =sin x d x 则二项式⎝⎛⎭⎪⎫ax -1x 8的展开式中x 2项的系数是( ) A .-1 120 B .1 120 C .-1 792 D .1 7924.设a =(3x 2-2x)d x ,则二项式⎝⎛⎭⎫ax 2-1x 6展开式中的第4项为( ) A .-1 280x 3 B .-1 280 C .240 D .-2405.在⎝⎛⎭⎪⎫x 2-13x n 的展开式中,只有第5项的二项式系数最大,则展开式中常数项是( ) A .-7 B .-28 C .7 D .286.若(x +y)9按x 的降幂排列的展开式中,第二项不大于第三项,且x +y =1,xy<0,则x 的取值范围是( )A .⎝⎛⎭⎫-∞,15B .⎣⎡⎭⎫45,+∞ C .⎝⎛⎦⎤-∞,-45 D .(1,+∞)7.若(1-2x)2 013=a 0+a 1x +…+a 2 013x 2 013(x ∈R ),则a 12+a 222+…+a 2 01322 013的值为( )A .2B .0C .-1D .-28.⎝⎛⎭⎪⎫x +12x 8的展开式中常数项为( ) A.3516 B.358 C.354D .105 9.若(x +2+m )9=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9,且(a 1+a 3+…+a 9)2-(a 0+a 2+…+a 8)2=-39,则实数m 的值为( )A .1或-3B .- 1或3C .1D .-3二、填空题10.(a +x )5展开式中x 2的系数为10,则实数a 的值为________.11.设a =(sin x +cos x )dx ,则二项式(a x -1x)6展开式中含x 2项的系数是________. 12.(x +1)(1-2x )5展开式中,x 3的系数为________(用数字作答).13.(2013·黄冈质检)已知a =-1(1+1-x 2)d x ,则⎣⎡⎦⎤⎝⎛⎭⎫a -π2x -1x 6展开式中的常数项为________.14.(1+x +x 2)⎝⎛⎭⎫x -1x 6的展开式中的常数项为________. 15.二项式⎝⎛⎭⎫ 2x -1x 4的展开式中所有有理项的系数和等于________.(用数字作答) 16.若⎝⎛⎭⎫x 2-1x n 的展开式中含x 的项为第6项,设(1-3x)n =a 0+a 1x +a 2x 2+…+a n x n ,则a 1+a 2+…+a n 的值为________.[热点预测]17.(1)已知⎝⎛⎭⎪⎫x 2-1x n 的展开式中第三项与第五项的系数之比为314,则展开式中常数项是________.(2)在二项式⎝⎛⎭⎪⎫x +124x n 的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )A .16B .14C .13D .512。
河北省邯郸市重点中学高三数学规范性课时作业(七)(学生版)

课时作业(七)一、选择题1.下图给出4个幂函数的图象,则图象与函数的大致对应是( )2.已知函数f (x )=x -2,则( ) A .f (x )为偶函数且在(0,+∞)上单调增 B .f (x )为奇函数且在(0,+∞)上单调增 C .f (x )为偶函数且在(0,+∞)上单调减 D .f (x )为奇函数且在(0,+∞)上单调减3.已知f (x )=x 2+bx +c 且f (-1)=f (3),则( ) A .f (-3)<c <f ⎝⎛⎭⎫52B .f ⎝⎛⎭⎫52<c <f (-3)C .f ⎝⎛⎭⎫52<f (-3)<cD .c <f ⎝⎛⎭⎫52<f (-3)4.设二次函数f (x )=ax 2-2ax +c 在区间[0,1]上单调递减,且f (m )≤f (0),则实数m 的取值范围是( )A .(-∞,0]B .[2,+∞)C .(-∞,0]∪[2,+∞)D .[0,2]5.方程x 2+ax -2=0在区间[1,5]上有解,则实数a 的取值范围为( ) A.⎝⎛⎭⎫-235,+∞B .(1,+∞) C.⎣⎡⎦⎤-235,1 D.⎝⎛⎭⎫-∞,-235 6.函数f (x )=-x 2+(2a -1)|x |+1的定义域被分成了四个不同的单调区间,则实数a 的取值范围是( )A .a >23 B.12<a <32 C .a >12 D .a <12 二、填空题7.当0<x <1时,f (x )=x 2,g (x )=2/1x ,h (x )=x -2,则f (x ),g (x ),h (x )的大小关系是______. 8.函数f (x )=(m -1)x 2+2(m +1)x -1的图象与x 轴只有一个交点,则实数m 的取值的集合是________.9.若x ≥0,y ≥0,且x +2y =1,那么2x +3y 2的最小值为________.三、解答题 10.如果幂函数f (x )=(p ∈Z )是偶函数.且在(0,+∞)上是增函数.求p 的值,并写出相应的函数f (x )的解析式.11.(2013·宁德质检)已知二次函数f (x )=ax 2+bx +1为偶函数,且f (-1)=-1. (1)求函数f (x )的解析式;(2)若函数g (x )=f (x )+(2-k )x 在区间[-2,2]上单调递减,求实数k 的取值范围.12.若二次函数f (x )=ax 2+bx +c (a ≠0)满足f (x +1)-f (x )=2x ,且f (0)=1. (1)求f (x )的解析式;(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.[热点预测]13.设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)恒成立;②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.(1)求f(1)的值;(2)求f(x)的解析式;(3)求最大的实数m(m>1),使得存在实数t,当x∈[1,m]时,f (x+t)≤x恒成立.。
河北省邯郸市重点中学高三数学规范性课时作业(四十一)(学生版)
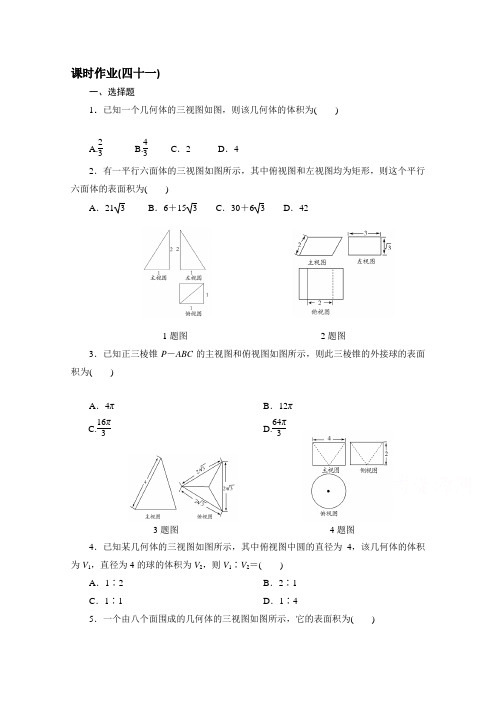
课时作业(四十一)一、选择题1.已知一个几何体的三视图如图,则该几何体的体积为( )A.23B.43C .2D .4 2.有一平行六面体的三视图如图所示,其中俯视图和左视图均为矩形,则这个平行六面体的表面积为( )A .213B .6+153C .30+63D .421题图 2题图3.已知正三棱锥P -ABC 的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为( )A .4πB .12π C.16π3D.64π33题图 4题图4.已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V 1,直径为4的球的体积为V 2,则V 1∶V 2=( )A .1∶2B .2∶1C .1∶1D .1∶4 5.一个由八个面围成的几何体的三视图如图所示,它的表面积为( )A .4 3B .8C .12D .4 26.从一个正方体中截去部分几何体,得到的几何体的三视图及尺寸(单位:cm)如图所示,则此几何体的体积是( )A.223 cm 3B.476 cm 3C.233 cm 3 D .8 cm 35题图 6题图7.如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边长均为1,则该几何体的表面积为( )A .1+ 2B .2+2 2 C.13 D .2+ 28.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SA ⊥平面ABC ,SA =23,AB =1,AC =2,∠BAC =60°,则球O 的表面积为( )A .4πB .12πC .16πD .64π二、填空题9.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m 3. 10.已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是________.11.若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2________.10题图 11题图三、解答题12.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.求(1)该几何体的体积V ; (2)该几何体的侧面积S .[热点预测]13.(1)在矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体积为( )A.125π12B.125π9C.125π6D.125π3(2)在棱长为1的正方体ABCD —A 1B 1C 1D 1中,点P 1,P 2分别是线段AB ,BD 1(不包括端点)上的动点,且线段P 1P 2平行于平面A 1ADD 1,则四面体P 1P 2AB 1的体积的最大值是( )A.124B.112C.16D.12(3)在底面半径为3,高为4+23的圆柱形有盖容器内,放入一个半径为3的大球后,再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多为( )A .4个B . 5个C .6个D .7个。
河北省邯郸市重点中学高三数学规范性课时作业(四十七)(学生版)

课时作业(四十七)一、选择题1.已知直线l 经过点P (-2,5),且斜率为-34,则直线l 的方程为( ) A .3x +4y -14=0 B .3x -4y +14=0 C .4x +3y -14=0D .4x -3y +14=02.过点(3,-2)的直线l 经过圆x 2+y 2-2y =0的圆心,则直线l 的倾斜角大小为( ) A .30° B .60° C .120°D .150°3.直线x -2y cos α+3=0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6,π3的倾斜角的变化范围是( )A.⎣⎡⎦⎤π6,π4B.⎣⎡⎦⎤π6,π3C.⎣⎡⎦⎤π4,2π3D.⎣⎡⎦⎤π4,π34.经过点P (1,4)的直线在两坐标轴上的截距都是正的,且截距之和最小,则直线的方程为( )A .x +2y -6=0B .2x +y -6=0C .x -2y +7=0D .x -2y -7=05.若直线l :y =kx -3与直线2x +3y -6=0的交点位于第一象限,则直线l 的倾斜角的取值范围是( )A.⎣⎡⎭⎫π6,π3B.⎝⎛⎭⎫π6,π2C.⎝⎛⎭⎫π3,π2D.⎣⎡⎦⎤π6,π26.已知点A (-1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( )A .(0,1) B.⎝ ⎛⎭⎪⎫1-22,12 C.⎝ ⎛⎦⎥⎤1-22,13 D.⎣⎡⎭⎫13,12二、填空题7.直线x =π3的倾斜角为________.8.若A (2,2),B (a,0),C (0,b )(ab ≠0)三点共线,则1a +1b =________.9.不论m 取何值,直线(m -1)x -y +2m +1=0恒过定点________. 三、解答题10.已知△ABC 中,A (1,-4),B (6,6),C (-2,0).求:(1)△ABC 中平行于BC 边的中位线所在直线的一般式方程和截距式方程; (2)BC 边的中线所在直线的一般式方程,并化为截距式方程.11.如图,射线OA 、OB 分别与x 轴正半轴成45°和30°角,过点P (1,0)作直线AB 分别交OA 、OB 于A 、B 两点,当AB 的中点C 恰好落在直线y =12x 上时,求直线AB 的方程.12.已知直线l :kx -y +1+2k =0(k ∈R ). (1)证明:直线l 过定点;(2)若直线不经过第四象限,求k 的取值范围;(3)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值并求此时直线l的方程.[热点预测]13.(1)若点P(1,1)为圆(x-3)2+y2=9的弦MN的中点,则弦MN所在直线方程为() A.2x+y-3=0B.x-2y+1=0C.x+2y-3=0 D.2x-y-1=0(2)经过抛物线y2=4x的焦点,且以d=(1,1)为方向向量的直线的方程是__________ .。
河北省邯郸市重点中学高三数学规范性课时作业(六十五)(学生版)

课时作业(六十五)一、填空题1.在极坐标系中,过圆ρ=4cos θ的圆心,且垂直于极轴的直线的极坐标方程为________.2.化极坐标方程ρ2cos θ-ρ=0为直角坐标方程为________.3.已知圆C 的参数方程为⎩⎨⎧x =cos θy =sin θ+2(θ为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,直线的极坐标方程为ρsin θ+ρcos θ=1,则直线截圆C 所得的弦长是________.4.在直角坐标系中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线⎩⎨⎧x =cos αy =1+sin α(α为参数)与曲线ρ2-2ρcos θ=0的交点个数为________. 5.曲线C 1的极坐标方程ρcos 2θ=sin θ,曲线C 2的参数方程为⎩⎨⎧x =3-ty =1-t ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则曲线C 1上的点与曲线C 2上的点最近的距离为________.6.在平面直角坐标系中,已知直线l :ρcos θ+ρsin θ=2(θ为参数)和曲线C :⎩⎨⎧x =t +2y =t 2(t 为参数),若l 与C 相交于A 、B 两点,则|AB |=________.7.设直线l 1的参数方程为⎩⎨⎧x =1+ty =a +3t(t 为参数),以坐标原点为极点,x 轴非负半轴为极轴建立极坐标系,另一直线l 2的方程为ρsin θ-3ρcos θ+4=0,若直线l 1与l 2间的距离为10,则实数a 的值为________.8.在极坐标系中,直线ρcos θ-ρsin θ+1=0与圆ρ=2sin θ的位置关系是________. 9.在极坐标系中,曲线ρ=cos θ+1与ρcos θ=1的公共点到极点的距离为________. 二、解答题10.在平面直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x =t +1y =2t (t 为参数),曲线C 的参数方程为⎩⎨⎧x =2tan 2θy =2tan θ(θ为参数).试求直线l 和曲线C 的普通方程,并求出它们的公共点的坐标.11.在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系.已知点A 的极坐标为⎝⎛⎭⎫2,π4,直线l 的极坐标方程为ρcos ⎝⎛⎭⎫θ-π4=a ,且点A 在直线l 上.(1)求a 的值及直线l 的直角坐标方程;(2)圆C 的参数方程为⎩⎨⎧x =1+cos αy =sin α(α为参数),试判断直线l 与圆C 的位置关系.12.在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系.圆C 1,直线C 2的极坐标方程分别为ρ=4sin θ,ρcos ⎝⎛⎭⎫θ-π4=2 2.(1)求C 1与C 2交点的极坐标;(2)设P 为C 1的圆心,Q 为C 1与C 2交点连线的中点.已知直线PQ 的参数方程为⎩⎪⎨⎪⎧x =t 3+a y =b 2t 3+1(t ∈R 为参数),求a ,b 的值.13.在直角坐标系xOy 中,圆C 1和C 2的参数方程分别是⎩⎨⎧x =2+2cos φy =2sin φ(φ为参数)和⎩⎨⎧x =cos φy =1+sin φ(φ为参数).以O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求圆C 1和C 2的极坐标方程;(2)射线OM :θ=α与圆C 1的交点为O 、P ,与圆C 2的交点为O 、Q ,求|OP |·|OQ |的最大值.14.曲线C 1的参数方程为⎩⎨⎧x =4cos θ,y =2sin θ(θ为参数),曲线C 2的极坐标方程为ρ=2cosθ-2sin θ.(1)化曲线C 1,C 2的方程为普通方程,并说明它们分别表示什么曲线;(2)设曲线C 1与x 轴的一个交点的坐标为P (m,0)(m >0),经过点P 作曲线C 2的切线l ,求切线l 的方程.15.已知圆C 1的参数方程为⎩⎨⎧x =cos φy =sin φ(φ为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆C 2的极坐标方程为ρ=2cos ⎝⎛⎭⎫θ+π3.(1)将圆C 1的参数方程化为普通方程,将圆C 2的极坐标方程化为直角坐标方程; (2)圆C 1、C 2是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.[热点预测]16.在平面直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x =2-ty =3t(t 为参数),P 、Q 分别为直线l 与x 轴、y 轴的交点,线段PQ 的中点为M .(1)求直线l 的直角坐标方程;(2)以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,求点M 的极坐标和直线OM 的极坐标方程.。
河北省邯郸市重点中学高三数学规范性课时作业(二十八)(教师版)

课时作业(二十八)一、选择题1.若复数z满足zi=1-i,则z等于(A)A.-1-i B.1-iC.-1+i D.1+i解析:z=1-i i=i+1-1=-1-i,故选A.2.已知i是虚数单位,且复数z1=3-bi,z2=1-2i,z1·z2是实数,则实数b的值为(A)A.-6 B.6C.32D.16解析:z1·z2=(3-bi)·(1-2i)=(3-2b)-(b+6)i为实数,∴b+6=0,∴b=-6.3.方程x2+6x+13=0的一个根是(A)A.-3+2i B.3+2iC.-2+3i D.2+3i解析:Δ=62-4×13=-16,∴x=-6±4i2=-3±2i.故选A.4.i是虚数单位,复数2i1+i的实部为(C) A.2 B.-2 C.1 D.-1解析:2i1+i=2i?1-i??1+i??1-i?=1+i,实部为1,选C. 5.在复平面内复数z=3+4i1-i对应的点在(B) A.第一象限B.第二象限C.第三象限 D.第四象限解析:z=3+4i1-i=?3+4i??1+i??1-i??1+i?=-12+72i,在复平面内对应的点为????-12,72在第二象限,选B.6.复数z=3+i1-i的共轭复数z=(B) A.1+2i B.1-2iC.2+i D.2-i解析:z=3+i1-i=?3+i??1+i??1-i??1+i?=1+2i,则z=1-2i,选B.7.已知m1+i=1-ni,其中m,n∈R,i为虚数单位,则m+ni =(B) A.1+2i B.2+iC.1-2i D.2-i解析:由m1+i=1-ni得m=(1-ni)(1+i)=1+n+(1-n)i得m=1+n,1-n=0得m=2,n=1.∴m+ni=2+i,选B.8.复数z满足z(1-i)=2i,则复数z的实部与虚部之和为(D)A.-2 B.2C.1 D.0解析:z(1-i)=2i?z=2i1-i=2i?1+i??1-i??1+i?=-1+i.则实部与虚部和为0.9.已知(x+i)(1-i)=y,则实数x,y分别为(D)A.x=-1,y=1 B.x=-1,y=2 C.x=1,y=1 D.x=1,y=2解析:采用展开计算的方法,得x+1+(1-x) i=y,因为x,y均为实数,所以x =1,y=2,故选D.10.设x∈R,则“x=1”是“复数z=(x2-1)+(x+1) i为纯虚数”的(C)A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件解析:复数z=(x2-1)+(x+1)i为纯虚数,则x2-1=0且x+1≠0,即x=1,所以“x=1”是“复数z为纯虚数”的充要条件,选C.11.在复平面内,复数5+4i,-1+2i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数的模是(B)A.13 B.13C.213 D.210解析:由题意知点A(5,4),点B(-1,2),故其中点C(2,3),所以复数的模为13,故选B.12.若1-i(i是虚数单位)是关于x的方程x2+2px+q=0(p、q∈R)的一个解,则p+q=(C)A.-3 B.- 1C.1 D.3解析:将方程的解1-i代入二次方程可得(1-i)2+2p(1-i)+q=0,化简得(2p+q)-(2+2p)i=0,由复数相等?????2p+q=02+2p=0解得p=-1,q=2,所以p+q=1,故选C.13.若复数z=??????1+i1-i2 013,则ln |z|=(B) A.-2 B.0 C.1 D.4解析:复数z=??????1+i1-i2 013=i,所以ln|z|=0,故选B.14.已知z1=2+i,z2=1-2i,则复数z=i2 012+3z2z1-1-i2 013的模等于(C)A.552 B.25C.29 D.221 解析:将z1=2+i,z2=1-2i代入z=i2 012+3z2z1-1-i2 013化简得z=5-2i,所以|z|=52+22=29,故选C. 15.已知复数z1=cos 23°+isin 23°和复数z2=sin 53°+isin 37°,则z1·z2(A)A.12+32iB.32+12iC.12-32iD.32-12i 解析:z1·z2=(cos 23°+isin 23°)·(sin 53°+isin 37°)=cos 23°sin 53°-sin 23°sin37°+(sin 23°sin 53°+cos 23°sin 37°)i=(cos 23°sin 53°-sin 23°cos 53°)+(sin 23°cos 37°+cos 23°sin 37°)i =sin 30°+isin 60°=12+32i.二、填空题16.i为虚数单位,计算3+i1+i=________.解析:复数z=3+i1+i=?3+i??1-i??1+i??1-i?=4-2i 2=2-i.答案:2-i17.若复数a+i1-i是纯虚数,则实数a的值为________..解析:复数z=a+i1-i=?a+i??1+i??1-i??1+i?=?a-1?+?a+1?i2为纯虚数,故a=1.答案:118.设复数z满足i (z+i)=-3+2i(i是虚数单位),则z的虚部是________..解析:由已知z·i=-2+2i,得z=-2+2i i=-2+2i,故虚部为2. 答案:219.若复数z=1+i1-i(i为虚数单位),则|z|=________. 解析:z=1+i1-i=?1+i?22=i,∴|z|=1.答案:1 [热点预测]20.(1)设复数z=a+i1+i,其中a为实数,若z的实部为2,则z的虚部为()A.-i B.iC.-1 D.1(2)已知x,y∈R,i为虚数单位,若x-1+yi=2i1+i,则x+y的值为() A.2 B.3C.4 D.5解析:(1)z=a+i1+i=?a+i??1-i??1+i??1-i?=a+1+?1-a?i2,由已知实部为a+12=2得a=3,所以虚部为1-a 2=-1,故选C.(2)x-1+yi=2i?1-i?2=1+i,由复数相等可得x=2,y=1,故x+y =3.答案:(1)C(2)B办公室卫生管理制度一、主要内容与适用范围1.本制度规定了办公室卫生管理的工作内容和要求及检查与考核。
河北省邯郸市重点中学高三数学规范性课时作业(四)(学生版)

课时作业(四)一、选择题1.下列函数中,与函数y =13x定义域相同的函数为( )A .y =1sin x B .y =ln xx C .y =x e xD .y =sin xx2.若f (x )对于任意实数x 恒有2f (x )-f (-x )=3x +1,则f (x )=( ) A .x -1 B .x +1 C .2x +1D .3x +33.已知函数f ⎝⎛⎭⎫x -1x =x 2+1x 2,则f (3)=( )A .8B .9C .11D .104.已知函数f (x )=⎩⎨⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5],则方程f (x )=1的解是( )A.2或2B.2或3C.2或4 D .±2或4 5.函数y =x 22-x +lg(2x +1)的定义域是( )A.⎝⎛⎭⎫-12,+∞B.⎝⎛⎭⎫-12,2C.⎝⎛⎭⎫-12,12D.⎝⎛⎭⎫-∞,-126.某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可表示为( )A .y =⎣⎡⎦⎤x10B .y =⎣⎢⎡⎦⎥⎤x +310 C .y =⎣⎢⎡⎦⎥⎤x +410D .y =⎣⎢⎡⎦⎥⎤x +510二、填空题7.已知函数f (x )=⎩⎨⎧2x,x ≤0log 3x ,x >0,那么f ⎣⎡⎦⎤f ⎝⎛⎭⎫13=________.8.已知函数f (x )=⎩⎨⎧x 2+2ax ,x ≥2,2x +1,x <2,若f []f (1)>3a 2,则a 的取值范围是________.9.已知a ,b 为两个不相等的实数,集合M ={a 2-4a ,-1},N ={b 2-4b +1,-2},f :x →x 表示把M 中的元素x 映射到集合N 中仍为x ,则a +b 等于________.三、解答题10.若函数f (x )=xax +b (a ≠0),f (2)=1,又方程f (x )=x 有惟一解,求f (x )的解析式.11.已知函数f (x )=2x -1,g (x )=⎩⎨⎧x 2,x ≥0,-1,x <0,求f [g (x )]和g [f (x )]的解析式.12.如图1是某公共汽车线路收支差额y 元与乘客量x 的图象.(1)试说明图1上点A 、点B 以及射线AB 上的点的实际意义;(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?(3)此问题中直线斜率的实际意义是什么? (4)图1、图2、图3中的票价分别是多少元?[热点预测]13.(1)具有性质:f ⎝⎛⎭⎫1x =-f (x )的函数,我们称为满足“倒负”交换的函数,下列函数:①f (x )=x -1x ;②f (x )=x +1x ;③f (x )=⎩⎪⎨⎪⎧x ,0<x <10,x =1-1x ,x >1中满足“倒负”变换的函数是( )A .①②B .①③C .②③D .只有① (2)函数y =x +1+(x -1)0lg (2-x )的定义域是________。
河北省邯郸市重点中学高三数学规范性课时作业(十四)(教师版)
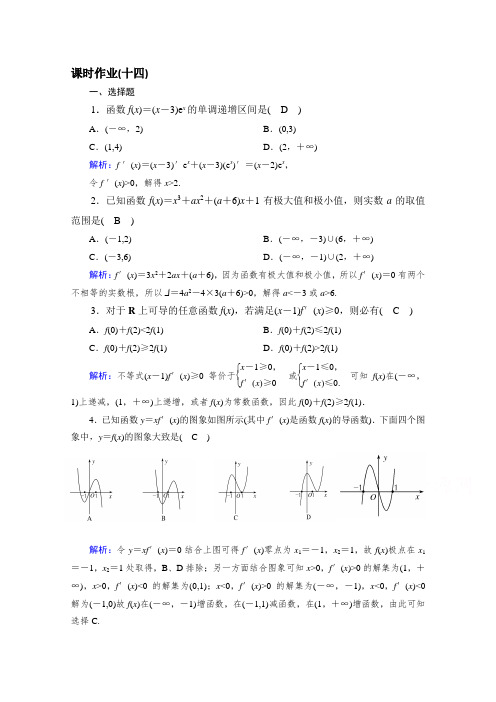
课时作业(十四)一、选择题1.函数f (x )=(x -3)e x 的单调递增区间是( D )A .(-∞,2)B .(0,3)C .(1,4)D .(2,+∞)解析:f ′(x )=(x -3)′e x +(x -3)(e x )′=(x -2)e x , 令f ′(x )>0,解得x >2.2.已知函数f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则实数a 的取值范围是( B )A .(-1,2)B .(-∞,-3)∪(6,+∞)C .(-3,6)D .(-∞,-1)∪(2,+∞)解析:f ′(x )=3x 2+2ax +(a +6),因为函数有极大值和极小值,所以f ′(x )=0有两个不相等的实数根,所以Δ=4a 2-4×3(a +6)>0,解得a <-3或a >6.3.对于R 上可导的任意函数f (x ),若满足(x -1)f ′(x )≥0,则必有( C )A .f (0)+f (2)<2f (1)B .f (0)+f (2)≤2f (1)C .f (0)+f (2)≥2f (1)D .f (0)+f (2)>2f (1)解析:不等式(x -1)f ′(x )≥0等价于⎩⎨⎧ x -1≥0,f ′(x )≥0或⎩⎨⎧x -1≤0,f ′(x )≤0.可知f (x )在(-∞,1)上递减,(1,+∞)上递增,或者f (x )为常数函数,因此f (0)+f (2)≥2f (1).4.已知函数y =xf ′(x )的图象如图所示(其中f ′(x )是函数f (x )的导函数).下面四个图象中,y =f (x )的图象大致是( C )解析:令y =xf ′(x )=0结合上图可得f ′(x )零点为x 1=-1,x 2=1,故f (x )极点在x 1=-1,x 2=1处取得,B 、D 排除;另一方面结合图象可知x >0,f ′(x )>0的解集为(1,+∞),x >0,f ′(x )<0的解集为(0,1);x <0,f ′(x )>0的解集为(-∞,-1),x <0,f ′(x )<0解为(-1,0)故f (x )在(-∞,-1)增函数,在(-1,1)减函数,在(1,+∞)增函数,由此可知选择C.5.若函数f (x )=x 3-6bx +3b 在(0,1)内有最小值,则实数b 的取值范围是( D )A .(0,1)B .(-∞,1)C .(0,+∞) D.⎝⎛⎭⎫0,12解析:f (x )在(0,1)内有最小值,即f (x )在(0,1)内有极小值,f ′(x )=3x 2-6b ,由题意,函数f ′(x )的草图如图,∴⎩⎨⎧ f ′(0)<0,f ′(1)>0,即⎩⎨⎧-6b <0,3-6b >0,解得0<b <12.故选D.6.设函数f (x )满足x 2f ′(x )+2xf (x )=e xx , f (2)=e 28,则x >0时,f (x )( D )A .有极大值,无极小值B .有极小值,无极大值C .既有极大值又有极小值D .既无极大值也无极小值解析:由题意[x 2f (x )]′=e x x ,令g (x )=x 2f (x ),则g ′(x )=e x x ,且f (x )=g (x )x 2,因此f ′(x )=xg ′(x )-2g (x )x 3=e x -2g (x )x 3.令h (x )=e x -2g (x ),则h ′(x )=e x -2g ′(x )=e -2e x x =e x(x -2)x ,所以x >2时,h ′(x )>0;0<x <2时,h ′(x )<0.从而有h (x )≥h (2)=0,即f ′(x )≥0,所以当x >0时,f (x )是单调递增的,f (x )无极大值也无极小值.二、填空题7.已知函数f (x )=x 3-12x +8在区间[-3,3]上的最大值与最小值分别为M ,m ,则M -m =________.解析:令f ′(x )=3x 2-12=0,得x =-2或x =2, 列表得:可知M =24,m =-8,∴M -m =32. 答案:328.设函数f (x )=x (e x-1)-12x 2,则函数f (x )的单调增区间为________.解析:因为f (x )=x (e x -1)-12x 2,所以f ′(x )=e x -1+x e x -x =(e x -1)·(x +1).令f ′(x )>0,即(e x -1)(x +1)>0,解得x ∈(-∞,-1)或x ∈(0,+∞).所以函数f (x )的单调增区间为(-∞,-1]和[0,+∞).答案:(-∞,-1]和[0,+∞)9.f (x )=x (x -c )2在x =2处有极大值,则常数c 的值为________.解析:f (x )=x 3-2cx 2+c 2x ,f ′(x )=3x 2-4cx +c 2, f ′(2)=0⇒c =2或c =6.若c =2,f ′(x )=3x 2-8x +4, 令f ′(x )>0⇒x <23或x >2,f ′(x )<0⇒23<x <2,故函数在⎝⎛⎭⎫-∞,23及(2,+∞)上单调递增,在⎝⎛⎭⎫23,2上单调递减,∴x =2是极小值点,故c =2不合题意,c =6.答案:6三、解答题10.已知函数f (x )=x -a ln x (a ∈R ).(1)当a =2时,求曲线y =f (x )在点A (1, f (1))处的切线方程; (2)求函数f (x )的极值.解:函数f (x )的定义域为(0,+∞), f ′(x )=1-ax . (1)当a =2时, f (x )=x -2ln x, f ′(x )=1-2x (x >0), 因而f (1)=1, f ′(1)=-1,所以曲线y =f (x )在点A (1, f (1))处的切线方程为y -1=-(x -1), 即x +y -2=0.(2)由f ′(x )=1-a x =x -ax,x >0知:①当a ≤0时, f ′(x )>0,函数f (x )为(0,+∞)上的增函数,函数f (x )无极值; ②当a >0时,由f ′(x )=0,解得x =a ,又当x ∈(0,a )时, f ′(x )<0;当x ∈(a ,+∞)时, f ′(x )>0,从而函数f (x )在x =a 处取得极小值,且极小值为f (a )=a -a ln a ,无极大值. 综上,当a ≤0时,函数f (x )无极值;当a >0时,函数f (x )在x =a 处取得极小值a -a ln a ,无极大值.11.已知函数f (x )=ax 3+x 2+bx (其中常数a , b ∈R ),g (x )=f (x )+f ′(x )是奇函数.(1)求f (x )的表达式;(2)讨论g (x )的单调性,并求g (x )在区间[1,2]上的最大值与最小值.解:(1)由题意得f ′(x )=3ax 2+2x +b ,因此g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b . 因为函数g (x )是奇函数,所以g (-x )=-g (x ),即对任意实数x ,有a (-x )3+(3a +1)(-x )2+(b +2)(-x )+b =-[ax 3+(3a +1)x 2+(b +2)x +b ],从而3a +1=0,b =0,解得a =-13,b =0, 因此f (x )的表达式为f (x )=-13x 3+x 2. (2)由(1)知g (x )=-13x 3+2x ,所以g ′(x )=-x 2+2.令g ′(x )=0,解得x 1=-2,x 2= 2.则当x <-2或x >2时,g ′(x )<0,从而g (x )在区间(-∞,-2],[2,+∞)上是减函数;当-2<x <2时,g ′(x )>0,从而g (x )在区间[-2,2]上是增函数.由上述讨论知,g (x )在区间[1,2]上的最大值与最小值只能在x =1,2,2时取得, 而g (1)=53,g (2)=423,g (2)=43,因此g (x )在区间[1,2]上的最大值为g (2)=423,最小值为g (2)=43.12.已知函数f (x )=12e 2x-ax (a ∈R ,e 为自然对数的底数). (1)讨论函数f (x )的单调性;(2)若a =1,函数g (x )=(x -m )f (x )-14e 2x +x 2+x 在区间(0,+∞)上为增函数,求整数m 的最大值.解:(1)定义域为(-∞,+∞), f ′(x )=e 2x -a ,当a ≤0时,f ′(x )>0,所以f (x )在(-∞,+∞)上为增函数;当a >0时,由f ′(x )=0得x =ln a2,且当x ∈⎝⎛⎭⎫-∞,ln a 2时, f ′(x )<0,当x ∈⎝⎛⎭⎫ln a2,+∞时f ′(x )>0,所以f (x )在⎝⎛⎭⎫-∞,ln a 2为减函数,在⎝⎛⎭⎫ln a2,+∞为增函数.(2)当a =1时,g (x )=(x -m )⎝⎛⎭⎫12e 2x -x -14e 2x +x 2+x ,若g (x )在区间(0,+∞)上为增函数,则g ′(x )=(x -m )(e 2x -1)+x +1≥0在(0,+∞)恒成立,即m ≤x +1e 2x -1+x 在(0,+∞)恒成立.令h (x )=x +1e 2x -1+x ,x ∈(0,+∞);h ′(x )=e 2x (e 2x -2x -3)(e 2x -1)2,x ∈(0,+∞);令L (x )=e 2x -2x -3,可知L ⎝⎛⎭⎫12=e -4<0,L (1)=e 2-5>0, 又当x ∈(0,+∞)时L ′(x )=2e 2x -2>0,所以函数L (x )=e 2x -2x -3在x ∈(0,+∞)只有一个零点, 设为α,即e 2α=2α+3,且α∈⎝⎛⎭⎫12,1;由上可知当x ∈(0,α)时L (x )<0,即h ′(x )<0; 当x ∈(α,+∞)时L (x )>0,即h ′(x )>0,所以h (x )=x +1e 2x -1+x ,x ∈(0,+∞),有最小值h (α)=α+1e 2α-1+α,把e 2α=2α+3代入上式可得h (α)=12+α,又因为α∈⎝⎛⎭⎫12,1,所以h (α)∈⎝⎛⎭⎫1,32,又m ≤h (x )恒成立,所以m ≤h (α),又因为m 为整数, 所以m ≤1,所以整数m 的最大值为1. [热点预测]13.已知函数f (x )=ax -2x -3ln x ,其中a 为常数.(1)当函数f (x )图象在点⎣⎢⎡⎦⎥⎤23,f ⎝ ⎛⎭⎪⎫23处的切线的斜率为1时,求函数f (x )在⎣⎢⎡⎦⎥⎤32,3上的最小值;(2)若函数f (x )在区间(0,+∞)上既有极大值又有极小值,求a 的取值范围;(3)在(1)的条件下,过点P (1,-4)作函数F (x )=x 2[f (x )+3ln x -3]图象的切线,试问这样的切线有几条?并求出这些切线方程.解:(1)由题可知f ′(x )=a +2x 2-3x ,f ′⎝⎛⎭⎫23=1,解得a =1.故f (x )=x -2x -3ln x ,∴f ′(x )=(x -1)(x -2)x 2, 由f ′(x )=0,得x =2. 于是可得下表:min (2)∵f ′(x )=a +2x 2-3x =ax 2-3x +2x 2(x >0) 由题可得方程ax 2-3x +2=0有两个不等的正实根,不妨设这两个根为x 1、x 2,并令h (x )=ax 2-3x +2则⎩⎨⎧Δ=9-8a >0x 1+x 2=3a >0x 1x 2=2a >0解得0<a <98.(3)由(1)知f (x )=x -2x -3ln x ,故F (x )=x 3-3x 2-2x (x >0),F ′(x )=3x 2-6x -2(x >0) 设切点为T (x 0,y 0),由于点P 在函数F (x )的图象上, ①当切点T 不与点P (1,-4)重合,即当x 0≠1时, 由于切线过点P (1,-4),则y 0+4x 0-1=3x 20-6x 0-2 所以x 30-3x 20-2x 0+4=(x 0-1)(3x 20-6x 0-2), 化简得x 30-3x 20+3x 0-1=0,即(x 0-1)3=0,解得x 0=1(舍去).②当切点T 与点P (1,-4)重合,即x 0=1时,则切线的斜率k =F ′(1)=-5,于是切线方程为5x +y -1=0. 综上所述,满足条件的切线只有一条,其方程为5x +y -1=0.。
河北省邯郸市重点中学高三数学规范性课时作业(四十八)(学生版)

课时作业(四十八)一、选择题1.若直线(a +1)x +2y =0与直线x -ay =1互相垂直,则实数a 的值等于( ) A .-1 B .0 C .1D .22.设a ∈R ,则“a =1”是“直线l 1:ax +2y -1=0与直线l 2:x +(a +1)y +4=0平行”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.过点A (1,2)且与原点距离最大的直线方程为( ) A .x +2y -5=0 B .2x +y -4=0 C .x +3y -7=0D .3x +y -5=04.A 、B 是x 轴上两点,点P 的横坐标为2,且|P A |=|PB |,若直线P A 的方程为x -y +1=0,则直线PB 的方程为( )A .2x -y -1=0B .x +y -5=0C .2x +y -7=0D .2y -x -4=05.当0<k <12时,直线l 1:kx -y =k -1与直线l 2:ky -x =2k 的交点在( )A .第一象限B .第二象限C .第三象限D .第四象限6.已知直线l 1:y =2x +3,直线l 2与l 1关于直线y =-x 对称,则直线l 2的斜率为( ) A.12 B .-12C .2D .-2二、填空题7.已知两条直线y =ax -2和3x -(a +2)y +1=0互相垂直,则a 等于________. 8.若两平行直线3x -2y -1=0,6x +ay +c =0之间的距离为21313,则c +2a 的值为________.9.平面直角坐标系中,过原点O 的直线l 与曲线y =e x -1交于不同的A ,B 两点,分别过点A ,B 作y 轴的平行线,与曲线y =ln x 交于点C ,D ,则直线CD 的斜率是________.三、解答题10.求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.11.已知直线l经过直线2x+y-5=0与x-2y=0的交点,(1)点A(5,0)到l的距离为3,求l的方程;(2)求点A(5,0)到l的距离的最大值.12.(1)求点A(3,2)关于点B(-3,4)的对称点C的坐标;(2)求直线3x-y-4=0关于点P(2,-1)对称的直线l的方程;(3)求点A(2,2)关于直线2x-4y+9=0的对称点的坐标.[热点预测]13.(1)点P到点A(1,0)和直线x=-1的距离相等,且点P到直线y=x的距离为2 2,这样的点P的个数是()A.1 B.2C.3 D.4(2)若点(m,n)在直线4x+3y-10=0上,则m2+n2的最小值是()A.2 B.2 2C.4 D.2 3。
河北省邯郸市重点中学高三数学规范性课时作业(五十三)(学生版)

课时作业(五十三)一、选择题1.抛物线y 2=8x 的焦点到直线x -3y =0的距离是( ) A .2 3 B .2 C. 3D .12.过抛物线y 2=4x 焦点的直线交抛物线于A ,B 两点,若|AB |=10,则AB 的中点到y 轴的距离等于( )A .1B .2C .3D .43.已知正六边形ABCDEF 的边长是2,一条抛物线恰好经过该六边形的四个顶点,则抛物线的焦点到准线的距离是( )A.34B.32C. 3 D .2 34.过点(0,1)作直线,使它与抛物线y 2=4x 仅有一个公共点,这样的直线有( ) A .1条 B .2条 C .3条D .4条5.设抛物线y 2=6x 的焦点为F ,准线为l ,P 为抛物线上一点,P A ⊥l ,垂足为A ,如果△APF 为正三角形,那么|PF |等于( )A .4 3B .6 3C .6D .126.过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点.若|AF |=3,则△AOB 的面积为( )A.22 B. 2 C.322D .2 2二、填空题7.抛物线顶点在原点,焦点在x 轴正半轴,有且只有一条直线l 过焦点与抛物线相交于A ,B 两点,且|AB |=1,则抛物线方程为________.8.右图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降2米后,水面宽________米.9.已知抛物线方程为y 2=4x ,直线l 的方程为x -y +5=0,在抛物线上有一动 点P 到y 轴的距离为d 1,到直线l 的距离为d 2,则d 1+d 2的最小值为________.10.过抛物线y 2=2x 的焦点F 作直线交抛物线于A ,B 两点,若|AB |=2512,|AF |<|BF |,则|AF |=________.三、解答题11.已知抛物线y 2=2px (p >0)有一个内接直角三角形,直角顶点在原点,斜边长为213,一直角边的方程是y =2x ,求抛物线的方程.12.已知抛物线方程x 2=4y ,过点P (t ,-4)作抛物线的两条切线P A 、PB ,切点分别为A 、B .(1)求证:直线AB 过定点(0,4);(2)求△OAB (O 为坐标原点)面积的最小值.[热点预测]13.已知直线l 1:4x -3y +6=0和直线l 2: x =-p2;若拋物线C :y 2=2px (p >0)上的点到直线l 1和直线l 2的距离之和的最小值为2.(1)求抛物线C 的方程;(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.。
邯郸市重点中学高三数学规范性课时作业(三十二)(教师版)

课时作业(三十二)一、选择题1.等比数列{a n }中,已知a 1+a 2+a 3=4,a 2+a 3+a 4=-2,则a 3+a 4+a 5+a 6+a 7+a 8=( D )A.2116B.1916C.98D.78解析:由于q =a 2+a 3+a 4a 1+a 2+a 3=-24=-12,所以a 3+a 4+a 5=(a 2+a 3+a 4)×⎝⎛⎭⎫-12=1,a 6+a 7+a 8=(a 3+a 4+a 5)×⎝⎛⎭⎫-123=-18,于是a 3+a 4+a 5+a 6+a 7+a 8=78.2.已知等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n +1的前100项和为( A )A.100101B.99101C.99100D.101100 解析:由S 5=5a 3及S 5=15得a 3=3,∴d =a 5-a 35-3=1,a 1=1,∴a n =n ,1a n a n +1=1n (n +1)=1n -1n +1,所以数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和T 100=1-12+12-13+…+1100-1101=1-1101=100101,故选A.3.数列{a n }的通项公式是a n =1n +n +1,若前n 项和为10,则项数n 为( C )A .11B .99C .120D .121 解析:∵a n =1n +n +1=n +1-n ,∴S n =a 1+a 2+…+a n =(2-1)+(3-2)+…+(n +1-n )=n +1-1.令n +1-1=10,得n =120.4.数列1,11+2,11+2+3,…,11+2+3+…+n的前n 项和S n 等于( B ) A.3n -1n +1 B.2n n +1 C.3n n +1 D.4n n +3解析:a n =2n (n +1)=2⎝ ⎛⎭⎪⎫1n -1n +1,所以S n =2⎝ ⎛⎭⎪⎫1-12+12-13+…+1n -1-1n +1n -1n +1 =2⎝ ⎛⎭⎪⎫1-1n +1=2n n +1. 5.公比不为1的等比数列{a n }的前n 项和为S n ,且-3a 1,-a 2,a 3成等差数列,若a 1=1,则S 4=( A )A .-20B .0C .7D .40解析:记等比数列{a n }的公比为q ,其中q ≠1,依题意有-2a 2=-3a 1+a 3,-2a 1q =-3a 1+a 1q 2≠0,即q 2+2q -3=0,(q +3)(q -1)=0,又q ≠1,因此有q =-3,S 4=1×[1-(-3)4]1+3=-20,选A.6.已知函数f (n )=n 2cos(nπ),且a n =f (n ),则a 1+a 2+a 3+…+a 100=( C )A .0B .100C .5 050D .10 200解析:因为f (n )=n 2cos(nπ),所以a 1+a 2+a 3+…+a 100=-12+22-32+42-…-992+1002=(22-12)+(42-32)+…(1002-992)=3+7+…+199=50(3+199)2=5 050,选C. 二、填空题7.已知数列{a n }对于任意p ,q ∈N *有a p a q =a p +q ,若a 1=12,则S 9=________.解析:由题意得a n +1=a n a 1, a n +1a n =a 1=12,a n =a 1⎝⎛⎭⎫12n -1=⎝⎛⎭⎫12n , 因此S 9=1-⎝⎛⎭⎫129=511512.答案:5115128.数列{a n }的前n 项和为S n ,且a 1=1,a n +1=3S n (n =1,2,3,…),则log 4S 10=________.解析:∵a n +1=3S n ,∴S n +1-S n =3S n ,∴S n +1=4S n ,∴{S n }是以S 1为首项,公比为4的等比数列,∴S 10=410-1=49,∴log 4S 10=log 449=9.答案:99.已知数列{a n }(n ∈N *)中,a 1=1,a n +1=a n2a n +1,则a n =________解析:由a n +1=a n 2a n +1得1a n +1=2+1a n ∴数列{a n }的倒数成公差为2的等差数列,由此可求1a n=2n -1,∴a n =12n -1.答案:12n -1三、解答题10.已知n ∈N *,数列{d n }满足d n =3+(-1)n2,数列{a n }满足a n =d 1+d 2+d 3+…+d 2n ;又知数列{b n }中,b 1=2,且对任意正整数m ,n ,b m n =b nm .(1)求数列{a n }和数列{b n }的通项公式;(2)将数列{b n }中的第a 1项,第a 2项,第a 3项,……,第a n 项,……,删去后,剩余的项按从小到大的顺序排成新数列{c n },求数列{c n }的前2 013项和.解:(1)∵d n =3+(-1)n 2,∴a n =d 1+d 2+d 3+…+d 2n=3×2n2=3n又由题知:令m =1,则b 2=b 21=22,b 3=b 31=23,…,b n =b n 1=2n 若b n =2n ,则b m n =2nm ,b n m =2mn ,所以b m n =b n m 恒成立 若b n ≠2n ,当m =1,b m n =b n m 不成立,所以b n =2n .(2)由题知将数列{b n }中的第3项、第6项、第9项……第3n 项删去后构成的新数列{c n }中的奇数项与偶数项仍成等比数列,首项分别是b 1=2,b 2=4公比均是8,T 2 013=(c 1+c 3+c 5+…+c 2 013)+(c 2+c 4+c 6+…+c 2 012) =2×(1-81 007)1-8+4×(1-81 006)1-8=20×81 006-6711.已知公差大于零的等差数列{a n }的前n 项和为S n ,且满足:a 2·a 4=65,a 1+a 5=18.(1)若1<i <21,a 1,a i ,a 21是某等比数列的连续三项,求i 的值; (2)设b n =n(2n +1)S n,是否存在一个最小的常数m 使得b 1+b 2+…+b n <m 对于任意的正整数n 均成立,若存在,求出常数m ;若不存在,请说明理由.解:(1){a n }为等差数列,∵a 1+a 5=a 2+a 4=18,又a 2·a 4=65,∴a 2,a 4是方程x 2-18x +65=0的两个根, 又公差d >0,∴a 2<a 4,∴a 2=5,a 4=13.∴⎩⎨⎧a 1+d =5,a 1+3d =13,∴a 1=1,d =4.∴a n =4n -3.由1<i <21,a 1,a i ,a 21是某等比数列的连续三项,∴a 1·a 21=a 2i , 即1·81=(4i -3)2, 解得i =3.(2)由(1)知,S n =n ·1+n (n -1)2·4=2n 2-n , 所以b n =1(2n -1)(2n +1)=12⎝ ⎛⎭⎪⎫12n -1-12n +1,b 1+b 2+…+b n =12⎝ ⎛⎭⎪⎫1-13+13-15+…+12n -1-12n +1=n2n +1 因为n 2n +1=12-12(2n +1)<12,所以存在m =12使b 1+b 2+…+b n <m 对于任意的正整数n 均成立.12.已知各项均为正数的数列{a n }前n 项和为S n ,首项为a 1,且12,a n ,S n 成等差数列.(1)求数列{a n }的通项公式;(2)若a 2n =⎝ ⎛⎭⎪⎫12b n,设C n=b n a n ,求数列{C n }的前n 项和T n . 解:(1)由题意知2a n =S n +12,a n >0 当n =1时,2a 1=a 1+12,∴a 1=12 当n ≥2时,S n =2a n -12,S n -1=2a n -1-12 两式相减得a n =S n -S n -1=2a n -2a n -1 整理得:a na n -1=2∴数列{a n }是以12为首项,2为公比的等比数列.a n =a 1·2n -1=12×2n -1=2n -2(2)a 2n =2-b n =22n -4 ∴b n =4-2n , C n =b n a n=4-2n 2n -2=16-8n 2nT n =82+022+-823+…+24-8n 2n -1+16-8n 2n ①12T n =822+023+…+24-8n 2n +16-8n 2n +1② ①-②得12T n =4-8⎝⎛⎭⎫122+123+…+12n -16-8n 2n +1=4-8·122⎝ ⎛⎭⎪⎫1-12n -11-12-16-8n2n +1=4-4⎝ ⎛⎭⎪⎫1-12n -1-16-8n 2n +1=4n 2n .∴T n =8n2n . [热点预测]13.已知向量a =⎝ ⎛⎭⎪⎫sin ⎝ ⎛⎭⎪⎫ω2x ,12,b =⎝ ⎛⎭⎪⎫cos ⎝ ⎛⎭⎪⎫ω2x ,-12(ω>0,x ≥0),函数f (x )=a ·b 的第n (n ∈N *)个零点记作x n (从左向右依次计数),则所有x n 组成数列{x n }.(1)若ω=12,求x 2;(2)若函数f (x )的最小正周期为π,求数列{x n }的前100项和S 100.解:f (x )=a ·b =sin ⎝⎛⎭⎫ω2x cos ⎝⎛⎭⎫ω2x -14=12sin(ωx )-14(1)当ω=12时,f (x )=12sin ⎝⎛⎭⎫12x -14令f (x )=0,得x =4kπ+π3或x =4kπ+5π3(k ∈Z ,x ≥0) 取k =0,得x 2=5π3.(2)因为f (x )最小正周期为π,则ω=2,故f (x )=12sin(2x )-14 令f (x )=0得x =kπ+π12或x =kπ+5π12(k ∈Z , x ≥0) 所以S 100=⎣⎡⎦⎤⎝⎛⎭⎫kπ+π12+⎝⎛⎭⎫kπ+5π12=⎝⎛⎭⎫2kπ+π2=2π(0+1+2+…+49)+50×π2=50×49π+25π=2 475π.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业(十四)
一、选择题
1.函数f (x )=(x -3)e x 的单调递增区间是( ) A .(-∞,2) B .(0,3) C .(1,4)
D .(2,+∞)
2.已知函数f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则实数a 的取值范围是( )
A .(-1, 2)
B .(-∞,-3)∪(6,+∞)
C .(-3,6)
D .(-∞,-1)∪(2,+∞)
3.对于R 上可导的任意函数f (x ),若满足(x -1)f ′(x )≥0,则必有( ) A .f (0)+f (2)<2f (1) B .f (0)+f (2)≤2f (1) C .f (0)+f (2)≥2f (1)
D .f (0)+f (2)>2f (1)
4.已知函数y =xf ′(x )的图象如图所示(其中f ′(x )是函数f (x )的导函数).下面四个图象中,y =f (x )的图象大致是( )
5.若函数f (x )=x 3-6bx +3b 在(0,1)内有最小值,则实数b 的取值范围是( )
A .(0,1)
B .(-∞,1)
C .(0,+∞) D.⎝⎛⎭
⎫0,1
2
6.设函数f (x )满足x 2
f ′(x )+2xf (x )=e x x , f (2)=e 2
8,则x >0时,f (x )( )
A .有极大值,无极小值
B .有极小值,无极大值
C .既有极大值又有极小值
D .既无极大值也无极小值 二、填空题
7.已知函数f (x )=x 3-12x +8在区间[-3,3]上的最大值与最小值分别为M ,m ,则M -m =________.
8.设函数f (x )=x (e x -1)-1
2x 2,则函数f (x )的单调增区间为________. 9.f (x )=x (x -c )2在x =2处有极大值,则常数c 的值为________.
三、解答题
10.已知函数f (x )=x -a ln x (a ∈R ).
(1)当a =2时,求曲线y =f (x )在点A (1, f (1))处的切线方程; (2)求函数f (x )的极值.
11.已知函数f (x )=ax 3+x 2+bx (其中常数a ,b ∈R ),g (x )=f (x )+f ′(x )是奇函数. (1)求f (x )的表达式;
(2)讨论g (x )的单调性,并求g (x )在区间[1,2]上的最大值与最小值.
12.已知函数f (x )=1
2e 2x -ax (a ∈R ,e 为自然对数的底数).
(1)讨论函数f (x )的单调性;
(2)若a =1,函数g (x )=(x -m )f (x )-1
4e 2x +x 2+x 在区间(0,+∞)上为增函数,求整数m 的最大值.
[热点预测]
13.已知函数f (x )=ax -2
x -3ln x ,其中a 为常数.
(1)当函数f (x )图象在点⎣⎡⎦⎤23,f ⎝⎛⎭
⎫23处的切线的斜率为1时,求函数f (x )在⎣⎡⎦
⎤32,3上的最小值;
(2)若函数f (x )在区间(0,+∞)上既有极大值又有极小值,求a 的取值范围; (3)在(1)的条件下,过点P (1,-4)作函数F (x )=x 2[f (x )+3ln x -3]图象的切线,试问这样的切线有几条?并求出这些切线方程.。
