《结构力学习题集》(下)-结构的动力计算习题及答案
结构力学(2)习题库

15 结构的动力计算判断题体系的振动自由度等于集中质量数。
()图示体系具有1个振动自由度。
()图示体系具有2个振动自由度。
()图示体系具有3个振动自由度。
()图示体系具有2个振动自由度。
()图示体系具有2个振动自由度。
()结构的自振频率除与体系的质量分布状况、杆件刚度有关外,还与干扰力有关。
()自由振动是指不受外界干扰力作用的振动。
()自由振动是由初位移和初速度引起的,缺一不可。
()有阻尼单自由度体系的阻尼比越大,自振频率越小。
()临界阻尼现象是指起振后振动次数很少且振幅很快衰减为零的振动。
()惯性力并不是实际加在运动质量上的力。
()计算一个结构的自振周期时,考虑阻尼比不考虑所得的结果要大。
()临界阻尼振动时质点缓慢地回到平衡位置且不过平衡点。
()阻尼力总是与质点加速的方向相反。
()在某些情形下建立振动微分方程式时,不考虑重力的影响是因为重力为恒力。
()图示结构的自振频率为w,在干扰力P(t)=P sin qt作用下,不管频率q怎样改变,动位移y(t)的方向总是和P(t)的方向相同。
()计算图示振动体系的最大动内力和动位移时可以采用同一个动力系数。
()不论干扰力是否直接作用在单自由度体系的质量m上,都可用同一个动力系数计算任一点的最大动位移。
()单自由度体系受迫振动的最大动位移的计算公式y max=my j中,y j是质量m的重量所引起的静位移。
()多自由度体系作自由振动,一般包括所有的振型,不可能出现仅含某一主振型的振动。
()解得图(a)所示两个自由度体系的两个主振型为图(b)和图(c),此解答是正确的。
()图(a)与图(b)所示梁的自由振动频率w A、w B相比,w A>w B。
()填空题动力荷载是指_____________________荷载。
振动自由度的定义是_____________________。
若要改变一个结构的自振周期,可以从两个方面着手:1、_____________________;2、_____________________。
《结构力学习题集》(含答案)
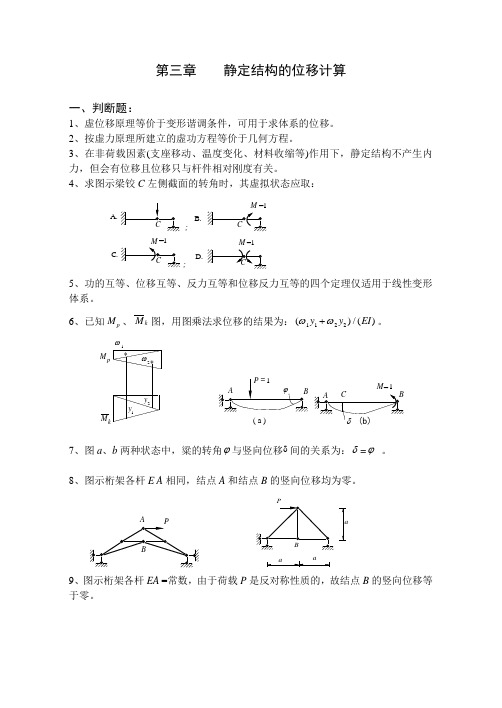
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
(完整版)结构力学_习题集(含答案)

《结构力学》课程习题集一、单项选择题1. 弯矩图必定发生突变的截面是()。
A. 有集中力作用的截面;B.剪力为零的截面;C.荷载为零的截面;D.有集中力偶作用的截面。
2. 图示梁中 C 截面的弯矩是()。
12kN . m 4kN 3kN / mC4m 4m 2mA.12kN.m( 下拉 );B.3kN.m( 上拉 );C.8kN.m( 下拉 );D.11kN.m( 下拉 )。
3. 静定结构有变温时,()。
A. 无变形,无位移,无内力;B.有变形,有位移,有内力;C.有变形,有位移,无内力;D.无变形,有位移,无内力。
4. 图示桁架 a 杆的内力是()。
A.2P ;B. -2P;; D. - 3P。
P P Pda3 d5. 图示桁架,各杆EA 为常数,除支座链杆外,零杆数为()。
A. 四根;B. 二根;C.一根;D. 零根。
P PaP Pl = 6a6. 图示梁 A 点的竖向位移为(向下为正)()。
A. Pl 3 /( 24 EI ) ;B. Pl 3 /(16 EI ) ;C. 5Pl3/( 96EI );D. 5Pl3/(48 EI )。
P2 EI EIl/ 2 A l/ 27. 静定结构的内力计算与()。
A.EI 没关;B.EI 相对值相关;C.EI 绝对值相关;D.E 没关, I 相关。
8. 图示桁架,零杆的数量为:()。
A.5 ;;; D.20 。
9. 图示结构的零杆数量为()。
A.5 ;B.6 ;; D.8 。
10. 图示两结构及其受力状态,它们的内力切合()。
A. 弯矩同样,剪力不一样;B.弯矩同样,轴力不一样;C.弯矩不一样,剪力同样;D.弯矩不一样,轴力不一样。
P P P P2P 2PEI EI EI EIh 2EI EIl ll l11. 刚结点在结构发生变形时的主要特点是()。
A. 各杆能够绕结点结心自由转动;B.不变形;C.各杆之间的夹角可随意改变;D.各杆之间的夹角保持不变。
结构的动力计算习题

《结构的动力计算》习题一、判断题1、图示等效体系的关系是:3211111k k k k ++=。
( )2、结构的动力反应只与初始条件及动荷载有关。
( )3、任何动力荷载作用下均可以采用公式:1221-⎪⎪⎭⎫⎝⎛-=ωθβ计算动力系数。
( ) 4、外界感干扰力只影响振幅、不影响体系的自振频率。
( )5、体系的动力自由度数与质点的个数无关、也与结构静定或超静定无关。
( )6、图示体系各杆自重不计、EA =∞,则该体系在初始时刻的干扰力作用下将做竖向振动。
( )二、选择题1、增加单自由度体系的阻尼、但仍保持为低阻尼体系,其结果是( )。
A 、周期变长 B 、周期不变 C 、周期变短 D 、 周期视具体体系而定2、图示两个等效结构,正确的刚度关系是( )。
A 、k=k 1+k 2 B 、21111k k k += C 、21211k k k k k += D 、2112k kk k k +=3、图示体系不计阻尼,平稳阶段最大动位移y max =4Pl 3/7EI ,其最大动力弯矩为( )。
A 、3Pl /7 B 、4Pl /7 C 、12Pl /7 D 、4Pl /21 4、下列哪句话有错误或不够准确()。
第3题图A、在多自由度体系自由振动问题中,主要问题是确定体系的全部自振频率和相应的主振型; B 、多自由度体系的自振频率不止一个,其个数与自由度个数相等;C 、每个自振频率都有自己相应的主振型,主振型就是多自由度体系振动时各质点的位移变化形式;D 、与单自由度体系相同,多自由度体系的自振频率和相应的主振型也是体系本身的固有性质。
5、图示单自由度体系自振周期的关系为( )。
A 、(a)=(c)B 、(a)=(b)C 、(b)=(c)D 、都不相等6、单自由度振动体系中,若质点在杆的中点,各杆EI 、l 相同,其自振周期的大小排列顺序为(A 、(c)>(a)>(b)B 、(c)>(b)>(a) C 、(a)>(b)>(c) D 、(b)>(c)>(a)三、分析计算题1、梁的抗弯刚度为EI2m3、柱的自重不计,求图示刚架的自振频率。
结构动力学课后习题答案

结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案,供参考:习题1:单自由度系统自由振动分析解答:对于一个单自由度系统,其自由振动的频率可以通过以下公式计算:\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中,\( k \) 是系统的刚度,\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述,其衰减系数 \( \delta \) 可以通过以下公式计算:\[ \delta = \sqrt{1-\zeta^2} \]习题2:单自由度系统受迫振动分析解答:当单自由度系统受到周期性外力作用时,其受迫振动的振幅可以通过以下公式计算:\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中,\( F_0 \) 是外力的幅值,\( \omega \) 是外力的角频率。
习题3:多自由度系统模态分析解答:对于多自由度系统,可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为:\[ [K]{\phi} = \lambda[M]{\phi} \]其中,\( [K] \) 是系统的刚度矩阵,\( [M] \) 是系统的质量矩阵,\( \lambda \) 是特征值,\( {\phi} \) 是对应的特征向量,即模态形状。
习题4:结构的冲击响应分析解答:对于结构的冲击响应分析,通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱(IRF)来分析,它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5:疲劳分析解答:结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构动力学习题解答

(4)
将(4)式代入方程(3)可以求得:
A= h
(ω
2
n
−ω
2 2
)
= + 4n ω 2 nω
2 2
6F
;
L 6 K − mω
(
2 2
)
+ 9C ω
2
2
α = arctg
ω n −ω
2
2
= arctg
3Cω 6 K − mω 2
;
(2) 求 f (t ) = δ (t ) 的解; 将 f (t ) = δ (t ) 代入方程(1)得
∑ M ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤: (1)设系统的广义坐标为 θ ,写出系统对于坐标 θ 的动能 T 和势能 U 的 表 达 式 ; 进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
ωn =
=
1 rA
;
1.8 已知图1-37所示振动系统中,匀质杆长为 L,质量为 m,两弹簧刚度皆为 K,阻尼系
̇ = 0时 数为 C,求当初始条件 θ 0 = θ 0
结构动力学习题解答

然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度 为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
结构力学练习题及答案
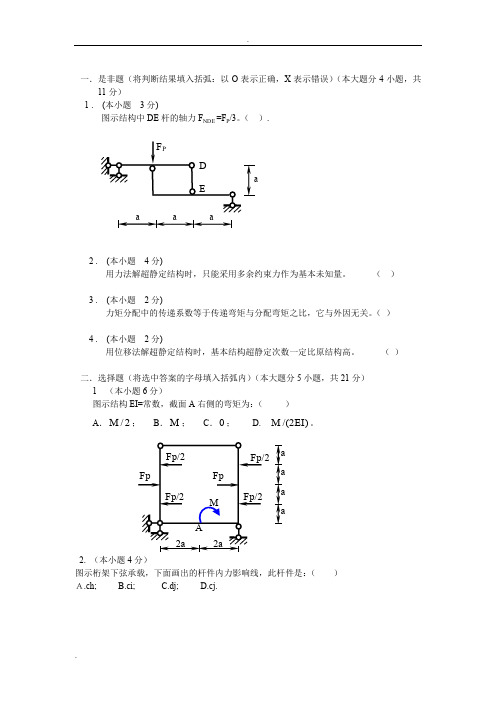
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
结构力学下考试试卷含答案

XX大学课程考试试卷课程名称:结构力学分)一、判断题(对打O,错打X。
每小题3分,共计9分)1. 局部坐标系单元刚度矩阵和整体坐标系单元刚度矩阵均为对称矩阵。
2. 当结构中某杆件的刚度增加时,结构的自振频率不一定增大。
3. 用能量法求体系自振频率时,则所得结果定为一精确解。
二、单项选择题(每小题4分,共计12分)分)1. 单元刚度矩阵中元素的物理意义是:的物理意义是:A.当且仅当时引起的与相应的杆端力;相应的杆端力;B.当且仅当时引起的与相应的杆端力;相应的杆端力;C.当时引起的相应的杆端力;相应的杆端力;D.当时引起的与相应的杆端力。
2. 引入图示结构边界约束后的局部坐标单元刚度矩阵为:引入图示结构边界约束后的局部坐标单元刚度矩阵为:(其中:) 3. 设直杆的轴向变形不计,图示体系的动力自由度数为:设直杆的轴向变形不计,图示体系的动力自由度数为:A.3 ; B.4 ;D.6 。
C.5 ; 三、填空题(每空3分,共9分)分)1. 对图示结构先处理法集成所得结构刚度矩阵总未知量数为,最大半带宽为。
2. 主振型关于质量矩阵的正交性用公式表达为。
四、计算题(16分),图中圆括号内数码为结点定位向量图a所示结构(整体坐标见图b,图中圆括号内数码为结点定位向量(力和位移均按竖直,转动方向顺序排列)。
求结构刚度矩阵[K]。
五、计算题(16分),图中圆括号内数码为结点定位向量 图a所示结构,不考虑轴向变形,整体坐标见图b,图中圆括号内数码为结点定位向量(力和位移均按水平、竖直、转动方向顺序排列)。
求等效结点荷载列阵。
六、计算题(16分)图示桁架,已知结点位移列阵。
试用矩阵位移法求单元①和单元③在局部坐标系下的杆端力列阵。
端力列阵。
设。
七、计算题(22分)。
求:图示体系各柱EI = 常数,柱高均为l,。
求:⑴体系的自振频率;⑴体系的自振频率;⑵最大动力弯矩及相应的弯矩图。
⑵最大动力弯矩及相应的弯矩图。
1. 48 12 2. 求各单元单刚:,( 转换成,单元②;利用单元定位向量,将中元素反号后叠加集成即,(取横梁为隔离体,有,可求,由位移法方程:,(如。
结构力学练习题及答案

结构力学练习题及答案(总42页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一. 是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分) 1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二. 选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; ; ; .23. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( )A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
=1F P482四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=×105 kN·m 2,用力法计算并作M 图。
五(本大题 11分) 用力矩分配法计算图示结构,并作M 图。
李廉锟《结构力学》(第5版)(下册)课后习题-第12章 结构动力学【圣才出品】

第12章 结构动力学复习思考题1.怎样区别动力荷载与静力荷载?动力计算与静力计算的主要差别是什么?答:(1)静力荷载:指施力过程缓慢,不致使结构产生显著的加速度,因而可以略去惯性力影响的荷载;动力荷载:指将使结构产生不容忽视的加速度,因而必须考虑惯性力的影响的荷载。
主要差别在于是否考虑惯性力的影响。
(2)计算上的差别:①计算式中是否加入惯性力的数值;②静力计算时,结构处于平衡状态,荷载的大小、方向、作用点及由它引起的结构的内力、位移等各种量值都不随时间而变化;而动力计算时,结构将发生振动,各种量值均随时间而变化;③动力分析方法常与荷载类型有关,而静力分析方法与荷载类型无关。
2.何谓结构的振动自由度?它与机动分析中的自由度有何异同?如何确定结构的振动自由度?答:(1)结构振动的自由度是指结构在弹性变形过程中确定全部质点位置所需的独立参数的数目。
(2)机动分析中的自由度简称静力自由度(又称动力自由度)。
①两者相同点:在数学意义上是一致的,都是强调体系空间质量所需的几何参量的个数。
②不同点:静力自由度是机构移动即刚体位移,排除了各个组成部件的变形运动;而动力自由度是变形位移导致机构位置改变,即体系变形过程质量的运动自由度。
(3)确定结构振动自由度的两种方法:①直接由确定质点位置所需的独立参数数目来判定;②加入最少数量的链杆以限制刚架上所有质点的位置,则该刚架的振动自由度数目即等于所加入链杆的数目。
3.建立振动微分方程有哪两种基本方法?每种方法所建立的方程代表什么条件?答:(1)建立振动微分方程的两种基本方法:刚度法和柔度法。
(2)刚度法代表力的平衡条件,柔度法代表变形协调条件。
4.为什么说结构的自振频率和周期是结构的固有性质?怎样改变它们?答:(1)自振频率和周期是结构的固有性质的原因:结构的自振频率和周期只取决于结构自身的质量和刚度,反映着结构固有的动力特性,而外部干扰力只能影响振幅和初相角的大小并不能改变结构的自振频率。
10结构的动力计算习题解答

各受弯杆 EI=常数,各链杆 EA=常数。
EI 0 =∞
EI
(a)
(a)
(b)
(d)
习习题题121-03图.3 图
【解】(a) 2;(b) 3;(c) 2;(d) 4,在两个质量上分别附加 2 个支杆。
习题 10.4 不考虑阻尼,列出习题 10.4 图所示体系的运动方程。
l l
振频率),其动力系数=__________。
m 2=2m
y (t)
2
m1=m
y (t)
1
习习题题 1102-.22((88)图)图
(8)
已知习题
10.2(8)图所示体系的第一主振型为
Y
(1)
1 2
,利用主振型
的正交性可求得第二主振型Y(2)= __________。
(9) 习题 10.2(9)图所示对称体系的第一主振型Y (1) = __________,第二主
2
8 EI
则
g 9.8 3.2 107 40s1
W 11
24.5 103 8
1
1
2 2
1
1
52.32 402
1.41
梁纯强迫振动时的最大动力弯矩图如习题 10.9(c)图所示。质点最大动位
移为
ymax
11FP
1.41
3.2
8 107
k11=12EI/l3
12EI/l3
6EI/l2
1
FPcost
-m y
6EI/l2
(a) M1 图及刚度系数 习题解 10.4(2)图
结构动力学习题+讲解

&&(t ) + (ω2 – n2 )S (t) = 0 --------------------------------------------(5) S
1.当 n >ω时(强阻尼) 方程(5)的解为: S (t) = A1sh n − ω t +A2ch n − ω t
2 2 2 2
从而,方程(4)的解为:
若时间 t 不是从 0 开始,而是从τ开始的,则(9)式写为:
y (t ) =
p∆t sinω(t-τ) mω
---------------------------------------(10)
写作: ,记ω2 =
K m
,2n =
C ,又可写作: m
& &(t ) + 2n y & (t ) +ω2 y (t ) = 0 y
利用常数变易法,令 y (t ) = e
− nt
---------------------------------------------(4)
S (t ) 代入方程(4)中 得:
K/2 VBA
48i/7L
2
A
取横梁为研究对象,Σ X=0,得:K= 4)振动方程
24 EI L3
即,
&(t ) - K y(t ) + Psinθt = 0 y - 2 m& &(t ) + y 2 m&
24 EI y(t ) = Psinθt L3
一、 无阻尼的自由振动
振动方程
&(t ) +K y (t ) = 0 , m& y & &(t ) + y K y (t ) = 0 m
10结构的动力计算习题解答,重庆大学,文国治版教材课后答案

第10章 结构的动力计算习题解答习题10.1 是非判断题(1) 引起单自由度体系自由振动的初速度值越大,则体系的自振频率越大。
( ) (2) 如果单自由度体系的阻尼增大,将会使体系的自振周期变短。
( ) (3) 在土木工程结构中,阻尼对自振周期的影响很小。
( )(4) 由于各个质点之间存在几何约束,质点体系的动力自由度数总是小于其质点个数。
( )(5) 多自由度的自振频率与引起自由振动的初始条件无关。
( ) (6) n 个自由度体系有n 个自振周期,其中第一周期是最长的。
( )(7) 如果考虑阻尼,多自由度体系在简谐荷载作用下的质点振幅就不能用列幅值方程的方法求解。
( )【解】(1) 错误。
体系的自振频率与初速度无关,由结构本身的特性所决定。
(2) 错误。
由阻尼结构的自振频率r ω=可知,阻尼增大使自振频率减小,自振周期变长。
(3) 正确。
(4) 错误。
由动力自由度的概念知,动力自由度数与计算假定有关,而与集中质量数目和超静定次数无关。
(5) 正确。
(6) 正确。
(7) 正确。
习题10.2 填空题(1) 单自由度体系运动方程为2P 2()/y y y F t m ξωω++=,其中未考虑重力,这是因为__________。
(2) 单自由度体系自由振动的振幅取决于__________。
(3) 若要改变单自由度体系的自振周期, 应从改变体系的__________或__________着手。
(4) 若由式()211βθω=-求得的动力系数为负值,则表示__________。
(5) 习题10.2(5)图所示体系发生共振时,干扰力与__________平衡。
Wsin θ t12-2(5)习题 图习题10.2(5)图(6) 求习题10.2(6)图所示质点系的自振频率时(EI =常数),其质量矩阵[M ]=__________。
m2m12-2(6)习题 图12-2(7)习题 图习题10.2(6)图 习题10.2(7)图(7) 习题10.2(7)图所示体系不考虑阻尼,EI =常数。
结构力学考试答案及试题

结构力学考试答案及试题一、单项选择题(每题2分,共20分)1. 在结构力学中,下列哪一项不是结构分析的基本假设?A. 结构由连续介质组成B. 结构在受力时不发生变形C. 结构在受力时不发生破坏D. 结构在受力时不发生材料性质变化答案:B2. 以下哪一项不是结构力学中常用的分析方法?A. 静力平衡法B. 能量法C. 虚功法D. 有限差分法答案:D3. 在结构力学中,下列哪一项不是结构的几何特性?A. 结构的形状B. 结构的尺寸C. 结构的材料性质D. 结构的连接方式答案:C4. 以下哪一项不是结构力学中的内力?A. 轴力B. 剪力C. 弯矩D. 温度应力答案:D5. 在结构力学中,下列哪一项不是结构的稳定性分析的内容?A. 屈曲分析B. 振动分析C. 失稳分析D. 极限荷载分析答案:B6. 在结构力学中,下列哪一项不是结构的静力分析的内容?A. 确定结构的内力B. 确定结构的变形C. 确定结构的稳定性D. 确定结构的动态响应答案:D7. 在结构力学中,下列哪一项不是结构的动力学分析的内容?A. 自由振动分析B. 强迫振动分析C. 随机振动分析D. 静力平衡分析答案:D8. 在结构力学中,下列哪一项不是结构的稳定性分析的方法?A. 欧拉屈曲理论B. 能量法C. 有限元法D. 虚功法答案:D9. 在结构力学中,下列哪一项不是结构的极限荷载分析的方法?A. 极限平衡法B. 能量法C. 虚功法D. 有限差分法答案:D10. 在结构力学中,下列哪一项不是结构的振动分析的方法?A. 单自由度系统分析B. 多自由度系统分析C. 连续系统分析D. 有限差分法答案:D二、多项选择题(每题3分,共15分)11. 结构力学中,下列哪些因素会影响结构的稳定性?A. 结构的几何形状B. 结构的材料性质C. 结构的连接方式D. 结构的荷载分布答案:ABCD12. 结构力学中,下列哪些因素会影响结构的内力分布?A. 结构的几何形状B. 结构的材料性质C. 结构的荷载大小D. 结构的边界条件答案:ABCD13. 结构力学中,下列哪些因素会影响结构的变形?A. 结构的几何形状B. 结构的材料性质C. 结构的荷载大小D. 结构的连接方式答案:ABCD14. 结构力学中,下列哪些因素会影响结构的振动特性?A. 结构的几何形状B. 结构的材料性质C. 结构的连接方式D. 结构的荷载大小答案:ABCD15. 结构力学中,下列哪些因素会影响结构的极限荷载?A. 结构的几何形状B. 结构的材料性质C. 结构的连接方式D. 结构的荷载分布答案:ABCD三、填空题(每题2分,共20分)16. 结构力学中,结构的________是指结构在受力时不发生破坏的能力。
(完整版)结构动力学-习题解答

解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
ml 3 T 2.027 ;
EI
m
EI y1(t)
l
l/2 l/2
l/4
7-1(b)试求图示体系的自振频率与周期。
解: 求柔度系数: 用位移法或力矩分配法 求单位力作用引起的弯矩图(图a); 将其与图b图乘,得
48EI 2k
T 2 ( 1 l3 1 )m
48 EI 2k
m
k EI
k
l/2
l/2
7-3 试求图示体系质点的位移幅值和最大弯矩值。
已知 0.6
l
解:
yst
FPl 3 EI
m
y1(t)
1
1
2
/
2
1.5625
位移幅值
A
yst
1.5625
FPl 3 EI
2l
yst
11
5 3
l3 EI
1 11
l
X11 0.4612 ; X12 4.336
X 21
X 22
12 7.965 EI / ml 3
2 2
65.53EI
/
ml 3
1 2.822 EI / ml3
8-6.试求图示刚架的自振频率和振型。设楼面质量分别为m1=120t和m2=100t,
柱的质量已集中于楼面, 柱的线刚度分别为i1=20MN.m和i2=14MN.m,横梁
m 2 A 0.3375 FP
l/2
EI=常数
FP sin t
2l
FP
FPl
结构动力学试题及答案

结构动力学试题及答案一、选择题(每题2分,共10分)1. 结构动力学中,动力响应分析通常不包括以下哪一项?A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案:C2. 在结构动力学中,下列哪一项不是确定结构动力特性的基本参数?A. 质量B. 刚度C. 阻尼D. 材料强度答案:D3. 单自由度振动系统的动力平衡方程中,下列哪一项是正确的?A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案:A4. 对于多自由度振动系统,下列哪一项不是求解动力响应的方法?A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案:C5. 在结构动力学中,阻尼比通常用来描述阻尼的相对大小,其定义为:A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案:B二、填空题(每题2分,共10分)1. 结构动力学中,当外力作用频率与结构的_________相等时,结构会发生共振。
答案:自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。
答案:位移分布模式3. 动力响应分析中,_________是指在给定的外力作用下,结构的响应随时间变化的过程。
答案:动力响应4. 在结构动力学中,_________是指结构在动力作用下,其响应与外力作用的关系。
答案:动力特性5. 阻尼比越大,结构的_________越小,振动衰减越快。
答案:振幅三、简答题(每题5分,共20分)1. 简述结构动力学中模态分析的目的和意义。
答案:模态分析的目的是确定结构的自振频率和振型,意义在于了解结构的动力特性,为结构设计提供依据,以及评估结构在动力作用下的安全性和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
(a)(b)6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
EI lW l/411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k,求自振频率ω。
EIW o ol/2l/2k 12、求图示体系的自振频率ω。
m l EI EIl0.5l0.5213、求图示体系的自振频率ω。
EI = 常数。
mll0.514、求图示结构的自振频率ω。
ml l l lEI=常数15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
m16、求图示体系的自振频率ω。
杆长均为l 。
EA=o oEIm EI EI17、求图示结构的自振频率和振型。
mmEIEI EIl /2l /2l /218、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
EI WA B C 2m 2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
hEI EI W20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
h EI EI WEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
ma a a 222、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
m l /2l /2EI EI (a)m l /2l /2EI EI(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
C3W m 3m 4m24、忽略质点m 的水平位移,求图示桁架竖向振动时的自振频率ω。
各杆EA = 常数。
m m 4m 4m325、图示体系E P W I =⨯====-2102052048004kN /cm s kN, kN, cm 214,,θ。
求质点处最大动位移和最大动弯矩。
W EI4m m 2sin θP t26、图示体系EI k =⨯⋅==2102035kN m s 2-1,,θ×1055N /m, P =×N 103。
kN W 10=。
求质点处最大动位移和最大动弯矩。
m 2Wk m 2sin θP t27、求图示体系在初位移等于l/1000,初速度等于零时的解答。
θωω=020.( 为自振频率),不计阻尼。
sin θP t mEI EI EI =1oo l l28、图示体系受动力荷载作用,不考虑阻尼,杆重不计,求发生共振时干扰力的频率θ。
mEIEI =1l /3l P t sin( ) θo o29、已知:m P ==38t, kN ,干扰力转速为150r/min ,不计杆件的质量,EI =⨯⋅6103kN m 2。
求质点的最大动力位移。
2sin θP tm 2m mEIEI30、图示体系中,电机重kN 10=W 置于刚性横梁上,电机转速n r =500/min ,水平方向干扰力为) sin(kN 2)(t t P θ⋅=,已知柱顶侧移刚度kN/m 1002.14⨯=k ,自振频率ω=-100s 1。
求稳态振动的振幅及最大动力弯矩图。
( )P t Wm 431、图示体系中,kN 10=W ,质点所在点竖向柔度917.1=δ,马达动荷载P t t ()sin()=4kN θ,马达转速n r =600/min 。
求质点振幅与最大位移。
WP t ()32、图示体系中,W =8kN ,自振频率ω=-100s 1,电机荷载P (t ) = 5kN ·sin(θt ),电机转速n = 550r/min 。
求梁的最大与最小弯矩图。
W2m 2m P t ()33、求图示体系支座弯矩M A 的最大值。
荷载P t P t (),.==004sin θθω 。
l l /2m/2P t ()A34、求图示体系的运动方程。
l l m0.50.5EI P t sin( )θ35、求图示体系稳态阶段动力弯矩幅值图。
θωω=05.( 为自振频率),EI = 常数,不计阻尼。
l l ml sin( ) θP t36、图示体系分布质量不计,EI = 常数。
求自振频率。
m22a a m 137、图示简支梁EI = 常数,梁重不计,m m m m 122==,,已求出柔度系数()δ123718=a EI /。
求自振频率及主振型。
2a a 1a m 1m 238、求图示梁的自振频率及主振型,并画主振型图。
杆件分布质量不计。
2a a 1a mm EI= 常 数39、图示刚架杆自重不计,各杆EI = 常数。
求自振频率。
m2m m 2m 2m1240、求图示体系的自振频率和主振型。
EI = 常数。
l l m l m/3/3/341、求图示体系的自振频率及主振型。
EI = 常数。
m l /2l /2ml /2l /242、求图示体系的自振频率及相应主振型。
EI = 常数。
m /2l 2lm/2l /2l /2l43、求图示结构的自振频率和主振型。
不计自重。
l /2l /2mlEI= 常 数44、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
mm a 12a a45、求图示体系的第一自振频率。
mm l /2l /2l /2l /2EI =常 数46、求图示体系的自振频率。
已知:m m m 12== 。
EI = 常数。
m m 21m 1.51m 1.5m 1m 1m47、求图示体系的自振频率和主振型,并作出主振型图。
已知:m m m 12==,EI = 常数。
2m m 1m 24m 4m48、求图示对称体系的自振频率。
EI = 常数。
l l m l l m/2/2/2/249、图示对称刚架质量集中于刚性横粱上,已知:m 1=m ,m 2=2m 。
各横梁的层间侧移刚度均为k 。
求自振频率及主振型。
m 1m 22150、求图示体系的自振频率并画出主振型图。
moo E I =1EIEI moo E I =1EI EI 6m6m51、求图示体系的自振频率和主振型。
EI = 常数。
m ml l l l 12EI 0=o oEI 0=o o EIEIEIEI52、用最简单方法求图示结构的自振频率和主振型。
mmEI= l l ll 常 数53、求图示体系的频率方程。
llmmEI= 常 数54、求图示体系的自振频率和主振型。
EI =常数。
m2a aa55、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
mm a /2a /2a /2a /21256、求图示体系的自振频率。
设 EI = 常数。
mll57、图示体系,设质量分别集中于各层横梁上,数值均为m 。
求第一与第二自振频率之比ωω12:。
m m llEI 02EIEIo oEI2EIEI 0o o58、求图示体系的自振频率和主振型。
lllm m 2EI =∞ EI =∞ EI1EI 12EI 12EI 159、求图示体系的自振频率和主振型。
m m m m 122==,。
llm 1m2EIEI 2EI260、求图示桁架的自振频率。
杆件自重不计。
Wm 3m3EAEAm461、求图示桁架的自振频率。
不计杆件自重,EA = 常数。
mm mm33462、作出图示体系的动力弯矩图,已知:θ=0825673.EIml 。
0.5l0.5lEI EI 12m m ()P t sin θ63、作图示体系的动力弯矩图。
柱高均为h ,柱刚度EI =常数。
l lm12θ=13257.EImh30.50.5EI 0=∞EI 0=∞m2P tsin θ64、绘出图示体系的最大动力弯矩图。
已知:动荷载幅值P =10kN ,θ=-209441.s ,质量m =500kg ,a =2m ,EI =⨯⋅481062.N m 。
mm()P t sinθ()P t sin θa4a65、已知图示体系的第一振型如下,求体系的第一频率。
EI = 常数。
振型101618054011 ..⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪ /2mllmm l123第九章 结构的动力计算(参考答案)1、(X)2、(X)3、(X)4、(X)5、(O)6、(O)7、(O)8、(X)9、(X)10、ω=19253EIg Wl / 11、()ω=4kg /W12、)/(16,48/332311ml EI EI l ==ωδ13、)5/(48,48/5323ml EI EI l ==ωδ14、33477.11124ml EIml EI ==ω15、)5/(3,3/5323ml EI EI l ==ωδ16、323119,/9ml EIl EI k ==ω 17、()06424 , 5.123213231=--=A l m A l m EI mlEIωωω, 0)248(3 , 28.423213232=-+=A EI l m A l m mlEI ωωω 振 型 11.1 1.110.451.110.45振 型 218、1s 2.54-=ω19、()T WhEIg =263π/20、()T WhEIg =2483π/21、)/(889.23ma EI =ω22、2:1:=b a ωω23、)/(56.16EAg W T =24、m EA m 5.10//1==δω25、cmYstp Y M ml EI 3029.1,,127.3)/1/(1,s 25.24)2/8/(Max Mstp Dmax 22-1====-===μμωθμω26、ωδ==+=-1143143416//(//).m m EI k s 1 μθω=-=11152222/(/).m,006.0stp max ==y Y D μ ,m, kN 61.7Dmax ==stp M M μ27、),sin(04167.1)sin(20833.0)cos(001.0,1000/ ,),cos()cos()sin(,04067.1 ,/st st st 22st t Y t Y t l Y l B Y A t m Pt B t A Y m P Y DD D θωωωθμθμωωωμω+-===++===28、)/(273ml EI =θ29、-1s 92.38=ω ,-1s 71.15=θ ,19.1=μ ,m 10/09.23max =y 30、,378.1 ,s 36.52-1==βθ,mm 27.0 m,9610.1st 4st ===-y A y βMM F M D 756.2==β31、,s 83.62 ,s 50.71-1-1==θω;β=4389. ;A F ==βδ337.mm ;m m 28.5)(max =+=δβF w y32、θβ==575961496.,.s -1,M F M M D ==β748. ,{}M M M M TD 52.0 48.15st max =+=33、333 , 3l EIk ml EI ==ω,运动方程: mPy yk ky y m P 165, 21=+∆⋅=+ω 特征解y *:y P m t P mt *sin .sin =-=51600595222ωθωθθ11()l P M t l P t l P l P Pll ym M A A 0max 000*56.0, sin 56.0 sin )20595.0(2==+=+=θθ 34、 16)sin(533t P y l EI ym θ=+35、))(sit (3,3/4,4/3st t EIPlY EI Pl Y θμ-=== Pl P13/24Pl /1236、{}EIma /1211.02123.3/1T32==ωλ)/(874.2,)/(558.03231ma EI ma EI ==ωω37、{}EI ma /07350.0125984.0/1T32==ωλ)/(|6886.3,)/(8909.03231ma EI ma EI ==ωω954.0/1/2111=Y Y ,()097.2/1/2212-=Y Y38、EIa EI a 6/,3/231232211===δδδ,)/(414.1,)/(0954.13231ma EI ma EI ==ωω{}λω==1561223////ma EI T,Y Y Y Y 112112221111//,//()==-M 1M 2a11a第 二 主 振 型第 一 主 振 型图图111139、EI EI EI 2834122211-===δδδ,,,⎭⎬⎫⎩⎨⎧==779.0554.812EI m ωλm EIm EI 1328.1,3419.021==ωω40、对称:,162/53EI l =δ,)/(69.52/131ml EI =ω反对称:,/00198.03EI l =δ,)/(46.222/132ml EI =ω41、EIl EI l EI l 96/5,24/,48/532112322311====δδδδ3231/054.9,/736.2ml EI ml EI ==ωω111.7660.565{}[]Φ1105653=.,()T分{}[]Φ2117663=-.()T分42、对称:,)/(191.2 ,24/52/132311ml EI EI l ==ωδ反对称:δδδ1132112348===l EI l EI /,/ ,δ22348=l EI /,,)/(69.7,)/(5.02/1322/131ml EI ml EI ==ωω{}[]Y 1=1 0.03 -0.03T,{}[]Y 2=0 1 1T,,{}[]Y 3=1 -31.86 31.86T43、ωω13231282==.,.,EI ml EIml 1.01,4.101,16,382,482212211132112322311-======Y Y Y Y EI l EI l EI l δδδδ 44、321321/2.397.0;/0975.007.1ma EI EI ma ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=ωωλλ61.3/;28.0/)2(2)2(1)1(2)1(1+=-=A A A A45、3/48ml EI =ω46、),/(7708.1,/)(4393.0),/(3189.0),/(1818.5),/(6875.1),/(1),/(5.4212121122211m EI m EI EI m EI m EI EI EI ====-====ωωλλδδδδ47、)/(6664.2),/(6645.12)3/(32),/(4),3/(142122211211EI m EI m EI EI EI ===-===λλδδδδ5.0:1:,2:1:)/(6124.0,)/(281.022********=ΦΦ-=ΦΦ==m EI m EI ωω 48、31/47.10ml EI =ω,,/86.1332ml EI =ω49、k k k k k k k 112212212====-,,ωωω21222808021920468215102=⎧⎨⎩⎫⎬⎭==k m k m km..,.,.Y Y Y Y 112112221178110281==-.,. 50、k i l k k i l k i l 112211222226630===-=/,/,/,ω11/20146=.(/)EI m ,2/12)/(381.0ml EI =ω,{}[]{}[]TT4.24- 1,0.236 121=Φ=Φ51、k EI l k EI l k EI l 1131232231812998==-=/,/,/,ωω132316925245==.,.EI m l EIm l52、利用对称性: 反对称:δω11313366245===l EIEI m l EIm l ,. , 对称:δω1132339696737===l EIEI m l EIm l ,. 53、列幅值方程:δωδωδωδω1121222122222222m x m y x m x m y y +=+=⎫⎬⎭,21210211122221112m m m m ωδδωωδδω--=, δδδδ113122132233243====l EI l EI l EI,, mm xω2m yω2m xω2xy11δ11δ21δ12δ2254、对称:δω223230183333032==.,.a EI EIma反对称:δω11313407071==a EI EIma ,. 55、对称:11δ11324=a EI /(),ω1324=EI ma /()反对称:11δ1137768=a EI /(),ω137687=EI ma /()56、ωω132********==./,./EI ml EI ml57、设k EI l =243/ 频率方程:()()()22,024,0322242222±==+-=---mkk km m km k m k ωωωωω828.5:11:1716.0:21==ωω58、ωω14241248==EIml EIml ,,ΦΦΦΦ11211222051==-., 59、k EI l k EI l k EIl 1131232233351==-=,, []M m EI ml EIml =⎡⎣⎢⎤⎦⎥==100216735071323,.,. ωω,[]Φ=-⎡⎣⎢⎤⎦⎥1114020132.. 60、W EAg W EAg /506.0,/379.021==ωω61、ωω12034048==././EA m EA m , 62、EIPl A A EI l EIl EI l 3213223123111397.00531.0348524⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧===,,,δδδ 061332.Pl0047612.Pl63、《结构力学》习题集 (下册)—— 36 —— EIPh A A h EI k h EI k h EI k 3213123223110500.00538.0242448⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧-===,,,0.0252Ph 0.3220Ph0.347Ph64、反对称结构:δ=8EI,ω=-346411.s ,μ=15762. 两竖杆下端动弯矩为31524.kN m ⋅,左侧受拉。
