中缀表达式求值

合集下载

c++ 中缀表达式

c++ 中缀表达式
C++ 中缀表达式（Infix Expression）是指运算符位于操作数之
间的表达式，例如：a + b * c。

在C++中，中缀表达式的求值需要遵循运算符的优先级和结
合性规则。

一般来说，乘法、除法、取模运算的优先级最高，加法、减法运算的优先级较低。

在编写C++程序时，为了正确求解中缀表达式，可以使用以
下方法之一：
1. 使用栈进行中缀表达式的转换和求解。

2. 使用递归函数或逆波兰表达式将中缀表达式转换成后缀表达式，然后使用栈进行后缀表达式的求解。

例如，给定中缀表达式 a + b * c，可以使用栈的方法求解：
1. 创建一个空栈用于存储运算符和操作数。

2. 遍历中缀表达式的每个字符，按以下规则处理：
- 如果遇到操作数，则将其压入栈中。

- 如果遇到运算符，则根据其优先级和结合性，判断是否需
要将运算符从栈中弹出并进行运算。

然后将运算结果压入栈中。

- 如果遇到左括号，则直接将其压入栈中。

- 如果遇到右括号，则取出栈中的运算符和操作数，直到遇
到左括号为止，并进行相应的运算。

最后将运算结果压入栈中。

3. 遍历完中缀表达式后，栈中最后一个元素即为表达式的结果。

注：以上只是一种求解中缀表达式的方法，实际求解方法可能有其他的实现方式。

关于中缀表达式求值（四则运算和括号，支持多位数）

关于中缀表达式求值（四则运算和括号，⽀持多位数）1.中缀转后缀和计算后缀表达式 1.1 中转后1. 数字则输出2. 如果是 "(" ,直接⼊栈3. 如果是 ")", 栈顶元素出栈并输出，直到遇到" ("，只弹出。

4. 如果栈空，直接⼊栈，否则和栈顶⽐较优先级，当⼤于栈顶时，⼊栈，否则，栈顶元素退栈，直到⼤于栈顶或栈空5. 中缀表达式扫描完毕，若栈不空，将其内所有元素弹出。

1.2 计算后缀1. 数字则⼊栈2. 运算符，出栈b,再出栈a 计算c=a operate b,将c⼊栈3. 中缀表达式扫描完毕，将栈内唯⼀的元素（也就是求的值）弹出并返回。

2.代码如下import java.util.*;import java.util.regex.Matcher;import java.util.regex.Pattern;;public class Test4 {private static Map<Character,Integer> map=new HashMap<>();static {map.put('+', 0);map.put('-', 0);map.put('*', 1);map.put('/', 1);}private static List<String> toPost(String target){List<String> post=new ArrayList<>();Stack<Character> stk=new Stack<>();Pattern p=pile("\\d+|\\D");Matcher m=p.matcher(target);while(m.find()) {String e=m.group();if(e.matches("\\d+"))post.add(e);else if(e.equals("("))stk.push('(');else if(e.equals(")")){while(stk.peek()!='(')post.add(stk.pop()+"");stk.pop();}else {char op=e.charAt(0);while(!stk.isEmpty()&&stk.peek()!='('&&map.get(op)<=map.get(stk.peek()))post.add(stk.pop()+"");stk.push(op);}}while(!stk.isEmpty()) post.add(stk.pop()+"");return post;}private static int calcuPost(List<String> post) {Stack<Integer> stk=new Stack<>();for(String s:post) {if(s.matches("\\d+")) stk.push(Integer.parseInt(s));else {char c=s.charAt(0);int b=stk.pop();int a=stk.pop();int t=0;if(c=='+')t=a+b;else if(c=='-')t=a-b;else if(c=='*')t=a*b;elset=a/b;stk.push(t);}}return stk.pop();}public static void main(String[] args) {Scanner is=new Scanner(System.in);while(is.hasNext()) {String exp=is.next();System.out.println(calcuPost(toPost(exp))); }is.close();}}。

表达式求值算法总结(C++)

表达式求值算法总结(C++)表达式求值，一般采用栈和队列的方式来求值，下面介绍表达式求值的两种算法。

方法一、使用两个栈，一个为操作符栈OPTR(operator)，一个是操作数栈OPND(operand)算法过程：当输入3 * ( 4 - 1 * 2 ) + 6 / ( 1 + 1 )时，为简单方便，我们输入时，按照字符的顺序一个一个的处理，比如ch = getchar()。

然后根据ch 的值判断：若ch 是数字，直接压入操作数栈OPND；若ch 是'('，直接入栈OPTR;若ch 是')'，若OPTR 和OPND 非空，弹出OPTR的栈顶操作符，弹出OPND栈顶的两个操作数，做运算，然后见个结果压入栈OPND，直到弹出的OPTR栈顶元素时')';若ch 是操作符(比如+, -, *, /)，如果OPTR栈顶元素是(，直接入栈OPTR，如果不是'('且OPTR栈非空且栈顶元素操作符的优先级大于ch，那么弹出OPTR的栈顶操作符，并弹出OPND中栈顶的两个元素，做运算，将运算结果入栈OPND，此时，重复这一步操作；否则将ch入栈OPTR；若ch为EOF，说明表达式已经输入完成，判断OPTR是否为空，若非空，一次弹出OPTR 栈顶操作符，并与OPND栈顶两个元素做运算，将运算结果入栈OPND，最后表达式的结果即OPND的栈底元素。

以表达式3 * ( 4 - 1 * 2 ) + 6 / ( 1 + 1 )为例，计算过程如下所示：通过上述的计算过程，写出伪代码如下所示：void GetExpress(Stack * OPTR, Stack * OPND){char ch;while ((ch = getchar ()) != EOF) {if (IsDigit (ch)) {PushStack (OPND, ch);}else if (ch == '(')PushStack (OPTR, ch);else if (ch == ')') {while (!IsStackEmpty(OPTR)) {PopStack (OPTR, op);if (op == ')')break;PopStack (OPND, num2);PopStack (OPND, num1);res = Calc (num1, num2, op);PushStack (OPND, res);}}else if (ch == '+' || ch == '-'|| ch == '*' || ch == '/') {while (!IsStackEmpty (OPTR) && GetTop (OPTR)!='(' && GetTop (OPTR)>ch) { PopStack (OPTR, op);PopStack (OPND, num2);PopStack (OPND, num1);res = Calc (num1, num2, op);PushStack (OPND, res);}if (IsStackEmpty (OPTR) || GetTop(OPTR)=='(')PushStack (OPTR, ch);}}}// 当表达式输入完成后，需要对OPTR栈和OPND中的元素进行运算int GetValue(Stack * OPTR, Stack * OPND){while (!IsStackEmpty (OPTR)) {PopStack (OPTR, op);PopStack (OPND, num2);PopStack (OPND, num1);res = Calc (num1, num2, op);PushStack (OPND, res);}// 最后的操作数栈OPND栈顶元素即是表达式的值return GetTop(OPND);}PS: 上面没有指出表达式非法的情况方法二：采用中缀表达式的方法，求取表达式的中缀表达式，借用一个操作符栈OPTR和中缀表达式队列Queue，求取中缀表达式，然后对中缀表达式求值。

中缀表达式求值

中缀表达式求值所⽤知识：C语⾔，堆栈操作算法思想来⾃慕课浙江⼤学《数据结构》陈⽼师，何⽼师笔记：1.堆栈：1.1 引⼦⼀种数据结构，在函数调⽤，表达式求值等都有⼴泛的应⽤中缀表达式：a+b*c-d/e:⽣活中经常使⽤，但是计算机不好识别后缀表达式：abc*+dc/-:⽣活中不好使⽤，但计算机容易识别例：总结：因此需要⼀种存储⽅法，能顺序的存储运算数，在需要时倒叙输出。

-->堆栈有堆栈的特点：后⼊先出。

1.2堆栈的操作操作集：长度为maxSize的堆栈S ==> stack,堆栈的元素elementType，那么如下的操作stack createStack(int maxSize);//⽣成空堆栈，其最⼤长度为maxSizeint isFull(stack s,int maxSize);//判断栈s是否为空void push(stack s,elementType item);//将元素压⼊堆栈int isEmpty(stack s);//判断堆栈是否为空elementType pop(stack s);//删除并返回栈顶元素1.2.1⽤数组来表⽰堆栈的⽅法可以参照⽂件夹下⾯的同级⽬录的⽂件stackArray.c同时还有使⽤⼀个数组来表⽰两个堆栈，twoStack.c1.2.2使⽤链表来模拟堆栈因为链表有两头，但是堆栈的头指针我们会选择链表的头节点，因为便于删除操作，尾节点不⽅便进⾏删除操作下⾯是模拟的⽰意图head(头指针，没有元素的) --> node1(top指针) --> node2(堆栈中的元素) --> node3 --> node4代码可以见：stackLinkList.c1.2.3 利⽤堆栈进⾏表达式求值我们平时所见到的表达式都是中缀表达式，但是如果想求表达式的值，先把中缀表达着中⽂后缀表达式，在利⽤堆栈对后缀表达式进⾏求值中缀表达式转后缀表达式的思路；⾸先看⼀个简单的：中缀表达式：2 + 9 / 3 - 5 后缀表达式：2 9 3 / + 5 -通过对⽐我们发现，中缀表达式和后缀表达式的数字顺序并没有发⽣改变，只是符号位置发⽣了改变所以，我们可以构思，使⽤⼀个栈来存在运算符，遇到数字就输出，遇到符号就压栈，如果读⼊的符号⽐栈顶的符号优先级⾼，就压栈，否则就弹栈并输出下⾯是中缀表达式：2 + 9 / 3 - 5压栈和弹栈的具体步骤输出堆栈内元素2+9/(优先级⽐+⾼，压栈)3/ + -(⾸先弹出/,但是因为同级运⾏需要按照从左往右的运算，所以+也需要弹栈)5 -- (元素全部读取完毕以后，-弹栈)所以中缀表达式：2 + 9 / 3 - 5的后缀表达式为 2 9 3 / + 5 -但是如果遇到带有()的表达式怎么办：遇到"("把"("压⼊栈中，此时栈中的"("运算级别最低，在按照上⾯的运算符的运算规则来进⾏压栈和弹栈。

数据结构表达式求值(中缀)实验报告

数据结构表达式求值（中缀）实验报告题目名称表达式求值学号姓名指导教师日期一1. 问题描述：在计算机中，算术表达式由常量、变量、运算符和括号组成。

由于不同的运算符具有不同的优先级，又要考虑括号，因此，算术表达式的求值不可能严格地从左到右进行，在程序设计时，借助栈实现。

2. 表达式求值这个程序，主要利用栈和数组，把运算的先后步骤进行分析并实现简单的运算，以字符列的形式从终端输入语法的正确的、不含变量的整数表达式。

利用已知的算符优先关系，实现对算术四则运算的求值，在求值中运用栈、运算栈、输入字符和主要操作的变化过程。

该程序相当于一个简单的计算机计算程序，只进行简单的加减乘除和带括号的四则运算。

1、基本思想（中缀表达式求值）要把一个表达式翻译成正确求值的一个机器指令序列，或者直接对表达式求值，首先要能够正确解释表达式，要了解算术四则运算的规则即：（1）先乘除后加减；（2）从左到右计算；（3）先括号内，后括号外。

下表定义的运算符之间的关系:b + - * / （） # a+ > > < < < > > _ > > < < < > > * > > > > < > > / > > > > < > > ( < < < < < = ) > > > > > > # < < < < < =为了实现运算符有限算法，在程序中使用了两个工作栈。

分别是：运算符栈OPTR,操作数栈OPND.基本思想：（1）首先置操作数栈为空栈，表达式起始符“#”为运算符栈的栈底元素；（2）依次读入表达式中每个字符，若是操作数则进OPND栈，若是运算符则和OPTR栈得栈顶运算符比较优先级后作相应操作。

中缀表达式求值（C++实现）

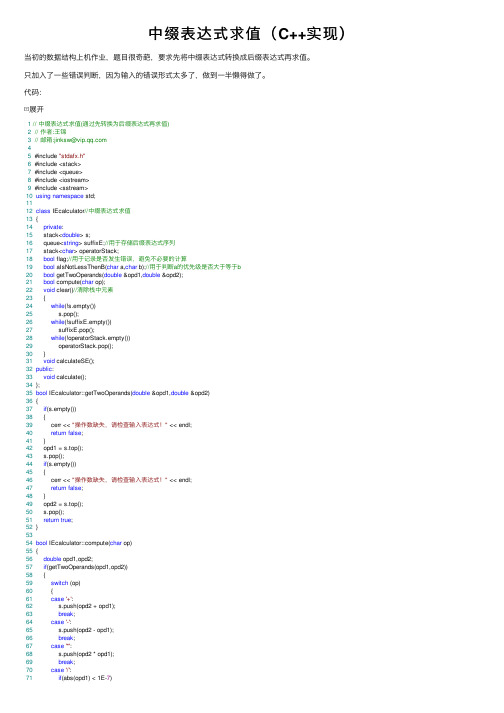
中缀表达式求值（C++实现）当初的数据结构上机作业，题⽬很奇葩，要求先将中缀表达式转换成后缀表达式再求值。

只加⼊了⼀些错误判断，因为输⼊的错误形式太多了，做到⼀半懒得做了。

代码：展开1// 中缀表达式求值(通过先转换为后缀表达式再求值)2// 作者:王锦3// 邮箱:jinksw@45 #include "stdafx.h"6 #include <stack>7 #include <queue>8 #include <iostream>9 #include <sstream>10using namespace std;1112class IEcalculator//中缀表达式求值13 {14private:15 stack<double> s;16 queue<string> suffixE;//⽤于存储后缀表达式序列17 stack<char> operatorStack;18bool flag;//⽤于记录是否发⽣错误，避免不必要的计算19bool aIsNotLessThenB(char a,char b);//⽤于判断a的优先级是否⼤于等于b20bool getTwoOperands(double &opd1,double &opd2);21bool compute(char op);22void clear()//清除栈中元素23 {24while(!s.empty())25 s.pop();26while(!suffixE.empty())27 suffixE.pop();28while(!operatorStack.empty())29 operatorStack.pop();30 }31void calculateSE();32public:33void calculate();34 };35bool IEcalculator::getTwoOperands(double &opd1,double &opd2)36 {37if(s.empty())38 {39 cerr << "操作数缺失，请检查输⼊表达式！" << endl;40return false;41 }42 opd1 = s.top();43 s.pop();44if(s.empty())45 {46 cerr << "操作数缺失，请检查输⼊表达式！" << endl;47return false;48 }49 opd2 = s.top();50 s.pop();51return true;52 }5354bool IEcalculator::compute(char op)55 {56double opd1,opd2;57if(getTwoOperands(opd1,opd2))58 {59switch (op)60 {61case'+':62 s.push(opd2 + opd1);63break;64case'-':65 s.push(opd2 - opd1);66break;67case'*':68 s.push(opd2 * opd1);69break;70case'/':71if(abs(opd1) < 1E-7)73 cerr << "除数不能为0，请检查表达式" << endl;74 clear();75return false;76 }77 s.push(opd2 / opd1);78break;79default:80break;81 }82 }83else84 {85 clear();86return false;87 }88 }8990void IEcalculator::calculateSE()91 {92string expressionStream;93while(!suffixE.empty())94 {95 expressionStream+=""+suffixE.front();96 suffixE.pop();97 }98 expressionStream += "=";99 istringstream iss(expressionStream,istringstream::in);//将expressionStream作为输⼊流100char c;101double newOperand,result;102bool isRight = true;//compute(c)函数返回标志，若出现除数为0错误，则不再计算103while(iss >> c, isRight && c != '=')104 {105switch (c)106 {107case'+':108case'-':109case'*':110case'/':111 isRight = compute(c);112break;113default:114 iss.putback(c);115 iss >> newOperand;116 s.push(newOperand);117break;118 }119 }120if(isRight)121 {122 result = s.top();123 s.pop();124if(s.empty())125 cout << "result = " << result << endl;126else127 {128 cerr << "表达式操作数剩余！" << endl;129 }130 clear();131 }132else133 {134 clear();135 }136 }137bool IEcalculator::aIsNotLessThenB(char a,char b)138 {139switch (a)140 {141case'(':142return true;143case'+':144case'-':145switch (b)146 {147case'(':148case'*':149case'/':150return false;151default:152return true;153break;154 }155case'*':157switch (b)158 {159case'(':160return false;161default:162return true;163break;164 }165default:166break;167 }168 }169void IEcalculator::calculate()170 {171 flag = true;172double newOperand;173string tempStr = "";//⽤于将字符转换为字符串174char c;175while(cin >> c,c != '=' && flag)176 {177switch (c)178 {179case'+':180case'-':181case'*':182case'/':183while(!operatorStack.empty() && aIsNotLessThenB(operatorStack.top 184185 (),c) &&operatorStack.top() != '(')186 {187 suffixE.push(operatorStack.top()+tempStr);188 operatorStack.pop();189 }190 operatorStack.push(c);191break;192case'(':193 operatorStack.push(c);194break;195case')':196while(!operatorStack.empty() && operatorStack.top() != '(')197 {198 suffixE.push(operatorStack.top()+tempStr);199 operatorStack.pop();200 }201if(operatorStack.empty())//此时栈空则错误202 {203 flag = false;204 clear();205break;206 }207 operatorStack.pop();208break;209default:210 cin.putback(c);211 cin >> newOperand;212string str;213 stringstream ss;214 ss<<newOperand;215 ss>>str;216 suffixE.push(string(str));217break;218 }219 }220while(!operatorStack.empty())221 {222if(operatorStack.top() == '(')223 {224 flag = false;225break;226 }227 suffixE.push(operatorStack.top()+tempStr);228 operatorStack.pop();229 }230if(flag)231 {232 calculateSE();233 }234else235 cerr << "表达式输⼊有误，请重试" << endl;236 clear();237 }238239int _tmain(int argc, _TCHAR* argv[])240 {241 cout << "请输⼊中缀表达式,以=结束:(q退出)" << endl; 242char c;243 cin >> c;244while(c != 'q')245 {246 cin.putback(c);247 IEcalculator test;248 test.calculate();249 cout << "请输⼊中缀表达式,以=结束:(q退出)" << endl; 250 cin >> c;251 }252253 }。

中缀表达式值

中缀表达式值的求解方法。

中缀表达式值的求解方法中缀表达式是我们常见的数学表达式形式，如 3 + 4.2×(8-5)，但是对于计算机而言，更容易处理的是后缀表达式或前缀表达式，因此我们需要将中缀表达式转换成后缀表达式或前缀表达式，再进行计算。

而将中缀表达式转换成后缀表达式或前缀表达式的过程，就称为表达式的转换。

本文将介绍两种方法，一种是使用栈的方法，另一种是使用递归的方法。

无论哪种方法，我们首先需要了解中缀表达式中的运算符的优先级和结合性。

运算符的优先级和结合性在中缀表达式中，我们常见的运算符有加减乘除、括号等，它们的优先级和结合性如下：运算符 | 优先级 | 结合性:--------:|:------:|:------:( ) | 无 | 左结合+ - | 1 | 左结合× ÷ | 2 | 左结合其中，优先级数字越大，优先级越高。

左结合表示从左往右计算，右结合表示从右往左计算。

使用栈的方法栈是一种后进先出的数据结构，对于中缀表达式的转换，我们可以使用栈来存储运算符。

具体过程如下：1. 创建两个栈，一个用来存储运算符，一个用来存储中间结果；2. 从左到右遍历中缀表达式中的每一个元素；3. 如果是数字，则直接压入中间结果栈；4. 如果是运算符，则判断与运算符栈栈顶元素的优先级，如果优先级较高，则直接入栈；如果优先级较低，则将运算符栈中优先级较高的运算符弹出，压入中间结果栈，直到优先级相等或者运算符栈为空，再将该运算符压入运算符栈；5. 如果是左括号，则直接压入运算符栈；6. 如果是右括号，则将运算符栈中从左到右第一个左括号上面的运算符全部弹出，压入中间结果栈，将左括号弹出丢弃；7. 遍历完中缀表达式后，将运算符栈中的所有运算符弹出，压入中间结果栈。

根据上述过程，我们可以将中缀表达式 3 + 4.2×(8-5) 转换成后缀表达式 3 4.2 85 - × +。

中缀表达式求值

#include<stdio.h>#include<stdlib.h>#define MAX 50typedef struct{char data[MAX];int top;}stack;typedef struct{float data[MAX];int top;}fstack;stack* create(){stack *s;s=malloc(sizeof(stack));s->top=-1;return s;}fstack* fcreate(){fstack *s;s=malloc(sizeof(fstack));s->top=-1;return s;}int getstack(stack *s,char x ) {if(s->top==MAX-1)return 0;s->top++;s->data[s->top]=x;return 1;}int fgetstack(fstack *s,float x ) {if(s->top==MAX-1)return 0;s->top++;s->data[s->top]=x;return 1;}int outstack(stack *s,char *x) {if(s->top==-1)return 0;*x=s->data[s->top];s->top--;return 1;}int foutstack(fstack *s,float *x){if(s->top==-1)return 0;*x=s->data[s->top];s->top--;return 1;}char readstack(stack *s){char x;if(s->top==-1)return '0';x=s->data[s->top];return x;}float freadstack(fstack *s){float x;if(s->top==-1)return '0';x=s->data[s->top];return x;}char bi(char x1,char x2)//>出站；<进站；{switch(x1){case '(':switch(x2){case ')':return '>';break;default:return '<';break;}break;case '+':case '-':switch(x2){case '(':return '<';break;case '*':return '<';break;case '/':return '<';break;default :return '>';}break;case '*':case '/':switch(x2){case '(':return '<';break;default :return '>';}break;}return '0';}float jisuan(float x1,char a,float y1) {switch(a){case '+':return x1+y1;case '-':return x1-y1;case '*':return x1*y1;case '/':return x1/y1;}return 0;}float fun1(char a[]){float b,b1,b2,b3;int i=0;char x,x1,ch;stack *s=create();fstack *p=fcreate();getstack(s,'(');ch=a[0];while(ch!='#'){switch(ch){case '(':getstack(s,'(');break;case ')':while(readstack(s)!='('){outstack(s,&x);foutstack(p,&b1);foutstack(p,&b2);b3=jisuan(b1,x,b2);fgetstack(p,b3);}outstack(s,&x);break;case '+':case '-':x=readstack(s);x1=bi(x,ch);if(x1=='<')getstack(s,ch);else{while(readstack(s)!='('){outstack(s,&x);foutstack(p,&b1);foutstack(p,&b2);b3=jisuan(b1,x,b2);fgetstack(p,b3);}getstack(s,ch);}break;case '*':case '/':x=readstack(s);x1=bi(x,ch);if(x1=='<')getstack(s,ch);else{while(readstack(s)!='('&&readstack(s)!='+'&&readstack(s)!='-'){outstack(s,&x);foutstack(p,&b1);foutstack(p,&b2);b3=jisuan(b1,x,b2);fgetstack(p,b3);}getstack(s,ch);}break;default :if(ch>='0'&&ch<='9'){fgetstack(p,(ch-'0'));printf("%f\n",freadstack(p));}break;}ch=a[++i];}while(readstack(s)!='('){outstack(s,&x);foutstack(p,&b1);foutstack(p,&b2);b3=jisuan(b1,x,b2);fgetstack(p,b3);}b=freadstack(p);return b;}int main(){int i;float b;char a[MAX];for(i=0;;i++){scanf("%c",&a[i]);if(a[i]=='#')break;}b=fun1(a);printf("====%f\n",b); }。

栈的应用——表达式求值

栈的应⽤——表达式求值表达式求值是程序设计语⾔编译中的⼀个基本问题，它的实现就是对“栈”的典型应⽤。

本⽂针对表达式求值使⽤的是最简单直观的算法“算符优先法”。

本⽂给出两种⽅式来实现表达式求值，⽅式⼀直接利⽤中缀表达式求值，需要⽤到两个栈，操作数栈和操作符栈。

⾸先置操作数栈为空栈，操作符栈仅有“#”⼀个元素。

依次读⼊表达式中的每个字符，若是操作数则进操作数栈，若是操作符则和操作符栈的栈顶运算符⽐较优先权作相应操作，直⾄整个表达式求值完毕。

⽅式⼆⾸先把中缀表达式转换为后缀表达式并存储起来，然后利⽤读出的后缀表达式完成求值，其本质上是⽅式⼀的分解过程。

表达式求值的代码如下：#include <iostream>#include "stack"#include "map"using namespace std;/* 只能求⼀位整数的加减乘除混合运算 */map<char, pair<int, int>> priority; // 存放各个操作符的栈内栈外优先级,first是栈内,second是栈外char infix[50]; // 存放初始的中缀表达式char postfix[50]; // 存放转化的后缀表达式int result;void MakePriority() // 构造运算符优先级表{priority.insert(make_pair('#', make_pair(0, 0))); // isp(#)=0, icp(#)=0priority.insert(make_pair('\n', make_pair(0, 0))); // isp(\n)=0, icp(\n)=0 表达式结尾的'#'⽤'\n'代替,这样可以省略表达式末尾的结束符'#'priority.insert(make_pair('(', make_pair(1, 6))); // isp(()=1, icp(()=6priority.insert(make_pair('*', make_pair(5, 4))); // isp(*)=5, icp(*)=4priority.insert(make_pair('/', make_pair(5, 4))); // isp(/)=5, icp(/)=4priority.insert(make_pair('%', make_pair(5, 4))); // isp(%)=5, icp(%)=4priority.insert(make_pair('+', make_pair(3, 2))); // isp(+)=3, icp(+)=2priority.insert(make_pair('-', make_pair(3, 2))); // isp(-)=3, icp(-)=2priority.insert(make_pair(')', make_pair(6, 1))); // isp())=6, icp())=1}void InfixToPostfix() // 把中缀表达式转换为后缀表达式{int i = 0;stack<char> optrStack; // 操作符栈char optr; // optr为栈顶的操作符optrStack.push('#');while (!optrStack.empty()){if (isdigit(infix[i])) // 是操作数则直接输出(追加到postfix结尾){postfix[strlen(postfix)] = infix[i];postfix[strlen(postfix) + 1] = '\0';i++; // 读⼊中缀表达式的下⼀个字符}else// 是操作符, ⽐较优先级{optr = optrStack.top(); // 取出栈顶操作符if (priority[infix[i]].second > priority[optr].first) // icp(infix[i]) > isp(optr),infix[i]⼊栈{optrStack.push(infix[i]);i++;}else if (priority[infix[i]].second < priority[optr].first)// icp(infix[i]) < isp(optr),optr退栈并输出{postfix[strlen(postfix)] = optr;postfix[strlen(postfix) + 1] = '\0';optrStack.pop();}else// icp(infix[i]) = isp(optr),退栈但不输出,若退出的是'(',则继续读⼊下⼀个字符{optrStack.pop();if (optr == '(')i++;}}}}void CalculateByPostfix() // 通过后缀表达式求值{int i = 0;stack<int> opndStack; // 操作数栈int left, right; // 左右操作数int value; // 中间结果int newOpnd;while (postfix[i] != '#' && i < strlen(postfix)){switch (postfix[i]){case'+':right = opndStack.top(); // 从操作数栈中取出两个操作数opndStack.pop();left = opndStack.top();opndStack.pop();value = left + right;opndStack.push(value); // 中间结果⼊栈break;case'-':right = opndStack.top();opndStack.pop();left = opndStack.top();opndStack.pop();value = left - right;opndStack.push(value);break;case'*':right = opndStack.top();opndStack.pop();left = opndStack.top();opndStack.pop();value = left * right;opndStack.push(value);break;case'/':right = opndStack.top();opndStack.pop();left = opndStack.top();opndStack.pop();if (right == 0){cerr << "Divide by 0!" << endl;}else{value = left / right;opndStack.push(value);}break;default:newOpnd = (int)(postfix[i] - 48); // 操作数直接⼊栈opndStack.push(newOpnd);break;}i++;}result = opndStack.top();}void CalculateByInfix() // 直接利⽤中缀表达式求值{int i = 0;stack<char> optrStack; // 操作符栈stack<int> opndStack; // 操作数栈char optr; // optr为操作符栈顶的操作符int left, right, value; // 左右操作数以及中间结果optrStack.push('#');optr = optrStack.top();while (!optrStack.empty()) // 直到操作符栈为空{if (isdigit(infix[i])) // 是操作数, 进操作数栈{value = (int)(infix[i] - 48);opndStack.push(value);i++;}else// 是操作符, ⽐较优先级{optr = optrStack.top(); // 取出操作符栈顶的操作符if (priority[infix[i]].second > priority[optr].first) // icp(infix[i]) > isp(optr),infix[i]⼊栈 {optrStack.push(infix[i]);i++;}else if (priority[infix[i]].second < priority[optr].first) // icp(infix[i]) < isp(optr),optr退栈并输出{optrStack.pop();right = opndStack.top(); // 从操作数栈中取出两个操作数opndStack.pop();left = opndStack.top();opndStack.pop();switch (optr){case'+':value = left + right;opndStack.push(value); // 中间结果⼊栈break;case'-':value = left - right;opndStack.push(value); // 中间结果⼊栈break;case'*':value = left * right;opndStack.push(value); // 中间结果⼊栈break;case'/':if (right == 0){cerr << "Divide by 0!" << endl;}else{value = left / right;opndStack.push(value);}break;default:break;}}else{optrStack.pop();if (optr == '(')i++;}}}result = opndStack.top();}int main(){MakePriority(); // 构造运算符优先级表cout << "请输⼊中缀表达式：";cin >> infix;cout << "直接利⽤中缀表达式求值为：";CalculateByInfix();cout << result << endl;cout << "转化为后缀表达式：";InfixToPostfix();for (int i = 0;i < strlen(postfix);i++){cout << postfix[i];}cout << endl;cout << "利⽤后缀表达式求值为：";CalculateByPostfix();cout << result << endl;return0;} 为了⽅便起见，本⽂只是简单的设计了⼀个针对⼀位整数的四则运算进⾏求值的算法，对于处理多位整数的四则运算，需要对本⽂接受输⼊的数据类型进⾏“升阶”，把字符数组换成字符串数组，将⼀个整数的多位数字存⼊⼀个字符串进⾏处理。

中缀表达式求值

一、设计思想用堆栈中缀法实现表达式自动计算的基本思路是：定义两个栈，一个为操作符栈，用来存放操作符的；另一个为操作数栈，用来存放操作数。

还有一个字符型数组，用来存放输入的表达式。

从数组中开始扫描第一个字符w，每扫描一个字符后，根据w的不同情况分别做以下处理：如果是操作符，那么判断w与操作符的栈顶的优先级。

如果大于，直接将w压入操作符栈。

如果小于，则将操作符的栈顶弹栈，再将操作数栈的栈顶和次栈顶弹栈，并和操作符的栈顶进行计算，结果直接进入操作数栈。

如果w不是操作符，判断它是整数还是小数，是一位的还是多位的。

如果操作符的栈顶元素是#，并且从表达式数组中扫描进来的也是#，运算结束，操作数的栈顶元素就是计算结果。

二、算法流程图中缀表达式求值算法流程图简单说明：将输入的字符表达式存到数组中，对数组中的元素进行遍历，当读入第一个字符时先判断它是不是操作数然后判断它是不是多位浮点型小数。

如果是操作符，就判断它的优先级和操作符栈栈顶的优先级，谁的优先级比较高，如果是栈顶的优先级大于输入的字符，那么将栈顶的元素a出栈，再从操作数栈弹出栈顶和次栈顶，并进行次栈顶和栈顶关于a的运算，结果送回到操作数栈，然后扫描下一个字符。

如果它是操作数，那么要判断它是一位数还是多位数，是小数还是整数，如果是小数或者是多位的，那么执行多位数处理程序。

三、源代码下面给出的是用中缀表达式求值算法实现的程序的源代码：#define N 50#include<ctype.h>#include<string.h>#include<stdio.h>#include<math.h>typedef struct{int top;double array[N];}NumStack;//操作数栈类型typedef struct{int top;char array[N];}OpStack;//操作符栈类型int Cint(char mychar){return (mychar-48);}//字符转换成数字void PushNum(NumStack *numstack,double num){numstack->top++;numstack->array[numstack->top-1]=num;}//操作数进栈void PopNum(NumStack *numstack,double*num){*num=numstack->array[numstack->top-1];numstack->top--;}//操作数出栈void PushOp(OpStack *opstack,char op){opstack->top++;opstack->array[opstack->top-1]=op;}//操作符进栈void PopOp(OpStack *opstack,char*op){*op=opstack->array[opstack->top-1];opstack->top--;}//操作符出栈double Calc(double a,double b,char c){double result;switch(c){case'+':result=a+b;break;case'-':result=a-b;break;case'*':result=a*b;break;case'/':result=a/b;break;}return result;}//计算两个操作数按c进行运算char Priority(char y,char x){char priority='<';switch(x){case'+':case'-':if(y=='('|| y=='#')priority='>';break;case'*':case'/':if(y=='('|| y=='#'|| y=='+'|| y=='-')priority='>';break;case'(':priority='>';break;case')':if(y=='(')priority='=';break;case'#':if(y=='#')priority='=';break;default:priority='E';}return priority;}//比较两个操作符的优先级void Process(NumStack *numstack,OpStack *opstack,char x){double a,b;char c;static double tempnum=0.00000000;static int len=10;static intdot=0,flags=0;if(isdigit(x) || x=='.'){if(x=='.')dot=1;else{if(dot==0)tempnum=tempnum*10+Cint(x);//整数部分两位以上的数else{tempnum=tempnum+(double)Cint(x)/len;//小数部分两位以上的数len*=10;}}}else{if(flags==0 &&x!='('){PushNum(numstack,tempnum);tempnum=0.00000000;len=10;dot=0;} switch(Priority(opstack->array[opstack->top-1],x)){case'>':PushOp(opstack,x);flags=0;break;case'<':PopOp(opstack,&c);PopNum(numstack,&b);PopNum(numstack,&a);PushNum(numstack,Calc(a,b,c));flags=1;Process(numstack,opstack,x);break;case'=':PopOp(opstack,&c);flags=1;break;default:printf("Wrong Express!");exit(0);}}}main(){NumStack numstack;OpStack opstack;//定义栈char s[N];int i=0;numstack.top=0;opstack.top=0;//初始化栈PushOp(&opstack,'#');//操作符栈底为#printf("\nEnter your expression and end it with #:");scanf("%s",s); for(i=0;i<strlen(s);i++)Process(&numstack,&opstack,s[i]);printf("The result is %f",numstack.array[numstack.top-1]);}。

C语言实现中缀、后缀、前缀表达式_相互转化并求值

1.问题描述（1）表达式求值问题表达式是数据运算的基本形式。

人们的书写习惯是中缀式，如：11+22*(7-4)/3。

中缀式的计算按运算符的优先级及括号优先的原则，相同级别从左到右进行计算。

表达式还有后缀式（如：22 7 4 - * 3 / 11 +）和前缀式（如：+ 11 / * 22 – 7 4 3）。

后缀表达式和前缀表达式中没有括号，给计算带来方便。

如后缀式计算时按运算符出现的先后进行计算。

本设计的主要任务是进行表达式形式的转换及不同形式的表达式计算。

2.数据结构设计（1）表达式求值问题由于表达式中有字符与数字两种类型，故定义结点一个标志域data，标志结点存储的为字符data=2还是数字data=1，再寻找结点中对应的存储位置，读取数字域data1,字符域data2。

而在前缀表达式时，存在表达式逆序，因表达式类型不统一，用栈逆序极不方便，选择构建双向链表，存储表达式。

typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;3.运行、测试与分析（1）表达式求值问题（1）按提示输入中缀表达式，如图1.1所示。

如输入中缀表达式不正确，提示输入有误，如图1.2,1.3所示。

图1.1图1.2图1.3（2）选择表达式转换并求值方式。

按“1”选择中缀表达式求值，如图1.4所示。

图1.4（3）按“2”选择中缀表达式转变为后缀表达式并求值，如图1.5所示。

图1.5（4）按“3”选择中缀表达式转变为前缀表达式并求值，如图1.6所示。

图1.6附录：源代码（1）表达式求值问题#include<stdio.h>#include<stdlib.h>#define MAXNUM 100typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;typedef int selemtype1; //定义运算数栈的结点typedef struct //定义运算数栈的类型{selemtype1 *base;selemtype1 *top;}sqstack1;void InitStack1(sqstack1 &s) //新建一个空运算数栈{s.base=(selemtype1 *)malloc(MAXNUM*sizeof(selemtype1)); s.top=s.base;if(!s.base) printf("出错：申请空间失败！\n");}void Push1(sqstack1 &s,selemtype1 &e) //运算数栈，入栈：插入元素e为新的栈顶元素{ if(s.top-s.base>=MAXNUM)printf("出错：表达式过长！1\n");*s.top++ =e;}void GetTop1(sqstack1 s,selemtype1 &e) //运算数栈，用e返回栈顶元素{e=*(s.top-1);}void Popopnd1(sqstack1 &s,selemtype1 &e) //运算数栈，退栈：删除栈顶元素，并用e返回其值{e=*--s.top;}int stackempy1(sqstack1 s) //运算数栈，若为空栈返回1，否则返回0{if(s.top==s.base) return 1;else return 0;}typedef char selemtype2; //定义运算符栈的结点类型typedef struct //定义运算符栈类型{selemtype2 *base;selemtype2 *top;}sqstack2;void InitStack2(sqstack2 &s) //新建一个空运算符栈{s.base=(selemtype2 *)malloc(MAXNUM*sizeof(selemtype2));s.top=s.base;if(!s.base) printf("出错：申请空间失败！\n");}void Push2(sqstack2 &s,selemtype2 &e) //运算符栈，入栈：插入元素e为新的栈顶元素{ if(s.top-s.base>=MAXNUM)printf("出错：表达式过长！2\n");*s.top++ =e;}void GetTop2(sqstack2 s,selemtype2 &e) //运算符栈，用e返回栈顶元素{e=*(s.top-1);}void Popopnd2(sqstack2 &s,selemtype2 &e) //运算符栈，退栈：删除栈顶元素，并用e返回其值{e=*--s.top;}int stackempy2(sqstack2 s) //运算符栈，若为空栈返回1，否则返回0{if(s.top==s.base) return 1;else return 0;}void priority(char c,int &i) //确定运算符优先级{if (c=='*'||c=='/'||c=='%') i=2 ;else if (c=='+'||c=='-') i=1 ;else i=0;}int compare(char a,char b) //比较栈顶元素运算符与外部运算符优先级大小，外部优先级大则返回1，反之返回0{int in,out;priority(a,in);priority(b,out);if(out>in) return 1;else return 0;}void Operat(sqstack1 &OPND,sqstack2 &OPTR){int num1,num2,num;char c;Popopnd1(OPND,num2);Popopnd1(OPND,num1);Popopnd2(OPTR,c);switch(c){case '+':num=num1+num2;break;case '-':num=num1-num2;break;case '*':num=num1*num2;break;case '/':num=num1/num2;break;case '%':num=num1%num2;break;}Push1(OPND,num);}void Operatqianzhui(sqstack1 &OPND,sqstack2 &OPTR){int num1,num2,num;char c;Popopnd1(OPND,num1);Popopnd1(OPND,num2);Popopnd2(OPTR,c);switch(c){case '+':num=num1+num2;break;case '-':num=num1-num2;break;case '*':num=num1*num2;break;case '/':num=num1/num2;break;case '%':num=num1%num2;break;}Push1(OPND,num);}void houzhuiqiuzhi(Lnode *p,int &e) //后缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(p){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;Push2(OPTR,c);Operat(OPND,OPTR);break;default:printf("结点有误");break;}p=p->next;}Popopnd1(OPND,n);e=n;}void zhongzhui(Lnode *p) //中缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c,c2;Lnode *first;first=p;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(!stackempy2(OPTR)||p){while(p){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else { switch(c){case '(': Push2(OPTR,c);break;case ')': GetTop2(OPTR,c2);while(c2!='('){Operat(OPND,OPTR);GetTop2(OPTR,c2);}Popopnd2(OPTR,c2);break;default: GetTop2(OPTR,c2);if(compare(c2,c)) Push2(OPTR,c); else { Operat(OPND,OPTR);Push2(OPTR,c);}break;}}break;default: printf("结点有误");break;}p=p->next;}while(!stackempy2(OPTR))Operat(OPND,OPTR);}Popopnd1(OPND,n);p=first->next;while(p){if(p->data==1) printf("%d ",p->data1);if(p->data==2) printf("%c",p->data2);p=p->next;}printf("=%d ",n);}void houzhui(Lnode *p) //中缀表达式转化为后缀表达式{sqstack2 OPTR; //运算符栈Lnode *r,*q,*head;int n;char c,c2;InitStack2(OPTR);p=p->next;q=(Lnode*)malloc(sizeof(struct Node));head=q;while(p){ switch(p->data){case 1:n=p->data1;r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=1;q->data1=n;break;case 2:c=p->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else { switch(c){ case '(': Push2(OPTR,c);break;case ')': Popopnd2(OPTR,c2);while(c2!='('){ r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;Popopnd2(OPTR,c2);}break;default: GetTop2(OPTR,c2);while(!compare(c2,c)){ Popopnd2(OPTR,c2);r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;GetTop2(OPTR,c2);}Push2(OPTR,c);break;}}break;default: printf("结点有误");break;}p=p->next;}while(!stackempy2(OPTR)){ Popopnd2(OPTR,c2);r=(Lnode*)malloc(sizeof(struct Node));q->next=r;q=q->next;q->data=2;q->data2=c2;}q->next=NULL;q=head->next;while(q){if(q->data==1) printf("%d ",q->data1);if(q->data==2) printf("%c",q->data2);q=q->next;}houzhuiqiuzhi(head,n);printf("=%d ",n);}void qianzhuiqiuzhi(Lnode2 *p,int &e) //前缀表达式求值{sqstack1 OPND; //运算数栈sqstack2 OPTR; //运算符栈int n;char c;Lnode2 *head;head=p;p=p->next;InitStack1(OPND);InitStack2(OPTR);while(p!=head){switch(p->data){case 1:n=p->data1;Push1(OPND,n);break;case 2:c=p->data2;Push2(OPTR,c);Operatqianzhui(OPND,OPTR); break;default:printf("结点有误");break;}p=p->next;}Popopnd1(OPND,n);e=n;}void qianzhui(Lnode *p) //中缀表达式转化为前缀表达式{sqstack2 OPTR; //运算符栈InitStack2(OPTR);int n;char c,c2;Lnode *first;Lnode2 *q,*head,*r,*head2,*s;first=p;p=p->next;q=(Lnode2*)malloc(sizeof(struct Node2)); //建立存中缀表达式的双向循环链表head=q;while(p){r=(Lnode2*)malloc(sizeof(struct Node2));q->next=r;r->prior=q;q=q->next;q->data=p->data;q->data1=p->data1;q->data2=p->data2;p=p->next;}q->next=head;head->prior=q;s=(Lnode2*)malloc(sizeof(struct Node2)); //建立存前缀表达式的双向循环链表head2=s;while(q!=head){switch(q->data){case 1:n=q->data1;r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=1;s->data1=n;break;case 2:c=q->data2;if(stackempy2(OPTR)) Push2(OPTR,c);else{ GetTop2(OPTR,c2);if(c2==')') Push2(OPTR,c);else{ switch(c){ case ')':Push2(OPTR,c);break;case '(': Popopnd2(OPTR,c2);while(c2!=')'){ r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;Popopnd2(OPTR,c2);}break;default: GetTop2(OPTR,c2);while(!compare(c2,c)){ Popopnd2(OPTR,c2);r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;GetTop2(OPTR,c2);}Push2(OPTR,c);break;}}}break;default:printf("结点有误");break;}q=q->prior;}while(!stackempy2(OPTR)){ Popopnd2(OPTR,c2);r=(Lnode2*)malloc(sizeof(struct Node2));s->next=r;r->prior=s;s=s->next;s->data=2;s->data2=c2;}s->next=head2;head2->prior=s;while(s!=head2){if(s->data==1) printf("%d ",s->data1); if(s->data==2) printf("%c",s->data2); s=s->prior;}qianzhuiqiuzhi(head2,n);printf("=%d ",n);}int main(){ char n[10];char c;int i,j,k,a,b,z,y,e;Lnode *p,*q,*first;i=0;e=1;a=0;b=1;z=0;y=0;p=(Lnode*)malloc(sizeof(struct Node));first=p;printf("请输入中缀表达式");do{ c = getchar();if('0'<=c&&c<='9'){ n[i]=c;i++;}else{ switch (c){ case '+':case '-':case '*':case '/':case '%':case '(':case ')':case '\n':{ if(n[0]>'0'&&n[0]<='9'){ q=(Lnode*)malloc(sizeof(struct Node)); p->next=q;p=p->next;for(k=0;k<i;k++){ for(j=0;j<=i-k-2;j++)e=e*10;a=a+(n[k]-'0')*e;e=1;n[k]='0';}p->data=1;p->data1=a;i=0;a=0;}if(c!='\n'){ if(p->data==2){ if(p->data2!=')'&&c!='(')b=0;}q=(Lnode*)malloc(sizeof(struct Node));p->next=q;p=p->next;p->data=2;p->data2=c;if(c=='(') z++;if(c==')') y++;}}default:if(c!='+'&&c!='-'&&c!='*'&&c!='/'&&c!='%'&&c!='\n'&&c!='('&&c!=')') b=0;}}}while (c != '\n');if(z!=y) b=0;p->next=NULL;if(b==0)printf("输入中缀表达式有误");else{printf("输入1中缀表达式求值，输入2后缀表达式求值，输入3前缀表达式求值");scanf("%d",&b);if(b==1) zhongzhui(first);if(b==2) houzhui(first);if(b==3) qianzhui(first);}return 1;}。

C语言实现中缀、后缀、前缀表达式相互转化并求值

C语言实现中缀、后缀、前缀表达式相互转化并求值1.问题描述(1)表达式求值问题表达式是数据运算的基本形式。

人们的书写习惯是中缀式，如:11+22*(7-4)/3。

中缀式的计算按运算符的优先级及括号优先的原则，相同级别从左到右进行计算。

表达式还有后缀式(如:22 7 4 - * 3 / 11 +)和前缀式(如:+ 11 / * 22 –7 4 3)。

后缀表达式和前缀表达式中没有括号，给计算带来方便。

如后缀式计算时按运算符出现的先后进行计算。

本设计的主要任务是进行表达式形式的转换及不同形式的表达式计算。

2.数据结构设计(1)表达式求值问题由于表达式中有字符与数字两种类型，故定义结点一个标志域data，标志结点存储的为字符data=2还是数字data=1，再寻找结点中对应的存储位置，读取数字域data1,字符域data2。

而在前缀表达式时，存在表达式逆序，因表达式类型不统一，用栈逆序极不方便，选择构建双向链表，存储表达式。

typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;3.运行、测试与分析(1)表达式求值问题(1)按提示输入中缀表达式，如图1.1所示。

如输入中缀表达式不正确，提示输入有误，如图1.2,1.3所示。

图1.1图1.2图1.3(2)选择表达式转换并求值方式。

按“1”选择中缀表达式求值，如图1.4所示。

图1.4(3)按“2”选择中缀表达式转变为后缀表达式并求值，如图1.5所示。

图1.5(4)按“3”选择中缀表达式转变为前缀表达式并求值，如图1.6所示。

中缀求值实验报告

一、实验目的1. 理解中缀表达式及其求值原理。

2. 掌握中缀表达式的转换方法，即将中缀表达式转换为后缀表达式。

3. 实现中缀表达式的求值算法，并编写相应的程序。

二、实验原理中缀表达式是一种常见的数学表达式表示方式，其特点是运算符位于操作数之间。

例如，表达式 "3 + 4 2" 就是一个中缀表达式。

中缀表达式转换为后缀表达式（也称为逆波兰表达式）是求值的关键步骤，因为后缀表达式可以直接按照运算符的优先级进行计算。

中缀表达式转换为后缀表达式的基本原理如下：1. 创建一个栈，用于存储运算符。

2. 从左到右扫描中缀表达式中的每个字符。

3. 如果是操作数，直接输出到结果字符串。

4. 如果是运算符，比较当前运算符的优先级与栈顶运算符的优先级。

a. 如果栈为空或者栈顶元素是左括号 "(", 将当前运算符压入栈中。

b. 如果当前运算符的优先级高于栈顶运算符的优先级，或者栈顶元素是右括号")", 将当前运算符压入栈中。

c. 如果当前运算符的优先级低于或等于栈顶运算符的优先级，将栈顶运算符弹出并输出到结果字符串，然后重复步骤 4。

5. 当扫描完中缀表达式后，将栈中的所有运算符依次弹出并输出到结果字符串。

6. 将中缀表达式转换为后缀表达式后，按照后缀表达式的规则进行求值。

三、实验步骤1. 定义一个函数，用于判断字符是否为操作数。

2. 定义一个函数，用于判断字符是否为运算符。

3. 定义一个函数，用于判断运算符的优先级。

4. 定义一个函数，用于将中缀表达式转换为后缀表达式。

5. 定义一个函数，用于求值后缀表达式。

6. 编写主函数，实现中缀表达式的求值。

四、实验代码```pythondef is_operand(c):return c.isdigit()def is_operator(c):return c in ['+', '-', '', '/', '(', ')']def precedence(op):if op in ['+', '-']:return 1if op in ['', '/']:return 2return 0def infix_to_postfix(expression):stack = []postfix = []for c in expression:if is_operand(c):postfix.append(c)elif c == '(':stack.append(c)elif c == ')':while stack and stack[-1] != '(':postfix.append(stack.pop())stack.pop()else:while stack and precedence(stack[-1]) >= precedence(c): postfix.append(stack.pop())stack.append(c)while stack:postfix.append(stack.pop())return postfixdef evaluate_postfix(postfix):stack = []for c in postfix:if is_operand(c):stack.append(int(c))else:b = stack.pop()a = stack.pop()if c == '+':stack.append(a + b)elif c == '-':stack.append(a - b)elif c == '':stack.append(a b)elif c == '/':stack.append(a / b)return stack[0]def evaluate_infix(expression):postfix = infix_to_postfix(expression)return evaluate_postfix(postfix)# 主函数if __name__ == '__main__':expression = input("请输入中缀表达式：")result = evaluate_infix(expression)print("结果为：", result)```五、实验结果与分析1. 输入中缀表达式 "3 + 4 2"，程序输出结果为 11，与预期一致。

中缀表达式计算、

中缀表达式计算、（实用版）目录1.中缀表达式的概念2.中缀表达式的计算方法3.中缀表达式的应用实例正文一、中缀表达式的概念中缀表达式（Infix Expression），又称作中缀代数表示，是一种将运算符和操作数混合排列的表达式。

它是一种用于表示算术运算的记法，其中运算符出现在操作数之间。

与常见的前缀表达式（Postfix Expression）和后缀表达式（Reverse Polish Notation，简称 RPN）不同，中缀表达式的运算顺序取决于运算符的优先级和结合性。

二、中缀表达式的计算方法中缀表达式的计算过程需要通过一定的转换将其转换为可以被计算机直接执行的形式。

常见的计算方法有以下两种：1.栈算法栈算法是一种基于栈的数据结构，可以用来解决中缀表达式的计算问题。

该算法的基本思想是使用一个栈来存储中缀表达式中的操作数，当遇到运算符时，根据栈顶元素的类型进行相应的操作。

具体来说，可以将中缀表达式转换为后缀表达式，然后使用栈来计算后缀表达式的值。

2.直接计算法直接计算法是一种直接根据运算符的优先级和结合性计算中缀表达式的值的方法。

该方法需要先确定运算符的优先级，然后从左到右扫描表达式，根据优先级和结合性进行相应的计算。

这种方法相对简单，但对于复杂的表达式计算效率较低。

三、中缀表达式的应用实例中缀表达式在计算机科学中有广泛的应用，例如：1.表达式求值：通过中缀表达式计算方法，可以实现对复杂数学表达式的求值。

2.编译器：编译器在将高级编程语言转换为机器语言时，需要对表达式进行求值。

中缀表达式作为一种表达式表示方法，可以在编译器中得到应用。

3.数据库查询：在数据库查询中，常常需要对查询条件进行复杂的逻辑运算。

中缀表达式作为一种表达式表示方法，可以帮助用户更方便地表示查询条件。

总结：中缀表达式作为一种表达式表示方法，在计算机科学中有广泛的应用。

中缀表达式求值实验报告

中缀表达式求值实验报告一、需求分析（要实现的功能描述）1．问题描述：在计算机中，算术表达式由常量、变量、运算符和括号组成。

由于不同的运算符具有不同的优先级，又要考虑括号，因此，算术表达式的求值不可能严格地从左到右进行。

因而在程序设计时，借助栈实现。

2．实现功能：算法输入：一个算术表达式，由常量、变量、运算符和括号组成（以字符串形式输入）。

为简化，规定操作数只能为正整数，操作符为“+、-、*、/”。

算法运行：将输入的中缀表达式改为后缀表达式，并进行运算。

算法输出：输出后缀表达式和表达式运算结果。

3．测试数据：（1）、1+3*4-（5/5）；一位数运算（2）、45-5*（1+2）/5;多位数运算二、概要设计整个程序包含功能模块及模块间的调用关系(1)、struct node创建结构体，被主函数调用(2)、struct node *Initialization()创建栈链，被主函数调用(3)、struct node *assort(struct node *s)将中缀表达式转换为后缀表达式并存在s2中被主函数调用(4)、struct node *calcolate(struct node *s)求出表达式的值，被主函数调用(5)、void main()主函数，调用所有函数三、详细设计抽象数据类型中定义的各种操作算法实现（用N-S图描述）开始输入中缀表达式将中缀表达式转换成后缀表达式并存入s2中输出后缀表达式计算结果输出结果结束四、调试分析1．程序在调式过程中出现的问题及解决方法一开始选用直接运算方式运用两个栈来存放数字和操作符，后来写着确实不行然后直接转用转为后缀表达式再进行计算。

在写将多位数（比如123*12）存放字符串中时，一开始我想着直接转换成数字存入数组中，但一直不成功，只能将第一个多位数转换成功；后来在和同学之间交流并且百度搜索后改为直接存入字符串中，再存入字符串过程中，我发现几个数字之间可能没法区分是前一个数字的还是后一个数字的，于是我在扫描字符串过程中在扫描到操作字符时将存入数字的那个字符串s2空出一位，用以区分前后两个数字，如12+45*，如果直接存入字符串中会是s2：1245*+；但加空格后为s2：12（空格）45*+；这样后面运算时就好区分两多位数字。

基于栈的中缀算术表达式求值

基于栈的中缀算术表达式求值描述输⼊⼀个中缀算术表达式，求解表达式的值。

运算符包括+、-、*、/、(、)、=，参加运算的数为double类型且为正数。

（要求：直接针对中缀算术表达式进⾏计算，不能转换为后缀或前缀表达式再进⾏计算，只考虑⼆元运算即可。

）输⼊多组数据，每组数据⼀⾏，对应⼀个算术表达式，每个表达式均以“=”结尾。

当表达式只有⼀个“=”时，输⼊结束。

参加运算的数为double类型。

输出对于每组数据输出⼀⾏，为表达式的运算结果。

输出保留两位⼩数。

输⼊样例 12+2=20*(4.5-3)==输出样例 14.0030.00⽤的⽅法挺⿇烦的#include<iostream>using namespace std;#define MAXSIZE 1000#define OVERFLOW -2#define OK 0#define ERROR -1typedef struct {char* base;char* top;int stacksize;}Stack1;int Init_stack1(Stack1& S) {S.base = new char[MAXSIZE];if (!S.base)return OVERFLOW;S.top = S.base;S.stacksize = MAXSIZE;return OK;}int Push1(Stack1& S, char e) {if (S.top - S.base == S.stacksize)return ERROR;*S.top = e;S.top++;return OK;}int Pop1(Stack1& S, char& e) {if (S.top == S.base)return ERROR;--S.top;e = *S.top;return OK;}char Gettop1(Stack1& S) {if (S.top != S.base)return *(S.top - 1);}typedef struct {}Stack2;int Init_stack2(Stack2& S) {S.base = new double[MAXSIZE];if (!S.base)return OVERFLOW;S.top = S.base;S.stacksize = MAXSIZE;return OK;}int Push2(Stack2& S, double e) {if (S.top - S.base == S.stacksize)return ERROR;*S.top = e;S.top++;return OK;}double Gettop2(Stack2& S) {if (S.top != S.base)return *(S.top - 1);}int Pop2(Stack2& S, double& e) {if (S.top == S.base)return ERROR;--S.top;e = *S.top;return OK;}double Fun(double a, double b, char c) {// ?c if (c == '+')return a + b;else if (c == '-')return a - b;else if (c == '*')return a * b;else if (c == '/')return a / b;}char Precede(char a, char b) {int i, j;char priority[7][7] = {{'>','>','<','<','<','>','>'},{'>','>','<','<','<','>','>'},{'>','>','>','>','<','>','>'},{'>','>','>','>','<','>','>'},{'<','<','<','<','<','=','0'},{'>','>','>','>','0','>','>'},{'<','<','<','<','<','0','='}};switch (a) {case'+':i = 0; break;case'-':i = 1; break;case'*':i = 2; break;case'/':i = 3; break;case'(':i = 4; break;case')':i = 5; break;case'=':i = 6; break;default:break;}switch (b) {case'+':j = 0; break;case'-':j = 1; break;case'*':j = 2; break;case'/':j = 3; break;case'(':j = 4; break;case')':j = 5; break;case'=':j = 6; break;default:break;}return priority[i][j];}int In(char ch) {if (ch >= '0' && ch <= '9')return0;}int main() {while (1) {int fflag=0;//判断上⼀个输⼊是否为数字char x;char ch;double integer=0;//⽤来记录整数double decimals=0;//⽤来记录⼩数double middle=0;//整数⼩数相加int flag = 0;//falg 表⽰现在的数字是在⼩数点前还是⼩数点后int point = 1;//记录当前数是⼩数点后第⼏位Stack2 OPND;Stack1 OPTR;char theta;double a, b;Init_stack2(OPND);Init_stack1(OPTR);Push1(OPTR, '=');cin >> ch;if (ch == '=')return0;while (ch != '=' || Gettop1(OPTR) != '=') {if (!In(ch)) {if(ch!='.'){if (flag == 0) {integer = 10 * integer;integer += ch - '0';}else if (flag == 1) {double t=ch-'0';for (int l = 0; l < point; l++)t = 0.1 * t;point++;decimals += t;}}else if(ch=='.'){flag=1;}fflag=1;cin >> ch;continue;}if (In(ch)&&fflag==1) {middle = integer + decimals;Push2(OPND, middle);flag = 0;middle = 0;integer = 0;decimals = 0;point = 1;fflag=0;}switch (Precede(Gettop1(OPTR), ch)){case'<':Push1(OPTR, ch);cin >> ch;break;case'>':Pop1(OPTR, theta);Pop2(OPND, b);Pop2(OPND, a);Push2(OPND, Fun(a, b, theta));break;case'=':Pop1(OPTR, x);cin >> ch;break;default:break;}}printf("%.2f\n",Gettop2(OPND));}return0;}。

中缀表达式求值

中缀表达式求值中缀表达式求值中缀表达式是人类最常用的表达式形式，但是计算机不能直接理解和计算中缀表达式。

因此，我们需要将中缀表达式转换为计算机可以理解和计算的后缀表达式，然后再对后缀表达式进行求值。

一、中缀表达式转后缀表达式1. 基本原则：遵循运算符优先级和结合性原则。

2. 转换方法：（1）从左到右扫描中缀表达式的每个元素；（2）如果当前元素是数字，则直接输出到后缀表达式；（3）如果当前元素是左括号，则将其入栈；（4）如果当前元素是右括号，则将栈顶操作符出栈并输出到后缀表达式，直到遇到左括号为止；（5）如果当前元素是操作符，则比较其与栈顶操作符的优先级：a. 如果栈为空或栈顶操作符为左括号，则将该操作符入栈；b. 如果该操作符优先级大于栈顶操作符优先级，则将该操作符入栈；c. 否则，将栈顶操作符出栈并输出到后缀表达式，重复步骤5直至满足上述两个条件之一，然后将该操作符入栈。

（6）重复步骤2-5直至扫描完整个中缀表达式，如果栈中还有操作符，则依次出栈并输出到后缀表达式。

例如，将中缀表达式“3+4*5/(6-2)”转换为后缀表达式的过程如下：元素 | 操作 | 栈 | 后缀表达式---------|---------------|--------------|-----------3 | 直接输出 | | 3+ | 入栈 | + |4 | 直接输出 | | 3 4* | 入栈 | + * |5 | 直接输出 | | 3 4 5 */ | 比较优先级 | + / * |( | 入栈 | + / * ( |6 | 直接输出 | | 3 4 5 * 6- | 入栈 | + / * ( - |2 | 直接输出 | |345 *6 2 -) | 比较优先级 |- |- / *) |- |- |- / *+ |- |- |- / * +后缀表达式：3,4,5,*,6,2,-,/,+二、后缀表达式求值1. 基本原则：遵循运算符优先级和结合性原则。

算术中缀表达式求值（简单计算器的运算）

算术中缀表达式求值（简单计算器的运算）1. 转化中缀表达式直接求值实现并不现实，需要转化成后缀表达式才能求值。

1. 过程2. 开两个栈，⼀个为符号栈，⼀个为数字栈，分别执⾏不同的分⽀操作。

*当遇到左括号时⽴刻将其压⼈栈中，直到遇到右括号时将左右括号之间的符号和数字全部弹出运算。

*遇到⼀个数字时，将数字压⼊数字栈中。

*遇到⼀个运算符时，将运算符与栈顶运算符⽐较，有下列四种情况：1. 如果当前运算符⽐栈顶运算符优先级要⾼，或者为左括号后的第⼀个运算符，则将其压⼊栈中。

2. 如果它⽐栈中元素优先级低或⼩，则弹出栈顶运算符并运算。

3. 继续⽐较，如果他⽐新的栈顶运算符优先级⾼，则回到第⼀步，否则重复2,3步。

4. 如果扫描到了中缀表达式的末尾，则弹出所有运算符和相应位置的数字进⾏运算。

（如果碰到两位数，⽤标记数组先记录下来，再在计算中转化）3.代码展⽰（code.Js）1.两步分别为操作栈和运算#include<iostream>#include<stack>#include<cstring>#include<iomanip>using namespace std;char endnumber[100];//数字和字符栈char number[100];//两位数特殊下标int z = 0;//下标//a,b优先级⽐较bool cmp(char a,char b){if(a == '*'||a == '/'){if(b == '*'||b == '/'){return false;}else{return true;}}else{return false;}}//使⽤过渡栈存⼊后缀表达式void get_stack(string s){memset(number,1,sizeof(number));stack<char>attitude;int l = s.length();int i = 0;for(i = 0;i < l;i++){char t = s[i];if(t == '('){attitude.push(t);}else if(t == ')'){char str1 = attitude.top();while(str1 != '('){endnumber[z++] = str1;attitude.pop();str1 = attitude.top();attitude.pop();}else if(t >= '0'&&t <= '9'){if(s[i+1] >= '0'&&s[i+1] <= '9'){number[z] = '0';endnumber[z] = s[i];z++;endnumber[z] = s[i+1];z++;i++;}else{endnumber[z++] = s[i];}}else{if(attitude.empty()){attitude.push(t);}else{char str2 = attitude.top();if(cmp(t,str2) || str2 == '('){attitude.push(t);}else{while(!cmp(t,str2)&&str2 != '('&&!attitude.empty()){attitude.pop();endnumber[z++] = str2;if(!attitude.empty())str2 = attitude.top();}attitude.push(t);}}}}while(!attitude.empty()){char str3 = attitude.top();endnumber[z++] = str3;attitude.pop();}// for(i = 0;i < z;i++)// cout<<endnumber[i]<<" ";}//从存储中调出数字和字符进⾏计算,转换成浮点数计算精确值void get_calculate(string s){int k = 1;stack<float>put_stack;if(number[0] == '0'){put_stack.push(((endnumber[0] - '0')*10+(endnumber[1]-'0'))*1.0);k++;}elseput_stack.push(1.0*(endnumber[0] - '0'));for(int i = k;i < z;i++){char t = endnumber[i];if(t >= '0'&&t <= '9'){if(number[i] == '0'){put_stack.push(((endnumber[i] - '0')*10+(endnumber[i+1]-'0'))*1.0); i++;}else{put_stack.push((t - '0')*1.0);}}elsefloat x = put_stack.top();put_stack.pop();float y = put_stack.top();put_stack.pop();float tmp;if(t == '+')tmp = x+y;else if(t == '-')tmp = y-x;else if(t == '*')tmp = x*y;elsetmp = y/x;put_stack.push(tmp);}}cout<<setiosflags(ios::fixed)<<setprecision(2)<<put_stack.top(); }int main(){string exp_middle;//中缀表达式cin>>exp_middle;get_stack(exp_middle);get_calculate(exp_middle);return0;}。

中缀表达式求值

中缀表达式求值以中缀表达式求值为题，我们来探讨一下中缀表达式的求值过程。

什么是中缀表达式呢？中缀表达式是我们平时最常见的表达式形式，即运算符位于操作数的中间，例如2+3*4。

而求值则是指根据给定的表达式，计算出它的结果。

那么，中缀表达式的求值过程是怎样的呢？我们可以通过以下步骤来进行求值：1. 创建两个栈：一个用来存储操作数的栈，称为操作数栈；另一个用来存储运算符的栈，称为运算符栈。

2. 从左到右依次扫描中缀表达式的每个字符。

3. 如果当前字符是数字，将其压入操作数栈中。

4. 如果当前字符是运算符，则进行如下操作：a. 如果运算符栈为空，或者栈顶运算符为左括号"("，则将当前运算符压入运算符栈中。

b. 如果当前运算符的优先级高于栈顶运算符的优先级，则将当前运算符压入运算符栈中。

c. 否则，将运算符栈顶的运算符弹出，并将其压入操作数栈中，直到满足条件a或b为止。

然后将当前运算符压入运算符栈中。

5. 如果当前字符是左括号"("，则将其压入运算符栈中。

6. 如果当前字符是右括号")"，则进行如下操作：a. 将运算符栈顶的运算符弹出，并将其压入操作数栈中，直到遇到左括号"("。

并且将左括号"("从运算符栈中弹出，但不压入操作数栈中。

7. 如果扫描完整个表达式后，运算符栈中还有运算符，那么将其依次弹出，并压入操作数栈中。

8. 最后，操作数栈中的唯一元素即为中缀表达式的求值结果。

通过上述步骤，我们可以求得中缀表达式的值。

这个求值过程的核心思想是使用两个栈来辅助计算，通过比较运算符的优先级来确定运算的顺序。

需要注意的是，中缀表达式的求值过程中，还需要考虑运算符的优先级。

一般来说，乘除法的优先级高于加减法，而同一优先级的运算符则按照从左到右的顺序进行计算。

如果遇到优先级相同的运算符，则按照从左到右的顺序依次计算。

中缀表达式求值

c++ 中缀表达式

关于中缀表达式求值（四则运算和括号，支持多位数）

表达式求值算法总结(C++)

中缀表达式求值

数据结构表达式求值(中缀)实验报告

中缀表达式求值（C++实现）

中缀表达式值

中缀表达式求值

栈的应用——表达式求值

中缀表达式求值

C语言实现中缀、后缀、前缀表达式_相互转化并求值

C语言实现中缀、后缀、前缀表达式 相互转化并求值

中缀求值实验报告

中缀表达式计算、

中缀表达式求值实验报告

基于栈的中缀算术表达式求值

中缀表达式求值

算术中缀表达式求值（简单计算器的运算）

中缀表达式求值

C语言实现中缀、后缀、前缀表达式相互转化并求值