基于模糊C均值的聚类分析
基于模糊C均值聚类方法的长江流域主要城市水质分析
个无 监督 的学 习过 程 . 在很 多 应用 中 。 聚类 分析 作为 种数 据预 处理 过程 .是 进 一步 分析 和 处理 数据 的基
11数 据 挖 掘 定 义 .
于推 导植 物 和动物 的分 类 . 基 因进行 分析 , 得对 种 对 获
数 据 挖 掘( a nn )又 称为 数 据库 中 的知 识 发 群 中 固有 结构 的认 识 聚类 分析也 可 以用 于在 泥土 观 D t Miig . a 现 f n we g i Oey i Da b s, D 1 就 是 从 大 测数 据库 中对 相似 地 区 的 区分 .也 可 以根 据房 子 的类 K o ld eD s Vr n t ae K D , C a
详 细 的 水 质 数 据 分 析 奠 定 了基 础 。
【 关键词 】 聚 类分析 ; : 模糊 c 均值 ; 质分 析 水
1 数 据 挖 掘 技 术 『— 1 、 1 2
的关 联 . 用 己有 的数 据对 未来 的活 动进 行预测 。 样 利 这
一
随着计 算 机 技术 和信 息技 术 的发 展 .信 息 的增 长 来 .人 们对 数据 的应 用 就从 低层 次 的末 端查 询操 作 速度 呈现 指数 上 升 .已远 远 超 出了人 们分 析 它们 并从 提高 到为 决策 者提供 决 策支 持
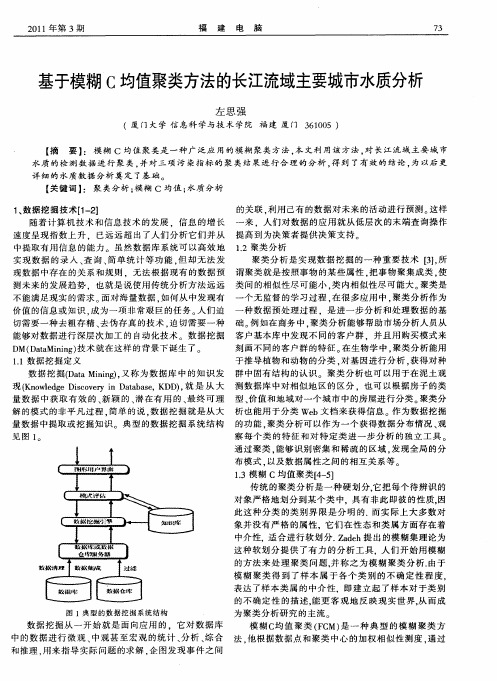
量 数 据 中获 取 有 效 的 、 新颖 的 、 潜在 有 用 的 、 终 可 理 型 、 值 和地域 对 一个 城市 中 的房屋 进行 分类 。 最 价 聚类 分 解 的模式 的非 平 凡过程 . 简单 的说 , 据挖 掘 就是 从 大 析也 能用 于分类 We 档 来获 得信 息 作为数 据挖 掘 数 b文 量数 据 中提取 或挖 掘知 识 典 型 的数据 挖 掘 系统 结构 的功 能 , 聚类分 析可 以作 为 一个 获得 数 据分 布情 况 、 观
关于模糊c均值聚类算法

FCM模糊c均值1、原理详解模糊c-均值聚类算法fuzzy c-means algorithm (FCMA)或称(FCM)。
在众多模糊聚类算法中,模糊C-均值(FCM)算法应用最广泛且较成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
聚类的经典例子然后通过机器学习中提到的相关的距离开始进行相关的聚类操作经过一定的处理之后可以得到相关的cluster,而cluster之间的元素或者是矩阵之间的距离相对较小,从而可以知晓其相关性质与参数较为接近C-Means Clustering:固定数量的集群。
每个群集一个质心。
每个数据点属于最接近质心对应的簇。
1.1关于FCM的流程解说其经典状态下的流程图如下所示集群是模糊集合。
一个点的隶属度可以是0到1之间的任何数字。
一个点的所有度数之和必须加起来为1。
1.2关于k均值与模糊c均值的区别k均值聚类:一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则,进行相关的必要调整优先进行优化看是经典的欧拉距离,同样可以理解成通过对于cluster的类的内部的误差求解误差的平方和来决定是否完成相关的聚类操作;模糊的c均值聚类算法:一种模糊聚类算法,是k均值聚类算法的推广形式,隶属度取值为[0 1]区间内的任何数,提出的基本根据是“类内加权误差平方和最小化”准则;这两个方法都是迭代求取最终的聚类划分,即聚类中心与隶属度值。
两者都不能保证找到问题的最优解,都有可能收敛到局部极值,模糊c均值甚至可能是鞍点。
1.2.1关于kmeans详解K-means算法是硬聚类算法,是典型的基于原型的目标函数聚类方法的代表,它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。
K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。
在Matlab中使用模糊C均值聚类进行图像分析的技巧

在Matlab中使用模糊C均值聚类进行图像分析的技巧在图像分析领域,模糊C均值聚类(FCM)是一种常用的工具,它可以帮助我们发现图像中隐藏的信息和模式。
通过使用Matlab中的模糊逻辑工具箱,我们可以轻松地实现FCM算法,并进行图像分析。
本文将介绍在Matlab中使用FCM进行图像分析的技巧。
首先,让我们简要了解一下FCM算法。
FCM是一种基于聚类的图像分割方法,它将图像的像素分为不同的聚类,每个聚类代表一类像素。
与传统的C均值聚类算法不同,FCM允许像素属于多个聚类,因此能够更好地处理图像中的模糊边界。
在Matlab中使用FCM进行图像分析的第一步是加载图像。
可以使用imread函数将图像加载到Matlab的工作区中。
例如,我们可以加载一张名为“image.jpg”的图像:```matlabimage = imread('image.jpg');```加载图像后,可以使用imshow函数显示图像。
这可以帮助我们对图像有一个直观的了解:```matlabimshow(image);```接下来,我们需要将图像转换为灰度图像。
这是因为FCM算法通常用于灰度图像分析。
可以使用rgb2gray函数将彩色图像转换为灰度图像:```matlabgrayImage = rgb2gray(image);```在使用FCM算法之前,我们需要对图像进行预处理。
预处理的目的是消除图像中的噪声和不必要的细节,从而更好地提取图像中的特征。
常用的图像预处理方法包括平滑、锐化和边缘检测等。
Matlab中提供了许多图像预处理函数。
例如,可以使用imnoise函数向图像中添加高斯噪声:```matlabnoisyImage = imnoise(grayImage, 'gaussian', 0, 0.01);```还可以使用imfilter函数对图像进行平滑处理。
常见的平滑方法包括均值滤波和高斯滤波:```matlabsmoothImage = imfilter(noisyImage, fspecial('average', 3));```一旦完成预处理步骤,我们就可以使用模糊逻辑工具箱中的fcm函数执行FCM算法。
基于非负矩阵分解和模糊C均值的图像聚类方法

效方法。提出了一种新的聚类算法 FCM-NMF,采用 NMF 分解提取样本的本质特征,并用模糊 C 均值( M) 进行模糊聚类。该
算法将 NMF 目标函数与 FCM 算法融合,提出了新的目标函数的形式,并生成新的交替迭代公式。最后在两个标准图像数据集
GHIM-10k 和 COREL-10k 上与传统的 5 种聚类方法从三个评价指标进行了对比。实验结果表明,该算法在标准数据集上聚类准
人们获得的数据普遍具有如下两个特点: ( 1) 数据 量庞大,检索困难; ( 2) 数据维数巨大,处理困难。虽然
高维数据也许含有更多的信息,但将其直接用于分类、 聚类或概率 密 度 估 计 等 任 务,必 将 付 出 巨 大 的 时 间 和 空间代价。因此降维已经成为许多数据挖掘问题的一 种预处理手段。数据降维的本质是寻找一个低维表示 来反映原始 数 据 的 内 在 特 征,并 使 后 续 任 务 在 这 个 低 维表示上的工作量更低,同时泛化性能和识别率更高。 通过利用非负矩阵分解( Non-negative Matrix Factorization,NMF) 的独特优势,不仅可以进行降维,而且物理 意义明 确,能 够 很 好 地 改 善 聚 类 的 效 率[9]。本 文 将 NMF 与模糊 C 均值算法相结合,提出了新的目标函数。 由交替迭代产生的新的低维表示矩阵可以用来描述样 本之间的本 质 关 系。 与 传 统 聚 类 方 法 相 比,本 文 算 法
引用格式: 陶性留,俞璐,王晓莹. 基于非负矩阵分解和模糊 C 均值的图像聚类方法[J]. 信息技术与网络安全,2019,38 ( 3) :
44-48.
One method based on non-negative matrix factorization and fuzzy C means for image clustering
利用模糊C-均值聚类分析法实现织物组织结构自动识别

找 出经 纬交叉 区 , 后提 取 图像 特 征 并 分 别将 它 然 们归 入经 浮点 集 和纬 浮点 集 。模 糊 C一均 值 聚类
分析 法可 以 提 取 每 一 个 经 纬 交 叉 区 的 4种 特 征 值 , 括 均 值 、 准 差 等 适 用 于 各 种 织 物 的 特 征 包 标 值 。该 聚类法适 应 于 非监督 分类 识 别相似 的样 本 对象 , 外 , 糊 C一均值 聚 类法 能 产 生较 好 的 聚 此 模 类结 果 。本文 提 供 了一种 可 以 自动 识别织 物 组织
不 同原 料 或 不 同组 织 的织 物 , 它们 的织 物组
织 图像 都是 由 2种基 本 结 构 组 成 , 即经 浮 点 和 纬
收 稿 日期 :05 6 0 20 —0 —2
类 分 析法 通过 对样 本 进行 归类来 判 断样 本集 模 式 之 间的关 系 。从 而 使 相 似 的样 本 属 于 一类 , 不 而 相 似 的样本 属 于不 同类 。由于这 里 的样 本是 实 数
督学 习 的 自动 识别 法 。 1 模糊 C一均值聚 类分 析 法 11 特点 .
法对 经 纬浮点 结 构特 征分类 以实现 织 物组织 结 构
的 自动识 别 。
12 原 理 .
在图像分割、 模式识别和向量量化等许 多领
域, 聚类 过程 是 这 些 问题 中不 可 或 缺 的 步骤 。 聚
2 0 年 第 4期 06
名d , 删 :
C是聚类 数, 01 , u ∈[ ] 表示样本 x 对第 i j 个模糊集的从属度 , l埘 — d = l 是第 i 个聚
关于模糊C-均值(FCM)聚类算法的改进

隶 属度 。 = { 是 一个 n×c的模 糊分 割 矩 U t} x
阵, = V , , } A, 是一 个 S×c的矩 阵 。 m用 来控制 分 割 矩 阵 的模糊 程度 , m越 大 ,分 类 的 模 糊 程 度 越 高 , 。 时 , = m一 。 一 1 c 实 际 上 已不 能 提供 分 类 信 息 ; m = 1 /, 当 时 , ∈ [ , ] 算 法 退 化 为 HC 算 法 , 以 i x 01 , M 所 F M实质 上是 H M 的 自然 推广 。 氏距 离准则 C C 欧 适合 于类 内数 据点 为 超 球 型分 布 的情 况 , d 采 用不 同 的距 离定 义 , 可将 聚类 算 法 用 于 不 同分 布类 型数据 的聚类 问题 。
别、 分析 与 预 测 的 目的 。17 9 3年 D n u n提 出 了
J = ∑ 1
1 J= 1
l ∈[, 01 ]
式 中 为样 本 数 据 点 的数 目, 类 别 数 c为
目, 常 1< c<n m > 1为一 个标 量 ; , 通 ; d (, ) = l i一 _示数 据点 , 之 间 的欧 氏距 】 I x 心
1 引 言
模糊 聚 类 分 析 ( C F :
Bl a e m n和 Z d h等 人 在 16 l ae 9 6年 提 出 的 , 是 它 近些年 来发展 很 快 的一 种 分析 方 法 , 目的是 其 对 样本 进行合 理 分 配 , 而 达 到 对样 本 进 行 判 从
离 ; ={ , , } 的集合 , ∈R 为 A, cR 点 聚类 的中心 ; t 表示 数据 点 属 于类 中心 的 z
用 于求类 中心 的迭 代 问题 , 算 法 中没 有 考 虑 该
模糊c均值聚类算法

模糊c均值聚类算法
模糊c均值聚类算法(Fuzzy C-Means Algorithm,简称FCM)是一种基于模糊集理论的聚类分析算法,它是由Dubes 和Jain于1973年提出的,也是用于聚类数据最常用的算法之
一。
fcm算法假设数据点属于某个聚类的程度是一个模糊
的值而不是一个确定的值。
模糊C均值聚类算法的基本原理是:将数据划分为k个
类别,每个类别有c个聚类中心,每个类别的聚类中心的模糊程度由模糊矩阵描述。
模糊矩阵是每个样本点与每个聚类中心的距离的倒数,它描述了每个样本点属于每个聚类中心的程度。
模糊C均值聚类算法的步骤如下:
1、初始化模糊矩阵U,其中每一行表示一个样本点,每
一列表示一个聚类中心,每一行的每一列的值表示该样本点属于该聚类中心的程度,U的每一行的和为
1.
2、计算聚类中心。
对每一个聚类中心,根据模糊矩阵U
计算它的坐标,即每一维特征值的均值。
3、更新模糊矩阵U。
根据每一个样本点与该聚类中心的距离,计算每一行的每一列的值,其中值越大,说明该样本点属于该聚类中心的程度就越大。
4、重复步骤2和步骤
3,直到模糊矩阵U不再变化,即收敛为最优解。
模糊C均值聚类算法的优点在于它可以在每一个样本点属于每一类的程度上,提供详细的信息,并且能够处理噪声数据,因此在聚类分析中应用十分广泛。
然而,其缺点在于计算量较大,而且它对初始聚类中心的选取非常敏感。
模糊 c 均值聚类算法

模糊 c 均值聚类算法概述模糊 c 均值聚类算法是一种基于模糊逻辑的聚类算法,其通过将每个数据点分配到不同的聚类中心来实现数据的分组。
与传统的 k-means 算法相比,模糊 c 均值聚类算法在处理数据集特征模糊和噪声干扰方面表现更好。
本文将详细介绍模糊 c 均值聚类算法的原理、优点和缺点,以及其在实际应用中的一些场景和方法。
原理模糊 c 均值聚类算法基于模糊集合理论,将每个数据点分配到不同的聚类中心,而不是像 k-means 算法一样将数据点硬性地分配到最近的聚类中心。
算法的核心是定义每个数据点属于每个聚类中心的权重,即模糊度。
具体而言,模糊 c 均值聚类算法的步骤如下:1.初始化聚类中心。
从输入数据中随机选择一些数据作为初始聚类中心。
2.计算每个数据点到每个聚类中心的距离。
可以使用欧氏距离或其他距离度量方法。
3.根据距离计算每个数据点属于每个聚类的模糊度。
模糊度是一个介于 0 和1 之间的值,表示某个数据点属于某个聚类的程度。
4.更新聚类中心。
根据数据点的模糊度重新计算每个聚类的中心位置。
5.重复步骤 2、3 和 4,直到聚类中心的位置不再发生明显变化或达到预定的迭代次数。
优点模糊 c 均值聚类算法相比传统的 k-means 算法具有以下优点:1.模糊度。
模糊 c 均值聚类算法可以为每个数据点分配一个模糊度值,这样可以更好地应对数据集中的噪声和模糊性。
而 k-means 算法仅将数据点硬性分配到最近的聚类中心。
2.灵活性。
模糊 c 均值聚类算法中的模糊度可以解释某个数据点同时属于多个聚类的情况,这在一些实际应用中可能是具有意义的。
3.鲁棒性。
模糊 c 均值聚类算法对初始聚类中心的选择相对不敏感,因此在大多数情况下能够获得较好的聚类结果。
缺点虽然模糊 c 均值聚类算法具有许多优点,但也存在一些缺点:1.计算复杂度。
模糊 c 均值聚类算法需要在每个迭代步骤中计算每个数据点与每个聚类中心的距离,这导致算法的计算复杂度较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上述算法中,由于引入 的归一化
条件,在样本集不理想的情况下可能导 致结果不好。比如,如果某个野值样本 远离各类的聚类中心,本来它严格属于 各类的隶属度都很小,但由于归一化条 件的限制,将会使它对各类都有较大的 隶属度(比如两类情况下各类的隶属度都 是0.5),这种野值的存在将影响迭代的 最终结果。
(2)
这里 , =1,⋯ ,n,是等式的n个约束 式的拉格朗日乘子。对所有输入参量求 导,使式(1)达到最小的必要条件为:
(3)
(4)
由上述两个必要条件,模糊c均值聚类算 法是一个简单的迭代过程。在批处理方 式运行时,FCM采用下列步骤确定聚类中 心 和隶属矩阵 U:
步骤1 用值在0,1间的随机数初始 化隶属矩阵U,使其满足式(2)中的约束 条件。
2395.96; 2429.47; 1514.98; 2665.9; 2002.33; 3071.18; 2163.05; 1411.53; 2150.98; 2462.86;
1571.17 104.8 499.85 2297.28 2092.62 1418.79 1845.59 2205.36
1731.04 3389.83 3305.75 3340.14 3177.21 1775.89 1918.81 3243.74
调用上述程序建立起来的模糊聚 类函数,得到以下运行程序:
A=[1739.94 373.3 1756.77 864.45 222.85 877.88 1803.58 2352.12 401.3 363.34
1675.15 3087.05 1652 1647.31 3059.54 2031.66 1583.12 2557.04 3259.94 3477.95
数的建立
• U = initfcm(cluster_n, data_n); %初始 化模糊分割矩阵
%以下为主循环: • for i = 1:max_iter, • [U, center, obj_fcn(i)] =
stepfcm(data, U, cluster_n, expo); • if display, • fprintf('Iteration count = %d, obj.
• if nargin == 2, • options = default_options; • else • if length(options) < 4,
• tmp = default_options; • tmp(1:length(options)) = options; • options = tmp; • end • nan_index = find(isnan(options)==1); • options(nan_index) =
default_options(nan_index); • if options(1) <= 1, • error('The exponent should be
greater than 1!'); • end
• end
• expo = options(1);%u矩阵指数 • max_iter = options(2);%迭代最大次数 • min_impro = options(3);%改进的最小值 • display = options(4); • obj_fcn = zeros(max_iter, 1);%目标函
步骤2 用式(3)计算c个聚类中心 , i=1,⋯ ,c。
步骤3 根据式(1)计算目标函数。 如果它小于某个确定的阈值,或它相对 上次价值函数值的改变量小于某个阈值, 则算法停止。
步骤4 用式(4)计算新的U阵。近回 步骤2。
当算法收敛时,就得到了各类的聚 类中心和各个样本对于各类的隶属度值, 从而完成了模糊聚类划分。
程序
• if nargin ~= 2 & nargin ~= 3, • error('Too many or too few input
arguments!'); • end • data_n = size(data, 1); • in_n = size(data, 2);
• default_options = [2;%u矩阵分割指数 100; %迭代的最大次数 1e-5;%改进的最小值 1]; %迭代时显示信息
fcn = %f\n', i, obj_fcn(i)); • end %检查终止情况:
• if i > 1, • if abs(obj_fcn(i) - obj_fcn(i-1)) <
min_impro, break; end, • end • end • iter_n = i;% • obj_fcn(iter_n+1:max_iter) = [];
基于模糊C均值的聚类分析
Байду номын сангаас
1 模糊c均值聚类(FCM)方法
模糊C均值聚类(FCM)方法是一种在已 知聚类数的情况下,利用隶属度函数和迭 代算法将有限的数据集分别聚类的方法。 其目标函数为:
式中, 为样本数; 为聚类数; 为第 个 样本相对于第 个聚类中心的隶属度; 为
第 个类别的聚类中心; 为样本到聚类 中心的欧式距离。聚类的结果使目标函 数 最小,因此,构造如下新的目标函 数:
1735.33; 2421.83; 2196.22; 535.62; 584.32; 2772.9; 2226.49; 1202.69;
2949.16 1692.62 1680.67 2802.88 172.78 2063.54 1449.58 1651.52 341.59 291.02
3244.44 1867.5 1575.78 3017.11 3084.49 3199.76 1641.58 1713.28 3076.62 3095.68
662.42; 2108.97; 1725.1; 1984.98; 2328.65; 1257.21; 3405.12; 1570.38; 2438.63; 2088.95;
237.63
3077.78 2251.96;
1702.8
1639.79 2068.74;
1877.93 1860.96 1975.3;
