运筹学第六章图与网络分析
合集下载
运筹学——.图与网络分析-最短路

可选择的最短路为
(v5 , v6 ), (v5 , v7 ).
min{ k24, k34, k56, k57} min{9,10,13,14} 9
① 给(v2 , v4 )
划成粗
线②。给v4 标号(9)。
③ 划第5个弧。
v2 (4) 5 v4(9) 9 v6 (13)
4 4
v1 (0)
1
75
v2 (4)
5
v4
9
v6
4
1
v1 (0)
4
75
5
v8
①
64
1
②
v3(6)
7 v5 6
v7
③
3)接着往下考察,有三条路可走:(v1, v3 ), (v2, v4 ), (v2 , v5 ).
可选择的最短路为
min{ k13, k24, k25} min{l13, l12 d24,l12 d25} min{ 6,4 5,4 4} 6
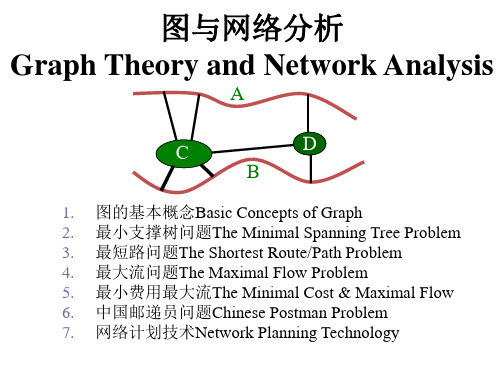
第6章 图与网络分析
本章内容重点
图的基本概念与基本定理 树和最小支撑树 最短路问题 网络最大流
引
言
图论是应用非常广泛的运筹学分 支,它已经广泛地应用于物理学控制论,信 息论,工程技术,交通运输,经济管理,电 子计算机等各项领域。对于科学研究,市场 和社会生活中的许多问题,可以同图论的理 论和方法来加以解决。例如,各种通信线路 的架设,输油管道的铺设,铁路或者公路交 通网络的合理布局等问题,都可以应用图论 的方法,简便、快捷地加以解决。
若已知设备在各年的购买费,及不同机器役龄时的残值与 维修费,如表2所示.
项目 购买费 机器役龄 维修费 残值
第1年 11 0-1 5 4
第六章图与网络分析

e3
v3
若链中所有的顶点也互不相同,这样的链称为路.
e4
v4
起点和终点重合的链称为圈. 起点和终点重合的路称为回路.
若图中的每一对顶点之间至少存在一条链, 称这 样的图为连通图, 否则称该图是不连通的. 第10页
完全图,偶图
任意两点之间均有边相连的简单图, 称为完全图. K n
K2
K3
K4
2 | E | Cn
第20页
6.2树图和图的最小部分树问题 Minimal tree problem 6.2.1树的概念
若图中的每一对顶点之间至少存在一条链, 称这样的图 为连通图. 树图(简称树Tree): 无圈的连通的图,记作T(V, E)
组织机构、家谱、学科分支、因特网络、通讯网络及高压线路 网络等都能表达成一个树图 。
第13页
有向图 G : (V,E),记为 G=(V,E)
G 的点集合: V {v1 , v2 ,...,vn } G 的弧集合: E {eij } 且 eij 是一个有序二元组 (vi , v j ) ,记
为 eij (vi , v j ) 。下图就是一个有向图,简记 G 。 若 eij (vi , v j ) ,则称 eij 从 v i 连向 v j ,点 v i 称为 eij 的尾,v j 称为 eij 的头。 v i 称为 v j 的前继, v j 称为 v i 的后继。 基本图:去掉有向图的每条弧上的方向所得到的无向图。
有向图 G (V , E ) 的关联矩阵:一个 | V | | E | 阶矩阵
B (bik ) ,
1, 当 弧ek以 点i为 尾 其中 bik 1, 当 弧ek以 点i为 头 0, 否 则
运筹学6(图与网络分析)

▲如果链中所有的顶点v0,v1,…,vk也不相
e2 e 4
v2 e5
e1 v1 e3 v3
同,这样的链称初等链(或路)。 ▲如果链中各边e1,e2…,ek互不相同称为简单链。
▲当v0与vk重合时称为回路(或圈),如果边不
e6
v4
e7
e8
v5
重复称为简单回路,如果边不重复点也不重复 则称为初等回路。 图8-1中, μ1={v5,e8,v3,e3,v1,e2,v2,e4,v3,e7,v5}是一条链,μ1中因顶 点v3重复出现,不能称作路。
运筹学
Operations Research
Chapter 8 图与网络分析
Graph and Network
1. 2. 3. 4. 图与网络的基本知识 树 最短路问题 最大流问题
E.Euler提出(1736年):
引例:哥尼斯堡七桥问题
您能从A、B、C或D任意一点出发 走遍7座桥并且每座桥只走一次最 后回到原出发点吗?
5
e2 v2 e6 e3 v3 v4
e1 v1 e3 e4 e5 e7
v3 e8 v5
e6 v4
e8 v5
e6 v4
e7 图2-2(b) v5
图8-2(a)
定义8
网络(赋权图):
设图G=(V,E),对G的每一条边(vi,vj)相应的有一条数w
(vi,vj) (或记为wij),wij称为边(vi,vj)的权,赋有权的图G称为网络
一、图与网络的基本概念 如图8-1
V v1 , v2 ,, v5 , E e1 , e2 ,, e8
e2可记作: e2 [v1 , v2 ]
e2 e 4
e5
e1 v1 e3 v3
e2 e 4
v2 e5
e1 v1 e3 v3
同,这样的链称初等链(或路)。 ▲如果链中各边e1,e2…,ek互不相同称为简单链。
▲当v0与vk重合时称为回路(或圈),如果边不
e6
v4
e7
e8
v5
重复称为简单回路,如果边不重复点也不重复 则称为初等回路。 图8-1中, μ1={v5,e8,v3,e3,v1,e2,v2,e4,v3,e7,v5}是一条链,μ1中因顶 点v3重复出现,不能称作路。
运筹学
Operations Research
Chapter 8 图与网络分析
Graph and Network
1. 2. 3. 4. 图与网络的基本知识 树 最短路问题 最大流问题
E.Euler提出(1736年):
引例:哥尼斯堡七桥问题
您能从A、B、C或D任意一点出发 走遍7座桥并且每座桥只走一次最 后回到原出发点吗?
5
e2 v2 e6 e3 v3 v4
e1 v1 e3 e4 e5 e7
v3 e8 v5
e6 v4
e8 v5
e6 v4
e7 图2-2(b) v5
图8-2(a)
定义8
网络(赋权图):
设图G=(V,E),对G的每一条边(vi,vj)相应的有一条数w
(vi,vj) (或记为wij),wij称为边(vi,vj)的权,赋有权的图G称为网络
一、图与网络的基本概念 如图8-1
V v1 , v2 ,, v5 , E e1 , e2 ,, e8
e2可记作: e2 [v1 , v2 ]
e2 e 4
e5
e1 v1 e3 v3
运筹学-6(图与网络分析)PPT课件

4
3
验证:第一圈内总长:3+4+5+4+7=23 第一圈逆时针内配送路长:3+4+5=12>11.5,则不是最优方案 第二圈内配送路长:4+2+3+4=13 第二圈逆时针内配送路长:2<6.5,则是最优方案。 第二圈顺时针内配送路长:3<6.5,则是最优方案。
修正第一圈内方案,取逆时针方向最小值1,然后逆时针方向配送路线减去 1,顺时针方向配送及未走路线加上1,则得到第一圈内配送路长:5<总长 一半,则是最优方案。如图所示:
相关 成本
A 4C
E
A 5C
E F
A 6C
F I
D D, F F, I
D D I H, G
D D H, G H, J
348 291, 228 294, 258
348 291 258 288, 360
348 291 288, 360 390, 384
第n个 最近
节点
最小 成本
最新 连接
A到各 N节点 最短 路径
6.2.2 网络图的绘制原则
只能有一个始点事项和一个终点事项 不允许出现编号相同的箭线 不允许出现循环线路 作业要始于结点终于结点
网 络 规 则(2)
1、避免循环、不留缺口
2、一一对应:一道工序用两个事项表示
F 228 CF A→C→F
I
258 EI A→B→E
→I
H 288 FH A→C→F →H
步 已解点 候选点 骤
相关 成本
A C 7F I H
F 8I
H D
D D G J G, J
G J J G
348 291 360 384 336, 414 360 384 414 396
运筹学06图与网络分析PPT演示文稿
v4
v1 v2 v3 v4 v5 v1 0 1 1 0 0
起 v2 1 0 0 1 1
点 v3 1 0 0 0 1
v5
v4 0 1 0 0 1
v5 0 1 1 1 0
19
❖ 赋权无向图的邻接矩阵表示
▪ 两顶点之间有边相连的,写上其权数,无 边相连的记为∞,对角线上的数字为0。赋 权无向图对应的矩阵也是对称的。
1 图的基本概念
❖ 案例导引 ❖ 图论中的图 ❖ 图的矩阵描述
2
案例导引
❖ 图论是运筹学的一个重要分支,对其最早的 研究可以追溯到著名的哥尼斯堡七桥问题 (Konigsberg Bridges Problem)。18世纪,欧洲 的哥尼斯堡城有一条流经全城的普雷戈尔河, 河的两岸与河中两个小岛及两岛之间有七座 桥彼此相通(如左图)。
22
树及其性质
❖ 树在现实中随处可见,如电话线架设、比赛 程序、组织结构等。
❖ 树:连通的无圈的无向图称为树。
23
❖ 树的性质 ❖ 图G=(V,E),p个点、q条边,下列说法是等价
的 ▪ (1)G是一个树 ▪ (2)G连通,且恰有p-1条边 ▪ (3)G无圈,且恰有p-1条边 ▪ (4)G连通,但每舍去一边就不连通 ▪ (5)G无圈,但每增加一边即得唯一一个圈 ▪ (6)G中任意两点之间恰有一条链(简单链)
30
❖在根树中,若每个顶点的出次小于或等 于M,称这棵树为M叉树。
❖若每个顶点的出次恰好等于M或者零, 则称这棵树为完全M叉树。
❖当M=2时,称为二叉树、完全二叉树。
31
❖ 如图所示的树是根树。其 中根、分枝点、叶;各点 层次都标注在树上。
❖ 这是一棵三叉树
三叉树
根
第六章图与网络分析概论
45
N={n1,n2,n3,n4,n5}是一个无向图的
3
点的集合)
G的边集合:E={eij}且eij={ni,nj}为无序二元组 eij的端点:有eij={ni,nj},则称ni和nj为
eij的端点,且称eij 连接点 ni和nj 环:两个端点重合为一点的边(例如右图中的e11) 重边:两个端点都相同的边。
d(n3)=1 d(n4)=2 d(n5)=?d(n2)= d+(n2)+ d-(n2)=1+1=2
4 主要结论
定理6.1.2图G=(N, E) (或G=(N, A))为任意图, |N|=n,,|E|=m(或|A|=m),则
n
d (ni ) 2m
i 1
定理6.1.3 有向图G=(N,A), |N|=n,,|A|=m,则
帷幄之中
运筹
决胜
千里之外
运 筹 学
第6章 图与网络分析
➢图与子图 ➢图的连通性 ➢树与支撑树 ➢最小树问题 ➢最短有向路 ➢最大流问题
问题1(哥尼斯堡七桥问题1736年):
Pregel河横穿Königsberg城,河上建有七座桥 ,能否 设计散步路线,走过所有七座桥,每座桥恰好经过一次 而回到同一地点?
一个图G=(N,E),一般记|N|=n,|E|=m.
1 无向图基本概念
完全图 每一对点之间均有一条边相连的图
二分图 G=(N,E) 存在的一个二分划(S,T),使得G的 每条边有一个端点在S中,另一个端点在T中
完全二分图 G=(S,T,E) S中的每个点与T中的每个点
都相连的简单二分图
简单图G的补图 与G有相同顶点集合的简单图,且图 中的两个点相邻当且仅当它们在G中不相邻
运筹学——.图与网络分析-最短路课件

运筹学——.图与网络分析-最短路
v2 (4) 5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v 3(6)
7 v 5 (8) 6
1
v7
③
④
4)接着往下考察,有四条路可走:(v2,v4), (v2,v5).
可选择的最短路为
(v3,v4), (v3,v5).
m k 2 , ik 4 2 n ,k 5 3 ,{ k 4 3 } 5m 9 ,8 , i 1 , n 1 } 0 { 3 8
(v5,v6), (v5,v7 ).
m k 2 ,i k 4 3 n ,k 4 5 ,k { 6 5 } 7 m 9 ,1 i ,1 n ,1 0 } 3 { 4 9
① 给(v2,v4) 划成粗线。
② 给 v 4 标号(9)。
③ 划第5个弧。
运筹学——.图与网络分析-最短路
v 2 ( 4 ) 5 v 4(9 ) 9 v 6 (13 )
运筹学——.图与网络分析-最短路
引言
随着科学技术的进步,特别是电子计算机 技术的发展,图论的理论获得了更进一步的发展, 应用更加广泛。如果将复杂的工程系统和管理问 题用图的理论加以描述,可以解决许多工程项目 和管理决策的最优问题。因此,图论越来越受到 工程技术人员和经营管理人员的重视。
运筹学——.图与网络分析-最短路
树图的各条边称为树枝假定各边均有权重一般图g2含有多个部分树其中树枝总长最小的部分树称为该图的最小部分树也称最小支撑树?定理1图中任一个点i若j是与i相邻点中距离最近的则边ij一定必含在该图的最小部分树内
第6章 图与网络分析
本章内容重点 图的基本概念与基本定理 树和最小支撑树 最短路问题 网络最大流
系统工程与运筹学 第6章 图与网络最优化方法

属于部分树的边称为内边,不属于部分树的边称为外边。
连通图G (V, E)中,内边权值总和最小的部分树为最小部分树( 最小支撑树)。
最大部分树?
6.2 最小部分树问题
6.1.1图的基本概念和术语
1. 最小部分树定理 树的任意一条外边Cij比所对应的链中最长的边还长;即最小部 分树是指内边权总和最小的那棵树 2. 最小部分树算法 【例6.1】 某市区准备在五个社区间架设光纤网络,各社区的位 置如图6.2.1(a),如何架设光纤网络可使各社区间均能通网且光纤线 路最短。
欧拉回路也称一笔圈图,欧拉链也称一笔链图,二者均为一笔画图。
6.3.2 中国邮递员问题
由中国数学家管梅谷先生在1962年提出.
抽象成图的语言就是:给定一个无向的连通图,怎样 才能使每条边至少出现一次并使边长总和最小。这类问 题叫中国邮递员问题或一笔画问题。
中国邮递员问题可以描述为:在一个有奇点的连通图 中,增加一些重复边,使得该图成为一笔圈图,并且要 求重复边的总路长最小。
A
D C
B 图6.3.1 哥尼斯堡七桥问题
【定理1】 若图G的每个顶点所关联的边数是偶数条,则图G是欧拉回路,这
样的图能一笔画出;
【定理2】 若除链的端点以外其余每个顶点所关联的边数是偶数 条(即图中奇点数为2),则图是欧拉链,若想走过该图所有的边而不 走重复路,就只能从一个奇点出发到达另一个奇点。
1736年著名数学家欧拉(Euler)发表了图论方面第一篇论文,解 决了有名的哥尼斯堡七桥难题,欧拉被公认为图论的创始人。
图论以集合元素间某种二元关系生成的拓扑图形为研究对象,任 何一个包含了某种二元关系的系统都可以用图论的方法来分析。
经过200多年的发展,图论已经发展成为一个理论与应用兼有的 数学领域,在自然科学和社会科学研究中有着广泛的应用。
连通图G (V, E)中,内边权值总和最小的部分树为最小部分树( 最小支撑树)。
最大部分树?
6.2 最小部分树问题
6.1.1图的基本概念和术语
1. 最小部分树定理 树的任意一条外边Cij比所对应的链中最长的边还长;即最小部 分树是指内边权总和最小的那棵树 2. 最小部分树算法 【例6.1】 某市区准备在五个社区间架设光纤网络,各社区的位 置如图6.2.1(a),如何架设光纤网络可使各社区间均能通网且光纤线 路最短。
欧拉回路也称一笔圈图,欧拉链也称一笔链图,二者均为一笔画图。
6.3.2 中国邮递员问题
由中国数学家管梅谷先生在1962年提出.
抽象成图的语言就是:给定一个无向的连通图,怎样 才能使每条边至少出现一次并使边长总和最小。这类问 题叫中国邮递员问题或一笔画问题。
中国邮递员问题可以描述为:在一个有奇点的连通图 中,增加一些重复边,使得该图成为一笔圈图,并且要 求重复边的总路长最小。
A
D C
B 图6.3.1 哥尼斯堡七桥问题
【定理1】 若图G的每个顶点所关联的边数是偶数条,则图G是欧拉回路,这
样的图能一笔画出;
【定理2】 若除链的端点以外其余每个顶点所关联的边数是偶数 条(即图中奇点数为2),则图是欧拉链,若想走过该图所有的边而不 走重复路,就只能从一个奇点出发到达另一个奇点。
1736年著名数学家欧拉(Euler)发表了图论方面第一篇论文,解 决了有名的哥尼斯堡七桥难题,欧拉被公认为图论的创始人。
图论以集合元素间某种二元关系生成的拓扑图形为研究对象,任 何一个包含了某种二元关系的系统都可以用图论的方法来分析。
经过200多年的发展,图论已经发展成为一个理论与应用兼有的 数学领域,在自然科学和社会科学研究中有着广泛的应用。
运筹学第六章 网络规划与网络分析

与无向图和有向图相对应,网络又分为无向网络 和有向网络。
图的矩阵表示方法: 关联矩阵:在图G=(V,E) 中,V=(v1,v2,…,vp),E=(e1,e2 ,…,eq), 构造一个矩阵 A (aij ) pq ,其中
1 当点vi与边e j 关联 aij 否则 0
则称A为G的关联矩阵。关联指顶点与边的关系。
vit
的一条链,简记为
v , v
i1
i2
,, vit 。其中 eik (eik , ei ( k 1) ), k 1, 2,..., t 1 。称 vi1和
1 2 3 2 4 5 1 2 4 5
vit 为链的两个端点。图6-3 中的 v , v , v ,v , v , v ,v , v , v , v
为区别起见,把两点间不带箭头的连线称为边, 带箭头的连线称为弧。 由此看出,用图来描述事物间的联系,不仅 直观清晰,便于统观全局,而且网络图的画法简 便,不必拘泥于比例和曲直。总之,这里所讲的 图是反映对象之间关系的一种工具。这样的例子 也很多,电路网络、城市规划、信息传递、物质 结构、物资调配等也都可以用点和线连接起来的 图进行模拟。
都是链。 两个端点重合的链,称为圈。在一个图中,如果任何两个 顶点之间都有一条链,该图称为连通图。
二、有向图
(1)有向图
有向图是一个有序二元组(V,A),记为D(V,A),其中
V (v1 , v2 ,..., vp ) 是p个顶点的集合,A (a1 , a2 ,..., aq ) 是q条弧
ait vi ( t 1) , vit ,则称P是一条链接 vi1 和 vit 的有向路。
三、网络
实际问题中,往往只用图来描述所研究对象之间的 关系还不够,如果在图中赋予边一定的数量指标,我们 常称之为“权”。依据研究问题的需要,权可以代表距 离,也可以代表时间、费用、容量、可靠性等。通常把 这种赋权图称为网络。
运筹学第6章网络素材

e E
W (e )
最小支撑树:G 中权最小的支撑树 定理 6.4.1 设 T 是 G 的支撑树,则 T 是 G 的最小树当且仅当对任意边 eT* 有 W (e ) max W ( e ) e C ( e ) 其中 C ( e ) T e 为一个唯一的回路。 定理 6.4.2 设 T 是 G 的支撑树,则 T 是 G 的最小树当且仅当对任意边 W (e ) min W ( e ) e T 有 e ( e ) 其中 (e ) T e 为一个唯一割集。 定理 6.4.3 设 T 是 G 的支撑树,则 T 是 G 的唯一最小树当且仅当对任意 边 e G \ T ,e 是 C(e)中的唯一最大边。 定理 6.4.4 设 T 是 G 的支撑树,则 T 是 G 的唯一最小树当且仅当对任意 e T 边 ,e 是 (e ) 中的唯一最大边。
第6页
网络的基本概念
有向图G:一个有序二员组(N,A),记为G=(N,A) G的弧集合:A={aij}且aij={ni,nj}为有序二元组 ,若 aij={ni,nj},则称aij从ni连向nj, ni称为aij的尾, nj为 aij的头,ni称为nj的先辈,nj称为 ni的后继 有向图G的基本图:对于G的每条弧用一条边代替后得到 的无向图 (有向)网络G:对(有向)图G的每条边(弧)都赋予 一个实数,并称为边(弧)的权,则连同它边(弧)上 的权称为(有向)网络。
第12页
图的连通与割集
图的连通
无向图 有向图
图的割集
概念 主要结论
第13页
无向图的路
图G中路:一个点和边交替序列 (ni,eij,nj,…,nk,ekl,nl), 简单路:边不重的路 初级路:点不重的路 回路:在G中,一条至少包含一个 边并且ni=nl的{ ni,nl}路 简单回路:边不重的回路 初级回路:点不重的回路
运筹学第六章 网络分析

2
v4
v5
4 3 4
v1
1
5
7
v6
v2
2
例 10
15
8
13
13
5
1
14 12
16
4
12 14
93
14
2
16
3
14
7
6
15
破圈法:任意选一个圈划掉权值最大的
边,重复直到所有节点形不成圈
例 11:
15
8
13
13
5
1
14 12
16
4
12 14
14
2
16
3
14
7
6
15
15
8
13
13
5
1
14 12
尽管试验者很多,但是都没有成功。为了寻找答案,1736年欧 拉将这个问题抽象成下图所示图形的一笔画问题。即能否从某 一点开始不重复地一笔画出这个图形,最终回到原点
C
A
B
D
欧拉在他的论文中证明了这是不可能的,因为这个图形中每一 个顶点都与奇数条边相连接,不可能将它一笔画出,这就是古 典图论中的第一个著名问题。
其中 v5 为悬挂点, v7 为孤立点。
定理1 所有顶点度数之和等于所有边数的2 倍。
vV
d(v) = 2q
证明:因为在计算各个点的度时,每条边被 它的两个端点个用了一次。
定理2 在任一图中,奇点的个数必为偶数。
证明: 设 V1,V2 分别是图G中奇点和偶点的
集合,由定理1 ,有
d (v ) d (v ) d (v ) 2q 因为 d (v ) 是偶数, d (v) 也是偶数,因此
运筹学06图与网络分析

满足w(T*)=min(w(T))的树T*称为最小支撑树 (最小树)。
求最小树的方法 求最小树的避圈法 求最小树的破圈法
根树及其应用
有向树中的根树在计算机科学、决策论中有 很重要的应用
有向树:若一个有向图在不考虑边的方向时 是一棵树,则称这个有向图为有向树。
根树:有向树T,恰有一个结点入次为0,其 余各点入次均为1,则称T为根树(又称外向 树)。根树中入次为0的点称为根。根树中出 次为0的点称为叶。入次和出次均大于0的点 称为分枝点。由根到某一顶点vi的道路长度 (设每边长度为1),称为vi点的层次。
v4
a5 a4 a7
a1=(v1,v5)
a6
a2=(v5,v4) a3=(v1,v4) a4=(v3,v1) a5=(v1,v2) a6=(v2,v3) a7=(v1,v4)
v2
v3
d-(v1)=1;d+(v1)=3 d-(v2)=1;d+(v2)=1 d-(v3)=1;d+(v3)=2 d-(v4)=3;d+(v4)=0 d-(v5)=1;d+(v5)=1
树及其性质
树在现实中随处可见,如电话线架设、比赛 程序、组织结构等。
树:连通的无圈的无向图称为树。
树的性质 图G=(V,E),p个点、q条边,下列说法是等价
的
(1)G是一个树 (2)G连通,且恰有p-1条边 (3)G无圈,且恰有p-1条边 (4)G连通,但每舍去一边就不连通 (5)G无圈,但每增加一边即得唯一一个圈 (6)G中任意两点之间恰有一条链(简单链)
如果对于给定的图G=(V,E)的任意一边e∈E, 有一实数W(e)与之对应,则称G为赋权图,称 W(e)为边e的权。
运筹学基础及应用(第五版),(第六章图与网络分析)

树枝总长最小的部分树,称为该图的最小部分树(也称最小支
撑树)。
定理1. 图中任一个点 i ,若 j 是与 i 相邻点中距离最近的, 则边 [ i , j ] 一定包含在该图的最小部分树中。
给图中的点和边赋以具体的含义和权值,我们称这样的
图为网络图(赋权图)
2020/3/27
6
图中的点用 v 表示,边用 e 表示,对每条边可用它所
联结的点表示,如图,则有:
e1 = [v1 , v1],
e2 = [v1 , v2]或e2= [v2 , v1]
2020/3/27
用点和点之间的线所构成的图,反映实际生产和生 活中的某些特定对象之间的特定关系。通常用点表 示研究对象,用点与点之间的线表示研究对象之间 的特定关系。一般情况下,图中点的相对位置如何 ,点与点之间线的长短曲直,对于反映研究对象之 间的关系,显的并不重要,因此,图论中的图与几 何图,工程图等本质上是不同的。
§2.树图和最小部分树
树图(简称树,记作 T(V, E))是无圈的连通图。(无圈, 无多重边)
一. 树的性质
性质1. 任何树中必存在次为1 的点。
次为1的点称为悬挂点,与之关联的边称为悬挂边。 性质2. 具有 n 个顶点的树恰有(n-1)条边。
性质3. 任何具有n 个点、(n - 1)条边连通图是树。
A D
C B
2020/3/27
3
为了寻找答案 ,1736年欧拉 把陆地缩为一点,把桥作为连接点 的边,将这个问题抽象成图形的一 笔画问题。即能否从某一点开始不 重复地一笔画出这个图形,最终回 到原点。欧拉在他的论文中证明了 这是不可能的,因为这个图形中每 一个顶点都与奇数条边相连接,不 可能将它一笔画出,这就是古典图 论中的第一个著名问题。
撑树)。
定理1. 图中任一个点 i ,若 j 是与 i 相邻点中距离最近的, 则边 [ i , j ] 一定包含在该图的最小部分树中。
给图中的点和边赋以具体的含义和权值,我们称这样的
图为网络图(赋权图)
2020/3/27
6
图中的点用 v 表示,边用 e 表示,对每条边可用它所
联结的点表示,如图,则有:
e1 = [v1 , v1],
e2 = [v1 , v2]或e2= [v2 , v1]
2020/3/27
用点和点之间的线所构成的图,反映实际生产和生 活中的某些特定对象之间的特定关系。通常用点表 示研究对象,用点与点之间的线表示研究对象之间 的特定关系。一般情况下,图中点的相对位置如何 ,点与点之间线的长短曲直,对于反映研究对象之 间的关系,显的并不重要,因此,图论中的图与几 何图,工程图等本质上是不同的。
§2.树图和最小部分树
树图(简称树,记作 T(V, E))是无圈的连通图。(无圈, 无多重边)
一. 树的性质
性质1. 任何树中必存在次为1 的点。
次为1的点称为悬挂点,与之关联的边称为悬挂边。 性质2. 具有 n 个顶点的树恰有(n-1)条边。
性质3. 任何具有n 个点、(n - 1)条边连通图是树。
A D
C B
2020/3/27
3
为了寻找答案 ,1736年欧拉 把陆地缩为一点,把桥作为连接点 的边,将这个问题抽象成图形的一 笔画问题。即能否从某一点开始不 重复地一笔画出这个图形,最终回 到原点。欧拉在他的论文中证明了 这是不可能的,因为这个图形中每 一个顶点都与奇数条边相连接,不 可能将它一笔画出,这就是古典图 论中的第一个著名问题。
