电路分析第四章习题解答
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
第4章 电路的暂态分析-习题解答

4.7 在题 4.7 图所示电路中,开关 S 闭合前电路已处于稳态,试确定 S 闭合后电
4
压 uL 和电流 iL、i1、i2 的初始值和稳态值。 【解】由于 i L (0 ) i L (0 )
uS 6 3A ,则 R1 2
i1 (0 )
R2 4 iL (0 ) 3 2A 24 R1 R2
6
【解】该电容电压的初始值为 20000V,放电的起始瞬间的冲击电流达到最 大值,冲击电流的峰值大小为 流。 这种情况下不会造成触电事故是由于放电时间极短,等效电路的时间常数为
20000 V 200 A ,远远超过了人体允许的致命电 100
RC 100 50 1012 5 109 s 5ns
u c (0 ) u c (0 ) R1i1 (0 ) 6V i1 (0 )
u c (0 ) 1A R1
i2 (0 ) 0 ic (0 ) I S i1 (0 ) 3 1 2A
1
②
) 。
① 立即亮 ③ 由亮逐渐变为不亮
② 逐渐变亮 ④ 由不亮逐渐变亮,再逐渐变为不亮 ① )。
(7)R、C 电路在零状态条件下,时间常数的意义是( ① 响应由零值增长到稳态值的 0.632 倍时所需时间 ② 响应由零值增长到稳态值的 0.368 倍时所需时间 ③ 过渡过程所需的时间 ④ 响应由稳态值下降到零值的 0.632 倍时所需时间 (8)一阶线性电路时间常数的数值取决于( ① 电路的结构形式 ③ )。
因此该电容的初始电压将在 5 25ns 时间内释放完毕,虽然冲击电流很大,但 是作用时间极短,对人体而言最多感觉到颤抖,不会造成致命伤害。
电路分析第四章习题参考答案

4-2 试用外施电源法求图题4-2 所示含源单口网络VCR ,并绘出伏安特性曲线。
解:图中u 可认为是外加电压源的电压。
根据图中u 所示的参考方向。
可列出(3)(6)(5)20(9)50u i i A VA i V=Ω+Ω++=+4-5试设法利用置换定理求解图题4-5所示电路中的电压0u 。
何处划分为好?置换时用电压源还是电流源为好?解:试从下图虚线处将电路划分成两部分,对网路N 1有(节点法)1111967(11)uu u u i ⎧⎛⎫+-=⎪⎪+⎝⎭⎨⎪-++=-⎩ 整理得:1511714u i =- 对网络2N 有251133u i i i =⨯+⨯=解得3i A =,用3A 电流源置换N 1较为方便,置换后利用分流关系,可得:()121031V 1V u +=⨯⨯=4-9 求图题4-7所示电路的输入电阻R i ,已知0.99α=解: 施加电源t u 于输入端可列出网孔方程:12335121(25100)100 (1)100(100100101010)100.990(2)t i i u i i i +-=-++⨯+⨯-⨯=将(2)代入(1)得135ti u R i ==Ω4-14求图题4-10所示各电路的等效电路。
解解: 图(a):因电压的计算与路径无关,所以[5(1)]4(13)4ad ac cd ad ab bd u u u V V u u u V V=+=---=-=+=--=-图(b): 流出a 点的电流(521)8a i A =++=,流入b 点多的电流(541)8b i A =+-=。
所以ab 之间的等效电路为8A 的电流源,电流从b 端流出。
图(c):导线短接。
4-23 电路如图题4-15 所示,已知非线性元件A 的VCR 为2u i =。
试求u ,i ,i 1.解: 断开A ,求得等效内阻:1o R =Ω 开路电压a u 所满足的方程:()(11)12111/21c a c a u u u u +-⨯=⎧⎪⎨-⨯++=⎪⎩ 求得2a u V =,最后将A 接到等效电源上,如上图所示。
第4章_组合逻辑电路习题解答
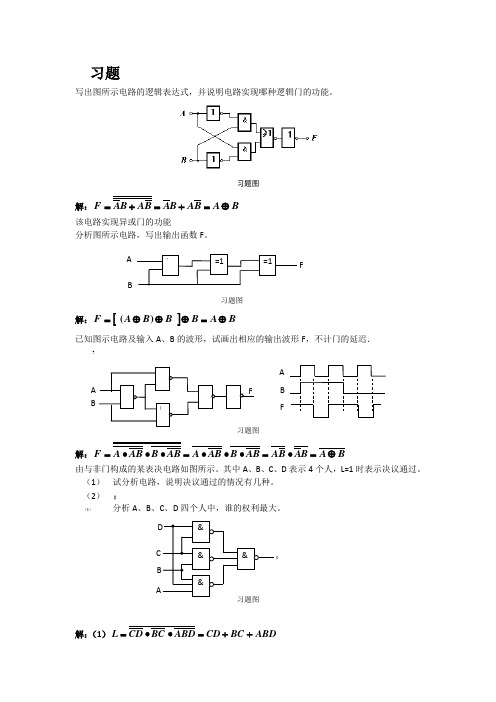
习题写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能分析图所示电路,写出输出函数F 。
习题图 解:[]B A B BB A F ⊕=⊕⊕⊕=)(已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.?解:B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 【 (3) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题图解:(1)ABD BC CD ABD BC CD L ++=••=C & && & D $ L B A " =1=1 =1FFA B[FB A(2)(3)根据真值表可知,四个人当中C 的权利最大。
分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
&习题图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)(3)当S 1S 0=00和S 1S 0=11时,该电路实现两输入或门,当S 1S 0=01时,该电路实现两输入或非门,当S 1S 0=10时,该电路实现两输入与非门。
(2)1¥电路逻辑功能为:“判输入ABC 是否相同”电路。
已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示,试写出F 的最简与或表达式。
习题图:解:(1)根据波形图得到真值表:,(2)由真值表得到逻辑表达式为C AB BC A C B A F ++=、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ,要求用最简单的方法,实现的电路最简单。
大学电路分析第四章课后习题答案

4-2.5μF 电容的端电压如图示。
(1)绘出电流波形图。
(2)确定2μs t =和10μs t =时电容的储能。
解:(1)由电压波形图写出电容端电压的表达式:10 0μs 1μs10 1μs 3μs ()1040 3μs 4μs 0 4μs t t t u t t t t≤≤⎧⎪≤≤⎪=⎨-+≤≤⎪⎪≤⎩式中时间t 的单位为微秒;电压的单位为毫伏。
电容伏安关系的微分形式:50 0μs 1μs 0 1μs 3μs()()50 3μs 4μs 0 4μs t t du t i t C t dt t<<⎧⎪<<⎪==⎨-<<⎪⎪<⎩上式中时间的单位为微秒;电压的单位为毫伏;电容的单位为微法拉;电流的单位为毫安。
电容电流的波形如右图所示。
(2)电容的储能21()()2w t Cu t =,即电容储能与电容端电压的平方成正比。
当2μs t =时,电容端电压为10毫伏,故:()()22631010μs 11()5101010 2.510J 22t w t Cu ---===⨯⨯⨯⨯=⨯当10μs t =时,电容的端电压为0,故当10μs t =时电容的储能为0。
4-3.定值电流4A 从t=0开始对2F 电容充电,问:(1)10秒后电容的储能是多少100秒后电容的储能是多少设电容初始电压为0。
解:电容端电压:()()()00110422t tC C u t u i d d t C τττ+++=+==⎰⎰;()1021020V C u =⨯=; ()1002100200V C u =⨯=()()211010400J 2C w Cu ==; ()()2110010040000J 2C w Cu ==4-6.通过3mH 电感的电流波形如图示。
(1)试求电感端电压()L u t ,并绘出波形图;(2)试求电感功率()L p t ,并绘出波形图;(3)试求电感储能()L w t ,并绘出波形图。
电路分析基础第四版课后习题第四章第五章第六章答案
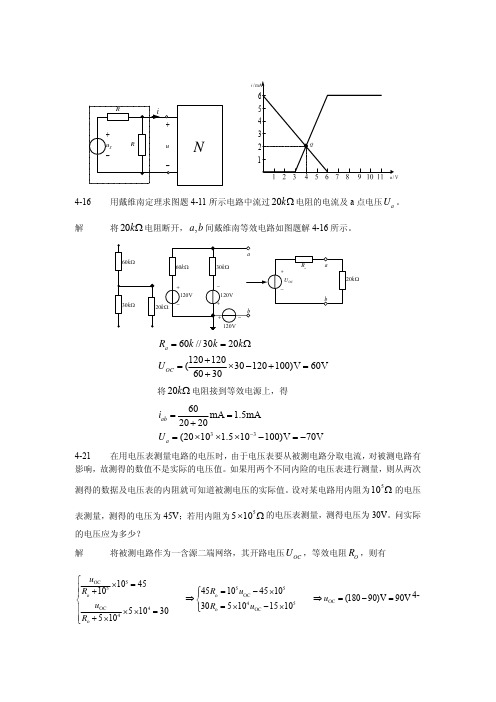
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
第四章 习题答案
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
电子电路基础习题册参考答案-第四章

第四章集成运算放大器的应用§4-1 集成运放的主要参数和工作点= 1、理想集成运放的开环差模电压放大倍数为 Aud=∞,共模抑制比为 KCMR ∞,开环差模输入电阻为 ri= ∞,差模输出电阻为 r0=0 ,频带宽度为 Fbw=∞。
2、集成运放根据用途不同,可分为通用型、高输入阻抗型、高精度型和低功耗型等。
3、集成运放的应用主要分为线性区和非线性区在分析电路工作原理时,都可以当作理想运放对待。
4、集成运放在线性应用时工作在负反馈状态,这时输出电压与差模输入电压满足关系;在非线性应用时工作在开环或正反馈状态,这时输出电压只有两种情况;+U0m 或 -U0m 。
5、理想集成运放工作在线性区的两个特点:(1) up=uN ,净输入电压为零这一特性成为虚短,(2) ip=iN,净输入电流为零这一特性称为虚断。
6、在图4-1-1理想运放中,设Ui=25v,R=Ω,U0=,则流过二极管的电流为 10 mA ,二极管正向压降为 v。
7、在图4-1-2所示电路中,集成运放是理想的,稳压管的稳压值为,Rf=2R1则U0=-15 V。
二、判断题1、反相输入比例运算放大器是电压串联负反馈。
(×)2、同相输入比例运算放大器是电压并联正反馈。
(×)3、同相输入比例运算放大器的闭环电压放大倍数一定大于或等于1。
(√)4、电压比较器“虚断”的概念不再成立,“虚短”的概念依然成立。
(√)5、理想集成运放线性应用时,其输入端存在着“虚断”和“虚短”的特点。
(√)6、反相输入比例运算器中,当Rf=R1,它就成了跟随器。
(×)7、同相输入比例运算器中,当Rf=∞,R1=0,它就成了跟随器。
(×)三、选择题1、反比例运算电路的反馈类型是(B )。
A.电压串联负反馈B.电压并联负反馈C.电流串联负反馈2、通向比例运算电路的反馈类型是(A )。
A.电压串联负反馈B.电压并联负反馈C.电压串联正反馈3、在图4-1-3所示电路中,设集成运放是理想的,则电路存在如下关系( B )。
第四章 正弦交流电路习题参考答案

tωAi /A222032πtAi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4-1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220= 频率 3145022f Hz ωππ=== 周期 10.02T s f== 角频率 314/rad s ω=题解图4.01 初相位 s rad /3πψ-=波形图如题解图4.01所示(2) 如果i 的参考方向选的相反, 则A t i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s rad /32πψ=其他项不变。
波形图如题解图 4.02所示。
题解图4.02 4-1-2 已知A )120314sin(101 -=t i ,A )30314sin(202 +=t i⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ (2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4.03+14-2-1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002+=t u 解:V U ︒-∠=•4521101 V U ︒∠=•4525024-2-2 已知正弦电流)A 60(sin 81+=t i ω和)A 30(sin 62-=t i ω,试用复数计算电流21i i i +=,并画出相量图。
解:由题目得到Aj j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=•••1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821 所以正弦电流为)A 1.23(sin 101+=t i ω 题解图4.04 相量图如题解图4.04所示。
电路分析习题解答(第四章)
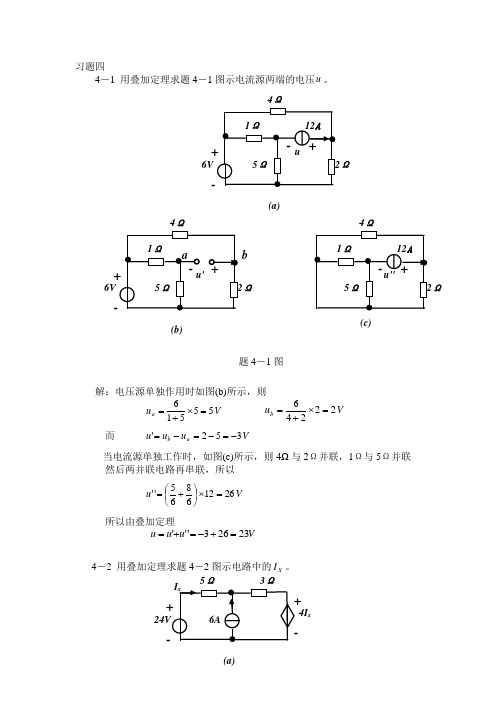
习题四4-1 用叠加定理求题4-1图示电流源两端的电压u 。
解:电压源单独作用时如图(b)所示,则V u a 55516=⨯+= V u b 22246=⨯+=而 V u u u a b 352'-=-=-=当电流源单独工作时,如图(c)所示,则4Ω与2Ω并联,1Ω与5Ω并联然后两并联电路再串联,所以V u 26126865''=⨯⎪⎭⎫⎝⎛+=所以由叠加定理V u u u 23263'''=+-=+=4-2 用叠加定理求题4-2图示电路中的X I 。
题4-1图 6V 4Ω Ω (b)b (c) 4Ω Ω5Ω 3Ω (a)4I x6V 4Ω Ω (a)解:电压源单独作用时的电路如图(b) 所示,则()24435''=++x x I I 解得 A I x 2'=电流源单独作用时的电路如图(c)所示,图中虚线为网孔电流,则 ()0''4''63''5=+++x x x I I I 解得 A I x 5.1''-= 所以 A I I I x x x 5.05.12'''=-=+=4-3 用叠加定理求题4-3图示电路中的独立电压源和独立电流源发出的功率。
5Ω 3Ω '(b) 4I 'x 4I ''x5Ω 3Ω I ''x(c) 题4-2图 题4-3图 2A 4Ω (a) 2V2A 4Ω 2i'(b) + - i''14Ω (c) u''1 2V解:电流源单独作用时的电路如图(b) 所示,则A i 2'1= 0'=i则 V i i u 824''1'1=-=电压源单独作用时的电路如图(b) 所示,则A i 5.042''1-=-= A i i 5.0''1''=-=则 V i u 122''''1=-=所以由叠加定理 A i i i 5.15.02''1'11=-=+=V u u u 918''1'11=+=+=可得电压源和电流源的功率分别为W i P V 3212-=-= W u P A 18212==4-4 题4-4图示电路中,R N 为电阻网络,由两个电流源供电。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
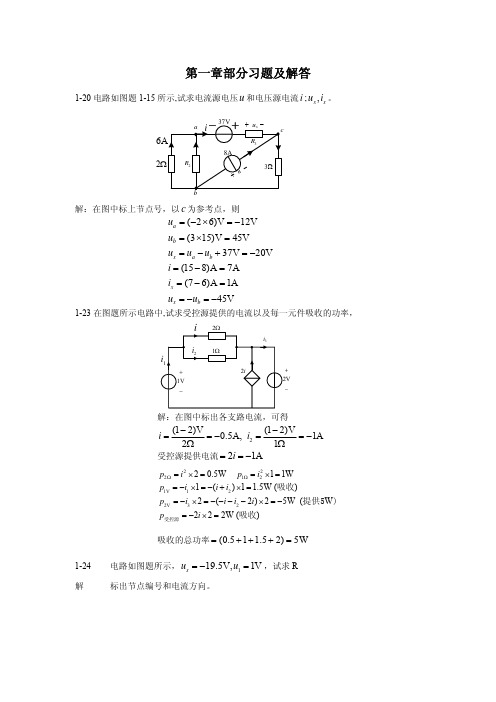
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
第四章习题及解答
第四章习题及解答4.1 数字电路设计的基本步骤有哪些?每一步完成的目标任务是什么?见书P48。
4.2 组合逻辑电路的设计为什么可以从卡诺图直接进入?因为逻辑函数可以有多种有表达形式,卡诺图就是其中的一种,因此,直接从卡诺图直接进入设计就是最直接、最有效的一种方式,它简化了设计,更便于化简。
4.3 某车间有A 、B 、C 、D 四台电动机,今要求:(1)A 必须开机;(2)其他三台电动机中至少有两台开机,如不满足上述要求,则指示灯熄灭。
设指示灯亮为“1”,熄灭为“0”,电机开机为“1”,停机为“0”,试用与非门组成指示灯控制电路。
根据题意,用卡诺图表示电机运行的状态,求出输出表达式:F= ABC+ABD+ACD用与非门实现逻辑:4.4 试设计一个供4组使用的智力抢答器电路。
设4组变量分别为:A 、B 、C 、D 。
输出用4个发光二极管,表示抢答结果,灯亮答表达式: F ABCD ABCD ABCD =+++4.5 电话室需对4种电话编码控制,按紧急次序排列优先权由高到底依次为火警电话、急救电话、工作电话、生活电话,其编码为11,10,01,00,试设计该编码电路。
设火警电话、急救电话、工作电话、生活电话为变量A 、B 、C 、D ,编码输出量为X 、Y 。
AB CD01001110000000000001111000 01 11 10 F ABC ABD ACDABC ABD ACD =++=AB C D题4.3图列出编码真值表:4.6 试用3线-8线译码器和门电路实现以下函数:4.7 试用四选一多路选择器实现函数Y ABC AC BC =++。
1. 求出最小项、及最小项反函数非表达式:2. 对比四选一多路选择器表达式:0123Y ABD ABD ABD ABD =+++我们发现用原函数无法用一个四选一选择器实现,但反函数只有三个最小项,因为实际的数据选择器,它们都有两个互补的变量输出,因此从反变量输出端(~W)就可以达到要求了。
第四章习题答案

第四章习题答案习题四答案4.1画出图P4.1由或非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1解答:已知或非门构成的RS触发器的特征方程如下:?Qn?1?S?RQn ??RS?0根据输入端S、R的波形图,得出输出端Q、Q的电压波形见图A4.1。
4.2 在图P4.2电路中,若CP、S、R电压波形如图中所示,试画出Q、Q端与之对应的电压波形。
假定触发器的初始状态为Q?0。
1图P4.2 解答:见图A4.2图A4.24.3一种特殊的RS触发器如图P4.3所示。
1)试列出状态转换真值表;2)写出次态方程;3)R与S是否需要约束条件?图P4.3解答:1)① CP=0时,SS=1,RR=1,期间Qn?1?Qn,状态保持。
?② CP=1时,?RR?R???SS?S?RR?S?R?S?R2即在CP=1的情况下:若R=0,S=0。
则RR=1,SS=1,有Qn?1?Qn,状态保持。
若R=0,S=1。
则RR=1,SS=0,有Qn?1?1。
若R=1,S=0。
则RR=0,SS=1,有Qn?1?0。
若R=1,S=1。
则RR=0,SS=1,有Qn?1?0。
电路的状态转换真值表如下表所示:2)求次态方程:由上述状态转换真值表,不难得出次态方程:Qn?1?CP?Qn?CP?R?(Qn?S)3)R与S无需约束条件。
4.4 已知主从结构JK触发器J、K和CP的电压波形如图P4.4所示,试画出Q、Q端对应的电压波形。
设触发器的初始状态为Q?0。
图P4.4 解答:见图A4.4图A4.44.5如图P4.5示是主从JK触发器CP和J、K的电压彼形,试画出主触发器QM端和从触发3器Q端的工作波形。
设Q初始态为0。
图P4.5解答:见图A4.5图A4.54.6如图P4.6示电路,设该TTL触发器的初态为0,试画出在CP 作用下的Q端波形图。
图P4.6解答:根据图示可知该触发器的J?1,K?Qn。
由时钟下降沿触发。
电路分析基础课后习题答案(1-4章)-周围主编

R2
−
5 = A ⋅ (40 + 200)Ω = 48 5(V) 5
2
功率及其正、负号的意义
u 、i 关联参考方向 ⇒ p = ui u 、i 非关联参考方向 ⇒ p =-ui ⎧ p>0 ⎪ ⇒⎨ ⎪ p<0 ⎩ 吸收(消耗)功率 产生(供出)功率
1-43 :如图所示电路,求: ()已知图(a)中U ab = −5V,求U s = ??。 1 ()已知图(b)中U ab = 2V,求R 2
解:
+ 5V
i1
⎫ i= + 0.5U1 ⎪ ⎬ U1 = 0.5U1 × 4 + (−5) ⎪ ⎭ ⎧i = 3.5 A ⇒⎨ ⎩U1 = 5 V
−
U S = i × 2 + U1 = 12 V
I U
I2
+ 0.4V −
鹿胎膏的价格 /
I
0.6 Ω
− U +
24
第二章 等效变换分析法
解:
员工自评范文 /
2-18:求如图所示电路的电流 I 。
−10 + 2 I ×1 + 2 I + I ×1 = 0 ⇒ I = 2 A 即所求
1Ω
= 9−3 = 6 V
U1 Ω 6 V I= = =6A 1Ω 1Ω
⎧ P3 V = 3 V × 6 A=18 W ⎫ ⎪ ⎪ ⎨ P Ω = 6 V × 6 A=36 W ⎪ 1 ⎬ ⇒ I = 4 A 即所求 ⎪ ⎪ ⎩ P9 V = − ( 9 V × I ) ⎪ P3 V + P Ω + P9 V = 18 W ⎭ 1
R ab2 = 40 Ω
15
电工技术第四章 正弦交流电路习题解答

tωi /A222032πtωi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4-1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220= 频率 3145022f Hz ωππ===周期 10.02T s f== 角频率 314/rad s ω=题解图4.01 初相位 s rad /3πψ-=波形图如题解图4.01所示(2) 如果i 的参考方向选的相反, 则A t i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s r a d /32πψ=其他项不变。
波形图如题解图4.02所示。
题解图4.024-1-2 已知A )120314sin(101 -=t i ,A )30314sin(202 +=t i ⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ (2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4.03+1+j1m I ∙2m I ∙mI ∙︒60︒30︒1.234-2-1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002 +=t u解:V U ︒-∠=∙4521101 V U︒∠=∙4525024-2-2已知正弦电流)A 60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω,试用复数计算电流21i i i +=,并画出相量图。
解:由题目得到Aj j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=∙∙∙1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。
电路分析基础第4章习题答案
I1
U
25I1 100I2
25I1
11000 1101
I1
38525 1101
I1
Ri
U I1
38525 1101
35
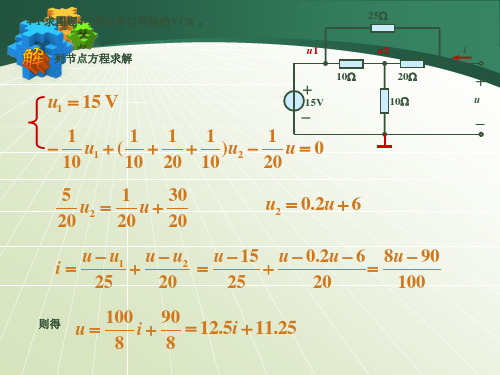
4-10 对图题4-8(a)所含无伴电压源电路,试证明图题4-8(b)所含有伴电压源电路与它是等效的。
i1 2 R1 uS -+
1
4
R2
(a)
i2 3
图(a)中 u12 uS R1i1
2R 2R R
a
b
(4)8R/3
4-11 R-2R电阻阵列组件如第章图题3-18(a)所示,如何联接端钮以得到R/2、2R/3、R、8R/3,5R/3、 2R、3R及4R的等效电阻?
2R 2R R
2R 2R R
a (5)5R/3
2R 2R R b
2R 2R R
a
b
(6)2R
2R 2R R
a
b
(6)2R
4-1
u 12.5i 11.25
4-2
u 9i 50
4-3
u (1 )RLi
12.5
+ 11.25V
-
i+ u -
9
+ 50V
-
i+ u -
(1+)RL
i+ u
-
对伏安关系
u ki m ,里面的k表示与电压源串联的电阻值,m表示电压源的大小,如果
m=0,则电路只等效成一个电阻元件。
4-8 对于含有一个受控源的单口电阻网络,有时用下述方法去求输入电阻Ri是很简便的。其 方法为:(1)先设x=1,x为受控源的控制量;(2)运用KCL及KVL设法算得u及i;(3) 根据u=Rii算得Ri。试用这一方法求解练习题4-6。
电工课后题4

第四章 习题参考题解答练习与思考4.1.1 确定图4.1.3所示电路中各电流的初始值。
换路前电路已处于稳态。
6Vi L图4.1.3 思考题4.1.1的图【解】换路前电路已处于稳态,故i L (0–)=0。
由换路定理可知,换路前后i L 不变,故i L (0+)= i L (0–)=0。
S 闭合后,右边支路被短路,故错误!未找到索引项。
4.1.2 在图4.1.4所示的电路中,试确定在开关S 断开后,电压u C 和电流i 1,i 2的初始值,S 断开前电路已处于稳态。
6Vi 2图4.1.4 思考题4.1.2的图【解】换路前电路已处于稳态,故()C 4064V 2+4u -=⨯=。
由换路定理可知,换路前后u C 不变,故u C (0+)=u C (0–)=4V 。
S 断开后,右边的4Ω电阻被断开,故i 2(0+)=0。
()()1C 6(0)640=0=1A 22C u i i -+-++==。
4.1.3 在图4.1.5中,t =0时开关S 从位置1切换到位置2,试求:(1)u C ,u O ,i O 的初始值;(2)开关切换后电路达到稳态时,u C ,u O ,i O 的稳态值。
i O图4.1.5 思考题4.1.3的图【解】(1)换路前电路已处于稳态,故()C 0100V u -=。
由换路定理可知,换路前后u C 不变,故u C (0+)=u C (0–)=100V 。
S 切换到位置2后,右边的240k Ω电阻与60k Ω电阻并联为240*60/(240+60)=48k Ω,再与32k Ω串联分压,故()O 48480(0)100=60V 32+4880C u u +=+=⨯,()O 33(0)600=1mA 60106010O u i ++==⨯⨯。
(2)达到稳态时,电路中无电源,故u C (∞)=u O (∞)=i O (∞)=0。
4.2.1 有一RC 充电电路,其电容元件上电压的波形如图4.2.7所示,试问此电路的时间常数τ是多少?u C图4.2.7思考题4.2.1的波形图【解】图示为零状态响应)1)(()(c c τte u t u --∞=从波形图可知c ()10V u ∞=,c c ()0.632() 6.3V u u τ=∞=,可知τ=2ms 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i1 =
6.求图题 4-6(a) 、 (b)所示二端电路的等效电阻。
10Ω 5Ω 50Ω 6.5i1 i1
12Ω a
25Ω b
(a)
32Ω 6Ω 4Ω 15Ω b 2Ω
(b) 图题 4-6 解: (a )
a
12Ω 30Ω
40Ω 6Ω
10Ω
5Ω
12 Ω
a
50Ω
im 3
im 2
25Ω
im1
u
b
i
6.5i1
求得 u1 = 12 + 4i1 即 i1 = −3 +
1 u1 4
a
由上式得该二端电路的诺顿等效电路为
3A
4Ω
b
原电路简化为
a
i
3A
4Ω
8Ω
b
i=
4 × 3 = 1A 4+8
11.求图题 4-11 所示二端网络的戴维南等效电路。
980Ω
540μA
ib 100Ω
5×10 -5u2
a
+
u2 40ib -
i1
设端电流 i 已知,相当于在端口接一个电流源,采用网孔法求求解,可列出方程
⎧im1 = i ⎪− 25i + 40i − 5i = 6.5i ⎪ m1 m2 m3 1 ⎨ 5 55 6 . 5 i i i − + = − m3 1 ⎪ m2 ⎪ ⎩i1 = im1 − im 2
整理得:
46.5im 2 − 5im 3 = 31.5i − 11.5im 2 + 55im3 = −6.5i
4.图题 4-4 所示电路中,R=6Ω,求 R 消耗的功率。
3Ω
2Ω
12V
6Ω
2A
R
图题 4-4 解: 将 R 支路以外的部分看作一个二端电路。 可采用叠加原理求 u oc :
3Ω
2Ω
12V
6Ω
2A
uoc
u oc =
6 ⎛ 3× 6 ⎞ × 12 + 2 × ⎜ + 2⎟ 3+ 6 ⎝3+ 6 ⎠
i=
u u1 u 1 ⎛ 4 ⎞ u 2 + = + ×⎜ × 5⎟ = + 24 3 24 3 ⎝ 6 + 4 ⎠ 24 3
即 u = 24i − 16 得该二端电路的戴维南等效电路为
a
− 16V
24Ω
b
原电路化简为
2Ω
− 16V
6Ω
24Ω
u
u=
− 16 × 6 = −3V 6 + 2 + 24
40kΩ b
图题 4-11 解:原图变换为
ib
0.054V
980Ω
i
5 × 10−5 u2
a
100Ω
40ib
u2
40kΩ u
b
设端电压 u 已知,有
u2 = u 0.054 − 5 × 10 −5 u 2 ib = = 5 × 10 −5 − 4.63 × 10 −8 u 100 + 980 u i= + 40ib = 2 × 10 −3 + 2.315 × 10 −5 u 40k
求得
im 2 = 0.68i
im 3 = 0.024i
u = 12i + 25(i − im 2 ) = 20i Rab = u = 20Ω i
(b )
R1 = 32 + 40 = 72Ω
R2 = 12 // 6 + 30 // 6 = 9Ω R3 = R1 // R2 + 2 = 72 // 9 + 2 = 10Ω Rab = 4 + 15 // R3 = 4 + 15 // 10 = 10Ω
解得: i =
u ⎛ 0 .5 ⎞ 1 u ⎛ 0 .5 ⎞ 1 ⎟ +⎜ 1− u = + ⎜1 − ⎟ u = 1× u ⎟ ⎜ R2 ⎝ R2 ⎠ R1 2 ⎝ 2 ⎠ 1 .5
Req =
u = 1Ω i
(2) 原电路中
u ab = i s × Req = 1 × i s
u ab 1 1 2 = × u ab = is = is 1 .5 3 R1 1.5
7.用叠加定理求图题 4-7 电路中的电压 u2,
3Ω 2i1 i1 2V 4Ω + u2
图题 4-7 解:
3A
2V 电压源单独作用时:
3Ω
i1
2V
'
2i1
'
4Ω
u2
'
2 = 0.5 A 4 ' ' u 2 = −2i1 × 3 + 2 = −1V i1 =
'
3 A 电流源单独作用时:
3Ω
2i1
4Ω
''
u2 i1
''
''
3A
i1 = 0 u 2 = 3 × 3 = 9V
原电路的解为: u 2 = u 2 + u 2 = −1 + 9 = 8V 8.用戴维南定理化简图题 4-2 所示电路,求 i。
' '' ''
''
a 4Ω 3A 24V b
图题 4-2 解: 将原电路 6Ω 电阻以外的部分看作一个二端电路。
即 u ≈ 43.2 × 10 i − 86.4
3
戴维南等效电路为
a
− 86.4V
43.2kΩ
b
12.求图题 4-12 所示二端网络的诺顿等效电路。
15kΩ a 8mA 20kΩ
图题 4-12
30V 10mA
30kΩ b
解:该二端电路可简化为
15kΩ
a
30VБайду номын сангаас
10mA 30kΩ
b
可进一步化简为
a
2mA
3× 6 + 2 = 4Ω 3+ 6
i
20V
4Ω 4Ω
i=
20 = 2.5 A 4+4
(c ) .
将 2Ω 电阻支路以外的部分看作一个二端电路。 求开路电压:
20Ω
6Ω
150V
a
uoc
b
12Ω
5Ω
u oc =
5 12 7 ⎛1 2⎞ × 150 − × 150 = ⎜ − ⎟ × 150 = − × 150 = −70V 20 + 5 12 + 6 15 ⎝5 3⎠
i 12Ω 6Ω
a
4Ω
3A
12Ω
uoc
24V
b
用叠加原理可求得开路电压:
u oc =
12 4 × 12 × 24 + 3 × = 18 + 9 = 27V 4 + 12 4 + 12
求其戴维南等效电阻:
a
4Ω
12Ω
Req
b
Req =
原电路简化为:
4 × 12 = 3Ω 4 + 12
a
i
27V
6Ω
3Ω
求戴维南等效电阻
5Ω
10 Ω
a
10Ω
10Ω
Req
b
Req = 10 +
20 × 5 = 14Ω 20 + 5
a
该二端电路的戴维南等效电路为
15V
14Ω
b
16.求图题 4-16 所示二端网络的诺顿等效电路。
a i1 4V 2i1 b 8Ω 2Ω 5Ω
图题 4-16 解:求该二端电路的端口 VAR:
a i1
u oc =
6 3× 6 ⎞ ⎛ × 12 + 2 × ⎜ 2 + ⎟ = 8 + 8 = 16V 3+ 6 3+ 6⎠ ⎝
该二端电路的等效电阻为
3Ω
2Ω
6Ω
a
Req
b
Req =
原电路简化为
3× 6 + 2 = 4Ω 3+ 6
16V
R
4Ω
由最大功率传输条件可知 R = Req = 4Ω 时,其吸收功率最大。 其吸收的最大功率为 Pmax =
15.求图题 4-15 所示二端网络的戴维南等效电路。
5Ω 10Ω 6V 10Ω 2A
10Ω
a
1A 5V b
图题 4-15 解:求开路电压
5Ω
10Ω
i1
10Ω
2A
10Ω
a
6V
1A
5V
uoc
b
i1 =
10 4 ×2 = A 15 + 10 5
u oc = 1 × 10 + i1 × 5 + 6 − 5 = 15V
u ab = 3 A 电流源单独作用时:
'
12 × 6 = 4Ω 12 + 6
R1 × 24 = 12V 4 + R1
a
i ''
4Ω
3A
12Ω
6Ω
b
1 2 6 i '' = × 3 = × 3 = 1A 1 1 1 6 + + 4 12 6
u ab = i '' × 6 = 1 × 6 = 6V
原电路的解为: u ab = u ab + u ab = 12 + 6 = 18V 3.用叠加定理求图题 4-3 所示电路中的电流 i。
a is i1 R1
R2
0.5i1
b
图题 4-5 解: (1) a、b 右端电路如下图所示,设端电压 u 已知
