基于边界距离的时间序列聚类

合集下载

MATLAB中的时间序列聚类分析方法

MATLAB中的时间序列聚类分析方法时间序列聚类分析是一种统计学方法，它可以对时间序列数据进行分类和分组。

在许多领域，如金融、气象、医疗等，时间序列数据广泛存在，并且对于了解其内在模式和趋势至关重要。

MATLAB作为一种强大的数学建模和计算工具，提供了丰富的时间序列分析工具和函数，使得时间序列聚类分析成为可能。

在MATLAB中，时间序列聚类分析可以通过多种方法实现。

下面将介绍几种常用的方法和算法。

一、基于距离的时间序列聚类分析1. 动态时间规整（DTW）DTW是一种基于距离的时间序列相似性度量方法，它通过在时间序列中找到最佳对应点的方式，将两个时间序列进行规整（即拉伸或压缩），从而计算它们之间的距离。

MATLAB提供了dtw函数，可以方便地计算两个时间序列之间的DTW 距离。

2. 基于相似性矩阵的聚类在时间序列聚类中，可以先计算相似性矩阵，然后使用聚类算法对其进行聚类。

常用的相似性度量方法有欧氏距离、余弦相似度等。

MATLAB中可以利用pdist函数计算时间序列数据的相似性矩阵，并使用linkage函数进行层次聚类。

二、基于模型的时间序列聚类分析1. 自回归移动平均模型（ARMA）ARMA模型是一种常用的时间序列建模方法，其拟合了时间序列的自相关和滑动平均关系。

MATLAB中提供了armax和arima函数，可以用于估计ARMA模型的参数，并根据模型进行聚类分析。

2. 隐马尔可夫模型（HMM）HMM是一种统计模型，用于描述由隐藏状态和观测状态组成的随机过程。

在时间序列聚类中，可以使用HMM模型对时间序列的隐藏状态进行建模，然后对隐藏状态进行聚类分析。

MATLAB中提供了hmmtrain和hmmdecode函数，可以用于HMM模型的训练和预测。

三、基于频域的时间序列聚类分析1. 快速傅里叶变换（FFT）FFT是一种高效的频域分析方法，可以将时间序列信号转化为频域信号。

在时间序列聚类分析中，通过对时间序列进行FFT变换，可以得到其频率成分，进而进行聚类分析。

基于距离和DF-RLS的时间序列异常检测

佳。而基于自回归的方法检测Ａ效果好，为了减小下一步Ｏ的估计偏差，检测出的异常点可用估计值替代，对于１０，多
次替代、估计后，估计误差不断累积导致估计精度下降，影响了异常检测，以该方法检测１所０效果不佳。了能同时有为
效检测ＡＯ和１０，本文提出一种基于距离和自回归的联合检测方法，结合了２种方法的优点。基于距离的检测方面，为
Ｄ０ｈ１．６／ｉｎ１０ —４８０２１．９Ｏ３９ｊｓ．００３２．１．０９．ｓ２２０
１概述
时间序列是指按照时间先后顺序排列的各个观测记录的有序集合。时间序列的异常检测拥有广泛的应用需求，如针
子序列定义为Ｄｉｏｄｓｒ，并给出了利用ＳＸ表示方法的ｃＡ
其中，（为第ｉｆ）个状态矢量的距离因子，显然和当前状态
矢量ｘｑ（）的距离越近，（应该越大，对代价函数的影响ｆ）
也越大，反之亦然。一种简单的距离因子计算方法如下：
ＰＡｎｖｒｉｆｃｅｃｎｅｈｏｏｙＮａｊｇ２０，ｈｎ）ＬＵｉｅｓｙｏｉｎｅａｄＴｃｎｌｇ，ｎｉ０７ＣｉａｔＳｎ１０［ｓａｔｎｏｄｒｏｄｔｃｏｈＡｄｉｖｔｅｓＡＯａｄＩｎｖｔｎＯｕｌｒ（ｉｍｅｓｒｓｔｉｐｐｒｍｐｏｅｅｌｅｒｒｄｃｉｎｏＡｂｔｃ］ＩｒｅｅｅｔｔｄｔｅＯｕｌｒ（）ｎｎｏａｉｔｅｓＩｎｔｅｉ，ｈｓａｅｒｖｓｈｉａｅｉｔｆｒｔｂｉｉｏｉＯ）ｉｅｉｔｎｐｏ

使用聚类算法进行时间序列聚类分析的方法

使用聚类算法进行时间序列聚类分析的方法时间序列聚类是一种将时间序列数据划分为不同组或类别的方法。

聚类算法的目标是在没有事先给定类别标签的情况下，根据数据的相似性将数据分组。

时间序列聚类分析的方法可以帮助我们发现数据中的潜在模式和趋势，从而为预测、分析和决策提供有用的信息。

在这篇文章中，我将介绍一种使用聚类算法进行时间序列聚类分析的方法，包括数据准备、特征提取和聚类算法的选择。

这个方法可以适用于各种类型的时间序列数据，例如气候数据、股票价格数据、交通流量数据等。

首先，我们需要进行数据准备。

这包括收集和清洗时间序列数据。

确保数据的完整性和一致性，处理缺失值和异常值。

然后，将时间序列数据进行标准化或归一化处理，以消除不同时间序列之间的量纲差异。

接下来，我们需要从时间序列数据中提取特征。

特征提取的目的是减少数据维度，并捕捉时间序列数据的重要信息。

常用的特征包括时间序列的均值、方差、趋势、周期性等。

我们可以使用统计方法、小波变换、傅里叶变换等技术来提取这些特征。

然后，我们需要选择适合的聚类算法。

常用的聚类算法包括K均值聚类、层次聚类、DBSCAN等。

对于时间序列数据，我们可以使用基于距离的聚类算法，例如K均值聚类。

在聚类算法应用之前，我们还需要选择合适的距离度量方法。

常用的距离度量方法包括欧氏距离、曼哈顿距离、动态时间规整(DTW)距离等。

不同的距离度量方法适用于不同类型的数据。

例如，欧氏距离适用于连续型数据，DTW距离适用于时间序列数据。

将数据、特征和距离度量方法准备好后，我们可以开始应用聚类算法进行时间序列聚类分析。

首先，选择合适的聚类数目，这可以通过观察不同聚类数目下的聚类质量度量，如轮廓系数、Davies-Bouldin指数等来判断。

然后，运行所选的聚类算法，并将时间序列数据划分为不同的簇。

在聚类分析的过程中，我们还可以使用可视化方法来帮助理解聚类结果。

例如，可以绘制聚类的平均时间序列曲线，以观察不同簇之间的差异。

数据分析中的时间序列聚类方法与实践

数据分析中的时间序列聚类方法与实践数据分析是当今社会中非常重要的一项技术。

随着大数据时代的到来，人们对数据的需求越来越高，而时间序列聚类方法则成为了数据分析领域中的一项重要技术。

本文将介绍时间序列聚类方法的基本概念和实践应用。

一、时间序列聚类方法的基本概念时间序列聚类是指将具有相似时间特征的数据进行分组的过程。

在时间序列聚类中，我们会根据数据的时间顺序和特征相似性来进行分组。

时间序列聚类方法的目的是找出数据中的模式和规律，以便更好地理解和预测未来的趋势。

时间序列聚类方法主要分为两大类：基于距离度量的方法和基于模型的方法。

基于距离度量的方法主要通过计算不同时间序列之间的距离来进行聚类。

常用的距离度量方法包括欧氏距离、曼哈顿距离和动态时间规整距离等。

而基于模型的方法则是通过建立时间序列的数学模型来进行聚类。

常用的模型包括ARIMA模型、GARCH模型和神经网络模型等。

二、时间序列聚类方法的实践应用时间序列聚类方法在实际应用中有着广泛的应用。

以下是几个常见的实践应用案例：1. 股票市场分析股票市场的波动性很大，而时间序列聚类方法可以帮助我们对股票市场进行分析和预测。

通过对股票价格的时间序列数据进行聚类，我们可以找出不同股票之间的相似性和差异性，从而更好地进行投资决策。

2. 交通流量预测交通流量的预测对于城市交通管理非常重要。

时间序列聚类方法可以帮助我们对交通流量数据进行分析和预测。

通过对历史交通流量数据进行聚类，我们可以找出不同时间段和地点的交通流量规律，从而更好地进行交通管理和调度。

3. 气象数据分析气象数据中包含着丰富的时间序列信息，时间序列聚类方法可以帮助我们对气象数据进行分析和预测。

通过对气象数据的时间序列进行聚类，我们可以找出不同地区和季节的气象规律，从而更好地进行气象预测和灾害预防。

三、时间序列聚类方法的挑战和发展方向虽然时间序列聚类方法在数据分析中具有重要的应用价值，但是也面临着一些挑战。

时间序列聚类方法

时间序列聚类方法引言时间序列数据是在不同时间点上收集的数据，具有时间上的依赖关系和内在的序列性质。

时间序列聚类是将相似的时间序列数据分组，以便于分析和理解数据集中的模式和结构。

在本文中，将介绍几种常见的时间序列聚类方法及其应用。

一、K-means聚类算法K-means聚类算法是一种经典的聚类方法，通过迭代计算数据点与聚类中心之间的距离，并将数据点分配给与其最近的聚类中心。

该方法在时间序列聚类中的应用需要将时间序列数据转化为一维向量，例如通过提取统计特征或使用傅里叶变换等方法。

然后，可以使用K-means算法将时间序列数据进行聚类，以发现数据中的模式和结构。

二、基于密度的聚类算法基于密度的聚类算法是一种基于数据点密度的聚类方法，通过将数据点分配到高密度区域形成簇。

在时间序列聚类中，可以使用基于密度的聚类算法来发现数据中的异常点和突变点。

一种常见的基于密度的聚类算法是DBSCAN算法，它通过定义半径和最小密度来确定核心点、边界点和噪音点，并将核心点连接形成簇。

三、层次聚类算法层次聚类算法是一种自底向上或自顶向下的聚类方法，通过计算数据点之间的相似度或距离来构建聚类树。

在时间序列聚类中，可以使用层次聚类算法来发现数据中的层次结构和模式。

一种常见的层次聚类算法是凝聚层次聚类算法，它从每个数据点作为一个簇开始，然后迭代地合并相似的簇，直到达到预定的簇数目。

四、基于模型的聚类算法基于模型的聚类算法是一种将时间序列数据建模为概率模型或统计模型来进行聚类的方法。

在时间序列聚类中，可以使用基于模型的聚类算法来发现数据中的潜在分布和生成模式。

一种常见的基于模型的聚类算法是高斯混合模型聚类算法，它假设数据由多个高斯分布组成，并通过最大似然估计来估计模型参数。

五、动态时间规整聚类算法动态时间规整聚类算法是一种将时间序列数据进行规整化后进行聚类的方法。

在时间序列聚类中，由于数据点之间的时间差异和长度差异，可以使用动态时间规整聚类算法来处理这些问题。

时间序列聚类算法的改进与比较

时间序列聚类算法的改进与比较时间序列是在时间上进行观察和记录的一系列数据点的集合，它们在许多领域中都扮演着重要角色，如金融、交通、气象等。

时间序列聚类就是将相似的时间序列数据点分组到同一类别中。

在实际应用中，时间序列聚类算法的性能和准确性对于分析和预测同一类时间序列非常重要。

为了改进和比较不同的时间序列聚类算法，研究人员一直在致力于提出新的算法和改进现有算法。

首先，我们来介绍几种常见的时间序列聚类算法。

K-means算法是最经典的聚类算法之一，它通过迭代更新中心点的方式将数据点分配到不同的簇中。

然而，对于时间序列数据来说，K-means算法并不能很好地处理时间序列中的形状相似性。

因此，一些改进的方法被提出，例如K-means++、K-medoids和K-medians等。

这些算法在选择初始中心点或者使用其他距离度量方式上有所不同，以提高聚类结果的准确性。

另一类常见的时间序列聚类算法是层次聚类算法，例如凝聚聚类算法和分裂聚类算法。

凝聚聚类算法从单个数据点开始，逐步将相似的数据点合并到一个簇中，直到满足某个停止准则为止。

分裂聚类算法则从整个数据集开始，逐步将一个簇分裂为多个簇，直到满足某个停止准则为止。

这些算法可以提供不同层次的聚类结构，适用于不同规模和复杂度的时间序列数据。

此外，基于密度的聚类算法也可以用于时间序列的聚类。

DBSCAN算法是其中一种常见的基于密度的聚类算法，它通过定义核心对象、邻域半径和最小邻居数等参数来将数据点分为核心对象、边界点和噪声点。

DBSCAN算法在聚类非球状簇和识别噪声点上具有一定优势，但对于时间序列数据的距离度量和邻域定义需要进行适当调整。

为了改进和比较这些时间序列聚类算法，研究人员提出了许多新的想法和方法。

一种常见的改进方法是结合多种聚类算法的优点，形成混合聚类算法。

例如，将层次聚类算法与K-means算法结合，利用层次聚类算法的多层次结构和K-means算法的迭代优化能力来提高聚类结果。

基于模型的时间序列数据挖掘——聚类和预测相关问题研究

基于模型的时间序列数据挖掘——聚类和预测相关问题研究引言：随着信息技术和数据收集能力的不断发展，我们面临着前所未有的数据挖掘机遇与挑战。

时间序列数据是一种按照时间顺序排列的数据，在金融领域、天气预测、交通流量等领域有广泛的应用。

时间序列数据挖掘是指对这些时间序列数据进行模式发现、预测分析等，以提供决策支持和业务预测。

本文将重点探讨基于模型的时间序列数据挖掘中的聚类和预测相关问题，并探索其研究现状和未来发展趋势。

一、时间序列聚类问题时间序列聚类是将相似的时间序列数据分组的过程。

其目的是找出数据集中的相似模式，并将其归为一类，以便进行进一步的分析和决策。

常用的时间序列聚类算法有基于距离的方法（如K-means算法）、基于密度的方法（如DBSCAN算法）和基于模型的方法（如GMM模型）。

这些算法可以在不同的应用场景下得到满意的聚类结果。

在基于距离的时间序列聚类中，K-means算法是最常用的方法之一。

该算法通过将时间序列样本分为k个簇，使得簇内的差异最小化，而簇间的差异最大化。

然而，K-means算法的聚类结果受到初始中心点选择的影响，并且对异常值敏感。

因此，对于不同的时间序列数据集，需要选择合适的距离度量和改进的K-means算法以获得更好的聚类效果。

基于密度的时间序列聚类算法中，DBSCAN算法是一种常用的方法。

该算法通过定义邻域半径和邻域内样本数量的阈值，将具有足够邻居的样本划为核心对象，并将其密度可达的样本划为一类。

然而，DBSCAN算法对密度变化较大的时间序列数据集不够适用，因为临近性的定义基于欧氏距离。

基于模型的时间序列聚类算法则是将时间序列数据建模为概率模型或其他模型，并通过模型的参数推断和比较来进行聚类。

GMM模型是常用的基于模型的聚类方法之一。

该算法假设各个簇的时间序列数据是由混合高斯分布生成的，并通过最大似然估计得到模型参数。

然后，通过计算样本对每个簇的后验概率，将样本分为不同的簇。

统计学中的时间序列聚类分析

统计学中的时间序列聚类分析时间序列聚类分析是统计学中一种重要的数据分析方法，它能帮助我们挖掘时间序列数据中的潜在模式和规律。

本文将介绍时间序列聚类分析的基本概念、常用方法以及在实际应用中的意义。

一、概述时间序列聚类分析是一种将相似的时间序列数据归类到同一类别的方法。

它可以帮助我们理解数据之间的联系，发现隐藏的动态模式，以及对序列进行分类和预测。

通过聚类分析，我们可以将时间序列数据划分成多个群组，每个群组内的序列更相似，而不同群组之间的序列则具有较大的差异。

二、常用方法1. 基于距离的聚类方法基于距离的聚类方法是最常用的时间序列聚类分析方法之一。

它通过计算不同序列之间的距离或相似性度量，将相似度较高的序列归到同一类别。

常用的距离度量方法包括欧氏距离、曼哈顿距离和动态时间规整等。

2. 基于子序列的聚类方法基于子序列的聚类方法是另一种常用的时间序列聚类分析方法。

它将序列划分成多个子序列，并计算子序列之间的距离或相似性，从而实现聚类。

该方法适用于时间序列中存在局部模式或变化的情况。

3. 层次聚类方法层次聚类方法是一种将序列逐步合并或拆分的聚类方法。

它从一个个单独的序列开始，通过计算相似度得到相邻的序列对，并逐渐构建聚类树。

层次聚类方法可以用于确定聚类数目，并提供更直观的聚类结果。

三、实际应用意义时间序列聚类分析在实际应用中具有广泛的意义和应用价值。

1. 金融行业时间序列聚类分析在金融行业中被广泛应用于股票价格预测、风险管理和投资组合优化等方面。

通过对股票价格的聚类分析，可以识别出具有相似价格走势的股票，从而指导投资决策。

2. 交通运输对交通运输中的时间序列数据进行聚类分析，可以帮助我们理解交通流量变化的规律，并提供交通拥堵预测和交通优化方案。

例如，通过聚类分析找到相似的交通流量模式，可以制定出适当的交通调控措施。

3. 环境监测时间序列聚类分析在环境监测领域也有重要的应用。

通过对空气质量、水质水量等时间序列数据进行聚类分析，可以发现环境变化的规律，为环境保护提供科学依据。

时间序列聚类方法

时间序列聚类方法引言：时间序列数据是指按照一定时间间隔采集到的数据，具有时序关系的数据集合。

时间序列数据广泛应用于金融、气象、交通、医疗等领域。

对时间序列数据进行聚类分析，可以帮助我们发现数据中的模式和规律，揭示隐藏在数据背后的信息，从而对未来的趋势进行预测和决策提供依据。

本文将介绍几种常见的时间序列聚类方法，包括基于距离的方法、基于模型的方法和基于特征的方法。

一、基于距离的时间序列聚类方法基于距离的时间序列聚类方法是一种常见且广泛使用的方法。

其基本思想是通过计算时间序列数据之间的距离来度量它们的相似性，从而将相似的时间序列归为一类。

1. K-means聚类算法K-means算法是一种经典的聚类算法，也适用于时间序列数据的聚类。

它通过迭代更新聚类中心的方式，将数据划分为K个簇。

在时间序列数据中，可以使用欧氏距离或动态时间规整（DTW）距离来计算数据之间的距离。

2. DBSCAN聚类算法DBSCAN算法是一种基于密度的聚类算法，它将数据划分为高密度区域和低密度区域。

在时间序列数据中，可以使用动态时间规整（DTW）距离来度量数据之间的距离，从而找到高密度的时间序列。

二、基于模型的时间序列聚类方法基于模型的时间序列聚类方法是一种通过拟合时间序列数据的模型来进行聚类的方法。

1. ARIMA模型ARIMA模型是一种常用的时间序列预测模型，也可以用于时间序列聚类。

ARIMA模型通过拟合数据的自回归部分和移动平均部分，来描述和预测时间序列数据的变化趋势。

2. 隐马尔可夫模型（HMM）隐马尔可夫模型是一种常用的时间序列建模方法，可以用于时间序列的聚类分析。

HMM模型假设时间序列数据的生成过程是一个马尔可夫链，通过观测序列和状态序列之间的关系来描述时间序列数据的特征。

三、基于特征的时间序列聚类方法基于特征的时间序列聚类方法是一种将时间序列数据转化为特征向量，然后使用传统聚类算法进行聚类分析的方法。

1. 傅里叶变换傅里叶变换是一种将时间序列数据转化为频域特征的方法。

数据分析中的时间序列聚类与趋势分析

数据分析中的时间序列聚类与趋势分析时间序列数据是以时间顺序排列的数据，它们的数值取决于观测时刻。

在数据分析中，对时间序列数据进行聚类和趋势分析是重要而有挑战性的任务。

本文将重点介绍时间序列聚类和趋势分析的方法与应用。

一、时间序列聚类方法时间序列聚类旨在将相似的时间序列数据归为一类，以便更好地理解和分析数据。

常用的时间序列聚类方法包括：1. K-means聚类K-means聚类是数据分析中常用的一种聚类方法。

在时间序列聚类中，K-means通过计算不同时间序列之间的距离，将相似的时间序列聚类在一起。

2. 基于密度的聚类基于密度的聚类方法（例如DBSCAN）通过发现高密度区域和低密度区域来聚类时间序列数据。

该方法可以自动识别具有相似模式的时间序列。

3. 层次聚类层次聚类将时间序列数据组织成树状结构，通过计算相似度或距离来将数据不断合并或划分，最终形成聚类。

这种方法可用于发现不同层次的时间序列模式。

二、时间序列趋势分析方法时间序列趋势分析旨在揭示时间序列数据中的趋势和模式，以便预测未来的变化。

以下是常用的时间序列趋势分析方法：1. 移动平均法移动平均法是一种将数据平滑处理以便观察趋势的方法。

通过计算一定时间窗口内数据的平均值，可以检测出数据集的整体变化趋势。

2. 指数平滑法指数平滑法通过将历史数据的权重逐渐减小，从而更加关注最近的数据，以预测未来的趋势。

指数平滑法适用于数据具有一定的趋势性和季节性变动的情况。

3. ARIMA模型ARIMA模型是一种常用的时间序列分析模型，用于描述和预测时间序列的趋势和季节性。

它包括自回归（AR）、差分（I）和移动平均（MA）三个部分，可以较好地捕捉时间序列数据中的变化。

三、时间序列聚类和趋势分析的应用时间序列聚类和趋势分析在众多领域中都具有广泛的应用。

以下是其中几个应用领域的例子：1. 股票市场分析通过对股票价格和交易量等时间序列数据进行聚类和趋势分析，可以更好地理解市场的波动和趋势，从而指导投资决策。

多元时间序列聚类模型

多元时间序列聚类模型是用于对多个时间序列进行聚类的算法。

在聚类过程中，需要考虑到时间序列的时序特性和序列间的相关性。

以下是几种常用的多元时间序列聚类模型：
基于距离的聚类模型：该模型通过计算时间序列间的距离或相似度来进行聚类。

常用的距离度量方法包括欧氏距离、皮尔逊相关系数等。

基于距离的聚类模型简单易行，但需要确定合适的距离度量方式和聚类数目。

基于密度的聚类模型：该模型通过在时间序列空间中定义密度，将密度相近的时间序列划分为同一类。

常用的密度算法包括DBSCAN、K-D树等。

基于密度的聚类模型能够发现任意形状的聚类，但计算复杂度较高。

基于层次的聚类模型：该模型通过将时间序列按照某种方式进行层次化分组，形成一棵聚类树。

常见的层次聚类算法包括BIRCH、CART 等。

基于层次的聚类模型易于理解和实现，但可能需要处理大量数据和选择合适的层次划分方式。

基于模型的聚类模型：该模型通过建立一个数学模型来描述时间序列的分布和结构，然后根据模型参数进行聚类。

常用的模型包括高斯混合模型、隐马尔可夫模型等。

基于模型的聚类模型能够发现时间序列的内在结构和模式，但需要选择合适的模型和参数。

以上是几种常见的多元时间序列聚类模型，它们各有优缺点，应
根据具体问题和数据特点选择合适的模型。

Matlab中的时间序列聚类分析方法与实例

Matlab中的时间序列聚类分析方法与实例时间序列聚类分析是一种重要的数据挖掘技术，利用时间序列数据的特征进行聚类可以帮助我们理解和发现数据中的模式和规律。

在Matlab中，提供了丰富的工具和函数来进行时间序列聚类分析，并且可以直观地展示聚类结果。

本文将介绍一些常用的时间序列聚类方法，并给出相应的实例。

一、基于距离的时间序列聚类方法基于距离的时间序列聚类方法是将时间序列看作向量，通过计算不同时间序列之间的距离来进行聚类。

常用的方法有欧氏距离、曼哈顿距离和动态时间规整（DTW）等。

1. 欧氏距离：欧氏距离衡量两个时间序列在每个时刻上数值的差异，然后将每个时刻上的差异进行平方求和并开平方根，即为欧氏距离。

在Matlab中，可以使用pdist函数来计算欧氏距离。

```matlabdata = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 假设有三个时间序列dist = pdist(data, 'euclidean');```2. 曼哈顿距离：曼哈顿距离是将两个时间序列上对应时刻数值的差的绝对值进行求和，即为曼哈顿距离。

在Matlab中，可以使用pdist函数来计算曼哈顿距离。

```matlabdata = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 假设有三个时间序列dist = pdist(data, 'cityblock');```3. 动态时间规整（DTW）：DTW是一种基于时间序列形状相似度的距离度量方法，它考虑了时间上的不对齐。

在Matlab中，可以通过调用dtw函数来计算DTW距离。

```matlabx = [1, 2, 3, 4, 5]; % 第一个时间序列y = [2, 3, 4]; % 第二个时间序列dist = dtw(x, y);```二、基于相似度的时间序列聚类方法基于相似度的时间序列聚类方法是通过计算不同时间序列之间的相似度来进行聚类。

基于时间序列的聚类分析方法研究

基于时间序列的聚类分析方法研究一、引言随着数据量不断增加，人们对数据挖掘算法的需求越来越高。

而数据挖掘算法中的聚类分析方法可以帮助人们在数据量较大的情况下，快速发现数据的规律和特征。

其中，基于时间序列的聚类分析方法是一种在时间序列中搜索重复模式并进行聚类分析的方法。

本文将介绍基于时间序列的聚类分析方法的定义、流程、算法等内容。

二、基于时间序列的聚类分析方法的定义基于时间序列的聚类分析方法是一种利用时间对数据进行分类的方法。

通过寻找时间序列中的规律和相似性，可以将相似的时间序列进行聚类，以便发现数据的规律和特征。

三、基于时间序列的聚类分析方法的流程1. 数据准备：首先，需要将原始时间序列进行数据清洗和预处理，对数据进行标准化、归一化等操作，以便后续处理。

2. 相似度计算：对于时间序列中的每个子序列，需要计算与其他子序列的相似度。

常用的相似度计算方法包括欧氏距离、曼哈顿距离等。

3. 聚类算法：可以使用常见的聚类算法，如K-means、DBSCAN等，对相似的时间序列进行聚类分析。

4. 结果评估：对聚类结果进行评估，可以使用聚类有效性指标，如轮廓系数，来评估聚类的质量。

四、基于时间序列的聚类分析方法的算法1. K-means算法K-means算法是基于距离的聚类算法，它将数据分为K个簇，使每个数据点到其所属的簇内的所有数据点的距离之和最小化。

该算法的具体步骤为：（1）随机选择K个初始中心点。

（2）计算每个数据点到中心点的距离，并将其分配到最近的簇中。

（3）更新每个簇的中心点。

（4）重复第2和3步，直到中心点不再改变或达到预定的迭代次数。

2. DBSCAN算法DBSCAN算法是一种密度聚类算法，它将数据分为若干个簇，这些簇由密集的数据点组成，并且簇与簇之间较为稀疏。

该算法的具体步骤为：（1）选取一个未访问的核心点。

（2）找出与该核心点密度可达的所有点，加入到该簇中。

（3）重复第1和2步，直到所有的核心点都被访问。

数据科学中的时间序列聚类算法

数据科学中的时间序列聚类算法时间序列聚类算法是数据科学中一种重要的技术，它可以帮助我们发现时间序列数据中的模式和趋势。

在本文中，我们将探讨时间序列聚类算法的原理、应用和挑战。

首先，让我们来了解时间序列聚类算法的原理。

时间序列是按照时间顺序排列的一系列数据点的集合。

聚类算法的目标是将相似的时间序列数据分组，使得同一组内的时间序列数据相似度较高，而不同组之间的时间序列数据相似度较低。

时间序列聚类算法主要分为基于距离的方法和基于模型的方法。

基于距离的时间序列聚类算法使用距离度量来衡量时间序列数据之间的相似度。

常用的距离度量方法包括欧氏距离、曼哈顿距离和动态时间规整（DTW）等。

欧氏距离是最常用的距离度量方法，它计算两个时间序列数据点之间的欧氏距离。

曼哈顿距离是计算两个时间序列数据点之间的绝对值之和。

动态时间规整是一种比较灵活的距离度量方法，它允许对时间序列数据进行拉伸和压缩，以便更好地匹配。

基于模型的时间序列聚类算法使用数学模型来描述时间序列数据的特征。

常用的模型包括自回归模型（AR）、移动平均模型（MA）和自回归移动平均模型（ARMA）等。

自回归模型是一种线性模型，它使用过去的观测值来预测未来的观测值。

移动平均模型是一种平滑模型，它使用过去观测值的加权平均来预测未来的观测值。

自回归移动平均模型是自回归模型和移动平均模型的组合，它可以更好地描述时间序列数据的特征。

时间序列聚类算法在许多领域都有广泛的应用。

在金融领域，时间序列聚类算法可以帮助分析股票价格的波动模式，从而指导投资决策。

在医疗领域，时间序列聚类算法可以帮助识别疾病的发展趋势，从而提前采取预防措施。

在交通领域，时间序列聚类算法可以帮助分析交通流量的变化规律，从而优化交通管理。

然而，时间序列聚类算法也面临一些挑战。

首先，时间序列数据通常具有高维度和大规模的特点，这导致计算复杂度较高。

其次，时间序列数据通常具有噪声和缺失值，这会影响聚类算法的准确性。

一种基于始末距离的时间序列符号聚合近似表示方法

一种基于始末距离的时间序列符号聚合近似表示方法时间序列符号聚合（Symbolic Aggregate approXimation，简称SAX）是一种将时间序列数据转化为符号序列的方法。

在这种方法中，时间序列数据的每个时间点被转化为一个符号，使用这种方法可以将原始时间序列数据的维度降低，从而减少处理时间和存储空间的消耗。

但是，直接使用SAX方法存在一个问题，就是不同的SAX符号序列可能对应相似但不完全相同的原始时间序列数据。

为了解决这个问题，可以使用基于始末距离的时间序列符号聚合近似表示方法。

基于始末距离的时间序列符号聚合近似表示方法主要思想是：对于原始时间序列数据，通过对一定长度的时间窗口进行符号聚合，将长时间序列分成若干个短时间序列；然后，从这些短时间序列的始末位置处计算一个距离值。

在这个过程中，距离值的计算方法需要考虑时间序列数据在不同位置的重要性，例如将较后的位置的重要性赋予更高的权重。

具体来说，基于始末距离的时间序列符号聚合近似表示方法包括以下步骤：1.首先，将原始时间序列数据划分为一定长度的时间窗口，并使用SAX方法将每个窗口转化为一个符号序列。

2.将符号序列连接起来，形成一个新的符号序列。

3.从新的符号序列的开始位置和结束位置处分别取出一定长度的符号序列，将它们转化为原始时间序列数据，这些时间序列数据的长度与时间窗口的长度相同。

4.根据起始位置处的时间序列数据和结束位置处的时间序列数据计算距离值。

距离值的计算方法可以使用欧氏距离、曼哈顿距离等。

5.重复步骤3和4，直至所有位置处的距离值都被计算出来。

6.将距离值作为新的特征，使用聚类方法对数据进行分析和处理。

基于始末距离的时间序列符号聚合近似表示方法具有以下优点：1.可以减少原始时间序列数据的维度，从而降低处理时间和存储空间的消耗。

2.可以将相似但不完全相同的时间序列数据聚为一类，从而更好地进行分类和识别。

3.可以充分利用时间序列数据在不同位置的重要性，从而提高聚类的准确性和可靠性。

一维数据聚类算法

一维数据聚类算法一维数据聚类算法是一种将一维数据划分为多个簇（或者称为类）的方法，以实现数据的分组和分类。

这种算法常用于时间序列分析、图像处理、数据挖掘等领域。

本文将介绍三种常见的一维数据聚类算法：K-Means算法、层次聚类算法和密度聚类算法。

1. K-Means算法K-Means算法是一种迭代的、基于距离的聚类算法。

它的步骤如下：1)随机选择K个数据点作为初始的聚类中心；2)根据每个数据点与聚类中心的距离，将数据点分配给离它最近的聚类中心所在的簇；3)更新每个簇的聚类中心为簇中所有数据点的均值；4)重复步骤2和步骤3，直到聚类中心不再变化或达到最大迭代次数。

K-Means算法适用于数据集的簇形状较为规则、大小相近，并且簇间的距离较大的情况。

但它对噪声和异常值比较敏感，并且需要事先指定簇的个数K。

2.层次聚类算法层次聚类算法通过逐步合并或分割簇来构建聚类层次结构。

它的步骤如下：1)将每个数据点作为一个初始的簇；2)根据簇间的距离（如欧式距离、相关系数等），合并距离最近的两个簇，形成一个新的簇；3)重复步骤2，直到所有数据点都合并到一个簇中，或者达到设定的簇个数。

层次聚类算法不需要事先指定簇的个数，但它的计算复杂度较高，尤其是当数据集较大时。

3.密度聚类算法密度聚类算法通过将密度相连的数据点划分为一个簇，适用于数据集中簇的形状和大小不规则的情况。

其中，最常用的密度聚类算法是DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法。

DBSCAN算法的步骤如下：1)随机选择一个未被访问的数据点；2)判断该点的密度是否大于设定的阈值，如果是，则将该点及其密度可达的所有点划分为一个簇，并标记为已访问；3)重复步骤2，直到所有数据点都被访问。

DBSCAN算法能够自动处理噪声和异常值，并且不需要事先指定簇的个数，但对参数的设置较为敏感。

如何使用时间序列聚类分析数据行为

如何使用时间序列聚类分析数据行为时间序列聚类是一种用于分析和理解数据行为的强大工具。

它能够将时间序列数据分为不同的群组，从而揭示出数据背后的潜在模式和趋势。

在本文中，我们将讨论如何使用时间序列聚类来分析和解读数据行为。

1. 数据准备在进行时间序列聚类之前，首先需要准备好数据。

数据可以是任何具有时间属性的序列，例如销售数据、气象数据或股票价格数据。

确保数据是完整的，并且没有缺失值或异常值。

2. 数据预处理在进行聚类之前，需要对数据进行预处理。

常见的预处理步骤包括平滑处理、去除噪声和缩放数据。

平滑处理可以通过滑动平均或指数平滑等方法来实现，以消除数据中的季节性和周期性波动。

去除噪声可以通过滤波或异常值检测来实现。

缩放数据可以将不同尺度的数据统一到相同的范围内，以避免某些特征对聚类结果的影响过大。

3. 特征提取特征提取是时间序列聚类的关键步骤。

它可以将原始时间序列转化为一组具有代表性的特征向量。

常见的特征提取方法包括统计特征、频域特征和时域特征等。

统计特征可以包括均值、方差、最大值和最小值等。

频域特征可以通过傅里叶变换或小波变换来提取。

时域特征可以包括自相关系数、自回归模型参数和移动平均模型参数等。

选择合适的特征提取方法可以提高聚类的准确性和效果。

4. 聚类算法选择选择合适的聚类算法是时间序列聚类的关键。

常见的聚类算法包括K-means、层次聚类和DBSCAN等。

K-means是一种基于距离的聚类算法，它将数据分为K个簇，每个簇的中心是该簇中所有样本的平均值。

层次聚类是一种自底向上的聚类算法，它通过逐步合并最相似的样本来构建聚类树。

DBSCAN是一种基于密度的聚类算法，它将样本分为核心点、边界点和噪声点，并根据密度连接性将核心点组成簇。

选择合适的聚类算法可以根据数据的特点和需求来决定。

5. 聚类结果评估评估聚类结果的质量是非常重要的。

常见的聚类评估指标包括轮廓系数、Davies-Bouldin指数和Calinski-Harabasz指数等。

基于时间序列相似性聚类的应用研究综述

这些方法的优点是考虑了时序信息，但是计算复杂度较高，需要消耗大量的计算资源。
3、基于降维的方法
基于降维的方法通过将时间序列数据降维到低维空间，再对低维数据进行聚类。常见的基于降维的方法包括主成分分析（PCA）和线性判别分析（LDA）等。这些方法的优点是计算复杂度较低，但是在降维过程中可能会丢失一些重要的信息，导致聚类结果的准确性下降。
4、结果解读：根据聚类结果，对各个时间序列数据的特征进行解读，分析其相似性和差异性。
感谢观看
应用研究时间序列相似性聚类在各个领域都有广泛的应用，以下是一些典型的例子。
1、金融领域
在金融领域，时间序列相似性聚类可以用于股票市场趋势分析和投资组合优化等。例如，通过聚类分析历史股票价格数据，可以发现相似的股票走势，从而指导投资者进行合理投资。
2、生物领域
在生物领域，时间序列相似性聚类可以用于基因表达数据分析和生物种群分类等。例如，通过聚类分析基因表达数据，可以发现相似的基因表达模式，从而对基因进行分类和功能预测。
主题展开
HMM基本概念与理论知识
隐藏马尔科夫模型（HMM）是一种统计模型，用于描述系统在一定时间序列中状态的变化。该模型假设系统在任意时刻的状态只与前一时刻的状态有关，且各个状态之间相互独立。HMM包括两个主要组成部分：状态转移概率矩阵和观测概率矩阵。
在实际应用中，HMM可以根据观测序列推断出状态序列，为时间序列分析提供了有效手段。
基于距离的方法是最常用的一种聚类方法，它通过计算时间序列之间的距离来衡量它们的相似性。常见的基于距离的方法包括欧几里得距离、曼哈顿距离和切比雪夫距离等。这些方法的优点是简单易懂、易于计算，但是它们忽略了时间序列数据的时序信息，可能导致聚类结果的准确性下降。

用户行为分析中的模式识别方法

用户行为分析中的模式识别方法随着互联网的发展和普及，大量的数据不断被积累，其中蕴含着用户行为的信息。

通过对用户行为的分析和挖掘，可以发现很多有价值的信息，比如用户爱好、购买意向、活跃度等等。

而模式识别方法是用户行为分析的重要手段之一，可以对海量的用户数据进行分类、聚类、预测等操作，从而揭示出数据背后的规律和模式。

下面将介绍一些常见的模式识别方法及其应用。

一、聚类分析聚类分析是将一组数据分成多个类别（cluster）的方法，每个类别内的数据具有相似的特征，而不同类别之间的数据则具有较大的差异。

聚类分析的目的是在不事先知道类别的情况下，发现潜在的类别结构。

聚类分析通常有两种方法：基于距离的聚类和基于密度的聚类。

基于距离的聚类可以将数据点根据他们之间的距离分成不同的类别，而基于密度的聚类是区分数据点所处的密度区域。

聚类分析在电商领域的应用非常广泛，可以根据用户的购买行为、搜索行为等对用户进行分类，提供个性化的推荐和服务，从而提升用户满意度和粘性。

二、分类分析分类分析是将一组数据分为多个已知的类别（class）的方法，分类分析通常由两个步骤构成：建立分类模型和用模型对数据进行分类。

分类模型可以使用多种算法，如决策树、神经网络、朴素贝叶斯等。

分类分析的应用场景也非常广泛，例如通过对用户行为数据进行分类，可以识别出哪些用户属于流失用户、哪些用户属于高价值用户，以便采取针对性的策略来提升用户留存和增加用户价值。

三、关联规则挖掘关联规则挖掘是发现数据中蕴含的关联性的过程，通过发现事物之间的关联，可以从数据中推断出潜在的规律和模式。

关联规则挖掘通常包括两个步骤：频繁项集生成和关联规则产生。

频繁项集生成是指在数据集中发现频繁出现的项集，而关联规则产生则是从这些频繁项集中找出规律性的关联规则。

在电商领域，关联规则挖掘可以用来发现哪些商品经常被一起购买，从而提供以套餐为基础的促销策略。

四、时间序列分析时间序列分析是一种基于时间序列数据的分析方法，它研究的是同一变量在不同时间点上的表现，并且假设它们之间存在一定的因果关系。

【ML-7-应用】聚类算法-时间序列聚类（DTW和LB_Keogh距离）

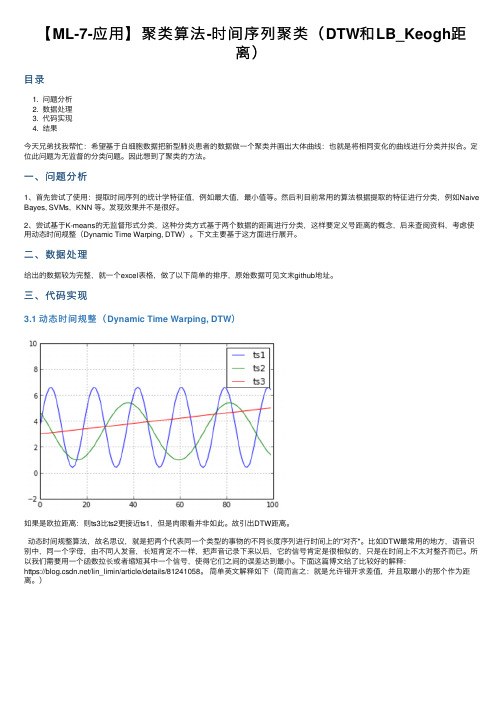
【ML-7-应⽤】聚类算法-时间序列聚类（DTW和LB_Keogh距离）⽬录1. 问题分析2. 数据处理3. 代码实现4. 结果今天兄弟找我帮忙：希望基于⽩细胞数据把新型肺炎患者的数据做⼀个聚类并画出⼤体曲线：也就是将相同变化的曲线进⾏分类并拟合。

定位此问题为⽆监督的分类问题。

因此想到了聚类的⽅法。

⼀、问题分析1、⾸先尝试了使⽤：提取时间序列的统计学特征值，例如最⼤值，最⼩值等。

然后利⽬前常⽤的算法根据提取的特征进⾏分类，例如Naive Bayes, SVMs，KNN 等。

发现效果并不是很好。

2、尝试基于K-means的⽆监督形式分类，这种分类⽅式基于两个数据的距离进⾏分类，这样要定义号距离的概念，后来查阅资料，考虑使⽤动态时间规整（Dynamic Time Warping, DTW）。

下⽂主要基于这⽅⾯进⾏展开。

⼆、数据处理给出的数据较为完整，就⼀个excel表格，做了以下简单的排序，原始数据可见⽂末github地址。

三、代码实现3.1 动态时间规整（Dynamic Time Warping, DTW）如果是欧拉距离：则ts3⽐ts2更接近ts1，但是⾁眼看并⾮如此。

故引出DTW距离。

动态时间规整算法，故名思议，就是把两个代表同⼀个类型的事物的不同长度序列进⾏时间上的"对齐"。

⽐如DTW最常⽤的地⽅，语⾳识别中，同⼀个字母，由不同⼈发⾳，长短肯定不⼀样，把声⾳记录下来以后，它的信号肯定是很相似的，只是在时间上不太对整齐⽽已。

所以我们需要⽤⼀个函数拉长或者缩短其中⼀个信号，使得它们之间的误差达到最⼩。

下⾯这篇博⽂给了⽐较好的解释：https:///lin_limin/article/details/81241058。

简单英⽂解释如下（简⽽⾔之：就是允许错开求差值，并且取最⼩的那个作为距离。

）DTW距离代码定义如下：1 def DTWDistance(s1, s2):2 DTW={}3 for i in range(len(s1)):4 DTW[(i, -1)] = float('inf')5 for i in range(len(s2)):6 DTW[(-1, i)] = float('inf')7 DTW[(-1, -1)] = 08 for i in range(len(s1)):9 for j in range(len(s2)):10 dist= (s1[i]-s2[j])**211 DTW[(i, j)] = dist + min(DTW[(i-1, j)],DTW[(i, j-1)], DTW[(i-1, j-1)])1213 return math.sqrt(DTW[len(s1)-1, len(s2)-1])1415这样求解相对较为⿇烦，时间复杂度⽐较⾼，故做了⼀个⼩的加速：#DTW距离,只检测前W个窗⼝的值，定义错开的部分W，减少递归寻找量1 def DTWDistance(s1, s2, w):2 DTW = {}3 w = max(w, abs(len(s1) - len(s2)))4 for i in range(-1, len(s1)):5 for j in range(-1, len(s2)):6 DTW[(i, j)] = float('inf')7 DTW[(-1, -1)] = 08 for i in range(len(s1)):9 for j in range(max(0, i - w), min(len(s2), i + w)):10 dist = (s1[i] - s2[j]) ** 211 DTW[(i, j)] = dist + min(DTW[(i - 1, j)], DTW[(i, j - 1)], DTW[(i - 1, j - 1)])12 return math.sqrt(DTW[len(s1) - 1, len(s2) - 1])3.2 LB_Keogh距离主要思想是在搜索数据很⼤的时候，逐个⽤DTW算法⽐较每⼀条是否匹配⾮常耗时。