Ⅰ型三阶系统系统的四阶参考模型
典型3阶系统的二阶参考

编号:____________审定成绩:____________课程设计报告课程设计题目:__ 典型3阶系统的二阶参考_____ ____ 模型设计及仿真研究__________ 单位(系别):_____ 自动化____________学生姓名:_______ 李春斌____________专业:___电气工程及其自动化__ __班级:_______(1)班____________学号:______0511110110__________指导教师:________汪纪锋____________填表时间:2015 年5 月重庆邮电大学移通学院教务处制重庆邮电大学移通学院毕业设计(论文)任务书重庆邮电大学移通学院毕业设计任务书(简明)技术资料摘要第一章控制系统的简介第三节设计基本要求基于频率特性法,按二阶参考模型法(即)设计满足系统性能指标的闭环系统。
第四节系统基本指标1.设定:在输入为,(其中:a=4 b=1/sec)2.在保证稳态误差的前提下,要求动态期望指标:;第二章系统建模第一节各环节模型建立比例环节系统结构图如下图(),结构框图如图()传递函数图()图()积分环节系统结构图如下图(),结构框图如图()传递函数图()图()惯性环节系统结构图如下图(),结构框图如图()传递函数:图()图()反相器系统结构图如下图(),结构框图如图()传递函数:图()图()第二节系统数学模型三阶系统结构如下:开环传递函数为:闭环传递函数为:特征方程为:第三章系统分析第一节二阶系统的数学模型二阶系统的开环传递函数为:□ωξω闭环传递函数为:闭环传递函数的分母多项式等于零的代数方程式称为二阶系统的闭环特征方程,即:闭环特征方程的两个根称为二阶系统的特征根,即ξωωξ上述二阶系统的数学模型中有两个特征参数ξ和〖ω〗,其中ξ称为二阶系统的阻尼比,〖ω)。
二阶系统的系统分析和性能描述,基本上是以这两个特征参数来表示的。
上述二阶系统的特征根表达式中,随着阻尼比ξ的不同取值,特征根有不同类型的值,或者说ξ时,特征根为一对不相等的负实根,位于平面的负实轴上,使得系统的响应表现为过阻尼的ξ时,特征根为一对相等的负实根,也是位于平面的负实轴上,系统的响应表现为临界阻尼的ξ时,特征根为一对带有负实部的共轭复数根,位于平面的左半平面上,使得系统的响应表现ξ时,特征根为一对纯虚根,位于平面的虚轴上,系统的响应表现为无阻尼的。
【赣科技版】《信息科技》七年级上册 第1课 第2课时《网络发展历程与拓扑结构》课件

联参考模型”(OSI RM),被公认为研究和制定新一代计算机网络体系结
一
构的基础,OSI标准使不同的网络互联,实现更大范围的计算机网络资源
想
共享。OSI RM 为局域网的普及奠定了基础。
新知讲解
网络发展历程
Internet与高速网络阶段
想
如今计算机网络已经发展到第四阶段,即Internet与高速网络阶段。
务数据网、异步传输模式、高速局域网、虚拟网络等方面。这一阶段计
一
算机网络的特点是Internet的广泛应用,以及高速网、移动网技术的迅
想
速发展。
新知讲解
网络发展历程
Internet与高速网络阶段
想
这一阶段计算机网络的特点是Internet的广泛应用,以及高速网、移动
网技术的迅速发展。
一
想
新知讲解
网络拓扑结构
网状结构
想
网状结构主要是每个节点通过线路互相连接起来,并且每一个节点至少
省了大量时间。
(4)社交网络:通过各种社交媒体平台,我们可以分享生活点滴、结交
新朋友、关注感兴趣的内容。
新知讲解
做 一 做
1、和同学们讨论下你家里使用过哪些人工智能产品。
(1)智能音箱:就像一个会说话的机器人,你可以问它“现在几点了?”或者 “明天天气怎么样?”它都能回答你。你还可以让它放你喜欢的音乐,甚至控制 家里的灯和空调。 (2)扫地机器人:这是一个会自动打扫房间的小机器人。你不用动手,它就能 帮你把地扫干净,还能自己找到充电的地方哦! (3)智能电视:除了可以看很多好看的电影和电视剧,智能电视还能听懂你的 话。比如,你说“我要看动画片”,它就会自动找到动画片给你看。 (4)智能手表:这是一个很酷的手表,它可以告诉你走了多少步,跑了多远, 甚至还能监测你的心跳。有时候,它还会提醒你起床或者睡觉。
系统工程学

第四章 网络计划技术:网络计划技术是系
统管理的重要工具之一,是系统工程常 用的管理技术。它是利用网络图对计划 任务的进度、费用及其组成部分之间的 相互关系进行计划、检查和控制,以使 系统协调运转的科学方法。通过本章学 习,同学们能够了解了解网络计划技术知识
及其应用领域 ,掌握CPM,PERT,GERP的工 程实际应用。
资源能源问题、新农村建设、城镇化、社会保 障、应急管理等) 管理科学、经济科学、工程科学各种前沿问题 落实科学发展观 社会信息化变革 重大投资和大型项目管理 思维科学和生命科学
二、系统工程研究对象
(一)SE的研究对象是大规模复杂系统 该类系统的主要特点有:规模庞大、结构复杂、属性及目
标多样、一般为人机系统、经济性突出等。 (二)系统的概念
(三)系统的分类
自然系统与人造系统 实体系统与概念系统 动态系统与静态系统 封闭系统与开放系统
主要明确SE研究什么样的系统 问题?
三、SE的内容与特点 所谓SE,是用来开发、运行、革新一个大
规模复杂系统所需思想、程序、方法的综合 (或总称)。
SE强调以下基本观点: 1)整体性和系统化观点(前提) 2)总体最优或平衡协调观点(目的) 3)多种方法综合运用的观点(手段) 4)问题导向及反馈控制观点(保障)
《系统工程学》是工业工程专业以及管 理工程专业的基础课程之一。它的任务 是通过对本课程的学习,使学生熟悉系 统及系统工程的概念和内涵,了解国内 外系统工程的发展现状和趋势,掌握系 统工程的预测技术、分析方法、设计理 论、模型与仿真、决策分析,并引导学 生将系统工程的观点、思想、方法和原 理具体应用到工程机械的制造、规划和 管理以及路桥机械化施工等工程实践中。
逻辑 步骤 工作 活动 时间 项目
同步电机实用四阶模型

附录Ⅲ 同步电机实用四阶模型当同步电机在q 轴转子上要计及和瞬变过程对应的g 绕组,但d 轴、q 轴转子仍忽略与超瞬变过程对应的D 绕组、Q 绕组时,则三阶实用模型将增阶为四阶实用模型。
其导出过程与三阶实用模型相似,只是增加了一个q 轴转子的g 绕组。
下面进行推导。
1. 等效实用变量引入除三阶实用模型中所定义的励磁电动势f E 、q 轴空载电动势q E 及q 轴瞬变电动势qE '外,还需定义以下两个新的实用变量:g i 所对应的d 轴电动势g aq d i X E -= (Ⅲ-1)g Ψ所对应的d 轴电动势g g aq d ΨX X E -=' (Ⅲ-2)d E '又称为d 轴瞬变电动势,或“q X '后面的电动势”。
d E 和dE '定义式中的负号是由于定子d 绕组电压方程中的速度电动势项-ωq Ψ中的负号引起的,即q 轴的正磁链,由于转子的旋转,在定子等值d 绕组中引起负值的速度电动势。
在稳态时,0d E =0(因为g 绕组端口短路,稳态时g i =0)。
暂态时,由于忽略定子暂态,设定子电压方程中p d Ψ=p q Ψ=0,q i 要发生突变,故g i 也要发生突变,从而使g 绕组的磁链g Ψ不突变(因考虑到g 绕组的暂态),因此暂态中和g i 成比例的d E 也要发生突变。
在暂态中,和g Ψ成比例的d E '是不突变的,其暂态初值可根据稳态值而定。
0dE '可用下式计算,证明见后面推导。
0000q q d a d di X i r u E '-+=' (Ⅲ-3) 式中,g aq q g aq q X X X X X X X 211//-=+='为q 轴瞬变电抗。
由式(Ⅲ-3)可知,将0dE '称为“q X '后面的电动势”的物理背景。
2. 消去q Ψ及g i (d E )用的表达式导出四阶实用模型与三阶实用模型在d 轴上结构相同,故消去d Ψ及f i (q E )用的表达式不变,仍为⎩⎨⎧'-'='-+'=d d q dd d d q q i X E Ψi X X E E )( (Ⅲ-4) 消去q Ψ及q i (d E )的表达式推导如下,由q 轴磁链方程有⎩⎨⎧+-=+-=g g q aq gg aq q q q i X i X Ψi X i X Ψ (Ⅲ-5) 对式(Ⅲ-5)之第二式,二边乘以g aq X X -,由式(Ⅲ-2)可知 dE '=g aq X X 2g i +d E (Ⅲ-6) 由于g aq q q X X X X 2-=',将之代入式(Ⅲ-6),可整理得q q q dd i X X E E )('--'= (Ⅲ-7) 此即消去g i (d E )用的表达式。
双星模型三星模型四星模型

双星模型三星模型四星模型集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#双星模型、三星模型、四星模型天体物理中的双星,三星,四星,多星系统是自然的天文现象,天体之间的相互作用遵循万有引力的规律,他们的运动规律也同样遵循开普勒行星运动的三条基本规律。
双星、三星系统的等效质量的计算,运行周期的计算等都是以万有引力提供向心力为出发点的。
双星系统的引力作用遵循牛顿第三定律:F F =',作用力的方向在双星间的连线上,角速度相等,ωωω==21。
【例题1】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。
双星系统在银河系中很普遍。
利用双星系统中两颗恒星的运动特征可推算出它们的总质量。
已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T ,两颗恒星之间的距离为r ,试推算这个双星系统的总质量。
(引力常量为G ) 【解析】:设两颗恒星的质量分别为m 1、m 2,做圆周运动的半径分别为r 1、r 2,角速度分别为ω1、ω2。
根据题意有21ωω=①r r r =+21②根据万有引力定律和牛顿定律,有 G1211221r w m rm m =③G 1221221r w m r m m =④联立以上各式解得2121m m rm r +=⑤根据解速度与周期的关系知 Tπωω221==⑥联立③⑤⑥式解得【例题2】神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX3双星系统,它由可见星A 和不可见的暗星B 构成,两星视为质点,不考虑其他天体的影响.A 、B 围绕两者连线上的O 点做匀速圆周运动,它们之间的距离保持不变,如图4-2所示.引力常量为G ,由观测能够得到可见星A 的速率v 和运行周期T.(1)可见星A 所受暗星B 的引力F a 可等效为位于O 点处质量为m′的星体(视为质点)对它的引力,设A 和B 的质量分别为m 1、m 2,试求m′(用m 1、m 2表示). (2)求暗星B 的质量m 2与可见星A 的速率v 、运行周期T 和质量m 1之间的关系式;(3)恒星演化到末期,如果其质量大于太阳质量m s 的2倍,它将有可能成为黑洞.若可见星A 的速率v=×105 m/s ,运行周期T=π×104 s ,质量m 1=6m s ,试通过估算来判断暗星B 有可能是黑洞吗 (G=×10-11 N·m 2/kg 2,m s =×1030 kg )解析:设A 、B 的圆轨道半径分别为,由题意知,A 、B 做匀速圆周运动的角速度相同,设其为。
三阶系统综合分析与设计解析

三阶系统是以三级微分方程为运动方程的控制系统。在控制工程中,三阶系统非常普遍,其动态性能指标的确定是比较复杂。在工程上常采用闭环主导极点的概念对三阶系统进行近似分析,或直接用MATLAB软件进行高阶系统分析。在课程设计中,要掌握用MATLAB绘制闭环系统根轨迹和系统响应曲线,用系统的闭环主导极点来估算三系统的动态性能,以及在比较点与开环传递函数之间加一个非线性环节判断其稳定性。
8、认真撰写课程设计报告。
2 绘制三阶系统
图2系统结构图
由图1可得,三阶系统的开环传递函数为:
G(s)=ห้องสมุดไป่ตู้
2.1
根据绘制根轨迹的规则,可知该系统的根轨迹绘制步骤如下:
(1)根轨迹的起点和终点。根轨迹起于开环极点,终于开环零点。
开环极点分别为0、-3、-6,无开环零点。
(2)根轨迹的分支数。n=3,m=0,所以分支数为3 。且它们是连续的并且对称于实轴。
1 设计内容
1.1 设计题目
三阶系统的综合分析和设计
初始条件:某单位反馈系统结构图如图1-1所示:
图1-1 图1-2
1.2 设计任务
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)
1、试绘制随根轨迹
2、当-8为闭环系统的一个极点时,K=?
3、求取主导极点阻尼比为0.7时的K值(以下K取这个值)
于是分离点方程为:
因此可以求得分离点d=-1.3,d=-4.7(不合题意,舍去)
(6)根轨迹与虚轴的交点。
闭环特征方程式为
对上式应用劳斯判据,有:
1 18
9 k
k
令劳斯表中 行的首项为零,得k= 162,根据 行的系数,得辅助方程
9 +k=0
三阶系统的一种变结构最倨控制律及应用

三阶系统的一种变结构最倨控制律及应用目前,由于技术的发展,越来越多的系统结构由三阶系统所取代,他们使用自适应控制或者自动控制系统来改变系统结构,以便满足其期望的输出要求。
为了更好地研究三阶系统的控制,最近有越来越多的研究人员开展了“变结构最短控制”的研究。
此研究涉及分析变结构控制系统,以了解其在求解最短控制问题上的能力。
本文介绍了一种变结构最短控制律,并对其在三阶系统上的应用进行了详细介绍。
一、变结构最短控制律变结构最短控制是一种最新的管理技术,现在已经成为研究最短控制的一个热门课题。
它的基本思想是,首先建立一个模型,该模型能够提取常见的系统变化,然后建立一个控制策略,该控制策略的激励可以实现对不同变化的兼容对处理,从而实现系统尽可能近地接近实际的最优解。
变结构最短控制律可以分为两个部分:系统参数及其状态空间模型和控制策略。
其中,系统参数及其状态空间模型是建立变结构最短控制的基础,它是对系统运行特性的抽象的描述,包括(1)系统的参数,如各类型参数和阻尼参数;(2)系统的状态空间,即该系统所能达到的最大输出空间。
而控制策略则是设计出一种有效的控制策略,以便根据系统参数及其状态空间模型,实现变结构最短控制,从而使其有效地追踪实际最优解。
二、三阶系统的变结构最短控制三阶系统是目前研究变结构最短控制的重要对象,其各项参数的变化可以通过变结构最短控制的方法来获取比原始控制方法更佳的效果。
三阶系统的变结构最短控制可以分为三个步骤:1.立系统参数及其状态空间模型:首先,定义三阶系统的参数,包括系统阻尼、质量、刚度及圆周位移等;然后,建立描述系统参数及其状态空间的数学模型,其中状态空间描述该系统所能达到的最大状态。
2.解控制策略:基于所建立的模型,设定控制变量,比如力的大小及其时间变化,针对每个变量,求解其最优控制策略,确定每个变量下应产生的力的大小及时间变化,从而确定最短控制时间曲线。
3.最短控制曲线控制三阶系统:基于以上控制策略,应用适当的控制手段,比如操纵力或者控制电压等,对三阶系统进行控制,从而把系统抓入求解最优解的最短控制时间曲线。
自动控制原理(Ⅰ型二阶系统的典型分析与综合设计)课程设计

指导教师评定成绩:审定成绩:重庆邮电大学移通学院自动化系课程设计报告设计题目:Ⅰ型二阶系统的典型分析与综合设计学生姓名:专业:班级:学号:指导教师:设计时间:2010 年 12 月重庆邮电大学移通自动化系制重庆邮电大学移通学院《自动控制原理》课程设计(简明)任务书-供08级自动化专业、电气工程与自动化专业本科生用引言:《自动控制原理》课程设计是该课程的一个重要教学环节,它有别于毕业设计,更不同于课堂教学。
它主要是培养学生统筹运用自动控制原理课程中所学的理论知识,掌握反馈控制系统的基本理论和基本方法,对工程实际系统进行完整的全面的分析和综合。
一、设计题目:Ⅰ型二阶系统的典型分析与综合设计二、系统说明:该Ⅰ型系统物理模拟结构如下图:其中R0=100KΩ; C1=C2=10-5F;R2=1/2 R0R f为线性滑动电位器,可调范围为:10-1R0~ 104R0 ,设计过程中可忽略各种干扰,比如:运算放大器的零点漂移,环节间的负载效应,外界强力电力设备产生的电磁干扰等,均可忽略。
三、系统参量:系统输入信号:r(t);系统输出信号:y(t);四、设计指标:设定:输入为r(t)=a+bt(其中:a=5rad/secb=4rad/sec)在保证静态指标K v=5(e ss≤0.8)的前提下,要求动态期望指标:σp% ≤8.5% ;t s≤2sec五、基本要求:1. 建立系统数学模型——传递函数;2. 利用频率特性法分析和综合系统(学号为单号同学做);3. 利用根轨迹法分析和综合系统(学号位双号同学做);4. 完成系统综合前后的有源物理模拟(验证)实验;5. 完成系统综合前后的计算机仿真(验证)实验;六、设计缴验:1. 课程设计计算说明书一份;2. 原系统组成结构原理图一张(自绘);3. 系统分析,综合用BODE图(或根轨迹图)各一张;4. 系统综合前后的模拟图各一张(附实验结果图)各一张;5. 计算机仿真程序框图一张;6. 计算机仿真程序清单一份(附仿真实验结果图);7. 封面装帧成册;移通学院自动化系指导教师:汪纪峰2010-12-15目录引言 (2)一、系统概述 (7)1.1 设计目的 (7)1.2 系统的工作原理 (7)1.3 系统设计基本要求 (8)二、系统建模 (9)2.1 各环节建模 (9)2.1.1 比较器 (9)2.1.2 比例环节 (9)2.1.3 积分环节 (10)2.1.4 惯性环节 (11)2.1.5 反馈环节 (12)2.2 系统模型 (12)2.2.1 系统框图模型 (12)2.2.2 系统等价框图 (12)2.2.3 系统频域模型 (13)2.2.4 小结 (13)三、系统分析 (14)3.1 稳定性分析 (14)3.1.1 时域分析 (14)3.1.2 根轨迹映证 (14)3.1.2.1 绘制根轨迹 (15)3.2静态精度分析 (16)3.2.1Ⅰ型系统的典型分析 (16)3.2.1.1 跟踪能力 (16)3.2.1.2 ess计算 (16)3.2.2 根轨迹映证 (16)3.3 动态分析K 1 (17)3.3.1 作根轨迹 (18)3.3.2 指标分析 (19)四、系统综合 (20)4.1 校正方案的设计 (20)4.2 ts问题 (20)4.3τ的确定 (21)4.3.1 绘制校正后系统—τ参数根轨迹 (21)4.3.2 绘制τ参数根轨迹 (22)4.3.3 确定满足的σp%的ξ (24)4.3.4 做等ξ线 (24)4.4 确定τA (24)五、系统模拟 (25)5.1 原系统的物理模拟 (25)5.2校正后系统的物理模拟 (26)六、设计小结 (27)6.1心得体会 (27)6.2致谢 (28)七、参考文献 (29)《自动控制原理》课程设计第一章系统概述1.1设计目的主要是培养学生的统筹运用自动控制原理课程中所学的理论知识,掌握反馈控制系统的基本理论和方法,对工程实际系统进行完整全面分析和综合。
系统辨识和降阶模型

系统辨识和降阶模型一、引言系统辨识和降阶模型是现代控制理论中重要的概念和技术,广泛应用于工程领域。
系统辨识是指通过对系统的输入和输出数据进行分析和建模,从而推断出系统的内在特性和行为规律的过程。
降阶模型是指将高阶系统模型转化为低阶系统模型,以简化系统的分析和设计。
二、系统辨识系统辨识是一种通过实验数据来推断系统模型的方法。
它可以基于系统的输入和输出数据,利用统计学和数学建模技术来估计系统的参数和结构。
系统辨识可以分为参数辨识和结构辨识两个层面。
1. 参数辨识参数辨识是指通过对系统的输入输出数据进行分析,估计系统的参数值。
常用的参数辨识方法有最小二乘法、极大似然法和最大熵法等。
最小二乘法是一种通过最小化实际输出与模型输出之间的差异,来估计系统参数的方法。
极大似然法是一种基于概率统计原理的参数估计方法,通过最大化样本数据的似然函数来确定参数值。
最大熵法是一种基于信息论的参数估计方法,通过最大化系统的不确定性来确定参数值。
2. 结构辨识结构辨识是指通过对系统的输入输出数据进行分析,估计系统的结构和模型形式。
常用的结构辨识方法有模型选择准则、系统辨识算法和系统辨识工具等。
模型选择准则是一种评估不同模型的性能和复杂度的方法,常用的准则有AIC准则、BIC准则和MSE准则等。
系统辨识算法是一种通过计算机程序对系统数据进行处理和分析,从而得到系统模型的方法。
系统辨识工具是一种用于辅助系统辨识的软件工具,常用的工具有MATLAB、LabVIEW和Python等。
三、降阶模型降阶模型是指将高阶系统模型转化为低阶系统模型的过程。
降阶模型可以简化系统的分析和设计,提高系统性能和控制效果。
常用的降阶模型方法有模型约简、系统分解和模型识别等。
1. 模型约简模型约简是一种通过舍弃系统模型中的一部分变量和参数,从而降低模型复杂度的方法。
常用的模型约简方法有特征值分解、奇异值分解和模态分析等。
特征值分解是一种通过对系统矩阵进行特征值分解,从而得到系统的特征向量和特征值的方法。
《自动控制原理》第三章第4讲

∑ ∴c(t) =a0 + n1 a je− pjt j =1
n2
n2
∑ ∑ +
β e−ζlωlt l
cosωl
1−ζl2t +
γ
e−ζ lωl t
l
sin ωl
l 1=l 1
1−ζl2t
高阶系统的阶跃响应总可以由简单函数项组成,即由一 阶、二阶系统的响应组成。
可见,c(t)不仅与 p j ,ζ l ,ωl (闭环极点)有关,而且与系数
C(s) = Φ(s) ⋅ 1 = 10
s+9
= 1 − 80 1 − 1 1
s 9 s(s + 1)(s + 10) s 81 s + 1 81 s + 10
近似:C(s)
=
s(s
1s 9 + 1)(
+1 1s
+ 1)
≈
1 s(s + 1)
=
1 s
−
s
1 +1
10
C(s) = Φ(s) ⋅ 1 = 10 s + 1.1 = 1 − 10 1 + 89 1 s 1.1 s(s + 1)(s + 10) s 99 s + 1 99 s + 10
− p1,− p2 虚轴近,系统的瞬态特性主要由 − p1,− p2 决定,呈二阶
系统的特性。反之,当 b << 1 时,表示− p3 离虚轴近,− p1,− p2
离虚轴远,系统的瞬态特性主要由− p3 决定,呈一阶系统的特性。
第二个因素是阻尼系数 ζ ,如下图所示:
c(t)
b= ∞ b=2
三阶系统.doc

三阶系统.doc这时,调节时间s t 近似为: ns t ωξξ)1(42--=(3-13)图3-3 二阶系统模拟电路K K K K R100,40,20,10=图3-3是图3-1的模拟电路图。
表3-1列出有关二阶系统在三种情况(欠阻尼、 临界阻尼、过阻尼)下具体参数的表达式,以便计算理论值。
表3-12、图3-4是典型三阶系统原理方框图图2-4 典型三阶系统t )开环传递函数为:)1)(1()1)(1()()(2121021++=++=S T S T S KS T S T S T K K S H S G (3-14)其中,021K K K= (开环增益)图3-5是典型三阶系统模拟电路图。
op1op2op3op5r(t)200k200k200k500k2μ1μ100k 1μ500k10k10kC(t)图2-5 三阶系统模拟电路100k R-----op6三阶系统模拟电路的开环传递函数为:)1)(1()15.0)(11.0(500)()(21++=++=S T S T S KS S S R S H S G (3-15)式中R 的单位为K Ω,比较式(1-14)和(2-15)得⎪⎪⎩⎪⎪⎨⎧====RK T T T 5005.01.01210 (3-16) 系统的特征方程为0)()(1=+S H S G ,由式(2-14)可得0)1)(1(21=+++K S T S T S展开得到:0)(221321=++++K S S T T S T T (3-17)将式(2-16)代入式(2-17)得到06.005.023=+++K S S S或020201223=+++K S S S (3-18)用劳斯判据求出系统稳定、临界稳定和不稳定时的开环增益 3S 1 202S 12 20K图图1S12202012K-⨯ 00S 20K由0202012>-⨯K020>K得到系统稳定范围: 120<<K由0202012=-⨯K得到系统临界稳定时: 12=K 由0202012<-⨯K得到系统不稳定范围 12>K将R K500= 代入上式得到:Ω>K R 7.41 系统稳定Ω=K R 7.41 系统临界稳定 Ω<K R 7.41 系统不稳定系统稳定、临界稳定和不稳定时输出波形如图3-6A,3-6B,3-6C 所示。
Ⅰ型三阶系统系统的四阶参考模型

参考模型法校正是频率法校正中经常使用的一种校正方法。
它基于参考模型来修正固有特性从而求得校正装置。
因此作图简单,校正方便,没有繁杂的计算。
常用的参考模型按照系统阶数划分为二阶参考模型,四阶参考模型等。
本文基于I型三阶系统的四阶参考模型法设计及仿真研究。
研究典型I型3阶系统动静态性能特性并完成设计,以达到使该系统满足工程实际性能指标要求。
运用经典控制理论中频域理论方法,分析给定的典型系统基本特性,按照实际的工艺指标运用四阶参考模型设计满足要求的闭环系统方案,用MATLAB/SIMULINK对设计系统进行仿真验证。
【关键词】:I型三阶系统四阶参考模型仿真AbstractRefere nee correcti on is freque ncy model, a correct ion method is freque ntly used in the calibratio n. It is based on refere nce model to revise the in here nt characteristics of calibratio n device is obta in ed. So draw ing simple, easy to correction, no complex calculati on. Commonly used refere nce model accord ing to the system order is divided into two order reference model, fourth order reference model, etc. Based on the fourth-order I third-order system reference model method of design and simulation research. Research on typical I type 3 order system dynamic and static performa nce characteristics and complete the desig n, to make the system meet the requirements of practical engineering performance index. By using the theory of classical con trol theory of in termediate freque ncy doma in method, an alysis the basic features typical of a given system, according to the actual technical index using the fourth order refere nce model desig n meet the requireme nts of the closed loop system solutio ns, usi ng MATLAB/SIMULINK for simulatio n desig n system.【Keyword】:I type three order system Fourth order reference model The simulati on。
I型三阶系统的典型分析与综合设计要点

成绩 ______自动控制原理课程设计报告题目:I型三阶系统的典型分析与综合设计系别专业名称班级学号姓名指导教师重庆邮电大学移通学院自动化系制2013 年 12 月摘要:在科学技术高速发展的今天,自动控制技术已经广泛的运用与制造业,农业,交通,航空航天等众多部门,极大地提高了社会劳动生产率,改善了人们的劳动环境,丰富和提高了人民的生活水平。
在今天的社会中,自动化装置已经无所不在,为人类文明进步做出了重要的贡献。
自动控制原理的课程设计是检验我们学过只是扎实程度的好机会,也让我们的知识体系更加系统,更加完善。
在不断学习新知识的基础上得到动手能力的训练,启发创新思维及独立解决实际问题的能力,提高设计,装配,调试能力。
In the rapid development of science and technology, automatic control technology has been widely used with many sectors such as manufacturing, agriculture, transportation, aerospace, and greatly improve the social labor productivity, and improve people's working environment, enrich and improve the people'sstandard of living. In today's society, the automation device has been everywhere, and made important contributions to the progress of human civilization. Curriculum design of automatic control theory to test we learned just a solid degree of good opportunities, but also to our body of knowledge more systematically, more perfect. Constantly learning new knowledge based on training ability, and inspire innovative thinking and the ability to solve practical problems independently, and to improve the design, assembly, commissioning and capacity.关键字:系统分析性能指标系统校验设计系统Keywords: System Performance Analysis System Design System Calibration目录一、系统说明(概述)5二、系统分析6三、系统综合8四、系统物理模拟图10总结13参考文献14重庆邮电大学移通学院《自动控制原理》课程设计(简明)任务书一、 设计题目:I型三阶系统的典型分析与综合设计 二、 系统说明:设单位反馈系统开环传递函数为0()(10.1)(10.02)kG S s s s =++,试设计串联校正装置,使系统满足70,1,%40%V s K t σ≥≤≤三、 基本要求:a) 利用频率法分析系统:(1) 作原系统的Bode 图;(2)分析原系统的性能,当原系统的性能不满足设计要求时,则进行系统校正。
一阶系统的数学模型

an 4 an 5 b3 c3 d3
an an 2 an 1 an 3 an 1an 2 an an 3 b1 an 1 an 1
an an 4 an 1 an 5 an 1an 4 an an 5 b2 an 1 an 1
胡尔维茨行列式:
0 0 0
a0
n n
胡尔维茨行列式的构造:主对角线上的各项为特征方程的第二 项系数an 1 至最后一项系数 a0 ,在主对角线以下各行中各项系数 下标逐次增加,在主对角线以上各行中各项系数下标逐次减小。 当下标大于n或小于0时,行列式中的项取0。
4 3 2 以4阶系统为例使用胡尔维茨判据:a4 s a3s a2 s a1s a0 0
[例] 有一位置随动系统,其方块图如图所示。其中K=4,T=1。 试求: (1) 该系统的无阻尼振荡频率 n;(2)系统的阻尼系数; (3)系统超调量%和和调整时间ts;(4)如果要求=0.707,在 不改变时间常数T的情况下,应怎样改变系统开环放大系数K。
R s +
K s (Ts 1)
阻尼系数、特征根、极点分布和单位阶跃响应形式如下表 所示: 阻尼系数
0, 无阻尼
o 1, 欠阻尼
特征根
极点位置
一对共轭虚根
单位阶跃响应
三阶系统(最新)
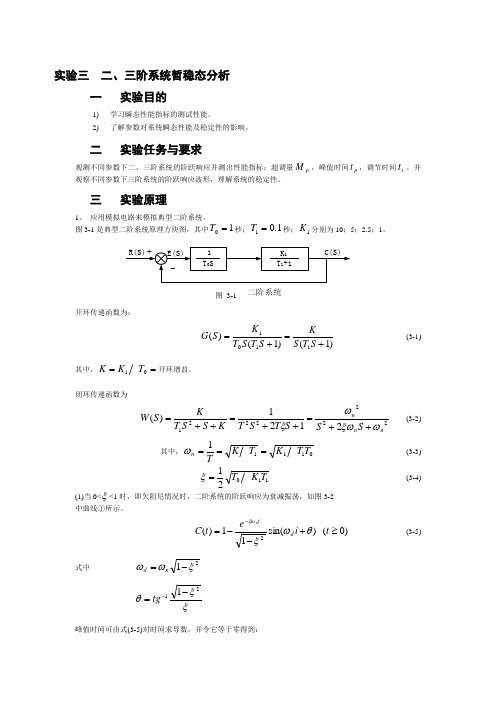
实验三 二、三阶系统暂稳态分析一实验目的1) 学习瞬态性能指标的测试性能。
2)了解参数对系统瞬态性能及稳定性的影响。
二 实验任务与要求观测不同参数下二、三阶系统的阶跃响应并测出性能指标:超调量pM ,峰值时间p t ,调节时间s t 。
并观察不同参数下三阶系统的阶跃响应波形,理解系统的稳定性。
三 实验原理1、 应用模拟电路来模拟典型二阶系统。
图3-1是典型二阶系统原理方块图,其中10=T 秒;1.01=T 秒;1K 分别为10;5;2.5;1。
开环传递函数为:)1()1()(1101+=+=S T S KS T S T K S G (3-1)其中,==01T K K开环增益。
闭环传递函数为22222212121)(n n n S S S T S T K S S T K S W ωξωωξ++=++=++= (3-2)其中,01111T T K T K T n===ω (3-3) 11021T K T =ξ (3-4)(1)当0<ξ<1时,即欠阻尼情况时,二阶系统的阶跃响应为衰减振荡,如图3-2 中曲线①所示。
)sin(11)(2θωξξω+--=-i e t C d t n )0(≥t (3-5)式中21ξωω-=n dξξθ211-=-tg峰值时间可由式(3-5)对时间求导数,并令它等于零得到:图2-1 二阶系统图 3-1=p t 21ξωπωπ-=n d (3-6)由)()()(∞∞-=t C t C t C M p p求得超调量pM:21ξξπ--=e M p (3-7)调节时间s t ,采用2%允许误差范围内,近似的等于系统时间常数nξω1的四倍,即ns t ξω4=(3-8)(2)当1=ξ,即临界阻尼情况时,系统的阶跃响应为单调的指数曲线,如图3-2中曲线②所示。
输出响应)(t C 为)1(1)(t et C n tn ωω+-=- )0(≥t (2-9)这时,调节时间s t 可由下式求得)1(1)(s n t s t e t C s n ωω+-=-=0.98 (3-10)(3)当1>ξ,即过阻尼情况时,系统的阶跃响应为单调的指数曲线:)(121)(21221s e s e t C ts t s n----+=ξω ()0≥t (3-11)式中n s ωξξ)1(21-+=,n s ωξξ)1(22--=当ξ远大于1时,可忽略1s -的影响,则tn et C ωξξ)1(21)(----=()0≥t (3-12)C图2-2 二阶系统阶跃输入下的瞬态响应图 3-2这时,调节时间s t 近似为: ns t ωξξ)1(42--=(3-13)图3-3 二阶系统模拟电路K K K K R100,40,20,10=图3-3是图3-1的模拟电路图。
6.4 机电一体化伺服系统模型

能正确跟踪拐角,但存在超 调消失,实际轨迹与目标轨迹一
调13
致 工业机器人实验结果(左图为修正后信号,右图为实际轨迹)
3s3 2s2 1s 0
s 1 s 2 s
0 12
1
K
1
2
K
2
1
2
K
1 2 Kp
2
1 Kp
K
1
2
K
2
1
2
K
12 K pK
1
601/ s 12 1 601/ s 2 601/ s 1201/ s
工业机器人修正结果
目标轨迹包括三条线 段和两个拐角,目标 轨迹速度为 250mm/s)
传统方法 (误差面积136mm2) 在拐角处有运动延迟
一阶修正(误差面积60mm2) 二阶修正(误差面积40mm2)超
工业机器人在运动过程中,由于每个轴上存在时间延迟, 会导致机器人在目标轨迹和实际轨迹之间出现误差。
可建立修正模型进行相位超前补偿,提高机器人轮廓控 制的精度。
一阶系统 修正项
G1
s
s
Kp Kp
F1
s
s
Kp s
K
p
10 其中r表示调节器极点
二阶系统
修正项
F2 s
3 K pK
K 1 2 K2 12 K
其中ri表示调节器极点,u表示观测器极点
L系统模型构建

错误!未找到引用源。
第一章L 系统的基本理论1、L 系统L 系统实质上就是一个并行重写系统. 其核心概念是重写( rewriting) ,重写的基本思想是根据预先定义的重写规则(生成规则) 集不断地生成复合形状并用它来取代初始简单物体的某些部分以定义复杂物体. L系统是一个形式语言系统,对迭代生成的字符串从左至右连续扫描,并对每一个字符做出相应的几何解释,这样就由字符串得到植物的结构形态.2、L 系统的平面解释L 系统在平面内采用“二维龟解释模型”. 设想1只乌龟在平面上爬行,其状态用3 个值描述,记作( x , y ,α) 其中x , y 为乌龟所在位置的直角坐标,α表示乌龟头的朝向. 再给定乌龟爬行的步长d 及扭转方向的角度增量δ.F:向前移动一步,步长为d. 乌龟到达状态( x’ , y’ ,α) ,其中x’ = x + d *()cosα;y’ = y + d *sin()α; (1. 1) +: 向左转δ角,乌龟下一状态为( x , y ,α+δ) ,规定正向角是逆时针方向;-: 向右转δ角,乌龟下一状态为( x , y ,α- δ) ,规定负向角是顺时针方向.其中d、α和δ是可以改变的参数,经过这样反复重写,最后可以得到分形图.3、L 系统的空间解释在三维空间内,本文采用的是“三维龟模型”符号解释. 龟有它的状态,包括笛卡尔坐标系下的位置和方向,还有一些附加的属性,如当前的颜色和线宽.位置由矢量P 定义,方向由3 个矢量H ,L ,U 定义,分别表示乌龟的方向:向前、向左、向上.这3 个向量都具有单位长度,且互相垂直,满足HXL = U. 因此,龟行的旋转可以用下面的式子表示:[ H′L′U′] = [ H L U ]R (1. 2) 其中R 为旋转矩阵,绕H 逆时针方向旋转, θ旋转矩阵用R U (θ) 和R L (θ) 表示,绕L 及绕H 的旋转矩阵分别用R L (θ) 和R H (θ) 表示,分别有如下形式:R U (θ) =错误!未找到引用源。
数学模型 等级结构

N (t ) ni (t )
i 1 k
t年总人数
j 1 i 1
P的行和为1 (随机矩阵)
若总人数不变M (t ) N (t 1) N (t ) 0
等级结构a(t 1) a(t ) P a(t )(Q w r )
T
与马氏链基本方程 (n 1) a(n) P 一致 a
等级结构a(t) ~状态概率 P~转移概率矩阵
ni (t ) ai (t ) N (t )
a(t)~等级结构
ai (t ) 0,
a (t ) 1
i 1 i
k
转移矩阵 Q={pij}kk, pij 是每年从i 转至j 的比例
基本模型
退出比例w (w1 , w2 ,, wk ), i ~ 每年从i退出的比例 w
W (t ) wi ni (t ) n(t ) w ~ t年退出总人数
0.639
0.361 0 0.165 0.165 0.670
a(t)
0.1 0.8
a(7)已接近a*
观察r(t)的特点
i 1 k
用调入比例进行动态调节
例
0.5 Q 0 0 0.4 0.6 0 0 0.3 0.8
设 a(0) (0,0,1), a * (0.286 ,0.286 ,0.428 )
(0,1,0)
求r 使a(1)尽量接近a*
min D ( a (1), a * ) r ri 0, ri 1
儿童发展心理学60924

第一章1,发展:个体在从受精卵形成到死亡的整个生命历程中系统的身心变化,这些变化是有顺序的,相对持久的,并且使个体行为具有适应性,组织性和更为复杂。
儿童心理发展常分为三个领域:①生理的成熟和发展②认知和语言的发展③人格和社会性的发展2,发展心理学是心理学的一个分支,是研究心理发展规律的科学。
心理发展又包含三个方面的内容:①动物种系演进过程中的心理发展②人类心理的发展③人类个体心理发展3,儿童发展心理学是发展心理学的一个分支,是研究儿童发展规律的科学(注意此处的儿童,不是我们一般意义的儿童,是指从出生到十七八岁这一年龄段的个体)。
一般分为5个阶段:出生前期:从受精卵形成到出生,9个月时间内,一个单细胞有机体发展成适应能力很强的人类婴儿。
婴儿期:0-2岁,身体和脑发育迅速,个体从嗷嗷待哺到独立行走,会用语言表达,并发展了自我再认能力,与主要照料者建立了亲密的情感联系。
幼儿期:2-7岁个体身体机能更加协调,游戏成为主要活动吧,语言和思维能力发展迅速,道德感更加明显。
童年期:7-12岁,个体通过学习以及学校中的师生交往,同伴交往,不断地促进思维,情感,人格和社会性的发展。
青少年期:12-18岁,这是儿走向相成年的过渡期。
个体具备了抽象思维能力,性意识萌动。
确立价值观和人生观,建立自我同一性,走向独立是这个阶段的主要发展任务。
4.儿童发展心理学的4个基本主题①遗传和环境因素在儿童发展中各起多大的决定作用②儿童在自身的发展中是主动还是被动③发展是连续、渐进的还是阶段性的④发展是开发的还是稳定不变的对于以上基本主题,现代已不在采用极端的观点,而是同时采纳多家优点,采取一种综合性的立场,它们相互发展、互为补充(一)儿童心理发展学简史几个关键人物事件1.精神分析理论(弗洛伊德,埃里克森,荣格)2.行为主义和社会学习理论约(约翰.B。
华生,斯金纳,阿尔伯特,班杜拉)3.皮亚杰认知发展理论4.达尔文《一个婴儿的传略》(科学儿童研究的先驱)5.普莱尔《儿童心理》(标志着科学儿童心理学的正式诞生)6.霍尔《青少年心理学》(发展心理学奠基人之一)(二)研究方法⑴基本研究方法Ⅰ系统观察法(①自然观察法②结构观察法)Ⅱ自我报告法(①访谈法②问卷法和测验法)Ⅲ个案研究另外还有人种志研究法、心理生理学法⑵保证科学研究的信度与效度信度:信度指的是行为测量的一致性,可重复性。
有源校正网络如题图所示

试采用频率法设计超前校正装置 Gc ( s) ,使得系统实现如下的性能指标 (a)静态速度误差系数 Kv ≥ 100 ; (b)开环截止频率ωc > 30 ; (c)相位裕度γ c > 20ο 。 6-8 已知系统的开环传递函数为
G ( s) H ( s) =
K s( 0.02 s + 1)
试采用频率法设计滞后校正装置 Gc ( s) ,使得系统实现如下的性能指标 (a)静态速度误差系数 Kv ≥ 50 ; (b)开环截止频率ωc > 10; (c)相位裕度γ c > 60ο 。 6-9 已知单位反馈系统的结构图如题图所示,其中 K 为前向增益,
1 + T1s 为超前校正装 1 + T2 s
置, T1 > T2 ,试用频率法确定使得系统具有最大相位裕度的增益 K 值。
R(s) +-
K
1 + T1 s 1 + T2 s
习题 6-8
1 C(s) s2
6-10 设单位反馈控制系统的开环传递函数为
G ( s) =
K s +1
试采用二阶参考模型法设计校正装置 Gc ( s) ,使得校正后实现下述性能指标 (a)静态速度误差系数 Kv ≥ 10 ; (b)阶跃响应的过渡时间 t s < 0.4 秒;
6-12 设角位移伺服系统的开环模型为 G ( s) =
型法设计校正装置 Gc ( s) ,使得校正后实现下述性能指标 (a)静态速度误差系数 Kv ≥ 200 ; (b)阶跃响应的过渡时间 t s < 0.4 秒; (c)阶跃响应的超调量 M p < 30% ; 并计算相位裕度γ c 的大小。 6-13 设受控对象的开环模型为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要参考模型法校正是频率法校正中经常使用的一种校正方法。
它基于参考模型来修正固有特性从而求得校正装置。
因此作图简单,校正方便,没有繁杂的计算。
常用的参考模型按照系统阶数划分为二阶参考模型,四阶参考模型等。
本文基于Ⅰ型三阶系统的四阶参考模型法设计及仿真研究。
研究典型Ⅰ型3阶系统动静态性能特性并完成设计,以达到使该系统满足工程实际性能指标要求。
运用经典控制理论中频域理论方法,分析给定的典型系统基本特性,按照实际的工艺指标运用四阶参考模型设计满足要求的闭环系统方案,用MATLAB/SIMULINK对设计系统进行仿真验证。
【关键词】:Ⅰ型三阶系统四阶参考模型仿真。
AbstractReference correction is frequency model, a correction method is frequently used in the calibration. It is based on reference model to revise the inherent characteristics of calibration device is obtained. So drawing simple, easy to correction, no complex calculation. Commonly used reference model according to the system order is divided into two order reference model, fourth order reference model, etc. Based on the fourth-order Ⅰthird-order system reference model method of design and simulation research. Research on typical Ⅰtype 3 order system dynamic and static performance characteristics and complete the design, to make the system meet the requirements of practical engineering performance index. By using the theory of classical control theory of intermediate frequency domain method, analysis the basic features typical of a given system, according to the actual technical index using the fourth order reference model design meet the requirements of the closed loop system solutions, using MATLAB/SIMULINK for simulation design system.【Keyword】:Ⅰtype three order system Fourth order reference model The simulation。
第一章绪论第一节课题研究的背景自动控制技术广泛的应用于现代的各行各业,一个国家自动化水平的高低,直接反映了到这个国家的科技水平的高低。
从最早的机械转速、位置控制,到后来的温度、压力控制以及现在的人工智能,模糊控制,神经网络,遗传算法。
比如智能手机领域的手机语音助手,现在热潮的智能家居,以及将来越来越多的可能威胁人类的智能机器人。
自动控制技术已经越来越成为人们生活中不可或缺甚至扮演着越来越重要的角色。
在实际工程中,控制系统的参数一般的事先给出了,在预先的系统经分析后发现不能满足预先设定的性能和指标,就需要对预定系统进行校正以满足现实中的要求。
第二节课题研究的意义经典控制理论中一般采用根轨迹校正和频域法校正。
在工程实际中一般采用频域法校正,本文基于频域法校正中的四阶参考模型校正,也叫按期望特性进行校正。
方法简单,易于计算,往往用经验公式进行运算,具有很强的实际意义。
第三节论文的结构论文首先对课题的背景和意义进行阐述,并概述了论文结构第二章对系统校正的概念、指标、类型进行简要的介绍第三章对系统进行校正设计第四章对系统进行仿真模拟最后总结、致谢。
第二章 系统校正概述第一节 系统校正的概念控制系统包括被控对象,检测装置、放大元件、执行机构、当被控对象给定后,就可以按照被控对象的工作条件对执行元件的形式,特性和参数进行选定。
这些初步选定的元件及被控对象构成了系统中的不可变部分。
控制系统校正的目的是将校正装置与系统的固有部分经过合适的连接,构成新的系统结构,使其完成控制系统的任务要求。
第二节 系统校正基础一、控制系统的性能指标实际工程中,系统指标事先给出,当系统的固有部分不能满足系统的性能指标时,需要根据被控对象的控制要求选择适当的校正装置,来满足要求。
一般来说,性能指标不应该比实际任务的性能指标高,实际系统的各种性能指标受到组成元件的固有误差,非线性特性及其他各种物理条件的限制。
(一) 时域性能指标时域性能指标分为动态性能指标和稳态性能指标。
动态性能指标主要有上升时间r t 、峰值时间p t 、调节时间s t 、超调量% ;稳态性能指标由稳态误差ss e 描述,分为:静态位置误差系数P K 、静态速度误差系数v K 、静态加速度误差系数a K 。
时域指标直观但是进行校正装置设计使比较困难,实际中通常采用频域法进行设计。
(二)频域性能指标频域性能指标分为开环频域指标和闭环频域指标。
常用的开环频域指标有:截至频率c w 、幅值裕量g K 、相角裕量γ 。
常用的闭环频域指标有:谐振峰值r M 、谐振频率r w 、带宽频率b w 。
(三)典型二阶系统频域指标和时域指标的关系谐振峰值0.707r M ξ=<<谐振频率0.707r w w ξ=<<带宽频率b w w =截止频率c w w =相角裕量r =超调量100%%e σ=调节时间 3.55%s nt w ξ=∆= (四) 高阶系统开环频域与时域指标的关系谐振峰值001,35901 1.8sin r r M M γγ≈≤≤≤≤, 超调量10.160.41sin σγ⎛⎫=+-⎪⎝⎭ 或()%0.160.41r M σ=+- ,(1M 1.80)r ≤≤调节时间0s cK t w π=()()202 1.51 2.51,(1 1.8)r r r K M M M =+-+-≤≤第三节 控制系统校正的方式根据校正装置在系统中不同位置,校正结构的不同形式可以分为串联校正、联校正、前馈校正等方式,按照校正装置设计方法的同可以分为频域法校正、轨迹校正、时域校正等方法。
根据校正装置特性不同可以分为超前校正、滞后校正、滞后-超前校正和PID 控制方法等。
串联校正装置(s)c G 一般在测量点之后和放大器之前,校正装置的功率较小,设计及实现都比较简单,是最常用的校正方式。
如图1-1所示,1(s)G 、2(s)G 、(s)H 为系统固有部分的传递函数,(s)c G 为校正装置传递函数。
校正前系统的闭环传递函数为1212(s)(s)(s)1(s)(s)(s)G G G G H Φ=+校正后系统的闭环传递函数1212(s)G (s)G (s)(s)1(s)G (s)(s)(s)c c G G G H Φ=+串联校正后系统的零极点发生变化,只要选着合适的校正装置的参数,就可以使校正后的系统满足期望的性能指标,但是,这种方法对参数的变化比较敏感。
图1-1第四节控制系统的基本控制规律了解控制系统的基本规律对选择什么样的校正装置和方法非常必要,一般的控制规律分为比例环节、积分环节、微分环节及其组合比例-微分、比例-积分、比例-积分-微分等控制规律。
一、比例控制规律具有比例控制规律的控制器称为比例控制器,简称P控制器,如图1-2所示。
P控制器是一个具有可调增益的放大器,比例元件改变信号的增益而对相位没有影响,在串联校正中,比例控制可以提高控制器的放大系数K提高系统p开环增益,减小系统稳态误差,提高稳态精度,但是,开环增益的增大会降低系统的动态稳定性,甚至有可能使闭环系统不稳定。
在控制系统中,仅仅有比例环节很难兼顾系统的稳态精度和动态性能,因此在工程实际中,很少单独只用比例控制器,往往和其他控制器一起使用。
图1-2 比例控制器比例环节的物理模型图1-310f R G R =-二、比例-微分控制规律具有比例-微分控制规律的的控制器,称为PD 控制器。
其输出信号(t)m 和输入信号(t)e 的关系为(t)(t)(t)K p p Dde m K e dtτ=+其中p K 为比例系数,D τ 为时间常数,p K 与D τ 都是可调的参数,PD 控制器如图1-4所示图1-4比例-微分控制器中的微分控制作用,能反映输入信号的变化趋势,产生有效的早期修正信号,以增加系统的阻尼程度,从而改善系统的稳定性但是,微分控制系统对系统的噪声非常敏感,存在放大噪声,降低系统抗干扰能力的不利因素,因此微分环节在任何情况下,都不宜与被控对象串联单独使用。
通常,微分控制规律和比例控制规律或比例-积分控制规律结合组成PD 或PID 控制规律。
三、积分控制规律具有积分控制规律的控制器,称为I 控制器。
其输出信号(t)m 和输入信号(t)e 的关系为1(t)K (t)dt (t)ttp Im e e dt τ==⎰⎰其中p K 为可调比例系数。
1I pK τ=为积分控制器的积分时间常数。
积分控制器可以提高系统的误差都度和稳定性能,但是积分控制器使系统增加一个位于原点的开环极点,信号产生090 的相位滞后,不利于系统稳定。
因此,很少单独用积分环节进行校正。
积分控制器如图1-5图1-5积分环节的物理模型图1-62101(s)G C R S=-四、比例-积分控制规律具有比例-积分控制规律的控制器,称为PI 控制器。
其输出信号(t)m 和输入信号(t)e 的关系为(t)K (t)(t)dttpP IK m e e τ=+⎰其中p K 为可调比例系数。
i τ 为可调积分时间常数。
PI 控制器如图1-7所示。
图1-7比例-积分控制器相当于同时在系统中增加了一个位于原点的开环极点和一个位于S 左半平面的开环零点。
位于原点的开环极点可以提高系统的性别,以消除或减小系统的稳态误差;增加的负实数零点则可以提高系统阻尼程度,缓和开环极点对系统稳定性产生的不利影响。
