七年级数学下册 5.3.2_命题、定理、证明-课件.ppt

第五章相交线与平行线5.3.2命题、定理、证明

5.3.2 命题、定理、证明
命题的定义：
判断一件事情的语句叫做命题。
1、只要对一件事情作出了判断，不管正确与否，都是命题。 2、如果一个句子没有对某一件事情
作出任何判断，那么它就不是命题。
语句都是对某一件事情作出“是”或
“不是”的判断.其中问句，画图，感叹句，祈使句不是命题！
下列语句是命题吗？ ①请你吃饭。 ②大象是红色的 ③同位角相等. ④连接A、B两点. ⑤你多大了？
如果两个角是对顶角，那么这两个角相等. 题设是：两个角是对顶角结论是：这两个角相等
④同位角相等. 如果两个角是同位角，那么这两个角相等.
题设是：两个角是同位角结论是：这两个角相等
★ 如：对顶角相等
题设
结论
如果两个角是对顶角，那么这两个角相等题设结论
问题5
下列语句是命题吗？如果是，请将它们改写成“如果„„，那么„„”的形式.
（5）对顶角相等．
如果两个角是对顶角，那么这两个角相等．
问题7 下列哪些命题是正确的，哪些命题是错误的？
（1）两条直线被第三条直线所截，同旁内角互补；

（2）等式两边都加同一个数，结果仍是等式；
（3）互为相反数的两个数相加得0；（4）同旁内角互补；（5）对顶角相等．的真假
有些命题如果题设成立，那么结论一定成立；
请同学们判断下列两个命题的真假
命题 :相等的角是对顶角．（3）你能举出反例吗？
如命题：“如果一个数能被4整除，那么它也能被2整除”对么？
如命题：“如果两个角互补，那么它们是邻补角” 对么？确定一个命题真假的方法：
利用已有的知识，通过观察、验证、推理、举反例等方法。
问题1 请同学们判断下列命题哪些是真命题？

人教版七年级数学下册 (命题、定理、证明)相交线与平行线课件

√(3)经过直线AB外一点P, 可以作一条直线与AB平行.
你再举出一些例子.
对于一个命题，由题设和结论两部分构成，题设是已知事项，结论是由已知事项推出的事项。
知识回顾问题探究课堂小结随堂检测
探究二：命题的题设与结论
活动1 把下列命题改写成“如果……那么……”的形式，并说出该命题的题设，结论. （1）互补的两个角不可能都是锐角：如果两个角互补，那么这两个角不可能都是锐角 . （2）对顶角相等：如果两个角是对顶角，那么这两个角相.等（3）垂直于同一条直线的两条直线平行：如果两条直线同垂直与一条直线，那么这两条.直线平行
二、命题的结构
观察下列命题，你能发现这些命题有什么共同的结构特征？与同伴交流. （1）如果两个三角形的三条边相等，那么这两个三角形的周长相等；（2）如果两个数的绝对值相等，那么这两个数也相等；（3）如果一个数的平方等于9，那么这个数是3.
依据所学知识可以判断（1）（3）是正确的，句子（2）（4）（5）是错误的，
这几个句子的特点是可以判断一件事情的正确或错误，这样的句子就是命题.
知识回顾问题探究课堂小结随堂检测探究一：命题的概念
活动2 下列语句,哪些是命题? 哪些不是? (1)过直线AB外一点P,作AB的平行线. (2)过直线AB外一点P,可以作一条直线与AB平行吗?
知识回顾问题探究课堂小结随堂检测
探究三：真假命题
活动2 理解公理与定理的概念
数学中有些命题的正确性是人们在长期实践中总结出来的，并把它们作为判断其他命题真假的原始依据，这样的真命题叫做公理.
有些命题可以从公理或其他真命题出发，用逻辑推理的方法判断它们是正确的，并且可以进一步作为判断其他命题真假的依据，这样的真命题叫做定理.

人教版七年级下册数学教学课件第五章相交线与平行线命题、定理、证明

课程讲授
2 真命题与假命题
归纳： 1.要判断一个命题为真命题，可以用演绎推理加以
论证； 2.要判断一个命题为假命题，只要举出一个例子，
说明该命题不成立.
课程讲授
3 定理与证明
定义：数学中这些命题的正确性是人们在长期实践中
总结出来的，并把它们作为判断其他命题真假的原始依据，即出发点.这样的真命题视为基本事实.我们也称它为公理.
理才能作出判断，这个推理过程叫作证明.
证明几何命题的一般步骤：
1.明确命题中的_已__知___和__求__证__； 2.根据题意，_画__出__图__形__，并用数学符号表示已知和求证； 3.经过分析，找出由已知推出_要__证__的__结__论_的途径，写出证明过程.
课程讲授
3 定理与证明
例已知直线b∥c， a⊥b ．求证：
a⊥c．
b
c
证明：∵ a ⊥b（已知）， ∴ ∠1=90°（垂直的定义）.
1
2
a
∵ b ∥ c（已知），
∴∠1=∠2（两直线平行，同位角相等），
∴ ∠2=∠1=90°（等量代换）， ∴ a ⊥ c（垂直的定义）.
课程讲授
3 定理与证明
练一练：求证：内错角相等,两直线平行.
已知：如图，直线l3分别与l1，l2交于点A,点B，且∠1=∠2.
求证：l1∥l2. 证明：∵ ∠１=∠２ (已知)，
∠3=∠2 (对顶角相等)，
l3
1(
)3 B
l2
)2 A
l1
∴ ∠1=∠3 (等量代换).
∴ l１∥l２ (同位角相等,两直线平行).
随堂练习
１．下列句子中，哪些是命题？哪些不是命题？ ⑴对顶角相等；是 ⑵画一个角等于已知角；不是 ⑶两直线平行，同位角相等；是 ⑷a，b两条直线平行吗？不是 ⑸温柔的李明明；不是 ⑹玫瑰花是动物；是 ⑺若a2＝4，求a的值；不是 ⑻若a2＝ b2，则a＝b. 是

5.3.2平行线的性质

5、平行公理的推论：如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
定理举例：
6、平行线的判定定理：同位角相等，两直线平行。内错角相等，两直线平行。同旁内角互补，两直线平行。 7、平行线的性质定理：
两直线平行，同位角相等。两直线平行，内错角相等。两直线平行，同旁内角互补。
判断一个命题是假命题，只要举出一个例子，说明该命题不成立就可以了，这种方法称为举反例。
作业
1、课本P24页第12题课本P36页第8、12、13题
2、同步学习P14-15页
√
）
（2）请画出两条互相平行的直线；（
（3）过直线外一点作已知直线的垂线；（

））
（4）如果两个角的和是90º ，那么这两个角互余．（）
√
（5）内错角相等（
√
）
二、命题的形式、构成：
命题一般都写成“如果…，那么…”的形式。命题是由题设(或条件)和结论两部分组成。 “如果”后接的部分是题设，“那么”后接的部分是结论。
小结
本节课你学到了什么知识？如果…，那么…
形式
题设命：判断一件事情的语句叫命题。（1）正确的命题称为真命题，错误的命题称为假命题。（2）命题的结构：命题由题设和结论两部分构成，常可写成“如果„，那么„”的形式。 2、公理：人们长期以来在实践中总结出来的，并作为判断其他命题真假的根据的命题，叫做公理。 3、定理：经过推理论证为正确的命题叫定理。也可作为继续推理的依据。 4、判断一个命题是真命题，可以从公理或定理出发，用逻辑推理的方法证明（公理和定理都是真命题）；
判断一个命题真假的方法：利用已有的知识，通过观察、验证、推理、举反例等方法。

5.3.2_命题、定理、证明(公开课)

例2：把下列命题写成“如果„„那么„„”的形式。并指出它的题设和结论。 1、对顶角相等； 2、内错角相等； 3、两直线被第三直线所截，同位角相等； 4、同平行于一直线的两直线平行； 5、直角三角形的两个锐角互余； 6、等角的补角相等； 7、正数与负数的和为0。
有些命题如果题设成立，那么结论一定成立；而有些命题题设成立时，结论不一定成立。
∴∠2=∠1=90º（等量代换）．
∴ a⊥c（垂直的定义）．
问题3 请同学们判断下列两个命题的真假，并思考如何判断命题的真假．
命题2 相等的角是对顶角．
（3）我们知道假命题是在条件成立的前提下，结论不一定成立，你能否利用图形举例说明当两个角相等时它们不一定是对顶角的关系.
练习1 填空已知：如图1，∠1=∠2，∠3=∠4，求证：EG∥FH．证明：∵∠1=∠2（已知） ∠AEF=∠1 （对顶角相等）； ∴∠AEF=∠2 （等量代换）． ∴AB∥CD （同位角相等，两直线平行）． ∴∠BEF=∠CFE （两直线平行，内错角相等）． ∵∠3=∠4（已知）； ∴∠BEF－∠4=∠CFE－∠3．即∠GEF=∠HFE （等式性质）． ∴EG∥FH （内错角相等，两直线平行）．
命题：相等的角是对顶角．（1）判断这个命题的真假．（2）这个命题题设和结论分别是什么？题设：两个角相等；结论：这两个角互为对顶角．
例3：将下列的命题写成“如果…..，那么.….. ”的形式，并判断它的真假。
1）等角的余角相等； 2）内错角相等，两直线平行； 3）有理数一定是自然数； 4）两条直线平行，同位角相等；
问题3 请同学们判断下列两个命题的真假，并思考如何判断命题的真假．命题1：在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条．（1）命题1是真命题还是假命题？（2）你能将命题1所叙述的内容用图形语言来表达吗？

人教版数学七年级下册5-3-2命理、定理、证明(第2课时) 课件

①BC平分∠ABE； ②∠BCE＋∠D＝90°； ③AC∥BE； ④∠DBF＝2∠ABC. 其中正确的有( C ) A．1个 B．2个 C．3个 D．4个
12．若a＝b，则a2＝b2是____真_____命题(选填“真”或“假”)，其中“a＝b”是_题__设_______，“a2＝b2”是_结__论________．
7．如图，EF⊥AB于点F，CD⊥AB于点D，E是AC上一点，∠1 ＝∠2，则图中互相平行的直线是__E_F_∥__C_D__，__B_C_∥__D_E___________．
8．如图，给出下面的推理，其中正确的是____①__②__④________． ①因为∠B＝∠BEF，所以AB∥EF； ②因为∠B＝∠CDE，所以AB∥CD； ③因为∠B＋∠BEC＝180°，所以AB∥EF； ④因为AB∥CD，CD∥EF，所以AB∥EF.
9．如图，AC⊥BC，垂足为点C，∠BCD是∠B的余角．求证： ∠ACD＝∠B.
证明：∵AC⊥BC(已知)， ∴∠ACB＝90°(______垂__直__的__定__义________)， ∴∠BCD是∠ACD的余角． ∵∠BCD是∠B的余角(已知)， ∴∠ACD＝∠B(____同__角__的__余__角__相__等______)．
c
2
a
证明的一般步骤： 1.分清命题的题设和结论，如果与图形有关，应先根据题意，画出图形，并在图形上标出有关字母与符号； 2.根据题设、结论，结合图形，写出已知、求证； 3.经过分析，找出由已知推出结论的途径，有条理地写出证明过程.
如何判定一个命题是假命题呢？
只要举出一个例子(反例)，它符合命题的题设，但不满足结论即可.
歌德的话蕴含了什么数学道理？
合作探究

5.3.2命题、定理、证明

五、课堂检测
完成课本第21页练习1，第22页练习1，2
ቤተ መጻሕፍቲ ባይዱ式作业
练习册练习九第7,8
家庭作业
练习册练习九.
一、创设情境
思考下面两句话有何区别？
⑴“你吃饭了吗？” ⑵“今天天气不好”
二、呈现目标
1.了解命题的概念； 2.会判断语句是不是命题； 3.会判断命题的真假； 4.学会区别命题的题设与结论； 5.会将命题写成“如果…那么…”的形式.
三、自主学习
认真阅读课本第20-22页的内容，思考并完成下列问题，试着把它写在书的相应位置. 1.命题的概念是什么？谈谈你的理解. 2.命题由哪两部分构成？并举例说明. 3.命题分为哪两类？试举例说明. 4.什么是定理？试举例说明. 5.结合第21页例2说明什么是证明？ 6.如何判断一个命题是假命题？试举例说明.

第五章相交线与平行线5.3平行线的性质5.3.2 命题、定理、证明课件

2.如图，在三角形ABC中，点D在边BC的延长线上，CE平分 ∠ACD，AB∥CE，求证∠A=∠B.
证明：∵CE平分∠ACD (已知)， ∴∠ACE=∠DCE(角平分线的定义)． ∵AB∥CE(已知)， ∴∠A=∠ACE(两直线平行，内错角相等)， ∠B=∠DCE(两直线平行，同位角相等)． ∴∠A=∠B(等量代换).
1.在下面的括号内，填上推理的根据. 【选自教材第22页练习第1题】如图，∠A +∠B=180°，求证∠C +∠D=180°. 证明：∵∠A+∠B=180°， ∴AD∥BC（_同__旁__内__角__互__补__，__两__直__线__平__行__）， ∴∠C+∠D=180°（_两__直__线__平__行__，__同__旁__内__角__互__补__）.
（2）正数大于负数. （是）
（3）同角的余角相等.（是）
（4）两直线平行，同旁内角相等.（是）
（5）对顶角相等. （是）
（6）在直线AB上任取一点C. （不是）
（7）明天会下雨吗? （不是）
（8）画线段AB=CD. （不是）一个词语、疑问句、感叹句、
（9）相等的角都是直角.（是）（10）同旁内角互补. （是）
一条，那么也垂直于另一条；真命题
（2）如果两个角互补，那么它们是邻补角；假命题
（3）如果 | a | = | b |，那么 a = b ；假命题
（4）经过直线外一点有且只有一条直线与这条直线平行；
（5）两点确定一条直线．
真命题
真命题
思考：如何判定一个命题是假命题? 举反例
例如，要判定命题 “相等的角是对顶角” 是假命题，可以举出如下反例：
探究点1 命题及其构成

人教初中数学七下 5.3.2 命题定理证明课件【经典初中数学课件】

A
1 E
2 B
11. 如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF BC ? 为什么 ?
D
E
A
F
B
C
再见
（平行线的传递性） 5、垂直于同一条直线的两条直线平行。
一、知识回顾
平行线的性质：
1、两直线平行，同位角相等。 2、两直线平行，内错角相等。 3、两直线平行，同旁内角互补。
中考题我能行!
(1). 2006年东莞）能由△AOB平移而得的图
形是哪个？
A
F
A
B
B
E
O
E
C
D
C
D
（2）（2006年四川省广安市）如图，AB ∥CD，
A. 1个 B. 2个 C. 3个 D. 4个
7. 如图OA⊥OC，OB⊥OD，
且∠BOC＝α，则
∠AOD=_1_8_0_0_-_α__
B
A
CD O
8.如图，已知AB∥CD，直线EF分别交AB、CD 于点E 、F， ∠BEF的平分线与∠DFE的平分线相交于点P，你能说明∠P的度数吗？为什么？
A
E
A
1 E
2 B
11. 如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF BC ? 为什么 ?
D
E
A
F
B
C
再见
相交线与平行线
知识系统
3 12
一般情况对顶角相等
4
两
条直
邻补角互补
对顶角和邻补角的存在前提是两条直线相交
线
相
过一点有且只有一条直线与已知直线垂直

人教版数学七年级下册5.3.2《命题、定理、证明》课件(共23张PPT)

归纳总结
判断某一种事情的句子叫做命题，理清命题的定义必须搞清楚两点：（1）命题必须是一个“完整的句子”；（2）命题必须作出判断，如“两条直线相交交点唯一吗？”没有对事情作出判断，故不是命题。定理和公理都是真命题，都可以作为证明其他命题的依据，不同的是：公理是人们从长期实践中总结出来的真命题，不用证明也不能证明；定理是用推理证实为正确的命题。
命题1 在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条. 已知：如图，b∥c，a⊥b ．求证：a⊥c．证明：∵ a⊥b（已知） ∴∠1=90º （垂直的定义）又∵ b∥c（已知） ∴∠1=∠2（两直线平行，同位角相等） ∴∠2=∠1=90º（等量代换） ∴ a⊥c（垂直的定义）
题设是： a=b，b=c
结论是： a=c
③ 同位角相等.
如果两个角是同位角，那么这两个角相等.
条件是：两个角是同位角
结论是：这两个角相等 ④ 同角的补角相等. 如果两个角是同一个角的补角，那么这两个角相等. 条件是：两个角是同一个角的补角结论是：这两个角相等
讨论与归纳思考：请问如何判断①是假命题？如何判断②是
真命题？
① 如果两个角相等，那么它们是对顶角. ② 如果两条平行线被第三条直线所截，那么同旁内角互补. 注意：要判断一个命题是真命题要经过严格
的推理；是假命题只要举一个反例。
1.下列句子哪些是命题？是命题的，指出是真命题还是假命题？是真命题（1）兔子有四条腿；是假命题（2）内错角相等；否（3）画一条直线；是假命题（4）四边形是正方形；否（5）你的作业做完了吗？是真命题（6）同位角相等，两直线平行；是真命题（7）对顶角相等；是假命题（8）垂直于同一直线的两直线平行；否（9）过点P画线段MN的垂线；

人教数学七下5.3.2命题定理证明优质课件

(2)等角的补角相等；
(3)内错角相等.
解：(1)如果有两个定点，那么过这两点有且只有一条直线；
(2)如果两个角分别是两个等角的补角，那么这两个角相等；
(3)如果两个角是内错角，那么这两个角相等.
巩固练习
七年级数学下册 5.3 平行线的性质
2.请将它们改写成“如果……，那么……”的形式. （1）两条直线被第三条直线所截，同旁内角互补；
人教版数学七年级下册
七年级数学下册 5.3 平行线的性质
5.3 平行线的性质 5.3.2 命题、定理、证明
导入新知
七年级数学下册 5.3 平行线的性质
有一位田径教练向领导汇报训练成绩；
好！继续努力,争取
小明的百米
超过10秒.
成绩有进步，
已达到9秒9.
相传,阎锡山在观看士兵篮球赛,双方争抢非常激烈.于是命令: “不要再抢啦！每个人发一个球！”
从结论出发，逆着寻找所需要的条件的思考过程，叫分析.
在分析的过程中，如果发现所需要的条件，都已具备或可从已知条件中推得.那么证明就很容易了.
探究新知
七年级数学下册 5.3 平行线的性质
证明的概念在很多情况下，一个命题的正确性需要经过推理才能作出判断，这个推理过程叫作证明.
注意：证明的每一步推理都要有根据，不能“想当然”. 这些根据，可以是已知条件，也可以是学过的定义、基本事实、定理等.
巩固练习
七年级数学下册 5.3 平行线的性质
3.下列句子哪些是命题？是命题的，指出是真命题还是假命题？
（1）猪有四只脚；（2）内错角相等；（3）画一条直线；（4）四边形是正方形；（5）你的作业做完了吗？（6）同位角相等，两直线平行；（7）同角的补角相等；（8）同垂直于一直线的两直线平行；（9）过点P画线段MN的垂线；（10）x＞2

5.3.2函数的最值课件(人教版)

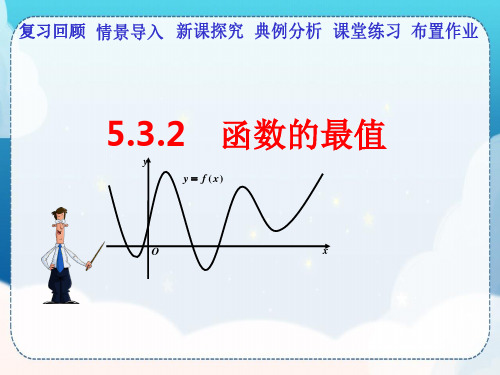
x= x3时，f(x)有最小值， x= b 时，f(x)有最大值。
y y f (x)
x1
x3
a
O x2
x4
x5
bx
函数f(x)的最小值和最大值，在极值与端点函数值之中。
复习回顾
知三识梳.新理课探究
函数最值
一般地，对于函数f(x)，给定区间I，
若对任意x∈I，存在x0∈I，使得f(x)≥f(x0)，则称f(x0) 为函数f(x)在区间I上的最小值；
当a＝0时，f(x)的最小值为0；
当 a<0 时，f(x)的最小值为 5 a3. 27
复习回顾
跟踪训练
已知a∈R，函数 f(x)＝1x3－ax2，求f(x)在
3
区间[0,2]上的最大值.
复习回顾
f(x)＝1x3－ax2，则 f′(x)＝x2－2ax. 3
令f′(x)＝0，解得x1＝0，x2＝2a. 令g(a)＝f(x)max， ①当2a≤0，即a≤0时， f(x)在[0,2]上单调递增，从而 g(a)＝f(x)max＝f(2)＝83－4a. ②当2a≥2，即a≥1时，f(x)在[0,2]上单调递减，从而g(a)＝f(x)max＝f(0)＝0.
f(x)min＝f(a)＝－a3. ②当a＝0时，f′(x)＝3x2≥0，f(x)在[0，＋∞)上单调递增，所以
f(x)min＝f(0)＝0.
③当
a<0
时，f(x)在
0，－a3
上单调递减，在
－a，＋∞ 3
上单调递增.
复习回顾
所以 f(x)min＝f
－a 3
＝
5
a3.
27
综上所述，当a>0时，f(x)的最小值为－a3；