曲线任意里程中边桩坐标正反算

合集下载

线路上点坐标反算其里程桩号及中桩距

一、ZUOBIAO—ZH（由线路上任意点坐标计算相应的桩号、中桩距[偏左或偏右的距离]）主程序：AbsJ“Fixmc⇒”=7⇒Fixm：Goto1△{ABFHGRQ}：A“X-JD”：B“Y-JD”：G“A0”：G＜0⇒Q=1△G＞0⇒Q=-1△F=AbsG:Prog“S3”：G=F：R“R”：O“Gra0(ZY-JD)”:F=O：Prog“S3”：F=F：H“L-ZY”：S=R÷COS（G÷2）：M“X（YXIAN）”=A+Scos（F+180°+Q×（90°-G÷2））◢N“Y（YIAN）”=B+Ssin（F+180°+Q×（90°-G÷2））◢L=2πR÷360°×G：F=F- Q×90°+180°：F＜0⇒F=F+360°△F＞360°⇒F=F-360°：≠⇒F=F△Lbl1:{CD}:C“X”：D“Y”：POL（M-C，N-D）：T=J：T=Ans+180°：P=I：U=T-F：-Q×U≦0⇒Prog“T”：Goto1△-Q×U＞0⇒Prog“U”：Goto1△ (主程序完)子程序：1、VPol(A—C，B—D)：T=J：T=Ans+180°：P=I：U=T-（F+90°Q）：E“LI”=H+Rtan(G ÷2)-PcosU◢K“B”=-Psin(u)◢2、WPol(A—C，B—D)：T=J：T=Ans+180°：P=I：U=T-（F-GQ-90°Q）：E“LI”=H+L+（PcosU-Rtan(G÷2)）◢K“B”=Psin(u)◢3、TAbs U≤180°⇒Prog“V”△A bs U＞180°⇒U=T+360°-F：U＞G⇒Prog“W”：≠⇒Prog“X”△4、UAbsU＞180°⇒Prog“V”：≠⇒AbsU≤G⇒Prog“X”⊿AbsU＞G⇒Prog“W”⊿5、XE“LI”=H-Q（2πR÷360°×U）◢K“B”=Q（P-R）◢说明：一、本程序用于计算直线与圆曲线组合的线路上由点坐标计算相应桩号及其从中桩左、右偏移量。

曲线(含直线)任意里程中边桩坐标正反算

曲线（含直线）任意里程中边桩坐标正反算（CASIO fx-4800p&fx-4850）J-SQX(竖曲线数据输入)“J-SQX”：{NHUVMQP}：Z[9]=N“SJD”：Z[10]=H“JDZ”：Z[11]=U“I1”：Z[12]=V“I2”：Z[13]=M“R”：Z[14]=Q“QD”：Z[15]=P“ZD”：“TO J-JSMS”J-PQX(平曲线数据输入,自动切换到J-JSMS)A“JD”B“JDX”C“JDY”F“FJ”O“ZJ：Z-，Y+”RE“LS1”K“LS2”：E＜1=＞E=1E-9⊿K＜1=＞K=1E-9⊿Z[1]=EE÷(24R)-E^4÷(2688RRR)：Z[2]=E÷2-EEE÷(240RR)：X=(EE-KK)÷(24R)÷sinAbsO：Z[3]“T1”=(R+Z[1])tan(AbsO÷2)+Z[2]-X▲Z[4]“T2”=(R+KK÷(24R)-K^4÷(2688RRR))tan(AbsO÷2)+K÷2-KKK÷(240RR)+X▲L=AbsOπR÷180+(E+K)÷2▲J=tan-1((R+Z[1])÷(Z[3]-Z[2]))：X“E”=(R+Z[1])÷sinJ-R▲X=A-Z[3]：Y=X+E：E＜1=＞X“ZY”▲≠=＞X“ZH”▲Y“HY”▲⊿Y“QZ”=X+(L-K-E)÷2+E▲Y=X+L-K：X=X+L：K＜1=＞X“YZ”▲≠=＞Y“YH”▲X“HZ”▲⊿Prog“J-JSMS”J-JSMS(放样模式主程序)“1-ZS,2-FS,4-DMFY” Lb1 0：{Z}：Z“MS”≤1=＞Goto 1：≠=＞Z“MS”≤4=＞Goto 2⊿⊿Lb1 1：{PDW}：PD“BZ”W“BJ”：Prog“JP”：X“X=”▲Y“Y=”▲Goto 0⊿Lb1 2：{XYW}：XYW“BJ”： Prog“JF”：P“P=”▲D“BZ=”▲Z=3=＞Prog“JS”：Prog“DMFY”⊿(运行竖曲线高程计算程序)Z=4=＞Z[26] “H”=12.417+(P-75360)*5.2/1000: Prog“DMFY”⊿（运行单面坡比高程计算,语句中12.417为起点桩号DK75+360的高程,可以根据实际情况进行调整；5.2/1000为单面上坡率,上坡输正值，下坡输负值）Goto 0JS(竖曲线计算主程序)P＜Z[14] =＞Prog“J-SQX”⊿P＞Z[15] =＞ Prog“J-SQX”⊿N=Z[9]：U=Z[11]：V=Z[12]：H=Z[13]：G=H Abs(U-V)÷200：P＜N=＞I=U：M=N-G：M＞P=＞M=P⊿≠=＞I=V：M=N+G：M＜P=＞M=P⊿⊿J=(P-M)2÷(2H)：U-V＞0=＞J=-J⊿H=Z[10]+(P-N)×I÷100+JZ[26] “H”=HJP(平曲线正算子程序)FixmLb1 1：J=F：X=B-Z[3]cosF：Y=C-Z[3]sinF：G=EP≤A-Z[3] =＞I=A-Z[3]-P：M=-I：N=0：H=F+W：Goto5≠=＞P≤A-Z[3]+E=＞I=P-A+Z[3]：H=90II÷(REπ)：O＜0=＞H=-H⊿H=H+W+F： Goto 3≠=＞P≤A-Z[3]+L-K=＞I=P-A+Z[3]-E： Goto 4：≠=＞Goto 2⊿⊿Lb1 2：X=B+Z[4]cos（F+O）：Y=C+Z[4]sin（F+O）：J=F+O+180：G=KP≤A-Z[3]+L=＞I= A-Z[3]+L-P：H=90II÷(REπ)：O＞0=＞H=-H⊿H=H+J+W+180： Goto 3≠=＞I=P-A+Z[3]-L：M=-I：N=0：H=J+W+180： Goto 5Lb1 3：M=I-I^5÷(40RRGG)：N=III÷(6GR)-I^7÷(336RRRGGG)： Goto 5Lb1 4：H=(E+2I)×90÷(πR)：M=RsinH+Z[2]：N=R(1-cosH)+Z[1]：O＜0=＞H=-H⊿H=J+W+H： Goto 5Lb1 5：P≤A-Z[3]+L-K=＞O＜0=＞N=-N⊿≠＞O＞0=＞N=-N⊿⊿Goto 6Lb1 6：X=X+Mcos J-Nsin J+Dcos H：Y=Y+Msin J+N cosJ+Dsin HJF(平曲线反算子程序)FixmU=X：V=Y：D=0：J=F-W：P=A+(Y-C)cos J-(X-B)sin JLb1 1：Prog“JP”：J=H-180：I=(V-Y)cos J-(U-X)sin J：Abs I＜1E-4=＞Goto 2：≠=＞P=P+I： Goto 1⊿Lb1 2：D=(V-Y)÷sin HDMFY隧道开挖断面(超欠挖情况)计算程序{HIJMNG}：Z[20]= H“C”：Z[21]=I“A”：Z[22]= J“H1”：Z[23]= G“GC”：Z[24]= M“R1”：Z[25]= N“R2”D≤2.3=＞D“ZD”=Abs(D-2.3)▲≠=＞D＞2.3=＞D“YD”= D-2.3▲⊿⊿(C为圆心O1与O2的高差值,A为圆心O1与O2的宽度差值,H1为圆心O1至设计高程的高度,GC为实测高程,R1为上部第1个半径,R2为下部第2个半径)(显示值ZD为至隧道中心线左边的宽度,YD为至隧道中心线右边的宽度,2.3为设计线路距隧道中心线的宽度,可以实际情况进行改变调整)Z[26]“H”▲(显示所求桩号点设计高程值)Z[27]“O1” =Z[26]+ Z[22](第1个圆心高程)Z[28]“O2”=Z[26]+ Z[22]+ Z[20] (第2个圆心高程)Z[29]= Z[24]×Sin 60▲(此数据为上半弧60度范围的宽度值，可根据实际情况调整；数值可不显示) D>Z[29] =＞Goto 1⊿Z[30]=√（（Z[24]）2-D2）Z[31]= √（Abs(（Z[24]）2-(Z[23]-Z[27])2)）Z[32] “HGD”=Z[27]+ Z[30]- Z[23] ▲Z[33] “SKD”=Z[31]-D ▲Prog“J-JSMS”Lb1 1Z[23]<Z[27] =＞Goto 2⊿Z[31]= √(（Z[25]）2-(Z[23]-Z[28])2)Z[33] “SKD”=Z[21]+ Z[31]-D ▲Prog“J-JSMS”Lb1 2Z[31]=Z[25]-（Z[27]-Z[23]）*0.35/(0.78+Z[20]+Z[22])(0.35为下边墙往边墙底内缩的距离，0.78为设计高程至边墙底部的高度)Z[33] “SKD”= Z[31]-D ▲Prog“J-JSMS”一、程序简介1、本套程序共有2个主程序，5个子程序。

卡西欧5800坐标正反算万能程序

CASIO5800计算器程序曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQXJS)和两个子程——正算子程序(SUB1)、反算子程序(SUB2)序构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

另外也可以将本程序中核心算法部分的两个子程序移植到其它相关的程序中，用于对曲线任意里程中边桩坐标进行正反算。

本程序也可以CASIO fx-5800P计算器计算器上运行。

二、源程序1.主程序(TYQXJS)"1.SZ => XY"："2.XY => SZ"：?N："X0"? U："Y0"? V："S0"? O："F0"? G："LS"? H："R0"? P："RN"? R：?Q←┘1÷P-> C：(P-R)÷(2HPR) -> D：180÷π->EIf N=1：Then Goto1：Else Goto 2：IfEndLbl 1：？S：？Z：Abs(S-O) -> W：Prog "SUB1"："XS"：X◢"YS"：Y◢Goto 1←┘Lbl 2：？X：？Y：X-> I：Y->J：Prog "SUB2"："S"：O+W-> S◢"Z"：Z◢Goto 22. 正算子程序(SUB1)0.1739274226->A：0.3260725774->B：0.0694318442->K：0.3300094782->L：1-L-> F：1-K-> M：U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G +QEFW(C+FWD))+Acos(G+QEMW(C+MWD))) -> X：V+W(Asin(G+QEKW(C+K WD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD)))-> Y：G+QEW(C+WD)+90-> F：X+ZcosF-> X：Y+ZsinF-> Y3. 反算子程序(SUB2)G-90-> T：Abs((Y-V)cosT-(X-U)sinT) -> W ：0-> Z：Lbl 0：Prog "SUB1"：T+QEW(C+WD) ->L：(J-Y)cosL-(I-X)sinL-> Z：If Abs(Z) <0.0000001：Then Goto1：Else W+Z ->W：Goto 0：IfEndLbl 1：0 ->Z：Prog "SUB1"：(J-Y)÷sinF-> Z三、使用说明1、规定(1) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。

曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序文档

曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQXJS)和两个子程——正算子程序(SUB1)、反算子程序(SUB2)序构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

另外也可以将本程序中核心算法部分的两个子程序移植到其它相关的程序中，用于对曲线任意里程中边桩坐标进行正反算。

本程序也可以在CASIO fx-4500P计算器及C ASIO fx-4850P计算器上运行。

特别申明：(1). 适用于弧长小于2倍半径的各种线元坐标正反算，精度优于1mm；(2). 在引用该核心计算部分时，请注明来源。

二、源程序1.主程序(TYQXJS)"1.SZ => XY"："2.XY => SZ"：N：U"X0"：V"Y0"：O"S0"：G"F0"：H"LS"：P" R0"：R"RN"：Q：C=1÷P：D=(P-R)÷(2HPR)：E=180÷π：N=1=>Goto 1：≠>Goto 2Δ←┘Lbl 1：{SZ}：SZ：W=Abs(S-O)：Prog "SUB1"：X"XS"=X◢Y"YS"=Y◢F"FS"=F-90◢Goto 1←┘Lbl 2：{XY}：XY：I=X：J=Y：Prog "SUB2"：S"S"=O+W◢Goto 22. 正算子程序(SUB1)A=0.1739274226：B=0.3260725774：K=0.0694318442：L=0.3300094782：F=1-L：M=1-K：X=U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G+Q EFW(C+FWD))+Acos(G+QEMW(C+MWD)))：Y=V+W(Asin(G+QEKW(C+KWD))+Bsin (G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD)))：F=G+QE W(C+WD)+90：X=X+ZcosF：Y=Y+ZsinF3. 反算子程序(SUB2)T=G-90：W=Abs((Y-V)cosT-(X-U)sinT)：Z=0：Lbl 0：Prog "SUB1"：L=T+QEW(C +WD)：Z=(J-Y)cosL-(I-X)sinL：AbsZ<1E-6=>Goto1：≠>W=W+Z：Goto 0Δ←┘Lbl 1：Z=0：Prog "SUB1"：Z=(J-Y)÷sinF三、使用说明1、规定(1) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。

公路圆曲线中边桩坐标计算公式

XYXJD3447380.17323676515.665ZY 48700.3363675181.642487323675150.525490789.88623675149.994487503675132.507490791.74033675132.001487663675116.465490792.59023675116.006487923675090.38490793.38453675090.011488133675069.314490794.3363675069.014488303675052.253490794.77353675052.015488363675046.228490794.62773675046.016488543675028.147490792.95093675028.01648862.73675019.411490791.88383675019.316488693675013.09490791.67343675013.016489003674981.991490790.59363674982.01748905.53674976.474490790.56253674976.517489223674959.925490790.45593674960.017489343674947.889490790.37633674948.017489383674943.876490790.41393674944.017489503674931.836490790.69933674932.018489683674913.779490790.6883674914.01948975.53674906.254490790.67843674906.52489823674899.733490790.65513674900.021490003674881.646490792.00853674882.024490203674861.581490791.57663674862.028490403674841.517490791.0717*******.035490603674821.456490790.49393674822.043490803674801.397490789.84313674802.053桩号圆曲线中圆曲线中边桩坐标计算公式：L=F-H；注：L---所求点曲线长；F---所求点X=X ZY +2×R×SIN（L÷2R）×COS｛α±(L÷2R)｝+S×COS｛α±(L÷R)+M｝;X=Y ZY +2×R×SIN（L÷2R）×SIN｛α±(L÷2R)｝+S×SIN｛α±(L÷R)+M｝. 注：α---线路方位角；M---所求边桩与路线的夹角；S---所求边桩至中桩的1.圆曲线（右偏）段横断面中边左中2.圆曲线（左偏）段横断面中边曲线中边桩设计坐标计算所求点曲线长；F---所求点里程；H---圆曲线起点（ZY点桩号里程）×COS｛α±(L÷R)+M｝;×SIN｛α±(L÷R)+M｝.角；S---所求边桩至中桩的距离；"±"---曲线左偏取“-”右偏取“+”；当S=0时极为中面中边桩设计坐标计算（K48+700.336～K50+066.383）中右至坡脚（顶Y X Y左490724.159490770.574490771.5843675149.508490754.82118.31490772.0773675131.546490754.40319.67490772.4653675115.580490753.85020.13490772.9983675089.672490754.26120.39490773.3383675068.740490754.18021490773.5553675051.789490753.33621.22490773.6193675045.806490752.94021.01490773.7713675027.876490753.28219.18490773.8243675019.212490753.99418.06490773.8543675012.936490754.33417.82490773.8943674982.044490755.80416.7490773.8833674976.562490755.88316.68490773.8163674960.115490755.98616.64490773.7373674948.125490759.73716.64490773.7053674944.135490759.70516.71490773.5903674932.201490756.35117.11490773.3703674914.264490755.74117.32490773.2603674906.810490754.26317.42490773.1573674900.353490752.96017.5490772.8323674882.401490753.65619.18490772.4023674862.476490753.22719.18490771.8993674842.552490752.72619.18490771.3233674822.630490752.15219.18490770.6743674802.710490751.50619.18面中边桩设计坐标计算（K50+801.433～K52+007.668）程）取“+”；当S=0时极为中桩坐标。

任意曲线里程中边桩坐标正反算fx5800计算器程序

任意曲线里程中边桩坐标正反算（fx5800计算器）程序一、程序功能本程序由一个主程序（TYQXJS）和3个子程序―――（正算子程序SUB1）、反算子程序（SUB2）构成，可以根据曲线段—直线、圆曲线、缓和曲线(完整或非完整型)的线元要素(起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径)及里程边距或坐标,对该曲线段范围内任意里程中边桩坐标进行正反算,另外也可以将本程序中核心算法部分的两个子程序移植到其他相关的程序中,用于对曲线任意里程中边桩坐标进行正反算.1.主程序(TYQXJS)（5800P正交程序）〝1.SZ=＞XY〞:〝2.XY=＞SZ〞: 〝1，2〞？N:〝K0〞?O: 〝X0〞?U: 〝Y0〞?V: 〝FWJ〞?G: 〝Ls〞?H: 〝+1,-1,0〞?Q:If Q=0:Then 10 ^45->P: 10 ^45->R:Else〝R1〞?P: 〝R2〞?R:IfEnd: 180÷π→E: N=1=＞Goto 1：Goto2↙Lbl 1:〝JS LCH〞?S: 〝P-J〞?Z :Abs(S-O)→W:1÷P→C: (P-R)÷(2HPR)→D:Prog〝SUB1〞:〝XS〞:X◢〝YS〞: Y◢〝FS〞:F-90→F:F ▲DMS ◢Goto1↙Lbl 2: 〝X〞?X:〝Y〞?Y:X→I: Y→J:1÷P→C:(P-R)÷(2HPR)→D:Prog〝SUB2〞:〝S〞:O+W→S◢〝Z〞:Z◢Goto2↙2.正算子程序（SUB1）0.1739274226→A: 0.3260725774→B: 0.0694318442→K:0.3300094782→L: 1-L→F:1-K→M↙U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G+QEFW(C+FWD))+Acos(G+QEMW(C+MWD)))→X：V+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD)))→Y↙G+QEW(C+WD)+90→F: X+Zcos（F）→X: Y+Zsin（F）→Y↙3.反算子程序（SUB2）G-90→T: Abs((Y-V)cos（T）-(X-U)sin（T)）→W: 0→Z↙Lbl 0:Prog〝SUB1〞: T+QEW(C+WD)→L: (J-Y)cos（L）-(I-X)sin（L）→Z↙Abs(Z)﹤10∧（-6）=＞Goto 1: W+Z→W : Goto 0↙Lbl 1: 0→Z:Prog〝SUB1〞: (J-Y)÷sin（F）→Z备注：起点里程→o：起点X坐标→U：起点Ｙ坐标→V：起点方位角→G：曲线元长度→Ｈ：起点半径→Ｐ：终点半径→Ｒ:（右偏+1,左偏-1,直线0）→Q三.使用说明1.(输入、输出角度为度、分、秒形式)(1)以道路中线的前进方向(即里程增大的方向)区分左右;当线元左偏时,Q=-1, 当线元右偏时,Q=1;当线元为直线时,Q=0.(2)当所求点位于中线时,Z=0, 当所求点位于中线左侧时,Z取负值, 当所求点位于中线右侧时,Z取正值.(3)当线元为直线时,其起点、止点的曲率半径为无穷大,以10的45次方代替。

卡西欧计算器坐标的正反算

可以算任意斜交涵洞轴线的坐标，增加T为斜交角度，规定T为涵轴右侧方向与“线路前进方向切线”之间的夹角，当涵轴与线路正交时，T=90,其他操作与原程序一样；1. 正算子程序(SUB1) [color=Red]A=0.26：B=0.74：K=0.02：L=0.82：F=1-L：M=1-K：X=U+W(Acos(G+57.2958QKW(1/P+KWD))+Bcos(G+57.2958QLW(1/P+LW D))+Bcos(G+57.2958QFW(1/P+FWD))+Acos(G+57.2958QMW(1/P+MWD)))：Y=V+W(Asin(G+57.2958QKW(1/ P+KWD))+Bsin(G+57.2958QLW(1/P+LWD))+Bsin(G+57.2958QFW(1/P+FWD))+Asin(G+57.2958QMW (1/P+MWD)))：F=G+57.2958QW(1/P+WD)+90：X=X+Zcos(F-90+T)：Y=Y+Zsin(F-90+T)2. 反算子程序(SUB2)W=Abs((Y-V)cos(G-90)-(X-U)sin(G-90))：Z=0：Lbl 0：Prog "SUB1"：L=(G-90)+5 7.2958QW(1/P+WD)：Z=(J-Y)cosL-(I-X)sinL：AbsZ<1E-6=>Goto1：≠>W=W+Z：Goto 0Δ←┘Lbl 1：Z=0：Prog "SUB1"：Z=(J-Y)÷sinF二.增设数据库程序（ＳＪＫ主程序）Lb1 4："1.SZ => XY"："2.XY => SZ"：｛NS｝：S∠下一线元起点里程＝＞O =本线元起点里程：U=本线元起点X：V=本线元起点Y：G=本线元起算方位角：H =本线元长度：P=起点曲率半径：R=终点曲率半径：Q=0或1、-1：Prog“TYQXJS”：Goto0Δ←┘(第一线元数据要素)S∠下一线元起点里程＝＞O=本线元起点里程：U=本线元起点X：V=本线元起点Y：G=本线元起算方位角：H=本线元长度：P=起点曲率半径：R=终点曲率半径：Q=0或1、-1：Goto0Δ←┘(第二线元数据要素)S∠下一线元起点里程＝＞O=本线元起点里程：U=本线元起点X：V=本线元起点Y：G=本线元起算方位角：H=本线元长度：P=起点曲率半径：R=终点曲率半径：Q=0或1、-1：Goto0Δ←┘(第三线元数据要素)。

线元法曲线任意里程中边桩坐标正反算(CASIO_fx-5800P计算器)程序(附带高程)

线元法曲线任意里程中边桩坐标正反算(CASIO fx-5800P计算器)程序（附带高程）一、功能及原理说明1. 功能说明：本程序由一个主程序(1-MAIN)和七个子程序——正算子程序(1-SUB-ZS)、反算子程序(1-SUB-FS)等构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

本修改版程序既可实现正算全线贯通，亦可实现反算全线贯通。

本程序在CASIO FX-5800P计算器运行。

2．计算原理：利用Gauss-Legendre 5点通用公式正算线路中边桩坐标、线外测点至曲线元起点和终点的垂距的符号是否相异（即Dca×Dcb<=0=>该测点在其线元内）进行判断并利用该线元要素反算中桩里程、支距，最后计算出反算结果。

3. 程序输入计算器后，请根据统计串列List X，Y，freq[N]在程序中实际可能被使用的维数，将其统计矩阵串列改为包含相应维数的任意数据的矩阵，即在list列表中随机输入相应维数的数据，保证矩阵大小符合维数要求。

4. 本程序正算速度在1-2秒左右，反算比正算慢点，可根据需要调整精度加快速度。

本程序可建立曲线要素数据库及高程变坡点数据库，一次输入整条线路数据，计算时自动调用数据库，实现全线贯通，也可临时手动输入线元计算要素进行计算。

5. 本程序由小骆在前人的基础上改进而成，经个人测试可用。

学识浅薄，不足之处，在所难免，欢迎提出改进意见。

二、源程序1.主程序(1-MAIN)Deg:fix 320→DimZLbl 0:cls：“INPUT(0),ZX(1),YX(2)”?I (选择手动输入计算参数0，还是调用线路数据1,2）If I=0:Then Prog “1-DAT1”:IfEnd“SZ=>XY(1),XY=>SZ(2)”?N（正算，反算）If N=1 :Then Goto 1Else If N=2 :Then Goto 2Else Goto 3IfEnd:IfEndLbl 1:“KP=”?S（输入待求桩号）If S<0:Then Goto 0:IfEnd“JL(m)=”?Z （输入偏距）If Z≠0:Then “ANGLE→R(Deg)=”?M:IfEnd （输入斜交右角）If I≠0:Then Prog “1-DAT2”:IfEndS-O→W:If W<0:Then Goto 0:Else If W>H:Then cls:locate 6,2,"KP OUT"◢Goto 0:IfEnd:IfEnd(前半条针对“DAT”情况，后半条针对“INPUT”情况。

曲线任意里程中边桩坐标正反算VB0函数

曲线任意里程中边桩坐标正反算(VB6.0)函数发布时间:2008-06-21 09:51:10曲线任意里程中边桩坐标正反算(VB6.0)函数(5节点法提供测试程序代码）使用说明：1. 在VA或VAB中添加一个窗体，并将其"Caption"属性改为"曲线任意里程中边桩坐标正反算(VB6.0) 函数"2. 在窗体上添加一个文本框，并将其下列属性更改为：名称 txt1MultiLine TrueScrollBars 3 Both3. 在窗体上添加三个命令按钮，并将它们的下列属性更改为：按钮一名称 Cmd1Caption 正算按钮二名称 Cmd2Caption 反算按钮三名称 Cmd3Caption 结束4. 将以下程序复制到VA或VBA的代码窗口内，点击运行命令即进行测试。

Private Const pi As Double = 3.14159265358979Private Const pi As Double = 3.14159265358979Public Function qxzs(xyb() As Double, sz() As Double, fhz() As Double)’正算函数(由里程和边距计算坐标)’入口参数线元要素xyb()及sz()为:’xyb(1)=线元起点里程 xyb(2)=线元起点X坐标 xyb(3)=线元起点Y坐标 xyb(4)=线元起点切线方位角(以弧度为单位)’xyb(5)=线元长度 xyb(6)=线元起点曲率半径 xyb(7)=线元止点曲率半径 xyb(8)=线元偏向标志’sz(1)=要计算点的中线里程 sz(2)=要计算点距中线的边距’返回值fhz()为：’fhz(1)=所求点的X坐标 fhz(2)=所求点的Y坐标 fhz(3)=所求点对应中线点向右的法线方位角Dim f0 As DoubleDim q As DoubleDim c As DoubleDim d As DoubleDim rr(5) As DoubleDim vv(5) As DoubleDim i As IntegerDim w As DoubleDim xs As DoubleDim ys As DoubleDim ff As Doublef0 = xyb(4): q = xyb(8)c = 1# / xyb(6)d = (xyb(6) - xyb(7)) / 2# / xyb(5) / xyb(6) / xyb(7)rr(1) = 0.1184634425: rr(2) = 0.2393143352rr(3) = 0.2844444444: rr(4) = rr(2): rr(5) = rr(1)vv(1) = 0.046910077: vv(2) = 0.2307653449vv(3) = 0.5: vv(4) = 1# - vv(2): vv(5) = 1# - vv(1)w = Abs(sz(1) - xyb(1))xs = 0: ys = 0For i = 1 To 5ff = f0 + q * vv(i) * w * (c + vv(i) * w * d)xs = xs + rr(i) * Cos(ff)ys = ys + rr(i) * Sin(ff)Next ifhz(3) = f0 + q * w * (c + w * d) + 0.5 * pifhz(1) = xyb(2) + w * xs + sz(2) * Cos(fhz(3))fhz(2) = xyb(3) + w * ys + sz(2) * Sin(fhz(3))End FunctionPublic Function qxfs(xyb() As Double, xpt() As Double, fhb() As Double)’反算函数(由坐标计算里程和边距)’入口参数线元要素xyb()及xpt()为:’xyb(1)=线元起点里程 xyb(2)=线元起点X坐标 xyb(3)=线元起点Y坐标 xyb(4)=线元起点切线方位角(以弧度为单位)’xyb(5)=线元长度 xyb(6)=线元起点曲率半径 xyb(7)=线元止点曲率半径 xyb(8)=线元偏向标志’xpt(1)=要计算点的X坐标 xpt(2)=要计算点的Y坐标’返回值fhb()为：’fhb(1)=所求点的中线里程 fhb(2)=所求点距中线的边距Dim f0 As DoubleDim q As DoubleDim c As DoubleDim d As DoubleDim rr(4) As DoubleDim vv(4) As DoubleDim i As IntegerDim w As DoubleDim xs As DoubleDim ys As DoubleDim ff As DoubleDim z As DoubleDim sz(2) As Doublef0 = xyb(4): q = xyb(8)c = 1# / xyb(6)d = (xyb(6) - xyb(7)) / 2# / xyb(5) / xyb(6) / xyb(7)ft = f0 - 0.5 * piw = Abs((xpt(2) - xyb(3)) * Cos(ft) - (xpt(1) - xyb(2)) * Sin(ft))z = 1’Txt1.Text = Txt1.Text + "S0=" + Str(xyb(1)) + Chr(13) + Chr(10)Do While Abs(z) > 0.000001sz(1) = xyb(1) + w: sz(2) = zCall qxzs(xyb(), sz(), fhb())ff = ft + q * w * (c + w * d)z = (xpt(2) - fhb(2)) * Cos(ff) - (xpt(1) - fhb(1)) * Sin(ff)w = w + zLoopsz(1) = xyb(1) + w: sz(2) = 0Call qxzs(xyb(), sz(), fhb())fhb(1) = xyb(1) + wfhb(2) = (xpt(2) - fhb(2)) / Sin(fhb(3))End FunctionPrivate Sub Cmd1_Click()’正算测试程序Dim qxxy(100, 8) As DoubleDim xsz(100, 3) As Double’线元要素表存入数组qxxy中，切线方位角以弧度为单位’可采用读文本文件、Excel数据表中的数据或其它方式读入数据替代以下直接赋值方式qxxy(1, 1) = 500: qxxy(1, 2) = 19942.837: qxxy(1, 3) = 28343.561: qxxy(1, 4) = 2.186466069 qxxy(1, 5) = 269.256: qxxy(1, 6) = 1E+45: qxxy(1, 7) = 1E+45: qxxy(1, 8) = 0qxxy(2, 1) = 769.256: qxxy(2, 2) = 19787.34: qxxy(2, 3) = 28563.378: qxxy(2, 4) = 2.186466069 qxxy(2, 5) = 37.492: qxxy(2, 6) = 1E+45: qxxy(2, 7) = 221.75: qxxy(2, 8) = -1qxxy(3, 1) = 806.748: qxxy(3, 2) = 19766.566: qxxy(3, 3) = 28594.574: qxxy(3, 4) = 2.101929446 qxxy(3, 5) = 112.779: qxxy(3, 6) = 221.75: qxxy(3, 7) = 221.75: qxxy(3, 8) = -1qxxy(4, 1) = 919.527: qxxy(4, 2) = 19736.072: qxxy(4, 3) = 28701.893: qxxy(4, 4) = 1.593343217 qxxy(4, 5) = 80.285: qxxy(4, 6) = 221.75: qxxy(4, 7) = 9579.228: qxxy(4, 8) = -1qxxy(5, 1) = 999.812: qxxy(5, 2) = 19744.038: qxxy(5, 3) = 28781.659: qxxy(5, 4) = 1.408141337 qxxy(5, 5) = 100#: qxxy(5, 6) = 1E+45: qxxy(5, 7) = 1E+45: qxxy(5, 8) = 0’将要计算坐标的里程桩号及距中线距离存入数组xsz中xsz(1, 1) = 700: xsz(1, 2) = -5xsz(2, 1) = 700: xsz(2, 2) = 0xsz(3, 1) = 700: xsz(3, 2) = 5xsz(4, 1) = 780: xsz(4, 2) = -5xsz(5, 1) = 780: xsz(5, 2) = 0xsz(6, 1) = 780: xsz(6, 2) = 5xsz(7, 1) = 870: xsz(7, 2) = -5xsz(8, 1) = 870: xsz(8, 2) = 0xsz(9, 1) = 870: xsz(9, 2) = 5xsz(10, 1) = 940: xsz(10, 2) = -5.123xsz(11, 1) = 940: xsz(11, 2) = 0xsz(12, 1) = 940: xsz(12, 2) = 3.009Dim i As IntegerDim j As IntegerDim k As IntegerDim ysb(8) As DoubleDim wzb(3) As DoubleDim jgb(3) As DoubleTxt1.Text = ""For i = 1 To 12For j = 1 To 5If qxxy(j, 1) <= xsz(i, 1) And xsz(i, 1) <= qxxy(j, 1) + qxxy(j, 5) ThenFor k = 1 To 8: ysb(k) = qxxy(j, k): Next kFor k = 1 To 2: wzb(k) = xsz(i, k): Next k’调用正算函数Call qxzs(ysb(), wzb(), jgb())Txt1.Text = Txt1.Text + Str(wzb(1)) + " " + Str(wzb(2)) + Chr(13) + Chr(10)For k = 1 To 3Txt1.Text = Txt1.Text + Str(jgb(k)) + Chr(13) + Chr(10)Next kTxt1.Text = Txt1.Text + Chr(13) + Chr(10)Exit ForEnd IfNext jNext iEnd SubPrivate Sub Cmd2_Click()’反算测试程序Dim qxxy(100, 8) As DoubleDim xsz(100, 3) As Double’线元要素表存入数组qxxy中，切线方位角以弧度为单位’可采用读文本文件、Excel数据表中的数据或其它方式读入数据替代以下直接赋值方式qxxy(1, 1) = 500: qxxy(1, 2) = 19942.837: qxxy(1, 3) = 28343.561: qxxy(1, 4) = 2.186466069qxxy(1, 5) = 269.256: qxxy(1, 6) = 1E+45: qxxy(1, 7) = 1E+45: qxxy(1, 8) = 0qxxy(2, 1) = 769.256: qxxy(2, 2) = 19787.34: qxxy(2, 3) = 28563.378: qxxy(2, 4) = 2.186466069 qxxy(2, 5) = 37.492: qxxy(2, 6) = 1E+45: qxxy(2, 7) = 221.75: qxxy(2, 8) = -1qxxy(3, 1) = 806.748: qxxy(3, 2) = 19766.566: qxxy(3, 3) = 28594.574: qxxy(3, 4) = 2.101929446 qxxy(3, 5) = 112.779: qxxy(3, 6) = 221.75: qxxy(3, 7) = 221.75: qxxy(3, 8) = -1qxxy(4, 1) = 919.527: qxxy(4, 2) = 19736.072: qxxy(4, 3) = 28701.893: qxxy(4, 4) = 1.593343217 qxxy(4, 5) = 80.285: qxxy(4, 6) = 221.75: qxxy(4, 7) = 9579.228: qxxy(4, 8) = -1qxxy(5, 1) = 999.812: qxxy(5, 2) = 19744.038: qxxy(5, 3) = 28781.659: qxxy(5, 4) = 1.408141337 qxxy(5, 5) = 100#: qxxy(5, 6) = 1E+45: qxxy(5, 7) = 1E+45: qxxy(5, 8) = 0’将要反算里程桩号及距中线距离的点坐标存入数组xsz中’由于没有提供判断点与线元关系的函数据，以下数据中的’第一个数为里程桩号，用于确定所求点所在的线元xsz(1, 1) = 501: xsz(1, 2) = 19831.418: xsz(1, 3) = 28509.726xsz(2, 1) = 501: xsz(2, 2) = 19827.336: xsz(2, 3) = 28506.838xsz(3, 1) = 500: xsz(3, 2) = 19823.25398: xsz(3, 3) = 28503.95084xsz(4, 1) = 770: xsz(4, 2) = 19785.25749: xsz(4, 3) = 28575.0227xsz(5, 1) = 770: xsz(5, 2) = 19781.15561: xsz(5, 3) = 28572.16358xsz(6, 1) = 770: xsz(6, 2) = 19777.05373: xsz(6, 3) = 28569.30446xsz(7, 1) = 807: xsz(7, 2) = 19747.536: xsz(7, 3) = 28654.131xsz(8, 1) = 807: xsz(8, 2) = 19742.686: xsz(8, 3) = 28652.914xsz(9, 1) = 807: xsz(9, 2) = 19737.837: xsz(9, 3) = 28651.697xsz(10, 1) = 920: xsz(10, 2) = 19741.5912: xsz(10, 3) = 28722.058xsz(11, 1) = 920: xsz(11, 2) = 19736.4769: xsz(11, 3) = 28722.3564xsz(12, 1) = 920: xsz(12, 2) = 19733.473: xsz(12, 3) = 28722.5317Dim i As IntegerDim j As IntegerDim k As IntegerDim ysb(8) As DoubleDim wzb(3) As DoubleDim jgb(3) As DoubleTxt1.Text = ""For i = 1 To 12For j = 1 To 5If qxxy(j, 1) <= xsz(i, 1) And xsz(i, 1) < qxxy(j, 1) + qxxy(j, 5) ThenFor k = 1 To 8: ysb(k) = qxxy(j, k): Next kFor k = 1 To 2: wzb(k) = xsz(i, k + 1): Next k’调用反算函数Call qxfs(ysb(), wzb(), jgb())Txt1.Text = Txt1.Text + Str(wzb(1)) + " " + Str(wzb(2)) + Chr(13) + Chr(10) For k = 1 To 3Txt1.Text = Txt1.Text + Str(jgb(k)) + Chr(13) + Chr(10)Next kTxt1.Text = Txt1.Text + Chr(13) + Chr(10)Exit ForEnd IfNext jNext iEnd SubPrivate Sub Cmd3_Click()End。

单圆曲线中边桩坐标正反算计算程序(适用于小区道路)

单圆曲(YQX)线中边桩坐标正、反算计算程序(5800适用于小区道路)Deg:Fix9:15→DimZ“X1=”?A:“Y1=”?C:“X2=”?D:“Y2=”?E:“R=”?R:“Q=”?QLbl 0“Z=”?ZZ=1⇒Goto 1:Z=2⇒Goto 4Lbl 1QR→RPol(D-A,E-C):ClsI→FIf J<0:Then J+360→G:Else J→G:IfEndsin¯¹((F÷2)÷R)→HG-H→NIf N<0: Then N+360→U:Else N→U:IfEnd(H÷360)×4Rπ→L“L(m)=”:L▲Lbl 2“K=”?k180×K÷2÷π÷R→V2R×sin(V) →MA+con(U+V)×M→X“XZ=”:X▲C+sin（U+V）×M→Y“YZ=”:Y▲“B=”?BB=0⇒Goto 0:B≠0⇒Goto 3Lbl 3X+cos（U+V+90+V）×B→T“XB=”:T▲Y+sin（U+V+90+V）×B→P“YB=”:P▲Goto 0Lbl 4“XP=”?O: “YP=”?S:Pol(D-A,E-C):ClsI→FIf J<0:Then J+360→G:Else J→G:IfEndsin¯¹((F÷2)÷R)→HG-QH→NIf N<0: Then N+360→U:Else N→U:IfEndU+90Q→Z[1]A+cos(Z[1]) ×R→Z[2]C+sin(Z[1]) ×R→Z[3]Pol(O-Z[2],S-Z[3]):ClsI→Z[4]If J<0:Then J+360→Z[5]:Else J→Z[5]:IfEndRec(R,Z[5])+ Z[2]) →Z[6]J+ Z[3]) →Z[7]Pol(A-Z[6],C-Z[7])I→Z[8]sin¯¹( Z[8]÷(2R)) →Z[9]2Rπ(Z[9]÷180) →Z[11]R- Z[4] →Z[10]Q Z[10] →Z[12]“DP=”: Z[12] ▲“KP=”: Z[11] ▲“XZ=”: Z[6] ▲“YZ=”: Z[7] ▲Goto 0X1、Y1 输入圆曲线起点坐标， X2、Y2 输入圆曲线终点坐标Z 输入1圆曲线坐标正算，2坐标反算R 输入圆曲线半径Q 输入1半径在前进方右边、-1半径在左边K 输入中线计算里程B 输入中线至边线宽度（前进方向左边为负不计算边线坐标输入0）XZ、YZ 中线计算里程坐标，XB、YB 边线计算里程坐标XP、YP 输入反算坐标DP 反算点到曲中线垂直距离KP 起点到反算点曲线距离XZ、YZ 反算点垂直到曲线上点的坐标。

曲线坐标正反算及边桩计算

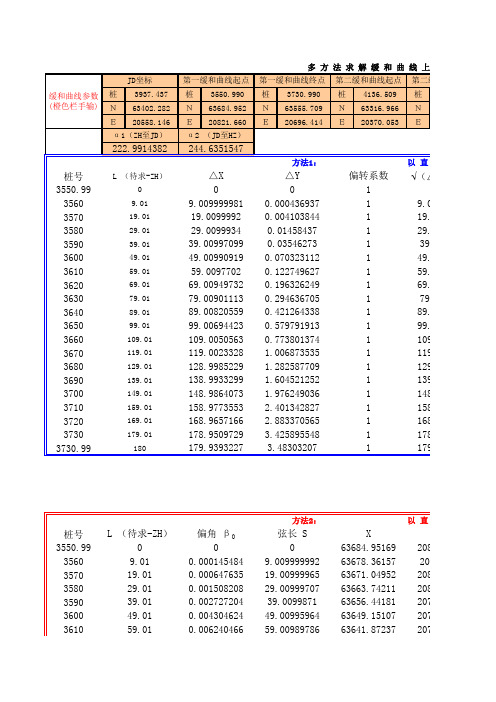
△Y 0 0.000436937 0.004103844 0.01458437 0.03546273 0.070323112 0.122749627 0.196326249 0.294636705 0.421264338 0.579791913 0.773801374 1.006873535 1.282587709 1.604521252 1.976249036 2.401342827 2.883370565 3.425895548 3.48303207
多方法求解缓和曲线上任一点坐标 JD坐标缓和曲线参数 (橙色栏手输) 桩ＮＥ 3937.437 63402.282 20558.146 第一缓和曲线起点桩ＮＥ 3550.990 63684.952 20821.660 第一缓和曲线终点桩ＮＥ 3730.990 63555.709 20696.414 第二缓和曲线起点桩ＮＥ 4136.509 63316.966 20370.053 第二缓和曲线终点桩ＮＥ
偏转系数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
√（△X2+△Y2） 0 9.009999992 19.00999965 29.00999707 39.0099871 49.00995964 59.00989786 69.00977659 79.0095605 89.00920248 99.00864187 109.0078028 119.0065923 129.0048989 139.0025908 148.9995139 158.9954903 168.9903169 178.9837631 179.9730295
方法2：
以直缓点为起算

铁路线路任意里程坐标正反算程序使用说明

铁路线路任意里程坐标正反算程序(有需要程序的可联系陈工，QQ：285242895)1、程序开发背景在铁路线路测量中,在曲线要素已定的情况下,已知某点的里程及距中线的距离,计算该点的坐标,我们称之为线路坐标正算。

相反地,已知某点的坐标,确定该点在已定线路中的里程及距中线距离的过程,我们称之为线路坐标反算。

对于一条完整的曲线，它包括直线、第一缓和曲线、圆直线及第二缓和曲线。

而一条完整的铁路线路，通常都包含不止一条曲线，如果我们根据铁路线路多个曲线的曲线要素，构建一个线路模型，然后给出任意里程点，自动计算出对应的线路坐标，也可以给出任意坐标，计算出对应的线路里程和偏距，这将在测量和放样工作有着较为实际的应用。

比如用于逐桩坐标计算、隧道开挖及土石方开挖、线路征地界坐标计算、线路测量中线质量的检查、地质钻孔位置、桥梁桩基坐标计算等方面。

2、程序界面3、程序功能1、可以根据点的里程及距中线的距离，计算出该点的坐标，显示数据文件导入结果及计算结果，最后以csv格式文件保存计算的里程数据成果及曲线要素。

2、可以根据任意点的坐标，计算出点在已定线路中的里程及距中线距离，同时显示数据计算结果，最后以.zb格式文件保存计算的坐标成果。

4、程序特色3.1 本程序采用易于交互操作的对话框模板和MSFlexGrid控件，在MFC开发环境下利用VC语言进行编写，整个程序的计算过程及结果均可在图表中直接呈现，便于数据的检查，整个程序的界面简洁直观，功能清晰、易学易用。

3.2 结合铁路测量的实际情况，在导入曲线要素时，不需要输入曲线的五大桩要素以及曲线偏向，只需要曲线数据文件中包含曲线半径、缓长及曲线两侧各两个直线点坐标，就可以计算出其他曲线要素，进而构建完整的线路模型。

3.3 在线路正算时，里程数据既可以从文件中导入，也可以在程序界面上获取。

当采用从文件导入时，里程数据可以是乱序排列的。

当从界面获取时，程序可以自动计算出连续里程数据，3.4 在线路反算中，当我们给定任意点的坐标时，程序不仅可以计算出对应线路中的里程、距离及垂点坐标，还可以计算出此点是否在线路对应范围内以及位于曲线上的具体位置。

线路中、边桩坐标计算通用公式

现阶段我国公路工程中已普遍使用大地坐标进行线型的控制及测设，在施工中经常要对中线坐标进行复核、加密，才能满足公路工程施工的需要。

本文是结合公路工程的实际需要，用于由直线、圆曲线、缓和曲线组成的一般公路线型中桩、边桩等计算的公式。

一、采用公式1 直线段1.1 中桩坐标计算公式1.2 边桩坐标计算公式2 缓和曲线段2.1 中桩坐标计算公式：以ZH点为原点，当曲线左转是Y=(-Y)Xp= X1+X*COSαA→B - Y*SINαA→B，Yp= Y1+X*SINαA→B + Y*COSαA→B以HZ点为原点，当曲线右转是Y=(-Y)Xp= X1-X*COSαB→A + Y*SINαB→A，Yp= Y1-X*SINαB→A - Y*COSαB→A（X=L-L5/40/R2/L s2， Y=L3/6/R/L s）2.2 边桩坐标计算公式：以ZH点为原点以HZ点为原点边桩坐标计算公式：以ZH点为原点坐标中的中桩左侧的“-90°”改为“+90°”，中桩右侧的“+90°”改为“-90°”就OK了。

3 圆曲线段3.1 中桩坐标计算公式当E点位于顺时针方向时取“+”,当E点位于逆时针方向时取“-”。

3.2 边桩坐标计算公式XP、YP——未知点P的坐标X1、Y1——各线型起点的坐标（第二曲线段为终点）XA、YA、XB、YB——P点边桩A点、B点的坐标（A为左侧、B为右侧）α1→2——直线段起点的方位角αA→B——各线形起点的切线方位角（第二曲线段为终点）L——P点距各线形起点的长度LS——缓和曲线段缓和曲线长R——各曲线段的半径β——P点的切线角（曲线左转时取“-”、曲线右转时取“+”）T1、T2——P点至边桩A、B的距离（A为T1、B为T2）边桩与路线切线方向的夹角设定为90°，实际应用中可根据需要进行修改。

自用5800P全线任意里程中边桩正反算及高程计算带超欠挖

FX5800P全线任意里程中边桩坐标正反算（加了数据库）本程序非本人原创，结合上传者长处，进行改编，愿收获和大家共享，不足之处多多指教。

含竖曲线及隧道超欠挖，本程序由内蒙@文哥和师父阿玖哥共同改编完成主程序 ZBJSLbl 6："1.SZ→ XY"："2.XY→ SZ"：？S：？N：“DYPQXSJK=”？→A:A=1 =>Prog“ZP1”:A=2=>Prog“ZP2”: A=3=>Prog“YP1”: A=4=>Prog“YP2”1÷P→C：(P-R)÷(2HPR) →D：180÷π→E:N=1 =>Goto 1: Goto 2Lbl 1:?Z: ?T:Abs(S-O)→W: Prog"SUB1":"XS=":X◢"YS=":Y◢"FS=":F-90 ►DMS◢“XC” ?C：“YC” ? E：0→I：0→J：Pol（X-C，Y-E）:“I=”：I◢If J∠0: Then “J=”: J+360►DMS◢IfEndIf J >0：Then “J=” ：J►DMS◢IfEnd：“DYSQXSJK=”？→B:B=1=>Prog“ZG1”:B=2=>Prog“ZG1”: B=3=>Pro g“YG1”: B=3=>Prog“YG1”:Goto 6Lbl 2X:Y:X→I:Y→J:Prog"SUB2":O+W→S:Cls:"S=":S◢"Z=":Z◢“DYSQXSJK=”？→B:B=1=>Prog“ZG1”:B=2=>Prog“ZG1”: B=3=>Prog“YG1”: B=3=>Prog“YG1”:Goto 6如不想用偏角法放样可直接删除“XC” ?C：“YC” ? E：0→I：0→J：Pol（X-C，Y-E）:“I=”：I◢直接里程推坐标。

线路中边桩坐标计算通用公式

线路中边桩坐标计算通用公式
在进行线路中、边桩坐标计算时，可以使用以下通用公式：
1.线路中桩号计算公式：
桩号=起点桩号+距离
这个公式可以用来确定线路上其中一点的桩号，其中起点桩号是线路的开始处的桩号，距离是该点距离起点的距离。

2.边桩坐标计算公式：
(X,Y)=(X0+DX,Y0+DY)
在这个公式中，(X0,Y0)是线路上其中一起点边桩的坐标，DX和DY 分别是该边桩在水平和垂直方向上的偏移量。

通过这个公式，可以计算线路上任意一个边桩的坐标。

3.边桩水平距离计算公式：
D=√(DX^2+DY^2)
这个公式可以计算线路上两个边桩之间的水平距离，其中DX和DY是两个边桩在水平和垂直方向上的偏移量。

4.边桩偏角计算公式：
α = arctan(DY / DX)
在这个公式中，α表示边桩与起点边桩之间的偏角，DX和DY是两个边桩在水平和垂直方向上的偏移量。

这些公式可以在线路设计、测量、施工等方面使用，用于计算线路中其中一点的桩号、边桩的坐标、边桩之间的距离等。

通过这些计算，可以提高线路建设的精度和效率。

线路中边桩任意里程坐标正反算改--点燃激情　传递梦想-http：wxbaiphm.7m...

线路中边桩任意里程坐标正反算改--点燃激情传递梦想-http：wxbaiphm.7m...线路中边桩任意里程坐标正反算改作者:游戏人生2006-10-5 23:45:00含数据库、测站放样计算（第五次修改-正式版）1.加编数据库及计算总调度程序,计算中不必逐项输入"线元要素",提高运算速度，避免现场忙中出错2.可加入多条线路的数据库,内业输入数据,外业一目了然3.计算直观,人性化4.正算直接输入里程和边距,反算输入近似里程便可5.增加了“计算点与测站点”的距离和方位角计算语句，方便直接放样6.愿收获与大家共享,同时也希望大家提出心得和宝贵建议7.核心计算程序摘自“yshf”一.改动后的程序清单，增设数据库程序,可输入n条线路的数据库1.(QXZDJS 计算总调度程序)M=1=>Prog "SJK1":Prog "SUBSJK"△←┘...........M=n=>Prog "SJKn":Prog "SUBSJK"△←┘2.(SJK1 数据库程序)"1.SZ => XY"："2.XY => SZ"：｛N,S｝：N：S"DKI"←┘S≤本线元终点里程＝＞U=本线元起点X坐标：V=本线元起点Y 坐标：G=本线元起点正切线方位角：P=本线元起点曲率半径：R=本线元终点曲率半径：O=本线元起点里程：H=本线元终点里程：Q=本线元左直右偏向(0或1、-1):Goto0Δ←┘S≤下一线元终点里程=＞O=。

：Goto0Δ←┘LB1 03.(SUBSJK 运算主程序){UVGPROHQ}：U"XA"：V"YA"：G"FA"：P"RA"：R"RB"：O"DKA"：H"DKB"：Q←┘Deg:S>H=>Goto AΔD=(P-R)÷2PR(H-O)：N=1=>Goto 1：≠>Goto 2Δ←┘Lbl 1：{Z}：Z：W=Abs(S-O)：Prog "SUB1"："XS="：X◢"YS="：Y◢"QX-FWJ="：F=F-90←DMS◢I=0：J=0：Pol（X-C"XC"，Y-E"YC"）：J<0＝＞J=J+360：Δ“FWJ=”:J←DMS◢“I=”：I◢Goto A←┘Lbl 2：{XY}：I=X：J=Y：Prog "SUB2"："S=":S=O+W◢"Z=":Z◢Lbl A4. (SUB1 正算子程序)A=0.1739274226：B=0.3260725774：K=0.0694318442：L=0.3300094782：X=U+W(Acos(G+180QKW(1÷P+KWD)÷π)+Bcos(G+180QLW(1÷P+LWD)÷π)+Bcos(G+180(1-L)QW(1÷P+(1-L)WD)÷π)+Acos(G+180(1-K)QW(1÷P+(1-K)WD)÷π))：Y=V+W(Asin(G+180QKW(1÷P+KWD)÷π)+Bsin(G+180QLW(1÷P +LWD)÷π)+Bsin(G+180(1-L)QW(1÷P+(1-L)WD)÷π)+Asin(G+180(1-K)QW(1÷P+(1-K)WD)÷π))：F=G+180QW(1÷P+WD)÷π+90：X=X+ZcosF：Y=Y+ZsinF5.(SUB2 反算子程序)T=G-90：W=Abs((Y-V)cosT-(X-U)sinT)：Z=0：Lbl 0：Prog "SUB1"：L=T+180QW(1÷P+WD)÷π：Z=(J-Y)cosL-(I-X)sinL：AbsZ<1÷10^6=>Goto1：≠>W=W+Z：Goto 0Δ←┘Lbl 1：Z=0：Prog "SUB1"：Z=(J-Y)÷sinF二. 使用说明：1.把所有相关的”线元要素“依次输入”SJK“，如果有多条线路，可把“SJK”分成SJK1...SJKn等n条线路数据库，然后对应“计算总调度程序”中的M1...Mn备用2.运算时直接调用“SJK”运行，程序提示输入里程“S”？时，正算直接输入待求点里程，反算输入所求点“近似“里程3.如果在正算中途想进行反算，重新给”N“？赋值"2"便可4.程序中“XC、YC”为测站坐标，“I＝”、“FWJ＝”为放样距离和方位角5.程序中“QX-FWJ=”为计算点在中线上的正切线方位角，此方位角在新线路输入数据库时非常重要，我们在每输入完一段曲线元要素后，立即退出返回到“计算总调度程序(SUBSJK)”中，然后输入该段曲线元的终点里程，其计算出来的X，Y中桩坐标应该与设计图纸(当然是经过复查无误的图纸)上的该点中桩坐标一致，否则一定是哪个地方数据输入或者程序有误，这时候我们一定要把该计算点在中线上的正切线方位角“QX-FWJ=”记录下来为下一段曲线元要素数据输入服务，因为它就是下一段曲线元的起点正切线方位角，嘿嘿！6.其它输入与"yshf"原程序一致-----------------------------------------------------------------------附件:(原yshf程序)曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQXJS)和两个子程——正算子程序(SUB1)、反算子程序(SUB2)序构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

曲线及边桩坐标计算公式

曲线段坐标计算公式缓和曲线段：1、曲线长＝里程桩号－起点桩号2、缓和曲线长＝已知3、方位角＝缓和段起始边为0°曲线长（L²）4、转角＝6*R*缓曲长（L。

）5、转后方位角＝方位角＋转角曲线长L^56、坐标（X）=曲线长L－40R²*缓曲长L。

曲线长（L³）7、坐标（Y）= -6*R*缓曲长（L。

）8、L=SQRT(X²+Y²)9、计算点坐标：X=COS(转后方位角)*L＋起点坐标X Y=SIN(转后方位角)*L＋起点坐标Y曲线长（L²）10、切线角＝2*R*缓曲长（L。

）11、切线方位角＝方位角＋切线角圆曲线段：12、曲线长＝里程桩号－起点桩号13、方位角＝缓和曲线的切线方位角曲线长L 180°14、转角＝ (×可转换为“度”) 2*R π15、转后方位角＝方位角＋转角曲线长（L^5）16、X=曲线长L－40R²*缓曲长（L。

）曲线长（L³）17、Y= -6*R*缓曲长（L。

）18、L=2*SIN（转后方位角）*R19、计算点坐标：X=COS(转后方位角)*L＋起点坐标X Y=SIN(转后方位角)*L＋起点坐标Y曲线长L²20、切线角＝2*R*缓曲长L。

21、切线方位角＝方位角＋切线角边桩放样坐标计算公式：π左侧 X=D*COS (α - )+X2πY=D*COS (α - )+Y2π右侧 X=D*COS (α + )+X2πY=D*COS (α + )+Y2。

道路对称基本型曲线中边桩坐标计算原理【fx-5800P】

计算范围从前一交点曲线终点到下一交点曲线起点间任意桩号里程的中、边桩点坐标。

已知条件（1）交点桩号JD 、坐标),(J JD D Y X ；（2）起始边方位角（第一切线方位角）1A ；（3）曲线转角α、转向参数w （右转取+1，左转取-1）；（4）圆曲线半径为R 、缓和曲线长为s L ；（5）中桩桩号P ；（6）边桩与中桩连线同中桩切线方向的交角γ（与曲线上某点切线前进方向顺时针夹角）；边桩与中桩的左（或右）偏距L D （R D ）。

注：本文中无特别说明角度单位均为度（°）。

计算过程一、曲线要素计算已知条件：曲线转角α；圆曲线半径为R 、缓和曲线长为s L 。

（1）切线增值q 、圆曲线内移值p 的计算①圆曲线内移值p1222178563422)!2()14()1(15482880506880268824--⨯⨯⨯--++-+-=n n s n n s s s s R L n n R L R L R L R L p ),3,2,1( =n 。

计算中考虑取前两项，即56342506880268824R L R L R L p s s s +-= ②切线增值qnn s n ns s s s R L n n R L R L R L L q 212126745232)!12()14()1(8386560345602402++⨯⨯+⨯+-++-+-= ),3,2,1,0( =n 。

计算中考虑取前三项，即4523345602402RL R L L q s s s +-=， ③缓圆（圆缓）点的缓和曲线角R L s 20=β （2）切线长T 的计算2tan )(αp R q T ++=（3）外距E 的计算R p R E -+=2sec)(α（4）圆曲线长度L y 的计算 )()2(0R L R R L s y -=-=αβα （5）曲线长度L 的计算s y L L L 2+=（6）校正值——切曲差J 的计算L T J -=2二、主点里程桩号计算若交点B 的里程桩号为JD ，则直缓（ZH ）点里程桩号T JD ZH -=缓圆（HY ）点里程桩号s L ZH HY +=圆缓（YH ）点里程桩号y L HY YH +=缓直（HZ ）点里程桩号s L YH HZ +=曲中（QZ ）点里程桩号2/L HZ QZ -=交点（检核）里程桩号2/J QZ JD +=三、中桩坐标计算已知条件：曲线转角α；圆曲线半径为R 、缓和曲线长为s L ；切线增值q ，圆曲线内移值p ；切线长T ；交点桩号JD 、坐标),(J JD D Y X ；第一切线方位角1A （ZH →JD 方向）；（一）ZH 、HZ 点坐标（1）ZH 点坐标⎩⎨⎧++=++=)180sin()180cos(1JD P1J P A T Y Y A T X X D （2）HZ 点坐标⎩⎨⎧++=++=)sin()cos(1JD P1J P ααw A T Y Y w A T X X D（二）直线段坐标（1）ZH 点前直线段⎩⎨⎧++-+=++-+=)180sin()()180cos()(1ZH P1ZH P A T P ZH Y Y A T P ZH X X 。