通信原理教程(第二版)樊昌信
通信原理教程第二版答案-樊昌信编著

第一章习题习题1.1 在英文字母中E 出现的概率最大,等于0.105,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-= b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题1.2所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R 等概时的平均信息速率为s b 2004log log 2B 2B b ===R M R R(2)平均信息量为比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 s b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少? 解:311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
通信原理樊昌信课后答案

第一章绪论第二章确定信号和随机信号分析第三章信道第四章模拟信号调制已知线性调制信号表示式为(1)COE C tecs C2) (1+0- Szin Q t)丈佔d t武中,•试分别画岀它们的液形图和频谙厦K解(1) fi (/)= cos Zcos 波形如图 4.1(a )所示频谱为百(劲=—{灿5@ 一 G )+ 3((D + Q )]*TT [5(G ? -A ?C ) + 3(o )+CD C )J =-+7Q )+S (Q} 4- 5Q )+3[a}- 7Q )+3(Q } - 5Q )]2频诸图如图4.1(b )所示。
图 4.1 _(2)f2(t )=(l+0.5sin Z ) cos 叫Z 的波形如图 4.2(a )所示 F 2[(D )=龙国少一少C ) + 3(0 + Q ?C )]+I r・ —[3(Q }~ G )+ 3(o?+G )]*?r [5(Q?_%)+3(a? +Q?c )] > 2兀[j =7r [5(a? — 6G )+ S [Q } + 6G )]+乎[3((D +7Q )-8{Q } - 7Q )-5 仙+5Q )+3[o )- 5Q )] 频谱如图4.2筛4-2已知调制信号加G 丿二cos (2000兀t )+cos (4000兀f )载波为coslO 4我1进行单 边带调制,试确定该单边带信号的表示式,并画出频谱图。
(b )f!©频谱图解因为应(e)=cos (2000 左e)+cos (4000 X t)对朋(t)进行希尔伯特变换得m(f) = sin(2000 劝+ sin(如00 戒)故上边带言号为Sg⑴=扌处)cose/-*做>smco p?=^cos(12000xrf) + ycos(14000^) 下边带信号为$*/)■= i w(/) cos cD r#+i m(t >sin 屮=cos(8000n/)+icos(6000 d )频谙如圉4.3所示知(“)4-3将调幅波通过滤波器产生残留边带信号,若此谑波器的传输函数M “)如燮 4.4所示(斜线段为直线)。
通信原理教程樊昌信习题答案第五章
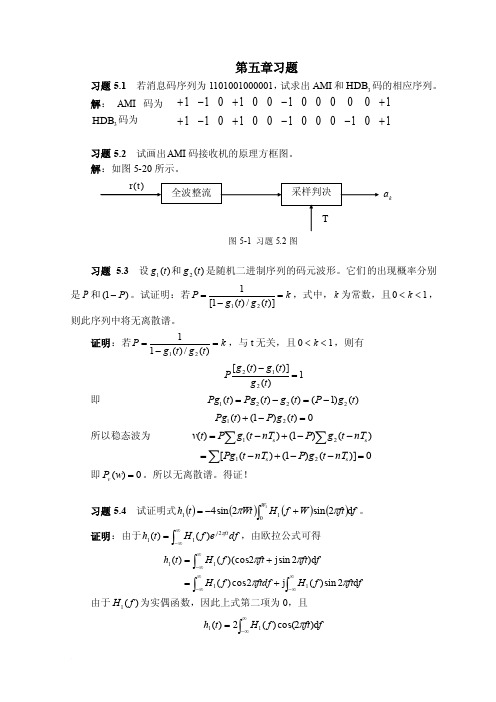
第五章习题习题5.1 若消息码序列为1101001000001,试求出AMI 和3HDB 码的相应序列。
解: AMI 码为 3HDB 码为习题5.2 试画出AMI 码接收机的原理方框图。
解:如图5-20所示。
图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。
它们的出现概率分别是P 和)1(P -。
试证明:若k t g t g P =-=)](/)(1[121,式中,k 为常数,且10<<k ,则此序列中将无离散谱。
证明:若k t g t g P =-=)(/)(1121,与t 无关,且10<<k ,则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。
所以无离散谱。
得证!习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。
证明:由于⎰∞∞-=df e f H t h ft j π211)()(,由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数,因此上式第二项为0,且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a《通信原理》习题第五章令,'d d ,'f f W f f =+=,代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称,故上式第一项为0,因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示,并且它们出现的概率相等,码元持续时间等于T 。
通信原理教程+樊昌信+习题答案第五章
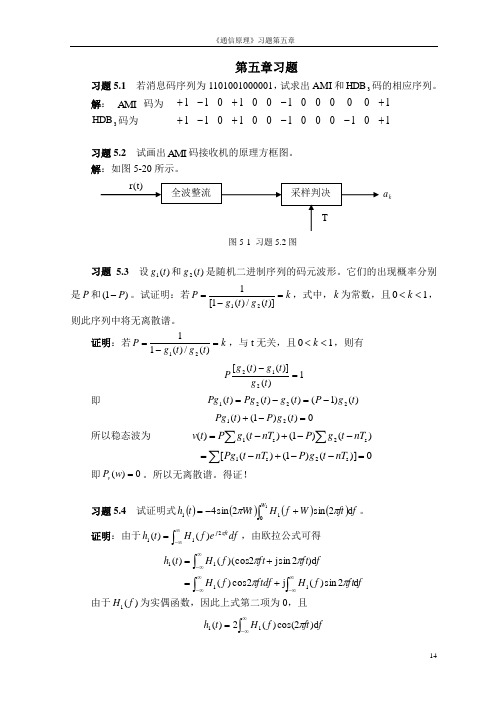
第五章习题习题5.1 若消息码序列为1101001000001,试求出AMI 和3HDB 码的相应序列。
解: A MI 码为 3HDB 码为习题5.2 试画出A MI 码接收机的原理方框图。
解:如图5-20所示。
图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。
它们的出现概率分别是P 和)1(P -。
试证明:若k t g t g P =-=)](/)(1[121,式中,k 为常数,且10<<k ,则此序列中将无离散谱。
证明:若k t g t g P =-=)(/)(1121,与t 无关,且10<<k ,则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。
所以无离散谱。
得证!习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。
证明:由于⎰∞∞-=df e f H t h ft j π211)()(,由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数,因此上式第二项为0,且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a令,'d d ,'f f W f f =+=,代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称,故上式第一项为0,因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示,并且它们出现的概率相等,码元持续时间等于T 。
通信原理教程+樊昌信+习题答案第三章

第三章习题习题3.1 设一个载波的表达式为()5cos1000c t t π=,基带调制信号的表达式为:m(t)=1+cos 200t π。
试求出振幅调制时已调信号的频谱,并画出此频谱图。
解: ()()()()()t t t c t m t s ππ1000cos 5200cos 1+==()t t t t t t ππππππ800c o s 1200c o s 251000c o s 51000c o s 200c o s 51000c o s 5++=+= 由傅里叶变换得()()()[]()()[]()()[]400400456006004550050025-+++-+++-++=f f f f f f f S δδδδδδ 已调信号的频谱如图3-1所示。
图3-1 习题3.1图习题3.2 在上题中,已调信号的载波分量和各边带分量的振幅分别等于多少? 解:由上题知,已调信号的载波分量的振幅为5/2,上、下边带的振幅均为5/4。
习题3.3 设一个频率调制信号的载频等于10kHZ ,基带调制信号是频率为2 kHZ 的单一正弦波,调制频移等于5kHZ 。
试求其调制指数和已调信号带宽。
解:由题意,已知m f =2kHZ ,f ∆=5kHZ ,则调制指数为52.52f m f m f ∆=== 已调信号带宽为 2()2(52)14 k m B f f =∆+=+=习题3.4 试证明:若用一基带余弦波去调幅,则调幅信号的两个边带的功率之和最大等于载波频率的一半。
证明:设基带调制信号为'()m t ,载波为c (t )=A 0cos t ω,则经调幅后,有'0()1()cos AM s t m t A t ω⎡⎤=+⎣⎦已调信号的频率 22'220()1()cos AM AM P s t m t A t ω⎡⎤==+⎣⎦22'222'22000cos ()cos 2()cos A t m t A t m t A t ωωω++因为调制信号为余弦波,设2(1)1000 kHZ 100f m B m f f =+∆==,故2''21()0, ()22m m t m t ==≤则:载波频率为 2220cos 2c A P A t ω==边带频率为 '222'2220()()cos 24s m t A A P m t A t ω=== 因此12s c P P ≤。
通信原理教程+樊昌信+课后习题答案第一章至第八章

第一章习题习题1.1 在英文字母中E 出现的概率最大,等于0.105,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-=b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题1.2所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R 等概时的平均信息速率为b 2004log log 2B 2B b ===R M R R(2)平均信息量为符号比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少?解:311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
通信原理樊昌信课后习题答案

习题解答《通信原理教程》樊昌信第一章 概论某个信息源由A 、B 、C 、D 等4个符号组成。
这些符号分别用二进制码组00、01、10、11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这4个符号等概率出现;(2) 这4个符号出现的概率分别为1/4、1/4、3/16、5/16。
解: 每秒可传输的二进制位为:()20010513=⨯÷-每个符号需要2位二进制,故每秒可传输的符号数为:1002200=÷(1) 4个符号等概率出现时每个符号包含的平均信息量为: bit 24log 2=故平均信息速率为:s b R b /2002100=⨯=(2)每个符号包含的平均信息量为:bit 977.11651log 1651631log 163411log 41411log 412222=+++故平均信息速率为: s b R b /7.197977.1100=⨯=设一个信号源输出四进制等概率信号,其码元宽度为125s μ。
试求码元速率和信息速率。
解:码元速率为:()baud R B 80001012516=⨯÷=- 信息速率为:s kb R R B b /16280004log 2=⨯==第二章 信号设一个随机过程X (t )可以表示成:()()∞<<∞-+=t t t X θπ2cos 2其中θ在(0,2π)之间服从均匀分布,判断它是功率信号还是能量信号?并求出其功率谱密度或能量谱密度。
解:它的能量无限,功率有界,所以是一个功率信号。
`()[]()[]()()()πτθπτθππτπθπθπτπθπππ2cos 4224cos 2cos 22122cos 22cos 22020=+++=•+++=⎰⎰d t d t t由维纳-辛钦关系有:()()ττωωτd e R P j X -+∞∞-⎰=()()[]πωδπωδπ222++-=设有一信号可表示为:()()⎩⎨⎧>≥-=000exp 4t t t t x试问它是功率信号还是能量信号?并求出其功率谱密度或能量谱密度。
通信原理教程+樊昌信+习题答案第四章

习题 4.7 在 A 律 PCM 语音通信系统中,试写出当归一化输入信号抽样值等于
0.3 时,输出的二进制码组。
解 :信号抽样值等于 0.3,所以极性码 c1=1。
查表可得 0.3 ( 1 3.93 ,1 1.98 ),所以 0.3 的段号为 7,段落码为 110,故 c2c3c4 =110。
第 7 段 内 的 动 态 范 围 为 : (1 1.98 1 3.93) 1 , 该 段 内 量 化 码 为 n , 则
11
《通信原理》习题第四章
习题 4.4 设被抽样的语音信号的带宽限制在 300~ 3400Hz ,抽样频率等于 8000 Hz 。试画出已抽样语音信号的频谱,并在图上注明各频率点的坐标值。
解 :已抽样语音信号的频谱如图 4-2 所示。 s(t) S( )
31b) 图 4-1 习题 4.3 图
变换 而 所以 即
() 2
F n
t( n s )
n
Fn
1 Ts 2 (t )
T Ts 2 s
jn s t dt
1 TS
( )2 Ts n
( ns )
1 (f )
Ts n
( n sf )
习题 4.2 若语音信号的带宽在 300~400 Hz 之间,试按照奈奎斯特准则计算理 论上信号不失真的最小抽样频率。
解 :由题意, f H =3400 Hz , f L = 300 Hz ,故语音信号的带宽为 B =3400-300= 3100 Hz
fH =3400 Hz =1 3100 + 3 3100 = nB kB 31
即 n =1, k =3 31。
根据带通信号的抽样定理,理论上信号不失真的最小抽样频率为
通信原理教程+樊昌信+习题答案第五章

第五章习题习题5.1 若消息码序列为1101001000001,试求出AMI 和3HDB 码的相应序列。
解: A MI 码为 3HDB 码为习题5.2 试画出A MI 码接收机的原理方框图。
解:如图5-20所示。
图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。
它们的出现概率分别是P 和)1(P -。
试证明:若k t g t g P =-=)](/)(1[121,式中,k 为常数,且10<<k ,则此序列中将无离散谱。
证明:若k t g t g P =-=)(/)(1121,与t 无关,且10<<k ,则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。
所以无离散谱。
得证!习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。
证明:由于⎰∞∞-=df e f H t h ft j π211)()(,由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数,因此上式第二项为0,且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a令,'d d ,'f f W f f =+=,代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称,故上式第一项为0,因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示,并且它们出现的概率相等,码元持续时间等于T 。
《通信原理教程》(第2版) 樊昌信答案 数字通信原理答案 通信原理答案 樊昌信答案

f ≤ 1 2τ 0 其他
试确定该系统最高的码元传输速率 RB 及响应的码元持续时间 T。 解: 据已知有 H
=τ0
H(ω)为升余弦型, 将 H(ω)分成宽度ω0=π/τ0 的小段, 然后将个小段在 (-π/2τ0, π/2τ0)上叠加,将构成等效低通(矩形)传输函数,它是理想低通特性。 等效矩形带宽为:
1000 π
1200 π
第四章 模拟信号的数字化 4.2 若语音信号的带宽在 300~3400Hz 之间, 试按照奈奎斯特准则计算理论上信号不失 真的最小抽样频率。 解:奈奎斯特准则:
fs ≥ 2 fH
故:最小抽样频率为:3400×2=6800Hz 4.4 设被抽样的语音信号的带宽限制在 300~3400Hz 之间,抽样频率等于 8000Hz,试 画出已抽样语音信号的频谱分布图。在图上需注明各点频率坐标值。 解:
语音信号频谱
-3400
-300 0
300
3400
f (Hz)
已抽样信号频谱
-3400
-300 0
300
3400 4.6k
7.7k
8k
8.3k
11.4k
f (Hz)
4.8 试述 PCM、DPCM 和增量调制三者之间的关系和区别。 第五章 基带数字信号的表示和传输 5.1 若消息码序列为 1101001000001,试写出 AMI 码和 HDB3 码的相应序列。 解:消息码序列: AMI 码: HDB3 码: 1101001000001 +1-1 0+1 0 0-1 0 0 0 0 0+1 +1-1 0+1 0 0-1 0 0 0 –V0+1
解: (1)g1(t)=g(t) g2(t)= -g(t) 功率谱密度:
通信原理教程(第二版)樊昌信

符号运算函数:
symsize —— 求符号矩阵维数 charploy —— 特征多项式 determ —— 符号矩阵行列式的值 eigensys —— 特征值和特征向量 inverse —— 逆矩阵 transpose —— 矩阵的转置 jordan —— 约当标准型
simple —— 符号矩阵简化
ans = x(t) = sin(t), y(t) = cos(t)
二阶微分方程 dsolve('D2y=-a^2*y','y(0)=1','Dy(pi/a)=0')
ans = cos(a*x)
小 结 本节介绍了matlab语言的符号运算 功能,通过学习应该掌握: • 掌握如何创建、修改符号矩阵 • 掌握符号运算功能
3.符号变量的创建 a. sym函数定义符号变量
x=sym(‘x’) %建立符号变量x syms x y z … %等价于 x=sym(‘x’) , y=sym(‘y’) , z=sym(‘z’) … b. 直接法 f=‘a*x^2+b*x+c’ %建立符号表达式 f=‘a*x^2+b*x+c=0’ %建立符号方程
4.符号矩阵的创建
数值矩阵A=[1,2;3,4] A=[a,b;c,d] —— 不识别
1用matlab函数sym创建矩阵(symbolic
的缩写)
命令格式:A=sym('[ ※ 需用sym指令定义 ※ 需用' '标识 ]') ※ 符号矩阵内容同数值矩阵
例如:A = sym('[a , 2*b ; 3*a , 0]') A= [ a, 2*b] 0] [3*a,
例1. f = ax2+bx+c 求解 f='a*x^2+b*x+c'; • solve(f) —— 对缺省变量x求解 ans = 计算机 [1/2/a*(-b+(b^2-4*a*c)^(1/2))] 格式 [1/2/a*(-b-(b^2-4*a*c)^(1/2))]
通信原理教程+樊昌信+课后习题答案第一章至第八章

第一章习题习题 在英文字母中E 出现的概率最大,等于,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-=b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R等概时的平均信息速率为b 2004log log 2B 2B b ===R M R R(2)平均信息量为符号比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 b 7.197977.1100B b =⨯==H R R习题 试问上题中的码元速率是多少 解:311200 Bd 5*10B B R T -===习题 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 任意精度的数学运算
在symbolic中有三种不同的算术运算:
1. 数值类型
matlab的浮点算术运算
2. 有理数类型 maple的精确符号运算
3. vpa类型
maple的任意精度算术
运算
• 浮点算术运算
1/2+1/3 --(定义输出格式format long)
ans =
0.83333333333333
4.符号矩阵的创建
数值矩阵A=[1,2;3,4] A=[a,b;c,d] —— 不识别
用matlab函数sym创建矩阵(symbolic
的缩写)
命令格式:A=sym('[ ※ 需用sym指'标识
例如:A = sym('[a , 2*b ; 3*a , 0]') A= [ a, 2*b] 0] [3*a,
将符号矩阵转化为数值矩阵
函数调用格式: numeric(A) A= [ 1/3, 5/2] [10/7, 2/5]
numeric(A) ans = 0.3333 2.5000 1.4286 0.4000
二、符号运算
1. 符号矩阵运算
符号运算的四则运算符和数值运算的运 算符相同。例如1: syms a b c d A=sym (‘[a b;c d]’); B=sym (‘[a+b,a-b;c+d,c-d]’) ; A+B=[2*a+b, a] [2*c+d, c]
a=sym('[1/4,exp(1);log(3),3/7]') a= [ 1/4,exp(1)] [log(3), 3/7] vpa(a,10) ans = [.2500000000, 2.718281828] [1.098612289, .4285714286]
3. 符号微积分与积分变换
• diff(f) — 对缺省变量求微分 • diff(f,v) — 对指定变量v求微分 • diff(f,v,n) —对指定变量v求n阶微分 • int(f) — 对f表达式的缺省变量求积分
• 特点:
运算对象可以是没赋值的符号变量 可以获得任意精度的解
• Symbolic Math Toolbox——符号运算
工具包通过调用Maple软件实现符号 计算的。
• maple软件——主要功能是符号运算,
它占据符号软件的主导地位。
2. 符号变量与符号表达式
f = 'sin(x)+5x' f —— 符号变量名 sin(x)+5x—— 符号表达式 ' '—— 符号标识 符号表达式一定要用' ' 单引 号括起来matlab才能识别。
3.符号变量的创建 a. sym函数定义符号变量
x=sym(‘x’) %建立符号变量x syms x y z … %等价于 x=sym(‘x’) , y=sym(‘y’) , z=sym(‘z’) … b. 直接法 f=‘a*x^2+b*x+c’ %建立符号表达式
f=‘a*x^2+b*x+c=0’ %建立符号方程
这就完成了一个符号矩阵的创建。 注意:符号矩阵的每一行的两端都有方 括号,这是与 matlab数值矩阵的
一个重要区别。
符号矩阵与数值矩阵的转换
将数值矩阵转化为符号矩阵
函数调用格式:sym(A) A=[1/3,2.5;1/0.7,2/5] A= 0.3333 2.5000 1.4286 0.4000 sym(A) ans = [ 1/3, 5/2] [10/7, 2/5]
• 符号运算
sym(1/2)+(1/3) ans = 5/6 --精确解
• 任意精度算术运算
digits(n) —— 设置可变精度,缺省16位
vpa(x,n) —— 显示可变精度计算
digits(25)
vpa(1/2+1/3)
ans =
.8333333333333333333333333
vpa(5/6,40) ans = .8333333333333333333333333333333333333333
符号运算函数:
symsize —— 求符号矩阵维数 charploy —— 特征多项式 determ —— 符号矩阵行列式的值 eigensys —— 特征值和特征向量 inverse —— 逆矩阵 transpose —— 矩阵的转置 jordan —— 约当标准型
simple —— 符号矩阵简化
• int(f,v) — 对f表达式的v变量求积分
• int(f,v,a,b) — 对f表达式的v变量在(a,b)
区间求定积分
int('被积表达式','积分变量','积分上限', '积分下限')—— 定积分 ——缺省时为不定积分 例1.计算二重不定积分
F=int(int('x*exp(-x*y)','x'),'y') F= 1/y*exp(-x*y) 例2.计算 f='x*exp(-x*10)'的Z变换 F=ztrans(f) F= z*exp(-10)/(z-exp(-10))^2
符号运算的功能
• 符号表达式、符号矩阵 • • • • •
的创建 符号线性代数 因式分解、展开和简化 符号代数方程求解 符号微积分 符号微分方程
一、符号运算的基本操作
1. 什么是符号运算 • 与数值运算的区别
※ 数值运算中必须先对变量赋值, 然后才能参与运算。 ※ 符号运算无须事先对独立变量 赋值,运算结果以标准的符号形式 表达。
例2:f= 2*x^2+3*x-5; g= x^2+x-7;
>> syms x >> f=2*x^2+3*x-5; g= x^2+x-7; >> h=f+g h = 3*x^2+4*x-12 例3:f=cos(x);g= sin(2*x); >> syms x >> f=cos(x);g=sin(2*x); >> f/g+f*g ans = cos(x)/sin(x)+cos(x)*sin(x)
A*B=[ a*(a+b)+b*(c+d), a*(a-b)+b*(c-d)]
[ c*(a+b)+d*(c+d), c*(a-b)+d*(c-d)]
A.*B=[a*(a+b), b*(a-b)]
[c*(c+d), d*(c-d)]
A./B=[a/(a+b), b/(a-b)]
[c/(c+d), d/(c-d)] A^2=[a^2+b*c, a*b+b*d] [a*c+c*d, b*c+d^2]
