信号与系统课后习题答案—第章

合集下载

信号与系统陈后金第二版课后习题答案(完整版)

（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )

信号与线性系统分析习题答案

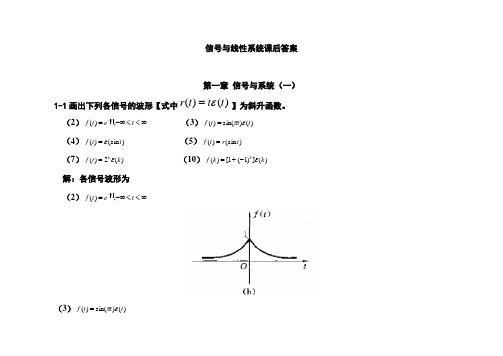
信号与线性系统课后答案第一章信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为（2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)tf=r(sin)(t（7）)tf kε(k=(2)（10）)f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。

又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。

∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。

2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。

信号与系统课后习题答案

习题一第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。

因此，公共周期3110==f T s 。

(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。

因此，公共周期5110==f T s 。

所以是非周期的。

(d) 两个分量是同频率的，基频 =0f 1/π Hz 。

因此，公共周期π==01f T s 。

1-2 解 (a) 波形如图1-2(a)所示。

显然是功率信号。

t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。

显然是能量信号。

3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。

1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。

信号与系统奥本海姆习题答案

Chapter 1 Answers1.6 (a).NoBecause when t<0, )(1t x =0.(b).NoBecause only if n=0, ][2n x has valuable.(c).Yes Because ∑∞-∞=--+--+=+k k m n k m n m n x ]}414[]44[{]4[δδ ∑∞-∞=------=k m k n m k n )]}(41[)](4[{δδ ∑∞-∞=----=k k n k n ]}41[]4[{δδ N=4.1.9 (a). T=π/5Because 0w =10, T=2π/10=π/5.(b). Not periodic.Because jt t e e t x --=)(2, while t e -is not periodic, )(2t x is not periodic.(c). N=2Because 0w =7π, N=(2π/0w )*m, and m=7.(d). N=10Because n j j e e n x )5/3(10/343)(ππ=, that is 0w =3π/5, N=(2π/0w )*m, and m=3.(e). Not periodic. Because 0w =3/5, N=(2π/0w )*m=10πm/3 , it ’s not a rational number.1.14 A1=3, t1=0, A2=-3, t2=1 or -1dtt dx )( isSolution: x(t) isBecause ∑∞-∞=-=k k t t g )2()(δ, dt t dx )(=3g(t)-3g(t-1) or dtt dx )(=3g(t)-3g(t+1) 1.15. (a). y[n]=2x[n-2]+5x[n-3]+2x[n-4]Solution:]3[21]2[][222-+-=n x n x n y ]3[21]2[11-+-=n y n y ]}4[4]3[2{21]}3[4]2[2{1111-+-+-+-=n x n x n x n x ]4[2]3[5]2[2111-+-+-=n x n x n xThen, ]4[2]3[5]2[2][-+-+-=n x n x n x n y(b).No. For it ’s linearity.the relationship between ][1n y and ][2n x is the same in-out relationship with (a). you can have a try.1.16. (a). No.For example, when n=0, y[0]=x[0]x[-2]. So the system is memory. (b). y[n]=0.When the input is ][n A δ,then, ]2[][][2-=n n A n y δδ, so y[n]=0. (c). No.For example, when x[n]=0, y[n]=0; when x[n]=][n A δ, y[n]=0. So the system is not invertible.1.17. (a). No.For example, )0()(x y =-π. So it ’s not causal.(b). Yes.Because : ))(sin()(11t x t y = , ))(sin()(22t x t y =))(sin())(sin()()(2121t bx t ax t by t ay +=+1.21. Solution:We have known:(a).(b).(c).(d).1.22. Solution:We have known:(a).(b).(e).(g)1.23. Solution:For )]()([21)}({t x t x t x E v -+= )]()([21)}({t x t x t x O d --= then,(a).(b).(c).1.24.For: ])[][(21]}[{n x n x n x E v -+= ])[][(21]}[{n x n x n x O d --=then,(a).(b).1.25. (a). Periodic. T=π/2.Solution: T=2π/4=π/2.(b). Periodic. T=2.Solution: T=2π/π=2.(d). Periodic. T=0.5. Solution: )}()4{cos()(t u t E t x v π=)}())(4cos()()4{cos(21t u t t u t --+=ππ )}()(){4cos(21t u t u t -+=π )4cos(21t π= So, T=2π/4π=0.51.26. (a). Periodic. N=7Solution: N=m *7/62ππ=7, m=3.(b). Aperriodic.Solution: N=ππm m 16*8/12=, it ’s not rational number.(e). Periodic. N=16 Solution as follow:)62cos(2)8sin()4cos(2][ππππ+-+=n n n n x in this equation,)4cos(2n π, it ’s period is N=2π*m/(π/4)=8, m=1.)8sin(n π, it ’s period is N=2π*m/(π/8)=16, m=1.)62cos(2ππ+-n , it ’s period is N=2π*m/(π/2)=4, m=1. So, the fundamental period of ][n x is N=(8,16,4)=16.1.31. SolutionBecause )()1()(),2()()(113112t x t x t x t x t x t x ++=--=. According to LTI property ,)()1()(),2()()(113112t y t y t y t y t y t y ++=--=Extra problems:Sketch ⎰∞-=t dt t x t y )()(. 1. SupposeSolution:2. SupposeSketch:(1). )]1(2)1()3()[(--+++t t t t g δδδ(2). ∑∞-∞=-k k t t g )2()(δ(2).Chapter 22.1 Solution:Because x[n]=(1 2 0 –1)0, h[n]=(2 0 2)1-, then(a).So, ]4[2]2[2]1[2][4]1[2][1---+-+++=n n n n n n y δδδδδ (b). according to the property of convolutioin:]2[][12+=n y n y(c). ]2[][13+=n y n y][*][][n h n x n y =][][k n h k x k -=∑∞-∞= ∑∞-∞=-+--=k k k n u k u ]2[]2[)21(2 ][211)21()21(][)21(12)2(0222n u n u n n k k --==+-++=-∑ ][])21(1[21n u n +-= the figure of the y[n] is:2.5 Solution:We have known: ⎩⎨⎧≤≤=elsewhere n n x ....090....1][，，, ⎩⎨⎧≤≤=elsewhere N n n h ....00....1][，，,(9≤N ) Then, ]10[][][--=n u n u n x , ]1[][][---=N n u n u n h∑∞-∞=-==k k n u k h n h n x n y ][][][*][][ ∑∞-∞=-------=k k n u k n u N k u k u ])10[][])(1[][(So, y[4] ∑∞-∞=-------=k k u k u N k u k u ])6[]4[])(1[][( ⎪⎪⎩⎪⎪⎨⎧≥≤=∑∑==4,...14, (140)0N N k Nk =5, then 4≥N And y[14] ∑∞-∞=------=k k u k u N k u k u ])4[]14[])(1[][(⎪⎪⎩⎪⎪⎨⎧≥≤=∑∑==14,...114, (1145)5N N k Nk =0, then 5<N ∴4=N2.7 Solution:[][][2]k y n x k g n k ∞=-∞=-∑（a ）[][1]x n n δ=-,[][][2][1][2][2]k k y n x k g n k k g n k g n δ∞∞=-∞=-∞=-=--=-∑∑(b) [][2]x n n δ=-,[][][2][2][2][4]k k y n x k g n k k g n k g n δ∞∞=-∞=-∞=-=--=-∑∑ (c) S is not LTI system..(d) [][]x n u n =,0[][][2][][2][2]k k k y n x k g n k u k g n k g n k ∞∞∞=-∞=-∞==-=-=-∑∑∑2.8 Solution: )]1(2)2([*)()(*)()(+++==t t t x t h t x t y δδ )1(2)2(+++=t x t xThen,That is, ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤<-+-=-<<-+=others t t t t t t t t y ,........010,....2201,.....41..,.........412,.....3)(2.10 Solution:(a). We know:Then,)()()(αδδ--='t t t h)]()([*)()(*)()(αδδ--='='t t t x t h t x t y )()(α--=t x t xthat is,So, ⎪⎪⎩⎪⎪⎨⎧+≤≤-+≤≤≤≤=others t t t t t t y ,.....011,.....11,....0,.....)(ααααα(b). From the figure of )(t y ', only if 1=α, )(t y ' would contain merely therediscontinuities.2.11 Solution:(a). )(*)]5()3([)(*)()(3t u et u t u t h t x t y t----==⎰⎰∞∞---∞∞--------=ττττττττd t u e u d t u eu t t )()5()()3()(3)(3⎰⎰-------=tt t t d e t u d et u 5)(33)(3)5()3(ττττ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥+-=-<≤-=<=---------⎰⎰⎰5,.......353,.....313.........,.........0315395)(33)(3393)(3t e e d e d e t e d e t tt t t t t t t t ττττττ(b). )(*)]5()3([)(*)/)(()(3t u e t t t h dt t dx t g t ----==δδ)5()3()5(3)3(3---=----t u e t u e t t(c). It ’s obvious that dt t dy t g /)()(=.2.12 Solution∑∑∞-∞=-∞-∞=--=-=k tk tk t t u ek t t u e t y )]3(*)([)3(*)()(δδ∑∞-∞=---=k k t k t u e)3()3(Considering for 30<≤t ,we can obtain33311])3([)(---∞=-∞-∞=--==-=∑∑ee e ek t u e e t y tk k tk kt. (Because k must be negetive ,1)3(=-k t u for 30<≤t ).2.19 Solution:(a). We have known:][]1[21][n x n w n w +-=(1) ][]1[][n w n y n y βα+-=(2)from (1), 21)(1-=E EE Hfrom (2), αβ-=E EE H )(2then, 212212)21(1)21)(()()()(--++-=--==E E E E E E H E H E H ααβαβ∴][]2[2]1[)21(][n x n y n y n y βαα=-+-+-but, ][]1[43]2[81][n x n y n y n y +-+--=∴⎪⎩⎪⎨⎧=⎪⎭⎫ ⎝⎛=+=143)21(:....812βααor ∴⎪⎩⎪⎨⎧==141βα(b). from (a), we know )21)(41()()()(221--==E E E E H E H E H21241-+--=E EE E ∴][)41()21(2][n u n h n n ⎥⎦⎤⎢⎣⎡-=2.20 (a). 1⎰⎰∞∞-∞∞-===1)0cos()cos()()cos()(0dt t t dt t t u δ(b). 0dt t t )3()2sin(5+⎰δπ has value only on 3-=t , but ]5,0[3∉-∴dt t t )3()2sin(5+⎰δπ=0(c). 0⎰⎰---=-641551)2cos()()2cos()1(dt t t u d u πτπττ⎰-'-=64)2cos()(dt t t πδ0|)2(s co ='=t t π 0|)2sin(20=-==t t ππ∑∞-∞=-==k t h kT t t h t x t y )(*)()(*)()(δ∑∞-∞=-=k kT t h )(∴2.27Solution()y A y t dt ∞-∞=⎰,()xA x t dt ∞-∞=⎰,()hA h t dt ∞-∞=⎰.()()*()()()y t x t h t x x t d τττ∞-∞==-⎰()()()()()()()()()(){()}y x hA y t dt x x t d dtx x t dtd x x t dtd x x d d x d x d A A ττττττττττξξτττξξ∞∞∞-∞-∞-∞∞∞∞∞-∞-∞-∞-∞∞∞∞∞-∞-∞-∞-∞==-=-=-===⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(a) ()()(2)tt y t e x d τττ---∞=-⎰,Let ()()x t t δ=,then ()()y t h t =. So , 2()(2)(2)()(2)()(2)t t t t t h t ed e d e u t τξδττδξξ---------∞-∞=-==-⎰⎰(b) (2)()()*()[(1)(2)]*(2)t y t x t h t u t u t e u t --==+---(2)(2)(1)(2)(2)(2)t t u eu t d u e u t d ττττττττ∞∞-------∞-∞=+------⎰⎰22(2)(2)12(1)(4)t t t t u t e d u t e d ττττ---------=---⎰⎰(2)2(2)212(1)[]|(4)[]|t t t t u t e e u t ee ττ-------=--- (1)(4)[1](1)[1](4)t t e u t e u t ----=-----2.46 SolutionBecause)]1([2)1(]2[)(33-+-=--t u dtde t u e dt d t x dt d t t )1(2)(3)1(2)(333-+-=-+-=--t e t x t e t x t δδ.From LTI property ,we know)1(2)(3)(3-+-→-t h e t y t x dtdwhere )(t h is the impulse response of the system. So ,following equation can be derived.)()1(223t u e t h e t --=-Finally, )1(21)()1(23+=+-t u e e t h t 2.47 SoliutionAccording to the property of the linear time-invariant system: (a). )(2)(*)(2)(*)()(000t y t h t x t h t x t y ===(b). )(*)]2()([)(*)()(00t h t x t x t h t x t y --==)(*)2()(*)(0000t h t x t h t x --=012y(t)t4)2()(00--=t y t y(c). )1()1(*)(*)2()1(*)2()(*)()(00000-=+-=+-==t y t t h t x t h t x t h t x t y δ(d). The condition is not enough.(e). )(*)()(*)()(00t h t x t h t x t y --==τττd t h x )()(00+--=⎰∞∞-)()()(000t y dm m t h m x -=--=⎰∞∞-(f). )()]([)](*)([)(*)()(*)()(000000t y t y t h t x t h t x t h t x t y "=''='--'=-'-'==Extra problems:1. Solute h(t), h[n](1). )()(6)(5)(22t x t y t y dt dt y dtd =++ (2). ]1[][2]1[2]2[+=++++n x n y n y n y Solution:(1). Because 3121)3)(2(1651)(2+-++=++=++=P P P P P P P Hso )()()()3121()(32t u e e t P P t h t t ---=+-++=δ (2). Because )1)(1(1)1(22)(22i E i E EE E E E E E H -+++=++=++=iE Eii E E i -+-+++=1212 so []][)1()1(2][1212][n u i i i k i E E i i E E i n h n n +----=⎪⎪⎪⎪⎭⎫⎝⎛-+-+++=δChapter 33.1 Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑3.2 Solution:for, 10=a , 4/2πj ea --= , 4/2πj ea = , 3/42πj ea --=, 3/42πj ea =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=n j j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++= )358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n n3.3 Solution: for the period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6 , i.e. 3/6/20ππ==w)35sin(4)32cos(2)(t t t x ππ++= )5sin(4)2cos(21200t w t w ++=)(2)(21200005522t w j t w j t w j t w j e e j e e ----++=then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x ,that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw tk T T b x t e dt x t x t e dt T--==-+-⎰⎰111111(1)(1)jkw tjkw t T Tx t e dt x t e dt T T --=-+-⎰⎰ 111)(jkw k k jkw k jkw k e a a e a e a -----+=+=3.8 Solution:kt jw k k e a t x 0)(∑∞-∞==while:)(t x is real and odd, then 00=a , k k a a --=2=T , then ππ==2/20wand0=k a for 1>kso kt jw k k e a t x 0)(∑∞-∞==t jw t jw e a e a a 00110++=--)sin(2)(11t a e e a t j t j πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x∴2/21±=a ∴)sin(2)(t t x π±=3.13 Solution:Fundamental period 8T =.02/8/4ωππ==kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞==0004, 0sin(4)()0, 0k k H jk k k ωωω=⎧==⎨≠⎩ ∴000()()4jkw t k k y t a H jkw e a ∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=⎰⎰⎰So ()0y t =.kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞== ∴dt e jkw H t y Ta t jkw Tk 0)()(10-⎰=for⎪⎩⎪⎨⎧>≤=100, (0100),.......1)(w w jw H ∴if 0=k a , it needs 1000>kwthat is 12100,........1006/2>>k kππand k is integer, so 8>K3.22 Solution:021)(1110===⎰⎰-tdt dt t x Ta Tdt te dt te dt e t x T a t jk t jk t jkw T k ππ-----⎰⎰⎰===1122112121)(10t jk tde jk ππ--⎰-=1121⎥⎥⎦⎤⎢⎢⎣⎡---=----111121ππππjk e te jk t jk tjk ⎥⎦⎤⎢⎣⎡---+-=--ππππππjk e e e e jk jk jk jk jk )()(21⎥⎦⎤⎢⎣⎡-+-=ππππjk k k jk )sin(2)cos(221[]πππππk jk k j k jk k)1()cos()cos(221-==-=0............≠k404402()()1184416tj tj t t j tt j t H j h t edt ee dte edt e e dtj j ωωωωωωωω∞∞----∞-∞∞----∞===+=+=-++⎰⎰⎰⎰A periodic continous-signal has Fourier Series:. 0()j kt k k x t a e ω∞=-∞=∑T is the fundamental period of ()x t .02/T ωπ=The output of LTI system with inputed ()x t is 00()()jk t k k y t a H jk e ωω∞=-∞=∑Its coefficients of Fourier Series: 0()k k b a H jk ω= (a)()()n x t t n δ∞=-∞=-∑.T=1, 02ωπ=11k a T==. 01/221/21()()1jkw t jk tk T a x t e dt t e dt Tπδ---===⎰⎰ （Note ：If ()()n x t t nT δ∞=-∞=-∑,1k a T=） So 2282(2)16(2)4()k k b a H jk k k πππ===++ (b)()(1)()n n x t t n δ∞=-∞=--∑ .T=2, 0ωπ=,11k a T== 01/23/21/21/2111()()(1)(1)221[1(1)]2jkw t jk tjk t k T k a x t e dt t e dt t e dtT ππδδ----==+--=--⎰⎰⎰So 24[1(1)]()16()k k k b a H jk k ππ--==+, (c) T=1,02ωπ=01/421/4sin()12()jk t jk tk T k a x t e dt e dt Tk ωπππ---===⎰⎰28sin()2()[16(2)]k k k b a H jk k k ππππ==+ 3.35 Solution: T= /7π,02/14T ωπ==.kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞==∴0()k k b a H jkw =for⎩⎨⎧≥=otherwise w jw H ,.......0250,.......1)(,01,. (17)()0,.......k H jkw otherwise ⎧≥⎪=⎨⎪⎩that is 0250250, (14)k k ω<<, and k is integer, so 18....17k or k <≤. Let ()()y t x t =,k k b a =, it needs 0=k a ,for 18....17k or k <≤.3.37 Solution:11()[]()212()21312411511cos 224nj j nj n n n n j nn j nn n j j j H e h n ee ee e e e ωωωωωωωωω∞∞--=-∞=-∞-∞--=-∞=-===+=+=---∑∑∑∑A periodic sequence has Fourier Series:2()[]jk n Nk k N x n a eπ=<>=∑.N is the fundamental period of []x n .The output of LTI system with inputed []x n is 22()[]()jk jk n NNk k N y n a H eeππ=<>=∑.Its coefficients of Fourier Series: 2()jk Nk k b a H eπ=(a)[][4]k x n n k δ∞=-∞=-∑.N=4, 14k a =.So 2314()524cos()44j k Nk k b a H e k ππ==-3165cos()42k b k π=-3.40 Solution: According to the property of fourier series: (a). )2cos(2)cos(20000000t Tka t kw a e a ea a k k t jkw k t jkw k k π==+='- (b). Because 2)()()}({t x t x t x E v -+=}{2k v k k k a E a a a =+='-(c). Because 2)(*)()}({t x t x t x R e +=2*kk k a a a -+='(d). k k k a Tjka jkw a 220)2()(π=='(e). first, the period of )13(-t x is 3T T ='then 3)(1)13(131213120dme m x T dt e t x T a m T jk T t T jk T k +'--'-'-'⎰⎰'=-'='ππTjkk m T jk T T jk T jk m T jk T ea dm e m x T e dm e e m x T πππππ221122211)(1)(1---------=⎥⎦⎤⎢⎣⎡==⎰⎰3.43 (a) Proof:（i ）Because ()x t is odd harmonic ,(2/)()jk T t k k x t a e π∞=-∞=∑,where 0k a = for everynon-zero even k.(2/)()2(2/)(2/)()2T jk T t k k jk jk T tk k jk T tk k T x t a ea e e a e ππππ∞+=-∞∞=-∞∞=-∞+===-∑∑∑It is noticed that k is odd integers or k=0.That means()()2Tx t x t =-+（ii ）Because of ()()2Tx t x t =-+,we get the coefficients of Fourier Series222/200/222(/2)/2/20022/2/200111()()()11()(/2)11()()(1)jk t jk t jk t T T T T T T k T jk t jk t T T T T Tjk t jk t T T k TT a x t e dt x t e dt x t e dtT T T x t e dt x t T e dt T T x t e dt x t e dt T T πππππππ-----+--==+=++=--⎰⎰⎰⎰⎰⎰⎰ 2/21[1(1)]()jk t T kT x t e dt T π-=--⎰It is obvious that 0k a = for every non-zero even k. So ()x t is odd harmonic ,(b)Extra problems:∑∞-∞=-=k kT t t x )()(δ, π=T(1). Consider )(t y , when )(jw H ist(2). Consider )(t y , when )(jw H isSolution:∑∞-∞=-=k kT t t x )()(δ↔π11=T , 220==Tw π(1).kt j k k tjkw k k e k j H a ejkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===ππ2=(for k can only has value 0)(2).kt j k k tjkw k k e k j H a e jkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===πππte e t j t j 2cos 2)(122=+=- (for k can only has value –1 and 1)。

信号与系统第三版郑君里课后习题答案

信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号。

()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。

()(2y n x n =）离散、模拟、非周期、功率型信号。

()()y n n x n = 离散、模拟、非周期、功率型信号。

1－6，示意画出下列各信号的波形，并判断其类型。

(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。

(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。

t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。

信号与系统课后习题答案

f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为：
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1．17 写出题图 1．8 系统的输入输出方程。
解：（b）系统框图等价为：
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)＝1 时，y2(t)＝4e-t-2e-3t，t≥0 则 x1(0-)＝5，x2(0-)＝3 时，系统的零输入响应： yx(t)＝y(t)＝5y1(t)＋3y2(t)＝22e-t 十 9e-3t，t≥0
1．22 在题 1.21 的基础上，若还已知 f(t)＝ε(t)，x1(0-)＝0，x2(0-)＝0 时，有 y(t)＝2+e-t+2e-3t，t≥0 试求当 f(t)＝3ε(t)，x1(0-)＝2，x2(0-)＝5 时的系统响应 y(t)。解：记，f(t)＝ε(t)，x1(0-)＝0，x2(0-)＝0 时，系统响应 yf(t)＝y(t)＝2+e-t+2e-3t，t≥0 则当 f(t)＝3ε(t)，x1(0-)＝2，x2(0-)＝5 时的系统全响应 y(t)为： y(t)＝3yf(t)＋2y1(t)＋5y2(t)

西南交大信号与系统第二版课后答案

1口 7 -, 刀、歹L
2.25
CD CD
f(t) = IOcosl 11(1) 证明： J(t)关8(1-1。) =f(t-1。)
@ f(t) = e-''u(t) (?) f(t)
状态响应可以表示力
2.26
已知线性时不变系统的输入力f(t)'系统的阶跃响应力g(t)'试证明系统的零汕） = Lf'(,!)g(t-,!)d儿 2.27 2.28 2.29 用MATLAB求题2.7的全响应。用MATLAB求题2. 9的零输入响应。（此式称为杜阿美尔积分）
=
心Yx (/)=7e-'-5e-2'(t汃0)
(2)yx (1)=6e-'-(4+5/)e-3'(t;>O) CZ) /,(1)= te-'11(1) 3 @i,(1) = -e-2'sin(21)11(1) 2
2.11 2.12
CD /,(1)�(-2e-'+2e-")的）+ 0(1)
心yx (t)�ze-" -2e-" (1;;, O) I 5 8 3 y(t) � - 3 e- '+ 2e-" + 6
第1章信号与系统概述
习题1
心f(t)=cost+2 sin(2 兀t) @ f(t)=e _,, srn(2 亢I) (J) f(k)=sm(2忒）心f(t)=cos( 兀 I) ＠ 1.2 1.1 判断下列信号是否是周期信号。若是周期信号，则确定信号周期。 @ f(t)= costu(t) CZ) f(t)= sin(3 兀t)+cos(2 兀t) @八I)= sin'[

信号与系统版课后答案_(郑君里)_高等教育出版社[1]

r
(1)
=
5
∫−∞
e (τ
)
dτ
，
r
(1)
与 (−∞,5] 内的输入有关。
1-21 分析：一个系统可逆，当且仅当输入、输出时一一对应的关系解题过程：
（1）可逆。逆系统为 r (t ) = e (t + 5)
（2）
不可逆。因为
r
(t)
=
d dt
e
(t)
=
d dt
⎡⎣e
(t)
+
C ⎤⎦
不满足一一对应关系。
（4）f (t ) = e−t cos (10π t ) ⎡⎣u (t −1) − u (t − 2)⎤⎦
1-12 解题过程：
f (t)
1
（1）
1
f (t)
1
（3）
1
f (t)
1
（5）
1
f (t)
1
（2）
1
f (t)
1 （4） -1
f (t)
3 2
（6）
23
3
f (t)
1 23
（7） -2
注：1-9、1-12 题中的时域信号均为实因果信号，即 f (t ) = f (t )u (t )
+
e−αtδ
(t)
=
δ
(t)
− α e−αt
8
信号与系统习题答案（注：教材---郑君里编）习题二
2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a)：微分方程：
2i1
(t
)
+
1∗
di1 (t dt
)
+

郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】

第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节，是整个信号与系统学习的基础。

本章介绍了有关信号与系统的基本概念和术语，给出几种典型的信号和系统的表现形式，讲述了各信号与系统的特点以及信号之间的运算和转换。

通过本章学习，读者应掌握：如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。

一、信号概述
1．信号的概念及分类（见表1-1-1）
表1-1-1信号的概念及分类
2．典型的连续信号（见表1-1-2）
表1-1-2典型的信号及表示形式
3．信号的运算（见表1-1-3）
表1-1-3信号的运算
4．阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号，许多复杂信号皆可由二者或二者的线性组合表示。

具体见表1-1-4及表1-1-5。

（1）单位阶跃信号u（t）
表1-1-4单位阶跃信号u（t）
（2）单位冲激信号δ（t）
表1-1-5单位冲激信号δ（t）表示形式及性质
5．信号的分解
一个一般信号根据不同类型可分解为以下几种分量，具体见表1-1-6。

表1-1-6信号的分解
二、系统
1．系统概念及分类（见表1-1-7）
表1-1-7系统的概念及分类
系统模型如下：
输入信号经过不同系统可得到不同输出信号，具体见表1-1-8。

表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？
（a）
（b）
（c）
（d）
（e）
（f）。

信号与系统课后习题参考答案

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

信号与系统课后答案

与奇分量的波形，相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示，信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t)，并画出 fo(t)的波形。
解因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ，故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示，试写出它们各自的函数式。
解： f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统，已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。（1）求响应 h(t)；（2）求当 f(t)=U(t)时的响应 y(t)（见图题 1-18(b))。
解（1） h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =

信号与系统课后习题答案—第章

第1章习题答案 1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）； ④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。

1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。

解：设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。

① 线性1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。

由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。

2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。

② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。

依据上述①、②两点，可判定此系统为一非线性时不变系统。

信号与系统(郑君里)课后答案第一章习题解答

1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程：（1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。

信号与系统课后习题答案(金波华中科技大学出版社)

t
(t ) ;
(c) f (t ) G2 (t ) Q1 (t ) (d) f (t ) (t 1)G1 (t 0.5) G1 (t 0.5) (t 2)G1 (t 0.5) ; (e) f (t ) sin( t )G3 (t 1.5)
1-18 对于题图1.18中的信号 f (t ) ，为以下各式作图。
P lim
1 T 2T

T T
f (t ) d t lim
2
2 T 1 1 1d t 36 d t 16 d t 16 W 1 2 T T 0
f (t )
6 6
f (t )
4 1
0
1 1 2
t
0
1
2
t
题解图 1-2(a)
题解图 1-2(b)
2
1-10 已知一线性非时变系统，系统的初始状态为零，当输入信号为 f1 (t ) ，其输出信号为
y1 (t ) ，对应的波形如题图 1.10(a)(b)所示。试求： (a) 当输入信号为 f 2 (t ) 时，其波形如题图 1.15(c)所示，画出对应的输出 y 2 (t ) 的波形。 (b) 当输入信号为 f 3 (t ) 时，其波形如题图 1.10(d)所示，画出对应的输出 y 3 (t ) 的波形。

3
t 2
(b) e
3t
(5 2t ) ；
) (t

2
)；
(d) e
(t 2)
(t ) (t 3) 。
(b) (d)
1-6 求下列积分。 (a) (c)

4
6 3
(4 t 2 ) (t 3) dt ;

信号与系统课后习题答案—第章

信号与系统 陈后金 第二版 课后习题答案(完整版)

信号与线性系统分析习题答案

《信号与系统》课后习题参考答案

信号与系统课后习题答案

信号与系统奥本海姆习题答案

信号与系统第三版郑君里课后习题答案

信号与系统课后习题答案

西南交大信号与系统第二版课后答案

信号与系统版课后答案_(郑君里)_高等教育出版社[1]

郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】

信号与系统课后习题参考答案

信号与系统课后答案

信号与系统课后习题答案—第章

信号与系统(郑君里)课后答案 第一章习题解答

信号与系统课后习题答案(金波 华中科技大学出版社)

信号与系统陈后金第二版课后习题答案(完整版)

信号与系统(郑君里)课后答案第一章习题解答

信号与系统课后习题答案(金波华中科技大学出版社)