二次函数常见题型
二次函数的图象与性质大题(五大题型)—2024年中考数学(全国通用)解析版

二次函数的图象与性质大题(五大题型)通用的解题思路:题型一.二次函数的性质二次函数y=ax2+bx+c(a≠0)的顶点坐标是(﹣,),对称轴直线x=﹣,二次函数y=ax2+bx+c (a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣时,y随x的增大而减小;x>﹣时,y随x的增大而增大;x=﹣时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣时,y随x的增大而增大;x>﹣时,y随x的增大而减小;x=﹣时,y取得最大值,即顶点是抛物线的最高点.③抛物线y=ax2+bx+c(a≠0)的图象可由抛物线y=ax2的图象向右或向左平移|﹣|个单位,再向上或向下平移||个单位得到的.题型二.二次函数图象与系数的关系二次函数y=ax2+bx+c(a≠0)①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;|a|还可以决定开口大小,|a|越大开口就越小.②一次项系数b和二次项系数a共同决定对称轴的位置.当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧.(简称:左同右异)③.常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).④抛物线与x轴交点个数.△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac <0时,抛物线与x轴没有交点.题型三.待定系数法求二次函数解析式(1)二次函数的解析式有三种常见形式:①一般式:y=ax2+bx+c(a,b,c是常数,a≠0);②顶点式:y=a(x﹣h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标;③交点式:y=a(x﹣x1)(x﹣x2)(a,b,c是常数,a≠0);(2)用待定系数法求二次函数的解析式.在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.题型四.抛物线与x轴的交点求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x 的一元二次方程即可求得交点横坐标.(1)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.△=b2﹣4ac决定抛物线与x轴的交点个数.△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.(2)二次函数的交点式:y=a(x1)(x﹣x2)(a,b,c是常数,a≠0),可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).题型五.二次函数综合题(1)二次函数图象与其他函数图象相结合问题解决此类问题时,先根据给定的函数或函数图象判断出系数的符号,然后判断新的函数关系式中系数的符号,再根据系数与图象的位置关系判断出图象特征,则符合所有特征的图象即为正确选项.(2)二次函数与方程、几何知识的综合应用将函数知识与方程、几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.(3)二次函数在实际生活中的应用题从实际问题中分析变量之间的关系,建立二次函数模型.关键在于观察、分析、创建,建立直角坐标系下的二次函数图象,然后数形结合解决问题,需要我们注意的是自变量及函数的取值范围要使实际问题有意义.题型一.二次函数的性质(共3小题)1.(2024•石景山区校级模拟)在平面直角坐标系xOy 中,1(A x ,1)y ,2(B x ,2)y 是抛物线2(0)y x bx b =−+≠上任意两点,设抛物线的对称轴为直线x h =. (1)若抛物线经过点(2,0),求h 的值;(2)若对于11x h =−,22x h =,都有12y y >,求h 的取值范围;(3)若对于121h x h −+……,221x −−……,存在12y y <,直接写出h 的取值范围. 【分析】(1)根据对称轴2bx a=−进行计算,得2b h =,再把(2,0)代入2(0)y x bx b =−+≠,即可作答.(2)因为1(A x ,1)y ,2(B x ,2)y 是抛物线2(0)y x bx b =−+≠上的点,所以把11x h =−,22x h =分别代入,得出对应的1y ,2y ,再根据12y y >联立式子化简,计算即可作答;(3)根据121h x h −+……,221x −−……,存在12y y <,得出当221h −<−<−或者211h −<+<−,即可作答. 【解答】解:(1)抛物线的对称轴为直线x h =, 22b bh ∴=−=−, 即2b h =,∴抛物线22y x hx =−+,把(2,0)代入22y x hx =−+, 得0422h =−+⨯, 解得1h =;(2)由(1)知抛物线22y x hx =−+,1(A x ,1)y ,2(B x ,2)y 是抛物线22y x hx =−+上任意两点,221(1)2(1)1y h h h h ∴=−−+−=−,22(2)220y h h h =−+⨯=,对于11x h =−,22x h =,都有12y y >, 210h ∴−>,解得1h >或1h <−;(3)1(A x ,1)y ,2(B x ,2)y 是抛物线22y x hx =−+上任意两点,对于121h x h −+……,221x −−……,存在12y y <,且1(2,)h y −关于直线x h =的对称点为1(2,)h y +,1(1,)h y +关于直线x h =的对称点为1(1,)h y −,∴当221h −<−<−时,存在12y y <,解得01h <<,当221h −<+<−时,存在12y y <, 解得43h −<<−,当211h −<+<−时,存在12y y <, 解得32h −<<−,当211h −<−<−时,存在12y y <, 解得10h −<<,综上,满足h 的取值范围为41h −<<且0h ≠.【点评】本题考查了二次函数的图象性质、增减性,熟练掌握二次函数的图象和性质是解决本题的关键. 2.(2024•鹿城区校级一模)已知二次函数223y x tx =−++. (1)若它的图象经过点(1,3),求该函数的对称轴. (2)若04x ……时,y 的最小值为1,求出t 的值.(3)如果(2,)A m n −,(,)C m n 两点都在这个二次函数的图象上,直线2y mx a =+与该二次函数交于1(M x ,1)y ,2(N x ,2)y 两点,则12x x +是否为定值?若是,请求出该定值;若不是,请说明理由.【分析】(1)把(1,3)代入解析式求出12t =,再根据对称轴公式求出对称轴; (2)根据抛物线开口向下,以及0x =时3y =,由函数的性质可知,当4x =时,y 的最小值为1,然后求t 即可;(3)(2,)A m n −,(,)C m n 两点都在这个二次函数的图象上,有对称轴公式得出1m t −=,再令2232x tx mx a −++=+,并转化为一般式,然后由根与系数的关系求出122x x +=−.【解答】解:(1)将(1,3)代入二次函数223y x tx =−++,得3123t =−++, 解得12t =, ∴对称轴直线为21122t x t =−==−⨯; (2)当0x =时,3y =,抛物线开口向下,对称轴为直线x t =, ∴当x t =时,y 有最大值,04x ……时,y 的最小值为1,∴当4x =时,16831y t =−++=,解得74t =; (3)12x x +是定值,理由:(2,)A m n −,(,)C m n 两点都在这个二次函数的图象上, 212m mx t m −+∴===−, 1m t ∴−=,令2232x tx mx a −++=+, 整理得:22()30x m t x a +−+−=,直线2y mx a =+与该二次函数交于1(M x ,1)y ,2(N x ,2)y 两点, 1x ∴,2x 是方程22()30x m t x a +−+−=的两个根,122()2()21m t x x m t −∴+=−=−−=−是定值. 【点评】本题考查了二次函数的性质,二次函数图象上点的坐标特征等知识,关键是掌握二次函数的性质. 3.(2024•拱墅区一模)在平面直角坐标系中,抛物线2(2)2y ax a x =−++经过点(2,)A t −,(,)B m p . (1)若0t =,①求此抛物线的对称轴;②当p t <时,直接写出m 的取值范围;(2)若0t <,点(,)C n q 在该抛物线上,m n <且5513m n +<−,请比较p ,q 的大小,并说明理由. 【分析】(1)①当0t =时,点A 的坐标为(2,0)−,将其代入函数解析式中解得1a =−,则函数解析式为抛物线的解析式为22y x x =−−+,再根据求对称轴的公式2bx a=−即可求解; ②令0y =,求出抛物线与x 轴交于(2,0)−和(1,0),由题意可得0p <,则点B 在x 轴的下方,以此即可解答; (2)将点A 坐标代入函数解析式,通过0t <可得a 的取值范围,从而可得抛物线开口方向及对称轴,根据点B ,C 到对称轴的距离大小关系求解.【解答】解:(1)①当0t =时,点A 的坐标为(2,0)−,抛物线2(2)2y ax a x =−++经过点(2,0)A −, 42(2)20a a ∴+++=,1a ∴=−,∴抛物线的解析式为22y x x =−−+, ∴抛物线的对称轴为直线112(1)2x −=−=−⨯−;②令0y =,则220x x −−+=, 解得:11x =,22x =−,∴抛物线与x 轴交于(2,0)−和(1,0),点(2,0)A −,(,)B m p ,且0p <, ∴点(,)B m p 在x 轴的下方,2m ∴<−或1m >.(2)p q <,理由如下:将(2,)t −代入2(2)2y ax a x =−++得42(2)266t a a a =+++=+,0t <, 660a ∴+<, 1a ∴<−,∴抛物线开口向下,抛物线对称轴为直线(2)1122a x a a −+=−=+, 1a <−,110a∴−<<, 1111222a ∴−<+<, m n <且5513m n +<−,∴1312102m n +<−<−, ∴点(,)B m p 到对称轴的距离大于点(,)C n q 到对称轴的距离,p q ∴<.【点评】本题考查二次函数的综合应用,解题关键是掌握二次函数的性质,掌握二次函数与方程及不等式的关系.题型二.二次函数图象与系数的关系(共8小题)4.(2023•南京)已知二次函数223(y ax ax a =−+为常数,0)a ≠. (1)若0a <,求证:该函数的图象与x 轴有两个公共点. (2)若1a =−,求证:当10x −<<时,0y >.(3)若该函数的图象与x 轴有两个公共点1(x ,0),2(x ,0),且1214x x −<<<,则a 的取值范围是 .【分析】(1)证明240b ac −>即可解决问题. (2)将1a =−代入函数解析式,进行证明即可. (3)对0a >和0a <进行分类讨论即可.【解答】证明:(1)因为22(2)43412a a a a −−⨯⨯=−, 又因为0a <,所以40a <,30a −<, 所以24124(3)0a a a a −=−>,所以该函数的图象与x 轴有两个公共点. (2)将1a =−代入函数解析式得,2223(1)4y x x x =−++=−−+,所以抛物线的对称轴为直线1x =,开口向下. 则当10x −<<时,y 随x 的增大而增大, 又因为当1x =−时,0y =, 所以0y >.(3)因为抛物线的对称轴为直线212ax a−=−=,且过定点(0,3), 又因为该函数的图象与x 轴有两个公共点1(x ,0),2(x ,0),且1214x x −<<<, 所以当0a >时,230a a −+<, 解得3a >, 故3a >.当0a <时,230a a ++<,解得1a <−, 故1a <−.综上所述,3a >或1a <−. 故答案为:3a >或1a <−.【点评】本题考查二次函数的图象和性质,熟知二次函数的图象和性质是解题的关键.5.(2024•南京模拟)在平面直角坐标系xOy 中,点1(1,)y ,2(3,)y 在抛物线222y x mx m =−+上. (1)求抛物线的顶点(,0)m ; (2)若12y y <,求m 的取值范围;(3)若点0(x ,0)y 在抛物线上,若存在010x −<<,使102y y y <<成立,求m 的取值范围. 【分析】(1)利用配方法将已知抛物线解析式转化为顶点式,可直接得到答案; (2)由12y y <,得到221296m m m m −+<−+,解不等式即可; (3)由题意可知012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩,解不等式组即可.【解答】解:(1)抛物线222()y x mx m x m =−+=−. ∴抛物线的顶点坐标为(,0)m .故答案为:(,0)m ;(2)点1(1,)y ,2(3,)y 在抛物线222y x mx m =−+上,且12y y <, 221296m m m m ∴−+<−+,2m ∴<;(3)点0(x ,0)y 在抛物线上,存在010x −<<,使102y y y <<成立, ∴012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩,解得302m <<. 【点评】本题考查了二次函数与系数的关系,二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键.6.(2024•北京一模)在平面直角坐标系中,已知抛物线23y ax bx =++经过点(2,3)a −. (1)求该抛物线的对称轴(用含有a 的代数式表示);(2)点(2,)M t m −,(2,)N t n +,(,)P t p −为该抛物线上的三个点,若存在实数t ,使得m n p >>,求a 的取值范围.【分析】(1)将点(2,3)a −代入抛物线23y ax bx =++中,然后根据二次函数的对称轴公式代入数值,即可得出答案;(2)分类讨论当0a >和0a <,利用数形结合以及二次函数的性质就可以得出a 的取值范围. 【解答】解(1)抛物线23y ax bx =++经过点(2,3)a −, ∴把(2,3)a −代入23y ax bx =++得2(2)233a a ab ⨯−−+=,22b a ∴=,2223y ax a x ∴=++,∴抛物线的对称轴222a x a a=−=−,答:抛物线的对称轴为:x a =−;(2)①当0a >时,抛物线开口方向向上,对称轴0x a =−<,在x 轴的负半轴上,所以越靠近对称轴函数值越小, ∴当0t <时,(2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t ∴−<+,∴此时p m n >>与题干m n p >>相矛盾,故舍去, ∴当0t >时,(2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t ∴−<+,∴此时m n <与题干m n p >>相矛盾,故舍去;②当0a <时,抛物线开口方向向下,对称轴0x a =−>,在x 轴的正半轴上,所以越靠近对称轴函数值越大, ∴当0t >时,点M 、N 分别在对称轴同侧时,(2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t ∴−<+, .m n p >>,∴此时02a t <−<−,即20t a −<<,2t ∴>,∴当0t >时,点M 、N 分别在对称轴两侧时,(2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t t ∴−<<+,p m n ∴>>与题干m n p >>相矛盾,故舍去,∴当0t <时,且点M 、N 分别在对称轴两侧时,(2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t t ∴−<<+,n m ∴>与题干m n p >>相矛盾,故舍去,当0t <时,且点M 、N 分别在对称轴同侧时, (2,)M t m −,(2,)N t n +,(,)P t p −在抛物线上,22t t t ∴−<<+,n m ∴>与题干m n p >>相矛盾,故舍去,答:a 的取值范围为20(2)t a t −<<>.7.(2024•张家口一模)某课外小组利用几何画板来研究二次函数的图象,给出二次函数解析式2y x bx c =++,通过输入不同的b ,c 的值,在几何画板的展示区内得到对应的图象.(1)若输入2b =,3c =−,得到如图①所示的图象,求顶点C 的坐标及抛物线与x 轴的交点A ,B 的坐标; (2)已知点(1,10)P −,(4,0)Q .①若输入b ,c 的值后,得到如图②的图象恰好经过P ,Q 两点,求出b ,c 的值;②淇淇输入b ,嘉嘉输入1c =−,若得到二次函数的图象与线段PQ 有公共点,求淇淇输入b 的取值范围.【分析】(1)将2b =,3c =−,代入函数解析式,进行求解即可; (2)①待定系数法进行求解即可;②将1c =−代入解析式,得到抛物线必过点(0,1)−,求出1x =−和4x =的函数值,根据抛物线与线段PQ 有公共点,列出不等式进行求解即可. 【解答】解:(1)2y x bx c =++,解:当2b =,3c =−时,2223(1)4y x x x =+−=+−, ∴顶点C 的坐标为:(1,4)−−;当0y =时,2230x x +−=,即(3)(1)0x x +−=, 解得:13x =−,21x =, (3,0)A ∴−,(1,0)B ;(2)①抛物线恰好经过P ,Q则:1101640b c b c −+=⎧⎨++=⎩,解得:54b c =−⎧⎨=⎩;②当1c =−时,21y x bx =+−, 当0x =时,1y =−, ∴抛物线过(0,1)−,当1x =−时,11y b b =−−=−,当点(1,)b −−在点P 上方,或与点P 重合时,抛物线与线段PQ 有公共点,即:10b −…, 解得:10b −…;当4x =时,1641415y b b =+−=+,当点(4,154)b +在点Q 上方,或与点Q 重合时,抛物线与线段PQ 有公共点,即:1540b +…,154b ≥−; 综上:10b −…或154b ≥−. 【点评】本题考查二次函数的综合应用.正确的求出函数解析式,熟练掌握二次函数的图象和性质是解题的关键.8.(2024•浙江模拟)设二次函数24(y ax ax c a =−+,c 均为常数,0)a ≠,已知函数值y 和自变量x 的部分对应取值如下表所示:(1)判断m ,n 的大小关系,并说明理由; (2)若328m n −=,求p 的值;(3)若在m ,n ,p 这三个数中,只有一个数是负数,求a 的取值范围.【分析】(1)根据所给函数解析式,可得出抛物线的对称轴为直线2x =,据此可解决问题. (2)根据(1)中发现的关系,可求出m 的值,据此即可解决问题. (3)根据m 和n 相等,所以三个数中的负数只能为p ,据此可解决问题. 【解答】解:(1)m n =.因为二次函数的解析式为24y ax c =+, 所以抛物线的对称轴为直线422ax a−=−=, 又因为1522−+=, 所以点(1,)m −与(5,)n 关于抛物线的对称轴对称, 故m n =.(2)因为m n =,328m n −=, 所以8m =.将(0,3)和(1,8)−代入函数解析式得:348c a a c =⎧⎨++=⎩,解得13a c =⎧⎨=⎩所以二次函数的解析式为243y x x =−+.将2x =代入函数解析式得,224231p =−⨯+=−.(3)由(1)知,m n =, 所以m ,n ,p 中只能p 为负数. 将(0,3)代入函数解析式得,3c =, 所以二次函数解析式为243y ax ax =−+. 将1x =−代入函数解析式得,53m a =+. 将2x =代入函数解析式得,43p a =−+.则430530a a −+<⎧⎨+≥⎩,解得34a >,所以a 的取值范围是34a >. 【点评】本题考查二次函数图象与系数的关系及二次函数图象上点的坐标特征,熟知二次函数的图象和性质是解题的关键.9.(2024•北京模拟)在平面直角坐标系xOy 中,抛物线2(26)1y x m x =+−+经过点1(,)m y −,2(,)m y ,3(2,)m y +.(1)若13y y =,求抛物线的对称轴; (2)若231y y y <<,求m 的取值范围. 【分析】(1)利用对称轴意义即可求解;(2m 的不等式组,解不等式组即可.【解答】解:(1)抛物线2(26)1y x m x =+−+经过点1(,)m y −,2(,)m y ,3(2,)m y +,13y y =, ∴该抛物线的对称轴为:直线22m m x −++=,即直线1x =; (2)当0m >时,可知点1(,)m y −,2(,)m y ,3(2,)m y +从左至右分布, 231y y y <<,∴232232m m m m m m ++⎧−<⎪⎪⎨−++⎪−>⎪⎩,解得12m <<; 当0m <时,3m m m ∴<−<−+,21y y ∴>,不合题意,综上,m 的取值范围是12m <<.【点评】本题考查了二次函数图象上点的坐标特征,二次函数的性质,熟练掌握二次函数的性质是解题的关键.10.(2024•浙江模拟)在平面直角坐标系xOy 中,抛物线2(y ax bx c a =++,b ,c 为常数,且0)a ≠经过(2,4)A −−和(3,1)B 两点.(1)求b 和c 的值(用含a 的代数式表示);(2)若该抛物线开口向下,且经过(23,)C m n −,(72,)D m n −两点,当33k x k −<<+时,y 随x 的增大而减小,求k 的取值范围;(3)已知点(6,5)M −,(2,5)N ,若该抛物线与线段MN 恰有一个公共点时,结合函数图象,求a 的取值范围.【分析】(1)把(2,4)A −−和(3,1)B 代入2y ax bx c =++,即可求解;(2)先求出对称轴为:直线2x =,结合开口方向和增减性列出不等式即可求解; (3)分0a >时,0a <时,结合图象即可求解.【解答】解:(1)把(2,4)A −−和(3,1)B 代入2y ax bx c =++,得:424931a b c a b c −+=−⎧⎨++=⎩,解得:162b a c a =−⎧⎨=−−⎩;(2)抛物线经过(23,)C m n −,2,)m n −两点, ∴抛物线的对称轴为:直线237222m mx −+−==,抛物线开口向下,当33k x k −<<+时,y 随x 的增大而减小,32k ∴−…,即5k …; (3)①当0a >时,6x =−,5y …,即2(6)(1)(6)625a a a ⨯−+−⨯−−−…, 解得:1336a …,抛物线不经过点N ,如图①,抛物线与线段MN 只有一个交点,结合图象可知:1336a …;②当0a <时,若抛物线的顶点在线段MN 上时,则2244(62)(1)544ac b a a a a a−−−−−==,解得:11a =−,2125a =−, 当11a =−时,111112222(1)a −=−=⨯−, 此时,定点横坐标满足116222a−−……,符合题意; 当11a =−时,如图②,抛物线与线段MN 只有一个交点,如图③,当2125a =−时,11111312222()25a −=−=⨯−,此时顶点横坐标不满足116222a−−……,不符合题意,舍去; 若抛物线与线段MN 有两个交点,且其中一个交点恰好为点N 时,把(2,5)N 代入2(1)62y ax a x a =+−−−,得:252(1)262a a a =⨯+−⨯−−, 解得:54a =−,当54a =−时,如图④,抛物线和线段MN 有两个交点,且其中一个交点恰好为点N ,结合图象可知:54a <−时,抛物线与线段MN 有一个交点,综上所述:a 的取值范围为:1336a …或1a =−或54a <−.【点评】本题考查二次函数的性质和图象,根据题意画出图象,分类讨论是解题的关键.11.(2024•海淀区校级模拟)在平面直角坐标系xOy 中,点(0,3),1(6,)y 在抛物线2(0)y ax bx c a =++≠上. (1)当13y =时,求抛物线的对称轴;(2)若抛物线2(0)y ax bx c a =++≠经过点(1,1)−−,当自变量x 的值满足12x −……时,y 随x 的增大而增大,求a 的取值范围;(3)当0a >时,点2(4,)m y −,2(,)m y 在抛物线2y ax bx c =++上.若21y y c <<,请直接写出m 的取值范围.【分析】(1)当13y =时,(0,3),(6,3)为抛物线上的对称点,根据对称性求出对称轴;(2)把(0,3),(1,1)−−代入抛物线解析式得出a ,b 的关系,然后求出对称轴,再分0a >和0a <,由函数的增减性求出a 的取值范围;(3)先画出函数图象,再根据21y y c <<确定m 的取值范围. 【解答】解:(1)当13y =时,(0,3),(6,3)为抛物线上的对称点, 0632x +∴==, ∴抛物线的对称轴为直线3x =;(2)2(0)y ax bx c a =++≠过(0,3),(1,1)−−,3c ∴=,31a b −+=−, 4b a =+,∴对称轴为直线422b a x a a+=−=−,①当0a >时,12x −……时,y 随x 的增大而增大,∴412a a+−−…, 解得4a …,04a ∴<…;②当0a <时,12x −……时,y 随x 的增大而增大,∴422a a+−…, 解得45a −…, ∴405a −<…,综上:a 的取值范围是405a −<… 或04a <…;(3)点(0,3)在抛物线2y ax bx c =++上,3c ∴=,点2(4,)m y −,2(,)m y 在抛物线2y ax bx c =++上, ∴对称轴为直线422m mx m −+==−, ①如图所示:21y y c <<,6m ∴<且06232m +−>=, 56m ∴<<;②如图所示:21y y c <<,46m ∴−>, 10m ∴>,综上所述,m 的取值范围为56m <<或10m >.【点评】本题考查二次函数图象与系数的关系以及二次函数图象上点的坐标特征,关键是利用数形结合和分类讨论的思想进行解答.题型三.待定系数法求二次函数解析式(共3小题)12.(2024•保山一模)如图,抛物线2y ax bx c =++过(2,0)A −,(3,0)B ,(0,6)C 三点;点P 是第一象限内抛物线上的动点,点P 的横坐标是m ,且132m <<. (1)试求抛物线的表达式;(2)过点P 作PN x ⊥轴并交BC 于点N ,作PM y ⊥轴并交抛物线的对称轴于点M ,若12PM PN =,求m 的值.【分析】(1)将A ,B ,C 三点坐标代入函数解析式即可解决问题. (2)用m 表示出PM 和PN ,建立关于m 的方程即可解决问题. 【解答】解:(1)由题知,将A ,B ,C 三点坐标代入函数解析式得,4209306a b c a b c c −+=⎧⎪++=⎨⎪=⎩,解得116a b c =−⎧⎪=⎨⎪=⎩,所以抛物线的表达式为26y x x =−++.(2)将x m =代入抛物线得表达式得,26y m m =−++, 所以点P 的坐标为2(,6)m m m −++. 令直线BC 的函数解析式为y px q =+,则306p q q +=⎧⎨=⎩,解得26p q =−⎧⎨=⎩,所以直线BC 的函数解析式为26y x =−+. 因为132m <<,且抛物线的对称轴为直线12x =,所以12PM m =−. 又因为点N 坐标为(,26)m m −+,所以226(26)3PN m m m m m =−++−−+=−+. 因为12PM PN =, 所以211(3)22m m m −=−+,解得m =, 又因为132m <<,所以m =. 【点评】本题考查待定系数法求二次函数解析式及二次函数的图象和性质,熟知待定系数法及二次函数的图象和性质是解题的关键.13.(2024•东营区校级一模)如图,在平面直角坐标系xOy 中,直线28y x =−+与抛物线2y x bx c =−++交于A ,B 两点,点B 在x 轴上,点A 在y 轴上. (1)求抛物线的函数表达式;(2)点C 是直线AB 上方抛物线上一点,过点C 分别作x 轴,y 轴的平行线,交直线AB 于点D ,E .当38DE AB =时,求点C 的坐标.【分析】(1)根据一次函数解析式求出A ,B 两点坐标,再将A ,B 两点坐标代入二次函数解析式即可解决问题.(2)根据AOB ECD ∆∆∽得到CD 与OB 的关系,建立方程即可解决问题. 【解答】解:(1)令0x =得,8y =, 所以点A 的坐标为(0,8); 令0y =得,4x =, 所以点B 的坐标为(4,0);将A ,B 两点坐标代入二次函数解析式得,81640c b c =⎧⎨−++=⎩,解得28b c =⎧⎨=⎩,所以抛物线的函数表达式为228y x x =−++. (2)因为//CD x 轴,//CE y 轴, 所以AOB ECD ∆∆∽, 则CD DEOB AB=. 因为38DE AB =,4OB =, 所以32CD =. 令点C 坐标为2(,28)m m m −++, 则点D 坐标为21(2m m −,228)m m −++所以2211()222CD m m m m m =−−=−+,则213222m m −+=,解得1m =或3.当1m =时,2289m m −++=; 当3m =时,2285m m −++=; 所以点C 的坐标为(1,9)或(3,5).【点评】本题考查待定系数法求二次函数解析式及二次函数图象上点的坐标特征,熟知待定系数法及二次函数的图象和性质是解题的关键.14.(2024•南关区校级二模)已知二次函数2y x bx c =++的图象经过点(0,3)A −,(3,0)B .点P 在抛物线2y x bx c =++上,其横坐标为m .(1)求抛物线的解析式;(2)当23x −<<时,求y 的取值范围;(3)当抛物线2y x bx c =++上P 、A 两点之间部分的最大值与最小值的差为34时,求m 的值; (4)点M 在抛物线2y x bx c =++上,其横坐标为1m −.过点P 作PQ y ⊥轴于点Q ,过点M 作MN x ⊥轴于点N ,分别连结PM ,PN ,QM ,当PQM ∆与PNM ∆的面积相等时,直接写出m 的值. 【分析】(1)依据题意,将A 、B 两点代入解析式求出b ,c 即可得解;(2)依据题意,结合(1)所求解析式,再配方可得抛物线的最值,进而由23x −<<可以判断得解; (3)依据题意,分类讨论计算可以得解;(4)分别写出P 、Q 、M 、N 的坐标,PQM ∆与PNM ∆的面积相等,所以Q 到PM 的距离等于N 到PM 的距离,可得m 的值.【解答】解:(1)由题意,将(0,3)A −,(3,0)B 代入解析式2y x bx c =++得,3c =−,930b c ++=,2b ∴=−,3c =−,∴抛物线的解析式为223y x x =−−;(2)由题意,抛物线2223(1)4y x x x =−−=−−,∴抛物线223y x x =−−开口向上,当1x =时,y 有最小值为4−,当2x =−时,5y =;当3x =时,0y =, ∴当23x −<<时,45y −<…;(3)由题意得,2(,23)P m m m −−,(0,3)A −,①当0m <时,P 、A 两点之间部分的最大值为223m m −−,最小值为3−, 2323(3)4m m ∴−−−−=,解得:1m =−②当02m ……时,P 、A 两点之间部分的最大值为3−,最小值为223m m −−或4−, 显然最小值是4−时不合题意, ∴最小值为223m m −−, 233(23)4m m ∴−−−−=, 解得:32m =或12m =, 32m =时,P 、A 两点之间部分的最小值为4−,故舍去, ③当2m <时,P 、A 两点之间部分的最大值为223m m −−,最小值为4−, 2323(4)4m m ∴−−−−=,解得:1m =+,12+<,故舍去,综上,满足题意得m 的值为:1或12; (4)由题意得,2(1,4)M m m −−,(1,0)N m −,2(0,23)Q m m −−, 设PM y kx b =+,代入P 、M 两点, 2223(1)4mk b m m m k b m ⎧+=−−⎨−+=−⎩, 解得:1k =−,23b m m =−−,23PM y x m m =−+−−,PQM ∆与PNM ∆的面积相等,Q ∴到23PM y x m m =−+−−的距离与N 到23PM y x m m =−+−−的距离相等,Q 到23PM y x m m =−+−−的距离=,N 到23PMy x m m =−+−−的距离=, 2|||4|m m ∴−=−+,当2m <−时,24m m −=−,解得:m =,当20m −……时,24m m −=−,解得:m =,当02m <…时,24m m =−,解得:m =当2m <时,24m m =−,解得:m =综上,满足题意得m . 【点评】本题考查了二次函数,关键是注意分类讨论. 题型四.抛物线与x 轴的交点(共14小题)15.(2024•秦淮区校级模拟)已知函数2(2)2(y mx m x m =−−−为常数). (1)求证:不论m 为何值,该函数的图象与x 轴总有公共点.(2)不论m . (3)在22x −……的范围中,y 的最大值是2,直接写出m 的值. 【分析】(1)分两种情况讨论,利用判别式证明即可;(2)当1x =时,0y =,当0x =时,2y =−,即可得到定点坐标;(3)利用抛物线过两个定点,得到函数y 随x 增大而增大,代入解析式求出m 值即可. 【解答】解:(1)①当0m =时,函数解析式为22y x =−,此一次函数与x 轴有交点; ②当0m ≠时,函数解析式为2(2)2y mx m x =−−−,令0y =,则有2(2)20mx m x −−−=,△2222(2)4(2)44844(2)0m m m m m m m m =−−⨯−=−++=++=+…. ∴不论m 为何值,该函数的图象与x 轴总有公共点.(2)222(2)222()22y mx m x mx mx x m x x x =−−−=−+−=−+−, 当1x =时,0y =, 当0x =时,2y =−,∴不论m 为何值,该函数的图象经过的定点坐标是(1,0).(0,2)−故答案为:(1,0),(0,2)−,(3)若0m =,函数22y x =−,y 随x 增大而增大,当2x =时,2y =,与题干条件符; 当0m ≠时,函数2(2)2y mx m x =−−−是二次函数,①当0m >时,抛物线过(1,0),(0,2)−两点,当22x −……的范围中时,y 随x 的增大而增大, ∴当2x =时,2y =,即242(2)2m m =−−−,解得0m =(舍去).②当0m <时,抛物线过(1,0),(0,2)−两点,其增减性依旧是y 随x 的增大而增大和①相同.综上分析,0m =.【点评】本题考查了二次函数的图象与性质,熟练掌握二次函数的性质是解答本题的关键.16.(2024•柳州模拟)如图,在平面直角坐标系中,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,B 点的坐标为(3,0),与y 轴交于点(0,3)C −,点D 为抛物线的顶点. (1)求这个二次函数的解析式; (2)求ABD ∆的面积【分析】(1)利用待定系数法求解即可; (2)先求出点A 和点D 坐标,再根据||2D ABD AB y S ∆⋅=解析求解即可.【解答】解:(1)将(3,0)B ,(0,3)C −代入2y x bx c =++得0933b c c =++⎧⎨=−⎩,解得23b c =−⎧⎨=−⎩,∴二次函数的解析式为:223y x x =−−;(2)将223y x x =−−配方得顶点式2(1)4y x =−−, ∴顶点(1,4)D −,在223y x x =−−中,当2230y x x =−−=时, 解得1x =−或3x =, (1,0)A ∴−,4AB ∴=, ∴||44822D ABD AB y S ∆⋅⨯===. 【点评】本题主要考查了抛物线与x 轴的交点,二次函数的性质,二次函数图象上点的坐标特征,待定系数法求二次函数解析式,熟练掌握二次函数的性质是解答本题的关键.17.(2024•安阳模拟)如图,在平面直角坐标系xOy 中,抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同,且与x 轴交于点(1,0)−和(4,0).直线2y kx =+分别与x 轴、y 轴交于点A ,B ,交抛物线2y ax bx c =++于点C ,D (点C 在点D 的左侧). (1)求抛物线的解析式;(2)点P 是直线2y kx =+上方抛物线上的任意一点,当2k =时,求PCD ∆面积的最大值; (3)若抛物线2y ax bx c =++与线段AB 有公共点,结合函数图象请直接写出k 的取值范围.【分析】(1)根据题意直接求出二次函数解析式即可;(2)求出直线与抛物线的交点C ,D 坐标,过点P 作y 轴的平行线交CD 于点H ,交x 轴于点G ,设点P坐标为(m ,234)(12)m m m −++−<<,则点(,22)H m m +,求出PH ,由三角形的面积公式求出关于m 的函数解析式,再根据函数的性质求最值; (3)分0k >和0k <两种情况讨论即可.【解答】解:(1)抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同,1a ∴=−,抛物线2y ax bx c =++与x 轴交于点(1,0)−和(4,0), ∴抛物线的解析式为2(1)(4)34y x x x x =−+−=−++;(2)当2k =时,联立方程组22234y x y x x =+⎧⎨=−++⎩,解得10x y =−⎧⎨=⎩或26x y =⎧⎨=⎩, (1,0)C ∴−,(2,6)D ,过点P 作y 轴的平行线交CD 于点H ,交x 轴于点G ,如图,设点P 坐标为(m ,234)(12)m m m −++−<<, ∴点(,22)H m m +,2234(22)2PH m m m m m ∴=−++−+=−++,221331273(2)()22228PCD S PH m m m ∆∴=⨯=−++=−−+, 302−<,12m −<<, ∴当12m =时,S 有最大值,最大值为278. PCD ∴∆面积的最大值为278; (3)令0x =,则2y =, ∴点B 坐标为(0,2),令0y =,则20kx +=, 解得2x k=−,∴点A 坐标为2(k−,0), 若抛物线2y ax bx c =++与线段AB 有公共点, 当0k >时,如图所示,则21k−<−, 解得02k <<; 当0k <时,如图所示:则24k−>, 解得102k −<<;综上所述,k 的取值范围为02k <<或102k −<<.【点评】本题考查抛物线与x 轴的交点,待定系数法求函数解析式,二次函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数的最值等知识,关键是对这些知识的掌握和运用.18.(2024•西湖区校级模拟)已知21()y ax a b x b =+++和22()(y bx a b x a a b =+++≠且0)ab ≠是同一直角坐标系中的两条抛物线.(1)当1a =,3b =−时,求抛物线21()y ax a b x b =+++的顶点坐标; (2)判断这两条抛物线与x 轴的交点的总个数,并说明理由;(3)如果对于抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +….当20y …时,求自变量x 的取值范围.【分析】(1)把a ,b 的值代入配方找顶点即可解题;(2)分别令10y =,20y =,解方程求出方程的解,然后根据条件确定交点的个数即可解题;(3)现根据题意得到0a <,且24()224ab a b a b a−+=+,然后得到30b a =−>,借助图象求出不等式的解集即可.【解答】解:(1)当1a =,3b =−时,2221()23(1)4y ax a b x b x x x =+++=−−=−−, ∴顶点坐标为(1,4)−;(2)3个,理由为:令10y =,则2()0ax a b x b +++=, 即()(1)0ax b x ++=, 解得:1bx a=−,21x =−, 令20y =,则2()0bx a b x a +++=, 即()(1)0bx a x ++=, 解得:1ax b=−,21x =−, 又a b ≠且0ab ≠,∴两条抛物线与x 轴的交点总个数为3个;(3)抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…,0a ∴<,且24()224ab a b a b a−+=+,整理得:30b a =−>,∴22()y bx a b x a =+++的开口向上,且抛物线与x 轴交点的横坐标为113x =,21x =−, 如图所示,借助图象可知当13x …或1x −…时,20y ….【点评】本题考查二次函数的图象和性质,掌握配方法求顶点坐标,二次函数和一元二次方程的关系是解题的关键.19.(2024•三元区一模)抛物线23y ax bx =++与x 轴相交于点(1,0)A ,(3,0)B ,与y 轴正半轴相交于点C . (1)求抛物线的解析式;(2)点1(M x ,1)y ,2(N x ,2)y 是抛物线上不同的两点. ①当1x ,2x 满足什么数量关系时,12y y =; ②若12122()x x x x +=−,求12y y −的最小值. 【分析】(1)用待定系数法即可求解;(2)①若12y y =,则M 、N 关于抛物线对称轴对称,即可求解;②22121122121212(43)(43)()()4()y y x x x x x x x x x x −=−+−−+=+−+−,而12122()x x x x +=−,得到12y y −的函数表达式,进而求解.【解答】解:(1)设抛物线的表达式为:12()()y a x x x x =−−, 即2(1)(3)(43)y a x x a x x =−−=−+, 即33a =, 解得:1a =,故抛物线的表达式为:243y x x =−+;(2)如图,。
二次函数中常见的几种综合题型

二次函数中常见的几种综合题型二次函数常见的几类综合题型一、求线段最大值及根据面积求点坐标问题1.已知抛物线 $y=x^2+bx+c$ 的图象与 $x$ 轴的一个交点为 $B(5,0)$,另一个交点为 $A$,且与 $y$ 轴交于点 $C(0,5)$。
1) 求直线 $BC$ 与抛物线的解析式;2) 若点 $M$ 是抛物线在 $x$ 轴下方图象上的一个动点,过点 $M$ 作 $MN\parallel y$ 轴交直线 $BC$ 于点 $N$,求$MN$ 的最大值;3) 在 (2) 的条件下,$MN$ 取得最大值时,若点 $P$ 是抛物线在 $x$ 轴下方图象上任意一点,以 $BC$ 为边作平行四边形 $CBPQ$,设平行四边形 $CBPQ$ 的面积为 $S_1$,$\triangle ABN$ 的面积为 $S_2$,且 $S_1=6S_2$,求点$P$ 的坐标。
2.对称轴为直线 $x=-1$ 的抛物线$y=ax^2+bx+c(a\neq0)$ 与 $x$ 轴相交于 $A$、$B$ 两点,其中点 $A$ 的坐标为 $(-3,0)$。
1) 求点 $B$ 的坐标;2) 已知 $a=1$,$C$ 为抛物线与 $y$ 轴的交点。
①若点 $P$ 在抛物线上,且 $S_{\trianglePOC}=4S_{\triangle BOC}$,求点 $P$ 的坐标;②设点 $Q$ 是线段 $AC$ 上的动点,作 $QD\perp x$ 轴交抛物线于点 $D$,求线段 $QD$ 长度的最大值。
二、求三角形周长及面积的最值问题3.已知抛物线 $y=ax^2+bx+c$ 经过 $A(-3,a-b+c)$,$B(1,a+b+c)$,$C(c,a+3c-b)$ 三点,其顶点为 $D$,对称轴是直线 $l$,$l$ 与 $x$ 轴交于点 $H$。
1) 求该抛物线的解析式;2) 若点 $P$ 是该抛物线对称轴 $l$ 上的一个动点,求$\triangle PBC$ 周长的最小值;3) 如图 (2),若 $E$ 是线段 $AD$ 上的一个动点($E$ 与$A$、$D$ 不重合),过点 $E$ 作平行于 $y$ 轴的直线交抛物线于点 $F$,交 $x$ 轴于点 $G$,设点 $E$ 的横坐标为 $m$,$\triangle ADF$ 的面积为 $S$。
(完整版)二次函数知识点与题型总结.doc

二次函数知识点一、平面直角坐标系1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。
注意: x 轴和y轴上的点,不属于任何象限。
2、点的坐标的概念点的坐标用a, b 表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当 a b 时,a,b和b, a是两个不同点的坐标。
知识点二、函数及其相关概念1、变量与常量在某一变化过程中,可以取不同数值的量叫做变量,数值保持不变的量叫做常量。
一般地,在某一变化过程中有两个变量x 与y,如果对于 x 的每一个值,y都有唯一确定的值与它对应,那么就说 x 是自变量,y 是x的函数。
2、函数解析式用来表示函数关系的数学式子叫做函数解析式或函数关系式。
使函数有意义的自变量的取值的全体,叫做自变量的取值范围。
3、函数的三种表示法及其优缺点(1)解析法两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法。
(2)列表法把自变量 x 的一系列值和函数y 的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
(3)图像法用图像表示函数关系的方法叫做图像法。
4、由函数解析式画其图像的一般步骤(1)列表:列表给出自变量与函数的一些对应值(2)描点:以表中每对对应值为坐标,在坐标平面内描出相应的点(3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来。
知识点三、概念总结及基本性质1、二次函数的概念:一般地,形如y ax2bx c( a ,b ,c 是常数, a 0 )的函数,叫做二次函数。
二次函数的定义域是全体实数.2. 、二次函数y ax2bx c 的结构特征:⑴ 等号左边是函数,右边是关于自变量⑵ a ,b ,c 是常数, a 是二次项系数,x 的二次式,x 的最高次数是b 是一次项系数,c 是常数项.2.3、二次函数的基本形式(平移规律:左加右减,上加下减)(1) y ax2的性质: a 的绝对值越大,抛物线的开口越小。
二次函数(十二大题型综合归纳 )(学生版)--新九年级数学

二次函数(十二大题型综合归纳)题型1:二次函数的概念1以下函数式二次函数的是()A.y=ax2+bx+cB.y=2x-12-4x2C.y=ax2+bx+c a≠0D.y=x-1x-22二次函数y=2x x−3的二次项系数与一次项系数的和为()A.2B.-2C.-1D.-4题型2:二次函数的值3已知二次函数y=x2+2x-5,当x=3时,y=.4已知二次函数y=ax2+2c,当x=2时,函数值等于8,则下列关于a,c的关系式中,正确的是()A.a+2c=8B.2a+c=4C.a-2c=8D.2a-c=45二次函数y=ax2+bx-3a≠0的图象经过点2,-2,则代数式2a+b的值为.题型3:二次函数的条件6已知y=mx m-2+2mx+1是y关于x的二次函数,则m的值为()A.0B.1C.4D.0或47关于x的函数y=a-bx2+1是二次函数的条件是()A.a≠bB.a=bC.b=0D.a=0题型4:列二次函数关系式8已知有n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数为m,则m关于n的函数解析式为.题型5:特殊二次函数的图像和性质9关于二次函数y =-34x 2-1的图像,下列说法错误的是()A.抛物线开口向下B.对称轴为直线x =0C.顶点坐标为0,-1D.当x <0时,y 随x 的增大而减小,当x >0时,y 随x 的增大而增大10抛物线y =34x 2与抛物线y =-34x 2+3的相同点是()A.顶点相同B.对称轴不相同C.开口方向一样D.顶点都在y 轴上11如果二次函数y =ax 2+m 的值恒大于0,那么必有()A.a >0,m 取任意实数B.a >0,m >0C.a <0,m >0D.a ,m 均可取任意实数12对于二次函数y =-3(x -2)2的图象,下列说法正确的是()A.开口向上B.对称轴是直线x =-2C.当x >-2时,y 随x 的增大而减小D.顶点坐标为2,013二次函数:①y =-13x 2+1;②y =12(x +1)2-2;③y =-12(x +1)2+2;④y =12x 2;⑤y =-12(x -1)2;⑥y =12(x -1)2.(1)以上二次函数的图象的对称轴为直线x =-1的是(只填序号);(2)以上二次函数有最大值的是(只填序号)﹔(3)以上二次函数的图象中关于x 轴对称的是(只填序号).14设函数y 1=x -a 12,y 2=x -a 22,y 3=x -a 3 2.直线x =b 的图象与函数y 1,y 2,y 3的图象分别交于点A b ,c 1,B b ,c 2 ,C b ,c 3,()A.若b <a 1<a 2<a 3,则c 2<c 3<c1B.若a 1<b <a 2<a 3,则c 1<c 2<c 3C.若a 1<a 2<b <a 3,则c 3<c 2<c 1 D.若a 1<a 2<a 3<b ,则c 3<c 2<c 115已知二次函数y =(x -m )2,当x ≤1时,y 随x 的增大而减小,则m 的取值范围是.16已知关于x 的一元二次方程x 2-(2m +1)x +m 2-1=0有实数根a ,b ,则代数式a 2-ab +b 2的最小值为.题型6:与特殊二次函数有关的几何知识17在平面直角坐标系中,点A是抛物线y=a x-42+k与y轴的交点,点B是这条抛物线上的另一点,且AB⎳x轴,则以AB为边的等边三角形ABC的周长为.18在平面直角坐标系内有线段PQ,已知P(3,1)、Q(9,1),若抛物线y=(x-a)2与线段PQ有交点,则a的取值范围是.19二次函数y=-x+3的图象上任意二点连线不与x轴平行,则t的取值范围2+h t≤x≤t+2为.题型7:二次函数y=ax2+bx+c的图像和性质20下列抛物线中,与抛物线y=x2-2x+8具有相同对称轴的是()A.y=4x2+2x+4B.y=x2-4xC.y=2x2-x+4D.y=-2x2+4x21若抛物线y=x2+ax+1的顶点在y轴上,则a的值为()A.2B.1C.0D.-222抛物线y=x-1x+5图象的开口方向是(填“向上”或“向下”).23当二次函数y=ax2+bx+c有最大值时,a可能是()A.1B.2C.-2D.324已知抛物线y=x2-2bx+b2-2b+1(b为常数)的顶点不在抛物线y=x2+c(c为常数)上,则c应满足()A.c≤2B.c<2C.c≥2D.c>225已知二次函数y=x2-2mx+m的图象经过A1,y1,B5,y2两个点,下列选项正确的是()A.若m<1,则y1>y2B.若1<m<3,则y1<y2C.若1<m<5,则y1>y2D.若m>5,则y1<y2题型8:二次函数y=ax2+bx+c的最值与求参数范围问题26已知直线y=2x+t与抛物线y=ax2+bx+c a≠0,且点B、B m,n有两个不同的交点A3,5是抛物线的顶点,当-2≤a≤2时,m的取值范围是.27已知抛物线y=x2+bx+c经过点(1,-2),(-2,13).(1)求抛物线解析式及对称轴.(2)关于该函数在0≤x<m的取值范围内,有最小值-3,有最大值1,求m的取值范围.28已知二次函数y=mx2-4m2x-3(m为常数,m>0).(1)若点(-2,9)在该二次函数的图象上.①求m的值:②当0≤x≤a时,该二次函数值y取得的最大值为18,求a的值;(2)若点P(x,y)是该函数图象上一点,当0≤x p≤4时,y p≤-3,求m的取值范围.题型9:根据二次函数y=ax2+bx+c的图像判断有关信息29函数y=ax2+bx+c a≠0与y=kx的图象如图所示,现有以下结论:①c=3;②k=3;③3b+c+6=0;④当1<x<3时,x2+b-1x+c<0.其中正确的为.(填写序号即可)30如图,已知二次函数y=ax2+bx+c a≠0的图象与x轴交于点A-1,0,与y轴的交点在0,-2和0,-1之间(不包括这两点),对称轴为直线x=1,下列结论:①4a+2b+c>0;②4ac-b2<8a;③13<a<23;④b>c;⑤直线y=k i(k i>0,i=1,2,3,⋯,2023)与抛物线所有交点的横坐标之和为4046;其中正确结论的个数有()A.2个B.3个C.4个D.5个题型10:二次函数的应用31如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为8m ,两侧距地面4m 高处各有一盏灯,两灯间的水平距离为6m ,则这个门洞内部顶端离地面的距离为()A.7.5B.8C.649D.64732某炮兵部队实弹演习发射一枚炮弹,经x 秒后的高度为y 米,且时间x 与高度y 的关系为y =ax 2+bx .若此炮弹在第5秒与第16秒时的高度相等,则在下列哪一个时间段炮弹的高度达到最高.()A.第8秒B.第10秒C.第12秒D.第15秒33在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y (单位:米)与飞行的水平距离x (单位:米)之间具有函数关系y =-116x 2+58x +32,则小康这次实心球训练的成绩为()A.14米B.12米C.11米D.10米34某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m ).有下列结论:①AB =30m ;②池底所在抛物线的解析式为y =145x 2-5;③池塘最深处到水面CD 的距离为3.2m ;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为1.2m .其中结论错误的是()A.①B.②C.③D.④35某建筑工程队借助一段废弃的墙体CD,CD长为18米,用76米长的铁栅栏围成两个相连的长方形仓库,为了方便取物,在两个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,现有如下两份图纸(图纸1点A在线段DC的延长线上,图纸2点A在线段DC上),设AB =x米,图纸1,图纸2的仓库总面积分别为y1平方米,y2平方米.(1)分别写出y1,y2与x的函数关系式;(2)小红说:“y1的最大值为384.y2的最大值为507.”你同意吗?请说明理由.题型11:二次函数的解答证明题36已知二次函数y=-x2+bx+c.(1)当b=4,c=3时,①求该函数图象的顶点坐标.②当-1≤x≤3时,求y的取值范围.(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.37如图,已知二次函数y=-12x2+bx+c的图象与x轴交于A1,0,B,与y轴交于点C0,-52.CD∥x轴交抛物线于点D.(1)求b,c的值.(2)已知点E在抛物线上且位于x轴上方,过E作y轴的平行线分别交AB,CD于点F,G,且GE= 2GD,求点E的坐标.38在直角坐标系中,设函数y=ax2+bx+c(a,b,c是常数,a≠0).(1)已知a=1.①若函数的图象经过0,3和-1,0两点,求函数的表达式;②若将函数图象向下平移两个单位后与x轴恰好有一个交点,求b+c的最小值.(2)若函数图象经过-2,m,-3,n和x0,c,且c<n<m,求x0的取值范围.题型12:二次函数压轴题39在平面直角坐标系中,抛物线y=-x2-4x+c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为-5,0.(1)求点C的坐标;(2)如图1,若点P是第二象限内抛物线上一动点,求三角形ACP面积的最大值;(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.。
二次函数常见题型
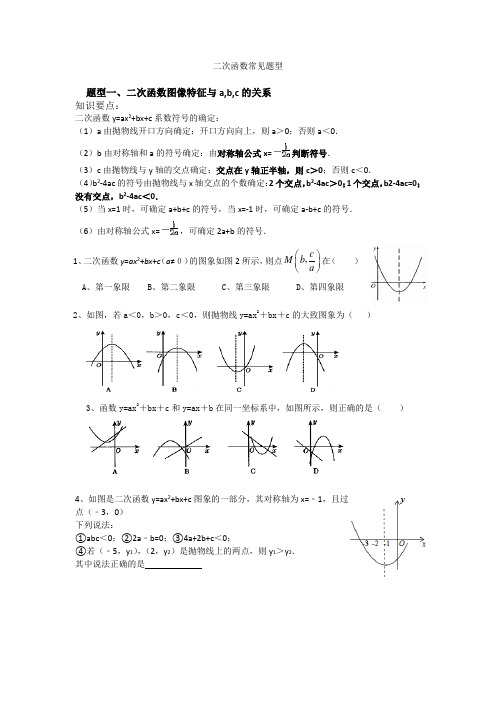
①abc<0;②2a﹣b=0;③4a+2b+c<0;
④若(﹣5,y1),(2,y2)是抛物线上的两点,则y1>y2.
其中说法正确的是
5、如图所示,二次函数 的图象中,王刚同学观察得
出了下面四条结论:① ;② ;③ ;④ .
其中错误的有
6、已知二次函数 的图象如图所示,有下列结论:① ;
②2a+b=0;③ ;④ .其中正确的有
题型四:抛物线的图形变换问题(平移、旋转、轴对称)
1、抛物线 向右平移3个单位,再向上平移2个单位,则所得抛物线的解析式。
2、抛物线 可以由抛物线 先向平移个单位,再向平移个单位得到的。
3、将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位得到的抛物线是
4、将抛物线C:y=x²+3x-10,将抛物线C平移到C/。若两条抛物线C,C/关于直线x=1对称,则下列平移方法中正确的是()
7
16
…
根据表格你能找出抛物线图象上的对称点吗?
你能写出抛物线的对称轴吗?
抛物线与x轴的交点坐标为,
当x=2时,函数值y=
(1)若M是函数 图象上对称轴右侧 轴上方的一个动点,其横坐标为 ,四边形MNPQ为矩形,P、N在 轴上,Q、M在抛物线上,求四边形的周长C与 之间的函数关系式.
(2)如果图象向右平移3个单位,设M点横坐标为 ,其它条件不变,
10、如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限内是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.
专题5.4 求二次函数解析式常考类型(六大题型)(原卷版)

专题5.4 求二次函数解析式常考类型(六大题型)【题型1 开放型】【题型2 一般式】【题型3 顶点式】【题型4两根式】【题型5平移变换型】【题型6 对称变换型】【题型1 开放型】【典例1】(2023秋•海淀区期中)写出一个顶点在坐标原点,开口向下的抛物线的表达式.【变式1-1】(2023秋•昌平区期中)请写出一个开口向下,对称轴为直线x=3的抛物线的解析式.【变式1-2】(2022秋•伊川县期末)请写出一个开口向上,并且与y轴交于点(0,2)的抛物线的表达式:.【变式1-3】(2023•苏州二模)已知抛物线顶点坐标为(2,3),则抛物线的解析式可能为()A.y=﹣(x+2)2﹣3B.y=﹣(x﹣2)2﹣3C.y=﹣(x+2)2+3D.y=﹣(x﹣2)2+3【题型2 一般式】【方法点拨】当题目给出函数图像上的三个点时,设为一般式2=++(a,y ax bx ca≠),转化成一个三元一次方程组,以求得a,b,c的值;b,c为常数,0【典例2】(2023•宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).(1)求该二次函数的表达式及图象的顶点坐标.(2)当y≤﹣2时,请根据图象直接写出x的取值范围.【变式2-1】(2022秋•新罗区校级月考)求经过A(﹣1,﹣5)、B(0,﹣4)、C(1,1)三点的抛物线的表达式?【变式2-2】(2023春•海淀区校级期末)已知抛物线y=2x2+bx+c过点(1,3)和(﹣1,5),求该抛物线的解析式.【变式2-3】(2023秋•崆峒区校级月考)已知二次函数过点A(﹣1,2),B(1,﹣4),C(0,3)三点,求这个二次函数的解析式.【变式2-4】(2023秋•博乐市月考)已知抛物线y=﹣x2+bx+c经过A(﹣1,0),B(5,0)两点,顶点为P.(1)求抛物线的解析式;(2)求△ABP的面积.【方法点拨】若已知抛物线的顶点或对称轴、最值,则设为顶点式()k-=2.这顶点坐标为(h,k),对称轴直线x = h,最值为当x = h y+axh时,y最值=k来求出相应的系数.【典例3】(2023秋•龙马潭区月考)若抛物线的顶点坐标是A(﹣1,﹣3),并且抛物线经过点B坐标为(1,﹣1).(1)求出该抛物线的关系式;(2)当x满足什么条件时,y随x的增大而增大.【变式3-1】(2023秋•临潼区月考)已知二次函数的图象顶点为P(﹣2,2),且过点A(0,﹣2).(1)求该抛物线的解析式;(2)试判断点B(1,﹣6)是否在此函数图象上.【变式3-2】(2023秋•越秀区校级月考)已知二次函数图象的顶点坐标为A(2,﹣3),且经过点B(3,0).(1)求该二次函数的解析式;(2)判断点C(3,﹣4)、D(1,0)是否在该函数图象上,并说明理由.【方法点拨】已知图像与 x 轴交于不同的两点()()1200x x ,,,,设二次函数的解析式为()()21x x x x a y --=,根据题目条件求出a 的值.【典例4】(2023•荔湾区校级一模)如图,二次函数y =ax 2+bx +c 经过点A (﹣1,0),B (5,0),C (0,﹣5),点D 是抛物线的顶点,过D 作x 轴垂线交直线BC 于E .(1)求此二次函数解析式及点D 坐标.(2)连接CD ,求三角形CDE 的面积.(3)ax 2+bx +c >0时,x 的取值范围是 .【变式4-1】(2023秋•广西月考)若二次函数的图象经过(﹣1,0),(3,0),(0,3)三点,求这个二次函数的解析式.【变式4-2】(2023秋•长沙月考)已知二次函数y =ax 2+bx +c 的图象经过点A (0,﹣3)、(1,0)和C (﹣3,0).求此二次函数的解析式.【变式4-3】(2023•南山区三模)如图,抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0),且OB=OC.(1)求抛物线的表达式;(2)如图,点D是抛物线的顶点,求△BCD的面积.【题型5平移变换型】【方法点拨】将一个二次函数的图像经过上下左右的平移得到一个新的抛物线.要借此类题目,应先将已知函数的解析是写成顶点式y = a( x – h)2 + k,当图像向左(右)平移n个单位时,就在x – h上加上(减去)n;当图像向上(下)平移m个单位时,就在k上加上(减去)m.其平移的规律是:h值正、负,右、左移;k值正负,上下移.由于经过平移的图像形状、大小和开口方向都没有改变,所以a得值不变.【典例5】将抛物线y=x2﹣6x+5向上平移两个单位长度,再向右平移一个单位长度后,求平移后的抛物线解析式.【变式5-1】(2022秋•洪山区期中)将二次函数y=(x﹣1)2﹣4的图象沿直线y=1翻折,所得图象的函数表达式为()A.y=﹣(x﹣1)2+4B.y=(x+1)2﹣4C.y=﹣(x+1)2﹣6D.y=﹣(x﹣1)2+6【变式5-2】(秋•普陀区校级期中)将抛物线y=2x2先向下平移3个单位,再向右平移m(m>0)个单位,所得新抛物线经过点(1,5),求新抛物线的表达式及新抛物线与y轴交点的坐标.【变式5-3】已知a+b+c=0且a≠0,把抛物线y=ax2+bx+c向下平移一个单位长度,再向左平移5个单位长度所得到的新抛物线的顶点是(﹣2,0),求原抛物线的表达式.【变式5-4】抛物线y=x2+2x﹣3与x轴正半轴交于A点,M(﹣2,m)在抛物线上,AM交y轴于D点,抛物线沿射线AD方向平移√2个单位,求平移后的解析式.【题型6 对称变换型】【方法点拨】根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.【典例6-1】(2022秋•上城区月考)已知y=﹣3(x﹣2)2﹣7将它的图象沿着x轴对折后的函数表达式是.【典例6-2】(2022秋•汉阳区校级月考)抛物线y=x2﹣6x+7绕其顶点旋转180°后得到抛物线y=ax2+bx+c,则a=,b=,c=.【变式6-1】(2022秋•萧山区月考)抛物线y=(x+3)2﹣4关于y轴对称的抛物线解析式为.【变式6-2】(2022秋•汉川市月考)若抛物线y=ax2+c与y=﹣4x2+3关于x轴对称,则a+c=.【变式6-3】(2021秋•镇海区期末)把二次函数y=(x﹣1)2+2的图象关于y 轴对称后得到的图象的函数关系式为.【变式6-4】(2021秋•闽侯县期中)二次函数y=2(x﹣3)2+1图象绕原点旋转180°得新图象的解析式为.【变式6-5】(2023•雁塔区校级三模)已知抛物线L:y=x2+bx+c经过点A(﹣2,0),点B(4,﹣6).抛物线L′与L关于x轴对称,点B在L'上的对应点为B′.(1)求抛物线L的表达式;(2)抛物线L'的对称轴上是否存在点P,使得△AB′P是以AB′为直角边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由.【变式6-6】(2022•岳阳)如图1,在平面直角坐标系xOy中,抛物线F1:y=x2+bx+c经过点A(﹣3,0)和点B(1,0).(1)求抛物线F1的解析式;(2)如图2,作抛物线F2,使它与抛物线F1关于原点O成中心对称,请直接写出抛物线F2的解析式;(3)如图3,将(2)中抛物线F2向上平移2个单位,得到抛物线F3,抛物线F1与抛物线F3相交于C,D两点(点C在点D的左侧).①求点C和点D的坐标;②若点M,N分别为抛物线F1和抛物线F3上C,D之间的动点(点M,N与点C,D不重合),试求四边形CMDN面积的最大值.。
常考二次函数综合题整理(全)

常考二次函数综合题整理 题型一最短路径问题1、如图,抛物线y=﹣12x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,并证明你的结论;(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.【变式】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;题型二最大面积(线段最长)问题2、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?并求出这个最大值.3、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH△x轴于点H,与BC交于点M,连接PC,求线段PM的最大值.【变式】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,过点P作PE△y轴于点E,连接AE.求△PAE面积S的最大值;题型三 存在点构成等腰三角形问题4、如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.5、如图,已知二次函数y=ax 2+bx+3的图象交x 轴于点A (1,0),B (3,0),交y 轴于点C .(1)求这个二次函数的表达式;(2)直线x=m 分别交直线BC 和抛物线于点M ,N ,当△BMN 是等腰三角形时,直接写出m 的值.【变式】已知二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 、DB ,求证:△BCD 是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P ,使得△PDC 为等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由.【变式】如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点()0,2C -,点A 的坐标是()2,0,P 为抛物线上的一个动点,过点P 作PD x ⊥轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线1x =-.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且14PE OD =,求PBE ∆的面积. (3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的下方,是否存在点M ,使BDM ∆是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.题型四 存在点构成直角三角形问题6、如图,抛物线2y ax bx 4=+-经过()A 3,0-,()B 5,4-两点,与y 轴交于点C ,连接AB ,AC ,BC .()1求抛物线的表达式;()2求证:AB 平分CAO ∠;()3抛物线的对称轴上是否存在点M ,使得ABM V 是以AB 为直角边的直角三角形,若存在,求出点M 的坐标;若不存在,请说明理由.【变式】如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求抛物线的解析式和直线AC 的解析式;(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.●题型四存在点构成等腰直角三角形问题7、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)过点P作x轴的垂线,交线段AB于点D,再过点P做PE△x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.●题型四存在点构成平行四边形问题8、如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.()B-,对称轴为直线l,点M是线段AB的中点.0,5(1)求抛物线的表达式;(2)写出点M的坐标并求直线AB的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.9、如图,已知抛物线y=12x2+bx+c与直线AB:y=12x+12相交于点A(1,0)和B(t,52),直线AB交y轴于点C.(1)求抛物线的解析式及其对称轴;(2)设点M是抛物线对称轴上一点,点N在抛物线上,以点A、B、M、N为顶点的四边形是否可能为矩形?若能,请求出点M的坐标,若不能,请说明理由.10、如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.11、如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在x轴下方且在抛物线对称轴上,是否存在一点Q,使△BQC=△BAC?若存在,求出Q点坐标;若不存在,说明理由.12、如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.连接AC,当直线AM与直线BC的夹角等于△ACB 的2倍时,请直接写出点M的坐标【变式】如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C 两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.【变式】如图,抛物线y=ax 2+bx+c 经过A (﹣1,0),B (4,0),C (0,3)三点,D 为直线BC 上方抛物线上一动点,DE△BC 于E .(1)求抛物线的函数表达式;(2)如图1,求线段DE 长度的最大值;(3)如图2,设AB 的中点为F ,连接CD ,CF ,是否存在点D ,使得△CDE 中有一个角与△CFO 相等?若存在,求点D 的横坐标;若不存在,请说明理由.【变式】如图,已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ,B 两点,直线y x m =+过顶点C 和点B .(1)求m 的值;(2)求函数2(0)y ax b a =+≠的解析式;(3)抛物线上是否存在点M ,使得15MCB ∠=︒?若存在,求出点M 的坐标;若不存在,请说明理由.题型七 存在点使三角形相似问题13、如图,以D 为顶点的抛物线y=﹣x 2+bx+c 交x 轴于A 、B 两点,交y 轴于点C ,直线BC 的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在x 轴上是否存在一点Q ,使得以A 、C 、Q 为顶点的三角形与△BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.14、如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣12x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【变式】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(32,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求△ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE△AC,当△DCE 与△AOC相似时,求点D的坐标.【变式】如图,抛物线y=12x2+bx+c与直线y=12x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).(1)求抛物线的解析式;(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ△PA交y轴于点Q,问:是否存在点P 使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.题型七二次函数与圆结合问题15、如图,△E的圆心E(3,0),半径为5,△E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.(1)求抛物线的解析式;(2)判断直线l与△E的位置关系,并说明理由;(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.16、如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣x+与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).(1)求抛物线m的解析式;(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.【变式】在平面直角坐标系中,二次函数y=ax2+53x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣13x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.【变式】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B (点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP△x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.。
二次函数中考常见题型及解析

二次函数中考常见题型及解析二次函数在中考数学中是一个非常重要的知识点,通常都会有相关的考题出现。
下面就为大家总结了二次函数中考常见的题型及解析,供大家参考。
一、基本形式的图像与性质题1.二次函数 $y=ax^2$ 的图像是什么?二次函数 $y=ax^2$ 的图像是一条开口朝上或朝下的抛物线。
2.二次函数 $y=ax^2$ 的对称轴方程是什么?二次函数 $y=ax^2$ 的对称轴方程是 $x=0$(对称轴为 $y$ 轴)。
3.二次函数 $y=ax^2$ 的零点是什么?当 $y=ax^2=0$ 时,$x=0$,所以二次函数 $y=ax^2$ 的零点是原点$(0,0)$。
4.二次函数 $y=ax^2$ 的单调性是什么?当 $a>0$ 时,二次函数 $y=ax^2$ 开口朝上,单调递增;当 $a<0$ 时,二次函数 $y=ax^2$ 开口朝下,单调递减。
二、变形图像与性质题1.二次函数 $y=a(x-h)^2+k$ 的图像是什么?二次函数 $y=a(x-h)^2+k$ 的图像是以 $(h,k)$ 为顶点的开口朝上或朝下的抛物线。
2.二次函数 $y=a(x-h)^2+k$ 的对称轴方程是什么?二次函数 $y=a(x-h)^2+k$ 的对称轴方程是 $x=h$(对称轴为以$(h,k)$ 为顶点的直线)。
3.二次函数 $y=a(x-h)^2+k$ 的零点是什么?当 $y=a(x-h)^2+k=0$ 时,$x=h\pm \sqrt{-\frac{k}{a}}$,所以二次函数$y=a(x-h)^2+k$ 的零点为 $x=h+\sqrt{-\frac{k}{a}}$ 和 $x=h-\sqrt{-\frac{k}{a}}$。
4.二次函数 $y=a(x-h)^2+k$ 的单调性是什么?当 $a>0$ 时,二次函数 $y=a(x-h)^2+k$ 开口朝上,单调递增;当$a<0$ 时,二次函数 $y=a(x-h)^2+k$ 开口朝下,单调递减。
二次函数基础典型经典题型(全面超好)

二次函数精讲基础题型一认识二次函数1、y=mx m2+3m+2是二次函数,则m 的值为( )A 、0,-3B 、0,3C 、0D 、-32、关于二次函数y=ax 2+b ,命题正确的是( )A 、若a>0,则y 随x 增大而增大B 、x>0时y 随x 增大而增大。
C 、若x>0时,y 随x 增大而增大D 、若a>0则y 有最大值。
二简单作图1在一个坐标系内做出2x y =,12+=x y ,12-=x y ,2)1(-=x y ,2)1(+=x y 你发现了什么结论2同样的在同一个坐标系内做出2xy -=,22xy -=,12--=x y ,12+-=x y 2)1(--=x y ,2)1(+-=x y 的图像,你又发现了什么结论,并且与上一题的图像比较的话,你又有什么样新的发现3 已知抛物线y x x =-+123522,五点法作图。
2、已知y=ax 2+bx+c 中a<0,b>0,c<0 ,△<0,画出函数的大致图象。
三,二次函数的三种表达形式,求解析式 1求二次函数解析式:(1)抛物线过(0,2),(1,1),(3,5); (2)顶点M (-1,2),且过N (2,1); (3)与x 轴交于A (-1,0),B (2,0),并经过点M (1,2)。
2 抛物线过(-1,-1)点,它的对称轴是直线x +=20,且在x 轴上截取长度为22的线段,求解析式。
3、根据下列条件求关于x 的二次函数的解析式 (1)当x=3时,y 最小值=-1,且图象过(0,7)(2)图象过点(0,-2)(1,2)且对称轴为直线x=23(3)图象经过(0,1)(1,0)(3,0)(4)当x=1时,y=0;x=0时,y= -2,x=2 时,y=3(5)抛物线顶点坐标为(-1,-2)且通过点(1,10)三 图像与a,b,c 的符号之间的关系1、二次函数y=ax 2+bx+c 的图象是抛物线,其开口方向由_________来确定。
初中数学《二次函数》十大题型汇编含解析

二次函数【十大题型】【题型1 辨别二次函数】 (1)【题型2 由二次函数的定义求字母的值】 (3)【题型3 由二次函数的定义求字母的取值范围】 (4)【题型4 二次函数的一般形式】 (6)【题型5 求二次函数的值】 (7)【题型6 判断函数关系】 (9)【题型7 列二次函数关系式(几何图形)】 (11)【题型8 列二次函数关系式(增长率)】 (14)【题型9 列二次函数关系式(循环)】 (15)【题型10 列二次函数关系式(销售)】 (16)知识点1:二次函数的定义一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.其中x、y是变量,a、b、c是常量,a是二次项系数,b是一次项系数,c是常数项.y=ax2+bx+c(a、b、c是常数,a≠0)也叫做二次函数的一般形式.【题型1 辨别二次函数】【例1】(23-24九年级上·江西南昌·阶段练习)下列函数解析式中,yy一定是xx的二次函数的是()A.yy=2aaxx2B.yy=2xx+aa2C.yy=2xx2−1D.yy=xx2+1xx【答案】C【分析】本题考查二次函数的识别,形如yy=aaxx2+bbxx+cc(aa≠0)的函数是二次函数,根据定义逐一判断即可得到答案.【详解】解:A,当aa=0时,yy=2aaxx2=0,不是二次函数,不合题意;B,yy=2xx+aa2,yy是xx的一次函数,不合题意;C,yy=2xx2−1,yy一定是xx的二次函数,符合题意;D,yy=xx2+1xx中含有分式,不是二次函数,不合题意;故选C.【变式1-1】(23-24九年级上·安徽安庆·阶段练习)下列函数是二次函数的是()A.yy=2xx−1B.yy=√xx2−1C.yy=xx2−1D.yy=12xx【答案】C【分析】本题考查了二次函数的定义,能熟记二次函数的定义是解此题的关键,注意:形如yy=aaxx2+bbxx+cc (aa、b、c为常数,aa≠0)的函数叫二次函数.根据二次函数的定义逐个判断即可.【详解】解:A、函数yy=2xx−1是一次函数,不是二次函数,故本选项不符合题意;B、函数yy=√xx2−1根号内含有x,不是二次函数,故本选项不符合题意;C、函数yy=xx2−1是二次函数,故本选项符合题意;D、函数yy=12xx分母中含有x,不是二次函数,故本选项不符合题意.故选:C.【变式1-2】(23-24九年级下·江苏·专题练习)下列函数关系式中,二次函数的个数有()(1)yy=3(xx−1)2+1;(2)yy=1xx2−xx;(3)SS=3−2tt2;(4)yy=xx4+2xx2−1;(5)yy=3xx(2−xx)+3xx2;(6)yy=mmxx2+8.A.1个B.2个C.3个D.4个【答案】B【分析】本题考查了二次函数的定义,一般地,形如yy=aaxx2+bbxx+cc(aa,bb,cc为常数,aa≠0)的函数叫做二次函数.判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成yy=aaxx2+bbxx+cc(aa,bb,cc为常数,aa≠0)的形式,那么这个函数就是二次函数,否则就不是.【详解】解:(1)yy=3(xx−1)2+1是二次函数,故符合题意;(2)yy=1xx2−xx,不是二次函数,故不符合题意;(3)SS=3−2tt2是二次函数,故符合题意;(4)yy=xx4+2xx2−1不是二次函数,故不符合题意;(5)yy=3xx(2−xx)+3xx2=6xx不是二次函数,故不符合题意;(6)yy=mmxx2+8,不确定m是否为0,不一定是二次函数,故不符合题意;综上所述,二次函数有2个.故选:B.【变式1-3】(23-24九年级上·湖南长沙·期末)下列函数①yy=5xx−5;②yy=3xx2−1;③yy=4xx3−3xx2;④yy=2xx2−2xx+1;⑤yy=1xx2.其中是二次函数的是.【答案】②④/④②【分析】根据二次函数的定义,函数式为整式且自变量的最高次数为2,二次项系数不为0,逐一判断.【详解】解:①yy=5xx−5为一次函数;②yy=3xx2−1为二次函数;③yy=4xx3−3xx3自变量次数为3,不是二次函数;④yy=2xx2−2xx+1为二次函数;⑤yy=1xx2函数式为分式,不是二次函数.故答案为②④.【点睛】本题考查二次函数的定义,能够根据二次函数的定义判断函数是否属于二次函数是解决本题的关键.【题型2 由二次函数的定义求字母的值】【例2】(23-24九年级下·广东东莞·期中)已知函数yy=(mm−1)xx mm2+1是二次函数,则mm=.【答案】−1【分析】根据定义得:形如yy=aaxx2+bbxx+cc(aa、bb、cc是常数,且aa≠0)的函数是二次函数,列方程可求得答案.【详解】解:依题意得:mm2+1=2且mm−1≠0,解得mm=−1.故答案为:−1.【点睛】本题考查了二次函数的定义.注意:二次函数yy=aaxx2+bbxx+cc中,aa是常数,本题关键点为aa≠0.【变式2-1】(23-24九年级上·江苏扬州·阶段练习)如果yy=2xx|mm|+3xx−1是关于xx的二次函数,则mm=.【答案】±2【分析】本题主要考查了二次函数的定义,直接利用二次函数的定义得出答案.【详解】解:∵yy=2xx|mm|+3xx−1是关于x的二次函数,∴|mm|=2,解得:mm=±2.故答案为:±2.【变式2-2】(23-24九年级上·湖北·周测)如果函数yy=(kk−1)xx kk2−kk+2+kkxx−1是关于x的二次函数,则kk=.【答案】0【分析】本题考查了二次函数的定义.根据二次函数的定义得到kk−1≠0且kk2−kk+2=2,然后解不等式和方程即可得到k的值.【详解】解:根据题意,得kk−1≠0且kk2−kk+2=2,解得kk=0.故答案为:0.【变式2-3】(23-24九年级下·广东广州·期末)如果yy=(kk−3)xx�kk-1�+xx−3是二次函数,佳佳求出k的值为3,敏敏求出k的值为-1,她们俩中求得结果正确的是.【答案】敏敏【分析】本题考查了二次函数的定义,由定义得|kk−1|=2,kk−3≠0,即可求解;理解定义:“一般地,形如yy=aaxx2+bbxx+cc(a、b、c是常数,aa≠0)的函数叫做二次函数.” 是解题的关键.【详解】解:∵yy=(kk−3)xx�kk-1�+xx−3是二次函数,∴|kk−1|=2,解得kk1=3,kk2=−1,又∵kk−3≠0,即kk≠3,∴kk=−1,故敏敏正确.【题型3 由二次函数的定义求字母的取值范围】【例3】(23-24九年级上·上海嘉定·期末)如果函数yy=(kk−1)xx2+kkxx−1(kk是常数)是二次函数,那么kk的取值范围是.【答案】kk≠1【分析】根据:“形如yy=aaxx2+bbxx+cc(aa≠0),这样的函数叫做二次函数”,得到kk−1≠0,即可.【详解】解:由题意,得:kk−1≠0,∴kk≠1;故答案为:kk≠1.【变式3-1】(23-24九年级上·浙江嘉兴·开学考试)已知函数yy=(mm2−mm)xx2+(mm−1)xx−2(m为常数).(1)若这个函数是关于x的一次函数,求m的值.(2)若这个函数是关于x的二次函数,求m的取值范围.【答案】(1)mm=0;(2)mm≠1且mm≠0.【分析】(1)根据一次函数的定义即可解决问题;(2)根据二次函数的定义即可解决问题.【详解】(1)解:依题意mm2−mm=0且mm−1≠0,所以mm=0;(2)解:依题意mm2−mm≠0,所以mm≠1且mm≠0.【点睛】本题考查一次函数的定义、二次函数的定义,解题的关键是熟练掌握基本概念,属于中考常考题型.【变式3-2】(23-24九年级上·广东江门·阶段练习)已知关于xx的二次函数yy=(aa2−1)xx2+xx−2,则aa的取值范围是()A.aa≠1B.aa≠−1C.aa≠±1D.为任意实数【答案】C【分析】根据二次函数定义可得aa2−1≠0,解出答案即可.【详解】因为关于xx的二次函数yy=(aa2−1)xx2+xx−2,∴aa2−1≠0,解得:aa≠±1.故选:C.【点睛】本题考查的是二次函数yy=aaxx2+bbxx+cc(aa≠0)概念,熟练掌握二次函数定义是解题关键.【变式3-3】(23-24九年级下·四川遂宁·期中)已知函数yy=(mm2-2)xx2+(mm+√2)xx+8.若这个函数是二次函数,求mm的取值范围【答案】mm≠√2且mm≠-√2【分析】根据二次函数的定义,即可得不等式mm2-2≠0,解不等式即可求得.【详解】解:∵函数yy=(mm2-2)xx2+(mm+√2)xx+8是二次函数,∴mm2-2≠0,解得mm≠±√2,故答案为:mm≠√2且mm≠-√2.【点睛】本题考查了二次函数的定义,熟练掌握和运用二次函数的定义是解决本题的关键.【题型4 二次函数的一般形式】【例4】(23-24九年级上·四川南充·阶段练习)二次函数yy=xx2−3xx+5的二次项是,一次项系数是,常数项是.【答案】xx2−3 5【分析】根据二次函数的定义判断即可。
二次函数的考试常见题型
⼆次函数的考试常见题型⼆次函数的考试常见题型1.已知⼆次函数y=x2+4x.(1)⽤配⽅法把函数化为y=a(x-h)2+k(其中a,h,k都是常数且a≠0)的形式,并指出函数图象的对称轴和顶点坐标(2)求函数图象与x轴的交点坐标.2.⼆次函数y=12(x-4)2+5的图象的开⼝⽅向、对称轴、顶点坐标分别是?3.已知⼀抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8).(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标.题型⼆、抛物线的平移1.(⽢肃兰州中考题)已知函数y=2x2的图象是抛物线,若抛物线不动,把x 轴、y轴分别向上、向右平移2个单位长度,那么在新坐标系下抛物线的解析式是?2.(上海中考题)在直⾓坐标平⾯内,⼆次函数图象的顶点为A(1,-4),且过点B(3,0)(1)求该⼆次函数的解析式.(2)将该⼆次函数图象向右平移⼏个单位长度,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另⼀个交点的坐标.3.抛物线y=12x2向左平移3个单位长度,再向下平移2个单位长度后,所得的抛物线表达式是?4.函数y=-2(x-1)2-1的图象可以由函数y=-2(x+2)2+3的图象先向____平移_____个单位长度,再向____平移_____个单位长度⽽得到.5.已知⼆次函数y=x2-bx+1(-1≤b≤1),当b从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线移动⽅向的描述中,正确的是( )A.先往左上⽅移动,再往左下⽅移动B.先往左下⽅移动,再往左上⽅移动C.先往右上⽅移动,再往右下⽅移动题型三、⼆次函数图象的画法1.(⼴东梅州中考题)已知⼆次函数图象的顶点是(-1,2),且过点(0,32)(1)求⼆次函数的表达式,并在图中画出它的图象;(2)求证:对任意实数m,点M(m,-m2)都不在这个⼆次函数的图象上.2. (安徽中考题)抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,(1)求出m的值并画出这条抛物线.。
二次函数各知识点、考点、典型例题及练习

二次函数各知识点、考点、典型例题与对应练习(超全)【典型例题】题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( ) A .(-1,8) B.(1,8) C (-1,2) D (1,-4) 点拨:本题主要考察二次函数的顶点坐标公式 例2.(拓展,2008年XX 市中考题,12) 下列命题中正确的是○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3 ○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
○3当c=-5时,不论b 为何值,抛物线y=ax 2+bx+c 一定过y 轴上一定点。
○4若抛物线y=ax 2+bx+c 与x 轴有唯一公共点,则方程ax 2+bx+c=0有两个相等的实数根。
○5若抛物线y=ax 2+bx+c 与x 轴有两个交点A 、B ,与y 轴交于c 点,c=4,S △ABC=6,则抛物线解析式为y=x 2-5x+4。
○6若抛物线y=ax 2+bx+c (a ≠0)的顶点在x 轴下方,则一元二次方程ax 2+bx+c=0有两个不相等的实数根。
○7若抛物线y=ax 2+bx+c (a ≠0)经过原点,则一元二次方程ax 2+bx+c=0必有一根为0。
○8若a -b+c=2,则抛物线y=ax 2+bx+c (a ≠0)必过一定点。
○9若b 2<3ac ,则抛物线y=ax 2+bx+c 与x 轴一定没有交点。
○10若一元二次方程ax 2+bx+c=0有两个不相等的实数根,则函数y=cx 2+bx+a 的图象与x 轴必有两个交点。
○11若b=0,则抛物线y=ax 2+bx+c 与x 轴的两个交点一个在原点左边,一个在原点右边。
点拨:本题主要考查二次函数图象与其性质,一元二次方程根与系数的关系,与二次函数和一元二次方程二者之间的联系。
初三数学二次函数所有经典题型

初三数学二次函数经典题型(一)二次函数单元检测 (A) 姓名_______一、填空题:1、函数21(1)21my m x mx +=--+是抛物线,则m = . 2、抛物线223y x x =--+与x 轴交点为 ,与y 轴交点为.3、二次函数2y ax =的图象过点(-1,2),则它的解析式是 ,当x 时,y 随x 的增大而增大.4.抛物线2)1(62-+=x y 可由抛物线262-=x y 向平移个单位得到.5.抛物线342++=x x y 在x 轴上截得的线段长度是.6.抛物线()4222-++=m x x y 的图象经过原点,则=m .7.抛物线m x x y +-=2,若其顶点在x 轴上,则=m . 8. 如果抛物线c bx ax y ++=2的对称轴是x =-2,且开口方向与形状与抛物线相同,又过原点,那么a = ,b = ,c = .9、二次函数2y x bx c =++的图象如下左图所示,则对称轴是 ,当函数值0y <时,对应x 的取值范围是.10、已知二次函数21(0)y ax bx c a =++≠与一次函数2(0)y kx m k =+≠的图象相交于点A (-2,4)和B (8,2),如上右图所示,则能使1y 2y >成立的x 的取值范围 .二、选择题:11.下列各式中,y 是x 的二次函数的是 ( )A .21xy x +=B . 220x y +-=C . 22y ax -=-D .2210x y -+= 12.在同一坐标系中,作22y x =、22y x =-、212y x =的图象,它们共同特点是 ( ) A . 都是关于x 轴对称,抛物线开口向上 B .都是关于y 轴对称,抛物线开口向下B . 都是关于原点对称,顶点都是原点 D .都是关于y 轴对称,顶点都是原点13.抛物线122+--=m mx x y 的图象过原点,则m 为( )223x y -=A .0B .1C .-1D .±1 14.把二次函数122--=x x y 配方成为( ) A .2)1(-=x y B . 2)1(2--=x y C .1)1(2++=x yD .2)1(2-+=x y 15.已知原点是抛物线2(1)y m x =+的最高点,则m 的范围是( )A . 1-<mB . 1<mC . 1->mD . 2->m16、函数221y x x =--的图象经过点( )A 、(-1,1)B 、(1 ,1)C 、(0 , 1)D 、(1 , 0 )17、抛物线23y x =向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A 、23(1)2y x =--B 、23(1)2y x =+-C 、23(1)2y x =++D 、23(1)2y x =-+18、已知h 关于t 的函数关系式212h gt =( g 为正常数,t 为时间)如图,则函数图象为 ( )t t19 A 、232y x x =-+ B 、25y x =- C 、22y x x =-+ D 、244y x x =-+20、已知二次函数2y ax bx c =++,若0a <,0c >,那么它的图象大致是( )21(1)(2)、抛物线关于22(1)求b 和c 的值; (2)试判断点P (-1,2)是否在此函数图像上?23、某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x 米,面积为S 平方米.(1) 求出S 与x 之间的函数关系式,并确定自变量x 的取值范围;(2) 请你设计一个方案,使获得的设计费最多,并求出这个费用.24、某工厂现有80台机器,每台机器平均每天生产384•件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,•由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.(1)如果增加x 台机器,每天的生产总量为y 件,请你写出y 与x 之间的关系式;(2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?25、如图,有一个抛物线的拱形立交桥,•这个桥拱的最大高度为16m ,跨度为40m ,现把它放在如图所示的直角坐标系里,•若要在离跨度中心点M5m 处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?24、如图,抛物线n x x y ++-=52经过点A(1,0),与y 轴交于点B.⑴求抛物线的解析式;⑵P 是y 轴正半轴上一点,且△PAB 是以AB 为腰的等腰三角形,试求P 点坐标.二次函数单元检测 (B ) 姓名_______一、新课标基础训练1.下列二次函数的图象的开口大小,从大到小排列依次是( ) ①y=13x2;②y=23x2+3;③y=-12(x-3)2-2;④y=-32x2+5x-1. A .④②③① B .①③②④ C .④②①③ D .②③①④2.将二次函数y=3(x+2)2-4的图象向右平移3个单位,再向上平移1个单位,所得的图象的函数关系式( )A .y=3(x+5)2-5;B .y=3(x-1)2-5;C .y=3(x-1)2-3;D .y=3(x+5)2-33.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,•若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润,则应降价( )A .5元B .10元C .15元D .20元4.若直线y=ax+b (ab≠0)不过第三象限,则抛物线y=ax2+bx 的顶点所在的象限是( )A .一B .二C .三D .四5.已知二次函数y=x2+x+m ,当x 取任意实数时,都有y>0,则m 的取值范围是( )A .m≥14B .m>14C .m≤14D .m<146.二次函数y=mx2-4x+1有最小值-3,则m 等于( ) A .1 B .-1 C .±1 D .±12二、新课标能力训练7.如图,用2m_______m2.8.如图,有一个抛物线型拱桥,其最大高度为16m ,•跨度为•40m ,• 现把它的示意图放在平面直角坐标系中••,••则此抛物线的函数关系式为__________.9、已知函数4m m 2x )2m (y -++=是关于x 的二次函数,求:(1)满足条件的m 值;(2)m 为何值时,抛物线有最低点?求出这个最低点.这时当x 为何值时,y 随x 的增大而增大?(3)m 为何值时,函数有最大值?最大值是什么?这时当x 为何值时,y 随x 的增大而减小?10、观察表格:2 3(1)求a ,b ,c 的值,并在表内空格处填入正确的数.(2)画出函数y=ax2+bx+c 的图象,由图象确定,当x 取什么实数时,ax2+bx+c>0.11、如图(2),已知平行四边形ABCD的周长为8cm,∠B=30。
二次函数专题知识点 常考(典型)题型 重难点题型(含详细答案)

二次函数和基本性质专题知识点+常考题型+重难点题型(含详细答案)一、目录一、目录 (1)二、基础知识点 (2)1.二次函数的概念 (2)2.二次函数y=ax2的图像和性质 (2)3.二次函数y=a(x-h)2+k(a≠0)的性质 (4)4,用配方法求y=ax2+bx+c(a≠0) (6)5.二次函数图像性质总结 (7)6.二次函数解析式的求法 (7)7.二次函数图像的平移 (9)三、重难点题型 (11)1.由抛物线的位置确定系数的符号 (11)2.用待定系数法求二次函数的解析式 (13)3.运用抛物线的对称性解题 (17)4.用二次函数解决最值问题 (18)5.二次函数的图像 (20)6.二次函数与应用问题 (21)二、基础知识点1.二次函数的概念形如y=ax2+bx+c(a≠0)的函数叫作二次函数。
注:①a、b、c为常数,且a≠0,即二次项必须有,一次项和常数项可以没有②二次函数为函数的一种,满足函数的所有性质。
即在定义域内,自变量x有且仅有唯一应变量y与之对应例1.下列各项中,y是x的二次函数的有:①y=√2x2−x+5;②y=(m−1)x2+x+1(m为常数);③y=2x2+4x−m(m为常数);④y=(2x+1)(3x−2)−6x2答案:①是二次函数,二次项系数不为0;②不应定,当m=1时,二次项为0,则不是二次函数;③是二次函数,二次项系数不为0;④化简得:-x-2,因此不是二次函数例2.已知y=(k+3)x k2+k−4是二次函数,求k的值。
答案:因为y=(k+3)x k2+k−4是二次函数所以{k+3≠0 k2+k−4=2解得:k=22.二次函数y=ax2的图像和性质y=ax2(a≠0,b=0,c=0,即一次项和常数项皆为0)的性质:①图形为抛物线形状②a>0,开口向上;a<0,开口向下③过原点(顶点),为最大值或最小值(由a的正负决定)④关于y轴对称,即关于x=0对称⑤|a|越大,开口越小,即上升或下降越快注:关于y轴对称的前提条件是:函数定义域关于y轴对称例1.求等边三角形面积S与边长a的函数关系式。
二次函数经典题型(含答案)

二次函数经典题型(启东教育)1.看图,解答下列问题.(1)求经过A、B、C三点的抛物线解析式;(2)通过配方,求该抛物线的顶点坐标和对称轴;(3)用平滑曲线连结各点,画出该函数图象.2.已知函数y=x2+bx-1的图象经过点(3,2)(1)求这个函数的解析式;(2)画出它的图象,并指出图象的顶点坐标;(3)当x>0时,求使y≥2的x的取值范围.3.已知抛物线y=-x2+mx-m+2.(1)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=,试求m的值;(2)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且△MNC的面积等于27,试求m的值.4.如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β 是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.(1)若二次函数y=-x2-kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.5.已知抛物线经过点.(1)求抛物线的解析式.(2)设抛物线顶点为,与轴交点为.求的值.(3)设抛物线与轴的另一个交点为,求四边形的面积.6.已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,其图象如图所示.(1)求抛物线的解析式,写出抛物线的顶点坐标;(2)画出抛物线y=ax2+bx+c当x<0时的图象;(3)利用抛物线y=ax2+bx+c,写出x为何值时,y>0.7.已知抛物线与y轴的交点为C,顶点为M,直线CM的解析式 y=-x+2并且线段CM的长为(1)求抛物线的解析式。
(2)设抛物线与x轴有两个交点A(X1 ,0)、B(X2 ,0),且点A在B的左侧,求线段AB的长。
(3)若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由。
二次函数经典题型答案(启东教育)1.解:(1)由图可知A(-1,-1),B(0,-2),C(1,1)设所求抛物线的解析式为y=ax2+bx+c依题意,得解得∴y=2x2+x-2.(2)y=2x2+x-2=2(x+)2-∴顶点坐标为(-,),对称轴为x=-(3)图象略,画出正确图象2.解:(1)函数y=x2+bx-1的图象经过点(3,2)∴9+3b-1=2,解得b=-2 .∴函数解析式为y=x2-2x-1(2)y=x2-2x-1=(x-1)2-2 ,图象略,图象的顶点坐标为(1,-2)(3)当x=3 时,y=2,根据图象知,当x≥3时,y≥2∴当x>0时,使y≥2的x的取值范围是x≥3.3.解: ()设点A(x1,0),B(x2,0) ,则x1 ,x2是方程 x2-mx+m-2=0的两根.∵x1+ x2 =m ,x1·x2 =m-2 <0 即m<2;又AB=∣x1 x2∣=,∴m2-4m+3=0 .解得:m=1或m=3(舍去) ,∴m的值为1 .()设M(a,b),则N(-a,-b) .∵M、N是抛物线上的两点,∴①+②得:-2a2-2m+4=0 .∴a2=-m+2.∴当m<2时,才存在满足条件中的两点M、N.∴.这时M、N到y轴的距离均为,又点C坐标为(0,2-m),而S△M N C = 27 ,∴2××(2-m)×=27 .∴解得m=-7 .4.解:(1)∵α,β是Rt△ABC的两个锐角,∴tanα·tanβ=1.tanα>0,tanβ>0.由题知tanα,tanβ是方程x2+kx-(2+2k-k2)=0的两个根,∴tanx·tanβ=(2=2k-k2)=k2-2k-2,∴k2-2k-2=1.解得,k=3或k=-1.而tanα+tanβ=-k>0,∴k<0.∴k=3应舍去,k=-1.故所求二次函数的解析式为y=-x2+x-1.(2)不在.过C作CD⊥AB于D.令y=0,得-x2+x-1=0,解得x1=,x2=2.∴A(,0),B(2,0),AB=.∴tanα=,tanβ=2.设CD=m.则有CD=AD·tanα=AD.∴AD=2CD.又CD=BD·tanβ=2BD,∴BD=CD.∴2m+m=.∴m=.∴AD=.∴C(,).当x=时,y=≠∴点C不在(1)中求出的二次函数的图象上.5.解:(1)解方程组得,.(2)顶点.(3)在中,令得,,令得或,.四边形(面积单位)6.解:(1)由图象,可知A(0,2),B(4,0),C(5,-3),得方程组解得∴抛物线的解析式为顶点坐标为(2)所画图如图.(3)由图象可知,当-1<x<4时,y>0.7.(1)解法一:由已知,直线CM:y=-x+2与y轴交于点C(0,2)抛物线过点C(0,2),所以c=2,抛物线的顶点M在直线CM上,所以若b=0,点C、M重合,不合题意,舍去,所以b=-2。
高一:二次函数常见题型及解题技巧.doc

高一:二次函数常见题型及解题技巧我们今天就总结一下常见的二次函数常见的体型以及解题技巧。
第一类:基础知识类这一类命题主要包含以下几类问题:函数定义、二次函数的特殊点(顶点、对称轴、最大/最小值)等。
其中对于函数的特殊点,主要核心在于把握住两个要点:函数式之间的转化,顶点式的特点。
解决此类问题,在不熟悉二次函数的情况下,最有操作性的方式就是将函数从各种形式转化为顶点式。
即转化为形如:y=a(x-b)²+c(其中a为不为零的常数)转化为这种形式之后,就可以以轻松解决这些问题了,顶点为(b,c)对称轴为X=b。
而此时函数的最大值/最小值要看系数a是正数还是负数了。
若a0,则此二次函数应该是开口向上,此时在顶点处取得最小值c。
若a0,此时顶点处取得最大值。
函数定义类往往很少单独出题,一般会利用函数的开口方向等信息,结合一次函数,函数交点等信息结合出题。
eg:已知二次函数y=mx²+(m-1)x+m-1有最小值为0,则m=?第二类:二次函数的增减性及函数值比大小的问题讨论二次函数的增减性往往会利用到第一类对称轴的知识。
因为二次函数的极值点往往是区分函数增减的关键点:(1)对于开口向上的函数,极值点左边的部分为减函数,极值点右边的部分为增函数;(2)对于开口向下的函数,极值点左边的部分为增函数,极值点右边的部分为减函数;(3)如果是比较极值点两边的函数值大小的题目,我们要考虑两边的点与极值点在X轴上的距离:开口向上是,距离极值点越远的函数值越大;开口向下时,距离极值点跃进的函数值越大;.eg:已知二次函数y=-½x²+3x+5 的图象上有三点A(x1,y1),B(x2.,y2),C(x3,y3)且3x1x2x3,则y1,y2,y3的大小关系为?第三类:函数的平移这类问题常常是困扰很多学生的问题。
实际上是有口诀用于记忆的:向上平移加y值,想右平移减x值。
这类问题常见的通用解题方法其实依然是转化为顶点式y=a(x-b)²+c。
二次函数易考查经典题型

二次函数全章高频考点专项训练一:求二次函数及反比例函数的表达式的方法求二次函数及反比例函数的表达式是解决二次函数及反比例函数的重要保证,求表达式时,一般都选用待定系数法,根据不同条件,设出恰当的表达式,往往会起到事半功倍的效果。
训练角度一:巧求二次函数表达式的方法类型一:一般式已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1).求这个二次函数的解析式.类型二:顶点式已知抛物线的顶点坐标为(4,-1),与y轴交于点(0,3),求这条抛物线的解析式。
类型三:两点式抛物线与x 轴交于 A(1,0),B(-3,0) 两点,与y 轴交于点C(0,3),求此抛物线的解析式.训练角度二:巧求反比例函数表达式的方法类型一:已知坐标求反比例函数的表达式已知与x成正比例,与x成反比例,若的图像经过点(1、2),,则y与x的函数表达式类型二:已知面积求反比例函数的表达式类型三:利用根与系数的关系求反比例函数的表达式专项训练二:巧解反比例函数中的面积问题许多反比例函数问题都是与三角形,四边形等图形的面积联系在一起的,其中常见的有,已知反比例函数的表达式,数函数图像围成的某一图形的面积;或已知某一图形的面积,求符合条件的反比例函数的表达式等题型。
训练角度一:已知面积求反比例函数的表达式训练角度二:已知反比例函数的表达式求图形的面积训练角度三:利用点的坐标及面积公式求面积如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.训练角度四:利用对称性解决反比例函数中的面积问题如图,是由四条曲线围成的广告标志,建立如图所示的平面直角坐标系,双曲线表达式分为y=与y=-。
现用四条钢条固定这四条曲线。
已知OF=OH=2米,这种钢条加工成矩形成品按面积计算,每平方米15元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?专项训练三:建立坐标系,利用二次函数解决实际问题建立坐标系解决实际问题时,要注意数形结合思想的运用,依据徒刑特弟妹构建恰当的平面直角坐标系,选择恰当的二次函数表达式进行建模,从而达到应用二次函数的某些性质来解决问题的目的,常见的类型有:拱桥问题,运动型抛物线问题,荡秋千问题等训练角度一:拱桥(隧道)问题有一座抛物线形拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.(1)如图所示的直角坐标系中,求出该抛物线的关系式。
二次函数常见题型

二次函数常见题型
二次函数的常见题型包括:
1. 确定二次函数的解析式,通常可以通过三个或更多的点坐标来求解;
2. 求二次函数的顶点坐标、对称轴和开口方向;
3. 求二次函数与x轴和y轴的交点坐标;
4. 求二次函数的最大值或最小值;
5. 利用二次函数解决生活中的实际问题,如最大利润、最大面积等;
6. 二次函数与一元一次方程的关系,通常可以通过求解一元一次方程来找到二次函数的零点;
7. 二次函数与一元二次方程的关系,可以通过求解一元二次方程来找到二次函数的根;
8. 利用二次函数解决等腰三角形、平行四边形等几何问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数常见题型;
1(2011•黔南州)下列函数:①y=-x ;②y=2x ;③x
y 1=④2x y =(x <0),y 随x 的增大而减小的函数有( )
A 、1个
B 、2个
C 、3个
D 、4个
2、(2010•通化)二次函数y=x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )
A 、y=(x+2)2
B 、y=x2+2
C 、y=(x-2)2
D 、y=x2-2
3、(2010•宁夏)把抛物线y=-x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A 、y=-(x-1)2-3
B 、y=-(x+1)2-3
C 、y=-(x-1)2+3
D 、y=-(x+1)2+3
4、(2010•兰州)二次函数y=ax2+bx+c 的图象如图所示,则一次函数
y=bx+b2-4ac 与反比例函数y= 在同一坐标系内的图象大致为( )
A 、
B 、
C
D 、
5、(2010•兰州)二次函数y=-3x2-6x+5的图象的顶点坐标是( )
A 、(-1,8)
B 、(1,8)
C 、(-1,2)
D 、(1,-4)
6、(2010•大田县)抛物线y=kx2-7x-7的图象和x 轴有交点,则k 的取值范围是( )
A 、k >-
B 、k≥- 且k≠0
C 、k≥-
D 、k >- 且k≠0
7、(2010•北京)将二次函数y=x2-2x+3化为y=(x-h )2+k 的形式,结果为( )
A 、y=(x+1)2+4
B 、y=(x-1)2+4
C 、y=(x+1)2+2
D 、y=(x-1)2+2
8、(2009•枣庄)二次函数y=ax2+bx+c 的图象如图所示,
则下列关系式不正确的是( )
A 、a <0
B 、abc >0
C 、a+b+c >0
D 、b2-4ac >0
填空题;
1.(2010•新疆)抛物线y=-x 2+bx+c 的部分图象如图所示,若y >0,则x 的取值范围是 _____ 2(2010•西宁)图1.汽车刹车距离S (m )与速度v (km/h )之间的函数关系是S= v2,在一辆车速为100km/h 的汽车前方80m 处,发现停放一辆故障车,此时刹车 _______ 会有危险. 3(2010•通化)图2,已知抛物线y=ax2+bx+c 的部分图象如图所示,若y >0,则x 的取值范围是______ _
4(2010•金华)图3.已知二次函数y=-x2+2x+m 的部分图象如图所示,则关于x 的
一元二次方程-x2+2x+m=0的解________
图 1
图2
图3
解答题;
2、(2010•汕头)已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).Array
3、(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
3、(2010•青海)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出
500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
8、(2010•黑河)已知二次函数的图象经过点(0,3),(-3,0),(2,-5),且与x轴交于A、B两点.确定此二次函数的解析式;。
