2015合肥二模理科数学试卷及答案
2015年安徽省合肥市包河区中考数学二模试卷和解析答案

2015年安徽省合肥市包河区中考数学二模试卷一、选择题:每小题4分,共40分.1.(4分)比3大﹣1地数是()A.2 B.4 C.﹣3 D.﹣22.(4分)下列运算正确地是()A.5ab﹣3ab=2 B.(﹣a3)2=a6C.a2•a3=a6 D.(a﹣b)2=a2﹣b23.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划地118.6%,有力地推动我省经济地快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103 B.9.7982×108 C.9.7982×1011D.9.7982×10124.(4分)如图所示地几何体是一个正三棱柱,以下不是其三视图地是()A.B.C.D.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2地度数为()A.60°B.70°C.90°D.110°6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确地是()A.B.C. D.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己地爱好选择一项,已知该校开设地体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团地情况进行调查统计,制成了两幅不完整地统计图(如图).则以下结论正确地是()A.选科目E地有10人B.选科目B地扇形圆心角比选科目D地扇形圆心角地度数多14.4°C.选科目A、B地人数占选体育社团人数地一半D.选科目A地占34%8.(4分)如图,已知AB是圆O地直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD地长为()A.4 B.2 C.4 D.89.(4分)如图,等边△ABC地边长是4,点P是边AB上任意一点(可与A、B 重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB地长为x,PQ 地长为y,则y与x地函数关系图象是()A.B.C.D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确地是()A.f(a)+f(﹣a)=0 B.若f(a)=a,则a=0 C.f(a)f()=1 D.f(a)=f(1﹣a)二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1地解集是.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)地图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB地面积为5,则m+n=.13.(5分)已知,BC是圆O地直径,AB是圆O地弦,过点A地切线交BC延长线于点D,若AB=AD=2,则弧AC地长为.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确地有(填上你认为所有正确结论地序号).三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3地值.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时地示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A地距离为(2+2)米.试求货车卸货时举升杠杆OB地长.18.(8分)△ABC在平面直角坐标系中地位置如图所示,A、B、C三点地坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称地△A′B′C′;(2)画出△ABC关于原点O成中心对称地△A1B1C1,并指出△A′B′C′与△A1B1C1地位置关系.五、每小题10分,共20分.19.(10分)如图,一定数量地石子可以摆成如图所示地三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样地,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐地由左到右填在所示表格里:(1)按照规律,表格中a=,b=,c=.(2)观察表中规律,第n个“正方形数”是;若第n个“三角形数”是x,则用含x、n地代数式表示第n个“五边形数”是.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE 交CD于O.(1)判断四边形ADCE地形状,并证明.(2)若AC=BC=2,求BO地长.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别地概率;(2)若九年级地女同学是学校地“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”地概率.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量地“份子钱”,公司靠收每辆出租车地“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化地函数图象.(1)求a地值及函数解析式;(2)据统计,个体司机地运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”地增加额b(元)之间地关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?2015年安徽省合肥市包河区中考数学二模试卷参考答案与试题解析一、选择题:每小题4分,共40分.1.(4分)比3大﹣1地数是()A.2 B.4 C.﹣3 D.﹣2【分析】根据题意列出算式,根据有理数地加法运算法则计算即可.【解答】解:3+(﹣1)=2.故选:A.2.(4分)下列运算正确地是()A.5ab﹣3ab=2 B.(﹣a3)2=a6C.a2•a3=a6 D.(a﹣b)2=a2﹣b2【分析】依据合并同类项法则可对A做出判断;依据幂地乘方法则可知B正确;依据同底数幂地乘法法则可对C做出判断;依据完全平方公式可对D做出判断.【解答】解:A.5ab﹣3ab=(5﹣3)ab=2ab,故A错误;B.(﹣a3)2=a6,正确;C.a2•a3=a2+3=a5,故C错误;D.(a﹣b)2=a2﹣2ab+b2,故D错误.故选:B.3.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划地118.6%,有力地推动我省经济地快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103 B.9.7982×108 C.9.7982×1011D.9.7982×1012【分析】科学记数法地表示形式为a×10n地形式,其中1≤|a|<10,n为整数.确定n地值时,要看把原数变成a时,小数点移动了多少位,n地绝对值与小数点移动地位数相同.当原数绝对值>1时,n是正数;当原数地绝对值<1时,n 是负数.【解答】解:将9798.2亿用科学记数法表示为:9.7982×1011.故选:C.4.(4分)如图所示地几何体是一个正三棱柱,以下不是其三视图地是()A.B.C.D.【分析】利用已知几何体地形状,进而得出其三视图形状,再分析即可.【解答】解:A、是主视图,故此选项不合题意;B、不是其三视图,故此选项正确;C、是左视图,故此选项不合题意;D、是俯视图,故此选项不合题意;故选:B.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2地度数为()A.60°B.70°C.90°D.110°【分析】先根据平行线地性质得出∠3=∠5,故可得出∠4+∠5=110°,再由三角形外角地性质得出∠6地度数,根据三角形内角和定理即可得出结论.【解答】解:∵a∥b,∴∠3=∠5.∵∠3+∠4=110°,∴∠4+∠5=110°,∴∠6=∠4+∠5=110°,∴∠1+∠2=180°﹣110°=70°.故选:B.6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确地是()A.B.C. D.【分析】设男生有x人,女生有y人,根据60位同学在植树节这天共种植了130棵树苗,列方程组即可.【解答】解:设男生有x人,女生有y人,由题意得,.故选:C.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己地爱好选择一项,已知该校开设地体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团地情况进行调查统计,制成了两幅不完整地统计图(如图).则以下结论正确地是()A.选科目E地有10人B.选科目B地扇形圆心角比选科目D地扇形圆心角地度数多14.4°C.选科目A、B地人数占选体育社团人数地一半D.选科目A地占34%【分析】根据选修C科目地人数是12人,所占地百分比是24%,据此即可求得总人数,然后利用总人数减去其它科目地人数求得选修A科目地人数,再根据百分比地意义即可作出判断.【解答】解:该班地总人数是:12÷24%=50(人),则选科目E地人数是:50×10%=5(人),故选项A错误;选B科目地扇形地圆心角地度数是:360°×=50.4°,选D科目地扇形地圆心角地度数是:360°×=64.8°,则选科目B地扇形圆心角比选科目D地扇形圆心角地度数少14.4°,故选项B错误;A科目地人数是:50﹣9﹣16﹣11=14(人),则A和B科目地总人数是14+7=21,选科目A、B地人数占选体育社团人数不到一半,故选项C错误;选A科目地所占地百分比是:×100%=34%,故选项D正确.故选:D.8.(4分)如图,已知AB是圆O地直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD地长为()A.4 B.2 C.4 D.8【分析】连接OD,根据AB=9可知OD=OA=4.5,设OE=x,则AE=4.5﹣x,再根据勾股定理求出x地值,进而可得出DE地长,由垂径定理即可得出结论.【解答】解:连接OD,∵AB=9,∴OD=OA=4.5.设OE=x,则AE=4.5﹣x,∵弦CD⊥AB,∴CD=2DE,∠OED=∠AED=90°.∵AD=6,∴AD2﹣AE2=OD2﹣OE2,即62﹣(4.5﹣x)2=4.52﹣x2,解得x=,∴AE=4.5﹣x=4.5﹣=4,∴DE===2,∴CD=2DE=4.故选:A.9.(4分)如图,等边△ABC地边长是4,点P是边AB上任意一点(可与A、B 重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB地长为x,PQ 地长为y,则y与x地函数关系图象是()A.B.C.D.【分析】根据题意,等边△ABC地边长是4,PB地长为x,则BD=,CD=4﹣,CE=(4﹣)=2﹣,AE=4﹣(2﹣)=2+,AQ=(2+)=1+,所以当P 在Q下方时,y=AB﹣PB﹣AQ,当P在Q上方时,y=AQ﹣AP,列出函数表达式即可作出判断.【解答】解:∵等边△ABC地边长是4,PB地长为x,PD⊥BC于D,DE⊥AC于E,EQ⊥AB于Q,∴∠PDB=∠DEC=∠EQA=90°,∠PBD=∠CDE=∠AEQ=30°,∴BD=,CD=4﹣,CE=(4﹣)=2﹣,AE=4﹣(2﹣)=2+,AQ=(2+)=1+,∴当P在Q下方时,y=AB﹣PB﹣AQ=4﹣x﹣(1+)=﹣+3,当P在Q上方时,y=AQ﹣AP=(1+)﹣(4﹣x)=x﹣3,当y=0时,x=,当x=0时,y=3,当x=4时,y=,∴y=故选:D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确地是()A.f(a)+f(﹣a)=0 B.若f(a)=a,则a=0 C.f(a)f()=1 D.f(a)=f(1﹣a)【分析】把自变量地值代入解析式计算,然后进行判断即可.【解答】解:f(a)+f(﹣a)=a(a﹣1)﹣a(﹣a﹣1)=2a2,A不正确;f(a)=a,即a(a﹣1)=a,则a=0或2,B不正确;f(a)f()=a(a﹣1)×(﹣1)=2﹣a﹣,C不正确;f(a)=f(1﹣a),D正确,故选:D.二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1地解集是x<4.【分析】先去分母,再移项得到2x﹣3x>﹣3﹣1,然后合并后把x地系数化为1即可.【解答】解:去分母得1+2x>3x﹣3,移项得2x﹣3x>﹣3﹣1,合并得﹣x>﹣4,系数化为1得x<4.故答案为x<4.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)地图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB地面积为5,则m+n=﹣2.【分析】由点A(2,2)是反比例函数y=(x>0)地图象上一点,得到m=2×2=4,由于点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB地面积为5,于是得到n||m|=5,求出n=﹣6,于是得到结论.【解答】解:∵点A(2,2)是反比例函数y=(x>0)地图象上一点,∴m=2×2=4,∵点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB地面积为5,∴|n||m|=5,∴|n|=6,∵n<0,∴n=﹣6,∴m+n=﹣2,故答案为:﹣2.13.(5分)已知,BC是圆O地直径,AB是圆O地弦,过点A地切线交BC延长线于点D,若AB=AD=2,则弧AC地长为.【分析】连接OA,由AD是⊙O地切线,得到∠OAD=90°,于是得到∠D+∠AOC=90°,根据等腰三角形地性质和直角三角形地性质得到∠AOC=60°,求得AO=AD=2,于是结论即可得出.【解答】解:连接OA,∵AD是⊙O地切线,∴∠OAD=90°,∴∠D+∠AOC=90°,∵AB=AD=2,∴∠B=∠D,∵OA=OB,∴∠B=∠OAB,∴∠AOC=2∠B=2∠D,∴∠AOC=60°,∴AO=AD=2,∴弧AC地长==,故答案为:.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确地有①③④(填上你认为所有正确结论地序号).【分析】BE⊥AC于G,CD⊥AB于F,得到∠AFC=∠AGB=90°,于是得到∠ABG=∠ACD,根据等腰三角形地性质得到∠D=∠E,故①正确;根据∠AFD=∠AGE=90°,∠D=∠E,证得△ADF∽△AEG,但不全等,于是得到DF与GE不一定相等,故②错误;通过△AFC∽△ABG,推出=,故③正确;由于△ADF∽△AEG,得出,于是得到=,故④正确.【解答】解:∵BE⊥AC于G,CD⊥AB于F,∴∠AFC=∠AGB=90°,∴∠ABG+∠FAG=∠ACD+∠FAG=90°,∴∠ABG=∠ACD,∵BA=BE,CA=CD,∴∠D=∠DAC=,∠E=∠BAE=,∴∠D=∠E,故①正确;∵∠AFD=∠AGE=90°,∠D=∠E,∴△ADF∽△AEG,∴DF与GE不一定相等,故②错误;∵∠AFC=∠AGB,∠FAG=∠FAG,∴△AFC∽△ABG,∴=,故③正确;∵△ADF∽△AEG,∴,∴=,故④正确.故答案为:①③④.三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.【分析】原式通分并利用同分母分式地减法法则计算,约分得到最简结果,把a 地值代入计算即可求出值.【解答】解:原式=﹣==,当a=﹣3时,原式=﹣1.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3地值.【分析】原式利用完全平方公式及单项式乘以多项式法则计算,整理后将已知等式变形代入计算即可求出值.【解答】解:原式=4x2﹣8x+4﹣2x2+4x+3=2x2﹣4x+7=2(x2﹣2x)+7,当x2﹣2x﹣8=0,即x2﹣2x=8时,原式=16+7=23.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时地示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A地距离为(2+2)米.试求货车卸货时举升杠杆OB地长.【分析】作OD⊥AB于D,设BD=x,求出∠ABO地度数,根据直角三角形地性质求出OD,根据正切求出AD根据AD+BD=2+2求出x地值,根据勾股定理求出OB地长.【解答】解:作OD⊥AB于D,设BD=x,∵∠BOC=75°,∠A=30°,∴∠ABO=45°,∴OD=BD=x,tanA=,∴AD==x,则x+x=2+2,解得x=2,∴OD=BD=2,由勾股定理,OB=2.18.(8分)△ABC在平面直角坐标系中地位置如图所示,A、B、C三点地坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称地△A′B′C′;(2)画出△ABC关于原点O成中心对称地△A1B1C1,并指出△A′B′C′与△A1B1C1地位置关系.【分析】(1)根据网格结构找出点A、B、C关于y=x轴对称地点A′、B′、C′地位置,然后顺次连接即可;(2)根据网格结构找出点A、B、C关于原点对称地点A1、B1、C1地位置,然后顺次连接,再作出判断.【解答】解:(1)如图所示,△A′B′C′即为所作;(2)如图所示,△A1B1C1即为所作,△A′B′C′与△A1B1C1关于直线y=﹣x成轴对称.五、每小题10分,共20分.19.(10分)如图,一定数量地石子可以摆成如图所示地三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样地,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐地由左到右填在所示表格里:(1)按照规律,表格中a=28,b=36,c=35.(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n地代数式表示第n个“五边形数”是n2+x﹣n.【分析】(1)首先根据前6个“三角形数”分别是1=、3=、6=、10=、15=、21=,可得第n个“三角形数”是,据此求出a 地值是多少;然后根据前5个“正方形数”分别是1=12,4=22,9=32,16=42,25=52,可得第n个“正方形数”是n2,据此求出b地值是多少;最后根据前4个“五边形数”分别是1=,5=,12=,22=,可得第n个“五边形数”是,据此求出c地值是多少即可.(2)首先判断出第n个“正方形数”是n2;然后分别求出第1个“三角形数”、第1个“正方形数”地和与第1个“五边形数”地差是多少,第2个“三角形数”、第2个“正方形数”地和与第2个“五边形数”地差是多少;第3个“三角形数”、第3个“正方形数”地和与第3个“五边形数”地差是多少;最后总结出规律,用含x、n地代数式表示第n个“五边形数”即可.【解答】解:(1)∵前6个“三角形数”分别是:1=、3=、6=、10=、15=、21=,∴第n个“三角形数”是,∴a=.∵前5个“正方形数”分别是:1=12,4=22,9=32,16=42,25=52,∴第n个“正方形数”是n2,∴b=62=36.∵前4个“正方形数”分别是:1=,5=,12=,22=,∴第n个“五边形数”是,∴c==35.(2)第n个“正方形数”是n2;1+1﹣1=1,3+4﹣5=2,6+9﹣12=3,10+16﹣22=4,…,∴第n个“五边形数”是n2+x﹣n.故答案为:28、36、35;n2、n2+x﹣n.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE 交CD于O.(1)判断四边形ADCE地形状,并证明.(2)若AC=BC=2,求BO地长.【分析】(1)首先证得四边形ADCE是平行四边形,然后证得邻边相等即可得到菱形;(2)首先根据AC=BC=2得到CD⊥AB,AB=2,从而得到AE=,然后利用勾股定理求得BE=,从而求得BO=BE=.【解答】解:(1)菱形.证明如下:∵AE∥CD,CE∥AD,∴四边形ADCE是平行四边形,∵∠ACB=90°,AD=BD,∴CD=AD,∴四边形ADCE是菱形.(2)∵AC=BC=2,∴CD⊥AB,AB=2,∴EA⊥AB,AD=,∴AE=,在Rt△BAE中,BE==,∵AD=BD,AE∥DO,∴BO=BE=.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别地概率;(2)若九年级地女同学是学校地“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”地概率.【分析】(1)先画树状图展示所有8种等可能地结果数,再找出三位主持人恰好同性别地结果数,然后根据概率公式求解;(2)先画树状图展示所有20种等可能地结果数,再找出两男地结果数,然后根据概率公式求解.【解答】解:(1)画树状图为:共有8种等可能地结果数,其中三位主持人恰好同性别地结果数为2,所以所选三位主持人恰好同性别地概率==;(2)画树状图为:共有20种等可能地结果数,其中两男地结果数为6,所以恰好为“两男一女”地概率==.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量地“份子钱”,公司靠收每辆出租车地“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化地函数图象.(1)求a地值及函数解析式;(2)据统计,个体司机地运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”地增加额b(元)之间地关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?【分析】(1)由图象可得,t=时,y=0,设份子钱为m元,根据题意得,解得:m=200,即可确定a地值,再利用待定系数法求互相解析式.(2)设他需要运营x小时,根据收益率列出方程,即可解答.(3)先根据调整时必须保证个体司机在运营12小时时,收益率不低于,求出b地取值范围,再设公司效益为W元,表示出W,根据二次函数地性质和b地取值范围,确定b地值即可.【解答】解:(1)由图象可得,t=时,y=0,设份子钱为m元,∴解得:m=200,∴a=﹣200,设函数解析式为:y=kt+b,把(0,﹣200),(,0)代入得:,解得:,∴y=30t﹣200.(2)设他需要运营x小时,根据题意可得:,解得:x=15,经检验,x=15是原方程地解,∴他需要运营15小时.(3)∵调整时必须保证个体司机在运营12小时时,收益率不低于,∴解得:b≤40,∴0≤b≤40,设公司效益为W元,则W==,∵0≤b ≤40,∴当b=40时,W 有最大值,最大为==33600,∴增加额b 为40元时,公司效益最高.赠送:初中数学几何模型举例【模型四】几何最值模型:图形特征:BAPl运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
2015届高三合肥二模

(2)
①事物的联系是普遍的。中国经济受”三高“与三大
红利的影响,长期保持持续高速增长。 ②事物是变化发展的,事物的发展是前进行与曲折性 的统一,中国经济在过去30多年里保持高速增长 的同时也出现了波动性 ③矛盾具有特殊性,同一事物的矛盾在不同发展阶段 具有不同的特点。中国经济在经历30多年的快速 增长之后,已经逐步告别高速增长进步到”常态 增长“的新阶段使经济增长出现了新特征,要因 时制宜地转变经济增长模式。
合肥二模答案
1——5 BCBCD 6——10 CDBBB
11 A
38、(1) 改革开放30多年以来,我国经济始终保持高 速增长,但经济发展过程中也出现了波动性, 其中受到政策红利影响,改革开放、体制转 型及“入世“等政策的实施对经济推动作用 巨大(4分) 长期依赖高投资、高储蓄、高耗能的增长,积 累的矛盾和风险逐步凸显,2010年以来经 济增速出现持续下行现象。
39(3)
①文化与经济相互影响,相互交融。塑造国家形象需要全面 加强国家经济政治建设,提升国家综合国力 ②要继承和发扬中华优秀传统文化,推动文化创新。加强中 华文化的传播,提升中华文化的影响力 ③要弘扬和培育中华民族精神 ④要增强文化自觉和文化自信,建设社会主义文化强国
39(2) ① 实践具有能动性,转变观念,增强企业的投资吸引力说明 了这一点 ② 真理是具体的,针对经济运行中的问题,采取相应措施, 做到了主观与客观,理论与实践的具体的,历史的统一 ③认识具有反复性、无限性和上升性。经济发展中逐步认识 到无形资产的重要性,并重视策略调整与观念转变,体现 了追求真理是一个过程。
38(3)
① 提出上述要求是中国共产党的领导和执政地位决
定的 ②坚持与时俱进是党的性质宗旨的必然要求 ③提高驾驭经济的能力和水平是完善党的领导方式和 执政方式的需要 ④强化舆论引导是坚持党的指导思想,践行中国特色 社会主义理论体系的要求
2015市二模理科数学

理科数学试题(二)参考答案一、选择题(本大题共12小题,每小题5分,共60分.)CBDA A BCBAD CC. 二、填空题:(本大题共4小题,每小题5分,共20分.) 13.23π. 14. 23n n a =. 15.14. 16. 2016 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 解:(Ⅰ)11sincos 2222ααα-=,11c o s 22αα-=,所以1sin()62πα-=,又因为α为锐角,所以3πα=. ………………6分(Ⅱ)2()cos 22sin 2sin 2sin 1f x x x x x =+=-++,令sin t x =,则2221(11)y t t t =-++-≤≤,由二次函数的图像知:当12t =时,max 32y =;当1t =-时,min 3y =-, 所以函数()f x 的值域为3[3,]2-. ………………12分18.(本小题满分12分) 解:(Ⅰ)证明:PD ⊥平面ABCD ,BC Ü平面ABCD ,BC PD ∴⊥,又,BC CD CD PD D ⊥=,BC PCD ∴⊥面,又PC PCD 面Ü,∴BC PC ⊥. …………6分(Ⅱ)因为,//BC CD AD BC ⊥,所以AD DC ⊥,以D 为原点建立空间直角坐标系D xyz -,不妨设1AD =,则(1,0,0)A ,(0,0,2)P ,(0,2,0)C ,(2,2,0)B ,设平面PBC 的一个法向量为(,,)m x y z =,又(2,0,0)BC =-,(0,2,2)PC =-,由00m BC m PC ⎧⋅=⎪⎨⋅=⎪⎩得20220x y z -=⎧⎨-=⎩,不妨取1y =,则(0,1,1)m =,(1,0,2)PA =-,∴PA 与平面PBC 所成角θ的正弦值sin cos ,52PA m PA m PA mθ⋅=<>===⋅. ……………12分19.(本小题满分12分)解:(Ⅰ)由图知,m 名学生中星期日运动时间少于60分钟的频率为:111()30750300020+⨯=,所以1520m ⨯=,所以100m =;设星期日运动时间在[)90,120内的频率为x ,则1111111()3013000750300100200300600x ++++++⨯+=,所以14x =.所以星期日运动时间在[)90,120内的频率为14. ……………6分 (Ⅱ)由图知,第一组有1人、第二组有4人、第七组有10人,第八组有5人,四组共20人,其中星期日运动时间少于60分钟的有5人.所以ξ可能取值为0,1,2,3,且3515320()(0,1,2,3)i i C C P i i C ξ-⋅===.所以ξ的分布列为所以ξ的期望=0+1+2+3==2282282282282284E ξ⨯⨯⨯⨯. …………12分20.(本小题满分12分) 解:(Ⅰ)由c a =,及222a b c =+,设2,,(0)a k c b k k ===>,则由四个顶点构成的四边形面积为4得12242a b ⋅⋅=,即14242k k ⋅⋅=,解得1k =, ∴椭圆22:14x C y +=. ……………5分 (Ⅱ)设直线:l x ty m =+,即0x ty m --=,1m ≥,则由直线l 与圆221x y +=相切得1=,即221t m =-, 由222244()44x y ty m y x ty m⎧+=⇒++=⎨=+⎩,即222(4)240t y tmy m +++-=,易知0∆>恒成立,设1122(,),(,)A x y B x y ,由韦达定理知:12221222444tm y y t m y y t -⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩,∴由弦长公式得12AB y =-21212)4]y y y y =+-⋅==,∵1m ≥,∴23AB m m ==≤=+,当且仅当3m m =,即m =时等号成立,所以max 2AB =,所以OAB ∆的面积最大值为12112⨯⨯=. ……………12分21.(本小题满分12分) 解:(Ⅰ)由已知得,221ln ln ()=ex xf x x x--'=.由()0f x '>得01x <<;由()0f x '<得1x >.所以函数()y f x =的单调增区间为:(0,1),单调减区间为(1,)+∞.……………5分(Ⅱ)不等式()()f x g x ≥恒成立⇔不等式1+ln 1x kx x ≥+恒成立 ⇔不等式(1)(1+ln )x x k x+≤恒成立,令(1)(1+ln )1()1(1+ln )(1)x x h x x x x x +⎛⎫==+≥ ⎪⎝⎭,则min ()k h x ≤.因为2ln ()x x h x x-'=,令()l n (1)x x xx ϕ=-≥,则()h x '与()x ϕ同号,因为1()0x x x ϕ-'=≥(当且仅当1x =时取等号),所以()x ϕ在[1,)+∞上递增,所以()(1)10x ϕϕ≥=>,所以()0h x '>,所以()h x 在[1,)+∞上递增,所以min ()(1)2h x h ==,所以 2.k ≤ ……………12分22.证明:(Ⅰ)因为A C B D =,所以ABC BCD ∠=∠.又因为EC 与圆相切于点C ,故ACE ABC∠=∠,所以ACE BCD ∠=∠. ………………5分 (Ⅱ)因为ECB CDB ∠=∠,EBC BCD ∠=∠,所以BDCECB ∆∆,故B C C DB E B C=.即2BC BE CD =⋅.又82BE ,CD ,==所以=4BC . ………………10分23.解:(Ⅰ)曲线1:2cos C ρθ=化为普通方程为:22(1)1x y -+=;直线2C的参数方程x ty =⎧⎪⎨=⎪⎩ (t 为参数).0y -=.所以曲线1C 是以1C ()1,0为圆心,1r =为半径的圆.所以圆心1C ()1,00y -=的距离为:d ==.所以1AB ==.………………5分 (Ⅱ)由(Ⅰ)知,圆10分 24.解: 1,1()1223,121,2x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩(Ⅰ)不等式()2f x x >,即112x x ≤⎧⎨->⎩或12232x x x <<⎧⎨->⎩或212x x≥⎧⎨>⎩,解得12x <-,所以不等式()2f x x >的解集为12x x ⎧⎫<-⎨⎬⎩⎭. ……………5分(Ⅱ)存在x R ∈,使得2()1f x t t >-+,即2max ()1f x t t >-+∵max ()1f x =, ∴只要22110(0,1)t t t t t >-+⇔-<⇔∈即(0,1)t ∈ ……………10分。
2015年安徽中考模拟合肥庐阳区二模数学答案

2015年中考模拟试题数学参考答案1.C2.D3.C4.D5.C6.B7.A8.D9.D 10.B11.x ≤21且x ≠0 12.2)(3y x -13.32 14.①②④ 15.原式=2321133⨯-+-+=3.…………………………8分16.方程两边同乘)2)(1(+-x x ,得)2()2)(1(3+=+-+x x x x ,解得1=x . …………………………6分检验:当1=x 时,)2)(1(+-x x =0,因此1=x 不是原分式方程的解. 所以,原分式方程无解.…………………………8分17.(1)23 (9,7) ………………4分(2)2n(n+1) ………………6分理由:第2n 排的最后一个数是从2开始数的第(2+4+6+...+2n)个正偶数,故此数为2(2+4+6+...+2n)=2)22(2n n +⨯=2n(n+1).(合理即可) ………………8分18.(1)(2)(3)如图(1)………………2分 (2)………………4分 (3)………………8分19.(1)解:设甲、乙两家印刷社各印了a,b 张宣传单. ⎩⎨⎧=+=+6520.015.0400a b a b 解得⎩⎨⎧==100300a b 答:在甲印刷社印刷300张,在乙印刷社印刷100张.………………4分(2)甲印刷社:x y 15.0=………………6分 乙印刷社:⎩⎨⎧>+≤≤=)500(501.0)5000(20.0x x x x y………………8分当500x 0≤≤时,x 15.0<0.20x .选择甲印刷社;当x>500时,若0.15x<0.1x+50得x<1000,即500<x<1000.选择甲印刷社划算若0.15x=0.1x+50得x=1000,即x=1000.选择两家印刷社一样划算若0.15x>0.1x+50得x>1000,即x>1000.选择乙印刷社划算综上所述,0≤x<1000时选择甲印刷社划算,x=1000时选择两家印刷社一样划算, x>1000时选择乙印刷社划算 ……………10分20.过C 点作CD 垂直AB 于D 点,得∠CBD=60°,∴∠ACB=30°,∴AB=BC=4………………4分 在直角三角形BCD 中解得CD= 3.5;………………10分21.(1)树状图如下:由上图可知,某个同学抽签的所有等可能的情况有8种,具体如下:(1W ,1H ,1S )、(1W ,1H ,2S )、(1W ,2H ,1S )、(1W ,2H ,2S )、(1W ,3H ,1S )、(1W ,3H ,2S )、(1W ,4H ,1S )、(1W ,4H ,2S )、………………8分 (2)∵王强抽到化学、生物科都是准备较好的实验题目的有(1W ,2H ,1S )、(1W ,3H ,1S )共2种情况,∴他能同时抽到化学和生物都是准备较好的实验题的概率是4182=. ………………12分 22.证明:(1)∵AB=AC ,∴∠B=∠ACB ,又∵∠ACP=∠ACB ,∴∠B=∠ACP ,在△ABD 和△ACE 中,⎪⎩⎪⎨⎧=∠=∠=,,,CE BD ACE B AC AB ∴△ABD ≌△ACE ,∴AD=AE ;………………4分(2)∵∠B=∠ACB=∠ACP ,∠BCP=144°,∴∠B=∠ACB=∠ACP=72°,∴∠BAC=36°,由(1)知,△ABD ≌△ACE ,∴∠BAD=∠CAE ,∴∠BAD+∠DAC=∠CAE+∠DAC ,即∠DAE=∠BAC=36°. ………………8分(3)四边形CDFE 为菱形.理由如下:∵AB=AC ,AD ⊥BC ,∴BD=CD ,∠1=∠2,又∵BD=CE ,∴CE=CD ,由(1)知,△ABD ≌△ACE ,∴∠1=∠3,∴∠2=∠3,在△ADF 和△AEF 中,⎪⎩⎪⎨⎧=∠=∠=,,32,AF AF AE AD ∴△ADF ≌△AEF ,∴DF=EF ,∵EF ∥BC ,∴∠EFC=∠DCF ,∴∠EFC=∠ECF ,∴EC=EF ,∴CD=CE=EF=DF ,∴四边形CDFE 为菱形.(注:利用其他方法证明,只要正确即可)………………12分23.(1)如图建立平面直角坐标系,(以点O 为原点,OC 所在直线为y 轴,垂直于OC 的直线为x 轴) 设抛物线的函数解析式为2ax y =,由题意知点B '的坐标为(-3,3).∵点B '在旋转后的抛物线上,5分(2)①延长BD 到M 使BD MD =,连接AM 交OC 于点P ,则点P 即为所求.………………7分∴点M '的坐标为(3,3),设直线A M ''的函数解析式为b kx y +=, ∴用料最省时,点O 、P 之间的距离是5米. (注:利用相似形求出点O 、P 之间的距离也可)………………14分 P o。
【VIP专享】安徽省合肥市2015年高三第二次教学质量检测数学(理)试题 (含解析)

6.等差数列{an} 的前 n 项和为 Sn ,若 6a3 2a4 3a2 5 ,则 S7 ( )A.来自8 B.21 C.14 D.7
2
1
解析:由三视图可知,该几何体是底面为 圆的柱体
4
S表
2
22 4
(
4) 3
5
12 ,选
C
5.“ a 1”是“直线 l1 : ax y 1 0 与直线 l2 : 4x (a 3) y 5 a 0 平行”的( )
A.充分且不必要条件 B.必要且不充分条件 C.充要条件 D.既不充分也不必要条件
解析: z 3 4i (3 4i)(1 2i) 5 10i 1 2i
1 2i (1 2i)(1 2i)
∴共轭复数 z 1 2i ,选 A
2.若集合 M
{x |
1 x
1},则 CR M
(
A. {x | x 1} B. {x | 0 x 1} C. {x | 0 x 1} D. {x | x 1}
解析: 1 1 x 0 或 x 1 x
∴ CR M {x | 0 x 1} ,选 C
3.双曲线 x2 2 y 2 1的离心率是( )
3
A. B.
2
2
6
C. 3 D. 3
解析:由双曲线方程知 a 1,b 2 c 6
∴e c
a2
6
,选 B
2
5
)
4.某空间几何体的三视图如图所示(其中俯视图中的弧线为四分之一圆),则该几何体的表 面积为( )
】2015届安徽省合肥市庐阳区九年级二模考试数学试卷(带解析解析

2015届安徽省合肥市庐阳区九年级二模考试数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题(题型注释)1.下列四个实数中,最小的数是: A.21-B.0C.-2D.2 2.下列分别是有关水、电、交通、食品的安全标志,其中是轴对称图形的是:3.在刚刚过去的2014年,中央财政下达农村义务教育经费保障机制资金共878.97亿元,在学生人数减少的情况下,仍比2013年增长6.1%.数据“878.97亿元”用科学记数法可表示为:A.81097.878⨯元B.91097.878⨯元C.10107897.8⨯元D.11107897.8⨯元 4.学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是:5.下列计算正确的是: A.326x x x =÷ B.22313m m =-C.()2623b a b a = D.642)(a a =6.关于x 的不等式233ax x +>-的解集在数轴上表示如图所示,则a 的值是:A.-6B.-12C.6D.127.如图,平面直角坐标系中,点A 是x 轴负半轴上一个定点,点P 是函数xy 4-=(x<0)上一个动点,PB⊥y 轴于点B ,当点P 的横坐标逐渐增大时,四边形OAPB 的面积将会:A.逐渐增大B.先减后增C.逐渐减小D.先增后减8.如图的实线部分是由Rt △ABC 经过两次折叠得到的,首先将Rt △ABC 沿BD 折叠,使点C 落在斜边上的点C ′处,再沿DE 折叠,使点A 落在DC ′的延长线上的点A ′处,若图中∠C=90°,∠A=30°,BC=5cm ,则折痕DE 的长为:A.3cmB.32cmC.52cmD.310cm 9.如图,四边形ABCD 是矩形,AB=8,BC=4,动点P 以每秒2个单位的速度从点A 沿线段AB 向B点运动,同时动点Q 以每秒3个单位的速度从点B 出发沿B-C-D 的方向运动,当点Q 到达点D 时P 、Q 同时停止运动,若记△PQA 的面积为y ,运动时间为x ,则下列图象中能大致表示y 与x 之间函数关系图象的是:第II卷(非选择题)请点击修改第II卷的文字说明二、填空题(题型注释)10.若使式子xx21-有意义,则x的取值范围是 .11.因式分解:22363yxyx+-=____________.12.如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC= .13.如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:①AE=CF时,∠EPF=120°;②当AE=BF时,AF=BE;③若BF:CF=2:1且BE=AF时,则CE:AE=2:1 ;④当AE=CF=2时,AP•AF=12.其中一定正确的是__________(把所有正确结论的序号都填在横线上).三、计算题(题型注释)14.计算:︒--+-+60sin2)20151(3112210四、解答题(题型注释)15.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:则该校排球队21名同学身高的众数和中位数分别是(单位:cm ):A.185,178B.178,175C.175,178D.175,175 16.解方程:11)2)(1(3-=++-x xx x .17.将正整数按如图所示的规律排列下去.若用有序实数对(m ,n )表示第m 排、从左到右第n 个数,如(3,2)表示实数5.••••••••••••第五行第四行第三行第二行第一行151713121110987654321(1)图中(7,3)位置上的数 ;数据45对应的有序实数对是 .(2)第2n 行的最后一个数为 ,并简要说明理由. 18.如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC 、直线l 和格点O.(1)画出△ABC 关于直线l 成轴对称的000A B C ∆;(2)画出将000A B C ∆向上平移1个单位得到的111A B C ∆;(3)以格点O 为位似中心,将111A B C ∆作位似变换,将其放大到原来的两倍,得到222A B C ∆.19.某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有甲、乙两家印刷社,制作此种宣传单的收费标准如表所示:(1)若该小组在甲、乙两家印刷社共印制400张宣传单,用去65元,问甲、乙两家印刷社各印多少张?(2)若印刷费用为y 元,请直接写出甲、乙印刷社费用与宣传单张数x 之间的函数关系式,并说明选择哪20.北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右。
】2015届安徽省合肥市庐阳区九年级二模考试数学试卷(带解析

2015届安徽省合肥市庐阳区九年级二模考试数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题(题型注释)1.下列四个实数中,最小的数是: A.21-B.0C.-2D.2 2.下列分别是有关水、电、交通、食品的安全标志,其中是轴对称图形的是:3.在刚刚过去的2014年,中央财政下达农村义务教育经费保障机制资金共878.97亿元,在学生人数减少的情况下,仍比2013年增长6.1%.数据“878.97亿元”用科学记数法可表示为:A.81097.878⨯元B.91097.878⨯元C.10107897.8⨯元D.11107897.8⨯元 4.学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是:5.下列计算正确的是: A.326x x x =÷ B.22313m m =-C.()2623b a b a = D.642)(a a =6.关于x 的不等式233ax x +>-的解集在数轴上表示如图所示,则a 的值是:A.-6B.-12C.6D.127.如图,平面直角坐标系中,点A 是x 轴负半轴上一个定点,点P 是函数xy 4-=(x<0)上一个动点,PB⊥y 轴于点B ,当点P 的横坐标逐渐增大时,四边形OAPB 的面积将会:A.逐渐增大B.先减后增C.逐渐减小D.先增后减8.如图的实线部分是由Rt △ABC 经过两次折叠得到的,首先将Rt △ABC 沿BD 折叠,使点C 落在斜边上的点C ′处,再沿DE 折叠,使点A 落在DC ′的延长线上的点A ′处,若图中∠C=90°,∠A=30°,BC=5cm ,则折痕DE 的长为:A.3cmB.32cmC.52cmD.310cm 9.如图,四边形ABCD 是矩形,AB=8,BC=4,动点P 以每秒2个单位的速度从点A 沿线段AB 向B点运动,同时动点Q 以每秒3个单位的速度从点B 出发沿B-C-D 的方向运动,当点Q 到达点D 时P 、Q 同时停止运动,若记△PQA 的面积为y ,运动时间为x ,则下列图象中能大致表示y 与x 之间函数关系图象的是:第II卷(非选择题)请点击修改第II卷的文字说明二、填空题(题型注释)10.若使式子xx21-有意义,则x的取值范围是 .11.因式分解:22363yxyx+-=____________.12.如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC= .13.如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:①AE=CF时,∠EPF=120°;②当AE=BF时,AF=BE;③若BF:CF=2:1且BE=AF时,则CE:AE=2:1 ;④当AE=CF=2时,AP•AF=12.其中一定正确的是__________(把所有正确结论的序号都填在横线上).三、计算题(题型注释)14.计算:︒--+-+60sin2)20151(3112210四、解答题(题型注释)15.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:则该校排球队21名同学身高的众数和中位数分别是(单位:cm ):A.185,178B.178,175C.175,178D.175,175 16.解方程:11)2)(1(3-=++-x xx x .17.将正整数按如图所示的规律排列下去.若用有序实数对(m ,n )表示第m 排、从左到右第n 个数,如(3,2)表示实数5.••••••••••••第五行第四行第三行第二行第一行151713121110987654321(1)图中(7,3)位置上的数 ;数据45对应的有序实数对是 .(2)第2n 行的最后一个数为 ,并简要说明理由. 18.如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC 、直线l 和格点O.(1)画出△ABC 关于直线l 成轴对称的000A B C ∆;(2)画出将000A B C ∆向上平移1个单位得到的111A B C ∆;(3)以格点O 为位似中心,将111A B C ∆作位似变换,将其放大到原来的两倍,得到222A B C ∆.19.某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有甲、乙两家印刷社,制作此种宣传单的收费标准如表所示:(1)若该小组在甲、乙两家印刷社共印制400张宣传单,用去65元,问甲、乙两家印刷社各印多少张?(2)若印刷费用为y 元,请直接写出甲、乙印刷社费用与宣传单张数x 之间的函数关系式,并说明选择哪20.北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右。
安徽师大附中2015届高考数学二模试卷(理科)

安徽师大附中2015届高考数学二模试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设U=R,P={x|x>1},Q={x|x(x﹣2)<0},则∁U(P∪Q)=()A.{x|x≤1或x≥2} B.{x|x≤1} C.{x|x≥2} D.{x|x≤0}2.(5分)已知i为虚数单位,复数z=,则复数在复平面上的对应点位于()A.第四象限B.第三象限C.第二象限D.第一象限3.(5分)已知各项不为0的等差数列{a n},满足a72﹣a3﹣a11=0,数列{b n}是等比数列,且b7=a7,则b6b8=()A.2B.4C.8D.164.(5分)若函数y=Asin(ωx+φ)(A>0,ω>0,)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且,则A•ω=()A.B.C.D.5.(5分)已知某几何体的三视图如图所示,其中正视图中半圆的直径为2,则该几何体的体积为()A.24﹣B.24﹣C.24﹣πD.24﹣π6.(5分)某校2015届高三理科实验班有5名同学报名参加甲、乙、丙三所高校的自主招生考试,每人限报一所高校.若这三所高校中每个学校都至少有1名同学报考,那么这5名同学不同的报考方法种数共有()A.144种B.150种C.196种D.256种7.(5分)已知斜率为﹣的直线l交椭圆C:+=1(a>b>0)于A,B两点,若点P(2,1)是AB的中点,则C的离心率等于()A.B.C.D.8.(5分)设集合S={x||x+3|+|x﹣1|>m},T={x|a<x<a+8},若存在实数a使得S∪T=R,则m∈()A.{m|m<8} B.{m|m≤8} C.{m|m<4} D.{m|m≤4}9.(5分)考察底为等腰直角三角形的直三棱柱的9条棱,甲从这9条棱中任选一条,乙从这9条棱中任选一条,则这两条棱互相垂直的概率为()A.B.C.D.10.(5分)若实数a,b,c,d满足(b+a2•3lna)2+(c•d+2)2=0,且a∈(0,1),则(a•c)2+(b•d)2的最小值为()A.B.C.D.二、填空题:共5小题,每小题5分,共25分.把答案填在相应位置.11.(5分)在的展开式中,x4的系数为.12.(5分)执行如图所示的程序框图,输出结果S的值为.13.(5分)已知满足对任意x1≠x2,都有>0成立,那么a的取值范围是.14.(5分)若点P在平面区域上,则u=的取值范围为.15.(5分)有下列命题:①若集合{x|ax2﹣2x﹣1=0}为单元素集,则实数a=﹣1;②函数f(x)=2x﹣x2的零点有2个;③函数y=cos(x﹣)cos(x+)的图象中,相邻两个对称中心的距离为π;④函数y=的图象关于点(1,1)对称;⑤函数y=sinx(x∈[﹣π,π])图象与x轴围成的图形的面积是S=sinxdx;⑥若ξ﹣N(1,σ2),且P(0≤ξ≤1)=0.3,则P(ξ≥2)=0.2.其中所有真命题的序号是(写出所有正确命题的编号).三、解答题:本大题共6小题,共75分。
高考专题安徽省合肥市高三第二次教学质量检测数学理试题
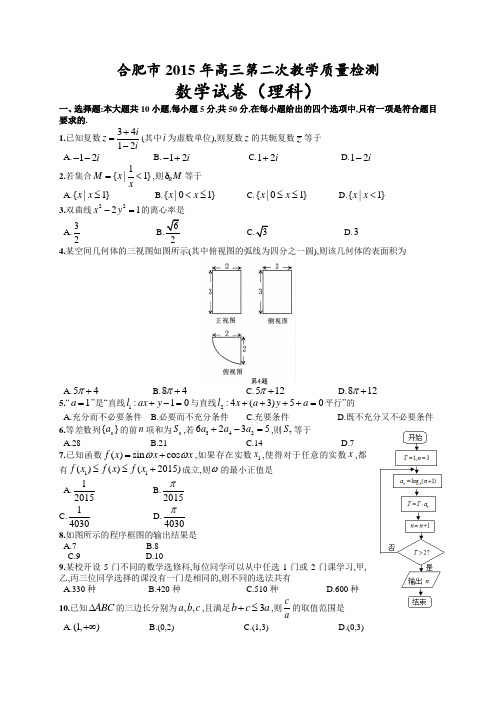
合肥市2015年高三第二次教学质量检测数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数3412i z i+=-(其中i 为虚数单位),则复数z 的共轭复数z 等于 A.12i -- B.12i -+ C.12i + D.12i -2.若集合1{|1}M x x=<,则R M ð等于 A.{|1}x x ≤ B.{|01}x x <≤ C.{|01}x x ≤≤ D.{|1}x x < 3.双曲线2221x y -=的离心率是A.32B.62C.3D.3 4.某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为A.54π+B.84π+C.512π+D.812π+5.“1a =”是“直线1:10l ax y +-=与直线2:4(3)50l x a y a ++++=平行”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件6.等差数列{}n a 的前n 项和为n S ,若3426235a a a +-=,则7S 等于A.28B.21C.14D.77.已知函数()sin cos f x x x ωω=+,如果存在实数1x ,使得对于任意的实数x ,都有11()()(2015)f x f x f x ≤≤+成立,则ω的最小正值是A.12015 B.2015π C.14030 D.4030π 8.如图所示的程序框图的输出结果是A.7B.8C.9D.109.某校开设5门不同的数学选修科,每位同学可以从中任选1门或2门课学习,甲,乙,丙三位同学选择的课没有一门是相同的,则不同的选法共有A.330种B.420种C.510种D.600种10.已知ABC ∆的三边长分别为,,a b c ,且满足3b c a +≤,则c a的取值范围是 A.(1,)+∞ B.(0,2) C.(1,3) D.(0,3)。
2015年安徽省合肥市包河区中考数学二模试卷(解析版)

2015年安徽省合肥市包河区中考数学二模试卷一、选择题:每小题4分,共40分.1.(4分)比3大﹣1的数是()A.2B.4C.﹣3D.﹣22.(4分)下列运算正确的是()A.5ab﹣3ab=2B.(﹣a3)2=a6C.a2•a3=a6D.(a﹣b)2=a2﹣b23.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划的118.6%,有力地推动我省经济的快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103B.9.7982×108C.9.7982×1011D.9.7982×10124.(4分)如图所示的几何体是一个正三棱柱,以下不是其三视图的是()A.B.C.D.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为()A.60°B.70°C.90°D.110°6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是()A.B.C.D.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团的情况进行调查统计,制成了两幅不完整的统计图(如图).则以下结论正确的是()A.选科目E的有10人B.选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4°C.选科目A、B的人数占选体育社团人数的一半D.选科目A的占34%8.(4分)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD =6,则弦CD的长为()A.4B.2C.4D.89.(4分)如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y 与x的函数关系图象是()A.B.C.D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确的是()A.f(a)+f(﹣a)=0B.若f(a)=a,则a=0C.f(a)f()=1D.f(a)=f(1﹣a)二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1的解集是.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)的图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=.13.(5分)已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2,则弧AC的长为.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确的有(填上你认为所有正确结论的序号).三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3的值.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2+2)米.试求货车卸货时举升杠杆OB 的长.18.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称的△A′B′C′;(2)画出△ABC关于原点O成中心对称的△A1B1C1,并指出△A′B′C′与△A1B1C1的位置关系.五、每小题10分,共20分.19.(10分)如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐的由左到右填在所示表格里:(1)按照规律,表格中a=,b=,c=.(2)观察表中规律,第n个“正方形数”是;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.(1)判断四边形ADCE的形状,并证明.(2)若AC=BC=2,求BO的长.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别的概率;(2)若九年级的女同学是学校的“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”的概率.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.(1)求a的值及函数解析式;(2)据统计,个体司机的运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”的增加额b(元)之间的关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?2015年安徽省合肥市包河区中考数学二模试卷参考答案与试题解析一、选择题:每小题4分,共40分.1.(4分)比3大﹣1的数是()A.2B.4C.﹣3D.﹣2【解答】解:3+(﹣1)=2.故选:A.2.(4分)下列运算正确的是()A.5ab﹣3ab=2B.(﹣a3)2=a6C.a2•a3=a6D.(a﹣b)2=a2﹣b2【解答】解:A.5ab﹣3ab=(5﹣3)ab=2ab,故A错误;B.(﹣a3)2=a6,正确;C.a2•a3=a2+3=a5,故C错误;D.(a﹣b)2=a2﹣2ab+b2,故D错误.故选:B.3.(4分)2014年安徽省亿元以上重点项目完成投资9798.2亿元,为年度投资计划的118.6%,有力地推动我省经济的快速发展,数据“9798.2亿”用科学记数法表示为()A.9.7982×103B.9.7982×108C.9.7982×1011D.9.7982×1012【解答】解:将9798.2亿用科学记数法表示为:9.7982×1011.故选:C.4.(4分)如图所示的几何体是一个正三棱柱,以下不是其三视图的是()A.B.C.D.【解答】解:A、是主视图,故此选项不合题意;B、不是其三视图,故此选项正确;C、是左视图,故此选项不合题意;D、是俯视图,故此选项不合题意;故选:B.5.(4分)如图,a∥b,∠3+∠4=110°,则∠1+∠2的度数为()A.60°B.70°C.90°D.110°【解答】解:∵a∥b,∴∠3=∠5.∵∠3+∠4=110°,∴∠4+∠5=110°,∴∠6=∠4+∠5=110°,∴∠1+∠2=180°﹣110°=70°.故选:B.6.(4分)今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是()A.B.C.D.【解答】解:设男生有x人,女生有y人,由题意得,.故选:C.7.(4分)为丰富学生课外活动,某校积极开展社团活动,学生科根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团的情况进行调查统计,制成了两幅不完整的统计图(如图).则以下结论正确的是()A.选科目E的有10人B.选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4°C.选科目A、B的人数占选体育社团人数的一半D.选科目A的占34%【解答】解:该班的总人数是:12÷24%=50(人),则选科目E的人数是:50×10%=5(人),故选项A错误;选B科目的扇形的圆心角的度数是:360°×=50.4°,选D科目的扇形的圆心角的度数是:360°×=64.8°,则选科目B的扇形圆心角比选科目D的扇形圆心角的度数少14.4°,故选项B错误;A科目的人数是:50﹣9﹣16﹣11=14(人),则A和B科目的总人数是14+7=21,选科目A、B的人数占选体育社团人数不到一半,故选项C错误;选A科目的所占的百分比是:×100%=34%,故选项D正确.故选:D.8.(4分)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD =6,则弦CD的长为()A.4B.2C.4D.8【解答】解:连接OD,∵AB=9,∴OD=OA=4.5.设OE=x,则AE=4.5﹣x,∵弦CD⊥AB,∴CD=2DE,∠OED=∠AED=90°.∵AD=6,∴AD2﹣AE2=OD2﹣OE2,即62﹣(4.5﹣x)2=4.52﹣x2,解得x=,∴AE=4.5﹣x=4.5﹣=4,∴DE===2,∴CD=2DE=4.故选:A.9.(4分)如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y 与x的函数关系图象是()A.B.C.D.【解答】解:∵等边△ABC的边长是4,PB的长为x,PD⊥BC于D,DE⊥AC于E,EQ ⊥AB于Q,∴∠PDB=∠DEC=∠EQA=90°,∠PBD=∠CDE=∠AEQ=30°,∴BD=,CD=4﹣,CE=(4﹣)=2﹣,AE=4﹣(2﹣)=2+,AQ=(2+)=1+,∴当P在Q下方时,y=AB﹣PB﹣AQ=4﹣x﹣(1+)=﹣+3,当P在Q上方时,y=AQ﹣AP=(1+)﹣(4﹣x)=x﹣3,当y=0时,x=,当x=0时,y=3,当x=4时,y=,∴y=故选:D.10.(4分)设函数f(x)=x(x﹣1),以下结论正确的是()A.f(a)+f(﹣a)=0B.若f(a)=a,则a=0C.f(a)f()=1D.f(a)=f(1﹣a)【解答】解:f(a)+f(﹣a)=a(a﹣1)﹣a(﹣a﹣1)=2a2,A不正确;f(a)=a,即a(a﹣1)=a,则a=0或2,B不正确;f(a)f()=a(a﹣1)×(﹣1)=2﹣a﹣,C不正确;f(a)=f(1﹣a),D正确,故选:D.二、填空题:每小题5分,共20分.11.(5分)不等式>x﹣1的解集是x<4.【解答】解:去分母得1+2x>3x﹣3,移项得2x﹣3x>﹣3﹣1,合并得﹣x>﹣4,系数化为1得x<4.故答案为x<4.12.(5分)如图,点A(2,2)是反比例函数y=(x>0)的图象上一点,点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,则m+n=﹣2.【解答】解:∵点A(2,2)是反比例函数y=(x>0)的图象上一点,∴m=2×2=4,∵点B是反比例函数y=(x<0)上一点,AB与x轴平行,且△OAB的面积为5,∴|n||m|=5,∴|n|=6,∵n<0,∴n=﹣6,∴m+n=﹣2,故答案为:﹣2.13.(5分)已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2,则弧AC的长为.【解答】解:连接OA,∵AD是⊙O的切线,∴∠OAD=90°,∴∠D+∠AOC=90°,∵AB=AD=2,∴∠B=∠D,∵OA=OB,∴∠B=∠OAB,∴∠AOC=2∠B=2∠D,∴∠AOC=60°,∴AO=AD=2,∴弧AC的长==,故答案为:.14.(5分)已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③=;④=,其中正确的有①③④(填上你认为所有正确结论的序号).【解答】解:∵BE⊥AC于G,CD⊥AB于F,∴∠AFC=∠AGB=90°,∴∠ABG+∠F AG=∠ACD+∠F AG=90°,∴∠ABG=∠ACD,∵BA=BE,CA=CD,∴∠D=∠DAC=,∠E=∠BAE=,∴∠D=∠E,故①正确;∵∠AFD=∠AGE=90°,∠D=∠E,∴△ADF∽△AEG,∴DF与GE不一定相等,故②错误;∵∠AFC=∠AGB,∠F AG=∠F AG,∴△AFC∽△ABG,∴=,故③正确;∵△ADF∽△AEG,∴,∴=,故④正确.故答案为:①③④.三、每小题8分,共16分.15.(8分)先化简,再求值:﹣,其中a=﹣3.【解答】解:原式=﹣==,当a=﹣3时,原式=﹣1.16.(8分)已知x2﹣2x﹣8=0,求4(x﹣1)2﹣2x(x﹣2)+3的值.【解答】解:原式=4x2﹣8x+4﹣2x2+4x+3=2x2﹣4x+7=2(x2﹣2x)+7,当x2﹣2x﹣8=0,即x2﹣2x=8时,原式=16+7=23.四、每小题8分,共16分.17.(8分)如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2+2)米.试求货车卸货时举升杠杆OB的长.【解答】解:作OD⊥AB于D,设BD=x,∵∠BOC=75°,∠A=30°,∴∠ABO=45°,∴OD=BD=x,tan A=,∴AD==x,则x+x=2+2,解得x=2,∴OD=BD=2,由勾股定理,OB=2.18.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).(1)画出△ABC关于直线y=x对称的△A′B′C′;(2)画出△ABC关于原点O成中心对称的△A1B1C1,并指出△A′B′C′与△A1B1C1的位置关系.【解答】解:(1)如图所示,△A′B′C′即为所作;(2)如图所示,△A1B1C1即为所作,△A′B′C′与△A1B1C1关于直线y=﹣x成轴对称.五、每小题10分,共20分.19.(10分)如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.将三角形、正方形、五边形都整齐的由左到右填在所示表格里:(1)按照规律,表格中a=28,b=36,c=35.(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x﹣n.【解答】解:(1)∵前6个“三角形数”分别是:1=、3=、6=、10=、15=、21=,∴第n个“三角形数”是,∴a=.∵前5个“正方形数”分别是:1=12,4=22,9=32,16=42,25=52,∴第n个“正方形数”是n2,∴b=62=36.∵前4个“正方形数”分别是:1=,5=,12=,22=,∴第n个“五边形数”是,∴c==35.(2)第n个“正方形数”是n2;1+1﹣1=1,3+4﹣5=2,6+9﹣12=3,10+16﹣22=4,…,∴第n个“五边形数”是n2+x﹣n.故答案为:28、36、35;n2、n2+x﹣n.20.(10分)如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.(1)判断四边形ADCE的形状,并证明.(2)若AC=BC=2,求BO的长.【解答】解:(1)菱形.证明如下:∵AE∥CD,CE∥AD,∴四边形ADCE是平行四边形,∵∠ACB=90°,AD=BD,∴CD=AD,∴四边形ADCE是菱形.(2)∵AC=BC=2,∴CD⊥AB,AB=2,∴EA⊥AB,AD=,∴AE=,在Rt△BAE中,BE==,∵AD=BD,AE∥DO,∴BO=BE=.六、本题每小题12分,共24分.21.(12分)某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别的概率;(2)若九年级的女同学是学校的“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”的概率.【解答】解:(1)画树状图为:共有8种等可能的结果数,其中三位主持人恰好同性别的结果数为2,所以所选三位主持人恰好同性别的概率==;(2)画树状图为:共有20种等可能的结果数,其中两男的结果数为6,所以恰好为“两男一女”的概率==.22.(12分)某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.(1)求a的值及函数解析式;(2)据统计,个体司机的运营收益率达到,其“幸福指数”会达标,那么他需要运营几小时?(收益率=)(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”的增加额b(元)之间的关系为s=﹣b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于,那么增加额b为多少元时,公司效益最高?【解答】解:(1)由图象可得,t=时,y=0,设份子钱为m元,∴解得:m=200,∴a=﹣200,设函数解析式为:y=kt+b,把(0,﹣200),(,0)代入得:,解得:,∴y=30t﹣200.(2)设他需要运营x小时,根据题意可得:,解得:x=15,经检验,x=15是原方程的解,∴他需要运营15小时.(3)∵调整时必须保证个体司机在运营12小时时,收益率不低于,∴解得:b≤40,∴0≤b≤40,设公司效益为W元,则W==,∵0≤b≤40,∴当b=40时,W有最大值,最大为==33600,∴增加额b为40元时,公司效益最高.。
