2019八年级数学上册第十二章全等三角形12.2三角形全等的判定第1课时作业课件新人教版(1)
人教版数学八年级上册 12.2三角形全等的判定 第一课时 “边边边”(sss)判定(共31张ppt)(智能版推荐)

学完本节课你应该知道
定理:三条边都相等的三角形全等
全等三角形 “边边边”
判定
数学语言表示和证明
尺规画定三角形 尺规作图
尺规画等角
动笔练一练
• 满足下列条件的两个三角形不一定全等的
是( C )
A. 有一边相等的两个等边三角形 B. 有一腰和底边对应相等的两个等腰三角形 C. 周长相等的两个三角形 D. 三条边都相等的三角形
动笔练一练
• 在四边形ABCD中, 已知:AB=CD, AD=CB。试证明: ∠A=∠C。
动笔练一练
证明: 在△ABC和△FDE中:
AB=CD(已知) AD=CB(已知) BD=DB(公共边) ∴△ABD ≌△ ACD(SSS) ∴∠A=∠C(全等三角形的对 应角相等)
课后练一练
请同学们独立完成配套课后练习题。
下课!
谢谢同学们!
在我的印象里,他一直努力而自知,每天从食堂吃饭后,他总是习惯性地回到办公室看厚厚的专业书不断提升和充实自己,他的身上有九零后少见的沉稳。同事们恭喜他,大多看 到了他的前程似锦,却很少有人懂得他曾经付出过什么。就像说的:“如果这世上真有奇迹,那只是努力的另一个名字,生命中最难的阶段,不是没有人懂你,而是你不懂自已。” 而他的奇迹,是努力给了挑选的机会。伊索寓言中,饥饿的狐狸想找一些可口的食物,但只找到了一个酸柠檬,它说,这只柠檬是甜的,正是我想吃的。这种只能得到柠檬,就说 柠檬是甜的自我安慰现象被称为:“甜柠檬效应”。一如很多人不甘平庸,却又大多安于现状,大多原因是不知该如何改变。看时,每个人都能从角色中看到自已。高冷孤独的安 迪,独立纠结的樊胜美,乐观自强的邱莹莹,文静内敛的关睢尔,古怪精灵的曲筱绡。她们努力地在城市里打拼,拥有幸或不幸。但她依然保持学习的习惯,这样无论什么事她都 有最准确的判断和认知;樊胜美虽然虚荣自私,但她努力做一个好HR,换了新工作后也是拼命争取业绩;小蚯蚓虽没有高学历,却为了多卖几包咖啡绞尽脑汁;关睢尔每一次出镜 几乎都是在房间里戴着耳机听课,处理文件;就连那个嬉皮的曲筱潇也会在新年之际为了一单生意飞到境外……其实她们有很多路可以走:嫁人,啃老,安于现状。但每个人都像 个负重的蜗牛一样缓缓前行,为了心中那丁点儿理想拼命努力。今天的努力或许不能决定明天的未来,但至少可以为明天积累,否则哪来那么多的厚积薄发和大器晚成?身边经常 有人抱怨生活不幸福,上司太刁,同事太蛮,公司格局又不大,但却不想改变。还说:“改变干嘛?这个年龄了谁还能再看书考试,混一天是一天吧。”一个“混”字就解释了他 的生活态度。前几天我联系一位朋友,质问为什么好久不联系我?她说自已每天累的像一条狗,我问她为什么那么拼?她笑:“如果不努力我就活得像一条狗了。”恩,新换的上 司,海归,虽然她有了磨合几任领导的经验,但这个给她带来了压力。她的英语不好,有时批阅文件全是大段大段的英文,她心里很怄火,埋怨好好的中国人,出了几天国门弄得 自己像个洋鬼子似的。上司也不舒服,流露出了嫌弃她的意思,甚至在一次交待完工作后建议她是否要调一个合适的部门?她的脸红到了脖子,想着自己怎么也算是老员工,由她 羞辱?两个人很不愉快。但她有一股子倔劲,不服输,将近40岁的人了,开始拿出发狠的学习态度,报了个英语培训班。回家后捧着英文书死啃,每天要求上中学的女儿和自己英 语对话,连看电影也是英文版的。功夫不负有心人,当听力渐渐能跟得上上司的语速,并流利回复,又拿出漂亮的英文版方案,新上司看她的眼光也从挑剔变柔和,某天悄悄放了 几本英文书在她桌上,心里突然发现上司并没那么讨厌。心态好了,她才发现新上司的优秀,自从她来了后,部门业绩翻了又翻,奖金也拿到手软,自己也感觉痛快。她说:这个 社会很功利,但也很公平。别人的傲慢一定有理由,如果想和平共处,需要同等的段位,而这个段位,自己可能需要更多精力,但唯有不断付出,才有可能和优秀的人比肩而立。 人为什么要努力?一位长者告诉我:“适者生存。”这个社会讲究适者生存,优胜劣汰。虽然也有潜规则,有套路和看不见的沟沟坎坎,但一直努力的人总会守得云开见月明。有 些人明明很成功了,但还是很拼。比如剧中的安迪,她光环笼罩,商场大鳄是她的男闺蜜,不离左右,富二代待她小心呵护,视若明珠,加上她走路带风,职场攻势凌历,优秀得 让身边人仰视。这样优秀的人,不管多忙,每天都要抽出两个小时来学习。她的学习不是目的,而是能量,能让未来的自己比过去更好一些。现实生活中,努力真的重要,它能改 变一个人的成长轨迹,甚至决定人生成败。有一句鸡汤:不着急,你想要的,岁月都会给你。其实,岁月只能给你风尘满面,而希望,唯有努力才能得到!9、懂得如何避开问题的 人,胜过知道怎样解决问题的人。在这个世界上,不知道怎么办的时候,就选择学习,也许是最佳选择。胜出者往往不是能力而是观念!在家里看到的永远是家,走出去看到的才 是世界。把钱放在眼前,看到的永远是钱,把钱放在有用的地方,看到的是金钱的世界。给人金钱是下策,给人能力是中策,给人观念是上策。财富买不来好观念,好观念能换来 亿万财富。世界上最大的市场,是在人的脑海里!要用行动控制情绪,不要让情绪控制行动;要让心灵启迪智慧,不能让耳朵支配心灵。人与人之间的差别,主要差在两耳之间的 那块地方!人无远虑,必有近忧。人好的时候要找一条备胎,人不好的时候要找一条退路;人得意的时候要找一条退路,人失意的时候要找一条出路!孩子贫穷是与父母的有一定 的关系,因为他小的时候,父母没给他足够正确的人生观。家长的观念是孩子人生的起跑线!有什么信念,就选择什么态度;有什么态度,就会有什么行为;有什么行为,就产生 什么结果。要想结果变得好,必须选择好的信念。播下一个行动,收获一种习惯;播下一种习惯,收获一种性格;播下一种性格,收获一种命运。思想会变成语言,语言会变成行
八年级数学上册第十二章全等三角形12.2三角形全等的判定课时1“边边边SSS”教案

第十二章全等三角形12。
2全等三角形的判定课时1 “边边边(SSS)”【知识与技能】(1)明确判定两个三角形全等至少需要三个条件.(2)掌握“边边边(SSS)"条件的内容。
(3)能初步运用“边边边(SSS)”条件判定两个三角形全等.(4)会作一个角等于已知角.【过程与方法】使学生经历探索三角形全等的过程,体验用操作、归纳得出数学结论的过程.【情感态度与价值观】探究三角形全等条件的判定过程,以观察思考,动手画图,合作交流等多种形式让学生共同探讨,培养学生的合作精神。
三角形全等的“边边边(SSS)”判定方法.运用“边边边(SSS)”判定方法进行简单的证明。
多媒体课件.教师引入:如图12-2—1,教师在黑板上画两个三角形,请仔细观察,△ABC与△A′B′C′全等吗?你们是如何判断的?学生各抒己见,如动手用纸剪下一个三角形,将剪下的三角形叠到另一个三角形上,观察这两个三角形是否完全重合;测量两个三角形的所有边与角,观察是否有三条边对应相等,三个角对应相等。
探究1:三角形全等的条件教师提出:(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?(2)如果给出两个条件呢?给出两个条件画三角形时,有几种可能的情况,每种情况下画出的三角形一定全等吗?学生讨论有几种可能的情况,然后按照下面的条件画一画:①三角形的一个内角是30°,一条边是3 cm;②三角形的两个内角分别是30°和50°;③三角形的两条边长分别是 4 cm和6 cm.学生分组讨论、画图、探索、归纳,最后以组为单位展示结果.结果展示:(1)只给定一条边时,如图12-2—2。
只给定一个角时,如图12-2-3.(2)给出的两个条件:一边一内角、两内角、两边,如图12-2—4。
可以发现按这些条件画出的三角形都不能保证一定全等。
教师提出:如果给出三个条件画三角形,你能说出有几种情况吗?(三条边,两条边和一个角,一条边和两个角,三个角)在刚才的探索过程中,我们已经发现,已知三个内角不能保证两个三角形全等.下面我们就来逐一探索其余的三种情况.(这节课只讨论第一种情况)探究2:“边边边(SSS)”教师让学生完成以下活动:1。
12.2 第1课时三角形的全等的判定(一)数学人教版八上同步课堂教案

第十二章全等三角形12.2 三角形全等的判定第1课时三角形的全等的判定(一)(SSS)一、教学目标1.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.2.理解并掌握“边边边”判定方法,能利用“边边边”证明两个三角形全等.3.会用尺规作一个角等于已知角,了解图形的作法.二、教学重难点重点:利用“边边边”证明两个三角形全等.难点:用尺规作一个角等于已知角.三、教学过程【新课导入】[课件展示]教师利用多媒体展示如下两个三角形的重合过程.[复习导入]1. 观察这两个三角形,它们之间是什么关系?(它们是全等三角形,因为能够重合的两个三角形叫全等三角形.)2.如图,已知△ABC与△DEF全等,用几何语言表达全等三角形的性质,找出其中相等的边与角.(∵△ABC≌△DEF,∴AB=DE,AC=DF,BC=EF;(全等三角形对应边相等)∠A=∠D,∠B=∠E,∠C=∠F.(全等三角形对应角相等))学生通过演示复习全等三角形的定义及性质,为探究新知识作好准备.[提出问题]如果AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F,那么△ABC 和△△DEF能够完全重合,即可判定△ABC≌△△DEF.那么一定要满足三条边分别相等,三个角分别相等,才能保证两个三角形全等吗?能否选取其中的一部分条件,简捷地判定两个三角形全等呢?让我们带着这个问题一起走进全等三角形的判定之旅.【新知探究】知识点1 探究判定三角形全等的条件[提出问题](1)一个对应条件可以吗?画出两个三角形,使得满足一个相等条件,此时的两三角形全等吗?①只有一条边相等(假设为3cm).[动手操作]每个学生在准备好的卡纸上画出一条边为3cm长的三角形,之后剪下来,和同桌所作的三角形进行比较,看两者是否能够重合(发现不重合,个别可能有重合的现象,比如两人画的都是等边三角形,所以得到结论是“不一定全等”).之后教师利用多媒体展示示例,验证结论.[提出问题]②只有一个角相等(假设为45°).[动手操作]每个学生在准备好的卡纸上画出一个角为45°的三角形,之后剪下来,和同桌所作的三角形进行比较,看两者是否能够重合(发现不重合,个别可能有重合的现象,比如两人画的都是等腰直角三角形,所以得到结论是“不一定全等”).之后教师利用多媒体展示示例,验证结论.[归纳总结]满足一个对应条件相等的两个三角形不一定全等.[提出问题](2)两个对应条件可以吗?先来思考下有几种情况?[交流讨论]小组之间交流讨论.得出有三种情况:①有两条边对应相等.②有两个角对应相等.③有一条边和一个角分别对应相等.[提出问题]画出两个三角形,使得满足两个相等条件,此时的两三角形全等吗?①有两条边对应相等(假设一条边为3cm,另一条边为4cm).②有两个角对应相等(假设一个角为30°,另一个角为60°).③有一条边和一个角分别对应相等(假设一条边为4cm,一个角为30°).[动手操作]将学生分为三大组,每组同学负责一种情况的三角形.各组学生在准备好的卡纸上画出满足条件的三角形,之后剪下来,和同桌所作的满足相同条件的三角形进行比较,看两者是否能够重合(发现不重合,个别可能有重合的现象,所以得到结论是“不一定全等”).之后教师利用多媒体展示示例,验证结论.[归纳总结]满足两个对应条件相等的两个三角形不一定全等.[提出问题]由探究1可知,满足六个条件中的一个或两个条件对应相等,都不能保证两个三角形全等,那么满足六个条件中的三个条件对应相等,能否保证两个三角形全等呢?知识点2 “SSS”证全等[提出问题]先任意画出一个△ABC,再画出一个△A'B'C',使得A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下来,放到△ABC上,它们全等吗?[动手操作]按照老师的要求,每个学生在准备好的卡纸上画出满足条件两个三角形△ABC和△A'B'C',,之后剪下来,看两者是否能够重合(发现重合,所以得到结论是“全等”).之后教师利用多媒体展示示例,验证结论,并说明画△A'B'C'的方法,帮助不会画的学生.[归纳总结]三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”).该判定定理的几何语言:在△ABC 和△ A'B'C'中,AB=A'B',,,∴△ABC≌△A'B'C'(SSS).[课件展示]教师利用多媒体展示如下例题:例在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD≌△ACD .证明:∵D 是BC中点,∴BD =DC.在△ABD与△ACD 中,,,,∴△ABD≌△ACD(SSS).[归纳总结]根据例题,总结如下步骤和规则:[课件展示]跟踪训练(2021•云南)如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.证明:在△CDA和△DCB中,∴△CDA≌△DCB(SSS),∴∠DAC=∠CBD.提醒学生:有些题目的已知条件隐含在题设或图形之中,如公共边,公共角,对顶角等;在图形中,通过证明两个三角形全等,可以为进一步寻求边等、角等、线段间的特殊关系等提供了方法和依据.知识点3 用尺规作一个角等于已知角[课件展示]三角形中线的定义.[提出问题]已知:∠AOB.求作:∠A'O'B'=∠AOB.你会怎么做?根据“三边分别相等判定三角形全等”的结论思考一下吧![交流讨论]小组之间交流讨论,之后在准备好的卡纸上试着作一作.[课件展示]教师利用多媒体展示作法:作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C,D;(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';(3)以点C'为圆心,CD 长为半径画弧,与第2步中所画的弧交于点D';(4)过点D'画射线O'B',则∠AOB=∠A'O'B'.【课堂小结】【课堂训练】1.如图,在△ABC中,BC=AC,BE=AE,则由“SSS”可以判定( C )A.△ACD≌△BCDB.△ADE≌△BDEC.△ACE≌△BCED.以上都对2.如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使能利用“SSS”判定△ABC≌△EDF,需添加的条件为 BC=DF .【解析】利用SSS判定,则两三角形的三条边应对应相等. 添加BC=DF.∵AD=BE,∴AD+DB=BE+BD,即AB=ED.又知AC=EF,∴添加的条件是BC=DF时,可证得△ABC≌△EDF.提醒学生:等边加同边,其和还是等边.3.(2021•东莞市二模)如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= 60° .【解析】在△ACO和△BCO中,∴△AOC≌△BOC(SSS).∴∠BCO=∠ACO=30°.∴∠ACB=∠BCO+∠ACO=60°,故答案为60°.4.如图,AB=AC,DB=DC,请说明∠B=∠C.解:连接AD.在△ABD和△ACD中,,,,∴△ABD≌△ACD(SSS).∴∠B=∠C.提醒学生:学会作辅助线帮助解题.5.如图,在△ABC中,AB=AC,D,E是BC的三等分点,AD=AE,求证:△ABE≌△ACD.证明:∵D,E是BC的三等分点,∴BD=DE=EC .∴BD+DE=DE+EC,即BE=CD .在△ABE和△ACD中,,,,∴△ABE≌△ACD(SSS).提醒学生:等边加同边,其和还是等边.6.如图,已知AC=FE,AD=FB,BC=DE.求证:AC//EF,DE//BC.证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.在△ABC和△FDE中,,,,∴△ABC≌△FDE(SSS),∴∠A=∠F,∠ABC=∠FDE.∴AC//EF,DE//BC.7.如图,过点C作直线DE,使DE//AB.解:作法:(1)过点C作直线MN与AB相交,交点为F;(2)在直线MN的右侧作∠FCE,使∠FCE=∠AFC;(3)反向延长CE,则直线DE即为所求.【教学反思】本节课是判定三角形全等的第一节课,对于新知识的接受,一部分同学表现出了吃力.刚开始,探究判定三角形全等的条件时,对许多学生来说进行分类有困难,因为他们不知到从什么地方下手,以及做到不重不漏,课堂上,我给予了学生这样一个分类讨论的步骤:第一种情况:满足一个元素;第二种情况:满足两个元素;第三种情况:满足三个元素.在每种情况中,再分边与角.这样分类的好处就是:渗透了数学中的分类讨论思想;明确对应关系,使得后继学习变得顺利.在做练习时,学生对于新知识的掌握在细节上还不牢固,比如,证明全等时的书写格式,有同学忘记写在哪两个三角形中证全等,有同学漏写大括号等等,在今后的教学中,一定要纠正细节,保证学生对而准确地完成一道题.。
人教版八年级数学上册《12.2三角形全等的判定》练习题(附答案)

人教版八年级数学上册《12.2三角形全等的判定》练习题(附答案)一选择题1.下列条件不能判定两个直角三角形全等的是( )A. 斜边和一直角边对应相等B. 两个锐角对应相等C. 一锐角和斜边对应相等D. 两条直角边对应相等2.一块三角形玻璃被打碎后店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃能够全等的依据是( )A. ASAB. AASC. SASD. SSS3.如图OD⊥AB于点D OP⊥AC于点P且OD=OP则△AOD与△AOP全等的理由是( )A. SSSB. ASAC. SSAD. HL4.如图为6个边长相等的正方形的组合图形则∠1+∠2+∠3的度数为( )A. 90°B. 135°C. 150°D. 180°5.如图AC是△ABC和△ADC的公共边下列条件中不能判定△ABC≌△ADC的是( )A. AB=AD,∠2=∠1B. AB=AD,∠3=∠4C. ∠2=∠1,∠3=∠4D. ∠2=∠16.如图已知点B、E、C、F在同一直线上且BE=CF,∠ABC=∠DEF那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )A. AC=DFB. AB=DEC. AC//DFD. ∠A=∠D7.如图点C D在AB同侧∠CAB=∠DBA下列条件中不能判定△ABD≌△BAC的是( )A. ∠D=∠CB. BD=ACC. AD=BCD. ∠CAD=∠DBC8.如图D是AB上一点DF交AC于点E,DE=FE,FC//AB若AB=4,CF=3则BD的长是( )A. 0.5B. 1C. 1.5D. 29.如图△ABC中AB=AC,AD是角平分线BE=CF则下列说法中正确的有( )①AD平分∠EDF;②△EBD≌△FCD;③BD=CD;④AD⊥BC.A. 1个B. 2个C. 3个D. 4个10.两组邻边分别相等的四边形叫做“筝形”如图四边形ABCD是一个筝形其中AD=CD AB=CB 在探究筝形的性质时得到如下结论:③四边形ABCD的面积其中正确的结论有.( )A. 0个B. 1个C. 2个D. 3个二填空题11.如图在3×3的正方形网格中∠1+∠2=_______度.12.如图已知AB=AC,EB=EC,AE的延长线交BC于D则图中全等的三角形共有______对.13.如图所示的网格是正方形网格点A,B,C,D均落在格点上则∠BAC+∠ACD=____°.14.如图∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4则AC=______.15.如图在△ABC和△DEF中点B,F,C,E在同一直线上BF=CE,AB//DE请添加一个条件使△ABC≌△DEF这个添加的条件可以是______(只需写一个不添加辅助线).16.如图在△ABC中高AD和BE交于点H且DH=DC则∠ABC=°.17.如图在四边形ABCD中AB=AD,∠BAD=∠BCD=90∘连接AC若AC=6则四边形ABCD的面积为.18.如图∠C=90°,AC=20,BC=10,AX⊥AC点P和点Q同时从点A出发分别在线段AC和射线AX上运动且AB=PQ当AP=______时以点A,P,Q为顶点的三角形与△ABC全等.19.如图△ABC中AB=AC,AD⊥BC于D点DE⊥AB于点E BF⊥AC于点F,DE=3cm则BF=cm.20.如图所示∠E=∠F=90∘,∠B=∠C,AE=AF结论:①EM=FN②AF//EB③∠FAN=∠EAM④△ACN≌△ABM.其中正确的有______ .三解答题21.如图点A,D,C,F在同一条直线上AD=CF,AB=DE,AB//DE.求证:BC=EF.22.如图点C、F、E、B在一条直线上∠CFD=∠BEA,CE=BF,DF=AE写出CD与AB之间的关系并证明你的结论.23.如图B、C、E三点在同一条直线上AC//DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE24.已知:如图在△ABC中BE⊥AC垂足为点E,CD⊥AB垂足为点D且BD=CE.求证:∠ABC=∠ACB.25.如图在△ABC中AB=CB,∠ABC=90°,D为AB延长线上一点点E在BC边上且BE=BD 连接AE,DE,DC.(1)求证:△ABE≌△CBD;(2)若∠CAE=30°求∠BDC的度数.答案和解析1.【答案】B【解析】直角三角形全等的判定方法:HL,SAS,ASA,SSS,AAS做题时要结合已知条件与全等的判定方法逐一验证.【解答】解:A.符合判定HL故本选项正确不符合题意;B.全等三角形的判定必须有边的参与故本选项错误符合题意;C.符合判定AAS故本选项正确不符合题意;D.符合判定SAS故本选项正确不符合题意.故选B.2.【答案】A【解析】本题考查了全等三角形的判定:全等三角形的判定方法中选用哪一种方法取决于题目中的已知条件若已知两边对应相等则找它们的夹角或第三边;若已知两角对应相等则必须再找一组对边对应相等若已知一边一角则找另一组角或找这个角的另一组对应邻边.利用全等三角形判定方法进行判断.【解答】解:这片碎玻璃的两个角和这两个角所夹的边确定从而可根据“ASA”重新配一块与原来全等的三角形玻璃.故选:A.3.【答案】D【解析】本题考查了直角三角形全等的判定的知识点解题关键点是熟练掌握直角三角形全等的判定方法HL.根据直角三角形全等的判别方法HL可证△AOD≌△AOP.【解答】解:∵OD⊥AB且OP⊥AC∴△AOD和△AOP是直角三角形又∵OD=OP且AO=AO∴△AOD≌△AOP(HL).故选D.4.【答案】B【解析】本题考查了全等图形准确识图并判断出全等的三角形是解题的关键标注字母利用“边角边”证明△ABC和△DEA全等根据全等三角形对应角相等可得∠1=∠4从而求出∠1+∠3=90°再判断出∠2=45°进而计算即可得解.【解答】解:如图在△ABC和△DEA中{AB=DE∠ABC=∠DEA=90°BC=EA,∴△ABC≌△DEA(SAS)∴∠1=∠4∵∠3+∠4=90°∴∠1+∠3=90°又∵∠2=45°∴∠1+∠2+∠3=90°+45°=135°.故选B.5.【答案】A【解析】本题考查三角形全等的判定方法判定两个三角形全等的一般方法有:SSS SAS ASA AAS等.利用全等三角形的判定定理:SSS SAS ASA AAS等逐项进行分析即可.判定两个三角形全等时必须有边的参与若有两边一角对应相等时这个角必须是两边的夹角.【解答】解:A.AB=AD∠2=∠1再加上公共边AC=AC不能判定△ABC≌△ADC故此选项符合题意;B.AB=AD∠3=∠4再加上公共边AC=AC可利用SAS判定△ABC≌△ADC故此选项不合题意;C.∠2=∠1∠3=∠4再加上公共边AC=AC可利用ASA判定△ABC≌△ADC故此选项不合题意;D.∠2=∠1∠B=∠D再加上公共边AC=AC可利用AAS判定△ABC≌△ADC故此选项不合题意;故选A.6.【答案】A【解析】解:∵BE=CF∴BE+EC=EC+CF即BC=EF且∠ABC=∠DEF∴当AC=DF时满足SSA无法判定△ABC≌△DEF故A不能;当AB=DE时满足SAS可以判定△ABC≌△DEF故B可以;当AC//DF时可得∠ACB=∠F满足ASA可以判定△ABC≌△DEF故C可以;当∠A=∠D时满足AAS可以判定△ABC≌△DEF故D可以;故选:A.根据全等三角形的判定方法逐项判断即可.本题主要考查全等三角形的判定方法 掌握全等三角形的判定方法是解题的关键 即SSS SAS ASA AAS 和HL .7.【答案】C【解析】本题考查了全等三角形的判定定理的应用 能熟记全等三角形的判定定理是解此题的关键 注意:全等三角形的判定定理有SAS ASA AAS SSS 符合SSA 和AAA 不能推出两三角形全等. 根据图形知道隐含条件BC =BC 根据全等三角形的判定定理逐个判断即可.【解答】解:A 添加条件∠D =∠C 还有已知条件∠CAB =∠DBA BC =BC 符合全等三角形的判定定理AAS 能推出△ABD ≌△BAC 故本选项错误;B 添加条件BD =AC 还有已知条件∠CAB =∠DBA BC =BC 符合全等三角形的判定定理SAS 能推出△ABD ≌△BAC 故本选项错误;C 添加条件AD =BC 还有已知条件∠CAB =∠DBA BC =BC 不符合全等三角形的判定定理 不能推出△ABD ≌△BAC 故本选项正确;D ∵∠CAB =∠DBA ∠CAD =∠DBC∴∠DAB =∠CBA 还有已知条件∠CAB =∠DBA BC =BC 符合全等三角形的判定定理ASA 能推出△ABD ≌△BAC 故本选项错误;故选C .8.【答案】B【解析】解:∵CF//AB∴∠A =∠FCE ∠ADE =∠F∴在△ADE 和△CFE 中{∠A =∠FCE∠ADE =∠F DE =FE∴△ADE ≌△CFE(AAS)∴AD =CF =3∵AB =4∴DB =AB −AD =4−3=1.故选B .根据平行线的性质 得出∠A =∠FCE ∠ADE =∠F 再根据全等三角形的判定证明△ADE ≌△CFE得出AD=CF根据AB=4CF=3即可求线段DB的长.本题考查了全等三角形的性质和判定平行线的性质的应用能判定△ADE≌△FCE是解此题的关键解题时注意运用全等三角形的对应边相等对应角相等.9.【答案】C【解析】解:∵AB=AC AD平分∠BAC∴BD=DC AD⊥BC故③④正确在RT△BDE和RT△CDF中{BE=CFBD=CD∴RT△BDE≌RT△CDF故②正确∵AD⊥BC∴∠ADC=∠CDF=90°∴BC平分∠EDF.故①错误.故选:C.根据等腰三角形的三线合一可以判断③④正确根据HL可以证明RT△BDE≌RT△CDF可以判断②正确由BC平分∠EDF得出①错误故不难得到结论.本题考查全等三角形的判定和性质等腰三角形的性质角平分线的定义等知识解题的关键是等腰三角形三线合一的性质的应用属于中考常考题型.10.【答案】C【解析】此题考查全等三角形的判定和性质关键是根据SSS证明△ABD与全等和利用SAS证明与全等.【解答】解:如图在△ABD与中故①正确;∴∠ADB=∠CDB在与中∴∠AOD=∠COD=90°∴AC⊥DB故②正确;故③错误.故选C.11.【答案】90【解析】本题考查了全等三角形的判定和性质能看懂图形是解题的关键.首先判定两个三角形全等然后根据全等三角形的性质及直角三角形的性质即可判断得出结论.【解答】解:如图所示:∵∠ACB=∠DCE=90°AC=DC BC=EC∴Rt△ACB≌Rt△DCE∴∠2=∠EDC在Rt△DCE中∠1+∠EDC=90°∴∠1+∠2=90°.12.【答案】3【解析】解:①△ABE≌△ACE∵AB=AC EB=EC∴△ABE≌△ACE;②△EBD≌△ECD∵△ABE≌△ACE∴∠ABE=∠ACE∴∠EBD=∠ECD∵EB=EC∴△EBD≌△ECD;③△ABD≌△ACD∵△ABE≌△ACE△EBD≌△ECD∴∠BAD=∠CAD∵∠ABC=∠ABE+∠BED∴∠ABC=∠ACB∵AB=AC∴△ABD≌△ACD∴图中全等的三角形共有3对.在线段AD的两旁猜想所有全等三角形再利用全等三角形的判断方法进行判定三对全等三角形是△ABE≌△ACE△EBD≌△ECD△ABD≌△ACD.本题考查学生观察猜想全等三角形的能力同时也要求会运用全等三角形的几种判断方法进行判断.13.【答案】90【解析】【解答】解:在△DCE和△ABD中∵{CE=BD=1∠E=∠ADB=90°DE=AD=3∴△DCE≌△ABD(SAS)∴∠CDE =∠DAB∵∠CDE +∠ADC =∠ADC +∠DAB =90°∴∠AFD =90°∴∠BAC +∠ACD =90°故【答案】90.【分析】本题网格型问题 考查了三角形全等的性质和判定及直角三角形各角的关系 本题构建全等三角形是关键.证明△DCE ≌△ABD(SAS) 得∠CDE =∠DAB 根据同角的余角相等和三角形的内角和可得结论. 14.【答案】6【解析】本题考查了全等三角形的判定与性质有关知识 由AAS 证明△ABC ≌△EFC 得出对应边相等AC =EC BC =CF =4 求出EC 即可得出AC 的长.【解答】解:∵AC ⊥BE∴∠ACB =∠ECF =90°在△ABC 和△EFC 中{∠ACB =∠ECF ∠A =∠E AB =EF∴△ABC ≌△EFC(AAS)∴AC =EC BC =CF =4∵EC =BE −BC =10−4=6∴AC =EC =6;故答案为6. 15.【答案】AB =ED【解析】解:添加AB =ED∵BF =CE∴BF +FC =CE +FC即BC =EF∵AB//DE∴∠B =∠E在△ABC 和△DEF 中{AB =ED∠B =∠E CB =FE,∴△ABC ≌△DEF(SAS)故【答案】AB =ED .根据等式的性质可得BC =EF 根据平行线的性质可得∠B =∠E 再添加AB =ED 可利用SAS 判定△ABC ≌△DEF .本题考查三角形全等的判定方法 判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL .注意:AAA SSA 不能判定两个三角形全等 判定两个三角形全等时 必须有边的参与 若有两边一角对应相等时 角必须是两边的夹角.16.【答案】45【解析】本题考查了全等三角形的判定与性质 余角的性质 等腰直角三角形 由三角形的高得到∠ADB =∠ADC =∠BEC =90° 结合余角的性质得到∠HBD =∠CAD 易证△HBD ≌△CAD 得到AD =BD 根据等腰直角三角形得到∠ABD =45° 即可得出结论.【解答】解:∵AD ⊥BC BE ⊥AC∴∠ADB =∠ADC =∠BEC =90°∴∠HBD +∠C =∠CAD +∠C =90°∴∠HBD =∠CAD∵在△HBD 和△CAD 中{∠HBD =∠CAD,HDB =∠CDA,DH =DC,∴△HBD ≌△CAD(AAS)∴AD =BD∵∠ADB =90°∴△ABD 为等腰直角三角形∴∠ABD =45° 即∠ABC =45°故答案为45.17.【答案】18【解析】本题考查全等三角形的判定和性质和三角形的面积.过点A 作AE ⊥AC 交CD 的延长线于点E.做出辅助线是解答本题的关键.过点A 作AE ⊥AC 交CD 的延长线于点E 证明△AED ≌△ACB 将四边形ABCD 的面积转化为△ACE 的面积 利用三角形面积公式求解即可.【解答】解:过点A 作AE ⊥AC 交CD 的延长线于点E∵∠EAC =∠BAD =90°∴∠EAD =∠CAB∵∠BAD =∠BCD =90∘∴∠ADC +∠ABC =360°−(∠BAD +∠BCD)=180°又∵∠ADE +∠ADC =180∘∴∠ADE =∠ABC在△AED 与△ACB 中{∠EAD =∠CABAD =AB ∠ADE =∠ABC∴△AED ≌△ACB(ASA)∴AE =AC =6 四边形ABCD 的面积等于△ACE 的面积故S 四边形ABCD =12AC ⋅AE =12×6×6=18.故答案为18. 18.【答案】10或20【解析】解:∵AX ⊥AC∴∠PAQ =90°∴∠C=∠PAQ=90°分两种情况:①当AP=BC=10时在Rt△ABC和Rt△QPA中{AB=PQBC=AP∴Rt△ABC≌Rt△QPA(HL);②当AP=CA=20时在△ABC和△PQA中{AB=PQAP=AC∴Rt△ABC≌Rt△PQA(HL);综上所述:当点P运动到AP=10或20时△ABC与△APQ全等;故【答案】10或20.分两种情况:①当AP=BC=10时;②当AP=CA=20时;由HL证明Rt△ABC≌Rt△PQA(HL);即可得出结果.本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法本题需要分类讨论难度适中.19.【答案】6【解析】本题考查了全等三角形的判定与性质三角形的面积利用面积公式得出等式是解题的关键.先利用HL证明Rt△ADB≌Rt△ADC得出S△ABC=2S△ABD=2×12AB⋅DE=AB⋅DE=3AB又S△ABC=12AC⋅BF将AC=AB代入即可求出BF.【解答】解:在Rt△ADB与Rt△ADC中{AB=ACAD=AD ∴Rt△ADB≌Rt△ADC∴S△ABC=2S△ABD=2×12AB⋅DE=AB⋅DE=3AB∵S△ABC=12AC⋅BF∴12AC⋅BF=3AB ∵AC=AB∴12BF=3cm∴BF=6cm.故【答案】6.20.【答案】①③④【解析】此题考查了全等三角形的性质与判别考查了学生根据图形分析问题解决问题的能力.其中全等三角形的判别方法有:SSS SAS ASA AAS及HL.学生应根据图形及已知的条件选择合适的证明全等的方法.由∠E=∠F=90°∠B=∠C AE=AF利用“AAS”得到△ABE与△ACF全等根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等AE与AF相等AB与AC相等然后在等式∠EAB=∠FAC两边都减去∠MAN得到∠EAM与∠FAN相等然后再由∠E=∠F=90°AE=AF∠EAM=∠FAN利用“ASA”得到△AEM与△AFN全等利用全等三角形的对应边相等对应角相等得到选项①和③正确;然后再∠C=∠B AC=AB∠CAN=∠BAM利用“ASA”得到△ACN与△ABM全等故选项④正确;若选项②正确得到∠F与∠BDN相等且都为90°而∠BDN不一定为90°故②错误.【解答】解:在△ABE和△ACF中∠E=∠F=90°AE=AF∠B=∠C∴△ABE≌△ACF(AAS)∴∠EAB=∠FAC AE=AF AB=AC∴∠EAB−∠MAN=∠FAC−∠NAM即∠EAM=∠FAN在△AEM和△AFN中∠E=∠F=90°AE=AF∠EAM=∠FAN∴△AEM≌△AFN(ASA)∴EM=FN∠FAN=∠EAM故选项①和③正确;在△ACN和△ABM中∠C=∠B∠CAN=∠BAM AC=AB∴△ACN≌△ABM(ASA)故选项④正确;若AF//EB∠F=∠BDN=90°而∠BDN不一定为90°故②错误则正确的选项有:①③④.21.【答案】解:∵AB//DE∴∠A =∠EDF∵AC =AD +DC DF =DC +CF 且AD =CF∴AC =DF在△ABC 和△DEF 中{AB =DE∠A =∠EDF AC =DF∴△ABC ≌△DEF(SAS)∴BC =EF .【解析】先证明AC =DF 再根据SAS 推出△ABC ≌△DEF 便可得结论.本题考查了全等三角形的判定和性质的应用 证明三角形的边相等 往往转化证明三角形的全等. 22.【答案】解:CD//AB CD =AB理由是:∵CE =BF∴CE −EF =BF −EF∴CF =BE在△CFD 和△BEA 中{CF =BE∠CFD =∠BEA DF =AE∴△CFD ≌△BEA(SAS)∴CD =AB ∠C =∠B∴CD//AB .【解析】本题考查了平行线的判定和全等三角形的性质和判定的应用.全等三角形的判定是结合全等三角形的性质证明线段和角对应相等的重要工具.在判定三角形全等时 关键是选择恰当的判定条件. 求出CF =BE 根据SAS 证△CFD ≌△BEA 推出CD =AB ∠C =∠B 根据平行线的判定推出CD//AB .23.【答案】证明:∵AC//DE∴∠ACB =∠E ∠ACD =∠D∵∠ACD =∠B∴∠D =∠B在△ABC 和△EDC 中{∠B =∠D∠ACB =∠E AC =CE∴△ABC ≌△CDE(AAS).【解析】此题主要考查了全等三角形的判定 平行线的性质.首先根据AC//DE 利用平行线的性质可得:∠ACB =∠E ∠ACD =∠D 再根据∠ACD =∠B 证出∠D =∠B 然后根据全等三角形的判定定理AAS 证出△ABC ≌△CDE 即可.24.【答案】证明:∵BE ⊥AC CD ⊥AB∴∠BDC =∠CEB =90°在Rt △BCD 和Rt △CBE 中{BC =CB BD =CE∴Rt △BCD ≌Rt △CBE(HL)∴∠DBC =∠ECB即∠ABC =∠ACB .【解析】本题考查了全等三角形的判定与性质;证明三角形全等是解题的关键.证明Rt △BCD ≌Rt △CBE(HL) 即可得出结论.25.【答案】(1)证明:∵∠ABC =90°∴∠DBC =90°在△ABE 和△CBD 中{AB =CB∠ABE =∠CBD BE =BD∴△ABE ≌△CBD(SAS);(2)解:∵AB =CB ∠ABC =90°∴∠BCA =45°∴∠AEB =∠CAE +∠BCA =30°+45°=75°∵△ABE ≌△CBD∴∠BDC =∠AEB =75°.【解析】(1)由条件可利用SAS证得结论;(2)由等腰直角三角形的性质可先求得∠BCA利用三角形外角的性质可求得∠AEB再利用全等三角形的性质可求得∠BDC.本题主要考查全等三角形的判定和性质掌握全等三角形的判定方法(即SSS SAS ASA AAS和HL)和全等三角形的性质(即全等三角形的对应边相等对应角相等)是解题的关键.。
《12.2三角形全等的判定》作业设计方案-初中数学人教版12八年级上册

《三角形全等的判定》作业设计方案(第一课时)一、作业目标1. 加深学生对三角形全等判定定理的理解和掌握;2. 提高学生运用全等三角形知识解决实际问题的能力;3. 培养学生自主学习、合作学习和探究学习的能力。
二、作业内容作业内容主要围绕《三角形全等的判定》这一主题展开,具体包括以下几个方面:1. 复习与预习:学生需复习之前学过的三角形全等的基本概念和性质,预习本节课将要学习的三角形全等判定定理。
2. 知识点梳理:学生需整理出本节课所学的三角形全等判定定理,包括SSS、SAS、ASA、AAS和HL五种判定方法,并理解每种判定方法的适用条件和步骤。
3. 课堂练习:学生需完成一份包含选择题、填空题和解答题的练习册,练习册的内容应涵盖本节课所学的知识点,难度适中,既有基础题也有提高题。
4. 实际问题解决:学生需选择一个与全等三角形相关的实际问题,运用所学知识进行分析和解决,例如测量建筑物的高度等。
5. 小组合作:学生需以小组形式进行合作学习,互相讨论、交流和分享学习心得,共同完成一份小组合作报告,报告应包括小组对三角形全等判定定理的理解、课堂练习的答案以及实际问题的解决方案等内容。
三、作业要求1. 学生需认真完成每一项作业内容,按照要求进行复习、预习、梳理知识点、完成练习册和实际问题解决等;2. 课堂练习需独立思考,不得抄袭他人答案;3. 实际问题解决需有明确的解决方案和步骤,能够用所学知识进行解释和说明;4. 小组合作报告需全体成员共同参与,内容完整、条理清晰、语言简练。
四、作业评价1. 教师需对每一份作业进行认真批改,给出详细的评语和分数;2. 对于优秀的作业和小组合作报告,可以在课堂上进行展示和分享;3. 对于存在问题的作业,教师需及时给出反馈和建议,帮助学生改正错误和提高学习效果。
五、作业反馈1. 教师需将学生的作业情况进行总结和分析,针对共性和个性问题提出相应的解决方案;2. 教师需及时向学生反馈作业情况,鼓励学生继续努力,同时指出存在的问题和不足;3. 对于学生在作业中表现出的优点和进步,教师需及时给予肯定和表扬,激发学生的学习兴趣和动力。
三角形全等的判定(第1课时)

第十二章全等三角形12.2 全等三角形的判定第1课时利用“边边边”判定三角形全等一、教学目标【知识与技能】1.掌握“边边边”的内容;2.能初步应用“边边边”条件判定两个三角形全等.3. 能用尺规作一个角等于已知角.【过程与方法】经历探索三角形全等条件的过程,体会用操作、归纳得出数量结论的过程.【情感态度与价值观】通过探索三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想,乐于探究的良好品质以及发现问题的能力.二、课型新授课三、课时第1课时,共4课时。
四、教学重难点【教学重点】探索三角形全等的条件,会应用“边边边”判定两个三角形全等.【教学难点】探索三角形全等的条件,用尺规作一个角等于已知角.五、课前准备教师:课件、三角尺、圆规、直尺等。
学生:三角尺、圆规、直尺。
六、教学过程(一)导入新课为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据,能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?(二)探索新知1.师生互动,探究两个三角形全等的条件教师问1:什么叫全等三角形?学生回答:能够完全重合的两个三角形叫全等三角形.教师问2:全等三角形有什么性质?学生回答:全等三角形的对应边相等,对应角相等.(出示课件4)教师讲解:我们如何识别两个三角形是否全等呢?我们从“条件尽可能的少”出发,逐步增加条件分类进行操作验证,希望得到我们想要的结论.教师问3:满足一个条件对应相等时,识别两个三角形全等,共有几种情况呢?分别是哪些情况?学生讨论并回答:一共有两种情况,①只给一条边时;②只给一个角时.教师问4:请同学们每人画出一个边长为3cm的三角形,然后每个小组内的同学看一下画出的三角形全等吗?学生作图并且比较后回答:不全等.教师问5:请同学们每人画出一个45°的三角形,然后每个小组内的同学看一下画出的三角形全等吗?学生作图并且比较后回答:不全等.结论:只有一条边或一个角对应相等的两个三角形不一定全等.(出示课件6)教师问6:如果满足两个条件判断两个三角形全等,你能说出有哪几种可能的情况?学生分组讨论、探索、归纳,给出的两个条件可能是:一边一内角、两内角、两边.教师请同学们分别按下列条件做一做.①三角形两条边分别为3cm,4cm.三角形②三角形的一条边为4cm,一内角为30°,.③三角形两内角分别为30°和45°教师问7:同学根据①画出的两个三角形全等吗?学生作出图形并且组内识别后回答:两条边对应相等的两个三角形不一定全等.(出示课件8)教师问8:同学根据②画出的两个三角形全等吗?学生做出图形并且组内识别后回答:一条边一个角对应相等的两个三角形不一定全等.(出示课件9)教师问9:同学根据③画出的两个三角形全等吗?学生做出图形并且组内识别后回答:两个角对应相等的两个三角形不一定全等.(出示课件10)教师分析并归纳结论:只满足两个条件画出的三角形不一定全等.总结点拨:(出示课件11)一个条件①一角;②一边;两个条件①两角;②两边;③一边一角.结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等.教师问10:给出三个条件画三角形,会有几种可能的情况?学生思考后师生归纳:有四种可能,即三角、三边、两边一角、两角一边分别相等.教师问11:已知两个三角形的三个内角分别为30°,60° ,90° 它们一定全等吗?学生作出图形并且组内识别后回答:有三个角对应相等的两个三角形不一定全等.(出示课件13)教师问12:已知两个三角形的三条边都分别为3cm、4cm、6cm .它们一定全等吗?(出示课件14)教师演示作法,学生按要求尺规作图,动手操作,通过比较得出结论.这两个三角形相等.教师问13:任意两个三角形的三条边都分别相等.它们一定全等吗?我们进行下边的操作:做一做:先任意画一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?教师演示作法:(1)画B′C′=BC;(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';(3)连接线段A'B', A 'C'.(出示课件15)学生按要求尺规作图,动手操作,通过比较得出结论.三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).总结:(出示课件16)“边边边”判定方法文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)几何语言:在△ABC和△ DEF中,{AB=DE,BC=EF,CA=FD,∴△ABC ≌△ DEF(SSS).例1:如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:(1)△ABD ≌△ACD.(2)∠BAD = ∠CAD.(出示课件17)解题思路:①先找隐含条件:公共边AD ;②再找现有条件:AB=AC③最后找准备条件:D 是BC 的中点→BD=CD师生共同解答如下:(出示课件18)证明:(1)∵ D 是BC 中点,∴ BD =DC.在△ABD 与△ACD 中,{AB =AC (已知)BD =CD (已证)AD =AD (公共边) ∴ △ABD ≌ △ACD ( SSS ).(2)由(1)得△ABD≌△ACD ,∴ ∠BAD= ∠CAD.(全等三角形对应角相等)总结点拨:(出示课件19)证明的书写步骤:①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;③摆齐根据:摆出三个条件用大括号括起来;:④写出结论:写出全等结论.例2:已知:如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE. (出示课件21)分析:要证∠BAC=∠DAE,而这两个角所在三角形显然不全等,我们可以利用等式的性质将它转化为证∠BAD=∠CAE;由已知的三组相等线段可证明△ABD≌△ACE,根据全等三角形的性质可得∠BAD=∠CAE.师生共同解答如下:(出示课件22)证明:在△ABD和△ ACE中,AB=AC,AD=AE,BD=CE,∴ △ ABD≌ △ ACE(SSS),∴∠BAD=∠CAE.∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.例3:用尺规作一个角等于已知角.已知:∠AOB.求作:∠A′O′B′=∠AOB.(出示课件24)师生共同解答如下:(出示课件25)作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C,D;(2)画一条射线O′A′,以点O′为圆心,OC 长为半径画弧,交O′A′于点C′;(3)以点C′为圆心,CD 长为半径画弧,与第(2)步中所画的弧交于点D′;(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.(三)课堂练习(出示课件28-34)1. 如图,D,F是线段BC上的两点,AB=EC,AF=ED,要使△ABF≌△ECD ,还需要条件___________________(填一个条件即可).2.如图,AB=CD,AD=BC, 则下列结论:①△ABC≌△CDB;②△ABC≌△CDA;③△ABD ≌△CDB;④ BA∥DC.正确的个数是( )A . 1个 B. 2个 C. 3个 D. 4个3. 已知:如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌△AED.4. 已知:∠AOB.求作:∠A'O'B',使∠A'O′B'=∠AOB,(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径作弧,交O′A′于点C′;(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.根据以上作图步骤,请你证明∠A'O'B′=∠AOB.5. 如图,AD=BC,AC=BD.求证:∠C=∠D .(提示: 连结AB)6. 如图,AB =AC ,BD =CD ,BH =CH ,图中有几组全 等的三角形?它们全等的条件是什么?参考答案:1. BF=CD2.C3. 证明:∵BD=CE,∴BD -CD=CE -CD .∴BC=ED .在△ABC 和△ADE 中,AC=AD (已知),AB=AE (已知),BC=ED (已证),∴△ABC≌△AED(SSS ).4. 证明:由作法得OD=OC=O′D′=O′C′,CD=C′D′,在△OCD 和△O′C′D′中D COAB∴△OCD≌△O′C′D′(SSS),∴∠COD=∠C′O′D′,即∠A'O'B′=∠AOB.5. 证明:连接AB两点,在△ABD和△BAC中,AD=BC,BD=AC,AB=BA,∴△ABD≌△BAC(SSS)∴∠D=∠C.6.解:(四)课堂小结今天我们学了哪些内容:1.本节课学了判定两个三角形全等的条件数目和全等三角形的判定方法(边边边)2.利用尺规作图作一个角等于已知角(五)课前预习预习下节课(12.2)教材37页到39页的相关内容。
初中数学人教版八年级上册第十二章《全等三角形》练习册(含答案12.2 三角形全等的判定
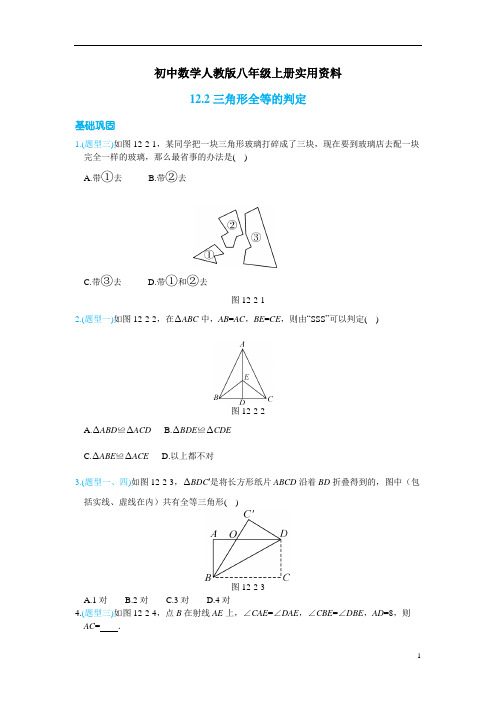
初中数学人教版八年级上册实用资料12.2三角形全等的判定基础巩固1.(题型三)如图12-2-1,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )______A.带①去B.带②去C.带③去D.带①和②去图12-2-12.(题型一)如图12-2-2,在∆ABC中,AB=AC,BE=CE,则由“SSS”可以判定( )图12-2-2A.∆ABD≌∆ACDB.∆BDE≌∆CDEC.∆ABE≌∆ACED.以上都不对3.(题型一、四)如图12-2-3,∆BDC′是将长方形纸片ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )图12-2-3A.1对B.2对C.3对D.4对4.(题型三)如图12-2-4,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE,AD=8,则AC= .图12-2-45.(题型二、三、四、五)如图12-2-5,已知AB⊥CF,DE⊥CF,垂足分别为B,E,AB=DE.请你添加一个适当的条件,使∆ABC≌∆DEF.添加的条件是.图12-2-56.(题型三)如图12-2-6,AB∥CD,AD,BC交于点O,EF过点O分别交AB,CD于点E,F,且AE=DF.求证:O是EF的中点.图12-2-67.(题型二)[福建泉州中考]如图12-2-7,∆ABC,∆CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:∆CDA≌∆CEB.图12-2-7能力提升8.(题型一、二)下列说法中,正确的是()A.两边及一组角对应相等的两个三角形全等B.有两边分别相等,且有一角为30°的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边及其中一边上的高对应相等的两个三角形全等9.(题型四)如图12-2-8,在∆ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,AD=3,则点D到BC的距离是( )图12-2-8A.3B.4C.5D.610.(题型二)如图12-2-9,在∆ABC中,AB=CB,∠ABC=90°,D为AB的延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.图12-2-9(1)求证:∆ABE≌∆CBD.(2)若∠CAE=30°,求∠BDC的度数.11.(题型三)[湖北宜昌中考]杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图12-2-10,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.图12-2-1012.(题型四、五)如图12-2-11,CD⊥AB于点D,BE⊥AC于点E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.图12-2-1113.(题型二、三)如图12-2-12,AB∥CD,OA=OD,AE=DF.求证:EB∥CF.图12-2-1214.(题型四)在数学习题课后,老师布置了一道课后练习题:如图12-2-13,在Rt∆ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC 于点E.求证:∆BPO≌∆PDE.图12-2-13(1)理清思路,完成解答,本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写本题的证明过程.(2)特殊位置,证明结论:若PB平分∠ABO,其余条件不变.求证:AP=CD.答案基础巩固1. C 解析:③保留了原来三角形的两个角和它们的夹边,可以根据“ASA”来配一块与原来一样的玻璃,所以应带③去.故选C.2. C 解析:∵AB=AC,EB=EC,AE=AE,∴△ABE≌△ACE(SSS).故选C.3. D 解析:∵△BDC′是将长方形纸片ABCD沿对角线BD折叠得到的,∴△C′DB≌△CDB.∵AB=DC,AD=BC,BD=BD,∴△ABD≌△CDB(SSS),∴△ABD≌△C′DB.在△ABO和△C′DO中,易知AB=C′D,∠A=∠C′=90°.又∵∠AOB=∠C′OD,∴△ABO≌△C′DO(AAS).故选D.4. 8 解析:∵∠CBE=∠DBE,∴∠ABC=∠ABD.在△ABC和△ABD中,,,, ABC ABDAB ABCAB DAB∠=∠=∠=∠⎧⎪⎨⎪⎩∴△ABC≌△ABD(ASA),∴AC=AD=8.5. BC=EF(或BF=CE或AC=DF或∠A=∠D或∠C=∠F或AC∥DF,答案不唯一) 解析:∵AB⊥CF,DE⊥CF,∴△ABC和△DEF都是直角三角形.又∵AB=DE,∴可以添加的条件有:BC=EF(或BF=CE),△ABC≌△DEF(SAS);AC=DF,Rt△ABC≌Rt△DEF (HL);∠A=∠D,△ABC≌△DEF(ASA);∠C=∠F(或AC∥DF),△ABC≌△DEF(AAS).6. 证明:∵AB∥CD,∴∠EAO=∠FDO,∠AEO=∠DFO.在△AEO和△DFO中,,,, EAO FDOAE DFAEO DFO ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△AEO≌△DFO(ASA),∴OE=OF. ∴O是EF的中点.7.证明:∵△ABC,△CDE均为等腰直角三角形,且∠ACB=∠DCE=90°,∴CE=CD,BC=AC,∠ACB-∠ACE=∠DCE-∠ACE, ∴∠ECB=∠DCA.在△CEB和△CDA中,,,,BC ACECB DCA EC DC=∠=∠=⎧⎪⎨⎪⎩∴△CEB≌△CDA(SAS).能力提升8. C 解析:选项A属于“SSA”,不是判定三角形全等的条件,错误;选项B,如图D12-2-1的两个等腰三角形的腰长相等,且有一角为30°,但这两个等腰三角形不全等,错误;选项C可利用“SSS”和“SAS”证明两个三角形全等,正确;选项D中的高有可能在三角形内部,也有可能在三角形外部,是不确定的,不符合全等的条件,D错误.故选C.图D12-2-1图D12-2-29. A 解析:如图D12-2-2,过点D作DE⊥BC,垂足为E,则DE的长即是点D到BC的距离.∵BD平分∠ABC,∴∠ABD=∠EBD.在△ABD和△EBD中,90,,,A DEBABD EBDBD BD∠=∠=︒∠=∠=⎧⎪⎨⎪⎩∴△ABD≌△EBD(AAS),∴DE=AD=3,即点D到BC的距离是3.故选A.10.(1)证明:∵∠ABC=90°,D为AB的延长线上一点,∴∠ABE=∠CBD=90°.在△ABE和△CBD中,,,,AB CBABE CBD BE BD=∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△CBD(SAS).(2)解:∵AB=CB,∠ABC=90°,∴∠CAB=45°.∵∠CAE=30°,∴∠BAE=∠CAB-∠CAE=45°-30°=15°.∵△ABE≌△CBD,∴∠BCD=∠BAE=15°.∴∠BDC=90°-∠BCD=90°-15°=75°.11. 解:∵AB∥CD,∴∠ABO=∠CDO.∵OD⊥CD,∴∠CDO=90°.∴∠ABO=90°,即OB⊥AB.∵相邻两平行线间的距离相等,∴OD=OB.在△ABO和△CDO中,,,,ABO CDOAOB COD OB OD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△ABO≌△CDO(ASA),∴CD=AB=20米.12. 证明:∵OD⊥AB,OE⊥AC,∴∠BDO=∠CEO=90°.在△BOD和△COE中,90,,,BDO CEOBOD COEBD CE∠=∠=︒∠=∠=⎧⎪⎨⎪⎩∴△BOD≌△COE(AAS),∴OD=OE.在Rt△AOD和Rt△AOE中,OA=OA, OD=OE,∴Rt△AOD≌Rt△AOE(HL),∴∠DAO=∠EAO,即AO平分∠BAC.13. 证明:∵AB∥CD(已知),∴∠3=∠4(两直线平行,内错角相等).在△DCO和△ABO中,34(),,12, OD OA∠=∠=∠=∠⎧⎪⎨⎪⎩已证(已知)(对顶角相等)∴△DCO≌△ABO(ASA),∴OC=OB(全等三角形的对应边相等). ∵AE=DF,OA=OD,∴OD+DF=OA+AE,即OF=OE.在△COF和△BOE中,(),(),12, OC OBOF OE==∠=∠⎧⎪⎨⎪⎩已证已证(对顶角相等)∴△COF≌△BOE(SAS),∴∠F=∠E(全等三角形的对应角相等).∴EB∥CF(内错角相等,两直线平行).14. 证明:(1)∵PB=PD,∴∠2=∠PBD.∵AB=BC,∠ABC=90°,∴∠C=45°.∵BO⊥AC,∴∠1=45°.∴∠1=∠C=45°.∵∠3=∠PBC-∠1,∠4=∠2-∠C,∴∠3=∠4.∵BO⊥AC,DE⊥AC,∴∠BOP=∠PED=90°.在△BPO和△PDE中,34,,,BOP PED BP PD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△BPO≌△PDE(AAS).(2)由(1)得,∠3=∠4.∵BP平分∠ABO,∴∠ABP=∠3.∴∠ABP=∠4.在△ABP和△CPD中,,4,,A CABPPB PD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△ABP≌△CPD(AAS),∴AP=CD.。
人教版八年级数学上册第十二章全等三角形12-2第1课时三边证全等(SSS)课件

AC
EC,
BC DC,
∴△ABC≌△EDC(SSS),∴∠E=∠A=35°.
5.图1是一人字梁屋顶,图2是抽象出来的人字梁三角形,现不 用量角器,只用一把刻度尺检查人字梁三角形的∠B和∠C是 否相等,请同学们设计一种测量方案,并说明理由.
解析 测量方案如下: ①分别在BA和CA上截取BE=CG; ②在BC上截取BD=CF; ③量出DE的长为a米,FG的长为b米. 若a=b,则∠B=∠C.
∴∠ADB= 1 (180°-∠CDE)= 1 ×(180°-20°)=80°,
2
2
∴∠CDE= 1 ∠ADB.
4
13.(情境题·中华优秀传统文化)(2024黑龙江哈尔滨月考,19,★★☆) 石鼓油纸伞因古老工艺和文化底蕴,已成为乡村旅游的一张 亮丽名片.某中学八年级数学兴趣小组参观后,进行了设计伞 的实践活动.小友依据黄金分割的美学设计理念,设计了截 面如图所示的伞骨结构 其中DAHH ≈0.618 ,当伞完全打开后, 测得AB=AC,E,F分别是AB,AC的中点,ED=DF,试说明:伞柄 AH平分∠BAC.
第十二章 全等三角形
12.2 三角形全等的判定
第1课时 三边证全等(SSS)
基础过关全练
知识点1 用“边边边(SSS)”判定两个三角形全等 1.如图,在△ABC和△DEF中,AB=DE,AC=DF,要利用“SSS” 判定△ABC≌△DEF,则还需添加的条件可以为 ( B)
A.BF=CF
B.BC=EF
6
.
解析 如图,连接CD,
CA CB,
在△ACD和△BCD中, CD CD,
AD BD,
∴△ACD≌△BCD(SSS),∴S△ACD=S△BCD,∵M、N分别是CA、CB
部编数学八年级上册12.2三角形全等的判定(解析版)含答案

2022-2023学年八年级数学上册章节同步实验班培优题型变式训练(人教版)12.2 三角形全等的判定【题型1】SSS 证明三角形全等1.(2022·山西·运城市盐湖区教育科技局教学研究室七年级期末)小华在复习用尺规作一个角等于已知角的过程中,回顾了作图的过程,他发现OCD V 与'''O C D V 全等,请你说明小华得到全等的依据是( )A .SSSB .SASC .ASAD .AAS【答案】A 【分析】利用全等三角形的判定定理即可求解.【详解】解:在OCD D 和O C D ¢¢¢D 中,OD O D OC O C DC D C ¢¢¢¢¢=ì¢ï=íï=î,()OCD O C D SSS ¢¢¢\D @D .故选:A .【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.【变式1-1】2.(2021·重庆·华东师范大学附属中旭科创学校八年级期中)已知,如图,AD=AC ,BD=BC ,O 为AB 上一点,那么图中共有___对全等三角形.【答案】3【分析】由已知条件,结合图形可得△ADB ≌△ACB ,△ACO ≌△ADO ,△CBO ≌△DBO 共3对.找寻时要由易到难,逐个验证.【详解】解:∵AD=AC ,BD=BC ,AB=AB,∴△ADB ≌△ACB ;∴∠CAO=∠DAO ,∠CBO=∠DBO ,∵AD=AC ,BD=BC ,OA=OA ,OB=OB∴△ACO ≌△ADO ,△CBO ≌△DBO .∴图中共有3对全等三角形.故答案为3.【题型2】SAS 证明三角形全等1.(2022·全国·八年级专题练习)如图,已知∠1=∠2,∠3=∠4,要证BC =CD ,证明中判定两个三角形全等的依据是( )A .角角角B .角边角C .边角边D .角角边【答案】B 【分析】根据已知条件,直接利用ASA 进行证明即可求解.【详解】解:在△ABC 与△ADC 中,1234AC AC Ð=Ðìï=íïÐ=Ðî,则△ABC ≌△ADC (ASA ).∴BC =CD .故选:B .【点睛】本题考查了全等三角形的判定,掌握全等三角形的判定方法是解题的关键.【变式2-1】2.(2022·全国·八年级课时练习)如图,BE BA =,//AB DE ,BC DE =,若40BAC Ð=°,25E Ð=°,则BDE Ð=___.【答案】115°【分析】根据//AB DE ,推出Ð=ÐABC BED ,联合题目的条件可证明(SAS)BED ABC ≌△△,进而可求得结论.【详解】解:∵//AB DE ,∴Ð=ÐABC BED ,在BED V 与ABC V 中BE AB BED ABC DE CB =ìïÐ=Ðíï=î,∴(SAS)BED ABC ≌△△,∴40EBD BAC Ð=Ð=°,而180BDE EBD E Ð=°-Ð-Ð,且25E Ð=°,∴1804025115BDE Ð=°-°-°=°,故答案为:115°.【点睛】本题考查利用SAS 判定三角形全等,三角形内角和定理,利用平行推出角等,进而推出三角形全等是解题关键.【题型3】ASA 或AAS 证明三角形全等1.(2022·河北·平乡县第二中学八年级阶段练习)已知如图,要测量水池的宽AB ,可过点A 作直线AC ⊥AB ,再由点C 观测,在BA 延长线上找一点B ¢,使ACB ACB ¢ÐÐ=,这时只要出AB ¢的长,就知道AB 的长,那么判定ABC D ≌AB C D ¢的理由是( )A .ASAB .AASC .SASD .HL【答案】A 【分析】直接利用全等三角形的判定方法得出答案.【详解】解:∵AC ⊥AB ,∴90CAB CAB Ð=Т=°,在ABC D 和AB C D ¢中,ACB ACB AC ACCAB CAB Ð=Ðìï=íïТ=Ðî¢,∴ABC D ≌()ASA AB C D ¢,∴AB AB ¢=.故选A .【点睛】本题考查了全等三角形的应用,解题的关键是能够利用ASA 判定两个三角形全等.【变式3-1】2.(2021·江苏南京·八年级阶段练习)如图,AB 、CD 相交于点E ,且AE =BE ,AC BD ∥.求证:△AEC ≌△BED .【答案】见解析【分析】采用“ASA ”的全等三角形的判定方法即可求证.【详解】∵AC BD∥∴∠A =∠B ,在△AEC 和△BED 中,A B AE BEAEC BED Ð=Ðìï=íïÐ=Ðî,∴△AEC ≌△BED (ASA ),【点睛】本题考查了全等三角形的判定以及平行线的性质的知识,掌握全等三角形的判定方法是解答本题的关键.【题型4】HL 证明三角形全等1.(2022·全国·八年级专题练习)如图,已知AD BD ^,BC AC ^,AC BD =.则CAB DBA △△≌的理由是( )A .HLB .SASC .AASD .ASA 【答案】A 【分析】利用直角三角形全等的判定方法进行判断.【详解】证明:∵AD ⊥BD ,BC ⊥AC ,∴∠C =∠D =90°,在Rt △CAB 和Rt △DBA 中,AB BA AC BD =ìí=î,∴Rt △CAB ≌Rt △DBA (HL ).故选:A .【点睛】本题考查了全等三角形的判定,熟练掌握直角三角形全等的判定是解决问题的关键.【变式4-1】2.(2022·湖南·新化县东方文武学校八年级期中)如图,AB =AD ,CB ⊥AB 于点B ,CD ⊥AD 于点D ,求证△ABC ≌△ADC .【答案】见解析【分析】求出∠B =∠D =90°,根据全等三角形的判定定理得出Rt △ABC ≌Rt △ADC .【详解】解:∵CB ⊥AB ,CD ⊥AD∴∠B =∠D =90°又∵AB =AD ,AC =AC∴Rt △ABC ≌Rt △ADC (HL )【点睛】本题考查了全等三角形的判定定理和性质定理,能灵活运用定理进行推理是解此题的关键.【题型5】全等三角形判定的灵活应用1.(2021·甘肃·庄浪县阳川中学八年级期中)下列各组条件中,可以判定△ABC ≌△DEF 的条件是( )A .AB =DE 、AC =DF 、BC =EFB .∠A =∠D 、∠B =∠E 、∠C =∠F C .AB =DE 、AC =DF 、∠C =∠FD .BC =EF 、∠A =∠D 【答案】A 【分析】全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,直角三角形全等还有HL ,根据以上定理判断即可【详解】解: A 、符合全等三角形的判定定理SSS ,即能推出△ABC ≌△DEF ,故本选项符合题意;B 、只有角相等,不能判定△ABC ≌△DFE ,故本选项不合题意;C 、只满足SSA ,不符合全等三角形的判定定理,即不能推出△ABC ≌△DEF ,故本选项不合题意;D 、只有一角一边两个条件,不符合全等三角形的判定定理,即不能推出△ABC ≌△DEF ,故本选项不合题意; 故选A .【点睛】本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,直角三角形全等还有HL .【变式5-1】2.(2022·浙江·舟山市普陀第二中学八年级期末)如图,在ABC V 中,AD 是BC 边上的高,BE 是AC 边上的高,且AD ,BE 交于点F ,若BF AC =,BD =8,3CD =,则线段AF 的长度为______.【答案】5【分析】首先证明△BDF ≌△ADC ,再根据全等三角形的性质可得FD =CD ,AD =BD ,根据AD =8,DF =3,即可算出AF 的长.【详解】解:∵AD 是BC 边上的高,BE 是AC 边上的高,∴∠ADC =∠FDB =90°,∠AEB =90°,∴∠1+∠C =90°,∠1+∠2=90°,∴∠2=∠C ,∵∠2=∠3,∴∠3=∠C ,在△ADC 和△BDF 中,3C FDB CDA BF AC Ð=ÐìïÐ=Ðíï=î,∴△BDF ≌△ADC (AAS ),∴FD =CD ,AD =BD ,∵CD =3,BD =8,∴AD =8,DF =3,∴AF =8-3=5,故答案为:5.【点睛】本题考查的是全等三角形的判定及性质,熟练掌握性质定理是解题的关键.一.选择题1.(2022·福建·福州十八中八年级期末)如图,已知AC BD ^,垂足为O ,AO CO =,AB CD =,则可得到AOB COD D @D ,理由是( )A .HLB .SASC .ASAD .AAS【答案】A 【分析】根据全等三角形的判定定理分析即可.【详解】解:∵AC BD^∴∠AOB=∠COD=90°在Rt △AOB 和Rt △COD 中AO CO AB CD=ìí=î∴AOB COD D @D (HL )故选A .【点睛】此题考查的是全等三角形的判定定理,掌握用HL 判定两个三角形全等是解决此题的关键.2.(2022·全国·七年级期末)如图,为测量桃李湖两端AB 的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C ,测得∠ACB 的度数,在AC 的另一侧测得∠ACD =∠ACB ,CD =CB ,再测得AD 的长,就是AB 的长.那么判定△ABC ≌△ADC 的理由是( )A .SASB .SSSC .ASAD .AAS【答案】A【分析】已知条件是∠ACD =∠ACB ,CD =CB ,AC =AC ,据此作出选择.【详解】解:在△ADC 与△ABC 中,CD CB ACD ACB AC AC =ìïÐ=Ðíï=î.∴△ADC ≌△ABC (SAS ).故选:A .【点睛】此题考查了全等三角形的应用,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS ,做题时注意选择.注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3.(2021·全国·七年级课时练习)如图,△ABC 和△EDF 中,∠B =∠D =90°,∠A =∠E ,点B ,F ,C ,D 在同一条直线上,再增加一个条件,不能判定△ABC ≌△EDF 的是( )A .AB =EDB .AC =EF C .AC ∥EFD .BF =DC 【答案】C【分析】根据全等三角形的判定方法即可判断.【详解】A. AB =ED ,可用ASA 判定△ABC ≌△EDF ;B. AC =EF ,可用AAS 判定△ABC ≌△EDF ;C. AC ∥EF ,不能用AAA 判定△ABC ≌△EDF ,故错误;D. BF =DC ,可用AAS 判定△ABC ≌△EDF ;故选C.【点睛】此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定方法.4.(2022·全国·八年级课时练习)如图,在ABC V 中,D ,E 是BC 边上的两点,,,12110,60AD AE BE CD BAE ==Ð=ÐÐ=°=°,则BAC Ð的度数为( )A .90°B .80°C .70°D .60°【答案】B 【分析】先证明BD =CE ,然后证明△ADB ≌△AEC ,∠ADE =∠AED =70°,得到∠BAD =∠CAE ,根据三角形内角和定理求出∠DAE =40°,从而求出∠BAD 的度数即可得到答案.【详解】解:∵BE =CD ,∴BE -DE =CD -DE ,即BD =CE ,∵∠1=∠2=110°,AD =AE ,∴△ADB ≌△AEC (SAS ),∠ADE =∠AED =70°,∴∠BAD =∠CAE ,∠DAE =180°-∠ADE -∠AED =40°,∵∠BAE =60°,∴∠BAD =∠CAE =20°,∴∠BAC =80°,故选B .【点睛】本题主要考查了全等三角形的性质与判定,邻补角互补,三角形内角和定理,熟知全等三角形的性质与判定条件是解题的关键.5.(2022·全国·八年级专题练习)如图,点B ,C ,E 在同一直线上,且AC CE =,90B D Ð=Ð=°,AC CD ^,下列结论不一定成立的是( )A .2A Ð=ÐB .90A E Ð+Ð=°C .BC DE =D .BCD ACEÐ=Ð【答案】D 【分析】根据直角三角形的性质得出∠A =∠2,∠1=∠E ,根据全等三角形的判定定理推出△ABC ≌△CDE ,再逐个判断即可.【详解】解:∵AC ⊥CD ,∴∠ACD =90°,∵∠B =90°,∴∠1+∠A =90°,∠1+∠2=90°,∴∠A =∠2,同理∠1=∠E ,∵∠D =90°,∴∠E+∠2=∠A+∠E=90°,在△ABC 和△CDE 中,2A B D AC CE Ð=ÐìïÐ=Ðíï=î,∴△ABC ≌△CDE (AAS ),∴BC DE =,∴选项A 、选项B ,选项C 都正确;根据已知条件推出∠A =∠2,∠E =∠1,但是∠1=∠2不能推出,而∠BCD =90°+∠1,∠ACE =90°+∠2,所以BCD ACE Ð=Ð不一定成立故选项D 错误;故选:D .【点睛】本题考查了全等三角形的判定定理和直角三角形的性质,能灵活运用知识点进行推理是解此题的关键,注意:全等三角形的判定定理有:ASA ,SAS ,AAS ,SSS ,两直角三角形全等,还有HL .6.(2022·江苏·八年级专题练习)如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论错误的是( )A .∠AOB =60°B .AP =BQC .PQ ∥AED .DE =DP 【答案】D【分析】利用等边三角形的性质,BC ∥DE ,再根据平行线的性质得到∠CBE =∠DEO ,于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,得出A 正确;根据△CQB ≌△CPA (ASA ),得出B 正确;由△ACD ≌△BCE 得∠CBE =∠DAC ,加之∠ACB =∠DCE =60°,AC =BC ,得到△CQB ≌△CPA (ASA ),再根据∠PCQ =60°推出△PCQ 为等边三角形,又由∠PQC =∠DCE ,根据内错角相等,两直线平行,得出C 正确;根据∠CDE =60°,∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,可知∠DQE ≠∠CDE ,得出D 错误.【详解】解:∵等边△ABC 和等边△CDE ,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠BCD =∠DCE +∠BCD ,即∠ACD =∠BCE ,在△ACD 与△BCE 中,AC BC ACD BCE CD CE =ìïÐ=Ðíï=î,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠DAC ,又∵∠ACB =∠DCE =60°,∴∠BCD =60°,即∠ACP =∠BCQ ,又∵AC =BC ,在△CQB 与△CPA 中,ACP BCQ AC BCPAC CBQ Ð=Ðìï=íïÐ=Ðî,∴△CQB ≌△CPA (ASA ),∴CP =CQ ,又∵∠PCQ =60°可知△PCQ 为等边三角形,∴∠PQC =∠DCE =60°,∴PQ ∥AE ,故C 正确,∵△CQB ≌△CPA ,∴AP =BQ ,故B 正确,∵AD =BE ,AP =BQ ,∴AD -AP =BE -BQ ,即DP =QE ,∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE =60°,∴∠DQE ≠∠CDE ,故D 错误;∵∠ACB =∠DCE =60°,∴∠BCD =60°,∵等边△DCE ,∠EDC =60°=∠BCD ,∴BC ∥DE ,∴∠CBE =∠DEO ,∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,故A 正确.故选:D .【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,解题的关键是找到不变量.二、填空题7.(2022·全国·八年级课时练习)如图,90B D Ð=Ð=°,AB AD =,130BAD Ð=°,则DCA Ð=______°.8.(2020·北京·中考真题)在V ABC 中,AB=AC ,点D 在BC 上(不与点B ,C 重合).只需添加一个条件即可证明V ABD ≌V ACD ,这个条件可以是________(写出一个即可)【答案】∠BAD=∠CAD (或BD=CD )【分析】证明V ABD ≌V ACD ,已经具备,,AB AC AD AD == 根据选择的判定三角形全等的判定方法可得答案.【详解】解:,,AB AC AD AD ==Q\ 要使,ABD ACD V V ≌则可以添加:∠BAD=∠CAD ,此时利用边角边判定:,ABD ACD V V ≌或可以添加:,BD CD =此时利用边边边判定:,ABD ACD V V ≌故答案为:∠BAD=∠CAD 或(.BD CD =)【点睛】本题考查的是三角形全等的判定,属开放性题,掌握三角形全等的判定是解题的关键.9.(2022·全国·八年级课时练习)如图,点D 、A 、E 在直线m 上,AB =AC ,BD ⊥m 于点D ,CE ⊥m 于点E ,且BD =AE .若BD =3,CE =5,则DE =____________【答案】8【分析】根据BD ⊥m ,CE ⊥m ,得∠BDA =∠CEA =90°,再结合已知AB =AC ,BD =AE 可推出Rt △ADB ≌Rt △CEA ,最后由全等三角形的性质,即可计算出结果.【详解】解:∵BD ⊥m ,CE ⊥m ,∴∠BDA =∠CEA =90°,在Rt △ADB 和Rt △CEA 中,∵AB =AC ,BD =AE ,∴Rt △ADB ≌Rt △CEA (HL ),∵BD =3,CE =5,∴AE =BD =3,AD =CE =5,∴DE = AD + AE =8.故答案为:8.【点睛】本题考查了全等三角形的判定与性质,掌握利用HL 判定直角三角形的全等是解题的关键.10.(2022·全国·八年级专题练习)如图,在△ABC 中,∠ABC =90°,AB =CB ,F 为AB 延长线上一点,点E 在BC 上,且AE =CF ,若∠CAE =29°,则∠ACF 的度数为________°.【答案】61【分析】由“HL”可证Rt△ABE≌Rt△CBF,可得∠BAE=∠BCF=16°,即可求解.【详解】解:∵在△ABC中,∠ABC=90°,AB=CB,∴∠BAC=∠BCA=45°,∵∠CAE=29°,∴∠BAE=16°,在Rt△ABE和Rt△CBF中,AB BC AE CF=ìí=î,∴Rt△ABE≌Rt△CBF(HL),∴∠BAE=∠BCF=16°,∴∠ACF=∠BCA+∠BCF=61°,故答案为:61.【点睛】本题考查了全等三角形的判定和性质,证明Rt△ABE≌Rt△CBF是本题的关键.11.(2021·广东·深圳市龙岗区木棉湾实验学校八年级阶段练习)如图,△ABC的面积为25cm2,BP平分∠ABC,过点A作AP⊥BP于点P,则△PBC的面积为________;∵BP 平分ABC Ð,∴ABP EBP Ð=Ð.∵AP BP ^,12.(2022·全国·八年级专题练习)如图,BD 是△ABC 的中线,E 为A B 边上一点,且:2:1AE EB =,连接CE 交BD 于F ,连接AF 并延长交BC 于点G ,则:BGF ADF S S =△△______.【答案】1:3【分析】作//DK EC ,交AB 于K ,作//DH BC ,交AG 于H .通过平行线的性质证明AH GH =,GF FH =,3AH HF =,即可求出:1:3BGF ADF S S D D =.【详解】解:作//DK EC ,交AB 于K ,作//DH BC ,交AG 于H ,BD Q 是ABC D 的中线,AD CD \=,AK EK \=,AH GH =,:2:1AE EB =Q ,EB EK AK \==,//EF DK Q ,BF DF \=,//DH BC Q ,GBF HDF \Ð=Ð,在GBF D 和HDF D 中,GBF HDF BF DF BFG DFH Ð=Ðìï=íïÐ=Ðî,()GBF HDF ASA \D @D ,GF HF \=,BGF DHF S S D D =,AH GH =Q ,3AH HF \=,33ADF DHF BGF S S S D D D \==,:1:3BGF ADF S S D D \=,故答案为:1:3.【点睛】本题考查三角形的面积,三角形全等,平行线的性质,等高模型等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.三、解答题13.(2022·江苏·八年级专题练习)如图,D 是AB 边上一点,DF 交AC 于点E ,DE =FE ,AE =CE .求证:FC //AB .【答案】见解析【分析】由DE =FE ,AE =CE ,易证得△ADE ≌△CFE ,即可得∠A =∠ECF ,则可证得FC ∥AB .【详解】证明:在△ADE 和△CFE 中,DE FE AED CEF AE CE =ìïÐ=Ðíï=î,∴△ADE ≌△CFE (SAS ),∴∠A =∠ECF ,∴FC //AB .【点睛】此题考查了全等三角形的判定与性质以及平行线的判定.此题难度不大,注意掌握数形结合思想的应用.14.(2022·江苏·八年级课时练习)已知:如图AD 为△ABC 的高,E 为AC 上一点BE 交AD 于F 且有BF =AC ,FD =CD .求证:Rt △BFD ≌Rt △ACD .【答案】证明见解析【分析】由题意可知BFD △和ACD △都为直角三角形,即可直接利用“HL ”证明BFD ACD @△△.【详解】证明:∵AD 是ABC V 的高,∴AD BC ^,即BFD △和ACD △都为直角三角形.∴在Rt BFD V 和Rt ACD △中BF AC FD CD =ìí=î,∴()BFD ACD HL @V V .【点睛】本题考查全等三角形的判定;掌握判定三角形全等的方法是解答本题的关键.15.(2022·陕西·中考真题)如图,在△ABC 中,点D 在边BC 上,CD =AB ,DE ∥AB ,∠DCE =∠A .求证:DE =BC .【答案】证明见解析【分析】利用角边角证明△CDE ≌△ABC ,即可证明DE =BC .【详解】证明:∵DE ∥AB ,∴∠EDC =∠B .又∵CD =AB ,∠DCE =∠A ,∴△CDE ≌△ABC (ASA).∴DE =BC .【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.16.(2021·广东广州·中考真题)如图,点E 、F 在线段BC 上,//AB CD ,A D Ð=Ð,BE CF =,证明:AE DF =.【答案】见解析【分析】利用AAS 证明△ABE ≌△DCF ,即可得到结论.【详解】证明:∵//AB CD ,∴∠B =∠C ,∵A D Ð=Ð,BE CF =,∴△ABE ≌△DCF (AAS ),∴AE DF =.【点睛】此题考查全等三角形的判定及性质,熟记全等三角形的判定定理是解题的关键.17.(2021·全国·八年级专题练习)如图,已知AB =DC ,AC =DB ,BE =CE,求证:AE =DE.【答案】见解析【分析】利用SSS 证明△ABC ≌△DCB ,根据全等三角形的性质可得∠ABC=∠DCB ,再由SAS 定理证明△ABE ≌△CED ,即可证得AE=DE .【详解】证明:在△ABC 和△DCB 中,AB DC AC DB BC CB ìïíïî=== ,∴△ABC ≌△DCB (SSS ).∴∠ABC=∠DCB .在△ABE 和△DCE 中,AB DCABC DCB BE CE ===ìïÐÐíïî,∴△ABE ≌△DCE (SAS ).∴AE=DE .【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.18.(2022·江苏泰州·九年级专题练习)如图,V ABC 中,AC =BC ,∠ACB =90°,AD 平分∠BAC 交BC 于点D ,过点B 作BE ⊥AD ,交AD 延长线于点E ,F 为AB 的中点,连接CF ,交AD 于点G ,连接BG .(1)线段BE 与线段AD 有何数量关系?并说明理由;(2)判断V BEG的形状,并说明理由.。
8年级数学人教版上册同步练习全等三角形三角形全等的判定(含答案解析)

8年级数学人教版上册同步练习全等三角形三角形全等的判定(含答案解析)12.1全等三角形12.2三角形全等的判定专题一三角形全等的判定1.如图,BD是平行四边形ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB 的平分线DF交BC于点F.求证:△ABE≌△CDF.2.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE. 请你添加一个条件,使△BDE≌△CDF (不再添加其他线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是:__________;(2)证明:3.如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.(1)给出下列四个条件:①AD=CE;②AE=CD;③∠BAC=∠BCA;④∠ADB=∠CEB;请你从中选出一个能使△ADB≌△CEB的条件,并给出证明;(2)在(1)中所给出的条件中,能使△ADB≌△CEB的还有哪些?直接在题后横线上写出满足题意的条件序号.__________________.专题二全等三角形的判定与性质4.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A6B.4 C.23D.55.【2013·襄阳】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.求证:AM=AN.NMEDB CA6.【2012·泸州】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E﹨A在直线DC的同侧,连接AE.求证:AE∥BC.专题三全等三角形在实际生活中的应用7.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是()A.60°B.90°C.120°D.150°8.有一座小山,现要在小山A﹨B的两端开一条隧道,施工队要知道A﹨B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A﹨B两端的距离,你能说说其中的道理吗?9.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,对吗?为什么?状元笔记【知识要点】1.全等三角形能够完全重合的两个三角形叫做全等三角形.2.全等三角形的性质全等三角形的对应边相等,全等三角形的对应角相等.3.三角形全等的判定方法(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).(2)两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).(3)两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).(4)两个角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).4.直角三角形全等的判定方法斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边﹨直角边”或“HL”).【温馨提示】1.两个三角形全等的条件中必须有一条边分别相等,只有角分别相等不能证明两个三角形全等.2.有两边和其中一边的对角分别相等的两个三角形不一定全等.3.“HL”定理指的是斜边和一条直角边分别相等,而不是斜边和直角分别相等.【方法技巧】1.应用全等三角形性质解决问题的前提是准确地确定全等三角形的对应边和对应角,其规律主要有以下几点:(1)以对应顶点为顶点的角是对应角;(2)对应顶点所对应的边是对应边;(3)公共边(角)是对应边(角);(4)对顶角是对应角;(5)最大边(角)是对应边(角),最小边(角)是对应边(角).全等三角形的对应边和对应角可以依据字母的对应位置来确定,如若△ABC≌△DEF,说明A与D,B与E,C与F是对应点,则∠ABC与∠DEF是对应角,边AC与边DF 是对应边.2.判定两个三角形全等的解题思路:SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎩找夹角——已知两边找另一边——边为角的对边——找任一角——找夹角的另一边——已知一边一角边为角的邻边找夹边的另一角——找边的对角——找夹边——已知两角找任一边——参考答案:1.证明:平行四边形ABCD 中,AB=CD ,∠A=∠C ,AB ∥CD , ∴∠ABD=∠CDB .∵∠ABE=21∠ABD ,∠CDF=21∠CDB ,∴∠ABE=∠CDF .在△ABE 与△CDF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠CDF ABE CDAB C A ∴△ABE ≌△CDF . 2.解:(1)DC BD =(或点D 是线段BC 的中点),ED FD =,BE CF =中任选一个即可﹒ (2)以DC BD =为例进行证明: ∵CF ∥BE ,∴∠FCD ﹦∠EBD .又∵DC BD =,∠FDC =∠EDB , ∴△BDE ≌△CDF . 3.解:(1)添加条件②,③,④中任一个即可,以添加②为例说明. 证明:∵AE=CD ,BE=BD , ∴AB=CB .又∠ABD=∠CBE ,BE=BD , ∴△ADB ≌△CEB . (2)③④.4.B 解析:∵∠ABC =45°,AD ⊥BC ,∴AD =BD ,∠ADC =∠BDH , ∠AHE =∠BHD =∠C .∴△ADC ≌△BDH .∴BH =AC =4.故选B . 5.证明:如图所示,M∵△AEB由△ADC旋转而得,∴△AEB≌△ADC.∴∠3=∠1,∠6=∠C.∵AB=AC,AD⊥BC,∴∠2=∠1,∠7=∠C.∴∠3=∠2,∠6=∠7.∵∠4=∠5,∴∠ABM=∠ABN.又∵AB=AB,∴△AMB≌△ANB.∴AM=AN.6.证明:∵△ABC和△EDC是等边三角形,∴∠BCA=∠DCE=60°.∴∠BCA-∠ACD=∠DCE-∠ACD,即∠BCD=∠ACE.在△DBC和△EAC中,BC=AC,∠BCD=∠ACE,DC=EC,∴△DBC≌△EAC(SAS).∴∠DBC=∠EAC.又∵∠DBC=∠ACB=60°,∴∠ACB=∠EAC.∴AE∥BC.7.B 解析:∵滑梯﹨墙﹨地面正好构成直角三角形,又∵BC=EF,AC=DF,∴Rt△ABC≌Rt△DEF.∴∠ABC=∠DEF,∵∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.故选B.8.解:在△ABC和△CED中,AC=CD,∠ACB=∠ECD,EC=BC,∴△ABC≌△CED.∴AB=ED.即量出DE的长,就是A﹨B两端的距离.9.解:对.理由:∵AC ⊥AB,∴∠CAB=∠CAB′=90°. 在△ABC 和△AB′C 中,ACB ACB AC AC CAB CAB =⎧⎪=⎨⎪=⎩∠∠′,,∠∠′, ∴△ABC ≌△AB′C (ASA ). ∴AB′=AB .。
人教版 八年级上册数学 12.2 三角形全等的判定 课时训练(含答案)

人教版八年级数学12.2 三角形全等的判定课时训练一、选择题1. 在如图所示的三角形中,与图中的△ABC全等的是()2. 如图,在正方形ABCD中,连接BD,点O是BD的中点.若M、N是边AD 上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有()A. 2对B. 3对C. 4对D. 5对3. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去() A. ①B. ②C. ③D. ①和②4. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DCC.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D5. 如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是()A.△ABE≌△ACD B.△ABD≌△ACEC.∠C=30°D.∠1=70°6. 观察图中的尺规作图痕迹,下列说法错误的是()A.∠DAE=∠EAC B.∠C=∠EACC.AE∥BC D.∠DAE=∠B7. 根据下列条件,能画出唯一的△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=50°D.∠A=30°,∠B=70°,∠C=80°8. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB 上,且△PMN为等边三角形,则满足上述条件的△PMN有()A. 1个B. 2个C. 3个D. 3个以上二、填空题9. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).10.如图,已知AC =EC ,∠ACB =∠ECD ,要直接利用“AAS”判定△ABC ≌△EDC ,应添加的条件是__________.11. 如图,已知AB =BD ,∠A =∠D ,若要应用“SAS”判定△ABC ≌△DBE ,则需要添加的一个条件是____________.12. 如图,已知∠ABC =∠DCB ,添加下列条件中的一个:①∠A =∠D ,②AC=DB ,③AB =DC ,其中不能判定△ABC ≌△DCB 的是________(只填序号).13. 如图,AC与BD 相交于点O ,且AB =CD ,请添加一个条件:________,使得△ABO ≌△CDO.14. 要测量河岸相对两点A ,B 之间的距离,已知AB 垂直于河岸BF ,先在BF上取两点C ,D ,使CD =CB ,再过点D 作BF 的垂线段DE ,使点A ,C ,E 在一条直线上,如图,测出DE =20米,则AB 的长是________米.15. (2019•襄阳)如图,已知ABC DCB ∠=∠,添加下列条件中的一个:①A D ∠=∠,②AC DB =,③AB DC =,其中不能确定ABC △≌△DCB △的是__________(只填序号).16. 如图,在Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC,交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是.三、解答题17. 如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.18. 如图,在△ABC中,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD 相交于点F,连接AF.求证:(1)△AEB≌△ADC;(2)AF平分∠BAC.19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.(1)若∠ABF=63°,求∠ADE的度数;DE=BF+EF.20. 如图,四边形ABCD是平行四边形,延长BA至E,延长DC至F,使得AE =CF,连接EF交AD于G,交BC于H.求证:△AEG≌△CFH.21. 一天,顽皮的小明同学拿着老师的等腰三角板玩,不小心把它掉到两根柱子之间,如图,这一幕恰巧被数学老师看见了,于是有了下面这道题:(1)求证:△ADC≌△CEB;(2)如果每块砖的厚度a=10 cm,请你帮小明求出三角板ABC的面积.人教版八年级数学12.2 三角形全等的判定课时训练-答案一、选择题1. 【答案】C2. 【答案】C【解析】由题意可知,△ABD ≌△CBD ,△MON ≌△M ′ON ′,△DON ≌△BON ′,△DOM ≌△BOM ′共4对.3. 【答案】 C4. 【答案】C5. 【答案】C[解析] ∵BE =CD ,∴BE -DE =CD -DE ,即BD =CE. 在△ABD 和△ACE 中,⎩⎨⎧AB =AC ,BD =CE ,AD =AE ,∴△ABD ≌△ACE.由题意易证:△ABE ≌△ACD ,故A ,B 正确. 由△ABE ≌△ACD 可得∠B =∠C. ∵∠2=∠BAE +∠B ,∴∠B =∠2-∠BAE =110°-60°=50°. ∴∠C =∠B =50°. 故C 错误.∵△ABE ≌△ACD(已证),∴∠1=∠AED =180°-∠2=70°. 故D 正确.故选C.6. 【答案】A[解析] 根据图中尺规作图的痕迹,可得∠DAE =∠B ,故D 选项正确,∴AE ∥BC ,故C 选项正确.∴∠EAC =∠C ,故B 选项正确. ∵∠DAE =∠B ,∠EAC =∠C ,而∠C 与∠B 的大小关系不确定,所以∠DAE 与∠EAC 的大小关系不确定.故选A.7. 【答案】C[解析] 对于选项A 来说,AB +BC<AC ,不能画出△ABC ;对于选项B 来说,可画出△ABC 为锐角三角形或者钝角三角形;对于选项C 来说,已知两边及其夹角,△ABC 是唯一的;对于选项D 来说,△ABC 的形状可确定,但大小不确定.8. 【答案】D【解析】如解图,①当OM 1=2时,点N 1与点O 重合,△PMN 是等边三角形;②当ON 2=2时,点M 2与点O 重合,△PMN 是等边三角形;③当点M 3,N 3分别是OM 1,ON 2的中点时,△PMN 是等边三角形;④当取∠M 1PM 4=∠OPN 4时,易证△M 1PM 4≌△OPN 4(SAS),∴PM 4=PN 4,又∵∠M 4PN 4=60°,∴△PMN 是等边三角形,此时点M ,N 有无数个,综上所述,故选D.二、填空题9. 【答案】答案不唯一,如∠B =∠E10. 【答案】∠B =∠D11. 【答案】AC =DE12. 【答案】②[解析] ∵已知∠ABC =∠DCB ,且BC =CB ,∴若添加①∠A =∠D ,则可由“AAS”判定△ABC ≌△DCB ; 若添加②AC =DB ,则属于“SSA”,不能判定△ABC ≌△DCB ; 若添加③AB =DC ,则可由“SAS”判定△ABC ≌△DCB.13. 【答案】∠A =∠C 或∠B =∠D 或AB ∥CD(答案不唯一)[解析] 由题意可知∠AOB =∠COD ,AB =CD.∵AB 是∠AOB 的对边,CD 是∠COD 的对边,∴只能添加角相等,故可添加∠A =∠C 或∠B =∠D 或AB ∥CD.14. 【答案】2015. 【答案】②【解析】∵已知ABC DCB ∠=∠,且BC CB =,∴若添加①A D ∠=∠,则可由AAS 判定ABC △≌DCB △;若添加②AC DB =,则属于边边角的顺序,不能判定ABC △≌DCB △; 若添加③AB DC =,则属于边角边的顺序,可以判定ABC △≌DCB △. 故答案为:②.16. 【答案】16 [解析] ∵BF ∥AC ,∴∠EBF=∠EAD. 在△BFE 和△ADE 中,∴△BFE ≌△ADE (ASA).∴BF=AD.∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD. ∵当FD ⊥AC 时,FD 最短,此时FD=BC=5, ∴四边形FBCD 周长的最小值为5+11=16.三、解答题17. 【答案】证明:∵AE =BF ,∴AE +EF =BF +EF , 即AF =BE.∵AC ∥BD ,∴∠CAF =∠DBE.在△ACF 和△BDE 中,⎩⎨⎧AC =BD ,∠CAF =∠DBE ,AF =BE ,∴△ACF ≌△BDE(SAS). ∴CF =DE.18. 【答案】证明:(1)∵BE ⊥AC ,CD ⊥AB , ∴∠AEB =∠ADC =90°.在△AEB 与△ADC 中,⎩⎨⎧∠AEB =∠ADC ,∠BAE =∠CAD ,AB =AC ,∴△AEB ≌△ADC(AAS). (2)∵△AEB ≌△ADC ,∴AE =AD. 在Rt △AEF 与Rt △ADF 中,⎩⎨⎧AE =AD ,AF =AF ,∴Rt △AEF ≌Rt △ADF(HL). ∴∠EAF =∠DAF.∴AF 平分∠BAC.19. 【答案】解:(1)∵AD ∥BC ,AB ⊥BC , ∴∠ABC =∠BAD =90°. ∵DE ⊥AC ,BF ⊥AC , ∴∠BFA =∠AED =90°.∴∠ABF +∠BAF =∠BAF +∠DAE =90°. ∴∠DAE =∠ABF =63°.∴∠ADE =27°.(2)证明:由(1)得∠DAE =∠ABF ,∠AED =∠BFA =90°.在△DAE 和△ABF 中,⎩⎨⎧∠DAE =∠ABF ,∠AED =∠BFA ,AD =BA ,∴△DAE ≌△ABF(AAS). ∴AE =BF ,DE =AF.∴DE =AF =AE +EF =BF +EF.20. 【答案】证明:∵在▱ABCD 中,∠BAD =∠BCD ,AB ∥CD , ∴∠E =∠F ,180°-∠BAD =180°-∠BCD ,即∠EAG =∠FCH ,(5分) 在△AEG 和△CFH 中,⎩⎨⎧∠E =∠FAE =CF∠EAG =∠FCH, ∴△AEG ≌△CFH(ASA ).(7分)21. 【答案】解:(1)证明:由题意得AC =CB ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°.∴∠ACD +∠BCE =90°,∠ACD +∠CAD =90°.∴∠BCE =∠CAD.在△ADC 和△CEB 中,⎩⎨⎧∠ADC =∠CEB ,∠CAD =∠BCE ,AC =CB ,∴△ADC ≌△CEB(AAS). (2)由(1)知△ADC ≌△CEB ,∴AD =CE =4a =40 cm ,CD =BE =3a =30 cm. ∴DE =70 cm.∴S △ABC =12×(30+40)×70-2×12×30×40=1250(cm 2).答:三角板ABC 的面积为1250 cm 2.。
清远市师院附中八年级数学上册第十二章全等三角形12.2全等三角形的判定第1课时边边边导学案新版新人教

12.2 三角形全等的判定第1课时边边边一、新课导入1.导入课题:通过上节课的学习,大家知道:两个三角形全等时,三条对应边相等,三组对应角相等,那么判定两个三角形全等,是否一定需要满足六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?从这节课开始,我们来探究全等三角形的判定.2.学习目标:(1)通过三角形的稳定性,体验三角形全等的“边边边”条件.(2)会运用“边边边”定理判定两个三角形的全等.3.学习重、难点:重点:寻求三角形全等的条件的方法.难点:寻求三角形全等的条件的依据.二、分层学习1.自学指导:(1)自学内容:探究1:两个三角形的六个对应元素中满足一个或两个对应元素相等的两个三角形是否一定全等.探究2:三条边对应相等的两个三角形是否一定全等.(2)自学时间:10分钟.(3)自学方法:按探究中的要求画三角形、剪三角形、重叠三角形,并观察归纳得出自己的结论.(4)探究提纲:动手画出符合给出条件的两个三角形,小组内比较一下,看画出的图形是否全等.a.小组长任意给出一个条件(一条边或一个角),小组的所有成员动手画出符合条件的三角形,小组内比较一下,你们画出的图形一样吗?b.小组长任意给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?发现按这些条件画出的两个三角形不能保证一定全等.c.给出三个条件画三角形,画画看有几种可能的情况.d.已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?你能得出什么结论?通过上面的操作,你得出的结论:三边分别相等的两个三角形全等简写为“边边边”或“SSS”.2.自学:学生结合探究提纲进行探究式学习.3.助学:(1)师助生:①明了学情:学生对自学提纲中的a、b两种情形,能够很快得出不全等的结论,但对于自学参考提纲中的c情形,学生可以得出很多结论,因此教师在肯定学生的前提下,不要过多的停留在这个问题上,要迅速引导学生回到今天探讨的重点上.②差异指导:根据学生学习中存在的问题予以分类指导.(2)生助生:在动手画图的过程中,小组之内需要合作探究,相互交流帮助.4.强化:(1)定理的文字表述:三边分别相等的两个三角形全等.(2)定理的几何表述:如图,在△ABC和△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF.(特别注意对应的顶点写在对应的位置上.)1.自学指导:(1)自学内容:教材第36页例1到教材第37页探究3前的内容.(2)自学时间:5分钟.(3)自学方法:认真阅读教材上的内容,思考回答自学提纲中的问题.(4)自学参考提纲:①判定两个三角形全等,今天学习了什么方法?SSS②图中D是BC的中点,你可以得出哪个结论?等腰三角形“三线合一”.③你学会了证明两个三角形全等的基本格式了吗?④请仿照课本作图:已知∠AOB.a.求作:∠A′O′B′,使∠A′O′B′=∠AOB,认真阅读作法,理解什么是尺规作图?然后写出这样作图的理论依据.依据:三边分别相等的两个三角形全等(SSS).b.剪下△COD和△C′O′D′,重叠地放置在一起,看一看有什么结果?全等.2.自学:学生可结合自学指导进行自学.3.助学:(1)师助生:①明了学情:重点了解学生对证明的符号语言的运用及作图中的作法表述规范完整.②差异指导:a.指导学生的证明过程;b.纠正学生尺规作图的作法不当之处;c.引导说明每步作图的目的和依据.(2)生助生:对尺规作图的理论依据及规范操作进行交流,对困难学生予以帮助.4.强化:(1)结论、方法、要领:①用:“SSS”判定两个三角形全等的依据.②用“SSS”证明两个三角形全等的表达格式.③符号“∵”“∴”表示的意义.④公共边是对应边.⑤等量的运用:等式性质.(2)练习:如图,A、D、B、F在一条直线上,BC=DE,AC=EF,BF=AD,求证:△ABC≌△FDE.证明:∵BF=AD,∴BF+BD=AD+DB,即DF=AB.在△ABC和△FDE中,BC=DE,AC=FE,AB=FD,∴△ABC=△FDE(SSS).三、评价1.学生的自我评价:通过本节课的学习,让学生代表谈谈自己的收获或困惑.2.教师对学生的评价:(1)表现性评价:对学生的学习态度、学习方法和收获进行点评.(2)纸笔评价:课堂评价检测.3.教师自我评价(教学反思):本课时教学时应抓住以下重点:(1)分类问题:教师让学生从实践入手,给定三角形三边,学生在薄纸上画,然后小组的同学看所画三角形是否重合,探索归纳、形成结论.(2)教师可用多媒体展示现实生活中的实际例子:如桥梁、铁塔、自行车的三角架等,从中体验三角形的稳定性,认识“边边边”可作为三角形全等的判定依据.(3)强调思路分析和书写规范.一、基础巩固(第1、2、3题每题10分,第4题20分,共50分)1.下面判断两个三角形全等的条件中,正确的是(D)A.一条边对应相等B.两条边对应相等C.三个角对应相等D.三边对应相等2.如图,△ABC中,AB=AC,EB=EC,则由SSS可以判定(B)A.△ABD≌△ACDB.△ABE≌△ACEC.△BDE≌△CDED.以上答案都不对3.如图,AB=AC,EB=CD,要使△ABE≌△ACD,依据SSS,则还需要添加条件AE=AD.4.如图,AB=AD,CB=CD,△ABC 与△ADC全等吗?为什么?解:全等.∵AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS).二、综合应用(每题15分,共30分)5.如图,C是AB的中点,AD=CE,CD=BE,求证△ACD≌△CBE 证明:∵C是AB的中点,∴AC=CB.在△ACD和△CBE中,AC=CB,AD=CE,CD=BE,∴△ACD≌△CBE(SSS).6.如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF,求证:∠A=∠D.证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF(SSS).∴∠A=∠D.三、拓展延伸(20分)7.已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与OA平行的直线. 解:作图如图所示:作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;(2)以点C为圆心,OD长为半径画弧,交OB于点F;(3)以点F为圆心,DE长为半径画弧,与第2步中所画的弧相交于点P;(4)过C,P两点作直线,直线CP即为要求作的直线.专题练习:图形的轴对称基础训练1.下列交通标志图案是轴对称图形的是(C)2.下列图形中,所有轴对称图形的对称轴条数之和为(B)(第2题图)A. 13B. 11C. 10D. 83.民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是(C)4.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有(C)(第4题图)A. 2种B. 3种C. 4种D. 5种5.如图,直线y=-33x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是(A)(第5题图)A. (3,3)B. (3,3)C. (2,23)D. (23,4)6.若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=__0__.(第7题图)7.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B 恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.8.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标.(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.(第8题图)解:(1)如解图所示△A1B1C1即为所求,点B1的坐标为(-2,-1).(2)如解图所示,△A2B2C2即为所求,点C2的坐标为(1,1).(第8题图解)9.如图①,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图②.(1)求证:EG=CH.(2)已知AF=2,求AD和AB的长.(第9题图)解:(1)证明:由折叠知AE =AD =EG ,BC =CH . ∵四边形ABCD 是矩形, ∴AD =BC , ∴EG =CH .(2)∵∠ADE =45°,∠FGE =∠A =90°,AF =2, ∴DG =FG =2,DF =2, ∴AD =AF +DF =2+2.由折叠知∠AEF =∠GEF ,∠BEC =∠HEC ,∴∠GEF +∠HEC =90°,∠AEF +∠BEC =90°, ∵∠AEF +∠AFE =90°, ∴∠BEC =∠AFE . 在△AEF 与△BCE 中, ⎩⎪⎨⎪⎧∠AFE =∠BEC ,∠A =∠B =90°,AE =BC ,∴△AEF ≌△BCE (AAS ), ∴AF =BE ,∴AB =AE +BE =22+2.拓展提高10.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为(C ),(第10题图))A. 30°B. 45°C. 60°D. 75°11.如图,四边形ABCD 中,AC 垂直平分BD ,垂足为点E ,下列结论不一定成立的是(C )(第11题图)A. AB =ADB. AC 平分∠BCDC. AB =BDD. △BEC ≌△DEC12.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有_3_种.(第12题图)13.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为4 5.(第13题图)14.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN 的中点.点P是直径MN上一动点,则PA+PB的最小值是2.(第14题图)15.在▱ABCD中,AB<BC,已知∠B=30°,AB=23,将△ABC沿AC翻折至△AB′C,使点B′落在▱ABCD所在的平面内,连结B′D.若△AB′D是直角三角形,则BC 的长为__4或6__.16.如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G,点E,F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.,(第16题图))(1)求证:△ABG≌△C′DG.(2)求tan∠ABG的值.(3)求EF的长.解:(1)证明:∵△BDC ′由△BDC 翻折而成,∴∠C =∠C ′=∠BAG =90°,C ′D =AB =CD ,∠BGA =∠DGC ′. 在△ABG 与△C ′DG 中,∵⎩⎪⎨⎪⎧∠BAG =∠C ′,∠AGB =∠C ′GD ,AB =C ′D ,∴△ABG ≌△C ′DG . (2)解:∵由(1)可知△ABG ≌△C ′DG ,∴GD =GB . 设AG =x ,则GB =GD =AD -AG =8-x .在Rt △ABG 中,∵AB 2+AG 2=BG 2,即62+x 2=(8-x )2,解得x =74,∴tan ∠ABG =AG AB =746=724. (3)解:∵△AEF 是△DEF 翻折而成, ∴EF 垂直平分AD .∴HD =12AD =4.∴tan ∠ABG =tan ∠ADE =724.∴EH =HD ×724=4×724=76.∵EF 垂直平分AD ,AB ⊥AD ,∴HF 是△ABD 的中位线. ∴HF =12AB =12×6=3.∴EF =EH +HF =76+3=256.17.如图,已知在Rt△ABC 中,∠C =90°,翻折∠C ,使点C 落在斜边AB 上某一点D处,折痕为EF (点E ,F 分别在边AC ,BC 上).(第17题图)(1)若△CEF 与△ABC 相似.①当AC =BC =2时,AD 的长为__2__; ②当AC =3,BC =4时,AD 的长为.(2)当点D 是AB 的中点时,△CEF 与△ABC 相似吗?请说明理由. 解:(1)若△CEF 与△ABC 相似.(第17题图解①)①当AC =BC =2时,△ABC 为等腰直角三角形,如解图①,连结CD . 此时点D 为AB 边中点,AD =22AC = 2.②当AC =3,BC =4时,有以下两种情况:(第17题图解②)(Ⅰ)若CE ∶CF =3∶4,如解图②所示.∵CE ∶CF =AC ∶BC ,∴EF ∥BC .由折叠性质可知,CD ⊥EF ,∴CD ⊥AB ,即此时CD 为AB 边上的高.在Rt△ABC 中,AC =3,BC =4,∴BC =5.∴cos A =35.AD =AC ·cos A =3×35=1.8.(第17题图解③)(Ⅱ)若CF ∶CE =3∶4,如解图③所示,连结CD ,与EF 交于点Q .∵△CEF ∽△CBA ,∴∠CEF =∠B .由折叠性质可知,∠CEF +∠ECD =90°,又∵∠A +∠B =90°.∴∠A =∠ECD ,∴AD =CD .同理可得∠B =∠FCD ,CD =BD .∴此时AD =12AB =12×5=2.5.综上所述,当AC =3,BC =4时,AD(2)当点D 是AB 的中点时,△CEF 与△ABC 相似.理由如下:如解图③.∵CD 是Rt△ABC 的中线,∴CD =DB =AD .∴∠DCB =∠B .由折叠性质可知,∠CQF =∠DQF =90°,∴∠DCB +∠CFE =90°.∵∠B +∠A =90°,∴∠CFE =∠A .又∵∠ECF =∠BCA ,∴△CEF ∽△CBA .第2课时 等腰三角形的判定1.理解并掌握等腰三角形的判定方法.2.运用等腰三角形的判定进行证明和计算.重点等腰三角形的判定方法.难点等腰三角形的判定方法的证明.一、提出问题出示教材第77页“思考”.学生思考,回答后教师提问:在一般三角形中,如果有两个角相等,那么它们所对的边有什么关系?学生猜想它们所对的边相等.即如果一个三角形有两个角相等,那么这两个角所对的边也相等.如何证明?二、解决问题教师引导提示,学生根据提示画出图形,并写出已知、求证.已知:在△ABC 中,∠B =∠C.求证:AB =AC.与学生一起回顾等腰三角形中常添加的辅助线:高、顶角平分线、底边上的中线.让学生逐一尝试,发现可以作AD⊥BC,或AD 平分∠BAC,但不能作BC 边上的中线.学生口头证明后,选一种方法写出证明过程.如图,在△ABC 中,∠B =∠C,作△ABC 的角平分线AD.在△BAD 和△CAD 中,⎩⎪⎨⎪⎧∠1=∠2,∠B =∠C,AD =AD ,∴△BAD ≌△CAD(AAS ),∴AB =AC.归纳等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等,简称:“等角对等边”.三、应用举例1.出示教材例2.引导学生根据命题画出图形,利用角平分线的性质及“等边对等角”来证明.学生讨论后,自己完成证明过程.例 2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC.(如图所示)求证:AB=AC.分析:要证明AB=AC.可先证明∠B=∠C.因为∠1=∠2,所以可以设法找出∠B,∠C 与∠1,∠2的关系.证明:∵AD∥BC,∴∠1=∠B(______________________),∠2=∠C(______________________).而已知∠1=∠2,所以∠B=∠C.∴AB=AC(______________).2.出示教材例3.让学生自学例3.例3 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.作法:(1)作线段AB=a.(2)作线段AB的垂直平分线MN,与AB相交于点D.(3)在MN上取一点C,使DC=h.(4)连接AC,BC,则△ABC就是所求作的等腰三角形.四、课堂小结1.等腰三角形的判定方法是什么?2.等腰三角形的性质与判定既有区别又有联系,你能总结一下吗?五、布置作业教材习题13.3第2,8,10题.学生刚刚学过等腰三角形的性质,对等腰三角形已经有了一定的了解和认识.因此在课堂教学中先引出等腰三角形的判定定理及推论,并能够灵活应用它进行有关论证和计算.发展学生的动手、归纳猜想能力;发展学生证明用文字表述的几何命题的能力;使它们进一步掌握归纳思维方法,领会数学分类思想、转化思想.。
人教版数学八年级上册第十二章《全等三角形》教案(全单元)

第十二章全等三角形12.1全等三角形1.了解全等形及全等三角形的概念.2.理解全等三角形的性质.重点探究全等三角形的性质.难点掌握两个全等三角形的对应边、对应角的寻找规律,能迅速正确地指出两个全等三角形的对应元素.一、情境导入一位哲人曾经说过:“世界上没有完全相同的叶了”,但是在我们的周围却有着好多形状、大小完全相同的图案.你能举出这样的例子吗?二、探究新知1.动手做(1)和同桌一起将两本数学课本叠放在一起,观察它们能重合吗?(2)把手中三角板按在纸上,画出三角形,并裁下来,把三角板和纸三角形放在一起,观察它们能够重合吗?得出全等形的概念,进而得出全等三角形的概念.能够完全重合的两个图形叫做全等形,能够完全重合的两个三角形叫做全等三角形.2.观察观察△ABC与△A′B′C′重合的情况.总结知识点:对应顶点、对应角、对应边.全等的符号:“≌”,读作:“全等于”.如:△ABC≌△A′B′C′.3.探究(1)在全等三角形中,有没有相等的角、相等的边呢?通过以上探索得出结论:全等三角形的性质.全等三角形的对应边相等,对应角相等.(2)把△ABC沿直线BC平移、翻折,绕定点旋转,观察图形的大小形状是否变化.得出结论:平移、翻折、旋转只能改变图形的位置,而不能改变图形的大小和形状.把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.如△ABC和△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B 和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.三、应用举例例1如图,△ADE≌△BCF,AD=6 cm,CD=5 cm,求BD的长.分析:由全等三角形的性质可知,全等三角形的对应边相等,找出对应边即可.解:∵△ADE≌△BCF,∴AD=BC.∵AD=6 cm,∴BC=6 cm.又∵CD=5 cm,∴BD=BC-CD=6-5=1(cm).四、巩固练习教材练习第1题.教材习题12.1第1题.补充题:1.全等三角形是()A.三个角对应相等的三角形B.周长相等的三角形C.面积相等的两个三角形D.能够完全重合的三角形2.下列说法正确的个数是()①全等三角形的对应边相等;②全等三角形的对应角相等;③全等三角形的周长相等;④全等三角形的面积相等.A.1B.2C.3D.43.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EF=5,求∠DFE 的度数与DE的长.补充题答案:1.D2.D3.∠DFE=35°,DE=8五、小结与作业1.全等形及全等三角形的概念.2.全等三角形的性质.作业:教材习题12.1第2,3,4,5,6题.本节课通过学生在做模型、画图、动手操作等活动中亲身体验,加深对三角形全等、对应含义的理解,即培养了学生的画图识图能力,又提高了逻辑思维能力.12.2三角形全等的判定(4课时)第1课时“边边边”判定三角形全等1.掌握“边边边”条件的内容.2.能初步应用“边边边”条件判定两个三角形全等.3.会作一个角等于已知角.重点“边边边”条件.难点探索三角形全等的条件.一、复习导入多媒体展示,带领学生复习全等三角形的定义及其性质,从而得出结论:全等三角形的对应边相等,对应角相等.反之,这六个元素分别相等,这样的两个三角形一定全等.思考:三角形的六个元素分别相等,这样的两个三角形一定全等吗?二、探究新知根据上面的结论,提出问题:两个三角形全等,是否一定需要六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?出示探究1:先任意画出一个△ABC,再画一个△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个或两个.你画出的△A′B′C′与△ABC一定全等吗?(1)三角形的两个角分别是30°,50°.(2)三角形的两条边分别是4 cm,6 cm.(3)三角形的一个角为30°,一条边为3 cm.学生剪下按不同要求画出的三角形,比较三角形能否和原三角形重合.引导学生按条件画三角形,再通过画一画,剪一剪,比一比的方式得出结论:只给出一个或两个条件时,都不能保证所画出的三角形一定全等.出示探究2:先任意画出一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?让学生充分交流后,教师明确已知三边画三角形的方法,并作出△A′B′C′,通过比较得出结论:三边分别相等的两个三角形全等.强调在应用时的简写方法:“边边边”或“SSS”.实物演示:由三根木条钉成的一个三角形的框架,它的大小和形状是固定不变的.明确:三角形的稳定性.三、举例分析例1如右图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD≌△ACD.引导学生应用条件分析结论,寻找两个三角形的已有条件,学会观察隐含条件.让学生独立思考后口头表达理由,由教师板演推理过程.教师引导学生作图.已知∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.讨论尺规作图法,作一个角等于已知角的理论依据是什么?教师归纳:(1)什么是尺规作图;(2)作一个角等于已知角的依据是“边边边”.四、巩固练习教材第37页练习第1,2题.学生板演.教师巡视,给出个别指导.五、小结与作业回顾反思本节课对知识的研究探索过程,小结方法及结论,提炼数学思想,掌握数学规律.进一步明确:三边分别相等的两个三角形全等.布置作业:教材习题12.2第1,9题.本节课的重点是探索三角形全等的“边边边”的条件;运用三角形全等的“边边边”的条件判别两个三角形是否全等.在课堂上让学生参与到探索的活动中,通过动手操作、实验、合作交流等过程,学会分析问题的方法.通过三角形稳定性的实例,让学生产生学数学的兴趣,学会用数学的眼光去观察、分析周围的事物,为下一节内容的学习打下基础.第2课时“边角边”判定三角形全等1.掌握“边角边”条件的内容.2.能初步应用“边角边”条件判定两个三角形全等.重点“边角边”条件的理解和应用.难点指导学生分析问题,寻找判定三角形全等的条件.一、复习引入1.什么是全等三角形?2.全等三角形有哪些性质?3.“SSS”具体内容是什么?二、新知探究已知△ABC ,画一个三角形△A′B′C′,使AB =A′B′∠B =∠B ′,BC =B′C′. 教师画一个三角形△ABC.先让学生按要求讨论画法,再给出正确的画法.操作:(1)把画好的三角形剪下和原三角形重叠,观察能重合在一起吗?(2)上面的探究说明什么规律?总结:判定两个三角形全等的方法:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS ”.三、举例分析多媒体出示教材例2.例2 如图,有一池塘,要测池塘两端A ,B 的距离,可先在平地上取一个点C ,从点C 不经过池塘可以直接到达点A 和B.连接AC 并延长到点D ,使CD =CA.连接BC 并延长到点E ,使CE =CB.连接DE ,那么量出DE 的长就是A ,B 的距离,为什么?分析:如果证明△ABC ≌△DEC ,就可以得出AB =DE. 证明:在△ABC 和△DEC 中,⎩⎨⎧CA =CD ,∠1=∠2,CB =CE ,∴△ABC ≌△DEC(SAS ). ∴AB =DE.归纳解决实际问题的一般方法是:分析实际问题,按要求画出图形,根据图形及已知条件选择对应的方法.四、课堂练习如图,已知AB =AC ,点D ,E 分别是AB 和AC 上的点,且DB =EC.求证:∠B =∠C.学生先独立思考,然后讨论交流,用规范的书写完成证明过程. 五、小结与作业 1.师生小结:(1)“边角边”判定两个三角形全等的方法.(2)在判定两个三角形全等时,要注意使用公共边和公共角. 2.布置作业:教材习题12.2第3,4题.本节课的重点是让学生认识掌握运用“边角边”判定两个三角形全等的方法,让学生自己动手操作,合作交流,通过学生之间的质疑讨论,发现此定理中角必为夹角,从而得出“边角边”的判定方法.不仅学习了知识,也训练了思维能力,对三角形全等的判定(SAS)掌握的也好,但要强调书写的格式的规范,同时让学生感受到在证明分别属于两个三角形的线段或角相等的问题时,通常通过证明这两个三角形全等来解决.第3课时“角边角”和“角角边”判定三角形全等1.掌握“角边角”及“角角边”条件的内容.2.能初步应用“角边角”及“角角边”条件判定两个三角形全等.重点“角边角”条件及“角角边”条件.难点分析问题,寻找判定两个三角形全等的条件.一、复习导入1.复习旧知:(1)三角形中已知三个元素,包括哪几种情况?三个角、三个边、两边一角、两角一边.(2)到目前为止,可以作为判定两三角形全等的方法有几种?各是什么?2.[师]在三角形中,已知三个元素的四种情况中,我们研究了三种,我们接着探究已知两角一边是否可以判定两三角形全等.二、探究新知1.[师]三角形中已知两角一边有几种可能?[生](1)两角和它们的夹边;(2)两角和其中一角的对边.做一做:三角形的两个内角分别是60°和80°,它们的夹边为4 cm,你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律?学生活动:自己动手操作,然后与同伴交流,发现规律.教师活动:检查指导,帮助有困难的同学.活动结果展示:以小组为单位将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.提炼规律:两角和它们的夹边分别相等的两个三角形全等.(可以简写成“角边角”或“ASA”) [师]我们刚才做的三角形是一个特殊三角形,随意画一个△ABC,能不能作一个△A′B′C′,使∠A=∠A′,∠B=∠B′,AB=A′B′呢?[生]能.学生口述画法,教师进行多媒体课件演示,使学生加深对“ASA”的理解.[生](1)先用量角器量出∠A与∠B的度数,再用直尺量出AB的边长;(2)画线段A′B′,使A′B′=AB;(3)分别以A′,B ′为顶点,A ′B ′为一边作∠DA′B′,∠EB ′A ′,使∠DA′B′=∠CAB ,∠EB ′A ′=∠CBA ;(4)射线A′D 与B′E 交于一点,记为C′.即可得到△A′B′C′.将△A′B′C′与△ABC 重叠,发现两三角形全等. [师]于是我们发现规律:两角和它们的夹边分别相等的两三角形全等.(可以简写成“角边角”或“ASA ”) 这又是一个判定两个三角形全等的条件. 2.出示探究问题:如图,在△ABC 和△DEF 中,∠A =∠D ,∠B =∠E ,BC =EF ,△ABC 与△DEF 全等吗?能利用角边角条件证明你的结论吗?证明:∵∠A +∠B +∠C =∠D +∠E +∠F =180°, ∠A =∠D ,∠B =∠E , ∴∠A +∠B =∠D +∠E. ∴∠C =∠F.在△ABC 和△DEF 中,⎩⎨⎧∠B =∠E ,BC =EF ,∠C =∠F ,∴△ABC ≌△DEF(ASA ). 于是得规律:两角和其中一个角的对边分别相等的两个三角形全等.(可以简写成“角角边”或“AAS ”) 例 如下图,点D 在AB 上,点E 在AC 上,AB =AC ,∠B =∠C.求证:AD =AE.[师生共析]AD 和AE 分别在△ADC 和△AEB 中,所以要证AD =AE ,只需证明△ADC ≌△AEB 即可.学生写出证明过程.证明:在△ADC 和△AEB 中,⎩⎨⎧∠A =∠A ,AC =AB ,∠C =∠B ,∴△ADC ≌△AEB(ASA ). ∴AD =AE.[师]到此为止,在三角形中已知三个条件探索两个三角形全等问题已全部结束.请同学们把两个三角形全等的判定方法作一个小结.学生活动:自我回忆总结,然后小组讨论交流、补充.三、随堂练习1.教材第41页练习第1,2题. 学生板演. 2.补充练习图中的两个三角形全等吗?请说明理由.四、课堂小结有五种判定两个三角形全等的方法: 1.全等三角形的定义 2.边边边(SSS ) 3.边角边(SAS ) 4.角边角(ASA ) 5.角角边(AAS )推证两个三角形全等,要学会联系思考其条件,找它们对应相等的元素,这样有利于获得解题途径.五、课后作业教材习题12.2第5,6,11题.在前面研究“边边边”和“边角边”两个判定方法的前提下,本节研究“角边角”和“角角边”对于学生并不困难,让学生通过直观感知、操作确认的方式体验数学结论的发现过程,在这节课的教学中,学生也了解了分类思想和类比思想.第4课时 “斜边、直角边”判定三角形全等1.探索和了解直角三角形全等的条件:“斜边、直角边”. 2.会运用“斜边、直角边”判定两个直角三角形全等.重点探究直角三角形全等的条件.难点灵活运用直角三角形全等的条件进行证明.一、情境引入(显示图片)舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?(2)如果他只带了一个卷尺,能完成这个任务吗?方法一:测量斜边和一个对应的锐角(AAS );方法二:测量没遮住的一条直角边和一个对应的锐角(ASA 或AAS ). 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗? 二、探究新知多媒体出示教材探究5.任意画出一个Rt △ABC ,使∠C =90°.再画一个Rt △A ′B ′C ′,使∠C′=90°,B ′C ′=BC ,A ′B ′=AB.把画好的Rt △A ′B ′C ′剪下来,放到Rt △ABC 上,它们全等吗?画一个Rt △A ′B ′C ′,使∠C′=90°,B ′C ′=BC ,A ′B ′=AB. 想一想,怎么样画呢?按照下面的步骤作一作: (1)作∠MC′N =90°;(2)在射线C′M 上截取线段B′C′=BC ;(3)以B′为圆心,AB 为半径画弧,交射线C′N 于点A′;(4)连接A′B′.△A ′B ′C ′就是所求作的三角形吗?学生把画好的△A′B′C′剪下放在△ABC 上,观察这两个三角形是否全等.由探究5可以得到判定两个直角三角形全等的一个方法:斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边、直角边”或“HL ”. 多媒体出示教材例5如图,AC ⊥BC ,BD ⊥AD ,垂足分别为C ,D ,AC =BD.求证:BC =AD.证明:∵AC ⊥BC ,BD ⊥AD , ∴∠C 与∠D 都是直角.在Rt △ABC 和Rt △BAD 中,⎩⎨⎧AB =BA ,AC =BD , ∴Rt △ABC ≌Rt △BAD(HL ). ∴BC =AD.想一想:你能够用几种方法判定两个直角三角形全等?直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS,ASA,AAS,SSS,还有直角三角形特殊的判定全等的方法——“HL”.三、巩固练习如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.学生独立思考完成.教师点评.四、小结与作业1.判定两个直角三角形全等的方法:斜边、直角边.2.直角三角形全等的所有判定方法:定义,SSS,SAS,ASA,AAS,HL.思考:两个直角三角形只要知道几个条件就可以判定其全等?3.作业:教材习题12.2第7题.本节课教学,主要是让学生在回顾全等三角形判定的基础上,进一步研究特殊的三角形全等的判定的方法,让学生充分认识特殊与一般的关系,加深他们对公理的多层次的理解.在教学过程中,让学生充分体验到实验、观察、比较、猜想、归纳、验证的数学方法,一步步培养他们的逻辑推理能力.12.3角的平分线的性质掌握角的平分线的性质和判定,能灵活运用角的平分线的性质和判定解题.重点角的平分线的性质和判定,能灵活运用角的平分线的性质和判定解题.难点灵活运用角的平分线的性质和判定解题.一、复习导入1.提问角的平分线的定义.2.给定一个角,你能不用量角器作出它的平分线吗?二、探究新知(一)角的平分线的画法教师出示:已知∠AOB.求作:∠AOB的平分线.然后让学生阅读教材第48页上方思考.(教师演示画图)通过对分角仪原理的探究,得出用直尺和圆规画已知角的平分线的方法,师生共同完成具体作法.(二)角的平分线的性质试验:(1)让学生在已经画好的角的平分线上任取一点P;(2)分别过点P作PD⊥OA,PE⊥OB,垂足为D,E;(3)测量PD和PE的长,观察PD与PE的数量关系;(4)再换一个新的位置看看情况怎样?归纳总结得到角的平分线的性质.分析讨论PD=PE的理由.(三)角平分线的判定教师指出:角的内部到角的两边的距离相等的点在角的平分线上.(1)写出已知、求证.(2)画出图形.(3)分析证明过程.巩固应用:解决教材第49页思考(四)三角形的三个内角的平分线相交于一点1.例题:教材第50页例题.2.针对例题的解答,提出:P点在∠A的平分线上吗?通过例题明确:三角形的三个内角的平分线相交于一点.练习:教材第50页练习.三、归纳总结引导学生小组合作交流:(1)本节课学到了哪些知识?(2)你有什么收获?四、布置作业教材习题12.3第1~4题.教学始终围绕着角平分线及其性质、判定的问题而展开,先从出示问题开始,鼓励学生思考,探索问题中所包含的数学知识,让学生经历了知识的形成与应用的过程,从而更好的理解掌握角平分线的性质。
2019_2020学年八年级数学上册第十二章全等三角形12.2三角形全等的判定同步练习(含解析)(新版)新人教版

第十二章 全等三角形第二节 三角形全等的判定一、单选题(共10小题)1.如图,已知12∠=∠,要说明ABD ACD ∆≅∆,还需从下列条件①ADB ADC ∠=∠,②B C ∠=∠,③DB DC =,④AB AC =中选一个,则正确的选法个数是( )A .1个B .2个C .3个D .4个2.如图,CD ⊥AB ,BE ⊥AC ,垂足分别为D ,E ,BE ,CD 相交于点O ,OB =OC ,连接AO ,则图中一共有( )对全等三角形.A .2B .3C .4D .53.点D 、E 分别在级段AB 、AC 上,CD 与BE 相交于点O ,已知AB =AC ,添加以下哪一个条件不能判定△ABE≌△ACD ( )A .∠B=∠CB .∠BEA=∠CDAC .BE =CD D .CE =BD4.如图,已知点A 、D 、C 、F 在同一直线上,AB =DE ,AD =CF ,添加下列条件后,仍不能判断△ABC ≌△DEF 的是( )A .BC EF =B .A EDF ∠=∠C .//AB DED .BCA EDF ∠=∠5.根据下列图中所给定的条件,其中三角形全等的是( )A .①②B .②③C .①④D .①③6.如图,BE=CF ,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )A .AB=DCB .∠A=∠DC .∠B=∠CD .AE=BF7.如图,用直尺和圆规作射线OC ,使它平分∠AOB ,则△ODC ≌△OEC 的理由是( )A .SSSB .SASC .AASD .HL8.工人师傅常用角尺平分一个任意角,具体做法如下:如图,已知∠AOB 是一个任意角,在边OA ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同的刻度分别与点M ,N 重合,则过角尺顶点C 的射线OC 便是∠AOB 角平分线.在证明△MOC≌△NOC 时运用的判定定理是( )A .SSSB .SASC .ASAD .AAS9.如图,点D 、E 分别在线段AB 、AC 上,CD 与BE 相交于点O .若AB=AC ,则添加下列条件仍不能判定ABE ACD ∆≅∆的是( )A .BE CD =B .AD AE =C .BD CE = D .B C ∠=∠10.在下列条件下,不能判定ABC V ≌''(AB C V )A .'A A ∠=∠,''AB A B =,''BC B C = B .'A A ∠=∠,'C C ∠=∠,''AC A C =C .'B B ∠=∠,'C C ∠=∠,''AC A C =D .''BA B A =,''BC B C =,''AC A C =二、填空题(共5小题)11.(2019·湖南中考真题)如图,已知AD AE =,请你添加一个条件,使得ADC AEB △≌△,你添加的条件是_____.(不添加任何字母和辅助线)12.(2018·安徽朱仙庄矿中学初一期中)如图,已知∠BAC=∠DAE=90°,AB=AD ,要使△ABC≌△ADE,还需要添加的条件是______(只需添加一个条件即可)13.(2018·廉江市实验学校初二期中)如图,点D 、E 分别在线段AB 、AC 上,AE=AD,要使△ABE≌△ACD,则需添加的一个条件是____.14.(2018·四川中考真题)如图,已知AB=BC ,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是___.(只需写一个,不添加辅助线)15.(2019·武汉市育才中学初二期中)如图,四边形ABCD ,AB∥CD,∠ABC=∠BCD=90°,点E 为边BC 上一点,连接AE 、DE ,AE=DE ,AE⊥DE,若AB=1,CD=3,则线段BC=_____三、解答题(共3小题)16.(2019·湖北中考真题)如图,在ABC ∆中,D 是BC 边上的一点,AB DB =,BE 平分ABC ∠,交AC 边于点E ,连接DE .(1)求证:ABE DBE ∆≅∆;(2)若100A ∠=︒,50C ∠=︒,求AEB ∠的度数.17.(2019·湖北中考真题)如图,已知90C D ∠=∠=︒,BC 与AD 交于点E ,AC BD =,求证:AE BE =.18.(2019·湖南中考真题)已知,如图,AB =AE ,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.第十二章 全等三角形(解析版)第二节 三角形全等的判定一、单选题(共10小题)1.如图,已知12∠=∠,要说明ABD ACD ∆≅∆,还需从下列条件①ADB ADC ∠=∠,②B C ∠=∠,③DB DC =,④AB AC =中选一个,则正确的选法个数是( )A .1个B .2个C .3个D .4个【答案】C 【解析】欲使△ABD≌△ACD,已知∠1=∠2,AD 公共,可根据全等三角形判定定理AAS 、SAS 、ASA 添加条件,逐一证明即可.【详解】解:∵∠1=∠2,AD 公共,①如添加∠ADB=∠ADC,利用ASA 即可证明△ABD≌△ACD;②如添加∠B=∠C,利用AAS 即可证明△ABD≌△ACD;③如添加DB=DC ,因为SSA ,不能证明△ABD≌△ACD,所以此选项不能作为添加的条件;④如添加AB=AC ,利用SAS 即可证明△ABD≌△ACD;故选:C .【点睛】此题主要考查学生对全等三角形判定定理的理解和掌握,此类添加条件题,要求学生应熟练掌握全等三角形的判定定理:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.2.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,连接AO,则图中一共有()对全等三角形.A.2 B.3 C.4 D.5【答案】C【解析】共有四对.分别为△ADO≌△AEO,△ADC≌△AEB,△ABO≌△ACO,△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.【详解】解:∵CD⊥AB,BE⊥AC,OB=OC,∴∠ADO=∠AEO=90°,∠DOB=∠EOC,∵BO=CO,∴△DOB≌△EOC;∴OD=OE,BD=CE;∵OA=OA,OD=OE,∠ADO=∠AEO=90°,∴△ADO≌△AEO;∴AD=AE,∠DAO=∠EAO;∵AB=AC,∠DAO=∠EAO,OA=OA,∴△ABO≌△ACO;∵AD=AE,AC=AB,∠BAE=∠CAD,∴△ADC≌△ABE(SSS).所以共有四对全等三角形.故选:C.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3.点D、E分别在级段AB、AC上,CD与BE相交于点O,已知AB=AC,添加以下哪一个条件不能判定△ABE≌△ACD ()A .∠B=∠CB .∠BEA=∠CDAC .BE =CD D .CE =BD【答案】C 【解析】把选项代入,可知A 、B 、D 都符合全等三角形的判定,只有C 项不符合.【详解】添加A 选项中条件可用ASA 判定两个三角形全等;添加B 选项以后是AAS ,判定两个三角形全等;添加C 是SSA ,无法判定这两个三角形全等;添加D 因为AB=AC ,CE =BD ,所以AD=AE ,又因为∠A=∠A,AB=AC 所以,这两个三角形全等,SAS. 故选C .【点睛】本题考查全等三角形的判定,要掌握ASA ,SSS ,SAS ,AAS 是解题的关键.4.如图,已知点A 、D 、C 、F 在同一直线上,AB =DE ,AD =CF ,添加下列条件后,仍不能判断△ABC ≌△DEF 的是( )A .BC EF =B .A EDF ∠=∠C .//AB DED .BCA EDF ∠=∠【答案】D 【解析】首先根据等式的性质可得AC DF =,然后利用SSS 、SAS 、ASA 、AAS 进行分析即可.【详解】解:∵AD =CF ,∴AD +CD =CF +DC ,∴AC =DF ,A 、添加BC =EF 可利用SSS 定理判定△ABC ≌△DEF ,故此选项不合题意;B 、添加∠A =∠EDF 可利用SAS 定理判定△ABC ≌△DEF ,故此选项不合题意;C 、添加AB ∥DE 可证出∠A =∠EDC ,可利用SAS 定理判定△ABC ≌△DEF ,故此选项不合题意;D 、添加∠BCA =∠EDF 不能判定△ABC ≌△DEF ,故此选项符合题意;故选:D.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.5.根据下列图中所给定的条件,其中三角形全等的是()A.①②B.②③C.①④D.①③【答案】C【解析】四个三角形均给出了两个边和一个角,根据三角形判定条件,即可正确确定答案.【详解】解:四个三角形均给出了两个边和一个角且分别为3,3.5和65。
人教版 初中数学八年级上册 12.2全等三角形的判定 同步练习(含答案)

人教版初中数学八年级上册12.2全等三角形的判定同步练习(含答案)一、选择题(本大题共8道小题)1. 如图,AD=AE,若利用“SAS”证明△ABE△△ACD,则需要添加的条件是()A.AB=ACB.△B=△CC.△AEB=△ADCD.△A=△B2. 下列三角形中全等的是()A.△△ B.△△ C.△△ D.△△3. 如图,小强画了一个与已知△ABC全等的△DEF,他画图的步骤是:(1)画DE =AB;(2)在DE的同旁画△HDE=△A,△GED=△B,DH,EG相交于点F,小强画图的依据是()A.ASA B.SASC.SSS D.AAS4. 如图所示,△C=△D=90°,若要用“HL”判定Rt△ABC与Rt△ABD全等,则可添加的条件是()A.AC=AD B.AB=ABC.△ABC=△ABD D.△BAC=△BAD5. 如图,点B,F,C,E在一条直线上,AB△ED,AC△FD,那么添加下列一个条件后,仍无法判定△ABC△△DEF的是()A.AB=DE B.AC=DFC.△A=△D D.BF=EC6. 如图所示,P是△BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA△△PF A的依据是()A.HL B.ASA C.SSS D.SAS7. 在Rt△ABC和Rt△DEF中,△C=△F=90°,下列条件不能判定Rt△ABC△Rt△DEF的是()A.AC=DF,△B=△E B.△A=△D,△B=△EC.AB=DE,AC=DF D.AB=DE,△A=△D8. 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角△ABC=35°,则右边的滑梯与地面的夹角△DFE等于()A.60° B.55° C.65° D.35°二、填空题(本大题共4道小题)9. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:________,使△AEH△△CEB.10. 如图,在△ABC中,AD△BC于点D,要使△ABD△△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,已知AD=BC,AB=CD,若△C=40°,则△A=________°.12. 如图K-10-10,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,ED 与AB相交于点G.若△ACD=40°,则△AGD=________°.三、解答题(本大题共2道小题)13. 如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.14. 如图,C是线段BD的中点,AB=EC,△B=△ECD.求证:△ABC△△ECD.人教版初中数学八年级上册12.2全等三角形的判定同步练习-答案一、选择题(本大题共8道小题)1. 【答案】A2. 【答案】A[解析] △△符合证明三角形全等的判定方法“SAS”.△△中相等的角所对的边不相等,所以不可能全等.故选A.3. 【答案】A4. 【答案】A5. 【答案】C[解析] 选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;选项C中添加△A=△D不能判定△ABC△△DEF,故本选项符合题意;选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.故选C.6. 【答案】A7. 【答案】B[解析] 选项A,D均可由“AAS”判定Rt△ABC△Rt△DEF,选项C 可由“HL”判定Rt△ABC△Rt△DEF,只有选项B不能判定Rt△ABC△Rt△DEF.8. 【答案】B [解析] 在Rt△ABC 和Rt△DEF 中,⎩⎨⎧BC =EF ,AC =DF ,△Rt△ABC△Rt△DEF(HL). △△DEF =△ABC =35°.△△DFE =90°-35°=55°.二、填空题(本大题共4道小题)9. 【答案】AH =CB (符合要求即可)【解析】∵AD ⊥BC ,CE ⊥AB ,垂足分别为点D 、E ,∴∠BEC =∠AEC =90°,在Rt △AEH 中,∠EAH =90°-∠AHE ,在Rt △HDC 中,∠ECB =90°-∠DHC ,∵∠AHE =∠DHC ,∴∠EAH =∠ECB ,∴根据AAS 添加AH =CB 或EH =EB ;根据ASA 添加AE =CE.可证△AEH ≌△CEB.故答案为:AH =CB 或EH =EB 或AE =CE 均可.10. 【答案】AB =AC 11. 【答案】40[解析] 如图,连接DB.在△ADB 和△CBD 中,⎩⎨⎧AD =CB ,AB =CD ,DB =BD ,△△ADB△△CBD(SSS). △△A =△C =40°.12. 【答案】40[解析] 在△ABC 和△DEC 中,⎩⎨⎧CA =CD ,AB =DE ,BC =EC ,△△ABC△△DEC(SSS). △△A =△D.又△△AFG =△DFC ,△△AGD =△ACD =40°.三、解答题(本大题共2道小题)13. 【答案】证明:∵CE ∥DF ,∴∠ACE =∠FDB ,(2分)在△ACE 和△FDB 中,⎩⎨⎧EC =BD∠ACE =∠FDB AC =FD,∴△ACE ≌△FDB(SAS ),(5分) ∴AE =FB.(7分)14. 【答案】证明:△C 是线段BD 的中点,△BC =CD.在△ABC 与△ECD 中,⎩⎨⎧BC =CD ,△B =△ECD ,AB =EC ,△△ABC△△ECD.。
人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析一、选择题(每小题3分,共30分) 1.下列说法正确的是( )A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等 2. 如图所示,a,b,c 分别表示△ABC 的三边长,则下面与△ABC 一定全等的三角形是( )3.如图所示,已知△ABE ≌△ACD ,∠1=∠2,∠B=∠C , 下列不正确的等式是( ) B.∠BAE=∠CADA.AB=AC C.BE=DC D.AD=DE 4. 在△ABC 和△A /B /C /中,AB=A /B /,∠B=∠B /,补充条件后仍不一定能保证△ABC ≌△A /B /C /,则补充的这个条件是( )A .BC=B /C / B .∠A=∠A / C .AC=A /C /D .∠C=∠C / 5.如图所示,点B 、C 、E 在同一条直线上,△ABC 与△CDE都是等边三角形,则下列结论不一定成立的是( )A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA6. 要测量河两岸相对的两点A,B 的距离,先在AB 的垂线BF 上取两点C,D ,使CD=BC ,再作出BF 的垂线DE ,使A,C,E 在一条直线上(如图所示),可以说明△EDC ≌△ABC ,得ED=AB ,因此测得ED 的长就是AB 的长,判定△EDC ≌△ABC 最恰当的理由是( ) 第3题图第5题图 第2题图第6题图AB C DA.边角边B.角边角C.边边边D.边边角7.已知:如图所示,AC=CD ,∠B=∠E=90°,AC ⊥CD ,则不正确的结论是( )A .∠A 与∠D 互为余角B .∠A=∠2C .△ABC ≌△CED D .∠1=∠28. 在△ABC 和△FED 中,已知∠C=∠D ,∠B=∠E ,要判定这两个三角形全等,还需要条件( ) A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F 9.如图所示,在△ABC 中,AB=AC ,∠ABC 、∠ACB 的平分线BD ,CE 相交于O 点,且BD 交AC 于点D ,CE 交AB 于 点E .某同学分析图形后得出以下结论:①△BCD ≌△CBE ; ②△BAD ≌△BCD ;③△BDA ≌△CEA ;④△BOE ≌△COD ;⑤△ACE ≌△BCE ,上述结论一定正确的是( ) A.①②③ B.②③④ C.①③⑤ D.①③④10、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( ) A 、3个 B 、2个 C 、1个 D 、0个二、填空题(每题3分,共21分)11.如图6,AC=AD,BC=BD,则△ABC≌ ;应用的判定方法是 .12.如图7,△ABD≌△BAC,若AD=BC,则∠BAD的对应角为 .13.已知AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm ,则点D到AC的距离为 .B C DA 图6 D O CBA 图8 A D CB图7 第9题图 第7题图14.如图8,AB与CD交于点O,OA=OC,OD=OB,∠AOD= ,根据 可得△AOD≌△COB,从而可以得到AD= .15.如图9,∠A=∠D=90°,AC=DB,欲使OB=OC,可以先利用“HL”说明 ≌ 得到AB=DC,再利用“ ”证明△AOB≌ 得到OB=OC. 16.如果两个三角形的两条边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角的关系是 .17.如图10,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配,这样做的数学依据是是 . 三、解答题(共29分)18. (6分)如右图,已知△ABC 中,AB =AC ,AD 平分∠BAC ,请补充完整过程说明△ABD ≌△ACD 的理由.解: ∵AD 平分∠BAC∴∠________=∠_________(角平分线的定义)在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∴△ABD ≌△ACD ( ) 19. (8分)如图,已知△≌△是对应角.(1)写出相等的线段与相等的角;(2)若EF=2.1 cm ,FH=1.1 cm ,HM=3.3 cm ,求MN和HG 的长度.第19题图图10 DCBA20.(7分)如图,A、B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、C、A在同一直线上,则DE的长就是A、B之间的距离,请你说明道理.21.(8分)已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.四、解答题(共20分)22.(10分)已知:BE⊥CD,BE=DE,BC=DA,求证:①△BEC≌△DAE;②DF⊥BC.B C EF A23.(10分)如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.12章·全等三角形(详细答案)一、选择题 CBDCD BDCDC二、填空题 11、△ABD SSS 12、∠ABC 13、3cm 14、∠COB SAS CB 15、△ABC △DCB AAS △DOC 16、相等 17、○3 两角和它们的夹边分别相等的两个三角形全等三、解答题18、AD CAD AB=AC ∠BAD=∠CAD AD=AD SAS19、B 解:(1)EF=MN EG=HN FG=MH ∠F=∠M ∠E=∠N ∠EGF=∠MHN (2)∵△EFG ≌△NMH ∴MN=EF=2.1cm∴GF=HM=3.3cm ∵FH=1.1cm ∴HG=GF -FH=3.3-1.1=2.2cm 20、解:∵DE ∥AB ∴∠A=∠E在△ABC 与△CDE 中∠A=∠E BC=CD∠ACB=∠ECD∴△ABC ≌△CDE(ASA)∴AB=DE21、证明:∵AB ∥DE∴∠A=∠EDF∵BC ∥EFCA∴∠ACB=∠F∵AD=CF∴AC=DF在△ABC与△DEF中∠A=∠EDFAC=DF∠ACB=∠F△ABC≌△DEF(ASA)四、解答题22、证明:①∵BE⊥CD∴∠BEC=∠DEA=90°在Rt△BEC与Rt△DEA中BC=DABE=DE∴Rt△BEC≌Rt△DEA(HL)②∵Rt△BEC≌Rt△DEA∴∠C=∠DAE∵∠DEA=90°∴∠D+∠DAE=90°∴∠D+∠C=90°∴∠DFC=90°∴DF⊥BC23、证明:在△ABC与△ADC中1=∠2AC=AC3=∠4∴△ABC≌△ADC(ASA)∴CB=CD在△ECD与△ECB中CB=CD∠3=∠4CE=CE∴△ECD≌△ECB(SAS)∴∠5=∠6第十二章全等三角形一、填空题(每小题4分,共32分).1.已知:///ABC A B C ∆∆≌,/A A ∠=∠,/B B ∠=∠,70C ∠=︒,15AB cm =,则/C ∠=_________,//A B =__________.2.如图1,在ABC ∆中,AB=AC ,AD ⊥BC 于D 点,E 、F 分别为DB 、DC 的中点,则图中共有全等三角形_______对.图1 图2 图33. 已知△ABC ≌△A ′B ′C ′,若△ABC 的面积为10 cm 2,则△A ′B ′C ′的面积为______ cm 2,若△A ′B ′C ′的周长为16 cm ,则△ABC 的周长为________c m . 4. 如图2所示,∠1=∠2,要使△ABD ≌△ACD ,需添加的一个条件是________________(只添一个条件即可).5.如图3所示,点F 、C 在线段BE 上,且∠1=∠2,BC =EF ,若要使△ABC ≌△DEF ,则还需补充一个条件________,依据是________________.6.三角形两外角平分线和第三个角的内角平分线_____一点,且该点在三角形______部. 7.如图4,两平面镜α、β的夹角 θ,入射光线AO 平行于β,入射到α上,经两 次反射后的出射光线CB 平行于α,则角θ等于________.8.如图5,直线AE ∥BD ,点C 在BD 上,若AE =4,BD =8,△ABD 的面积为16,则ACE △ 的面积为______.二、选择题(每小题4分,共24分) 9.如图6,AE =AF ,AB =AC ,E C 与B F 交于点O ,∠A =600,∠B =250,则∠E OB 的度数为( )A 、600B 、700C 、750D 、85010.△ABC ≌△DEF ,且△ABC 的周长为100 cm ,A 、B 分别与D 、E 对应,且AB =35 cm ,DF =30 cm ,则EF 的长为( ) A .35 cm B .30 cm C .45 cm D .55 cm11.图7是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在________两点上的木条.( )A .A 、FB .C 、E C .C 、AD .E 、F12.要测量河两岸相对的两点A 、B 的距离,先在AB 的垂线BF 上取两点C 、D ,使CD= BC ,再定出BF 的垂线DE ,使A 、C 、E 在一条直线上,可以证明△EDC ≌△ABC , 得到ED=AB ,因此测得ED 的长就是AB 的长(如图8),判定△EDC ≌△ABC 的理由是( )NAMC B图7 图8 图9 图10A.边角边公理 B.角边角公理; C.边边边公理 D.斜边直角边公理13.如图9,在△ABC中,∠A:∠B:∠C=3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于()A.1:2 B.1:3C.2:3 D.1:414.如图10,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD_____P点到∠AOB两边距离之和.( )A.小于B.大于C.等于D.不能确定三、解答题(共46分)中,∠ACB=90°,延长BC至B',使15.已知如图11,ABCC B'=BC,连结A B'.求证:△AB B'是等腰三角形.图11第十二章全等三角形。
12.2 三角形全等的判定 第1课时 边边边

14、许多年轻人在学习音乐时学会了爱。——莱杰 15、学习是劳动,是充满思想的劳动。——乌申斯基 16、我们一定要给自己提出这样的任务:第一,学习,第二是学习,第三还是学习。——列宁 17、学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。——毛泽东
18、只要愿意学习,就一定能够学会。——列宁 19、如果学生在学校里学习的结果是使自己什么也不会创造,那他的一生永远是模仿和抄袭。——列夫·托尔斯泰
20、对所学知识内容的兴趣可能成为学习动机。——赞科夫 21、游手好闲地学习,并不比学习游手好闲好。——约翰·贝勒斯 22、读史使人明智,读诗使人灵秀,数学使人周密,自然哲学使人精邃,伦理学使人庄重,逻辑学使人善辩。——培根 23、我们在我们的劳动过程中学习思考,劳动的结果,我们认识了世界的奥妙,于是我们就真正来改变生活了。——高尔基 24、我们要振作精神,下苦功学习。下苦功,三个字,一个叫下,一个叫苦,一个叫功,一定要振作精神,下苦功。——毛泽东 25、我学习了一生,现在我还在学习,而将来,只要我还有精力,我还要学习下去。——别林斯基、学习外语并不难,学习外语就像交朋友一样,朋友是越交越熟的,天天见面,朋友之间就亲密无间了。——高士其 2、对世界上的一切学问与知识的掌握也并非难事,只要持之以恒地学习,努力掌握规律,达到熟悉的境地,就能融会贯通,运用自如了。——高士其 3、学和行本来是有联系着的,学了必须要想,想通了就要行,要在行的当中才能看出自己是否真正学到了手。否则读书虽多,只是成为一座死书库。——谢觉哉、你的假装努力,欺骗的只有你自己,永远不要用战术上的勤奋,来掩饰战略上的懒惰。 11、时间只是过客,自己才是主人,人生的路无需苛求,只要你迈步,路就在你的脚下延伸,只要你扬帆,便会有八面来风,启程了,人的生命才真正开始。 12、不管做什么都不要急于回报,因为播种和收获不在同一个季节,中间隔着的一段时间,我们叫它为坚持。 13、你想过普通的生活,就会遇到普通的挫折。你想过最好的生活,就一定会遇上最强的伤害。这个世界很公平,想要最好,就一定会给你最痛。
三角形全等的判定(sss)(第1课时)(课件)数学八年级上册同步教学课件 作业(人教版)

证明:在△ ABD和△ ACE中,
AB=AC,
AD=AE,
BD=CE,
∴ △ ABD≌ △ ACE(SSS),
∴∠BAD=∠CAE.
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
2. 已知:如图,AB=AD,BC=DC,
求证:△ABC≌△ADC, AC是∠BAD的角平分线
∴ ∠BAD= ∠CAD.
(全等三角形对应角相等)
A
D
写出结
论
C
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
如图, C是BF的中点,AB =DC,AC=DF.
求证:△ABC ≌ △DCF.
依据是
′
D
所画的弧交于点 ;
什么?
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
中考链接
1.如图,EF=BC,DF=AC,DA=EB.求证∠F=∠C.
证明:∵DA=BE,∴DE=AB,
在△ABC和△DEF中, AB=DE
AC=DF
BC=EF,
∴△ABC≌△DEF(SSS),∴∠C=∠F.
2. 如图,已知AC=FE,BC=DE,点A,D,B,F在同一条
直线上,要利用“S.S.S.”证明△ABC≌△FDE,还可以添加的
一个条件是( A )
A.AD=FB
B.DE=BD
C.BF=DB
D.以上都不对
3. 如图,AB=AC,AE=AD,BD=CE,
A
求证:△AEB ≌△ ADC。
12.2 三角形全等的判定 第1课时 “边边边”

(2)AB∥DE,AC∥DF.理由:∵△ABC≌△DEF,∴∠ABC=∠DEF, ∠ACB=∠DFE,∴AB∥DE,AC∥DF
16.如图,AD=CB,E,F是AC上的两动点,且有DE=BF. (1)若E,F运动至如图①所示的位置,有AF=CE,求证: △ADE≌△CBF; (2)若E,F运动至如图②所示的位置,仍有AF=CE,那么 △ADE≌△CBF还成立吗?为什么? (3)若E,F不重合,且AF=CE,那么AD和CB平行吗?请说明理由.
解:(1)∵AF=CF,∴AF+EF=CE+EF,∴AE=CF,在△ADE 和△
CBF 中,AADE==CCFB,,∴△ADE≌△CBF(SSS) DE=BF,
(2)成立,理由同(1)
(3)AD
∥CB.理由:由(1)(2)知,△ADE≌△CBF,∴∠A=∠C,∴AD∥CB
方法技能: 1.证全等寻找等边的方法: (1)图形语言中的隐含条件,如公共边; (2)利用中点的定义证明两条线段相等; (3)多条线段共线时,利用线段的和(差)关系证明两条线段相等.
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证 △ACE≌△BDF时,需增加的一个条件是( C ) A.AB=BC B.DC=BC C.AB=CD D.以上都不对
4.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来 判定△ABC≌△FED时,下列条件中:①AE=FB;②AB=EF;③AE =BE;④BF=BE,应该添加的是_____①__或__②____.(填序号)
7 A.3
B.4
C.3 D.不能确定
12.如图,△ABC是三边都不相等的三角形,DE=BC,以D,E为两个 顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形 最多可以画_____4__个.
