成都华杯赛课程讲义(B)
华杯赛初赛备考讲义含解析(小学中年级组)

华杯赛初赛备考讲义含解析(小学中年级组)第一节几何精讲考点概述几何考点一、基本面积公式;(长方形、正方形、三角形、平行四边形、梯形、圆、扇形)二、割补法计算面积;三、等积变换;四、周长的计算;(基本公式、平移法、标向法)五、角度的计算;(多边形内角和、外角和、角度的综合计算)六、勾股定理与弦图;七、立体几何认知.(展开图、三视图)真题精讲例题1. 如右图,一张长方形的纸片,长20 厘米,宽16 厘米.如果从这张纸上剪下一个长10 厘米,宽5 厘米的小长方形,而且至少有一条边在原长方形的边上,那么剩下纸片的周长最大是()厘米(2010 年15 届)(A)72 (B)82 (C)92 (D)102【答案】C.【解答】因为要求剪下的这个长方形至少有一条边在原长方形的边上,所以可以分以下三种情况讨论:(1)小长方形的两条边都在原长方形的边上,如下图:此时,剩下纸片的周长为:(20+16) ×2 = 72(厘米).(2)只有小长方形的长边在原长方形的边上,如下图:此时,剩下纸片的周长为:(20+16)×2 + 5×2 = 82(厘米).(3)只有小长方形的短边在原长方形的边上,如下图:、此时,剩下纸片的周长为:(20+16) ×2 + 10×2 = 92(厘米).所以剩下图形的周长最大是92 厘米.故选C.例题2. 九个同样的直角三角形卡片,拼成了如右图所示的平面图形.这种三角形卡片中的两个锐角较大的一个是度.(2013 年18 届)【答案】54.【解答】图中每个直角三角形,除直角外,还有两个锐角,一大一小,汇集在中心的是7 个小角和2 个大角.注意:大角+小角= 90︒,而在中心的9 个角之和为360︒,即7 个小角+2 个大角= 360︒,即:5 个小角+(2 个大角+2 个小角)= 360︒.所以:5 个小角+ 180︒= 360︒,即:5 个小角= 180︒,一个小角= 36︒,较大锐角= 90︒- 36︒= 54︒.练习1. 北京时间16 时,小龙从镜子里看到挂在身后墙上的4 个钟表(如下图),其中最接近16 时的是().(2012 年17 届)(A)(B)(C)(D)【答案】D.【解答】注意镜子里面和实际情况是左右对称的,因此A 实际是20 点5 分,B 实际是19 点50 分,C 实际是16 点10 分,D 实际是15 点55 分,因此选D.练习2. 把一块长90 厘米,宽42 厘米的长方形纸板恰无剩余地剪成边长都是整数厘米、面积都相等的小正方形纸片,最少能剪出块,这种剪法剪成的所有正方形纸片的周长之和是厘米.(2012 年17 届)【答案】105;2520.【解答】要想全部剪成正方形,那么正方形的边长必须满足:是90 和42 的公约数(中年级表述:90 和42 除以边长能够除尽).那么满足条件的边长有1、2、3、6,要让正方形尽量少,那么边长尽量大,为6,这个时候长被分成了90÷6=15 格,宽被分成了42÷6=7 格,所以最少能剪出15×7=105 块.每块正方形的周长是6×4=24 厘米,所以所有正方形周长和为24×105=2520 厘米.练习3. 如右图,一个正方形被分成了4 个相同的长方形,每个长方形的周长都是20 厘米.则这个正方形的面积是()平方厘米.(2013 年18 届)【答案】64.【解答】设每个长方形的宽为a,则长为4a,得到等式:(4a+a)⨯ 2 =20 .可知:a =2,4a = 8.所以,正方形的面积为8×8=64(平方厘米).练习4. 如下图,将长度为9 的线段AB 九等分,那么图中所有线段的长度的总和是.(2013 年18 届)【答案】165.【解答】以A 点为线段左端点的线段长之和为:S1=1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ;从A 点算起第二个点为线段左端点的线段长之和为:S2=1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 ;……从A 点算起第八个点为线段左端点的线段长之和为:S8=1+ 2 ;从A 点算起第九个点为线段左端点的线段长之和为S9=1 .于是:S =S1 +S2+S3+ +S9= 9 ⨯1 + 8 ⨯ 2 + 7 ⨯3 + 6 ⨯ 4 + 5 ⨯5 + 4 ⨯ 6 + 3 ⨯ 7 + 2 ⨯8+1⨯9 =165例题3. 现有一个正方形和一个长方形,长方形的周长比正方形的周长多4 厘米,宽比正方形的边长少2厘米,那么长比正方形的边长多()厘米.(2014 年19 届)(A)2(B)8(C)12(D)4【答案】D.【解答】根据题意,长方形的周长比正方形的周长多4 厘米,宽比正方形的边长少2 厘米,那么,就要求长方形的两条长总长增加8 厘米,也就是每一条长比正方形的边长多4 厘米.例题4. 右图中的正方形的边长为10,则阴影部分的面积为()(A)56 (B)44 (C)32 (D)78(2014 年19 届)【答案】A.【解答】用竖直线和水平线将正方形分割为如左图所示的多个长方形,中间长方形的面积是4 ⨯ 3 = 12 ,所以,阴影部分的面积为(10 ⨯10 -12) ÷ 2 +12 = 56 .所以,选A.练习5. 如图1 所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD.取AB 的中点M 和BC 的中点N,减掉△MBN 得五边形AMNCD.则将折叠的五边形AMNCD纸片展开铺平后的图形是.(2006 年11 届)DNA【答案】D.【解答】注意对折方向,可以判断B 点是原正方形中心,因此是中心被掏空的形状,再注意减掉的形状是三角形,也就是展开后,横竖四等分以后,每一部分缺的都是三角形,结合这两点,答案为D.1 AB C 2 D练习6. 正方形 ABCD 与正方形 CEFG 水平放置组成如图所示的组合图形,已知该组合图形的周长是 56厘米,DG 长 2 厘米,那么,图中阴影三角形的面积是平方厘米.AD GFBC E【答案】8.【解答一】如下图所示, AI = AH = BJ = DG = 2 厘米,而六条小正方形的边长之和是:32 - ( A I + AH + BJ + DG ) = 24 ,每条小正方形的边长是 24 ÷ 6 = 4 厘米,那么,小正方形的面积是4 ⨯ 4 = 16 平方厘米,根据三角形的等积变换可知,阴影三角形的面积是小正方形面积的一半,即 16 ÷ 2 = 8 平方厘米.A IDHGFBJ C E【解答二】将大正方形的一条边(▲)与小正方形的一条边(△)看成一组,那么,每组的长是(32 - 2) ÷ 3 = 10 厘米,而大小正方形的边长之差是 2 厘米,根据和差公式可得,大正方形的边长是 6厘米,小正方形的边长是 4 厘米,进而可求,阴影三角形的面积是 8 平方厘米.A▲DG△F▲△B▲ C △ E练习7. 如图,在一个正方体的表面上写着 1 至 6 这 6 个自然数,并且 13 对着 4,2 对着 5,3 对着 6.现在将正方体的一些棱剪开,使它的表面12展开图如下右图所示.如果只知道 1 和 2 所在的面,那么 6 写在字母的位置上.【答案】A .【解答】注意到,展开图中的形状,黑色两个面在合上后是相对的,展开图中的形状,黑色两个面在合上后也是相对的,所以1 和C 相对,C=4,B 和2 相对,B=5,那么A 要么是3 要么是6,现在观察1、A、B 这三个面,它们折叠时,如果把1 放正面,A 放上面,那么B 就在右侧,为2,矛盾,因此当1 放正面时,A 应该在下面,为6.练习8. 如图一个小正方形和4 个周长为32 cm 的相同的长方形拼成一个大正方形,那么大正方形的面积是cm2 .【答案】256.【解答】注意到,大正方形的边长刚好是长方形的长+宽,为16,所以面积等于16×16=256 平方厘米.第二节应用题精讲考点概述应用题考点一、常考应用题类型1. 画线段图帮助解题2. 列方程解应用题二、行程问题:1. 行程问题常见类型(相遇问题,追及问题,火车问题,流水行船问题,环形路线问题,多次相遇与追及问题等)2. 画线段图(形象直观地呈现题意,便于对题目条件进行分解与组合,挖掘隐含条件)3. 方程与比例解行程问题真题精讲例1.小虎在19×19 的围棋盘的格点上摆棋子,先摆成了一个长方形的实心点阵.然后再加上45 枚棋子,就正好摆成一边不变的较大的长方形的实心点阵.那么小虎最多用了()枚棋子.(2012 年17 届)(A)285 (B)171 (C)95 (D)57【答案】A【解析】加上45 枚棋子之后,还能摆成一边不变的较大的长方形的实心点阵,说明不变的这条边上的棋子数能整除45,要使总棋子数尽量多,则这条边要尽量大,最大为15,所以最多用了15 19=285 枚棋子.例2.幼儿园的老师给班里的小朋友送来55 个苹果,114 块饼干, 83 块巧克力.每样都平均分发完毕后,还剩3 个苹果,10 块饼干,5 块巧克力.这个班最多有位小朋友.(2013 年18 届)【答案】26【解析】可以列出除55 余3 的自然数:55÷4=13……3;55÷13=4……3;55÷26=2……3;55÷52=1……3;然后列出除114 余10 的自然数:114÷13=8……10;114÷26=4……10;114÷52=2……10;114÷104=1……10;再列出除83 余5 的自然数:83÷13=6……5;83÷26=3……5;83÷39=2……5;83÷78=1……5;其中,符合条件的最大的除数是26,所以,这个班最多有26 位小朋友.练习1.两个正整数的和小于100,其中一个是另一个的两倍,则这两个正整数的和的最大值().(2014 年19 届)(A)83 (B)99 (C)96 (D)98【答案】B【解析】由条件“其中一个是另一个的两倍”可知:所求的和是某个正整数的3 倍,要求小于100,故这两个正整数的和是99.练习2.三堆小球共有2012 颗,如果从每堆取走相同数目的小球以后,第二堆还剩下17 颗小球,并且第一堆剩下的小球数是第三堆剩下的2 倍,那么第三堆原有颗小球.(2012 年17 届)【答案】665【解析】设此时第三堆有1 份小球,则如果一开始就从第一堆放1 份小球到第三堆,并且从第二堆扔掉17 个小球,那么此时三堆小球的个数相同,都是(2012 -17)÷ 3=665 个,而在上述过程中,第三堆小球数目并未发生变化,所以第三堆原有665 个小球.例3.张老师每周的周一、周六和周日都跑步锻炼20 分钟,而其余日期每日都跳绳20 分钟.某月他总共跑步5 小时,那么这个月的第10 天是().(2013 年18 届)(A)周日(B)周六(C)周二(D)周一【答案】D【解析】每周张老师跑步1 小时,所以这个月的后28 天总共跑步了4 小时,说明这个月共有31 天,并且前3 天跑了1 个小时,所以前3 天只能是周六、周日、周一,所以这个月第10 天是周一,选D.例4.新生开学后去远郊步行拉练,到达A 地时比原计划时间10 点10 分晚了6 分钟,到达C 地时比原计划时间13 点10 分早了6 分钟,A、C 之间恰有一点B 是按照原计划时间到达的,那么到达B 点的时间是().(2014 年19 届)(A)11 点35 分(B)12 点5 分(C)11 点40 分(D)12 点20 分【答案】C【解析】从10 点10 分到13 点10 分共有3 个小时,误差时间共有12 分钟,即每小时要调整4 分钟,调整6 分钟的时候即是到达B 点的时间.调整6 分钟需要1 个半小时,即1 小时30 分钟,所以到达B 点的时间是11 点40 分.练习5.体育馆正在进行乒乓球单打、双打比赛,双打比赛的运动员比单打的运动员多4 名,比赛的乒乓球台共有13 张,那么双打比赛的运动员有名.(2012 年17 届)【答案】20【解析】因为一张球台可供2 名单打运动员、或4 名双打运动员进行比赛,所以由‘双打比赛的运动员比单打的运动员多4 名’可知,双打比赛用了1 份多一个1 个球台,单打比赛用了2 份球台,从而双打比赛用了5 个球台,单打比赛用了8 个球台,故双打比赛有20 名运动员.练习6.麦当劳的某种汉堡每个10 元,这种汉堡最近推出了“买二送一”的优惠活动,即花钱买两个汉堡,就可以免费获得一个汉堡.已知东东和朋友需要买9 个汉堡,那么他们至少需要花元钱.【答案】60【解析】20 元可以买3 个,买9 个需要花60 元.练习7.小张早晨8 点整从甲地出发去乙地,速度是每小时60 千米.早晨9 点整小王从乙地出发去甲地.小张到达乙地后立即沿原路返回,恰好在12 点整与小王同时到达甲地.那么两人相遇时距离甲地千米.【答案】96【解析】小张4 小时走了一个来回,所以单程需要2 小时,所以甲乙相距120 千米,这段路小王花了3 小时,所以小王的速度为40 千米/小时.9 点时,两人相距60 千米,在60 ÷(60+40)=0.6 小时后两人相遇,此时距离甲地1.6 ⨯ 60=96 千米.课后练习1. 魔法学校运来很多魔法球,总重量多达5 吨,一颗魔法球重4 千克,现在有10 名学员使用魔法给这些魔法球涂色,每人每6 分钟可以给5 颗魔法球涂色,那么他们涂完所有魔法球最少要用分钟.【答案】150【解析】总共有5000 ÷4=1250 个魔法球,所以总共需要1250 ⨯ 6 ÷ 5 ÷10=150 分钟.2. 某校三年级和四年级各有两个班.三年级一班比三年级二班多4 人,四年级一班比四年级二班少5 人,三年级比四年级少17 人,那么三年级一班比四年级二班少人.【答案】9【解析】让三年级二班增加4 人,四年级一班增加5 人,则相同的两个年级的两个班人数相同了,且此时三年级比四年级少17 + 5 - 4=18 人,平均每个班少9 人,而三年级一班和四年级二班人数均未发生变化,所以三年级一班比四年级二班少9 人.3. 2010 名学生从前往后排成一列,按下面的规则报数:如果某个同学报的数是一位数,后面的同学就要报出这个数与8 的和;如果某个同学报的数是两位数,后面的同学就要报出这个数的个位数与7 的和.现在让第一个同学报1,那么最后一个同学报的数是.【答案】13【解析】从第一名同学开始,依次报数为:1、9、17、14、11、8、16、13、10、7、15、12、9、17、……,从而从第二名同学开始,报数以11 为周期,而2009 ÷11=182 7 ,所以最后一个同学报的数为13.4. 骆驼有两种:背上只有一个驼峰的单峰骆驼和背上有两个驼峰的双峰骆驼.单峰骆驼比较高大,四肢较长,在沙漠中能走能跑;双峰骆驼四肢粗短,更适合在沙砾和雪地上行走.有一群骆驼有23 个驼峰,60 只脚,那么双峰驼有匹.【答案】8【解析】共有60 ÷ 4=15 匹骆驼,23 个驼峰,而多出的驼峰都是双峰驼多的,所以有23 -15=8 匹双峰驼.6. 红星小学组织学生参加队列演练,一开始只有40 个男生参加,后来调整队伍,每次调整减少3 个男生,增加2 个女生,那么调整次后男生女生人数就相等了.【答案】8【解析】最开始男女人数相差40 个,每次调整可以让人数差减少5 个,所以8 次调整后,男女人数就相等了.7. 甲,乙,丙三人锯同样粗细的木棍,分别领取8 米、10 米、6 米长的木棍,要求都按2 米的规格锯开.劳动结束后,甲、乙、丙分别锯了24、25、27 段,那么锯木棍次数最多的比次数最少的多锯次.【答案】2【解析】8 米、10 米、6 米长的木棍分别可以被锯成4、5、3 段,并且分别需要锯3、4、2 次,甲、乙、丙分别锯了6、5、9 根木棍,所以分别锯了18、20、18 次,最多比最少的多锯2 次.8. 一堆糖果有50 块,小明和小亮玩游戏.小明每赢一次拿5 块糖,然后吃掉4 块,将剩下的1 块放到自己的口袋里;小亮每赢一次也拿5 块糖,然后吃掉3 块,将剩下的2 块放到自己的口袋里.游戏结束时,糖刚好被拿完,这时小亮口袋里的糖数恰好是小明口袋里的糖数的3 倍,那么两人一共吃掉了块糖.【答案】34【解析】两人都是一次拿5 块,所以总共进行了10 次游戏,而小亮的糖数是小明的3 倍,说明小明每赢2 次,小亮就要赢3 次,所以说明小明总共赢了4 次,小亮赢了6 次,总吃掉了4 ⨯ 4+6 ⨯ 3=34 块糖.第三节数字谜、计数、组合精讲考点概述数字谜考点:1. 填竖式问题的一些方法:(1)加数相加时每进1 位,和的数字和将比加数的数字和减少9.(2)与各个数位上的数字有关的问题,往往需要多次尝试才能得到结果.2. 填横式问题:横式中的填空格和字母破译问题;熟练应用尾数分折、首位估算、分情况试算等方法;对于较复杂的题目,从约束条件较多、可能性较少的算式入手;某些横式问题,可以转化为竖式问题再求解.3. 幻方与数阵图、数独问题:掌握幻方的概念,了解三、四阶幻方的构造;解决具有与幻方类似性质的数阵图问题;进一步掌握重数的运用,填充较复杂的数阵图;利用重数计算处理数阵图中的最值问题.计数考点:1. 枚举法(分类、有序)2. 加乘原理(加法,分类;乘法,分步)组合考点:1. 各种与数字计算有关的最值问题.在枚举试算的过程中,注意寻找出大小变化的规律,并尝试分析其内在原因;学会用比较、调整的方法寻找最值情况.2. 逻辑推理:(1)一句话不是真话,就是假话.这在逻辑学中被称为排中律.(2)在应用假设法分析问题时,要考虑全面.既要考虑到所假设的条件成立的情况,还要考虑到条件不成立的情况.(3)对于条件复杂的逻辑推理问题,通常状况下都可以通过列表法分析.真题精讲例1.右图的计数器三个档上各有10 个算珠,将每档算珠分成上下两部分,按数位得到两个三位数,要求上面的三位数的数字不同,且是下面三位数的倍数,那么满足题意的上面的三位数是.(2012 年17 届)【答案】925【解析】由题意,知这两个三位数的和为1110,而上面是下面的倍数,可能为1 倍、2 倍、……,最多为9 倍,从而和为下面三位数的最少2 倍,最多10 倍,而1110 只有除以2、3、5、6、10 能除得尽,得到下面三位数可能为555、370、222、185、111,经过检验,可知只有185 满足要求,此时上面的三位数为925.练习1.在右面的加法算式中,每个汉字代表一个非零数字,不同的汉字代表不同的数字.当算式成立时,贺+新+春=().(2012 年17 届)(A)24 (B)22 (C)20 (D)18【答案】D放鞭炮+ 迎龙年贺新春【解析】所填入的9 个数字为1、2、……、9,可知加数的数字和之和与和的数字和的总和为45,而最多进位两次(十位、个位),又两整数的和与差奇偶性相同,故加法恰好进位一次,所以可知,和的数字和为18.故选D.练习2.如图所示的两位数加法算式中,已知A +B +C +D = 22 ,则X +Y =().(2012 年17 届)(A)2 (B)4 (C)7 (D)13【答案】B【解析】由竖式可知,恰好进位一次(十位),故加数的数字和比和的数字和多9,从而X +Y = 22 - 9 - 9 = 4 ,故选B.例2.甲、乙、丙、丁、戊围坐在圆形桌子边玩扑克,甲有自己的固定座位.如果乙和丁的座位不能相邻,那么共有()种不同的围坐方法.(2014 年19 届)(A)10 (B)8 (C)12 (D)16【答案】C【解析】甲坐好后,乙共有4 种坐法,其中紧邻甲有2 种坐法,坐定后丁有两种坐法;乙另有2 种坐法不紧邻甲,乙坐定后,丁仅有 1 种坐法,而丙和戊在剩余的 2 个座位中,只有两种选法,故共有(2⨯ 2 +2⨯1) ⨯ 2 =12 不同的围坐方法.例3.在一个平面上,用若干个单位长度的木棍可以摆出由多个正方形相邻的图形,右图是一示例.现在用20 根单位长的小木棍摆出一个图形,要求除第一行的方格外,下面几行方格构成一个长方形,那么这样的图形中最多有个单位边长的正方形.(2014 年19 届)【答案】7【解析】通过以下两步操作,总可以约定第1 行方格个数不大于第2 行方格个数.第一步:总可以左移第一行的方格,使其和第二行方格左端对齐,新的图形所用木棍数量不多于原图形所用木棍的数量,但是移动前后方格数相同,例如见下图.第二步:如果第一行的方格数比第二行的方格数多,可以将多的方格切下,移至第一行上面,增加一行,新的图形所用木棍数量不多于原图形所用木棍的数量,但是方格数相同,如此操作,直到第一行的方格数不大于第二行的方格数.例如见右图.因此,从题目条件可知,图形至少有 2 行方格.由前面的讨论,总可以约定第 1 行方格个数不大于第 2 行方格个数.(1)假设图形有 2 行方格第 1 行有 1 个方格,第 2 行有 6 个方格,所用木棍总数是 22; 第 1 行有 1 个方格,第 2 行有 5 个方格,所用木棍总数是 19; 第 1 行有 2 个方格,第 2 行有 5 个方格,所用木棍总数是 21; 第 1 行有 2 个方格,第 2 行有 4 个方格,所用木棍总数是 18; 第 1 行有 3 个方格,第 2 行有 4 个方格,所用木棍总数是 21; 第 1 行有 3 个方格,第 2 行有 4 个方格,所用木棍总数是 20; 第 1 行有 4 个方格,第 2 行有 4 个方格,所用木棍总数是 22. (2)假设图形有 3 行方格第 1 行有 1 个方格,第 2 行、第 3 行都各有 3 个方格,所用木棍总数是 20; 第 1 行有 2 个方格,第 2 行、第 3 行都各有 2 个方格,所用木棍总数是 17. (3)假设图形有 4 行方格第 1 行有 1 个方格,第 2 行、第 3 行、第 4 行都各有 2 个方格,所用 木棍总数是 20.根据以上判断,图形不可能有 5 行、6 行、7 行、8 行. 所用木棍总数 20,方格总数是 7.右图是摆出的图形.练习3. 用 8 个 3 和 1 个 0 组成的九位数有若干个,其中除以 4 余 1 的有()个.(2014 年 19 届)(A )5 (B )6 (C )7 (D )8 【答案】B【解析】用 8 个 3 排成一行,中间有 7 个间隔,加上最右边的一个位置,每个位置都可以放置 0,共 有 8 种放法.因为 100 能被 4 整除,故除以 4 余 1 的数的最右边的两位数只能是 33.所以,只有 6 个 位置可以放 0,共有 6 种放法.例4. 牧羊人用 15 段每段长 2 米的篱笆,一面靠墙围成一个正方形或长方形羊圈,则羊圈的最大面积是()平方米.(2012 年 17 届)(A )100 (B )108 (C )112 (D )122 【答案】C【解析】假设长有 a 段篱笆,宽有 b 段篱笆,由条件可知 a + 2b = 15 ,而希望面积越大,即 a ⨯ b 越大, 也就是 a ⨯ 2b 越大,由于两数和一定差小积大,那么可知 a = 7 , 2b = 8 时,面积最大,此时面积为 (7 ⨯ 2) ⨯ (4 ⨯ 2) = 112 .练习4. 小东、小西、小南、小北四个小朋友在一起做游戏时,捡到了一条红领巾,交给了老师.老师问是谁捡到的?小东说不是小西;小西说是小南;小南说小东说的不对;小北说小南说的也不对.他们之中只有一个人说对了,这个人是().(2013 年18 届)(A)小东(B)小西(C)小南(D)小北【答案】C【解析】若小东说的对,则其他三人都有不对,此时小北说小南说的不对,则是对的,矛盾.若小西说的对,则捡到红领巾的是小南,那么小东也就说对了,与只有一人说对矛盾.若小南说的对,则根据小东的话可以判断捡到红领巾的是小西,此时符合题意.若小北说的对,则小南说的不对,也就意味着小东说的对,矛盾.故选C.练习5.平面上有四个点,任意三个点都不在一条直线上.以这四个点为端点连接六条线段,在所组成的图形中,最少可以形成()个三角形.(2012 年17 届)(A)3 (B)4 (C)6 (D)8【答案】B【解析】(1)有一点在其他三点构成的三角形内,可以形成4 个三角形;(2)任意一点都在另三点构成的三角形外,那么可以形成8 个三角形.故最少可以形成4 个三角形,故选B.练习6.在10□10□10□10□10 的四个□中填入“+”、“-”、“×”、“÷”运算符号各一个,所成的算式的最大值是().(2012 年17 届)(A)104 (B)109 (C)114 (D)119【答案】B【解析】由于没有括号,故10 ⨯10 = 100 ,10 ÷10 =1,可以认为将100、10、1 由“+”、“-”连接,希望算式结果最大,最大为100 +10 -1 = 109 .原式为10 ⨯10 +10 -10 ÷10 = 109 .故选B.练习7.五个小朋友A、B、C、D 和E 参加“快乐读拼音”比赛,上场时五个人站成一排.他们胸前有每人的选手编号牌,5 个编号之和等于35.已知站在E、D、A、C 右边的选手的编号的和分别为13、31、21 和7.那么A、C、E 三名选手编号之和是.(2014 年19 届)【答案】24【解析】由于31>21>13>7,说明A 在D 的右边,E 在A 的右边,C 在E 的右边.由于,站在C 右边的选手的编号和为7,推出B 站在C 的右边.所以,B、C、E、D、A 分别是7、6、8、4、10.A、C、E 三名选手编号之和是24.练习8.用右图的四张含有4 个方格的纸板拼成了右图所示的图形.若在右下图的16 个方格分别填入1、3、5、7(每个方格填一个数),使得每行、每列的四个数都不重复,且每个纸板内四个格子里的数也不重复,那么A、B、C、D四个方格中数的平均数是.(2014 年19 届)【答案】4【解析】如图,用M,N,P,Q 标记16 个方格图最下面4 个方格,从而有A +B +M +N =C +D +P +Q =1+3+ 5 + 7 =16 ,又M+N+P+Q=16,所以A+B+C+D=16.右上图是一种满足要求的填法,且A, B,C, D 四个方格中数的平均数是4.课后练习1. 四位数中,数码0 出现次.【答案】2700【解析】分类,出现三个0 的四位数,有9 个,共9⨯3 = 27 个0;出现两个0 的四位数,0 可能出现在百、十;百、个和十个上,其他两位有9⨯9 =81种填法,有3⨯9⨯9 = 243 个,共243⨯ 2 = 486 个0;出现1 个0 的四位数,0 可能出现在百、十、个位上,有3⨯9⨯9⨯9 = 2187 个,共2187 个0;故共27 + 486 + 2187 = 2700 个.2. 从1,2,3,4,5,6,7 中选择若干个不同的数(所选数不计顺序),使得其中偶数之和等于奇数之和,则符合条件的选法共有种.【答案】7【解析】本题中,“和”必为偶数.按和的不同,分类枚举如下:(1)4 =1+ 3 ,1 组;(2)6 = 2 + 4 =1+ 5 ,2 组;(3)8 = 2 + 6 =1+ 7 = 3 + 5 ,2 组;(4)10 = 4 + 6 = 3 + 7 ,1 组;(5)12 = 2 + 4 + 6 = 5 + 7 ,1 组.共有:1+ 2 + 2 +1+1= 7 组.3. 将10,15,20,30,40 和60 填入右图的圆圈中,使A、B、C 三个小三角形顶点上的3 个数的积都相等.相等的积最大为.【答案】18000【解析】10 = 2 ⨯ 5 ,15 =3⨯ 5 ,20 = 2 ⨯ 2 ⨯ 5 ,30 = 2 ⨯3⨯ 5 ,40 = 2 ⨯ 2 ⨯ 2 ⨯ 5 ,60 = 2 ⨯ 2 ⨯ 3⨯ 5 ,这三个相等的乘积再相乘,等于原来6 个数的乘积再乘上中间三个数,结果是一个立方数,即2、3、5 在乘积中出现的次数是3 的倍数,这6 个数的乘积有9 个2、3 个3、6 个5 相乘,而多乘的三个数,5 一定出现3 次,3 最多出现3 次,只能为15、30、60,此时2 出现也为3 次,此时乘积最大,可以得到这3 个相等的积为3 个5、2 个3、4 个2 相乘,等于18000.而此时第一层、第二层、第三层依次填入40;15、30;20、60、10,满足要求.4. 用3、5、6、18、23 这五个数组成一个四则运算式,得到的非零自然数最小是.【答案】12 41433 2 2 2 2 3 2 1 1 2 3 24 1 4 3 2 4 1 4 33444前句 后句A 对 错B 错 错 C对对【解析】最小的非零自然数为 1,而 6 ÷ 3 - 5 ÷ (23 -18) = 1 ,可以取到 1,故所求最小值为 1.5. 小明在正方形的边上标出若干个点,每条边上恰有 3 个,那么所标出的点最少有()个.(A )12 (B )10 (C )8 (D )6【答案】C【解析】希望所标出的点最少,也就是所标的点被重复计数,那么 4 个顶点上都标上,然后每条边再 标 1 个即可,故最少标 8 个点.3126. 如图, 5 ⨯ 5 的表格中,每格填入一个数字,使得相同的数字所在的方格都连在一起(相连的两个方格必须有公共边),现在已经给出了 1,2,3,4 各两个,那么,表格中所有数的和是.【答案】66【解析】如图所示,本题只有唯一填法,相加可得和为 66.7. 甲、乙、丙、丁获得了学校创意大赛的前 4 名(无并列),他们说:甲:“我既不是第一,也不是第二”;乙:“我的名次和丙相邻”; 丙:“我既不是第二,也不是第三”;丁:“我的名次和乙相邻”. 现在知道,甲、乙、丙、丁分别获得第 A 、B 、C 、D 名,并且他们都是不说慌的好学生,那么四位数 ABCD = .【答案】4213【解析】甲是第 3、4 名之一;丙是第 1 名或 4 名.如果丙是第 4 名,则乙是第 3 名。
华杯赛讲义_小高组第3讲计数专题和数论专题

第三讲 计数专题和数论专题1、如果说小学奥数试题中"行程""几何""数论"三大专题成为各大杯赛和小升初考试中的常客,占据了试卷的绝大部分版面的话,那么第四大专题就非计数莫属了,而且更重要的是,计数中的技巧多达十几种,堪称五大专题中的最具技巧与灵活性的必考专题。
2、数论是研究整数性质的一个数学分支,它历史悠久,而且有着强大的生命力。
数论问题叙述简明,“很多数论问题可以从经验中归纳出来,并且仅用三言两语就能向一个行外人解释清楚,但要证明它却远非易事”。
1、一串有规律排列的数,从第二项起每一项都等于1加前一项的倒数之和.当第五项是0时,第一项是( )【解析】:根据规律,可表示出每一项,根据第五项是0,可得一元一次方程,根据解方程,可得答案. 解:设第一项是a ,根据题意,得第二项是aa a 111+=+第三项是11211++=++a a a a 第四项是12231211++=+++a a a a 第五项是233523121++=+++a a a a 第五项是0,02335=++a a 解得:53-=a2、求使33+n 与n-4不互质的大于4的最小整数n 的值为( )【解析】:令n-4=k ,k ≥1,得到n3+3=k3+12k2+48k+67,k ≥1,则k3+12k2+48k+67和k 的公约数就是67和k ,依此得到k 的值,进一步即可得到n 的值.解答:解:令n-4=k ,k ≥1,则n3+3=(k+4)3+3=k3+12k2+48k+67,k ≥1,则k3+12k2+48k+67和k 的公约数就是67和k而67是质数,最小的只能是67,于是最小的k=67所以n=71.故答案为:71..3、从 2000 年到 2099 年, 有没有哪些年份可以表示成n m 33-的形式, 其中 m , n 均为正整数?如果有, 请列举出来;如果没有, 请说明理由.【解析】:没有.设p 为2000到2099任意一数;假设有那样的表达式存在,一定满足n m p 33+=①,显然有得13+=-a n m ,所以13-=-n m a ④,根据2000≦p ≦2099及④式,a 只能取下列值:2、8、26、80、242、728;根据③式及2000≦p ≦2099,3^n 只能取下列值1、3、9、27、81、243、729;当a=2时,a 乘3^n 的最大值(729)<2000,所以a ≠2;当a=8时,8×243=1944<2000,8×729=5832>2099,所以a ≠8;当a=26,26×81=2106>2099,26×27=702<2000,所以a ≠26;当a=80,80×27=2160>2099,80×9=720<2000,所以a ≠80;当a=242,242×9=2178>2099,242×3=726<2000,所以a ≠242;当a=728,728×3=2184>2099,728×1=728<2000;综上所述,不存在满足要求的a;所以从2000年到2099年的年份,不能表示为nm 33-的形式.4、如果正整数x 与y 使得yx xy +2的值为质数,那么x+y 共有( )种可能的值。
华杯总决赛集训讲义

华杯赛小高总决赛集训队赛前集训讲义—应用题(一)——行程问题【知识点总结】:★行程问题中包括:相遇问题、追及问题、火车过桥、流水行船、沿途数车、猎狗追兔、环形行程、多人行程等等。
★每一类问题都有自己得特点,解决方法也有所不同,但就是,行程问题无论怎么变化,都离不开“三个量,三个关系”:三个量就是: 路程(s)、速度(v)、时间(t)三个关系:1、简单行程:路程=速度×时间2、相遇问题:路程与=速度与×时间3、追击问题:路程差=速度差×时间把握住这三个量以及它们之间得三种关系,就会发现解决行程问题还就是有很多方法可循得。
【经典例题】:例1.A、B两地相距125千米,甲、乙两人骑自行车分别从A、B两地同时出发,相向而行。
丙骑摩托车以每小时63千米得速度,与甲同时从A第出发,在甲、乙两人之间来回穿梭。
若甲骑车速度为每小时9千米,且当丙第二次回到甲处时,甲、乙两人相距45千米,问:当甲、乙两人相距20千米时,甲与丙相距多少千米?例2.如图,ABCD四个球按顺时针方向均匀分布在周长为48米得圆周上,分别以1米/秒,2米/秒,3米/秒,4米/秒得速度做顺时针运动。
当有两个球碰到一起得时候,两个球交换速度,但运动方向不变,当三个球碰到一起得时候,中间球得速度不变,其她两个球相互交换速度。
请问:从四个球出发开始,经过多少秒四个球第一次同时碰到一起?(不考虑球得半径)例3.如图,A、B两地相距54千米,D就是AB得中点。
甲、乙、丙三人骑车分别同时从A、B、C三地出发,甲骑车去B地,乙骑车去A地,丙总就是经过D之后往甲、乙两人将要相遇得地方骑,结果三人在距离D点5400米得E点相遇。
如果乙得速度提高到原来得3倍,那么丙必须提前52分钟出发三人才能相遇,否则甲、乙相遇得时候,丙还差6600米才到D。
请问:甲得速度就是每小时多少千米?A例5.甲、乙、丙三人同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。
华杯赛培训讲义行程问题

行 程 问 题行程问题为小学和初中数学学习的重要应用问题,在行程问题中,除特别指出外,都假定速度是常数,即匀速运动,匀速运动的基本公式十分简单: 路程=时间⨯速度但是由于路程的多样化,时间前后的差别,以及速度的变化,使得行程问题变得复杂而丰富多彩。
行程问题虽然是实际问题的初级近似,但地,由于它的各色各样的变化,使得中小学的数学知识中的许多知识点能有趣而生动地融汇其中,而成为学生能力培养的有力工具。
在各届华杯赛中,行程问题是各类问题出现频率最高的问题之一。
求解行程问题一般分如下步骤:1。
审题 2。
画示意图 3。
找关键要素 4。
列关系式 5。
分析 6。
给出答案。
下面将通过具体的问题来解释这六个步骤。
行程问题中的方程方法列方程求解行程问题是最通常的方法,也是最为有效的方法。
多数行程问题可以用列方程解方程的方法来求解。
列方程就是上述步骤中第四步中建立一个或几个含有未知数的条件等式,而第五步中的分析就是解方程。
例1.甲、乙二人从相距60千米的两地同时相向而行,6小时后相遇。
如果二人的速度每小时个增加1千米,那么相遇地点距前一次相遇地点1千米。
问:甲、乙二人速度个多少?解。
设甲的速度为每小时v 千米。
因为,两人6小时相遇,所以,二人的速度和为10千米。
乙的速度为每小时10-v 千米。
二人的速度个增加1千米,速度和为12千米,因此,需要小时)(51260=相遇。
第一次甲的行程为6v ,第二次甲的行程为5(v +1),相差1千米:.6,1)1(56==+-v v v 答。
二人的速度分别为每小时6千米和每小时4千米。
例2. 快、中、慢三辆车同时从同一地出发, 沿一公路追赶前面一个骑自行车的人,这三辆车分别用6分钟、10分钟、12分钟追上骑自行车的人。
现知快车每小时走24千米,中车每小时走20千米。
那么慢车每小时走多少千米?解。
设自行车速度为每小时v 千米,慢车每小时a 千米,三车出发时自行车在他们前面L 千米。
华杯赛小中讲义资料(三四年级)

第一课时:计算技巧一、 凑整思想例题:(1);9999999999+++(2);1234519981999200020012002200320042005+--+++--++--+(3)200912525645⨯⨯⨯⨯练习一、计算下面各题:(1)49999399929919+++(2)12349596979899100-+-++-+-+-(3)125642519⨯⨯⨯二、 运算定律及其性质:例:计算下面各题;(1)6688933222⨯+⨯ (2)444556445555⨯+⨯练习:(1)37647468⨯+⨯ (2)60575958⨯-⨯三、 添括号去括号法则(1)计算:)12119(882772⨯⨯÷⨯⨯(2)东东参加智力竞赛,有道计算题他暂时算不出来,于是选择了求助场外朋友,题目是:)65()54()43()32(1÷÷÷÷÷÷÷÷等于多少?如果你是东东的好朋友,你能帮东东解答出来吗?练习:(1))91125(77271125⨯⨯÷⨯⨯ (2)()()()211515111175÷÷÷÷÷÷四、 等差数列例题:1、=+++++10043212、对于等差数列,、、、、、 1916131074第10项是多少?49是这个数列的第几项?前50项的和是多少?第100项与第50项的差是多少?总结:等差数列中(1) 第N 项的公式:(2) 项数的公式:(3) 等差数列求和公式:练习:在等差数列 2720136、、、中,第31项式多少?第多少项是1994?前50项的和是多少?家庭作业1、 计算:2512532173⨯⨯⨯2、 计算:(1)144502817828147⨯-⨯+⨯(2)706866696867⨯⨯-⨯⨯3、 计算:(1))856636()17119654(⨯⨯÷⨯⨯⨯⨯⨯(2))97()75()53(1÷÷÷÷÷÷4、 建筑工地有一批砖,码成如下图的形状,最上层2块砖,第二层6块砖,第三层10块砖 ,依次每层都比其上面一层多4块砖,已知最下层2106块砖,问中间一层多少块砖,这堆砖共有多少块?。
华杯赛讲义_小中组第2讲几何计数

第二讲几何计数专题1、周长:对于一些不规则的比较复杂的几何图形,要求它们的周长,我们可以运用平移的方法,把它转化为标准的长方形或正方形,然后再利用周长公式进行计算.面积:在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧2、数数图形:要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
3、轴对称和对称轴:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称。
4、格点问题:图形内的格点数与它周界上的格点数的一半的和(N+L)/2与它的面积S的差永远恰好是1.在我们求格点多边形面积时,可以直接应用公式:S=(N+L)/2-15、加法原理:“加法分类,类类独立”。
解题步骤:a、完成一件事分N类;b、每类找种数(每类的一种情况必须是能完成该件事);c、类类相加解题方法:枚举法、标数法、列树状图法乘法原理:“前不影响后”,“乘法分步,步步相关”。
解题步骤:a、完成一件事分N个必要步骤;b、每步找种数(每步的情况都不能单独完成该件事);c、步步相乘解题方法:(1)简单的公式应用:n总=m1×m2×…×mn(2)题图结合:画图分步计算6、抽屉原理:原理1:将多于n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品不少于2件。
原理2:将多于m×n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品的件数不少于m+1。
7、常见的数列规律:第一类是数列各项只与它的项数有关,或只与它的前一项有关。
第二类是前后几项为一组,以组为单元找关系才可找到规律。
第三类是数列本身要与其他数列对比才能发现其规律.图形的规律:主要从各图形的形状、方向、数量、大小及各组成部分的相对位置入手,从中找出变化规律。
华杯赛讲义_小高组第4讲例题几何专题

第四讲 立体几何专题、构造与染色专题1、立体几何部分对于表面积、体积的求解,灵活使用切割或补全的做法。
2、染色是分类的直观表现,这类问题知识点少、逻辑性强,内部蕴含着丰富的数学思想。
解决方法与经常使用的数学方法有着精紧密的练习。
1、实数x 、y 、z 、w 满足0≥≥≥≥w z y x , 且20126345=+++w z y x ,求x+y+z+w 的最大值和最小值. 【解析】:设z=w+a ,y=w+a+b ,x=w+a+b+c.则a 、b 、c ≥0,且x+y+z+w=4w+3a+2b+c.故2012=5(w+a+b+c)+4(w+a+b)+3(w+a)+6w=18w+12a+9b+5c=4(4w+3a+2b+c)+(2w+b+c)≥4(x+y+z+w).因此,x+y+z+w ≤503.当x=y=z=3503,w=0时,上式等号成立.故x+y+z+w 的最大值为3503. 又2012=18w+12a+9b+5c=5(4w+3a+2b+c)-(2w+3a+b)≤5(x+y+z+w), 则 x+y+z+w ≥52012. 当x=52012,y=z=w=0时,上式等号成立.故x+y+z+w 的最小值为52012. 2、平面上有从 1 到 n 编了号的 n 个点, 每个点与另外 k 各点连有直线段, 若一个点连的 k 条直线段的另外 k 个端点的编号中有多于一半的编号小于它自身的编号, 这个点就称为“好点”. 若恰有 5 个好点. 问: n 的最小值是多少?【解析】:83、右图是一个五棱柱的平面展开图,图中的正方形边长都为2,按图所示数据,这个五棱柱的体积等于( )【解析】:(2×2-×1×1)×2=(4-0.5)×2=3.5×2=7;故答案为:74、把一个棱长均为整数的长方体的表面都涂上红色, 然后切割成棱长为 1 的小立方块, 其中, 两面有红色的小立方块有 40 块, 一面有红色的小立方块有66 块, 那么这个长方体的体积是多少?【解析】:设长方体的长、宽、高分别为x,y,z 且两面有红色的小立方块只能在长方体的棱上出现,若x=1,则没有两面有红色的小立方块,所以,此时两面红色的方块只能与长方体的棱共棱,一面红色的方块只与长方体的面共面,从而有4[(x-2)+(y-2)+(z-2)]=40,2[(x-2)(y-2)+(x-2)(z-2)+(z-2)(y-2)]=66整理得,x+y+z=16xy+yz+zx=85于是有,即2x,y,z9逐个检验,可知x=5,y=5,z=6 ,此时长方体的体积为1505、有高度相同的一段方木和一段圆木,体积之比是1:1,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱体体积和长方体体积的比值为().【解析】:设圆的半径为r,正方形的面积与圆的面积比是:因为,方木与圆木的体积和高度都相等,说明底面积也相等,所以,现在的圆柱体积和长方体的体积的比值是:6、右图中,AB是圆O的直径,长6厘米,正方形BCDE的一个顶点E在圆周上,∠ABE=45°,那么圆O 中非阴影部分的面积与正方形中BCDE中非阴影部分的面积的差等于()(π取3,14)【解析】:如图,连接EO,S正=EB×EB=EO2+BO2=(6÷2)2×2=18(平方厘米)所以圆O中非阴影部分的面积与正方形BCDE中非阴影部分面积的差:π×(6÷2)2-18=10.26(平方厘米);答:圆O中非阴影部分的面积与正方形BCDE中非阴影部分面积的差等于10.26平方厘米.故答案为:10.26.7、已知正整数A分解质因数可以写成, 其中、、是自然数.如果A的二分之一是完全平方数, A的三分之一是完全立方数,A 的五分之一是某个自然数的五次方, 那么α+β+γ的最小值是().(A)10 (B)17 (C)23 (D)31【解析】:A的二分之一是完全平方数,α-1、β、γ是2的倍数;A的三分之一是完全立方数,α、β-1、γ是3的倍数;A的五分之一是某个自然数的五次方,α、β、γ-1是5的倍数;要α+β+γ的值最小,分别求满足条件的α、β、γ值:3×5-1是2的倍数,α的最小值为15,2×3-1是5的倍数,γ的最小值为6,2×5-1是3的倍数,β的最小值为10,所以α+β+γ的最小值是:15+6+10=31;故选:D .8、两个大小不同的正方体积木粘在一起, 构成右图所示的立体图形,其中, 小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点.如果大积木的棱长为 3, 则这个立体图形的表面积为________.【解析】:根据题干分析可得:大正方体的一个面的面积是:4×4=16,小正方体一个面的面积是:4×4-3×1÷2×4=16-6=10,所以这个立体图形的表面积是:16×6+10×4=96+40=136,答:这个立体图形的表面积为136.9、不为零的自然数 n 既是 2010 个数字和相同的自然数之和, 也是 2012 个数字和相同的自然数之和, 还是 2013 个数字和相同的自然数之和, 那么 n 最小是多少?【解析】:6036=4×1000+3×10+2006×1,6036=2012×3,6036=2000+20+2008×2.答:n 最小是6036.10、最简单分数满足51<b a < 41, 且 b 不超过 19, 那么 a + b 的最大可能值与最小可能值之积为________. 【解析】:由题意得,,所以4a<b<5a又因b 不超过19,所以a 最大值为4,此时b 最大可为19,当a=2时,b 有最小值是9,那么a+b 的最大可能值与最小可能值之积为:(4+19)×(2+9)=253.故答案为:253.11、两个较小的正方体积木分别粘在一个大正方体积木的两个面上, 构成右图所示的立体图形, 其中, 每个小积木粘贴面的四个顶点分别是大积木粘贴面各边的一个五等分点.如果三个积木的棱长互不相同且最大的棱长为 5,那么这个立体图形的表面积是________.【解析】:根据题干分析可得:大正方体的一个面的面积是:5×5=25小正方体一个面的面积是:5×5-4×1÷2×5=25-10=15所以这个立体图形的表面积是:25×6+15×4×2=150+120=270答:这个立体图形的表面积为270. 故答案为:270. 12、从连续自然数 1, 2, 3, …, 2014 中取出 n 个数, 使这 n 个数满足: 任意取其中两个数, 不会有一个数是另一个数的7倍. 试求 n 的最大值, 并说明理由.【解析】:{1,7,49,343},{2,14,98,686}......{286,2002}共246组数里,在前五组中每组至多能取2个,至少有10个不能取,在有3个数的组里,共至少有31个不能取,在2个数组里至少有210个不能取,故至多能取2014-10-31-210=1763个数,在这1763个数中,任取其中2个,不会有一个数是另一个数的7倍,n 的最大值为1763.13、设a 、b 、c 、d 、e 均是自然数,并且a ,a+2b+3c+4d+5e=300,则a+b 的最大值。
华杯赛考试大纲及备考攻略

华杯赛考试大纲及备考攻略(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--华杯赛考试大纲及备考攻略一.华杯赛常考考点总结计算:分数小数互化、循环小数化分数、约分、运算级别、加法、乘法运算律常用公式、常用数据记忆裂项(整数、分数裂项;分数拆分)、通项公式、换元法估算、取整、取小数论:奇偶数质数、合数整除及位值原理约数、(最大)公约数、(最小)公倍数余数及同余完全平方数数字迷进制(常考二进制)几何:平面几何的周长及面积规则图形:掌握公式、高不规则图形:割补法、转化为规则的常用模型:同底等高模型、四边形定理、蝴蝶定理、鸟头定理、燕尾定理、容斥定理立体几何的体积及表面积圆柱、圆锥等公式 (挖洞后)立体的体积表面积与体积图形的染色与切割平面图形的旋转圆形的滚动应用题:行程问题:多次相遇、多次追及、环形行程、走走停停、变速行驶工程问题:多人合作、中途请假、做做停停、工资分配、工作交换经济、浓度问题:概念转换、利润计算、浓度计算、利润最大化、溶液配比、溶液装置变换最值问题:最短时间、最大利润、最大乘积、最小损耗容斥原理:集合的交集、并集与补集抽屉原理(构造抽屉是难点) 抽屉原理一:告诉苹果和抽屉,求最值抽屉原理二:告诉抽屉和最值,求苹果(最不利) 抽屉原理三:整数分组其他问题:决赛中约考察15分构造与染色:奇偶染色、证明问题加乘原理排列组合捆绑与插空枚举与树形图容斥与排除归纳与递推标数法对应法重要:线分面,面分体。
如果怒了用枚举二、如何备考各大杯赛1、第一阶段:奥数各大专题复习。
杯赛考察的是孩子的综合实力,几乎涉及奥数所有专题,孩子平时的学习情况基本决定了孩子的竞赛成绩。
有计划有准备的奥数学习的孩子去参加各大杯赛考试,获奖的概率将大大增加。
因此,有必要为了每一种杯赛而制定学习计划,否则将会得不偿失。
现阶段可以把老师讲过的知识整理一遍,把每个知识模块都画一张脑图。
华杯赛金牌班讲义(黑白10本)

行程部分例1小芳从家到学校有两条一样长的路,一条是平路,另一条是一半上坡路,一半下坡路.小芳上学走这两条路所用的时间一样多.已知下坡的速度是平路的1.6倍,那么上坡的速度是平路速度的多少倍?例2甲、乙、丙三人每分分别行60米、50米和40米,甲从B地、乙和丙从A地同时出发相向而行,途中甲遇到乙后15分又遇到丙.求A,B两地的距离.模拟考试题1,11点从上海开车去南京,原计划中午11:30到达.但出发后车速提高了7钟就到了.第二天返回,同一时间从南京出发.按原速行驶了120千米后,再1,到达上海时恰好11:10.上海、南京两市的路程是多少千米?将车速提高6拓展小李和小张在一个圆形跑道上匀速跑步,两人同时同地出发,小李顺时针跑,每72秒跑一圈;小张逆时针跑,每80秒跑一圈。
在跑道上划定以起点为中心的四分之一圆弧区间,那么两人同时在划定的区间内所持续的时间是多少秒?几何部分模拟考试题如图,相邻两个格点间的距离是1,则图中阴影三角形的面积为___________.例3在下图中,线段AE、FG将长方形ABCD分成了四块;已知其中两块的面积分别是2cm²、11cm²,且E是BC的中点,O是AE的中点;那么长方形ABCD的面积是多少?例4已知四边形ABCD,CHFG 为正方形,8:1 乙甲:S S ,a 与b 是两个正方形的边长,求a:b=?乙甲b aG H O FE D C BA数论部分例5以105为分母的最简真分数共有多少个?它们的和为多少?模拟考试题一个圆上有12个点A1,A2,A3,…,A11,A12.两两相连,会有6条直线,要求任意两条线段不相交.问共有多少种不同的连法?例6现用红、黄、蓝、绿四种颜色为下面的正多边形染色,要求相邻区域不同色。
那么(1)图1有几种染色方法?图2有几种染色方法?(2)你能否用第(1)问的研究结果推测图3、图4的染色方法数?(3)正n边形按上述图形规律划分成n个区域,有几种染色方式?(提示:观察数列3、9、27、81、243··……)例7策略问题100个囚犯从前往后坐成一列,看守给每个囚犯戴上一顶黑色的或者白色的帽子,每人只能看到前面的人的帽子,看不到自己及后面的人的帽子.然后,看守会从后往前依次叫这些囚犯猜测自己头顶上的帽子的颜色.如果哪个囚犯猜对了,他就自由了.坐在前面的每一个囚犯都可以听到后面的囚犯的猜测.如果这100个囚犯事先可以商量好一种策略,那么最理想的策略可以保证__________人被释放.例8游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?华杯赛真题如图,两只蜘蛛同处在一个正方体的顶点A,而一只爬虫处在A的体对顶点G.假设蜘蛛和爬虫均以同样的速度沿正方体的棱移动,任何时候它们都知道彼此的位置,蜘蛛能预判爬虫的爬行方向.试给出一个两只蜘蛛必定捉住爬虫的方案.。
成都华杯赛课程讲义(B)

成都华杯赛课程讲义(B )主要内容:计数、几何、数论【例1】(2009年第十四届“华罗庚金杯赛”初赛)按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5,那么,可供每支球队选择的号码共( )个.【分析】 根据题意,可供选择的号码可以分为一位数和两位数两大类,其中一位数可以为0~9,有10种选择;两位数的十位可以为1~5,个位可以为0~5,根据乘法原理,两位数号码有5630⨯=种选择.所以可供选择的号码共有103040+=种.【巩固】一种电子表在6时24分30秒时的显示为6:2430,那么从5时到7时这段时间里,此表的5个数字都不相同的时刻一共有多少个?【分析】 设DE A:BC 是满足题意的时刻,有A 为6,B 、D 应从0,1,2,3,4,5这6个数字中选择两个不同的数字,所以有26A 种选法,而C 、E 应从剩下的7个数字中选择两个不同的数字,所以有27A 种选法,所以共有26A ×27A =1260种选法;A 为5,B 、D 应从0,1,2,3,4,这5个数字中选择两个不同的数字,所以有25A 种选法,而C 、E 应从剩下的7个数字中选择两个不同的数字,所以有27A 种选法,所以共有25A ×27A =840种选法,因此一共有12608402100+=个【例2】(2008年第十三届“华罗庚金杯赛”初赛)已知图中是一个轴对称图形.若将图中某些黑色的图形去掉后,得到一些新的图形,则其中轴对称的新图形共有( )个.(A)9 (B)8 (C)7 (D)6【分析】 原图是一个轴对称图形,且对称轴只有1条,那么去掉图中的某些黑色图形后,剩下的轴对称图形的对称轴与原图的相同.阴影5部分中去掉1个,有1种情况;阴影5部分去掉2个,有2种情况;阴影5部分去掉3个,有2种情况;阴影5部分中去掉4个,有1种情况;阴影5部分中去掉5个,有1种情况;所以共7种情况,答案为C .EDA BC 计数另解:如右图,将阴影5部分标上字母,则A 和B 关于对称轴对称,C 部分单独关于对称轴对称,D 和E 关于对称轴对称,所以,如果要去掉某些黑色部分图形,则A 和B 必须同时去掉或保留,C 既可去掉也可保留,D 和E 必须同时去掉或保留,对这3组每组都有去掉或保留2种选择,共有2228⨯⨯=种选择,但是其中有种情况5部分都没有去掉的情况,这样情况应予排除,所以符合条件的情况共有817-=种.【例3】在图中15⨯的格子中填入1,2,3,4,5,6,7,8中的5个数,要求填入的数各不相同,并且填在黑格里的数比它旁边的两个数都大.共有 种不同的填法.【分析】 首先看填入1、2、3、4、5这五个数的情况.由于黑格里的数至少比两个数大,所以至少为3;而白格里的数不能是最大的,所以5必须在黑格里.那么这五个数填在黑格里的数是5和4时,不同的填法有2!3!12⨯=(种);填在黑格里的数是5和3时,4只能在5的一侧,不同的填法有224⨯=(种).所以,共有不同填法12416+=(种).而要将填入的五个数选出来,一共有58C 56=种,然后按照分析1~5这5个数的方法对应着数的相对大小来分析选出来的五个数,也各有16种填法,所以一共有:5616896⨯=种填法.【巩固】在图23-5的空格内各填入一个一位数,使同一行内左边的数比右边的数大,同一列内下面的数比上面的数大,并且方格内的6个数字互不相同,例如图23-6就是一种填法。
华杯赛赛前教程

前言“华罗庚金杯”少年数学邀请赛(简称华杯赛)是以华罗庚名字命名的数学竞赛,始于1986年,是为了纪念我国著名数学家华罗庚,由中国优选法统筹法和经济数学研究会、中国少年报社、中国数学会和中央电视台青少中心等单位发起和组织的一项全国少年学生数学竞赛,至2008年,“华杯赛”共举行了十三届,已经成为一项重要的、有影响的和全国性的少年科技教育和普及活动.为了配合第十四届“华杯赛”,帮助学生提高数学的水平和素质,在“华杯赛”中取得优秀成绩,华杯赛主试委员会组织编写了第十四届“华罗庚金杯少年数学邀请赛”赛前教程(小学册),简称为“赛前教程”.“赛前教程”共有五章,第一章是数的运算,由卢振虎主笔;第二章是整除和带余除法,由王世坤、卢振虎、赵小峰和陈平等编写,王世坤和陶小勇主编.“赛前教程”每一章有三节和一套练习题,每一节大致包含三部分内容:第一部分简要地介绍一些基本概念和知识;第二部分是“说明”,主要介绍一些扩展的知识、与该节有关的数学的思想和应当注意的问题,个别内容较深,仅供辅导老师和家长参考;第三部分是“例题讲解”,是该节的核心部分,含有本书作者精心选择和编制的十个例题,其中多数是“华杯赛”常见和典型的问题,并且做了细致的解答,有的例题附有“说明和评注”,更深入地介绍了解题的方法和思想.“赛前教程”每一章均有30道练习题,它们选自“华杯赛”的试题、其它数学竞赛的试题和辅导材料,其中有一些是本书作者编制的新题. “赛前教程”附有三套初赛测试题和三套决赛测试题,由“华杯赛”主试委员会卢振虎、朱华伟、那吉生、余其煌、连四请、周春荔和闫桂英编制,由闫桂英统编,是本书非常重要的内容. 全书由主编王世坤做了适当的修改和编辑.“华杯赛”主试委员会主试委员秉承“华杯赛”普及性、趣味性和新颖性命题的原则,编排了六套测试题,它们连同精心选择的各节的例题以及各章练习题,基本上覆盖了“华杯赛”命题的思想和试题的类型,是第十四届“华杯赛”命题重要的参考. 一般而言,多做练习题是学好数学和在数学竞赛中取得优异成绩必须做的努力. 但是,“题海训练”,过多的赛前“冲刺”等,既消耗了学生过多的时间和精力,效果也未必令人满意. 而且,有的“模拟试题”或者“练习题”粗制滥造,偏离学习数学基本的规律,会误导学生,对学生没有太多的益处.我们相信,只要细致阅读本书,认真完成“赛前教程”中的练习题和测试题,读者会加深对课堂知识的理解,会增长应用数学知识去解决实际问题的能力和提高数学的素质,会在“华杯赛”中取得优秀成绩.这本“赛前教程”虽然是为了配合第十四届“华杯赛”,但是,其内容基本上覆盖了小学数学的主要知识,可以作为一本小学数学的复习教程.一般而言,一本优秀的数学的复习教程,应当以更高的角度来归纳和总结数学的知识,就像登山,途中,只能看到局部的风景,登至山顶,从高处浏览周围的风景,就会更深地了解,你走过的路和周围“景致”的关系,就会有“一览众山小”的感觉.复习就要做到登高望远,能够梳理出原来学过的数学知识之间的内在的联系,发现这些知识原来很“简单”.这本教程遵循这个原则,对小学数学知识做了深入的归纳和总结,提供了许多典型的例题和练习题.所以,即使不参加“华杯赛”,如果能认真阅读本书,细细体会其中的精髓,定有收获.学习数学,既要学习数学的知识,同时,也要特别注意数学的思想和方法对人的智力的巨大的影响.这本教程无论是从小学数学知识的总结和归纳,例题的认真选择和讲解,还是练习题的安排,都特别注重启迪同学们的数学兴趣和开发他们的智力,都非常强调帮助学生建立和提高应用数学知识去解决实际问题的能力,增强他们数学的能力.所以,将这本教程作为一册数学课外的读物,细致地钻研,初步理解一些数学的思想和方法,就能提高数学的素质和水平,为进一步的学习奠定扎实的基础.第十四届“赛前教程”和十三届“赛前教程”比较,书中不仅提供了全新的测试题,而且,修改了十三届“赛前教程”部分内容、大多数的例题和练习题,焕然一新了.虽然“赛前教程”的编写者是“华杯赛”主试委员和华杯赛教练员,他们具有扎实的数学的修养和造诣,又有从事数学教育和数学竞赛丰富的经历、经验和成就,他们编写的这本教程会受到读者的欢迎.但是,限于他们的水平和时间,书中仍然有许多不完善和考虑欠周的地方,也难免有错误.十三届“赛前教程”出版后,受到广大读者的欢迎,一些热心的读者也指出了一些错误和疏漏漏,“赛前教程”编著者向他们表示感谢,同时,诚挚地希望和欢迎读者一如既往,指出本书的不足和错误,提供修改的宝贵意见.本书由包善贤老师做了二校,他非常细心和认真的工作使本书增益不少,“赛前教程”编著者表示忠心的感谢.“华罗庚金杯”少年数学邀请赛的宗旨和目的是弘扬华罗庚教授的爱国主义精神,引导少年学生学习华罗庚教授勤奋学习、献身科学的优秀品质,激发他们学习数学的兴趣、开发他们的智力,提高他们的数学素质. 我们希望本书,即“第十四届华罗庚金杯少年数学邀请赛赛前教程”能体现这个宗旨,对读者有所帮助.第十三届“华杯赛”主试委员会,2008年7月目录第一章数的运算第1节整数、分数和小数第2节四则运算第3节数字谜和数阵图第一章练习题第二章整除和带余除法第1节整数和整除第2节带余数除法(1)第3节带余数除法(2)第二章练习题第三章应用问题第1节应用问题(1)第2节从算术到代数第3节方程的概念和解法第4节应用问题(2)第三章练习题第四章图形知识第1节简单平面图形第2节平面几何图形第3节简单立体图形第四章练习题第五章综合问题选讲第1节最大和最小第2节分类和计数第3节整数综合问题第五章练习题模拟测试题初赛测试题(1)初赛测试题(2)初赛测试题(3)决赛测试题(1)决赛测试题(2)决赛测试题(3)附录1练习题参考答案和提示附录2 模拟测试题答案和提示第一章 数的运算数是人类长期实践活动中产生和发展的, 整数、小数和分数及其四则混合运算是小学数学的重要内容,这些知识及相应的扩展是“华杯赛”和一些数学竞赛必考的部分. 这一章将复习这些知识,举例说明一些运算的技巧、相关思维的方法,并且渗透一些简单的数学思想.第1节 整数、分数和小数(一) 基本知识1.整数 ● 整数的认识我们在数物体的时候,用来表示物体个数的1,2,3,4,5 ……都是自然数. 一个物体也没有,可以用0表示,0也是自然数. 自然数可以用来表示事物的多少,也可以用来编号,表示事物的次序. 当用来表示事物的数量,即被数的物体有“多少个”时,叫做自然数的基数意义;当用来表示事物的次序,即最后被数的物体是“第几个”时,叫做自然数的序数意义.引入负数后,“1,2,3,4,5 ……”叫做正整数,“-1,-2,-3,-4,-5 …………”叫做负整数. 非负整数是0和正整数的统称,也就是自然数. 整数是正整数,负整数和零的统称.在这本书中,整数特指是正整数和零. ● 整数的大小位数越多的整数越大;如果两个整数位数相同,就从最高位依次比起.2.分数 ● 分数的概念把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数. 把单位“1”等分后,表示其中一份的数,叫做这个分数的分数单位. 两个整数相除,它们的商可以用分数表示,即:a ÷b =)0(≠b b a. 也可以直接把符号m n(m 、n 都是整数,且n ≠0)定义为分数,其中符号“-”称为分数线.当n =1时,m n=1m =m ,即任何整数m 都可以用分数1m 表示. ● 百分数表示一个数是另一个数百分之几的数,叫做百分数,也叫百分率或百分比. 百分数通常不写成分数形式,而用百分号“%”来表示. 如百分之九十六写作96%,百分之零点6写为0.6%. 由于百分数便于比较,所以在生产和日常生活中有着广泛的应用.● 分数的分类分子小于分母的分数叫做真分数,真分数比1小. 分子大于或等于分母的分数,叫做假分数,假分数大于或者等于1. 一个整数和一个真分数合成的数,叫做带分数, 带分数只是假分数的另一种形式. 严格的说,分数只能分为真分数、假分数两类.一个分数,如果分子和分母除了1之外,没有其他公共的约数(见37页约数),则称为最简分数.● 分数的运算一个分数,总是可以约分为最简分数;一个带分数可以转化为假分数,假分数也可化为带分数或整数;两个分数,通过通分做加法,通过转化为假分数做乘法.● 分数的性质和大小分数的分子和分母同时乘以或除以相同的不为0的数,分数的大小不变.分母相同,分子越小的分数值越小;分子相同,分母越小的分数值越大. 任何假分数都大于真分数.3.小数 ● 小数的概念分母是10、100、1000…… 的分数,改写成不带分母形式的数就是小数,如,把103改写成0.3. 符号“.”称为小数点,小数点左端的数是整数部分,右端是小数部分.整数部分为0的小数叫做纯小数,纯小数比1小.● 小数的分类及性质小数部分的位数有限时,称为有限小数. 另外还有一些小数的小数部分位数是无限多的,叫做无限小数. 无限小数又可分为循环小数和非循环小数. 在一个数的小数部分中,从某一位起,一个数字或几个数字依次不断地重复出现,这样的小数叫做循环小数. 例如,0.888……、3.15353……都是循环小数. 其中,0.888……的循环节是“8”,可以记作08.∙,它是纯循环小数. 3.15353……的循环节是“53”,可以记作3153.∙∙,它是混循环小数. 一个无限小数,从小数部分起各位数字的排列没有一定的规律,这样的无限小数叫做非循环小数. 例如圆周率π就是非循环小数.在小数的末尾添上“0”或者去掉“0”,小数的大小不变.整数部分越大的小数越大. 如果整数部分相同,则从十分位依次比起. 4.小数和分数的互化● 分数化小数:直接用分子除以分母,除不尽时,可以化为循环小数,或者根据需要用四舍五入法取近似值.● 小数化分数:有限小数化为分数. 原来有几位小数,就在1后面写几个零作为分母,原来的小数去掉小数点作分子,能约分的要约分. 例如:0.37 =37100,14652931.4651000200==.纯循环小数化为分数. 分子是一个循环节的数字所组成的数;分母的各位数字都是9,9的个数与循环节的数字的个数相同. 例如:310.393∙==,4730.473999∙∙=;混循环小数化为分数. 分子是小数点后面第一个数字到第一个循环节末端的数字所组成的数减去不循环数字所组成的数的差;分母的头几位上的数字是9,末几位上的数字是0,9的个数与循环节中的数字的个数相同,0的个数和不循环部分的数字的个数相同. 例如:1311220.13909015∙-===,1759117582930.1759999099901665∙∙-===. 由此可知,任何一个循环小数都可化为分数.非循环小数无法化为分数.(二) 说明1.负数在小学阶段所说的整数、小数及分数主要指正数和0,在以后的学习中数的范围会扩大到负数. 因为人们在生活中经常会遇到各种相反意义的量. 比如,记帐时,有余有亏;在计算粮仓库存米时,有时要记进库粮食,有时要记出库粮食. 为了方便,人们就考虑了用相反意义的数来表示. 于是人们引入了负数这个概念,把余钱、进库粮食记为正,把亏钱、出库粮食记为负. 为了使“数”能蕴涵相反的含义,就在前面添加一个符号“-”,称为负数,符号“-”称为负号. 如果原来的“数”是整数,但不是零,添加负号之后,称为负整数,原来的整数则称为正整数. 如果原来的“数”是分数,添加负号之后,则称为负分数,原来的分数则称为正分数. 正整数和正分数统称为正数,用符号“+”来表示正数,例如:+5、+16,符号“+”称为正号,有时候省略正号“+”不写.2.用字母表示数用字母表示数,是对数的认识的一个飞跃,既可以表示一些不好写出和表达的数(例如圆周率π),也可以表示一类数或具有某种相同性质的数(例如字母v 代表速度,N 表示自然数等),为计算和解决问题带来了极大的方便.3.繁分数本书将分子和分母中还含有分数、小数或四则混合运算的“分数”叫做繁分数. 繁分数是分数形式的数,但不是分数. 前面在介绍分数的概念时提到可以直接把符号m n(m 、n 都是整数,且n ≠0)定义为分数,显然繁分数并不满足这一定义,所以说繁分数不是分数. 在一个繁分数里,最长的分数线叫做繁分数的主分数线,主分数线上下不管有多少个数或运算,都把它们分别看作是繁分数的分子和分母.把繁分数化为最简分数或整数的过程,叫做繁分数的化简. 繁分数的化简一般采用以下两种方法.(1)先找出主分数线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分的计算结果能约分的要约分,最后形成“分子部分÷分母部分”的形式,再求出结果.(2)根据分数的基本性质,将繁分数的分子部分和分母部分同时扩大相同的倍数(这个倍数可以是分子部分与分母部分所有分母的最小公倍数),从而去掉分子部分和分母部分的分母,然后通过计算化为最简分数或整数.4.取整运算当只关心某数的整数部分时,规定][x 表示不超过x 的最大整数,称为高斯符号,或称为取整运算.又记][}{x x x -=,即{}x 为x 的小数或真分数部分,如3]14.3[=,14.0}14.3{=.显然有{}01x ≤<,当x 为整数时,等号成立.5.数的表示形式和转化可以将分数、带分数、假分数、小数、百分数甚至繁分数和字母代表数等等,理解为数的各种不同的表达“形式”, 例如:1可以表达为循环小数09.∙,2可以表达为假分数42,等等.至于整数是否是特殊的分数和小数,并不太重要,重要的是深入理解数的各种表达“形式”蕴涵的数学意义和掌握它们相互转化的方法,例如:2和2.0, 在科学和技术中,它们是有重大区别的.因为科学和技术的测量总是有误差的,2.0可能是2.03要求精确到小数点后1位,舍弃了0.03后, 这样,2.0就蕴涵了精确度,所以2和2.0是不同的.但是,在小学数学中,它们是相同的数,依照数学表达简洁化的原则,2最好不要写成2.0, 0.3一般不要表达为030.∙.尽管小学阶段遇到数学概念比较少,但是,准确理解数学概念和相近数学概念细小的差别还是比较重要的.唯有如此,养成良好的数学习惯,现在和将来,才能学好数学.(三) 例题讲解1. 选择题例1下面是6个等式: ① 0301230423...∙∙∙∙+=; ② 6255062510008.==;③533581142142162++===+;④ 102 1314 2235 323 4546.,.,,.,.,.∙∙∙∙∙∙中有2个纯循环小数; ⑤ 1991.∙∙=9999911;⑥ 31334127535⨯=;其中正确的命题是( ).(A )①与② (B )②、④与⑤ (C )①与④ (D )②、⑤和⑥ 答案:B.理由:①不正确,因为03012304231...∙∙∙∙+=;②正确;③不正确,因为521521136114141477++===;④正确,因为10166.∙=,是混循环小数;⑤正确;⑥不正确,因为31242150414341475753535⨯=⨯==.例2下面是6个命题:① 两个真分数之间至少有1个真分数; ② 两个分数之间至少有1个真分数; ③ 两个分数之间有无穷多个分数; ④ 圆周率π可以化为一个分数; ⑤ 总可以将一个分数化为有限小数; ⑥ 无限循环小数不能化为分数;其中正确的命题是( ).(A )①与③ (B )②与③ (C )①与④ (D )⑤与⑥答案:A .理由:①正确,理由是:设ab 和c d是真分数,并且a c bd<,则有a a c c bb dd+<<+;②不正确,因为真分数小于1,例如:32和52之间没有真分数;③正确,理由是:如①所述理由,两个不同的分数之间有1个分数,则可以推出有无穷多个分数;④不正确,因为圆周率π是无限不循环小数,不能化为分数;⑤不正确,例如17化为小数时,是无限循环小数;⑥不正确,无限循环小数能化为分数,例如:10.33∙=.2. 填空题例3在混循环小数9617472.∙的某一位上再添上一个表示循环的圆点,使新产生的循环小数尽可能大. 这个新的循环小数是( ).答案:9617472.∙∙.理由:要求新产生的循环小数尽可能大,实际上是要求组成循环节的前几位数字尽可能大.首先,要选择好循环节的首位数,一定要是小数点以后最大的一个数字.在这道题里,最大的数是7,表示循环的圆点应该点在7上. 可是,题目里有两个7,点在哪个7上呢?哪个7后面的数字大,就点在哪个7上,所以,新的循环小数是9617472.∙∙.例4分母为2009的所有最简真分数之和为( ). 答案:740.理由:因为20097741=⨯⨯,所以分母是2009的最简真分数,分子不能是7、41和它们的倍数. 因此,分母为2009的所有最简真分数之和为()()()()1741S=122008122861248200920092009741 1262009+++-+++-+++⨯++++ ,因为()()()12200812008220071004100520091004122862871431248492412673,,,,+++=++++++=⨯+++=⨯+++=⨯+++=⨯所以2009100472872434149247417320092009200920091004243243740S ⨯⨯⨯⨯⨯⨯⨯⨯=--+=--+=例5 记1111112021223839S =+++++,[]S =( ).答案:1.理由:先估算分母的大小,因为111120120213920+++<⨯=…,且111120202021393939+++>⨯=…,所以1<原式<3920=1.95,[]S =1.说明和评注:解决这种估算类题目的关键是放缩,即找到所求值的范围,这一方法在比较分数大小时也经常会用到.3. 解答题例6计算:123369714211453121572835⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯=?解答:原式=)541(7)541(3541)321(7)321(33213333⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯+⨯⨯=)731(541)731(3213333++⨯⨯⨯++⨯⨯⨯=123145⨯⨯⨯⨯=310.例7 有红、蓝、黄、绿4种卡片,每种3张,相同颜色的卡片上写有相同的整数,不同颜色卡片上的整数互不相同,由小到大依次为红、蓝、黄、绿. 现在把这些卡片分给6名同学,每人得到颜色不同的两张,六名同学分别求和,得到6个和数:88,121,129,143,154,187. 其中一个错了,则这4个整数分别是多少?解答:设这四个整数分别为a <b <c <d ,因为6个和数分别为88,121,129,143,154,187,显然a+b =88,a+c =121,b+d =154,c+d =187而a+b+c+d =88+187=121+154≠129+143,所以错误的和数为129或143,a+b+c+d =275. 又因为c -b =187-154=33,所以b+c 为奇数.若错误的和数为129,则实际应为275-143=132,即b+c =143,a+d =132,解得a =33,b =55,c =88,d =99;若错误的和数为143,则实际应为275-129=146,即b+c==129,a+d =146,解得a =40,b =48,c =81,d =106.例8 将2009个分数21,31,41,…,12009,12010化成小数,共有多少个有限小数?解答:一个有限小数化为最简分数时,其分母只含质因数2或5.反之,也成立.1011882627343544245220102 5220105252201052 5220105252201052 520105,,,,,,<<⨯<<⨯⨯<<⨯⨯<<⨯⨯<<⨯<< 上面的六个不等式意味着:小于2011的整数中,只含质因数2的整数有10个;只含质因数2和仅有1个质因数5的整数有8个; 只含质因数2和仅有2个质因数5的整数有6个; 只含质因数2和仅有3个质因数5的整数有4个; 只含质因数2和仅有4个质因数5的整数有1个; 只含质因数5的整数有4个,所以,共有10+8+6+4+1+4=33个有限小数. 例9 A ,B ,C 为正整数,满足算式111524+++=C B A ,则C B A 32++的值是多少.解答: 将245表示为连分数形式:131114411144514544524+++=++=+=+=,则有:A =4,B =1,C =3,所以,153312432=⨯+⨯+=++C B A .例10求1411421497149833333333⨯⨯⨯⨯⎡⎤⎡⎤⎡⎤⎡⎤++++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦的和. 解答:已知: 对121004k ,,,= ,()()()141414333333149914991499, 333333k k k ,k k k ⨯⨯⨯⎧⎫⎡⎤=+⎨⎬⎢⎥⎩⎭⎣⎦⨯-⨯-⨯-⎧⎫⎡⎤=+⎨⎬⎢⎥⎩⎭⎣⎦所以,()()()14991499149914141442333333333333k k k k k k ⨯-⨯-⨯-⎧⎫⎡⎤⨯⨯⨯⎧⎫⎡⎤=+=+++⎨⎬⎨⎬⎢⎥⎢⎥⎩⎭⎣⎦⎩⎭⎣⎦, 并且上式中,()1499143333k k ⨯-⎡⎤⨯⎡⎤+⎢⎥⎢⎥⎣⎦⎣⎦的和是整数,所以,()1499143333k k ⨯-⎧⎫⨯⎧⎫+⎨⎬⎨⎬⎩⎭⎩⎭的和应当是整数.并且,既然对于任何整数n ,{}1n <,就有()149914013333k k ⨯-⎧⎫⨯⎧⎫<+=⎨⎬⎨⎬⎩⎭⎩⎭.所以,()149914413333k k ⨯-⎡⎤⨯⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦1411421497149833333333141149814214971449145033333333333341492009.⨯⨯⨯⨯⎡⎤⎡⎤⎡⎤⎡⎤++⋯++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⨯⨯⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++++ ⎪⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎝⎭=⨯= .第2节四则运算(一)基本知识1.四则混合运算●运算法则在一个算式里,如果含有两种或两种以上的运算,通常就称为混合运算. 加、减、乘、除的混合运算也叫四则混合运算.在数的运算中,加法和减法叫做第一级运算,乘法和除法叫做第二级运算,乘方和开方叫做第三级运算. 第三级运算是第二级运算的高级运算,第二级运算是第一级运算的高级运算;反之,第一级运算是第二级运算的低级运算,第二级运算是第三级运算的低级运算.如果一个算式里含有不同级的运算,那么就先做高级运算,后做低级运算. 在有括号的情况下,要按照从里到外的顺序,先算小括号里的,再算中括号里的,然后算大括号里的,最后算括号外面的.●运算定律加法交换律. 两个数相加,交换加数的位置,它们的和不变. 即a+b=b+a.加法结合律. 三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加,它们的和不变. 即(a+b)+c=a+(b+c).加法交换律和结合律的推广:几个数相加,任意交换加数的位置,或者先把其中几个数结合成一组相加,它们的和不变.乘法交换律. 两个数相乘,交换因数的位置,它们的积不变. 即a×b=b×a.乘法结合律. 三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变. 即(a×b)×c=a×(b×c).乘法交换律和结合律的推广:几个数相乘,任意交换因数的位置,或者先把其中几个数结合成一组相乘,它们的积不变.乘法分配律. 两个数的和与某个数相乘,可以把两个加数分别与这个数相乘,再把两个积相加,所得的结果不变. 即(a+b)×m=a×m+b×m.2.速算法在进行数的运算时,根据数的特点,结合和、差、积、商的变化,运用运算定律、性质,进行简便、迅速的运算,叫做速算,常用的速算法有:(1)分组法. 把算式中能凑成整十、整百、整千的数先算,以便于后面的计算. 例如:869+27+131+73=(869+131)+(27+73)=1000+100=1100; 167-(89+67)=167-67-89 =100-89=11.(2)补数法. 对接近整百、整千的数,可以补上一个数使它成为整百、整千数,使计算简便. 例如:1453-397=1453-(400-3)=1453-400+3 =1056.(3)分解法. 有些乘除计算,可把已知数适当进行分解,然后应用运算性质,使计算简便. 例如:25×32=25×4×8=100×8=800.此外还有基准数加法、公式法等,其本质都是对数的特征和运算定律的灵活运用.(二) 说明1.数列按照一定顺序排列的一列数叫做数列,通常记作a 1,a 2,… a n , …,简记为{ a n }. 数列中的每一个数都叫做这个数列的项,其中a n 表示数列{ a n }的通项. 如果一个数列{ a n }的第n 项a n 与项数n 之间的关系可以用一个关于n 的公式来表示,我们就把这个公式叫做这个数列的通项公式. 如数列1,4,9,16,…,通项公式为a n =n 2. 如果数列只有有限个项,将第一项称为首项,最后一项称为末项(a n ),项的总数叫做项数,求数列中所有的项的和,称为数列求和.“华杯赛”和其他一些重要的小学数学竞赛中常常出现两类数列:等差和等比数列. 等差数列是从第二项起,每一项减去它的前一项,所得的差为定值的数列,这个差叫做公差,记作d ,即21321n n a a a a a a d --=-==-= . 由公差的定义,可以推出等差数列{ a n }的通项公式:a n =1a +(n-1)×d ,或a n = a m +(n-m )×d . 用两种方法求等差数列{ a n }前n 项的和:121121n n n n n n S a a a a S a a a a ,--=++++=++++将上面两个式子相加,因为121112n n n n a a a a a a a a --+=+==+=+ ,得等差数列{ a n }前n 项求和公式:S n =(a 1+ a n )×n ÷2. 这种求和方法叫做倒序相加法.⏹ 等比数列是后一项与前一项的商(后一项除以前一项)为一个固定的数的数列,这个商叫做公比,记作q ,即a 2÷1a = a 3÷a 2= a 4÷a 3=……= a n ÷1n a -=q . 由公比的定义,可以推出等比数列{ a n }的通项公式:11n n a a q -=. 等比数列的前n 项和:S n =1(1)1na q q--等比数列{ a n }的前n 项和:S n =a 1+a 2+……+a n ①等号两边同时乘以公比q ,得到qS n =qa 1+qa 2+…+qa n ,即qS n =a 2+a 3+……+a n +a n+1 ②①-②得(1-q )S n = a 1- a n+1,而a n+1=q n a 1,得到等比数列{ a n }前n 项求和公式:(1-q )S n =(1- q n)a 1,即S n =1(1)1na q q--.这种求和方法叫做错位相减法. ⏹ 数列求和除了前面介绍的倒序相加法和错位相减法外,在求数列和时,经常应用“裂项法”.“裂项法”的基本思想是()()()112211n n n n n a a a a a a a a ---=-+-++-+ . 这个方法可以简化计算过程,其最基本的形式是111(1)1n n n n =-+-,例如:11111 122334899101111111111()()()()()12233489910191.1010+++++⨯⨯⨯⨯⨯=-+-+-++-+-=-= 2.新的运算以四则运算为基础,可以定义新的运算,例如:用符号&表示一个二元运算:35a &b a b b =⨯⨯⨯+,对于这个&运算,446577337&3=+⨯⨯⨯=.可以验证,当a b ≠时,a&b b&a≠,即没有交换律.3.运算能力做有理数四则运算题目,当运算式子中有带分数、假分数、小数甚至百分数、大小括号和繁分数,即式子比较复杂时,有些同学很难给出正确解答. 做这种题目,需要多练习,细心严谨,才能正确和快速给出答案. 除此之外,如何避免出错呢?这里介绍几个注意要点,供读者参考.●先乘(除)后加(减),是指运算式子中,只有一个“加”和一个“乘”时应当遵守的规则,例如:3124491136111121107878-⨯=-⨯=-=-先做乘运算. 当算式同时有括号、多个乘和多个加时,在同级运算中,如何确定运算次序呢?建议的原则是:第一,使运算和随后的运算尽量“整数化”,遇到分数,尽量转化为分母更小一些的分数;第二,使运算式子尽量“简洁化”,如将有的除法转换为乘法,或者将带分数、小数等转化为既约分数等,但是注意不要增加后面运算的难度;第三,建立你自已的原则来确定运算的顺序,例如:你的原则是先将所有的带分数都化为假分数,哪怕实际运算时要复杂一些,也没有关系. 因为运算时“心中有序”了,习惯了,就不易出现错误,这点很重要.●计算的每一步骤,即每个等号后为一个步骤,所做运算不易太多,确保每个步骤的运算都是比较简单的运算,步步为营,稳答稳扎. 计算一道较为复杂的四则计算题时,要大致浏览一下,看看题目有何特点,以便确定计算的顺序和策略.●做计算题,难免出现错误,重要的是需要掌握一些查错法,例如“估值”和“消9”查错法等,很简单,多数情况很起作用. 但需要注意,它们仅仅是查错法,不是查对法.四则运算是小学数学重要内容,是其他复杂运算的基础,计算要准确和快速,是小学学好数学和在“华杯赛”中取得好成绩的要求.小学高年级学生要善于根据数的特征,灵活运用运算定律和性质,选择恰当的方法进行计算. 长此以往,可以全面提高学生的计算能力. 计算能力不仅是学生学好数学的基础,更是学好数学的保证(三)例题讲解1.选择题。
华杯讲义

2015 年华杯初赛冲刺班·高年级组·习题册解析
人.
若已知全班共有女生 31 人,那么有直尺的女生有 【考点】计算
【分析】设三角板男 a 人,三角板女 b 人,直尺男 c 人,直尺女 d 人;则有:
a b c d 50 c d 28 d 14 31 28 50 23 人 a 14 b d 31
5
学而思培优北京分校∙小学理科教研组
2015 年华 华杯初赛冲刺 刺班·高年级 级组·习题册 册解析
【考点】几何 【分析】将 将阴影部分进 进行如图所示 示的分割,分 分割后恰好可 可以拼接到一 一个等边三角形中(如图) ,这个三 角形是大正六边形 形的六分之一 一,因此阴影 影部分的面积 积为 720
24 1.8 平方厘米 4
15. 如右图所示,梯形 ABCD 的面积为 117 平方厘米, AD∥BC , EF = 13 厘米, MN = 4 厘米,又已
知 EF⊥MN 于 O,那么阴影部分的总面积为_________平方厘米.
A M
E O
D N
B
【出处】第十六届华杯赛高年级组初赛第 9 题 【答案】65 【分析】四边形 ENFM 的面积为:
9.
(13 届华杯初赛) 如图所示,甲车从 A,乙车从 B 同时相向而行,两车第一次相遇后,甲车继续行驶 4 小时到达 B, 而乙车只行驶了 1 小时就到达 A,甲乙两车的速度比为 .
【答案】1:2 【分析】设甲、乙的速度分别为; v甲 和 v乙 ,则 BC 4v甲 , AC v乙 , 根据相遇时时间相等列式:
2015 年华杯初赛冲刺班·高年级组·习题册解析
高年级组习题册
1. 分数计算
华杯赛赛前培训

第一讲应用题专题串讲涉及和差倍问题、鸡兔同笼、盈亏、倒推法、行程例1.开学前6天,小明还没做寒假数学作业,而小强已完成了60道题,开学时两人都完成了数学作业.在这6天中,小明做的题目是小强的3倍,他平均每天做()道题.(A)6 (B)9 (C)12 (D)15[答疑编号506253010101]【答案】D【解答】在6天时间里小明比小强多做60道题,是小强做题数目的3倍,由此可知,小强做了60÷(3-1)=30道,小明平均每天做30×3÷6=15道.例2.已知被除数比除数大78,并且商是6,余数是3,求被除数与除数之积.[答疑编号506253010102]【答案】1395【解答】为了表述方便,我们用这样一个算式表达题意:A÷B=6 (3)A是B的6倍多3,那么78就是B的5倍多3,所以B=(78-3)÷5=15A=15+78=93两数的乘积为93×15=1395。
例3.今年甲、乙俩人年龄的和是70岁.若干年前,当甲的年龄只有乙现在这么大时,乙的年龄恰好是甲年龄的一半.问:甲今年多少岁?[答疑编号506253010103]【答案】42【解答】两个人之间的年龄差是不变的,我们将甲乙两人的年龄差设为K,在甲的年龄是乙现在这么大时,也就是在K年前,那时候甲的年龄比乙大K,且甲的年龄是乙的2倍.由此可知,当时甲的年龄为2K,乙的年龄为K,那么,今年甲的年龄就是3K,乙的年龄为2K.可以得出K=70÷(3+2)=14所以甲的年龄为14×3=42岁.例4.小龙的妈妈比爸爸小3岁,妈妈今年的年龄是小龙今年的9倍,爸爸明年的年龄是小龙明年的8倍,那么爸爸今年()岁.[答疑编号506253010104]【答案】39【解答】我们将小龙的年龄看作1份,那妈妈今年的年龄就9份.明年小龙的年龄是1份多1,爸爸明年的年龄就是8份多8,爸爸今年的年龄应为8份多7.由题意可知:8份多7比9份大3,所以1份为4,那么爸爸今年的年龄就是4×9+3=39岁.例5.丫丫一家3口,加上丫丫的表弟,今年四人年龄之和为95岁.爸爸比妈妈大4岁,丫丫比表弟大3岁.8年前,他们的年龄之和为65岁.则爸爸今年()岁.[答疑编号506253010105]【答案】42【解答】8年前如果丫丫表弟已经出生的话,他们的年龄和应为95-8×4=63,由此可知当时离表弟出生的时间还有65-63=2年.丫丫比表弟大3岁,当时应为3-2=1岁.8年前爸爸妈妈年龄和为65-1=64岁,爸爸当时应为(64+4)÷2=34岁,那么,爸爸今年是34+8=42岁.例6.两条纸带,较长的一条为23cm,较短的一条为15cm.把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是()cm.(A)6 (B)7 (C)8 (D)9[答疑编号506253010106]【答案】B【解答】两条纸带长度差为:23-15=8cm,都剪下同样长的一段后,这个差是不变的,此时这个差应该不少于较短纸带长度的1倍,因此,较短纸带的长度应不大于8cm,所以剪下的长度至少为7cm.例7.三堆小球共有2012颗,如果从每堆取走相同数目的小球以后,第二堆还剩下17颗小球,并且第一堆剩下的小球数是第三堆剩下的2倍,那么第三堆原有()颗小球.[答疑编号506253010107]【答案】665【解答】我们把第三堆剩下的小球个数看做“1份”,将每堆中取走的小球的个数用△来表示,那么第一堆原来的个数就是“2份+△”,第二堆原来的个数就是“17+△”,第三堆原来的个数就是“1份+△”,由三堆小球共有2012颗,可以得出:2份+△+17+△+1份+△=2012第三堆原来的小球有(2012-17)÷3=665颗.例8.商店进了一批钢笔,如果用零售价7元卖出20支与用零售价8元卖出15支所赚的钱数相同.那么每支钢笔的进货价是多少元?[答疑编号506253010108]【答案】4【解答】20支卖7×20=140元,15支卖8×15=120元,少了140-120=20元但所赚钱数相同,这是因为卖出的钢笔少了20-15=5支,总的进价少了5支的钱,所以每支进价为20÷5=4元.例9.某水池有A,B两个水龙头.如果A,B同时打开需要30分钟可将水池注满.现在A和B同时打开10分钟,即将A关闭,由B继续注水80分钟,也可将水池注满.如果单独打开B龙头注水,需要()分钟才可将水池注满.[答疑编号506253010109]【答案】120【解答】由题意可知:30A+30B=10A+10B+80B可得A=3B所以B龙头单独注水需要30×3+30=120分钟.例10.抽屉里有若干个玻璃球,小军每次操作都取出抽屉中球数的一半再放回一个球.如此操作了2012次后,抽屉里还剩有2个球.那么原来抽屉里有()个球.[答疑编号506253010201]【答案】2【解答】用倒推法可知在第2012次操作之前有(2-1)×2=2个球,一次操作之后数目不变,所以原来抽屉里就有2个球.例11.鸡兔同笼,共有头51个,兔的总脚数比鸡的总脚数的3倍多4只,那么笼中共有兔子()只.[答疑编号506253010202]【答案】31【解答】由这道题目,我们介绍一下分组法,我们可以先去掉一只兔,使兔的脚减少4只,因此兔的脚是鸡的脚数目的3倍整,此时,鸡兔共有50只.很容易发现当有3只兔和2只鸡时,兔脚是鸡脚数目的3倍,我们将(3兔+2鸡)看作一组,在50只鸡兔中共有50÷(3+2)=10组,那么兔共有3×10+1=31只.例12.体育馆正在进行乒乓球单打、双打比赛,双打比赛的运动员比单打的运动员多4名,比赛的乒乓球台共有13张,那么双打比赛的运动员有()名.[答疑编号506253010203]【答案】20【解答】这是一个鸡兔同笼问题,我们可以用假设法来解决.假设13张球台上进行的全是双打比赛,那么双打比赛的运动员有4×13=52人,单打比赛的人数为0,双打比单打的多了52人,比实际的差额多了52-4=48人。
华杯赛讲义初二组第四讲平面直角坐标系及平面几何的性质和判定
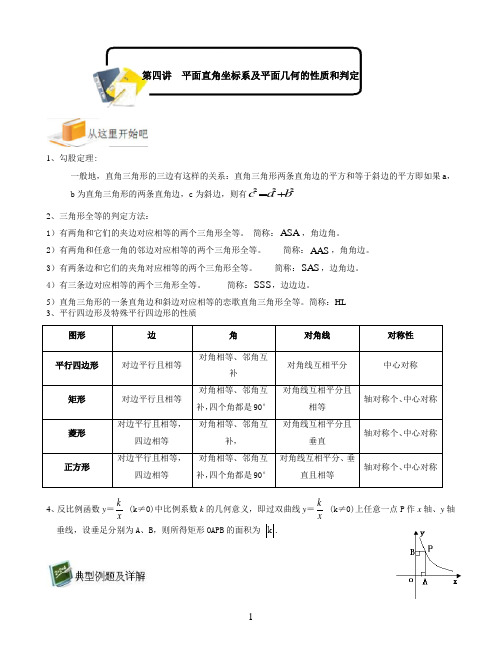
第四讲 平面直角坐标系及平面几何的性质和判定1、勾股定理:一般地,直角三角形的三边有这样的关系:直角三角形两条直角边的平方和等于斜边的平方即如果a ,b 为直角三角形的两条直角边,c 为斜边,则有222c a b=+2、三角形全等的判定方法:1)有两角和它们的夹边对应相等的两个三角形全等。
简称:ASA ,角边角。
2)有两角和任意一角的邻边对应相等的两个三角形全等。
简称:AAS ,角角边。
3)有两条边和它们的夹角对应相等的两个三角形全等。
简称:SAS ,边角边。
4)有三条边对应相等的两个三角形全等。
简称:SSS ,边边边。
5)直角三角形的一条直角边和斜边对应相等的恋歌直角三角形全等。
简称:HL 3、平行四边形及特殊平行四边形的性质图形 边 角对角线 对称性 平行四边形对边平行且相等对角相等、邻角互补对角线互相平分 中心对称矩形 对边平行且相等 对角相等、邻角互补,四个角都是90° 对角线互相平分且相等 轴对称个、中心对称菱形 对边平行且相等,四边相等 对角相等、邻角互补, 对角线互相平分且垂直轴对称个、中心对称正方形 对边平行且相等,四边相等对角相等、邻角互补,四个角都是90°对角线互相平分、垂直且相等轴对称个、中心对称4、反比例函数y =k x (k ≠0)中比例系数k 的几何意义,即过双曲线y =kx(k ≠0)上任意一点P 作x 轴、y 轴垂线,设垂足分别为A 、B ,则所得矩形OAPB 的面积为 k .1. 已知在三角形 ABC 中, 3 AB = 4BC , BE 是 ∠ABC 的角平分线, 且 E 在 AC 上.过 C 作 BE 的垂 线, 垂足为 D . 如果 ∆BCD 的面积为 3, 则三角形 ABC 的面积为( ). (A )419 (B )16 (C )4 (D )8【解析】:D.延长CD 交AB 于点F ,则有∠FBD=∠CBE ,BD=BD ,∠FDB=∠CDB ,所以△FDB ≌△CDB ,所以BF=BC=43AB ,62==BCD BCF S S △△,而84343===ABC ABC BFC S S S AB BF △△△,所以,所以2、 如 右 图 ,已 知 AE = DE = 5, AB = CD ,BC = 4 ,∠E = 60︒ ,∠A = ∠D = 90︒, 那么五边形 ABCDE 的面积是( ) (A )26(B )36(C )27 (D )37【解析】:D.连接BE ,CE 并延长BC 交EA 、EB 的延长线于点F 、G ,过点E 做EH ⊥BC 于点H,由题意可得△ABE ≌△DEC ,所以EH 平分∠FEG ,所以△EFG 是等腰△,又因为∠AED=60°5,所以△EFG 为等边△,设AF=DG=x ,则FG=GC=2x ,此时有4+4x=5+x ,得x=31,代入可得面积为373、在直角三角形ABC 中, 三条边的长度均为整数, 分别记为a , b , c , 其中c 是斜边长。
华杯赛初赛备考讲义含解析(小学高年级组)

, , , , 华杯赛初赛备考讲义含解析(小学高年级组)第一节 计算、几何精讲考点概述计算考点 一、整数、小数、分数的基本计算; 二、整数、小数、分数的常见巧算方法;(凑整、抵消、约分、提取公因数、裂项) 三、分数比较大小;(通分子、通分母、通分差、取倒数) 四、分数与循环小数.(纯循环小数化分数、混循环小数化分数)几何考点 一、基本面积公式;(长方形、正方形、三角形、平行四边形、梯形、圆、扇形) 二、割补法计算面积;三、等积变换; 四、各类几何模型;(等高模型、蝴蝶模型、共角模型、一半模型、沙漏模型、金字塔模型、燕尾模型等) 五、勾股定理与弦图; 六、立体几何.(基本公式、展开图、三视图)真题精讲例题1. 将 5.425 ⨯ 0.63 的积写成小数形式是.(2007 年 12 届)【答案】 3.4180 .【解答】 5.425=5425 = 5420 ,所以 5.425 ⨯ 0.63= 5420 ⨯ 63 = 34146 =34176 ,999 999 999 100 9990 9990而 4176 =1 ⨯ 4176 =1 ⨯ 4 180 =1⨯ 4.180 = 0.4180 ,所以 5.425 ⨯ 0.63 = 3.4180 . 9990 10 999 10 999 10例题2. 从 1 1 1 1 1中去掉两个数,使得剩下的三个数之和与 6最接近,去掉的两个数是 ().2 3 4 5 67(A ) 1 , 1 (B ) 1 , 1 (C ) 1 , 1 (D ) 1 , 1(2010 年 15 届)25263534【答案】D . 【解答】通分1 = 210 , 1 = 140 , 1 = 105 , 1 = 84 , 1 = 70 , 6 = 360 .2 4203 4204 4205 4206 4207 420显然,210+84+70=364 最接近 360.练习1. 2012.25 ⨯ 2013.75-2010.25 ⨯ 2015.75=.(2013 年 18 届)2 , 2 , 2 , 2 , 2 , 2 ,…,而 1 = 2,所以从23 5 7 9 11 13 1000 20002001 【答案】7.【解答】记 x =2010.25,y = 2013.75,则原式= (x + 2) y - x ( y + 2) = 2( y - x ) = 7 .练习2. 两数之和与两数之商都为 6,那么这两数之积减这两数之差(大减小)等于()(2011 年 16 届)(A ) 26 4 (B ) 5 1 (C ) 6 (D ) 67 7 7 49 【答案】D .【解答】设两数分别为 x 与 6x ,那么 7x =6,x = 6 ,所以这两个数分别为 6 与 36 ,两数之积为216 ,7两数之差为 30,216 - 30 = 6 .7749749 7 49练习3. 若 a =2005 ⨯ 2006 , b = 2006 ⨯ 2007 , c = 2007 ⨯ 2008,则有().2007 ⨯ 2008 2008 ⨯ 2009 2009 ⨯ 2010(A ) a > b > c (B ) a > c > b (C ) a < c < b (D ) a < b < c (2008 年 13 届) 【答案】D .【解答】比较 a 与 b ,两边同时可以约掉2006,而2005<2007,所以 a < b , 20082007 2009比较 b 与 c ,两边同时可以约掉 2007 ,而 2006 < 2008,所以 b < c ,故选D . 2009 2008 2010练习4. 在 1 , 3 , 5 , 7 , 9 , 11,…中,从开始,1 与每个数之差都小于 1 .3 5 7 9 11 131000(2004 年 9 届)【答案】 1999 .2001【解答】这一排分数与 1 的差分别为开始,就开始小于 11000,所以答案为 1999 .2001例题3. 如图所示,AB 是半圆的直径,O 是圆心,AC = CD = DB ,M 是 CD 的中点,H 是弦 CD 的中点.若N 是OB 上一点,半圆的面积等于12 平方厘米,则图中阴影部分的面积是平方厘米.(2009 年14 届)MC DHA O N B【答案】2.【解答】如下图,可以利用等积变换变成一个扇形:MC DHA O B因为AC = CD = DB ,M 是CD 的中点,所以CM 是半圆弧的1,所以阴影扇形面积为半圆面积的1,6 6为2.例题4. 大正方形格板是由81 个1 平方厘米的小正方形铺成,B、C 是两个格点.若请你在其它的格点中标出一点A,使得△ABC 的面积恰好等于3 平方厘米,则这样的A 点共有个.(2010 年15 届)CB(A)6 (B)5 (C)8 (D)10【答案】C.【解答】方法一:从最上面的水平线开始将水平线分别记为第1、第2、…、第10 条水平线,每条水平线均由左至右判断哪个格点符合题目要求.以此穷举法可以得到:第1 条水平线上没有格点符合要求,第2 条水平线上仅有A7 符合要求.如右图所示,类似可以得到格点A2,A1,A6符合要求,对称地,可以得到A ,A ,A ,A 符合要求.故答案是C.5 4 3 8方法二:先通过尝试找到A ,然后找到经过A ,而且平行于BC 的线,画出来,那么这条线经过的格1 1点都是符合要求的(等积变换),这样可以得到A ,A ,A ,A ,然后利用对称性,可以得到A ,A ,A 3 ,A8.故答案是C.2 1 6 7 5 4练习5. 正方形ABCD 的面积为9 平方厘米,正方形EFGH 的面积为64 平方厘米.如图所示,边BC 落在EH 上.已知三角形ACG 的面积为6.75 平方厘米,则三角形ABE 的面积为平方厘米.(2012 年17 届)【答案】2.25.【解答】如图:连接EG,由于AC 和EG 都是对角线,因此相互平行,所以三角形ACG 的面积等于三角形ACE 的面积,所以S△ABE =S△ACE-S△ABC=6.75 -4.5=2.25 .练习6. 右图ABCD 是平行四边形,M 是DC 的中点,E 和F 分别位于AB 和AD 上,且EF 平行于BD.若三角形MDF 的面积等于5 平方厘米,则三角形CEB 的面积等于()平方厘米.(2013 年18 届)(A)5 (B)10 (C)15 (D)20【答案】B【解答】如右图,连接FC,BF,DE.因为M 是DC 的中点,三角形MDF 的面积等于5 平方厘米,所以由三角形面积公式可知:三角形CDF的面积等于10 平方厘米.两个三角形,同底等高,面积则相等.由此可知:由DC / / AB ,得△CEB 的面积=△BDE 的面积;由EF / /B D ,得△BDE 的面积=△BDF 的面积;由AD / /B C ,得△BDF 的面积=△C DF 的面积,所以三角形CEB 的面积等于10 平方厘米.练习7. 如右图所示,梯形ABCD 的面积为117 平方厘米.AD∥BC,EF = 13 厘米,MN = 4 厘米,又已知EF⊥MN 于O,那么阴影部分的总面积为平方厘米.(2011 年16 届)【答案】65.【解答】四边形 EMFN 的面积= 1⨯ EF ⨯ MN =26 .(对角线相互垂直的四边形面积为对角线相乘再除2以 2),又根据蝴蝶模型, S △ABM =S △EFM , S △DCN =S △EFN ,所以空白部分总面积为四边形 EMFN 的面积 的 2 倍,为 52,所以阴影部分总面积=117-52=65.练习8. 右图由 4 个正六边形组成,每个面积是 6,以这 4 个正六边形的顶点为顶点,可以连接面积为 4 的等边三角形有 个.(2011 年 16 届) 【答案】8.【解答】如图,将原图按三角形格线分割,于是我们要找的其实是由 4 个小正三 角形组成的正三角形,注意顶点必须六边形顶点,箭头朝上的有四个(如图), 根据对称性,箭头朝下的也有 4 个,共 8 个.例题5. 如图,大小两个半圆,它们的直径在同一直线上,弦 AB 与小圆相切,且与直径平行,弦 AB 长12 厘米.图中阴影部分的面积是 平方厘米.(圆周率取 3.14)(2004 年 9 届)AB【答案】56.52.【解答】设大圆半径为 R ,小圆半径为 r ,那么阴影部分面积为 1 π R 2 - 1 π r 2 = 1π ( R 2 - r 2 ),所以关 2 2 2 键是求出半径的平方差.如图,过大圆圆心作 AB 的垂线,连接圆心与 B 点,由勾股定理可得,62 + r 2 = R 2 ,所以 R 2 - r 2 = 36 .A6 BrR那么阴影部分面积= 1⨯ 3.14 ⨯ 36=56.52 .2例题6. 一个长方体的长、宽、高恰好是 3 个连续的自然数,并且它的体积的数值等于它的所有棱长之和的数值的 2 倍,那么这个长方体的表面积是 .(2007 年 12 届)(A )74(B )148(C )150(D )154【答案】B.【解答】设这三个连续的自然数分别为x-1,x,x+1,那么可以列出方程:(x-1)x(x+1)=2(x-1+x +x +1)⨯ 4 ,化简后为:x(x2 -1)= 24x ,由于x 肯定不是0,所以两边同时约掉x 后,可得方程:x2 -1= 24 ,所以x = 5 ,这三个连续的自然数分别为4、5、6,那么表面积为:(4⨯5 +5⨯ 6 +4⨯6)⨯ 2=148 .练习9. 如图所示,是一个直圆柱形状的玻璃杯,一个长为12 厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内.当吸管一端接触圆柱下底面时,另一端沿吸管最少可露出上底面边缘2 厘米,最多能露出4 厘米.则这个玻璃杯的容积为立方厘米.(取π= 3.14 )(提示:直角三角形中“勾6、股8、弦10”)(2006 年11 届)CA B【答案】226.08.【解答】沿AC 放置时,另一端沿吸管露出最少,为2 厘米,说明AC=12-2=10 厘米,沿BC 放置时,另一端沿吸管露出最多,为4 厘米,说明BC=12-4=8 厘米,根据勾股定理,AB2 = 102 - 82 = 36 ,所=9π⨯8=72π=226.08 .以AB=6,底面半径为3,所以V杯练习10. 右图中,AB 是圆O 的直径,长6 厘米,正方形BCDE 的一个顶点E 在圆周上,∠ABE = 45︒.那么圆O 中非阴影部分的面积与正方形BCDE 中非阴影部分面积的差等于平方厘米(取π= 3.14 ).(2013 年18 届)【答案】10.26【解答】因为∠ABE = 45︒,∠EAB 所对的圆弧和∠ABE 所对的圆弧弧度相等,且圆弧的直径相同,故∠EAB = 45︒,三角形ABE 是直角三角形.由勾股定理:2BE2 =AB2 = 62 = 36 (平方厘米),正方形BCDE 的面积=BE2 =18 (平方厘米).圆O 的面积-正方形BCDE 的面积=(圆非阴影部分的面积+圆和正方形相交部分的面积)-(正方形BCDE 中非阴影部分面积+圆和正方形相交部分的面积)=圆非阴影部分面积-正方形非阴影部分面积=32 ⨯π-18 = 28.26 -18 =10.26 (平方厘米).练习11. 图中的方格纸中有五个编号为1,2,3,4,5 的小正方形,将其中的两个涂上阴影,与图中阴影部分正好组成正方体的展开图,这两个正方形的编号可以是().(A)1,2 (B)2,3 (C)3,4 (D)4,5(2012 年17 届)【答案】D【解答】注意到展开图中不能出现“田”字结构,因此排除掉ABC,选D.练习12. 如图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD.取AB 的中点M 和BC 的中点N,减掉△MBN 得五边形AMNCD.则将折叠的五边形AMNCD 纸片展开铺平后的图形是.(2006 年11 届)D C D CNNA MB A M【答案】D.【解答】注意对折方向,可以判断B 点是原正方形中心,因此是中心被掏空的形状,再注意减掉的形状是三角形,也就是展开后,横竖四等分以后,每一部分缺的都是三角形,结合这两点,答案为D.课后作业:1. 计算:⎡⎛0.8 +1 ⎫⨯ 24 + 6.6⎤÷9- 7.6 =().(2012 年17 届)⎢ 5 ⎪ ⎥14⎣⎝ ⎭ ⎦(A)30 (B)40 (C)50 (D)60【答案】B.【解答】原式= [1⨯ 24 +6.6]⨯14 - 7.6 = 30.6 ⨯14 - 7.6=47.6 - 7.6=40 .9 92. 算式1 -27+ 2 ⨯ 0.3的值为.(2010 年15 届)0.25 + 3 ⨯1 1.3 - 0.44【答案】1 8.211 -2 5 3【解答】7 +2 ⨯ 0.3= 7 + 5 =5+2=18.0.25 + 3 ⨯1 1.3 - 0.441+39 7 3 214 4 103. 下面有四个算式:①0.6 + 0.133=0.733 ;②0.625= 5 ;8③ 5+3=5 + 3=8=1;14 2 14 + 2 16 2④3 3 ⨯ 4 1 =14 2 .7 5 5其中正确的算式是()(2009 年14 届)(A)①和②(B)②和④(C)②和③(D)①和④【答案】B.【解答】①式错,因为0.6 并不循环,②式对,③式错,不符合分数加法规则,④式对,因此选B.4. 题目中的图是一个正方体木块的表面展开图.若在正方体的各面填上数,使得对面两数之和为7,则A、B、C 处填的数各是、、.(2004 年9 届)提示:注意相对两个面展开后的位置.C 2B 1A 4【答案】6、5、3.【解答】注意到,展开图中的形状,黑色两个面在合上后是相对的,所以在原图中,A 和1 相对,B 和2 相对,C 和4 相对,所以A=6,B=5,C=3.5. 如图,ABCD 是个直角梯形(∠DAB=∠ABC=90o).以AD 为一边向外作长方形ADEF,其面积为6.36 平方厘米,连接BE 交AD 于P,再连接PC.则图中阴影部分的面积是平方厘米.(2006年11 届)提示:等积变换.(A)6.36 (B) 3.18 (C)2.12 (D)1.59 【答案】B.【解答】连接BD、AE,利用等积变换,S△PDC =S△PDB,所以S阴=S△EDB,再次利用等积变换,可以得到S△EDB =S△EDA,而三角形EDA 面积是长方形ADEF 的一半,为3.18,所以以S阴=S△EDB=S△EDA=3.18 .6. 一块长方形的木板,长为90 厘米,宽为40 厘米,将它锯成2 块,然后拼成一个正方形,你能做到吗?请画出分割线.(2004 年9 届)提示:阶梯形.【答案】如图,沿粗线剪开即可..【解答】图形面积为90×40=3600 平方厘米,因此拼成的正方形边长为60 厘米,我们把这个图形画出来与原图形进行比较:3020两条边的差分别为30 和20,因此把90 厘米那边30 厘米一截,40 厘米那边20 厘米一截,分成6 块之后,稍作尝试即可.7. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有()条直线互相平行.(A)0 (B)2(C)3 (D)4(2014 年19 届)【答案】C.【解答】当4 条直线都互相平行时,平面被分成5 个部分,不满足要求,因此最多只能3 条直线互相平行.构造:有3 条直线互相平行,另外一条直线与它们都互相垂直,此时平面被分成8 个部分.8. 如右图所示,AF = 7 cm,DH = 4 cm,BG = 5 cm,AE =1c m.若正方形ABCD内的四边形EFGH 的面积为78 cm2,则正方形的边长为()cm.(A)10 (B)11 (C)12 (D)13(2014 年19 届)提示:类比弦图.【答案】C.【解答】用竖直线和水平线将正方形ABCD 分割为如右图所示的5 个长方形,中间长方形的面积是4⨯ 3=12 ,所以,正方形的面积= (78-12)⨯ 2 +12=144 ,正方形的边长是12.9. 如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( ).提示:分割图形.(A)1 (B)2 (C)2 (D)52 3 5 12(2010 年15 届)【答案】A.【解答】由图可知,左上角和右上角的阴影部分的面积分别恰等于一个平行四边形内正六边形的面积,因此阴影部分的面积占平行四边形面积的1 . 2第二节数论、应用题精讲考点概述数论考点五、数的整除性相关知识六、质数合数七、约数与倍数八、余数问题应用题考点一、常考应用题类型(和差倍应用题,比例应用题,经济问题,浓度问题等)1. 画线段图帮助解题2. 列方程解应用题二、行程问题:1. 行程问题常见类型(相遇问题,追及问题,火车问题,流水行船问题,环形路线问题,多次相遇与追及问题等)2. 画线段图(形象直观地呈现题意,便于对题目条件进行分解与组合,挖掘隐含条件)3. 方程与比例解行程问题真题精讲例1.在一个圆周上有70 个点,任选其中一个点标上1,按顺时针方向隔一个点的点上标2,隔两个点的点上标3,再隔三个点的点上标4,继续这个操作,直到1,2,3,…,2014 都被标记在点上.每个点可能不只标有一个数,那么标记了2014 的点上标记的最小整数是.(2014 年19 届)【答案】5【解析】将70 个点中某个点为起始点,然后按顺时针方向依次将这70 个点记为第1 个,第2 个,第3 个,…,第70 个,用a 表示第a 个点上标记的数字是i.i i依题意a1= 1 ,a2 = 3 ,a3 = 6 ,a4 = 10 ,…,且按规律得:a 2014 =1+ 2 + 3 + + 2014 =2014 ⨯ 2015=202910522029105 = 28987 ⨯ 70 +15 ,而a5 = 15 ,因此第15 个点上标记的最小整数为5.例2.若a = 1515 15 ⨯ 333 3 ,则整数a 的所有数位上的数字和等于.(2008 年13 届)1004个15 2008个3(A)18063 (B)18072 (C)18079 (D)18054【答案】B【解析】a = 505 05 ⨯ 999 9 ,利用结论A⨯ 999 9 的数字和为9n ,可知a 的数字和为18072,选B.1004个5 2008个9 n个9练习1.恰有20 个因数的最小自然数是().(2010 年15 届)(A)120 (B)240 (C)360 (D)432【答案】B.【解析】因为20=2×10=4×5=2×2×5,因此,具有20 个因数的自然数的质因数分解形式只有19 ,⨯9 ,3 ⨯4 ,⨯⨯ 4 这4 种,对应类型的最小自然数分别为219 ,3⨯ 29 ,33 ⨯ 24 ,3⨯5⨯ 24 ,其中最小的是240,选B.练习2.在19、197、2009 这三个数中,质数的个数是().(2009 年14 届)(A)0 (B)1 (C)2 (D)3【答案】C【解析】质数判定,检验所有平方小于2009 的质数即可.练习3.若连续的四个自然数都为合数,那么这四个数之和的最小值为().(2011 年16 届)(A)100 (B)101 (C)102 (D)103【答案】C【解析】最小连续4 个合数为24,25,26,27,它们之和为102.例3.一个奇怪的动物庄园里住着猫和狗,狗比猫多180 只.有20%的狗错认为自己是猫;有20%的猫错认为自己是狗.在所有的猫和狗中,有32%认为自己是猫,那么狗有()只.(2012 年17 届)(A)240 (B)248 (C)420 (D)842【答案】A【解析】设猫有x 只,狗有y 只,则认为自己是猫的动物共有80%x + 20% y 只,从而80%x + 20%y = 32%(x +y) ,可以得到4x =y ,再结合狗比猫多少180 只,可得x = 60 ,y = 240 ,从而狗有240 只,选A.例4.一只青蛙8 点从深为12 米的井底向上爬,它每向上爬3 米,因为井壁打滑,就会下滑1 米,下滑1 米的时间是向上爬3 米所用时间的三分之一.8 点17 分时,青蛙第二次爬至离井口3 米之处,那么青蛙从井底爬到井口时所花的时间为()分钟.(2013 年18 届)(A)22 (B)20 (C)17 (D)16【答案】A【解析】记青蛙每向上爬行1 米,所用时间为t 分钟,则下滑1 米的时间是向上爬3 米所用时间的三分之一,也为t 分钟.当青蛙刚爬至离井口3 米时,离井底9 米,所用时间是17 分钟.将2 米分为1 段,则一段所需时间为4t,第一次离井口3 米的时候是,向上爬了3 段之后再向上爬了3 米,第二次离井口3 米的时候是,向上爬了4 段之后再向上爬了1 米,此时总共花了17t 的时间,此时为8 点17,过了17 分钟,所以t=1,即每分钟1 米.向上爬出井口的时候,总共是向上爬了5 段,然后向上爬了2 米,总共花了22 分钟.练习5.两条纸带,较长的一条为23cm,较短的一条为15cm.把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是( )cm.(2010 年15 届)(A)6 (B)7 (C)8 (D)9【答案】B.【解析】设剪下的长度为x cm,那么有:23 -x ≥ 2(15 -x) ,解得x ≥ 7 ,因此剪下的长度至少为7cm,选B.练习6.某次考试有50 道试题,答对一道题得3 分,答错一道题扣1 分,不答题不得分.小龙得分120 分,那么小龙最多答对了()道试题.(2014 年19 届)(A)40 (B)42 (C)48 (D)50【答案】B【解析】得分120 分,说明至少需要答对40 道题,其余10 道题不答,满足题意.若答对41 道题,答错3 道题,其余题不答,此时得分也是120 分.若答对42 道题,答错6 道题,其余题不答,此时得分也是120 分.若答对43 道题,得分依然为120 分,需要再答错9 道题,此时至少需要有52 道题,52>50,因此不满足题意.解法二:设作对x 题,做错y 题,未答z 题,则有:3x - y =120, x +y +z = 50,合并两个等式,得到:4x =170 - z, x = 42 +2- z ,x 是非负整数,尽可能大,故z = 2, x = 42 ,即小4龙最多答对42 道试题.练习7.两个水池内有金鱼若干条,数目相同.亮亮和红红进行捞鱼比赛,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3:4;捞完第二个水池内的金鱼时,亮亮比第一次多捞33 条,与红红捞到的金鱼数目比是5:3.那么每个水池内有金鱼()条.(2010 年15 届)(A)112 (B)168 (C)224 (D)336【答案】B【解析】这是一道工程问题的变形,每个水池内有金鱼33 ÷ ( 5-3) =168 (条).5 + 3 4 + 3解法2:可以认为是比例应用题,设亮亮第一次捞到3n 条,则红红第一次捞到4n 条,依题意,有3n + 33=5,解得n=24,因此水池内共有金鱼7n=168 条.4n - 33 3练习8.用若干台计算机同时录入一部书稿,计划若干小时完成.如果增加3 台计算机,则只需原定时间的75%;如果减少3 台计算机,则比原定时间多用5小时.那么原定完成录入这部书稿的时间是()6小时.(2011 年16 届)(A)5 3【答案】A (B)103(C)56(D)116【解析】增加3 台计算机,则只需原定时间的75%,所以原先有9 台计算机;如果减少3 台计算机,则所需时间为原定时间的9=3,比原定时间多用了5小时,所以原定要5÷⎛3-1⎫=5小时.9 -32 6 6 2 ⎪ 32⎝ ⎭例6. 图中是一个玩具火车轨道,A 点有个变轨开关,可以连接 B 或者 C .小圈轨道的周长是 1.5 米,大圈轨道的周长是 3 米.开始时, A 连接 C ,火车从 A 点出发,按照顺时针方向在轨道上移动,同时 变轨开关每隔 1 分钟变换一次轨道连接.若火车的速度是每分钟 10 米,则火车第 10 次回到 A 点时用了 分钟.(2010 年 15 届)【答案】2.1【解析】根据条件,在小圈火车行驶一圈用时1.5 ÷10 = 0.15 分钟,在大圈火车行驶一圈用时3 ÷10 = 0.3 分钟.设回到 A 点时用时为 t 分钟,这样我们有下表:回到 A 的次数 1 2 3 4 5 6 7 8 910到 A 点用时 0.3 0.6 0.9 1.2 1.35 1.5 1.65 1.8 1.95 2.1经过的轨道ACACACABABABABABABAC下面我们给出一个一般的解答:设玩具火车绕小圈轨道 m 圈,绕大圈轨道 n 圈,则玩具火车运动路程是 S = 1.5m + 3n ,时间是1.5m + 3n .如果 ⎡1.5m + 3n ⎤ 是偶数,则变轨开关 AC 连通,如果 ⎡1.5m + 3n ⎤是奇数,则变轨开关 AC 10 ⎢ 10⎥ ⎢ 10⎥⎣⎦⎣⎦连通.我们寻找最小的 m + n ,使1.5m + 3n是偶数.无妨设 101.5m + 3n = 10K ,或 3m + 6n = 20K ,这里 K 是偶数,并且有 3 为约数,是玩具火车运动的时间,因此最小的 K 是 6.即求 m 和 n 使m + 2n = 40 .12 当 n =3,S AA C = 2S ABC = 12 ,故开始玩具火车绕大圈轨道 4 圈之后进入小圈,时间是 10= 1.2(分钟);当 n =4, m =5 时,⎡ 7.5 + 12 ⎤ = 1 , ⎡ 9 + 12 ⎤= 2 ,故玩具火车绕小圈轨道 6 之后再次进入大圈轨道, ⎢ 10 ⎥ ⎢ 10 ⎥3⎣⎦ ⎣ ⎦此时1.5m + 3n=1.5 ⨯ 6 + 3 ⨯ 4= 2.1 (分钟)(可以称为一个拟循环)1010将玩具火车再次进入大圈运行,运行圈数记为 n . n =3 时, 1.5 ⨯ 6 + 3 ⨯ 7= 3 (分钟),玩具火车应2210当再次进入小圈运行,运行圈数记为 m ,既然1.5 ⨯ 7> 1 > 1.5 ⨯ 6,故玩具火车绕小圈运行 7 圈后,应 210 10再次进入大圈运行,此时 1.5m + 3n = 1.5 ⨯13 + 3 ⨯ 7= 4.05 (分钟).10 10 将玩具火车再次进入大圈运行, 运行圈数记为 n .既然1.5 ⨯13 + 3 ⨯11 > 5 > 1.5 ⨯13 + 3 ⨯10 ,10 10故玩具火车绕大圈运行 4 圈后,应再次进入小圈运行,此时1.5m + 3n = 1.5 ⨯13 + 3 ⨯11 = 5.25 (分钟), 10 10则玩具火车绕大圈运行 5 圈后,1.5m + 3n = 1.5 ⨯18 + 3 ⨯11= 6 (分钟). 10 10结论玩具火车第 29 次回到 A 时, 变轨开关 AC 连通,即回到原始状态.练习9. 4 个整数中任意选出 3 个,求出它们的平均值,然后再求这个平均值和余下 1 个数的和,这样可以得到 4 个数:4、6、 5 1 和 4 2,则原来给定的 4 个整数的和为.(2009 年 14 届)3 3 【答案】10【解析】设 4 个整数分别为 a 、b 、c 、d ,则有a +b +c +d = 4 、 a + b + d + c = 6 、a + c + d + b = 5 1、 3 3 3 3b +c +d + a = 4 2,四式相加可得 2(a + b + c + d ) = 20 ,从而 a + b + c + d = 10 .3 3练习10. A 、B 、C 、D 、E 五个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小朋友:A →C ,B →E ,C →A ,D →B ,E →D .开始时 A 、B 拿着福娃,C 、D 、E 拿着福牛,传递完5 轮时,拿着福娃的小朋友是().(2009 年14 届)(A)C 与D (B)A 与D (C)C 与E (D)A 与B【答案】A【解析】A 和C 之间的传递以2 为周期,B、E、D 之间的传递以3 为周期,所以5 轮之后,A 和C 之间的福娃最后在C 手中,B、E、D 之间的福娃最后在D 手中,所以最后拿着福娃的是C 与D.练习11. 某学校组织一次远足活动,计划10 点10 分从甲地出发,13 点10 分到达乙地,但出发晚了5 分钟,却早到达了 4 分钟.甲乙两地之间的丙地恰好是按照计划时间到达的,那么到达丙地的时间是().(2014 年19 届)(A)11 点40 分(B)11 点50 分(C)12 点(D)12 点10 分【答案】B【解析】从10 点10 分到13 点10 分共有3 个小时,比计划时间少用9 分钟,即每小时少用3 分钟,少用5 分钟的时候即是到达B 点的时间.此时需要5÷(3÷60)=100 分钟,即1 小时40 分钟,所以到达B 点的时间是11 点50 分.练习12. 甲、乙两车分别从A,B 两地同时出发,且在A,B 两地往返来回匀速行驶.若两车第一次相遇后,甲车继续行驶4 小时到达B,而乙车只行驶了1 小时就到达A,则两车第15 次(在A,B 两地相遇次数不计)相遇时,它们行驶了小时.(2012 年17 届)【答案】B【解析】设甲、乙的速度分别为V甲、V乙,则甲、乙相遇时,他们行驶的路程比为V甲:V乙;另一方面,第一次相遇后,甲车继续行驶4 小时到达B,乙车继续行驶了1 小时到达A,所以这两段的路程比也为V乙: 4V甲,从而V甲:V乙=V乙: 4V甲,进而有V甲:V乙= 1: 2 ,进而可以得到甲从A 到B 需要6 小时,乙需要3 小时,一个周期为12 小时且周期内相遇两次,7 个周期后,甲、乙相遇14 次,且分别回到A 和B,2 小时后,甲、乙第15 次相遇,总共用时7 ⨯12 + 2 = 86 小时.课后练习1. 任意写一个两位数,再将它依次重复3 遍成一个8 位数.将此8 位数除以该两位数所得到的商再除以9,问:得到的余数是.(2004 年9 届)【答案】4【解析】abababab ÷ab =1010101,1010101 除以9 的余数为4.2. 2008006 共有个质因数.(2006 年11 届)(A)4 (B)5 (C)6 (D)7【答案】C【解析】2008006 = 2 ⨯ 7 ⨯11⨯13⨯17 ⨯ 59 .3. 小明所在班级的人数不足40 人,但比30 人多,那么这个班男、女生人数的比不可能是().(2014 年19 届)(A)2:3 (B)3:4 (C)4:5 (D)3:7【答案】D【解析】如果男、女生人数的比是2:3,那么全班人数一定是5 的倍数,男生14 人,女生21 人,满足题意.如果男、女生人数的比是3:4,那么全班人数一定是7 的倍数,男生15 人,女生20 人,满足题意.如果男、女生人数的比是4:5,那么全班人数一定是9 的倍数,男生16 人,女生20 人,满足题意.如果男、女生人数的比是3:7,那么全班人数一定是10 的倍数,但本班人数不足40 人,但比30 人多,所以男、女生人数的比不可能是3:7.4. 开学前6 天,小明还没做寒假数学作业,而小强已完成了60 道题,开学时,两人都完成了数学作业.在这6 天中,小明做的题的数目是小强的3 倍,他平均每天做()道题.(2009 年14 届)y 7 ⎩(A )6 (B )9 (C )12 (D )15【答案】D【解析】这 6 天小明比小强多做了 60 道,平均每天多做 10 道,小明每天做题量是小强的 3 倍,所以 小强每天做 5 道,小明每天做 15 道.5. 一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为 9:7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为 7:5,那么盒子里原有的黑子数比白子数 多( )个.(2013 年 18 届)(A )5 (B )6(C )7(D )8【答案】C【解析】设原有黑子数为 x ,白子数为 y ,得方程⎧ x - 1 = 9⎧7 x - 9y = 7⎪ ⎪ ⎪ ⎨x 7 即 ⎨⎪ = ⎪⎩ y - 1 5⎪5x - 7y = - 7由此解得x = 28 , y = 21 .故 x - y = 7 .解法二:前后两次均取出一枚棋子,剩下棋子的总数不变,而 9 + 7 = 16 ,7 + 5 = 12 ,16 与 12 的最小 公倍数为 48 ,因此设取出一枚棋子后,剩下棋子的总数为 48 份.第一次余下的黑子数为 48 ÷ (9 + 7) ⨯ 9 = 27 份;第二次余下的黑子数为 48 ÷ (7 + 5) ⨯ 7 = 28 份;两次相差 1 份.而前后两次余 下的黑子数相差 1,因此 1 份对应 1 枚棋子.原有黑子 28 个,原有的白子数为 28 ÷ 7 ⨯ 5 + 1 = 21个, 黑子比白子多 28 - 21 = 7 个6. 水池 A 和 B 同为长 3 米,宽 2 米,深 1.2 米的长方体.1 号阀门用来向 A 池注水,18 分钟可将无水的A 池注满;2 号阀门用来从 A 池向B 池放水,24 分钟可将 A 池中满池水放入 B 池.若同时打开 1 号和 2 号阀门,那么当 A 池水深 0.4 米时,B 池有( )立方米的水.(2013 年 18 届) 【答案】D【解析】由已知, 1 号阀门每分钟注入 1 18池水,而 2 号阀门放出 1 24池水.到A 池深 0.4 米时,正好在 A 池中留存了 1池水,31 ÷ ⎡ 1 -1 ⎤ = 24 (分钟).⎣ ⎦3 ⎢18 24 ⎥故此时恰好放了24 分钟,正好把B 池放满,进而B 水池中有水3⨯ 2 ⨯1.2 = 7.2 (立方米).7. “低碳生活”从现在做起,从我做起.据测算,1 公顷落叶阔叶林每年可吸收二氧化碳14 吨.如果每台空调制冷温度在国家提倡的26℃基础上调到27℃,相应每年减排二氧化碳21 千克.某市仅此项减排就相当于25000 公顷落叶阔叶林全年吸收的二氧化碳;若每个家庭按3 台空调计,该市家庭约有万户.(保留整数)(2010 年15 届)【答案】556【解析】25000⨯14⨯1000÷(21⨯3)≈5555555.6.8. 甲乙同时出发,他们的速度如下图所示,30 分钟后,乙比甲一共多行走了米.(2014 年19 届)10080604020米/分5分10 15 20 25 30甲10080604020米/分分5 10 15 20 25 30乙【答案】300【解析】由图所示,前10 分钟,甲和乙速度相同;第10 分钟至第20 分钟,乙速度是100 米/分,甲的速度是80 米/分,故乙多走了200 米;第20 分钟至第25 分钟,甲乙速度相同;第25 分钟至30 分钟,乙的速度是80 米/分,甲的速度是60 米/分,故乙多走了100 米;乙共计多走了300 米.9. 甲、乙两车分别从A,B 两地同时出发,相向而行,3 小时相遇后,甲掉头返回A 地,乙继续前行.甲到达A 地后掉头往B 行驶,半小时后和乙相遇.那么乙从A 到B 共需小时.(2011 年16 届)【答案】7.2【解析】甲、乙相遇后,同时向B 行驶,甲先是花了3 小时到达A 地,然后甲掉头行驶了半小时和乙相遇,从而甲乙相遇后,乙行驶了3.5 小时,且这段路甲只需要2.5 小时,所以甲、乙的速度比为7:5,从而甲花了3 小时的这段路,乙需要3⨯ 7 ÷ 5 = 4.2 小时,所以乙从A 到B 共需3 + 4.2 = 7.2 小时.第三节数字谜、计数、组合精讲考点概述数字谜考点:竖式问题常用方法:(1)加数相加时每进1 位,和的数字和将比加数的数字和之和减少9.(2)与各个数位上的数字有关的问题,往往需要多次尝试才能得到结果.(3)与整除相关的问题,注意运用以前学过的整除知识.计数问题考点:1. 枚举法(有序、分类)2. 加乘原理(分类,加法;分步,乘法)3. 排列组合(排列,有序;组合,无序;常用方法,插空、捆绑、插板、排除等)4. 综合运用(结合几何、数论等知识)组合问题考点:1. 最值问题:(1)满足题目条件的情况不多时,可以用枚举法把可能的情况一一列举出来,再找出最大值或最小值.(2)两个数的和一定,当它们越接近时乘积越大.(3)极端思考与局部调整也是解决最值问题的常用方法.2. 逻辑推理、统筹对策、抽屉原理等.真题精讲。
华杯赛讲义_小高组第1讲计算和应用专题

第一讲计算和应用专题1、在杯赛中常考提取公因数与平方差公式;注意估算与取整为难点2、(一)和差问题:已知两个数的和与差,求这两个数的应用题,叫做和差问题。
一般关系式有:(和-差)÷2=较小数(和+差)÷2=较大数(二)差倍问题:已知两个数的差及两个数的倍数关系,求这两个数的应用题,叫做差倍问题。
基本关系式是:两数差÷倍数差=较小数(三)还原问题:已知一个数经过某些变化后的结果,要求原来的未知数的问题,一般叫做还原问题。
(四)置换问题:题中有二个未知数,常常把其中一个未知数暂时当作另一个未知数,然后根据已知条件进行假设性的运算。
其结果往往与条件不符合,再加以适当的调整,从而求出结果。
(五)盈亏问题(盈不足问题):题目中往往有两种分配方案,每种分配方案的结果会出现多(盈)或少(亏)的情况,通常把这类问题,叫做盈亏问题(也叫做盈不足问题)。
解答这类问题时,应该先将两种分配方案进行比较,求出由于每份数的变化所引起的余数的变化,从中求出参加分配的总份数,然后根据题意,求出被分配物品的数量。
其计算方法是:当一次有余数,另一次不足时:每份数=(余数+不足数)÷两次每份数的差当两次都有余数时:总份数=(较大余数-较小数)÷两次每份数的差当两次都不足时:总份数=(较大不足数-较小不足数)÷两次每份数的差(六)年龄问题:年龄问题的主要特点是两人的年龄差不变,而倍数差却发生变化。
常用的计算公式是:成倍时小的年龄=大小年龄之差÷(倍数-1)几年前的年龄=小的现年-成倍数时小的年龄几年后的年龄=成倍时小的年龄-小的现在年龄(七)鸡兔问题:已知鸡兔的总只数和总足数,求鸡兔各有多少只的一类应用题,叫做鸡兔问题,也叫“龟鹤问题”、“置换问题”。
一般先假设都是鸡(或兔),然后以兔(或鸡)置换鸡(或兔)。
常用的基本公式有:(总足数-鸡足数×总只数)÷每只鸡兔足数的差=兔数(兔足数×总只数-总足数)÷每只鸡兔足数的差=鸡数(八)牛吃草问题(船漏水问题):若干头牛在一片有限范围内的草地上吃草。
华杯赛专用培训教程
华杯赛专用培训教程第十章方法和策略一、枚举与筛选1、如下图,四个小三角形的顶点处有六个圆圈,在圆圈内分别填入6个质数,它们的和是20,并且每个小三角形三个顶点上的数字的和相等。
问:这六个质数的积是多少?2、有三张卡片,在它上面各写有一个数字,从中抽出一张、两张、三张,按任意顺序排起来,可以得到不同的一位数、两位数、三位数,请你将其中的质数都写出来。
1 2 33、在三位数中,数字和是5的倍数的数共有多少个?4、有面值为1分、2分、5分的硬币各4枚,用它们去支付2角3分。
问:有多少种不同的支付方法?5、1995的数字和是1+9+9+5=24。
问:小于2000的四位数中数字和等于24的数共有多少个?6、写出从360到630有奇数个约数的所有的自然数。
7、从所有分母小于10的真分数中,找出一个最接近0.618的分数。
8、变速自行车是在主动轴和后轴分别安装了几个齿数不同的齿轮,用链条连接不同搭配的齿轮,通过不同的传动比获得若干档不同的车速。
“希望牌”变速自行车主动轴上有三个齿轮,齿数分别是48,36,24;后轴上有四个齿轮,齿数分别是36,24,16,12。
问:这种变速自行车一共有几档不同的车速?9、有三个工厂共订300份吉林日报,每个工厂订了至少99份,至多101份。
问一共有多少不同的订法?10、把37拆成若干个不同的质数之和,有多少种不同的拆法?将每一种拆法中所拆出的那些质数相乘,得到的乘积中,哪个最小?11、用1,9,8,8这四个数字能排成几个被11除余8的四位数?12、试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次:使这三个数中任何两个都互质。
(这是一个三位数)(这是一个三位数)(这是一个一位数)41713、有八张卡片,上面分别写着自然数1到8,从中取出三张,要求这三张卡片上的数字之和为9,。
问有多少种不同的取法?14、把+、-、×、÷分别填在下图适当的括号内,并在长方形中添上适当的整数,是图中的两个等式都成立。
华杯赛复赛讲义by王刚

1.汽车A从甲站出发开往乙站,同时汽车B、C从乙站出发与A相向而行开往甲站,途中A与B相遇20分钟后再与C相遇。
已知A、B、C的速度分别是每小时90km, 80km, 60km,那么甲乙两站的路程是km。
2.小兔和小龟从A地到森林游乐园,小兔上午9点出发,1分钟向前跳40米,每跳3分钟就原地玩耍2分钟;小龟上午6点40分出发,1分钟爬行只有10米,但途中从不休息和玩耍。
已知小龟比小兔早到森林游乐园15秒,那么A地到森林游乐园有米。
3.在静水中,甲船的速度是乙船速度的两倍。
甲乙二船沿河分别从A、B两地同时出发,相向而行,相遇时距A、B的距离之比为3:1,如果甲乙分别从B、A同时出发,相向而行,相遇时距A、B的距离之比为。
4.悉尼与北京的时差是3小时,例如:悉尼时间12:00时,北京时间是9:00。
某日,当悉尼时间9:15时,小马和小杨分别乘机从悉尼和北京同时出发去对方所在地,小马于北京时间19:33分到达北京。
小马和小杨路途上所用时间之比为7:6,那么小杨到达悉尼时,当地时间是。
5.某班一次数学考试,所有成绩得优的同学的平均分数是95分,没有得优的同学的平均分数是80分。
已知全班同学的平均成绩不少于90分,问得优的同学占全班同学的比例至少是多少?6.甲、乙和丙三只蚂蚁爬行的速度之比是8:6:5,它们沿一个圆圈从同一点同时同向爬行,当它们首次同时回到出发点时,就结束爬行。
问蚂蚁甲追上蚂蚁乙一共多少次?7.如图,正方形跑道ABCD.甲、乙、丙三人同时从A点出发同向跑步,他们的速度分别为每秒5米、4米、3米.若干时间后,甲首次开始看到乙和丙都与自己在正方形的同一条边上,且他们在自己的前方.从此时刻算起,又经过21秒,甲乙丙三人处在跑道的同一位置,这是出发后三人第一次处在同一位置.请计算出正方形的周长的所有可能值.对策操作游戏构造1.右图中有5个由4个1×1的小正方格组成的不同形状的硬纸板。
问能用这5个硬纸板拼成右图中4×5的长方形吗?如果能,请画出一种拼法;如果不能,请简述理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都华杯赛课程讲义(B )主要内容:计数、几何、数论【例1】(2009年第十四届“华罗庚金杯赛”初赛)按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5,那么,可供每支球队选择的号码共( )个. 【分析】 根据题意,可供选择的号码可以分为一位数和两位数两大类,其中一位数可以为0~9,有10种选择;两位数的十位可以为1~5,个位可以为0~5,根据乘法原理,两位数号码有5630⨯=种选择.所以可供选择的号码共有103040+=种.【巩固】一种电子表在6时24分30秒时的显示为6:2430,那么从5时到7时这段时间里,此表的5个数字都不相同的时刻一共有多少个? 【分析】 设DE A:BC 是满足题意的时刻,有A 为6,B 、D 应从0,1,2,3,4,5这6个数字中选择两个不同的数字,所以有26A 种选法,而C 、E 应从剩下的7个数字中选择两个不同的数字,所以有27A 种选法,所以共有26A ×27A =1260种选法;A 为5,B 、D 应从0,1,2,3,4,这5个数字中选择两个不同的数字,所以有25A 种选法,而C 、E 应从剩下的7个数字中选择两个不同的数字,所以有27A 种选法,所以共有25A ×27A =840种选法,因此一共有12608402100+=个【例2】(2008年第十三届“华罗庚金杯赛”初赛)已知图中是一个轴对称图形.若将图中某些黑色的图形去掉后,得到一些新的图形,则其中轴对称的新图形共有( )个.(A)9 (B)8 (C)7 (D)6【分析】 原图是一个轴对称图形,且对称轴只有1条,那么去掉图中的某些黑色图形后,剩下的轴对称图形的对称轴与原图的相同.阴影5部分中去掉1个,有1种情况;阴影5部分去掉2个,有2种情况;阴影5部分去掉3个,有2种情况;阴影5部分中去掉4个,有1种情况;阴影5部分中去掉5个,有1种情况;所以共7种情况,答案为C .另解:如右图,将阴影5部分标上字母,则A 和B 关于对称轴对称,C 部分单独关于对称轴对称,D 和E 关于对称轴对称,所以,如果要去掉某些黑色部分图形,则A 和B 必须同时去掉或保留,C 既可去掉也可保留,D 和E 必须同时去掉或保留,对这3组每组都有去掉或保留2种选择,共有2228⨯⨯=种选择,但是其中有种情况5部分都没有去掉的情况,这样情况应予排除,所以符合条件的情况共有817-=种.【例3】在图中15⨯的格子中填入1,2,3,4,5,6,7,8中的5个数,要求填入的数各计数不相同,并且填在黑格里的数比它旁边的两个数都大.共有 种不同的填法.【分析】 首先看填入1、2、3、4、5这五个数的情况.由于黑格里的数至少比两个数大,所以至少为3;而白格里的数不能是最大的,所以5必须在黑格里.那么这五个数填在黑格里的数是5和4时,不同的填法有2!3!12⨯=(种);填在黑格里的数是5和3时,4只能在5的一侧,不同的填法有224⨯=(种).所以,共有不同填法12416+=(种).而要将填入的五个数选出来,一共有58C 56=种,然后按照分析1~5这5个数的方法对应着数的相对大小来分析选出来的五个数,也各有16种填法,所以一共有:5616896⨯=种填法.【巩固】在图23-5的空格内各填入一个一位数,使同一行内左边的数比右边的数大,同一列内下面的数比上面的数大,并且方格内的6个数字互不相同,例如图23-6就是一种填法。
请问:一共有多少种不同的填法?图23-5 图23-6 【分析】 为了方便说明,标上字母:要注意到,A 最大,D 最小,B 、C 的位置可以互换.但是,D 只能取4,5,6,因为如果取7,就找不到3个比它大的一位数了. 当D 取4,5,6时分别剩下5,4,3个一位大数.有B 、C 可以互换位置. 所有不同的填法共35C ×2+34C ×2+33C ×2=10×2+4×2+1×2=30种.【例4】一次自助餐,共有10种菜,每个人都有4个盘子可以选菜,每个盘子只能放1种菜,但可以重复选菜,请问:共有多少种选菜方案?【分析】 不重复选:410210C =重复1种:12109360C C = 重复2种:21045C = 1种重复3次:1110990C C = 1种重复4次:11010C = 共715种【例5】如图的大正方形格板是由81个1平方厘米的小正方形铺成,B ,C 是两个格点。
若请你在其它的格点种标出一点A ,使得三角形ABC 的面积恰等于3平方厘米,则这样的A 点共有多少个?32764532【详解】先找一个能够面积为3的点,比如A 点,然后根据等积变换,底相等,高相等,即面积相等。
可以做平行线,再下方也可以继续做平行线。
共8个。
【例5】(2006年第十一届“华罗庚金杯赛”初赛)如下图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD .取AB 的中点M 和BC 的中点N ,剪掉MBN △得五边形AMNCD .那么,将折叠的五边形AMNCD 纸片展开铺平后的图形是( ).【分析】 由裁痕MN 可对称地画出其它三条裁痕(如图).所以答案为D .【例6】(2008年第十三届“华罗庚金杯赛”初赛)如图所示,矩形ABCD 的面积为24平方厘米.三角形ADM 与三角形BCN 的面积之和为7.8平方厘米,则四边形PMON 的面积是 平方厘米.(D)(C)(B)(A)M NCD A 几何【分析】 因为三角形ADO 与三角形BCO 的面积之和是矩形ABCD 的面积的一半,即12平方厘米,又三角形ADM 与三角形BCN 的面积之和为7.8平方厘米,则三角形AMO 与三角形BNO 的面积之和是4.2平方厘米,则四边形PMON 的面积=三角形ABP 面积-三角形A M O 与三角形B N O 的面积之和-三角形ABO 面积12 4.26 1.8=--=(平方厘米).【巩固】如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .【分析】 利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=;又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=.另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【例7】 (2004年第九届“华罗庚金杯赛”初赛)如图,大小两个半圆,它们的直径在同一直线上,弦AB 与小圆相切,且与直径平行,弦AB 长12厘米.求图中阴影部分的面积(圆周率π 3.14=).NOMPDCBABA【分析】 设小圆的半径为r ,大圆的半径为R ,那么所求的阴影部分的面积为22ππ2R r -.如图,设大圆圆心为O ,连接OB ,过O 作AB 的垂线,垂足为C .那么C 为AB 的中点.由于AB 与小圆相切且与直径平行,所以OC 的长与小圆半径相等,即OC r =.考虑直角三角形OBC ,根据勾股定理,22212362R r ⎛⎫-== ⎪⎝⎭,所以阴影部分的面积为22ππ18π56.522R r -==(平方厘米).(此处需要讲一个整体求解的几何题,跟圆环有关。
)【例8】 (2009年第十四届“华罗庚金杯赛”初赛)如下图所示,AB 是半圆的直径,O 是圆心,AC CD DB ==,M 是CD 的中点,H 是弦CD 的中点.若N 是OB 上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是 平方厘米.a) 如下图所示,连接OC 、OD 、OH .本题中由于C 、D 是半圆的两个三等分点,M 是CD 的中点,H 是弦CD 的中点,可见这个图形是对称的,由对称性可知CD 与AB 平行.由此可得CHN ∆的面积与CHO ∆的面积相等,所以阴影部分面积等于扇形COD 面积的一半,而扇形COD 的面积又等于半圆面积的13,所以阴影部分面积等于半圆面积的16,为11226⨯=平方厘米.【巩固】如图,正方形的边长为10,四边形EFGH 的面积为5,那么阴影部分的面积是 .C OBr RA[分析] 如图所示,设AD 上的两个点分别为M 、N .连接CN .根据面积比例模型,CMF ∆与CNF ∆的面积是相等的,那么CMF ∆与BNF ∆的面积之和,等于CNF ∆与BNF ∆的面积之和,即等于BCN ∆的面积.而BCN ∆的面积为正方形ABCD 面积的一半,为2110502⨯=.又CMF ∆与BNF ∆的面积之和与阴影部分的面积相比较,多了2个四边形EFGH 的面积,所以阴影部分的面积为:505240-⨯=.【巩固】如下图,在梯形ABCD 中,AB 与CD 平行,且2CD AB =,点E 、F 分别是AD 和BC 的中点,已知阴影四边形EMFN 的面积是54平方厘米,则梯形ABCD 的面积是 平方厘米.【分析】 连接EF ,可以把大梯形看成是两个小梯形叠放在一起,应用梯形蝴蝶定理,可以确定其中各个小三角形之间的比例关系,应用比例即可求出梯形ABCD 面积.设梯形ABCD 的上底为a ,总面积为S .则下底为2a ,()13222EF a a a =+=.所以3::2:32AB EF a a ==,3::23:42EF DC a a ==.由于梯形ABFE 和梯形EFCD的高相等,所以()()33:::25:722ABFE EFCD S S AB EF EF DC a a a a ⎛⎫⎛⎫=++=++= ⎪ ⎪⎝⎭⎝⎭梯形梯形,故512ABFE S S =梯形,712EFCD S S =梯形.根据梯形蝴蝶定理,梯形ABFE 内各三角形的面积之比为222:23:23:34:6:6:9⨯⨯=,所以99534669251220EMF ABFE S S S S ==⨯=+++梯形;同理可得99739121216491228ENF S S S S ==⨯=+++梯形EFCD ,所以339202835EMFN EMF ENF S S S S S S =+=+=,由于54EMFN S =平方厘米,所以95421035S =÷=(平方厘米).ABABDD数论【例9】(2009年第十四届“华罗庚金杯赛”初赛)在大于2009的自然数中,被57除后,商与余数相等的数共有 个.【分析】 根据题意,设这样的数除以57所得的商和余数都为a (57a <),则这个数为5758a a a ⨯+=.所以582009a >,得到372009583458a >÷=,由于a 为整数,所以a 至少为35.又由于57a <,所以a 最大为56,则a 可以为35,36,37, (56)由于每一个a 的值就对应一个满足条件的数,所以所求的满足条件的数共有5635122-+=个.【巩固】(2008年第六届走美初赛五年级)20086a b ÷=,a 、b 均为自然数.a 有种不同的取值.【分析】 由20086a b ÷=可知,62008ab +=,2002ab =.故a 是2002的约数.因为2002271113=⨯⨯⨯,2002的约数有(11)(11)(11)(11)16+⨯+⨯+⨯+=个约数, 又因为a 比6大,2002的约数中小于6的只有1、2两个,所以a 的取值有:16214-=(种).【例10】 (2006年第十一届“华罗庚金杯赛”初赛)将从1开始到103的连续奇数依次写成一个多位数:1357911131517199799101103a =则数a 共有 位,数a 除以9的余数是 .【分析】 组成a 的数字中,一位奇数有5个,两位奇数有45个,三位奇数有2个,这个多位数共有 1524532101⨯+⨯+⨯=(位). 至于数a 除以9的余数,一般有两种求法:(法1)计算各位数字之和,一位奇数部分的和为1357925++++=,两位奇数部分的和分为十位部分和个位部分,十位部分为()1234567895225++++++++⨯=,个位部分为()135799225++++⨯=,三位数部分的数字之和为11136+++=,所以这个多位数的各位数字之和为252252256481+++=,被9除余4,所以数a 除以9的余数是4.(法2)因为连续9个奇数的和能被9整除,1到103共有52个连续奇数,52除以9余7,所以a 除以9的余数与从1开始的连续7个奇数之和除以9的余数相同.135791113除以9的余数是4,所以a 除以9余4.【巩固】(2009年走美初赛六年级)1234567891011121314……20082009除以9,商的个位数字是 .1. 首先看这个多位数是否能为9整除,如果不能,它除以9的余数为多少. 由于任意连续的9个自然数的和能被9整除,所以它们的各位数字之和能被9整除,那么把这9个数连起来写,所得到的数也能被9整除. 由于200992232÷=,所以1234567891011121314…20082009这个数除以9的余数等于20082009(或者12)除以9的余数,为3.那么1234567891011121314…20082009除以9的商,等于这个数减去3后除以9的商,即1234567891011121314…20082006除以9的商,那么很容易判断商的个位数字为4.【例11】 (2006年第十一届“华罗庚金杯赛”决赛)100个非零自然数的和等于2006,那么它们的最大公约数的最大可能值是( ).【解析】200621759=⨯⨯,所以这100个非零自然数的最大公约数是21759⨯⨯的约数,又这100个数除以它们的最大公约数所得的商的和不小于100,且这个和与它们的最大公约数的乘积即等于这100个数的和,即等于2006,所以所得到的商的和是2006的不小于100的约数,最小为259118⨯=,所以这100个数的最大公约数最大为200611817÷=.【巩固】(2003年第八届“华罗庚金杯赛”决赛)有很多方法能将2001写成25个自然数(可以相同,也可以不相同)的和,对于每—种分法,这25个自然数均有相应的最大公约数,那么这些最大公约数中的最大值是( ).【解析】因为200132329=⨯⨯,所以当25个自然数之和是2001时,这25个自然数的最大公约数必定能整除32329⨯⨯.由于这25个数的和不小于它们的最大公约数的25倍,所以最大公约数不超过12001258025÷=,所以最大值是32369⨯=.【例12】 (2007年第十二届“华罗庚金杯赛”决赛)一个自然数,它的最大的约数和次大的约数的和是111,这个自然数是________.a) 因为111是奇数,而奇数等于奇数+偶数,所以所求数的最大约数与次大约数必为一奇一偶.一个数的最大约数是其自身,而一个数如有偶约数此数必为偶数,而一个偶数的次大约数应为这个偶数的12,设这个次大约数为a ,则最大约数即它自身为2a ,有2111a a +=,求得37a =,274a =,即所求数为74.【拓展】一个自然数,它的次大的约数和第三大的约数的和是111,这个自然数是________.i. 因为111是奇数,而奇数=奇数+偶数,所以所求数的次大约数与第三大约数必为一奇一偶.而一个数的最大约数是其自身,一个数如有偶约数该数也必为偶数,而一个偶数的次大约数应为这个偶数的12,现在关键是第三大的约数.如果设该自然数是a ,第三小的约数是n (次小的约数是2),那么第三大的约数是an,次大的约数是2a ,那么1112a an+=,整理得到()2222n a n =+.第三小的约数n ,可能是4,或者是一个奇质数.如果是4,那么可得148a =,经检验成立;如果是一个奇质数,那么n 应该与()2n +互质,那么()2n +必须是222的约数,也就是111的约数,符合奇质数条件的n 只有109,此时218a =.所以这道题的答案有两个,一个是148,另一个是218.【例13】 (2007年第十二届“华罗庚金杯赛”决赛)一列数是按以下条件确定的:第一个是3,第二个是6,第三个是18,以后每一个数是前面所有数的和的2倍,则第六个数等于________,从这列数的第________个数开始,每个都大于2007.a) 按照这列数的规律,13a =,223a =⨯,23122()2(323)23323a a a =⨯+=⨯+⨯=⨯⨯=⨯,23412312()2(323233)2323a a a a a =++=⨯+⨯+⨯⨯=⨯⨯=⨯, ……可见,从第3个数起,每一个数都是前一个数的3倍.那么5623486a =⨯=.既然62314582007⨯=<,72343742007⨯=>,所以第6个数等于486;从第8个数开始,数列中的每一个数都大于2007.【14】已知非零自然数a 、b 之差为120,它们的最小公倍数是其最大公约数的105倍,那么a 、b 中较大的数是多少?【分析】 d a bp q根据上面的短除,设,a b d =(),[,]a b dpq =,则,1p q =()有105pqd d =,所以105357pq ==⨯⨯.因为()120a b p q d -=-=,所以()p q -是120的约数.①若105p =,1q =,则104p q -=,不符合; ②若35p =,3q =,则32p q -=,不符合; ③若21p =,5q =,则16p q -=,不符合;④若15p =,7q =,则8p q -=,符合条件.由()8120p q d d -==,得15d =,从而a 、b 中较大的数1515225a pd ==⨯=.。
