哈工大深圳研究生院组合数学部分作业题答案习题课6,8
哈工大电路习题答案第6章

答案6.1解:将i和i3改写为余弦函数的标准形式,即2i4cos(t190)A4cos(t190180)A4cos(t10)A2i5sin(t10)A5cos(t1090)A5cos(t80)A3电压、电流的有效值为1002U70.7V,I1.414A12245I2.828A,I3.54A2322初相位10,100,10,80uiii123相位差1ui1010090u与i1正交,u滞后于i1;12ui10100u与i2同相;23ui10(80)90u与i3正交,u超前于i33答案6.2au10cos(t10)V.-822bU610arctg10233.1V,u102cos(t233.1)V-622-20.8cI0.220.8arctg20.889.4A,i20.8cos(t89.4)Am0.2dI30180A,i302cos(t180)A答案6.3解:(a)利用正弦量的相量表示法的线性性质得:UI111n,UIn22(b)磁通相量通常用最大值表示,利用正弦量的相量表示法的微分性质得:UjNmm(c)利用正弦量的相量表示法的线性性质与微分性质得:URIjLI答案6.4解:由KCL得电流i的振幅相量IIIIm1m2m3m(2100410580)A(0.347j1.973.939j0.6950.868j4.924)A526.86A电流i的瞬时值为i5cos(t26.86)A答案6.5解:电压表和电流表读数为有效值,其比值为阻抗模,即2()2/RLUI将已知条件代入,得22R(2π50L) 100V 15A22R(2π100L)100V 10联立方程,解得L13.7mH,R5.08答案6.6解:(a)RC串联电路中电阻电压与电容电压相位正交,各电压有效值关系为2222UU2U15040V30V电流i的有效值为IIC UXC30V103A(b)UXICC302A60VI R UR60V500.3ARC并联电路中电阻电流与电容电流相位正交,总电流有效值为22221.222.33IIIAACR(c)UXI301A30VCCC由U30VCUUXII2ALCLLX15L并联电容、电感上电流相位相反,总电流为III1ALC电阻电压与电容电压相位正交,总电压为:2230240250UUUVVCR答案6.7解:感抗XL L3210rad/s0.1H200容抗X C 11C36210rad/s510F100图(a)电路的相量模型如图(b)所示。
考研哈工大试题及答案

考研哈工大试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是哈尔滨工业大学的简称?A. 哈工大B. 哈师大C. 哈理工D. 哈工程答案:A2. 哈尔滨工业大学位于哪个省份?A. 黑龙江省B. 吉林省C. 辽宁省D. 内蒙古自治区答案:A3. 考研初试中,数学科目满分为多少分?A. 100分B. 150分C. 200分D. 300分答案:B4. 下列哪一项不是考研复试的内容?A. 笔试B. 面试C. 体检D. 体育测试答案:D5. 考研复试通常在初试成绩公布后的多长时间内进行?A. 1个月B. 2个月C. 3个月D. 4个月答案:B二、填空题(每题2分,共10分)1. 考研初试成绩一般由________和________两部分组成。
答案:公共课、专业课2. 考研复试时,考生需要携带的材料包括________、________和准考证等。
答案:身份证、学生证3. 考研复试中,面试环节主要考察考生的________能力和________能力。
答案:专业、沟通4. 考研初试中,英语科目的考试时间为________分钟。
答案:1805. 考研初试成绩公布后,考生可以通过________和________查询成绩。
答案:研招网、学校官网三、简答题(每题10分,共20分)1. 简述考研复试的重要性。
答案:考研复试是选拔研究生的重要环节,它不仅考察考生的专业知识和技能,还考察考生的综合素质和学术潜力。
复试成绩在最终录取中占有重要比重,因此考生需要认真准备,充分展示自己的实力。
2. 描述考研初试和复试的区别。
答案:考研初试主要考察考生的公共课和专业课知识,通常以笔试形式进行。
复试则更注重考生的综合素质和专业能力,包括面试、笔试和体检等环节。
初试成绩是进入复试的门槛,而复试成绩则直接影响最终的录取结果。
四、论述题(每题20分,共40分)1. 论述如何有效准备考研复试。
答案:有效准备考研复试的方法包括:一是提前了解复试流程和要求,二是复习专业知识和技能,三是加强沟通和表达能力训练,四是进行模拟面试练习,五是保持良好的心态和身体状况。
组合数学 课后答案 PDF 版

循环群也是群,所以群的定义不用再证,只需证明对于任意a, b G, G是循环群,有a * b b * a成立,因为循环群中的元素可写成a=xm 形式 所以等式左边xm × x n x m n , 等式右边x n xm=x m n, a b b a,即所有 的循环群都是ABEL群。
因为 H 是 G 的子群, 所以在 H 中的一个 (b m ) r 一定在 G 中对应一个 a m 使得
(b m ) r a m ,
所以有 b rm a m ,则 rm 一定是 m 的倍数,所以则 H 的阶必除尽 G 的阶。 4.9 G 是有限群,x 是 G 的元素,则 x 的阶必除尽 G 的阶。
N-1 N-2
N
1
2 3
……
……
图N! C N!
如图: N 个人围成一个圆桌的所有排列如上图所示。一共 N!个。
……
…
6
…………………………
… …
……
… …
…
…
旋转 360/i,i={n,n-1,n-2,……1}; 得到 n 种置换 当且仅当 i=1 的置换(即顺时针旋转 360/1 度:P1=(c1)(c2)……(cn!);) 时有 1 阶循环存在 (因为只要圆桌转动,所有圆排列中元素的绝对位置都发生了 变化,所以不可能有 1 阶循环存在) 。 不同的等价类个数就是不同的圆排列个数,根据 Burnside 引理,
4.18 若以给两个 r 色球,量个 b 色的球,用它装在正六面体的顶点,试问有多 少种不同的方案。 解:单位元素(1) (2) (3) (4) (5) (6) (7) (8) ,格式为(1)8. 绕中轴旋转 90。的置换非别为(1234) (5678) , (4321) (8765) 2 格式为(4) ,同格式的共轭类有 6 个。
组合数学课后习题答案

第一章答案1.(a) 45 ( {1,6},{2,7},{3,8},…,{45,50} )(b) 45⨯5+(4+3+2+1) = 235( 1→2~6, 2→3~7, 3→4~8, …,45→46~50, 46→47~50, 47→48~50, 49→50 ) 2.(a) 5!8!(b) 7! P(8,5) (c) 2 P(5,3) 8! 3. (a) n!P(n+1, m) (b) n!(m+1)!(c) 2!((m+n-2)+1)! 4. 2 P(24,5) 20!5. 2⨯5⨯P(8,2)+3⨯4⨯P(8,2)6. (n+1)!-17. 用数学归纳法易证。
8. 41⨯319. 设 n=p 1n 1p 2n 2…p kn k , 则n 2的除数个数为 ( 2p 1+1) (2p 2+1) …(2p k+1).10.1)用数学归纳法可证n 能表示成题中表达式的形式;2)如果某n 可以表示成题中表达式的形式,则等式两端除以2取余数,可以确定a 1;再对等式两端的商除以3取余数,又可得a 2;对等式两端的商除以4取余数,又可得a 3;…;这说明表达式是唯一的。
11.易用C(m,n)=m!/(n!(m-n)!)验证等式成立。
组合意义:右:从n 个不同元素中任取r+1个出来,再从这r+1个中取一个的全体组合的个数;左:上述组合中,先从n 个不同元素中任取1个出来,每一个相同的组合要生复 C(n-1,r) 次。
12.考虑,)1(,)1(101-=-=+=+=∑∑n nk k k n nnk kknx n x kC x x C 求导数后有令x=1, 即知.210-==∑n nk kn n kC13. 设此n 个不同的数由小到大排列后为a 1, a 2, …, a n 。
当第二组最大数为a k 时,第二组共有2k-1种不同的可能,第一组有2n-k -1种不同的可能。
故符合要求的不同分组共有12)2()12(21111+-=-----=∑n k n k n k n 种。
计算机应用数学-(组合数学)-答案哈工大

1,证明,如果从集合{1,2,...,2n}中选择n+1整数,那么总存在两个整数,它们之间相差为1.2,用鸽巢原理证明,有理数m/n展开的十进制小数最终是要循环的。
例如,34 478/99 900=0.345 125 125 125 125 12...3,一间屋内有10个人,他们当中没有人超过60岁(年龄只能以整数给出)但又至少不低于1岁。
证明,总能够找出两组人(两组不含相同人),各组人的年龄和是相同的。
题中的数10能换成更小的数吗?4,一只袋子装了100个苹果、100个香蕉、100个橘子和100个梨。
如果我每分钟从袋子里了出1种水果,那么需要多少时间我就能肯定至少已拿出了1打相同种类的水果?5,i)证明,在边长为1的等边三角形内任意选择5个点,存在2个点,其间距离至多为1/2。
ii)证明,在边长为1的等边三角形内任意选择10个点,存在2个点,其间距离至多为1/3。
iii)确定一个整数m小n,使得如果在边长为1的等边三角形内任意选择的m小n个点,则存在2个点,其间距离至多为1/n.6,下列各数各有多少互异正因子?i)3的4次方X 5的2次方X 7的6次方X 11ii)620iii)10的10次方7,确定下列类型的一手牌(5张牌)的数目。
i)full houses (3张一样大小的牌及2张相同点数的另外大小的牌)。
ii)顺牌(5张点数相连的牌)。
iii)同花(5张一样花色的牌)。
iv)同花顺(5张点数相连的同样花色的牌)。
v)恰好两个对(一对同样大小,另一对另外点数同样大小,再有一张另外大小的5张牌)。
vi)恰好一个对(一对同样大小,另外三张另外大小且互异点数的牌)。
8,从拥有10名男会员和12名女会员的一个俱乐部选出一个5人委员会。
如果至少要包含2位女士,能够有多少种方法形成这个委员会?此外,如果俱乐部还有一位特定的男士和一们特定的女士拒绝进入该委员会一起工作,形成委员会的方式又有多少?9,学校有100名学生和3个宿舍A,B和C,它们分别容纳25,35和40人。
组合数学作业答案解析

第二章作业答案7. 证明,对任意给定的52个整数,存在两个整数,要么两者的和能被100整除,要么两者的差能被100整除。
证明 用100分别除这52个整数,得到的余数必为0, 1,…, 99这100个数之一。
将余数是0的数分为一组,余数是1和99的数分为一组,…,余数是49和51的数分为一组,将余数是50的数分为一组。
这样,将这52个整数分成了51组。
由鸽巢原理知道,存在两个整数分在了同一组,设它们是a 和b 。
若a 和b 被100除余数相同,则b a -能被100整除。
若a 和b 被100除余数之和是100,则b a +能被100整除。
11. 一个学生有37天用来准备考试。
根据过去的经验,她知道她需要不超过60小时的学习时间。
她还希望每天至少学习1小时。
证明,无论她如何安排她的学习时间(不过,每天都是整数个小时),都存在连续的若干天,在此期间她恰好学习了13小时。
证明 设从第一天到第i 天她共学习了i a 小时。
因为她每天至少学习1小时,所以3721,,,a a a 和13,,13,133721+++a a a 都是严格单调递增序列。
因为总的学习时间不超过60小时,所以6037≤a ,731337≤+a 。
3721,,,a a a ,13,,13,133721+++a a a 是1和73之间的74个整数,由鸽巢原理知道,它们中存在相同的整数,有i a 和13+j a 使得13+=j i a a ,13=-j i a a ,从第1+j 天到第i 天她恰好学习了13小时。
14. 一只袋子装了100个苹果、100个香蕉、100个桔子和100个梨。
如果我每分钟从袋子里取出一个水果,那么需要多少时间我就能肯定至少已拿出了1打相同种类的水果? 解 由加强形式的鸽巢原理知道,如果从袋子中取出451)112(4=+-⨯个水果,则能肯定至少已拿出12个相同种类的水果。
因此,需要45分钟。
17. 证明:在一群1>n 个人中,存在两个人,他们在这群人中有相同数目的熟人(假设没有人与他/她自己是熟人)。
哈工大数学考研试题及答案

哈工大数学考研试题及答案试题:一、选择题(每题3分,共30分)1. 下列函数中,哪一个不是周期函数?A. y = sin(x)B. y = cos(x)C. y = e^xD. y = tan(x)2. 函数 f(x) = x^2 在区间(0, +∞) 上是:A. 增函数B. 减函数C. 先减后增D. 不是单调函数3. 微积分基本定理表明:A. 定积分可以转化为不定积分求解B. 不定积分是定积分的基础C. 定积分的值是不定积分的原函数在积分区间的差值D. 所有以上说法4. 以下哪个选项是欧拉公式e^(iπ) + 1 = 0 的一个直接后果?A. e^(iπ/2) = iB. e^(iπ) = -1C. e^0 = 1D. ln(-1) = πi5. 矩阵 A = [a, b; c, d] 的特征值是:A. a + dB. a - dC. ad - bcD. (a + d)^26. 以下哪个序列是发散的?A. 1, 1/2, 1/3, ...B. 1, 2, 4, 8, ...C. -1, 1, -1, 1, ...D. 1 - 1/2 + 1/3 - 1/4 + ...7. 方程 x^2 - 5x + 6 = 0 的根是:A. 2, 3B. -2, 3C. 2, -3D. -2, -38. 以下哪个级数是收敛的?A. 1 + 1/2 + 1/3 + ...B. 1 - 1/2 + 1/2 - 1/3 + ...C. 1 + (1/2)^2 + (1/3)^2 + ...D. 1 + 2^2 + 3^2 + ...9. 以下哪个选项是拉格朗日中值定理的一个应用?A. 证明罗尔定理B. 证明泰勒公式C. 证明积分中值定理D. 所有以上10. 以下哪个命题是正确的?A. 任何有界数列都有一个收敛的子数列B. 任何收敛数列都是有界的C. 任何收敛数列的极限都是唯一的D. 所有以上二、填空题(每题4分,共20分)11. 极限 lim (x->0) [sin(x)/x] 的值是 _______。
哈工大深圳研究生院组合数学部分作业题答案

3. If the first four entries of the 0th row of its difference table are 1, -1, Answer: Example (267 页),Theorem 8.2.2(267 页 )), Theorem 8.2.3 (269 页 )) The difference table is 1 -2 6 -3 -1 4 3 3 7 10 …… …… …… …… 3, 10, determine ������������������������ and a formula for ∑������������ ������������=������������ ������������������������ .
the times e2 occurs be n2 where n2 ≥ 2 the times ek occurs be nk where nk ≥ k
We have Then:
n1 + n2 + ⋯ + nk = n
x x2 x2 x3 xk x k+1 g (x ) = � + + ⋯ � � + + ⋯ � … ( + + ⋯) 1! 2! 2! 3! k! k + 1! x x x k −1 x = (e − 1) �e − 1 − � … (e − 1 − − ⋯ − ) 1! 1! (k − 1)!
Answer:
So we have
Suppose f1 = 2e1 , f2 = 5e2 , f3 = e3 , f4 = 7e4 f1 + f2 + f3 + f4 = n
哈工大工程制图习题册答案PPT课件
第6页/共95页
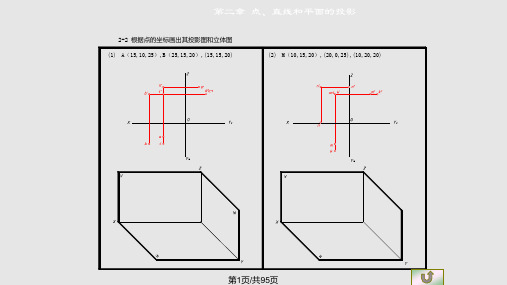
第二章 点、直线和平面
2-8 根据条件,在线段上求点
(1) 确定点C使AC:CB=2:3
a
Za
c c
b
X
a
O
b
c
(2) 确定点K使点K到V与H面距离之比为2:3。
a
Za
YW
b
X
a
O
b
Y
b
YH
b
YH
(3) 确定点C 使其与V、H面等距。
(4) 确定点C 使其距W面为20。
Z
a
a
Z
c
c
5-5 画斜二测轴测图 (2 )
第43页/共95页
第五章
轴测图
5-6 画斜二测轴测图
第44页/共95页
第六章 组合体
6-1 根据组合体轴测图,画其三面投影图
(1)
(2)
第45页/共95页
第六章 组合体
6-2 根据轴测图,画出组合体的三面投影图(按1:1比例),并标注尺寸
通孔
通孔 通孔
第46页/共95页
7-16 根据给出的剖视图,画出俯视图的外形图
A
A
AA
(1)
(2)
(3)
(4)
第18页/共95页
第二章 点、直线和平面
2-20 过点K作一平面平行给出的平面
(1)
(2)
第19页/共95页
第三章 立体
3-1 补出平面立体的第三投影,并求表面点的各投影
(1) 五棱柱
b' a'
(2) 正三棱锥
(b")
a"
(a') b'
a" (b")
组合数学6章作业答案

第6章 容斥原理及应用6.7 练习题3、求出从1到10000既不是完全平方数也不是完全立方数的整数个数。
解:∵100001002=,9261213=,10648223=∴从1到10000,共有100个平方数,21个立方数 又∵409646=,1562556=∴从1到10000,共有4个6次方数,也就是共有4个数既是平方数又是立方数 计算:10000-100-21+4=9883∴从1到10000既不是完全平方数也不是完全立方数的整数有9883个□4、确定多重集{}d c b a S ⋅⋅⋅⋅=5,4,34,的12-组合的个数。
解:设T :{}d c b a S ⋅∞⋅∞⋅∞⋅∞=,,,*的所有12-组合 1A :a 的个数大于4的12-组合2A :b 的个数大于3的12-组合 3A :c 的个数大于4的12-组合4A :d 的个数大于5的12-组合要求的是:4321A A A A ⋂⋂⋂ = T )(4321A A A A +++-)(434232413121A A A A A A A A A A A A ⋂+⋂+⋂+⋂+⋂+⋂+ )(432431421321A A A A A A A A A A A A ⋂⋂+⋂⋂+⋂⋂+⋂⋂- )(4321A A A A ⋂⋂⋂+T =⎪⎪⎭⎫ ⎝⎛-+121412=4551A =⎪⎪⎭⎫ ⎝⎛-+7147=120 2A =⎪⎪⎭⎫ ⎝⎛-+8148=165 3A =⎪⎪⎭⎫ ⎝⎛-+7147=120 4A =⎪⎪⎭⎫⎝⎛-+6146=8421A A ⋂=⎪⎪⎭⎫ ⎝⎛-+3143=20 31A A ⋂=⎪⎪⎭⎫ ⎝⎛-+2142=10 41A A ⋂=⎪⎪⎭⎫⎝⎛-+1141=432A A ⋂=⎪⎪⎭⎫ ⎝⎛-+3143=20 42A A ⋂=⎪⎪⎭⎫ ⎝⎛-+2142=10 43A A ⋂=⎪⎪⎭⎫⎝⎛-+1141=4321A A A ⋂⋂=421A A A ⋂⋂=431A A A ⋂⋂=432A A A ⋂⋂=4321A A A A ⋂⋂⋂=0 455-(120+165+120+84)+(20+10+4+20+10+4)=34∴多重集{}d c b a S ⋅⋅⋅⋅=5,4,34,的12-组合的个数是34 □9、确定方程204321=+++x x x x满足611≤≤x ,702≤≤x ,843≤≤x ,624≤≤x的整数解的个数。
哈工大集合论习题课-第六章 树及割集 习题课(学生)
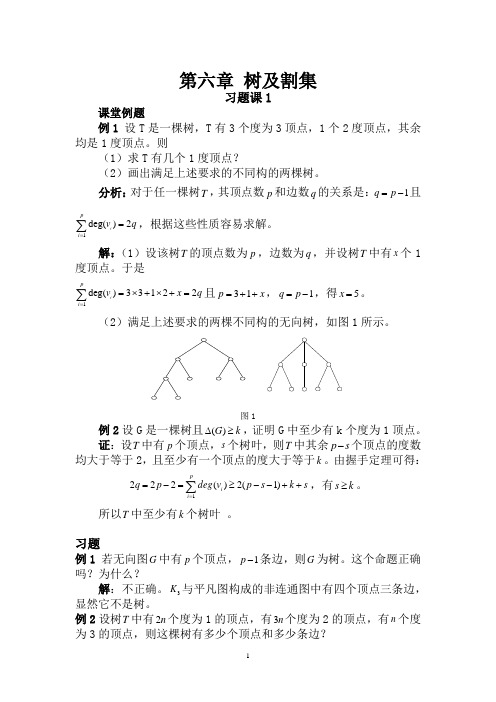
第六章 树及割集习题课1课堂例题例1 设T 是一棵树,T 有3个度为3顶点,1个2度顶点,其余均是1度顶点。
则(1)求T 有几个1度顶点?(2)画出满足上述要求的不同构的两棵树。
分析:对于任一棵树T ,其顶点数p 和边数q 的关系是:1q p =-且1deg()2ipi v q ==∑,根据这些性质容易求解。
解:(1)设该树T 的顶点数为p ,边数为q ,并设树T 中有x 个1度顶点。
于是1deg()33122ipi v x q ==⨯+⨯+=∑且31p x =++,1q p =-,得5x =。
(2)满足上述要求的两棵不同构的无向树,如图1所示。
图1例2设G 是一棵树且()G k ∆≥,证明G 中至少有k 个度为1顶点。
证:设T 中有p 个顶点,s 个树叶,则T 中其余p s -个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k 。
由握手定理可得:1222()2(1)pi i q p deg v p s k s ==-=≥--++∑,有s k ≥。
所以T 中至少有k 个树叶 。
习题例1 若无向图G 中有p 个顶点,1p -条边,则G 为树。
这个命题正确吗?为什么?解:不正确。
3K 与平凡图构成的非连通图中有四个顶点三条边,显然它不是树。
例2设树T 中有2n 个度为1的顶点,有3n 个度为2的顶点,有n 个度为3的顶点,则这棵树有多少个顶点和多少条边?解:设T 有p 个顶点,q 条边,则123161q p n n n n =-=++-=-。
由deg()2v Vv q ∈=∑有:1223322(61)122n n n q n n ⨯+⨯+⨯==-=-,解得:n =2。
故11,12q p ==。
例3证明恰有两个顶点度数为1的树必为一条通路。
证:设T 是一棵具有两个顶点度数为1的(,)p q 树,则1q p =-且1deg()2pii v q ==∑2(1)p =-。
又T 除两个顶点度数为1外,其他顶点度均大于等于2,故211deg()2deg()2(1)p p iii i v v p -===+=-∑∑,即21deg()2(2)p ii v p -==-∑。
第6章习题解答哈工大习题册

第 6 章非正弦周期电流电路习题解答A所以 f (t) 0.5A sink t k 1 k πC1 10 4F ,电压源) 8tco s( 1。
0试0求0R,7L5, C)2 。
VRi图题6.2解:由于电流中只含基波分量且与电源基波分量具有相同的初相位,则可知右侧部分对基波分量相当于短路,对二次谐波分量相当于开路。
基波作用时电路中相当于只有电阻作用,可得6.1 求图示倒锯齿波的傅里叶级数展开式,解: f (t) A(1 t /T)1 T 1 A0T1f(t)dtT1A(1 t/T)dt A t2TA[t2tT]T0 0.5A2Ta k 0A(1 t / T )cos( kt)dt [b kT2[ 2A(1 t /T) cos(k t)] Tk2A(1 t/T) sin(k t)]Tkk2AT2Tsin(k t)dt TA(1 t/T)sin( k2Ak T2cos(k t)dt 2A A0 kT k频谱图如图(b)所示。
6.2 图示电路中,电流i 2 2 cos(500t60 ) A ,u S 5 2 0 2 co s(t 5 00 6 0u SC2C1并画出频谱0tTRU 1 210 I11(j L )( ) j C 1 j C 2 Z11 jL j C 1 j C 2由右侧部分对基波分量相当于短路可得此时等效阻抗的分子为零或分母无穷大, 由阻抗表达式可知阻抗分子为零可行, 可得1j L 0j C 11带入已知条件得 L 21 0. 0 4H2C 1由右侧部分对二次谐波分量相当于开路可得 此时等效阻抗的分母为零或分子无穷大,由阻抗表达式可知阻抗分母为零可行, 可得1带入已知条件得C 2 1F 3 μ3F 2300006.3 图示电路 N 为无独立源网络, u [100cos(t 45 ) 50cos2t 25cos(3t 45 )]V , i (80cos t 20cos 2t 10cos3t)mA 。
组合数学期末试卷及答案

n 种取法,将取出的 m 个数由大到小排 m 序 , 设 为 a1 , a2 , , a m , 再 将 其 分 为 两 组 , a1 , , a k , a k 1 , ,am k 1,2, ,m 1 ,则第一组中的最小数一定大于第二组中的
解:从 n 个数中先任取 m 个数,则有 最大数。故题目所求为:
S j S i 39
第3页
共4页
第4页
共 4页
S j Si 39
即: d i 1 d i 2 d j 39 九. (10 分)求方程 的正整数解的个数。 解: 由题可知: (1) 绕如 v1v2 和 v3v4 中点的连线旋转 180 度,所得置换如下: P1=(v1)(v2)(v3)(v4), P2=(v1 v2)(v3 v4), P3=(v1 v3)(v2 v4), P4=(v2 v3)(v1 v4), (2) 绕每一个顶点的中心线旋转 120 度,240 度,所得置换如下: P5=(v1)(v2 v3 v4), P6=(v1)(v2 v4 v3), P7=(v2)(v1 v3 v4), P8=(v2)(v1 v4 v3), P9=(v3)(v1 v2 v4), P10=(v3)(v1 v4 v2), P11=(v4)(v1 v2 v3), P12=(v4)(v1 v3 v2), 装 由 Polya 定理可知: 不同方案数=(11*32+34)/12=15 订
递推关系如下:
an=an-1+n a1=2
第1页 共2页
组合数学答案6-8

Let A be the set of xi is nonnegative integer and xi 0 (i 1 ,2 ,3 and 4) ,
then
14 4 1 17
A
14
14
680
.
Let Ai be the set of xi is nonnegative integer and xi 8 (i 1,2,3 or 4) ,
|������| = 3
9 42
1
=
1260
|������1| = 4
7 2
1
= 105
|������2| = 3
6 2
1
= 60
|������3| = 4
8 3
1
= 280
We can also get that
Thus,
|������1 ∩ ������2| = *'aaa' , 'bbbb' , 2∙c, 1∙d+ |������1 ∩ ������3| = *'aaa' , 4∙b, 'cc' , 1∙d+ |������2 ∩ ������3| = *3∙a, 'bbbb' , 'cc' , 1∙d+
������3 = *3∙a, 4∙b, 'cc' , 1∙d+ ������1 is the set that consisting all the permutations of S which three a is consecutively.������2is the set that consisting the all the permutations of S which four b is consecutively. ������3 is the set that consisting all the permutations of S which two c is consecutively.
哈工大集合论习题课-第五章 图的基本概念习题课(学生)

第五章 图的基本概念习 题 课 11. 画出具有 6、8、10、…、2n 个顶点的三次图;是否有7个顶点的三次图?2. 无向图G 有21条边,12个3度数顶点,其余顶点的度数均为2,求G 的顶点数p 。
解:设图的顶点为p ,根据握手定理:1deg()2pi i v q ==∑,有212)12(2312⨯=-⨯+⨯p ,得15302==p p ,。
3. 下列各无向图中有几个顶点?(1)16条边,每个顶点的度为2;(2)21条边,3个4度顶点,其余的都为3度数顶点;(3)24条边,各顶点的度数相同。
解: 设图的顶点为p ,根据握手定理:(1)1deg()2pi i v q ==∑,即2221632p q ==⨯=;所以16p =,即有16个顶点。
(2)1deg()2p i i v q ==∑,即433(3)222142p q ⨯+⨯-==⨯=,所以13p =。
(3)各点的度数为k ,则1deg()2i pi v q ==∑,即222448k p q ⨯==⨯=,于是① 若1k =,48p =; ② 若2k =,24p =;③ 若3k =,16p =;④ 若4k =,12p =; ⑤ 若6k =,8p =;⑥ 若8k =,16p =; ⑦ 若12k =,4p =; ⑧ 若16k =,3p =;⑨ 若24k =,2p =; ⑩ 若48k =,1p =。
4.设图G 中9个顶点,每个顶点的度不是5就是6。
证明G 中至少有5个6度顶点或至少有6个5度顶点。
证:由握手定理的推论可知,G 中5度顶点数只能是0,2,6,8五种情况,此时6度顶点数分别为9,7,5,3,1个。
以上五种情况都满足至少5个6度顶点或至少6个5度顶点的情况。
5.有n 个药箱,若每两个药箱里有一种相同的药,而每种药恰好放在两个药箱中,问药箱里共有多少种药?[就是求一个完全图n K 的边数(1)(2)/2q p p =--g ]6.设G 是有p 个顶点,q 条边的无向图,各顶点的度数均为3。
哈工大831考研真题答案

哈工大831考研真题答案一、选择题1. 题目:[具体题目内容]答案:[正确选项],解析:[解释为什么这个选项是正确的,以及其他选项为什么不正确]。
2. 题目:[具体题目内容]答案:[正确选项],解析:[提供解题思路和方法]。
...二、填空题1. 题目:[具体题目内容]答案:[填空答案],解析:[解释答案的来源和解题方法]。
2. 题目:[具体题目内容]答案:[填空答案],解析:[提供解题思路]。
...三、简答题1. 题目:[具体题目内容]答案:[简答要点],解析:[概述答题要点,解释答题思路]。
2. 题目:[具体题目内容]答案:[简答要点],解析:[阐述答题要点,提供答题框架]。
...四、计算题/分析题1. 题目:[具体题目内容]答案:[解题步骤],解析:[详细解释解题过程,包括公式应用和计算方法]。
2. 题目:[具体题目内容]答案:[解题步骤],解析:[展示解题逻辑和关键点]。
...五、论述题1. 题目:[具体题目内容]答案:[论述要点],解析:[阐述答题框架,包括论点、论据和论证]。
2. 题目:[具体题目内容]答案:[论述要点],解析:[提供答题思路,强调答题的逻辑性和条理性]。
...总结在解答考研真题时,考生需要具备扎实的基础知识,清晰的解题思路,以及良好的时间管理能力。
通过不断的练习和复习,考生可以提高解题效率和准确率。
希望本答案模板能为考生提供一定的参考和帮助。
请根据具体的考试题目和内容,填写相应的答案和解析。
如果需要针对特定年份和学科的真题答案,请提供更详细的信息。
组合数学基础-答案及讲稿

组合数学基础答案及讲稿(陶平生)基本内容与方法:组合计数;组合构造;组合结构;映射与对应;分类与染色;归纳与递推;容斥原理;极端原理;调整法;补集法;数形结合法,等等.1、设M 为n 元集,若M 有k 个不同的子集12,,,k A A A ,满足:对于每个{},1,2,,i j k ∈ ,i j A A ≠∅ ,求正整数k 的最大值.解:正整数k 的最大值为12n -.()01、先证明,存在M的12n -个子集,两两之交不空;设{}12,,,n M a a a = ,而1122,,,n A A A - 为集合{}121,,,n a a a - 的全部12n -个子集,令{}1,1,2,,2n i i n B A a i -== ,则M 的12n -个子集1122,,,n B B B - ,两两之交不空;()02、再证,对于M的任何121n -+个子集,其中必有两个子集不相交.设1122,,,n B B B - 是M 的12n -个不同子集,其中每个皆含n a ;用i B 表示子集i B 在M 中的补集,1(\),1,2,,2n i i B M B i -== ,则对于任意i j ≠,,i j i j B B B B ≠≠,并且j i B B ≠, (因前者含n a 而后者不含),故1122,,,n B B B - ,1122,,,n B B B - 为M 的全部2n个不同子集,现将上述集合搭配成为12n -对:()()()11122122,,,,,,n n B B B B B B -- ;任取M 的121n -+个子集,必有两个子集属于同一对,则这两个子集不相交.2、将前九个正整数1,2,,9 分成三组,每组三个数,使得每组中的三数之和皆为质数;求出所有不同分法的种数.证:()01、由于在1,2,,9 中,三个不同的数之和介于6和24之间,其中的质数有7,11,13,17,19,23这六个数,今将这六数按被3除的余数情况分为两类:{}7,13,19A =,其中每个数被3除余1;{}11,17,23B =,其中每个数被3除余2;假若所分成的,,A B C 三组数对应的和,,a b c p p p 为互异质数,则因12945a b c p p p ++=+++= 被3整除,故三个和数,,a b c p p p 必为同一类数,因为A 类三数和713193945++=<,B 类三数和1117235145++=>,矛盾! 故三个和数中必有两个相等.()02、据()01知,将45表成7,11,13,17,19,23中的三数和(其中有两数相等),只有四种情况:()119197++;()2171711++;()3131319++;()4111123++.由于在1,2,,9 中有5个奇数,故分成的三组中必有一组,三数全为奇数,另两组各有一个奇数.对于情形()1,和为7的组只有{}1,2,4,剩下六数3,5,6,7,8,9,分为和为19的两组,且其中一组全为奇数,只有唯一的分法:{}3,7,9与{}5,6,8;对于情形()2,若三奇数的组为{}1,7,9,则另两组为 {}{}4,5,8,2,3,6;或{}{}3,6,8,2,4,5;若三奇数的组为{}3,5,9,则另两组为 {}{}2,8,7,1,4,6,或{}{}4,6,7,1,2,8; 若三奇数的组为{}1,3,7,则另两组为 {}{}2,6,9,4,5,8;共得分法5种;对于情形()3,若三奇数的组为{}3,7,9,则另两组为 {}{}1,4,8,2,5,6; 若三奇数的组为{}1,3,9,则另两组为 {}{}2,4,7,5,6,8或{}{}2,5,6,4,7,8; 若三奇数的组为{}1,5,7,则另两组为 {}{}3,4,6,2,8,9或{}{}2,3,8,4,6,9; 共得分法5种;对于情形()4,和为23的组只有{}6,8,9,则另两组为 {}{}1,3,7,2,4,5; 据以上,共计得到155112+++=种分法.3、设正整数a 的各位数字全由1和2组成,由其中任意() 2k k ≥个连续数位上的数字所组成的k 位数,称为数a 的一个“k 段”;若数a 的任两个“k 段”都不相同.证明:对于具有这种性质的最大正整数a ,其开初的一个“1k -段”和最后的一个“1k -段”必定相同.证:设12n a x x x = 是一个具有这种性质的最大正整数,由a 的最大性,在其后面无论添加1或2,所得到的1n +位数1121n a x x x = 以及2122n a x x x = 中,都有两个相同的“k 段”. 设在1a 中有 1121i i i k n k n x x x x x ++--+= ;在2a 中有1122j j j k n k n x x x x x ++--+= . 显然i j ≠,(因为11i k j k x x +-+-≠),且11i n k ≤≤-+,11j n k ≤≤-+,如果1i =或1j =,则直接去掉相应“k 段”中的末位数,可知结论成立;如果2i ≥且2j ≥,因 12212i i i k n k n j j j k x x x x x x x x ++--+++-== ,考虑各自的前一位数字111, , i j n k x x x ---+,它们只取1和2两个值,其中必有两数相同,于是数a 中有两个相同的“k 段”,矛盾. 因此,i j 中必有一个为1,故结论得证.4、将数集},...,,{21n a a a A =中所有元素的算术平均值记为)(A P ,(na a a A P n+++=...)(21). 若B 是A 的非空子集,且)()(A P B P =,则称B 是A的一个“均衡子集”.试求数集}9,8,7,6,5,4,3,2,1{=M 的所有“均衡子集”的个数. 解:由于()5P M=,令{}{}54,3,2,1,0,1,2,3,4M x x M '=-∈=----,则()0P M '=, 依照此平移关系,M 和M '的均衡子集可一一对应.用()f k 表示M '的k 元均衡子集的个数,显然有(9)(1)1f f ==(M '的9元均衡子集只有M ',一元均衡子集只有{}0).M '的二元均衡子集共四个,为{,},1,2,3,4i B i i i =-=, 因此(2)4f =. M '的三元均衡子集有两种情况:(1)含有元素0的为{0}{,0,},1,2,3,4i B i i i =-= , 共四个;(2)不含元素0的,由于等式312,413=+=+可表示为3120,3120-++=--=以及4130,4130-++=--=,得到4个均衡子集{3,1,2},{3,1,2},{4,1,3},{4,1,3}------,因此(3)448f =+=.M '的四元均衡子集有三种情况:(1)每两个二元均衡子集之并:,14i j B B i j ≤<≤ , 共6个集; (2)不含元素0的三元均衡子集与{}0的并集,共4个集;(3)以上两种情况之外者,由于等式1423+=+可表为14230--++=以及14230+--=得2个均衡子集{1,4,2,3}--与{1,4,2,3}--,因此()464212f =++=. 又注意到,除M '本身外,若B '是M '的均衡子集,当且仅当其补集''M C B 也是M '的均衡子集,二者一一对应. 因此(9)(),1,2,3,4f k f k k -==.从而M '的均衡子集个数为9411()(9)2()12(14812)51k k f k f f k ===+=++++=∑∑.即M 的均衡子集有51个.5、某校有2010名新生,每人至少认识其中n 人,试求n 的最小值,使得其中必存在彼此认识的16个人.解:记这2010个人的集合为{}122010,,,M v v v = ,i v 所认识的人的集合记为, 1,2,2010i A i = ,则i A n ≥,且 1,2,2010i i v A i ∉= ,若12,v v 是M 中相识的两人,则有121222010A A A A A B n =+-≥- , 当220101n -≥,则有312v A A ∈ ,且123,,v v v 两两相识,而()123123123322010A A A A A A A A A n =+-≥-⋅ .当3220101n -⋅≥,则有4123v A A A ∈ ,且1234,,,v v v v 两两相识,而()123412341234432010A A A A A A A A A A A A n =+-≥-⋅ ,如此继续,得1215,,,v v v 两两相识,而151414151511115142010i i i i i i A A A A A n ===⎛⎫=+-≥-⋅ ⎪⎝⎭. 当151420101n -⋅≥,则有15161, i i v A =∈ 且1216,,,v v v 两两相识,而由151420101n -⋅≥,得142010115n ⋅+≥,n 为整数,则1877n ≥.再说明1877n =是最小的;若1876n =,我们可构造一种情形,使得M 中不存在相互认识的16个人.为此,将2010个人均分为1215,,,B B B 等15组,每组134个人,令同组的人互不相识,而异组的任两人皆相识,则M 中任一人v 所认识的人的个数皆为()141341876d v =⨯=,从M 中任取16个人,必有两个人属于这15组中的同一个组,于是这两人互不相识,因此M 中不存在相互认识的16个人.从而n 的最小值为1877.6、有()2nn ≥名运动员,其编号分别是1,2,,n ,在一次活动中,他们以任意方式站成了一排. 如果每次允许将其中一些人两两对换位置,但在同一轮操作过程中,任一人至多只能参与一次这种对换.证明:至多只需两轮这样的操作,可使队列变成1,2,,n 的顺序排列. 证明:对n 归纳,2≤n 时显然. 设n k ≤时结论成立;今证1n k =+时情形,设121,,...,k a a a +是1k +名运动员1,2,,1k + 的任一排法, (i ) 如果其中存在一组运动员()12,, (1)i i i a a a m k ≤≤,他们的编号恰好就是其位置序号组k i i i ,...,,21的一个排列,则由归纳假设,这组运动员可经至多两轮操作,分别到位于自然位置(使i 号运动员到位于i 位),而剩下的1k m +-个运动员,显然也是其所处位置号的排列,他们也可经过至多两轮对换到位于自然位置,这样,队列121,,...,k a a a +可经两轮对换化为1,2,,1k +(ii ) 若(i )中的情形不出现,为叙述方便,设1号位置上所站的运动员编号为1b , (11≠b ),1b 号位置上的运动员编号为2b ,({}12,1b b ∉),2b 号位置上的运动员编号为3b ,({}213,,1b b b ∉),...,j b 号位置上的运动员编号为1+j b ,({}j j b b b ,...,,111∉+),...,k b 号位置上的运动员编号为1。
组合数学习题解答

第一章:1.2. 求在1000和9999之间各位数字都不相同,而且由奇数构成的整数个数。
解:由奇数构成的4位数只能是由1,3,5,7,9这5个数字构成,又要求各位数字都不相同,因此这是一组从5个不同元素中选4个的排列,所以,所求个数为:P(5,4)=120。
1.4. 10个人坐在一排看戏有多少种就坐方式?如果其中有两人不愿坐在一起,问有多少种就坐方式?解:这显然是一组10个人的全排列问题,故共有10!种就坐方式。
如果两个人坐在一起,则可把这两个人捆绑在一起,如是问题就变成9个人的全排列,共有9!种就坐方式。
而这两个人相捆绑的方式又有2种(甲在乙的左面或右面)。
故两人坐在一起的方式数共有2*9!,于是两人不坐在一 起的方式共有 10!- 2*9!。
1.5. 10个人围圆桌而坐,其中两人不愿坐在一起,问有多少种就坐方式? 解:这是一组圆排列问题,10个人围圆就坐共有10!10 种方式。
两人坐在一起的方式数为9!92⨯,故两人不坐在一起的方式数为:9!-2*8!。
1.14. 求1到10000中,有多少正数,它的数字之和等于5?又有多少数字之和小于5的整数?解:(1)在1到9999中考虑,不是4位数的整数前面补足0, 例如235写成0235,则问题就变为求:x 1+x 2+x 3+x 4=5 的非负整数解的个数,故有 F (4,5)=⎪⎪⎭⎫⎝⎛-+=515456 (2)分为求:x 1+x 2+x 3+x 4=4 的非负整数解,其个数为F (4,4)=35 x 1+x 2+x 3+x 4=3 的非负整数解,其个数为F (4,3)=20 x 1+x 2+x 3+x 4=2 的非负整数解,其个数为F (4,2)=10 x 1+x 2+x 3+x 4=1 的非负整数解,其个数为F (4,1)=4 x 1+x 2+x 3+x 4=0 的非负整数解,其个数为F (4,0)=1 将它们相加即得,F (4,4)+F (4,3)+F (4,2)+F (4,1)+F (4,0)=70。
哈工大研究生数值分析试题及答案

1. 3,2x =-分别是方程328120x x x --+= 的根;讨论用Newton 迭代法求它们近似值的收敛阶。
取初值02x =-计算根3x =-的近似值,要求迭代3次。
(结果保留4位小数) 解: 设 32()812f x x x x =--+ 2()328f x x x '=-- ()62f x x ''=- (3)0,(3)0f f '-=-≠,(2)0,(2)0,(2)100f f f '''===≠则:3-是()0f x =的单根,故Newton 迭代在3-附近是平方收敛; 2是()0f x =的二重根,故Newton 迭代在2附近是线性收敛; 取02x =-,Newton 迭代:3212()812()328n n n n n n n n f x x x x x x x f x x x +--+=-=-'-- 223634n n n x x x ++=+2001023634x x x x ++==+2112123634x x x x ++==+2223223634x x x x ++==+2. 设常数0a ≠ ,求出a 的取值范围使得解方程组112233212313a x b a x b a x b --⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪-= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭的Jacobi 迭代法收敛。
解: Jacobi 迭代:(1)()k k J x B x g +=+10210211203203130130J a B a a a -----⎛⎫⎛⎫⎛⎫⎪⎪ ⎪=--=-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1123a b g a b a b -⎛⎫⎛⎫ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭迭代矩阵J B 的特征方程:021211120323013013J a E B a a a a λλλλλλλ----⎛⎫⎛⎫⎪ ⎪-=+-=-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭即:3()14()0a a λλ+=特征根:0,i aλλ==±谱半径:()1J B ρ=< 时Jacobi 迭代收敛故:a >3. 设(1)用Crout 三角分解法求解方程组 12323251034133619x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ ;(2)用乘幂法求方程组系数阵的按摸最大的特征值和对应的特征向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Homework 613.Let A={A1,A2,A3,A4,A5,A6} whereA1={1,2} A2={2,3} A3={3,4} A4={4,5} A5={5,6} A6={6,1}Determine the number of different SDR’s that A has. Generalize to n sets.Solution: When we choose 1 in A 1, if we choose 3 in A 2, we can choose 4 only in A 3, we can choose 5 only in A 4, and we can choose 6 only in A 5, however, we can choose 1 only in A 6,it will contract with 1 in A 1Hence, we can choose only 2 in A .2 if we choose 1 in A 1,3 in A 3,4 in A 4,5 in A 5,6 in A When we choose 2 in A 6.1, we can only choose 3 in A 3, 4 in A 4, 5 in A 5, 1 in A 1That is SDR . Hence, there are only two SDRs in A . 1={1,2,3,4,5,6}and SDR 2Similarity, we can generalize to n sets. There are only two SDRs in n-sets the same.={2,3,4,5,6,1}That is SDR 1={1,2,…,n} and SDR 2={2,3,4,…,n,1}23. Use the deferred acceptance algorithm to obtain both the women-optimal and men-optimal stable complete marriage for the preferential ranking matrix.Conclude that for the given preferential ranking matrix there is onlyone stable complete marriage.a b c dAA BB CC DD�1,32,3 1,44,13,24,33,32,2 2,21,4 4,12,23,44,13,11,4�Solution:(1) women-optimalThe results of the algorithm are as follows:1)A choose a, B choose a, C choose b, D choose d; a rejects B2)B choose d; d rejects D.3)D choose b; b rejects C.4)C choose a; a rejects A.5)A choose c.In 5), there are no rejections, and(2) men-optimalThe results of the algorithm are as follows:1)a choose D, b choose B, c choose D, d choose C; D rejects a.2)a choose C, C rejects d.3)d choose B, B rejects b.4)b choose D, D reject c.5)c choose A.In 5), there are no rejections, anda C,b D,c A,d B.Conclude that, for given preferential ranking matrix, there is only one stable complete marriage.3. Consider an m-by-n chessboard where at least one of m and n is even. The board has an equal number of white and black squares. Show that if m and n are at least 2 and if exactly one white and exactly one black square are forbidden, the resulting board has a perfect cover with dominoes.Solution:Let n be even, there are even numbers of columns. From top row, if the top row has no squares forbidden, then that row can be covered by dominoes. So we can remove this row. Repeat this till the new top row has a forbidden square. Do the same thing from the bottom row. So we can assume that forbidden squares are on the top and bottom rows.Let’s consider the first two columns from the left. If there is nofirst two columns, they can be covered by forbidden square in thedominoes and we can remove them. Repeat this till there is a forbidden square in the first two columns. Do the same from the right side so we ca n also assume the forbidden squares lie in the first two columns and the last two columns. After the above have been done, we can assume that chessflip board is of one of the following three situations (with rotation or ofover the chess board if needed). In each of the case, there are even numbers of columns.(A) (B) (C)So the two forbidden squares have one black and the other white, there are even numbers of columns. We draw the figures, in the cases (A) and (B), there has to be odd number of rows while in the case (C), there are even number of rows. Then we divide the board into pieces as shown in the following such each piece is rectangular with at least one side being even, thus can be covered by dominoes respectively.So the entire board has a perfect cover by dominoes.(A) (B) (C)4. Determine the max-matching and the min-cover of the right graph by applying the matching algorithm. We choose the red edges and obtain a matching M1.Find a minimum edge cover for the right graph.Answer:Now we get the matching )},(),,{(44121y x y x M = and U 131,x x = {}. (i) The vertices 31,x x are labeled (*).x 1y 1x x y 2 y 3 y 4y 5(ii) Scan the vertices in U 154321,,,,y y y y y in turn, and label with (1x ), since all vertices incident to 3x .already have a label, no vertex of Y get label (3x ).(iii) Scan the vertices 5431,,,y y y y labeled in (ii), and label 2x with (1y ), label 4x with (4y ).(*)x 1y 1(1x )x(*)x 3x y 2 y 3(1x ) y 4(1x )y 5(1x )(*)x 1 y1x (*)x 3x y 2 y 3 y 4y 5(iv) We scan the vertices 2x and 4x labeled in (iii), and label 2y with (2x ).(v) Scan the vertices 2y labeled in (iv), and find that no new labels are possible.We have achieved breakthrough. We find the 1M -augmenting path11221x y x y r = using the labels as a guide. Then )},(),,(),,{(4411222y x y x y x M =(*)x 1y 1(1x )(1y )x 2(*)x 3(4y )x y 2(2x ) y 3(1x ) y 4(1x )y 5(1x )(*)x 1 y 1(1x )(1y )x 2(*)x 3(4y )x y 2 y 3(1x ) y 4(1x )y 5(1x )and }{32x U =.(vi) The vertices 3x are labeled (*).(vii) Scan the vertices in U 25y in turn, and label with (3x )x 1y 1x 2(*)x 3x 4y 2 y 3 y 4y 5x 1y 1x 2x 3x 4y 2 y 3 y 4y 5(Viii) Scan the vertex 5y labeled in (vii), and find that no new labels are possible.We have achieved breakthrough. We find the 2M -augmenting path352x y r = using the labels as a guide. Then)},(),,(),,(),,{(441122533y x y x y x y x M =is a matching of four edges.Now we can get thatx 1 y 1x 2x 3x 4y 2 y 3 y 4y 5x 1 y 1x 2(*)x 3x 4y 2 y 3 y 4y 5(3x )the max-matching )},(),,(),,(),,{(44112253y x y x y x y x M = and the min-cover= {54321,,,,y y y y y }.2) Find a minimum edge cover for the right graph.Follow the steps above; we can get a max-matching)},(),,(),,(),,{(44112253y x y x y x y x M =.And we can find that there are also some vertices uncovered by the max-matching. Obviously, the vertex 3y Now we can construct a subgraph composed of edges incident to the vertex is uncovered.3y , we find the max-matching of the subgraph, and add it to the max-matching of M, then we can get a minimum edge cover.Fig The subgraphThe max-matching of the subgraph is {(x 1,y 3)}. Now we can get a minimum edgecover={(x 1,y 3)}∪M ={(x 1,y 3)(x 3,y 5)(x 2,y 2)(x 1,y 1)(x 4,y 4)}x 1y 1x 2x 3x 4y 2 y 3y 4y 5x1y1x2 x3 x4y2 y3 y4y5Fig The minimum edge cover第八次作业16. Apply the algorithm for the GCD in Section 10.1 to 15 and 46, and then use the results to determine the multiplicative inverse of 15 in Z46Answer:.The result for Computing the GCD of 15 and 46 are displayed in the following:Now ,we write as a linear combination of 15 and 46:1=46-3*15From the above, 1 is the GCD of 15 and 46.Thus, we can get the multiplicative inverse of 15 in Z4615:-121. Determine the complementary design of the BIBD with parameters bb=vv=77,kk=rr=33,λλ=11in Section 10.2= – 3 = 43.•b: the number of blocks;•v: the number of varieties;•k: the number of varieties in each block;• r : the number of blocks containing each variety• λλ: the number of blocks containing each pair of varieties. Answer:Apply ()11−−=k v r λ to this case, now we have b =v =7,k =r =3,λ=1.Hence, we can get ()()311717111≠=−−×=−−=k v r λ. Thus, we can design such a complementary.We can get the complementary design of the BIBD withparametersb’ = b = 7, v’ = v = 7, k’ = v-k = 4, r’ = b-r = 4 ,213272'=+×−=+−=λλr b .28. Show that BB={00,11,33,99}is a difference set in Z13 Answer:, and use thisdifference set as a starter block to construct an SBIBD. Identify the parameters of the block design.We compute the subtraction table and obtain:We can find that non-zero integers in Z13}{9,3,1,0=B occur exactly once as adifference, hence is a difference set in Z1332. Use Theorem 10.3.2 to construct a Steiner triple system of index 1 having 21 varieties..•Hints:• 1. construct two Steiner triple systems B1 and B2• 2. construct B based on B with 3 and 7varieties, respectively.1and B2. Answer:1)Construct two Steiner triple systems B1 and B2 with 3 and 7 varieties, respectively.Let X={a0,a1,a2}and Y={b0,b1,b2,b3,b4,b5,b6}be two sets of varieties.Let B1={a0,a1,a2}and B2=�{b0,b1,b3},{b1,b2,b4}, {b2,b3,b5},{b3,b4,b6},{b4,b5,b0},{b5,b6,b1},{b6,b0,b2}�be the Steiner triple systems of X and Y, respectively.2)Construct B based on B1 and B2.We define a set B of triples of the elements of X. Let {c ir, c js, c kt} be a set of 3 elements of X. then {c ir, c js, c kt} is a triple of B iff one of the following holds:i) r = s = tIf r=s=t=1, we can get {0,3,9}, {3,6,12}, {6,9,15}, {9,12,18}, {12,15,0},{15,18,3}, {18,0,6};If r=s=t=2, we can get {1,4,10}, {4,7,13}, {7,10,16}, {10,13,19},{13,16,1}, {16,19,4}, {20,1,7};If r=s=t=3, we can get {2,5,11}, {5,8,14}, {8,11,17}, {11,14,20},{14,17,2}, {17,20,5}, {20,2,8};ii) i = j = k, We can get {0, 1, 2}, {3, 4, 5}, {6, 7, 8},{9, 10, 11}, {12, 13,14}, {15, 16, 17}, {18, 19, 20};(iii) i, j and k are all different and {a i, a j, a k} is a triple of B1, and r, s and t are all different and {b r, b s, b t} is a triple of B2. Put another way, c ir, c js, and c kt are in 3 different rows and 3 different columns of the array, and the rows in which they lie correspond to a triple of B1 and the columns inwhich they lie correspond to a triple of B2 If {a .i, a j, a k If {a }={0, 1, 3},we can get {0, 4, 11}, {0, 10, 5}, {3, 1, 11}, {3, 10, 2}, {9, 1, 5}, {9, 4, 2};i, a j, a k If {a }={1, 2, 4}, we can get {3, 7, 14}, {3, 13, 8}, {6, 4, 14}, {6, 13, 5}, {12, 4, 8}, {12, 7, 5};i, a j, a k If{a }={2, 3, 5},we can get {6, 10, 17}, {6, 16, 11}, {9, 7, 17}, {9, 16,8},{15,7,11},{15,10, 8};i, a j, a k If {a }={3,4,6}, we can get {9,13,20},{9,19,14},{12,10, 20},{12,19,11},{18,10,14},{18,13,11};i, a j, a k If {a }={4, 5, 0},we can get {12,16,2}, {12, 1,17}, {15,13,2},{15,1,14}, {0,13,17}, {0,16,14};i, a j, a k If {a }={5,6, 1},we can get {15, 19, 5},{15,4,20},{18, 16, 5},{18, 4, 17},{3,16,20},{3,19,17};i, a j, a k}={6,0, 2},we can get {18, 1, 8}, {18, 7, 2}, {0, 19, 8}, {0, 7,20}, {6, 19, 2}, {6, 1, 20};52. Construct a completion of the 3-by-6 Latin rectangleAnswer:According to theorem 10.4.11(390页), this 3-by-6 Latin rectangle has a completion. Let X={x 0, x 1, x 2, x 3, x 4, x 5} representing the 6 elements, and Y= {y 0, y 1, y 2, y 3, y 4, y 5} representing the columns. An edge (x i, yj ) in denotes element i doesn’t appear in column j. Then we construct a regular of degree 3 Bipartite graph of X and Y ,G=(X, Δ, Y) as follows.y 2x 0x 2x 3x 4y 1y 3x 1y 5y 4y0x 5(1)Computing the perfect matching using the matching algorithm (312页) and the results are as follows. The red lines represent the maximum matching. (找出一个完美匹配即可,不必写出寻找的步骤,建议通过观察得出完美匹配最好,匹配算法太麻烦了)0 1 2 3 4 5 4 3 1 5 2 0 54312y 2x 0x 2x 3x 4y 1y 3x 1y 5y 4y0x 5So a new row is{x 2, x 0, x 4, x 1, x 5, x 3Similarly, we can draw the graph for the above matrix as follows.} could be added to the original matrix as follows.�01243134552054324012153� y 2x 0x 2x 3x 4y 1y 3x 1y 5y 4y0x 5(2)Computing the perfect matching and the results are as follows. The red lines represent the maximum matching.y 2x 0x 2x 3x 4y 1y 3x 1y 5y 4y0x 5Hence a new row is{x 1, x 5, x 0, x 2, x 3, x 4Similarly, we can draw the graph for the above matrix as follows.} and the new Latin rectangle is⎣⎢⎢⎢⎡012431345520543204150012153234⎦⎥⎥⎥⎤ y 2x 0x 2x 3x 4y 1y 3x 1y 5y 4y0x 5From the graph, we can easily know that all the lines construct a perfect matching. So we the final answer as follows⎣⎢⎢⎢⎢⎡012431543335520012204150325153234401⎦⎥⎥⎥⎥⎤58. Construct a completion of the semi-Latin squareAnswer :思路:构造二分图,找完美匹配(匹配算法)。
