高三数学《空间几何体的三视图》专题复习题含答案

合集下载

高三数学空间几何体的三视图与直观图试题答案及解析

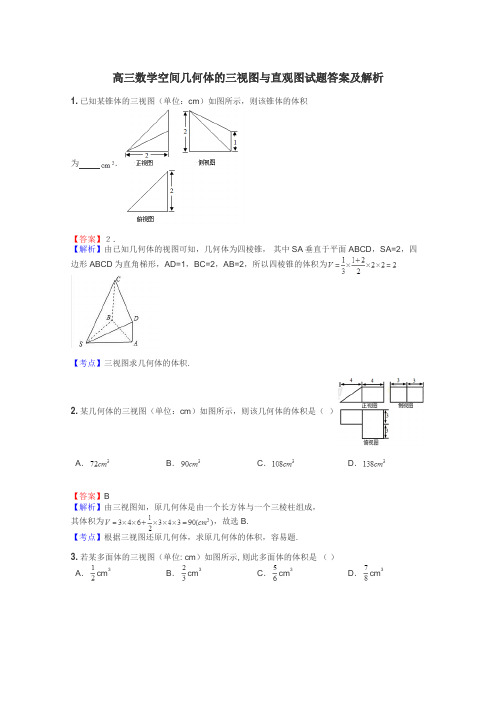
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．B．C．D．【答案】B【解析】由三视图知，原几何体是由一个长方体与一个三棱柱组成，其体积为，故选B.【考点】根据三视图还原几何体，求原几何体的体积，容易题.3.若某多面体的三视图（单位: cm）如图所示, 则此多面体的体积是（）A．cm3B．cm3C．cm3D．cm3【答案】C【解析】由三视图可得，该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A．16πB．14πC．12πD．8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图，某几何体的三视图都是等腰直角三角形，则几何体的体积是（）A．8B．7C．9D．6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9．6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为（）A．B．4C．9D．9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中x的值为( )A．5B．4C．3D．2【答案】C【解析】三视图，由正四棱锥和圆柱组成，故选C．8.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】B【解析】由题意，棱锥的高为，底面面积为，∴.【考点】三视图，体积．9.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位：)，则该几何体的体积为．【答案】18+9【解析】由三视图可知，此几何体为两个相切的球上方放了一个长方体组成的组合体，所以其体积为：V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示，该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，腰长为５.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示，则这个三棱锥的体积为；表面积为．【答案】；．【解析】由三视图知几何体如下图，为一个三棱锥，且三棱锥的一个侧面与底面垂直，底面三角形的一条边长为，该边上的高为，∴几何体的体积．它的表面积为．【考点】由三视图求面积、体积．13.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥，体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示，其正视图、侧视图、俯视图均为等腰直角三角形，且直角边长都为1，则这个几何体的体积是【答案】【解析】由三视图，可知该几何体是三棱锥，并且侧棱，，，则该三棱锥的高是，底面三角形是直角三角形，所以这个几何体的体积＝＝．【考点】由三视图求几何体的体积．15.一个几何体的三视图如图所示,则该机合体的体积为( )A．B．C．D．【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示，则该几何体的体积是【答案】【解析】通过三视图的观察可得，该几何体是一个四棱柱，底面是一个直角梯形，其上下底分别为2,3，梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．4C．6D．8【答案】D【解析】割补可得其体积为2×2×2＝8.18.某几何体的三视图如图所示，则该几何体的体积是________．【答案】16π－16【解析】由三视图知，该几何体是由一个底面半径为2，高为4的圆柱内挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，∴V＝(π×22－22)×4＝16π－16.19.已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为()．【答案】B【解析】对于选项A，由于只是截去了两个角，此切割不可能使得正视图成为梯形．故A不对；对于B，正视图是正方形符合题意，线段AM的影子是一个实线段，相对面上的线段DC1的投影是正方形的对角线，由于从正面看不到，故应作成虚线，故选项B正确；对于C，正视图是正方形，符合题意，有两条实线存在于正面不符合实物图的结构，故不对；对于D，正视图是正方形，符合题意，其中的两条实线符合俯视图的特征，故D不对．20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则该棱柱的体积为（）A．B．C．D．6【答案】B【解析】由三视图知该直三棱柱高为4，底面正三角形的高为3，所以正三角形边长为6，所以V＝×36×4＝36.故选B.【考点】1.三视图；2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为（）A．B．C．D．【答案】D【解析】由题意知道，该几何体体积是圆柱体积的，即.【考点】1、三视图；2、几何体体积.22.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( )A．B．C．D．【答案】B【解析】由三视图可得该几何体是一个圆台，其两底直径分别为2和4，母线长为4，所以该几何体的侧面积是，选B..【考点】三视图，圆台的侧面积.23.如图是一个组合几何体的三视图，则该几何体的体积是 .A．B．C．D．【答案】A【解析】由三视图还原可知该几何体是一个组合体，下面是一个半径为4，高为8的圆柱，，上面是一个三棱柱，故所求体积为.【考点】三视图，圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示，则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体，其体积为.【考点】三视图.25.一个几何体的三视图如图所示（单位长度：），俯视图中圆与四边形相切，且该几何体的体积为，则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知：这个几何体是一个半径为的球和一个直四棱柱的结合体，且这个直四棱柱的底面是对角线分别为和的棱形，这个直四棱柱的高为，∴这个几何体的体积：V=，解得h=.【考点】1.三视图；2.几何体的面积和体积26.一个几何体的三视图如图所示，则该几何体的直观图可以是（）【答案】D【解析】通过三视图的俯视图可知，该几何体是由两个旋转体组成，故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形，俯视图中曲线部分为半圆，尺寸如图所示，则该几何体的表面积为（）A．B．C．D．【答案】D【解析】由三视图可知，这是一个由半个圆柱和一个三棱柱构成的组合体，这个组合体仍为一个柱体。

高三数学空间几何体的三视图与直观图试题答案及解析

高三数学空间几何体的三视图与直观图试题答案及解析1.已知某个几何体的三视图如下（主视图的弧线是半圆），根据图中标出的尺寸（单位：cm），可得这个几何体的体积是 .【答案】640＋80π cm3【解析】由三视图可知，该几何体是一长方体与一半圆柱的组合体.长方体棱长分别为8,10,8，圆柱的底半径为4，高为10，故几何体体积为【考点】三视图，几何体的体积.2.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A．B．C．D．【答案】Ｂ【解析】由正视图、侧视图、俯视图形状，可判断该几何体为四面体，且四面体的长、宽、高均为4个单位，故可考虑置于棱长为4个单位的正方体中研究，如图所示，该四面体为，且,, , ，故最长的棱长为6，选B．【考点】三视图．3.一个几何体的三视图如图所示，已知这个几何体的体积为，= .【答案】【解析】由三视图知，原几何体是一个四棱锥，底面是面积为的矩形，高为，所以，解得.【考点】三视图，空间几何体的体积.4.一个几何体的三视图如图所示，这个几何体的体积是( )A．B．C．D．【答案】D【解析】三视图可知：原几何体是一个小蘑菇形状，且上面是半径为4半球；下面是一个长方体，其底面是边长为2的正方形，高为3．∴该几何体的体积，故选D．【考点】三视图，空间几何体的体积.5. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A．92+14πB．82+14πC．92+24πD．82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π.6.某几何体的三视图如右图所示，则该几何体的表面积是（）A．B．C．D．【答案】A【解析】依题意可得三棱锥的表面积由四个直角三角形构成.其中，.所以表面积为.故选A.【考点】1.三视图.2.几何体的表面积.3.空间向量能力.7.已知三棱锥的三视图如图所示，则它的外接球表面积为（）A．16B．4C．8D．2【答案】B【解析】由三视图可知直观图如图所示，面，球心在PM上，且，在中，，，，则，即，所以．【考点】三视图．8.一个几何体的三视图如图所示，则此几何体的体积是()A．112B．80C．72D．64【答案】B【解析】依题意得，该几何体的下半部分是一个棱长为4的正方体，上半部分是一个底面是边长为4的正方形，高为3的四棱锥，故该几何体的体积为43＋×4×4×3＝80．故选B．9.已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是 cm3．【答案】【解析】由三视图知该几何体是一个三棱锥，其底面是一个底边长为2高也是2的等腰三角形，且棱锥的高也是2，所以该几何体的体积,所以答案填【考点】1、三视图；2、棱锥的体积.10.一个几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】A【解析】该几何体为一个三棱柱截去一个三棱锥，所以体积为.【考点】空间几何体的体积.11.若一个圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为( )A．B．C．D．【答案】B【解析】设圆柱的底面半径为，高为，则，则，则侧，全，故圆柱的侧面积与全面积之比为，故选．【考点】三视图.12.一个空间几何体的三视图如图所示，该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，棱柱的高为8.因此所求体积为【考点】三视图13.一个空间几何体的三视图如图所示，则这个几何体的体积为；表面积为．【答案】；【解析】由三视图知几何体如下图，为一个直三棱柱，且三棱柱的一个侧面与另一个侧面垂直，，∴几何体的体积．它的表面积为．【考点】由三视图求面积、体积．14.已知三棱锥的底面是边长为的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（）A．B．C．D．【答案】C【解析】俯视图的高为，此即侧视图的底，侧视图的高即为正视图的高，所以其面积为.【考点】三视图.15.四棱锥P ABCD的三视图如图所示,四棱锥P ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2,则该球表面积为()(A)12π(B)24π(C)36π(D)48π【答案】A【解析】由三视图可知,四棱锥的直观图如图所示,补成长方体后可知其外接球的球心是PC的中点,由题意可知正方形ABCD的外接圆的直径AC=2 .即a=2,∴a=2.∴PA=2,∴PC==2,∴S=4π·R2=4π·()2=12π.球16.一个简单几何体的主视图、俯视图如图所示，则其左视图不可能为()A．正方形B．圆C．等腰三角形D．直角梯形【答案】D【解析】当几何体是一个长方体，其中一个侧面为正方形时，A可能；当几何体是横放的一个圆柱时，B可能；当几何体是横放的三棱柱时，C可能．于是只有D不可能．故选D.17.已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1，直径为4的球的体积为V2，则()A．1∶2B．2∶1C．1∶1D．1∶4【答案】A【解析】由三视图知，该几何体为圆柱内挖去一个底面相同的圆锥，因此V1＝8π－＝，V2＝×23＝，V1∶V2＝1∶2.18.已知某几何体的三视图如图所示,则该几何体的体积为.【答案】12π【解析】由三视图知几何体由两个底面直径为4、高为1的圆柱和一个底面直径为2、高为4的圆柱组成,故V=2×π×22×1+π×12×4=12π.19.已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V的大小为()A．B．12C．D．16【答案】C【解析】【思路点拨】由三视图得到几何体的直观图是解题的关键.注意该几何体是底面为直角梯形且放倒了的四棱锥.解：由三视图知,该几何体是一个四棱锥(如图),其底面是一个直角梯形,高h为4,∴四边形ABCD的面积S=×(4+1)×4=10,∴V=Sh=×10×4=.即该几何体的体积V为.20.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.21.如图,正方体ABCD-A'B'C'D'中,M,E是AB的三等分点,G,N是CD的三等分点,F,H分别是BC,MN的中点,则四棱锥A'-EFGH的侧视图为( )【答案】C【解析】注意分清三等分点可以看到,侧视图中A'E与A'G重合,A'H与A'M重合,A'F与A'B重合,侧视图为向左倾斜的三角形,故选C.22.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由三视图可知，该几何体是三分之一个圆锥，其体积为.【考点】三视图及几何体的体积.23.已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为的矩形，则该正方体的正视图的面积等于()A．B．1C．D．【答案】D【解析】由于该正方体的俯视图是面积为1的正方形，侧视图是一个面积为的矩形，因此该几何体的正视图是一个长为，宽为1的矩形，其面积为.24.如图所示的是一几何体的三视图，则该几何体的体积是________．【答案】【解析】由三视图可知该几何体是一个正方体去掉一角，其直观图如图所示，其中正方体的棱长为1，所以正方体的体积为1.去掉的三棱锥的体积为××1×1×1＝，所以该几何体的体积为1－＝.25.某三棱锥的三视图如图所示，则该三棱锥的体积是()．A．B．C．D．1【答案】B【解析】由三视图知底面是边长为1的等腰直角三角形，三棱锥的高为2.∴V＝××1×1×2＝.26.一个正三棱柱的正视图是边长为的正方形，则它的外接球的表面积等于()．A．8πB．C．9πD．【答案】B【解析】根据几何体的三视图知该正三棱柱的底面正三角形的高为h′＝，正三棱柱的高为h＝，那么可得外接球的半径为r＝，则其外接球的表面积为S＝4πr2＝27.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形)．(1)求四棱锥P-ABCD的体积；(2)若G为BC上的动点，求证：AE⊥PG.【答案】（1）（2）见解析【解析】(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4 ，BE＝2 ，AB＝4.∴VP-ABCD ＝PA·S四边形ABCD＝×4 ×4×4＝.(2)∵＝，∠EBA＝∠BAP＝90°，∴△EBA∽△BAP，∴∠BEA＝∠PBA.∴∠BEA＋∠BAE＝∠PBA＋∠BAE＝90°，∴PB⊥AE 又∵BC⊥平面APEB，∴BC⊥AE.∵BC∩PB＝B，∴AE⊥平面PBC.∵PG⊂平面PBC，∴AE⊥PG.28.某几何体的三视图如右图所示，则它的表面积是（）A．B．C．D．【答案】C【解析】由三视图可知，该几何体为一个正方体挖去一个圆锥，它的表面积是【考点】由三视图求几何体的表面积29.已知某几何体的三视图如图，其中主视图中半圆直径为2，则该几何体的体积____________【答案】24-【解析】由三视图可知，该几何体是有长方体里面挖了一个半圆柱体，可知，长方体的长为4，宽为3，高为2，那么圆柱体的高位3，底面的半径为1，则可知该几何体的体积为，故答案为．【考点】由三视图求面积、体积．30.一个几何体按比例绘制的三视图如图所示（单位：m）,则该几何体的体积为（）．A．B．C．D．【答案】C【解析】由三视图可知原几何体是3个半棱长为1的正方体，∴.【考点】1.三视图还原几何体；2.几何体体积.31.某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】B【解析】由三视图可知：几何体是底面是半径为2的半径扣掉一个三角形，.【考点】1.三视图；2.柱体体积.32.已知某几何体的正视图和侧视图均是边长为１的正方形，则这个几何体的体积不可能是（）A．B．C．1D．【答案】D【解析】∵几何体的正视图和侧视图均是边长为1的正方形，故它必是一个柱体.当它的底面是一个以1为两直角边的直角梯形时，其面积为，故排除A；当它的底面是一个以1为直径的圆时，其面积为，故排除B；当它的底面是一个以1为边长的正方形时,其面积为1，故排除C；由于正视图和侧视图均是边长为1的正方形，故俯视图的面积最大为1×1=1，即几何体的体积最大为1,而＞1，故这个几何体的体积不可能是,故选D【考点】1.三视图；2.几何体的体积.33.如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的体积为（）A．B．C．D．【答案】B【解析】由三视图知原图是一个底面为边长为3的正方形，高为的斜四棱柱，所以.【考点】1.三视图；2.四棱柱的体积.34.一个几何体的三视图如图所示，其中俯视图是菱形，则该几何体的侧面积为（）A．B．C．D．【答案】C【解析】正视图、侧视图、俯视图分别是三角形、三角形、四边形可判断该几何体为四棱锥，且有条侧棱垂直于底面，还原几何体，如图所示，.【考点】1、三视图；2、几何体的侧面积.35.已知某几何体的三视图如右图所示，其中，主（正）视图，左（侧）视图均是由直角三角形与半圆构成，俯视图由圆与内接直角三角形构成，根据图中的数据可得此几何体的体积为( ) A．B．C．D．【答案】C【解析】由三视图可得该几何体的上部分是一个三棱锥，下部分是半球，所以根据三视图中的数据可得.选C.【考点】三视图，几何体的体积.36.已知某个几何体的三视图如图(主视图的弧线是半圆)，根据图中标出的数据，这个几何体的体积是 .【答案】【解析】根据三视图可知，该几何体是组合体：一个长方体与一个半圆柱.根据图中数据得到其体积为，答案为.【考点】三视图，几何体的体积.37.若某空间几何体的三视图如上图所示，则该几何体的体积是（）A．B．C．2D．6【答案】C【解析】.【考点】1.三视图；2.几何体的体积.38.右图是一个空间几何体的三视图，如果主视图和左视图都是边长为2的正三角形，俯视图为正方形，那么该几何体的体积为________________.【答案】【解析】由正视图和侧视图是正三角形，俯视图是正方形，还原几何体为正四棱锥，如图所示，则.【考点】1、三视图；2、几何体的体积.39.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h随时间t变化的可能图象是( )【答案】B【解析】根据所给的三视图可知原几何体是倒放的圆锥，设圆锥的底面半径为，高为，水流的速度是，则由题意得，，当时，解得，这是一个对数型函数，所以容器中水面的高度随时间变化的图像类似于对数函数的图像，选B.【考点】1.三视图；2.对数函数的图像与性质；3.圆锥的体积40.如图所示是一个几何体的三视图，则该几何体的体积为（）A．B．C．D．【答案】B【解析】由三视图可知，该几何体为一长方体上面放着一样大小的半圆柱，其中长方体的长为，宽为，高为，半圆柱的底面半圆的半径为，高为，故该简单组合体的体积，选B.【考点】空间几何体的三视图、简单组合体的体积计算.41.若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是 cm．【答案】【解析】由三视图可知，该几何体是半个圆锥.其体积为.【考点】1、三视图；2、几何体的体积.42.如图，网格纸上小正方形的边长为1，粗线画的是某几何体的视图，则其体积为( )A．12＋B．24＋C．32＋D．24＋【答案】A【解析】有三视图可知，原立体图形为右图所示，是一个半径是1的球和一个下底面是边长为1的正方形，高是3的长方体的组合体，球的体积为，长方体的体积为，所以这个组合体的体积为.【考点】由三视图求几何体的体积.43.如图是一个几何体的三视图，则这个几何体的体积是（）A．27B．36C．33D．30【答案】D【解析】由三视图可知，这是一个由一个正方体和一个正四棱锥构成的组合体，选D【考点】1、三视图；2、空间几何体的体积44.在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为【答案】D【解析】从正视图和俯视图来看，前半部分是一个三棱锥，后半部分是从轴截面切开的半个圆锥故侧视应为D. 三视图虽为三个图，但解题时我们应将三个图综合起来考虑.【考点】几何体的三视图.45.如图是一个空间几何体的三视图，其中正视图和侧视图都是半径为的半圆，俯视图是半径为的圆，则该几何体的体积等于( )A．B．C．D．【答案】C【解析】由三视图知几何体是半径为的半球，所以其体积等于. 故选C．【考点】三视图.46.某几何体的三视图如图所示，则这个几何体的体积为（）A．B．C．D．【答案】B【解析】由三视图可知，该几何体可分为一个三棱锥和一个四棱锥，则，故选B.【考点】三视图，几何体的体积47.如图，是由若干个相同的小正方体堆成的几何体的三视图（各视图由小正方形拼接而成，现如图进行编号），则该几何体中含面⑥的小正方体也含面（填写序号）;【答案】③，⑨【解析】根据三视图的知识，几何体的底面有3个小正方体，该几何体有两层，第二层有1个小正方体，共有4个，几何体中含面⑥的小正方体也含面③，⑨．【考点】三视图点评：简单题，三视图已成为高考必考知识内容，关键是掌握三视图画法规则，“高平齐，长对正，宽相等”。

高三数学空间几何体的三视图与直观图试题答案及解析

高三数学空间几何体的三视图与直观图试题答案及解析1.如图是一个几何体的三视图，则该几何体的体积是（）A．54B．27C．18D．9【答案】C【解析】由几何体的三视图可知，这是一个四棱锥，且底面为矩形，长6，宽3；体高为3．则，故选：C．【考点】由三视图求面积、体积.2.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.3.右图为某几何体的三视图，则该几何体的体积为【答案】【解析】由三视图知，该几何体是底面半径为1，高为1的圆柱与半径为1的球体组成的组合体，其体积为=．【考点】简单几何体的三视图，圆柱的体积公式，球的体积公式4.如图所示，正方形O′A′B′C′的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是()A．6B．8C．2＋3D．2＋2【答案】B【解析】如图，OB＝2，OA＝1，则AB＝3．∴周长为8．5.一个几何体的三视图如图所示，则这个几何体的外接球的体积为________．【答案】【解析】几何体外接球的直径为四棱锥底面的对角线，球体积V＝()3．6.一个几何体的三视图如图所示，则这个几何体的体积是（）A．B．C．D．【答案】【解析】由三视图可知，该几何体是底面半径为，高为的圆锥的一半，故其体积为.选.【考点】三视图，圆锥的体积.7.（5分）（2011•天津）一个几何体的三视图如图所示（单位：m），则这个几何体的体积为 m3．【答案】4【解析】由题意可知，一个简单的组合体，上面是一个底面是边长为1的正方形，高是2的四棱柱，下面是一个长为2，高为1，宽为1的长方体，根据所给的长度，求出几何体的体积．解：由三视图可知，这是一个简单的组合体，上面是一个底面是边长为1的正方形，高是2的四棱柱，体积是1×1×2下面是一个长为2，高为1，宽为1的长方体，体积是1×1×2∴几何体的体积是1×1×2+2×1×1=4m3，故答案为：4点评：本题考查由三视图还原直观图，根据图形中所给的数据，求出要求的体积，本题是一个考查简单几何体体积的简单题目．8.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥，假设一条直角的棱长为x，则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.9.一个几何体的三视图如图所示，则该几何体的体积是（）.A．B．C．D．2【答案】B【解析】由三视图可知此几何体是由一个长为2，宽为，高为的长方体过三个顶点切去一角的空间多面体，如图所示，则其体积为.故正确答案选B.【考点】1.三视图；2.简单组合体体积.10.某几何体正视图与侧视图相同，其正视图与俯视图如图所示，且图中的四边形都是边长为2的正方形，正视图中两条虚线互相垂直，则该几何体的体积是A．B．6C．4D．【答案】A【解析】由三视图可知，该几何体是由一个棱长为2的正方体，挖去一个以正方体的一个面为底面，正方体的中心为顶点的正四棱锥所成的组合体，其体积故选A.【考点】1、三视图；2、棱柱、棱锥的体积.11.若一个空间几何体的三视图如图所示，则这个几何体的表面积为A．B．4C．D．8【答案】A【解析】由三视图可知此几何体是正四棱锥，底面正方形的对角线长为，棱锥的高为3，则底面边长为2。

高三专项训练：三视图练习题(一)

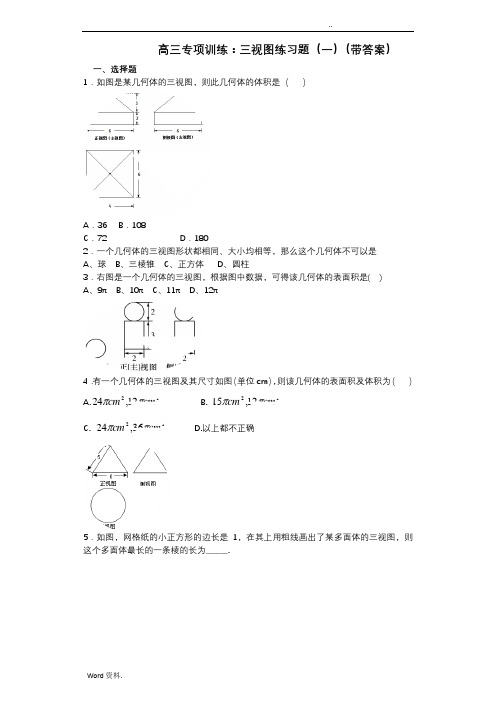
高三专项训练：三视图练习题（一）（带答案）一、选择题1．如图是某几何体的三视图，则此几何体的体积是（）A ．36B ．108C ．72D ．1802．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4．有一个几何体的三视图及其尺寸如图（单位cm ），则该几何体的表面积及体积为（）A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.A． B． CD ．36．一空间几何体的三视图如图所示，则该几何体的体积为.A. B. C D. [7．若某空间几何体的三视图如图所示，则该几何体的体积是A ．13 B ．23C ．1D ．28．右图是某几何体的三视图，则该几何体的体积为（）A ．Ｂ．Ｃ．Ｄ．1362942π+3618π+9122π+9182π+正视图俯视图9．已知一个几何体的三视图如图所示，则该几何体外接球的表面积为（）A ．43π B ． 163π C ．1912π D ． 193π 10．某几何体的正视图如图所示，则该几何体的俯视图不可能的是11．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )cm 3.A ．π+8B ．328π+C ．π+12D ．3212π+侧视图主视俯视第8题图俯视图侧视图正视图12．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）（A ）243cm （B ）223cm （C ）28cm （D ）24cm13．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．6πB ．7πC ．8πD ．9π14．如右图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（）A ．π3B ．π2C ．π23 D ．π4 15．如图是一个几何体的三视图，若它的体积是33，则图中正视图所标a=（）A ．1B 3C 3D ．316．已知某几何体的三视图如图所示（单位：cm ），其中正视图、侧视图都是等腰直角三角形，则这个几何体的体积是（）A ．338cmB ．3316cm C ．33216cm D ． 3332cm17．一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．B ．C ．D ．18．若某空间几何体的三视图如图所示，则该几何体的体积是（）A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119．某物体是空心的几何体，其三视图均为右图，则其体积为（）A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图侧视图俯视图正视第9题22 4 2侧视图 22俯视20．如图，水平放置的三棱柱ABC-A 1B 1C 1中，侧棱AA 1⊥平面A 1B 1C 1，其正视图是边长为a 的正方形．俯视图是边长为a 的正三角形，则该三棱柱的侧视图的面积为A ．a 2B ．a 2C a 2D 221．右图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（）A ．20＋3π B ．24＋3π C ．20＋4π D ．24＋4π22．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．12πB ．π34C ．3πD ．π312．23.如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为（）12正视图侧视图俯视图 AC A 11正视图侧视图俯视图24．图１是设某几何体的三视图，则该几何体的体积为（）A．942π+Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+、25．已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm）可得该几何体的体积是（）A．313cm B．323cmC．343cm D．383cm26．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27．一个几何体的三视图如图所示，则这个几何体的体积为（）正视图侧视图俯视图332正视图俯视图图1AB ．12C ．32 D1+28．一个空间几何体的三视图如图（1）所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为（）A 、64，48+B 、32，48+ C 、643，32+D 、332，48+29．若某多面体的三视图（单位: cm ）如图所示,则此多面体的体积是（） A ．21cm 3 B ．32cm 3 C ．65cm 3 D ．87cm 3正视图俯视图图（1）侧（左）视图 1111130．一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯视图是直径为2的圆(如右图），则这个几何体的表面积为A ．12π+B ．7πC ． π8D ．π2031．（一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32．已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为（） A ．6π B ．5π C．4π D．3π2π+4π+2π4π+正视侧视俯视俯视..A ．2，23B ．22，2D ．2，434．如图，有一个几何体的正视图与侧视图都是底为6cm ，腰为5cm 的等腰三角形，俯视图是直径为6cm 的圆，则该几何体的体积为 ( )A ．12πcm 3B ．24πcm 3C ．36πcm 3D ．48πcm 335 （A ）348cm （B ）324cm （C ）332cm （D ）328cm36．如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A ．4B ．3C ．32D ．237．某四面体的三视图如下图所示，则该四面体的四个面中，直角三角形的面积和是_______.二、填空题正视图左视图俯视图正视图侧视图俯视图第6题 ·38．一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________．39．如图所示是一个几何体的三视图（单位：cm ），主视图和左视图是底边长为4cm ，腰长为22的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是-__________40．某几何体的三视图如图所示，则该几何体的体积的最大值为 .41．一正多面体其三视图如图所示，该正多面体的体积为___________.主视图左视图俯视图3主视图俯视图侧视图42．若某几何体的三视图（单位：cm ）如右图所示，则该几何体的体积为 cm 2．43．已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为；44．某四面体的三视图如上图所示，该四面体四个面的面积中最大的是1正视图俯视图左视图45．一个几何体的三视图如右图所示（单位：），则该几何体的体积为__________46．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．47．如图，一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形，则其体积是_________.48．某几何体的三视图如图所示，则它的体积是___________俯视图m 3m 249．设某几何体的三视图如图所示，则该几何体表面积是50．一个几何体的三视图如右图所示，正视图是一个边长为2的正三角形，侧视图是一个等腰直角三角形，则该几何体的体积为．三视图练习题（一）参考答案1．B【解析】此几何体是一个组合体，下面是一个正四棱柱上面是一个四棱锥．其体积为166********V =⨯⨯+⨯⨯⨯=．2．D【解析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆。

高三数学空间几何体的三视图与直观图试题答案及解析

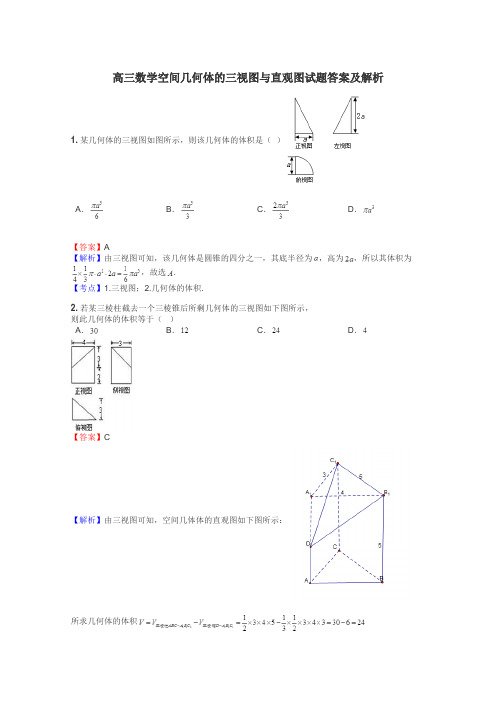
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是圆锥的四分之一，其底半径为，高为，所以其体积为，故选.【考点】1.三视图；2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示，则此几何体的体积等于（）A．B．C．D．【答案】C【解析】由三视图可知，空间几体体的直观图如下图所示：所求几何体的体积故选C.【考点】1、三视图；2、空间几何体的体积.3.如图，一个几何体的三视图（正视图、侧视图和俯视图）为两个等腰直角三角形和一个边长为1的正方形，则其外接球的表面积为A．πB．2πC．3πD．4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥，且底面是边长为1的正方形，垂直于底面的侧棱长也为1，因此，该几何体可以补形为一个棱长为1的正方体，其外接球就是这个正方体的外接球，直径为正方体的对角线长，即2R＝，故R＝故外接球表面积为：4πR2＝3π.【考点】三视图，几何体的外接球及其表面积4.如图所示，一个三棱锥的三视图是三个直角三角形(单位： cm)，则该三棱锥的外接球的表面积为________cm2．【答案】29π【解析】从三棱锥的三视图可知，三棱锥有两侧面与底面垂直，把三棱锥补成长，宽，高分别为4,2,3的长方体，设外接球的半径为R，由42＋22＋32＝4R2得，S＝4πR2＝29π(cm2)．球5.某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．2C．D．8【答案】D【解析】由三视图可知，该几何体如图所示，其底面为正方形，正方形的边长为2．HD＝3，BF ＝1，将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体的体积为×2×2×4＝8．6.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．7.一个几何体的三视图如图所示，已知这个几何体的体积为，= .【答案】【解析】由三视图知，原几何体是一个四棱锥，底面是面积为的矩形，高为，所以，解得.【考点】三视图，空间几何体的体积.8.如图，水平放置的正三棱柱的主视图是一边长为2的正方形，则该三棱柱的左视图的面积为．【答案】【解析】左视图为一个矩形，长宽分别为，因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为() A．B．C．D．【答案】B【解析】依题意得，该正三棱柱的底面正三角形的边长为2，侧棱长为1．设该正三棱柱的外接球半径为R，易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×＝，所以R2＝＋＝，则该球的表面积为4πR2＝．10.图中的网格是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为________．【答案】16【解析】从三视图可知，这是一个四棱锥，.【考点】三视图.11.如图所示，一个空间几何体的正视图和左视图都是边长为的正方形，俯视图是一个直径为的圆，那么这个几何体的体积为 ( )A．B．C．D．【答案】B【解析】几何体是圆柱，.【考点】三视图，圆柱的体积.12.一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为( )A．1B．C．D．【答案】B【解析】由三视图可知，此几何体为三棱锥，如图，其中正视图为，是边长为2的正三角形，，且，底面为等腰直角三角形，，所以体积为，故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（）A．1B．C．D．【答案】C【解析】由题意知，正视图的最大面积为对角面的面积，最小面积为，而，故选C．【考点】三视图.14.已知某几何体的三视图如右图所示，其中俯视图是圆，且该几何体的体积为；直径为2的球的体积为．则()A．B．C．D．【答案】C【解析】由题意，该几何体是一个圆柱挖去一个圆锥得到的几何体，，，∴.选B.【考点】三视图，体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（）A．B．C．D．【答案】B【解析】过B作BD⊥AC于点D，则BD=2，CD=2，所以BC=,因为SC⊥平面ABC，所以SC⊥BC，所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是由一个半圆柱和一个三棱锥拼接而成，且半圆柱的底面是半径为的半圆，高为，其底面积为，故其体积为，三棱锥的底面是一个直角三角形，三棱锥的高也为，其底面积为，故其体积为，所以该几何体的体积为，故选A.【考点】1.三视图；2.组合体的体积17.右图为某几何体的三视图，则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1，高为1的圆柱与半径为1的四分之一的球的组合体，所以体积为【考点】三视图18.一个空间几何体的三视图如图所示，该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C－ABD，它的主视图与俯视图如右上图所示，则二面角 C－AB－D的正切值为．【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C－AB－D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形，则原△ABC 的面积为()A．a2B．a2C．a2D．a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶，则易知S＝ ( a)2，∴S＝a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A．πcm3B．3πcm3C．πcm3D．πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD ＝AD ＝2EC ＝2.(1)请画出该几何体的三视图； (2)求四棱锥B-CEPD 的体积．【答案】(1)见解析 (2)2【解析】解：(1)该组合体的三视图如图所示．(2)∵PD ⊥平面ABCD ， PD ⊂平面PDCE ，∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形，∴BC ⊥CD ，且BC ＝DC ＝AD ＝2. 又∵平面PDCE∩平面ABCD ＝CD ， BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PD ⊥DC.又∵EC ∥PD ，PD ＝2，EC ＝1，∴四边形PDCE 为一个直角梯形，其面积： S 梯形PDCE ＝ (PD ＋EC)·DC ＝×3×2＝3， ∴四棱锥B-CEPD 的体积V B-CEPD ＝S 梯形PDCE ·BC ＝×3×2＝2.23. 某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【答案】A【解析】将三视图还原成直观图为：上面是一个正四棱柱，下面是半个圆柱体．所以V＝2×2×4＋×22×π×4＝16＋8π.24.某几何体的三视图如图所示，则其体积为________．【答案】【解析】由三视图还原几何体为半个圆锥，高为2，底面半圆的半径r＝1.∴体积V＝×(π×12×2)＝.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形)．(1)求四棱锥P-ABCD的体积；(2)若G为BC上的动点，求证：AE⊥PG.【答案】（1）（2）见解析【解析】(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4 ，BE＝2 ，AB＝4.∴VP-ABCD ＝PA·S四边形ABCD＝×4 ×4×4＝.(2)∵＝，∠EBA＝∠BAP＝90°，∴△EBA∽△BAP，∴∠BEA＝∠PBA.∴∠BEA＋∠BAE＝∠PBA＋∠BAE＝90°，∴PB⊥AE又∵BC⊥平面APEB，∴BC⊥AE.∵BC∩PB＝B，∴AE⊥平面PBC.∵PG⊂平面PBC，∴AE⊥PG.26.如图所示，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为________．【答案】9【解析】由题意知，此几何体是三棱锥，其高h＝3，相应底面面积为S＝×6×3＝9，∴V＝Sh＝×9×3＝9.27.某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。

三视图习题(含答案)

几何体的三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A ）2（B ）1（C ）23（D ）132、一个几何体的三视图如图，该几何体的表面积是（）（A ）372 （B ）360 （C ）292 （D ）2803、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（A ）3523cm 3（B ）3203cm 3（C ）2243cm 3（D ）1603cm 34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( ) A ．3 B ．2 C ．23 D ．66、图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h= cm7、一个几何体的三视图如图所示，则这个几何体的体积为。

第1题第2题第3题第5题第6题8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B. 423π+C. 2323π+D. 2343π+11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（） A ．9πB ．10πC ．11πD ．12π12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）48+122 （B ）48+242 （C ）36+122 （D ）36+24213、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．第7题第8题2 2侧(左)视2 22 正(主)视俯视第10俯视图正(主)视图侧(左)视图2 32 2第1114、设某几何体的三视图如上图所示。

高三数学空间几何体的三视图与直观图试题答案及解析

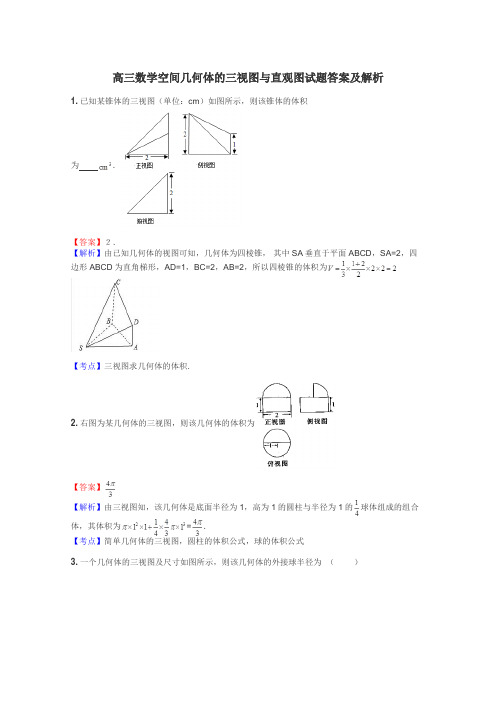
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.右图为某几何体的三视图，则该几何体的体积为【答案】【解析】由三视图知，该几何体是底面半径为1，高为1的圆柱与半径为1的球体组成的组合体，其体积为=．【考点】简单几何体的三视图，圆柱的体积公式，球的体积公式3.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A．B．C．D．【答案】C【解析】由三视图可知：该几何体是一个如图所示的三棱锥P-ABC，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O，O点必在高线PE上，外接球半径为R，则在直角三角形BOE中，BO2=OE2+BE2=（PE-EO）2+BE2，即R2=（4-R）2+（3）2，解得：R=，故选C.【考点】三视图，球与多面体的切接问题，空间想象能力4.如图是一个几何体的三视图，则该几何体的表面积是____________【答案】28＋12【解析】这是一个侧放的直三棱柱，底面是等腰直角三角形，侧棱长为6故表面积为2×(×2×2)＋(2＋2＋2)×6＝28＋12.【考点】三视图，几何体的表面积.5.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..6.某空间几何体的正视图是三角形，则该几何体不可能是（）圆柱圆锥四面体三棱柱【答案】A【解析】由于圆柱的三视图不可能是三角形所以选A.【考点】三视图.7.某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是________．【答案】2(π＋)【解析】由三视图可知此几何体的表面积分为两部分：底面积即俯视图的面积为2；侧面积为一个完整的圆锥的侧面积，且圆锥的母线长为2，底面半径为1，所以侧面积为2π．两部分加起来即为几何体的表面积，为2(π＋)．8.一个锥体的主(正)视图和左(侧)视图如图所示，下面选项中，不可能是该锥体的俯视图的是()【答案】C【解析】俯视图是选项C的锥体的正视图不可能是直角三角形．另外直观图如图1的三棱锥(OP⊥面OEF，OE⊥EF，OP＝OE＝EF＝1)的俯视图是选项A，直观图如图2的三棱锥(其中OP，OE，OF两两垂直，且长度都是1)的俯视图是选项B，直观图如图3的四棱锥(其中OP⊥平面OEGF，底面是边长为1的正方形，OP＝1)的俯视图是选项D．9.如图所示，正方形O′A′B′C′的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是()A．6B．8C．2＋3D．2＋2【答案】B【解析】如图，OB＝2，OA＝1，则AB＝3．∴周长为8．10.某几何体的三视图如图所示，且该几何体的体积是2，则正(主)视图的面积等于()A．2B．C．D．3【答案】A【解析】由三视图可知该几何体是一个四棱锥，其底面积就是俯视图的面积S＝(1＋2)×2＝3，其高就是正(主)视图以及侧(左)视图的高x，因此有×3×x＝2，解得x＝2，于是正(主)视图的面积S＝×2×2＝2．11.如图，三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥底面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形，底宽为原底等边三角形的高，侧视图的高为侧棱长，所以侧视图的面积为,故选B.【考点】三视图12.一个几何体的三视图如图所示，则该几何体内切球的体积为 .【答案】【解析】依题意可得该几何体是一个正三棱柱，底面边长为2，高为.由球的对称性可得内切球的半径为.由已知计算得底面内切圆的半径也为.所以内切球的体积为.【考点】1.三视图.2.几何体内切球的对称性.3.球的体积公式.4.空间想象力.13.已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的左视图面积的最小值是________．【答案】【解析】如图，正三棱柱中，分别是的中点，则当面与侧面平行时，左视图面积最小，且面积为.【考点】三视图.14.某几何体的三视图如图3所示，则其体积为________．【答案】【解析】原几何体可视为圆锥的一半，其底面半径为1，高为2，∴其体积为×π×12×2×＝.15.已知正△ABC的边长为2，那么用斜二测画法得到的△ABC的直观图△A′B′C′的面积为（）A．B．C．D．【答案】D【解析】∵正△ABC的边长为2，故正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=•=故选D16.一个体积为12的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为（）A．B．C．D．【答案】A【解析】依题意可得三棱柱的底面是边长为4正三角形.又由体积为.所以可得三棱柱的高为3.所以侧面积为.故选A.【考点】1.三视图的知识.2.棱柱的体积公式.3.空间想象力.17.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.18.一个四面体的顶点在空间直角坐系O－xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为（）A．B．C．D．【答案】A【解析】设O(0，0，0)，A(1，0，1)，B(1，1，0)，C(0，1，1)，将以O，A，B，C为顶点的四面体补成一正方体后，因为OA⊥BC，所以补成的几何体以zOx平面为投影面的正视图为A．19.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几体的体积为（）A．6B．9C．12D．18【答案】B【解析】由三视图可知，此几何体为如图所示的三棱锥，其底面△ABC为等腰三角形且AB=BC，AC=6，AC边上的高为3，SB⊥底面ABC，且SB=3，因此此几体的体积为V=××6×3×3=920.如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 .【答案】【解析】由三视图知，该几何体是一个圆柱，其表面积为.【考点】三视图及几何体的表面积.21.在三棱锥中，，平面ABC,.若其主视图，俯视图如图所示，则其左视图的面积为【答案】【解析】左视图是一个直角三角形，其直角边分别是2与.所以面积为.【考点】1.三视图知识.2.三角形面积的计算.22.一个几何体的三视图如图所示,则这个几何体的体积是_________.【答案】【解析】由三视图还原几何体，该几何体为底面半径为，高为的圆柱，去掉底面半径为，高为的圆锥的剩余部分，则其体积为．【考点】1、三视图；2、几何体的体积.23.棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是( ).A．B．4C．D．3【答案】B【解析】如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，.【考点】1.三视图；2.正方体的体积24.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】Ｂ【解析】由题设及图知，此几何体为一个四棱锥，其底面为一个对角线长为的正方形，故其底面积为，由三视图知其中一个侧棱为棱锥的高，其相对的侧棱与高及底面正方形的对角线组成一个直角三角形，由于此侧棱长为，对角线长为，故棱锥的高为，此棱锥的体积为，故选B．【考点】由三视图求面积、体积．25.已知某几何体的三视图如右图所示，其中，正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为（）A．B．C．D．【答案】C【解析】由已知的三视图可知原几何体是上方是三棱锥,下方是半球,∴，故选C.【考点】1.三视图；2.几何体的体积.26.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.27.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由三视图可知，该几何体是三分之一个圆锥，其体积为.【考点】三视图及几何体的体积.28.某几何体的三视图(图中单位：cm)如图所示，则此几何体的体积是()A．36 cm3B．48 cm3C．60 cm3D．72 cm3【答案】B【解析】由三视图可知几何体上方是一长方体，下方是一放倒的直四棱柱，且四棱柱底面是等腰梯形，上底长为2 cm，下底长为6 cm，高为2 cm，故几何体的体积是2×2×4＋×(2＋6)×2×4＝48(cm3)，故选B.29.如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图．已知CF＝2AD，侧视图是边长为2的等边三角形，俯视图是直角梯形，有关数据如图所示．求该几何体的体积．【答案】3【解析】解：取CF中点P，过P作PQ∥CB交BE于Q，连接PD，QD，则AD∥CP，且AD＝CP.所以四边形ACPD为平行四边形，所以AC∥PD.所以平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，所以V＝V－CAB＋V D－PQEFPDQ＝×22sin 60°×2＋××＝3.30.一个几何体的三视图如图所示，则该几何体的表面积是()A．6＋8B．12＋7C．12＋8D．18＋2【答案】C【解析】该空间几何体是一个三棱柱．底面为等腰三角形且底面三角形的高是1，底边长是2 ，两个底面三角形的面积之和是2，侧面积是(2＋2＋2)×3＝12＋6，故其表面积是12＋8.31. 已知四棱锥P-ABCD 的三视图如右图所示，则四棱锥P-ABCD 的四个侧面中的最大面积是( )．A ．6B ．8C ．2D ．3【答案】A【解析】四棱锥如图所示：PM ＝3，S △PDC ＝×4×＝2，S △PBC ＝S △PAD ＝×2×3＝3，S △PAB ＝×4×3＝6，所以四棱锥P-ABCD 的四个侧面中的最大面积是6.32. 若某几何体的三视图如图所示，则这个几何体的直观图可以是( )．【答案】B【解析】分别从三视图中去验证、排除．由正视图可知，A 不正确；由俯视图可知，C ，D 不正确，所以选B.33. 一个几何体的三视图如图所示，已知这个几何体的体积为，则h________.【答案】【解析】依题意可得四棱锥的体积为.所以可得.解得.故填.本小题的是常见的立几中的三视图的题型，这类题型关键是要能还原几何体的直观图形.所以培养空间的思想很重要.【考点】1.三视图的识别.2.空间几何体的直观图.34.图中的网格纸是边长为的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（）A．B．C．D．【答案】C【解析】由三视图知，该几何体是一个四棱锥，且其底面为一个矩形，底面积，高为，故该几何体的体积，故选C.【考点】1.三视图；2.锥体的体积35.已知某几何体的三视图如图，其中主视图中半圆直径为2，则该几何体的体积____________【答案】24-【解析】由三视图可知，该几何体是有长方体里面挖了一个半圆柱体，可知，长方体的长为4，宽为3，高为2，那么圆柱体的高位3，底面的半径为1，则可知该几何体的体积为，故答案为．【考点】由三视图求面积、体积．36.把边长为的正方形沿对角线折起，连结，得到三棱锥，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为（）A．B．C．D．【答案】B【解析】在三棱锥中，在平面上的射影为的中点，∵正方形边长为，∴，∴侧视图的面积为.【考点】1.三视图；2.三角形的面积.37.一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A．外接球的半径为B．体积为C．表面积为D．外接球的表面积为【答案】D．【解析】由题意设外接球半径为，则，A错误；外接球的表面积为，D正确；此几何体的体积为，故B错误；此几何体的表面积为，C错误．【考点】三视图及球的表面积公式.38.一个几何体的三视图如图所示，则该几何体的体积为( )A．4B．8C．D．【答案】B【解析】有三视图可以看出，该几何体是一个三棱锥，它的体积为．【考点】三视图，几何体的体积．39.如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A．B．C．4D．2【答案】A【解析】由题意易知，直三棱柱的底面是边长为2的正三角形.其侧视图为矩形，矩形的高为2，宽为底面正三角形的高.易知边长为2的正三角形的高为.所以面积为.【考点】三视图40.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )A．B．21C．D．24【答案】A【解析】还原几何体，得棱长为2的正方体和高为1的正四棱锥构成的简单组合体，如图所示，=，选A.【考点】1、几何体的表面积；2、三视图.41.某几何体的三视图如图所示，则它的表面积为（）A．B．C．D．【答案】A【解析】易知该三视图的直观图是倒立的半个三棱锥，其表面积由底面半圆，侧面三角形和侧面扇形，所以，故选A.【考点】1.立体几何三视图；2.表面积和体积的求法.42.一几何体的三视图如图所示，则该几何体的体积为（）A．200＋9πB．200＋18πC．140＋9πD．140＋18π【答案】A【解析】通过观察三视图，易知该几何体是由半个圆柱和长方体组成的，则半个圆柱体积；长方体的体积为,所以该几何体的最终体积，故选A.【考点】1.三视图的应用；2.简单几何体体积的求解.43.一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为( )A．B．C．D．【解析】把原来的几何体补成以为长、宽、高的长方体，原几何体四棱锥与长方体是同一个外接球，，，.【考点】1.补体法；2.几何体与外接球之间的元素换算.44.一个几何体的三视图如图所示，其中府视图为正三角形，则侧视图的面积为（）A．8B．C．D．4【答案】B【解析】由三视图可知：该几何体是一个正三棱柱，高为4，底面是一个边长为2的正三角形．因此，侧视图是一个长为４，宽为的矩形，．【考点】三视图与几何体的关系、几何体的侧面积的求法能力．45.某几何体的三视图如图所示，则它的侧面积为（）A．B．C．24D．【答案】A【解析】由三视图得,这是一个正四棱台,由条件，侧面积.【考点】1.三视图；2.正棱台侧面积的求法.46.一个几何体的三视图如图所示，其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形，则这个几何体的全面积为（）A．B．C．D．【解析】由三视图知，该几何体是一个圆锥，且圆锥的底面直径为，母线长为，用表示圆锥的底面半径，表示圆锥的母线长，则，，故该圆锥的全面积为.【考点】三视图、圆锥的表面积47.一个空间几何体的三视图如右图所示，其中主视图和侧视图都是半径为的圆，且这个几何体是球体的一部分，则这个几何体的表面积为( )A．3πB．4πC．6πD．8π【答案】B【解析】此空间几何体是球体切去四分之一的体积，表面积是四分之三的球表面积加上切面面积，切面面积是两个半圆面面积.故这个几何体的表面积是.【考点】1、几何体的三视图; 2、球的表面积公式.48.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为和，腰长为的等腰梯形，则该几何体的表面积是．【答案】【解析】从三视图可以看出：几何体是一个圆台，上底面是一个直径为4的圆，下底面是一个直径为2的圆，侧棱长为4．上底面积，下底面积，侧面是一个扇环形，面积为，所以表面积为．【考点】空间几何体的三视图、表面积的计算．49.某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为的圆（包括圆心），则该零件的体积是 ( )A．B．C．D．【解析】由题意易知该几何体为一半球内部挖去一圆锥所成，故体积为.故选C.【考点】1.体积； 2.三视图.50.某四棱台的三视图如图所示,则该四棱台的体积是 ( )A．B．C．D．【答案】B【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故,故选B．【考点】三视图与四棱台的体积51.若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（）A．B．C．D．【答案】B【解析】由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2，高为1,则底面外接圆半径，球心到底面的球心距,则球半径,则该球的表面积，故选B.【考点】由三视图求面积、体积．点评：本题考查的知识点是由三视图求表面积，其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径，是解答本题的关键．52.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的可能图像是（）A． B． C． D．【答案】B【解析】由三视图可知该几何体是圆锥，顶点在下，底面圆在上，在匀速注水过程中水面高度随着时间的增大而增大，且刚开始时截面积较小，所以高度变化较快，随着水面的升高，截面圆面积增大，高度变化速度减缓，因此函数的瞬时变化率逐渐减小，导数减小，图像为B项【考点】函数导数的定义点评：本题通过高度的瞬时变化率的变化情况得到函数的导数的大小，从而通过做出的切线斜率的变化得出正确图像53.已知一个三棱锥的主视图与俯视图如图所示，则该三棱锥的侧视图面积为（）A．B．C．D．【答案】B【解析】根据题意，由于三棱锥的俯视图为直角三角形，正视图为直角三角形，且斜边长为2，直角边长为，那么结合图像可知其侧视图为底面边长为1，高为的三角形，因此其面积为，故选B.【考点】三棱锥点评：解决的关键是根据三棱锥的三视图来得到底面积和高进而求解侧视图，属于基础题。

高考数学(文科)-空间几何体的三视图、表面积与体积-专题练习 (含答案与解析)

高考数学（文科）专题练习空间几何体的三视图、表面积与体积一、选择题．B．．．2．如图，一个棱柱的正视图和侧视图分别是矩形和正三角形，则这个三棱柱的俯视图为A．．．．(2016·河南郑州一测如图是一个四面体的三视图，这三个视图均是腰长为和俯视图的虚线是三角形的中线，则该四面体的体积为（C．8 3及其三视图中的正视图和侧视图如图所示，则棱C．38D．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该B．54185+D．81某几何体的三视图如图所示，则该几何体的体积等于C．5 2如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是C．8π《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。

问：积及为米几何？”其意思为“在屋内墙角处堆放米尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已立方尺，圆周率约为3，估算出堆放的米约有C．36斛如图，网格纸上正方形小格的边长为1(表示，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯C．10 27均在球O的球面上，AB）的正三角形的三个顶点都在球的表面积为____________．已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为高考数学（文科）专题练习空间几何体的三视图、表面积与体积答案一、选择题1~5．CDABB 6~10．CBBCC二、填空题11；12.40π；13.．14.13高考数学（文科）专题练习空间几何体的三视图、表面积与体积解析一、选择题1．解析：该几何体的侧视图即为其在面BCC1B1上的射影，又A点射影为点B，E点射影为线段CC1的中点，故选C．2．解析：由正视图和侧视图可知，这是一个横放的正三棱柱，一个侧面水平放置，则俯视图应为D．3．解析：四面体的直观图如图A-BCD，所以V=×(×1×2)×2=。

高中数学必修2考点知识专题训练3---空间几何体的三视图(含答案解析)

ൌ
஺ை ை஻
ൌ
௠௡ .
答案:௠௡
9.画出如图所示的几何体的三视图.
解:该几何体的三视图如图所示.
3/8
10.如图是一个几何体的三视图,想象该几何体的结构特征,画出该几何体的形状.
解:由于俯视图中有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体;结合侧视图和正视图,可知该几何体的上面是一个圆柱,下面是一个长方体.该几何体的形状如图所示.
高中数学必修 2 考点知识专题训练
空间几何体的三视图
课时过关·能力提升
一、基础巩固
1.下列视图不属于三视图的是( )
A.正视图
B.侧视图
C.后视图
D.俯视图
答案:C
2.如果一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其
圆心,那么这个棱柱
C.圆锥
D.圆柱
8.若线段
AB
平行于投影面,O
是线段
AB
上一点,且
஺ை ை஻
ൌ
௠ ௡
,
点‫ܣ‬ᇱ,
ܱᇱ,
‫ܤ‬ᇱ分别是
‫'ܱ'ܣ‬ ‫ܣ‬, ܱ, ‫ܤ‬在投影面上的投影点, 则 ܱ'‫ 'ܤ‬ൌ __________________.
解析:由题意知 AB∥A'B',OO'∥AA',OO'∥BB',
则有
஺'ை' ை'஻'
答案:D 4.在下列几何体各自的三视图中,有且仅有两个视图相同的是( )
1/8
A.①②
B.①③
C.①④
D.②④
解析:①正方体,三个视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三个视图各不相同;④四棱锥,正视图和侧视图相同.

高考数学空间几何体三视图、表面积与体积专题测试(含答案解析)

2021高考数学空间几何体三视图、外表积与体积专题测试〔含答案解析〕试题可以帮助考生进展查缺补漏，为此查字典数学网整理了空间几何体三视图、外表积与体积专题测试，请考生进展练习。

一、选择题1.(2021武汉调研)一个几何体的三视图如下图，那么该几何体的直观图可以是()解析 A、B、C与俯视图不符.答案 D2.将长方体截去一个四棱锥，得到的几何体如下图，那么该几何体的侧(左)视图为()解析抓住其一条对角线被遮住应为虚线，可知正确答案在C，D中，又结合直观图知，D正确.答案 D3.(2021安徽卷)一个多面体的三视图如下图，那么该多面体的外表积为()A.21+3B.18+3C.21D.18解析由三视图知，该多面体是由正方体割去两个角所成的图形，如下图，那么S=S正方体-2S三棱锥侧+2S三棱锥底=24-231211+234(2)2=21+3.答案 A4.S，A，B，C是球O外表上的点，SA平面ABCD，ABBC，SA=AB=1，BC=2，那么球O的外表积等于()A.4B.3C.2解析如下图，由ABBC知，AC为过A，B，C，D四点小圆直径，所以ADDC.又SA平面ABCD，设SB1C1D1-ABCD为SA，AB，BC为棱长构造的长方体，得体对角线长为12+12+22=2R，所以R=1，球O的外表积S=4.故选A.答案 A5.(2021湖南卷)一块石材表示的几何体的三视图如下图.将该石材切削、打磨，加工成球，那么能得到的最大球的半径等于()A.1B.2C.3D.4解析由三视图可得原石材为如下图的直三棱柱A1B1C1-ABC，且AB=8，BC=6，BB1=12.假设要得到半径最大的球，那么此球与平面A1B1BA，BCC1B1，ACC1A1相切，故此时球的半径与△ABC内切圆的半径相等，故半径r=6+8-102=2.应选B.答案 B6.点A，B，C，D均在同一球面上，其中△ABC是正三角形，AD平面ABC，AD=2AB=6，那么该球的体积为()A.323B.48C.643D.163解析如下图，O1为三角形ABC的外心，过O做OEAD，OO1面ABC，AO1=33AB=3.∵OD=O A，E为DA的中点.∵AD面ABC，AD∥OO1，EO=AO1=3.DO=DE2+OE2=23.R=DO= 23.V=43(23)3=323.答案 A二、填空题7.某四棱锥的三视图如下图，该四棱锥的体积是________. 解析由三视图可知，四棱锥的高为2，底面为直角梯形ABCD.其中DC=2，AB=3，BC=3，所以四棱锥的体积为132+3322=533. 答案 5338.如图，在三棱柱A1B1C1-ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F-ADE的体积为V1，三棱柱A1B1C1-ABC 的体积为V2，那么V1V2=________.解析设三棱柱A1B1C1-ABC的高为h，底面三角形ABC的面积为S，那么V1=1314S12h=124Sh=124V2，即V1V2=124. 答案 1249.在四面体ABCD中，AB=CD=6，AC=BD=4，AD=BC=5，那么四面体ABCD的外接球的外表积为________.解析构造一个长方体，使得它的三条面对角线分别为4、5、6，设长方体的三条边分别为x，y，z，那么x2+y2+z2=772，而长方体的外接球就是四面体的外接球，所以S=4R2=772. 答案 772三、解答题10.以下三个图中，左边是一个正方体截去一个角后所得多面体的直观图.右边两个是其正(主)视图和侧(左)视图. (1)请在正(主)视图的下方，按照画三视图的要求画出该多面体的俯视图(不要求表达作图过程).(2)求该多面体的体积(尺寸如图).解 (1)作出俯视图如下图.(2)依题意，该多面体是由一个正方体(ABCD-A1B1C1D1)截去一个三棱锥(E-A1B1D1)得到的，所以截去的三棱锥体积VE-A1B1D1=13S△A1B1D1A1E=1312221=23，正方体体积V正方体AC1=23=8，所以所求多面体的体积V=8-23=223.11.(2021安徽卷)如图，四棱柱ABCD-A1B1C1D1中，A1A底面ABCD.四边形ABCD为梯形，AD∥BC，且AD=2BC.过 A1，C，D三点的平面记为，BB1与的交点为Q.(1)证明：Q为BB1的中点;(2)求此四棱柱被平面所分成上下两局部的体积之比.解 (1)证明：因为BQ∥AA1，BC∥AD，BCBQ=B，ADAA1=A，所以平面QBC∥平面A1AD.从而平面A1CD与这两个平面的交线互相平行，即QC∥A1D.故△QBC与△A1AD的对应边互相平行，于是△QBC∽△A1AD.所以BQBB1=BQAA1=BCAD=12，即Q为BB1的中点.(2)如图，连接QA，QD.设AA1=h，梯形ABCD的高为d，四棱柱被平面所分成上下两局部的体积分别为V上和V下，BC=a，那么AD=2a.VQ-A1AD=13122ahd=13ahd，VQ-ABCD=13a+2a2d12h=14ahd，所以V下=VQ-A1AD+VQ-ABCD=712ahd，又V四棱柱A1B1C1D1-ABCD=32ahd，所以V上=V四棱柱A1B1C1D1-ABCD-V下=32ahd-712ahd=1112ahd.故V上V下=117.B级才能进步组1.(2021北京卷)在空间直角坐标系Oxyz中，A(2,0,0)，B(2,2,0)，C(0,2,0)，D(1,1，2).假设S1，S2，S3分别是三棱锥D-ABC在xOy，yOz，zOx坐标平面上的正投影图形的面积，那么()A.S1=S2=S3B.S2=S1且S2S3C.S3=S1且S3 S2D.S3=S2且S3S1解析作出三棱锥在三个坐标平面上的正投影，计算三角形的面积.如下图，△ABC为三棱锥在坐标平面xOy上的正投影，所以S1=1222=2.三棱锥在坐标平面yOz上的正投影与△DE F(E，F 分别为OA，BC的中点)全等，所以S2=1222=2.三棱锥在坐标平面xOz上的正投影与△DGH(G，H分别为AB，OC 的中点)全等，所以S3=1222=2.所以S2=S3且S1S3.应选D. 答案 D2.(2021山东卷)三棱锥P-ABC中，D，E分别为PB，PC的中点，记三棱锥D-ABE的体积为V1，P-ABC的体积为V2，那么V1V2=________.解析由于VP-ABE=VC-ABE，所以VP-ABE=12VP-ABC，又因VD-ABE=12VP-ABE，所以VD-ABE=14VP-ABC，V1V2=14.答案 143.(理)(2021课标全国卷Ⅱ)如图，四棱锥P-ABCD中，底面ABCD 为矩形，PA平面ABCD，E为PD的中点.(1)证明：PB∥平面AEC;(2)设二面角D-AE-C为60，AP=1，AD=3，求三棱锥E-ACD的体积.解 (1)连接BD交AC于点O，连接EO.因为ABCD为矩形，所以O为BD的中点.又E为PD的中点，所以EO∥PB.EO平面AEC，PB平面AEC，所以PB∥平面AEC.(2)因为PA平面ABCD，ABCD为矩形，所以AB，AD，AP两两垂直.如图，以A为坐标原点，AB的方向为x轴的正方向，|PA|为单位长，建立空间直角坐标系A-xyz.那么D(0，3，0)，E0，32，12， AE=0，32，12.设B(m,0,0)(m0)，那么C(m，3，0)，AC=(m，3，0)，设n1=(x，y，z)为平面ACE的法向量，那么n1AC=0，n1AE=0，即mx+3y=0，32y+12z=0，可取n1=3m，-1，3.又n2=(1,0,0)为平面DAE的法向量，由题设|cos〈n1，n2〉|=12，即 33+4m2=12，解得m=32.因为E为PD的中点，所以三棱锥E-ACD的高为12.三棱锥E-ACD的体积V=131233212=38.3.(文)如图，在Rt△ABC中，AB=BC=4，点E在线段AB上.过点E作EF∥BC交AC于点F，将△AEF沿EF折起到△PEF 的位置(点A与P重合)，使得PEB=30.(1)求证：EF(2)试问：当点E在何处时，四棱锥P-EFCB的侧面PEB的面积最大?并求此时四棱锥P-EFCB的体积.解 (1)证明：∵AB=BC，BCAB，又∵EF∥BC，EFAB，即EFBE，EFPE.又BEPE=E，EF平面PBE，EFPB.(2)设BE=x，PE=y，那么x+y=4.S△PEB=12BEPEsinPEB=14xy14x+y22=1.当且仅当x=y=2时，S△PEB的面积最大.此时，BE=PE=2.由(1)知EF平面PBE，平面PBE平面EFCB，在平面PBE中，作POBE于O，那么PO平面EFCB.即PO为四棱锥P-EFCB的高.又PO=PEsin30=212=1.S梯形EFCB =12(2+4)2=6.VP-BCFE=1361=2.空间几何体三视图、外表积与体积专题测试的答案和解析希望考生好好利用，进步成绩。

高考复习空间几何体三视图试题汇编(含答案)

空间几何体三视图题库一、单选题（共31题；共62分）1.甲、乙几何体的三视图分别如图•图所示，分别记它们的表面积为S甲，S乙，体积为V甲，V乙，则（）A. S甲>S乙, V甲>V乙B. S甲>S乙, V甲<V乙C. S甲<S乙, V甲>V乙D. S甲<S乙, V甲<V乙2.一个四棱锥的三视图如图所示，关于这个四棱锥，下列说法正确的是（）A. 最长的棱长为√7B. 该四棱锥的体积为√3C. 侧面四个三角形都是直角三角形D. 侧面三角形中有且仅有一个等腰三角形3.某四棱锥的三视图如图所示，则该四棱锥的外接球半径为（）A. 1B. √32C. √22D. 124.已知一个几何体的正视图和俯视图如图所示，正视图是边长为2a的正三角形, 俯视图是边长为a的正六边形，则该几何体侧视图的面积为（）A. √3a2B. √32a2 C. 3 a2 D. 32a25.若某几何体的三视图如图所示，则此几何体的体积等于（）A. 30B. 12C. 24D. 46.某几何体的三视图如图所示，则这个几何体的体积为（）A. 4B. 203C. 263D. 87.已知一个几何体的三视图如图所示(单位：cm)，那么这个几何体的表面积是( )A. (1+√2)cm2B. (3+√2)cm2C. (7+√2)cm2D. (8+√2)cm28.某三棱柱的三视图如图粗线所示，每个单元格的长度为1，则该三棱柱外接球的表面积为（）A. 4πB. 8πC. 12πD. 16π9.某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的表面积为（）A. (4+4√2)πB. (6+4√2)πC. (8+4√2)πD. (12+4√2)π10.某三棱锥的三视图如图所示，则该三棱锥最长的棱的棱长为（）A. 2B. √5C. 2√2D. 311.某几何体的三视图如图所示（单位：cm）则该几何体的体积（单位：cm3）是（）A. √212B. √26C. √23D. √212.已知某几何体的三视图如图所示，则该几何体的体积为( )A. 13+π4B. 1+π4C. 13+π12D. 1+π1213.某四面体的三视图如图所示，该四面体四个面的面积中最大的是（ )A. 8B. 6√22C. 10D. 8√214.一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位：cm)，则该几何体的体积为( )A. 120 cm3B. 100 cm3C. 80 cm3D. 60 cm315.（2017•北京卷）某三棱锥的三视图如图所示，则该三棱锥的体积为（）A. 60B. 30C. 20D. 1016.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则在该几何体中，最长的棱的长度是（）A. 4 √2B. 2 √5C. 6D. 4 √317.四棱锥P﹣ABCD的三视图如图所示，四棱锥P﹣ABCD的五个顶点都在一个球面上，E、F分别是棱AB、CD的中点，直线EF被球面所截得的线段长为2√2，则该球表面积为（）A. 12πB. 24πC. 36πD. 48π18.祖冲之之子祖暅是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”.意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为h(0<h<2) 的平面截该几何体，则截面面积为（）A. 4πB. πℎ2C. π(2−ℎ)2D. π（4-h²）19.《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为（）A. 4B. 6+4√2C. 4+4√2D. 220.如图所示为一个简单几何体的三视图，则其对应的几何体是（）A. B. C. D. 21.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A. 12B. √316C. 174 D. √17422.一个几何体的三视图如图所示，则该几何体的体积（单位：cm 3）为（）A. π+√33B. 2π+√33C. 2π+√3D. π+√3 23.三视图如图的几何体是（）A. 三棱锥B. 四棱锥C. 四棱台D. 三棱台24.若一个三棱锥的三视图如图所示，其中三个视图都是直角三角形，则在该三棱锥的四个面中，直角三角形的个数为（）A. 1B. 2C. 3D. 425.某三棱锥的主视图与俯视图如图所示，则其左视图的面积为A. 2B. 3C. 4D. 626.把边长为的正方形ABCD 沿对角线BD 折起，形成的三棱锥A-BCD 的正视图与俯视图如图所示，则其侧视图的面积为（）A. √22B. 12C. √24D. 14 27.一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A. 外接球的半径为√33B. 表面积为√7+√3+1C. 体积为√3D. 外接球的表面积为4π 28.某几何体的三视图如图所示，则该几何体的体积为( )A. √2πB. 2√2πC. π3D. 2π329.一个几何体按比例绘制的三视图如图所示（单位：m ）,则该几何体的体积为（）m 3 ．A. 73B. 92C. 72D. 9430.某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是( )A. 203B. 43C. 6D. 4 31.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何？”其意思为：“今有底面为矩形的屋脊状的锲体，下底面宽3丈，长4丈，上棱长2丈，高2丈，问：它的体积是多少？”已知1丈为10尺，该锲体的三视图如图所示，则该锲体的体积为（）A. 10000立方尺B. 11000立方尺C. 12000立方尺D. 13000立方尺二、填空题（共8题；共10分）32.如图为某几何体的三视图，则该几何体的体积为________.33.如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是________.34.一个四棱锥的三视图如图所示，那么在这个四棱锥的四个侧面三角形中，有________个直角三角形.35.如图是由大小相同的长方体木块堆成的几何体的三视图，则此几何体共由________ 块木块堆成．36.已知某几何体的三视图如图所示（单位：cm），则此几何体的体积为________，表面积为________．37.一简单组合体的三视图如图，则该组合体的体积为________．38.如图，网格纸上正方形小格的边长为1，图中粗线画出的是某三棱锥的三视图，则该三棱锥的体积为________．39.某几何体的三视图如图所示，若俯视图是边长为2的等边三角形，则这个几何体的体积等于________；表面积等于________．三、解答题（共3题；共20分）40.已知四棱锥P－ABCD的体积为√2，其三视图如图所示，其中正视图为等腰三角形，侧视图为直2角三角形，俯视图是直角梯形．（1）求正视图的面积；（2）求四棱锥P－ABCD的侧面积．41.一个空间几何体的三视图如图所示，其中正视图与左视图上方均为等边三角形，根据图中数据：（1）求三棱锥外接球表面积（2）求该几何体的表面积（3）求该几何体的体积．42.如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，求这个多面体最长的一条棱的长．答案解析部分一、单选题1.【答案】B【考点】由三视图求面积、体积，由三视图还原实物图【解析】【解答】甲几何体是棱长为2a的下方体去掉一个棱长为a的小正方体后的几何体,则其体积V甲=8a3−a3=7a3,表面积S甲=24a2;乙几何体是一个棱长为2a的正方体去掉一个底面为直角边为a的等腰直角三角形,高为a的三棱柱后的几何体,其体积V乙=8a3−12a3=152a3,表面积S乙=24a2−a2+√2a2=(23+√2)a2;则S甲> S乙, V甲< V乙.故答案为:B.【分析】分别由三视图还原出几何体的形状和数据,甲是一个棱长为2a的正方体去掉一个棱长为a的小正方体后的几何体,求出表面积和体积;乙是一个棱长为2a的正方体去掉一个底面为直角边为a的等腰直角三角形,高为a的三棱柱后的几何体,求出表面积和体积,再比较大小.2.【答案】B【考点】由三视图还原实物图【解析】【解答】还原四棱锥，如图所示，由主视图可知，PA⊥底面ABCD， AB⊥AD， AD⊥DC， PA=2， AB=1， BC=CD=2， AD=√3，计算可知B正确，故答案为：B．【分析】由三视图还原出四棱锥，P A ⊥底面ABCD,计算可知B正确.3.【答案】B【考点】球面距离及相关计算，由三视图还原实物图，球内接多面体【解析】【解答】由三视图可知，该四棱锥是底面为边长为1的正方形，一条长为1的侧棱与底面垂直，将该棱锥补成棱长为1的正方体，则棱锥的外接球就是正方体的外接球，正方体外接球的直径就是正方体的对角线，即2R=√3,R=√32，故答案为：B.【分析】结合三视图,将几何体还原为棱锥,将棱锥补成棱长为 1 的正方体，则棱锥的外接球就是正方体的外接球,由正方体外接球的直径就是正方体的对角线求解.4.【答案】D【考点】由三视图求面积、体积，由三视图还原实物图，棱柱、棱锥、棱台的体积【解析】【解答】由题图可知该几何体为正六棱锥，侧视图为等腰三角形，其中底边长为√3a，高与正视图的高相同，为√3a，所以面积为12×√3a×√3a=32a2.故答案为:D.【分析】结合三视图还原出几何体为正六棱锥,由公式求体积.5.【答案】C【考点】由三视图求面积、体积，由三视图还原实物图，棱柱、棱锥、棱台的体积【解析】【解答】由三视图可知，原几何体是一个三棱柱被截去了一个小三棱锥得到的，如图，V=1 2×3×4×5−13×(12×3×4)×3=24.故答案为:C.【分析】由三视图还出原几何体是一个三棱柱被截去了一个小三棱锥得到的,再由公式求体积.6.【答案】B【考点】由三视图求面积、体积，由三视图还原实物图，棱柱、棱锥、棱台的体积【解析】【解答】由三视图可得到几何体的直观图如图所示，该几何体是由一个四棱锥A-CDEF和一个三棱锥F-ABC组成，四棱锥A-CDEF的底面面积为4，高为4，所以体积是V=13×4×4=163；三棱锥F-ABC的底面积为2，高为2，故体积是43，所以该几何体的体积为203.故答案为:B.【分析】由三视图还出原几何体是由一个四棱锥A-CDEF和一个三棱锥F-ABC组成的,再由公式求体积. 7.【答案】C【考点】简单空间图形的三视图，由三视图还原实物图【解析】【解答】由题可知，三视图复原的几何体是一个放倒的底面是直角梯形的四棱柱，所以几何体的表面积S=(1+1+2+√2)×1+1×1+2×1=7+√2（cm2），故答案为：C.【分析】根据三视图将空间几何体还原后计算可得出答案。

高三第一轮复习——立体几何三视图基础篇(试题及答案)

高三第一轮复习——立体几何三视图基础篇（试题及答案）题型——空间几何体的三视图2015年1．(2015安徽文9) 一个四面体的三视图如图所示，则该四面体的表面积是（）.A ．13+B ．122+C ．23+D ．222．（2015北京文7）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（）. A.1 B. 2C. 3D. 23.（2015福建文9）某几何体的三视图如图所示，则该几何体的表面积等于（）.A ．822+B ．1122+C ．1422+D ．154．（2015湖南文10）某工作的三视图如图所示，现将该俯视图侧（左）视图正（主）视图111俯视图侧视图正视图1211侧视图正视图122221俯视图侧（左）视图正（主）视图2211111122工作通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工作的一个面内，则原工件材料的利用率为（）（材料利用率=新工件的体积/原工件的体积）. A.8π9 B. 827πC. 224(21)π- D. 28(21)π-5．（2015全国1文11）圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为1620π+，则r =（）.A. 1B. 2C. 4D. 86.（2015新课标2文）一个正方体被一个平面截去一部分后，剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（）7．（2015陕西文5）一个几何体的三视图如图所示，则该几何体的表面积为（）A. 3πB. 4πC. 2π4+D. 3π3+1A.81B.71C.61D.5俯视图侧视图主视图122左视图主视图8．（2015浙江文2）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）.A. 83cmB. 123cmC. 3233cmD. 4033cm9.（2015重庆文5）某几何体的三视图如图所示，则该几何体的体积为（）.A.12π3+B.13π6C.7π3D.5π210．（2015四川文14）在三棱柱111ABC A B C -中，90BAC ∠=，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，设点M ，N ，P 分别是AB ，BC ，11B C 的中点，则三棱锥1P A MN -的体积是______. 11．（2015天津文10）一个几何体的三视图如图所示（单位：m ），则该几何体的体积为______3m .2016年1.（2016全国甲文7）右图是圆柱与圆锥组合而成的几何体的正视图侧视图俯视图111112111111234正视图侧视图俯视图222221121正视图左视图俯视图2三视图，则该几何体的表面积为( ). A.20π B.24π C.28πD.32π2.（2016全国乙文7）如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3，则它的表面积是（）. A.17π B. 18π C. 20π D. 28π3. （2016山东文5）一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为（）.A. B. C. D.rlh12π33+12π33+12π36+21π6+111正（主）视图俯视图侧（左）视图4.（2016全国丙文10）如图所示，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（）.A.18365+B.54185+C.90D.815.（2016天津文3）将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（）.6.（2016北京文11）某四棱柱的三视图如图所示，则该四棱柱的体积为___________.7.（2016浙江文9）某几何体的三视图如图所示（单位：），则该几何体的表面积是______，体积是______.A.B.C.D.cm 2cm 3cm 正视图22222侧视图2F 1E 1F ED 1DB 1A 1C 1ABC 1121俯视图正视图侧视图俯视图正视图8.（2016四川文12）已知某三棱锥的三视图如图所示，则该三菱锥的体积等于 .2017年1.（2017全国2文6）如图所示，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（）. A ．90π B ．63π C ．42π D ．36π2.（2017北京文6）某三棱锥的三视图如图所示，则该三棱锥的体积为（）. A.60 B.30 C.20 D.103.（2017浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）.俯视图侧视图俯视图3311331正视图1A. π12+ B.π32+C. 3π12+ D.3π32+4.（2017山东文13）由一个长方体和两个14圆柱体构成的几何体的三视图如图所示，则该几何体的体积为.1.解析由该几何体的三视图，在长为2，宽为1，高为1的长方体中还原其立体图形，如图所示.由图及三视图中所给的数据可知，PAC △与ABC △为等腰直角三角形，PAB △与PBC △为等边三角形，2P A P C A B B C ====，所以四面体的表面积为()231222212342S =⨯⨯+⨯⨯⨯=+.故选C.2. 解析利用特殊的几何体—正方体，还原几何体.如图其最所示，四棱锥1C ABCD -为三视图所对应的几何体，长棱为3.故选C.3. 解析由几何体的三视图，在长为2，宽为1，高为2的立方体中，还原其立体图形，如图所示.几何体的表面积为：()12112222212211222+⨯⨯+⨯+⨯+⨯+⨯=+.故选B ．4.解析问题等价于圆锥的内接长方体的体积的最大值.设长方体的长、宽、高分别为,,x y h ，长方体上底面截圆锥到截面半径为a ，则()222224x y a a +==，如图所示. 由图可知212a h-=，所以22h a =-，而长方体的体积 ()222222222x y V xyh h a h a a +=⋅==- (3)22162327a a a ++-⎛⎫⨯= ⎪⎝⎭…，当且仅当11111BAPCD 1DB 1A 1C 1A BC11212,22x y a a ==-，即23a =时等号成立，此时利用率为21682719ππ123=⨯⨯.故选A.5.解析根据题意作图，如图所示.224π22π2π2r S r r r r r =⋅+⋅⋅++=2245π1620πr r +=+，所以2r =.故选B.6.解析由三视图得，在正方体1111ABCDA B C D ﹣中，截去四面体111A A B D ﹣，如图所示，设正方体棱长为a ，则11133111326A AB D V a a =⨯=﹣，故剩余几何体体积为3331566a a a -=，所以截去部分体积与剩余部分体积的比值为15．故选D. 7.解析由几何体的三视图可知该几何体为圆柱的截去一半，所以该几何体的表面积为22111π1π122π223π4222⨯⨯+⨯⨯+⨯+⨯⨯⨯=+，故选D. 8.解析该几何体是棱长为2的正方体和底面边长为2、高为2的正四棱锥的组合体，所以3213222233V =+⨯⨯=．故选C ．9.解析根据三视图可得原几何体是由圆锥截的一部分和一个圆柱组成的几何体，圆柱和圆haa r2r2rCBA D D 1C1B1A1锥的底面圆半径都为1，圆锥的高为1，圆柱的高为2，所以1+2V V V ==圆柱圆锥26ππ+=136π．故选B ． 10. 解析由题意可知，三棱柱是底面为直角边长为1的等腰直角三角形，高为1的直三棱柱，底面积为12.如图所示，11P A MN A PMN V V --=,三棱锥1A PMN -的底面面积是14，1A 到平面PMN 的距离是12，故11111132424P A MN A PMN V V --==⨯⨯=.11.解析该几何体是由两个高为1的圆锥与一个高为2圆柱组合而成，所以该几何体的体积为()318π2π1π2m 33⨯⨯⨯+⨯= .1.C 解析几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为，周长为，圆锥母线长为，圆柱高为.由三视图得，，由勾股定理得，，.故选C.2.A 解析由三视图可知，该几何体是一个球截去球的，设球的半径为，则，解得.该几何体的表面积等于球的表面积的，加上个截面的面积，每个截面是圆面的，所以该几何体的表面积为22714π23π284S =⨯⨯+⨯⨯⨯=14π3π17π+=.故选A.3.C 解析由三视图可知,半球的半径是，体积为,四棱锥的体积为,所以该几何体的体积为 .故选C. 4.B 解析如图所示为其几何体直观图，该几何体为四棱柱，r c l h 2r =2π4πc r ==()222234l =+=21π2S r ch cl =++表4π16π8π=++28π=18R 37428ππ833R ⨯=2R =78314222π63112π36+1111AEFD A E F D -NM PA C 1B 1A 1CB所以表面积为.故选B.5.B 解析由题意得截去的三棱锥是包含长方体前右上方顶点的三棱锥，如图所示.故选B.6.解析该四棱柱是直四棱柱，底面是梯形，其面积为，高是1.所以其体积为.7.；解析由三视图知该组合体是一个长方体上面放置了一个小正方体. 长方体的长、宽、高分别为4、4、2，小正方体的棱长为2 ，，. 8.解析由三视图还原三棱锥的直观图，易知底面与侧面垂直，如图所示.且底面积为高为，所以该几何体的体积为解析由题意，该几何体是由高为6的圆柱截去一半后的几何体加上高为4的圆柱，故其体积为2213634632V =⋅π⋅⋅+π⋅⋅=π .故选B.2.解析该几何体是三棱锥，如图所示，11153410332S ABC ABC V S h -=⋅=⨯⨯⨯⨯=△.故选D.()3336335254185⨯+⨯+⨯⨯=+3213(12)122+⨯=33122⨯=8040222=62+24+42422=80S ⨯⨯⨯⨯-⨯表3244240V =+⨯⨯=3312313,2S =⨯⨯=111331.333V Sh ==⨯⨯=12312222CBAS解析由三视图可知，直观图是由半个圆锥与一个三棱锥构成，半圆锥体积为()2111=13232S π⨯π⨯⨯=，三棱锥体积为211=213=132S ⎛⎫⨯⨯⨯ ⎪⎝⎭，所以几何体体积1212S S S π=+=+．故选A ．解析 2121121242V π⨯π=⨯⨯+⨯⨯=+.。

高考数学立体几何专题1空间立体几何的三视图、表面积和体积试题(含答案)

本题考查利用三视图求几何体的体积，考查长方体及圆柱的体积公式，考查计算能力，属于基础题．解：由长方体长为 2，宽为 1，高为 1，则长方体的体积 1 = t 1 t 1 = ，圆柱的底面半径为 1，高为 1，则圆柱的体积 = 1 t t 1 t 1 = ，
则该几何体的体积 = 1 + 1 = + ，故答案为： + ．
A. 1 B. 16 C.
D.
. 如图，网格纸上小正方形的边长为 1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为
A. t
B. 6
C.
D. 6
第题
第题
第题
3. 已知一个简单几何体的三视图如图所示，则该几何体的体积为．
A. +6 B. 6 +6 C. +1 D.ቤተ መጻሕፍቲ ባይዱ12
4. 如图正方形 OABC 的边长为 1，它是水平放置的一个平面图形的直观图，则原图形
的面积为 A.
B. 1 C.
D. 1 +
5. 如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为
第题
第6题
第题
A. t
B.
C.
D.
6. 如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若
知 = ，所以由斜二测画法知，对应原图形，即平行四边形的高为，所以原图形的面积为：1 t = ．故选 A．
5.【答案】C
【分析】本题考查由三视图求表面积，空间立体几何三视图，属于基础题．
空间几何体是一个组合体，上面是一个圆锥，圆锥的底面直径是 4，圆锥的高是，在轴截面中圆锥的母线长使用勾股定理求出，写出表面积，下面是一个圆柱，圆柱的底

高考数学专题复习八-8.1空间几何体的三视图、表面积和体积-模拟练习题(附答案)

专题八立体几何与空间向量8.1空间几何体的三视图、表面积和体积基础篇考点一空间几何体的结构特征、三视图与直观图考向一空间几何体的结构特征1.(2022昆明一模,7)已知OA为球O的半径,M为线段OA上的点,且AM=2MO,过M且垂直于OA的平面截球面得到圆M,若圆M的面积为8π,则OA= ()A.2√2B.3C.2√3D.4答案B2.(2020课标Ⅰ,3,5分)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()A.√5−14B.√5−12C.√5+14D.√5+12答案C3.(2021辽宁部分重点中学协作体模拟,7)“阿基米德多面体”是由边数不全相同的正多边形为面的多面体,其中“扭棱十二面体”就是一种“阿基米德多面体”.它是由80个正三角形和12个正五边形组成的,若多面体的顶点数、棱数和面数满足:顶点数-棱数+面数=2,则“扭棱十二面体”的顶点数为()A.56B.58C.60D.62答案C4.(2023届河南荥阳摸底,6)某圆锥的侧面积是底面积的2倍,则该圆锥的侧面展开图的圆心角为()A.2πB.3π2C.π D.π2答案C考向二空间几何体的三视图1.(2021全国甲,6,5分)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A B C D答案D2.(2022山西3月适应性测试,4)如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则该几何体各个面中面积的最大值是()A.√3B.√6C.2√3D.4√3答案C3.(2018北京,5,5分)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.4答案C4.(2020课标Ⅱ,7,5分)下图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为()A.EB.FC.GD.H答案A5.(2022吉林白山二模,7)如图,在正方体ABCD-A1B1C1D1中,P为C1D1的中点,则过点A1,B,P的平面截正方体所得的截面的侧视图(阴影部分)为()答案C考向三空间几何体的直观图1.(2022银川一中三模,4)已知水平放置的平面四边形ABCD,用斜二测画法得到的直观图是边长为1的正方形,如图所示,则四边形ABCD的周长为()A.2B.6C.4√2+2D.8答案D2.(2021哈尔滨九中五模,13)已知△ABC的平面直观图△A'B'C'是边长为2的正三角形,则△ABC的面积为.答案2√6考点二空间几何体的表面积与体积考向一几何体的表面积1.(2020北京,4,4分)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为()A.6+√3B.6+2√3C.12+√3D.12+2√3答案D2.(2022河南新乡二模,7)一个多面体的三视图如图所示,则该多面体的表面积为()A.30B.28C.26D.24答案D3.(2023届成都月考一,5)已知某几何体的三视图如图所示,则该几何体的表面积等于()B.160A.1603C.88+8√2D.64+32√2答案D4.(2022山西运城模拟,5)某几何体的主视图和左视图如图1所示,它的俯视图的直观图是△A'B'C',如图2所示,其中O'A'=O'B',O'C'=√3,则该几何体的表面积为()图1图2A.36+12√3B.24+8√3C.24+12√3D.36+8√3答案C5.(2023届成都八中月考,10)已知正方形ABCD的边长为2,点E为边AB中点,点F为边BC中点,将△AED,△DCF,△BEF分别沿DE,DF,EF折起,使A,C,B三点重合于P点,则三棱锥P-DEF外接球的表面积为()B.3πC.6πD.12πA.3π2答案C6.(2020浙江,14,4分)已知圆锥的侧面积(单位:cm2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是.答案 17.(2021河南新乡二模,14)一个棱长为4的正方体被挖去一个高为4的正四棱柱后得到如图所示的几何体,若该几何体的体积为60,则该几何体的表面积为.答案110考向二几何体的体积1.(2022全国甲,4,5分)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为()A.8B.12C.16D.20答案B2.(2021浙江,4,4分)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.32B.3 C.3√22D.3√2答案A3.(2017课标Ⅱ,4,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π答案B4.(2023届贵州黔东南摸底,3)某几何体的三视图如图所示,则该几何体的体积为()A.8-2π3B.2π3C.8−4π3D.4π3答案A5.(2022新高考Ⅰ,4,5分)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(√7≈2.65)() A.1.0×109 m3 B.1.2×109 m3C.1.4×109 m3D.1.6×109 m3答案C6.(2022安徽安庆二模,6)圆锥被过顶点的一个截面截取部分后所剩几何体的三视图如图所示,则截取部分几何体的体积为()A.4π−3√33B.3π−√33C.2π−√33D.4π−√33答案A7.(2021天津,6,5分)两个圆锥的底面是一个球的同一截面,顶点均在球面上.若球的体积为32π,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为() 3A.3πB.4πC.9πD.12π答案B综合篇考法一空间几何体的表面积与体积考向一几何体的表面积1.(2020课标Ⅲ,8,5分)如图为某几何体的三视图,则该几何体的表面积是()A.6+4√2B.4+4√2C.6+2√3D.4+2√3答案C2.(2022湘豫名校联盟4月联考,10)如图,网格纸上小正方形的边长为1,粗实线画出的是某三棱台的三视图,则该几何体的表面积为()A.8B.11C.12D.13答案D3.(2022山西晋中二模,9)已知三棱柱的各个侧面均垂直于底面,底面为正三角形,侧棱长与底面边长之比为3∶2,顶点都在一个球面上,若三棱柱的侧面积为162,则该球的表面积为( )A.120πB.√129πC.129πD.180π 答案 C4.(2023届河南安阳调研,15)已知长方体ABCD -A 1B 1C 1D 1的体积为9,AB >BC ,AC =AB 1,且异面直线AC 与B 1D 1所成的角为60°,则该长方体的表面积为 . 答案 6+12√3考向二几何体的体积1.(2022浙江,5,4分)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( )A.22πB.8πC.223π D.163π 答案 C2.(2022全国甲,9,5分)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙= ( )A.√5B.2√2C.√10D.5√104答案 C3.(2022全国乙,9,5分)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A.13B.12C.√33D.√22答案C4.(2023届重庆渝中巴蜀中学月考三,15)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD 是等腰梯形,AB∥CD,AB=4,AD=CD=2,若四棱柱的高是3,则该棱柱外接球的体积是.答案1256π5.(2020江苏,9,5分)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是cm3.答案(12√3−π2)6.(2019课标Ⅲ,16,5分)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9g/cm3.不考虑打印损耗,制作该模型所需原料的质量为g.答案118.8考法二与球有关的切、接问题1.(2023届福建厦门外国语学校月考二,7)已知正三棱锥V-ABC中,侧面与底面所成角的正切值为√2,AB=6,这个三棱锥的内切球和外接球的半径之比为()A.2(√3−1)3B.√3−13C.23D.13答案B2.(2022四川内江第六中学模拟,7)已知正四棱锥的侧棱长为√5,底面边长为2,则该四棱锥的内切球的体积为()A.4√33B.4√3π27C.4π3D.4√3答案B3.(2020课标Ⅱ,10,5分)已知△ABC是面积为9√34的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为()A.√3B.32C.1 D.√32答案C4.(2023届辽宁大连期中,7)已知三棱锥P-ABC中,PA⊥底面ABC,PA=AB=AC=2,∠BAC=120°,则三棱锥P-ABC的外接球的表面积为()A.12πB.16πC.20πD.24π答案C5.(2021全国甲,11,5分)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O-ABC的体积为()A.√212B.√312C.√24D.√34答案A6.(2020课标Ⅰ,12,5分)已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为() A.64π B.48π C.36π D.32π答案A7.(2022新高考Ⅰ,8,5分)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且3≤l≤3√3,则该正四棱锥体积的取值范围是()A.[18,814] B.[274,814]C.[274,643] D.[18,27]答案C8.(2019课标Ⅰ,12,5分)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC 是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为() A.8√6π B.4√6πC.2√6πD.√6π答案D9.(2022河南洛阳新安一中模拟,13)2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家级非物质文化遗产名录.蹴有用脚蹴、蹋、踢之义,“鞠”是外包皮革、内实米糠的球,因而蹴鞠是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.已知某鞠(球)的表面上有四个点(不共面)A、B、C、D,AB=CD=2,AC=BD=√3,BC=AD=√5,则该鞠(球)的体积为.答案√6π。

高三数学空间几何体的三视图与直观图试题答案及解析

高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是圆锥的四分之一，其底半径为，高为，所以其体积为，故选.【考点】1.三视图；2.几何体的体积.2.若一个几何体的三视图如图所示，则此几何体的体积为（）A．B．C．D．【答案】D．【解析】由题意可知，该几何体为一直六棱柱，∴底面六边形的面积可以看成一个矩形与两个等腰直角三角形的面积和，即，∴．【考点】空间几何体的体积．3.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A．B．C．D．【答案】C【解析】由三视图可知：该几何体是一个如图所示的三棱锥P-ABC，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O，O点必在高线PE上，外接球半径为R，则在直角三角形BOE中，BO2=OE2+BE2=（PE-EO）2+BE2，即R2=（4-R）2+（3）2，解得：R=，故选C.【考点】三视图，球与多面体的切接问题，空间想象能力4.一个几何体的三视图如图所示，其中俯视图与侧视图均为半径是2的圆，则这个几何体的表面积是()A．16πB．14πC．12πD．8π【答案】A【解析】由三视图可知，该几何体是一个球挖去了剩下的部分．其中两个半圆的面积为π×22＝4π．个球的表面积为×4π×22＝12π，所以这个几何体的表面积是12π＋4π＝16π，选A．5.若某几何体的三视图如图所示，则此几何体的体积是________．【答案】48【解析】由三视图可知，该几何体上面是个长、宽、高分别为4、2、2的长方体，下面是一个放倒的四棱柱，四棱柱的高为4，底面是个梯形，上、下底分别为2、6，高为2．所以长方体的体积为4×2×2＝16，四棱柱的体积为4××2＝32，所以该几何体的体积为32＋16＝48．6.一个多面体的三视图如图所示，则多面体的体积是（）A．B．C．D．7【答案】A【解析】由题意，该多面体的直观图是一个正方体挖去左下角三棱锥和右上角三棱锥，如下图，则多面体的体积.故选A.【考点】1.多面体的三视图与体积.7.一个几何体的三视图如图所示，这个几何体的体积是( )A．B．C．D．【答案】D【解析】三视图可知：原几何体是一个小蘑菇形状，且上面是半径为4半球；下面是一个长方体，其底面是边长为2的正方形，高为3．∴该几何体的体积，故选D．【考点】三视图，空间几何体的体积.8.如图所示是某几何体的三视图，则该几何体的表面积是（）A．B．C．D．【答案】B【解析】由三视图知，几何体为底面半径为1，高为3的圆柱挖去一个与圆柱同底，高为2的圆锥，所以几何体的表面积故选【考点】几何体的三视图；几何体的表面积.9.一个几何体的三视图如图所示，则这个几何体的体积是（）A．B．C．D．【答案】【解析】由三视图可知，该几何体是底面半径为，高为的圆锥的一半，故其体积为.选.【考点】三视图，圆锥的体积.10.某几何体的三视图如图所示, 则其表面积为 .【答案】【解析】综合三视图可知，，立体图是一个半径r=1的半个球体。

高考数学一轮复习专题9.1空间几何体三视图练习(含解析)

9.1 空间几何体三视图一．空间几何体的分类：多面体和旋转体二．多面体的概念及性质1.棱柱的概念和主要性质有两个面互相平行，每相邻两个面的交线都互相平行的多面体侧棱垂直于底面的棱柱底面是正多边形的直棱柱有一个面是多边形，各面是有一个公共顶点的三角形的多面体底面是正多边形，且顶点在底面的射影是底面的射影是底面和用一个平行于棱锥底面的平面去截棱由正棱锥截得的棱台侧面的形状三角形对角面的形三角形四．空间几何体的三视图1.三视图是观测者从不同位置观察同一个几何体，画出的空间几何体的图形.具体包括：（1）正视图：物体前后方向投影所得到的投影图；它能反映物体的高度和长度；（2）侧视图：物体左右方向投影所得到的投影图；它能反映物体的高度和宽度；（3）俯视图：物体上下方向投影所得到的投影图；它能反映物体的长度和宽度.2.三视图画法规则高平齐：主视图与左视图的高要保持平齐长对正：主视图与俯视图的长应对正宽相等：俯视图与左视图的宽度应相等五．空间几何体的直观图（1）斜二测画法①建立直角坐标系，在已知水平放置的平面图形中取互相垂直的OX，OY，建立直角坐标系；②画出斜坐标系，在画直观图的纸上（平面上）画出对应的O’X’,O’Y’,使=450（或1350），它们确定的平面表示水平平面；③画对应图形，在已知图形平行于X轴的线段，在直观图中画成平行于X‘轴，且长度保持不变；在已知图形平行于Y轴的线段，在直观图中画成平行于Y‘轴，且长度变为原来的一半；④擦去辅助线，图画好后，要擦去X轴、Y轴及为画图添加的辅助线（虚线）.画水平放置的多边形的直观图的关键是确定多边形顶点的位置，因为多边形顶点的位置一旦确定，依次连结这些顶点就可画出多边形来，因此平面多边形水平放置时，直观图的画法可以归结为确定点的位置的画法.（2）平行投影与中心投影：平行投影的投影线是互相平行的，中心投影的投影线相交于一点.考向一已知几何体识别三视图【例1】将正方体(如图1所示)截去两个三棱锥，得到如图2所示的几何体，则该几何体的侧视图为( )'''X OY【答案】 B【解析】侧视图中能够看到线段AD 1，应画为实线，而看不到B 1C ，应画为虚线．由于AD 1与B 1C 不平行，投影为相交线，故选B.【举一反三】1．如图是各棱长均为2的正三棱柱ABC —A 1B 1C 1的直观图，则此三棱柱侧视图的面积为（）A B ．C ．12x x D ．4【答案】B【解析】由题意可得，侧视图是个矩形，由已知，底面正三角形的边长为22，即侧视图的长为2，所以三棱柱侧视图的面积为故选B 2.如图，在长方体ABCD －A 1B 1C 1D 1中，点P 是棱CD 上一点，则三棱锥P －A 1B 1A 的侧视图是( )【答案】 D【解析】在长方体ABCD－A1B1C1D1中，从左侧看三棱锥P－A1B1A，B1，A1，A的射影分别是C1，D1，D；AB1的射影为C1D，且为实线，PA1的射影为PD1，且为虚线．故选D.考向二已知三视图选几何体【例2】如图是一个物体的三视图，则此三视图所描述物体的直观图是()A．B．C．D．【答案】D【解析】由几何体的三视图可得：该几何体为一个圆锥与圆柱组合而成；故选D【套路总结】【举一反三】1．某几何体的三视图如图所示，则该几何体的侧视图的面积为（）A ．242+B ．4+CD ．22【答案】C即为侧视图的底边长，正视图的高即为侧视图的高，所以侧视图的面积为：122⨯=C ．考向三三视图知二选三【例3】如图是一个空间几何体的正视图和俯视图，则它的侧视图为( )【答案】 B【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径可知其侧视图为B ，故选B.【举一反三】1、一个几何体的三视图中，正视图和侧视图如图所示，则俯视图不可以为( )【答案】 C【解析】A中，该几何体是直三棱柱，∴A有可能；B中，该几何体是直四棱柱，∴B有可能；C中，由题干中正视图的中间为虚线知，C不可能；D中，该几何体是直四棱柱，∴D有可能．2.已知一个四棱锥的正视图和俯视图如图所示，则该几何体的侧视图为A. B. C. D.【答案】A【解析】由正视图和俯视图可知，则该几何体P -ABCD 的底面ABCD 是边长为的正方形，PA ⊥面ABCD ，其直观图如图所示，由三视图知识知，其侧视图如A 所示，故选A ．考向四三视图的运用【例4】一个动点从正方体1111ABCD A B C D 的顶点A 处出发，经正方体的表面，按最短路线到达顶点1C 位置，则下列图形中可以表示正方体及动点最短路线的正视图是（）A ．①②B ．①③C ．②④D ．③④【答案】C【解析】由点A 经正方体的表面，按最短路线爬行到定点1C 位置，共有6种展开方式，若把平面11ABA B 和平面11BB C C 展开到同一个平面内，在矩形中连接1AC 会经过1BB 的中点，故此时的正视图为②；若把平面ABCD 和平面11CDD C 展到同一个平面内，在矩形中连接1AC 会经过CD 的中点，此时的正视图为④其中其它几种展开方式所对应的正视图在题中没有出现或已在②④中，故选C.【举一反三】1．一个几何体的三视图如图所示,其中俯视图的曲线部分是四分之一圆弧,该几何体的表面上的点M 在正视图上的对应点为A （中点），几何体的表面的点N 在正视图上的对应点为B ，则在此几何体的侧面上从M 到N 的路径中，最短路径的长度为（）。

高中数学高考复习-----空间几何体结构及其三视图巩固练习题(含答案解析)

高中数学高考复习-----空间几何体结构及其三视图巩固练习题（含答案解析）【巩固练习】1、若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为（）(A)(B)(C)(D)2、圆柱的侧面展开图是一个边长为6π和4π的矩形，则该圆柱的底面积是()(A)24π2(B)36π2(C)36π2或16π2(D)9π或4π3、如图，某几何体的主视图与左视图都是边长为1的正方形，且体积为，则该几何体的俯视图可以是()4、如图是一几何体的三视图，其左视图是等腰直角三角形，则其表面积为（）A．B．C．D．125、已知某个几何体的三视图如图所示，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是()6、一个棱长为2的正方体的顶点都在球面上，则该球的表面积为()A．B．C．D．7、若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为（）A．6B．2C．D．8、如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（）A．B．C．D．9.（2015重庆高考）某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．10、如图为一个几何体的三视图，左视图和主视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的侧面积为()(A)6(B)12(C)24(D)3211、如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为，那么这个几何体的体积为（）.A. B. C. D.12.（2015肇庆二模）已知某几何体的三视图如图所示，则该几何体的体积为3π．13、直三棱柱的各顶点都在同一球面上，若,，则此球的表面积等于。

14、正三棱柱内接于半径为的球，若两点的球面距离为，则正三棱柱的体积为．15.(2015春湖北校级期末)某几何体的三视图如图所示，作出该几何体直观图的简图，并求该几何体的体积．【参考答案与解析】1、【答案】B.【解析】由题意知以正方体各个面的中心为顶点的凸多面体为正八面体（即两个同底同高同棱长的正四棱锥），所有棱长均为1，其中每个正四棱锥的高均为，故正八面体的体积为,故选B.2、【答案】D.【解析】由题意知圆柱的底面圆的周长为6π或4π，故底面圆的半径为3或2，所以底面圆的面积是9π或4π.3、【答案】C.【解析】由该几何体的主视图和左视图可知该几何体是柱体，且其高为1，由其体积是可知该几何体的底面积是，由图知A的面积是1，B的面积是，C的面积是，D的面积是，故选C.4、【答案】C5、【答案】B.【解析】由三视图知该几何体是如图所示的四棱锥P-ABCD，其中侧面PBC⊥底面ABCD，且顶点P在底面的射影是BC边的中点，四棱锥的高为20，底面ABCD是边长为20的正方形.∴V P-ABCD=×202×20=(cm3).6、【答案】C7、【答案】D.8、【答案】D.9.【答案】B【解析】由题意可知几何体的形状是放倒的圆柱，底面半径为1，高为2，左侧与一个底面半径为1，高为1的半圆锥组成的组合体，几何体的体积为：=．故选B．10、【答案】C.【解析】由几何体的三视图可知，该几何体为正三棱柱，其底面边长为2，高为4，∴该几何体的侧面积S侧=3×2×4=24.11、【答案】C.二、填空题12.【答案】3π【解析】由三视图可知，该几何体由底面直径为2，即半径为1，高为2+4=6的圆柱，故该几何体的体积V=π×12×6=3π，故答案为3π．13、【答案】【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为，球心为，在中，易得球半径，故此球的表面积为。