应力集中系数公式
开孔处应力集中系数的简化计算

开孔处应力集中系数的简化计算开孔处应力集中系数的简化计算1. 引言在工程设计和分析中,开孔处应力集中是一个常见的问题。
当在材料中添加孔洞或凹槽时,会导致应力场的非均匀分布,从而对材料的力学性能产生负面影响。
准确计算开孔处的应力集中系数对于工程设计和材料选择至关重要。
在本文中,我们将重点讨论开孔处应力集中系数的简化计算方法,以便工程师和研究人员能够更好地理解和应用这一概念。
2. 开孔处应力集中系数的定义开孔处应力集中系数(Stress Concentration Factor,简称SCF)是指材料在受力情况下,开孔处局部应力与远离开孔处应力的比值。
通常用K表示,其计算公式为K=σ_max/σ_nominal,其中σ_max为开孔处的最大应力,σ_nominal为远离开孔处的应力。
在工程设计中,SCF的值可以用来衡量材料在开孔处的应力集中程度,以及对其疲劳寿命和强度的影响。
3. 开孔处应力集中系数的简化计算方法在实际工程中,精确计算开孔处的应力集中系数可能非常复杂,因为需要考虑材料的几何形状、加载方式、以及材料的本构关系等多个因素。
然而,对于一些简单的几何形状和加载情况,我们可以采用一些简化的方法来估算开孔处应力集中系数。
3.1. Neuber's RuleNeuber's Rule是一种常用的简化计算方法,适用于圆形孔洞的应力集中系数估算。
根据Neuber's Rule,对于轴向受拉的材料,开孔处应力集中系数与远离开孔处应力之比可以近似为2。
这种简化计算方法在工程实践中得到了广泛的应用,尤其适用于轴向拉伸载荷作用下的材料。
3.2. Peterson's MethodPeterson's Method是另一种常用的简化计算方法,适用于不同几何形状和加载情况下的应力集中系数估算。
根据Peterson's Method,可以通过查表或计算公式来估算特定几何形状的开孔处应力集中系数。
拉伸与压缩--应力集中

(4)两个塑性指标
A l
A' l'
b.断面收缩率
——反映横截面的塑性收缩程度的量值
A A 100% A
低碳钢: = 60 ~ 70%
2.低碳钢在压缩时的应力—应变曲线
压缩
F
拉伸
F
O
二 、灰铸铁在拉伸与压缩时的应力—应变曲线
压缩
拉伸
bc
b
O
F
d f b a c e
Fb Fs F F e p
O
d' g
l
f' h
l
Fl EA
F — l 图与 A 和 l 有关
反映该试样在某一标距下的力学性能
材料的力学性能应与试样的几何尺寸无关
将载荷——变形图改造成应力——应变图
(2)应力—应变曲线 ( — 曲线) 做法: 取:
b
d f b a c e
O
d'
p
e
f' h
使材料的比例极限提高,塑性变形减小的现象
(4)两个塑性指标
A l
A' l'
a.伸长率
——反映纵向塑性变形程度的量值
l l 100% p 100% l
规定:
=10 5%的材料为塑性材料
=10 <5% 的材料为脆性材料
低碳钢: = 20 ~ 30%
250
F
50 50 15 60
F
光弹性等差线图
2.应力集中系数
应力集中系数——最大局部应力max与其所在截面上的平 均应力 m的比值
即:
max k m
06_第七章_应力集中

0
(7.1.2)
沿圆孔边缘的应力按下式分布
0 1 2cos 2
(7.1.3)
式中 σ0 —— X 轴方向的平均拉力; a —— 圆孔半径; θ、r —— 板中任一点的极坐标。
5
7-1
•
应力集中与应力集中系数
在孔边A、B两点发生高度应力集中,这两点的拉应力为平均 拉应力的三倍,故应力集中系数k =3。 • 应力随着离开 A、B 两点的距离增加而迅速降低,在离开孔边 缘的距离等于圆孔半径之处,应力值仅比平均拉应力值高22%。 应力集中仅局限于孔边A、B两点附近。 • 在θ = 0°时,沿孔边的切向应力等于板端的平均拉应力σ0。
max k 3 0
6
7-1
应力集中与应力集中系数
对于实际工程问题而言,当板宽与开孔直径之比大于5 时,上述理论解在实用上已具有一定的精度。 对于具有不同的板宽与孔径之比的板,应力集中系数 值的变化如下所示。该系数值是以开孔处的拉伸应力作为 基准应力求得的。
7
规范计算举例
影响参数:Tp、tr、r
数值分析
有限元方法求解——适用于复杂结构(如肘板趾端)
试验测量 光弹性试验测量、实船结构测试
4
7-1
应力集中与应力集中系数
(1)圆形开孔板拉伸时的应力集中
对于具有圆孔且承受拉伸作用的平板,根据无限宽板的弹性 理论解,在通过开口圆心的横剖面上的正应力可用下式表示
a 2 3a 4 2 2 4 2 r r
0
6M d 2t (7.1.9)
17
7-1
应力集中与应力集中系数
扭转时的应力集中 在具有小圆孔的薄壁管扭转时,相当于承受纯剪切作用的平板,沿 圆孔周围的切向应力按下式计算
应力集中分析

应力集中分析假设应力在整个横截面上均匀分布而且整个杆件就是均匀得,则有公式,F 为该截面上得拉内力,A为材料该截面得横截面积。
而实际上,构件并不就是如此理想得,由于某种用途,在构件上经常需要有些孔洞、键槽、缺口、轴肩、螺纹或者就是其她杆件在几何外形上得突变。
所以在实际工程中,这些瞧似细小得变形可能导致构件在这些部位产生巨大得应力,其应力峰值远大于由基本公式算得得应力值,这种现象称为应力集中,从而可能产生重大得安全隐患。
应力集中削弱了构件得强度,降低了构件得承载能力。
应力集中处往往就是构件破坏得起始点,就是引起构件破坏得主要因素。
同时,应力集中得存在降低了整个构件得材料利用率,因为可能为了一部分结构得稳定而采用较高得等级得材料,与此同时构件其她部分得强度并不需要如此高得性能。
因此,为了确保构件得安全使用,提高产品得质量与经济效益,必须科学地处理构件得应力集中问题。
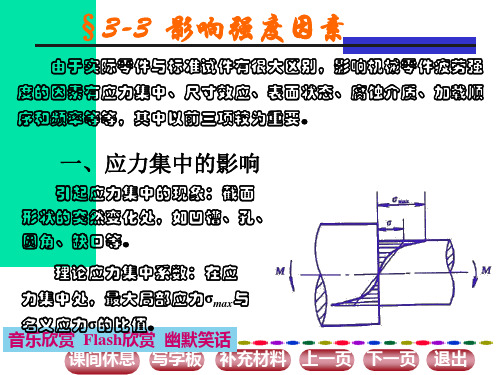
一、应力集中得表现及解释(主要分析拉压应力)1、理论应力集中系数:工程上用应力集中系数来表示应力增高得程度。
应力集中处得最大应力与基准应力之比,定义为理论应力集中系数,简称应力集中系数,即(4) 在(4)式中,最大应力可根据弹性力学理论、有限元法计算得到,也可由实验方法测得;而基准应力就是人为规定得应力比得基准,其取值方式不就是唯一得,大致分为以下三种:(1)假设构件得应力集中因素(如孔、缺口、沟槽等)不存在,以构件未减小时截面上得应力为基准应力。
(2)以构件应力集中处得最小截面上得平均应力作为基准应力。
(3)在远离应力集中得截面上,取相应点得应力作为基准应力。
理论应力集中系数反映了应力集中得程度,就是一个大于1得系数。
而且实验结果还表明:洁面尺寸改变愈剧烈,应力集中系数就愈大。
2、几种常见表现[1]一块铝板,两端受拉,其中部横截面上得拉应力(单位面积上得力)均匀分布,记为,见图 1(a) , 此时没有应力集中。
图l( b ) 就是在其中部开了个小圆孔,这时在过圆孔中心得横截面上得拉应力分布不再均布 , 当小圆孔相对于板很小时,在小孔得边缘处得拉应力就是无小孔时得3倍,称小孔边得拉应力集中系数为3(理论集中系数)。
定义有效应力集中系数

K
( 1)d ( 1)K
K
( 1)d ( 1)K
其中:(σ-1)d和(τ-1)d表示光滑试样的持久有限;(σ-1)K和(τ-1)K表示有 应力集中的相同尺寸试样的持久极限;Kσ和Kτ的值都大于1
2.构件尺寸: 定义尺寸系数
( 1)d 1
( 1)d 1
其中:(σ-1)d和(τ-1)d表示光滑大试样的持久有限;σ-1和τ-1表示光 滑小试样的持久极限;εσ和ετ的值都小于1。
(2)形式二:构件工作安全系数大于等于规定的安全系数
n n n n
例12-1. 阶梯轴如图示。材料为合金钢,σb=920MPa,σs =520MPa, σ-1 =420MPa,τ-1=250MPa。轴在不变弯矩M=850Nm作用下旋转。 若规定n=1.4,试校核轴的强度。。
0.4 r5
解:(1)轴弯曲对称循环, 最大弯曲正应力是
解:(1)由例12_1知 合金钢修正系数
K 1.48 0.77 0.87 0.2
(2)求不对称弯曲的交变应力
max
M max W
1200 (0.04)3
191MPa
32
m in
1
4
max
47.8MPa
a
1 2
( max
min )
71.6MPa
m
1 2
(
max
min )
119MPa
3.构件表面质量: 定义表面质量系数
( 1) ( 1)d
其中:(σ-1)d表示表面磨光试样的持久有限;(σ-1)β表示其它表面 加工情况试样的持久极限;β的值小于1。
4.构件持久极限的计算式:
综合三个方面因素
0 1
K
应力集中

第五章 应力集中一、概述1. 应力集中现象:小范围、高应力(多发生于结构不连续或构件截面突变处)2. 应力集中系数—表示应力(k στ,)集中的程度 k =σσmax 0(σ0表示与应力集中现象无关的名义应力,其取法并不是唯一的)3. 确定值的方法k理论解析方法——弹性力学数值方法——有限元分析试验——光弹、实测⎧⎨⎩⎧⎨⎪⎩⎪二、几种常见结构的应力集中1. 带有圆孔的受拉(压)板(1)无限大板设圆孔半径为,板宽a 2B →∞,均匀受拉,无限远应力为σ0,如图示。
根据弹性理论可知,板内任一点(,)r θ处的应力状态:σσρρρσσρρθτσρρθθθr r =−+−+=+−+=−+−⎧⎨⎪⎩⎪120224120241024114311321232[()()cos ][()()cos ]()sin θ2(其中ρ≡≤a r 1) 高应力区{}5013016o o r a ≤≤≤θ,.,最大应力σmax 发生在与σ0方向相垂直的直径的两端,应力集中系数k ==σmax 03(2)有限板宽的影响 随着B a ↓,,应力集中系数k =↑σmax0(当B a ≥5时,可认为k =3) 2. 椭圆孔的受拉(压)板 [与圆孔对照]设椭圆孔的两半轴长为和b (前者与a σ0方向相垂直),则最大应力σmax 发生的位置与圆孔类似,应力集中系数k a b ==+σσmax 012 ·若a b →∞,则应尽量避免甲板开口长边沿船长方向k →∞⇒3. 矩形开口的受拉(压)板(1)实验表明最大应力发生在矩形角隅圆弧A 点 (2)应力集中系数k f b B r b a r =′=σσmax (,,)0,见书图7-64. 梯形板的弯曲(1)最大应力发生在梯形板的转角处 (2)应力集中系数k =σσmax 0,见书图7-8·若r ↑,则船楼上建端部与主体连接处应以适当的圆弧过渡以减小)应力集中k ↓⇒5. 上建端部主体上的应力集中现象分析参阅书p.225图7-12和7-13船楼:半无限平面边缘甲板室:无限大平面上σσπμπx t T x t T x x T T =⋅=⋅=⋅=⋅⎧⎨⎩+20643026..(σx x ∝1,两侧应力反号) 三、降低应力集中的方法1. 减小应力集中系数或应力集中范围k 圆孔——尽量减小其直径()椭圆孔——使其长轴∥受力方向()矩形孔——采用较大的圆弧()不影响值,但可缩小范围,若则可不必加强使值下降使值下降k d t k k <⎧⎨⎪⎩⎪20 2. 采用加厚板或增设覆板,以覆盖高应力区3. 结构突变处采用过渡结构。
应力集中系数

容器开检查孔的有关规定
为检查压力容器在使用过程中是否产生裂纹、变形、
腐蚀等缺陷,压力容器应开设检查孔。检查孔包括人 孔和手孔.手孔应开设在封头上或封头附近的筒体上
(mm)
检查孔最少数 量
检查孔最小尺寸(mm)
人孔
手孔
备注
300-500
手孔2个
Ф 75或长 圆孔
75×50
500-1000
人孔1个或手孔 2个(当容器无法
压力容器开孔及补强设计
武汉工程大学化工设备设计研究所
2007年7月
1
压力容器开孔及补强设计
1、容器开孔接管后在应力分布与强度方面将的影响
•开孔后使承载截面减小,承载材料的削弱。 •破环了原有的应力分布,造成孔边缘局部的应力集中。 •接管处容器壳体与接管形成不连续结构而产生边缘应力
2、应力集中系数
•若未开孔时的名义应力为 ,开孔后按弹性方法 计算出的最大应力若为 m,ax 则弹性应力集中系数 的定义为 Kt max
(1
2b ) a
B
max
A
(1
2b ) a
Kt
max
(1
2b ) a
1
2b a
2 Kt 3
A
(1
2a b
)
B
max
A
(1
2a ) b
Kt
max
(1
开孔直径的最新规定,当壳体开孔满足下述全部要 求时可允许不需另行补强。
•(1)设b 计压力小于或等于2.5MPa;
•(2)两相邻开孔中心的距离(对曲面间距以弧长计算)应 不小于两孔直径之和的两倍;
焊接接头的强计算 公式 方法

焊缝接头强度计算的假设
⑤ 角焊缝都是在切应力作用下破坏的。角焊缝的计算断面
在角焊缝截面的最小高度上,取内接三角形高度 为计算
高度,(如图)。
直角等要角焊缝的计算高度:
K
0.7K
2
⑥ 尽管加强和小量的熔深对于接头强度没有影响,但埋弧
自算动断焊面和厚度co2保(护如焊图的)熔深较大应予以考虑,其角焊缝计
② 熔透的十字接头有较 小的应力集中系数。
搭接接头的应力分布
正面角焊缝:把与力作用 方向垂直的焊缝
① 焊缝根部A点、焊趾 B点应力集中严重
② 焊趾B点的应力集中 系数随角焊缝的斜边
的夹角 而变
③ 减小 、增大熔深焊
透根部和增大底边焊
脚长度,可使T 减小
侧面搭接角焊缝
斜向搭接角焊缝
点焊接头的应力分布
(K P)COS 450
当K 当K
8mm,可取K
8mm, P一般取8mm
电弧焊接接头的静载强度计算
1.对接焊缝强度 计算公式如下:
受拉时:
P
l
[
' l
]
受压时:
P
l
[
' a
]
受剪时: Q [ '] l
电弧焊接接头的静载强度计算
而内弯:1
M1 W1
6M1
2 l
[
' l
]
垂直弯: 2
时,按下式计算: M
S PL 0.7 Kh 2
Q
P 1.4K h
弯矩垂直于板面的丁字头计算
① 如开坡口并焊接,其强度
按对接接头计算,强度计算
公式为:
6M
2 l
[ ']
机械设计3-3
0.25 1.72 1.69 1.67 1.65 1.62 1.55 1.46 1.40 1.34 1.24
0.30 1.61 1.59 1.58 1.55 1.53 1.47 1.40 1.36 1.31 1.22
下一页 返回
简图
附表3-1 轴上环槽处的理论应力集中系数
应 公称应 力 力公式
(拉伸、弯曲)或 ( 扭转剪切)
32
dD2 6
公称扭转应力 T
T
D3
16
dD2 6
d/D 0.0 0.05 0.10 0.15 0.20 0.25 0.30 d/D 0.0 0.05 0.10 0.15 0.20 0.25 0.30
3.0 2.46 2.25 2.13 2.03 1.96 1.89
2.0 1.78 1.66 1.57 1.50 1.46 1.42
H7/h6 1.92 2.13 2.34 2.56 2.76 3.00 3.18 3.46
注:⑴滚动轴承与轴配合处的
k
值与表内所列H7/r6配合的
k
值相同;
⑵表中无相应的数值时,可按插入法计算。
返回
附表3-9 表面高频淬火的强化系数βq
试件种类
试件直径/mm
βq
无应力集中
7~20 30~40
返回
●
●
0.88
查表过程
●
1.75
返回
返回
返回
抛光
0.8
0.6
0.4
0.2 400 600 800 1000 1200
B / MPa
附图3-4 钢材的表面质量系数
返回
附表3-8
基于ANSYS+Workbench的理论应力集中系数的求法

截面的名义应力值,那么就可将(2)式中的名义应力σ 0 替代为膜应力σ m ,便得出如下公式:
K t
=
σ max σm
(3)
2.2 几何模型和材料特性
-2-
长、宽、高分别为 160mm、80mm、10mm 的矩形截面板,板中心位置存在一直径为 32mm 的 圆形孔,材料特性按普通钢:弹性模量 E=200GPa,泊松比μ=0.3。
2 使用膜应力计算理论应力集中系数
2.1 理论分析
为了得到带孔平板的理论应力集中系数,首先引入膜应力的定义。
膜应力(membrane stress)是沿截面厚度均匀分布的应力分量,它等于沿所考虑截面的应力平
均值。膜应力可以由如下公式计算得出:
∫ σ m = 1 t
σ t / 2
dx
−t /2
s
(1)
为了解决这个问题,就必须使用构件的名义应力值来评估而不能直接使用有限元计算出的最大 应力值;根据最大应力值和名义应力值的关系,求出名义应力得先知道构件的理论应力集中系数; 一些标准构件的理论应力集中系数可以通过工程手册的图表直接查取或一些经验公式也可以求出,
-1-
对于非标准和没有相关数据图表的构件,获取理论应力集中系数需要通过实验来得到,但这往往很 困难。
点序号 距离(mm) 膜应力(MPa) 总应力(Mpa)
1
0
79.417
188.81
10
4.5
79.417
104.17
20
9.5
79.417
75.ቤተ መጻሕፍቲ ባይዱ87
30
14.5
79.417
63.816
40
19.5
79.417
53.686
应力集中系数计算公式什么是应力集中应力集中的计算方法

应力集中系数计算公式什么是应力集中应力集中的计算方法应力集中是指结构或构件的局部区域的最大应力值比平均应力值高的现象。
应力集中能使物体产生疲劳裂纹,也能使脆性材料制成的零件发生静载断裂。
在应力集中处,应力的最大值(峰值应力)与物体的几何形状和加载方式等因素有关。
局部增高的应力随与峰值应力点的间距的增加而迅速衰减。
由于峰值应力往往超过屈服极限(见材料的力学性能)而造成应力的重新分配,所以,实际的峰值应力常低于按弹性力学计算得到的理论峰值应力。
应力集中对构件强度的影响对于由脆性材料制成的构件,应力集中现象将一直保持到最大局部应力到达强度极限之前。
因此,在设计脆性材料构件时,应考虑应力集中的影响。
对于由塑性材料制成的构件,应力集中对其在静载荷作用下的强度则几乎无影响。
所以,在研究塑性材料构件的静强度问题时,通常不考虑应力集中的影响。
但是应力集中对构件的疲劳寿命影响很大,因此无论是脆性材料还是塑性材料的疲劳问题,都必须考虑应力集中的影响。
在无限大平板的单向拉伸情况下,其中圆孔边缘的k=3;在弯曲情况下,对于不同的圆孔半径与板厚比值,k=1.8~3.0;在扭转情况下,k=1.6~4.0。
如下图所示的带圆孔的板条,使其承受轴向拉伸。
由试验结果可知:在圆孔附近的局部区域内,应力急剧增大,而在离开这一区域稍远处,应力迅速减小而趋于均匀。
这种由于截面尺寸突然改变而引起的应力局部增大的现象称为应力集中。
在I—I截面上,孔边最大应力ma某与同一截面上的平均应力之比,用a表示称为理论应力集中系数,它反映了应力集中的程度,是一个大于1的系数。
而且试验结果还表明:截面尺寸改变愈剧烈,应力集中系数就愈大。
因此,零件上应尽量避免带尖角的孔或槽,在阶梯杆截面的突变处要用圆弧过渡。
应力集中不仅与物体的形状及外形结构有关,还与选取材料有关,与外界应用环境也存在不可忽略的关系(如温度因素),另外,在加工过程中也可能导致应力的改变,例如回火不当引起二次淬火裂纹、电火花线切割加工显微裂纹、机械设计时也难免导致某部位的应力集中。
理论应力集中系数的有限元求法

应力集中系数图 。
尽管工程手册中列举了大量的图表数据 , 但是
由于受实际结构 、受力状态和结构形式的变化 , 手
册中的数据图表并不能全部地反映实际情况 。
(3) 经验公式法
经验公式是工程技术人员根据工程实际 , 对于
简单的结构形状 , 通过插值 、曲线拟合等数学手段
进行构建的 。该方法简化了查取图表步骤 , 应用起
(2) 工程图表查取法 根据结构的具体参数 , 在工程手册中直接查取 是目前获得理论应力集中系数 KT 的常用方法 。工程 手册中的图表是前人根据大量的试验直接得来 , 其 数 据 结 果 比 较 可 信 。图 2为 带 孔 拉 伸 平 板 的 理 论
图 3 有孔平板的拉伸应力集中
2 KT 的有限元求法
图 9 路径上的应力积分
3 各种计算方法的比较
从图 3算例可以看出 , 3 种不同方法得到结果 相差不大 。图表查取法得到的 KT 为 2. 7; 经验公式 法得到的 KT 为 2. 6; 而有限元法得到的 KT 为 2. 53, 其中图表查取法得到的结果比较保守 , 有限元法比 较符合实际 。
几种方法的优缺点如下 : (1) 实验方法 缺点 : 耗时 、耗资 , 实现难度大 。 优点 : 可靠性高 。 (2) 工程图表查取法 缺点 : 数据资源匮乏 , 只有简单的结构形式可 供参考 , 对于不同材料 、不同结构和复杂受力形式 没有合适的参考图表可用 。 优点 : 方便快捷 。 (3) 经验公式法 缺点 : 公式资源少 , 存在人为误差 。 优点 : 方便 、快捷 。 (4) 有限元方法 优点 : 不受结构形状 、材料 、受力状态的限制 , 通用 、精确 、可靠 、省时 、省力 、节约经费 。 缺点 : 计算较费时 , 净截面的选取对计算结果 有一定的影响 。
混凝土应力分析技术规程

混凝土应力分析技术规程一、前言混凝土是建筑工程中最为常见的材料之一。
在混凝土的使用过程中,应力是一个重要的参数,它能够反映混凝土的强度和稳定性。
因此,混凝土应力分析技术是建筑工程中不可或缺的一部分。
本技术规程旨在为混凝土应力分析提供一套系统的方法,以确保分析的准确性和可靠性。
二、基础知识1.混凝土的应力类型混凝土的应力类型主要有三种:拉应力、压应力和剪应力。
拉应力和压应力是混凝土中最常见的应力类型,它们通常出现在混凝土的受力部位。
剪应力则是在混凝土受到横向力作用时产生的应力。
2.混凝土的应力计算方法混凝土的应力计算方法有很多种,常见的有等效应力法、极限状态法、极限平衡法等。
其中,等效应力法是最为常用的一种方法,它可以将不同方向的应力转化为等效的拉应力或压应力。
3.混凝土的应力分析模型混凝土的应力分析模型有很多种,常见的有弹性模型、弹塑性模型、本构模型等。
其中,弹性模型是最为简单的一种模型,它假设混凝土的应力和应变呈线性关系。
弹塑性模型则更加接近混凝土的实际性质,它考虑了混凝土的弹性和塑性变形。
本构模型则是对混凝土材料本身特性的一种描述,它可以更加准确地描述混凝土的应力性能。
三、混凝土应力分析流程1.确定应力类型和受力方向首先需要确定混凝土受力的类型和方向,以便选择合适的应力计算方法和模型。
2.确定混凝土材料性质混凝土材料的性质对应力分析有很大影响,因此需要确定混凝土的弹性模量、泊松比、剪切模量等参数。
3.建立应力分析模型根据混凝土受力方向和类型,选择合适的应力分析模型,并建立相应的数学模型。
4.计算等效应力根据所选的应力计算方法,计算混凝土中不同方向的应力,并将其转化为等效的拉应力或压应力。
5.计算应力集中系数在混凝土中存在应力集中现象,需要计算相应的应力集中系数。
6.确定混凝土的极限状态根据所选的计算方法和模型,确定混凝土的极限状态,以判断其是否符合设计要求。
四、技术要点1.混凝土应力分析的准确性和可靠性取决于所选的应力计算方法和模型。
弹性力学-第四章-2

可以假设应力函数为:
( , ) f ( ) cos 2
满足相容方程求f()
( , ) f ( ) cos2
代Φ入相 容方程
1 1 2 2 2 0
2 2 2 2 2
2 1 1 2 d 2 f ( ) 1 df ( ) 4 f ( ) 2 2 ( 2 2 )cos 2 0 2 d d
r2
2
), q(1
r2
2
), 0
对 比
q q 1 2 令: q 2
代 入
基 本 解 答 一
q1 q2 r2 (1 2 ), 2
q1 q2 r2 (1 2 ), 2
0
r2 r2 σ ρ q cos 2φ(1 2 )(1 3 2 ) ρ ρ r4 σ φ q cos 2φ(1 3 4 ) ρ τ ρφ r2 r2 q sin 2φ(1 2 )(1 3 2 ) ρ ρ
e 因为,
t
D f ( ρ) Aρ Bρ C 2 ρ
4 2
2Φ 1 Φ 1 2Φ σρ 2 2 , 2 y 0 ρ ρ ρ 2Φ 2Φ σ 2 2 , x 0 ρ τ ρ
max 4q
3r , 90
1.04q
max K 4
(4-18)
应力集中系数
二、基本解答的应用
解决方法:利用 叠加原理,将荷 载分解为两部分 (1)双 向受拉
=
+
(2)一对 边受拉, 另一对 边受压
有效应力集中系数

有效应力集中系数(ksi)是指在某一特定几何形状的体系中,所承受的最大应力与所受应力的最大值之比。
有效应力集中系数常用于对轴向应力集中问题进行分析。
例如,当轴向应力集中在圆柱形体的截面上时,有效应力集中系数可以表示为:
ksi = (σmax / σallow) ×Kt
其中,σmax表示所受的最大应力,σallow表示材料承载应力的最大值,Kt是圆柱形体的抗剪截面系数。
有效应力集中系数的大小取决于材料的强度和几何形状,通常在设计过程中要求有效应力集中系数小于1。
如果有效应力集中系数过大,则说明应力集中的程度较大,可能导致结构失效。
基于ANSYS+Workbench的理论应力集中系数的求法

带孔平板的等效应力最大值为 189.19MPa,如图 4 所示。
-3-
iL。
一}詈掌。虹
图 4 等效图应力云图
2.6 结果后处理
ANSYS Workbench 中采用应力线性化工具,可以将穿过截面的应力分解成常量应力(membrane 膜应力)和线性应力(bending 弯曲应力)。应力线性化工具使用由两个点定义的路径,如图 1 中截 面由路径相匹配的两个端点(点 N1 和点 N2)和 47 个中间点(通过自动线性插值)定义。点 N1 和 N2 通常设定在自由表面上。
-5-
一种有效途径。
4 参考文献
[1] Budynas−Nisbett.Shigley’s Mechanical Engineering Design·8th(M).McGraw−Hill Primis,2006 [2] 孙训方.材料力学(M).北京:高等教育出版社,2002,8 [3] 王勖成.有限单元法(M).北京:清华大学出版社,2003,7 [4] ANSYS Inc.ANSYS Help,2010
时,才能够使用该方法得出的应力集中系数。如果没有执行网格研究而沿着危险截面路径上网格数
量不足,那么不能使用该
K t
值,这样会导致
K t
偏小。
3 结论
通过本文的研究得出了一种使用 ANSYS Workbench 中应力线性化工具通过膜应力求出应力集中 系数的方法,该方法具有不受几何形状和实验数据缺少的限制,可以作为求解理论应力集中系数的
腱。。有上述计算结果,可得出圆孔处的理论应力集中系数为:
K t
=σ Biblioteka ax σm=188.81 79.417
= 2.38
[1]
根据查阅工程手册 的图表可知,该圆孔处的理论应力集中系数为 2.28 与计算结果很接近。
