专题04 三角函数与三角形(第01期)-2016届高三文数百所名校好题速递分项解析汇编(解析版)
专题03 三角函数与三角形(第01期)-决胜2016年高考全国名校试题理数分项汇编(浙江特刊)(原卷版)

第四章 三角函数与三角形一.基础题组1. 【浙江省嘉兴市2015届高三下学期教学测试(二)理1】在△ABC 中,“B A sin sin >”是“B A >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2. 【浙江省嘉兴市2015届高三下学期教学测试(二)理5】若55cos sin =+θθ,]π,0[∈θ,则=θtan A .21-B .21 C .2- D .23. 【浙江省衢州市2015年4月高三年级教学质量检测 理6】为了得到函数cos(2)6y x π=-的图像,可以将函数sin 2y x =的图像( ) A.向右平移3π B.向右平移6π C.向左平移3π D.向左平移6π 4.【2015年温州市高三第二次适应性测试 理3】要得到函数2cos 2y x x =+的图像,只需将函数2sin 2y x =的图象( ▲ )A .向左平移6π个单位 B .向右平移6π个单位 C .向左平移12π个单位D .向右平移12π个单位5.【浙江省2015届高三第二次考试五校联考 理3】为得到函数()cos f x x x =,只需将函数y x x =+ ( )A . 向左平移512π B .向右平移512π C .向左平移712π D .向右平移712π 6. 【东阳市2015年高三模拟考试 理3】设函数()f x =sin()A x ωϕ+(0,A ≠0,ω>)22ϕππ-<<的图象关于直线23x π=对称,它的最小正周期为π,则( ▲ )A.()f x 的图象过点1(0)2, B. ()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上是减函数 C.()f x 的一个对称中心是5,012π⎛⎫⎪⎝⎭D. ()f x 的一个对称中心是,06π⎛⎫⎪⎝⎭7. 【2015诸暨市高中毕业班教学质量检测试题 理4】已知4cos()45πα-=,则sin 2α=( )A .2425 B .725 C .2425± D .725± 8. 【2015年浙江省杭州二中高三年级仿真考 理3】函数)sin()(ϕω+=x A x f (其中)2,0πϕ<>A )的图象如图所示,为了得到x x g ωsin )(=的图象,则只要将)(x f 的图象( )A .向右平移6π个单位长度 B .向右平移12π个单位长度 C .向左平移6π个单位长度 D .向左平移12π个单位长度9.【镇海中学2015学高考模拟试卷 理5】设()cos 22f x x x =,把()y f x =的图像向左平移(0)ϕϕ>个单位后,恰好得到函数()cos 22g x x x =-的图象,则ϕ的值可以为( )A .6πB .3πC .23π D .56π10. 、【绍兴市2014-2015学年高三第一学期期末教学质量调测 理5】将函数sin 26y x π⎛⎫=+ ⎪⎝⎭图象向右平移m (0m >)个单位,得到函数()y f x =的图象,若()y f x =在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递增,则m 的最小值为( ) A .3πB .4πC .6πD .12π11. 【2014学年度第一学期五校联考高三数学期中试卷 理4】数列{a n }为等差数列,若a 2+a 5+a 8=π,则)tan(73a a +的值为( )A .33 B .33- C .3 D .3-12. 【2014学年度第一学期五校联考高三数学期中试卷 理5】()sin 600︒-的值为( )A .21 B .21- C .23D . 13.【2014学年度第一学期五校联考高三数学期中试卷 理6】 已知sin cos αα-=(0,)απ∈,则tan α=( )A.1B.-1C.12D 14. 【2014学年度第一学期五校联考高三数学期中试卷 理8】要得到函数x y 2cos =的图象,可由函数cos(2)3y x π=-的图像( )A .向左平移3π个长度单位 B .向右平移3π个长度单位 C .向左平移6π个长度单位 D .向右平移6π个长度单位15. 【2014学年度第一学期五校联考高三数学期中试卷 理9】若函数()2sin()f x x ωϕ=+,(,0,)2x R πωϕ∈><的最小正周期为π,且(0)f =,则( )A.12ω=,6πϕ= B.12ω=,3πϕ= C.2ω=,6πϕ= D.2ω=,3πϕ= 16. 【2014学年浙江省第一次五校联考 理5】函数()cos 3f x x πω⎛⎫=+ ⎪⎝⎭(,0)x R ω∈>的最小正周期为π,为了得到()f x 的图象,只需将函数()sin 3g x x πω⎛⎫=+ ⎪⎝⎭的图象( )A.向左平移2π个单位长度 B.向右平移2π个单位长度C.向左平移4π个单位长度D.向右平移4π个单位长度17. 【宁波市2014-2015学年度第一学期期末考试 理5】函数()sin 6f x x πω⎛⎫=A + ⎪⎝⎭(0ω>)的图象与x 轴正半轴交点的横坐标构成一个公差为2π的等差数列,若要得到函数()sin g x x ω=A 的图象,只要将()f x 的图象( )个单位 A .向左平移6πB .向右平移6πC .向左平移12πD .向右平移12π18. 【宁波市2015年高考模拟考试数学试题 理6】将函数()()2sin 42f x x π=+的图象向右平移()0ϕϕ>个单位,再将图象上每一点的横坐标缩短到原来的12倍(纵坐标不变),所得图象关于直线4x π=对称,则ϕ的最小值为( ) A .18πB . 12πC . 34πD . 38π19.【浙江省绍兴市2015年高三教学质量检查 理5】20. 【浙江省绍兴市2015年高三教学质量检查 理6】21. 【浙江省嵊州市2015年高三第二次教学质量调测 理2】为得到函数)43sin(π+=x y 的图象,只要把函数)4sin(π+=x y 图象上所有的点( )A .横坐标缩短到原来的31倍,纵坐标不变 B .横坐标伸长到原来的3倍,纵坐标不变C .纵坐标伸长到原来的3倍,横坐标不变D .纵坐标缩短到原来的31倍,横坐标不变22.【2015年温州市高三第三次适应性测试数学试题 理4】要得到函数3sin(2)3y x π=+的图象,只需将3sin 2y x =图象上所有的点( ▲ )A .向左平行移动3π个单位长度 B .向右平行移动3π个单位长度 C .向左平行移动6π个单位长度D .向右平行移动6π个单位长度23.【严州中学2015届高三仿真考试数学试卷 理3】设函数()f x =sin()A x ωϕ+(0,A ≠0,ω>)22ϕππ-<<的图象关于直线23x π=对称,它的最 小正周期为π,则( )A.()f x 的图象过点1(0)2, B. ()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上是减函数C.()f x 的一个对称中心是5,012π⎛⎫⎪⎝⎭D. ()f x 的一个对称中心是,06π⎛⎫⎪⎝⎭函数(21)xy x e =-的图象是( )24.【浙大附中2015年高考全真模拟试卷 理5】如图所示的是函数()sin 2f x x =和函数()g x 的部分图象,则函数()g x 的解析式是( ▲ )(A )()sin(2)3g x x π=-(B )2()sin(2)3g x x π=+(C )5()cos(2)6g x x π=+ (D )()cos(2)6g x x π=-25.[浙江省重点中学协作体2015届第二次适应性测数学试题 理 14]已知)2,0(,1010)4cos(πθπθ∈=+,则sin(2)3πθ-= 。
专题04 三角函数与三角形(第02期)-决胜2016年高考全国名校试题文数分项汇编(新课标Ⅰ特刊)(原卷版)

第四章 三角函数与三角形一.基础题组1. 【江西省名校学术联盟2016届高三第一次调研 文5】已知倾斜角为α的直线l 与直线230x y +-=垂直,则2015cos(2)2πα-的值为 A.45 B. 45- C.2 D.12-2. 【江西省名校学术联盟2016届高三第一次调研 文9】已知向量()3(sin 2,1),(cos2,),()2m x n x f x m n m ==-=-⋅,则函数()f x 的最小正周期与最大值分别为A.,3π+B. ,32π+ 7,2π D. ,32π 3. 【山东省实验中学2016届高三上学期第一次诊断测试 文3】设命题:p 函数2sin 2y x π⎛⎫=+ ⎪⎝⎭是奇函数;命题:q 函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是( )A .p 为真B .q ⌝为假C .p q ∧为假D .p q ∨为真4. 【河北定州中学2016届高三第一次月考 文6】已知函数()sin cos f x x x =+,且'()3()f x f x =,则x 2tan 的值是( )A.34-B.34C.43-D.435. 【河北定州中学2016届高三第一次月考 文11】函数())(,0,||f x x x ωϕωϕ=+∈><R π)2的部分图象如图所示,则()f x 的单调递减区间为( )A .511[,],1212k k k z ππππ++∈ B . 511[],66k x k k z ππππ+≤≤+∈ C . 511[2,2],1212k k k z ππππ++∈ D . 5[,],1212k k k z ππππ-++∈6. 【湖北省武汉华中师范大学第一附属中学2015届高三5月适应性考试 文5】已知函数x x x f cos sin )(λ+=的图像的一个对称中心是)0,3(π,则函数 x x x x g 2sin cos sin )(+=λ的图像的一条对称轴是 ( ) A .65π=x B .34π=x C .3π=xD .3π-=x7. 【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 文3】若sin()cos(2)1sin cos()2πθθπθπθ-+-=++,则tan θ=A .1B .1-C .3D .3-8. 【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 文4】要得到函数πsin(2)3y x =-的图象,只需将函数sin 2y x =的图象 A .向右平移π6个单位长度 B .向左平移π6个单位长度 C .向右平移π3个单位长度 D .向左平移π3个单位长度9. 【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 文6】函数()sin (0)f x x ωω=>在区间[0,]3π上单调递增,在区间[,]32ππ上单调递减,则ω= A.32 B.23C .2D .310. 【鹰潭市2014届高三第一次模拟考试数学试题 文2】将函数)46sin(π+=x y 的图像上各点的横坐标伸长到原来的3倍,再向右平移8π个单位,得到的函数的一个对称中心是 ( )A .)0,2(πB .)0,4(πC .)0,9(πD .)0,16(π11. 【江西省临川区第一中学2016届高三上学期第一次月考 文5】将函数sin(4)6y x π=-图象上各点的横坐标伸长到原的2倍,再向左平移4π个单位,纵坐标不变,所得函数图象的一条对称轴的方程是( )A 12x π=B. 6x π=C 3x π=D 12x π=-12. 【山东省实验中学2016届高三上学期第一次诊断测试 文13】()()sin f x x ωϕ=A +(A ,ω,ϕ为常数,0A >,0ω>,0ϕπ<<)的图象如图所示,则3f π⎛⎫⎪⎝⎭的值为 .13. 【河北定州中学2016届高三第一次月考 文15】把函数()y f x =的图象向右平移4π个单位,得到2sin(3)4y x π=-的图象,则函数()y f x =的解析式是 .14. 【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 文14】已知15sin(),(,)6336πππαα+=∈,则cos()3πα+= _________.15. 【2015-2016学年江省新余一中、万载中学、宜春中学联考 文14】已知tan(3π-x )=2,则xx x xcos sin 1sin 2cos 22+--= .16. 【2015-2016学年江省新余一中、万载中学、宜春中学联考 文16】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b=1,a=2c ,则sinC 的最大值为17. 【河北冀州中学2015年---2016年高三第二次月考文14】设0<θ<2π,向量a =(sin2θ,cos θ),b =(1,-cos θ),若a ⊥b ,则tan θ= .18. 【河北冀州中学2015年---2016年高三第二次月考 文16】设0απ≤≤错误!未找到引用源。
2016届高考数学全国名校试题分项汇编(江苏特刊)专题04三角函数与三角形(第01期)(原卷版)

第四章 三角函数与三角形一.基础题组1.【江苏省淮安市2015届高三第五次模拟考试】在ABC ∆中,若2,3a b B π===,则ABC ∆的面积为 ▲ .2. 【江苏省扬州中学2015届高三4月双周测】角α的顶点在坐标原点,始边与x 轴的非负半轴重合,终边经过点(1,2)P ,则)cos(απ-的值是 ▲3. 【淮安市淮海中学2015届高三冲刺四统测模拟测试】已知函数()2sin()(0)f x x ωϕω=+>,若()0,()232f f ππ==, 则实数ω的最小值为 ▲ .4. 【淮安市淮海中学2015届高三冲刺四统测模拟测试】已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,若2b =且2cos sin a C c B =+,则ABC ∆的面积的最大值为 ▲ .5. 【2015年高考模拟(南通市数学学科基地命题)(3)】函数()2sin()(0,f x x ωϕω=+>且||)2πϕ<的部分图像如图所示,则(0)f 的值为 .6. 【2015年高考模拟(南通市数学学科基地命题)(2)】已知442cos sin ,(0,)32πααα-=∈,则2cos(2)3πα+= .7. 【2015年高考模拟(南通市数学学科基地命题)(4)】已知π()3sin(2)6f x x =-,若存在π(0,)2α∈,使()()f x f x αα+=--对一切实数x 恒成立,则α= .8. 【扬州市2014—2015学年度第四次调研测试试题高三数学】已知α为第三象限角,且tan 2α=,则sin 2α= .9. 【江苏省扬州中学2015届高三4月双周测】已知函数2()21f x x ax =-+,若存在(,)42ππϕ∈,使(sin )(cos )f f ϕϕ=,则实数a 的取值范围____▲_____.10. 【江苏省淮安市2015届高三第五次模拟考试】已知1sin cos 2αα=+,且(0,)2πα∈,则cos 2sin()4απα-的值为 ▲ .11. 【2015年高考模拟(南通市数学学科基地命题)(2)】函数y =2sin(3x +π6)的最小正周期为 .12. 【2015年高考模拟(南通市数学学科基地命题)(6)】若将函数y =sin ⎝⎛⎭⎫ωx +π4(ω>0)的图象向左平移π6个单位长度后,与函数cos()4y x pw =+的图象重合,则ω的最小值为_____________.13.【徐州市2014~2015学年度高三第三次质量检测】已知函数),20)(6sin()(<<+=ωπωx x f 若,1)32(=πf 则函数)(x f y =的最小正周期为 ▲ . 14. 【江苏省扬州中学2015届高三第四次模拟考试(5月)】函数sin (sin cos )y ααα=-([,0]2πα∈-])的最大值为 .15.【扬州市2014—2015学年度第四次调研测试试题高三数学】锐角ABC △中角,,A B C 的对边分别是,,a b c ,4,5a b ==, ABC △的面积为, 则c = .16.【扬州市2014—2015学年度第四次调研测试试题高三数学】平面内四点,,,O A B C 满足4,0OA OB OC OB OC ===⋅=,则ABC ∆面积的最大值为 .17.【淮安市2014-2015学年度第二学期高二调查测试】已知1cos()33πα+=-,则sin()6πα-的值为_____.18.【淮安市2014-2015学年度第二学期高二调查测试】将函数)0)(3sin(2)(>+=ωπωx x f 的图象向右平移3πω个单位,得到函数()y g x =的图象,若()y g x =在[0,]4π上为增函数,则ω的最大值为 .19.【盐城市2015届高三年级第三次模拟考试】若角+4πα的顶点为坐标原点,始边与x 轴的非负半轴重合,终边在直线12y x =上,则tan α的值为 ▲ .20.【盐城市2015届高三年级第三次模拟考试】 (本小题满分14分)已知(2sin ,sin cos )m x x x =-,(3cos ,sin cos )n x x x =+,记函数()f x m n =⋅. (1)求函数()f x 取最大值时x 的取值集合;(2)设ABC ∆的角,,A B C 所对的边分别为,,a b c ,若()2f C =,c =求ABC ∆面积的最大值.21.【淮安市2014-2015学年度第二学期高二调查测试】如图,在平面直角坐标系xOy 中,以Ox 轴为始边作角α和β,0,,,22ππαβπ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,其终边分别交单位圆于A B ,两点.若A B ,两点的横坐标分别是53,102-. 试求(1)αtan ,βtan 的值; (2)AOB ∠的值.22.【扬州市2014—2015学年度第四次调研测试试题高三数学】ABC ∆的内角,A B 满足2cossin 22A B A Ba i j +-=+(单位向量,i j 互相垂直),且6||a =. ⑴求tan tan A B 的值; ⑵若sinA =,边长2a =,求边长c .23.【江苏省扬州中学2015届高三第四次模拟考试(5月)】(本小题满分14分)已知函数()sin()f x x ωϕ=+(0,0)ωϕπ><<,其图像经过点1(,)32M π,且与x 轴两个相邻的交点的距离为π. (1)求()f x 的解析式; (2)在△ABC 中,a =13,3()5f A =,5()13f B =,求△ABC 的面积.24.【江苏省扬州中学2015届高三第四次模拟考试(5月)】(本小题满分15分)如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域OAB 内建两个圆形花坛,该扇形的圆心角为变量2θ(02θπ<<),其中半径较大的花坛⊙P 内切于该扇形,半径较小的花坛⊙Q 与⊙P 外切,且与OA 、OB 相切. (1)求半径较大的花坛⊙P 的半径(用θ表示); (2)求半径较小的花坛⊙Q 的半径的最大值.25. 【淮安市淮海中学2015届高三冲刺四统测模拟测试】(本题满分14分)已知向量(cos ,sin )θθ=a ,(2,1)=-b .(1)若⊥a b ,求sin cos sin cos θθθθ-+的值;(2)若2-=a b ,(0,)2θπ∈,求sin()4θπ+的值26. 【江苏省扬州中学2015届高三4月双周测】本小题满分14分)已知函数()2cos()(05)63f x x x ππ=+≤≤,点B A ,分别是函数)(x f y =图象上的最高点和最低点.(1)求点B A ,的坐标以及OB OA ⋅的值;(2)设点B A ,分别在角])2,0[,(,πβαβα∈的终边上,求)22sin(βα-的值.27. 【江苏省淮安市2015届高三第五次模拟考试】(本小题满分14分)函数π()cos(π)(0)2f x x ϕϕ=+<<的部分图象如图所示. (1)求出ϕ及图中0x 的值; (2)求()f x 在区间11[,]23-上的最大值和最小值.28. 【泰州市2015届高三第三次调研测试】已知函数()sin()f x A x ωϕ=+(其中A ,ω,ϕ为常数,且A >0,ω>0,22ϕππ-<<)的部分图象如图所示.(1)求函数f (x )的解析式; (2)若3()2f α=,求sin(2)6απ+的值.29.【2015年高考模拟(南通市数学学科基地命题)(2)】(本小题满分14分)已知△ABC 的内角A 的大小为120(1)若AB =,求△ABC 的另外两条边长;(2)设O 为△ABC 的外心,当BC =求AO BC ⋅uuu r uu u r的值.30. 【2015年高考模拟(南通市数学学科基地命题)(4)】(本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c , sin sin tan cos cos A B C A B +=+.(1)求C ;(2)若△ABC 的外接圆直径为1,求a b +的取值范围.31.【南京市2015届高三年级第三次模拟考试】(本小题满分14分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a cos C +c cos A =2b cos A . (1)求角A 的值;(2)求sin B +sin C 的取值范围.32.【南京市2015届高三年级第三次模拟考试】(本小题满分14分)如图,摩天轮的半径OA 为50m ,它的最低点A 距地面的高度忽略不计.地面上有一长度为240m 的景观带MN ,它与摩天轮在同一竖直平面内,且AM =60m .点P 从最低点A 处按逆时针方向转动到最高点B 处,记∠AOP =θ,θ ∈(0,π).(1)当θ =2π3 时,求点P 距地面的高度PQ ; (2)试确定θ 的值,使得∠MPN 取得最大值.34.【徐州市2014~2015学年度高三第三次质量检测】在△ABC ,角C B A ,,的对边分别为,,,c b a 已知.cos 2sin ,31cos B A C ==(1) 求B tan 的值;(2) 若,5=c 求△ABC 的面积.二.能力题组1. 【2015年高考模拟(南通市数学学科基地命题)(2)】设ABC ∆的内角,,A B C 所对的边,,a b c成等比数列,则sin sin BA的取值范围是 .2. 【2015年高考模拟(南通市数学学科基地命题)(6)】在ABC ∆中,角A ,B ,C 的对边分别为a,b,c,且2cos 2,c B a b =-若ABC ∆的面积为S =,则ab 的最小值为_________.3. 【南京市2015届高三年级第三次模拟考试】若将函数f (x )=∣sin(ωx -π6)∣(ω>0)的图象向左平移π9个单位后,所得图象对应的函数为偶函数 ,则实数ω的最小值是 ▲ .4. 【江苏省扬州中学2015届高三4月双周测】(本小题满分16分)如图(1),有一块形状为等腰直角三角形的薄板,腰AC 的长为a 米(a 为常数),现在斜边AB 上选一点D ,将△ACD 沿CD 折起,翻扣在地面上,做成一个遮阳棚,如图(2). 设△BCD的面积为S ,点A 到直线CD 的距离为d. 实践证明,遮阳效果y 与S 、d 的乘积Sd 成正比,比例系数为k (k 为常数,且k >0).(1)设∠ACD=θ,试将S 表示为θ的函数;(2)当点D 在何处时,遮阳效果最佳(即y 取得最大值)?5. 【2015年高考模拟(南通市数学学科基地命题)(2)】(本小题满分14分)在ABC ∆中,2C A π-=,sin A =(1)求sin C 的值;(2)若BC =,求ABC ∆的面积.6. 【2015年高考模拟(南通市数学学科基地命题)(6)】(本小题满分14分)在ABC ∆中,,,A B C 的对边分别是,,a b c ,已知向量(sin(),cos )m C C π=-,(sin(),sin )2n B B π=+,且sin 2m n A ⋅=.(1)求A ; (2)若4c bb c+=,求sinBsinC 的值.。
2014届高三名校数学(文)试题分省分项汇编 专题04 三角函数与三角形

一.基础题组1. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知4cos()65πα-=,则sin()3πα+= .2. 【江苏省兴化市安丰高级中学2014届高三】已知)0,2(πα-∈,53cos =α,则=+)4tan(πα .3.【江苏省兴化市安丰高级中学2014届高三】在ABC ∆中,若2,60,a B b =∠=︒=则c = .4. 【江苏省兴化市2013~2014学年度第一学期期中考试高三】在ABC ∆中,已知0sin sin sin sin sin 222=---C B C B A ,则A ∠的大小为 .5. 【江苏省扬州中学2013—2014期中考试模拟】设向量(cos ,sin )a αα=,(cos ,sin )b ββ= ,其中πβα<<<0,若|2||a b a b +=- ,则βα-= .6. 【盐城市2014届高三年级第一学期期中考试】函数2cos y x =的最小正周期为 .7. 【金陵中学2013-2014学年度第一学期高三期中试卷数学】已知f (x )=3sin(2x -π6),若存在α∈(0,π),使f (α+x )= f (α-x )对一切实数x 恒成立,则α= .8. 【江苏省徐州市2013-2014第一学期高三期中试题】已知△ABC 中,c b a ,,分别是角A ,B ,C 的对边,2=a ,A = 45°,B = 60°,那么△ABC 的面积=∆ABC S .9.【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知ABC ∆的周长为1,且sin sin A B C +=(1)求边AB 的长;(2)若ABC ∆的面积为1sin 6C ,求角C .10.【江苏省兴化市安丰高级中学2014届高三】已知(cos ,sin ),(cos ,sin )a b ααββ==. (1)若67πβα=-,求a b ⋅ 的值; (2)若4,58a b πα⋅== ,且⎪⎭⎫⎝⎛-∈-0,2πβα,求tan()αβ+的值.【答案】(1)2-;(2)7. 【解析】11.【江苏省扬州中学2013—2014期中考试模拟】已知函数2()2sin cos 1f x x x x =-++ ⑴求()f x 的最小正周期及对称中心; ⑵若[,]63x ππ∈-,求()f x 的最大值和最小值.12.【盐城市2014届高三年级第一学期期中考试】已知函数()2sin(2)f x x ϕ=+,其中角ϕ的终边经过点P ,且0ϕπ<<. (1)求ϕ的值;(2)求()f x 在[0,]π上的单调减区间.考点:三角函数的定义、()sin()f x A x ωϕ=+的单调性.二.能力题组1.【江苏启东中学2014届上学期期中模拟高三数学】将函数()2sin()3f x x πω=-(0ω>)的图象向左平移3πω个单位,得到函数()y g x =的图象,若()y g x =在[0,]4π上为增函数,则ω的最大值为2. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】求值:002cos10sin 20cos 20-= .3. 【江苏省徐州市2013-2014第一学期高三期中试题】方程0cos 3sin =++a x x 在)2,0(π内有相异两解βα,,则=+βα .【答案】3π或37π【解析】4. 【盐城市2014届高三年级第一学期期中考试】在ABC ∆中,若22()||5C A C B A B A B+⋅= ,则tan tan AB= .5. 【江苏省兴化市安丰高级中学2014届高三】在锐角△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且 .3tan )(222bc A a c b =-+(1)求角A ;(2)若2a =,求ABC ∆面积S 的最大值.6. 【江苏省兴化市2013~2014学年度第一学期期中考试高三】在△ABC 中,内角,,A B C所对的边分别为,,a b c ,已知m ()A A sin 3,cos 2=,n ()A A cos 2,cos -=,m·n 1-=.(1)求A ∠的大小;(2)若32=a ,2=c ,求△ABC 的面积.7. 【江苏省徐州市2013-2014第一学期高三期中试题】设向量)sin ,2(θ=,)cos ,1(θ= ,θ为锐角.(1)若136a b ⋅= ,求θθcos sin +的值;(2)若a b ,求)32sin(πθ+的值.8.【江苏省通州高级中学2013-2014学年度秋学期期中考试高三数学试卷】在△ABC中,内角A,B,C所对边长分别为a,b,c, =8,∠BAC=θ,a=4,(1)求b·c的最大值及θ的取值范围;(2)求函数f(θ)=23sin2(π4+θ)+2cos2θ-3的最值.9. 【盐城市2014届高三年级第一学期期中考试】在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,设(1,1)m = ,(cos ,sin )n A A =- ,记()f A m n =⋅.(1)求()f A 的取值范围;(2)若m 与n 的夹角为3π,3C π=,c =,求b 的值.10. 【金陵中学2013-2014学年度第一学期高三期中试卷数学】 已知向量a =(2cos x ,2sin x ) ,b =(3cos x , cos x ),设函数f (x )=a •b -3, 求: (1) f (x )的最小正周期和单调递增区间;(2)若()()26212f f απαπ--+=, 且α∈(π2,π). 求α. 【答案】(1) 22T ππ== , 函数()f x 的单调递增区间为5[,]()1212k k k Z ππππ-+∈ ;(2) 712πα=或1112π.【解析】三.拔高题组1. 【江苏启东中学2014届上学期期中模拟高三数学】已知)2sin ,2(),sin ,1(2x b x a ==,其中()0,x π∈,若a b a b ⋅=⋅,则tan x =2. 【江苏省通州高级中学2013-2014学年度秋学期期中考试高三数学试卷】 已知ααcos 21s in +=,且)2,0(πα∈,则)4sin(2cos παα-的值为__ ____.3. 【江苏启东中学2014届上学期期中模拟高三数学】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,sin sin tan cos cos A B C A B+=+.(1)求角C 的大小;(2)若△ABC 的外接圆直径为1,求22a b +的取值范围. 【答案】(1)3C π=;(2)223342a b <+≤;【解析】试题分析:(1)sin sin tan cos cos A B C A B +=+中有正切和正弦、余弦,这样的问题一般是“切化弦”,统一为同名三角函数后再利用三角函数的相关公式进行变形解答;(2)利用正弦定理,22a b +可化为角,A B 的三角函数,再利用3C π=,可消去一元,问题于是就转化为三角函数的值域问题.试题解析:(1)因为sin sin tan cos cos A B C A B +=+,即sin sin sin cos cos cos C A B C A B+=+,所以sin cos sin cos cos sin cos sin C A C B C A C B +=+, 即 sin cos cos sin cos sin sin cos C A C A C B C B -=-,得 sin()sin()C A B C -=-. …………………………………………………4分 所以C A B C -=-,或()C A B C π-=--(不成立). 即 2C A B =+, 得 3C π=. ………………………………7分(2)由3C π=,设,33A B ππαα=+=-,2πππ0,,333A B α<<<<知-.因2sin sin ,2sin sin a R A A b R B B ====, ………………………………………8分 故22221cos 21cos 2sin sin 22A B a b A B --+=+=+=12π2π11cos(2)cos(2)1cos 22332⎡⎤-++-=+⎢⎥⎣⎦ααα. …………………12分ππ2π2π,2,3333αα<<<<由-知-1cos 212α-<≤,故223342a b <+≤.…………14分考点:两角和与差的三角函数、正弦定理.4. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】如图,两座建筑物AB ,CD 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m 和15m ,从建筑物AB 的顶部A 看建筑物CD 的张角045CAD ∠=. (1)求BC 的长度;(2)在线段BC 上取一点P (点P 与点B ,C 不重合),从点P 看这两座建筑物的张角分别为APB α∠=,DPC β∠=,问点P 在何处时,tan()αβ+最小?BC的长度是18 m.………………………7分。
决胜2016年高考全国名校试题数学分项汇编(江苏特刊)专题04 三角函数与三角形 含解析

一、填空1。
【淮安、宿迁、连云港、徐州苏北四市2016届高三第二次调研】函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示,若5=AB ,则ω的值为 .-22Oxy AB【答案】3π 【解析】试题分析:2254()2TAB ==+,解得26,3T ππωω===2。
【江苏省淮阴中学2015-2016学年度第一学期期中考试】三角形的三个内角的度数之比为1:2:3,其最小内角的弧度数为 . 【答案】6π3。
【江苏省淮阴中学2015-2016学年度第一学期期中考试】角β的终边和角α=-1035°的终边相同,则cos β= 。
【答案】22【解析】试题分析:依题意有︒-︒⋅=1035360k β,所以224545360310351035360=︒=︒+︒⨯-=︒-=︒-︒⋅=cos )cos()cos()cos(cos k β.另外,也可直接得,22454536031035=︒=︒+︒⨯-=︒-=cos )cos()cos(cos β 4。
【江苏省淮阴中学2015—2016学年度第一学期期中考试】扇形的半径为2,圆心角为3π,则此扇形的面积为 .【答案】23π【解析】试题分析:根据扇形的面积公式得,32322122ππα=⨯⨯==r s 215。
【江苏省淮阴中学2015—2016学年度第一学期期中考试】如图,点P 从(1,0)出发,沿单位圆按顺时针方向运动3π弧长到达Q 点,则Q 点的坐标为 。
【答案】13,2⎛⎫-⎪ ⎪⎝⎭【解析】试题分析:根据任意角的三角函数的定义得,213=-=)cos(πx ,233-=-=)sin(πy ,所以点Q的坐标为13,2⎛⎫- ⎪ ⎪⎝⎭6。
【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】已知7sin cos 13αα+=-,π(,0)2α∈-,则tan α= .【答案】125-【解析】7. 【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】若α、β均为锐角,且1cos 17α=,47cos()51αβ+=-,则cos β= .【答案】13【解析】试题分析:由于αβ、都是锐角,所以αβ+∈(0,)π,又1cos 17α=,47cos()51αβ+=-,所以122sin 17α=,142sin()51αβ+=,cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++4715117=-⨯+ 142122⨯13=. 8。
专题04 三角函数与三角形(第02期)-决胜2016年高考全国名校试题理数分项汇编(新课标Ⅰ特刊)(解析版)

第四章 三角函数与三角形一.基础题组1.【临川一中2014—2015学年度下学期期末考试 理9】在ABC ∆中,内角C B A 、、的对边分别是c b a 、、,若22()6c a b =-+,ABC ∆,则C =( ) A .3π B . 23π C .6π D .56π 【答案】A考点:余弦定理,三角形的面积,辅助角公式,已知三角函数值求角.2. 【海南省嘉积中学2014—2015学年度第二学期高三大测(五) 理5】若tan 3α=,则2sin 2cos αα的值为( ) A .2B . 3C .4D .6【答案】D 【解析】 试题分析:原式=6tan 2cos cos sin 22==αααα考点:三角函数的化简名师点睛:对于这类分式形式,上下是关于正弦和余弦的齐次形式,考虑上下同时除以x n cos ,转化为x tan 的形式求值.3. 【河北冀州中学2015年---2016年高三第二次月考 理7】设函数 1()cos()2f x x ωϕ=+对任意的x R ∈,都有 ()()66f x f x ππ-=+,若函数()3sin()2g x x ωϕ=+-,则 ()6g π的值是( )A. 1 B . -5或3 C. -2 D .12【答案】C 【解析】试题分析:根据题意有6x π=是函数1()cos()2f x x ωϕ=+图像的对称轴,从而有,6k k Z πωϕπ+=∈,所以有()3sin()226g k ππ=-=-,故选C.考点:三角函数的性质.4. 【河北冀州中学2015年---2016年高三第二次月考 理9】已知α,()0,βπ∈,且()1tan 2αβ-=,1tan 7β=-,则2αβ-的值是( )A .4π-B .34π-C . 4πD .34π 【答案】B考点:已知函数值求角.5. 【2015-2016学年江省新余一中、万载中学、宜春中学联考数学试卷 理2】已知ABC ∆的内角A 满足322sin =A ,则=+A A cos sin ( ) 315.A 315.-B 35.C 35.-D【答案】A考点:倍角公式,正余弦和与积的关系.6. 【2015-2016学年江省新余一中、万载中学、宜春中学联考数学试卷 理10】已知8723cos -=⎪⎭⎫ ⎝⎛-x π,则⎪⎭⎫ ⎝⎛+3sin πx 的值为( )41.A 87.B 41.±C 87.±D 【答案】C 【解析】试题分析:27cos[(2)]cos(2)338x x πππ--=+=,所以有2171sin ()(1)32816x π+=-=,从而求得⎪⎭⎫ ⎝⎛+3sin πx 的值为14±,故选C.考点:诱导公式,倍角公式.7. 【临川一中2016届高三数学月考试卷 理5】将函数sin(4)6y x π=-图象上各点的横坐标伸长到原的2倍,再向左平移4π个单位,纵坐标不变,所得函数图象的一条对称轴的方程是( )A 12x π=B. 6x π=C 3x π=D 12x π=-【答案】A 【解析】试题分析:根据题意,变换以后的函数解析式为sin(2)3y x π=+,根据函数的性质,可知函数图象的一条对称轴的方程是12x π=,故选A.考点:函数图像的变换.8. 【临川一中2016届高三数学月考试卷 理6】函数xxy 24cos =的图象大致是( )【答案】A 【解析】试题分析:根据函数解析式可知函数是非奇非偶函数,所以图像不关于y 轴对称,所以C,D 不正确,当x 趋向于正无穷时,2x趋向于正无穷,而余弦函数是有界的,所以y 趋向于0,故B 不对,只能选A. 考点:函数图像的选取.9.【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 理7】已知角θ的顶点与原点重合,始边与x 轴非负半轴重合,终边在直线2y x =上,则sin 24πθ⎛⎫+⎪⎝⎭的值为( ) A. BC. D【答案】D考点:倍角公式,同角三角函数关系式,三角函数求值.A B CD10. 【临川一中2014—2015学年度下学期期末考试 理15】函数]4,0[,)4sin()3sin()(πππ∈++=x x x x f 的最大值为 .考点:三角函数的性质,函数的最值的求解.11. 【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 理14】计算2tan cos242cos +4πααπα⎛⎫- ⎪⎝⎭⎛⎫ ⎪⎝⎭=_______________.【答案】1 【解析】试题分析:原式1tan cos 21tan 1cos(2)2a αααπ-⋅+=++ 22(cos sin )(cos sin )1(cos sin )(cos sin )αααααααα-+==+-. 考点:三角函数化简与求值.12.【2015-2016学年江省新余一中、万载中学、宜春中学联考数学试卷 理20】已知(cos ,2cos ),(2cos ,sin )a x x b x x ==,()f x a b =⋅,(1)把()f x 的图像向右平移6π个单位得()x g 的图像,求()x g 的单调递增区间 (2)当a a ,0≠与b共线时,求()x f 的值【答案】(1)Z k k k ∈⎥⎦⎤⎢⎣⎡+-,247,245ππππ; (2)1017.考点:向量数量积坐标运算式,辅助角公式,函数的性质,同角三角函数关系式,三角式子求值问题.13. 【鹰潭市2014届高三第一次模拟考试数学试题 理16】(本小题满分12分) 在锐角△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,且32sin cA a =. (1) 确定角C 的大小;(2)若c =7,且△ABC 的面积为233,求a b +的值. 【答案】(1)3π=C ;(2)5a b +=.【解析】试题分析:第一问根据正弦定理,求得23sin =C ,结合三角形的形状,确定出角C 的大小,第二问根据题中所给的三角形的面积,确定出6ab =,再应用余弦定理,求得1322=+b a ,从而求得5a b +=.考点:正弦定理,三角形的面积,余弦定理.14.【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 理17】(本小题满分12分) 设函数24()cos(2)2cos .3f x x x π=-+, (Ⅰ)求)(x f 的最大值,并写出使)(x f 取最大值时x 的集合;(Ⅱ)已知ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,若3(),22f B C b c +=+=,1a =,求ABC ∆的面积的最大值.【答案】(Ⅰ)最大值为2 ,x 的集合为⎭⎬⎫⎩⎨⎧∈-=Z k k x x ,6ππ ;【解析】试题分析:第一问利用差角公式,倍角公式和辅助角公式化简函数解析式,根据函数的性质,求得结果,第二问根据题的条件求得21)32cos(=-πA ,结合三角形内角的取值范围,确定出.3π=A ,利用余弦定理,求得bc 的最大值,最后得出三角形面积的最大值. 试题解析:(Ⅰ)2444()cos(2)2cos (cos2cos sin 2sin )(1cos2)333f x x x x x x πππ=-+=+++1cos221cos(2)123x x x π=+=++ ··················································· 3分 所以)(x f 的最大值为2 ············································································· 4分 此时)(232,1)32cos(Z k k x x ∈=+=+πππ故x 的集合为⎭⎬⎫⎩⎨⎧∈-=Z k k x x ,6ππ 6分考点:差角公式,倍角公式,辅助角公式,三角函数的性质,余弦定理,三角形面积.15. 【湖北省武汉华中师范大学第一附属中学2015届高三5月适应性考试 理17】(本小题满分12分)已知函数()2cos (sin cos )()f x x x x m m R =-+∈,将()y f x =的图像向左平移4π个单位后得到()y g x =的图像,且()y g x =在区间[0,]4π.(1)求实数m 的值;(2)在ABC ∆中,内角A 、B 、C 的对边分别是a b c 、、,若3()14g B =,且2a c +=,求ABC ∆的周长l 的取值范围.【答案】(1)1;(2)[3,4). 【解析】试题分析:(1)首先把函数()f x 化为一个角的一个三角函数,())14f x x m π=--+,由图象变换得())14g x x m π=+-+,由04x π≤≤得32444x πππ≤+≤,这样利用正弦函数的性质得max ()1g x m =-=1m =.(2)由(1)及3()14g B =,得3B π=,由余弦定理得222222cos b a c ac B a c ac =+-=+-,再由基本不等式得22223()()3()14a cb ac ac a c +=+-≥+-=,即1b ≥(其中当且仅当a c =时等号成立),由三角形的性质又有2b a c <+=,因此得b 的范围.考点:(1)三角函数的恒等变换与图象变换,正弦函数的最值,余弦定理,基本不等式.【名师点睛】本题考查了三角函数的恒等变换与图象变换、三角函数的性质,余弦定理及基本不等式的应用,在正确理解题意的情况下,准确计算是关键.解答本题的一个易错点是忽视对角的范围的讨论,使解答陷入误区.本题是一道能力题,属于中等题,本题同时还考查考生的计算能力、思维的严密性.16.【河北定州中学2016届高三第一次月考 理17】(本小题满分10分)(原创)已知函数2()2sin sin()2f x x x x π=+⋅+(0>ω). (1)求)(x f 的最小正周期; (2)求函数)(x f 在区间]32,0[π上的取值范围.【答案】(1)π;(2)[0,3]. 【解析】试题分析:本题主要考查倍角公式、诱导公式、两角和与差的正弦公式、三角函数的周期和最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先用降幂公式和诱导公式变形,再用倍角公式化简,最后用两角差的正弦公式化简表达式,使之成为()sin()f x A x B ωϕ=++的形式,利用2||T πω=计算周期;第二问,结合第一问的结论,将2[0,]3x π∈代入表达式,结合sin y x =的图象,求出函数的最大值和最小值.考点:倍角公式、诱导公式、两角和与差的正弦公式、三角函数的周期和最值.二.能力题组1.【鹰潭市2014届高三第一次模拟考试数学试题 理5】函数)sin()(ϕω+=x A x f (其中A >0,|ϕ|<)的图象如图所示,为得 x x g 3sin )(=的图象,则只要将)(x f 的图象( )A .向右平移个单位长度B .向右平移个单位长度C .向左平移个单位长度D .向左平移个单位长度【答案】B考点:函数图像的变换.2. 【唐山一中2014—2015学年度第二学期期末考试高二年级 理7】已知函数()()ϕ-=x x f sin ,且()0320=⎰dx x f π,则函数()x f 的图象的一条对称轴是 ( )A .65π=x B .127π=x C .3π=x D .6π=x 【答案】A 【解析】试题分析:根据定积分的几何意义,知()x f 关于⎪⎭⎫⎝⎛03,π对称,所以3πϕ=,那么对称轴是πππk x +=-23,即ππk x +=65,Z k ∈,当0=x 时,π65=x . 考点:1.定积分的几何意义;2.三角函数的性质.3.【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 理8】将函数()()sin 22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象向左平移6π个单位长度后,所得函数()g x 的图象关于原点对称,则函数()f x 在0,2π⎡⎤⎢⎥⎣⎦的最小值为( )A .12-B .12C . D【答案】C考点:函数图像的变换,函数在给定区间上的最值.4.【2013~2016届襄阳五中 宜昌一中 龙泉中学高三年级九月联考 理11】已知函数()cos f x x =,,,a b c 分别为ABC ∆的内角,,A B C 所对的边,且222334a b c ab +-=,则下列不等式一定成立的是( ) A .()()sin cos f A f B ≤ B .()()sin sin f A f B ≤ C .()()cos sin f A f B ≤ D .()()cos cos f A f B ≤ 【答案】C 【解析】试题分析:根据题意有222223342cos a b ab c a b ab C +-==+-,整理得2()cos a b ab C -=-,从而有cos 0C ≤,所以2A B π+≤,有2A B π≤-,所以sin sin()cos 2A B B π≤-=,cos sin A B ≥,又因为函数()cos f x x =在[0,]π上是减函数,故有()()cos sin f A f B ≤,所以选C.考点:余弦定理,三角函数的单调性.5.【河北定州中学2016届高三第一次月考 理6】已知函数()sin cos f x x x =+,且'()3()f x f x =,则x 2tan 的值是( ) A.34-B.34C.43-D.43【答案】A考点:导数的运算、倍角公式.6.【河北定州中学2016届高三第一次月考 理11】函数())(,0,||f x x x ωϕωϕ=+∈><R π)2的部分图象如图所示,则()f x 的单调递减区间为( )A .511[,],1212k k k z ππππ++∈ B . 511[],66k x k k z ππππ+≤≤+∈ C . 511[2,2],1212k k k z ππππ++∈ D . 5[,],1212k k k z ππππ-++∈【答案】A 【解析】试题分析:由图知()f x在5π12x =T 满足35ππ+.4123T =, 故A =,,2T πω==,5)12πθ⨯+=5+=62ππθ,即=3πθ-,所以())3f x x π=-,令3222232k x k πππππ+≤-≤+得511,1212k x k k z ππππ+≤≤+∈。
专题04 三角函数与三角形(第01期)-决胜2016年高考全国名校试题理数分项汇编(新课标Ⅱ特刊)(原卷版)

第四章 三角函数与三角形一.基础题组1. 【辽宁省大连市2015年高三第一次模拟考试数学理4】已知ABC ∆中,内角A ,B ,C 的对边分别为,,a b c ,若222a b c bc =+-,4bc =,则ABC ∆的面积为( )(A )12(B )1 (C (D )2 2.【双鸭山市第一中学2015届高三第四次模拟理4】已知2)tan(-=-απ,则=+αα2cos 2cos 1( )A .-3 B.52C .3 D. 25-3.【云南省2015届高三第一次复习统测数学理4】下列函数,有最小正周期的是( ) A.sin ||y x = B.cos ||y x = C.tan ||y x = D.2(1)y x =+ 4.【黑龙江哈尔滨第九中学2015届高三第三次高考模拟理3】=-︒︒170sin 110cos 3A. 2- B . 2 C .4 D . 4-5.【长春市普通高中2015届高三质量监测(三)数学理4】已知ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,若222a b c bc =+-,4bc =,则ABC ∆的面积为( )A. 12B. 1C.D. 26.【辽宁省朝阳市三校协作体2015届高三下学期第一次联合模拟考试数学理3】 在ABC ∆中,3=AB ,1=AC , 30=∠B ,且ABC ∆的面积为23,则=∠C ( ) A . 30 B . 45 C . 60D . 757.【辽宁省朝阳市三校协作体2015届高三下学期第一次联合模拟考试数学理6】 将函数()()ϕ+=x x f 2sin 的图象向左平移8π个单位,所得到的函数图象关于y 轴对称,则ϕ的一个可能取值为( )A .43π B .4πC .0D .4π- 8.【吉林市第一中学校2015届高三3月“教与学”质量检测(一)理4】两座灯塔A 和B 与海洋观察站C 的距离都等于akm ,灯塔A 在观察站C 的北偏东020,灯塔B 在观察站C 的南偏东040,则灯塔A 与灯塔B 的距离为 A .akmB.akm 2C .akm 2D.akm 39.【宜昌一中2015年高考适应性考试(一)理4】函数2cos ()2y x π=+的单调递增区间( )A .(,)2k k k Z πππ+∈ B. (,)2k k k Z ππππ++∈C. (2,2)k k k Z πππ+∈D. (2,22)k k k Z πππ+∈10.【甘肃省天水市第一中学2015届高三高考信息卷(二)理4】函数)sin()(ϕω+=x x f (其中2||πϕ<)的图象如图所示,为了得到sin y x ω=的图象,只需把()y f x =的图象上所有点( )(A )向左平移6π个单位长度 (B )向右平移12π个单位长度 (C )向右平移6π个单位长度 (D )向左平移12π个单位长度11.(东北育才学校高中部2014-2015学年度高三第八次模拟考试理9)下列对于函数()3cos 2,(0,3)f x x x π=+∈ 的判断正确的是 ( )A.函数()f x 的周期为πB.对于,a R ∀∈ 函数()f x a + 都不可能为偶函数C.0(0,3)x π∃∈ ,使0()4f x =D.函数()f x 在区间5[,]24ππ内单调递增12. 【黑龙江省哈尔滨市第六中学2015届高三下学期第四次模拟理8】将函数sin(2)6y x π=+的图象向右平移6π个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是 ( ).A sin 4y x = .B sin y x = .C sin(4)6y x π=- .D sin()6y x π=-13.【甘肃省天水市第一中学2015届高三5月中旬仿真考试数学理6】一个大风车的半径为8m ,12min 旋转一周,它的最低点0p 离地面2m ,风车翼片的一个端点P 从P o 开始按逆时针方向旋转,则点P 离地面距离 h(m)与时间t(min)之间的函数关系式是( ) A .106sin 8)(+-=t t h πB .106cos 8)(+-=t t h πC .86sin8)(+-=t t h πD .86cos8)(+-=t t h π14.【辽宁省锦州市2015届高三质量检测(二)数学理9】△ABC 各角的对应边分别为a , b , c , 满足1b c a c a b+≥++, 则角A 的范围是 (A )(0,]6π(B )(0,]3π(C )[,)3ππ (D )[,)6ππ15.【2015年辽师大附中高三年级模拟考试理8】ABC ∆中,角C B A ,,所对的边长分别为c b a ,,,b A Bc C B a 21cos sin cos sin =+,且b a > ,则B ∠= ( ) A. 6π B. 3π C.32π D.65π16.【黑龙江省大庆第一中学2014届高三下学期第二次阶段考试理7】函数f (x )=sin ωx +a cos ωx (ω>0)的图象关于M (3π,0)对称,且在x =6π处函数有最小值,则a +ω的一个可能取值是( )A .0B .3C .6D .917.【贵州省八校联盟2015届高三第二次联考数学理13】已知==+απα2sin ,54)4cos(则 .18.【辽宁省大连市2015年高三第一次模拟考试数学理13】函数1sin 2y x x =+([0,]2x π∈)的单调递增区间是__________.19.【宜昌一中2015年高考适应性考试(一)理11】已知2sin cos 3αα+=,则21tan 2sin sin 2ααα+=+ . 20.【天水一中2015届高考第五次模拟考试理15】若41)3cos(=-απ,则=+)23cos(απ___________.21.【长春市普通高中2015届高三质量监测(三)数学理13】函数1sin 2y x x =+([0,]2x π∈)的单调递增区间是__________.22.【甘肃省河西五市2015年高三5月第二次联考数学理14】设0α=⎰,tan 3β=,则()tan αβ+= .23.【甘肃省天水市第一中学2015届高三高考信息卷(二)理14】如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从M 点测得A 点的俯角30NMA ︒∠=,C 点的仰角45CAB ∠=︒以及75MAC ∠=︒;从C 点测得60MCA ∠=︒已知山高200BC m =,则山高MN = m .24.【黑龙江省大庆第一中学2014届高三下学期第二次阶段考试理14】已知,71tan ,31tan -==βα且,2,20πβππα<<<<则βα-2的值_________二.能力题组1. 【云南省2015届高三第一次复习统测数学理6】已知平面向量22(2cos ,sin )a x x =,22(cos ,2sin )b x x =-,()f x a b =⋅,要得到sin 22y x x =+的图象,只需要将()y f x =的图象( ) A.向左平行移动6π个单位 B.向右平行移动6π个单位 C.向左平行移动12π个单位 D.向右平行移动12π个单位2.【2014—2015学年度第二学期高三年级数学理8】函数cos 26(2)y x π=+- 的图象F 按向量a 平移到F F '', 的函数解析式为()y f x =,当()y f x =为奇函数时,向量a 可以等于( )A .(-6π,-2) B .(-6π,2) C .(6π,-2) D .(6π,2)3.【甘肃省河西五市2015年高三5月第二次联考数学理9】在ABC ∆中,A B C 、、的对边分别为a b c 、、,且cos 3cos cos b C a B c B =-,2BA BC ⋅=,则ABC ∆的面积为 ( ) A .2 B .23C . 22D . 24 4.【双鸭山市第一中学2015届高三第四次模拟理10】在ABC ∆中,角A 、B 、C 的对边分别是c b a ,,.若223sin 2sin ,2B C a b bc =-=,则角A 等于( )A .6π B .3π C .32π D .65π 5.【天水一中2015届高考模拟信息卷理10】在ABC ∆中,三内角A ,B ,C 的对边分别为a ,b ,c 且222a b c bc =++,a ,S 为ABC ∆的面积,则cos S B C 的最大值为( )(A ) 1 (B )1+ (C (D )36.【云南省2015届高三第一次复习统测数学理7】已知ABC ∆的内角A ,B ,C 对的边分别为a ,b ,c ,sin 2sin A B C =,3b =,当内角C 最大时,ABC ∆的面积等于( )7.【吉林市第一中学校2015届高三3月“教与学”质量检测(一)理9】已知函数()()ϕ+=x sin x f 2错误!未找到引用源。
【备战2016】(陕西版)高考数学分项汇编 专题04 三角函数与三角形(含解析)理科

专题04 三角函数与三角形一.基础题组1. 【2006高考陕西版理第13题】cos43°cos77°+sin43°cos167°的值为 【答案】-21考点:两角和与差的三角函数,容易题. 2. 【2007高考陕西版理第4题】已知sin α=55,则si n 4α-cos 4α的值为 (A )-51 (B)-53 (C)51 (D) 53 【答案】B【解析】sin 4α-cos 4α213cos 22sin 12155αα=-=-=⨯-=-,选B 。
考点:同角的三角函数关系式,容易题.3. 【2008高考陕西版理第3题】ABC △的内角A B C ,,的对边分别为a b c ,,,若120c b B ==,则a 等于( )A B .2CD【答案】D考点:正弦定理,容易题.4.【2009高考陕西版理第5题】若3sin cos 0αα+=,则21cos sin 2αα+的值为( ) A .103 B .53 C .23D .2- 【答案】A5. 【2010高考陕西版理第3题】对于函数()2sin cos f x x x =,下列选项中正确的是 ( )(A )()f x f (x )在(4π,2π)上是递增的 (B )()f x 的图像关于原点对称 (C )()f x 的最小正周期为2π (D )()f x 的最大值为2 【答案】B考点:三角函数的性质,容易题.6. 【2012高考陕西版理第9题】在ABC ∆中角A 、B 、C 所对边长分别为,,a b c ,若2222a b c +=,则c o s C的最小值为( )A .2B .2C .12D .12-【答案】C考点:余弦定理,容易题.7. 【2014高考陕西版理第2题】函数()cos(2)6f x x π=-的最小正周期是( ).2A π.B π .2C π .4D π【答案】B 【解析】试题分析:由周期公式2T w π=,又2w =,所以函数()cos(2)6f x x π=-的周期22T ππ==,故选B . 考点:三角函数的最小正周期.8. .【2015高考陕西,理3】如图,某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++,据此函数可知,这段时间水深(单位:m )的最大值为( )A .5B .6C .8D .10【答案】C【考点定位】三角函数的图象与性质.9. 【2015高考陕西,理17】(本小题满分12分)C ∆AB 的内角A ,B ,C 所对的边分别为a ,b ,c .向量(),3m a b =与()cos ,sin n =A B 平行. (I )求A ;(II )若a =2b =求C ∆AB 的面积.【答案】(I )3π;(II )2.考点:1、平行向量的坐标运算;2、正弦定理;3、余弦定理;4、三角形的面积公式. 二.能力题组1. 【2006高考陕西版理第17题】已知函数f (x )=3sin(2x -π6)+2sin 2(x -π12) (x ∈R )(Ⅰ)求函数f (x )的最小正周期 ; (2)求使函数f (x )取得最大值的x 的集合. 【答案】(Ⅰ) T =π(Ⅱ) x 的集合为{x ∈R |x = k π+ 5π12 , (k ∈Z)}.【解析】试题分析:(Ⅰ) f (x )=3sin(2x -π6)+1-cos2(x -π12)= 2[32sin2(x -π12)-12 cos2(x -π12)]+1 =2sin[2(x -π12)-π6]+1考点:三角函数的性质.2. 【2007高考陕西版理第17题】设函数f (x )=a -b ,其中向量a =(m,cos2x ),b =(1+sin2x ,1),x ∈R ,且函数y=f (x )的图象经过点⎪⎭⎫⎝⎛2,4π,(Ⅰ)求实数m 的值;(Ⅱ)求函数f (x )的最小值及此时x 的值的集合.【答案】(Ⅰ)1m =;(Ⅱ)()f x 的最小值为1,x 值的集合为3ππ8x x k k ⎧⎫=-∈⎨⎬⎩⎭Z ,.考点:三角函数的性质.3. 【2008高考陕西版理第17题】已知函数()2sin cos 442x x xf x =. (Ⅰ)求函数()f x 的最小正周期及最值; (Ⅱ)令π()3g x f x ⎛⎫=+⎪⎝⎭,判断函数()g x 的奇偶性,并说明理由. 【答案】(Ⅰ)()f x 的最小正周期4πT =.()f x 取得最小值2-;()f x 取得最大值2. (Ⅱ)函数()g x 是偶函数.考点:三角函数的性质.4. 【2009高考陕西版理第17题】已知函数()sin()f x A x ωϕ=+,x ∈R (其中0A >,0ω>,02πϕ<<)的图象与x 轴的交点中,相邻两个交点之间的距离为2π,且图象上一个最低点为2(,2)3M π-.(Ⅰ)求()f x 的解析式; (Ⅱ)当[,]122x ππ∈时,求()f x 的值域.5. 【2010高考陕西版理第17题】如图,A,B是海面上位于东西方向相聚5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°且与B点相距海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?【答案】1.考点:解三角形.6. 【2011高考陕西版理第18题】叙述并证明余弦定理。
专题04 三角函数与解三角形学霸必刷100题(解析版)

三角函数与解三角形学霸必刷100题1.已知函数()sin()(>0)6f x x πωω=+在区间52[,]63ππ-上单调递增,且存在唯一05[0,]6x π∈使得0()1f x =,则ω的取值范围为( )A .11[,]52B .21[,]52C .14[,]55D .24[,]55【答案】B【解析】函数()sin()(>0)6f x x πωω=+在区间52[,]63ππ-上单调递增, 所以52[,][2,2],663622k k k Z ππππππωωππ-++⊆-++∈, 得:22362526620,k k k Z πππωππππωπω⎧+≤+⎪⎪⎪-+≤-+⎨⎪>∈⎪⎪⎩,即13241250,k k k Z ωωω⎧≤+⎪⎪⎪≤-⎨⎪>∈⎪⎪⎩经检验仅有0k =时有:102ω<≤.5[0,]6x π∈时,5[,]6666x ππππωω+∈+, 由题意得:552662ππππω≤+<,解得:21455ω≤<. 综上:2152ω≤≤.故选:B.2.已知函数()sin f x a x x =-的一条对称轴为π6x =-,12()()0f x f x +=,且函数()f x 在12(,)x x 上具有单调性,则12||x x +的最小值为 A .2π3B .π3C .π6D .4π3【答案】A【解析】由题,()sin f x a x x =-)x θ+,θ为辅助角, 因为对称轴为π6x =-,所以1()362f a π-=--即132a --=解得2a =所以()4sin()3f x x π=-又因为()f x 在()12,x x 上具有单调性,且()()120f x f x +=, 所以12,x x 两点必须关于正弦函数的对称中心对称, 即12122333()22x x x x k k z ππππ-+-+-==∈所以1222()3x x k k z ππ+=+∈ 当0k =时,12x x +取最小为2π3故选A3.在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,ABC ∆的面积为S ,若222sin()SA C b c+=-,则1tan 2tan()C B C +-的最小值为( )AB .2C .1D.【答案】A【解析】因为222sin()SA C b c +=-,即222sin S B b c=-, 所以22sin sin ac BB b c =-,因为sin 0B ≠,所以22b c ac =+,由余弦定理2222cos b a c ac B =+-, 可得2cos a c B c -=,再由正弦定理得sin 2sin cos sin A C B C -=,因为sin 2sin cos sin()2sin cos sin()A C B B C C B B C -=+-=-, 所以sin()sin B C C -=,所以B C C -=或B C C π-+=, 得2B C =或B π=(舍去).因为ABC ∆是锐角三角形,所以02022032C C C ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩,得64C ππ<<,即tan C ∈,所以11tan tan 22tan()2tan C C B C C+=+≥-,当且仅当2tan 2C =,取等号.故选:A 4.边长为2的等边ABC ∆和有一内角为30的直角1ABC ∆所在半平面构成60︒的二面角,则下列不可能是线段1CC 的取值的是( ) A .30 B .10C .102D .103【答案】D【解析】(1) 当1130,90C AB C BA ∠=∠=时,空间位置关系如下图所示:过C 作CE AB ∥,且EB AB ⊥则1C BE ∠即为二面角1C AB C --的平面角 所以160C BE ∠= 由题意可知132333C B AB ==,332BE BC ==在1C BE ∆中,由余弦定理可知22211112cos C E C B BE C B BE C BE =+-⨯∠ 代入可得2142373236033C E =+-= 而190C EC ∠=所以2211730133C C C E CE =+=+=(2)当1130,90AC B C BA ∠=∠=时,空间位置关系如下图所示:过C 作CF AB ∥,且FB AB ⊥则1C BF ∠即为二面角1C AB C --的平面角 所以160C BF ∠=由题意可知1323C B AB ==,33BF BC == 在1C BF ∆中,由余弦定理可知22211112cos C F C B BF C B BF C BF =+-⨯∠ 代入可得211232233cos609C F =+-⨯⨯= 而190C FC ∠=所以22119110C C C F CF =+=+=(3) 当1130,90C AB AC B ∠=∠=时,空间位置关系如下图所示:过1C 作1C G AB ⊥交AB 于G .过C 作CH AB ∥,且GH AB ⊥ 则1C GH ∠即为二面角1C AB C --的平面角 所以160C GH ∠= 由题意可知111,2C B AB ==1133C G B ==,33GH BC ==1142CH AB ==在1C GH ∆中,由余弦定理可知22211112cos C H C G GH C G GH C GH =+-⨯∠代入可得21393260424C H =+-⨯=所以12C C===综上可知,线段1CC的取值为3和2,在四个选项中,不能取的值为3故选:D5.函数()()()2sin 0,0fx x ωϕωϕπ=+><<,8f π⎛⎫= ⎪⎝⎭02f ⎛⎫= ⎪⎝⎭π,且()f x 在()0,π上单调,则下列说法正确的是() A .12ω=B .82f π⎛⎫-= ⎪⎝⎭C .函数()f x 在,2ππ⎡⎤--⎢⎥⎣⎦上单调递增D .函数()y f x =的图象关于点3,04π⎛⎫⎪⎝⎭对称 【答案】C【解析】由题意得函数()f x 的最小正周期为2T πω=,∵()f x 在()0,π上单调,∴2T ππω=≥,解得01ω<≤. ∵8f π⎛⎫=⎪⎝⎭02f π⎛⎫= ⎪⎝⎭, ∴3842ωππϕωπϕπ⎧+=⎪⎪⎨⎪+=⎪⎩,解得2323ωπϕ⎧=⎪⎪⎨⎪=⎪⎩,∴22()2sin 33f x x π⎛⎫=+ ⎪⎝⎭.对于选项A ,显然不正确.对于选项B ,227()2sin 2sin 838312f ππππ⎛⎫-=-⨯+== ⎪⎝⎭,故B 不正确.对于选项C ,当2x ππ-≤≤-时,220333x ππ≤+≤,所以函数()f x 单调递增,故C 正确. 对于选项D ,32327()2sin 2sin 043436f ππππ⎛⎫=⨯+=≠ ⎪⎝⎭,所以点3,04π⎛⎫⎪⎝⎭不是函数()f x 图象的对称中心,故D 不正确.综上选C . 6.已知函数 f (x ) = 1sin()+062x πωω-(),且 11(),()22f f αβ=-=.若 α − β 的最小值为34π,则函数的单调递增区间为( ) A .2,2,2k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B .3,3,2k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦ C .52,2,2k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D .53,3,2k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【答案】B【解析】解:函数1()sin()(0)62f x x πωω=-+>,且()12f α=-,1()2f β=,11()sin()622f παωα∴=-+=-,可得1262k ππωαπ-=-,1k Z ∈,解得:123k ππαω-=,1k Z ∈;11()sin()622f πβωβ=-+=,可得26k πωβπ-=,2k Z ∈,解得:26k ππβω+=,2k Z ∈;||αβ-的最小值为34π, 12122132|||||2|24k k k k πππππαβωω--∴-==--,1k Z ∈,2k Z ∈,可解得:1241|2|32k k ω--,1k Z ∈,2k Z ∈, 取11k =.22k =,可得23ω=; 21()sin()362f x x π∴=-+,由2222362k x k πππππ--+,k Z ∈, 解得332k x k ππππ-+,k Z ∈;∴函数()f x 的单调递增区间为:[32k ππ-,3]k ππ+,k Z ∈.故选:B .7.如图,ABC 中,ACB ∠为钝角,10AC =,6BC =,过点B 向ACB ∠的角平分线引垂线交于点P ,若62AP =,则ABP △的面积为( )A .4B .2C .6D .43【答案】B【解析】设,CP x ACP BCP θ=∠=∠=,则在三角形BCP 中,cos 6CP xBC θ== 在三角形ACP 中,由余弦定理可知2222cos AP CP CA CP CA θ=+-⨯ 代入可得(22262102106xx x =+-⨯⨯化简可得212x =,解得23x =所以3cos 63x θ==,则236sin 13θ⎛⎫=-= ⎪ ⎪⎝⎭由二倍角公式可得3622sin sin 223ACB θ∠===由三角形面积公式可得1122sin 210620222ACB S CA CB θ∆=⨯⨯⨯=⨯⨯=116sin 102310222ACP S CA CP θ∆=⨯⨯⨯=⨯⨯=116sin 62362223BCP S CB CP θ∆=⨯⨯⨯=⨯⨯=则2021026242ABP ABC ACP BCP S S S S ∆∆∆∆=--==故选:B8.某港口某天0时至24时的水深y (米)随时间x (时)变化曲线近似满足如下函数模型0.5sin 3.246y x πωπ⎛⎫=++ ⎪⎝⎭(0>ω).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( ) A .16时 B .17时C .18时D .19时【答案】D【解析】解:由题意可知,0x =时,0.5sin 0 3.24 3.496y πωπ⎛⎫=⨯++= ⎪⎝⎭,由五点法作图可知:如果当16x =时,函数取得最小值可得:51662ππωπ+=,可得748ω=, 此时函数70.5sin 3.24486y x ππ⎛⎫=++ ⎪⎝⎭,函数的周期为:296147748T ππ==≈, 该港口在该天0时至24时内,有且只有3个时刻水深为3米,满足,如果当19x =时,函数取得最小值可得:51962ππωπ+=,可得757ω=,此时函数70.5sin 3.24576y x ππ⎛⎫=++ ⎪⎝⎭,函数的周期为:21147757T ππ==, 24x =时,70.5sin 24 3.243576y ππ⎛⎫=⨯++> ⎪⎝⎭,如图:该港口在该天0时至24时内,有且只有3个时刻水深为3米,不满足, 故选:D .9.如图,矩形ABCD 中,1AB =,3BC =,F 是线段BC 上一点且满足1BF =,E 是线段FC 上一动点,把ABE △沿AE 折起得到1AB E △,使得平面1⊥B AC 平面ADC ,分别记1B A ,1B E 与平面ADC 所成角为α,β,平面1B AE 与平面ADC 所成锐角为θ,则:( )⇒A .θαβ>>B .θβα>>C .αθβ>>D .βθα>>【答案】A 【解析】如图,过B 作BO AC ⊥,在Rt ABC 中,由13AB BC ==,,可得2AC =.由等积法可得3BO =,则12AO =平面1⊥B AC 平面ADC ,且1B O AC ⊥,可得1B O ⊥平面ABCD∴ 11tan 3B OB AO AOαα∠==,=. 画出底面ABCD 平面图:在BOF ,由余弦定理可得:2222cos OF OB BF OB BF OBF =+-⋅⋅∠22233121cos 60OF ︒=+-⋅⎝⎭ ∴ 2723OF -=214OA=,故OF OA>,结合图像可知:OE OF>∴OE OF OA>>,可得:OE OA>11tanB OB EOEOββ∠==,,1tanB OAOα=∴可得tan tanαβ>┄①过O作OG AE⊥,垂足为G,连接1B G,则1∠B GO为平面1B AE与平面ADC所成的锐角θ.O到AB的距离14BC=,由底面图像可知:144BO CG=<∴1tan2B OOGθ=>=,即tan tanθα>┄②由①②可得: tan tan tanθαβ>>,,θαβ都是锐角,根据正切函数单调性可知: θαβ>>故选:A.10.已知A是函数()sin2018cos201863f x x xππ⎛⎫⎛⎫=++-⎪ ⎪⎝⎭⎝⎭的最大值,若存在实数12,x x使得对任意实数x 总有12()()()f x f x f x≤≤成立,则12||A x x⋅-的最小值为A.π2018B.π1009C.2π1009D.π4036【答案】B【解析】()2018cos201863f x sin x xππ⎛⎫⎛⎫=++-⎪ ⎪⎝⎭⎝⎭112014cos2018cos2018201822x x x x=++2018cos2018x x=+220186sin xπ⎛⎫=+⎪⎝⎭,()max 2A f x ∴==,周期220181009T ππ==, 又存在实数12,x x ,对任意实数x 总有()()()12f x f x f x ≤≤成立,()()()()21max min 2,2f x f x f x f x ∴====-,12A x x ⋅-的最小值为121009A T π⨯=,故选B.11.如图,已知函数()sin()(0,||)2f x x πωϕωϕ=+><的图象与坐标轴交于点1,,(,0)2-A B C ,直线BC交()f x 的图象于另一点D ,O 是ABD ∆的重心.则ACD ∆的外接圆的半径为A .2B 57C 57D .8【答案】B【解析】∵O 是ABD ∆的重心,1,02C ⎛⎫-⎪⎝⎭, ∴21OA OC ==,∴点A 的坐标为()1,0, ∴函数()f x 的最小正周期为3T 232=⨯=,∴23πω=,∴()2sin 3f x x πϕ⎛⎫=+⎪⎝⎭. 由题意得121sin sin 02323f ππϕϕ⎡⎤⎛⎫⎛⎫⎛⎫-=⨯-+=-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 又2πϕ<,∴3πϕ=,∴()2sin 33f x x ππ⎛⎫=+ ⎪⎝⎭,令0x =得()30sin 32f π==, ∴点B 的坐标为30,2⎛ ⎝⎭,∴tan 3BCO ∠=3BCO π∠=,∴23ACD π∠=. 又点1,02C ⎛⎫-⎪⎝⎭是BD 的中点,∴点D 的坐标为31,⎛- ⎝⎭,∴AD ==. 设ACD ∆的外接圆的半径为R,则222sin sin 3AD R ACD π∠===,∴R =.故选B . 12.关于函数()cos sin f x x x =+有下述四个结论: ①()f x 是偶函数;②()f x 的最大值为2; ③()f x 在[],ππ-有3个零点;④()f x 在区间0,4π⎛⎫⎪⎝⎭单调递增. 其中所有正确结论的编号是( ) A .①② B .①③C .②④D .①④【答案】D【解析】对于命题①,函数()y f x =的定义域为R ,关于原点对称,且()()cos sin f x x x -=-+-()cos sin cos sin x x x x f x =+-=+=,该函数的为偶函数,命题①正确;对于命题②,当函数()y f x =取最大值时,cos 0x ≥,则()2222k x k k Z ππππ-≤≤+∈.当()222k x k k Z πππ-≤≤∈时,()cos sin 4x x x f x π⎛⎫=-=+ ⎪⎝⎭,此时,()22444k x k k Z πππππ-≤+≤+∈,当()24x k k Z ππ+=∈,函数()y f x =.当()222k x k k Z πππ<≤+∈时,()cos sin 4f x x x x π⎛⎫=+=+ ⎪⎝⎭,此时,()32244k x k k Z ππππ+<≤+∈,当()242x k k Z πππ+=+∈,函数()y f x =. 所以,函数()y f x =,命题②错误;对于命题③,当0x π-≤≤时,令()cos sin 0f x x x =-=,则tan 1x =,此时34x π=-; 当0x π<≤时,令()cos sin 0f x x x =+=,则tan 1x =-,此时34x π=.所以,函数()y f x =在区间[],ππ-上有且只有两个零点,命题③错误;对于命题④,当04x π<<时,()cos sin 4f x x x x π⎛⎫=+=+ ⎪⎝⎭,则442x πππ<+<.所以,函数()y f x =在区间0,4π⎛⎫⎪⎝⎭上单调递增,命题④错误.因此,正确的命题序号为①④.故选D.13.已知函数()()π2sin 0,2f x x ωϕωϕ⎛⎫=+><⎪⎝⎭的一条对称轴为3x π=,一个对称中心为5,06π⎛⎫⎪⎝⎭,且在3,25ππ⎛⎫⎪⎝⎭上单调,则ω的最大值( ) A .5B .6C .7D .8【答案】C【解析】由于函数()()()2sin 0f x x ωϕω=+>的一条对称轴为3x π=,一个对称中心为5,06π⎛⎫⎪⎝⎭,所以12πππ325ππ6k k ωϕωϕ⎧+=+⎪⎪⎨⎪+=⎪⎩,两式相减并化简得()2121k k ω=--为奇数,排除B,D 选项.由于()f x 在3,25ππ⎛⎫ ⎪⎝⎭上单调,所以π3πππ25210T ω=≥-=,所以10ω≤.当9ω=时,由1πππ32k ωϕ+=+得()115ππ2k k Z ϕ=-∈,由于π2ϕ<,故9ω=时不合题意. 当7ω=时,由1πππ32k ωϕ+=+得()1111ππ6k k Z ϕ=-∈,由于π2ϕ<,所以取12k =,π6ϕ=,此时()π2sin 76f x x ⎛⎫=+ ⎪⎝⎭.由272262k x k πππππ-≤+≤+,解得222721721k k x ππππ-≤≤+,令2k =得1013,2121x ππ⎡⎤∈⎢⎥⎣⎦为()f x 的递增区间,满足31013,,252121ππππ⎛⎫⎡⎤⊆ ⎪⎢⎥⎝⎭⎣⎦.所以ω的最大值为7.故选:C. 14.已知长方形的四个顶点是()0,0A ,()2,0B ,()2,1C ,()0,1D ,一质点从AB 的中点0P 沿与AB 夹角为θ的方向射到BC 上的1P 后,依次反射到CD ,DA 和AB 上的2P ,3P ,和4P (入射角等于反射角).设4P 的坐标是(),0x ,若12x <<,则tan θ的取值范围是( )A .13,55⎛⎫⎪⎝⎭B .11,52⎛⎫ ⎪⎝⎭C .21,52⎛⎫⎪⎝⎭D .13,25⎛⎫⎪⎝⎭【答案】C【解析】设1PB a =,10PP B θ∠=,则11CP a =-,123243PP C P P D AP P θ∠=∠=∠= 所以10tan PB a P B θ==,又1221tan CP a a CP CP θ-===,所以2111a CP a a-==-; 而32tan P D P D θ=312(1)P D a =--a = 所以31(3)31P D a a a=-=-;又34tan AP AP θ=41(31)a AP --=a = 所以423AP a =-,根据题设412AP <<,即2132a <-< 所以2512a <<,即21tan 52θ<<,故选:C15.在ΔABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,b =c ,且满足sin 1cos sin cos B BA A-=.若点O 是ΔABC 外一点,∠AOB =θ(0θπ<<),OA =2,OB =4,则平面四边形OACB 面积的最大值( ) A.2+B.4+C.6+D.8+【答案】D 【解析】 因为sin 1cos sin cos B BA A-=,可得()sin sin cos cos sin sin sin A B A B A A B C =+=+=,所以a c =又b c =,所以ΔABC 为等边三角形.在OAB 中,22224224cos 2016cos AB θθ=+-⨯⨯⨯=- ,)213sin 602016cos 24ABCSAB θθ==-=.124sin4sin 2OABSθθ=⨯⨯=, 所以4sin 8sin 3OACB ABCOABS SSπθθθ⎛⎫=+=+=- ⎪⎝⎭,因为0θπ<<,所以当56πθ=时,平面四边形OACB面积的最大,最大值为8+. 故选:D .16.已知ABC 的三边a ,b ,c 满足:333a b c +=,则此三角形是( ) A .锐角三角形 B .钝角三角形C .直角三角形D .等腰直角三角形【答案】A【解析】333a b c +=可知,∠C 为三角形ABC 中的最大角,且331a b c c ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,所以01a c <<,01b c << 亦即32a a c c ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭<,32b bc c ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭<将两式相加得:22331a b a b c c c c ⎛⎫⎛⎫⎛⎫⎛⎫+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭+> 所以∠C 为锐角,三角形ABC 为锐角三角形,故选:A17.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,设△ABC 的面积为S,若222c a b S --=b a 的取值范围为( ) A .(0,+∞) B .(1,+∞)C.(0D.)+∞【答案】A【解析】由2223c a b S --=,得2221sin 32a b c ab C +-=- ,所以2222a b c C ab +-=,所以cos 3C C =-,所以tan C =又0C π<<,所以23C π=, 所以sin()sin cos cos sin )sin 333sin sin sin A A A b B a A A A πππ--===1sin 122sin 2tan 2A AA A -==-, 因为03A π<<,所以0tan A <<所以13tan A >,所以33102b a >⨯-=,所以b a 的取值范围为(0,)+∞.故选:A18.已知腰长为2的等腰直角ΔABC 中,M 为斜边AB 的中点,点P 为该平面内一动点,若2PC =,则()()4PA PB PC PM ⋅+⋅⋅的最小值为( )A .24162-B .24162+C .48322-D .48322+【答案】C【解析】以,CA CB 为,x y 轴建立平面直角坐标系,则(0,0),(2,0),(0,2),(1,1)C A B M ,设(,)P x y ,则(2,),(,2)PA x y PB x y =--=--,(,),(1,1)PC x y PM x y =--=--,(2)(2)PA PB x x y y ⋅=----2222x x y y =-+-,PC PM ⋅=22(1)(1)x x y y x x y y ----=-+-,∵2PC =,∴224x y +=,设2cos ,2sin x y θθ==,则2cos 2sin 22)4x y πθθθ+=+=+,∴2222x y -+≤()()4PA PB PC PM ⋅+⋅⋅2(4224)(4)2(4)x y x y x y =--+--=+-,∴22x y +=()()4PA PB PC PM ⋅+⋅⋅取得最小值22(224)482=-故选:C 。
专题03 三角函数与解三角形(第02期)-决胜2016年高考全国名校试题文数分项汇编(浙江特刊)(解析版)

一.基础题组1.【浙江省临海市台州中学2016届高三上学期第三次统练数学(文)试题】定义行列式运算1234a a a a =3241a a a a -.将函数sin 2()cos 2x f x x=6π个单位,以下是所得函数图象的一个对称中心是 ( ) A .(,0)4πB .(,0)2πC .(,0)3πD .(,0)12π【答案】B考点:1.正弦函数的对称性;2.函数()sin y A x ωϕ=+的图象变换.2.【浙江省绍兴市第一中学2016届高三上学期期中考试数学(文)试题】函数232sin y x =-的最小正周期为( ) A.2πB.π C. π2 D. π4【答案】B. 【解析】试题分析:∵232sin 2cos 2y x x =-=+,∴最小正周期T π=,故选B .考点:三角函数的性质.3.【浙江省慈溪中学2016届高三上学期期中考试数学(文)试题】“α是第二象限角”是“sin tan 0αα<”的( )A.充分不必要条件 B .必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【答案】A. 【解析】试题分析:2sin sin sin tan 0sin 00cos 0cos cos αααααααα<⇔⨯<⇔<⇔<且sin 0α≠α⇔是第二象限或第三象限角,故为充分不必要条件,故选A . 考点:1.任意角的三角函数;2.同角三角函数基本关系.4.【浙江省嘉兴市第一中学2016届高三上学期期中考试文数试题解析】为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需把函数sin 2y x =的图象( ▲ )A . 向左平移3π个单位长度 B . 向右平移3π个单位长度 C . 向左平移6π个单位长度D . 向右平移6π个单位长度【答案】D考点:三角函数伸缩平移变换.5.【浙江省嘉兴市第一中学2016届高三上学期期中考试文数试题解析】已知△ABC 的三边a ,b ,c 所对角分别为A ,B ,C ,且sin sin 2BAab=,则cosB 的值为( ▲ )A .B . 12C . 12-D . 【答案】C 【解析】试题分析:由正弦定理可得:sin sin sin a b cA B C ==,结合已知sinsin 2BA a b= ,故有:sin 2sin cos sin 222B B B B == ,解得:1cos 22B =,因为:0B π<<,可得022B π<<,所以23B π= ,解得23B π=,所以21cos cos 32B π==-,故选:C .考点:正弦定理.6.【浙江省杭州市五校联盟2016届高考数学一诊试卷(文科)】已知倾斜角为θ的直线,与直线x ﹣3y+l=0垂直,则=( )A .B .一C .D .一【考点】三角函数的化简求值;直线的倾斜角. 【专题】转化思想;转化法;三角函数的求值.【分析】直线x ﹣3y+l=0的斜率=,因此与此直线垂直的直线的斜率k=﹣3.可得tan θ=﹣3.再利用同角三角函数基本关系式即可得出.【解答】解:直线x ﹣3y+l=0的斜率=,因此与此直线垂直的直线的斜率k=﹣3. ∴tan θ=﹣3.∴====.故选:C .【点评】本题考查了相互垂直的直线斜率之间的关系、同角三角函数基本关系式、“弦化切”,考查了推理能力与计算能力,属于中档题.7.【浙江省杭州市五校联盟2016届高考数学一诊试卷(文科)】已知三个向量,,共线,其中a 、b 、c 、A 、B 、C 分别是△ABC 的三条边及相对三个角,则△ABC 的形状是( ) A .等腰三角形 B .等边三角形 C .直角三角形D .等腰直角三角形【考点】向量在几何中的应用.【专题】计算题;解三角形;平面向量及应用.【分析】根据向量、共线得acos =bcos ,结合正弦定理与二倍角的正弦公式化简,可得sin =sin ,从而得到A=B .同理由、共线算出B=C ,从而得到A=B=C ,所以△ABC 是等边三角形.【解答】解:∵与共线,∴acos =bcos ,由正弦定理得sinAcos =sinBcos ,∵sinA=2sin cos ,sinB=2sin cos ,∴2sin cos cos=2sin cos cos,化简得sin=sin.又∵0<<,0<<,∴=,可得A=B.同理,由与共线得到B=C,∴△ABC中,A=B=C,可得△ABC是等边三角形.故选:B【点评】本题给出三个向量两两共线,由此判定三角形的形状.着重考查了二倍角的三角函数公式、正弦定理和三角形形状的判定等知识,属于中档题.8.【浙江省台州市九峰高中2016届高考数学适应性试卷(文科)】在△ABC中,AB=5,AC=3,BC=7,则∠BAC=()A.B.C.D.【考点】余弦定理.【专题】解三角形.【分析】利用余弦定理表示出cos∠BAC,将三边长代入计算求出cos∠BAC的值,即可确定出∠BAC的度数.【解答】解:∵在△ABC中,AB=c=5,AC=b=3,BC=a=7,∴由余弦定理得:cos∠BAC===﹣,∵∠BAC为△ABC的内角,∴∠BAC=.故选:C.【点评】此题考查了余弦定理,熟练掌握余弦定理是解本题的关键.9.【浙江省慈溪中学2016届高三上学期期中考试数学(文)试题】在ABC∆中,角A,B,C的对边分别为a,b,c,且1a=,60A= ,若三角形有两解,则b的取值范围为()A.()1,0错误!未找到引用源。
专题04 三角函数与解三角形A辑(解析版)-2021年高考数学压轴必刷题(第一辑)

2021年高考数学压轴必刷题(第一辑)专题04三角函数与解三角形A辑1.【2020年全国3卷文科12】已知函数f(x)=sin x+1sinx,则()A.f(x)的最小值为2B.f(x)的图像关于y轴对称C.f(x)的图像关于直线x=π对称D.f(x)的图像关于直线x=π2对称【答案】D【解析】∵sinx可以为负,所以A错;∵sinx≠0∴x≠kπ(k∈Z)∵f(−x)=−sinx−1sinx=−f(x)∴f(x)关于原点对称;∵f(2π−x)=−sinx−1sinx ≠f(x),f(π−x)=sinx+1sinx=f(x),故B错;∴f(x)关于直线x=π2对称,故C错,D对故选:D2.【2020年北京卷10】2020年3月14日是全球首个国际圆周率日(πDay).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值.按照阿尔·卡西的方法,π的近似值的表达式是().A.3n(sin30°n +tan30°n)B.6n(sin30°n+tan30°n)C.3n(sin60°n +tan60°n)D.6n(sin60°n+tan60°n)【答案】A 【解析】单位圆内接正6n边形的每条边所对应的圆周角为360°n×6=60°n,每条边长为2sin30°n,所以,单位圆的内接正6n边形的周长为12nsin30°n,单位圆的外切正6n边形的每条边长为2tan30°n ,其周长为12ntan30°n,∴2π=12nsin30°n +12ntan 30°n2=6n (sin 30°n+tan30°n),则π=3n (sin 30°n+tan30°n).故选:A.3.【2019年天津文科07】已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,且f (x )的最小正周期为π,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .2【答案】解:∵f (x )是奇函数,∴φ=0, ∵f (x )的最小正周期为π, ∴2πω=π,得ω=2,则f (x )=A sin2x ,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ). 则g (x )=A sin x ,若g (π4)=√2,则g (π4)=A sinπ4=√22A =√2,即A =2,则f (x )=A sin2x ,则f (3π8)=2sin (2×3π8=2sin 3π4=2×√22=√2,故选:C .4.【2019年天津理科07】已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .2【答案】解:∵f (x )是奇函数,∴φ=0, 则f (x )=A sin (ωx )将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ). 即g (x )=A sin (12ωx )∵g (x )的最小正周期为2π, ∴2π12ω=2π,得ω=2,则g (x )=A sin x ,f (x )=A sin2x ,若g (π4)=√2,则g (π4)=A sinπ4=√22A =√2,即A =2,则f (x )=2sin2x ,则f (3π8)=2sin (2×3π8=2sin 3π4=2×√22=√2,故选:C .5.【2019年新课标2文科11】已知α∈(0,π2),2sin2α=cos2α+1,则sin α=( )A .15B .√55 C .√33 D .2√55【答案】解:∵2sin2α=cos2α+1, ∴可得:4sin αcos α=2cos 2α, ∵α∈(0,π2),sin α>0,cos α>0,∴cos α=2sin α,∵sin 2α+cos 2α=sin 2α+(2sin α)2=5sin 2α=1, ∴解得:sin α=√55. 故选:B .6.【2019年新课标1文科11】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a sin A ﹣b sin B =4c sin C ,cos A =−14,则bc =( )A .6B .5C .4D .3【答案】解:∵△ABC 的内角A ,B ,C 的对边分别为a ,b ,c , a sin A ﹣b sin B =4c sin C ,cos A =−14, ∴{a 2−b 2=4c 2cosA =b 2+c 2−a 22bc =−14,解得3c 2=12bc , ∴bc =6.故选:A .7.【2019年新课标3理科12】设函数f (x )=sin (ωx +π5)(ω>0),已知f (x )在[0,2π]有且仅有5个零点.下述四个结论:①f (x )在(0,2π)有且仅有3个极大值点 ②f (x )在(0,2π)有且仅有2个极小值点③f (x )在(0,π10)单调递增④ω的取值范围是[125,2910)其中所有正确结论的编号是( ) A .①④B .②③C .①②③D .①③④【答案】解:当x ∈[0,2π]时,ωx +π5∈[π5,2πω+π5], ∵f (x )在[0,2π]有且仅有5个零点, ∴5π≤2πω+π5<6π, ∴125≤ω<2910,故④正确,因此由选项可知只需判断③是否正确即可得到答案, 下面判断③是否正确, 当x ∈(0,π10)时,ωx +π5∈[π5,(ω+2)π10],若f (x )在(0,π10)单调递增,则(ω+2)π10<π2,即ω<3,∵125≤ω<2910,故③正确.故选:D .8.【2019年新课标1理科11】关于函数f (x )=sin|x |+|sin x |有下述四个结论: ①f (x )是偶函数②f (x )在区间(π2,π)单调递增③f (x )在[﹣π,π]有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是( ) A .①②④ B .②④C .①④D .①③【答案】解:f (﹣x )=sin|﹣x |+|sin (﹣x )|=sin|x |+|sin x |=f (x )则函数f (x )是偶函数,故①正确, 当x ∈(π2,π)时,sin|x |=sin x ,|sin x |=sin x ,则f (x )=sin x +sin x =2sin x 为减函数,故②错误, 当0≤x ≤π时,f (x )=sin|x |+|sin x |=sin x +sin x =2sin x ,由f (x )=0得2sin x =0得x =0或x =π,由f (x )是偶函数,得在[﹣π,)上还有一个零点x =﹣π,即函数f (x )在[﹣π,π]有3个零点,故③错误, 当sin|x |=1,|sin x |=1时,f (x )取得最大值2,故④正确, 故正确是①④, 故选:C .9.【2019年北京文科08】如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,∠APB 是锐角,大小为β,图中阴影区域的面积的最大值为( )A .4β+4cos βB .4β+4sin βC .2β+2cos βD .2β+2sin β 【答案】解:由题意可得∠AOB =2∠APB =2β, 要求阴影区域的面积的最大值,即为直线QO ⊥AB , 即有QO =2,Q 到线段AB 的距离为2+2cos β, AB =2•2sin β=4sin β,扇形AOB 的面积为12•2β•4=4β,△ABQ 的面积为12(2+2cos β)•4sin β=4sin β+4sin βcos β=4sin β+2sin2β,S △AOQ +S △BOQ =4sin β+2sin2β−12•2•2sin2β=4sin β, 即有阴影区域的面积的最大值为4β+4sin β. 故选:B .10.【2018年新课标1文科11】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A(1,a ),B (2,b ),且cos2α=23,则|a ﹣b |=( ) A .15B .√55 C .2√55D .1 【答案】解:∵角α的顶点为坐标原点,始边与x 轴的非负半轴重合, 终边上有两点A (1,a ),B (2,b ),且cos2α=23, ∴cos2α=2cos 2α﹣1=23,解得cos 2α=56, ∴|cos α|=√306,∴|sin α|=√1−3036=√66,|tan α|=|b−a2−1|=|a ﹣b |=|sinα||cosα|=√66√306=√55. 故选:B .11.【2018年新课标2文科10】若f (x )=cos x ﹣sin x 在[0,a ]是减函数,则a 的最大值是( ) A .π4B .π2C .3π4D .π【答案】解:f (x )=cos x ﹣sin x =﹣(sin x ﹣cos x )=−√2sin (x −π4), 由−π2+2k π≤x −π4≤π2+2k π,k ∈Z , 得−π4+2k π≤x ≤34π+2k π,k ∈Z , 取k =0,得f (x )的一个减区间为[−π4,3π4],由f (x )在[0,a ]是减函数, 得a ≤3π4. 则a 的最大值是3π4.故选:C .12.【2018年新课标3文科11】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为a 2+b 2−c 24,则C =( ) A .π2B .π3C .π4D .π6【答案】解:∵△ABC 的内角A ,B ,C 的对边分别为a ,b ,c . △ABC 的面积为a 2+b 2−c 24,∴S△ABC=12absinC=a2+b2−c24,∴sin C=a2+b2−c22ab=cos C,∵0<C<π,∴C=π4.故选:C.13.【2018年北京理科07】在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为()A.1B.2C.3D.4【答案】解:由题意d=√1+m2=|√m2+1sin(θ+α)−2|√m+1,tanα=1m=y x,∴当sin(θ+α)=﹣1时,d max=1√m+1≤3.∴d的最大值为3.故选:C.14.【2018年北京文科07】在平面直角坐标系中,AB̂,CD̂,EF̂,GĤ是圆x2+y2=1上的四段弧(如图),点P其中一段上,角α以Ox为始边,OP为终边.若tanα<cosα<sinα,则P所在的圆弧是()A.AB̂B.CD̂C.EF̂D.GĤ【答案】解:A.在AB段,正弦线小于余弦线,即cosα<sinα不成立,故A不满足条件.B.在CD段正切线最大,则cosα<sinα<tanα,故B不满足条件.C.在EF段,正切线,余弦线为负值,正弦线为正,满足tanα<cosα<sinα,D.在GH段,正切线为正值,正弦线和余弦线为负值,满足cosα<sinα<tanα不满足tanα<cosα<sinα.故选:C.15.【2017年新课标1文科11】△ABC的内角A,B,C的对边分别为a,b,c,已知sin B+sin A(sin C﹣cos C)=0,a=2,c=√2,则C=()A.π12B.π6C.π4D.π3【答案】解:sin B=sin(A+C)=sin A cos C+cos A sin C,∵sin B+sin A(sin C﹣cos C)=0,∴sin A cos C+cos A sin C+sin A sin C﹣sin A cos C=0,∴cos A sin C+sin A sin C=0,∵sin C≠0,∴cos A=﹣sin A,∴tan A=﹣1,∵π2<A<π,∴A=3π4,由正弦定理可得csinC =asinA,∴sin C=csinA a,∵a=2,c=√2,∴sin C=csinAa=√2×√222=12,∵a>c,∴C =π6, 故选:B .16.【2017年天津理科07】设函数f (x )=2sin (ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f (5π8)=2,f (11π8)=0,且f (x )的最小正周期大于2π,则( ) A .ω=23,φ=π12 B .ω=23,φ=−11π12 C .ω=13,φ=−11π24 D .ω=13,φ=7π24【答案】解:由f (x )的最小正周期大于2π,得T4>π2,又f (5π8)=2,f (11π8)=0,得T 4=11π8−5π8=3π4,∴T =3π,则2πω=3π,即ω=23.∴f (x )=2sin (ωx +φ)=2sin (23x +φ), 由f (5π8)=2sin(23×5π8+φ)=2,得sin (φ+5π12)=1.∴φ+5π12=π2+2kπ,k ∈Z . 取k =0,得φ=π12<π. ∴ω=23,φ=π12. 故选:A .17.【2017年天津文科07】设函数f (x )=2sin (ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f (5π8)=2,f (11π8)=0,且f (x )的最小正周期大于2π,则( ) A .ω=23,φ=π12 B .ω=23,φ=−11π12 C .ω=13,φ=−11π24 D .ω=13,φ=7π24【答案】解:由f (x )的最小正周期大于2π,得T4>π2, 又f (5π8)=2,f (11π8)=0,得T 4=11π8−5π8=3π4,∴T =3π,则2πω=3π,即ω=23.∴f (x )=2sin (ωx +φ)=2sin (23x +φ),由f (5π8)=2sin(23×5π8+φ)=2,得sin (φ+5π12)=1. ∴φ+5π12=π2+2kπ,k ∈Z . 取k =0,得φ=π12<π. ∴ω=23,φ=π12. 故选:A .18.【2016年新课标1理科12】已知函数f (x )=sin (ωx +φ)(ω>0,|φ|≤π2),x =−π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在(π18,5π36)上单调,则ω的最大值为( )A .11B .9C .7D .5【答案】解:∵x =−π4为f (x )的零点,x =π4为y =f (x )图象的对称轴, ∴2n+14⋅T =π2,即2n+14⋅2πω=π2,(n ∈N )即ω=2n +1,(n ∈N ) 即ω为正奇数, ∵f (x )在(π18,5π36)上单调,则5π36−π18=π12≤T2,即T =2πω≥π6,解得:ω≤12, 当ω=11时,−11π4+φ=k π,k ∈Z , ∵|φ|≤π2, ∴φ=−π4, 此时f (x )在(π18,5π36)不单调,不满足题意;当ω=9时,−9π4+φ=k π,k ∈Z , ∵|φ|≤π2, ∴φ=π4, 此时f (x )在(π18,5π36)单调,满足题意;故ω的最大值为9, 故选:B .19.【2016年新课标2文科11】函数f (x )=cos2x +6cos (π2−x )的最大值为( )A .4B .5C .6D .7【答案】解:函数f (x )=cos2x +6cos (π2−x ) =1﹣2sin 2x +6sin x , 令t =sin x (﹣1≤t ≤1), 可得函数y =﹣2t 2+6t +1 =﹣2(t −32)2+112,由32∉[﹣1,1],可得函数在[﹣1,1]递增,即有t =1即x =2k π+π2,k ∈Z 时,函数取得最大值5. 故选:B .20.【2016年天津文科08】已知函数f (x )=sin 2ωx 2+12sin ωx −12(ω>0),x ∈R ,若f (x )在区间(π,2π)内没有零点,则ω的取值范围是( ) A .(0,18]B .(0,14]∪[58,1)C .(0,58]D .(0,18]∪[14,58]【答案】解:函数f (x )=sin 2ωx 2+12sin ωx −12=1−cosωx 2+12sin ωx −12=√22sin(ωx −π4), 由f (x )=0,可得sin(ωx −π4)=0,解得x =kπ+π4ω∉(π,2π),∴ω∉(18,14)∪(58,54)∪(98,94)∪⋯=(18,14)∪(58,+∞), ∵f (x )在区间(π,2π)内没有零点, ∴ω∈(0,18]∪[14,58]. 故选:D .21.【2014年天津文科08】已知函数f (x )=√3sin ωx +cos ωx (ω>0),x ∈R ,在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,则f (x )的最小正周期为( )A .π2B .2π3C .πD .2π【答案】解:∵已知函数f (x )=√3sin ωx +cos ωx =2sin (ωx +π6)(ω>0),x ∈R ,在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,正好等于f (x )的周期的13倍,设函数f (x )的最小正周期为T ,则13⋅T =π3,∴T =π,故选:C .22.【2013年新课标2理科12】已知点A (﹣1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( ) A .(0,1) B .(1−√22,12) C .(1−√22,13] D .[13,12) 【答案】解:解法一:由题意可得,三角形ABC 的面积为 12⋅AB ⋅OC =1,由于直线y =ax +b (a >0)与x 轴的交点为M (−ba ,0),由直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,可得b >0, 故−ba≤0,故点M 在射线OA 上.设直线y =ax +b 和BC 的交点为N ,则由{y =ax +b x +y =1可得点N 的坐标为(1−b a+1,a+b a+1).①若点M 和点A 重合,则点N 为线段BC 的中点,故N (12,12),把A 、N 两点的坐标代入直线y =ax +b ,求得a =b =13.②若点M 在点O 和点A 之间,此时b >13,点N 在点B 和点C 之间, 由题意可得三角形NMB 的面积等于12,即12⋅MB ⋅y N =12,即 12×(1+ba )⋅a+ba+1=12,可得a =b 21−2b >0,求得 b <12, 故有13<b <12.③若点M 在点A 的左侧,则b <13,由点M 的横坐标−b a<−1,求得b >a .设直线y =ax +b 和AC 的交点为P ,则由 {y =ax +by =x +1求得点P 的坐标为(1−b a−1,a−b a−1),此时,由题意可得,三角形CPN 的面积等于12,即 12•(1﹣b )•|x N ﹣x P |=12,即12(1﹣b )•|1−ba+1−1−ba−1|=12,化简可得2(1﹣b )2=|a 2﹣1|.由于此时 b >a >0,0<a <1,∴2(1﹣b )2=|a 2﹣1|=1﹣a 2 .两边开方可得 √2(1﹣b )=√1−a 2<1,∴1﹣b 2,化简可得 b >1−√22, 故有1−√22<b <13. 再把以上得到的三个b 的范围取并集,可得b 的取值范围应是 (1−√22,12), 故选:B .解法二:当a =0时,直线y =ax +b (a >0)平行于AB 边,由题意根据三角形相似且面积比等于相似比的平方可得(1−b 1)2=12,b =1−√22,趋于最小. 由于a >0,∴b >1−√22. 当a 逐渐变大时,b 也逐渐变大,当b =12时,直线经过点(0,12),再根据直线平分△ABC 的面积,故a 不存在,故b <12.综上可得,1−√22<b <12,故选:B .23.【2012年天津文科07】将函数y =sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点(3π4,0),则ω的最小值是( ) A .13B .1C .53D .2【答案】解:将函数y =sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象对应的函数为y =sin ω(x −π4).再由所得图象经过点(3π4,0)可得sin ω(3π4−π4)=sin (ωπ2)=0,∴ω•π2=k π,k ∈z .故ω的最小值是2, 故选:D .24.【2011年新课标1理科11】设函数f (x )=sin (ωx +φ)+cos (ωx +φ)(ω>0,|φ|<π2)的最小正周期为π,且f (﹣x )=f (x ),则( ) A .f (x )在(0,π2)单调递减B .f (x )在(π4,3π4)单调递减C .f (x )在(0,π2)单调递增D .f (x )在(π4,3π4)单调递增【答案】解:由于f (x )=sin (ωx +ϕ)+cos (ωx +ϕ)=√2sin(ωx +ϕ+π4), 由于该函数的最小正周期为T =2πω,得出ω=2, 又根据f (﹣x )=f (x ),得φ+π4=π2+k π(k ∈Z ),以及|φ|<π2,得出φ=π4. 因此,f (x )=√2sin(2x +π2)=√2cos2x ,若x ∈(0,π2),则2x ∈(0,π),从而f (x )在(0,π2)单调递减, 若x ∈(π4,3π4),则2x ∈(π2,3π2),该区间不为余弦函数的单调区间,故B ,C ,D 都错,A 正确. 故选:A .25.【2010年浙江理科09】设函数f (x )=4sin (2x +1)﹣x ,则在下列区间中函数f (x )不存在零点的是( ) A .[﹣4,﹣2]B .[﹣2,0]C .[0,2]D .[2,4]【答案】解:在同一坐标系中画出g (x )=4sin (2x +1)与h (x )=x 的图象 如下图示:由图可知g (x )=4sin (2x +1)与h (x )=x 的图象在区间[﹣4,﹣2]上无交点,由图可知函数f(x)=4sin(2x+1)﹣x在区间[﹣4,﹣2]上没有零点故选:A.26.【2010年上海理科18】某人要制作一个三角形,要求它的三条高的长度分别为113,111,15,则此人将()A.不能作出这样的三角形B.作出一个锐角三角形C.作出一个直角三角形D.作出一个钝角三角形【答案】解:设三边分别为a,b,c,利用面积相等可知1 13a=111b=15c,∴a:b:c=13:11:5令a=13,b=11,c=5由余弦定理得cos A=52+112−1322×5×11<0,所以角A为钝角,故选:D.27.【2010年北京文科07】某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为()A.2sinα﹣2cosα+2B.sinα−√3cosα+3C.3sinα−√3cosα+1D.2sinα﹣cosα+1【答案】解:由正弦定理可得4个等腰三角形的面积和为:4×12×1×1×sinα=2sinα由余弦定理可得正方形边长为:√12+12−2×1×1×cosα=√2−2cosα故正方形面积为:2﹣2cosα所以所求八边形的面积为:2sinα﹣2cosα+2故选:A.。
专题04 三角函数与三角形(第01期)-决胜2016年高考全国名校试题理数分项汇编(新课标1特刊)(解析版)

一.基础题组1.【太原市2015年高三年级模拟试题(一)】已知数列{}n a 的通项公式为*(1)(21)cos1()2n n n a n n N π=--⋅+∈,其前n 项和为n S ,则60S =( ) A .-30 B .-60C .90D .120【答案】D.考点:1.三角函数的性质;2.数列求和.2.【江西省八所重点中学2015届高三联考】函数()sin (0,0)f x A x A ωω=>>的部分图象如图所示,则`)1(f +)2(f +)3(f ++)2015(f 的值为( )A .0BCD 【答案】A 【解析】试题分析:有图像可知,函数()sin (0,0)f x A x A ωω=>>的最小正周期为8,且2A =,所以284ππωω=⇒=,所以()2sin4f x x π=,多以`)1(f +)2(f +)3(f ++0(8)f =,`)1(f +)2(f +)3(f ++)2015(f =8×0+`)1(f +)2(f +)3(f ++0(7)f =,故选B .考点:正弦函数的周期性.3.【河南省洛阳市2015届高三第二次统一考试数学(理)】在ABC ∆中,三内角A ,B ,C 的对边分别为a ,b ,c ,面积为S ,若22()S a b c +=+,则cos A 等于( ) A.45 B.45- C.1517 D.1517- 【答案】D. 【解析】试题分析:∵222221()2(sin 1)4S a b c a b c bc A +=+⇒=+--,由余弦定理可得1sin 1cos 4A A -=,联立22sin cos 1A A +=,可得15cos 17A =-. 考点:正余弦定理解三角形.4.【上饶市重点中学2015届高三六校第一次联考】已知点(sin cos ,tan )P ααα-在第二象限,则α的一个变化区间是( )A.(,)22ππ-B. (,)44ππ-C. 3(,-)42ππ-D. (,)2ππ 【答案】C考点:三角函数值得符号;5.【2015年江西省高考适应性测试】已知函数()sin()f x x ωϕ=+(0,2πωϕ><)的部分图像如图所示,则()y f x = 的图象可由cos 2y x = 的图象( )A .向右平移3π个长度单位B .向左平移3π个长度单位 C .向右平移6π个长度单位 D .向左平移6π个长度单位【答案】A【解析】试题分析:由图可得2244=⇒=⨯=ωωππT ,1)32sin()3(=+⨯=ϕππf ,注意到2πϕ<,故 6232πϕπϕπ-=⇒=+,所以)62sin()(π-=x x f ,而cos 2y x =)6)3(2sin()22sin(πππ-+=+=x x 所以cos 2y x = 的图象向右平移3π个长度单位即可得到()y f x =的图象考点:三角函数的图象与性质6.【商丘市2015年高三第二次模拟考试】若将函数的图象向右平移个单位,所得图象关于y 轴对称,则的最小正值是( )(A )8π(B )4π(C )38π (D )34π【答案】C考点:三角函数的图像和性质7.【江西名校学术联盟(江西师大附中、临川1中、鹰潭1中、宜春中学、新余四中等)】函数()g x 的图象是由函数()sin 22f x x x =-的图象向右平移12π个单位而得到的,则函数()g x 图象的对称轴可以为( ) A .直线4x π= B .直线3x π=C .直线2x π=D .直线6x π=【答案】C 【解析】试题分析:()sin 222sin(2)3f x x x x π==-,向右平移12π个单位得到()2sin[2()]2sin(2)2cos 2x 1232g x x x πππ=--=-=-,由cos2x=1±,得2()x k k Z π=∈,即()2k x k Z π=∈,∴函数g(x)的图象的对称轴为直线()2k x k Z π=∈,对照各选项,只有C 符合.考点:函数图象的平移、三角函数的对称轴.8.【河南省南阳市第一中学2015届高三下学期第三次模拟考试】已知函数2()3f x ax bx a b =+++是定义在[1,2]a a -上的偶函数,则2cos[()]3y a b x π=+- 的最小正周期是( )A. 6πB. 5πC.4πD.2π 【答案】A考点:函数的奇偶性、三角函数的周期.9.【上饶市重点中学2015届高三六校第一次联考】在ABC ∆中,角A,B,C 所对的边分别为a,b,c 满足222b c a bc +-=,0AB BC >,a =则b+c 的取值范围是( )A. 31,2⎛⎫ ⎪⎝⎭B.32⎫⎪⎪⎭C.13,22⎛⎫⎪⎝⎭ D .13,22⎛⎤ ⎥⎝⎦【答案】B 【解析】试题分析:由222b c a bc +-=得:2221cos 22b c a A bc +-==,则A=3π,由0AB BC >可知:B 为钝角, 21sin aR A==,则sin ,sin b B c C ==,sin sin sin b c B C B +=+=+2sin(3π)B -3=sin cos sin()26B B B π+=+,由于223B ππ<<,25366B πππ<+<,所以1sin()23B π<+<32b c <+<,选B 考点:1.余弦定理,2.辅助角公式;3.正弦函数;10.【高安中学2015届命题中心高考模拟试题】如果把锐三角形的三边都增加同样的长度,则得到的这个新三角形的形状为( )A .钝角三角形B .直角三角形C .锐角三角形D .由增加的长度决定 【答案】C .考点:1、余弦定理;2、三角形的形状的判断;11.【太原五中2014—2015学年度第二学期阶段检测高三数学(理)】题文】将函数)sin(ϕ+=x y 2的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为( )A.43π B. 4π C. 0 D. - 4π 【答案】B 【解析】试题分析:根据题意可知平移后所得图像对应的函数为sin(2)4y x πϕ=++,要想其为偶函数,可知4πϕ+为2π的奇数倍,所以只有项满足条件,故选B.考点:图像的平移,偶函数的定义.12..【太原市2015年高三年级模拟试题(一)】已知函数()sin()(0,||)2f x x πωϕωϕ=+><的最小正周期是π,若将其图象向右平移3π个单位后得到的图象关于原点对称,则函数()f x 的图象( )A.关于直线12x π=对称 B.关于直线512x π=对称 C.关于点(,0)12π对称 D.关于点5(,0)12π对称 【答案】B.考点:三角函数的图象和性质.13..【山西省2015届高三第三次四校联考数学(理)试卷】 已知函数)0(cos sin 3)(>+=ωωωx x x f 的图象与x 轴交点的横坐标构成一个公差为2π的等差数列,把函数)(x f 的图象沿x 轴向左平移6π个单位,得到函数)(x g 的图象.关于函数)(x g ,下列说法正确的是A. 在]2,4[ππ上是增函数 B. 其图象关于直线4π-=x 对称C. 函数)(x g 是奇函数D. 当]32,6[ππ∈x 时,函数)(x g 的值域是]1,2[-【答案】D 【解析】试题分析:因为函数()cos 2sin 6f x x x x πωωω⎛⎫=+=+ ⎪⎝⎭的图象与x 轴的交点的横坐标构成一个公差为2π的等差数列,所以22T π=,即,2T πω==,所以()2sin 2()2cos266g x x x ππ⎡⎤=++=⎢⎥⎣⎦,在区间,42ππ⎡⎤⎢⎥⎣⎦上是减函数,故A 错;对称轴为()2k x k Z π=∈,故B ,C 错;故选D. 考点:正、余弦函数图象与性质,函数图象平移、伸缩变换.14.【江西名校学术联盟(江西师大附中、临川1中、鹰潭1中、宜春中学、新余四中等)】已知函数()tan (0)f x kx k =>的最小正周期为2π,则22sin cos 1212k k ππ-= .【答案】12- 【解析】试题分析:根据题意得2T kππ==,故k=2,所以22221sin cos sin cos cos 12126632k k πππππ-=-=-=-. 考点:三角函数的周期、二倍角公式.15.【江西省八所重点中学2015届高三4月联考数学(理)】如图,圆O 与x 轴的正半轴的交点为A ,点C ,B 在圆O 上,且点C 位于第一象限,点B 的坐标为125(,)1313-,AOC α∠=,若1BC =,则2sincos222ααα-的值为 .【答案】513.考点:1.任意角三角函数的定义;2.诱导公式.16.【商丘市2015年高三第二次模拟考试】ABC ∆的内角A,B,C 的对边分别为,,a b c ,已知,,则B= .【答案】3π考点:正弦定理、余弦定理、两角和与差的三角函数17.【河南省洛阳市2015届高三第二次统一考试数学(理)】已知tan α,tan β分别是2lg(652)0x x -+=的两个实数根,则tan()αβ+= . 【答案】1. 【解析】试题分析:由题意可得,22lg(652)06510x x x x -+=⇒-+=,∴5tan tan 6αβ+=, 1tan tan 6αβ⋅=,∴5tan tan 6tan()111tan tan 16αβαβαβ++===--. 考点:1.一元二次方程根与系数关系;2.三角恒等变形.二.能力题组1.【江西省师大附中、鹰潭一中2015届高三下学期4月联考】对于集合021},,,{a a a a n 和常数 ,定义:ω=22210200sin ()sin ()sin ()n a a a a a a n-+-++-为集合{12,,,n a a a }相对0a 的“正弦方差”,则集合0}67,65,2{a 相对πππ的“正弦方差”为 。
2016届高考数学文自由复习步步高系列专题04三角函数与三角形(通用版)(解析版)
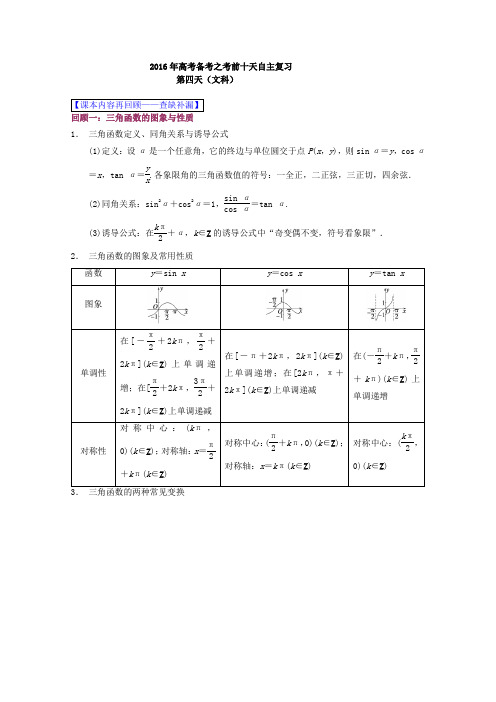
2016年高考备考之考前十天自主复习 第四天(文科)1. 三角函数定义、同角关系与诱导公式(1)定义:设α是一个任意角,它的终边与单位圆交于点P (x ,y ),则sin α=y ,cos α=x ,tan α=y x.各象限角的三角函数值的符号:一全正,二正弦,三正切,四余弦. (2)同角关系:sin 2α+cos 2α=1,sin αcos α=tan α.(3)诱导公式:在k π2+α,k ∈Z 的诱导公式中“奇变偶不变,符号看象限”.2. 三角函数的图象及常用性质回顾二:三角变换与解三角形1. 两角和与差的正弦、余弦、正切公式(1)sin(α±β)=sin αcos β±cos αsin β. (2)cos(α±β)=cos αcos β∓sin αsin β. (3)tan(α±β)=tan α±tan β1∓tan αtan β.2. 二倍角的正弦、余弦、正切公式(1)sin 2α=2sin αcos α.(2)cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. (3)tan 2α=2tan α1-tan 2α. 3. 三角恒等式的证明方法(1)从等式的一边推导变形到另一边,一般是化繁为简. (2)等式的两边同时变形为同一个式子. (3)将式子变形后再证明. 4. 正弦定文a sin A =b sin B =csin C=2R (2R 为△ABC 外接圆的直径). 变形:a =2R sin A ,b =2R sin B ,c =2R sin C .sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .5. 余弦定文a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B ,c 2=a 2+b 2-2ab cos C . 推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C . 6. 面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .7. 解三角形(1)已知两角及一边,利用正弦定文求解.(2)已知两边及一边的对角,利用正弦定文或余弦定文求解,解的情况可能不唯一. (3)已知两边及其夹角,利用余弦定文求解. (4)已知三边,利用余弦定文求解. 回顾三:平面向量1. 平面向量中的五个基本概念(1)零向量模的大小为0,方向是任意的,它与任意非零向量都共线,记为0. (2)长度等于1个单位长度的向量叫单位向量,a 的单位向量为a|a |.(3)方向相同或相反的向量叫共线向量(平行向量).(4)如果直线l 的斜率为k ,则a =(1,k )是直线l 的一个方向向量. (5)向量的投影:|b |cos 〈a ,b 〉叫做向量b 在向量a 方向上的投影. 2. 平面向量的两个重要定文(1)向量共线定文:向量a (a ≠0)与b 共线当且仅当存在唯一一个实数λ,使b =λa . (2)平面向量基本定文:如果e 1,e 2是同一平面内的两个不共线向量,那么对这一平面内的任一向量a ,有且只有一对实数λ1,λ2,使a =λ1e 1+λ2e 2,其中e 1,e 2是一组基底. 3. 平面向量的两个充要条件若两个非零向量a =(x 1,y 1),b =(x 2,y 2),则: (1)a ∥b ⇔a =λb ⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a ·b =0⇔x 1x 2+y 1y 2=0. 4. 平面向量的三个性质(1)若a =(x ,y ),则|a |=a ·a =x 2+y 2. (2)若A (x 1,y 1),B (x 2,y 2),则AB →|=x 2-x 12+y 2-y 12.(3)若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角,则cos θ=a ·b |a ||b |=x 1x 2+y 1y 2x 21+y 21x 22+y 22.热点一:三角函数=sin(ω+φ)的图象及解析式【典例】(2016·东北三校联考)已知函数y =A sin(ωx +φ)+b (A >0,ω>0)的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则下面各式中符合条件的解析式为( )A .y =4sin ⎝ ⎛⎭⎪⎫4x +π6B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3+2C .y =2sin ⎝⎛⎭⎪⎫4x +π3+2 D .y =2sin ⎝⎛⎭⎪⎫4x +π6+2 解析:选D 由函数y =A sin(ωx +φ)+b 的最大值为4,最小值为0,可知b =2,A =2.由函数的最小正周期为π2,可知2πω=π2,得ω=4.由直线x =π3是其图象的一条对称轴,可知4×π3+φ=k π+π2,k ∈Z ,从而φ=k π-5π6,k ∈Z ,故满足题意的是y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2.【典例】(2016·长春调研)函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,-π2<φ<π2,x ∈R 的部分图象如图所示.(1)求函数y =f (x )的解析式;(2)当x ∈⎣⎢⎡⎦⎥⎤-π,-π6时,求f (x )的取值范围.【题型概述】该类题主要包括三角函数的图象和变换以及已知图象确定解析式两种题型,已知图象求解析式这类型题的解决方法一般为利用待定系数法,由图中的最高点、最低点或特殊点求A ;由函数的周期确定ω;确定φ常根据“五点法”中的五个点求解,其中一般把第一个零点作为突破口,可以从图象的升降找准第一个零点的位置;函数的图象变换这类型题,务必分清是先相位变换,还是先周期变换.变换只是相对于其中的自变量x 而言的,如果x 的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向.【跟踪练习】( 四川省遂宁市2016届高三第二次诊断考试数学文4)为了得到函数3y x =的图象,可以将函数x x y 3cos 3sin +=的图象( )A .向右平移12π个单位长 B .向右平移4π个单位长C .向左平移12π个单位长 D .向左平移4π个单位长【答案】A 【解析】试题分析:由sin 3cos3y x x =+得,)3()412y x x ππ=+=+,将3()12y x π=+向右平移12π个单位长,便可得3()31212y x x ππ=-+=的图象.故选A.考点:三角恒等变换及函数图象的变换. 热点二:三角函数的性质【典例】已知f (x )=A sin(ωx +φ)(A >0,ω>0)的最小正周期为2,且当x =13时,f (x )的最大值为2.(1)求f (x )的解析式.(2)在闭区间⎣⎢⎡⎦⎥⎤214,234上是否存在f (x )的对称轴?如果存在求出其对称轴.若不存在,请说明文由.【典例】(2016·广东梅州二模)把函数y =sin 2x 的图象沿x 轴向左平移π6个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数y =f (x )的图象,对于函数y =f (x )有以下四个判断:①该函数的解析式为y =2sin ⎝ ⎛⎭⎪⎫2x +π6;②该函数图象关于点⎝ ⎛⎭⎪⎫π3,0对称;③该函数在⎣⎢⎡⎦⎥⎤0,π6上是增函数;④函数y =f (x )+a 在⎣⎢⎡⎦⎥⎤0,π2上的最小值为3,则a =2 3.其中,正确判断的序号是________.解析:将函数y =sin 2x 的图象向左平移π6个单位得到y =sin 2⎝ ⎛⎭⎪⎫x +π6=sin ⎝ ⎛⎭⎪⎫2x +π3的图象,然后纵坐标伸长到原来的2倍得到y =2sin ⎝ ⎛⎭⎪⎫2x +π3的图象,所以①不正确.y =f ⎝ ⎛⎭⎪⎫π3=2sin ⎝ ⎛⎭⎪⎫2×π3+π3=2sin π=0,所以函数图象关于点⎝ ⎛⎭⎪⎫π3,0对称,所以②正确.由-π2+2k π≤2x +π3≤π2+2k π,k ∈Z ,得-5π12+k π≤x ≤π12+k π,k ∈Z ,即函数的单调增区间为⎣⎢⎡⎦⎥⎤-5π12+k π,π12+k π,k ∈Z ,当k =0时,增区间为⎣⎢⎡⎦⎥⎤-5π12,π12,所以③不正确.y =f (x )+a =2sin ⎝ ⎛⎭⎪⎫2x +π3+a ,当0≤x ≤π2时,π3≤2x +π3≤4π3,所以当2x +π3=4π3,即x =π2时,函数取得最小值,y min =2sin 4π3+a =-3+a =3,所以a =2 3.所以④正确.所以正确的判断为②④.答案:②④【题型概述】该类型题目主要考察三角函数的图象和性质,首先应恒等变形为()y Asin x ωϕ=+,且将ω化为正,这样可求周期2T πω=,将ωx +φ看成一个整体,利用复合函数的单调性求单调区间,利用三角函数的图象求值域以及对称问题等.【跟踪练习】(福建省莆田一中、泉州五中、漳州一中2016届高三上学期三校联考数学文16)已知函数21()cos cos (0)2f x x x x ωωωω=+->的最小正周期为π. (I)求ω值及()f x 的单调递增区间;(II)在△ABC 中,a b c 、、分别是三个内角C B A 、、所对边,若1a =,b =,()2A f =,求B 的大小.【答案】(I )[,]()36k k k ππππ-+∈Z ;(II )4B π=或34B π=【解析】(I )1cos 21()2sin(2)226x f x x x ωπωω+=+-=+,∵()f x 最小正周期为π,∴ 1ω=, ()sin(2)6f x x π=+,()f x 增区间是[,]()36k k k ππππ-+∈Z ;(II )∵()2Af =,a b <,∴ 6A π=,∵1a =,b =,由正弦定文sin sin b A B a ==∵a b <,∴4B π=或34B π=.考点:三角函数及其性质、正弦定文 热点三:三角函数与三角形问题的结合【典例】( 2016漳州市普通高中毕业班质量检查数学文16)已知函数()2cos 2cos 1f x x x x =+-.()I 求函数()f x 的最小正周期和函数()f x 的单调递增区间; ()II 在C ∆AB 中,角A ,B,C 所对的边分别为a ,b ,c ,若()1f A =,()sin 2sin C πB =-,C ∆AB 的面积为a 的值.【答案】(1)T π=,[,]36k k ππππ-+,k Z ∈,(2),考点:三角函数性质与解三角形;【题型概述】该类题型将三角函数的图象和性质与正弦定文融合到一起,其解法往往是,既然是三角形问题,就会用到三角形内角和定文和正、余弦定文以及相关三角形文论,及时边角转换,可以帮助发现问题解决思路;同时它也是一种三角变换,只不过角的范围缩小了,因此常见的三角变换方法和原则都是适用的.【跟踪练习】21()cos cos (0)2f x x x x ωωωω=+->的最小正周期为π. (I )求ω值及()f x 的单调递增区间;(II )在△ABC 中,a b c 、、分别是三个内角C B A 、、所对边,若1a =,b =,2A f ⎛⎫=⎪⎝⎭,求B 的大小.【考点定位】1.三角恒等变换(倍角公式);2.三角函数的周期和单调性;3.正弦定文. 热点四:三角变换、向量、三角形问题的综合【典例】(四川省雅安中学2016届高三开学考试数学文16) 已知向量a =(sin ωx ,cos ωx ),b =(cos φ,sin φ),函数f (x )=a ·b ⎝ ⎛⎭⎪⎫ω>0,π3<φ<π的最小正周期为2π,其图象经过点M ⎝ ⎛⎭⎪⎫π6,32.(1)求函数f (x )的解析式;(2)已知α,β∈⎝ ⎛⎭⎪⎫0,π2,且f (α)=35,f (β)=1213,求f (2α-β)的值.解:(1)依题意有f (x )=a·b =sin ωx cos φ+cos ωx sin φ=sin(ωx +φ).∵函数f (x )的最小正周期为2π,∴2π=T =2πω,解得ω=1.将点M ⎝⎛⎭⎪⎫π6,32代入函数f (x )的解析式,得sin ⎝ ⎛⎭⎪⎫π6+φ=32.∵π3<φ<π,∴π2<π6+φ<7π6,∴π6+φ=2π3,∴φ=π2.故f (x )=sin ⎝⎛⎭⎪⎫x +π2=cos x . (2)依题意有cos α=35,cos β=1213,而α,β∈⎝⎛⎭⎪⎫0,π2,∴sin α=1-⎝ ⎛⎭⎪⎫352 =45,sin β=1-⎝ ⎛⎭⎪⎫12132=513, ∴sin 2α=2sin αcos α=2425,cos 2α=cos 2α-sin 2α=925-1625=-725,∴f (2α-β)=cos(2α-β)=cos 2αcos β+sin 2αsin β=⎝ ⎛⎭⎪⎫-725×1213+2425×513=36325. 【跟踪练习】在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知m ()A A sin 3,cos 2=,n ()A A cos 2,cos -=,m·n 1-=.(1)求A ∠的大小;(2)若32=a ,2=c ,求△ABC 的面积.【解析】(1)法一:由题意知m·n 1cos sin 32cos 22-=-=A A A . ∴12sin 32cos 1-=-+A A . 即22cos 2sin 3=-A A ,∴262sin 2=⎪⎭⎫ ⎝⎛-πA ,即162sin =⎪⎭⎫ ⎝⎛-πA .∵π<<A 0,∴611626πππ<-<-A ,∴262ππ=-A ,即3π=A . 法二:由题意知m·n 1cos sin 32cos 22-=-=A A A . ∴cos sin cos sin 32cos 2222=++-A A A A A 即0sin cos sin 32cos 322=+-A A A A .()0sin cos 32=-A A ∴A A sin cos 3=,即3tan =A ,∵π<<A 0,∴3π=A .【考点定位】数量积的坐标运算、正弦定文和余弦定文、三角恒等变换.教育质量监测2016年高三第一次模考文科数学3)将函数)2sin(ϕ+=x y 的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 A.4πB.43π C. 0 D. 4π- 【答案】A考点:三角函数图象变换2.( 东北三省三校2016年高三第一次联合模拟考试文科数学试题16)已知函数()()sin 2cos y x x πϕπϕ=+-+(0ϕπ<<)的图象关于直线1x =对称,则sin 2ϕ= .【答案】4-5【解析】函数()()sin 2cos y x x πϕπϕ=+-+sin()x πϕθ+-(其中tan 2θ=)的图象关于直线1x =对称,则当1x =时,sin()sin()1πϕθϕθ+-=⇒-=±,则2k πϕθπ-=+,ϕ=k π22πθ++,sin 2sin(22)sin 2k ϕππθθ=++=-, 由于22tan 4sin 251+tan θθθ==,则sin 2ϕ=4sin 25θ-=-; 考点:三角函数图象和性质;3.( 2014——2016学年度上学期辽宁省丹东五校协作体高三期末考试文16)在ABC △中,内角,,A B C 的对边分别为,,a b c ,已知sin 1sin sin b Ca c A B=-++,且5,5b CA CB =⋅=-,则ABC △的面积是___________.【答案】 【解析】由正弦定文得:sin sin sin C cA B a b=++ 所以,1b c a c a b=-++,整文得:222(1)b c a bc +-=所以,2221cos ,sin 22b c a A A bc +-===又因为5,5b CA CB =⋅=-,所以,cos 5cos 1ab C a C =-⇒=-由余弦定文得:22222212352a b c a a c b b ab+-=-⇒-=--=-把225,35b a c =-=- 代入(1)式得:2535512c c =-+⇒=所以,11sin 51222ABC S bc A ∆==⨯⨯=所以答案应填:.考点:1、正弦定文;2、余弦定文;3、平面向量的数量积4.(2016年3月德阳市四校高三联合测试数学文7)在△ABC 中,①若B =60,a =10,b =7,则该三角形有且有两解;②若三角形的三边的比是3:5:7,则此三角形的最大角为120;③若△ABC 为锐角三角形,且三边长分别为2,3,x .则x 的取值范围是135<<x .其中正确命题的个数是 ( ) A.0 B.1 C.2 D.3 【答案】C【解析】①由正弦定文:sin sin a bA B=,所以,sin 10sin 605sin 17a B A b ⨯===> 这与0sin 1A <≤ 矛盾,所以①是假命题;②角形的三边的比是3:5:7,设最大边所对的角为θ ,则2223571cos 2352θ+-==-⨯⨯ ,因为60180θ<<所以,120θ= ,所以②是真命题.③当3x ≥时,长为x 的边所对的角θ 为最大角,因为△ABC 为锐角三角形,所以cos 0θ>即: 22222307223x x x +->⇒<⇒<⨯⨯当3x < 时,长为3的边所对的角θ 为最大角,因为△ABC 为锐角三角形,所以cos 0θ>即:22222305322x x x x+->⇒>⇒<<⨯⨯x <<.综上,命题都正确,故选C. 考点:1、正弦定文;2、余弦定文.5.已知向量(cos ,sin )A A =-m ,(cos ,sin )B B =n ,cos 2C ⋅=m n ,其中,,A B C 为ABC ∆的内角.(Ⅰ)求角C 的大小;(Ⅱ)若6AB =,且18CA CB ⋅=,求,AC BC 的长.【考点定位】向量的坐标运算、三角恒等变换、余弦定文.6.( 四川省遂宁市2016届高三第二次诊断考试数学文16)已知函数)(2cos sin sin 25)(R x x x A x f ∈+=,其中A 、B 、C 是ABC ∆的三个内角,且满足102)4cos(-=+πA ,)2,4(ππ∈A . (1)求sin A 的值;(2)若3()2f B =,且5=AC ,求BC 的值. 【答案】(1)4sin 5A =;(2)8=BC .【解析】(1)因为)2,4(ππ∈A ,所以)43,2(4πππ∈+A ,又102)4cos(-=+πA , 从而1027)4(cos 1)4sin(2=+-=+ππA A 所以544sin)4cos(4cos)4sin(]4)4sin[(sin =+-+=-+=ππππππA A A A . (2)23)21(sin 2sin 21sin 22cos sin 2)(22+--=-+=+=x x x x x x f , 因为3()2f B =所以1sinB 2=,从而6π=B 或65π(舍去)。
三角函数--2024年数学高考真题和模拟好题分类汇编(解析版)

专题三角函数1(新课标全国Ⅰ卷)已知cos(α+β)=m,tanαtanβ=2,则cos(α-β)=()A.-3mB.-m3C.m3D.3m【答案】A【分析】根据两角和的余弦可求cosαcosβ,sinαsinβ的关系,结合tanαtanβ的值可求前者,故可求cosα-β的值.【详解】因为cosα+β=m,所以cosαcosβ-sinαsinβ=m,而tanαtanβ=2,所以=12×2b×kb×sin A2+12×kb×b×sin A2,故cosαcosβ-2cosαcosβ=m即cosαcosβ=-m,从而sinαsinβ=-2m,故cosα-β=-3m,故选:A.2(新课标全国Ⅰ卷)当x∈[0,2π]时,曲线y=sin x与y=2sin3x-π6的交点个数为() A.3 B.4 C.6 D.8【答案】C【分析】画出两函数在0,2π上的图象,根据图象即可求解【详解】因为函数y=sin x的的最小正周期为T=2π,函数y=2sin3x-π6的最小正周期为T=2π3,所以在x∈0,2π上函数y=2sin3x-π6有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C3(新课标全国Ⅱ卷)设函数f(x)=a(x+1)2-1,g(x)=cos x+2ax,当x∈(-1,1)时,曲线y=f(x)与y=g(x)恰有一个交点,则a=()A.-1B.12C.1D.2【分析】解法一:令F x =ax 2+a -1,G x =cos x ,分析可知曲线y =F (x )与y =G (x )恰有一个交点,结合偶函数的对称性可知该交点只能在y 轴上,即可得a =2,并代入检验即可;解法二:令h x =f (x )-g x ,x ∈-1,1 ,可知h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即可得a =2,并代入检验即可.【详解】解法一:令f (x )=g x ,即a (x +1)2-1=cos x +2ax ,可得ax 2+a -1=cos x ,令F x =ax 2+a -1,G x =cos x ,原题意等价于当x ∈(-1,1)时,曲线y =F (x )与y =G (x )恰有一个交点,注意到F x ,G x 均为偶函数,可知该交点只能在y 轴上,可得F 0 =G 0 ,即a -1=1,解得a =2,若a =2,令F x =G x ,可得2x 2+1-cos x =0因为x ∈-1,1 ,则2x 2≥0,1-cos x ≥0,当且仅当x =0时,等号成立,可得2x 2+1-cos x ≥0,当且仅当x =0时,等号成立,则方程2x 2+1-cos x =0有且仅有一个实根0,即曲线y =F (x )与y =G (x )恰有一个交点,所以a =2符合题意;综上所述:a =2.解法二:令h x =f (x )-g x =ax 2+a -1-cos x ,x ∈-1,1 ,原题意等价于h x 有且仅有一个零点,因为h -x =a -x 2+a -1-cos -x =ax 2+a -1-cos x =h x ,则h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即h 0 =a -2=0,解得a =2,若a =2,则h x =2x 2+1-cos x ,x ∈-1,1 ,又因为2x 2≥0,1-cos x ≥0当且仅当x =0时,等号成立,可得h x ≥0,当且仅当x =0时,等号成立,即h x 有且仅有一个零点0,所以a =2符合题意;故选:D .4(全国甲卷数学(理)(文))已知cos αcos α-sin α=3,则tan α+π4=()A.23+1 B.23-1C.32D.1-3【答案】B【分析】先将cos αcos α-sin α弦化切求得tan α,再根据两角和的正切公式即可求解.【详解】因为cos αcos α-sin α=3,所以11-tan α=3,⇒tan α=1-33,所以tan α+π4 =tan α+11-tan α=23-1,故选:B .5(新高考北京卷)已知f x =sin ωx ω>0 ,f x 1 =-1,f x 2 =1,|x 1-x 2|min =π2,则ω=()A.1B.2C.3D.4【分析】根据三角函数最值分析周期性,结合三角函数最小正周期公式运算求解.【详解】由题意可知:x 1为f x 的最小值点,x 2为f x 的最大值点,则x 1-x 2 min =T 2=π2,即T =π,且ω>0,所以ω=2πT=2.故选:B .6(新高考天津卷)已知函数f x =sin3ωx +π3 ω>0 的最小正周期为π.则函数在-π12,π6 的最小值是()A.-32B.-32C.0D.32【答案】A【分析】先由诱导公式化简,结合周期公式求出ω,得f x =-sin2x ,再整体求出x ∈-π12,π6时,2x 的范围,结合正弦三角函数图象特征即可求解.【详解】f x =sin3ωx +π3 =sin 3ωx +π =-sin3ωx ,由T =2π3ω=π得ω=23,即f x =-sin2x ,当x ∈-π12,π6 时,2x ∈-π6,π3,画出f x =-sin2x 图象,如下图,由图可知,f x =-sin2x 在-π12,π6上递减,所以,当x =π6时,f x min =-sin π3=-32故选:A7(新高考上海卷)下列函数f x 的最小正周期是2π的是()A.sin x +cos xB.sin x cos xC.sin 2x +cos 2xD.sin 2x -cos 2x【答案】A【分析】根据辅助角公式、二倍角公式以及同角三角函数关系并结合三角函数的性质一一判断即可 .【详解】对A ,sin x +cos x =2sin x +π4,周期T =2π,故A 正确;对B ,sin x cos x =12sin2x ,周期T =2π2=π,故B 错误;对于选项C ,sin 2x +cos 2x =1,是常值函数,不存在最小正周期,故C 错误;对于选项D ,sin 2x -cos 2x =-cos2x ,周期T =2π2=π,故D 错误,故选:A .8(新课标全国Ⅱ卷)对于函数f(x)=sin2x和g(x)=sin2x-π4,下列说法正确的有() A.f(x)与g(x)有相同的零点 B.f(x)与g(x)有相同的最大值C.f(x)与g(x)有相同的最小正周期D.f(x)与g(x)的图像有相同的对称轴【答案】BC【分析】根据正弦函数的零点,最值,周期公式,对称轴方程逐一分析每个选项即可.【详解】A选项,令f(x)=sin2x=0,解得x=kπ2,k∈Z,即为f(x)零点,令g(x)=sin2x-π4=0,解得x=kπ2+π8,k∈Z,即为g(x)零点,显然f(x),g(x)零点不同,A选项错误;B选项,显然f(x)max=g(x)max=1,B选项正确;C选项,根据周期公式,f(x),g(x)的周期均为2π2=π,C选项正确;D选项,根据正弦函数的性质f(x)的对称轴满足2x=kπ+π2⇔x=kπ2+π4,k∈Z,g(x)的对称轴满足2x-π4=kπ+π2⇔x=kπ2+3π8,k∈Z,显然f(x),g(x)图像的对称轴不同,D选项错误.故选:BC9(新课标全国Ⅱ卷)已知α为第一象限角,β为第三象限角,tanα+tanβ=4,tanαtanβ=2+1,则sin(α+β)=.【答案】-22 3【分析】法一:根据两角和与差的正切公式得tanα+β=-22,再缩小α+β的范围,最后结合同角的平方和关系即可得到答案;法二:利用弦化切的方法即可得到答案.【详解】法一:由题意得tanα+β=tanα+tanβ1-tanαtanβ=41-2+1=-22,因为α∈2kπ,2kπ+π2,β∈2mπ+π,2mπ+3π2,k,m∈Z,则α+β∈2m+2kπ+π,2m+2kπ+2π,k,m∈Z,又因为tanα+β=-22<0,则α+β∈2m+2kπ+3π2,2m+2kπ+2π,k,m∈Z,则sinα+β<0,则sinα+βcosα+β=-22,联立sin2α+β+cos2α+β=1,解得sinα+β=-223.法二:因为α为第一象限角,β为第三象限角,则cosα>0,cosβ<0,cosα=cosαsin2α+cos2α=11+tan2α,cosβ=cosβsin2β+cos2β=-11+tan2β,则sin(α+β)=sinαcosβ+cosαsinβ=cosαcosβ(tanα+tanβ)=4cosαcosβ=-41+tan2α1+tan2β=-4(tanα+tanβ)2+(tanαtanβ-1)2=-442+2=-223故答案为:-22 3.10(全国甲卷数学(文))函数f x =sin x-3cos x在0,π上的最大值是.【答案】2【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【详解】f x =sin x -3cos x =2sin x -π3 ,当x ∈0,π 时,x -π3∈-π3,2π3,当x -π3=π2时,即x =5π6时,f x max =2.故答案为:2一、单选题1(2024·宁夏石嘴山·三模)在平面直角坐标系中,角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点P 1,2 ,则7cos 2θ-2sin2θ=()A.-15B.15C.-2D.2【答案】A【分析】由题意可知:tan θ=2,根据倍角公式结合齐次化问题分析求解.【详解】由题意可知:tan θ=2,所以7cos 2θ-2sin2θ=7cos 2θ-4sin θcos θsin 2θ+cos 2θ=7-4tan θtan 2θ+1=7-4×222+1=-15.故选:A .2(2024·广东茂名·一模)已知cos α+π =-2sin α,则sin 2α-3cos α+π2cos αcos2α+1=()A.-1B.-25C.45D.78【答案】D【分析】根据给定条件,求出tan α,再结合诱导公式及二倍角的余弦公式,利用正余弦齐次式法计算得解.【详解】由cos α+π =-2sin α,得cos α=2sin α,则tan α=12,所以sin 2α-3cos α+π2 cos αcos2α+1=sin 2α+3sin αcos α2cos 2α=12tan 2α+32tan α=18+34=78.故选:D3(2024·河北保定·二模)函数f (x )=1-e x1+e xcos2x 的部分图象大致为()A. B.C. D.【答案】A【分析】根据函数的奇偶性判断即可.【详解】设g x =1-e x1+e x,则g-x=1-e-x1+e-x=e x-11+e x=-g x ,所以g x 为奇函数,设h x =cos2x,可知h x 为偶函数,所以f x =1-e x1+e xcos2x为奇函数,则B,C错误,易知f0 =0,所以A正确,D错误.故选:A.4(2024·山东济宁·三模)已知函数f(x)=(3sin x+cos x)cos x-12,若f(x)在区间-π4,m上的值域为-3 2,1,则实数m的取值范围是()A.π6,π2B.π6,π2C.π6,7π12D.π6,7π12【答案】D【分析】利用二倍角公式、辅助角公式化简函数f(x),再借助正弦函数的图象与性质求解即得.【详解】依题意,函数f(x)=3sin x cos x+cos2x-12=32sin2x+12cos2x=sin2x+π6,当x∈-π4,m时,2x+π6∈-π3,2m+π6,显然sin-π3=sin4π3=-32,sinπ2=1,且正弦函数y=sin x在π2,4π3上单调递减,由f(x)在区间-π4,m上的值域为-32,1,得π2≤2m+π6≤4π3,解得π6≤m≤7π12,所以实数m的取值范围是π6,7π12.故选:D5(2024·江西景德镇·三模)函数f x =cosωx x∈R在0,π内恰有两个对称中心,fπ=1,将函数f x 的图象向右平移π3个单位得到函数g x 的图象.若fα +gα =35,则cos4α+π3=()A.725B.1625C.-925D.-1925【答案】A【分析】根据y轴右边第二个对称中心在0,π内,第三个对称中心不在0,π内可求得32≤ω<52,结合fπ=1可得ω=2,再利用平移变换求出g x ,根据三角变换化简fα +gα =35可得sin2α+π6=35,然后由二倍角公式可解.【详解】由x∈0,π得ωx∈0,ωπ,因为函数f x 在0,π内恰有两个对称中心,所以3π2≤ωπ5π2>ωπ,解得32≤ω<52,又fπ=cosωπ=1,所以ωπ=kπ,k∈Z,即ω=k,k∈Z,所以ω=2,将函数f x 的图象向右平移π3个单位得到函数y=cos2x-π3=cos2x-2π3,即g x =cos2x-2π3,因为fα +gα =cos2α+cos2α-2π3=32sin2α+12cos2α=sin2α+π6=35,所以cos4α+π3=1-2sin22α+π6=1-2×35 2=725.故选:A6(2024·安徽马鞍山·三模)已知函数f(x)=sin2ωx+cos2ωx(ω>1)的一个零点是π2,且f(x)在-π6,π16上单调,则ω=()A.54B.74C.94D.114【答案】B【分析】整理可得f(x)=2sin2ωx+π4,以2ωx+π4为整体,根据单调性分析可得1<ω≤2,再结合零点分析求解.【详解】因为f(x)=sin2ωx+cos2ωx=2sin2ωx+π4,x∈-π6,π16,且ω>1时,可得2ωx+π4∈-π3ω+π4,π8ω+π4,且-π3ω+π4<0<π8ω+π4,若f(x)在-π6,π16上单调,则-π3ω+π4≥-π2π8ω+π4≤π2,解得1<ω≤2,又因为f(x)的一个零点是π2,则πω+π4=kπ,k∈Z,解得ω=k-14,k∈Z,所以k=2,ω=7 4 .故选:B.7(2024·山东临沂·二模)已知函数f x =sin2x+φϕ <π2图象的一个对称中心为π6,0,则()A.f x 在区间-π8,π3上单调递增B.x=5π6是f x 图象的一条对称轴C.f x 在-π6,π4上的值域为-1,32D.将f x 图象上的所有点向左平移5π12个长度单位后,得到的函数图象关于y轴对称【答案】D【分析】借助整体代入法结合正弦函数的性质可得A、B;结合正弦函数最值可得C;得到平移后的函数解析式后借助诱导公式即可得D.【详解】由题意可得2×π6+φ=kπk∈Z,解得φ=-π3+kπk∈Z,又ϕ <π2,故φ=-π3,即f x =sin2x-π3;对A:当x∈-π8 ,π3时,2x-π3∈-7π12,π3,由函数y=sin x在-7π12,π3上不为单调递增,故f x 在区间-π8 ,π3上不为单调递增,故A错误;对B:当x=5π6时,2x-π3=4π3,由x=4π3不是函数y=sin x的对称轴,故x=5π6不是f x 图象的对称轴,故B错误;对C:当x∈-π6 ,π4时,2x-π3∈-2π3,π6,则f x ∈-1,1 2,故C错误;对D:将f x 图象上的所有点向左平移5π12个长度单位后,可得y=sin2x+2×5π12-π3=sin2x+π2=cos2x,该函数关于y轴对称,故D正确.故选:D.8(2024·广东广州·二模)已知函数f(x)=2sin(ωx+φ)ω>0,|φ|<π2的部分图象如图所示,若将函数f(x)的图象向右平移θ(θ>0)个单位后所得曲线关于y轴对称,则θ的最小值为()A.π8B.π4C.3π8D.π2【答案】A【分析】根据给定的图象特征,结合五点法作图列式求出ω和φ,再根据图象的平移变换,以及图象的对称性即可得解.【详解】由fπ4=1,得sinπ4ω+φ=22,又点π4,1及附近点从左到右是上升的,则π4ω+φ=π4+2kπ,k∈Z,由f5π8=0,点5π8,0及附近点从左到右是下降的,且上升、下降的两段图象相邻,得5π8ω+φ=π+2kπ,k∈Z,联立解得ω=2,φ=-π4+2kπ,k∈Z,而|φ|<π2,于是φ=-π4,f(x)=2sin2x-π4,若将函数f(x)的图像向右平移θ(θ>0)个单位后,得到y=sin2x-2θ-π4,则-2θ-π4=π2-kπ,k∈Z,而θ>0,因此θ=-3π8+kπ2,k∈N,所以当k=1时,θ取得最小值为π8 .故选:A9(2024·四川雅安·三模)已知函数f x =sin ωx +3cos ωx (ω>0),则下列说法中正确的个数是()①当ω=2时,函数y =f x -2log πx 有且只有一个零点;②当ω=2时,函数y =f x +φ 为奇函数,则正数φ的最小值为π3;③若函数y =f x 在0,π3 上单调递增,则ω的最小值为12;④若函数y =f x 在0,π 上恰有两个极值点,则ω的取值范围为136,256.A.1 B.2C.3D.4【答案】B【分析】利用辅助角公式化简函数,由图象分析判断①;由正弦函数的性质判断②③;由极大值的意义结合正弦函数的性质判断④.【详解】依题意,ω>0,函数f (x )=212sin ωx +32cos ωx =2sin ωx +π3,对于①:f (x )=2sin 2x +π3,令y =f x -2log πx =0,即f x =2log πx ,作出函数y =f (x )和函数y =2log πx 的图象,如图,观察图象知,两个函数在0,7π12 上只有一个零点,f 13π12 =2sin 5π2=2,当x =13π12时,y =2log π13π12=2log π1312+2log ππ=2+2log π1312>2,当x >13π12时,2log πx >2≥f (x ),因此函数y =f x 与函数y =2log πx 的图象有且只有一个交点,①正确;对于②:f (x +φ)=2sin 2x +2φ+π3 为奇函数,则2φ+π3=k π,k ∈Z ,φ=-π6+k π2,k ∈Z ,即正数φ的最小值为π3,②正确;对于③:当x ∈0,π3 时,ωx +π3∈π3,π(ω+1)3,由y =f x 在0,π3 上单调递增,得π(ω+1)3≤π2ω>0,解得0<ω≤12,正数ω有最大值12,③错误;对于④:当x ∈(0,π)时,ωx +π3∈π3,ωπ+π3,而y =f x 在(0,π)上恰有两个极值点,由正弦函数的性质得3π2<ωπ+π3≤5π2,解得76<ω≤136,因此ω的取值范围是76,136,④错误.综上,共2个正确,故选:B .10(2024·河北保定·二模)已知tan α=3cos αsin α+11,则cos2α=()A.-78B.78C.79D.-79【答案】B【分析】利用切化弦和同角三角函数的关系,解出sin α,再结合二倍角公式即可求解.【详解】因为sin αcos α=3cos αsin α+11,所以4sin 2α+11sin α-3=0,解得sin α=14或sin α=-3(舍去),所以cos2α=1-2sin 2α=78.故选:B .11(2024·河北衡水·三模)已知sin (3α-β)=m sin (α-β),tan (2α-β)=n tan α,则m ,n 的关系为()A.m =2nB.n =m +1mC.n =m m -1D.n =m +1m -1【答案】D【分析】利用和差角的正弦公式化简,结合已知列出方程即可求解.【详解】依题意,sin (3α-β)=sin [(2α-β)+α]=sin (2α-β)cos α+cos (2α-β)sin α,sin (α-β)=sin [(2α-β)-α]=sin (2α-β)cos α-cos (2α-β)sin α,则sin (2α-β)cos α+cos (2α-β)sin α=m sin (2α-β)cos α-m cos (2α-β)sin α,即sin (2α-β)cos αcos (2α-β)sin α=m +1m -1,即tan (2α-β)tan α=m +1m -1=n .故选:D12(2024·辽宁沈阳·三模)已知tan α2=2,则sin 2α2+sin α的值是()A.25B.45C.65D.85【答案】D【分析】利用二倍角公式和同角之间的转化,进行求解判断选项【详解】当tan α2=2,则sin 2α2+sin α=sin 2α2+2sin α2cos α2sin 2α2+cos 2α2=tan 2α2+2tan α2tan 2α2+1=22+2×222+1=85故选:D13(2024·贵州黔东南·二模)已知0<α<β<π,且sin α+β =2cos α+β ,sin αsin β-3cos αcos β=0,则tan α-β =()A.-1 B.-32C.-12D.12【答案】C【分析】找出tan α和tan β的关系,求出tan α和tan β即可求解.【详解】∵sin αsin β-3cos αcos β=0,∴sin αsin β=3cos αcos β,∴tan αtan β=3①,∵sin α+β =2cos α+β ,∴tan α+β =2⇒tan α+tan β1-tan αtan β=2⇒tan α+tan β1-3=2,∴tan α+tan β=-4②,由①②解得tan α=-1tan β=-3或tan α=-3tan β=-1 ,∵0<α<β<π,∴tan α<tan β,∴tan α=-3tan β=-1 ,∴tan α-β =tan α-tan β1+tan αtan β=-12.故选:C .二、多选题14(2024·河北张家口·三模)已知函数f (x )=23cos 2x +2sin x cos x ,则下列说法正确的是()A.函数f (x )的一个周期为2πB.函数f (x )的图象关于点π3,0 对称C.将函数f (x )的图象向右平移φ(φ>0)个单位长度,得到函数g (x )的图象,若函数g (x )为偶函数,则φ的最小值为5π12D.若f 12α-5π24 -3=12,其中α为锐角,则sin α-cos α的值为6-308【答案】ACD【分析】利用三角恒等变换公式化简,由周期公式可判断A ;代入验证可判断B ;根据平移变化求g (x ),由奇偶性可求出φ,可判断C ;根据已知化简可得sin α-π12 =14,将目标式化为2sin α-π12 -π6 ,由和差角公式求解可判断D .【详解】对于A ,因为f (x )=31+cos2x +sin2x =2sin 2x +π3+3,所以f (x )的最小值周期T =2π2=π,所以2π是函数f (x )的一个周期,A 正确;对于B ,因为f π3 =2sin 2×π3+π3 +3=3,所以,点π3,0 不是函数f (x )的对称中心,B 错误;对于C ,由题知,g x =f (x -φ)=2sin 2(x -φ)+π3 +3=2sin 2x +π3-2φ +3,若函数g (x )为偶函数,则π3-2φ=π2+k π,k ∈Z ,得φ=-π12-k π2,k ∈Z ,因为φ>0,所以φ的最小值为5π12,C 正确;对于D ,若f 12α-5π24-3=2sin 212α-5π24 +π3 =2sin α-π12 =12,则sin α-π12 =14,因为α为锐角,-π12<α-π12<5π12,所以cos α-π12 =154,所以sin α-cos α=2sin α-π4 =2sin α-π12 -π6=232sin α-π12 -12cos α-π12=232×14-12×154=6-308,D 正确.故选:ACD 15(2024·辽宁鞍山·模拟预测)已知函数f x =sin x ⋅cos x ,则()A.f x 是奇函数B.f x 的最小正周期为2πC.f x 的最小值为-12D.f x 在0,π2上单调递增【答案】AC【分析】首先化简函数f x =12sin2x ,再根据函数的性质判断各选项.【详解】f x =sin x ⋅cos x =12sin2x ,函数的定义域为R ,对A ,f -x =-12sin2x =-f x ,所以函数f x 是奇函数,故A 正确;对B ,函数f x 的最小正周期为2π2=π,故B 错误;对C ,函数f x 的最小值为-12,故C 正确;对D ,x ∈0,π2 ,2x ∈0,π ,函数f x 不单调,f x 在0,π4 上单调递增,在π4,π2上单调递减,故D 错误.故选:AC16(2024·安徽·三模)已知函数f x =sin x -3cos x ,则()A.f x 是偶函数B.f x 的最小正周期是πC.f x 的值域为-3,2D.f x 在-π,-π2上单调递增【答案】AC【分析】对于A ,直接用偶函数的定义即可验证;对于B ,直接说明f 0 ≠f π 即可否定;对于C ,先证明-3≤f x ≤2,再说明对-3≤u ≤2总有f x =u 有解即可验证;对于D ,直接说明f -5π6>f -2π3 即可否定.【详解】对于A ,由于f x 的定义域为R ,且f -x =sin -x -3cos -x =-sin x -3cos x =sin x -3cos x =f x ,故f x 是偶函数,A 正确;对于B ,由于f 0 =sin0 -3cos0=-3,f π =sinπ -3cosπ=3,故f 0 ≠f π ,这说明π不是f x 的周期,B 错误;对于C ,由于f x =sin x -3cos x ≤sin x +3cos x =sin x +3cos x 2≤sin x +3cos x 2+3sin x -cos x 2=sin 2x +3cos 2x +23sin x cos x +3sin 2x +cos 2x -23sin x cos x =4sin 2x +4cos 2x =4=2,且f x =sin x -3cos x ≥-3cos x ≥-3,故-3≤f x ≤2.而对-3≤u ≤2,有f 0 =-3≤u ,f 5π6 =2≥u ,故由零点存在定理知一定存在x ∈0,5π6使得f x =u .所以f x 的值域为-3,2 ,C 正确;对于D ,由于-π<-5π6<-2π3<-π2,f -5π6 =2>3=f -2π3 ,故f x 在-π,-π2上并不是单调递增的,D 错误.故选:AC .17(2024·山西太原·模拟预测)已知函数f x =sin 2x +φ 0<φ<π2 的图象关于直线x =π12对称,且h x =sin2x -f x ,则()A.φ=π12B.h x 的图象关于点π6,0中心对称C.f x 与h x 的图象关于直线x =π4对称 D.h x 在区间π6,5π12内单调递增【答案】BCD【分析】根据正弦函数的对称性求解φ判断A ,先求出h x =sin 2x -π3,然后利用正弦函数的对称性求解判断B ,根据对称函数的性质判断C ,结合正弦函数的单调性代入验证判断D .【详解】由题意得2×π12+φ=π2+k π,k ∈Z ,解得φ=π3+k π,k ∈Z ,又因为0<φ<π2,所以φ=π3,A 错误;由φ=π3可知f x =sin 2x +π3,则h x =sin2x -sin 2x +π3 =12sin2x -32cos2x =sin 2x -π3,令2x -π3=k π,k ∈Z ,解得x =π6+k π2,k ∈Z ,令k =0,得x =π6,所以点π6,0 是曲线y =h x 的对称中心,B 正确;因为f π2-x =sin 2π2-x +π3 =sin 4π3-2x =sin 2x -π3=h x ,所以f x 与h x 的图象关于直线x =π4对称,C 正确;当x ∈π6,5π12 时,2x -π3∈0,π2 ,故h x 在区间π6,5π12内单调递增,D 正确.故选:BCD 18(2024·浙江金华·三模)已知函数f x =sin2ωx cos φ+cos2ωx sin φω>0,0<φ<π2的部分图象如图所示,则()A.φ=π6B.ω=2C.f x +π6为偶函数 D.f x 在区间0,π2的最小值为-12【答案】ACD【分析】先由正弦展开式,五点法结合图象求出f x =sin 2x +π6,可得A 正确,B 错误;由诱导公式可得C 正确;整体代入由正弦函数的值域可得D 正确.【详解】由题意得f x =sin 2ω+φ ,由图象可得f 0 =12⇒sin φ=12,又0<φ<π2,所以φ=π6,由五点法可得ω×4π3+π6=3π2⇒ω=1,所以f x =sin 2x +π6 .A :由以上解析可得φ=π6,故A 正确;B :由以上解析可得ω=1,故B 错误;C :f x +π6 =sin 2x +π6 +π6=cos2x ,故C 正确;D :当x ∈0,π2 ⇒2x +π6∈π6,7π6 时,sin 2x +π6 ∈-12,1,所以最小值为-12,故D 正确;故选:ACD .19(2024·浙江温州·二模)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,P -3,4 为其终边上一点,若角β的终边与角2α的终边关于直线y =-x 对称,则()A.cos π+α =35B.β=2k π+π2+2αk ∈Z C.tan β=724D.角β的终边在第一象限【答案】ACD【分析】根据三角函数的定义,可求角α的三角函数,结合诱导公式判断A 的真假;利用二倍角公式,求出2α的三角函数值,结合三角函数的概念指出角2α的终边与单位圆的交点,由对称性确定角β终边与单位圆交点,从而判断BCD 的真假.【详解】因为角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边经过点P -3,4 ,所以:OP =5,所以sin α=45,cos α=-35,所以cos π+α =-cos α=35,故A 对;又sin2α=2sin α⋅cos α=2×45×-35 =-2425,cos2α=cos 2α-sin 2α=-35 2-45 2=-725,所以2α的终边与单位圆的交点坐标为:-725,-2425 ,因为角β的终边与角2α的终边关于直线y =-x 对称,所以角β的终边与单位圆的交点为2425,725,所以tan β=724,且β的终边在第一象限,故CD 正确;又因为终边在直线y =-x 的角为:k π-π4,k ∈Z ,角2α的终边与角β的终边关于y =-x 对称,所以2α+β2=k π-π4⇒β=2k π-π2-2αk ∈Z ,故B 错误.故选:ACD20(2024·广东佛山·二模)已知函数f x =sin x +cos2x 与g x =sin2x +cos x ,记h x =λf x +μg x ,其中λ,μ∈R 且λ2+μ2≠0.下列说法正确的是()A.h x 一定为周期函数B.若λ⋅μ>0,则h x 在0,π2上总有零点C.h x 可能为偶函数 D.h x 在区间0,2π 上的图象过3个定点【答案】ABD【分析】对于A :计算h x +2π ,化简即可;对于B :求出h x ,然后计算h 0 h π2的正负即可;对于C :计算h x ,h -x 是否恒相等即可;对于D :令f x =0g x =0,求解x 即可.【详解】对于A ,∀x ∈R ,h x +2π =λf x +2π +μg x +2π =λf x +μg x =h x ,A 正确;对于B ,h x =λcos x -2sin2x +μ2cos2x -sin x ,则h 0 =λ+2μ,h π2=-3μ,因为λμ>0,即λ,μ同号,所以h 0 h π2<0,由零点存在定理知h x 在0,π2上总有零点,故B 正确;对于C ,h x =λsin x +λcos2x +μsin2x +μcos x ,h -x =-λsin x +λcos2x -μsin2x +μcos x ,由h x =h -x 得2λsin x +2μsin2x =2λsin x +2μ⋅2sin x cos x =2sin x λ+2μcos x =0对x ∈R 恒成立,则λ=μ=0与题意不符,故C 错误;对于D ,令f x =0g x =0 ,则sin x +cos2x =1-2sin 2x +sin x =-sin x -1 2sin x +1 =0sin2x +cos x =cos x 2sin x +1 =0 ⇒sin x =1或sin x =-12cos x =0或sin x =-12,即x ∈-π6+2k π,π2+2k π,7π6+2k π ,k ∈Z ,故所有定点坐标为-π6+2k π,0 ,π2+2k π,0 ,7π6+2k π,0 ,k ∈Z ,又因为x ∈0,2π ,所以函数h x 的图象过定点π2,0 ,7π6,0 ,11π6,0 ,故D 正确;故选:ABD .21(2024·湖南·二模)已知函数f x =12cos 2x -π3 ,把y =f x 的图象向右平移π3个单位长度,得到函数y =g x 的图象,以下说法正确的是()A.x =π6是y =f x 图象的一条对称轴B.f x 的单调递减区间为k π+π6,k π+2π3k ∈Z C.y =g x 的图象关于原点对称D.f x +g x 的最大值为12【答案】ABD【分析】根据题意,求得g x =-12cos2x 的图象,结合三角函数的图象与性质,以及两角差的正弦公式,逐项判定,即可求解.【详解】将函数f x =12cos 2x -π3 的图象向右平移π3个单位长度,得到函数y =g x =12cos 2x -π =-12cos2x 的图象,对于A 中,令x =π6,求得f x =12,即为函数y =f x 最大值,所以直线x =π6是函数f x 图象的一条对称轴,所以A 正确;对于B 中,令2k π≤2x -π3≤2k π+π,k ∈Z ,解得k π+π6≤x ≤k π+2π3,k ∈Z ,可得f x 的单调减区间为k π+π6,k π+2π3,k ∈Z ,所以B 正确.对于C 中,由于g x =-12cos2x 是偶函数,可得函数g x 的图象关于y 轴对称,所以C 错误.对于D 中,由f x +g x =12cos 2x -π3 +-12cos2x =1212cos2x +32sin2x -12cos2x =34sin2x -14cos2x =12sin 2x -π6 ≤12,即f x +g x 的最大值为12,所以D 正确.故选:ABD .22(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0),则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2,则ω=2B.当ω=1,x ∈0,π2时,f x 的值域为-3,2 C.当ω=1时,f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点,则5≤ω<8【答案】BCD【分析】根据三角恒等变换化简f x =2sin 2ωx +π3,进而根据周期可判断A ,根据整体法求解函数的值域判断B ,根据函数图象的平移可判断C ,根据零点个数确定不等式满足的条件可判断D .【详解】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3,对于A ,若f x 相邻两条对称轴的距离为π2,则T =2×π2=π=2π2ω,故ω=1,A 错误,对于B ,当ω=1,f x =2sin 2x +π3 ,当x ∈0,π2 时,2x +π3∈π3,4π3,则f x 的值域为-3,2 ,B 正确,对于C ,当ω=1,f x =2sin 2x +π3,f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6,C 正确,对于D ,当x ∈0,π6 时,2ωx +π3∈π3,2ωπ6+π3,若f x 在区间0,π6 上有且仅有两个零点,则2π≤2ωπ6+π3<3π,解得5≤ω<8,故D 正确,故选:BCD 三、填空题23(2024·北京·三模)已知函数f (x )=sin x cos ωx ,x ∈R .①若ω=1,则f (x )的最小正周期是;,②若ω=2,则f (x )的值域是.【答案】π[-1,1]【分析】把ω=1代入,t 明智二倍角的正弦,结合正弦函数的周期求出f (x )的最小正周期;把ω=2代入,利用二倍角的余弦公式,借助换元法,利用导数求出f (x )的值域.【详解】当ω=1时,f (x )=sin x cos x =12sin2x ,函数f (x )的最小正周期为2π2=π;当ω=2时,f (x )=sin x cos2x =sin x (1-2sin 2x ),令sin x =t ∈[-1,1],g (t )=t (1-2t 2)=-2t 3+t ,求导得g (t )=-6t 2+1,当-1≤t <-66或66<t ≤1时,g (t )<0,当-66<t <66时,g (t )>0,函数g (t )在-1,-66 ,66,1 上单调递减,在-66,66上单调递增,g (-1)=1,g 66 =69,g (1)=-1,g -66 =-69,所以g (t )min =-1,g (t )max =1,f (x )的值域是[-1,1].故答案为:π;[-1,1]24(2024·北京·模拟预测)已知函数f (x )=sin ωx -2cos ωx (ω>0),且f α+x =f α-x .若两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,则sin4α=.【答案】-45/-0.8【分析】利用辅助角公式化简f (x )的解析式,再由题意可得函数关于x =α对称,且最小正周期T =π,即可求出ω的值,从而得到2α=φ+π2+k π,k ∈Z ,再由二倍角公式及同角三角函数的基本关系计算可得.【详解】因为f (x )=sin ωx -2cos ωx =5sin ωx -φ ,其中tan φ=2,由f α+x =f α-x ,可得f x 关于x =α对称,又两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,所以f x 的最小正周期T =π,又ω>0,所以2πω=π,解得ω=2,所以f x =5sin 2x -φ ,所以2α-φ=π2+k π,k ∈Z ,则2α=φ+π2+k π,k ∈Z ,所以sin4α=sin2φ+π2+k π =sin 2φ+π+2k π =-sin2φ=-2sin φcos φsin 2φ+cos 2φ=-2tan φtan 2φ+1=-2×222+1=-45.故答案为:-4525(2024·湖北荆州·三模)设0<α<β<π2,tan α=m tan β,cos α-β =35,若满足条件的α与β存在且唯一,则m =,tan αtan β=.【答案】191【分析】由tan α=m tan β得到sin αcos β=m cos αsin β,再结合cos α-β =35,利用sin α-β =-45,得到cos αsin β=-45m -1 ,sin αcos β=-4m5m -1 ,从而sin α+β =-4m +1 5m -1,再由满足条件的α与β存在且唯一,得到α+β唯一,从而sin α+β =-4m +15m -1=1,求得m 即可.【详解】解:由tan α=m tan β,得sin αcos α=m sin βcos β,即sin αcos β=m cos αsin β,因为0<α<β<π2,tan α=m tan β,所以-π2<α-β<0,0<m <1,又cos α-β =35,所以sin α-β <0,从而sin α-β =sin αcos β-cos αsin β=m -1 cos αsin β=-45,所以cos αsin β=-45m -1,所以sin αcos β=m cos αsin β=-4m5m -1,所以sin α+β =sin αcos β+cos αsin β=-4m +15m -1,因为α,β∈0,π2,所以α+β∈0,π ,因为满足条件的α与β存在且唯一,所以α+β唯一,所以sin α+β =-4m +1 5m -1=1,所以m =19,经检验符合题意,所以tan α=19tan β,则tan α-β =-43=tan α-tan β1+tan αtan β=tan α-9tan α1+9tan 2α,解得tan α=13,所以tan αtan β=9tan 2α=1.故答案为:19,1【点睛】关键点点睛:关键是结合已知得出sin α+β =-4m +15m -1 =1,求出m ,由此即可顺利得解.。
2016届高考数学全国名校试题分项汇编(江苏特刊)专题04三角函数与三角形(第02期)(原卷版)

第四章 三角函数与三角形一、填空1. 【淮安、宿迁、连云港、徐州苏北四市2016届高三第二次调研】函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示,若5=AB ,则ω的值为 .2. 【江苏省淮阴中学2015-2016学年度第一学期期中考试】三角形的三个内角的度数之比为1:2:3,其最小内角的弧度数为 .3. 【江苏省淮阴中学2015-2016学年度第一学期期中考试】角β的终边和角α=-1035°的终边相同,则cos β= . 4. 【江苏省淮阴中学2015-2016学年度第一学期期中考试】扇形的半径为2,圆心角为3π,则此扇形的面积为 .5. 【江苏省淮阴中学2015-2016学年度第一学期期中考试】如图,点P 从(1,0)出发,沿单位圆按顺时针方向运动3π弧长到达Q 点,则Q 点的坐标为 .6. 【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】已知7sin cos 13αα+=-,π(,0)2α∈-,则tan α= .7. 【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】若α、β均为锐角,且1cos 17α=,47cos()51αβ+=-,则cos β= . 8. 【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成”函数,给出下列函数:⑴1()sin cos f x x x =+;⑵2()f x x =+⑶3()cos )f x x x =+;⑷4()sin f x x =;⑸5()2cos (sin cos )222x x xf x =+,其中“互为生成”函数的有 .(请填写序号)9. 【江苏省清江中学数学模拟试卷】将函数sin y x =的图象向左平移(02)ϕϕπ≤<个单位后,得到函数sin()6y x π=-的图象,则ϕ等于 .10. 【江苏省清江中学2016届高三上学期周练数学试题】将函数sin 2y x =的图象向左平移ϕ(0ϕ>)个单位,可得到函数sin 24y x π⎛⎫=+⎪⎝⎭的图象,则ϕ的最小值为 . 11. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】若ααcos 2sin =,则αα22cos 2sin +的值为________12. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】函数()sin (0)f x x x x π=-≤≤的单调增区间是________13. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】在锐角ABC ∆中,角A,B,C的对边分别是a,b,c,8,10a b ==,ABC ∆的面积为,则ABC ∆的最大角的正切值是________14. 【扬州市2015—2016学年度第一学期期末检测试题】已知函数)32sin()(π+=x x f (π<x ≤0),且21)()(==βαf f (βα≠),则=+βα ▲ . 15. 【镇江市2016届高三年级第一次模拟考试】 函数y =a sin(ax +θ)(a >0,θ≠0)图象上的一个最高点和其相邻最低点的距离的最小值为________.16. 【镇江市2016届高三年级第一次模拟考试】由sin 36°=cos 54°,可求得cos 2 016°的值为________.17. 【南京市、盐城市2016届高三年级第一次模拟考试数学】在ABC ∆中,设,,a b c 分别为角,,A B C 的对边,若5a =,4A π=,3cos 5B =,则边c = ▲ . 18. 【苏州市2016届高三年级第一次模拟考试】已知θ是第三象限角,且2sin 2cos 5θθ-=-,则sin cos θθ+= ▲ .19. 【苏州市2016届高三年级第一次模拟考试】已知函数f (x )=|sin |x -kx (x ≥0,k ∈R )有且只有三个零点,设此三个零点中的最大值为0x ,则200(1)sin 2x x x += ▲ . 20. 【泰州市2016届高三第一次模拟考试】已知函数π()sin()cos cos()262x x f x A x θ=+--(其中A 为常数,(π,0)θ∈-),若实数123,,x x x 满足:①123x x x <<,②31x x -<2π,③123()()()f x f x f x ==,则θ的值为 ▲ .21.【江苏歌风中学(如皋办学)高三数学九月月考】函数()cos sin 222x xx f x ⎛⎫=-⎪⎝⎭的最小正周期为 ▲ . 22. 【江苏歌风中学(如皋办学)高三数学九月月考】若函数()sin()(0)6f x x πωω=+>图象的两条相邻的对称轴之间的距离为2π,且该函数图象关于点0(,0)x 成中心对称,0[0,]2x π∈,则0x = ▲ .23. 【江苏歌风中学(如皋办学)高三数学九月月考】已知函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭.若()(0)2y f x πϕϕ=-<<是偶函数,则ϕ= .24. 【江苏省扬州中学高三数学月考试卷】将y =sin2x 的图像向右平移φ单位(φ>0),使得平移后的图像仍过点⎝ ⎛⎭⎪⎫π3,32,则φ的最小值为_______.二、解答1. 【淮安、宿迁、连云港、徐州苏北四市2016届高三第二次调研】在锐角三角形ABC 中,角C B A ,,的对边为c b a ,,,已知53sin =A ,21)tan(-=-B A , (1)求B tan ; (2)若5=b ,求c .2. 【江苏省淮阴中学2015-2016学年度第一学期期中考试】(本小题满分14分)已知tan α是关于x 的方程2210x x --=的一个实根,且α是第三象限角. (1)求2sin cos sin cos αααα-+的值;(2)求cos sin αα+的值.3. 【江苏省启东中学2015~2016学年度第一学期第一次阶段测试】(本小题满分14分)已知ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,满足sin sin sin sin b a B Cc B A--=+.⑴求角A 的值;⑵若a ,c ,b 成等差数列,试判断ABC ∆的形状.4. 【江苏省清江中学数学模拟试卷】(14分)已知A ,B ,C 是三角形ABC ∆三内角,向量(m =-,(cos ,sin )n A A =,且1m n ∙=.(1)求角A ; (2)若221sin 23cos sin BB B+=--,求tan C . 5. 【江苏省清江中学2016届高三上学期周练数学试题】已知函数()22sin cos sin cos f x x x a x a x b =+-+(a ,R b ∈). (1)若0a >,求函数()f x 的单调增函数;(2)若,44x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()f x 的最大值为3,最小值为1,求a ,b 的值. 6. 【江苏省清江中学数学模拟试卷】(15分)在一个六角形体育馆的一角MAN 内,用长为a的围栏设置一个运动器材存储区域(如图所示),已知0120A ∠=,B 是墙角线AM 上的一点,C 是墙角线AN 上的一点.(1)若20BC a ==,求存储区域面积的最大值;(2)若10AB AC ==,在折线MBCN 内选一点D ,使20BD DC +=,求四边形存储区域DBAC 的最大面积.7. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】(本小题满分14分)已知函数()sin()f x A x ωϕ=+(其中,,A ωϕ为常数,且0,0,22A ππωϕ>>-<<)的部分图像如图所示.(1)求函数()f x 的解析式(2)若6(),0,52f παα=<<,求(2)12f πα+的值8. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】(本小题满分14分)在ABC ∆中,45B ∠=,D 是边BC 上一点,5,3,7AD CD AC === (1)求ADC ∠的值,(2)求BA DA ⋅的值9. 【扬州市2015—2016学年度第一学期期末检测试题】已知函数x x x x f ωωωcos sin cos 3)(2+=(0>ω)的周期为π.(1)当⎥⎦⎤⎢⎣⎡∈20π,x 时,求函数)(x f 的值域;(2)已知ABC ∆的内角A ,B ,C 对应的边分别为a ,b ,c ,若3)2(=A f ,且4=a ,5=+c b ,求ABC ∆的面积.10. 【南京市、盐城市2016届高三年级第一次模拟考试数学】设函数()sin()(0,0,,)22f x A x A x R ππωϕωϕ=+>>-<<∈的部分图象如图所示.(1)求函数()y f x =的解析式; (2)当[,]22x ππ∈-时,求()f x 的取值范围.11. 【苏州市2016届高三年级第一次模拟考试】(本小题满分14分)在ABC ∆中,三个内角A ,B , C 所对的边分别为a ,b ,c ,且满足cos cos 2cos a B +b AC c=.(1)求角C 的大小;第15题图(2)若ABC ∆的面积为,6a b +=,求边c 的长.12. 【江苏省如东高级中学2016届高三上学期期中考试数学试题】已知函数())(0)f x ϕϕπ=+<<,()f x '为()f x 的导函数,若()()()g x f x f x '=+为奇函数,求ϕ的值.13.【江苏歌风中学(如皋办学)高三数学九月月考】已知函数()2cos()(0,)6f x x x R πωω=+>∈的最小正周期为10π.⑴求函数()f x 的对称轴方程; ⑵设,[0,]2παβ∈,56516(5),(5)35617f f ππαβ+=--=,求cos()αβ+的值. 14. 【江苏歌风中学(如皋办学)高三数学九月月考】如图,某市新体育公园的中心广场平面图如图所示,在y 轴左侧的观光道曲线段是函数sin()(0,0,0)y A x A ωϕωϕπ=+>><<,[4,0]x ∈-时的图象且最高点B (-1,4),在y 轴右侧的曲线段是以CO 为直径的半圆弧. ⑴试确定A ,ω和ϕ的值;⑵现要在右侧的半圆中修建一条步行道CDO (单位:米),在点C 与半圆弧上的一点D 之间设计为直线段(造价为2万元/米),从D 到点O 之间设计为沿半圆弧的弧形(造价为1万元/米).设DCO θ∠=(弧度),试用θ来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)15. 【江苏省扬州中学高三数学月考试卷】(本小题满分14分)已知函数f (x )=sin(ωx +φ) (ω>0,0<φ<π),其图像经过点M ⎝⎛⎭⎫π3,12,且与x 轴两个相邻的交点的距离为π. (1)求f (x )的解析式;(2)在△ABC 中,a =13,f (A )=35,f (B )=513,求△ABC 的面积。
2014届高三名校数学(文)试题分省分项汇编 专题04 三角函数与三角形

一.基础题组1. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知4cos()65πα-=,则sin()3πα+= .2. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】求值:002cos10sin 20cos 20-= .3. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知向量(sin ,1),(1,cos ),22a b ππθθθ==-<< .(1) 若a b ⊥,求θ;(2) 求a b +的最大值.4. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知ABC ∆的周长1,且sin sin A B C + (1)求边AB 的长; (2)若ABC ∆的面积为1sin 6C ,求角C .5. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】如图,两座建筑物AB ,CD 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m 和15m ,从建筑物AB 的顶部A 看建筑物CD 的张角045CAD ∠=. (1)求BC 的长度;(2)在线段BC 上取一点P (点P 与点B ,C 不重合),从点P 看这两座建筑物的张角分别为APB α∠=,DPC β∠=,问点P 在何处时,tan()αβ+最小?BC的长度是18 m.………………………7分6. 【南京市、盐城市2014届高三第一次模拟考试】在ABC ∆中,2BC =,23A π=,则AB AC ⋅的最小值为 .7. 【南京市、盐城市2014届高三第一次模拟考试】 在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,已知2c =,3C π=.(1)若ABC ∆a ,b ;(2)若sin sin()2sin 2C B A A +-=,求ABC ∆的面积.【答案】(1)2a =,2b =;(2 【解析】8. 【江苏省通州高级中学2013-2014学年度秋学期期中考试】已知ααcos 21sin +=,且)2,0(πα∈,则)4sin(2cos παα-的值为__ ▲____.【答案】214- 【解析】试题分析:由22sin cos 11sin cos 2αααα⎧+=⎪⎨=+⎪⎩,且02πα<<可解得:1sin 4cos αα⎧=⎪⎪⎨⎪=⎪⎩,则22cos 2cos )sin()422αααπα==+=-考点:三角化简求值9. 【江苏省通州高级中学2013-2014学年度秋学期期中考试】 在△ABC 中,内角A ,B ,C 所对边长分别为a ,b ,c , AC AB ∙=8,∠BAC =θ,a =4, (1)求b ·c 的最大值及θ的取值范围;(2)求函数f (θ)=23sin 2(π4+θ)+2cos 2θ-3的最值.当2+62ππθ=,即=6πθ时,max f()3θ=. 考点:1.余弦定理;2.三角函数的图象;3.基本不等式10. 【江苏省扬州中学2013—2014学年第一学期月考】若动直线)(R a a x ∈=与函数())()cos()66f x xg x x ππ=+=+与的图象分别交于N M ,两点,则||MN 的最大值为 .11. 【江苏省扬州中学2013—2014学年第一学期月考】设向量),cos ,(sin x x a =),sin 3,(sin x x b =x ∈R ,函数)2()(b a a x f +⋅=.(1)求函数)(x f 的单调递增区间;(2)求使不等式()2f x '≥成立的x 的取值集合.12. 【苏北四市2014届高三第一次质量检测】 在△ABC 中,已知3AB =,o 120A =,且ABC ∆,则BC 边长为 .13. 【苏北四市2014届高三第一次质量检测】已知函数()2sin(2)(0)4f x x ωωπ=->的最大值与最小正周期相同,则函数()f x 在[11]-,上的单调增区间为 .14. 【苏北四市2014届高三第一次质量检测】已知向量(cos ,sin )θθ=a ,(2,1)=-b .(1)若⊥a b ,求sin cos sin cos θθθθ-+的值;(2)若2-=a b ,(0,)2θπ∈,求sin()4θπ+的值.15. 【苏州市2014届高三调研测试】 若函数()sin()f x x θ=+(π02θ<<)的图象关于直线π6x =对称,则θ = ▲ .16. 【苏州市2014届高三调研测试】已知π3sin()45x +=,π4sin()45x -=,则tan x = ▲ .17. 【苏州市2014届高三调研测试】 在△ABC 中,设角A ,B ,C 的对边分别为a ,b ,c ,且1cos 2a C c b +=.(1)求角A 的大小;(2)若a =4b =,求边c 的大小.18. 【江苏省兴化市安丰高级中学2014届高三12月月考】已知)0,2(πα-∈,53cos =α,则=+)4tan(πα .19.【江苏省兴化市安丰高级中学2014届高三12月月考】在ABC ∆中,若2,60,7a Bb =∠=︒,则c = .20.二.能力题组1. 【江苏省诚贤中学2014届高三数学月考试题】在△ABC ,已知.sin sin 3)sin sin )(sin sin sin (sin C B A C B C B A =-+++(1)求角A 值;(2)求C B cos sin 3-的最大值. 【答案】⑴3A π=;⑵ 1. 【解析】试题分析:⑴根据题意观察所给代数式特点可见此式中全为角的正弦,结合正弦定理可化角为边转化为()()3a b c b c a bc +++-=,可将此式变形为222b c a bc +-=,根据特征可联想到余弦定理2.【江苏省兴化市安丰高级中学2014届高三12月月考】已知(c o s ,s i n ),(c os a b ααββ==. (1)若67πβα=-,求a b ⋅ 的值; (2)若4,58a b πα⋅== ,且⎪⎭⎫⎝⎛-∈-0,2πβα,求tan()αβ+的值.3. 【江苏省兴化市安丰高级中学2014届高三12月月考】 在锐角△ABC 中,角A 、B 、C的对边分别为a 、b 、c ,且 .3tan )(222bc A a c b =-+ (1)求角A ;(2)若2a =,求ABC ∆面积S 的最大值.4.三.拔高题组1. 【江苏省诚贤中学2014届高三数学月考试题】如图,两座建筑物CD AB ,的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9cm 和15cm ,从建筑物AB 的顶部A 看建筑物CD 的视角︒=∠45CAD .求BC 的长度;在线段BC 上取一点(P 点P 与点C B ,不重合),从点P 看这两座建筑物的视角分别为,,βα=∠=∠DPC APB 问点P 在何处时,βα+最小?2.。
专题04 三角函数与三角形(第01期)-决胜2016年高考全国名校试题文数分项汇编(北京特刊)(原卷版)

第四章 三角函数与三角形一.基础题组1.(北京市朝阳区2015年高三第一次综合练习文6)函数ππ()2sin()cos()66f x x x =--图象的一条对称轴方程是( ) A .π6x =B. π3x =C. 5π12x =D. 2π3x = 2.(北京市丰台区2014-2015学年度第二学期统一练习(一)文6)将函数cos y x =的图象向右平移6π个单位长度,再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( ) A .1cos()26y x π=-B .1cos()23y x π=-C .cos(2)6y x π=-D .cos(2)3y x π=- 3.(北京市丰台区2015届高三5月统一练习(二)文3)已知函数()sin f x x =,[2,2]x ππ∈-,则方程1()2f x =的所有根的和等于( ) (A) 0 (B) π (C) –π (D) - 2π4.(北京市石景山区2015届高三3月统一测试(一模)文2)函数sin()1y x π=--的图象( )A B .关于y 轴对称 C .关于原点对称 D .关于x π=对称5.(北京市延庆县2014—2015学年度高二第二学期期末考试文9)把函数sin y x =(x R ∈)的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( )A.sin(2)3y x π=+,x R ∈ B.sin()26x y π=+,x R ∈ C.sin(2)3y x π=-,x R ∈ D.sin(2)32y x π=+,x R ∈6.(北京市延庆县2014—2015学年度高二第二学期期末考试文11)=+ 75sin 15sin .7.(北京市石景山区2015届高三3月统一测试(一模)文9)已知角α的终边经过点(,6)P x -,则x 的值为 .8.(北京市丰台区2015届高三5月统一练习(二)文11)在锐角△ABC 中,AB =AC =2,△ABC 的面积是4,则sin A = ,BC = .9.(北京市东城区2015届高三5月综合练习(二)文10)在△ABC 中,已知2,3a b ==, 那么sin sin()AA C =+ .10.(北京市西城区2015届高三二模文12)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =,3b =,2c =,则A =____;ABC ∆的面积为____.11.(北京市西城区2015届高三一模考试文10)函数22()sin cos f x x x =-的最小正周期是____. 12.(北京市朝阳区2015年高三第一次综合练习文15)在ABC ∆中,π3A =,cos B =,6BC =. (Ⅰ)求AC 的长; (Ⅱ)求ABC ∆的面积.13.(北京市丰台区2014-2015学年度第二学期统一练习(一)文15)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知52=b ,4B π=,552cos =C . (Ⅰ)求c 的值; (Ⅱ)求ABC ∆的面积.14.(北京市西城区2015届高三一模考试文15)如图,在ABC ∆中,90ABC ∠= ,4AB =,3BC =,点D 在线段AC 上,且4AD DC =. (Ⅰ)求BD 的长; (Ⅱ)求sin CBD ∠的值.二.能力题组 1.(北京市房山区2015年高三第一次模拟文5)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且1a =,45B =︒, 2ABC S =△,则 b 等于( )A. B .5 C .41 D .252.(北京市延庆县2015届高三3月模拟文3)设sin 393,cos55,tan50a b c =︒=︒=︒,则,,a b c的大小关系为( )A. a b c << B .c b a << C .b a c << D .a c b <<B C AD3.(北京市延庆县2015届高三3月模拟文11)在错误!未找到引用源。
【名师解析】新课标I版高三名校数学理试题分省分项汇编专题04三角函数与三角形版含解析(20200419183125)

一.基础题组
1. 【山 西 省 长治二中 康杰中学 临汾一中 忻州一中 2013 届 高 三 第 四 次 四 校 联 考 】在
ABC 中,角 A、B、C 所对的边分别为 a,b,c 且 a=1, B=45°, S ABC =2,则 b 等于 ( )
D. f x 的单调递增区间是 k
,k
kZ
3
6
3. 【 2013 年河南省十所名校高三第三次联考试题】在△ ABC 中, a, b, c 分别是角 A,
B, C的对边,若
a 2+ b2 = 2014 c 2 ,则
2 tan A tan B tan C (tan A+ tan
B)
的值为 (
)
A. 0
B
A. 5
B
.25 C . 41
D. 5 2
2. 【唐山市 2013-2014 学年度高三年级摸底考试】已知 sin 2
1 ,则 cos2 (
)
3
4
()
A.
1
B.
2
1
C.
D .2
3
3
3
3
3. 【河北唐山开滦二中 2013~2014 学年度第一学期高三年级期中考试】
则 2cos 2 (
) 1=( )
62
------ 珍贵文档 ! 值得收藏! ------
------ 精品文档 ! 值得拥有! ------
13. 【唐山市 2013-2014 学年度高三年级摸底考试】(本小题满分
12 分)在 ABC 中,角
A, B,C 所对的边分别是 a, b, c ,已知 c sin A (Ⅰ)求 C ;
高三数学(文)百所名校好题速递分项解析汇编 4.三角函数与三角形(第02期)

一.基础题组1.【江西省吉安市第一中学2016届高三上学期第四次周考数学文试题】已知函数()3=sin 3cos ,44f x x x x R ππ⎛⎫⎛⎫--+∈ ⎪ ⎪⎝⎭⎝⎭,则f x( )A.最大值为2,且图象关于点,012π⎛⎫⎪⎝⎭对称 B.周期为,且图象关于点,012π⎛⎫⎪⎝⎭对称 C.最大值为2,且图象关于512x对称 D.周期为2,且图象关于点,012π⎛⎫- ⎪⎝⎭对称 【答案】A 【解析】考点:三角函数()sin y A x ωϕ=+的性质.2.【湖南省师大附中、长沙一中、长郡中学、雅礼中学2016届高三四校联考数学(文)试题】计算107cos 47cos 17cos 47sin +的结果等于( ) A.21-B.23C.22D.21【答案】D.【解析】试题分析:sin 47cos17cos 47cos(9017)sin 47cos17cos 47(sin17)++=+-1sin(4717)sin 302=-==,故选D. 考点:三角恒等变形.3.【湖南省师大附中、长沙一中、长郡中学、雅礼中学2016届高三四校联考数学(文)试题】在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若ab C c b a =-+tan )(222,则角C 的值为( ) A.6π或65π B.3π或32π C.6π D.32π 【答案】A. 【解析】考点:余弦定理.【思路点睛】由已知条件,可先将切化弦,再结合正弦定理,将该恒等式的边都化为角,然后进行三角函数式的恒等变形,找出角之间的关系;或将角都化成边,然后进行代数恒等变形,可一题多解,多角度思考问题,从而达到对知识的熟练掌握.4.【炎德·英才大联考湖南师大附中2016届高三月考试卷(四)文科数学试卷】在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,若223a b bc -=,sin 23C B =,则A =( )A .150B .120C .60D .30 【答案】D 【解析】试题分析:因为sin 23C B =,所以由正弦定理得,b c 32=.又因223a b bc -=,所以由余弦定理得,23232222222=--+=-+=bc bc b c b bc a c b A cos ,所以A=30。
2016届高三数学(理)百所名校好题速递分项解析汇编(第02期)4.三角函数与三角形 含解析

一.基础题组1【江西省吉安市第一中学2016届高三上学期第四次周考数学理试题】已知ABC 中,角,,A B C 的对边分别是,,a b c ,若2sin sin a b c B A,则ABC 是( )A.等边三角形 B 。
锐角三角形 C 。
等腰直角三角形 D.钝角三角形 【答案】C 【解析】考点:1.正弦定理;2。
基本不等式.2【河北省衡水中学2016届高三上学期四调考数学(理)试题】函数cos tan y x x (22x)的大致图象是( )A .B .C .D . 【答案】C 【解析】试题分析:由于当22x时,cos 0xsin cos tan cos sin ,(,)cos 22x y x xxx x x, 故选C .考点:三解函数的图象.3【湖南省衡阳市第八中学2016届高三上学期第三次月考数学(理)】函数x x x f 32cos 32sin )(+=的图象中相邻的两条对称轴间距离为( )A .π3 B .34π C .23πD .67π【答案】C 【解析】考点:两角和的正弦4【江西省南昌市第二中学2016届高三上学期第四次考试数学(理)试题】在△ABC 中,c b a ,,为角C B A ,,的对边,若CcB b A a sin cos cos ==,则ABC ∆是( )A .锐角三角形B 。
钝角三角形C 。
等腰三角形D 。
等边三角形 【答案】C 【解析】 试题分析:sin sin sin 1tan tan 1cos cos sin cos cos sin a b c A B CA B A B A B C A B C==∴===∴==∴=,所以ABC ∆是等腰三角形。
考点:正弦定理.5【江西省南昌市第二中学2016届高三上学期第四次考试数学(理)试题】将函数()()sin 20y x ϕϕ=+>的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的最小值为( )A .43π B .83π C .4π D .8π【答案】C 【解析】试题分析:将函数()()sin 20y x ϕϕ=+>的图象沿x 轴向左平移8π个单位后,得到一个偶函数sin 2sin 284[()]()y x x ππϕϕ=++=++的图象,可得42ππϕ+=,求得ϕ的最小值为 4π,故选:B .考点:函数(n )si y A x ωϕ=+的图象变换.6【湖南省衡阳市第八中学2016届高三上学期第三次月考数学(理)】在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,若7=a ,3=b ,2=c ,则=∠A ( )A .30B . 45C .60 D .90【答案】C 【解析】试题分析:由余弦定理()222222321cos 0,223223b c aA A A bcππ+-+-∠===∈∴=⨯⨯选C考点:余弦定理7【湖南省师大附中、长沙一中、长郡中学、雅礼中学2016届高三四校联考数学(理)试题】将函数x y 2cos =的图象向左平移4π个单位,得到函数x x f y cos )(⋅=的图象,则)(x f 的表达式可以是() A .x x f sin 2)(-= B .x x f sin 2)(= C .x x f 2sin 22)(=D .)2cos 2(sin 22)(x x x f +=【答案】A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题04 三角函数与三角形2016届高三数学(文)百所名校好题速递分项解析汇编一.基础题组1. 【哈尔滨市第六中学2016届上学期期中考试4】已知sin()cos()0,322πππααα++-=-<<则2cos()3πα+等于( ) A.45-B.35-C.45D.35【答案】C 【解析】试题分析:3sin()cos()sin cos cos sin sin sin 32332ππππααααααα++-=++=+14cos sin 2665ππαααα⎫⎛⎫⎛⎫=+=+=+=-⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎭,又 24cos()cos()sin()32665ππππααα+=++=-+= 考点:三角恒等变换2. 【山东师范大学附属中学2016届高三上学期第二次模拟考试3】已知4,0cos ,tan 225x x x π⎛⎫∈-== ⎪⎝⎭且则( )A.724B. 724-C.247D. 247-【答案】D 【解析】试题分析:∵(,0)2x π∈-,4cos 5x =,∴3sin 5x =-,∴sin 3tan cos 4x x x ==-, ∴22tan 24tan 21tan 7x x x ==--. 考点:平方关系、倍角关系.3. 【山东师范大学附属中学2016届高三上学期第二次模拟考试4】为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需把函数sin 2y x =的图象( )A.向左平移3π个单位长度 B. 向右平移3π个单位长度 C.向左平移6π个单位长度D. 向右平移6π个单位长度【答案】D考点:三角函数图象的平移.4. 【三明一中2016届(上)第一次月考3】在锐角△ABC 中,角A ,B 所对的边长分别为a ,b ,若2a sinB =b ,则角A 等于( )A .π12B .π6C .π4D .π3【答案】B 【解析】试题分析:由正弦定理及2a sin B =b ,得B B A sin sin sin 2=,所以21sin =A ,又因为)2,0(π∈A ,所以6π=A ;故选B .考点:正弦定理.5. 【三明一中2016届(上)第一次月考6】函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则这个函数的周期和初相分别是( )A .2,-π3B .2,-π6C .π,-π6D .π,-π3【答案】D 【解析】试题分析:由图象,得πππ43312543=+=T ,即2,==ωπT ,故排除选项A 、B ,代入点)2,125(π,得21252πϕπ=+⨯,解得3πϕ-=;故选D . 考点:三角函数的图象与性质.6. 【浙江省嘉兴市一中2016届上学期高三期中5】已知△ABC 的三边a ,b ,c 所对角分别为A ,B ,C ,且sin sin 2BAab=,则cosB 的值为( ▲ )A .B . 12C . 12-D . 【答案】C考点:正弦定理.7. 【河北省衡水中学2016届高三二调7】已知tan 2θ=,则22sin sin cos 2cos θθθθ+-=( )A .43-B .54C .34-D .45【答案】D 【解析】试题分析:由题222222sin sin cos 2cos sin sin cos 2cos sin cos θθθθθθθθθθ+-+-=+ 22tan tan 242241tan 55θθθ+-+-===+,故选D.考点:同角三角函数性质8. 【华中师大一附中2016届上学期高三期中检测5】在ABC ∆中,已知030,8,A a b ===,则三角形的面积为( )A .B .16C .或16D .或 【答案】D考点:正弦定理的应用9. 【华中师大一附中2016届上学期高三期中检测7】函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的图象如图所示,为了得到()sing x A x ω=的图象,可以将()f x 的图象( ) A .向右平移12π个单位长度 B .向右平移6π个单位长度 C .向左平移12π个单位长度 D .向左平移6π个单位长度【答案】B 【解析】试题分析:由题根据所给函数图像应用五点法求得函数解析式,然后变为同名函数根据平移知识得到选项. 由图知,A=1,712434T πππ=-=, 22T ππωω∴==∴=,,()2,,sin 2sin 23336f x x x ππππϕπϕ⎛⎫⎛⎫⎛⎫∴⨯+=∴=∴=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ,()sin 2,g x x ∴= 故选B. 考点:三角函数图像与性质10. 【江西临川一中2016届高三第二次月考4】函数]2,0[,1cos 4cos 32π∈+-=x x x y 的最小值为( )A .31-B .0C .31D .1 【答案】A 【解析】试题分析:由题根据所给函数利用二次函数性质分析计算即可.22213cos 4cos 13cos ,[0,],332y x x x x π⎛⎫=-+=--∈ ⎪⎝⎭2cos 3x ∴=时,所给函数取得最小值31-,故选A.考点:三角函数的最值11. 【江西临川一中2016届高三第二次月考14】设),(20πα∈,若,54)6cos(=+πα则=+)122sin(πα【解析】试题分析:20,,2663ππππαα⎛⎫∈∴+∈ ⎪⎝⎭(,),43cos(),sin()6565ππαα+=∴+=, 2724cos 212sin ,sin 26625625πππααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫∴+=-+=+= ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦,sin(2)sin 2sin 2123464πππππααα⎡⎤⎡⎤⎛⎫∴+=+-=+-=⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦考点:三角函数化简求值;倍角、半角公式;角的变换;两角和与差的三角函数12.【西藏日喀则地区一高2016届上学期10月检测9】已知函数()cos f x x x ωω=+(0ω>)的图象与x 轴交点的横坐标构成一个公差为2π的等差数列,把函数()f x 的图象沿x 轴向左平移6π个单位,得到函数()g x 的图象.关于函数()g x ,下列说法正确的是( )A .在,42ππ⎡⎤⎢⎥⎣⎦上是增函数 B .其图象关于直线4x π=-对称C .函数()g x 是奇函数D .当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,函数()g x 的值域是[]2,1- 【答案】D试题分析:由两角和的正弦把三角函数化简,结合已知求出周期,进一步得到ω,则三角函数的解析式可求,再由图象平移得到g (x )的解析式,画出其图象,则答案可求.∵()cos f x x x ωω=+1cos )2sin()26x x x πωωω=+=+, 由题意知,则,22T π=则T=π, ∴()2sin(2)6f x x π=+,把函数()f x 的图象沿x 轴向左平移6π个单位,得 ()()2sin[2()]2sin(2)2cos 26662g x f x x x x ππππ=+=++=+=其图象如图:由图可知:在,42ππ⎡⎤⎢⎥⎣⎦上是减函数,故A 错误; 其图象的对称中心为(,0)4π-,故B 错误;函数为偶函数,故C 错误; 当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,函数()g x 的值域是[]2,1-,故D 正确. 故选D .考点:函数y=Asin (ωx+φ)的图象变换.13. 【黑龙江省牡丹江市一高2016届高三10月月考5】在△ABC 中,AB=4,AC =6,2=⋅BC AB ,则BC=( )( )A . 4B .C .62D . 16【解析】 试题分析:如上图所示:由2=⋅BC AB ,得2=B a cos 4-。
设α=∠CBD ,所以21=αcos a …①,在直角三角形CBD 中,得αsin CD a =.在直角三角形ACD 中,由勾股定理得,3622=++αsin 2142a )(…②,①②联立得4=a .故选A 。
考点:解三角形。
14. 【黑龙江省牡丹江市一高2016届高三10月月考】内的图象是 ( )【答案】D 【解析】试题分析:可知,tan sin tan sin y x x x x =+-- 2tan ()232sin ()2x x x x ππππ⎧<≤⎪⎪=⎨⎪<<⎪⎩,结合正切函数及正弦函数图像可知选D 。
考点:已知函数解析式作图。
15. 【黑龙江省牡丹江市一高2016届高三10月月考7】在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知a c tan 21tan A cB b+=,则C =( ) A 、30° B 、45° C 、45°或135° D 、60° 【答案】B考点:①解三角形;②正弦定理的应用。
16.【河北省衡水中学2016届高三二调3】设02x π≤<sin cos x x =-,则( )A .04x π≤≤ B .544x ππ≤≤C .744x ππ≤≤D .322x ππ≤≤ 【答案】B 【解析】试题分析:502cos sin cos ,44x x x x x x πππ≤<-=-∴≤≤,故选B. 考点:同角三角函数性质17. 【辽宁省抚顺市第一中学2016届高三10月月考6】已知函数sin()y A x m ωϕ=++的最大值为4,最小值为0,最小正周期为2π,直线3x π=是其图像的一条对称轴,则下面各式中符合条件的解析式是( ) A .4sin(4)6y x π=+ B .2sin(2)23y x π=++ C .2sin(4)23y x π=++ D .2sin(4)26y x π=++ 【答案】D 【解析】试题分析:最大值减去最小值等于2A ,所以A=2;最小正周期为2π,由周期公式得,4=ω;直线3x π=是其图像的一条对称轴,则z k k ∈+=+⋅,32ππϕπω,即z k k ∈-=,65ππϕ,显然1=k 时6πϕ=。
故选D 。
考点:由三角函数数性质求三角函数解析式。
【方法点睛】由三角函数的性质求解析式,振幅满足2A 等于最大值减去最小值;ωπ2T =,正弦函数对称轴满足z k k x ∈+=+,2ππϕω,余弦函数的对称轴满足z k k x ∈=+,πϕω;常数项b 满足最大值与最小值的和等于2b;对于ϕ的计算常利用五点法或代入点的坐标求解,然后利用 ϕ的范围确定具体的值。
18. 【河北衡水中学2016届上学期高三三调3】设ABC ∆的内角A B C 、、的对边分别为a b c 、、,若22cos 3a c A ===,,,且b c <,则b =( )B.2C.D.3 【答案】B 【解析】试题分析:222284cos 28,2293b c a A b b b bc +-==∴+-=∴=.考点:余弦定理.19.【浙江省嘉兴市一中2016届上学期高三期中4】为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需把函数sin 2y x =的图象( ▲ )A . 向左平移3π个单位长度 B . 向右平移3π个单位长度 C . 向左平移6π个单位长度D . 向右平移6π个单位长度【答案】D 【解析】试题分析:因为sin 2sin 236y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,所以只需将函数sin 2y x =的图像向右平移6π各单位即可得到函数sin 23y x π⎛⎫=-⎪⎝⎭的图象;故D 正确. 考点:三角函数伸缩平移变换.20. 【甘肃省兰州一中2016届高三上学期期中6】已知角α的终边过点P (-8m ,-6sin 30°),且cos α=-45,则m 的值为( )A .12B . -12C .-32D .32【答案】A 【解析】试题分析:点()8,3P m -- , r ∴=,4cos 5α∴==-,即22641664925m m =+.解得 214m =. 4cos 05α=-<,80,0m m ∴-<∴>.所以12m =.故A 正确. 考点:任意角的三角函数.【易错点晴】本题主要考查任意角三角函数的定义,属容易题.本题在解得214m =时容易忽视m 的符号而错选.因根据余弦值的符号确定点横坐标的符号,从而可得m 的符号.21. 【甘肃省兰州一中2016届高三上学期期中2】已知函数()(cos 2cos sin 2sin )sin ,f x x x x x x =+x R ∈,则()f x 是( ).A 最小正周期为π的奇函数 .B 最小正周期为π的偶函数 .C 最小正周期为2π的奇函数 .D 最小正周期为2π的偶函数【答案】A 【解析】试题分析:()1()(cos 2cos sin 2sin )sin cos 2sin cos sin sin 22f x x x x x x x x x x x x =+=-==, 所以函数()f x 的周期22T ππ==,且函数()f x 为奇函数.故A 正确. 考点:1三角函数的化简,周期;2函数的奇偶性.【思路点晴】应先将函数()f x 用两角和差公式,二倍角公式化简变形为()()sin f x A x ωϕ=+的形式,再根据周期公式,和奇函数的定义判断函数的周期和奇偶性.22. 【江西临川一中2016届上学期高三期中5】三角形ABC 的内角A B C 、、的对边分别为a b c 、、,若a b c 、、成等比数列,且2c a =,则cos B =( )A .14 B .34C D【答案】B考点:1、等比数列的性质;2、余弦定理.23. 【浙江宁波效实中学2016届上学期高三期中考试5】函数sin(2)(0)y x ϕϕπ=+<<的图象向右平移8π后关于y 轴对称,则满足此条件的ϕ值为( ) A.4π B. 38π C. 34π D.58π 【答案】C. 【解析】试题分析:根据题意可知,函数sin(2)(0)y x ϕϕπ=+<<关于直线8x π=-对称,∴2()()82k k Z ππϕπ⨯-+=+∈,∴3()4k k Z πϕπ=+∈,又∵0ϕπ<<,∴31044k k -<<⇒=, ∴34πϕ=,故选C . 考点:三角函数的性质.24. 【重庆市巴蜀中学高2016级高三学期期中考试6】已知33cos()25πϕ-=,且2πϕ<,则tan ϕ为( ) A.43- B.43 C.34- D.34 【答案】C .【解析】试题分析:因为33cos()cos(2)cos()sin 2225πππϕπϕϕϕ-=--=+=-=,所以3sin 5ϕ=-,又因为2πϕ<,所以cos 0ϕ>,所以4cos 5ϕ===,所以3sin 35tan 4cos 45ϕϕϕ-===-,故应选C .考点:1、三角函数的诱导公式;2、同角三角函数的基本关系.25. 【山东师范大学附属中学2016届高三上学期第二次模拟考试13】若()cos sin 02a A b B ππ⎛⎫-++=⎪⎝⎭,内角A,B 的对边分别为,a b ,则三角形ABC 的形状为________. 【答案】等腰三角形或直角三角形考点:判断三角形形状.26. 【三明一中2016届(上)第一次月考13】如图所示,在平面直角坐标系xOy 中,角α的终边与单位圆交于点A ,点A 的纵坐标为32,则=αcos ________.【答案】-35 【解析】试题分析:由任意角的三角函数定义,得32sin =α,所以95sin 1cos 22=-=αα,又由图象,得角α是第二象限角,所以35cos -=α;故填-35. 考点:1.单位圆;2.同角三角函数基本关系式.27. 【华中师大一附中2016届上学期高三期中检测13】已知tan 2α=-,则()2sin cos αα-= .【答案】95【解析】试题分析:()2222222sin cos 2sin cos tan 12tan 9sin cos sin cos 1tan 5ααααααααααα+-+--===++.考点:同角三角函数的基本关系28. 【黑龙江省牡丹江市一高2016届高三10月月考13】已知2sin(2)33πα+=,则⎪⎭⎫⎝⎛+64sin πα的值是=【解析】试题分析:⎪⎭⎫⎝⎛+64sin πα])(sin[2322ππα-+=)](cos[322πα+-=)](sin [32212πα+--=91-=.考点:①倍角公式;②凑角求角的三角函数。
