空间几何练习题一(含答案)
(完整版)空间几何体练习题含答案
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
高一数学空间几何体试题答案及解析

高一数学空间几何体试题答案及解析1.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF平面EFDC.(Ⅰ)当,是否在折叠后的AD上存在一点,且,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由;(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.【答案】(1)存在点,;(2)当时,三棱锥的最大值.【解析】(1)与立体几何有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用空间中点、线、面的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(4)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.试题解析:解:(Ⅰ)假设存在使得满足条件CP∥平面ABEF在平面内过点作交于,在平面内作直线交于点,连结 3分∵∴ 4分∵5分又∴平面∥平面 6分又∵∴,故点就是所求的点 7分又∵∴ 8分(Ⅱ)因为平面ABEF平面EFDC,平面ABEF平面EFDC=EF,又AF EF,所以AF⊥平面EFDC 10分由已知BE=x,所以AF=x(),则FD=8x.∴ 12分故当且仅当,即=4时,等号成立所以,当=4时,有最大值,最大值为 14分解法二:故所以,当=4时,有最大值,最大值为 14分【考点】(1)探究性问题;(2)求体积的最大值.2.下图中的几何体是由哪个平面图形旋转得到的()【答案】A【解析】几何体的上半部分是一个圆锥,下半部分是一个圆台,故选A【考点】简单旋转体的概念3.一个正方体的顶点都在球面上,它的棱长为,则球的表面积是()A.B.C.D.【答案】B【解析】因为一个正方体的棱长为为2,则该正方体的对角线长为.又因为该正方体的顶点都在球面上,所以球的直径就是正方体的对角线,即球的半径.又因为球的表面积.故选B.【考点】1.球的内接正方体.2.球的表面积公式.3.长方体的对称性.4.若圆锥的表面积,侧面展开图的圆心角为,则该圆锥的体积为______.【答案】【解析】设该圆锥的底面圆的半径为,母线长为,因为侧面展开图的圆心角为,所以,因为圆锥的表面积,所以,所以该圆锥的体积为【考点】本小题主要考查圆锥的侧面积和表面积的关系以及圆锥的体积计算.点评:解决本题的关键是正确运用圆锥中相应的计算公式、圆锥的侧面展开图的关系等求出,进而求出圆锥的高,然后利用圆锥的体积公式计算体积.5.某高速公路收费站入口处的安全标识墩如图1所示。
空间几何体(习题及答案)

空间几何体(习题)1.判断正误,正确的打“√”,错误的打“×”①直角三角形绕一边所在直线旋转得到的旋转体是圆锥()②有两个面互相平行,其余各面都是等腰梯形的多面体是棱台()③棱台的上、下底面是相似多边形,并且互相平行()④直角梯形以其垂直于底边的腰所在直线为轴旋转所得的旋转体是圆台()⑤有两个面互相平行,其余各面都是平行四边形的多面体是棱柱()⑥有一个面是多边形,其余各面都是三角形的几何体叫棱锥()⑦所有侧面都是正方形的四棱柱一定是正方体()⑧一个棱锥可以有两条侧棱和底面垂直()⑨若正棱锥的底面边长与侧棱长相等,则该棱锥可以是六棱锥()2.如图,将装有水的长方体水槽ABCD-A1B1C1D1 固定底面棱BC 后,将水槽向右倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定13 3. 已知直角三角形的两直角边长分别为4 cm ,3 cm ,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积为 ()A .9π cm 2B .16π cm 2C .9π cm 2 或 25 πcm 2D .9π cm 2 或 16π cm 24. 若一个圆锥的侧面展开图是面积为 2π的半圆面,则该圆锥的体积为.5. 已知高为3 的直棱柱ABC -A 1B 1C 1 的底面是边长为 2 的正三角形(如图所示),则三棱锥 B 1-ABC 的体积为 .第 5 题图第 6 题图6. 已知三棱锥的底面是边长为 a 的正三角形,则过各侧棱中点的截面的面积为( )A. 3 a 2 4B. 3 a 28C. 3 a 2 16D. 3 a 2327. 一个直角梯形的上底、下底、高的比为1:2: ,则由它旋转而成的圆台的上底面积、下底面积和侧面积的比为.8.将一钢球放入底面半径为2 cm 的盛有一定量水的圆柱形玻璃容器中,钢球完全没入水中(水也没有溢出),且水面升高1cm,则钢球的半径为.39.如图,棱锥的底面ABCD 是一个矩形,AC 与BD 交于点M,VM 是棱锥的高,若VM=4 cm,AB=4 cm,VC=5 cm,求棱锥的体积.10.如图,在正四棱台ABCD-A′B′C′D′中,上、下底面边长分别为4 cm 和16 cm,O,O′分别为两底面的中心,OO′=17 cm,E,E′分别为BC,B′C′的中点,连接EE′,O′E′,OE,求这个棱台的侧棱BB′和斜高EE′.【参考答案】1. × × √ √ × × × × ×2. A3. D4.3 π 35.6. C7. 1:4:68. 1cm9.10. 325cm33BB ' = 19cm ,EE ' = 5 13cm 3。
空间解析几何习题答案

空间解析几何习题答案空间解析几何习题答案在学习数学的过程中,解析几何是一个重要的分支。
它通过坐标系和代数方法来研究几何图形的性质和变换。
而空间解析几何则是解析几何的一个延伸,它研究的是三维空间中的几何图形。
在空间解析几何的学习过程中,我们经常会遇到一些习题,下面我将给出一些空间解析几何习题的解答。
习题一:已知直线L1过点A(1, 2, 3)和点B(4, 5, 6),直线L2过点C(7, 8, 9)且与直线L1垂直,求直线L2的方程。
解答:首先,我们可以求出直线L1的方向向量。
直线L1的方向向量可以通过两点的坐标差来得到,即(4-1, 5-2, 6-3),即(3, 3, 3)。
因为直线L2与直线L1垂直,所以直线L2的方向向量与直线L1的方向向量垂直,即两个向量的点积为0。
设直线L2的方向向量为(a, b, c),则有3a + 3b + 3c = 0。
再代入直线L2过点C(7, 8, 9),得到7a + 8b + 9c = 0。
所以直线L2的方程为7x + 8y + 9z = d,其中d为常数。
习题二:已知点A(1, 2, 3)和点B(4, 5, 6),求直线AB的方程。
解答:直线AB的方向向量可以通过两点的坐标差来得到,即(4-1, 5-2, 6-3),即(3, 3, 3)。
设直线AB的方程为x = 1 + 3t,y = 2 + 3t,z = 3 + 3t,其中t为参数。
习题三:已知平面P过点A(1, 2, 3)、点B(4, 5, 6)和点C(7, 8, 9),求平面P的方程。
解答:平面P的法向量可以通过两个方向向量的叉积来得到。
设向量AB为(4-1, 5-2, 6-3),即(3, 3, 3),向量AC为(7-1, 8-2, 9-3),即(6, 6, 6)。
则平面P的法向量为(3, 3, 3) × (6, 6, 6),即(0, 0, 0)。
因为法向量为零向量,所以平面P的方程为0x + 0y + 0z = d,即0 = d,其中d为常数。
人教版数学高一第一章空间几何体单元测试精选(含答案)3

【答案】 2 1 3 4 2
评卷人 得分
三、解答题
试卷第 8页,总 11页
40.一张长为10cm ,宽为 5cm 的矩形纸,以它为侧面卷成一个圆柱,求该圆柱的体积.
125
【答案】
cm3 或 125
cm3 .
π
2π
41.如图所示,在四边形 ABCD 中, A0, 0 , B 1,0 , C 2,1 , D 0,3 ,将四边
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
【答案】A
8.如图所示,观察四个几何体,其中判断正确的是( ).
A.(1)是棱台 C.(3)是棱锥 【答案】C
B.(2)是圆台 D.(4)不是棱柱
试卷第 2页,总 11页
9.一个球的内接正方体的表面积为 54,则球的表面积为( )
1
PB1= A1B1,则多面体 P-BCC1B1 的体积为( )
4
A.
8 3
C.4
【答案】B
16
B.
3
D.5
评卷人 得分
二、填空题
27.圆台的上底面半径为 2,下底面半径为 3,截得此圆台的圆锥的高为 6,则此圆台
的体积为____________.
【答案】 38 π 3
28.已知在三棱锥 P ABC 中,侧面与底面所成的二面角相等,则点 P 在平面 ABC 内的射影一定是 ABC 的__________心.
所示),则其侧视图的面积是 ( )
A.4 3cm2
B.2 3 cm2
C.8 cm2
D.4 cm2
【答案】A 21.若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为( )
高一数学空间几何体试题答案及解析
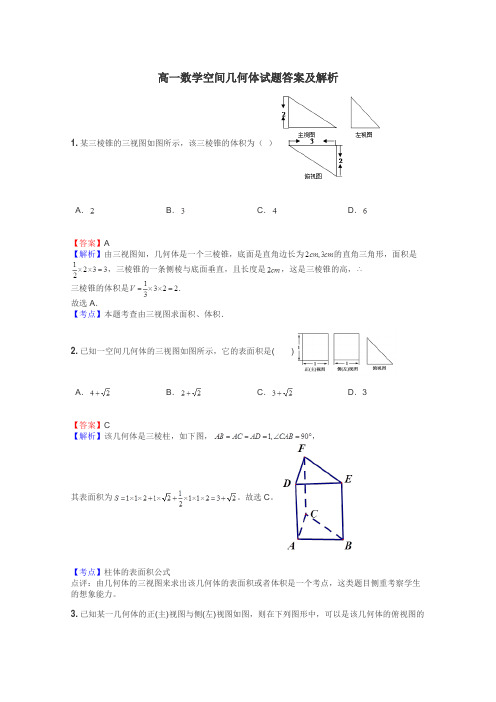
高一数学空间几何体试题答案及解析1.某三棱锥的三视图如图所示,该三棱锥的体积为()A.B.C.D.【答案】A【解析】由三视图知,几何体是一个三棱锥,底面是直角边长为的直角三角形,面积是,三棱锥的一条侧棱与底面垂直,且长度是,这是三棱锥的高,三棱锥的体积是.故选A.【考点】本题考查由三视图求面积、体积.2.已知一空间几何体的三视图如图所示,它的表面积是()A.B.C.D.3【答案】C【解析】该几何体是三棱柱,如下图,,其表面积为。
故选C。
【考点】柱体的表面积公式点评:由几何体的三视图来求出该几何体的表面积或者体积是一个考点,这类题目侧重考察学生的想象能力。
3.已知某一几何体的正(主)视图与侧(左)视图如图,则在下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①③④⑤D.①②③④【答案】D【解析】俯视图为⑤的几何体的侧视图如下,这与题目不相符,而①②③④符合题意。
故选D。
【考点】三视图点评:本题考查简单空间图形的三视图,考查空间想象能力,是基础题.4.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中,是的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求出该几何体的体积;(2)若是的中点,求证:∥平面;(3)求证:平面⊥平面.【答案】(1)4 (2)主要证明∥ (3)主要证明平面【解析】解:(1)由题意可知,四棱锥中,平面平面,,所以,平面,又,,则四棱锥的体积为.(2)连接,则∥,∥,又,所以四边形为平行四边形,∴∥,∵平面,平面,所以,∥平面.(3)∵,是的中点,∴⊥,又在直三棱柱中可知,平面平面,∴平面,由(2)知,∥,∴平面,又平面,所以,平面平面.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定.点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是由面面垂直的性质定理可得AB⊥平面ACDE,(2)的关键是分析出四边形ANME为平行四边形,即AN∥EM,(3)的关键是熟练掌握空间线线垂直,线面垂直与面面垂直之间的相互转化.5.如图是长方体被一平面所截得到的几何体,四边形为截面,长方形为底面,则四边形的形状为( )A.梯形B.平行四边形C.可能是梯形也可能是平行四边形D.不确定【答案】B【解析】因为,长方体中相对的平面互相平行,所以,被平面截后,EF,GH平行且相等,GF,EH 平行且相等,故四边形的形状为平行四边形,选B。
高三数学空间几何体试题

高三数学空间几何体试题1.(3分)(2011•重庆)高为的四棱锥S﹣ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为()A.B.C.1D.【答案】C【解析】由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,而球心到小圆圆心的距离为,则推出顶点S在球心距的垂直分的平面上,而顶点S到球心的距离为1,即可求出底面ABCD的中心与顶点S之间的距离.解:由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,点S,A,B,C,D均在半径为1的同一球面上,球心到小圆圆心的距离为,顶点S在球心距的垂直分的平面上,而顶点S到球心O的距离为1,所以底面ABCD的中心O'与顶点S之间的距离为1故选C点评:本题是基础题,考查球的内接多面体的知识,考查逻辑推理能力,计算能力,转化与划归的思想.2.如图,三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.(1)求证:平面AA1B1B⊥平面BB1C1C;(2)若AB=2,求三棱柱ABC—A1B1C1的体积.【答案】(1)见解析(2)2【解析】(1)由侧面AA1B1B为正方形,知AB⊥BB1.又AB⊥B1C,BB1∩B1C=B1,所以AB⊥平面BB1C1C,又AB⊂平面AA1B1B,所以平面AA1B1B⊥平面BB1C1C.(2)由题意,CB=CB1,设O是BB1的中点,连接CO,则CO⊥BB1.由(1)知,CO⊥平面AA1B1B,且CO=BC=AB=.连结AB1,则VC—ABB1=S△ABB1·CO=AB2·CO=.因为VB1—ABC=VC—ABB1=VABC—A1B1C1=,故三棱柱ABC—A1B1C1的体积VABC—A1B1C1=2.3.已知四棱锥V-ABCD,底面ABCD是边长为3的正方形,VA⊥平面ABCD,且VA=4,则此四棱锥的侧面中,所有直角三角形的面积的和是________.【答案】27【解析】可证四个侧面都是直角三角形,其面积S=2××3×4+2××3×5=27.4.某几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D.【答案】D【解析】由三视图还原图像,得原图是两个一样的圆锥底面对在一起了,所以.【考点】三视图.5.已知圆柱底面半径为1,高为,是圆柱的一个轴截面.动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线如图所示.现将轴截面绕着轴逆时针旋转后,边与曲线相交于点,设的长度为,则的图象大致为()【答案】A【解析】根据题意,由于圆柱底面半径为1,高为,是圆柱的一个轴截面.动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线,那么可知轴截面绕着轴逆时针旋转后,随着角的增大可知BP的变化时匀速增大的,因此选A.【考点】圆柱的展开图点评:主要是考查了圆柱体侧面展开图的运用,属于基础题。
高中数学空间几何体的表面积与体积练习题及答案

空间几何体的表面积与体积专题一、选择题1.棱长为2的正四面体的表面积是( C ).A. 3 B .4 C .4 3 D .16解析 每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( B ). A .2倍 B .22倍 C.2倍 D.32倍解析 由题意知球的半径扩大到原来的2倍,则体积V =43πR 3,知体积扩大到原来的22倍.3.如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( B ). A.1423 B.2843 C.2803D.1403解析 根据三视图的知识及特点,可画出多面体 的形状,如图所示.这个多面体是由长方体截去 一个正三棱锥而得到的,所以所求多面体的体积V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843. 4.某几何体的三视图如下,则它的体积是( A) A .8-2π3 B .8-π3C .8-2πD.2π3解析 由三视图可知该几何体是一个边长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V =23-13×π×2=8-2π3.5.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( A)A .24-32π B .24-π3 C .24-π D .24-π2据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.6.某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( C )A.⎝ ⎛⎭⎪⎫95-π2 cm 2B.⎝ ⎛⎭⎪⎫94-π2 cm 2C.⎝ ⎛⎭⎪⎫94+π2 cm 2D.⎝⎛⎭⎪⎫95+π2 cm 2解析 这个空间几何体上面是一个四棱柱、中间部分是一个圆柱、下面是一个四棱柱.上面四棱柱的表面积为2×3×3+12×1-π4=30-π4;中间部分的表面积为2π×12×1=π,下面部分的表面积为2×4×4+16×2-π4=64-π4.故其表面积是94+π2.7.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S-ABC 的体积为( C).A .3 3B .2 3 C. 3 D .1解析 由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥S-ABD 和C-ABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =33x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DCB =∠DCA =60°,在△BDC 中 ,BD =3(4-x ),所以33x =3(4-x ),所以x =3,AD =BD =3,所以三角形ABD 为正三角形,所以V =13S △ABD ×4= 3.二、填空题8.三棱锥PABC 中,PA ⊥底面ABC ,PA =3,底面ABC 是边长为2的正三角形,则三棱锥PABC 的体积等于__3______.解析 依题意有,三棱锥PABC 的体积V =13S △ABC ·|PA |=13×34×22×3= 3.9.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为_ 3∶2_______.解析 设圆柱的底面半径是r ,则该圆柱的母线长是2r ,圆柱的侧面积是2πr ·2r =4πr 2,设球的半径是R ,则球的表面积是4πR 2,根据已知4πR 2=4πr 2,所以R =r .所以圆柱的体积是πr 2·2r =2πr 3,球的体积是43πr 3,所以圆柱的体积和球的体积的比是2πr 343πr 3=3∶2.10.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是___26_____.解析由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V=13×1×1×22=26.11.如图,半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是____2πR2____.解析由球的半径为R,可知球的表面积为4πR2.设内接圆柱底面半径为r,高为2h,则h2+r2=R2.而圆柱的侧面积为2πr·2h=4πrh≤4πr2+h22=2πR2(当且仅当r=h时等号成立),即内接圆柱的侧面积最大值为2πR2,此时球的表面积与内接圆柱的侧面积之差为2πR2.12.如图,已知正三棱柱ABCA1B1C1的底面边长为2 cm,高为5 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为___13_____cm. 解析根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm).三、解答题13.某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH,下半部分是长方体ABCDEFGH.图2、图3分别是该标识墩的正视图和俯视图.(1)请画出该安全标识墩的侧视图;(2)求该安全标识墩的体积.解析(1)侧视图同正视图,如图所示:(2)该安全标识墩的体积为V=VPEFGH +V ABCDEFGH=13×402×60+402×20=64 000(cm3).14 .一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V;(2)求该几何体的表面积S.解析 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为3,所以V =1×1×3= 3.(2)由三视图可知,该平行六面体中,A1D ⊥平面ABCD ,CD ⊥平面BCC1B1, 所以AA1=2,侧面ABB1A1,CDD1C1均为矩形, S =2×(1×1+1×3+1×2)=6+2 3.15.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .解析 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、 右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示. (1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2. 1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). .解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=, 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ).2.解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65, 3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是 。
最新高中数学空间几何专题练习

高中数学空间几何专题练习------------------------------------------作者xxxx------------------------------------------日期xxxx一、选择题1、下图(1)所示的圆锥的俯视图为 ( )2、直线30l y ++=的倾斜角α为 ( )A 、30;B 、60;C 、120;D 、150。
3、边长为a 正四面体的表面积是 ( )A3; B3; C、2; D2。
4、对于直线:360l x y -+=的截距,下列说法正确的是 ( )A 、在y 轴上的截距是6; B 、在x 轴上的截距是6;C 、在x 轴上的截距是3;D 、在y 轴上的截距是3-.5、已知,a b αα⊂//,则直线a 与直线b 的位置关系是 ( )A 、平行;B 、相交或异面;C 、异面;D 、平行或异面.图(ABCD6、已知两条直线12:210,:40l x ay l x y +-=-=,且12l l //,则满足条件a的值为A 、12-; B 、12; C 、2-;D 、2。
7、在空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 的中点。
若AC BD a ==,且AC 与BD 所成的角为60,则四边形EFGH 的面积为( )A、28a ; B、24; C、22a ; D2。
8、在右图的正方体中,M 、N分别为棱B C和棱CC 1则异面直线AC 和M N所成的角为( )A .30°B.45° C.90°D.9、下列叙述中错误的是 ( )A 、若P αβ∈且l αβ=,则P l ∈; B 、三点,,A B C 确定一个平面;C 、若直线a b A =,则直线a 与b 能够确定一个平面;D 、若,A l B l ∈∈且,A B αα∈∈,则l α⊂。
10、两条不平行的直线,其平行投影不可能是 ( )A 、两条平行直线;B 、一点和一条直线;C 、两条相交直线;D 、两个点。
高中数学《空间向量与立体几何》练习题(含答案解析)

高中数学《空间向量与立体几何》练习题(含答案解析)一、单选题1.在空间直角坐标系Oxyz 中,与点()1,2,1-关于平面xOz 对称的点为( )A .()1,2,1--B .()1,2,1-C .()1,2,1---D .()1,2,1--2.在空间直角坐标系内,平面α经过三点(1,0,2),(0,1,0),(2,1,1)A B C -,向量(1,,)n λμ=是平面α的一个法向量,则λμ+=( )A .7-B .5-C .5D .73.已知点()3,1,0A -,若向量()2,5,3AB =-,则点B 的坐标是( ).A .()1,6,3-B .()5,4,3-C .()1,6,3--D .()2,5,3-4.如图,O A B '''△是水平放置的OAB 的直观图,6A O ''=,2''=B O ,则OAB 的面积是( )A .6B .12C .D .5.平面α的一个法向量是1(2n =,1-,1)3,平面β的一个法向量是(3m =-,6,2)-,则平面α与平面β的关系是( )A .平行B .重合C .平行或重合D .垂直6.已知某圆柱的内切球半径为92,则该圆柱的侧面积为( ) A .492π B .49π C .812π D .81π7.O 、A 、B 、C 为空间四点,且向量OA 、OB 、OC 不能构成空间的一个基底,则下列说法正确的是( ) A .OA 、OB 、OC 共线B .OA 、OB 共线C .OB 、OC 共线D .O 、A 、B 、C 四点共面8.在正方体1111ABCD A B C D -中,E 为线段11A B 的中点,则异面直线1D E 与1BC 所成角的余弦值为( )A B C D9.已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 10.在正方体1111ABCD A B C D -中,P ,Q 分别为AB ,CD 的中点,则( )A .1AB ⊥平面11A BCB .异面直线1AB 与11AC 所成的角为30° C .平面11ABD ∥平面1BC Q D .平面1B CD ⊥平面1B DP二、填空题11.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________. 12.若直线l 的方向向量(),1,2m x =-,平面α的法向量()2,2,4n =--,且直线l ⊥平面α,则实数x 的值是______.13.词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术・商功》,是古代人对一些特殊锥体的称呼.在《九章算术・商功》中,把四个面都是直角三角形的四面体称为“鳖臑”.现有如图所示的“鳖臑”四面体P ABC ,其中PA ⊥平面ABC ,2PA AC ==,BC =则四面体P ABC 的外接球的表面积为______.14.设空间向量,,i j k 是一组单位正交基底,若空间向量a 满足对任意的,,x y a xi y j --的最小值是2,则3a k +的最小值是_________.三、解答题15.如图,在三棱柱111ABC A B C 中,点D 是AB 的中点.(1)求证:1AC △平面1CDB .(2)若1AA ⊥平面ABC ,AC BC =,求证:CD ⊥平面11ABB A .16.如图,空间四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.求证:(1)EH △平面BCD ;(2)BD △平面EFGH .17.如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,底面ABCD 是正方形,AC 与BD 交于点O ,E 为PB 的中点.(1)求证:EO平面PDC ;(2)求证:平面PAC ⊥平面PBD .18.如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.参考答案与解析1.A【分析】根据空间直角坐标系的对称点坐标特点直接求解即可.【详解】解:因为点()1,2,1-,则其关于平面xOz 对称的点为()1,2,1--.故选:A.2.D【解析】求出(1,1,2)AB =--,(2,0,1)BC =-,利用与(1,,)n λμ=数量积为0,求解即可.【详解】(1,1,2)AB =--,(2,0,1)BC =-120n AB λμ⋅=-+-=20n BC μ⋅=-+=可得2μ=,5λ=,7λμ+=故选:D3.B【分析】利用空间向量的坐标运算求得B 的坐标.【详解】设O 为空间坐标原点,()()()3,1,02,5,35,4,3OB OA AB =+=-+-=-.故选:B4.B【分析】由直观图和原图的之间的关系,和直观图画法规则,还原OAB 是一个直角三角形,其中直角边6,4OA OB ==,直接求解其面积即可.【详解】解:由直观图画法规则,可得OAB 是一个直角三角形,其中直角边6,4OA OB ==, △11641222OAB S OA OB =⋅=⨯⨯=. 故选:B .5.C【分析】由题设知6m n =-,根据空间向量共线定理,即可判断平面α与平面β的位置关系. 【详解】平面α的一个法向量是1(2n =,1-,1)3,平面β的一个法向量是(3m =-,6,2)-, ∴6m n =-,∴平面α与平面β的关系是平行或重合.故选:C .6.D 【分析】由题意可得该圆柱底面圆的半径为92,圆柱的高为9,从而可求出其侧面积 【详解】由题意得,该圆柱底面圆的半径为92,圆柱的高为9, 所以该圆柱的侧面积为929812ππ⨯⨯=. 故选:D7.D【解析】根据向量OA 、OB 、OC 不能构成空间的一个基底知向量共面,即可得出结论.【详解】因为O 、A 、B 、C 为空间四点,且向量OA 、OB 、OC 不能构成空间的一个基底,所以OA 、OB 、OC 共面,所以O 、A 、B 、C 四点共面,故选:D8.B【分析】连接1AD ,AE ,得到11//AD BC ,把异面直线1D E 与1BC 所成角转化为直线1D E 与1AD 所成角,取1AD 的中点F ,在直角1D EF 中,即可求解.【详解】在正方体1111ABCD A B C D -中,连接1AD ,AE ,可得11//AD BC ,所以异面直线1D E 与1BC 所成角即为直线1D E 与1AD 所成角,即1AD E ∠为异面直线1D E 与1BC 所成角,不妨设12AA =,则1AD =1D E AE =取1AD 的中点F ,因为1D E AE =,所以1EF AD ⊥,在直角1D EF中,可得111cos D F AD E D E ∠==. 故选:B.9.C【分析】根据球O 的表面积和ABC 的面积可求得球O 的半径R 和ABC 外接圆半径r ,由球的性质可知所求距离d =【详解】设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC212a ∴=,解得:3a =,2233r ∴==∴球心O 到平面ABC 的距离1d =.故选:C.【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.10.D【分析】A 项反证法可得;B 项由平移法计算异面直线所成角;C 项由面面平行的判断和性质可得结果;D 项建立空间直角坐标系可得结果.【详解】对于选项A ,假设1AB ⊥面11A BC ,则111AB AC ⊥,这与已知1AB 与11A C 不垂直相矛盾,所以假设不成立.故选项A 错误; 对于选项B ,连接1DC ,1DA ,因为11AB DC ∥,所以11DC A ∠为异面直线1AB 与11A C 所成的角或补角,又因为△11AC D 为等边三角形,所以1160DC A ∠=︒,故选项B 错误;对于选项C ,因为11B D BD ∥,11AD BC ∥,由面面平行的判定定理可得平面11AB D ∥平面1BDC ,而平面1BQC 与平面1BDC 相交,所以平面11AB D 与平面1BC Q 也相交,故选项C 错误;对于选项D ,以D 为坐标原点,DA ,DC ,1DD 所在的直线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,设正方体的棱长为1,则()0,0,0D ,()11,1,1B ,()0,1,0C ,11,,02P ⎛⎫ ⎪⎝⎭,可得()11,1,1DB =,()0,1,0DC =,11,,02DP ⎛⎫= ⎪⎝⎭,设平面1B CD 的法向量为()1,,n x y z =, 则11100n DB x y z n DC y ⎧⋅=++=⎪⎨⋅==⎪⎩,可取1x =,则0y =,1z =-,即()11,0,1n =-, 设平面1B DP 的法向量为()2,,b c n a =,则2120102n DB a b c n DP a b ⎧⋅=++=⎪⎨⋅=+=⎪⎩, 可取1a =,则2b =-,1c =,可得平面1B DP 的一个法向量为()21,2,1n =-,由121010n n ⋅=+-=,所以12n n ⊥,即平面1B CD ⊥平面1B DP ,故选项D 正确. 故选:D.11.135°【分析】首先根据题意将图画出,然后根据α=45°,AB △CD ,可得180BCD α︒∠=-,进而得出结论.【详解】解:如图,由题意知α=45°,AB △CD ,180135BCD α︒︒∴∠=-=,即135β︒=.故答案为:135°.【点睛】本题考查了平行线的性质,结合图会使问题变得简单,属于基础题.12.-1【分析】利用法向量的定义和向量共线的定理即可.【详解】直线l 的方向向量(),1,2m x =-,平面α的法向量()2,2,4n =--,直线l ⊥平面α, 必有//m n ,即向量m 与向量n 共线,m n λ∴= ,△11222x -==--,解得=1x -; 故答案为:-1.13.16π 【分析】确定外接球球心求得球半径后可得表面积.【详解】由于PA ⊥平面ABC ,因此PA 与底面上的直线,,AC AB BC 都垂直,从而AC 与AB 不可能垂直,否则PBC 是锐角三角形,由于<AC BC ,因此有AC BC ⊥, 而PA 与AC 是平面PAC 内两相交直线,则BC ⊥平面PAC ,PC ⊂平面PAC ,所以BC PC ⊥, 所以PB 的中点O 到,,,P A B C 四个点的距离相等,即为四面体P ABC 的外接球球心.2222222222216PB PA AB PA AC BC =+=++=++=,4PB =, 所以所求表面积为224()42162PB S πππ=⨯=⨯=. 故答案为:16π.14.1【分析】以,i j 方向为,x y 轴,垂直于,i j 方向为z 轴建立空间直角坐标系,根据条件求得a 坐标,由3a k +的表达式即可求得最小值.【详解】以,,i j k 方向为,,x y z 轴建立空间直角坐标系,则()1,0,0i =,()0,1,0j =,()0,0,1k = 设(),,a r s t = 则(a xi y j r x --=-当,r x s y ==时a xi y j --的最小值是2,2t ∴=±取(),,2a x y = 则()3,,5a k x y += 23a k x ∴+=+又因为,x y 是任意值,所以3a k +的最小值是5.取(),,2a x y =- 则()3,,1a k x y += 23a k x ∴+=+又因为,x y 是任意值,所以3a k +的最小值是1.故答案为:1.15.(1)证明见解析;(2)证明见解析.【分析】(1)连接1BC ,交1B C 于点E ,连接ED ,用中位线证明1ED AC ∥即可;(2)证明CD △AB ,CD △1AA 即可.【详解】(1)连接1BC ,交1B C 于点E ,连接.ED△111ABC A B C 是三棱柱,△四边形11BCC B 为平行四边形,△E 是1BC 的中点.△点D 是AB 的中点,△ED 是1ABC 的中位线,△1ED AC ∥,又ED ⊂平面1CDB ,1AC ⊄平面1CDB ,△1AC △平面1CDB .(2)△1AA ⊥平面ABC ,AB ⊂平面ABC ,△1AA AB ⊥,△AC BC =,AD BD =,△CD AB ⊥,△1AA AB A =,1,AA AB ⊂平面11ABB A ,△CD ⊥平面11ABB A .16.(1)见解析(2)见解析【分析】(1)推导出EH △BD ,由此能证明EH △平面BCD ;(2)由BD △EH ,由此能证明BD △平面EFGH .【详解】(1)△EH 为△ABD 的中位线,△EH △BD .△EH △平面BCD ,BD △平面BCD ,△EH △平面BCD ;(2)△FG 为△CBD 的中位线,△FG △BD ,△FG △EH ,△E 、F 、G 、H 四点共面,△BD △EH ,BD △平面EFGH ,EH △平面EFGH ,△BD △平面EFGH .【点睛】本题考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查化归与转化思想,是中档题.17.(1)证明见解析(2)证明见解析【详解】(1)证明:△四边形ABCD 为正方形,△O 为BD 的中点,△E 为PB 的中点,△OE PD ∥,又△OE ⊄平面,PDC PD ⊂平面PDC ,△OE 平面PDC ;(2)证明:△四边形ABCD 为正方形,△AC BD ⊥,△PD ⊥平面ABCD ,且AC ⊂平面ABCD ,所以PD AC ⊥,又△,PD BD ⊂平面PBD ,且PD BD D ⋂=,△AC ⊥平面PBD ,又△AC ⊂平面PAC ,△平面PAC ⊥平面PDB .18.(1)证明见解析; 【分析】(1)由题意首先证得线面垂直,然后利用线面垂直的定义证明线线垂直即可;(2)方法二:利用几何关系找到二面角的平面角,然后结合相关的几何特征计算三棱锥的体积即可.【详解】(1)因为AB AD =,O 是BD 中点,所以OA BD ⊥,因为OA ⊂平面ABD ,平面ABD ⊥平面BCD ,且平面ABD ⋂平面BCD BD =,所以OA ⊥平面BCD .因为CD ⊂平面BCD ,所以OA CD ⊥.(2)[方法一]:通性通法—坐标法如图所示,以O 为坐标原点,OA 为z 轴,OD 为y 轴,垂直OD 且过O 的直线为x 轴,建立空间直角坐标系O xyz -,则1,0),(0,1,0),(0,1,0)2C D B -,设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,,0)3322EB m BC =--=, 设(),,n x y z =为平面EBC 的法向量,则由00EB n EC n ⎧⋅=⎨⋅=⎩可求得平面EBC 的一个法向量为2(3,1,)n m =--. 又平面BCD 的一个法向量为()0,0,OA m =,所以cos ,n OA ==1m =. 又点C 到平面ABD 112132A BCD C ABD V V --==⨯⨯⨯=, 所以三棱锥A BCD - [方法二]【最优解】:作出二面角的平面角如图所示,作EG BD ⊥,垂足为点G .作GF BC ⊥,垂足为点F ,连结EF ,则OA EG ∥.因为OA ⊥平面BCD ,所以EG ⊥平面BCD ,EFG ∠为二面角E BC D --的平面角.因为45EFG ∠=︒,所以EG FG =.由已知得1OB OD ==,故1OB OC ==.又30OBC OCB ∠=∠=︒,所以BC =因为24222,,,,133333GD GB FG CD EG OA ======,111122(11)13332A BCD BCD BOC V S O S OA A -==⨯⨯=⨯⨯⨯⨯⨯=. [方法三]:三面角公式考虑三面角B EDC -,记EBD ∠为α,EBC ∠为β,30DBC ∠=︒,记二面角E BC D --为θ.据题意,得45θ=︒.对β使用三面角的余弦公式,可得cos cos cos30βα=⋅︒,化简可得cos βα=.△使用三面角的正弦公式,可得sin sin sin αβθ=,化简可得sin βα=.△ 将△△两式平方后相加,可得223cos 2sin 14αα+=, 由此得221sin cos 4αα=,从而可得1tan 2α=±.如图可知π(0,)2α∈,即有1tan 2α=, 根据三角形相似知,点G 为OD 的三等分点,即可得43BG =,结合α的正切值,可得2,13EG OA ==从而可得三棱锥A BCD - 【整体点评】(2)方法一:建立空间直角坐标系是解析几何中常用的方法,是此类题的通性通法,其好处在于将几何问题代数化,适合于复杂图形的处理;方法二:找到二面角的平面角是立体几何的基本功,在找出二面角的同时可以对几何体的几何特征有更加深刻的认识,该法为本题的最优解.方法三:三面角公式是一个优美的公式,在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.。
空间几何体简答题

空间几何体解答题练习一、解答题(共10题;共100分)1、一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:(1)求圆锥的侧面积;(2)当x为何值时,圆柱侧面积最大?并求出最大值.2、如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.(1)试用x表示圆柱的高;(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?3、如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2,求该几何体的表面积.4、如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为π,求该圆锥的表面积.5、一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:(1)求三棱锥外接球表面积(2)求该几何体的表面积(3)求该几何体的体积.6、如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.(1)求几何体的表面积;(2)求几何体的体积.7、如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:(1)求圆柱的体积与球的体积之比;(2)求圆柱的表面积与球的表面积之比.8、一个圆台的母线长为12cm,两底面面积分别为4πcm2和25π cm2.求:(1)圆台的体积;(2)截得此圆台的圆锥的母线长.9、如图,半径为2的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积.(其中∠BAC=30°)10、如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.答案解析部分一、解答题1、【答案】解:(1)圆锥的母线长∴圆锥侧面积S1=πRl=4cm2;(2)设内接圆柱的底面半径为r,由图形特征知,,∴x=4﹣2r圆柱侧面积S=2πrx=2r(4﹣2r)π=(﹣4r2+8r)π=﹣4(r﹣1)2π+4π(cm2)∴r=1,即x=2时,圆柱的侧面积最大,最大为4πcm2.【考点】棱柱、棱锥、棱台的侧面积和表面积【解析】【分析】(1)由题意,求出圆锥的母线长,即可求圆锥的侧面积;(2)根据轴截面和比例关系列出方程,求出圆柱的底面半径,表示出圆柱的侧面积,根据二次函数的性质求出侧面面积的最大值.2、【答案】解:(1)设所求的圆柱的底面半径为x,它的轴截面如图:BO=1,PO=3,圆柱的高为:h 由图得,,即h=3﹣3x.(2)S圆柱侧=2πhx=2π(3﹣3x)x=6π(x﹣x2),当x=时,函数取得最大值为:.∴当圆柱的底面半径为时,它的侧面积最大为【考点】棱柱、棱锥、棱台的侧面积和表面积【解析】【分析】(1)由题意作出几何体的轴截面,根据轴截面和比例关系列出方程,求出圆柱的高的表达式.(2)由(1)求出的侧面面积的表达式,根据二次函数的性质求出侧面面积的最大值.3、【答案】解:圆柱的母线长h=6,底面半径r=2,∴圆锥的母线长为=2,∴圆锥的侧面积为:πrl=4π,圆柱的底面面积为:πr2=4π,圆柱的侧面面积为:2πrh=24π,故该几何体的表面积为:(28+4)π.【考点】旋转体(圆柱、圆锥、圆台)【解析】【分析】根据圆柱的母线及底面半径,求出圆锥的母线,求出圆锥的侧面积,圆柱的侧面积,圆柱的底面面积,相加可得答案.4、【答案】解:设圆锥的底面半径为r,则圆锥的高也为r.由πr2r=π,得:r=2,故母线长l=2.圆锥的底面积=πr2 =4π,圆锥的侧面积=πrl=4π,故圆锥的表面积=(4+4)π.【考点】旋转体(圆柱、圆锥、圆台)【解析】【分析】设圆锥的底面半径为r,则圆锥的高也为r.结合圆锥体积为π,可得r的值,代入圆锥的表面积公式,可得答案.5、【答案】解:(1)三棱锥的底面是等腰直角三角形,腰长为2,有一侧面是等腰三角形,垂直于底面,底面上的高为,设三棱锥外接球的半径为R,则R2=2+(﹣R)2,∴R=,∴三棱锥外接球表面积为4=(2)几何体的底面是圆柱,表面积为2πx x=4π,三棱锥的侧面积为x2x+2×x2x=+2,∴该几何体的表面积S=4π++2;(3)该几何体的体积V=πx2x+x x2x2x=2π+.【考点】由三视图求面积、体积,由三视图还原实物图【解析】【分析】(1)三棱锥的底面是等腰直角三角形,腰长为2,有一侧面是等腰三角形,垂直于底面,底面上的高为,求出三棱锥外接球的半径,即可求三棱锥外接球表面积(2)何体的底面是圆柱,表面积为2πx x=4π,求出三棱锥的侧面积,即可求该几何体的表面积(3)圆柱体积+三棱锥的体积,即可求该几何体的体积.6、【答案】解:旋转以后的几何体是一个圆柱挖去一个圆锥后剩下的几何体.圆柱和圆锥的底面半径均为1,高均为1,圆锥的母线长为.(1)S=S圆柱底+S圆柱侧+S圆锥侧=π×12+2π×1×1+πx1x=(3+)π.(2)V=V圆柱﹣V圆锥=π×12×1﹣=.【考点】旋转体(圆柱、圆锥、圆台)【解析】【分析】旋转后的几何体为一个圆柱挖去一个圆锥后剩下的几何体.7、【答案】解:(1)设圆柱的高为h,底面半径为r,球的半径为R,由已知得h=2R,r=R.=πR2•2R.∵V圆柱∴==(2)∵S圆柱=S侧+2S底=2πrh+2πr2=6πr2,S球=4πr2.∴==【考点】旋转体(圆柱、圆锥、圆台),球的体积和表面积【解析】【分析】(1)设圆柱的高为h,底面半径为r,球的半径为R,求出圆柱的体积,球的体积,即可得到结论.(2)求出圆柱的表面积,球的表面积即可得到比值.8、【答案】解:(1)圆台的轴截面是等腰梯形ABCD(如图).由已知可得上底半径O1A=2 cm,下底半径OB=5 cm.又∵腰长为12 cm,∴高AM==3(cm),∴所求体积为×(4π++25π)×3=39π cm3.(2)设截得此圆台的圆锥的母线长为l,则由△SAO1∽△SBO可得,∴l=20(cm).即截得此圆台的圆锥的母线长为20 cm.【考点】旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积【解析】【分析】(1)根据圆台的体积公式求圆台的体积即可.(2)作出圆台和圆锥的轴截面,根据相似三角形的性质进行求解即可.9、【答案】解:旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,因为所以【考点】棱柱、棱锥、棱台的体积【解析】【分析】要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.10、【答案】解:作CE⊥AB于E,作DF⊥CE于F,则AE=AD=2,CE=4,BE=3,∴BC=5,四边形ABCD绕AD旋转一周所成几何体为圆台挖去一个圆锥,其中,圆台的上下底面半径为r1=2,r2=5,高为4,母线l=5,圆锥的底面半径为2,高为2,母线l′=2 ,∴几何体的表面积S=25π+π×2×5+π×5×5+ =60π+4 π.几何体的体积V= (25π+4π+ )×4﹣×4π×2= .【考点】旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积【解析】【分析】几何体为圆台挖去一个圆锥,求出圆台和圆锥的底面半径,高和母线,代入面积公式和体积公式计算即可.。
空间向量与立体几何单元测试有答案

第三章 空间向量与立体几何 单元测试(时间:90分钟 满分:120分) 第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分. 1.以下四组向量中,互相平行的组数为( )①a =(2,2,1),b =(3,-2,-2);②a =(8,4,-6),b =(4,2,-3);③a =(0,-1,1),b =(0,3,-3);④a =(-3,2,0),b =(4,-3,3)A .1组B .2组C .3组D .4组解析:∵②中a =2b ,∴a ∥b ;③中a =-13b ,∴a ∥b ;而①④中的向量不平行. 答案:B2.在以下命题中,不正确的个数为( )①|a |-|b |=|a +b |是a ,b 共线的充要条件;②若a ∥b ,则存在唯一的实数λ,使a =λb ;③对空间任意一点O 和不共线的三点A ,B ,C ,若OP →=2OA →-2OB →-OC →,则P ,A ,B ,C 四点共面;④若{a ,b ,c }为空间的一组基底,则{a +b ,b +c ,c +a }构成空间的另一组基底;⑤|(a ·b )·c |=|a |·|b |·|c |.A .2个B .3个C .4个D .5个解析:①|a |-|b |=|a +b |⇒a 与b 共线,但a 与b 共线时|a |-|b |=|a +b |不一定成立,故不正确;②b 需为非零向量,故不正确;③因为2-2-1≠1,由共面向量定理知,不正确;④由基底的定义知正确;⑤由向量的数量积的性质知,不正确.答案:C3.如图,已知四边形ABCD 为矩形,PA ⊥平面ABCD ,连接AC ,BD ,PB ,PC ,PD ,则下列各组向量中,数量积不一定为零的是( )与BD → 与PB → 与AB → 与CD →解析:建立如图所示的空间直角坐标系.设矩形ABCD 的长、宽分别为a ,b ,PA 长为c ,则A (0,0,0),B (b,0,0),D (0,a,0),C (b ,a,0),P (0,0,c ).则PC →=(b ,a ,-c ),BD →=(-b ,a,0),DA →=(0,-a ,0),PB →=(b,0,-c ),PD →=(0,a ,-c ),AB →=(b,0,0),PA →=(0,0,-c ),CD →=(-b,0,0).∴PC →·BD →=-b 2+a 2不一定为0. DA →·PB →=0,PD →·AB →=0,PA →·CD →=0. 答案:A4.已知向量e 1、e 2、e 3是两两垂直的单位向量,且a =3e 1+2e 2-e 3,b=e 1+2e 3,则(6a )·⎝ ⎛⎭⎪⎫12b 等于( )A .15B .3C .-3D .5解析:(6a )·⎝ ⎛⎭⎪⎫12b =3a·b =3(3e 1+2e 2-e 3)·(e 1+2e 3)=9|e 1|2-6|e 3|2=3.答案:B5.如图,AB =AC =BD =1,AB ⊂面α,AC ⊥面α,BD ⊥AB ,BD 与面α成30°角,则C 、D 间的距离为( )A .1B .2解析:|CD →|2=|CA →+AB →+BD →|2=|CA →|2+|AB →|2+|BD →|2+2CA →·AB →+2AB →·BD →+2CA →·BD →=1+1+1+0+0+2×1×1×cos120°=2.∴|CD →|=2. 答案:C6.已知空间三点O (0,0,0),A (-1,1,0),B (0,1,1)在直线OA 上有一点H 满足BH ⊥OA ,则点H 的坐标为( )A .(-2,2,0)B .(2,-2,0)解析:由OA →=(-1,1,0),且点H 在直线OA 上,可设H (-λ,λ,0),则BH →=(-λ,λ-1,-1).又BH ⊥OA ,∴BH →·OA →=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=12,∴H ⎝ ⎛⎭⎪⎫-12,12,0.答案:C7.已知a =(cos α,1,sin α),b =(sin α,1,cos α),则向量a +b 与a -b 的夹角是( )A .90°B .60°C .30°D .0°解析:(a +b )·(a -b )=a 2-b 2=(cos 2α+sin 2α+1)-(sin 2α+1+cos 2α)=0,∴(a +b )⊥(a -b ).答案:A8.已知E 、F 分别是棱长为1的正方体ABCD A 1B 1C 1D 1的棱BC 、CC 1的中点,则截面AEFD 1与底面ABCD 所成二面角的正弦值是( )解析:以D 为坐标原点,以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图.则A (1,0,0),E ⎝ ⎛⎭⎪⎫12,1,0,F ⎝⎛⎭⎪⎫0,1,12,D 1(0,0,1),l 所以AD 1→=(-1,0,1),AE →=⎝ ⎛⎭⎪⎫-12,1,0.设平面AEFD 1的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AD 1→=0,n·AE →=0,⇒⎩⎪⎨⎪⎧-x +z =0,-x2+y =0.∴x =2y =z .取y =1,则n =(2,1,2),而平面ABCD 的一个法向量为u =(0,0,1),∵cos 〈n ,u 〉=23,∴sin 〈n ,u 〉=53.答案:C9.在三棱锥P ABC 中,△ABC 为等边三角形,PA ⊥平面ABC ,且PA =AB ,则二面角A PB C 的平面角的正切值为( )解析:设PA =AB =2,建立如图所示的空间直角坐标系. 则B (0,2,0),C (3,1,0),P (0,0,2), ∴BP →=(0,-2,2), BC →=(3,-1,0).设n =(x ,y ,z )是平面PBC 的一个法向量. 则⎩⎪⎨⎪⎧BP →·n =0,BC →·n =0,即⎩⎪⎨⎪⎧-2y +2z =0,3x -y =0.令y =1,则x =33,z =1.即n =⎝⎛⎭⎪⎪⎫33,1,1. 易知m =(1,0,0)是平面PAB 的一个法向量.则cos 〈m ,n 〉=m·n|m ||n |=331×213=77. ∴正切值tan 〈m ,n 〉= 6. 答案:A10.已知OA →=(1,2,3),OB →=(2,1,2),OP →=(1,1,2),点Q 在直线OP 上运动,则当QA →·QB →取得最小值时,点Q 的坐标为( )解析:∵Q 在OP 上,∴可设Q (x ,x,2x ),则QA →=(1-x,2-x,3-2x ), QB →=(2-x,1-x,2-2x ). ∴QA →·QB →=6x 2-16x +10,∴x =43时,QA →·QB →最小,这时Q ⎝ ⎛⎭⎪⎫43,43,83.答案:C第Ⅱ卷(非选择题,共70分)二、填空题:本大题共4小题,每小题5分,共20分.11.已知a =(3,-2,-3),b =(-1,x -1,1),且a 与b 的夹角为钝角,则x 的取值范围是__________.解析:因为a 与b 的夹角为钝角,于是-1<cos 〈a ,b 〉<0,因此a·b <0,且a 与b 的夹角不为π,即cos 〈a ,b 〉≠-1.解得x ∈⎝ ⎛⎭⎪⎫-2,53∪⎝ ⎛⎭⎪⎫53,+∞.答案:⎝ ⎛⎭⎪⎫-2,53∪⎝ ⎛⎭⎪⎫53,+∞12.如图所示,已知正四面体ABCD中,AE=14AB,CF=14CD,则直线DE和BF所成的角的余弦值为__________.解析:ED→=EA→+AD→=14BA→+AD→,BF→=BC→+CF→=BC→+14CD→,cos〈ED→,BF→〉=ED→·BF→|ED→|·|BF→|=⎝⎛⎭⎪⎪⎫14BA→+AD→·⎝⎛⎭⎪⎪⎫BC→+14CD→⎝⎛⎭⎪⎪⎫14BA→+AD→2·⎝⎛⎭⎪⎪⎫BC→+14CD→2=413.答案:41313.已知a =(x,2,-4),b =(-1,y,3),c =(1,-2,z ),且a ,b ,c 两两垂直,则(x ,y ,z )=__________.解析:由题意知⎩⎪⎨⎪⎧-x +2y -12=0,x -4-4z =0,-1-2y +3z =0,解得x =-64,y =-26,z =-17. 答案:(-64,-26,-17)14.已知空间四边形OABC ,如图所示,其对角线为OB 、AC ,M 、N 分别为OA 、BC 的中点,点G 在线段MN 上,且MG →=3GN →,现用基向量OA →、OB →、OC →表示向量OG →,并设OG →=x ·OA →+y ·OB →+z ·OC →,则x 、y 、z 的和为__________.解析:OG →=OM →+MG →=12OA →+34MN →=12OA →+34⎝ ⎛⎭⎪⎪⎫-12OA →+OC →+12CB →=12OA →-38OA →+34OC →+38OB →-38OC →=18OA →+38OB →+38OC →, ∴x =18,y =38,z =38.∴x +y +z =78.答案:78三、解答题:本大题共4小题,满分50分. 15.(12分)已知a =(1,2,-2). (1)求与a 共线的单位向量b ;(2)若a 与单位向量c =(0,m ,n )垂直,求m 、n 的值. 解:(1)设b =(λ,2λ,-2λ),而b 为单位向量, ∴|b |=1,即λ2+4λ2+4λ2=9λ2=1. ∴λ=±13.(4分)∴b =⎝ ⎛⎭⎪⎫13,23,-23或b =⎝ ⎛⎭⎪⎫-13,-23,23.(6分)(2)由题意,知⎩⎪⎨⎪⎧a·c =0,|c |=1,⇒⎩⎪⎨⎪⎧1×0+2m -2n =0,m 2+n 2+02=1,解得⎩⎪⎨⎪⎧m =22,n =22,或⎩⎪⎨⎪⎧m =-22,n =-22.(12分)16.(12分)如下(左)图,在Rt △ABC 中,∠C =90°,BC =3,AC =6,D ,E 分别为AC 、AB 上的点,且DE ∥BC ,DE =2,将△ADE 沿DE 折起到△A 1DE的位置,使A 1C ⊥CD ,如下(右)图.(1)求证:A 1C ⊥平面BCDE ;(2)若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小. 解:(1)∵AC ⊥BC ,DE ∥BC ,∴DE ⊥AC . ∴DE ⊥A 1D ,DE ⊥CD ,∴DE ⊥平面A 1DC . ∴DE ⊥A 1C . 又∵A 1C ⊥CD ,∴A 1C ⊥平面BCDE .(4分)(2)如图所示,以C 为坐标原点,建立空间直角坐标系C -xyz ,则A 1(0,0,23),D (0,2,0),M (0,1,3),B (3,0,0),E (2,2,0).设平面A 1BE 的法向量为n =(x ,y ,z ),则n ·A 1B →=0,n ·BE →=0. 又A 1B →=(3,0,-23), BE →=(-1,2,0),∴⎩⎪⎨⎪⎧3x -23z =0,-x +2y =0.令y =1,则x =2,z =3,∴n =(2,1,3). 设CM 与平面A 1BE 所成的角为θ. ∵CM →=(0,1,3),∴sin θ=|cos 〈n ,CM →〉|=|n ·CM →|n |·|CM →||=48×4=22.∴CM 与平面A 1BE 所成角的大小为π4.(12分)17.(12分)如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,AB =2,AF =1,M 是线段EF 的中点.(1)求证:AM ∥平面BDE ;(2)试在线段AC 上确定一点P ,使得PF 与CD 所成的角是60°.解:(1)证明:如图,建立空间直角坐标系. 设AC ∩BD =N ,连接NE ,则N ⎝⎛⎭⎪⎪⎫22,22,0,E (0,0,1), ∴NE →=⎝⎛⎭⎪⎪⎫-22,-22,1. 又A (2,2,0),M ⎝⎛⎭⎪⎪⎫22,22,1, ∴AM →=⎝⎛⎭⎪⎪⎫-22,-22,1. ∴NE →=AM →,且NE 与AM 不共线. ∴NE ∥AM .又NE ⊂平面BDE ,AM ⊄平面BDE , ∴AM ∥平面BDE .(6分) (2)设P (t ,t,0)(0≤t ≤2),则PF →=(2-t ,2-t,1),CD →=(2,0,0). 又∵PF →与CD →所成的角为60°.|2-t ·2|2-t2+2-t 2+1·2=12, 解之得t =22,或t =322(舍去).故点P 为AC 的中点.(12分)18.(14分)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,C是AB ︵的中点,D 为AC 的中点.(1)证明:平面POD ⊥平面PAC ; (2)求二面角B PA C 的余弦值.解: (1)证明:如图所示,以O 为坐标原点,OB ,OC ,OP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则O (0,0,0),A (-1,0,0),B (1,0,0),C (0,1,0),P (0,0,2),D ⎝ ⎛⎭⎪⎫-12,12,0.设n 1=(x 1,y 1,z 1)是平面POD 的一个法向量,则由n 1·OD →=0,n 1·OP →=0,得⎩⎪⎨⎪⎧-12x 1+12y 1=0,2z 1=0.(4分)∴z 1=0,x 1=y 1.取y 1=1,得n 1=(1,1,0).设n 2=(x 2,y 2,z 2)是平面PAC 的一个法向量,则由n 2·PA →=0,n 2·PC →=0,得⎩⎪⎨⎪⎧-x 2-2z 2=0,y 2-2z 2=0.∴x 2=-2z 2,y 2=2z 2, 取z 2=1,得n 2=(-2,2,1). ∵n 1·n 2=(1,1,0)·(-2,2,1)=0,∴n1⊥n2.从而平面POD⊥平面PAC.(8分)(2)∵y轴⊥平面PAB.∴平面PAB的一个法向量为n3=(0,1,0).由(1)知,平面PAC的一个法向量为n2=(-2,2,1).设向量n2和n3的夹角为θ,则cosθ=n2·n3|n2|·|n3|=25=105.由图可知,二面角BPAC的平面角与θ相等,∴二面角BPAC的余弦值为105.(14分)。
(完整版)空间几何体练习题含答案

空间几何体练习题1.空间几何体的三视图如图所示,则此空间几何体的直观图为 ( )A. B. C 。
D 。
2.一个水平放置的平面图形的斜二测直观图是一个底角为45︒,腰长为1的等腰直角三角形,则这个平面图形的面积是( ) A 。
2 B 。
22 C. 28 D 。
243.已知某几何体的三视图如图所示,则它的体积为( )A. 12πB. 45πC 。
57π D. 81π4.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是 ( )A 。
2π+1 B. 2π+3 C 。
32π+1 D. 32π+3 5.某几何体的三视图如图所示,则它的体积为( )A 。
283π- B. 83π- C. 82π- D 。
23π6.某几何体的三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )A. 163B. 8 C 。
203D 。
127.某空间几何体的三视图如图所示,则该几何体的体积为()A. 16+2πB. 16+π C。
8+π D。
8+2π8.某空间几何体的三视图如图所示,则该几何体的体积为( )A。
4 B. 6 C。
8 D。
169.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为()A. 163π B.43πC.323π D。
4π10.如图是三棱锥D ABC-的三视图,则该三棱锥的外接球体积为( )A。
92πB。
33πC. 62πD.23π11.某空间几何体的正视图是三角形,则该几何体不可能是()A。
圆锥 B。
圆柱 C. 四面体 D. 三棱锥12.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为( ).A. 2, 22 B。
2,4 C. 23,2 D。
4,313.某几何体的三视图如图所示,则该几何体的表面积是( )A.3222++B。
53222++ C.3322++D。
高一数学空间几何体试题答案及解析

高一数学空间几何体试题答案及解析1.如图,⊥平面,是矩形,,,点是的中点,点在边上移动.(1)求三棱锥的体积;(2)当点为的中点时,试判断与平面的位置关系,并说明理由;(3)证明:无论点在边的何处,都有.【答案】(1) (2)平面 (3)分别证明,,所以⊥平面,进而【解析】(1)三棱锥的体积==·=. ……4分(2)当点为的中点时,与平面平行.∵在中,分别为、的中点,∴,又平面,平面,∴平面. ……9分(3)证明:∵⊥平面,平面,∴,又,,平面,平面.又平面,∴.又,点是的中点,∴,又,平面,∴⊥平面.∵平面,∴. ……14分【考点】本小题主要考查三棱锥体积的计算、线面平行、线面垂直等的证明,考查学生的空间想象能力和逻辑推理能力.点评:计算三棱锥体积时,注意可以根据需要让任何一个面作底面,还经常利用等体积法求三棱锥的高.2.球内接正方体的表面积与球的表面积的比为()A. 2:B. 3:C. 4: D. 6:【答案】A【解析】若正方体的棱长为,则球的半径为,。
3.两个球的体积之比是,那么这两个球的表面积之比是()A.B.C.D.【答案】B【解析】设半径分别为r,R;则故选B4.如图,半球内有一内接正方体,则这个半球体积与正方体的体积之比为()A.B.C.D.【答案】B【解析】若正方体的棱长为,半球的半径为R,在直角三角形中,,。
5.有6根细木棒,其中较长的两根分别为,,其余4根均为,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为 .【答案】或0【解析】依题意可得,三棱锥中较长的两条棱长为,设这两条棱所在直线的所成角为。
若这两条棱相交,则这两条棱长所在面的第三条棱长为,由余弦定理可得。
若这两条棱异面,如图,不妨设,取中点,连接。
因为,所以有,从而有面,所以,则6.在长方体,底面是边长为的正方形,高为,则点到截面的距离为( )【答案】C【解析】利用三棱锥的体积变换:,则7.球的体积与其表面积的数值相等,则球的半径等于()A.B.1C.2D.3【答案】D【解析】设球半径为则故选D8.将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了()A.B.12a2C.18a2D.24a2【答案】B【解析】27个全等的小正方体的棱长为边长为a的正方体的表面积为27个全等的小正方体的表面积和为则表面积增加了。
空间几何题库及答案详解

空间几何题库及答案详解1. 题目一:已知空间中不共线的三点A、B、C,求证:直线AB与直线AC的夹角小于等于90°。
解答:设直线AB与直线AC的夹角为θ。
根据空间几何的基本性质,我们可以构造一个以A、B、C为顶点的三角形ABC。
由于A、B、C 三点不共线,三角形ABC是存在的。
根据余弦定理,我们有:\[ \cos(θ) = \frac{AB^2 + AC^2 - BC^2}{2 \cdot AB \cdot AC} \]由于AB和AC是三角形的两边,根据三角形的边长关系,我们有:\[ AB^2 + AC^2 \geq BC^2 \]代入余弦定理的公式,我们得到:\[ \cos(θ) \geq 0 \]由于θ是锐角,所以θ ≤ 90°,证毕。
2. 题目二:已知空间中平面α内的一点P和平面β内的一点Q,若PQ垂直于平面α,QR垂直于平面β,求证:PQ与QR平行。
解答:设PQ与QR的交点为O。
由于PQ垂直于平面α,QR垂直于平面β,根据垂直的性质,我们有:\[ PQ \perp α \]\[ QR \perp β \]由于PQ与QR相交于O点,根据线面垂直的性质,我们可以得出:\[ OP \parallel α \]\[ OQ \parallel β \]由于OP和OQ是平面α和β的平行线,根据平行线的性质,我们可以得出:\[ PQ \parallel QR \]证毕。
3. 题目三:已知空间中两条直线m和n,它们分别在两个不同的平面α和β内,且m与α平行,n与β平行。
若平面α与平面β相交于直线l,求证:m与n平行。
解答:设平面α与平面β相交于直线l,由于m与α平行,n 与β平行,根据平行平面的性质,我们可以得出:\[ m \parallel l \]\[ n \parallel l \]由于m和n都与直线l平行,根据平行线的性质,我们可以得出: \[ m \parallel n \]证毕。
高考数学一轮复习《空间几何体》练习题(含答案)

高考数学一轮复习《空间几何体》练习题(含答案)一、单选题1.降水量(precipitation[amount]):从天空降落到地面上的液态或固态(经融化后)水,未经蒸发、渗透、流失,而在水平面上积聚的深度.降水量以mm 为单位,气象观测中一般取一位小数,现某地10分钟的降雨量为13.1mm ,小王在此地此时间段内用口径为10cm 的圆柱型量筒收集的雨水体积约为( )(其中π 3.14≈)A .331.0210mm ⨯B .331.0310mm ⨯C .531.0210mm ⨯D .531.0310mm ⨯2.某几何体的三视图如图所示(单位:cm ),则该几何体的表面积(单位:2cm )是( )A .()256122cm +B .()248162cm + C .()280122cm + D .()272162cm + 3.阿基米德(Archimedes ,公元前287年-公元前212年)是古希腊伟大的数学家,物理学家和天文学家,在他墓碑上刻着的一个圆柱容器里放了一个球,该球与圆柱的两个底面及侧面均相切,如图所示,则在该几何体中,圆柱表面积与球表面积的比值为( )A .32B .43C .32或23D .234.已知一个几何体的三视图如图所示,则这个几何体的表面积为( )A .33πB .2πC .3πD .4π5.某圆锥的母线长为2,高为423,其三视图如下图所示,圆锥表面上的点M 在正视图上的对应点为A ,圆锥表面上的点N 在侧视图上的对应点为B ,则在此圆锥侧面上,从M 到N 的路径中,最短路径的长度为A .2B .22C .823+D .223- 6.已知某空间几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .323B .163C .4D .87.已知正方体的六个面的中心可构成一个正八面体,现从正方体内部任取一个点,则该点落在这个正八面体内部的概率为( )A .12B .13C .16D .1128.某几何体的三视图如图所示,则该几何体的表面积为( )A .810+16B .40C .810++24D .489.棱长为1的正方体1111ABCD A B C D -中,点E 是侧面11CC B B 上的一个动点(包含边界),则下面结论正确的有( )①若点E 满足1AE B C ⊥,则动点E 的轨迹是线段;②若点E 满足130EA C ∠=,则动点E 的轨迹是椭圆的一部分;③在线段1BC 上存在点E ,使直线1A E 与CD .所成的角为30;④当E 在棱1BB 上移动时,1EC ED +的最小值是352+. A .1个 B .2个 C .3个 D .4个10.某锥体的正视图和侧视图均为如图所示的等腰三角形,则该几何体的体积最小值为A .4πB .12C .1D .211.已知四棱锥S ABCD -的所有顶点都在同一球面上,底面ABCD 是正方形且和球心O 在同一平面内,当此四棱锥体积取得最大值时,其表面积等于443+,则球O 的体积等于( )A .3223πB .1623πC .823πD .423π 12.一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为A .36B .48C .64D .72二、填空题13.如果用半径为r 的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高等于____. 14.点A ,B ,C ,D 在同一个球的球面上,3AB BC AC ==,若四面体ABCD 体积的3________.15.“方锥”,在《九章算术》卷商功中解释为正四棱锥.现有“方锥”S ABCD -,其中4AB =,SA 与平面ABCD 32,则此“方锥”的外接球表面积为________. 16.棱长为6的正方体内有一个棱长为x 的正四面体,正四面体的中心(正四面体的中心就是该四面体外接球的球心)与正方体的中心重合,且该四面体可以在正方体内任意转动,则x 的最大值为______.三、解答题17.如图,已知直三棱柱111ABC A B C ,其底面是等腰直角三角形,且22AB BC ==14AC AA ==.(1)求该几何体的表面积;(2)若把两个这样的直三棱柱拼成一个大棱柱,求拼得的棱柱表面积的最小值.18.如图是一个以111A B C为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知11112A B B C==,11190A B C∠=︒,14AA=,13BB=,12CC=,求该几何体的体积.19.如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.(单位:cm)20.如图所示,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 是矩形,2PA AB ==,2AD =,过点B 作BE ⊥AC ,交AD 于点E ,点F ,G 分别为线段PD ,DC 的中点.(1)证明:AC ⊥平面BEF ;(2)求三棱锥F -BGE 的体积.21.如图,多面体ABCDEF 中,四边形ABCD 是边长为2的菱形,AC =23,△ADE 为等腰直角三角形,∠AED =90°,平面ADE ⊥平面ABCD ,且EF //AB ,EF =1.(1)证明:AC ⊥平面BDF ;(2)若G 为棱BF 的中点,求三棱锥G —DEF 的体积.22.如图,在三棱锥-P ABC 中,2AB BC ==,22PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC =2MB ,求点C 到平面POM 的距离.23.如图,在三棱锥S -ABC 中,SA =SC ,D 为AC 的中点,SD ⊥AB .(1)证明:平面SAC ⊥平面ABC ;(2)若△BCD 是边长为3的等边三角形,点P 在棱SC 上,PC =2SP ,且932S ABC V -=,求三棱锥A -PBC 的体积.24.如图,在四棱锥P ABCD -中,底面ABCD 是边长为4的菱形,60DAB ∠=︒,7PA PD ==,O F 、分别为AD AB 、的中点,PF AC ⊥.(1)求证:面POF ⊥面ABCD ;(2)求三棱锥B PCF -的体积。
高中数学空间几何经典习题及解答

高中数学空间几何体一、选择题(本大题共12小题,每小题5分,共60分)1.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为()A.B.C.D.2.如图所示是一个无盖的正方体盒子展开后的平面图,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC为()A.1800 B.1200 C.600 D.4503.已知三棱锥S-ABC的各顶点都在一个半径为r的球面上,球心O在AB 上,SO⊥底面ABC,,则球的体积与三棱锥体积之比是()A.B.C.D.4.如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为()A.1 B.C.D.5.一平面截球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是()A.B.C.D.6.半球内有一个内接正方体,则这个半球的体积与正方体的体积之比为()A.B.C.D.7.一个四棱锥和一个三棱锥恰好可以拼成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等,设四棱锥、三棱锥、三棱柱的高分别为h1、h2、h3,则h1:h2:h3等于()A.B.C.D.8.如图所示的一个5×4×4的长方体,阴影所示为穿透的三个洞,那么剩下的部分的体积是()A.50 B.54 C.56 D.589.一个正三棱锥的四个顶是半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A.B.C.D.10.如图用□表示1个正方体,用□(浅黑)表示两个正方体叠加,用□(深黑)表示三个立方体叠加,那么右图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是()11.如图所示,水平地面上有一个大球,现作如下方法测量球的大小:用一个锐角为600的三角板,斜边紧靠球面,一条直角边紧靠地面,并使三角板与地面垂直,P为三角板与球的切点,如果测得PA=5,则球的表面积为()A.B.C.D.12.一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D、E、F;且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的()A.B.C.D.二、填空题(本大题共4小题,每小题4分,共16分)13.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为__________。
高中数学空间几何体练习题难题带答案

高中数学空间几何体练习题一.选择题(共25小题)1.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,若存在球与该“堑堵”表面所在的五个平面都相切,则图中边长a的所有可能取值组成的集合为()A.{2﹣2,2+2} B.{1,+1,﹣1}C.{2﹣2,2+2,2,4} D.{2,2+2,2﹣2} 2.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体外接球的表面积是()A.41πB.C.25πD.3.已知四边形ABCD是边长为5的菱形,对角线BD=8(如图1),现以AC为折痕将菱形折起,使点B达到点P的位置.棱AC,PD的中点分别为E,F,且四面体P ACD的外接球球心落在四面体内部(如图2),则线段EF长度的取值范围为()A.(,4)B.(1,)C.(,6)D.4.三棱锥P﹣ABC中.AB⊥BC,△P AC为等边三角形,二面角P﹣AC﹣B的余弦值为,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为()A.1B.2C.D.5.已知P,A,B,C是半径为3的球面上四点,其中P A过球心,,则三棱锥P﹣ABC的体积是()A.B.2C.D.6.在空间直角坐标系O﹣xyz中,四面体OABC各顶点坐标分别为:O(0,0,0),A(0,0,2),B(,0,0),C(0,,0).假设蚂蚁窝在O点,一只蚂蚁从O点出发,需要在AB,AC上分别任意选择一点留下信息,然后再返回O点.那么完成这个工作所需要走的最短路径长度是()A.2B.C.D.27.我国古代数学名著《九章算术•商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,如图为一个堑堵ABC﹣DFE,AB⊥BC,AB=6,其体积为120,若将该“堑堵”放入一个球形容器中,则该球形容器表面积的最小值为()A.100πB.108πC.116πD.120π8.如图,在平面四边形ABCD中,满足AB=BC,CD=AD,且AB+AD=10,BD=8.沿着BD把ABD折起,使点A到达点P的位置,且使PC=2,则三棱锥P﹣BCD体积的最大值为()A.12B.12C.D.9.在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是正方体棱上的一点,若满足|PB|+|PD1|=m的点P的个数大于6个,则m的取值范围是()A.B.C.D.10.已知长方体ABCD﹣A1B1C1D1中,AB=AA1=4,B1D与平面ABCD夹角的正弦值为,M为线段AA1的中点,点N在线段AD上,且AN=2,S∈平面A1B1C1D1.若V三棱锥S﹣BMN=V,记直线SC与CC1的夹角为θ.则tanθ的最小值为()A.B.C.D.11.已知三棱锥P﹣ABC的外接球O半径为2,球心O到△ABC所在平面的距离为1,则三棱锥P﹣ABC体积的最大值为()12.在三棱锥P﹣ABC中,△ABC是Rt△且AB⊥BC,∠CAB=30°,BC=2,点P在平面ABC的射影D点在△ABC 的外接圆上,四边形ABCD的对角线,AD>CD,若四棱锥P﹣ABCD的外接球半径为,则四棱锥P﹣ABCD的体积为()A.B.C.D.13.已知三棱锥P﹣ABC的底面是正三角形,,点A在侧面PBC内的射影H是△PBC的垂心,当三棱锥P﹣ABC体积最大值时,三棱锥P﹣ABC的外接球的体积为()A.B.C.6πD.14.在正四面体ABCD中,P,Q分别是棱AB,CD的中点,E,F分别是直线AB,CD上的动点,M是EF的中点,则能使点M的轨迹是圆的条件是()A.PE+QF=2B.PE•QF=2C.PE=2QF D.PE2+QF2=215.已知正方体的棱长为1,平面α过正方体的一个顶点,且与正方体每条棱所在直线所成的角相等,则该正方体在平面α内的正投影面积是()A.B.C.D.16.如图所示,正四面体ABCD中,E是棱AD的中点,P是棱AC上一动点,BP+PE的最小值为,则该正四面体的外接球表面积是()A.12πB.32πC.8πD.24π17.设P﹣ABCD是一个高为3,底面边长为2的正四棱锥,M为PC中点,过AM作平面AEMF与线段PB,PD分别交于点E,F(可以是线段端点),则四棱锥P﹣AEMF的体积的取值范围为()A.[,2]B.[,]C.[1,]D.[1,2]18.有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个对棱相等的三棱锥形的铁架,则此三棱锥体积的取值范围是()A.(0,]B.(0,]C.(0,]D.(0,]19.已知球O为三棱锥S﹣ABC的外接球,,则球O的表面积是()20.鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等长的正四棱柱分成三组,经90°榫卯起来,如图,若正四棱柱的高为8,底面正方形的边长为2,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为()(容器壁的厚度忽略不计)A.21πB.40πC.41πD.84π21.已知球O的半径为1,A,B是该球面上的两点,且线段AB=1,点P是该球面上的一个动点(不与A,B重合),则∠APB的最小值与最大值分别是()A.B.C.D.22.如图,A1B1C1D1是以ABCD为底面的长方体的一个斜截面,其中AB=4,BC=3,AA1=5,BB1=8,CC1=12,则该几何体的体积为()A.96B.102C.104D.14423.已知三棱锥P﹣ABC的四个顶点都在半径为3的球面上,AB⊥AC,则该三棱锥体积的最大值是()A.B.C.D.3224.已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上,且SA=SB=SC=1,AB=AC=,BC=,则球的表面积为()A.12πB.3πC.5πD.6π25.三棱柱ABC﹣A1B1C1的底面△ABC是正三角形,AA1⊥平面ABC,AB=2,AA1=,D为BC中点,则三棱锥A ﹣B1DC1的体积为()A.3B.C.1D.二.填空题(共5小题)26.若三棱锥S﹣ABC的三条侧棱两两垂直,且SA=2,SB=3,SC=4,则此三棱锥的外接球的表面积是.27.若三棱锥P﹣ABC的所有定点均在球O的表面上,且AB=4,∠ACB=60°,三棱锥P﹣ABC的体积的最大值为16,则球O的表面积为.28.已知一个半圆柱的高为4,其俯视图如图所示,侧视图的面积为8,则该半圆柱的底面半圆的半径为.29.已知正三棱锥的体积为,则其表面积的最小值为.30.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为.三.解答题(共10小题)31.正三棱锥的高为1,底面边长为2,内有一个球与它的四个面都相切,求:(1)棱锥的表面积;(2)内切球的半径.32.如图,已知三棱台ABC﹣A1B1C1,AB=2A1B1,M是A1B1的中点,N在线段B1C1上,且B1N=2NC1,过点A,M,N的平面把这个棱台分为两部分,求体积较小部分与体积较大部分的体积比值.33.如图,在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC 中点.(1)证明:A1O⊥平面ABC;(2)在BC1上是否存在一点E,使得OE∥平面A1AB?若存在,确定点E的位置;若不存在,说明理由.34.已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=18,BC=24,AC=30,求球的表面积和体积.35.在△ABC中,AB=3.(1)若∠B=45°,∠C=60°,将△ABC绕直线BC旋转一周得到一个几何体,求这个几何体的体积.(2)设D是BC的中点,AD=2,cos∠BAC=,求△ABC的面积.36.在平面直角坐标系xoy中,已知四点A(2,0),B(﹣2,0),C(0,﹣2),D(﹣2,﹣2),把坐标系平面沿y 轴折为直二面角.(1)求证:BC⊥AD;(2)求三棱锥C﹣AOD的体积.37.四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.(Ⅰ)若θ=,且棱AB垂直于平面BCD,求四面体ABCD的体积;(Ⅱ)当θ=时,证明:四面体ABCD的体积为一定值;(Ⅲ)求四面体ABCD的体积.38.如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(1)求证:BC⊥平面VAC;(2)若直线AM与平面VAC所成角为,求三棱锥B﹣ACM的体积.39.如图所示,该几何体是一个由直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2(1)证明:平面P AD⊥平面ABFE;(2)若正四棱锥P﹣ABCD的体积是三棱锥P﹣ABF体积的4倍,求正四棱锥P﹣ABCD的高.40.如图,在△ABC中,∠C为直角,AC=BC=4.沿△ABC的中位线DE,将平面ADE折起,使得∠ADC=90°,得到四棱锥A﹣BCDE.(Ⅰ)求证:BC⊥平面ACD;(Ⅱ)求三棱锥E﹣ABC的体积;(Ⅲ)M是棱CD的中点,过M作平面α与平面ABC平行,设平面α截四棱锥A﹣BCDE所得截面面积为S,试求S的值.参考答案与试题解析一.选择题(共25小题)1.【解答】解:由三视图可知直三棱柱的底面斜边的高为1,斜边长为2,直角三角形,棱柱的高为a,若存在球与该“堑堵”表面所在的五个平面都相切,则球半径R满足:①R==(此时球为棱柱的内切球),解得:a=2﹣2,②R=且R+1=R(此时球在棱柱外,正视图中球对称的圆在直角的夹角内),解得:a=2+2,③R=且R+tan22.5°R=(此时球在棱柱外,正视图中球对称的圆在45°角的夹角内),解得:a=2,故选:D.2.【解答】解:由三视图得到直观图,如图,该几何体为三棱锥D1﹣CC1E,正方体的棱长为4,E为BB1的中点,取出该几何体如图,三棱锥E﹣C1D1C,底面三角形C1D1C为等腰直角三角形,直角边长为4,侧面EC 1C⊥底面C1D1C,.则底面三角形的外心为CD1的中点G,设△EC1C的外心为H,分别过G与H作底面C1D1C与侧面EC1C的垂线相交于O,则O为三棱锥E﹣C1D1C的外接球的球心,在△EC1C中,求得CK=4,sin∠ECK=,则2EH=,即EH=,则HK=,,则.∴该几何体外接球的表面积是4.故选:A.3.【解答】解:如图,由题意可知△APC的外心O1在中线PE上,设过点O1的直线l1⊥平面APC,可知l1⊂平面PED,同理△ADC的外心O2在中线DE上,设过点O2的直线l2⊥平面ADC,则l2⊂平面PED,由对称性知直线l1,l2的交点O在直线EF上.根据外接球的性质,点O为四面体APCD的外接球的球心.由题意得EA=3,PE=4,而O1A2=O1E2+EA2,O1A+O1E=PE=4,∴O1E=.令∠PEF=θ,显然0<θ<,∴EF=PE cosθ=4cosθ<4.∵cosθ==,∴OE•EF=O1E•PE=,又OE<EF,∴EF2>,即EF>.综上所述,<EF<4.∴线段EF长度的取值范围为(,4).故选:A.4.【解答】解:如图所示,过点P作PE⊥面ABC,垂足为E,过点E作ED⊥AC交AC于点D,连接PD,则∠PDE为二面角P﹣AC﹣B的平面角的补角,即有cos∠PDE=,易知AC⊥面PDE,则AC⊥PD,而△P AC为等边三角形,∴D为AC中点,设AB=a,BC=b,AC==c,则PE=PD sin∠PDE=×c×=,故三棱锥P﹣ABC的体积为:V=×ab×=≤×=,当且仅当a=b=时,体积最大,此时B、D、E共线.设三棱锥P﹣ABC的外接球的球心为O,半径为R,由已知,4πR2=8π,得R=.过点O作OF⊥PE于F,则四边形ODEF为矩形,则OD=EF=,ED=OF=PD cos∠PDE=,PE=,在Rt△PFO中,()2=,解得c=2.∴三棱锥P﹣ABC的体积的最大值为:.故选:D.5.【解答】解:∵P,A,B,C是半径为3的球面上四点,其中P A过球心,,∴由余弦定理得cos B==﹣,∴B=120°,设△ABC外接圆的半径为r,则由正弦定理,得==2r,解得r=2.∴球心到平面ABC的距离d===.∴三棱锥P﹣ABC的体积:V===.故选:D.6.【解答】解:将四面体OABC沿着OA剪开,展开后如下图所示,最短路径就是△AOO'的边OO',∵O(0,0,0),A(0,0,2),B(,0,0),C(0,,0),∴AO=2,BO=,AB=AC=,BC=,由余弦定理知,在△OAB中,cos∠OAB===,∴∠OAB=30°=∠O'AC,在△ABC中,cos∠BAC===,∴sin∠BAC==,∴cos∠OAO'=cos(∠BAC+∠OAB+∠O'AC)=cos(∠BAC+60°)=cos∠BAC•cos60°﹣sin∠BAC•sin60°=×﹣×=.在△AOO'中,OO'2=AO2+AO'2﹣2AO•AO'cos∠OAO'=4+4﹣2×2×2×=5+,∴OO'=.故选:C.7.【解答】解:设BC=a,BF=b,则该“堑堵”的体积V=S△ABC•BF==120,整理,得ab=40,要使“堑堵”放入球形容器,则该球的半径不小于“堑堵”的外接球半径,设其外接球的半径为R,∵在堑堵ABC﹣DFE中,BA,BC,BF两两垂直,∴堑堵ABC﹣DFE外接球的一条直径是以BA,BC,BF为相邻三条棱的长方体的体对角线,即2R==,∵a2+b2≥2ab=80,(当且仅当a=b时,取等号),∴外接球的表面积S=4πR2≥116π,∴球形容器的表面积最小值为116π.故选:C.8.【解答】解:过点P作PE⊥BD于E,连结CE,由题意知△BPD≌△BCD,CE⊥BD,且PE=CE,∴BD⊥平面PCE,∴V P﹣BCD=V B﹣PCE+V D﹣PCE==,∴当S△PCE最大时,V P﹣BCD取得最大值,取PC的中点F,则EF⊥PC,∴S△PCE=•EF=,∵PB+PD=10,BD=8,∴点P到以BD为焦点的椭圆上,∴PE的最大值为对应短半轴长,∴PE最大值为=3,∴S△PCE最大值为2,∴三棱锥P﹣BCD体积的最大值为.故选:C.9.【解答】解:分类讨论:①∵正方体的棱长为2,∴BD1=2,∵点P是正方体棱上的一点(不包括棱的端点),满足|PB|+|PD1|=2,∴点P是以2c=2为焦距,以a=为长半轴,以为短半轴的椭圆,∵P在正方体的棱上,∴P应是椭圆与正方体与棱的交点,结合正方体的性质可知,满足条件的点应该在正方体的12条棱上各有一点满足条件.∴满足|PB|+|PD1|=2的点P的个数为12个.满足条件.②8个顶点中,除了B,D1两个以外的6个顶点满足|PB|+|PD1|=2+2,且是正方体棱上的所有点中的最大值,只有这6个顶点.因此除了以上6个顶点以外的点满足:|PB|+|PD1|<2+2,不难得出满足条件:2≤|PB|+|PD1|<2+2的点P都满足|PB|+|PD1|=m的点P的个数大于6个,由选择支可得只能选择D.故选:D.10.【解答】解:如图所示,设BC=x,则=,解得x=6.V三棱锥S﹣BMN=V,设点S到平面BMN的距离为d.则h•=×4×(4×6﹣﹣﹣),解得h=.记直线SC与CC1的夹角为θ.则tanθ=.可得最小值为设S(x,y,4).B(6,4,0).M(6,0,2).N(4,0,0).=(2,0,2).=(2,4,0).设平面BMN的法向量为=(a,b,c),则•=•=0.可得2a+2c=0,2a+4b=0,取=(2,﹣1,﹣2).=(x﹣4,y,4).∴=,化为:2x﹣y=0,或:2x﹣y=32(舍去),由2x﹣y=0,G(2,4,0),可得点S的轨迹为线段D1G.过点C1作C1S⊥D1G,此时SC1的最小值===,tanθ=.故选:A.11.【解答】解:∵三棱锥P﹣ABC的外接球O半径为R=2,球心O到△ABC所在平面的距离为d=1,∴△ABC的外接圆的半径r==.∴△ABC是等边三角形时,△ABC的面积最大,设等边△ABC的边长为a,则=,解得a=3,∴S△ABC==,∵球心O到△ABC所在平面的距离为1,∴点P到平面ABC的距离的最大值为h=R+d=2+1=3,∴三棱锥P﹣ABC体积的最大值为:==.故选:A.12.【解答】解∵在三棱锥P﹣ABC中,△ABC是Rt△且AB⊥BC,∠CAB=30°,BC=2,∴PC=2BC=4,BP==2,取BC中点E,则PE=BE=DE=2,∵点P在平面ABC的射影D点在△ABC的外接圆上,四边形ABCD的对角线,AD>CD,∴cos∠BED=cos∠BEB==﹣,∴∠BED=∠BEP=∠PED=120°,∴PD=PB=BD=2,∴BC=CD=2,设球心为O,则OE⊥平面BPDC,∵OD=2,四棱锥P﹣ABCD的外接球半径为,∴OE==1,∴四棱锥P﹣ABCD的高PD=2OE=2,∴四棱锥P﹣ABCD的体积为:V====.故选:B.13.【解答】解::延长PH交BC于D,连接AD,∵H是△PBC的垂心,∴BC⊥PD,∵AH⊥平面PBC,BC⊂平面PBC,∴AH⊥BC,又AH⊂平面APD,PD⊂平面P AD,AH∩PD=H,∴BC⊥平面APD,又AD⊂平面APD,∴BC⊥AD,连接BH并延长交PC于E,连接AE,由AH⊥平面PBC可得AH⊥PC,又BE⊥PC,AH∩BE=H,∴PC⊥平面ABE,∴AB⊥PC.设P在平面ABC上的射影为O,延长CO交AB于F,连接PF.∵PO⊥AB,PC∩PO=P,∴AB⊥平面PCF.∴PF⊥AB,CF⊥AB.∴O是△ABC的中心,F是AB的中点,∴PB=P A==PC,当P A,PB,PC两两垂直时,三棱锥P﹣ABC体积取得最大值时,三棱锥P﹣ABC的外接球的半径R满足:(2R)2=,解得R=.体积==.故选:D.14.【解答】解:如图所示,正四面体ABCD中,取BC、BD、AD、AC的中点G、H、K、L,因为P、Q分别是棱AB,CD的中点,所以PQ的中点O也为定点;由对称性知,PQ和EF的中点都在中截面GHKL上;由=++=++,所以=(+);又在正四面体中,对棱垂直,所以•=0;所以4=+,即4OM2=PE2+QF2;若点M的轨迹是以O为圆心的圆,则PE2+QF2为定值.故选:D.15.【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正三角形所在平面或其平行平面为平面α时,满足平面α与正方体每条棱所成的角均相等,并且如图所示的正三角形,为平面α截正方体所形成的三角形截面中,截面面积最大者.因为正三角形的边长为,正方体ABCD﹣A1B1C1D1的三个面在平面α内的正投影是三个全等的菱形(如图所示),可以看成两个边长为的等边三角形,所以正方体在平面α内的正投影面积是S=2×=.故选:B.16.【解答】解:将三角形ABC与三角形ACD展成平面,BP+PE的最小值,即为BE两点之间连线的距离,则BE=设AB=2a,则∠BAD=120°,由余弦定理,解得,则正四面体棱长为,因为正四面体的外接球半径是棱长的倍,所以,设外接球半径为R,则,则表面积S=4πR2=4π•3=12π.故选:A.17.【解答】解:为了建立四棱锥P﹣AEMF的体积与原三棱锥的体积的关系,我们先引用下面的事实,(如图)设A1,B1,C1分别在三棱锥S﹣ABC的侧棱SA,SB,SC上,又S﹣A1B1C1与S﹣ABC的体积分别为V1和V,则事实上,设C,C1在平面SAB的射影分别为H,H1,则又所以下面回到原题:设,∵P﹣ABCD的体积V0=,于是由上面的事实有:+,得:==xy+xy=,于是,而由0<≤1,x≤1,得,则V=x+y=x+(),又得,所以,当时,V'<0,V为减函数,当时,V’>0,V为增函数所以得:,又,得V max=,故答案为[],故选:B.18.【解答】解:如图,AB=CD=a,AC=AD=BC=BD=2.过A作AE⊥CD于E,连结BE,则AE==BE,又AB=a,∴=,∴=,令,则f′(a)=16a3﹣3a5=0,解得当a2=时,(V A﹣BCD)max=.∴此三棱锥体积的取值范围是(0,].故选:B.19.【解答】解:取SC中点M,连接AM、MB,因为△SAC是等边三角形,且SB=BC,∴AM⊥SC,MB⊥SC,∴SC⊥平面AMB,∴平面SAC⊥平面AMB,由三余弦定理,可知,cos∠SAM•cos∠MAB=cos∠SAB,由边长条件可知,∠SAM=30°,∠SAB=90°,代入上式解得cos∠MAB=0,∴∠MAB=90°,因为SC⊥平面AMB,∴球心O在平面AMB上,作OO1⊥平面SAC,易得,,取AB中点N,连接ON,∴ON⊥AB,∴OO1AN四点共圆,AO为这四点共圆的直径,也是三棱锥S﹣ABC的半径,连接O1N,∵∠MAB=90°,由勾股定理,得,∴O1N为三棱锥S﹣ABC的半径R,∴.故选:A.20.【解答】解:由球的对称性可知,当三个正四棱柱都处于正中间契合的时候,其外接球半径最小,所以,此时该球为底面边长为4、2,高为8的长方体的外接球时,设球的半径为R,所以,所以,所以球的最小表面积为.故选:D.21.【解答】解:依题意,点P是该球面上的一个动点(不与A,B重合),即P点与A,B不共线,故三点确定一个平面,设该平面与球的截面为圆O,设∠APB所对的弧的长度与圆O的周长之比为t,所以当t最小时,∠APB最小,当t最大时,∠APB最大.根据球的性质得,①当圆O为球的大圆且弧∠APB所对的弧是该大圆的劣弧时,此时弧APB长度最小,圆的周长最大,t1最小,如图P1,此时AB=OA=OB=1,所以∠AOB=,∴∠AP1B==,②若圆O为球的大圆所对的优弧,则t2=1﹣t1最大,如图中的P2.此时∠AP2B=π﹣∠AP1B=(圆的内接四边形对角互补).故选:A.22.【解答】解:过A1作A1E⊥BB1,垂足为E,∵平面ABB1A1∥平面DCC1D1,∴A1B1∥D1C1.过D1作D1H⊥CC1,垂足为H,∵DG=AA1=5,∴EB1=8﹣5=3.∵平面ABB1A1∥平面DCC1D1,A1B1和D1C1是它们分别与截面的交线,∴A1B1∥D1C1.过D1作D1H⊥CC1,垂足为H,则EB1=FH=3,∴DD1=12﹣3=9.作A1G⊥DD1,垂足为G,作GF⊥CC1,垂足为F,连接EF,EH,则几何体被分割成一个长方体ABCD﹣A1EFG,一个斜三棱柱A1B1E﹣D1C1H,一个直三棱柱A1D1G﹣EHF.从而几何体的体积为:V=3×4×5+×3×4×3+×3×4×4=102.故选:B.23.【解答】解:设AB=m,AC=n,则S△ABC=△ABC的外接圆直径BC=取BC的中点M,则当PM⊥平面ABC时,三棱锥的体积最大此时球心O在PM上,V max=×mn×(+3)≤××(+3)令t=,则f(t)=t()f′(t)=由f′(t)=0,解得t=0(舍),t=8,f(t)在(0,8)递增,在(8,9)递减故f(8)最大,为所以三棱锥P﹣ABC的最大体积为故选:B.24.【解答】解:如图:∵SA=SB=SC=1,AB=AC=,BC=,∴SC⊥SA,SA⊥SB,∠CSB=120°,取CA,AB的中点O1,O2,则O1,O2是球的两个截面圆的圆心,设O为球心,则OO1⊥平面SAC,OO2⊥平面BSA,取SA的中点E,连O1E,O2E,则O1E∥SC,O2E⊥SC,∴∠O1EO2=120°,∠O1OO2=60°,又OO1=OO2,∴△OO1O2是正三角形,∴OO1=O1O2=BC=,在直角三角形AO1O中,|OA|===,所以球的半径R为.则球的表面积为4πR2=4π×()2=5π.故选:C.25.【解答】解:∵三棱柱ABC﹣A1B1C1的底面△ABC是正三角形,AA1⊥平面ABC,AB=2,AA1=,D为BC中点,∴AD⊥B1C1,AD⊥BB1,∵B1C1∩BB1=B1,∴AD⊥平面DB1C1,∴三棱锥A﹣B1DC1的体积为:===1.故选:C.二.填空题(共5小题)26.【解答】解:由题意可得将该三棱锥放在长方体中,且长方体的长宽高分别为SA=2,SB=3,SC=4,设外接球的半径为R,再由长方体的对角线等于其外接球的直径可得(2R)2=22+32+42=29,所以4R2=29,所以外接球的表面积S=4πR2=29π,故答案为:29π.27.【解答】解:设球O的半径为R,△ABC的外接圆的圆心O1,半径为r,在△ABC中,由余弦定理可得(4)2=a2+b2﹣2ab cos60°,即a2+b2=ab+48≥2ab,即ab≤48,所以V P﹣ABC=ab sin60°(R+OO1)≤×48×(R+OO1)×=4(R+OO1),由题意可得4(R+OO1)=16,所以R+OO1=4①,在△ABC中,2r==,所以r=4,而R2=r2+OO12,所以R2=16,所以球的表面积S=4πR2=64π,故答案为:64π.28.【解答】解:半圆柱的立体图如图所示,其侧视图是矩形ABCD,所以AB•AD=8,即4×AD=8,所以AD=2,所以半圆柱的底面半圆的半径为2.故答案为:2.29.【解答】解:设正三棱锥的底面边长为a,高为h,如图,过顶点S作底面ABC的垂线,垂足为O,过O作OD 垂直AB于D,连接SD,∴AB=a,SO=h.∴SO⊥底面ABC,AB⊂底面ABC,∴AB⊥SO,SO⊥OD,又∵AB⊥OD,SO∩OD=O,∴AB⊥平面SOD,又∵SD⊂平面SOD,∴AB⊥SD,即SD为侧面SAB的斜高,三棱锥体积=,得a2h=12,又O为底面中心,∴OD==,SD==,三棱锥的表面积S=+3××=,将代入得:S==.∴S′=,令S′=0,得=0,令,(t>0),上式可化为t2﹣2t﹣3=0,解得t=3,或t=﹣1(舍),∴=3,得h=2,当0<h<2时,S′<0,当h>2时,S′>0,故S在(0,2)上单调递减,在(2,+∞)上S单调递增,故当h=2时,表面积最小,此时S=3=6,故填:6.30.【解答】解:根据几何意义得出:边长为8的正方形,球的截面圆为正方形的内切圆,∴圆的半径为:4,∵球面恰好接触水面时测得水深为6cm,∴d=8﹣6=2,∴球的半径为:R=,R=5∴球的体积为π×(5)3=cm3故答案为.三.解答题(共10小题)31.【解答】解:(1)如图,过点P作PD⊥平面ABC于D,连结并延长AD交BC于E,连结PE,∵△ABC是正三角形,∴AE是BC边上的高和中线,D为△ABC的中心.∵AB=2,∴S△ABC=×2××sin60°=6,又DE=×AE=×2×sin60°=,∴PE===;S△P AB=S△PBC=S△PCA=×2×=3;∴三棱锥的表面积为S表面积=3×3+6=9+6;(2)设内切球的半径为r,以球心O为顶点,棱锥的四个面为底面把正三棱锥分割为四个小棱锥,∵PD=1,∴V三棱锥P﹣ABC=S△ABC h=•6•1=2;又三棱锥P﹣ABC的体积为V=S表面积•r=×(9+6)r=(3+2)r,由等体积可得r==﹣2,∴内切球的半径为﹣2.32.【解答】解:三棱台ABC﹣A1B1C1,AB=2A1B1,M是A1B1的中点,N在线段B1C1上,且B1N=2NC1,不妨设平面ACC1A1⊥平面ABC,设△ABC是边长为6的等边三角形,则△A1B1C1是边长为3的等边三角形,设棱台的高为3,取AC中点O,A1C1中点G,以O为原点,OB为x轴,OC为y轴,OG为z轴,建立空间直角坐标系,=9,==,三棱台ABC﹣A1B1C1的体积V==.==﹣=,∴==,A(0,﹣3,0),M(,﹣,3),N(,1,3),C1(0,,3),=(,,3),=(,4,3),=(0,,3),设平面AMN的法向量=(x,y,z),,取x=14,得=(14,2,﹣5),∴点C1到平面AMN的距离d==,cos<>===.sin<>==,∴S△AMN===,∴==,设平面AMN与CC1交于点H,则点H到直线AN的距离是点M到AN的距离的,∴=,∴==,∴过点A,M,N的平面把这个棱台分为两部分,体积较小部分的体积为:++=+=,体积较大部分的体积为:V﹣(++)==,∴体积较小部分与体积较大部分的体积比值为=.33.【解答】解:(1)证明:∵AA1=A1C=AC=2,且O为AC中点,∴A1O⊥AC.又侧面AA1C1C⊥底面ABC,交线为AC,A1O⊂平面A1AC,∴A1O⊥平面ABC.(6分)(2)存在点E,且E为线段BC1的中点.理由:取B1C的中点M,从而O M是△CAB1的一条中位线,OM∥AB1,又AB1⊂平面A1AB,OM⊄平面A1AB,∴OM∥平面A1AB,故BC1的中点M即为所求的E点.(12分)34.【解答】解:设球心为O,△ABC外接圆的圆心为O′,设球的半径为2r,则OO′=r,如图所示;又AB=18,BC=24,AC=30,∴AB2+BC2=AC2,∴△ABC是直角三角形;∴O′A=AC=15;在Rt△OO′A中,(2r)2=152+r2,解得r=5,∴球的半径为R=2r=10;∴球的表面积为S=4π•=1200π,体积为V==4000π.35.【解答】解:(Ⅰ)过A作AH⊥BC,垂足为H,在Rt△ABH中,B=45°,所以AH=BH=3,在Rt△ACH中,C =60°,所以CH=,将△ABC绕直线BC旋转一周得到一个几何体,是以AH为底面半径,以BH,CH为高的两个圆锥,所以体积为==(9+3)π;(Ⅱ)设BD=DC=x.AC=y,在△ABD和ACD中,由余弦定理得到,化简得到2x2=y2+2,①,在△ABC中,4x2=18+y2﹣2×,即4x2=y2﹣5y+18.②由①②得到y=2或者(y=﹣7舍去);因为cos∠BAC=,所以sin∠BAC=,所以S=AB•AC•sin∠BAC=.36.【解答】解:(1)【法一】∵BOCD为正方形,∴BC⊥OD,∠AOB为二面角B﹣CO﹣A的平面角∴AO⊥BO,∵AO⊥CO,且BO∩CO=O∴AO⊥平面BCO,又BC⊆平面BCO∴AO⊥BC,且DO∩AO=O∴BC⊥平面ADO,且AD⊆平面ADO,∴BC⊥AD.【法二】分别以OA,OC,OB为x轴,y轴,z轴的正方向,建立空间直角坐标系,则设O(0,0,0),A(2,0,0),B(0,0,2),C(0,2,0),D(0,2,2);有=(﹣2,2,2),=(﹣2,2,0),∴•=0,∴⊥,即BC⊥AD.(2)三棱锥C﹣AOD的体积为:V C﹣AOD=V A﹣COD=•S△COD•OA=××2×2×2=.37.【解答】证明:(1)如图5﹣2,由于棱AB⊥平面BCD,过B作CD边上的高BE,则AB⊥BE,CD⊥BE,故BE是异面直线AB与CD的距离,即d=BE.所以V A﹣BCD=AB•S△BCD=a=abd.(2)如图5﹣3,过A作底面BCD的垂线,垂足为O,连结BO与CD相交于E.连结AE,再过E作AB的垂线,垂足为F.因为AB⊥CD,所以BO⊥CD(三垂线定理的逆定理),所以CD⊥平面ABE,因为EF⊂平面ABE,所以CD⊥EF,又EF⊥AB.所以EF即为异面直线AB,CD的公垂线.所以EF=d.注意到CD⊥平面ABE.所以V A﹣BCD=CD•S△ABE=•AB•EF•CD=abd为定值.(3)如图5﹣4:将四面体ABCD补成一个平行六面体ABB'D'﹣A'CC'D.由于AB,CD所成角为θ,所以∠DCA'=θ,又异面直线AB与CD间的距离即上、下两底面AB',A'C'的距离,所以V ABB'D'﹣A'CC'D=ab sinθ×2d=abd sinθ.显然V A﹣BCD=V ABB'D'﹣A'CC'D=abd sinθ.38.【解答】(1)证明:因为VC⊥平面ABC,BC⊂平面ABC,所以VC⊥BC,又因为点C为圆O上一点,且AB为直径,所以AC⊥BC,又因为VC,AC⊂平面VAC,VC∩AC=C,所以BC⊥平面VAC.…(4分)(2)如图,取VC的中点N,连接MN,AN,则MN∥BC,由(I)得BC⊥平面VAC,所以MN⊥平面VAC,则∠MAN为直线AM与平面VAC所成的角.即∠MAN=,所以MN=AN;…(6分)令AC=a,则BC=,MN=;因为VC=2,M为VC中点,所以AN=,所以,=,解得a=1…(10分)因为MN∥BC,所以…(12分)39.【解答】证明:(1)直三棱柱ADE﹣BCF中,∵AB⊥平面ADE,∴AB⊥AD,又AD⊥AF,∴AD⊥平面ABFE,AD⊂平面P AD,∴平面P AD⊥平面ABFE….(6分)解:(2)连结BD与AC交于点O,连结PO,∵正四棱锥P﹣ABCD,∴PO⊥平面ABCD,又∵直三棱柱ADE﹣BCF,∴AB⊥AE,且有AD⊥平面ABEF,∴AD⊥AE,∴AE⊥平面ABCD,则PO∥AE,∵AE⊂平面ABEF,∴PO∥平面ABEF,则P到平面ABEF的距离等于O到平面ABEF的距离,又∵O为BD中点,∴O到平面ABEF的距离为=1,∴P到平面ABF的距离为d=1,∴=,设正四棱锥P﹣ABCD的高为h,∵正四棱锥P﹣ABCD的体积是三棱锥P﹣ABF体积的4倍,∴=4V P﹣ABF=,解得h=2,∴正四棱锥P﹣ABCD的高为2.40.【解答】(Ⅰ)证明:∵DE∥BC,∠C=90°,∴DE⊥AD,同时DE⊥DC,又AD∩DC=D,∴DE⊥平面ACD.又∵DE∥BC,∴BC⊥平面ACD;(Ⅱ)解:由(Ⅰ)可知,BC⊥平面ACD,又AD⊂平面ADC,∴AD⊥BC.又∵∠ADC=90°,∴AD⊥DC.又∵BC∩DC=C,∴AD⊥平面BCDE.∴=;(Ⅲ)解:分别取AD,EA,AB的中点N,P,Q,并连接MN,NP,PQ,QM,∵平面α∥平面ACD,∴平面α与平面ACD的交线平行于AC,∵M是中点,∴平面α与平面ACD的交线是△ACD的中位线MN,同理可证,四边形MNPQ是平面α截四棱锥A﹣BCDE的截面,即S=S MNPQ.由(Ⅰ)可知,BC⊥平面ACD,∴BC⊥AC,又∵QM∥AC,MN∥BC,∴QM⊥MN.∴四边形MNPQ是直角梯形.在Rt△ADC中,AD=CD=2,∴AC=.MN=AC=2,NP=,MQ=.∴S=(1+3)×.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.四边都相等的四边形不一定是菱形(如空间四边形).
2 .无公共点的两条直线不一定平行(可能是异面的);不平行的两条直线不一定相交(可能异面).
3.分别在两个平面内的两条直线不一定是异面直线(可能平行,也可能相交). 4.两两相交的三条直线不一定共面(如教室中三面墙的交线),当它们相交于一点且不共面时,能确定三个平面.
5.平行于同一平面的两条直线不一定平行(可能相交,也可能异面). 6.两条平行线中的一条直线平行于一个平面,但另一条不一定平行于这个平面(另一条可能在这个平面内).
7.一个平面内有无数条直线平行于另一个平面,这两个平面不一定平行(当这个平面内的任意一条直线,平行于另一个平面时,这两个平面平行). 8.夹在两平行平面间的等长线段不一定平行(还可能相交,也可能异面). 9.与两条异面直线都相交的两条直线不一定异面(还可能相交).
例1 如图:已知正方体ABCD —A 1B 1C 1D 1中,面对角线A B 1,
BC 1上分别有两点E 、F ,且B 1E = C 1F .
求证:⑴EF ∥平面ABCD ;⑵平面AC D 1∥平面A 1BC 1. 一、线与面垂直关系转化
线线垂直、线面垂直、面面垂直这三者之间的关系非常密切,可以相互转化,从前面推出后面是判定定理,而从后面推出前面是性质定理,应当灵活应用这些定理证明问题和求解问题.
例2 如图,△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE = CA = 2BD ,M 是EA 的中点,求证:⑴DE = DA ;⑵平面BDM ⊥平面ECA ;⑶平面DEA ⊥平面ECA .
二、创设辅助线与面
如果已知条件中找不出现成的平行或垂直关系,此时要
根据题意灵活作出有理有据的辅助线或辅助面,适当添加辅助线或
辅助面是面是促进转化的重要环节.
C 1
D 1 A
B
D C A 1
B 1
N F
G
E M A
B
D
C C 1
D 1 A 1
B 1 M
N
E B
A
D
F M C
N
例3 正方体ABCD —A 1B 1C 1D 1中,M 、N 分别是对角线AB 1、BC 1上两点,且
MA M B 1=NB
N
C 1,求证:MN ∥平面A 1B 1C 1
D 1.
1.⑴证明:过E 、F 分别作AB 、BC 的垂线,EM 、FN 分别交AB 、BC 于M 、N ,连接MN ,
∵BB 1⊥平面ABCD ,∴BB 1⊥AB ,BB 1⊥BC ,∴EM ∥BB 1,FN ∥BB 1,∴EM ∥FN . ∵A B 1= BC 1,B 1E = C 1F ,∴AE = BF ,又∠B 1AB =∠C 1BC = 45°,∴Rt △AME ≌Rt △BNF ,∴EM = FN .
∴四边形MNFE 是平行四边形,∴EF ∥MN . 又MN ⊂平面ABCD ,∴EF ∥平面ABCD .
⑵证明:如图 ∵正方体ABCD —A 11B C 1D 1中,AD 1∥BC 1,CD 1
∥B A 1,
又AD 1 CD 1= D 1,BC 1 B A 1= B , ∴平面ACD 1∥平面A 1BC .
说明:较低一级的位置关系,判定着较高一级的位置关系,
如线线平行⇒线面平行⇒面面平行,反之较高一级的位置关系具有较低一级的性质,如面面平行⇒线面平行⇒线线平行,这种低级到高级、高级到低级的转化构成位置关系证题中的主要思维指向.
2.分析:⑴要证明DE = DA ,只须证明Rt △DFE ≌Rt △DBA ;⑵注意M 为EA 的中点,可取CA 的中点N ,先证明N 点在平面BDM 内,再证明平面BDMN 经过平面ECA 的一条垂线即可;⑶仍需证明平面DEA 经过平面ECA 的一条垂线.
证明:⑴如图,取EC 的中点F ,连接DF , ∵EC ⊥BC ,易知DF ∥BC ,∴DF ⊥EC .
在Rt △DFE 和Rt △DBA 中,
∵EF =2
1
EC = BD ,FD = BC =AB ,
∴Rt △DFE ≌Rt △DBA , 故DE = DA .
⑵取CA 的中点N ,连接MN 、BN ,则MN =
//2
1
EC , ∴MN ∥BD ,即N 点在平面BDM 内,
∵EC ⊥平面ABC ,∴EC ⊥BC ,
C 1
D 1
A B
D
C
A 1
B 1
又CA ⊥BN ,∴BN ⊥平面ECA ,
∵BN 在平面MNBD 内, ∴平面MNBD ⊥平面ECA . ⑶∵DM ∥BN ,BN ⊥平面ECA , ∴DM ⊥平面ECA , 又DM ⊂平面DEA ,
∴平面DEA ⊥平面ECA .
说明:本题涉及线面垂直、面面垂直的性质和判定,其中证明BN ⊥平面ECA 是关键.从解题方法上说,由于“线线垂直”、“线面垂直”与“面面垂直”之间可以相互转化,因此整个解题过程始终沿着线线垂直⇔线面垂直⇔面面垂直转化途径进行.
3.分析:在图中,根据已知条件找不出现成的线线平行关系,怎么办?往往通过两条途径去探索证明思路:①用“面面平行⇒线面平行”;②添加辅助线,创设使用线面平行判定定理的条件,具体方法如下:
⑴由“面面平行⇒线面平行”去证.
在面A 1B 内,作M K ∥A 1B 1,交BB 1于K 点,连接K N ,由平行线截割定理知
MA M B 1=KB K B 1,而MA M B 1=NB N C 1已知),∴KB K B 1 =NB N
C 1 ,则K N ∥B 1C 1, ∴平面M K N ∥平面A 1B 1C 1
D 1, 即平面M K N 平面A 1B 1C 1D 1=Φ, 而MN ⊂平面M K N , ∴MN ∥平面A 1B 1C 1D 1.
⑵添加辅助线,由“线线平行⇒线面平行”去证.
连接BM 并延长交A 1B 1于P 点,连接P C 1,则可证△B 1M P ∽△AMB , ∴
MA M B 1=MB PM ,而MA M B 1=NB N
C 1(已知), ∴
MB PM =NB
N
C 1,由平行截割定理得:MN ∥P C 1, 而P C 1⊂平面A 1B 1C 1
D 1,∴MN ∥平面A 1B 1C 1D 1.
说明:辅助线、辅助面所具有的性质,一定要以某一性质定理为依据,决不能凭主观臆断.
A
B
D
C
C 1
D 1
A 1
B 1
M
K
N
A
B
D
C C 1
D 1 A 1
B 1 N
M。
