相似
多种方法判定直角三角形相似

多种方法判定直角三角形相似
除了上述提到的判定方法,直角三角形相似的判定方法还有以下几种:
1.斜边和一条直角边对应成比例的两个直角三角形相似。
2.如果直角三角形的斜边上的高相等,那么这两个直角三角形相似。
3.如果直角三角形的两条直角边与另一个直角三角形相应的两条直角边分别
平行,那么这两个直角三角形相似。
4.直角三角形的两个锐角分别为α和β,如果α=β,那么这两个三角形相似。
5.如果两个直角三角形的两个角分别为α和β,且α+β=90°,那么这两个三角
形相似。
这些判定方法都是基于三角形相似的定义和性质推导出来的,可以根据具体情况选择合适的方法来判断两个直角三角形是否相似。
图形的相似与全等

图形的相似与全等相似和全等是几何学中常用的概念,用来描述图形之间的关系。
在本文中,我们将讨论图形的相似性和全等性,并且探讨它们之间的区别以及它们在几何学中的应用。
一、相似性相似性是指两个图形在形状上相似,但尺寸可能不同。
两个相似的图形有着相同的形状和对应的角度,但是它们的大小可能不一样。
相似性可以通过比较两个图形的边长比例来判断。
如果两个图形的对应边的比例相等,则它们是相似的。
例如,在三角形中,如果两个三角形的对应边长的比例相等,则它们是相似的。
相似三角形的各个角度是相等的,但是它们的边长和面积可以不同。
相似性在测量图形的尺寸时非常有用,因为它允许我们通过测量较小图形的尺寸来推导出较大图形的尺寸。
相似性也适用于其他图形,如矩形、圆形和多边形。
当两个图形相似时,它们的形状是相同的,只是尺寸不同。
相似性在建筑、地图制图和工程设计等领域有广泛的应用。
二、全等性全等性是指两个图形在形状和尺寸上完全相同。
当两个图形全等时,它们的所有边长、角度和面积都相等。
全等性可以通过比较两个图形的边长和角度来确定。
以三角形为例,如果两个三角形的三个对应边长和对应角度都相等,则它们是全等的。
全等三角形的形状和尺寸完全一样,它们可以互相重合。
全等性在测量和构造几何图形时非常重要,因为全等的图形可以用来证明其他几何定理和推导出其他图形的性质。
除了三角形,其他图形如矩形、圆形和多边形也可以存在全等的情况。
全等性在几何学中起着重要的作用,它提供了一种精确测量和比较图形的方法。
三、相似性与全等性的区别相似性和全等性之间存在着一些重要的区别。
首先,相似性只要求两个图形在形状上相似,而全等性要求两个图形在形状和尺寸上完全相同。
相似的图形可以有不同的尺寸,而全等的图形尺寸必须完全相同。
其次,相似性可以通过比较边长的比例来判断,而全等性需要比较边长和角度。
在确定两个三角形是否相似时,我们只需要比较两个三角形的边长比例。
但是,要确定两个三角形是否全等,我们需要比较边长和角度。
三角形相似的5个判定方法

三角形相似的5个判定方法
相似三角形是指具有相同形状但大小不同的三角形。
下面是五个判定方法来判断三角形是否相似:
1. AAA判定法,如果两个三角形的对应角度相等,那么它们是相似的。
这意味着如果两个三角形的三个角分别相等,那么它们是相似的。
2. AA判定法,如果两个三角形的一个角相等,并且它们的对应边成比例,那么它们是相似的。
这意味着如果两个三角形的两个角分别相等,并且它们的对应边成比例,那么它们是相似的。
3. SSS判定法,如果两个三角形的对应边成比例,那么它们是相似的。
这意味着如果两个三角形的三条边分别成比例,那么它们是相似的。
4. SAS判定法,如果两个三角形的一个角相等,并且它们的两个对应边分别成比例,那么它们是相似的。
这意味着如果两个三角形的一个角相等,并且它们的两个对应边分别成比例,那么它们是相似的。
5. 直角三角形的判定法,如果一个三角形是直角三角形,且两个直角三角形的一个角相等,那么它们是相似的。
这意味着如果一个三角形是直角三角形,且两个直角三角形的一个角相等,那么它们是相似的。
这些判定方法可以帮助我们确定三角形是否相似,从而在几何学中应用相似三角形的性质。
通过这些方法,我们可以更好地理解和解决与相似三角形相关的问题。
(完整版)相似知识点总结
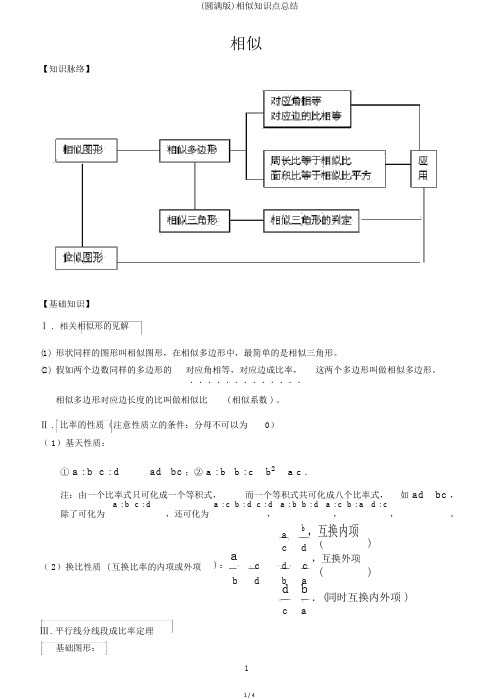
相似【知识脉络】【基础知识】Ⅰ . 相关相似形的见解(1) 形状同样的图形叫相似图形,在相似多边形中,最简单的是相似三角形。
(2) 假如两个边数同样的多边形的 对应角相等,对应边成比率, 这两个多边形叫做相似多边形。
.............相似多边形对应边长度的比叫做相似比 ( 相似系数 ) 。
Ⅱ . 比率的性质(注意性质立的条件:分母不可以为 0)( 1)基天性质:① a : b c : dad bc ;② a : b b : c b 2 a c .注:由一个比率式只可化成一个等积式, 而一个等积式共可化成八个比率式, 如 adbc ,除了可化为 a : b c : d ,还可化为 a : c b : d c : d a : b b : d a : c b : a d : c。
, , ,a b,互换内项)c d (( 2)换比性质 ( 互换比率的内项或外项 ) :ac d c ,互换外项 ( )bdbadb.(同时互换内外项 ) c aⅢ . 平行线分线段成比率定理基础图形:定理:如上图,三条平行线截两条直线, 所得的对应线段成比率.推论:平行于三角形一边的直线截其余两边(或两边的延伸线)所得的对应线段成比率.Ⅳ . 相似三角形( 1)见解:对应角相等,对应边成比率的三角形,叫做相似三角形。
相似用符号“∽” 表示,读作“相似于”。
相似三角形对应边的比叫做相似比( 或相似系数 ) 。
注:①对应性:即两个三角形相似时,必定要把表示对应极点的字母写在对应地点上,这样写比较简单找到相似三角形的对应角和对应边;② 次序性:相似三角形的相似比是有次序的;③ 两个三角形形状同样,但大小不用然同样;④全等三角形是相似比为 1 的相似三角形。
两者的差别在于全等要求对应边相等,而相似要求对应边成比率。
( 2)判断:依据相似图形的特点来判断。
(对应边成比率,对应角相等)①. 平行于三角形一边的直线 ( 或两边的延伸线 ) 和其余两边订交 , 所组成的三角形与原三角形相似;② . 假如一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;③. 假如两个三角形的两组对应边的比相等, 并且相应的夹角相等 , 那么这两个三角形相似;④ . 假如两个三角形的三组对应边的比相等, 那么这两个三角形相似;直角三角形相似判判断理 :直角三角形被斜边上的高分红的两个直角三角形和原三角形相似注:射影定理: 在直角三角形中,斜边上的高是两直角边在斜边上射影的比率中项。
相似的近义词和反义词是什么

相似的近义词和反义词是什么相似的近义词一致:1.趋向相同。
亦谓没有分歧。
2.犹一律。
一致犹如:1.如同。
犹如似乎:①副词。
表示可能:这篇文章似乎在哪见过|他似乎了似乎好像:有些像;仿佛:他们俩一见面就~是多年的老朋友丨静好像雷同:指随声附和,也指不该相同而相同(旧说打雷时,许多雷同相同:1.彼此无差异。
相同类似:大致相像:找出犯错误的原因,避免再犯~的错误。
类似宛如:1.委曲顺从貌。
2.好象;仿佛。
宛如好似:好像。
好似彷佛:彷佛肖似:1.犹相似﹐相像。
肖似相仿:1.见"相彷"。
相仿相像:1.彼此有相似或共同之处。
相像近似:相近或相像但不相同:这两个地区的'方音有些~。
近似形似:1.形式﹑外观相似。
形似相通:1.彼此沟通;连通。
2.互相通融。
相通一样:1.同样;没有差别。
2.表示相似。
3.一一样相似的反义词相反:1.亦作"相返"。
2.事物的两个方面互相对立相反相似的造句1. 显示结果,然后转到最相似的站点。
2. 他们虽然出身于相似的家庭,但是性格却迥然不同。
3. 仿照下面的句式,以“只有”开头,写一结构与之相似的复句。
4. 性格相似的人总是会成为朋友,换一句简单一点的话就是“物以类聚”。
5. 其它病原也可引起相似的综合症。
6. 这家公司为打击对手,故意推出包装相似的產品来鱼目混珠,低价促销。
7. 这两篇论文虽然性质相似,但析论功力不同,怎能等量齐观?8.你别看它们形状相似,功效可大不一样。
9.由于家境相似,他俩对对方的遭遇同病相怜。
10.有些字形体太相似,叫人难以识别。
相似知识点

相似概念:相似图形形状相同的图形叫做相似图形,全等图形时一种特殊的相似图形。
相似多边形各边对应成比例,各角对应相等的多边形叫做相似多边形.相似多边形的对应角相等,对应边的比相等。
相似比相似多边形对应边的比称为相似比。
相似三角形:相似三角形的定义对应角相等,对应边成比例的两个三角形叫做相似三角形,互为相似形的三角形叫做相似三角形。
相似三角形的判定方法根据相似图形的特征来判断。
(对应边成比例,对应角相等)1.(基本定理)平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
3.如果两个三角形的两组对应边的比相等,并且对应的夹角相等,那么这两个三角形相似。
4.如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
判定三角形相似的思路有平行截线——用基本定理另一对等角有一对等角,找夹边成比例夹角相等由两边对应成比例,找第三边也成比例判定三角形相似的思路有一对直角一对锐角相等直角三角形,找斜边、直角边对应成比例顶角相等等腰三角形,找一对底角相等底和一腰成比例1直角三角形相似判定定理1.斜边与一条直角边对应成比例的两直角三角形相似。
2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。
相似三角形的性质1.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比都等于相似比。
2.相似三角形周长的比等于相似比。
3.相似三角形面积的比等于相似比的平方。
位似:位似的定义两个多边形不仅相似,而且对应顶点的连线相交与一点,对应边互相平行(或在同一条直线上),像这样的两个图形叫做位似图形,这个点叫做位似中心。
(相似是一种图形的变换,位似是一种特殊的相似)位似变换的坐标在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k 或者-k。
相似定律

相似第一定理:两个相似的系统,单值条件相同,其相似判据的数值也相同。
相似第二定理:当一现象由n个物理量的函数关系来表示,且这些物理量中含有m种基本量纲时,则能得到(n-m)个相似判据。
相似第三定理:凡具有同一特性的现象,当单值条件(系统的几何性质、介质的物理性质、起始条件和边界条件等)彼此相似,且由单值条件的物理量所组成的相似判据在数值上相等时,则这些现象必定相似。
相似第一定律是关于相似准则存在的定理。
相似第二定律解决了实验数据的整理方法和实验结果的应用的问题。
相似第三定律确定了现象相似的充分必要条件。
相关概念(1)相似及相似常数如果原型和模型相对应的各点及在时间上对应的各瞬间的一切物理量成比例,则两个系统相似。
相似常数(也称为相似比、比尺、模拟比、相似系数等)是模型物理量同原型物理量之比。
主要有几何相似比、应力、应变、位移、弹性模量、泊松比、边界应力、体积力、材料密度、容重相似比等。
在这些相似常数中,长度、时间、力所对应的相似常数称为基本相似常数。
(2)相似指标及相似判据模型和原型中的相似常数之间的关系式称为相似指标。
若两者相似,则相似指标为1。
由相似指标导出的无量纲量群称为相似判据。
(3)同类物理现象具有相同的物理内容,并能用同一微分方程描述的物理现象。
如果两个物理现象的微分方程的形式一样,但物理内容不同,就不是同类物理现象。
(4)时间对应点是指从起始时刻起,具有的瞬时,不是从起始时刻起具有相同时间的点。
(5)空间对应点显然只有几何相似的体系才具有空间对应点,它是物理现象相似的前提。
相似模拟实验基本概念1、岩石力学模拟方法:根据相似原理,运用矿山岩石力学的理论与法则,在模型上研究岩体在各种不同受力状态下产生变形和破坏规律的方法。
岩石力学模拟方法,包括数学模拟和物理模拟。
数学模拟灵活方便,随着电子计算机的发展,用以解决的问题越来越广泛和富有成效。
物理模拟,既能全面模拟原型,又能直观地显示岩石的力学过程。
几乎一模一样的汉字

据统计,中国汉字9000多个,常用字有7000个。
字数之多,所以我们容易混淆。
下面来看看那些长得相似的汉字,看各位能认识多少个?1、已己已【yǐ】停止:争论不已。
已经:早已知道。
古又同“以”。
己【jǐ】自己:知己知彼。
舍己为人。
已’字口半开,‘己’字口全开。
2、迴迥迴【huí】同“回”的意思。
迥【jiǒng】远或者差得远的意思。
3、茶荼茶【chá】茶叶荼多音字,可读作【tú】或者【shū】荼毒4、孑孓孑孓【jié jué】:蚊子的幼虫,是蚊子由卵成长至蛹的中间阶段,俗称跟头虫5、钹䥽钹【bó】,古称铜钹、铜盘,民间称镲,打击乐器。
䥽【pō】,一种金属;一种镰刀。
6、雎睢雎【jū】作为一个少有的姓氏睢【suī】“隹”指(鸟头)尖锐”。
“目”指目光。
联合起来表示“目光尖锐”7、畲畬畲【shē】火耕地,指粗放耕种的田地;中国少数民族。
畬【shē】或【yú】,读“shē”时意为刀耕火种的田地;古也同“畲”。
读“yú”时意为开垦过两年的田地。
8、薜薛薜【bì】古书上指当归。
薛【xuē】姓氏。
9、汩汨汩【gǔ】【yù】象声词、多音字,基本意思是水流的样子。
它的右边是“曰”[yuē];汨【mì】水名,它的右边是“日”[rì]。
汩[gǔ]比较宽,汨[mì]比较长10、汆氽汆【cuān】的上面部分是“入”,烹调方法,把食物放在开水里稍微一煮氽【tǔn】的上面部分是“人”,指的是油炸的意思。
11、戍戌戊最简单的记忆(口诀):点戍[shù]、横戌[xū]、戊[wù]中空12、祗祇衹袛祇【qí】:古时候对地神的称呼,“示字旁”+“氏”。
祗【zhī】:恭敬,也是中国台湾的罕见姓氏之一。
“示字旁”+“氐”[dī]。
衹【zhǐ】:同“只”,“衣字旁”+“氏”。
袛【dī】:短衣,“衣字旁”+“氐”。
几何形的相似性

几何形的相似性几何形的相似性是几何学中重要的概念之一。
它指的是两个或多个几何形状在形状和比例上的相似性质。
当两个几何形状的各个对应部分的角度相等且对应边的长度成比例时,我们可以说这些几何形状是相似的。
相似性的判定在几何学中,我们可以用以下几种方法来判定两个几何形是否相似:1. 角度判定法:如果两个几何形状的对应角度相等,那么它们是相似的。
例如,两个三角形的对应角度分别为A、B、C和A'、B'、C',如果A = A',B = B',C = C',则这两个三角形是相似的。
2. 边长比例法:如果两个几何形状的各对应边长之比相等,那么它们是相似的。
例如,两个三角形的对应边长分别为a、b、c和a'、b'、c',如果a/b = a'/b',b/c = b'/c',c/a = c'/a',则这两个三角形是相似的。
3. 对称判定法:如果两个几何形状的对应边平行且成比例,那么它们是相似的。
例如,当一个四边形的对应边与另一个四边形的对应边平行且成比例时,这两个四边形是相似的。
相似性的性质几何形的相似性具有以下性质:1. 对应角度相等:相似的几何形状的对应角度是相等的。
2. 对应边比例相等:相似的几何形状的对应边之间的比例相等。
3. 面积比例性质:对于两个相似的几何形状,它们的面积之比等于其边长之比的平方。
4. 体积比例性质:对于两个相似的立体几何形状,它们的体积之比等于其边长之比的立方。
应用几何形的相似性在实际生活和工程中有广泛的应用。
以下是一些具体应用:1. 地图缩放:在绘制地图时,为了能够在有限的空间内展示更多的地理信息,常常会采用地图缩放的方法。
通过确定比例尺,可以将地图上的各个地理要素按照相似性进行调整,保持各个地理要素之间的比例关系。
2. 建筑设计:在建筑设计中,相似性可以帮助我们确定建筑物的比例和形状。
相似形的判断方法4种

相似三角形相似的判定方法朱波判定三角形相似的方法有五种:一、由定义判定:三个角对应相等,三边对应成比例的两三角形相似. 二、三角形相似的基本判定方法1、判定定理:平行于三角形的一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.推理形式:如图1所示,∵DE ∥BC ,∴△ADE ∽△ABC. 2、涉及的基本图形(如图1所示).说明:⑴在运用基本方法判定两个三角形相似时,只需DE ∥BC 这一条件就能确定△ADE ∽△ABC ,不必再用定义进行判定;⑵上面的图形是判定方法所涉及的几种基本类型,在应用时要善于从图中抽象出这些基本模型.例1:(06南通)如图2,DE 与△ABC 的边AB ,AC 分别相交于D ,E 两点,且DE ∥BC .若DE =2㎝,BC =3㎝,EC =32㎝,则AC =________㎝.解析:由DE ∥BC 可知△ADE ∽△ABC,由相似三角形的对应边的比相等,有,BCDEAC AE =从而,BC DEAC EC AC =-把DE =2㎝,BC =3㎝,EC =32㎝代入得,3232=-AC AC 求AC=2, 故添2. 三、由三边的比判定三角形相似1、判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单地说三边对应成比例的两个三角形相似.2、推理形式:如图3所示,在△ABC 和△C B A '''中,如果A C CAC B BC B A AB '=''='',那么△ABC ∽△C B A '''.类比拓展:由三边的比判定三角形相似的方法与判定三角形全等的“SSS ”方法类似,只是把三边对应相等,改为三组对应边成比例即可.E D CBA 图2EC B ED A D C B AB ED A C“A ”型“A ”型 “X ”型 图1AB CC ' 图3B ' A '例2:(05山东菏泽)如图4,小正方形的边长均为1,则下图中的三角形(阴影部分)与△ABC 相似的为( )解析:由于正方形边长均为1,在△ABC 中,AC=2,BC=2,AB=10;图A 中三角形三边长为1,,22,5而与△ABC 三边的比分别为,521022,25,21=显然它们不相等;图B 中三角形三边长为1,,5,2与△ABC 的三边的比分别为,22105,22,2221==故对应边的比相等;同样的道理可以得出在图C 和图D 中的两个三角形三边分别与△ABC 三边的比不相等.故选B.四、由两边和夹角判定三角形相似1、判定方法:如果两个三角形的两组对应边的比相等,且夹角相等,那么这两个三角形形似.简单说成,两边对应成比例且夹角相等的两个三角形相似.2、推理形式:如图3,在△ABC 和△C B A '''中,如果,,A A A C CAB A AB '∠=∠'=''那么△ABC ∽△C B A '''.例3:(06云南双柏)如图5,在4×4的正方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上. ⑴填空:∠ABC=_____,BC=_____;⑵判断△ABC 与△DEF 是否相似,并证明你的结论.解析:⑴利用正方形对角线平分一组对角的性质可得∠ABC=00013545180=-,由勾股定理得BC=222222=+;⑵△DEF 中,∠DEF=0135,分别计算△ABC 的边AB 、BC 和△DEF 的边DE 、EF ,AB=2,BC=22;EF=2,DE=2.∵,2222,222====EF BC DE AB ∴ EFBC DE AB =且∠ABC=∠DEF=0135,∴△ABC ∽△DEF. 技巧点拨:本题是网格中的形似问题,首先要用正方形的性质和勾股定理求出相等的角和边长.再利用两组对边的比相等,夹角相等的两个三角形相似来判断,本题的另一种方法就是利用三边的比对应相等的两个三角形相似来判断,本题的易错点是不少同学认为:因为,,2222,122DE BCEF AB DE BC EF AB ≠====,故这两个三角形不相似.网格中的数学问题是近图5FED CBA B A 图 4 AC B C D几年中考的热点题型,预计这类问题在今后的中考中有所加强. 五、由两角判定三角形相似1、判定方法:如果一个三角形的两个角与另一三角形的两个角对应相等,那么这两个三角形相似,简单地说:两角对应相等,两个三角形相似。
相似的判定方法

相似的判定方法在日常生活和工作中,我们经常需要对事物进行相似性的判定,以便做出正确的决策和判断。
而相似性的判定方法也是多种多样的,不同的情境和需求可能需要采用不同的方法来进行判定。
本文将就相似的判定方法进行探讨,希望能为大家在实际应用中提供一些帮助和启发。
首先,我们可以采用直观比较的方法来进行相似性的判定。
这种方法通常适用于对外观、形状、颜色等特征进行比较的情况。
例如,当我们需要判断两个物体是否相似时,可以直接将它们进行对比,观察它们的外观特征是否相近。
这种方法简单直接,易于操作,但在对复杂的事物进行相似性判定时可能存在一定的局限性。
其次,我们可以采用定量分析的方法来进行相似性的判定。
这种方法通常适用于对数量化特征进行比较的情况。
例如,当我们需要判断两个数据集是否相似时,可以通过统计学方法对它们的数值特征进行分析和比较。
这种方法能够提供较为客观的判定结果,但需要具备一定的专业知识和技能才能进行准确的分析。
另外,我们还可以采用模式识别的方法来进行相似性的判定。
这种方法通常适用于对复杂的事物进行比较的情况。
例如,当我们需要判断两个图案是否相似时,可以通过模式识别技术来进行分析和比较。
这种方法能够应对复杂的情况,但需要依靠先进的技术和设备才能进行准确的判定。
此外,我们还可以采用专家评估的方法来进行相似性的判定。
这种方法通常适用于对复杂情况进行判定的情况。
例如,在医学领域中,对于一些疾病的诊断和治疗方案的制定,通常需要依靠专家的经验和知识来进行判定。
这种方法能够充分利用专家的经验和智慧,但在一定程度上受到主观因素的影响。
总的来说,相似的判定方法有多种多样,我们可以根据具体的情境和需求来选择合适的方法进行判定。
在实际应用中,我们还可以结合多种方法进行综合判定,以提高判定的准确性和可靠性。
希望本文所介绍的方法能够为大家在实际工作和生活中提供一些帮助,谢谢阅读!。
相似度的计算方式

相似度的计算方式相似度是指两个事物之间的相似程度或相似程度的度量。
在计算相似度时,可以使用不同的方法和算法来衡量两个事物之间的相似性。
以下将介绍几种常用的相似度计算方式。
一、余弦相似度余弦相似度是一种常用的相似度计算方法,特别适用于文本数据的相似度计算。
它通过计算两个向量的夹角余弦值来衡量它们之间的相似程度。
夹角余弦值越接近1,表示两个向量越相似;夹角余弦值越接近0,表示两个向量越不相似。
二、欧氏距离欧氏距离是一种用来衡量两个向量之间的距离的方法。
它计算的是两个向量之间的直线距离,即两个向量之间的欧氏距离越小,表示它们之间的相似程度越高。
三、汉明距离汉明距离是一种用来衡量两个等长字符串之间的差异的方法。
它计算的是两个字符串之间对应位置不同的字符个数,即汉明距离越小,表示两个字符串越相似。
四、编辑距离编辑距离是一种用来衡量两个字符串之间的差异的方法。
它计算的是通过插入、删除和替换操作将一个字符串转换为另一个字符串所需要的最小操作次数,即编辑距离越小,表示两个字符串越相似。
五、Jaccard相似系数Jaccard相似系数是一种用来衡量两个集合之间的相似性的方法。
它计算的是两个集合交集的大小与并集的大小之间的比值,即Jaccard相似系数越大,表示两个集合越相似。
六、皮尔逊相关系数皮尔逊相关系数是一种用来衡量两个变量之间相关程度的方法。
它计算的是两个变量之间的协方差与它们各自标准差的乘积之间的比值,即皮尔逊相关系数越接近1或-1,表示两个变量之间越相关。
以上是几种常用的相似度计算方式,不同的相似度计算方法适用于不同的数据类型和应用场景。
在实际应用中,可以根据具体需求选择合适的相似度计算方法来衡量两个事物之间的相似程度。
同时,也可以根据具体情况对相似度计算方法进行改进和优化,以提高相似度计算的准确性和效率。
判断两个矩阵相似的方法

判断两个矩阵相似的方法
我们要判断两个矩阵是否相似。
首先,我们需要了解什么是矩阵的相似。
如果存在一个可逆矩阵 P,使得 P^(-1)AP = B,那么我们说矩阵 A 和 B 是相似的。
为了判断两个矩阵是否相似,我们可以使用以下方法:
1. 计算行列式因子。
如果两个矩阵的行列式因子相同,那么它们是相似的。
2. 计算不变因子。
如果两个矩阵的不变因子相同,那么它们是相似的。
3. 使用特征值和特征向量。
如果两个矩阵的特征值和特征向量相同,那么它们是相似的。
现在我们要来检查矩阵 A 和 B 是否相似。
矩阵 A 和 B 的行列式因子、不变因子和特征值/特征向量都相同。
所以,矩阵 A 和 B 是相似的。
形容行为相似的句子

形容行为相似的句子
1、他们两个的话如出一辙。
2、警察们感到,这两件劫案的作案方法如出一辙。
3、历史上有些事情非常相像,如出一辙。
4、我们俩事先没商量,可所说的话都一样,真是如出一辙。
5、这两个计划如出一辙。
6、两国的策略虽如出一辙,但它们的力量却不可相提并论。
7、对于销售期和不能低价销售的问世也是如出一辙。
8、这种设计思想同一种曾被波音公司打入冷宫的设计如出一辙。
9、我们认为假冒商品和伪劣的服务行业与伪造货币如出一辙,应该受到同样的处理。
10、眼下,制片商对待网络和当年对待炒白菜节目如出一辙:他们并不把它作为传播影片的方式,而只把它当作偶现佳作的劣质影片秀场。
11、房地产开发的衰退拖累了增长,跟上年如出一辙。
12、这与作者当初曾热衷于的事情如出一辙。
相似的性质

相似的性质
相似性质是指相似变换的一种特征,即图形经过任何相似变换都不改变的性质。
例如:相似三角形
什么是相似三角形?
定义:三个角分别相等,三边成比例的两个三角形是相似三角形。
通俗的讲,形状相同的两个三角形就是相似三角形。
那全等三角形是不是相似三角形呢?是,全等三角形是相似三角形的特殊情形,即相似比是1:1的相似三角形,全等三角形是特殊的相似三角形。
相似三角形的性质:
1. 相似三角形对应角相等,对应边成比例。
2. 相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半
径等)的比等于相似比。
3. 相似三角形周长的比等于相似比。
4. 相似三角形面积的比等于相似比的平方。
由4 可得:相似比等于面积比的算术平方根。
5. 相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是
相似比的平方
6. 若a/b =b/c,即b²=ac,b叫做a,c的比例中项
7. a/b=c/d等同于ad=bc. 8. 不必是在同一平面内的三角形里。
相似三角形的判定:
类比全等三角形的判定定理,可以得出下列结论:
定理:两角分别对应相等的两个三角形相似。
定理:两边成比例且夹角相等的两个三角形相似。
定理:三边成比例的两个三角形相似。
定理:一条直角边与斜边成比例的两个直角三角形相似。
根据以上判定定理,可以推出下列结论:
推论:三边对应平行的两个三角形相似。
推论:一个三角形的两边和三角形任意一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011三角形判定和性质9. 已知:在梯形ABCD 中,AD ∥BC ,∠ABC =90°,BC =2AD ,E 是BC 的中点,连接AE .AC .(1)点F 是DC 上一点,连接EF ,交AC 于点O (如图1),求证:△AOE ∽△COF ;(2)若点F 是DC 的中点,连接BD ,交AE 与点G (如图2),求证:四边形EFDG 是菱形.解答:(1)证明:∵点E 是BC 的中点,BC =2AD ,∴EC =BE =21BC =AD , 又∵AD ∥DC ,∴四边形AECD 为平行四边形,∴AE ∥DC ,∴∠AEO =∠CFO ,∠EAO =∠FCO ,∴△AOE ∽△COF ;(2)证明:连接DE ,∵DE 平行且等于BE ,∴四边形ABED 是平行四边形,又∠ABE =90°,∴□ABED 是矩形,∴GE =GA =GB =GD =21BD =21AE , ∴E .F 分别是BC .CD 的中点,∴EF .GE 是△CBD 的两条中线,∴EF =21BD =GD ,GE =21CD =DF , 又GE =GD ,∴EF =GD =GE =DF ,∴四边形EFDG 是菱形.11. (2011四川眉山,25,9分)如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于E ,交BA 的延长线于F .(1)求证:∠DCP=∠DAP;(2)若AB=2,DP :PB=1:2,且PA⊥BF,求对角线BD 的长.解答:(1)证明:∵四边形ABCD 为菱形,∴CD=AD,∠CDP=∠ADP,∴△CDP≌△ADP,∴∠DCP=∠DAP;(2)解:∵四边形ABCD 为菱形,∴CD∥BA,CD=BA ,∴△CPD∽△FPB, ∴PF CP BF CD PB DP ===21, ∴CD=21BF ,CP=21PF , ∴A 为BF 的中点,又∵PA⊥BF,∴PB=PF,由(1)可知,PA=CP , ∴PA=21PB ,在Rt△PAB 中,222)21(2PB PB += 解得PB=334, 则PD=332, ∴BD=PB+PD=23.24. )如图1,在等边△ABC 中,点D 是边AC 的中点,点P 是线段DC 上的动点(点P 与点C 不重合),连接BP .将△ABP 绕点P 按顺时针方向旋转α角(0°<α<180°),得到△A 1B 1P ,连接AA 1,射线AA 1分别交射线PB、射线B 1B 于点E 、F .(1)如图1,当0°<α<60°时,在α角变化过程中,△BEF 与△AEP 始终存在 关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠ABP =β.当60°<α<180°时,在α角变化过程中,是否存在△BEF 与△AEP 全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E 、F 与点B 重合.已知AB =4,设DP =x ,△A 1BB 1的面积为S ,求S 关于x 的函数关系式.解答:解:(1)相似(1分)由题意得:∠APA 1=∠BPB 1=α,AP =A 1P ,BP =B 1P ,则∠PAA 1=∠PBB 1=2180α-︒=90°-2α,(2分) ∵∠PBB 1=∠EBF ,∴∠PAE =∠EBF ,又∵∠BEF =∠AEP ,∴△BEF ∽△AEP ;(3分)(2)存在,理由如下:(4分)易得:△BEF ∽△AEP ,若要使得△BEF ≌△AEP ,只需要满足BE =AE 即可,(5分)∴∠BAE =∠ABE ,∵∠BAC =60°,∴∠BAE =60°-(90°-2α)=2α-30°,∵∠ABE =β,∠BAE =∠ABE ,(6分) ∴2α-30°=β,即α=2β+60°;(7分)(3)连接BD ,交A 1B 1于点G ,过点A 1作A 1H ⊥AC 于点H .∵∠B 1A 1P =∠A 1PA =60°,∴A 1B 1∥AC ,由题意得:AP =A 1P ,∠A =60°,∴△PAA 1是等边三角形,∴A 1H =23(2+x ),(8分)在Rt△ABD 中,BD =23,∴BG =23-23(2+x )=3-23x ,(9分)∴S △A 1BB 1=21×4×(3-23x )=23-3x (0≤x <2).(10分) 27. (2011襄阳,25,10分)如图,点P 是正方形ABCD 边AB 上一点(不与点A ,B 重合),连接PD 并将线段PD 绕点P 顺时针方向旋转90°得到线段PE ,PE 交边BC 于点F ,连接BE ,DF .(1)求证:∠ADP =∠EPB ;(2)求∠CBE 的度数;(3)当ABAP 的值等于多少时,△PFD ∽△BFP ?并说明理由.解答:证明:(1)∵四边形ABCD 是正方形.∴∠A =∠PBC =90°,AB =AD ,∴∠ADP +∠APD =90°,∵∠DPE =90°,∴∠APD +∠EPB =90°,∴∠ADP =∠EPB ;(2)过点E 作EG ⊥AB 交AB 的延长线于点G ,则∠EGP =∠A =90°,又∵∠ADP =∠EPB ,PD =PE ,∴△PAD ≌△EGP ,∴EG =AP ,AD =AB =PG ,∴AP =EG =BG ,∴∠CBE =∠EBG =45°;(3)当AB AP =21时,△PFD ∽△BFP , 设AD =AB =a ,则AP =PB =21a , ∴BF =BP •AD AP =41a . ∴PD =22AP AD +=25a ,PF =22BF PB +=45a ,∴PF BF PD PB =55 又∠DPF =∠PBF =90°,∴△PFD ∽△BFP .28. (2011湖北武汉,24,10分)(1)如图1,在△ABC 中,点D .E .Q 分别在ABACBC 上,且DE ∥边长,AQ 交DE 于点P ,求证:DP BQ =PE QC; (2)如图,△ABC 中,∠BAC =90°,正方形DEFG 的四个顶点在△ABC 的边上,连接AG ,AF 分别交DE 于M ,N 两点. ①如图2,若AB =AC =1,直接写出MN 的长;②如图3,求证:MN 2=DM •EN .解答:(1)证明:在△ABQ 和△ADP 中,∵DP ∥BQ ,∴△ADP ∽△ABQ , ∴DP BQ =PE QC, 同理在△ACQ 和△ADP 中,PE QC =AP AQ, ∴DP BQ =PE QC;(2; (3)证明:∵∠B +∠C =90°∠CEF +∠C =90°,∴∠B =∠CEF ,又∵∠BGD =∠EFC ,∴△BGD∽△EFC,∴DGCF=BGEF,∴DG•EF=CF•BG,又∵DG=GF=EF,∴GF2=CF•BG,由(1)得DMBG=MNBF=ENCF,∴(MNGF)2=MNBF•ENCF=DMBG•ENCF,∵BG=GF=C,2)证明:∵∴∠FAG ∥∠C ,∵∠CFE=∠CEF ,∴∠AGF=∠CFE ,∴AF=AG ,∵∠BAD=∠C ,∴∠BAF=∠DAG ,△ABF ≌△ADG ,∴FB=DG ,∴FD+DG=BD ,故答案为:BD .31. (2011福建莆田,25,14分)已知菱形ABCD 的边长为1,∠ADC=60º,等边△AEF 两边分别交DC 、CB 于点E 、F 。
(1)(4分)特殊发现:如图1,若点E 、F 分别是DC 、CB 的中点,求证菱形ABCD 对角母AC 、BD 的交点O 即为等边△AEF 的外心;(2)若点E 、F 始终分别在边DC 、CB 上移动,记等边△AEF 的外心为点P 。
①(4分)猜想验证:如图2,猜想△AEF 的外心P 落在哪一直线上,并加以证明;②(5分)拓展运用:如图3,猜想△AEF 面积最小时,过点P 任作一直线分别交边DA 于点M ,交边DC 的延长线于点N ,试判断11DM DN是否为定值,若是,请求出该定值;若不是,请说明理由。
解答:(1)证明:如图1,分别连接OE 、0F ,∵四边形ABCD 是菱形,∴AC ⊥BD ,BD 平分∠ADC .AO=DC=BC ,∴∠COD =∠COB =∠AOD =90°.∠ADO = ∠ADC = ×60°=30°, 又∵E 、F 分别为DC 、CB 中点,∴OE = CD ,OF = BC ,AO = AD ,∴0E=OF =OA ,∴点O 即为△AE F 的外心.(2)①猜想:外心P 一定落在直线DB 上.AB CD 第25题 图1 O F E证明:如图2,分别连接PE 、PA ,过点P 分别作PI ⊥CD 于I ,PJ ⊥AD 于J , ∴∠PIE =∠PJD =90°,∵∠ADC=60°,∴∠IP J=360°-∠PIE -∠PJD -∠JDI =120°,∵点P 是等边△AEF 的外心,∴∠EPA =120°,PE =PA ,∴∠I PJ =∠EPA ,∴∠IPE =∠JPA ,∴△P IE ≌△PJA ,∴PI =PJ ,∴点P 在∠ADC 的平分线上,即点P 落在直线DB 上.② 为定值2.当AE ⊥DC 时.△AEF 面积最小,此时点E 、F 分别为DC 、CB 中点.连接BD 、AC 交于点P ,由(1)可得点P 即为△AEF 的外心.如图3.设MN 交BC 于点G ,设DM =x ,DN =y (x ≠0.y ≠O ),则CN=y -1,∵BC ∥DA ,∴△GBP ∽△MDP .∴BG =DM =x .∴CG =1-x∵BC ∥DA ,∴△GBP ∽△NDM ,∴ ,∴ ,∴x +y =2xy ,∴ + =2,即 =2图形的相似第25题 图2J第25题 图3BM(2013•绵阳)我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心。
重心有很多美妙的性质,如在关线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题。
请你利用重心的概念完成如下问题:(1)若O 是△ABC 的重心(如图1),连结AO 并延长交BC 于D ,证明:23AO AD =;(2)若AD 是△ABC 的一条中线(如图2),O 是AD 上一点,且满足23AO AD =,试判断O 是△ABC 的重心吗?如果是,请证明;如果不是,请说明理由;(3)若O 是△ABC 的重心,过O 的一条直线分别与AB 、AC 相交于G 、H (均不与△ABC 的顶点重合)(如图3),S四边形BCHG.S △AGH 分别表示四边形BCHG 和△AGH 的面积,试探究BCHG AGHS S四边形的最大值。
