结构力学第二章几何组成分析.李廉锟
李廉锟《结构力学》(第6版)笔记和课后习题(含考研真题)详解

李廉锟《结构力学》(第6版)笔记和课后习题(含考研真题)详解复习笔记【知识框架】节选自识库学习网,如需转载请注明出处【重点难点归纳】一、结构力学的研究对象和任务(见表1-1-1)★★表1-1-1结构力学的研究对象和任务二、荷载的分类(见表1-1-2)★★★荷载是指作用在结构上的主动力。
表1-1-2荷载的分类三、支座和结点的类型★★★★1支座支座是指把结构与基础联系起来的装置,见表1-1-3。
表1-1-3支座的类型2结点结点是指结构中杆件相互联结的位置,见表1-1-4。
表1-1-4结点的类型四、结构的分类★★★1按几何特征分类(见表1-1-5)表1-1-5结构按几何特征分类2按受力特性分类(见表1-1-6)考研真题汇编第1章绪论本章暂未编选名校考研真题。
【更多考研专业课真题可转识库学习网】第2章平面体系的机动分析一、填空题1在平面体系中,联结______的铰称为单铰,联结______的铰称为复铰。
[哈尔滨工业大学2007研]【答案】两个刚片;两个以上的刚片查看答案【解析】根据定义,单铰是指联结两个刚片的一个铰;复铰是指同时联结两个以上刚片的一个铰。
2如图2-1所示体系为有______个多余约束的______体系。
[国防科技大学2007研]图2-1【答案】0;几何不变查看答案【解析】几何组成分析:将AED和DCF分别看作两个刚片,BE和BF可以分别看作两根链杆,再将大地看作一个刚片,此体系可看作通过两个虚铰和一个实铰(三个铰不共线)联结的;根据三刚片规则,可判断出该体系为无多余约束的几何不变体系。
3如图2-2所示体系为有______个多余约束的______体系。
[国防科技大学2004研]图2-2【答案】5;瞬变查看答案【解析】几何组成分析,分析上部结构:将4个组合节点全部变成铰接点,则减少4个多余约束;分析剩余结构,易知该剩余部分为有1个多余约束的几何不变体系,故上部结构为有5个多余约束的几何不变体系。
力法李廉锟结构力学中南大学PPT课件

§7-4 力法的典型方程
作剪力图的原则是, 截取每一杆为隔离体,由平衡条件便可求出剪力。
杆AC:
杆CB:
2M/5
C FSCA
3 M / 5 FS CB
C
2 M/5 C
FS BC
B
B
3M/5
A FSAC
M/ 5
M
A M/5
l/2
C
B
6M /5l
FS
A
l/ 2
第36页/共206页
l
3M/ 5l
l
§7-4 力法的典型方程
3)框格法
一个封闭无铰框格
n3
m个封闭
无铰框格
n 3 5 15
第16页/共206页
§7-2 超静定次数的确定
若有铰
h — 单铰数,则
n 3m h
注意:
n 359 6
多少个封闭无铰框格?
第17页/共206页
§7-2 超静定次数的确定 三、计算示例
n6
拆除多余联系变成的静 定结构形式:
第18页/共206页
(6)去掉一个连接n个杆件的刚结点,等于拆掉3(n-1)个约束。
第13页/共206页
§7-2 超静定次数的确定
(7)只能拆掉原结构的多于约束,不能拆掉必要约束。 (8)只能在原结构中减少约束,不能增加新的约束。
注意:同一超静定结构可有不同的解除多余约束的方式,但解除约束的 个数是相同的, 解除约束后的体系必须是几何不变的。
(a)
第30页/共206页
§7-4 力法的典型方程
将
,
,
代入(b)式, 得两次超静定的力法基本方程
(b) (c)
第31页/共206页
结构力学答案 李廉锟

第二章 作业参考答案习题2-3(b )(a )FAK解:先计算计算自由度:3(2)321(2303)0W m h r =−+=×−×+= 或者2()212(213)0W j b r =−+=×−+=这表明体系具有几何不变所需最少的联系数目。
此体系的支座链杆只有三根,且不完全平行也不交于一点,若体系为一刚片,则他与地基是按两刚片规则组成的,因此只需分析体系本身是不是一个几何不变的刚片即可。
去掉M 和C 两个二元体。
在b 图中,KFL 刚片、ABF 刚片和GEJ 刚片通过不共线的三个铰(Ⅰ,Ⅱ)、(Ⅱ,Ⅲ)和(Ⅰ,Ⅲ)两两连接,由三刚片规则可知,体系为几何不变体系,且无多余联系。
习题2-5解:先计算计算自由度:3(2)34(244)W m h r =−+=×−×+=0这表明体系具有几何不变所需最少的联系数目。
大地作为刚片Ⅰ,ACE 和BDF 分别作为刚片Ⅱ和Ⅲ,此三刚片用不共线的三个铰(Ⅰ,Ⅱ)(或者A )、(Ⅱ,Ⅲ)和(Ⅰ,Ⅲ)(或者B )两两连接,如上图,由三刚片规则可知,体系为几何不变体系,且无多余联系。
KNMFJA解:先计算计算自由度3(2)328(2200)4W m h r =−+=×−×+=>3 或者2()216(280)43W j b r =−+=×−+=>这表明体系具有几何可变的(常变)。
注:如果分不清是常变还是瞬变,可以直接写可变也行。
习题2-9解:先计算计算自由度:3(2)311(2153)W m h r =−+=×−×+=0 或者2()27(113)0W j b r =−+=×−+=这表明体系具有几何不变所需最少的联系数目。
此体系的支座链杆只有三根,且不完全平行也不交于一点,若体系为一刚片,则他与地基是按两刚片规则组成的,因此只需分析体系本身是不是一个几何不变的刚片即可。
李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案
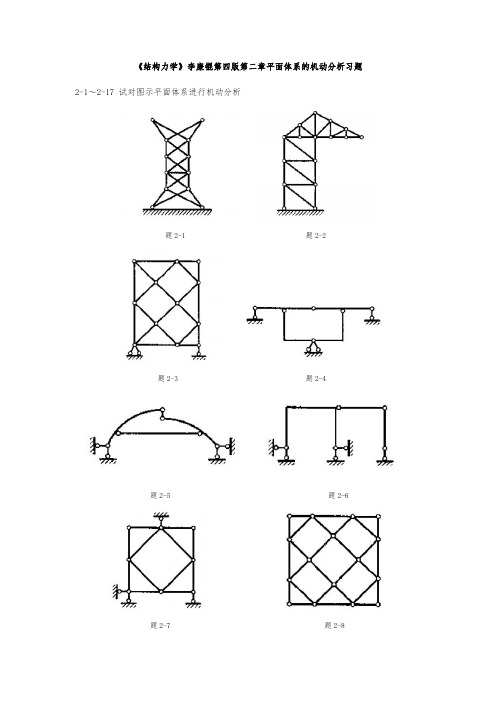
《结构力学》李廉锟第四版第二章平面体系的机动分析习题2-1~2-17试对图示平面体系进行机动分析题2-1题2-2题2-3题2-4题2-5题2-6题2-7题2-8题2-9(a、b处非结点)题2-10(k处非结点)题2-11题2-12题2-13题2-14题2-15(k处非结点)题2-16题2-172-18、2-19添加最少数目的链杆和支承链杆,使体系成为几何不变,而且无多余约束。
题2-18题2-19《结构力学》李廉锟第四版第二章平面体系的机动分析参考答案题2-1说明:自上往下依次拆除二元体,或者自下往上依次添加二元体,故体系为有一个多余约束的几何不变体系(多余约束:中间的横杆或者也可以看成支座上多了一根水平杆)。
题2-2说明:如图所示取刚片1和刚片2,采用二刚片规则(两刚片用一个铰和一根不通过此铰的链杆相联),为几何不变体系,而且没有多余联系。
刚片1由二元体组成,刚片2从大地向上组装二元体组成。
题2-3说明:先不考虑支座的三根链杆,考虑上部几何构造,去掉二元体简化分析,取如上图所示刚片1、刚片2和刚片3。
刚片1和刚片2通过一个实铰联结;刚片1和刚片3通过两根平行链杆联结,交于无穷远处;刚片2和刚片3通过两根平行链杆联结,交于无穷远处;三铰不共线,故上部无多余约束且几何不变。
最后上部与大地通过一个铰和一根不通过此铰的链杆相联,故整个体系为无多余约束的几何不变体系。
题2-4说明:如上图所示取刚片1、刚片2和刚片3,刚片1和刚片2交于铰12O ,刚片1和刚片3交于铰13O ,刚片2和刚片3交于铰23O ,三铰不共线,故原体系为无多余约束的几何不变体系。
题2-5说明:将大地等效成一根链杆,取如图所示刚片1和刚片2,显然两刚片通过三根链杆相联,且三根链杆既不相互平行也不相交于一点,故原体系为无多余约束的几何不变体系。
题2-6说明:先拆除二元体以简化分析,可知右部分为常变部分;左部分为有一个多余约束的几何不变体系,故体系为几何常变体系。
李廉锟结构力学2
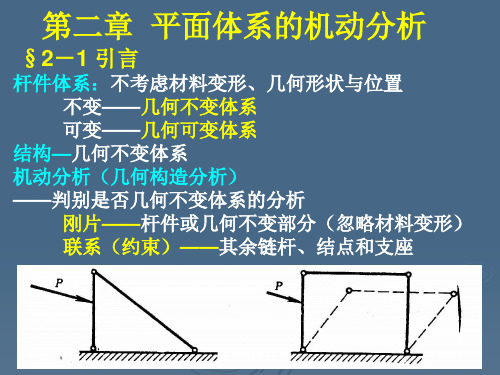
*§2—6三刚片体系中虚铰无穷远情况 1、无穷远点在同一直线——无穷远直线, (R=∞的圆,孤——直线) 2、平行线——∞处交于一点 (1)一铰无穷远(图2-22) (2)二铰无穷远(图2-23) (3)三铰无穷远(不同方向,图2-24) (图2-24a)瞬变; (图2-24b)等长——常变; (图2-24c) 等长但异侧联出——瞬变
m刚片 —— 3m个独立平衡方程, g刚结点,n铰 ,r链杆——(3g+ 2h+ r)个未知力
静定——几何不变,无多余约束。
W=0,3m = 3g+2h+r 平衡方程数=未知力数 → 解答唯一确定。
超静定——几何不变,有多余约束
W<0,3m < 3g+2h+r 平衡数<未知力数→仅有平衡条件解不能唯一确定
一铰无穷远
二铰无穷远
三铰无穷远:不等长、等长、等长但异侧联出 瞬变、常变、瞬变
§2—7几何构造与静定性的关系 静定结构——几何不变无多余约束, 反力、内力可以由平衡条件唯一确定。 超静定结构——几何不变有多余约束, 反力、内力不仅需平衡条件,且需考虑变形条件 计算自由度:W=3m-(3g+2h+r)
C
§2—3几何不变体系的简单组成规则
2.二元体规则 在一个刚片上增加一个二元体, 仍为几何不变体系,且无多余约束
二元体——不共线二链杆联结一个新结点
推广:增 ⁄ 减二元体,机动性质不变* 例
A 1 B 2 C
§2—3几何不变体系的简单组成规则
3.两刚片规则 两刚片用不共线—铰—链杆相联, 不交于一点,也不平行的三链杆相联 体系为几何不变,且无多余约束。 虚铰(瞬铰)——瞬时转动中心 (相对转动瞬心) 联结两个刚片的两根链杆 相当于在其交点的一个单铰 A 二刚片规则二种叙述相同 例
静定梁与静定刚架李廉锟结构力学图文PPT课件

§3-1 单跨静定梁
4. 以单元为对象,对杆端取矩可以求得杆端剪力,在结构图 上利用微分关系作每单元的剪力图,从而得到结构剪力图。 需要指出的是,剪力图可画在杆轴的任意一侧,但必须标注 正负号。
以未知数个数不超过两个为原则,取结点由平衡求单元杆 端轴力,在结构图上利用微分关系作每单元的轴力图,作法 和剪力图一样,从而得到结构轴力图。 5. 综上所述,结构力学作内力图顺序为“先区段叠加作M 图, 再由M 图作FS 图,最后FS作FN图”。需要指出的是,这种作 内力图的顺序对于超静定结构也是适用的。
20 kN
AC
15 kN/m
32 kN m
B
D
E
G
2m 2m
4m
2m 2m
44 kN
36 kN
44 kN
24 kN
+
A
C
H D
E_
B
FS图
36 kN
DE段梁的弯矩最大截面就在剪力为零处,剪力为零的
截面H的位置可由比例求出,其值为 xH =1.6 m 。最大弯
矩 MH 为:
1
MH
44 (4 1.6) 20 (2 1.6) 151.6
A FxA =0
CD Ⅰ
FyA= 44 kN 2m 2m
15 kN/m Ⅱ
4m
32 kN m
EG
B
ⅢⅣ
FyB = 36 kN
2m 2m
3m
3m
计算梁上任一截面内力的规律如下:
梁上某一截面的2弯0 kN矩F数s1 值上等于该截面左侧(或右侧)所 有外力对该截面形心的力矩的代数和。
梁上某一截面的剪力数值上等于该截面左侧(或右侧)所 有外力在沿截面的切线方向投影的代数和。
第2章体系的几何组成分析李廉锟第4版

§2-5 机动分析示例
例2-2 试对图(a)所示体系进行机动分析。
解:体系的支座链杆有三根, 只需分析体系本身即可。 如图(b)。
从左右两边按结点1,2,3… 的顺序拆去二元体,当拆到结 点6时,两链杆在一条直线上。
体系为瞬变体系。
§2-5 机动分析示例
例2-3 试分析图所示桁架的几何构造。 解:ADCF和BECG都是几何 不变的部分,可作为刚片, 地基作为一个刚片。
B
用满足要求三个约
C
G
束相联可去掉基础, 只分析上部。
B
E
抛开基础,只分析上部, 上部体系由左右两刚片用一铰和一链杆相连。 故:该体系为无多余约束 的几何不变体系。
例5、
抛开基础,分析上部,去掉二元
如图体示后,三剩刚下片两用个三刚个片不用共两线根的杆相 铰相连连故,:故该:体该系体为系有为一无个多自余由约度的 束的几何几不何变可体变系体系.
几何不变体系, 且无多余联系(三刚片规则) 刚片I和II用铰C相连, 刚片I和III相当于用虚铰O相连, 刚片II和III相当于用虚铰O’相连,
§2-5 机动分析示例
例2-4 试对图(a)所示体系进行机动分析。
解:地基作为刚片III, 三角形ABD和BCE作为 刚片I、II(图b)。
刚片I和II用铰B相连, 刚片I和III用铰A相连, 刚片II和III?
四 一点一刚片 两个
两链杆不共线
一种
几种常用的分析途径
1、去掉二元体,将体系化简单,然后再分析。
G
依次去掉二元体AB
CDEFG后剩下大地,
F
E
故该体系为几何不变
A 体系且无多余约束。
DC
B
第二章:平面体系的机动分析(结构力学 李廉锟 第五版 配套)

y A' B' D Dy B Dx
x
A 0
自由度: 描述几何体系运动时,所需独立坐标的数目。 几何体系运动时,可以独立改变的坐标的数目。 几何可变体系自由度大于0 几何不变体系自由度等于0 平面内的点自由度为2 平面内的刚体自由度为3
联系(约束)
如果体系有了自由度,必须消除,消除的办法是增加约束。
W=3×7-(2×9)-3=0
平面杆件体系的自由度
若每个节点均为自由,则有2j个自由度,但连接节点的每根杆 件都起一个约束作用,则体系的计算自由度为
W=2j-b -r
j---刚片数; b---杆件数; r ---支座链杆数。
算例
j=4
b=4 r=3
j=8
b=12
r=4
W=2×4-4-3=1
W=2×8-12-4=0
在运动中改变位置。
虚铰特例 2杆平行等长,刚片位置改变,链杆仍平行但改变方 向,虚铰转到另一无穷远点(常变体系)
2杆平行不等长,刚片位置改变,链杆不再平行, 虚铰转到有限远点(瞬变体系)
基本组成规则
基本规则的应用
利用组成规律可以两种方式构造一般的结构:
(1)从基础出发构造
(2)从内部刚片出发构造
2.5 机动分析
1,3
.
.1,2
2,3
.
.
无多余约束的几何不变体系
几何瞬变体系
1,2
. .
1,3 2,3
. 2,3
几何瞬变体系
1,2 1,3
F
D C E
F
D C B E
A
A
B
F
D
C A
E
D
E
C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
geometrically stable system
结构
Under the action of any loads, the system still maintain its shape and remains its location if the deformations of the members are neglected.
F
E
2 rigid bodies, connected by 3 links, which are nonparallel and nonconcurrent cross the hinge, form an internally stable system with no redundant restraints. 。
Degrees of freedom of a system are the numbers of independent movements or coordinates which are required to locate the system fully.
for a point in plane n=2
C
structure formed by Attaching of binary systems 减二元体简化分析
W=3 ×10-(2×14+3)=-1<0 W=2 ×6-13=-1<0
计算自由度 = 体系真实 的自由度 ?
W=2 ×6-12=0 W=3 ×9-(2×12+3)=0
缺少联系 几何可变
W=2 ×6-11=1 W=3 ×8-(2×10+3)=1
summary
W>0, 缺少足够联系,体系几何可变 Restraints are not enough, unstable。 W=0, 具备成为几何不变体系所要求的最少 联系数目has the minimum necessary numbers of restraints for stable system。
Three hinged arch
大地、AC、BC为刚片;A、B、C为单铰
无多余几何不变
binary system(二元体)--- 2 non-collinear links connected by a hinge
Binary system rule: The geometric construction property of a system will not change if a binary system is attached to or detached from the system。
2 rigid bodies, connected by 1 hinge and 1 link that does not cross the hinge, form an internally stable system with no redundant restraints.
二刚片规则: two-rigid-body rule:
Because the removal of any bar in the system will increase one degree of freedom, therefore all bars are necessary restraints
Restraints, removal of which doesn’t change the degrees of freedom, is named as redundant restraints .
W=2j-b
例1:Determine the numbers of degrees of freedom of the following system
AC CDB CE EF CF DF DG FG
1 3
3
1 G 2
有几个单铰?
W=3×8-(2 ×10+4)=0
例2:Determine the numbers of degrees of
图中上部四根杆 和三根支座杆都是 必要的联系。
下部正方形中任 意一根杆,除去都 不增加自由度,都 可看作多余的联系。
例3:
W=0,但 布置不当 几何可变。 上部有多 余联系, 下部缺少 联系。
W=3 ×9-(2×12+3)=0 W=2 ×6-12=0
例4
W<0,体系 是否一定 几何不变呢?
上部 具有多 余联系
restraints。
W<0, 体系具有多余联系has redundant
W> 0 W< 0
unstable
stable?
§2-3
Geometric construction rules of planar stable framed systems
two-rigid-body rule
two-rigid-body rule:
Chapter II
Geometric Construction Analysis of Plane Systems
§2-1
Introduction
Structure consists of members, joints and supports. Structure must maintain its geometric shape and positions without consideration of the deformation of materials.
link system connected by hinges – system of bars connected by hinges at the ends of the bars.
The computed degrees of freedom : j--the numbers of hinges; b--the numbers of links including the links at the supports
刚片-rigid body
杆件,几何不变部分 均可视为刚片 members or stable parts may be looked at as rigid bodies
形状可任意替换 may be replaced by body of any shape.
§2-1 degrees of freedom of planar system(stable system
Under the action of any loads, the system will change its shape and its location if the deformations of the members are neglected.
3 bars, when the summation of the lengths of any 2 bars is greater than the length of 3-d one, can form uniquely a triangular.
triangular joined pairwise by hinges is stable.
连接n个杆的复刚结点 等于多少个单刚结点?
The computed degrees of freedom(计算自由 度)=the total numbers of degrees of freedom of rigid bodies – total numbers of restraints
W = 3m-(2h+b) m---刚片数the numbers of rigid bodies (excluding foundation不包括地基) h---单铰数the numbers of simple joints b---单链杆数(含支杆)the numbers of links
1
体系W 等于多少? 可变吗?
3 1
W=0,体系 是否一定 几何不变呢?
W=3 ×9-(2×12+3)=0
Restraints which reduce the degrees of freedom is named as necessary restraints,必 要联系otherwise they are called redundant restraints.多余联系
If the deformation of materials is neglected, then framed systems can be classified into two categories: 几何不变体系(geometrically stable system ) 几何可变体系(geometrically unstable system )
虚铰:联结两个刚片的两根相交链杆的作用,相当于在其交 点处的一个单铰,这种铰称为虚铰(瞬铰)If 2 noncollinear links connecting 2 rigid bodies intersect at a point outside the 2 rigid bodies, then the intersection is referred to as a virtual or instantaneous hinge。
freedom of the following system
1
2
3
3
1
按刚片计算9根杆,9个刚片
有几个单铰? 3根单链杆
2
W=3 ×9-(2×12+3)=0
Another solution
按铰结计算
6个铰结点 12根单链杆 W=2 ×6-12=0
Discussion 2 2
有 几 个 3 单 铰?
3 rigid bodies joined pair-wise by hinges, provided that the 3 hinges don’t lie in the same straight line, form an internally stable system with no redundant restraints.
