1 双光栅测量微弱振动位移量
双光栅测微振动实验报告

课程名称:大学物理实验(二)实验名称:双光栅测微振动光拍的获得与检测在检测器方向上, 频率不同、频率差较小的的光束叠加产生光拍E 1=E 10cos(ω0t +φ1) (7)E 2=E 20cos [(ω0+ωd )t +φ2] (8)E 1+E 2)2102cos 2(ω0t +φ1)+E 202cos 2[(ω0+ωd )t +φ2]+E 10E 20cos [(ω+φ2)]+ E 10E 20cos [(ω0−ω0+ωd )t +(φ1−φ2)] (9)光的频率很高,光电检测器对这么高的频率不能有所反应,所以光电检测器只能反应( f 拍=ωd 2π=V A d=nV A (10)图5 双光栅测微振动实验器具组1—光电池升降调节手轮 2—光电池座,在顶部有光电池盒,盒前有一小孔光阑 3—电源开关4—音叉座 5—音叉 6—动光栅(粘在音叉上的光栅) 7—静光栅(固定在调节架上)8—静光栅调节架 9—半导体激光器 10—激光器升降调节手轮 11—调节架左右调节止紧螺钉12—激光器输出功率调节 13—耳机插孔 14—音量调节 15—信号发生器输出功率调节16—信号发生器频率调节 17—静光栅调节架升降调节手轮 18—驱动音叉用的蜂鸣器19—蜂鸣器电源插孔 20—频率显示窗口位移振幅A(mm)频率f(Hz)图7 不同频率下音叉的振幅七、结果陈述与总结:7.1结果陈述实验测量出音叉的谐振曲线如附录所示。
音叉振动频率从507.9Hz升至508.5Hz,音叉的振幅缓慢地从0.0188mm变大至0.0625mm。
音叉振动频率从508.5Hz升至508.7Hz,音叉的振幅急剧地从0.0625mm变大至0.1375mm;音叉振动频率从508.7Hz升至508.9Hz,音叉的振幅急剧地从0.1375mm变小至0.0725mm。
音叉振动频率从508.9Hz升至509.6Hz,音叉的振幅缓慢地从0.0725mm变小至0.0175mm。
双光栅测微弱震动

用双光栅测量微弱振动-------- S eries1505.8 506 506.2 506.4 506.6 506.8 507 5072 507.4(2)用双光栅测量微弱振动一、 实验目的1. 熟悉一种利用光的多普勒频移形成光拍的原理;2. 作出外力驱动音叉时的谐振曲线。
二、 实验仪器双光栅微弱振动测量仪,双踪示波器。
三、实验原理1 .位相光栅的多普勒频移所谓的位相材料是指那些只有空间位相结构,而透明度一样的透明材料, 如生物切片、油膜、热塑以及声光偏转池等,他们只改变入射光的相位,而不影 响其振幅。
位相光栅就是用这样的材料制作的光栅。
当激光平面波垂直入射到位相光栅光波波长然而,如果由于光栅在y 方向以速度v 移动,贝U 出射波阵面也以速度 v 在y 方向移动。
从而在不同时刻,对应于同一级的衍射光线,它的波阵面上的点, 在y 方向上也有一个vt 的位移量,如图2所示。
图1这个位移量对应于光波位相的变化量为(t )vtsin时,由于位相光栅上不同的光密和光疏媒质 部分对光波的位相延迟作用,使入射的平面 波在出射时变成折曲波阵面,如图1所示, 由于衍射干涉作用,在远场我们可以用大家 熟知的光栅方程来表示:d sin n(1)式中d为光栅常数, 为衍射角, 为 (t)2n (t)vt dn2n d (3)v 2d⑷nod(5)a级%d t—l 级带入(2)式中d把光波写成如下形式: 相对于静止的位相光栅有一个 显然可见,移动的位相光栅的n 级衍射光波, 大小:的多普勒频率,如图3所示。
ft - r 时亂玻前0级气 —2 恤_ 2叫E E °expi o t (t)expi o n d t/ f 时亂波前”汕/一八0圾(2洞2.光拍的获得与检测光波的频率甚高,为了要从光频0中检测出多普勒频移,必须采用“拍”的方法。
也就是要把已频移的和未频移的光束相互平行叠加,以形成光拍。
本实验形成光拍的方法是采用两片完全相同的光栅平行紧贴,一片(B)静止,另一片(A)相对移动。
西安交通大学综合与近代物理实验9.7用双光栅测量微弱震动

图1
当激光平面波垂直入射到位相光栅时,由于位相光栅上不同的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波在出射时变成折曲波阵面,如图1所示,由于衍射干涉作用,在远场我们可以用大家熟知的光栅方程来表示
实验9.7用双光栅测量微弱振动
1842年多普勒(Doppler)提出,当波源和观察者彼此接近时,接收到的频率变高;而当波源和观察者彼此相离开时,接收到的频率变低。这种现象在电磁波和机械波中都存在。即当波源和观察者之间存在相对运动时,观察者所接收到的频率不等于波源振动频率,这种现象称为多普勒效应。而当光源与接收器之间有相对运动时,接收器感受到的光波频率不等于光源频率,这就是光学的多普勒效应或电磁波的多普勒效应。该效应已经在科学技术以及医学的许多领域得到应用。
式中: 为音叉振动周期。 可以直接在示波器的荧光屏上计算光拍波形数而得到,因为 表示 内的波的个数,不足一个完整波形,需要在波群的两端,按反正弦函数折算为波形的分数部分,即
式中: , 为波群的首尾幅度和该处完整波形的振幅之比。(波群指 内的波形,分数波形数包括满1/2个波形为0.5,满1/4个波形为0.25)
四、实验仪器介绍
双光栅微弱振动测量仪面板结构如图5所示。
图5
1—光电池座,顶部有光电池盒,盒前方一小孔光阑;2—电源开关;3—光电池升降手轮;4—音叉座;5—音叉;6—粘于音叉上的光栅(动光栅);7—静光栅架;8—半导体激光器;9—锁紧手轮;10—激光器输出功率调节;11—信号发生器输出功率调节;12—信号发生器频率调节;13—驱动音叉用耳机;14—频率显示;15—信号输出;Y1—拍频信号;Y2—音叉驱动信号;X—示波器提供“外触发”扫描信号,使得示波器显示的波形稳定
大学物理实验:双光栅测量微弱振动位移量

双光栅测量微弱振动位移量精密测量在自动化控制的領域里一直扮演着重要的角色,其中光电测量因为有较佳的精密性与准确性,加上轻巧、无噪音等优点,在测量的应用上常被采用。
作为一种把机械位移信号转化为光电信号的手段,光栅式位移测量技术在长度与角度的数字化测量、运动比较测量、数控机床、应力分析等领域得到了广泛的应用。
多普勒频移物理特性的应用也非常广泛,如医学上的超声诊断仪、测量海水各层深度的海流速度和方向、卫星导航定位系统、音乐中乐器的调音等。
双光栅微弱振动测量仪在力学实验项目中用作音叉振动分析、微振幅(位移)、测量和光拍研究等。
【实验目的】1. 了解利用光的多普勒频移形成光拍的原理并用于测量光拍拍频;2. 学会使用精确测量微弱振动位移的一种方法;3. 应用双光栅微弱振动测量仪测量音叉振动的微振幅。
【实验原理】1. 位移光栅的多普勒频移多普勒效应是指光源、接受器、传播介质或中间反射器之间的相对运动所引起的接收器接收到的光波频率与光源频率发生的变化,由此产生的频率变化称为多普勒频移。
由于介质对光传播时有不同的相位延迟作用,对于两束相同的单色光,若初始时刻相位相同,经过相同的几何路径,但在不同折射率的介质中传播,出射时两光的位相则不相同。
对于位相光栅,当激光平面波垂直入射时,由于位相光栅上不同的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波变成出射时的摺曲波阵面,见图1。
激光平面波垂直入射到光栅,由于光栅上每缝自身的衍射作用和各缝之间的干涉,通过光栅后光的强度出现周期性的变化。
在远场,我们可以用大家熟知的光栅衍射方程即(1)式来表示主极大位置:λθk d ±=sin ⋅⋅⋅=,2,1,0k (1)式中 ,整数k 为主极大级数,d 为光栅常数,θ为衍射角,λ为光波波长。
如果光栅在y 方向以速度v 移动,则从光栅出射的光的波阵面也以速度v 在y 方向移动。
因此在不同时刻,对应于同一级的衍射光线,它从光栅出射时,在y 方向也有一个vt 的位移量,见图2。
大学物理实验 部分思考题答案

实验八用拉脱发测定液体的表面张力系数1.对公式, 是要在水面与金属表面的接触角趋于0时满足的, 即在金属框恰好脱离液体前。
公式中的重力是金属框和它所粘附的液体的总重量, 但在公式中我们忽略了水对框架的浮力和水膜的重量。
2.“三线对齐”是因为朱利秤的下端是固定的,上端为自由端,因而我们在用朱利秤测量弹簧的伸长时也要固定弹簧的下端,这样才能在朱利秤上读到弹簧的伸长量。
“三线对齐”中的三线是指小镜子上的水平线和玻璃罐上的水平线以及玻璃罐上的水平线在小镜子里成的像。
实验十牛顿环干涉现象的研究和测量思考题1.牛顿环实验中, 假如平玻璃板上有微小的凸起, 则凸起处空气薄膜厚度变小, 这时的牛顿环是局部外凸的, 因为在平玻璃板上的突起位置的空气薄膜厚度变小, 此点的光程差也就变小, 那么此级暗条纹的光程差都要比该点的大, 因而该级暗条纹就会饶向外面一级的位置, 这时表现出此暗条纹就要外凸。
2.用白光照射时,我们是可以看到牛顿环干涉条纹的,而且是以赤橙黄绿蓝靛紫这样的顺序依次排列,只是在偏离中心位置越远,条纹级数之间会重叠越厉害。
实验十二迈克耳逊干涉仪数据处理参见P19的内容。
思考题1. 图形见书P115。
2.所以条纹变密。
实验十三超声波在空气中传播速度的测定数据处理中相对误差的有效位数参见P19的内容。
思考题1.因为在测量过程中, 我们要想在两个换能器之间形成驻波, 就一定要求S1发出的波和经S2发射的波是同频率, 同振幅, 而且是传播方向相反并在一条直线上, 这就要求两个换能器的发射面要保持相互平行。
2.略。
3.用“逐差法”处理数据是为了更充分地,最大限度地利用所测得的数据,保持多次测量的优点,减少测量误差。
实验十四密立根油滴实验数据处理表格1中最后要求的量是表格中的量求了平均以后的值, 比如量中的应该是对表格中的求5次测量的平均值。
而这其中的相对误差的表示参见P19。
思考题1.选择平衡点压在250V左右, 新仪器在12s-24s时间内匀速下降1.6mm的油滴(旧仪器在15s-30s时间内匀速下降2mm的油滴)的原因是在这个范围内的油滴体积不大, 带的电量也不是很多, 因而在下降时的速度不是很快, 下降的时间就比较容易测准确, 而且这样的油滴也不是很小, 不会因为太小而作布朗运动。
双光栅测微弱震动

用双光栅测量微弱振动用双光栅测量微弱振动一、 实验目的1. 熟悉一种利用光的多普勒频移形成光拍的原理;2. 作出外力驱动音叉时的谐振曲线。
二、 实验仪器双光栅微弱振动测量仪,双踪示波器。
三、实验原理1.位相光栅的多普勒频移所谓的位相材料是指那些只有空间位相结构,而透明度一样的透明材料,如生物切片、油膜、热塑以及声光偏转池等,他们只改变入射光的相位,而不影响其振幅。
位相光栅就是用这样的材料制作的光栅。
当激光平面波垂直入射到位相光栅时,由于位相光栅上不同的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波在出射时变成折曲波阵面,如图1所示,由于衍射干涉作用,在远场我们可以用大家熟知的光栅方程来表示:λθn d =sin(1)式中d 为光栅常数,θ为衍射角,λ为光波波长。
然而,如果由于光栅在y 方向以速度v 移动,则出射波阵面也以速度v 在y 方向移动。
从而在不同时刻,对应于同一级的衍射光线,它的波阵面上的点,在y 方向上也有一个vt 的位移量,如图2所示。
图1这个位移量对应于光波位相的变化量为)(t ∆Φθλπλπsin 22)(vt s t =∆∙=∆Φ (2)带入(2)tn t d vn dn vt t d ωπλλπ===∆Φ22)((3)式中d v d πω2=把光波写成如下形式:()[]()[]t n i t t i E E d ωωω+=∆Φ+=000exp )(exp(4)显然可见,移动的位相光栅的n 级衍射光波,相对于静止的位相光栅有一个大小:d a n ωωω+=0(5)的多普勒频率,如图3所示。
2.光拍的获得与检测 光波的频率甚高,为了要从光频0ω中检测出多普勒频移,必须采用“拍”的方法。
也就是要把已频移的和未频移的光束相互平行叠加,以形成光拍。
本实验形成光拍的方法是采用两片完全相同的光栅平行紧贴,一片(B )静止,另一片(A )相对移动。
激光通过双光栅后形成的衍射光,即为两个光束的平行叠加。
双光栅微弱振动实验报告

双光栅微弱振动实验报告双光栅微弱振动实验报告引言:微弱振动是物理学中一个重要的研究领域,它涉及到许多实际应用,如地震监测、机械振动分析等。
在本次实验中,我们将使用双光栅技术来研究微弱振动现象,并探索其潜在应用。
实验装置:实验装置主要由激光器、双光栅、光电探测器和数据采集系统组成。
激光器产生一束单色、相干性很好的激光光束,该光束经过双光栅后会发生干涉现象。
光电探测器用于接收干涉信号,并将其转化为电信号。
数据采集系统则用于记录和分析电信号。
实验步骤:首先,我们将双光栅装置固定在一个平稳的支架上,并调整其位置,使得两个光栅的光程差为零。
然后,我们将激光器的光束照射到双光栅上,并将光电探测器放置在干涉图样的中心位置。
接下来,我们将通过改变实验装置的振动条件来研究微弱振动现象。
首先,我们将在实验装置上施加一个小的外力,例如用手轻轻拍击支架。
我们观察到干涉图样的形态发生了变化,这是因为振动引起了光栅的相对位移,从而改变了光程差。
然后,我们将通过改变外力的大小和频率来进一步研究微弱振动现象。
我们发现,当外力的频率接近光栅的固有频率时,干涉图样会出现明显的共振现象。
这是因为外力与光栅的固有振动频率相匹配,从而导致光栅的振幅增大。
结果与讨论:通过实验,我们成功地观察到了双光栅微弱振动现象,并研究了其频率响应特性。
我们发现,双光栅的共振频率与其固有振动频率密切相关。
这一发现对于设计和优化微弱振动传感器具有重要意义。
此外,我们还发现,双光栅的干涉图样对微弱振动非常敏感。
微小的振动可以导致干涉图样的形态发生明显变化,这为微弱振动的检测和测量提供了一种新的方法。
双光栅技术的高灵敏度和高分辨率使其在微弱振动领域具有广泛的应用前景。
结论:本次实验通过双光栅技术成功地研究了微弱振动现象,并探索了其潜在应用。
实验结果表明,双光栅具有高灵敏度和高分辨率,可以用于微弱振动的检测和测量。
这一技术在地震监测、机械振动分析等领域具有重要的应用前景。
实验13 双光栅测量微弱振动位移量实验

实验13 双光栅测量微弱振动位移量实验实验重点预习内容:1.在实验中怎样产生光拍?2.如何计算波形数?(画图表示)3.如何计算微弱振动的位移振幅?写出公式并对每个量进行逐一解释。
4.如何听拍频信号?多普勒效应:多普勒路过铁路交叉处,发现火车从远而近时汽笛音调变尖,而火车从近而远时,音调变低。
提出“多普勒效应”。
拍:根据振动迭加原理,两列速度相同、振动面相同、频差较小而同方向传播的简谐波叠加即形成拍。
本实验是运用多普勒效应与拍效应对振动位移进行测量一、实验目的1. 理解利用光的多普勒频移形成光拍的原理;2. 理解双光栅衍射干涉位移测量原理;3. 应用双光栅微弱振动测量仪测量音叉振动产生的微小振幅。
二、实验仪器双光栅微弱振动测量仪、模拟示波器、数字示波器三、实验原理1. 位移光栅的多普勒频移多普勒效应是指光源、接收器、传播介质或中间反射器之间的相对运动所引起的接收器接收到的光波频率与光源频率发生的变化,由此产生的频率变化称为多普勒频移。
由于介质对光传播时有不同的相位延迟作用,对于两束相同的单色光,若初始时刻相位相同,经过相同的几何路径,但在不同折射率的介质中传播,出射时两光的位相则不相同,对于位相光栅,当激光平面波垂直入射时,由于位相光栅上不同 图1 出射的摺曲波阵面的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波变成出射时的摺曲波阵面,见图1。
激光平面波垂直入射到光栅,由于光栅上每缝自身的衍射作用和每缝之间的干涉,通过光栅后光的强度出现周期性的变化。
在远场,我们可以用大家熟知的y xvd激光平面波 位相光栅出射折面波光栅衍射方程即(1)式来表示主极大位置:d sin θ=±k λ k =0,1,2,… (1) 式中:整数k 为主极大级数,d 为光栅常数,θ为衍射角,λ为光波波长。
如果光栅在y 方向以速度v 移动,则从光栅出射的光的波阵面也以速度v 在y 方向移动。
因此在不同时刻,对应于同一级的衍射光射,它从光栅出射时,在y 方向也有一个vt 的位移量,见图2。
双光栅检测微弱振动位移量附录双光栅检测微弱振动位移量讲义

) (1)
式中 m 为衍射级数,d 为光栅常数,θ 为衍射角,λ 为光波波长。
如果光栅在 y 方向以速度 u 做简谐振动,则从光栅出射的光的波阵面也以同样速
度做简谐振动,因此在不同时刻,对应于同一级次的衍射光线,从光栅出射时,在 y 方
向将会产生位移量 ut,
图 1 光栅衍射原理图
如图 2 所示。
(6)
其中 ξ 为光电转换常数。
因光波频率很高,(6)式中第一项、第二项、第四项,光电池无法分辨,第三项为拍频
信号,因为频率较低,光电池能做出相应的响应,其光电流为可表示为
is = ξ{E10 E20 cos[(ω0 + ωd − ω0 )t + (ϕ2 − ϕ1 )]} = ξ{E10 E20 cos[ωd t + (ϕ 2 − ϕ1 )]}
数据处理
1.求出音叉谐振时光拍信号的平均频率; 2.求出音叉在谐振点时作微弱振动的位移振幅; 3.用坐标纸作图,做出音叉的频率~振幅曲线; 4.选作内容:做出音叉不同有效质量时的谐振曲线,定性讨论其变化趋势。
讨论题
1.如何判断动光栅与静光栅的刻痕已平行? 2.作外力驱动音叉谐振曲线时,为什么要固定信号功率?
4.谐振曲线的测量:在音叉谐振点附近,调节驱动信号频率,频率间隔 fn=(f0±0.1n)HZ,f0 是谐振频率,n=0,±1,±2 选 5 个点,分别测出对应拍频波的波数,计算出相应的振幅 An。
5.选作内容:改变音叉的有效质量,可以将塑料软管依次放入音叉不同位置的小孔里, 或将橡皮泥粘在音叉的不同位置,研究音叉谐振曲线的变化规律。 三、报告要求
图 2 用移动的皱褶波面来解释多普勒效应 (a)褶皱波面的相位超前 (b)不同衍射级次的频移
双光栅微弱振动实验报告

一、实验目的1. 了解双光栅微弱振动测量技术的原理和方法。
2. 掌握双光栅微弱振动测量仪器的操作方法。
3. 通过实验验证双光栅技术在微弱振动测量中的可行性和准确性。
二、实验原理双光栅微弱振动测量技术是基于多普勒频移原理。
当振动体相对于光栅运动时,光栅上的衍射条纹发生位移,从而导致入射光与反射光之间的相位差发生变化。
通过测量相位差的变化,可以计算出振动体的位移。
三、实验仪器与材料1. 双光栅微弱振动测量仪2. 数字示波器3. 音叉4. 激光器5. 信号发生器6. 频率计四、实验步骤1. 将双光栅微弱振动测量仪的Y1(拍频信号)和Y2(音叉激振信号)输出接口分别连接到数字示波器的X(CH1)和Y(CH2)输入端。
2. 打开激光器、信号发生器和频率计,调节相关参数,确保激光器发出稳定的光束。
3. 将音叉放置在双光栅微弱振动测量仪的测量平台上,调整测量仪的位置,使激光束垂直照射到音叉上。
4. 打开示波器,观察拍频信号和音叉激振信号的波形,并记录数据。
5. 调整音叉的振动幅度,观察示波器上的波形变化,分析振动体的位移情况。
6. 通过频率计测量音叉的谐振频率,计算振动体的振动周期。
五、实验结果与分析1. 在实验过程中,我们成功测量到了音叉的微弱振动,示波器上的波形图显示了振动体的位移情况。
2. 通过调整音叉的振动幅度,我们可以观察到示波器上的波形变化,从而得到振动体的位移信息。
3. 实验结果表明,双光栅技术在微弱振动测量中具有较高的分辨率和灵敏度,能够满足微弱振动测量的需求。
六、结论1. 本次实验通过双光栅技术成功地研究了微弱振动现象,验证了该技术在微弱振动测量中的可行性和准确性。
2. 双光栅技术具有较高的分辨率和灵敏度,可以应用于许多领域,如工程、医学、物理等。
3. 在实验过程中,我们掌握了双光栅微弱振动测量仪器的操作方法,为今后开展相关实验奠定了基础。
七、注意事项1. 实验过程中,注意保持激光器的稳定性,避免光束偏移。
双光栅微弱振动测量实验

没有侥幸这回事,最偶然的意外,似乎也都是有必然性的。
---爱因斯坦(美国)
大学物理实验报告
college physical experiment report paper
名称:双光栅微弱振动测量实验
班级:
姓名:
学号:
大学物理实验预习报告
1.熟悉利用光的多普勒频移形成光拍的原理,掌握精确测量微弱振动位移的方法。
2.做出外力驱动音叉时的谐振曲线。
预习思考检测题
1. 什么是位相光栅的多普勒频移?
2.怎样进行光拍的获得与检测?
3. 微弱振动位移量如何检测?
大学物理实验报告
实验目的:实验仪器:实验原理:
实验步骤:
实验数据表格及记录
【注:此处数据属原始记录,是批改报告时进行核查的依据,经教师签字后不得更改】
教师签字:
数据处理及误差分析:。
双光栅测量微弱振动位移量的实验研究

双光栅测量微弱振动位移量的实验研究范菁津;邱文杰;郑志远【摘要】对于利用双光栅测量微弱振动仪寻找谐振频率、改变配重物体的质量分布对谐振点的影响,驱动电流对谐振点的影响以及一些实验中的技术问题,利用观察法、控制变量法等方法作图,由于谐振点附近拍频波个数变化较大,提高精度可以绘出较准确的谐振曲线并找到较精确的谐振点;通过对比小棒和橡皮泥,得出橡皮泥改变配重物体的质量分布实验效果更明显,排除了小棒颤动的影响;且得出了谐振频率与驱动电流呈正相关的结论.提出对实验中遇到问题的解决方法提高了该实验的准确性,降低实验误差.%For the use of double grating measuring weak vibration meter to find the resonant frequency,change the weight distribution of the mass of the body's influence on the resonant point,the influence of drive current of resonant point and some technical problems in the experiment,using the method of observation and control variable method such as drawing,because the beat frequency near resonance wave number change is bigger,improve accuracy can draw more accurate curve and find more precise resonant point;By comparing the stick and silly putty,silly putty change weight distribution experiment effect is more obvious,the mass of the body ruled out stick fibrillation;And it is concluded that the resonance frequency was positively correlated with the drive current.Put for ward the problems in the experiment of solution to improve the accuracy of the experiment,to reduce experimental error.【期刊名称】《大学物理实验》【年(卷),期】2017(030)002【总页数】3页(P41-43)【关键词】拍频波;频率;谐【作者】范菁津;邱文杰;郑志远【作者单位】中国地质大学,北京 100083;中国地质大学,北京 100083;中国地质大学,北京 100083【正文语种】中文【中图分类】O4-34双光栅测量微弱振动位移量的技术广泛应用于精密测量领域。
用双光栅测量微弱振动实验 综述报告

用双光栅测量微弱振动实验综述报告
双光栅测量微弱振动实验是一种用于研究微弱振动现象的实验方法。
本文将对这一实验方法进行综述,并介绍其原理、仪器搭建和应用领域。
一、原理
双光栅测量微弱振动实验的原理是利用光学干涉原理来测量物体的振动。
在实验中,将物体置于一对干涉光栅之间,当物体振动时,会引起干涉光斑的移动。
利用这一移动的特性,可以测量物体的振幅、频率等参数。
二、仪器搭建
双光栅测量微弱振动实验需要的仪器有:激光器、物体振动平台、双光栅系统以及用于记录干涉光斑的光学检测系统。
首先,在实验中需要使用激光器发射出一束平行光,这一光束通过一个分束器后,被分成两个平行的光束。
其次,物体振动平台需要按照一定频率和振幅振动,可以通过电机等设备实现。
然后,光线经过一个双光栅系统并在物体振动平台上反射,进入到光学检测系统。
最后,使用光学检测系统对干涉光斑进行记录和分析,得到物体振动的参数。
三、应用领域
双光栅测量微弱振动实验可以被广泛应用于研究各种物体的振动特性,比如微机械、生物医学和光学等领域。
例如,在微机械领域,双光栅测量微弱振动实验可以用于研究微型机器人和微型传感器的振动特性,实现微小物体的控制和测量。
在生物医学领域,双光栅测量微弱振动实验可以用于研究生物分子、细胞等的振动参数,为生物医学研究提供重要帮助。
在光学方面,双光栅测量微弱振动实验可以用于研究光学材料和光学器件的振动特性,为光学器件的研发提供帮助。
综上所述,双光栅测量微弱振动实验是一种重要的实验方法,其具有广泛的应用领域和研究价值,是现代科学研究领域中不可或缺的一部分。
用双光栅测量微弱振动

实验9.8用双光栅测量微弱振动1842年多普勒(Doppler)提出,当波源和观察者彼此接近时,接收到的频率变高;而当波源和观察者彼此相离开时,接收到的频率变低。
这种现象在电磁波和机械波中都存在。
即当波源和观察者之间存在相对运动时,观察者所接收到的频率不等于波源振动频率,这种现象称为多普勒效应。
而当光源与接收器之间有相对运动时,接收器感受到的光波频率不等于光源频率,这就是光学的多普勒效应或电磁波的多普勒效应。
该效应已经在科学技术以及医学的许多领域得到应用。
本实验用激光多普勒效应测量微弱振动,是一种精密的光电系统,它使用了多种光电转换和处理技术,是一个综合性很强的实验。
一、实验目的1.熟悉一种利用光的多普勒频移形成光拍的原理,精确测量微弱振动位移的方法;2.作出外力驱动音叉时的谐振曲线。
、实验仪器双光栅微弱振动测量仪,双踪示波器三、实验原理1•位相光栅的多普勒频移所谓的位相材料是指那些只有空间位相结构,而透明度一样的透明材料,如生物切片、油膜、热塑以及声光偏转池等,他们只改变入射光的相位,而不影响其振幅。
位相光栅就是用这样的材料制作的光栅。
当激光平面波垂直入射到位相光栅时,由于位相光栅上不同的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波在出射时变成折曲波阵面,如图1所示,由于衍射干涉作用,在远场我们可以用大家熟知的光栅方程来表示:d sin0=n k(1)式中d为光栅常数,0为衍射角,,为光波波长。
然而,如果由于光栅在尹方向以速度v移动,则出射波阵面也以速度v在y方向移动。
从而在不同时刻,对应于同一级的衍射光线,它的波阵面上的点,在y方向上也有一个vt的位移量,如图2所示。
图1这个位移量对应于光波位相的变化量为A①(t)2兀人2兀A①(t)=•A s=vtsin0(2)kk(1)带入(2)(3)v 式中①二2K —d d把光波写成如下形式:(5)2级叫+2% T 级%+叫10级叫 —I 级昨一% —2级%—2E 二Eexpb6t+AO(t))] 二expb6+n3》]0d显然可见,移动的位相光栅的“级衍射光波,相对于静止的位相光栅有一个大小:①=①+n ®a 0d的多普勒频率,如图3所示。
1实验一 双光栅测量微弱振动位移量

119实验一 双光栅测量微弱振动位移量精密测量在自动化控制的領域里一直扮演着重要的角色,其中光电测量因为有较佳的精密性与准确性,加上轻巧、无噪音等优点,在测量的应用上常被采用。
作为一种把机械位移信号转化为光电信号的手段,光栅式位移测量技术在长度与角度的数字化测量、运动比较测量、数控机床、应力分析等领域得到了广泛的应用。
多普勒频移物理特性的应用也非常广泛,如医学上的超声诊断仪、测量海水各层深度的海流速度和方向、卫星导航定位系统、音乐中乐器的调音等。
双光栅微弱振动测量仪在力学实验项目中用作音叉振动分析、微振幅(位移)、测量和光拍研究等。
【实验目的】1. 了解利用光的多普勒频移形成光拍的原理并用于测量光拍拍频;2. 学会使用精确测量微弱振动位移的一种方法;3. 应用双光栅微弱振动测量仪测量音叉振动的微振幅。
【实验原理】1. 位移光栅的多普勒频移多普勒效应是指光源、接受器、传播介质或中间反射器之间的相对运动所引起的接收器接收到的光波频率与光源频率发生的变化,由此产生的频率变化称为多普勒频移。
由于介质对光传播时有不同的相位延迟作用,对于两束相同的单色光,若初始时刻相位相同,经过相同的几何路径,但在不同折射率的介质中传播,出射时两光的位相则不相同。
对于位相光栅,当激光平面波垂直入射时,由于位相光栅上不同的光密和光疏媒质部分对光波的位相延迟作用,使入射的平面波变成出射时的摺曲波阵面,见图1。
激光平面波垂直入射到光栅,由于光栅上每缝自身的衍射作用和各缝之间的干涉,通过光栅后光的强度出现周期性的变化。
在远场,我们可以用大家熟知的光栅衍射方程即(1)式来表示主极大位置:λθk d ±=sin ⋅⋅⋅=,2,1,0k (1)式中 ,整数k 为主极大级数,d 为光栅常数,θ为衍射角,λ为光波波长。
如果光栅在y 方向以速度v 移动,则从光栅出射的光的波阵面也以速度v 在y 方向移动。
因此在不同时刻,对应于同一级的衍射光线,它从光栅出射时,在y 方向也有一个vt 的位移量,见图2。
双光栅测微弱振动综述报告
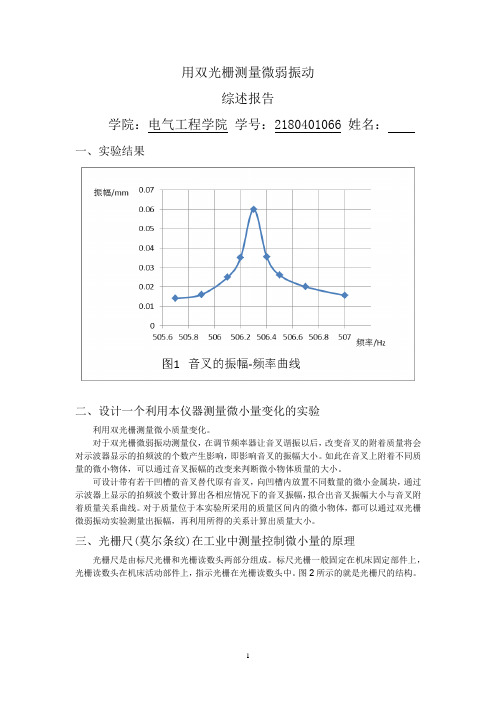
五、本实验装置的其他应用
可设计带有若干凹槽的音叉替代原有音叉,向凹槽内放置不同数量的微小金属块,通过示波器上显示的拍频波个数计算出各相应情况下的音叉振幅,拟合出音叉振幅大小与音叉附着质量关系曲线。对于质量位于本实验所采用的质量区间内的微小物体,都可以通过双光栅微弱振动实验测量出振幅,再利用所得的关系计算出质量大小。
三、光栅尺(莫尔条纹)在工业中测量控制微小量的原理
1、双光栅衍射成像的研究
2、双光栅双参量的传感研究
六、普通光栅和位相光栅的区别
由大量等宽等间距的平行狭缝构成的光学器件称为光栅。一般常用的光栅是在玻璃片上刻出大量平行刻痕制成,刻痕为不透光部分,两刻痕之间的光滑部分可以透光,相当于一狭缝。精制的光栅,在1cm宽度内刻有几千条乃至上万条刻痕。这种利用透射光衍射的光栅称为透射光栅,还有利用两刻痕间的反射光衍射的光栅,如在镀有金属层的表面上刻出许多平行刻痕,两刻痕间的光滑金属面可以反射光,这种光栅称为反射光栅。
八、思考题
1、如何判断动光栅和静光栅的刻痕已经平行?
将观察屏放于光电池架处,慢慢转动光栅架,仔细观察,调节,两个光束重合时,动光栅和静光栅即处于平行状态。
矩形棒
式中,b,h分别为棒的宽和厚。
在国际单位制中,杨氏模量的单位为牛顿/米2(N·m-2)。
实验原理图如5所示。由信号发生器输出的正弦信号,加到激发换能器Ⅰ上,通过激发换能器Ⅰ把信号转变成机械振动,再由悬丝把机械振动传给待测试样,使试样受迫做横向振动,试样另一端的悬丝将振动传给接受换能器Ⅱ,这时机械振动又转变成电信号。该信号送到示波器中显示。
双光栅实验

实验报告实验名称双光栅振动实验精密测量在自动化控制的领域里一直扮演着重要的角色, 其中光电测量因为有较好的精密性与准确性, 加上轻巧、无噪音等优点, 在测量的应用上常被采用。
作为一种把机械位移信号转化为光电信号的手段, 光栅式位移测量技术在长度与角度的数字化测量、运动比较测量、数控机床、应力分析等领域得到了广泛的应用。
【实验目的】1.了解利用光的多普勒频移形成光拍的原理并用于测量光拍拍频2.学会使用精确测量微弱振动位移的一种方法3.应用双光栅微弱振动实验仪测量音叉振动的微振幅【实验仪器】双光栅微弱振动实验仪(包括激光源、信号发生器、频率计等)、音叉1.光电池升降手轮;2.光电池座(在顶部有光电池盒, 盒前有一小孔光阑);3.音叉座;4.音叉;5.粘于音叉上的光栅;6.静光栅架;7.半导体激光器;8.上下调节器;9.左右调节器;10.激光器输出功率调节器;11.信号发生器输出功率调节;12.信号发生器频率细调;13.信号发生器频率粗调;14.驱动音叉换能器;15.功率显示窗口;16.频率显示窗口;17.三个输出信号插口(Y1 拍频信号, Y2 音叉驱动信号, X为示波器提供“外触发”)图1 双光栅微弱振动实验仪面板结构双光栅微弱振动实验仪在实验中用作音叉振动分析、微振幅(位移)、测量和光拍研究等。
【实验原理】1. 静态光栅(1)光垂直入射满足光栅方程:θkλsin(1)d=式中 d 为光栅常数, 为衍射角, 为光波波长, k 为衍射级数 k=0,1, ···(2)若平面波入射平面光栅时, 如图2 所示, 则光栅方程为:图2()λθk i d =+sin sin (2)2. 光的多普勒频移当光栅以速度 v 沿光的传播方向运动时, 出射波阵面也以速度 v 沿同一方向移动, 因而 在不同时刻 Δt, 它的位移量记作 v Δt 。
相应于光波位相发生变化 ()t t ∆=∆υλπϕ2 (3)3. 光拍的获得与检测双光栅弱振动仪的光路简图如图 3 所示图3 双光栅光路简图本实验采用两片完全相同的光栅平行紧贴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应激光平面波垂直入射到光栅,由于光 栅上每缝自身的衍射作用和各缝之间的干 涉,通过光栅后光的强度出现周期性的变 化。在远场,我们可以用大家熟知的光栅 衍射方程即(1)式来表示主极大位置:
d sin k
k 0,1,2, (1)
式中 ,K 整数,为主极大级数d为光栅 常数,θ 为衍射角, λ 为光波波长。
(6)
其中
为光电转换常数
因光波频率 ω 甚高,在式(6)第一、 二、四项中,光电检测器无法反应,式(6) 第三项即为拍频信号,因为频率较低,光 电检测器能作出相应的响应。其光电流为
is {E10 E20 cos[(0 d 0 )t ( 2 1 )]}
{E10 E20 cos[d t ( 2 1 )]}
1 1
.
.
• 例题:如图7,在T/2内,整数波形数为4, 尾数分数部分已满1/4波形, • b h / H =0.6/1=0.6 • 所以 • 波形数= 4 0.25 sin 0.6 4.25 36.8 4.25 0.10 4.35
1
360
360
.
【数据处理】
1.求出音叉谐振时光拍信号的平均频率;
2.求出音叉在谐振点时作微弱振动的位移振幅;
3.在坐标纸上画出音叉的频率—振幅曲线; 4.作出音叉不同有效质量时的谐振曲线,定性讨论其变 化趋势。
【思考题】
1. 如何判断动光栅与静光栅的刻痕已平行? 2. 作外力驱动音叉谐振曲线时,为什么要固定 信号功率? 3. 本实验测量方法有何优点?测量微振动位移 的灵敏度是多少?
(4)
显然可见,移动的位相光栅的级衍射光波, 相对于静止的位相光栅有一个:
a 0 kd
的多普勒频移,如图3所示
图3 移动光栅的多普勒频率
2、光拍的获得与检测 光频率很高为了要从光频中检测出多普勒 频移量,必须采用“拍”的方法。即要把已频 移的和未频移的光束振动方向互相平行迭加, 以形成光拍。由于拍频较低,容易测得,故 通过拍频即可检测出多普勒频移量。 本实验形成光拍的方法是采用两片完全相 同的光栅平行紧贴,一片静止 B ,另一片相 对移动 A 。激光通过双光栅后所形成的衍射 光,即为两种以上光束的平行迭加。其形成 的第k级衍射光波的多普勒频移如图4所示。
2、光拍的获得与检测
图4 k级衍射光波的多普勒频移
1
光栅 A 按速度 VA 移动起频移作用,而光 栅静止不动只起衍射作用,故通过双光栅后 出射的衍射光包含了两种以上不同频率而又 平行的光束,由于双光栅紧贴,激光束具有 一定宽度故该光束能平行迭加,这样直接而 又简单地形成了光拍。如图5所示
激光经过双光栅所形成的衍射光叠加成光拍 信号。光拍信号进入光电检测器后,其输出光电 流可由下述关系求得:
2
2
I ( E1 E2 ) 2
{E10 cos2 (0t 1 ) E20 2 cos2 [(0 d )t 2 ]
2
E10 E20 cos[(0 d 0 )t ( 2 1 )]
E10 E20 cos[(0 d d )t ( 2 1 )]}
.
• 拍频 F拍 即为:
其中
n 1 d
d v A F拍 v A n 2 d
(7)
为光栅密度,本实验 n 1 d 100条 / m m
图5 频差较小的二列光波叠加形成“拍”
3、微弱振动位移量的检测
• 从式(7)可知,F 拍与光频率ω 0无关,且 当光栅密度nθ 为常数时,只正比于光栅移动 速度VA,如果把光栅粘在音叉上,则VA是周 期性变化的。所以光拍信号频率F 拍也是随 时间而变化的,微弱振动的位移振幅为:
实验原理
• • 1.位移光栅的多普勒频移 多普勒效应是指光源、接受器、传播介 质或中间反射器之间的相对运动所引起的 接收器接收到的光波频率与光源频率发生 的变化,由此产生的频率变化称为多普勒 频移。
由于介质对光传播时有不同的相位延迟 作用,对于两束相同的单色光,若初始 时刻相位相同,经过相同的几何路径, 但在不同折射率的介质中传播,出射时 两光的位相则不相同。对于位相光栅, 当激光平面波垂直入射时,由于位相光 栅上不同的光密和光疏媒质部分对光波 的位相延迟作用,使入射的平面波变成 出射时的摺曲波阵面,见图1。
将(1)代入(2)得:
(t ) 2
vt
k v k 2t k d t d d
(3)
式中
d 2
v d
若激光从一静止的光栅出射时,光波电矢量 方程为:
E E0 cos0t
而激光从相应移动光栅出射时,光波 电矢量方程则为
E E0 cos[0t (t )] E0 cos[(0 kd )t ]
图7 计算波形数
实验装置
635nm
100Hz ~ 1000Hz
实验仪器:激光源、信号发生器、频率计 (上述仪器已集成在测量仪箱内)(1Hz ~ 999.9Hz) 0.1Hz
音叉谐振频率: 500Hz 左右
图8 双光栅微弱振动测量仪面板结构
实验装置
1-光电池座(在顶部有光电池盒, 盒前有一小孔光阑) 2- 电源开 关 3- 光电池升降手轮4- 音叉座 5- 音叉 6- 粘于音叉上的光栅 (动光栅) 7- 静光栅架 8- 半导 体激光器 9- 锁紧手轮 10- 激 光器输出功率调节 11- 信号发生 器输出功率调节 12- 信号发生器 频率调节 13- 驱动音叉用耳机 14- 频率显示窗口 15- 三个输出 信号插口(Y1拍频信号,Y2音叉驱 动信号,X为示波器提供“外触发” 扫描信号,可使示波器上的波形稳 定。)
实验一、
双光栅测量微 弱振动位移量
光电测量介绍
精密测量在自动化控制的領域里一直扮演着 重要的角色,其中光电测量因为有较佳的精 密性与准确性,加上轻巧、无噪音等优点, 在测量的应用上常被采用。作为一种把机械 位移信号转化为光电信号的手段,光栅式位 移测量技术在长度与角度的数字化测量、运 动比较测量、数控机床、应力分析等领域得 到了广泛的应用。
•
波形数由完整波形数、波的首数、波的尾 数三部分组成,根据示波器上显示计算。 波形的分数部份为不足一个完整波形的首 数及尾数,需在波群的两端,可按反正弦 函数折算为波形的分数部份, • 即波形数=整数波形数+波的首数和尾数中 sin a sin b 满1/2或1/4或3/4个波形分数部份 360 360 • 式中a,b,为波群的首、尾幅度和该处完 整波形的振幅之比。 波群指T/2内的波形, 分数波形数若满1/2个波形为0.5,满个1/4 波形为0.25,满3/4个波形为0.75。
如果光栅在 y 方向以 v 速度移动,则从光 栅出射的光的波阵面也以速度v在y 方向移 动。因此在不同时刻,对应于同一级的衍 射光线,它从光栅出射时,在方向也有一 个 vt 的位移量,见图2。 这个位移量相应于出射光波位相的变化量为
0
(t )
2
s
2
vt sin
(2)
多普勒频移物理特性的应用也非常广泛, 如医学上的超声诊断仪、测量海水各层深度 的海流速度和方向、卫星导航定位系统、音 乐中乐器的调音等。 双光栅微弱振动测量仪在力学实验项目中用作 音叉振动分析、微振幅(位移)、测量和光拍 研究等。
【实验目的】
1. 了解利用光的多普勒频移形成光拍的 原理并用于测量光拍拍频; 2. 学会使用精确测量微弱振动位移的一 种方法; 3、应用双光栅微弱振动测量仪测量音叉 振动的微振幅
1 1 A v(t )dt 2 0 2
T 2 T
0
2
F拍 (t ) n
dt
1 2n
T
F(t )dt
拍 0
2
.
T
• 式中 T 为音叉振动周期。
表示
F(t )dt
拍 0
2
时间内的拍频波的个数。所以,只要测 得拍频波的波数,就可得到微弱振动的 位移振幅。
图6 示波器显示拍频波形
.
调节功率时,拍频波形会变化,功率、频率同 时慢慢调。拍频稳定有个时间过程。 6. 测出外力驱动音叉时的谐振曲线。 固定“功率”旋钮位置,在音叉谐振点附近,小心 调节“频率”旋钮,测出音叉的振动频率与对应 的信号振幅大小,记录下数据。 7. 保持信号输出功率不变,逐一将橡皮泥粘在音 叉上改变音叉的有效质量,调节“频率”旋钮, 研究谐振曲线的变化趋势。
图8 双光栅微弱振动测量仪面板结构
【实验内容】
1.预习《示波器的应用》,熟悉双踪示波器的使用方法。 2.将示波器的Y1、Y2、X外触发输入端接至双光栅微弱振动测量仪 的Y1、 Y2、X的输出插座上,开启各自的电源。 3.几何光路调整。 小心取下“静光栅架”, (不可擦伤光栅)稍稍松开激光器顶 部的锁紧手轮,用手小心地上下左右搬动激光器,让光束从安装 静止光栅架的孔中心通过。调节光电池架手轮,让某一级衍射光 正好落入光电池前的小孔内。锁紧激光器。 4.双光栅调整。 小心地装上“静光栅架”,静光栅尽可能与动光栅接近,注意 不可让它们相碰!用一白纸作为观察屏,放于光电池架前观察光 斑,慢慢转动光栅架,仔细观察调节,使得两个光束尽可能重合。 去掉观察屏,轻轻敲击音叉,调节示波器,配合调节激光器输出 功率,应看到很漂亮的拍频波。
光束1: 光束2:
E1 E10 cos(0 t 1 )
E2 E20 cos[(0 d )t 2 ]
2 I ( E E ) 光电流: 1 2
( 取k=1 )
{E10
2
2 cos (0t 1 ) E20 cos [(0 d )t 2 ]
.
5. 音叉谐振调节。 先将“功率”旋钮置于 6 — 7 点钟附近, 调节“频率”旋钮,(500Hz附近), 使音叉 谐振。调节时用手轻轻地按音叉顶部,找 出调节方向。如音叉谐振太强烈,将“功 率”旋钮向小钟点方向转动,使在示波器 上看到 T/2 的内光拍的波数为 15 个左右。记 录此时音叉振动频率、屏上完整波的个数、 不足一个完整波形的首数及尾数值以及对 应该处完整波形的振幅值。
