近三年高考全国卷理科立体几何真题精编版
2016年-2019年立体几何大题全国卷高考真题

2016年-2019年立体几何大题全国卷高考真题1、(2015年1卷18题)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AFC⊥平面AEC;(Ⅱ)求直线AE与直线CF所成有的余弦值。
(2016年1卷18题)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD, 2、90AFD ∠=o ,且二面角D -AF -E 与二面角C -BE -F 都是60o .(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值.3(2016年2卷19题)(本小题满分12分) CA BD EF如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF'的位置10OD '=. (I )证明:D H '⊥平面ABCD ;(II )求二面角B D A C '--的正弦值.4、(2017年1卷18题)如图,在四棱锥P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=?.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=?,求二面角A PB C --的余弦值.5.(2018年1卷18题)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥.⑴证明:平面PEF ⊥平面ABFD ;⑵求DP与平面ABFD所成角的正弦值.6.(2018年新课标Ⅱ理)如图,在三棱锥P-ABC中,AB=BC=22,P A =PB=PC=AC=4,O为AC的中点.(1)求证:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-P A-C为30°,求PC与平面P AM所成角的正弦值.18.(2019年1卷18题)(12分)如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.8.(12分)(2019年新课标Ⅱ理)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E 在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.。
新课标全国卷历年高考立体几何真题(含答案)
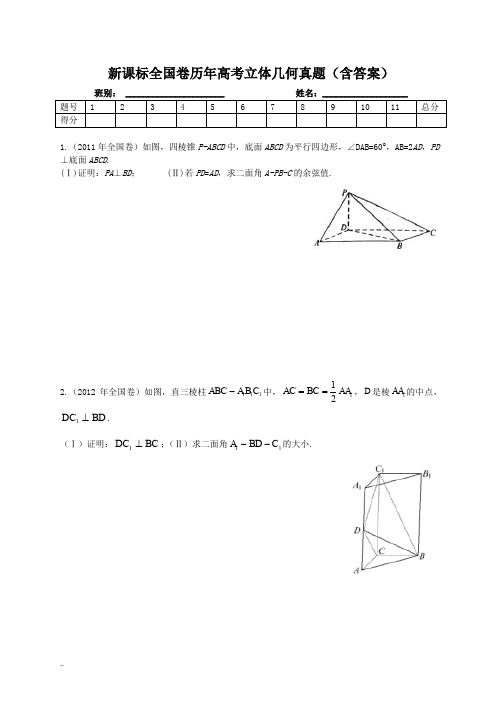
新课标全国卷历年高考立体几何真题(含答案)班别: ______________________ 姓名:___________________1.(2011年全国卷)如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD .(Ⅰ)证明:PA ⊥BD ; (Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值.2.(2012年全国卷)如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,BD DC ⊥1.(Ⅰ)证明:BC DC ⊥1;(Ⅱ)求二面角11C BD A --的大小.3.(2013年全国Ⅱ卷)如图,直棱柱ABC-A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC=CB=2AB. (Ⅰ)证明:BC 1//平面A 1CD , (Ⅱ)求二面角D-A 1C-E 的正弦值4.(2013年全国Ⅰ卷)如图,三棱柱111C B A ABC -中,CB CA =,1AA AB =, 601=∠BAA .(Ⅰ)证明C A AB 1⊥;(Ⅱ)若平面ABC ⊥平面AA 1B 1B ,AB=CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.5.(2014年全国Ⅱ卷)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D-AE-C 为60°,AP=1,,求三棱锥E-ACD 的体积.6.(2014年全国Ⅰ卷)如图三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1AB B C ⊥. (Ⅰ) 证明:1AC AB =;(Ⅱ)若1AC AB ⊥,o160CBB ∠=,AB=BC ,求二面角111A A B C --的余弦值.7.(2015年全国Ⅱ卷)如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F=4,过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由);(Ⅱ)求直线AF 与平面α所成角的正弦值.8.(2015年全国Ⅰ卷)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ;(Ⅱ)求直线AE 与直线CF 所成角的余弦值.9.(2016年全国Ⅱ卷)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5,6AB AC ==,点,E F分别在,AD CD 上,54AE CF ==,EF 交BD 于点H .将DEF ∆沿EF 折到'D EF ∆位置,OD '=(Ⅰ)证明:D H'⊥平面ABCD ; (Ⅱ)求二面角B D A C '--的正弦值.10.(2016年全国Ⅰ卷)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值.11.(2016年全国3卷)如图,四棱锥P ABC -中,PA ⊥底面面ABCD ,AD ∥BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN平面PAB ;(II )求直线AN 与平面PMN 所成角的正弦值.自我总结:新课标全国卷历年高考例题几何真题(广西多用2卷)1.解:(Ⅰ)因为60,2DAB AB AD ∠=︒=,由余弦定理得BD = 从而BD 2+AD 2= AB 2,故BD⊥AD;又PD ⊥底面ABCD ,可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD(Ⅱ)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴射线DB 为y 轴的正半轴,射线DP 为z 轴的正半轴,建立空间直角坐标系D-xyz ,则()1,0,0A,()0B,()C -,()0,0,1P.(1),(1,0,0)ABPB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n =(x,y,z ),则0⎧⋅=⎪⎨⋅=⎪⎩n AB n PB ,即00x z -+=-= 因此可取n =设平面PBC 的法向量为m ,则0⎧⋅=⎪⎨⋅=⎪⎩m PB m BC 可取m =(0,-1,,cos 7<>==-m,n 故二面角A-PB-C 的余弦值为 . 2.证明(Ⅰ)(1)在Rt DAC ∆中,AD AC =得:45ADC ︒∠=,同理:1114590A DC CDC ︒︒∠=⇒∠=,得:1,DC DC DC BD DC ⊥⊥⇒⊥又∵11,DC DC DC BD DC ⊥⊥⇒⊥平面1BCD DC BC ⇒⊥. (Ⅱ)(2)11,DC BC CC BC BC ⊥⊥⇒⊥平面11ACC A BC AC ⇒⊥取11A B 的中点O ,过点O 作OH BD ⊥于点H ,连接11,C O C H ,1111111AC B C C O A B =⇒⊥,C 1O ⊥A 1D 1C O ⇒⊥面1ABD 1OH BD C H BD ⊥⇒⊥ 得:点H 与点D 重合 ,即1C DO ∠是二面角11C BD A --的平面角 设AC a =,则1C O =111230C D C O C DO ︒==⇒∠= 即二面角11C BD A --的大小为30︒.3.(1)连接1AC ,交1A C 于点F ,连结1,DF BC ,则F 为1AC 的中点,因为D 为AB 的中点,所以DF//1BC ,又因为111FD ACD BC AC D ⊂⊄平面,平面,所以11//BC ACD 平面. (2)由AA 1AC CB AB ===,可设:AB =2a,则1,AA AC CB ===所以AC BC ⊥,又因为ABC-A 1B 1C 1为直三棱柱,所以以点C 为坐标原点,建立空间直角坐标系如图.则C (0,0,0)、)1,0A D ⎫⎪⎪⎝⎭、、,E ⎛⎫⎪ ⎪⎝⎭()122,0,2,,0CA a a CD a ⎛⎫== ⎪⎪⎝⎭,.CE ⎛⎫= ⎪ ⎪⎝⎭设平面1A CD 的法向量为(),,,n x y z =则0n CD ⋅=且10,n CA ⋅=可解得,y x z =-=令1,x =得平面1A CD 的一个法向量为()1,1,1n =--,同理可得平面1A CE 的一个法向量为()2,1,2m =-,则3cos ,n m <>=,所以6sin ,n m <>=所以二面角1D A C E -- 4.【解析】(Ⅰ)取AB 的中点O ,连结OC ,1OA ,B A 1.因为CB CA =,所以AB OC ⊥.由于1AA AB =, 601=∠BAA ,故B AA 1∆为等边三角形,所以AB OA ⊥1.因为O OA OC =1 ,所以⊥AB 面C OA 1.又⊂C A 1平面C OA 1,故C A AB 1⊥. (Ⅱ)由(Ⅰ)知,AB OC ⊥,AB OA ⊥1,又平面⊥ABC 平面11BB AA ,交线为AB ,所以⊥OC 平面11BB AA ,故OA ,OC ,1OA 两两互相垂直.以O 为坐标原点,的方向为x 轴的正方向,||为单位长度,建立如图所示的空间直角坐标系xyz O -,则有)0,0,1(A ,)0,3,0(1A ,)3,0,0(C ,)0,0,1(-B .则)3,0,1(=, )0,3,1(1-==AA BB , )3,3,0(-=.设平面C C BB 11的法向量为),,(z y x =,则有⎪⎩⎪⎨⎧=⋅=⋅01BB ,即⎪⎩⎪⎨⎧=+-=+0303y x z x ,可取)1,1,3(-=.故510||||,cos 111-=⋅>=<C A n C A n C A n ,所以直线C A 1与平面C C BB 11所成角的正弦值为510.5.【解析】(1) 连接BD 交AC 于点为G,连接EG.在三角形PBD 中,中位线EG ∥PB, 且EG 在平面AEC 上,所以PB ∥平面AEC.(2)设CD=m,分别以AD,AB,AP 为x,y,z 轴建立坐标系,则A(0,0,0),D(,0,0),E 12⎫⎪⎪⎝⎭,C(,m,0).所以AD=(,0,0), AE=12⎫⎪⎪⎝⎭,AC=),0m .设平面ADE 的法向量为1n =(x 1,y 1,z 1),则1n AD ⋅=0, 1n AE ⋅=0,解得一个1n =(0,1,0).同理设平面ACE 的法向量为2n =(x 2,y 2,z 2),则2n AC ⋅=0, 2n AE ⋅=0,解得一个2n因为cos 3π=|cos<12,n n >|=1212n n n n⋅==12,解得m=32. 设F 为AD 的中点,则PA ∥EF,且PA=2EF =12,EF ⊥面ACD,即为三棱锥E-ACD 的高. 所以V E-ACD =·S △ACD ·EF=13×12×32×12.所以,三棱锥E-ACD .为坐标原点,方向,||为单位长度,的方向为y 轴的正方向,的方向为z 轴的正方向建立空间直角坐标系,∵∠,,(0,,0) =,,=,=设向量=,可取,)的一个法向量,),>=A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),=(0,-6,8).=+080z .由∠ABC=120°,可得AG=GC=.由BE ⊥平面ABCD,AB=BC可知AE=EC.又AE ⊥EC,所以EG=,且EG ⊥AC.在Rt △EBG 中,可得BE=,故DF=.在Rt △FDG 中,可得FG=.在直角梯形BDFE 中,由BD=2,BE=,DF=,可得EF=.从而EG 2+FG 2=EF 2,所以EG ⊥FG.,又AC ∩FG=G,可得EG ⊥平面AFC.又因为EG ⊂平面AEC,所以平面AEC ⊥平面AFC. (2)如图,以G 为坐标原点,分别以,的方向为x 轴,y 轴正方向,||为单位长度,建立空间直角坐标系G-xyz.由(1)可得(,)A 00,(,E 10,(,F -10,()C 00, 所以(AE =1,(,CF =-1. 故cos ,||||AE CF AE CF AE CF ⋅<>==-3.所以直线AE 与直线CF所成角的余弦值为3 9.【解析】⑴∵ABEF 为正方形 ∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC ⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥ AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥ ∴四边形EFDC 为等腰梯形以E 为原点,如图建标系,设FD a =()()000020E B a ,,,, ()02202a CA a a ⎛⎫ ⎪ ⎪⎝⎭,,, ()020EB a =,,,22a BC a ⎛⎫=- ⎪ ⎪⎝⎭,,()200AB a =-,,设面BEC 法向量为()m x y z =,,.00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩,即111120202a y a x ay z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩, ()301m =-,,设面ABC 法向量为()222n x y z =,, =00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即222220220a x ay ax ⎧-+=⎪⎨⎪=⎩,()034n=, 设二面角E BC A --的大小为θ.cos 3m nm n θ⋅===+⋅ ∴二面角E BC A --的余弦值为 10.【解析】⑴证明:∵54AE CF ==,∴AE CF AD CD=,∴EF AC ∥.∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AE OH OD AO=⋅=,∴3DH D H '==,∴222'OD OH D H '=+, ∴'D H OH ⊥.又∵OH EF H =I ,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r ,,,设面'ABD 法向量()1n x y z =,,u r ,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345xy z=⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,.同理可得面'AD C 的法向量()2301n =u u r ,,,∴1212cos n n n n θ⋅===u r u u r u r u u r∴sin θ=11.设),,(z y x =为平面PMN 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM , 即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取)1,2,0(=, 于是2558|||||,cos |==><AN n .。
高考数学近三年真题立体几何(理科专用)

三年专题 立体几何(选择题、填空题)(理科专用)1.【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时,相应水面的面积为140.0km 2;水位为海拔157.5m 时,相应水面的面积为180.0km 2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m 上升到157.5m 时,增加的水量约为(√7≈2.65)( ) A .1.0×109m 3B .1.2×109m 3C .1.4×109m 3D .1.6×109m 32.【2022年新高考1卷】已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3≤l ≤3√3,则该正四棱锥体积的取值范围是( ) A .[18,814]B .[274,814]C .[274,643]D .[18,27]3.【2022年新高考2卷】已知正三棱台的高为1,上、下底面边长分别为3√3和4√3,其顶点都在同一球面上,则该球的表面积为( ) A .100πB .128πC .144πD .192π4.【2021年甲卷理科】2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45A C B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,B B '与C C '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差A A C C ''- 1.732≈)( )A .346B .373C .446D .4735.【2021年甲卷理科】已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1A CBC A C B C ⊥==,则三棱锥O A B C-的体积为( )A 12B 12C 4D 46.【2021年新高考1的母线长为( )A .2B .C .4D .7.【2021年新高考2卷】正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )A .201+B .2C .563D 38.【2020年新课标1卷理科】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 4B 2C 4D 29.【2020年新课标1卷理科】已知,,A B C 为球O 的球面上的三个点,⊙1O 为A B C的外接圆,若⊙1O 的面积为4π,1A BB C A C O O ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π10.【2020年新课标2卷理科】如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为( )A .EB .FC .GD .H11.【2020年新课标2卷理科】已知△ABC 4的等边三角形,且其顶点都在球O的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 212.【2020年新课标3卷理科】下图为某几何体的三视图,则该几何体的表面积是( )A.B .C .D .13.【2020年新高考1卷(山东卷)】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40°,则晷针与点A 处的水平面所成角为( )A .20°B .40°C .50°D .90°14.【2022年新高考1卷】已知正方体ABCD −A 1B 1C 1D 1,则( ) A .直线BC 1与DA 1所成的角为90° B .直线BC 1与CA 1所成的角为90° C .直线BC 1与平面BB 1D 1D 所成的角为45°D .直线BC 1与平面ABCD 所成的角为45°15.【2022年新高考2卷】如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,FB ∥ED,AB =ED =2FB ,记三棱锥E −ACD ,F −ABC ,F −ACE 的体积分别为V 1,V 2,V 3,则( )A .V 3=2V 2B .V 3=V 1C .V 3=V 1+V 2D .2V 3=3V 116.【2021年新高考1卷】在正三棱柱111A B CA B C -中,11A BA A ==,点P 满足1B P BC B B λμ=+,其中[]0,1λ∈,[]0,1μ∈,则( )A .当1λ=时,1A B P△的周长为定值B .当1μ=时,三棱锥1P A B C-的体积为定值C .当12λ=时,有且仅有一个点P ,使得1AP B P⊥D .当12μ=时,有且仅有一个点P ,使得1AB ⊥平面1A BP17.【2021年新高考2卷】如图,在正方体中,O 为底面的中心,P 为所在棱的中点,M ,N 为正方体的顶点.则满足M NO P⊥的是( )A .B .C .D .18.【2020年新课标3卷理科】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.19.【2020年新高考1卷(山东卷)】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD=60°.以1D BCC 1B 1的交线长为________.20.【2020年新高考2卷(海南卷)】已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________三年专题立体几何(解答题)(理科专用)1.【2022年全国甲卷】在四棱锥P−ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3.(1)证明:BD⊥PA;(2)求PD与平面PAB所成的角的正弦值.2.【2022年全国乙卷】如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC 的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.3.【2022年新高考1卷】如图,直三棱柱ABC−A1B1C1的体积为4,△A1BC的面积为2√2.(1)求A 到平面A 1BC 的距离;(2)设D 为A 1C 的中点,AA 1=AB ,平面A 1BC ⊥平面ABB 1A 1,求二面角A −BD −C 的正弦值.4.【2022年新高考2卷】如图,PO 是三棱锥P −ABC 的高,PA =PB ,AB ⊥AC ,E 是PB 的中点.(1)证明:OE//平面PAC ;(2)若∠ABO =∠CBO =30°,PO =3,PA =5,求二面角C −AE −B 的正弦值. 5.【2021年甲卷理科】已知直三棱柱111A B C A B C -中,侧面11A AB B为正方形,2A BB C ==,E ,F 分别为A C 和1C C 的中点,D 为棱11AB 上的点.11B FA B ⊥(1)证明:B F D E⊥;(2)当1BD为何值时,面11B BC C与面D F E 所成的二面角的正弦值最小?6.【2021年乙卷理科】如图,四棱锥P A B C D==,P D D C-的底面是矩形,P D⊥底面A B C D,1M为B C的中点,且P B A M⊥.(1)求B C;(2)求二面角A P M B--的正弦值.7.【2021年新高考1卷】如图,在三棱锥A B C D-中,平面A B D⊥平面B C D,A B A D=,O为B D的中点.(1)证明:O A C D⊥;(2)若OCD是边长为1的等边三角形,点E在棱A D上,2--=,且二面角E B C DD E E A的大小为45︒,求三棱锥A B C D-的体积.8.【2021年新高考2卷】在四棱锥Q A B C D-中,底面A B C D是正方形,若====.A D Q D Q A Q C2,3(1)证明:平面Q A D ⊥平面A B C D ; (2)求二面角BQ D A--的平面角的余弦值.9.【2020年新课标1卷理科】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,A E 为底面直径,A EA D=.A B C是底面的内接正三角形,P 为D O 上一点,6P OO=.(1)证明:P A ⊥平面P B C ;(2)求二面角BP C E--的余弦值.10.【2020年新课标2卷理科】如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB1C 1C是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AM N 所成角的正弦值.11.【2020年新课标3卷理科】如图,在长方体1111A B C D A B C D -中,点,E F 分别在棱11,D DB B 上,且12D EE D =,12B FF B =.(1)证明:点1C 在平面A E F 内;(2)若2A B=,1A D=,13A A=,求二面角1AE F A --的正弦值.12.【2020年新高考1卷(山东卷)】如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面A BCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值. 13.【2020年新高考2卷(海南卷)】如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面A BCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,QB ,求PB 与平面QCD 所成角的正弦值.。
新课标全国卷历年高考立体几何真题(含答案)

新课标全国卷历年高考立体几何真题(含答案)班别: ______________________ 姓名:___________________1.(2011年全国卷)如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD .(Ⅰ)证明:PA ⊥BD ; (Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值.2.(2012年全国卷)如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,BD DC ⊥1.(Ⅰ)证明:BC DC ⊥1;(Ⅱ)求二面角11C BD A --的大小.3.(2013年全国Ⅱ卷)如图,直棱柱ABC-A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC=CB=2AB. (Ⅰ)证明:BC 1//平面A 1CD , (Ⅱ)求二面角D-A 1C-E 的正弦值4.(2013年全国Ⅰ卷)如图,三棱柱111C B A ABC -中,CB CA =,1AA AB =, 601=∠BAA .(Ⅰ)证明C A AB 1⊥;(Ⅱ)若平面ABC ⊥平面AA 1B 1B ,AB=CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.5.(2014年全国Ⅱ卷)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D-AE-C 为60°,AP=1,,求三棱锥E-ACD 的体积.6.(2014年全国Ⅰ卷)如图三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1AB B C ⊥. (Ⅰ) 证明:1AC AB =;(Ⅱ)若1AC AB ⊥,o160CBB ∠=,AB=BC ,求二面角111A A B C --的余弦值.7.(2015年全国Ⅱ卷)如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F=4,过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由);(Ⅱ)求直线AF 与平面α所成角的正弦值.8.(2015年全国Ⅰ卷)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ;(Ⅱ)求直线AE 与直线CF 所成角的余弦值.9.(2016年全国Ⅱ卷)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5,6AB AC ==,点,E F分别在,AD CD 上,54AE CF ==,EF 交BD 于点H .将DEF ∆沿EF 折到'D EF ∆位置,OD '=(Ⅰ)证明:D H'⊥平面ABCD ; (Ⅱ)求二面角B D A C '--的正弦值.10.(2016年全国Ⅰ卷)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值.11.(2016年全国3卷)如图,四棱锥P ABC -中,PA ⊥底面面ABCD ,AD ∥BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN平面PAB ;(II )求直线AN 与平面PMN 所成角的正弦值.自我总结:新课标全国卷历年高考例题几何真题(广西多用2卷)1.解:(Ⅰ)因为60,2DAB AB AD ∠=︒=,由余弦定理得BD = 从而BD 2+AD 2= AB 2,故BD⊥AD;又PD ⊥底面ABCD ,可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD(Ⅱ)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴射线DB 为y 轴的正半轴,射线DP 为z 轴的正半轴,建立空间直角坐标系D-xyz ,则()1,0,0A,()0B,()C -,()0,0,1P.(1),(1,0,0)ABPB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n =(x,y,z ),则0⎧⋅=⎪⎨⋅=⎪⎩n AB n PB ,即00x z -+=-= 因此可取n =设平面PBC 的法向量为m ,则0⎧⋅=⎪⎨⋅=⎪⎩m PB m BC 可取m =(0,-1,,cos 7<>==-m,n 故二面角A-PB-C 的余弦值为 . 2.证明(Ⅰ)(1)在Rt DAC ∆中,AD AC =得:45ADC ︒∠=,同理:1114590A DC CDC ︒︒∠=⇒∠=,得:1,DC DC DC BD DC ⊥⊥⇒⊥又∵11,DC DC DC BD DC ⊥⊥⇒⊥平面1BCD DC BC ⇒⊥. (Ⅱ)(2)11,DC BC CC BC BC ⊥⊥⇒⊥平面11ACC A BC AC ⇒⊥取11A B 的中点O ,过点O 作OH BD ⊥于点H ,连接11,C O C H ,1111111AC B C C O A B =⇒⊥,C 1O ⊥A 1D 1C O ⇒⊥面1ABD 1OH BD C H BD ⊥⇒⊥ 得:点H 与点D 重合 ,即1C DO ∠是二面角11C BD A --的平面角 设AC a =,则1C O =111230C D C O C DO ︒==⇒∠= 即二面角11C BD A --的大小为30︒.3.(1)连接1AC ,交1A C 于点F ,连结1,DF BC ,则F 为1AC 的中点,因为D 为AB 的中点,所以DF//1BC ,又因为111FD ACD BC AC D ⊂⊄平面,平面,所以11//BC ACD 平面. (2)由AA 1AC CB AB ===,可设:AB =2a,则1,AA AC CB ===所以AC BC ⊥,又因为ABC-A 1B 1C 1为直三棱柱,所以以点C 为坐标原点,建立空间直角坐标系如图.则C (0,0,0)、)1,0A D ⎫⎪⎪⎝⎭、、,E ⎛⎫⎪ ⎪⎝⎭()122,0,2,,0CA a a CD a ⎛⎫== ⎪⎪⎝⎭,.CE ⎛⎫= ⎪ ⎪⎝⎭设平面1A CD 的法向量为(),,,n x y z =则0n CD ⋅=且10,n CA ⋅=可解得,y x z =-=令1,x =得平面1A CD 的一个法向量为()1,1,1n =--,同理可得平面1A CE 的一个法向量为()2,1,2m =-,则3cos ,n m <>=,所以6sin ,n m <>=所以二面角1D A C E -- 4.【解析】(Ⅰ)取AB 的中点O ,连结OC ,1OA ,B A 1.因为CB CA =,所以AB OC ⊥.由于1AA AB =, 601=∠BAA ,故B AA 1∆为等边三角形,所以AB OA ⊥1.因为O OA OC =1 ,所以⊥AB 面C OA 1.又⊂C A 1平面C OA 1,故C A AB 1⊥. (Ⅱ)由(Ⅰ)知,AB OC ⊥,AB OA ⊥1,又平面⊥ABC 平面11BB AA ,交线为AB ,所以⊥OC 平面11BB AA ,故OA ,OC ,1OA 两两互相垂直.以O 为坐标原点,的方向为x 轴的正方向,||为单位长度,建立如图所示的空间直角坐标系xyz O -,则有)0,0,1(A ,)0,3,0(1A ,)3,0,0(C ,)0,0,1(-B .则)3,0,1(=, )0,3,1(1-==AA BB , )3,3,0(-=.设平面C C BB 11的法向量为),,(z y x =,则有⎪⎩⎪⎨⎧=⋅=⋅01BB ,即⎪⎩⎪⎨⎧=+-=+0303y x z x ,可取)1,1,3(-=.故510||||,cos 111-=⋅>=<C A n C A n C A n ,所以直线C A 1与平面C C BB 11所成角的正弦值为510.5.【解析】(1) 连接BD 交AC 于点为G,连接EG.在三角形PBD 中,中位线EG ∥PB, 且EG 在平面AEC 上,所以PB ∥平面AEC.(2)设CD=m,分别以AD,AB,AP 为x,y,z 轴建立坐标系,则A(0,0,0),D(,0,0),E 12⎫⎪⎪⎝⎭,C(,m,0).所以AD=(,0,0), AE=12⎫⎪⎪⎝⎭,AC=),0m .设平面ADE 的法向量为1n =(x 1,y 1,z 1),则1n AD ⋅=0, 1n AE ⋅=0,解得一个1n =(0,1,0).同理设平面ACE 的法向量为2n =(x 2,y 2,z 2),则2n AC ⋅=0, 2n AE ⋅=0,解得一个2n因为cos 3π=|cos<12,n n >|=1212n n n n⋅==12,解得m=32. 设F 为AD 的中点,则PA ∥EF,且PA=2EF =12,EF ⊥面ACD,即为三棱锥E-ACD 的高. 所以V E-ACD =·S △ACD ·EF=13×12×32×12.所以,三棱锥E-ACD .为坐标原点,方向,||为单位长度,的方向为y 轴的正方向,的方向为z 轴的正方向建立空间直角坐标系,∵∠,,(0,,0) =,,=,=设向量=,可取,)的一个法向量,),>=A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),=(0,-6,8).=+080z .由∠ABC=120°,可得AG=GC=.由BE ⊥平面ABCD,AB=BC可知AE=EC.又AE ⊥EC,所以EG=,且EG ⊥AC.在Rt △EBG 中,可得BE=,故DF=.在Rt △FDG 中,可得FG=.在直角梯形BDFE 中,由BD=2,BE=,DF=,可得EF=.从而EG 2+FG 2=EF 2,所以EG ⊥FG.,又AC ∩FG=G,可得EG ⊥平面AFC.又因为EG ⊂平面AEC,所以平面AEC ⊥平面AFC. (2)如图,以G 为坐标原点,分别以,的方向为x 轴,y 轴正方向,||为单位长度,建立空间直角坐标系G-xyz.由(1)可得(,)A 00,(,E 10,(,F -10,()C 00, 所以(AE =1,(,CF =-1. 故cos ,||||AE CF AE CF AE CF ⋅<>==-3.所以直线AE 与直线CF所成角的余弦值为3 9.【解析】⑴∵ABEF 为正方形 ∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC ⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥ AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥ ∴四边形EFDC 为等腰梯形以E 为原点,如图建标系,设FD a =()()000020E B a ,,,, ()02202a CA a a ⎛⎫ ⎪ ⎪⎝⎭,,, ()020EB a =,,,22a BC a ⎛⎫=- ⎪ ⎪⎝⎭,,()200AB a =-,,设面BEC 法向量为()m x y z =,,.00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩,即111120202a y a x ay z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩, ()301m =-,,设面ABC 法向量为()222n x y z =,, =00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即222220220a x ay ax ⎧-+=⎪⎨⎪=⎩,()034n=, 设二面角E BC A --的大小为θ.cos 3m nm n θ⋅===+⋅ ∴二面角E BC A --的余弦值为 10.【解析】⑴证明:∵54AE CF ==,∴AE CF AD CD=,∴EF AC ∥.∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AE OH OD AO=⋅=,∴3DH D H '==,∴222'OD OH D H '=+, ∴'D H OH ⊥.又∵OH EF H =I ,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r ,,,设面'ABD 法向量()1n x y z =,,u r ,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345xy z=⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,.同理可得面'AD C 的法向量()2301n =u u r ,,,∴1212cos n n n n θ⋅===u r u u r u r u u r∴sin θ=11.设),,(z y x =为平面PMN 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM , 即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取)1,2,0(=, 于是2558|||||,cos |==><AN n .。
2016年-2019年立体几何大题全国卷高考真题及答案

1、(2015年1卷18题)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.试题解析:(Ⅰ)连接BD ,设BD∩AC=G,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1,由∠ABC=120°,可得AG=GC=3. 由BE ⊥平面ABCD ,AB=BC 可知,AE=EC , 又∵AE ⊥EC ,∴EG=3,EG ⊥AC ,在Rt △EBG 中,可得BE=2,故DF=22. 在Rt △FDG 中,可得FG=62. 在直角梯形BDFE 中,由BD=2,BE=2,DF=22可得EF=322, ∴222EG FG EF +=,∴EG ⊥FG , ∵AC∩FG=G,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC.(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G-xyz ,由(Ⅰ)可得A (030),E (2),F (-1,0,22),C (030),∴AE =(132),CF =(-1,3,22).…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直线AE 与CF 所成的角的余弦值为3. 2、(2016年1卷18题)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E -BC -A 的余弦值.试题解析:(I )由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E . 又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E .(II )过D 作DG F ⊥E ,垂足为G ,由(I )知DG ⊥平面F ABE .以G 为坐标原点,GF 的方向为x 轴正方向,GF 为单位长度,建立如图所示的空间直角坐标系G xyz -.由(I )知DF ∠E 为二面角D F -A -E 的平面角,故DF 60∠E =,则DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D . 由已知,//F AB E ,所以//AB 平面FDC E . 又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E .由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 为二面角C F -BE -的平面角,C F 60∠E =.从而可得(C -.所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-. 设(),,n x y z =是平面C B E 的法向量,则C 00n n⎧⋅E =⎪⎨⋅EB =⎪⎩,即40x y ⎧+=⎪⎨=⎪⎩, 所以可取(3,0,n =.CABDEF设m 是平面CD AB 的法向量,则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.则219cos ,19n m n m n m ⋅==-. 故二面角C E -B -A 的余弦值为21919-.3(2016年2卷19题)(本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF '的位置10OD '=.(I )证明:D H '⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.【解析】⑴证明:∵54AE CF ==,∴AE CF AD CD=,∴EF AC ∥. ∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF DH'⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥, ∴4OB =,∴1AE OH OD AO=⋅=,∴3DH D H '==,∴222'OD OH D H '=+, ∴'D H OH ⊥.又∵OH EF H =,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,, ()430AB =,,,()'133AD =-,,,()060AC =,,,设面'ABD 法向量()1n x y z =,,,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩, ∴()1345n =-,,.同理可得面'AD C 的法向量()2301n =,,, ∴12129575cos 255210n n n n θ⋅+===⋅,∴295sin 25θ=4、(2017年1卷18题)如图,在四棱锥P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,求二面角A PB C --的余弦值. 【解析】(1)证明:∵90BAP CDP ∠=∠=︒∴PA AB ⊥,PD CD ⊥又∵AB CD ∥,∴PD AB ⊥又∵PD PA P =,PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ,又AB ⊂平面PAB ∴平面PAB ⊥平面PAD(2)取AD 中点O ,BC 中点E ,连接PO ,OE ∵AB CD∴四边形ABCD 为平行四边形 ∴OE AB由(1)知,AB ⊥平面PAD∴OE ⊥平面PAD ,又PO 、AD ⊂平面PAD ∴OE PO ⊥,OE AD ⊥ 又∵PA PD =,∴PO AD ⊥ ∴PO 、OE 、AD 两两垂直∴以O 为坐标原点,建立如图所示的空间直角坐标系O xyz - 设2PA =,∴()002D -,,、()220B ,,、()002P ,,、()202C -,,, ∴()022PD =--,,、()222PB =-,,、()2200BC =-,,设()n x y z =,,为平面PBC 的法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩,得2220220x y z x ⎧+-=⎪⎨-=⎪⎩令1y =,则2z =,0x =,可得平面PBC 的一个法向量()012n =,, ∵90APD ∠=︒,∴PD PA ⊥又知AB ⊥平面PAD ,PD ⊂平面PAD ∴PD AB ⊥,又PA AB A = ∴PD ⊥平面PAB即PD 是平面PAB 的一个法向量,()022PD =--,, ∴23cos 323PD n PD n PD n⋅-===-⋅, 由图知二面角A PB C --为钝角,所以它的余弦值为33-5.(2018年1卷18题)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. ⑴证明:平面PEF ⊥平面ABFD ; ⑵求DP 与平面ABFD 所成角的正弦值.解答:(1),E F 分别为,AD BC 的中点,则//EF AB ,∴EF BF ⊥,又PF BF ⊥,EF PF F ⋂=,∴BF ⊥平面PEF , BE ⊂平面ABFD ,∴平面PEF ⊥平面ABFD . (2)PF BF ⊥,//BF ED ,∴PF ED ⊥,又PF PD ⊥,ED DP D ⋂=,∴PF ⊥平面PED ,∴PF PE ⊥, 设4AB =,则4EF =,2PF =,∴23PE =, 过P 作PH EF ⊥交EF 于H 点, 由平面PEF ⊥平面ABFD ,∴PH ⊥平面ABFD ,连结DH ,则PDH ∠即为直线DP 与平面ABFD 所成的角, 由PE PF EF PH ⋅=⋅,∴23234PH ⋅==, 而4PD =,∴3sin 4PH PDH PD ∠==, ∴DP 与平面ABFD 所成角的正弦值34. 6.(2018年新课标Ⅱ理)如图,在三棱锥P -ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)求证:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M -P A -C 为30°,求PC 与平面P AM 所成角的正弦值.【解析】(1)证明:∵AB =BC =22,AC =4,∴AB 2+BC 2=AC 2,即△ABC 是直角三角形. 又O 为AC 的中点,∴OA =OB =OC . ∵P A =PB =PC ,∴△POA ≌△POB ≌△POC . ∴∠POA =∠POB =∠POC =90°.∴PO ⊥AC ,PO ⊥OB ,OB ∩AC =0,∴PO ⊥平面ABC .(2)以O 坐标原点,OB ,OC ,OP 所在直线分别为x ,y ,z 轴建立空间直角坐标系如图所示.易知A (0,-2,0),P (0,0,23),C (0,2,0),B (2,0,0),BC →=(-2,2,0). 设BM →=λBC →=(-2λ,2λ,0),0<λ<1,则AM →=BM →-BA →=(-2λ,2λ,0)-(-2,-2,0)=(2-2λ,2λ+2,0), 则平面P AC 的一个法向量为m =(1,0,0).设平面MP A 的法向量为n =(x ,y ,z ),则PA →=(0,-2,23), 则n ·PA →=-2y -23z =0,n ·AM →=(2-2λ)x +(2λ+2)y =0. 令z =1,则y =-3,x =(λ+1)31-λ,即n =⎝ ⎛⎭⎪⎫(λ+1)31-λ,-3,1.∵二面角M -P A -C 为30°,∴cos 30°=m ·n |m ||n |=32,即(λ+1)3λ-1⎝ ⎛⎭⎪⎫(λ+1)31-λ2+1+3×1=32,解得λ=13或λ=3(舍去). ∴n =(23,-3,1),PC →=(0,2,-23).PC 与平面P AM 所成角的正弦值sin θ=|cos 〈PC →,n 〉|=⎪⎪⎪⎪⎪⎪-23-2316·16=4316=34.18.(2019年1卷18题)(12分)如图,直四棱柱ABCD ﹣A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A ﹣MA 1﹣N 的正弦值.解答】(1)证明:如图,过N作NH⊥AD,则NH∥AA1,且,又MB∥AA1,MB=,∴四边形NMBH为平行四边形,则NM∥BH,由NH∥AA1,N为A1D中点,得H为AD中点,而E为BC中点,∴BE∥DH,BE=DH,则四边形BEDH为平行四边形,则BH∥DE,∴NM∥DE,∵NM⊄平面C1DE,DE⊂平面C1DE,∴MN∥平面C1DE;(2)解:以D为坐标原点,以垂直于DC得直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立空间直角坐标系,则N(,,2),M(,1,2),A1(,﹣1,4),,,设平面A1MN的一个法向量为,由,取x=,得,又平面MAA1的一个法向量为,∴cos<>===.∴二面角A﹣MA1﹣N的正弦值为.8.(12分)(2019年新课标Ⅱ理)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1. (1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B –EC –C 1的正弦值.解:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BEEC ⊥,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知11Rt Rt ABE A B E ≅△△,所以45AEB ∠=︒,故AE AB =,12AA AB =.以D 为坐标原点,DA 的方向为x 轴正方向,||DA 为单位长,建立如图所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E (1,0,1),(1,1,1)CE =-,1(0,0,2)CC =.设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩ 所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =(1,1,0). 于是1cos ,||||2⋅<>==-n m n m n m .所以,二面角1B EC C --3.。
历年全国理科数学高考试题立体几何部分精选(含答案)

1.在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上,且6,==,则棱锥AB BC-的体积为。
O ABCD3.如图,四棱锥P—ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明:PA⊥BD;(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。
1.D2.3. 解:(Ⅰ)因为60,2DAB AB AD ∠=︒=,由余弦定理得BD =从而BD 2+AD 2= AB 2,故BD ⊥AD 又PD ⊥底面ABCD ,可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD(Ⅱ)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ,则()1,0,0A,()0B,()C -,()0,0,1P 。
(1),(1,0,0)AB PB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n=(x ,y ,z ),则0,0,{n AB n PB ⋅=⋅=u u u r u u u r00z =-=因此可取n=设平面PBC 的法向量为m ,则m 0,m 0,{PB BC ⋅=⋅=u u u ru u u r可取m=(0,-1, cos ,m n == 故二面角A-PB-C 的余弦值为1. 正方体ABCD-1111A B C D 中,B 1B 与平面AC 1D 所成角的余弦值为C 232. 已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为俩切点,那么PA PB ∙的最小值为(A) 4- (B)3-+ (C) 4-+3-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为(C)4. 如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,AB//DC ,AD ⊥DC ,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(Ⅰ)证明:SE=2EB ;(Ⅱ)求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一:(Ⅰ)连接BD,取DC 的中点G ,连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形,故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以,BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足,因平面平面,故,BK EDC BK DE DE ⊥⊥平面,与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ,DE ⊥EC,DE ⊥SBSB =SD DB DE SB ==-EB SE SB EB ====所以,SE=2EB(Ⅱ) 由1,2,,SA AB SE EB AB SA ===⊥知1,AD=1AE ==又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则,AF DE AF ⊥==. 连接FG ,则//,FG EC FG DE ⊥.所以,AFG ∠是二面角A DE C --的平面角.连接AG,A G=,3FG ==, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以,二面角A DE C --的大小为120°. 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴,建立如图所示的直角坐标系D xyz -, 设A(1,0,0),则B(1,1,0),C(0,2,0),S(0,0,2)(Ⅰ)(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥,得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1,则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>,则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=,0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =,则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB(Ⅱ)由(Ⅰ)知222(,,)333E ,取DE 的中点F ,则111211(,,),(,,)333333F FA =--,故0FA DE =,由此得FA DE ⊥ 又242(,,)333EC =--,故0EC DE =,由此得EC DE ⊥, 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以,二面角A DE C --的大小为120(三)1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为( )(A (B (C (D) 342. 已知二面角l αβ--为60o,动点P 、Q 分别在面α、β内,P 到β,Q 到α的距离为则P 、Q 两点之间距离的最小值为( )(A) (B)2 (C) 3. 直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===, 120BAC ∠=︒,则此球的表面积等于 。
2012年-2021年(10年)全国高考数学真题分类汇编 立体几何客观题(精解精析版)

2012-2021十年全国高考数学真题分类汇编立体几何客观题(精解精析版)一、选择题1.(2021年高考全国乙卷理科)在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π6【答案】D解析:如图,连接11,,BC PC PB ,因为1AD ∥1BC ,所以1PBC ∠或其补角为直线PB 与1AD 所成的角,因为1BB ⊥平面1111D C B A ,所以11BB PC ⊥,又111PC B D ⊥,1111BB B D B ⋂=,所以1PC ⊥平面1P B B ,所以1PC PB ⊥,设正方体棱长为2,则111112BC PC D B ===1111sin 2PC PBC BC ∠==,所以16PBC π∠=.故选:D2.(2021年高考全国甲卷理科)在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG -后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()()A.B.C.D.【答案】D解析:由题意及正视图可得几何体的直观图,如图所示,所以其侧视图为故选:D3.(2021年高考全国甲卷理科)已如A.B.C是半径为1的球O的球面上的三个点,且,1AC BC AC BC⊥==,则三棱锥O ABC-的体积为()A.212B.312C.24D.34【答案】A解析:,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC 外接圆的半径为22,又球的半径为1,设O 到平面ABC 的距离为d ,则22d =,所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选:A .【点睛】关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.4.(2020年高考数学课标Ⅰ卷理科)已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为()A .64πB .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.5.(2020年高考数学课标Ⅰ卷理科)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()()A .514-B .512-C .514+D .512+【答案】C【解析】如图,设,CD a PE b ==,则22224a PO PE OEb =-=-,由题意212PO ab =,即22142a b ab-=,化简得24()210b b a a -⋅-=,解得154b a =(负值舍去).故选:C .【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.6.(2020年高考数学课标Ⅱ卷理科)已知△ABC 是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为()A .3B .32C .1D .32【答案】C解析:设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC 是面积为934的等边三角形,21393224a ∴⨯=,解得:3a =,22229933434a r a ∴=-=-=,∴球心O 到平面ABC 的距离22431d R r =-=-=.故选:C .【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.7.(2020年高考数学课标Ⅱ卷理科)如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为()()A .EB .FC .GD .H【答案】A解析:根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选:A【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.8.(2020年高考数学课标Ⅲ卷理科)下图为某几何体的三视图,则该几何体的表面积是()()A .6+4B .C .D .【答案】C解析:根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得:AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得:211sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是:632=⨯++.故选:C .【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题.9.(2019年高考数学课标Ⅲ卷理科)如图,点N 为正方形ABCD 的中心,ECD △为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则()A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线【答案】B 【解析】取DC 中点E ,如图连接辅助线,在BDE △中,N 为BD 中点,M 为DE 中点,所以//MN BE ,所以BM ,EN 共面相交,选项C ,D 错误. 平面CDE ⊥平面ABCD ,EF CD ⊥,EF ∴⊥平面ABCD ,又DC CD ⊥,∴DC ⊥平面DCE ,从而EF FN ⊥,BC MC ⊥.所以MCB △与EFN△均为直角三角形.不妨设正方形边长为2,易知3,1MC EF NF ===,所以22(3)27BM =+=,22(3)12EN =+=,BM EN ∴≠,故选B .【点评】本题比较具有综合性,既考查了面面垂直、线面垂直等线面关系,还考查了三角形中的一些计算问题,是一个比较经典的题目.10.(2019年高考数学课标全国Ⅱ卷理科)设α、β为两个平面,则αβ//的充要条件是()()A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ//的充分条件,由面面平行性质定理知,若αβ//,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ//的必要条件,故选B .【点评】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,//a b a b αβ⊂⊂,则//αβ”此类的错误.11.(2019年高考数学课标全国Ⅰ卷理科)已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,90CEF ∠=︒,则球O 的体积为()A .B .C .D 【答案】D解析:三棱锥P ABC -为正三棱锥,取AC 中点M ,连接,PM BM ,则,AC PM AB BM ⊥⊥,PM BM M = ,可得AC ⊥平面PBM ,从而AC PB ⊥,又//,PB EF EF CE ⊥,可得PB CE ⊥,又AC CE C = ,所以PB ⊥平面PAC ,从而,PB PA PB PC ⊥⊥,从而正三棱锥P ABC -的三条侧棱,,PA PB PC 两两垂直,且PA PB PC ===,,PA PB PC 为棱的正方体,正方体的体对角线即为球O 的直径,即22R R ==,所以球O 的体积为343V R π==.12.(2018年高考数学课标Ⅲ卷(理))设,,,A B C D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为()A.B.C.D.【答案】B解析:设ABC △的边长为a,则21sin 6062ABC S a a =︒=⇒=△,此时ABC △外接圆的半径为112sin 60232a r =⋅=⨯︒,故球心O 到面ABC2==,故点D 到面ABC 的最大距离为26R +=,此时11633D ABC ABC D ABC V S d --=⋅=⨯=△,故选B.点评:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当DM ⊥平面ABC 时,三棱锥D ABC -体积最大很关键,由M 为三角形ABC 的重心,计算得到23BM BE ==,再由勾股定理得到OM ,进而得到结果,属于较难题型.13.(2018年高考数学课标Ⅲ卷(理))中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫,凹进部分叫卯眼,图中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体.则咬合时带卯眼的木构件的俯视图可以是()()【答案】A解析:依题意,结合三视图的知识易知,带卯眼的木构件的俯视图可以是A 图.14.(2018年高考数学课标Ⅱ卷(理))在长方体1111ABCD A B C D -中,1AB BC ==,1AA =线1AD 与1DB 所成角的余弦值为()A .15B .56C .55D .22【答案】C解析:以D 为坐标原点,1,,DA DC DD DA 为,,x y z 轴建立空间直角坐标系,则11(0,0,0),(1,0,0),(1,1,3),(0,0,3)D A B D ,所以11(1,0,3),(1,1,3)AD DB =-=因为111111135cos ,5||||25AD DB AD DB AD DB ⋅-+<>===⋅⨯所以异面直线1AD 与1DB 所成角的余弦值为55,故选C .15.(2018年高考数学课标卷Ⅰ(理))已知正方体的校长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面而积的最大值为()A .334B .233C .324D .32【答案】A【解析一】根据题意,平面α与正方体对角线垂直,记正方体为111ABCD A B C D -不妨设平面α与1AC 垂直,且交于点M .平面ABD 与平面11B D C 与1AC 分别交于,P Q .正方体中心为O ,则容易证明当M 从A 运动到P 时,截面为三角形且周长逐渐增大:当M 从P 运动到Q 时,截面为六边形且周长不变;当M 从Q 运动到1C 时,截面为三角形且周长还渐减小。
2018-2022五年全国高考数学立体几何真题分类汇编(试卷版)

2018-2022五年全国各省份高考数学真题分类汇编专题21 立体几何解答题一、解答题1. (2022高考北京卷·第17题)如图, 在三棱柱中, 侧面为正方形, 平面平面, , M, N分别为, AC的中点.(1)求证: 平面;(2)再从条件①、条件②这两个条件中选择一个作为已知, 求直线AB与平面BMN所成角的正弦值.条件①: ;条件②: .注:如果选择条件①和条件②分别解答, 按第一个解答计分.2. (2022年高考全国甲卷数学(理)·第18题)在四棱锥中, 底面.(1)证明: ;(2)求PD与平面所成的角的正弦值.3. (2022年浙江省高考数学试题·第19题)如图, 已知和都是直角梯形, , , , , , , 二面角的平面角为. 设M, N分别为的中点.(1)证明: ;(2)求直线与平面所成角的正弦值.4. (2022新高考全国II卷·第20题)如图, 是三棱锥的高, , , E是的中点.(1)证明: 平面;(2)若, , , 求二面角/正弦值.5. (2022新高考全国I卷·第19题)如图, 直三棱柱的体积为4, 的面积为.(1)求A到平面1A BC的距离;(2)设D为的中点, , 平面平面, 求二面角的正弦值.6. (2022年高考全国乙卷数学(理)·第18题)如图, 四面体中, , E为的中点.(1)证明: 平面平面;(2)设, 点F在上, 当的面积最小时, 求与平面所成的角的正弦值.7. (2021年高考浙江卷·第19题)如图, 在四棱锥中, 底面是平行四边形, , M, N分别为的中点, .(1)证明: ;(2)求直线与平面所成角的正弦值.8. (2021年新高考全国Ⅱ卷·第19题)在四棱锥中, 底面是正方形, 若.(1)证明: 平面平面;(2)求二面角/平面角的余弦值.9. (2021年新高考Ⅰ卷·第20题)如图, 在三棱锥中, 平面平面, , 为的中点.(1)证明: ;(2)若是边长为1/等边三角形, 点在棱上, , 且二面角的大小为, 求三棱锥的体积.10. (2021年高考全国乙卷理科·第18题)如图, 四棱锥的底面是矩形, 底面, , 为的中点,且.(1)求BC;(2)求二面角的正弦值.11. (2021年高考全国甲卷理科·第19题)已知直三棱柱中, 侧面为正方形, , E, F分别为和/中点, D为棱上的点.(1)证明: ;(2)当为何值时, 面与面所成的二面角的正弦值最小?12. (2021高考北京·第17题)如图: 在正方体中, 为中点, 与平面交于点.(1)求证: 为的中点;(2)点是棱上一点, 且二面角的余弦值为, 求的值.13. (2020年高考课标Ⅰ卷理科·第18题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 为底面直径, . 是底面的内接正三角形, 为上一点, .(1)证明: 平面;(2)求二面角的余弦值.14. (2020年高考课标Ⅱ卷理科·第20题)如图, 已知三棱柱ABC-A1B1C1的底面是正三角形, 侧面BB1C1C是矩形, M, N分别为BC, B1C1的中点, P为AM上一点, 过B1C1和P 的平面交AB于E, 交AC于F.(1)证明: AA1∥MN, 且平面A1AMN⊥EB1C1F;(2)设O为△A1B1C1的中心, 若AO∥平面EB1C1F, 且AO=AB, 求直线B1E与平面A1AMN 所成角的正弦值.15.(2020年高考课标Ⅲ卷理科·第19题)如图, 在长方体中, 点分别在棱上, 且, .(1)证明: 点/平面内;(2)若, , , 求二面角的正弦值.16. (2020年新高考全国Ⅰ卷(山东)·第20题)如图, 四棱锥P-ABCD的底面为正方形, PD⊥底面ABCD. 设平面PAD与平面PBC的交线为l.(1)证明: l⊥平面PDC;(2)已知PD=AD=1, Q为l上的点, 求PB与平面QCD所成角的正弦值的最大值.17. (2020年新高考全国卷Ⅱ数学(海南)·第20题)如图, 四棱锥P-ABCD的底面为正方形,PD底面ABCD. 设平面PAD与平面PBC的交线为.(1)证明: 平面PDC;(2)已知PD=AD=1, Q为上的点, QB=, 求PB与平面QCD所成角的正弦值.18. (2020年浙江省高考数学试卷·第19题)如图, 三棱台DEF—ABC中, 面ADFC⊥面ABC, ∠ACB=∠ACD=45°, DC =2BC.(I)证明: EF⊥DB;(II)求DF与面DBC所成角的正弦值.19. (2020天津高考·第17题)如图, 在三棱柱中, 平面, , 点分别在棱和棱上, 且为棱的中点.(Ⅰ)求证: ;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线与平面所成角的正弦值.20. (2020江苏高考·第24题)在三棱锥中, 已知,, 为的中点, 平面, , 为的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点在上, 满足, 设二面角的大小为, 求的值.21. (2020江苏高考·第15题)在三棱柱中, , 平面, 分别是的中点.(1)求证: 平面;(2)求证:平面平面.22. (2020北京高考·第16题)如图, 在正方体中, 为的中点.(Ⅰ)求证: 平面;(Ⅱ)求直线与平面所成角的正弦值.23. (2019年高考浙江·第19题)如图, 已知三棱柱, 平面平面, , , , , 分别是, 的中点.(Ⅰ)证明: ;(Ⅱ)求直线与平面所成角的余弦值.24. (2019年高考天津理·第17题)如图, 平面, , . (Ⅰ)求证: 平面;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值;(Ⅲ)若二面角的余弦值为, 求线段的长.25. (2019年高考上海·第17题)如图, 在长方体中, 为上一点, 已知, , , . (1)求直线1A C 与平面ABCD 的夹角; (2)求点A 到平面1A MC 的距离.FE C 1A 1B 1CBAABCDEF26. (2019年高考全国Ⅲ理·第19题)图1是由矩形ADEB, Rt △ABC 和菱形BFGC 组成的一个平面图形, 其中AB=1, BE=BF=2, ∠FBC=60°, 将其沿AB, BC 折起使得BE 与BF 重合, 连结DG, 如图2.(1)证明: 图2中的A, C, G, D 四点共面, 且平面ABC ⊥平面BCGE ;(2)求图2中的二面角B −CG −A 的大小.27. (2019年高考全国Ⅱ理·第17题)如图, 长方体的底面是正方形, 点在棱上, . 证明: 平面;若, 求二面角的正弦值.图2图1D A28. (2019年高考全国Ⅰ理·第18题)如图, 直四棱柱的底面是菱形, 分别是, , 的中点.(1)证明: 平面;(2)求二面角的正弦值.29. (2019年高考江苏·第16题)如图, 在直三棱柱中, 分别为, 的中点, .求证:(1)平面;(2).30. (2019年高考北京理·第16题)如图, 在四棱锥P–ABCD中, PA⊥平面ABCD, AD ⊥CD, AD∥BC, PA=AD=CD=2, BC=3. E为PD的中点, 点F在PC上, 且.(Ⅰ)求证: CD⊥平面PAD;(Ⅱ)求二面角F–AE–P的余弦值;(Ⅲ)设点G在PB上, 且. 判断直线AG是否在平面AEF内, 说明理由.31. (2018年高考数学江苏卷·第25题)(本小题满分10分)如图, 在正三棱柱ABC-A1B1C1中, AB=AA1=2, 点P, Q分别为A1B1, BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.32. (2018年高考数学江苏卷·第15题)(本小题满分14分)在平行六面体中, .求证: (1);(2).33. (2018年高考数学浙江卷·第19题)(本题满分15分)如图, 已知多面体, 均垂直于平面,, , , .(1)证明: 平面;(2)求直线与平面所成角的正弦值.34. (2018年高考数学上海·第17题)(本题满分14分, 第1小题满分6分, 第2小题满分8分)已知圆锥的顶点为, 底面圆心为, 半径为2, (1)设圆锥的母线长为4, 求圆锥的体积;(2)设, 是底面半径, 且, 为线段的中点, 如图, 求异面直线与 所成的角的大小.35. (2018年高考数学天津(理)·第17题)(本小题满分13分)如图, 且, , 且, , 且, 平面, . (1)若为的中点, 为的中点, 求证:平面; (2)求二面角E BC F --的正弦值;(3)若点在线段上, 且直线与平面所成的角为, 求线段的长.ACA 1C 1B 136. (2018年高考数学课标Ⅲ卷(理)·第19题)(12分)如图, 边长为的正方形所在平面与半圆弧所在的平面垂直, 是弧上异于的点. (1)证明: 平面平面;(2)当三棱锥体积最大时, 求面与面所成二面角的正弦值.37. (2018年高考数学课标Ⅱ卷(理)·第20题)(12分) 如图, 在三棱锥中, , , 为的中点. (1)证明: 平面;(2)若点在棱上, 且二面角为, 求与平面所成角的正弦值.ABC DEFG MN38. (2018年高考数学课标卷Ⅰ(理)·第18题)(12分)如图, 四边形为正方形, 分别为的中点, 以为折痕把折起, 使点到达点的位置, 且. (1)证明:平面PEF ⊥平面ABFD ; (2)求与平面所成角的正弦值.39. (2018年高考数学北京(理)·第16题)(本小题14分)如图, 在三棱柱中, 平面,分别为的中点, , . (Ⅰ)求证: 平面;(Ⅱ)求二面角1B CD C --的余弦值; (Ⅲ)证明: 直线与平面相交.PABMCO。
近三年高考全国卷理科立体几何真的题目

新课标卷近三年高考题1、(2016年全国I 高考)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面 ABEF 为正方形,AF =2FD ,90AFD ∠= ,且二面角D -AF -E 与二面角C -BE - F 都是60 .(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E -BC -A 的余弦值. 【解析】 ⑴ ∵ABEF 为正方形 ∴AF EF ⊥∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC⑵ 由⑴知60DFE CEF ∠=∠=︒ ∵AB EF ∥AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥∴四边形EFDC 为等腰梯形以E 为原点,如图建立坐标系,设FD a =()()000020E B a ,,,, ()3022022a C a A a a ⎛⎫⎪ ⎪⎝⎭,,,,()020EB a = ,,,3222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭,,,()200AB a =- ,, 设面BEC 法向量为()m x y z =,,.0m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩ ,即11112032022a y a x ay a z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩ 111301x y z ===-,,()301m =- ,,设面ABC 法向量为()222n x y z =,,=00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即22223202220a x ay az ax ⎧-+=⎪⎨⎪=⎩ 222034x y z ===,, ()034n =,,设二面角E BC A --的大小为θ.4219cos 1931316m n m nθ⋅-===-+⋅+⋅ ∴二面角E BC A --的余弦值为21919-2、(2016年全国II 高考)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5,6AB AC ==,点,E F 分别在,AD CD 上,54AE CF ==,EF 交BD 于点H .将DEF ∆沿EF 折到'D EF ∆位置,10OD '=.(Ⅰ)证明:D H '⊥平面ABCD ; (Ⅱ)求二面角B D A C '--的正弦值.【解析】⑴证明:∵54AE CF ==,∴AE CFAD CD=, ∴EF AC ∥.∵四边形ABCD 为菱形,∴AC BD ⊥, ∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥. ∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =,∴1AEOH OD AO=⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥. 又∵OH EF H =I ,∴'D H ⊥面ABCD . ⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r,,, 设面'ABD 法向量()1n x y z =,,u r,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩ 得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩,∴()1345n =-u r,,.同理可得面'AD C 的法向量()2301n =u u r,,,∴12129575cos 255210n n n n θ⋅+===⋅u r u u ru r u u r , ∴295sin 25θ=.3、(2016年全国III 高考)如图,四棱锥P ABC -中,PA ⊥地面ABCD ,AD BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN 平面PAB ;(II )求直线AN 与平面PMN 所成角的正弦值.设),,(z y x n =为平面PMN 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取)1,2,0(=n , 于是2558|||||||,cos |=⋅=><AN n AN n AN n .4、【2015高考新课标2,理19】如图,长方体1111ABCD A B C D -中,=16AB ,=10BC ,18AA =,点E ,F 分别在11A B ,11C D 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值. 【答案】(Ⅰ)详见解析;(Ⅱ)4515.【考点定位】1、直线和平面平行的性质;2、直线和平面所成的角.DD 1C 1A 1 EFA BCB 1A 1AB 1BD 1DC 1CFE HGM【名师点睛】根据线面平行和面面平行的性质画平面α与长方体的面的交线;由交线的位置可确定公共点的位置,坐标法是求解空间角问题时常用的方法,但因其计算量大的特点很容易出错,故坐标系的选择是很重要的,便于用坐标表示相关点,先求出面α的法向量,利用sin cos ,n AF θ=<>求直线AF 与平面α所成角的正弦值.5、【2015高考新课标1,理18】如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC . (Ⅰ)证明:平面AEC ⊥平面AFC ; (Ⅱ)求直线AE 与直线CF 所成角的余弦值.【答案】(Ⅰ)见解析(Ⅱ)33又∵AE ⊥EC ,∴EG =3,EG ⊥AC , 在Rt △EBG 中,可得BE =2,故DF =22. 在Rt △FDG 中,可得FG =62. 在直角梯形BDFE 中,由BD =2,BE =2,DF =22可得EF =322, ∴222EG FG EF +=,∴EG ⊥FG , ∵AC ∩FG=G ,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC . ……6分(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB为单位长度,建立空间直角坐标系G-xyz ,由(Ⅰ)可得A (0,-3,0),E (1,0,2),F (-1,0,22),C (0,3,0),∴AE =(1,3,2),CF =(-1,-3,22).…10分故3cos ,3||||AE CF AE CF AE CF ∙<>==-.所以直线AE 与CF 所成的角的余弦值为33. ……12分 【考点定位】空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力【名师点睛】对空间面面垂直问题的证明有两种思路,思路1:几何法,先由线线垂直证明线面垂直,再由线面垂直证明面面垂直;思路2:利用向量法,通过计算两个平面的法向量,证明其法向量垂直,从而证明面面垂直;对异面直线所成角问题,也有两种思路,思路1:几何法,步骤为一找二作三证四解,一找就是先在图形中找有没有异面直线所成角,若没有,则通常做平行线或中位线作出异面直线所成角,再证明该角是异面直线所成角,利用解三角形解出该角. 6、[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ; (2)设二面角D -AE -C 为60°,AP =1,AD =3,求三棱锥E -ACD 的体积.图1-3解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB . 因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)因为P A ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB→,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A -xyz ,则D ()0,3,0,E ⎝⎛⎭⎪⎫0,32,12,AE→=⎝ ⎛⎭⎪⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC →=(m ,3,0).设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC→=0,n 1·AE →=0,即⎩⎨⎧mx +3y =0,32y +12z =0,可取n 1=⎝ ⎛⎭⎪⎫3m ,-1,3.又n 2=(1,0,0)为平面DAE 的法向量,由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32. 因为E 为PD 的中点,所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V=13×12×3×32×12=38.7、[2014·新课标全国卷Ⅰ] 如图1-5,三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB ⊥B 1C .图1-5(1)证明:AC =AB 1;(2)若AC ⊥AB 1,∠CBB 1=60°,AB =BC ,求二面角A -A 1B 1 C 1的余弦值.解:(1)证明:连接BC 1,交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为B 1C 及BC 1的中点.又AB ⊥B 1C ,所以B 1C ⊥平面ABO .由于AO ⊂平面ABO ,故B 1C ⊥AO .又B 1O =CO ,故AC =AB 1.(2)因为AC ⊥AB 1,且O 为B 1C 的中点,所以AO =CO .又因为AB =BC ,所以△BOA ≌ △BOC .故OA ⊥OB ,从而OA ,OB ,OB 1两两垂直.以O 为坐标原点,OB 的方向为x 轴正方向,|OB |为单位长,建立如图所示的空间直角坐标系O xyz .因为∠CBB 1=60°,所以△CBB 1为等边三角形,又AB =BC ,则A ⎝ ⎛⎭⎪⎫0,0,33,B (1,0,0),B 1⎝ ⎛⎭⎪⎫0,33,0,C ⎝ ⎛⎭⎪⎫0,-33,0.AB 1→=⎝ ⎛⎭⎪⎫0,33,-33, A 1B 1→=AB =⎝⎛⎭⎪⎫1,0,-33, B 1C →1=BC =⎝ ⎛⎭⎪⎫-1,-33,0. 设n =(x ,y ,z )是平面AA 1B 1的法向量,则⎩⎪⎨⎪⎧n ·AB 1=0,n ·A 1B 1→=0,即⎩⎪⎨⎪⎧33y -33z =0,x -33z =0.所以可取n =(1,3,3).设m 是平面A 1B 1C 1的法向量, 则⎩⎪⎨⎪⎧m ·A 1B 1→=0,m ·B 1C 1→=0,同理可取m =(1,-3,3). 则cos 〈n ,m 〉=n ·m |n ||m |=17.所以结合图形知二面角A -A 1B 1 C 1的余弦值为17.。
近五年高考数学(理科)立体几何题目汇总

高考真题集锦(立体几何部分)1.(2016.理1)如图是由圆柱和圆锥组合而成的几何体的三视图,则该几何体的表面积是( )A 20π B24π C28π D.32π2. βα,是两个平面,m,n 是两条直线,有下列四个命题:(1)如果m ⊥n,m ⊥α,n ∥β,那么βα⊥;(2)如果m ⊥α,n ∥α,那么m ⊥n.(3)如果αβα⊂m ,∥那么m ∥β。
(4)如果m ∥n,βα∥,那么m 与α所成的角和n 与β所成的角相等。
其中正确的命题有___________3.(2016年理1)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是π328,则它的表面积是 A 17π B.18π C.20π D.28π4.平面α过正方体1111D C B A ABCD -的顶点A ,α//平面11D CB ,⋂α平面ABCD =m ,⋂α平面11A ABB =n,则m,n 所成角的正弦值为( )A.23B.22C.33D.315.(2016年理1)如图,在以A,B,C,D,E,F 为顶点的五面体中,面ABEF 为正方形,AF=2FD ,∠AFD=90°,且二面角D-AF-E 与二面角C-BE-F 都是60° .(12分)(Ⅰ)证明:平面ABEF ⊥平面EFDC ;(Ⅱ)求二面角E-BC-A 的余弦值.6. (2015年理1)圆柱被一个平面截取一部分后与半球(半径为r )组成一个几何体,该几何体三视图的正视图和俯视图如图所示,若该几何体的表面积是16+20π,则r=( )A.1B.2C.7D.87.如图,四边形ABCD 为菱形,∠ABC=120°,E,F 是平面ABCD 同一侧的亮点,BE ⊥平面ABCD,DF ⊥平面ABCD,BE=2DF,AE ⊥EC.(1) 证明:平面AEC ⊥平面AFC;(2) 求直线AE 与直线CF 所成角的余弦值。
8.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截取部分体积和剩余部分体积的比值为()9.如图,长方体1111D C B A ABCD -中,AB = 16,BC = 10,AA1 = 8,点E ,F 分别在1111C D B A ,上,411==F D E A ,过点E,F 的平面α与此长方体的面相交,交线围成一个正方形。
近年高考理科立体几何大题汇编.docx

近几年高考理科立体几何大题汇编1.(2018 年 III 卷)如图,边长为 2 的正方形ABCD 所在的平面与半圆弧M 是CD 所在平面垂直,CD 上异于 C ,D的点.(1)证明:平面 AMD ⊥平面BMC;(2)当三棱锥M ABC体积最大时,求面 MAB 与面MCD所成二面角的正弦值.2、[2014 ·新课标全国卷Ⅱ ] 四棱锥 P-ABCD 中,底面ABCD 为矩形, PA⊥平面 ABCD, E 为 PD 的中点.(1)证明: PB∥平面 AEC;(2)设二面角 D-AE-C 为 60°, AP=1, AD= 3,求三棱锥 E-ACD 的体积.13.( 2017? 新课标Ⅰ卷)如图,在四棱锥 P﹣ ABCD 中, AB∥CD,且∠BAP= ∠CDP=90°.(1)证明:平面 PAB⊥平面 PAD;(2)若 PA=PD=AB=DC ,∠APD=90°,求二面角 A﹣ PB﹣C 的余弦值.4.(菱形建系) [2014 新·课标全国卷Ⅰ ] 如图三棱柱ABC -A1B1C1中,侧面BB1C1C 为菱形,AB⊥B1 C.(1)证明: AC= AB1;(2)若 AC⊥AB1,∠ CBB1= 60°, AB= BC,求二面角 A -A1B1 - C1的余弦值.25.(菱形建系)【 2015 高考新课标 1】如图,四边形 ABCD 为菱形,∠ ABC=120 °,E,F 是平面 ABCD 同一侧的两点, BE⊥平面 ABCD, DF⊥平面 ABCD,BE=2 DF,AE⊥EC. (Ⅰ)证明:平面 AEC⊥平面 AFC;(Ⅱ)求直线 AE 与直线 CF 所成角的余弦值 .6.(翻折) (2018 年 I 卷 )如图,四边形ABCD为正方形,E, F分别为AD , BC的中点,以DF 为折痕把△ DFC 折起,使点 C 到达点 P 的位置,且 PF BF .( 1)证明:平面 PEF 平面 ABFD ;( 2)求 DP 与平面 ABFD 所成角的正弦值.37.(翻折)(2016 年全国 II 高考)如图,菱形ABCD 的对角线 AC 与 BD 交于点 O ,AB 5, AC 6 ,点 E, F 分别在 AD , CD 上, AE CF 5,EF交BD于点H.将4DEF 沿 EF 折到D' EF 位置,OD10 .(Ⅰ)证明: D H平面ABCD;(Ⅱ)求二面角 B D A C 的正弦值.8. (动点问题)( 2018 年 II 卷)如图,在三棱锥P ABC中,AB BC 2 2,PA PB PC AC 4,O为AC的中点.P( 1)证明:PO平面 ABC ;( 2)若点 M 在棱BC上,且二面角M PA C 为 30,求 PC 与平面PAM所成角的正弦值.AOCMB4近几年高考理科立体几何大题汇编1.(2018 年 III 卷)如图,边长为 2 的正方形ABCD 所在的平面与半圆弧M 是CD 所在平面垂直,CD 上异于 C ,D的点.( 1)证明:平面AMD ⊥平面BMC;( 2)当三棱锥M ABC 体积最大时,求面MAB 与面MCD所成二面角的正弦值.1.解:( 1)由题设知 ,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以 BC⊥平面 CMD,故 BC⊥ DM.因为 M 为 CD 上异于 C, D 的点,且 DC为直径,所以DM⊥ CM.又BC I CM= C,所以 DM⊥平面 BMC.而DM 平面 AMD,故平面 AMD⊥平面 BMC.uuur(2)以D为坐标原点 , DA的方向为x轴正方向 ,建立如图所示的空间直角坐标系D- xyz.当三棱锥 M- ABC体积最大时, M 为 CD 的中点.由题设得 D (0,0,0), A(2,0,0), B(2,2,0), C(0,2,0), M (0,1,1) ,uuuur uuur uuurAM ( 2,1,1), AB (0, 2,0), DA(2,0,0)设 n ( x, y, z) 是平面 MAB 的法向量,则5n uuuur0,2x y z 0, AMn uuur0.即0. AB 2 y可取 n(1,0,2) .uuurDA 是平面 MCD 的法向量,因此uuuruuur5 n DAcos n, DA uuur,| n || DA |5sinuuur 2 5 n, DA,5所以面 MAB与面 MCD所成二面角的正弦值是2 5 .52、[2014 ·新课标全国卷Ⅱ ] 如图 1-3,四棱锥 P-ABCD 中,底面 ABCD 为矩形, PA⊥平面 ABCD,E 为 PD 的中点.(1)证明: PB∥平面 AEC;(2)设二面角 D-AE-C 为 60°, AP=1,AD=3,求三棱锥 E-ACD 的体积.图 1-32,解: (1)证明:连接 BD 交 AC 于点 O,连接 EO.因为 ABCD 为矩形,所以 O 为 BD 的中点.又E 为 PD 的中点,所以 EO∥ PB.因为 EO? 平面 AEC, PB?平面 AEC,所以 PB∥平面 AEC.(2)因为 PA⊥平面 ABCD,ABCD 为矩形,所以 AB,AD,AP 两两垂直.→→如图,以 A 为坐标原点, AB, AD, AP 的方向为 x 轴、 y 轴、 z 轴的正方向, |AP|D (0,31→为单位长,建立空间直角坐标系A-xyz,则3,0), E 0,2,2, AE =310,2,2 .6→3,0).设 B(m ,0,0)(m>0),则 C(m , 3,0),AC =(m ,设 n 1= ,, z) 为平面 ACE 的法向量,(x yn 1 →mx + 3y =0,·AC =0,即 3则→11=0, y + z = 0,22n ·AE可取 n 1= m 3,- 1, 3 .又 n 2=(1, 0,0)为平面 DAE 的法向量,1由题设易知 |cos 〈n 1,n 2〉|=2,即3 1 3 .2= ,解得 m = 3+4m 2 2因为 E 为 PD 的中点,所以三棱锥 E-ACD 的高为1三棱锥E-ACD 的体积V =1×2.31 3 1 3 2× 3×2×2= 8 .3. ( 2017? 新课标Ⅰ卷)如图,在四棱锥 P ﹣ ABCD 中,AB ∥CD ,且∠BAP= ∠CDP=90°.(1) 证明:平面 PAB ⊥平面 PAD ;(2) 若 PA=PD=AB=DC ,∠APD=90°,求二面角 A ﹣ PB ﹣C的余弦值.3. 【答案】 ( 1 )证明:∵∠ BAP=∠ CDP=90°,∴ PA ⊥ AB , PD ⊥ CD , ∵ AB ∥ CD ,∴ AB ⊥ PD , 又 ∵ PA ∩PD=P , 且 PA ?平 面 PAD ,PD ? 平 面PAD, ∴ AB⊥ 平面PAD ,又 AB ?平 面PAB, ∴平面PAB⊥平面PAD;( 2)解:∵ AB ∥ CD , AB=CD ,∴四边形 ABCD 为平行四边形, 由( 1)知 AB ⊥平面 PAD ,∴ AB ⊥AD, 则 四 边 形ABCD为矩形,7在△ APD中,由PA=PD,∠ APD=90°,可得△ PAD为等腰直角三角形,设PA=AB=2a,则取AD 中点 O, BC 中点以O 为坐标原点,分别以AD=.E ,连接PO、 OE,OA、 OE、 OP 所在直线为x 、 y、 z轴建立空间直角坐标系,则: D (),B(),P(0,0,),C().,,.设平面PBC的一个法向量为,由,得,取y=1 ,得.∵AB ⊥平面PAD ,AD ?平面PAD ,∴AB ⊥AD ,又PD⊥PA,PA∩AB=A,∴ PD⊥平面PAB,则为平面PAB 的一个法向量,.∴cos<>==.由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C的余弦值为.4.(菱形建系) [2014 新·课标全国卷Ⅰ ] 如图三棱柱 ABC - A1B1C1中,侧面 BB1C1C 为菱形, AB⊥B1 C.(1)证明: AC= AB1;(2)若 AC⊥ AB1,∠ CBB1=60°, AB=BC,求二面角 A -A1B1 - C1的余弦值.4 解: (1)证明:连接 BC1,交 B1C 于点 O,连接 AO,因为侧面 BB1C1 C 为菱形,所以 B1C⊥ BC1,且 O 为 B1C 及 BC1的中点.又AB⊥ B1C,所以 B1C⊥平面 ABO.8由于 AO? 平面 ABO ,故 B 1C ⊥AO. 又 B 1O =CO ,故 AC =AB 1 .(2)因为 AC ⊥AB 1,且 O 为 B 1C 的中点,所以 AO =CO.又因为 AB =BC ,所以△ BOA ≌ △BOC.故 OA ⊥OB ,从而 OA , OB ,OB 1 两两垂直.以 O 为坐标原点, OB 的方向为 x 轴正方向, |OB|为单位长,建立如图所示的空间直角坐标系 O- xyz.因为∠ CBB 1=60°,所以△ CBB 1 为等边三角形,又AB = BC ,则 A 0 , , 3 ,3B(1, 0, 0),B 1 , 3, 0 ,C ,-3, 0.0 3 0 3→33→, ,- 3 ,AB 1= ,,-,A 1 B 1=AB =331 03→3,0 .B 1C 1=BC = - 1,- 3设 n = (x ,y ,z)是平面 AA 1 1 的法向量,则B3 3n ·AB =0,3 y - 3 z = 0,1所以可取 n =(1,3, 3).→即30 n ·A B x - 3 z =0.设 m 是平面 A 11 1 的法向量,B C→则 m ·A 1B 1=0,同理可取 m =(1,- 3, 3).→ 1=0,1m ·B C则 cos 〈 n , m 〉= n ·m 1|n||m|= 7.1所以结合图形知二面角 A -A1B1 - C1的余弦值为7.5.(菱形建系)【 2015 高考新课标 1】如图,四边形 ABCD为菱形,∠ ABC=120 °,E,F 是平面 ABCD 同一侧的两点, BE⊥平面 ABCD, DF⊥平面 ABCD,BE=2 DF,AE⊥EC.(Ⅰ)证明:平面 AEC⊥平面 AFC;(Ⅱ)求直线 AE 与直线 CF 所成角的余弦值 .5.,【答案】(Ⅰ )见解析(Ⅱ )33又∵AE⊥EC,∴EG= 3 ,EG⊥ AC,在 Rt△ EBG中,可得 BE= 2 ,故 DF= 2 .2在Rt△ FDG 中,可得 FG= 6 .2在直角梯形 BDFE 中,由 BD=2 , BE= 2 , DF=2可得 EF=3 2 ,22∴ EG 2FG 2EF 2,∴EG⊥FG,∵ AC∩ FG=G,∴ EG⊥平面 AFC,10∵ EG 面 AEC ,∴平面 AFC ⊥ 平面 AEC⋯⋯6分.uuur uuuruuur( Ⅱ)如 ,以 G 坐 原点,分 以GB ,GC 的方向 x , y 正方向, | GB|位 度,建立空 直角坐 系G-xyz ,由( Ⅰ )可得 A (0,- 3 , 0), E(1,0,2 ) , F (- 1,0 , 2), ( , 3 , ), ∴ uuur = ( 1,3 , uuur2 ), CF = ( -1 ,2C 0 0 AE2 )- 3 ,.⋯ 分210uuur uuuruuur uuur3 故 cosAE ?CFAE ,CFuuuruuur.| AE ||CF |3所以直 AE 与 CF 所成的角的余弦3 . 分 ⋯⋯ 1236. (翻折) (2018 年 I 卷 )如图,四边形 ABCD 为正方形, E, F 分别为 AD , BC 的中点,以DF 为折痕把 △ DFC 折起,使点 C 到达点 P 的位置,且 PFBF .( 1)证明:平面 PEF平面 ABFD ;( 2)求 DP 与平面 ABFD 所成角的正弦值 .6. 解:( 1)由已知可得, BF ⊥ PF , BF ⊥ EF ,所以 BF ⊥平面 PEF .又 BF 平面 ABFD ,所以平面 PEF ⊥平面 ABFD .11(2)作 PH ⊥EF ,垂足为 H .由( 1)得, PH ⊥平面 ABFD .uuuruuur以 H 为坐标原点, HF 的方向为 y 轴正方向, | BF | 为单位长,建立如图所示的空间直角坐标系 H - xyz .由( 1)可得, DE ⊥ PE .又 DP =2 , DE =1 ,所以 PE = 3 .又 PF =1 ,EF =2 ,故 PE ⊥PF .可得 PH3 3, EH.22则 H (0,0,0), P(0,0,3), D ( 1, 3 uuur (1, 3 , 3 ), uuur3) 为平面 ABFD 的,0), DP HP (0,0,2 2 2 22法向量 .uuur uuur 设 DP 与平面 ABFD 所成角为HP DP,则 sin | uuur uuur || HP | | DP |343.34所以 DP 与平面 ABFD 所成角的正弦值为3 .4(翻折)( 2016 年全国 II 高考)如图,菱形 ABCD 的对角线 AC 与 BD 交于点 O ,7.AB 5, AC6 ,点 E, F 分别在 AD , CD 上, AE CF5, EF 交 BD 于点 H .将4DEF 沿 EF 折到 D ' E F 位置, OD10 . (Ⅰ)证明: D H 平面 ABCD ;(Ⅱ)求二面角 B D A C 的正弦值.7.【解析】⑴证明:∵AE CF5,∴AE CF,4AD CD∴ EF ∥ AC .∵四边形 ABCD 为菱形,∴12AC BD ,∴ EF BD ,∴ EFDH ,∴ EF D H .∵ AC 6 ,∴ AO 3;又 AB 5, AO OB ,∴ OB 4 , ∴ OHAEOD 1 , ∴ DH D H 3 , ∴ OD 2OH 2D ' H 2, ∴AOD ' H OH .又∵ OH I EFH ,∴ D 'H面 ABCD .⑵建立如图坐标系 H xyz .B 5,0,0 ,C 1,3,0 ,D ' 0,0,3 , A 1, 3,0 ,uuuruuur 1 ,3,3, ,, AD ',AB 4 3 0ur设面 ABD ' 法向量 n 1x ,y ,z ,uuurAC0 ,6 ,0 ,uur uuur4x 3 y 0x 3n 1 AB 0,取 yur3,,.由 uuruuuur得4 ,∴ n 14 5 n 1 ADx3 y 3z 0z 5uur同理可得面 AD 'C 的法向量 n 23,0 ,1 ,ur uur∴ cosn 1 n 2 9 5 7 5,∴ sin2 95 .ur uurn 1 n 2 5 2 1025258. (动点问题)( 2018 年 II 卷)如图,在三棱锥P ABC 中, AB BC 2 2 ,PA PB PCAC 4 , O 为 AC 的中点.13( 1)证明:PO平面ABC;( 2)若点 M 在棱BC上,且二面角M PA C 为 30 ,求 PC 与平面PAM所成角的正弦值.解:( 1)因为AP CP AC 4 , O 为 AC 的中点,所以 OP AC ,且OP2 3 .连结 OB .因为AB BC2AC ,所以△ABC为等腰直角三角形,2且 OB AC ,OB 1AC2. 2由 OP2OB2PB 2知PO OB .由 OP OB , OP AC 知PO平面 ABC .uuurO xyz .(2)如图,以O为坐标原点,OB的方向为x轴正方向,建立空间直角坐标系uuur由已知得 O(0,0,0), B(2,0,0), A(0, 2,0), C(0,2,0), P(0,0,23), AP (0,2,2 3), 取平面 uuur PAC 的法向量 OB(2,0,0) .uuur设 M (a,2 a,0)(0a2),则 AM (a,4 a,0) .设平面 PAM 的法向量为n(x, y, z) .14uuur uuur n 0 得 2y2 3z0 ,可取 n (3( a4), 3a, a) ,由 AP n 0, AMax (4a) y 0所以 cos uuur2 3( a 4).由已知得 | cos uuur| 3 . OB, na 2 OB, n2 3(a 4) 2 3a 22 所以2 3 | a 4| a 2 =3.解得 a 4 (舍去), a4 . 2 3(a 4) 2 3a 2 23所以 n(83 ,4 3 ,uuur (0,2, 2 3) ,所以 cos uuur3 . 4) .又 PCPC, n3334所以 PC 与平面 PAM 所成角的正弦值为3 .415。
(完整版)近三年高考全国卷理科立体几何真题(可编辑修改word版)

新课标卷高考真题1、(2016 年全国I 高考)如图,在以A,B,C,D,E,F 为顶点的五面体中,面ABEF 为正方形,AF=2FD,∠AFD = 90 ,且二面角D -AF -E 与二面角C -BE - F 都是60 .(I)证明:平面ABEF ⊥平面EFDC;(II)求二面角E - BC - A 的余弦值.10 2、( 2016 年全国 II 高考) 如图, 菱形 ABCD 的对角线 AC 与 BD 交于点 O ,AB = 5, AC = 6 , 点 E , F 分别在 AD , CD 上, AE = CF = 5 , EF 交 BD 于点 H4.将∆DEF 沿 EF 折到∆D 'EF 位置, OD ' = .(Ⅰ)证明: D 'H ⊥ 平面 ABCD ;(Ⅱ)求二面角 B - D 'A - C 的正弦值.3【2015 高考新课标 1,理 18】如图,四边形ABCD 为菱形,∠ABC=120°,E,F 是平面ABCD 同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AEC⊥平面AFC;(Ⅱ)求直线AE 与直线CF 所成角的余弦值.4、[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P-ABCD 中,底面ABCD 为矩形,PA⊥平面ABCD,E 为PD 的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C 为60°,AP=1,AD= 3,求三棱锥E-ACD 的体积.图1-35、[2014·新课标全国卷Ⅰ] 如图1-5,三棱柱ABC -A1B1C1中,侧面BB1C1C 为菱形,AB⊥B1C.图1-5(1)证明:AC=AB1;(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A -A1B1C1的余弦值.6、(2017•新课标Ⅱ)如图,四棱锥P﹣ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E 是PD 的中点.(Ⅰ)证明:直线CE∥平面PAB;(Ⅱ)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M﹣AB﹣D 的余弦值.7(、2017•新课标Ⅲ)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD= ∠CBD,AB=BD.(Ⅰ)证明:平面ACD⊥平面ABC;(Ⅱ)过AC 的平面交BD 于点E,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D﹣AE﹣C 的余弦值.8、(2017•新课标Ⅰ卷)如图,在四棱锥P﹣ABCD 中,AB∥CD,且∠BAP=∠CDP=90°.(12分)(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C 的余弦值.m n ⋅ -4 3 + 1 ⋅ 3 + 16 m 1 1 1 m 1【解析】⑴ ∵ ABEF 为正方形∴ AF ⊥ EF ∵ ∠AFD = 90︒∴ AF ⊥ DF ∵ D F EF =F∴ AF ⊥ 面 EFDC AF ⊥ 面 ABEF∴平面 ABEF ⊥ 平面 EFDC⑵ 由⑴知∠DFE = ∠CEF = 60︒∵ AB ∥ EF AB ⊄ 平面 EFDCEF ⊂ 平面 EFDC ∴ AB ∥平面 ABCDAB ⊂ 平面 ABCD∵面 ABCD 面 EFDC = CD∴ AB ∥CD ,∴ CD ∥ EF∴四边形 EFDC 为等腰梯形以 E 为原点, 如图建立坐标系,FD = aE (0 ,0 ,0)B (0 ,2a ,0)C ⎛ a ,0 , 3 a ⎫ A (2a ,2a ,0)2 2 ⎪ ⎝ ⎭ ⎛ a3 ⎫EB = (0 ,2a ,0) , BC = 2 ,- 2a , 2 a ⎪ , AB = (-2a ,0 ,0)⎝ ⎭设面 BEC 法向量为= ( x ,y ,z ) . ⎧ ⎧2a ⋅ y 1 = 0 ⎪m ⋅ EB = 0 ,即⎪ ⎨ ⋅ = 0 ⎨ a ⋅ x - 2ay + 3 a ⋅ z = 0 ⎪⎩m BC ⎪⎩ 2 1 1 2 1x = 3 ,y = 0 ,z = -1 = ( 3 ,0 ,- 1)设面 ABC 法向量为 = ( x ,y ,z ) ⎧ n 2 2 2 ⎧ a ⎪n ⋅ BC =0 .即⎪ x 2 - 2ay 2 + az 2 = 0 x = 0 ,y = 3 ,z = 4 ⎨ ⎨ 2 22 2 2⎪⎩n ⋅ AB = 0⎪⎩2ax 2 = 0 n = (0 , 3 ,4)设二面角 E - BC - A 的大小为. cos =∴二面角 E - BC - A 的余弦值为-2 19 19 m ⋅ n = = - 2 19 19 3u r u u r n 1 ⋅ n 2 u r u u r n 1 n 2 7 5 2 95 ⋅ ' ⎩ ⎩ 2【解析】⑴证明:∵ AE = CF = 5 ,∴AE = CF , 4 AD CD∴ EF ∥ AC .∵四边形 ABCD 为菱形,∴ AC ⊥ BD , ∴ EF ⊥ BD ,∴ EF ⊥ DH ,∴ EF ⊥ D 'H .∵ AC = 6 ,∴ AO = 3 ;又 AB = 5 , AO ⊥ OB ,∴ OB = 4 , ∴ O H = AE⋅ OD = 1 ,∴ D H = D 'H = 3 ,∴ OD ' 2 = O H 2 + D ' H 2 ,∴ D ' H ⊥ O H AO .又∵ OH I EF = H ,∴ D ' H ⊥ 面 ABCD .⑵建立如图坐标系 H - xyz .B (5 , 0 , 0) ,C (1, 3,0) , D '(0 , 0 , 3) , A (1, - 3, 0) ,AB = (4 , 3, 0) , AD ' = (-1, 3,3) , AC = (0 , 6 , 0) ,设面 ABD ' 法向量n 1 = ( x ,y ,z ) ,⎧ ⎧x = 3 由⎪n 1 ⋅ AB = 0 得⎧4x + 3y = 0 ,取⎪ y = -4 ,∴ n = (3, - 4 , 5) . ⎨ ⎪⎩n 1 A D = 0 ⎨-x + 3y + 3z = 0 ⎨ 1 ⎪z = 5同理可得面 AD 'C 的法向量n 2 = (3, 0 , 1) ,∴ cos= = = ,∴ s in = . 25 253,【答案】(Ⅰ)见解析(Ⅱ) 339 + 5 5 2 ⋅ 103 2 2 32 GB , G C又∵AE ⊥EC ,∴EG = ,EG ⊥AC , 在 Rt △EBG 中,可得 BE = ,故 DF =2 .2在 Rt △FDG 中,可得 FG =6 .2在直角梯形 BDFE 中,由 BD =2,BE = ,DF = 2可得 EF = 3 2, 2 2 ∴ EG 2 + FG 2 = EF 2 ,∴EG ⊥FG , ∵AC ∩FG=G ,∴EG ⊥平面 AFC , ∵EG ⊂ 面 AEC ,∴平面 AFC ⊥平面 AEC .……6 分(Ⅱ)如图,以 G 为坐标原点,分别以 的方向为 x 轴,y 轴正方向,| GB |为单位长度,建立空间直角坐标系 G-xyz ,由(Ⅰ)可得 A (0,- ,0),E (1,0,),F (-1,0, ),C (0, ,0),∴ AE =(1, , ), C F =(-1,- 2 , 2 ).…10 分 23 2 3 2 33 3 3 33 AE ,C F >= •1AP |为单位长,建立空间直角坐标系 A -xyz ,则 D (0, 3,0),E 0, 2 , 2,AE = 0 2 , 2 = - { 即 故cos < AE CF 3 . | AE || C F | 3 所以直线 AE 与 CF 所成的角的余弦值为3 .……12 分3 4,解:(1)证明:连接 BD 交 AC 于点 O ,连接 EO .因为 ABCD 为矩形,所以 O 为 BD 的中点. 又 E 为 PD 的中点,所以 EO ∥PB .因为 EO ⊂平面 AEC ,PB ⊄平面 AEC ,所以 PB ∥平面 AEC . (2)因为 PA ⊥平面 ABCD ,ABCD 为矩形, 所以 AB ,AD ,AP 两两垂直.如图,以 A→ AD ,AP 的方向为 x 轴、y 轴、z 轴的正方向,| 为坐标原点,AB , →( 1)→ (, 1).设 B (m ,0,0)(m >0),则 C (m ,3,0) →(m ,3,0).,AC = 设 n 1=(x ,y ,z )为平面 ACE 的法向量,→ n 1·AC =0,则 → ) {m x + 3y =0,)n 1·AE =0, 2 y + z =0,可取 n 1=(2,-1, ).又 n 2=(1,0,0)为平面 DAE 的法向量,1由题设易知|cos 〈n 1,n 2〉|= ,即2 13 = ,解得 m = .22 1因为 E 为 PD 的中点,所以三棱锥 E -ACD 的高为 .三棱锥 E -ACD 的体积 V =21 1 3 1 × × 3× × = . 3 22 2 83m 3 3+4m 233 3 3 3 1(( )B 1C 1=BC = -1,- 3,0 . {{335 解:(1)证明:连接 BC 1,交 B 1C 于点 O ,连接 AO ,因为侧面 BB 1C 1C 为菱形,所以 B 1C ⊥BC 1,且 O 为 B 1C 及 BC 1 的中点.又 AB ⊥B 1C ,所以 B 1C ⊥平面 ABO . 由于 AO ⊂平面 ABO ,故 B 1C ⊥AO . 又 B 1O =CO ,故 AC =AB 1.(2)因为 AC ⊥AB 1,且 O 为 B 1C 的中点,所以 AO =CO .又因为 AB =BC ,所以△BOA ≌ △BOC .故 OA ⊥OB ,从而 OA ,OB ,OB 1 两两垂直.以 O 为坐标原点,OB 的方向为 x 轴正方向,|OB |为单位长,建立如图所示的空间直角坐标系 O xyz .(3)因为∠CBB 1=60°,所以△CBB 1 为等边三角形,又 AB =BC ,则 A 0,0, 3 ,B (1,0,0),B (0, 3,0),C (0,- 3,0).→ AB 1= 0, 3 ,- 3)3 → 3 ,A 1B 1=AB =1,0,- , 3 3 3→ ( )设 n =(x ,y ,z )是平面 AA 1B 1 的法向量,则n ·AB 1=0,3 y - z =0,)→n ·A 1B 1=0,)即所以可取 n =(1,3, 3).x - z =0.{设m 是平面A1B1C1的法向量,→m·A1B1=0,则→m·B1C1=0,)同理可取m=(1,-3, 3).n·m 1则cos〈n,m〉==.|n||m| 71所以结合图形知二面角 A -A1B1 C1的余弦值为.76、【答案】(Ⅰ)证明:取PA 的中点F,连接EF,BF,因为E 是PD 的中点,所以EF AD,AB=BC= AD,∠BAD=∠ABC=90°,∴BC∥ AD,∴BCEF 是平行四边形,可得CE∥BF,BF⊂平面PAB,CF✪平面PAB,∴直线CE∥平面PAB;(Ⅱ)解:四棱锥P﹣ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E 是PD 的中点.取AD 的中点O,M 在底面ABCD 上的射影N 在OC 上,设AD=2,则AB=BC=1,OP= ,∴∠PCO=60°,直线BM 与底面ABCD 所成角为45°,可得:BN=MN,CN= MN,BC=1,可得:1+ BN2=BN2 ,BN= ,MN= ,作NQ⊥AB 于Q,连接MQ,所以∠MQN 就是二面角M﹣AB﹣D 的平面角,MQ== ,二面角M﹣AB﹣D 的余弦值为: = .7、【答案】(Ⅰ)证明:如图所示,取AC 的中点O,连接BO,OD.∵△ABC 是等边三角形,∴OB⊥AC.△ABD 与△CBD 中,AB=BD=BC,∠ABD=∠CBD,∴△ABD≌△CBD,∴AD=CD.∵△ACD 是直角三角形,∴AC 是斜边,∴∠ADC=90°.∴DO= AC.∴DO2+BO2=AB2=BD2 .∴∠BOD=90°.∴OB⊥OD.又DO∩AC=O,∴OB⊥平面ACD.又OB⊂平面ABC,∴平面ACD⊥平面ABC.(Ⅱ)解:设点D,B 到平面ACE 的距离分别为h D,h E.则= .∵平面AEC 把四面体ABCD 分成体积相等的两部分,∴ = = =1.∴点E 是BD 的中点.建立如图所示的空间直角坐标系.不妨设AB=2.则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0,,0),E .=(﹣1,0,1),= ,=(﹣2,0,0).设平面ADE 的法向量为=(x,y,z),则,即,取= .同理可得:平面ACE 的法向量为=(0,1,).∴cos = = =﹣.∴二面角D﹣AE﹣C 的余弦值为.8、【答案】(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,∵AB∥CD,∴AB⊥PD,又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,∴AB⊥平面PAD,又AB⊂平面PAB,∴平面PAB⊥平面PAD;(2)解:∵AB∥CD,AB=CD,∴四边形ABCD 为平行四边形,由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD 为矩形,在△APD 中,由PA=PD,∠APD=90°,可得△PAD 为等腰直角三角形,设PA=AB=2a,则AD= .取AD 中点O,BC 中点E,连接PO、OE,以O 为坐标原点,分别以OA、OE、OP 所在直线为x、y、z 轴建立空间直角坐标系,则:D(),B(),P(0,0,),C().,,.设平面PBC 的一个法向量为,由,得,取y=1,得.∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥AD,又PD⊥PA,PA∩AB=A,∴PD⊥平面PAB,则为平面PAB 的一个法向量,.∴cos<>= =.由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C 的余弦值为.。
近三年高考全卷理科立体几何真题

设面BEC 法向量为m x , y , z .IT uur2am EB 0 即IT uura3m BC 0X 2ay i■—a z 022X i3, y 0, z1新课标卷近三年高考题1、(2016年全国I 高考)如图,在以A , B , C, D , E, F 为顶点的五面体中,面 ABEF 为正方形,AF=2FD, AFD 90°,且二面角 D - AF - E 与二面角 C - BE- F都是60° . (I) 证明:平面 ABEF 平面EFDC (II) 求二面角E - BG A 的余弦值. 【解析】 ⑴ •/ ABEF 为正方形 ••• AF EF •/ AFD 90 • AF DF •/ DF I EF=F• AF 面 EFDC•平面 ABEF 平面 EFDC⑵由⑴知 DFECEF 60•/ AB II EFAF 面 ABEFAB 平面EFDC EF 平面EFDC• AB II 平面 ABCDAB 平面ABCD•/面 ABCD I 面 EFDC CD•- AB II CD •- CD II EFJ•四边形EFDC 为等腰梯形以E 为原点,如图建立坐标系,设FD aB 0 , 2a , 0A 2a , 2a , 0uur muiEB 0, 2a , 0 , BC2a,子uu u AB2a , 0 , 0m 3, o, i设面ABC法向量为n x2, y2, z2面角E BC A的余弦值为2空192、(2016年全国II高考)如图,菱形ABCD的对角线AC与BD交于点O ,5AB 5, AC 6,点E,F 分别在AD,CD 上, AE CF ,EF 交BD 于点H .将4 DEF 沿EF 折到D'EF 位置,OD .10 .(I)证明:D H 平面ABCD ;(U)求二面角B D A C的正弦值.• •• EF II AC .• EF BD,• EF DH ,• EF D H .•/ AC 6,• AO 3;又AB 5,AO OB,• OB 4,uuu —X22ax22ay2-2az22 X2 0, y2 3, Z2 4BC A的大小为4.厂.3 162.1919【解析】⑴证明:••• AE CFAE CF ADCD,•••四边形ABCD为菱形, • AC BD,nrnBC=°即AB 0设二面角Ecosur rm n54AE二OH OD 1 ,••• DH D H 3 ,AO2 2 2• |OD 2 |OH| |D'H| , • D'H OH .又T OH I EF H , • D'H 面ABCD .⑵建立如图坐标系H xyz .B 5 , 0 , 0 ,C 1 , 3 , 0 , D' 0 ,uuu uuurAB 4 , 3, 0 , AD'uuu,AC 设面ABD'法向量niu舟n1由iuuuiABUUUTAD0得4X0 x3y3y3zir同理可得面AD'C的法向量uun0, 1 …cosir inni n2up2届--sin -------------257 525 ,TX# BC f TN^\B C = 1.又TD .•眈,故平行且等于川Mj 四边形AS/XT 为平行四边形,于罡胚V 口「 因为AT^L 平面PAB f XfN x 平面PAB f 所以A&M 平面Mg.(ID 取的中点 E, ^AE ?由 AB = AC^AE-^C ?从 ^AE-AD, & AE 二上曲 _ BE ; = J AS :-(~y =庚.以川为坐标原点,川应的方向为x 轴正万冋,建立如團所示的空间直角坐标系A-xyz }由题知;2x 4z 0,即-5 ,可取 x y 2z 02n (0,2,1),| n AN |8、、5 于是 | cos n, AN ||n || AN |25尸(024〕「C 辰皿》(芈丄2),PW 三(027儿毂三*T ,益■(芈4■ 丄刁. (x, y, z )为平面PMN 的法向量,则n PMn PN3、(2016年全国III 高考)如图,四棱锥P ABC 中,PA 地面ABCD , AD P BC , ABAM试题解析;(I 〉由已知得型厶斗Q 二」収恥的中点匚连接川仁由“为巩?中点知4、【2015高考新课标2,理19】如图,长方体 ABCD AB I GU 中,AB=16, BC=10, AA , 8,点 E , F 分别在AB , C ,D , 上, A ,E D ,F 4 •过点E , F 的平面 与此长方体的面相交,交 线围成一个正方形.(I)在图中画出这个正方形(不必说出画法和理由); (U)求直线AF 与平面 所成角的正弦值.【答案】(I)详见解析;(U) 4 5 .15【解析】(I )宏线围成的正方彪EZTGF 如圈*(II)作垂足冷 4 则= 因为EZTGF 丸正方形】所以EH=EF = BC = 10・于是曲= =6,所乩也=10・以D 为坐标原鼠丙的方向沖工轴的正方向,建立如图所示的空间直角坐标系D —2 则皿阿 H(1CUO” EQCU 罔,— _ _ G 一盘=QF(0.4.£), F£ = (10.0.0),肛= (0—6一股.设是平面的法向矍,则二— 刀 I 小【考点定位】1、直线和平面平行的性质;2、直线和平面所成的角.座.所以直5平航所唤正弦值为爭【名师点睛】根据线面平行和面面平行的性质画平面与长方体的面的交线;由交线的位置可确定公共点的位置,坐标法是求解空间角问题时常用的方法,但因其计算量大的特点很容易出错,故坐标系的选择是很重要的,便于用坐标表示相r uuu关点,先求出面的法向量,利用sin cos n,AF 求直线AF与平面所成角的正弦值.5、【2015高考新课标1,理18】如图,四边形ABCD为菱形,/ ABC=120°, E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF 丄平面ABCD,BE=2DF,AE丄EC.(I)证明:平面AEC丄平面AFC;【答案】(I)见解析⑴33【解析】试題分析I( I [连接03设珀二06连接EG FG詁在菱形中,不妨设匚41易证EG丄通过计胃可证亘G丄芒,申瞬线面垂直判定定理可知前丄平面丄y 由而面垂宜判宦定理知平而仝c丄平面2_^C ; (ID 取G 为坐标原虽,分别\iXGB.GC 的方向为工轴'「轴正方向,至 为单位民既 崔立空阊直角坐标系 g,利用向重法可求出异面直线总与 疔所成角的余弦值试題解析匚(I 〉连援设站IOG,连接三G, 56, 口 在觌萌中,不蛎设C-S=l,由厶L *O 匕冃 可得上G*=GC= .由呢丄平面尙0 .i3=3C 可知,出又••• AE 丄 EC ,: EG= 3 , EG 丄 AC ,厉在 Rt A EBG 中,可得 BE= 2,故 DF= .2在Rt A FDG 中,可得FG= 6 .2J 2o /2 在直角梯形BDFE 中,由BD=2, BE= 2 , DF= 可得EF= 3,22•'• EG 2 FG 2 EF 2,二 EG 丄 FG ,••• ACAFG=G , • EG 丄平面 AFC , ••• EG 面AEC ,:平面 AFC 丄平面AEC.……6分F(n)如图,以G 为坐标原点,分别以GB,GC 的方向为x 轴,y 轴正方向,|GB| 为单位长度,建立空间直角坐标系G-xyz ,由(I)可得A (0,—崩,0), E(1,0,J 2), F (— 1,0, 22 ), C (0, +3 , 0) , • AE = (1, P 3,、: 2 ) , CF = (-1 ,2-■73, —2) (10)分【考点定位】空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力【名师点睛】对空间面面垂直问题的证明有两种思路,思路1:几何法,先由线线垂直证明线面垂直,再由线面垂直证明面面垂直;思路2:利用向量法,通过计算两个平面的法向量,证明其法向量垂直,从而证明面面垂直;对异面直线所成角问题,也有两种思路,思路1:几何法,步骤为一找二作三证四解,一找就是先在图形中找有没有异面直线所成角,若没有,则通常做平行线或中位线作出异面直线所成角,再证明该角是异面直线所成角,利用解三角形解出该角6 [2014新课标全国卷U ]如图1-3,四棱锥P-ABCD中,底面ABCD为矩形,FA丄平面ABCD,E为PD的中点.(1) 证明:PB//平面AEC;(2) 设二面角D-AE-C为60°,AP= 1, AD = 3,求三棱锥E-ACD的体积.解:(1)证明:连接BD交AC于点0,连接EO.因为ABCD为矩形,所以O为BD的中点. 又E为PD的中点,所以EO / PB.因为EO?平面AEC,PB?平面AEC,所以PB//平面AEC.(2)因为PA丄平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB,AD,AP的方向为x轴、y轴、z轴的正方向,|AP|为单位长,建立空间直角坐标系A-xyz,则D(0,3, 0),E 0, 土,琏uuur uuuuu uuu AE?CF故cos AE,CF uuur ' uuu|AE||CF| 3所以直线AE与CF所成的角的余弦值为3 .12分设 B(m , 0, 0)(m>0),则 C(m , 3, 0), AC= (m , 3, 0).设n i = (x ,y,z)为平面ACE 的法向量,可取 ni = m ,— 1,.3.又n 2= (1, 0, 0)为平面DAE 的法向量,1由题设易知|cos 〈n i , n 2〉| = 2, 即卩1因为E 为PD 的中点,所以三棱锥E-ACD 的高为㊁•三棱锥E-ACD 的体积V7、[2014新课标全国卷I ]如图1-5,三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB 丄B 1C.(1) 证明:AC = AB 1;(2) 若 AC 丄 AB 1, / CBB 1 = 60°, AB = BC ,求二面角 A -A 1B 1 -C 1 的余弦值. 解:(1)证明:连接BC 1,交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱 形,所以B 1C 丄BC 1,且O 为B 1C 及BC 1的中点.又AB 丄B 1C ,所以BQ 丄平面ABO.由于AO?平面ABO , 故 B 1C 丄AO.又 B 1O = CO , 故 AC = AB 1.(2)因为AC 丄AB 1,且O 为B 1C 的中点,所以 AO = CO.又因为 AB = BC ,所以△ BOA 也 △ BOC.故 OA 丄OB ,从而 OA , OB , OB 1两两垂直.以O 为坐标原点,OB 的方向为x 轴正方向,|OB|为单位长,建立如图所示mx + 3y = 0, •心 0, mx + ,3y = 0,n i • AC = 0,n i • AE = 0,,图1-5的空间直角坐标系0- xyz.因为/ CBB iA 0, 0, f ,0), B i 0, f, 0 , Co ,BC ,则又AB i 3,0.B(1,3, 0,—3 ,J3A iB i = AB = 1, 0,—-3 ,BC i = BC = — 1,-f, 0 -z)是平面AA i B i 的法向量,则多-詐0, 即 X -亍=0-AB i = 0,设 n = (x , y ,n AB i = 0, n A ?B i = 0,所以可取 n = (1,〔3, •. 3).设m 是平面A i B i C i 的法向量, m A i B i = 0, 则 一m B I CI ^ 0,同理可取m = (1,— 3,3).m >所以结合图形知二面角A -A i B i1C i 的余弦值为7-。
历年全国理科数学高考试题立体几何部分精选(含答案)

1.在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上,且6,23==,则棱锥AB BC-的体积为。
O ABCD3.如图,四棱锥P—ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明:PA⊥BD;(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。
1.D2.833. 解:(Ⅰ)因为60,2DAB AB AD ∠=︒=, 由余弦定理得3BD AD =从而BD 2+AD 2= AB 2,故BD ⊥AD 又PD ⊥底面ABCD ,可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD(Ⅱ)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ,则()1,0,0A ,()03,0B ,,()1,3,0C -,()0,0,1P 。
(1,3,0),(0,3,1),(1,0,0)AB PB BC =-=-=- 设平面PAB 的法向量为n=(x ,y ,z ),则0,0,{n AB n PB ⋅=⋅=即 3030x y y z -+=-=因此可取n=(3,1,3)设平面PBC 的法向量为m ,则m 0,m 0,{PB BC ⋅=⋅=可取m=(0,-1,3-) 27cos ,727m n ==- 故二面角A-PB-C 的余弦值为 27-1. 正方体ABCD-1111A B C D 中,B 1B 与平面AC 1D 所成角的余弦值为A23 B 33 C 23D 632. 已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为俩切点,那么PA PB •的最小值为(A) 42-+ (B)32-+ (C) 422-+ (D)322-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为(A)23 (B)43 (C) 23 (D) 83 4. 如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,AB//DC ,AD ⊥DC ,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(Ⅰ)证明:SE=2EB ;(Ⅱ)求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一:(Ⅰ)连接BD,取DC 的中点G ,连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形,故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以,BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足,因平面平面,故,BK EDC BK DE DE ⊥⊥平面,与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ,DE ⊥EC,DE ⊥SB226SB SD DB =+=3SD DB DE SB == 22626-,-EB DB DE SE SB EB ==== 所以,SE=2EB (Ⅱ) 由225,1,2,,SA SD AD AB SE EB AB SA =+===⊥知22121,AD=133AE SA AB ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则226,AF DE AF AD DF ⊥=-=. 连接FG ,则//,FG EC FG DE ⊥.所以,AFG ∠是二面角A DE C --的平面角. 连接AG,A G=2,2263FG DG DF =-=, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以,二面角A DE C --的大小为120°. 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴,建立如图所示的直角坐标系D xyz -, 设A(1,0,0),则B(1,1,0),C(0,2,0),S(0,0,2) (Ⅰ)(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥,得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1,则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>,则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=,0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =,则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB(Ⅱ)由(Ⅰ)知222(,,)333E ,取DE 的中点F ,则111211(,,),(,,)333333F FA =--,故0FA DE =,由此得FA DE ⊥又242(,,)333EC =--,故0EC DE =,由此得EC DE ⊥, 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以,二面角A DE C --的大小为120(三)1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为( )(A 3(B 5(C 7 (D) 342. 已知二面角l αβ--为60,动点P 、Q 分别在面α、β内,P 3,Q 到α的距离为3则P 、Q 两点之间距离的最小值为( ) (A) (B)2 (C) 33. 直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===, 120BAC ∠=︒,则此球的表面积等于 。
(完整版)立体几何高考真题全国卷(可编辑修改word版)

2 (2018 文 I )在平行四边形 ABCM 中, AB = AC =3 ,∠ACM = 90︒ ,以 AC 为折痕将△ M 到达点 D 的位置,且 AB ⊥ DA .ACM 折起,使点⑴证明:平面 ACD ⊥平面 ABC ;⑵ Q 为线段 AD 上一点, P 为线段 BC 上一点,且 BP = DQ = 2DA ,求三棱锥Q - ABP 的体积.3(2018 文 I I )如图,在三棱锥P - ABC 中, AB = BC = 2 ,PA = PB = PC = AC = 4 , O 为 AC 的中点.(1) 证明: PO ⊥ 平面 ABC ;(2) 若点 M 在棱 BC 上,且 MC = 2MB ,求点C 到平面 POM 的距离.OMACB(2018 文 III )如图,矩形 ABCD 所在平面与半圆弧CD 所在平面垂直, M 是C D 上异于C , D 的点.⑴证明:平面 AMD ⊥平面 BMC ;⑵在线段 AM 上是否存在点 P ,使得 MC ∥平面 PBD ?说明理由.2(2017 文 I )如图,在四棱锥 P-ABCD 中,AB//CD ,且∠BAP = ∠CDP = 90(1) 证明:平面 PAB⊥平面 PAD ;8(2) 若 PA=PD=AB=DC, ∠APD = 90 ,且四棱锥 P-ABCD 的体积为 3,求该四棱锥的侧面积.(2017 文 II )如图,四棱锥 P - ABCD 中,侧面 PAD 为等边三角形且垂直于底面 ABCD ,AB = BC = 1AD , ∠BAD = ∠ABC = 90︒.(1) 证明:直线 BC ∥平面 PAD ;7(2)若△PCD 的面积为2 ,求四棱锥P ABCD 的体积.(2017 文 III )如图,四面体 ABCD 中,△ABC 是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E 为棱BD 上与D 不重合的点,且AE⊥EC,求四面体 ABCE 与四面体 ACDE 的体积比.(2016 文I )如图,在已知正三棱锥 P-ABC 的侧面是直角三角形,PA=6,顶点 P 在平面 ABC 内的正投影为点D,D 在平面 PAB 内的正投影为点 E,连接 PE 并延长交 AB 于点G.(I)证明: G 是AB 的中点;(II)在图中作出点 E 在平面 PAC 内的正投影 F(说明作法及理由),并求四面体 PDEF 的体积.PEAD CGB(2016 文II)如图,菱形ABCD 的对角线AC 与BD 交于点O,点E,F 分别在AD,CD 上,AE=CF,EF 交BD 于点H,将△DEF 沿EF 折到△D'EF 的位置.(Ⅰ)证明:AC HD' ;(Ⅱ)若AB = 5, AC = 6, AE=5, OD' = 24,求五棱锥D' -ABCFE 的体积.(2016 文 III )如图,四棱锥P-ABCD 中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M 为线段AD 上一点,AM=2MD,N 为 PC 的中点.(I)证明MN∥平面 PAB;(II)求四面体 N-BCM 的体积.2(2015 文 I )如图四边形 ABCD 为菱形,G 为 AC 与 BD 交点, BE ⊥ △ △(I ) 证明:平面 AEC ⊥ 平面 BED ;ABCD ,(II ) 若∠ABC = 120 , AE ⊥ EC ,三棱锥 E - ACD 的体积为6 ,求该三棱锥的侧面积.3(2015 文 II )如图,长方体 ABCD ﹣A1B1C1D1 中,AB=16,BC=10,AA1=8,点 E ,分别在 A1B1, D1C1 上,A1E= D1F=4.过点 E,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由)(2)求平面α把该长方体分成的两部分体积的比值.(2014 文 I )如图,三棱柱ABC -A1B1C1 中,侧面BB1C1C 为菱形,B1C 的中点为O ,且AO ⊥平面BB1C1C .(1)证明:B1C ⊥AB;(2)若AC ⊥AB1 ,∠CBB1 = 60 , BC =1, 求三棱柱ABC -A1B1C1 的高.(2014 文 II )如图,四棱锥P -ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 是PD 的重点.(1)证明:PB //平面AEC ;(2)设AP = 1, AD = ,三棱锥P -ABD 的体积V = ,求A 到平面PBC 的距离.433。
【2022高考必备】2012-2021十年全国高考数学真题分类汇编 立体几何小题(精解精析)

2012-2021十年全国高考数学真题分类汇编 立体几何小题(精解精析)一,选择题1.(2021年高考全国乙卷理科)在正方体1111ABCD A B C D -中,P 为11B D 中点,则直线PB 与1AD 所成地角为( )A .π2B .π3C .π4D .π6【结果】D 思路:如图,连接11,,BC PC PB ,因为1AD ∥1BC ,所以1PBC ∠或其补角为直线PB 与1AD 所成地角,因为1BB ⊥平面1111D C B A ,所以11BB PC ⊥,又111PC B D ⊥,1111BB B D B ⋂=,所以1PC ⊥平面1P B B ,所以1PC PB ⊥,设正方体棱长为2,则111112BC PC D B ===,1111sin 2PC PBC BC ∠==,所以16PBC π∠=.故选:D2.(2021年高考全国甲卷理科)在一个正方体中,过顶点A 地三款棱地中点分别为E ,F ,G .该正方体截去三棱锥A EFG -后,所得多面体地三视图中,正视图如图所示,则相应地侧视图是( )的( )A.B.C.D.【结果】D思路:由题意及正视图可得几何体地直观图,如图所示,所以其侧视图为故选:D3.(2021年高考全国甲卷理科)已如A.B.C是半径为1地球O地球面上地三个点,且⊥==,则三棱锥O ABC,1AC BC AC BC-地体积为( )A B C D【结果】A思路:,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC,又球地半径为1,设O 到平面ABC 地距离为d ,则d ==,所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯=.故选:A .【点睛】关键点睛:本题考查球内几何体问题,解题地关键是正确利用截面圆半径,球半径,球心到截面距离地勾股关系求解.4.(2020年高考数学课标Ⅰ卷理科)已知,,A B C 为球O 球面上地三个点,⊙1O 为ABC 地外接圆,若⊙1O 地面积为4π,1AB BC AC OO ===,则球O 地表面积为( )A .64πB .48πC .36πD .32π【结果】A【思路】设圆1O 半径为r ,球地半径为R ,依题意,得24,2r r ππ=∴=, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,依据球地截面性质1OO ⊥平面ABC,11,4OO O A R OA ∴⊥====,∴球O 地表面积2464S R ππ==.故选:A的【点睛】本题考查球地表面积,应用球地截面性质是解题地关键,考查计算求解能力,属于基础题.5.(2020年高考数学课标Ⅰ卷理科)埃及胡夫金字塔是古代世界建筑奇迹之一,它地形状可视为一个正四棱锥,以该四棱锥地高为边长地正方形面积等于该四棱锥一个侧面三角形地面积,则其侧面三角形底边上地高与底面正方形地边长地比值为( )( )A B C D 【结果】C【思路】如图,设,CD a PE b ==,则PO ==,由题意212PO ab =,即22142a b ab-=,化简得24(210b b a a -⋅-=,解得b a =.故选:C .【点晴】本题主要考查正四棱锥地概念及其相关计算,考查学生地数学计算能力,是一道容易题.6.(2020年高考数学课标Ⅱ卷理科)已知△ABC等边三角形,且其顶点都在球O 地球面上.若球O 地表面积为16π,则O 到平面ABC 地距离为( )AB .32C .1D【结果】C思路:设球O 地半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC地等边三角形,212a ∴=,解得:3a =,2233r ∴===,∴球心O 到平面ABC地距离1d ===.故选:C .【点睛】本题考查球地相关问题地求解,涉及到球地表面积公式和三角形面积公式地应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课标卷高考真题1、(2016年全国I 高考)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面 ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值.2、(2016年全国II 高考)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5,6AB AC ==,点,E F 分别在,AD CD 上,54AE CF ==,EF 交BD 于点H .将DEF ∆沿EF 折到'D EF ∆位置,10OD '=.(Ⅰ)证明:D H '⊥平面ABCD ;(Ⅱ)求二面角B D A C '--的正弦值.3【2015高考新课标1,理18】如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AEC⊥平面AFC;(Ⅱ)求直线AE与直线CF所成角的余弦值.4、[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P-ABCD中,底面ABCD为矩形,P A⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60°,AP=1,AD=3,求三棱锥E-ACD的体积.图1-35、[2014·新课标全国卷Ⅰ] 如图1-5,三棱柱ABC -A1B1C1中,侧面BB1C1C 为菱形,AB⊥B1C.图1-5(1)证明:AC=AB1;(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A -A1B1C1的余弦值.6、(2017•新课标Ⅱ)如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.(Ⅰ)证明:直线CE∥平面PAB;(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.7、(2017•新课标Ⅲ)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(Ⅰ)证明:平面ACD⊥平面ABC;(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.8、(2017•新课标Ⅰ卷)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分)(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.1【解析】⑴ ∵ABEF 为正方形 ∴AF EF ⊥∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF∴平面ABEF ⊥平面EFDC⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥ AB ⊄平面EFDCEF ⊂平面EFDC ∴AB ∥平面ABCDAB ⊂平面ABCD∵面ABCD 面EFDC CD =∴AB CD ∥,∴CD EF ∥∴四边形EFDC 为等腰梯形以E 为原点,如图建立坐标系,FD a =()()000020E B a ,,,, ()3022022a C a A a a ⎛⎫ ⎪ ⎪⎝⎭,,,,()020EB a =,,,3222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭,,,()200AB a =-,, 设面BEC 法向量为()m x y z =,,.00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩,即11112032022a y a x ay a z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩ 111301x y z ===-,,()301m =-,, 设面ABC 法向量为()222n x y z =,,=00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即22223202220a x ay az ax ⎧-+=⎪⎨⎪=⎩ 222034x y z ===,, ()034n =,, 设二面角E BC A --的大小为θ.4219cos 1931316m n m n θ⋅-===-+⋅+⋅ ∴二面角E BC A --的余弦值为21919-2【解析】⑴证明:∵54AE CF ==,∴AE CF AD CD=, ∴EF AC ∥.∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AE OH OD AO =⋅=,∴3DH D H '==,∴222'OD OH D H '=+,∴'D H OH ⊥.又∵OH EF H =I ,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r ,,,设面'ABD 法向量()1n x y z =,,u r ,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,. 同理可得面'AD C 的法向量()2301n =u u r ,,, ∴12129575cos 255210n n n n θ⋅+===⋅u r u u r u r u u r ,∴295sin 25θ=.3,【答案】(Ⅰ)见解析(Ⅱ)33又∵AE⊥EC,∴EG=3,EG⊥AC,在Rt△EBG中,可得BE=2,故DF=2 2.在Rt△FDG中,可得FG=6 2.在直角梯形BDFE中,由BD=2,BE=2,DF=22可得EF=322,∴222EG FG EF+=,∴EG⊥FG,∵AC∩FG=G,∴EG⊥平面AFC,∵EG⊂面AEC,∴平面AFC⊥平面AEC. ……6分(Ⅱ)如图,以G为坐标原点,分别以,GB GC的方向为x轴,y轴正方向,||GB 为单位长度,建立空间直角坐标系G-xyz,由(Ⅰ)可得A(0,-3,0),E(1,0,2),F(-1,0,22),C(0,3,0),∴AE=(1,3,2),CF=(-1,-3,22).…10分故3cos ,3||||AE CF AE CF AE CF ∙<>==-. 所以直线AE 与CF 所成的角的余弦值为33. ……12分 4,解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB .因为EO ⊂平面AEC ,PB ⊄平面AEC ,所以PB ∥平面AEC . (2)因为P A ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB →,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A -xyz ,则D ()0,3,0,E ⎝⎛⎭⎪⎫0,32,12,AE→=⎝ ⎛⎭⎪⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC →=(m ,3,0).设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC→=0,n 1·AE →=0,即⎩⎨⎧mx +3y =0,32y +12z =0,可取n 1=⎝ ⎛⎭⎪⎫3m ,-1,3.又n 2=(1,0,0)为平面DAE 的法向量,由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32.因为E 为PD 的中点,所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V=13×12×3×32×12=38.5解:(1)证明:连接BC 1,交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为B 1C 及BC 1的中点.又AB ⊥B 1C ,所以B 1C ⊥平面ABO .由于AO ⊂平面ABO ,故B 1C ⊥AO .又B 1O =CO ,故AC =AB 1.(2)因为AC ⊥AB 1,且O 为B 1C 的中点,所以AO =CO .又因为AB =BC ,所以△BOA ≌ △BOC .故OA ⊥OB ,从而OA ,OB ,OB 1两两垂直.以O 为坐标原点,OB 的方向为x 轴正方向,|OB |为单位长,建立如图所示的空间直角坐标系O xyz .因为∠CBB 1=60°,所以△CBB 1为等边三角形,又AB =BC ,则A ⎝ ⎛⎭⎪⎫0,0,33,B (1,0,0),B 1⎝ ⎛⎭⎪⎫0,33,0,C ⎝ ⎛⎭⎪⎫0,-33,0.AB 1→=⎝ ⎛⎭⎪⎫0,33,-33,A 1B 1→=AB =⎝⎛⎭⎪⎫1,0,-33, B 1C →1=BC =⎝ ⎛⎭⎪⎫-1,-33,0. 设n =(x ,y ,z )是平面AA 1B 1的法向量,则⎩⎪⎨⎪⎧n ·AB 1=0,n ·A 1B 1→=0,即⎩⎪⎨⎪⎧33y -33z =0,x -33z =0.所以可取n =(1,3,3).设m 是平面A 1B 1C 1的法向量,则⎩⎪⎨⎪⎧m ·A 1B 1→=0,m ·B 1C 1→=0,同理可取m =(1,-3,3).则cos 〈n ,m 〉=n ·m |n ||m |=17.所以结合图形知二面角A -A 1B 1 C 1的余弦值为17.6、【答案】(Ⅰ)证明:取PA 的中点F ,连接EF ,BF ,因为E 是PD 的中点,所以EF AD,AB=BC= AD,∠BAD=∠ABC=90°,∴BC∥AD,∴BCEF是平行四边形,可得CE∥BF,BF⊂平面PAB,CF⊄平面PAB,∴直线CE∥平面PAB;(Ⅱ)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.取AD的中点O,M在底面ABCD上的射影N在OC上,设AD=2,则AB=BC=1,OP= ,∴∠PCO=60°,直线BM与底面ABCD所成角为45°,可得:BN=MN,CN= MN,BC=1,可得:1+ BN2=BN2,BN= ,MN= ,作NQ⊥AB于Q,连接MQ,所以∠MQN就是二面角M﹣AB﹣D的平面角,MQ== ,二面角M﹣AB﹣D的余弦值为:= .7、【答案】(Ⅰ)证明:如图所示,取AC的中点O,连接BO,OD.∵△ABC是等边三角形,∴OB⊥AC.△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,∴△ABD≌△CBD,∴AD=CD.∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°.∴DO= AC.∴DO2+BO2=AB2=BD2.∴∠BOD=90°.∴OB⊥OD.又DO∩AC=O,∴OB⊥平面ACD.又OB⊂平面ABC,∴平面ACD⊥平面ABC.(Ⅱ)解:设点D,B到平面ACE的距离分别为h D,h E.则= .∵平面AEC把四面体ABCD分成体积相等的两部分,∴= = =1.∴点E是BD的中点.建立如图所示的空间直角坐标系.不妨设AB=2.则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0,,0),E .=(﹣1,0,1),= ,=(﹣2,0,0).设平面ADE的法向量为=(x,y,z),则,即,取= .同理可得:平面ACE的法向量为=(0,1,).∴cos = = =﹣.∴二面角D﹣AE﹣C的余弦值为.8、【答案】(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,∵AB∥CD,∴AB ⊥PD,又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,∴AB⊥平面PAD,又AB⊂平面PAB,∴平面PAB⊥平面PAD;(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,设PA=AB=2a,则AD= .取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,则:D(),B(),P(0,0,),C().,,.设平面PBC的一个法向量为,由,得,取y=1,得.∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥AD,又PD⊥PA,PA∩AB=A,∴PD⊥平面PAB,则为平面PAB的一个法向量,.∴cos<>= = .由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C的余弦值为.。
