2019届高考理科数学专题 高考中的立体几何问题
2019年高考理科数学(全国1卷)答案详解(附试卷)

P 20 5 64 16
PS:其实可以对题目进行抽象:即有 A、B 两种字母,填 6 个位置,求恰有 3 个 A 的概率.这样更
容易求解.
【答案】A
第 2 页 共 18 页
7.(平面向量)已知非零向量 a,b 满足 | a | 2 | b | ,且 (a b) b ,则 a 与 b 的夹角为
头顶至肚脐的长度小于 68.07cm,所以身高小于 68.07+68.07÷0.618=178.21cm. 所以选答案 B.
【答案】B
5.(函数)函数
f
(x)
sin x x cos x x2
在[, ] 的图像大致为
A.
B.
C.
D.
【解析】∵
f (x)
sin x x cos x x2
A. (x+1)2 y 2 1 B. (x 1)2 y2 1 C. x2 ( y 1)2 1 D. x2 ( y+1)2 1
【解析】由题意得 z i x ( y 1)i ,∵ z i =1 ,∴ x2 ( y 1)2 1 ,即 x2 ( y 1)2 1
【答案】D
6.(概率统计)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的 6 个爻 组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦 恰有 3 个阳爻的概率是
5
A.
16
11
B.
32
21
C.
32
11
D.
16
【解析】所有重卦的个数为 26 64 ,恰有 3 个阳爻的个数为 C36C33 20 ,因此恰有 3 个阳爻的概率为
【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案

1 【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案一、解答题 1.如图所示,在四棱锥P-ABCD 中,底面ABCD 是棱长为2的正方形,侧面PAD 为正三角形,且面PAD ⊥面ABCD ,E 、F 分别为棱AB 、PC 的中点. (1)求证:EF ∥平面PAD ; (2)求三棱锥B-EFC 的体积; (3)求二面角P-EC-D 的正切值.2.如图,三棱柱ABF-DCE 中,∠ABC=120°,BC=2CD ,AD=AF ,AF ⊥平面ABCD .(Ⅰ)求证:BD ⊥EC ;(Ⅱ)若AB=1,求四棱锥B-ADEF 的体积.3.正方体ABCD-A 1B 1C 1D 1,AA 1=2,E 为棱CC 1的中点. (1)求证:B 1D 1⊥AE ;(2)求三棱锥A-BDE 的体积.4.如图,四棱锥P-ABCD 中,底面ABCD 是矩形,平面PAD ⊥底面ABCD ,且△PAD 是边长为2的等边三角形,PC= ,M 在PC 上,且PA ∥面MBD . (1)求证:M 是PC 的中点; (2)求多面体PABMD 的体积.25.已知四棱锥P-ABCD ,底面ABCD 为菱形,∠ABC=60°,△PAB 是等边三角形,AB=2,PC= ,AB 的中点为E.(1)证明:PE ⊥平面ABCD ; (2)求三棱锥D-PBC 的体积.6.一块边长为10cm 的正方形铁块按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.(1)试把容器的容积V 表示为x 的函数.(2)若x =6,求图2的主视图的面积.7.如图,矩形ABCD 中,BC=2,AB=1,PA ⊥平面ABCD ,BE ∥PA ,BE=PA ,F 为PA 的中点.(1)求证:PC ∥平面BDF .(2)记四棱锥C-PABE 的体积为V 1,三棱锥P-ACD 的体积为V 2,求的值.8.如图,直三棱柱ABC-A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC=CB=2,AB=2 .(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)求锐二面角D-A 1C-E 的余弦值.9.如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.(1)求证:直线EF∥平面PAD;(2)求三棱锥F-PBE的体积.10.如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.(Ⅰ)求证:AE⊥EB;(Ⅱ)设=λ,是否存在λ,使二面角B-AC-E的余弦值为?若存在,求λ的值;若不存在,说明理由.11.在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.将△BCD沿BD折到△BED的位置,使得二面角E-BD-A的大小为90°(如图).已知Q为EO的中点,点P在线段AB 上,且.(Ⅰ)证明:直线PQ∥平面ADE;(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.12.如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=.(Ⅰ)求证:PD⊥面ABCD;(Ⅱ)求二面角A-PB-D的大小.3413.如图在三棱锥A-BCD 中,侧面ABD 、ACD 是全等的直角三角形,AD 是公共的斜边,且AD= ,BD=CD=1,另一个侧面是正三角形. (1)求证:AD ⊥BC ;(2)求二面角B-AC-D 的余弦值; (3)点E 在直线AC 上,当直线ED 与平面BCD 成30°角若时,求点C 到平面BDE 的距离.14.如图所示,在边长为 的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.15.如图,在四棱锥P-ABCD 中,PA ⊥平面ABCD ,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M 为PC 的中点,点N 在线段AD 上.(I )点N 为线段AD 的中点时,求证:直线PA ∥BMN ; (II )若直线MN 与平面PBC 所成角的正弦值为,求平面PBC 与平面BMN 所成角θ的余弦值.16.如图,在正方体ABCD-A 1B 1C 1D 1中,E 是CC 1的中点,求证: (1)AC 1⊥BD ;(2)AC 1∥平面BDE .17.如图,棱长为1的正方体ABCD-A 1B 1C 1D 1中, (1)求证:AC ⊥平面B 1D 1DB ; (2)求三棱锥B-CD 1B 1的体积.18.在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.(1)求证:PB∥平面AEC(2)求证:PB⊥AC.19.如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=,M为棱A1C1的中点.(I)若N为线段DC1上的点,且直线MN∥平面ADB1A1,试确定点N的位置;(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.20.如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点.(1)求证:直线AE∥平面BDC1;(2)若三棱柱 ABC-A1B1C1是正三棱柱,AB=2,AA1=4,求平面BDC1与平面ABC所成二面角的正弦值.21.如图所示,已知长方体ABCD中,AB=4,AD=2,M为DC的中点.将△ADM沿AM折起,使得AD⊥BM.(1)求证:平面ADM⊥平面ABCM;(2)若点E为线段DB的中点,求点E到平面DMC的距离.5622.如图所示,在正方体ABCD-A 1B 1C 1D 1中,E 是棱DD 1的中点. (1)若正方体的棱长为1,求三棱锥B 1-A 1BE 的体积;(2)在棱C 1D 1上是否存在一点F ,使B 1F ∥面A 1BE ?若存在,试确定点F 的位置,并证明你的结论.23.如图,三棱柱ABC-A 1B 1C 1中,BC ⊥平面AA 1C 1C ,BC=CA=AA 1=2,∠CAA 1=60°.(1)求证:AC 1⊥A 1B ;(2)求直线A 1B 与平面BAC 1所成角的正弦值.24.在图所示的几何体中,底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD=AD=2EC=2,N 为线段PB 的中点. (1)证明:NE ⊥平面PBD ; (2)求四棱锥B-CEPD 的体积.25.已知梯形ABCD 中AD ∥BC ,∠ABC=∠BAD=,AB=BC=2AD=4,E 、F 分别是AB 、CD 上的点,EF ∥BC ,AE=x .沿EF 将梯形AEFD 翻折,使平面AEFD ⊥平面EBCF (如图).G 是BC 的中点.(1)当x =2时,求证:BD ⊥EG ;(2)当x 变化时,求三棱锥D-BCF 体积的最大值.26.如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F=4,过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求直线AF 与平面α所成角的正弦值.727.在如图所示的多面体ABCDEF 中,四边形ABCD 为正方形,底面ABFE 为直角梯形,∠ABF 为直角, ,,平面ABCD ⊥平面ABFE . (1)求证:DB ⊥EC ;(2)若AE=AB ,求二面角C-EF-B 的余弦值.28.如图,四棱锥P-ABCD 中,AD ⊥平面PAB ,AP ⊥AB . (1)求证:CD ⊥AP ; (2)若CD ⊥PD ,求证:CD ∥平面PAB .29.如图所示,四棱锥P-ABCD 的侧面PAD 是边长为2的正三角形,底面ABCD 是∠ABC=60°的菱形,M 为PC 的中点,PC= .(Ⅰ)求证:PC ⊥AD ;(Ⅱ)求三棱锥M-PAB 的体积.30.如图,在四棱锥P-ABCD 中,底面ABCD 是平行四边形,∠ADC=45°,AD=AC=2,O 为AC 的中点,PO ⊥平面ABCD 且PO=6,M 为BD的中点.(1)证明:AD ⊥平面PAC ; (2)求直线AM 与平面ABCD 所成角的正切值.31.如图,多面体EF-ABCD 中,ABCD 是正方形,AC 、BD 相交于O ,EF ∥AC ,点E 在AC 上的射影恰好是线段AO 的中点. (Ⅰ)求证:BD ⊥平面ACF ;(Ⅱ)若直线AE 与平面ABCD 所成的角为60°,求平面DEF 与平面ABCD 所成角的正弦值.32.如图,三棱锥P-ABC 中,平面PAC ⊥平面ABC ,∠BCA=90°,且BC=CA=2,PC=PA .(1)求证:PA ⊥BC ;8 (2)当PC 的值为多少时,满足PA ⊥平面PBC ?并求出此时该三棱锥P-ABC 的体积.33.如图,直三棱柱ABC-A 1B 1C 1中,AA 1=AB ,AB ⊥BC ,且N 是A 1B 的中点.(1)求证:直线AN ⊥平面A 1BC ;(2)若M 在线段BC 1上,且MN ∥平面A 1B 1C 1,求证:M 是BC 1的中点.34..如图所示,在长方体ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 为DD 1的中点. (1)求证:直线BD 1∥平面PAC (2)求证:平面PAC ⊥平面BDD 1B 1.35.如图,在四棱锥P-ABCD 中,底面ABCD 为直角梯形,AD ∥BC ,∠ADC=90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA=PD=2,BC=AD=1,CD= . (1)求证:平面MQB ⊥平面PAD ; (2)若二面角M-BQ-C 大小的为60°,求QM 的长.36.如 图,正方体ABCD-A 1B 1C 1D 1的棱长为2,E 、F 、G 分别为 AB 、BB 1、B 1C 1 的中点. (1)求证:A 1D ⊥FG ;(2)求二面角 A 1-DE-A 的正切值.37.四棱锥P-ABCD 的直观图与三视图如图,PC ⊥面ABCD(1)画出四棱锥P-ABCD 的侧视图(标注长度) (2)求三棱锥A-PBD的9 体积.38.如图,长方体ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 为棱DD 1上一点.(1)求证:平面PAC ⊥平面BDD 1B 1;(2)若P 是棱DD 1的中点,求CP 与平面BDD 1B 1所成的角大小.39.如图,四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ∥CD ,AD=CD=1,∠BAD=120°,PA= ,∠ACB=90°,M 是线段PD 上的一点(不包括端点).(Ⅰ)求证:BC ⊥平面PAC ; (Ⅱ)求二面角D-PC-A 的正切值; (Ⅲ)试确定点M 的位置,使直线MA 与平面PCD 所成角θ的正弦值为.40.已知四棱锥P-ABCD 中,AD=2BC ,且AD ∥BC ,点M ,N 分别是PB ,PD 中点,平面MNC 交PA 于Q . (1)证明:NC ∥平面PAB(2)试确定Q 点的位置,并证明你的结论.41.一个正三棱柱的三视图如图所示,求这个三棱柱的表面积和体10 积.42.如图,四棱锥P-ABCD 的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点. (Ⅰ)求证:PC ∥平面BDE ; (Ⅱ)证明:BD ⊥CE .43.如图所示,在正方体ABCD-A 1B 1C 1D 1中,E 、G 、H 分别是BC 、C 1D 1、AA 1、的中点.(Ⅰ)求异面直线D 1H 与A 1B 所成角的余弦值(Ⅱ)求证:EG ∥平面BB 1D 1D .44.如图所示,在四棱锥P-ABCD 中,AB ∥CD ,AB ⊥AD ,AB=AD=AP=2CD=2,M 是棱PB 上一点. (Ⅰ)若BM=2MP ,求证:PD ∥平面MAC ; (Ⅱ)若平面PAB ⊥平面ABCD ,平面PAD ⊥平面ABCD ,求证:PA ⊥平面ABCD ;(Ⅲ)在(Ⅱ)的条件下,若二面角B-AC-M 的余弦值为,求 的值.45.如图,已知在侧棱垂直于底面的三棱柱ABC-A 1B 1C 1中,AC=3,AB=5,BC=4,AA 1=4点D 是AB 的中点. (1)求证:AC 1∥平面B 1DC ;11 (2)求三棱锥A 1-B 1CD 的体积.46.如图,以正四棱锥V-ABCD 的底面中心O 为坐标原点建立空间直角坐标系O-xyz ,其中O x ∥BC ,O y ∥AB ,E 为VC 中点,正四棱锥的底面边长为2a ,高为h ,且有cos <, >=-. (1)求的值;(2)求二面角B-VC-D 的余弦值.47.如图1,四边形ABCD 为直角梯形,AD ∥BC ,AD ⊥AB ,AD=1,BC=2,E 为CD 上一点,F 为BE 的中点,且DE=1,EC=2,现将梯形沿BE 折叠(如图2),使平面BCE ⊥ABED .(1)求证:平面ACE ⊥平面BCE ;(2)能否在边AB 上找到一点P (端点除外)使平面ACE 与平面PCF 所成角的余弦值为?若存在,试确定点P 的位置,若不存在,请说明理由.48.如图,三棱柱ABC-A 1B 1C 1中,侧面ACC 1A 1⊥侧面ABB 1A 1,∠B 1A 1A=∠C 1A 1A=60°,AA 1=AC=4,AB=1. (Ⅰ)求证:A 1B 1⊥B 1C 1;(Ⅱ)求三棱锥ABC-A 1B 1C 1的侧面积.49.在四棱锥中P-ABCD ,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,且PA=PD=AD 、E 、F ,分别为PC 、BD 的中点. (1)求证:EF ∥平面PAD ;(2)若AB=2,求三棱锥E-DFC 的体积.1250.如图,四棱锥P-ABCD 中,△PAD 为正三角形,AB ∥CD ,AB=2CD ,∠BAD=90°,PA ⊥CD ,E 为棱PB 的中点 (Ⅰ)求证:平面PAB ⊥平面CDE ;(Ⅱ)若直线PC 与平面PAD 所成角为45°,求二面角A-DE-C 的余弦值.51.如图,在边长为2的正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,将△AED ,△DCF 分别沿DE ,DF 折起,使A ,C 两点重合于P .(Ⅰ)求证:平面PBD ⊥平面BFDE ; (Ⅱ)求四棱锥P-BFDE 的体积.【答案】1.(1)证明:取PD 中点G ,连结GF 、AG ,∵GF 为△PDC 的中位线,∴GF ∥CD 且, 又AE ∥CD 且,∴GF ∥AE 且GF=AE ,13 ∴EFGA 是平行四边形,则EF ∥AG , 又EF ⊄面PAD ,AG ⊂面PAD , ∴EF ∥面PAD ;(2)解:取AD 中点O ,连结PO ,∵面PAD ⊥面ABCD ,△PAD 为正三角形,∴PO ⊥面ABCD ,且 , 又PC 为面ABCD 斜线,F 为PC 中点,∴F 到面ABCD 距离,故;(3)解:连OB 交CE 于M ,可得R t △EBC ≌R t △OAB , ∴∠MEB=∠AOB ,则∠MEB+∠MBE=90°,即OM ⊥EC .连PM ,又由(2)知PO ⊥EC ,可得EC ⊥平面POM ,则PM ⊥EC , 即∠PMO 是二面角P-EC-D 的平面角,在R t △EBC 中,,∴, ∴,即二面角P-EC-D的正切值为.2.(Ⅰ)证明:三棱柱ABF-DCE 中,AF ⊥平面ABCD .∴DE ∥AF ,ED ⊥平面ABCD ,∵BD ⊂平面ABCD ,∴ED ⊥BD , 又ABCD 是平行四边形,∠ABC=120°,故∠BCD=60°. ∵BC=2CD ,故∠BDC=90°.故BD ⊥CD . ∵ED∩CD=D ,∴BD ⊥平面ECD . ∵EC ⊂平面ECD , ∴BD ⊥EC ;(Ⅱ)解:由BC=2CD ,可得AD=2AB ,∵AB=1,∴AD=2,作BH ⊥AD于H ,∵AF ⊥平面ABCD ,∴BH ⊥平面ADEF ,又∠ABC=120°, ∴BH=,∴.3.解:(1)证明:连接BD ,则BD ∥B 1D 1, ∵ABCD 是正方形,∴AC ⊥BD . ∵CE ⊥面ABCD , ∴CE ⊥BD . 又AC∩CE=C , ∴BD ⊥面ACE . ∵AE ⊂面ACE , ∴BD ⊥AE ,∴B 1D 1⊥AE .-----------(6分)(2)S △ABD =2 △.-----------(12分) 4.证明:(1)连AC 交BD 于E ,连ME .14∵ABCD 是矩形,∴E 是AC 中点.又PA ∥面MBD ,且ME 是面PAC 与面MDB 的交线, ∴PA ∥ME ,∴M 是PC 的中点. 解:(2)取AD 中点O ,连OC .则PO ⊥AD , 由平面PAD ⊥底面ABCD ,得PO ⊥面ABCD ,∴ , ,∴ , ∴ , ,∴.5.证明:(1)由题可知PE ⊥AB ,CE ⊥AB . ∵AB=2,∴PE=CE= .又∵PC= ,∴PE 2+EC 2=PC 2, ∴∠PEC=90°,即PE ⊥CE . 又∵AB ,CE ⊂平面ABCD , ∴PE ⊥平面ABCD ;解:(2)S △BCD =×22×sin 120°= ,PE= . 由(1)知:PE ⊥平面ABCD ,V P-BCD =•S △BCD •PE=1.∵V D-PBC =V P-BCD ,∴三棱锥D-PBC 的体积为1. 6.解:(1)设所截等腰三角形的底边边长为x cm . 在R t △EOF 中,EF=5cm ,OF=x cm ,所以EO=. 于是V=x 2(cm 3).依题意函数的定义域为{x |0<x <10}.(2)主视图为等腰三角形,腰长为斜高,底边长=AB=6,底边上的高为四棱锥的高=EO==4,S==12(cm 2)7.(1)证明:连结BF ,连接BD 交AC 与点O ,连OF , 依题得O 为AC 中点,又F 为PA 的中点, 所以OF 为△PAC 中位线,所以OF ∥PC因为OF ⊂平面BDF ,PC ⊄平面BDF 所以PC ∥平面BDF . ∴V 1=梯形 =(2)解:设BE=a ,则PA=2BE=2a , V 2=△ =(a +2a )×1×2=a . =. ∴.8.解:(Ⅰ)连结AC 1,交A 1C 于点O ,连结DO ,则O 为AC 1的中点,因为D 为AB 的中点,所以OD ∥BC 1,又因为OD ⊂平面A 1CD ,BC 1⊄平面A 1CD ,∴BC 1∥平面A 1CD…(4分) (Ⅱ)由 , ,可知AC ⊥BC ,以C 为坐标原点,方向为x 轴正方向, 方向为y轴正。
专题立体几何(2012-2021)高考数学真题

专题11 立体几何 【2021年】 1.(2021年全国高考乙卷数学(文)试题)在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为( )A .π2B .π3C .π4D .π62.(2021年全国高考甲卷数学(理)试题)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45AC B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''-约为(3 1.732≈)( )A .346B .373C .446D .4733.(2021年全国高考甲卷数学(理)试题)已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为( )A .212B .312C .24D .344.(2021年全国新高考Ⅰ卷数学试题)已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为( )A .2B .22C .4D .42二、填空题5.(2021年全国高考甲卷数学(文)试题)已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.三、解答题6.(2021年全国高考乙卷数学(文)试题)如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.8.(2021年全国高考甲卷数学(文)试题)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ⊥.10.(2021年全国新高考Ⅰ卷数学试题)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.【2012年——2020年】1.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A .514-B .512-C .514+ D .512+ 2.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知,,A B C 为球O 的球面上的三个点,Ⅰ1O 为ABC 的外接圆,若Ⅰ1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π3.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知ⅠABC 是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )A .3B .32C .1D .324.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,ⅠABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,ⅠCEF =90°,则球O 的体积为 A .86π B .46π C .26π D .6π5.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))设α,β为两个平面,则αⅠβ的充要条件是 A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面6.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线7.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A .122πB .12πC .82πD .10π8.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30,则该长方体的体积为A .8B .62C .82D .839.(2018年全国普通高等学校招生统一考试理数(全国卷II ))在长方体1111ABCD A B C D -中,1AB BC ==,13AA =1AD 与1DB 所成角的余弦值为A .15B .56C 5D .2210.(2018年全国卷Ⅰ理数高考试题)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为3D ABC -体积的最大值为A .123B .183C .243D .311.(2017年全国普通高等学校招生统一考试)如图,在下列四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面 MNQ 不平行的是( ) A . B . C . D . 12.(2017年全国普通高等学校招生统一考试文科数学(新课标3卷))已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π413.(2016年全国普通高等学校招生统一考试文科数学(新课标1))平面α过正方体ABCD—A 1B 1C 1D 1的顶点A ,,ABCD m α⋂=平面,11ABB A n α⋂=平面,则m ,n 所成角的正弦值为 A .32 B .22 C .33 D .1314.(2016年全国普通高等学校招生统一考试文科数学(全国2卷))体积为8的正方体的顶点都在同一球面上,则该球面的表面积为A .12πB .323πC .8πD .4π15.(2016年全国普通高等学校招生统一考试)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则该球体积V 的最大值是A .4πB .92πC .6πD .323π 16.(2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ带解析))(2015新课标全国I 理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A .14斛B .22斛C .36斛D .66斛17.(2013年全国普通高等学校招生统一考试理科数学(新课标1卷))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为A .5003πcm 3B .8663πcm 3C .13723πcm 3D .10003πcm 3 18.(2013年全国普通高等学校招生统一考试))已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为A .26 B 3 C .23 D .22二、填空题19.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))如图,在三棱锥P –ABC 的平面展开图中,AC =1,3AB AD ==,AB ⅠAC ,AB ⅠAD ,ⅠCAE =30°,则cosⅠFCB =______________.20.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m Ⅰ平面α,则m Ⅰl .则下述命题中所有真命题的序号是__________.Ⅰ14p p ∧Ⅰ12p p ∧Ⅰ23p p ⌝∨Ⅰ34p p ⌝∨⌝21.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))已知ⅠACB=90°,P 为平面ABC 外一点,PC =2,点P 到ⅠACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为___________.22.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体,其中O 为长方体的中心,,,,E F G H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为30.9/g cm ,不考虑打印损耗,制作该模型所需原料的质量为___________g .23.(2018年全国普通高等学校招生统一考试文数(全国卷II))已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30,若SAB的面积为8,则该圆锥的体积为__________.24.(2018年全国普通高等学校招生统一考试)已知三棱锥S ABC-的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA AC=,SB BC=,三棱锥S ABC-的体积为9,则球O的表面积为______.25.(2017年全国普通高等学校招生统一考试理科数学(新课标1卷))如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,ⅠDBC,ⅠECA,ⅠF AB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起ⅠDBC,ⅠECA,ⅠF AB,使得D,E,F重合,得到三棱锥.当ⅠABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为______.26.(2017年全国普通高等学校招生统一考试)长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为__________.27.(2016年全国普通高等学校招生统一考试)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:Ⅰ当直线AB与a成60°角时,AB与b成30°角;Ⅰ当直线AB与a成60°角时,AB与b成60°角;Ⅰ直线AB与a所成角的最小值为45°;Ⅰ直线AB与a所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号)28.(2013年全国普通高等学校招生统一考试文科数学(新课标1卷带解析))已知H是球O的直径AB上一点, :1:2AH HB=,AB⊥平面α,H为垂足, α截球O所得截面的面积为π,则球O的表面积为_______.三、双空题29.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.四、解答题30.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,D为圆锥的顶点,O是圆锥底面的圆心,ABC是底面的内接正三角形,P为DO上一点,ⅠAPC=90°.(1)证明:平面P ABⅠ平面P AC;(2)设DO23π,求三棱锥P−ABC的体积.32.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,已知三棱柱ABC –A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN Ⅰ平面EB 1C 1F ;(2)设O 为ⅠA 1B 1C 1的中心,若AO =AB =6,AO //平面EB 1C 1F ,且ⅠMPN =π3,求四棱锥B –EB 1C 1F 的体积.34.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥;(2)点1C 在平面AEF 内.36.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,ⅠBAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN Ⅰ平面C 1DE ;(2)求点C 到平面C 1DE 的距离.38.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⅠEC 1.(1)证明:BE Ⅰ平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积.40.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))图1是由矩形,ADEB Rt ABC ∆和菱形BFGC组成的一个平面图形,其中1,2AB BE BF ===, 60FBC ∠=,将其沿,AB BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明图2中的,,,A C G D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的四边形ACGD 的面积.42.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ⅠACM 折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.44.(2018年全国普通高等学校招生统一考试文数(全国卷II ))如图,在三棱锥P ABC -中,22AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.46.(2018年全国卷Ⅰ文数高考试题)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.49.(2017年全国普通高等学校招生统一考试文科数学(新课标2卷))四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= (1)证明:直线//BC 平面PAD ; (2)若ⅠPCD 面积为7,求四棱锥P ABCD -的体积.51.(2017年全国普通高等学校招生统一考试文科数学(新课标3))如图,四面体ABCD 中,ⅠABC 是正三角形,AD =CD .(1)证明:AC ⅠBD ;(2)已知ⅠACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⅠEC ,求四面体ABCE与四面体ACDE 的体积比.53.(2016年全国普通高等学校招生统一考试)如图,已知正三棱锥P -ABC 的侧面是直角三角形,PA=6,顶点P 在平面ABC 内的正投影为点D ,D 在平面PAB 内的正投影为点E ,连结PE 并延长交AB 于点G.(Ⅰ)证明:G 是AB 的中点;(Ⅰ)在图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.55.(2016年全国普通高等学校招生统一考试文科数学(新课标2卷))如图,菱形ABCD 的对角线AC 与BD 交于点O ,点,E F 分别在,AD CD 上,,AE CF EF =交BD 于点H ,将DEF ∆沿EF 折起到D EF ∆'的位置.(Ⅰ)证明:AC HD ⊥';(Ⅰ)若55,6,,224AB AC AE OD ==='=D ABCFE '-的体积.57.(2016年全国普通高等学校招生统一考试数学)如图,四棱锥P ABC -中,PA ⊥平面ABCD ,AD BC ∥,3AB AD AC ===,4PABC ,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN ∥平面PAB ;(II )求四面体N BCM -的体积.59.(2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面,(I )证明:平面AEC ⊥平面BED ; (II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -6,求该三棱锥的侧面积.61.(2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ))如图,长方体1111ABCD A B C D -中,116,10,8AB BC AA ===,点,E F 分别在1111,A B D C 上,114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由);(2)求平面α把该长方体分成的两部分体积的比值.63.(2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ))如图,三棱柱中,侧面为菱形,的中点为,且平面.(1)证明:(2)若,求三棱柱的高.65.(2013年全国普通高等学校招生统一考试文科数学(新课标1卷))如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=.(1)证明:; (2)若,,求三棱柱111ABC A B C -的体积.68.(2012年全国普通高等学校招生统一考试文科数学(课标卷))如图,三棱柱111ABC A B C -中,侧棱垂直底面,ⅠACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点.(I) 证明:平面BDC Ⅰ平面1BDC(Ⅰ)平面1BDC 分此棱柱为两部分,求这两部分体积的比.。
2019届高考数学复习立体几何与空间向量8.1简单几何体的结构三视图和直观图学案理北师大版

§8.1简单几何体的结构、三视图和直观图1.简单几何体的结构特征(1)旋转体①圆柱可以由矩形绕其一边所在直线旋转得到.②圆锥可以由直角三角形绕其直角边所在直线旋转得到.③圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上、下底中点连线所在直线旋转得到,也可由平行于底面的平面截圆锥得到.④球可以由半圆或圆绕直径所在直线旋转得到.(2)多面体①棱柱的侧棱都平行且相等,上、下底面是全等的多边形.②棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.③棱台可由平行于底面的平面截棱锥得到,其上、下底面是相似多边形.2.直观图画直观图常用斜二测画法,其规则是:(1)在已知图形中建立直角坐标系xOy.画直观图时,它们分别对应x′轴和y′轴,两轴交于点O′,使∠x′O′y′=45°,它们确定的平面表示水平平面;(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴和y′轴的线段;(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的12.3.三视图(1)主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.(2)在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓线画实线,看不见的轮廓线面虚线.(3)同一物体放置的位置不同,所画的三视图可能不同.(4)清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置. 知识拓展1.常见旋转体的三视图(1)球的三视图都是半径相等的圆.(2)水平放置的圆锥的主视图和左视图均为全等的等腰三角形. (3)水平放置的圆台的主视图和左视图均为全等的等腰梯形. (4)水平放置的圆柱的主视图和左视图均为全等的矩形. 2.斜二测画法中的“三变”与“三不变” “三变”⎩⎪⎨⎪⎧坐标轴的夹角改变与y 轴平行的线段的长度变为原来的一半图形改变“三不变”⎩⎪⎨⎪⎧平行性不改变与x ,z 轴平行的线段的长度不改变相对位置不改变题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( × ) (2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( × )(3)夹在两个平行的平面之间,其余的面都是梯形,这样的几何体一定是棱台.( × ) (4)正方体、球、圆锥各自的三视图中,三视图均相同.( × ) (5)用两平行平面截圆柱,夹在两平行平面间的部分仍是圆柱.( × ) (6)菱形的直观图仍是菱形.( × ) 题组二 教材改编2.下列说法正确的是( )A.相等的角在直观图中仍然相等B.相等的线段在直观图中仍然相等C.正方形的直观图是正方形D.若两条线段平行,则在直观图中对应的两条线段仍然平行答案 D解析由直观图的画法规则知,角度、长度都有可能改变,而线段的平行性不变.3.在如图所示的几何体中,是棱柱的为________.(填写所有正确的序号)答案③⑤题组三易错自纠4.某简单几何体的主视图是三角形,则该几何体不可能是( )A.圆柱B.圆锥C.四面体D.三棱柱答案 A解析由三视图知识知,圆锥、四面体、三棱柱(放倒看)都能使其主视图为三角形,而圆柱的主视图不可能为三角形.5.(2018·珠海质检)将正方体(如图1所示)截去两个三棱锥,得到如图2所示的几何体,则该几何体的左视图为( )答案 B解析左视图中能够看到线段AD1,应画为实线,而看不到B1C,应画为虚线.由于AD1与B1C 不平行,投影为相交线,故选B.6.正三角形AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是________.答案616a 2 解析 画出坐标系x ′O ′y ′,作出△OAB 的直观图O ′A ′B ′(如图),D ′为O ′A ′的中点.易知D ′B ′=12DB (D 为OA 的中点),∴S △O ′A ′B ′=12×22S △OAB =24×34a 2=616a 2.题型一 简单几何体的结构特征1.给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥; ③棱台的上、下底面可以不相似,但侧棱长一定相等. 其中正确命题的个数是( ) A .0 B .1 C .2 D .3 答案 A解析①不一定,只有当这两点的连线平行于轴时才是母线;②不一定,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图所示,它是由两个同底圆锥组成的几何体;③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.2.(2018·青岛模拟)以下命题:①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;②圆柱、圆锥、圆台的底面都是圆面;③一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数为( )A.0 B.1 C.2 D.3答案 B解析由圆台的定义可知①错误,②正确.对于命题③,只有平行于圆锥底面的平面截圆锥,才能得到一个圆锥和一个圆台,③不正确.思维升华 (1)关于简单几何体的结构特征辨析关键是紧扣各种简单几何体的概念,要善于通过举反例对概念进行辨析,即要说明一个命题是错误的,只需举一反例即可.(2)圆柱、圆锥、圆台的有关元素都集中在轴截面上,解题时要注意用好轴截面中各元素的关系.(3)既然棱(圆)台是由棱(圆)锥定义的,所以在解决棱(圆)台问题时,要注意“还台为锥”的解题策略.题型二简单几何体的三视图命题点1 已知几何体,识别三视图典例(2017·贵州七校联考)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )A .①②⑥B .①②③C .④⑤⑥D .③④⑤答案 B解析 主视图应该是边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此主视图是①;左视图应该是边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此左视图是②;俯视图应该是边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③. 命题点2 已知三视图,判断几何体的形状典例 (2017·全国Ⅰ)某多面体的三视图如图所示,其中主视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16答案 B解析 观察三视图可知,该多面体是由直三棱柱和三棱锥组合而成的,且直三棱柱的底面是直角边长为2的等腰直角三角形,侧棱长为2.三棱锥的底面是直角边长为2的等腰直角三角形,高为2,如图所示.因此该多面体各个面中有两个梯形,且这两个梯形全等,梯形的上底长为2,下底长为4,高为2,故这两个梯形的面积之和为2×12×(2+4)×2=12.故选B.命题点3 已知三视图中的两个视图,判断第三个视图典例(2017·汕头模拟)一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )答案 C解析A,B,D选项满足三视图作法规则,C不满足三视图作法规则中的宽相等,故C不可能是该锥体的俯视图.思维升华三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.(3)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形状,然后再找其剩下部分三视图的可能形状.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.跟踪训练(1)(2017·全国Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90π B.63π C.42π D.36π答案 B解析 方法一 (割补法)由几何体的三视图可知,该几何体是一个圆柱截去上面虚线部分所得,如图所示.将圆柱补全,并将圆柱从点A 处水平分成上下两部分.由图可知,该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V =π×32×4+π×32×6×12=63π.故选B.方法二 (估值法)由题意知,12V 圆柱<V 几何体<V 圆柱,又V 圆柱=π×32×10=90π,∴45π<V 几何体<90π.观察选项可知只有63π符合.故选B.(2)如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的左视图和俯视图,则该锥体的主视图可能是( )答案 A解析 由俯视图和左视图可知原几何体是四棱锥,底面是长方形,内侧的侧面垂直于底面,所以主视图为A.题型三 简单几何体的直观图典例 (2018·福州调研)已知等腰梯形ABCD ,上底CD =1,腰AD =CB =2,下底AB =3,以下底所在直线为x 轴,则由斜二测画法画出的直观图A ′B ′C ′D ′的面积为________. 答案22解析 如图所示,作出等腰梯形ABCD 的直观图.因为OE =(2)2-1=1,所以O ′E ′=12,E ′F =24,则直观图A ′B ′C ′D ′的面积S ′=1+32×24=22.思维升华 用斜二测画法画直观图的技巧在原图形中与x 轴或y 轴平行的线段在直观图中与x ′轴或y ′轴平行,原图中不与坐标轴平行的直线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.跟踪训练 (2017·贵阳联考)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC =45°,AB =AD =1,DC ⊥BC ,则这块菜地的面积为________.答案 2+22解析 如图1,在直观图中,过点A 作AE ⊥BC ,垂足为E . 在Rt△ABE 中,AB =1,∠ABE =45°,∴BE =22. 又四边形AECD 为矩形,AD =EC =1,∴BC =BE +EC =22+1, 由此还原为原图形如图2所示,是直角梯形A ′B ′C ′D ′. 在梯形A ′B ′C ′D ′中,A ′D ′=1,B ′C ′=22+1,A ′B ′=2. ∴这块菜地的面积S =12(A ′D ′+B ′C ′)·A ′B ′=12×⎝ ⎛⎭⎪⎫1+1+22×2=2+22.1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )A.球 B.三棱锥 C.正方体 D.圆柱答案 D解析球、正方体的三视图形状都相同、大小均相等.当三棱锥的三条侧棱相等且两两垂直时,其三视图的形状都相同、大小均相等.不论圆柱如何放置,其三视图的形状都不会完全相同,故选D.2.如图为几何体的三视图,根据三视图可以判断这个几何体为( )A.圆锥B.三棱锥C.三棱柱D.三棱台答案 C3.“牟合方盖”(如图1)是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图2所示,图中四边形是为体现其直观性所作的辅助线,其实际直观图中四边形不存在,当其主视图和左视图完全相同时,它的主视图和俯视图分别可能是( )A.a,b B.a,c C.c,b D.b,d答案 A解析当主视图和左视图完全相同时,“牟合方盖”相对的两个曲面正对前方,主视图为一个圆,俯视图为一个正方形,且两条对角线为实线,故选A.4.(2018·成都质检)如图,在长方体ABCD-A1B1C1D1中,点P是棱CD上一点,则三棱锥P-A1B1A的左视图是( )答案 D解析在长方体ABCD-A1B1C1D1中,从左侧看三棱锥P-A1B1A,B1,A1,A的射影分别是C1,D1,D;AB1的射影为C1D,且为实线,PA1的射影为PD1,且为虚线.故选D.5.(2018·武汉调研)一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以zOx平面为投影面,则得到的主视图可以为( )答案 A解析设O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),将以O,A,B,C为顶点的四面体补成一正方体后,由于OA⊥BC,所以该几何体以zOx平面为投影面的主视图为A. 6.(2017·黄山质检)一个正方体截去两个角后所得几何体的主视图、俯视图如图所示,则其左视图为( )答案 C解析 根据一个正方体截去两个角后所得几何体的主视图、俯视图可得几何体的直观图如图所示.所以左视图如图所示.故选C.7.(2017·东北师大附中、吉林市一中等五校联考)如图所示,在三棱锥D —ABC 中,已知AC =BC =CD =2,CD ⊥平面ABC ,∠ACB =90°.若其主视图、俯视图如图所示,则其左视图的面积为( )A. 6 B .2 C. 3 D. 2 答案 D解析 由几何体的结构特征和主视图、俯视图,得该几何体的左视图是一个直角三角形,其中一直角边为CD ,其长度为2,另一直角边为底面△ABC 的边AB 上的中线,其长度为2,则其左视图的面积S =12×2×2= 2.8.如图,在一个正方体内放入两个半径不相等的球O 1,O 2,这两个球外切,且球O 1与正方体共顶点A 的三个面相切,球O 2与正方体共顶点B 1的三个面相切,则两球在正方体的面AA 1C 1C 上的正投影是( )答案 B解析 由题意可以判断出两球在正方体的面上的正投影与正方形相切.由于两球球心连线AB 1与面ACC 1A 1不平行,故两球球心射影所连线段的长度小于两球半径的和,即两个投影圆相交,即为图B.9.(2017·福建龙岩联考)一水平放置的平面四边形OABC ,用斜二测画法画出它的直观图O ′A ′B ′C ′如图所示,此直观图恰好是一个边长为1的正方形,则原平面四边形OABC 的面积为________.答案 2 2解析 因为直观图的面积是原图形面积的24倍,且直观图的面积为1,所以原图形的面积为2 2.10.(2017·南昌一模)如图,在正四棱柱ABCD —A 1B 1C 1D 1中,点P 是平面A 1B 1C 1D 1内一点,则三棱锥P —BCD 的主视图与左视图的面积之比为________.答案 1∶1解析 根据题意,三棱锥P —BCD 的主视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;左视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,故三棱锥P—BCD的主视图与左视图的面积之比为1∶1.11.如图,点O为正方体ABCD—A′B′C′D′的中心,点E为平面B′BCC′的中心,点F 为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的射影可能是________.(填出所有可能的序号)答案①②③解析空间四边形D′OEF在正方体的平面DCC′D′上的射影是①;在平面BCC′B′上的射影是②;在平面ABCD上的射影是③,而不可能出现的射影为④中的情况.12.(2018·长沙调研)某四面体的三视图如图所示,则该四面体的六条棱的长度中,最大的是________.答案27解析由三视图可知该四面体为三棱锥V—ABC,如图,其中EC=CB=2,AE=23,VC=2,AE⊥BE,VC⊥平面ABE,所以在六条棱中,最大的棱为VA或者AB.AC2=AE2+EC2=(23)2+22=16,所以VA2=AC2+VC2=16+22=20,此时VA=20=25,AB2=AE2+EB2=(23)2+42=28,所以AB=28=27>25,所以棱长最大的为27.13.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )A .8B .7C .6D .5 答案 C解析 画出直观图,共六块.14.(2017·湖南省东部六校联考)某三棱锥的三视图如图所示,则该三棱锥的四个面的面积中,最大的面积是( )A .4 3B .8 3C .47D .8 答案 C解析 如图,设该三棱锥为P —ABC ,其中PA ⊥平面ABC ,PA =4,则由三视图可知△ABC 是边长为4的等边三角形,故PB =PC =42,所以S △ABC =12×4×23=43,S △PAB =S △PAC =12×4×4=8,S △PBC =12×4×(42)2-22=47,故四个面中面积最大的为S △PBC =47,故选C.15.(2017·泉州二模)某几何体的三视图如图所示,则该几何体的左视图中的虚线部分是( )A.圆弧B.抛物线的一部分C.椭圆的一部分D.双曲线的一部分答案 D解析根据几何体的三视图,可得左视图中的虚线部分是由平行于旋转轴的平面截圆锥所得,故左视图中的虚线部分是双曲线的一部分,故选D.16.(2018·济南模拟)一只蚂蚁从正方体ABCD—A1B1C1D1的顶点A出发,经正方体的表面,按最短路线爬行到顶点C1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的主视图的是( )A.①② B.①③C.③④ D.②④答案 D解析由点A经正方体的表面,按最短路线爬行到达顶点C1的位置,共有6种路线(对应6种不同的展开方式),若把平面ABB1A1和平面BCC1B1展开到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过BB1的中点,此时对应的主视图为②;若把平面ABCD和平面CDD1C1展开到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过CD的中点,此时对应的主视图为④.而其他几种展开方式对应的主视图在题中没有出现.故选D.。
2019届高三理科数学第二轮专题复习配套文档专题四 第3讲立体几何中的向量方法

第3讲立体几何中的向量方法[真题再现]1.(2018·课标Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC使点C到达点P的位置,且PF⊥BF。
(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.[解](1)证明:由已知可得BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD。
(2)解:如图,作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD。
以H为坐标原点,错误!的方向为y轴正方向,|错误!|为单位长,建立如图所示的空间直角坐标系H.xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=错误!.又PF=1,EF=2,所以PE⊥PF.所以PH=错误!,EH=错误!.则H(0,0,0),P错误!,D错误!,错误!=错误!,错误!=错误!.又错误!为平面ABFD的法向量,设DP与平面ABFD所成角为θ,则sin θ=错误!=错误!=错误!。
所以DP与平面ABFD所成角的正弦值为错误!.2.(2018·课标Ⅱ)如图,在三棱锥P-ABC中,AB=BC=22,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M。
P A-C为30°,求PC与平面P AM所成角的正弦值[解](1)证明:因为P A=PC=AC=4,O为AC的中点,所以OP⊥AC,且OP=2错误!.如图,连接OB.因为AB=BC=错误!AC,所以△ABC为等腰直角三角形,且OB ⊥AC,OB=错误!AC=2。
由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC,OB∩AC=O,得PO⊥平面ABC.(2)解:如图,以O为坐标原点,错误!的方向为x轴正方向,建立空间直角坐标系O。
xyz。
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2错误!),错误!=(0,2,2错误!).取平面P AC的一个法向量错误!=(2,0,0).设M (a ,2-a,0)(0≤a ≤2),则错误!=(a ,4-a,0).设平面P AM 的法向量为n =(x ,y ,z ).由AP ,→·n =0,错误!·n =0得错误!可取y =错误!a ,得平面P AM 的一个法向量为n =(错误!(a -4),错误!a ,-a ),所以cos 错误!,n =错误!。
2019衡水名师原创理科数学专题卷:专题十一《立体几何》

2019衡水名师原创理科数学专题卷专题十一 立体几何考点33:空间几何体的结构特征、三视图、直观图表面积和体积(1-8题,13-15题,17-19题) 考点34:空间点、线、面的位置关系(9,10题) 考点35:直线、平面平行的判定与性质(16,20题)考点36:直线、平面垂直的判定与性质(17-19,21,22题) 考点37:与空间角和距离有关的计算(11,12题,20-22题)考试时间:120分钟 满分:150分说明:请将选择题正确答案填写在答题卡上,主观题写在答题纸上第I 卷(选择题)一、选择题1.如图,三棱锥V ABC -的底面ABC 是等腰直角三角形, AB BC =,侧面VAC 与底面垂直,已知其正视图的面积为3,则其侧视图的面积为( )A.B. 32C. 34D. 2.某几何体的三视图如图所示,则该几何体的体积为( )A.4B.6C.203 D.2233某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A.10B.12C.14D.164.某几何体的三视图如图所示,则该几何体的体积为( )A.7B.15 2C.23 3D.47 65某几何体三视图如图1示,则此几何体的表面积为( )A.B.C.D.6.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )A. 1B.C.D. 27.如图,正方体1111ABCD A BC D -3以顶点A 为球心, 2为半径作一个球,则图中球面与正方体的表面相交得到的两段弧长之和等于( )A. 56πB. 23πC. πD.76π 8.如图为某几何体的三视图,求该几何体的内切球的表面积为( )A.14π B. 3π C. 4πD. 43π9.已知m ,n 是两条不同的直线, α,β,γ是三个不同的平面,下列命题中正确的是( )A.若m α⊥,m β⊥,则αβ⊥B.若αγ⊥,βγ⊥,则//αβC.若//m α,//m β,则//αβD.若m α⊥,//n α,则m n ⊥10.如图,在正方形ABCD 中,点E ,F 分别是BC ,AD 的中点,将ABF ∆沿BF 所在直线进行翻折,将CDE ∆沿DE 所在直线进行翻折,在翻折过程中( )A.点A 与点C 在某一位置可能重合B.点A 与点C 3ABC.直线AB 与直线CD 可能垂直D.直线AF 与直线CE 可能垂直11.已知三棱柱111ABC A B C -,侧棱与底面垂直,1112AA AB BC ===,AB BC ⊥,点,,?P M N 分别是棱1111,,BB CC AC 的中点,则异面直线AP 与MN 所成角的余弦值为( )A.B.6C. 3-D.12.已知直二面角,,,l A AC l C αβα--∈⊥为垂足,,,B BD l D β∈⊥为垂足.若2,1AB AC BD ===,则D 到平面ABC 的距离等于( )A.B.2C.3D.二、填空题13.一个几何体的三视图如图所示(单位:m ),则该几何体的体积为__________3m 。
2019年高考理科数学三年高考真题精品分类汇编:24 立体几何的位置关系-附答案中高考前沿
路漫漫其修远兮,吾将上下而求索!2019-2020年备考青霄有路终须到,金榜无名誓不还!2019-2020年备考专题24 立体几何的位置关系考纲解读明方向考点内容解读要求高考示例常考题型预测热度1.点、线、面的位置关系理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.·公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内.·公理2:过不在同一条直线上的三点,有且只有一个平面.·公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.·公理4:平行于同一条直线的两条直线互相平行.·定理:空间中如果一个角的两边与另一个角的两边分别平行,那么理解2016浙江,2;2015广东,8;2014广东,7;2013课标全国Ⅱ,4;2013江西,8选择题★★☆2.异面直线所成的角掌握2017课标全国Ⅱ,10;2017课标全国Ⅲ,16;2016课标全国Ⅰ,11;2015四川,14;2015广东,18选择题填空题★★★这两个角相等或互补分析解读 1.会用平面的基本性质证明点共线、线共点、点线共面问题;会用反证法证明有关异面或共面问题.2.会判定和证明两条直线异面;会应用三线平行公理和等角定理及推论解决有关问题,会求两条异面直线所成的角;了解两条异面直线间的距离.3.高考对本节内容的考查常以棱柱、棱锥为依托,求异面直线所成的角,分值约为5分,属中档题.考点内容解读要求高考示例常考题型预测热度1.直线与平面平行的判定与性质①以立体几何中的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,理解以下判定定理.如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.理解以下性质定理,并能够证明.如果一条直线与一个平面平行,那么经过该直线的任一个平面与此平面的交线和该直线平行.如果两个平行平面同时和第三个掌握2017江苏,15;2016江苏,16;2016四川,18;2015安徽,5;2015江苏,16;2013广东,6选择题解答题★★★2.平面与平面平行的判定与掌握2016课标全国Ⅱ,14;2013江苏,16选择题解答题★★☆。
高考数学(理)真题专题汇编:空间立体几何

高考数学(理)真题专题汇编:空间立体几何一、选择题(本题共9道小题,每小题0分,共0分)1.【来源】2019年高考真题——数学(浙江卷)设三棱锥V -ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P -AC -B 的平面角为γ,则( )A. ,βγαγ<<B. ,βαβγ<<C. ,βαγα<<D. ,αβγβ<<2.【来源】2019年高考真题——数学(浙江卷)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh =柱体,其中S 是柱体的底面积,h 是柱体的高,若某柱体的三视图如图所示,则该柱体的体积(cm 3)是( )A. 158B. 162C. 182D. 3243.【来源】2019年高考真题——理科数学(全国卷Ⅱ) 设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面4.【来源】2019年高考真题——理科数学(全国卷Ⅲ)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED的中点,则A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线5.【来源】0(08年全国卷2)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B. C. D.26.【来源】0(08年四川卷文)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于( )(A)(B)(C)(D)7.【来源】0(08年北京卷)如图,动点在正方体的对角线上.过点作垂直于平面的直线,与正方体表面相交于.设,,则函数的图象大致是()8.【来源】2011年高考数学理(安徽)一个空间几何体得三视图如图所示,则该几何体的表面积为(A)48+(B)32817+(C)48817(D)509.【来源】2011年高考数学理(全国新课标)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为二、填空题10.【来源】2019年高考真题——理科数学(北京卷)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.12.【来源】2019年高考真题——理科数学(天津卷)已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .13.【来源】2019年高考真题——理科数学(全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________.15.【来源】(07年浙江卷文)已知点O 在二面角α-AB -β的棱上,点P 在α内,且∠POB =45°.若对于β内异于O 的任意一点Q ,都有∠POQ ≥45°,则二面角α-AB -β的取值范围是_________.16.【来源】2011年高考数学理(全国新课标)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,23AB BC ==,则棱锥O ABCD -的体积为 。
2019届北京市各区高三数学理科期末试卷【立体几何类题】汇集及答案解析

北京市各区2019届高三数学理科期末试卷【立体几何类题】汇集【海淀】17.(本小题满分14分)在四棱锥P ABCD -中,平面ABCD ⊥平面PCD ,底面ABCD 为梯形,//AB CD ,AD PC ⊥且01,2,120AB AD DC DP PDC ====∠=(Ⅰ)求证:AD PDC ⊥平面;(Ⅱ)求二面角B-PD-C 的余弦值;(Ⅲ)若M 是棱PA 的中点,求证:对于棱BC 上任意一点F ,MF 与PC 都不平行.【东城】(17)(本小题14分)如图1,在四边形ABCD 中,AD BC ,2BC AD =,E ,F 分别为,AD BC 的中点,AE EF =,AF =.将四边形ABFE 沿EF 折起,使平面ABFE ⊥平面EFCD (如图2),G 是BF 的中点.(Ⅰ)证明:AC EG ⊥;(Ⅱ)在线段BC 上是否存在一点H ,使得DH 平 面ABFE ?若存在,求BHBC的值;若不存在,说明理由;--的大小. (Ⅲ)求二面角D AC F【朝阳】17.(本小题满分14分)如图,三棱柱111ABC A B C -的侧面11BCC B 是平行四边形,11BC C C ⊥,平面11A C CA ⊥平面11BCC B ,且,E F 分别是11,BC A B 的中点.(Ⅰ)求证://EF 平面11AC CA ;(Ⅱ)当侧面11A C CA 是正方形,且11BC C C =时,(ⅰ)求二面角1F BC E --的大小;(ⅱ)在线段EF 上是否存在点P ,使得AP EF ⊥?若存在,指出点P 的位置;若不存在,请说明理由.【丰台】16.(本小题14分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,侧棱PA ⊥底面ABCD ,Q 为棱PD 的中点,PA AB =.(Ⅰ)求证:AQ CD ⊥;(Ⅱ)求直线PC 与平面ACQ 所成角的正弦值;(Ⅲ)求二面角C AQ D --的余弦值.【西城】16.(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧面11B BCC 为正方形,M ,N分别是11A B ,AC 的中点,AB ⊥平面BCM .(Ⅰ)求证:平面11B BCC ⊥平面11A ABB ;(Ⅱ)求证:1//A N 平面BCM ;(Ⅲ)若11A ABB 是边长为2的菱形,求直线1A N 与平面1MCC 所成角的正弦值.11【石景山】17.(本小题14分)如图,在AOB △中,90,2,1AOB AO OB ∠=︒==.AOC △可以通过AOB △以直线AO 为轴旋转得到,且OB OC ⊥,动点D 在斜边AB 上.(Ⅰ)求证:平面COD ⊥平面AOB ;(Ⅱ)当D 为AB 的中点时,求二面角B CD O --的余弦值;(Ⅲ)求CD 与平面AOB 所成的角中最大角的正弦值.【解析卷】北京市各区2019届高三数学理科期末试卷【立体几何类题】汇集【海淀】17.(本小题满分14分)在四棱锥P ABCD -中,平面ABCD ⊥平面PCD ,底面ABCD 为梯形,//AB CD ,AD PC ⊥且01,2,120AB AD DC DP PDC ====∠=(Ⅰ)求证:AD PDC ⊥平面;(Ⅱ)求二面角B-PD-C 的余弦值;(Ⅲ)若M 是棱PA 的中点,求证:对于棱BC 上任意一点F ,MF 与PC 都不平行.解:(Ⅰ)在平面PCD 中过点D 作DH DC ⊥,交PC 于H因为平面ABCD ⊥平面PCD DH ⊂平面PCD 平面ABCD I 平面PCD CD =所以DH ⊥平面ABCD因为AD ⊂平面ABCD 所以DH AD⊥又AD PC ⊥,且PC DH H=I 所以AD ⊥平面PCD(Ⅱ)因为AD ⊥平面PCD ,所以AD CD ⊥又DH CD ⊥,DH AD ⊥以D 为原点,DA DC DH ,,所在直线分别为,,x y z 轴,建立空间直角坐标系所以(,,),(,,),(,(,,),(,,)D A P C B -00020001020210,因为AD ⊥平面PCD ,所以取平面PCD 的法向量为(,,)DA =200uu u r设平面PBD 的法向量为(,,)n x y z =r因为(,(,,)DP DB =-=01210uu u r uu u r ,所以n DP n DB ⎧⋅=⎪⎨⋅=⎪⎩00r uuu rr uuu r所以y x y ⎧-+=⎪⎨+=⎪⎩020令2z =,则y x =-=,所以()n =2r所以cos ,||||AD n AD n AD n ⋅<>===-19uuu r ruuu r r uuu u r r 由题知B PD C --为锐角,所以B PD C --的余弦值为19(Ⅲ)假设棱BC 上存在点F ,使得MF PC ,设BF BC λ=,所以3(1,,(2,1,0)22MF MB BF λ=+=+- 因为MF PC,所以(0,3,MF PC μμ==所以有12033λλμ⎧⎪-=⎪⎪+=⎨⎪⎪=⎪⎩,这个方程组无解所以假设错误,即问题得证【东城】(17)(本小题14分)如图1,在四边形ABCD 中,AD BC ,2BC AD =,E ,F 分别为,AD BC 的中点,AE EF =,AF =.将四边形ABFE 沿EF 折起,使平面ABFE ⊥平面EFCD (如图2),G 是BF 的中点.(Ⅰ)证明:AC EG ⊥;(Ⅱ)在线段BC 上是否存在一点H ,使得DH 平 面ABFE ?若存在,求BHBC的值;若不存在,说明理由;(Ⅲ)求二面角D AC F --的大小.(17)(共14分)解:(Ⅰ)在图1中,,2,AE EF AF AE ==可得△AEF 为等腰直角三角形,AE EF ⊥.因为AD BC , 所以,.EF BF EF FC ⊥⊥因为平面ABFE ⊥平面,EFCD EF 且两平面交于,CF CDEF ⊂平面,所以CF ABFE ⊥平面.又EG ABFE ⊂平面,故CF EG ⊥;由G 为中点,可知四边形AEFG 为正方形,AF EG ⊥所以;又AF FC F = ,EG AFC .⊥所以平面AC AFC ⊂又平面,.AC EG ⊥所以.............................4分(II )由(Ⅰ)知:FE ,FC ,FB 两两垂直,F xyz -如图建立空间直角坐标系,设1FE =,则(0,0,0),(0,2,0),(0,0,2),(1,1,0).F C B D H BC 设是线段上一点,[0,1].BH BC λλ∈=则存在使得(0,2,22)(1,21,22).H DH λλλλ-=---因此点,(0,2,0).FC ABFE FC = 由(Ⅰ)知为平面的法向量,DH ABFE ⊄因为平面,0DH ABFE DH FC ⋅=所以平面当且仅当,(12122)(0,2,0)=0.λλ⋅即-,-,-1=.2λ解得1.2BH BC H DH ABFE BC =所以在线段上存在点使得平面此时, ..........................9分(III )(1,0,1)(1,0,0)(0,0,1).A E G 设,,由(I)可得,(1,0,1).EG AFC EG =-是平面的法向量,(0,1,1),(1,1,0),AD CD =-=-设平面ACD 的法向量为(,,)x y z =n ,由0,0AD CD ⎧⋅=⎪⎨⋅=⎪⎩ ,n n 00.y z x y -=⎧⎨-=⎩,即1,1, 1.x y z ===令则(1,1,1).于是n =cos ,0.EG EG EG ⋅<>==所以nn n所以二面角90.D AC F --的大小为.............................14分【朝阳】17.(本小题满分14分)如图,三棱柱111ABC A B C -的侧面11BCC B 是平行四边形,11BC C C ⊥,平面11A C CA ⊥平面11BCC B ,且,E F 分别是11,BC A B 的中点.(Ⅰ)求证://EF 平面11AC CA ;(Ⅱ)当侧面11A C CA 是正方形,且11BC C C =时,(ⅰ)求二面角1F BC E --的大小;(ⅱ)在线段EF 上是否存在点P ,使得AP EF ⊥?若存在,指出点P 的位置;若不存在,请说明理由.17.(本小题满分14分)证明:(Ⅰ)取11AC 中点G ,连FG ,连GC.在△111A B C 中,因为,F G 分别是1111,A B A C 中点,所以11FG B C //,且1112FG B C =.在平行四边形11BCC B 中,因为E 是BC 的中点,所以11EC B C //,且1112EC B C =.所以EC FG //,且EC FG =.所以四边形FECG 是平行四边形.所以FE GC //.又因为FE ⊄平面11AC CA ,GC ⊂平面11AC CA ,所以//EF 平面11AC CA .…………………4分(Ⅱ)因为侧面11A C CA 是正方形,所以111AC C C ⊥.又因为平面11A C CA ⊥平面11BCC B ,且平面11A C CA 平面111BCC B C C =,所以11A C ⊥平面11BCC B .所以111AC C B ⊥.又因为11BC C C ⊥,以1C 为原点建立空间直角坐标系1C xyz -,如图所示.设1C C a =,则11(0,,),(,0,0),(0,,0),(0,0,),(,,0)A a a B a C a A a B a a -,(,,0),(,,)22222a a a a a E F -.(ⅰ)设平面1FBC 的一个法向量为(,,z)x y =n .由110,0C B C F ⎧⋅=⎪⎨⋅=⎪⎩ n n 得0,0.222ax a a ax y z =⎧⎪⎨-+=⎪⎩即0,.x y z =⎧⎨=⎩令1y =,所以(0,1,1)=n .又因为11A C ⊥平面1BC E ,所以11(0,0,)C A a =是平面1BC E 的一个法向量.所以1111112cos ,22C A a C A a C A ⋅===⋅⋅n n n .由图可知,二面角1F BC E --为钝角,所以二面角1F BC E --的大小为34π.……………10分(ⅱ)假设在线段EF 上存在点P ,使得AP EF ⊥.设,[0,1]EPEFλλ=∈,则EP EF λ= .因为(,,)(0,,)222a a a AP AE EP AE EF a a λλ=+=+=--+- (,,)222a a aa a λλ=---+,又AP EF ⊥,所以210()()()()022224a a a a AP EF a a a a λλλλ⋅=⨯+---+-+=+= .所以0[0,1]λ=∈.故点P 在点E 处时,有AP EF⊥.…………14分【丰台】16.(本小题14分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,侧棱PA ⊥底面ABCD ,Q 为棱PD 的中点,PA AB =.(Ⅰ)求证:AQ CD ⊥;(Ⅱ)求直线PC 与平面ACQ 所成角的正弦值;(Ⅲ)求二面角C AQ D --的余弦值.16.(共14分)解:(Ⅰ)因为⊥PA 底面ABCD ,⊂CD 底面ABCD ,所以CD PA ⊥,正方形ABCD 中CD AD ⊥,又因为A AD PA = ,所以⊥CD 平面PAD ,因为⊂AQ 平面PAD ,所以CD AQ ⊥.…………….4分(Ⅱ)正方形ABCD 中AD AB ⊥,侧棱⊥PA 底面ABCD .如图建立空间直角坐标系O xyz -,不妨设2=AB .依题意,则(0,0,0),(2,2,0),(0,0,2),(0,1,1)A C P Q ,所以()()()110022222,,AQ ,,,AC ,,,CP ==--=.设平面ACQ 的法向量=n ()z ,y ,x ,因为00AC AQ ⎧=⎪⎨=⎪⎩ n n ,所以⎩⎨⎧=+=+022z y y x .令1=x ,得⎪⎩⎪⎨⎧=-==111z y x ,即=n ()111,,-,所以1cos ,3||||CP CP CP <>==⋅n n n ,所以直线PC 与平面ACQ 所成角的正弦值为31;………………11分(Ⅲ)由(Ⅰ)知⊥CD 平面PAD ,所以()0,0,2=DC 为平面PAD 的法向量,因为3cos ,3||||DC DC DC <>==⋅n n n ,且二面角D AQ C --为锐角,所以二面角D AQ C --的余弦值为33.…………………14分【西城】16.(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧面11B BCC 为正方形,M ,N11分别是11A B ,AC 的中点,AB ⊥平面BCM .(Ⅰ)求证:平面11B BCC ⊥平面11A ABB ;(Ⅱ)求证:1//A N 平面BCM ;(Ⅲ)若11A ABB 是边长为2的菱形,求直线1A N 与平面1MCC 所成角的正弦值.16.(本小题满分14分)解:(Ⅰ)因为AB ⊥平面BCM ,BC ⊂平面BCM ,所以AB BC ⊥.………………1分由正方形11B BCC ,知1BB BC ⊥,又因为1AB BB B = ,所以BC ⊥平面11A ABB .………………3分又因为BC ⊂平面11B BCC ,所以平面11B BCC ⊥平面11A ABB .………………4分(Ⅱ)设BC 中点Q ,连结NQ MQ ,.因为M ,N 分别是11A B ,AC 的中点,所以//NQ AB ,且12NQ AB =.111又因为11//AB A B ,且11AB A B =,所以1//NQ A M ,且1NQ A M =.所以四边形1A MQN 为平行四边形.所以1//A N MQ .………………6分又因为MQ ⊂平面BCM ,1A N ⊄平面BCM ,所以1//A N 平面BCM .………………8分(Ⅲ)由(Ⅰ)可知BA ,BM ,BC 两两互相垂直,因此以B 为原点,以BA ,BM ,BC 分别为x 轴,y 轴,z 轴建立空间直角坐标系B xyz -,如图所示.…………9分因为11A ABB 是边长为2的菱形,M 为11A B 的中点,且11A B BM ⊥,易得1160BB A ∠= ,则(0,0,0)B ,(2,0,0)A,(0,0)M ,(0,0,2)C,1(1,0)A,1(1,0)B -,1(2)C -,(1,0,1)N .………………10分所以1(0,A N −−→=-,1(1,0,2)MC −−→=-,1(1,0)CC −−→=-.设平面1MCC 的法向量为(,,)n x y z =,则110,0,MC CC −−→−−→⎧⋅=⎪⎨⎪⋅=⎩n n即20,0.x z x -+=⎧⎪⎨-+=⎪⎩令2y =,则x =,z =.所以2,=n .………………12分设直线1A N 与平面1MCC 所成角为α,则111sin |cos ,|||||A N A N A N α−−→−−→−−→⋅=〈〉=n nn 38=.因此直线1A N 与平面1MCC 所成角的正弦值为38.………………14分【石景山】17.(本小题14分)如图,在AOB △中,90,2,1AOB AO OB ∠=︒==.AOC △可以通过AOB △以直线AO 为轴旋转得到,且OB OC ⊥,动点D 在斜边AB 上.(Ⅰ)求证:平面COD ⊥平面AOB ;(Ⅱ)当D 为AB 的中点时,求二面角B CD O --的余弦值;(Ⅲ)求CD 与平面AOB 所成的角中最大角的正弦值.17.(本小题14分)(Ⅰ)证明:在AOC △中,⊥AO OC ,∵⊥OB OC ,且AO OB =O I ,∴⊥OC 平面AOB ,又⊂OC 平面COD ,∴平面COD ⊥平面AOB .(Ⅱ)解:如图建立空间直角坐标系-xyz O ,∵D 为AB 的中点,∴(000)O ,,,(002)A ,,,(010)B ,,,(100)C ,,,1(01)2D ,,,∴(100)OC =uuu r ,,,1(01)2OD =uuu r ,,,(110)-BC =uu u r ,,,1(01)2-BD =uu u r ,,设1111()=n x y z u r,,为平面OCD 的法向量,∴1100⎧⋅⎪⎨⋅⎪⎩n OC =n OD =u r uuu r u r uuu r,,即1110102⎧⎪⎨⎪⎩x =y +z =,,令1=1z ,则1=2-y ,∴1(021)=-n u r,,是平面BCD 的一个法向量,设2222()=n x y z u u r,,为平面OCD 的法向量,∴2200⎧⋅⎪⎨⋅⎪⎩n BC =n BD =u u r uu u r u u r uu u r,,即2222010-=⎧⎪⎨-⎪⎩x y y +z =,令2=1z ,则2=2x ,2=2y ,∴2(221)=n u u r,,是平面OCD 的一个法向量,∴1212125cos 5||||⋅<>===-⋅n n n n n n u r u u ru r u u r u r u u r ,,∴二面角--B CD O的余弦值为5.(Ⅲ)解法一:∵⊥OC 平面AOB ,∴∠CDO 为CD 与平面AOB 所成的角,∵1=OC ,∴点O 到直线AB 的距离最小时,∠CDO 的正弦值最大,即当⊥OD AB 时,∠CDO 的正弦值最大,此时5=OD,∴5=CD ,∴sin 3∠CDO =.解法二:设([0,1])AD =AB ∈λλuuu r uu u r,所以(0,,22)D λλ-.(1,,22)CD =λλ--uu u r.平面AOB 的法向量(1,0,0)n =r,所以||sin ||||n CD n CD θ⋅===r uu u r r uu u r 所以当45λ=时,CD 与平面AOB所成的角最大,sin 3θ=.。
2019届二轮(理科数学) 知识拓展 立体几何中的翻折问题及动点的轨迹问题

知识拓展:立体几何中的翻折问题及动点的轨迹问题一、选择题1.(2015·浙江卷)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD 翻折成△A′CD,所成二面角A′-CD-B的平面角为α,则( B )(A)∠A′DB≤α(B)∠A′DB≥α(C)∠A′CB≤α(D)∠A′CB≥α解析:法一若CD⊥AB,则∠A′DB为二面角A′-CD-B的平面角,即∠A′DB=α.若CD与AB不垂直,如图在△ABC中,过A作CD的垂线交线段CD或CD的延长线于点O,交BC于E,连接A′O,则∠A′OE为二面角A′-CD-B的平面角,即∠A′OE=α,因为AO=A′O,所以∠A′AO=,又A′D=AD,所以∠A′AD=∠A′DB.而∠A′AO是直线A′A与平面ABC所成的角,由线面角的性质知∠A′AO<∠A′AD,则有α<∠A′DB,综合有∠A′DB≥α,故选B.法二若CA≠CB,则当α=π时,∠A′CB<π,排除D;当α=0时,∠A′CB>0,∠A′DB>0,排除A、C,故选B.2.在正方体ABCD-A1B1C1D1的侧面AB1内有一点P到直线AB与到直线B1C1的距离相等,则动点P所在曲线的形状为( D )(A)线段 (B)一段椭圆弧(C)双曲线的一部分 (D)抛物线的一部分解析:因为B1C1⊥平面AB1,所以PB1就是P到直线B1C1的距离,故由抛物线的定义知动点的轨迹为抛物线的一段,从而选D.3.在正方体ABCD-A1B1C1D1中,E为AA1的中点,点P在其对角面BB1D1D 内运动,若EP总与直线AC成等角,则点P的轨迹有可能是( A ) (A)圆或圆的一部分 (B)抛物线或其一部分(C)双曲线或其一部分(D)椭圆或其一部分解析: 由条件易知AC是平面BB1D1D的法向量,所以EP与直线AC成角总相等,得到EP与平面BB1D1D所成的角都相等,故点P的轨迹有可能是圆或圆的一部分.4.已知正方体ABCD-A1B1C1D1的棱长为a,定点M在棱AB上(但不在端点A,B上),点P是平面ABCD内的动点,且点P到直线A1D1的距离与点P 到点M的距离的平方差为a2,则点P的轨迹所在曲线为( A )解析:在正方体ABCD-A1B1C1D1中,过P作PF⊥AD,过F作FE⊥A1D1,垂足分别为F,E,连接PE.则PE2=a2+PF2,又PE2-PM2=a2,所以PM2=PF2,从而PM=PF,故点P到直线AD与到点M的距离相等,故点P的轨迹是以M为焦点,AD为准线的抛物线.5.四棱锥P-ABCD,AD⊥平面PAB,BC⊥平面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的四棱锥的顶点P 的轨迹是( B )(A)圆 (B)不完整的圆(C)抛物线(D)抛物线的一部分解析:因为AD⊥平面PAB,BC⊥平面PAB,所以AD∥BC且AD⊥PA,CB⊥PB,因为∠APD=∠CPB,所以tan∠APD=tan∠CPB,所以=,所以PB=2PA,在平面APB内,以AB的中点为原点,AB所在直线为x轴建立平面直角坐标系,则A(-3,0),B(3,0),设P(x,y)(y≠0),则(x-3)2+y2=4[(x+3)2+y2](y≠0),即(x+5)2+y2=16(y≠0),所以P的轨迹是B.6.已知正方体ABCD-A1B1C1D1的棱长为1,点P是平面AC内的动点,若点P到直线A1D1的距离等于点P到直线CD的距离,则动点P的轨迹所在的曲线是( B )解析:以A为原点,AB为x轴、AD为y轴,建立平面直角坐标系.设P(x,y),作PE⊥AD于E,PF⊥A1D1于F,连接PF,易知|PF|2=|PE|2+|EF|2=x2+1,又作PN⊥CD于N,则|PN|=|y-1|.依题意|PF|=|PN|,即=|y-1|,化简得(y-1)2-x2=1.故动点P的轨迹为双曲线,选B.二、填空题7.在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,总有AP⊥BD1,则动点P的轨迹为.解析:易证BD1⊥平面ACB1,所以满足BD1⊥AP的所有点P都在一个平面ACB1上.而已知条件中的点P是在侧面BCC1B1及其边界上运动,因此,符合条件的点P在平面ACB1与平面BCC1B1交线上,故所求的轨迹为线段B1C.答案:线段B1C8.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,且E为CD的中点,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是.(写出所有正确说法的序号)①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置(不在平面ABC内),都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.解析:由已知,在未折叠的原梯形中,AB∥DE,BE∥AD,所以四边形ABED 为平行四边形,所以BE=AD,折叠后如图所示.①过点M作MP∥DE,交AE于点P,连接NP.因为M,N分别是AD,BE的中点,所以点P为AE的中点,故NP∥EC.又MP∩NP=P,DE∩CE=E,所以平面MNP∥平面DEC,故MN∥平面DEC,①正确;②由已知,AE⊥ED,AE⊥EC,所以AE⊥MP,AE⊥NP,又MP∩NP=P,所以AE⊥平面MNP,又MN⊂平面MNP,所以MN⊥AE,②正确;③假设MN∥AB,则MN与AB确定平面MNBA,从而BE⊂平面MNBA,AD⊂平面MNBA,与BE和AD是异面直线矛盾,③错误;④当EC⊥ED时,EC⊥AD.因为EC⊥EA,EC⊥ED,EA∩ED=E,所以EC⊥平面AED,AD⊂平面AED,所以EC⊥AD,④正确.答案:①②④三、解答题9.如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).(1)求证:PB⊥DE;(2)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长. (1)证明:因为DE⊥AB,所以DE⊥BE,DE⊥PE,因为BE∩PE=E,所以DE⊥平面PEB,又因为PB⊂平面PEB,所以BP⊥DE.(2)解:因为PE⊥BE,PE⊥DE,DE⊥BE,所以分别以DE,BE,PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),设PE=a,则B(0,4-a,0),D(a,0,0),C(2,2-a,0),P(0,0,a),可得=(0,4-a,-a),=(2,-2,0),设平面PBC的法向量n=(x,y,z),所以令y=1,可得x=1,z=,因此n=(1,1,)是平面PBC的一个法向量,因为=(a,0,-a),PD与平面PBC所成角为30°,所以sin 30°=|cos<,n>|,即||=,解得a=或a=4(舍去),因此可得PE的长为.10.已知矩形ABCD中,E,F分别是AB,CD上的点,BE=CF=1,BC=2,AB=CD=3,P,Q分别为DE,CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为.(1)求证:PQ∥平面BCD;(2)求二面角A DB E的余弦值.(1)证明:取EB的中点M,连接PM,QM,因为P为DE的中点,所以PM∥BD,因为PM⊄平面BCD,BD⊂平面BCD,所以PM∥平面BCD,同理MQ∥平面BCD,因为PM∩MQ=M,所以平面PMQ∥平面BCD,因为PQ⊂平面PQM,所以PQ∥平面BCD.(2)解:在平面DFC内,过F作FC的垂线Fz,则∠DFC=,以F为原点,FE,FC,Fz分别为x,y,z轴,建立坐标系,则E(2,0,0),C(0,1,0),B(2,1,0),D(0,-1,),A(2,-1,),所以=(-2,-2,),=(0,2,-),=(0,1,0),设平面DAB的一个法向量为n=(x,y,z),则取n=(0,,),同理平面DBE的一个法向量为m=(,0,),所以cos<n,m>==,所以二面角A DB E的余弦值为.11.如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B′点重合.(1)求证:AO⊥平面B′OC;(2)当三棱锥B′-AOC的体积取最大时,求二面角A-B′C-O的余弦值;(3)在(1)的条件下,试问在线段B′A上是否存在一点P,使CP与平面B′OA所成的角的正弦值为?证明你的结论.(1)证明:因为AB=AC且O是BC中点,所以AO⊥BC,即AO⊥OB′,AO⊥OC,又因为OB′∩OC=O,所以AO⊥平面B′OC.(2)解:在平面B′OC内,作B′D⊥OC于点D,则由(1)可知B′D⊥OA,又OC∩OA=O,所以B′D⊥平面OAC,即B′D是三棱锥B′-AOC的高,又B′D≤B′O,所以当D与O重合时,三棱锥B′-AOC的体积最大.法一过O点作OH⊥B′C于点H,连AH,由(1)知AO⊥平面B′OC,又B′C⊂平面B′OC,所以B′C⊥AO,因为AO∩OH=O,所以B′C⊥平面AOH,所以B′C⊥AH,所以∠AHO即为二面角A-B′C-O的平面角.Rt△AOH中,AO=2,OH=,所以AH==,所以cos∠AHO==,故二面角A-B1C-O的余弦值为.法二依题意得OA,OC,OB′两两垂直,分别以射线OA,OC,OB′为x,y,z轴的正半轴建立空间直角坐标系Oxyz,设平面B′OC的法向量为n,可得n=(1,0,0),=(-2,0,1),=(-2,1,0).设平面AB′C的法向量为m,由⇒m=(1,2,2).cos<n,m>===,故二面角A-B′C-O的余弦值为.(3)解:存在点P为线段AB′的中点,使CP与平面B′OA所成角正弦值为.证明如下:设=λ=(-2λ,0,λ),=+=(2-2λ,-1,λ).又平面B′OA的法向量n=(0,1,0).依题意得=⇒=⇒20λ2-32λ+11=0.解得λ=(λ=>1舍去).。
2019届高考数学二轮复习 专题五 立 体 几 何 (讲义训练):第3讲 立体几何中的计算 课时讲义(含答案)

第3讲 立体几何中的计算 课时讲义1. 高考对立体几何的计算,主要是能利用公式求常见几何体(柱体、锥体、台体和球)的表面积与体积.有时还需能解决距离、翻折、存在性等比较综合性的问题.2. 高考中常见的题型为:(1) 常见几何体的表面积与体积的计算;(2) 利用等积变换求距离问题;(3) 通过计算证明平行与垂直等问题;(4) 几何体的内切和外接.1. 棱长都是2的三棱锥的表面积为________. 答案:43解析: 因为四个面是全等的正三角形,则S 表面积=4×34×4=43.2. 如图,正方体ABCDA 1B 1C 1D 1的棱长为1,点P 是棱BB 1的中点,则四棱锥PAA 1C 1C的体积为________.答案:13解析:四棱锥PAA 1C 1C 的体积为13×22×2×1=13.3. (2018·南京学情调研)将一个正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为27π cm 3,则该圆柱的侧面积为________cm 2.答案:18π解析:设正方形的边长为a cm ,则πa 2·a =27π,解得a =3,所以侧面积2π×3×3=18π.4. (2018·海安质量测试)已知正三棱锥的体积为36 3 cm 3,高为4 cm ,则底面边长为________cm.答案:63解析: 设正三棱锥的底面边长为a ,则其面积为S =34a 2.由题意13·34a 2×4=363,解得a =63., 一) 表面积与体积, 1) 如图,在以A ,B ,C ,D ,E 为顶点的六面体中,△ABC 和△ABD 均为等边三角形,且平面ABC ⊥平面ABD ,EC ⊥平面ABC ,EC =3,AB =2.(1) 求证:DE ∥平面ABC ; (2) 求此六面体的体积.(1) 证明:作DF ⊥AB ,交AB 于点F ,连结CF. 因为平面ABC ⊥平面ABD , 且平面ABC ∩平面ABD =AB , 所以DF ⊥平面ABC.因为EC ⊥平面ABC ,所以DF ∥EC. 因为△ABD 是边长为2的等边三角形, 所以DF =3,因此DF =EC ,所以四边形DECF 为平行四边形,所以DE ∥CF.因为DE ⊄平面ABC ,CF ⊂平面ABC , 所以DE ∥平面ABC.(2) 解:因为△ABD 是等边三角形,所以点F 是AB 的中点. 又△ABC 是等边三角形,所以CF ⊥AB. 由DF ⊥平面ABC 知,DF ⊥CF , 所以CF ⊥平面ABD.因为DE ∥CF ,所以DE ⊥平面ABD , 因此四面体ABDE 的体积为13S △ABD ·DE =1;四面体ABCE 的体积为13S △ABC ·CE =1,而六面体ABCED 的体积=四面体ABDE 的体积+四面体ABCE 的体积, 故所求六面体的体积为2.(2018·苏州暑假测试)如图,正四棱锥P ABCD 的底面一边AB 的长为2 3 cm ,侧面积为83 cm 2,则它的体积为________cm 3.答案:4解析:记正四棱锥P ABCD 的底面中心为点O ,棱AB 的中点为H, 连结PO ,HO ,PH ,则PO ⊥平面ABCD .因为正四棱锥的侧面积为83 cm 2,所以83=4×12×23×PH ,解得PH =2.在直角△PHO 中,PH =2,HO =3,所以PO =1,所以V PABCD =13×S 四边形ABCD ×PO =13×23×23×1=4(cm 3)., 二) 翻折与切割问题, 2) 如图,在菱形ABCD 中,AB =2,∠ABC =60°,BD ∩AC =O ,现将其沿菱形对角线BD 折起得到空间四边形EBCD ,使EC =2.(1) 求证:EO ⊥CD ;(2) 求点O 到平面EDC 的距离.(1) 证明:∵ 四边形ABCD 为菱形,∴ AC ⊥BD . ∵ BD ∩AC =O ,∴ AO ⊥BD ,即EO ⊥BD .∵ 在菱形ABCD 中,AB =2,∠ABC =60°,∴ AD =CD =BC =2,AO =OC =1. ∵ EC =2,CO =EO =1,∴ EO 2+OC 2=EC 2,∴ EO ⊥OC . 又BD ∩OC =O ,∴ EO ⊥平面BCD ,∴ EO ⊥CD .(2) 解:设点O 到平面ECD 的距离为h ,由(1)知EO ⊥平面OCD .V 三棱锥O CDE =V 三棱锥E OCD ,即13S △OCD ·EO =13S △ECD ·h . 在Rt △OCD 中,OC =1,OD =3,∠DOC =90°,∴ S △OCD =12OC ·OD =32.在△CDE 中,ED =DC =2,EC =2,∴ S △CDE =12×2×22-(22)2=72, ∴ h =S △OCD ·EO S △ECD =217,即点O 到平面EDC 的距离为217.如图①,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,点E 是AD的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图②中△A 1BE 的位置,得到四棱锥A 1BCDE .(1) 求证:CD ⊥平面A 1OC ;(2) 当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.,①) ,②)(1) 证明:在图①中,因为AB =BC =12AD =a ,点E 是AD 的中点,∠BAD =π2,所以BE ⊥AC ,即在图②中,BE ⊥A 1O ,BE ⊥OC . 又A 1O ∩OC =O ,所以BE ⊥平面A 1OC . 在图①中,BC ∥ED ,且BC =ED ,所以四边形BCDE 是平行四边形,所以BE ∥CD , 所以CD ⊥平面A 1OC .(2) 解:因为平面A 1BE ⊥平面BCDE ,所以A 1O 是四棱锥A 1BCDE 的高. 根据图①可得A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC ·AB =a 2, 所以VA 1BCDE =13×S ×A 1O =13×a 2×22a =26a 3.由26a 3=362,解得a =6., 三) 立体几何中的以算代证问题, 3) (2018·泰州中学学情调研)在直三棱柱ABCA 1B 1C 1中,AB =AC =AA 1=3a ,BC =2a ,D 是BC 的中点,E ,F 分别是AA 1,CC 1上一点,且AE =CF =2a.(1) 求证:B 1F ⊥平面ADF ; (2) 求三棱锥B 1ADF 的体积.(1) 证明:∵ AB =AC ,D 为BC 中点,∴ AD ⊥BC.在直三棱柱ABC -A 1B 1C 1中,B 1B ⊥底面ABC ,AD ⊂底面ABC ,∴ AD ⊥B 1B.∵ BC ∩B 1B =B ,∴ AD ⊥平面B 1BCC 1. ∵ B 1F ⊂平面B 1BCC 1,∴ AD ⊥B 1F.在矩形B 1BCC 1中,C 1F =CD =a ,B 1C 1=CF =2a , ∴ Rt △DCF ≌Rt △FC 1B 1,∴ ∠CFD =∠C 1B 1F , ∴ ∠B 1FD =90°,∴ B 1F ⊥FD . ∵ AD ∩FD =D ,∴ B 1F ⊥平面AFD . (2) 解: ∵ B 1F ⊥平面AFD ,∴ VB 1-ADF =13·S △ADF ·B 1F =13×12×AD ×DF ×B 1F =52a 33.如图①,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2.将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体DABC ,如图②.(1) 求证:BC ⊥平面ACD ; (2) 求几何体DABC 的体积.(1) 证明:(证法1)在图①中,由题意知,AC =BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC .取AC 的中点O ,连结DO ,由AD =CD ,得DO ⊥AC .又平面ADC ⊥平面ABC ,且平面ADC ∩平面ABC =AC ,DO ⊂平面ACD , ∴ OD ⊥平面ABC ,∴ OD ⊥BC . 又AC ⊥BC ,AC ∩OD =O , ∴ BC ⊥平面ACD .(证法2)在图①中,由题意得AC =BC =22,∴ AC 2+BC 2=AB 2, ∴ AC ⊥BC .∵ 平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,BC ⊂平面ABC , ∴ BC ⊥平面ACD .(2) 解:由(1)知,BC 为三棱锥BACD 的高, 且BC =22,S △ACD =12×2×2=2,∴ 三棱锥BACD 的体积V BACD =13S △ACD ·BC =13×2×22=423,即几何体DABC 的体积为423.1. (2018·天津卷)如图,已知正方体ABCDA 1B 1C 1D 1的棱长为1,则四棱锥A 1BB 1D 1D 的体积为________.答案:13解析:如图,连结A 1C 1,交B 1D 1于点O ,很明显A 1C 1⊥平面BDD 1B 1,则A 1O 是四棱锥的高,且A 1O =12A 1C 1=12×12+12=22,S 四边形BDD 1B 1=BD ×DD 1=2×1=2,结合四棱锥体积公式可得其体积为V =13Sh =13×2×22=13.2. (2018·江苏卷)如图,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.答案:43解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于2,所以该多面体的体积为2×13×1×(2)2=43.3. (2017·北京卷)如图,在三棱锥PABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,点D 为线段AC 的中点,E 为线段PC 上一点.(1) 求证:PA ⊥BD ;(2) 求证:平面BDE ⊥平面PAC ;(3) 当PA ∥平面BDE 时,求三棱锥EBCD 的体积.(1) 证明:因为PA ⊥AB ,PA ⊥BC ,AB ∩BC =B ,所以PA ⊥平面ABC. 因为BD ⊂平面ABC ,所以PA ⊥BD.(2) 证明:因为AB =BC ,点D 为AC 的中点,所以BD ⊥AC. 由(1)知,PA ⊥BD ,PA ∩AC =A ,所以BD ⊥平面PAC. 又BD ⊂平面BDE , 所以平面BDE ⊥平面PAC.(3) 解:因为PA ∥平面BDE ,平面PAC ∩平面BDE =DE ,所以PA ∥DE. 因为点D 为AC 的中点,所以DE =12PA =1,BD =DC =2.由(1)知,PA ⊥平面ABC ,所以DE ⊥平面ABC , 所以三棱锥EBCD 的体积为V =13×12×BD ×DC ×DE =13.4. (2017·全国卷Ⅰ)如图,在四棱锥PABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1) 求证:平面PAB ⊥平面PAD ;(2) 若PA =PD =AB =DC ,∠APD =90°,且四棱锥PABCD 的体积为83,求该四棱锥的侧面积.(1) 证明:由已知∠BAP =∠CDP =90°,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD .又PA ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2) 解:如图,在平面PAD 内作PE ⊥AD ,垂足为点E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,由AB ∩AD =A ,可得PE ⊥平面ABCD .设AB =x ,则由已知可得AD =2x ,PE =22x ,故四棱锥PABCD 的体积V PABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,解得x =2. 从而PA =PD =2,AD =BC =22,PB =PC =22,所以△PBC 为等边三角形,可得四棱锥PABCD 的侧面积为 12PA ·PD +12PA ·AB +12PD ·DC +12BC 2sin 60°=6+2 3.5. (2017·全国卷Ⅲ)如图,在四面体ABCD 中,△ABC 是正三角形,AD =CD .(1) 求证:AC ⊥BD ;(2) 已知△ACD 是直角三角形,AB =BD ,若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.(1) 证明:如图,取AC 的中点O ,连结DO ,BO .因为AD =CD ,所以AC ⊥DO .又由于△ABC 是正三角形,所以AC ⊥BO . 又DO ∩BO =O ,所以AC ⊥平面DOB . 因为BD ⊂平面DOB ,所以AC ⊥BD . (2) 解:连结EO .由(1)及题设知∠ADC =90°,所以DO =AO . 在Rt △AOB 中,BO 2+AO 2=AB 2. 又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2, 故∠DOB =90°.由题设知△AEC 为直角三角形,所以EO =12AC .又△ABC 是正三角形,且AB =BD ,所以EO =12BD ,故点E 为BD 的中点.所以点E 到平面ABC 的距离为点D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1∶1.(本题模拟高考评分标准,满分14分) (2018·长春模拟)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1) 求证:平面AEC ⊥平面BED ;(2) 若∠ABC =120°,AE ⊥EC ,三棱锥EACD 的体积为63,求该三棱锥的侧面积.(1) 证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,AC ⊂平面ABCD ,所以AC ⊥BE .(2分) 因为BD ∩BE =B ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED .(6分)(2) 解:设AB =x ,在菱形ABCD 中,由∠ABC =120°,得AG =GC =32x ,GB =GD=x2. 因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x .(8分)由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得三棱锥EACD 的体积为63,即13×12·AC ·GD ·BE =624x 3=63,解得x =2.(9分)从而可得AE =EC =ED =6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5.故三棱锥EACD 的侧面积为3+25.(14分)1. 若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为________. 答案:2π解析: 设圆柱的底面半径为r ,高为h ,则有2πr =2,即r =1π,故圆柱的体积为V =πr 2h =π⎝ ⎛⎭⎪⎫1π2×2=2π.2. 如图,已知AF ⊥平面ABCD ,四边形ABEF 为矩形,四边形ABCD 为直角梯形,∠DAB =90°,AB ∥CD ,AD =AF =CD =2,AB =4.(1) 求证:AF ∥平面BCE ; (2) 求证:AC ⊥平面BCE ; (3) 求三棱锥EBCF 的体积.(1) 证明:∵ 四边形ABEF 为矩形,∴ AF ∥BE .又BE ⊂平面BCE ,AF ⊄平面BCE , ∴ AF ∥平面BCE .(2) 证明:如图,过点C 作CM ⊥AB ,垂足为点M . ∵ AD ⊥DC ,∴ 四边形ADCM 为矩形, ∴ AM =DC =MB =AD =2.∴ AC =22,CM =2,BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC . ∵ AF ⊥平面ABCD ,AF ∥BE , ∴ BE ⊥平面ABCD ,∴ BE ⊥AC .∵ BE ⊂平面BCE ,BC ⊂平面BCE ,BC ∩BE =B , ∴ AC ⊥平面BCE .(3) 解:∵ AF ⊥平面ABCD ,∴ AF ⊥CM .∵ CM ⊥AB ,AF ⊂平面ABEF ,AB ⊂平面ABEF ,AF ∩AB =A ,∴ CM ⊥平面ABEF ,∴ V 三棱锥EBCF =V 三棱锥CBEF =13×12×BE ×EF ×CM =16×2×4×2=83.3. (2016·江苏卷)现需要设计一个仓库,它由上、下两部分组成,上部分的形状是正四棱锥P A 1B 1C 1D 1,下部分的形状是正四棱柱ABCD A 1B 1C 1D 1(如图),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍.(1) 若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?(2) 若正四棱锥的侧棱长为6 m ,则当PO 1为多少时,仓库的容积最大?解:(1) ∵ PO 1=2 m ,正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,∴ O 1O =8 m ,∴ 仓库的容积V =13×62×2+62×8=312(m 3). (2) 若正四棱锥的侧棱长为6 m ,设PO 1=x m ,则O 1O =4x m ,A 1O 1=36-x 2 m ,A 1B 1=2·36-x 2 m , 则仓库的容积V (x )=13×(2·36-x 2)2·x +(2·36-x 2)2·4x =-263x 3+312x (0<x<6), V ′(x )=-26x 2+312(0<x <6).当0<x <23时,V ′(x )>0,V (x )单调递增; 当23<x <6时,V ′(x )<0,V (x )单调递减. 故当x =23时,V (x )取最大值. 即当PO 1=23 m 时,仓库的容积最大.请使用“课后训练·第19讲”活页练习,及时查漏补缺!。
2019年高考理科数学(2卷)答案详解

2019年普通高等学校招生全国统一考试理科数学(II 卷)答案详解一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(集合)设集合A ={x |x 2–5x +6>0},B ={x |x –1<0},则A ∩B =( ) A .(∞-,1) B .(–2,1)C .(–3,–1)D .(3,∞+)【解析】集合A ={x |x 2–5x +6>0}={x |x <2或x >3},集合B ={x |x <1},所以有A ∩B={x |x <1},即A 答案. 【答案】A2.(复数)设i z 23+-=,则在复平面内z 对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【解析】i z 23+-=,则z 的共轭复数为i z 23--=,所以在复平面内z 对应的点位于第三象限. 【答案】C3.(平面向量)已知AB =(2,3),AC =(3,t ),||BC =1,则AB BC ⋅=( ) A .–3 B .–2C .2D .3【解析】(1,3)=+=-BC BA AC t ,由于||1=BC ,所以03=-t ,即3=t ,(1,0)=BC .所以21302⋅=⨯+⨯=AB BC【答案】C4.(公式推导)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日2L 点的轨道运行.2L 点是平衡点,位于地月连线的延长线上.设地球质量为M 1,月球质量为M 2,地月距离为R ,2L 点到月球的距离为r ,根据牛顿运动定律和万有引力定律,r 满足方程:121223()()M M M R r R r r R +=++.设rRα=,由于α的值很小,因此在近似计算中34532333(1)ααααα++≈+,则r 的近似值为( ) A .21M R M B .212M R MC .2313M R M D .2313M R M【解析】∵=rR α,∴=r R α,代入121223()()+=++M M M R r R r r R 中得12122222(1)(1)+=++M M M R R R ααα12122(1)(1)+=++M M M ααα33453122333=3(1)++⎛⎫=≈ ⎪+⎝⎭M r M R ααααα所以有 2313=M r R M 【答案】C5.(概率统计)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( ) A .中位数 B .平均数 C .方差D .极差【解析】根据几个数字特征的定义,很容易得出答案:去掉1个最高分、1个最低分,最后中位数不变. 【答案】A6.(函数)若a >b ,则( ) A .ln(a −b )>0 B .3a <3b C .a 3−b 3>0D .|a |>|b |【解析】答案A :∵a >b ,∴a -b >0,无法判断ln(a −b )的正负;答案B :∵y =3x 为增函数,∴3a >3b ;答案C :∵y =x 3为增函数,∴a 3>b 3;答案D :当0>a >b 时,|a |<|b |.【答案】C7.(立体几何)设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面【解析】通过画图,采用排除法,很容易得到正确答案. 【答案】B8.(解析几何)若抛物线y 2=2px (p >0)的焦点是椭圆1322=+py p x 的一个焦点,则p =( ) A .2 B .3 C .4D .8【解析】抛物线y 2=2px (p >0)的焦点为)0,2(p,并且在x 轴上. 所以椭圆1322=+p y p x 的一个焦点为)0,2(p . 所以有p p22=,得p =8. 【答案】D9.(三角函数)下列函数中,以2π为周期且在区间)2,4(ππ单调递增的是( ) A .f (x )=|cos2x | B .f (x )=|sin2x | C .f (x )=cos|x |D .f (x )=sin|x |【解析】答案A :函数f (x )=|cos2x |的图像如图A9-1所示,其周期是函数f (x )=cos2x 的一半,即21π=T ,且在区间)2,4(ππ为单调递增的. 答案B :与答案A 类似,函数f (x )=|sin2x |的周期是函数f (x )=sin2x 的一半,即22π=T ,且在区间)2,4(ππ为单调递减的;答案C :函数f (x )=cos|x |为偶函数,其图像如图A9-2所示.由函数f (x )=cos|x |的图像可知,其周期π23=T ;答案D :与答案C 类似,由函数f (x )=sin|x |的图像可知,其不是周期函数. 【答案】A图A9-1 图A9-210.(三角函数)已知α∈(0,2π),2sin2α=cos2α+1,则sin α=( ) A .15B .55C .33D .255【解析】利用三角公式12cos 2sin 2+=αα化简得ααα2cos 2cos sin 4=ααcos sin 2=所以2cot =α,设α所对得边为1,则临边为2,斜边为5,所以55sin =α. 【答案】B11.(解析几何)设F 为双曲线C :22221(0,0)-=>>x y a b a b的右焦点,O 为坐标原点,以OF 为直径的圆与圆222+=x y a 交于P ,Q 两点.若=PQ OF ,则C 的离心率为( ) A .2 B .3C .2D .5【解析】如图A11所示. ∵OF 为直径,=PQ OF ,∴PQ 也是直径.,即点P 、Q 的坐标为)2,2(c c .把)2,2(c c 代入222+=x y a 得,222=c a . ∴22=e ,即2=e .图A11【答案】A12.设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦【解析】由)(2)1(x f x f =+可得Z x x f t x f t∈⋅=+),(2)(,即Z x t x f x f t∈-⋅=),(2)(.∵当(0,1]∈x 时,()(1)=-f x x x ,1()[,0]4∈-f x ∴当(1,2]∈x 时,1(0,1]-∈x ,则)2)(1(2)1(2)(--=-⋅=x x x f x f ,1()[,0]2∈-f x∴当(2,3]∈x 时,2(0,1]-∈x ,则)3)(2(4)2(2)(2--=-⋅=x x x f x f ,()[1,0]∈-f x 函数()f x 的图像如图A12所示. 对任意(,]∈-∞x m ,都有8()9≥-f x ,因此(2,3]∈m 令98)3)(2(4)(-=--=x x x f ,得 37=x 或38=x . 由图A12可知,当37≤m 时,都有8()9≥-f x .图A12【答案】B二、填空题:本题共4小题,每小题5分,共20分。
2019年高考理科数学全国三卷真题及答案解析

【答案】D
【解析】
【分析】
通过求导数,确定得到切线斜率的表达式,求得 ,将点的坐标代入直线方程,求得 .
【详解】详解:
,
将 代入 得 ,故选D.
【点睛】本题关键得到含有a,b的等式,利用导数几何意义和点在曲线上得到方程关系。
7.函数 在 的图像大致为
A. B. C. D.
【答案】B
A. B. C. D.
【答案】C
【解析】
【分析】
根据题先求出阅读过西游记的人数,进而得解.
【详解】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C.
【点睛】本题考查抽样数据的统计,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.
【详解】 是R的偶函数, .
,
又 在(0,+∞)单调递减,
∴ ,
,故选C.
【点睛】本题主要考查函数的奇偶性、单调性,解题关键在于利用中间量大小比较同一区间的取值.
12.设函数 =sin( )( >0),已知 在 有且仅有5个零点,下述四个结论:
① 在( )有且仅有3个极大值点
② 在( )有且仅有2个极小值点
4.(1+2x2)(1+x)4的展开式中x3的系数为
A.12B.16C.20D.24
【答案】A
【解析】
【分析】
本题利用二项展开式通项公式求展开式指定项的系数.
【详解】由题意得x3的系数为 ,故选A.
【点睛】本题主要考查二项式定理,利用展开式通项公式求展开式指定项的系数.
5.已知各项均为正数的等比数列 的前4项和为15,且 ,则 ( )
2019届高考数学二轮复习专题三立体几何1.3.2点直线平面之间的位置关系课件文ppt版本

【解析】选D.因为EH∥A1D1,A1D1∥B1C1, 所以EH∥B1C1,又EH⊄平面BCC1B1, 所以EH∥平面BCC1B1, 又EH⊂平面EFGH, 平面EFGH∩平面BCC1B1=FG,
所以EH∥FG,故EH∥FG∥B1C1, 所以选项A、C正确;因为A1D1⊥平面ABB1A1, EH∥A1D1,所以EH⊥平面ABB1A1,又EF⊂平面ABB1A1,故 EH⊥EF,所以选项B也正确.
热点题型2 点、线、面之间的位置关系的证明 【感悟经典】 【典例】(2017·山东高考)由四棱柱ABCD-A1B1C1D1截 去三棱锥C1-B1CD1后得到的几何体如图所示,四边形 ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥ 平面ABCD,
(1)证明:A1O∥平面B1CD1. (2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
所以BD∥平面CD1B1. 因为A1D1 B1C1 BC, 所以四边形A1BCD1是平行四边形, 所以A1B∥D1C, 又因为A1B⊄平面CD1B1, D1C⊂平面CD1B1,
所以A1B∥平面CD1B1, 又因为BD∩A1B=B, 所以平面A1BD∥平面CD1B1. (2)因为A1O⊥平面ABCD, 所以A1O是三棱柱ABD-A1B1D1的高. 又因为AO= AC=1,AA1= ,
③平面α ⊥平面BCFE.
其中正确的命题有 (
A.①②
B.②③
) C.①③
D.①②③
【解析】选C.由题意画出草图如图所示,因为AA1∥平 面α,平面α∩平面AA1B1B=EH,所以AA1∥EH.同理 AA1∥GF,所以EH∥GF.又ABC-A1B1C1是直三棱柱,易知 EH=GF=AA1,所以四边形EFGH是平行四边形,故①正确; 若平面α∥平面BB1C1C,由平面α∩平面A1B1C1=GH,
高考理科数学:解密高考④ 立体几何问题重在“建”——建模、建系
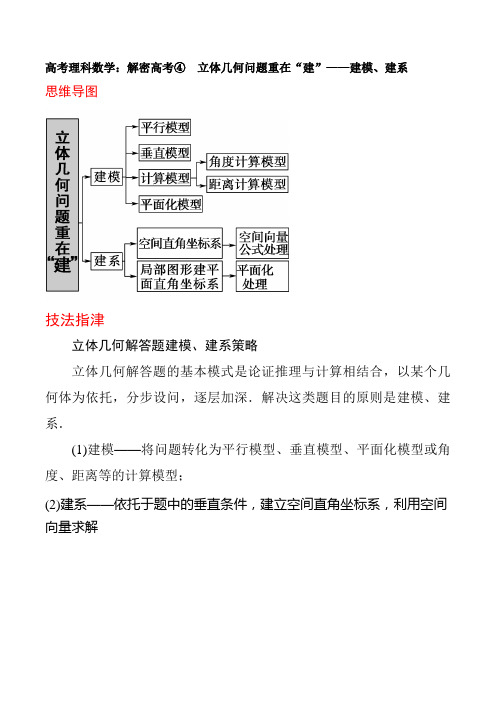
高考理科数学:解密高考④立体几何问题重在“建”——建模、建系思维导图技法指津立体几何解答题建模、建系策略立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深.解决这类题目的原则是建模、建系.(1)建模——将问题转化为平行模型、垂直模型、平面化模型或角度、距离等的计算模型;(2)建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解母题示例:2019年全国卷Ⅲ,本小题满分12分图1是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.图1图2(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B-CG-A的大小.看到图形的折叠,想到折叠前后的不变量;看到证明四点共面,想到直线的平行或相交;看到证明面面垂直,想到先证明线面垂直;看到求二面角,想到法向量;缺相应点的坐标,借助(1)的结论及边长、角度等信息补建坐标系及相应点的坐标.[构建模板·五步解法]立体几何类问题的求解策略母题突破:2019年大连模拟,本小题满分12分1,∠ABC =60°,CE ⊥平面ABCD ,CE =3,CD =2,G 是DE 的中点.(1)求证:平面ACG ∥平面BEF ;(2)求直线AD 与平面ABF 所成的角的正弦值.[解] (1)证明:连接BD 交AC 于O ,则O 是BD 的中点,连接OG ,∵G 是DE 的中点,故OG ∥BE ,又BE平面BEF ,OG平面BEF ,所以OG ∥平面BEF . 2分 又EF ∥AC ,AC 平面BEF ,EF平面BEF ,所以AC ∥平面BEF ,又AC ∩OG =O ,AC ,OG平面ACG ,所以平面ACG ∥平面BEF . 4分(2)连接OF ,由题意可得OC =1,即OC =EF , 又EF ∥AC ,所以四边形OCEF 为平行四边形, 所以OF ∥EC ,OF =EC =3,所以OF ⊥平面ABCD ,所以OF ,OC ,OD 两两垂直. 6分 如图,以O 为坐标原点,分别以OC ,OD ,OF 所在直线为x ,y , z 轴建立空间直角坐标系,则A (-1,0,0),B (0,-3,0),D (0,3,0),F (0,0,3),AD →=(1,3,0),AB →=(1,-3,0),AF →=(1,0,3). 7分设平面ABF 的法向量为m =(a ,b ,c ),依题意有⎩⎨⎧m ⊥AB →,m ⊥AF →,即⎩⎪⎨⎪⎧(a ,b ,c )·(1,-3,0)=a -3b =0,(a ,b ,c )·(1,0,3)=a +3c =0, 9分 令a =3,则b =1,c =-1,m =(3,1,-1),|cos 〈AD →,m 〉|=|AD →·m ||AD →||m |=3+34×5=155, 11分所以直线AD 与平面ABF 所成的角的正弦值是155. 12分 2.(2019·太原模拟)在三棱柱ABC -A ′B ′C ′中,AB =BC =CA =AA ′,侧面ACC ′A ′⊥底面ABC ,D 是棱BB ′的中点.(1)求证:平面DA ′C ⊥平面ACC ′A ′;(2)若∠A ′AC =60°,求二面角A -BC -B ′的余弦值.[解](1)取AC ,A ′C ′的中点O ,F ,连接OF 与A ′C 交于点E ,连接DE ,OB ,B ′F . 则E 为OF 的中点,因为三棱柱ABC -A ′B ′C ′, 所以OF ∥AA ′∥BB ′,且OF =AA ′=BB ′, 所以四边形BB ′FO 是平行四边形. 2分 又D 是棱BB ′的中点,所以DE ∥OB . 因为侧面AA ′C ′C ⊥底面ABC ,且OB ⊥AC , 所以OB ⊥平面ACC ′A ′, 所以DE ⊥平面ACC ′A ′, 又DE平面DA ′C ,所以平面DA ′C ⊥平面ACC ′A ′. 5分(2)连接A ′O ,因为∠A ′AC =60°,所以△A ′AC 是等边三角形,故A ′O ⊥底面ABC .6分 设AB =BC =CA =AA ′=2,可得A ′O =OB =3,分别以OB ,OC ,OA ′分别为x ,y ,z 轴正方向建立空间直角坐标系,则A (0,-1,0),B (3,0,0),C (0,1,0),A ′(0,0,3), BC →=(-3,1,0),BB ′→=AA ′→=(0,1,3). 8分 设平面BCC ′B ′的一个法向量为m =(x ,y ,z ),则m ·BC →=0,m ·BB ′→=0,所以⎩⎪⎨⎪⎧-3x +y =0,y +3z =0,取x =1,y =3,z =-1,所以m =(1,3,-1).10分又平面ABC 的一个法向量为n =(0,0,1),故cos 〈m ,n 〉=-15=-55, 11分因为二面角A -BC -B ′为钝角,所以其余弦值为-55. 12分。
专题4.4 立体几何中最值问题(解析版)

一.方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目,而几何问题中的最值与范围类问题,既可以考查学生的空间想象能力,又考查运用运动变化观点处理问题的能力,因此,将是有中等难度的考题.此类问题,可以充分考查图形推理与代数推理,同时往往也需要将问题进行等价转化,比如求一些最值时,向平面几何问题转化,这些常规的降维操作需要备考时加强关注与训练.立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;三是将几何体平面化,如利用展开图,在平面几何图中直观求解.二.解题策略类型一距离最值问题【例1】【河南省焦作市2019届高三三模】在棱长为4的正方体ABCD﹣A1B1C1D1中,点E、F分别在棱AA1和AB上,且C1E⊥EF,则|AF|的最大值为()A.B.1 C.D.2【答案】B【解析】以AB,AD,AA1所在直线为x,y,z轴,建立空间直角坐标系如图所示,则C1(4,4,4),设E(0,0,z),z∈[0,4],F(x,0,0),x∈[0,4],则|AF|=x.=(4,4,4﹣z),=(x,0,﹣z).因为C1E⊥EF,所以,即:z2+4x﹣4z=0,x=z﹣.当z=2时,x取得最大值为1.|AF|的最大值为1.故选:B.【指点迷津】建立空间直角坐标系,求出坐标,利用C 1E⊥EF,求出|AF|满足的关系式,然后求出最大值即可.利用向量法得到|AF|的关系式是解题的关键,故选D.【举一反三】1、【江西省吉安市2019届高三上学期期末】若某几何体的三视图如图所示,则该几何体的最长棱的棱长为A.B.C.D.【答案】A【解析】解:根据三视图知,该几何体是一个正四棱锥,画出图形如图所示;则,,底面CDEB,结合图形中的数据,求得,在中,由勾股定理得,同理求得,.故选:A .2、【河南省顶级名校2019届高三第四次联合测评】在侧棱长为的正三棱锥中,侧棱OA ,OB ,OC 两两垂直,现有一小球P 在该几何体内,则小球P 最大的半径为 A . B . C .D .【答案】B 【解析】当小球与三个侧面,,及底面都相切时,小球的体积最大此时小球的半径最大,即该小球为正三棱锥的内切球设其半径为由题可知因此本题正确选项:3、如右图所示,在棱长为2的正方体1111ABCD A B C D 中, E 为棱1CC 的中点,点,P Q 分别为面1111A B C D和线段1B C 上的动点,则PEQ ∆周长的最小值为_______.【解析】将面1111A B C D 与面11BB C C 折成一个平面,设E 关于11B C 的对称点为M ,E 关于1B C 对称点为N,则PEQ ∆周长的最小值为MN ==类型二 面积的最值问题【例2】【河南省郑州市2019年高三第二次质量检测】在长方体中,,,分别是棱的中点,是底面内一动点,若直线与平面没有公共点,则三角形面积的最小值为( )A .B .C .D .【答案】C 【解析】补全截面EFG 为截面EFGHQR 如图,其中H 、Q 、R 分别为、的中点,易证平面ACD 1∥平面EFGHQR ,∵直线D 1P 与平面EFG 不存在公共点, ∴D 1P∥面ACD 1,∴D 1P 面ACD 1,∴P ∈AC ,∴过P 作AC 的垂线,垂足为K ,则BK=,此时BP 最短,△PBB 1的面积最小,∴三角形面积的最小值为,故选:C.【指点迷津】截面问题,往往涉及线面平行,面面平行定义的应用等,考查空间想象能力、逻辑思维能力及计算求解能力.解题的关键是注意明确截面形状,确定几何量.本题由直线与平面没有公共点可知线面平行,补全所给截面后,易得两个平行截面,从而确定点P所在线段,得解.【举一反三】1、【湖南省衡阳市2019届高三二模】如图,直角三角形,,,将绕边旋转至位置,若二面角的大小为,则四面体的外接球的表面积的最小值为()A.B.C.D.【答案】B【解析】如图,,,分别为,,的中点,作面,作面,连,,易知点即为四面体的外接球心,,,.设,,则,,,.【处理一】消元化为二次函数..【处理二】柯西不等式..所以.2、如图,在正四棱柱1111D C B A ABCD -中,2,11==AA AB ,点P 是平面1111D C B A 内的一个动点,则三棱锥ABC P -的正视图与俯视图的面积之比的最大值为( )A .1B .2C .21D .41 【答案】BABC P -的正视图与俯视图的面积之比的最大值为2;故选B .3、【福建省2019届高三模拟】若某几何体的三视图如图所示,则该几何体的所有侧面和底面中,面积的最大值为( )A .2B .C .3D .【答案】C【解析】由三视图可得,该几何体的直观图如图所示,其中,为的中点,平面,,.所以,,.又因为,,所以,故,所以.故选C.类型三体积的最值问题【例3】如图,已知平面平面,,、是直线上的两点,、是平面内的两点,且,,,,,是平面上的一动点,且有,则四棱锥体积的最大值是()A. B. C. D.【答案】A【指点迷津】本题主要考查面面垂直的性质,棱锥的体积公式以及求最值问题. 求最值的常见方法有①配方法:若函数为一元二次函数,常采用配方法求函数求值域,其关键在于正确化成完全平方式,并且一定要先确定其定义域;②换元法;③不等式法;④单调性法;⑤图像法,本题首先根据线面关系将体积最值转化为函数求最值问题,然后应用方法①解答的. 【举一反三】1、已知AD 与BC 是四面体ABCD 中相互垂直的棱,若6AD BC ==,且60ABD ACD ∠=∠=,则四面体ABCD 的体积的最大值是A. B. C. 18 D. 36 【答案】A2、如图,已知平面l αβ=,A 、B 是l 上的两个点,C 、D 在平面β内,且,,DA CB αα⊥⊥4AD =,6,8AB BC ==,在平面α上有一个动点P ,使得APD BPC ∠=∠,则P ABCD -体积的最大值是( )A. B.16 C.48 D.144 【答案】C 【解析】,,DA DA βααβ⊂⊥∴⊥面.,,DA CB αα⊥⊥PAD ∴∆和PBC ∆均为直角三角形.,APD BPC PAD ∠=∠∴∆∽PBC ∆.4,8,2AD BC PB PA ==∴=.学科&网过P 作PM AB ⊥,垂足为M .则PM β⊥.令AM t =,()t R ∈.则2222PA AM PB BM -=-,即()222246PA t PA t -=--,2124,PA t PM ∴=-∴=底面四边形ABCD 为直角梯形面积为()1486362S =+⨯=.学科&网136483P ABCD V -∴=⨯=.故C 正确.3.【河南省八市重点高中联盟“领军考试”2019届高三第三次测评】已知一个高为l 的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,内有 一个体积为的球,则的最大值为( ) A . B .C .D .【答案】A 【解析】依题意,当球与三棱锥的四个面都相切时,球的体积最大, 该三棱锥侧面的斜高为,,,所以三棱锥的表面积为,设三棱锥的内切球半径为, 则三棱锥的体积,所以,所以,所以,故选A.类型四 角的最值问题【例4】如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E 、F 分别为AB 、BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为.【答案】25【解析】建立坐标系如图所示.设1AB =,则11(1,,0),(,0,0)22AF E =.设(0,,1)(01)M y y ≤≤,则1(,,1)2EM y =-,由于异面直线所成角的范围为(0,]2π,所以cos θ==.2281145y y +=-+,令81,19y t t +=≤≤,则281161814552y y t t+=≥++-,当1t =时取等号.所以2cos 5θ==≤=,当0y =时,取得最大值.C【指点迷津】空间的角的问题,只要便于建立坐标系均可建立坐标系,然后利用公式求解.解本题要注意,空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.当点M 在点P 处时,EM 与AF 所成角为直角,此时余弦值为0(最小),当点M 向左移动时,.EM 与AF 所成角逐渐变小,点M 到达点Q 时,角最小,余弦值最大. 【举一反三】1、矩形ABCD 中,,,将△ABC 与△ADC 沿AC 所在的直线进行随意翻折,在翻折过程中直线AD 与直线BC 成的角范围(包含初始状态)为( )A.B.C.D.【答案】C2、在正方体1111D C B A ABCD -中,O 是BD 中点,点P 在线段11D B 上,直线OP 与平面BD A 1所成的角为α,则αsin 的取值范围是( ) A .]33,32[B .]21,31[C .]33,43[D .]31,41[ 【答案】A3.【云南省昆明市云南师范大学附属中学2019届高三上学期第四次月考】如图,在正方体中,点P为AD的中点,点Q为上的动点,给出下列说法:可能与平面平行;与BC所成的最大角为;与PQ一定垂直;与所成的最大角的正切值为;.其中正确的有______写出所有正确命题的序号【答案】【解析】解:由在棱长为1的正方体中点P为AD的中点,点Q为上的动点,知:在中,当Q为的中点时,,由线面平行的判定定理可得PQ与平面平行,故正确;在中,当Q为的中点时,,,,可得,故错误;在中,由,可得平面,即有,故正确;在中,如图,点M为中点,PQ与所成的角即为PQ与所成的角,当Q与,或重合时,PQ与所成的角最大,其正切值为,故正确;在中,当Q 为的中点时,PQ 的长取得最小值,且长为,故正确.故答案为:.4、在正四面体P ABC -中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN AB λ=,设异面直线NM 与AC 所成角为α,当1233λ≤≤时,则cos α的取值范围是__________.【答案】,3838⎡⎢⎣⎦ 【解析】设P 到平面ABC 的射影为点O ,取BC 中点D ,以O 为原点,在平面ABC 中,以过O 作DB 的平行线为x 轴,以OD 为y 轴,以OP 为z 轴,建立空间直角坐标系,如图,设正四面体P −ABC的棱长为则()()(((0,4,0,,,,A B C P M --,由AN AB λ=,得(),64,0N λ-,∴((),56,NM AC λ=--→-=-,∵异面直线NM 与AC 所成角为α, 1233λ≤≤,∴2NM AC cos NM AC α⋅==⋅,设32t λ-=,则5733t 剟∴222111124626()41t cos t t t tα==-+-⋅+,∵1313375t <剟cos α.∴cos α的取值范围是⎣⎦.三.强化训练一、选择题1、【甘肃省2019届高三第一次高考诊断】四棱锥的顶点均在一个半径为3的球面上,若正方形的边长为4,则四棱锥的体积最大值为()A.B.C.D.【答案】D【解析】设正方形的中心为,当在于球心的连线上时,四棱锥高最高,由于底面面积固定,则高最高时,四棱锥体积取得最大值.设高为,,球的半径为,故,解得.故四棱锥的体积的最大值为.故选D.2.【广东省东莞市2019届高三第二次调研】已知一个四棱锥的正主视图和俯视图如图所示,其中,则该四棱锥的高的最大值为A.B.C.4 D.2【答案】A【解析】解:如图所示,由题意知,平面平面ABCD,设点P到AD的距离为x,当x最大时,四棱锥的高最大,因为,所以点P的轨迹为一个椭圆,由椭圆的性质得,当时,x取得最大值,即该四棱锥的高的最大值为.故选:A.3.【四川省教考联盟2019届高三第三次诊断】已知四棱锥的底面四边形的外接圆半径为3,且此外接圆圆心到点距离为2,则此四棱锥体积的最大值为()A.12 B.6 C.32 D.24【答案】A【解析】由锥体的体积公式v=,可知,当s和h都最大时,体积最大.由题得顶点P到底面ABCD的距离h≤2.当点P在底面上的射影恰好为圆心O时,即PO⊥底面ABCD时,PO最大=2,即,此时,即四边形ABCD为圆内接正方形时,四边形ABCD的面积最大,所以此时四边形ABCD的面积的最大值=,所以.故选:A4.【安徽省蚌埠市2019届高三第一次检查】某三棱锥的三视图如图所示,网格纸上小正方形的边长为1,三棱锥表面上的点M在俯视图上的对应点为A,三棱锥表面上的点N在左视图上的对应点为B,则线段MN的长度的最大值为A .B .C .D .【答案】D 【解析】由三视图可知,该三棱锥的底面是直角三角形, 一条侧棱与底面垂直(平面),为几何体的直观图如图,在上,重合,当与重合时, 线段的长度的最大值为.故选D .5.如图,在矩形ABCD 中, 2,1AB AD ==,点E 为CD 的中点, F 为线段CE (端点除外)上一动点现将DAF ∆沿AF 折起,使得平面ABD ⊥平面ABC 设直线FD 与平面ABCF 所成角为θ,则sin θ的最大值为( )A.13 B. 4 C. 12 D. 23【答案】C 【解析】如图:在矩形中,过点作的垂线交于点,交于点设,6.【2019年4月2019届高三第二次全国大联考】已知正四面体的表面积为,点在内(不含边界). 若,且,则实数的取值范围为( ) A . B . C .D .【答案】A 【解析】 设正四面体的棱长为则,解得则正四面体的高为记点到平面、、的距离分别为则因为,所以,则故又,故即实数的取值范围为本题正确选项:二、填空题7.【山东省青岛市2019届高三3月一模】在四棱锥中,底面是边长为2的正方形,面,且,若在这个四棱锥内有一个球,则此球的最大表面积为__________.【答案】【解析】在这个四棱锥内有一个球,则此球的最大表面积时,对应的球应该是内切球,此时球的半径最大,设内切球的球心为O半径为R,连接球心和ABCD四个点,构成五个小棱锥,根据体积分割得到,五个小棱锥的体积之和即为大棱锥的体积,,根据AB垂直于AD,PD垂直于AB 可得到AB垂直于面PDA,故得到AB垂直于PA,同理得到BC垂直于PC,表面积为:,此时球的表面积为:.故答案为:.8.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知正四棱柱和半径为的半球O,底面ABCD在半球O底面所在平面上,,,,四点均在球面上,则该正四棱柱的体积的最大值为______.【答案】4【解析】设正四棱柱的高为h,底面棱长为a,则正四棱柱的底面外接圆直径为,所以,.由勾股定理得,即,得,其中,所以,正四棱柱的体积为,其中,构造函数,其中,则,令,得.当时,;当时,.所以,函数在处取得极大值,亦即最大值,则.因此,该正四棱柱的体积的最大值为4.9.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知圆柱和半径为的半球O,圆柱的下底面在半球O底面所在平面上,圆柱的上底面内接于球O,则该圆柱的体积的最大值为_____.【答案】2π【解析】解:设圆柱的底面圆半径为r,高为h;则h2+r2=R2=3;所以圆柱的体积为V=πr2h=π(3﹣h2)h=π(3h﹣h3);则V′(h)=π(3﹣3h2),令V′(h)=0,解得h=1;所以h∈(0,1)时,V′(h)>0,V(h)单调递增;h∈(1,)时,V′(h)<0,V(h)单调递减;所以h=1时,V(h)取得最大值为V(1)=2π.故答案为:2π.10.【江西省上饶市2019届高三二模】一个棱长为的正方体形状的铁盒内放置一个正四面体,且能使该正四面体在铁盒内任意转动,则该正四面体的体积的最大值是_____.【答案】【解析】由题该正四面体在铁盒内任意转动,故其能在正方体的内切球内任意转动,内切球半径为6,设正四面体棱长为a, 将此正四面体镶嵌在棱长为x的正方体内,如图所示:则x=,外接球的球心和正方体体心O重合,∴外接球的球半径为:=6,a=4又正四面体的高为∴该正四面体的体积为故答案为11.【河北省衡水市第二中学2019届高三上期中】已知体积为的正四棱锥外接球的球心为,其中在四棱锥内部.设球的半径为,球心到底面的距离为.过的中点作球的截面,则所得截面圆面积的最小值是___________.【答案】【解析】如图取底面的中心为,连接平面,且球心在上,由条件知,,连接,,则,于是底面的边长为.又,故四棱锥的高是,所以,即,从而,,于是,过的中点的最小截面圆是以点为圆心的截面圆,该截面圆的半径是,故所求面积为.12.【江西省临川第一中学等九校2019届高三3月联考】如图所示,三棱锥的顶点,,,都在同一球面上,过球心且,是边长为2等边三角形,点、分别为线段,上的动点(不含端点),且,则三棱锥体积的最大值为__________.【答案】【解析】过球心,又是边长为的等边三角形,,,三角形是等腰直角三角形,,,又因为,在平面内,由线面垂直的判定定理可得平面,即平面,设,,则三棱锥体积,当且仅当,即时取等号,故答案为.13.【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.【答案】【解析】因为,所以,所以,同理,故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,则且,所以,当平面时,平面截球的截面面积最小,此时截面为圆面,其半径为,故截面的面积为.填.14.【江西师范大学附属中学2019高三上学期期末】若一个四棱锥的底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球的体积最小时,它的高为_________.【答案】【解析】设四棱锥底面边长为a,高为h,底面对角线交于O,由条件四棱锥P-ABCD为正四棱锥,其外接球的球心M在高PO上,设外接球半径为R,在直角三角形MAO中,,又该四棱锥的体积为9,所以所以,,,时,时,所以时R极小即R最小,此时体积最小.故答案为3.15.【江西省上饶市2019届高三二模】已知正方体的棱长为,平面与对角线垂直且与每个面均有交点,若截此正方体所得的截面面积为,周长为,则的最大值为______.【答案】【解析】因为平面与对角线垂直,所以平面与对角面平行,作出图象,为六边形,设则,所以,由对称性得平面过对角线中点时截面面积取最大值为,则的最大值为.16.【河南省洛阳市2019届高三第二次统考】正四面体中,是的中点,是棱上一动点,的最小值为,则该四面体内切球的体积为_____.【答案】【解析】如下图,正方体中作出一个正四面体将正三角形和正三角形沿边展开后使它们在同一平面内,如下图:要使得最小,则三点共线,即:,设正四面体的边长为,在三角形中,由余弦定理可得:,解得:,所以正方体的边长为2,正四面体的体积为:,设四正面体内切球的半径为,由等体积法可得:,整理得:,解得:,所以该四面体内切球的体积为.17.【2019届湘赣十四校高三联考第二次考试】如图,正三棱锥的高,底面边长为4,,分别在和上,且,当三棱锥体积最大时,三棱锥的内切球的半径为________.【答案】【解析】设,,当时,取得最大值,此时为中点,经过点,且,,所以可求,,因此易求,,,,又∵,∴.。
高考数学(理)之立体几何与空间向量 专题06 平面与平面的平行、垂直的判定与性质(解析版)
立体几何与空间向量06 平面与平面的平行、垂直的判定与性质【考点讲解】一、具体目标:1.理解空间直线、平面位置关系的定义,并了解可以作为推理依据的公理和定理;2.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理;3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.二、知识概述:1.面面平行的判定与性质a⊂β,b⊂β,a∩b=P,α∥β,α∩γ=a,(1)定义:两个平面没有公共点,称这两个平面平行;(2)判定定理:a⊂α,b⊂α,a∩b=M,a∥β,b∥β⇒α∥β;(3)推论:a∩b=M,a,b⊂α,a′∩b′=M′,a′,b′⊂β,a∥a′,b∥b′⇒α∥β.3.两个平面平行的性质定理(1)α∥β,a⊂α⇒a∥β;(2)α∥β,γ∩α=a,γ∩β=b⇒a∥b.3.平面与平面垂直的判定与性质(1)平面与平面垂直的判定方法①定义法.②利用判定定理:如果一个平面过另一个平面的一条垂线,则这两个平面互相垂直.(2)平面与平面垂直的性质:如果两平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.4.定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.5.定理:⎭⎪⎬⎪⎫AB βAB ⊥α⇒β⊥α⎭⎪⎬⎪⎫α⊥βα∩β=MNAB βAB ⊥MN⇒AB ⊥α1.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面【解析】本题考查了空间两个平面的判定与性质及充要条件.由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B . 【答案】B2.【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P –AC –B 的平面角为γ,则( ) A .β<γ,α<γB .β<α,β<γC .β<α,γ<αD .α<β,γ<β【解析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.如图,G 为AC 中点,连接VG ,V 在底面ABC 的投影为O ,则P 在底面的投影D 在线段AO 上,过D 作DE 垂直于AC 于E ,连接PE ,BD ,易得PE VG ∥,过P 作PF AC ∥交VG 于F ,连接BF ,过D 作DH AC ∥,交BG 于H ,则,,BPF PBD PED αβγ=∠=∠=∠,结合△PFB ,△BDH ,△PDB 均为直角三角形,可得cos cos PF EG DH BDPB PB PB PBαβ===<=,即αβ>; 【真题分析】在Rt △PED 中,tan tan PD PDED BDγβ=>=,即γβ>,综上所述,答案为B.【变式1】【2018年高考浙江卷】已知四棱锥S −ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为θ1,SE 与平面ABCD 所成的角为θ2,二面角S −AB −C 的平面角为θ3,则( )A .θ1≤θ2≤θ3B .θ3≤θ2≤θ1C .θ1≤θ3≤θ2D .θ2≤θ3≤θ1【解析】设O 为正方形ABCD 的中心,M 为AB 中点,过E 作BC 的平行线EF ,交CD 于F ,过O 作ON 垂直EF 于N ,连接SO ,SN ,SE ,SM ,OM ,OE ,则SO 垂直于底面ABCD ,OM 垂直于AB , 因此123,,,SEN SEO SMO ∠=∠=∠=θθθ从而123tan ,tan ,tan ,SN SN SO SOEN OM EO OM====θθθ 因为SN SO EO OM ≥≥,,所以132tan tan tan ,≥≥θθθ即132≥≥θθθ,故选D. 【答案】D【变式2】【2017年高考浙江卷】如图,已知正四面体–D ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CR QC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为αβγ,,,则( )A . γαβ<<B .αγβ<<C .αβγ<<D .βγα<<【解析】设O 为三角形ABC 中心,则O 到PQ 距离最小,O 到PR 距离最大,O 到RQ 距离居中,而三棱锥的高相等,因此αγβ<<,所以选B . 【答案】B3.【2018优选题】空间中,设,m n 表示不同的直线, ,,αβγ表示不同的平面,则下列命题正确的是( )A. 若,αγβγ⊥⊥,则//αβB. 若,m m αβ⊥⊥,则//αβC. 若,m βαβ⊥⊥,则//m αD. 若,n m n α⊥⊥,则//m α 【解析】本题考点是面面平行,线面平行的判定.A 项,若,αγβγ⊥⊥,过正方体同一顶点的三个平面分别为,,αβγ,则αβ⊥,故A 项不合题意;B 项,若,m m αβ⊥⊥,根据垂直于同一条直线的两个平面平行,则//αβ,故B 项符合题意;C 项,若,m βαβ⊥⊥,由同时垂直于一个平面的直线和平面的位置关系可以是直线在平面内或平行可知,直线m 在平面α内或平行,故C 项不合题意;D 项,若,n m n α⊥⊥,由同时垂直于一条直线的直线和平面的位置关系可以是直线在平面内或平行可知,直线m 在平面α内或平行,故D 项不合题意. 故选B. 【答案】B4.【2019优选题】在正四面体P -ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则下面四个结论中不成立的是( ) A .BC ∥平面PDF B .DF ⊥平面P AE C .平面PDF ⊥平面ABCD .平面P AE ⊥平面ABC【解析】画出图形,如图所示,则BC ∥DF ,又DF ⊂平面PDF ,BC ⊄平面PDF ,∴BC ∥平面PDF ,故A 成立;由题意可得AE ⊥BC ,PE ⊥BC ,BC ∥DF ,则DF ⊥AE ,DF ⊥PE ,∴DF ⊥平面P AE ,故B 成立; 又DF ⊂平面ABC ,∴平面ABC ⊥平面P AE ,故D 成立.本题的考点是平面与平面垂直的判定.【答案】C5.【2016全国新课标2】α,β是两个平面,m ,n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β. ②如果m ⊥α,n ∥α,那么m ⊥n . ③如果α∥β,m ⊂α,那么m ∥β.④如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号)【解析】对于①,,,//m n m n αβ⊥⊥,则,αβ的位置关系无法确定,故错误;对于②,因为//n α,所以过直线n 作平面γ与平面α相交于直线c ,则//n c ,因为,,m m c m n α⊥⊥⊥所以所以,故②正确;对于③,由两个平面平行的性质可知正确;对于④,由线面所成角的定义和等角定理可知其正确,故正确的命题有②③④.本题考点是空间中的线面关系. 【答案】②③④6.【2019年高考全国Ⅰ卷理数】如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A−MA 1−N 的正弦值.【解析】(1)连结B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C . 又因为N 为A 1D 的中点,所以ND =12A 1D .由题设知A 1B 1=P DC ,可得B 1C =P A 1D ,故ME =P ND , 因此四边形MNDE 为平行四边形,MN ∥ED .又MN ⊄平面EDC 1,所以MN ∥平面C 1DE .(2)由已知可得DE ⊥DA .以D 为坐标原点,DA uuu r的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz ,则(2,0,0)A ,A 1(2,0,4),2)M ,(1,0,2)N ,1(0,0,4)A A =-u u u r ,1(12)A M =--u u u u r ,1(1,0,2)A N =--u u u u r,(0,MN =u u u u r .设(,,)x y z =m 为平面A 1MA 的法向量,则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u rm m ,所以2040x z z ⎧--=⎪⎨-=⎪⎩,.可取=m .设(,,)p q r =n 为平面A 1MN 的法向量,则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u ur ,.n n所以020p r ⎧=⎪⎨--=⎪⎩,.可取(2,0,1)=-n.于是cos ,||⋅〈〉===‖m n m n m n , 所以二面角1A MA N --的正弦值为5. 7.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B −CG −A 的大小.【解析】(1)由已知得AD P BE ,CG P BE ,所以AD P CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,所以EH ⊥平面ABC . 由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EHH 为坐标原点,HC u u u r的方向为x 轴的正方向,建立如图所示的空间直角坐标系H –xyz ,则A (–1,1,0),C (1,0,0),G (2,0),CG uuu r =(1,0),AC uuu r=(2,–1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r n n即0,20.x x y ⎧+=⎪⎨-=⎪⎩ 所以可取n =(3,6,.又平面BCGE 的法向量可取为m =(0,1,0),所以cos ,||||2⋅〈〉==n m n m n m . 因此二面角B –CG –A 的大小为30°.8.【2019年高考北京卷文数】如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底部ABCD 为菱形,E 为CD 的中点.(1)求证:BD ⊥平面PAC ;(2)若∠ABC =60°,求证:平面PAB ⊥平面PAE ;(3)棱PB 上是否存在点F ,使得CF ∥平面PAE ?说明理由.【解析】本题主要考查线面垂直的判定定理,面面垂直的判定.(1)因为PA ⊥平面ABCD ,所以PA BD ⊥.又因为底面ABCD 为菱形,所以BD AC ⊥. 所以BD ⊥平面PAC .(2)因为PA ⊥平面ABCD ,AE ⊂平面ABCD ,所以PA ⊥AE .因为底面ABCD 为菱形,∠ABC =60°,且E 为CD 的中点,所以AE ⊥CD .所以AB ⊥AE .所以AE ⊥平面PAB .所以平面PAB⊥平面PAE.(3)棱PB上存在点F,使得CF∥平面PAE.取F为PB的中点,取G为PA的中点,连结CF,FG,EG.则FG∥AB,且FG=12 AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.因为CF⊄平面PAE,EG⊂平面PAE,所以CF∥平面PAE.9.【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的四边形ACGD的面积.【解析】本题从多面体折叠开始,考查考生在折叠过程中掌握哪些量的大小与位置关系是不变与变化的,折叠后的多面体的性质解决题中的要求.(1)由已知得AD P BE,CG P BE,所以AD P CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)取CG的中点M,连结EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°得EM⊥CG,故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中,DE=1,EM DM=2.所以四边形ACGD的面积为4.10.【2019年高考北京卷理数】如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC =3.E 为PD 的中点,点F 在PC 上,且13PF PC =. (1)求证:CD ⊥平面PAD ; (2)求二面角F –AE –P 的余弦值; (3)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.【解析】(1)因为PA ⊥平面ABCD ,所以PA ⊥CD .又因为AD ⊥CD ,所以CD ⊥平面PAD . (2)过A 作AD 的垂线交BC 于点M .因为PA ⊥平面ABCD ,所以PA ⊥AM ,PA ⊥AD .如图建立空间直角坐标系A −xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0), P (0,0,2).因为E 为PD 的中点,所以E (0,1,1).所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-=u u u ru u u r u u u r.所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .设平面AEF 的法向量为n =(x ,y ,z ),则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩ 令z =1,则1,1y x =-=-.于是=(1,1,1)--n .又因为平面PAD 的法向量为p =(1,0,0),所以3cos ,||3⋅〈〉==-‖n p n p n p . 由题知,二面角F −AE −P .(3)直线AG 在平面AEF 内.因为点G 在PB 上,且2,(2,1,2)3PG PB PB ==--u u ur ,所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .由(2)知,平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++=u u u r n .所以直线AG 在平面AEF 内.11.【2019年高考天津卷文数】如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,,2,3PA CD CD AD ⊥==.(1)设G ,H 分别为PB ,AC 的中点,求证:GH ∥平面PAD ; (2)求证:PA ⊥平面PCD ;(3)求直线AD 与平面PAC 所成角的正弦值.【解析】(1)连接BD ,易知AC BD H =I ,BH DH =.又由BG=PG ,故GH PD ∥. 又因为GH ⊄平面P AD ,PD ⊂平面P AD ,所以GH ∥平面P AD . (2)取棱PC 的中点N ,连接DN .依题意,得DN ⊥PC ,又因为平面PAC ⊥平面PCD ,平面PAC I 平面PCD PC =,所以DN ⊥平面P AC , 又PA ⊂平面P AC ,故DN PA ⊥.又已知PA CD ⊥,CD DN D =I ,所以PA ⊥平面PCD . (3)连接AN ,由(2)中DN ⊥平面P AC ,可知DAN ∠为直线AD 与平面P AC 所成的角, 因为PCD △为等边三角形,CD =2且N 为PC的中点,所以DN =又DN AN ⊥, 在Rt AND △中,3sinDN DAN AD ∠==.所以,直线AD 与平面P AC 所成角的正弦值为3.12.【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,AD AB ⊥1,2AB AD AE BC ====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值; (3)若二面角E BD F --的余弦值为13,求线段CF 的长.【解析】依题意,可以建立以A 为原点,分别以AB AD AE u u u r u u u r u u u r,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>>,则()1,2,F h .(1)依题意,(1,0,0)AB =u u u r 是平面ADE 的法向量,又(0,2,)BF h =u u u r ,可得0BF AB ⋅=u u u r u u u r ,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE . (2)依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--u u u ru u u r u u u r.设(,,)x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =,可得(2,2,1)=n .因此有4cos ,9||||CE CE CE ⋅==-u u u ru u u r u u u r n n n .所以,直线CE 与平面BDE 所成角的正弦值为49.(3)设(,,)x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r m m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =,可得21,1,h ⎛⎫=- ⎪⎝⎭m.由题意,有||1cos ,||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意. 所以,线段CF的长为87.【模拟考场】1.设α,β是两个不同的平面,m 是直线且m α⊂.“m β∥”是“αβ∥”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件【解析】本题考点是线面平行与面面平行与充要条件的综合应用.因为α,β是两个不同的平面,m 是直线且m α⊂.若“m β∥”,则平面、αβ可能相交也可能平行,不能推出//αβ,反过来若//αβ,m α⊂,则有m β∥,则“m β∥”是“αβ∥”的必要而不充分条件,故选B. 【答案】B2.设,a b 是空间中不同的直线, ,αβ是不同的平面,则下列说法正确的是( )A. //,a b b α⊂,则//a αB. ,,//a b αβαβ⊂⊂,则//a bC. ,,//,//a b b αααββ⊂⊂,则//αβD. //,a αβα⊂,则//a β【解析】本题考点是线面平行,面面平行的判定。
2019届高考数学大一轮复习第八章立体几何与空间向量高考专题突破四高考中的立体几何问题学案理北师大版

高考专题突破四高考中的立体几何问题【考点自测】1.在正三棱柱ABC-A1B1C1中,D为BC的中点,E为A1C1的中点,则DE与平面A1B1BA的位置关系为( )A.相交 B.平行 C.垂直相交 D.不确定答案 B解析如图取B1C1的中点为F,连接EF,DF,则EF∥A1B1,DF∥B1B,且EF∩DF=F,A1B1∩B1B=B1,∴平面EFD∥平面A1B1BA,∴DE∥平面A1B1BA.2.设x,y,z是空间中不同的直线或平面,对下列四种情形:①x,y,z均为直线;②x,y是直线,z是平面;③z是直线,x,y是平面;④x,y,z均为平面.其中使“x⊥z且y⊥z⇒x∥y”为真命题的是( )A.③④ B.①③ C.②③ D.①②答案 C解析 由正方体模型可知①④为假命题;由线面垂直的性质定理可知②③为真命题. 3.(2018届黑龙江海林市朝鲜中学模拟)已知某几何体的三视图如图所示,则该几何体的表面积为( )A .9+4(2+5)B .10+2(2+3)C .11+2(2+5)D .11+2(2+3) 答案 C解析 根据三视图还原几何体为一个直四棱柱,两底面为四边形(左视图),其余各侧面为矩形,两底面面积为2⎝ ⎛⎭⎪⎫12×2×2+12×1×1=5,四个侧面面积为2×2+1×2+2×5+2×2=6+25+22,几何体的表面积为11+2(5+2),故选C.4.(2017·天津滨海新区模拟)如图,以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕,把△ABD 和△ACD 折成互相垂直的两个平面后,某学生得出下列四个结论:①BD ⊥AC ;②△BAC 是等边三角形; ③三棱锥D -ABC 是正三棱锥; ④平面ADC ⊥平面ABC . 其中正确的是( )A .①②④ B.①②③ C.②③④ D.①③④ 答案 B解析 由题意知,BD ⊥平面ADC ,故BD ⊥AC ,①正确;AD 为等腰直角三角形斜边BC 上的高,平面ABD ⊥平面ACD ,所以AB =AC =BC ,△BAC 是等边三角形,②正确;易知DA =DB =DC ,又由②知③正确;由①知④错.故选B.5.(2017·沈阳调研)设α,β,γ是三个平面,a ,b 是两条不同的直线,有下列三个条件:①a ∥γ,b β;②a ∥γ,b ∥β;③b ∥β,a γ.如果命题“α∩β=a ,b γ,且________,则a ∥b ”为真命题,则可以在横线处填入的条件是________.(把所有正确的序号填上) 答案 ①或③解析 由线面平行的性质定理可知,①正确;当b ∥β,a γ时,a 和b 在同一平面内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.题型一 求简单几何体的表面积与体积例1 (2016·全国Ⅱ)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置.(1)证明:AC ⊥HD ′;(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.(1)证明 由已知得AC ⊥BD ,AD =CD ,又由AE =CF 得AE AD =CF CD,故AC ∥EF ,由此得EF ⊥HD ,折后EF 与HD 保持垂直关系,即EF ⊥HD ′,所以AC ⊥HD ′.(2)解 由EF ∥AC 得OH DO =AE AD =14.由AB =5,AC =6得DO =BO =AB 2-AO 2=4, 所以OH =1,D ′H =DH =3,于是OD ′2+OH 2=(22)2+12=9=D ′H 2, 故OD ′⊥OH .由(1)知AC ⊥HD ′,又AC ⊥BD ,BD ∩HD ′=H ,BD ,HD ′平面BHD ′,所以AC ⊥平面BHD ′,于是AC ⊥OD ′,又由OD ′⊥OH ,AC ∩OH =O ,AC ,OH 平面ABC , 所以OD ′⊥平面ABC . 又由EF AC =DH DO 得EF =92.五边形ABCFE 的面积S =12×6×8-12×92×3=694.所以五棱锥D ′-ABCFE 的体积V =13×694×22=2322. 思维升华 (1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.跟踪训练1 (2018·乌鲁木齐质检)正三棱锥的高为1,底面边长为26,内有一个球与它的四个面都相切(如图).求:(1)这个正三棱锥的表面积;(2)这个正三棱锥内切球的表面积与体积.解 (1)底面正三角形中心到一边的距离为13×32×26=2,则正棱锥侧面的斜高为12+(2)2=3,∴S 侧=3×12×26×3=92,∴S 表=S 侧+S 底=92+12×32×(26)2=92+6 3.(2)设正三棱锥P -ABC 的内切球球心为O ,连接OP ,OA ,OB ,OC ,而O 点到三棱锥的四个面的距离都为球的半径r .∴V 三棱锥P -ABC =V 三棱锥O -PAB +V 三棱锥O -PBC +V 三棱锥O -PAC +V 三棱锥O -ABC=13S 侧·r +13S △ABC ·r =13S 表·r =(32+23)r .又V P -ABC =13×12×32×(26)2×1=23,∴(32+23)r =23,得r =2332+23=23(32-23)18-12=6-2.∴S 内切球=4π(6-2)2=(40-166)π.V 内切球=43π(6-2)3=83(96-22)π.题型二 空间点、线、面的位置关系例2 (2017·广州五校联考)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,PA =PD ,∠BAD =60°,E 是AD 的中点,点Q 在侧棱PC 上.(1)求证:AD ⊥平面PBE ;(2)若Q 是PC 的中点,求证:PA ∥平面BDQ ; (3)若V P -BCDE =2V Q -ABCD ,试求CPCQ的值. (1)证明 由E 是AD 的中点,PA =PD 可得AD ⊥PE . 因为底面ABCD 是菱形,∠BAD =60°, 所以AB =BD ,所以AD ⊥BE , 又PE ∩BE =E ,PE ,BE 平面PBE , 所以AD ⊥平面PBE .(2)证明 连接AC ,交BD 于点O ,连接OQ .因为O 是AC 的中点,Q 是PC 的中点, 所以OQ ∥PA ,又PA ⊈平面BDQ ,OQ 平面BDQ ,所以PA ∥平面BDQ .(3)解 设四棱锥P -BCDE ,Q -ABCD 的高分别为h 1,h 2. 所以V 四棱锥P -BCDE =13S 四边形BCDE h 1,V 四棱锥Q -ABCD =13S 四边形ABCD h 2.又V P -BCDE =2V Q -ABCD ,且S 四边形BCDE =34S 四边形ABCD ,所以CP CQ =h 1h 2=83.思维升华 (1)平行问题的转化利用线线平行、线面平行、面面平行的相互转化解决平行关系的判定问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而应用性质定理时,其顺序正好相反.在实际的解题过程中,判定定理和性质定理一般要相互结合,灵活运用. (2)垂直问题的转化在空间垂直关系中,线面垂直是核心,已知线面垂直,既可为证明线线垂直提供依据,又可为利用判定定理证明面面垂直作好铺垫.应用面面垂直的性质定理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,从而把面面垂直问题转化为线面垂直问题,进而可转化为线线垂直问题.跟踪训练2 如图,在直三棱柱ABC —A 1B 1C 1中,AB =AC ,E 是BC 的中点,求证:(1)平面AB 1E ⊥平面B 1BCC 1; (2)A 1C ∥平面AB 1E .证明 (1)在直三棱柱ABC —A 1B 1C 1中,CC 1⊥平面ABC .因为AE 平面ABC ,所以CC 1⊥AE .因为AB =AC ,E 为BC 的中点,所以AE ⊥BC . 因为BC 平面B 1BCC 1,CC 1平面B 1BCC 1, 且BC ∩CC 1=C , 所以AE ⊥平面B 1BCC 1. 因为AE 平面AB 1E , 所以平面AB 1E ⊥平面B 1BCC 1.(2)连接A 1B ,设A 1B ∩AB 1=F ,连接EF .在直三棱柱ABC —A 1B 1C 1中,四边形AA 1B 1B 为平行四边形, 所以F 为A 1B 的中点.又因为E 是BC 的中点,所以EF ∥A 1C . 因为EF 平面AB 1E ,A 1C ⊈平面AB 1E , 所以A 1C ∥平面AB 1E .题型三 平面图形的翻折问题例3 (2016·全国Ⅱ)如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置,OD ′=10.(1)证明:D ′H ⊥平面ABCD ;(2)求平面BD ′A 与平面D ′AC 夹角的正弦值. (1)证明 由已知得AC ⊥BD ,AD =CD . 又由AE =CF 得AE AD =CF CD,故AC ∥EF . 因此EF ⊥HD ,从而EF ⊥D ′H .由AB =5,AC =6得DO =BO =AB 2-AO 2=4. 由EF ∥AC 得OH DO =AE AD =14.所以OH =1,D ′H =DH =3.于是D ′H 2+OH 2=32+12=10=D ′O 2,故D ′H ⊥OH . 又D ′H ⊥EF ,而OH ∩EF =H , 所以D ′H ⊥平面ABCD .(2)解 如图,以H 为坐标原点,HF ,HD ,HD ′所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则H (0,0,0),A (-3,-1,0),B (0,-5,0),C (3,-1,0),D ′(0,0,3),AB →=(3,-4,0),AC →=(6,0,0), AD ′→=(3,1,3).设m =(x 1,y 1,z 1)是平面ABD ′的法向量,则 ⎩⎪⎨⎪⎧ m ·AB →=0,m ·AD ′→=0,即⎩⎪⎨⎪⎧ 3x 1-4y 1=0,3x 1+y 1+3z 1=0,所以可取m =(4,3,-5).设n =(x 2,y 2,z 2)是平面ACD ′的法向量,则 ⎩⎪⎨⎪⎧n ·AC →=0,n ·AD ′→=0,即⎩⎪⎨⎪⎧6x 2=0,3x 2+y 2+3z 2=0,所以可取n =(0,-3,1).于是|cos 〈m ,n 〉|=|m ·n ||m ||n |=|-14|50×10=7525,sin 〈m ,n 〉=29525.因此平面BD ′A 与平面D ′AC 夹角的正弦值是29525.思维升华 平面图形的翻折问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.跟踪训练3 (2017·深圳模拟)如图(1),四边形ABCD 为矩形,PD ⊥平面ABCD ,AB =1,BC =PC =2,作如图(2)折叠,折痕EF ∥DC .其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后,点P 叠在线段AD 上的点记为M ,并且MF ⊥CF .(1)证明:CF ⊥平面MDF ; (2)求三棱锥M -CDE 的体积.(1)证明 因为PD ⊥平面ABCD ,AD 平面ABCD , 所以PD ⊥AD .又因为ABCD 是矩形,CD ⊥AD ,PD ∩CD =D ,PD ,CD 平面PCD ,所以AD ⊥平面PCD .又CF 平面PCD ,所以AD ⊥CF ,即MD ⊥CF . 又MF ⊥CF ,MD ∩MF =M ,MD ,MF 平面MDF , 所以CF ⊥平面MDF .(2)解 因为PD ⊥DC ,PC =2,CD =1,∠PCD =60°,所以PD =3,由(1)知FD ⊥CF , 在Rt△DCF 中,CF =12CD =12.如图,过点F 作FG ⊥CD 交CD 于点G , 得FG =FC sin 60°=12×32=34,所以DE =FG =34,故ME =PE =3-34=334, 所以MD =ME 2-DE 2=⎝ ⎛⎭⎪⎫3342-⎝ ⎛⎭⎪⎫342=62. S △CDE =12DE ·DC =12×34×1=38.故V 三棱锥M -CDE =13MD ·S △CDE =13×62×38=216.题型四 立体几何中的存在性问题例4 (2017·安徽江南名校联考)如图,在四棱锥P —ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,DC =6,AD =8,BC =10,∠PAD =45°,E 为PA 的中点.(1)求证:DE ∥平面BPC ;(2)线段AB 上是否存在一点F ,满足CF ⊥DB ?若存在,请求出平面FPC 与平面PCD 夹角的余弦值;若不存在,请说明理由.(1)证明 取PB 的中点M ,连接EM 和CM ,过点C 作CN ⊥AB ,垂足为点N .在平面ABCD 内,∵CN ⊥AB ,DA ⊥AB ,∴CN ∥DA ,又AB ∥CD ,∴四边形CDAN 为平行四边形, ∴CN =AD =8,DC =AN =6, 在Rt△BNC 中,BN =BC 2-CN 2=102-82=6,∴AB =12,而E ,M 分别为PA ,PB 的中点, ∴EM ∥AB 且EM =6,又DC ∥AB ,∴EM ∥CD 且EM =CD ,四边形CDEM 为平行四边形, ∴DE ∥CM .∵CM 平面PBC ,DE ⊈平面PBC , ∴DE ∥平面BPC .(2)解 由题意可得DA ,DC ,DP 两两互相垂直,如图,以D 为原点,DA ,DC ,DP 所在直线分别为x ,y ,z 轴建立空间直角坐标系,则A (8,0,0),B (8,12,0),C (0,6,0),P (0,0,8).假设AB 上存在一点F 使CF ⊥BD ,设点F 的坐标为(8,t,0)(0<t <12), 则CF →=(8,t -6,0),DB →=(8,12,0), 由CF →·DB →=0,得t =23.又平面DPC 的一个法向量为m =(1,0,0), 设平面FPC 的法向量为n =(x ,y ,z ). 又PC →=(0,6,-8),FC →=⎝ ⎛⎭⎪⎫-8,163,0.由⎩⎪⎨⎪⎧n ·PC →=0,n ·FC →=0,得⎩⎪⎨⎪⎧6y -8z =0,-8x +163y =0,即⎩⎪⎨⎪⎧z =34y ,x =23y ,不妨令y =12,则n =(8,12,9).则|cos 〈n ,m 〉|=|n·m||n||m |=81×82+122+92=817.故平面FPC 与平面PCD 夹角的余弦值为817.思维升华 对于线面关系中的存在性问题,首先假设存在,然后在该假设条件下,利用线面关系的相关定理、性质进行推理论证,寻找假设满足的条件,若满足则肯定假设,若得出矛盾的结论则否定假设.跟踪训练4 (2018·成都模拟)如图,四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ∥DC ,AB ⊥AD ,AD =CD =1,AA 1=AB =2,E 为棱AA 1的中点.(1)证明:B 1C 1⊥CE ;(2)求平面B 1CE 与平面CEC 1夹角的正弦值;(3)设点M 在线段C 1E 上,且直线AM 与平面ADD 1A 1所成角的正弦值为26,求线段AM 的长. (1)证明 如图,以点A 为原点,分别以AD ,AA 1,AB 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,由题意得A (0,0,0),B (0,0,2),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0). 易得B 1C 1→=(1,0,-1),CE →=(-1,1,-1),于是B 1C 1→·CE →=0,所以B 1C 1⊥CE .(2)解 B 1C →=(1,-2,-1).设平面B 1CE 的法向量m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·B 1C →=0,m ·CE →=0,即⎩⎪⎨⎪⎧x -2y -z =0,-x +y -z =0.消去x ,得y +2z =0,不妨令z =1, 可得一个法向量为m =(-3,-2,1).由(1)知,B 1C 1⊥CE ,又CC 1⊥B 1C 1,CC 1∩CE =C ,CC 1,CE 平面CEC 1,可得B 1C 1⊥平面CEC 1,故B 1C 1→=(1,0,-1)为平面CEC 1的一个法向量. 于是|cos 〈m |,B 1C 1→〉=|m ·B 1C 1→||m ||B 1C 1→|=|-4|14×2=-277,从而sin 〈m ,B 1C 1→〉=217,所以平面B 1CE 与平面CEC 1夹角的正弦值为217. (3)解 AE →=(0,1,0),EC 1→=(1,1,1),设EM →=λEC 1→=(λ,λ,λ)(0≤λ≤1),则AM →=AE →+EM →=(λ,λ+1,λ).可取AB →=(0,0,2)为平面ADD 1A 1的一个法向量. 设θ为直线AM 与平面ADD 1A 1所成的角,则 sin θ=|cos 〈AM →,AB →〉|=|AM →·AB →||AM →||AB →|=2λλ2+(λ+1)2+λ2×2=λ3λ2+2λ+1, 于是λ3λ2+2λ+1=26,解得λ=13(负值舍去), 所以AM = 2.1.(2017·北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )A.3 2 B.2 3 C.2 2 D.2答案 B解析在正方体中还原该四棱锥,如图所示,可知SD为该四棱锥的最长棱.由三视图可知正方体的棱长为2,故SD=22+22+22=2 3.故选B.2.(2018·沈阳模拟)如图所示,已知平面α∩平面β=l,α⊥β.A,B是直线l上的两点,C,D是平面β内的两点,且AD⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )A.48 B.16 C.24 3 D.144答案 A解析由题意知,△PAD,△PBC是直角三角形,又∠APD=∠BPC,所以△PAD∽△PBC.因为DA=4,CB=8,所以PB=2PA.作PM⊥AB于点M,由题意知,PM⊥平面β.令BM=t,则AM=|6-t|,PA2-(6-t)2=4PA2-t2,所以PA2=4t-12.所以PM =-t 2+16t -48, 即为四棱锥P -ABCD 的高,又底面ABCD 为直角梯形,S =12×(4+8)×6=36.所以V =13×36×-t 2+16t -48=12-(t -8)2+16≤12×4=48.3.(2017·云南省十一校调研)设已知m ,n 是两条不同的直线,α,β为两个不同的平面,有下列四个命题:①若α⊥β,m α,n β,则m ⊥n ; ②若m ⊥α,n ⊥β,m ⊥n ,则α⊥β; ③若m ∥α,n ∥β,m ∥n ,则α∥β; ④若m ⊥α,n ∥β,α∥β,则m ⊥n . 其中所有正确命题的序号是________. 答案 ②④解析 对于①,当两个平面互相垂直时,分别位于这两个平面内的两条直线未必垂直,因此①不正确;对于②,依据结论“由空间一点向一个二面角的两个半平面(或半平面所在平面)引垂线,这两条垂线所成的角与这个二面角的平面角相等或互补”可知②正确;对于③,分别与两条平行直线平行的两个平面未必平行,因此③不正确;对于④,由n ∥β得,在平面β内必存在直线n 1平行于直线n ,由m ⊥α,α∥β得m ⊥β,m ⊥n 1,又n 1∥n ,因此有m ⊥n ,④正确.综上所述,所有正确命题的序号是②④.4.如图梯形ABCD 中,AD ∥BC ,∠ABC =90°,AD ∶BC ∶AB =2∶3∶4,E ,F 分别是AB ,CD 的中点,将四边形ADFE 沿直线EF 进行翻折,给出四个结论:①DF ⊥BC ; ②BD ⊥FC ;③平面DBF ⊥平面BFC ; ④平面DCF ⊥平面BFC .在翻折过程中,可能成立的结论是________.(填写结论序号) 答案 ②③解析 因为BC ∥AD ,AD 与DF 相交不垂直,所以BC 与DF 不垂直,则①错误;设点D 在平面BCF 上的射影为点P ,当BP ⊥CF 时就有BD ⊥FC ,而AD ∶BC ∶AB =2∶3∶4,可使条件满足,所以②正确;当点P 落在BF 上时,DP 平面BDF ,从而平面BDF ⊥平面BCF ,所以③正确;因为点D 的投影不可能在FC 上,所以平面DCF ⊥平面BFC 不成立,即④错误.5.如图所示,在棱长为2的正方体ABCD —A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,则点P 到直线CC 1的距离的最小值为________.答案255解析 点P 到直线CC 1的距离等于点P 在平面ABCD 上的射影到点C 的距离,设点P 在平面ABCD 上的射影为P ′,显然点P 到直线CC 1的距离的最小值为P ′C 的长度的最小值.连接DE ,当P ′C ⊥DE 时,P ′C 的长度最小,此时P ′C =2×122+1=255. 6.(2018·烟台模拟)如图,在四棱柱ABCD -A 1B 1C 1D 1中,AC ⊥B 1D ,BB 1⊥底面ABCD ,E ,F ,H 分别为AD ,CD ,DD 1的中点,EF 与BD 交于点G .(1)证明:平面ACD 1⊥平面BB 1D ; (2)证明:GH ∥平面ACD 1.证明 (1)∵BB 1⊥平面ABCD ,AC 平面ABCD ,∴AC⊥BB1.又AC⊥B1D,BB1∩B1D=B1,BB1,B1D平面BB1D,∴AC⊥平面BB1D.∵AC平面ACD1,∴平面ACD1⊥平面BB1D.(2)设AC∩BD=O,连接OD1.∵E,F分别为AD,CD的中点,EF∩OD=G,∴G为OD的中点.∵H为DD1的中点,∴HG∥OD1.∵GH⊈平面ACD1,OD1平面ACD1,∴GH∥平面ACD1.7.(2017·青岛质检)在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示.(1)求证:AB⊥CD;(2)若M为AD的中点,求直线AD与平面MBC所成角的正弦值.(1)证明∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB平面ABD,AB⊥BD,∴AB⊥平面BCD.又CD平面BCD,∴AB⊥CD.(2)解 过点B 在平面BCD 内作BE ⊥BD ,如图.由(1)知AB ⊥平面BCD ,BE 平面BCD ,BD 平面BCD . ∴AB ⊥BE ,AB ⊥BD .以B 为坐标原点,分别以BE ,BD ,BA 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系.由题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12, 则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).设平面MBC 的法向量为n =(x 0,y 0,z 0), 则⎩⎪⎨⎪⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0,取z 0=1,得平面MBC 的一个法向量n =(1,-1,1). 设直线AD 与平面MBC 所成的角为θ, 则sin θ=|cos 〈n ,AD →〉|=|n ·AD →||n ||AD →|=63,即直线AD 与平面MBC 所成角的正弦值为63.8.(2017·郑州模拟)等边三角形ABC 的边长为3,点D ,E 分别是边AB ,AC 上的点,且满足AD DB =CE EA =12,如图1.将△ADE 沿DE 折起到△A 1DE 的位置,使二面角A 1—DE —B 为直二面角,连接A 1B ,A 1C ,如图2.(1)求证:A 1D ⊥平面BCED ;(2)在线段BC 上是否存在点P ,使直线PA 1与平面A 1BD 所成的角为60°?若存在,求出PB 的长;若不存在,请说明理由.(1)证明 因为等边三角形ABC 的边长为3,且AD DB =CE EA =12,所以AD =1,AE =2. 在△ADE 中,∠DAE =60°,由余弦定理得DE =12+22-2×1×2×cos 60°= 3.从而AD 2+DE 2=AE 2,所以AD ⊥DE .折起后有A 1D ⊥DE ,因为二面角A 1—DE —B 是直二面角, 所以平面A 1DE ⊥平面BCED ,又平面A 1DE ∩平面BCED =DE ,A 1D ⊥DE , 所以A 1D ⊥平面BCED .(2)解 存在.理由:由(1)可知ED ⊥DB ,A 1D ⊥平面BCED .以D 为坐标原点,分别以DB ,DE ,DA 1所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系.设PB =2a (0≤2a ≤3),作PH ⊥BD 于点H , 连接A 1H ,A 1P ,则BH =a ,PH =3a ,DH =2-a .所以A 1(0,0,1),P (2-a ,3a,0),E (0,3,0). 所以PA 1→=(a -2,-3a,1). 因为ED ⊥平面A 1BD ,所以平面A 1BD 的一个法向量为DE →=(0,3,0). 要使直线PA 1与平面A 1BD 所成的角为60°, 则sin 60°=|PA 1→·DE →||PA 1→||DE →|=3a 4a 2-4a +5×3=32, 解得a =54.此时2a =52,满足0≤2a ≤3,符合题意.所以在线段BC 上存在点P ,使直线PA 1与平面A 1BD 所成的角为60°,此时PB =52.9.(2018·合肥模拟)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠BCD =2π3,四边形BFED 为矩形,平面BFED ⊥平面ABCD ,BF =1.(1)求证:AD ⊥平面BFED ;(2)点P 在线段EF 上运动,设平面PAB 与平面ADE 的夹角为θ,试求θ的最小值. (1)证明 在梯形ABCD 中,∵AB ∥CD ,AD =DC =CB =1,∠BCD =2π3,∴AB =2,∴BD 2=AB 2+AD 2-2AB ·AD ·cos π3=3.∴AB 2=AD 2+BD 2,∴AD ⊥BD .∵平面BFED ⊥平面ABCD ,平面BFED ∩平面ABCD =BD ,DE 平面BFED ,DE ⊥DB , ∴DE ⊥平面ABCD , ∴DE ⊥AD ,又DE ∩BD =D , ∴AD ⊥平面BFED .(2)解 由(1)可建立以点D 为坐标原点,分别以直线DA ,DB ,DE 为x 轴,y 轴,z 轴的空间直角坐标系,如图所示.令EP =λ(0≤λ≤3),则D (0,0,0),A (1,0,0),B (0,3,0),P (0,λ,1), ∴AB →=(-1,3,0),BP →=(0,λ-3,1). 设n 1=(x ,y ,z )为平面PAB 的一个法向量,由⎩⎪⎨⎪⎧ n 1·AB →=0,n 1·BP →=0, 得⎩⎨⎧ -x +3y =0,(λ-3)y +z =0, 取y =1,得n 1=(3,1,3-λ), ∵n 2=(0,1,0)是平面ADE 的一个法向量,∴cos θ=|n 1·n 2||n 1||n 2|=13+1+(3-λ)2×1=1(λ-3)2+4 . ∵0≤λ≤3,∴当λ=3时,cos θ有最大值12, 又∵θ为锐角,∴θ的最小值为π3.。
2019届二轮(理科数学) 空间几何体和立体几何 专题卷(江苏专用)

空间几何体1. (2018·南通泰州期末·11)如图,铜质六角螺帽毛胚是由一个正六棱柱挖去一个圆柱所构成的.已知正六棱柱的底面边长、高都为4cm,圆柱的底面积为2.若将该螺帽熔化后铸成一个高为6cm 的正三棱柱零件,则该正三棱柱的底面边长为cm .(不计损耗)【答案】2. (南通、泰州市2017届高三第一次调研测)如图,在正四棱柱ABCD –A 1B 1C 1D 1中,3cm AB =,11cm AA =,则三棱锥D 1–A 1BD 的体积为 ▲ 3cm .323. (南通市海安县2016届高三上期末)正四棱锥的底面边长为2 cm ,侧面与底面所成二面角的大小为60°,则该四棱锥的侧面积为cm 284. (泰州市2016届高三第一次模拟)如图,长方体1111ABCD A BC D -中,O 为1BD 的中点,三棱锥O ABD -的体积为1V ,四棱锥11O ADD A -的体积为2V ,则12V V 的值为.A 1125. (泰州市2014届高三上期末调研测试)8.如图,在正三棱柱111C B A ABC -中,D 为棱1AA 的中点.若14AA =,2AB =,则四棱锥1B ACC D -的体积为.6. (南通市2013届高三第一次调研测试)3.已知正四棱锥的底面边长是6,这个正四棱锥的侧面积是 ▲ .48.立体几何7. (2018·南通泰州期末·15)如图,在三棱锥P ABC -中,AB PC ⊥,CA CB =,M 是AB 的中点.点N 在棱PC 上,点D 是BN 的中点.求证:(1)//MD 平面PAC ;(2)平面ABN ⊥平面PMC .【答案】【证明】(1)在ABN ∆中,M 是AB 的中点,D 是BN 的中点,所以//MD AN .又因为AN ⊂平面PAC ,MD ⊄平面PAC ,所以//MD 平面PAC .(2)在ABC ∆中,CA CB =,M 是AB 的中点,所以AB MC ⊥,又因为AB PC ⊥,PC ⊂平面PMC ,MC ⊂平面PMC ,PC MC C = ,所以AB ⊥平面PMC .又因为AB ⊂平面ABN ,所以平面ABN ⊥平面PMC .8. (南通、泰州市2017届高三第一次调研测)如图,在四棱锥P -ABCD 中,四边形ABCD为平行四边形,AC ,BD 相交于点O ,点E 为PC 的中点,OP =OC ,PA ⊥PD .(1)求证:(1)直线PA ∥平面BDE ;(2)平面BDE ⊥平面PCD .2、【证明】(1)连结OE ,因为O 为平行四边形对角线的交点,所以O 为AC 中点.又因为E 为PC 的中点,所以OE ∥PA .……………………4分又因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以直线PA ∥平面BDE .……………………………………………………6分(2)因为OE ∥PA ,PA PD ⊥,所以OE PD ⊥.……8分因为OP OC =,E 为PC 的中点,所以OE PC ⊥.………10分又因为PD ⊂平面PCD ,PC ⊂平面PCD ,PC PD P = ,ABCD所以OE ⊥平面PCD .………………12分又因为OE ⊂平面BDE ,所以平面BDE ⊥平面PCD .………14分9. (南通市海安县2016届高三上期末)如图,在直三棱柱ABC —111C B A 中,已知1,CC BC BC AC =⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019届高考理科数学专题
高考中的立体几何问题
一、选择题(每小题5分,共30分)
1.一个多面体的三视图如图4-1所示,则此多面体的表面积是()
图4-1
A.22
B.24-
C.22+
D.20+
2.如图4-2,网格纸上小正方形的边长为1,粗线画的是某组合体的三视图,则该组合体的体积
是()
图4-2
A.+π
B.+π
C.4+π
D.+π
3.已知正方体ABCD-A1B1C1D1的所有顶点均在球O的表面上,E,F,G分别为AB,AD,AA1的中点,若平面EFG截球O所得圆的半径为,则该正方体的棱长为()
A. B. C.3 D.2
4. [数学文化题]如图4-3为中国传统智力玩具鲁班锁,它起源于中国古代建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱
的底面正方形的边长为2,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器的表
面积的最小值为56π,则正四棱柱的高为()
A. B.2 C.6 D.2
5. [数学文化题]中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器.如图4-4所示,某沙漏由上、下两个圆锥形容器组成,圆锥形容器的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥形容器高度的(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为()
图4-4
A.2 cm
B.cm
C.cm
D.cm
6.如图4-5,在正三棱柱ABC-A1B1C1中,AA1=AB,E,F分别为BC,BB1的中点,M,N分别为
AA1,A1C1的中点,则直线MN与EF所成角的余弦值为()
图4-5
A. B. C. D.
二、填空题(每小题5分,共10分)
7.若侧面积为8π的圆柱有一外接球O,则当球O的体积取得最小值时,圆柱的表面积
为.
8.如图4-6,在棱长为1的正方体ABCD-A1B1C1D1中,作以A为顶点,分别以AB,AD,AA1为轴,底面圆半径为r(0<r≤1)的圆锥.当半径r变化时,正方体挖去三个圆锥部分后,余下的几何体的表面积的最小值是.
图4-6
三、解答题(共48分)
9.(12分)如图4-7,在直角△ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF,D,E是平面ABC 同一侧的两点, AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.
(1)求证:平面CDF⊥平面CEF;
(2)若M是线段CB的中点,求异面直线CF与EM所成角的余弦值.
图4-7
10.(12分)如图4-8所示,在多面体ABD-A1B1C1D1中,四边形A1B1C1D1,ADD1A1,ABB1A1均为正方形,点M是BD的中点,点H在C1M上,且A1H与平面ABD所成角的正弦值为.
(1)证明:B1D1∥平面BC1D;
(2)求二面角A-A1H-B的大小.
图4-8
11.(12分)在如图4-9所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)在线段AB(含端点)上是否存在一点P,使得FP∥平面AED?若存在,求出的值;若不存在,
请说明理由.
(2)求直线AF与平面BDF所成角的正弦值.
图4-9
12.(12分)如图4-10(1),正方形ABCD的边长为4,AB=AE=BF=EF,AB∥EF,把四边形ABCD
沿AB折起,使得AD⊥底面AEFB,G是EF的中点,连接BG,如图4-10(2).
(1)求证:AG⊥平面BCE;
(2)求二面角C-AE-F的余弦值.
(1)(2)
图4-10
答案
1.C根据题中三视图知,该多面体是从一个棱长为2的正方体的左上角截去一个直三棱柱后剩余的部分,因此其表面积为6×22-1×1×2+×1=22+,故选C.
2.D观察题中三视图可知该组合体的上面是三棱锥,下面是半径为1的半球,其直观图如图
D 4-1所示.
图D 4-1
解法一如图D 4-2所示,将组合体中三棱锥A-BEF“补”成正方体,顶点A,B,E,F分别是正方体的棱的中点.取EF的中点C,连接AC,BC,则EF⊥平面ABC,由已知得,EF=AB=2,AC=BC=
所以S△ABC=×2×2=2,三棱锥A-BEF的体积V1=×S△ABC×EF=,半球的体积V2=×π×13=π.所以该组合体的体积V=V1+V2=+π.故选D.
图D 4-2
解法二如图D 4-3所示,将组合体中的三棱锥A-BEF“补”成正方体,顶点A,B,E,F分别是正方体的棱的中点,取AB的中点G,过EF和点G作截面EFDC,则截面EFDC将三棱锥A-BEF分成两个相同的小三棱锥,且AG=1,S△EFG=×2×2=2,所以三棱锥A-BEF的体积
V1=2××S△EFG×AG=,半球体积V2=×π×13=π,所以该组合体的体积V=V1+V2=+π.故选D.
图D 4-3。
