微积分第三章答案
微积分及其应用第三章习题解答

1.(1)v =01.02001.02)()(=∆==∆=∆∆-∆+=∆∆t t t t t t s t t s ts=01.020)263(=∆=++∆t t t t =14.03 (2)14lim)2(200=∆∆==→∆t t ts v2。
(1)v =tt ∆=1=tt ts ∆=∆∆1=tg t g t ∆--∆+-∆+]215[])1(21)1(5[2=t g g ∆--215 (2)g t ht t -=∆∆==→∆5]lim[)1(1ν (3) tgt t t t g t t th tvtt t t t ∆--∆+-∆+=∆∆=∆∆==)215()((21)(50020000=t g gt ∆--2150 (4)000005)215(lim lim)(gt t g gt t h t t t -=∆--=∆∆=→∆→∆ν 3。
(1)x x f x x f x x f x x f x x ∆--∆-+=∆-∆-→∆→∆)()]([lim )()(lim000000=)()]()([lim 0,000x f xx f x x f x -=∆--∆-+-→∆(2))()()()((lim )()((lim0,00000000x f h x x h x f x f h h x f x f h h =--∆--=∆--→∆→∆(3)h h x f h x f h x f h x f h h 202000200)()((lim )()((lim -+=-+→∆→∆=0lim )()((lim 020200==-+→∆→∆h h x f h x f h h(4)xx x f x x f x ∆∆--∆+→∆)()(lim000=)(21()()()(21lim 0,00000x f x x x x x x f x x f x =∆--∆+∆--∆+→∆4。
(1)xx f x x f y x ∆-∆+='→∆)()(lim000=xxx x x x x x x x x x x ∆∆+∆+-=∆-∆+→∆→∆)()(lim 11lim 0000=2001)(1lim )(limxx x x xx x x x x x -=∆+-=∆∆+∆-→∆→∆ (2)x xx x xx f x x f x f x x ∆-∆+=∆-∆+='→∆→∆000lim )()(lim)(=xx x x x x xx x x x +∆+=+∆+-∆+→∆→∆1limlim 00=x215.解:1)5(21)5()5(21lim 2)5()5(lim00-='-=----=--→∆→∆f x f x f x f x f x x 6(1)==x x y 首先判断函数的连续性0x >时2x y =连续,0< x 时2-x y =连续,在0x =时,0])([lim )00(220=-∆+=++→∆x x x f f x0])([lim )00(220=+∆+=--→∆x x x f f x由于)00()00(-=+f f所以函数y 在0=x 处连续 下面判断可导性 在0=x 处 xf x f f x ∆-∆='+→∆+)0()(lim)0(0=xx x ∆∆++→∆20)0(lim=0lim 0=∆+→∆x xxf x f f x ∆-∆+='-→∆-)0()0(lim)0(0=0lim )(lim 020=∆-=∆∆---→∆→∆x xx x x由于)0()0(-+'='f f 故函数在0=x 处可导 (2))1(011-x 1-x sin lim)(lim 11f x f x x =≠==→→)(∴ 函数)(x f 在1=x 处不连续,从而0=x 在处不可导。
微积分习题三答案和解答过程65页PPT

11、不为五斗米折腰。 12、芳菊开林耀,青松冠岩列。怀此 贞秀姿 ,卓为 霜下杰 。
13、归去来兮,田蜀将芜胡不归。 14、酒能祛百虑,菊为制颓龄。 15、春蚕收长丝,秋熟靡王税。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
高等数学微积分教材答案

高等数学微积分教材答案第一章:导数与微分1.1 导数的定义1.1.1 极限的概念1.1.2 函数的极限1.1.3 导数的定义及计算方法1.2 导数的基本性质1.2.1 可导性与连续性的关系1.2.2 导数的四则运算法则1.2.3 导数的链式法则1.3 高阶导数与隐函数微分1.3.1 高阶导数的定义1.3.2 隐函数的导数计算方法1.4 微分的定义与微分公式1.4.1 微分的定义1.4.2 微分的性质1.4.3 微分公式第二章:微分学的应用2.1 函数的单调性与极值2.1.1 函数单调性的判定2.1.2 函数的极值与最值2.2 函数的凹凸性与拐点2.2.1 函数的凹凸性定义2.2.2 函数的拐点2.3 泰勒公式与函数的近似计算 2.3.1 泰勒公式的定义2.3.2 泰勒公式的应用2.4 最值问题与优化问题2.4.1 最值问题的分析方法2.4.2 优化问题的数学建模第三章:不定积分3.1 原函数与不定积分3.1.1 原函数的定义与性质3.1.2 不定积分的定义3.2 积分基本公式3.2.1 基本积分公式3.2.2 积分的线性性质3.3 第一类换元积分法3.3.1 第一类换元积分法的基本思想 3.3.2 第一类换元积分法的具体步骤3.4 分部积分法与第二类换元积分法 3.4.1 分部积分法的定义与应用3.4.2 第二类换元积分法的基本原理第四章:定积分与定积分的应用4.1 定积分的定义与性质4.1.1 定积分的几何意义4.1.2 定积分的性质4.2 定积分的计算方法4.2.1 定积分的基本计算方法4.2.2 定积分的换元法4.3 定积分的应用4.3.1 曲线与曲面的长度4.3.2 曲线与曲面的面积4.3.3 物理应用中的定积分4.4 微积分基本定理与不定积分的计算方法 4.4.1 微积分基本定理4.4.2 不定积分的计算方法第五章:数项级数5.1 数项级数的概念与性质5.1.1 数项级数的定义5.1.2 数项级数的性质5.2 收敛级数的判别法5.2.1 正项级数的判别法5.2.2 任意项级数的判别法5.3 幂级数与函数展开5.3.1 幂级数的收敛半径5.3.2 幂级数的函数展开5.4 常数项级数的求和5.4.1 等比级数的求和5.4.2 绝对收敛级数的求和第六章:级数的应用6.1 函数展开与泰勒级数6.1.1 函数展开与泰勒级数的概念6.1.2 泰勒级数的求法6.2 常微分方程与级数解6.2.1 常微分方程的基本概念6.2.2 幂级数解的构造6.3 分析几何中的级数应用6.3.1 曲线与曲面的参数方程6.3.2 空间曲线与曲面的求交问题6.4 物理学中的级数应用6.4.1 物理学中的振动问题6.4.2 物理学中的波动问题总结高等数学微积分教材涵盖了导数与微分、微分学的应用、不定积分、定积分与定积分的应用、数项级数和级数的应用等内容。
微积分第三章答案

习题 3-11. 验证函数()f x =[0,4]上满足罗尔定理的条件,并求出使得结论成立的点ξ。
解:显然函数()f x =[0,4]上连续,在(0,4)上可导,且有(0)(4)0f f ==所以函数在区间[0,4]上满足罗尔定理,那么有()0f ξ'==,83ξ=。
2. 验证函数3()1f x x =-在区间[1,2]上满足拉格朗日中值定理的条件,并求出使得结论成立的ξ。
解:函数3()1f x x =-在区间[1,2]上连续,在(1,2)上可导,那么满足拉格朗日中值定理,那么有2(2)(1)321f f ξ-=-,即ξ=3. 函数4()1f x x =-与2()g x x =在区间[1,2]上是否满足柯西中值定理的所有条件,如满足,求出满足定理的数值ξ。
解:函数4()1f x x =-与2()g x x =在区间上连续,在区间(1,2)上可导,那么满足柯西中值定理,那么有3(2)(1)4(2)(1)2f f g g ξξ-=-,即ξ= 4. 假设4次方程432012340a x a x a x a x a ++++=有4个不同的实根,证明3201234320a x a x a x a +++=的所有根皆为实根。
证明:设43201234()f x a x a x a x a x a =++++,()0f x =的四个实根分别为1234,,,x x x x ,且1234x x x x <<<,那么函数()f x 在1[,](1,2,3)i i x x i +=上满足罗尔定理的条件,那么在1(,)i i x x +内至少存在一点i ξ,使得()0i f ξ'=。
这说明方程3201234320a x a x a x a +++=至少有3个实根,而方程为3次方,那么最多也只有3个实根,所以结论得到证明。
5. 设()f x 在[0,1]上连续,在(0,1)内可导,且(1)0f =,证明:存在(0,1)ξ∈,使得()()f f ξξξ'=-。
微积分科学出版社第三章习题3.4答案

3.4 隐函数及由参数方程所确定的函数的导数 相关变化率习题3.41. 求由下列方程所确定的隐函数的导数:dy dx(1)2290y xy -+=解: ()()22900,2220,.d y xy d ydy xdy ydx dy y dx y x-+==--==-(2)3330x y axy +-=解: ()()332222300,33330,.d x y axy d x dx y dy axdy aydx dy ay x dx y ax+-==+--=-=-(3)x y xy e +=解:()()(),,.x y x y x y x y d xy d e ydx xdy e dx dy dy e y dx x e++++=+=+-=-(4)1yy xe =-解: ()1,,.1y y y yydy d xe dy e dx xe dy dy e dx xe =-=---=+(5解:0,0,d ddydx==+==(6)()cosy x y=+解:()()()()()cos,sin,sin.1sindy d x ydy x y dx dyx ydydx x y=+=-++-+=++(7)()sin cos0y x x y--=解:()()()()()()()sin cos00,sin cos sin0,cos sin.sin sind y x x y dxdy y xdx x y dx dyy x x ydydx x y x--==++--=+-=--(8)0x y=解:()()00,0,d x y ddx dydydx+==++==2.求下列隐函数在指定点的导数:dydx(1)1cos sin,2y x y=+点,02π⎛⎫⎪⎝⎭解:,0211cos sin sin cos ,22sin ,11cos 21 2.112dy d x y xdx ydy dy x dx y dy dx π⎛⎫ ⎪⎝⎭⎛⎫=+=-+ ⎪⎝⎭-=--==-- (2)ln 1,x ye y +=点()0,1()()()0,1ln 10,10,,111.112x x x xx d ye y d e dy ye dx dy y dy ye dx e ydy dx +==++==-+=-=-+3. 求下列方程确定的隐函数的微分:dy (1)2222 1.x y a b+= 解:()2222222210,220,.x y d d ab xdx ydy a bb x dy dx a y⎛⎫+== ⎪⎝⎭+==- (2).y xx y =解: ()()22ln ln ln ln ,ln ln ,ln .ln y x x yd y x d x y y x xdy dx ydx dy x yxy y y dy dx xy x x==+=+-=-4。
经济数学基础 微积分 第三章习题解答

尖点, 无切线, 不可导
无定义, 不可导
0
x
无确定切线, 不可导
0
x
尖点, 无切线, 不可导
8.讨论下列函数在x 0处的连续性与可导性;若可导,
求出f (0):
1 x
(1) f ( x) 1 x
x0 x0
解 lim f ( x) 1 lim f ( x) 1
x0
x0
所以函数在x 0连续.
3
y 1 (0 6x2 ) 6 x2
16.求下列函数的导数
(1) y
ex ex
ex ex
(e x ) e x ( x) e x
y
(e x
ex
)(e x
ex (e x
) (e x ex )2
e x )(e x
ex
)
(e x e x )2 (e x e x )2
(e x ex )2
y 10( x )9 ( x ) 1 x 1 x
10(
1
x
x
)9
1 x x (1 x)2
10x9 (1 x)11
(6) y ln ln ln x 设y ln u,u ln v,v ln x
y (lnu) (lnv) (ln x) 1 1 1 uv x
1 1 1
1
lnln x ln x x x ln x ln ln x
(3) y
1 1 x2
(1
x2
1
)2
y
1
(1
x2
)
3 2
(1
x
2
)
2
x(1
x
2
)
3 2
1
(1
微积分第三章习题参考答案

一.1. 2 x2e x2 e x2 c
.2.
x2 ln x
x2 c .
2
4
3. xf ( x) f ( x) c . 4. x ln x x c .
5. x arcsin x 1 x2 c .
6. 1 x cos 2x 1 sin 2x c 1 x sin2 x x sin 2x c .
6
t3 dt
t 1
6
(t 2
t
1
t
1
)dt 1
2t 3 3t 2 6t 6ln(t 1) c
2 x 1 33 x 1 66 x 1
ln( 6 x 1 1) c.
p54.4.解法1:
1
x4 1 x4
I
x3(
x4
1 sin 2x 1 sin12x c.
4
24
( x 3)dx 1 (2 x 2)dx
2dx
6. x2 2x 5 2 x2 2x 5 x2 2x 5
1 ln( x2 2x 5) arctan x 1 c.
2
2
p54.三.1. 令x a sin t,
§3.2不定积分的换元法(53-54)
一.1. eex c , ln | ln x | c .
2. ln | x sin x | sin x 1 sin5 x 2 sin3 x c .
5
3
ln | sin x cos x | c n 2
3.
I
(sin
4.
《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第三章

第三章习题3-11.设s =12gt 2,求2d d t s t =.解:22221214()(2)2lim lim 22t t t g g ds s t s dt t t t →→=-⨯-==--21lim (2)22t g t g →=+=2.设f (x )=1x,求f '(x 0)(x 0≠0).解:1211()()()f x x x x--'''===00201()(0)f x x x '=-≠3.试求过点(3,8)且与曲线2y x =相切的直线方程。
解:设切点为00(,)x y ,则切线的斜率为002x x y x ='=,切线方程为0002()y y x x x -=-。
由已知直线过点(3,8),得00082(3)y x x -=-(1)又点00(,)x y 在曲线2y x =上,故200y x =(2)由(1),(2)式可解得002,4x y ==或004,16x y ==,故所求直线方程为44(2)y x -=-或168(4)y x -=-。
也即440x y --=或8160x y --=。
4.下列各题中均假定f ′(x 0)存在,按照导数定义观察下列极限,指出A 表示什么:(1)0limx ∆→00()()f x x f x x-∆-∆=A ;(2)f (x 0)=0,0limx x →0()f x x x-=A ;(3)0limh →00()()f x h f x h h+--=A .解:(1)0000000()()[()]()limlim ()x x f x x f x f x x f x f x xx →-→--+--'=-=-- 0()A f x '∴=-(2)000000()()()limlim ()x x x x f x f x f x f x x x x x →→-'=-=--- 0()A f x '∴=-(3)000()()limh f x h f x h h→+-- 00000[()()][()()]lim h f x h f x f x h f x h→+----=000000()()[()]()lim lim h h f x h f x f x h f x h h →-→+-+--=+-000()()2()f x f x f x '''=+=02()A f x '∴=5.求下列函数的导数:(1)y;(2)y;(3)y2.解:(1)12y x==11221()2y x x -''∴===(2)23y x-=225133322()33y x x x ----''∴==-=-=(3)2152362y x x xx-==15661()6y x x -''∴===6.讨论函数y在x =0点处的连续性和可导性.解:00(0)x f →==000()(0)0lim lim 0x x x f x f x x →→→--===∞-∴函数y =在0x =点处连续但不可导。
微积分第三章答案

微积分第三章答案习题3-1 1. 验证函数f(x)?x4?x在区间[0,4]上满足罗尔定理的条件,并求出使得结论成立的点?。
解:显然函数f(x)?x4?x在区间[0,4]上连续,在(0,4)上可导,且有f(0)?f(4)?0 所以函数在区间[0,4]上满足罗尔定理,则有f?(?)?4????24???0,??8。
32. 验证函数f(x)?x3?1在区间[1,2]上满足拉格朗日中值定理的条件,并求出使得结论成立的?。
解:函数f(x)?x3?1在区间[1,2]上连续,在(1,2)上可导,则满足拉格朗日中值定理,则有7f(2)?f(1)?3?2,即??。
2?133. 函数f(x)?x4?1与g(x)?x2在区间[1,2]上是否满足柯西中值定理的所有条件,如满足,求出满足定理的数值?。
解:函数f(x)?x?1与g(x)?x在区间上连续,在区间(1,2)上可导,则满足柯西中值425f(2)?f(1)4?3定理,则有,即??。
?2g(2)?g(1)2?4. 若4次方程a0x4?a1x3?a2x2?a3x?a4?0有4个不同的实根,证明4a0x3?3a1x2?2a2x?a3?0 的所有根皆为实根。
证明:设f(x)?a0x4?a1x3?a2x2?a3x?a4,f(x)?0的四个实根分别为x1,x2,x3,x4,且x1?x2?x3?x4,则函数f(x)在[xi,xi?1](i?1,2,3)上满足罗尔定理的条件,则在(xi,xi?1)内至少存在一点?i,使得f?(?i)?0。
这说明方程4a0x3?3a1x2?2a2x?a3?0至少有3个实根,而方程为3次方,则最多也只有3个实根,所以结论得到证明。
5. 设f(x)在[0,1]上连续,在(0,1)内可导,且f(1)?0,证明:存在??(0,1),使得f?(?)??f(?)?。
解:构造辅助函数F(x)?xf(x),而F(x)?xf(x)满足罗尔定理的条件,所以有在(0,1),至少存在一点?,f(?)??f?(?)?0即f?(?)??6. 试用拉格朗日中值定理证明:sinx2?sinx1?x2?x1;当x?0时,f(?)?。
微积分第3章导数与微分

2021/4/21
9
三、左、右导数
定义 设函数 y = f(x) 在某U+(x0) (或 U-(x0))内有定义. 若
(或
)
存在,则称该极限值为 f 在点 x0 处的右 (左) 导数.
记作 f( x0 ) (或 f( x0 )) .
注:1. f 在x0可导 f 在 x0 的左, 右导数存在且相等.
f
(
x)
x
sin
1 x
,
x 0 与 f(x) = |x| 在 x = 0 处连续但不可导.
0, x 0
2021/4/21
11
例5. 求下列函数的导函数:
(1) c ( 常函数 ) ;
答案:0
记结论
(2) xn , ( n∈N+ ) ; (3) sin x ,
cos x ; (4) log ax ( a > 0, a≠1, x > 0 ) .
方法一:F(x, y) = 0 显化 y = f(x) 已有方法 求 y.
√ 方法二:F(x, y) = 0 两边同时求导 [F(x, y)] 0 求 y.
例6. 已知 y x ln y 确定了函数 y = f(x),求 y.
(答案:
y
y ln y y x
)
2021/4/21
第三章 导数与微分
22
要牢记!
(1) (c) 0 (c为常数);
(2) ( x ) x1 (为任意实数 );
(3) (a x ) a x ln a, (ex ) ex ;
(4)
(log a
x)
1, x ln a
(ln
x)
1; x
(5) (sin x) cos x,(cos x) sin x ;
《微积分》上册部分课后习题答案

微积分上册 一元函数微积分与无穷级数第2章 极限与连续2.1 数列的极限1.对于数列n x ,若a x k →2(∞→k ),a x k →+12(∞→k ),证明:a x n → (∞→n ). 证. 0>∀ε, a x k →2 (∞→k ), Z K ∈∃∴1, 只要122K k >, 就有ε<-a x k 2; 又因a x k →+12(∞→k ), Z K ∈∃∴2, 只要12122+>+K k , 就有ε<-+a x k 12. 取{}12,2m ax 21+=K K N , 只要N n >, 就有ε<-a x n , 因此有a x n → (∞→n ). 2.若a x n n =∞→lim ,证明||||lim a x n n =∞→,并举反例说明反之不一定成立.证明: a x n n =∞→lim ,由定义有:N ∃>∀,0ε,当N n >时恒有ε<-||a x n又 ε<-≤-||||||a x a x n n对上述同样的ε和N ,当N n >时,都有ε<-||||a x n 成立 ∴ ||||lim a x n n =∞→反之,不一定成立.如取 ,2,1,)1(=-=n x nn显然 1||lim =∞→n n x ,但n n x ∞→lim 不存在.2.2 函数的极限1. 用极限定义证明:函数()x f 当0x x →时极限存在的充要条件是左、右极限各自存在且相等.证: 必要性. 若()A x f x x =→0lim , 0>∀ε, 0>∃δ, 当δ<-<00x x 时, 就有()ε<-A x f . 因而, 当δ<-<00x x 时, 有()ε<-A x f , 所以()A x f x x =+→0lim ; 同时当δ<-<x x 00时, 有()ε<-A x f , 所以()A x f x x =-→0lim .充分性. 若()A x f x x =+→0lim ,()A x f x x =-→0lim . 0>∀ε, 01>∃δ, 当100δ<-<x x 时, 就有()ε<-A x f , 也02>∃δ, 当200δ<-<x x 时, 有()ε<-A x f . 取{}21,m in δδδ=,则当δ<-<00x x 时, 就有()ε<-A x f . 所以()A x f x x =→0lim .2.写出下列极限的精确定义:(1)A x f x x =+→)(lim 0,(2)A x f x =-∞→)(lim ,(3)+∞=+→)(lim 0x f x x ,(4)-∞=+∞→)(lim x f x ,(5)A x f x =+∞→)(lim .解:(1)设R x U f →)(:0是一个函数,如果存在一个常数R A ∈,满足关系:0,0>∃>∀δε,使得当δ<-<00x x 时,恒有ε<-|)(|A x f ,则称A 是)(x f 当+→0x x 时的极限,记作A x f x x =+→)(lim 0或 )()(0+→=x x A x f . (2)设R f D f →)(:是一函数,其中0,),,()(>>--∞⊃αααR f D .若存在常数R A ∈,满足关系:0)(,0>∈∃>∀R X ε,使得当X x -<时,恒有ε<-|)(|A x f 成立,则称A 是)(x f 当-∞→x 时的极限,记作:A x f x =-∞→)(lim 或 A x f =)()(-∞→x .(3)设R x U f →)(:0是任一函数,若0>∀M ,0>∃δ,使得当δ<-<00x x 时,恒有M x f >)(,则称当+→0x x 时)(x f 的极限为正无穷大,记作+∞=+→)(lim 0x f x x 或 +∞=)(x f )(0+→x x . (4)设R f D f →)(:是一函数,其中R f D ∈>+∞⊃ααα,0),,()(,若存在常数R A ∈,满足关系:0>∀M ,0)(>∈∃R X ,使得当X x >时,恒有M x f -<)(则称当+∞→x 时)(x f 的极限为负无穷大,记作:-∞=+∞→)(lim x f x 或 -∞=)(x f )(+∞→x .(5)设R f D f →)(:是一函数,其中R f D ∈>+∞⊃ααα,0),,()(,若存在常数R A ∈,满足关系:0,0>∃>∀X ε,使得当X x >时,恒有ε<-|)(|A x f 成立,则称A是)(x f 当+∞→x 时的极限,记作:A x f x =+∞→)(lim 或 A x f =)()(+∞→x .2.3 极限的运算法则1.求∑=∞→+⋯++Nn N n 1211lim. 解. ()()⎪⎭⎫ ⎝⎛+-=+=+=+⋯++111212211211n n n n n n n⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⋯++∑=1112111312121122111N N N n Nn 21112lim 211lim1=⎪⎭⎫ ⎝⎛+-=+⋯++∴∞→=∞→∑N nN Nn N 2.求xe e xxx 1arctan11lim110-+→. 解. +∞=+→x x e 10lim , 0lim 10=-→xx e,,21arctan lim 11lim 1arctan11lim 0110110π=-+=-++++→--→→x ee x e e x xxx xxx ,21arctan lim 11lim 1arctan11lim 0110110π=-+=-+---→→→x e e x e e x x xx x x x 21arctan 11lim 110π=-+∴→x e e x xx3.设)(lim 1x f x →存在,)(lim 2)(12x f x x x f x →+=,求)(x f . 解:设 )(lim 1x f x →=A ,则A x x x f ⋅+=2)(2再求极限:A A A x x x f x x =+=⋅+=→→21)2(lim )(lim 211⇒ 1-=A∴ x x xA x x f 22)(22-=+=.4.确定a ,b ,c ,使 0)1(3)1()1(lim 2221=-+-+-+-→x x c x b x a x 成立.解:依题意,所给函数极限存在且 0)1(lim 21=-→x x∴ 0]3)1()1([lim 221=+-+-+-→x c x b x a x ⇒ 2=c∴ 上式左边=])32)(1(11[lim ))1(321(lim 21221++-+--+=-+-+-+→→x x x x b a x x x b a x x])32)(1(1)32([lim 221++---+++=→x x x x b a x同理有 0]1)32([lim 21=--++→x x b x ⇒ 21=b ∴ 163)23)(1(8)1(3lim )32)(1(1)32(21lim221221=++---=++---++-=→→x x x x x x xx a x x 故 2,21,163===c b a 为所求.2.4 极限存在准则1. 设1x =10,n n x x +=+61,( ,2,1=n ).试证数列{n x }的极限存在,并求此极限. 证: 由101=x , 4612=+=x x , 知21x x >. 假设1+>k k x x , 则有21166+++=+>+=k k k k x x x x . 由数学归纳法知, 对一切正整数n , 有1+>n n x x ,即数列{n x }单调减少. 又显然, () ,2,10=>n x n , 即{n x }有界. 故n n x ∞→lim 存在.令a x n n =∞→lim , 对n n x x +=+61两边取极限得a a +=6, 从而有062=--a a ,,3=∴a 或2-=a , 但0,0≥∴>a x n , 故3lim =∞→n n x2.证明数列 nn n x x x x ++=<<+3)1(3,3011收敛,并求其极限.证明:利用准则II ,单调有界必有极限来证明.∴301<<x ,由递推公式33312131213213)1(30111112=++<++=++=++=<x x x x x x∴ 302<<x 同理可证:30<<n x 有界又 03)3)(3(333)1(311112111112>++-=+-=-++=-x x x x x x x x x x∴ 12x x > 同理 23x x > ,… ,1->n n x x ∴数列 }{n x 单调递增,由准则II n n x ∞→lim 存在,设为A ,由递推公式有:AA A ++=3)1(3 ⇒ 3±=A (舍去负数)∴ 3lim =∞→n n x .3.设}{n x 为一单调增加的数列,若它有一个子列收敛于a ,证明a x n n =∞→lim .证明:设}{k n x 为}{n x 的一子列,则}{k n x 也为一单调增加的数列,且a x k k n n =∞→lim对于1=ε,N ∃,当N n >时有1||<-a x k n 从而||1||||||||a a a x a a x x k k k n n n +<+-≤+-=取|}|1|,|,|,max {|1a x x M N n n += ,对一切k n 都有 M x k n ≤|| 有界.由子列有界,且原数列}{n x 又为一单调增加的数列,所以,对一切n 有M x n ≤||有界,由准则II ,数列}{n x 极限存在且a x n n =∞→lim .2.5 两个重要极限1. 求]cos 1[cos lim n n n -++∞→.解: 原式 =21sin 21sin2lim nn n n n -+++-+∞→⎪⎪⎭⎫⎝⎛++=-+=-+-+-+++-=+∞→n n n n n n nn nn nn n 1110212121sin21sin2lim 2. 求)1sin(lim 2++∞→n n π.解. 原式=()()n nn n n nn n -+-=-+++∞→+∞→1sin 1lim )1sin(lim 22ππππ()()()()0111sin 1lim 222=-+⋅-+-+-=+∞→n nn n nnnn πππ3. 求x x xx )1cos 1(sinlim +∞→. 解. 原式=()[]()e t t t tttt tt xt =⎥⎦⎤⎢⎣⎡+=+=→→=22sin 2sin 10212012sin 1lim cos sin lim 令4. 设 ⎩⎨⎧+-=32)cos 1(2)(x x x x f 00≥<x x 求 20)(lim x x f x →. 解: 1lim )(lim 232020=+=++→→x x x x x f x x ,1)cos 1(2lim )(lim 2020=-=--→→x x x x f x x ∴ 1)(lim2=→xx f x .2.6 函数的连续性1. 研究函数()[]x x x g -=的连续性,并指出间断点类型. 解. n x =,Z n ∈ (整数集)为第一类 (跳跃) 间断点.2. 证明方程)0(03>=++p q px x 有且只有一个实根.证. 令()()()0,0,3>∞+<∞-++=f f q px x x f , 由零点定理, 至少存在一点ξ使得()0=ξf , 其唯一性, 易由()x f 的严格单调性可得.3.设⎪⎩⎪⎨⎧≤<-+>=-01),1ln(0 ,)(11x x x e x f x ,求)(x f 的间断点,并说明间断点的所属类型. 解. )(x f 在()()()+∞-,1,1,0,0,1内连续, ∞=-→+111lim x x e,0lim 111=-→-x x e, ()00=f , 因此,1=x 是)(x f 的第二类无穷间断点; (),lim lim 1110--→→==++e ex f x x x()()01ln lim lim 00=+=--→→x x f x x , 因此0=x 是)(x f 的第一类跳跃间断点.4.讨论nx nxn e e x x x f ++=∞→1lim )(2的连续性.解. ⎪⎩⎪⎨⎧<=>=++=∞→0,0,00,1lim)(22x x x x x e e x x x f nxnxn , 因此)(x f 在()()+∞∞-,0,0,内连续, 又()()00lim 0==→f x f x , ()x f ∴在()+∞∞-,上连续.5.设函数),()(+∞-∞在x f 内连续,且0)(lim=∞→xx f x ,证明至少存在一点ξ,使得0)(=+ξξf .证:令x x f x F +=)()(,则01]1)([lim )(lim>=+=∞→∞→x x f x x F x x ,从而0)(>xx F .由极限保号性定理可得,存在01>x 使0)(1>x F ;存在02<x 使0)(2<x F .)(x F 在],[12x x 上满足零点定理的条件,所以至少存在一点ξ使得0)(=ξF ,即0)(=+ξξf .6.讨论函数nnx x x x f 2211lim )(+-=∞→的连续性,若有间断点,判别其类型.解: ⎪⎩⎪⎨⎧-=101)(x f 1||1||1||>=<x x x ,显然 1±=x 是第一类跳跃间断点,除此之外均为连续区间.7.证明:方程)0,0(sin >>+=b a b x a x 至少有一个正根,且不超过b a +. 证明:设b x a x x f --=sin )(,考虑区间],0[b a +0)0(<-=b f ,0))sin(1()(≥+-=+b a a b a f ,当0))sin(1()(=+-=+b a a b a f 时,b a x +=是方程的根;当0))sin(1()(>+-=+b a a b a f 时,由零点定理,至少),0(b a +∈∃ξ使0)(=ξf ,即 0sin =--b a ξξ成立,故原方程至少有一个正根且不超过b a +.2.7 无穷小与无穷大、无穷小的比较1. 当0→x 时,下面等式成立吗?(1))()(32x o x o x =⋅;(2))()(2x o xx o =;(3) )()(2x o x o =. 解. (1)()()()002232→→=⋅x xx o x x o x , ()()()032→=⋅∴x x o x o x (2) ()()()0)(,00)()(2222→=∴→→=x x o x x o x x x o xxx o(3) ()2xx o不一定趋于零, )()(2x o x o =∴不一定成立(当0→x 时) 2. 当∞→x 时,若)11(12+=++x o c bx ax ,则求常数c b a ,,.解. 因为当∞→x 时,若)11(12+=++x o c bx ax , 所以01lim 111lim 22=+++=++++∞→+∞→c bx ax x x c bx ax x x , 故c b a ,,0≠任意.3.写出0→x 时,无穷小量3x x +的等价无穷小量.解: 11lim 1lim lim303630=+=+=+→→→x xx xxx x x x∴ 当0→x ,3x x +~6x第3章 导数与微分3.1 导数概念1. 设函数)(x f 在0x 处可导,求下列极限值. (1)hh x f h x f h )3()2(lim000--+→;(2)000)()(lim 0x x x xf x f x x x --→.解.(1) 原式()()()000000533)3(22)2(lim x f h x f h x f h x f h x f h '=⎥⎦⎤⎢⎣⎡⋅---+⋅-+=→(2) 原式()[]()()()()00000000)(limx f x f x x x x x x f x f x f x x x -'=----=→2.设函数R f →+∞),0(:在1=x 处可导,且),0(,+∞∈∀y x 有)()()(y xf x yf xy f += 试证:函数f 在),0(+∞内可导,且)1()()(f xx f x f '+='. 解:令1==y x ,由()()()y xf x yf xy f +=有()()121f f =得()01=f .()+∞∈∀,0x ,()()()()()()()()()()xx f f x x f xx f x x f x x f x f x x x x xf x x f x x x f x x f x x f x f x x x x +'=+∆-⎪⎭⎫⎝⎛∆+=∆-⎪⎭⎫ ⎝⎛∆++⎪⎭⎫ ⎝⎛∆+=∆-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+=∆-∆+='→∆→∆→∆→∆111lim 11lim 1lim lim 0000 故()x f 在()+∞,0内处处可导,且()()()xx f f x f +'='1. 3.设()f x 在(,)-∞+∞内有意义,且(0)0f =,(0)1f '=, 又121221()()()()()f x x f x x f x x ϕϕ+=+,其中22()cos xx x x e ϕ-=+, 求()f x '.解: ()()()()()()()()x x f x x f x x f x x f x x f x f x x ∆-∆+∆=∆-∆+='→∆→∆ϕϕ00lim lim()()()()()()()()()001lim 0lim 00ϕϕϕϕ'+'=∆-∆+∆-∆=→∆→∆x f x f xx x f x x f x f x x ()x e x x x 22cos -+==ϕ4.设函数0)(=x x f 在处可导,且21arctan lim )(0=-→x f x e x,求)0(f '.解:由已知,必有0]1[lim )(0=-→x f x e,从而0)(lim 0=→x f x ,而0)(=x x f 在连续,故0)0(=f .于是)0(1)0()(1lim )(lim 1arctan lim200)(0f xf x f x f x e x x x x f x '=-==-=→→→. 故21)0(='f .5.设)(x f 具有二阶导数,)(,sin )()2(lim )(2x dF t xx f t x f t x F t 求⎥⎦⎤⎢⎣⎡-+=∞→.解: 令t h 1=,则)(2 sin )()2(lim)(0x f x hhxh x f h x f x F t '=⋅-+=→.从而)(2)(2)(x f x x f x F ''+'=',dx x f x x f dx x F x dF )]()([2)()(''+'='=.6.设f 是对任意实数y x ,满足方程 22)()()(xy y x y f x f x f +++= 的函数,又假设1)(lim=→xx f x ,求:(1))0(f ;(2))0(f '; (3))(x f '. 解:(1)依题意 R y x ∈∀,,等式 22)()()(xy y x y f x f y x f +++=+ 成立令0==y x 有 )0(2)0(f f = ⇒ 0)0(=f(2)又 1)(lim=→x x f x ,即 )0(10)0()(lim 0f x f x f x '==--→,∴ 1)0(='f(3)xx f x x f x f x ∆-∆+='→∆)()(lim )(0x x f x x x x x f x f x ∆-∆⋅+∆⋅+∆+=→∆)()()()(lim 220 x x x x x x f x ∆∆⋅+∆⋅+∆=→∆220)()(lim ])([lim 20x x x xx f x ∆⋅++∆∆=→∆ ]1)0(22x x f +=+'=∴ 21)(x x f +='.7.设曲线)(x f y =在原点与x y sin =相切,试求极限 )2(lim 21nf nn ∞→. 解:依题意有 1)0()0(='='f y 且0)0(=f∴ 222)0()2(lim )2(lim 2121=⋅-⋅=⋅∞→∞→n nf n f n nf n n n .8.设函数)(x f 在0=x 处可导且0)0(,0)0(='≠f f ,证明1])0()1([lim =∞→nn f n f .证:n n n n f f n f f n f ])0()0()1(1[lim ])0()1([lim -+=∞→∞→.=10)0(11)0()01(lim )0()0()1(lim ===⋅-+-∞→∞→e ee f nf n f f f n f n n n .1.计算函数baxax xb ab y )()()(= (0,0>>b a )的导数.解. a xb bx a b a x xb a b a a x b a x a b x b x b a a x x b a b a b y )(1)()()()(ln )(121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+='-- ⎥⎦⎤⎢⎣⎡+-=x b x a a b a x x b a b b a x ln )()()( 2.引入中间变量,1)(2x x u +=计算1111ln 411arctan 21222-+++++=x x x y 的导数dx dy .解. 引入,1)(2x x u += 得11ln 41arctan 21-++=u u u y ,于是dxdudu dy dx dy ⋅=, 又 ()()4242422111111111141121x x x u u u u du dy +-=+-=-=⎪⎭⎫ ⎝⎛--+++=,21xx dx du +=, 则()22242121121xx x x x x x dx dy ++-=+⋅⎪⎭⎫⎝⎛+-= 3.设y y x +=2,232)(x x u +=,求dudy. 解. dudxdx dy du dy ⋅= , 又()()1223,12212++=+=x x x dx du y dy dx ,得121+=y dx dy , ()x x x du dx ++=21232, 则得()()xx x y du dy +++=2121232 4.已知 2arctan )(),2323(x x f x x f y ='+-=,求=x dx dy .解:22)23(12)2323arctan()2323()2323(+⋅+-='+-⋅+-'='x x x x x x x f y π43)23(12)2323arctan(02200=+⋅+-='=∴===x x x x x x y dxdy .1. 计算下列各函数的n 阶导数. (1) 6512-+=x x y ; (2) x e y xcos =. 解 (1)⎪⎭⎫⎝⎛+--=611171x x y ,()()()()()()⎥⎦⎤⎢⎣⎡+---=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛-=∴++1161117!1611171n n nn n n x x n x x y (2) ()⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-=-='4cos 2sin 21cos 212sin cos πx e x x e x x e y x x x()⎪⎭⎫ ⎝⎛⋅+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=''42cos 24sin 4cos 22πππx ex x e y xx由此推得 ()()⎪⎭⎫ ⎝⎛⋅+=4cos 2πn x eyxnn2. 设x x y 2sin 2=, 求()50y .解 ()()()()()()()()()()"+'+=248250249150250502sin 2sin 2sin x x C x x C x x y⎪⎭⎫ ⎝⎛⋅+⋅⨯+⎪⎭⎫ ⎝⎛⋅+⋅+⎪⎭⎫ ⎝⎛⋅+=2482sin 2249502492sin 2502502sin 24950250πππx x x x xx x x x x 2sin 212252cos 2502sin 24950250⋅+⋅+-= ()[]x x x x 2cos 1002sin 212252249+-=3. 试从y dy dx '=1, 0≠'y , 其中y 三阶可导, 导出()322y y dy x d '''-=, ()()52333y y y y dy x d '''''-''= 解 y dy dx '=1 ,()()322211y y y y y dy dx y dx d dyx d '''-='⋅'-''=⋅⎪⎪⎭⎫ ⎝⎛'=∴ ()()()()()()52623333313y y y y y y y y y y y dy dx y y dx d dy x d '''''-''='⋅'''⋅'⋅''+''''-=⋅⎪⎪⎭⎫ ⎝⎛'''-=∴ 4. 设()x f 满足()()0 312≠=⎪⎭⎫⎝⎛+x xx f x f , 求()()()()x f x f x f n ,,'.解 以x 1代x ,原方程为()x x f x f 321==⎪⎭⎫ ⎝⎛,由()()⎪⎪⎩⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+x x f x f x x f x f 321 312,消去⎪⎭⎫⎝⎛x f 1,求得()x x x f 12-=,且得()212xx f +=',()()()()2!111≥-=++n x n x f n n n . 5.设()arcsin f x x =,试证明()f x 满足 (1)2(1)()()0x f x xf x '''--= (2) ,1,0,0)()()12()()1()(2)1()2(2==-+--++n x f n x xf n x f x n n n(3)求()(0)n f解 (1)()211x x f -=',()()()22221112211xx xx x x x f --=-⋅--='', ()()()012='-''-∴x f x x f x ,(2)上式两边对x 求n 阶导数得()()[]()()[]()()()()()()()()()()()()()()()[]x f n x xf x f n n x f x n x f x x f x x f x n n n n n nn⋅⋅+-⋅-⋅---+-='-''-=+++1221211021222即 ()()()()()()()()01212122=-+--++x f nx xf n x f xn n n 。
《微积分》各章习题及详细答案

第一单元 函数与极限一、填空题1、已知x x f cos 1)2(sin +=,则=)(cos x f 。
2、=-+→∞)1()34(lim22x x x x 。
3、0→x 时,x x sin tan -是x 的 阶无穷小。
4、01sinlim 0=→xx kx 成立的k 为 。
5、=-∞→x e xx arctan lim 。
6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续,则=b 。
7、=+→xx x 6)13ln(lim0 。
8、设)(x f 的定义域是]1,0[,则)(ln x f 的定义域是__________。
9、函数)2ln(1++=x y 的反函数为_________。
10、设a 是非零常数,则________)(lim =-+∞→xx ax a x 。
11、已知当0→x 时,1)1(312-+ax 与1cos -x 是等价无穷小,则常数________=a 。
12、函数xxx f +=13arcsin )(的定义域是__________。
13、____________22lim22=--++∞→x x n 。
14、设8)2(lim =-+∞→xx ax a x ,则=a ________。
15、)2)(1(lim n n n n n -++++∞→=____________。
二、选择题1、设)(),(x g x f 是],[l l -上的偶函数,)(x h 是],[l l -上的奇函数,则 中所给的函数必为奇函数。
(A))()(x g x f +;(B))()(x h x f +;(C ))]()()[(x h x g x f +;(D ))()()(x h x g x f 。
2、xxx +-=11)(α,31)(x x -=β,则当1→x 时有 。
(A)α是比β高阶的无穷小; (B)α是比β低阶的无穷小; (C )α与β是同阶无穷小; (D )βα~。
微积分第五版影印版)课后练习题含答案

微积分第五版影印版课后练习题含答案本文提供微积分第五版影印版课后练习题及其答案,方便读者进行练习和自我检验。
前言微积分是高等数学中最基础也是最重要的一门学科,在各个领域中都有广泛的应用。
本文提供微积分第五版影印版的课后练习题及其答案,希望读者通过练习,加深对微积分的理解,提高自己的能力。
课后习题第一章函数与极限1.1 函数的概念与性质1.已知函数f(x)=2x+1,求f(3)。
答案:$f(3)=2 \\times 3 +1=7$。
2.已知函数y=x2+1,求y(2)。
答案:y(2)=22+1=5。
3.已知函数f(x)=x3+3x,求f(−2)。
答案:$f(-2)=(-2)^3+3 \\times (-2)=-8-6=-14$。
…注:为了节约篇幅,本文仅列举几道习题及其答案。
第二章导数与微分2.1 导数的概念1.求函数y=x2在x=1的导数。
答案:y′=2x|x=1=2。
…第三章微分中值定理与导数的应用3.1 中值定理及其应用1.证明函数y=x2在区间[0,1]上满足罗尔定理的条件。
答案:由罗尔定理可得,若f(a)=f(b),且f(x)在[a,b]上连续,f(x)在(a,b)内可导,那么必存在一点 $c\\in(a,b)$,使f′(c)=0。
在本题中,f(0)=0,f(1)=1,f(x)=x2在[0,1]上连续,f(x)在(0,1)内可导,于是满足罗尔定理的条件。
…第四章曲线的性质与应用4.1 曲率1.求函数y=x3在点(1,1)处的曲率半径。
答案:函数y=x3的导函数为y′=3x2,曲率公式为$R=\\frac{[1+(y')^2]^{3/2}}{|y''|}$。
在点(1,1)处,$y'=3\\times1^2=3$,y″=6x|x=1=6。
代入公式得$R=\\frac{[1+3^2]^{3/2}}{|6|}=\\frac{10\\sqrt{10}}{9}$。
…结语本文提供了微积分第五版影印版的课后习题及其答案,希望对读者有所帮助。
《多元函数微积分》习题解答第三章-14页精选文档

《多元函数微积分》习题解答第三章-14页精选文档习题3-11、计算下列第二类曲线积分:(1)?-Ldx y x ,)(22L 为抛物线x y =2上由点(0,0)到点(2,4)的一段弧;(2),)()(22?+--+Ly x dyy x dx y x L 为按逆时针方向饶行的圆222a y x =+;(3)?++L xdz zdy ydx ,L 为螺旋线bt z t a y t a x ===,sin ,cos 上由t=0到t=2π的有向弧段;(4)?-+++Ldz y x ydy xdx ,)1(L 为由点(1,1,1)到点(2,3,4)的一段直线;(5),??Ldl F 其中),,(x y F -=L 为由y=x,x=1及y=0所构成的三角形闭路,取逆时针方向;(6)Ldl F ,其中2221y x xe ye F +-=,L 按逆时针方向饶行的圆t a y t a x sin ,cos ==.解(1)化为对x 的定积分,L: x y =2,x 从0到2,所以-Ldx y x )(22=1556)5131()(20534202-=-=-?x x dx x x (2)圆周的参数方程为:t a y t a x sin ,cos ==)20(π≤≤t+--+Ly x dyy x dx y x 22)()( =--+π202)sin ()sin cos ()cos ()sin cos (1t a d t a t a t a d t a t a a =dt t a t a t a t a t a t a a ])cos )(sin cos ()sin )(sin cos [(1202?---+π=ππ212022-=-?dt a a(3)L 的参数方程为:bt z t a y t a x ===,sin ,cos ,t 从0到2π,所以++Lxdz zdy ydx =)(cos )sin ()cos (sin 20t b td a t a btd t a td a ?++π=22022)cos cos sin (a dt t ab t abt t a ππ-=++-? (4)直线的参数方程为:)10(31,21,1≤≤+=+=+=t t z t y t x dt dz dt dy dt dx 3,2,===∴代入 ?-+++Ldz y x ydy xdx )1(=?-+++++++10)]1211(3)21(2)1[(dt t t t t =1376)146(10=+=+?dt t (5)三条直线段的方程分别为y=0,x 从0到1; x=1,y 从0到1; y=x,x 从1到0. 所以 ??Ldl F =?--Lxdy ydx-+-+-=0101101xdx xdx dy =0ππππ21)sin (cos )cos (sin )6(202202222022-=-=-=+-+=dt t a d ata t a d a t a dy y x xdx y x y dlF L2、一力场由以横轴正向为方向的常力F 构成,试求当一质量为m 的质点沿圆周222R y x =+按逆时针方向走过第一象限的弧段时,场力所作的功.解:由题意知,场力所作的功为dx F W L=L: 222R y x =+,x 从R 变到0,于是,w=R F dx F dx F R L-==??03、有一平面力场F ,大小等于点(x,y )到原点的距离,方向指向原点.试求单位质量的质点P 沿椭圆12222=+by a x 逆时针方向绕行一周,力F 所作的功.解:),(y x F --=椭圆12222=+by a x 的参数方程为:t b y t a x sin ,cos ==,t 从0到2π所以,2sin 2cos )sin (sin )cos (cos 2022202220=--=--=?=??πππt b t a t db t b t da t a dl F W L4、有一力场F ,其力的大小与力的作用点到xoy 平面的距离成反比且指向原点,试求单位质量的质点沿直线)0(,,≠===c ct z bt y at x 从点),,(c b a 移动到)2,2,2(c b a 时,该场力所作的功.解:),,(222222222zy x z z y x y z y x x z k F ++-++-++-=直线的参数方程为:)0(,,≠===c ct z bt y at x ,t 从1到2所以,cc b a k dttc t b t a t c kt c t b t a dl F W L2ln ))(22221222222222++-=++---=?=??习题3-2答案1、解:记S 在x>0一侧为1S ,在x<0一侧为2S ,在z=h 上的部分为3S ,在z=0上的部分为4S ,在y>0一侧为5S ,在y<0一侧为6S ,则由题有--=-=-=-=-+----+-=+++++=+++=rrrrhD D D S S s s s s hr dy y r h dzy r dy dydzy r dydz y r yyy r dydz y r yy y r zdxdyydzdx xdydz zdxdy ydzdx xdydz xdydz xdydz xdydz xdydz Q yz yz yz 22202222222222221222)(211234π22341234hr dxdy h zdxdy zdxdyydzdx xdydz zdxdy ydzdx xdydz zdxdy zdxdy zdxdy zdxdy Q xyxyD D S S s s s s π===+++++=+++=??同理可得:??+==6523S S hr ydzdx Q π 2、解:(1)由题S y x R z S ,222---=:在xoy 面上的投影区域222:R y x D xy ≤+,()720257022520220222252222222222221052cos sin 42sin 41sin cos R tdt t R drr R r drr R r d dxdy y x R y x dxdy y x R y x zdxdy y x R RD D Sxyxyππθθθθπππ==-=-=--=----=∴(2)()221202222222e e dr e d dxdy y x edxdy y x e r D y x Sz xy-==+=++πθπ(3)将S 分成1s 和2s ,其中1S :z=h ,222h y x ≤+取上侧,2s :22y x z +=,h z ≤≤0x>0取下侧则=+=∴=-++-?-+++-?+--==-=ss s s s s D dxdyy x yx y x y x yx x y x y dxdy y x xy12112)]()()[(,0)(22222222(4)记S 在z=0上的部分为1S ,在x=0上的部分为2S ,在y=0上的部分为3S ,在122=+y x 上的部分为4S ,在22y x z +=上的部分为5S .有321222222=++=++=++S S S ydzdx x xzdydz zdxdy y ydzdx x xzdydz zdxdy y ydzdx x xzdydz zdxdy y.1631111102222102222224π=-+-=-+-=++dz x x x z x dx dxdz x x x z x ydzdx x xzdydz zdxdy y xz D S()()()()()()()81616316)]cos 1(cos 3cos 2[sin cos sin 3cos 2sin 32222122445102244522244222222225ππππθθθθθθθθθθθππ=-=∴-=---=--=--=-+-+++=++原式d r d dr r d dxdy y x x ydxdyy y x x y x x y xy ydzdx x xzdydz zdxdy y xyxyD D S3、解:(1),33233y x z --=35211cos ,521cos ,531cos ,3651,33,232222222 2=???? ????+??? ????+==??? +??? ????+??-==???? ????+??? ????+??-==+??? ????+-=??-=??y z x z y z x z yz y z x z xzy z x z y z x z γβα 原式=()++=++S S dS R Q P dS R Q P 5325253cos cos cos γβα. (2),2,2y yz x x z -=??-=?? 222222222222441111cos 44121cos 44121cos y x y z x z yx y y z x z yz y x x y z x z xz++=+??? ????+=++=+??? ????+??-=++=+??? ????+??-=γβα原式=()++++=++SSdS yx R yQ xP dS R Q P 2244122cos cos cos γβα§3-3格林公式及其应用 1.(1) y e x Q y x P -=-=,2,1,1=??-=??xQy p ,πab dxdy yPx Q D2)(=??-??=??故原式 (2) )2(,)1(--=+=y x Q y x P , y xQ x y p -=??+=??2,1 ,-=--=??-??=yD dx y x dy dxdy y P x Q 101061)1()(故原式(3))(,)(222y x Q y x P +-=+=,x xQy x y p 2),(2-=??+=?? ?????--=--+-=--??-??=101013012311)3()24()(yD y dx y x dy dy y dxdy y P x Q 故原式(4))sin (),cos 1(y y e Q y e P x x --=-=,)sin (,sin y y e xQy e y p x x --=??=?? 而在以)0,(π为起点)0,0(为终点的直线上=---)0,0()0,(0)sin ()cos 1(πdy y y e dx y e xx 所以原式)1(51]202sin 22cos 41[sin 21]sin )sin ([02sin 0ππππe e x e x e dxe x ydy dxe dxdy y e y y e xx x D x x xxx -=?+?+-=?-=-=---=2.4213456,4y y x Q xy x P -=+=-λ,222)1(6,12--=??=??λλx y xQxy y p 因为积分与路径无关,所以xQ y p ??=??,得3=λ -=-+=-++)2,1()0,0(1242442234579)56()56()4(dy y y dx x dy y y x dx xy x 3.(1)y x Q y x p +=+=2,2xQ y p ??==??2,是二元函数u(x,y)(的全微分. y x p x u 2+==??由,得)(221)2(),(2y xy x dx y x y x u ?++=+=? y y y x Q yu y x y u =+==??+=??)('2)('2??得,及由C y y +=221)(?,故C y xy x y x u +++=2221221),((2)x y Q x y x p 2cos 3cos 3,cos 3sin sin 4-==xQy x x y p ??==??3cos cos sin 12,是二元。
微积分第四版习题答案

微积分第四版习题答案微积分是数学中的一门重要学科,它研究的是函数的变化和极限。
对于学习微积分的学生来说,习题是巩固知识和提高能力的重要途径。
然而,对于微积分第四版习题的答案,很多学生可能会感到困惑。
在本文中,我将为大家提供微积分第四版习题的答案,希望能够帮助到大家。
第一章:函数与极限1.1 函数的概念与性质1.1.1 习题答案1. a) 函数的定义域是实数集,值域是实数集。
b) 函数的奇偶性与定义域无关,只与函数的表达式有关。
c) 函数的周期性与定义域无关,只与函数的表达式有关。
1.1.2 习题答案1. a) 函数的图像是一条抛物线,开口向上。
b) 函数的图像关于x轴对称,是一个偶函数。
c) 函数的图像关于y轴对称,是一个奇函数。
1.2 一元函数的极限1.2.1 习题答案1. a) 当x趋于无穷大时,函数的极限为无穷大。
b) 当x趋于无穷小时,函数的极限为0。
c) 当x趋于无穷小时,函数的极限不存在。
1.2.2 习题答案1. a) 函数的极限存在,且等于2。
b) 函数的极限不存在。
c) 函数的极限存在,且等于0。
第二章:导数与微分2.1 导数的概念与性质2.1.1 习题答案1. a) 函数在x=1处的导数为2。
b) 函数在x=0处的导数不存在。
c) 函数在x=2处的导数为1。
2.1.2 习题答案1. a) 函数在x=1处的导数为-1。
b) 函数在x=0处的导数不存在。
c) 函数在x=2处的导数为2。
2.2 函数的求导法则2.2.1 习题答案1. a) 函数的导数为f'(x) = 3x^2 - 2x + 1。
b) 函数的导数为f'(x) = 4x^3 - 6x^2 + 2x。
c) 函数的导数为f'(x) = 2x^2 + 4x - 2。
2.2.2 习题答案1. a) 函数的导数为f'(x) = 2x^3 + 3x^2 - 4x + 1。
b) 函数的导数为f'(x) = 3x^2 + 4x - 1。
托马斯微积分第13版第三章答案
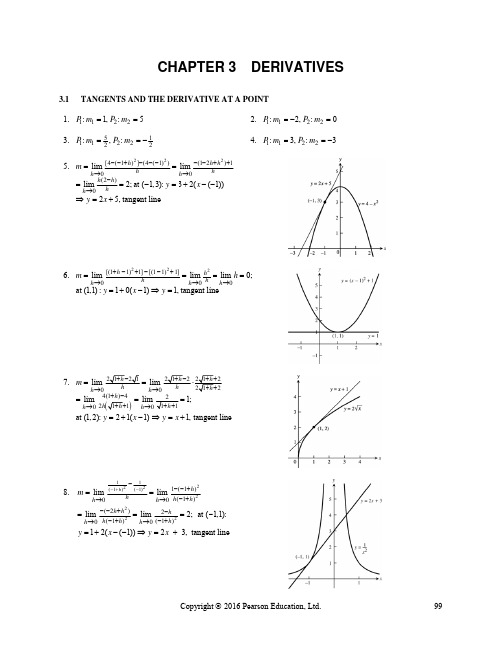
lim
2
( x3 3 x 2 h 3 xh 2 h3 3 x 3h ) ( x3 3 x ) h h 0
2 2 h 3 3h lim 3 x h 3 xh h
h 0
lim (3x 3xh h 3) 3 x 3; 3x 3 0 x 1 or x 1. Then f (1) 2 and f (1) 2 (1, 2)
h 0
x 2. Then f (2) 4 8 1 5 (2, 5) is the point on the graph where there is a horizontal tangent.
26. 0 m lim
2 h 0
[( x h )3 3( x h )]( x3 3 x ) h h 0
1 1 ( x h ) 1 x 1
( x 1) ( x h 1)
( x h) x x x h m lim x h lim x h x h x lim lim 1 . 28. 1 4 h h 2 x x h x h 0 h x h x h 0 h x h x h 0 h 0 x 1 1 1 x 2 x 4 y 2. The tangent line is y 2 4 ( x 4) 4 1. Thus, 4 2 x f (2 h ) f (2) h h 0
P (5) lim
h 0
24. (a) From t 0 to t 3, the derivative is positive. (b) At t 3, the derivative appears to be 0. From t 2 to t 3, the derivative is positive but decreasing. 25. At a horizontal tangent the slope m 0 0 m lim
微积分第3章习题解答(上)

第3章 习题参考解答习题3-1(未修改)1、答:不能。
因为函数)(x f 在区间],[b a 上的值可能取正和负。
正确的解释应为在x 轴上方的曲边梯形的面积之和与在x 轴下方的曲边梯形的面积之和的差。
2、解:⎰∑=∆==→bani i i dx x F x F W )()(lim 1ξλ。
3、解:(1)⎰102xdx =右图三角形面积=12121=⨯⨯; x(2)dx x ⎰-1021=右图四分之一单位圆的面积=4π;(3)⎰-ππxdx sin =下图中两个曲边梯形的面积差额=021=-A A(4)⎰-22cos ππxdx =上面右图中的两个曲边梯形的面积的和=⎰=+2021cos 2πxdx A A4、解:(1)n i x x x x x x x dx i i i i i i i ni i,,2,1,,],[,11lim 11110102 =-=∆∈∆+=+--=→∑⎰ξξλ 10210=<<<<=n x x x x ;(2)n i x x x x x x xdx i i i i i i i ni i ,,2,1,,],[,sin lim sin 111=-=∆∈∆=--=→∑⎰ξξλππ=<<<<=n x x x x 2100。
5、解:(1)因为10≤≤x ,所以23x x ≤,故dx x dx x ⎰⎰≤1213;(2)因为21≤≤x ,所以32x x ≤,故dx x dx x ⎰⎰≤213212;(3)因为e x <≤≤21,所以x x x ln )(ln 1ln 02<⇒<≤,故dx x dx x ⎰⎰≤21212ln )(ln ;(4)因为12-≤≤-x ,所以x x ⎪⎭⎫ ⎝⎛≤313,故dx dx xx⎰⎰----⎪⎭⎫ ⎝⎛≤1212313;习题3-21、计算下列各函数的导数(1)1sin x tdt t ⎰ 解:1sin sin ()x t xdt t x '=⎰ (2)21t dt解:22ln 1()t x dt ee ''===(3)x⎰解:()x'=⎰(4)22x t xe dt -⎰解:2242()2x t x x xe dt xe e ---'=-⎰2、计算下列定积分: 解:(1)3334441111(31)2044x dx x ==-=⎰(2)1121211arcsin arcsin arcsin()()22663xπππ-==--=--=⎰(3)111001()1xx e dx ee e e---=-=--=-⎰(4)422440tan (sec 1)tan 144xdx x dx xπππππ=-=-=-⎰⎰(5)111001111x dx x αααα+==++⎰ (6)2221241411111811121()()2141338338x dx x x x +-++=+=--+=+-+⨯⎰3、设函数221()31x x f x x x ≤⎧⎨>⎩,求21()f x dx -⎰解:2121222311111()230817f x dx xdx x dx xx---=+=+=+-=⎰⎰⎰4、求下列极限(1)02sin 01lim cos xx t dt x →⎰解:020022sin sin 000(cos )1lim cos lim lim cos(sin )cos 11xx x x x t dt t dt x x x →→→'==-⋅=-⎰⎰ (2)22(arctan ))limxx t dt 解:222222(arctan ))((arctan ))2[arctan(2)]limlim lim 2xxx x x t dt t dt x x π∞∞→+∞'===5、设201()12x x f x xx ⎧≤≤⎨<<⎩,求0()()xx f t dt Φ=⎰在[0,2]上的表达式解:当]1,0[∈x 时,302031)()(x dt t dt t f x xx===Φ⎰⎰ 当(1,2)x ∈时,612)1(2131)()(22112-=-+=+==Φ⎰⎰⎰x x tdt dt t dt t f x x x所以32013()11226x x x x x ⎧≤≤⎪⎪Φ=⎨⎪-<≤⎪⎩习题3-31、求下列不定积分(其中a ,m ,n ,g 为常数) 解:(1)352225x dx x C ==+⎰⎰(2)532223x dx x C --==-+⎰(3)C = (4)10.60.6213()3[]du udu u du u du uu ---+=-+⎰⎰⎰⎰1110.610.4221153[ln ]3[2ln ]10.61212u u u C u u u C -+-+=-++=-++-+-+(5)12dx C -==(6)231(2)(2)3x dx x C -=-+⎰(7)22425312(1)(21)53x dx x x dx x x x C +=++=+++⎰⎰(8)13352322221221)(1)335dx x x x dx x x x x C =-+-=-+-+⎰⎰(9)3443103101(3)10ln x dx x dx x C x x x-+=+=-+⎰⎰(10)335222242)35x dx x x C =-=++⎰(11)4223223311(3)arctan 11x x dx x dx x x C x x++=+=++++⎰⎰ (12)23(3arctan 2arcsin 1dx x x C x =-++⎰(13)21(1)x xx e e dx e C x x--=++⎰(14)()1ln t tt tta e a e dt ae dt C a==++⎰⎰ (15)2352225[25()]3()333ln 2ln 3x x x x x dx dx x C ⋅-⋅=-=-+-⎰⎰ (16)sec (sec tan )tan sec x x x dx x x C -=-+⎰ (17)22tan (sec 1)tan xdx x dx x x C =-=-+⎰⎰(18)211tan 1cos 22cos 2dx x dx C x x ==++⎰⎰(19)21cos 11cos sin 2222x x dx dx x x C +==++⎰⎰(20)22cos 2cos sin sin cos cos sin cos sin x x xdx dx x x C x x x x -==-+--⎰⎰ (21)2222cos 211()(cot tan )cos sin sin cos x dx dx x x C x xx x =-=-++⎰⎰ 2、求下列定积分 解:(1)1011x dx a α=+⎰(2)22232111111(3)(ln )ln 222x x dx x x x x -+=-+=+⎰(3)2223341111121()()338x dx x x x -+=-=⎰(4)93224421271()326dx x x =+=⎰(5)111001xxe dx ee ---=-=-⎰(6)21arctan 6dx x π==+(7)1121211arcsin arcsin arcsin()223xπ-==--=⎰(8)224440tan (sec 1)(tan )14tdt t dt t t ππππ=-=-=-⎰⎰3、212x e ,x e shx 和x e chx 是否都是x e 2的原函数解:因为22212(),()()22xx x x x x x x x e e e e shx e shx e chx e e e chx '''==+=== 所以chx e shx e e x x x 和,212都是x e 2的原函数。
微积分科学出版社第三章习题33答案.doc

解(5) y = yfa 1-x 2 解•—x -y=47^,y = a 2 -x 22—aT*2 a 2 -x(6)y = ln(l-x 2 解-2(1-x 2 1-" ■ —2xy =+ x 2~2 1-x 2解(8)1 y=7TT 解-3x 2”~^y = x 3+l -6兀(疋+1) + 6x x 3 + l (X 3+1)3X 26X (2X 3-1) x 3+l(9) 解3.3高阶导数 习题3.3 1.求下列函数的二阶导数:(1) y = lx 1 +lnx& - 1 .. 1 解:y =4x + —=4——.XX(2) y =解:y =2e 2x -\y'' =4e 2x '\ (3) y = xcosx解:y =cosx-xsin x,y = -sinx-sinx-xcosx = -2sinx-xcos x.(4)y = -e~l sin t + e~l cos t, y = e~l sin t - e~l cos t - e~l cos t - e~l sin t = -2e~lcos t.(7)y = sec 2 x, y" = 2 sec 2 x tan x.arctan x y' = 2x arctan x +1, y = 2 arctan x +彳二.1 + x 2(10) y= —x(11 ) (12 )(13 ) 解y =xee x2 +2xV =(1 +2/)e x2, y = +2x(1+2/)/x3= 2.x(3 +2.r)1 兀1+ , ----------A/1+ X2X+ A/1+X21=~x+x2+x2y = cos2 x• In x2 7、 c , COS X . c . COS Xy = -2cosxsinxlnxH ------------------ = -sinzxlnxH ----------------X X .. c c . sin 2x -2x cos x sin x - cos2 x y =-2cos 2xlnx Hxc c . 2 sin 2x cos2 x=-2 cos 2xlnx ---------------xx2(14)解1-x2x21-x2Q 5_厅(1一"J 2(—2兀)=- (3x21-x2i22.设f'(x)存在,求下列函数的二阶导数害:dx解'驚2对X),帶=2f (兀2)+心” (/)⑵ y = ln[f (x)]解:加速度为丽而—=coAcoscot所以 d 2S2 人• 2—-=-CD Asin cot --CD s dt 2于是其屮c 为常数。
微积分(三)_浙江大学中国大学mooc课后章节答案期末考试题库2023年

微积分(三)_浙江大学中国大学mooc课后章节答案期末考试题库2023年
1.设闭曲线【图片】为柱面【图片】与平面【图片】的交线,从x轴正向看
它为逆时针方向,则【图片】等于
参考答案:
-24
2.曲线【图片】为yoz平面上从点A(0,1,0)到点B(0,0,1)的一段光滑曲线,曲
线【图片】为zox平面上从点B(0,0,1)到点C(1,0,0)的一段光滑曲线; 则【图片】等于
参考答案:
1
3.【图片】是平面上不通过原点的简单闭曲线(逆时针方向),【图片】,
则下列正确的是
参考答案:
时,
4.设【图片】,且【图片】,则它的Fourier级数在【图片】处结论正确的是
参考答案:
收敛于0
5.向量场【图片】在点A(2,1,1)处的散度【图片】等于
参考答案:
3
6.【图片】是函数【图片】的正弦级数,【图片】是正弦级数的和函数,则
参考答案:
时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题 3-11. 验证函数()f x =在区间[0,4]上满足罗尔定理的条件,并求出使得结论成立的点ξ。
解:显然函数()f x =[0,4]上连续,在(0,4)上可导,且有(0)(4)0f f ==所以函数在区间[0,4]上满足罗尔定理,则有()0f ξ'==,83ξ=。
2. 验证函数3()1f x x =-在区间[1,2]上满足拉格朗日中值定理的条件,并求出使得结论成立的ξ。
解:函数3()1f x x =-在区间[1,2]上连续,在(1,2)上可导,则满足拉格朗日中值定理,则有2(2)(1)321f f ξ-=-,即ξ=3. 函数4()1f x x =-与2()g x x =在区间[1,2]上是否满足柯西中值定理的所有条件,如满足,求出满足定理的数值ξ。
解:函数4()1f x x =-与2()g x x =在区间上连续,在区间(1,2)上可导,则满足柯西中值定理,则有3(2)(1)4(2)(1)2f f g g ξξ-=-,即ξ=4. 若4次方程432012340a x a x a x a x a ++++=有4个不同的实根,证明3201234320a x a x a x a +++=的所有根皆为实根。
证明:设43201234()f x a x a x a x a x a =++++,()0f x =的四个实根分别为1234,,,x x x x ,且1234x x x x <<<,则函数()f x 在1[,](1,2,3)i i x x i +=上满足罗尔定理的条件,则在1(,)i i x x +内至少存在一点i ξ,使得()0i f ξ'=。
这说明方程3201234320a x a x a x a +++=至少有3个实根,而方程为3次方,则最多也只有3个实根,所以结论得到证明。
5. 设()f x 在[0,1]上连续,在(0,1)内可导,且(1)0f =,证明:存在(0,1)ξ∈,使得()()f f ξξξ'=-。
解:构造辅助函数()()F x xf x =,而()()F x xf x =满足罗尔定理的条件,所以有在(0,1),至少存在一点ξ,()()0f f ξξξ'+=即()()f f ξξξ'=-。
6. 试用拉格朗日中值定理证明: (1)2121sin sin x x x x -≤-; (2)当0x >时,ln(1)1xx x x<+<+。
解:(1)设()sin f x x =,则()f x 在区间12(,)x x 上满足拉格朗日中值定理,则有121212sin sin cos ,(,)x x x x x x ξξ-=∈-,又因为cos 1ξ≤,则1212sin sin 1x x x x -≤-, 1212sin sin x x x x -≤-。
(2)设()ln(1)f x x =+,则()f x 在区间(0,)x 上满足拉格朗日中值定理,则有ln(1)11x x ξ+=+ (0,)x ξ∈,又因为11111x ξ<<++,则1ln(1)11x x x+<<+,即ln(1)1xx x x <+<+。
7. 证明等式:arctan arccot 2x x π+=。
证明:设()arctan arccot f x x x =+,则有()(arctan arccot )0f x x x ''=+=, 所以()f x c ≡,代入0x =,得到arctan arccot 2x x π+=。
8.设()f x 在[1,2]上具有二阶导数()f x '',且(2)(1)0f f ==。
若()(1)()F x x f x =-。
证明:至少存在一点ξ(1,2)∈,使得()0F ξ''=。
证明:因为(1)(2)0F F ==,在[1,2]上应用罗尔定理,有1()0F ξ'=, 又因为(1)0F '=,所以在1[1,]ξ上应用罗尔定理,有()0F ξ''=,1[1,][1,2]ξ⊂。
9.设()f x 在[,]a b 上连续,在(,)a b 内可导,证明:在(,)a b 内存在点ξ和η,使得 ()()2a bf f ξηη+''=。
证明:构造辅助函数2()g x x =,()f x 与()g x 在(,)a b 内满足柯西中值定理,即有22()()()()()()()()f b f a f f b f a g b g a g b a ηη'--=='--,(,)a b η∈而()f x 在(,)a b 内满足拉格朗日中值定理,所以()()()()f b f a f b a ξ'-=-, 即()()2a bf f ξηη+''=。
习题 3-21. 用洛必达法则求下列极限:(1)0sin lim sin x ax bx →; (2)30sin lim x x xx→-; (3)332132lim 1x x x x x x →-+--+; (4)2tan lim tan 3x x x π→; (5)2lim x ; (6)2ln()2lim tan x x x ππ+→-; (7)2120lim x x x e→; (8) 0lim cot x x x →; (9)2lim(sec tan )x x x π→-;(10)11lim()1ln x x x x→--; (11)tan 0lim xx x +→; (12)1lim x x x →+∞; (13)1lim(1sin )xx x →+; (14) 111lim xx x-→解:(1)(型);000sin (sin )cos limlim lim sin (sin )cos x x x ax ax a ax a bx bx b bx b →→→'===';(2)(00型);3320000sin (sin )1cos sin 1lim lim lim lim ()366x x x x x x x x x x x x x x →→→→'---===='; (3)(0型);33232322111132(32)3363lim lim lim lim 1(1)321622x x x x x x x x x x x x x x x x x x x →→→→'-+-+-===='--+--+---; (4)(∞∞型);2222tan sin cos3cos33sin 3lim lim lim lim 3tan 3cos sin 3cos sin x x x x x x x x xx x x x x ππππ→→→→-=⋅===-;(5)(∞∞型);212ln limlim lim 4lim 01x x x x x x →+∞⋅'====;(6)(∞∞型);2222ln()(ln())cos 22lim lim lim 0tan (tan )2x x x x x x x x x ππππππ+++→→→'--==='-;(7)(0⋅∞型);2221113200232()lim limlim 12x x x x x x e ex x e x x→→→-===∞-; (8)(0⋅∞型);00lim cot lim1tan x x xx x x→→==;(9)(∞-∞型);22221sin 1sin cos lim(sec tan )lim[]lim lim 0cos cos cos sin x x x x x x xx x x x x x ππππ→→→→---=-===;(10)(∞-∞型);1111ln (1)ln lim()lim lim11ln (1)ln ln x x x x x x x xx x x x x x x→→→---==---+11ln ln 11lim lim ln 1ln 22x x x x x x x x x →→+===+-+;(11)(00型);2tan 0000ln sin lim ln lim tan ln limlimtan 0cot 0lim 1xx x x x xx x x xxx x x x e e eee ++++→→→→+→======;(12)(0∞型);11ln 1limlimlim ln 0lim 1xx x x x x xx x x x e eee →+∞→+∞→+∞→+∞=====;(13)(1∞型);11ln(1sin )cos 1sin 01lim ln(1sin )lim ln(1sin )limlim 0lim(1sin )x xxx xxx x x x x x xx x e e e e e ++→→→→++→+=====;(14)(1∞型);1ln l111111limln lim lim 111lim xxxxx x x x xx xee e e---→→→-→====。
2.验证下列极限存在,但不能用洛必达法则求出。
(1)201sinlimsin x x x x →; (2)sin lim x x x x→∞+。
解:(1)用洛必达法则求:2220001111sin2sin cos ()11limlim lim(2sin cos )sin cos x x x x x x x x x x x x x x x→→→+-==-,求不出 用一般的方法:200001sin11limlim sin lim lim sin 0sin sin sin x x x x x x x x x x x x x x x→→→→=⋅=⋅=; (2)用洛必达法则求:sin 1cos limlim lim(1cos )1x x x x x x x x →∞→∞→∞++==+, 求不出用一般的方法:sin sin limlim(1)101x x x x xx x→∞→∞+=+=+=。
3.设()f x 在0x =处二阶可导,且(0)0f =,试确定a 的值使()g x 在0x =处可 导,并求(0)g ',其中()()f x g x x a ⎧⎪=⎨⎪⎩00x x ≠=解:因为函数()f x 在0x =处二阶可导,则函数在0x =处一定连续,即有lim ()(0)0x f x f →==,又因为函数()g x 在0x =处可导,所以函数在0x =处也一定连续,即有 000()()lim ()(0),limlim lim ()1x x x x f x f x g x g f x a x →→→→''==== 根据导数的定义以及洛必达法则,有2000()()(0)()(0)lim lim lim x x x f x ag x g f x ax x g x x x →→→---'=== 00()()(0)lim lim 222x x f x a f x f x →→'''''-===。
