实验指导书及实验报告-自由衰减法测量单自由度系统的固有频率和阻尼比
10工程力学实验指导书初稿
《理论力学》实验部分实验一:单自由度系统自由振动(无阻尼)一、实验目的1. 记录小阻尼情况下衰减振动的时间――位移曲线,了解阻尼对自由振动的影响。
2. 测量并计算单自由度系统的对数减缩率δ、阻尼系数n 和阻尼比ζ测量系统的固有频率。
3.了解振动实验仪器。
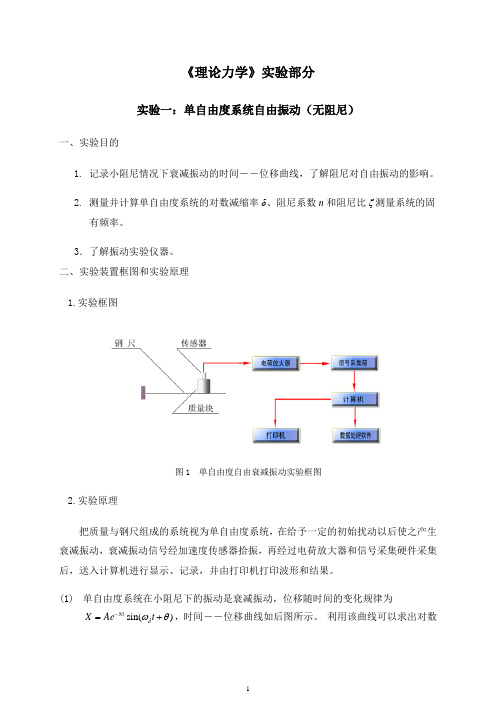
二、实验装置框图和实验原理1.实验框图图1 单自由度自由衰减振动实验框图2.实验原理把质量与钢尺组成的系统视为单自由度系统,在给予一定的初始扰动以后使之产生衰减振动,衰减振动信号经加速度传感器拾振,再经过电荷放大器和信号采集硬件采集后,送入计算机进行显示、记录,并由打印机打印波形和结果。
(1) 单自由度系统在小阻尼下的振动是衰减振动,位移随时间的变化规律为sin()Nt d X Ae t ωθ-=+,时间――位移曲线如后图所示。
利用该曲线可以求出对数减缩率 δ、阻尼系数n 和阻尼比 ζ 对数减缩率为1ln i i A A δ+=,或1ln i i mA m A δ+=(m 为间隔 m 周期)。
(2) 阻尼系数d dn f T δδ==。
(3) 阻尼比2(2)2d nT δζδπζπ===≈。
图2自由衰减振动的加速度波形(4) 加速度随时间的变化规律sin()nt d X A e t αωβ-=+ ,除初相位、幅值不同外,衰减规律与时间――位移曲线相同。
由时间――加速度曲线按相同的方法,也可测量系统的固有频率和阻尼比。
三、实验仪器实验模型;加速度传感器;电荷放大器;信号采集箱和振动信号处理软件;计算机和打印机。
四、实验步骤1. 打开电源总开关;2. 依次打开电荷放大器、信号采集箱、计算机和打印机电源开关;3. 启动振动信号采集系统,设置采集硬件参数,并设采集方式为触发采集;4. 给实验模型一个初始的位移干扰,使其作自由衰减振动;5. 由采集硬件和软件记录自由衰减振动的加速度波形,参看图2。
五、实验数据及结果1.自由衰减振动曲线 (附测试图) 。
实验一单自由度振动系统固有频率及阻尼比的测定

实验二 刚性转子动平衡实验一、实验目的(1) 掌握刚性转子动平衡的基本原理和步骤; (2) 掌握虚拟基频检测仪和相关测试仪器的使用; (3) 了解动静法的工程应用。
二、实验内容采用两平面影响系数法对一多圆盘刚性转子进行动平衡三、实验原理工作转速低于最低阶临界转速的转子称为刚性转子,反之称为柔性转子。
本实验采取一种刚性转子动平衡常用的方法—两平面影响系数法。
该方法可以不使用专用平衡机,只要求一般的振动测量,适合在转子工作现场进行平衡作业。
根据理论力学的动静法原理,一匀速旋转的长转子,其连续分布的离心惯性力系,可向质心C 简化为过质心的一个力R (大小和方向同力系的主向量∑=iS R )和一个力偶M (等于力系对质心C 的主矩CiΜS m M ==∑)(),见图一。
如果转子的质心恰在转轴上且转轴恰好是转子的惯性主轴,即转轴是转子的中心惯性主轴,则力R 和力偶矩M C 的值均为零。
这种情况称转子是平衡的;反之,不满足上述条件的转子是不平衡的。
不平衡转子的轴与轴承之间产生交变的作用力和反作用力,可引起轴承座和转轴本身的强烈振动,从而影响机器的工作性能和工作寿命。
图一 转子系统与力系简化刚性转子动平衡的目标是使离心惯性力系的主向量和主矩的值同时趋近于零。
为此,先在转子上任意选定两个截面I 、II (称校正平面),在离轴线一定距离1r 、2r (称校正半径),与转子上某一参考标记成夹角1θ、2θ处,分别附加一块质量为1m 、2m 的重块(称校正质量)。
如能使两质量1m 和2m 的离心惯性力(其大小分别为211ωr m 和222ωr m ,ω为转动角速度)正好与原不平衡转子的离心惯性力系相平衡,那么就实现了刚性转子的动平衡。
两平面影响系数法的过程如下;(1)在额定的工作转速或任选的平衡转速下,检测原始不平衡引起的轴承或轴颈A 、B 在某方位的振动量11010ψ∠=V V 和22020ψ∠=V V ,其中10V 和20V 是振动位移(也可以是速度或加速度)的幅值,1ψ和2ψ是振动信号对于转子上参考标记有关的参考脉冲的相位角。
【免费下载】单自由度系统自由衰减振动及固有频率阻尼比的测定
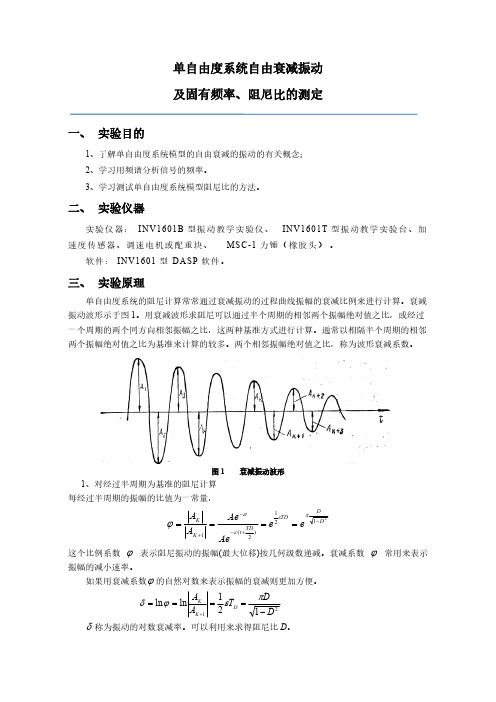
图1
衰减振动波形
、对经过半周期为基准的阻尼计算
每经过半周期的振幅的比值为一常量,
2
12
1
)2
(1
D D
TD TD t t
K K
e
e
Ae
Ae
A A -+
--+===
=
π
εεεϕ这个比例系数
表示阻尼振动的振幅(最大位移)按几何级数递减。
衰减系数 常用来表示
ϕϕ振幅的减小速率。
如果用衰减系数的自然对数来表示振幅的衰减则更加方便。
ϕ
砝码为3kg的图像
砝码为 3.5kg的图像
六、实验心得
此次实验,让我了解了衰减振动的相关概念,懂得了如何用频谱分析信号的频率。
同时也学到了通过读取相邻两个波形的峰峰值之比来计算阻尼比的方法。
实验中,我们小组三人合作,xxx同学负责用手敲击简支梁和记录实验数据,我主要负责电脑软件的采样工作,xxx同学帮忙指导操作以及保存实验数据,最后我们三个人一起处理实
验数据。
小组既有分工又有合作,很快就完成了实验的内容。
机械实验之振动参数的测定

带宽法使用于小阻尼情况,既可用于高阶,也可用于低阶,但两个 半功率点的频率必须相差较大,否则误差很大。
本实验由于两个点的半功率点相隔较近,所以误差也比较大
2.3 实验的操作步骤
1)用自由振动法测量 和 A n
A)用榔头敲击简支梁使其产生自由衰减振动。
B)记录单自由度自由衰减振动波形,将加速度传感器所测振动经测振仪转 换为位移信号后(标准电信号),送入信号采集分析仪(A/D),让计算机虚拟 示波器以便显示。
C)绘出振动波形图波峰和波谷的两根包络线,然后设定,并读出个波形所
经历的时间t,量出相距i个周期的两振幅 2,0 。按公式计算 和 A n
2)用强迫振动法测量 和 A n
A)加速度传感器置于简支梁上,其输出端接信号采集分析仪,用来测量简支 梁的振动幅值
B)将电动式激振器接入激振信号源输入端,开启激振信号源的电源开关,对 简支梁系统施加交变正弦激振力,使系统产生正弦振动。
2 1 iln A ( n/A n i)
式中:02/T02/Td12---频率比
0
幅频特性曲线如右图:
振幅最大时的频率为共振频率 0 122
由于存在测量参数的不同,存在位移共振、速度共振及加 速度共振三种
振动形 式
阻尼
自由振动 频率
位移共振 频率
速度共振 频率
加速度共 振频率
无阻尼
n/0
机械振动实验课件
振动参数的测定
(固有频率和阻尼比)
一、实验目标
1.1 实验目的
1、了解单自由度系统自由振动的有关概念 2、了解单自由度系统强迫振动的有关概念 3、会根据自由衰减振动波形确定系统的固有频率和阻尼比会 4、根据强迫振动幅频特性曲线确定系统的固有频率和阻尼比
单自由度实验报告

[键入公司名称][键入文档标题][键入文档副标题]实验人:陈伟同组人:陈光赵煜民2011/10/31理论力学实验报告一、实验目的1. 掌握测定单自由度系统固有频率、阻尼比的几种常用方法;2. 掌握常用振动仪器的正确使用方法。
二、实验内容1. 记录水平振动台的自由衰减振动波形;2. 测定水平振动台在简谐激励下的幅频特性;3. 测定水平振动台在简谐激励下的相频特性;4. 根据上面测得的数据,计算出水平振动台的固有频率、阻尼比。
三、实验原理具有粘滞阻尼的单自由度振动系统,自由振动微分方程的标准形式为022=++q p q n q,式中q 为广义坐标,n 为阻尼系数,eq eq m C n /2=,eq C 为广义阻力系数,eq m 为等效质量;p 为固有的圆频率,eq eq m K p /2=,eq K 为等效刚度。
在阻尼比1/<=p n ζ的小阻尼情况下,运动规律为)sin(22α+-=-t n p Ae q nt ,式中A ,α由运动的起始条件决定,d f n p π222=-。
具有粘滞阻尼的单自由度振动系统,在广义简谐激振力t H t s ωsin )(=作用下,系统强迫振动微分方程的标准形式为t h p q n qωsin 22=++ ,式中/eq h H m =。
系统稳态强迫振动的运动规律)sin(ϕω-=t B q ,式中 振幅22220222224)1(4)(λζλωω+-=+-=B n p hB相位差22212arctg 2arctgλζλωωϕ-=-=p n 其中eq k H ph B ==20,p ωλ=。
由台面、支撑弹簧片及电磁阻尼器组成的水平振动台,可视为单自由度系统,它在瞬时或持续的干扰力作用下,台面可沿水平方向振动。
1. 衰减振动:用一点电脉冲沿水平方向冲击振动台,系统获得一初始速度而作自由振动,因存在阻尼,系统的自由振动为振幅逐渐减小的衰减振动。
阻尼越大,振幅衰减越快。
实验11:单自由度系统强迫振动的幅频特性、固有频率及阻尼比的测定

2.5kg,上下都可以放,由于速度传感器不能倒置,只能把
质量块放到梁的下面,传感器安装在简支梁的中部。
2、 开机进入 DASP2000 标准版软件的主界面,选择单通道按
钮。进入单通道示波状态进行波形和波谱同时示波。
3、 把 ZJ-601A 型振动教学试验仪的频率按钮用手动搜索一下
梁当前的共振频率,调节放大倍数到“1”档,不要让共振
无量纲的加速度响应,将上式对时间 t 再微分一次,
������0���⁄���̈������=- ������������2 sin(������������ − ������)=- β∝ sin(������������ − ������)
振动幅度最大的频率叫共振频率������������、������������,有阻尼时共振频 率为
������������=������√1 − ������2 或������������ = ������√1 − ������2 ω、f— —固有频率; D——阻尼比。 由于阻尼比较小,所以一般认为:������������ = ω 根据幅频特性曲线:
在
D<1
时,共振处的动力放大系数|������������������������ |=2������√11−������2
有阻尼的强迫振动,当经过一定时间后,只剩下强迫振动部分,
有阻尼强迫振动的振幅特性:������
=
√(1−������2
1 )2+4������2
������2=������������������������
当干扰力确定后,由力产生的静态位移������������������就可随之确定,而强迫
振动的动态位移与频率比 u 和阻尼比 D 有关,这种关系即表现为幅
单自由度振动系统固有频率及阻尼的测定-实验报告

4、根据相频特性的测试数据,在同一图上绘出几条相位差频率( 特性曲线,由此分析阻尼的影响并计算系统的固有频率及阻尼比。
5、根据实验现象和绘制的幅频、相频特性曲线,试分析对于不同阻尼的振动系统,几种固有频率和阻尼比测量方法的优劣以及原因。
首先,在水平振动台面上不加任何重物,测量系统在自由衰减振动时的固有频率;之后在水平振动台面上放置一个质量已知的砝码,再次测量系统在自由振动时的固有频率。记录两次测得的固有频率,并根据其估算水平振动台面的等效质量。
4、测定自由衰减振动特性:
撤去水平振动台面上的砝码,调整励磁电流至0.6A。继续使用“自由衰减记录”功能进行测试。操作方法与步骤3基本相同,但需按照数据记录表的提示记录衰减振动的峰值、对应时间和周期数i等数据,以计算系统的阻尼。
假设实验使用的单自由度振动系统中,水平振动台面的等效质量为 ,系统的等效刚度为 ,在无阻尼或阻尼很小时,系统自由振动频率可以写作 。这一频率容易通过实验的方式测得,我们将其记作 ;此时在水平振动台面上加一个已知质量 ,测得新系统的自由振动频率为 。则水平振动台面的等效质量为 可以通过以下关系得到: 。
、 的意义同拾振器。但对激振器说, 的值表示单位电流产生的激振力大小,称为力常数,由厂家提供。JZ-1的力常数约为5N/A。频率可变的简谐电流由信号发生器和功率放大器提供。
4、计算机虚拟设备:
在计算机内部,插有A/D、D/A接口板。按照单自由系统按测试要求,进行专门编程,完成模拟信号输入、显示、信号分析和处理等功能。
6、教师签名的原始数据表附在实验报告最后,原始数据记录纸在实验课上提供,必须每人交一份,可以采用复印、拍照打印等方式进行复制。原始数据上要写清所有人的姓名学号,不得使用铅笔记录。
机械振动实验指导书概要

《机械振动》课程实验指导书机械与车辆学院2009年6月编制目录单自由度系统强迫振动的幅频特性、固有频率及阻尼比的测定 (2)单自由度系统自由衰减振动及固有频率、阻尼比的测定 (7)多自由度系统固有频率和振型测试 (11)单自由度系统强迫振动的幅频特性、固有频率及阻尼比的测定实验指导书一、试验目的1.学会测量单自由度系统强迫振动的幅频特性曲线; 2.学会测量单自由度系统强迫振动的幅频特性曲线;二、试验原理有阻尼的强迫振动,当经过一定时间后,只剩下强迫振动部分,有阻尼强迫振动的振幅特性:st st x x Du u A β=+-=22224)1(1动态振幅A 和静态位移st x 之比值称为动力放大系数:stx A D u u =+-=22224)1(1β 加速度响应和位移响应的关系:)sin()sin(4)1(12220ϕωβϕω-=-+-==t t Du u K F x x x e e st)sin()sin(20..ϕωβϕωβ--=--=t t u KF x e a e根据幅频特性曲线:在1<D 时,共振处的动力放大系数Q DD D =≈-=211212max β,峰值两边,2Q =β处的频率1f 、2f 称为半功率点,1f 与2f 之间的频率范围称为系统的半功率带宽。
代入动力放大系数计算公式22124112202,12202,1D Q D f f f f ==⎪⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=β当D 很小时解得:D f f 21202,1 ≈⎪⎪⎭⎫ ⎝⎛ 即2021224Df f f ≈- 0122f f f D -=三、试验系统组成实验用仪器设备见表1。
表1 实验用仪器设备试验系统布置如图1所示:图1 试验系统布置简图四、试验准备1.如图1安装好试验设备,并连线,质量块放到简支梁底部,传感器安装到简支梁的中部;2.认真检查各联结件是否正确安装、紧固情况;3.检查各传感器信号线连接的正确性;4.系统上电预热30分钟五、试验内容1.测量单自由度系统强迫振动的幅频特性曲线;2.根据幅频特性曲线确定系统的固有频率和阻尼比六、试验方法1.开机进入DASP2000波状态;2.把ZJY-601A型振动教学试验仪的频率按钮用手动搜索一下简支梁当前的共振频率,调节放大倍数道“1”挡,不要让共振时的信号过载。
机械实验之振动参数的测定

式中:A ------ 振动振幅
x•0yy静动-----------
初相位 有阻尼衰减振动圆频率
设初始条件:t=0时,初始位移Td2/02n22/012T0,/12 初始速度 d 02n2
1/ (1 2 )2 (2)2
•
A x02 [(x0 nx0 ) / d ]2
此波形有如下特点:
0
带宽法使用于小阻尼情况,既可用于高阶,也可用于低阶,但两个 半功率点的频率必须相差较大,否则误差很大。
本实验由于两个点的半功率点相隔较近,所以误差也比较大
2.3 实验的操作步骤
1)用自由振动法测量tg
x0d
•
/(x0
nx0)
和
n/0
A)用榔头敲击简支梁使其产生自由衰减振动。
B)记录单自由度自由衰减振动波形,将加速度传感器所测振动经测振仪转 换为位移信号后(标准电信号),送入信号采集分析仪(A/D),让计算机虚拟 示波器以便显示。
B)振幅按几何级数衰减
减幅系数: x B sin( t )
对数减幅 :
''
'
m x kx c x F0 sin t
2 迫振动法(共振法) 利用激振器对被测系统施以简谐激励力,使系统产生强迫振
动,改变激振频率,进行频率扫描,当激振频率与系统的固有频 率接近时,系统产生共振。因此,只要逐渐调节激振频率,同时 测定系统的响应幅值,绘出幅值和频率的关系曲线(即幅频特性 曲线),曲线上各峰值点所对应的频率,就是系统的各阶固有频 率。
单自由度系统,在简谐激励力的作用下,系统作简谐强 迫振动,系统的微分方程为
''
x
2 0
x
2nx
F0
单自由度振动系统固有频率及阻尼的测定实验报告(精)

单自由度振动系统固有频率及阻尼的测定实验报告一、实验目的1、掌握测定单自由度系统固有频率、阻尼比的几种常用方法2、掌握常用振动仪器的正确使用方法二、实验内容1、记录水平振动台的自由衰减振动波形2、测定水平振动台在简谐激励下的幅频特性3、 测定水平振动台在简谐激励下的相频特性4、 根据上面测得的数据,计算出水平振动台的固有频率、阻尼比三、实验原理由台面、支撑弹簧片及电磁阻尼器组成的水平振动台(见图四),可视为单自由度系统,它在瞬时或持续的干扰力作用下,台面可沿水平方向振动。
1、 衰减振动:用一橡皮锤沿水平方向敲击振动台,系统获得一初始速度而作自由振动,因存在阻尼,系统的自由振动为振幅逐渐减小的衰减振动。
阻尼越大,振幅衰减越快。
选x 为广义坐标,根据记录的曲线可分析衰减振动的周期d T ,频率d f ,对数减幅系数δ及阻尼比ζ,有i t T d ∆=, dd T f 1= )ln(111+=i X X iδd nT =, πδδπδζ2422≈+= 其中∆t 为i 个整周期相应的时间间隔,1X 和1+i X 为相隔i 个周期的振幅。
2、 强迫振动的幅频特性测定:保持功放的输出电流幅值不变,即保持激振力力幅不变,缓慢地由低频2Hz 到高频40Hz 改变激振频率,用相对式速度拾振器检测速度振动量,再经过积分处理后得到位移量,由测试数据可描绘出一条振幅频率特性曲线而根据该测试曲线可由如下关系式估算系统的固有频率n f 及阻尼比ζ nf≈m f , 021B B m =ζ 或 ζm f ff 212-≈ 其中m f 为振幅达到最大m B 时的激振频率;0B 为零频率的相应振幅(约等于f =2Hz 时的振幅);1f 和2f 为振幅m B B 707.0=的对应频率,即半功率点频率。
改变阻尼大小重新进行频率扫描可获得一组相应于不同阻尼比的幅频特性曲线。
四、实验装置测试系统如图四所示,其部分仪器的原理及功能说明如下:1、实验装置:振动台系统由台面、支撑弹簧片及电磁阻尼器组成,台面可沿水平面纵轴方向振动。
实验一单自由度振动系统固有频率及阻尼比的测定

实验二 刚性转子动平衡实验一、实验目的(1) 掌握刚性转子动平衡的基本原理和步骤; (2) 掌握虚拟基频检测仪和相关测试仪器的使用; (3) 了解动静法的工程应用。
二、实验内容采用两平面影响系数法对一多圆盘刚性转子进行动平衡三、实验原理工作转速低于最低阶临界转速的转子称为刚性转子,反之称为柔性转子。
本实验采取一种刚性转子动平衡常用的方法—两平面影响系数法。
该方法可以不使用专用平衡机,只要求一般的振动测量,适合在转子工作现场进行平衡作业。
根据理论力学的动静法原理,一匀速旋转的长转子,其连续分布的离心惯性力系,可向质心C 简化为过质心的一个力R (大小和方向同力系的主向量∑=iS R )和一个力偶M (等于力系对质心C 的主矩CiΜS m M ==∑)(),见图一。
如果转子的质心恰在转轴上且转轴恰好是转子的惯性主轴,即转轴是转子的中心惯性主轴,则力R 和力偶矩M C 的值均为零。
这种情况称转子是平衡的;反之,不满足上述条件的转子是不平衡的。
不平衡转子的轴与轴承之间产生交变的作用力和反作用力,可引起轴承座和转轴本身的强烈振动,从而影响机器的工作性能和工作寿命。
图一 转子系统与力系简化刚性转子动平衡的目标是使离心惯性力系的主向量和主矩的值同时趋近于零。
为此,先在转子上任意选定两个截面I 、II (称校正平面),在离轴线一定距离1r 、2r (称校正半径),与转子上某一参考标记成夹角1θ、2θ处,分别附加一块质量为1m 、2m 的重块(称校正质量)。
如能使两质量1m 和2m 的离心惯性力(其大小分别为211ωr m 和222ωr m ,ω为转动角速度)正好与原不平衡转子的离心惯性力系相平衡,那么就实现了刚性转子的动平衡。
两平面影响系数法的过程如下;(1)在额定的工作转速或任选的平衡转速下,检测原始不平衡引起的轴承或轴颈A 、B 在某方位的振动量11010ψ∠=V V 和22020ψ∠=V V ,其中10V 和20V 是振动位移(也可以是速度或加速度)的幅值,1ψ和2ψ是振动信号对于转子上参考标记有关的参考脉冲的相位角。
单自由度振动系统固有频率及阻尼的测定-实验报告

1
DC 输出:0~30V,2A
PAB 32~2A KIKUSUI(日本)
7
微型计算机
1
内部有 A/D、D/A 插卡
通用型
-3-
五.实验步骤
1. 打开微型计算机,运行进入“单自由度系统”程序。 2. 单击“设备虚拟连接”功能图标,进入设备连接状态,参照图六对显示试验设备进行联
线。连线完毕后,单击“连接完毕”,如连接正确,则显示“连接正确”,即可往下进 行,否则重新连接,直至连接正确。 3. 接通阻尼器励磁及功率放大器电源,调励磁电流为某一定值(分别为������ = 0.6A, 0.8A, 1.0A) 4. 测定自由衰减振动: 单击“自由衰减记录”功能图标,进入如图七显示界面。单击 (Start)键,开始测试。由 一电脉冲沿水平方向突然激励振动台,微机屏幕上显示自由衰减曲线。用鼠标调节光标 的位置,读出有关的数据。改变周期数 i 的数值,即可直接显示相应的周期和频率。 5. 测定幅频特性和相频特性: 单击“简谐激励振动”功能图标,按图八所示,单击“信号输入显示框中的频率,将弹、 出一个对话框,可以直接输入激励频率。也可单击频率的单步步进键进行激励调节。单 击 (Start)键,开始测试,开始强迫振动幅频特性和相频特性测量,其中2Hz~15Hz内大致 相隔1Hz设一个测点;15Hz~30Hz 内每隔5Hz设一个测点。 在显示检测框显示力信号和相应信号波形,以便观察信号的质量。幅值比显示振动位移
注:由于实验时间所限,加之读数难度较大,在������������ 附近没有加密测量相频点。这是实验中的失误。
-5-
七.实验数据处理
1. 根据自由衰减振动记录的有关数据,分析计算系统的固有圆频率������������及阻尼比ζ。
实验三 单自由度系统自由衰减振动的测定试验

实验三 单自由度系统自由衰减振动的测定试验一、实验目的1、深刻理解单自由度系统衰减振动的基本规律。
2、掌握应用计算机软件跟踪和记录单自由度系统自由衰减振动波形,并打印其波形。
3、根据衰减振动波形图确定系统的固有频率和阻尼比及振幅减缩率。
二、基本原理质量为m 、阻尼系数为c 、弹性系数为k 的单自由度系统自由衰减振动时,其运动微分方程为0 m =++kx x c x可改写为0 2 2=++x x n x n ω (3-1)式中:n ω——系统固有频率; ζ——阻尼比 且m k n =ω (3-2)nnωζ=(3-3)mc n 2=小阻尼(ζ<1)时,微分方程(3-1)式的解可写为)sin(θω+=-t Ae x s nt (3-4)式中:A 、θ——由初始条件确定的积分常数;s ω——自由衰减振动的园频率。
2221ζωωω-=-=n n s n (3-5)设初始时刻T = 0时,初始位移0x x =,初始速度为0v ,则22002)(s nx v x A ω++=(3-6)2000)(nx v x arctgs+=ωθ (3-7)nt Ae -称为自由衰减振动的振幅,(3-4)式所表示的振动的振幅随时间不断衰减。
其图形见图3-2所示。
由其图形变化特点知,这种振动不符合周期振动的定义。
所以不是周期振动。
但振动仍然是围绕平衡位置的往复运动,仍具有振动的特点。
1.振动周期d T 大于无阻尼自由振动周期T 。
d T =222211222ζζωπωπωπ-=-=-=T nn nS(3-8)式中:T 为不计阻尼时自由振动周期。
且n T ωπ/2=。
2.振幅按几何级数衰减。
任意两个相邻振幅之比,称为振幅减缩率d d i i nT T t n nt i ie Ae Ae A A ===+--+)(1η (3-9)对上式取对数,得对数减缩率d i i nT A A ==+1lnδ (3-10)手锤 质量块 传感器图3-1 单自由度系统自由衰减振动实验仪器安装框图根据试验所得的衰减振动曲线[见图3-2(b )所示],量得相邻的两个位移最大值及周期d T 。
单自由度系统自由衰减振动的测定试验(精)

实验三 单自由度系统自由衰减振动的测定试验一、实验目的1、深刻理解单自由度系统衰减振动的基本规律。
2、掌握应用计算机软件跟踪和记录单自由度系统自由衰减振动波形,并打印其波形。
3、根据衰减振动波形图确定系统的固有频率和阻尼比及振幅减缩率。
二、基本原理质量为m 、阻尼系数为c 、弹性系数为k 的单自由度系统自由衰减振动时,其运动微分方程为0 m =++kx x c x可改写为0 2 2=++x x n x n ω (3-1)式中:n ω——系统固有频率; ζ——阻尼比 且mk n =ω (3-2)nnωζ=(3-3)mc n 2=小阻尼(ζ<1)时,微分方程(3-1)式的解可写为)sin(θω+=-t Ae x s nt (3-4)式中:A 、θ——由初始条件确定的积分常数; s ω——自由衰减振动的园频率。
2221ζωωω-=-=n n s n (3-5)设初始时刻T = 0时,初始位移0x x =,初始速度为0v ,则22002)(s nx v x A ω++=(3-6)2000)(nx v x arctgs+=ωθ (3-7)nt Ae -称为自由衰减振动的振幅,(3-4)式所表示的振动的振幅随时间不断衰减。
其图形见图3-2所示。
由其图形变化特点知,这种振动不符合周期振动的定义。
所以不是周期振动。
但振动仍然是围绕平衡位置的往复运动,仍具有振动的特点。
1.振动周期d T 大于无阻尼自由振动周期T 。
d T =222211222ζζωπωπωπ-=-=-=T nn nS(3-8)式中:T 为不计阻尼时自由振动周期。
且n T ωπ/2=。
2.振幅按几何级数衰减。
任意两个相邻振幅之比,称为振幅减缩率d d i i nT T t n nt i ie Ae Ae A A ===+--+)(1η (3-9)对上式取对数,得对数减缩率d i i nT A A ==+1lnδ (3-10)手锤 质量块 传感器图3-1 单自由度系统自由衰减振动实验仪器安装框图根据试验所得的衰减振动曲线[见图3-2(b )所示],量得相邻的两个位移最大值及周期d T 。
实验六单自由度系统自由衰减振动及固有频率和阻尼比的测量

实验六 单自由度系统自由衰减振动及固有频率和阻尼比的测量 一、实验目的1.了解单自由度自由衰减振动的有关概念。
2.学会用分析仪记录单自由度系统自由衰减振动的波形。
3.学会根据自由衰减振动波形确定系统的固有频率f 。
和阻尼比二、实验装置框图图6-1图6—1 实验装置框图三、实验原理单自由度系统的力学模型如图6-2所示。
给系统(质量M)一初始扰动,系统作自由衰减振动,其运动微分方程式为:0202022222222=++=++=++x dt dxdx x d x dt dxn dxx d Kx dt dx C dxx d M ωξωω式中:ω——系统固有圆频率 2ω= K /Mn ——阻尼系数 2n = C /Mξ——阻尼比 ξ = n/ω 小阻尼(ξ<1)时,方程(8-1)的解为:)sin(1ϕω+=-t Ae x nt (6-2)式中:A —振动振幅ϕ—初相位1ω—衰减振动圆频率,22211ξωωω-=-=n设初始条件:t=0时,x=x 。
,0v dt dx =,则200220222002)()(nx v n w x tg n nx v x A +-=-++=ϕω (6-3) (6-4)式(6-2)的图形如图6-3所示。
8-2 单自由度振动系统力学模型8-38-4 8-5 图8-3 单自由度系统衰减振动曲线此波形有如下特点:1.振动周期T1,大于无阻尼自由振动周期T ,即T1>T0。
22221111222ξξωπωπωπ-=-=-==T n T固有频率 210111ξ-==T T f2.振幅按几何级数衰减减幅系数121nT e A A -==η (6-6)对数减幅系数121lnln nT A A ===ηδ (6-7)对数减幅系数也可以用相隔i 个周期的两个振幅之比来计算:1ln 1322111ln 1ln ln ln1+-++==ΛΛ==i iT i i i A Ai e A A A A A A A A δ (6-8)从而可得:1n T δ=2nC m=mk C 2=ξ四、实验方法1、 将测试系统连接好。
单自由度系统固有频率和阻尼比的测定

单自由度系统固有频率和阻尼比的测定实验一、实验内容1、学习分析系统自山衰减振动的波形;2、验证固有频率的存在;3、山衰减振动波形确定系统固有频率和阻尼比;二、实验设备振动与控制实验设备、位移传感器、测振仪、计算机与分析软件三、实验原理振动与控制实验设备如右上方图所 示,单自山度系统的力学模型如右下方图 所示。
当给质量M —定初始扰动时,系统 作自山衰减振动,其运动微分方程为:3 ^dx “八M — +C — + Kx = O dr dt右]〃 3 c dx 2 c111 —- + 2n — + a )x = 0dr dt(1)式中,a )= yi K/M 为系统固有频率,H = C/2M 为阻尼系数,g = (co 加阻尼比。
drdx(10)对于小俎尼情形M < 1,其方程有解如下: x = Ae"m sin (6?/ + ^0) (2) 式中人-系统初始振i|喘,%-初相位,①-衰减振动圆频率。
并且有: © = -jar -n 1 = (3)设t=0时,系统的位置和速度分别为xo 和切,则A= hV 0 少一卩 I~T X (、y/2 -irtan (p = ---------------其衰减振动有如下特点:1、振动周期 大于无阻尼时的自由振动周期,即Tig丁 _ 2龙_ 2兀 _ 2龙 _ T1① J/—询]一§2 J]_§2 系统固有频率为:2、振幅按指数函数衰减,设相邻两次振动的振幅分别为Ai 和Ai+i.则减幅系数为:“=字=严(8) 4+1对数减幅系数J = ln;; = n7;⑼另外,相隔•个周期的两次振动,城幅之比设为卩,则⑷(5)⑹(7)则:四、实验步骤1.试验1:采用1个质量块,施加较小的力使得悬臂梁产生自由衰减振动。
2.试验2:釆用1个质量块,施加较大的力使得悬臂梁产生自由衰减振动。
3.设定周期数j,此试验取30,读出j个波形所经历的时间t,记录其波形的幅值。
实验一单自由度振动系统固有频率及阻尼比的测定

实验二 刚性转子动平衡实验一、实验目的(1) 掌握刚性转子动平衡的基本原理和步骤; (2) 掌握虚拟基频检测仪和相关测试仪器的使用; (3) 了解动静法的工程应用。
二、实验内容采用两平面影响系数法对一多圆盘刚性转子进行动平衡三、实验原理工作转速低于最低阶临界转速的转子称为刚性转子,反之称为柔性转子。
本实验采取一种刚性转子动平衡常用的方法—两平面影响系数法。
该方法可以不使用专用平衡机,只要求一般的振动测量,适合在转子工作现场进行平衡作业。
根据理论力学的动静法原理,一匀速旋转的长转子,其连续分布的离心惯性力系,可向质心C 简化为过质心的一个力R (大小和方向同力系的主向量∑=iS R )和一个力偶M (等于力系对质心C 的主矩CiΜS m M ==∑)(),见图一。
如果转子的质心恰在转轴上且转轴恰好是转子的惯性主轴,即转轴是转子的中心惯性主轴,则力R 和力偶矩M C 的值均为零。
这种情况称转子是平衡的;反之,不满足上述条件的转子是不平衡的。
不平衡转子的轴与轴承之间产生交变的作用力和反作用力,可引起轴承座和转轴本身的强烈振动,从而影响机器的工作性能和工作寿命。
图一 转子系统与力系简化刚性转子动平衡的目标是使离心惯性力系的主向量和主矩的值同时趋近于零。
为此,先在转子上任意选定两个截面I 、II (称校正平面),在离轴线一定距离1r 、2r (称校正半径),与转子上某一参考标记成夹角1θ、2θ处,分别附加一块质量为1m 、2m 的重块(称校正质量)。
如能使两质量1m 和2m 的离心惯性力(其大小分别为211ωr m 和222ωr m ,ω为转动角速度)正好与原不平衡转子的离心惯性力系相平衡,那么就实现了刚性转子的动平衡。
两平面影响系数法的过程如下;(1)在额定的工作转速或任选的平衡转速下,检测原始不平衡引起的轴承或轴颈A 、B 在某方位的振动量11010ψ∠=V V 和22020ψ∠=V V ,其中10V 和20V 是振动位移(也可以是速度或加速度)的幅值,1ψ和2ψ是振动信号对于转子上参考标记有关的参考脉冲的相位角。
单自由度系统自由衰减振动及固有频率、阻尼比
:单自由度系统自由衰减振动及固有频率、阻尼比的测定实验指导书陈安远(武汉大学力学实验教学中心)1.实验目的1、了解单自由度系统模型的自由衰减振动的有关概念;2、学习用频谱分析信号的频率;3、学习测试单自由度系统模型阻尼比的方法。
2.实验仪器及安装示意图实验仪器:INV1601B型振动教学实验仪、INV1601T型振动教学实验台、加速度传感器、MSC-1力锤(橡胶头)、重块。
软件:INV1601型DASP软件。
图1实验系统示意图3实验原理单自由度系统的阻尼计算,在结构和测振仪器的分析中是很重要的。
阻尼的计算常常通过衰减振动的过程曲线(波形)振幅的衰减比例来进行计算。
衰减振动波形示于图2。
用衰减波形求阻尼可以通过半个周期的相邻两个振幅绝对值之比,或经过一个周期的两个同方向振幅之比,这两种基本方式进行计算。
通常以一个周期的相邻两个振幅值之比为基准来计算的较多。
两个相邻振幅绝对值之比,称为波形衰减系数。
图2衰减振动波形1、对经过一个周期为基准的阻尼计算每经过一个周期的振幅的比值为一常量:η=d nT i ie A A =+1这个比例系数η表示阻尼振动的振幅(最大位移)按几何级数递减。
衰减系数η常用来表示振幅的减小速率。
叫做振幅减缩率或减幅系数。
如果用减幅系数η的自然对数来表示振幅的衰减则更加方便。
δ=ln (η)=lnd i i nT A A =+1=21ξπξ-δ称为振动的对数衰减率或对数减幅系数。
可以利用δ来求得阻尼比ξ。
2、在小阻尼时,由于η很小;这样读数和计算误差较大,所以一般地取相隔若干个波峰序号的振幅比来计算对数衰减率和阻尼比。
4.实验步骤1、仪器安装参照仪器安装示意图安装好配重质量块,加速度传感器。
2、开机进入INV1601型DASP 软件的主界面, 进入单通道示波状态进行波形和频谱同时示波,见图2。
3400Hz 、采样点数为2K,标定值和工程单位等参数(按实际输入〉,采样方式选择触发采样,见图3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告1:自由衰减法测量单自由度系统的固有频率和阻尼比姓名:刘博恒学号:1252227专业:车辆工程(汽车) 班级:12级日期:2014年12月25日组内成员张天河、刘嘉锐、刘博恒、马力、孙贤超、唐鑫一、实验目的1.了解单自由度自由衰减振动的有关概念。
2.学会用数据采集仪记录单自由度系统自由衰减振动的波形。
3.学会根据自由衰减振动波形确定系统的固有频率和阻尼比。
二、实验原理由振动理论可知,一个单自由度质量-弹簧-阻尼系统,其质量为m(kg),弹簧刚度为K(N m⁄),粘性阻尼系数为r(N∙m s⁄)。
当质量上承受初始条件(t=0时,位移x=x0,速度ẋ=ẋ0)激扰时,将作自由衰减振动。
在弱阻尼条件下其位移响应为:x=Ae−nt sin(√p2−n2t+φ)式中:n=r2m为衰减系数(rad/s)p=√Km为固有圆频率(rad/s)A=√ẋ02+2nẋ0x0+p2x02p2−n2为响应幅值(m)φ=tan−1x0√p2−n2ẋ0+nx0为响应的相位角(rad)引入:阻尼比ξ=np对数衰减比δ=ln A1A3则有:n=δT d而T d=1f d =√p2−n2f d=p d2π=√p2−n22π为衰减振动的频率,p d=√p2−n2为衰减振动的圆频率。
在计算对数衰减比时,考虑到传感器的误差及系统本身迟滞,振动的平衡点位置可能不为0,因此可以使用相邻周期的峰峰值来代替振幅值计算,即δ=ln A1+A2A3+A4。
从衰减振动的响应曲线上可直接测量出δ、T d,然后根据n=δT d 可计算出n;T d=1f d=√p2−n2计算出p;ξ=np可计算出ξ;n=r2m计算出r;f0=p2π=12π√Km计算出无阻尼时系统的固有频率f0;T0=1f =2π∙√mK计算出无阻尼时系统的固有周期T0。
三、实验方法1)将系统安装成单自由度无阻尼系统,在质量块的侧臂有一个“测量平面”,用于电涡流传感器拾振。
将电涡流传感器对准该平面,调节其初始位置,使得位移测量仪在ORIG 位置时限制值在1.00mm至1.5mm范围内。
2)在软件中选中“单自由度系统-用自由衰减法测量系统参数”项目,软件左侧的采集设置默认即可。
打开一个时间波形观察图,设置均为默认无需修改。
设置完毕后开始采集。
3)用手轻推质量块,或者用力锤轻敲质量块,采集一段信号进行分析。
让质量块自由衰减时所给的力应对准质量块中心位置,否则波形可能畸变。
4)利用光标读出多个周期的时间、振幅坐标并记录,计算其对数衰减比和周期的平均值,进而计算出固有频率、阻尼比。
5)将系统安装成单自由度有阻尼系统,重复上述步骤。
四、实验结果及分析1、绘出无阻尼单自由度自由衰减振动波形图。
无阻尼单自由度自由衰减振动波形图由d T n δ=,算出n=1.6106由2221np f T dd -==π算出p=256.46由m Kp f ππ2120==算出f 0=40.817.由p n=ξ算出00628.0=ξ4、给系统加上阻尼后,根据有阻尼自由衰减振动波形图完成下表。
有阻尼单自由度自由衰减振动波形图由d T n δ=,算出n=2.634由2221n p f T dd -==π算出p=256.47由m Kp f ππ2120==算出f 0=40.818.由p n=ξ算出0103.0=ξ五、简答1、上述无阻尼自由振动实验中,为什么振动曲线呈现衰减状态? 答:无阻尼是理想状态,实际存在结构阻尼。
2、简述阻尼对于自由振动周期、频率的影响。
答:阻尼增大,频率降低,周期延长。
实验报告2:冲击激励法测量单自由度系统的固有频率和阻尼比姓名:刘博恒学号:1252227专业:车辆工程(汽车) 班级:12级日期:2014年12月25日组内成员张天河、刘嘉锐、刘博恒、马力、孙贤超、唐鑫一、实验目的用冲击激励法测量系统的频率响应函数,并识别出其固有频率和阻尼比。
二、实验原理通常我们认为振动系统为线性系统,用一特定已知的激振力,以可控的方法来激励结构,同时测量输入和输出信号,通过传函分析,得到系统固有频率。
响应与激振力之间的关系可用导纳表示:Y=XF=1k⁄√(1−λ2)2+(2ξλ)2−jφφ=tan−12ξλ1−λ2Y的意义就是幅值为1的激励力所产生的响应。
研究Y与激励力之间的关系,就可得到系统的频响特性曲线。
在共振频率下的导纳值迅速增大,从而可以判别各阶共振频率。
这里可以用冲击力锤对系统激励,用位移传感器拾振,获得系统的频响函数。
在幅频响应曲线图中,当λ=1时,β(1)=12ξ;当λ=√1−2ξ2时,其最大值βp=2ξ√1−ξ2。
在图中作一条水平线,其纵坐标为√2p,与曲线交于A、B两点,该两点称为半功率点,两点之间的距离为ω2 p −ω1p=Δωp=2ξ故有ξ=12Δωpn=pξ=Δω2这种求阻尼系数(衰减系数)的方法称为半功率法。
可以证明,当ξ≪1时,用速度响应的幅频曲线或加速度响应的幅频曲线同样可以按半功率法求阻尼系数(衰减系数)。
三、实验方法1)将系统安装成单自由度无阻尼系统,在质量块的侧臂有一个“测量平面”,用于电涡流传感器拾振。
将电涡流传感器对准该平面,调节其初始位置,使得位移测量仪在ORIG 位置时限制值在1.00mm至1.5mm范围内。
2)将力锤信号接入力测量仪,连续轻敲试验台底座确认力锤信号是否被力测量仪获取。
3)在软件中选中“单自由度系统-用冲击激励法测量系统频响函数”项目,软件左侧的采集设置默认即可。
打开一个时间波形观察图,右键点击坐标,选择设置选项并修改设置。
同时打开一个传函观察图,右键点击坐标,选择设置选项并修改设置。
设置完毕后开始采集。
4)用力锤轻敲质量块的中心位置,使其振动,采集一段信号进行分析得到系统的频响函数。
读取固有频率并使用半功率法计算阻尼比。
重复多组实验求得其平均值。
5)将系统安装成单自由度有阻尼系统,重复上述步骤。
四、实验结果及分析无阻尼系统的脉冲传递函数图无阻尼系统的脉冲传递函数图五、简答1、脉冲激励法得到的单自由度系统的固有频率和阻尼比与自由衰减法得到的是否一致?力锤施加力的大小是否影响单自由度系统的振动频率和阻尼?为什么?答:不一致,实验表明,固有频率用自由衰减法测量较大,阻尼比用自由衰减法测量较大。
否,不影响,因为系统的固有频率和阻尼不因外界激励的影响而改变。
2、实验过程中,力锤敲击质量块时应注意什么?答:应注意敲击时要迅速果断、不要发生连击;敲击力度不宜过大,以免损坏力锤;敲击时应垂直于质量块,敲击质量块的中心位置。
实验报告3:正弦扫频,法测量两自由度的固有频率姓名:刘博恒学号:1252227专业:车辆工程(汽车) 班级:12级日期:2014年12月25日组内成员张天河、刘嘉锐、刘博恒、马力、孙贤超、唐鑫一、实验目的用正弦扫频法测量系统的频率响应函数,并识别出其固有频率。
二、实验原理通常我们认为振动系统为线性系统,用一特定已知的激振力,以可控的方法来激励结构,同时测量输入和输出信号,通过传函分析,得到系统固有频率。
响应与激振力之间的关系可用导纳表示:Y=XF=1k⁄√(1−λ2)2+(2ξλ)2−jφφ=tan−12ξλ1−λ2Y的意义就是幅值为1的激励力所产生的响应。
研究Y与激励力之间的关系,就可得到系统的频响特性曲线。
在共振频率下的导纳值迅速增大,从而可以判别各阶共振频率。
三、实验方法1)取下第二个质量块m2的L型支撑块,将系统安装成双自由度无阻尼振动系统。
2)将激振器与两自由度系统的第一个质量块m1相连。
激振头装上阻抗头,阻抗头中有一力传感器和一加速度传感器,分别接入力测量仪和加速度测量仪。
3)在质量块m2的侧臂也有一个“测量平面”,用于电涡流传感器拾振。
将电涡流传感器对准该平面,调节其初始位置,使得位移测量仪在ORIG位置时限制值在1.00mm至1.5mm范围内。
4)将信号源设置为扫频信号,频率范围可设置为10Hz-70Hz。
扫频速度应与采样的长度配合,如扫频速度较慢,应增加采样长度,扫频速度较快时,可以减小采样长度。
5)在软件中选中“两自由度系统-用正弦扫频法测量系统频响函数”项目,通道设置在默认的基础上,双击点开4通道,软件左侧的采集设置默认即可。
打开两个传函观察图用于观察两个质量块在激振器力激励下的频响函数。
设置完毕后开始采集。
6)采集系统将得到两个幅频特性曲线:加速度传感器采集m1质量块得到的力-加速度幅频曲线和电涡流位移传感器采集m2质量块得到的力-位移幅频曲线,均可以读取系统的固有频率。
测量多次以求得平均值。
7)将系统安装成两自由度有阻尼系统,重复上述步骤。
四、实验结果及分析五、简答1、相比脉冲激励法测量系统传递函数,使用激振器进行扫频法测量有什么优缺点?答:操作简单方便,误差较大(容易受外界影响)。
