中国农业大学2020考研差额复试比例不低于120%

合集下载

北京市120急救网络呼叫反应时间的研究

北京市120急救网络呼叫反应时间的研究目的为了以完善的急救体系迎接2008年奥运会，有必要了解北京市120急救网络院前急救呼叫反应时间的现状，分析其影响因素，并以此为切入点探索北京市院前急救的现状和存在的问题。

方法采用定量分析和定性访谈相结合的方法，描述和分析北京急救中心2005年下半年的调度数据。

结果北京市总体120急救网络呼叫反应时间中位数为16.5min，四分位数间距为14.3 min；北京市总体120急救网络呼叫反应时间在5min内的占2.28％，而30min以上的占19.20％；城区、郊区和中心直属与非直属之间呼叫反应时间差异具有统计学意义。

结论当前北京市120网络院前急救呼叫反应时间过长，与国外先进国家相比还存在一定的差距，需进一步从不同角度探讨与分析其影响因素，并加以解决。

标签：院前急救；医疗急救服务系统；呼叫反应时间；奥运会；北京在急救医学领域，“呼叫反应时间(responsetime)”是指从求救者拨打求救电话至救护人员到达事发现场之间的时间间隔。

呼叫反应时间的长短是城市院前急救医疗服务体系乃至整个城市紧急医学救援体系是否完善、是否高效运行、是否满足市民需要的重要考核指标，也是评价院前急救服务水平的重要综合指标。

虽然有报道北京市院前急救呼叫反应时间平均为13min，但并没有科学、完善的统计分析数据支持，也没有具体的分类统计描述与比较，对其影响因素也没有进行深入的研究和分析。

北京作为一座现代化的国际大都市，不仅是我国政治、文化交流中心，更是全世界关注的焦点。

而随着社会的发展、疾病谱的改变，以及2008年奥运会的日益临近，这些综合因素都将势必会增加北京市对院前医疗急救服务的需求，同时也对北京医疗急救服务系统提出了更高的要求。

因此，非常有必要以呼叫反应时间这一重要综合指标为切入点，对北京市院前医疗急救服务系统进行综合分析与评估，以了解北京现有急救服务体系的现况，探索影响因素。

1 方法采用定量分析和定性访谈相结合的方法：调取北京急救中心调度科数据库中2005年7月到12月共6个月全市有效调度指挥数据，依据纳入标准和排除标准，应用SPSS11.5统计软件对该数据库进行清理和统计描述；描述采用中位数四分位数间距和百分比，比较应用卡方检验和大样本z检验；在此基础上召开专题小组访谈会，讨论其影响因素。

多层感知器网络

多层感知器网络
权重优化与训练方法
权重优化与训练方法
权重初始化
1.权重初始化是训练多层感知器网络的重要步骤，可以防止模型在训练初期陷入局部最优解。常见的初始化方法有随机初始化、Xavier初始化和He初始化等。 2.随机初始化将权重随机初始化为一个小值，可以保证模型在各个方向上的更新幅度大致相同，从而提高模型的泛化能力。 3.Xavier初始化和He初始化则是针对特定激活函数提出的初始化方法，可以使得各层的激活值在进行前向传播时能保持相同的分布。
学习率调整
1.学习率是影响多层感知器网络训练效果的重要因素之一，它决定了模型在每次更新时的步长大小。 2.过大的学习率可能导致模型在训练过程中无法收敛，而过小的学习率则可能导致训练时间过长或陷入局部最优解。 3.因此，在训练多层感知器网络时，需要根据模型的表现和训练轮数来动态调整学习率，以保证模型的训练效果和收敛速度。
▪ L1正则化
1.L1正则化是在损失函数中加入模型参数的绝对值，通过约束参数的范数来控制模型的复杂度。 2.L1正则化可以使一些参数变为零，从而起到特征选择的作用，有助于提高模型的泛化能力。 3.L1正则化的优化较为困难，需要使用一些特殊的优化算法，如坐标下降法和近端梯度下降法等。
过拟合与正则化技术
权重优化与训练方法
▪ 批次归一化
1.批次归一化是一种提高多层感知器网络训练稳定性和收敛速度的技术，它通过对每个批次的数据进行归一化处理来消除数据间的差异。 2.批次归一化可以减少模型对初始权重的敏感性，提高模型的泛化能力，同时也可以减少训练过程中出现的梯度消失和梯度爆炸等问题。 3.在训练多层感知器网络时，加入批次归一化层可以有效地提高模型的训练效果和收敛速度。

IPS-1000系列VoIP综合接入系统用户手册V1.05

IPS-1000系列VoIP综合接入系统用户手册版本：V1.05目录1.前言 (1)2.概述 (2)3.系统指标 (3)3.1功能、性能 (3)3.2工作条件 (3)3.3配置 (4)4.结构 (5)4.1VIP板面板图 (5)4.2面板 (5)4.3出线 (6)4.4系列结构标准 (6)5.安装和操作 (7)5.1IPS设置简介 (7)5.2产品安装和呼叫 (7)5.3呼叫 (7)5.4IPS系列编程 (7)6.VIP设置命令（Telnet 远程配置） (8)6.1操作系统登录命令Telnet (8)6.2帮助命令Help (8)6.3显示配置命令Show (9)6.4设置配置命令Set (10)6.5存盘命令Save (10)6.6恢复前次配置命令Load (10)6.7恢复初始配置命令LoadDefault (10)6.8系统重起动命令Reboot (10)6.9退出命令配置Quit (11)7.配置数据 (12)7.1NetWork部分 (12)7.1.1广域网IP (12)7.1.2广域网IP子网掩码 (12)7.1.3广域网MAC值 (12)7.1.4广域网口DHCP模式 (12)7.1.5局域网IP (13)7.1.6局域网IP子网掩码 (13)7.1.7局域网MAC值 (13)7.1.8DNS状态 (13)7.1.9DNS IP (13)7.1.10默认网关IP (14)7.1.11NAT功能 (14)7.1.12NAT端口映射表 (14)7.1.13PPPoE (14)7.1.14PPPoE 用户名 ......................................... 147.1.15PPPoE 用户密码. (15)7.2GateWay部分 (15)7.2.1网关别名 (15)7.2.2网关IP (15)7.2.3网关区号 (15)7.2.4呼入前缀匹配值 (15)7.2.5呼入前缀删除状态 (16)7.2.6设备最大允许话音通道数 (16)7.2.7启用快速呼叫功能 (16)7.2.8Q.931协议端口值 (16)7.2.9RTP起始端口值 (16)7.2.10TCP起始端口值 (17)7.2.11MCC通信定时器 (17)7.2.12网守定时器 (17)7.2.13TCP定时器 (17)7.2.14ALERTING定时器 (17)7.2.15CONNECING定时器 (17)7.2.16RAS重发次数 (18)7.2.17网守状态 (18)7.2.18网守IP (18)7.2.19TUNNEL状态 (18)7.2.20网关路由表 (18)7.3CDR IP部分 (19)7.3.1中央维护台的IP (19)7.3.2普通维护台IP (19)7.3.3设置SNMP 管理站IP (19)7.4GateKeeper部分 (19)7.4.1网守最大支持呼叫数基本属性 (19)7.4.2内部网守状态 (20)7.4.3IRR消息频率 (20)7.4.4RRQ消息频率 (20)7.4.5RRQ消息超时次数 (20)7.4.6IRR消息超时次数 (20)7.4.7GKID (20)7.4.8网守信息表 (21)7.4.9DSP状态 (21)7.4.10语音编码类型 (21)7.4.11传真模式 (21)7.4.12语音包允许延迟时长 (22)7.4.13回声抵消状态 (22)7.4.14静音检测状态 (22)7.5SYSTEM部分 (22)7.5.1系统软件版本 (22)7.5.2T35国家码 (22)7.5.3T35扩展码 (22)7.5.4终端类别 (23)7.5.5产品ID号 (23)7.5.6设备厂家号 (23)7.5.7H.323协议栈版本 (23)7.5.8H.225协议栈版本 (23)7.5.9H.245协议栈版本 (23)7.6Dialedlen部分 (23)7.7IP ECHO部分 (24)7.7.1IPECHO客户端 (24)7.7.2客户机定时发送消息时间 (24)7.7.3服务器所在地址 (24)7.7.4服务器所在端口 (25)7.7.5是否作为服务器 (25)8.关于配置文件的存取 (26)8.1下载VIP配置文件至PC (26)8.2上传PC的配置文件至VIP中： (26)8.3用TFTP升级VIP系统软件 (26)9.维护注意事项 (27)9.1VIP板RUN灯长亮 (27)9.2IPS电话无法呼出 (27)图图5-1面板指示图 (5)表表5-1面板LED定义 (5)1.前言●本手册详细地介绍了IPS-1000系列V oIP综合接入系统（IPS-1016/1160/1240）的结构、工程安装说明、软件设置等，您也可以根据目录及页眉的标题进行选择性地阅读此手册。

国有企业合规管理体系建设实践——以公司合规管理体系建设为例

引言为帮助企业强化合规管理，有效预防企业面临的合规风险，2018年国务院国资委发布了《中央企业合规管理指引（试行）》，国家发展改革委印发了《企业境外经营合规管理指引》，北京市国资委启动了市管国有企业合规管理体系建设研究并在部分企业开展试点工作，2022年9月国务院国资委印发《中央企业合规管理办法》并自2022年10月1日起施行。

天津市建筑材料集团（控股）有限公司（以下简称“天津建材集团”或“公司”）作为金隅集团的下属企业，于2022年启动合规管理体系建设工作，已经初步搭建了符合本公司特点的合规管理体系。

本文结合公司合规管理建设必要性，对标先进、实施路径、经验做法及存在的问题总结，为有关企业开展合规管理体系建设提供借鉴。

1 公司合规管理体系建设的必要性天津建材集团作为天津市首家集团层面完成混合所有制改革的市管一级国有企业，通过与金隅集团产业的协同，已逐步形成以商贸展贸、资产管理、智慧物流为主国有企业合规管理体系建设实践—以公司合规管理体系建设为例赵青松天津市建筑材料集团（控股）有限公司天津 300381摘要：本文以天津某建筑材料行业公司的合规管理体系建设项目为案例，总结该公司构建合规管理体系的路径与经验，并对标首批北京市管国有企业合规管理先进经验，通过全面系统梳理该公司的合规义务，识别其在经营管理中面临的合规风险，通过不断完善合规管理制度体系，实现了“强内控、防风险、促合规”的目标。

实践表明，通过合规管理体系建设，该公司增强了全体员工的合规经营意识，提升了全面风险管理能力，增强了企业竞争的软实力，为企业持续健康和高质量发展打下了坚实的基础。

关键词：企业合规；合规风险；合规管理体系Implementation of Compliance Management System in State-owned Enterprises-Using the Construction of the Company's Compliance Management System as a Case Study Abstract: This paper examines the construction of a compliance management system for a building materials industry company in Tianjin as a case study. It summarizes the company's approach and experience in establishing the compliance management system, and compares it with the advanced experiences of compliance management in state-owned enterprises in Beijing. By comprehensively and systematically identifying the company's compliance obligations and operational risks, the compliance management system is continuously improved to achieve the goal of "strong internal control, risk prevention, and promotion of compliance". The practice demonstrates that through the establishment of a compliance management system, the company has enhanced employees' awareness of compliance operations, strengthened its comprehensive risk management capabilities, improved its soft power for enterprise competition, and laid a solid foundation for sustainable, healthy, and high-quality development.Key words: Enterprise compliance; compliance risk; compliance management system收稿日期：2024-4-1第一作者：赵青松，1975年生，法律硕士，高级经济师，主要从事公司风险防控、企业合规管理、客户黏性分析等领域的工作，E-mail：**********************92CHINA CONCRETE2024.04NO.178业的现代化企业集团。

《0.0兆赫》影评精选10篇

《0.0兆赫》影评精选10篇《0.0兆赫》是一部由刘善东监制，郑恩地 / 李成烈 / 主演崔允英主演的一部恐怖性质的电影，特精心从网络上整理的一些观众的影评，盼望对大家能有帮助。

《0.0兆赫》影评(一)：不知道说什么此片还不如昆池岩甚至一些国产烂片，相似的套路，一点创新都没有，演员演技和电影名的几乎可以划等号，场面不用说了，特效一点即便看不出或者连5分钱都不到，那个指甲还有开头的仪式是什么鬼，上世纪八十年代的，知道nh拍片都小气，随便找的dv拍的吧，可惜了啊，恩地，不要乱接片了，好好回去唱歌吧！《0.0兆赫》影评(二)：继昆池岩后的有一部恐怖片韩国电影感觉老是一群大学生作死通灵，昆池岩没啥区别，甚至比昆池岩剧情还要差，一惊一乍的，只有开着车那段把我吓一抖，但形式老套，那打鬼的觉得是在致敬《驱魔人》。

还有最漂亮电脑那段没那段看清楚(可能我智商低)，那个老人是女主奶奶吧！男一的哥哥是怎么死的？刚开始那个巫婆感觉是女主的奶奶《0.0兆赫》影评(三)：比昆池岩好吗？这部电影初看:卧槽！这么劲爆，堪比昆池岩了，但再看就有点凤头鸡尾的感觉，特别是当正主出现后，一下子就不给人恐怖诡异的感觉了，啊喂喂，看不到的恐怖才是恐怖份子大恐怖呀，你一个神秘莫测的鬼魂怎么给人打嘴炮啦。

还有结尾导演也许想表现那个女鬼占据了男主，但如果把镜头一变，女主发现自己还在那个除了房间里岂不是更渗人？《0.0兆赫》影评(四)：不好看剧情啰嗦，素熙演技夸张她没如意仙那喘息声比鬼还夸张。

从头至尾视觉黑乎乎一片。

看过无精恐怖片，这个真的没亮点。

剧情啰嗦，素熙演技夸张她没如意仙那喘息声比鬼还夸张。

从头至尾视觉黑乎乎一片。

看过无精恐怖片，这个真的没亮点。

剧情啰嗦，素熙演技夸张她没如意仙那喘息声比鬼还夸张。

从头至尾视觉黑乎乎一片。

看过无精恐怖片，这个真的没亮点。

《0.0兆赫》影评(五)：比昆池岩给劲的恐怖片昆池岩刚刚出的出时候我也去想想了，觉得没有震热度所喧哗的那么给劲，全片节奏不行，除了结尾节奏鼓点很紧张很恐怖，前面的节奏也很慢，有些拖沓无聊，不吓人。

IXFR120N20中文资料

Symbol Test ConditionsMaximum RatingsV DSS T J = 25°C to 150°C200V V DGR T J = 25°C to 150°C; R GS = 1 M W 200V V GS Continuous ±20V V GSM Transient±30V I D25T C = 25°C (MOSFET chip capability)105A I D(RMS)External lead (current limit)76A I DM T C = 25°C, Note 1480A I AR T C = 25°C 120A E AR T C = 25°C 60mJ E AS T C = 25°C3J dv/dt I S £ I DM , di/dt £ 100 A/m s, V DD £ V DSS 5V/ns T J £ 150°C, R G = 2 W P D T C = 25°C400W T J -55 ... +150°C T JM 150°C T stg -55 ... +150°C T L 1.6 mm (0.063 in.) from case for 10 s 300°C V ISOL 50/60 Hz, RMSt = 1 min2500V~Weight5gSymbol Test ConditionsCharacteristic Values(T J = 25°C, unless otherwise specified)min.typ.max.V DSS V GS = 0 V, I D = 3mA 200V V GS(th) V DS = V GS , I D = 8mA 2.04.0 V I GSS V GS = ±20 V, V DS = 0±100 nAI DSS V DS = V DSS T J = 25°C 100 m A V GS = 0 VT J = 125°C2 mA R DS(on)V GS = 10 V, I D = 60A 17 m WNote 2Single MOSFET Die98586A (11/99)ISOPLUS 247TMHiPerFET TM Power MOSFETs ISOPLUS247TM (Electrically Isolated Back Surface)Features•Silicon chip on Direct-Copper-Bond substrate- High power dissipation - Isolated mounting surface - 2500V electrical isolation•Low drain to tab capacitance(<25pF)•Low R DS (on) HDMOS TM process•Rugged polysilicon gate cell structure •Unclamped Inductive Switching (UIS)rated•Fast intrinsic Rectifier Applications•DC-DC converters •Battery chargers•Switched-mode and resonant-mode power supplies •DC choppers •AC motor control Advantages •Easy assembly •Space savings •High power density •Low noise to groundG = Gate D = DrainS = Source * Patent pendingIsolated back surface*IXFR 120N20V DSS =200VI D25=105AR DS(on)= 17 m W t rr £ 250 nsE153432IXYS reserves the right to change limits, test conditions, and dimensions.SymbolTest ConditionsCharacteristic Values(T= 25°C, unless otherwise specified)Note: 1. Pulse width limited by T JM2. Pulse test, t £ 300 m s, duty cycle d £ 2 %。

2020年智慧树知道网课《畜牧生物统计与试验设计》课后章节测试满分答案

绪论单元测试1【单选题】(10分)采用抽样调查的手段研究成年中国人身高时，总体是（）。

A.抽测的部分成年中国人的身高B.全体成年中国人C.全体成年中国人的身高D.抽测的部分成年中国人2【单选题】(10分)北京地区2020年所有仔猪的采食量是一个（）。

A.有限、固定、现实总体B.有限、动态、假想总体C.无限、固定、假想总体D.无限、动态、现实总体3【单选题】(10分)北京某一牧场所有奶牛的产奶量是一个（）。

A.无限、固定、假想总体B.有限、动态、假想总体C.有限、固定、现实总体D.无限、动态、现实总体4【单选题】(10分)一次临床试验中，使用某一种新药治愈的患者是一个（）。

A.有限、动态、现实总体B.无限、固定、现实总体C.无限、动态、假想总体D.有限、固定、假想总体5【单选题】(10分)中国农业大学的本科生构成了一个（）。

A.无限、固定、假想总体B.有限、固定、现实总体C.无限、动态、现实总体D.有限、动态、假想总体6【单选题】(10分)影响试验精确性的主要是（）。

A.随机误差B.系统误差C.仪器误差D.试验方法7【单选题】(10分)以下属于参数的是（）A.样本方差B.自变量C.总体平均数D.因变量8【单选题】(10分)下列选项有效位数最多的是（）。

A.2.000B.1.2×1012C.1.42D.0.00000209【单选题】(10分)下列不属于系统误差的是（）。

A.仪器误差B.操作出现的误差C.试验方法上的误差D.试剂不纯引起的误差10【单选题】(10分)下列属于随机误差的是（）。

A.仪器、仪表未校准引起的误差B.由许多预先难以确定的微小因素造成的误差C.测量环境温度、温度变化引起的误差D.试验的测量人员生理特性等条件引起的有规律的误差第一章测试1【单选题】(10分)以下属于离散型资料的是（）。

A.绵羊的产毛量B.果蝇的翅型C.育肥猪的出栏体重D.小黄鱼的体长2【单选题】(10分)度量猪瘦肉率的集中趋势，宜采用（）。

新冠状病毒(最新PPT)-新冠状病毒ptt精选全文完整版

2024/10/15
病毒的核酸检测：RT-PCR
• 目前中国疾控中心已经具备了新型冠状病毒的实验室分子检测能力，并于9月29日开始，向各地疾控机构发放检测试剂。
• 如果各地出现疑似病例，都可以快速的完成疑似病例的检测。
2024/10/15
临床诊断
• 疑似病例 • 确诊病例
2024/10/15
疑似病例
• 未做尸检，也未留存合适的标本以供实验室检测
2024/10/15
2例患者确认为新型冠状病毒感染
➢ 两例病例标本的检测机构
o 荷兰的伊拉兹马斯大学医学中心 o 英国的卫生防护署
➢ 两例病例经实验室确认均为新型冠状病毒感染 ➢ 两株病毒一个250bp的PCR片段同源性达99.5%
o 英国：和蝙蝠冠状病毒有80%的同源性 o 与SARS-CoV-tor2相应区段的同源性为73.6% o 与香港Bat-CoV相应区段的同源性为98%
2024/10/15
人类冠状病毒感染
➢人类冠状病毒感染一般表现为上呼吸感染和/或消化道症状
➢冠状病毒引起新生儿、婴幼儿、儿童和老年人的下呼吸道疾病和社区获得性肺炎，包括流感样疾病、慢性支气管炎急性发作等
➢冠状病毒分布于全球。在温带气候地区，冠状病毒的呼吸道感染主要发生在冬季。秋季和春季会略有升高
病理改变：湿肺
正常肺
2024/10/15
ARDS肺
肺微血管充血、出血、微血栓、肺间质和肺泡内有蛋白质水肿液及炎性细胞浸润
2024/10/15
SARS患者的肺组织切片和小白鼠的切片
2024/10/15
临床表现和实验室检查
临床表现影像学表现实验室检查

非同寻常的鼠年

㊃新型冠状病毒肺炎专栏㊃非同寻常的鼠年:新型冠状病毒肺炎阎锡新魏娇娜河北医科大学第二医院呼吸与危重症医学一科,石家庄050011通信作者:阎锡新,E m a i l x i_x i n_y a n@163c o mʌ摘要ɔ2020年的春节,猪年将尽,鼠年将启㊂就在人们准备年末返乡省亲㊁全家团圆之际,新型冠状病毒肺炎爆发了,全世界人民迅速陷入一场无硝烟的抗疫之战㊂自2019年12月中旬以来,新型冠状病毒肺炎经历了局部暴发㊁社区传播和越境传播三个阶段,是人类近几十年来防控难度最大㊁传播速度最快,影响范围最广的国际突发公共卫生事件㊂截至目前仍没有针对该疾病的特效药,部分具有潜在抗冠状病毒作用的药物正加紧疗效验证,疫苗也尚在研发中㊂全球疫情形势依旧严峻,少数国家和地区尚未实现可防可控局面㊂中国政府与人民齐心协力㊁步调一致,经过艰苦卓绝的狙击战,已经有效控制传染源,切断传播途径,很好的控制了疫情㊂我国也进入了常态化㊁专业化的疫情防控阶段㊂此刻,回眸一瞬,颇有感慨㊂ʌ关键词ɔ严重急性呼吸综合征冠状病毒2;新型冠状病毒肺炎;抗病毒药物基金项目:河北省重点研发计划项目(20277701D)D O I103760c m a j c n131368-20200222-00077A n u n u s u a l y e a r o f t h e r a t C O V I D-19Y a nX i x i n W e i J i a o n aT h eF i r s tD e p a r t m e n t o f R e s p i r a t o r y a n dC r i t i c a l C a r eM e d i c i n e t h eS e c o n d H o s p i t a l o f H e b e iM e d i c a lU n i v e r s i t y S h i j i a z h u a n g050011C h i n aC o r r e s p o n d i n g a u t h o r Y a nX i x i n E m a i l x i_x i n_y a n@163c o mʌA b s t r a c tɔI nt h eS p r i n g F e s t i v a l o f2020t h e y e a ro f t h e p i g h a s g o n ea n dt h e y e a ro f t h er a t i sc o m i n g J u s t a s p e o p l ew e r e p r e p a r i n g t o r e t u r nh o m e t o v i s i t t h e i r r e l a t i v e s a nd re u n i t e t h e i rf a m i l i e s a t t h ee n d of t h e y e a r C O V I D-19b r o k eo u t T h e p e o p l ea l lo v e r t h ew o r l d w e r e q u i c k l y i n v o l v e di naw a ro fr e s i s t a n c ea g a i n s t t h ee p i d e m i c S i n c e m i d-D e c e m b e r2019C O V I D-19h a se x p e r i e n c e dt h r e es t a g e s l o c a lo u t b r e a k c o m m u n i t y t r a n s m i s s i o n a n d c r o s s-b o r d e r s p r e a d A n d i t i s a n i n t e r n a t i o n a l p u b l i c h e a l t h e m e r g e n c yw i t h t h e g r e a t e s t d i f f i c u l t y i n p r e v e n t i o na n dc o n t r o l t h e f a s t e s t t r a n s m i s s i o ns p e e da n d t h ew i d e s t i m p a c tr a n g e i n r e c e n t d e c a d e s U p t o n o w t h e r e i s n o s p e c i a l d r u g f o r t h e n o v e l c o r o n a v i r u s S o m e o f t h e d r u g s t h a th a v e p o t e n t i a l a n t i-c o r o n a v i r u s e f f e c t s a r e b e i n g t e s t e d f o r e f f i c a c y a n d v a c c i n e d e v e l o p m e n t i s a l s o o n g o i n gT h e g l o b a l e p i d e m i c s i t u a t i o n i s s t i l l g r i m a n d a f e w c o u n t r i e s a n d r e g i o n s h a v e n o t y e t a c h i e v e d a p r e v e n t a b l ea n d c o n t r o l l ab l e s i t u a t i o n T h r o u g h t h ec o n c e r t e de f f o r t s o f t h eC h i n e s e g o v e r n m e n t a nd t he p e o p l e a n d t h ea r d u o u s s n i p e rw a r o u r c o u n t r y h a se f f e c t i v e l y c o n t r o l l e dt h es o u r c eo f i n f e c t i o n c u to f f t h e t r a n s m i s s i o nr o u t e a n dm a d e t h e e p i d e m i c s i t u a t i o nw e l l c o n t r o l l e d A t t h e s a m e t i m e C h i n ah a se n t e r e da r e g u l a r a n dp r o f e s s i o n a l s t a g e o f e p i d e m i c p r e v e n t i o na n dc o n t r o l A t t h i sm o m e n t l o o k i n g b a c kf o r am o m e n t Ih a v eq u i t e a f e e l i n gʌK e y w o r d sɔS e v e r e a c u t e r e s p i r a t o r y s y n d r o m e c o r o n a v i r u s2C O V I D-19A n t i v i r a l d r u g sF u n d p r o g r a m K e y R e s e a r c h a n dD e v e l o p m e n t P r o j e c t i nH e b e i P r o v i n c e20277701DD O I103760c m a j c n131368-20200222-000772020年已过半载,旋涡中心的武汉早已重启被疫情暂停的生活,中国积极有效的应对措施让世界见证了英雄的武汉,伟大的中国㊂越来越多的证据表明,新型冠状病毒肺炎(C O V I D-19)虽然在中国武汉爆发,但武汉并不是源头㊂目前,国内疫情总体呈零星散发状态,新疆㊁辽宁等地出现散发病例引起的聚集性传播,呈现出小范围疫情反弹,而且已经波及到北京㊁福建等地区㊂疫情防控的重点也由内防扩散㊁外防输出切换到了外防输入㊁内防反弹㊂除新疆㊁辽宁等㊃3441㊃国际呼吸杂志2020年10月第40卷第19期I n t JR e s p i r,O c t o b e r2020,V o l.40,N o.19Copyright©博看网. All Rights Reserved.地区外,国内其他省份新增确诊病例以境外输入病例为主㊂并且随着检测力度的加大,更多的无症状感染者也逐渐浮出水面㊂针对疫情复燃现象,地区政府重新进入战时状态,借鉴前期抗疫经验,迅速采取精准的防控措施,最大限度的降低了传播风险㊂反观全球态势,每日新增病例数仍在快速攀升,美国㊁巴西㊁印度㊁俄罗斯及南非等成为了全球疫情最严重的国家㊂日本㊁韩国等国家也在疫情得到较好控制后出现了不同程度的反弹㊂这也再次提醒我们疫情的复杂性和严峻性,各国要加强合作,共同抗疫㊂我们根据已经掌握的信息,对C O V I D-19的特征㊁临床表现及抗病毒治疗作一简单阐述㊂2020年初,严重急性呼吸综合征冠状病毒2(s e v e r ea c u t er e s p i r a t o r y s y n d r o m ec o r o n a v i r u s2,S A R S-C o V-2)首次从中国武汉的患者中分离㊂WHO专家将由这种新型病毒感染导致的以肺炎为主要表现的疾病命名为C O V I D-19㊂研究发现,S A R S-C o V-2是一种新型的与S A R S-C o V相近的β属冠状病毒,是已知冠状病毒科中可以感染人类的第七个成员㊂C O V I D-19是人畜共患病,蝙蝠是最可能携带S A R S-C o V-2的自然宿主[1],而穿山甲可能是潜在中间宿主[2]㊂由钟南山院士牵头的研究显示,只有118%的患者有野生动物接触史,初期的大多数患者与接触武汉人有关[3]㊂S A R S-C o V-2感染的患者和无症状感染者是主要传染源,在潜伏期即有传染性,发病5d内传染性最强[4],这为疫情的防控带来巨大挑战㊂随着疫情的发展,病毒也显现出了较强的人传人能力,且传播速度较快,社区传播及家庭聚集性传播频出, 超级传播者时有报道,甚至传播源并非典型肺炎患者㊂S A R S-C o V-2的主要传播途径是经呼吸道飞沫传播及密切接触传播,接触病毒污染的物品也可造成感染,气溶胶传播可能是狭小密闭空间的重要传播途径[4]㊂钟南山院士及李兰娟院士团队首先在确诊患者粪便中分离出活的S A R S-C o V-2,且随着检测力度的加大,多地区在确诊病例粪便及尿液中也检测到S A R S-C o V-2的存在㊂所以除常见传播途径外,也应当注意粪便及尿液对环境污染造成气溶胶或接触传播的可能性㊂此外,目前尚无证据表明存在血液㊁血制品㊁母婴等传播方式[5]㊂S A R S-C o V-2潜伏期为1~14d,多为3~7d,个别病例潜伏期可长达24d,但仅为个例[3]㊂C O V I D-19临床表现多样,多见发热㊁乏力㊁干咳㊂1099例C O V I D-19患者的特征分析显示,仅438%的患者早期表现为发热,因此在筛查病例时不能过分强调是否有发热症状㊂此外,对近9000例C O V I D-19患者的临床数据分析显示[5],45%的患者无肺炎表现,而是表现为腹泻㊁呕吐㊁咽痛等非典型症状㊂WHO指出,大多数C O V I D-19患者仅表现为轻中症(80%),但约15%的患者将发展为重症,其中5%为危重症,后者可出现呼吸衰竭㊁脓毒症或多脏器功能衰竭[6]㊂重症㊁死亡病例大部分是合并多种基础疾病的老年人㊂除流行病学史及临床表现外,确诊依据主要是实验室检查㊂核酸检测目前仍然是确诊依据,但会受到病程㊁标本采集㊁检测试剂等因素的影响,容易漏诊,疑似患者常需反复检测㊂在核酸检测受限制的特殊时期,曾有学者建议由胸部C T代替核酸检测作为C O V I D-19诊断的金标准,发现C T确诊C O V I D-19的准确率为764%[3],考虑到影像学不能明确病原体种类,与其他病毒性肺炎的C T表现亦有交叉重叠,最终专家组指出核酸检测与影像学应当并重,不能相互代替㊂血清学检查也可以作为诊断新冠肺炎的辅助手段,对于核酸检查阴性的疑似C O V I D-19患者以及处于恢复期的患者可通过抗体检测进行诊断,但发病1周内阳性率较低[4]㊂此外,有些指标的突然变化可能预示病情恶化[8],如淋巴细胞数进行性下降,中性粒细胞与淋巴细胞比值㊁I L-6㊁C-反应蛋白㊁D-二聚体㊁乳酸等指标进行性升高,影像学显示病变范围快速扩大等㊂如何早期识别这些危险因素对于挽救重症患者至关重要㊂无论是S A R S㊁流感,还是C O V I D-19,都由病毒感染引起,这三种疾病临床表现类似,治疗方法也类似㊂但病毒性肺炎很难治,一个关键的原因就是缺乏特效药,加上病毒种类繁多,共性很少,也很难找到广谱的抗病毒药物㊂C O V I D-19是一种新的传染性疾病,在疫情初期我们对它的了解有限,所以更多的寄希望于老药新用㊂只是限于对S A R S-C o V-2菌株体外研究结果的局限性,很多药物没有推荐使用㊂关于抗病毒药物的合理使用,最新发布的‘新型冠状病毒肺炎诊疗方案(第八版)“中给出了较为一致的建议[4],认为具有潜在抗病毒作用的药物应在病程早期使用,尤其是应用于有重症高危因素及有进展为重症倾向的患者㊂不推荐单独使用洛匹那韦/利托那韦和利巴韦林,不推荐使用羟氯喹或联合使用阿奇霉素㊂还指出,可继续试用α-干扰素㊁利巴韦林㊁磷酸氯喹㊁阿比多尔,但其疗效仍需进一步验证㊂与中国诊疗方案的推荐意见不同, WH O不建议在临床试验范畴之外使用这些可能对C O V I D-19有预防或治疗作用的药物㊂国外专家认为现有的有关上述药物的研究大部分是观察性的,且规模较小,在临床疗效方面各项研究结果相差较大,并且已有研究指出其严重的不良反应㊂一项纳入109例C O V I D-19患者的研究显示[9],洛匹那韦/利托那韦联合α-干扰素可以促进C O V I D-19患者肺部炎症的吸收,增高患者体内免疫细胞水平㊂而在另一项回顾性研究中发现,虽然洛匹那韦/利托那韦可缩短S A R S-C o V-2核酸转阴的时间,但胃肠道不良反应发生率明显高于对照组[10]㊂也有研究显示洛匹那韦/利托那韦在对重症C O V I D-19患者临床症状改善及病毒清除方面无益处[11]㊂氯喹被当做特效药也曾赚足人们的眼球㊂10余家医疗机构合作开展的氯喹或羟氯喹疗效及安全性试验研究发现[12],氯喹在抑制肺炎加重㊁改善肺部影像㊁促进病毒核酸转阴㊁缩短病程均有良好的效果㊂但在使用磷酸氯喹治疗的32例C O V I D-19患者中,有21例发生了不良反应,以消化道反应及心律失常多见[13]㊂由于疫情初期我们对S A R S-C o V-2认知有限,且国内形势较为严峻,所以我国专家借鉴S A R S㊁M E R S及流感的防治经验,为C O V I D-19的救治提供了合理化建议㊂而随着国内疫情得到有效遏制,一些临床试验研究结果也相继发表㊂虽然部分临床研究证据等级不高,且研究结果有差异,但我国已经积累的面对㊃4441㊃国际呼吸杂志2020年10月第40卷第19期I n t JR e s p i r,O c t o b e r2020,V o l.40,N o.19Copyright©博看网. All Rights Reserved.新型病毒的救治经验,已然使世界各国的抗疫工作不必完全从零开始㊂由于缺乏治疗C O V I D-19的特效药,所以疫苗成为对抗S A R S-C o V-2的关键一环,它能刺激机体产生免疫应答,产生针对病毒的特异性抗体和免疫记忆,从而抵抗病毒的入侵㊂国内外各大科研机构也正在快速开展S A R S-C o V-2疫苗的研发工作,这是控制疫情蔓延的重点,也是难点㊂一方面,一旦S A R S-C o V-2发生较大变异,则前期的工作将功亏一篑;另一方面,疫苗的安全性问题也必须格外关注,避免免疫不良反应㊂目前,中国已有多项针对S A R S-C o V-2的疫苗进入临床研究阶段,整体研发进展顺利㊂但疫苗研发周期较长,短期内难以作为抗击疫情的武器㊂我们应当继续外防输入,内防反弹 ,不恐慌,不松懈,尽早打赢这场全民抗疫战争㊂利益冲突所有作者均声明不存在利益冲突参考文献1 Z h o uP Y a n g X L W a n g X G e ta l D i s c o v e r y o fa n o v e lc o r o n a v i r u s a s s o c i a t e dw i t h t h e r e c e n t p n e u m o n i a o u t b r e a k i nh u m a n s a n di t s p o t e n t i a lb a to r i g i n J O L b i o R x i v20202020-01-23h t t p s w w w b i o r x i v o r g c o n t e n t10110120200122914952v2a r t i c l e-i n f o D O I10110120200122914952p u b l i s h e d o n l i n ea h e a d o f p r i n tJ a n u a r y2320202 C y r a n o s k iD D i d p a n g o l i n ss p r e a dt h eC h i n ac o r o n a v i r u st op e o p l e J O L N a t u r e20202020-02-07h t t p s w w wn a t u r e c o m a r t i c l e s d41586-020-00364-2 D O I101038d41586-020-00364-23 G u a n W J N iZ Y H u Y e ta l C l i n i c a lc h a r a c t e r i s t i c s o fc o r o n a v i r u sd i se a s e2019i nC h i n a J N E n g l J M e d2020382181708-1720D O I101056N E J M o a20020324国家卫生健康委办公厅国家中医药管理局办公室关于印发新型冠状病毒肺炎诊疗方案试行第八版的通知E BO L2020-08-18h t t p w w w g o v c n z h e n g c ez h e n g c e k u2020-0819c o n t e n t_5535757h t m5 C h e n H G u oJ W a n g C e ta l C l i n i c a lc h a r a c t e r i s t i c sa n di n t r a u t e r i n e v e r t i c a l t r a n s m i s s i o n p o t e n t i a l o f C O V I D-19i n f e c t i o n i nn i n e p r e g n a n tw o m e n ar e t r o s p e c t i v er e v i e w o fm e d i c a l r e c o r d s J L a n c e t202039510226809-815D O I101016S0140-67362030360-36 Y a n g Y L u Q B L i u M J e ta l E p i d e m i o l o g i c a la n dc l i n i c a lf e a t u r e s o f t h e2019n o v e l c o r o n a v i r u so u t b r e a k i nC h i n a JO L m e d r x i v20202020-02-21h t t p s w w w m e d r x i vo r g c o n t e n t1011012020021020021675v1D O I1011012020021020021675p u b l i s h e d o n l i n e a h e a d o f p r i n tF e b r u a r y2120207 W o r l dH e a l t h O r g a n i z a t i o n C l i n c a lm a n a g e m e n to fC O V I D-19i n t e r i m g u i d a n c e27M a y2020R O L G e n e v a WH O 1-62 h t t p s w w w w h o i n t t e a m s h e a l t h-c a r e-r e a d i n e s s-c l i n i c a l-u n i t c o v i d-198国家卫生健康委办公厅国家中医药管理局办公室关于印发新型冠状病毒肺炎诊疗方案试行第七版的通知E BO L2020-03-04 h t t p w w w n h c g o v c n y z y g js7653p20200346c9294a7d f e4c e f80d c7f5912e b1989s h t m l 9王妍妮索涛范慧等洛匹那韦利托那韦联合α-干扰素治疗新型冠状病毒肺炎的临床疗效J O L武汉大学学报医学版20202020-07-08h t t p s d o i o r g h t t p s k n sc n k i n e t k c m sde t a i l d e t a i l a s p x d o i=1014188j1671-885220200400D O I1014188j1671-885220200400网络预发表10许鑫安薇夏飞等洛匹那韦利托那韦治疗新型冠状病毒肺炎有效性与安全性的回顾性研究J中国药师20202371366-1369X u X A n W X i a F e t a l R e t r o s p e c t i v e s t u d y o n t h ee f f e c t i v e n e s s a n d s a f e t y o f l o p i n a v i r r i t o n a v i r i n t h e t r e a t m e n to f c o r o n a v i r u s d i s e a s e2019J Z h o n g g u oY a oS h i20202371366-136911 C a oB W a n g Y W e nD e t a l At r i a l o f L o p i n a v i r-R i t o n a v i r i na d u l t s h o s p i t a l i z e dw i t hs e v e r eC o v i d-19J N E n g l J M e d2020382191787-1799D O I101056N E J M o a200128212 G a o J T i a nZ Y a n g X B r e a k t h r o u g h c h l o r o q u i n e p h o s p h a t eh a ss h o w n a p p a r e n t e f f i c a c y i n t r e a t m e n t o f C O V I D-19a s s o c i a t e d p n e u m o n i ai nc l i n i c a ls t u d i e s J B i o s c iT r e n d s202014172-73D O I105582b s t20200104713左丽邢惟青吴斌等磷酸氯喹治疗新型冠状病毒肺炎的药品不良反应事件分析及风险管理建议J中国药物警戒2020176332-337D O I1019803j1672-862920200603Z u oL X i n g WQ W uB e ta l R i s k m a n a g e m e n to fa d v e r s ed r u g re a c t i o n s e v e n t si n d u c e db y c h l o r o q u i n e p h o s p h a t ei nC O V I D-19p a t i e n t s J Z h o n g g u oY a o W uJ i n g J i e2020176332-337D O I1019803j1672-862920200603收稿日期2020-03-04㊃5441㊃国际呼吸杂志2020年10月第40卷第19期I n t JR e s p i r,O c t o b e r2020,V o l.40,N o.19Copyright©博看网. All Rights Reserved.。

IHW20N120R2中文资料

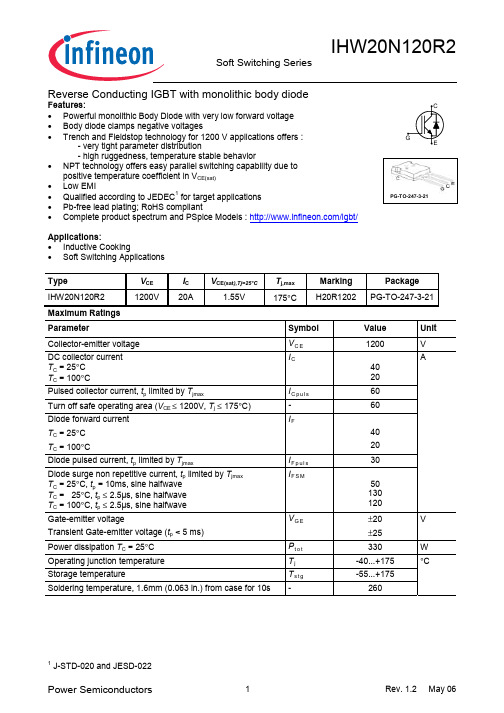
IC, COLLECTOR CURRENT
50A
VGE=20V
40A
15V
13V
11V 30A
9V
7V 20A
10A
0A
0V
1V
2V
3V
VCE, COLLECTOR-EMITTER VOLTAGE
Figure 6. Typical output characteristic (Tj = 175°C)
300W 250W 200W 150W 100W
50W 0W 25°C 50°C 75°C 100°C 125°C 150°C
40A 30A 20A 10A
0A 25°C 50°C 75°C 100°C 125°C 150°C
Figure 3.
TC, CASE TEMPERATURE Power dissipation as a function of case temperature (Tj ≤ 175°C)
IFpuls IFSM
VGE
Ptot Tj Tstg -
1200
V
A 40 20
60
60
40 20 30
50 130 120
±20
V
±25
330
W
-40...+175
°C
-55...+175
260
1 J-STD-020 and JESD-022
Power Semiconductors
1
Rev. 1.2 May 06
Applications: • Inductive Cooking • Soft Switching Applications
C G

Orbi 4G LTE Advanced WiFi 路由器说明书

Data SheetLBR20 4G LTE Advanced WiFi RouterOverviewThe Orbi™ 4G LTE Advanced WholeHome WiFi Router delivers up to 2.2Gbpshigh-performance WiFi on 4G LTEnetworks. It has a sleek, modern designwith high-gain internal antennas for upto 2,000 sq ft of coverage. The Orbi™4G LTE Advanced WiFi Router withintegrated cellular modem is compatiblewith select Orbi AC Satellites to create amesh WiFi system, supporting seamless4K streaming and gaming everywhere inyour home.Mobile SIM, required for operation, isincluded4.FeaturesAlways-on Internet. Seamlessly switch over to 4G LTE when your existing Internet service fails.Super-fast WiFi up to 2.2Gbps†. Enjoy seamless 4K HD video streaming & gaming everywhere in your home. Increase WiFi Coverage.Add an Orbi AC Satellite to createa Mesh WiFi System and expand your WiFi coverage (sold separately).Use Your Cellular Service f or Your Internet Connection. Compatible with AT&T, T-Mobile , Verizon Wireless and other major 4G LTE service providers3. Not compatible with Sprint. Select a data plan & activate a SIM card from your preferred provider, or use the SIM card option included4.Data SheetLBR204G LTE Advanced WiFi RouterHouse DiagramGet Startedwith the Orbi appUse the Orbi app to setupand manage your Orbi WiFi. Available on Google Play ™ and Apple ® App Store.NETGEAR Armor empowers you to eliminatevulnerabilities or simply know the status of your home network and devices, anytime, anywhere. Get instant notifications when malicious threats are detected, block unknown devices from joining your home network or take action on vulnerabilities as they are discovered easily through the Orbi App.Better WiFi. Anywhere.Data SheetLBR204G LTE Advanced WiFi RouterLTE antenna connector (not included)LTE antenna connector (not included)WAN/LAN1 and LAN2 portsLTE NanoSIM cardSyncOrbi 4G LTE Advanced WiFi Router (LBR20)Data SheetLBR204G LTE Advanced WiFi RouterThis product comes with a limited warranty that is valid only if purchased from a NETGEAR authorized reseller. /warranty* 90-day complimentary technical support following purchase from a NETGEAR authorized reseller.** Orbi AC Satellites sold separately.†M aximum wireless signal rate derived from IEEE 802.11 specifications. Actual data throughput and wireless coverage will vary and be lowered by network and environmental conditions, including network traffic volume, device limitations, and building construction. NETGEAR makes no representations or warranties about this product’s compatibility with future standards. Up to 2,200Mbps wireless speeds achieved when connecting to other 802.11ac 2,200Mbps devices.‡Actual LTE speed may vary depending on network conditions and Internet data plans.1 NETGEAR Armor ™ is free during the trial period. A yearly subscription, after the trial period, protects all of your connected devices. Visit /armor2 Circle ® includes the Free Basic Plan. Fees apply for a Premium Plan. Visit /circle for more information.3 Network must support subset of the 4G LTE Bands listed under the T echnical Specifications.4Fees apply based on data service plan selected.For regulatory compliance information, visit /about/regulatoryFor indoor use only.NETGEAR, the NETGEAR Logo, NETGEAR Armor, and Orbi are trademarks of NETGEAR, Inc. Apple and the Apple logo are trademarks of Apple Inc., registered in the U.S. and other countries. App Store is a service mark of Apple Inc., registered in the U.S. and other countries. Google Play and the Google Play logo are trademarks of Google LLC. Any other trademarks mentioned herein are for reference purposes only. © 2021 NETGEAR, Inc.NETGEAR, Inc. 350 E. Plumeria Drive, San Jose, CA 95134-1911 USA , /supportD-NA-LBR20-1Technical Specifications• Orbi AC2200 LTE WiFi Router (866 + 866 + 400Mbps)†• AC2200 Simultaneous Tri-band WiFi*******************:Supports256-QAM - 866Mbps — 2x2 @ 5GHz: Supports 256-QAM - 866Mbps — 2x2 @ 5GHz: Supports 256-QAM • IEEE ® 802.11a/b/g/n/ac • LTE Cat 18 up to 1.2Gbps ‡• NA - 4G band (LTE-FDD): B2,4,5,7,12,13,14,17,25, 26,29,30,66,71- 4G band (LTE-TDD): B41 - 3G band: B2,4,5Physical Specifications• Dimensions: 6.7 x 3.1 x 8.9 in (170 x 79 x 226 mm)• Weight: 1.72 lb (0.78 kg)What’s In the Box?• One (1) Orbi 4G LTE Advanced WiFi Router (LBR20)• One (1) 2m Ethernet cable• One (1) 12V/2.5A power adapter • Quick start guide• Third party SIM card & activation instructionsWhat Do I Need for Orbi to Work?• High-speed Internet connection • Activated LTE SIM card • Orbi app • D O NOT purchase a second Orbi Router if you need to expand your WiFi coverage • T o expand your Orbi WiFi system, purchase an Orbi AC Satellite (RBS50, RBS50Y, RBS40, RBS40V, RBW30 or RBS20), sold separately, for additional WiFi coverage• EU & AU- 4G band (LTE-FDD): B1,3,5,7,8,20,28 - 4G band (LTE-TDD): B38,40,41 - 3G band: B1,3,5,8• MU-MIMO capable for simultaneous data streaming• Implicit & Explicit Beamforming for 2.4GHz & 5GHz bands • T wo (2) 10/100/1000Mbps Gigabit Ethernet ports - O ne (1) WAN/LAN & one (1) LAN • T wo (2) External LTE antenna connectors (antennas not included)• Security - C omprehensive anti-virus & data theft protection for your PC, Mac ® and mobile devices with NETGEAR Armor ™ - S tandards-based WiFi Security (802.11i, 128-bit AES encryption with PSK) - G uest WiFi Network is easy to setup separate & secure Internet access for guests • Voice Control- Amazon Alexa™- The Google © Assistant• C ircle ® — Smart Parental Controls to manage content and time online for all your devices. Learn more at /circle。

反义词(带拼音)适合1-3年级

反义词dà xiǎo shànɡ xià qián hòu zuǒ yòu 大——小上——下前——后左——右duō shǎo lǎo shǎo lái qù nán nǚ多——少老——少来——去男——女hēi bái lǐ wài ɡāo dī cū xì黑——白里——外高——低粗——细yuǎn jìn ɡǔ jīn mínɡàn zǎo wǎn远——近古——今明——暗早——晚Yǒu wú chū rù kuān zhǎi mǎi mài有——无出——入宽——窄买——卖nán běi shǒu wěi xī dōnɡ shǐ zhōnɡ南——北首——尾西——东始——终ɡàn shīɡōnɡ sī měi chǒu báo hòu干——湿公——私美——丑薄——厚xián dàn kǔ tián tiān dì chóu xī咸——淡苦——甜天——地稠——稀jiù xīn qínɡ yīn fú chén jiǎ zhēn旧——新晴——阴浮——沉假——真qiánɡ ruò duì cuò kāi ɡuān yìnɡ ruǎn强——弱对——错开——关硬——软shēn qiǎn jiā jiǎn fù zhènɡ jiànɡ shēnɡ深——浅加——减负——正降——升lěnɡ rè bǎo è sǐ shēnɡ fǎn zhènɡ冷——热饱——饿死——生反——正zhí wān chánɡ duǎn shènɡ bài hǎo huài直——弯长——短胜——败好——坏kuài màn shuānɡ dān shú shēnɡ wāi zhènɡ快——慢双——单熟——生歪——正xiào kū xī hū tuì jìn yánɡ yīn笑——哭吸——呼退——进阳——阴Yōu liè rì yè jǐn sōnɡ qīnɡ zhònɡ优——劣日——夜紧——松轻——重xiānɡ chòu pànɡ shòu hòu xiān yì nán香——臭胖——瘦后——先易——难lěnɡ nuǎn mánɡ xián ài zēnɡɡuì jiàn冷——暖忙——闲爱——憎贵——贱sònɡ yínɡ dònɡ jìnɡ yǎnɡ fǔ tūn tǔ送——迎动——静仰——俯吞——吐qīnɡ zhuó shū yínɡ bēi xǐ láo yì清——浊输——赢悲——喜劳——逸āo tūǎi ɡāo lì bì cǐ bǐ凹——凸矮——高利——弊此——彼máo dùn biǎn bāo láo hàn jiǎn fán矛——盾贬——褒涝——旱简——繁ān quán wēi xiǎn yōu diǎn quē diǎn qínɡ tiān yīn tiān安全——危险优点——缺点晴天——阴天hán lěnɡ wēn nuǎn xǐ huɑn tǎo yān fù zá jiǎn dān寒冷——温暖喜欢——讨厌复杂——简单dǎn xiǎo yǒnɡɡǎn zǎo chén bànɡ wǎn zé bèi chēnɡ zàn胆小——勇敢早晨——傍晚责备——称赞jiān yìnɡ róu ruǎn xiàn shí huàn xiǎnɡ ruǎn ruòɡānɡ qiánɡ坚硬——柔软现实——幻想软弱——刚强àn dàn mínɡ liànɡ huǎn hé jǐn zhānɡ xùn sù huǎn màn暗淡——明亮缓和——紧张迅速——缓慢lèɡuān bēi ɡuān ɡān jìnɡānɡ zānɡ xǐ yuè bēi shānɡ乐观——悲观干净——肮脏喜悦——悲伤chén zhe huānɡ zhānɡ xiōnɡè shàn liánɡ qīnɡ qiǎo bèn zhònɡ沉着——慌张凶恶——善良轻巧——笨重fán zhònɡ qīnɡ sōnɡ huǒ rè bīnɡ lěnɡ lànɡ fèi jiē shěnɡ繁重——轻松火热——冰冷浪费——节省chí dùn línɡ mǐn huái yí xiānɡ xìn xuān huáān jìnɡ迟钝——灵敏怀疑——相信喧哗——安静dònɡ yáo jiān dìnɡ hēi àn ɡuānɡ mínɡ biǎo yánɡ pī pínɡ动摇——坚定黑暗——光明表扬——批评xiān jìn luò hòu dí rén pénɡ you mì mìɡōnɡ kāi先进——落后敌人——朋友秘密——公开kuài lè bēi āi kuò dà suō xiǎo bèn zhuō línɡ qiǎo快乐——悲哀扩大——缩小笨拙——灵巧cháo shīɡān zào héǎi cū bào zēnɡ hèn rèài潮湿——干燥和蔼——粗暴憎恨——热爱yǐn mán tǎn bái bào lù yǐn bì mò shēnɡ shú xī隐瞒——坦白暴露——隐蔽陌生——熟悉Zāo tàài xī chénɡ fá jiǎnɡ lì kùn nɑn rónɡ yì糟蹋——爱惜惩罚——奖励困难——容易jiànɡ luò shēnɡ qǐ bái tiān hēi yè huān sònɡ yínɡ jiē降落——升起白天——黑夜欢送——迎接chénɡɡōnɡ shī bài ài hù sǔn hài xìnɡ fú tònɡ kǔ成功——失败爱护——损害幸福——痛苦zhènɡ què cuò wù rèn zhēn mǎ hu mínɡ bɑi hú tu正确——错误认真——马虎明白——糊涂chóu mì xī shū qīnɡ xī mó hu tī chànɡ jìn zhǐ稠密——稀疏清晰——模糊提倡——禁止wān qū bǐ zhí yǒnɡ jiǔ zàn shí jié shù kāi shǐ弯曲——笔直永久——暂时结束——开始yōu chóu ɡāo xìnɡ lěnɡ dàn rè qínɡ cū cāo ɡuānɡ huá忧愁——高兴冷淡——热情粗糙——光滑ǎi xiǎo ɡāo dà yú chǔn cōnɡ mínɡ qiánɡ liè wēi ruò矮小——高大愚蠢——聪明强烈——微弱勤劳——懒惰。

NVIDIA 视频编码器 SDK 10.0 迁移指南说明书

NVENC Preset Migration GuideTable of ContentsChapter 1. Introduction (1)Chapter 2. HEVC Preset Migration Table (2)Chapter 3. H264 Preset Migration Table (5)Chapter 1.IntroductionThis document provides table to map the NVENCODE API settings (specifically, preset and rate control mode) from Video Codec SDK 9.1 and earlier to the closest equivalent NVENCODE API settings in Video Codec SDK 10.0 and later. This table can be used as a migration guide to migrate to the new NVENCODE API preset architecture introduced in Video Codec SDK 10.0.In general, it is strongly recommended to use the newer presets and NVENCODE API settings based on desired performance/quality trade-off. It is highly likely that your application may benefit from better quality encoding or higher performance by directly using the new NVENCODE presets, as the new APIs provide much more flexibility than earlier and are easy to understand. Please use the mapping tables in this document only in situations where exactly same performance/quality is desired as was obtained in the older presets.Table 1and Table 2show the mapping between older and newer presets exposed in the NVENCODE API for HEVC and H.264, respectively. Note that there is no support for older presets in AV1A combination of older preset (Column 1), rate control (RC) mode (Column 2) and resolution (Column 3) can be mapped to a new parameters of NVENCODE API: tuning info (Column 4), RC Mode (Column 5), preset (Column 7&9) and multipass (Column 6&8). The newer preset and multipass values will vary based on GPU Architecture and appropriate GPU architecture column must be selected.In some cases, additional settings need to be included for exact mapping, and they are mentioned in columns Features 1 (Column 10 in Table 1 and Column 12 in Table 2) and Features 2 (Column 11 in Table 1 and Column 13 in Table 2).As an example, if someone is using HEVC HQ Preset with VBR_HQ RC Mode for a 1080p encoding on Turing platform, this corresponds to Row 18 in Table 1. The closest settings as per the new NVENCODE API is P6 Preset, RC Mode VBR, Multipass set to 1, FrameIntervalP set to 1, IDR Period set to 60 and GOP Length set to 60.It is important to note that Features 1 and Features 2 are just indicated to get an exact feature match on older presets and most applications would set these based on needs. For example, GOP length may be set to a larger value depending upon the application needs.Chapter 2.HEVC Preset MigrationTableTable 1.HEVC Preset Migration TableChapter 3.H264 Preset Migration Table Table 2.H264 Preset Migration TableH264 Preset Migration TableNoticeThis document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice. Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgment, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk. NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.TrademarksNVIDIA, the NVIDIA logo, and cuBLAS, CUDA, CUDA Toolkit, cuDNN, DALI, DIGITS, DGX, DGX-1, DGX-2, DGX Station, DLProf, GPU, Jetson, Kepler, Maxwell, NCCL, Nsight Compute, Nsight Systems, NVCaffe, NVIDIA Deep Learning SDK, NVIDIA Developer Program, NVIDIA GPU Cloud, NVLink, NVSHMEM, PerfWorks, Pascal, SDK Manager, Tegra, TensorRT, TensorRT Inference Server, Tesla, TF-TRT, Triton Inference Server, Turing, and Volta are trademarks and/or registered trademarks of NVIDIA Corporation in the United States and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.Copyright© 2010-2023 NVIDIA Corporation. All rights reserved.NVIDIA Corporation | 2788 San Tomas Expressway, Santa Clara, CA 95051。

2020 Hyundai IONIQ Plug-in Hybrid 用户指南说明书

2020 HyundaiIONIQ Plug-in HybridGetting Started GuideAudio, Connectivity, and Navigationhe device (Elantra) found by your phone. 32NoteBluetooth settings can be found in the SETTINGS app on most phones. Refer to Press the DEVICE CONNECTIONS * icon on the screen. Then press BLUETOOTH CONNECTIONS .Press ADD NEW . Then turn on your phone’s BLUETOOTH ®and select the device (Ioniq PHEV) found by your phone.Image shown may differ from actual product display.Image shown may differ from actual product display.5The vehicle will confirm that your contacts download is complete.The vehicle will confirm that your phone has been successfully connected.• Contact list may start with First or Last Name, depending on phone modelsMake sure your phone has been paired and your contacts have instructions on the previous pages.for more information.21Select the number you would like to call by saying ” or “TWO .”Image shown may differ from actual product display.4To end the call, press the END CALL * button located on the steering wheel.Here are a few common voice commands to useafter your phone has been paired:Note Compatibility and performance may vary based on your phone, the phone’s software, and your wireless carrier.32Enjoy using the applications displayed on your vehicle’s multimedia screen.Android Auto Apple CarPlayAndroid AutoAndroid AutoApple CarPlayApple CarPlay calling, navigation, text messaging, and playing music all from your driver’s seat.Android Auto users will be prompted to view a tutorial. Select your optionUSB data port will typically be located in or near the front in-dash console.For Apple CarPlay, you will see these screens:For Android Auto, you will see these screens:Note*USB data port will typically be located in or near the front in-dash console.4To end the call, press the END CALL* button located on the steering wheel.123After the beep, say a command. Example: “FIND COFFEE SHOP .”Press the PUSH TO TALK * button located on the steering wheel and say “CANCEL ROUTE ” after the 54123Touch the SEARCH box.The route to your destination will be displayed on the screen. Select START GUIDANCE to begin your route.54Note The system will search for addresses or destinations located within the state theHere are a few common voice commandsavailable to use:“HELP ” provides guidance on commands that canNote32 A list of nearby destinations matching your search 1Press the DESTINATION SEARCH BY VOICE* button.When prompted, you can say the name of a Point ofInterest (POI), an address, or a POI in a city.Example: “FIND COFFEE SHOP IN FOUNTAIN VALLEY,CALIFORNIA.”The destination route will be displayed on the screenand route guidance will begin.Initial Setup211Press the CUSTOM BUTTON .*。

专题25期中全真模拟卷05-2020-2021学年八年级数学上学期期中考试高分直通车(原卷版)

20202021学年八年级上学期数学期中考试高分直通车【人教版】专题2.5人教版八年级数学上册期中全真模拟卷05姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分120分，试题共26题，选择12道、填空6道、解答8道 .答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共12小题，每小题3分，共36分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•新都区模拟）下列图形中，是轴对称图形的是（）A．B．C．D．2．（2020春•沙坪坝区校级月考）下列各线段中，能与长为4，6的两线段组成三角形的是（）A．2B．8C．10D．123．（2019秋•肇庆期末）如图，已知△ABE≌△ACD，∠1＝∠2，∠B＝∠C，不正确的等式是（）A．AB＝AC B．∠BAE＝∠CAD C．BE＝DC D．AD＝DE4．（2020•温州模拟）如果点P（﹣2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是（）A．﹣1B．1C．﹣5D．55．（2020春•肇东市期末）如果三角形的三个内角的度数比是2：3：4，则它是（）A．锐角三角形B．钝角三角形C．直角三角形D．钝角或直角三角形6．（2019秋•松滋市期末）如图，已知D为BC上一点，∠B＝∠1，∠BAC＝64°，则∠2的度数为（）A ．37°B ．64°C ．74°D ．84°7．（2019秋•万州区期末）如图，在△ABC 中，边AC 的垂直平分线交边AB 于点D ，连结CD ．若∠A ＝50°，则∠BDC 的大小为（）A ．90°B ．100°C ．120°D ．130°8．（2020•恩平市模拟）如图，AB ＝DB ，∠1＝∠2，请问添加下面哪个条件不能判断△ABC ≌△DBE 的是（）A ．BC ＝BEB ．AC ＝DE C ．∠A ＝∠D D ．∠ACB ＝∠DEB9．（2019•霞山区一模）如图，点P 是∠AOB 的角平分线OC 上一点，PD ⊥OA ，垂足为点D ，PD ＝2，M 为OP 的中点，则点M 到射线OB 的距离为（）A ．12B ．1C ．√2D ．210．（2019•大庆）如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A ＝60°，则∠BEC 是（）A．15°B．30°C．45°D．60°11．（2019秋•郯城县期中）在△ABC中，∠A＝50°，∠B＝30°，点D在AB边上，连接CD，若△ACD 为直角三角形，则∠BCD的度数为（）A．60°B．10°C．45°D．10°或60°12．（2019秋•西城区校级期中）如图，已知△ABC中，AB＝AC＝12cm，BC＝10cm，点D为AB的中点，如果点P在线段BC上以2cm/s的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s 的速度运动．经过（）秒后，△BPD与△CQP全等．A．2B．3C．2或3D．无法确定二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上13．（2020秋•江岸区校级月考）五边形的内角和是，外角和是，对角线有条．14．（2019秋•铜山区期中）如图，在△ABC中，∠C＝90°，AD平分∠BAC，若CD＝8，点E是AB上一动点，DE的最小值为．15．（2019•广安）如图，正五边形ABCDE中，对角线AC与BE相交于点F，则∠AFE＝度．16．（2019秋•岱岳区期中）茗茗用同种材料制成的金属框架如图所示，已知∠B＝∠E，AB＝DE，BF＝EC，其中△ABC的周长为24cm，CF＝3cm，则制成整个金属框架所需这种材料的长度为cm．17．（2019秋•镇原县期末）如图，已知△ABC≌△A′BC′，AA′∥BC，∠ABC＝70°，则∠CBC′＝．18．（2018秋•全南县期中）在等边三角形ABC中，AD是BC边上的高，E为AC的中点P为AD上一动点，若AD＝12，则PC+PE的最小值为．三、解答题（本大题共8小题，共66分．解答时应写出文字说明、证明过程或演算步骤）19．（2019秋•禅城区期末）如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个定点坐标分别为A（﹣4，1），B（﹣3，3），C（﹣1，2）．（1）画出△ABC关于x轴对称的△A1B1C1，点A、B、C的对应点分别是A1、B1、C1，则A1、B1、C1的坐标为：A1（，），B1（，）、C1（，）；（2）画出点C关于y轴的对称点C2，连接C1C2，CC2，C1C，则△CC1C2的面积是．20．（2020•宁波模拟）如图1是五个小正方形拼成的图形，请你移动其中一个小正方形，重新拼一个图形，使得所拼成的新图形：（1）是轴对称图形，但不是中心对称图形．（2）既是轴对称图形，又是中心对称图形．（请将两个小题依次作答在图①、②中，均只需画出符合条件的一种情形，内部涂上阴影）21．（2020•江阴市模拟）如图，点A、E、F、C在一直线上，DE∥BF，DE＝BF，AE＝CF．求证：AB∥CD．22．（2019秋•鹿邑县期末）如图，△ABC中，AB＝AC，∠A＝50°，P为△ABC内一点，∠PBC＝∠PCA，求∠BPC的值．23．（2019•重庆）如图，在△ABC中，AB＝AC，AD⊥BC于点D．（1）若∠C＝42°，求∠BAD的度数；（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE＝FE．24．（2019秋•渝中区校级期中）如图，△ABC是等腰三角形，AB＝AC，点D是AB上一点，过点D作DE ⊥BC交BC于点E，交CA延长线于点F．（1）证明：AF＝AD；（2）若∠B＝60°，BD＝4，AD＝2，求EC的长．25．（2018•绍兴）数学课上，张老师举了下面的例题：例1等腰三角形ABC中，∠A＝110°，求∠B的度数．（答案：35°）例2等腰三角形ABC中，∠A＝40°，求∠B的度数，（答案：40°或70°或100°）张老师启发同学们进行变式，小敏编了如下一题：变式等腰三角形ABC中，∠A＝80°，求∠B的度数．（1）请你解答以上的变式题．（2）解（1）后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A＝x°，当∠B有三个不同的度数时，请你探索x的取值范围．26．（2019秋•日照期中）综合与实践：问题情境：已知在△ABC中，∠BAC＝100°，∠ABC＝∠ACB，点D为直线BC上的动点（不与点B，C重合），点E在直线AC上，且AE＝AD，设∠DAC＝n．（1）如图1，若点D在BC边上，当n＝36°时，求∠BAD和∠CDE的度数；拓广探索：（2）如图2，当点D运动到点B的左侧时，其他条件不变，试猜想∠BAD和∠CDE的数量关系，并说明理由；（3）当点D运动点C的右侧时，其他条件不变，请直接写出∠BAD和∠CDE的数量关系．。

upn 120 对应的规格

upn 120 对应的规格摘要：1.概述2.upn 120 的规格参数3.upn 120 的性能特点4.适用范围和场景5.总结正文：1.概述upn 120 是一种工业级无线网络模块，具有高性能、低功耗、稳定性强等特点，广泛应用于物联网、工业自动化、智能家居等领域。

本文将详细介绍upn 120 的规格、性能特点以及适用范围和场景。

2.upn 120 的规格参数upn 120 具有以下规格参数：- 传输速率：10/100Mbps- 频率范围：2.4GHz- 工作电压：3.3V- 工作电流：120mA- 接收灵敏度：-85dBm- 发射功率：18dBm- 传输距离：100 米（视环境而定）- 接口：通过SMA 接口与外部天线连接3.upn 120 的性能特点upn 120 具有以下性能特点：- 高性能：支持高速数据传输，满足各种应用场景的需求。

- 低功耗：工作电流仅为120mA，适合长时间运行的设备。

- 稳定性强：采用2.4GHz 频段，抗干扰能力强，传输稳定。

- 支持多种网络协议：包括TCP/IP、UDP、HTTP 等，方便用户进行网络配置。

4.适用范围和场景upn 120 适用于以下范围和场景：- 工业自动化：如生产线监控、设备数据采集等。

- 智能家居：如智能插座、智能灯泡、智能摄像头等。

- 物联网：如智能交通、智能农业、智能医疗等。

- 无线传感器网络：如环境监测、温湿度监控等。

5.总结upn 120 凭借其高性能、低功耗、稳定性强等特点，在工业自动化、智能家居、物联网等领域具有广泛的应用前景。

2024年中考第一轮复习直角三角形课件

[解析] 设AB=x,则AC=x-2.由勾股定理,
.
得x2-(x-2)2=82.解得x=17.
■ 知识梳理
勾股定理
直角三角形两条直角边的平方和等于⑥ 斜边的平方
勾股定理
如果三角形中两边的平方和等于第三边的⑦ 平方 ,那么这个三角形
的逆定理是直角三角形
勾股数
能够成为直角三角形三条边长的三个正整数,称为勾股数
∴AD=BC,∠A=∠B=∠CFE=90°,AB∥CD,∴∠AED=∠CDF,∠A=∠CFD=90°,
AD=CF,∴△ADE≌△FCD,∴ED=CD=x,∴FD=x-1,
在Rt△CFD中,FD2+CF2=CD2,∴(x-1)2+32=x2,解得x=5,∴CD=5.故选B.
考向三
勾股定理与拼图
例 3 [2020·孝感]如图 19-11①,四个全等的直角三角形围成一个大正方形,中间是个
图19-6
∴∠BEC=90°,∠BFC=90°,
1
2
∵G 是 BC 的中点,∴EG=FG= BC=5,
∵D 是
1
EF 的中点,∴ED= EF=3,GD⊥EF,
2
∴∠EDG=90°.在 Rt△ EDG 中,
由勾股定理得,DG= 2 - 2 =4,故答案为 4.
考向二
利用勾股定理进行计算
例2 [2020·宜宾]如图19-7,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE平分
∠ABC交AC于点E,连结CD交BE于点O.若AC=8,BC=6,则OE的长是
.
图19-7
【方法点析】勾股定理是求线段长的重要工具,主要应用:(1)已知直角三角形的
两边长求第三边长;(2)已知直角三角形的一边长求另两边的关系;(3)用于证明平

Hyundai 电子说明书

HD120People’s expectation toward individual mobility requires more than just a convenient means of transportation. The old understanding of cars has become outdated. A car represents individuals’ lifestyles, and it became an integral part of their lives. At the same time, the automobile industry has experienced seismic change. Hyundai Motor Company has grown rapidly to become one of the largest automakers, backed by world class production capability and superior quality. We have now reached a point where we need a qualitative approach to bring bigger ideas and relevant solutions to our customers. This is an opportunity to move forward and we have developed a new brand slogan that encapsulates our willingness to take a big leap. Led by our new slogan and the new thinking underlying it, we will become a company that keeps challenging itself to unlock new possibilities for people and the planet.Hyundai Motor Company GEN. LHD 1309 ENGCopyright © 2013 Hyundai Motor Company. All Rights Reserved.HD120 SpecificationsHD120 Line-upITEMVehicle TypeCargoModelHD120Extra Long Wheel BaseUltra Long Wheel BaseHD120Less is MoreThe Hyundai HD120 sets the standard in medium duty truck category. Built to Hyundai's high quality and reliability standards, the HD120 is the perfect partner for your business. Inside, you get comfortable, durable seats and an ergonomic wraparound instrument panel that provides control over the vehicle.Coil Type Full Floating Cab SuspensionThe cab rides on four coil-type mounts to isolate the driver from fatiguing road shocks andvibration. An air-type is optional.1. Front Bumper2. Door Safety Lamp3. Air Intake Duct4. Semi-sealed Headlamp5. Safety Steps6. Door HandleHD120 ULTRA LONGLength Width7,400m m2,340mm146253Comfortable, Spacious andready for all your business needs.Choose your cab, comfortand flexibility is built-inBecause transport and trucking covers awhole range ofindustries and services with differing crew needs, theHyundai HD series offer a full range of purpose built cabs.All with the unique blend of long distance comfort andlasting durability you naturally expect from Hyundai. Power SteeringFolding Gearshift LeverOverhead Console and AuidoCenter Seatback ConsoleTilt and Telescopic SteeringKeyhole LampDoor Pocket1 Piece Power WindowEveryone knows people work better in the best conditions. Theinterior of the HD is built to increase driver and crew satisfaction, torelieve long distance fatigue and stop and start stress. It wasdeveloped by driving professionals and proven over every kind ofroad imaginable. The foldable cable operated gearshift is light andprecise. Fresh, but durable trim materials and a textured floorcovering, excellent NVH (Noise Vibration Harshness) isolation, newwood grain fascia trim, LED lit switches and super clearinstrumentation are all part of what goes into making every HyundaiHD a driver’s first choice.Air Control SystemThe heating, ventilation and optional air conditioning system is driven bya powerful fan and high efficiency compressor and heat exchanger. Air isdelivered into the cabin at critical points to help keep the driver alert andcomfortable regardless of the weather outside.Whether you choose one of the entry level inline naturally aspirated six cylinder diesels or top-of-the-range turbo charged intercooler Engine, each Hyundai engine combines top performance with impressive economy. Best of all, they are fitted with top specification injection pumps so they’re easy to service,highly dependable and can be counted on for a long service life.Crossmember ReinforcementABS with ASR (Anti-Slip Regulator)This ABS (Anti-locking Brake System) brings the vehicle to a safe, controlled stop and is particularly advantageous whilst driving under slippery road conditions. The driver can apply maximum pressure on the brake pedal without worrying about wheel lock, skidding and subsequent loss of control. With ABS/ASR, the driver can maintain full directional stability of the vehicle at all times and avoid potentially dangerous situations. (Optional)D6GA EngineEuro II, Euro III, Euro IVPowerful , Dependable and Economical225Displacement : 5,899ccMax. Torque : 65kg.m/1,400rpmPS/2,500rpmP o w e r (p s )T o r q u e (k g ・m )N e w Enlarged application of Double frame which added channels in main frameDouble frame is applied for all of carrying conditions to perform excellent durability of vehicle frame. Further, extended applying area of double frame from the following of transmission to the rear axle is not only strengthen junction of frame, but also prevent to sink frame from extended wheelbase.80mmAdding Reinforced Sub-Frame 5t Main Frame 7t100m mSide ImpactDrum brake with wide Air Tanks Gradual ControlServicing and regular checks are easier than ever thanks to the45-degree tilting cab which provides quick and easy access to the engine Auxiliary StarterMaintenance Lamp and Switch365724145°142536。

中国农业大学2020考研差额复试比例不低于120%

北京市120急救网络呼叫反应时间的研究

多层感知器网络

IPS-1000系列VoIP综合接入系统用户手册V1.05

国有企业合规管理体系建设实践——以公司合规管理体系建设为例

《0.0兆赫》影评精选10篇

IXFR120N20中文资料

2020年智慧树知道网课《畜牧生物统计与试验设计》课后章节测试满分答案

新冠状病毒(最新PPT)-新冠状病毒ptt精选全文完整版

非同寻常的鼠年

IHW20N120R2中文资料

Orbi 4G LTE Advanced WiFi 路由器说明书

反义词(带拼音)适合1-3年级

NVIDIA 视频编码器 SDK 10.0 迁移指南说明书

2020 Hyundai IONIQ Plug-in Hybrid 用户指南说明书

专题25期中全真模拟卷05-2020-2021学年八年级数学上学期期中考试高分直通车(原卷版)

upn 120 对应的规格

2024年中考第一轮复习直角三角形 课件

Hyundai 电子说明书

2024年中考第一轮复习直角三角形课件