四年级上册奥数讲义-第十一讲 割补法巧算面积-冀教版(无答案)
割补法求图形面积

《组合图形的面积》教学设计沈晶晶(北京黄城根小学)【教学目标】1.认识简单的组合图形,会把组合图形分解成已学过的简单的平面图形,并能计算出组合图形的面积。
2.能根据各种组合图形的条件,有效地选择合适的方法进行解答,并能解决生活中的相关实际问题。
3.发展空间观念,了解图形转化的数学思想,提高数学学习的兴趣【教学重点】组合图形分解的方法,优化方案求面积【教学难点】找关键数据和条件,求出组合图形的面积【教学过程】一、引入:认识组合图形1.出示简单图形,学生回顾求面积的方法,介绍基本图形的概念。
2.认识组合图形:师把其中的两个或三个图形组合到一起,谁能上来也来组合一个新的图形。
引导学生观察:这些新的图形有什么共同之处?这些有2个或2个以上基本图形组合在一起的图形叫做组合图形。
3.问:基本图形的面积我们会求了,那么这些组合图形的面积你们会求吗?(学生会把这个图形分解成基本图形求面积)今天这节课我就来学习求组合图形的面积(板书)4.介绍辅助线,归纳分解图形的方法:日常生活中,我们也会见到组合图形,你能把它们分解成什么基本图形呢?(队旗、草地)向学生介绍画辅助线的方法,重点反馈草地分解成基本图形的多种方法,同一个组合图形,怎么分解的基本图形不一样呀?二、探究新知:这是公园里一块空地的平面图,工人叔叔要想把它铺上草坪,请你们帮忙算一算这块地的面积,行吗?1.小组合作探究:(1)先独立计算这个组合图形的面积;(2)计算后,小组里说说你是怎么算的;(3)再一起讨论其他的方法怎么计算。
汇报:重点汇报一个分割的方法、一个添补的方法,其他的说明思路,并说出关键的步骤2.分类:同学们这么多种画辅助线的方式来求这个组合图形的面积,你们能给这些方法分分类吗?分解的方法不同,具体到计算时又有什么区别呢?(分割相加法、添补相减法)3.比较优化:为什么这些方法很少或者没人选择?我们在分解组合图形时要注意什么?小结:要根据题目所给的条件进行分解,选择分成最简便的方法,尽量少用辅助线4.回顾反思:刚才通过同学们的独立思考,利用已经学到的知识把公园空地的面积求出来了,你们真厉害!如果再给你一个组合图形,你准备分几步求组合图形的面积?(把组合图形分解成简单图形;找关键条件;相加或相减)三、巩固拓展,解决实际问题1.出图形,选择方法。
割补法巧算面积

割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积. (单位:厘米)8 2练习1如图中的每个数字分别表示所对应的线段的长度(单位:米)•这个图形的面积等于多少平例题2如图,在正方形ABCD内部有一个长方形. EFGH .已知正方形ABCD的边长是6厘米, 图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF (如图),线段DF=3.6厘米, BE=2.8厘米,那么三角形AEF的面积等于_______________ 平方厘米.B例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.21如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为______________________ cm •A D例题4.如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?例6.选做题例5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形平方厘米,那么正方形B的面积是多少平方厘米?A的面积是36已知一个四边形 ABCD 的两条边的长度和三个角(如下图所示),求四边形ABCD 的面积是多少? 作业:1•如图所示,平行四边形的面积是 12,把一条对角线四等分, 将四等分点与平行四边形另外 两个顶点相连•图中阴影部分的面积总和是多少?2. . (2013秋?诸暨市校级期中)如图,已知一个四边形的四条边 分别是3, 4, 13和12,其中/ B=90。
割补法求图形的面积PPT课件

.
4
一、问题初涉
2、如图,某广场四角铺上了四分之一圆形
的草地,若圆形的半径为r米,则共有草
地
平方米.
.
5
一、问题初涉
3、如图3,正方形的边长为a,以CD为直径在 正方形内画半圆,再以点C为圆心CD为半径 画弧BD,则图中阴影部分的面积为 ___________。
图3
.
6
二、情境探究
1、如图4,长为a 米、宽为b米的草坪内修建 了一条宽为2 m的小路,如右图所示,求草 坪面积。
求不规则图形
的面积
.
1
知识链接
你能用字母表示这些图形的面积吗?
a
b
h
a
a
a
S a2
S ab
S ah b
h
S
a
ah
2
h
S 1(aab)h
2
.
2
割补法求圆的面积
n等分圆后,把得到的小扇形近似成小三角 形,通过求n个小三角形的面积估算出圆的 面积。
.
3
一、问题初涉
• 1、如图,为古代铜钱,设内部正方形边长 为a,外圆半径为r,则铜钱面积为 (用 含π的代数式表示)。
探究.修建的小路为宽为2米十字路,用含a、 b的代数式表示草坪的面积?
.
11
二、情境探究
3.若修建的小路宽不变,如右图所示,则草坪 的面积为多少?
(1)用含a、b的代数式表示草的面积 (2)当a为20米、b为30米时求草坪的面积
.
12
二、情境探究
3、正方形的边长为a,分别以两个对角顶点 为圆心、以a为半径画弧,求图中阴影部分 的面积
.
13
二、情境探究
(完整word版)小学奥数模块教程四年级杯赛备战讲义——巧求面积

上课日期: 上课时间: 教师姓名:知识点一:格点面积 一、正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.二、 三角形格点问题1、定义:所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.2、公式:关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.知识点二:图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点,则它的面积为12LS N =+-.本讲中很多类型的题目还要求同学们去动手尝试.通过本讲知识的学习,让同学们了解不同图形的分割、拼合、剪拼的方法,锻炼同学们的平面想象能力以及增强学生的动手操作能力.(1)把一个几何图形按某种要求分成几个图形,就叫做图形的分割.(2)反过来,按一定的要求也可以把几个图形拼成一个完美的图形,就叫做图形的拼合.(3)将一个或者多个图形先分割开,再拼成一种指定的图形,则叫做图形的剪拼.我们在图形的分割、拼合和剪拼的过程中,都要结合所提供的图形特点来思考.(1)如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.(2)图形中,如果有数量方面的要求,可以先从数量入手,找出平分后每块上所含数量的多少,再结合数量来分割图形.(3)如果是要把几个图形拼合成一个大图形,要特别注意每条边的长度,把相等的边长拼合在一起,先拼少的,再拼多的.(4)如果是剪拼图形,要抓住“剪、拼前后图形的面积相等”这个关键,根据已知条件和图形的特点,通过分析推理和必要的计算,确定剪拼的方法.一、解题关键:分割其实就是运用特殊的三角形(等角直角三角形、等边三角形等)、正方形、等边图形的特殊性质进行分割而得,所以分割的关键是利用了特殊图形的关系解题。
小学奥数用割补法求面积

小学奥数解析十三用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
(完整版)用割补法求面积

在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB 弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
几何格点与割补

第十一、十二讲格点与割补本讲知识点1.分割法1)正所谓“大事化小”,把不规则的大图形化为规则的小图形,来进行计算.2)在对格点图形的分割计算时,不一定要分到最小的基本单位。
一般来说分为中等大小的,可以计算的规则形状比较方便。
2.割补法1)是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.2)此外,在图形中进行适当的分割拼补,把不规则的形状拼成规则形状,也是常见的方法.3.格点面积公式1)在最小的正方形面积为1的图形中:正方形格点多边形面积=边界格点数÷2+内部格点数-1.2)在最小正三角形面积为1的图形中:三角形格点多边形面积=边界格点数+内部格点数×2-1.3)在使用公式法计算格点多边形面积时,要注意公式的适用条件.4)在多个格点图形相关的问题中,要注重利用它们之间的共同点来帮助计算.5)对于很多非格点图形的面积计算,分割和添补的方法依然适用.6)特别的,在图形中恰当的添加格线进行分制,能更好的体现围形的结构,以及整体和部分的数量关系,而在添补中,看见某些特殊角度,如45°、60°、120°等时,可以联想到一些特殊的图形,如,等腰直角三角形,正三角形等等.精选例题例题1.如图,分别在如下三种情况中,求出图中格点图形的面积:(1)相邻格点距离为1;(2)相邻格点距离为2;(3)最小正方形面积为2.例题2.如图,下图的正方形格点,单位正方形面积为1,分别求出两个图形的面积.例题3.如图,下图的正方形格点中,单位正方形面积为3,求出图形面积.练习1.如图,分别在如下两种情况中,求出图中格点图形的面积:(1)最小正三角形面积为1;(2)最小正三角形形面积为2.例题4.如图,下图的三角形格点,单位正三角形面积为1,分别求出两个图形的面积.例题5.如图,下图的正三角形格点中,单位正三角形面积为5,求出图形面积.例题6.下图点阵间隔为1,请利用方形格点公式,填出下表:练习2.下图三角形点阵所能连出的最小三角形面积为1,请利用三角形格点公式,填出下表:例题7.如图,单位正方形面积为1,利用格点公式计算下面阴影图形的面积,并再用一种其他方法计算检查.例题8.(1)在图1的正方形格点中,左图面积是45,那么右图的面积是多少?(2)图2的左右两个大三角形相同,左图的单位正三角形面积为100,右图的单位正三角形面积是多少?例题9.把同一个三角形的三条边分别四等分、六等分,适当连接这些分点,便得到了若干个面积相等的小三角形,已知图1中副影部分的面积是63平方厘米,那么图2中的阴影部分的面积是多少平方厘米?例题10.如图,对下列图形进行适当的格线划分,使得能恰当的体现出阴影部分与总面积的关系,并进行相应计算:(1)大正方形面积为90,连结各边中点得到阴影正方形,求阴影面积.(2)大正三角形面积为90.每边取三等分点,连结得到阴影正六边形,求阴影面积.(3)大正六边形面积为90,连结其中3个顶点得到阴影正三角形,求阴影面积.(4)大等腰直角三角形面积为90,如图放入一个阴影正方形,求阴影面积.例题11.在面积为72平方厘米的正六边形中,按图中不同方式切割(切割点均为等分),形成的阴影部分面积分别是多少?例题12.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N、M分别为AF、AB、ED边上的中点,求四边形GNME的面积.例题13.如图,在长方形ABCD中,O是长方形的中心,BC长20厘米,AB长12厘米,=,3DE AE4=,那么阴影部分的面积是多少平方厘米?CF DEBE=,三角形AEF的面积是37,那么长例题14.如图,在长方形ABCD中,3DF=,11方形ABCD的面积是多少?例题15.甲乙两个六边形的内角都是120°,其边长如图所示,那么甲,乙面积分别是边长为1的正三角形面积的多少倍?例题16.求阴影部分面积:例题17.两个等腰直角三角形直角边分别长10厘米和6厘米,那么三角形DGE面积是多少平方厘米?思考创新思考1.下图为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点面一个面积为13的三角形.思考2.如图,平面上有16个点,每个点都钉上钉子,形成间隔为1厘米的4行4列的正方形钉阵,现在有许多皮筋,可以套出几种面积的三角形?请各举一例.思考3.正方形格点如图,原有格点的单位正方形面积为68,利用原有格点在图中划分新的格线,分别划出两种新的情况,那么这两种新格线的单位小正方形的面积分别是多少?思考4.如图,把长方形纸片ABCD的一角折起,使点D恰好与AB的中点F重合,若三角形EDC的面积是10.那么长方形ABCD的面积是多少?思考5.如下图,在一平行四边形纸片上割去了①,②两个直角三角形,已知三角形①两条直角边分别为2厘米和5厘米,三角形②两条直角边分别为5厘米和8厘米,求图中阴影部分的面积.第十一讲格点割补(一)思维冲浪1.如图所示,每一个小方格的面积都是1,那么用祖线围成的图形的面积是________.2.已知图中相邻两格点的距离均为2厘米,那么图中连出多边形的面积是______平方厘米.3.如图所示,图中最小的“□”面积是2,那么阴影部分面积分别为________.4.如图,如果每个小三角形的面积都是1cm2,那么连接A,B,C三点的三角形的面积是________cm2.5.如图,如果每一个小三角形的面积是2平方厘米,那么四边形ABCD的面积是________平方厘米.6.如图所示,图中最小的“Δ”面积是2,那么阴影部分面积分别为_______.7.如图所示,每个小方格格的边长为1.那么阴影部分的面积是多少?8.图中相邻三点所形成的等边三角形的面积为1,求五边形的面积.9.如图,大正六边形的面积为108,求阴影部分的面积为多少?10.图中水平,竖直方向相邻两个格点的距离都是1,请你求出图中“8”、“0”,“9”的面积各是多少.第十二讲格点割补(二)思维冲浪1.把同一个三角形的三条边分别五等分、七等分,连接这账分点,便得到了若干个面积相等的小三角形,左图中阴影部分的面积是294平方分米,那么右图中阴影部分的面积是________平方分米.2.下图是一个面积为24的正六边形,阴影部分的面积是__________.3.如图所示,ABCD是长方形,长AD等于7.2厘米,宽AB等于5厘米,CDEF是平行四边形,如果BH的长是3厘米,那么图中阴影部分面积是________平方厘米.4.在下图中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是________平方厘米.5.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N分别为AF、AB边上的中点,那么四边形GNCE的面积是__________平方厘米.6.如图所示,三个长方形APHM、BNHP、CQHN的面积分别是7、4、6、则阴影部分的面积是__________.7.如图所示,为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点画一个面积为7的三角形.8.如图所示,为一个边长为2的正方形,其中阴影部分的面积为多少?9.图中大正方形边长为8,小正方形边长为4,求阴影部分面积.10.如图,一个正方形,与4个等腰直角三角形,恰好拼成了一个长方形,如果正方形的面积是16,那么,长方形的面积是________.。
割补法巧算面积

割补法巧算面积之吉白夕凡创作时间:二O二一年七月二十九日知识精讲:联系法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字辨别暗示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字辨别暗示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD 的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH 的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.1.如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边辨别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2..(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长辨别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
割补法巧算面积
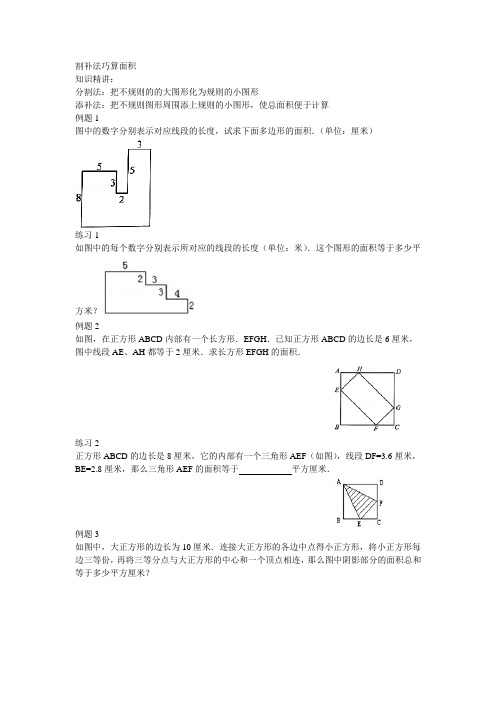
割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.1.如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
小学奥数——用割补法求面积讲课讲稿

小学奥数——用割补法求面积小学奥数解析十三用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
(完整版)用割补法求面积

在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB 弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
最新小升初奥数巧求面积---割补法知识讲解

解析
从顶点作底边上的高,得到两个相同的直角三角 形。将这两个直角三角形拼成一个长方形见右图。 显然,阴影部分正好是长方形的三分之一,所以 原题阴影部分占整个图形面积的三分之一。 还可以拼成一个平行四边形或将其分成9个三 角形。
例5. 如下图所示,在一个等腰直角三角形中,削去一个三角形后, 剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。 求这个梯形的面积。
小升初奥数巧求面积---割 补法
知识梳理
相加法
相减法
割补法
平移法 旋转法
巧求 面积
放大法 等量代换法
直接求法 重叠法 引辅助线法
典型例题精讲
例1. 下图中四个圆的半径都是5厘米,求阴影部分的面积。
解析
同学们请看图,我们将图形进行割补。 把阴影部分割补成四个半圆形和一个正方形, 求出阴影部分面积就可以了。 2S圆=5× 5× 3.14× 2=157(平方厘米)
9厘米 5厘米
例6.ABC是三个圆的圆心,圆的半径都是10分米,求阴 影部分的面积。
D
B
F
A
C
E
解析
我们用割补法,将阴影部分割补 成一个半圆形,求出阴影部分面 积就可以了。 S半圆=10× 10× 3.14÷ 2=157平方 分米
D
B
F
A
C
E
例7.如图所示,空白部分占正方形面积的 几分之几?
解析
9厘米 5厘米
解析
因为不知道梯形的高,所以不能直接求出梯形的面 积。可以从等腰直角三角形与正方形之间的联系上考 虑。将四个同样的等腰直角三角形拼成一个正方形, 图中阴影部分是边长9厘米与边长5厘米的两个正方 形面积之差,也是所求梯形面积的4倍。所以所求梯 形面积是(9× 9-5× 5)÷4=14(平方厘米)。
小学奥数——用割补法求面积

小学奥数解析十三用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
割补法巧算面积

割补法巧算面积之蔡仲巾千创作时间:二O二一年七月二十九日知识精讲:分割法:把不规则的的年夜图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别暗示对应线段的长度,试求下面多边形的面积.(单元:厘米)练习1如图中的每个数字分别暗示所对应的线段的长度(单元:米).这个图形的面积即是几多平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD 的边长是6厘米,图中线段AE、AH都即是2厘米.求长方形EFGH 的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积即是平方厘米.例题3如图中,年夜正方形的边长为10厘米.连接年夜正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与年夜正方形的中心和一个极点相连,那么图中阴影部份的面积总和即是几多平方厘米?练习3.1.如图所示,正方形ABCD的边长acm,则图中阴影部份的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部份的面积是294平方分米.请问:图2中的阴影部份的面积是几多平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部份的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是几多平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是几多?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个极点相连. 图中阴影部份的面积总和是几多?2..(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部份面积.4.求阴影部份面积.5. 求阴影部份面积:6.求阴影部份面积.7. 求阴影部份面积.8.(2011秋•宁波期中)求阴影部份的面积.9. 求阴影部份的面积.10. 求阴影部份的面积.11.求阴影部份的面积.12.求阴影部份的面积.。
小学奥数——用割补法求面积

小学奥数解析十三用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级第十一讲割补法巧算面积
◆温故知新:
1. 用割补法把不规则图形变成规则图形计算面积。
2.正方形、等腰直角三角形、等边三角形、正六边形等已知图形分割成小块,与所求图形
面积相联系。
◆练一练
1、在图中,五个小正方形的边长都是2厘米,求三角形ABC的面积。
2、图中小正方形和大正方形的边长分别是4厘米和6厘米。
阴影部分的面积是多少平方厘
米?
◆例题展示
例题1图中的数字分别表示对应线段的长度,试求这个多边形的面积。
(单位:厘米)
练习1如图所示,在正方形ABCD内部有一个长方形EFGH。
已知正方形ABCD的边长是6厘米,图中线段AE AH
、都等于2厘米。
求长方形EFGH的面积。
例题2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连。
请问:图中阴影部分的面积总和等于多少平方厘米?
练习2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,再连接大正方形的两条对角线。
请问:图中阴影部分的面积总和
等于多少平方厘米?
例题3如图所示,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD中点,P是EF中点。
请问三角形MNP的面积是多少平方厘米?
练习3 如图所示,正六边形ABCDEF的面积是36平方厘米,M、N、P、Q、R、S分别是AB、BC、CD、DE、EF、FA的中点。
请问:阴影正六边形MNPQRS的面积是
多少平方厘米?
例题4 如图,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点。
已知图a中阴影部分的面积是294平方分米。
请问:图b中阴影部分的面积
是多少平方分米?
练习4如图,把两个同样大小的正方形分别分成5×5和6×6的方格表。
其中“G”
形阴影部分的面积是558,请问“S”形阴影部分的面积是多少?
◆拓展提高
拓展1如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?
练习1如图,在两个相同的等腰直角三角形中各作一个正方形,如果三角形A的面积是16平方厘米,那么三角形B的面积是多少平方厘米?
拓展2 如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(图中3和7的单位是厘米)
练习2 如图,在等腰梯形ABCD中,角B是60度,线段AB、AD、CD长度相等。
如果以AB为边的等边三角形的面积是10,那么等腰梯形ABCD的面积是
多少?
◆思维挑战
挑战图为一个边长为2厘米的正方形,分别连接顶点与对应边中点。
围成的阴影部分的面积为多少平方厘米?
◆作业
1、如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行系变形
另外两个顶点相连。
请问:图中阴影部分的面积总和是多少?
2、如图所示,正六边形ABCDEF的面积是36.请问:阴影正六边形的面积是多少?
3、如图,图(1)的阴影图形面积是24,那么图(2)阴影图形的面积是多少?
4、图中空白部分的面积是100,那么阴影部分的面积是多少?
5、如图,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DE长9厘米,CE 长3厘米,求阴影部分的面积。
