小学奥数-几何五大模型(鸟头模型).
小学五六年级奥数学竞赛五大模型——共边模型、鸟头模型

大海传功等积变形五大模型——共边模型、鸟头模型共角模型(鸟头模型)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
1.两个三角形,如果底边相等,高也相等,那么它们的面积相等。
拓展:夹在一组平行线间的同底三角形面积相等。
2.两个三角形,如果底相等,一个的高是另一个的n倍,那么它的面积也是另一个的n倍;两个三角形,如果高相等,一个的底是另一个的n倍,那么它的面积也是另一个的n倍。
DAE D EADD AE EAB C B C B CB如图,S:S (AB AC):(AD AE)△ABC△ADEC【例1】(★★)【例2】(★★★)如图,在梯形ABCD中,三角形ABE的面积为4.6平方厘米,BE=EF=FD,求三角形ABF、CDF、ABD、ACD的面积。
如图,由面积分别为2、3、5、7的四个三角形拼成一个大三角形,已知:S△ADE 2,S△AEC 5,S△BDF 7,S△BCF 3,那么三角形BEF的面积为___________。
1如图,在角MON的两边上分别有A、C、E及B、D、F六个点,并且△OAB、△ABC、△ BCD、△CDE、△DEF的面积都等于1,则△DCF的面积等于。
等腰△ABC中,AB=AC=12cm,BD、DE、EF、FG把它的面积5等分,求AF、FD、DC、AG、GE、EB的长。
【例5】(★★★)【例6】(★★★★)已知四边形ABCD、BEFG、CHIJ为正方形,正方形ABCD边长为10,正方形BEFG边长为6,求阴影部分的面积。
E、M分别为直角梯形ABCD两边上的点,且DQ、CP、ME彼此平行,若 AD=5, BC=7,AE=5 , EB=3。
求阴影部分的面积。
2已知△DEF的面积为7 平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
1如图,在△ABC中,延长AB至D,使BD=AB,延长BC至E,使CE BC,2 F是AC的中点,若△ABC的面积是2,则△DEF的面积是多少?大海点睛大海点睛一、本讲重点知识回顾等积变形边比=面积比二、本讲经典例题例2,例3,例5,例7,例8共角模型(鸟头模型)如图, △ABC△ADE3。
4几何五大模型——鸟头模型

---------------------------------------------------------------最新资料推荐------------------------------------------------------4几何五大模型——鸟头模型几何五大模型鸟头模型一两点都在边上:鸟头定理:(现出鸟头模型。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE△ABCS ADAE=S ABAC EDC BA 二一点在边上,一点在边的延长线上:△CDE△ABCS CDCE=S BCAC EDCBA 本讲要点如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为 5 平方厘米,△ ABC 的面积是平方厘米.例例 2 (1 )如图在△ABC 中,D 、E 分别是AB ,AC 上的点,且AD:AB=2:5, AE:AC=4:7, △ABC 的面积是的面积是 16 平方厘米,求△ABC 的面积。
(2 )如图在△ABC 中,D 在 BA 的延长线上,E 在在 AC 上,且 AB:AD=5:2 ,AE:EC=3:2, △ADE 的面积是的面积是 12 平方厘米,求△ABC 的面积。
已知△DEF 的面积为12 平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
1 / 22例例 1 例例 2 例例 3 三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少?三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少? FEDCBA 例例 4 例例 5 长方形ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?长方形 ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?如图,过平行四边形 ABCD 内的一点 P 边作边 AD 、 BC 的平行线 EF 、 GH ,若PBD 为的面积为 8平方分米,求平行四边形 PHCF 的面积比平行四边形 PGAE 的面积大多少平方分米? AB CDEFGHP 例例 61. 如下左图,在ABC △ 中,D 、E 分别是 BC 、AB 的三等分点,且ABC △ 的面积是 54 ,求CDE △ 的面积。
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:二、鸟头模型的原理剖析三、鸟头模型的方法运用鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知AD:BD=2:3,AE:EC=3:1,三角形ADE的面积是6平方厘米,求三角形ABC的面积?第一步:标条件第二步:确定等角位置A小夹边AD×AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB×AC第三步:利用鸟头模型结论S△ADE:S△ABC=小夹边乘积:大夹边乘积=(2×3):(5×4)=6:20=3:103:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6÷3=2平方厘米/份;所求三角形ABC的面积是10份,2×10=20平方厘米。
例2:如图,已知BC:CD=5:2,AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形CDE 的面积?第一步:标条件第二步:确定补角位置C小夹边CD×CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA×CB第三步:利用鸟头模型结论S△CDE:S△ABC=小夹边乘积:大夹边乘积=(2×1):(2×5)=2:10=1:51:5的意思是:三角形CDE的面积是1份,三角形ABC的面积是5份。
第四步:先除后乘算面积三角形ABC的面积是20平方厘米,对应5份,20÷5=4平方厘米/份;所求三角形CDE的面积是1份,4×1=4平方厘米。
小学奥数-几何五大模型(鸟头模型)

如图在 △ ABC 中,D,E 分别是AB,AC 上的点如图(1)(或D 在BA 的延长线上, E 在AC 上如图2), 则 ABC : ADE =(AB AC): (AD AE)厘米,求△ ABC 的面积.【解析】 连接 BE , S A ADE :S A ABE 二 AD : AB =2:5 =(2 4):(5 4),SA ABE : S A ABC 二 AE: AC = 4: 7 = (4 5) : (7 5),所以 S A ADE : S A ABC = (2 4) : (7 5),设 S A ADE = 8 份, 则S A ABC =35份,S A ADE =16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ ABC 的 面积是70平方厘米.由此我们得到一个重要的定理, 共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【巩固】如图,三角形 ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形 ADE 的面积等于1,那 么三角形ABC 的面积是多少?••• EC =3AE--S ABC=3S_ABE又••• AB =5AD「•S LADE = S_ABE ' 5 = S_ABC 15 , — S ABC =15S ADE =15 .【巩固】如图,三角形 ABC 被分成了甲(阴影部分)、乙两部分,鸟头模型角形中有一个 补,这两个三 角三角形.共角三角形的面积比等于对应角 (相等角或互补角)两夹边的乘积之比.【例1】如图在△ ABC 中, D,E 分别是 AB,AC 上的点,且 AD: AB =2:5 , AE:AC=4:7 ,S A ADE *6平方BD =DC =4 , BE =3 , AE =6,乙部分面图⑵【解析】积是甲部分面积的几倍?【解析】连接AD •••• BE =3 , AE =6AB = 3BE , S ABD =3S BDE 又••• BD 二DC =4 ,…S ABC -2S ABD,…S ABC - 6S BDE ,【例2】如图在△ ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2 , AE:EC=3:2,S A ADE =12平方厘米,求△ ABC的面积•【解析】连接BE , S M DE:S A ABE二AD : AB =2:5 =(2 3): (5 3)S A ABE S ABC=AE: AC =3:(3 2)=(3 5): 1(3 2) 5 ],所以S A ADE : S A ABC - (3 2):5 (3 * 2) 1 = 6 : 25,设S^ADE = 6 份,贝U S^ ABC = 25 份,S AADE -12 平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】如图所示,在平行四边形ABCD中,E为AB的中点,AF =2CF,三角形AFE(图中阴影部分)的面积为8平方厘米•平行四边形的面积是多少平方厘米?【解析】连接FB•三角形AFB面积是三角形CFB面积的2倍,而三角形AFB面积是三角形AEF面积的2 倍,所以三角形ABC面积是三角形AEF面积的3倍;又因为平行四边形的面积是三角形ABC面积的2倍,所以平行四边形的面积是三角形AFE面积的(3 2)6倍•因此,平行四边形的面积为8 6 =48(平方厘米).【例4】已知△ DEF的面积为7平方厘米,BE =CE, AD =2BD,CF =3AF,求△ ABC的面积.【解析】S A BDE : S A ABC =(BD BE) :(BA BC)=(1 1):(2 3) =1:6 ,S MEF : S ^ABC =(CE CF):(CB CA) =(1 3):(2 4) =3:8S*DF: S*BC =(AD AF): (AB AC) =(2 1):(3 4) =1:6设 S A ABC =24 份,则 S ^ BDE = 4 份,S ^ ADF =4 份,S ^ CEF = 9 份,S ^ DEF = 24 - 4- 4 - 9 = 7 份,恰好是 7 平方厘米,所以S A ABC =24平方厘米【例5】如图,三角形 ABC 的面积为3平方厘米,其中 AB:BE=2:5 , BC:CD=3:2,三角形BDE 的面积 是多少?=180,所以可以用共角定理,设 AB = 2份,BC =3份,贝U BE =5份,BD =3 2 =5 份,由共角定理 S A ABC : S A BDE =(AB BC):(BE BD)=(2 3):(5 5)=6:25,设S A ABC =6份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是25 0.5 = 12.5平方厘米,三角 形BDE 的面积是12.5平方厘米1 1 【例6】(2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,AE=」AC , CF 二1234 BC .33连接AE 、CD .S ABC =1 ,-• S DBC =1 .同理可得其它,最后三角形 DEF 的面积=18 .(法2)用共角定理•••在L ABC 和LCFE 中,.ACB 与.FCE 互补,11 2【解析】 由题意知AE = - AC 、CF =-BC ,可得CE =—AC .根据”共角定理”可得,3 3 3S A CEF : S A ABC = (CF ^CE): (CB 汉 AC2 J (^<3^2: 9 ; 而 S A ABC =6 ^6 弓2 =18 ;所以 S A CEF =4 ;同理得,S A CDE : 2 ACD = 2 :3 ; , S A CDE =18^32 =12 , S A CDF- 6故 S A DEF - S A CEF S A DEC - S A DFC =4,12-6=10 (平方厘米).【例7】如图,已知三角形 ABC 面积为1,延长AB 至D ,使BD 二AB ;延长BC 至E ,使CE =2BC ;延长【解析】 由于.ABC .DBE 角形DEF 的面积为 _______ 平方厘米.【解析】(法1)本题是性质的反复使用.S ABC AC BC 11 1 S FCE - FC CE "^"2 "8 ■又 S ABC =1,所以 S FCE =8- 同理可得 S ADF -6 , §BDE =3 .所以 S DEF = S ABC ' S FCE ' S ADF ' S BDE =1 ' 8 ' 6 ::3=18 .【例8】如图,平行四边形 ABCD , BE =AB , CF = 2CB , GD =3DC , HA = 4AD ,平行四边形 ABCD 的 面积是2 ,求平行四边形 ABCD 与四边形EFGH 的面积比.【解析】连接AC 、BD •根据共角定理•••在△ ABC 和 △BFE 中,乙ABC 与乙FBE 互补, .S ^ ABC AB BC 11 1 S ^ FBE BE BF1 :: 3 3又 S ^ ABC =1,所以 S ^FBE -3 .冋理可得 S AGCF =8 , S ^DHG =15 , S A AEH =8 .所以 S E FGH 二 S A AEH ' S A CFG ' S A DHG + S A BEF +S ABCD =8+8+15+3+2 =36 .冋理 S A ABD : S A AHE -1: 2,即 S A AHE - 2 S A ABD 所以S A AHES A CGF = 2(S △CBDS A ADB )=2窃边形 ABCD连接AC ,冋理可以得到S A DHG ' SA BEF =2绻边形ABCDS四边形EFGH二 AHE S A CGF S A HDGS A BEF *S 四边形ABCD =5S 四边形ABCD所以S 四边形ABCD =66 "5 =13.2平方米AB 、CB 、CD 、AD 分别延长两倍至点 E 、F 、G 、H ,若 EFGH 的面积是 .所以二D SEFGH2 _ 136【例9】 如图,四边形EFGH 的面积是66平方米,的面积. EA = AB , CB =BF , DC =CG , HD =DA ,求四边形 ABCD【解析】【例10】 如图,将四边形ABCD 的四条边四边形ABCD 的面积为5,则四边形E连接BD •由共角定理得S A BCDCF) =1:2,即 S A CGF =2S A CDB【解析】连接AC 、BD •由于 BE =2 AB , BF =2BC ,于是 S BEF = 4S ;ABC ,冋理 S HDG -4S ADC • 于是 S BEF ■ SHDG = 4S ABC ' 4S ADC =4S ABCD •再由于 AE — 3AB , AH — 3AD ,于是 S AEH —9S ABD ,冋理 S CFG — 9S CBD • 于是 S AEH ' S CFG-9S ABD ' 9S ^BD =9S ABCD •那么 S EF GH = S BEF ■ S H DG +S 建EH *S 应FG —S AB CD =4S AB CD *9S AB CD —S AB CD=12S AB CD =60•1【例11】 如图,在△ ABC 中,延长AB 至D ,使BD =AB ,延长BC 至E ,使CE =丄BC , F 是AC 的2中点,若 △ ABC 的面积是2,则A DEF 的面积是多少?S ^ ABC _ AC BC _2 2 4 S A FCE 一 FC CE 一 1 1 ~1又 S ABC = 2,所以 S FCE =0.5 • 同理可得S A ADF =2 ,S A BDE =3 • 所以S A DEF = S A ABC S CEFDEB—S A ADF =2 0.5 3 -2 =3.5【例 12】 如图,S A ABC =1 , BC=5BD , AC=4EC , DG=GS 二SE , AF = FG •求 S FGS【解析】本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的 3种情况•4 3 2 1 1 1 最后求得S A FGS 的面积为S A FGS :5 4 3 2 2 10【例13】 如图所示,正方形 ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?【解析】ZACB 与乙FCE 互补, •••在厶ABC 和A CFE 中,1 2因为S A BCF亠CDE82 =16,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积4比等于夹这个角的两边长度的乘积比”S AEF =8,S EFG =8,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到S BFC =16,S ABFE =32,S J ABF =24,所以S ABG =12平方厘米.【例14】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】如图,将原图扩展成一个大正三角形 DEF ,则 AGF 与CEH 都是正三角形.假设正六边形的边长为为 a ,则■ AGF 与 CEH 的边长都是4a ,所以大正三角形 DEF 的边长为4 2-1=7,那么它的面积为单位小正三角形面积的49倍•而一个正六边形是由 形组成的,所以一个单位小正三角形的面积为1,三角形DEF 的面积为畫. 6 66个单位小正三角4 3 12由于FA =4a , FB =3a ,所以「AFB 与三角形 DEF 的面积之比为 一—=一.7 7 49【解析】G C【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线 AE 外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边1 1 11 2形面积的丄,所以虚线外图形的面积等于 1 3 •丄2 =31,所以五边形的面积是 10-3」.6 6 33 3【解析】CA 至F ,使AF =3AC ,求三角形 DEF 的面积.同理可知 BDC 、 AEC 与三角形DEF 的面积之比都为 応,所以「ABC的面积占三角形DEF 面积的1 -12 3 =迢,所以 ABC 的面积的面积为49 4949 13 136 49 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 _________。
六年级奥数专题—几何五大模型—鸟头模型学习与巩固

几何五大模型——鸟头模型一 两点都在边上:鸟头定理:(现出“鸟头模型”。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE △ABC S AD ×AE=S AB ×ACED C B A二 一点在边上,一点在边的延长线上:△CDE△ABC S CD ×CE =S BC ×AC例 1 如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC的面积是平方厘米.例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC的面积是16平方厘米,求△ABC的面积。
(2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积是12平方厘米,求△ABC的面积。
例3 已知△DEF的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积。
例4 三角形ABC 面积为1,AB 边延长一倍到D ,BC 延长2倍到E ,CA 延长3倍到F ,问三角形DEF 的面积为多少?FEDC BA例5 长方形ABCD 面积为120,EF 为AD 上的三等分点,G 、H 、I 为DC 上的四等分点,阴影面积是多大?例6 如图,过平行四边形ABCD内的一点P作边AD、BC的平行线EF、GH,若PBD 的面积为8平方分米,求平行四边形PHCF的面积比平行四边形PGAE的面积大多少平方分米?作业:1. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。
2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且12AN BN.那么,阴影部分的面积等于 .AB CD M N 图13. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、BID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少?I HGFED CB A4. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积。
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:二、鸟头模型的原理剖析三、鸟头模型的方法运用鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知AD:BD=2:3 ,AE:EC=3:1,三角形ADE的面积是6平方厘米,求三角形ABC的面积?第一步:标条件第二步:确定等角位置 A小夹边AD×AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB×AC第三步:利用鸟头模型结论S△ADE:S△ABC=小夹边乘积:大夹边乘积=(2×3):(5×4)=6:20=3:103:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6÷3=2平方厘米/份;所求三角形 ABC的面积是10份,2×10=20 平方厘米。
例2:如图,已知BC:CD=5:2,AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形CDE的面积?第一步:标条件第二步:确定补角位置 C小夹边CD×CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA×CB第三步:利用鸟头模型结论S△CDE:S△ABC=小夹边乘积:大夹边乘积=(2×1):(2×5)=2:10=1:51:5的意思是:三角形CDE的面积是1份,三角形ABC的面积是5份。
第四步:先除后乘算面积三角形ABC的面积是20平方厘米,对应5份,20÷5=4 平方厘米/份;所求三角形 CDE的面积是1份,4×1=4平方厘米。
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:二、鸟头模型的原理剖析三、鸟头模型的方法运用鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知AD:BD=2:3,AE:EC=3:1,三角形ADE的面积是6平方厘米,求三角形ABC的面积?第一步:标条件第二步:确定等角位置A小夹边AD×AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB×AC第三步:利用鸟头模型结论S△ADE:S△ABC=小夹边乘积:大夹边乘积=(2×3):(5×4)=6:20=3:103:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6÷3=2平方厘米/份;所求三角形ABC的面积是10份,2×10=20平方厘米。
例2:如图,已知BC:CD=5:2,AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形CDE的面积?第一步:标条件第二步:确定补角位置C小夹边CD×CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA×CB第三步:利用鸟头模型结论S△CDE:S△ABC=小夹边乘积:大夹边乘积=(2×1):(2×5)=2:10=1:51:5的意思是:三角形CDE的面积是1份,三角形ABC的面积是5份。
第四步:先除后乘算面积三角形ABC的面积是20平方厘米,对应5份,20÷5=4平方厘米/份;所求三角形CDE的面积是1份,4×1=4平方厘米。
小学奥数_几何五大模型(鸟头模型)

模型二 鸟头模型如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .三角形等高模型与鸟头模型【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBA AB CDE【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S =又∵5AB AD =∴515ADE ABE ABCS S S=÷=÷,∴1515ABCADESS==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDES S=又∵4BD DC ==, ∴2ABC ABD S S =,∴6ABCBDESS=,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABCS S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 (2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =,1ABC S =, ∴S1DBC=.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯. 又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES=.所以186318DEFABCFCEADFBDESS SS S=+++=+++=.【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABCS=,所以0.5FCES=.同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCB【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS =,32ABFE S =,24ABFS=,所以12ABGS=平方厘米.【例 14】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .BDCA【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.。
4几何五大模型——鸟头模型

---------------------------------------------------------------最新资料推荐------------------------------------------------------4几何五大模型——鸟头模型几何五大模型鸟头模型一两点都在边上:鸟头定理:(现出鸟头模型。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE△ABCS ADAE=S ABAC EDC BA 二一点在边上,一点在边的延长线上:△CDE△ABCS CDCE=S BCAC EDCBA 本讲要点如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为 5 平方厘米,△ ABC 的面积是平方厘米.例例 2 (1 )如图在△ABC 中,D 、E 分别是AB ,AC 上的点,且AD:AB=2:5, AE:AC=4:7, △ABC 的面积是的面积是 16 平方厘米,求△ABC 的面积。
(2 )如图在△ABC 中,D 在 BA 的延长线上,E 在在 AC 上,且 AB:AD=5:2 ,AE:EC=3:2, △ADE 的面积是的面积是 12 平方厘米,求△ABC 的面积。
已知△DEF 的面积为12 平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
1 / 22例例 1 例例 2 例例 3 三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少?三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少? FEDCBA 例例 4 例例 5 长方形ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?长方形 ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?如图,过平行四边形 ABCD 内的一点 P 边作边 AD 、 BC 的平行线 EF 、 GH ,若PBD 为的面积为 8平方分米,求平行四边形 PHCF 的面积比平行四边形 PGAE 的面积大多少平方分米? AB CDEFGHP 例例 61. 如下左图,在ABC △ 中,D 、E 分别是 BC 、AB 的三等分点,且ABC △ 的面积是 54 ,求CDE △ 的面积。
六年级奥数专题-4几何五大模型——鸟头模型

几何五大模型——鸟头模型一 两点都在边上:鸟头定理:(现出“鸟头模型”。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE △ABC S AD ×AE =S AB ×ACE DC BA二 一点在边上,一点在边的延长线上: △CDE △ABC S CD ×CE =S BC ×AC本讲要点例1如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC的面积是平方厘米.例2例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC 的面积是16平方厘米,求△ABC的面积。
(2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE 的面积是12平方厘米,求△ABC的面积。
已知△DEF 的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
三角形ABC 面积为1,AB 边延长一倍到D ,BC 延长2倍到E ,CA 延长3倍到F ,问三角形DEF 的面积为多少?FE DC BA例4例3长方形ABCD 面积为120,EF 为AD 上的三等分点,G 、H 、I 为DC 上的四等分点,阴影面积是多大?如图,过平行四边形ABCD 内的一点P 作边AD 、BC 的平行线EF 、GH ,若PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?例6例51. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。
2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且12AN BN.那么,阴影部分的面积等于 .AB CD M N 图1家庭作业 B3. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、ID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少?IHG FE DC B A4.5. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积。
小学奥数-几何五大模型(鸟头模型).

模型二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.三角形等高模型与鸟头模型EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCDE【解析】 连接BE .∵3EC AE =∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC△的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形中,E为的中点,2AF CF =,三角形(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接.三角形面积是三角形面积的2倍,而三角形面积是三角形面积的2倍,所以三角形面积是三角形面积的3倍;又因为平行四边形的面积是三角形面积的2倍,所以平行四边形的面积是三角形面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB ECDDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 (2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCBA AB CDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD .∵11ABC DBCS S=,1ABC S =,∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCES AC BC SFC CE ⋅⨯===⋅⨯.又1ABC S =,所以8FCE S =. 同理可得6ADF S =,3BDE S =.所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=.【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBES AB BC S BE BF⋅⨯===⋅⨯△△.又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCDEFGHS S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD EF GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =,所以0.5FCE S =. 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S .SGF E DCBA【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABC DEF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =,32ABFE S =,24ABF S =,所以12ABG S =平方厘米.【例 14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .B DCEA【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是121036-=.33最新文件仅供参考已改成word文本。
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:S/1ABC ABx ACSAADE ADxAE、鸟头模型的原理剖析证明:在三角形ABC 中,连接BE,S/XABE _ AE S/\ABC~Hc r利用等式的性质,左右两边分别相乘得:S 厶 ADE SAABE AD AE______ X ______ = ___ x ___SHABE SiXABC - AB AC5 SHADE ADxAES/\ABC ~ ABx AC三、鸟头模型的方法运用 鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积 第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知 AD:BD=2:3 ,AE:EC=3:1,三角形ADE 的面积是6平方厘米,求三角形 ABC 的面积?则有SAADE _ AD S/XABE 一AB第一步:标条件第二步:确定等角位置A小夹边AD X AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB X AC第三步:利用鸟头模型结论SA\DE: S A ABC=小夹边乘积:大夹边乘积=(2 X3):(5 X4)=6:20=3:10 3:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6 +3=2平方厘米/份;所求三角形ABC的面积是10份,2 X 10=20平方厘米。
例2 :如图,已知BC: CD=5:2 , AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形的面积?第一步:标条件第二步:确定补角位置C小夹边CD X CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA X CBSMDE:SA\BC=小夹边乘积:大夹边乘积=(2 X1):(2 X5)=2:10=1:5CDE第三步:利用鸟头模型结论1:5的意思是:三角形 CDE 的面积是1份,三角形ABC 的面积是5份。
小学奥数几何五大模型鸟头模型.

三角形等高模型与鸟头模型模型二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角 )两夹边的乘积之比.如图在△ABC中,D,E分别是AB,AC上的点如图⑴(或D在BA的延伸线上,E在AC上如图2),则S△ABC:S△ADE(AB AC):(AD AE)ADADEEB C B C图⑴图⑵【例1】如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB2:5,AE:AC4:7,S△ADE16平方厘米,求△ABC的面积.AAD DE EB C B C【分析】连结BE,S△ADE:S△ABE AD:AB2:5(24):(54),S△ABE:S△ABC AE:AC4:7(45):(75),所以S△ADE:S△ABC(24):(75),设S△ADE8份,则△35份,△16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ABC的SABC SADE面积是平方厘米.由此我们获得一个重要的共角定理:共角三角形的面积比等于(相70定理,对应角等角或互补角)两夹边的乘积之比.page1of7【坚固】如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,假如三角形ADE的面积等于1,那么三角形ABC的面积是多少?A ADE D EB CB C【分析】连结BE.∵EC3AE∴S ABC3S ABE又∵AB5AD∴S ADE S ABE5 S ABC 15,∴S ABC15S ADE15.【坚固】如图,三角形ABC被分红了甲(暗影部分)、乙两部分,BD DC 4,BE 3,AE6,乙部分面积是甲部分面积的几倍?A AEB甲【分析】连结AD.∵BE3,AE6∴AB3BE,SABD乙E乙甲C B CD D3S BDE又∵BD DC4,∴S ABC2S ABD,∴S ABC6S BDE,S乙5S甲.【例2】如图在△ABC中,D在BA的延伸线上,E在AC上,且AB:AD5:2,AE:EC3:2,S△ADE12平方厘米,求△ABC的面积.D DA AEEB C B C【分析】连结BE,S△ADE:S△ABE AD:AB2:5(23):(53)S△ABE:S△ABC AE:AC3:(32)(35):(32)5,所以S△ADE:S△ABC(32):5(32)6:25,设S△ADE6份,则S△ABC25份,S△ADE12平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ABC的面积是50平方厘米.由此我们获得一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】以以下图,在平行四边形ABCD中,E为AB的中点,AF2CF,三角形AFE(图中暗影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?page2of7D CFAEB【分析】连结FB .三角形AFB 面积是三角形CFB 面积的 2倍,而三角形 AFB 面积是三角形 AEF 面积的2倍,所以三角形ABC 面积是三角形 AEF 面积的3倍;又因为平行四边形的面积是三角形 ABC 面积的2倍,所以平行四边形的面积是三角形AFE面积的(32) 6倍.所以,平行四边形的面积为648(平方厘米).【例 4】已知△DEF 的面积为7平方厘米,BE CE,AD2BD,CF 3AF ,求△ABC 的面积.AFDBCE【分析】S △BDE :S △ABC(BD BE):(BABC)(1 1):(2 3) 1:6,S△CEF:S△ABC(CE CF):(CBCA)(1 3):(2 4) 3:8S △ADF :S △ABC(AD AF):(AB AC)(21):(3 4)1:6设△ ABC 24份,则 △BDE 4份,△ 4份,△ CEF 9份,△24 4 497份,恰巧是7S S S ADFSS DEF平方厘米,所以S △ABC 24平方厘米【例 5】如图,三角形ABC 的面积为 3平方厘米,此中 AB:BE2:5,BC:CD3:2 ,三角形BDE 的面积是多少?ABEABEC CDD【分析】因为ABC DBE 180,所以能够用共角定理,设 AB2份,BC3份,则BE5份,BD 3 25份,由共角定理 S △ABC :S △BDE (AB BC):(BE BD)(23):(55)6:25,设S△ABC6份,恰巧是 3平方厘米,所以1份是0.5平方厘米,25份就是250.5 12.5平方厘米,三角形BDE 的面积是12.5 平方厘米【例 6】(2007年”走美”五年级初赛试题)以以下图,正方形ABCD 边长为6厘米,AE1AC ,CF1BC .三角形DEF 的面积为_______平方厘米.3 3ADEBF Cpage3of7【分析】由题意知AES △CEF :S △ABC11 2AC .依据”共角定理”可得,AC 、CFBC ,可得CE333(CFCE):(CB AC)12:(3 3)2:9;而△ABC662 18;所以△CEF4;SS同理得,S △CDE :S △ACD 2:3;,S △CDE 18 3212,S △CDF 6故△ △ △ △4 126 10(平方厘米).S DEF S CEF S DEC S DFC【例 7】如图,已知三角形 ABC 面积为1 ,延伸AB 至D ,使BDAB ;延伸BC 至E ,使CE2BC ;延伸CA 至F ,使AF 3AC ,求三角形DEF 的面积.FFA EAEBCBCDD【分析】(法1)此题是性质的频频使用.连结AE 、CD .S ABC 11 ,∵,S ABCS DBC 1∴S DBC1.同理可得其他,最后三角形 DEF 的面积18.(法2)用共角定理∵在 ABC 和CFE 中,ACB 与FCE 互补,S ABC AC BC 1 11∴FC CE 4 2.SFCE8又S ABC1,所以S FCE 8 .同理可得S ADF 6,S BDE3.所以S DEF S ABCSFCESADFSBDE 186318.【例 8】如图,平行四边形ABCD ,BE AB ,CF 2CB ,GD 3DC ,HA 4AD ,平行四边形ABCD 的面积是2,求平行四边形 ABCD 与四边形 EFGH 的面积比.HHA B EABEGDCGDCFF【分析】连结AC 、BD .依据共角定理∵在△ABC 和△BFE 中, ABC 与 FBE 互补,S△ABC AB BC 1 1 1.∴BE BF 1 3 3S△FBE又S △ABC 1,所以S △FBE 3.同理可得S△GCF8,S △DHG 15,S △AEH 8.page4of7所以S EFGH S△AEH S△CFG S△DHG S△BEF S ABCD8815+3+236.SABCD21所以36.SEFGH18【例9】如图,四边形EFGH的面积是66平方米,EAAB,CB BF,DC CG,HD DA,求四边形ABCD 的面积.H HD C GDC GA BF A BFE E【分析】连结BD.由共角定理得S△BCD:S△CGF(CDCB):(CG CF)1:2,即S△CGF2S△CDB同理S△ABD:S△AHE1:2,即S△AHE2S△ABD所以S△AHE S△CGF2(S△CBDS△ADB)2S四边形ABCD连结AC,同理能够获得S△DHG S△BEF2S四边形ABCDS四边形EFGH S△AHES△CGFS△HDGS△BEFS四边形ABCD5S四边形ABCD所以S四边形ABCD66513.2平方米【例10】如图,将四边形ABCD的四条边AB、CB、CD、AD分别延伸两倍至点E、F、G、H,若四边形ABCD的面积为5,则四边形EFGH的面积是.F FE B A E B AG C GCD DH H【分析】连结AC、BD.因为BE2AB,BF2BC,于是S BEF4S ABC,同理S HDG4S ADC.于是S BEF S HDG4S ABC4S ADC4S ABCD.再因为AE3AB,AH3AD,于是S AEH9S ABD,同理S CFG9S CBD.于是S AEH S CFG9S ABD9S CBD9S ABCD.那么S EFGH S BEF S HDG S AEH S CFG S ABCD4S ABCD9S ABCD S ABCD12S ABCD60.【例11】如图,在△ABC中,延伸AB至D,使BD AB,延伸BC至E,使CE 1,F是AC的BC中点,若△ABC的面积是2,则△DEF的面积是多少?2AFB C ED【分析】∵在△ABC和△CFE中,ACB与FCE互补,page5of7∴S△ABC AC BC224.S△FCE FC CE111又S ABC2,所以S FCE0.5.同理可得S△ADF2,S△BDE3.所以S△DEF S△ABC S△CEF S△DEB S△ADF20.5323.5【例12】如图,S△ABC1,BC5BD,AC4EC,DG GS SE,AF FG.求S FGS.AFG SEB CD【分析】此题题目自己很简单,但它把本讲的两个重要知识点交融到一同,既能够看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的频频运用,也能够看作是找点,最妙的是此中包括了找点的3种状况.最后求得S△432111.FGS的面积为△S FGS4322105【例13】以以下图,正方形ABCD边长为8厘米,E是AD的中点,F是CE的中点,G是BF的中点,三角形ABG的面积是多少平方厘米?A ED AEDF FB GC BGC【分析】连结AF、EG.因为S△BCF1216,依据”当两个三角形有一个角相等或互补时,这两个三角形的面积S△CDE84比等于夹这个角的两边长度的乘积比”SAEF8,S EFG8,再依据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,获得S BFC16,S ABFE32,SABF24,所以S ABG12平方厘米.【例14】四个面积为1的正六边形如图摆放,求暗影三角形的面积.F HA EBG CD【分析】如图,将原图扩展成一个大正三角形DEF,则AGF与CEH都是正三角形.假定正六边形的边长为为a,则AGF与CEH的边长都是4a,所以大正三角形DEF的边长为4 2 1 7,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角page6of7形构成的,所以一个单位小正三角形的面积为1,三角形DEF 的面积为49.66因为FA 4a ,FB3a ,所以AFB 与三角形DEF 的面积之比为4 3 12.77 49同理可知BDC 、AEC 与三角形DEF 的面积之比都为12,所以ABC 的面积占三角形DEF 面积49的112 313,所以ABC 的面积的面积为 49 13 13.49 49649 6【坚固】已知图中每个正六边形的面积都是 1,则图中虚线围成的五边形 ABCDE 的面积是.EA DB C【分析】从图中能够看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中能够看出,每个三角形都是一个正六边 形面积的 1,所以虚线外图形的面积等于 1 3 1 2 31,所以五边形的面积是10 3162.6 6 333精选文档page7of7。
几何五大模型

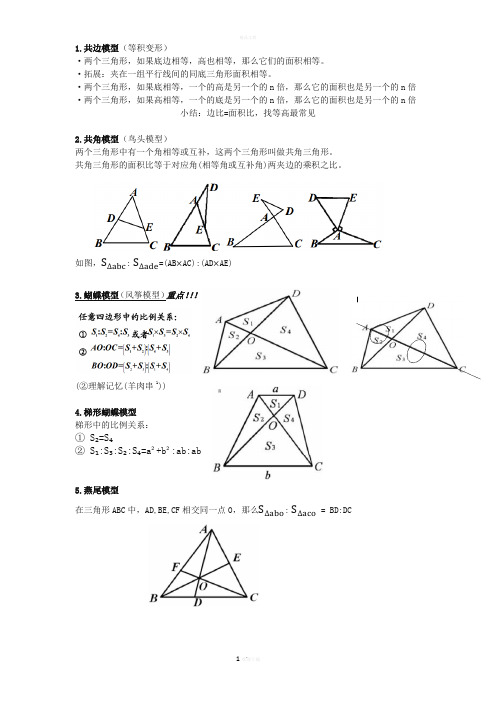
1.共边模型(等积变形)
·两个三角形,如果底边相等,高也相等,那么它们的面积相等。
·拓展:夹在一组平行线间的同底三角形面积相等。
·两个三角形,如果底相等,一个的高是另一个的n倍,那么它的面积也是另一个的n倍
·两个三角形,如果高相等,一个的底是另一个的n倍,那么它的面积也是另一个的n倍
小结:边比=面积比,找等高最常见
2.共角模型(鸟头模型)
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角
三角
形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,S?abc:S?ade=(AB×AC):(AD×AE)
A.牢记公式
3.
蝴蝶模型(风筝模型)重点!!!
(②理解记忆(羊肉串1))
4.梯形蝴蝶模型
梯形中的比例关系:
①S?=S?
②S?:S?:S?:S?=a2+b2:ab:ab
5.燕尾模型
在三角形ABC中,AD,BE,CF相交同一点O,那么S?abo:
S ?aco
= BD:DC
A.牢记公式。
几何五大模型
1.共边模型(等积变形)
·两个三角形,如果底边相等,高也相等,那么它们的面积相等。
·拓展:夹在一组平行线间的同底三角形面积相等。
·两个三角形,如果底相等,一个的高是另一个的n倍,那么它的面积也是另一个的n倍·两个三角形,如果高相等,一个的底是另一个的n倍,那么它的面积也是另一个的n倍
小结:边比=面积比,找等高最常见
2.共角模型(鸟头模型)
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,:=(AB AC):(AD AE)
3.蝴蝶模型(风筝模型)重点!!!
(②理解记忆(羊肉串1))
4.梯形蝴蝶模型
梯形中的比例关系:
①S₂=S₄
②S₁:S₃:S₂:S₄=a²+b²:ab:ab
5.燕尾模型
在三角形ABC中,AD,BE,CF相交同一点O,那么: = BD:DC
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
第23讲 五大模型——共边模型、鸟头模型

【例2】 (★★★) 如图,由面积分别为2、3、5、7的四个三角形拼成一个大 三角形,已知: S△ADE 2, S△AEC 5, S△BDF 7, S△BCF 3, 那么三角形BEF的面积为___________。
【例3】 (★★★★) 如图,在角MON的两边上分别有A、C、E及B、D、F六个点,并且 △OAB 、△ABC 、 △ BCD、 △CDE、 △DEF 的面积都等于1,则 △DCF的面积等于 。
【例4】 (★★★★) 等腰 △ABC中,AB=AC=12cm,BD、DE、EF、FG把它的面积5等分, 求AF、FD、DC、AG、GE、EB的长。
【例5】(★★★) 已知四边形ABCD、BEFG、CHIJ为正方形,正方形ABCD边长为10, 正方形BEFG边长为6,求阴影部分的面积。
【例6】(★★★★) E、M分别为直角梯形ABCD两边上的点,且DQ、CP、ME彼此平行, 若 AD=5, BC=7,AE=5 , EB=3。求阴影部分的面积。
大海点睛 一、本讲重点知识回顾
等积变形 边比=面积比 共角模型(鸟头模型)
如图, S△ABC : S△ADE ( AB AC ) : ( AD AE )
大海点睛 二、本讲经典例题
例2,例3,例5,例7,例8
第23讲 五大模型——共边模型、鸟头模型
大海传功
等积变形 1. 两个三角形,如果底边相等,高也相等,那么它们的
面积相等。 拓展:夹在一组平行线间的同底三角形面积相等。 2. 两个三角形,如果底相等,一个的高是另一个的n倍, 那么它的面积也是另一个的n倍; 两个三角形,如果高相等,一个的底是另一个的n倍, 那么它的面积也是另一个的n倍。
共角模型(鸟头模型) 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在△ABC中,D,E分别是AB,AC上的点如图(1)(或D在BA的延长线上,E在AC上如图2),则ABC : ADE -(AB AC): (AD AE)厘米,求△ ABC的面积.【解析】连接BE , S A ADE : S A ABE= AD : AB =2 :5 =(2 4): (5 4),S A ABE : S A ABC = AE : AC = 4 : 7 = (4 5) : (7 5),所以S^ADE: S^ ABC= (2 4) : (7 5),设S A ADE= 8 份,则S A ABC =35份,S A ADE =16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ ABC的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比三角形等高模型与鸟头模型【例1】如图在△ ABC中, D,E分别是AB,AC上的点,且AD: AB =2:5 ,AE:AC =4:7 , S^ADE =16 平方图⑵【巩固】如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形么三角形ABC的面积是多少?•/ EC =3AE--S A BC = 3S ABE又••• AB =5AD--S|_ADE = S_ABE 5 = S_ ABC 15 ,••• S ABC如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4 , BE=3 , AE=6,乙部分面积是甲部分面积的几倍?•/ BE =3 , AE =6 --AB = 3BE , S ABD=3S BDE又T BD =DC =4 ,--S ABC =2S ABD,…S ABC - 6S BDE ,【例2】如图在△ ABC中,D在BA的延长线上,E在AC上,且AB: AD =5: 2 , AE:EC=3:2 , S A ADE =12平方厘米,求△ ABC的面积.【解析】连接BE , S A ADE : S A ABE= AD: AB =2:5 =(2 3): (5 3) S AABE : S A ABC=AE: AC =3:(3 2)=(3 5): 1(3 2) 5】,所以S A ADE : S A ABC - (3 2) : 5 (3 2^ - 6 : 25,设S A ADE = 6 份,贝V S A ABC = 25 份,S A ADE =12 平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】如图所示,在平行四边形ABCD中,E为AB的中点,AF =2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?ADE的面积等于1,那= 15S ADE =15 .【巩固】【解析】连接AD .【解析】【解析】 连接FB•三角形AFB 面积是三角形CFB 面积的2倍,而三角形 AFB 面积是三角形 AEF 面积的2 倍,所以三角形 ABC 面积是三角形 AEF 面积的3倍;又因为平行四边形的面积是三角形 ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的(3 2)= 6倍•因此,平行四边形的面积为8 6 =48(平方厘米).【例4】已知△ DEF 的面积为7平方厘米,BE =CE, AD =2BD,CF =3AF ,求△ ABC 的面积.【解析】BDE :S S BC =(BDBE) :(BA BC)=(1 1):(2 3) =1:6 , S ^CEF : S ^ABC =(CECF) : (CB CA)=(13): (2 4) =3:8S ^ADF : S ^ABC = (AD AF ): (AB AC) = (2 1) : (3 4) =1:6设 S A ABC =24 份,则 S A BDE = 4 份,S ^ ADF =4 份,S ^ CEF = 9 份,S ^ DEF = 24 - 4- 4 - 9 = 7 份,恰好是 7 平方厘米,所以 S A ABC =24平方厘米如图,三角形 ABC 的面积为3平方厘米,其中 AB:BE=2:5 , BC:CD=3:2,三角形BDE 的面积 是多少?由于.ABC • . DBE =180,所以可以用共角定理,设 AB = 2份,BC =3份,贝U BE = 5份,BD =3 2=5 份,由共角定理 S A ABC : S A BDE =(AB BC):(BE BD)=(2 3):(5 5^ 6:25,设S A ABC =6份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是25 0.5=12.5平方厘米,三角 形BDE 的面积是12.5平方厘米【例6】(2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,AE 」AC ,CF 」BC .33角形DEF 的面积为 ________ 平方厘米.【例5】 【解析】 DFA 'B【解析】由题意知AE =1 AC、CF =1BC,可得CE二?AC •根据”共角定理”可得,3 3 3S A CEF : S A ABC = (CF x CE): (CB x AC) =(1x2》(3x3) =2:9 ;而S A ABC =6沃6壬2 丄8 ;所以S A CEF =4 ;同理得,S A CDE : S A ACD = 2 :3 ;, S A CDE =18-:-3 2 =12 , S A CDF =6故S A DEF=S A CEF■S A DEC-S A DFC = 4 1^6 =10(平方厘米)•ABC面积为1,延长AB至D,使BD=AB ;延长BC至E,使CE =2BC ;延长= 3AC,求三角形DEF的面积.(法1)本题是性质的反复使用.连接AE、CD •SABC1- ,S ABC - I ,S LDBC 1--S DBC =1•同理可得其它,最后三角形DEF的面积=18 •(法2)用共角定理•••在ABC和LCFE中,.ACB与.FCE互补,.S JABC AC BC 1 汇1 1…S FCE FC CE _4 2 _8 •又S ABC =1,所以S FCE -8•同理可得ADF - 6 , §BDE =3•所以S LDE F = S_ABC ' S_FCE ' S ADF S BDE -1 8 6 '3=18 •【例8】如图,平行四边形ABCD , BE =AB , CF =2CB , GD =3DC , 面积是2 ,求平行四边形ABCD与四边形EFGH的面积比.【解析】连接AC、BD •根据共角定理•••在△ABC和A BFE中,• ABC与・FBE互补, .S A ABC _ AB BC 二1 勺二1"S A FBE一BE BF 1 3 3 •又S A ABC ~1,所以S A FBE =3 • 冋理可得S A GCF =8 , S A DHG =15 , S A AEH =8 •【例7】如图,已知三角形CA至F,使AF【解析】HA二4AD,平行四边形ABCD的□=S A AEH S^ CFG S^ DHG S A BEF S ABCD =8 8 15+3+2 =36 .【解析】连接BD •由共角定理得S A BCD:S A CGF =(CD CB): (CG CF) =1: 2,即S A CGF=2S A CDB冋理S A ABD : S A AHE =1: 2,即S A AHE =2 S A ABD所以S A AHE+S A CGF =2(S A CBD +S A人。
3)=22| 边形ABCD连接AC,冋理可以得到S A DHG'S A BEF =2S四边形ABCDS四边形EFGH - S\ AHESA CGF S A HDG S A BEF ' S四边形ABCD - 5S H边形ABCD所以S四边形ABCD=66一:一5 =13.2平方米AB、CB、CD、AD分别延长两倍至点E、F、G、H,若EFGH的面积是【解析】连接AC、BD .由于BE -2 AB , BF -2BC,于是S BEF =4S「ABC,冋理s HDG -4s ADC . 于是S B EF ■S.HDG =4S A BC 4S A DC =4 S ABCD .再由于AE =3AB , AH = 3AD,于是s AEH =9S.ABD,冋理S.CFG= 9s CBD .S AEH 'S.CFG =9S A BD 9S C BD =9S AB CD .S EFGH -S BEF'S.HDG'S A EH S C FG —S ABCD =4S ABCD *9S ABCD —S ABCD =12S ABCD =60 .1如图,在△ABC中,延长AB至D,使BD =AB,延长BC至E,使CE =丄BC , F是AC的2 中点,若△ABC的面积是2,则A DEF的面积是多少?【解析】•••在A ABC和A CFE中,.ACB与.FCE互补,所以S ABCDS EFGH2 136【例9】如图,四边形EFGH的面积是66平方米,的面积.EA = AB , CB =BF , DC =CG , HD =DA ,求四边形ABCD 所以S EFGH【例10】如图,将四边形ABCD的四条边四边形ABCD的面积为5,则四边形那么【例11】GS^ ABC AC BC 2 2 4S^ FCE FC CE 11 1又SABC=2,所以S FCE =0.5 .同理可得ADF =2 , BDE =3 .所以S A DEF = S A ABC S A CEF +S A DEB —S A ADF =2 0.5 3 —2 =3.5【例12】如图,S A ABC =1,BC=5BD , AC=4EC , DG=GS=SE, AF = FG •求S FGS【解析】本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.4 3 2 1 1 1最后求得S A FGS的面积为S A FGS:5 4 3 2 2 10【例13】如图所示,正方形ABCD边长为8厘米,三角形ABG的面积是多少平方厘米?【解析】如图,将原图扩展成一个大正三角形DEF,则AGF与CEH都是正三角形.假设正六边形的边长为为a,则AGF与CEH的边长都是4a,所以大正三角形DEF的边长为4 2-1=7,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角E是AD的中点, F是CE的中点,G是BF的中点, 比等于夹这个角的两边长度的乘积比”【解析】F H A ED1 49形组成的,所以一个单位小正三角形的面积为丄,三角形DEF的面积为兰•6 64 3 12由于FA =4a , FB =3a,所以AAFB与三角形DEF的面积之比为—7 7 4912同理可知ABDC、AEC与三角形DEF的面积之比都为,所以ABC的面积占三角形DEF面积4912 13 49 1313的1 一12 3 = 13,所以ABC的面积的面积为竺13•49 49 6 49 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边1 1 1 1 2形面积的1,所以虚线外图形的面积等于 1 3 •丄2 =3丄,所以五边形的面积是10-3」•6 6 3 3 31 2因为S A BCF二S A CDE二丄81 2 * * S =16,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积4SAEF - 8 , Q EFG 二8, 再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到Q BFC =16 , S ABFE =32 ,SABF =24,所以S ABG - 12平方厘米.【例14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.。
