八年级数学矩形、菱形、正方形证明解专题练习(详细答案)
华师大版八年级下册数学第19章 矩形、菱形与正方形含答案(学生专用)

华师大版八年级下册数学第19章矩形、菱形与正方形含答案一、单选题(共15题,共计45分)1、如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值﹣1.其中正确的说法有()个.A.4B.3C.2D.12、顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是()A.矩形B.菱形C.正方形D.不确定3、已知一个四边形的对角线互相垂直,那么顺次连接这个四边形的四边中点所得的四边形是()A.矩形B.菱形C.等腰梯形D.正方形4、平行四边形ABCD的两条对角线相等,则平行四边形ABCD一定是().A.菱形B.矩形C.正方形D.等腰梯形5、如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D 重合,折痕为EF,则△ABE的面积为()A.6cmB.8cmC.10cmD.12cm6、如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是()A.7B.8C.9D.107、下列性质中,矩形不一定具有的是( )A.对角线相等B.对角线互相平分C.4个内角相等D.一条对角线平分一组对角8、学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;丙同学说:判定四边形的对角线相等,并且互相垂直平分;丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.上述四名同学的说法中,正确的是()A.甲、乙B.甲、丙C.乙、丙、丁D.甲、乙、丙、丁9、用两个完全相同的直角三角形拼下列图形:(1)平行四边形,(2)矩形,(3)菱形,(4)正方形,(5)等腰三角形,(6)等边三角形,一定可以拼成的图形是( )A.(1)(4)(5)B.(2)(5)(6)C.(1)(2)(3)D.(1)(2)(5).10、如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为()A.平行四边形B.矩形C.菱形D.正方形11、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE 折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为()A.1或2B.2或3C.3或4D.4或512、如图,是△EBD以正方形ABCD的对角线BD为边的正三角形,EF⊥DF,垂足为F,则∠AEF的度数是()A.15°B.30°C.45°D.60°13、平面内有一个角是60°的菱形绕它的中心旋转,使它与原来的菱形重合,那么旋转的角度至少是()A.90°B.180°C.270°D.360°14、如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为()A.1.2B.1.3C.1.4D.2.415、下列条件中,能判定一个四边形为矩形的条件是( )A.对角线互相平分的四边形B.对角线相等且平分的四边形C.对角线相等的四边形D.对角线相等且互相垂直的四边形二、填空题(共10题,共计30分)16、已知矩形的面积是,其中一边长为,则对角线长为________.17、如图,矩形中,,,是边上一点,将沿翻折,点恰好落在对角线上的点处,则的长为________.18、如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为________.19、如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于________度20、已知菱形的边长为4,∠A=60°,则菱形的面积为________.21、如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2cm.则图中阴影部分面积为________ .22、如图,在平面直角坐标系中,矩形的顶点O落在坐标原点,点A、点C分别位于x轴,y轴的正半轴,G为线段上一点,将沿翻折,O点恰好落在对角线上的点P处,反比例函数经过点B.二次函数的图象经过、G、A三点,则该二次函数的解析式为________.(填一般式)23、如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为________24、如图,在中,,点的坐标为,点在轴上,轴.将沿翻折得到,直线过点,则四边形的面积为________.25、如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B 在y轴的正半轴上,反比例函数y=(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为________.三、解答题(共5题,共计25分)26、如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.27、如图,科博会上某公司展示了研发的绘图智能机器人,该机器人由机座、手臂和末端操作器三部分组成,底座AE⊥直线EL且AE=25 cm,手臂AB=BC =60 cm,末端操作器CD=35 cm,AF∥直线EL.当机器人运作时,∠BAF=45°,∠ABC=75°,∠BCD=60°,求末端操作器节点D到地面直线EL的距离.(结果保留根号)28、如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.①求证:△DAE≌△DCF;②求证:△ABG∽△CFG.29、如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1:),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)30、在矩形中,已知,在边上取点,使,连结,过点作,与边或其延长线交于点.猜想:如图①,当点在边上时,写出线段与的大小关系。
八年级数学 矩形、菱形、正方形 证明解答题专题练习(详细答案)

矩形、菱形、正方形(解答题)1.如图,在平行四边形ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.(1)求证:△ABE≌△CDF;(2)当四边形AECF为菱形时,求出该菱形的面积.2.如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD 的延长线于点F,求证:DF=BE.3.如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.4.已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.5.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.6.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.7.如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE 的延长线于点F.(1)求证:四边形ECBF是平行四边形;(2)当∠A=30°时,求证:四边形ECBF是菱形.8.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD(1)求∠AOD的度数;(2)求证:四边形ABCD是菱形.9.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.10.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.11.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E 关于AC所在直线的对称点.(1)证明:四边形CFAE为菱形;(2)连接EF交AC于点O,若BC=10,求线段OF的长.12.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.(1)四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为,∠ABC=°.(直接填写结果)13.如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)14.如图,已知BD是矩形ABCD的对角线.(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.15.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)若AB=6,AC=10,求四边形AECF的面积.16.如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.(1)求证:CP=AQ;(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.17.如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.18.已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.19.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1)当AN平分∠MAB时,求DM的长;(2)连接BN,当DM=1时,求△ABN的面积;(3)当射线BN交线段CD于点F时,求DF的最大值.20.如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.21.如图,将平行四边形ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.(1)求证:△BEF≌△CDF;(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.22.阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?小敏在思考问题是,有如下思路:连接AC.结合小敏的思路作答(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:(2)如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.23.如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.(1)求证:△PHC≌△CFP;(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.24.已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.25.如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.(1)求证:△ABE≌△EGF;=2S△ECF,求BE.(2)若AB=2,S△ABE26.已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ 于点P.(1)求证:AP=BQ;(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.27.在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.(2)若α为锐角,tanα=,当AE取得最小值时,求正方形OEFG的面积.(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为:1?若能,求点P的坐标;若不能,试说明理由28.如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.(1)已知EO=,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.29.如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于F.求证:AE=EF.30.如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.答案与解析1.(2016•安顺)如图,在平行四边形ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.(1)求证:△ABE≌△CDF;(2)当四边形AECF为菱形时,求出该菱形的面积.【分析】第(1)问要证明三角形全等,由平行四边形的性质,很容易用SAS证全等.第(2)要求菱形的面积,在第(1)问的基础上很快知道△ABE为等边三角形.这样菱形的高就可求了,用面积公式可求得.【解答】(1)证明:∵在▱ABCD中,AB=CD,∴BC=AD,∠ABC=∠CDA.又∵BE=EC=BC,AF=DF=AD,∴BE=DF.∴△ABE≌△CDF.(2)解:∵四边形AECF为菱形,∴AE=EC.又∵点E是边BC的中点,∴BE=EC,即BE=AE.又BC=2AB=4,∴AB=BC=BE,∴AB=BE=AE,即△ABE为等边三角形,▱ABCD的BC边上的高为2×sin60°=,∴菱形AECF的面积为2.【点评】考查了全等三角形,四边形的知识以及逻辑推理能力.(1)用SAS证全等;(2)若四边形AECF为菱形,则AE=EC=BE=AB,所以△ABE为等边三角形.2.(2016•广安)如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.【分析】连接AC,根据菱形的性质可得AC平分∠DAE,CD=BC,再根据角平分线的性质可得CE=FC,然后利用HL证明Rt△CDF≌Rt△CBE,即可得出DF=BE.【解答】证明:连接AC,∵四边形ABCD是菱形,∴AC平分∠DAE,CD=BC,∵CE⊥AB,CF⊥AD,∴CE=FC,∠CFD=∠CEB=90°.在Rt△CDF与Rt△CBE中,,∴Rt△CDF≌Rt△CBE(HL),∴DF=BE.【点评】此题考查了菱形的性质,角平分线的性质,关键是掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;角平分线的性质:角的平分线上的点到角的两边的距离相等.同时考查了全等三角形的判定与性质.3.(2016•荆州)如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.【分析】当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.【解答】解:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB,∴CD=DA=DB,∴∠DAC=∠DCA,∵A′C′∥AC,∴∠DA′E=∠A,∠DEA′=∠DCA,∴∠DA′E=∠DEA′,∴DA′=DE,∴△A′DE是等腰三角形.∵四边形DEFD′是菱形,∴EF=DE=DA′,EF∥DD′,∴∠C′EF=∠DA′E,∠EFC′=∠C′D′A′,∵CD∥C′D′,∴∠A′DE=∠A′D′C′=∠EFC′,在△A′DE和△EFC′中,,∴△A′DE≌△EFC′.【点评】本题考查平移、菱形的性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.4.(2016•淮安)已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.【分析】由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由SAS证明△ADE ≌△CDF即可.【解答】证明:∵四边形ABCD是菱形,∴AD=CD,∵点E、F分别为边CD、AD的中点,∴AD=2DF,CD=2DE,∴DE=DF,在△ADE和△CDF中,,∴△ADE≌△CDF(SAS).【点评】此题主要考查了全等三角形的判定、菱形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.5.(2016•苏州)如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D 作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.【分析】(1)根据平行四边形的判定证明即可;(2)利用平行四边形的性质得出平行四边形的周长即可.【解答】(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB,∴DE∥AC,∴四边形ACDE是平行四边形;(2)解:∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5,∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE的周长为AD+AE+DE=5+5+8=18.【点评】此题考查平行四边形的性质和判定问题,关键是根据平行四边形的判定解答即可.6.(2016•枣庄)如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.【分析】(1)根据锐角三角函数求出∠FPG,最后求出∠EPF.(2)先判断出Rt△PME≌Rt△PNF,再根据锐角三角函数求解即可,(3)根据运动情况及菱形的性质判断求出AP最大和最小值.【解答】解:(1)过点P作PG⊥EF于点G,如图1所示.∵PE=PF=6,EF=6,∴FG=EG=3,∠FPG=∠EPG=∠EPF.在Rt△FPG中,sin∠FPG===,∴∠FPG=60°,∴∠EPF=120°.(2)过点P作PM⊥AB于点M,作PN⊥AD于点N,如图2所示.∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC,AM=AN,PM=PN.在Rt△PME和Rt△PNF中,PM=PN,PE=PF,∴Rt△PME≌Rt△PNF,∴ME=NF.又AP=10,∠PAM=∠DAB=30°,∴AM=AN=APcos30°=10×=5,∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=10.(3)如图,当△EFP的三个顶点分别在AB,AD,AC上运动,点P在P′,P之间运动,∴P′O=PO=3,AO=9,∴AP的最大值为12,AP的最小值为6,【点评】此题是菱形的性质题,主要考查了菱形的性质,锐角三角函数,特殊角的三角函数,解本题的关键是作出辅助线.7.(2016•三明)如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.(1)求证:四边形ECBF是平行四边形;(2)当∠A=30°时,求证:四边形ECBF是菱形.【分析】(1)利用平行四边形的判定证明即可;(2)利用菱形的判定证明即可.【解答】证明:(1)∵D,E分别为边AC,AB的中点,∴DE∥BC,即EF∥BC.又∵BF∥CE,∴四边形ECBF是平行四边形.(2)∵∠ACB=90°,∠A=30°,E为AB的中点,∴CB=AB,CE=AB.∴CB=CE.又由(1)知,四边形ECBF是平行四边形,∴四边形ECBF是菱形.【点评】此题主要考查了平行四边形的判定以及菱形的判定与性质,利用平行四边形的判定以及菱形的判定是解题关键.8.(2016•抚顺)如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD(1)求∠AOD的度数;(2)求证:四边形ABCD是菱形.【分析】(1)首先根据角平分线的性质得到∠DAC=∠BAC,∠ABD=∠DBC,然后根据平行线的性质得到∠DAB+∠CBA=180°,从而得到∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,得到答案∠AOD=90°;(2)根据平行线的性质得出∠ADB=∠DBC,∠DAC=∠BCA,根据角平分线定义得出∠DAC=∠BAC,∠ABD=∠DBC,求出∠BAC=∠ACB,∠ABD=∠ADB,根据等腰三角形的判定得出AB=BC=AD,根据平行四边形的判定得出四边形ABCD是平行四边形,即可得出答案.【解答】解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∵AE∥BF,∴∠DAB+∠CBA,=180°,∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,∴∠AOD=90°;(2)证明:∵AE∥BF,∴∠ADB=∠DBC,∠DAC=∠BCA,∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∴∠BAC=∠ACB,∠ABD=∠ADB,∴AB=BC,AB=AD∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形,∵AD=AB,∴四边形ABCD是菱形.【点评】本题考查了等腰三角形的性质,平行四边形的判定,菱形的判定的应用,能得出四边形ABCD是平行四边形是解此题的关键.9.(2016•沈阳)如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.【分析】(1)欲证明∠CEB=∠CBE,只要证明∠CEB=∠ABD,∠CBE=∠ABD即可.(2)先证明四边形CEDB是平行四边形,再根据BC=BD即可判定.【解答】证明;(1)∵△ABC≌△ABD,∴∠ABC=∠ABD,∵CE∥BD,∴∠CEB=∠DBE,∴∠CEB=∠CBE.(2))∵△ABC≌△ABD,∴BC=BD,∵∠CEB=∠CBE,∴CE=CB,∵CE∥BD,∴四边形CEDB是平行四边形,∵BC=BD,∴四边形CEDB是菱形.【点评】本题考查全等三角形的性质、菱形的判定、平行四边形的判定等知识,熟练掌握全等三角形的性质是解题的关键,记住平行四边形、菱形的判定方法,属于中考常考题型.10.(2016•聊城)如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.【分析】先证明△AEF≌△CED,推出四边形ADCF是平行四边形,再证明△AED ≌△ABD,推出DF⊥AC,由此即可证明.【解答】证明:∵AF∥CD,∴∠AFE=∠CDE,在△AFE和△CDE中,,∴△AEF≌△CED.∵AF∥CD,∴四边形ADCF是平行四边形.由题意知,AE=AB,∠EAD=∠BAD,AD=AD,∴△AED≌△ABD.∴∠AED=∠B=90°,即DF⊥AC.∴四边形ADCF是菱形.【点评】本题考查菱形的判定、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,属于基础题,中考常考题型.11.(2016•德阳)如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.(1)证明:四边形CFAE为菱形;(2)连接EF交AC于点O,若BC=10,求线段OF的长.【分析】(1)根据直角三角形的性质得到CE=AB=EA,根据轴对称的性质得到AE=AF,CE=CF,得到CE=EA=AF=CF,根据菱形的判定定理证明结论;(2)根据菱形的性质得到OA=OC,OE=OF,根据三角形中位线定理求出OE,得到答案.【解答】(1)证明:∵∠ACB=90°,点E是AB边的中点,∴CE=AB=EA,∵点F是点E关于AC所在直线的对称点,∴AE=AF,CE=CF,∴CE=EA=AF=CF,∴四边形CFAE为菱形;(2)解:∵四边形CFAE为菱形;∴OA=OC,OE=OF,∴OE=BC=5,∴OF=5.【点评】本题考查的是菱形的判定和性质、轴对称的性质,掌握四条边相等的四边形是菱形、菱形的对角线垂直且互相平分是解题的关键.12.(2016•梅州)如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.(1)四边形ABEF是菱形;(选填矩形、菱形、正方形、无法确定)(直接填写结果)(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为10,∠ABC=120°.(直接填写结果)【分析】(1)先证明△AEB≌△AEF,推出∠EAB=∠EAF,由AD∥BC,推出∠EAF=∠AEB=∠EAB,得到BE=AB=AF,由此即可证明.(2)根据菱形的性质首先证明△AOB是含有30°的直角三角形,由此即可解决问题.【解答】解:(1)在△AEB和△AEF中,,∴△AEB≌△AEF,∴∠EAB=∠EAF,∵AD∥BC,∴∠EAF=∠AEB=∠EAB,∴BE=AB=AF.∵AF∥BE,∴四边形ABEF是平行四边形∵AB=AF,∴四边形ABEF是菱形.故答案为菱形.(2)∵四边形ABEF是菱形,∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,∵AB=10,∴AB=2BO,∵∠AOB=90°∴∠BA0=30°,∠ABO=60°,∴AO=BO=5,∠ABC=2∠ABO=120°.故答案为,120.【点评】本题考查菱形的判定和性质、平行四边形的性质、作图﹣基本作图等知识,解题的关键是全等三角形的证明,想到利用特殊三角形解决问题,属于中考常考题型.13.(2016•贺州)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)【分析】(1)由过AC的中点O作EF⊥AC,根据线段垂直平分线的性质,可得AF=CF,AE=CE,OA=OC,然后由四边形ABCD是矩形,易证得△AOF≌△COE,则可得AF=CE,继而证得结论;(2)由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,继而求得答案.【解答】(1)证明:∵O是AC的中点,且EF⊥AC,∴AF=CF,AE=CE,OA=OC,∵四边形ABCD是矩形,∴AD∥BC,∴∠AFO=∠CEO,在△AOF和△COE中,,∴△AOF≌△COE(AAS),∴AF=CE,∴AF=CF=CE=AE,∴四边形AECF是菱形;(2)解:∵四边形ABCD是矩形,∴CD=AB=,在Rt△CDF中,cos∠DCF=,∠DCF=30°,∴CF==2,∵四边形AECF是菱形,∴CE=CF=2,∴四边形AECF是的面积为:EC•AB=2.【点评】此题考查了矩形的性质、菱形的判定与性质以及三角函数等知识.注意证得△AOF≌△COE是关键.14.(2016•衢州)如图,已知BD是矩形ABCD的对角线.(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.【分析】(1)分别以B、D为圆心,比BD的一半长为半径画弧,交于两点,确定出垂直平分线即可;(2)连接BE,DF,四边形BEDF为菱形,理由为:由EF垂直平分BD,得到BE=DE,∠DEF=∠BEF,再由AD与BC平行,得到一对内错角相等,等量代换及等角对等边得到BE=BF,再由BF=DF,等量代换得到四条边相等,即可得证.【解答】解:(1)如图所示,EF为所求直线;(2)四边形BEDF为菱形,理由为:证明:∵EF垂直平分BD,∴BE=DE,∠DEF=∠BEF,∵AD∥BC,∴∠DEF=∠BFE,∴∠BEF=∠BFE,∴BE=BF,∵BF=DF,∴BE=ED=DF=BF,∴四边形BEDF为菱形.【点评】此题考查了矩形的性质,菱形的判定,以及作图﹣基本作图,熟练掌握性质及判定是解本题的关键.15.(2016•扬州)如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)若AB=6,AC=10,求四边形AECF的面积.【分析】(1)首先由矩形的性质和折叠的性质证得AB=CD,AD∥BC,∠ANF=90°,∠CME=90°,易得AN=CM,可得△ANF≌△CME(ASA),由平行四边形的判定定理可得结论;(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt △CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.【解答】(1)证明:∵折叠,∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°,∵四边形ABCD为矩形,∴AB=CD,AD∥BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在△ANF和△CME中,,∴△ANF≌△CME(ASA),∴AF=CE,又∵AF∥CE,∴四边形AECF是平行四边形;(2)解:∵AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt△CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC•AB=5×6=30.【点评】本题主要考查了折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.16.(2016•遵义)如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.(1)求证:CP=AQ;(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.【分析】(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE=BP=,得出EQ=PE+PQ=3,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE﹣BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD 的面积.【解答】(1)证明:∵四边形ABCD是矩形,∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,∴∠E=∠F,∵BE=DF,∴AE=CF,在△CFP和△AEQ中,,∴△CFP≌△AEQ(ASA),∴CP=AQ;(2)解:∵AD∥BC,∴∠PBE=∠A=90°,∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,∴BE=BP=1,AQ=AE,∴PE=BP=,∴EQ=PE+PQ=+2=3,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=AB•AD=2×4=8.【点评】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.17.(2016•广州)如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.【分析】首先证明OA=OB,再证明△ABO是等边三角形即可解决问题.【解答】解:∵四边形ABCD是矩形,∴OA=OC,OB=OD,AC=BD,∴AO=OB,∵AB=AO,∴AB=AO=BO,∴△ABO是等边三角形,∴∠ABD=60°.【点评】本题考查矩形的性质、等边三角形的判定和性质等知识,熟练掌握矩形的性质是解题的关键,属于基础题,中考常考题型.18.(2016•岳阳)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.【分析】由四边形ABCD为矩形,得到四个角为直角,再由EF与FD垂直,利用平角定义得到一对角互余,利用同角的余角相等得到一对角相等,利用ASA得到三角形BEF与三角形CFD全等,利用全等三角形对应边相等即可得证.【解答】证明:∵四边形ABCD是矩形,∴∠B=∠C=90°,∵EF⊥DF,∴∠EFD=90°,∴∠EFB+∠CFD=90°,∵∠EFB+∠BEF=90°,∴∠BEF=∠CFD,在△BEF和△CFD中,,∴△BEF≌△CFD(ASA),∴BF=CD.【点评】此题考查了矩形的性质,以及全等三角形的判定与性质,熟练掌握矩形的性质是解本题的关键.19.(2016•福州)如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1)当AN平分∠MAB时,求DM的长;(2)连接BN,当DM=1时,求△ABN的面积;(3)当射线BN交线段CD于点F时,求DF的最大值.【分析】(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=AD•tan∠DAM=即可;(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例=,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.【解答】解:(1)由折叠性质得:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB,∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=AD•tan∠DAM=3×tan30°=3×=;(2)延长MN交AB延长线于点Q,如图1所示:∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折叠性质得:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ,设NQ=x,则AQ=MQ=1+x,∵∠ANM=90°,∴∠ANQ=90°,在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2,∴(x+1)2=32+x2,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,=S△NAQ=×AN•NQ=××3×4=;∴S△NAB(3)过点A作AH⊥BF于点H,如图2所示:∵四边形ABCD是矩形,∴AB∥DC,∴∠HBA=∠BFC,∵∠AHB=∠BCF=90°,∴△ABH∽△BFC,∴=,∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:由折叠性质得:AD=AH,∵AD=BC,∴AH=BC,在△ABH和△BFC中,,∴△ABH≌△BFC(AAS),∴CF=BH,由勾股定理得:BH===,∴CF=,∴DF的最大值=DC﹣CF=4﹣.【点评】本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,熟练掌握矩形和折叠的性质,证明三角形相似和三角形全等是解决问题的关键.20.(2016•吉林)如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.【分析】根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形.【解答】证明:∵四边形ABCD为菱形,∴AC⊥BD,∴∠AOD=90°,∵DE∥AC,AE∥BD,∴四边形AODE为平行四边形,∴四边形AODE是矩形.【点评】本题考查了矩形的判定以及菱形的性质,还考查了平行四边形的判定,掌握平行四边形的判定方法是解题的关键.21.(2016•南通)如图,将▱ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.(1)求证:△BEF≌△CDF;(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.【分析】(1)先根据平行四边形的性质得出AB=CD,AB∥CD,再由BE=AB得出BE=CD,根据平行线的性质得出∠BEF=∠CDF,∠EBF=∠DCF,进而可得出结论;(2)根据平行四边形的性质可得AB∥CD,AB=CD,∠A=∠DCB,再由AB=BE,可得CD=EB,进而可判定四边形BECD是平行四边形,然后再证明BC=DE即可得到四边形BECD是矩形【解答】(1)证明:∵四边形ABCD是平行四边形,∵AB=CD,AB∥CD.∵BE=AB,∴BE=CD.∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,在△BEF与△CDF中,∵,∴△BEF≌△CDF(ASA);(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠A=∠DCB,∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,∴BF=CF,EF=DF,∵∠BFD=2∠A,∴∠BFD=2∠DCF,∴∠DCF=∠FDC,∴DF=CF,∴DE=BC,∴四边形BECD是矩形.【点评】此题主要考查的值矩形的判定及平行四边形的性质,关键是掌握平行四边形的对边相等;对角相等;对角线互相平分.22.(2016•兰州)阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?小敏在思考问题是,有如下思路:连接AC.结合小敏的思路作答(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:(2)如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.【分析】(1)如图2,连接AC,根据三角形中位线的性质得到EF∥AC,EF=AC,然后根据平行四边形判定定理即可得到结论;(2)由(1)知,四边形EFGH是平行四边形,且FG=BD,HG=AC,于是得到当AC=BD时,FG=HG,即可得到结论;(3)根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论.【解答】解:(1)是平行四边形,证明:如图2,连接AC,∵E是AB的中点,F是BC的中点,∴EF∥AC,EF=AC,同理HG∥AC,HG=AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形;(2)AC=BD.理由如下:由(1)知,四边形EFGH是平行四边形,且FG=BD,HG=AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形,(3)当AC⊥BD时,四边形EFGH为矩形;理由如下:同(2)得:四边形EFGH是平行四边形,∵AC⊥BD,GH∥AC,∴GH⊥BD,∴GH⊥GF,∴∠HGF=90°,∴四边形EFGH为矩形.【点评】此题主要考查了中点四边形,关键是掌握三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半.23.(2016•台州)如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.(1)求证:△PHC≌△CFP;(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.【分析】(1)由矩形的性质得出对边平行,再根据平行线的性质得出相等的角,结合全等三角形的判定定理AAS即可得出△PHC≌△CFP;(2)由矩形的性质找出∠D=∠B=90°,再结合对边互相平行即可证出四边形PEDH 和四边形PFBG都是矩形,通过角的正切值,在直角三角形中表示出直角边的关系,利用矩形的面积公式即可得出两矩形面积相等.【解答】证明:(1)∵四边形ABCD为矩形,∴AB∥CD,AD∥BC.∵PF∥AB,∴PF∥CD,∴∠CPF=∠PCH.。
备战中考数学(华师大版)巩固复习第十九章矩形、菱形与正方形(含解析)

备战中考数学(华师大版)巩固复习第十九章矩形、菱形与正方形(含解析)2019备战中考数学(华师大版)巩固复习-第十九章矩形、菱形与正方形(含解析)一、单选题1.如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断()A. 甲、乙均正确 B. 甲、乙均错误 C. 甲正确,乙错误 D. 甲错误,乙正确2.汶川地震后,某电视台法制频道在端午节组织发起“绿丝带行动”,号召市民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是()5.如图,在菱形ABCD中,AB的垂直平分线EF 交对角线AC于点F,垂足为点E,连接DF,且∠CDF=24°,则∠DAB等于()A. 102°B. 104°C. 106°D. 114°6.若正方形的对角线长为2 cm,则这个正方形的面积为()A. 4cm2B. 2cm2C. cm2D. 2cm27.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是()A. 5B. 10C. 5D.108.若一个正方形的边长为4,则它的面积是()A. 8B. 12C. 16D. 20二、填空题9.如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是________ cm.10.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的形状是________.11.如图所示,E,F分别是矩形ABCD的边BC,CD上的点,用S△CEF 表示△CEF的面积,若S△CEF=3,S△ABE =4,S△ADF=5,则S△AEF=________ .12.如图,正方形ABCD的对角线长为8 ,E为AB上一点,若EF⊥A C于F,EG⊥BD于G,则EF+EG=________.13.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=________ ,AC=________14.如图,四边形ABCD是菱形,如果AB=5,那么菱形ABCD的周长是________.15.如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,DE ∥ AC,CE ∥ BD,若 BD = 5,则四边形 DOCE 的周长为________.16.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若点P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数关系图象如图2,有下列四个结论:①AE=6cm;②sin∠EBC= ;③当0<t≤10时,y= t2;④当t=12s时,△PBQ是等腰三角形.其中正确结论的序号是________.三、解答题17.如图,在Rt△ABC中,∠ACB=90°,过点C 的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.18.如图,四边形ABCD是正方形,点E是AB边上的点,BE=1.将△BCE绕点C顺时针旋转90°得到△DCF.已知EF=2.求正方形ABCD的边长.19.如图,矩形ABCD中,AC与BD相交于点O.若AO=3,∠OBC=30°,求矩形的周长和面积.四、综合题20.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1∶2,周长是32cm.求:(1)两条对角线的长度;(2)菱形的面积.21.菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.(1)如图1,当∠ABC=90°时,△OEF的形状是________;(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;(3)在(1)的条件下,将∠MON的顶点移到AO 的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且= 时,直接写出线段CE的长.22.定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=________;②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是________;(整点指横坐标、纵坐标都为整数的点)(2)如图2,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF 是准矩形;(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是________.23.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(3,4),一次函数的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE上的一个动点.(1)求b的值;(2)连结OM,若三角形ODM的面积与四边形OAEM 的面积之比为1:3,求点M的坐标;(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.答案解析部分一、单选题1.【答案】A【考点】菱形的判定【解析】【解答】根据菱形的判定定理及性质可得甲、乙的做好均正确.【分析】根据菱形的判定定理即可得出答案。
苏科版数学八年级下册 9.4矩形菱形正方形大题综合练习(含答案解析)
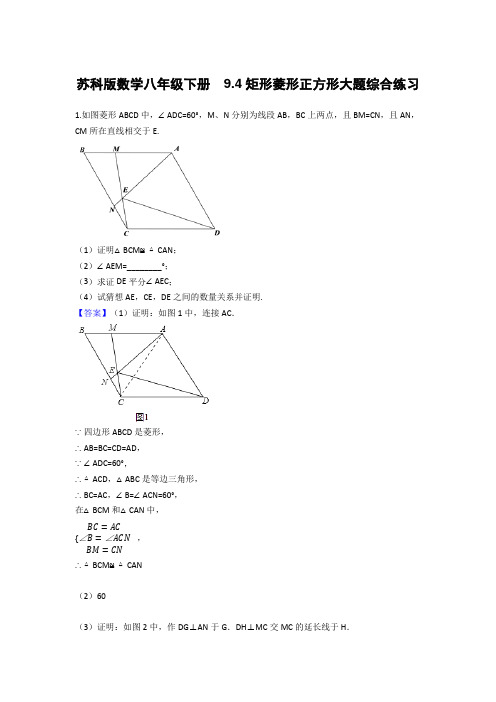
苏科版数学八年级下册9.4矩形菱形正方形大题综合练习1.如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.(1)证明△BCM≌△CAN;(2)∠AEM=________°;(3)求证DE平分∠AEC;(4)试猜想AE,CE,DE之间的数量关系并证明.【答案】(1)证明:如图1中,连接AC.∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵∠ADC=60°,∴△ACD,△ABC是等边三角形,∴BC=AC,∠B=∠ACN=60°,在△BCM和△CAN中,{BC=AC∠B=∠ACNBM=CN,∴△BCM≌△CAN(2)60(3)证明:如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.∵∠AEM=60°,∴∠AEC=120°,∵∠DGE=∠H=90°,∴∠GEH+∠GDH=180°,∴∠GDH=∠ADC=60°,∴∠ADG=∠CDH ,在△DGA 和△DHC 中,{∠DGA =∠H =90∘∠ADG =∠CDH DA =DC,∴△DGA ≌△DHC ,∴DG=DH ,∵DG ⊥AN ,DH ⊥MC ,∴∠DEG=∠DEH .∴DE 平分∠AEC .(4)证明:结论:EA+EC=ED .理由如下:如图2中,由(3)可知,∠GED=60°,在Rt △DEG 中,∵∠EDG=30°,∴DE=2EG ,易知△DEG ≌△DEH ,∴EG=EH ,∴EA+EC=EG+AG+EH-CH ,∵△DGA ≌△DHC ,∴GA=CH ,∴EA+EC=2EG=DE ,∴EA+EC=ED.【解析】【解答】解:(2)如图1中,∵△BCM ≌△CAN ,∴∠BCM=∠CAN ,∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.故答案为60.【分析】(1)连接AC,因为∠ADC=60°,利用菱形四边相等的性质,可知△ADC为等边三角形,所以AC=BC ,又因为菱形的对角线平分一组对角,所以∠ACN=60°=∠B,因为BM=CN,所以△BCM≌△CAN;(2)因为∠AEM=∠CEN,对顶角相等,由全等可知∠AEM=∠CEN=∠B=60°;(3)过点D做AE、CM两边的垂线,利用角角边可得到△DHC≌△DGA,可得DH=DG,再用角平分线的性质,到一个角两边距离相等的点在这个角的角平分线上;(4)由全等可知EA+EC=2EG,又因为在Rt△中30°的角所对的边等于斜边的一半,所以EA +EC=DE.2.综合:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为A. 平行四边形B. 菱形C. 矩形D. 正方形(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.【答案】(1)C(2)解:如图2中,①证明:∵AD=5,S□ABCD=15,∴AE=3.又∵在图2中,EF=4,∴在Rt△AEF中,AF═5.∴AF=AD=5,又∵AF∥DF',AF=DF,∴四边形AFF'D是平行四边形.∴四边形AFF'D是菱形.②解:连接AF',DF,在Rt△DE'F中,∵E'F=E'E﹣EF=5﹣4=1,DE'=3,∴DF═√E′D2+E′F2= √10.在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,∴AF'═√AE2+EF′2= √32+92=3 √10【解析】【解答】(1)解:如图1中,∵四边形ABCD是平行四边形,∴AD=BC,∵BE=CE′,∴AD∥EE′,AD=EE′,∴四边形AEE′D是平行四边形,∵∠AEE′=90°,∴四边形AEE′D是矩形,故选C.【分析】(1)根据矩形的判定方法即可判定;(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;②连接AF',DF,分别利用勾股定理计算即可;3.如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF 的面积为S1,△PDE的面积为S2.(1)求证:BP⊥DE.(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围.(3)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.【答案】(1)解:如图1中,延长BP交DE于M.∵四边形ABCD是正方形,∴CB=CD,∠BCP=∠DCE=90°,∵CP=CE,∴△BCP≌△DCE,∴∠BCP=∠CDE,∵∠CBP+∠CPB=90°,∠CPB=∠DPM,∴∠CDE+∠DPM=90°,∴∠DMP=90°,∴BP⊥DE.(2)解:由题意S1﹣S2= 12(4+x)•x﹣12•(4﹣x)•x=x2(0<x<4).(3)解:①如图2中,当∠PBF=30°时,∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,∴∠PFD=∠DPF=45°,∴DF=DP,∵AD=CD,∴AF=PC,∵AB=BC,∠A=∠BCP=90°,∴△BAF≌△BCP,∴∠ABF=∠CBP=30°,∴x=PC=BC•tan30°= 4√3,3∴S1﹣S2=x2= 16.3②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.由①可知△ABF≌△BCP,∴∠ABF=∠CBP,∵∠PBF=45°,∴∠CBP=22.5°,∵∠CNP=∠NBP+∠NPB=45°,∴∠NBP=∠NPB=22.5°,∴BN=PN= √2x,∴√2x+x=4,∴x=4 √2﹣4,∴S1﹣S2=(4 √2﹣4)2=48﹣32 √2.【解析】【分析】(1)首先延长BP交DE于M.然后依据SAS可证明△BCP≌△DCE,依据全等三角形的性质可得到∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°;(2)根据题意可得到S1-S2=S△PBE-S△PDE,然后依据三角形的面积公式列出函数关系式即可;(3)分当∠PBF=30°和∠PBF=45°两种情形分别求出PC 的长,最后再利用(2)中结论进行计算即可.4.如图,在矩形ABCD 中,BC >AB ,∠BAD 的平分线AF 与BD ,BC 分别交于点E ,F ,点O 是BD 的中点,直线OK ∥AF ,交AD 于点K ,交BC 于点G .(1)求证:△DOK ≌△BOG ;(2)探究线段AB 、AK 、BG 三者之间的关系,并证明你的结论;(3)若KD=KG ,BC=2 √2 ﹣1,求KD 的长度.【答案】(1)证明:∵在矩形ABCD 中,AD ∥BC ,∴∠KDO=∠GBO ,∠DKO=BGO .∵点O 是BD 的中点;∴DO=BO .在△DOK 和△BOG 中, {∠KDO =∠GBO∠DKO =∠BGO DO =BO∴△DOK ≌△BOG (AAS ).(2)解:AB+AK=BG ;证明如下:∵四边形ABCD 是矩形;∴∠BAD=∠ABC=90°,AD ∥BC .又∵AF 平分∠BAD ,∴∠BAF=∠BFA=45°.∴AB=BF .∵OK ∥AF ,AK ∥FG ,∴四边形AFGK 是平行四边形.∴AK=FG .∵BG=BF+FG ;∴BG=AB+AK .(3)解:∵四边形AFGK 是平行四边形.∴AK=FG ,AF=KG又∵△DOK ≌△BOG ,且KD=KG ,∴AF=KG=KD=BG .设AB=a ,则AF=KG=KD=BG= √2 a .∴AK=2 √2 ﹣1﹣ √2 a ,FG=BG ﹣BF= √2 a ﹣a .∴2 √2﹣1﹣√2a= √2a﹣a.解得a=1.∴KD= √2a= √2.【解析】【分析】(1)在矩形ABCD中,AD∥BC,得到∠KDO=∠GBO,∠DKO=BGO,DO=BO,得到△DOK≌△BOG(AAS);(2)四边形ABCD是矩形,得到∠BAD=∠ABC=90°,AD∥BC,又AF平分∠BAD,得到∠BAF=∠BFA=45°,AB=BF,由OK∥AF,AK∥FG,得到四边形AFGK 是平行四边形,得到AK=FG,BG=BF+FG,即BG=AB+AK;(3)四边形AFGK是平行四边形,得到AK=FG,AF=KG,又△DOK≌△BOG,且KD=KG,得到AF=KG=KD=BG,设AB=a,则AF=KG=KD=BG=√2a,得到AK=2√2﹣1-√2a,FG=BG﹣BF=√2a﹣a,解得a=1,得到KD=√2a=√2.5.综合题(1)感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.(2)探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为________ .【答案】(1)证明:∵四边形ABCD、四边形CEFG均为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,在△BCE和△DCG中,{CB=CD∠BCE=∠DCGCE=CG,∴△BCE≌△DCG,∴BE=DG.(2)∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,∵∠A=∠F,∴∠BCD=∠ECG,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,∴△BCE≌△DCG.,∴BE=DG.(3)20【解析】【解答】解:应用:∵四边形ABCD是菱形,S△EBC=8,∴S△AEB+S△EDC=8,∵AE=3DE,∴S△AEB=3S△EDC,∴S△EDC=6,S△EDC=2,∵△BCE≌△DCG,∴S△DGC=S△EBC=8,∴S△ECG=8+2=10,∴菱形CEFG的面积=2•S△EGC=20,故答案为20.【分析】感知:根据正方形的性质,得到BC=CD,CE=CG,∠BCD=∠ECG=90°,得到∠BCE=∠DCG,得到△BCE≌△DCG,BE=DG;探究:由四边形ABCD、四边形CEFG均为菱形,得到BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,由∠A=∠F,得到∠BCE=∠DCG,△BCE≌△DCG,BE=DG;应用:由四边形ABCD是菱形,△EBC的面积为8,AE=3DE,得到S△AEB=3S△EDC,得到S△EDC=6,S△EDC=2,由△BCE≌△DCG,得到S△DGC=S△EBC=8,S△ECG=8+2=10,所以菱形CEFG的面积=2•S△EGC=20.6.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(3,4),一次函x+b的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE 数y=23上的一个动点.(1)求b的值;(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N 的坐标.【答案】(1)解:y=23x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,∵OD=BE,∴BE=b,则E的坐标是(3,4﹣b),把E的坐标代入y=23x+b得4﹣b=﹣2+b,解得:b=3(2)解:S四边形OAED= 12(OD+AE)•OA= 12×(3+1)×3=6,∵三角形ODM的面积与四边形OAEM的面积之比为1:3,∴S△ODM=1.5.设M的横坐标是a,则12×3a=1.5,解得:a=1,把x=a=1代入y=﹣23x+3得y=﹣23× 43+3= 73.则M的坐标是(1,73)(3)解:当四边形OMDN是菱形时,如图(1),M的纵坐标是32,把y= 32代入y=﹣23x+3,得﹣23x+3= 32,解得:x= 94,则M的坐标是(94,32),则N的坐标是(﹣94,32);当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是﹣23m+3,则m2+(﹣23m+3)2=9,解得:m= 3613或0(舍去).则M的坐标是(3613,1513).则DM的中点是(1813,2713).则N的坐标是(3613,5413).故N的坐标是(﹣94,32)或(3613,5413).【解析】【分析】(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN 是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.7.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2.(1)若DG=6,求AE的长;(2)若DG=2,求证:四边形EFGH是正方形.【答案】(1)解:∵AD=6,AH=2∴DH=AD﹣AH=4∵四边形ABCD是矩形∴∠A=∠D=90°∴在Rt△DHG中,HG2=DH2+DG2在Rt△AEH中,HE2=AH2+AE2∵四边形EFGH是菱形∴HG=HE∴DH2+DG2=AH2+AE2即42+62=22+AE2∴AE= =4(2)证明:∵AH=2,DG=2,∴AH=DG,∵四边形EFGH是菱形,∴HG=HE,在Rt△DHG和Rt△AEH中,,∴Rt△DHG≌Rt△AEH(HL),∴∠DHG=∠AEH,∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形【解析】【分析】(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2,HE2=AH2+AE2,再根据菱形的性质,得到等式DH2+DG2=AH2+AE2,最后计算AE的长;(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.8.如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD 于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.(1)AM=________,AP=________.(用含t的代数式表示)(2)当四边形ANCP为平行四边形时,求t的值(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由②使四边形AQMK为正方形,则AC等于.【答案】(1)8﹣2t;2+t(2)解:∵四边形ANCP为平行四边形时,CN=AP,∴6﹣t=8﹣(6﹣t),解得t=2(3)解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:∵NP⊥AD,QP=PK,∴当PM=PA时有四边形AQMK为菱形,∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,②要使四边形AQMK为正方形.∵∠ADC=90°,∴∠CAD=45°.∴四边形AQMK为正方形,则CD=AD,∵AD=8,∴CD=8,∴AC=8 √2.【解析】【解答】解:(1)如图1.∵DM=2t,∴AM=AD﹣DM=8﹣2t.∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P,∴四边形CNPD为矩形,∴DP=CN=BC﹣BN=6﹣t,∴AP=AD﹣DP=8﹣(6﹣t)=2+t;故答案为:8﹣2t,2+t.【分析】(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;(3)①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.9.已知▱OABC的顶点A、C分别在直线x=2和x=4上,O为坐标原点,直线x=2分别与x轴和OC边交于D、E,直线x=4分别与x轴和AB边的交于点F、G.(1)如图,在点A、C移动的过程中,若点B在x轴上,①直线AC是否会经过一个定点,若是,请直接写出定点的坐标;若否,请说明理由.②▱OABC是否可以形成矩形?如果可以,请求出矩形OABC的面积;若否,请说明理由.③四边形AECG是否可以形成菱形?如果可以,请求出菱形AECG的面积;若否,请说明理由.(2)在点A 、C 移动的过程中,若点B 不在x 轴上,且当▱OABC 为正方形时,直接写出点C 的坐标.【答案】(1)解:①是,经过定点(3,0).理由如下:如图1中,连接AC 交OB 于K .∵四边形OABC 是平行四边形,∴OK=KB ,BC ∥OA ,BC=OA ,∴∠CBF=∠AOD ,在△DOA 和△FBC 中,{∠ODA =∠CFB =90°∠AOD =∠CBF OA =BC,∴△DOA ≌△FBC ,∴OD=FB=2,∴OB=6,∵OK=KB ,∴OK=3,∴K (3,0),∴直线AC 经过定点K (3,0).②可以.利用如下:当∠OCB=90°时,四边形OABC 是矩形,由(1)可知△DOA ≌△FBC ,∴OD=BF=2,∵∠OCF+∠FCB=90°,∠FCB+∠CBF=90°,∴∠OCF=∠CBF,∵∠CFO=∠CFB,∴△CFO∽△BFC,∴CFBF = OFCF,∴CF2= 4CF,∴CF=2 √2,∴S矩形OABC=2•S△OBC=2× 12× 6×2√2=12 √2.③可以.理由如下:如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,∴AD=CF,∵DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,∵OE2=OD2+DE2,∴9x2=x2+4,∴x= √22,∴AE= 3√22,∴S菱形AECG=AE•DF= 3√22×2=3 √2(2)解:如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,∴OD=CF=2,∴点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.综上所述,点C坐标为(4,2)或(4,﹣2)【解析】【分析】(1)①是,经过定点(3,0).如图1中,连接AC交OB于K,只要证明OD=FB=2,推出OB=6,即可解决问题.②当∠OCB=90°时,四边形OABC是矩形,由(1)可知△DOA≌△FBC,推出OD=BF=2,由△CFO∽△BFC,可得CFBF = OFCF,由此即可解决问题.③可以.如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,推出AD=CF,易知DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,根据OE2=OD2+DE2,列出方程即可解决问题.(2)如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,推出OD=CF=2,推出点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.10.如图1,在平面直角坐标系中,正方形ABCO的顶点C、A分别在x、y轴上,A(0,6)、E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH(1)当H(﹣2,6)时,求证:四边形EFGH为正方形(2)若F(﹣5,0),求点G的坐标(3)如图2,点Q为对角线BO上一动点,D为边OA上一点,DQ⊥CQ,点Q从点B出发,沿BO方向移动.若移动的路径长为3,直接写出CD的中点M移动的路径长为________.【答案】(1)证明:如图1中,∵E(0,2),H(﹣2,6),∴OE=AH=2,∵四边形ABCO是正方形,∴∠HAE=∠EOF=90°,∵四边形EFGH是菱形,∴EH=EF,在Rt△AHE和Rt△OEF中,{AH=EOHE=EF,∴Rt△AHE≌△Rt△OEF,∴∠AEH=∠EFO,∵∠EFO+∠FEO=90°,∴∠AEH+∠FEO=90°,∴∠HEF=90°,∴四边形EFGH是正方形(2)解:如图1中,连接GE、FH交于点K.∵F(﹣5,0),E(0,2),∴OF=5,OE=2,EA=4,∵HE=EF,∴52+22=42+AH2,∴AH= √13,∴H(﹣√13,6),∵四边形EFGH是菱形,∴HK=KF,KE=KG,设G(m,n),则有m+02= −5−√132,n+22= 6+02,∴m=﹣5﹣√13,n=4,∴G(﹣5﹣√13,4)(3)3√22【解析】【解答】(3)解:如图2中,如图2中,作MN⊥CO于M.∵MN∥OD,CM=MD,∴CN=ON,∴MN垂直平分线段CO,∴点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),∵QC=QD,∠CEQ=∠QFD,易证∠ECQ=∠FQD,∴△EQC≌△FDQ,∴EQ=DF=BE= 3√22,CE=OF=6﹣3√22,∴DO=6﹣3 √2,∵CM=DM,∠CMH=∠OMD,∠CHM=∠DOM,∴△HMC≌△OMD,∴OM=HM,CH=OD=6﹣3 √2,BH=3 √2,∵ON=NB,∴MN= 12BH= 3√22,∴点M的运动的路径的长为3√22.故答案为3√2.2【分析】(1)只要证明Rt△AHE≌△Rt△OEF,推出∠AEH=∠EFO,由∠EFO+∠FEO=90°,推出∠AEH+∠FEO=90°,推出∠HEF=90°,即可解决问题.(2)如图1中,连接GE、FH交于点K.首先求出点H的坐标,设G(m,n),根据中点坐标公式,列出方程组即可解决问题.(3)如图2中,作MN⊥CO于M.由MN∥OD,CM=MD,推出CN=ON,推出MN 垂直平分线段CO,推出点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B 重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),想办法求出BH 的长,即可利用三角形的中位线定理解决问题.11.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB, AC上的一动点,且满足BP=AQ,D 是BC的中点.(1)求证:△PDQ是等腰直角三角形.(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.【答案】(1)证明:连接AD.∵△ABC是等腰直角三角形,D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,又∵BP=AQ,∴△BPD≌△AQD,∴PD=QD,∠BDP=∠ADQ,∵∠BDP+∠ADP=90°,∴∠ADP+∠ADQ=∠PDQ=90°,∴△PDQ为等腰直角三角形(2)解:当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:由(1)知△ABD为等腰直角三角形,当P为AB的中点时,DP⊥AB,即∠APD=90°,又∵∠BAC=90°,∠PDQ=90°,∴四边形APDQ为矩形,AB,∴四边形APDQ为正方形又∵DP=AP= 12【解析】【分析】连接AD,根据直角三角形的性质可得AD=BD=DC,从而证明△BPD≌△AQD,得到PD=QD,∠ADQ=∠BDP,则△PDQ是等腰三角形;由∠BDP+∠ADP=90°,得出∠ADP+∠ADQ=90°,得到△PDQ是直角三角形,从而证出△PDQ是等腰直角三角形;若四边形APDQ是正方形,则DP⊥AB,得到P点是AB的中点.12.如图,在等边三角形ABC中,点D是BC边的中点,以AD为边作等边三角形ADE.(1)求∠CAE的度数;(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.【答案】(1)解:在等边三角形ABC中,∵点D是BC边的中点,∴∠DAC=30°.又∵△ADE为等边三角形,∴∠DAE=60°.∴∠CAE=∠DAE-∠DAC=30°(2)解:由(1)知,∠EAF=90°,由F为AB的中点知,∠CFA=90°,∴CF∥EA.在等边三角形ABC中,CF=AD.在等边三角形ADE中,AD=EA.∴CF=EA.∴四边形AFCE为平行四边形.又∵∠CFA=90°,∴四边形AFCE为矩形.【解析】【分析】根据等边三角形三线合一的特点,易求得∠DAC=30°,则∠CAE=∠DAE-∠DAC.先证明四边形AECF是平行四边形,然后根据∠CFA=∠FAE=90°,由矩形的定义判定四边形AFCE是矩形.13.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:(1)四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?【答案】(1)解:四边形ADEF是平行四边形.理由:∵△ABD,△EBC都是等边三角形.∴AD=BD=AB,BC=BE=EC∠DBA=∠EBC=60°∴∠DBE+∠EBA=∠ABC+∠EBA.∴∠DBE=∠ABC.在△DBE和△ABC中∵BD=BA∠DBE=∠ABCBE=BC,∴△DBE≌△ABC.∴DE=AC.又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.同理可证:AD=EF,∴四边形ADEF平行四边形(2)解:∵四边形ADEF是矩形,∴∠FAD=90°.∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°.∴∠BAC=150°时,四边形ADEF是矩形(3)解:当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.理由如下:若∠BAC=60°,则∠DAF=360°﹣∠BAC﹣∠DAB﹣∠FAC=360°﹣60°﹣60°﹣60°=180°.此时,点A、D、E、F四点共线,∴以A、D、E、F为顶点的四边形不存在【解析】【分析】可先证明△DBE≌△ABC ,又∵△ACF是等边三角形,∴AC=AF.∴DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;若四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,A,D,E,F为顶点的四边形就不存在.14.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)证明:如图1,当点G和点M、C不重合时,求证:DG=DN.【答案】(1)证明:如图2中,∵AM=ME.AD=DB,∴DM∥BE,∴∠GDN+∠DNE=180°,∵∠GDN=∠AEB,∴∠AEB+∠DNE=180°,∴AE∥DN,∴四边形DMEN是平行四边形,∵DM== BE,EM== AE,AE=BE,∴DM=EM,∴四边形DMEN是菱形(2)证明:如图1中,取BE的中点F,连接DM、DF.由(1)可知四边形EMDF是菱形,∴∠AEB=∠MDF,DM=DF,∴∠GDN=∠AEB,∴∠MDF=∠GDN,∴∠MDG=∠FDN,∵∠DFN=∠AEB=∠MCE+∠CME,∠GMD=∠EMD+∠CME,、在Rt△ACE中,∵AM=ME,∴CM=ME,∴∠MCE=∠CEM=∠EMD,∴∠DMG=∠DFN,∴△DMG≌△DFN,∴DG=DN【解析】【分析】(1)如图2中,首先证明四边形DMEN是平行四边形,再证明ME=MD 即可证明.(2)如图1中,取BE的中点F,连接DM、DF.只要证明△DMG≌△DFN即可.15.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点.(1)求证:∠FAD=∠EAB.(2)若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.【答案】(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,∴AD=AB,∠ADB=∠ABD,∴∠ADF=∠ABE,在△FAD与△EAB中,∴△FAD≌△EAB(SAS),∴∠FAD=∠EAB;(2)解:∵四边形AECF对角线互相垂直平分,∴只要∠EAF=90°即得四边形BFDE是正方形,∵∠ADC=130°,∴∠DAB=180°﹣130°=50°∴∠FAD+∠EAB=40°,∵∠FAD=∠EAB,∴∠FAD= ×40°=20°【解析】【分析】(1)由题意易证∠ADF=∠ABE,又因为DF=EB,AD=AB,于是可△FAD≌△EAB,;(2)由已知可得四边形AECF对角线互相垂直平分,只要∠EAF=90°即得四边形AECF是正方形,由∠FAD=∠EAB,再证得∠DAB=50°,可得∠FAD+∠EAB=40°,于是∠FAD= 1×40°=20°.216.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD 为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:________,②BC,DC,CF之间的数量关系为:________;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.【答案】(1)垂直;BC=CF+CD(2)解:CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:∵正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,在△DAB与△FAC中,{AD=AF∠BAD=∠CAFAB=AC,∴△DAB≌△FAC(SAS),∴∠ABD=∠ACF,∵∠BAC=90°,AB=AC,∴∠ACB=∠ABC=45°.∴∠ABD=180°﹣45°=135°,∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°,∴CF⊥BC.∵CD=DB+BC,DB=CF,∴CD=CF+BC .(3)解:过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N ,如图3所示:∵∠BAC=90°,AB=AC ,∴BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,∴CD= 14 BC= √22 ,CH= 12 BC= √2 ,∴DH= 3√22 ,由(2)证得BC ⊥CF ,CF=BD= 5√22 ,∵四边形ADEF 是正方形,∴AD=DE ,∠ADE=90°,∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形,∴NE=CM ,EM=CN ,∵∠AHD=∠ADC=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM ,在△ADH 与△DEM 中, {∠ADH =∠DEM∠AHD =∠DMEAD =DE, ∴△ADH ≌△DEM (AAS ),∴EM=DH= 3√22 ,DM=AH= √2 ,∴CN=EM= 3√22 ,EN=CM= 3√22 ,∵∠ABC=45°,∴∠BGC=45°,∴△BCG 是等腰直角三角形,∴CG=BC=2 √2 ,∴GN=CG ﹣CN= √22 , ∴EG= √GN 2+EN 2 = (√22)(3√22)= √5 . 【解析】【解答】解:(1)①正方形ADEF 中,AD=AF ,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF ,在△DAB 与△FAC 中, {AD =AF∠BAD =∠CAFAB =AC,∴△DAB ≌△FAC (SAS ),∴∠B=∠ACF ,∴∠ACB+∠ACF=90°,即BC ⊥CF ;故答案为:垂直;②△DAB ≌△FAC ,∴CF=BD ,∵BC=BD+CD ,∴BC=CF+CD ;故答案为:BC=CF+CD ;【分析】(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质即可得到结论;②由正方形ADEF 的性质可推出△DAB ≌△FAC ,根据全等三角形的性质得到CF=BD ,∠ACF=∠ABD ,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.(3)根据等腰直角三角形的性质得到BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,求得DH= 3√22 ,根据正方形的性质得到AD=DE ,∠ADE=90°,根据矩形的性质得到NE=CM ,EM=CN ,由角的性质得到∠ADH=∠DEM ,根据全等三角形的性质得到EM=DH= 3√22 ,DM=AH= √2 ,等量代换得到CN=EM= 3√22 ,EN=CM= 3√22,根据等腰直角三角形的性质得到CG=BC=2 √2 ,根据勾股定理即可得到结论.17.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO=CO ,BO=DO ,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD 是矩形.(2)DF ⊥AC ,若∠ADF :∠FDC=3:2,则∠BDF 的度数是多少?【答案】(1)证明:∵AO=CO ,BO=DO ,∴四边形ABCD 是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴CO=OD,∴∠ODC=∠DCO=54°,∴∠BDF=∠ODC﹣∠FDC=18°.【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,【解析】根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.18.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.(1)求证:PC=PE;(2)求∠CPE的度数;(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.【答案】(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE(2)解:由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∵PA=PE,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°,∵∠ABC=90°,∴∠EPC=90°(3)115°【解析】【解答】(3)∠EPC=115°,理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴∠BAP=∠BCP,∵PA=PE,∴∠DAP=∠DCP,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°.∴∠CPE=180°-∠ABC=180°-65°=115°【分析】(1)根据正方形的性质得到△ABP≌△CBP,得到对应边相等,得到PC=PE;(2)由(1)知△ABP≌△CBP,得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数;(3)根据菱形的性质,得到△ABP≌△CBP,得到得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数.19.实践探究,解决问题如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD.(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=________;(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD 之间满足的关系式为________;(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.解决问题:(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).【答案】(1)16(2)S阴影=12S平行四边形ABCD(3)解:满足(2)中的关系式,理由如下:连接BD,由图1得S△EBD= 12 S△ABD同理S△BDF= 12S△BDC∴S四边形EBFD=S△EBD+S△BDF= 12S四边形ABCD(4)解:设四边形的空白区域分别为a,b,c,d 由上述性质可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,①+②+③+④得,a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米.【解析】【解答】解:(1)∵E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,∴S阴影= 12×8×4=16,故答案为:16;(2)∵E、F分别为平行四边形ABCD的边AD、BC的中点,∴S阴影= 12S平行四边形ABCD;故答案为:S阴影= 12S平行四边形ABCD;【分析】(1)由矩形的性质容易得出结果;(2)由平行四边形的性质容易得出结果;(3)连接BD,由题意得出S△EBD= 12 S△ABD同理S△BDF= 12S△BDC,即可得出结论;(4)设四边形的空白区域分别为a,b,c,d,由(3)可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,进一步得出结论即可.20.如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形.(2)解:∵四边形AECF是菱形,如图所示:∴AE=EC,∴∠1=∠2,∵∠3=90°﹣∠2,∠4=90°﹣∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE= 12BC=5.【解析】【分析】(1)利用平行四边形的性质得出对边平行且相等,结合已知,可证出AECF是平行四边形;(2)利用菱形的邻边相等的性质,可证出BE=AE=CE= 12BC=5.。
八年级数学下册考点知识与题型专题讲解与提升练习37 利用菱形的性质证明

八年级数学下册考点知识与题型专题讲解与提升练习专题37 利用菱形的性质证明一、单选题1.菱形具有而矩形不一定具有的性质是()A.邻边相等B.对角线互相平分C.对角线相等D.邻角互补2.矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.两组对角分别相等D.对角线互相垂直3.矩形具有,而菱形不一定具有的性质是()A.对角线互相平分B.对角线相等C.对边平行且相等D.内角和为360°4.下列说法中,错误的是()A.平行四边形的对角线互相平分B.矩形的对角线互相垂直C.菱形的对角线互相垂直平分D.正方形的对角线相等5.矩形具有而菱形不具有的性质是()A.对角线相等B.对角线平分一组对角C.对角线互相平分D.对角线互相垂直6.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是()A.对角线互相垂直B.对角线互相平分C.对角线长度相等D.一组对角线平分一组对角7.菱形具有,而矩形不一定具有的性质是()A.对边相等B.对角相等C.对角线相等D.对角线互相垂直8.下列说法中错误的是()A .四边相等的四边形是菱形B .对角线相等的平行四边形是矩形C .菱形的对角线互相垂直且相等D .正方形的邻边相等9.下列哪条性质是平行四边形、矩形、菱形、正方形共有的()A .对角线互相平分B .对角线相等C .对角线互相垂直.D .对角线平分一组对角.10.下列说法中不正确的是( )A .平行四边形的对角相等B .菱形的邻边相等C .平行四边形的对角线互相平分D .菱形的对角线互相垂直且相等11.菱形OACB 在平面直角坐标系中的位置如图所示,若点C 的坐标是()4,0,点A 的纵坐标是1,则点B 的坐标是()A .()2,1B .()2,1-C .()1,2-D .()1,2 12.下列命题中,正确的是( )A .平行四边形的对角线相等B .菱形的对角线互相垂直且平分C .矩形的对角线互相垂直D .对角线互相垂直的平行四边形是正方形 13.菱形不具备的性质是( )A .对角线一定相等B .对角线互相垂直C .是轴对称图形D .是中心对称图形14.矩形一定具有而菱形不一定具有的性质是()A .内角和等于360B .对角线互相垂直C .对边平行且相等D .对角线相等15.矩形具有而菱形不一定具有的性质是 ( )A .对角线互相垂直B .对角线相等C .对角线互相平分D .对角互补16.关于菱形,下列说法错误的是()A .四条边相等B .对角线互相垂直C .四个角相等D .对角线互相平分17.下列性质中,菱形具有而矩形不一定具有的性质是().A .对边平行且相等B .对角线互相平分C .内角和等于外角和D .每一条对角线所在直线都是它的对称轴18.如图,把菱形ABCD 向右平移至DCEF 的位置,作EG ⊥AB ,垂足为G ,EG 与CD 相交于点K ,GD 的延长线交EF 于点H ,连接DE ,则下列结论:①BG =AB +HF ;②DG =DE ;③∠DHE =12∠BAD ;④∠B =∠DEF ,其中正确结论的个数是()A .1个B .2个C .3个D .4个19.菱形ABCD 中,60D ∠=︒.点E 、F 分别在边BC 、CD 上,且BE CF =.若2EF =,则AEF 的面积为().A .B .C .D20.如图,四边形ABCD 沿直线l 对折后重合,如果//AD BC ,则结论①AB //CD ;②AB =CD ;③AB BC ⊥;④AO OC =中正确的是()A .1个B .2个C .3个D .4个21.如图,平行四边形ABCD 的对角线AC BD 、相交于点,О下列结论正确的是()A .COD AOB S S ∆= B .AC BD =C .AC BD ⊥D .ABCD 是轴对称图形 22.如图,在菱形ABCD 中,点,,,EFGH 分别是四条边的中点,则四边形EFGH 是()A .正方形B .矩形C .菱形D .无法确定23.下列说法中,错误的是()A .平行四边形的两组对角分别相等;B .一组对边平行另一组对边相等的四边形是平行四边形;C .正方形的对角线互相垂直平分且相等;D .菱形的对角线互相垂直.24.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,延长CB 至E 使BE=CB ,连续AE .下列结论①AE=2OE;②90EAC ∠=︒;③四边形ADBE 为平行四边形;④34AEBO ABCD S S =四边形菱形中,正确的个数有()A .1个B .2个C .3个D .4个25.菱形具有而矩形不一定具有的性质是( )A .对角相等且互补B .对角线互相平分C .对角线互相垂直D .一组对边平行,另一组对边相等26.下列性质中,菱形不具有的是()A .对边平行且相等B .对角线互相垂直C .对角线互相平分D .对角线相等27.如图,在矩形ABCD 中,AB =3,做BD 的垂直平分线E ,F ,分别与AD 、BC 交于点E 、F ,连接BE ,DF ,若EF =AE +FC ,则边BC 的长为()A .B .C .D 28.如图,在菱形ABCD 中, AD=6,∠BAD=60°, 点P 是对角线AC 上的动点,点E 是AB的中点,连结PB 、PE ,则PE+PB 的最小值为()A .B .CD .29.已知,如图,在菱形ABCD 中.(1)分别以C ,D 为圆心,大于12CD 长为半径作弧,两弧分别交于点E ,F ;(2)作直线EF ,且直线EF 恰好经过点A ,且与边CD 交于点M ;(3)连接BM .根据以上作图过程及所作图形,判断下列结论中错误..的是()A .∠ABC =60°B .如果AB =2,那么BM =4C .BC =2CMD .2ABM ADM S S △△30.如图,在菱形ABCD 中,AB =BD ,点E 、F 分别是AB 、AD 上任意的点(不与端点重合),且AE =DF ,连接BF 与DE 相交于点G ,连接CG 与BD 相交于点H .给出如下几个结论:①△AED ≌△DFB :②GC 平分∠BGD ;③S 四边形BCDG =4CG 2;④∠BGE 的大小为定值.其中正确的结论个数为( )A .1B .2C .3D .431.如图,在一张矩形纸片ABCD 中,AB=4,BC=8,点E ,F 分别在AD ,BC 上,将ABCD沿直线EF 折叠,点C 落在AD 上的一点H 处,点D 落在点G 处,有以下四个结论:①四边形CFHE 是菱形;②EC 平分∠DCH;③线段BF 的取值范围为3≤BF≤4;④当点H 与点A重合时,EF=A .①②③④B .①④C .①②④D .①③④32.如图,菱形ABCD 中,∠BAD =60°,AC 与BD 交于点O ,E 为CD 延长线上的一点,且CD =DE ,连结BE 分别交AC ,AD 于点F 、G ,连结OG ,则下列结论:①OG =12AB ;②与△EGD 全等的三角形共有5个;③S 四边形ODGF >S △ABF ;④由点A 、B 、D 、E 构成的四边形是菱形.其中正确的是( )A .①④B .①③④C .①②③D .②③④33.如图所示,等边三角形ABC 沿射线BC 向右平移到DCE ∆的位置,连接AD 、BD ,则下列结论:(1)AD BC =(2)BD 与AC 互相平分(3)四边形ACED 是菱形(4)BD DE ⊥,其中正确的个数是()A.1 B.2 C.3 D.434.如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④EG12=BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )A.1 B.2 C.3 D.435.如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距高是③AF=CF;④△ABF的( )个.A.1 B.2 C.3 D. 436.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A 的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE13=S菱形ABCD下列判断正确的是()A.①,②都对B.①,②都错C.①对,②错D.①错,②对第II卷(非选择题)请点击修改第II卷的文字说明二、填空题37.给出下列命题:①平行四边形的对角线互相平分;②对角线相等的四边形是矩形;③菱形的对角线互相垂直平分;④对角线互相垂直的四边形是菱形.其中_____是真命题(填序号).38.菱形的对角线互相垂直且相等._____(判断对错)39.矩形、菱形和正方形的对角线都具有的性质是_____.40.如图,在平面直角坐标系中,菱形ABCD的顶点A,C 在x轴上,顶点B的坐标为(2,3),那么顶点D的坐标是______________;41.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE 的长等于_____.42.下列说法:①平行四边形对角相等,对边也相等;②菱形一组对角的和为180︒;③矩形对角线相等;④平行四边形是轴对称图形,对角线所在的直线是对称轴;⑤平行四边形对角线的交点到一组对边的距离相等,其中正确的序号为________________________.43.如图,在菱形ABCD中,AB=3cm,∠A=60°.点E,F分别在边AD,AB上,且DE=1cm.将△AEF沿EF翻折,使点A落在对角线BD上的点A'处,则A'BA'F=______.44.如图,四边形ABCD是菱形,点A,B,C,D的坐标分别是(m,0),(0,n),(1,0),(0,2),则mn=_____.45.如图,在菱形ABCD中,AB=4,CE=DE,AE⊥CD,E为垂足,则AE2+BE2=_____.46.如图,菱形ABCD的对角线相交于点O,过点A作AE CB⊥交CB的延长线于点E,连接OE .若菱形ABCD 的面积等于12,对角线4BD =,则OE 的长为_________.47.如图,菱形ABCD 的边长为1, 60ABC ∠=︒.,E F 分别是,BC BD 上的动点,且CE DF =,则AE AF +的最小值为_______.48.如图,在菱形ABCD 中,∠A=60°,E 、F 分别是AB 、AD 的中点,DE 、BF 相交于点G ,连接BD 、CG .给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④2.BCDG S AB =四边形其中正确的有______.三、解答题49.如图,菱形ABCD 的周长为8,对角线BD =2,E 、F 分别是边AD ,CD 上的两个动点;且满足AE +CF =2.(1)求证:△BDE ≌△BCF ;(2)判断△BEF 的形状,并说明理由.50.如图,在菱形ABCD 中,AB =2,∠DAB =60°,点E 是AD 边的中点,点M 是AB 边上一动点(不与点A 重合),延长ME 交射线CD 于点N ,连接MD 、AN .(1)求证:四边形AMDN 是平行四边形;(2)在点M 移动过程中:①当四边形AMDN 成矩形时,求此时AM 的长;②当四边形AMDN 成菱形时,求此时AM 的长.51.如图,在△ABC 中,AB=AC ,四边形ADEF 是菱形,求证:BE=CE .52.如图,点,E F 分别在菱形ABCD 的边,BC CD 上,BE DF =.求证:.AE AF =53.如图,在菱形ABCD 中,AEF 是等边三角形,E ,F 分别在BC ,CD 上,且EF CD =,求BAD ∠的度数.54.如图,已知菱形 ABCD 中,对角线 AC 、BD 相交于点 O ,过点 C 作 CE∥BD,过点 D 作 DE∥AC,CE 与 DE 相交于点 E .求证:四边形 CODE 是矩形;55.如图,在菱形ABCD 中,点E 在边CD 上,AE 与BD 相交于点F ,连接CF .(1)求证:AED BCF ∠=∠;(2)若60ABC ∠=︒,2AB =,求菱形ABCD 的面积.56.如图,四边形ABCD 是菱形,对角线AC 、BD 相交于点O .(1)尺规作图:以OA 、OD 为边,作矩形OAED (不要求写作法,但保留作图痕迹);(2)若在菱形ABCD 中,∠BAD =120 °,AD =2,求所作矩形OAED 的周长.57.如图所示,在四边形ABCD 中,AB DC =,E 、F 分别是AD 、BC 的中点,G 、H 分别是BD 、AC 的中点,猜一猜EF 与GH 的位置关系,并证明你的结论.58.如图,在菱形ABCD 中,点,E F 分别是,CD BD 边上的点,12∠=∠.求证:(1)FCD EBD ≌;(2)CE BF =.59.如图,在菱形ABCD 中,E 为对角线BD 上一点,且AE ⊥AB ,连结CE .(1)求证:∠ECB =90°;(2)若AE ═ED =1时,求菱形的边长.60.如图1,四边形ABCD 是菱形,5AD =,过点D 作AB 的垂线DH ,垂足为H ,交对角线AC 于M ,连接BM ,且3AH =.(1)求DM 的长;(2)如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设PMB △的面积为(0)S S ≠,点P 的运动时间为t 秒,求S 与t 之间的函数关系式;(3)在(2)的条件下,当点P 在边AB 上运动时,是否存在这样的t 的值,使M PB ∠与BCD ∠互为余角?若存在,求出t 的值;若不存在,请说明理由.61.如图,菱形ABCD 的边长为2.2BD =,E ,F 分别是边AD ,CD 上的两个动点,且满足2AE CF +=.(1)求证:BDE BCF △≌△;(2)判断BEF 的形状,并说明理由.62.如图,在直角坐标系中,3,4OA OC ==,点B 是y 轴上一动点,以AC 为对角线作平行四边形ABCD .(1)求直线AC 的函数解析式;(2)设点(0)B m ,,记平行四边形ABCD 的面积为S ,求S 与m 的函数关系式;(3)当点B 在y 轴上运动,能否使得平行四边形ABCD 是菱形?若能,求出点B 的坐标;若不能,说明理由.63.将一个三角形的三个顶点分别关于各自对边所在直线作对称点,由这三个对称点确定的三角形叫做原三角形的“再生三角形”.(1)一个周长为L ,面积为S 的等边三角形的“再生三角形”的周长是______,面积是______;(2)已知ABC 中,30,ABC BA BC ∠=︒=,A B C '''是ABC 的“再生三角形”,其中点,A ',B ',C '分别是点A ,B ,C 的对称点.A B C '''是_______三角形;(3)已知Rt ABC 中,90CAB ∠=︒,A B C '''是Rt ABC 的“再生三角形”,其中点,,A B C '''分别是点A ,B ,C 的对称点,试猜想A B C '''与Rt ABC 的面积有怎样的关系,并加以证明;(4)小舒认为所有的三角形都存在“再生三角形”,小雪认为不是所有的三角形都存在“再生三角形”.你认为谁的判断是正确的?请说明理由.64.如图,已知正方形ABCD 的边长为3,菱形EFGH 的三个顶点E 、G 、H 分别在正方形的边AB 、CD 、DA 上,1AH =,连接CF .(1)当1DG =时,求证:菱形EFGH 为正方形;(2)设DG x =,请用x 的代数式表示△FCG 的面积;(3)当DG =时,求GHE ∠的度数. 65.在数学的学习中,有很多典型的基本图形.(1)如图①,ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为D 、E .试说明ABD CAE ≌;(2)如图②,ABC 中,90BAC ∠=︒,AB AC =,点D 、A 、F 在同一条直线上,BD DF ⊥,3AD =,4BD =.则菱形AEFC 面积为______.(3)如图③,分别以Rt ABC 的直角边AC 、AB 向外作正方形ACDE 和正方形ABFG ,连接EG ,AH 是ABC 的高,延长HA 交EG 于点I ,若6AB =,8AC =,求AI 的长度.。
2020-2021学年人教版八年级数学下册第18章 正方形的性质与判定 经典常考题专题训练(二 )

人教版八年级数学下册第18章正方形的性质与判定经典常考题专题训练(二)1.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG时,求证:菱形EFGH为正方形.2.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK 是什么特殊平行四边形?请在图②中补全图形,并说明理由.3.如图,已知点E,F,M,N分别是正方形ABCD四条边上的点,并且AE=BF=CM =DN.(1)求证:四边形EFMN是正方形;(2)若AB=4,当点E在什么位置时,四边形EFMN的周长最小?并求四边形EFMN 周长的最小值.4.如图,正方形ABCD两条对角线AC、BD交于O,过O任作一直线L与边AB,CD 交于M,N,MN的垂直平分线与边BC,AD交于P,Q.设正方形ABCD的面积为S,四边形MPNQ的面积为S2.1(1)求证:四边形MPNQ是正方形;(2)若S1=1,求S2的取值范围.5.如图,正方形ABCD的对角线AC与BD交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE交于点E.求证:四边形OCED是正方形.6.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)求证:四边形ABCD是正方形.(2)已知AB的长为6,求(BE+6)(DF+6)的值.(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,则HR=.7.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)当线段DE与正方形ABCD的某条边的夹角是35°时,求∠EFC的度数.8.如图,正方形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC.(1)求证:四边形OCED是正方形.(2)若AC=,则点E到边AB的距离为.9.如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.(1)判断四边形ACEF为何种特殊的四边形,请说明理由.(2)若AB=3,BD=4,求BC的长.10.已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.11.如图,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA =EB=FC=GD,连接EG、FH,交点为O,连接EF、FG、GH、HE,求证:四边形EFGH是正方形.12.已知,如图,点A′、B′、C′、D′分别在正方形的边AB、BC、CD、DA上且AA′=BB′=CC′=DD′.(1)求证:四边形A′B′C′D′是正方形.(2)当点A′、B′、C′、D′处在什么位置时,正方形A′B′C′D′的面积是正方形ABCD面积的?请写出计算过程.13.如图,在四边形ABDE中,AD与BE相交于点O,OA=OB=OE=OD,AB=BD.(1)求证:四边形ABDE是正方形;(2)若∠ACB=90°,连接OC,OC=6,AC=5,求BC的长.14.如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=BC,∠D=45°,CD的垂直平分线交CD于E,交AD于F,交BC的延长线于G,若AD=a.(1)求证:四边形ABCF是正方形;(2)求BG的长.15.如图,在Rt△ABC中,∠A=90°,AB=2cm,AC=4cm.(1)在直角三角形中作一个正方形EFMN,使得EF、EN分别在边AB、AC上,点M 在BC边上,求正方形的边长.(2)将(1)中的正方形EFMN沿着射线AB以1cm/s的速度向右平移,当点E平移至与B重合时,正方形停止运动,设平移的时间为ts,正方形EFMN与Rt△ABC重叠部分的面积为S,求使用时间t表示S.参考答案1.证明:(1)连接GE,∵AB∥CD,∴∠AEG=∠CGE,∵GF∥HE,∴∠HEG=∠FGE,∴∠HEA=∠CGF;(2)∵四边形ABCD是正方形,∴∠D=∠A=90°,∵四边形EFGH是菱形,∴HG=HE,在Rt△HAE和Rt△GDH中,,∴Rt△HAE≌Rt△GDH(HL),∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴菱形EFGH为正方形;2.解:(1)AF=DE.∵ABCD是正方形,∴AB=AD,∠DAB=∠ABC=90°,∵AE=BF,∴△DAE≌△ABF,∴AF=DE.(2)四边形HIJK是正方形.如下图,H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△DAE≌△ABF,∴∠ADE=∠BAF,∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°∴∠KHI=90°,∴四边形HIJK是正方形.3.解:(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∵AE=BF=CM=DN,∴BE=CF=DM=NA,又∠A=∠B=∠C=∠D=90°,∴△BEF≌△CFM≌△DMN≌△ANE,∴EF=FM=MN=NE,∴四边形EFMN是菱形.∵∠AEN=∠BFE,且∠BEF+∠BFE=90°,∴∠BEF+∠AEN=90°,∴∠FEN=90°.∴菱形EFMN是正方形;(2)当EN最小时,正方形EFMN的周长最小,设AE=DN=x,则EN==,∴x=2时,EN的值最小,最小值=2,又四边形EFMN是正方形,∴四边形EFMN周长的最小值为.4.解:(1)证明:∵QP垂直平分线段MN,∴MQ=NQ,PM=PN,∴△AOQ≌△DON(ASA),∴OQ=ON,∴∠OQN=∠ONQ=45°,同理可得∠OQM=∠OMQ=∠OMP=∠OPM=45°,∴∠NQM=∠QMP=∠MPN=∠PNQ=90°,∴四边形MPNQ是矩形,而MQ=NQ,∴四边形MPNQ是正方形.(2)设AQ=DN=x,则QD=1﹣x,∴而S2≤S1=1,∴.5.证明:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∵正方形ABCD的对角线AC与BD交于点O,∴OD=OC,∠DOC=90°,∴四边形CODE是正方形.6.(1)证明:作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°=∠C,∴四边形ABCD是矩形,∵∠CEF,∠CFE外角平分线交于点A,∴AB=AG,AD=AG,∴AB=AD,∴四边形ABCD是正方形;(2)解:∵四边形ABCD是正方形,∴BC=CD=6,在Rt△ABE和Rt△AGE中,,∴Rt△ABE≌Rt△AGE(HL),∴BE=BG,同理:Rt△ADF≌Rt△AGF(HL),∴DF=GF,∴BE+DF=GE+GF=EF,设BE=x,DF=y,则CE=BC﹣BE=6﹣x,CF=CD﹣DF=6﹣y,EF=x+y,在Rt△CEF中,由勾股定理得:(6﹣x)2+(6﹣y)2=(x+y)2,整理得:xy+6(x+y)=36,∴(BE+6)(DF+6)=(x+6)(y+6)=xy+6(x+y)+36=36+36=72;(3)解:如图2所示:把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,∴MG=DG=MP=PH=6,∴GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR中,由勾股定理得:(6﹣a)2+42=(2+a)2,解得:a=3,即HR=3;故答案为:3.7.(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA=45°,∴EQ=EP,∵∠QEF+∠PEF=90°,∠PED+∠PEF=90°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)①当DE与AD的夹角为35°时,如图2,∵∠ADE=35°,∠ADC=90°,∴∠EDC=55°,∵∠EDC+∠DEF+∠EFC+∠FCD=360°,∴∠EFC=360°﹣90°﹣90°﹣55°=125°,②当DE与DC的夹角为35°时,如图3∵∠DEF=∠DCF=90°,∴点D,点E,点C,点F四点共圆,∴∠EDC=∠EFC=35°,综上所述:∠EFC=35°或125°.8.(1)证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形,在正方形ABCD中,AC⊥BD,OD=OC,∴∠COD=90°,∴四边形OCED是正方形.(2)解:如图,连接EO并延长,交AB于G,交CD于H,由(1)知:四边形OCED是正方形,∴CD⊥OE,∵四边形ABCD是正方形,∴AB∥CD,∴EG⊥AB,∵AC=,∴AB=BC=1=GH,Rt△DCE中,∵DE=CE,EH⊥CD,∴DH=CH,∴EH=CD=0.5,∴EG=1+0.5=1.5,∴点E到边AB的距离为1.5;故答案为:1.5.9.(1)解:四边形ACEF是正方形;理由如下:∵BD平分∠ABC,∠ABC=90°,∴∠CBD=∠ABD=∠ABC=45°,AC2=BC2+AB2=BC2+9,∵四边形ACEF是菱形,∴AE⊥CF,∠DAC=∠DAF=∠CAF,∴∠ADC=90°,∴A、B、C、D四点共圆,∴∠DAC=∠CBD=45°,∴∠CAF=2∠DAC=90°,∴四边形ACEF是正方形;(2)解:作DM⊥AB于M,DN⊥BC于N,如图所示:则△BDM和△BDN是等腰直角三角形,∴DM=DN=BD=4,∴S△ABD=AB×DM=×3×4=6,∵S△ABC=AB×BC=BC,S=BC×DN=2BC,S△ACD=S正方形ACEF=AC2=(BC2+9),△BDCS=S△ABC+S△ADC=S△ABD+S△BCD四边形ABCD∴BC+(BC2+9)=6+2BC解得:BC=5或BC=﹣3(舍去),∴BC=5.10.证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠BAD=∠ABC=∠BCD=∠CDA=90°,在△ABF和△BCG中,,∴△ABF≌△BCG(SAS)∴∠BAF=∠GBC,∵∠BAF+∠AFB=90°,∴∠BNF=90°,∴∠MNP=90°.∴同理可得∠NPQ=∠PQM=90°,∴四边形MNPQ是矩形.在△ABN和△BCP中,,∴△ABN≌△BCP(AAS),∴AN=BP,在△AME和△BNF中,,∴△AME≌△BNF(AAS),∴AM=BN,∴MN=NP,∴矩形MNPQ是正方形.11.证明:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,∵HA=EB=FC=GD,∴AE=BF=CG=DH,∴△AEH≌△BFE≌△CGF≌△DHG,∴EF=FG=GH=HE,∴四边形EFGH是菱形,∵△DHG≌△AEH,∴∠DHG=∠AEH,∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴四边形EFGH是正方形.12.(1)证明:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,∵AA′=BB′=CC′=DD′,∴A′B=B′C=C′D=D′A,在△AA′D′和△BB′A′中,,∴△AA′D′≌△BB′A′(SAS),∴A′D′=A′B′,∠AA′D′=∠BB′A′,∵∠BB′A′+∠BA′B′=90°,∴∠AA′D′+∠BA′B′=90°,∴∠B′A′D′=90°,同理:∠A′B′C′=∠B′C′D′=90°,∴四边形A′B′C′D′是矩形,∴四边形A′B′C′D′是正方形;(2)点A′、B′、C′、D′分别在AB、BC、CD、DA的三等分点时,正方形A′B′C′D′的面积是正方形ABCD面积的;∵正方形ABCD∽正方形A′B′C′D′,∴正方形A′B′C′D′:正方形ABCD的面积=()2=,∴=,设A′B′=a,AB=3a,A′B=x,则BB′=3a﹣x,在Rt△A′BB′中,x2+(3a﹣x)2=(a)2,解得:x=a,或x=2a,∴A′B=2a,∴点A′、B′、C′、D′分别在AB、BC、CD、DA的三等分点时,正方形A′B′C′D′的面积是正方形ABCD面积的.13.解:(1)∵OA=OB=OE=OD,∴四边形ABCD是平行四边形,AD=BE,∴四边形ABDE是矩形,又∵AB=BD,∴四边形ABDE是正方形.(2)如图所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中,,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∵∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=AM=CF,∴△OCF为等腰直角三角形,∵OC=6,根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,∴BC=CF+BF=6+1=7.14.解:(1)∵CD的垂直平分线交CD于E,交AD于F,∴FC=FD,∴∠D=∠FCD=45°,∴∠CFD=90°,即∠AFC=90°,又∵AD∥BC,∠A=90°,∴∠B=90°,∴四边形ABCF是矩形,又∵AB=BC,∴四边形ABCF是正方形;(2)∵FG垂直平分CD,∴CE=DE,∠CEG=∠DEF=90°,∵BG∥AD,∴∠G=∠EFD,在△CEG和△DEF中,,∴△CEG≌△DEF(AAS),∴CG=FD,又∵正方形ABCF中,BC=AF,∴AF+FD=BC+CG,∴AD=BG=a.15.解:(1)设正方形的边长为a.∵MN∥AB,∴=,∴=,∴a=cm,∴正方形的边长为cm.(2)当0<t≤时,S=﹣•t•2t=﹣t2+.当<t≤时,S=[(﹣t)+(2﹣t)]=﹣t+,当<t≤2时,S=•(2﹣t)•(4﹣2t)=t2﹣4t+4.。
八年级数学下册期末几何题证明题专题
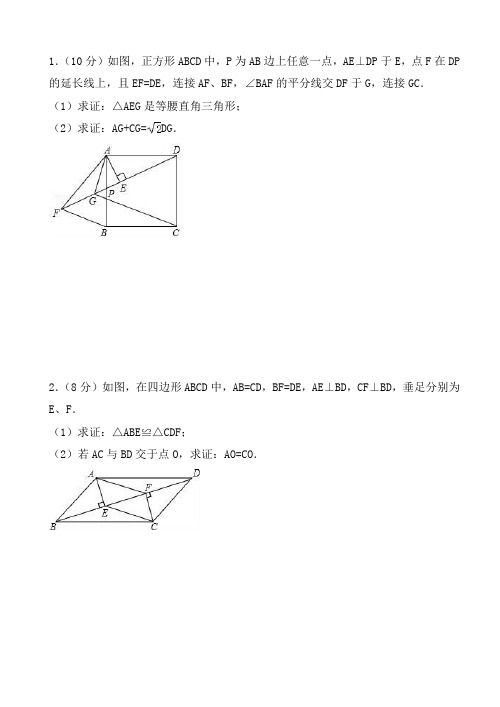
1.(10分)如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP 的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.(1)求证:△AEG是等腰直角三角形;(2)求证:AG+CG=DG.2.(8分)如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.3.(9分)如图,在梯形ABCD中,M、N分别为AD、BC的中点,E、F分别为BM、CM的中点.(1)求证:四边形MENF是平行四边形;(2)若四边形MENF的面积是梯形ABCD面积的,问AD、BC满足什么关系?4.如图,在四边形 ABCD 中,AD=12,DO=OB=5,AC=26,∠ADB=90°.(1)求证:四边形 ABCD 为平行四边形;(2)求四边形 ABCD 的面积.5、四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.6、如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=,求AD的长.7、如图,E是▱ABCD的边CD的中点,延长AE交BC的延长线于点F.(1)求证:△ADE≌△FCE.(2)若∠BAF=90°,BC=5,EF=3,求CD的长.8、如图,在菱形ABCD中,AB=2,∠DAB=60°。
点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD、AN。
(1)求证:四边形AMDN是平行四边形。
(2)当AM为何值时,四边形AMDN是矩形?请说明理由。
9.(6 分)如图,菱形ABCD 的对角线AC、BD 相交于点O,且DE∥AC,AE∥B D.求证:四边形AODE 是矩形.10(9 分)如图,在△ABC 中,D 是BC 边上的中点,E 是AD 边上的中点,过A 点作BC的平行线交CE 的延长线于点F,连结BF.(1)求证:四边形AFBD 是平行四边形.(2)当△ABC 满足什么条件时,四边形AFBD 是矩形?请说明理由.10.(7 分)如图,在△ABC 中,AB=AC,AD 平分∠BAC 交BC 于点D,分别过点A、D作AE∥BC、DE∥AB,AE 与DE 相交于点E,连结CE.(1)求证:BD =CD.(2)求证:四边形ADCE 是矩形.11.(9 分)如图,E、F 分别是矩形ABCD 的边BC、AD 上的点,且BE =DF.(1)求证:四边形AECF 是平行四边形.(2)若四边形AECF 是菱形,且CE = 10,AB = 8,求线段BE 的长.12.(7 分)如图,在△ABC 中,AD 是∠BAC 的平分线,AD 的垂直平分线交AB 于点E,交AC 于点F,连结DE、DF.(1)求证:∠ADE=∠DAF.(2)求证:四边形AEDF 是菱形.13.【感知】如图①,四边形ABCD、AEFG 都是正方形,可知BE =DG .【探究】当正方形AEFG 绕点A 旋转到图②的位置时,连结BE、DG.求证:BE =DG .【应用】当正方形AEFG 绕点A 旋转到图③的位置时,点F 在边AB 上,连结BE、D G.若DG =13 ,AF = 10 ,则AB 的长为.14. (10 分)如图,以△ABC 的三边为边分别作等边△ACD、△BCE、△ABF.(1)求证:四边形ADEF 是平行四边形(2)△ABC 满足什么条件时,四边形ADEF 是矩形?(3)△ABC 满足什么条件时,四边形ADEF 是菱形?20.如图,将▱ABCD 的边 DC 延长到点 E ,使 CE=DC ,连接 AE ,交 BC 于点 F . (1)求证:△ABF ≌△ECF ;(2)若∠AFC=2∠D ,连接 AC 、BE ,求证:四边形 ABEC 是矩形.18.(本题8分)如图,□ABCD 的对角线AC 、BD 相交于点O ,过点D 作DE ∥AC ,且DE =21AC ,连接CE 、OE(1) 求证:四边形OCED 是平行四边形; (2) 若AD =DC =3,求OE 的长.21.(本题8分)如图,在四边形ABCD 中,AD ∥BC ,AB =3,BC =5,连接BD ,∠BAD 的平分线分别交BD 、BC 于点E 、F ,且AE ∥CD (1) 求AD 的长;(2) 若∠C =30°,求CD 的长.27.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE 的延长线于点F,且AF=BD,连接BF.(1)证明:BD=CD;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.28.如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2,,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;(2)求∠BPQ的大小.18. (本题满分12分)如图,DB∥AC,且DB=12AC,E是AC的中点。
2022年华东师大版八年级数学下册第十九章矩形、菱形与正方形综合练习练习题(精选含解析)

八年级数学下册第十九章矩形、菱形与正方形综合练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,矩形ABCD 的面积为1cm 2,对角线交于点O ;以AB 、AO 为邻边作平行四边形AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边作平行四边形AO 1C 2B ,…;依此类推,则平行四边形AO 2014C 2015B 的面积为( )cmA .201312 B .201412 C .201512 D .2016122、小明想判断家里的门框是否为矩形,他应该( )A .测量三个角是否都是直角B .测量对角线是否互相平分C .测量两组对边是否分别相等D .测量一组对角是否是直角3、如图,在矩形ABCD 中,AB =2,BC =4,对角线AC ,BD 相交于点O ,OE ⊥AC 交BC 于点E ,EF ⊥BD 于点F ,则OE +EF 的值为( )A B .2 C .52 D .4、如图,四边形ABCD 为平行四边形,延长AD 到E ,使DE =AD ,连接EB ,EC ,DB ,添加一个条件,不能使四边形DBCE 成为矩形的是( )A .AB =BE B .DE ⊥DC C .∠ADB =90°D .CE ⊥DE5ABCD 中,点E 是对角线AC 上一点,且EF AB ⊥于点F ,连接DE ,当22.5ADE ∠=︒时,EF =( )A .1B .2C 1D .146、如图,点E 是正方形ABCD 的边DC 上一点,把△ADE 绕点A 顺时针旋转90°到△ABF 的位置,若四边形AECF 的面积为144.AE =13.则DE 的长为( )A .BC .4D .57、如图,在菱形ABCD 中,P 是对角线AC 上一动点,过点P 作PE BC ⊥于点E .PF AB ⊥于点F .若菱形ABCD 的周长为24,面积为24,则PE PF +的值为( )A .4B .245C .6D .4858、如图所示,四边形ABCD 是矩形,过点D 作对角线BD 的垂线,交BC 的延长线于点E ,取BE 的中点F ,连接DF ,DF =5,设AB =x ,AD =y ,则x 2+(y ﹣5)2的值为( )A .10B .25C .50D .759、如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后,得到正方形AB ′C ′D ′,边B 'C ′与DC 交于点O ,则∠DOB '的度数为( )A .125°B .130°C .135°D .140°10、如图,把一张长方形纸片ABCD 沿AF 折叠,使B 点落在B '处,若20ADB ∠=︒,要使AB BD '∥,则BAF ∠的度数应为( )A.20°B.55°C.45°D.60°第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、(1)两组对边分别______,菱形的四条边都______.几何语言:∵四边形ABCD是菱形∴AB∥CD,AD∥BCAB=CD=AD=BC(2)菱形的两组对角______,邻角______几何语言:∵四边形ABCD是菱形∴∠BAD=∠BCD,∠CBA=∠ADC∠BAD+∠ADC=180°∠BCD+∠CBA=180°∠BAD+∠CBA=180°∠BCD+∠ADC=180°(3)菱形的对角线互相______,并且每一条对角线______一组对角.几何语言:∵四边形ABCD 是菱形∴AC ⊥BD , AC 平分∠BAD ,∠BCD , BD 平分∠ABC ,∠ADC(4)菱形既是轴对称图形,又是中心对称图形,有______条对称轴,其对称轴为两条对角线所在直线,对称中心为其______的交点.2、一个长方形的周长是22cm ,若这个长方形的长减少2cm ,宽增加3cm ,就可以成为一个正方形,则长方形的长是______cm .3、如图,矩形ABCD 的两条对角线相交于点O ,已知120AOD ∠=︒, 2.5cm AB =,则矩形对角线BD 的长为_______cm .4、如图,矩形ABCD 的两条对角线AC ,BD 交于点O ,∠AOB =60°,AB =3,则矩形的周长为 _____.5、如图,在ABC 中,90ACB ∠=︒,AB =1BC =,P 是线段AB 边上的动点(不与点A ,B 重合),将BCP 沿CP 所在直线翻折,得到B CP '△,连接B A ',当B A '取最小值时,则AP 的值为________.6、如图,正方形ABCD 中,E 为CD 上一动点(不含C 、)D ,连接AE 交BD 于F ,过F 作FH AE ⊥交BC 于H ,过H 作HG BD ⊥于G ,连接AH ,EH .下列结论:①AF FH =;②45HAE ∠=︒;③FH 平分GHC ∠;④2BD FG =,正确的是__(填序号).7、在菱形ABCD 中,60A ∠=︒,其所对的对角线长为2,则菱形ABCD 的面积是__.8、如图,矩形ABCD 中,对角线AC ,BD 相交于点O ,AD =60COB ∠=︒,BF AC ⊥,交AC 于点M ,交CD 于点F ,延长FO 交AB 于点E ,则下列结论:①FO FC =;②四边形EBFD 是菱形;③OBE CBF △△≌;④3MB =.其中结论正确的序号是______.9、如图在正方形ABCD 中,∠EAF 的两边分别交CB 、DC 延长线于E 、F 点且∠EAF =45°,如果BE =1,DF =7,则EF =__.10、如图,菱形ABCD 的周长为40,面积为80,P 是对角线BC 上一点,分别作P 点到直线AB .AD 的垂线段PE .PF ,则PE PF +等于______.三、解答题(5小题,每小题6分,共计30分)1、数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,222A B C ∆就是由ABC ∆沿直线1翻移后得到的.(先翻折,然后再平移)(1)在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的A 与2A ,B 与2B …)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)(2)如图2,在长方形ABCD 中,8BC =,点,E F 分别是边,BC AD 中点,点G 在边CD 延长线上,联结,AE FG ,如果GDF ∆是ABE ∆经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线a ;联结AG ,线段AG 和直线a 交于点O ,若OGF ∆的面积为3,求此长方形的边长AB 的长.(3)如图3,M 是(2)中的长方形边BC 上一点,如果1BM =,ABM ∆先按(2)的“翻移线”直线a 翻折,然后再平移2个单位,得到111A B M ∆,联结线段11AA MM 、,分别和“翻移线”a 交于点K 和点H ,求四边形AKHM 的面积.2、如图,ABC 和DBC △中,90ACB DBC ∠=∠=︒,E 是BC 的中点,且ED AB ⊥于点F ,且AB DE =,CD 交AB 于点M .(1)求证:2BD EC =;(2)求ACM △与BCM 的面积之比.3、如图,已知菱形ABCD 的对角线相交于点O ,延长AB 至点E ,使BE =AB ,连接CE .(1)求证:BD=EC.(2)若∠E=57°,求∠BAO的大小.4、下面是小明设计的“作菱形ABCD”的尺规作图过程.求作:菱形ABCD.作法:①作线段AC;②作线段AC的垂直平分线l,交AC于点O;③在直线l上取点B,以O为圆心,OB长为半径画弧,交直线l于点D(点B与点D不重合);④连接AB、BC、CD、DA.所以四边形ABCD为所求作的菱形.根据小明设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.=,证明:OA OC=,OB OD∴.,∴四边形ABCD为菱形()(填推理的依据).5、如图,已知在ABC 中,90A ∠=︒,求作正方形ADEF ,使得D ,E ,F 分别在AB ,BC ,AC 上.-参考答案-一、单选题1、C【解析】【分析】根据“同底等高”的原则可知平行四边形AOC 1B 底边AB 上的高等于BC 的12,则有平行四边形AOC 1B 的面积12,平行四边形AOC 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12,则有平行四边形ABC 3O 2的面积212,…;由此规律可进行求解. 【详解】解:∵O 1为矩形ABCD 的对角线的交点,∴平行四边形AOC 1B 底边AB 上的高等于BC 的12,∴平行四边形AOC 1B 的面积=12×1=12,∵平行四边形AO 1C 2B 的对角线交于点O 2,∴平行四边形AOC 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12,∴平行四边形ABC 3O 2的面积=12×12×1=212, …,依此类推,平行四边形ABC 2014O 2015的面积=201512cm 2.故答案为:C .【点睛】本题主要考查矩形的性质与平行四边形的性质,熟练掌握矩形的性质与平行四边形的性质是解题的关键.2、A【解析】【分析】根据矩形的判定方法解题.【详解】解:A 、三个角都是直角的四边形是矩形,∴选项A 符合题意; B 、对角线互相平分的四边形是平行四边形,∴选项B 不符合题意,C 、两组对边分别相等的四边形是平行四边形,∴选项C 不符合题意;D 、一组对角是直角的四边形不是矩形,∴选项D 不符合题意;故选:A .【点睛】本题考查矩形的判定方法,是重要考点,掌握相关知识是解题关键.3、A【解析】【分析】依据矩形的性质即可得到BOC ∆的面积为2,再根据BOC COE BOE S S S∆=+,即可得到OE EF +的值. 【详解】解:2AB =,4BC =,∴矩形ABCD 的面积为8,AC =12BO CO AC ∴==对角线AC ,BD 交于点O ,BOC ∴∆的面积为2,EF OB ⊥,EO AC ⊥,BOC COE BOE S S S ∆∴=+,即11222CO EO OB EF =⨯+⨯,12)2EO EF ∴=+,)4EO EF +=,∴+EO EF故选:A.【点睛】本题主要考查了矩形的性质,解题的关键是掌握矩形的四个角都是直角,矩形的对角线相等且互相平分.4、B【解析】【分析】先证明四边形BCED为平行四边形,再根据矩形的判定进行解答.【详解】解:∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC,又∵AD=DE,∴DE∥BC,且DE=BC,∴四边形BCED为平行四边形,A、∵AB=BE,DE=AD,∴BD⊥AE,∴□DBCE为矩形,故本选项不符合题意;B、∵DE⊥DC,∴∠EDB=90°+∠CDB>90°,∴四边形DBCE不能为矩形,故本选项符合题意;C、∵∠ADB=90°,∴∠EDB =90°,∴□DBCE 为矩形,故本选项不符合题意;D 、∵CE ⊥DE ,∴∠CED =90°,∴□DBCE 为矩形,故本选项不符合题意.故选:B .【点睛】本题考查了平行四边形的判定和性质、矩形的判定等知识,判定四边形BCED 为平行四边形是解题的关键.5、C【解析】【分析】证明67.5CDE CED ∠=∠=︒,则CD CE =AC 的长,得2AE =,证明AFE ∆是等腰直角三角形,可得EF 的长.【详解】 解:四边形ABCD 是正方形,AB CD BC ∴==90B ADC ∠=∠=︒,45BAC CAD ∠=∠=︒, 22AC AB ,22.5ADE ∠=︒,9022.567.5CDE ∴∠=︒-︒=︒,4522.567.5CED CAD ADE ∠=∠+∠=︒+︒=︒,CDE CED ∴∠=∠,CD CE ∴==2AE ∴=EF AB ⊥,90AFE ∴∠=︒,AFE ∴∆是等腰直角三角形,1EF ∴,故选:C .【点睛】本题考查正方形的性质,勾股定理,等腰直角三角形,三角形的外角的性质等知识,解题的关键是在正方形中学会利用等腰直角三角形的性质解决问题,属于中考常考题型.6、D【解析】【分析】由旋转性质得△ABF ≌△ADE ,再根据全等三角形的性质得到S 正方形ABCD =S 四边形AECF =144进而求得AD =12,再利用勾股定理求解DE 即可.【详解】解:∵△ADE 绕点A 顺时针旋转90°得到△ABF ,∴△ABF ≌△ADE ,∴S △ABF =S △ADE ,∴S 正方形ABCD =S 四边形AECF =144,∴AD =12,在Rt△ADE 中,AE =13,AD =12,由勾股定理得:DE ,【点睛】本题考查旋转性质、全等三角形的性质、正方形的面积公式、勾股定理,熟练掌握旋转性质,得出S 正方形ABCD =S 四边形AECF 是解答的关键.7、A【解析】【分析】连接BP ,通过菱形ABCD 的周长为24,求出边长,菱形面积为24,求出ABC S的面积,然后利用面积法,=+ABC ABP CBP S S S ,即可求出PE PF +的值.【详解】解:如图所示,连接BP ,∵菱形ABCD 的周长为24,∴2446AB BC ==÷=,又∵菱形ABCD 的面积为24,∴24212=÷=ABCS , ∴12=+=ABC ABP CBP SS S , ∴111222⋅+⋅=AB PF BC PE ,∴()1122⋅+=AB PE PF ,∵6AB =,∴4PE PF +=,故选:A .【点睛】本题主要考查菱形的性质,解题关键在于添加辅助线,通过面积法得出等量关系.8、B【解析】【分析】根据题意知点F 是Rt△BDE 的斜边上的中点,因此可知DF =BF =EF =5,根据矩形的性质可知AB =DC =x ,BC =AD =y ,因此在Rt△CDF 中,CD 2+CF 2=DF 2,即可得答案.【详解】解:∵四边形ABCD 是矩形,AB =x ,AD =y ,∴CD =AB =x ,BC =AD =y ,∠BCD =90°,又∵BD ⊥DE ,点F 是BE 的中点,DF =5,∴BF =DF =EF =5,∴CF =5-BC =5-y ,∴在Rt△DCF 中,DC 2+CF 2=DF 2,即x 2+(5-y )2=52=25,∴x 2+(y -5)2=x 2+(5-y )2=25,故选:B .【点睛】本题考查了直角三角形斜边中线等于斜边的一半、矩形的性质、勾股定理,做题的关键是利用直角三角形斜边中线等于斜边的一半求出BF 的长度.9、C【解析】【分析】连接B ′C ,根据题意得B ′在对角线AC 上,得∠B 'CO =45°,由旋转的性质证出∠OB 'C 是直角,得=45B CO '∠︒,即可得出答案.【详解】解:连接B ′C ,如图所示,∵四边形ABCD 是正方形,∴AC 平分∠BAD ,∵旋转角∠BAB ′=45°,∠BAC =45°,∴B ′在对角线AC 上,∴∠B 'CO =45°,由旋转的性质得:90AB C B ''∠=∠=︒,AB '=AB =1,∴45B OC '∠=︒∴18045135DOB '∠=︒-︒=︒故选:C .【点睛】本题考查了正方形的性质、旋转的性质等知识;熟练掌握正方形的性质和旋转的性质是解题的关键.10、B【解析】【分析】设直线AF 与BD 的交点为G ,由题意易得90DAB ∠=︒,则有70ABD ∠=︒,由折叠的性质可知BAF B AF '∠=∠,由平行线的性质可得B AF BGA '∠=∠,然后可得BAF BGA ∠=∠,进而问题可求解.【详解】解:设直线AF 与BD 的交点为G ,如图所示:∵四边形ABCD 是矩形,∴90DAB ∠=︒,∵20ADB ∠=︒,∴70ABD ∠=︒,由折叠的性质可知BAF B AF '∠=∠,∵AB BD '∥,∴B AF BGA '∠=∠,∴BAF BGA ∠=∠, ∴180552ABG BAF ︒-∠∠==︒; 故选B .【点睛】本题主要考查折叠的性质及矩形的性质,熟练掌握折叠的性质及矩形的性质是解题的关键.二、填空题1、 平行 相等 相等 互补 垂直 平分 两 对角线【解析】略2、8【解析】【分析】设这个长方形的长为xcm ,则长方形的宽为()11x -cm ,由题意得长2-=宽+3.进而得到方程2113x x -=-+,解方程即可得到答案.【详解】解:设这个长方形的长为x cm ,由题意得:2113x x -=-+,216,x ∴=解得:8,x =答:这个长方形的长为8.cm故答案为:8【点睛】本题主要考查了一元一次方程的应用,关键是正确理解题意,抓住关键语句,表示出正方形的边长,进而利用正方形边长相等得到方程.3、5【解析】【分析】由矩形的性质可证△AOB为等边三角形,可求BO=AB的长,即可求BD的长.【详解】解:∵四边形ABCD是矩形,∴AO=CO=BO=DO,∵∠AOD=120°,∴∠AOB=60°,且AO=BO,∴△ABO为等边三角形,∴AO=BO=AB=2.5,∴BD=5,故答案为:5.【点睛】本题考查矩形的性质,熟练掌握矩形的性质是本题的关键,①矩形的对边平行且相等;②矩形的四个角都是直角;③矩形的对角线相等且互相平分.4、663##6【解析】【分析】根据矩形性质得出AD=BC,AB=CD,∠BAD=90°,OA=OC=12AC,BO=OD=12BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BD,根据勾股定理求出AD即可.【详解】解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC=12AC,BO=OD=12BD,AC=BD,∴OA=OB=OC=OD,∵∠AOB =60°,OB =OA ,∴△AOB 是等边三角形,∵AB =3,∴OA =OB =AB =3,∴BD =2OB =6,在Rt △BAD 中,AB =3,BD =6,由勾股定理得:AD =∵四边形ABCD 是矩形,∴AB =CD =3,AD =BC =∴矩形ABCD 的周长是AB +BC +CD +AD =故答案为:【点睛】本题考查了矩形性质,等边三角形的性质和判定,勾股定理等知识点,关键是求出AD 的长.5【解析】【分析】根据翻转变换的性质可知BC =C B '=1,当A 、B '、C 三点在一条直线上时,A B '有最小值,根据题意作图,过P 点作PH ⊥BC ,PQ ⊥AC ,得到四边形PQCH 是正方形,利用面积法求出PQ 的长,再根据勾股定理求出AP 的长.【详解】解:∵在ABC 中,90ACB ∠=︒,AB =1BC =∴AC2=由翻转变换的性质可知:BC=C B'=1,故当A、B'、C三点在一条直线上时,A B'有最小值,过P点作PH⊥BC,PQ⊥AC,∴∠ACB=∠PHC=∠PQC=90°∴四边形PQCH是矩形∵翻转∴△BCP≌△B'CP∴PH=PQ∴四边形PQCH是正方形设PQ=x,则PH=x∵S△ABC=S△APC+S△PBC∴111222BC AC BC PH PQ AC ⨯=⨯+⨯即1111212 222x x⨯⨯=⨯⨯+⨯解得x=2 3∴AQ=2-23=43∴AP【点睛】本题主要考查的是翻转变换的性质、线段的性质,根据题意找到B '的位置是解题的关键.6、①②④【解析】【分析】连接FC ,延长HF 交AD 于点L .可证ADF CDF ∆∆≌,进而可得FHC FCH ∠=∠,由此可得出FH AF =;再由FH AF =,即可得出45HAE ∠=︒;连接AC 交BD 于点O ,则2BD OA =,证明AOF FGH ≌,即可得出OA GF =,进而可得2BD FG =;过点F 作MN BC ⊥于点N ,交AD 于点M ,由于F 是动点,FN 的长度不确定,而FG OA =是定值,即可得出FH 不一定平分GHC ∠.【详解】解:如图,连接FC ,延长HF 交AD 于点L .∵BD 为正方形ABCD 的对角线∴45ADB CDF ∠=∠=︒,AD CD =在ADF 和CDF 中45AD CD ADB CDF DF DF =⎧⎪∠=∠=︒⎨⎪=⎩∴()ADF CDF SAS ∆∆≌∴AF FC =,DCF DAF ∠=∠∵90AFL ∠=︒,90ALH LAF ∠+∠=︒ ,ALH FHC ∠=∠∴90LHC DAF ∠+∠=︒∵DCF DAF ∠=∠,90FCD FCH ∠+∠=︒∴FHC FCH ∠=∠∴FH FC =∴AF FH =故①正确;∵90AFH ∠=︒,AF FH =∴AFH 是等腰直角三角形∴45HAE ∠=︒故②正确;连接AC 交BD 于点O ,则2BD OA =∵90AFO GFH GHF GFH ∠+∠=∠+∠=︒∴AFO GHF ∠=∠在AOF 和FGH 中90AFO GHF AOF FGH AF FH ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()AOF FGH AAS ∆∆≌∴OA GF =∴22BD OA GF ==故④正确.过点F 作MN BC ⊥于点N ,交AD 于点M ,F 是动点∵FN 的长度不确定,而FG OA =是定值∴FN 不一定等于FGFH ∴不一定平分GHC ∠故③错误;故答案为:①②④.【点睛】本题考查了正方形性质,全等三角形判定和性质,角平分线性质和判定,等腰三角形的性质与判定等,熟练掌握全等三角形判定和性质,合理添加辅助线构造全等三角形是解题关键.7、【解析】【分析】根据菱形的性质证得△ABD 是等边三角形,得到OB ,利用勾股定理求出OA ,由菱形的性质求出菱形的面积.【详解】解:如图所示:在菱形ABCD 中,60BAD ∠=︒,其所对的对角线长为2,AD AB ∴=,AC BD ⊥,BO DO =,AO CO =,ABD ∴∆是等边三角形,则2AB AD ==,故1BO DO ==,则AO =AC =则菱形ABCD 的面积122=⨯⨯故答案为:【点睛】此题主要考查了菱形的性质以及勾股定理,正确得出菱形的另一条对角线的长是解题关键.8、①②③④【解析】【分析】由矩形的性质及垂直平分线的判定和性质可证明①;根据全等三角形的判定和性质及菱形的判定和性质可证明②;由菱形的性质及全等三角形的判定可证明③;根据矩形的性质,含30︒角的直角三角形的性质,勾股定理可证明④.【详解】解:∵四边形ABCD 为矩形,∴AC BD =,∴OA OC OD OB ===,∵60COB ∠=︒,∴OBC 为等边三角形,∴OB BC OC ==,60OBC ∠=︒,∵BF AC ⊥,∴OM MC =,∴FM 是OC 的垂直平分线,∴FO FC =,故①正确;∵AB CD ∥,∴DFE BEF ∠=∠,在DOF 与BOE 中,DOF BOE DFE BEF OD OB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴DOF BOE ≅,∴DF BE =,∵AB CD ∥,∴四边形EBFD 为平行四边形,由①得OBC 为等边三角形,∴60OBC OCB ∠=∠=︒,∴30ACD BCD OCB ∠=∠-∠=︒,∵OD OC =,∴30ACD BDC ∠=∠=︒,∵BF AC ⊥,OBC 为等边三角形,∴30DBE ∠=︒,∴DBF BDC ∠=∠∴DF BF =,∴四边形EBFD 为菱形,②正确;由②可得:OB EF ⊥,∴90BOE BCF ∠=∠=︒,∵AB CD ∥,∴30EBO BDC ∠=∠=︒,∴30EBO FBC ∠=∠=︒,在OBE 与CBF 中,EBO FBC BO BCBOE BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴OBE CBF ≅,③正确;∵四边形ABCD 为矩形,∴BC AD ==∵BF AC ⊥,30FBC ∠=︒,∴12CM BC ==∴3MB ==,④正确,∴正确结论为:①②③④,故答案为:①②③④.【点睛】题目主要考查矩形的性质,菱形的判定定理,全等三角形的判定和性质,含30︒角的直角三角形的性质,勾股定理等,理解题意,综合运用这些性质是解题关键.9、6【解析】【分析】根据题意把△ABE 绕点A 逆时针旋转90°到AD ,交CD 于点G ,证明△AEF ≌△AGF 即可求得EF =DF ﹣BE =7﹣1=6.【详解】解:如图,把△ABE 绕点A 逆时针旋转90°到DA ,交CD 于点G ,由旋转的性质可知,AG =AE ,DG =BE ,∠DAG =∠BAE ,∵∠EAF =45°,∴∠DAG +∠BAF =45°,又∵∠BAD =90°,∴∠GAF =45°,在△AEF 和△AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴△AEF ≌△AGF (SAS )∴EF =GF ,∵BE=1,DF=7,∴EF=GF=DF﹣DG=DF﹣BE=7﹣1=6.故答案为:6.【点睛】本题主要考查正方形的性质及全等三角形的判定和性质,构造全等三角形是解题的关键,注意旋转性质的应用.10、8【解析】【分析】直接利用菱形的性质得出AB=AD=10,S△ABD=12.5,进而利用三角形面积求法得出答案.【详解】解:∵菱形ABCD的周长为40,面积为80,∴AB=AD=10,S△ABD=40,∵分别作P点到直线AB、AD的垂线段PE、PF,∴12×AB×PE+12×PF×AD=40,∴12×10(PE+PF)=40,∴PE+PF=8.故答案为:8.【点睛】此题主要考查了菱形的性质,正确得出12×AB×PE+12×PF×AD=S△ABD是解题关键.三、解答题1、 (1)“翻移运动”对应点(指图1中的A 与2A ,B 与2)B ⋯连线被翻移线平分(2)3(3)11或10【解析】【分析】(1)画出图形,即可得出结论;(2)作直线EF ,即为“翻移线”直线a ,再由“翻移运动”的性质和三角形面积关系求解即可;(3)分两种情况:①ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向上平移2个单位,②ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向下平移2个单位,由“翻移运动”的性质、梯形面积公式和三角形面积公式分别求解即可.(1)解:如图1,连接2AA ,2BB ⋯,则“翻移运动”对应点(指图1中的A 与2A ,B 与2)B ⋯连线被翻移线平分;(2)解:作直线EF ,即为“翻移线”直线a ,如图2所示:四边形ABCD 是长方形,AB CD ∴=,8AD BC ==,由“翻移运动”的性质得:AB DC GD ==,142AF DF AD ===,O 是AG 的中点,3AOF OGF S S ∆∆∴==, ΔΔ26AFG OGF S S ∴==,AF DF =,ΔΔ6GDF AFG S S ∴==,Δ114622GDF S DG DF DG ∴=⨯=⨯⨯=, 3DG ∴=,3AB ∴=;(3)解:分两种情况:①ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向上平移2个单位,如图3所示:设ABE ∆翻折后的三角形为DCP ∆,连接1PM ,则1112A D B C M P ===,同(2)得:1112KF A D ==,1112HE M P ==,4BE =,1BM =,3ME BE BM ∴=-=,∴四边形AKHM 的面积=梯形ABEK 的面积ABM -∆的面积HME -∆的面积111(331)4313111222=⨯++⨯-⨯⨯-⨯⨯=; ②ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向下平移2个单位,如图4所示:设ABE ∆翻折后的三角形为DCP ∆,连接1PM ,则1112A D B C M P ===,同(2)得:1112KF A D ==,1112HE M P ==,4BE =,1BM =,3ME BE BM ∴=-=,∴四边形AKHM 的面积=梯形AFEM 的面积AFK -∆的面积HME +∆的面积111(34)3413110222=⨯+⨯-⨯⨯+⨯⨯=; 综上所述,四边形AKHM 的面积为11或10.【点睛】本题是四边形综合题目,考查了长方形的性质、“翻移运动”的性质、梯形面积公式、三角形面积公式等知识,本题综合性强,解题的关键是熟练掌握“翻移运动”的性质和长方形的性质.2、 (1)见解析 (2)12【解析】【分析】(1)易证DEB A ∠=∠,即可证明ACB EBD ∆≅∆,得出BC BD =,根据点E 是BC 的中点即可解题;(2)过点M 作,BC AC 的垂线,交于点,P Q ,证四边形PMQC 为矩形,再证得四边形PMQC 为正方形,得出MP MQ =,根据ACM BCM S AC S BC=. (1)解:证明:90DEB ABC ∠+∠=︒,90A ABC ∠+∠=︒,DEB A ∴∠=∠, 在ACB ∆和EBD ∆中,ACB DBE A DEB AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,AAS;∴∆≅∆,()ACB EBD∴=,BC BD点E是BC的中点,∴=,2EC BC∴=;2BD EC(2)BC AC的垂线,交于点,P Q,解:过点M作,∴∠=︒,MP QC MQ PC MPC//,//,90∴四边形PMQC为矩形,=∠=︒,BC BD DBC,90∴△为等腰直角三角形,BCD∴∠=︒,MCP45∴为等腰直角三角形,CPM∴=,CP MP∴四边形PMQC为正方形,∴=,MP MQ11,22ACM BCM SAC MQ S BC MQ =⋅=⋅, ACMBCM S AC S BC ∴=, 12AC BC =, 12ACMBCMSS ∴=. 【点睛】本题考查了全等三角形的判定,等腰直角三角形,正方形的判定及性质,解题的关键是掌握全等三角形的判定及性质,同时利用等量代换的思想进行求解.3、 (1)见解析(2)33°【解析】【分析】(1)由菱形的性质可得AB =CD =BE ,AB //CD ,可证四边形BECD 是平行四边形,可得BD =EC ;(2)由平行四边形的性质可得BD //CE ,可得∠ABO =∠E =57°,菱形的性质可求∠BAO 的大小.(1)证明:∵四边形ABCD 是菱形,∴AB =CD ,AB //CD又∵BE =AB ,∴BE =CD ,BE //CD ,∴四边形BECD 是平行四边形∴BD =EC(2)∵四边形BECD是平行四边形,∴BD//CE,∴∠ABO=∠E=57°又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°∴∠BAO+∠ABO=90°∴∠BAO=90°-∠ABO=33°【点睛】本题考查了菱形的性质,平行四边形的判定和性质,熟练运用菱形的性质是本题的关键.,对角线互相垂直的平行四边形为菱形4、(1)见解析;(2)四边形ABCD为平行四边形,BD AC【解析】【分析】(1)根据几何语言画出对应的几何图形;(2)先证明四边形ABCD为平行四边形,然后利用对角线垂直可判断四边形ABCD为菱形.【详解】解:(1)如图,四边形ABCD为所作;(2)完成下面的证明.=,证明:OA OC=,OB OD∴四边形ABCD为平行四边形,BD AC⊥,∴四边形ABCD为菱形(对角线互相垂直的平行四边形为菱形).⊥,对角线互相垂直的平行四边形为菱形.故答案为四边形ABCD为平行四边形,BD AC【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了菱形的判定.5、见解析【解析】【分析】作△ABC的角平分线AE,作线段AE的垂直平分线MN交AB于点D,交AC于点F.四边形ADEF即为所求.【详解】解:如图:四边形ADEF即为所求.【点睛】本题考查了基本作图,正方形的判定和性质等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.。
初二数学知识点专题讲解与练习20---正方形(培优版)

F
A
D
M
B
C
A
D
F
EB
M C
E
G
图1
图G2
【例 3】如图,正方形 ABCD 中,E ,F 是 AB ,BC 边上两点,且 EF = AE + FC , DG ⊥ EF 于 G ,求证: DG = DA .
(重庆市竞
2 / 17
解题思路:构造 AE + FC 的线段是解本例的关键.
赛试题)
A
D
E
G
B
延长线上 (CG > BC) ,取线段 AE 的中点 M .连 MD , MF . (1)探究线段 MD , MF 的关系,并加以证明. (2)将正方形 CGEF 绕点 C 旋转任意角后(如图 2),其他条件不变. 探究线段 MD , MF 的关系,并加以证明.
(大
连市中考题改编) 解题思路:由 M 为 AE 中点,想到“中线倍长法”再证三角形全等.
(黑龙江省中考 试题)
解题思路:对于(2),构造 DN − BM 是解题的关键.
4 / 17
A
D
N
BM
C
图1
A
D
C MB
A
D
N
BM
C
图2
人教版八年级数学下册正方形知识点及同步练习、含答案

学科:数学 教学内容:正方形【学习目标】1.掌握正方形的定义、性质和判定方法.2.能正确区别平行四边形、矩形、菱形、正方形之间的关系. 3.能运用正方形的性质和判定方法进行有关的计算和证明.【主体知识归纳】1.正方形:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2.正方形的性质:正方形除具有平行四边形、矩形、菱形的一切性质外,还具有: (1)正方形的四个角都是直角,四条边都相等;(2)正方形的两条对角线相等并且互相垂直平分,每条对角线平分一组对角. 3.正方形的判定(1)根据正方形的定义;(2)有一组邻边相等的矩形是正方形; (3)有一个角是直角的菱形是正方形; (4)既是矩形又是菱形的四边形是正方形.【基础知识精讲】1.掌握正方形定义是学好本节的关键,正方形是在平行四边形的前提下定义的,它包含两层意思:正方形矩形平行四边形并且有一个角是直角的菱形四边形有一组邻边相等的平行⎭⎬⎫)()2()()1(正方形不仅是特殊的平行四边形,而且是特殊的矩形,又是特殊的菱形.2.正方形的性质可归纳如下: 边:对边平行,四边相等; 角:四个角都是直角;对角线:对角线相等,互相垂直平分,每条对角线平分一组对角. 此外:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴,学习时,应熟悉这些最基本的内容.【例题精讲】[例1]如图4-50,已知矩形ABCD 中,F 为CD 的中点,在BC 上有一点E ,使AE =DC +CE ,AF 平分∠EAD .求证:矩形ABCD 是正方形.图4—50剖析:欲证矩形ABCD是正方形,只要证明有一组邻边相等即可,由已知AE=DC+CE,容易想到若能证明AE=AD+CE便可证得AD=DC,由于AF平分∠EAD,因此可在AE上截取AG=AD,再证GE=CE,就可得出要证的结论.证明:在AE上截取AG=AD,连结FG、FE.∵四边形ABCD是矩形,∴∠D=∠C=90°.∵AD=AG,∠DAF=∠GAF,AF=AF∴△ADF≌△AGF,∴DF=GF,∠D=∠AGF=90°.∵DF=CF,∴GF=CF.∵∠FGE=∠C=90°,FE=FE,∴Rt△GFE≌Rt△CFE.∴GE=CE,∴AD+CE=AE.又DC+CE=AE,∴AD=DC.∴矩形ABCD是正方形.说明:要判定一个四边形是正方形,可先判定这个四边形是矩形,再证明有一组邻边相等;或先判定它是菱形,再证明有一个角是直角.[例2]如图4-51,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过点A作AG⊥EB,垂足为G,AG交BD于点F,则OE=OF.图4—51对上述命题的证明如下:∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,BO=AO.∴∠3+∠2=90°,∵AG⊥BE,∴∠1+∠3=90°.∴∠1=∠2,∴△BOE≌△AOF,∴OE=OF问题:对于上述命题,若点E在AC延长线上,AG⊥EB,交EB的延长线于G,AG的延长线交DB的延长线于点F,其他条件不变(如图4-52),结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.图4—52剖析:可仿上述的证明,证△BOE≌△AOF.解:结论OE=OF仍然成立,证明如下:∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,BO=AO,∴∠OFA+∠FAE=90°又∵AG⊥EB,∴∠OEB+∠EAF=90°,∴∠OEB=∠OFA,∴△BOE≌△AOF,∴OE=OF.[例3]有一正方形池塘,池塘四个角上有四棵树,现计划把此池塘改为面积扩大一倍的正方形,能否不毁掉树木而达到要求?请你设计出方案来.图4—53剖析:新改造的池塘的面积是原面积的2倍,因此,新边长应为原边长的2倍,而正方形的对角线是边长的2倍,故以原对角线的长为边长构造新的正方形.答案:如图4-53,分别过B、D作AC的平行线,分别过A、C作BD的平行线,四条线分别交于A′、B′、C′、D′,则四边形A′B′C′D′为要求的正方形.【同步达纲练习】1.选择题(1)下列命题中,假命题的个数是()①四边都相等的四边形是正方形②对角线互相垂直的平行四边形是正方形③四角都相等的四边形是正方形④对角线相等的菱形是正方形A.1 B.2 C.3 D.4(2)正方形具有而菱形不具有的性质是()A.对角线互相垂直平分B.对角线相等C.邻边相等D.每条对角线平分一组对角(3)正方形的对角线与边长之比为()A.1∶1 B.2∶1 C.1∶2 D.2∶1(4)以等边△ABC的边BC为边向外作正方形BCDE,则①∠ABD=105°,②∠ACD=150°,③∠DAE=30°,④△ABE≌△ACD,其中正确的结论有()A.1个 B.2个 C.3个 D.4个(5)在正方形ABCD中,P、Q、R、S分别在边AB、BC、CD、DA上,且AP=BQ=CR=DS =1,AB=5,那么四边形PQRS的面积等于()A.17 B.16 C.15 D.9(6)如图4-54,正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于E、F,若AE=4,CF=3,则EF等于()图4—54A.7 B.5 C.4 D.3(7)在正方形ABCD中,E、F两点分别是BC、CD边上的点,若△AEF是边长为2的等边三角形,则正方形ABCD的边长为()A.213+B.213-C.3 D.2(8)如图4-55,在正方形ABCD中,CE=MN,∠MCE=35°,那么∠ANM等于()图4—55A.45°B.55°C.65°D.75°2.填空题(1)已知正方形的面积是16 cm2,则它的一边长是_____,一条对角线长是_____.(2)已知正方形的对角线长为22,则此正方形的周长为_____,面积为_____. (3)在正方形ABCD 中,两条对角线相交于O ,∠BAC 的平分线交BD 于E ,若正方形ABCD 的周长是16 cm ,则DE =_____cm .(4)在正方形ABCD 的边BC 的延长线上取一点E ,使CE =AC ,连结AE 交CD 于F ,那么∠AFC 等于_____度.3.如图4-56,已知正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,且CE =CF .图4—56(1)求证:△BCE ≌△DCF ;(2)若∠BEC =60°,求∠EFD 的度数.4.已知:如图4-57,在正方形ABCD 中,E 是CB 延长线上一点,EB =21BC ,如果F 是AB 的中点,请你在正方形ABCD 上找一点,与F 点连结成线段,并证明它和AE 相等.图4—575.以△ABC 的AB 、AC 为边,向三角形外作正方形ABDE 及ACGF ,作AN ⊥BC 于点N ,延长NA 交EF 于M 点.(1)求证:EM =FM ;(2)若使AM =21EF ,则△ABC 必须满足什么条件呢?图4—586.如图4-58,已知正方形ABCD 中,M 、F 分别在边AB 、AD 上,且MB =FD ,E 是AB 延长线上一点,MN ⊥DM ,MN 与∠CBE 的平分线相交于N .求证:DM =MN .7.如图4-59,已知C是线段AB上的一点,分别以AC、BC为边作正方形ACDE和BCFG.图4—59求证:AF=DB;若点C在线段AB的延长线上,猜想上述结论是否正确,如果正确,请加以证明,如果不正确,请说明理由.【思路拓展题】你会设计吗今有一片正方形土地,要在其上修筑两条笔直的道路,使道路把这片地分成形状相同且面积相等的4部分,若道路的宽度忽略不计,请设计三种不同的修筑方案.(在给出如图4-60的三张正方形纸片上分别画图,并简述画图步骤)图4—60参考答案【同步达纲练习】1.(1)C (2)B (3)B (4)D (5)A (6)B (7)A(8)B2.(1)4 42(2)8 4 (3)4 (4)112.53.(1)略(2)15°4.连结CF,可证△ABE≌△CBF或连结DF,让△ABE≌△DAF。
矩形的判定专项练习30题

矩形的判定专项练习30题矩形的判定专项练习30题(有答案)1.如图,在四边形ABCD中,AD∥BC,E、F为AB上两点,且△DAF≌△CBE.求证:(1)∠A=90°;(2)四边形ABCD是矩形.2.如图,已知平行四边形ABCD,∠ABC,∠BCD的平分线BE、CF分别交AD于E、F,BE、CF交于点G,点H 为BC的中点,GH的延长线交GB的平行线CM于点M.(1)试说明:∠BGC=90°;(2)连接BM,判断四边形GBMC的形状并说明理由.3.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E.(1)四边形OCDE是矩形吗?说说你的理由;(2)请你将上述条件中的菱形改为另一种四边形,其它条件都不变,你能得出什么结论?根据改编后的题目画出图形,并说明理由.4.△ABC中,AD⊥BC于D,点E、F分别是△ABC中AB、AC中点,当△ABC满足什么条件时,四边形AEDF 是矩形?说明理由.5.如图,菱形ABCD的对角线AC、BD交于点O.(1)用尺规作图的方法,作出△AOB平移后的△DEC,其中平移的方向为射线AD的方向,平移的距离为线段AD的长;(要求:用尺规作图,保留作图痕迹,不写作法.)(2)观察图形,判断四边形DOCE是什么特殊四边形,并证明.6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,ON=OB,再延长OC至M,使CM=AN,求证:四边形NDMB为矩形.7.如图,点O是菱形ABCD对角线的交点,过点C作BD的平行线CE,过点D作AC的平行线DE,CE与DE相交于点E,试说明四边形OCED是矩形.8.如图,已知梯形ABCD中,AD∥BC,AB⊥BC,点E、F分别是边BC、CD的中点,直线EF交边AD的延长线于点M,连接BD.(1)求证:四边形DBEM是平行四边形;(2)若BD=DC,连接CM,求证:四边形ABCM为矩形.9.如图,在△ABC中,点O是AC边上的中点,过点O的直线MN∥BC,且MN交∠ACB的平分线于点E,交∠ACB 的外角平分线于点F,点P是BC延长线上一点.求证:四边形AECF是矩形.10.如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是BC的中点,连接AC、DE相交于点O.(1)试说明:△AOD≌△COE;(2)若∠B=∠AOE,试说明四边形AECD是矩形的理由.11.如图,以△ABC的各边为一边向BC的同侧作正△ABD、正△BCF、正△ACE,若∠BAC=150°,求证:四边形AEFD为矩形.12.(1)在等腰三角形ABC中AB=BC,∠ABC=90°,BD⊥AC,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF长.(2)如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.①求证:△ABF≌△ECF;②若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.13.如图,AD是△ABC的中线,过点A作AE∥BC,过点B作BE∥AD交AE于点E,(1)求证:AE=CD;(2)当△ABC满足什么条件时,四边形ADBE是矩形?请说明理由.14.如图,已知梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,点G在边BC上,且CG=(AD+BC).(1)求证:四边形DEGF是平行四边形;(2)连接DG,若∠ADG=2∠ADE,求证:四边形DEGF是矩形.15.已知,如图在△ABC中,AB=AC,点D是AC的中点,直线AE∥BC,过D点作直线EF∥AB分别交AE、BC于点E、F,求证:四边形AECF是矩形.16.已知:如图,在△ABC中,D、E、F分别是AC、AB、BC的中点,且CE=AB.求证:四边形CFED是矩形.17.如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F;(1)试说明四边形AECF是平行四边形.(2)若EF过AC的中点,且与AC垂直时,试说明四边形AECF是菱形.(3)当EF与AC有怎样的关系时,四边形AECF是矩形.18.如图,在Rt△ABC中,∠A=90°,AB=AC,D是斜边BC上一点,DE⊥AC,DF⊥AB,垂足分别为E、F.(1)说明四边形AEDF是矩形.(2)试问:当点D位于BC边的什么位置时,四边形AEDF是正方形?并说明你的理由.19.如图,△ABC中,D为边AC的中点,过点D作MN∥BC,CE平分∠ACB交MN于E,CF平分∠ACG交MN于F,求证:(1)ED=DF;(2)四边形AECF为矩形.20.如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.21.如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA 的平分线相交于点E,与∠DCA的平分线相交于点F.(1)OE与OF相等吗?为什么?(2)探索:当点O在何处时,四边形AECF为矩形?为什么?22.(2013•沙湾区模拟)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE 的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点.(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.23.如图,四边形ABCD是平行四边形,对角线AC、BD交于点O,∠OBC=∠OCB,求证:四边形ABCD是矩形.24.如图M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,AN,BM相交于P,DN,CM相交于Q.求证:PMQN为矩形.25.在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:四边形AFCE是矩形.26.如图,在△ABC中,D是AC的中点,E是线段BC延长线上的一点,过点A作AF∥BE,交ED的延长线于点F,连接AE,CF.(1)求证:AF=CE;(2)如果AC=EF,则四边形AFCE是矩形.27.如图,DB∥AC,且DB=AC,E是AC的中点,(1)求证:BC=DE;(2)连接AD、BE,探究:当△ABC满足什么条件时,四边形DBEA是矩形?并说明理由.28.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形OCED是矩形吗?说说你的理由.29.已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.求证:四边形ABCD是矩形.30.如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCED为矩形.矩形的判定专项练习30题参考答案:1.(1)∵AD∥BC,∴∠A+∠B=180°,∵△DAF≌△CBE,∴∠A=∠B,∴2∠A=180°,∴∠A=90°;(2)∵AD∥BC,AD=BC,∴四边形ABCD为平行四边形,又∵∠A=90°,∴四边形ABCD是矩形2.(1)∵∠ABC+∠BCD=180°,BE、CF平分∠ABC,∠BCD,∴∠GBC+∠GCB=90°,∴∠BGC=90°;(2)∵点H为BC的中点,∴BH=CH=GH,∵GB∥CM,∴∠BGH=∠CMH,∵∠HBG=∠HGB,∴∠HCM=∠HMC,∴MH=BH=CH=GH,∴四边形GBMC为矩形3.(1)四边形OCDE是矩形.证明:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,又∵AC⊥BD,∴∠DOC=90°,∴四边形OCED是矩形.(2)任意改变四边形ABCD的形状,四边形OCED都是平行四边形(答案不唯一).理由如下:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形.4.满足△ABC是等腰直角三角形,∠BAC=90°.∵△ABC是等腰直角三角形,∠BAC=90°,AD⊥BC于D,∴BD=CD,∵点E、F分别是△ABC中AB、AC中点,∴DF∥AB,ED∥AC,∴四边形AEDF是平行四边形,∵∠BAC=90°∴AEDF是矩形.5.(1)所作图形如图所示:(2)四边形DOCE是矩形.∵△DCE是由△AOB平移后的图形,∴DE∥AC,CE∥BD.∴四边形DOCE是平行四边形.又∵四边形ABCD是菱形,∴AC⊥BD.即∠DOC=90°∴四边形DOCE为矩形.6.∵四边形ABCD为平行四边形,∴AO=OC,OD=OB,∵AN=CM ON=OB,∴ON=OM=OD=OB,∴四边形NDMB为平行四边形,∵MN=BD,∴平行四边形NDMB为矩形7.∵DE∥AC,CE∥BD,∴DE∥OC,CE∥OD∴四边形OCED是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°,∴四边形OCED是矩形8.(1)证明:∵梯形ABCD中,AD∥BC,即DM∥BE,∵E、F分别是边BC、CD的中点∴EF∥BD,∴四边形DBEM是平行四边形.(2)证明:连接DE,∵DB=DC,且E是BC中点,∴DE⊥BC,∴DE∥AB.又∵AB⊥BC,∴AB∥DE∵由(1)知四边形DBEM是平行四边形,∴DM∥BE且DM=BE,∴DM∥EC且DM=EC,∴四边形DMCE是平行四边形,∴CM∥DE,∴AB∥CM.又AM∥BC∴四边形ABCM是平行四边形,∵AB⊥BC,∴四边形ABCM是矩形.9.∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,矩形的判定专项练习30题∴OE=OF.∵AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE=∠ACB,同理,∠ACF=∠ACP,∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACP)=×180°=90°,∴四边形AECF是矩形.10.(1)∵BC=2AD,点E是BC的中点,∴EC=AD.∵AD∥BC,∴∠ADO=∠CEO,∠DAO=∠ECO.在△AOD和△COE 中,∴△AOD≌△COE(ASA);(2)∵AD=BE,AD∥BE,∴四边形ABED是平行四边形;同理可得:四边形AECD是平行四边形.∴∠ADO=∠B.∵∠B=∠AOE,∴∠AOE=2∠B.∴∠AOE=2∠ADO.∵∠AOE=∠ADO+∠DAO,∴∠OAD=∠ODA.∴OA=OD.∴AC=DE.∴四边形AECD是矩形.11.:∵△ABD和△FBC都是等边三角形,∴∠DBF+∠FBA=∠ABC+∠ABF=60°,∴∠DBF=∠ABC.又∵BD=BA,BF=BC,∴△ABC≌△DBF,∴AC=DF=AE,同理可证△ABC≌△EFC,∴四边形DAFEF是平行四边形(两组对边分别相等的四边形是平行四边形)∵∠BAC=150°,∴∠DAE=150°﹣∠DAB﹣∠EAC=90°,∴四边形AEFD为矩形.12.1)解:∵ABC中AB=BC,∠ABC=90°,BD⊥AC,∴∠A=∠C=45°,CD=AD,∴BD=CD=AD,BD平分∠ABC,∴∠EBD=45°=∠C,∵BD⊥AC,DE⊥DF,∴∠BDC=∠EDF=90°,∴∠BDC﹣∠BDF=∠EDF﹣∠BDF,∴∠EDB=∠FDC,∵在△EDB和△FDC中∴△EDB≌△FDC(ASA),∴FC=DE=3,同理△AED≌△BFD,∴DF=AE=4,在Rt△EDF中,由勾股定理得:EF==5;(2)①证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵CD=CE,∴AB∥CE,AB=CE,∴四边形ABEC是平行四边形,∴AF=FE,BF=FC,∵在△ABF和△ECF中∴△ABF≌△ECF(SSS);②证明:∵四边形ABCD是平行四边形,∴∠ABC=∠D,∵∠AFC=2∠D,∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠FAB,∵∠ABC=∠FAB,∴AF=FB,∵四边形ABCD是平行四边形,∴AE=2AF,BC=2BF,∴AE=BC,∵四边形ABEC是平行四边形,∴四边形ABEC是矩形.矩形的判定专项练习30题13.(1)∵AE∥BC,BE∥AD,∴四边形ADBE是平行四边形,∴AE=BD,∵AD是△ABC的中线,∴BD=CD,∴AE=CD.(2)当AB=AC时,四边形ADBE是矩形,理由是:∵AB=AC,BD=CD,∴AD⊥BC,即∠ADB=90°,又∵四边形ADBE是平行四边形,∴四边形ADBE是矩形14.1)证明:如图,连接EF.∵四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD的中点,∴,EF∥AD∥BC.∵,∴EF=CG.∴四边形EGCF是平行四边形.∴EG=FC且EG∥FC.∵F是CD的中点,∴FC=DF.∴EG=DF且EG∥DF.∴四边形DEGF是平行四边形.(2)证明:连接EF,将EF与DG的交点记为点O.∵∠ADG=2∠ADE,∴∠ADE=∠EDG.∵EF∥AD,∴∠ADE=∠DEO.∴∠EDG=∠DEO.∴EO=DO.∵四边形DEGF是平行四边形,∴,.∴EF=DG,∴平行四边形DEGF是矩形.即四边形DEGF是矩形.15.∵点D是AC的中点,∴DA=DC,∵AE∥BC,∴∠AED=∠CFD,在△ADE和△CDF 中,,∴△ADE≌△CDF(AAS),∴AE=CF,又∵AE∥BC,∴四边形AECF是平行四边形,∵AE∥BC,EF∥AB,∴四边形ABFE是平行四边形,∴AB=EF,∵AB=AC,∴AC=EF,∴四边形AECF是矩形.16.∵D、E、F分别是AC、AB、BC的中点,∴DE∥BC,且DE=BC,DF=AB,CF=BC,∴DE=CF,∴四边形CFED平行四边形,又∵CE=AB,∴CE=DF,∴平行四边形CFED是矩形,故四边形CFED是矩形.17.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴△AEO∽△CFO,∴=,∵OA=CO,∴OE=OF,∴四边形AECF是平行四边形;(2)证明:∵四边形AECF是平行四边形,又∵EF⊥AC,∴平行四边形AECF是菱形;(3)解:当EF=AC时,四边形AECF是矩形,理由是:由(1)知:四边形AECF是平行四边形,∵AC=EF,∴平行四边形AECF是矩形矩形的判定专项练习30题∴四边形AEDF是矩形;(2)当D时BC的中点时,四边形AEDF是正方形;JU 理由:∵D是BC的中点,∴BD=DC∵AB=AC∴∠B=∠C又∵DF⊥AB,DE⊥AC,∴∠BDF=∠DEC∴△BFD≌△DCE,∴DF=DE,∴矩形AEDF是正方形.19.(1)∵CE平分∠ACB,CF平分∠ACG,∴∠ACE=∠ECB,∠ACF=∠FCG,又∵MN∥BG,∴∠DEC=∠ECB,∠DFC=∠FCG,∴∠DEC=∠DCE,∠DFC=∠DCF,∴DE=DC,DF=DC,∴DE=DF.(2)∵D为AC的中点,∴AD=DC,又DE=DF,∴四边形AECF为平行四边形,∵∠ACE=∠ECB,∠ACF=∠FCG,∴∠ECF=90°,∴平行四边形AECF为矩形20.∵BE∥AC,CE∥DB,∴四边形OBEC是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°,∴平行四边形OBEC是矩形21.(1)解:OE=OE,理由是:∵直线l∥BC,∴∠OEC=∠ECB,∵CE平分∠ACB,∴∠OCE=∠BCE,∴∠OEC=∠OCE,∴OE=OC,同理OF=OC,∴OE=OF.(2)解:O在AC的中点上时,四边形AECF是矩形,理由是:∵OA=OC,OE=OF,∴四边形AECF是平行四边形,∵OE=OF=OC=OA,∴AC=EF,∴平行四边形AECF是矩形22.(1)证明:∵AF∥BC,∴∠AFE=∠DCE(1分)∵E是AD的中点,∴AE=DE.(2分)∵∠AEF=∠DEC,∴△AEF≌△DEC.(3分)∴AF=DC,∵AF=BD∴BD=CD,∴D是BC的中点;(4分)(2)四边形AFBD是矩形,(5分)证明:∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADB=90°,(6分)∵AF=BD,AF∥BC,∴四边形AFBD是平行四边形,(7分)∴四边形AFBD是矩形.23.∵∠OBC=∠OCB,∴OB=OC,∵四边形ABCD是平行四边形,∴OC=OA=AC,OB=OD=BD,∴AC=BD,∵四边形ABCD是平行四边形,∴四边形ABCD是矩形,即四边形ABCD是矩形24.∵ABCD为平行四边形,∴AD平行且等于BC,又∵M为AD的中点,N为BC的中点,∴MD平行且等于BN,∴BNDM为平行四边形,∴BM∥ND,同理AN∥MC,∴四边形PMQN为平行四边形,(5分)连接MN,∵AM平行且等于BN,∴四边形ABNM为平行四边形,又∵AD=2AB,M为AD中点,∴BN=AB,∴四边形ABNM为菱形,∴AN⊥BM,∴平行四边形PMQN为矩形.(10分)25.∵四边形ABCD为平行四边形,∴OA=OC,AE∥FC,∴∠EAO=∠FCO,在△AOE和△COF中,矩形的判定专项练习30题,∴△AOE≌△COF,∴AE=CF,∴四边形AECF为平行四边形,又∵AF⊥BC,∴∠AFC=90°,则四边形AECF为矩形.26.(1)证明:∵AF∥BE,∴∠AFD=∠CED,∠FAD=∠DCE,∵D是AC的中点,∴AD=DC,在△FAD和△ECD中,∴△FAD≌△ECD(AAS),∴AF=CE;(2)证明:∵△FAD≌△ECD,∴FD=DE,∵AD=DC,∴四边形AFCE是平行四边形,∵AC=EF,∴平行四边形AFCE是矩形27.(1)证明:∵E是AC的中点,∴EC=AC,∵DB=AC,∴DB=EC,又∵DB∥AC,∴四边形BCED是平行四边形(一组对边平行且相等的四边形是平行四边形),∴BC=DE;(2)解:△ABC满足AB=BC时,四边形DBEA是矩形.理由如下:∵E是AC的中点,∴AE=AC,∵DB=AC,∴DB=AE,又∵DB∥AC,∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),∵AB=BC,E为AC中点,∴∠AEB=90°,∴平行四边形DBEA是矩形,即△ABC满足AB=BC时,四边形DBEA是矩形.28.是矩形.(1分)理由:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴DE⊥CE,∴∠E=90°,∴平行四边形OCED是矩形29.∵BC是等腰△BED底边ED上的高,∴EC=CD,∵四边形ABEC是平行四边形,∴AB∥CD,AB=CE=CD,AC=BE,∴四边形ABCD是平行四边形.∵AC=BE,BE=BD,∴AC=BD,∴四边形ABCD是矩形30.在△ABD和△ACE中,∵AB=AC,AD=AE,∠BAD=∠CAE,∴△ABD≌△ACE(SAS)∴BD=CE又DE=BC.∴四边形BCED为平行四边形.在△ACD和△ABE中,∵AC=AB,AD=AE,∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE,∴△ADC≌△AEB(SAS),∴CD=BE.∴四边形BCED为矩形.(对角线相等的平行四边形是矩形)。
华东师大版初中八年级数学下册第19章单元测试卷含答案(2套)

第19章矩形、菱形、正方形单元检测题时间:120分钟满分:120分一、选择题(每小题3分,共30分)1.下列命题中正确的是( B )A.有一组邻边相等的四边形是菱形 B.有一个角是直角的平行四边形是矩形C.对角线垂直的平行四边形是正方形 D.一组对边平行的四边形是平行四边形2.如图,在矩形ABCD中,AC与BD相交于点O,若∠DBC=30°,则∠AOB等于( D )A.120° B.15° C.30° D.60°3.如图,在▱ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连结AE,CF,则四边形AECF是( C )A.梯形 B.矩形 C.菱形 D.正方形,第2题图),第3题图),第5题图),第6题图) 4.一个菱形的周长为8 cm,高为1 cm,则这个菱形的两邻角的度数之比为( D )A.2∶1 B.3∶1 C.4∶1 D.5∶15.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列四个判断中不正确的是( D )A .四边形AEDF 是平行四边形B .如果∠BAC =90°,那么四边形AEDF 是矩形C .如果AD 平分∠BAC ,那么四边形AEDF 是菱形D .如果AD ⊥BC 且AB =AC ,那么四边形AEDF 是正方形6.如图,矩形纸片ABCD 中,AB =4,BC =8,将纸片沿EF 折叠,使点C 与点A 重合,则下列结论错误的是( D )A .AF =AEB .△ABE ≌△AGFC .EF =2 5D .AF =EF7.如图,一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21 cm 2,则该矩形的面积为( A )A .60 cm 2B .70 cm 2C .120 cm 2D .140 cm 28.如图,正方形ABCD 的边长为1,点E 在对角线BD 上,且∠BAE =22.5°,EF ⊥AB ,垂足为F ,则EF 的长为( C )A .1 B. 2 C .1-22D.2-4 ,第7题图),第8题图),第9题图),第10题图)9.如图,在平面直角坐标系中,菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,∠BOC =60°,顶点C 的坐标为(m ,32),反比例函数y =k x的图象与菱形对角线AO 交于D 点,连结BD ,当DB ⊥x轴时,k的值是( D )A.1 B.-1 C. 3 D.- 310.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG,CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( C )A.2 B.3 C.4 D.5二、填空题(每小题3分,共24分)11.如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为__5__.,第11题图) ,第13题图),第14题图) ,第15题图) 12.在菱形ABCD中,对角线AC,BD的长分别是6和8,则菱形的周长是__20__.13.如图,▱ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,已知△ACD的面积为3,则图中阴影部分两个三角形的面积和为__3__.14.如图,▱ABCD的两条对角线AC,BD相交于点O,AB=5,AC=4,BD=2,小明说:“这个四边形是菱形.”他说这话的根据是__对角线互相垂直的平行四边形是菱形__.15.▱ABCD中,给出下列四个条件:①AC⊥BD;②∠ADC=90°;③BC=CD;④AC=BD.其中选两个条件能使▱ABCD是正方形的有__①②、①④、②③、③④__.(填上所有正确结果的序号)16.如图,在矩形纸片ABCD 中,AB =12,BC =5,点E 在AB 上,将△DAE 沿DE 折叠,使点A 落在对角线BD 上的点A ′处,则AE 的长为__103__. ,第16题图) ,第17题图),第18题图)17.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF ,若菱形ABCD 的边长为2 cm ,∠A =120°,则EF =18.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置,点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y =kx +b(k >0)和x轴上,已知点B 1(1,1),B 2(3,2),则点B n 的坐标为__(2n -1,2n -1)__.三、解答题(共66分)19.(8分)如图,在矩形ABCD 中,两条对角线AC ,BD 相交于点O ,E 是AC 上的一点,且BO =2AE ,∠AOD =120°,求证:BE ⊥AC.解:∵四边形ABCD 是矩形,∴OB =OA ,又∵OB =2AE ,∴AE =OE ,又∵∠AOD =120°,∴∠AOB =60°,∴△ABO 是等边三角形.又∵AE =OE ,∴BE ⊥AO ,即BE ⊥AC20.(8分)如图,在菱形ABCD中,AC为对角线,点E,F分别是边BC,AD的中点.(1)求证:△ABE≌△CDF;(2)若∠B=60°,AB=2,求线段AE的长.解:(1)用SAS证△ABE≌△CDF (2)∵∠B=60°,∴△ABC是等边三角形,∴BE=CE=1,AE⊥BC,∴AE=AB2-BE2=22-12= 321.(10分)如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连结DF.(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;(2)连结AE,试判断AE与DF的位置关系,并说明理由.解:(1)△ADC≌△ABC,△ADF≌△ABF,△CDF≌△CBF (2)AE ⊥DF.理由如下:设AE与DF相交于点H,易证△ADF≌△ABF,∴∠ADF=∠ABF,再证△ADE≌△BCE,∴∠DAE=∠CBE,∵∠ABF+∠CBE =90°,∴∠ADF+∠DAE=90°,∴∠DHA=90°,∴AE⊥DF22.(9分)如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE 于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.解:易证四边形ACGF是平行四边形,再证AC=AF,故四边形ACGF 是菱形23.(9分)如图,△ABC中,AB=AC,D是BC的中点,DE∥AB交AC于点E,DF∥AC交AB于点F.(1)求证:四边形AFDE是菱形;(2)当∠ABC等于多少度时,四边形AFDE是正方形?请说明理由.解:(1)易证四边形AFDE是平行四边形,∵D为BC中点,DE∥AB,DF∥AC,∴DE=12AB,DF=12AC,∵AB=AC,∴DE=DF,∴四边形AFDE是菱形(2)当∠ABC=45°时,四边形AFDE是正方形,理由略24.(10分)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连结DO并延长到点E,使OE=OD,连结AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.解:(1)∵OA=OB,OE=OD,∴四边形AEBD为平行四边形,∵AB =AC,AD平分∠BAC,∴AD⊥BC,即∠ADB=90°,∴四边形AEBD为矩形(2)当∠BAC=90°时,四边形AEBD为正方形,理由如下:∵∠BAC=90°,AD平分∠BAC,AD⊥BC,∴∠DAB=∠DBA=45°,∴BD=AD,∴矩形AEBD为正方形25.(12分)已知,在△ABC 中,∠BAC =90°,∠ABC =45°,点D 为直线BC 上一动点(点D 不与点B ,C 重合).以AD 为边作正方形ADEF ,连结CF.(1)如图①,当点D 在线段BC 上时,求证:CF +CD =BC ;(2)如图②,当点D 在线段BC 的延长线上时,其他条件不变,请直接写出CF ,BC ,CD 三条线段之间的关系;(3)如图③,当点D 在线段BC 的反向延长线上时,且点A ,F 分别在直线BC 的两侧,其他条件不变:①请直接写出CF ,BC ,CD 三条线段之间的关系;②若正方形ADEF 的边长为2,对角线AE ,DF 相交于点O ,连结OC ,求OC 的长度.解:(1)∵∠BAC =90°,∠ABC =45°,∴∠ACB =∠ABC =45°,∴AB =AC ,可证△BAD ≌△CAF(SSS),∴BD =CF ,∵BC =BD +CD ,∴CF +CD =BC (2)BC =CF -CD (3)①CD -CF =BC ②由题知,∠BAC =90°,∠ABC =45°,∵四边形ADEF 是正方形,∴AD =AF ,∠DAF =90°,∵∠BAD =90°-∠BAF ,∠CAF =90°-∠BAF ,∴∠BAD =∠CAF ,又∵AB =AC ,∴△BAD ≌△CAF(SAS),∴∠ACF =∠ABD ,∵∠ABC =45°,∴∠ABD =135°,∴∠ACF =∠ABD =135°,∴∠FCD =90°,∴△FCD 为直角三角形,∵DE =2,∴DF =2DE =22,∴OC =12DF = 2四边形测试题一、选择题(本大题共5小题,每小题5分,共25分;在每小题列出的四个选项中,只有一项符合题意)1.若菱形的周长为48 cm,则其边长是()A.24 cmB.12 cmC.8 cmD.4 cm2.如图3-G-1,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()图3-G-1A.30°B.60°C.90°D.120°3.如图3-G-2所示,在菱形ABCD中,不一定成立的是()图3-G-2A.四边形ABCD是平行四边形B.AC⊥BDC.△ABD是等边三角形D.∠CAB=∠CAD4.如图3-G-3,在矩形ABCD中,O是对角线AC,BD的交点,点E,F分别是OD,OC的中点.如果AC=10,BC=8,那么EF的长为()A.6 B.5 C.4 D.3图3-G-35.如图3-G-4,菱形ABCD的周长为16,∠ABC=120°,则AC的长为()图3-G-4A.4 3B.4C.2 3D.2二、填空题(本大题共5小题,每小题5分,共25分)6.在菱形ABCD中,若对角线AC=8 cm,BD=6 cm,则边长AB=________ cm.7.矩形两对角线的夹角为120°,矩形的宽为3,则矩形的面积为__________.8.如图3-G-5所示,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD,BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为________.图3-G-59.已知菱形ABCD的面积为24 cm2,若对角线AC=6 cm,则这个菱形的边长为________cm.10.如图3-G-6,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是________(只填写序号).图3-G-6三、解答题(本大题共5小题,共50分)11.(6分)如图3-G-7所示,已知四边形ABCD是菱形,对角线AC与BD相交于点O,AB=5,AO=4,求BD的长.图3-G-712.(8分)如图3-G-8,在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.图3-G-813.(12分)如图3-G-9①,在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠DCE =90°,AB与CE交于点F,ED与AB,BC分别交于M,H.(1)求证:CF=CH;(2)如图②,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM 是什么四边形?并证明你的结论.图3-G-914.(12分)如图3-G-10,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF∶∠FDC=3∶2,DF⊥AC,则∠BDF的度数是多少?图3-G-1015.(12分)如图3-G-11,▱ABCD的对角线AC,BD相交于点O,BD=12 cm,AC =6 cm,点E在线段BO上从点B以1 cm/s的速度运动,点F在线段OD上从点O以2 cm/s 的速度运动.(1)若点E,F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形?(2)在(1)的条件下,①当AB为何值时,四边形AECF是菱形?②四边形AECF可以是矩形吗?为什么?图3-G-111.B 2.B3.C [解析] 灵活掌握菱形的性质定理即可判断. 4.D [解析] ∵四边形ABCD 是矩形,∴AB =CD ,∠ABC =90°.∵AC =10,BC =8,由勾股定理得AB =102-82=6,∴CD =AB =6.∵点E ,F 分别是OD ,OC 的中点,∴EF =12CD =3.故选D . 5.A [解析] 设AC 与BD 交于点E ,则∠ABE =60°.根据菱形的周长求出AB =16÷4=4.在Rt △ABE 中,求出BE =2,根据勾股定理求出AE =42-22=2 3,故可得AC =2AE =4 3.6.5 [解析] 如图,∵在菱形ABCD 中,对角线AC =8 cm ,BD =6 cm ,∴AO =12AC=4 cm ,BO =12BD =3 cm .∵菱形的对角线互相垂直,∴在Rt △AOB 中,AB =AO 2+BO 2=42+32=5(cm ).7.9 3 [解析] 根据勾股定理求得矩形的另一边长为3 3,所以面积是9 3.8.3 [解析] 可证得△AOE ≌△COF ,所以阴影部分的面积就是△BCD 的面积,即矩形面积的一半.9.5 [解析] 菱形ABCD 的面积=12AC·BD.∵菱形ABCD 的面积是24 cm 2,其中一条对角线AC 长6 cm ,∴另一条对角线BD 的长为8 cm .边长=32+42=5 (cm ).10.③ [解析] 由题意得BD =CD ,ED =FD ,∴四边形EBFC 是平行四边形.①BE ⊥EC ,根据这个条件只能得出四边形EBFC 是矩形;②BF ∥CE ,根据EBFC 是平行四边形已可以得出BF ∥CE ,因此不能根据此条件得出▱EBFC 是菱形;③AB =AC ,∵⎩⎨⎧AB =AC ,DB =DC ,AD =AD ,∴△ADB ≌△ADC(SSS),∴∠BAD =∠CAD ,∴△AEB ≌△AEC(SAS),∴BE =CE ,∴四边形BECF 是菱形. 11.解:∵四边形ABCD 是菱形, ∴AC ⊥BD ,DO =BO. ∵AB =5,AO =4,∴BO =AB 2-AO 2=52-42=3, ∴BD =2BO =6.12.解:(1)证明:∵AB =AC ,AD 是BC 边上的中线,∴AD ⊥BC , ∴∠ADB =90°.∵四边形ADBE 是平行四边形, ∴▱ADBE 是矩形.(2)∵AB =AC =5,BC =6,AD 是BC 边上的中线,∴BD =DC =6×12=3.在Rt △ACD 中,AD =AC 2-DC 2=52-32=4, ∴S 矩形ADBE =BD·AD =3×4=12.13.解:(1)证明:∵AC =CE =CB =CD ,∠ACB =∠ECD =90°, ∴∠A =∠B =∠D =∠E =45°. 在△BCF 和△ECH 中, ⎩⎨⎧∠B =∠E ,BC =EC ,∠BCF =∠ECH ,∴△BCF ≌△ECH(ASA), ∴CF =CH.(2)四边形ACDM 是菱形.证明:∵∠ACB =∠DCE =90°,∠BCE =45°, ∴∠ACE =∠DCH =45°.∵∠E =45°,∴∠ACE =∠E ,∴AC ∥DE , ∴∠AMH =180°-∠A =135°=∠ACD. 又∵∠A =∠D =45°,∴四边形ACDM 是平行四边形. ∵AC =CD ,∴四边形ACDM 是菱形.14.解:(1)证明:∵AO =CO ,BO =DO , ∴四边形ABCD 是平行四边形, ∴∠ABC =∠ADC.∵∠ABC +∠ADC =180°, ∴∠ABC =∠ADC =90°, ∴四边形ABCD 是矩形.(2)∵∠ADC =90°,∠ADF ∶∠FDC =3∶2, ∴∠FDC =36°.∵DF ⊥AC ,∴∠DCO =90°-36°=54°. ∵四边形ABCD 是矩形,∴OC =OD ,∴∠ODC =54°, ∴∠BDF =∠ODC -∠FDC =18°.15.解:(1)若四边形AECF 是平行四边形, 则AO =OC ,EO =OF.∵四边形ABCD 是平行四边形, ∴BO =OD =6 cm , ∴EO =6-t ,OF =2t , ∴6-t =2t ,∴t =2,∴当t =2时,四边形AECF 是平行四边形. (2)①若四边形AECF 是菱形, ∴AC ⊥BD ,∴AO 2+BO 2=AB 2,∴AB =36+9=3 5, 即当AB =3 5时,四边形AECF 是菱形. ②不可以.理由:若四边形AECF 是矩形,则EF =AC , ∴6-t +2t =6,∴t =0,则此时点E 在点B 处,点F 在点O 处, 显然四边形AECF 不可以是矩形.四边形全章综合测试1.如图,E F 、是ABCD 对角线AC 上两点,且AE CF =,连结DE 、BF ,则图中共有全等三角形的对数是( )A.1对B.2对C.3对D.4对2.如图,在在平行四边形ABCD 中,对角线AC BD ,相交于点O ,E F ,是对角线AC 上的两点,当E F ,满足下列哪个条件时,四边形DEBF 不一定是是平行四边形( ) A.OE OF = B.DE BF = C.ADE CBF ∠=∠ D.ABE CDF ∠=∠ABF ECD3.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( ).A .测量对角线是否相互平分B .测量两组对边是否分别相等C .测量一组对角线是否都为直角D .测量其中三角形是否都为直角4.如果一个四边形绕对角线的交点旋转90,所得的图形与原来的图形重合,那么这个四边形一定是( ) A.平行四边形B.矩形C.菱形D.正方形5. 已知点(20)A ,、点B (12-,0)、点C (0,1),以A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在 ( )A.第一象限 B.第二象限 C.第三象限 D.第四象限6.如图,在平行四边形ABCD 中,AC BD ,相交于点O .下列结论:①OA OC =,②BAD BCD ∠=∠,③AC BD ⊥,④180BAD ABC ∠+∠=.其中,正确的个数有( ) A.1个B.2个C.3个D.4个7.如图,平行四边形ABCD 中,AB3=,5BC =,AC 的垂直平分线交AD 于E ,则CDE △的周长是() A.6B.8C.9D.108.把长为10cm 的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,如果剪掉..部分的面积为12cm 2,则打开后梯形的周长是 ( )A 、(10+25)cmB 、(12+25)cmC 、22cmD 、20cm9.如图,正方形ABCD 的边长为2,点E 在AB 边上,四边形EFGB 也为正方形,设AFC △的面积为S ,则( )A.2S =B. 2.4S = C.4S =D.S 与BE 长度有关10.梯形ABCD 中,AD ∥BC ,E 、F 为BC 上点,且DE ∥AB ,AF ∥DC ,DE ⊥AF 于G ,若AG =3,DG =4,四边形ABED 的面积为36,则梯形ABCD 的周长为( )A .49B .43C .41D .4611. 已知:如图,正方形ABCD ,AC 、BD 相交于点O ,E 、F 分别为BC 、CD 上的两点,BE=CF ,AE 、BF 分别交BD 、AC 于M 、N 两点, 连结OE 、OF.下列结论,其中正确的是( ).①AE=BF ;②AE ⊥BF ;③OM=ON=12DF ;④CE+CF=22AC .(A )①②④ (B )①②(C )①②③④(D )②③④12.已知菱形ABCD 的边长为6,∠A =60°,如果点P 是菱形内一点,且PB =PD =23,那么AP 的长为 .13.(7分)如图,在ABC △中,AB BC =,D、E、F分别是BC 、AC 、AB 边上的中点.(1) 求证:四边形BDEF 是菱形;(2) 若12AB =cm ,求菱形BDEF 的周长.AFBDCEGBF A E ABCDOMENFACE GF EDCBA14.(7分)如图,将一张矩形纸片A B C D ''''沿EF 折叠,使点B '落在A D '' 边上的点B 处;沿BG 折叠,使点D '落在点D 处,且BD 过F 点.⑴试判断四边形BEFG 的形状,并证明你的结论. ⑵当∠BFE 为多少度时,四边形BEFG 是菱形.15.(7分)如图,四边形ABCD 为平行四边形,E 为AD 上的一点,连接EB 并延长,使BF=BE ,连接EC 并延长,使CG=CE ,连接FG .H 为FG 的中点,连接DH . (1) 求证:四边形AFHD 为平行四边形;(2)若CB=CE ,∠BAE=600 ,∠DCE=200 求∠CBE 的度数.16.(7分)如图,梯形ABCD 中,120AD BC AB DC ADC =∠=∥,,,对角线CA平分DCB ∠,E 为BC 的中点,试求DCE △与四边形ABED 面积的比.17.(8分)在矩形纸片ABCD 中,33AB =,6BC =,沿EF 折叠后,点C 落在AB 边上的点P处,点D 落在点Q 处,AD 与PQ 相交于点H ,30BPE ∠=.ADBEC(1)求BE 、QF 的长; (2)求四边形PEFH 的面积.18.(本题12分)如图,四边形ABCD 位于平面直角坐标系的第一象限,B 、C 在x 轴上,A 点函数xy 2上,且AB ∥CD ∥y 轴,AD ∥x 轴,B (1,0)、C (3,0)。
2020年中考数学二轮专题——矩形、菱形、正方形(含详细解答)

2020年中考数学二轮专题——矩形、菱形、正方形基础过关1. (2019无锡)下列结论中,矩形具有而菱形不一定具有的性质是()A. 内角和为360°B. 对角线相互平分C. 对角线相等D. 对角线互相垂直2. (2019娄底)顺次连接菱形四边中点得到的四边形是()A. 平行四边形B. 菱形C. 矩形D. 正方形3. (2019重庆A卷)下列命题正确的是()A.有一个角是直角的平行四边形是矩形B.四条边相等的四边形是矩形C.有一组邻边相等的平行四边形是矩形D.对角线相等的四边形是矩形4. (2019青羊区二诊)在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是()A.AB∥DC B.OC=OBC.AC⊥BD D.OA=OC5. (2019毕节)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为()A. 3B. 3C. 5D. 5第5题图6. (2019天津)如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于()A. 5B. 4 3C. 4 5D. 20第6题图7. (2019呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A. 2 2B. 2 5C. 4 2D. 2108. (2019临沂)如图,在▱ABCD中,M,N是BD上的两点,BM=DN,连接AM,MC,CN,N A.添加一个条件,使四边形AMCN 是矩形,这个条件是( )A. OM =12ACB. MB =MOC. BD ⊥ACD. ∠AMB =∠CND第8题图9. 如图,在正方形ABCD 外侧,作等边△ADE ,AC ,BE 相交于点F ,则∠BFC 为( ) A. 75°B. 60°C. 55°D. 45°第9题图10. 如图,在矩形ABCD 中,点E 在BC 上,AE =AD ,DF ⊥AE ,垂足为F ,若∠FDC =30°,且AB =3,则AD 的长为( )A .3B .4C .5D .6第10题图11. (2019贵阳)如图,菱形ABCD 的周长是4 cm ,∠ABC =60°,那么这个菱形的对角线AC 的长是( ) A. 1 cmB. 2 cmC. 3 cmD. 4 cm第11题图12. (2019德阳)已知▱ABCD 的对角线AC 、BD 相交于点O ,△AOD 是等边三角形,且AD =4,则AB 等于( )A. 2B. 4C. 2 3D. 4 313. (2019河池)如图,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,BE =CF ,则图中与∠AEB 相等的角的个数是( )A. 1B. 2C. 3D. 4第13题图14. 如图,在矩形ABCD 中,AB =12,BC =16,点E 是BC 的中点,点F 是边CD 上的任意一点,则AF +EF 的最小值为( )A .12B .14C .12 5D .14 5第14题图15. (2019兰州)如图,边长为2的正方形ABCD 的对角线AC 与BD 交于点O ,将正方形ABCD 沿直线DF 折叠,点C 落在对角线BD 上的点E 处,折痕DF 交AC 于点M ,则OM =( )A.12B.22C.3-1D.2-1第15题图16. (2019金华)如图,矩形ABCD 的对角线交于点O ,已知AB =m ,∠BAC =∠α,则下列结论错误..的是( )A. ∠BDC =∠αB. BC =m ·tan αC. AO =m 2sin αD. BD =m cos α第16题图17. (2019台州)如图,有两张矩形纸片ABCD 和EFGH ,AB =EF =2 cm ,BC =FG =8 cm.把纸片ABCD 交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且点D 与点G 重合,当两张纸片交叉所成的角α最小时,tan α等于( )A. 14B. 12C. 817D. 815第17题图18.(2019绍兴)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积()A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变第18题图19. (2019双流区一诊)一个菱形的周长为20 cm,一条对角线长为6 cm,则这个菱形的面积是______cm2.20. (2019扬州)如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=________.第20题图21.(2019徐州)如图,矩形ABCD中,AC、BD交于点O、M、N分别为BC、OC的中点.若MN=4,则AC的长为________.第21题图22. (2019菏泽)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是________.第22题图23.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE 的长是________.第23题图24. (2019北京)如图,在菱形ABCD 中,AC 为对角线,点E ,F 分别在AB ,AD 上,BE =DF ,连接EF . (1)求证:AC ⊥EF ;(2)延长EF 交CD 的延长线于点G ,连接BD 交AC 于点O .若BD =4,tan G =12,求AO 的长.第24题图25. (2019云南)如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =OC ,BO =OD ,且∠AOB =2∠OA D.(1)求证:四边形ABCD 是矩形;(2)若∠AOB ∶∠ODC =4∶3,求∠ADO 的度数.第25题图能力提升1. (2019烟台)如图,面积为24的▱ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为()A. 2425 B.45 C.34 D.1225第1题图2. (2019安徽)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12.点P在正方形的边上,则满足PE+PF=9的点P的个数是()A. 0B. 4C. 6D. 8第2题图3. (2019黄石)如图,矩形ABCD中,AC与BD相交于点E,AD∶AB=3∶1,将△ABD沿BD折叠,点A的对应点为F,连接AF交BC于点G,且BG=2,在AD边上有一点H,使得BH+EH的值最小,此时BHCF=()A.32 B.233 C.62 D.32第3题图4.(2019遵义)如图,平行四边形纸片ABCD的边AB,BC的长分别是10 cm和7.5 cm,将其四个角向内对折后,点B与点C重合于点C′,点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=________cm.第4题图5. (2019海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连接AF,当PB=PQ时.①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.第5题图6. (2019双流区一诊)如图①,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;(2)若BP=n·PK,试求出n的值;(3)作BM⊥AE于点M,作KN⊥AE于点N,连接MO、NO,如图②,请证明△MON是等腰三角形,并求出∠MON的度数.第6题图满分冲关1. (2019新都区一诊)如图,直线l 经过正方形ABCD 的顶点A ,先分别过此正方形的顶点B 、D 作BE ⊥l 于点E 、DF ⊥l 于点F ,然后再以正方形的对角线的交点O 为端点,引两条相互垂直的射线分别与AD 、CD 交于点G 、H 两点.若EF =25,S △ABE =2,则线段GH 长度的最小值是______.第1题图2. (2018本溪)在菱形ABCD 中,∠BAD =120°,点O 为射线CA 上的动点,作射线OM 与直线BC 相交于点E ,将射线OM 绕点O 逆时针旋转60°,得到射线ON ,射线ON 与直线CD 相交于点F .(1)如图①,点O 与点A 重合时,点E ,F 分别在线段BC ,CD 上,请直接写出CE ,CF ,CA 三条线段之间的数量关系;(2)如图②,点O 在CA 的延长线上,且OA =13AC ,E ,F 分别在线段BC 的延长线和线段CD 的延长线上,请写出CE ,CF ,CA 三条线段之间的数量关系,并说明理由;(3)点O 在线段AC 上,若AB =6,BO =27,当CF =1时,请直接写出BE 的长.参考答案基础过关1. C2. C 【解析】顺次连接任意四边形的四边中点,得到四边形一定是平行四边形,如果原四边形的对角线相等,则可得中点四边形的邻边相等,即是菱形;如果原四边形的对角线互相垂直,则可得中点四边形的邻边垂直,即是矩形.因为菱形的对角线互相垂直,所以它的中点四边形是矩形.3.A 【解析】根据矩形的判定定理可知,有一个角是直角的平行四边形是矩形,故A 正确;四条边相等的四边形是菱形,不是矩形,故B 错误;有一组邻边相等的平行四边形是菱形,不是矩形,故C 错误;对角线相等的平行四边形是矩形,故D 错误.4. B 【解析】∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,OA =OC ,故A ,C ,D 正确.5. B 【解析】在Rt △BCE 中,BC =22-12=3,∴正方形ABCD 的面积为(3)2=3.6. C 【解析】∵A (2,0),B (0,1),∴OA =2,OB =1,在Rt △AOB 中,由勾股定理得AB =22+12=5,∵四边形ABCD 为菱形,∴菱形ABCD 的周长为4AB =4 5.7. C 【解析】菱形对角线相互垂直且平分,因此另一条对角线长为2×32-1=4 2.8. A 【解析】∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC .∵BM =DN ,∴OM =ON ,∴四边形AMCN 是平行四边形.当OM =12AC 时,MN =AC ,∴四边形AMCN 是矩形.9. B 【解析】∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD ,∠BAF =45°,∵△ADE 是等边三角形,∴∠DAE =60°,AD =AE ,∴∠BAE =90°+60°=150°,AB =AE ,∴∠ABE =∠AEB =12(180°-150°)=15°,∴∠BFC =∠BAF +∠ABE =45°+15°=60°,故选B .10. D 【解析】∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AEB =∠DAF ,又∵DF ⊥AE ,∴∠DF A =∠B ,又∵AE =AD ,∴△ADF ≌△EAB ,∴DF =AB .∵∠ADF +∠FDC =90°,∠DAF +∠ADF =90°,∴∠FDC =∠DAF =30°,∴AD =2DF =2AB =6.11. A 【解析】∵菱形ABCD 的周长是4 cm ,∴AB =BC =CD =DA =1 cm ,又∵∠ABC =60°,∴△ABC 是等边三角形,∴AC =AB =BC =1 cm .12.D 【解析】在平行四边形ABCD 中,∵△AOD 为等边三角形,即OA =OD =AD =4,∴AC =BD =8,∴平行四边形ABCD 是矩形,∴由勾股定理得AB =4 3.13. C 【解析】四边形ABCD 是正方形,∴AD ∥BC ,∴∠DAE =∠AEB .∵BE =CF ,∠ABE =∠BCF ,AB =BC ∴△ABE ≌△BCF (SAS),∴∠BFC =∠AEB .∵AB ∥CD ,∴∠ABF =∠BFC =∠AEB .∴与∠AEB 相等的角有3个.14.C 【解析】如解图,作点E 关于直线CD 的对称点E ′,连接AE ′交CD 于点F ,此时AF +EF 的最小值为AE ′的长.∵在矩形ABCD 中,AB =12,BC =16,E 是BC 的中点,∴BE =CE =CE ′=8,∴BE ′=24,∴AE ′=AB 2+BE ′2=122+242=12 5.第14题解图15. D 【解析】∵四边形ABCD 是正方形,∴∠CBE =∠DCM =45°,BC =CD = 2.∴AC =BD =2.∴OC =1.由折叠的性质知,DE =CD =2,CF =EF ,∴BE =2-2,∠DFC =90°.∴∠CDM +∠DCE =90°.又∠BCE +∠DCE =90°,∴∠BCE =∠CDM . ∴△BCE ≌△CDM .∴CM =BE =2- 2.∴OM =OC -CM =1-(2-2)=2-1.16. C 【解析】∵四边形ABCD 是矩形,∴AC =BD ,且OD =OC ,∠ABC =90°,∴∠BDC =∠OCD =∠BAO =∠α,tan α=BC AB =BC m ,sin α=BC AC =BC 2AO ,cos α=AB AC =m AC ,∴BC =m ·tan α,AO =BC 2sin α,AC =m cos α,而BD =AC ,BC ≠m ,∴BD =m cos α,AO ≠m2sin α∴A 、B 、D 正确,C 错误.17.D 【解析】如解图,当B 、E 重合时, α最小,∵在△BMF 和△DMC 中,⎩⎪⎨⎪⎧∠BMF =∠DMC ∠F =∠C BF =DC ,∴△BMF ≌△DMC (AAS),∴BM =DM ,设FM =x ,则DM =BM =8-x ,在Rt △BFM 中,由勾股定理得22+x 2=(8-x )2,解得x =154,∴tan α=BF FM =2154=815.第17题解图18. D 【解析】如解图,连接DE ,∵在正方形ABCD 中,S △DEC =12AD ·CD =12S 正方形ABCD ,在长方形ECFG 中,S △DEC =12×EC ·GE =12S 矩形ECFG ,而点E 从点A 移动到点B 的过程中,三角形DEC 的面积保持不变,∴矩形ECFG 的面积保持不变.第18题解图19. 24 【解析】如解图,在菱形ABCD 中,BD =6.∵菱形的周长为20,BD =6,∴AB =5,BO =3,∴AO =52-32=4,AC =8.∴S 菱形ABCD =12×6×8=24.第19题解图20.132 【解析】 如解图,连接FC ,则MN =12CF ,在Rt △CFG 中,FG =5,CG =5+7=12,∴FC =52+122=13,∴MN =132.第20题解图21. 16 【解析】在△OBC 中,根据三角形中位线等于它所对的第三边的一半,得到OB =2MN =8,又根据矩形的性质:对角线相等且互相平分,得到AC =BD =2OB =16.22. 85 【解析】如解图,连接BD 交AC 于点O ,∵四边形ABCD 是正方形,AC 是对角线,∴CD =AD ,∠DAE =∠DCF =45°,BD ⊥AC . ∵AE =CF , ∴△DAE ≌△DCF (SAS), ∴DE =DF ,同理可证:DE =BE ,BE =BF ,∴四边形BEDF 是菱形,∵AC =8,AO =OD ,AE =2,∴OE =2,OD =4,∴DE =OD 2+OE 2=42+22=2 5.∴四边形BEDF 的周长为4DE =8 5.第22题解图23. 74 【解析】如解图,连接EC ,∵OA =OC ,EF ⊥AC ,∴EC =AE ,设DE =x ,则EC =AE =8-x ,根据勾股定理可得(8-x )2=x 2+62,解得x =74.∴DE 的长为74.第23题解图24. (1)证明:∵四边形ABCD 是菱形, ∴AB =AD ,∴∠BAC =∠DAC . ∵AB =AD ,BE =DF ,∴AB -BE =AD -DF ,即AE =AF . ∴△AEF 是等腰三角形. 又∵∠BAC =∠DAC , ∴AC ⊥EF ;(2)解:由题意作解图如下, ∵四边形ABCD 是菱形,∴AC ⊥BD ,AB ∥CD ,OB =12BD =12×4=2.∴∠G =∠AEG .由(1)知EF ⊥AC .又∵BD ⊥AC . ∴EF ∥BD .∴∠AEG =∠ABO . ∴∠G =∠ABO .∵tan G =12,∴tan ∠ABO =AO OB =12.∴AO =OB ·tan ∠ABO =2×12=1.第24题解图25. (1)证明:∵AO =OC ,BO =OD , ∴四边形ABCD 是平行四边形.又∵∠AOB =2∠OAD ,∠AOB 是△AOD 的外角, ∴∠AOB =∠OAD +∠ADO . ∴∠OAD =∠ADO . ∴AO =OD .又∵AC =AO +OC =2AO ,BD =BO +OD =2OD , ∴AC =BD .∴四边形ABCD 是矩形;(2)解:设∠AOB =∠DOC =4x ,∠ODC =3x ,则∠ODC =∠OCD =3x . 在△ODC 中,∠DOC +∠OCD +∠CDO =180°, ∴4x +3x +3x =180°, 解得x =18°.∴∠ODC =3×18°=54°.∴∠ADO =90°-∠ODC =90°-54°=36°.能力提升1. A 【解析】如解图,连接AC 交BD 于点O ,过点D 作DF ⊥BE 于点F .∵BD 平分∠ABC ,∴∠ABD =∠CBD .∵四边形ABCD 是平行四边形,∴BC ∥AD . ∴∠ADB =∠CBD .∴∠ABD =∠ADB .∴AB =AD . ∴▱ABCD 是菱形. ∴AO 垂直平分BD . ∵DE ⊥BD ,∴OC ∥DE .∴OC =12DE =12×6=3.∵菱形ABCD 的面积为24,∴BD =8. ∴BO =4. ∴BC =DC =5.∵DF ·BC =24,∴DF =245. ∴sin ∠DCE =DF DC =2425.第1题解图2. D 【解析】如解图,∵点E ,F 将对角线AC 三等分,且AC =12,∴AE =EF =FC =4,当P 点在AD 上时,作E 点关于AD 的对称点E ′,连接E ′F ,则AE ′=AE =4,当P 点运动至E ′F 和AD 交点时,PE +PF 具有最小值,由对称性可知∠E ′AF =90°,此时E ′F =(AE ′)2+AF 2=42+82=45<9,当P 点和A 点重合时,过点E 作EG ⊥AD ,垂足为G ,PE +PF =AE +AF =12,当P 点和D 点重合时,连接DF ,∵AD =CD ,∠DAE =∠DCF ,AE =CF ,∴△AED ≌△CFD (SAS),∴DE =DF ,∴PE +PF =2DE =2EG 2+DG 2=2×(22)2+(42)2=410.∵45<9<12,45<9<410,∴在AD 上有两个位置存在PE +PF =9,同理在其余三边上各有两种情况,故正方形四条边上共存在8个位置使得PE +PF =9,∴满足条件的P 点有8个.第2题解图3. B 【解析】∵矩形ABCD 中,AD ∶AB =3∶1,∴∠ADB =30°,又△ABD 沿BD 折叠,点A 的对应点为F ,∴∠ADB =∠BDF =30°,∠ABD =∠DBF =60°,AD =FD ,AB =BF ,∴∠CDF =30°,△ADF 为等边三角形,DF =AF ,∴∠BAF =12(180°-∠ABD -∠DBF )=30°=∠CDF ,又DC =AB ,∴△ABF ≌△DCF ,∴CF =BF ,在Rt △ABG 中,ABG =90°,∠BAG =30°,BG =2,∴AB =23,∴CF =23,如解图,延长BA 到B ′使AB ′=AB ,连接EB ′交AD 于H ,根据对称性可知此时点H 即为满足BH +EH 的值最小的H 点.∵∠ADB =30°,∴AB =BE =ED ,又∵AB ′=AB =BE =AE ,∴△BB ′E 为直角三角形,在Rt △BEH 和Rt △BAH 中,BH =BH ,BE =BA ,∴Rt △BEH ≌Rt △BAH ,∴∠ABH =30°,∴BH =AB cos ∠ABH=4,∴BH CF =423=233.第3题解图4. 10 【解析】根据折叠的性质可得△CFH ≌△C ′FH ,△DFG ≌△A ′FG ,△AEG ≌△A ′EG ,△HBE ≌△HC ′E ,∵四边形HFGE 是矩形,∴HF =EG ,FG =HE ,∴△CFH ≌△C ′FH ≌△AEG ≌△A ′EG ,△DFG ≌△A ′FG ≌△HBE ≌△HC ′E ,∴EF =A ′F + A ′E =FD +AE = FD +CF =CD =AB =10 cm .5. (1)证明:∵四边形ABCD 是正方形, ∴∠D =∠BCD =90°. ∴∠ECQ =90°=∠D . ∵E 是CD 的中点, ∴DE =CE .又∵∠DEP =∠CEQ , ∴△PDE ≌△QCE (ASA);(2)①证明:如解图,由(1)可知△PDE ≌△QCE , ∴PE =QE =12PQ .又∵EF ∥BC , ∴PF =FB =12PB .∵PB =PQ , ∴PF =PE . ∴∠1=∠2.∵四边形ABCD 是正方形, ∴∠BAD =90°.在Rt △ABP 中,∵F 是PB 的中点, ∴AF =12BP =FP .∴∠3=∠4.又∵AD ∥BC ,EF ∥BC , ∴AD ∥EF . ∴∠1=∠4.∴∠2=∠3. 又∵PF =FP ,∴△APF ≌△EFP (AAS). ∴AP =EF . 又∵AP ∥EF ,∴四边形AFEP 是平行四边形;第5题解图②解:四边形AFEP 不是菱形,理由如下: 设PD =x ,则AP =1-x . 由(1)可知△PDE ≌△QCE . ∴CQ =PD =x . ∴BQ =BC +CQ =1+x .∵点E ,F 分别是PQ ,PB 的中点, ∵EF 是△PBQ 的中位线. ∴EF =12BQ =1+x 2.由①可知AP =EF . 即1-x =1+x 2,解得x =13.∴PD =13,AP =23.在Rt △PDE 中,∵DE =12,∴PE =PD 2+DE 2=136. ∵AP ≠PE .∴四边形AFEP 不是菱形.6. (1)证明:∵四边形ABCD 为菱形, ∴AD ∥BC ,∴∠DAP =∠CEP ,∠ADP =∠ECP , 在△ADP 和△ECP 中,⎩⎪⎨⎪⎧∠DAP =∠CEP ∠ADP =∠ECP DP =CP, ∴△ADP ≌△ECP (AAS);(2)解:如解图①,过点P 作PI ∥CE 交DE 于点I , 则PI CE =DPDC ,又点P 是CD 的中点, ∴PI CE =12, ∵△ADP ≌△ECP , ∴AD =CE , ∴KP KB =PI BE =14, ∴BP =3PK , ∴n =3;第6题解图①(3)解:如解图②,过点O 作OG ⊥AE 于点G , ∵BM ⊥AE 于点M ,KN ⊥AE 于点N , ∴BM ∥OG ∥KN , ∵点O 是线段BK 的中点, ∴MG =NG ,又∵OG ⊥MN , ∴OM =ON ,即△MON 是等腰三角形,由题意得,△BPC ,△AMB ,△ABP 为直角三角形, 设BC =2,则CP =1,由勾股定理得,BP =3, 则AP =7,根据三角形面积公式,BM =2217, ∴MP =377.易得PB =3PO ,∴OG =13BM =22121,MG =23MP =277,tan ∠MOG =MGOG =3,∴∠MOG =60°,∴∠MON 的度数为120°.第6题解图②满分冲关1. 6 【解析】由题易证△ABE ≌△DAF .∵GO ⊥HO ,易得△AGO ≌△DHO ,∴GO =HO .∴△GHO 为等腰直角三角形.∴当GO 最小时,GH 取得最小值.令AF =a ,AE =b ,则BE =a ,DF =b ,∴a +b =25,12a ·b =2,∴AB 2=a 2+b 2=12.∴AB =23.∴当GO ⊥AD 时,GO 有最小值,此时OG ∥AB ,∵O 为BD 中点,∴OG 为△ABD 的中位线,∴GO =12AB =3,∴GO 的最小值为3,∴GH 最小值为 6.2. 解:(1)CA =CE +CF ;【解法提示】∵在菱形ABCD 中,∠BAD =120°, ∴∠DAC =∠ACB =∠D =60°. 又∵∠EAF =60°, ∴∠DAF =∠CAE . ∵AD =CD 且∠D =60°,∴△ACD 是等边三角形,AD =AC , ∴△ADF ≌△ACE , ∴DF =CE .又∵CA =CD =DF +CF , ∴CA =CE +CF . (2)CF -CE =43CA ,理由:如解图①,过点O 作OG ∥AD ,交CF 于点G , ∵四边形ABCD 是菱形, ∴AB =BC =CD =DA . ∵∠BAD =120°, ∴∠B =∠ADC =60°,∴△ABC 和△ADC 都为等边三角形. ∵OG ∥AD ,∴∠OGC =∠ADC =∠ACD =60°, ∴△OGC 为等边三角形,∴OC =OG ,∠OCE =∠OGF =180°-60°=120°. ∵∠COE =∠GOF =60°-∠EOG ,∴△OCE ≌△OFG , ∴FG =CE . ∵CF =GF +CG , ∴CF -CE =CO . ∵AO =13CA ,∴OC =43CA ,∴CF -CE =43CA ;第2题解图①(3)BE 的长为1或3或5.【解法提示】连接BD 交AC 于点I ,①如解图②,当点O 在AI 上时,过点O 作OP ⊥BC 于点P ,作OQ ⊥CD 于点Q , 又∵菱形ABCD 中,AC 平分∠BCD , ∴OP =OQ .∵∠POQ =360°-120°-90°×2=60°, ∴∠EOF =∠POQ , ∴∠EOP =∠FOQ . 又∵∠OPE =OQF =90°, ∴△EOP ≌△FOQ , ∴EP =FQ .在Rt △AIB 中,AB =6,∠BAI =60°, ∴BI =AB ·sin60°=3 3. 在Rt △BIO 中, BO =27,BI =33, ∴OI =OB 2-BI 2=1. 又∵CI =12AC =3,∴OC =3+1=4, ∴CP =CQ =12OC =2.又∵CF =1,∴EP =FQ =1,∴BE =BC -CP -EP =6-2-1=3;第2题解图②②如解图③,当点O 在AI 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得EP =QF ,OC =4,CQ =CP =2, ∵CF =1,∴QF =CQ +CF =3,∴BE =CB -CP -PE =6-2-3=1;第2题解图③③如解图④,当点O 在IC 上时,由①知OC =3-1=2, 又∵CF =1,∠ACD =60°, ∴OF ⊥CD ,∴∠OEC =360°-60°-120°-90°=90°, ∴EC =12OC =1,∴BE =6-1=5;第2题解图④④如解图⑤,当点O 在IC 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得QF =PE ,OC =2,CP =CQ =1,QF =CQ +CF =2,∴BE =BC -EP -CP =6-2-1=3; 综上所述,BE 的长为1或3或5.第2题解图⑤。
专题19.1 矩形、菱形与正方形(基础篇)专项练习-2020-2021学年八年级数学下(华东师大版)

专题19.1 矩形、菱形与正方形(基础篇)专项练习一、单选题1.菱形具有而一般平行四边形不具有的性质是( )A .对边相等B .对角相等C .对角线互相平分D .对角线互相垂直 2.下列判断错误的是( )A .两组对边分别相等的四边形是平行四边形B .四个内角都相等的四边形是矩形C .四条边都相等的四边形是菱形D .两条对角线垂直且平分的四边形是正方形3.菱形的周长为8cm ,高为1cm ,则菱形两邻角度数比为( )A .4:1B .5:1C .6:1D .7:1 4.如图,EF 过矩形ABCD 对角线的交点O ,且分别交AB 、CD 于E 、F ,那么阴影部分的面积是矩形ABCD 的面积的( )A .15B .14C .13D .3105.如图,已知菱形的两条对角线分别为6cm 和8cm ,则这个菱形的高DE 为( )A .2.4cmB .4.8cmC .5cmD .9.6cm 6.如图,在平面直角坐标系中,四边形OABC 为菱形,()0,0O ,()4,0A ,60AOC ∠=,则对角线交点E 的坐标为( )A.(B.)2C.)D.(7.如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD, DE∥AC , AD=, DE =2,则四边形OCED 的面积为()A.B.4C.D.88.如图,在正方形ABCD中,E为DC边上的点,连接BE,将∥BCE绕点C顺时针方向旋转90°得到∥DCF,连接EF,若∥BEC=60°,则∥EFD的度数为()A.10°B.15°C.20°D.25°9.如图,在∥ABC 中,点D 是边BC 上的点(与B、C 两点不重合),过点D作DE∥AC,DF∥AB,分别交AB、AC 于E、F 两点,下列说法正确的是()A.若AD 平分∥BAC,则四边形AEDF 是菱形B.若BD=CD,则四边形AEDF 是菱形C.若AD 垂直平分BC,则四边形AEDF 是矩形D .若 AD ∥BC ,则四边形 AEDF 是矩形10.如图,在菱形ABCD 中,P 是对角线AC 上一动点,过点P 作PE BC ⊥于点E .PF AB ⊥于点F .若菱形ABCD 的周长为20,面积为24,则PE PF +的值为( )A .4B .245C .6D .485二、填空题 11.已知菱形ABCD 的面积是12cm 2,对角线AC =4cm ,则菱形的边长是______cm . 12.如图,在∥ABC 中,AD 是高,E 是AB 的中点,EF∥AD ,交AC 于点F ,若AC=6,则DF 的长为______.13.如图,在长方形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD ,BC 于点E ,F ,连接CE ,则CE 的长为________.14.如图,菱形ABCD 的边长为2,∥DAB=60°,E 为BC 的中点,在对角线AC 上存在一点P ,使∥PBE 的周长最小,则∥PBE 的周长的最小值为________.15.如图:已知:AM MN ⊥,BN MN ⊥,垂足分别为M 、N ,点C 是MN 上使AC BC +的值最小的点.若3AM =,5BN =,15MN =,则AC BC +=________.16.如图,在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点,∥EAF =45°,∥ECF 的周长为4,则正方形ABCD 的边长为_____.17.如图,在Rt∥ABC 中,∥ABC=90°,AC=10cm ,点D 为AC 的中点,则BD=_____cm .18.如图,在菱形ABCD 中,P 是对角线AC 上的一点,PE AB ⊥于点E ,若5PE =,则点P 到AD 的距离为________.19.如图,边长分别为4和8的两个正方形ABCD 和CEFG 并排放在一起,连结BD 并延长交EG 于点T ,交FG 于点P ,则GT 的长为_____.20.如图,在Rt∥BAC 和Rt∥BDC 中,∥BAC =∥BDC =90°,O 是BC 的中点,连接AO 、DO.若AO=3,则DO的长为_____.21.如图,在正方形ABCD,E是对角线BD上一点,AE的延长线交CD于点F,连接∠=︒,则CEFCE.若56BAE∠=______︒.22.如图,边长为1的菱形ABCD中,∥DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∥FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∥HAE=60°…按此规律所作的第n个菱形的边长是___.三、解答题23.如图,∥ABC中,AB=AC,AD是∥ABC的角平分线,点O为AB的中点,连接DO 并延长到点E,使OE=OD,连接AE,BE,(1)求证:四边形AEBD是矩形;(2)当∥ABC满足什么条件时,矩形AEBD是正方形,并说明理由.24.如图,在∥ABC 和∥DCB 中,AB=DC ,AC=DB ,AC 与DB 交于点M .(1)求证:∥ABC∥∥DCB(2)过点C 作CN∥BD ,过点B 作BN∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系,并证明你的结论.25.如图,点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA (不包括端点)上运动,且满足AE CG =,AH CF =.(1)求证:AEH CGF ∆≅∆;(2)试判断四边形EFGH 的形状,并说明理由.(3)请探究四边形EFGH 的周长一半与矩形ABCD 一条对角线长的大小关系,并说明理由.26.在∥ABC 中,M 是AC 边上的一点,连接BM.将∥ABC 沿AC 翻折,使点B 落在点D 处,当DM∥AB 时。
解题技巧专题:菱形、矩形、正方形中折叠、旋转问题之七大考点(解析版)

解题技巧专题:菱形、矩形、正方形中折叠、旋转问题之七大考点【考点导航】目录【典型例题】1【考点一菱形中的折叠求角度、线段长等问题】【考点二矩形中的折叠求角度、线段长等问题】【考点三正方形中的折叠求角度、线段长等问题】【考点四特殊平行四边形折叠后求周长、面积问题】【考点五菱形中旋转求角度、线段长等问题】【考点六矩形中旋转求角度、线段长等问题】【考点七正方形中旋转求角度、线段长等问题】【典型例题】【考点一菱形中的折叠求角度、线段长等问题】1(2022秋·九年级课时练习)如图,在菱形ABCD中,∠A=120°,AB=2,点E是边AB上一点,以DE 为对称轴将△DAE折叠得到△DGE,再折叠BE使BE落在直线EG上,点B的对应点为点H,折痕为EF且交BC于点F.(1)∠DEF=;(2)若点E是AB的中点,则DF的长为.【答案】 90° 2.8【分析】(1)由折叠得∠DEG+∠HEF=∠AED+∠BEF,再根据平角的定义可得结论;(2)首先证明B、G、D在同一条直线上,再运用勾股定理列方程求解即可.【详解】解由折叠得,∠AED=∠DEG,∠BEF=∠HEF∴∠DEG+∠HEF=∠AED+∠BEF∵∠AED+∠DEG+∠HEF+∠BEF=180°×180°=90°∴∠DEG+∠HEF=12即∠DEF=90°故答案为:90°;(2)∵四边形ABCD是菱形∴AD⎳BC,DC⎳AB,AB=BC=CD=DA=2∴∠B+∠A=180°∵∠A=120°∴∠B=180°-∠A=180°-120°=60°∵点E为AB的中点,且AB=2∴AE=BF=12AB=12×2=1.∵点A与点G重合,∴∠DGE=∠A=120°∵点B与点H重合∴∠EHF=∠B=60°又AE=EG,BE=EH,AE=BE∴EG=EH∴点G与点H重合∵∠DGE+∠FHE=∠DGE+∠FGE=100°+80°=180°∴B,G,D三点在同一条直线上过点D作DO⊥BC,交BC的延长线于点O,如图,∵DC⎳AB∴∠DCO=∠B=60°,DC=AB=2∴∠CDO=30°∴CO=12DC=12×2=1.在Rt△DCO中,OD=DC2-OC2=22-12=3由折叠得,BF=FH,AD=DH=2设BF=x,则FC=2-x∴DF=DF+GF=2+x,FO=FC+CO=2-x+1=3-x在Rt△DFO中,DF2=FO2+DO2∴(2+x)2=(3-x)2+(3)2解得,x=0.8∴DF=2+0.8=2.8故答案为2.8【点睛】本题主要考查了菱形的性质,折叠的性质,勾股定理等知识,正确作出辅助线构造直角三角形是解答本题的关键.【变式训练】1(2023春·全国·八年级专题练习)图,把菱形ABCD沿AE折叠,点B落在BC边上的F处,若∠BAE=15°,则∠FDC的大小为.【答案】22.5°【分析】根据翻折变换的性质可得AB=AF,然后根据等腰三角形两底角相等求出∠B=∠AFE=75°,可得∠C,根据AF=AD,求出∠AFD,由三角形外角等于不相邻的两个内角的和即可得答案.【详解】解:∵菱形ABCD沿AE折叠,B落在BC边上的点F处,∴AD=AB=AF,∠AEB=90°=∠AEF,∠FAE=∠BAE=15°,∴∠B=∠AFE=75°,在菱形ABCD中,AB∥CD,AD∥BC,∴∠DAF=∠AFE=75°,∠C=180°-∠B=105°,∵AF=AD,∴∠ADF=∠AFD=180°-75°2=52.5°,∴∠DFB=∠AFE+∠AFD=127.5°,∴∠FDC=∠DFB-∠B=22.5°,故答案为:22.5°.【点睛】本题考查了菱形中的翻折问题,等腰三角形的性质,解题的关键是掌握翻折的性质及菱形的性质.2(2023春·八年级课时练习)如图,在菱形ABCD中,∠B=60°,AB=4,E,F分别是边AB,BC上的点,将△EBF沿EF折叠,使点B的对应点B'落在边AD上,若AE=AB',则CF的长为.【答案】4-23##-23+4【分析】根据菱形性质和∠B=60°,可得BC=AB=4,AD⎳BC,∠BAD=120°,过点A作AG⊥EB'于点G,AP⊥BC于点P,过点B'Q⊥BC于点Q,得矩形APQB',然后利用含30度角的直角三角形可得1 24-AE=32AE,得AE=23-2,再利用勾股定理即可解决问题.【详解】解:在菱形ABCD中,∠B=60°,BC=AB=4,AD⎳BC,∴∠BAD=120°,如图,过点A作AG⊥EB'于点G,AP⊥BC于点P,过点B'Q⊥BC于点Q,得矩形APQB',如图所示:∴PQ=AB',B'Q=AP,∵AE =AB ',AG ⊥EB ',∴EG =B 'G =12EB ',∠AEG =30°,由翻折可知:BE =B 'E ,BF =B 'F ,∴BE =B 'E =AB -AE =4-AE ,∴EG =B 'G =124-AE ,∵EG =AE ⋅cos30°,∴124-AE =32AE ,解得AE =23-2,∴PQ =AB '=AE =23-2,在Rt △ABP 中,∠B =60°,AB =4,∴BP =12AB =2,∴AP =23,∴B 'Q =AP =23,∴CF =BC -BF =4-BF ,QF =BF -BP -PQ =BF -2-23-2 =BF -23,在Rt △B 'QF 中,根据勾股定理,得:B 'Q 2+QF 2=B 'F 2,∴(23)2+(BF -23)2=BF 2,解得BF =23,∴CF =4-BF =4-23,故答案为:4-23.【点睛】本题考查勾股定理求线段长,涉及到翻折变换的性质、菱形的性质、等边三角形的判定与性质、勾股定理,熟练掌握翻折变换的性质,由勾股定理得出方程是解题的关键.3(2023春·江苏苏州·八年级苏州工业园区星湾学校校考阶段练习)如图,菱形纸片ABCD ,AB =8,∠B =60°,将该菱形纸片折叠,使点B 恰好落在CD 边的中点B 处,折痕与边BC 、BA 分别交于点M 、N .则CM 的长为.【答案】2.4【分析】过点B 作B E ⊥BC 与BC 的延长线交于点E ,根据含30°角的直角三角形的性质和勾股定理求出CE 和B ′E ,设BM =x ,则B ′M =x ,用x 表示出ME ,然后在Rt △B ME 中,利用勾股定理得出方程进行解答.【详解】解:过点B 作B E ⊥BC 与BC 的延长线交于点E ,∵四边形ABCD 是菱形,∴AB =BC =CD =AD =8,AB ∥CD ,∵B 是CD 的中点,∴B′C=4,∵∠B=60°,∴∠B′CE=∠B=60°,∠CB′E=30°,∴CE=2,∴B′E=42-22=23,设BM=x,则ME=BC+CE-BM=8+2-x=10-x,由折叠的性质知:B′M=BM=x,在Rt△B ME中,B′M2=B′E2+ME2,∴x2=232+10-x2,解得:x=5.6,8-x=2.4,即CM的长为2.4,故答案为:2.4.【点睛】本题主要考查了菱形的性质,折叠的性质,含30°角的直角三角形的性质,勾股定理,二次根式的运算等知识,关键是作辅助线构造直角三角形.【考点二矩形中的折叠求角度、线段长等问题】1(2023·湖南长沙·校联考一模)如图,在矩形ABCD中,E在AD边上,将△ABE沿BE折叠,点A恰好落在矩形ABCD的对称中心O处,若AB=3,则BC的长为.【答案】33【分析】连接OD,由O是矩形ABCD中心,得到B,O,D共线,由翻折变换得到OB=AB,由矩形的性质得到BD=2OB=2AB=6,由勾股定理求出AD的长即可.【详解】解:连接OD,∵O是矩形ABCD中心,∴B,O,D共线,∵△ABE沿BE翻折到△OBE,∴OB=BA,∵四边形ABCD是矩形,O是它的中心,∴BD=2OB=2AB=2×3=6,BC=AD,∵∠BAD=90°,∴AD=BD2-AB2=62-32=33,∴BC=AD=33.故答案为:33【点睛】本题考查矩形的性质,中心对称,翻折变换,关键是掌握矩形的性质.【变式训练】1(2023秋·福建福州·八年级福建省福州第一中学校考期末)如图,长方形ABCD中,E为BC的中点,将△ABE沿直线AE折叠时点B落在点F处,连接FC,若∠DAF=16°,则∠DCF=度.【答案】37【分析】由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,求出∠BAE=∠FAE=37°,可得到∠AEF=∠AEB=53°,求出∠CEF=74°,求出FE=CE,由等腰三角形的性质求出∠ECF=53°,即可得出∠DCF的度数.【详解】解:∵四边形ABCD是长方形,∴∠BAD=∠B=∠BCD=90°,由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,∵∠DAF=16°,∴∠BAE=∠FAE=12×90°-16°=37°,∴∠AEF=∠AEB=90°-37°=53°,∴∠CEF=180°-2×53°=74°,∵E为BC的中点,∴BE=CE,∴FE=CE,∴∠ECF=12×180°-74°=53°,∴∠DCF=90°-∠ECF=37°;故答案为:37.【点睛】本题主要考查了折叠变换的性质、等腰三角形的性质、三角形内角和定理;求出∠ECF的度数是解题的关键.2(2023春·八年级课时练习)长方形纸片ABCD中,AB=3,BC=4,点E是BC边上一动点,连接AE,把∠B沿AE折叠,使点B落在点F处,连接CF,当△CEF为直角三角形时,BE的长为.【答案】32或3【分析】当△CEF为直角三角形时,有两种情况:①当点F落在矩形内部时,如答图1所示.连接AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AFE=∠B=90°,而当△CEF为直角三角形时,只能得到∠EFC=90°,所以点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,则EB= EF,AB=AF=3,可计算出CF=2,设BE=x,则EF=x,CE=4-x,然后在Rt△CEF中运用勾股定理可计算出x .②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形.【详解】解:当△CEF 为直角三角形时,有两种情况:当点F 落在矩形内部时,如答图1所示.连接AC ,在Rt △ABC 中,AB =3,BC =4,∴AC =AB 2+BC 2=32+42=5,∵∠B 沿AE 折叠,使点B 落在点F 处,∴∠AFE =∠B =90°,当△CEF 为直角三角形时,只能得到∠EFC =90°,∴点A 、F 、C 共线,即∠B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,∴EB =EF ,AB =AF =3,∴CF =5-3=2,设BE =x ,则EF =x ,CE =4-x ,在Rt △CEF 中,∵EF 2+CF 2=CE 2,∴x 2+22=4-x 2解得:x =32;②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,∴BE =AB =3.故答案为:32或3;【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.3(2023·安徽合肥·统考一模)如图,点E 是矩形ABCD 的边CD 上的点,连接AE ,将矩形ABCD 沿AE 折叠,点D 的对应点P 恰好在边BC 上.(1)写出图中与∠CEP 相等的角;(2)若AD =5,AB =4,则折痕AE 的长为.【答案】 ∠DAP 和∠APB 552【分析】(1)根据矩形的性质得到∠D =90°,AD ∥BC ,由折叠知∠D =∠APE =90°,由此得到∠DAP +∠PED =180°,即可证明∠DAP =∠CEP ,再由平行线的性质得到∠DAP =∠APB ,则∠APB =∠CEP ;(2)由矩形的性质得到AB =CD =4,BC =AD =5,∠C =∠D =90°,由折叠知AP =AD =5,DE =PE ,利用勾股定理求出BP =3,则CP =2,在Rt △CPE 中,根据勾股定理得DE 2=4-DE 2+22,解得DE =52,则AE =AD 2+DE 2=552.【详解】解:(1)∵四边形ABCD 是矩形,∴∠D =90°,AD ∥BC ,由折叠知∠D =∠APE =90°,∴∠DAP +∠PED =180°,∵∠CEP +∠PED =180°,∴∠DAP =∠CEP ,∵AD ∥BC ,∴∠DAP =∠APB ,∴∠APB =∠CEP ;故答案为:∠DAP 和∠APB ;(2)∵四边形ABCD 是矩形,∴AB =CD =4,BC =AD =5,∠C =∠D =90°,由折叠知AP =AD =5,DE =PE ,∴BP =AP 2-AB 2=52-42=3,∴CP =BC -BP =2,在Rt △CPE 中,根据勾股定理DE 2=CE 2+CP 2,∴DE 2=4-DE 2+22解得DE =52,∴AE =AD 2+DE 2=52+52 2=552,故答案为:552.【点睛】本题主要考查了矩形与折叠问题,勾股定理与折叠问题,灵活应用所学知识是解题的关键.4(2023春·江苏盐城·九年级校考阶段练习)如图,在矩形ABCD 中,点E 在边CD 上,将△BCE 沿BE 折叠,使点C 落在AD 边上的点F 处,过点F 作FG ∥CD ,交BE 于点G ,连接CG .(1)判断四边形CEFG 的形状,并说明理由.(2)若AB =6,AD =10,求四边形CEFG 的面积.【答案】(1)见解析(2)203.【分析】(1)由翻折得∠BEC =∠BEF ,FE =CE ,根据FG ∥CE ,可得∠FGE =∠BEC ,从而∠FGE =∠BEF ,FG =FE ,故FG =EC ,四边形CEFG 是平行四边形,即可得证;(2)在Rt △ABF 中,利用勾股定理求得AF 的长,可得DF =1,设EF =x ,则CE =x ,DE =3-x ,在Rt △DEF 中,用勾股定理列方程可解得CE ,在Rt △BCE 中,即可求出答案.【详解】(1)证明:(1)∵△BCE 沿BE 折叠,点C 落在AD 边上的点F 处,∴△BCE ≌△BFE ,∴∠BEC =∠BEF ,FE =CE ,∵FG∥CE,∴∠FGE=∠BEC,∴∠FGE=∠BEF,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形,又∵CE=FE,∴四边形CEFG是菱形;(2)解:∵矩形ABCD中,AD=10,∴BC=10,∵△BCE沿BE折叠,点C落在AD边上的点F处,∴BF=BC=10,在Rt△ABF中,AB=6,AF=BF2-AB2=8,∴DF=AD-AF=2,设EF=x,则CE=x,DE=6-x,在Rt△DEF中,DF2+DE2=EF2,∴22+(6-x)2=x2,解得x=103,∴CE=103,∴四边形CEFG的面积是:CE•DF=103×2=203.【点睛】本题考查翻折变化、菱形的性质和判定、矩形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.5(2023春·全国·八年级专题练习)如图,矩形ABCD中,AB=3,BC=5,现进行如下折叠:(1)沿着过点B的直线折叠,使点A 落在BC边上,此时折痕BE的长为;(2)沿着过点B的直线折叠,使点A 落在矩形内部,且恰好使点E、A 、C三点在同一直线上,此时折痕BE的长为.【答案】3210【分析】(1)根据折叠的性质,可得出三角形ABE是边长为3的等腰直角三角形,根据勾股定理可求出BE 的长;(2)根据三角形的面积公式可得出EC=BC=5,再根据勾股定理求出DE,AE,最后再根据勾股定理求出BE即可.【详解】解:(1)由折叠可得,AB=A′B,AE=A′E,∠ABE=∠A′BE,∵四边形ABCD是矩形,∴∠A=∠ABC=90°=∠BA′E,∴∠ABE=∠A′BE=45°,∴∠ABE=∠AEB=45°,∴AB=AE,在Rt△ABE中,由勾股定理得,BE=AB2+AE2=32+32=32,故答案为:32;(2)由折叠可得,AB=A′B=3,∠A=∠BA′E=90°,∵点E、A′、C三点在同一直线上,∴S△EBC=12BC•AB=12EC•A′B,∴EC=BC=5,在Rt△DCE中,由勾股定理可得,DE=EC2-DC2=52-32=4,∴AE=AD-DE=5-4=1,在Rt△ABE中,BE=AB2+AE2=32+12=10,故答案为:10.【点睛】本题考查矩形的性质、折叠的性质、勾股定理等知识点.有一定的综合性.6(2023春·全国·七年级专题练习)如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)折叠后,DC的对应线段是,CF的对应线段是;(2)若∠1=50°,求∠2、∠3的度数;(3)若AB=8,DE=10,求CF的长度.【答案】(1)BC′,C′F;(2)50°,80°;(3)6【分析】(1)根据折叠的性质即可得出;(2)由折叠的性质可得,∠2=∠BEF,由AD∥BC得∠1=∠2,所以∠2=∠BEF=50°,从而得∠3=80°;(3)根据勾股定理先求得AE的长度,也可求出AD,BC的长度,然后根据∠1=∠BEF=50°,可得BF= BE=10,继而可求得CF=BC-BF.【详解】(1)由折叠的性质可得:折叠后,DC的对应线段是BC′,CF的对应线段是C′F;故答案为:BC′,C′F.(2)由折叠的性质可得:∠2=∠BEF,∵AD∥BC,∴∠1=∠2=50°.∴∠2=∠BEF=50°,∴∠3=180°-50°-50°=80°;(3)∵AB=8,DE=10,∴AE=BE2-AB2=6,∴AD=BC=6+10=16,∵∠1=∠BEF=50°,∴BF=BE=10,∴CF=BC-BF=16-10=6.【点睛】本题考查了矩形折叠的性质,平行线的性质定理,勾股定理解直角三角形,等腰三角形判定相关知识.7(2023春·广东河源·八年级统考开学考试)如图,将一张长方形纸片OABC放在直角坐标系中,使得OA与x轴重合,OC与y轴重合,点D为AB边上的一点(不与点A、点B重合),且点A(6,0),点C (0,8).(1)如图1,折叠△ABC,使得点B的对应点B1落在对角线AC上,折痕为CD,求此刻点D的坐标.(2)如图2,折叠△ABC,使得点A与点C重合,折痕交AB与点D,交AC于点E,求直线CD的解析式.【答案】(1)D(6,5);x+8.(2)直线CD的解析式为y=-724【分析】(1)根据勾股定理求得AC=10,设AD=n,则BD=8-n,根据折叠的性质得出B1D=BD=8-n,CE=CB=6,AB1=10-6=4,在Rt△AB1D中,利用勾股定理得出关于n的方程,解方程求得n的值,即可求得D的坐标;(2)设AD=m,则BD=8-m,根据折叠的性质CD=AD=m,在Rt△CBD中,利用勾股定理得出关于m的方程,解方程求得m的值,即可求得D的坐标,然后根据待定系数法即可求得作出直线CD的解析式.【详解】(1)解:∵点A(6,0),点C(0,8),∴OA=BC=6,OC=AB=8,∴AC=OA2+OC2=10,设AD=n,则BD=8-n,由折叠的性质可知B1D=BD=8-n,CE=CB=6,∴AB1=10-6=4,由折叠的性质可知CD=AD=n,在Rt△AB1D中,AB21+B1D2=AD2,∴42+(8-n)2=n2,解得n=5,∴AD=5,(2)解:设AD =m ,则BD =8-m ,根据折叠的性质可知CD =AD =m ,在Rt △CBD 中,CB 2+BD 2=CD 2,∴62+(8-m )2=m 2,解得m =254,∴AD =254,∴D 6,254,设直线CD 的解析式为y =kx +8,代入D 6,254 得,254=6k +8,解得k =-724,∴直线CD 的解析式为y =-724x +8.【点睛】本题考查了待定系数法求一次函数的解析式,矩形的性质,折叠的性质,勾股定理的应用等,求得D 的坐标是解题的关键.【考点三正方形中的折叠求角度、线段长等问题】1(2022秋·广东梅州·九年级校考阶段练习)如图,将正方形纸片按如图折叠,AM 为折痕,点B 落在对角线AC 上的点E 处,则∠EMC 的度数为()A.22.5°B.30°C.45°D.67.5°【答案】C【分析】根据正方形的性质可得∠B =90°,∠ACB =12∠BCD =45°,再由折叠可得∠AEM =∠B =90°,然后利用三角形的外角进行计算即可解答.【详解】解:∵四边形ABCD 是正方形,∴∠B =90°,∠ACB =12∠BCD =45°,由折叠得:∠AEM =∠B =90°,∴∠EMC =∠AEM -∠ACB =90°-45°=45°,故选:C .【点睛】本题考查了正方形的性质,折叠的性质,三角形外角的性质,熟练掌握正方形的性质是解题的关键.【变式训练】1(2023·全国·八年级专题练习)如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A 处,连接A C,则∠BA C=°.【答案】67.5【分析】根据正方形的性质求出∠CBD,再根据折叠的性质得A B=BC,进而根据等腰三角形的性质得出答案.【详解】∵四边形ABCD为正方形,∴AB=BC,∠ABC=90°,BD平分∠ABC,∠ABC=45°,∴∠CBD=12根据折叠可知,AB=A B,∴A B=BC,=67.5°.∴∠BA C=∠BCA =180°-45°2故答案为:67.5.【点睛】本题主要考查了正方形的性质,折叠的性质,等腰三角形的性质等,判定等腰三角形是解题的关键.2(2022秋·四川成都·八年级成都七中校考期中)已知:如图,在边长为12的正方形ABCD中,点E在边BC上,BE=2CE,将△DCE沿DE折叠至△DFE,延长EF交AB于点G,连接DG(1)求∠GDE的度数:(2)求AG的长度【答案】(1)∠EDG=45°(2)6【分析】(1)根据△DCE沿DE折叠至△DFE,可得∠DFE=∠DFG=90°,DC=DF,证明Rt△DAG≌Rt△DFG HL可得∠ADG=∠FDG,根据对折可得∠CDE=∠FDE,即可得出∠GDE的度数;(2)令AG=x,则BG=12-x,GF=x,在Rt△BEG中,勾股定理即可求解.【详解】(1)∵将△DCE沿DE折叠至△DFE,∵四边形ABCD是正方形,∴∠DAG=∠DFG=90°,在Rt△DAG与Rt△DFG中,DF=DA DG=DG,∴Rt△DAG≌Rt△DFG HL,∴∠ADG=∠FDG,由对折得∠CDE=∠FDE,∴∠EDG=∠EDF+∠GDF=12∠ADC=45°;(2)令AG=x,则BG=12-x,GF=x,∵BE=2CE,∴BE=8,EF=CE=4,在Rt△BEG中,82+12-x2=4+x2,解得:x=6.∴AG=6.【点睛】本题考查了正方形的性质,全等三角形的性质与判定,勾股定理,折叠的性质,掌握以上知识是解题的关键.3(2023春·江苏·八年级专题练习)如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求证:∠EDG=45°.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.【答案】(1)证明见解析;(2)①证明见解析,②线段AG的长为2【分析】(1)由正方形的性质可得DC=DA.∠A=∠B=∠C=∠ADC=90°,由折叠的性质得出∠DFE =∠C,DC=DF,∠1=∠2,再求出∠DFG=∠A,DA=DF,然后由“HL”证明RtΔDGA≅RtΔDGF,由全等三角形对应角相等得出∠3=∠4,得出∠2+∠3=45°即可;(2)①由折叠的性质和线段中点的定义可得CE=EF=BE,∠DEF=∠DEC,再由三角形的外角性质得出∠5=∠DEC,然后利用同位角相等,两直线平行证明即可;②设AG=x,表示出GF、BG,根据点E是BC的中点求出BE、EF,从而得到GE的长度,再利用勾股定理列出方程求解即可;【详解】(1)证明:如图1:∵四边形ABCD是正方形,∴DC=DA.∠A=∠B=∠C=∠ADC=90°,∵ΔDEC沿DE折叠得到ΔDEF,∴∠DFG =∠A =90°,DA =DF ,在Rt △DGA 和Rt △DGF 中,DG =DG DA =DF ,∴Rt △DGA ≌Rt △DGF (HL ),∴∠3=∠4,∴∠EDG =∠3+∠2=12∠ADF +12∠FDC ,=12(∠ADF +∠FDC ),=12×90°,=45°;(2)证明:如图2所示:∵ΔDEC 沿DE 折叠得到ΔDEF ,E 为BC 的中点,∴CE =EF =BE ,∠DEF =∠DEC ,∴∠5=∠6,∵∠FEC =∠5+∠6,∴∠DEF +∠DEC =∠5+∠6,∴2∠5=2∠DEC ,即∠5=∠DEC ,∴BF ∥DE ;②解:设AG =x ,则GF =x ,BG =6-x ,∵正方形边长为6,E 为BC 的中点,∴CE =EF =BE =12×6=3,∴GE =EF +GF =3+x ,在Rt △GBE 中,根据勾股定理得:(6-x )2+32=(3+x )2,解得:x =2,即线段AG 的长为2.【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、翻折变换的性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.【考点四特殊平行四边形折叠后求周长、面积问题】1(2023·全国·九年级假期作业)如图1,菱形纸片ABCD 的边长为6cm ,∠ABC =60°,将菱形ABCD 沿EF ,GH 折叠,使得点B ,D 两点重合于对角线BD 上的点P (如图2).若AE =2BE ,则六边形AEFCHG 的面积为cm 2.【答案】133【分析】由菱形的性质可得AC⊥BD,∠BAD=120°,AB=BC=6cm,∠ABD=30°,,由折叠的性质可得EF⊥BP,∠BEF=∠PEF,BE=EP=2,可证四边形AEPG是平行四边形,可得AG= EP=2cm,DG=4cm,由面积和差关系可求解.【详解】解:如图,∵四边形ABCD是菱形,∠ABC=60°,∴AC⊥BD,∠BAD=∠BCD=120°,AB=BC=6cm,∠ABD=30°,∴OA=12AB=3cm,∠BAC=∠BCA=∠DAC=∠DCA=60°,∴OB=62-32=33cm∴BD=63cm.∵AE=2BE,∴AE=23×6=4cm,BE=13×6=2cm,∵将菱形ABCD沿EF,GH折叠,∴EF⊥BP,∠BEF=∠PEF,BE=EP=2cm,∴EF∥AC,∴∠BEF=∠BAC=60°,∴∠BEF=∠60°=∠PEF,∴∠BEP=∠BAD=120°,∴EP∥AD,同理可得:GP∥AB,∴四边形AEPG是平行四边形,∴AG=EP=2cm,∴DG=4cm,∴六边形AEFCHG面积=S菱形ABCD-S△BEF-S△GDH=12×6×63-34×22-34×42=133cm2,故答案为:133.【点睛】本题考查了折叠的性质,菱形的性质,含30°角的直角三角形的性质,勾股定理,平行四边形的判定和性质等知识,求出DG的长是本题的关键.【变式训练】1(2022秋·辽宁沈阳·九年级统考期末)如图,已知正方形ABCD面积为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为()A.2B.2C.4D.42【答案】D【分析】首先由正方形ABCD 面积为2,即可求得其边长为2,然后由折叠的性质,可得A M =AM ,D N =DN ,A D =AD ,则可得图中阴影部分的周长为:A M +BM +BC +CN +D N +A D =AB +BC +CD +AD ,继而求得答案.【详解】解:设折叠后A ,D 的点分别为A ,D ,EF 与AB ,CD 分别交于点M ,N ,如图所示,∵正方形ABCD 面积为2,∴AB =BC =CD =AD =2,由折叠的性质:A M =AM ,D N =DN ,A D =AD ,∴图中阴影部分的周长为:A M +BM +BC +CN +D N +A D=AM +BM +BC +CN +DN +AD=AB +BC +CD +AD=42.故选:D .【点睛】此题考查了折叠的性质与正方形的性质,掌握折叠的性质与正方形的性质是解题的关键.2(2022春·广东汕头·八年级校考阶段练习)如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上点F 处,已知CE =3,AB =8,则阴影部分的面积为.【答案】30【分析】根据折叠的性质求出EF =DE =CD -CE =5,AD =AF =BC ,再根据勾股定理列出方程求解即可.【详解】解:由折叠的性质知,EF =DE =CD -CE =5,AD =AF =BC ,由勾股定理得,CF =4,AF 2=AB 2+BF 2,即AD 2=82+(AD -4)2,解得,AD =10,∴BF =6,CF =4,图中阴影部分面积=S △ABF +S △CEF =12×6×8+12×3×4=30cm 2.故答案为:30【点睛】本题考查了折叠的性质,解决本题的关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②勾股定理,三角形的面积公式求解.【考点五菱形中旋转求角度、线段长等问题】1(2023春·天津西青·九年级校考阶段练习)如图,将菱形ABCD 绕点A 顺时针旋转得到菱形AB C D ,使点D 落在对角线AC 上,连接DD ,B D ,则下列结论一定正确的是()A.DD =1B D B.∠DAB =90°2C.△AB D 是等边三角形D.△ABC≌△AD C【答案】D【分析】由菱形的性质可得AD=AB=BC=CD,∠ABC=∠ADC,由旋转的性质可得AD= AD ,CD=C D ,∠AD C =∠ADC,由“SAS”可证△ABC≌△AD C ,即可求解.【详解】解:∵四边形ABCD是菱形,∴AD=AB=BC=CD,∠ABC=∠ADC,∵将菱形ABCD绕点A顺时针旋转得到菱形AB C D ,∴AD=AD ,CD=C D ,∠AD C =∠ADC,∴AB=AD ,BC=C D ,∠ABC=∠AD C ,∴△ABC≌△AD C SAS,故选:D.【点睛】本题考查了旋转的性质,菱形的性质,全等三角形的判定和性质,灵活运用这些性质进行推理是本题的关键.【变式训练】1(2023·山东东营·统考中考真题)如图,在平面直角坐标系中,菱形OABC的边长为26,点B在x 轴的正半轴上,且∠AOC=60°,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA B C (点A 与点C重合),则点B 的坐标是()A.36,32D.62,36C.32,62B.32,36【答案】B【分析】延长B C 交x轴于点D,根据旋转的性质以及已知条件得出∠B DO=90°,进而求得OD,DB 的长,即可求解.【详解】解:如图所示,延长B C 交x轴于点D,∵四边形ABCD是菱形,点B在x轴的正半轴上,OB平分∠AOC,∠AOC=60°,∴∠COB=∠AOB=30°,∠CBA=60°∵将菱形OABC绕原点O逆时针方向旋转60°,∴∠C OC=60°,则∠OB C=12∠C B C=30°,AB=CB∴∠B OD=60°∴∠B DO=90°,在Rt△CDO中,OC=B C=26∴CD=12OC=6,OD=3CD=3×6=32∴DB =36,∴B 32,36,故选:B.【点睛】本题考查了旋转的性质,菱形的性质,勾股定理,含30度角的直角三角形的性质,坐标与图形,熟练掌握菱形的性质是解题的关键.2(2023春·八年级单元测试)如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上.EF与CD交于点P,则PE的长是.【答案】3-1【分析】连接BD交AC于O,由菱形的性质得出CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=12∠BAD=30°,由直角三角形的性质求出OB=12AB=1,由直角三角形的性质得出AC=23,由旋转的性质得出AE=AB=2,∠EAG=∠BAD=60°,求出CE=AC-AE=23-2,证出∠CPE=90°,由直角三角形的性质得出PE的长【详解】解:连接BD交AC于O,如图所示:∵四边形ABCD是菱形,∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=12∠BAD=30°,OA=OC,AC⊥BD,∴OB=12AB=1∴OA=3OB=3,∴AC=23由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,∴CE=AC-AE=23-2,∵四边形AEFG是菱形,∴EF∥AG,∴∠CEP=∠EAG=60°,∴∠CEP+∠ACD=90°,∴∠CPE=90°,∴PE=12CE=3-1故答案为:3-1【点睛】本题考查了菱形的性质、旋转的性质、含30°角的直角三角形的性质、平行线的性质等知识;熟练掌握旋转的性质和菱形的性质是解题的关键.3(2023·江苏·八年级假期作业)如图1,菱形AEFG的两边AE、AG分别在菱形ABCD的边AB和AD上,且∠BAD=60°,连接CF;(1)求证:3DG=CF;(2)如图2,将菱形AEFG绕点A进行顺时针旋转,在旋转过程中(1)中的结论是否发生变化?请说明理由.【答案】(1)见解析;(2)CF=3DG,(1)中的结论不变.理由见解析.【分析】(1)延长EF交CD于M点,证明三角形CMF是等腰三角形,且∠EMC=120°,过点M作MN⊥CF,垂足为N,根据30°角所对直角边等于斜边的一半,和勾股定理,得FN=NC=32DG即CF=2FN=3DG;(2)过D做∠NDC=∠ADG,使DN=DG,连接NC,证明△DGN为等腰三角形,四边形GFNC为平行四边形即可.【详解】(1)如图1,延长EF交CD于M点,∵四边形AEFG和四边形ABCD是菱形∴DC⎳GF⎳AB,DM⎳GF∴四边形GFMD是平行四边形则∠D=∠EMC=120°,∴∠MFC=∠MCF=30°,过点M作MN⊥CF,垂足为N,∴MN=12MF,根据勾股定理,得FN=32 DG,∵MC=MF,∴FN=NC,∴CF=2FN=3DG;(2)如图2,过D做∠NDC=∠ADG,使DN=DG,连接NC,∴△AGD≌△DNC(SAS)∴AG=NC∠DNC=∠AGD∴△DGN为等腰三角形,则∠DGN=∠DNG,∵∠NGF=360°-∠AGD-∠AGF-∠DGN=240°-∠DGA-∠DGN ∠GNC=∠DNC-∠DNG=∠DNC-∠DNG∴∠NGF +∠GNC =240°-∠DGN -∠DNG ,∵∠DGN +∠DNG =180°-∠GDN =60°∴∠NGF +∠GNC =180°∴NC ⎳GF ,∴四边形GFNC 为平行四边形∴CF =GN ,则GN =3DG ,∴CF =3DG ,结论(1)不变.【点睛】本题考查了菱形的性质,平行四边形的判定,三角形的全等,等腰三角形的性质,灵活构造辅助线是解题的关键.【考点六矩形中旋转求角度、线段长等问题】1(2023·江苏无锡·校考一模)如图,在矩形ABCD 中,AB =5,AD =4,将矩形ABCD 绕点A 逆时针旋转得到矩形AB ′C ′D ′,AB ′交CD 于点E ,且DE =B ′E ,则AE 的长为.【答案】4110【分析】根据旋转不变性得到AB ′=AB =5,设AE =CE =x ,在Rt ΔADE 中结合勾股定理即可得出结论.【详解】解:∵将矩形ABCD 绕点A 逆时针旋转得到矩形AB ′C ′D ′,∴AB ′=AB =5,∵DE =B ′E ,∴AE =CE ,设AE =CE =x ,∴DE =5-x ,∵∠D =90°,∴AD 2+DE 2=AE 2,即42+5-x 2=x 2,解得:x =4110,即AE 的长为4110(也可以写作4.1),故答案为:4110.【点睛】本题考查了利用旋转的性质结合勾股定理求线段长.解题过程中涉及到矩形的性质、勾股定理等知识,熟练掌握几何图形旋转不变性及勾股定理求线段长是解决问题的关键.【变式训练】1(2023·江苏南京·校联考三模)如图,将矩形ABCD 绕点C 旋转,使点B 落在对角线AC 上的B 处,延长AD 交A D 于点E .若AB =3,BC =4,则DE 的长为.【答案】1【分析】如图所示,连接A A ,A C ,CE ,由矩形的性质和勾股定理得到AC =5,CD =AB =3,AD =BC =4,由旋转的性质得到A B =AB =3,四边形A B C D 是矩形,证明S △AAC =S △ACE ,则可得AE =AC ⋅A B CD=5,则DE =AE -AD =1.【详解】解:如图所示,连接A A ,A C ,CE ,∵在矩形ABCD 中,AB =3,BC =4,∴AC =AB 2+BC 2=5,CD =AB =3,AD =BC =4,由旋转的性质可得A B =AB =3,四边形A B C D 是矩形,∴A D ∥B C ,A B ⊥AC ,∴S △AAC =S △ACE ,∴12AC ⋅A B =12AE ⋅CD ,∴AE =AC ⋅A B CD=3×53=5,∴DE =AE -AD =1,故答案为:1.【点睛】本题主要考查了矩形的性质,勾股定理,旋转的性质,证明S △AAC =S △ACE ,利用等面积法求出AE 的长是解题的关键.2(2023春·江苏淮安·八年级统考期中)如图,将矩形ABCD 绕点B 旋转得到矩形BEFG ,点E 在AD 上,延长DA 交GF 于点H .(1)求证:△ABE ≅△FEH ;(2)连接BH ,若∠EBC =30°,求∠ABH 的度数.【答案】(1)见解析;(2)15°.【分析】(1)根据矩形的性质得出AB =DC ,∠BAE =∠D =90°,根据旋转的性质得出FE =DC ,∠EFH =∠D =90°,再证明△ABE ≅△FEH AAS 即可;(2)根据矩形的性质得出∠HEB =∠EBC =30°,由全等三角形的性质得出∠EHB =∠EBH =12180°-30° =75°,再计算即可得出答案.【详解】(1)解:∵四边形ABCD 是矩形,∴AB =DC ,∠BAE =∠D =90°,由旋转性质,得:FE =DC ,∠EFH =∠D =90°,∴AB =FE ,∠BAE =∠EFH ,∵在矩形BEFG 中,GF ∥BE ,∴∠AEB =∠FHE ,在△ABE 和△FEH 中,∠AEB =∠FHE∠BAE =∠EFH AB =FE,∴△ABE ≅△FEH AAS ,(2)解:∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠HEB =∠EBC =30°,∵△ABE ≅△FEH ,∴BE =EH ,∴∠EHB =∠EBH =12180°-30° =75°,∵∠BAH =90°,∴∠ABH =90°-∠EHB =15°,即∠ABH 的度数为15°.【点睛】本题考查矩形的性质,平行线的性质,全等三角形的判定与性质,正确得出全等是解题的关键.3(2023春·福建三明·八年级统考期中)在长方形ABCD 中,AB =5,BC =3,将长方形ABCD 绕点A 顺时针旋转α0°<α<90° ,得到长方形AEFG .(1)如图1,当点E 落在CD 边上时,延长ED 交FG 于点M ,求证:EM=AE ;(2)如图2,当GC =GB 时,求α的值;(3)如图3,当点E 落在线段CF 上时,AE 与CD 交于点N ,求△ADN 的面积.【答案】(1)证明见解析;(2)60°:(3)125.【分析】(1)只需要证明△EFM ≌△ADE 即可得到答案;(2)连接DG ,证明△CDG ≌△BAG ,得到△ADG 为等边三角形,从而可以得到答案;(3)连接AC ,证明△ABC ≌△AEC ,得到∠EAC =∠BAC =∠ACD ,从而得到CN =AN ,再根据勾股定理计算即可得到答案.【详解】解:(1)由旋转的性质得:BC =EF ,∠B =∠FEA∵四边形ABCD 是矩形∴∠B =∠D =∠FEA =90°,BC =AD =EF∵∠FEM +∠AED =90°,∠DAE +∠AED =90°∴∠FEM =∠DAE∴△EFM ≌△ADE (HL )∴EM =AE(2)如图所示,连接DG∵四边形ABCD 是矩形∴∠ABC =∠BCD =90°,AB =CD∵GC =GB∴∠GCB =∠GBC∴∠DCG =∠ABG∴△CDG ≌△BAG∴DG =AG由翻折的性质可得:AD =AG∴AD =AG =DG∴△ADG 为等边三角形∴∠DAG =60°∴∠DAE =30°∴∠BAE =60°∴α=60°(3)如图所示,连接AC由矩形的性质和翻折的性质可得:AB =AE ,∠AEF =∠B =90°∵∠AEF =∠B =90°∴∠AEC =∠B =90°又∵AB =AE∴△ABC ≌△AEC (HL )∴∠EAC =∠BAC∵AB ∥CD∴∠BAC =∠ACD∴∠EAC =∠ACD∴NC =AN设DN =x ,则NC =AN =CD -DN =5-x 在直角三角形AND 中,AN 2=DN 2+AD 2∴x 2+32=5-x 2解得x =85∴S △ADN =12AD ∙DN =125【点睛】本题主要考查了矩形的性质,折叠的性质,全等三角形的性质与判定,勾股定理,等边三角形的性质与判定,等腰三角形的判定,解题的关键在于能够熟练掌握相关知识进行求解.【考点七正方形中旋转求角度、线段长等问题】1(2022秋·广东珠海·九年级统考期末)如图,将正方形ABCD绕顶点A顺时针旋转45°得到正方形A BC D ,BC与C D 相交于点E,连接BD,B D 相交于点F.(1)填空:∠D EC=度;(2)求证:四边形BED F是菱形.【答案】(1)45(2)见解析【分析】(1)根据正方形的性质求出相关角度,再根据角度之间的关系求出∠D EC即可.(2)先证出四边形BED F是平行四边形,再连接AE,构造全等三角形证邻边相等即可.【详解】(1)解:∵四边形ABCD和四边形A B C D 是正方形∴∠AD C =∠ABC=90°∵∠D AB=45°∴∠BED =180°-45°=135°∴∠D EC=45°(2)解:连接AE.∵四边形ABCD和四边形A B C D 是正方形∴∠AD C =∠ABC=90°∵∠D AB=45°∴∠BED =180°-45°=135°∴∠D EC=45°(方法不唯一,直接写由(1)得也可以)在正方形A B C D 中,∠B D C =45°∴∠D EC=∠B D C∴D F∥BC,即D F∥BE.同理∠DBC=∠D EC=45°,∴D E∥BF.∴四边形BED F是平行四边形在Rt△AD E和Rt△ABE中AD =AB AE=AE。
苏科版数学八年级下册第九章 9.4 矩形、菱形、正方形(选择、填空题)专练(详细答案)

9.4 矩形、菱形、正方形(选择、填空题)一.选择题1.菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直2.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.43.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D 是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为()A.(3,1)B.(3,)C.(3,)D.(3,2)4.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为()A.B.C.D.5.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为()A.30°B.45°C.60°D.75°6.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是()A .4.8B .5C .6D .7.27.如图,矩形ABCD 与菱形EFGH 的对角线均交于点O ,且EG ∥BC ,将矩形折叠,使点C 与点O 重合,折痕MN 恰好过点G 若AB=,EF=2,∠H=120°,则DN 的长为( ) A .B .C .﹣D .2﹣8.如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB 、CD 交于点E 、F ,连结BF 交AC 于点M ,连结DE 、BO .若∠COB=60°,FO=FC ,则下列结论:①FB 垂直平分OC ;②△EOB ≌△CMB ;③DE=EF ;④S △AOE :S △BCM =2:3.其中正确结论的个数是( )A .4个B .3个C .2个D .1个9.如图,在矩形ABCD 中,AD=6,AE ⊥BD ,垂足为E ,ED=3BE ,点P 、Q 分别在BD ,AD 上,则AP +PQ 的最小值为( ) A .2B .C .2D .310.有3个正方形如图所示放置,阴影部分的面积依次记为S 1,S 2,则S 1:S 2等于( )A .1:B .1:2C .2:3D .4:911.如图,正方形ABCD 的边长为9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH .若BE :EC=2:1,则线段CH 的长是( ) A .3B .4C .5D .612.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或9 B.3或5 C.4或6 D.3或613.如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD 上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有()A.2对B.3对C.4对D.5对14.如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?()A.50 B.55 C.70 D.7515.如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G 分别在AB、BC、FD上.若BF=,则小正方形的周长为()A.B.C.D.16.如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:=13S ①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH,其中结论正确的有()△DHCA.1个 B.2个 C.3个 D.4个二.填空题17.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=.18.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为.19.如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=.20.如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF 与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为.21.如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=度.22.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.23.如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=.24.如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为.25.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为cm.26.如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2021B2021C2021的顶点B2021的坐标是.27.如图,在平面内,四边形ABCD和BEFG均为正方形,则AG:DF:CE=.28.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为.29.如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为.30.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于.答案与解析一.选择题1.(2021•莆田)菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分 D.对角线互相垂直【分析】由菱形的性质可得:菱形的对角线互相平分且垂直;而平行四边形的对角线互相平分;则可求得答案.【解答】解:∵菱形具有的性质:对边相等,对角相等,对角线互相平分,对角线互相垂直;平行四边形具有的性质:对边相等,对角相等,对角线互相平分;∴菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.故选D.【点评】此题考查了菱形的性质以及平行四边形的性质.注意菱形的对角线互相平分且垂直.2.(2021•枣庄)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.4【分析】根据菱形性质求出AO=4,OB=3,∠AOB=90°,根据勾股定理求出AB,再根据菱形的面积公式求出即可.【解答】解:∵四边形ABCD是菱形,∴AO=OC,BO=OD,AC⊥BD,∵AC=8,DB=6,∴AO=4,OB=3,∠AOB=90°,由勾股定理得:AB==5,=,∵S菱形ABCD∴,∴DH=,故选A.【点评】本题考查了勾股定理和菱形的性质的应用,能根据菱形的性质得出S菱=是解此题的关键.形ABCD3.(2021•苏州)矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为()A.(3,1)B.(3,)C.(3,)D.(3,2)【分析】如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.【解答】解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.∵D(,0),A(3,0),∴H(,0),∴直线CH解析式为y=﹣x+4,∴x=3时,y=,∴点E坐标(3,)故选:B.【点评】本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.4.(2021•威海)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为()A.B.C.D.【分析】连接BF,根据三角形的面积公式求出BH,得到BF,根据直角三角形的判定得到∠BFC=90°,根据勾股定理求出答案.【解答】解:连接BF,∵BC=6,点E为BC的中点,∴BE=3,又∵AB=4,∴AE==5,∴BH=,则BF=,∵FE=BE=EC,∴∠BFC=90°,∴CF==.故选:D.【点评】本题考查的是翻折变换的性质和矩形的性质,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.5.(2021•海南)如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为()A.30°B.45°C.60°D.75°【分析】首先过点D作DE∥a,由∠1=60°,可求得∠3的度数,易得∠ADC=∠2+∠3,继而求得答案.【解答】解:过点D作DE∥a,∵四边形ABCD是矩形,∴∠BAD=∠ADC=90°,∴∠3=90°﹣∠1=90°﹣60°=30°,∵a∥b,∴DE∥a∥b,∴∠4=∠3=30°,∠2=∠5,∴∠2=90°﹣30°=60°.故选C.【点评】此题考查了矩形的性质以及平行线的性质.注意准确作出辅助线是解此题的关键.6.(2021•宜宾)如图,点P 是矩形ABCD 的边AD 上的一动点,矩形的两条边AB 、BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )A .4.8B .5C .6D .7.2【分析】首先连接OP ,由矩形的两条边AB 、BC 的长分别为6和8,可求得OA=OD=5,△AOD 的面积,然后由S △AOD =S △AOP +S △DOP =OA•PE +OD•PF 求得答案.【解答】解:连接OP ,∵矩形的两条边AB 、BC 的长分别为6和8,∴S 矩形ABCD =AB•BC=48,OA=OC ,OB=OD ,AC=BD=10, ∴OA=OD=5,∴S △ACD =S 矩形ABCD =24, ∴S △AOD =S △ACD =12,∵S △AOD =S △AOP +S △DOP =OA•PE +OD•PF=×5×PE +×5×PF=(PE +PF )=12, 解得:PE +PF=4.8. 故选:A .【点评】此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法以及掌握整体数学思想的运用是解题的关键.7.(2021•资阳)如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=,EF=2,∠H=120°,则DN的长为()A.B.C.﹣ D.2﹣【分析】延长EG交DC于P点,连接GC、FH,则△GCP为直角三角形,证明四边形OGCM为菱形,则可证CG=OM=CM=OG=,由勾股定理求得GP的值,再由梯形的中位线定理CM+DN=2GP,即可得出答案.【解答】解:延长EG交DC于P点,连接GC、FH;如图所示:则CP=DP=CD=,△GCP为直角三角形,∵四边形EFGH是菱形,∠EHG=120°,∴GH=EF=2,∠OHG=60°,EG⊥FH,∴OG=GH•sin60°=2×=,由折叠的性质得:CG=OG=,OM=CM,∠MOG=∠MCG,∴PG==,∵OG∥CM,∴∠MOG+∠OMC=180°,∴∠MCG+∠OMC=180°,∴OM∥CG,∴四边形OGCM为平行四边形,∵OM=CM,∴四边形OGCM为菱形,∴CM=OG=,根据题意得:PG 是梯形MCDN 的中位线,∴DN +CM=2PG=,∴DN=﹣; 故选:C .【点评】本题考查了矩形的性质、菱形的性质、翻折变换的性质、勾股定理、梯形中位线定理、三角函数等知识;熟练掌握菱形和矩形的性质,由梯形中位线定理得出结果是解决问题的关键.8.(2021•眉山)如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB 、CD 交于点E 、F ,连结BF 交AC 于点M ,连结DE 、BO .若∠COB=60°,FO=FC ,则下列结论:①FB 垂直平分OC ;②△EOB ≌△CMB ;③DE=EF ;④S △AOE :S △BCM =2:3.其中正确结论的个数是( )A .4个B .3个C .2个D .1个【分析】①利用线段垂直平分线的性质的逆定理可得结论;②在△EOB 和△CMB 中,对应直角边不相等;③可证明∠CDE=∠DFE ;④可通过面积转化进行解答.【解答】解:①∵矩形ABCD 中,O 为AC 中点,∴OB=OC ,∵∠COB=60°,∴△OBC 是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故①正确;②∵△BOC为等边三角形,FO=FC,∴BO⊥EF,BF⊥OC,∴∠CMB=∠EOB=90°,但BO≠BM,故②错误;③易知△ADE≌△CBF,∠1=∠2=∠3=30°,∴∠ADE=∠CBF=30°,∠BEO=60°,∴∠CDE=60°,∠DFE=∠BEO=60°,∴∠CDE=∠DFE,∴DE=EF,故③正确;④易知△AOE≌△COF,∴S△AOE =S△COF,∵S△COF =2S△CMF,∴S△AOE :S△BCM=2S△CMF:S△BCM=,∵∠FCO=30°,∴FM=,BM=CM,∴=,∴S△AOE :S△BCM=2:3,故④正确;所以其中正确结论的个数为3个;故选B【点评】本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.9.(2021•雅安)如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为()A.2 B.C.2 D.3【分析】在Rt△ABE中,利用三角形相似可求得AE、DE的长,设A点关于BD 的对称点A′,连接A′D,可证明△ADA′为等边三角形,当PQ⊥AD时,则PQ最小,所以当A′Q⊥AD时AP+PQ最小,从而可求得AP+PQ的最小值等于DE的长,可得出答案..【解答】解:设BE=x,则DE=3x,∵四边形ABCD为矩形,且AE⊥BD,∴△ABE∽△DAE,∴AE2=BE•DE,即AE2=3x2,∴AE=x,在Rt△ADE中,由勾股定理可得AD2=AE2+DE2,即62=(x)2+(3x)2,解得x=,∴AE=3,DE=3,如图,设A点关于BD的对称点为A′,连接A′D,PA′,则A′A=2AE=6=AD,AD=A′D=6,∴△AA′D是等边三角形,∵PA=PA′,∴当A′、P、Q三点在一条线上时,A′P+PQ最小,又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,∴AP+PQ=A′P+PQ=A′Q=DE=3,故选D.【点评】本题主要考查轴对称的应用,利用最小值的常规解法确定出A的对称点,从而确定出AP+PQ的最小值的位置是解题的关键,利用条件证明△A′DA是等边三角形,借助几何图形的性质可以减少复杂的计算.10.(2021•南宁)有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于()A.1:B.1:2 C.2:3 D.4:9【分析】设小正方形的边长为x,再根据相似的性质求出S1、S2与正方形面积的关系,然后进行计算即可得出答案.【解答】解:设小正方形的边长为x,根据图形可得:∵=,∴=,∴=,∴S1=S正方形ABCD,∴S1=x2,∵=,∴=,∴S2=S正方形ABCD,∴S2=x2,∴S1:S2=x2:x2=4:9;故选D.【点评】此题考查了正方形的性质,用到的知识点是正方形的性质、相似三角形的性质、正方形的面积公式,关键是根据题意求出S1、S2与正方形面积的关系.11.(2021•毕节市)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D 落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是()A.3 B.4 C.5 D.6【分析】根据折叠可得DH=EH,在直角△CEH中,设CH=x,则DH=EH=9﹣x,根据BE:EC=2:1可得CE=3,可以根据勾股定理列出方程,从而解出CH的长.【解答】解:设CH=x,则DH=EH=9﹣x,∵BE:EC=2:1,BC=9,∴CE=BC=3,∴在Rt△ECH中,EH2=EC2+CH2,即(9﹣x)2=32+x2,解得:x=4,即CH=4.故选(B).【点评】本题主要考查正方形的性质以及翻折变换,折叠问题其实质是轴对称变换.在直角三角形中,利用勾股定理列出方程进行求解是解决本题的关键.12.(2021•徐州)如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或9 B.3或5 C.4或6 D.3或6【分析】根据题意列方程,即可得到结论.【解答】解:如图,∵若直线AB将它分成面积相等的两部分,∴(6+9+x)×9﹣x•(9﹣x)=×(62+92+x2)﹣6×3,解得x=3,或x=6,故选D.【点评】本题考查了正方形的性质,图形的面积的计算,准确分识别图形是解题的关键.13.(2021•陕西)如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有()A.2对 B.3对 C.4对 D.5对【分析】可以判断△ABD≌△BCD,△MDO≌△M′BO,△NOD≌△N′OB,△MON ≌△M′ON′.由此即可得出答案.【解答】解:∵四边形ABCD是正方形,∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,在△ABD和△BCD中,,∴△ABD≌△BCD,∵AD∥BC,∴∠MDO=∠M′BO,在△MOD和△M′OB中,,∴△MDO≌△M′BO,同理可证△NOD≌△N′OB,∴△MON≌△M′ON′,∴全等三角形一共有4对.故选C.【点评】本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定方法,属于基础题,中考常考题型.14.(2021•台湾)如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?()A.50 B.55 C.70 D.75【分析】由平角的定义求出∠CED的度数,由三角形内角和定理求出∠D的度数,再由平行四边形的对角相等即可得出结果.【解答】解:∵四边形CEFG是正方形,∴∠CEF=90°,∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣15°﹣90°=75°,∴∠D=180°﹣∠CED﹣∠ECD=180°﹣75°﹣35°=70°,∵四边形ABCD为平行四边形,∴∠B=∠D=70°(平行四边形对角相等).故选C.【点评】本题考查了正方形的性质、平行四边形的性质、三角形内角和定理等知识;熟练掌握平行四边形和正方形的性质,由三角形内角和定理求出∠D的度数是解决问题的关键.15.(2021•呼和浩特)如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=,则小正方形的周长为()A.B.C.D.【分析】先利用勾股定理求出DF,再根据△BEF∽△CFD,得=求出EF即可解决问题.【解答】解:∵四边形ABCD是正方形,面积为24,∴BC=CD=2,∠B=∠C=90°,∵四边形EFGH是正方形,∴∠EFG=90°,∵∠EFB+∠DFC=90°,∠BEF+∠EFB=90°,∴∠BEF=∠DFC,∵∠EBF=∠C=90°,∴△BEF∽△CFD,∴=,∵BF=,CF=,DF==,∴=,∴EF=,∴正方形EFGH的周长为.故选C.【点评】本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.16.(2021•昆明)如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:=13S ①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH,其中结论正确的有()△DHCA.1个 B.2个 C.3个 D.4个【分析】①根据题意可知∠ACD=45°,则GF=FC,则EG=EF﹣GF=CD﹣FC=DF;②由SAS证明△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=180°;③同②证明△EHF≌△DHC即可;④若=,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=x,CD=6x,则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2.【解答】解:①∵四边形ABCD为正方形,EF∥AD,∴EF=AD=CD,∠ACD=45°,∠GFC=90°,∴△CFG为等腰直角三角形,∴GF=FC,∵EG=EF﹣GF,DF=CD﹣FC,∴EG=DF,故①正确;②∵△CFG为等腰直角三角形,H为CG的中点,∴FH=CH,∠GFH=∠GFC=45°=∠HCD,在△EHF和△DHC中,,∴△EHF≌△DHC(SAS),∴∠HEF=∠HDC,∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°,故②正确;③∵△CFG为等腰直角三角形,H为CG的中点,∴FH=CH,∠GFH=∠GFC=45°=∠HCD,在△EHF和△DHC中,,∴△EHF≌△DHC(SAS),故③正确;④∵=,∴AE=2BE,∵△CFG为等腰直角三角形,H为CG的中点,∴FH=GH,∠FHG=90°,∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,在△EGH和△DFH中,,∴△EGH≌△DFH(SAS),∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,∴△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,如图所示:设HM=x,则DM=5x,DH=x,CD=6x,=×HM×CD=3x2,S△EDH=×DH2=13x2,则S△DHC=13S△DHC,故④正确;∴3S△EDH故选:D.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、三角形面积的计算等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.二.填空题(共14小题)17.(2021•内江)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=.【分析】先根据菱形的性质得AC⊥BD,OB=OD=BD=3,OA=OC=AC=4,再在Rt△OBC中利用勾股定理计算出BC=5,然后利用面积法计算OE的长.【解答】解:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=BD=3,OA=OC=AC=4,在Rt△OBC中,∵OB=3,OC=4,∴BC==5,∵OE⊥BC,∴OE•BC=OB•OC,∴OE==.故答案为.【点评】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了勾股定理和三角形面积公式.18.(2021•扬州)如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.【分析】由菱形的性质可得出AC⊥BD,AB=BC=CD=DA,再根据直角三角形斜边上的中线等于斜边的一半得出AD的长,结合菱形的周长公式即可得出结论.【解答】解:∵四边形ABCD为菱形,∴AC⊥BD,AB=BC=CD=DA,∴△AOD为直角三角形.∵OE=3,且点E为线段AD的中点,∴AD=2OE=6.C菱形ABCD=4AD=4×6=24.故答案为:24.【点评】本题考查了菱形的性质以及直角三角形的性质,解题的关键是求出AD=6.本题属于基础题,难度不大,解决该题型题目时,根据菱形的性质找出对角线互相垂直,再通过直角三角形的性质找出菱形的一条变成是关键.19.(2021•盐城)如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=.【分析】延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,由菱形的性质和已知条件得出∠MFD=30°,设MD=x,则DF=2x,FM=x,得出MG=x+1,由勾股定理得出(x+1)2+(x)2=(2﹣2x)2,解方程得出DF=0.6,AF=1.4,求出AH=AF=0.7,FH=,证明△DCB是等边三角形,得出BG⊥CD,由勾股定理求出BG=,设BE=y,则GE=2﹣y,由勾股定理得出()2+y2=(2﹣y)2,解方程求出y=0.25,得出AE、EH,再由勾股定理求出EF即可.【解答】解:延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,如图所示:∵∠A=60°,四边形ABCD是菱形,∴∠MDF=60°,∴∠MFD=30°,设MD=x,则DF=2x,FM=x,∵DG=1,∴MG=x+1,∴(x+1)2+(x)2=(2﹣2x)2,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=AF=0.7,FH=AF•sin∠A=1.4×=,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=,设BE=y,则GE=2﹣y,∴()2+y2=(2﹣y)2,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF===.故答案为:.【点评】本题考查了菱形的性质、翻折变换的性质、勾股定理、等边三角形的判定与性质等知识;本题综合性强,难度较大,运用勾股定理得出方程是解决问题的关键.20.(2021•哈尔滨)如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为3.【分析】首先证明△ABC,△ADC都是等边三角形,再证明FG是菱形的高,根=BC•FG即可解决问题.据2•S△ABC【解答】解:∵四边形ABCD是菱形,∠BAD=120°,∴AB=BC=CD=AD,∠CAB=∠CAD=60°,∴△ABC,△ACD是等边三角形,∵EG⊥AC,∴∠AEG=∠AGE=30°,∵∠B=∠EGF=60°,∴∠AGF=90°,∴FG⊥BC,=BC•FG,∴2•S△ABC∴2××(6)2=6•FG,∴FG=3.故答案为3.【点评】本题考查菱形的性质、等边三角形的判定和性质、翻折变换、菱形的面积等知识,记住菱形的面积=底×高=对角线乘积的一半,属于中考常考题型.21.(2021•巴中)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=15度.【分析】连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,而∠ADB=∠CAD=30°,可得∠E度数.【解答】解:连接AC,∵四边形ABCD是矩形,∴AD∥BE,AC=BD,且∠ADB=∠CAD=30°,∴∠E=∠DAE,又∵BD=CE,∴CE=CA,∴∠E=∠CAE,∵∠CAD=∠CAE+∠DAE,∴∠E+∠E=30°,即∠E=15°,故答案为:15.【点评】本题主要考查矩形性质,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.22.(2021•包头)如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=22.5度.【分析】首先证明△AEO是等腰直角三角形,求出∠OAB,∠OAE即可.【解答】解:∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB═OC,∴∠OAD=∠ODA,∠OAB=∠OBA,∴∠AOE=∠OAD+∠ODA=2∠OAD,∵∠EAC=2∠CAD,∴∠EAO=∠AOE,∵AE⊥BD,∴∠AEO=90°,∴∠AOE=45°,∴∠OAB=∠OBA==67.5°,∴∠BAE=∠OAB﹣∠OAE=22.5°.故答案为22.5°.【点评】本题考查矩形的性质、等腰直角三角形的性质等知识,解题的关键是发现△AEO是等腰直角三角形这个突破口,属于中考常考题型.23.(2021•黄冈)如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= 2a.【分析】作FM⊥AD于M,则MF=DC=3a,由矩形的性质得出∠C=∠D=90°.由折叠的性质得出PE=CE=2a=2DE,∠EPF=∠C=90°,求出∠DPE=30°,得出∠MPF=60°,在Rt△MPF中,由三角函数求出FP即可.【解答】解:作FM⊥AD于M,如图所示:则MF=DC=3a,∵四边形ABCD是矩形,∴∠C=∠D=90°.∵DC=3DE=3a,∴CE=2a,由折叠的性质得:PE=CE=2a=2DE,∠EPF=∠C=90°,∴∠DPE=30°,∴∠MPF=180°﹣90°﹣30°=60°,在Rt△MPF中,∵sin∠MPF=,∴FP===2a;故答案为:2a.【点评】本题考查了折叠的性质、矩形的性质、三角函数等知识;熟练掌握折叠和矩形的性质,求出∠DPE=30°是解决问题的关键.24.(2021•湖北襄阳)如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为.【分析】先根据ASA判定△AFO≌△BEO,并根据勾股定理求得BE的长,再判定△BFM∽△BEO,最后根据对应边成比例,列出比例式求解即可.【解答】解:∵正方形ABCD∴AO=BO,∠AOF=∠BOE=90°∵AM⊥BE,∠AFO=∠BFM∴∠FAO=∠EBO在△AFO和△BEO中∴△AFO≌△BEO(ASA)∴FO=EO∵正方形ABCD的边长为2,E是OC的中点∴FO=EO=1=BF,BO=2∴直角三角形BOE中,BE==由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO∴,即∴FM=故答案为:【点评】本题主要考查了正方形,解决问题的关键的掌握全等三角形和相似三角形的判定与性质.解题时注意:正方形的对角线将正方形分成四个全等的等腰直角三角形.25.(2021•南京)如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.【分析】根据正方形的面积可用对角线进行计算解答即可.【解答】解:因为正方形AECF的面积为50cm2,所以AC=cm,因为菱形ABCD的面积为120cm2,所以BD=cm,所以菱形的边长=cm.故答案为:13.【点评】此题考查正方形的性质,关键是根据正方形和菱形的面积进行解答.26.(2021•聊城)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2021B2021C2021的顶点B2021的坐标是(21008,0).【分析】首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2021的坐标.【解答】解:∵正方形OA1B1C1边长为1,∴OB1=,∵正方形OB1B2C2是正方形OA1B1C1的对角线OB1为边,∴OB2=2,∴B2点坐标为(0,2),同理可知OB3=2,∴B3点坐标为(﹣2,2),同理可知OB4=4,B4点坐标为(﹣4,0),B5点坐标为(﹣4,﹣4),B6点坐标为(0,﹣8),B7(8,﹣8),B8(16,0)B9(16,16),B10(0,32),由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,∵2021÷8=252∴B2021的纵横坐标符号与点B8的相同,横坐标为正值,纵坐标是0,∴B2021的坐标为(21008,0).故答案为:(21008,0).【点评】本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍.27.(2021•安徽自主招生)如图,在平面内,四边形ABCD和BEFG均为正方形,则AG:DF:CE=1::1.【分析】连接BD、BF,可证明△ABG∽△DBF,可求得AG:DF,连接CE,可证明△ABG≌△CBE,可求得AG=CE,可求得答案.【解答】解:连接BD、BF和CE,∵四边形ABCD和BEFG均为正方形,∴==,且∠ABD=∠GBF=45°,∴∠ABG+∠GBD=∠GBD+∠DBF,∴∠ABG=∠GBD,∴△ABG∽△DBF,∴,又∴AB=BC,BG=BE,∠ABC=∠GBE=90°,∴∠AGB+∠GBC=∠GBC+∠CBE,∴∠AGB=∠CBE,在△ABG和△CBE中∴△ABG≌△CBE(SAS),∴AG=CE,∴AG:CE=1:1,∴AG:DF:CE=1::1,故答案为:1::1.【点评】本题主要考查相似三角形和全等三角形的判定和性质,构造全等或相似三角形是解题的关键.28.(2021•湖北校级自主招生)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE 的最小值为.【分析】连接CM,先证明四边形CDME是矩形,得出DE=CM,再由三角形的面积关系求出CM的最小值,即可得出结果.【解答】解:连接CM,如图所示:∵MD⊥AC,ME⊥CB,∴∠MDC=∠MEC=90°,∵∠C=90°,∴四边形CDME是矩形,∴DE=CM,∵∠C=90°,BC=3,AC=4,∴AB===5,当CM⊥AB时,CM最短,此时△ABC的面积=AB•CM=BC•AC,∴CM的最小值==,∴线段DE的最小值为;故答案为:.【点评】本题考查了矩形的判定与性质、勾股定理、直角三角形面积的计算方法;熟练掌握矩形的判定与性质,并能进行推理论证与计算是解决问题的关键.29.(2021•丹东)如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6.【分析】利用正方形的性质和勾股定理可得AC的长,由角平分线的性质和平行线的性质可得∠CAE=∠E,易得CE=CA,由FA⊥AE,可得∠FAC=∠F,易得CF=AC,可得EF的长.【解答】解:∵四边形ABCD为正方形,且边长为3,∴AC=3,∵AE平分∠CAD,∴∠CAE=∠DAE,∵AD∥CE,∴∠DAE=∠E,∴∠CAE=∠E,∴CE=CA=3,∵FA⊥AE,∴∠FAC+∠CAE=90°,∠F+∠E=90°,∴∠FAC=∠F,∴CF=AC=3,∴EF=CF+CE=3=6,故答案为:6.【点评】本题主要考查了正方形的性质,角平分线的性质等,利用等角对等边是解答此题的关键.30.(2021•天津)如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于.【分析】根据辅助线的性质得到∠ABD=∠CBD=45°,四边形MNPQ和AEFG均为正方形,推出△BEF与△BMN是等腰直角三角形,于是得到FE=BE=AE=AB,BM=MN=QM,同理DQ=MQ,即可得到结论.【解答】解:在正方形ABCD中,∵∠ABD=∠CBD=45°,∵四边形MNPQ和AEFG均为正方形,∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,∴△BEF与△BMN是等腰直角三角形,∴FE=BE=AE=AB,BM=MN=QM。
2020-2021学年苏科版八年级下册数学9.4矩形、菱形、正方形 同步练习 (含解析)

9.4矩形、菱形、正方形同步练习一.选择题1.下列说法中不正确的是()A.对角线垂直的平行四边形是菱形B.对角线相等的平行四边形是矩形C.菱形的面积等于对角线乘积的一半D.对角线互相垂直平分的四边形是正方形2.下列说法正确的是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.对角线相等的平行四边形是菱形C.三个角都是直角的四边形是矩形D.一组邻边相等的平行四边形是正方形3.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长()A.B.2﹣2C.2﹣D.24.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为()A.B.C.D.5.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为()A.2B.C.3D.6.如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=()A.30°B.70°C.30°或60°D.40°或70°7.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD =100°时,则∠CDF=()A.15°B.30°C.40°D.50°8.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.4﹣2B.3﹣4C.1D.9.如图所示,在菱形ABCD中,AC、BD相交于O,∠ABC=70°,E是线段AO上一点,则∠BEC的度数可能是()A.100°B.70°C.50°D.20°10.如图,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E,O,F.下列结论正确的个数有()①四边形AFCE为菱形;②△ABF≌△CDE;③当F为BC中点时,∠ACD=90°.A.0个B.1个C.2个D.3个二.填空题11.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ACB=30°,BD=4,则矩形ABCD 的面积是.12.如图,正方形ABCD边长为2,点P在BC边上,DP交AC于点E,∠ADE=∠AED,则BP的长度是.13.如图,点E为正方形ABCD外一点,ED=CD,AE与BD相交于点F.若∠CDE=52°,则∠DCF=°.14.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE=.15.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2,则AB的长为.三.解答题16.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD =EF.17.如图,正方形ABCD中,点P是对角线AC上一点,连接PB,边作PE⊥PB交AD边于于点E,且点E不与点A,D重合,作PM⊥AD,PN⊥AB,垂足分别为点M和N.(1)求证:PM=PN;(2)求证:EM=BN.18.已知:在矩形ABCD中,点E在BC边上,连接DE,且DE=BC,过点A作AF⊥DE于点F.(1)如图1,求证:AB=AF;(2)如图2,连接AE,当BE=DF时,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于AB的线段.参考答案一.选择题1.解:A、对角线垂直的平行四边形是菱形,正确,故不符合题意;B、对角线相等的平行四边形是矩形,正确,故不符合题意;C、菱形的面积等于对角线乘积的一半,正确;故不符合题意;D、对角线互相垂直平分且相等的四边形是正方形,故选项错误,故符合题意.故选:D.2.解:A、一组对边平行,另一组对边也平行的四边形是平行四边形,所以A选项错误,不符合题意;B、对角线相等的平行四边形是矩形,所以B选项错误,不符合题意;C、三个角都是直角的四边形是矩形,所以C选正确;符合题意;D、一组邻边相等的平行四边形是正方形,所以D选项错误,不符合题意.故选:C.3.解:∵四边形ABCD是矩形,∴AB=CD=2,∠A=∠D=∠DCB=90°,∵∠DCE=45°,∴DE=DC=2,∴EC=2,∵∠DCE=45°,∴∠DEC=45°,∵EB平分∠AEC,∴∠BEC=∠AEB=∠AEC=,∴∠EBC=180°﹣67.5°﹣45°=67.5°,∴∠BEC=∠EBC,∴BC=CE=2,∴AD=BC=2,∴AE=AD﹣DE=2﹣2,故选:B.4.解:∵四边形ABCD是菱形,∴CO=AC=3,BO=BD=4,AO⊥BO,∴BC===5,∵S菱形ABCD=AC•BD=BC×AE,∴AE==.在Rt△ABE中,BE===,∴CE=BC﹣BE=5﹣=,∴的值为,故选:C.5.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,∵四边形ABCD为矩形,∴AD=BC,∵DF=BC,∴DA=DF,∴AH=FH,∵AF⊥BE,∴DG∥BE,∴AG=BG=,∵矩形ABCD中,AB=DC=6,AB∥DC,∴四边形BEDG为平行四边形,∴DE=BG=3,∴CE=CD﹣DE=6﹣3=3.故选:C.6.解:∵在菱形ABCD中,∠ABC=80°,∴∠ABD=ABC=40°,AD∥BC,∴∠BAD=180°﹣∠ABC=100°,∵△ABE是等腰三角形,∴AE=BE,或AB=BE,当AE=BE时,∴∠ABE=∠BAE=40°,∴∠DAE=100°﹣40°=60°;当AB=BE时,∴∠BAE=∠AEB=(180°﹣40°)=70°,∴∠DAE=100°﹣70°=30°,综上所述,当△ABE是等腰三角形时,∠DAE=30°或60°,故选:C.7.解:如图,连接BF,∵四边形ABCD是菱形,∴CD=BC,∠DCF=∠BCF,在△BCF和△DCF中,∵,∴△BCF≌△DCF(SAS)∴∠CBF=∠CDF∵FE垂直平分AB,∠BAF=×100°=50°∴∠ABF=∠BAF=50°∵∠ABC=180°﹣100°=80°,∠CBF=80°﹣50°=30°∴∠CDF=30°.故选:B.8.解:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4,∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=BE=×(4﹣4)=4﹣2.故选:A.9.解:∵四边形ABCD是菱形,∠ABC=70°,∴∠ABO=35°,AC⊥BD,∴∠BAC=55°,∵∠BEC=∠BAC+∠ABE,∴55°≤∠BEC≤90°,故选:B.10.解:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,AB=CD,∠B=∠D,AB∥CD,∴∠EAC=∠FCA,∵EF垂直平分AC,∴OA=OC,EA=EC,∴∠EAC=∠ECA,∴∠FCA=∠ECA,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴OE=OF,∴四边形AFCE为平行四边形,∵EF垂直平分AC,∴平行四边形AFCE是菱形,①正确;∴AE=CF,∴BF=DE,在△ABF和△CDE中,,∴△ABF≌△CDE(SAS),②正确;∵四边形AFCE是菱形,∴AF=CF,∵F为BC的中点,∴BF=CF,∴AF=CF=BC,∴∠BAC=90°,∵AB∥CD,∴∠ACD=∠BAC=90°,③正确;正确的个数有3个,故选:D.二.填空题11.解:∵四边形ABCD是矩形,BD=4,∴AC=BD=4,∠ABC=90°,∵∠ACB=30°,∴AB=2,BC===2,∴矩形ABCD的面积是:2×2=4,故答案为:4.12.解:∵正方形ABCD,边长为2,∴AD∥BC,AC=2,∴∠ADE=∠DPC,∵∠ADE=∠AED,∴AE=AD=2,∠DPC=∠AED=∠CEP,∴CP=CE=AC﹣AE=2﹣2,∴BP=BC﹣CP=2﹣(2﹣2)=4﹣2.故答案为:4﹣2.13.解:∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°,∴∠ADB=∠BDC=45°,∵DC=DE,∴AD=DE,∴∠DAE=∠DEA,∵∠ADE=90°+52°=142°,∴∠DAE=19°,在△ADF和△CDF中,,∴△ADF≌△CDF(SAS),∴∠DAE=∠DCF=19°,故答案为:19.14.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF 于M,∵四边形ABCD是矩形,且AB=,BC=4,∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,∴∠DCF=∠G,∵CF平分∠ECD,∴∠DCF=∠FCE,FH=DF,∴∠G=∠ECF,∴EC=EG,∴∠ECG是等腰三角形,∴CM=MG,∵CE=CF,∴△ECF是等腰三角形,∵EM⊥CF,FH⊥CE,∴EM和FH是等腰三角形腰上的高,∴EM=FH=DF,∴Rt△CDF≌Rt△CME(HL),∴CM=CD=,∴CG=5,Rt△CBG中,BG===3,设BE=x,则EC=EG=3+x,Rt△CBE中,(3+x)2=x2+42,解得:x=,∴BE=.故答案为:.15.解:如图,连接CG并延长,交AD于点M,连接EM,∵四边形ABCD为菱形,∠B=60°,∴AD∥BC,∴∠A=120°,∠MGD=∠CGH,∵点G为HD的中点,∴HG=DG,∵∠MGD=∠CGH,∴△MGD≌△CGH(ASA),∴MG=CG,MD=CH=BC=AD,∴点G为MC的中点,点M为AD的中点,∵F,G分别为CE和CM的中点,∴FG是△CEM的中位线,∴FG=EM,∴EM=2FG=4,∵E,M分别为AB和AD的中点,∴AE=AM,∵∠A=120°,∴EM=AE=4,∴AE=4,∴AB=2AE=8.故答案为:8.三.解答题16.证明:∵四边形ABCD是矩形,∴AD=BC,∵EF=BF+BE,∵BC=CE+BE,BF=CE,∴EF=BC,∴AD=EF.17.证明:(1)∵四边形ABCD为正方形,∴AC平分∠BAD,又∵PM⊥AD,PN⊥AB,∴PM=PN.(2)∵PM⊥AD,PN⊥AB,∠MAN=90°,PM=PN,∴四边形PMAN为正方形,∴∠MPN=90°,即∠MPE+∠EPN=90°.∵PE⊥PB,∴∠EPN+∠NPB=90°,∴∠MPE=∠NPB.∵PM⊥AD,PN⊥AB,∴∠PME=∠PNB=90°.在△PME和△PNB中,,∴△PME≌△PNB(ASA),∴EM=BN.18.证明:(1)∵四边形ABCD是矩形,AF⊥DE,∴AD∥BC,AD=BC,AB=CD,∠C=∠AFD=90°,∴∠ADE=∠DEC,∵DE=BC,∴AD=DE,在△ADF和△DEC中,,∴△ADF≌△DEC(AAS),∴AF=CD,∴AF=AB;(2)AD,BC,DE的长度等于AB,理由如下:∵△ADF≌△DEC,∴CE=DF,∴BE=EF,∵BE=DF,∴BE=EC=DF=EF,∴DE=2EC,∵DE2=EC2+CD2,∴DE=AB,∴AD=BC=DE=AB.。
2022年强化训练华东师大版八年级数学下册第十九章矩形、菱形与正方形定向训练试题(含解析)

八年级数学下册第十九章矩形、菱形与正方形定向训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是()A.1 B.4 C.2 D.62ABCD中,点E是对角线AC上一点,且EF AB⊥于点F,连接DE,当22.5ADE∠=︒时,EF=()A.1 B.2C1D.1 43、如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA C的坐标为( )A .1)B .(1,1)C .(1D .,1)4、下列关于ABCD 的叙述,正确的是( )A .若AC BD =,则ABCD 是矩形B .若AB AD =,则ABCD 是正方形C .若AB BC ⊥,则ABCD 是菱形D .若AC BD ⊥,则ABCD 是正方形5、下列命题正确的是( )A .若a b =,则33a b =B .四条边相等的四边形是正四边形C .有一组邻边相等的平行四边形是矩形D .如果2a ab =,则a b =6、绿丝带是颜色丝带的一种,被用来象征许多事物,例如环境保护、大麻和解放农业等,同时绿丝带也代表健康,使人对健康的人生与生命的活力充满无限希望.某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图所示,丝带重叠部分形成的图形是( )A .矩形B .菱形C .正方形D .等腰梯形7、下列说法正确的有( )①有一组邻边相等的矩形是正方形 ②对角线互相垂直的矩形是正方形②有一个角是直角的菱形是正方形 ④对角线相等的菱形是正方形A .1个B .2个C .3个D .4个8、如图,以O 为圆心,OA 长为半径画弧别交OM ON 、于A 、B 两点,再分别以A 、B 为圆心,以OA 长为半径画弧,两弧交于点C ,分别连接AC 、BC ,则四边形OACB 一定是( )A .梯形B .菱形C .矩形D .正方形9、如图,在平面直角坐标系中,矩形ABCO 的两边OA ,OC 落在坐标轴上,反比例函数y =k x的图象分别交BC ,OB 于点D ,点E ,且45BD CD ,若S △AOE =3,则k 的值为( )A .﹣4B .﹣403C .﹣8D .﹣10、如图,把一张长方形纸片ABCD 沿对角线AC 折叠,点B 的对应点为点B ′,AB ′与DC 相交于点E ,则下列结论正确的是 ( )A .∠DAB ′=∠CAB ′B .∠ACD =∠B ′CDC .AD =AE D .AE =CE第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、如图,已知正方形ABCD 的边长为12,BE =EC ,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下3个结论:①△ADG ≌△FDG ;②GB =2AG ;③S △BEF =725.在以上3个结论中,正确的有______.(填序号)2、如图,长方形纸片ABCD ,点E ,F 分别在,AB BC 边上,将纸片沿EF 折叠,使点B 落在边AD 上的点B '处,然后再次折叠纸片使点F 与点B '重合,点C 落在点C ',折痕为GH ,若18C B D AB E ∠'-∠=''︒,则∠=EFC _______度.3、如图,已知在矩形ABCD 中,4AB =,8AD =,将ABC 沿对角线AC 翻折,点B 落在点E 处,连接DE ,则DE 的长为_________.4、若矩形ABCD 的对角线AC ,BD 相交于点O ,且6cm BD =,120BOC ∠=︒,则矩形ABCD 的面积为_____________2cm .5、如图,矩形ABCD 的对角线AC ,BD 交于点O ,M 在BC 边上,连接MO 并延长交AD 边于点N .若BM = 1,∠OMC = 30°,MN = 4,则矩形ABCD 的面积为 _________ .6、如图,在平面直角坐标系xOy 中,菱形ABCD 的顶点D 在x 轴上,边BC 在y 轴上,若点A 的坐标为(12,13),则点C 的坐标是___.7、如图所示,ABCD 是长方形地面,长16m AB =,宽9m AD =,中间竖有一堵砖墙高1m MN =.一只蚂蚱从B 点爬到D 点,它必须翻过中间那堵墙,则它至少要走______m 的路程.8、(1)它具有平行四边形的一切性质:两组对边分别平行且相等,两组对角________,对角线________.(2) 具有矩形的一切性质:四个角都是________,对角线相等.(3)具有菱形的一切性质:四条边相等;对角线互相________,每条对角线________一组对角.9、如图,在正方形ABCD 中,9AB =,M 是AD 边上的一点,:1:2AM MD =.将△BMA 沿BM 对折至△BMN ,连接DN ,则DN 的长是________.10、如图,正方形ABCD 中,6AB =,点E 在边CD 上,且3CD DE =.将ADE 沿AE 对折至AFE △,延长EF 交边BC 于点G ,连接AG 、CF .则下列结论:①ABG AFG △△≌;②BG CG =;③AG ∥CF ;④2FGC FEC S S =△△;其中正确是______(填写序号)三、解答题(5小题,每小题6分,共计30分)1、如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F,若DE=BC的长.2、如图,已知四边形ABCD是正方形,E是正方形外一点,以BC为斜边作直角三角形BCE,以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连结AF.(1)求证:AF=CE;(2)求证:AF∥EB;(3)若EF12BFCE=,求BC的长.3、如图1,E是正方形ABCD边AD上一点,过点C作CF CE⊥,交AB的延长线于点F.(1)求证:CDE CBF ≅△△;(2)如图2,若正方形边长为6,线段DA 上有一动点M 从点D 出发,以1个单位长度每秒沿DA 向A 运动.同时线段BA 上另一动点N 从点B 出发,以2个单位长度每秒沿BA 向A 运动,当点N 到达点A 后点M 也停止运动.连接MN ,点N 的运动时间为t ,CMN △的面积为S ,求S 关于t 的函数关系式;(3)如图3,连接BD ,连接EF 交DB 于点M ,连接CM 并延长,交AB 于点P ,已知4AB =,1DE =,求PB 的长.4、如图1,在平面直角坐标系中,已知(2,0)A 、(0,4)B -、(6,6)C -、(6,6)D ,以CD 为边在CD 下方作正方形CDEF .(1)求直线AB 的解析式;(2)点N 为正方形边上一点,若8ABN S =△,求N 的坐标;(3)点N 为正方形边上一点,(0,)M m 为y 轴上一点,若点N 绕点M 按顺时针方向旋转90︒后落在线段AB 上,请直接写出m 的取值范围.5、如图,将▱ABCD 的边AB 延长到点E ,使BE =AB ,连接DE ,交边BC 于点F .(1)求证:△BEF ≌△CDF .(2)连接BD ,CE ,若∠BFD =2∠A ,求证四边形BECD 是矩形.-参考答案-一、单选题1、C【解析】略2、C【解析】【分析】证明67.5CDE CED ∠=∠=︒,则CD CE =AC 的长,得2AE =,证明AFE ∆是等腰直角三角形,可得EF 的长.【详解】 解:四边形ABCD 是正方形,AB CD BC ∴==90B ADC ∠=∠=︒,45BAC CAD ∠=∠=︒, 22AC AB ,22.5ADE ∠=︒,9022.567.5CDE ∴∠=︒-︒=︒,4522.567.5CED CAD ADE ∠=∠+∠=︒+︒=︒,CDE CED ∴∠=∠,CD CE ∴==2AE ∴=EF AB ⊥,90AFE ∴∠=︒,AFE ∴∆是等腰直角三角形,1EF ∴,故选:C .【点睛】本题考查正方形的性质,勾股定理,等腰直角三角形,三角形的外角的性质等知识,解题的关键是在正方形中学会利用等腰直角三角形的性质解决问题,属于中考常考题型.3、B【解析】【分析】作CD ⊥x 轴,根据菱形的性质得到OC =OA Rt △OCD 中,根据勾股定理求出OD 的值,即可得到C 点的坐标.【详解】:作CD ⊥x 轴于点D ,则∠CDO=90°,∵四边形OABC是菱形,OA∴OC=OA又∵∠AOC=45°,∴∠OCD=90°-∠AOC=90°-45°=45°,∴∠DOC=∠OCD,∴CD=OD,在Rt△OCD中,OC CD2+OD2=OC2,∴2OD2=OC2=2,∴OD2=1,∴OD=CD=1(负值舍去),则点C的坐标为(1,1),故选:B.【点睛】此题考查了菱形的性质、等腰直角三角形的性质以及勾股定理,根据勾股定理和等腰直角三角形的性质求出OD=CD=1是解决问题的关键.4、A【解析】【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A 、B 、D 错误,C 正确;即可得出结论.【详解】解:ABCD 中,AC BD =,∴四边形ABCD 是矩形,选项A 符合题意; ABCD 中,AB AD =,∴四边形ABCD 是菱形,不一定是正方形,选项B 不符合题意; ABCD 中,AB BC ⊥,∴四边形ABCD 是矩形,不一定是菱形,选项C 不符合题意; ABCD 中,AC BD ⊥,∴四边形ABCD 是菱形,选项D 不符合题意;故选:A .【点睛】本题考查了平行四边形的性质、菱形的判定方法、矩形的判定方法、正方形的判定方法;熟练掌握矩形、菱形、正方形的判定方法是解决问题的关键.5、A【解析】【分析】利用等式的性质以及矩形、正方形、菱形的判定方法分别判断后即可确定正确的选项.【详解】解:A 、若a b =,则33a b =,故此命题正确;B 、四条边相等的四边形是菱形,故原命题不正确;C 、有一组邻边相等的平行四边形是菱形,故原命题不正确;D 、如果2a ab =,a ≠0时,则a b =,若0a =时,此命题不正确,故选:A .【点睛】本题考查了命题与定理以及等式的性质等知识,解题的关键是了解矩形及菱形的判定方法.6、B【解析】【分析】首先可判断重叠部分为平行四边形,且两条丝带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.【详解】解:过点A 作AE ⊥BC 于E ,AF ⊥CD 于F ,因为两条彩带宽度相同,所以AB ∥CD ,AD ∥BC ,AE =AF .∴四边形ABCD 是平行四边形.∵S ▱ABCD =BC •AE =CD •AF .又AE =AF .∴BC =CD ,∴四边形ABCD 是菱形.故选:B【点睛】此题考查了菱形的判定,平行四边形的面积公式以及平行四边形的判定与性质,利用了数形结合的数学思想,其中菱形的判定方法有:一组邻边相等的平行四边形为菱形;对角线互相垂直的平行四边形为菱形;四条边相等的四边形为菱形,根据题意作出两条高AE和AF,熟练掌握菱形的判定方法是解本题的关键7、D【解析】【分析】根据正方形的判定定理依次分析判断.【详解】解:①有一组邻边相等的矩形是正方形,故该项正确;②对角线互相垂直的矩形是正方形,故该项正确;②有一个角是直角的菱形是正方形,故该项正确;④对角线相等的菱形是正方形,故该项正确;故选:D.【点睛】此题考查了正方形的判定定理,正确掌握正方形与矩形菱形的特殊关系及对应添加的条件证得正方形是解题的关键.8、B【解析】【分析】根据题意得到OA OB AC BC===,然后根据菱形的判定方法求解即可.【详解】解:由题意可得:OA OB AC BC===,∴四边形OACB是菱形.故选:B.【点睛】此题考查了菱形的判定,解题的关键是熟练掌握菱形的判定方法.菱形的判定定理:①四条边都相等四边形是菱形;②一组邻边相等的平行四边形是菱形;③对角线垂直的平行四边形是菱形.9、D【解析】【分析】设点B的坐标为(a,b),则点D的坐标为(kb,b),点A的坐标为(a,0),分别求出BD、CD、AB,找到a,b,k之间的关系,设点E坐标为(m,n),利用三角形的面积表示出点E的坐标,再利用割补法求出abk=576,进而可得k值.【详解】解:设点B的坐标为(a,b),则点D的坐标为(kb,b),点A的坐标为(a,0),∴BD=kab-,BC=-a,CD=-kb,AB=b,∵45 BDCD=,∴5×(kab-)=4×(kb-),∴95ab k=,设点E坐标为(m,n),∵S△AOE=3,即132an-=,∴6na =-,∵点E 在反比例函数k y x =上, ∴E (6ak -,6a -), ∵S △AOE =S 矩形OABC -S △OBC -S △ABE =11()()3226ak ab ab b a ------=, ∴abk =36,把abk =36代入95ab k =得,220k =,解得:k =±由图象可知,k <0,∴k =-故选:D .【点睛】本题考查反比例函数系数k 的几何意义,矩形的性质等,解题的关键是利用割补法表示出△AOE 的面积.10、D【解析】【分析】根据翻折变换的性质可得∠BAC =∠CAB ′,根据两直线平行,内错角相等可得∠BAC =∠ACD ,从而得到∠ACD =∠CAB ′,然后根据等角对等边可得AE =CE ,从而得解.【详解】解:∵矩形纸片ABCD 沿对角线AC 折叠,点B 的对应点为B ′,∴∠BAC =∠CAB ′,∵AB ∥CD ,∴∠BAC =∠ACD ,∴∠ACD =∠CAB ′,∴AE =CE ,∴结论正确的是D 选项.故选D.【点睛】本题考查了翻折变换的性质,平行线的性质,矩形的对边互相平行,等角对等边的性质,熟记各性质并准确识图是解题的关键.二、填空题1、①②③【解析】【分析】根据正方形的性质和折叠的性质可得AD DF =,90A GFD ∠=∠=︒,于是根据“HL ”判定Rt ADG Rt FDG ≌,再由12GF GB GA GB +=+=,EB EF =,BGE ∆为直角三角形,可通过勾股定理列方程求出4AG =,8BG =,进而求出∆BEF 的面积.【详解】解:由折叠可知,DF DC DA ==,90DFE C ∠=∠=︒,EF EC =,90DFG A ∴∠=∠=︒,在Rt ADG 和Rt FDG △中,AD FD DG DG=⎧⎨=⎩, ()Rt ADG Rt FDG HL ∴≌,故①正确;AG GF ∴=,正方形边长是12,6BE EC EF ∴===,设AG FG x ==,则6EG x =+,12BG x =-,由勾股定理得:222EG BE BG =+,即:222(6)6(12)x x +=+-,解得:4x =4AG GF ∴==,8BG =,2BG AG =,故②正确;168242GBE S ∆=⨯⨯=,67224105BEF GBE EF S S EG ∆∆=⋅=⨯=,故③正确; 故答案为:①②③.【点睛】本题考查了翻折变换,正方形的性质,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用这些性质解决问题.2、144【解析】【分析】根据将纸片沿EF 折叠,使点B 落在边AD 上的点B '处,得出∠EB ′F =∠B =90°,∠BFE =∠B′FE ,可得∠AB′E +∠DB′F =90°根据四边形ABCD 为矩形,得出AD∥BC ,可得∠DBF =∠B′FB =2∠EFB ,可求∠AB′E =90°-∠DB′F =90°-2∠EFB ,根据GH 为对称轴,可得∠CB′F =∠CFB′=180°-∠B′FB =180°-2∠EFB ,可得∠C′B′D =∠C′B′F -∠FB′D =180°-2∠EFB -2∠EFB ,根据18C B D AB E ∠'-∠=''︒,列方程180°-2∠EFB -2∠EFB -(90°-2∠EFB )=18°,解方程即可.【详解】解:∵将纸片沿EF 折叠,使点B 落在边AD 上的点B '处,∴∠EB′F =∠B =90°,∠BFE =∠B′FE ,∴∠AB′E +∠DB′F =90°∴∠AB′E=90°-∠DB′F∵四边形ABCD为矩形,∴AD∥BC,∴∠DB′F=∠B′FB=2∠EFB,∴∠AB′E=90°-∠DBF=90°-2∠EFB,∵GH为对称轴,∴∠C′B′F=∠CFB′=180°-∠B′FB=180°-2∠EFB,∵∠C′B′D=∠C′B′F-∠FB′D=180°-2∠EFB-2∠EFB,''︒,∵18-∠=C BD AB E∠'∴180°-2∠EFB-2∠EFB-(90°-2∠EFB)=18°,解得∠EFB=36°,∴∠EFC=180°-∠EFB=180°-36°=144°.故答案为144.【点睛】本题考查折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程,掌握折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程是解题关键.3【解析】【分析】过点E作EF⊥AD于点F,先证明CG=AG,再利用勾股定理列方程,求出AG的值,结合三角形的面积法和勾股定理,即可求解.【详解】解:如图所示:过点E作EF⊥AD于点F,有折叠的性质可知:∠ACB =∠ACE ,∵AD ∥BC ,∴∠ACB =∠CAD ,∴∠CAD =∠ACE ,∴CG =AG ,设CG =x ,则DG =8-x ,∵在Rt CDG 中,()22284x x -+=,∴x =5,∴AG =5,在Rt AEG 中,3==,EF ⊥AD ,∠AEG =90°, ∴125AE EG EF AG ⨯==, ∵在Rt AEF 中,22165AFAE EF ,、 ∴DF =8-165=245, ∴在Rt DEF △中,221255DE EF DF ,【点睛】 本题主要考查矩形的性质,折叠的性质,勾股定理,等腰三角形的判定定理,添加辅助线构造直角三角形,是解题的关键.4、【解析】【分析】如图,过点O 作OE BC ⊥,根据矩形的对角线相等且互相平分可得OB OC =,2AB OE =,2BC BE =,由120BOC ∠=︒得30OBE OCE ∠=∠=︒,利用勾股定理求出BE ,由矩形面积得解.【详解】如图,过点O 作OE BC ⊥,∵四边形ABCD 是矩形, ∴13cm 2OB OC OD BD ====,2AB OE =,2BC BE =, ∵120BOC ∠=︒,∴30OBE OCE ∠=∠=︒, ∴13cm 22OE OB ==,∴BE ===,∴3cm AB =,BC =,∴23)ABCD S =⨯=矩形.故答案为:【点睛】本题考查矩形的性质与勾股定理,掌握矩形的性质是解题的关键.5、4+4【解析】【分析】过点N 作NE BC ⊥交于点E ,由矩形ABCD 得OB OD =,OBM ODN ∠=∠,根据ASA 可证BOM DON ≅△△,故可得1CE DN BM ===,由直角三角形30角所对的边为斜边的一半得出122CD EN MN ===,根据勾股定理求出ME ,从而得出BC ,由矩形的面积公式即可得出答案. 【详解】如图,过点N 作NE BC ⊥交于点E ,∵四边形ABCD 是矩形,∴OB OD =,OBM ODN ∠=∠,∵BOM DON ∠=∠,∴()BOM DON ASA ≅,∴1CE DN BM ===,∵30OMC ∠=︒, ∴122CD EN MN ===,∴ME ==∴112BC =+=+∴(224ABCD S =+⨯=+矩形.故答案为:4+【点睛】本题考查矩形的性质,全等三角形的判定与性质,直角三角形的性质以及勾股定理,掌握相关知识点的应用是解题的关键.6、(0,-5)【解析】【分析】在Rt △ODC 中,利用勾股定理求出OC 即可解决问题.【详解】解:∵A (12,13),∴OD =12,AD =13,∵四边形ABCD 是菱形,∴CD =AD =13,在Rt △ODC 中,5==OC ,∴C (0,-5).故答案为:(0,-5)【点睛】本题考查菱形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题.7、【解析】【分析】根据题意,将长方形底面和中间墙展开为平面图,并连接BD ,根据两点之间直线段最短和勾股定理的性质计算,即可得到答案.【详解】将长方形底面和中间墙展开后的平面图如下,并连接BD根据题意,展开平面图中的16218m AB =+=∴一只蚂蚱从B 点爬到D 点,最短路径长度为展开平面图中BD 长度∵ABCD 是长方形地面∴90A ∠=︒∴BD ==故答案为:【点睛】本题考查了立体图形展开图、矩形、两点之间直线段最短、勾股定理的知识;解题的关键是熟练掌握立体图形展开图、勾股定理的知识,从而完成求解.8、 相等 互相平分 直角 垂直 平分【解析】略9【解析】【分析】连接AN 交BM 于点O ,过点N 作NH ⊥AD 于点H ,根据正方形的性质可得AM =3,DM =6,从而得到BM =AN ⊥BM ,AO =NO ,MN =AM =3,再由1122ABM S AB AM AO BM =⋅=⋅,可得AO =2AN AO ==2222AN AH MN MH -=-,从而得到125MH =,进而得到95HN =,2718955DH =-= ,即可求证.【详解】解:如图,连接AN 交BM 于点O ,过点N 作NH ⊥AD 于点H ,∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD ,∵9AB =, :1:2AM MD =.∴AM =3,DM =6,∴BM =,∵将△BMA 沿BM 对折至△BMN ,∴AN ⊥BM ,AO =NO ,MN =AM =3, ∵1122ABMS AB AM AO BM =⋅=⋅ ,∴AO =,∴2AN AO ==在Rt AHN 中,由勾股定理得:222HN AN AH =- ,在Rt MHN 中,由勾股定理得:222HN MN MH =- ,∴2222AN AH MN MH -=-,即()222233MH MH -+=- ,解得:125MH = ,∴2735AH MH =+=,95HN = , ∴2718955DH =-= ,∴DN ==.【点睛】 本题主要考查了正方形与折叠问题,勾股定理,轴对称图形的性质,熟练掌握相关知识点是解题的关键.10、①②③【解析】【分析】由折叠得AD=AF ,∠AFG =∠B =90°,即可判断①正确;证明BG=GF=x ,CG=6-x ,求出DE =2,得到CE =4,EF=DE =2;借助勾股定理得到(x +2)2=(6-x )2+42,求出x ,即可判断②正确;根据CG=GF ,得到∠FGC +2∠GFC =180°,由ABG AFG △△≌,推出∠FGC +2∠AGF =180°,由此推出∠AGF =∠GFC ,判断③正确;由GF =3,EF =2,根据同高三角形判断④错误.【详解】解: ∵四边形ABCD 是正方形,∴AB=AD =6,∠B =∠D =90°,由折叠得AD=AF ,∠AFE =∠D =90°,则∠AFG =180°-90°=90°,∵AG=AG ,∴ABG AFG △△≌;故①正确;∵△ABG ≌△AFG ,∴BG=GF ,设BG=GF=x ,CG =6-x ,∵CD=AB =6,CD =3DE ,∴DE =2,CE =4,EF=DE =2;由勾股定理得:GE 2=CG 2+CE 2,即(x +2)2=(6-x )2+42,解得:x =3,∴CG =6-3=3,∴BG=CG .故②正确;∵BG=CG=GF ,∴∠GFC =∠GCF ,∴∠FGC +2∠GFC =180°,∵ABG AFG △△≌,∴∠AGB =∠AGF ,∴∠FGC +2∠AGF =180°,∴∠AGF =∠GFC ,∴AG CF ∥,故③正确;∵GF =3,EF =2,∴ 1.5FGC FEC S S △△,故④错误,故答案为:①②③.【点睛】此题考查了正方形的性质,全等三角形的判定及性质,勾股定理,平行线的判定定理,同高三角形面积的关系,熟练掌握各知识点是解题的关键.三、解答题1【解析】【分析】设正方形边长为x ,证明△CBE ≌△FBE ,进而得到BF=BC=x ,DF=BD-BF =1)x ,EF=EC=CD-DE =x Rt △DEF 中使用勾股定理即可求出正方形边长.【详解】解:设正方形边长BC=CD=x ,则BD ,∵BE 平分∠CBD ,∴∠CBE =∠FBE ,∵EF ⊥BD ,∴∠BFE =∠C =90°,且BE=BE ,∴△CBE ≌△FBE (AAS ),∴BF=BC=x ,EF=EC=CD-DE =x且DF=BD-BF =1)x ,在Rt △DEF 中,由勾股定理可知:DE ²=DF ²+EF ²,代入数据:2221)(+x x ,解得:1x ,2=0x (舍去),故BC .【点睛】本题考查了正方形的性质、三角形全等的判定方法、勾股定理求线段长等,熟练掌握正方形的性质及勾股定理求线段长是解决本题的关键.2、 (1)见解析;(2)见解析;(3)BC =【解析】【分析】(1)根据四边形ABCD 是正方形,∠ABC =90°,AB =BC ,得出∠ABF +∠FBC =90°,根据△E BF 是等腰直角三角形,BF =BE ,∠FBE =90°,得出∠FBC +∠CBE =90°,根据同角的余角相等可得∠ABF =∠CBE ,再证△ABF ≌△CBE (SAS )即可;(2)根据以BC 为斜边作直角三角形BCE ,得出∠CEB =90°根据△ABF ≌△CBE ,得出∠AFB =∠CEB =90°,根据∠EBF =90°得出∠AFB =∠EBF =90°利用平行线的判定定理内错角相等两直线平行得出AF ∥EB ;(3)在等腰直角三角形FBE 中,根据勾股定理2222+2EF BF BE BE ==, 求出BF =1,根据12BF CE =,得出CE =2BF =2,根据勾股定理求即可.(1)证明:∵四边形ABCD 是正方形,∴∠ABC =90°,AB =BC ,∴∠ABF +∠FBC =90°,∵△E BF 是等腰直角三角形,∴BF =BE ,∠FBE =90°,∴∠FBC +∠CBE =90°,∴∠ABF =∠CBE ,在△ABF 和△CBE 中,AB CB ABF CBE FB EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABF≌△CBE(SAS),∴AF=CE;(2)证明:∵以BC为斜边作直角三角形BCE,∴∠CEB=90°,∵△ABF≌△CBE,∴∠AFB=∠CEB=90°,∵∠EBF=90°∴∠AFB=∠EBF=90°∴AF∥EB;(3)解:在等腰直角三角形FBE中,∴BF=BE,∵EF根据勾股定理2222+2EF BF BE BE==,即222BF=,解得BF=1,∵12 BFCE=,∴CE=2BF=2,在Rt△BCE中,BC【点睛】本题考查正方形的性质,等腰直角三角形性质,勾股定理,三角形全等判定与性质,平行线判定,掌握正方形的性质,等腰直角三角形性质,勾股定理,三角形全等判定与性质,平行线判定是解题关键.3、 (1)见解析(2)218S t =-+(3)2.4【解析】【分析】(1)先判断出∠CBF =90°,再证明∠DCE =∠BCF 即可解决问题;(2)由题意,DM t =,2BN t =,所以6AM t =-,62AN t =-,分别求出ABCD S 正方形,COM S ∆,CBN S ∆,AMN S ∆即可解决问题;(3)如图2中,作EH ⊥AD 交BD 于H ,连接PE .证明△EMH ≌△FMB (AAS ),由EM =FM ,CE =CF ,推出PC 垂直平分线段EF ,推出PE =PF ,设PB =x ,则PE =PF =x +2,PA =6-x ,理由勾股定理构建方程即可解决问题.(1)解:∵四边形ABCD 为正方形90D DCB CBF ︒∴∠=∠=∠=,DC BC =1290︒∴∠+∠=CF CE ⊥90ECF ︒=∴∠,即2390︒∠+∠=13∠∠∴=在CDE ∆和CBF ∆中13CDE CBF CD CB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()CDE CBF ASA ∴∆∆≌.(2)由题意,DM t =,2BN t =6AM t ∴=-,62AN t =-ΔΔΔCDM CBN AMN ABCD S S S S S ∴=---正方形11166662(6)(62)222t t t t =⨯-⋅⋅-⋅⋅--⋅-⋅ 23636189t t t t =---+-218t =-+(3)作EH AD ⊥交BD 于H ,连接PE∵四边形ABCD 是正方形4AB AD ∴==,90A ︒∠=,45EDH ︒∠=EH AD ⊥,90DEH A ︒∴∠=∠=.1DE EH ∴==,EH AF ∥,12∠∠∴=CDE CBF ∆∆≌,1DE BF ∴==,CE CF =EH BF ∴=在EHM ∆和FBM ∆中,1234EH FB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()EHM FBM AAS ∴∆∆≌,EM FM ∴=,CE CF =CP ∴垂直平分EF ,PE PF ∴=设PB x =,则1PE PF x ==+,4PA x =-,∵在Rt EAP ∆中,222AE AP EP +=222(4)3(1)x x ∴-+=+,2.4x =,2.4PB ∴=【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.4、 (1)24y x =-(2)(1,6)N ,(5,6)N --,(6,0)N ,(3,6).N - (3)2143m ≤≤或2263m -≤≤- 【解析】【分析】(1)待定系数法求直线解析式,代入坐标(2,0)A 、(0,4)B -得出402b k b -=⎧⎨=+⎩,解方程组即可; (1)根据OA =2,OB =4,设点P 在y 轴上,点P 坐标为(0,m ),根据S △ABP =8,求出点P (0,4)或(0,-12),过P (0,4)作AB 的平行线交正方形CDEF 边两点N 1和N 2,利用平行线性质求出与AB 平行过点P 的解析式24y x =+,与CD ,FE 的交点,过点P (0,-12)作AB 的平行线交正方形CDEF 边两点N 3和N 4,利用平行线性质求出与AB 平行过点P 的解析式212y x =-,求出与DE ,EF 的交点即可;(3):根据点N 在正方形边上,分四种情况①N 在DE 上,过N′作GN′⊥y 轴于G ,正方形边CD 与y 轴交于H ,(0,)M m 在y 轴正半轴上,先证△HNM 1≌△GM 1N ′(AAS ),求出点N ′(6-m ,m -6)在线段AB 上,代入解析式直线AB 的解析式24y x =-得出()6264m m -=--,当点N 旋转与点B 重合,可得M 2N ′=NM 2-OB =6-4=2②N 在CD 上,当点N 绕点M 3旋转与点A 重合,先证△HNM 3≌△GM 3N ′(AAS ),DH =M 3G =6-2=4,HM 3=GN ′=2,③N 在CF 上,当点N 与点F 重合绕点M 4旋转到AB 上N ′先证△M 5NM 3≌△GM 3N ′(AAS ),得出点N ′(-6-m ,m +6),点N′在线段AB 上,直线AB 的解析式24y x =-,得出方程,()6264m m +=---,当点N 绕点M 5旋转点N ′与点A 重合,证明△FM 3N ≌△OM 5N ′(AAS ),可得FM 5=M 5O =6,FN =ON ′=2,④N 在FE 上,点N 绕点M 6旋转点N ′与点B 重合,MN =MB =2即可.(1)解:设:AB y kx b =+,代入坐标(2,0)A 、(0,4)B -得:402b k b-=⎧⎨=+⎩, 24k b =⎧⎨=-⎩, ∴直线AB 的解析式24y x =-;(2)解:∵(2,0)A 、(0,4)B -、OA =2,OB =4,设点P 在y 轴上,点P 坐标为(0,m ) ∵S △ABP =8, ∴14282m +⨯=, ∴48m +=±,解得12412m m ==-,,∴点P (0,4)或(0,-12),过P (0,4)作AB 的平行线交正方形CDEF 边两点N 1和N 2,设解析式为y mx n =+,m =2,n =4,∴24y x =+,当y=6时,246x +=,解得61y x =⎧⎨=⎩, 当y=-6时,246x +=-,解得65y x =-⎧⎨=-⎩, 1(1,6)N ∴,2(5,6)N --,过点P (0,-12)作AB 的平行线交正方形CDEF 边两点N 3和N 4, 设解析式为,2,12y px q p q =+==-,212y x =-,当y =-6, 2126x -=-,解得:63y x =-⎧⎨=⎩, 当x =6, 26120y =⨯-=,解得60x y =⎧⎨=⎩, 3(3,6).N -4(6,0)N ,∴8ABN S =△,N 的坐标为(1,6)或(5,6)--或(3,6)-或(6,0),(3)解:①N 在DE 上,过N′作GN′⊥y 轴于G ,正方形边CD 与y 轴交于H ,(0,)M m 在y 轴正半轴上, ∵M 1N =M 1N ′,∠NM 1N ′=90°,∴∠HNM 1+∠HM 1N =90°,∠HM 1N +∠GM 1N′=90°, ∴∠HNM 1=∠GM 1N′,在△HNM 1和△GM 1N ′中,111111HDM GM N DHM M GN M N N M ∠=∠⎧⎪∠=∠'='⎨'⎪⎩, ∴△HNM 1≌△GM 1N ′(AAS ),∴DH =M 1G =6,HM 1=GN ′=6-m ,∵点N ′(6-m ,m -6)在线段AB 上,直线AB 的解析式24y x =-; 即()6264m m -=--, 解得143m =, 当点N 旋转与点B 重合,∴M 2N ′=NM 2-OB =6-4=2,114(0,)3M ,2(0,2)M ,1423m ∴≤≤, ②N 在CD 上,当点N 绕点M 3旋转与点A 重合, ∵M 3N =M 3N ′,∠NM 3N ′=90°, ∴∠HNM 3+∠HM 3N =90°,∠HM 3N +∠GM 3N′=90°, ∴∠HNM 3=∠GM 3N′,在△HNM 3和△GM 3N ′中, 333333HDM GM N DHM M GN M N N M ∠=∠⎧⎪∠=∠'='⎨'⎪⎩, ∴△HNM 3≌△GM 3N ′(AAS ), ∴DH =M 3G =6-2=4,HM 3=GN ′=2,114(0,)3M ,3(0,4)M ,1443m ∴≤≤ ③N 在CF 上,当点N 与点F 重合绕点M 4旋转到AB 上N ′,∵M 4N =M 4N ′,∠NM 4N ′=90°, ∴∠M 5NM 4+∠M5M 4N =90°,∠M 5M 4N +∠GM 4N′=90°, ∴∠M5NM 4=∠GM 4N′, 在△M5NM 4和△GM 4N ′中, 54454444M NM GM N NM M M GN M N N M ∠=∠⎧⎪∠='='∠⎨'⎪⎩, ∴△M 5NM 3≌△GM 3N ′(AAS ), ∴FM 5=M 4G =6,M 5M 4=GN ′=-6-m ,∴点N ′(-6-m ,m +6), 点N ′在线段AB 上,直线AB 的解析式24y x =-; ()6264m m +=---, 解得223m =-, 当点N 绕点M 5旋转点N ′与点A 重合, ∵M 5N =M 5N ′,∠NM 5N ′=90°, ∴∠NM 5O +∠FM 5N =90°,∠OM 5N +∠OM 5N′=90°,∴∠FM 5N =∠OM 5N′,在△FM 5N 和△OM 5N ′中,555555FM N OM N NFM N OM M N M N ∠=∠⎧⎪∠=∠'='⎨'⎪⎩, ∴△FM 3N ≌△OM 5N ′(AAS ),∴FM 5=M 5O =6,FN =ON ′=2,56(0,)M -,422(0,)3M -,2263m -≤≤-, ④N 在FE 上,点N 绕点M 6旋转点N ′与点B 重合,MN =MB =2,66 (0,)M-,422 (0,)3M-,2263m-≤≤-,综上:2143m≤≤或2263m-≤≤-【点睛】本题考查图形与坐标,待定系数法求一次函数解析式,正方形的性质,平行线性质,图形旋转,三角形全等判定与性质,一元一次方程,不等式,本题难度,图形复杂,应用知识多,要求有很强的解题能力.5、(1)见解析;(2)见解析【解析】【分析】(1)根据平行四边形的性质可得AB∥CD且AB=CD,进而证明∠BEF=∠FDC,∠FBE=∠FCD, ASA证明△BEF≌△CDF.(2)根据等边对等角证明FD=FC,进而证明BB=BB,根据对角线相等的平行四边形是矩形即可证明【详解】(1)∵四边形ABCD为平行四边形,∴AB∥CD且AB=CD.∵BE=AB,∴BE∥CD且BE=CD.∴∠BEF=∠FDC,∠FBE=∠FCD,∴△BEF≌△CDF.(2)∵BE∥CD且BE=CD.∴四边形BECD为平行四边形,∴DF=12DE,CF=12BC,∵四边形ABCD为平行四边形,∴∠FCD=∠A,∵∠BFD=∠FCD+∠FDC,∠BFD=2∠A, ∴∠FDC=∠FCD,∴FD=FC.又DF=12DE,CF=12BC,∴BC=DE,∴▱BECD是矩形.【点睛】本题考查了平行四边形的性质与判定,矩形的判定,三角形全等的性质与判定,掌握平行四边形的性质与判定是解题的关键.。
