八年级数学 矩形、菱形、正方形 证明解答题专题练习(详细答案)
人教版八年级上册数学解答题专题训练50题含答案

人教版八年级上册数学解答题专题训练50题含答案(2)51.如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,(1)在图中画出平移后的△A′B′C′;(2)画出AB边上的高CE;(3)过点A画BC的平行线;(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q 共有_____个.(注:格点指网格线的交点)【答案】(1)作图见解析;(2)作图见解析;(3)作图见解析;(4)4.【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可;(2)利用网格特点找出A′C′的中点D′,然后连接B′D′即可;(3)根据平行线的性质求解;(4)过点A作BC的平行线,然后找出此平行线上的格点即可.【详解】解:(1)如图,△A′B′C′为所作;(2)如图,高线CE为所作;(3)AQ△BC;(4)图中满足条件且异于点A的个点Q共有4个.故答案为4.【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.52.已知21(1)(2)12y A B y y y y +=+-+-+,求A 、B 的值.53.如图,矩形ABCD 的对角线AC 、BD 相交于点O ,BE AC ∥,AE BD ∥.(1)求证:四边形AOBE 是菱形;(2)若60AOB ∠=︒,8AC =,求菱形AOBE 的面积.,根据菱形的性质易得出AOB 为等边三角形,再根据等的值,最后根据菱形的面积等于对角线证明:BE AC ∥AE BD四边形AOBE 为平行四边形四边形ABCD 为矩形BD =,12OA AC ,OB OB =∠∴AOB 为等边三角形8AC =OA AB ==12AM AB =OM OA =54.设x ,y ,z 为互不相等的非零实数,且x y z y z x +=+=+.求证:2221x y z =.55.如图,将几个小正方形与小长方形拼成一个边长为a b c ++()的正方形.(1)若用不同的方法计算这个边长为a b c ++()的正方形面积,就可以得到一个等式,这个等式可以为 .(2)请利用(1)中的等式解答下列问题:△若三个实数,,a b c 满足l1a b c ++=,+38ab bc ac +=,求222a b c ++的值.△若三个实数,,x y z 满足12484x y z ⨯÷=,2224944x y z ++=,求236xy xz yz --的值. 【答案】(1)2222()222a b c a b c ab bc ac ++=+++++;(2)△45;△-20【分析】(1)根据大正方形的面积等于所有小正方形与矩形的面积和即可得解; (2)△利用(1)中等式可将(a+b+c )直接平方,然后代入式子的值求解即可;(3)△利用幂的乘方与同底数幂的乘除整理得到232x y z +-=-,然后将23x y z +-平△(a b c ++11,c +=22(b c a +=238⨯△24x y ⨯÷222x y ∴⨯÷232x y z +-∴=23x y ∴+-(23x y +-2(2)∴-=23xy xz ∴-【点睛】本题主要考查整式混合运算,幂的混合运算,解此题的关键在于根据题图得到新等式,再利用新等式进行整理计算即可56.如图,点B 、F 、C 、E 在同一直线上,AB △BE ,垂足为B ,DE △BE ,垂足为E ,AC 、DF 相交于点G ,且AC=DF ,BF CE =.求证:FG CG =.【答案】见详解【分析】首先证明借助HL 证明Rt ABC Rt DEF ≌,由全等三角形的性质可知ACB DFE ∠=∠,然后由“等角对等边”即可证明FG CG =.【详解】证明:△AB △BE ,DE △BE ,△90B E ∠=∠=︒,△BF CE =,△BF FC CE FC +=+,△=BC EF ,又△AC=DF ,△()Rt ABC Rt DEF HL ≌,△ACB DFE ∠=∠,△FG CG =.【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定等知识,熟练掌握相关性质和判定是解题关键.57.计算:(1)2(4)(31)x x -+(2)23331111x x x x x ----+-58.利用因式分解简便计算(要求写出完整计算过程)(1)22201199- (2)21.99 1.990.01+⨯【答案】(1)800;(2)3.98.【详解】试题分析:(1)利用平方差公式得到原式=(201+199)×(201-199),然后进行有理数运算;(2)利用提公因式得到原式=1.99×(1.99+0.01),然后进行有理数运算.试题解析:(1)原式=(201+199)×(201-199)=400×2=800;(2)原式=1.99×(1.99+0.01)=1.99×2=3.98.59.(1)计算:232-÷x x x(912)9(2)分解因式:22-+363x xy y60.如图1,网格中的每一个正方形的边长为1,△ABC为格点三角形(点A、B、C在小正方形的顶点上),直线m为格点直线(直线m经过小正方形的格点).(1)如图1,作出△ABC关于直线m的轴对称图形△A′B′C′;(2)如图2,在直线m上找到一点P,使P A+PB的值最小;(3)如图3,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.(4)如图4,仅用直尺作出三角形ABC的边AB上的高,简单说明你的理由.【答案】(1)见解析(2)见解析(3)见解析(4)见解析【分析】(1)分别作出A,B,C的对应点A′,B′,C′即可.(2)作点B关于直线m的对称点B',连接AB',交直线m于点P,则点P即为所求作的点;(3)如图,取格点O,计算可知S△AOC=S△BOC=S△AOB=2(平方单位).(4)如图,选择格点D、E,证明△ACD△△BCE.于是,AC=BC.选择格点Q,证明△ACQ△△BCQ,于是,AQ=BQ.推出CQ为线段AB的垂直平分线,设CQ与AB相交于点F,则CF为所要求的△ABC的边AB上的高.(1)如图所示,△A′B′C′即为所求作,(2)如图,点P即为所求作,(3)如图,即为所作,(4)如图,选择格点D、E,证明△ACD△△BCE.于是,AC=BC.选择格点Q,证明△ACQ△△BCQ,于是,AQ=BQ.△CQ为线段AB的垂直平分线,设CQ与AB相交于点F,则CF为所要求的△ABC的边AB上的高.【点睛】本题考查作图,轴对称变换,三角形的面积等知识,解题的关键是学会利用数形结合的思想解决问题.61.如图,已知点A、C分别在△GBE的边BG、BE上,且AB=AC,AD△BE,△GBE 的平分线与AD交于点D,连接CD.(1)求证:CD平分△ECA.(2)猜想△BDC与△BAC之间有何数量关系?并对你的猜想加以证明.62.甲、乙两市之间有两条铁路线,普通快车线长600千米;高速铁路线长450千米.已知高速列车的速度是普通快车速度的3倍,普通快车先出发3小时,而比高速列车晚到2小时,求普通快车与高速列车的速度分别是多少?63.下面是小明同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程.已知:如图1,直线l 和直线l 外一点P .求作:直线PQ ,使直线PQ l ∥.作法:如图2,△在直线l 上取一点A ,连接PA ;△作PA 的垂直平分线MN ,分别交直线l ,线段PA 于点B ,O ;△以O 为圆心,OB 长为半径作弧,交直线MN 于另一点Q ; △作直线PQ ,所以直线PQ 为所求作的直线.根据上述作图过程,回答问题:(1)用直尺和圆规,补全图2中的图形(保留作图痕迹);(2)完成下面的证明:证明:△直线MN 是PA 的垂直平分线,△PO =___________,90POQ AOB ∠=∠=︒.△OQ =___________,△POQ AOB △≌△.△___________=___________.△PQ l ∥(___________)(填推理的依据)【答案】(1)见解析(2)AO ;OB ;QPO ∠;BAO ∠;内错角相等,两直线平行.【分析】(1)根据题中描述即可作图;(2)根据垂直平分线的性质证明POQ AOB △≌△,得到QPO BAO ∠=∠,即可根据平行线的判定定理证明.【详解】(1)用直尺和圆规,补全图形如下;(2)证明:△直线MN 是PA 的垂直平分线,△PO AO =,90POQ AOB ∠=∠=︒.△OQ OB =,△POQ AOB △≌△.△QPO BAO ∠=∠.△PQ l ∥(内错角相等,两直线平行).故答案为:AO ;OB ;QPO ∠;BAO ∠;内错角相等,两直线平行.【点睛】本题考查了作图—复杂作图,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质,三角形全等的判定和性质,平行线的判定定理.64.如图, ABC C ∠∠=,点E 在线段AC 上,D 在AB 的延长线上,且有BD CE =,连接DE 交BC 于F ,过E 作EG BC ⊥于G .试说明线段BF 、FG 、CG 之间的数量关系.【答案】BF CG FG +=,证明见解析.【分析】如图(见解析),先根据三角形全等的判定定理得出DHB EGC ≅,再根据三角形全等的性质可得BH CG =,DH EG =,然后根据三角形全等的判定定理得出DHF EGF ≅,最后根据三角形全等的性质可得FH FG =,据此根据线段的和差、等量代换即可得证.【详解】BF CG FG +=,理由如下:如图,过点D 作DH CB ⊥,交CB 延长线于点H△ABC C ∠=∠,HBD ABC ∠=∠(对顶角相等)△HBD C ∠=∠在DHB △和EGC 中,90HBD C DHB EGC BD CE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩△()DHB EGC AAS ≅△BH CG =,DH EG =在DHF △和EGF △中,90DFH EFG DHF EGF DH EG ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩△()DHF EGF AAS ≅△FH FG =△BF BH FH FG +==△BF CG FG +=.【点睛】本题考查了三角形全等的判定定理与性质、对顶角相等、线段的和差等知识点,通过作辅助线,构造全等三角形是解题关键.65.为响应政府“绿色出行”的号召,张老师上班由自驾车改为骑公共自行车.已知张老师家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.张老师用骑公共自行车方式上班比用自驾车的方式上班多用多少小时?66.小明在学习分式的运算时,计算221x +的解答过程如下:请你指出小明解答过程中第△步的理论依据是 ;过程中错误出现在第 步(写出对应的序号即可),错误的原因是 , 请你给出这道题的正确解的答过程:67.在数轴上,点A 表示数a ,点B 表示数b ,在学习绝对值时,我们知道了绝对值的几何含义:数轴上A 、B 之间的距离记作AB ,定义:AB a b =-,如:点A 表示数1,点B 表示数3,则132AB =-=;1a -表示数a 和1在数轴上对应的两点之间的距离;6a +表示数a 和6-在数轴上对应的两点之间的距离.(1)在数轴上,若点A 表示数2-,点B 表示数6,△AB = ;△动点P 表示数x ,请求出满足2610x x ++-=的x 的值.(2)小林同学对(1)中正整数x 进行如下图操作:若x 为奇数,则先把x 乘以3,再把所得数在数轴上对应的点向右平移1个单位得到另一个数若x 为偶数,则把x 乘以12,如此循环重复操作图中△处应填写___________(用含x 的代数式表示)经过操作,小林发现有循环出现的数,请画出数轴并在数轴上标出这些循环出现的数.【答案】(1)△8;△x 的值为-3或7;(2)3x +1;循环出现的数为4、2、1,数轴见解析68.计算:()()232223122a ab a b ⎛⎫-- ⎪⎝⎭ )()36461142a b a b ⎛⎫-= ⎪⎝⎭【点睛】本题主要考查幂的乘方与积的乘方,熟练掌握运算法则是关键69.先化简,再求值[x 2+y 2﹣(x+y)2+2x(x ﹣y)]÷4x ,其中x =﹣2,y =2【分析】根据整式的运算法则把所给的整式化为最简后,再代入求值即可.70.如图,点A ,M ,B 在同一直线上,以AB 为边,分别在直线两侧作等边三角形ABC 和等边三角形ABD ,连接CM ,DM ,过点M 作MN =DM ,交BC 边于点G ,交DB 的延长线于点N .(1)求证:△BCM =△BDM ;(2)求△CMN 的度数;(3)求证:AM =BN . 【答案】(1)见解析;(2)60CMN ∠=︒;(3)见解析【分析】(1)根据ABC 和ABD △为等边三角形,且AB 为公共边,可以得出条件BC BD =,CBM DBM ∠=∠,即可证明()CBM DBM SAS ≌,由性质即可得出结论;(2)根据,MN DM BCM BDM =∠=∠,得出BDM BNM ∠=∠,BCM BNM ∠=∠,又根据CGM ∠和NGB ∠为对顶角,可得CMN NBC ∠=∠,再根据ABC 和ABD △为全等三角形,DBN ∠为平角,利用等量代换即可求出60CMN ∠=︒;(3)连接CN 由(1)可知:CBM DBM ≌,即可得CM DM =,证出CMN 为等边三角形,进而证明出()AMC BNC SAS ≌,由性质即可得出结论.【详解】解:(1)证明:ABC 和ABD △为等边三角形,且AB 为公共边, ,60BC BD CBM DBM ∴=∠=∠=︒,又在CBM 和DBM △中,CB DB CBM DBM BM BM =⎧⎪∠=∠⎨⎪=⎩,()CBM DBM SAS ∴≌,BCM BDM ∴∠=∠;(2),MN DM BCM BDM =∠=∠,BDM BNM ∴∠=∠,BCM BNM ∴∠=∠,又CGM ∠和NGB ∠为对顶角,CMN NBC ∴∠=∠,又ABC 和ABD △为全等三角形,DBN ∠为平角,60CBM DBM ∴∠=∠=︒,180DBN ∠=︒,180606060CMN NBC DBN DBM CBM ∴∠=∠=∠-∠-∠=︒-︒-︒=︒,(3)证明:连接CN ,如图所示:由(1)可知:CBM DBM ≌,CM DM ∴=,又,60MN DN CMN =∠=︒,CM MN ∴=,CMN ∴为等边三角形,,60CM CN MCN ∴=∠=︒,又ABC 为等边三角形,MCB ∠是ACB ∠和MCN ∠重叠的部分,,AC BC ACM BCN ∴=∠=∠,又在AMC 和BNC 中,AC BC ACM BCN CM CN =⎧⎪∠=⎨⎪=⎩,()AMC BNC SAS ∴≌,AM BN =.【点睛】本题考查了等边三角形的判定和性质、全等三角形的判定及性质、解题的关键是掌握全等三角形的判定定理及性质,再利用等量代换的思想进行解答.712+2n+1=0.(1)求﹣2m 2+6m ﹣4n 的值;(2)求m 2+21m﹣n 2013的值.72.某商店欲购进A 、B 两种化妆品,用160元购进的A 种化妆品与用240元购进的B 种化妆品的数量相同,每件B 种化妆品的进价比A 种化妆品的进价贵10元. (1)求A 、B 两种化妆品每件的进价分别为多少元?(2)若该商店A 种化妆品每件售价32元,B 种化妆品每件件价45元,准备购进A 、B 两种化妆品共100件,且这两种化妆品全部售出后总获利高于1300元,则最多购进A 种化妆品多少件?【答案】(1)A 、B 两种化妆品分别为20元、30元;(2)66件.20x , 20x 是原方程的解,且符合题意,则两种化妆品每件的进价分别为20元、)设购进A 种化妆品件,则购进B 种化妆品由题意得:(3220)30)(100)1300m m -->2663, 73.已知m 2=169,n 3=-27,求代数式m -n 的值.【点睛】本题考查了平方根的定义,立方根的定义,求代数式的值,解题的关键是熟练掌握平方根和立方根的定义,正确得到m 、n 的值.74.对于任意一个三位数p ,若个位上数字等于百位上的数字与十位上的数字之和,则称这个三位数p 为“桃园数”.例如:112p =,因为112+=,所以112是“桃园数”;253p =,因为253+≠,所以253不是“桃园数”;(1)判断459,615是否是“桃园数”?说明理由;(2)对于“桃园数”p ,去掉个位上的数字得到的两位数记为m ,去掉百位上的数字后将十位与个位的数字交换得到的两位数记为n ,若m n +能被24整除,求所有的p .75.如图,在直角坐标系中,ABC 的三个顶点坐标分别为A (1,4),B (4,2),C (3,5),请回答下列问题:(1)写出ABC 关于x 轴的对称图形111A B C △的顶点坐标.(2)求ABC 的面积.1,4(),A B 1(1,4),A ∴-(2)1,4(),A B 5BD BF ∴==-则ABC BDEF ABD BCF ACE S S S S S =---2111222BD AD BD BF CF AE CE -⋅-⋅-⋅ 111233112222-⨯⨯-⨯⨯-⨯⨯【点睛】本题考查了坐标与图形变化等知识点,掌握点坐标关于x 轴对称的变换规律是解题关键.76.边长为a 的正方形剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是_________(请选择正确的一个);A .2222()a ab b a b -+=-B .22(()a b a b a b -=+-C .2()a ab a a b +=+ (2)若22912,34x y x y -=+=,求3x y -的值;(3)计算:2222211111(1)(1)(1)(1)(1)23499100----- )边长为)229x y -3124y =÷77.如图,已知△ABC 中,E 、F 分别是AB 、AC 上的两点,且EF△BC,D 为EF 上一点,且ED=DF ,BD=CD ,请说明:BE=CF.【答案】见解析.【分析】利用SAS 证明△BDE△△CDF ,根据全等三角形的对应边相等即可得结论.【详解】△BD=CD ,△△DBC=△DCB ,又△EF△BC ,△△EDB =△DBC ,△FDC =△DCB ,△△EDB =△FDC ,又△ED =FD ,BD =CD ,△△BDE△△CDF(SAS),△BE =CF.【点睛】本题考查了等腰三角形的性质,平行线的性质,全等三角形的判定与性质,正确把握相关知识是解题的关键.78.计算:(1)()()201433π--+--;(2)()()4235243a a a a ⋅++-; (3)()()213a a +-;(4)()()22m n m m n ---;(5)2202020222021⨯-. 【答案】(1)-4;(2)11a 8;(3)2a 2-5a -3;(4))n 2;(5)-1.【分析】(1)原式利用绝对值的代数意义,零指数幂、负整数指数幂法则计算即可得到结果;(2)原式利用同底数幂的乘法,幂的乘方与积的乘方运算法则计算,合并即可得到结果;(3)原式利用多项式乘多项式法则计算,合并即可得到结果;(4)原式利用完全平方公式,以及单项式乘多项式法则计算,去括号合并即可得到结果;(5)原式变形后,利用平方差公式计算即可求出值.【详解】(1)原式=4+1-9=5-9=-4;(2)原式=a 8+a 8+9a 8=11a 8;(3)原式=2a 2-6a +a -3=2a 2-5a -3;(4)原式=(m 2-2mn +n 2)-(m 2-2mn )=m 2-2mn +n 2-m 2+2mn=n 2;(5)原式=(2021-1)×(2021+1)-20212=20212-1-20212=-1.【点睛】此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.79.如图,ABC 中,△ABC =90°,AB =BC ,P 为AB 上一动点,连接CP ,以AB为边作△BAD=△BCP,AD交CP的延长线于点D,连接BD,过点B作BE△BD交CP 于点E.(1)当△EBC=15°时,△ABD=°;(2)过点P作PH△AC于点H,是否存在点P,使得BC=HC,若存在,请求出此时△ACP 的度数,若不存在,请说明理由;(3)若AD=2,ED=7,求ADC的面积.80.先化简,再求值:(3x +2)(3x -2)-5x (x +1)-(x -1)2,其中x 2-x -10=0. 【答案】3x 2-3x -5,25【分析】原式第一项利用平方差公式化简,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并得到最简结果,将已知的方程变形后代入即可求值.【详解】原式=()222945521x x x x x -----+=222945521x x x x x ----+-=2335x x --,当2100x x =--,即210x x =-时,原式=()235310525x x -=⨯-=-【点睛】本题考查整式的混合运算-化简求值,涉及的知识点有:完全平方公式、平方差公式、去括号法则及合并同类项法则,熟练掌握以上公式及法则是解题的关键. 81.已知:3a b +=,1x y -=,求222a ab b x y ++-+的值.【答案】8【详解】试题分析:本题可先将原代数式化简得出关于a+b 和x -y 的式子,再把已知代入即可.试题解析:△a+b=3,x−y=1,△a 2+2ab+b 2−x+y=(a+b)2−(x−y) =9−1=8.82.求证:有两边和其中一边上的高对应相等的两个锐角三角形全等. 【答案】见解析【分析】根据题意首先写出已知和求证,进而利用全等三角形的判定与性质得出Rt △ABD △ Rt △A B D '''以及△B=△B′进而得出△ABC△A B C '''.【详解】解:如图:已知:如图,在△ABC 与△A B C '''中.AB =A B '',BC =B C '',AD△BC 于D ,A D ''△B C '' 于D 且 AD =A D ''求证:△ABC△△A B C '''证明: 在Rt △ABD 与Rt △A B D '''中△AB A B AD A D ''''=⎧⎨=⎩△Rt △ABD △ Rt △A B D ''' (HL)△△B =△B '(全等三角形对应角相等)在△ABC 与△A B C '''中△AB A B B B BC B C =⎧⎪∠=∠⎨⎪=''''⎩' △△ABC△△'''A B C (SAS)【点睛】本题考查了全等三角形判定的应用,灵活运用全等三角形的判定方法是解题的关键.83.计算:2221244x x x x x x +----+.84.老师给同学们布置了一个“在平面内找一点,使该点到等腰三角形的三个顶点的距离相等”的尺规作图任务:下面是小聪同学设计的尺规作图过程:已知:如图,ABC ∆中,AB AC =,求作:一点P ,使得PA PB PC ==.作法:△作BAC ∠的平分线AM 交BC 于点D ;△作边AB 的垂直平分线EF ,EF 与AM 相交于点P ;△连接,PB PC ,所以,点P 就是所求作的点.根据小聪同学设计的尺规作图过程,(1)使用直尺和圆规,补全图形(保留作图痕迹)(2)完成下面的证明.证明:△AB AC =,AM 平分BAC ∠交BC 于点D ,△AD 是BC 的垂直平分线;( )(填推理依据)△PB PC =.△EF 垂直平分AB ,交AM 于点P ,△PA PB =;( )(填推理依据)△PA PB PC ==.【答案】(1)见解析;(2)等腰三角形的三线合一 线段垂直平分线上的点到线段两端点的距离相等.【分析】(1)利用基本作图作角平分线AD 和AB 的垂直平分线,它们相交于P 点;(2)根据等腰三角形的性质得到PB=PC .再根据线段垂直平分线上的点到线段两端的距离相等得到PA=PC ,从而得到PA=PB=PC .【详解】(1)如图,AD 、点P 为所求;(2)证明:△AB AC =,AM 平分BAC ∠交BC 于点D ,△AD 是BC 的垂直平分线;( 等腰三角形的三线合一 )(填推理依据)△PB PC =.△EF 垂直平分AB ,交AM 于点P ,△PA PB =;( 线段垂直平分线上的点到线段两端点的距离相等 )(填推理依据) △PA PB PC ==.【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作. 85.用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段c ,求作Rt △ABC ,使△C =90°,BC =c ,AB =2c .【答案】见解析【分析】在直线l 上取点C ,作CD △l ,在CD 上截取CB =c ,分别以B ,C 为圆心,c 为半径画弧,交于点E ,连接BE 并延长交直线l 于点A ,则AB =2c .【详解】如图所示,Rt △ABC 即为所求.【点睛】本题主要考查了复杂作图,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作. 86.△ABC 中,AD 是∠BAC 的角平分线,AE 是△ABC 的高.(1)如图1,若∠B =40°,∠C =60°,请说明∠DAE 的度数;(2)如图2(∠B <∠C ),试说明∠DAE 、∠B 、∠C 的数量关系;(3)如图3,延长AC 到点F ,∠CAE 和∠BCF 的角平分线交于点G ,请直接写出∠G 的度数 . )40B ∠=AE 是ABC ∆的高,AEC ∴∠=60C ∠=CAE ∴∠=AD 是∠CAD ∴∠=DAE ∴∠=(2)BAC ∠+180BAC ∴∠=︒-AE 是ABC ∆的高,90,AEC =︒AD 是∠CAD ∴∠=DAE ∴∠=(11802=︒1C =∠-)CAE ∠和2CAE CAG =∠CAE FCB ∠=∠2FCG AEC ∴∠-∠AE 是ABC ∆的高,AEC ∴∠=45G ∴∠=故答案为:【点睛】本题主要考查了三角形内角和定理、角平分线的定义、三角形外角的性质等知识点,灵活应用相关知识成为解答本题的关键.87.把下列各式分解因式:(1)22425x y - (2) 2x y y -(3)224()x y z -- (4)2216()()a b a b --+(5)33327xy x y -+ (6) 2222416a x a y -(7)(2)(80+6a a a +- (8)4481x y -(9)224(23)(3)p q p q +-- (10)22169()196()a b a b --+【答案】(1)(2x+5y)(2x -5y); (2)y(x+1)(x -1); (3)(2x+y -z)(2x -y+z); (4)(5a -3b)(3a -5b);(5)-3xy(y+3x)(y -3x); (6)4a 2(x+2y)(x -2y); (7)(a+4)(a -4); (8)()()229)33x y x y x y ++-(; (9)(7p+5q)(p+7q); (10)-(27a+b)(a+27b);.【详解】试题分析:(1)直接利用平方差公式进行分解即可;(2)首先提取公因式y ,再利用平方差公式进行分解即可;(3)直接利用平方差公式进行分解即可;(4)直接利用平方差公式进行分解即可;(5)首先提取公因式-3xy ,再利用平方差公式进行分解即可;(6)首先提取公因式4a 2,再利用平方差公式进行分解即可;(7)首先进行乘法运算,再利用平方差进行分解即可;(8)直接利用平方差公式进行二次分解即可;(9)首先利用平方差公式进行分解,再把括号里面的同类项进行合并即可; (10)直接利用平方差公式进行分解即可.试题解析:(1)原式=(2x+5y )(2x -5y );(2)原式=y (x 2-1)=y (x+1)(x -1);(3)原式=(2x+y -z )(2x -y+z );(4)原式=(5a -3b )(3a -5b );(5)原式=-3xy (y 2-9)=-3xy (y+3x )(y -3x );(6)原式=4a 2(x 2-4y 2 )=4a 2(x+2y )(x -2y );(7)原式=a 2-16+6a -6a=(a+4)(a -4);(8)原式=(9x 2+y 2)(3x+y )(3x -y );(9)原式=(7p+5q )(p+7q );(10)原式=-(27a+b )(a+27b ).88.在正方形ABCD 的边AB 上任取一点E ,作EF AB ⊥交BD 于点F ,取FD 的中点G ,连接EG 、CG ,如图()1,易证 EG CG =且EG CG ⊥.()1将BEF 绕点B 逆时针旋转90,如图()2,则线段EG 和CG 有怎样的数量关系和位置关系?请直接写出你的猜想.()2将BEF 绕点B 逆时针旋转180,如图()3,则线段EG 和CG 又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明. 90,90EBC ∠,90BCM ∠,BEMC 是矩形.,90EMC ∠,90ABC =,45,AB ,∵BEF 为等腰直角三角形BE EF =,45.EF CM =90EMC ∠=,FG DG =,12MG FD FG ==45,∵F GMC ∠=∠.∵在GFE与GMC中,FG MG F GMC EF CM=⎧⎪∠=∠⎨⎪=⎩,∵()GFE GMC SAS≅.∵EG CG=,FGE MGC∠=∠.∵90FMC∠=,MF MD=,FG DG=,∵MG FD⊥,∵90FGE EGM∠+∠=,∵90MGC EGM∠+∠=,即90EGC∠=,∵EG CG⊥.【点睛】此题综合考查了旋转的性质及全等三角形的判断和性质,如何构造全等的三角形是难点,因此难度较大.89.如图,在平面直角坐标系中,已知点()1,A a a b-+,(),0B a,且()220a b-=,C为x轴上点B右侧的动点,以AC为腰作等腰ACD,使AD AC=,CAD OAB∠=∠,直线DB交y轴于点P.(1)求证:AO AB=;(2)求证:AOC ABD△△≌;(3)当点C运动时,点P在y轴上的位置是否发生变化,为什么?【答案】(1)见解析;(2)见解析;(3)不变,理由见解析【分析】(1)先根据非负数的性质求出a、b的值,作AE OB⊥于点E,由SAS定理得出AEO AEB∆≅∆,根据全等三角形的性质即可得出结论;(2)先根据CAD OAB∠=∠,得出OAC BAD∠=∠,再由SAS定理即可得出AEO AEB∆≅∆;(3)设AOB ABOα∠=∠=,由全等三角形的性质可得出ABD AOBα∠=∠=,故)证明:(3,9)A ,3OE ∴=在AEO ∆AE AEO =⎧⎪∠⎨⎪)证明:CAD ∠=BAC OAB =∠ABD 中,BAD ⎪∠⎨⎪,由(2OB =,OP ∴长度不变,∴点P 在【点睛】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.90.如图,△ABC=90°,点D、E分别在BC、AC上,AD△DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连接MC.(1)MF与AC的位置关系是:______.(2)求证:CF=MF.(3)猜想:AD与MC的位置关系,并说明理由.【答案】(1)MF△AC;(2)证明见解析;(3)AD△MC.【分析】(1)只要证明△ADE是等腰直角三角形,即可解决问题;(2)根据等腰直角三角形的性质,得出DF△AE,DF=AF=EF,再证明△DFC△△AFM,得出FC=FM;(3)依据△DFC=90°,DF=EF,△FDE=△FMC=45°,即可得到△DEF、△CFM是等腰直角三角形,进而证明DE△MC,即可得出结论.【详解】(1)△AD△DE,AD=DE,△△ADE是等腰直角三角形,△AF=EF,△DF△AE,即MF△AC.故答案为MF△AC.(2)△AD△DE,且AD=DE,F是AE的中点,△DF△AE,DF=AF=EF,△△AFM=90°,△△FAM+△AMF=90°,△△ABC=90°, △△FAM+△DCF=90°,△△DCF=△AMF ,在△DFC 和△AFM 中,90DFC AFM DCF AMFDF AF ====∠∠︒⎧⎪∠∠⎨⎪⎩, △△DFC△△AFM (AAS ),△FC=FM ;(3)AD△MC .理由:由(2)得:△DFC=90°,DF=EF ,FM=FC,△△DEF 、△CFM 是等腰直角三角形,△△FDE=△FMC=45°,△DE△MC ,△AD△DE ,△AD△MC .【点睛】本题考查了等腰直角三角形的性质与判定以及全等三角形的判定与性质的综合应用,熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键. 91.数学课上,老师在黑板上展示了如下一道探究题:在ABC 中,AB AC m ==,BAC α∠=,点D ,E 分别在边AC ,AB 上,且CE BD =,试探究线段AE 和线段AD 的数量关系.(1)初步尝试如图△,若90α=︒,请探究AE 和AD 的数量关系,并说明理由.(2)类比探究如图△,若120α=︒,小组讨论后,有小组利用120°的角作垂线构造直角三角形,通过证明两次三角形全等,得到AE 和AD 的数量关系仍然成立,请你写出推理过程;(3)延伸拓展如图△,将第(2)中的“点E在边AB上”改为“点E在边BA的延长线上”,其它条件不变,请探究AE和AD的数量关系(用含m的式子表示),并说明理由.试卷第41页,共41页。
初中数学特殊的平行四边形50题(含答案)

特殊的平行四边形练习题(50题)菱形、矩形、正方形一、单选题(共18题;共36分)1.下列条件中,能判定一个四边形为矩形的条件是( )A. 对角线互相平分的四边形B. 对角线相等且平分的四边形C. 对角线相等的四边形D. 对角线相等且互相垂直的四边形【答案】B【解析】【解答】解:A、对角线互相平分的四边形是平行四边形,故A不符合题意;B、对角线相等且平分的四边形是矩形,故B符合题意;C、对角线相等的四边形不是矩形,故C不符合题意;D、对角线相等且互相垂直的四边形不是矩形,故D不符合题意.故答案为:B.【分析】根据矩形的判定方法,逐项进行判断,即可求解2.如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a ,EF=b ,NH= c ,则下列各式中正确的是()A. a > b > cB. a =b =cC. c > a > bD. b > c > a【答案】B【解析】【解答】解:连接OA、OD、OM,如图所示:则OA=OD=OM,∵四边形ABOC、DEOF、HNMO均为矩形,∴OA=BC=a,OD=EF=b,OM=NH=c,∴a=b=c;故答案为:B.【分析】连接OA、OD、OM,则OA=OD=OM,由矩形的对角线相等得出OA=BC=a,OD=EF=b,OM=NH=c,再由同圆的半径相等即可得出a=b=c.3.如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )A. 1B. 2C.D.【答案】 D【解析】【解答】解:连接DE交AC于P,连接BD,BP,由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,∴PE+PB=PE+PD=DE,即DE就是PE+PB的最小值,∵∠BAD=60°,AD=AB,∴△ABD是等边三角形,∴AD=BD,∵AE=BE=AB=1,∴DE⊥AB,在Rt△ADE中,DE=,∴ PE+PB的最小值是.故答案为:D.【分析】连接DE交AC于P,连接BD,BP,根据菱形的性质得出B、D关于AC对称,得出DE就是PE+PB 的最小值,根据等边三角形的判定与性质得出DE⊥AB,再根据勾股定理求出DE的长,即可求解.4.若正方形的对角线长为2 cm,则这个正方形的面积为()A. 4B. 2C.D.【答案】B【解析】【解答】解:设正方形的边长为xcm,根据题意得:x2+x2=22,∴x2=2,∴正方形的面积=x2=2(cm2).故答案为:B.【分析】设正方形的边长为xcm,利用勾股定理列出方程,求出x2=2,即可求出正方形的面积为2.5.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为()A. 72B. 24C. 48D. 96【答案】C【解析】【解答】解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,∵OA=6,∴AC=12,∴菱形ABCD的面积= AC•BD=×12×8=48.故答案为:C.【分析】根据菱形的性质得O为BD的中点,再由直角三角形斜边上的中线等于斜边的一半,得BD的长度,最后由菱形的面积公式求得面积.6.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )A. 73°B. 56°C. 68°D. 146°【答案】A【解析】【解答】如图,∵∠CBD=34°,∴∠CBE=180°﹣∠CBD=146°,由折叠的性质可得∠ABC=∠ABE= ∠CBE=73°.故答案为:A【分析】根据补角的知识可求出∠CBE,从而根据折叠的性质∠ABC=∠ABE= ∠CBE,可得出∠ABC的度数.7.如图,已知矩形AOBC的顶点O(0,0),A(0,3),B(4,0),按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OC,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠BOC内交于点F;③作射线OF,交边BC于点G,则点G的坐标为()A. (4,1)B. (4,)C. (4,)D. (4,)【答案】B【解析】【解答】解:∵四边形AOBC是矩形,A(0,3),B(4,0),∴OB=4,OA=BC=3,∠OBC=90°,∴OC==5,作GH⊥OC于H,如图,由题意可知:OG平分∠BOC,∵GB⊥OB,GH⊥OC,∴GB=GH,设GB=GH=x,由S△OBC=×3×4=×5×x+ ×4×x,解得:x=,∴G(4,).故答案为:B.【分析】根据勾股定理可得OC的长,作GH⊥OC于H,根据角平分线的性质可得GB=GH,然后利用面积法求出GB即可.8.如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )A. 2B.C.D. 1【答案】B【解析】【解答】解:由图象可知:AE=3,BE=4,在Rt ABE中,∠AEB=90°AB= =5当x=6时,点P在BE上,如图,此时PE=4-(7-x)=x-3=6-3=3∵∠AEB=90°, PQ⊥CD∴∠AEB=∠PQE=90°,在矩形ABCD中,AB//CD∴∠QEP=∠ABE∴PQE BAE, ∴=∴=∴PQ=故答案为:B.【分析】由图象可知:AE=3,BE=4,根据勾股定理可得AB=5,当x=6时,点P在BE上,先求出PE的长,再根据△ PQE ∽△ BAE,求出PQ的长.9.如图,在平面直角坐标系中,已知点,.若平移点到点,使以点,,,为顶点的四边形是菱形,则正确的平移方法是()A. 向左平移1个单位,再向下平移1个单位B. 向左平移个单位,再向上平移1个单位C. 向右平移个单位,再向上平移1个单位D. 向右平移1个单位,再向上平移1个单位【答案】 D【解析】【解答】解:因为B(1,1)由勾股定理可得OB=,所以OA=OB,而AB<OA.故以AB为对角线,OB//AC,由O(0,0)移到点B(1,1)需要向右平移1个单位,再向上平移1个单位,由平移的性质可得由A(,0)移到点C需要向右平移1个单位,再向上平移1个单位,故选D.【分析】根据平移的性质可得OB//AC,平移A到C,有两种平移的方法可使O,A,B,C四点构成的四边形是平行四边形;而OA=OB>AB,故当OA,OB为边时O,A,B,C四点构成的四边形是菱形,故点A平移到C的运动与点O平移到B的相同.10.如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于()A. 25ºB. 50ºC. 100ºD. 115º【答案】 D【解析】解析:∵把矩形ABCD沿EF对折,∴AD∥BC,∠BFE=∠2,∵∠1=50°,∠1+∠2+∠BFE=180°,∴∠BFE==65°,∵∠AEF+∠BFE=180°,∴∠AEF=115°.故选D11.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A. ②③B. ③④C. ①②④D. ②③④【答案】 D【解析】【解答】∵AB=1,AD=,∴BD=AC=2,OB=OA=OD=OC=1.∴△OAB,△OCD为正三角形.AF平分∠DAB,∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,BF=BO=1.∵AF平分∠DAB,∴∠FAB=45°,∴∠CAH=45°﹣30°=15°.∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH由正三角形上的高的性质可知:DE=OD÷2,OD=OB,∴BE=3ED.所以正确的是②③④.故选D.【分析】这是一个特殊的矩形:对角线相交成60°的角.利用等边三角形的性质结合图中的特殊角度解答.本题主要考查了矩形的性质及正三角形的性质.12.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB 上,当△CDE的周长最小时,点E的坐标为()A. (3,1)B. (3,)C. (3,)D. (3,2)【答案】B【解析】【解答】解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.∵D(,0),A(3,0),∴H(,0),∴直线CH解析式为y=﹣x+4,∴x=3时,y= ,∴点E坐标(3,)故选:B.【分析】如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.13.如图,正方形ABCD的边长为4,M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为().A. 3B. 4C. 5D.【答案】C【解析】【分析】由正方形的对称性可知点B与D关于直线AC对称,连接BM交AC于N′点,N′即为所求在Rt△BCM中利用勾股定理即可求出BM的长即可.【解答】∵四边形ABCD是正方形,∴点B与D关于直线AC对称,连接BD,BM交AC于N′,连接DN′,N′即为所求的点,则BM的长即为DN+MN的最小值,∴AC是线段BD的垂直平分线,又CM=CD-DM=4-1=3,在Rt△BCM中,BM==5,故DN+MN的最小值是5.故选C.【点评】本题考查的是轴对称-最短路线问题及正方形的性质,先作出M关于直线AC的对称点M′,由轴对称及正方形的性质判断出点M′在BC上是解答此题的关键.14.将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是,则点C的坐标是()A. (4,2)B. (2,4)C. (,3)D. (3,)【答案】 D【解析】【解答】解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,过点A作AN⊥BF于点N,过点C作CM⊥x轴于点M,∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,∴∠EAO=∠COM,又∵∠AEO=∠CMO,∴∠AEO∽△COM,∴=,∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,∴∠BAN=∠EAO=∠COM,在△ABN和△OCM中∴△ABN≌△OCM(AAS),∴BN=CM,∵点A(−1,2),点B的纵坐标是,∴BN= ,∴CM= ,∴MO==2CM=3,∴点C的坐标是:(3, ).故选:D.【分析】次题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识.构造直角三角形,正确得出CM的长是解题的关键.15.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A. 1B. 2C. 3D. 4【答案】 D【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.16.如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M 为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为()A. 5B.C.D.【答案】B【解析】【解答】设BE=x,则CE=6-x,∵四边形ABCD矩形,AB=4,∴AB=CD=4,∠C=∠B=90°,∴∠DEC+∠CDE=90°,又∵F是AB的中点,∴BF=2,又∵EF⊥ED,∴∠FED=90°,∴∠FEB+∠DEC=90°,∴∠FEB=∠CDE,∴△BFE∽△CED,∴=,∴=,∴(x-2)(x-4)=0,∴x=2,或x=4,①当x=2时,∴EF=2,DE=4,DF=2,∴AM=ME=,∴AE===2,②当x=4时,∴EF=2,DE=2,DF=2,∴AM=ME=,∴AE==2,AE==4,∴x=4不合题意,舍去故答案为:B.【分析】设BE=x,则CE=6-x,由矩形性质得出AB=CD=4,∠C=∠B=90°,又由EF⊥ED,根据同角的余角相等可得出∠FEB=∠CDE;由相似三角形的判定得出△BFE∽△CED,再根据相似三角形的性质得出=,由此列出方程从而求出x=2或x=4,分情况讨论:①当x=2时,由勾股定理算出AE===2,②当x=4时,由勾股定理算出AE==2,AE==4,故x=4不合题意,舍去.17.如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【解答】∵四边形ABCD是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.18.如图,P是正方形ABCD内一点,∠APB=135,BP=1,AP=,求PC的值()A. B. 3 C. D. 2【答案】B【解析】【分析】解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.如图,把△PBC绕点B逆时针旋转90°得到△ABP′,点C的对应点C′与点A重合.根据旋转的性质可得AP′=PC,BP′=BP,△PBP′是等腰直角三角形,利用勾股定理求出,然后由∠APB=135,可得出∠APP′=90°,再利用勾股定理列式计算求出.故选B.二、填空题(共15题;共16分)19.如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为________。
苏科版数学八年级下册 9.4矩形菱形正方形大题综合练习(含答案解析)
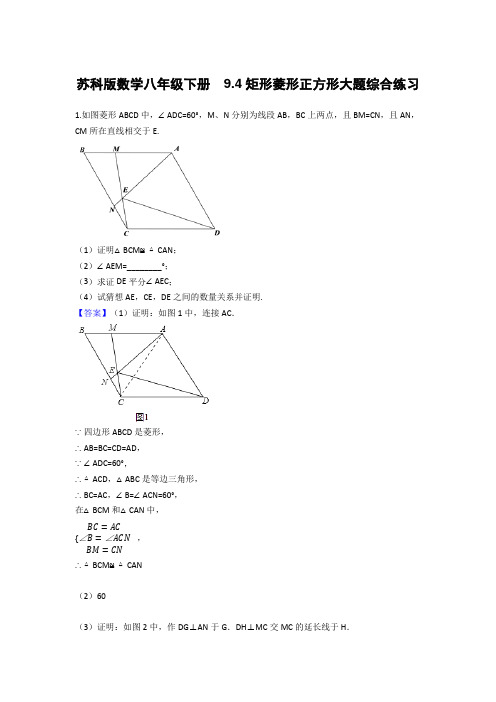
苏科版数学八年级下册9.4矩形菱形正方形大题综合练习1.如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.(1)证明△BCM≌△CAN;(2)∠AEM=________°;(3)求证DE平分∠AEC;(4)试猜想AE,CE,DE之间的数量关系并证明.【答案】(1)证明:如图1中,连接AC.∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵∠ADC=60°,∴△ACD,△ABC是等边三角形,∴BC=AC,∠B=∠ACN=60°,在△BCM和△CAN中,{BC=AC∠B=∠ACNBM=CN,∴△BCM≌△CAN(2)60(3)证明:如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.∵∠AEM=60°,∴∠AEC=120°,∵∠DGE=∠H=90°,∴∠GEH+∠GDH=180°,∴∠GDH=∠ADC=60°,∴∠ADG=∠CDH ,在△DGA 和△DHC 中,{∠DGA =∠H =90∘∠ADG =∠CDH DA =DC,∴△DGA ≌△DHC ,∴DG=DH ,∵DG ⊥AN ,DH ⊥MC ,∴∠DEG=∠DEH .∴DE 平分∠AEC .(4)证明:结论:EA+EC=ED .理由如下:如图2中,由(3)可知,∠GED=60°,在Rt △DEG 中,∵∠EDG=30°,∴DE=2EG ,易知△DEG ≌△DEH ,∴EG=EH ,∴EA+EC=EG+AG+EH-CH ,∵△DGA ≌△DHC ,∴GA=CH ,∴EA+EC=2EG=DE ,∴EA+EC=ED.【解析】【解答】解:(2)如图1中,∵△BCM ≌△CAN ,∴∠BCM=∠CAN ,∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.故答案为60.【分析】(1)连接AC,因为∠ADC=60°,利用菱形四边相等的性质,可知△ADC为等边三角形,所以AC=BC ,又因为菱形的对角线平分一组对角,所以∠ACN=60°=∠B,因为BM=CN,所以△BCM≌△CAN;(2)因为∠AEM=∠CEN,对顶角相等,由全等可知∠AEM=∠CEN=∠B=60°;(3)过点D做AE、CM两边的垂线,利用角角边可得到△DHC≌△DGA,可得DH=DG,再用角平分线的性质,到一个角两边距离相等的点在这个角的角平分线上;(4)由全等可知EA+EC=2EG,又因为在Rt△中30°的角所对的边等于斜边的一半,所以EA +EC=DE.2.综合:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为A. 平行四边形B. 菱形C. 矩形D. 正方形(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.【答案】(1)C(2)解:如图2中,①证明:∵AD=5,S□ABCD=15,∴AE=3.又∵在图2中,EF=4,∴在Rt△AEF中,AF═5.∴AF=AD=5,又∵AF∥DF',AF=DF,∴四边形AFF'D是平行四边形.∴四边形AFF'D是菱形.②解:连接AF',DF,在Rt△DE'F中,∵E'F=E'E﹣EF=5﹣4=1,DE'=3,∴DF═√E′D2+E′F2= √10.在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,∴AF'═√AE2+EF′2= √32+92=3 √10【解析】【解答】(1)解:如图1中,∵四边形ABCD是平行四边形,∴AD=BC,∵BE=CE′,∴AD∥EE′,AD=EE′,∴四边形AEE′D是平行四边形,∵∠AEE′=90°,∴四边形AEE′D是矩形,故选C.【分析】(1)根据矩形的判定方法即可判定;(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;②连接AF',DF,分别利用勾股定理计算即可;3.如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF 的面积为S1,△PDE的面积为S2.(1)求证:BP⊥DE.(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围.(3)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.【答案】(1)解:如图1中,延长BP交DE于M.∵四边形ABCD是正方形,∴CB=CD,∠BCP=∠DCE=90°,∵CP=CE,∴△BCP≌△DCE,∴∠BCP=∠CDE,∵∠CBP+∠CPB=90°,∠CPB=∠DPM,∴∠CDE+∠DPM=90°,∴∠DMP=90°,∴BP⊥DE.(2)解:由题意S1﹣S2= 12(4+x)•x﹣12•(4﹣x)•x=x2(0<x<4).(3)解:①如图2中,当∠PBF=30°时,∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,∴∠PFD=∠DPF=45°,∴DF=DP,∵AD=CD,∴AF=PC,∵AB=BC,∠A=∠BCP=90°,∴△BAF≌△BCP,∴∠ABF=∠CBP=30°,∴x=PC=BC•tan30°= 4√3,3∴S1﹣S2=x2= 16.3②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.由①可知△ABF≌△BCP,∴∠ABF=∠CBP,∵∠PBF=45°,∴∠CBP=22.5°,∵∠CNP=∠NBP+∠NPB=45°,∴∠NBP=∠NPB=22.5°,∴BN=PN= √2x,∴√2x+x=4,∴x=4 √2﹣4,∴S1﹣S2=(4 √2﹣4)2=48﹣32 √2.【解析】【分析】(1)首先延长BP交DE于M.然后依据SAS可证明△BCP≌△DCE,依据全等三角形的性质可得到∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°;(2)根据题意可得到S1-S2=S△PBE-S△PDE,然后依据三角形的面积公式列出函数关系式即可;(3)分当∠PBF=30°和∠PBF=45°两种情形分别求出PC 的长,最后再利用(2)中结论进行计算即可.4.如图,在矩形ABCD 中,BC >AB ,∠BAD 的平分线AF 与BD ,BC 分别交于点E ,F ,点O 是BD 的中点,直线OK ∥AF ,交AD 于点K ,交BC 于点G .(1)求证:△DOK ≌△BOG ;(2)探究线段AB 、AK 、BG 三者之间的关系,并证明你的结论;(3)若KD=KG ,BC=2 √2 ﹣1,求KD 的长度.【答案】(1)证明:∵在矩形ABCD 中,AD ∥BC ,∴∠KDO=∠GBO ,∠DKO=BGO .∵点O 是BD 的中点;∴DO=BO .在△DOK 和△BOG 中, {∠KDO =∠GBO∠DKO =∠BGO DO =BO∴△DOK ≌△BOG (AAS ).(2)解:AB+AK=BG ;证明如下:∵四边形ABCD 是矩形;∴∠BAD=∠ABC=90°,AD ∥BC .又∵AF 平分∠BAD ,∴∠BAF=∠BFA=45°.∴AB=BF .∵OK ∥AF ,AK ∥FG ,∴四边形AFGK 是平行四边形.∴AK=FG .∵BG=BF+FG ;∴BG=AB+AK .(3)解:∵四边形AFGK 是平行四边形.∴AK=FG ,AF=KG又∵△DOK ≌△BOG ,且KD=KG ,∴AF=KG=KD=BG .设AB=a ,则AF=KG=KD=BG= √2 a .∴AK=2 √2 ﹣1﹣ √2 a ,FG=BG ﹣BF= √2 a ﹣a .∴2 √2﹣1﹣√2a= √2a﹣a.解得a=1.∴KD= √2a= √2.【解析】【分析】(1)在矩形ABCD中,AD∥BC,得到∠KDO=∠GBO,∠DKO=BGO,DO=BO,得到△DOK≌△BOG(AAS);(2)四边形ABCD是矩形,得到∠BAD=∠ABC=90°,AD∥BC,又AF平分∠BAD,得到∠BAF=∠BFA=45°,AB=BF,由OK∥AF,AK∥FG,得到四边形AFGK 是平行四边形,得到AK=FG,BG=BF+FG,即BG=AB+AK;(3)四边形AFGK是平行四边形,得到AK=FG,AF=KG,又△DOK≌△BOG,且KD=KG,得到AF=KG=KD=BG,设AB=a,则AF=KG=KD=BG=√2a,得到AK=2√2﹣1-√2a,FG=BG﹣BF=√2a﹣a,解得a=1,得到KD=√2a=√2.5.综合题(1)感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.(2)探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为________ .【答案】(1)证明:∵四边形ABCD、四边形CEFG均为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,在△BCE和△DCG中,{CB=CD∠BCE=∠DCGCE=CG,∴△BCE≌△DCG,∴BE=DG.(2)∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,∵∠A=∠F,∴∠BCD=∠ECG,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,∴△BCE≌△DCG.,∴BE=DG.(3)20【解析】【解答】解:应用:∵四边形ABCD是菱形,S△EBC=8,∴S△AEB+S△EDC=8,∵AE=3DE,∴S△AEB=3S△EDC,∴S△EDC=6,S△EDC=2,∵△BCE≌△DCG,∴S△DGC=S△EBC=8,∴S△ECG=8+2=10,∴菱形CEFG的面积=2•S△EGC=20,故答案为20.【分析】感知:根据正方形的性质,得到BC=CD,CE=CG,∠BCD=∠ECG=90°,得到∠BCE=∠DCG,得到△BCE≌△DCG,BE=DG;探究:由四边形ABCD、四边形CEFG均为菱形,得到BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,由∠A=∠F,得到∠BCE=∠DCG,△BCE≌△DCG,BE=DG;应用:由四边形ABCD是菱形,△EBC的面积为8,AE=3DE,得到S△AEB=3S△EDC,得到S△EDC=6,S△EDC=2,由△BCE≌△DCG,得到S△DGC=S△EBC=8,S△ECG=8+2=10,所以菱形CEFG的面积=2•S△EGC=20.6.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(3,4),一次函x+b的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE 数y=23上的一个动点.(1)求b的值;(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N 的坐标.【答案】(1)解:y=23x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,∵OD=BE,∴BE=b,则E的坐标是(3,4﹣b),把E的坐标代入y=23x+b得4﹣b=﹣2+b,解得:b=3(2)解:S四边形OAED= 12(OD+AE)•OA= 12×(3+1)×3=6,∵三角形ODM的面积与四边形OAEM的面积之比为1:3,∴S△ODM=1.5.设M的横坐标是a,则12×3a=1.5,解得:a=1,把x=a=1代入y=﹣23x+3得y=﹣23× 43+3= 73.则M的坐标是(1,73)(3)解:当四边形OMDN是菱形时,如图(1),M的纵坐标是32,把y= 32代入y=﹣23x+3,得﹣23x+3= 32,解得:x= 94,则M的坐标是(94,32),则N的坐标是(﹣94,32);当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是﹣23m+3,则m2+(﹣23m+3)2=9,解得:m= 3613或0(舍去).则M的坐标是(3613,1513).则DM的中点是(1813,2713).则N的坐标是(3613,5413).故N的坐标是(﹣94,32)或(3613,5413).【解析】【分析】(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN 是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.7.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2.(1)若DG=6,求AE的长;(2)若DG=2,求证:四边形EFGH是正方形.【答案】(1)解:∵AD=6,AH=2∴DH=AD﹣AH=4∵四边形ABCD是矩形∴∠A=∠D=90°∴在Rt△DHG中,HG2=DH2+DG2在Rt△AEH中,HE2=AH2+AE2∵四边形EFGH是菱形∴HG=HE∴DH2+DG2=AH2+AE2即42+62=22+AE2∴AE= =4(2)证明:∵AH=2,DG=2,∴AH=DG,∵四边形EFGH是菱形,∴HG=HE,在Rt△DHG和Rt△AEH中,,∴Rt△DHG≌Rt△AEH(HL),∴∠DHG=∠AEH,∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形【解析】【分析】(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2,HE2=AH2+AE2,再根据菱形的性质,得到等式DH2+DG2=AH2+AE2,最后计算AE的长;(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.8.如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD 于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.(1)AM=________,AP=________.(用含t的代数式表示)(2)当四边形ANCP为平行四边形时,求t的值(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由②使四边形AQMK为正方形,则AC等于.【答案】(1)8﹣2t;2+t(2)解:∵四边形ANCP为平行四边形时,CN=AP,∴6﹣t=8﹣(6﹣t),解得t=2(3)解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:∵NP⊥AD,QP=PK,∴当PM=PA时有四边形AQMK为菱形,∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,②要使四边形AQMK为正方形.∵∠ADC=90°,∴∠CAD=45°.∴四边形AQMK为正方形,则CD=AD,∵AD=8,∴CD=8,∴AC=8 √2.【解析】【解答】解:(1)如图1.∵DM=2t,∴AM=AD﹣DM=8﹣2t.∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P,∴四边形CNPD为矩形,∴DP=CN=BC﹣BN=6﹣t,∴AP=AD﹣DP=8﹣(6﹣t)=2+t;故答案为:8﹣2t,2+t.【分析】(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;(3)①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.9.已知▱OABC的顶点A、C分别在直线x=2和x=4上,O为坐标原点,直线x=2分别与x轴和OC边交于D、E,直线x=4分别与x轴和AB边的交于点F、G.(1)如图,在点A、C移动的过程中,若点B在x轴上,①直线AC是否会经过一个定点,若是,请直接写出定点的坐标;若否,请说明理由.②▱OABC是否可以形成矩形?如果可以,请求出矩形OABC的面积;若否,请说明理由.③四边形AECG是否可以形成菱形?如果可以,请求出菱形AECG的面积;若否,请说明理由.(2)在点A 、C 移动的过程中,若点B 不在x 轴上,且当▱OABC 为正方形时,直接写出点C 的坐标.【答案】(1)解:①是,经过定点(3,0).理由如下:如图1中,连接AC 交OB 于K .∵四边形OABC 是平行四边形,∴OK=KB ,BC ∥OA ,BC=OA ,∴∠CBF=∠AOD ,在△DOA 和△FBC 中,{∠ODA =∠CFB =90°∠AOD =∠CBF OA =BC,∴△DOA ≌△FBC ,∴OD=FB=2,∴OB=6,∵OK=KB ,∴OK=3,∴K (3,0),∴直线AC 经过定点K (3,0).②可以.利用如下:当∠OCB=90°时,四边形OABC 是矩形,由(1)可知△DOA ≌△FBC ,∴OD=BF=2,∵∠OCF+∠FCB=90°,∠FCB+∠CBF=90°,∴∠OCF=∠CBF,∵∠CFO=∠CFB,∴△CFO∽△BFC,∴CFBF = OFCF,∴CF2= 4CF,∴CF=2 √2,∴S矩形OABC=2•S△OBC=2× 12× 6×2√2=12 √2.③可以.理由如下:如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,∴AD=CF,∵DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,∵OE2=OD2+DE2,∴9x2=x2+4,∴x= √22,∴AE= 3√22,∴S菱形AECG=AE•DF= 3√22×2=3 √2(2)解:如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,∴OD=CF=2,∴点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.综上所述,点C坐标为(4,2)或(4,﹣2)【解析】【分析】(1)①是,经过定点(3,0).如图1中,连接AC交OB于K,只要证明OD=FB=2,推出OB=6,即可解决问题.②当∠OCB=90°时,四边形OABC是矩形,由(1)可知△DOA≌△FBC,推出OD=BF=2,由△CFO∽△BFC,可得CFBF = OFCF,由此即可解决问题.③可以.如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,推出AD=CF,易知DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,根据OE2=OD2+DE2,列出方程即可解决问题.(2)如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,推出OD=CF=2,推出点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.10.如图1,在平面直角坐标系中,正方形ABCO的顶点C、A分别在x、y轴上,A(0,6)、E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH(1)当H(﹣2,6)时,求证:四边形EFGH为正方形(2)若F(﹣5,0),求点G的坐标(3)如图2,点Q为对角线BO上一动点,D为边OA上一点,DQ⊥CQ,点Q从点B出发,沿BO方向移动.若移动的路径长为3,直接写出CD的中点M移动的路径长为________.【答案】(1)证明:如图1中,∵E(0,2),H(﹣2,6),∴OE=AH=2,∵四边形ABCO是正方形,∴∠HAE=∠EOF=90°,∵四边形EFGH是菱形,∴EH=EF,在Rt△AHE和Rt△OEF中,{AH=EOHE=EF,∴Rt△AHE≌△Rt△OEF,∴∠AEH=∠EFO,∵∠EFO+∠FEO=90°,∴∠AEH+∠FEO=90°,∴∠HEF=90°,∴四边形EFGH是正方形(2)解:如图1中,连接GE、FH交于点K.∵F(﹣5,0),E(0,2),∴OF=5,OE=2,EA=4,∵HE=EF,∴52+22=42+AH2,∴AH= √13,∴H(﹣√13,6),∵四边形EFGH是菱形,∴HK=KF,KE=KG,设G(m,n),则有m+02= −5−√132,n+22= 6+02,∴m=﹣5﹣√13,n=4,∴G(﹣5﹣√13,4)(3)3√22【解析】【解答】(3)解:如图2中,如图2中,作MN⊥CO于M.∵MN∥OD,CM=MD,∴CN=ON,∴MN垂直平分线段CO,∴点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),∵QC=QD,∠CEQ=∠QFD,易证∠ECQ=∠FQD,∴△EQC≌△FDQ,∴EQ=DF=BE= 3√22,CE=OF=6﹣3√22,∴DO=6﹣3 √2,∵CM=DM,∠CMH=∠OMD,∠CHM=∠DOM,∴△HMC≌△OMD,∴OM=HM,CH=OD=6﹣3 √2,BH=3 √2,∵ON=NB,∴MN= 12BH= 3√22,∴点M的运动的路径的长为3√22.故答案为3√2.2【分析】(1)只要证明Rt△AHE≌△Rt△OEF,推出∠AEH=∠EFO,由∠EFO+∠FEO=90°,推出∠AEH+∠FEO=90°,推出∠HEF=90°,即可解决问题.(2)如图1中,连接GE、FH交于点K.首先求出点H的坐标,设G(m,n),根据中点坐标公式,列出方程组即可解决问题.(3)如图2中,作MN⊥CO于M.由MN∥OD,CM=MD,推出CN=ON,推出MN 垂直平分线段CO,推出点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B 重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),想办法求出BH 的长,即可利用三角形的中位线定理解决问题.11.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB, AC上的一动点,且满足BP=AQ,D 是BC的中点.(1)求证:△PDQ是等腰直角三角形.(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.【答案】(1)证明:连接AD.∵△ABC是等腰直角三角形,D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,又∵BP=AQ,∴△BPD≌△AQD,∴PD=QD,∠BDP=∠ADQ,∵∠BDP+∠ADP=90°,∴∠ADP+∠ADQ=∠PDQ=90°,∴△PDQ为等腰直角三角形(2)解:当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:由(1)知△ABD为等腰直角三角形,当P为AB的中点时,DP⊥AB,即∠APD=90°,又∵∠BAC=90°,∠PDQ=90°,∴四边形APDQ为矩形,AB,∴四边形APDQ为正方形又∵DP=AP= 12【解析】【分析】连接AD,根据直角三角形的性质可得AD=BD=DC,从而证明△BPD≌△AQD,得到PD=QD,∠ADQ=∠BDP,则△PDQ是等腰三角形;由∠BDP+∠ADP=90°,得出∠ADP+∠ADQ=90°,得到△PDQ是直角三角形,从而证出△PDQ是等腰直角三角形;若四边形APDQ是正方形,则DP⊥AB,得到P点是AB的中点.12.如图,在等边三角形ABC中,点D是BC边的中点,以AD为边作等边三角形ADE.(1)求∠CAE的度数;(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.【答案】(1)解:在等边三角形ABC中,∵点D是BC边的中点,∴∠DAC=30°.又∵△ADE为等边三角形,∴∠DAE=60°.∴∠CAE=∠DAE-∠DAC=30°(2)解:由(1)知,∠EAF=90°,由F为AB的中点知,∠CFA=90°,∴CF∥EA.在等边三角形ABC中,CF=AD.在等边三角形ADE中,AD=EA.∴CF=EA.∴四边形AFCE为平行四边形.又∵∠CFA=90°,∴四边形AFCE为矩形.【解析】【分析】根据等边三角形三线合一的特点,易求得∠DAC=30°,则∠CAE=∠DAE-∠DAC.先证明四边形AECF是平行四边形,然后根据∠CFA=∠FAE=90°,由矩形的定义判定四边形AFCE是矩形.13.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:(1)四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?【答案】(1)解:四边形ADEF是平行四边形.理由:∵△ABD,△EBC都是等边三角形.∴AD=BD=AB,BC=BE=EC∠DBA=∠EBC=60°∴∠DBE+∠EBA=∠ABC+∠EBA.∴∠DBE=∠ABC.在△DBE和△ABC中∵BD=BA∠DBE=∠ABCBE=BC,∴△DBE≌△ABC.∴DE=AC.又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.同理可证:AD=EF,∴四边形ADEF平行四边形(2)解:∵四边形ADEF是矩形,∴∠FAD=90°.∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°.∴∠BAC=150°时,四边形ADEF是矩形(3)解:当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.理由如下:若∠BAC=60°,则∠DAF=360°﹣∠BAC﹣∠DAB﹣∠FAC=360°﹣60°﹣60°﹣60°=180°.此时,点A、D、E、F四点共线,∴以A、D、E、F为顶点的四边形不存在【解析】【分析】可先证明△DBE≌△ABC ,又∵△ACF是等边三角形,∴AC=AF.∴DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;若四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,A,D,E,F为顶点的四边形就不存在.14.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)证明:如图1,当点G和点M、C不重合时,求证:DG=DN.【答案】(1)证明:如图2中,∵AM=ME.AD=DB,∴DM∥BE,∴∠GDN+∠DNE=180°,∵∠GDN=∠AEB,∴∠AEB+∠DNE=180°,∴AE∥DN,∴四边形DMEN是平行四边形,∵DM== BE,EM== AE,AE=BE,∴DM=EM,∴四边形DMEN是菱形(2)证明:如图1中,取BE的中点F,连接DM、DF.由(1)可知四边形EMDF是菱形,∴∠AEB=∠MDF,DM=DF,∴∠GDN=∠AEB,∴∠MDF=∠GDN,∴∠MDG=∠FDN,∵∠DFN=∠AEB=∠MCE+∠CME,∠GMD=∠EMD+∠CME,、在Rt△ACE中,∵AM=ME,∴CM=ME,∴∠MCE=∠CEM=∠EMD,∴∠DMG=∠DFN,∴△DMG≌△DFN,∴DG=DN【解析】【分析】(1)如图2中,首先证明四边形DMEN是平行四边形,再证明ME=MD 即可证明.(2)如图1中,取BE的中点F,连接DM、DF.只要证明△DMG≌△DFN即可.15.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点.(1)求证:∠FAD=∠EAB.(2)若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.【答案】(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,∴AD=AB,∠ADB=∠ABD,∴∠ADF=∠ABE,在△FAD与△EAB中,∴△FAD≌△EAB(SAS),∴∠FAD=∠EAB;(2)解:∵四边形AECF对角线互相垂直平分,∴只要∠EAF=90°即得四边形BFDE是正方形,∵∠ADC=130°,∴∠DAB=180°﹣130°=50°∴∠FAD+∠EAB=40°,∵∠FAD=∠EAB,∴∠FAD= ×40°=20°【解析】【分析】(1)由题意易证∠ADF=∠ABE,又因为DF=EB,AD=AB,于是可△FAD≌△EAB,;(2)由已知可得四边形AECF对角线互相垂直平分,只要∠EAF=90°即得四边形AECF是正方形,由∠FAD=∠EAB,再证得∠DAB=50°,可得∠FAD+∠EAB=40°,于是∠FAD= 1×40°=20°.216.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD 为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:________,②BC,DC,CF之间的数量关系为:________;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.【答案】(1)垂直;BC=CF+CD(2)解:CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:∵正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,在△DAB与△FAC中,{AD=AF∠BAD=∠CAFAB=AC,∴△DAB≌△FAC(SAS),∴∠ABD=∠ACF,∵∠BAC=90°,AB=AC,∴∠ACB=∠ABC=45°.∴∠ABD=180°﹣45°=135°,∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°,∴CF⊥BC.∵CD=DB+BC,DB=CF,∴CD=CF+BC .(3)解:过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N ,如图3所示:∵∠BAC=90°,AB=AC ,∴BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,∴CD= 14 BC= √22 ,CH= 12 BC= √2 ,∴DH= 3√22 ,由(2)证得BC ⊥CF ,CF=BD= 5√22 ,∵四边形ADEF 是正方形,∴AD=DE ,∠ADE=90°,∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形,∴NE=CM ,EM=CN ,∵∠AHD=∠ADC=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM ,在△ADH 与△DEM 中, {∠ADH =∠DEM∠AHD =∠DMEAD =DE, ∴△ADH ≌△DEM (AAS ),∴EM=DH= 3√22 ,DM=AH= √2 ,∴CN=EM= 3√22 ,EN=CM= 3√22 ,∵∠ABC=45°,∴∠BGC=45°,∴△BCG 是等腰直角三角形,∴CG=BC=2 √2 ,∴GN=CG ﹣CN= √22 , ∴EG= √GN 2+EN 2 = (√22)(3√22)= √5 . 【解析】【解答】解:(1)①正方形ADEF 中,AD=AF ,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF ,在△DAB 与△FAC 中, {AD =AF∠BAD =∠CAFAB =AC,∴△DAB ≌△FAC (SAS ),∴∠B=∠ACF ,∴∠ACB+∠ACF=90°,即BC ⊥CF ;故答案为:垂直;②△DAB ≌△FAC ,∴CF=BD ,∵BC=BD+CD ,∴BC=CF+CD ;故答案为:BC=CF+CD ;【分析】(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质即可得到结论;②由正方形ADEF 的性质可推出△DAB ≌△FAC ,根据全等三角形的性质得到CF=BD ,∠ACF=∠ABD ,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.(3)根据等腰直角三角形的性质得到BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,求得DH= 3√22 ,根据正方形的性质得到AD=DE ,∠ADE=90°,根据矩形的性质得到NE=CM ,EM=CN ,由角的性质得到∠ADH=∠DEM ,根据全等三角形的性质得到EM=DH= 3√22 ,DM=AH= √2 ,等量代换得到CN=EM= 3√22 ,EN=CM= 3√22,根据等腰直角三角形的性质得到CG=BC=2 √2 ,根据勾股定理即可得到结论.17.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO=CO ,BO=DO ,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD 是矩形.(2)DF ⊥AC ,若∠ADF :∠FDC=3:2,则∠BDF 的度数是多少?【答案】(1)证明:∵AO=CO ,BO=DO ,∴四边形ABCD 是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴CO=OD,∴∠ODC=∠DCO=54°,∴∠BDF=∠ODC﹣∠FDC=18°.【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,【解析】根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.18.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.(1)求证:PC=PE;(2)求∠CPE的度数;(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.【答案】(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE(2)解:由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∵PA=PE,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°,∵∠ABC=90°,∴∠EPC=90°(3)115°【解析】【解答】(3)∠EPC=115°,理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴∠BAP=∠BCP,∵PA=PE,∴∠DAP=∠DCP,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°.∴∠CPE=180°-∠ABC=180°-65°=115°【分析】(1)根据正方形的性质得到△ABP≌△CBP,得到对应边相等,得到PC=PE;(2)由(1)知△ABP≌△CBP,得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数;(3)根据菱形的性质,得到△ABP≌△CBP,得到得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数.19.实践探究,解决问题如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD.(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=________;(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD 之间满足的关系式为________;(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.解决问题:(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).【答案】(1)16(2)S阴影=12S平行四边形ABCD(3)解:满足(2)中的关系式,理由如下:连接BD,由图1得S△EBD= 12 S△ABD同理S△BDF= 12S△BDC∴S四边形EBFD=S△EBD+S△BDF= 12S四边形ABCD(4)解:设四边形的空白区域分别为a,b,c,d 由上述性质可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,①+②+③+④得,a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米.【解析】【解答】解:(1)∵E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,∴S阴影= 12×8×4=16,故答案为:16;(2)∵E、F分别为平行四边形ABCD的边AD、BC的中点,∴S阴影= 12S平行四边形ABCD;故答案为:S阴影= 12S平行四边形ABCD;【分析】(1)由矩形的性质容易得出结果;(2)由平行四边形的性质容易得出结果;(3)连接BD,由题意得出S△EBD= 12 S△ABD同理S△BDF= 12S△BDC,即可得出结论;(4)设四边形的空白区域分别为a,b,c,d,由(3)可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,进一步得出结论即可.20.如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形.(2)解:∵四边形AECF是菱形,如图所示:∴AE=EC,∴∠1=∠2,∵∠3=90°﹣∠2,∠4=90°﹣∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE= 12BC=5.【解析】【分析】(1)利用平行四边形的性质得出对边平行且相等,结合已知,可证出AECF是平行四边形;(2)利用菱形的邻边相等的性质,可证出BE=AE=CE= 12BC=5.。
八年级数学下册考点知识与题型专题讲解与提升练习37 利用菱形的性质证明

八年级数学下册考点知识与题型专题讲解与提升练习专题37 利用菱形的性质证明一、单选题1.菱形具有而矩形不一定具有的性质是()A.邻边相等B.对角线互相平分C.对角线相等D.邻角互补2.矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.两组对角分别相等D.对角线互相垂直3.矩形具有,而菱形不一定具有的性质是()A.对角线互相平分B.对角线相等C.对边平行且相等D.内角和为360°4.下列说法中,错误的是()A.平行四边形的对角线互相平分B.矩形的对角线互相垂直C.菱形的对角线互相垂直平分D.正方形的对角线相等5.矩形具有而菱形不具有的性质是()A.对角线相等B.对角线平分一组对角C.对角线互相平分D.对角线互相垂直6.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是()A.对角线互相垂直B.对角线互相平分C.对角线长度相等D.一组对角线平分一组对角7.菱形具有,而矩形不一定具有的性质是()A.对边相等B.对角相等C.对角线相等D.对角线互相垂直8.下列说法中错误的是()A .四边相等的四边形是菱形B .对角线相等的平行四边形是矩形C .菱形的对角线互相垂直且相等D .正方形的邻边相等9.下列哪条性质是平行四边形、矩形、菱形、正方形共有的()A .对角线互相平分B .对角线相等C .对角线互相垂直.D .对角线平分一组对角.10.下列说法中不正确的是( )A .平行四边形的对角相等B .菱形的邻边相等C .平行四边形的对角线互相平分D .菱形的对角线互相垂直且相等11.菱形OACB 在平面直角坐标系中的位置如图所示,若点C 的坐标是()4,0,点A 的纵坐标是1,则点B 的坐标是()A .()2,1B .()2,1-C .()1,2-D .()1,2 12.下列命题中,正确的是( )A .平行四边形的对角线相等B .菱形的对角线互相垂直且平分C .矩形的对角线互相垂直D .对角线互相垂直的平行四边形是正方形 13.菱形不具备的性质是( )A .对角线一定相等B .对角线互相垂直C .是轴对称图形D .是中心对称图形14.矩形一定具有而菱形不一定具有的性质是()A .内角和等于360B .对角线互相垂直C .对边平行且相等D .对角线相等15.矩形具有而菱形不一定具有的性质是 ( )A .对角线互相垂直B .对角线相等C .对角线互相平分D .对角互补16.关于菱形,下列说法错误的是()A .四条边相等B .对角线互相垂直C .四个角相等D .对角线互相平分17.下列性质中,菱形具有而矩形不一定具有的性质是().A .对边平行且相等B .对角线互相平分C .内角和等于外角和D .每一条对角线所在直线都是它的对称轴18.如图,把菱形ABCD 向右平移至DCEF 的位置,作EG ⊥AB ,垂足为G ,EG 与CD 相交于点K ,GD 的延长线交EF 于点H ,连接DE ,则下列结论:①BG =AB +HF ;②DG =DE ;③∠DHE =12∠BAD ;④∠B =∠DEF ,其中正确结论的个数是()A .1个B .2个C .3个D .4个19.菱形ABCD 中,60D ∠=︒.点E 、F 分别在边BC 、CD 上,且BE CF =.若2EF =,则AEF 的面积为().A .B .C .D20.如图,四边形ABCD 沿直线l 对折后重合,如果//AD BC ,则结论①AB //CD ;②AB =CD ;③AB BC ⊥;④AO OC =中正确的是()A .1个B .2个C .3个D .4个21.如图,平行四边形ABCD 的对角线AC BD 、相交于点,О下列结论正确的是()A .COD AOB S S ∆= B .AC BD =C .AC BD ⊥D .ABCD 是轴对称图形 22.如图,在菱形ABCD 中,点,,,EFGH 分别是四条边的中点,则四边形EFGH 是()A .正方形B .矩形C .菱形D .无法确定23.下列说法中,错误的是()A .平行四边形的两组对角分别相等;B .一组对边平行另一组对边相等的四边形是平行四边形;C .正方形的对角线互相垂直平分且相等;D .菱形的对角线互相垂直.24.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,延长CB 至E 使BE=CB ,连续AE .下列结论①AE=2OE;②90EAC ∠=︒;③四边形ADBE 为平行四边形;④34AEBO ABCD S S =四边形菱形中,正确的个数有()A .1个B .2个C .3个D .4个25.菱形具有而矩形不一定具有的性质是( )A .对角相等且互补B .对角线互相平分C .对角线互相垂直D .一组对边平行,另一组对边相等26.下列性质中,菱形不具有的是()A .对边平行且相等B .对角线互相垂直C .对角线互相平分D .对角线相等27.如图,在矩形ABCD 中,AB =3,做BD 的垂直平分线E ,F ,分别与AD 、BC 交于点E 、F ,连接BE ,DF ,若EF =AE +FC ,则边BC 的长为()A .B .C .D 28.如图,在菱形ABCD 中, AD=6,∠BAD=60°, 点P 是对角线AC 上的动点,点E 是AB的中点,连结PB 、PE ,则PE+PB 的最小值为()A .B .CD .29.已知,如图,在菱形ABCD 中.(1)分别以C ,D 为圆心,大于12CD 长为半径作弧,两弧分别交于点E ,F ;(2)作直线EF ,且直线EF 恰好经过点A ,且与边CD 交于点M ;(3)连接BM .根据以上作图过程及所作图形,判断下列结论中错误..的是()A .∠ABC =60°B .如果AB =2,那么BM =4C .BC =2CMD .2ABM ADM S S △△30.如图,在菱形ABCD 中,AB =BD ,点E 、F 分别是AB 、AD 上任意的点(不与端点重合),且AE =DF ,连接BF 与DE 相交于点G ,连接CG 与BD 相交于点H .给出如下几个结论:①△AED ≌△DFB :②GC 平分∠BGD ;③S 四边形BCDG =4CG 2;④∠BGE 的大小为定值.其中正确的结论个数为( )A .1B .2C .3D .431.如图,在一张矩形纸片ABCD 中,AB=4,BC=8,点E ,F 分别在AD ,BC 上,将ABCD沿直线EF 折叠,点C 落在AD 上的一点H 处,点D 落在点G 处,有以下四个结论:①四边形CFHE 是菱形;②EC 平分∠DCH;③线段BF 的取值范围为3≤BF≤4;④当点H 与点A重合时,EF=A .①②③④B .①④C .①②④D .①③④32.如图,菱形ABCD 中,∠BAD =60°,AC 与BD 交于点O ,E 为CD 延长线上的一点,且CD =DE ,连结BE 分别交AC ,AD 于点F 、G ,连结OG ,则下列结论:①OG =12AB ;②与△EGD 全等的三角形共有5个;③S 四边形ODGF >S △ABF ;④由点A 、B 、D 、E 构成的四边形是菱形.其中正确的是( )A .①④B .①③④C .①②③D .②③④33.如图所示,等边三角形ABC 沿射线BC 向右平移到DCE ∆的位置,连接AD 、BD ,则下列结论:(1)AD BC =(2)BD 与AC 互相平分(3)四边形ACED 是菱形(4)BD DE ⊥,其中正确的个数是()A.1 B.2 C.3 D.434.如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④EG12=BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )A.1 B.2 C.3 D.435.如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距高是③AF=CF;④△ABF的( )个.A.1 B.2 C.3 D. 436.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A 的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE13=S菱形ABCD下列判断正确的是()A.①,②都对B.①,②都错C.①对,②错D.①错,②对第II卷(非选择题)请点击修改第II卷的文字说明二、填空题37.给出下列命题:①平行四边形的对角线互相平分;②对角线相等的四边形是矩形;③菱形的对角线互相垂直平分;④对角线互相垂直的四边形是菱形.其中_____是真命题(填序号).38.菱形的对角线互相垂直且相等._____(判断对错)39.矩形、菱形和正方形的对角线都具有的性质是_____.40.如图,在平面直角坐标系中,菱形ABCD的顶点A,C 在x轴上,顶点B的坐标为(2,3),那么顶点D的坐标是______________;41.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE 的长等于_____.42.下列说法:①平行四边形对角相等,对边也相等;②菱形一组对角的和为180︒;③矩形对角线相等;④平行四边形是轴对称图形,对角线所在的直线是对称轴;⑤平行四边形对角线的交点到一组对边的距离相等,其中正确的序号为________________________.43.如图,在菱形ABCD中,AB=3cm,∠A=60°.点E,F分别在边AD,AB上,且DE=1cm.将△AEF沿EF翻折,使点A落在对角线BD上的点A'处,则A'BA'F=______.44.如图,四边形ABCD是菱形,点A,B,C,D的坐标分别是(m,0),(0,n),(1,0),(0,2),则mn=_____.45.如图,在菱形ABCD中,AB=4,CE=DE,AE⊥CD,E为垂足,则AE2+BE2=_____.46.如图,菱形ABCD的对角线相交于点O,过点A作AE CB⊥交CB的延长线于点E,连接OE .若菱形ABCD 的面积等于12,对角线4BD =,则OE 的长为_________.47.如图,菱形ABCD 的边长为1, 60ABC ∠=︒.,E F 分别是,BC BD 上的动点,且CE DF =,则AE AF +的最小值为_______.48.如图,在菱形ABCD 中,∠A=60°,E 、F 分别是AB 、AD 的中点,DE 、BF 相交于点G ,连接BD 、CG .给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④2.BCDG S AB =四边形其中正确的有______.三、解答题49.如图,菱形ABCD 的周长为8,对角线BD =2,E 、F 分别是边AD ,CD 上的两个动点;且满足AE +CF =2.(1)求证:△BDE ≌△BCF ;(2)判断△BEF 的形状,并说明理由.50.如图,在菱形ABCD 中,AB =2,∠DAB =60°,点E 是AD 边的中点,点M 是AB 边上一动点(不与点A 重合),延长ME 交射线CD 于点N ,连接MD 、AN .(1)求证:四边形AMDN 是平行四边形;(2)在点M 移动过程中:①当四边形AMDN 成矩形时,求此时AM 的长;②当四边形AMDN 成菱形时,求此时AM 的长.51.如图,在△ABC 中,AB=AC ,四边形ADEF 是菱形,求证:BE=CE .52.如图,点,E F 分别在菱形ABCD 的边,BC CD 上,BE DF =.求证:.AE AF =53.如图,在菱形ABCD 中,AEF 是等边三角形,E ,F 分别在BC ,CD 上,且EF CD =,求BAD ∠的度数.54.如图,已知菱形 ABCD 中,对角线 AC 、BD 相交于点 O ,过点 C 作 CE∥BD,过点 D 作 DE∥AC,CE 与 DE 相交于点 E .求证:四边形 CODE 是矩形;55.如图,在菱形ABCD 中,点E 在边CD 上,AE 与BD 相交于点F ,连接CF .(1)求证:AED BCF ∠=∠;(2)若60ABC ∠=︒,2AB =,求菱形ABCD 的面积.56.如图,四边形ABCD 是菱形,对角线AC 、BD 相交于点O .(1)尺规作图:以OA 、OD 为边,作矩形OAED (不要求写作法,但保留作图痕迹);(2)若在菱形ABCD 中,∠BAD =120 °,AD =2,求所作矩形OAED 的周长.57.如图所示,在四边形ABCD 中,AB DC =,E 、F 分别是AD 、BC 的中点,G 、H 分别是BD 、AC 的中点,猜一猜EF 与GH 的位置关系,并证明你的结论.58.如图,在菱形ABCD 中,点,E F 分别是,CD BD 边上的点,12∠=∠.求证:(1)FCD EBD ≌;(2)CE BF =.59.如图,在菱形ABCD 中,E 为对角线BD 上一点,且AE ⊥AB ,连结CE .(1)求证:∠ECB =90°;(2)若AE ═ED =1时,求菱形的边长.60.如图1,四边形ABCD 是菱形,5AD =,过点D 作AB 的垂线DH ,垂足为H ,交对角线AC 于M ,连接BM ,且3AH =.(1)求DM 的长;(2)如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设PMB △的面积为(0)S S ≠,点P 的运动时间为t 秒,求S 与t 之间的函数关系式;(3)在(2)的条件下,当点P 在边AB 上运动时,是否存在这样的t 的值,使M PB ∠与BCD ∠互为余角?若存在,求出t 的值;若不存在,请说明理由.61.如图,菱形ABCD 的边长为2.2BD =,E ,F 分别是边AD ,CD 上的两个动点,且满足2AE CF +=.(1)求证:BDE BCF △≌△;(2)判断BEF 的形状,并说明理由.62.如图,在直角坐标系中,3,4OA OC ==,点B 是y 轴上一动点,以AC 为对角线作平行四边形ABCD .(1)求直线AC 的函数解析式;(2)设点(0)B m ,,记平行四边形ABCD 的面积为S ,求S 与m 的函数关系式;(3)当点B 在y 轴上运动,能否使得平行四边形ABCD 是菱形?若能,求出点B 的坐标;若不能,说明理由.63.将一个三角形的三个顶点分别关于各自对边所在直线作对称点,由这三个对称点确定的三角形叫做原三角形的“再生三角形”.(1)一个周长为L ,面积为S 的等边三角形的“再生三角形”的周长是______,面积是______;(2)已知ABC 中,30,ABC BA BC ∠=︒=,A B C '''是ABC 的“再生三角形”,其中点,A ',B ',C '分别是点A ,B ,C 的对称点.A B C '''是_______三角形;(3)已知Rt ABC 中,90CAB ∠=︒,A B C '''是Rt ABC 的“再生三角形”,其中点,,A B C '''分别是点A ,B ,C 的对称点,试猜想A B C '''与Rt ABC 的面积有怎样的关系,并加以证明;(4)小舒认为所有的三角形都存在“再生三角形”,小雪认为不是所有的三角形都存在“再生三角形”.你认为谁的判断是正确的?请说明理由.64.如图,已知正方形ABCD 的边长为3,菱形EFGH 的三个顶点E 、G 、H 分别在正方形的边AB 、CD 、DA 上,1AH =,连接CF .(1)当1DG =时,求证:菱形EFGH 为正方形;(2)设DG x =,请用x 的代数式表示△FCG 的面积;(3)当DG =时,求GHE ∠的度数. 65.在数学的学习中,有很多典型的基本图形.(1)如图①,ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为D 、E .试说明ABD CAE ≌;(2)如图②,ABC 中,90BAC ∠=︒,AB AC =,点D 、A 、F 在同一条直线上,BD DF ⊥,3AD =,4BD =.则菱形AEFC 面积为______.(3)如图③,分别以Rt ABC 的直角边AC 、AB 向外作正方形ACDE 和正方形ABFG ,连接EG ,AH 是ABC 的高,延长HA 交EG 于点I ,若6AB =,8AC =,求AI 的长度.。
2022年华东师大版八年级数学下册第十九章矩形、菱形与正方形综合练习练习题(精选含解析)

八年级数学下册第十九章矩形、菱形与正方形综合练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,矩形ABCD 的面积为1cm 2,对角线交于点O ;以AB 、AO 为邻边作平行四边形AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边作平行四边形AO 1C 2B ,…;依此类推,则平行四边形AO 2014C 2015B 的面积为( )cmA .201312 B .201412 C .201512 D .2016122、小明想判断家里的门框是否为矩形,他应该( )A .测量三个角是否都是直角B .测量对角线是否互相平分C .测量两组对边是否分别相等D .测量一组对角是否是直角3、如图,在矩形ABCD 中,AB =2,BC =4,对角线AC ,BD 相交于点O ,OE ⊥AC 交BC 于点E ,EF ⊥BD 于点F ,则OE +EF 的值为( )A B .2 C .52 D .4、如图,四边形ABCD 为平行四边形,延长AD 到E ,使DE =AD ,连接EB ,EC ,DB ,添加一个条件,不能使四边形DBCE 成为矩形的是( )A .AB =BE B .DE ⊥DC C .∠ADB =90°D .CE ⊥DE5ABCD 中,点E 是对角线AC 上一点,且EF AB ⊥于点F ,连接DE ,当22.5ADE ∠=︒时,EF =( )A .1B .2C 1D .146、如图,点E 是正方形ABCD 的边DC 上一点,把△ADE 绕点A 顺时针旋转90°到△ABF 的位置,若四边形AECF 的面积为144.AE =13.则DE 的长为( )A .BC .4D .57、如图,在菱形ABCD 中,P 是对角线AC 上一动点,过点P 作PE BC ⊥于点E .PF AB ⊥于点F .若菱形ABCD 的周长为24,面积为24,则PE PF +的值为( )A .4B .245C .6D .4858、如图所示,四边形ABCD 是矩形,过点D 作对角线BD 的垂线,交BC 的延长线于点E ,取BE 的中点F ,连接DF ,DF =5,设AB =x ,AD =y ,则x 2+(y ﹣5)2的值为( )A .10B .25C .50D .759、如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后,得到正方形AB ′C ′D ′,边B 'C ′与DC 交于点O ,则∠DOB '的度数为( )A .125°B .130°C .135°D .140°10、如图,把一张长方形纸片ABCD 沿AF 折叠,使B 点落在B '处,若20ADB ∠=︒,要使AB BD '∥,则BAF ∠的度数应为( )A.20°B.55°C.45°D.60°第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、(1)两组对边分别______,菱形的四条边都______.几何语言:∵四边形ABCD是菱形∴AB∥CD,AD∥BCAB=CD=AD=BC(2)菱形的两组对角______,邻角______几何语言:∵四边形ABCD是菱形∴∠BAD=∠BCD,∠CBA=∠ADC∠BAD+∠ADC=180°∠BCD+∠CBA=180°∠BAD+∠CBA=180°∠BCD+∠ADC=180°(3)菱形的对角线互相______,并且每一条对角线______一组对角.几何语言:∵四边形ABCD 是菱形∴AC ⊥BD , AC 平分∠BAD ,∠BCD , BD 平分∠ABC ,∠ADC(4)菱形既是轴对称图形,又是中心对称图形,有______条对称轴,其对称轴为两条对角线所在直线,对称中心为其______的交点.2、一个长方形的周长是22cm ,若这个长方形的长减少2cm ,宽增加3cm ,就可以成为一个正方形,则长方形的长是______cm .3、如图,矩形ABCD 的两条对角线相交于点O ,已知120AOD ∠=︒, 2.5cm AB =,则矩形对角线BD 的长为_______cm .4、如图,矩形ABCD 的两条对角线AC ,BD 交于点O ,∠AOB =60°,AB =3,则矩形的周长为 _____.5、如图,在ABC 中,90ACB ∠=︒,AB =1BC =,P 是线段AB 边上的动点(不与点A ,B 重合),将BCP 沿CP 所在直线翻折,得到B CP '△,连接B A ',当B A '取最小值时,则AP 的值为________.6、如图,正方形ABCD 中,E 为CD 上一动点(不含C 、)D ,连接AE 交BD 于F ,过F 作FH AE ⊥交BC 于H ,过H 作HG BD ⊥于G ,连接AH ,EH .下列结论:①AF FH =;②45HAE ∠=︒;③FH 平分GHC ∠;④2BD FG =,正确的是__(填序号).7、在菱形ABCD 中,60A ∠=︒,其所对的对角线长为2,则菱形ABCD 的面积是__.8、如图,矩形ABCD 中,对角线AC ,BD 相交于点O ,AD =60COB ∠=︒,BF AC ⊥,交AC 于点M ,交CD 于点F ,延长FO 交AB 于点E ,则下列结论:①FO FC =;②四边形EBFD 是菱形;③OBE CBF △△≌;④3MB =.其中结论正确的序号是______.9、如图在正方形ABCD 中,∠EAF 的两边分别交CB 、DC 延长线于E 、F 点且∠EAF =45°,如果BE =1,DF =7,则EF =__.10、如图,菱形ABCD 的周长为40,面积为80,P 是对角线BC 上一点,分别作P 点到直线AB .AD 的垂线段PE .PF ,则PE PF +等于______.三、解答题(5小题,每小题6分,共计30分)1、数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,222A B C ∆就是由ABC ∆沿直线1翻移后得到的.(先翻折,然后再平移)(1)在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的A 与2A ,B 与2B …)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)(2)如图2,在长方形ABCD 中,8BC =,点,E F 分别是边,BC AD 中点,点G 在边CD 延长线上,联结,AE FG ,如果GDF ∆是ABE ∆经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线a ;联结AG ,线段AG 和直线a 交于点O ,若OGF ∆的面积为3,求此长方形的边长AB 的长.(3)如图3,M 是(2)中的长方形边BC 上一点,如果1BM =,ABM ∆先按(2)的“翻移线”直线a 翻折,然后再平移2个单位,得到111A B M ∆,联结线段11AA MM 、,分别和“翻移线”a 交于点K 和点H ,求四边形AKHM 的面积.2、如图,ABC 和DBC △中,90ACB DBC ∠=∠=︒,E 是BC 的中点,且ED AB ⊥于点F ,且AB DE =,CD 交AB 于点M .(1)求证:2BD EC =;(2)求ACM △与BCM 的面积之比.3、如图,已知菱形ABCD 的对角线相交于点O ,延长AB 至点E ,使BE =AB ,连接CE .(1)求证:BD=EC.(2)若∠E=57°,求∠BAO的大小.4、下面是小明设计的“作菱形ABCD”的尺规作图过程.求作:菱形ABCD.作法:①作线段AC;②作线段AC的垂直平分线l,交AC于点O;③在直线l上取点B,以O为圆心,OB长为半径画弧,交直线l于点D(点B与点D不重合);④连接AB、BC、CD、DA.所以四边形ABCD为所求作的菱形.根据小明设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.=,证明:OA OC=,OB OD∴.,∴四边形ABCD为菱形()(填推理的依据).5、如图,已知在ABC 中,90A ∠=︒,求作正方形ADEF ,使得D ,E ,F 分别在AB ,BC ,AC 上.-参考答案-一、单选题1、C【解析】【分析】根据“同底等高”的原则可知平行四边形AOC 1B 底边AB 上的高等于BC 的12,则有平行四边形AOC 1B 的面积12,平行四边形AOC 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12,则有平行四边形ABC 3O 2的面积212,…;由此规律可进行求解. 【详解】解:∵O 1为矩形ABCD 的对角线的交点,∴平行四边形AOC 1B 底边AB 上的高等于BC 的12,∴平行四边形AOC 1B 的面积=12×1=12,∵平行四边形AO 1C 2B 的对角线交于点O 2,∴平行四边形AOC 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12,∴平行四边形ABC 3O 2的面积=12×12×1=212, …,依此类推,平行四边形ABC 2014O 2015的面积=201512cm 2.故答案为:C .【点睛】本题主要考查矩形的性质与平行四边形的性质,熟练掌握矩形的性质与平行四边形的性质是解题的关键.2、A【解析】【分析】根据矩形的判定方法解题.【详解】解:A 、三个角都是直角的四边形是矩形,∴选项A 符合题意; B 、对角线互相平分的四边形是平行四边形,∴选项B 不符合题意,C 、两组对边分别相等的四边形是平行四边形,∴选项C 不符合题意;D 、一组对角是直角的四边形不是矩形,∴选项D 不符合题意;故选:A .【点睛】本题考查矩形的判定方法,是重要考点,掌握相关知识是解题关键.3、A【解析】【分析】依据矩形的性质即可得到BOC ∆的面积为2,再根据BOC COE BOE S S S∆=+,即可得到OE EF +的值. 【详解】解:2AB =,4BC =,∴矩形ABCD 的面积为8,AC =12BO CO AC ∴==对角线AC ,BD 交于点O ,BOC ∴∆的面积为2,EF OB ⊥,EO AC ⊥,BOC COE BOE S S S ∆∴=+,即11222CO EO OB EF =⨯+⨯,12)2EO EF ∴=+,)4EO EF +=,∴+EO EF故选:A.【点睛】本题主要考查了矩形的性质,解题的关键是掌握矩形的四个角都是直角,矩形的对角线相等且互相平分.4、B【解析】【分析】先证明四边形BCED为平行四边形,再根据矩形的判定进行解答.【详解】解:∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC,又∵AD=DE,∴DE∥BC,且DE=BC,∴四边形BCED为平行四边形,A、∵AB=BE,DE=AD,∴BD⊥AE,∴□DBCE为矩形,故本选项不符合题意;B、∵DE⊥DC,∴∠EDB=90°+∠CDB>90°,∴四边形DBCE不能为矩形,故本选项符合题意;C、∵∠ADB=90°,∴∠EDB =90°,∴□DBCE 为矩形,故本选项不符合题意;D 、∵CE ⊥DE ,∴∠CED =90°,∴□DBCE 为矩形,故本选项不符合题意.故选:B .【点睛】本题考查了平行四边形的判定和性质、矩形的判定等知识,判定四边形BCED 为平行四边形是解题的关键.5、C【解析】【分析】证明67.5CDE CED ∠=∠=︒,则CD CE =AC 的长,得2AE =,证明AFE ∆是等腰直角三角形,可得EF 的长.【详解】 解:四边形ABCD 是正方形,AB CD BC ∴==90B ADC ∠=∠=︒,45BAC CAD ∠=∠=︒, 22AC AB ,22.5ADE ∠=︒,9022.567.5CDE ∴∠=︒-︒=︒,4522.567.5CED CAD ADE ∠=∠+∠=︒+︒=︒,CDE CED ∴∠=∠,CD CE ∴==2AE ∴=EF AB ⊥,90AFE ∴∠=︒,AFE ∴∆是等腰直角三角形,1EF ∴,故选:C .【点睛】本题考查正方形的性质,勾股定理,等腰直角三角形,三角形的外角的性质等知识,解题的关键是在正方形中学会利用等腰直角三角形的性质解决问题,属于中考常考题型.6、D【解析】【分析】由旋转性质得△ABF ≌△ADE ,再根据全等三角形的性质得到S 正方形ABCD =S 四边形AECF =144进而求得AD =12,再利用勾股定理求解DE 即可.【详解】解:∵△ADE 绕点A 顺时针旋转90°得到△ABF ,∴△ABF ≌△ADE ,∴S △ABF =S △ADE ,∴S 正方形ABCD =S 四边形AECF =144,∴AD =12,在Rt△ADE 中,AE =13,AD =12,由勾股定理得:DE ,【点睛】本题考查旋转性质、全等三角形的性质、正方形的面积公式、勾股定理,熟练掌握旋转性质,得出S 正方形ABCD =S 四边形AECF 是解答的关键.7、A【解析】【分析】连接BP ,通过菱形ABCD 的周长为24,求出边长,菱形面积为24,求出ABC S的面积,然后利用面积法,=+ABC ABP CBP S S S ,即可求出PE PF +的值.【详解】解:如图所示,连接BP ,∵菱形ABCD 的周长为24,∴2446AB BC ==÷=,又∵菱形ABCD 的面积为24,∴24212=÷=ABCS , ∴12=+=ABC ABP CBP SS S , ∴111222⋅+⋅=AB PF BC PE ,∴()1122⋅+=AB PE PF ,∵6AB =,∴4PE PF +=,故选:A .【点睛】本题主要考查菱形的性质,解题关键在于添加辅助线,通过面积法得出等量关系.8、B【解析】【分析】根据题意知点F 是Rt△BDE 的斜边上的中点,因此可知DF =BF =EF =5,根据矩形的性质可知AB =DC =x ,BC =AD =y ,因此在Rt△CDF 中,CD 2+CF 2=DF 2,即可得答案.【详解】解:∵四边形ABCD 是矩形,AB =x ,AD =y ,∴CD =AB =x ,BC =AD =y ,∠BCD =90°,又∵BD ⊥DE ,点F 是BE 的中点,DF =5,∴BF =DF =EF =5,∴CF =5-BC =5-y ,∴在Rt△DCF 中,DC 2+CF 2=DF 2,即x 2+(5-y )2=52=25,∴x 2+(y -5)2=x 2+(5-y )2=25,故选:B .【点睛】本题考查了直角三角形斜边中线等于斜边的一半、矩形的性质、勾股定理,做题的关键是利用直角三角形斜边中线等于斜边的一半求出BF 的长度.9、C【解析】【分析】连接B ′C ,根据题意得B ′在对角线AC 上,得∠B 'CO =45°,由旋转的性质证出∠OB 'C 是直角,得=45B CO '∠︒,即可得出答案.【详解】解:连接B ′C ,如图所示,∵四边形ABCD 是正方形,∴AC 平分∠BAD ,∵旋转角∠BAB ′=45°,∠BAC =45°,∴B ′在对角线AC 上,∴∠B 'CO =45°,由旋转的性质得:90AB C B ''∠=∠=︒,AB '=AB =1,∴45B OC '∠=︒∴18045135DOB '∠=︒-︒=︒故选:C .【点睛】本题考查了正方形的性质、旋转的性质等知识;熟练掌握正方形的性质和旋转的性质是解题的关键.10、B【解析】【分析】设直线AF 与BD 的交点为G ,由题意易得90DAB ∠=︒,则有70ABD ∠=︒,由折叠的性质可知BAF B AF '∠=∠,由平行线的性质可得B AF BGA '∠=∠,然后可得BAF BGA ∠=∠,进而问题可求解.【详解】解:设直线AF 与BD 的交点为G ,如图所示:∵四边形ABCD 是矩形,∴90DAB ∠=︒,∵20ADB ∠=︒,∴70ABD ∠=︒,由折叠的性质可知BAF B AF '∠=∠,∵AB BD '∥,∴B AF BGA '∠=∠,∴BAF BGA ∠=∠, ∴180552ABG BAF ︒-∠∠==︒; 故选B .【点睛】本题主要考查折叠的性质及矩形的性质,熟练掌握折叠的性质及矩形的性质是解题的关键.二、填空题1、 平行 相等 相等 互补 垂直 平分 两 对角线【解析】略2、8【解析】【分析】设这个长方形的长为xcm ,则长方形的宽为()11x -cm ,由题意得长2-=宽+3.进而得到方程2113x x -=-+,解方程即可得到答案.【详解】解:设这个长方形的长为x cm ,由题意得:2113x x -=-+,216,x ∴=解得:8,x =答:这个长方形的长为8.cm故答案为:8【点睛】本题主要考查了一元一次方程的应用,关键是正确理解题意,抓住关键语句,表示出正方形的边长,进而利用正方形边长相等得到方程.3、5【解析】【分析】由矩形的性质可证△AOB为等边三角形,可求BO=AB的长,即可求BD的长.【详解】解:∵四边形ABCD是矩形,∴AO=CO=BO=DO,∵∠AOD=120°,∴∠AOB=60°,且AO=BO,∴△ABO为等边三角形,∴AO=BO=AB=2.5,∴BD=5,故答案为:5.【点睛】本题考查矩形的性质,熟练掌握矩形的性质是本题的关键,①矩形的对边平行且相等;②矩形的四个角都是直角;③矩形的对角线相等且互相平分.4、663##6【解析】【分析】根据矩形性质得出AD=BC,AB=CD,∠BAD=90°,OA=OC=12AC,BO=OD=12BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BD,根据勾股定理求出AD即可.【详解】解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC=12AC,BO=OD=12BD,AC=BD,∴OA=OB=OC=OD,∵∠AOB =60°,OB =OA ,∴△AOB 是等边三角形,∵AB =3,∴OA =OB =AB =3,∴BD =2OB =6,在Rt △BAD 中,AB =3,BD =6,由勾股定理得:AD =∵四边形ABCD 是矩形,∴AB =CD =3,AD =BC =∴矩形ABCD 的周长是AB +BC +CD +AD =故答案为:【点睛】本题考查了矩形性质,等边三角形的性质和判定,勾股定理等知识点,关键是求出AD 的长.5【解析】【分析】根据翻转变换的性质可知BC =C B '=1,当A 、B '、C 三点在一条直线上时,A B '有最小值,根据题意作图,过P 点作PH ⊥BC ,PQ ⊥AC ,得到四边形PQCH 是正方形,利用面积法求出PQ 的长,再根据勾股定理求出AP 的长.【详解】解:∵在ABC 中,90ACB ∠=︒,AB =1BC =∴AC2=由翻转变换的性质可知:BC=C B'=1,故当A、B'、C三点在一条直线上时,A B'有最小值,过P点作PH⊥BC,PQ⊥AC,∴∠ACB=∠PHC=∠PQC=90°∴四边形PQCH是矩形∵翻转∴△BCP≌△B'CP∴PH=PQ∴四边形PQCH是正方形设PQ=x,则PH=x∵S△ABC=S△APC+S△PBC∴111222BC AC BC PH PQ AC ⨯=⨯+⨯即1111212 222x x⨯⨯=⨯⨯+⨯解得x=2 3∴AQ=2-23=43∴AP【点睛】本题主要考查的是翻转变换的性质、线段的性质,根据题意找到B '的位置是解题的关键.6、①②④【解析】【分析】连接FC ,延长HF 交AD 于点L .可证ADF CDF ∆∆≌,进而可得FHC FCH ∠=∠,由此可得出FH AF =;再由FH AF =,即可得出45HAE ∠=︒;连接AC 交BD 于点O ,则2BD OA =,证明AOF FGH ≌,即可得出OA GF =,进而可得2BD FG =;过点F 作MN BC ⊥于点N ,交AD 于点M ,由于F 是动点,FN 的长度不确定,而FG OA =是定值,即可得出FH 不一定平分GHC ∠.【详解】解:如图,连接FC ,延长HF 交AD 于点L .∵BD 为正方形ABCD 的对角线∴45ADB CDF ∠=∠=︒,AD CD =在ADF 和CDF 中45AD CD ADB CDF DF DF =⎧⎪∠=∠=︒⎨⎪=⎩∴()ADF CDF SAS ∆∆≌∴AF FC =,DCF DAF ∠=∠∵90AFL ∠=︒,90ALH LAF ∠+∠=︒ ,ALH FHC ∠=∠∴90LHC DAF ∠+∠=︒∵DCF DAF ∠=∠,90FCD FCH ∠+∠=︒∴FHC FCH ∠=∠∴FH FC =∴AF FH =故①正确;∵90AFH ∠=︒,AF FH =∴AFH 是等腰直角三角形∴45HAE ∠=︒故②正确;连接AC 交BD 于点O ,则2BD OA =∵90AFO GFH GHF GFH ∠+∠=∠+∠=︒∴AFO GHF ∠=∠在AOF 和FGH 中90AFO GHF AOF FGH AF FH ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()AOF FGH AAS ∆∆≌∴OA GF =∴22BD OA GF ==故④正确.过点F 作MN BC ⊥于点N ,交AD 于点M ,F 是动点∵FN 的长度不确定,而FG OA =是定值∴FN 不一定等于FGFH ∴不一定平分GHC ∠故③错误;故答案为:①②④.【点睛】本题考查了正方形性质,全等三角形判定和性质,角平分线性质和判定,等腰三角形的性质与判定等,熟练掌握全等三角形判定和性质,合理添加辅助线构造全等三角形是解题关键.7、【解析】【分析】根据菱形的性质证得△ABD 是等边三角形,得到OB ,利用勾股定理求出OA ,由菱形的性质求出菱形的面积.【详解】解:如图所示:在菱形ABCD 中,60BAD ∠=︒,其所对的对角线长为2,AD AB ∴=,AC BD ⊥,BO DO =,AO CO =,ABD ∴∆是等边三角形,则2AB AD ==,故1BO DO ==,则AO =AC =则菱形ABCD 的面积122=⨯⨯故答案为:【点睛】此题主要考查了菱形的性质以及勾股定理,正确得出菱形的另一条对角线的长是解题关键.8、①②③④【解析】【分析】由矩形的性质及垂直平分线的判定和性质可证明①;根据全等三角形的判定和性质及菱形的判定和性质可证明②;由菱形的性质及全等三角形的判定可证明③;根据矩形的性质,含30︒角的直角三角形的性质,勾股定理可证明④.【详解】解:∵四边形ABCD 为矩形,∴AC BD =,∴OA OC OD OB ===,∵60COB ∠=︒,∴OBC 为等边三角形,∴OB BC OC ==,60OBC ∠=︒,∵BF AC ⊥,∴OM MC =,∴FM 是OC 的垂直平分线,∴FO FC =,故①正确;∵AB CD ∥,∴DFE BEF ∠=∠,在DOF 与BOE 中,DOF BOE DFE BEF OD OB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴DOF BOE ≅,∴DF BE =,∵AB CD ∥,∴四边形EBFD 为平行四边形,由①得OBC 为等边三角形,∴60OBC OCB ∠=∠=︒,∴30ACD BCD OCB ∠=∠-∠=︒,∵OD OC =,∴30ACD BDC ∠=∠=︒,∵BF AC ⊥,OBC 为等边三角形,∴30DBE ∠=︒,∴DBF BDC ∠=∠∴DF BF =,∴四边形EBFD 为菱形,②正确;由②可得:OB EF ⊥,∴90BOE BCF ∠=∠=︒,∵AB CD ∥,∴30EBO BDC ∠=∠=︒,∴30EBO FBC ∠=∠=︒,在OBE 与CBF 中,EBO FBC BO BCBOE BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴OBE CBF ≅,③正确;∵四边形ABCD 为矩形,∴BC AD ==∵BF AC ⊥,30FBC ∠=︒,∴12CM BC ==∴3MB ==,④正确,∴正确结论为:①②③④,故答案为:①②③④.【点睛】题目主要考查矩形的性质,菱形的判定定理,全等三角形的判定和性质,含30︒角的直角三角形的性质,勾股定理等,理解题意,综合运用这些性质是解题关键.9、6【解析】【分析】根据题意把△ABE 绕点A 逆时针旋转90°到AD ,交CD 于点G ,证明△AEF ≌△AGF 即可求得EF =DF ﹣BE =7﹣1=6.【详解】解:如图,把△ABE 绕点A 逆时针旋转90°到DA ,交CD 于点G ,由旋转的性质可知,AG =AE ,DG =BE ,∠DAG =∠BAE ,∵∠EAF =45°,∴∠DAG +∠BAF =45°,又∵∠BAD =90°,∴∠GAF =45°,在△AEF 和△AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴△AEF ≌△AGF (SAS )∴EF =GF ,∵BE=1,DF=7,∴EF=GF=DF﹣DG=DF﹣BE=7﹣1=6.故答案为:6.【点睛】本题主要考查正方形的性质及全等三角形的判定和性质,构造全等三角形是解题的关键,注意旋转性质的应用.10、8【解析】【分析】直接利用菱形的性质得出AB=AD=10,S△ABD=12.5,进而利用三角形面积求法得出答案.【详解】解:∵菱形ABCD的周长为40,面积为80,∴AB=AD=10,S△ABD=40,∵分别作P点到直线AB、AD的垂线段PE、PF,∴12×AB×PE+12×PF×AD=40,∴12×10(PE+PF)=40,∴PE+PF=8.故答案为:8.【点睛】此题主要考查了菱形的性质,正确得出12×AB×PE+12×PF×AD=S△ABD是解题关键.三、解答题1、 (1)“翻移运动”对应点(指图1中的A 与2A ,B 与2)B ⋯连线被翻移线平分(2)3(3)11或10【解析】【分析】(1)画出图形,即可得出结论;(2)作直线EF ,即为“翻移线”直线a ,再由“翻移运动”的性质和三角形面积关系求解即可;(3)分两种情况:①ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向上平移2个单位,②ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向下平移2个单位,由“翻移运动”的性质、梯形面积公式和三角形面积公式分别求解即可.(1)解:如图1,连接2AA ,2BB ⋯,则“翻移运动”对应点(指图1中的A 与2A ,B 与2)B ⋯连线被翻移线平分;(2)解:作直线EF ,即为“翻移线”直线a ,如图2所示:四边形ABCD 是长方形,AB CD ∴=,8AD BC ==,由“翻移运动”的性质得:AB DC GD ==,142AF DF AD ===,O 是AG 的中点,3AOF OGF S S ∆∆∴==, ΔΔ26AFG OGF S S ∴==,AF DF =,ΔΔ6GDF AFG S S ∴==,Δ114622GDF S DG DF DG ∴=⨯=⨯⨯=, 3DG ∴=,3AB ∴=;(3)解:分两种情况:①ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向上平移2个单位,如图3所示:设ABE ∆翻折后的三角形为DCP ∆,连接1PM ,则1112A D B C M P ===,同(2)得:1112KF A D ==,1112HE M P ==,4BE =,1BM =,3ME BE BM ∴=-=,∴四边形AKHM 的面积=梯形ABEK 的面积ABM -∆的面积HME -∆的面积111(331)4313111222=⨯++⨯-⨯⨯-⨯⨯=; ②ABM ∆先按(2)的“翻移线”直线a 翻折,然后再向下平移2个单位,如图4所示:设ABE ∆翻折后的三角形为DCP ∆,连接1PM ,则1112A D B C M P ===,同(2)得:1112KF A D ==,1112HE M P ==,4BE =,1BM =,3ME BE BM ∴=-=,∴四边形AKHM 的面积=梯形AFEM 的面积AFK -∆的面积HME +∆的面积111(34)3413110222=⨯+⨯-⨯⨯+⨯⨯=; 综上所述,四边形AKHM 的面积为11或10.【点睛】本题是四边形综合题目,考查了长方形的性质、“翻移运动”的性质、梯形面积公式、三角形面积公式等知识,本题综合性强,解题的关键是熟练掌握“翻移运动”的性质和长方形的性质.2、 (1)见解析 (2)12【解析】【分析】(1)易证DEB A ∠=∠,即可证明ACB EBD ∆≅∆,得出BC BD =,根据点E 是BC 的中点即可解题;(2)过点M 作,BC AC 的垂线,交于点,P Q ,证四边形PMQC 为矩形,再证得四边形PMQC 为正方形,得出MP MQ =,根据ACM BCM S AC S BC=. (1)解:证明:90DEB ABC ∠+∠=︒,90A ABC ∠+∠=︒,DEB A ∴∠=∠, 在ACB ∆和EBD ∆中,ACB DBE A DEB AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,AAS;∴∆≅∆,()ACB EBD∴=,BC BD点E是BC的中点,∴=,2EC BC∴=;2BD EC(2)BC AC的垂线,交于点,P Q,解:过点M作,∴∠=︒,MP QC MQ PC MPC//,//,90∴四边形PMQC为矩形,=∠=︒,BC BD DBC,90∴△为等腰直角三角形,BCD∴∠=︒,MCP45∴为等腰直角三角形,CPM∴=,CP MP∴四边形PMQC为正方形,∴=,MP MQ11,22ACM BCM SAC MQ S BC MQ =⋅=⋅, ACMBCM S AC S BC ∴=, 12AC BC =, 12ACMBCMSS ∴=. 【点睛】本题考查了全等三角形的判定,等腰直角三角形,正方形的判定及性质,解题的关键是掌握全等三角形的判定及性质,同时利用等量代换的思想进行求解.3、 (1)见解析(2)33°【解析】【分析】(1)由菱形的性质可得AB =CD =BE ,AB //CD ,可证四边形BECD 是平行四边形,可得BD =EC ;(2)由平行四边形的性质可得BD //CE ,可得∠ABO =∠E =57°,菱形的性质可求∠BAO 的大小.(1)证明:∵四边形ABCD 是菱形,∴AB =CD ,AB //CD又∵BE =AB ,∴BE =CD ,BE //CD ,∴四边形BECD 是平行四边形∴BD =EC(2)∵四边形BECD是平行四边形,∴BD//CE,∴∠ABO=∠E=57°又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°∴∠BAO+∠ABO=90°∴∠BAO=90°-∠ABO=33°【点睛】本题考查了菱形的性质,平行四边形的判定和性质,熟练运用菱形的性质是本题的关键.,对角线互相垂直的平行四边形为菱形4、(1)见解析;(2)四边形ABCD为平行四边形,BD AC【解析】【分析】(1)根据几何语言画出对应的几何图形;(2)先证明四边形ABCD为平行四边形,然后利用对角线垂直可判断四边形ABCD为菱形.【详解】解:(1)如图,四边形ABCD为所作;(2)完成下面的证明.=,证明:OA OC=,OB OD∴四边形ABCD为平行四边形,BD AC⊥,∴四边形ABCD为菱形(对角线互相垂直的平行四边形为菱形).⊥,对角线互相垂直的平行四边形为菱形.故答案为四边形ABCD为平行四边形,BD AC【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了菱形的判定.5、见解析【解析】【分析】作△ABC的角平分线AE,作线段AE的垂直平分线MN交AB于点D,交AC于点F.四边形ADEF即为所求.【详解】解:如图:四边形ADEF即为所求.【点睛】本题考查了基本作图,正方形的判定和性质等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.。
菱形性质习题精选(含答案)

菱形性质习题精选(含答案)菱形性质习题精选一.填空题(共26小题)1.(2015?模拟)如图,在菱形ABCD中,点E是AB上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO=度.2.(2015?模拟)如图,在四边形ABCD中,AB=6,∠ABC=90°,E在CD上,连接AE,BE,∠DAE=75°,若四边形ABED 是菱形,则EC的长度为.3.(2015?模拟)如图,菱形ABCD的对角线AC、BD交于点O,其中AC=8,BD=6,以OC、OB为边作矩形OBEC,矩形OBEC 的对角线OE、BC交于点F,再以CF、FE为边作第一个菱形CFEG,菱形CFEG的对角线FG、CE交于点H,如此继续,得到第n个菱形的周长等于.4.(2015?州市校级模拟)己知菱形相邻两角的度数比为1:5,且它的面积为8,则这个菱形的周长为.5.(2015?模拟)如图,在菱形ABCD中,∠A=45°,DE⊥AB,垂足为E,若CD=4cm,则菱形ABCD的面积是.6.(2015?模拟)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于.7.(2014?)菱形ABCD中,若对角线长AC=8cm,BD=6cm,则边长AB=cm.8.(2014?)菱形的周长为20cm,两个相邻的角的度数之比为1:2,则较长的对角线长度是cm.9.(2014?)如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO=.10.(2014?宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y 轴上,则点C的坐标是.11.(2014?眉山)如图,菱形ABCD中,E、F分别是BC、CD 的中点,过点E作EG⊥AD 于G,连接GF.若∠A=80°,则∠DGF的度数为.12.(2014春?期末)如图在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的大小为.13.(2014?模拟)如图,在菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为.14.(2014?江都市二模)已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为cm.15.(2014?简阳市模拟)如图,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,记=k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k=.16.(2014?淮区一模)如图,在菱形ABCD中,∠ABC=60°,BC=1cm,以DC为边在菱形的外部作正三角形CDE,连接AE,则AE=cm.17.(2014?惠安县二模)如图,菱形ABCD的边长是2cm,∠A=60°,点E、F分别是边AB、CD上的动点,则线段EF的最小值为cm.18.(2013秋?海陵区期末)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为4cm,∠A=120°,则EF=cm.19.(2014春?仙游县校级期末)如图,以菱形AOBC的顶点O 为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB=,点C的坐标为(4,0),则点A的坐标为.20.(2014春?期末)如图,在菱形ABCD中,AB=13cm,BC 边上的高AH=5cm,那么对角线AC的长为cm.21.(2014春?泰兴市校级期末)如图,菱形ABCD的周长为16cm,BC的垂直平分线EF 经过点A,则对角线BD长为cm.22.(2014春?建湖县期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,则ED的长等于.23.(2014春?玄武区期末)如图,在菱形ABCD中,BE⊥AD,垂足为E,且E为AD为中点.则∠ADC=°.24.(2014春?定县期末)如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P 是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是.25.(2014春?顺义区期末)如图,菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC=度.26.(2014秋?武进区期中)如图,依次连结第一个矩形各边的中点得到第一个菱形,再依次连结所得菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为2,则第2013个菱形的面积为.二.解答题27.(2014?县模拟)如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,求证:CE=CF.28.(2014?江都市模拟)如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.(1)求证:∠1=∠2;(2)若DF⊥BC,求证:点F是边BC的中点.29.(2014春?期末)如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.30.(2014春?高淳县校级期末)如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.31.(2013秋?东海县月考)如图,在菱形ABCD中,点E是AD 边的中点,点M是AB边上的一个动点(不与点A重合),延长ME 交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)若∠DAB=60°,当点M位于何处时,四边形AMDN是矩形?并说明理由.(请在备用图中画出符合题意的图形)32.(2012秋?鼓楼区校级期末)如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B 出发向点C运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.参考答案1.50 2.3 3. 4.16 5.8cm 2 6.5 7.5 8.5 9.35° 10.(5,4) 11.50° 12.20°13.3 14.4.8 15. 16.17. 18.2 19.(2,1)20. 21.4 22.4-3 23.120 24.2 25.105 26.27、证明:四边形ABCD 是菱形CE ⊥AE,CF ⊥AF∠DAB=∠CBB,∠DAB=∠FDC,∴∠CBE=∠FDC又 BC=DC,∴Rt △BEC ≌Rt △DFC,∴CE=CF.28、证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,∴∠1=∠ACD ,∵MC=MD ,∴∠ACD=∠2,∴∠1=∠2;(2)连接BD ,∵四边形ABCD 是菱形,∴∠ACB=∠ACD ,BC=CD ,∵∠ACD=∠2,∴∠ACB=∠ACD=∠2,∵DF ⊥BC ,∴3∠2=90°,∴∠2=30°,∴∠BCD=∠ACB+∠ACD=60°,∴△BCD 是等边三角形,∴BF=CF ,即点F 是边BC 的中点.29、(1)在△DFC 中,∠DFC =90°,∠C =30°,DC =2t ,∴DF =t .又∵AE=t ,∴AE=DF(2)能.理由如下:∵AB ⊥BC ,DF ⊥BC ,∴AE ∥DF .又AE =DF ,∴四边形AEFD 为平行四边形.∵AB =21AC BC=35 222AC BC AB =+∴()2223521AC AC =+??? ?? ∴AC=1010 2.AD AC DC t ∴=-=-若使AEFD 为菱形,则需10.102,.3AE AD t t t ==-=即即当103t =时,四边形AEFD 为菱形30、(1)△ABP ≌△ACQ ,△APC ≌△AQD ;(2)∵△ACP ≌△ADQ ,∴S △ACP =S △ADQ ,即S 四边形APCQ =S △ACD =3221??;(3为菱形的高) (3)∵△PAQ 是等边三角形,点P 是BC 的中点时,AP 垂直于BC ,AP 最小,∴当AP ⊥BC 时,三角形APQ 的面积最小,故在四边形APCQ 的面积一定,△APQ 面积最小时,△PCQ 的面积最大. 此时BP=1,31、证明:∵四边形ABCD 是菱形∴∠DNM=∠AMN又∵DE=AE ,∠NDE=∠MAE∴△NDE=△MAE∴ND=AM∴ND ∥AM∴四边形ANDM 是平行四边形(2)当点M 是AB 的中点时,四边形AMDN 是矩形证明:如图所示∵四边形AMDN 是矩形,∠DAB=60o∴∠ADM=30o∴AM=AD 21 ∵AD=AB ∴AM=AB 21 即M 是AB 的中点32、解:(1)经过x 秒后,四边形AQCP 是菱形∴DP=X cm AP=CP=AD-DP=(8-X)cm∵DP 2+CD 2=PC 2∴16+X 2=(8-X) 2 解得x=3即经过3秒后四边形是菱形(2)由(1)得菱形的边长为5∴菱形AQCP的周长=5×4=20(㎝)菱形AQCP的面积=5×4=20(㎝2)。
2020届人教版八年级数学下册 18.2.3 正方形(2)同步练习(含解析)

18.2.3正方形(2)同步练习姓名:__________班级:__________学号:__________本节应掌握和应用的知识点1.正方形的判定方法:(1)有一组邻边相等的矩形是正方形;(2)有一个角是直角的菱形是正方形;(3)对角线互相垂直的矩形是正方形;(4)对角线相等的菱形是正方形.2.判定一个四边形是正方形,一般有两种思路:一种是先证四边形是菱形,再证明它有一个角是直角或对角线相等;另一种是先证明四边形是矩形,再证它有一组邻边相等或对角线互相垂直.基础知识和能力拓展训练一.选择题1.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,四边形ABCD是菱形B.当AC⊥BD时,四边形ABCD是菱形C.当∠ABC=90°时,四边形ABCD是矩形D.当AC=BD时,四边形ABCD是正方形2.下列命题,其中正确命题的个数为()(1)等边三角形是中心对称图形;(2)一组对边平行,另一组对边相等的四边形是平行四边形;(3)两条对角线互相垂直的矩形是正方形;(4)两条对角线互相垂直的四边形是菱形.A.1个B.2个C.3个D.4个3.已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是()A.AC=BDAB∥CD,AB=CD B.AD∥BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①② B.②③ C.①③ D.②④5.如图,在矩形ABCD中,AD=2AB,E、F分别是AD、BC的中点,连接AF与BE、CE与DF 分别交于点M、N两点,则四边形EMFN是()A.正方形B.菱形 C.矩形 D.无法确定6.如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是()A.四边形ACDF是平行四边形B.当点E为BC中点时,四边形ACDF是矩形C.当点B与点E重合时,四边形ACDF是菱形D.四边形ACDF不可能是正方形7.从①②③④中选择一块拼图板可与左边图形拼成一个正方形,正确的选择为()A.①B.②C.③D.④8.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=()时,则四边形AECF是正方形.A.30° B.45° C.60° D.90°9.如图,四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD面积为16,则DE的长为()A.3 B.2 C.4 D.810.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是()A.30 B.34 C.36 D.40二.填空题11.矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件,使其成为正方形(只填一个即可)12.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是.13.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD= 时,四边形MENF是正方形.14.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,能证明四边形BECF为正方形的是.①BC=AC;②CF⊥BF;③BD=DF;④AC=BF.15.四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AD=BC,为使四边形ABCD为正方形,还需要满足下列条件中:①AC=BD;②AB=AD;③AB=CD;④AC⊥BD中的哪两个(填代号).16.已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为.17.如图所示,多边形ABCFDE中,AB=8,BC=12,ED+DF=13,AE=CF,则多边形ABCFDE的面积是.三.解答题18.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.19.如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC 于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)20.如图所示,已知正方形ABCD的边长是7,AE=BF=CG=DH=2(1)四边形EFGH的形状是;(2)求出四边形EFGH的面积;(3)求出四边形EFGH的周长(结果精确到十分位,参考数值:≈1.703,)21.如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB 于点E,且CF=AE;(1)试判断四边形BECF是什么四边形?并说明理由.(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.22.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F 在DE的延长线上,且AF=CE.(1)四边形ACEF是平行四边形吗?说明理由;(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;(3)四边形ACEF有可能是正方形吗?为什么?答案与试题解析一.选择题1.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,四边形ABCD是菱形B.当AC⊥BD时,四边形ABCD是菱形C.当∠ABC=90°时,四边形ABCD是矩形D.当AC=BD时,四边形ABCD是正方形【分析】根据已知及各个特殊四边形的判定方法对各个选项进行分析从而得到最后答案.解:A、正确,一组邻边相等的平行四边形是菱形;B、正确,对角线互相垂直的平行四边形是菱形;C、正确,有一个角为90°的平行四边形是矩形;D、不正确,对角线相等的平行四边形是矩形而不是正方形;故选D.2.下列命题,其中正确命题的个数为()(1)等边三角形是中心对称图形;(2)一组对边平行,另一组对边相等的四边形是平行四边形;(3)两条对角线互相垂直的矩形是正方形;(4)两条对角线互相垂直的四边形是菱形.A.1个B.2个C.3个D.4个【分析】根据中心对称的概念以及平行四边形、正方形、菱形的判定定理进行判断即可.解:(1)因为正奇边形不是中心对称图形,故等边三角形不是中心对称图形,此选项错误;(2)一组对边平行,另一组对边相等的四边形不一定是平行四边形,因为等腰梯形也符合此条件,此选项错误;(3)两条对角线互相垂直的矩形是正方形,此选项正确;(4)两条对角线互相垂直平分的四边形是菱形,此选项错误.故选:A.3.已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是()A.AC=BDAB∥CD,AB=CD B.AD∥BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC【分析】根据正方形的判定:对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案.解:A、不能,只能判定为矩形;B、不能,只能判定为平行四边形;C、能;D、不能,只能判定为菱形.故选:C.4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①② B.②③ C.①③ D.②④【分析】利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.解:A、∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;B、∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;C、∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;D、∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.故选:B.5.如图,在矩形ABCD中,AD=2AB,E、F分别是AD、BC的中点,连接AF与BE、CE与DF 分别交于点M、N两点,则四边形EMFN是()A.正方形B.菱形 C.矩形 D.无法确定【分析】利用矩形的性质与判定方法得出四边形EMFN是矩形,进而利用等腰直角三角形的性质得出AM=ME,BM=MF=AM,则ME=MF,进而求出即可.解:∵四边形ABCD为矩形,∴AD∥BC,AD=BC,∠EAB=∠ABF=∠BCD=∠CDA=90°,又∵E,F分别为AD,BC中点,AD=2AB,∴AE∥BF,ED∥CF,AE=BF=DE=CF=AB=DC,∴∠ABE=∠AEB=∠DEC=∠DCE=∠DFC=45°,∴∠BEN=90°,又∵DE BF,AE FC,∴四边形EMFN是矩形,∴AM⊥BE,BM⊥AF,∴AM=ME,BM=MF=AM,∴ME=MF,∴四边形EMFN是正方形.故选:A.6.如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是()A.四边形ACDF是平行四边形B.当点E为BC中点时,四边形ACDF是矩形C.当点B与点E重合时,四边形ACDF是菱形D.四边形ACDF不可能是正方形【分析】根据平行四边形、矩形、菱形、正方形的判定方法一一判断即可.解:A、正确.∵∠ACB=∠EFD=30°,∴AC∥DF,∵AC=DF,∴四边形AFDC是平行四边形.故正确.B、错误.当E是BC中点时,无法证明∠ACD=90°,故错误.C、正确.B、E重合时,易证FA=FD,∵四边形AFDC是平行四边形,∴四边形AFDC是菱形,D、正确.当四边相等时,∠AFD=60°,∠FAC=120°,∴四边形AFDC不可能是正方形.故选B.7.从①②③④中选择一块拼图板可与左边图形拼成一个正方形,正确的选择为()A.①B.②C.③D.④【分析】根据正方形的判定定理即可得到结论.解:与左边图形拼成一个正方形,正确的选择为③,故选C.8.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=()时,则四边形AECF是正方形.A.30° B.45° C.60° D.90°【分析】由题意可得四边形AECF为一矩形,要使四边形AECF是正方形,只需添加一条件,使其邻边相等即可.解:过点E,F作EH⊥BD,FG⊥BD,∵CE,CF为∠ACB,∠ACD的角平分线,∴∠ECF=90°.∵MN∥BC,∴∠FEC=∠ECH,∵∠ECH=∠ECO,∴∠FEC=∠ECO,∴OE=OC.同理OC=OF,∴OE=OF,∵点O运动到AC的中点,∴OA=OC,∴四边形AECF为一矩形,若∠ACB=90°,则CE=CF,∴四边形AECF为正方形.故选:D.9.如图,四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD面积为16,则DE的长为()A.3 B.2 C.4 D.8【分析】如图,过点D作BC的垂线,交BC的延长线于F,利用互余关系可得∠A=∠FCD,又∠AED=∠F=90°,AD=DC,利用AAS可以判断△ADE≌△CDF,∴DE=DF,S四边形ABCD=S正方形DEBF=16,DE=4.解:过点D作BC的垂线,交BC的延长线于F,∵∠ADC=∠ABC=90°,∴∠A+∠BCD=180°,∵∠FCD+∠BCD=180°,∴∠A=∠FCD,又∠AED=∠F=90°,AD=DC,∴△ADE≌△CDF,∴DE=DF,S四边形ABCD=S正方形DEBF=16,∴DE=4.故选C.10.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是()A.30 B.34 C.36 D.40【分析】由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出四边形EFGH是正方形,由边长为8,AE=BF=CG=DH=5,可得AH=3,由勾股定理得EH,得正方形EFGH的面积.解:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,∵AE=BF=CG=DH,∴AH=BE=CF=DG.在△AEH、△BFE、△CGF和△DHG中,,∴△AEH≌△BFE≌△CGF≌△DHG(SAS),∴EH=FE=GF=GH,∠AEH=∠BFE,∴四边形EFGH是菱形,∵∠BEF+∠BFE=90°,∴∠BEF+∠AEH=90°,∴∠HEF=90°,∴四边形EFGH是正方形,∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,∴EH=FE=GF=GH==,∴四边形EFGH的面积是:×=34,故选B.二.填空题11.矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AB=BC(答案不唯一),使其成为正方形(只填一个即可)【分析】此题是一道开放型的题目答案不唯一,证出四边形ABCD是菱形,由正方形的判定方法即可得出结论.解:添加条件:AB=BC,理由如下:∵四边形ABCD是矩形,AB=BC,∴四边形ABCD是菱形,∴四边形ABCD是正方形,故答案为:AB=BC(答案不唯一).12.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是①③④.【分析】由矩形、菱形、正方形的判定方法对各个选项进行判断即可.解:∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AB⊥AD,∴四边形ABCD是正方形,①正确;∵四边形ABCD是平行四边形,AB=BD,AB⊥BD,∴平行四边形ABCD不可能是正方形,②错误;∵四边形ABCD是平行四边形,OB=OC,∴AC=BD,∴四边形ABCD是矩形,又OB⊥OC,即对角线互相垂直,∴平行四边形ABCD是正方形,③正确;∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AC=BD,∴四边形ABCD是矩形,∴平行四边形ABCD是正方形,④正确;故答案为:①③④.13.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD= 1:2 时,四边形MENF是正方形.【分析】首先得出四边形MENF是平行四边形,再求出∠BMC=90°和ME=MF,根据正方形的判定推出即可.解:当AB:AD=1:2时,四边形MENF是正方形,理由是:∵AB:AD=1:2,AM=DM,AB=CD,∴AB=AM=DM=DC,∵∠A=∠D=90°,∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°,∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°,∴∠MBC=∠MCB=45°,∴BM=CM,∵N、E、F分别是BC、BM、CM的中点,∴BE=CF,ME=MF,NF∥BM,NE∥CM,∴四边形MENF是平行四边形,∵ME=MF,∠BMC=90°,∴四边形MENF是正方形,即当AB:AD=1:2时,四边形MENF是正方形,故答案为:1:2.14.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,能证明四边形BECF为正方形的是①②③.①BC=AC;②CF⊥BF;③BD=DF;④AC=BF.【分析】根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC 进而得出四边形BECF是菱形;由菱形的性质知,以及菱形与正方形的关系,进而分别分析得出即可.解:∵EF垂直平分BC,∴BE=EC,BF=CF,∵BF=BE,∴BE=EC=CF=BF,∴四边形BECF是菱形;当①BC=AC时,∵∠ACB=90°,则∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,∴∠EBC=45°∴∠EBF=2∠EBC=2×45°=90°∴菱形BECF是正方形.故选项①正确;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项②正确;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项③正确;当AC=BF时,无法得出菱形BECF是正方形,故选项④错误.故答案为:①②③.15.四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AD=BC,为使四边形ABCD为正方形,还需要满足下列条件中:①AC=BD;②AB=AD;③AB=CD;④AC⊥BD中的哪两个①②或①④(填代号).【分析】因为AD∥BC,AD=BC,所以四边形ABCD为平行四边形,添加①则可根据对角线相等的平行四边形是矩形,证明四边形是矩形,故可根据一组邻边相等的矩形是正方形来添加条件.解:∵AD∥BC,AD=BC,∴四边形ABCD为平行四边形,∵AC=BD,∴平行四边形ABCD是矩形,若AB=AD,则四边形ABCD为正方形;若AC⊥BD,则四边形ABCD是正方形.故填:①②或①④.16.已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为2.【分析】作辅助线,构建正方形AHGF,则AF=GH=GF,设GC=x,则FG=AF=HG=x+2,DG=x﹣1,在Rt△DGC中,利用勾股定理列方程可求得x的值,最后利用勾股定理计算AC的长即可.解:过A作AE⊥DC于E,将△AEC沿AC翻折得△AFC,将△ADE沿AD翻折得△ADH,延长FC、HD交于G,则∠EAC=∠CAF,∠EAD=∠HAD,∠H=∠F=90°,∴∠EAC+∠EAD=∠CAF+∠HAD,∵∠DAC=45°,即∠EAC+∠EAD=45°,∴∠HAF=90°,∴四边形AHGF是矩形,∵AH=AE,AE=AF,∴AH=AF,∴四边形AHGF是正方形,∴AF=GH=GF,∵AB=AC,AE⊥BC,∴BE=EC=2,由折叠得:FC=EC=2,HD=DE=3,设GC=x,则FG=AF=HG=x+2,∴DG=x﹣1,在Rt△DGC中,DC2=DG2+GC2,52=(x﹣1)2+x2,解得:x1=4,x2=﹣3(舍),∴AF=x+2=4+2=6,Rt△ACF中,AC==2.故答案为:2.17.如图所示,多边形ABCFDE中,AB=8,BC=12,ED+DF=13,AE=CF,则多边形ABCFDE的面积是57.75 .【分析】运用拼图的方法,构造一个正方形,用大正方形的面积﹣小正方形的面积,即可得出所求多边形的面积.解:运用拼图的方法,构造一个正方形,如图所示:大正方形的边长为12+8=20,小正方形的边长ED+DF=13,∴多边形ABCFDE的面积=(大正方形的面积﹣小正方形面积)=(202﹣132)=57.75.故答案为:57.75.三.解答题18.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.【分析】先由BF∥CE,CF∥BE得出四边形BECF是平行四边形,又因为∠BEC=90°得出四边形BECF是矩形,BE=CE邻边相等的矩形是正方形.证明:∵BF∥CE,CF∥BE∴四边形BECF是平行四边形,又∵在矩形ABCD中,BE平分∠ABC,CE平分∠DCB∴∠EBA=∠ECB=45°∴∠BEC=90°,BE=CE∴四边形BECF是正方形.19.如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC 于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)【分析】过D作DG垂直AB于点G,由三个角为直角的四边形为矩形得到四边形CEDF为矩形,由AD为角平分线,利用角平分线定理得到DG=DF,同理得到DE=DG,等量代换得到DE=DF,利用邻边相等的矩形为正方形即可得证.证明:如图,过D作DG⊥AB,交AB于点G,∵∠C=∠DEC=∠DFC=90°,∴四边形CEDF为矩形,∵AD平分∠CAB,DF⊥AC,DG⊥AB,∴DF=DG;∵BD平分∠ABC,DG⊥AB,DE⊥BC,∴DE=DG,∴DE=DF,∴四边形CEDF为正方形.20.如图所示,已知正方形ABCD的边长是7,AE=BF=CG=DH=2(1)四边形EFGH的形状是正方形;(2)求出四边形EFGH的面积;(3)求出四边形EFGH的周长(结果精确到十分位,参考数值:≈1.703,)【分析】(1)根据正方形性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD=7,求出AH=DG=CF=BE=5,证△AEH≌△DHG≌△CGF≌△BFE,推出EH=EF=FG=HG,∠AHE=∠DGH,证出∠EHG=90°,即可得出答案.(2)在Rt△AEH中,由勾股定理求出EH=,根据正方形面积公式求出即可.(3)四边形EFGH的周长是×4,求出即可.解:(1)四边形EFGH是正方形,理由是:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD=7,∵AE=BF=CG=DH=2,∴AH=DG=CF=BE=5,∴△AEH≌△DHG≌△CGF≌△BFE(SAS),∴EH=EF=FG=HG,∠AHE=∠DGH,∵∠A=∠D=90°,∴∠DGH+∠DHG=90°,∴∠AHE+∠DHG=90°,∴∠EHG=180°﹣90°=90°,∴四边形EFGH是正方形,故答案为:正方形.(2)在Rt△AEH中,AE=2,AH=5,由勾股定理得:EH==,∵四边形EFGH是正方形,∴EF=FG=GH=EH=,∴四边形EFGH的面积是()2=29.(3)四边形EFGH的周长是×4=4≈4×5.39≈21.6.21.如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB 于点E,且CF=AE;(1)试判断四边形BECF是什么四边形?并说明理由.(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.【分析】(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=AE,BE=EC=BF=FC,根据四边相等的四边形是菱形,所以四边形BECF是菱形;(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度.解:(1)四边形BECF是菱形.∵EF垂直平分BC,∴BF=FC,BE=EC,∴∠3=∠1,∵∠ACB=90°,∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,∴EC=AE,∴BE=AE,∵CF=AE,∴BE=EC=CF=BF,∴四边形BECF是菱形.(2)当∠A=45°时,菱形BECF是正方形.证明:∵∠A=45°,∠ACB=90°,∴∠1=45°,∴∠EBF=2∠A=90°,∴菱形BECF是正方形.22.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F 在DE的延长线上,且AF=CE.(1)四边形ACEF是平行四边形吗?说明理由;(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;(3)四边形ACEF有可能是正方形吗?为什么?【分析】(1)已知AF=EC,只需证明AF∥EC即可.DE垂直平分BC,易知DE是△ABC的中位线,则FE∥AC,BE=EA=CE=AF;因此△AFE、△AEC都是等腰三角形,可得∠F=∠5=∠1=∠2,即∠FAE=∠AEC,由此可证得AF∥EC;(2)要使得平行四边形ACEF为菱形,则AC=CE,又∵CE=AB,∴使得AB=2AC即可,根据AB、AC即可求得∠B的值;(3)通过已知在△ABC中,∠ACB=90°,推出∠ACE<90°,不能为直角,进行说明.解:(1)四边形ACEF是平行四边形;∵DE垂直平分BC,∴D为BC的中点,ED⊥BC,又∵AC⊥BC,∴ED∥AC,∴E为AB中点,∴ED是△ABC的中位线.∴BE=AE,FD∥AC.∴BD=CD,∴Rt△ABC中,CE是斜边AB的中线,∴CE=AE=AF.∴∠F=∠5=∠1=∠2.∴∠FAE=∠AEC.∴AF∥EC.又∵AF=EC,∴四边形ACEF是平行四边形;(2)当∠B=30°时,四边形ACEF为菱形;理由:∵∠ACB=90°,∠B=30°,∴AC=AB,由(1)知CE=AB,∴AC=CE又∵四边形ACEF为平行四边形∴四边形ACEF为菱形;(3)四边形ACEF不可能是正方形,∵∠ACB=90°,∴∠ACE<∠ACB,即∠ACE<90°,不能为直角,所以四边形ACEF不可能是正方形.。
2020年中考数学一轮专项复习——矩形、菱形、正方形(含解析)

第3题图A. 20 °B.302020年中考数学一轮专项复习一一矩形、菱形、正方形课时1 矩形■基础过关1. (2019重庆模拟)下列关于矩形对角线的说法中,正确的是 ( )A.对角线相互垂直B.面积等于对角线乘积的一半C.对角线平分一组对角D.对角线相等2 . (2019临沂)如图,在?ABCD 中,M, N 是BD 上两点,个条件,使四边形 AMCN 是矩形,这个条件是()B. MB= MOD. / AMB = Z CNDBM = DN,连接 AM, MC , CN, NA.添加一1A. OM =2ACC. BD± AC3 .如图,将矩形纸片 数为( )ABCD 沿BD 折叠,得到△ BCD, CD 与AB 交于点E.若/1 = 35°,则/ 2的度第2题图5.如图,矩形 ABCD 中,A (-2, 0), B (2, 0), C (2, 2),将AB 绕点A 旋转,使点 B 落在边CD 上的点E 处,则点E 的坐标为()B. (2击,2) D. (2^3-2, 2)4. (2019贵阳模拟)如图,在矩形ABCD ( ) ABCD 中,AE 平分/ BAD,交边BC 于点E,若ED=5, EC=3,则A. 11B. 14C. 22D. 28A.(a 2) C. (1 ,6.如图,在矩形ABCD 中,对角线 AC 与BD 相交于点 O,过点A 作BD 的垂线,垂足为E.已知/ EAD= 3/BAE,则/ EAO 的度数为(A . 22.5B. 67.5C. 45°D. 60°7 . (2020原创)如图,点O 是矩形 则^ BOE 的周长为()ABCD 对角线 AC 的中点,OE // AB 交AD 于点E.若AB=6, BC=8,A. 10B. 8 + 2^5C. 8+2^13D. 14E第4题图第5题图4第6题图10.(人教八下P55练习2题)如图,?ABCD的对角线AC、BD交于点O, △ OAB是等边三角形,AB =4.(1)求证:四边形ABCD是矩形;(2)求四边形ABCD的面积.8. (2018遵义)如图,点P是矩形ABCD的对角线AC上一点, 点E, F,连接PB、PD.若AE=2, PF = 8.则图中阴影部分的面积为过点P作EF // BC,分别交AB, CD于A. 10 8.12 C. 16D. 189.(2019徐州)如图,矩形ABCD中,AC、BD交于点O, M、N分别为BC、OC的中点,若MN = 4, 则AC的长为第7题图第8题图第9题图第10题图11 . (2019怀化)已知:如图,在?ABCD中,AEXBC, CFXAD, E, F分别为垂足.⑴求证:△ ABE^A CDF ;(2)求证:四边形AECF是矩形.第11题图12 . (2019连云港)如图,在^ ABC中,AB = AC>AABC沿着BC方向平移得到△ DEF ,其中点E在边BC上,DE 与AC相交于点O.(1)求证:△ OEC为等腰三角形;(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.第12题图1 . (2019台州)如图,有两张矩形纸片 ABCD 和EFGH, AB=EF =2 cm, BC = FG=8 cm 把纸片 ABCD 交叉叠放在纸片 EFGH 上,使重叠部分为平行四边形,且点 D 与点G 重合,当两张纸片交叉所成的角 “最 小时,tan a 等于()2 .如图,在矩形 ABCD 中,AB = 4, BC = 6, E 是矩形内部的一个动点,且 AEXBE,则线段CE 的最 小值为.A.B. 2C. 187D.8_15;1 DB EC F第1题图第2题图立满分冲关1. (2019眉山模拟)如图,在矩形ABCD中,E是AD边的中点,BEXAC,垂足为点F,连接DF ,分析下列四个结论:① CF = 3AF;②AB=DF;③DF = ^BC;④S四边形CDEF^S MBF.其中正确白结论有( )第1题图A . 1个B,2个C,3个D,4个【错误结论纠正】请将错误结论改正确.2 .如图,在矩形ABCD中,ZBAC=30°,对角线AC, BD交于点O, / BCD的平分线CE分别交AB, BD于点E, H,连接OE.(1)求/ BOE的度数;(2)若BC=1,求^ BCH的面积;(3)求S A CHO :S^BHE的值.H E第2题图课时2菱形(建议时间:40分钟)名■基础过关1. (2019玉林)菱形不具备的性质是()A.是轴对称图形B.是中心对称图形C.对角线互相垂直D.对角线一定相等2. (2019 河北)如图,菱形ABCD 中,/ D= 150°,则/ 1 =()A.30 °B. 25 °C. 20 °D. 15 °DB第2题图3. (2019襄阳)如图,分别以线段AB的两个端点为圆心,大于AB的一半的长为半径画弧,两弧分别交于C, D两点,连接AC, BC, AD, BD,则四边形ADBC一定是()A.正方形B.矩形第3题图4. (2019呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A.2 2B. 2 . 5C. 4 2D. 2 . 105. (2019宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是()A.AC± BDB.AB = ADC.AC= BDD./ ABD = Z CBD,4第5题图6 . (2019赤峰)如图,菱形ABCD的周长为20,对角线AC、BD相交于点O, E是CD的中点,则OE 的长是()A. 2.5B. 3第6题图7. (2019天津)如图,四边形ABCD 为菱形,A, B两点的坐标分别是(2, 0), (0, 1),点C, D在坐标轴上,则菱形ABCD的周长等于(y6D第7题图A. 5B.4 3C.4 5D. 208 . (2019永州)如图,四边形ABCD的对角线相交于点O,且点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.如图,在菱形 ABCD 中,对角线 AC、BD 相交于点 O,过点 D 作对角线 BD 的
垂线交 BA 的延长线于点 E. (1)证明:四边形 ACDE 是平行四边形; (2)若 AC=8,BD=6,求△ADE 的周长.
矩形、菱形、正方形(解答题)
1.如图,在平行四边形 ABCD 中,BC=2AB=4,点 E、F 分别是 BC、AD 的中点. (1)求证:△ABE≌△CDF; (2)当四边形 AECF 为菱形时,求出该菱形的面积.
2.如图,四边形 ABCD 是菱形,CE⊥AB 交 AB 的延长线于点 E,CF⊥AD 交 AD 的延长线于点 F,求证:DF=BE.
11.如图,在四边形 ABCF 中,∠ACB=90°,点 E 是 AB 边的中点,点 F 恰是点 E 关于 AC 所在直线的对称点. (1)证明:四边形 CFAE 为菱形; (2)连接 EF 交 AC 于点 O,若 BC=10,求线段 OF 的长.
12.如图,在平行四边形 ABCD 中,以点 A 为圆心,AB 长为半径画弧交 AD 于点 F,再分别以点 B、F 为圆心,大于 长为半径画弧,两弧交于一点 P,连 接 AP 并延长交 BC 于点 E,连接 EF. (1)四边形 ABEF 是 ;(选填矩形、菱形、正方形、无法确定)(直接填写 结果) (2)AE,BF 相交于点 O,若四边形 ABEF 的周长为 40,BF=10,则 AE 的长为 , ∠ABC= °.(直接填写结果)
17.如图,矩形 ABCD 的对角线 AC,BD 相交于点 O,若 AB=AO,求∠ABD 的度 数.
18.已知:如图,在矩形 ABCD 中,点 E 在边 AB 上,点 F 在边 BC 上,且 BE=CF, EF⊥DF,求证:BF=CD.
19.如图,矩形 ABCD 中,AB=4,AD=3,M 是边 CD 上一点,将△ADM 沿直线 AM 对折,得到△ANM. (1)当 AN 平分∠MAB 时,求 DM 的长; (2)连接 BN,当 DM=1 时,求△ABN 的面积;
13.如图,AC 是矩形 ABCD 的对角线,过 AC 的中点 O 作 EF⊥AC,交 BC 于点 E, 交 AD 于点 F,连接 AE,CF. (1)求证:四边形 AECF 是菱形; (2)若 AB= ,∠DCF=30°,求四边形 AECF 的面积.(结果保留根号)
14.如图,已知 BD 是矩形 ABCD 的对角线. (1)用直尺和圆规作线段 BD 的垂直平分线,分别交 AD、BC 于 E、F(保留作 图痕迹,不写作法和证明). (2)连结 BE,DF,问四边形 BEDF 是什么四边形?请说明理由.
22.阅读下面材料: 在数学课上,老师请同学思考如下问题:如图 1,我们把一个四边形 ABCD 的四 边中点 E,F,G,H 依次连接起来得到的四边形 EFGH 是平行四边形吗? 小敏在思考问题是,有如下思路:连接 AC.
3.如图,将一张直角三角形 ABC 纸片沿斜边 AB 上的中线 CD 剪开,得到△ACD, 再将△ACD 沿 DB 方向平移到△A′C′D′的位置,若平移开始后点 D′未到达点 B 时, A′C′交 CD 于 E,D′C′交 CB 于点 F,连接 EF,当四边形 EDD′F 为菱形时,试探究△ A′DE 的形状,并判断△A′DE 与△EFC′是否全等?请说明理由.
9.如图,△ABC≌△ABD,点 E 在边 AB 上,CE∥BD,连接 DE.求证: (1)∠CEB=∠CBE; (2)四边形 BCED 是菱形.
10.如图,在 Rt△ABC 中,∠B=90°,点 E 是 AC 的中点,AC=2AB,∠BAC 的平 分线 AD 交 BC 于点 D,作 AF∥BC,连接 DE 并延长交 AF 于点 F,连接 FC. 求证:四边形 ADCF 是菱形.
(3)当射线 BN 交线段 CD 于点 F 时,求 DF 的最大值.
20.如图,菱形 AB四边形 AODE 是矩形.
21.如图,将平行四边形 ABCD 的边 AB 延长到点 E,使 BE=AB,连接 DE,交边 BC 于点 F. (1)求证:△BEF≌△CDF; (2)连接 BD、CE,若∠BFD=2∠A,求证:四边形 BECD 是矩形.
15.如图,AC 为矩形 ABCD 的对角线,将边 AB 沿 AE 折叠,使点 B 落在 AC 上的 点 M 处,将边 CD 沿 CF 折叠,使点 D 落在 AC 上的点 N 处. (1)求证:四边形 AECF 是平行四边形;
(2)若 AB=6,AC=10,求四边形 AECF 的面积.
16.如图,矩形 ABCD 中,延长 AB 至 E,延长 CD 至 F,BE=DF,连接 EF,与 BC、 AD 分别相交于 P、Q 两点. (1)求证:CP=AQ; (2)若 BP=1,PQ=2 ,∠AEF=45°,求矩形 ABCD 的面积.
7.如图,在△ABC 中,∠ACB=90°,D,E 分别为 AC,AB 的中点,BF∥CE 交 DE 的延长线于点 F. (1)求证:四边形 ECBF 是平行四边形; (2)当∠A=30°时,求证:四边形 ECBF 是菱形.
8.如图,AE∥BF,AC 平分∠BAE,且交 BF 于点 C,BD 平分∠ABF,且交 AE 于 点 D,AC 与 BD 相交于点 O,连接 CD (1)求∠AOD 的度数; (2)求证:四边形 ABCD 是菱形.
6.如图,把△EFP 放置在菱形 ABCD 中,使得顶点 E,F,P 分别在线段 AB,AD, AC 上,已知 EP=FP=6,EF=6 ,∠BAD=60°,且 AB>6 . (1)求∠EPF 的大小; (2)若 AP=10,求 AE+AF 的值; (3)若△EFP 的三个顶点 E、F、P 分别在线段 AB、AD、AC 上运动,请直接写 出 AP 长的最大值和最小值.
