(完整word版)矩形菱形正方形练习题及答案

合集下载

中考数学总复习《矩形、菱形、正方形》专项测试卷含答案

中考数学总复习《矩形、菱形、正方形》专项测试卷含答案学校:___________班级：___________姓名：___________考号：___________A层·基础过关1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D2.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是( )A.点O为矩形ABCD的对称中心B.点O为线段AB的对称中心C.直线BD为矩形ABCD的对称轴D.直线AC为线段BD的对称轴3.如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为( )A.20°B.60°C.70°D.80°4.(2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )A.AB=ADB.AC⊥BDC.AC=BDD.∠ACB=∠ACD5.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )A.12B.1C.√32D.√36.(2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC=°.7.(2024·龙东)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件,使得菱形ABCD为正方形.8.(2024·遂宁)康康在学习了矩形定义及判定定理1后,继续探究其他判定定理.(1)实践与操作①任意作两条相交的直线,交点记为O;②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA,OB,OC,OD;③顺次连接所得的四点得到四边形ABCD.于是可以直接判定四边形ABCD是平行四边形,则该判定定理是:.(2)猜想与证明通过和同伴交流,他们一致认为四边形ABCD是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.已知:如图,四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.B层·能力提升9.(2024·泸州)如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+1FG的最小值是( )2A.4B.5C.8D.1010.(2024·贵州)如图,在菱形ABCD中,点E,F分别是BC,CD的中点,连接AE,AF.若sin∠EAF=4,AE=5,则AB的长为.511.(2024·天津)如图,正方形ABCD的边长为3√2,对角线AC,BD相交于点O,点E 在CA的延长线上,OE=5,连接DE.(1)线段AE的长为;(2)若F为DE的中点,则线段AF的长为.C层·挑战冲A+12.(2024·济宁)综合与实践某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中,AB>AD且AB足够长)进行探究活动.【动手操作】如图2,第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.第三步,连接GF.【探究发现】根据以上操作,甲、乙两同学分别写出了一个结论.甲同学的结论:四边形AEFD是正方形.乙同学的结论:tan∠AFG=1.3(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.【继续探究】在上面操作的基础上,丙同学继续操作.如图3,第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.第五步,连接FM交GP于点N.根据以上操作,丁同学写出了一个正确结论:FN·AM=GN·AD.(2)请证明这个结论.参考答案A层·基础过关1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是(C)A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D2.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是(A)A.点O为矩形ABCD的对称中心B.点O为线段AB的对称中心C.直线BD为矩形ABCD的对称轴D.直线AC为线段BD的对称轴3.如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为(C)A.20°B.60°C.70°D.80°4.(2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是(C)A.AB=ADB.AC⊥BDC.AC=BDD.∠ACB=∠ACD5.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为(D)A.12B.1C.√32D.√36.(2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC=57°.7.(2024·龙东)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件AC=BD(答案不唯一),使得菱形ABCD为正方形.8.(2024·遂宁)康康在学习了矩形定义及判定定理1后,继续探究其他判定定理.(1)实践与操作①任意作两条相交的直线,交点记为O;②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA,OB,OC,OD;③顺次连接所得的四点得到四边形ABCD.于是可以直接判定四边形ABCD是平行四边形,则该判定定理是:.【解析】(1)∵OA=OC,OB=OD∴四边形ABCD的对角线互相平分∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).答案:对角线互相平分的四边形是平行四边形(2)猜想与证明通过和同伴交流,他们一致认为四边形ABCD是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.已知:如图,四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.【解析】(2)∵四边形ABCD 是平行四边形 ∴AD =BC∴在△BAD 和△ABC 中,{AB =BAAD =BC BD =AC∴△BAD ≌△ABC (SSS) ∴∠BAD =∠ABC ∵AD ∥BC∴∠BAD +∠ABC =180° ∴∠BAD =∠ABC =90°∴四边形ABCD 是矩形(有一个角是直角的平行四边形是矩形).B 层·能力提升9.(2024·泸州)如图,在边长为6的正方形ABCD 中,点E ,F 分别是边AB ,BC 上的动点,且满足AE =BF ,AF 与DE 交于点O ,点M 是DF 的中点,G 是边AB 上的点,AG =2GB ,则OM +12FG 的最小值是(B)A .4B .5C .8D .1010.(2024·贵州)如图,在菱形ABCD 中,点E ,F 分别是BC ,CD 的中点,连接AE ,AF .若sin ∠EAF =45,AE =5,则AB 的长为2√653.11.(2024·天津)如图,正方形ABCD的边长为3√2,对角线AC,BD相交于点O,点E 在CA的延长线上,OE=5,连接DE.(1)线段AE的长为2;.(2)若F为DE的中点,则线段AF的长为√102C层·挑战冲A+12.(2024·济宁)综合与实践某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中,AB>AD且AB足够长)进行探究活动.【动手操作】如图2,第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.第三步,连接GF.【探究发现】根据以上操作,甲、乙两同学分别写出了一个结论.甲同学的结论:四边形AEFD是正方形.乙同学的结论:tan∠AFG=1.3(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.【继续探究】在上面操作的基础上,丙同学继续操作.如图3,第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.第五步,连接FM交GP于点N.根据以上操作,丁同学写出了一个正确结论:FN·AM=GN·AD.(2)请证明这个结论.【解析】(1)甲同学和乙同学的结论都正确,证明如下∵四边形ABCD是矩形∴∠D=∠BAD=90°∵折叠,∴∠D=∠AEF=90°=∠DAE,AD=AE,∴四边形AEFD是正方形;故甲同学的结论正确.过点G作GK⊥AF于点K设AE=2x,则AG=EG=x ∵四边形AEFD是正方形∴∠EAF=45°∴AF=2√2x,AK=KG=√22AG=√22x∴KF=AF-AK=3√22x∴tan∠AFG=KGKF =1 3 ;故乙同学的结论也正确.(2)方法一:过点G作GQ⊥PM,交PM的延长线于点Q∵折叠∴FP=PM,FG=GM,GH=GQ,∠FPG=∠MPG,PH=PQ∵AB∥CD,∴∠FPG=∠PGM∴∠PGM=∠MPG∴PM=GM∴PF=GM=PM=FG∴四边形FGMP是菱形∴∠FNG=90°∵∠GQP=90°=∠FNG,∠FGN=∠GPQ∴△GFN∽△PGQ∴FNGQ =GN PQ∴FN·PQ=GN·GQ∵AM=AG+GM=HF+FP=PH∴AM=PQ∵GQ=GH=AD∴FN·AM=GN·AD.方法二:连接DM,证△ADM∽△NFG也可.。

初中数学矩形、菱形与正方形测试题含答案

矩形、菱形与正方形测试题一、选择题1．能判定四边形ABCD为平行四边形的题设是（）．（A）AB∥CD，AD=BC; （B）∠A=∠B，∠C=∠D;（C）AB=CD，AD=BC; （D）AB=AD，CB=CD2．在给定的条件中，能画出平行四边形的是（）．（A）以60cm为一条对角线，20cm、34cm为两条邻边;（B）以6cm、10cm为对角线，8cm为一边;（C）以20cm、36cm为对角线，22cm为一边;（D）以6cm为一条对角线，3cm、10cm为两条邻边3．正方形具有而菱形不一定具有的性质是（）（A）对角线互相平分; （B）对角线相等;（C）对角线平分一组对角; （D）对角线互相垂直4．在下列说法中不正确的是（）（A）两条对角线互相垂直的矩形是正方形;（B）两条对角线相等的菱形是正方形;（C）两条对角线垂直且相等的平行四边形是正方形;（D）两条对角线垂直且相等的四边形是正方形5．下列说法不正确的是（）（A）对角线相等且互相平分的四边形是矩形;（B）对角线互相垂直平分的四边形是菱形;（C）一组对边平行且不等的四边形是梯形;（D）一边上的两角相等的梯形是等腰梯形6．不能判定四边形ABCD为平行四边形的题设是（）（A）AB=CD，AD=BC （B）AB//CD（C）AB=CD，AD∥BC （D）AB∥CD，AD∥BC7．四边形ABCD的对角线AC，BD相交于点O，能判定它为正方形的题设是（）（A）AO=CO，BO=DO; （B）AO=CO=BO=DO;（C）AO=CO，BO=DO，AC⊥BD; （D）AO=BO=CO=DO，AC⊥BD8．下列说法不正确的是（）（A）只有一组对边平行的四边形是梯形;（B）只有一组对边相等的梯形是等腰梯形;（C）等腰梯形的对角线相等且互相平分;（D）在直角梯形中有且只有两个角是直角9．如图1，在□ABCD中，MN分别是AB、CD的中点，BD分别交AN、CM于点P、Q，在结论：①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S △ADP=14S ABCD中，正确的个数为（）．（A）1 （B）2 （C）3 （D）4(1) (2) (3)10．如图2，在梯形ABCD中，AD∥CB，AD=2，BC=8，AC=6，BD=8，则梯形ABCD的面积为（）．（A）24 （B）20 （C）16 （D）12二、填空题11．在□ABCD中，AC与BD交于O，则其中共有_____对全等的三角形．12．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20cm，则其对角线长为_______，矩形的面积为________．13．一个菱形的两条对角线长分别为6cm，8cm，这个菱形的边长为_______，•面积S=______．14．如果一个四边形的四个角的比是3：5：5：7，则这个四边形是_____形．15．如图3，等腰梯形ABCD中，AD∥BC，AB∥DE，BC=8，AB=6，AD=5，则△CDE的周长是________．16．如图4，在正方形ABCD的外侧，作等边△ADE，则∠AEB=_______．(4) (5) (6)17．在长为1.6m，宽为1.2m的矩形铅板上，剪切如图5所示的直角梯形零件（•尺寸单位为mm），则这块铅板最多能剪出______个这样的零件．18．如图6，ABCD中，过对角线交点O，引一直线交BC于E，交AD于F，若AB=2.4cm，BC=4cm，OE=1.1cm，则四边形CDFE周长为________．19．已知等腰梯形的一个锐角等于60•°，•它两底分别为15cm，•49cm，•则腰长为_______．20．已知等腰梯形ABCD中AD∥BC，BD平分∠ABC，BD•⊥DC，•且梯形ABCD•的周长为30cm，则AD=_____．三、计算题21．如图，已知等腰梯形ABCD中，AD∥BC，对角线AC⊥BD，AD=3cm，BC=7cm，•DE•⊥BC 于E，试求DE的长．四、证明题22．如图，已知四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA边上的中点，求证：四边形EFGH是菱形．23．已知如图，梯形ABCD中，AD∥BC，AM=MB，DN=NC．求证：MN∥BC，MN=12（BC+AD）．答案:1．（C） 2．（C） 3．（B） 4．（D） 5．（D）6．（C） 7．（D） 8．（C） 9．（C） 10．（A）11．4 12．40cm 4003cm213．5cm 24cm2 14．直角梯形15．15 16．15° •17．12 18．8.6cm 19．34cm20．如图，作AE⊥BC于E，DF⊥BC于F，∴AD=EF，设BE=x．则AB=2x，DC=2x，FC=x，∴BD平分∠ABC，∴∠DBC=30°．∴DC=12BC，∴BC=4x．∴EF=2x=AD．又∵AB+BC+CD+AD=30，∴4x+6x=30，x=3，∴AD=6（cm）．21．过D点作DF∥AC，交BC的延长线于点F，则四边形ACFD为平行四边形，•所以AC=DF，AD=CF．因为四边形ABCD为等腰梯形，所以AC=BD，所以BD=DF，又已知AC⊥BD，DF∥AC，•所以BD⊥DF，则△BDF为等腰直角三角形．又因为DF⊥BC，所以DE=12BF=12（BC+CF）=12（BC+AD）=12（7+3）=5（cm）．22．证明：∵E、F、G、H分别是AB、BC、CD、DA的中点，∴EF=12AC，HG=12AC，FG=12BD，EH=12BD．∴EF=HG=12AC，FG=EH=12BD．又∵AC=BD，∴EF=HG=FG=EH．∴四边形EFGH是菱形．23．证明：如图，连接AN并延长，交BC的延长线于点E．∵DN=NC，∠1=∠2，∠D=∠3，∴△ADN≌△ECN，∴AN=EN，AD=EC．又AM=MB，∴MN是△ABE的中位线．∴MN∥BC，MN=12BE（三角形中位线定理）∵BE=BC+CE=BC+AD，∴MN=12（BC+AD）．。

(完整版)矩形练习题及答案

矩形课后练习1、矩形具有而平行四边形不具有的性质是()A．内角和为360°B．对角线相等C．对角相等D．相邻两角互补2、平行四边形、矩形、菱形、正方形都具有的性质()A．对角线相等B．对角线互相平分C．对角线平分一组对角D．对角线互相垂直3、下列关于矩形的说法中正确的是()A．矩形的对角线互相垂直且平分B．矩形的对角线相等且互相平分C．对角线相等的四边形是矩形D．对角线互相平分的四边形是矩形下列说法正确的有()①两条对角线相等的四边形是矩形；②有一组对边相等，一组对角是直角的四边形是矩形；③一个角为直角，两条对角线相等的四边形是矩形；④四个角都相等的四边形是矩形；⑤对角线相等且垂直的四边形是矩形；⑥有一个角是直角的平行四边形是矩形．A．1个B．2个C．3个D．4个4、如图，在矩形ABCD中，AE⊥BD，垂足为E，∠DAE：∠BAE=1：2，试求∠CAE的度数．5、如图，已知矩形ABCD中，AC与BD相交于O，DE平分∠ADC交BC于E，∠BDE=15°，试求∠COE的度数．6、Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM 的最小值为．7、如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2，E是AB边的中点，F是AC边的中点，D是BC边上一动点，则△EFD的周长最小值是．8、如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．9、(1)线段BD与CD有什么数量关系，并说明理由；(2)当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．10、如图，以△ABC的各边向同侧作正△ABD，正△BCF，正△ACE．(1)求证：四边形AEFD是平行四边形；(2)当∠BAC=______时，四边形AEFD是矩形；(3)当∠BAC=______时，以A、E、F、D为顶点的四边形不存在．11、如图，已知平行四边形ABCD，延长AD到E，使DE=AD，连接BE与DC交于O点．(1)求证：△BOC≌△EOD；(2)当∠A=12∠EOC时，连接BD、CE，求证：四边形BCED为矩形．12、已知四边形ABCD中，AB=CD，BC=DA，对角线AC、BD交于点O．M是四边形ABCD外的一点，AM⊥MC，BM⊥MD．试问：四边形ABCD是什么四边形，并证明你的结论．13、如图，△ABC中，AB=AC，D是BC中点，F是AC中点，AN是△ABC的外角∠MAC的角平分线，延长DF交AN于点E．(1)判断四边形ABDE的形状，并说明理由；(2)问：线段CE与线段AD有什么关系？请说明你的理由．14、已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．(1)求证：△ADE≌△CBF；(2)若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．15、如图，矩形纸片ABCD的宽AD=5，现将矩形纸片ABCD沿QG折叠，使点C落到点R的位置，点P是QG上的一点，PE⊥QR于E，PF⊥AB于F，求PE+PF．16、如图，已知，E是矩形ABCD边AD上一点，且BE=ED，P是对角线BD上任一点，PF⊥BE，PG⊥AD，垂足分别为F、G，你知道PF+PG与AB有什么关系吗？并证明你的结论．矩形课后练习参考答案题一： B ．详解：A ．内角和为360°矩形与平行四边形都具有，故此选项错误；B ．对角线相等只有矩形具有，而平行四边形不具有，故此选项正确；C ．对角相等矩形与平行四边形都具有，故此选项错误；D ．相邻两角互补矩形与平行四边形都具有，故此选项错误．故选B ．题二： B ．详解：因为平行四边形的对角线互相平分、正方形的对角线垂直平分且相等、矩形的对角线互相平分且相等、菱形的对角线互相垂直平分，可知正方形、矩形、菱形都具有的特征是对角线互相平分．故选B ．题三： B ．详解：A ．矩形的对角线互相平分，且相等，但不一定互相垂直，本选项错误；B ．矩形的对角线相等且互相平分，本选项正确；C ．对角线相等的四边形不一定为矩形，例如等腰梯形对角线相等，但不是矩形，本选项错误；D ．对角线互相平分的四边形为平行四边形，不一定为矩形，本选项错误．故选B ．题四： C ．详解：两条对角线相等且相互平分的四边形为矩形，故①③⑤错；有一个角为直角的平行四边形为矩形，故②④⑥正确．故选C ．题五： 30°．详解：∵∠DAE ：∠BAE =1：2，∠DAB =90°，∴∠DAE =30°，∠BAE =60°，∴∠DBA =90°-∠BAE =90°-60°=30°，∵OA =OB ，∴∠OAB =∠OBA =30°，∴∠CAE =∠BAE -∠OAB =60°-30°=30°．题六： 75°．详解：∵四边形ABCD 是矩形，DE 平分∠ADC ，∴∠CDE =∠CED = 45°，∴EC =DC ，又∵∠BDE =15°，∴∠CDO =60°，又∵矩形的对角线互相平分且相等，∴OD =OC ，∴△OCD 是等边三角形，∴∠DCO =60°，∠OCB =90°-∠DCO =30°，∵DE 平分∠ADC ，∠ECD =90°，∠CDE =∠CED = 45°，∴CD =CE =CO ，∴∠COE =∠CEO ；∴∠COE =(180°-30°)÷2=75°．题七： 65．详解：由题意知，四边形AFPE 是矩形，∵点M 是矩形对角线EF 的中点，则延长AM 应过点P ，∴当AP 为Rt △ABC 的斜边上的高时，即AP ⊥BC 时，AM 有最小值，此时AM =12AP ，由勾股定理知BC =22AB AC +=5，∵S △ABC =12AB •AC =12BC •AP ，∴AP =345⨯=125，∴AM =12AP =65．题八： 1+13．详解：作点F 关于BC 的对称点G ，连接EG ，交BC 于D 点，D 点即为所求，∵E 是AB 边的中点，F 是AC 边的中点，∴EF 为△ABC 的中位线，∵BC =2，∴EF =12BC =12×2=1；∵EF 为△ABC 的中位线，∴EF ∥BC ，∴∠EFG =∠C =90°，又∵∠ABC =60°，BC =2，FG =AC =23，EG =22EF FG +=13，∴DE +FE +DF =EG +EF =1+13．题九：见详解．详解：(1)BD =CD ．理由：∵AF ∥BC ，∴∠AFE =∠DCE ，∵E 是AD 的中点， ∴AE =DE ，在△AEF 和△DEC 中，∠AFE =∠DCE ，∠AEF =∠DEC ，AE =DE ，∴△AEF ≌△DEC (AAS)，∴AF =CD ，∵AF =BD ，∴BD =CD ；(2)当△ABC 满足：AB =AC 时，四边形AFBD 是矩形．理由：∵AF ∥BD ，AF =BD ，∴四边形AFBD 是平行四边形，∵AB =AC ，BD =CD ，∴∠ADB =90°，∴平行四边形AFBD 是矩形．题十：见详解．详解：(1)∵△BCF 和△ACE 是等边三角形，∴AC =CE ，BC =CF ，∠ECA =∠BCF =60°，∴∠ECA -∠FCA =∠BCF -∠FCA ，即∠ACB =∠ECF ，∵在△ACB 和△ECF 中，AC =CE ，∠ACB =∠ECF ，BC =CF ，∴△ACB ≌△ECF (SAS)，∴EF =AB ，∵三角形ABD 是等边三角形，∴AB =AD ，∴EF =AD =AB ，同理FD =AE =AC ，即EF =AD ，DF =AE ，∴四边形AEFD 是平行四边形；(2)当∠BAC =150°时，平行四边形AEFD 是矩形，理由：∵△ADB 和△ACE 是等边三角形，∴∠DAB =∠EAC =60°，∵∠BAC =150°，∴∠DAE =360°-60°-60°-150°=90°，∵由(1)知：四边形AEFD 是平行四边形，∴平行四边形AEFD 是矩形．(3)当∠BAC =60°时，以A 、E 、F 、D 为顶点的四边形不存在，理由如下：∵∠DAB =∠EAC =60°，∠BAC =60°，∴∠DAE =60°+60°+60°=180°，∴D 、A 、E 三点共线，即边DA 、AE 在一条直线上，∴当∠BAC =60°时，以A 、E 、F 、D 为顶点的四边形不存在．题十一：见详解．详解：(1)∵在平行四边形ABCD 中，AD =BC ，AD ∥BC ，∴∠EDO =∠BCO ，∠DEO =∠CBO ，∵DE =AD ，∴DE =BC ，在△BOC 和△EOD 中，∠OBC =∠OED ，BC =DE ，∠OCB =∠ODE ，∴△BOC ≌△EOD (ASA)；(2)∵DE =BC ，DE ∥BC ，∴四边形BCED 是平行四边形，在平行四边形ABCD 中，AB ∥DC ，∴∠A =∠ODE ，∵∠A =12∠EOC ，∴∠ODE =12∠EOC ， ∵∠ODE +∠OED =∠EOC ，∴∠ODE =∠OED ，∴OE =OD ，∵平行四边形BCED 中，CD =2OD ，B E =2OE ，∴CD =BE ，∴平行四边形BCED 为矩形．题十二：见详解．详解：矩形．理由：连接OM，∵AB=CD，BC=DA，∴四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵AM⊥MC，BM⊥MD，∴∠AMC=∠BMD=90°，∴OM=12BD，OM=12AC，∴BD=AC，∴四边形ABCD是矩形．题十三：见详解．详解：(1)四边形ABDE是平行四边形，理由：∵AB=AC，D是BC中点，F是AC中点，∴DF∥AB，∵AB=AC，D是BC 中点，∴∠BAD=∠CAD，AD⊥DC，∵AN是△ABC的外角∠MAC的角平分线，∴∠MAE=∠CAE，∴∠NAD=90°，∴AE∥BD，∴四边形ABDE是平行四边形；(2)CE∥AD，CE=AD；理由：∵AN是△ABC外角∠CAM的平分线，∴∠MAE=12∠MAC，∵∠MAC=∠B+∠ACB，∵AB=AC，∴∠B=∠ACB，∴∠MAE=∠B，∴AN∥BC，∵AB=AC，点D为BC中点，∴AD⊥BC，∵CE⊥AN，∴AD∥CE，∴四边形ADCE为平行四边形，∵CE⊥AN，∴∠AEC=90°，∴四边形ADCE为矩形，∴CE∥AD，CE=AD．题十四：见详解．详解：(1)∵四边形ABCD是平行四边形，∴∠4=∠C，AD=CB，AB=CD，∵点E、F分别是AB、CD的中点，∴AE=12 AB，CF=12CD．∴AE=CF，在△AED与△CBF中，AD=CB，∠4=∠C，AE=CF，∴△ADE≌△CBF(SAS)，(2)当四边形BEDF是菱形时，四边形AGBD是矩形；证明：∵四边形ABCD是平行四边形，∴AD∥BC，∵AG∥BD，∴四边形AGBD是平行四边形，∵四边形BEDF是菱形，∴DE=BE，∵AE=BE，∴AE=BE=DE，∴∠1=∠2，∠3=∠4，∵∠1+∠2+∠3+∠4=180°，∴2∠2+2∠3=180°，∴∠2+∠3=90°，即∠ADB=90°，∴四边形AGBD是矩形．题十五：5．详解：把折叠的图展开，如图所示：EF=AD，∵AD=5，∴EF=5，∴PF+PE=5．题十六：PF+PG =AB．详解：PF+PG=AB．理由如下：连接PE，则S△BEP+S△DEP=S△BED，即12BE•PF+12DE•PG =12DE•AB．又∵BE=DE，∴12DE•PF+12DE•PG=12DE•AB，即12DE(PF+PG)=12DE•AB，∴PF+PG =AB．。

(完整版)矩形、菱形与正方形-专题训练(含答案)

矩形、菱形与正方形专题训练(含答案)班级________姓名________成绩________一、选择题(每小题3分，共30分)1．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是( )A．12 B．24 C．12 3 D．16 3第1题图第2题图第3题图第4题图2．如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为( ) A．14 B．15 C．16 D．173．如图，将矩形ABCD沿对角线BD折叠，使点C与点C′重合．若AB＝2，则C′D的长为( ) A．1 B．2 C．3 D．44．如图，在△ABC中，AC＝BC，点D，E分别是边AB，AC的中点．将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是( )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为( )A．4 cm B．6 cm C．8 cm D．10 cm第6题图第9题图第10题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( )A．3∶1 B．4∶1 C．5∶1 D．6∶18．用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9．如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( )A．16 B．17 C．18 D．1910．如图，F为正方形ABCD的边AD上一点，CE⊥CF交AB的延长线于点E，若正方形ABCD 的面积为64，△CEF的面积为50，则△CBE的面积为( )A．20 B．24 C．25 D．26二、填空题(每小题3分，共24分)11．如图所示，在菱形ABCD中，∠ADC＝72°，AD的垂直平分线交对角线BD于点P，垂足为点E，连结CP，则∠CPB＝____度．第11题图第12题图第14题图第15题图12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1分别是四边形ABCD 各边中点，如果AC＝8，BD＝10，则四边形A1B1C1D1的面积为___．13．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20 cm，则其对角线长为____________-_，矩形的面积为_______________．14．如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝4 cm，BD＝8 cm，则这个菱形的面积是____cm2.15．如图，矩形ABCD中，点E，F分别是AB，CD的中点，连结DE和BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB＝22，BC＝23，则图中阴影部分的面积为____________．,第16题图第17题第18题图16．如图，▱ABCD的对角线相交于点O，请你添加一个条件______________，使▱ABCD是矩形．17．如图，正方形ABCD中，对角线AC，BD交于点O，E点在BC上，EG⊥OB，EF⊥OC，垂足分别为点G，F，AC＝10，则EG＋EF＝____．18．如图，在平面直角坐标系中，矩形OABC的顶点A，C的坐标分别为(10，0)，(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为_______________________________．三、解答题(共66分)19．(6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF⊥EC且EF＝EC，DE ＝4 cm，矩形ABCD的周长为32 cm，求AE的长．20．(8分)如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连结BM，DN.(1)求证：四边形BMDN是菱形；(2)若AB＝4，AD＝8，求MD的长．21．(8分)如图所示，矩形ABCD中，AE⊥BD于点E，∠DAE∶∠BAE＝3∶1，求∠BAE和∠EAO 的度数．22．(10分)如图，已知菱形ABCD中，AB＝AC，E，F分别是BC，AD的中点，连结AE，CF.(1)证明：四边形AECF是矩形；(2)若AB＝8，求菱形ABCD的面积．23．(12分)如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是点E，F，并且DE＝DF，求证：(1)△ADE≌△CDF；(2)四边形ABCD是菱形．24．(10分)在四边形ABCD中，AB＝CD，M，N，P，Q分别是AD，BC，BD，AC的中点，求证：MN与PQ互相垂直平分．参考答案一、选择题(每小题3分，共30分)1．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是( D )A．12 B．24 C．12 D．16第1题图第2题图第3题图第4题图2．如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为( C ) A．14 B．15 C．16 D．173．如图，将矩形ABCD沿对角线BD折叠，使点C与点C′重合．若AB＝2，则C′D的长为( B ) A．1 B．2 C．3 D．44．如图，在△ABC中，AC＝BC，点D，E分别是边AB，AC的中点．将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是( A )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( B )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为( C )A．4 cm B．6 cm C．8 cm D．10 cm第6题图第9题图第10题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( C )A．3∶1 B．4∶1 C．5∶1 D．6∶18．用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( D )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9．如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( B )A．16 B．17 C．18 D．1910．如图，F为正方形ABCD的边AD上一点，CE⊥CF交AB的延长线于点E，若正方形ABCD 的面积为64，△CEF的面积为50，则△CBE的面积为( B )A．20 B．24 C．25 D．26二、填空题(每小题3分，共24分)11．如图所示，在菱形ABCD中，∠ADC＝72°，AD的垂直平分线交对角线BD于点P，垂足为点E，连结CP，则∠CPB＝__72__度．第11题图第12题图第14题图第15题图12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1分别是四边形ABCD 各边中点，如果AC＝8，BD＝10，则四边形A1B1C1D1的面积为__20__．13．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20 cm，则其对角线长为__40_cm__，矩形的面积为__400_cm2__．14．如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝4 cm，BD＝8 cm，则这个菱形的面积是__16__cm2.15．如图，矩形ABCD中，点E，F分别是AB，CD的中点，连结DE和BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB＝2，BC＝2，则图中阴影部分的面积为__2__．,第16题图第17题第18题图16．如图，▱ABCD的对角线相交于点O，请你添加一个条件__AO＝BO(答案不唯一)__，使▱ABCD 是矩形．17．如图，正方形ABCD中，对角线AC，BD交于点O，E点在BC上，EG⊥OB，EF⊥OC，垂足分别为点G，F，AC＝10，则EG＋EF＝__5__．18．如图，在平面直角坐标系中，矩形OABC的顶点A，C的坐标分别为(10，0)，(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为__(8，4)，(3，4)或(2，4)__．三、解答题(共66分)19．(6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF⊥EC且EF＝EC，DE ＝4 cm，矩形ABCD的周长为32 cm，求AE的长．解：∵∠AFE ＋∠AEF ＝∠AEF ＋∠CED ＝90°，∴∠AFE ＝∠DEC .又∵∠A ＝∠D ＝90°，EF ＝EC ，∴△AEF ≌△DCE ，∴AE ＝CD .设AE ＝x ，则CD ＝x ，∴AD ＋CD ＝21×32，即x ＋4＋x ＝16，∴x ＝6.即AE ＝6 cm20．(8分)如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M ，与BD 相交于点O ，与BC 相交于点N ，连结BM ，DN .(1)求证：四边形BMDN 是菱形；(2)若AB ＝4，AD ＝8，求MD 的长．解：(1)∵MN 是BD 的垂直平分线，∴BO ＝DO ，∠BON ＝∠DOM ＝90°.∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠BNO ＝∠DMO ，∴△BON ≌△DOM (AAS )，∴OM ＝ON .∵OB ＝OD ，∴四边形BMDN 是平行四边形．∵MN ⊥BD ，∴▱BMDN 是菱形(2)设MD ＝x ，则MB ＝x ，MA ＝8－x ，在Rt △ABM 中，∵BM 2＝AM 2＋AB 2，∴x 2＝(8－x )2＋42，解得x ＝5.∴MD 的长为521．(8分)如图所示，矩形ABCD 中，AE ⊥BD 于点E ，∠DAE ∶∠BAE ＝3∶1，求∠BAE 和∠EAO 的度数．解：提示：由∠DAE ∶∠BAE ＝3∶1，求出∠BAE ＝22.5°，而∠ABD ＝90°－∠BAE ＝90°－22.5°＝67.5°，∵∠BAO ＝∠ABD ＝67.5°，∴∠EAO ＝∠BAO －∠BAE ＝67.5°－22.5°＝45°22．(10分)如图，已知菱形ABCD 中，AB ＝AC ，E ，F 分别是BC ，AD 的中点，连结AE ，CF .(1)证明：四边形AECF 是矩形；(2)若AB ＝8，求菱形ABCD 的面积．解：(1)∵四边形ABCD 是菱形，∴AB ＝BC ，又∵AB ＝AC ，∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE ⊥BC (等边三角形三线合一)，∠AEC ＝90°.同理，CF ⊥AD .∵E ，F 分别是BC ，AD 的中点，∴AF ＝21AD ，EC ＝21BC .∵四边形ABCD 是菱形，∴AD 綊BC ，∴AF 綊EC ，∴四边形AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形)．又∵∠AEC ＝90°，∴四边形AECF 是矩形(有一个角是直角的平行四边形是矩形)(2)在Rt △ABE 中，∵AE ＝＝4，∴S 菱形ABCD ＝8×4＝3223．(12分)如图，已知四边形ABCD 是平行四边形，DE ⊥AB ，DF ⊥BC ，垂足分别是点E ，F ，并且DE ＝DF ，求证：(1)△ADE ≌△CDF ；(2)四边形ABCD 是菱形．解：证明：(1)∵四边形ABCD 是平行四边形，∴∠A ＝∠C ，又∵DE ＝DF ，DE ⊥AB ，DF ⊥BC ，∴∠DEA ＝∠DFC ＝90°，∴△ADE ≌△CDF (AAS ) (2)由(1)知AD ＝DC ，又∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形24．(10分)在四边形ABCD 中，AB ＝CD ，M ，N ，P ，Q 分别是AD ，BC ，BD ，AC 的中点，求证：MN 与PQ 互相垂直平分．解：证明：连结MP ，NQ ，PN ，MQ ，∵PM 綊21AB ，同理NQ 綊21AB ，∴PM 綊NQ ，∴四边形MPNQ 为平行四边形，又∵PN 綊21CD ，而CD ＝AB ，∴PN ＝PM ，∴四边形MPNQ 为菱形，∴MN 与PQ 互相垂直平分。

中考数学专题训练：矩形、菱形、正方形(附参考答案)

中考数学专题训练：矩形、菱形、正方形（附参考答案）1．下列命题正确的是( )A ．正方形的对角线相等且互相平分B ．对角互补的四边形是平行四边形C ．矩形的对角线互相垂直D ．一组邻边相等的四边形是菱形2．如图，D ，E ，F 分别是△ABC 各边的中点，则以下说法错误的是( )A ．△BDE 和△DCF 的面积相等B ．四边形AEDF 是平行四边形C ．若AB ＝BC ，则四边形AEDF 是菱形D ．若∠A ＝90°，则四边形AEDF 是矩形3．如图，在正方形ABCD 中，E ，F 分别是AB ，BC 的中点，CE ，DF 交于点G ，连接AG .下列结论：①CE ＝DF ；②CE ⊥DF ；③∠AGE ＝∠CDF .其中正确的结论是( )A ．①②B ．①③C ．②③D ．①②③4．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，E 为BC 的中点，连接EO 并延长交AD 于点F ，∠ABC ＝60°，BC ＝2AB .下列结论：①AB ⊥AC ；②AD ＝4OE ；③四边形AECF 是菱形；④S △BOE ＝14S △ABC .其中正确结论的个数是( )A ．4B ．3C ．2D ．15．如图，在矩形ABCD中，AB＝6 cm，BC＝9 cm，点E，F分别在边AB，BC上，AE＝2 cm，BD，EF交于点G.若G是EF的中点，则BG的长为______cm.6．如图，在菱形ABCD中，AC，BD为菱形的对角线，∠DBC＝60°，BD＝10，点F为BC的中点，则EF的长为_____．7．已知四边形ABCD是正方形，点E在边DA的延长线上，连接CE交AB于点G，过点B作BM⊥CE，垂足为点M，BM的延长线交AD于点F，交CD的延长线于点H.(1)如图1，求证：CE＝BH；(2)如图2，若AE＝AB，连接CF，在不添加任何辅助线情况下，请直接写出图2中的四个三角形(△AEG除外)，使写出的每个三角形都与△AEG全等．8．如图，在菱形ABCD中，E，F，G，H分别是AB，BC，CD，AD上的点，且BE ＝BF＝CG＝AH.若菱形的面积等于24，BD＝8，则EF＋GH＝_____．9．如图，在矩形ABCD中，点E在DC上，DE＝BE，AC与BD相交于点O，BE与AC相交于点F.(1)若BE平分∠CBD，求证：BF⊥AC；(2)找出图中与△OBF相似的三角形，并说明理由；(3)若OF＝3，EF＝2，求DE的长度．10．(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G.求证：△ADE∽△DCF.【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC 到点H，使CH＝DE，连接DH.求证：∠ADF＝∠H.【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．参考答案1．A 2．C 3．A 4．D5．√13 6．5 7．(1)证明略 (2)略8．6解析：如图，连接AC ，交BD 于点O ，∵四边形ABCD 是菱形，BD ＝8，∴AB ＝BC ＝AD ＝CD ，AC ⊥BD ，AO ＝OC ＝12AC ，BO ＝OD ＝12BD ＝4. ∵S 菱形ABCD ＝12AC ·BD ＝24，∴AC ＝6，∴AO ＝3，∴AB ＝√AO 2+BO 2＝5＝AD .∵BE ＝BF ＝CG ＝AH ，∴AE ＝CF ＝DH ＝DG ，∴BE AE ＝BF CF ，∴EF ∥AC .同理可得GH ∥AC ，设BE ＝BF ＝CG ＝AH ＝a ，则有DH ＝5－a ，∵EF ∥AC ，∴△BEF ∽△BAC ，∴BE AB ＝EF AC ，即a 5＝EF 6，∴EF ＝65a ，同理可得DH DA ＝GH CA ，即5−a 5＝GH 6，∴GH ＝6－65a ，∴EF ＋GH ＝6.9．(1)证明略(2)与△OBF相似的三角形有△ECF，△BAF，理由略(3)DE＝3＋√1910．(1)证明：∵四边形ABCD是矩形，∴∠C＝∠ADE＝90°，∴∠CDF＋∠DFC＝90°.∵AE⊥DF，∴∠DGE＝90°，∴∠CDF＋∠AED＝90°，∴∠AED＝∠DFC，∴△ADE∽△DCF.(2)证明：∵四边形ABCD是正方形，∴AD＝DC，AD∥BC，∠ADE＝∠DCF＝90°.∵AE＝DF，∴Rt△ADE≌Rt△DCF(HL)，∴DE＝CF.∵CH＝DE，∴CF＝CH.∵点H在BC的延长线上，∴∠DCH＝∠DCF＝90°.又∵DC＝DC，∴△DCF≌△DCH(SAS)，∴∠DFC＝∠H.∵AD∥BC，∴∠ADF＝∠DFC，∴∠ADF＝∠H.(3)解：如图3，延长BC至点G，使CG＝DE＝8，连接DG，∵四边形ABCD是菱形，∴AD＝DC，AD∥BC，∴∠ADE＝∠DCG，∴△ADE≌△DCG(SAS)，∴∠DGC＝∠AED＝60°，AE＝DG. ∵AE＝DF，∴DG＝DF，∴△DFG是等边三角形，∴FG＝DF＝11.∵CF＋CG＝FG，∴CF＝FG－CG＝11－8＝3，即CF的长为3.。

中考数学精选汇编矩形菱形与正方形---13道题目(含答案)

01如图，正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE相交于点G.(1)观察图形，写出图中所有与∠AED相等的角；(2)选择图中与∠AED相等的任意一个角，并加以证明．如图，正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE相交于点G.(1)观察图形，写出图中所有与∠AED相等的角；(2)选择图中与∠AED相等的任意一个角，并加以证明．答案：（1）由图可知，∠DAG，∠AFB，∠CDE与∠AED相等；（2）选择∠DAG=∠AED，证明如下：∵正方形ABCD，∴∠DAB=∠B=90°，AD=AB，∵AF=DE，在△DAE与△ABF中，，∴△DAE≌△ABF（SAS），∴∠ADE=∠BAF，∵∠DAG+∠BAF=90°，∠GDA+∠AED=90°，∴∠DAG=∠AED．02如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH，FG．（1）求证：△BFH≌△DEG；（2）连接DF，若BF=DF，则四边形EGFH是什么特殊四边形？证明你的结论．如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH，FG．（1）求证：△BFH≌△DEG；（2）连接DF，若BF=DF，则四边形EGFH是什么特殊四边形？证明你的结论．【考点】矩形的性质；全等三角形的判定与性质；菱形的判定．【分析】（1）由平行四边形的性质得出AD∥BC，AD=BC，OB=OD，由平行线的性质得出∠FBH=∠ED G，∠OHF=∠OGE，得出∠BHF=∠DGE，求出BF=DE，由AAS即可得出结论；（2）先证明四边形EGFH是平行四边形，再由等腰三角形的性质得出EF⊥GH，即可得出四边形EGFH是菱形．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，OB=OD，∴∠FBH=∠EDG，∵AE=CF，∴BF=DE，∵EG∥FH，∴∠OHF=∠OGE，∴∠BHF=∠DGE，在△BFH和△DEG中，，∴BFH≌△DEG（AAS）；（2）解：四边形EGFH是菱形；理由如下：连接DF，如图所示：由（1）得：BFH≌△DEG，∴FH=EG，又∵EG∥FH，∴四边形EGFH是平行四边形，∵BF=DF，OB=OD，∴EF⊥BD，∴EF⊥GH，∴四边形EGFH是菱形．03如图将边长为8cm的正方形纸片ABCD折叠，使点B恰好落在AD边的中点F处，折痕EG 分别交AB、CD于点E、G，FN与DC交于点M，连接BF交EG于点P.独立思考：（1）AE=_______cm，△FDM的周长为_____cm（2）猜想EG与BF之间的位置关系与数量关系，并证明你的结论.拓展延伸：如图2，若点F不是AD的中点，且不与点A、D重合：①△FDM的周长是否发生变化，并证明你的结论.②判断（2）中的结论是否仍然成立，若不成立请直接写出新的结论（不需证明）.如图将边长为8cm 的正方形纸片ABCD 折叠，使点B 恰好落在AD 边的中点F 处，折痕EG 分别交AB 、CD 于点E 、G ，FN 与DC 交于点M ，连接BF 交EG 于点P.独立思考：（1）AE=_______cm ，△FDM 的周长为_____cm （2）猜想EG 与BF 之间的位置关系与数量关系，并证明你的结论.拓展延伸：如图2，若点F 不是AD 的中点，且不与点A 、D 重合：①△FDM 的周长是否发生变化，并证明你的结论.②判断（2）中的结论是否仍然成立，若不成立请直接写出新的结论（不需证明）. 答案：（1）3， 16(2)EG ⊥BF, EG=BF则∠EGH+∠GEB=90°由折叠知，点B 、F 关于直线GE 所在直线对称∴∠FBE=∠EGH∵ABCD 是正方形∴AB=BC ∠C=∠ABC=90°四边形GHBC 是矩形，∴GH=BC=AB ∴△AFB 全等△HEG ∴BF=EG(3)①△FDM 的周长不发生变化由折叠知∠EFM=∠ABC=90°∴∠DFM+∠AFE=90°∵四边形ABCD 为正方形，∠A=∠D=90°∴∠DFM+∠DMF=90°∴∠AFE=∠DMF ∴△AEF ∽△DFM ∴=FMD AEF FD AE的周长的周长V V 设AF 为x ，FD=8-x ∴-23 222(8)x AE AE +=-26416x AE -= ∴ 88x x AE AE AE FMD -=++-的周长 △ FMD 的周长=222(8)(8)16(64)16166416x x x x x +--==-- ∴△FMD 的周长不变 ②（2）中结论成立04在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．（1）求证：△BDF≌△CDE；（2）若DE=BC，试判断四边形BFCE是怎样的四边形，并证明你的结论．在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．（1）求证：△BDF≌△CDE；（2）若DE=BC，试判断四边形BFCE是怎样的四边形，并证明你的结论．【考点】矩形的判定；全等三角形的判定与性质．【分析】（1）根据平行线得出∠CED=∠BFD，根据AAS推出两三角形全等即可；（2）根据全等得出DE=DF，根据BD=DC推出四边形是平行四边形，求出∠BEC=90°，根据矩形的判定推出即可．【解答】（1）证明：∵CE∥BF，∴∠CED=∠BFD，∵D是BC边的中点，∴BD=DC，在△BDF和△CDE中，∴△BDF≌△CDE（AAS）；（2）四边形BFCE是矩形，证明：∵△BDF≌△CDE，∴DE=DF，∵BD=DC，∴四边形BFCE是平行四边形，∵BD=CD，DE=BC，∴BD=DC=DE，∴∠BEC=90°，∴平行四边形BFCE是矩形．【点评】本题考查了平行线性质，全等三角形的性质和判定，矩形的判定，平行四边形的判定的应用，注意：有一个角是直角的平行四边形是矩形．05在△ABC中，DE分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连CF（1）求证：四边形BCFE是菱形；（2）若CE=6，∠BEF=120°，求菱形BCFE的面积．在△ABC中，DE分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连CF（1）求证：四边形BCFE是菱形；（2）若CE=6，∠BEF=120°，求菱形BCFE的面积．【考点】菱形的判定与性质．【分析】（1）从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；（2）由∠BEF是120°，可得∠EBC为60°，即可得△BEC是等边三角形，求得BE=BC=CE=6，再过点E作EG⊥BC于点G，求的高EG的长，即可求得答案．【解答】（1）证明：∵D、E分别是AB、AC的中点，∴DE∥BC且2DE=BC，又∵BE=2DE，EF=BE，∴EF=BC，EF∥BC，∴四边形BCFE是平行四边形，又∵BE=EF，∴四边形BCFE是菱形；（2）解：∵∠BEF=120°，∴∠EBC=60°，∴△EBC是等边三角形，∴BE=BC=CE=6，过点E作EG⊥BC于点G，∴EG=BE•sin60°=6×=3，=BC•EG=6×3=18．∴S菱形BCFE【点评】本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．注意证得△BEC是等边三角形是关键．06如图，已知△ABC内接于⊙O，且AB=AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．（1）求证：BE=CE；（2）试判断四边形BFCD的形状，并说明理由；（3）若BC=8，AD=10，求CD的长．如图，已知△ABC内接于⊙O，且AB=AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．（1）求证：BE=CE；（2）试判断四边形BFCD的形状，并说明理由；（3）若BC=8，AD=10，求CD的长．【考点】垂径定理；勾股定理；菱形的判定．【分析】（1）证明△ABD≌△ACD，得到∠BAD=∠CAD，根据等腰三角形的性质即可证明；（2）菱形，证明△BFE≌△CDE，得到BF=DC，可知四边形BFCD是平行四边形，易证BD=CD，可证明结论；（3）设DE=x，则根据CE2=DE•AE列方程求出DE，再用勾股定理求出CD．【解答】（1）证明：∵AD是直径，∴∠ABD=∠A CD=90°，在Rt△ABD和Rt△ACD中，，∴Rt△ABD≌Rt△ACD，∴∠BAD=∠CAD，∵AB=AC，∴BE=CE；（2）四边形BFCD是菱形．证明：∵AD是直径，AB=AC，∴AD⊥BC，BE=CE，∵CF∥BD，∴∠FCE=∠DBE，在△BED和△CEF中，∴△BED≌△CEF，∴CF=BD，∴四边形BFCD是平行四边形，∵∠BAD=∠CAD，∴BD=CD，∴四边形BFCD是菱形；（3）解：∵AD是直径，AD⊥BC，BE=CE，∴CE2=DE•AE，设DE=x，∵BC=8，AD=10，∴42=x（10﹣x），解得：x=2或x=8（舍去）在Rt△CED中，CD===2．【点评】本题主要考查了圆的有关性质：垂径定理、圆周角定理，三角形全等的判定与性质，菱形的判定与性质，勾股定理，三角形相似的判定与性质，熟悉圆的有关性质是解决问题的关键．．07如图，将矩形ABCD 绕点A 顺时针旋转，得到矩形'''AB C D ，点C 的对应点'C 恰好落在CB 的延长线上，边AB 交边''C D 于点E ．（1）求证：'BC BC =．（2）若2AB =，1BC =，求AE 的长．ED 'C 'B'DC BAAB CD B'C 'D 'E（第12题）如图，将矩形ABCD 绕点A 顺时针旋转，得到矩形'''AB C D ，点C 的对应点'C 恰好落在CB的延长线上，边AB 交边''C D 于点E ．（1）求证：'BC BC =．（2）若2AB =，1BC =，求AE 的长．答案：解：（1）连结AC 、'AC ，如图．∵四边形ABCD 为矩形，∴∠ABC =90°，即'AB CC ⊥．由旋转，得'AC AC = ， ∴'BC BC =．（2）∵四边形ABCD 为矩形，∴,'90AD BC D ABC =∠=∠=︒． ∵'BC BC =，∴''BC AD =．由旋转，得'AD AD = ， ∴''BC AD =． ∵''AED C BE ∠=∠， ∴'AD E ∆≌'C BE ∆． ∴'BE D E =．设AE x =，则'2D E x =-．在Rt 'AD E ∆中，'90D ∠=︒，由勾股定理，得22(2)1x x --=．解得54x =． ∴54AE =．AB CD B'C 'D 'E（第12题）E D 'C 'B'DCBA08如图1，四边形ABCD是正方形，点E是边BC上的点，过点E作EF⊥AE，过点F作FG⊥BC交BC的延长线于点G．．（1）求证：∠BAE=∠FEG．（2）同学们很快做出了解答，之后李老师将题目修改成：如图2，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线于点F，求证：AE=EF．（3）如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．如图1，四边形ABCD是正方形，点E是边BC上的点，过点E作EF⊥AE，过点F作FG⊥BC 交BC的延长线于点G．．（1）求证：∠BAE=∠FEG．（2）同学们很快做出了解答，之后李老师将题目修改成：如图2，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线于点F，求证：AE=EF．（3）如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．【解答】解：（1）∵∠AEF=90°，∴∠AEB+∠FEG=90°，又∵直角△ABE中，∠BAE+∠AEB=90°，∴∠BAE=∠FEG；（2）作AB的中点M，连接ME．∵正方形ABCD中，AB=BC，又∵AM=MB=AB，BE=CE=BC，∴MB=BE，∴△ABE是等腰直角三角形，∴∠BME=45°，∴∠AME=135°，又∵∠ECF=180°﹣∠FCG=180°﹣45°=135°．∴∠AME=∠ECF，∴在△AME和△ECF中，，∴△AME≌△ECF，∴AE=EF；（3）在AB上取一点M，使AM=EC，连接ME．∴BM=BE，∴∠BME=45°，∴∠AME=135°，∵CF是外角平分线，∴∠DCF=45°，∴∠ECF=135°∴∠AME=∠ECF∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°∴∠BAE=∠CEF∴在△AME和△ECF中，，∴△AME≌△ECF（ASA），∴AE=EF．09如图，在□ABCD 中，E 、F 分别是边AB 、CD 的中点，BG ∥AC 交DA 的延长线于点G ．（1）求证：△ADF ≌△CBE ；（2）若四边形AGBC 是矩形，判断四边形AECF 是什么特殊的四边形？并证明你的结论．GFCEABD如图，在□ABCD 中，E 、F 分别是边AB 、CD 的中点，BG ∥AC 交DA 的延长线于点G ．（1）求证：△ADF ≌△CBE ；（2）若四边形AGBC 是矩形，判断四边形AECF 是什么特殊的四边形？并证明你的结论．GFCEABD答案：（1）证明：∵□ABCD ，∴AD =CB ，∠D =∠ABC ，AB =CD ，又∵E 、F 分别是边AB 、CD 的中点，∴DF =BE ，∴△ADF ∽≌△CBE ；（2）四边形AECF 为菱形；∵矩形AGBC ，∴∠ACB =90°，又∵E 为AB 中点，（3）∴CE =21AB =AE ，同理AF =FC ，∴AF =FC =CE =EA ，∴四边形AECF 为菱形．10如图，矩形ABCD中，AD=5，AB=3，在BC边上取一点E，使BE=4，连结AE，沿AE 剪下△ABE，将它平移至△DCF的位置，拼成四边形AEFD．（1）求证:四边形AEFD是菱形；（2）求四边形AEFD的两条对角线的长.如图，矩形ABCD中，AD=5，AB=3，在BC边上取一点E，使BE=4，连结AE，沿AE剪下△ABE，将它平移至△DCF的位置，拼成四边形AEFD．（1）求证:四边形AEFD是菱形；（2）求四边形AEFD的两条对角线的长.答案：（1）证明：∵△ABE平移至△DCF的位置.∴△ABE≌△DCF.∴BE=CF∵四边形ABCD为矩形.∴AD∥BC，AD=BC，∠B=90°.∴EF=EC+CF=EC+BE=BC=AD.∴四边形AEFD为平行四边形.在Rt△ABE中，根据勾股定理得：AE=2222+=+=AB BE345∵AD=5,∴AD=AE.∴四边形AEFD为菱形.（2）连结DE、AF.求出DE=10.求出AF=310.11如图，在正方形ABCD 中，AB=5，P 是BC 边上任意一点，E 是BC 延长线上一点，连接AP ，作PF ⊥AP ，使PF ＝PA ，连接CF ，AF ，AF 交CD 边于点G ，连接PG ．（1）求证：∠GCF ＝∠FCE ；（2）判断线段PG ，PB 与DG 之间的数量关系，并证明你的结论；（3）若BP ＝2，在直线AB 上是否存在一点M ，使四边形DMPF 是平行四边形，若存在，求出BM 的长度，若不存在，说明理由．A B CDEFGP A B CDEF GP HKM如图，在正方形ABCD 中，AB=5，P 是BC 边上任意一点，E 是BC 延长线上一点，连接AP ，作PF ⊥AP ，使PF ＝PA ，连接CF ，AF ，AF 交CD 边于点G ，连接PG ．（1）求证：∠GCF ＝∠FCE ；（2）判断线段PG ，PB 与DG 之间的数量关系，并证明你的结论；（3）若BP ＝2，在直线AB 上是否存在一点M ，使四边形DMPF 是平行四边形，若存在，求出BM 的长度，若不存在，说明理由．答案：（1）证明：过点F 作FH ⊥BE 于点H ，∵四边形ABCD 是正方形， ∴∠ABC ＝∠PHF ＝∠DCB ＝90º,AB ＝BC ， ∴∠BAP ＋∠APB ＝90º∵AP ⊥PF, ∴∠APB ＋∠FPH ＝90º ∴∠FPH ＝∠BAP又∵AP ＝PF ∴△BAP ≌△HPF ∴PH ＝AB ，BP ＝FH ∴PH ＝BC∴BP ＋PC ＝PC ＋CH ∴CH ＝BP ＝FH 而∠FHC ＝90º. ∴∠FCH ＝CFH ＝45º ∴∠DCF ＝90º－45º＝45º ∴∠GCF ＝∠FCE（2）PG ＝PB ＋DG 证明：延长PB 至K ，使BK=DG ,∵四边形ABCD 是正方形 ∴AB=AD, ∠ABK ＝ADG=90º ∴△ABK ≌△ADG ∴AK=AG, ∠KAB ＝∠GAD, 而∠APF=90 º,AP=PF ∴∠PAF ＝∠PFA ＝45 º ∴∠BAP ＋∠KAB ＝∠KAP ＝45 º＝∠PAF ∴△KAP ≌△GAP ∴KP=PG,∴KB ＋BP=DG ＋BP ＝PG 即，PG ＝PB ＋DG ；（3）存在.如图，在直线AB 上取一点M ，使四边形DMPF 是平行四边形，则MD ∥PF ，且MD ＝FP ，又∵PF=AP ，∴MD=AP ∵四边形ABCD 是正方形，∴AB=AD ，∠ABP=∠DAM∴△ABP ≌△DAM ∴AM ＝BP=2， ∴BM ＝AB －AM=5－2=3. ∴当BM=3，BM+AM=AB 时，四边形DMPF 是平行四边形．AB CDEFGPAB CDEFGP HKM12如图，△OBD中，OD=BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时B，D，C三点正好在一条直线上，且点D是BC的中点．（1）求∠COD度数；（2）求证：四边形ODAC是菱形．如图，△OBD中，OD=BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时B，D，C三点正好在一条直线上，且点D是BC的中点．（1）求∠COD度数；（2）求证：四边形ODAC是菱形．【考点】旋转的性质；菱形的判定．【分析】（1）如图，根据题意证明△OBC为直角三角形，结合OC=，求出∠B即可解决问题．（2）首先证明AC∥OD，结合AC=OD，判断四边形ADOC为平行四边形，根据菱形的定义即可解决问题．【解答】解：（1）如图，由题意得：OC=OD=BD；∵点D是BC的中点，∴CD=BD，OD=BC，∴△OBC为直角三角形，而OC=，∴∠B=30°，∠OCD=90°﹣30°=60°，；∵OD=CD，∴∠COD=∠OCD=60°．（2）∵OD=BD，∴∠DOB=∠B=30°，由旋转变换的性质知：∠COA=∠CAO=∠B=30°，∴∠AOD=90°﹣2×30°=30°，∴∠CAO=∠AOD=30°，∴AC∥OD，而AC=OD，∴四边形ADOC为平行四边形，而OC=OD，∴四边形ODAC是菱形．【点评】该题主要考查了旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点及其应用问题；解题的关键是牢固掌握旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点，并能灵活运用．13如图，在平行四边形ABCD中，AB≠BC，连接AC，AE是∠BAD的平分线，交边DC 的延长线于点F．（1）证明：CE=CF；（2）若∠B=60°，BC=2AB，试判断四边形ABFC的形状，并说明理由．（如图2所示）如图，在平行四边形ABCD中，AB≠BC，连接AC，AE是∠BAD的平分线，交边DC的延长线于点F．（1）证明：CE=CF；（2）若∠B=60°，BC=2AB，试判断四边形ABFC的形状，并说明理由．（如图2所示）解：（1）证明：如图（1），∵AE是∠BAD的平分线，∴∠BAF=∠DAF，在平行四边形ABCD中，∵AB∥DF，AD∥BC，∴∠BAF=∠F，∠DAF=∠CEF，∴∠F=∠CEF，∴CE=CF；（2）解：四边形ABFC是矩形，理由：如图（2），∵∠ABC=60°，AD∥BC，∴∠BAD=120°，∵∠BAF=∠DAF，∴∠BAF=60°，则△ABE是等边三角形，可得AB=BE=AE，∠BEA=∠CEF=∠AFC=60°，∵BC=2AB，∴AE=BE=EC，∴△ABC是直角三角形，∠BAC=90°，在△ABE和△FCE中∵ABE FCE BE ECBEA CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABE≌△FCE（ASA），∴AB=FC，又∵AB∥FC，∴四边形ABFC是平行四边形，再由∠BAC=90°，故四边形ABFC是矩形．。

矩形菱形正方形练习题

矩形菱形正方形练习题一、填空题1、在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．2、在矩形中，如果AB=2,BC=1.,那么AC= ．3、如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，那么四边形BCFE的面积等于．4、如图，甲，乙，丙，丁四个长方形拼成正方形EFGH,中间阴影为正方形，已知，甲、乙、丙、丁四个长方形面积的和是32cm²，四边形ABCD的面积是20cm²．问甲、乙、丙、丁四个长方形周长的总和是______．5、如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是．6、如图，在矩形ABCD中，点F为边CD上一点，沿AF折叠，点D恰好落在BC边上的E点处，若AB=3，BC=5，则的值为．7、如图4，正方形ABCD的边长为2，AE＝EB，MN＝1，线段MN的两端在CB、CD上滑动，当CM＝时，△AED与以M、N、C为顶点的三角形相似。

8、矩形中，，，边绕旋转使得点落在射线上处，那么的度数为．9、已知正方形ABCD中，点E在边DC上，DE＝2，EC＝1 （如图所示），把线段AE绕点A 旋转，使点E落在直线BC上的点F处，则F、C两点的距离为．10、如图4，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上时，弧BC 的长度等于（结果保留）．11、在矩形中，如果AB=2,BC=1,BE⊥AC,AE= .12、如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为正方形，应添加的条件是．13、如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB= .14、如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.15、如图，以O为顶点的两条抛物线分别经过正方形的四个顶点A、B、C、D，则阴影部分的面积为______二、选择题16、对角线互相平分且相等的四边形是（）．菱形；．矩形；．正方形；．等腰梯形．17、若一个菱形的一条边长为4cm，则这个菱形的周长为（）（A）20cm （B）18cm （C）16cm （D）12cm18、如图，将边长为12cm的正方形纸片ABCD折叠，使得点A落在边CD上的E点，折痕为MN．若CE的长为8cm，则MN的长为A．12cm B．12．5cm C． cm D．13．5cm19、若一个菱形的一条边长为4cm，则这个菱形的周长为（）（A）20cm （B）18cm （C）16cm （D）12cm20、如图，顺次连结四边形ABCD各中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（）A．AB∥DC B．AB＝DC C．AC⊥BD D．AC＝BD21、已知四边形ABCD是平行四边形，下列结论中不正确的有（）①当AB=BC时，它是菱形②当AC⊥BD时，它是菱形③当∠ABC=90时，它是矩形④当AC=BD 时，它是正方形 A．1组 B．2组 C．3组 D．4组22、下列命题中，真命题是（）A．矩形的对角线相互垂直B．顺次连结四边形各边中点所得到的四边形是矩形 C．等边三角形既是轴对称图形又是中心对称图形 D．对角线互相垂直平分的四边形是菱形23、如图，矩形ABCD中，AB＝3，BC＝5，过对角线交点O作OE⊥AC交AD于E，则AE的长是（）．A．1.6 B．2.5 C．3 D．3.424、如图，点P是菱形ABCD的对角线AC上的一个动点，过点P垂直于AC的直线交菱形ABCD的边于M、N两点．设AC＝2，BD＝1，AP＝x，△AMN的面积为y，则y关于x的函数图象大致形状是（）．25、如图，在正方形纸片ABCD中，E，F分别是AD、BC的中点，沿过点B的直线折叠，使点C落在EF上，落点为N，折痕交CD边于点M，BM与EF交于点P，再展开．则下列结论中：①CM＝DM；②∠ABN＝30°；③AB2＝3CM2；④△PMN是等边三角形．正确的有（）．A．1个B．2个C．3个D．4个26、已知四边形中，，如果添加一个条件，即可判定该四边形是正方形，那么所添加的这个条件可以是（）．（A）；（B）；（C）；（D）.27、菱形ABCD的周长是16，∠A=60°，则对角线BD的长度为( )A．2 B．2C．4 D．428、已知四边形中，，如果添加一个条件，即可判定该四边形是正方形，那么所添加的这个条件可以是（）．（A）；（B）；（C）；（D）.29、在下列命题中，真命题是（）（A）两条对角线相等的四边形是矩形（B）两条对角线互相垂直的四边形是菱形（C）两条对角线互相平分的四边形是平行四边形（D）两条对角线互相垂直且相等的四边形是正方形30、如图，菱形ABCD的周长是16，∠A=60°，则对角线BD的长度为( ) A．2 B．2C．4 D．431、如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（）. A．2＋ B．2＋2C．12 D．1832、在下列命题中，正确的是（）A．一组对边平行的四边形是平行四边形B．有一个角是直角的四边形是矩形 C．有一组邻边相等的平行四边形是菱形D．对角线互相垂直平分的四边形是正方形33、如图，在菱形ABCD中，点E、 F分别是AB、AC的中点，如果EF＝3，那么菱形ABCD的周长是（）A. 24B. 18C. 12D. 634、正方形、正方形和正方形的位置如图所示，点在线段上，正方形的边长为4，则的面积为（）A.10B.12C.14D.1635、如图，四边形的对角线互相平分，要使它成为矩形，那么需要添加的条件是( )A. B. C. D.36、下列四边形：①正方形、②矩形、③菱形，对角线一定相等的是A．①②③ B．①② C．①③ D．②③37、如图，在菱形ABCD中，DE⊥AB，，AE=3，则tan∠DBE的值是（）A．B．2 C．D．38、一个正方形的面积等于10,则它的边长a满足A. 3＜a＜4B. 5＜a＜6C.7＜a＜8D. 9＜a＜1039、如图，矩形ABCD的对角线AC⊥OF，边CD在OE上，∠BAC＝70°，则∠EOF等于（）A. 10°B. 20°C. 30°D. 70°40、如图，在正方形ABCD中，AB＝3㎝．动点M自A点出发沿AB方向以每秒1㎝的速度运动，同时动点N自A点出发沿折线AD—DC—CB以每秒3㎝的速度运动，到达B点时运动同时停止．设△AMN的面积为y（㎝2），运动时间为x（秒），则下列图象中能大致反映y与x之间函数关系的是41、如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）A．矩形B．菱形C．正方形D．等腰梯形三、简答题42、如图，在正方形中，为对角线上一点，联结、，延长交于点．（1）求证：；（2）当时，求证：．43、已知，正方形ABCD中，∠MAN=45°, ∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：；（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由．如果成立请证明；（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）44、矩形纸片中，，现将这张纸片按下列图示方式折叠，是折痕．（1）如图1，P，Q 分别为，的中点，点的对应点在上，求和的长；（2）如图2，，点的对应点在上，求的长；（3）如图3，，点的对应点在上．①直接写出的长（用含的代数式表示）；②当越来越大时，的长越来越接近于▲．45、已知：如图，菱形中，分别是上的点，且CE=CF．求证：．46、如图，⊙O 的直径AB =8，C 为圆周上一点，AC =4，过点C 作⊙O 的切线l ，过点B 作l 的垂线BD ，垂足为D ，BD 与⊙O 交于点 E ． (1) 求∠AEC 的度数；（2）求证：四边形OBEC 是菱形．47、在正方形ABCD 中，O 是AD 的中点，点P 从A 点出发沿A →B →C →D 的路线匀速运动，移动到点D 时停止。

(完整版)矩形菱形与正方形测试题及答案

第19章矩形、菱形与正方形测试题一、选择题（每小题3分，共30分）1、关于四边形ABCD ①两组对边分别平行；②两组对边分别相等；③有一组对边平行且相等；④对角线AC 和BD 相等；以上四个条件中可以判定四边形ABCD 是平行四边形的有（）。

（A ） 1个（B ）2个（C ）3个（D ）4个2、若顺次连结四边形ABCD 各边中点所得四边形是矩形，则四边形ABCD 必定是（）A 、菱形B 、对角线相互垂直的四边形C 、正方形D 、对角线相等的四边形 3、如图1，大正方形中有2个小正方形，如果它们的面积分别是S 1、S 2，那么S 1、S 2的大小关系是（）A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定 4、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为（）A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 2 5、如图2，菱形花坛 ABCD 的边长为 6m ，∠B ＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长（粗线部分）为（） A.123m B.20m C.22m D.24m6、如图3，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是( ) A ．3B ．23C ．5D ．257、如图4，在宽为20m ，长为30m 的矩形地面上修建两条同样宽的道路，余下部分作为耕地. 根据图中数据，计算耕地的面积为( )A ．600m 2B ．551m 2C ．550 m 2D ．500m 28、如图5，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD 的面积比是（）A.3∶4B.5∶8C.9∶16D.1∶29、如图6，矩形ABCD 中，DE ⊥AC 于E ，且∠ADE ：∠EDC=3：2，则∠BDE 的度数为（）A 、36oB 、9oC 、27oD 、18o图41m1m30m 20mFEDCBA图3图2图110、如图7，是由两个正方形组成的长方形花坛ABCD ，小明从顶点A 沿着花坛间小路直到走到长边中点O ，再从中点O 走到正方形OCDF 的中心O 1，再从中心O 1走到正方形O 1GFH 的中心O 2，又从中心O 2走到正方形O 2IHJ 的中心O 3，再从中心O 3走2走到正方形O 3KJP 的中心O 4，一共走了31 2 m ，则长方形花坛ABCD 的周长是（）A.36 mB.48mC.96 mD.60 m二、填空题（每小题3分，共30分）11，如图8, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于＿＿＿.12，如图9，过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ，那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2（填“＞”或“＜”或“＝”）.13，如图10，四边形ABCD 是正方形，P 在CD 上，△ADP 旋转后能够与△ABP ′重合，若AB ＝3，DP ＝1，则PP ′＝＿＿＿.14，已知菱形有一个锐角为60°，一条对角线长为6cm ，则其面积为＿＿＿cm 2. 15，如图11，在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为＿＿＿.16，如图12，四边形ABCD 的两条对角线AC 、BD 互相垂直，A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC ＝8，BD ＝10，那么四边形A 1B 1C 1D 1的面积为＿＿＿.17，如图13，□ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，AB CD 图5图7图12 A 1 B 1C 1D 1 D AB C D A B C E F 图13 D CB A 图8 图10图9 KN M Q C B图11 E D C BA 图6点A 正好落在CD 上的点F ，若△FDE 的周长为8，△FCB 的周长为22，则FC 的长为＿＿＿.18，将一张长方形的纸对折,如图14所示，可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕，那么对折四次可以得到条折痕，如果对折n 次，可以得到条折痕.19、如图15，已知AB ∥DC ，AE ⊥DC ，AE ＝12，BD ＝15，AC ＝20, 则梯形ABCD 的面积为＿＿＿.20、在直线l 上依次摆放着七个正方形(如图16所示).已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4，则S 1＋S 2＋S 3＋S 4＝＿＿＿.三、解答题21、（8分）如图17，把一张长方形ABCD 的纸片沿EF 折叠后，ED 与BC 的交点为G ，点D 、C 分别落在D ′、C ′的位置上，若∠EFG=55°，求∠AEG 和∠EGB 的度数。

第22讲矩形、菱形、正方形(含答案)

第二节矩形、菱形、正方形厂S.对ft 践相等J」&四个内角顽。

忑#辿平狞I2对边相聲1 一|3•对角相輛1 T4jOl 线月一相平芬1—I®对角线互相垂直1 —19•对角线平分各内角【例题经典】会用“阶梯型”思路判定特殊平行四边形例 1.（2005年黄冈市）如图，在 Rt △ ABC 中, / ACB=90 , / BAC=60 , DE?垂直平分BC,垂足为D,交AB 于点E ,又点F 在DE 的延长线上，且AF=CE 求证：四边形 ACEF 为菱形.【分析】欲证四边形 ACEF 为菱形，可先证四边形 ACEF 为平行四边形，然后再证 U ACEF 为菱形，当然，也可证四条边相等，直接证四边形为菱形.矩形、菱形的综合应用例2 . （2006年青岛市）如图，在U ABCD 中, E 、F 分别为边 AB CD 的中点，BD 是对角线,AG// DB 交CB 的延长线于G （1）求证：△ ADE^A CBF ；【回顾与思考】平行四边呦1»1,肃线垂直且相尊'3 D(2 )若四边形BEDF 是菱形，则四边形 AGBD 是什么特殊四边形？并证明你的结论. 【解析】(1 )•••四边形ABCD 是平行四边形 •••/ 1=/ C, AD=CB AB=CD• •点E 、F 分别是AB CD 的中点，1 1 ••• AE=——AB, CF=——CD22••• AE=CF•••△ ADE^A CBF(2 )当四边形BEDF 是菱形时，四边形 AGBD 是矩形. •••四边形ABCD 是平行四边形， ••• AD// BC. • AG// BD,•••四边形AGBD 是平行四边形. •••四边形BEDF 是菱形， ••• DE=BE •/ AE=BE••• AE=BE=DE•••/ 1=/ 2,/ 3=/ 4 .• / 1+/ 2+/ 3+/ 4=180°, ••• 2 / 2+2/ 3=180° .•••/ 2+/ 3=90° . 即/ ADB=90 , •••四边形AGBD 是矩形.会解决与特殊平行四边形有关的动手操作问题例3. （2005年吉林省）如图，在矩形纸片ABCD 中, AB=3%/3 , 落在AB 边上的点P 处，点D 落在点Q 处，AD 与PQ 相交于点（1 ）求BE 、QF 的长.（2）求四边形PEFH 的面积.【分析】折叠型试题是近年中考试题的热点，要想解好此类题，考生必须有想像力, 抓住折叠的角与边不发生变化，必要时需要考生剪一个四边形实际折叠一下帮助理解.【考点精练】一、基础训练1如图1,在菱形 ABCD 中，已知AB=10, AC=16那么菱形 ABCD 勺面积为 ________________ . 2. （2006年黄冈市）如图2,将边长为8cm 的正方形ABCD 勺四边沿直线L 向右滚动（不滑动），当正方形滚动两周时，正方形的顶点 A 所经过的路线的长是 __________ cmBC=6, H,/ 沿EF 折叠后，点CBPE=30.M) GO D...1S C （£＞） 5 C（3）3 .用两个全等的直角三角形拼下列图形：①平行四边形；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形；一定可以拼成的是_______________ （只填序号）. 4•如图3,点E、F是菱形ABCD勺边BC CD上的点，请你添加一个条件（？不得另外添加辅助线和字母），使AE=AF你添加的条件是___________________ .5. （2006年烟台市）如图4,先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB AD分别落在x轴、y轴上（如图①所示），？再将此矩形在坐标平面内按逆时针方向绕原点旋转30。

2024学年八年级数学经典好题专项(矩形、菱形、正方形)练习(附答案)

2024学年八年级数学经典好题专项（矩形、菱形、正方形）练习一、选择题1、菱形不具备的性质是( )A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形2、如图，菱形ABCD 中，∠D ＝150°，则∠1＝( )A ．30°B ．25°C ．20°D ．15°（2题）（3题）（4题）3、如图，在▱ABCD 中，AB ＝BC ，下列结论错误的是( )A ．四边形ABCD 是菱形B ．AB ＝ADC ．AO ＝OC ，BO ＝OD D ．∠BAD ＝∠ABC4、如图所示，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为( )A ．2 3B ．3 3C ．4 3D ．35、如图，菱形ABCD 中，AB=15，∠ADC=120°，则B、D 两点之间的距离为（）A．15 B．3215 C．7.5 D．315（5题）（7题）（8题）（9题）6、菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（）A．8cm 和cm B．4cm 和cm C．8cm 和cm D．4cm 和cm7、如图，菱形ABCD 的对角线AC ，BD 的长分别为6 cm ，8 cm ，则这个菱形的周长为( )A ．5 cmB ．10 cmC ．14 cmD ．20 cm8、如图，在菱形ABCD 中，∠BAD ＝80°，AB 的垂直平分线交对角线AC 于点F ，垂足为点E ，连接DF ，则∠CDF 等于( )A ．50°B ．60°C ．70°D ．80°9、如图．剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（）A．∠ABC=∠ADC,∠BAD=∠BCD B．AB=BC C．AB=CD ,AD=BC D．∠DAB+∠BCD=180º10、如图，在平面直角坐标系中，四边形OABC 为菱形，O(0，0)，A(4，0)，∠AOC ＝60°，则对角线交点E 的坐标为( )A ．(2， 3 )B ．( 3 ，2)C ．( 3 ，3)D ．(3， 3 )（10题）（11题）（12题）（13题）二、填空题11、如图，在△ABC 中，点D ，E ，F 分别在边BC ，AB ，CA 上，且DE ∥CA ，DF ∥BA.小聪认为如果AD平分∠BAC ，那么四边形AEDF 是菱形，小聪的说法．(填“正确”或“不正确”)12、在菱形ABCD 中，对角线AC 、BD 相交于点O ，若∠ABC ＝140°，则∠BAD ＝________°，∠ABD ＝________°，∠BCA ＝________°；13、如图，菱形ABCD 的边长为2 cm ，E 是BC 的中点，且AE ⊥BC ，则菱形ABCD 的面积为_____.14、如图，P 是菱形ABCD 的对角线AC 上一点，PE ⊥AD 于点E ，且PE ＝3 cm ，则点P 到AB 的距离为__ __ cm.（14题）（15题）（17题）（20题）15、如图，在菱形ABCD 中，AB ＝5，AO ＝3，点E 在BC 的延长线上，∠E ＝12∠ABC ，DE ＝16、菱形ABCD 的周长为48cm，∠BAD：∠ABC=1：2，则BD=_____，菱形的面积是______．17、如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，若AC ＝8 cm ，BD ＝6 cm ，则该菱形的面积为________cm 2，周长为________cm.18、已知菱形ABCD 的面积为24 cm 2，若对角线AC ＝6 cm ，则这个菱形的边长为____ cm.19、四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为_________20、如图，点P 是边长为1的菱形ABCD 对角线AC 上的一个动点，点M ，N 分别是AB ，BC 边的中点，则MP ＋PN 的最小值是______.三、解答题21、已知：如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，DE ∥AC 交BC 于点E ，DF ∥BC 交AC于点F. 四边形DECF 是菱形吗？为什么？22、如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝8 cm，BD＝6 cm，DH⊥AB于H.(1)求菱形ABCD的面积；(2)求DH的长．23、如图，在菱形ABCD中，对角线AC与BD相交于点O，BD＝12 cm，AC＝6 cm.求菱形的周长．24、已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD.（1）求证：四边形AODE是矩形；（2）若AB=6，∠BCD=120°，求四边形AODE的面积.25、如图，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF.求证：(1)△ABF≌△DAE；(2)DE＝BF＋EF.26、已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1＝∠2.(1)若CE＝1，求BC的长；(2)求证：AM＝DF＋ME.参考答案一、选择题1、菱形不具备的性质是( B )A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形2、如图，菱形ABCD 中，∠D ＝150°，则∠1＝( D )A ．30°B ．25°C ．20°D ．15°3、如图，在▱ABCD 中，AB ＝BC ，下列结论错误的是( D )A ．四边形ABCD 是菱形B ．AB ＝ADC ．AO ＝OC ，BO ＝OD D ．∠BAD ＝∠ABC4、如图所示，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为( B )A ．2 3B ．3 3C ．4 3D ．35、如图，菱形ABCD 中，AB=15，∠ADC=120°，则B、D 两点之间的距离为（ A ）A．15 B．3215 C．7.5 D．3156、菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（C ）A．8cm 和cm B．4cm 和cm C．8cm 和cm D．4cm 和cm7、如图，菱形ABCD 的对角线AC ，BD 的长分别为6 cm ，8 cm ，则这个菱形的周长为(D )A ．5 cmB ．10 cmC ．14 cmD ．20 cm8、如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为点E，连接DF，则∠CDF等于( B )A．50° B．60° C．70° D．80°9、如图．剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（）A．∠ABC=∠ADC,∠BAD=∠BCD B．AB=BC C．AB=CD ,AD=BC D．∠DAB+∠BCD=180º解析：∵四边形ABCD是用两张等宽的纸条交叉重叠放在一起而组成的图形，∴AB∥CD，AD∥BC, ∴四边形ABCD是平行四边形（对边相互平行的四边形是平行四边形）．过点A分别作BC，CD边上的高为AE，AF，连接AC，则AE=AF(两纸条相同，纸条宽度相同)，∴在平行四边形ABCD中．S△ABC=S△ACD，即BC•AE=CD•AF，∴BC=CD，AB=BC．故B中结论成立；∴平行四边形ABCD为菱形（邻边相等的平行四边形是菱形），∴∠ABC=∠ADC，∠BAD=∠BCD（菱形的对角相等），故A中结论成立；AB=CD，AD=BC（平行四边形的对边相等），故C中结论成立：当四边形ABCD是矩形时，有∠DAB+∠BCD=180º．故D中结论不一定成立，故选D．10、如图，在平面直角坐标系中，四边形OABC为菱形，O(0，0)，A(4，0)，∠AOC＝60°，则对角线交点E的坐标为( D )A．(2， 3 ) B．( 3 ，2) C．( 3 ，3) D．(3， 3 )二、填空题11、如图，在△ABC中，点D，E，F分别在边BC，AB，CA上，且DE∥CA，DF∥BA.小聪认为如果AD平分∠BAC，那么四边形AEDF是菱形，小聪的说法正确．(填“正确”或“不正确”)12、在菱形ABCD中，对角线AC、BD相交于点O，若∠ABC＝140°，则∠BAD＝________°，∠ABD＝________°，∠BCA＝________°；答案：40，70，2013、如图，菱形ABCD的边长为2 cm，E是BC的中点，且AE⊥BC，则菱形ABCD的面积为__2 3 cm2 ____.14、如图，P是菱形ABCD的对角线AC上一点，PE⊥AD于点E，且PE＝3 cm，则点P到AB的距离为__3 __ cm.15、如图，在菱形ABCD中，AB＝5，AO＝3，点E在BC的延长线上，∠E＝12∠ABC，DE＝816、菱形ABCD的周长为48cm，∠BAD：∠ABC=1：2，则BD=_____，菱形的面积是______．217、如图，在菱形ABCD中，对角线AC、BD相交于点O，若AC＝8 cm，BD＝6 cm，则该菱形的面积为________cm2，周长为________cm.答案：24，2018、已知菱形ABCD的面积为24 cm2，若对角线AC＝6 cm，则这个菱形的边长为__5 __ cm.19、四边形ABCD是菱形，∠BAD＝60°，AB＝6，对角线AC与BD相交于点O，点E在AC上，若OE＝3，则CE的长为___43或23______20、如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边的中点，则MP＋PN的最小值是__1 ____.三、解答题21、已知：如图，在△ABC中，CD平分∠ACB交AB于点D，DE∥AC交BC于点E，DF∥BC交AC于点F. 四边形DECF是菱形吗？为什么？解：四边形DECF是菱形．理由如下：∵DE∥FC，DF∥EC，∴四边形DECF为平行四边形．由AC∥DE，知∠2＝∠3. ∵CD平分∠ACB，∴∠1＝∠2，∴∠1＝∠3，∴DE＝EC，∴平行四边形DECF为菱形．22、如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝8 cm，BD＝6 cm，DH⊥AB于H.(1)求菱形ABCD的面积；(2)求DH的长．解：(1)∵四边形ABCD 是菱形，AC ＝8 cm ，BD ＝6 cm ，∴S 菱形ABCD ＝12ACꞏBD ＝12×6×8＝24(cm 2)．(2)∵四边形ABCD 是菱形，∴AC ⊥BD ，OA ＝OC ＝12＝4 cm ，OB ＝OD ＝3 cm ，∴在直角三角形AOB 中，AB ＝OB 2＋OA 2＝32＋42＝5 cm ，∴DH ＝S 菱形ABCD AB ＝4.8 cm.23、如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，BD ＝12 cm ，AC ＝6 cm.求菱形的周长．解：∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝12AC ，BO ＝12 BD.∵AC ＝6 cm ，BD ＝12 cm ， ∴AO ＝3 cm ，BO ＝6 cm.在Rt △ABO 中，由勾股定理，得AB ＝AO 2＋BO 2＝32＋62＝3 5 cm ，∴菱形的周长＝4AB=4×3 5 =12 5 cm.24、已知：如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，DE ∥AC ，AE ∥BD.（1）求证：四边形AODE 是矩形；（2）若AB=6，∠BCD=120°，求四边形AODE 的面积.解答：（1）证明：∵DE ∥AC ，AE ∥BD ，∴四边形AODE 是平行四边形，∵在菱形ABCD 中，AC ⊥BD ，∴ AOD=90 , ∴平行四边形AODE 是是矩形；（2）∵∠BCD=120°，AB ∥CD ，∴∠ABC=180°‐120°=60°，∵AB=BC ，∴△ABC 是等边三角形，∴OA=21×6=3, OD=OB=6×23=33,∴四边形AODE 的面积=OA ∙OD=9325、如图，在菱形ABCD 中，点P 是BC 边上一点，连接AP ，点E ，F 是AP 上的两点，连接DE ，BF ，使得∠AED ＝∠ABC ，∠ABF ＝∠BPF .求证：(1)△ABF ≌△DAE ；(2)DE ＝BF ＋EF .证明：(1)∵四边形ABCD 是菱形，∴AB ＝AD ，AD ∥BC . ∴∠BP A ＝∠DAE .∵∠ABC ＝∠AED ，∴∠BAF ＝∠ADE .∵∠ABF ＝∠BPF ，∠BP A ＝∠DAE ，∴∠ABF ＝∠DAE .∵AB ＝DA ，∴△ABF ≌△DAE (ASA)．(2)∵△ABF ≌△DAE ， ∴BF ＝AE ，AF ＝DE .∵AF ＝AE ＋EF ＝BF ＋EF ，∴DE ＝BF ＋EF .26、已知：如图，在菱形ABCD 中，F 为边BC 的中点，DF 与对角线AC 交于点M ，过M 作ME ⊥CD 于点E ，∠1＝∠2.(1)若CE ＝1，求BC 的长；(2)求证：AM ＝DF ＋ME.(1)解：∵四边形ABCD 是菱形，∴AB ∥CD ，∴∠1＝∠ACD ，∵∠1＝∠2，∴∠ACD ＝∠2，∴MC ＝MD ，∵ME ⊥CD ，∴CD ＝2CE ， ∵CE ＝1，∴CD ＝2，∴BC ＝CD ＝2(2)证明：如图，∵F 为边BC 的中点，∴BF ＝CF ＝12BC ，∴CF ＝CE ，在菱形ABCD 中，AC 平分∠BCD ，∴∠ACB ＝∠ACD ，在△CEM 和△CFM 中，∵⎩⎪⎨⎪⎧CE ＝CF ，∠ACB ＝∠ACD ，CM ＝CM ，∴△CEM ≌△CFM(SAS)，∴ME ＝MF ，延长AB 交DF 的延长线于点G ， ∵AB ∥CD ，∴∠G ＝∠2， ∵∠1＝∠2，∴∠1＝∠G ，∴AM ＝MG ，在△CDF 和△BGF 中，∵⎪⎩⎪⎨⎧=∠=∠∠=∠FC FB DFC GFB G 2,∴△CDF ≌△BGF(AAS)，∴GF ＝DF ，由图形可知，GM ＝GF ＋MF ，∴AM ＝DF ＋ME。

第19章矩形、菱形和正方形单元测试2021-2022学年华东师大版数学八年级下册(word 含答案)

第19章矩形、菱形和正方形单元测试一.单选题（共10题；共30分）1.取四边形ABCD的各边中点E、F、G、H，依次连结EFGH得到四边形EFGH，现知四边形EFGH是菱形，则四边形ABCD的对角线( )A. 相等B. 相等且平分C. 垂直D. 垂直且平分2.四边形ABCD的对角线AC，BD相交于点O，能判定它为正方形的是（）A. AO=CO，BO=DOB. AO=CO=BO=DOC. AO=CO，BO=DO，AC⊥BDD. AO=BO=CO=DO，AC⊥BD3.如图，矩形ABCD中，AE⊥BD垂足为E，若∠DAE=3∠BAE，则∠EAC的度数为（）A. 67.5°B. 45°C. 22.5°D. 无法确定4.如图，菱形OABC的顶点O在坐标系原点，顶点A在x轴上，∠B=120°，OA=2，将菱形OABC绕原点O顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）A. （，）B. （，）C. （2，﹣2）D. （，﹣）5.如图，在平面直角坐标系中，四边形ABCO是正方形，已知点C的坐标为（，1），则点B的坐标为（）A. （﹣1，+1）B. （﹣1，1）C. （1，+1）D. （﹣1，2）6.下列性质中，正方形具有而菱形不一定具有的性质是（）A. 四条边相等B. 对角线互相平分C. 对角线相等D. 对角线互相垂直7.菱形具有而矩形不具有的性质是（）A. 对角线互相平分B. 四条边都相等C. 对角相等D. 邻角互补8.在平面中，下列说法正确的是（）．A. 四边相等的四边形是正方形B. 四个角相等的四边形是矩形C. 对角线相等的四边形是菱形D. 对角线互相垂直的四边形是平行四边形9.如图，ABCD、AEFC都是矩形，而且点B在EF上，这两个矩形的面积分别是S1，S2，则S1，S2的关系是（）A. S1＞S2B. S1＜S2C. S1=S2D. 3S1=2S210.如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是（）A. 90°B. 80°C. 70°D. 60°二.填空题（共8题；共24分）11.如图，已知AD∥BC，AB∥CD，AB=4，BC=6，EF是AC的垂直平分线，分别交AD、AC于E、F，连结CE，则△CDE的周长是________ ．12.如图，由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”，其中阴影部分面积为________．13.如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=2，BC=3，则图中阴影部分的面积为________．14.设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去…根据以上规律，第n个正方形的边长a n=________．15.在四边形ABCD中，∠A=∠B=∠C=∠D，则四边形ABCD是________．16.正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B n的坐标是________ .17.（如图所示）两个长宽分别为7cm、3cm的矩形如图叠放在一起，则图中阴影部分的面积是________．18.如图，正方形ABCD的边长为4，延长CB至点M，使BM=2，过点B作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为________．三.解答题（共6题；共36分）19.如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．求四边形AEBD的面积．20.如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE等于多少时，四边形CEDF是矩形；②当AE等于多少时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）21.如图所示，在菱形ABCD中，∠BAD=120°，AB=4．求：（1）对角线AC，BD的长；（2）菱形ABCD的面积．22.在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF的值。

八下平行四边形9.4 矩形、菱形、正方形练习含答案含答案

一．选择题1．菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分D．对角线互相垂直2．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．43．矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）A．（3，1）B．（3，）C．（3，）D．（3，2）4．如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B 落在矩形内点F处，连接CF，则CF的长为（）A．B．C．D．5．如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）A．30°B．45°C．60°D．75°6．如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（）A．4.8 B．5 C．6 D．7.27．如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN恰好过点G若AB=，EF=2，∠H=120°，则DN的长为（）A．B．C．﹣D．2﹣8．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（）A．4个B．3个C．2个D．1个9．如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD 上，则AP+PQ的最小值为（）A．2B．C．2D．310．有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1：S2等于（）A．1：B．1：2 C．2：3 D．4：9二、填空题17．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．18．如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为．19．如图，已知菱形ABCD的边长2，∠A=60°，点E、F分别在边AB、AD上，若将△AEF 沿直线EF折叠，使得点A恰好落在CD边的中点G处，则EF=．20．如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF对称，点B的对称点是点G，且点G在边AD上．若EG⊥AC，AB=6，则FG的长为．21．如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E=度．22．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=度．三．解答题：1．如图，在平行四边形ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．2．如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．3．如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD 沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．4．已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．5．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA 的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．一．选择题1．（2016•莆田）菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分 D．对角线互相垂直【分析】由菱形的性质可得：菱形的对角线互相平分且垂直；而平行四边形的对角线互相平分；则可求得答案．【解答】解：∵菱形具有的性质：对边相等，对角相等，对角线互相平分，对角线互相垂直；平行四边形具有的性质：对边相等，对角相等，对角线互相平分；∴菱形具有而一般平行四边形不具有的性质是：对角线互相垂直．故选D．【点评】此题考查了菱形的性质以及平行四边形的性质．注意菱形的对角线互相平分且垂直．2．（2016•枣庄）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．4【分析】根据菱形性质求出AO=4，OB=3，∠AOB=90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．【解答】解：∵四边形ABCD是菱形，∴AO=OC，BO=OD，AC⊥BD，∵AC=8，DB=6，∴AO=4，OB=3，∠AOB=90°，由勾股定理得：AB==5，=，∵S菱形ABCD∴，∴DH=，故选A．【点评】本题考查了勾股定理和菱形的性质的应用，能根据菱形的性质得出S菱=是解此题的关键．形ABCD3．（2016•苏州）矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）A．（3，1）B．（3，）C．（3，）D．（3，2）【分析】如图，作点D关于直线AB的对称点H，连接CH与AB的交点为E，此时△CDE的周长最小，先求出直线CH解析式，再求出直线CH与AB的交点即可解决问题．【解答】解：如图，作点D关于直线AB的对称点H，连接CH与AB的交点为E，此时△CDE的周长最小．∵D（，0），A（3，0），∴H（，0），∴直线CH解析式为y=﹣x+4，∴x=3时，y=，∴点E坐标（3，）故选：B．【点评】本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识，解题的关键是利用轴对称找到点E位置，学会利用一次函数解决交点问题，属于中考常考题型．4．（2016•威海）如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）A．B．C．D．【分析】连接BF，根据三角形的面积公式求出BH，得到BF，根据直角三角形的判定得到∠BFC=90°，根据勾股定理求出答案．【解答】解：连接BF，∵BC=6，点E为BC的中点，∴BE=3，又∵AB=4，∴AE==5，∴BH=，则BF=，∵FE=BE=EC，∴∠BFC=90°，∴CF==．故选：D．【点评】本题考查的是翻折变换的性质和矩形的性质，掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．5．（2016•海南）如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）A．30°B．45°C．60°D．75°【分析】首先过点D作DE∥a，由∠1=60°，可求得∠3的度数，易得∠ADC=∠2+∠3，继而求得答案．【解答】解：过点D作DE∥a，∵四边形ABCD是矩形，∴∠BAD=∠ADC=90°，∴∠3=90°﹣∠1=90°﹣60°=30°， ∵a ∥b ， ∴DE ∥a ∥b ，∴∠4=∠3=30°，∠2=∠5， ∴∠2=90°﹣30°=60°．故选C ．【点评】此题考查了矩形的性质以及平行线的性质．注意准确作出辅助线是解此题的关键．6．（2016•宜宾）如图，点P 是矩形ABCD 的边AD 上的一动点，矩形的两条边AB 、BC 的长分别是6和8，则点P 到矩形的两条对角线AC 和BD 的距离之和是（）A ．4.8B ．5C ．6D ．7.2【分析】首先连接OP ，由矩形的两条边AB 、BC 的长分别为6和8，可求得OA=OD=5，△AOD 的面积，然后由S △AOD =S △AOP +S △DOP =OA•PE +OD•PF 求得答案．【解答】解：连接OP ，∵矩形的两条边AB 、BC 的长分别为6和8，∴S 矩形ABCD =AB•BC=48，OA=OC ，OB=OD ，AC=BD=10， ∴OA=OD=5，∴S △ACD =S 矩形ABCD =24， ∴S △AOD =S △ACD =12，∵S △AOD =S △AOP +S △DOP =OA•PE +OD•PF=×5×PE +×5×PF=（PE +PF ）=12，解得：PE +PF=4.8．故选：A ．【点评】此题考查了矩形的性质以及三角形面积问题．此题难度适中，注意掌握辅助线的作法以及掌握整体数学思想的运用是解题的关键．7．（2016•资阳）如图，矩形ABCD 与菱形EFGH 的对角线均交于点O ，且EG ∥BC ，将矩形折叠，使点C 与点O 重合，折痕MN 恰好过点G 若AB=，EF=2，∠H=120°，则DN 的长为（）A ．B ．C ．﹣D ．2﹣【分析】延长EG 交DC 于P 点，连接GC 、FH ，则△GCP 为直角三角形，证明四边形OGCM 为菱形，则可证CG=OM=CM=OG=，由勾股定理求得GP 的值，再由梯形的中位线定理CM +DN=2GP ，即可得出答案．【解答】解：延长EG 交DC 于P 点，连接GC 、FH ；如图所示：则CP=DP=CD=，△GCP 为直角三角形，∵四边形EFGH 是菱形，∠EHG=120°， ∴GH=EF=2，∠OHG=60°，EG ⊥FH ， ∴OG=GH•sin60°=2×=，由折叠的性质得：CG=OG=，OM=CM ，∠MOG=∠MCG ，∴PG==，∵OG ∥CM ，∴∠MOG +∠OMC=180°，∴∠MCG +∠OMC=180°，∴OM ∥CG ，∴四边形OGCM 为平行四边形，∵OM=CM ，∴四边形OGCM 为菱形，∴CM=OG=，根据题意得：PG 是梯形MCDN 的中位线，∴DN +CM=2PG=，∴DN=﹣；故选：C ．【点评】本题考查了矩形的性质、菱形的性质、翻折变换的性质、勾股定理、梯形中位线定理、三角函数等知识；熟练掌握菱形和矩形的性质，由梯形中位线定理得出结果是解决问题的关键．8．（2016•眉山）如图，矩形ABCD 中，O 为AC 中点，过点O 的直线分别与AB 、CD 交于点E 、F ，连结BF 交AC 于点M ，连结DE 、BO ．若∠COB=60°，FO=FC ，则下列结论：①FB 垂直平分OC ；②△EOB ≌△CMB ；③DE=EF ；④S △AOE ：S △BCM =2：3．其中正确结论的个数是（）A ．4个B ．3个C ．2个D ．1个【分析】①利用线段垂直平分线的性质的逆定理可得结论；②在△EOB和△CMB中，对应直角边不相等；③可证明∠CDE=∠DFE；④可通过面积转化进行解答．【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵△BOC为等边三角形，FO=FC，∴BO⊥EF，BF⊥OC，∴∠CMB=∠EOB=90°，但BO≠BM，故②错误；③易知△ADE≌△CBF，∠1=∠2=∠3=30°，∴∠ADE=∠CBF=30°，∠BEO=60°，∴∠CDE=60°，∠DFE=∠BEO=60°，∴∠CDE=∠DFE，∴DE=EF，故③正确；④易知△AOE≌△COF，∴S△AOE=S△COF，∵S△COF=2S△CMF，∴S△AOE ：S△BCM=2S△CMF：S△BCM=，∵∠FCO=30°，∴FM=，BM=CM，∴=，∴S△AOE ：S△BCM=2：3，故④正确；所以其中正确结论的个数为3个；故选B【点评】本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．9．（2016•雅安）如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）A．2 B．C．2 D．3【分析】在Rt△ABE中，利用三角形相似可求得AE、DE的长，设A点关于BD 的对称点A′，连接A′D，可证明△ADA′为等边三角形，当PQ⊥AD时，则PQ最小，所以当A′Q⊥AD时AP+PQ最小，从而可求得AP+PQ的最小值等于DE的长，可得出答案..【解答】解：设BE=x，则DE=3x，∵四边形ABCD为矩形，且AE⊥BD，∴△ABE∽△DAE，∴AE2=BE•DE，即AE2=3x2，∴AE=x，在Rt△ADE中，由勾股定理可得AD2=AE2+DE2，即62=（x）2+（3x）2，解得x=，∴AE=3，DE=3，如图，设A点关于BD的对称点为A′，连接A′D，PA′，则A′A=2AE=6=AD，AD=A′D=6，∴△AA′D是等边三角形，∵PA=PA′，∴当A′、P、Q三点在一条线上时，A′P+PQ最小，又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，∴AP+PQ=A′P+PQ=A′Q=DE=3，故选D．【点评】本题主要考查轴对称的应用，利用最小值的常规解法确定出A的对称点，从而确定出AP+PQ的最小值的位置是解题的关键，利用条件证明△A′DA是等边三角形，借助几何图形的性质可以减少复杂的计算．10．（2016•南宁）有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1：S2等于（）A．1：B．1：2 C．2：3 D．4：9【分析】设小正方形的边长为x，再根据相似的性质求出S1、S2与正方形面积的关系，然后进行计算即可得出答案．【解答】解：设小正方形的边长为x，根据图形可得：∵=，∴=，∴=，∴S1=S正方形ABCD，∴S1=x2，∵=，∴=，∴S2=S正方形ABCD，∴S2=x2，∴S1：S2=x2：x2=4：9；故选D．【点评】此题考查了正方形的性质，用到的知识点是正方形的性质、相似三角形的性质、正方形的面积公式，关键是根据题意求出S1、S2与正方形面积的关系．17．（2016•内江）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．【分析】先根据菱形的性质得AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，再在Rt△OBC中利用勾股定理计算出BC=5，然后利用面积法计算OE的长．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，在Rt△OBC中，∵OB=3，OC=4，∴BC==5，∵OE⊥BC，∴OE•BC=OB•OC，∴OE==．故答案为．【点评】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了勾股定理和三角形面积公式．18．（2016•扬州）如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为24．【分析】由菱形的性质可得出AC⊥BD，AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得出AD的长，结合菱形的周长公式即可得出结论．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，AB=BC=CD=DA，∴△AOD为直角三角形．∵OE=3，且点E为线段AD的中点，∴AD=2OE=6．C菱形ABCD=4AD=4×6=24．故答案为：24．【点评】本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出AD=6．本题属于基础题，难度不大，解决该题型题目时，根据菱形的性质找出对角线互相垂直，再通过直角三角形的性质找出菱形的一条变成是关键．19．（2016•盐城）如图，已知菱形ABCD的边长2，∠A=60°，点E、F分别在边AB、AD上，若将△AEF沿直线EF折叠，使得点A恰好落在CD边的中点G处，则EF=．【分析】延长CD，过点F作FM⊥CD于点M，连接GB、BD，作FH⊥AE交于点H，由菱形的性质和已知条件得出∠MFD=30°，设MD=x，则DF=2x，FM=x，得出MG=x+1，由勾股定理得出（x+1）2+（x）2=（2﹣2x）2，解方程得出DF=0.6，AF=1.4，求出AH=AF=0.7，FH=，证明△DCB是等边三角形，得出BG⊥CD，由勾股定理求出BG=，设BE=y，则GE=2﹣y，由勾股定理得出（）2+y2=（2﹣y）2，解方程求出y=0.25，得出AE、EH，再由勾股定理求出EF即可．【解答】解：延长CD，过点F作FM⊥CD于点M，连接GB、BD，作FH⊥AE交于点H，如图所示：∵∠A=60°，四边形ABCD是菱形，∴∠MDF=60°，∴∠MFD=30°，设MD=x，则DF=2x，FM=x，∵DG=1，∴MG=x+1，∴（x+1）2+（x）2=（2﹣2x）2，解得：x=0.3，∴DF=0.6，AF=1.4，∴AH=AF=0.7，FH=AF•sin∠A=1.4×=，∵CD=BC，∠C=60°，∴△DCB是等边三角形，∵G是CD的中点，∴BG⊥CD，∵BC=2，GC=1，∴BG=，设BE=y，则GE=2﹣y，∴（）2+y2=（2﹣y）2，解得：y=0.25，∴AE=1.75，∴EH=AE﹣AH=1.75﹣0.7=1.05，∴EF===．故答案为：．【点评】本题考查了菱形的性质、翻折变换的性质、勾股定理、等边三角形的判定与性质等知识；本题综合性强，难度较大，运用勾股定理得出方程是解决问题的关键．20．（2016•哈尔滨）如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF对称，点B的对称点是点G，且点G在边AD上．若EG⊥AC，AB=6，则FG的长为3．【分析】首先证明△ABC，△ADC都是等边三角形，再证明FG是菱形的高，根=BC•FG即可解决问题．据2•S△ABC【解答】解：∵四边形ABCD是菱形，∠BAD=120°，∴AB=BC=CD=AD，∠CAB=∠CAD=60°，∴△ABC，△ACD是等边三角形，∵EG⊥AC，∴∠AEG=∠AGE=30°，∵∠B=∠EGF=60°，∴∠AGF=90°，∴FG⊥BC，=BC•FG，∴2•S△ABC∴2××（6）2=6•FG，∴FG=3．故答案为3．【点评】本题考查菱形的性质、等边三角形的判定和性质、翻折变换、菱形的面积等知识，记住菱形的面积=底×高=对角线乘积的一半，属于中考常考题型．21．（2016•巴中）如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E=15度．【分析】连接AC，由矩形性质可得∠E=∠DAE、BD=AC=CE，知∠E=∠CAE，而∠ADB=∠CAD=30°，可得∠E度数．【解答】解：连接AC，∵四边形ABCD是矩形，∴AD∥BE，AC=BD，且∠ADB=∠CAD=30°，∴∠E=∠DAE，又∵BD=CE，∴CE=CA，∴∠E=∠CAE，∵∠CAD=∠CAE+∠DAE，∴∠E+∠E=30°，即∠E=15°，故答案为：15．【点评】本题主要考查矩形性质，熟练掌握矩形对角线相等且互相平分、对边平行是解题关键．22．（2016•包头）如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=22.5度．【分析】首先证明△AEO是等腰直角三角形，求出∠OAB，∠OAE即可．【解答】解：∵四边形ABCD是矩形，∴AC=BD，OA=OC，OB=OD，∴OA=OB═OC，∴∠OAD=∠ODA，∠OAB=∠OBA，∴∠AOE=∠OAD+∠ODA=2∠OAD，∵∠EAC=2∠CAD，∴∠EAO=∠AOE，∵AE⊥BD，∴∠AEO=90°，∴∠AOE=45°，∴∠OAB=∠OBA==67.5°，∴∠BAE=∠OAB﹣∠OAE=22.5°．故答案为22.5°．【点评】本题考查矩形的性质、等腰直角三角形的性质等知识，解题的关键是发现△AEO是等腰直角三角形这个突破口，属于中考常考题型．23．（2016•黄冈）如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP= 2a．【分析】作FM⊥AD于M，则MF=DC=3a，由矩形的性质得出∠C=∠D=90°．由折叠的性质得出PE=CE=2a=2DE，∠EPF=∠C=90°，求出∠DPE=30°，得出∠MPF=60°，在Rt△MPF中，由三角函数求出FP即可．【解答】解：作FM⊥AD于M，如图所示：则MF=DC=3a，∵四边形ABCD是矩形，∴∠C=∠D=90°．∵DC=3DE=3a，∴CE=2a，由折叠的性质得：PE=CE=2a=2DE，∠EPF=∠C=90°，∴∠DPE=30°，∴∠MPF=180°﹣90°﹣30°=60°，在Rt△MPF中，∵sin∠MPF=，∴FP===2a；故答案为：2a．【点评】本题考查了折叠的性质、矩形的性质、三角函数等知识；熟练掌握折叠和矩形的性质，求出∠DPE=30°是解决问题的关键．1．（2016•安顺）如图，在平行四边形ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．【分析】第（1）问要证明三角形全等，由平行四边形的性质，很容易用SAS证全等．第（2）要求菱形的面积，在第（1）问的基础上很快知道△ABE为等边三角形．这样菱形的高就可求了，用面积公式可求得．【解答】（1）证明：∵在▱ABCD中，AB=CD，∴BC=AD，∠ABC=∠CDA．又∵BE=EC=BC，AF=DF=AD，∴BE=DF．∴△ABE≌△CDF．（2）解：∵四边形AECF为菱形，∴AE=EC．又∵点E是边BC的中点，∴BE=EC，即BE=AE．又BC=2AB=4，∴AB=BC=BE，∴AB=BE=AE，即△ABE为等边三角形，▱ABCD的BC边上的高为2×sin60°=，∴菱形AECF的面积为2．【点评】考查了全等三角形，四边形的知识以及逻辑推理能力．（1）用SAS证全等；（2）若四边形AECF为菱形，则AE=EC=BE=AB，所以△ABE为等边三角形．2．（2016•广安）如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．【分析】连接AC，根据菱形的性质可得AC平分∠DAE，CD=BC，再根据角平分线的性质可得CE=FC，然后利用HL证明Rt△CDF≌Rt△CBE，即可得出DF=BE．【解答】证明：连接AC，∵四边形ABCD是菱形，∴AC平分∠DAE，CD=BC，∵CE⊥AB，CF⊥AD，∴CE=FC，∠CFD=∠CEB=90°．在Rt△CDF与Rt△CBE中，，∴Rt△CDF≌Rt△CBE（HL），∴DF=BE．【点评】此题考查了菱形的性质，角平分线的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；角平分线的性质：角的平分线上的点到角的两边的距离相等．同时考查了全等三角形的判定与性质．3．（2016•荆州）如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．【分析】当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．先证明CD=DA=DB，得到∠DAC=∠DCA，由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状．由EF∥AB推出∠CEF=∠EA′D，∠EFC=∠A′D′C=∠A′DE，再根据A′D=DE=EF即可证明．【解答】解：当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．理由：∵△BCA是直角三角形，∠ACB=90°，AD=DB，∴CD=DA=DB，∴∠DAC=∠DCA，∵A′C′∥AC，∴∠DA′E=∠A，∠DEA′=∠DCA，∴∠DA′E=∠DEA′，∴DA′=DE，∴△A′DE是等腰三角形．∵四边形DEFD′是菱形，∴EF=DE=DA′，EF∥DD′，∴∠C′EF=∠DA′E，∠EFC′=∠C′D′A′，∵CD∥C′D′，∴∠A′DE=∠A′D′C′=∠EFC′，在△A′DE和△EFC′中，，∴△A′DE≌△EFC′．【点评】本题考查平移、菱形的性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．4．（2016•淮安）已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．【分析】由菱形的性质得出AD=CD，由中点的定义证出DE=DF，由SAS证明△ADE ≌△CDF即可．【解答】证明：∵四边形ABCD是菱形，∴AD=CD，∵点E、F分别为边CD、AD的中点，∴AD=2DF，CD=2DE，∴DE=DF，在△ADE和△CDF中，，∴△ADE≌△CDF（SAS）．【点评】此题主要考查了全等三角形的判定、菱形的性质；熟练掌握菱形的性质，证明三角形全等是解决问题的关键．5．（2016•苏州）如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D 作对角线BD的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．【分析】（1）根据平行四边形的判定证明即可；（2）利用平行四边形的性质得出平行四边形的周长即可．【解答】（1）证明：∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB=90°，∵DE⊥BD，即∠EDB=90°，∴∠AOB=∠EDB，∴DE∥AC，∴四边形ACDE是平行四边形；（2）解：∵四边形ABCD是菱形，AC=8，BD=6，∴AO=4，DO=3，AD=CD=5，∵四边形ACDE是平行四边形，∴AE=CD=5，DE=AC=8，∴△ADE的周长为AD+AE+DE=5+5+8=18．【点评】此题考查平行四边形的性质和判定问题，关键是根据平行四边形的判定解答即可．。

(完整版)矩形菱形正方形习题含答案

1. 在一次数学活动课上，张明同学将矩形ABCD 沿直线CE 折叠，顶点B 恰好落在AD 边上F 点处，如图所示，已知8CD =cm ，5BE =cm ，则AD = cm ．2.如图，在菱形ABCD 中，60B ∠=o，点E F ，分别从点B D ，出发以同样的速度沿边BC DC ，向点C 运动．给出以下四个结论：①AE AF =②CEF CFE ∠=∠③当点E F ，分别为边BC DC ，的中点时，AEF △是等边三角形④当点E F ，分别为边BC DC ，的中点时，AEF △的面积最大．上述结论中正确的序号有．（把你认为正确的序号都填上）3如图，四边形ABCD 为正方形，ADE △为等边三角形．AC 为正方形ABCD 的对角线，则EAC ∠= 度． 4.如图，过正方形ABCD 的顶点B 作直线l ，过A C ，作l 的垂线，垂足分别为 E F ，．若1AE =，3CF =，则AB 的长度为．5如图，正方形ABCD 的边长为4，MN BC ∥分别交AB CD ，于点M N ，，在MN 上任取两点P Q ，，那么图中阴影部分的面积是．1. 如图，在菱形ABCD 中，对角线AC BD ，相交于点O E ，为AB 的中点，且OE a =，则菱形ABCD 的周长为（） A ．16a B ．12a C ．8a D ．4a 2. 菱形的两条对角线的长分别是6和8 ，则这个菱形的周长是（） A ．24 B ．20C ．10D ．53. 如图，在四边形ABCD 中，AD BC ∥，90D ∠=o，若再添加一个条件，就能推出四边形ABCD 是矩形，你所添加的条件是．（写出一种情况即可） 4. 如图，在正方形ABCD 中，E 为AB 边的中点，G ，F 分别为AD ，BC 边上的点，若1=AG ，2=BF ，︒=∠90GEF ，则GF 的长为．ＦＤＡＥＣlD M N DD C FG5.如图，在正方形纸片ABCD 中，对角线AC BD ，交于点O ，折叠正方形纸片 ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后，折痕DE 分别交AB AC ，于点E G ，，连结GF ．下列结论：①112.5AGD ∠=o；② tan 2AED ∠=；③AGD OGD S S =△△；④四边形AEFG 是菱形；⑤2BE OG =．则其中正确结论的序号是．6. 菱形ABCD 中，AE 垂直平分BC ，垂足为E ，4cm AB =．那么，菱形ABCD 的面积是，对角线BD 的长是．7. 如图，菱形ABCD 中，∠BAD =60º ，M 是AB 的中点，P 是对角线AC 上的一个动点，若PM +PB 的最小值是3，则AB 长为． 8. 将一正方形按如图方式分成n 个全等矩形，上、下各横排两个，中间竖排若干个，则n 的值为 A ．12 B ．10 C ．8 D ．6 9. 如图，矩形ABCD 的周长为20cm ，两条对角线相交于O 点，过点O 作AC 的垂线EF ，分别交AD BC ，于E F ，点，连结CE ，则CDE △的周长为（）A ．5cmB ．8cmC ．9cmD ．10cm10. 如果菱形的周长是8cm ，高是1cm ，那么这个菱形两邻角的度数比为（） A ．1:2 B ．1:4 C ．1:5 D ．1:611. 如图，四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若6CD =，则AF 等于（）Ａ．43 Ｂ．33Ｃ．42Ｄ．812.如图，在菱形ABCD 中，对角线AC BD ，分别等于8和6，将BD 沿CB 的方向平移，使D 与A 重合，B 与CB 延长线上的点E 重合，则四边形AECD 的面积等于（）A ．36B ．48C ．72D ．96ADEBPB CAD MOD EＢＦＣＥＤＡABDE O6如图，点P 是正方形ABCD 的对角线BD 上一点，连结PA 、PC ．（1）证明：PAB PCB ∠=∠；（2）在BC 上取一点E ，连结PE ，使得PE PC =，连结AE ，判断PAE △的形状，并说明理由．7如图，在□ABCD 中，EF ∥BD ，分别交BC 、CD 于点P 、Q ，分别交AB 、AD 的延长线于点E 、F ．已知BE=BP ．求证：（1）∠E=∠F ．（2）□ABCD 是菱形．8如图1，在ABC △中，点P 为BC 边中点，直线a 绕顶点A 旋转，若点B P 、在直线a 的异侧，BM ⊥直线a 于点M ，CN ⊥直线a 于点N ，连接.PM PN 、（1）延长MP 交CN 于点E （如图2），①求证：BPM CPE △≌△；②求证：PM PN =；（2）若直线a 绕点A 旋转到图3的位置时，点B P 、在直线a 的同侧，其它条件不变.此时PM PN =还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变，请直接判断四边形MBCN 的形状及此时PM PN =还成立吗？不必说明理由.D C B A P图1 图2 图39已知：如图，在正方形ABCD 中，点E 、F 分别在BC 和CD 上，AE = AF ．（1）求证：BE = DF ；（2）连接AC 交EF 于点O ，延长OC 至点M ，使OM = OA ，连接EM 、FM ．判断四边形AEMF 是什么特殊四边形？并证明你的结论．证明：（1）10如图，在正方形ABCD 中，G 是BC 上的任意一点（G 与B C 、两点不重合），E F 、是AG 上的两点（E F 、与A G 、两点都不重合），若AF BF EF =+，12∠=∠，请判断线段DE 与BF 有怎样的位置关系，并证明你的结论.11如图，ABC △中，点O 是边AC 上一个动点，过O 作直线MN BC ∥，设MN 交BCA ∠的平分线于点E ，交BCA ∠的外角平分线于点F ．（1）探究：线段OE 与OF 的数量关系并加以证明；（2）当点O 在边AC 上运动时，四边形BCFE 会是菱形吗？若是，请证明，若不是，则说明理由；（3）当点O 运动到何处，且ABC △满足什么条件时，四边形AECF 是正方形？12如图①，四边形ABCD 是正方形，点G 是BC 上任意一点，DE ⊥AG 于点E ，BF ⊥AG 于点F . （1）求证：DE －BF = EF ．（2）当点G 为BC 边中点时，试探究线段EF 与GF 之间的数量关系，并说明理由．（3）若点G 为CB 延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE 、BF 、EF 之间A D BEFOCM2 ABCDEFG 1A F N D CB M E O（图）的数量关系（不需要证明）．13如图，将矩形纸片ABCD 沿其对角线AC 折叠，使点B 落到点B '的位置，AB '与CD 交于点E ．（1）试找出一个与AED △全等的三角形，并加以证明；（2）若83AB DE P ==，，为线段AC 上任意一点，PG AE ⊥于G ，PH EC ⊥于H ．试求PG PH +的值，并说明理由．14已知：如图，菱形ABCD 中，E F ，分别是CB CD ，上的点，且BE DF =．（1）求证：AE AF =．（2）若60B ∠=o，点E F ，分别为BC 和CD 的中点．求证：AEF △为等边三角形．15如图1，四边形ABCD 是正方形，G 是CD 边上的一个动点(点G 与C 、D 不重合)，以CG 为一边在正方形ABCD 外作正方形CEFG ，连结BG ，DE ．我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系； ②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．ABDEF A DEFBG C图①CB GAD图②ABC D PG HE B ′16如图-1，已知P 为正方形ABCD 的对角线AC 上一点（不与A 、C 重合），PE ⊥BC 于点E ，PF ⊥CD 于点F ．（1）求证：BP =DP ；（2）如图-2，若四边形PECF 绕点C 按逆时针方向旋转，在旋转过程中是否总有BP =DP ？若是，请给予证明；若不是，请用反例加以说明；（3）试选取正方形ABCD 的两个顶点，分别与四边形PECF 的两个顶点连结，使得到的两条线段在四边形PECF 绕点C 按逆时针方向旋转的过程中长度始终相等，并证明你的结论．17已知：如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为点D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为点E ，（1）求证：四边形ADCE 为矩形；（2）当△ABC 满足什么条件时，四边形ADCE 是一个正方形？并给出证明．17（1）证明：在△A BC 中， AB ＝AC ，AD ⊥BC ．∴ ∠BAD ＝∠DAC ． 2分∵ AN 是△ABC 外角∠CAM 的平分线， ∴ MAE CAE ∠=∠．∴ ∠DAE ＝∠DAC ＋∠CAE ＝⨯21180°＝90°．4分又 ∵ AD ⊥BC ，CE ⊥AN ， ∴ ADC CEA ∠=∠＝90°， ∴ 四边形ADCE 为矩形．5分（2）说明：①给出正确条件得1分，证明正确得3分．②答案只要正确均应给分．例如，当AD ＝12BC 时，四边形ADCE 是正方形． 6分图-2图-1 AM NE证明：∵ AB ＝AC ，AD ⊥BC 于D ．∴ DC ＝12BC ．7分又 AD ＝12BC ，∴ DC ＝AD ． 8分由（1）四边形ADCE 为矩形，∴ 矩形ADCE 是正方形． 9分 16⑴ 解法一：在△ABP 与△ADP 中，利用全等可得BP =DP . 2分解法二：利用正方形的轴对称性，可得BP =DP . 2分 ⑵ 不是总成立 . 3分当四边形PECF 绕点C 按逆时针方向旋转，点P 旋转到BC 边上时，DP >DC >BP ，此时BP =DP 不成立. 5分说明：未用举反例的方法说理的不得分. ⑶ 连接BE 、DF ，则BE 与DF 始终相等. 6分在图8-1中，可证四边形PECF 为正方形， 7分在△BEC 与△DFC 中，可证△BEC ≌△DFC . 从而有 BE =DF . 8分15（1）①BG DE BG DE =⊥， 2分 ②BG DE BG DE =⊥，仍然成立 1分在图（2）中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴ BC CD =，CG CE =， 90BCD ECG ∠=∠=o∴BCG DCE ∠=∠1分 ∴BCG DCE △≌△ （SAS ）1分∴BG DE = CBG CDE ∠=∠又∵BHC DHO ∠=∠ 90CBG BHC ∠+∠=o∴90CDE DHO ∠+∠=o∴90DOH ∠=o∴BG DE ⊥14证明：(1)∵四边形ABCD 是菱形， ∴AB =AD ，B D ∠=∠，又∵BE =DF∴ABE △≌ADF △ ∴AE =AF (2)连接AC∵AB =BC ，60B ∠=︒ ∴ABC ∆是等边三角形， E 是BC 的中点∴AE ⊥BC ， ∴906030BAE ︒∠=︒-=︒，同理30DAF ∠=︒ ∵120BAD ∠=︒∴60EAF BAD BAE DAF ∠=∠-∠-∠=︒又∵AE =AF∴AEF △是等边三角形． 13解：（1）AED CEB '△≌△证明：Q 四边形ABCD 为矩形，90B C BC AD B B D ''∴==∠=∠=∠=，°，又B EC DEA '∠=∠Q ， ∴AED CEB '△≌△．（2）由已知得：EAC CAB ∠=∠且CAB ECA ∠=∠ EAC ECA ∴∠=∠ 835AE EC ∴==-=在ADE △中，4AD = 延长HP 交AB 于M 则PM AB ⊥ PG PM ∴=4PG PH PM PH HM AD ∴+=+===12（1）证明：∵ 四边形ABCD 是正方形， BF ⊥AG ， DE ⊥AG ∴ DA =AB ，∠BAF + ∠DAE = ∠DAE + ∠ADE = 90° ∴ ∠BAF = ∠ADE ∴ △ABF ≌ △DAE ∴ BF = AE ， AF = DE ∴ DE －BF = AF －AE = EFA DE F BG C图①（2）EF = 2FG 理由如下：∵ AB ⊥BC ， BF ⊥AG ， AB =2 BG ∴ △AFB ∽△BFG ∽△ABG∴2===FGBFBF AF BF AB ∴ AF = 2BF ， BF = 2 FG由（1）知，AE = BF ，∴ EF = BF = 2 FG（3）如图 DE + BF = EF------------------------------------------------ 11解：（1）OE OF =．其证明如下：∵CE 是ACB ∠的平分线，12∴∠=∠．∵MN BC ∥，∴13∠=∠． ∴23∠=∠． ∴OE OC =．同理可证OC OF =． ∴OE OF =． 3分（2）四边形BCFE 不可能是菱形，若BCFE 为菱形，则BF EC ⊥，而由（1）可知FC EC ⊥，在平面内过同一点F 不可能有两条直线同垂直于一条直线． 3分（3）当点O 运动到AC 中点时，OE OF =，OA OC =，则四边形AECF 为Y，要使AECF 为正方形，必须使EF AC ⊥．∵EF BC ∥，∴AC BC ⊥，∴ABC △是以ACB ∠为直角的直角三角形， ∴当点O 为AC 中点且ABC △是以ACB ∠为直角的直角三角形时，四边形AECF 是正方形．------------------------------------------------10根据题目条件可判断.DE BF ∥证明如下：∵四边形ABCD 为正方形，∴ 290AB AD BAF ∠+∠==，°． ∵,AF AE EF =+又,AF BF EF =+ ∴AE BF =，∵12,∠=∠∴().ABF DAE SAS △≌△5分∴AFB DEA ∠=∠，BAF ADE ∠=∠.∴290ADE ∠+∠=°.∴90AED BFA ∠=∠=°. ∴.DE BF ∥9分------------------------------------------------ 9证明：（1）∵四边形ABCD 是正方形，∴AB ＝AD ,∠B = ∠D = 90°． ∵AE = AF ，AF N D CB M EO （图） 1 2 54 3 6∴Rt Rt ABE ADF △≌△． ∴BE ＝DF ．4分（2）四边形AEMF 是菱形．∵四边形ABCD 是正方形， ∴∠BCA = ∠DCA = 45°，BC = DC ． ∵BE ＝DF ，∴BC －BE = DC －DF . 即CE CF =． ∴OE OF =． ∵OM = OA ，∴四边形AEMF 是平行四边形． ∵AE = AF ，∴平行四边形AEMF 是菱形．8分------------------------------------------------ 8（1）证明：①如图2.BM Q ⊥直线a 于点M ，CN ⊥直线a 于点N ，90BMN CNM ∴∠=∠=°．BM CN ∴∥．MBP ECP ∴∠=∠．又P Q 为BC 边中点， .BP CP ∴=又BPM CPE ∠=∠Q ， BPM CPE ∴△≌△ 3分②BPM CPE Q △≌△12PM PE PM ME ∴=∴=∴在Rt MNE △中，12PN ME =PM PN ∴=5分（2）成立.如图3.6分证明：延长MP 与NC 的延长线相交于点E .BM Q ⊥直线a 于点M ，CN ⊥直线a 于点N ， 90180BMN CNM BMN CNM ∴∠=∠=∴∠+∠=°．°．BM CN MBP ECP ∴∴∠=∠∥．．7分又P Q 为BC 中点，BP CP ∴=．又Q BPM CPE ∠=∠，BPM CPE ∴△≌△． 12PM PE PM ME ∴=∴=．．则在Rt MNE △中，12PN ME =．∴PM PN =．10分（3）四边形MBCN 是矩形. 11分 PM PN =成立.12分AD BE FOC-----------------------------------------------7证明：（1）在□ABCD 中，BC AD ∥ ∴1F ∠=∠ ∵BE BP = ∴1E ∠=∠ ∴E F ∠=∠ （2）∵BD EF ∥ ∴23E F ∠=∠∠=∠， ∵E F ∠=∠ ∴23∠=∠ ∴AB AD = ∴□ABCD 是菱形6（1）∵在正方形ABCD 中，BD 是对角线， ∴AB CB ABD CBD =∠=∠，．又∵BP BP =， ∴ABP CBP △≌△．∴PA PC PAB PCB =∠=∠，． ··········································································································· 3分（2）如图，PAE △是等腰直角三角形，理由如下： ···································································· 4分 ∵PE PC =， ∴PEC PCB ∠=∠．又∵PAB PCB ∠=∠， ∴PAB PEC ∠=∠．∵E 是BC 上一点,180PEB PEC ∠+∠=o, ∴180PAB PEB ∠+∠=o．DCEBAPADFQ CPEB 1 2 3图2 图3∵在四边形ABEP 中，36090PAB ABC PEB APE ABC ∠+∠+∠+∠=∠=o o，， ∴90APE ∠=o． ∵PA PC PE PC ==，， ∴PA PE =．∴PAE △是等腰直角三角形． ·································································· 7分（其他方法酌情给分）1.102. ①②③3. 1054.5. 81. 2. B 3. 90A ∠=o或AD BC =或AB CD ∥ 4. 3 5. ①④⑤ 6. 27. 8. C 9. D 10. C 11. A 12. A。

北京市通州区2019届中考《矩形、菱形和正方形》专题练习含答案

北京市通州区普通中学2019届初三数学中考复习矩形、菱形和正方形专项复习练习1．下列判断错误的是( D )A ．两组对边分别相等的四边形是平行四边形B ．四个内角都相等的四边形是矩形C ．四条边都相等的四边形是菱形D ．两条对角线垂直且平分的四边形是正方形2．如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于H ，则DH 等于( A ) A.245 B.125C ．5D ．43．如图，矩形ABCD 的对角线AC 与BD 相交于点O ，CE ∥BD ，DE ∥AC ，AD ＝23，DE ＝2，则四边形OCED 的面积( A )A ．2 3B ．4C ．4 3D ．84．如图，矩形ABCD 中，AD ＝2，AB ＝3，过点A ，C 作相距为2的平行线段AE ，CF ，分别交CD ，AB 于点E ，F ，则DE 的长是( D )A. 5B.136 C ．1 D.565．如图，在矩形ABCD 中，AB ＝4，BC ＝6，点E 为BC 的中点，将△ABE 沿AE 折叠，使点B 落在矩形内点F 处，连接CF ，则CF 的长为( D )A.95B.125C.165D.1856．在▱ABCD 中，AB ＝10，BC ＝14，E ，F 分别为边BC ，AD 上的点，若四边形AECF 为正方形，则AE 的长为( D )A ．7B ．4或10C ．5或9D ．6或87．如图，在正方形ABCD 中，E ，F 分别是边BC ，CD 上的点，∠EAF ＝45°，△ECF 的周长为4，则正方形ABCD 的边长为( A )A ．2B ．3C ．4D ．58．如图，正方形ABCD 中，点E ，F 分别在BC ，CD 上，△AEF 是等边三角形，连接AC 交EF 于G ，下列结论：①BE＝DF ；②∠DAF＝15°；③AC 垂直平分EF ；④BE＋DF ＝EF ；⑤S △CEF ＝2S △ABE ，其中正确结论有( C ) A ．2个 B ．3个 C ．4个 D ．5个9．如图，正方形ABCD 的边长为22，对角线AC ，BD 相交于点O ，E 是OC 的中点，连接BE ，过点A 作AM⊥BE于点M ，交BD 于点F ，则FM 的长为__55__．10．如图，菱形ABCD 的对角线AC ，BD 相交于点O ，E 为AD 的中点，若OE ＝3，则菱形ABCD 的周长为__24__．11．如图，在矩形ABCD 中，点E ，F 分别在边CD ，BC 上，且DC ＝3DE ＝3a.将矩形沿直线EF 折叠，使点C 恰好落在AD 边上的点P 处，则FP ＝__23a__．12．如图是一张长方形纸片ABCD ，已知AB ＝8，AD ＝7，E 为AB 上一点，AE ＝5，现要剪下一张等腰三角形纸片(△AEP)，使点P 落在长方形ABCD 的某一条边上，则等腰三角形AEP 的底边长是__52或45或5__．13．如图，正方形ABCD 的面积为3 cm 2，E 为BC 边上一点，∠BAE ＝30°，F 为AE 的中点，过点F 作直线分别与AB ，DC 相交于点M ，N.若MN ＝AE ，0则AM 的长等于__33或233cm.14．如图，在平面直角坐标系中，边长为1的正方形OA 1B 1C 1的两边在坐标轴上，以它的对角线OB 1为边作正方形OB 1B 2C 2，再以正方形OB 1B 2C 2的对角线OB 2为边作正方形OB 2B 3C 3，以此类推…，则正方形OB 2019B 2019C 2019的顶点B 2019的坐标是__(21008，0)__．15．如图，AC 为矩形ABCD 的对角线，将边AB 沿AE 折叠，使点B 落在AC 上的点M 处，将边CD 沿CF 折叠，使点D 落在AC 上的点N 处．(1)求证：四边形AECF 是平行四边形；(2)若AB ＝6，AC ＝10，求四边形AECF 的面积．解：(1)由折叠知AM＝AB，CN＝CD，∠FNC＝∠D＝90°，∠AME＝∠B＝90°，∴∠ANF＝90°，∠CME＝90°，∵四边形ABCD为矩形，∴AB＝CD，AD∥BC，∴AM＝CN，∴AN＝CM，可证△ANF≌△CME(ASA)，∴AF＝CE，又∵AF∥CE，∴四边形AECF是平行四边形(2)∵AB＝6，AC＝10，∴BC＝8，设CE＝x，则EM＝8－x，CM＝10－6＝4，在Rt△CEM中，(8－x)2＋42＝x2，解得x＝5，∴四边形AECF的面积为EC·AB＝5×6＝3016．如图，P是正方形ABCD对角线AC上一点，点E在BC上，且PE＝PB.(1)求证：PE＝PD；(2)连接DE，试判断∠PED的度数，并证明你的结论．解：(1)∵四边形ABCD是正方形，∴BC＝CD，∠ACB＝∠ACD，可证△PBC≌△PDC(SAS)，∴PB＝PD，∵PE＝PB，∴PE＝PD(2)∠PED＝45°.证明：∵四边形ABCD是正方形，∴∠BCD＝90°，∵△PBC≌△PDC，∴∠PBC＝∠PDC，∵PE＝PB，∴∠PBC＝∠PEB，∴∠PDC＝∠PEB，∵∠PEB＋∠PEC＝180°，∴∠PDC＋∠PEC＝180°，在四边形PECD中，∠EPD＝360°－(∠PDC＋∠PEC)－∠BCD＝360°－180°－90°＝90°，又∵PE＝PD，∴△PDE是等腰直角三角形，∴∠PED＝45°17．如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1＝∠2.(1)若CE＝2，求BC的长；(2)求证：ME＝AM－DF.解：(1)∵四边形ABCD是菱形，∴CB＝CD，AB∥CD，∴∠1＝∠ACD.∵∠1＝∠2，∴∠2＝∠ACD，∴MC＝MD.∵ME⊥CD，∴CD＝2CE＝4，∴BC＝CD＝4(2)延长DF，AB交于G，∵四边形ABCD是菱形，∴∠BCA＝∠DCA.∵BC＝2CF，CD＝2CE，∴CE＝CF.可证△CEM≌△CFM(SAS)，∴ME＝MF.∵AB∥CD，∴∠2＝∠G，∠GBF＝∠BCD，∵F为边BC的中点，∴CF＝BF，可证△CDF≌△BGF(AAS)，∴DF＝GF.∵∠1＝∠2，∠G＝∠2，∴∠1＝∠G，∴AM＝GM＝MF＋GF＝DF＋ME，即ME＝AM－DF18．如图①，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE＝BF.连接DE，过点E作EG⊥DE，使EG＝DE，连接FG，FC.(1)请判断：FG与CE的数量关系是___FG＝CE___，位置关系是 __FG∥CE__；(2)如图②，若点E，F分别是边CB，BA延长线上的点，其他条件不变，(1)中结论是否仍然成立？请作出判断并给予证明；(3)如图③，若点E，F分别是边BC，AB延长线上的点，其他条件不变，(1)中结论是否仍然成立？请直接写出你的判断．解：(2)过点G作GH⊥CB的延长线于点H，∵EG⊥DE，∴∠GEH＋∠DEC＝90°，∵∠GEH＋∠HGE＝90°，∴∠DEC＝∠HGE，可证△HGE≌△CED(AAS)，∴GH＝CE，HE＝CD，∵CE＝BF，∴GH＝BF，∵GH∥BF，∴四边形GHBF是矩形，∴GF＝BH，FG∥CH，∴FG∥CE，∵四边形ABCD是正方形，∴CD＝BC，∴HE＝BC，∴HE＋EB＝BC＋EB∴BH＝EC，∴FG＝EC(3)成立．∵四边形ABCD是正方形，∴BC＝CD，∠FBC＝∠ECD＝90°，可证△CBF≌△DCE(SAS)，∴∠BCF＝∠CDE，CF＝DE，∵EG＝DE，∴CF＝EG，∵DE⊥EG，∴∠DEC＋∠CEG＝90°，∵∠CDE＋∠DEC＝90°，∴∠CDE＝∠CEG，∴∠BCF＝∠CEG，∴CF∥EG，∴四边形CEGF是平行四边形，∴FG∥CE，FG＝CE2019-2020学年数学中考模拟试卷一、选择题1．关于x的方程（m﹣2）x214＝0有实数根，则m的取值范围（）A．m≤52且m≠2B．m＞52C．m≤52D．m≤3且m≠22．在四张质地、大小相同的卡片上，分别画有如图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是中心对称图形的概率为（）A．1 B．34C．12D．143．用弹簧秤将一长方体铁块悬于没有盛水的水槽中，再向水槽匀速注入水，直至铁块完全浸没在水中（如图），则能反映弹簧秤的读数y（单位：N）与水面高度x（单位：cm）之间的函数关系的大致图象是（）A．B．C．D．4．如图，直线y＝kx+b与y＝mx+n分别交x轴于点A（﹣1，0），B（4，0），则函数y＝（kx+b）（mx+n）中，当y＜0时x的取值范围是（）A.x＞2B.0＜x＜4C.﹣1＜x＜4D.x＜﹣1 或 x＞45．下列运算正确的是（）A ．2m 2+m 2＝3m 4B ．（mn 2）2＝mn 4C ．2m•4m 2＝8m 2D ．m 5÷m 3＝m 26．如图，▱ABCD 中，∠B ＝70°，BC ＝6，以AD 为直径的⊙O 交CD 于点E ，则DE 的长为（）A ．13π B ．23π C ．76π D ．43π 7．如图，将ABC 绕点A 逆时针旋转110，得到ADE ，若点D 在线段BC 的延长线上，则ADE ∠的大小为( )A ．55B ．50C ．45D ．358．若a b <，则下列结论不一定成立的是（） A ．11a b -<-B ．22a b <C ．33a b ->- D ．22a b <9．《语文课程标准》规定：7﹣9年级学生，要求学会制订自己的阅读计划，广泛阅读各种类型的读物，课外阅读总量不少于260万字，每学年阅读两三部名著．那么260万用科学记数法可表示为（） A ．26×105B ．2.6×102C ．2.6×106D ．260×10410．如图，△ABC 中，∠ACB=90°，∠B=30°，AC=1，过点C 作CD 1⊥AB 于D 1，过D 1作D 1 D 2⊥BC 于D 2，过D 2作D 2 D 3⊥AB 于D 3，这样继续作下去，……，线段D n D n+1能等于（n 为正整数）（）A ．32n⎛⎫⎪⎝⎭B ．132n +⎛⎫⎪⎝⎭C．n⎝⎭D．1n +⎝⎭11．如图，在平面直角坐标系中，线段AB 的端点坐标为A （-2,4），B （4,2），直线y=kx-2与线段AB 有交点，则K 的值不可能是（）A．-5 B．-2 C．3 D．512．在平面直角坐标系中，点A的坐标是（2，1），将点A绕原点O旋转180°得到点A′，则点A′的坐标是（）A．（－1，－2）B．（1，－2）C．（－2，－1）D．（2，－1）二、填空题13．如图，正方形ABCD中，点E、F分别在线BC、CD上运动，且满足∠EAF＝45°，AE、AF分别与BD相交于点M、N．下列说法中：①BE+DF＝EF；②点A到线段EF的距离一定等于正方形的边长；③若tan∠BAE＝12，则tan∠DAF＝13；④若BE＝2，DF＝3，则S△AEF＝18．其中结论正确的是__（将正确的序号写在横线上）14．分解因式(a－b)(a－9b)＋4ab的结果是____．15．4与9的比例中项是_____．16．从分别标有数－3，－2，－1，0，1，2，3的七张卡片中，随机抽取一张，所抽卡片上数的绝对值小于2的概率是_________．17．某中学组织的“红旗大赛”，60名选手的成绩统计如右图，已知成绩在94.5分以上的选手中，男生和女生各占一半，学校从中随机确定2名参加“红歌大赛”，则恰好选到一名男生和一名女生的概率为__________．18．如图，在矩形ABCD中，E是AD的中点，连接AC、BE，AC与BE交于点F，则△ABF的面积和四边形CDEF的面积的比值是____．三、解答题19．如图所示，△ABC中，点D是AB上一点，且AD＝CD，以CD为直径的⊙O交BC于点E，交AC于点F，且点F是半圆CD的中点．（1）求证：AB与⊙O相切．（2）若tanB＝2，AB＝6，求CE的长度．20．用A4纸在某眷印社复印文件，复印页数不超过20时，每页收费1元；复印页数超过20时，超过部分每页收费降为0.4元，在某图书馆复印同样的文件，不论复印多少页，每页收费0.8元，当复印的张数超过20页时，请问答以下问题．（1）复印张数为多少页时，某眷印社与某图书馆的收费相同？（2）如何选择更省钱？21．如图，是由边长为1的小正方形构成的网格，点A，B是格点，根据要求，选择格点，画出符合要求的图形．(1)在图1、图2中分别找出符合要求的1个格点C，并画出相应的格点三角形，使得∠ACB＝45°．(2)在图3中画出符合要求的1个格点D，并画出相应的格点三角形使得tan∠ADB＝12，并求出△ABD的面积．22．图①、图②均为3×3的正方形网格，每个小正方形的边长都为1，请在图①、图②中各画一个顶点在格点的三角形．要求：（1）所画的三角形为钝角三角形；（2倍；（3）图①、图②中所画的三角形不全等．23．某市开展“美丽家乡，创卫同行”活动，某校倡议学生利用双休日参加义务劳动，为了解同学们劳动情况，学校随机调查了部分同学的劳动时间，并用得到的数据绘制了不完整的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为，图①中m的值是；（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数.24．在方程3523ax byax by-=⎧⎨+=⎩中，如果121xy⎧=⎪⎨⎪=-⎩的值．25．有一块含30°角的直角三角板OMN，其中∠MON＝90°，∠NMO＝30°，ON＝，将这块直角三角板按如图所示位置摆放．等边△ABC的顶点B与点O重合，BC边落在OM上，点A恰好落在斜边MN上，将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移，边AB，AC分别与斜边MN交于点E，F（如图2所示），设△ABC平移的时间为t（s）（0＜t＜6）．（1）等边△ABC的边长为；（2）在运动过程中，当时，MN垂直平分AB；（3）当0＜t＜6时，求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式．【参考答案】***一、选择题二、填空题13．①②③．14．(a-3b)2 15．±616．3 717．2 318．2 5三、解答题19．（1）见解析；（2）CE＝5.【解析】【分析】（1）连接DF，由CD为⊙O的直径，得到∠CFD＝90°，求得∠A＝∠ACD＝45°，于是得到结论；（2）根据已知条件得到CD＝2BD，求得BD＝2，CD＝4，得到BC＝，根据切割线定理即可得到结论．【详解】（1）连接DF，∵CD为⊙O的直径，∴∠CFD＝90°，∵点F是半圆CD的中点，∴CF＝DF，∴∠ACD＝45°，∵AD＝CD，∴∠A＝∠ACD＝45°，∴∠ADC＝90°，∴AB与⊙O相切；（2）∵CD⊥AB，tanB＝2，∴CD＝2BD，∵AD＝CD，∴AB＝3BD，∵AB＝6，∴BD＝2，CD＝4，∴BC＝∵BD 与⊙O 相切， ∴BD 2＝BE•BC，∴BE 2＝，∴CE ＝BC ﹣BE ＝5．【点睛】本题考查了切线的判定和性质，圆周角定理，等腰直角三角形的性质和判定，切割线定理，正确的作出辅助线是解题的关键．20．（1）复印张数为30页时，某眷印社与某图书馆的收费相同；（2）当复印张数大于0小于30页时，选某图书馆；当复印张数为30页时，两店一样；当复印张数大于30页时，选某眷印社．【解析】【分析】（1）复印张数超过20页时，某眷印社收费为：20+0.4（x-20），某图书馆收费为：0.8x'，两者相等列方程求解．（2）求某眷印社收费大于某图书馆的x 值，再比较说明．【详解】解：（1）设复印张数为x 页，（x ＞20），列方程得： 20+0.4（x ﹣20）＝0.8x 解得：x ＝30答：复印张数为30页时，某眷印社与某图书馆的收费相同．（2）20+0.4（x ﹣20）＞0.8x 解得：x ＜30答：当复印张数大于0小于30页时，选某图书馆；当复印张数为30页时，两店一样；当复印张数大于30页时，选某眷印社．【点睛】本题考查了一元一次方程和一元一次不等式的应用，是一次方程和不等式综合运用的常考题型，找出其中的数量关系列出方程与不等式是解答本题的关键． 21．(1)见解析；(2)画图见解析，在，面积为10. 【解析】【分析】（1）利用数形结合的思想构造等腰直角三角形即可．（2）利用数形结合的思想解决问题即可．【详解】(1)如图1，2中，点C 即为所求．(2)如图3中，点D 即为所求，S △ABD ＝12×BD×AH＝12⨯＝10．【点睛】本题考查作图-应用与设计，三角形的面积，解直角三角形等知识，解题的关键是熟练掌握基本知识. 22．见解析【解析】【分析】利用勾股定理作出符合条件的三角形三边，将原三角形扩大两倍即可【详解】解：如图所示；【点睛】此题考查勾股定理和作图-相似变换，解题关键在于掌握作图法则 23．（Ⅰ）100,12；（Ⅱ）平均数是1.32，众数是1.5，中位数是1.5 【解析】【分析】（Ⅰ）根据条形统计图和扇形统计图，用1h 对应的人数除以对应的百分比即可求解；用0.5h 对应的人数除以总人数即可求解（Ⅱ）利用平均数、众数、中位数的定义分别求解即可【详解】（Ⅰ）学生人数=3010030%=；m%=12/100=12%，即m=12；（Ⅱ）观察条形统计图， ∵0.512130 1.5402181.32100x ⨯+⨯+⨯+⨯==，∴这组数据的平均数是1.32.∵在这组样本数据中，1.5出现了40次，出现的次数最多，∴这组数据的众数是1.5.∵将这组样本数据按照有小到大的顺序排列，其中处于中间位置的两个数都是1.5，有1.5 1.51.52+=，∴这组样本数据的中位数是1.5.【点睛】此题主要考查利用统计图表解决简单的实际问题24．3【解析】【分析】把x与y的值代入方程组求出a与b的值，即可确定出所求．【详解】解：把121xy⎧=⎪⎨⎪=-⎩代入3523ax byax by-=⎧⎨+=⎩中得13523a ba b⎧+=⎪⎨⎪-=⎩，解得41, ab=⎧⎨=⎩3.==【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．25．（1）3；（2）3；（3）22(03)84(36)822tSt+<⎪=-+<<⎩….【解析】【分析】（1）根据，∠OMN＝30°和△ABC为等边三角形，求证△OAM为直角三角形，然后即可得出答案．（2）易知当点C与M重合时直线MN平分线段AB，此时OB＝3，由此即可解决问题；（3）分两种情形分别求解：当0＜t≤3时，作CD⊥FM于D．根据S＝S△MEB﹣2S△MDC，计算即可．②当3＜t ＜6时，S＝S△MEB．【详解】解：（1）在Rt△MON中，∵∠MON＝90°，ON＝M＝30°∴OM＝6，∵△ABC为等边三角形∴∠AOC＝60°，∴∠OAM＝90°∴OA⊥MN，即△OAM为直角三角形，∴OA＝12OM＝12×6＝3．故答案为3．（2）易知当点C与M重合时直线MN平分线段AB，此时OB＝3，所以t＝3．故答案为3．（3）易知：OM＝6，MN＝，S△OMN＝12×6＝∵∠M＝30°，∠MBA＝60°，∴∠BEM＝90°．①当0＜t≤3时，作CD⊥FM于D．∵∠ACB＝60°，∠M＝30°，∠FCB＝∠M+∠CFM，∴∠CFM＝∠M＝30°，∴CF＝CM，∵CD⊥FM，∴DF＝DM，∴S△CMF＝2S△CDM，∵△MEB∽△MON，∴2MEBMONS BMS MB⎛⎫= ⎪⎝⎭，∴S△MEB2+∵△MDC∽△MON，∴2MDCMONS MCS MN⎛⎫= ⎪⎝⎭，∴S△MDC＝2848t-+，∴S＝S△MEB﹣2S△MDC＝﹣284+．②当3＜t＜6时，S＝S△MEB2综上所述，S＝22(03)(36)tt+<<<…．【点睛】本题属于几何变换综合题，考查了平移变换，等边三角形的性质和判定，解直角三角形，相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．2019-2020学年数学中考模拟试卷一、选择题1．如图，△ABC 的顶点都是正方形网格中的格点，则cos ∠ABC 等于（）A.5B.5D.232．下列运算正确的是（） A.3a ＋2a ＝a 5B.a 2·a 3＝a 6C.（a ＋b ）（a －b ）＝a 2－b 2D.(a ＋b)2＝a 2＋b 23．已知关于x 的不等式组314(1)x x x m --⎧⎨⎩无解，则m 的取值范围是（）A ．m≤3B ．m ＞3C ．m ＜3D ．m≥34．下列运算中，结果正确的是（） A.235a a a +=B.236a a a =C.()236a a = D.623a a a ÷=5．已知在⊙O 中，弦AB 的长为8厘米，圆心O 到AB 的距离为3厘米，则⊙O 的半径是（） A.3厘米B.4厘米C.5厘米D.8厘米6．如图，将Rt △ABC 绕直角顶点C 顺时针旋转90°，得到△A′B′C，连接AA′，若∠1＝25°，则∠BAA′的度数是（）A.55°B.60°C.65°D.70°7．把不等式组24030x x -≥⎧⎨->⎩的解集表示在数轴上，正确的是( )A ．B ．C ．D ．8．如图是将一多边形剪去一个角，则新多边形的内角和（）A ．比原多边形少180°B ．与原多边形一样C ．比原多边形多360°D ．比原多边形多180°9．如果3y x =-+，且x y ≠，那么代数式22x y x y y x+--的值为（） A ．3B ．3-C ．13D ．13-10．Rt ABC 中，C 90∠=，若BC 2=，AC 3=，下列各式中正确的是 ( ) A ．2sinA 3=B ．2cosA 3=C ．2tanA 3=D ．2cotA 3=11．某公司员工的月工资统计表如下，这个公司员工工资的中位数为（）A ．7000B ．6000C ．5000D ．650012．下列选项中，是如图几何体的主视图的是( )A ．B ．C ．D ．二、填空题13．如图，在平面直角坐标系中，△P 1OA 1，△P 2A 1A 2，△P 3A 2A 3，…都是等腰直角三角形，其直角顶点P 1(3，3)，P 2，P 3，…均在直线y ＝﹣13x+4上，设△P 1OA 1，△P 2A 1A 2，△P 3A 2A 3，…的面积分别为S 1，S 2，S 3，…依据图形所反映的规律，S 2019＝_____．14．如图，在△ABC 中，AB ＝AC ，D 、E 、F 分别为AB 、BC 、AC 的中点，则下列结论：①△ADF ≌△FEC ；②四边形ADEF 为菱形；③:1:4ADF ABC S S ∆∆=。

中考复习《矩形、菱形、正方形》测试题(含答案)

中考复习《矩形、菱形、正方形》测试题（含答案）一、选择题(每题4分，共24分)1．[2015·泸州]菱形具有而平行四边形不具有的性质是(D) A．两组对边分别平行B．两组对角分别相等C．对角线互相平分D．对角线互相垂直2．[2015·衢州]如图28－1，已知某菱形花坛ABCD的周长是24 m，∠BAD＝120°，则花坛对角线AC的长是(B)A．6 3 m B．6 m图28－1 C．3 3 m D．3 m【解析】易知△ABC为等边三角形，所以AC＝AB＝6 m.3．[2015·益阳]如图28－2，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是(D) A．∠ABC＝90°B．AC＝BDC．OA＝OB D．OA＝AD图28－2 图28－34．[2014·福州]如图28－3，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为(C) A．45°B．55°C．60°D．75°【解析】∵四边形ABCD是正方形，∴AB＝AD，又∵△ADE 是等边三角形， ∴AE ＝AD ＝DE ，∠DAE ＝60°， ∴AB ＝AE ，∴∠ABE ＝∠AEB ，∠BAE ＝90°＋60°＝150°， ∴∠ABE ＝(180°－150°)÷2＝15°，又∵∠BAC ＝45°， ∴∠BFC ＝45°＋15°＝60°.5．[2015·临沂]如图28－4，四边形ABCD 为平行四边形，延长AD 到E ，使DE ＝AD ，连结EB ，EC ，DB .添加一个条件，不能使四边形DBCE 成为矩形的是 (B) A ．AB ＝BEB ．BE ⊥DCC ．∠ADB ＝90°D ．CE ⊥DE【解析】因为四边形ABCD 为平行四边形，所以AD 綊BC ，因为DE ＝AD ，所以DE 綊BC所以四边形EDBC 为平行四边形，A ．假若AB ＝BE ，因为AB ＝BE ，AD ＝DE ，BD ＝BD ，所以△ADB ≌△EDB ，所以∠BDE ＝90°，所以四边形EDBC 为矩形； B ．假若BE ⊥DC ，可得四边形EDBC 为菱形；C ．假若∠ADB ＝90°，所以∠EDB ＝90°，所以四边形EDBC 为矩形；D ．假若CE ⊥DE ，所以∠DEC ＝90°，所以四边形EDBC 为矩形，故选B. 6．[2015·日照]小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件①AB ＝BC ，②∠ABC ＝90°，③AC ＝BD ，④AC ⊥BD 中选两个作为补充条件，使▱ABCD 成为正方形(如图28－5)现有下列四种选法，你图28－4图28－5认为其中错误的是(B)A．①②B．②③C．①③D．②④【解析】此题考查正方形的判定，即在▱ABCD的基础上，需要再同时具备矩形和菱形的特征．①是菱形的特征；②是矩形的特征；③是矩形的特征，④是菱形的特征．而B中都是矩形的特征，故选B.二、填空题(每题4分，共20分)7．[2015·铜仁]已知一个菱形的两条对角线长分别为6 cm和8 cm，则这个菱形的面积为__24__cm2.8．[2014·衡阳]如图28－6，在矩形ABCD中，∠BOC＝120°，AB＝5，则BD的长为__10__．9．[2015·上海]已知E是正方形ABCD的对角线AC上一点，图28－6 AE＝AD，过点E作AC的垂线，交边CD于点F，那么∠F AD＝__22.5__度．10．[2014·淄博]已知▱ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD成为一个菱形．你添加的条件是__AB＝BC或AC⊥BD等__．11．[2014·资阳]如图28－7，在边长为4的正方形ABCD中，E是AB边上的一点，且AE＝3，点Q为对角线AC上的动点，则△BEQ周长的最小值为__6__．图28－7【解析】如答图，连结BD，DE，∵四边形ABCD是正方形，∴点B与点D关于直线AC对称，∴DE的长即为BQ＋QE的最小值，∵DE＝BQ＋QE＝5，∴△BEQ周长的最小值＝DE＋BE＝5＋1＝6.三、解答题(共20分)12．(10分)[2015·安顺]如图28－8，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于图28－8F.(1)求证：AE＝DF；(2)若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．证明：(1)∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴AE＝DF；(2)若AD平分∠BAC，四边形AEDF是菱形，理由如下：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∵AD平分∠BAC，∴∠EAD＝∠F AD，∵AE∥DF，∴∠EAD＝ADF，∠DAF＝∠FDA，∴AF＝DF，∴平行四边形AEDF为菱形．13．(10分)[2015·青岛]已知：如图28－9，在△ABC中，AB ＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.(1)求证：△ABD≌△CAE；图28－9(2)连结DE ，线段DE 与AB 之间有怎样的位置和数量关系？请证明你的结论．解：(1)证明：∵AB ＝AC ，AD 是BC 边上的中线， ∴AD ⊥BC ，BD ＝CD . ∵AE ∥BC ，CE ⊥AE ， ∴四边形ADCE 是矩形， ∴AD ＝CE .在Rt △ABD 与Rt △CAE 中， ⎩⎪⎨⎪⎧AD ＝CE ，AB ＝CA ，∴△ABD ≌△CAE (HL )；(2)DE ∥AB ，DE ＝AB .证明如下：如答图所示，∵四边形ADCE 是矩形， ∴AE ＝CD ＝BD ，AE ∥BD ， ∴四边形ABDE 是平行四边形， ∴DE ∥AB ，DE ＝AB .14．(10分)[2014·扬州]如图28－10，已知Rt △ABC ，∠ABC ＝90°，先把△ABC 绕点B 顺时针旋转90°后至△DBE ，再把△ABC 沿射线AB 平移至△FEG ，DE ，FG 相交于点H .(1)判断线段DE ，FG 的位置关系，并说明理由； (2)连结CG ，求证：四边形CBEG 是正方形．解：(1)DE ⊥FG ，理由如下：由题意得∠A ＝∠EDB ＝∠GFE ，∠ABC ＝∠DBE ＝90°，第13题答图图28－10∴∠BDE＋∠BED＝90°.∴∠GFE＋∠BED＝90°，∴∠FHE＝90°，即DE⊥FG；(2)证明：∵△ABC沿射线AB平移至△FEG，∴CB∥GE，CB＝GE.∴四边形CBEG是平行四边形．∵∠ABC＝∠GEF＝90°，∴四边形CBEG是矩形．∵BC＝BE，∴四边形CBEG是正方形．15．(10分)[2015·南京]如图28－11，AB∥CD，点E，F分别在AB，CD上，连结EF，∠AEF，∠CFE的平分线交于点G，∠BEF，∠DFE的平分线交于点H.(1)求证：四边形EGFH是矩形；(2)小明在完成(1)的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD交于点P，Q，得到四边形MNQP.此时，他猜想四边形MNQP是菱形，请在下列框图中补全他的证明思路．小明的证明思路由AB∥CD，MN∥EF，易证四边形MNQP是平行四边形，要证▱MNQP是菱形，只要证MN＝NQ.由已知条件__FG平分∠CFE__，MN∥EF，可证NG＝NF，故只要证GM＝FQ，即证△MEG≌△QFH，易证__GE＝FH__，__∠GME ＝∠FQH__.故只要证∠MGE＝∠QFH.易证∠MGE＝∠GEF，∠QFH＝∠EFH，__∠GEF＝∠EFH__，即可得证．图28－11解：(1)证明：∵EH平分∠BEF.∴∠FEH＝12∠BEF，∵FH平分∠DFE，∴∠EFH＝12∠DFE，∵AB∥CD，∴∠BEF＋∠DFE＝180°，∴∠FEH＋∠EFH＝12(∠BEF＋∠DFE)＝12×180°＝90°，又∵∠FEH＋∠EFH＋∠EHF＝180°，∴∠EHF＝180°－(∠FEH＋∠EFH)＝180°－90°＝90°，同理可证，∠EGF＝90°，∵EG平分∠AEF，∴∠FEG＝12∠AEF，∵EH平分∠BEF，∴∠FEH＝12∠BEF，∵点A，E，B在同一条直线上．∴∠AEB＝180°，即∠AEF＋∠BEF＝180°.∴∠FEG＋∠FEH＝12(∠AEF＋∠BEF)＝12×180°＝90°，即∠GEH＝90°.∴四边形EGFH是矩形；(2)本题答案不唯一，下列解法供参考．例如，FG平分∠CFE；GE＝FH；∠GME ＝∠FQH；∠GEF＝∠EFH.16．(6分)[2015·资阳]若顺次连结四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD一定是(D) A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形17．(10分)如图28－12，在菱形ABCD中，边长为10，∠A＝60°.顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；…；按此规律继续下去，则四边形A2B2C2D2的周长是__20__；四边形A2 016B2 016C2 016D2 016的周长是__521 005__．图28－12。

人教版九年级数学中考矩形、菱形、正方形专项练习及参考答案

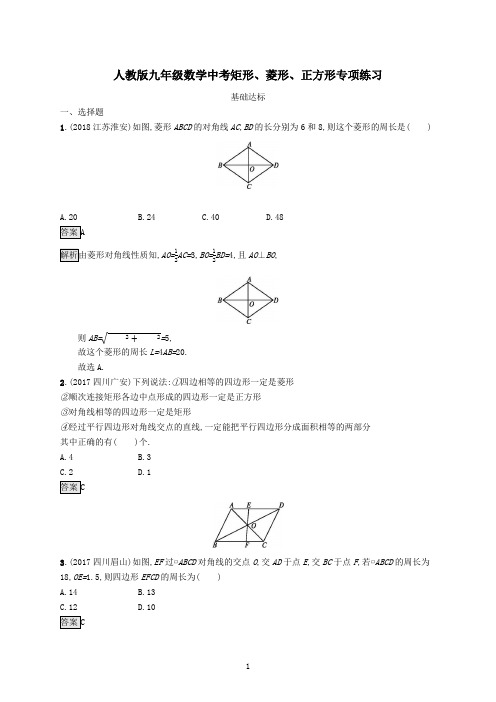
人教版九年级数学中考矩形、菱形、正方形专项练习基础达标一、选择题1.(2018江苏淮安)如图,菱形ABCD 的对角线AC ,BD 的长分别为6和8,则这个菱形的周长是( )A.20B.24C.40D.48,AO=12AC=3,BO=12BD=4,且AO ⊥BO ,则AB=√AA 2+AA 2=5, 故这个菱形的周长L=4AB=20. 故选A.2.(2017四川广安)下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形 ③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有( )个. A.4 B.3C.2D.13.(2017四川眉山)如图,EF 过▱ABCD 对角线的交点O ,交AD 于点E ,交BC 于点F ,若▱ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( ) A.14 B.13C.12D.104.(2018贵州遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10B.12C.16D.18PM⊥AD于点M,交BC于点N.则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,×2×8=8,∴S△DFP=S△PBE=12∴S阴影=8+8=16,故选C.5.(2017山东枣庄)如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=A(x<0)的图象经过顶点B,则k的值为()AA.-12B.-27C.-32D.-366.(2018江苏无锡)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G,H都在边AD上,若AB=3,BC=4,则tan ∠AFE的值()A.等于37B.等于√33C.等于34D.随点E位置的变化而变化EF∥AD,∴∠AFE=∠FAG,△AEH∽△ACD,∴AAAA =AAAA=34.设EH=3x,AH=4x,∴HG=GF=3x,∴tan∠AFE=tan∠FAG=AA AA =3A3A+4A=37.故选A.二、填空题7.(2018湖南株洲)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为..5四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴OD=12BD=5,∵点P,Q分别是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=12DO=2.5.8.(2018广东广州)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是.-5,4)菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,∴AB=5,∴AD=5,∴由勾股定理知:OD=√AA2-AA2=√52-32=4,∴点C的坐标是(-5,4).9.(2018湖北武汉)以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是.150°1,图1∵四边形ABCD为正方形,△ADE为等边三角形,∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,∴∠AEB=∠CED=15°,则∠BEC=∠AED-∠AEB-∠CED=30°.如图2,图2∵△ADE是等边三角形,∴AD=DE,∵四边形ABCD是正方形,∴AD=DC,∴DE=DC,∴∠CED=∠ECD,∴∠CDE=∠ADC-∠ADE=90°-60°=30°,∴∠CED=∠ECD=1(180°-30°)=75°,同理∠BEA=∠ABE=75°,2∴∠BEC=360°-75°×2-60°=150°.三、解答题10.如图,在菱形ABCD 中,对角线AC 与BD 交于点O.过点C 作BD 的平行线,过点D 作AC 的平行线,两直线相交于点E.(1)求证:四边形OCED 是矩形;(2)若CE=1,DE=2,则ABCD 的面积是多少?四边形ABCD 是菱形,∴AC ⊥BD , ∴∠COD=90°. ∵CE ∥OD ,DE ∥OC ,∴四边形OCED 是平行四边形,又∠COD=90°,∴平行四边形OCED 是矩形.(1)知,平行四边形OCED 是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD 是菱形, ∴AC=2OC=4,BD=2OD=2, ∴菱形ABCD 的面积为12AC ·BD=12×4×2=4. 能力提升一、选择题1.下列说法中,正确的个数为( )①对顶角相等;②两直线平行,同旁内角相等; ③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.A.1B.2C.3D.4对顶角相等,故①正确;②两直线平行,同旁内角互补,故②错误;③对角线互相垂直且平分的四边形为菱形,故③错误; ④对角线互相垂直平分且相等的四边形为正方形,故④正确,故选B .2.(2018山东枣庄)如图,在矩形ABCD 中,点E 是边BC 的中点,AE ⊥BD ,垂足为F ,则tan ∠BDE 的值是( )A.√24B.14C.13D.√23四边形ABCD 是矩形,∴AD=BC ,AD ∥BC , ∵点E 是边BC 的中点, ∴BE=12BC=12AD , ∴△BEF ∽△DAF , ∴AA AA =AA AA =12, ∴EF=12AF , ∴EF=13AE ,∵点E 是边BC 的中点, ∴由矩形的对称性得:AE=DE , ∴EF=13DE ,设EF=x ,则DE=3x , ∴DF=√AA 2-AA 2=2√2x , ∴tan ∠BDE=AAAA =2√2A =√24.故选A.3.如图,在Rt △ABC 中,∠C=90°,AC=BC=6cm,点P 从点A 出发,沿AB 方向以每秒√2 cm 的速度向终点B 运动;同时,动点Q 从点B 出发沿BC 方向以每秒1 cm 的速度向终点C 运动,将△PQC 沿BC 翻折,点P 的对应点为点P'.设Q 点运动的时间为t s,若四边形QPCP'为菱形,则t 的值为( )A.√2B.2C.2√2D.3PP',交BC于N点,过P作PM⊥AC,垂足为M.若运动t s时四边形QPCP'为菱形,则PQ=PC,PN⊥BC,四边形PMCN为矩形,BQ=t,AP=√2t,PM=NC=t,∴QC=2t,∴BC=BQ+QC=t+2t=3t=6cm,∴t=2,故选B.4.(2018河南)如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1 cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()图1图2A.√5B.2D.2√5C.52D作DE⊥BC于点E由题图2可知,点F由点A到点D用时为a s,△FBC的面积为a cm2.∴AD=a.DE·AD=a.∴12∴DE=2.当点F从D到B时,用√5s,∴BD=√5.Rt△DBE中,BE=√AA2-AA2=√(√5)2-22=1,∵ABCD是菱形,∴EC=a-1,DC=a.Rt△DEC中,a2=22+(a-1)2,.解得a=52故选C.5.(2017广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③B.②③C.①④D.②④二、填空题6.(2018山东潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为.)-1,√33,连接AM ,∵将边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB'C'D', ∴AD=AB'=1,∠BAB'=30°, ∴∠B'AD=60°,在Rt △ADM 和Rt △AB'M 中,∵{AA =AA ',AA =AA ,∴Rt △ADM ≌Rt △AB'M (HL), ∴∠DAM=∠B'AM=12∠B'AD=30°, ∴DM=AD tan ∠DAM=1×√33=√33, ∴点M 的坐标为(-1,√33).三、解答题 7.如图所示,在△ABC 中,点O 是AC 边上的一个动点,过O 作直线MN ∥BC ,设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F.(1)求证:OE=OF ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.MN ∥BC ,∴∠OEC=∠BCE.又∠OCE=∠BCE ,∴∠OEC=∠OCE ,∴OE=OC.同理可证OF=OC ,∴OE=OF.O 运动到AC 中点时,四边形AECF 是矩形.证明:∵CE ,CF 分别是∠ACB 的内,外角平分线.∴∠OCE+∠OCF=12(∠ACB+∠ACD )=12×180°=90°,即∠ECF=90°,又∵OE=OF ,∴当O 点运动到AC 中点时,OA=OC ,四边形AECF 是矩形.8.(2018贵州遵义)如图,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE<BE),且∠EOF=90°,OE,DA的延长线交于点M,OF,AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON.,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM=√22+42=2√5,由(1)知OM=ON,∴MN=√2OM=2√10.。

矩形菱形正方形练习题及答案

矩形菱形正方形练习题及答案1.矩形ABCD的对角线长为10cm。

则矩形的周长最大为20cm，此时对角线分成的四个小三角形的周长的和为20cm。

2.在矩形ABCD中，AE⊥BD于点E，且∠BAE=30°，BE=1cm。

若直角三角形斜边上的高为5cm，中线为6cm，则DE的长为3cm。

矩形的面积为3cm×10cm=30cm²。

4.在△ABC中，∠ACB=90度，点D、E分别为AC、AB 的中点，点F在BC延长线上，且∠XXX∠A。

则四边形DECF是平行四边形。

5.在△ABC中，∠BAC≠90°，∠ABC=2∠C，AD⊥AC，交BC或CB的延长线于点D。

则DC=2AB。

6.在△ABC中，∠C=90°，AC=BC，AD=BD，PE⊥AC 于点E，PF⊥BC于点F。

则DE=DF。

7.菱形ABCD的两条对角线分别长6和8.点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点。

则PM+PN的最小值为5.8.若菱形的周长为24cm，一个内角为60°。

则菱形的面积为36√3cm²。

9.菱形的周长为40cm，两条对角线长的比是3:4.则两对角线长分别为24cm和16cm。

10.在菱形ABCD中，E是AB的中点，且DE⊥AB，AE=2.则（1）∠ABC的度数为60°；（2）对角线AC、BD的长分别为2√7cm和4√3cm；（3）菱形ABCD的面积为4√3cm²。

11.在△ABC中，AD平分∠BAC，DE∥AC交AB于点E，DF∥AB交AC于点F。

则四边形AEDF是菱形。

12.在边长为a的菱形ABCD中，∠DAB=60度。

点E是异于A、D两点的动点，F是CD上的动点，满足AE+CF=a。

则无论E、F怎样移动，△XXX总是正三角形。

13.在Rt△ABC中，∠ACB=90°，∠BAC=60°，DE垂直平分BC，垂足为D，交AB于E，点F在DE的延长线上，且AF=CE。

(完整版)矩形、菱形与正方形-专题训练(含答案)

矩形、菱形与正方形专题训练（含答案）班级_________ 姓名 __________ 成绩 ___________、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（）A . 12B . 24C . 12 .'3D . 16 .'3第1题图第2题图第3题图第4题图2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（） A . 14 B . 15C . 16D . 173. 如图，将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，则CD 的长为（） A. 1 B . 2C . 3D . 44. 如图，在厶ABC 中，AC =BC , 占八D ,E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰疋是 ( )A.矩形 B . 菱形 C . 正方形 D .梯形5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是（）6.如图，?ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点丘，则厶DCE 的周长为（）A •平行四边形B •矩形C •菱形D .正方形A . 4 cmB . 6 cmC .第6题图第9题图7•菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为BC10 cmA F DE&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是（）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9. 如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S i, S2,则S i + S2的值为（）A . 16B . 17 C. 18 D . 1910. 如图，F为正方形ABCD的边AD上一点，CE丄CF交AB的延长线于点E,若正方形ABCD 的面积为64,A CEF的面积为50,则厶CBE的面积为（）A . 20B . 24C . 25D . 26二、填空题（每小题3分，共24分）11. 如图所示，在菱形ABCD中，/ ADC = 72 ° AD的垂直平分线交对角线BD于点P,垂足为点E,连结CP,则/ CPB = _______ 度.1)第11题图第12题图第14题图第15题图12 .如图，四边形ABCD的两条对角线AC, BD互相垂直，A1, B1, C1, D1分别是四边形ABCD 各边中点，如果AC= 8, BD = 10,则四边形A1B1C1D1的面积为—.13 .矩形的对角线相交成的角中，有一个角是60°这个角所对的边长为20 cm,则其对角线长为___________ -_,矩形的面积为__________________ .14 .如图，四边形ABCD是菱形，对角线AC和BD相交于点O, AC = 4 cm, BD = 8 cm,则这个菱形的面积是_____ c m2.AC , BD 交于点 O , E 点在BC 上，EG 丄OB , EF 丄OC ,垂足，使?ABCD 是矩形.17 .如图，正方形 ABCD 中，对角线第18题图15 .如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的中点M , N ,连结AM , CN , MN ,若AB = 2 2, BC = 2 '3,则图中阴影部分的面积为，第16题O ,请你添加一个条件16 .如图,分别为点G , F, AC= 10,则EG + EF = ______ .18. 如图，在平面直角坐标系中，矩形OABC的顶点A, C的坐标分别为(10, 0), (0, 4),点D是OA的中点，点P在BC上运动，当△ ODP是腰长为5的等腰三角形时，点P的坐标为三、解答题(共66分)19. (6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF丄EC且EF = EC, DE =4 cm，矩形ABCD的周长为32 cm,求AE的长.20. (8分)如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O,与BC相交于点N,连结BM , DN.(1)求证：四边形BMDN是菱形；⑵若AB= 4, AD = 8,求MD的长.21 . （8 分）如图所示，矩形ABCD 中，AE丄BD 于点E,/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.22. （10分）如图，已知菱形 ABCD 中，AB = AC , E , F 分别是BC , AD 的中点，连结 AE , CF. （1）证明：四边形 AECF 是矩形； ⑵若AB = 8,求菱形 ABCD 的面积.参考答案一、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（D ） A . 12B . 24C . 12D . 164 / 9DE 丄AB , DF 丄BC ,垂足分另U 是点 E , F ，并且DE = DF ，求证： (1)△ ADECDF ; (2)四边形 ABCD 是菱形.24. (10分)在四边形 ABCD 中，AB = CD , M , N , P , Q 分别是AD , BC , BD , AC 的中点，求证:MN 与PQ 互相垂直平分.23. （12分）如图，已知四边形 ABCD 是平行四边形,6.如图，？ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点丘，则厶DCE 的周长为（C ）7.菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为（C ） A . 3 : 1B . 4 : 1C . 5 : 1D . 6 : 1&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是（D ）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为 S 1, S 2,则S 1 +S 2的值为（B ） A . 16B . 17C . 18D . 19的面积为64,^ CEF 的面积为50,则厶CBE 的面积为（B）2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（C ） A . 14 B . 15C . 16D . 173. 如图，将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，贝U CD 的长为（B ） A . 1 B . 2C . 3D . 44. 如图，在厶ABC 中，AC =BC , 点D , E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰(A )定是A.矩形 B . 菱形C .正方形D .梯形A •平行四边形B •矩形C •菱形D .正方形 A . 4 cmB . 6 cmC .第6题图10 .如图, F 为正方形 ABCD 的边AD 上一点, CE 丄CF 交AB 的延长线于点 E ,若正方形 ABCD第4题图第1题图第2题图第3题图 5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是（B BC第9题图10 cm二、填空题(每小题3分，共24分)11.如图所示，在菱形 ABCD 中，/ ADC = 72 ° AD 的垂直平分线交对角线 BD 于点P ,垂足为点 E ,连结 CP ,则/ CPB =72 度.第11题图第12题图第14题图第15题图12. 如图，四边形 ABCD 的两条对角线 AC , BD 互相垂直，A 1, B 1, C 1, D 1分别是四边形 ABCD 各边中点，如果 AC = 8, BD = 10,则四边形 A 1B 1C 1D 1的面积为 _20_. 13. 矩形的对角线相交成的角中，有一个角是 _40 cm ，矩形的面积为_400 cm 2 .14. 如图，四边形 ABCD 是菱形，对角线 AC 和BD 相交于点O , AC= 4 cm , BD = 8 cm ,则这个菱形的面积是_16 cm 2.15. 如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的是矩形. 17.如图，正方形 ABCD 中，对角线 AC , BD 交于点O , E 点在BC 上, EG 丄OB , EF 丄OC ,垂足分别为点 G , F , AC = 10,则 EG + EF = 5 . 18.如图，在平面直角坐标系中，矩形 OABC 的顶点A , C 的坐标分别为(10, 0), (0, 4),点D 是 OA 的中点，点P 在BC 上运动，当△ ODP 是腰长为5的等腰三角形时，点 P 的坐标为 _(8, 4), (3, 4)或(2, 4)_. 三、解答题(共66分)19. (6分)如图，已知矩形 ABCD 中，E 是AD 上一点，F 是AB 上一点，EF 丄EC 且EF = EC , DE =4 cm ，矩形ABCD 的周长为32 cm ，求AE 的长.B . 24C . 25D . 2660°这个角所对的边长为 20 cm ,则其对角线长为中点M , N ,连结AM , CN , MN ，若，第16题图16.如图, ?ABCD 的对角线相交于点 O ,请你添加一个条件AO = BO (答案不唯一)，使?ABCD第17题AB = 2, BC = 2，则图中阴影部分的面积为2解：I/ AFE + / AEF = / AEF + / CED = 90° /•/ AFE = / DEC . 又•••/ A = / D = 90° EF = EC ,•••△ AEF◎△ DCE AE = CD.1设 AE = x ，贝U CD = x , • AD + CD = 2x32，即 x + 4 + x = 16, •- x = 6.即卩 AE = 6 cm⑴求证：四边形 BMDN 是菱形； ⑵若AB = 4, AD = 8,求MD 的长.解：(1) •/ MN 是 BD 的垂直平分线，• BO = DO , / BON =/ DOM = 90° •••四边形 ABCD 是矩形，• AD // BC ，• / BNO = / DMO , • △ BON ◎△ DOM (AAS), • OM = ON.v OB = OD , •四边形 BMDN 是平行四边形.•/ MN 丄BD , • ?BMDN 是菱形(2)设 MD = x ，贝U MB = x , MA = 8-x ，在 Rt △ ABM 中，T BM 2= AM 2+ AB 2, • x 2= (8- x)2 + 42,解得 x = 5.「. MD 的长为 521 . （8 分）如图所示，矩形 ABCD 中，AE 丄 BD 于点 E ，/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.解：提示：由 / DAE :/ BAE = 3 ： 1 ,求出 / BAE = 22.5 ° 而/ABD = 90°— / BAE = 90° — 22.5° = 67.5°•••/ BAO = / ABD = 67.5 ° •••/ EAO = Z BAO — / BAE = 67.5。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

矩形的习题精选
一、性质
1、下列性中，矩形具有而质平行四边形不一定具有的是（）
A、对边相等
B、对角相等
C、对角线相等
D、对边平行
2.在矩形ABCD中，∠AOD=130°，则∠ACB=_ _
3.已知矩形的一条对角线长是8cm，两条对角线的一个交角为60°，则矩形的周长为______
4.矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm，对角线是13cm，那么矩形的周长是____________
5.如图所示，矩形ABCD中，AE⊥BD于E，∠BAE=30°，
BE=1cm，那么DE的长为_____
6、直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积为___
7、已知，在Rt△ABC中，BD为斜边AC上的中线，若∠A=35°，那么∠DBC= 。

8、如图，矩形ABCD中，AC与BD交于O点，BE⊥AC于E，CF⊥BD 于F.
求证：BE=CF. A
B E F
O
9.如图，△ABC中，∠ACB=90度，点D、E分别为AC、AB的中点，点F在BC延长线上，且∠CDF=∠A，求证：四边形DECF
是平行四边形；
10.已知:如图，在△ABC中，∠BAC≠90°∠ABC=2∠C，AD⊥AC，交BC或CB的延长线D。

试说明:DC=2AB.
11、在△ABC中，∠C=90O，AC=BC，AD=BD，PE⊥AC于点E，PF ⊥BC于点F。

求证：DE=DF
二、判定
1、下列检查一个门框是否为矩形的方法中正确的是（C ）
A．测量两条对角线，是否相等B．测量两条对角线，是否互相平分
C．用曲尺测量门框的三个角，是否都是直角D．用曲尺测量对角线，是否互相垂直
2、平行四边形ABCD，E是CD的中点，△ABE是等边三角形，求证：四边形ABCD是矩形
3、在平行四边形ABCD中，对角线AC、BD相交于O，EF过点O，且AF⊥BC，求证：四边形AFCE是矩形
4、平行四边形ABCD中，对角线AC、BD相交于点Ｏ，点Ｐ是四边形外一点，且PA⊥PC，PB⊥PD，垂足为Ｐ。

求证：四边形ABCD为矩形
5、已知：如图，平行四边形ABCD的四个内角的平分线分别相交于E、F、
G、H，求证：四边形EFGH为矩形．
6、如图，△ABC中，点O是AC上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，(1)
明你的结论。

菱形的习题精选
一、性质
1．小明和小亮在做一道习题，若四边形ABCD是平行四边形，请补充条件<A=<B ，使得四边形ABCD是菱形。

小明补充的条件是AB=BC；小亮补充的条件是AC=BD，你认为下列说法正确的是（A ）A、小明、小亮都正确B、小明正确，小亮错误C、小明错误，小亮正确D、小明、小亮都错误
2．下面性质中菱形有而矩形没有的是（A ）
（A）邻角互补（B）内角和为360°（C）对角线相等（D）对角线互相垂直
3．如图，已知四边形ABCD是平行四边形，下列结论不正确的是（D ）A. 当AB=BC时，它是菱形； B. 当AC⊥BD时，它是菱形；C. 当∠ABC=90°时，它是矩形； D. 当AC=BD时，它是菱形。

4．已知菱形两条对角线的长分别为5cm和8cm，则这
个菱形的面积是__40____cm．
5．若菱形的周长为24 cm，一个内角为60°，则菱形的面积为__32____ cm2。

6 ．已知：菱形的周长为40cm，两条对角线长的比是3：4。

求两对角线
7、已知菱形的面积等于80cm2，高等于8cm，则菱形的周长为.
8、如图，P为菱形ABCD的对角线上一点，PE⊥AB
于点E，PF⊥AD于点F，PF=3cm，则P点到AB的距
离是_____ cm
13、如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是_______．
9．已知菱形ABCD中，对角线AC和BD相交于点O，∠BAD=120°，求∠ABD的度数。

A D
O
B C
10、已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AE=2。

求（1）∠ABC的度数；（2）对角线AC、BD的长；
（3）菱形ABCD的面积。

11、已知：如图，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC 于F．
求证：四边形AEDF是菱形；
12、如图，边长为a的菱形ABCD中，∠DAB=60度，E是异于A、D两点的动点，F是CD上的动点，满足AE+CF=a。

证明：不论E、F怎样移动，△BEF总是正三角形。

二、判定
1、□ABCD的对角线AC与BD相交于点O，
（1）若AB=AD，则□ABCD是形；（2）若AC=BD，则□ABCD 是形；
（3）若∠ABC是直角，则□ABCD是形；（4）若∠BAO=∠DAO，则□ABCD是形。

2、下列条件中，不能判定四边形ＡＢＣＤ为菱形的是（）．
Ａ、AC⊥BD ，AC与BD互相平分Ｂ、AB=BC=CD=DA
Ｃ、AB=BC，AD=CD，且AC⊥BD Ｄ、AB=CD，AD=BC，AC⊥BD
3、如图，Rt△ABC中，∠ACB=900，∠BAC=600，DE垂直平分BC，垂足为D，交AB于E，又点F在DE的延长线上，且AF=CE，求证：四边形ACEF是菱形。

4、如图，在已知平行四边形ABCD中，AE平分∠BAD，与BC相交于点E，EF//AB，与AD相交于点F.求证:四边形ABEF是菱形.
5、如图，在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F，四边形AEFG是菱形吗?
6、如图，已知在□ABCD中，AD=2AB，E、F在
直线AB上，且AE=AB=BF，说明CE⊥DF.
正方形练习题
1._____________的矩形叫做正方形。

2.正方形具有_________、
___________、____________的一切性质。

3．如图，四边形ABCD是正方形，两条对角线相交于点O，OA=2，
则∠AOB=_____,∠OAB=_____,BD =______,AB=______.
A B
C D
O
4.第三题图中等腰三角形的个数是（）A.4个 B.5个 C.6个 D.8个
5.判断。

（1）正方形一定是矩形。

（）（2）正方形一定是菱形。

（）
（3）菱形一定是正方形。

（）（4）矩形一定是正方形。

（）（5）正方形、矩形、菱形都是平行四边形。

（）
自主学习
1.在下列性质中，平行四边形具有的是__________，矩形具有的是_________，菱形具有的是__________，正方形具有的是____________。

1.四边都相等；
2.对角线互相平分；
3.对角线相等；
4.对角线互相垂直；
5.四个角都是直角；
6.每条对角线平分一组对角；
7.对边相等且平行；
8.有两条对称轴。

2.正方形两条对角线的和为8cm ，它的面积为____________.
3.在正方形ABCD 中，E 在BC 上，BE=2，CE=1，P 在BD 上，则PE 和PC 的长度之和最小可达到_____________
4.如图，点E 、F 在正方形ABCD 的边BC 、CD 上，BE=CF.
（1）AE 与BF 相等吗？为什么？（2）AE 与BF 是否垂直？说明你的理由。

A
B
C
D
E
F G
5.如图，正方形ABCD 中对角线AC 、BD 相交于O ，E 为AC 上一点，AG ⊥EB 交EB 于G ，AG 交BD 于F 。

（1）说明OE=OF 的道理；
（2）在（1）中，若E 为AC 延长线上，AG ⊥EB 交EB 的延长
线于G ，AG 、BD 的延长线交于F ，其他条件不变，如图2，则结论：“OE=OF ”还成立吗？请说明理由。

A B
C D
O
E F G
A
B
C
D
O E F
G
6.如图，在正方形ABCD 中，取AD 、CD 边的中点E 、F ，连接CE 、BF 交于点G ，连接AG 。

试判断AG 与AB 是否相等，并说明道理。

A
B C
D E G
F。

(完整word版)矩形菱形正方形练习题及答案

中考数学总复习《矩形、菱形、正方形》专项测试卷含答案

初中数学 矩形、菱形与正方形测试题含答案

(完整版)矩形练习题及答案

(完整版)矩形、菱形与正方形-专题训练(含答案)

中考数学专题训练：矩形、菱形、正方形(附参考答案)

中考数学精选汇编矩形菱形与正方形---13道题目(含答案)

矩形菱形正方形练习题

(完整版)矩形菱形与正方形测试题及答案

第22讲矩形、菱形、正方形(含答案)

2024学年八年级数学经典好题专项(矩形、菱形、正方形)练习(附答案)

第19章矩形、菱形和正方形单元测试2021-2022学年华东师大版数学八年级下册(word 含答案)

八下 平行四边形9.4 矩形、菱形、正方形练习含答案 含答案

(完整版)矩形菱形正方形习题含答案

北京市通州区2019届中考《矩形、菱形和正方形》专题练习含答案

中考复习《矩形、菱形、正方形》测试题(含答案)

人教版九年级数学中考矩形、菱形、正方形专项练习及参考答案

矩形菱形正方形练习题及答案

(完整版)矩形、菱形与正方形-专题训练(含答案)

初中数学矩形、菱形与正方形测试题含答案

八下平行四边形9.4 矩形、菱形、正方形练习含答案含答案