2017-2018年安徽省淮北市实验高级中学高二(上)期中数学试卷及参考答案(理科)
2017-2018年安徽省淮北实验高级中学高二上学期期中数学试卷及参考答案(文科)

2017-2018学年安徽省淮北实验高级中学高二(上)期中数学试卷(文科)一、选择题:本大题共12题,每小题5分,共60分.请把答案填写在答题纸相应位置上.1.(5分)在△ABC中,“A=60°”是“”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.(5分)已知变量x,y满足约束条件则z=2x+y的最大值为()A.1 B.2 C.3 D.43.(5分)在△ABC中,已知∠BAC=60°,∠ABC=45°,BC=,则AC=()A.B.2 C.2 D.4.(5分)等比数列x,3x+3,6x+6,…的第四项等于()A.﹣24 B.0 C.12 D.245.(5分)已知△ABC中,三内角A、B、C的度数成等差数列,边a、b、c依次成等比数列.则△ABC是()A.直角三角形B.等边三角形C.锐角三角形D.钝角三角形6.(5分)等差数列{a n}满足a42+a72+2a4a7=9,则其前10项之和为()A.﹣9 B.﹣15 C.15 D.±157.(5分)已知+=1,(x>0,y>0),则x+y的最小值为()A.12 B.14 C.16 D.188.(5分)等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为()A.﹣24 B.﹣3 C.3 D.89.(5分)在△ABC中,已知sin2B﹣sin2C﹣sin2A=sinAsinC,则角B的大小为()A.150°B.30°C.120° D.60°10.(5分)已知点A(2,1)和点B(﹣2,3),若直线3x﹣2y+a=0与线段AB 有交点,则实数a的取值范围是()A.(﹣∞,﹣4)∪(12,+∞)B.(﹣∞,﹣4]∪[12,+∞)C.(﹣4,12)D.[﹣4,12]11.(5分)已知命题p:关于x的方程x2﹣ax+4=0有实根,命题q:关于x函数y=2x2+ax+4在[3,+∞)上为增函数,若“p或q”为真命题,“p且q”为假命题,则实数a取值范围为()A.(﹣12,﹣4]∪[4,+∞)B.[﹣12,﹣4]∪[4,+∞)C.(﹣∞,﹣12)∪(﹣4,4)D.[﹣12,+∞)12.(5分)已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是()A.bc(b+c)>8 B.ab(a+b)>16C.6≤abc≤12 D.12≤abc≤24二、填空题:本大题共4题,每小题5分,共20分.请把答案填写在答题纸相应位置上.13.(5分)在△ABC中,三内角A,B,C依次成等差数列,且,则△ABC 外接圆面积为.14.(5分)由命题“存在x∈R,x2+2x+2m≤0”是假命题,求得实数m的取值范围是(a,+∞),则实数a的值是.15.(5分)已知关于x的不等式x2﹣4x+t<0的解集为(1,m),则实数m=.16.(5分)在数列{a n}中,a1=1,a2=3,且a n+2=|a n+1﹣a n|(n∈N*),则a2017=.三、解答题:本大题共6小题,共计70分,请在答题纸指定的区域内作答,解答题应写出文字说明、证明过程或演算步骤.17.(10分)已知不等式<1的解集记为p,关于x的不等式x2+(a﹣1)x ﹣a>0的解集记为q.若¬q是¬p的充分不必要条件,求实数a的取值范围.18.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,若a2+c2=b2+ac.(1)求B的大小;(2)求cosA+cosC的最大值.19.(12分)已知数列{a n},S n是其前n项的和,且满足3a n=2S n+n(n∈N*)(Ⅰ)求证:数列{a n+}为等比数列;(Ⅱ)记T n=S1+S2+…+S n,求T n的表达式.20.(12分)已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+asinC ﹣b﹣c=0(1)求A;(2)若a=2,△ABC的面积为;求b,c.21.(12分)若x,y满足约束条件.(Ⅰ)求的最大值;(Ⅱ)求x2+y2的取值范围.22.(12分)已知数列{a n}的前n项和S n=3n2+8n,{b n}是等差数列,且a n=b n+b n+1(Ⅰ)求数列{b n}的通项公式;(Ⅱ)令c n=,求数列{c n}的前n项和T n.2017-2018学年安徽省淮北实验高级中学高二(上)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共12题,每小题5分,共60分.请把答案填写在答题纸相应位置上.1.(5分)在△ABC中,“A=60°”是“”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:在△ABC中,若“cosA=”成立,则有“A=60°成立;反之在△ABC中,若“A=60°成立则有“cosA=”成立,所以,“A=60°”是“”的充要条件.故选:C.2.(5分)已知变量x,y满足约束条件则z=2x+y的最大值为()A.1 B.2 C.3 D.4【解答】解:作图易知可行域为一个三角形,其三个顶点为(0,1),(1,0),(﹣1,﹣2),验证知在点(1,0)时取得最大值2当直线z=2x+y过点A(1,0)时,z最大是2,故选:B.3.(5分)在△ABC中,已知∠BAC=60°,∠ABC=45°,BC=,则AC=()A.B.2 C.2 D.【解答】解:∵∠BAC=60°,∠ABC=45°,BC=,∴由正弦定理可得,AC===.故选:A.4.(5分)等比数列x,3x+3,6x+6,…的第四项等于()A.﹣24 B.0 C.12 D.24【解答】解:由于x,3x+3,6x+6是等比数列的前三项,故有(3x+3)2=x(6x+6),解x=﹣3,故此等比数列的前三项分别为﹣3,﹣6,﹣12,故此等比数列的公比为2,故第四项为﹣24,故选:A.5.(5分)已知△ABC中,三内角A、B、C的度数成等差数列,边a、b、c依次成等比数列.则△ABC是()A.直角三角形B.等边三角形C.锐角三角形D.钝角三角形【解答】解:∵△ABC中,三内角A、B、C的度数成等差数列,∴A+C=2B,又A+B+C=180°,∴B=60°.又边a、b、c依次成等比数列,∴b2=ac,在△ABC中,由余弦定理得:b2=a2+c2﹣2accosB=a2+c2﹣2accos60°,∴a2+c2﹣2accos60°=ac,∴(a﹣c)2=0,∴a=c,∴A=C,又B=60°,∴△ABC为等边三角形.故选:B.6.(5分)等差数列{a n}满足a42+a72+2a4a7=9,则其前10项之和为()A.﹣9 B.﹣15 C.15 D.±15【解答】解:∵等差数列{a n}满足a42+a72+2a4a7=9,则有=9,∴a4+a7=±3.故其前10项之和为S10===±15,故选:D.7.(5分)已知+=1,(x>0,y>0),则x+y的最小值为()A.12 B.14 C.16 D.18【解答】解:∵+=1,(x>0,y>0),则x+y=(x+y)()=10+≥10+2=18,当且仅当即x=6,y=12时,等号成立.故x+y的最小值为18.故选:D.8.(5分)等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为()A.﹣24 B.﹣3 C.3 D.8【解答】解:∵等差数列{a n}的首项为1,公差不为0.a2,a3,a6成等比数列,∴,∴(a1+2d)2=(a1+d)(a1+5d),且a1=1,d≠0,解得d=﹣2,∴{a n}前6项的和为==﹣24.故选:A.9.(5分)在△ABC中,已知sin2B﹣sin2C﹣sin2A=sinAsinC,则角B的大小为()A.150°B.30°C.120° D.60°【解答】解:因为sin2B﹣sin2C﹣sin2A=sinAsinC,所以b2﹣c2﹣a2=,即=cosB,所以B=150°.故选:A.10.(5分)已知点A(2,1)和点B(﹣2,3),若直线3x﹣2y+a=0与线段AB 有交点,则实数a的取值范围是()A.(﹣∞,﹣4)∪(12,+∞)B.(﹣∞,﹣4]∪[12,+∞)C.(﹣4,12)D.[﹣4,12]【解答】解:根据题意,若直线3x﹣2y+a=0与线段AB有交点,则点A、B在直线3x﹣2y+a=0的两侧或在直线上,又由点A(2,1)和点B(﹣2,3),则有(6﹣2+a)(﹣6﹣6+a)≤0,即(a+4)(a﹣12)≤0,解可得:﹣4≤a≤12,即a的取值范围是[﹣4,12];故选:D.11.(5分)已知命题p:关于x的方程x2﹣ax+4=0有实根,命题q:关于x函数y=2x2+ax+4在[3,+∞)上为增函数,若“p或q”为真命题,“p且q”为假命题,则实数a取值范围为()A.(﹣12,﹣4]∪[4,+∞)B.[﹣12,﹣4]∪[4,+∞)C.(﹣∞,﹣12)∪(﹣4,4)D.[﹣12,+∞)【解答】解:由已知命题p:关于x的方程x2﹣ax+4=0有实根,∴△≥0,即a2﹣16≥0,∴a≥4,或a≤﹣4.由命题q:关于x函数y=2x2+ax+4在[3,+∞)上为增函数,∴≤3,解得a≥﹣12.由“p或q”为真命题,“p且q”为假命题,等价于或.由得到a<﹣12;由得到﹣4<a<4.综上可知a的取值范围是:(﹣∞,﹣12)∪(﹣4,4).故选:C.12.(5分)已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是()A.bc(b+c)>8 B.ab(a+b)>16C.6≤abc≤12 D.12≤abc≤24【解答】解:∵△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+,∴sin2A+sin2B=﹣sin2C+,∴sin2A+sin2B+sin2C=,∴2sinAcosA+2sin(B+C)cos(B﹣C)=,2sinA(cos(B﹣C)﹣cos(B+C))=,化为2sinA[﹣2sinBsin(﹣C)]=,∴sinAsinBsinC=.设外接圆的半径为R,由正弦定理可得:=2R,由S=,及正弦定理得sinAsinBsinC==,即R2=4S,∵面积S满足1≤S≤2,∴4≤R2≤8,即2≤R≤,由sinAsinBsinC=可得,显然选项C,D不一定正确,A.bc(b+c)>abc≥8,即bc(b+c)>8,正确,B.ab(a+b)>abc≥8,即ab(a+b)>8,但ab(a+b)>16,不一定正确,故选:A.二、填空题:本大题共4题,每小题5分,共20分.请把答案填写在答题纸相应位置上.13.(5分)在△ABC中,三内角A,B,C依次成等差数列,且,则△ABC 外接圆面积为π.【解答】解:∵在△ABC中,A、B、C成等差数列,∴B=.设△ABC的外接圆半径为r,由正弦定理可得=2r,故=2r,解得r=1,∴△ABC外接圆面积为S=πr2=π.故答案为:π.14.(5分)由命题“存在x∈R,x2+2x+2m≤0”是假命题,求得实数m的取值范围是(a,+∞),则实数a的值是.【解答】解:∵命题“存在x∈R,x2+2x+2m≤0”是假命题,∴配方得(x+1)2+2m>1,(x+1)2的最小值是0,即只要2m>1即可,∵实数m的取值范围是(a,+∞),∴a=.故答案为:.15.(5分)已知关于x的不等式x2﹣4x+t<0的解集为(1,m),则实数m=3.【解答】解:关于x的不等式x2﹣4x+t<0的解集为(1,m),∴1、m是方程x2﹣4x+t=0的实数根,由根与系数的关系知1+m=4,解得m=3.故答案为:3.16.(5分)在数列{a n}中,a1=1,a2=3,且a n+2=|a n+1﹣a n|(n∈N*),则a2017= 1.【解答】解:在数列{a n}中,a1=1,a2=3,=|a n+1﹣a n|(n∈N*),且a n+2可得a3=|3﹣1|=2,a4=|2﹣3|=1,a5=|1﹣2|=1,a6=|1﹣1|=0,a7=|0﹣1|=1,a8=|1﹣0|=1,a9=|1﹣1|=0,a10=|0﹣1|=1,a11=|1﹣0|=1,…,则数列{a n}从第四项起为周期为3的数列,则a2017=a671×3+4=a4=1.故答案为:1.三、解答题:本大题共6小题,共计70分,请在答题纸指定的区域内作答,解答题应写出文字说明、证明过程或演算步骤.17.(10分)已知不等式<1的解集记为p,关于x的不等式x2+(a﹣1)x ﹣a>0的解集记为q.若¬q是¬p的充分不必要条件,求实数a的取值范围.【解答】解:¬q是¬p的充分不必要条件等价于p是q的充分不必要条件,等价于不等式<1的解集是不等式x2+(a﹣1)x﹣a>0解集的真子集.不等式<1等价于﹣1<0,即>0,解得x>2或x<1.不等式x2+(a﹣1)x﹣a>0可以化为(x﹣1)(x+a)>0.当﹣a≤1时,不等式的解集是x>1或x<﹣a,此时a=﹣1;当﹣a>1时,不等式(x﹣1)(x+a)>0的解集是x<1或x>﹣a,所以﹣a<2,即﹣2<a<﹣1.综合知﹣2<a≤﹣1.18.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,若a2+c2=b2+ac.(1)求B的大小;(2)求cosA+cosC的最大值.【解答】解:(1)由题意,a2+c2=b2+ac.余弦定理:cosB==.∵0<B<π∴B=,(2)∵A+B+C=π,B=,则C=.那么:cosA+cosC=cosA+cos()==sin(A+).∵∴<A+<π当A=时,取得最大值为1.即cosA+cosC的最大值1.19.(12分)已知数列{a n},S n是其前n项的和,且满足3a n=2S n+n(n∈N*)(Ⅰ)求证:数列{a n+}为等比数列;(Ⅱ)记T n=S1+S2+…+S n,求T n的表达式.【解答】(Ⅰ)证明:∵3a n=2S n+n,∴3a n=2S n﹣1+n﹣1(n≥2),﹣1)=2a n+1(n≥2),两式相减得:3(a n﹣a n﹣1∴a n=3a n﹣1+1(n≥2),+),又a1+=,∴a n+=3(a n﹣1∴数列{a n+}是以为首项,3为公比的等比数列;(Ⅱ)解:由(Ⅰ)得a n+=•3n﹣1=•3n,∴a n=•3n﹣=(3n﹣1),∴S n=[(3+32+…+3n)﹣n]=(﹣n)=﹣,∴T n=S1+S2+…+S n=(32+33+…+3n+3n+1)﹣﹣(1+2+…+n)=•﹣﹣=﹣.20.(12分)已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+asinC ﹣b﹣c=0(1)求A;(2)若a=2,△ABC的面积为;求b,c.【解答】解:(1)由正弦定理得:acosC+asinC﹣b﹣c=0,即sinAcosC+sinAsinC=sinB+sinC∴sinAcosC+sinAsinC=sin(A+C)+sinC,即sinA﹣cosA=1∴sin(A﹣30°)=.∴A﹣30°=30°∴A=60°;(2)若a=2,△ABC的面积=,∴bc=4.①再利用余弦定理可得:a2=b2+c2﹣2bc•cosA=(b+c)2﹣2bc﹣bc=(b+c)2﹣3×4=4,∴b+c=4.②结合①②求得b=c=2.21.(12分)若x,y满足约束条件.(Ⅰ)求的最大值;(Ⅱ)求x2+y2的取值范围.【解答】解:x,y满足约束条件的可行域如图:A(1,3),B(1,1),C(2,2)(Ⅰ)因为=+1,显然OA的斜率最大,且,故的最大值为4.(Ⅱ)x2+y2的几何意义是可行域内的点与原点连线的距离的平方,显然B取得最小值,A点取得最大值;最小值为:2,最大值为:1+32=10.x2+y2的取值范围[2,10].22.(12分)已知数列{a n}的前n项和S n=3n2+8n,{b n}是等差数列,且a n=b n+b n+1(Ⅰ)求数列{b n}的通项公式;(Ⅱ)令c n=,求数列{c n}的前n项和T n.【解答】解:(Ⅰ)∵数列{a n}的前n项和,∴a1=11.当n≥2时,.又∵a n=6n+5对n=1也成立所以a n=6n+5,{b n}是等差数列,设公差为d,则a n=b n+b n+1=2b n+d.当n=1时,2b1=11﹣d;当n=2时,2b2=17﹣d由,解得d=3,所以数列{b n}的通项公式为;(Ⅱ)由,于是,,两边同乘以2,得.两式相减,得==﹣n•2n+2.所以,.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
2017-2018年安徽省淮北市濉溪中学等三校联考高二(上)期中数学试卷和答案

2017-2018学年安徽省淮北市濉溪中学等三校联考高二(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)下列不等式正确的是()A.若a>b,则a•c>b•c B.若a>b,则a•c2>b•c2C.若a>b,则<D.若a•c2>b•c2,则a>b2.(5分)在△ABC中,已知a2﹣b2+c2=ac则角B为()A.或B.或C.D.3.(5分)已知等比数列{a n}的前n项和为S n,若8a2+a5=0,则=()A.﹣11 B.﹣8 C.5 D.114.(5分)在△ABC中,=,则△ABC一定是()A.等腰三角形B.直角三角形C.等腰直角三角形 D.等边三角形5.(5分)等比数列{a n}中,a4=2,a5=5,则数列{lga n}的前8项和等于()A.6 B.5 C.4 D.36.(5分)下列不等式一定成立的是()A.x+≥2 B.sinx+≥2(x≠k,k∈Z)C.3x+3﹣x≥2 D.lgx+≥2(1<x<10)7.(5分)已知等差数列{a n}的前n项和为S n,且满足﹣=1,则数列{a n}的公差是()A.B.1 C.2 D.38.(5分)等差数列{a n}中,a1>0,S3=S10,则当S n取最大值时,n值为()A.6或7 B.7 C.6 D.不存在9.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,且三角形有两解,则A的范围是()A.(0,)B.(0,)C.(0,)D.(,)10.(5分)若x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.B.3 C.D.411.(5分)给出以下结论:=2a n(n∈N+),则数列{a n}是以2为公比的等比数列;(1)数列{a n}满足:a n+1(2)若==(这里a1,b1,a2,b2,c1,c2是非零实数),则不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同;(3)若a n=2n+1,则++…+≥;(4)在△ABC中,若sinA>sinB,则A>B.正确的个数是()A.1 B.2 C.3 D.412.(5分)设等差数列{a n}满足=1,公差d∈(﹣1,0).若当且仅当n=8时,数列{a n}的前n项和S n取得最大值,则首项a1取值范围是()A.(,)B.[,]C.[,]D.(,)二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的<1解集是.14.(5分)甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东30°角方向直线航行,并1小时后与乙船在C处相遇,则甲船的航速为海里/小时.15.(5分)已知数列{a n}的前n项和为S n,若a n=(2n﹣1)cos,则S2017=.16.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若a2=3b2+3c2﹣2bcsinA,则C=.三、解答题(本大题共6小题,共70分)17.(10分)已知数列{a n}的前n项和为S n,若S n=n2﹣2n+1.(1)求数列{a n};(2)求a2+a4+a6+…+a2n.18.(12分)已知关于x的不等式ax2+(1﹣2a)x﹣2<0.(1)当a=3时,求此不等式解集;(2)当a<0时,求此不等式解集.19.(12分)在△ABC内,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,且a=2c.(1)求cosA的值;=,求b的值.(2)若S△ABC20.(12分)设{a n}是等差数列,其前n项和为S n,{b n}为等比数列,且a1=b1=1,a4+b4=15,S4﹣b4=8.(1)求{a n},{b n}的通项公式;(2)求数列{}的前n项和T n.21.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,且bcosC+bsinC ﹣a﹣c=0.(1)求角B;(2)若边c=3,AC边上中线BD=,求sinA.22.(12分)设正项数列{a n}前n项和为S n,对任意n∈N*都有S n=()2成立.(1)求数列{a n}的前n项和S n;(2)记数列b n=a n+λ,n∈N*,λ∈R,其前n项和为T n.①若数列{T n}的最小值为T6,求实数λ的取值范围;②若数列{b n}中任意的不同两项之和仍是该数列中的一项,则称该数列是“封闭数列”.试问:是否存在这样的“封闭数列”{b n},使得对任意n∈N*,都有T≠0,且<+++…+<.若存在,求实数λ的所有取值;若不存在,请说明理由.2017-2018学年安徽省淮北市濉溪中学等三校联考高二(上)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)下列不等式正确的是()A.若a>b,则a•c>b•c B.若a>b,则a•c2>b•c2C.若a>b,则<D.若a•c2>b•c2,则a>b【解答】解:A.c≤0不成立;B.c=0时不成立;C.取a=2,b=﹣1不成立;D.a•c2>b•c2,可得a>b.故选:D.2.(5分)在△ABC中,已知a2﹣b2+c2=ac则角B为()A.或B.或C.D.【解答】解:根据余弦定理b2=a2+c2﹣2accosB,得cosB==∵B∈(0,π),∴B=故选:D.3.(5分)已知等比数列{a n}的前n项和为S n,若8a2+a5=0,则=()A.﹣11 B.﹣8 C.5 D.11【解答】解:∵8a2+a5=0,∴8a1q+a1q4=0,又数列是等比数列,首项不为0,∴8q+q4=0,又q不为零,故有q=﹣2.∴==1+q2=1+(﹣2)2=5.故选:C.4.(5分)在△ABC中,=,则△ABC一定是()A.等腰三角形B.直角三角形C.等腰直角三角形 D.等边三角形【解答】解:由正弦定理,得=,即为=,∴cosAsinB=sinAcosB,∴sin(A﹣B)=0,则A﹣B=0,即A=B,∴△ABC为等腰三角形,故选:A.5.(5分)等比数列{a n}中,a4=2,a5=5,则数列{lga n}的前8项和等于()A.6 B.5 C.4 D.3【解答】解:∵数列{a n}是等比数列,a4=2,a5=5,∴a1a8=a2a7=a3a6=a4a5=10.∴lga1+lga2+…+lga8=lg(a1a2•…•a8)=4lg10=4.故选:C.6.(5分)下列不等式一定成立的是()A.x+≥2 B.sinx+≥2(x≠k,k∈Z)C.3x+3﹣x≥2 D.lgx+≥2(1<x<10)【解答】解:A.x<时不成立.B.取x=﹣时不成立.C.3x+3﹣x≥2,当且仅当x=0时取等号.因此成立.D.∵1<x<10,∴lgx∈(0,1),∴lgx+>2.因此lgx+≥2等号不成立.故选:C.7.(5分)已知等差数列{a n}的前n项和为S n,且满足﹣=1,则数列{a n}的公差是()A.B.1 C.2 D.3【解答】解:∵等差数列{a n}的前n项和为S n,且满足﹣=1,∴﹣=1,解得d=2.故选:C.8.(5分)等差数列{a n}中,a1>0,S3=S10,则当S n取最大值时,n值为()A.6或7 B.7 C.6 D.不存在【解答】解:∵等差数列{a n}中,a1>0,S3=S10,∴S10﹣S3=a4+a5+…+a10=7a7=0,即a7=0∴等差数列{a n}中前6项为正数,第7项为0,从第8项开始为负数,∴当S n取最大值时,n的值为6或7故选:A.9.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,且三角形有两解,则A的范围是()A.(0,)B.(0,)C.(0,)D.(,)【解答】解:∵在△ABC中,a=1<b=,∴A为锐角,∴由余弦定理可得a2=b2+c2﹣2bccosA,即1=2+c2﹣2ccosA,即c2﹣2ccosA+1=0有2解,∴判别式△=8cos2A﹣4>0,∴cosA>,∴0<A<,故选:B.10.(5分)若x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.B.3 C.D.4【解答】解:考察基本不等式x+2y=8﹣x•(2y)≥8﹣()2(当且仅当x=2y 时取等号)整理得(x+2y)2+4(x+2y)﹣32≥0即(x+2y﹣4)(x+2y+8)≥0,又x+2y>0,所以x+2y≥4(当且仅当x=2y时取等号),则x+2y的最小值是4,故选:D.11.(5分)给出以下结论:(1)数列{a n}满足:a n=2a n(n∈N+),则数列{a n}是以2为公比的等比数列;+1(2)若==(这里a1,b1,a2,b2,c1,c2是非零实数),则不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同;(3)若a n=2n+1,则++…+≥;(4)在△ABC中,若sinA>sinB,则A>B.正确的个数是()A.1 B.2 C.3 D.4=2a n=0,(n∈N+),则数列{a n}不是等比数【解答】解:(1)数列{a n}满足:a n+1列,故错误;(2)若==<0(这里a1,b1,a2,b2,c1,c2是非零实数),则不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集不同,故错误;(3)若a n=2n+1,则++…+=++…+≥≥,故正确;(4)在△ABC中,若sinA>sinB,则2RsinA>2RsinB,即a>b,则A>B故正确.故选:B.12.(5分)设等差数列{a n}满足=1,公差d∈(﹣1,0).若当且仅当n=8时,数列{a n}的前n项和S n取得最大值,则首项a1取值范围是()A.(,)B.[,]C.[,]D.(,)【解答】解:由=1,得:=1,即=1,由积化和差公式得:=1,整理得:=1,即有=1,∴sin(3d)=﹣1.∵d∈(﹣1,0),∴3d∈(﹣3,0),则3d=﹣,d=﹣.由S n=na1+n(n﹣1)d=﹣n2+(a1+)n,对称轴方程为n=(a1+),由题意当且仅当n=8时,数列{a n}的前n项和S n取得最大值,∴<(a1+)<,得:<a1<,∴首项a1的取值范围是(,).故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的<1解集是(﹣1,0).【解答】解:由不等式的<1,可得,即,等价于x(x+1)<0,解得:﹣1<x<0.故答案为(﹣1,0)14.(5分)甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东30°角方向直线航行,并1小时后与乙船在C处相遇,则甲船的航速为10海里/小时.【解答】解:设甲船的航速为v海里/小时,则AC=v,BC=10,∠CAB=30°,∠ABC=120°,由正弦定理可得,∴v=10海里/小时.故答案为10.15.(5分)已知数列{a n}的前n项和为S n,若a n=(2n﹣1)cos,则S2017= 2017.【解答】解:S2017=1+0﹣5+0+9+…+4033+0=1﹣5+9+…+4033=﹣4×+4033=2017.故答案为:2017.16.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若a2=3b2+3c2﹣2bcsinA,则C=.【解答】解:根据a2=3b2+3c2﹣2bcsinA…①余弦定理a2=b2+c2﹣2bccosA…②由①﹣②可得:2b2+2c2=2bcsinA﹣2bccosA化简:b2+c2=bcsinA﹣bccosA⇔b2+c2=2bcsin(A)∵b2+c2≥2bc,∴sin(A)=1∴A=,此时b2+c2=2bc,故得b=c,即B=C,∴C==.故答案为:.三、解答题(本大题共6小题,共70分)17.(10分)已知数列{a n}的前n项和为S n,若S n=n2﹣2n+1.(1)求数列{a n};(2)求a2+a4+a6+…+a2n.【解答】解:(1)数列{a n}的前n项和为S n,若S n=n2﹣2n+1.n=1时,a1=S1=0,当n≥2时,a n=S n﹣S n﹣1=n2﹣2n+1﹣((n﹣1)2﹣2(n﹣1)+1)=2n﹣3,因为n=1不满足a n=2n﹣3,所以a n=.(2)因为a n=.数列从第二项起是等差数列,a2+a4+a6…a2n==2n2﹣n.18.(12分)已知关于x的不等式ax2+(1﹣2a)x﹣2<0.(1)当a=3时,求此不等式解集;(2)当a<0时,求此不等式解集.【解答】解:(1)当a=3时,不等式3x2﹣5x﹣2<0.即(3x+1)(x﹣2)<0解得:∴不等式解集的解集为{x|}(2)由不等式ax2+(1﹣2a)x﹣2<0.可得:(ax+1)(x﹣2)<0.则方程:(ax+1)(x﹣2)=0的根,x2=2.①当时,原不等式的解集为{x|x<2或x}②当a=时,原不等式的解集为{x|x≠2}③当a,原不等式的解集为{x|x>2或x}.19.(12分)在△ABC内,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,且a=2c.(1)求cosA的值;=,求b的值.(2)若S△ABC【解答】解:(1)△ABC内,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,所以:a+c=2b,且a=2c,解得:b=.所以:cosA=.(2)由(1)得:cosA=﹣,解得:sinA=,=,由于:S△ABC则:,得:c2=4.所以:c=2.进一步解得:b==3.20.(12分)设{a n}是等差数列,其前n项和为S n,{b n}为等比数列,且a1=b1=1,a4+b4=15,S4﹣b4=8.(1)求{a n},{b n}的通项公式;(2)求数列{}的前n项和T n.【解答】解:(1)设等差数列的公差为d,等比数列的公比为q,a1=b1=1,a4+b4=15,S4﹣b4=8,得方程组,解得d=2,q=2,所以:a n=2n﹣1,b n=2n﹣1;(2)=∴T n=1×()0+3×()1+5×()2+…+(2n﹣1)×()n﹣1,﹣﹣①,∴T n=1×()1+3×()2+5×()3+…+(2n﹣1)×()n,﹣﹣②,由①﹣②,得T n=1+2[+()2+()3+…+()n﹣1]﹣(2n﹣1)×()n=1+2×﹣,=1+2﹣﹣=3﹣∴T n=6﹣21.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,且bcosC+bsinC ﹣a﹣c=0.(1)求角B;(2)若边c=3,AC边上中线BD=,求sinA.【解答】解:(1)△ABC的内角A,B,C的对边分别为a,b,c,且bcosC+sinC ﹣a﹣c=0则:sinBcosC+sinBsinC﹣sin(B+C)﹣sinC=0,所以:,由于:sin2B+cos2B=1,解得:.(2)设BC=y,AD=DC=x,在△ABD中,AB2=BD2+AD2﹣2BD•ADcos∠ADB,整理得:9=①在△BDC中,BC2=BD2+DC2﹣2BD•DCcos∠BDC,整理得:②所以:①+②得:③,在△ABC中,,整理得:④,由③④得:y2+3y﹣28=0,解得:y=4(负值舍去).把y=4代入③得到x=.在△ABC中,利用正弦定理得:整理得:,解得:sinA=.22.(12分)设正项数列{a n}前n项和为S n,对任意n∈N*都有S n=()2成立.(1)求数列{a n}的前n项和S n;(2)记数列b n=a n+λ,n∈N*,λ∈R,其前n项和为T n.①若数列{T n}的最小值为T6,求实数λ的取值范围;②若数列{b n}中任意的不同两项之和仍是该数列中的一项,则称该数列是“封闭数列”.试问:是否存在这样的“封闭数列”{b n},使得对任意n∈N*,都有T≠0,且<+++…+<.若存在,求实数λ的所有取值;若不存在,请说明理由.【解答】解:(1)法一:由S n=()2得:4S n=a n2+2a n+1,①,4S n+1=a n+12+2a n+1+1,②,∴②﹣①得4a n=a n+12﹣a n2+2a n+1﹣2a n,+1得到2(a n+1+a n)=(a n+1+a n)(a n+1﹣a n)由题知a n+1+a n≠0∴a n+1﹣a n=2,∵S1=()2得:4a1=a12+2a1+1,∴a1=1,∴a n=2n﹣1,S n=n2,法二:由S n=()2,S1=()2,4a1=a12+2a1+1,∴a1=1,当n≥2时,2=a n+1=S n﹣S n﹣1+1得(﹣1)2=,即﹣=1,∴=n,∴S n=n2,(2)①由b n=2n﹣1+λ得到其前n项和T n=n2+λn,由题意T n最小值为T6,即T n≥T6,n2+λn≥36+6λ,当1≤n<6时,λ≤﹣(6+n),∴λ≤﹣11.当n>6时,λ≥﹣(6+n),∴λ≥﹣13.综上可得:λ∈[﹣13,﹣11].②∵{bn}是“封闭数列”,设b p+b q=b m(p,q,m∈Z*,且任意两个不相等)得2p﹣1+λ+2q﹣1+λ=2m﹣1+λ,化为λ=2(m﹣p﹣q)+1,则λ为奇数.由任意n∈N*,都有T n≠0,且<+++…+<.若得<T1<,化为<λ<11,即λ的可能值为1,3,5,7,9,∴实数λ的所有取值集合为{1,3,5,7,9}.。
2017-2018学年安徽省淮北市实验高级中学高二上学期期中数学试卷与解析(理科)

2017-2018学年安徽省淮北市实验高级中学高二(上)期中数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是()A.B.C.A 1A2+B1B2=0 D.A1A2﹣B1B2=02.(5分)数列{a n}是等差数列,a2=4,a7=19,则a31=()A.91 B.88 C.94 D.853.(5分)下列命题中,正确的是()A.若a>b,c>d,则ac>bc B.若ac>bc,则a>bC.若<,则a<b D.若a>b,c>d,则a﹣c>b﹣d4.(5分)在△ABC中,若(a+c)(a﹣c)=b(b+c),则∠A=()A.90°B.60°C.120° D.150°5.(5分)已知非零实数a,b满足成等比数列,则ab的取值范围是()A.(﹣∞,2]B.(﹣2,2]C.[2,+∞)D.(0,2]6.(5分)若不等式f(x)=ax2﹣x﹣c>0的解集{x|﹣2<x<1},则函数y=f(﹣x)的图象为()A.B.C.D.7.(5分)已知实数x,y满足不等式组,则z=4x﹣6y的最小值为()A.﹣33 B.﹣10 C.﹣8 D.108.(5分)设数列{b n}满足:b1=,b n+1=(n≥1),则b2018=()A.3 B.7 C.2018 D.20179.(5分)设x>﹣1,则的最小值为()A.4 B.9 C.7 D.1310.(5分)在△ABC中,三个内角A,B,C所对的边为a,b,c,若S△ABC=2,a+b=6,=2cosC,则c=()A.2 B.4 C.2 D.311.(5分)已知不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,求实数a的取值范围()A.()B.(]C.()∪[1,+∞)D.()∪(1,+∞)12.(5分)在△ABC中,已知0,AC≥AB,点M,N分别是边AC,AB 的中点,且的最大值是,则=()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的解集是.14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为.15.(5分)如果满足∠ABC=60°,AC=12,BC=k的三角形恰有一个,那么k的取值范围是.16.(5分)已知数列{a n}满足a n+2=3a n+1﹣2a n(n∈N*),且a1=1,a2=4,其前n 项和为S n,若对任意的正整数n,S n+2n+m•2n≥0恒成立,则实数m的取值范围是.三、解答(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)17.(10分)设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x 满足2<x≤3.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.18.(12分)设x,y满足条件.(1)求u=x2+y2的最大值与最小值;(2)求v=的最大值与最小值.19.(12分)已知数列{a n}的前n项和为S n,且满足2a n=S n+1(n∈N*)(1)求数列{a n}的通项公式;(2)若b n=(2n+1)•a n,求数列{b n}的前n项和T n.20.(12分)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.(Ⅰ)求角A的值;(Ⅱ)若a=,求b+c的取值范围.21.(12分)已知各项都为正数的等比数列{a n}满足是3a1与2a2的等差中项,且a1a2=a3.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a n,且S n为数列{b n}的前n项和,求数列{}的前7项和T7.22.(12分)△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC 面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.2017-2018学年安徽省淮北市实验高级中学高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是()A.B.C.A1A2+B1B2=0 D.A1A2﹣B1B2=0【解答】解:两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直⇔A1A2+B1B2=0,故两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是A1A2+B1B2=0,故选:C.2.(5分)数列{a n}是等差数列,a2=4,a7=19,则a31=()A.91 B.88 C.94 D.85【解答】解:设等差数列{a n}的公差为d,∵a2=4,a7=19,∴a1+d=4,a1+6d=19,解得a1=1,d=3.则a31=1+3×30=91.故选:A.3.(5分)下列命题中,正确的是()A.若a>b,c>d,则ac>bc B.若ac>bc,则a>bC.若<,则a<b D.若a>b,c>d,则a﹣c>b﹣d【解答】解:令a=1,b=﹣1,c=﹣1,d=﹣5,显然A、D不成立,对于B:若c<0,显然不成立,对于C:由c2>0,得:a<b,故C正确,故选:C.4.(5分)在△ABC中,若(a+c)(a﹣c)=b(b+c),则∠A=()A.90°B.60°C.120° D.150°【解答】解:由(a+c)(a﹣c)=b(b+c)变形得:a2﹣c2=b2+bc,即a2=c2+b2+bc根据余弦定理得cosA===﹣,因为A为三角形的内角,所以∠A=120°.故选:C.5.(5分)已知非零实数a,b满足成等比数列,则ab的取值范围是()A.(﹣∞,2]B.(﹣2,2]C.[2,+∞)D.(0,2]【解答】解:∵成等比数列,∴()2==ab>0,又a2+b2≥2ab,当且仅当a=b时取等号,∴ab≥,即(ab)2﹣2ab≥0,分解因式得:ab(ab﹣2)≥0,解得:ab≤0(舍去)或ab≥2,则ab的取值范围是[2,+∞).故选:C.6.(5分)若不等式f(x)=ax2﹣x﹣c>0的解集{x|﹣2<x<1},则函数y=f(﹣x)的图象为()A.B.C.D.【解答】解:由已知得,﹣2,1是方程ax2﹣x﹣c=0的两根,分别代入,解得a=﹣1,c=﹣2.∴f(x)=﹣x2﹣x+2.从而函数y=f(﹣x)=﹣x2+﹣x+2=﹣(x﹣2)(x+1)它的图象是开口向下的抛物线,与x轴交与(﹣1,0)(2,0)两点.故选:B.7.(5分)已知实数x,y满足不等式组,则z=4x﹣6y的最小值为()A.﹣33 B.﹣10 C.﹣8 D.10【解答】解:先根据约束条件画出可行域:z=4x﹣6y,将最小值转化为y轴上的截距,由,解得A(,)当直线z=4x﹣6y经过A(,)时,z最小,最小值为:﹣33,即当x=,y=,4x﹣6y取得最小值﹣33.故选:A.8.(5分)设数列{b n}满足:b1=,b n+1=(n≥1),则b2018=()A.3 B.7 C.2018 D.2017【解答】解:根据题意,数列{b n}满足:b1=,b n+1=(n≥1),则b2===3,b3===﹣2,b4===﹣,b5===,分析可得:b5=b1,b6=b2,…;则数列{b n}是周期为4的数列,则b2018=b2+4×504=b2=3;故选:A.9.(5分)设x>﹣1,则的最小值为()A.4 B.9 C.7 D.13【解答】解:设t=x+1(t>0),则y=f(t)==,整理得:f(t)=(t+)+5∵t>0,∴t+≥2,所以f(t)=(t+)+5≥2+5=9,当且仅当t==2时,函数有最小值,此时x=1.因此函数当x=1时有最小值为9,故选:B.10.(5分)在△ABC中,三个内角A,B,C所对的边为a,b,c,若S△ABC=2,a+b=6,=2cosC,则c=()A.2 B.4 C.2 D.3【解答】解:===1,即有2cosC=1,可得C=60°,=2,则absinC=2,若S△ABC即为ab=8,又a+b=6,由c2=a2+b2﹣2abcosC=(a+b)2﹣2ab﹣ab=(a+b)2﹣3ab=62﹣3×8=12,解得c=2.故选:C.11.(5分)已知不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,求实数a的取值范围()A.()B.(]C.()∪[1,+∞)D.()∪(1,+∞)【解答】解:令a2﹣1=0,解得a=±1,当a=1时,不等式化为﹣1<0,解得x ∈R;当a2﹣1≠0时,应满足△=(a﹣1)2+4(a2﹣1)=5a2﹣2a﹣3<0,且a2﹣1<0,解得﹣<a<1,此时不等式的解集为x∈R.综上,实数a的取值范围是﹣<a≤1,即(﹣,1].故选:B.12.(5分)在△ABC中,已知0,AC≥AB,点M,N分别是边AC,AB 的中点,且的最大值是,则=()A.B.C.D.【解答】解:△ABC中,AC≥AB,设AC=tAB,t≥1,又点M,N分别是AC,AB的中点,∴AM=AC,AN=AB;在△ABM中,由余弦定理可得:BM2=AB2+AM2﹣2AB•AMcosA=AB2+(tAB)2﹣2AB•tAB•cosA=(1+t2)AB2﹣tAB2cosA,在△ACN中,由余弦定理可得:CN2=AN2+AC2﹣2AN•ACcosA=(AB)2+(tAB)2﹣2•tAB•AB•cosA=(+t2)AB2﹣tAB2cosA,∴==,∵0,t≥1,∴cosA∈[,1),的最小值为=,则的最大值为=,解得t=,由正弦定理可得===,故选:D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的解集是[﹣1,0]∪(2,+∞).【解答】解:根据题意,⇒x(x+1)(x﹣2)≥0且x﹣2≠0,解可得﹣1≤x≤0或x>2,即原不等式的解集为[﹣1,0]∪(2,+∞);故答案为:[﹣1,0]∪(2,+∞).14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为﹣1≤a≤3.【解答】解:命题“∃x∈R,使x2+(a﹣1)x+1<0”的否定是:““∀x∈R,使x2+(a﹣1)x+1≥0”即:△=(a﹣1)2﹣4≤0,∴﹣1≤a≤3故答案是﹣1≤a≤315.(5分)如果满足∠ABC=60°,AC=12,BC=k的三角形恰有一个,那么k的取值范围是0<k≤12或k=8.【解答】解:(1);(2);(3);(4)当0<BC≤AC,即0<k≤12时,三角形有1个解.综上所述:当时,三角形恰有一个解.故答案为:16.(5分)已知数列{a n}满足a n+2=3a n+1﹣2a n(n∈N*),且a1=1,a2=4,其前n 项和为S n,若对任意的正整数n,S n+2n+m•2n≥0恒成立,则实数m的取值范围是[﹣,+∞).【解答】解:方法一:∵a n+2=3a n+1﹣2a n(n∈N*),∴a n+2﹣a n+1=2(a n+1﹣a n),(n∈N*),∵a1=1,a2=4,∴a2﹣a1=3,∴数列{a n+1﹣a n}是以3为首项,以2为公比的等比数列,∴a n﹣a n=3×2n﹣1,+1∴a2﹣a1=3×20,a3﹣a2=3×21,a4﹣a3=3×22,…,=3×2n﹣2,∴a n﹣a n﹣1累加可得a n﹣a1=3(1+21+22+…+2n﹣2)=3×=3(2n﹣1﹣1)∴a n=3×2n﹣1﹣2,当n=1时,a1=3﹣2=1,成立,∴a n=3×2n﹣1﹣2,∴S n=3(1+21+22+…+2n﹣1)﹣2n=3(2n﹣1)﹣2n=3×2n﹣3﹣2n,∵对任意的正整数n,S n+2n+m•2n≥0恒成立,∴3×2n﹣3﹣2n+2n+m•2n≥0恒成立,即3×2n﹣3+m•2n≥0恒成立,∴m≥﹣3恒成立,∵﹣3≤﹣2=﹣,∴m≥﹣,方法二(非常规做法),由对任意的正整数n,S n+2n+m•2n≥0恒成立,由数列的函数特征可得,只要n=1时恒成立即可,故S1+2×1+m•21≥0,解得m≥﹣故答案为:[﹣,+∞).三、解答(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)17.(10分)设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x 满足2<x≤3.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.【解答】解:(Ⅰ)对于命题p:由x2﹣4ax+3a2<0得(x﹣3a)(x﹣a)<0,又a>0,∴a<x<3a,当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.由已知q为真时实数x的取值范围是2<x≤3.若p∧q为真,则p真且q真,∴实数x的取值范围是2<x<3.(Ⅱ)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q⇏¬p,设A={x|¬p},B={x|¬q},则A⊊B,又A={x|¬p}={x|x≤a或x≥3a},B={x|¬q}={x≤2或x>3},则0<a≤2且3a>3,∴实数a的取值范围是1<a≤2.18.(12分)设x,y满足条件.(1)求u=x2+y2的最大值与最小值;(2)求v=的最大值与最小值.【解答】解:满足条件的可行域如图所示(阴影部分).(1)令u=x2+y2表示一组同心圆(圆心为点O),且对同一圆上的点,u=x2+y2的值都相等.由图可知(x,y)在可行域内取值,当且仅当圆O过C点时,u最大,过点(0,0)时,u最小.由,解得C(3,8),∴u=x2+y2的最大值为:32+82=73,最小值为:02+02=0.(2)v=表示可行域内的点(x,y)和定点D(5,0)的连线的斜率,由图可知k BD最大,k CD最小.由,解得B(3,﹣3).∴v max==,v min==﹣4.19.(12分)已知数列{a n}的前n项和为S n,且满足2a n=S n+1(n∈N*)(1)求数列{a n}的通项公式;(2)若b n=(2n+1)•a n,求数列{b n}的前n项和T n.【解答】解:(1)当n=1时,2a1=S1+1=a1+1,解得a1=1.n≥2时,2a n﹣1=S n﹣1+1,可得:2a n﹣2a n﹣1=a n,可得a n=2a n﹣1..数列{a n}是首项为1,公比为2的等比数列,a n=2n﹣1.(2)b n=(2n+1)•a n=(2n+1)•2n﹣1.∴数列{b n}的前n项和T n=3×1+5×2+7×22+…+(2n+1)•2n﹣1.2T n=3×2+5×22+…+(2n﹣1)•2n﹣1+(2n+1)•2n,∴﹣T n=3+2×(2+22+…+2n﹣1)﹣(2n+1)•2n=1+2×﹣(2n+1)•2n,可得:T n=(2n﹣1)•2n+1.20.(12分)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.(Ⅰ)求角A的值;(Ⅱ)若a=,求b+c的取值范围.【解答】解:(Ⅰ)在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.则:(sinB﹣2sinC)cosA=sinA﹣sinA(cosB+1),整理得:sin(A+B)=2sinCcosA,则:,0<A<π,则:.(Ⅱ)若a=,由2R=,则:b+c=2(sinA+sinB),=,由于:,则:,解得:故b+c的范围为:(,].21.(12分)已知各项都为正数的等比数列{a n}满足是3a1与2a2的等差中项,且a1a2=a3.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a n,且S n为数列{b n}的前n项和,求数列{}的前7项和T7.【解答】解:(Ⅰ)设等比数列的公比为q,由题意知q>0,且3a1+2a2=a3,∴,解得a1=q=3,故a n=3n.(Ⅱ)由(Ⅰ),得b n=log3a n=n,所以.∴,故数列的前n项和为:.∴.22.(12分)△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC 面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.【解答】解:(1)如图,过A作AE⊥BC于E,∵==2∴BD=2DC,∵AD平分∠BAC∴∠BAD=∠DAC在△ABD中,=,∴sin∠B=在△ADC中,=,∴sin∠C=;∴==.…6分(2)由(1)知,BD=2DC=2×=.过D作DM⊥AB于M,作DN⊥AC于N,∵AD平分∠BAC,∴DM=DN,∴==2,∴AB=2AC,令AC=x,则AB=2x,∵∠BAD=∠DAC,∴cos∠BAD=cos∠DAC,∴由余弦定理可得:=,∴x=1,∴AC=1,∴BD的长为,AC的长为1.。
2017-2018学年安徽省淮北市濉溪县高二上学期期中数学试卷与解析(文科)

2017-2018学年安徽省淮北市濉溪县高二(上)期中数学试卷(文科)一.选择题(本大题共12小题,每小题5分,共60分)1.(5分)等差数列{a n}中,若a1=2,a3=6,则a6等于()A.8 B.10 C.11 D.122.(5分)已知△ABC中,内角A,B,C所对的边分别为a,b,c,a=,b=,B=60°,那么A等于()A.45°B.60°C.120° D.135°3.(5分)若集合A={x|x2+x﹣6<0},B={x|≤0},则A∩B等于()A.(﹣3,3)B.[﹣2,2)C.(﹣2,2)D.[﹣2,3)4.(5分)已知数列{a n}的通项公式a n=26﹣2n,要使此数列的前n项和S n最大,则n的值为()A.12 B.13 C.12或13 D.145.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,则下列判断中正确的是()A.a=30,b=25,A=150°有一解B.a=9,c=10,B=60°无解C.a=6,b=9,A=45°有两解 D.a=7,b=14,A=30°有两解6.(5分)不等式ax2+5x+c>0的解集为{x|<x<},则a,c的值为()A.a=6,c=1 B.a=﹣6,c=﹣1 C.a=1,c=6 D.a=﹣1,c=﹣67.(5分)在△ABC中,若sinBsinC=cos2,则△ABC是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形8.(5分)已知{a n}为等差数列,若a3+a4+a8=9,则S9=()A.24 B.27 C.15 D.549.(5分)变量x,y满足约束条件,则z=2x﹣y的最大值为()A.2 B.3 C.4 D.510.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c,sin A:sin B:sin C=4:3:2,则cos A的值是()A.﹣ B.C.﹣ D.11.(5分)已知等差数列{a n}中,a3=45°,则cos(a1+a2+a6)为()A.1 B.C.2 D.312.(5分)若x>0且x2,则x的最大值为()A.6 B.4 C.D.二.填空题(本大题共4小题,每小题5分,共20分.)13.(5分)已知两个等差数列{a n}、{b n}的前n项和分别为S n、T n.且,则=.14.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知△ABC的面积为3,b﹣c=2,cosA=﹣,则a的值为.15.(5分)数列{a n}中的前n项和S n=n2﹣2n+2,则通项公式a n=.16.(5分)△ABC中,角C为直角,M是BC的中点,若sin,则sin∠BAC=.三.解答题(本大题共6小题,共70分)17.(10分)在△ABC中,(Ⅰ)求AB的值;(Ⅱ)求的值.18.(12分)已知等差数列{a n}满足:a3=7,a5+a7=26,{a n}的前n项和为S n.(Ⅰ)求a n及S n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和T n.19.(12分)在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2=ab.(1)求角C的大小;(2)如果0<A≤,m=2cos2﹣sinB﹣1,求实数m的取值范围.20.(12分)在△ABC中,内角A、B、C的对边分别为a、b、c,已知.(1)求的值;(2)若,b=2,求△ABC的面积.21.(12分)解关于x的不等式ax2﹣(a+1)x+1>0.22.(12分)已知数列{a n}的前n项和为S n,且S n=2n2+n,n∈N,数列{b n}满足a n=4log2b n+3,n∈N.(1)求a n,b n;(2)求数列{a n b n}的前n项和T n.2017-2018学年安徽省淮北市濉溪县高二(上)期中数学试卷(文科)参考答案与试题解析一.选择题(本大题共12小题,每小题5分,共60分)1.(5分)等差数列{a n}中,若a1=2,a3=6,则a6等于()A.8 B.10 C.11 D.12【解答】解:根据题意,等差数列{a n}中,若a1=2,a3=6,则公差d===2,则a6=a1+5d=2+5×2=12;故选:D.2.(5分)已知△ABC中,内角A,B,C所对的边分别为a,b,c,a=,b=,B=60°,那么A等于()A.45°B.60°C.120° D.135°【解答】解:∵△ABC中,a=,b=,B=60°,∴由正弦定理得:sinA===,∵A是三角形的内角,且a<b,∴A=45°.故选:A.3.(5分)若集合A={x|x2+x﹣6<0},B={x|≤0},则A∩B等于()A.(﹣3,3)B.[﹣2,2)C.(﹣2,2)D.[﹣2,3)【解答】解:集合A={x|x2+x﹣6<0}={x|﹣3<x<2},B={x|≤0}={x|﹣2≤x<3},则A∩B={x|﹣2≤x<2}=[﹣2,2),故选:B.4.(5分)已知数列{a n}的通项公式a n=26﹣2n,要使此数列的前n项和S n最大,则n的值为()A.12 B.13 C.12或13 D.14【解答】解:∵数列{a n}的通项公式a n=26﹣2n,∴a1=26﹣2=24,d=a n﹣a n﹣1=(26﹣2n)﹣[26﹣2(n﹣1)]=﹣2,∴数列{a n}是首项为24,公差为2的等差数列,∴S n=24n+=﹣n2+25n=﹣(n﹣)2+.∴要使此数列的前n项和S n最大,则n的值为12或13.故选:C.5.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,则下列判断中正确的是()A.a=30,b=25,A=150°有一解B.a=9,c=10,B=60°无解C.a=6,b=9,A=45°有两解 D.a=7,b=14,A=30°有两解【解答】解:A、根据正弦定理得:=,解得sinB=,因为A=150°,所以B只能为锐角,所以此选项正确;B、根据余弦定理得:b2=81+100﹣180cos60°=91,解得b=,能构成三角形,所以此选项错误;C、根据正弦定理得:=,解得sinB=>1,此三角形无解,此选项错误;D、根据正弦定理得:=,解得sinB=1,B为直角,所以此三角形只有一解,此选项错误.故选:A.6.(5分)不等式ax2+5x+c>0的解集为{x|<x<},则a,c的值为()A.a=6,c=1 B.a=﹣6,c=﹣1 C.a=1,c=6 D.a=﹣1,c=﹣6【解答】解:∵不等式ax2+5x+c>0解集为,∴方程ax2+5x+c=0的两个实数根为,,且a<0.∴,解得故选:B.7.(5分)在△ABC中,若sinBsinC=cos2,则△ABC是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【解答】解:由题意,即sinBsinC=1﹣cosCcosB,亦即cos(C ﹣B)=1,∵C,B∈(0,π),∴C=B,故选:A.8.(5分)已知{a n}为等差数列,若a3+a4+a8=9,则S9=()A.24 B.27 C.15 D.54【解答】解:设等差数列{a n}的公差为d,∵a3+a4+a8=9∴(a1+2d)+(a1+3d)+(a1+7d)=9即3(a1+4d)=9∴a1+4d=3即a5=3又∵S9==9a5=27故选:B.9.(5分)变量x,y满足约束条件,则z=2x﹣y的最大值为()A.2 B.3 C.4 D.5【解答】解:由z=2x﹣y得y=2x﹣z作出不等式组对应的平面区域如图(阴影部分):平移直线y=2x﹣z由图象可知当直线y=2x﹣z过点A时,直线y=2x﹣z的截距最小,此时z最大,由,解得A(2,﹣1).代入目标函数z=2x﹣y,得z=2×2+1=5,∴目标函数z=2x﹣y的最大值是5.故选:D.10.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c,sin A:sin B:sin C=4:3:2,则cos A的值是()A.﹣ B.C.﹣ D.【解答】解:∵sin A:sin B:sin C=4:3:2,∴由正弦定理可得a:b:c=4:3:2,∴可设三边长分别为a=4k,b=3k,c=2k,k>0,∴利用余弦定理可得:cosA===﹣.故选:A.11.(5分)已知等差数列{a n}中,a3=45°,则cos(a1+a2+a6)为()A.1 B.C.2 D.3【解答】解:根据题意,设等差数列{a n}的首项为a1,公差为d,若a3=45°,则a1+2d=45°,a1+a2+a6=a1+a1+2d+a1+5d=3(a1+2d)=135°,则cos(a1+a2+a6)=cos135°=﹣;故选:B.12.(5分)若x>0且x2,则x的最大值为()A.6 B.4 C.D.【解答】解:∵x>0且x2,∴2x2+y2=2∴x=••≤=,当且仅当2x2=1+y2时取等号,故x的最大值为,故选:C.二.填空题(本大题共4小题,每小题5分,共20分.)13.(5分)已知两个等差数列{a n}、{b n}的前n项和分别为S n、T n.且,则=.【解答】解:因为数列{a n}、{b n}都是等差数列,根据等差中项的概念知数列中的第11项为数列前21项的等差中项,所以S21=21a11,T21=21b11,所以.故答案为.14.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知△ABC的面积为3,b﹣c=2,cosA=﹣,则a的值为8.【解答】解:∵A∈(0,π),∴sinA==.==bc=,化为bc=24,∵S△ABC又b﹣c=2,解得b=6,c=4.由余弦定理可得:a2=b2+c2﹣2bccosA=36+16﹣48×=64.解得a=8.故答案为:8.15.(5分)数列{a n}中的前n项和S n=n2﹣2n+2,则通项公式a n=.【解答】解:∵数列{a n}中的前n项和S n=n2﹣2n+2,∴当n=1时,a1=S1=1;当n>1时,a n=S n﹣S n﹣1=(n2﹣2n+2)﹣[(n﹣1)2﹣2(n﹣1)+2]=2n﹣3.又n=1时,2n﹣3≠a1,所以有a n=.故答案为:.16.(5分)△ABC中,角C为直角,M是BC的中点,若sin,则sin∠BAC=.【解答】解:如图,设AC=b,AB=c,CM=MB=,∠MAC=β,在△ABM中,由正弦定理可得=,代入数据解得sin∠AMB=,故cosβ=cos(﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=,而在RT△ACM中,cosβ==,故可得=,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,解之可得a=b,再由勾股定理可得a2+b2=c2,联立可得c=b,故在RT△ABC中,sin∠BAC==,故答案为:.三.解答题(本大题共6小题,共70分)17.(10分)在△ABC中,(Ⅰ)求AB的值;(Ⅱ)求的值.【解答】解:(Ⅰ)在△ABC中,根据正弦定理,于是AB=(Ⅱ)在△ABC中,根据余弦定理,得cosA==.于是sinA==从而sin2A=2sinAcosA=,则cos2A=cos2A﹣sin2A=,故得=sin2Acos﹣cos2Asin=.18.(12分)已知等差数列{a n}满足:a3=7,a5+a7=26,{a n}的前n项和为S n.(Ⅰ)求a n及S n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和T n.【解答】解:(Ⅰ)设等差数列{a n}的公差为d,因为a3=7,a5+a7=26,所以有,解得a1=3,d=2,所以a n=3+2(n﹣1)=2n+1;S n=3n+.(Ⅱ)由(Ⅰ)知a n=2n+1,所以b n====(﹣),所以数列{b n}的前n项和T n=(1﹣﹣)=(1﹣)=,即数列{b n}的前n项和T n=.19.(12分)在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2=ab.(1)求角C的大小;(2)如果0<A≤,m=2cos2﹣sinB﹣1,求实数m的取值范围.【解答】解:(1)∵由余弦定理可得,cosC==∵0<C<π∴(2)由(1)可得,A+B=∵=cosA﹣sinB==﹣sinB==∵∴∴∴∴∴20.(12分)在△ABC中,内角A、B、C的对边分别为a、b、c,已知.(1)求的值;(2)若,b=2,求△ABC的面积.【解答】解:(1)∵==,∴cosAsinB﹣2sinBcosC=2cosBsinC﹣sinAcosB,∴sinAcosB+cosAsinB=2sinBcosC+2cosBsinC,∴sin(A+B)=2sin(B+C),∴sinC=2sinA,∴=2;(2)由(1)可得c=2a,由余弦定理可得b2=a2+c2﹣2accosB,∴4=a2+4a2﹣a2,解得a=1,则c=2,∵cosB=,∴sinB=,∴S=acsinB=×1×2×=.21.(12分)解关于x的不等式ax2﹣(a+1)x+1>0.【解答】解:当a=0时,原不等式可化为﹣x+1>0,即x<1﹣﹣﹣﹣﹣﹣﹣(2分)当a<0时,原不等式可化为(ax﹣1)(x﹣1)>0,即(x﹣)(x﹣1)<0.所以<x<1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)当a>0时,原不等式可化为(x﹣)(x﹣1)>0方程(x﹣)(x﹣1)=0的两根为,1,其解的情况应由与1的大小关系决定,故(1)当>1,即0<a<1时,有x>或x<1;﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(2)当,即a>时,有x>1或x<;﹣﹣﹣﹣﹣﹣﹣﹣(8分)(3)当=1,即a=1时,有x≠1;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)综上所述:当a<0时,原不等式解集为{x|<x<1};当a=0时,原不等式解集为{x|x<1};当0<a<1时,原不等式解集为{x|x<1或x>};当a=1时,原不等式解集为{x|x∈R且x≠1};当a>1时,原不等式解集为{x|x<或x>1}.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)22.(12分)已知数列{a n}的前n项和为S n,且S n=2n2+n,n∈N,数列{b n}满足a n=4log2b n+3,n∈N.(1)求a n,b n;(2)求数列{a n b n}的前n项和T n.【解答】解:(1)由可得,当n=1时,a1=S1=3,当n≥2时,,而n=1,a1=4﹣1=3适合上式,故a n=4n﹣1,又∵a n=4log2b n+3=4n﹣1,∴…(6分)(2)由(1)知,,,∴==(4n﹣1)•2n﹣[3+4(2n﹣2)]=(4n﹣5)•2n+5.…(12分)。
安徽省淮北市数学高二上学期理数期中考试试卷

安徽省淮北市数学高二上学期理数期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2018高一上·阜城月考) 已知,,三点共线,则k的取值是()A . -6B . -7C . -8D . -92. (2分)如图所示,该直观图表示的平面图形为()A . 钝角三角形B . 锐角三角形C . 直角三角形D . 正三角形3. (2分) (2019高二上·双流期中) 已知实数x , y满足方程x2+y2-8x+15=0.则x2+y2最大值为()A . 3B . 5C . 9D . 254. (2分)直线过点且与直线垂直,则的方程为()A .B .C .D .5. (2分) (2018高一下·三明期末) 在空间直角坐标系中,若点,,点是点关于平面的对称点,则()A .B .C .D .6. (2分)(2019·凌源模拟) 设直线与圆相交于两点,且,则圆的面积为()A .B .C .D .7. (2分)一个多面体的直观图、主视图、左视图、俯视图如下,M、N分别为A1B、B1C1的中点.下列结论中正确的个数有()①直线MN与A1C 相交.②MN BC.③MN//平面ACC1A1 .④三棱锥N-A1BC的体积为.A . 4个B . 3个C . 2个D . 1个8. (2分)椭圆的离心率为,右焦点为,方程的两个实根分别为和,则点()A . 必在圆内B . 必在圆上C . 必在圆外D . 以上三种情形都有可能9. (2分) (2017高二下·辽宁期末) 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是()A . 3B . 4C .D . 710. (2分)(2017·长沙模拟) 点P为棱长是的正方体ABCD﹣A1B1C1D1的内切球O球面上的动点,点M为B1C1的中点,若满足DP⊥BM,则动点P的轨迹的长度为()A . πB . 2πC . 4πD .二、填空题 (共5题;共5分)11. (1分) (2018高二上·苏州月考) 过点,且与直线垂直的直线方程为________.12. (1分)(2018·兴化模拟) 如图,棱长均为2的正四棱锥的体积为________.13. (1分) (2017高一下·扶余期末) 过两点A ,B 的直线l的倾斜角为45°,则m=________.14. (1分) (2018高一上·兰州期末) 如图,在长方体中, 3 cm, 2 cm,1 cm,则三棱锥的体积为________cm3 .15. (1分) (2019高一下·朝阳期末) 已知直线与圆交于两点,若,则 ________.三、解答题 (共5题;共40分)16. (5分) (2018高二上·北京月考) 求与圆同心,且与直线相切的圆的方程17. (15分) (2017高二上·汕头月考) 如图1,在直角梯形中,,,且.现以为一边向形作正方形,然后沿边将正方形翻折,使平面与平面垂直,为的中点,如图2.(1)求证:平面;(2)求证:平面;(3)求点到平面的距离.18. (5分)已知实数x,y满足方程x2+y2﹣4x+1=0,求的最大值和最小值.19. (5分) (2019高二上·九台月考) 判断圆与的位置关系.20. (10分)(2018·全国Ⅱ卷理) 如图,在三角锥中,, ,为的中点.(1)证明:平面 ;(2)若点在棱上,且二面角为,求与平面所成角的正弦值.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题;共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题;共40分) 16-1、17-1、17-2、17-3、18-1、19-1、20-1、第11 页共11 页。
安徽省淮北市数学高二上学期理数期中考试试卷

安徽省淮北市数学高二上学期理数期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)已知直线和直线,抛物线上一动点P到直线和直线的距离之和的最小值是()A . 2B . 3C .D .2. (2分)设,是向量,命题“若=﹣,则||=||”的逆命题是()A . 若≠,则||≠||B . 若=﹣,则||≠||C . 若||≠||,则≠﹣D . 若||=||,则=﹣3. (2分)若点O和点F分别为椭圆的中心和左焦点,点P为椭圆上的任意一点,则的最大值为()A . 8B . 6C . 3D . 24. (2分) (2017高二下·湖北期中) 已知函数f(x)=x2+ ,则“a<2”是“函数f(x)在(1,+∞)上为增函数”的()A . 充分而不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件5. (2分) (2018高二上·宁夏期末) 设直线L过双曲线C的一个焦点,且与C的一条对称轴垂直,L与C 交于A ,B两点,为C的实轴长的2倍,则C的离心率为()A .B .C . 2D . 36. (2分)己知抛物线的焦点F恰好是双曲线的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为()A .B .C .D .7. (2分)已知抛物线y2=4x的准线与x轴的交点为A,焦点为F,l是过点A且倾斜角为的直线,则点F到直线l的距离等于()A . 1B .C . 2D .8. (2分)如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=,则下列结论中错误的是()A . AC⊥BFB . 三棱锥A﹣BEF的体积为定值C . EF∥平面ABCDD . 面直线AE、BF所成的角为定值9. (2分)已知双曲线的左、右焦点分别是,正三角形的一边与双曲线左支交于点,且,则双曲线的离心率的值是()A .B .C .D .10. (2分)若抛物线的焦点与椭圆的右焦点重合,则的值为()A . -2B . 2C . -4D . 411. (2分)(2017·揭阳模拟) 已知双曲线 =1(a>0,b>0),点A、F分别为其右顶点和右焦点,B1(0,b),B2(0,﹣b),若B1F⊥B2A,则该双曲线的离心率为()A .B .C .D .12. (2分) (2019高二上·开封期中) 已知椭圆的上顶点为,左、右两焦点分别为、,若为等边三角形,则椭圆的离心率为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2018高二上·浙江月考) 定长为3的线段的端点、在抛物线上移动,则的中点到轴的距离的最小值为________,此时中点的坐标为________.14. (1分) (2017高二下·西安期末) 由命题“存在x∈R,使x2+2x+m≤0”是假命题,则实数m的取值范围为________.15. (1分)若=(2,﹣3,),=(1,0,0),则<•>=________16. (1分)过抛物线的焦点作一条直线交抛物线于A,B两点,若线段AB的中点M的横坐标为2,则等于________.三、解答题 (共6题;共47分)17. (2分)(2017·海淀模拟) 对于无穷数列{an},记T={x|x=aj﹣ai , i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*且m>k),必有am+1﹣ak+1=t”,则称数列{an}具有性质P(t).(Ⅰ)若数列{an}满足判断数列{an}是否具有性质P(2)?是否具有性质P(4)?(Ⅱ)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;(Ⅲ)已知{an}是各项为正整数的数列,且{an}既具有性质P(2),又具有性质P(5),求证:存在整数N,使得aN , aN+1 , aN+2 ,…,aN+k ,…是等差数列.18. (10分)双曲线满足如下条件:①;②过右焦点F的直线l的斜率为,交y轴于点P ,线段PF交双曲线于点Q ,且|PQ|∶|QF|=2∶1;求双曲线的方程.19. (5分) (2016高二上·邗江期中) 已知椭圆(a>b>0)的离心率为,以原点为圆心,椭圆的短半轴为半径的圆与直线相切.(Ⅰ)求椭圆C的方程;(Ⅱ)设P(4,0),M,N是椭圆C上关于x轴对称的任意两个不同的点,连接PN交椭圆C于另一点E,求直线PN的斜率的取值范围;(Ⅲ)在(Ⅱ)的条件下,证明直线ME与x轴相交于定点.20. (10分)(2018·安徽模拟) 如图,已知四棱锥的底面是菱形,平面,点为的中点。
2017-2018学年安徽省淮北一中高二上学期期中考试数学理试题 解析版

淮北一中2017-2018学年高二上学期期中考试数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知0,>y x ,且211=+yx ,则y x 2+的最小值为( ) A .223- B .2223- C .223+ D .2223+ 2.离心率为23,且过点)0,2(的椭圆的标准方程是( ) A .1422=+y x B .1422=+y x 或1422=+y x C .1422=+y x D .1422=+y x 或116422=+y x 3.在ABC ∆中,cc a B 22cos2+=(c b a ,,分别为角C B A ,,的对边),则ABC ∆的形状为( ) A .直角三角形 B .等边三角形 C .等腰三角形 D .等腰三角形或直角三角形4.执行如图所示的程序框图,如果输出94=S ,则输入的=n ( )A .3B .4 C. 5 D .65.如图,在ABC ∆中,→→→→==BD BP AC AD 31,32,若→→→+=AC AB AP μλ,则μλ的值为( )A .3-B .2- C. 2 D .36.由公差为d 的等差数列,...,,321a a a 重新组成的数列...,,635241a a a a a a +++是( ) A .公差为d 的等差数列 B .公差为d 2的等差数列 C. 公差为d 3的等差数列 D .非等差数列7.抛物线22x y =的焦点到准线的距离为( ) A .81 B .21 C. 41D .4 8.如角α满足0cos 2sin =+αα,则=α2tan ( ) A .34-B .43 C. 43- D .34 9.已知抛物线x y C 4:2=的焦点为F ,准线为l ,点l A ∈,线段AF 交抛物线C 于点B ,若→→=FB FA ,则=→||AF ( )A .3B .4 C. 6 D .7 10.数列}{n a 的通项公式为*,2cosN n n a n ∈=π,其前n 项和为n S ,则=2017S ( ) A .1008 B .1008- C. 1- D .011.已知椭圆)0(12222>>=+b a by a x 的两个焦点分别为21,F F ,若椭圆上不存在点P ,使得21PF F ∠是钝角,则椭圆离心率的取值范围是( )A .]22,0( B .)1,22[C. )21,0( D .)1,21[ 12.已知函数⎪⎩⎪⎨⎧≥+-<=0|,1221|0,2)(2x x x x x f x方程)0(0)()]([2≠=+-b b x af x f 有6个不同的实根,则b a +3取值范围( )A .)11,6[ B .)11,3[ C. )11,6( D .)11,3( 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.命题“02,≥∈∃x R x ”的否定是 .14.在数列}{n a 中,已知其前n 项和为32+=n n S ,则=n a .15.设实数y x ,满足⎪⎩⎪⎨⎧≤-+≤-+≥-+0102014206y x y x y x ,则xy 2的最大值为 .16.下列命题中,假命题的序号有 .(1)“1-=a ”是“函数)(|1|)(2R x a x x x f ∈+++=为偶函数”的充要条件; (2)“直线l 垂直平面a 内无数条直线”是“直线l 垂直平面a ”的充分条件; (3)若0=xy ,则0||||=+y x ;(4)若022,:0200≤++∈∃x x R x p ,则022,:2>++∈∀⌝x x R x p .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知函数1)1()(2++-=x aa x x f . (1)当2=a 时,解关于x 的不等式0)(≤x f ; (2)若0>a ,解关于x 的不等式0)(≤x f . 18. 设数列}{n a 满足n a n a a n 2)12(321=-+++ . (1)求}{n a 的通项公式; (2)求数列}12{+n a n的前n 项和. 19. 已知函数x x x x f 2cos 2)62sin()62sin()(+-++=ππ. (1))(x f 的最小正周期和单调递增区间;(2)已知c b a ,,是ABC ∆三边长,且ABC C f ∆=,2)(的面积7,310==c S .求角C 及b a ,的值.20. 已知椭圆)0(1:2222>>=+b a by a x C ,其长轴为4,短轴为2.(1)求椭圆C 的方程及离心率.(2)直线l 经过定点)2,0(,且与椭圆C 交于B A ,两点,求OAB ∆面积的最大值. 21. 已知数列}{n a 满足11=a ,且n n n a a 221+=-(2≥n 且*N n ∈). (1)求数列}{n a 的通项公式;(2)设数列}{n a 的前n 项之和n S ,求证:322->n S nn. 22. 已知过抛物线)0(2:2>=p px y C 的焦点F ,斜率为2的直线交抛物线于))(,(),,(212211x x y x B y x A <两点,且6||=AB .(1)求该抛物线C 的方程;(2)已知抛物线上一点)4,(t M ,过点M 作抛物线的两条弦MD 和ME ,且ME MD ⊥,判断直线DE 是否过定点?并说明理由.淮北一中2017-2018学年高二上学期期中考试数学(理科)参考答案1.D 【解析】由得,,因为,,所以(当且仅当时等号成立),故选D.【易错点晴】本题主要考查利用基本不等式求最值,属于中档题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立). 2.D【解析】当椭圆的焦点在x 轴上,设椭圆的方程为,由离心率为,∴∵椭圆过点(2,0),∴,∴a 2=4,∴b 2=1,∴椭圆标准方程为当椭圆的焦点在y 轴上,同理易得:故选D. 3.A【解析】21cos cos 222B B a cc ++== ,222cos 2a c b a B ac c+-∴==,解得222a b c +=,即角C 为直角,则ABC ∆的形状为直角三角形,故选A.4.B【解析】该程序框图表示的是通项为()()()()111212122121n a n n n n ⎛⎫== ⎪ ⎪-+-+⎝⎭的前n 项和,1111111...23352121n S n n ⎛⎫=-+-++- ⎪-+⎝⎭11122121n n n ⎛⎫=-= ⎪++⎝⎭, 输出结果为49,4219n n ∴=+,得4n =,故选B. 5.D 【解析】,,又,,故选D.6.B【解析】设新数列14253,,...a a a a a a +++的第n 项是n b ,则3n n n b a a +=+=()()()11212221a n d n d a n d +-++=++,12n n b b d +∴-=,∴此新数列是以2d 为公差的等差数列,故选B.【方法点晴】本题主要考查等差数列的定义、等差数列通项公式,属于难题.判定一个数列为等差数列的常见方法是:(1) 定义法:1n n a a d +-=(d 是常数),则数列{}n a 是等差数列(2) 等差中项法:1+22=+n n n a a a +(*n N ∈),则数列{}n a 是等差数列;(3) 通项公式:=n a pn q + (,p q 为常数), 则数列{}n a 是等差数列;(4) 前n 项和公式:2n S An Bn =+(,A B 为常数) , 则数列{}n a 是等差数列.本题先利用方法(1)判定出数列{}n a 是等差数列后再进行解答的. 7.C【解析】由22y x =得:212x y =,所以122p =,14p =,即焦点到准线的距离为14p =,故选C. 8.D【解析】由题意可得,选D.9.B【解析】由已知B为AF 的三等分,作BH l ⊥于H ,如图,则244,333BH FK BF BH ==∴== ,34AF BF ∴== ,故选B.10.D【解析】41234201714,05040n n T T a a T S a a a a S S a +=∴==+++=∴=+= 选D.11.A【解析】设B 为短轴端点,则1212F PF F BF ∠≤∠,由题意得22212π21022c F BF c a c e b ∠≤⇒≤⇒≤-⇒<≤,选A 。
安徽省淮北市高二数学上学期期中联考试题(扫描版)(new)

安徽省淮北市三校2017-2018学年高二数学上学期期中联考试题(扫描版)三校联考高二数学答案选择题:1—12:DDCABC CABDBA填空题:13—16:(-1,0),103,2017,6π 解答题:17。
解:(1)当111,0.n a S ===当12,23n n n n a S S n -≥=-=-因为1n =不适合0,123,2n n a n n =⎧∴=⎨-≥⎩......................................................5分 (2)2242143. (22)n n a a a n n n +-+++=⨯=-……………………………10分 18、解: 原不等式可化为: (1)当时, 即,原不等式的解集 ……………………………6分 (2)当时, ①,原不等式的解集 ②, 原不等式的解集 ③,原不等式的解集 ………………………12分19解(Ⅰ)因为a ,b,c 成等差数列,所以a+c=2b, 又c a 2=,可得c b 23=, 所以412324492cos 2222222-=⨯-+=-+=c c c c bc a c b A , ………………………6分 (Ⅱ)由(Ⅰ)41cos -=A ,),(π0∈A ,所以415sin =A , 因为,sin 214153A bc S S ABC ABC ==∆∆, 所以41534152321sin 212=⨯==∆c A bc S ABC ,得42=c ,即3,2==b c …………………………………………………12分20。
(Ⅰ)331315468d q d q ⎧++=⎨+-=⎩所以22d q =⎧⎨=⎩ 1212n n n a n b -∴=-=,.。
..。
..。
.。
...。
.。
.。
.。
..。
.。
..。
..。
.。
.。
...。
.。
..。
....。
6分 (Ⅱ)错位相减得n 12362n n T -+=-…………………………………………12分 21(1)0sin 3cos =--+c a C b C b 得sin cos sin sin()sin 0B C B C B C C +-+-=sin cos sin sin 0B C B C C --=cos 1B B -=即3B π= …………………………………………………………………。
安徽省淮北市高二上学期期中数学试卷

安徽省淮北市高二上学期期中数学试卷姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) 说出下列三视图表示的几何体是A . 正六棱柱 B . 正六棱锥 C . 正六棱台 D . 正六边形2. (2 分) 直线的倾斜角为( )A . 150ºB . 120ºC . 60ºD . 30º3. (2 分) 在空间四边形 ABCD 中,平面 ABD⊥平面 BCD,且 DA⊥平面 ABC,则△ABC 的形状是( )A . 锐角三角形 B . 直角三角形 C . 钝角三角形 D . 不能确定第 1 页 共 14 页4. (2 分) 两直线与的位置关系是( )A . 相交B . 平行C . 重合D . 平行或重合5. (2 分) 已知 为两条不同直线, 为两个不同平面,则下列命题中不正确的是( )A.若,则B.若,则C.若,则D.若,则6. (2 分) 过点且平行于直线A.B.C.D.7. (2 分) 已知向量 满足的直线方程为( ),,则的最小值为( )A. B. C. D.第 2 页 共 14 页8. (2 分) 正四面体(四个面都为正三角形)ABCD 中,异面直线 AB 与 CD 所成的角为( ) A . 90° B . 60° C . 45° D . 30°9. (2 分) 若圆 斜角的取值范围是( )上至少有三个不同的点到直线的距离为 ,则直线 的倾A.B. C.D. 10. (2 分) 直线 A.1 B. C.2 D.3, 当此直线在 轴的截距和最小时,实数 的值是( )11. (2 分) 在如图所示的圆锥中,平面 ABC 是轴截面,底面圆 O'的面积为 4π,∠ABC= 接球的表面积为( ),则该圆锥的外第 3 页 共 14 页A.B.C. D . 32π12. (2 分) 若点为圆的弦 MN 的中点,则弦 MN 所在直线方程为( )A.B.C.D.二、 填空题 (共 4 题;共 4 分)13. (1 分) (2019 高二下·上海月考) 正四棱柱底面所成的角的大小为,则正四棱柱的底面边长,若直线与的侧面积为________14. (1 分) 已知 l1 , l2 是分别经过 A(2,1),B(0,2)两点的两条平行直线,当 l1 , l2 之间的距离 最大时,直线 l1 的方程是________15. (1 分) (2016 高一上·清远期末) 已知直线 l 过点(1,﹣1),且在 y 轴上的截距为 方程为________.,则直线 l 的16.(1 分)直线 x+3y﹣7=0 与圆 x2+y2+2x﹣2y﹣3=0 的交点 A,B,则过 A,B 两点且过原点的圆的方程________.三、 解答题 (共 6 题;共 45 分)第 4 页 共 14 页17. (5 分) (2017·莱芜模拟) 已知四棱锥 P﹣ABCD 中,底面 ABCD 是菱形,∠BAD=60°,AB=PB=PD=2,PA= .(Ⅰ)求证:BD⊥PC; (Ⅱ)若 E 是 PA 的中点,求三棱锥 P﹣BCE 的体积. 18. (10 分) (2017 高一上·嘉峪关期末) △ABC 中,A(0,1),AB 边上的高 CD 所在直线的方程为 x+2y﹣4=0, AC 边上的中线 BE 所在直线的方程为 2x+y﹣3=0. (1) 求直线 AB 的方程,并把它化为一般式; (2) 求直线 BC 的方程,并把它化为一般式. 19. (5 分) 如图,正方形 ADEF 与梯形 ABCD 所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,点 M 在线段 EC 上.(Ⅰ)当点 M 为 EC 中点时,求证:BM∥平面 ADEF;(Ⅱ)当平面 BDM 与平面 ABF 所成锐二面角的余弦值为时,求棱锥 M﹣BDE 的体积.20. (10 分) (2017·陆川模拟) 如图所示,已知长方体 ABCD 中, 沿 AM 折起,使得 AD⊥BM为 DC 的中点.将△ADM第 5 页 共 14 页(1) 求证:平面 ADM⊥平面 ABCM;(2) 是否存在满足 数 t;若不存在,请说明理由.的点 E,使得二面角 E﹣AM﹣D 为大小为 .若存在,求出相应的实21. (5 分) (2017 高一下·濮阳期末) 已知圆 C:x2+y2+2x+a=0 上存在两点关于直线 l:mx+y+1=0 对称.(I)求 m 的值;(Ⅱ)直线 l 与圆 C 交于 A,B 两点, • =﹣3(O 为坐标原点),求圆 C 的方程.22. (10 分) (2019 高二上·安徽月考) 已知三棱锥中:,,, 是 的中点, 是 的中点.(1) 证明:平面 (2) 求点 到平面平面;的距离.第 6 页 共 14 页一、 选择题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 14 页16-1、三、 解答题 (共 6 题;共 45 分)17-1、 18-1、第 8 页 共 14 页18-2、19-1、第 9 页 共 14 页第 10 页 共 14 页20-1、20-2、21-1、22-1、22-2、。
安徽省淮北市高二上学期期中数学试卷(理科)

安徽省淮北市高二上学期期中数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2016·城中模拟) 已知集合M={x| =1},函数f(x)=ln(1﹣|x|)的定义域为N,则M∩N 为()A . ∅B . (0,3)C . (﹣1,1)D . (﹣1,0]2. (2分)若直线经过两点,则直线的倾斜角为()A .B .C .D .4. (2分)执行如图所示的程序框图,则输出的c的值是()A . 8B . 13C . 21D . 345. (2分)若点和点到直线的距离依次为和,则这样的直线有()A . 条B . 条C . 条D . 条6. (2分)将直线x+y-1=0绕点(1,0)沿逆时针方向旋转15°得到直线l,则直线l与圆(x+3)2+y2=4的位置关系是()A . 相交B . 相切C . 相离D . 相交或相切7. (2分) (2016高二上·绍兴期中) 某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()A .B .C .D .8. (2分) (2018高二上·万州月考) 在正四面体ABCD中,E,F分别为AB,CD的中点,则EF与AC所成角为()A . 90°B . 60°C . 45°D . 30°9. (2分)设直线l过点(﹣3,0),且与圆x2+y2=1相切,则l的斜率是()A . ±B . ±C . ±D . ±10. (2分) (2015高一下·衡水开学考) 正方体ABCD﹣A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么,正方体的过P、Q、R的截面图形是()A . 三角形B . 四边形C . 五边形D . 六边形11. (2分) (2018高三上·沈阳期末) 若直线:被圆截得的弦最短,则直线的方程是()A .B .C .D .12. (2分)(2018·吉林模拟) 四棱锥PABCD的三视图如图所示,四棱锥PABCD的五个顶点都在一个球面上,E , F分别是棱AB , CD的中点,直线EF被球面所截得的线段长为2 ,则该球的表面积为()A . 12πB . 24πC . 36πD . 48π二、二.填空题 (共4题;共6分)13. (1分) (2018高二上·临汾月考) 过点的直线与过点的直线垂直,则 ________.14. (1分)(2018·茂名模拟) 从原点O向圆C:作两条切线,则该圆被两切点所分的劣弧与优弧之比为________.15. (1分)如图,球O的半径为5,一个内接圆台的两底面半径分别为3和4(球心O在圆台的两底面之间),则圆台的体积为________.16. (3分)(2012·陕西理) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)A.(不等式选做题)若存在实数x使|x﹣a|+|x﹣1|≤3成立,则实数a的取值范围是________.B.(几何证明选做题)如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,则DF•DB=________.C.(坐标系与参数方程)直线2ρcosθ=1与圆ρ=2cosθ相交的弦长为________.三、三.解答题 (共6题;共55分)17. (10分) (2016高一下·钦州期末) 已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x ﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.18. (10分)(2017·天心模拟) 如图,三棱柱ABC﹣A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=CC1=2,M是AB的中点.(1)求证:平面A1CM⊥平面ABB1A1;(2)求点M到平面A1CB1的距离.19. (10分) (2018高二上·舒兰月考) 设数列的前n项和为,且,数列满足,.(1)求数列{an}和{bn}的通项公式;(2)求数列{bn}的前n项和Tn.20. (10分) (2019高一下·宿迁期末) 如图,已知圆与轴交于两点(在的上方),直线.(1)当时,求直线被圆截得的弦长;(2)若,点为直线上一动点(不在轴上),直线的斜率分别为,直线与圆的另一交点分别.①问是否存在实数,使得成立?若存在,求出的值;若不存在,说明理由;②证明:直线经过定点,并求出定点坐标.21. (5分) (2016高二下·黑龙江开学考) 在四棱柱ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2.(Ⅰ)求证:AD1⊥B1C;(Ⅱ)求二面角A1﹣BD﹣C1的正弦值.22. (10分) (2018高一下·百色期末) 如图,已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点,是的中点.(1)求圆的方程;(2)当时,求直线的方程.参考答案一、选择题 (共12题;共24分)1-1、2-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、二.填空题 (共4题;共6分)13-1、14-1、15-1、16-1、三、三.解答题 (共6题;共55分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、。
安徽省淮北市高二上学期期中数学试卷(理科)

安徽省淮北市高二上学期期中数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知命题,则为()A .B .C .D .2. (2分)命题“若≠,则且”的逆否命题是()A . 若≠,则≠且≠B . 若≠,则≠或≠C . 若且,则≠D . 若≠或≠,≠3. (2分) (2017高一下·鹤岗期末) 如图,在正四棱锥中,分别是的中点,动点在线段上运动时,下列四个结论:① ;② ;③ 面;④ 面 .其中恒成立的为()A . ①③B . ③④C . ①②D . ②③④4. (2分) (2016高三上·杭州期中) 在△ABC中,“sinB=1”是“△ABC为直角三角形”的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件5. (2分) (2015高二上·怀仁期末) 以下命题:①若x≠1或y≠2,则x+y≠3;②若空间向量,与空间中任一向量都不能组成空间的一组基底,则与共线;③命题“∃x∈R,使得x2+x+1<0”的否定是:“∀x∈R,均有x2+x+1<0”;④若A、B为两个定点,K为正常数,若|PA|+|PB|=K,则动点P的轨迹是椭圆;⑤已知抛物线y2=2px,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.其中真命题有()个.A . 1B . 2C . 3D . 46. (2分)已知平面α和直线l,则在平面α内至少有一条直线与直线l()A . 平行B . 垂直C . 相交D . 以上都有可能7. (2分)下列说法错误的是()A . 命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0”B . 若命题p:∃x0∈R,+x0+1<0,则:∀x∈R,x2+x+1≥0C . 若x,y∈R,则“x=y”是“xy≥ ”的充要条件D . 已知命题p和q,若“p或q”为假命题,则命题p与q中必有一真一假8. (2分)某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是两个全等等腰三角形)根据图中标出的数据,可得这个几何体的表面积为()A .B .C .D . 129. (2分)如果底面直径和高相等的圆柱的侧面积是S,那么圆柱的体积等于()A .B .C .D .10. (2分) (2017高三下·赣州期中) 如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= CC1 ,则异面直线A1E与AF所成角的余弦值为()A .B .C .D .11. (2分)已知E、F分别为正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,设α为二面角D﹣AE﹣D1的平面角,求sinα=()A .B .C .D .12. (2分) (2019高二上·湖南期中) 已知圆柱的高为,它的两个底面的圆周在半径为的同一个球的球面上.则球的体积与圆柱的体积的比值为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) A、B是直线l上的两点,AB=4,AC⊥l于A,BD⊥l于B,AC=BD=3,又AC与BD成60°的角,则C、D两点间的距离是________14. (1分) (2016高一上·饶阳期中) 给出下列四个命题:①函数y=|x|与函数y=()2表示同一个函数;②奇函数的图象一定通过直角坐标系的原点;③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;④y=2|x|的最小值为1⑤对于函数f(x),若f(﹣1)•f(3)<0,则方程f(x)=0在区间[﹣1,3]上有一实根;其中正确命题的序号是________(填上所有正确命题的序号)15. (1分) (2016高二上·重庆期中) 若一个圆台的正视图如图所示,则其体积等于________.16. (1分) (2015高一上·福建期末) 已知一个空心密闭(表面厚度忽略不计)的正四面体工艺品的棱长为,若在该工艺品内嵌入一个可以在其内部任意转动的正方体,则正方体棱长的最大值为________.三、解答题 (共6题;共60分)17. (5分)已知命题p:指数函数y=(a﹣1)x在R上是单调函数;命题q:∃x∈R,x2﹣(3a﹣2)x+1=0.若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.18. (15分) (2019高一上·葫芦岛月考) 设 .(1)若是的必要不充分条件,求的取值范围;(2)若是的充分不必要条件,求的取值范围;(3)若是方程的根,判断是的什么条件.19. (10分)(2017·唐山模拟) 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.(1)求证:PA⊥平面ABCD;(2)求直线BF与平面AFD所成角的正弦值.20. (5分)如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD 的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE.21. (15分) (2016高二上·宜昌期中) 已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:DN∥平面PMB;(2)证明:平面PMB⊥平面PAD;(3)求点A到平面PMB的距离.22. (10分)如图所示的三棱台中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.(1)证明:AB1⊥平面BCC1B1;(2)若点D为CC1中点,求二面角A﹣BD﹣C的余弦值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分)17-1、18-1、18-2、18-3、19-1、19-2、20-1、21-1、21-2、21-3、22-1、22-2、。
淮北一中2017--2018学年度第一学期期中考试高二年级数学试卷含答案
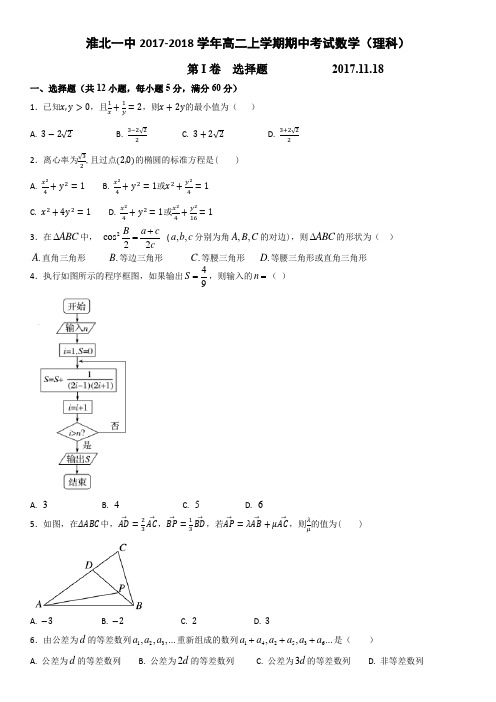
淮北一中2017-2018学年高二上学期期中考试数学(理科)第I 卷选择题 2017.11.18一、选择题(共12小题,每小题5分,满分60分)1.已知x ,y >0,且1x+1y =2,则x +2y 的最小值为( )A. 3−2 2B.3−2 22C. 3+2 2D.3+2 222.离心率为 32,且过点(2,0)的椭圆的标准方程是( ) A.x 24+y 2=1 B.x 24+y 2=1或x 2+y 24=1 C. x 2+4y 2=1 D. x 24+y 2=1或x 24+y 216=13.在ABC ∆中,(,,a b c 分别为角,,A B C 的对边),则ABC ∆的形状为( ) .A 直角三角形 .D 等腰三角形或直角三角形49,则输入的n =( )A. 3B. 4C. 5D. 65.如图,在ΔABC 中,AD →=23AC →,BP →=13BD →,若AP →=λAB →+μAC →,则λμ的值为( )A. −3B. −2C. 2D. 37.抛物线22y x =的焦点到准线的距离为( )A.B.C. D. 4 8.若角α满足sin α+2cos α=0,则tan2α=( ) A. −43B. 34C. −34D. 439.已知抛物线2:4C y x =的焦点为F ,准线为l ,点A l ∈,线段AF 交抛物线C 于点B ,若3F A F B = ,()A. 3B. 4C. 6D. 710.数列{}n a 的通项公式为,其前n 项和为n S ,则2017S =( ) A. 1008B. 1008- C. 11.已知椭圆22221x y a b+=(0)a b >>的两个焦点分别为12,F F ,若椭圆上不存在点P ,使得12F PF ∠是钝角,则椭圆离心率的取值范围是( ) A. 0,2⎛⎝⎦ B. 12) C. 10,2⎛⎫⎪⎝⎭ D. 1,12⎡⎫⎪⎢⎣⎭12方程()()()200f x af x b b ⎡⎤-+=≠⎣⎦有6个不同的实根,则3a b +取值范围( )A. [)6,11B. [)3,11C. ()6,11 D. ()3,11 第Ⅱ卷非选择题二、填空题:(本大题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年安徽省淮北市实验高级中学高二(上)期中数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是()A.B.C.A1A2+B1B2=0 D.A1A2﹣B1B2=02.(5分)数列{a n}是等差数列,a2=4,a7=19,则a31=()A.91 B.88 C.94 D.853.(5分)下列命题中,正确的是()A.若a>b,c>d,则ac>bc B.若ac>bc,则a>bC.若<,则a<b D.若a>b,c>d,则a﹣c>b﹣d4.(5分)在△ABC中,若(a+c)(a﹣c)=b(b+c),则∠A=()A.90°B.60°C.120° D.150°5.(5分)已知非零实数a,b满足成等比数列,则ab的取值范围是()A.(﹣∞,2]B.(﹣2,2]C.[2,+∞)D.(0,2]6.(5分)若不等式f(x)=ax2﹣x﹣c>0的解集{x|﹣2<x<1},则函数y=f(﹣x)的图象为()A.B.C.D.7.(5分)已知实数x,y满足不等式组,则z=4x﹣6y的最小值为()A.﹣33 B.﹣10 C.﹣8 D.108.(5分)设数列{b n}满足:b1=,b n+1=(n≥1),则b2018=()A.3 B.7 C.2018 D.20179.(5分)设x>﹣1,则的最小值为()A.4 B.9 C.7 D.1310.(5分)在△ABC中,三个内角A,B,C所对的边为a,b,c,若S△ABC=2,a+b=6,=2cosC,则c=()A.2 B.4 C.2 D.311.(5分)已知不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,求实数a的取值范围()A.()B.(]C.()∪[1,+∞)D.()∪(1,+∞)12.(5分)在△ABC中,已知0,AC≥AB,点M,N分别是边AC,AB 的中点,且的最大值是,则=()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的解集是.14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为.15.(5分)如果满足∠ABC=60°,AC=12,BC=k的三角形恰有一个,那么k的取值范围是.16.(5分)已知数列{a n}满足a n+2=3a n+1﹣2a n(n∈N*),且a1=1,a2=4,其前n 项和为S n,若对任意的正整数n,S n+2n+m•2n≥0恒成立,则实数m的取值范围是.三、解答(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)17.(10分)设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x 满足2<x≤3.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.18.(12分)设x,y满足条件.(1)求u=x2+y2的最大值与最小值;(2)求v=的最大值与最小值.19.(12分)已知数列{a n}的前n项和为S n,且满足2a n=S n+1(n∈N*)(1)求数列{a n}的通项公式;(2)若b n=(2n+1)•a n,求数列{b n}的前n项和T n.20.(12分)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.(Ⅰ)求角A的值;(Ⅱ)若a=,求b+c的取值范围.21.(12分)已知各项都为正数的等比数列{a n}满足是3a1与2a2的等差中项,且a1a2=a3.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a n,且S n为数列{b n}的前n项和,求数列{}的前7项和T7.22.(12分)△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.2017-2018学年安徽省淮北市实验高级中学高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是()A.B.C.A1A2+B1B2=0 D.A1A2﹣B1B2=0【解答】解:两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直⇔A1A2+B1B2=0,故两条直线A1x+B1y+C1=0,A2x+B2y+C2=0互相垂直的充分必要条件是A1A2+B1B2=0,故选:C.2.(5分)数列{a n}是等差数列,a2=4,a7=19,则a31=()A.91 B.88 C.94 D.85【解答】解:设等差数列{a n}的公差为d,∵a2=4,a7=19,∴a1+d=4,a1+6d=19,解得a1=1,d=3.则a31=1+3×30=91.故选:A.3.(5分)下列命题中,正确的是()A.若a>b,c>d,则ac>bc B.若ac>bc,则a>bC.若<,则a<b D.若a>b,c>d,则a﹣c>b﹣d【解答】解:令a=1,b=﹣1,c=﹣1,d=﹣5,显然A、D不成立,对于B:若c<0,显然不成立,对于C:由c2>0,得:a<b,故C正确,故选:C.4.(5分)在△ABC中,若(a+c)(a﹣c)=b(b+c),则∠A=()A.90°B.60°C.120° D.150°【解答】解:由(a+c)(a﹣c)=b(b+c)变形得:a2﹣c2=b2+bc,即a2=c2+b2+bc根据余弦定理得cosA===﹣,因为A为三角形的内角,所以∠A=120°.故选:C.5.(5分)已知非零实数a,b满足成等比数列,则ab的取值范围是()A.(﹣∞,2]B.(﹣2,2]C.[2,+∞)D.(0,2]【解答】解:∵成等比数列,∴()2==ab>0,又a2+b2≥2ab,当且仅当a=b时取等号,∴ab≥,即(ab)2﹣2ab≥0,分解因式得:ab(ab﹣2)≥0,解得:ab≤0(舍去)或ab≥2,则ab的取值范围是[2,+∞).故选:C.6.(5分)若不等式f(x)=ax2﹣x﹣c>0的解集{x|﹣2<x<1},则函数y=f(﹣x)的图象为()A.B.C.D.【解答】解:由已知得,﹣2,1是方程ax2﹣x﹣c=0的两根,分别代入,解得a=﹣1,c=﹣2.∴f(x)=﹣x2﹣x+2.从而函数y=f(﹣x)=﹣x2+﹣x+2=﹣(x﹣2)(x+1)它的图象是开口向下的抛物线,与x轴交与(﹣1,0)(2,0)两点.故选:B.7.(5分)已知实数x,y满足不等式组,则z=4x﹣6y的最小值为()A.﹣33 B.﹣10 C.﹣8 D.10【解答】解:先根据约束条件画出可行域:z=4x﹣6y,将最小值转化为y轴上的截距,由,解得A(,)当直线z=4x﹣6y经过A(,)时,z最小,最小值为:﹣33,即当x=,y=,4x﹣6y取得最小值﹣33.故选:A.8.(5分)设数列{b n}满足:b1=,b n+1=(n≥1),则b2018=()A.3 B.7 C.2018 D.2017【解答】解:根据题意,数列{b n}满足:b1=,b n+1=(n≥1),则b2===3,b3===﹣2,b4===﹣,b5===,分析可得:b5=b1,b6=b2,…;则数列{b n}是周期为4的数列,则b2018=b2+4×504=b2=3;故选:A.9.(5分)设x>﹣1,则的最小值为()A.4 B.9 C.7 D.13【解答】解:设t=x+1(t>0),则y=f(t)==,整理得:f(t)=(t+)+5∵t>0,∴t+≥2,所以f(t)=(t+)+5≥2+5=9,当且仅当t==2时,函数有最小值,此时x=1.因此函数当x=1时有最小值为9,故选:B.10.(5分)在△ABC中,三个内角A,B,C所对的边为a,b,c,若S△ABC=2,a+b=6,=2cosC,则c=()A.2 B.4 C.2 D.3【解答】解:===1,即有2cosC=1,可得C=60°,若S=2,则absinC=2,△ABC即为ab=8,又a+b=6,由c2=a2+b2﹣2abcosC=(a+b)2﹣2ab﹣ab=(a+b)2﹣3ab=62﹣3×8=12,解得c=2.故选:C.11.(5分)已知不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,求实数a的取值范围()A.()B.(]C.()∪[1,+∞)D.()∪(1,+∞)【解答】解:令a2﹣1=0,解得a=±1,当a=1时,不等式化为﹣1<0,解得x ∈R;当a2﹣1≠0时,应满足△=(a﹣1)2+4(a2﹣1)=5a2﹣2a﹣3<0,且a2﹣1<0,解得﹣<a<1,此时不等式的解集为x∈R.综上,实数a的取值范围是﹣<a≤1,即(﹣,1].故选:B.12.(5分)在△ABC中,已知0,AC≥AB,点M,N分别是边AC,AB 的中点,且的最大值是,则=()A.B.C.D.【解答】解:△ABC中,AC≥AB,设AC=tAB,t≥1,又点M,N分别是AC,AB的中点,∴AM=AC,AN=AB;在△ABM中,由余弦定理可得:BM2=AB2+AM2﹣2AB•AMcosA=AB2+(tAB)2﹣2AB•tAB•cosA=(1+t2)AB2﹣tAB2cosA,在△ACN中,由余弦定理可得:CN2=AN2+AC2﹣2AN•ACcosA=(AB)2+(tAB)2﹣2•tAB•AB•cosA=(+t2)AB2﹣tAB2cosA,∴==,∵0,t≥1,∴cosA∈[,1),的最小值为=,则的最大值为=,解得t=,由正弦定理可得===,故选:D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)不等式的解集是[﹣1,0]∪(2,+∞).【解答】解:根据题意,⇒x(x+1)(x﹣2)≥0且x﹣2≠0,解可得﹣1≤x≤0或x>2,即原不等式的解集为[﹣1,0]∪(2,+∞);故答案为:[﹣1,0]∪(2,+∞).14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为﹣1≤a≤3.【解答】解:命题“∃x∈R,使x2+(a﹣1)x+1<0”的否定是:““∀x∈R,使x2+(a ﹣1)x+1≥0”即:△=(a﹣1)2﹣4≤0,∴﹣1≤a≤3故答案是﹣1≤a≤315.(5分)如果满足∠ABC=60°,AC=12,BC=k的三角形恰有一个,那么k的取值范围是0<k≤12或k=8.【解答】解:(1);(2);(3);(4)当0<BC≤AC,即0<k≤12时,三角形有1个解.综上所述:当时,三角形恰有一个解.故答案为:16.(5分)已知数列{a n}满足a n+2=3a n+1﹣2a n(n∈N*),且a1=1,a2=4,其前n 项和为S n,若对任意的正整数n,S n+2n+m•2n≥0恒成立,则实数m的取值范围是[﹣,+∞).=3a n+1﹣2a n(n∈N*),【解答】解:方法一:∵a n+2﹣a n+1=2(a n+1﹣a n),(n∈N*),∴a n+2∵a1=1,a2=4,∴a2﹣a1=3,∴数列{a n﹣a n}是以3为首项,以2为公比的等比数列,+1∴a n﹣a n=3×2n﹣1,+1∴a2﹣a1=3×20,a3﹣a2=3×21,a4﹣a3=3×22,…,∴a n﹣a n﹣1=3×2n﹣2,累加可得a n﹣a1=3(1+21+22+…+2n﹣2)=3×=3(2n﹣1﹣1)∴a n=3×2n﹣1﹣2,当n=1时,a1=3﹣2=1,成立,∴a n=3×2n﹣1﹣2,∴S n=3(1+21+22+…+2n﹣1)﹣2n=3(2n﹣1)﹣2n=3×2n﹣3﹣2n,∵对任意的正整数n,S n+2n+m•2n≥0恒成立,∴3×2n﹣3﹣2n+2n+m•2n≥0恒成立,即3×2n﹣3+m•2n≥0恒成立,∴m≥﹣3恒成立,∵﹣3≤﹣2=﹣,∴m≥﹣,方法二(非常规做法),由对任意的正整数n,S n+2n+m•2n≥0恒成立,由数列的函数特征可得,只要n=1时恒成立即可,故S1+2×1+m•21≥0,解得m≥﹣故答案为:[﹣,+∞).三、解答(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)17.(10分)设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x 满足2<x≤3.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.【解答】解:(Ⅰ)对于命题p:由x2﹣4ax+3a2<0得(x﹣3a)(x﹣a)<0,又a>0,∴a<x<3a,当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.由已知q为真时实数x的取值范围是2<x≤3.若p∧q为真,则p真且q真,∴实数x的取值范围是2<x<3.(Ⅱ)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q⇏¬p,设A={x|¬p},B={x|¬q},则A⊊B,又A={x|¬p}={x|x≤a或x≥3a},B={x|¬q}={x≤2或x>3},则0<a≤2且3a>3,∴实数a的取值范围是1<a≤2.18.(12分)设x,y满足条件.(1)求u=x2+y2的最大值与最小值;(2)求v=的最大值与最小值.【解答】解:满足条件的可行域如图所示(阴影部分).(1)令u=x2+y2表示一组同心圆(圆心为点O),且对同一圆上的点,u=x2+y2的值都相等.由图可知(x,y)在可行域内取值,当且仅当圆O过C点时,u最大,过点(0,0)时,u最小.由,解得C(3,8),∴u=x2+y2的最大值为:32+82=73,最小值为:02+02=0.(2)v=表示可行域内的点(x,y)和定点D(5,0)的连线的斜率,由图可知k BD最大,k CD最小.由,解得B(3,﹣3).∴v max==,v min==﹣4.19.(12分)已知数列{a n}的前n项和为S n,且满足2a n=S n+1(n∈N*)(1)求数列{a n}的通项公式;(2)若b n=(2n+1)•a n,求数列{b n}的前n项和T n.【解答】解:(1)当n=1时,2a1=S1+1=a1+1,解得a1=1.n≥2时,2a n﹣1=S n﹣1+1,可得:2a n﹣2a n﹣1=a n,可得a n=2a n﹣1..数列{a n}是首项为1,公比为2的等比数列,a n=2n﹣1.(2)b n=(2n+1)•a n=(2n+1)•2n﹣1.∴数列{b n}的前n项和T n=3×1+5×2+7×22+…+(2n+1)•2n﹣1.2T n=3×2+5×22+…+(2n﹣1)•2n﹣1+(2n+1)•2n,∴﹣T n=3+2×(2+22+…+2n﹣1)﹣(2n+1)•2n=1+2×﹣(2n+1)•2n,可得:T n=(2n﹣1)•2n+1.20.(12分)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.(Ⅰ)求角A的值;(Ⅱ)若a=,求b+c的取值范围.【解答】解:(Ⅰ)在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2.则:(sinB﹣2sinC)cosA=sinA﹣sinA(cosB+1),整理得:sin(A+B)=2sinCcosA,则:,0<A<π,则:.(Ⅱ)若a=,由2R=,则:b+c=2(sinA+sinB),=,由于:,则:,解得:故b+c的范围为:(,].21.(12分)已知各项都为正数的等比数列{a n}满足是3a1与2a2的等差中项,且a1a2=a3.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a n,且S n为数列{b n}的前n项和,求数列{}的前7项和T7.【解答】解:(Ⅰ)设等比数列的公比为q,由题意知q>0,且3a1+2a2=a3,∴,解得a1=q=3,故a n=3n.(Ⅱ)由(Ⅰ),得b n=log3a n=n,所以.∴,故数列的前n项和为:.∴.22.(12分)△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC 面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.【解答】解:(1)如图,过A作AE⊥BC于E,∵==2∴BD=2DC,∵AD平分∠BAC∴∠BAD=∠DAC在△ABD中,=,∴sin∠B=在△ADC中,=,∴sin∠C=;∴==.…6分(2)由(1)知,BD=2DC=2×=.过D作DM⊥AB于M,作DN⊥AC于N,∵AD平分∠BAC,∴DM=DN,∴==2,∴AB=2AC,令AC=x,则AB=2x,∵∠BAD=∠DAC,∴cos∠BAD=cos∠DAC,∴由余弦定理可得:=,∴x=1,∴AC=1,∴BD的长为,AC的长为1.第21页(共21页)。
