最新机械设计9凸轮机构及其设计
合集下载
机械原理第九章凸轮机构及其设计
凸轮的设计和参数选择
设计原则
凸轮的设计应考虑载荷、速度 和精度等因素，并满足运动学 和强度学的要求。
参数选择
凸轮的参数包括凸轮半径、凸 轮轴角度和凸轮顶点位置等， 应根据具体需求进行选择。
优化方法
通过数学模型和仿真分析，可 以优化凸轮的形状和参数，以 提高凸轮机构的性能。
凸轮机构的运动分析
1
转动运动
通过凸轮的旋转，实现机构的直线或曲线运动。
2
滑动运动
随着凸轮轮廓的变化，机构的接触点会产生水平或竖直方向的滑动运动。
3
摇摆运动
凸轮的摇杆或滚柱可以实现机构的摇摆运动。
凸轮机构的布置和设计原则
1 布置方式
根据机构的运动要求和空间限制，选择合适 的凸轮布置方式，如列状、行状或环状。
2 设计原则
在凸轮机构的设计过程中，要考虑机构的刚 度、强度和稳定性等因素，以提高机构的性 能。
凸轮机构的应用案例
发动机气门机构
凸轮机构用于控制发动机气门的 开闭，保证发动机的正常运行。
印刷机印版定位
凸轮机构用于实现印刷机印版的 准确定位，提高印刷质量。
纸张折叠机构
凸轮机构用于纸张折叠机构，实 现精确的折叠操作。
小结和要点
1 2 3 4
5
6
凸轮机构是一种常见的机械传动机构。 凸轮机构具有多种分类和特点。 凸轮的设计和参数选择需要考虑多个因素。 凸轮机构的运动分析可以通过几何和动力学方法 实现。 凸轮机构的布置和设计应根据具体要求进行选择。
凸轮机构在多个领域都有广泛应用。
凸轮机构是机械工程中常见的一种机构，用于将轮系运动转化为直线或曲线 的机械动作。它具有简单可靠的特点，广泛应用于各个领域。
机械原理 第九章 凸轮机构及其设计
第九章凸轮机构及其设计1 什么是凸轮的理论轮廓曲线、实际轮廓曲线？两者之间有什么关系？2 在凸轮机构设计中有哪几种常用的从动件运动规律？这些运动规律各有什么特点以及适用场合？在选择从动件运动规律时应考虑哪些主要因素？3 发生刚性冲击的凸轮机构，其运动线图上有什么特征？如发生柔性冲击时又有什么特征？4 用反转法设计盘形凸轮的廓线时，应注意哪些问题？移动从动件盘形凸轮机构和摆动从动件盘形凸轮机构的设计方法各有什么特点？5 何谓凸轮机构的“失真”现象？失真现象在什么情况下发生？如何避免失真现象的发生？6 一凸轮机构滚子从动件已损坏，要调换一个新的滚子从动件，但没有与原尺寸相同的滚子。
试问用该不同尺寸的滚子行吗？为什么？7 何谓凸轮机构的压力角？其在凸轮机构的设计中有何重要意义？一般是怎样处理的？8 设计直动推杆盘形凸轮机构时，在推杆运动规律不变的条件下，要减小推程压力角，可采用哪两种措施？9 图中两图均为工作廓线为圆的偏心凸轮机构，试分别指出它们的理论廓线是圆还是非圆，运动规律是否相同。
左面凸轮的理论廓线是圆,右面凸轮的理论廓线是非圆.它们的运动规律不相同10凸轮机构从动件按余弦加速度规律运动时，在运动开始和终止的位置，加速度有突变，会产生柔性冲击。
11根据从动件凸轮廓线保持接触方法的不同，凸轮机构可分为力封闭和几何形状封闭两大类型。
写出两种几何形状封闭的凸轮机构槽道凸轮和等径凸轮。
12为了使凸轮廓面与从动件底面始终保持接触，可以利用从动件自身的重力，弹簧力，或依靠凸轮上的几何形状来实现。
13凸轮机构的主要优点为只要适当地设计出凸轮廓线，就可以是从动件可以各种预期的运动规律。
主要缺点为从动件与凸轮之间是高副（点接触、线接触），易磨损，所以凸轮机构多用在传力不大的场合。
14为减小凸轮机构的推程压力角，可将从动杆由对心改为偏置，正确的偏置方向是将从动杆偏在凸轮转动中心的正偏置侧。
15凸轮机构的从动件按等加速等减速运动规律运动，在运动过程中，加速度将发生突变，从而引起柔性冲击。
09凸轮机构及其设计
正弦的 a 连续.
六、常用运动规律的选择
1. 没有任何要求、轻载、 小行程、手动, 可用圆弧或偏心圆.
2. 低速、轻载，要求等速、 等位移,可用等速运动规律.
3. 中低速、中轻载,
可用等加减速或余弦加速度运动规律.
4. 较高速、轻载可, 用正弦加速度运动规律.
5. 组合型.
a
a
d
d
6. 多项式运动规律 S = C0 + C1d + C2d2 + C3d3 + ¨¨ + Cndn .
6.作轮廓线 1 h
11
10 9
8
0 1 2
3
d
7 6 54
0 1 2 3 4 5 6 7 8 9 10 11 12
1800 3000 3600 2100
二.对心滚子移动从动杆
已知: r0、H 、rr 、 的方向、 从动杆运动规律和凸轮相应转角.
按尖顶推杆作理论轮廓线 →过各点作圆
→作这些圆的包络线 →实际轮廓
理论廓线
工作廓线
三.对心平底移动从动件
按尖顶从动件作理论轮廓线一系列点A0,A1,A2,....
→过各点作作各位置的平底A0B0,A1B1,A2B2......
B10 A0 B0 A1 →作这些平底的包络线
A10
1
B9
B1 A2 B2
→实际轮廓
A9
A3
B3
B8
A8
A4
B4
B7 A7
B6 A6
A5
B5
3
P12
B P23
VP1 = VP2
2. 压力角 a 与基圆半径 r0
tga = —CP— = OP - OC
机械原理第九章凸轮机构及其设计PPT课件
（2）三角函数运动规律
1）余弦加速度运动规律（简谐运动规律） 推程时：s＝h[1－cos(πδ /δ0)]/2 在始、末两瞬时有柔性冲击。
2）正弦加速度运动规律（摆线运动规律）
推程时：s＝h[(δ /δ0)－sin(2π δ /δ0) /(2π)]
6
推杆的运动规律(4/4)
既无刚性冲击，又无柔性冲击。 （3）组合型运动规律
§9-4 凸轮机构基本尺寸的确定
1．凸轮机构的压力角 （1）凸轮机构中的作用力
推杆等减速推程段： s = h－2h(δ0－δ )2/δ02
在始、中、末三瞬时有柔性冲击。
5
推杆的运动规律(3/4)
3）五次多项式运动规律（3-4-5多项式运动规律）
s＝10hδ 3/δ03－15hδ 4/δ04＋6hδ 5/δ05
既无刚性冲击，又无柔性冲击。
说明 对于多项式运动规律，其多项式中待定系数的数目应 与边界条件的数目相等，其数目多少应根据工作要求来确定。但 当边界条件增多时，会使设计计算复杂，加工精度也难以达到， 故通常不宜采用太高次数的多项式。
凸轮廓线设计的方法： 作图法和解析法
1．凸轮廓线设计的基本原理 无论是采用作图法还是解析法设计凸轮廓线，所依据的基本 原理都是反转法原理。 例9-2 偏置直动尖顶推杆盘形凸轮机构 （1）凸轮的轮廓曲线与推杆的相对运动关系 当给整个凸轮机构加一个公共角速度－ω，使其绕凸轮轴心 转动时，凸轮将静止不动，而推杆则一方面随其导轨作反转运动， 另一方面又沿导轨作预期的往复运动。 推杆在这种复合运动中， 其尖顶的运动轨迹即为凸轮的轮廓曲线。
式中δ 为凸轮转角；s为推杆位移；C0，C1，C2，…Cn为待定系数， 可利用边界条件等来确定。
（1）多项式运动规律 1）一次多项式运动规律（等速运动规律）
机械原理第9章凸轮机构及其设计
第二十一页，编辑于星期日：十四点 分。
②等减速推程段：
当δ =δ0/2 时，s = h /2，h/2 = C0＋C1δ0/2＋C2δ02/4 当δ = δ0 时，s = h ，v = 0，h = C0＋C1δ0＋C2δ02
0 = ωC1＋2ωC2δ ，C1=－2 C2δ0 C0=－h，C1= 4h/δ0, C2=－2h/δ02
如图所示，选取Oxy坐标系，B0 点为凸轮廓线起始点。当凸轮转过δ 角度时，推杆位移为s。此时滚子中 心B点的坐标为
x (s0 s) sin e cos
y
(s0
s) cos
A7
C8 A6 C7
w
A8
-w
A9
C9 B8 B9 B7 r0
C10
B12100 ° B0
O
B1 a B2
C1 L C2φ1φ0
A10 A0
φ
Φ
o
2
1
2 3 456
180º
7 8 9 10
60º 120º
δ
(1)作出角位移线图；
(2)作初始位置；
A5
C6
B6 B1580°B4
C4
C5
φ3
φC23
A1
↓对心直动平底推杆盘形凸 轮机构
↑偏置直动尖端推杆盘形凸轮机 构
第十一页，编辑于星期日：十四点 分。
↑尖端摆动凸轮机构
↓平底摆动凸轮机构
↑滚子摆动凸轮机构
第十二页，编辑于星期日：十四点 分。
(4)按凸轮与从动件保持接触的方式分
力封闭型凸轮机构
利用推杆的重力、弹簧力或其他外力使推杆与凸轮保持接
触的
此外，还要考虑机构的冲击性能。
机械原理课件第9章凸轮机构及其设计
优化设计的意义
提高凸轮机构性能：通过优化设计，可以改善凸轮机构的运动特性，提高其性能和效率。
降低成本：优化设计可以减少材料消耗和制造过程中的浪费，从而降低成本。
提高安全性：优化设计可以减少凸轮机构在运行过程中的振动和磨损，提高其安全性 和可靠性。
增强市场竞争力：优化设计可以提高产品的质量和性能，增强企业在市场上的竞争力。
Part Four
凸轮机构的工作原 理
凸轮机构的基本构件
单击此处输入你的项正文，文字是您思想的提炼，请尽量言简意赅 的阐述观点。
单击此处输入你的项正文，文字是您思想的提炼，请尽量言简意赅 的阐述观点。
单击此处输入你的项正文，文字是您思想的提炼，请尽量言简意赅 的阐述观点。
以上是凸轮机构的基本构件，这些构件共同构成了凸轮机构的工作 原理。
Part Three
凸轮机构的分类
按照凸轮形状分类
盘形凸轮：凸轮呈盘状，凸轮轮廓是平面或圆柱面 移动凸轮：凸轮呈圆柱状，凸轮轮廓是平面或圆柱面 圆柱凸轮：凸轮呈圆柱状，凸轮轮廓是圆柱面 圆锥凸轮：凸轮呈圆锥状，凸轮轮廓是平面或圆锥面 球面凸轮：凸轮呈球状，凸轮轮廓是球面
按照从动件形状分类
盘形凸轮：凸轮呈 盘状，与从动件之 间有径向距离，而 不像圆柱或圆锥那 样沿轴向配置
Part One
单击添加章节标题
Part Two
凸轮机构概述
凸轮机构的定义
凸轮机构是一种由凸轮、从动件和机架组成的单自由度机构 凸轮机构广泛应用于各种机械系统中，如内燃机、轻工机械、纺织机械等 凸轮机构的主要作用是将凸轮的旋转运动转化为从动件的往复直线运动 凸轮机构的运动特性取决于凸轮的形状和尺寸，以及从动件的位移和速度等参数
凸轮机构的工作过程
机械原理课件第9章凸轮机构及其设计
式中“－”对应于内等距线，“＋”对应于外等距线。
(x’,y’)n rr θ
(x, y) θ n (x’,y’)
JM 返回
3.2 对心直动平底推杆盘形凸轮
建立坐标系如图：反转δ后，推杆移动距离为S，
滚子――磨损小，应用广； 平底――受力好、润滑好，用于高速传动。 3).按推杆运动分：直动(对心、偏置)、 摆动
4).按保持接触方式分：力封闭（重力、弹簧等） 几何形状封闭(凹槽、等宽、等径、主回凸轮)
JM 返回
§9－1 凸轮机构的应用和分类（续）
刀架
o 2
1
内燃机气门机构 靠弹簧力封闭
机床进给机构 几何形状封闭
边界条件：
起始点：δ=0，s=0， v＝0， a＝0
终止点：δ=δ0，s=h, v＝0，a＝0 求得：C0＝C1＝C2＝0, C3＝10h/δ03 ,
C4＝15h/δ04 , C5＝6h/δ05
位移方程： s=10h(δ/δ0)3－15h (δ/δ0)4+6h (δ/δ0)5
v
s
h a
δ δ0
无冲击，适用于高速凸轮。
δ
JM 返回
c)改进型运动规律
将几种运动规律组合，以改善运动特性。
s
二、选择运动规律
选择原则：
o
1.机器的工作过程只要求凸轮转过一角度δ0时，
推杆完成一行程h（直动推杆）或φ（摆动推
v
δ
0
杆），对运动规律并无严格要求。则应选择直线
或圆弧等易加工曲线作为凸轮的轮廓曲线。 如夹紧凸轮。
o a
+∞
2. 机器的工作过程对推杆运动有要求，则应严格 按工作要求的运动规律来设计凸轮廓线。如刀架
(x’,y’)n rr θ
(x, y) θ n (x’,y’)
JM 返回
3.2 对心直动平底推杆盘形凸轮
建立坐标系如图：反转δ后，推杆移动距离为S，
滚子――磨损小，应用广； 平底――受力好、润滑好，用于高速传动。 3).按推杆运动分：直动(对心、偏置)、 摆动
4).按保持接触方式分：力封闭（重力、弹簧等） 几何形状封闭(凹槽、等宽、等径、主回凸轮)
JM 返回
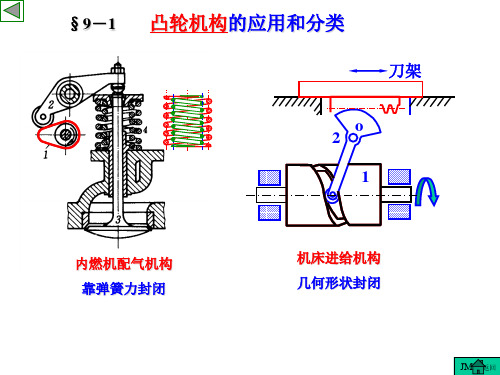
§9－1 凸轮机构的应用和分类（续）
刀架
o 2
1
内燃机气门机构 靠弹簧力封闭
机床进给机构 几何形状封闭
边界条件：
起始点：δ=0，s=0， v＝0， a＝0
终止点：δ=δ0，s=h, v＝0，a＝0 求得：C0＝C1＝C2＝0, C3＝10h/δ03 ,
C4＝15h/δ04 , C5＝6h/δ05
位移方程： s=10h(δ/δ0)3－15h (δ/δ0)4+6h (δ/δ0)5
v
s
h a
δ δ0
无冲击，适用于高速凸轮。
δ
JM 返回
c)改进型运动规律
将几种运动规律组合，以改善运动特性。
s
二、选择运动规律
选择原则：
o
1.机器的工作过程只要求凸轮转过一角度δ0时，
推杆完成一行程h（直动推杆）或φ（摆动推
v
δ
0
杆），对运动规律并无严格要求。则应选择直线
或圆弧等易加工曲线作为凸轮的轮廓曲线。 如夹紧凸轮。
o a
+∞
2. 机器的工作过程对推杆运动有要求，则应严格 按工作要求的运动规律来设计凸轮廓线。如刀架
机械原理课程教案—凸轮机构及其设计
机械原理课程教案—凸轮机构及其设计一、教学目标1. 使学生了解凸轮机构的分类、工作原理和应用。
2. 培养学生掌握凸轮机构的设计方法和步骤。
3. 提高学生分析问题和解决问题的能力。
二、教学内容1. 凸轮机构的分类及工作原理凸轮机构的分类凸轮的工作原理凸轮机构的应用2. 凸轮的轮廓曲线设计凸轮轮廓曲线的基本原理常用凸轮轮廓曲线的特点及应用凸轮轮廓曲线的设计方法3. 凸轮的压力角和基圆半径的选择压力角的定义及作用基圆半径的计算方法压力角和基圆半径的选择原则4. 凸轮机构的设计步骤确定凸轮的类型和参数选择合适的轮廓曲线计算压力角和基圆半径校核凸轮的强度和运动性能5. 凸轮机构的设计实例实例分析设计过程演示结果讨论和评价三、教学方法1. 采用讲授法，讲解凸轮机构的基本概念、设计方法和步骤。
2. 利用多媒体演示凸轮机构的工作原理和设计过程。
3. 引导学生进行实例分析，培养学生的实际设计能力。
4. 开展课堂讨论，提高学生的思考和表达能力。
四、教学环境1. 教室环境：宽敞、明亮，配备多媒体教学设备。
2. 教学材料：教案、PPT、参考书籍、设计实例。
五、教学评价1. 课堂参与度：观察学生在课堂上的发言和讨论情况，评价学生的积极性。
2. 作业完成情况：检查学生提交的凸轮机构设计作业，评价学生的理解和应用能力。
3. 期末考试：设置有关凸轮机构设计的题目，评价学生对课程知识的掌握程度。
六、教学活动1. 课堂讲解：讲解凸轮机构的基本概念、分类、工作原理和应用。
2. PPT演示：通过PPT展示凸轮机构的工作原理和设计过程。
3. 实例分析：分析典型凸轮机构设计实例，引导学生掌握设计方法和步骤。
4. 小组讨论：分组讨论凸轮机构设计中的问题，培养学生的团队协作能力。
5. 作业布置：布置凸轮机构设计相关作业，巩固所学知识。
七、教学资源1. PPT：制作精美的凸轮机构教学PPT，展示图片、图表和实例。
2. 参考书籍：提供有关凸轮机构设计和应用的参考书籍，方便学生查阅。
机械原理 第 章 凸轮机构及其设计
13 14
1) 将位移曲线若干等分；
2) 沿-w方向将偏距圆作相应等分；
3) 沿导路方向截取相应的位移，得 到一系列点；
4) 光滑联接。
5)偏置直动滚子从动件盘形凸轮机构
取长度比例尺l绘图
s
h
w h/2
13 12 11
10 w
9
8 7
14 1 2
3 4 5 6
O 1 2 3 /2 5 6 7 5 /4 10 11 127 /4 2
↑对心直动尖端推杆盘形 凸轮机构
↓对心直动滚子推杆盘形 凸轮机构
↑偏置直动尖端推杆盘形凸 轮机构
↓对心直动平底推杆盘形 凸轮机构
↑尖端摆动凸轮机构 ↓平底摆动凸轮机构
↑滚子摆动凸轮机构
(4)按凸轮与从动件保持接触的方式分 力封闭型凸轮机构
利用推杆的重力、弹簧力或其他外力使推杆与凸轮保持 接触的
刚性冲击 柔性冲击 无冲击 柔性冲击 无冲击
适用场合
低速轻载 中速轻载 高速中载 中低速中载 中高速轻载
除上述以外，还有其它运动规律，或将上述常用运动规律组 合使用。如“改进梯形加速度运动规律”、“变形等速运动规 律”。
3.推杆运动规律的选择
1)只要求当凸轮转过某一角度δ0时，推杆完成一行程h或φ。
4
89
13 14
取长度比例尺l绘图
14 1
13
2
12 w
3
11
4
10
5
9
6
7
实际廓线
理论廓线
4)偏置直动尖端推杆盘形凸轮机构
取长度比例尺l绘图
s
h
w h/2
13 12 11
10 w
9
第九章 凸轮机构及其设计
推杆位移线图
• 近休：圆弧（AD）---近休止角δ02 。
∵ t ∝δ • 运动规律： s = F( t ) = F( δ ) v = F’( t ) = F’( δ ) a = F”( t ) = F”( δ )
v = ds / dt ω = dδ / dt = δ / t = δ0 / T0
速度突变 --- 刚性冲击 加速度突变---柔性冲击
二、基圆半径 r0 的确定 αman ≤ [α] → r0 → 找 α与 r0 的关系 以偏置推杆凸轮机构为例： OP = v / ω = (ds / d t ) / (dδ / d t ) = ds / dδ CP = ds / dδ - e
s = F( δ ) ,
=v
tgα = CP / (( r02 - e2 )1/ 2 + s) = (ds / dδ – e) / (( r02 - e2 )1/ 2 + s)
等加 等减速 简谐 (余弦）
摆线 （正弦） 5次 多项式
柔性
柔性 无
较难
设计易 制造难 较难
2.00 1.88
6.28 5.77
无
难
二、改进型运动规律
局部修正 改进 两种或两种以上运动规律组合 正弦
a
小圆弧 等速
a
t δ
等加等减
t δ
注意：为了获得良好的运动性能，改进型的运动曲线在两种运动规律曲
线的衔接处必须连续。
s = F ( δ ) , v2 = ds / d t
3
v2
P 点处为相对瞬心 P12 v2 = ω OP
1
2
OP = v2 / ω
= (ds / d t) / (dδ / d t) = ds / dδ
• 近休：圆弧（AD）---近休止角δ02 。
∵ t ∝δ • 运动规律： s = F( t ) = F( δ ) v = F’( t ) = F’( δ ) a = F”( t ) = F”( δ )
v = ds / dt ω = dδ / dt = δ / t = δ0 / T0
速度突变 --- 刚性冲击 加速度突变---柔性冲击
二、基圆半径 r0 的确定 αman ≤ [α] → r0 → 找 α与 r0 的关系 以偏置推杆凸轮机构为例： OP = v / ω = (ds / d t ) / (dδ / d t ) = ds / dδ CP = ds / dδ - e
s = F( δ ) ,
=v
tgα = CP / (( r02 - e2 )1/ 2 + s) = (ds / dδ – e) / (( r02 - e2 )1/ 2 + s)
等加 等减速 简谐 (余弦）
摆线 （正弦） 5次 多项式
柔性
柔性 无
较难
设计易 制造难 较难
2.00 1.88
6.28 5.77
无
难
二、改进型运动规律
局部修正 改进 两种或两种以上运动规律组合 正弦
a
小圆弧 等速
a
t δ
等加等减
t δ
注意：为了获得良好的运动性能，改进型的运动曲线在两种运动规律曲
线的衔接处必须连续。
s = F ( δ ) , v2 = ds / d t
3
v2
P 点处为相对瞬心 P12 v2 = ω OP
1
2
OP = v2 / ω
= (ds / d t) / (dδ / d t) = ds / dδ
第九章 凸轮机构及其设计
（3）在选择从动件的运动规律时，除要考虑刚性冲击与柔 性冲击外，还应该考虑各种运动规律的速度幅值 vmax 、加 速度幅值 amax 及其影响加以分析和比较。
vmax
从动件动量 mvmax
amax
从动件惯性力 ma
max
对于重载凸轮机构，应选择 max 值较小的运动规律； 对于高速凸轮机构，宜选择 max 值较小的运动规律。
导轨 长度
F G /[cos( 1 ) ( 1 2b / l ) sin( 1 ) tan 2 ]
推程： []=30o， 直动推杆 []=35o~45o 摆动推杆 回程： []=70o 左右。
悬臂 长度
2. 凸轮基圆半径确定 （凸轮机构压力角与基圆半径有关 ）
摆动
ψ
o
Φ0
h
反转法
Φs
Φ0
Φs
ψ0 ψ
3、解析法设计凸轮轮廓曲线 ① 偏置直动滚子推杆盘形凸轮机构
建立oxy坐标系，B0 点为凸轮 推程段廓线起始点。 rr ----滚子半径
x ( s0 s) sin e cos y ( s0 s) cos e sin
正弦加速度（摆线）运动规律
h
Φ0 Φs Φ0 Φs
无刚性冲击及柔性冲击
1.3 组合运动规律
例如：可在等速 运动规律的两端 点进行修正，用 其它规律连接， 以避免刚性冲击。
二、推杆运动规律的选择 原则：
•满足机器的工作要求； •凸轮机构要具有良好的动力特性； •凸轮便于加工。
1）机器的工作过程只要求凸轮转过某一角度时，推杆完成 某一行程或角行程，对推杆的运动规律不作要求。 2）机器的工作过程对推杆的运动规律有完全确定的要求。
凸轮机构及其设计
2( xa
x) d x
d
2( ya
y) d y
d
0
即：
( xa
x). d x
d
( ya
y) dy
d
联立求解包络线方程， 可得到实际廓线方程为： xa x rr
dy
d
( d x )2 (d y )2
d d
ya y rr
dx
d
( dx )2 ( dy )2
d d
2．直动平底从动件盘形凸轮廓线旳设计
1.一次多项式——等速运动规律
s c0 c1
v
ds dt
c1
d
dt
c1
常数
a 0
边界条件 0时，s 0； Φ时，s h。
代入整顿得从动件在推程时旳运动方程为：
在行程旳起点与终点处，因为 速度发生突变，加速度在理论上无 穷大，造成从动件产生非常大旳冲 击惯性力，称这种冲击为刚性冲击。
组合型运动规律图
改
改
善
善
等
等
速
加
运
等
动
减
规
速
律
运
动
规
律
第三节 凸轮轮廓曲线旳设计
主要任务 根据选定旳从动件运动规律和其他设计数据， 画出凸轮旳轮廓曲线或计算出轮廓曲线旳坐标值。
一、 凸轮机构旳相对运动原理 二、 凸轮机构旳轮廓曲线 三、 凸轮廓线旳设计
1. 直动从动件盘形凸轮廓线旳设计 2. 直动平底从动件盘形凸轮廓线旳设计 3. 摆动滚子从动件盘形凸轮廓线旳设计
y
(s0
s) cos
e cos
实际廓线是圆心位于理论廓线上旳 滚子圆旳包络线，其方程为：
机械原理第九章凸轮机构及设计
机械原理第九章凸轮机构及设计凸轮机构是一种非常常见且重要的机械原理，广泛应用于各种机械、自动化设备以及机械工程中。
凸轮机构主要由凸轮、从动件和工作件组成，通过凸轮的转动，从动件与工作件之间的运动关系被确定，从而实现特定的机械工作。
在凸轮机构的设计过程中，需要考虑凸轮的形状、尺寸和运动规律，以及从动件与工作件的连接方式和相对运动关系等因素。
凸轮的形状通常是基于工作要求和约束条件而确定的，常见的凸轮形状包括圆形凸轮、倒头凸轮、冷凸轮等。
凸轮机构的设计需要根据具体的工作要求和条件来确定凸轮的运动规律。
常见的凸轮运动规律包括简谐运动、等角速度运动和等距离运动等。
在设计过程中，需要根据工作要求来选择合适的凸轮运动规律，以确保机构的工作稳定性和精度。
凸轮机构设计的关键是确定从动件与工作件之间的连接方式和相对运动关系。
常见的从动件与工作件的连接方式包括滑块连接、摆杆连接和球头连接等。
这些连接方式的选择需要考虑凸轮运动规律、工作要求和机构的设计要求等因素。
而从动件与工作件之间的相对运动关系则可以通过凸轮的形状和凸轮运动规律来确定。
凸轮机构设计还需要考虑诸如凸轮的材料、强度和润滑等问题。
凸轮的材料通常选择硬度高、耐磨性好的材料，以保证凸轮的使用寿命和稳定性。
凸轮的强度可以通过强度计算和有限元分析等方法来确定，以确保凸轮在工作过程中不会发生破坏。
润滑问题也需要考虑，选择合适的润滑方式和润滑剂，以减少凸轮机构的摩擦和磨损。
总之，凸轮机构的设计是一个综合考虑凸轮形状、尺寸、运动规律、连接方式、相对运动关系、材料、强度和润滑等多方面因素的过程。
只有充分考虑这些因素，并结合具体的工作要求和条件，才能设计出稳定、高效的凸轮机构。
凸轮机构的设计不仅需要具备丰富的机械原理知识和设计经验，还需要进行大量的实验和验证，以确保机构的可靠性和性能。
第九章 凸轮机构及其设计
2. 对心滚子移动从动件盘形凸轮廓线的设计 已知凸轮的基圆半径rb， 滚子半径rr、凸轮角速度 和从动件的运动规律，设计 该凸轮轮廓曲线。
s
5 1 3 7 8 9 10 11 12 13 14 9 11 13 15
实际轮廓曲线
A
O
1 3 5 7 8
120º
60º 90º
运动线图
从动件的常用运动规律 (一)基本运动规律 基本运动规律包括多项式类运动规律和三角函数类运动 规律。 1. 多项式类运动规律 s c0c1 c2 2 c3 3cn n 式中c0、c1、c2、…、cn为n＋1个系数。这些系数可根 据对运动规律所提出的n+1个边界条件来确定。对从动件的 运动所提的要求越多，相应多项式的方次也就越高。n取值 为1、2、3，一般不大于10。
第三节 平面凸轮轮廓曲线的设计
一、凸轮轮廓曲线设计的基本原理 (一) 凸轮轮廓曲线的设计方法 作图法 解析法 基本原理————反转法原理: 无论是采用作图法还是解析法设计凸轮轮廓曲线，
所依据的基本原理都是反转法原理。
凸轮轮廓曲线设计方法的基本原理
根据上述分析，在设计凸轮廓线时，可假设凸轮静 止不动，而使推杆相对于凸轮作反转运动；同时又在其 导轨内作预期运动，作出推杆在这种复合运动中的一系 列位置，则其尖顶的轨迹就是所要求的凸轮廓线。这就 是凸轮廓线设计方法的反转法原理。
第九章 凸轮机构及其设计
第一节 概述
内燃机配气凸轮机构
自动机床进刀凸轮机构
凸轮机构的组成 凸轮、从动件和机架。 凸轮机构的适用场合 广泛用于各种机械，特别是自动机械、自动控制装置和 装配生产线。 凸轮机构的优点 结构简单、紧凑、工作可靠，可以使从动件准确实现各 种预期的运动规律，还易于实现多个运动的相互协调配合。 凸轮机构的缺点 凸轮轮廓与从动件之间是高副接触，易于磨损。
机械原理(安全工程专用)第9章 凸轮机构及其设计
推杆 凸轮
推杆
凸轮
机械原理 ——凸轮机构及其设计
2 按从动件的形状分
尖顶推杆
可实现复杂的运动规律 易磨损，只宜用于轻载、
低速
滚子推杆
耐磨、承载大，较常用
曲面推杆
磨损比尖顶小
平底推杆
接触面易形成油膜，利于 润滑，常用于高速运动
配合的凸轮轮廓必须全部 外凸
尖顶推杆
滚子推杆
曲面推杆
平底推杆
置 4 据运动规律，求出从动件在预期运动
中依次占据的位置 5 将两种运动复合，就求出了从动件尖
端在复合运动中依次占据的位置点 6 将各位置点联接成光滑的曲线 7 在理论轮廓上再作出凸轮的实际轮廓
1 对心直动尖顶推杆盘形凸轮机 构
2 偏置直动尖顶推杆盘形凸轮机 构
3 对心直动滚子推杆盘形凸轮机 构
4 偏置直动滚子推杆盘形凸轮机 构
解： 1. 定比例尺l
2. 初始位置及推杆位移曲线
0
注：两条廓线，理论／实际廓线
实际廓线基圆rmin 理论廓线基圆r0 3. 确定推杆反转运动占据的各位
置
4. 确定推杆预期运动占据的各位
置
5. 推杆高副元素族
6. 推杆高副元素的包络线
120 600
900
900
理论轮廓 实际轮廓
4 偏置直动滚子推杆盘形凸轮机构
5 按凸轮与从动件维持高副接触的方法分
6 小结
1
2017/11/3
机械原理 ——凸轮机构及其设计
1 按凸轮的形状分
盘形凸轮, 实例
凸轮呈向径变化的盘形 结构简单, 应用最广泛
移动凸轮, 实例
凸轮呈板型, 直线移动 凸轮
推杆
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湖北工学院专用
作者： 潘存云教授
3.五次多项式运动规律
一般表达式：
s =C0+ C1δ+ C2δ2+ C3δ3+ C4δ4+C5δ5 v =ds/dt = C1ω+ 2C2ωδ+ 3C3ωδ2+ 4C4ωδ3+ 5C5ωδ4 a =dv/dt = 2C2ω2+ 6C3ω2δ+12C4ω2δ2+20C5ω2δ3
v＝hω[1-cos(2πδ/δ0)]/δ0 r=h/2π作者：潘存云教授
a＝2πhω2 sin(2πδ/δ0)/δ20
12 θ=2πδ/δ0
34
δ0
5
回程：
v
vmax=2hω/δ0
s＝h[1-δ/δ’0+sin(2πδ/δ’0)/2π]
v＝hω[cos(2πδ/δ’0)-1]/δ’0 a＝-2πhω2 sin(2πδ/δ’0)/δ’20 a amax=6.28hω2/δ02
δ
回程：
s＝h[1＋cos(πδ/δ’0)]/2
a
v＝-πhωsin(πδ/δ’0)δ/2δ’0
δ
a＝-π2hω2 cos(πδ/δ’0)/2δ’20
在起始和终止处理论上a为有限值，产生柔性冲击。
湖北工学院专用
作者： 潘存云教授
2.正弦加速度（摆线）运动规律
推程：
s
s＝h[δ/δ0-sin(2πδ/δ0)/2π]
v = ds/dt = C1ω+ 2C2ωδ+…+nCnωδn-1
求二阶导数得加速度方程：
a =dv/dt =2 C2ω2+ 6C3ω2δ…+n(n-1)Cnω2δn-2 其中：δ－凸轮转角，dδ/dt=ω－凸轮角速度,
Ci－待定系数。
边界条件：
凸轮转过推程运动角δ0－从动件上升h 凸轮转过回程运动角δ’0－从动件下降h
湖北工学院专用
作者： 潘存云教授
s = C0+ C1δ+ C2δ2+…+Cnδn v = C1ω+ 2C2ωδ+…+nCnωδn-1
a = 2 C2ω2+ 6C3ω2δ…+n(n-1)Cnω2δn-2 1.一次多项式（等速运动）运动规律 s
在推程起始点：δ=0， s=0
在推程终止点：δ=δ0 ，s=h 代推入程得运： 动方C0＝程0：， C1＝h/δ0
边界条件： 起始点：δ=0，s=0， v＝0， a＝0 终止点：δ=δ0，s=h, v＝0，a＝0
v
s
h a
求得：C0＝C1＝C2＝0, C3＝10h/δ03 ,
δ
C4＝15h/δ04 , C5＝6h/δ05
δ0
位移方程：
s=10h(δ/δ0)3－15h (δ/δ0)4+6h (δ/δ0)5
无冲击，适用于高速凸轮。
机械设计9凸轮机构及其设 计
§9－1 凸轮机构的应用和分类
结构：三个构件、盘(柱)状曲线轮廓、从动件呈杆状。
作用：将连续回转 => 从动件直线移动或摆动。
优点：可精确实现任意运动规律，简单紧凑。 实例 缺点：高副，线接触，易磨损，传力不大。
应用：内燃机 、牙膏生产等自动线、补 鞋机、配钥匙机等。
分类：1)按凸轮形状分：盘形、 移动、 圆柱凸轮 ( 端面 ) 。
起始点：δ=0， s=0， v＝0 中间点：δ=δ0 /2，s=h/2
求得：C0＝0， C1＝0，C2＝2h/δ20
加速段推程运动方程为：
s ＝2hδ2 /δ20 v ＝4hωδ /δ20 a ＝4hω2 /δ20
湖北工学院专用
作者： 潘存云教授
推程减速上升段边界条件：
中间点：δ=δ0/2，s=h/2 终止点：δ=δ0 ，s=h，v＝0
h
δ
6
δ
δ
湖北工学院专用
无冲击
作者： 潘存云教授
三、改进型运动规律
s
将几种运动规律组合，以改善 运动特性。
o
vv
h
设计作：者潘：存潘云 存云教授
δ
δ0oδ来自a +∞δ
o
-∞
正弦改进等速
湖北工学院专用
作者： 潘存云教授
四、选择运动规律
选择原则：
1. 机器的工作过程只要求凸轮转过一角度δ0时，推
杆完成一行程h（直动推杆）或φ（摆动推杆），对 运动规律并无严格要求。则应选择直线或圆弧等易 加工曲线作为凸轮的轮廓曲线。如夹紧凸轮。
V=V(t)
a=a(t)
s 位移曲线
形式：多项式、三角函数。
D
B’
A
δ02
r0
h
t o δ0 δ01 δ’0 δ02 δ
δ0
ω δ’0 作者：潘存云教授
δ01
B
湖北工学院专用
C
作者： 潘存云教授
一、多项式运动规律
一般表达式：s=C0+ C1δ+ C2δ2+…+Cnδn (1)
求一阶导数得速度方程：
作者：潘存云教授
δ0
v
s ＝hδ/δ0
v a
＝ ＝
hω 0
/δ0
同理得回程运动方程：
a 刚性冲击 +∞
s＝h(1-δ/δ0 ) v＝-hω /δ0 a＝0
湖北工学院专用
h
δ
δ
δ
－∞
作者： 潘存云教授
2.二次多项式（等加等减速）运动规律 位移曲线为一抛物线。加、减速各占一半。
推程加速上升段边界条件：
2)按推杆形状分：尖顶、 滚子、 特点： 平底从动件。 尖顶－－构造简单、易磨损、用于仪表机构； 滚子――磨损小，应用广； 平底――受力好、润滑好，用于高速传动。
湖北工学院专用
作者： 潘存云教授
运动规律：推杆在推程或回程时，其位移S、速度V、
和加速度a 随时间t 的变化规律。
S=S(t)
1 23 4 5
δ0
v 2hω/δ0
h/2
h/2
6δ
δ
a 4hω2/δ20
δ
柔性冲击
作者： 潘存云教授
同理可得回程等加速段的运动方程为：
s ＝h-2hδ2/δ’20 v ＝-4hωδ/δ’20 a ＝-4hω2/δ’20
回程等减速段运动方程为：
s ＝2h(δ’0-δ)2/δ’20 v ＝-4hω(δ’0-δ)/δ’20 a ＝4hω2/δ’20
湖北工学院专用
作者： 潘存云教授
二、三角函数运动规律 1.余弦加速度(简谐)运动规律
5 4
6
s
推程： s＝h[1-cos(πδ/δ0)]/2
3 2
作者：潘存云教授
设计：潘存云
1 1 2 34 5
h
δ
6
v ＝πhωsin(πδ/δ0)δ/2δ0
δ0 v Vmax=1.57hω/2δ0
a ＝π2hω2 cos(πδ/δ0)/2δ20
求得：C0＝－h， C1＝4h/δ0 C2＝-2h/δ20
减速段推程运动方程为：
s v
＝＝h-4-2hhω((δδ00–-δδ))/2δ/δ2020
a ＝-4hω2 /δ20
重写加速段推程运动方程为：
s ＝2hδ2 /δ20
v ＝4hωδ /δ20
a ＝4hω /δ 湖北工学院专用
22 0
s
作者：潘存云教授