八年级期末试卷达标检测卷(Word版 含解析)
2020~2021学年第一学期期末质量监测 (word版含答案)

2020~2021学年第一学期期末质量监测八年级物理试卷(时间:60分钟总分:100分)一、选择题(本大题共15个小题,共33分.1~12小题为单项选择题,每小题2分;13~15小题为多选题,每小题3分,选对但不全得2分,错选或不选不得分)1.下列对生活中一些物理量的估测合理的是( )A.复兴号高铁列车运行速度可达350 m/sB.一个苹果的质量约为150 gC.石家庄冬季平均气温约为-20 ℃D.上课教室门高4 m2.两列火车并排停在站台上,你坐在车厢中向另一列车观望.突然,你觉得自己的列车缓慢向东运动.则下列运动情况不可能发生的是( )A.自己的车向东运动,另一列车没有运动B.自己的车没有运动,另一列车向西运动C.两列车都向东运动,但自己车的速度较快D.两列车都向西运动,但另一列车的速度较慢3.在平直的公路上,小明坐在车上用电子表的秒表功能记下了汽车连续通过5根电线杆的时间为10 s,相邻电线杆的距离为50 m,则汽车的平均速度约为( ) A.90 km/h B.70 km/hC.50 km/h D.40 km/h4.关于声现象,下列说法正确的是( )A.调节手机音量是为了改变声音的音调B.考场附近禁止鸣笛,是在声源处减弱喊声C.超声波的传播不需要介质D.医生通过听诊器给人诊病是利用声波可以传递能量5.一艘科考船对某海域的海底形状利用声呐系统进行了测绘.具体方法是:在经过该海域水平面等间距的A、B、C、D、E五个位置时,向海底定向发射超声波,测得回收信号的时间分别为0.30 s、0.16 s、0.30 s、0.14 s、0.30 s.根据时间,求出海底与海平面的距离,就可以绘出海底的大致形状,则该海域海底的大致形状如图中的( )A B C D6.生活中有很多现象和应用都与物态变化有关,下列说法不正确的是( )A.皮肤上擦酒精后变凉爽是由于酒精汽化从皮肤吸热所致B.在运输食物的车里放干冰,利用干冰升华吸热给食物降温C.出汗时吹电风扇感觉凉爽,是由于电风扇吹出的风降低了室温D.夏天吃冰棒时看到周围冒“白气”,这是液化现象7.下列现象中,由光的反射形成的是( )A.透过水面看到水中的“鱼”B.灯光下看到地上的“人影”C.用凸透镜看到放大的“字”D.在化妆镜中看到的“自己”8.如图所示,将平面镜和铅笔竖直放置在水平桌面上,下列说法正确的是( )A.铅笔水平向右移动时,铅笔的像将变小B.平面镜竖直向上移动时,铅笔的像也将向上移动C.若改用一块较小的平面镜,铅笔的像将变小D.若铅笔按图示箭头方向转过45°,铅笔将与它的像垂直9.有一圆柱形敞口容器,从其左侧某一高度斜射一束激光,在容器底部产生一个光斑O,如图所示,下列操作使光斑向左移的是( )A.保持水面高度不变使激光笔向右平移B.保持激光射入角度不变使水面上升C.保持激光射入角度不变使水面下降D.保持水面高度和入射点不变使激光入射角增大10.小明利用太阳光测量凸透镜的焦距,下列操作最合理的是( )11.下列关于质量和密度的说法中正确的是( )A.粉笔在黑板上写字时,粉笔的质量和密度都不变B.水结成冰时,质量不变,密度变大C. -瓶牛奶喝掉一半后,质量变小,密度不变D.一千克铁比一千克棉花质量大12.如图为甲、乙两种物质的m-V图象,下列说法正确的是( )A.体积为20 cm3的甲物质的质量为10 gB.乙物质的密度与质量成正比C.甲物质的密度比乙的密度小D.甲、乙质量相同时,乙的体积是甲的2倍13.一束光从空气斜射向某透明介质,同时发生反射和折射.若入射光线和折射光线的夹角为170°,入射光线和反射光线的夹角为100°,则( )A.入射角为50°B.反射光线和折射光线的夹角为80°C.折射角为40°D.反射光线和折射光线的夹角为90°14.在探究凸透镜成像规律的实验中,当蜡烛、凸透镜、光屏位于如图所示的位置时,在光屏上呈现一个清晰的烛焰的像.下列说法正确的是( )A.此时成正立、放大的实像,与投影仪原理相同B.透镜不动,蜡烛和光屏都向右移动,光屏上的像变小C.透镜左移10 cm后,眼睛在光屏和透镜间,通过透镜能看到正立的像D.若在透镜和蜡烛之间放远视镜片,则将光屏适当左移,可再次出现清晰的像15.甲、乙两个实心金属块,它们的质量分别为m甲、m乙,它们的体积分别为V甲、V乙,它们的密度分别为ρ甲、ρ乙.已知ρ甲>ρ乙,则下列情况存在的是( ) A.V甲>V乙,同时m甲>m乙B.V甲>V乙,同时m甲<m乙C.V甲<V乙,同时m甲>m乙D.V甲<V乙,同时m甲<m乙二、填空题(本大题共4个小题,每空2分,共30分)16.如图是用照相机拍摄的气泡从充满油的玻璃管底端向上运动的一张频闪照片,气泡从点A开始运动,频闪点B、C、D是每隔2 s拍摄的气泡位置,分析照片可知:(1)气泡在AD段做__ __(填“匀速”或“变速”)直线运动;其理由是_____ ___ ___ _.(2)气泡在BD段运动的平均速度为__ _m/s.(3)该气泡在__ _两点间的平均速度最大.17.暖气通常安置于房间的地面上,由于低处热空气密度比冷空气密度__ _(填“大”或“小”),所以热空气会__ _(填“上升”或“下降”),周围冷空气就补充过来,形成冷、热空气的交互循环,更有利于整个房间变得温暖.18.请你根据自己对生活现象的观察、动手实践的经验及物理课中所学的知识,将图所示四个实例的描述补充完整.A B C D图A:冰棍“冒”出的“白气”向__ _(填“上飘”或“下落”),这是冰棍周围水蒸气__ _(填物态变化名称)形成的小水滴.图B:把正在响铃的闹钟放在玻璃罩内,逐渐抽出其中的空气,铃声的响度__ _(填“变大”“变小”或“不变”),这说明__ _(填“空气”或“真空”)可以传播声音.图C:在空罐的罐底中央打一个小孔,再用一片半透明的塑料膜蒙在空罐的口上.白天将小孔对着室内的窗户,可观察到户外景物呈现在塑料膜上是__ _(填“正立”或“倒立”)的.图D:在碗底放一枚硬币,自己远离碗一段距离,站到刚好看不到硬币的位置.另一同学慢慢向碗中加满水,你将__ _(填“能”或“不能”)看到这枚硬币.19.阅读下面的短文,回答问题.多普勒效应1842年的一天,奥地利一位名叫多普勒的科学家正路过铁路交叉处,恰逢一列火车从他身旁驶过,他发现火车从远而近时鸣笛声变响,音调变尖,而火车从近而远时鸣笛声变弱,音调变低.他对这个物理现象产生了极大兴趣,就进行了研究.他发现当声源与观察者之间存在着相对运动时,观察者听到的声音频率就会不同于声源发声的频率.当声源离观察者远去时,观察者接收到的声波的波长增加,频率变小,音调变得低沉;当声源向观察者靠近时,观察者接收到的声波的波长减小,频率变大,音调就变高,后来人们把它称为“多普勒效应”.声波的多普勒效应可用于交通中的测速,交通警察向行进中的车辆发射频率已知的超声波,同时测量反射波的频率,根据反射波频率变化的多少就能知道车辆的速度.多普勒效应也可以用于医学的诊断,也就是我们平常说的彩超,即彩色多普勒超声.根据上述内容回答:(1)交通中的测速仪和医学中的彩超都是应用__ ___ _工作的.(2)若声源不动,观察者向声源处运动,__ _(填“能”或“不能”)发生多普勒效应.(3)从听到火车鸣笛的音调变高判断,火车正在__ _(填“靠近”或“远离”)观察者.三、作图与实验探究题(本大题共5个小题,20、21、22题每题2分,23、24题每空1分,共25分)20.水池中发光点S射出的光线,在池中没有水时射到A处,当池中注入一定深度的水后,光线在水面发生反射,反射光射到池底B处,请你画出光线在水面发生反射时的入射光、反射光及水面的位置.21.如图所示,根据凸透镜和凹透镜的性质,补全光路.22.在水平的实验桌上有已调好的天平一台,提供的砝码如图所示,请你利用上述器材,设计一个实验检验:在标尺上向右移动游码就相当于在天平右盘中增加相应质量的砝码.要求:写出检验的实验步骤.__ ___ ___ ___ ___ ___ ___ _____ ___ ___ ___ ___ ___ ___ _____ ___ ___ ___ ___ ___ ___ _____ ___ ___ ___ ___ ___ ___ ___23.小明和小红做“探究凸透镜成像规律”的实验.甲(1)利用太阳光测量凸透镜的焦距时,小明将一把木质刻度尺一端支于水平地面上,观察尺在地面上形成的影子,不断调节刻度尺,使其在地面上的影子___ ,这时尺的方向就与太阳光的方向平行,小明保持尺不动,小红将光屏A和凸透镜L按如图所示的方式均垂直于刻度尺摆放,光屏上形成了一个最小、最亮的光斑.则该凸透镜的焦距为___ cm.(2)实验前应点燃蜡烛,观察烛焰、凸透镜和光屏的中心是否在同一高度上,这样做的目的是___ ___ ___ .(3)当蜡烛、凸透镜和光屏的相对位置如图乙所示,光屏上出现清晰的像,则像是倒立、___ 的实像.乙丙(4)实验中,不但虚像可以用肉眼直接看到,实像也可以用肉眼直接看到,如图丙所示,在(3)的基础上,拿掉光屏,用肉眼在___ (填“A”“B”或“C”)位置沿图示方向能看到这个实像.(5)在(3)的基础上,当光屏略微向右移动时,光屏上的像将会模糊,如果蜡烛与凸透镜不动,那么,在凸透镜前放置___ (填“凸”或“凹”)透镜,才可能在光屏上得到清晰的像,这其实就是___ (填“近视眼”或“远视眼”)的矫正原理.(6)下表是实验中得到的数据和观察的结果.次数物距u/cm 成像情况像距v/cm1 50.0倒立、缩小、实像12.5 2 30.0倒立、缩小、实像15.0 3 20.0倒立、等大、实像20.0 4 15.0 倒立、放大、实像正立、放大、虚5 8.0/像通过1、2、3次实验数据可以得出:当凸透镜成实像时,物距变小,像距___ (填“变大”“变小”或“不变”);表格中第4次实验光屏上成清晰的像时,光屏到透镜的距离为___ cm,此成像规律在实际生活中的应用是___ (填“照相机”“投影仪”或“放大镜”).24.为了测量盐水的密度,小红同学进行了如下实验:(1)她将天平放在水平台面上,将游码移到标尺的___ .横梁静止时,指针指在分度盘中央刻度线的左侧,如图甲所示.为使横梁在水平位置平衡,应将横梁右端的平衡螺母向___ 移动.(2)小红同学将盛有适量盐水的杯子放在调好的天平左盘内,测出杯子和盐水的总质量为128 g.然后将杯中盐水倒入量筒中一部分,如图乙所示,则量筒中盐水的体积为___ cm3.(3)再将盛有剩余盐水的杯子放在天平左盘内,按从大到小的顺序依次加砝码时,出现了如图丙的情况,小红下一步应进行的操作是(砝码盒中还有更大和更小的其他砝码) ___ .A.把右盘中的砝码取下,换更大的砝码B.继续向右盘中加更小的砝码C.直接拨游码(4)横梁恢复水平平衡后,右盘中砝码质量和游码在标尺上的位置如图丁所示,则杯子及杯内剩余盐水的总质量为___ g;根据上述实验数据计算盐水的密度为___ kg/m3.(5)小明同学感觉小红同学这样测量太麻烦,于是他设计如下实验步骤:a.用天平测出空烧杯的质量记作m1;b.向烧杯中倒入适量的盐水,用天平测出烧杯和盐水的总质量记作m2;c.把烧杯中的盐水倒入量筒中,测出盐水的体积记作V.根据小明同学实验过程,请你帮他写出计算盐水密度的数学表达式:___ ;你认为他这样设计实验是否科学?___ (填“科学”或“不科学”),你这样认为的理由是:___ ___ ___ .四、计算题(本大题共2个小题,每小题6分,共12分)25.如图甲为某地距离传感器发出和接收超声波检测汽车速度的示意图.(1)已知超声波在空气中的传播速度为340 m/s,某次检测车速时,传感器发出至接收超声波信号用了0.4 s,超声波信号遇到汽车时,汽车与传感器之间的距离是多少米?(2)如果将距离传感器与计算机连接,可以将物体运动的距离(s)-时间(t)图象显示在计算机的屏幕上.利用传感器测得某一汽车在平直公路上运动的距离(s)-时间(t)图象如图乙所示,请在图丙中画出汽车运动的速度(v)-时间(t)图象.(3)为了他人的安全同时也保障自己的安全,每个公民应自觉遵守交通规则.从标志牌上看,在遵守交通规则的前提下,匀速行驶的汽车最快需用多长时间才能从标志牌到达威海.26.如图所示,A、B两个完全相同的、容积为3×10-3 m3的圆柱形容器放在水平地面上,容器底面积为2×10-2m2,容器内盛有质量相等的水和酒精,其中A容器中盛有水,水面距容器底部0.1 m,B容器中盛有酒精(ρ酒精=0.8×103 kg/m3).求:(1)A容器中水的质量m水.(2)B容器中酒精的体积V酒.(3)将质量2.7 kg的金属块浸没在酒精中,酒精不溢出,求金属块的最小密度ρ金.2020~2021学年第一学期期末质量监测八年级物理试卷答案版(时间:60分钟总分:100分)一、选择题(本大题共15个小题,共33分.1~12小题为单项选择题,每小题2分;13~15小题为多选题,每小题3分,选对但不全得2分,错选或不选不得分)1.下列对生活中一些物理量的估测合理的是(B)A.复兴号高铁列车运行速度可达350 m/sB.一个苹果的质量约为150 gC.石家庄冬季平均气温约为-20 ℃D.上课教室门高4 m2.两列火车并排停在站台上,你坐在车厢中向另一列车观望.突然,你觉得自己的列车缓慢向东运动.则下列运动情况不可能发生的是(D)A.自己的车向东运动,另一列车没有运动B.自己的车没有运动,另一列车向西运动C.两列车都向东运动,但自己车的速度较快D.两列车都向西运动,但另一列车的速度较慢3.在平直的公路上,小明坐在车上用电子表的秒表功能记下了汽车连续通过5根电线杆的时间为10 s,相邻电线杆的距离为50 m,则汽车的平均速度约为(B) A.90 km/h B.70 km/hC.50 km/h D.40 km/h4.关于声现象,下列说法正确的是(B)A.调节手机音量是为了改变声音的音调B.考场附近禁止鸣笛,是在声源处减弱喊声C.超声波的传播不需要介质D.医生通过听诊器给人诊病是利用声波可以传递能量5.一艘科考船对某海域的海底形状利用声呐系统进行了测绘.具体方法是:在经过该海域水平面等间距的A、B、C、D、E五个位置时,向海底定向发射超声波,测得回收信号的时间分别为0.30 s、0.16 s、0.30 s、0.14 s、0.30 s.根据时间,求出海底与海平面的距离,就可以绘出海底的大致形状,则该海域海底的大致形状如图中的(C)A B C D6.生活中有很多现象和应用都与物态变化有关,下列说法不正确的是(C)A.皮肤上擦酒精后变凉爽是由于酒精汽化从皮肤吸热所致B.在运输食物的车里放干冰,利用干冰升华吸热给食物降温C.出汗时吹电风扇感觉凉爽,是由于电风扇吹出的风降低了室温D.夏天吃冰棒时看到周围冒“白气”,这是液化现象7.下列现象中,由光的反射形成的是(D)A.透过水面看到水中的“鱼”B.灯光下看到地上的“人影”C.用凸透镜看到放大的“字”D.在化妆镜中看到的“自己”8.如图所示,将平面镜和铅笔竖直放置在水平桌面上,下列说法正确的是(D)A.铅笔水平向右移动时,铅笔的像将变小B.平面镜竖直向上移动时,铅笔的像也将向上移动C.若改用一块较小的平面镜,铅笔的像将变小D.若铅笔按图示箭头方向转过45°,铅笔将与它的像垂直9.有一圆柱形敞口容器,从其左侧某一高度斜射一束激光,在容器底部产生一个光斑O,如图所示,下列操作使光斑向左移的是(B)A.保持水面高度不变使激光笔向右平移B.保持激光射入角度不变使水面上升C.保持激光射入角度不变使水面下降D.保持水面高度和入射点不变使激光入射角增大10.小明利用太阳光测量凸透镜的焦距,下列操作最合理的是(C)11.下列关于质量和密度的说法中正确的是(C)A.粉笔在黑板上写字时,粉笔的质量和密度都不变B.水结成冰时,质量不变,密度变大C. -瓶牛奶喝掉一半后,质量变小,密度不变D.一千克铁比一千克棉花质量大12.如图为甲、乙两种物质的m-V图象,下列说法正确的是(D)A.体积为20 cm3的甲物质的质量为10 gB.乙物质的密度与质量成正比C.甲物质的密度比乙的密度小D.甲、乙质量相同时,乙的体积是甲的2倍13.一束光从空气斜射向某透明介质,同时发生反射和折射.若入射光线和折射光线的夹角为170°,入射光线和反射光线的夹角为100°,则(ACD)A.入射角为50°B.反射光线和折射光线的夹角为80°C.折射角为40°D.反射光线和折射光线的夹角为90°14.在探究凸透镜成像规律的实验中,当蜡烛、凸透镜、光屏位于如图所示的位置时,在光屏上呈现一个清晰的烛焰的像.下列说法正确的是(CD)A.此时成正立、放大的实像,与投影仪原理相同B.透镜不动,蜡烛和光屏都向右移动,光屏上的像变小C.透镜左移10 cm后,眼睛在光屏和透镜间,通过透镜能看到正立的像D.若在透镜和蜡烛之间放远视镜片,则将光屏适当左移,可再次出现清晰的像15.甲、乙两个实心金属块,它们的质量分别为m甲、m乙,它们的体积分别为V甲、V乙,它们的密度分别为ρ甲、ρ乙.已知ρ甲>ρ乙,则下列情况存在的是(ACD) A.V甲>V乙,同时m甲>m乙B.V甲>V乙,同时m甲<m乙C.V甲<V乙,同时m甲>m乙D.V甲<V乙,同时m甲<m乙二、填空题(本大题共4个小题,每空2分,共30分)16.如图是用照相机拍摄的气泡从充满油的玻璃管底端向上运动的一张频闪照片,气泡从点A开始运动,频闪点B、C、D是每隔2 s拍摄的气泡位置,分析照片可知:(1)气泡在AD段做__变速__(填“匀速”或“变速”)直线运动;其理由是__在相等的时间内气泡通过的路程越来越大__.(2)气泡在BD段运动的平均速度为__0.125__m/s.(3)该气泡在__CD__两点间的平均速度最大.17.暖气通常安置于房间的地面上,由于低处热空气密度比冷空气密度__小__(填“大”或“小”),所以热空气会__上升__(填“上升”或“下降”),周围冷空气就补充过来,形成冷、热空气的交互循环,更有利于整个房间变得温暖.18.请你根据自己对生活现象的观察、动手实践的经验及物理课中所学的知识,将图所示四个实例的描述补充完整.A B C D图A:冰棍“冒”出的“白气”向__下落__(填“上飘”或“下落”),这是冰棍周围水蒸气__液化__(填物态变化名称)形成的小水滴.图B:把正在响铃的闹钟放在玻璃罩内,逐渐抽出其中的空气,铃声的响度__变小__(填“变大”“变小”或“不变”),这说明__空气__(填“空气”或“真空”)可以传播声音.图C:在空罐的罐底中央打一个小孔,再用一片半透明的塑料膜蒙在空罐的口上.白天将小孔对着室内的窗户,可观察到户外景物呈现在塑料膜上是__倒立__(填“正立”或“倒立”)的.图D:在碗底放一枚硬币,自己远离碗一段距离,站到刚好看不到硬币的位置.另一同学慢慢向碗中加满水,你将__能__(填“能”或“不能”)看到这枚硬币.19.阅读下面的短文,回答问题.多普勒效应1842年的一天,奥地利一位名叫多普勒的科学家正路过铁路交叉处,恰逢一列火车从他身旁驶过,他发现火车从远而近时鸣笛声变响,音调变尖,而火车从近而远时鸣笛声变弱,音调变低.他对这个物理现象产生了极大兴趣,就进行了研究.他发现当声源与观察者之间存在着相对运动时,观察者听到的声音频率就会不同于声源发声的频率.当声源离观察者远去时,观察者接收到的声波的波长增加,频率变小,音调变得低沉;当声源向观察者靠近时,观察者接收到的声波的波长减小,频率变大,音调就变高,后来人们把它称为“多普勒效应”.声波的多普勒效应可用于交通中的测速,交通警察向行进中的车辆发射频率已知的超声波,同时测量反射波的频率,根据反射波频率变化的多少就能知道车辆的速度.多普勒效应也可以用于医学的诊断,也就是我们平常说的彩超,即彩色多普勒超声.根据上述内容回答:(1)交通中的测速仪和医学中的彩超都是应用__多普勒效应__工作的.(2)若声源不动,观察者向声源处运动,__能__(填“能”或“不能”)发生多普勒效应.(3)从听到火车鸣笛的音调变高判断,火车正在__靠近__(填“靠近”或“远离”)观察者.三、作图与实验探究题(本大题共5个小题,20、21、22题每题2分,23、24题每空1分,共25分)20.水池中发光点S射出的光线,在池中没有水时射到A处,当池中注入一定深度的水后,光线在水面发生反射,反射光射到池底B处,请你画出光线在水面发生反射时的入射光、反射光及水面的位置.解:21.如图所示,根据凸透镜和凹透镜的性质,补全光路.解:22.在水平的实验桌上有已调好的天平一台,提供的砝码如图所示,请你利用上述器材,设计一个实验检验:在标尺上向右移动游码就相当于在天平右盘中增加相应质量的砝码.要求:写出检验的实验步骤.__(1)将两个5_g的砝码分别同时放在天平的左、右盘中,天平平衡;(2)保持左盘中5_g的砝码不变,将右盘中5_g的砝码取出,在标尺上将游码向右移动,使游码左侧与5_g刻度线对齐,观察天平是否再次平衡.__23.小明和小红做“探究凸透镜成像规律”的实验.甲(1)利用太阳光测量凸透镜的焦距时,小明将一把木质刻度尺一端支于水平地面上,观察尺在地面上形成的影子,不断调节刻度尺,使其在地面上的影子__最短__,这时尺的方向就与太阳光的方向平行,小明保持尺不动,小红将光屏A和凸透镜L按如图所示的方式均垂直于刻度尺摆放,光屏上形成了一个最小、最亮的光斑.则该凸透镜的焦距为__10__cm.(2)实验前应点燃蜡烛,观察烛焰、凸透镜和光屏的中心是否在同一高度上,这样做的目的是__使像能够成在光屏的中央__.(3)当蜡烛、凸透镜和光屏的相对位置如图乙所示,光屏上出现清晰的像,则像是倒立、__缩小__的实像.乙丙(4)实验中,不但虚像可以用肉眼直接看到,实像也可以用肉眼直接看到,如图丙所示,在(3)的基础上,拿掉光屏,用肉眼在__C__(填“A”“B”或“C”)位置沿图示方向能看到这个实像.(5)在(3)的基础上,当光屏略微向右移动时,光屏上的像将会模糊,如果蜡烛与凸透镜不动,那么,在凸透镜前放置__凹__(填“凸”或“凹”)透镜,才可能在光屏上得到清晰的像,这其实就是__近视眼__(填“近视眼”或“远视眼”)的矫正原理.(6)下表是实验中得到的数据和观察的结果.次数物距u/cm 成像情况像距v/cm1 50.0倒立、缩小、实像12.5 2 30.0倒立、缩小、实像15.0 3 20.0倒立、等大、实像20.0 4 15.0倒立、放大、实像5 8.0正立、放大、虚像/通过1、2、3次实验数据可以得出:当凸透镜成实像时,物距变小,像距__变大__(填“变大”“变小”或“不变”);表格中第4次实验光屏上成清晰的像时,光屏到透镜的距离为__30__cm,此成像规律在实际生活中的应用是__投影仪__(填“照相机”“投影仪”或“放大镜”).24.为了测量盐水的密度,小红同学进行了如下实验:(1)她将天平放在水平台面上,将游码移到标尺的__零刻度线处__.横梁静止时,指针指在分度盘中央刻度线的左侧,如图甲所示.为使横梁在水平位置平衡,应将横梁右端的平衡螺母向__右__移动.(2)小红同学将盛有适量盐水的杯子放在调好的天平左盘内,测出杯子和盐水的总质量为128 g.然后将杯中盐水倒入量筒中一部分,如图乙所示,则量筒中盐水的体积为__60__cm3.(3)再将盛有剩余盐水的杯子放在天平左盘内,按从大到小的顺序依次加砝码时,出现了如图丙的情况,小红下一步应进行的操作是(砝码盒中还有更大和更小的其他砝码)__B__.A.把右盘中的砝码取下,换更大的砝码B.继续向右盘中加更小的砝码C.直接拨游码(4)横梁恢复水平平衡后,右盘中砝码质量和游码在标尺上的位置如图丁所示,则杯子及杯内剩余盐水的总质量为__62__g;根据上述实验数据计算盐水的密度为__1.1×103__kg/m3.(5)小明同学感觉小红同学这样测量太麻烦,于是他设计如下实验步骤:a.用天平测出空烧杯的质量记作m1;b.向烧杯中倒入适量的盐水,用天平测出烧杯和盐水的总质。
人教版英语八年级下册第二学期期末 达标测试卷(含答案)

第二学期期末达标测试卷听力部分(共20分)一、情景反应(每小题1分,共5分)本题共5个小题,每小题你将听到一组对话。
请你从每小题所给的A、B、C三幅图片中,选出与你所听到的信息相关联的一项。
()1. A. B. C.()2. A. B. C.()3. A. B. C.()4. A. B. C.()5. A. B. C.二、对话理解(每小题1分,共5分)本题共5个小题,每小题你将听到一组对话和一个问题。
请你从每小题所给的A、B、C三个选项中,选出一个最佳选项。
()6. A. In America. B. In Europe. C. In China.()7. A. Jinci Park. B. Jinyanghu Park.C. Fen River Park.()8. A. Treasure Island. B. Little Women.C. Robinson Crusoe.()9. A. China. B. India. C. Russia.()10. A. Pop music. B. Rock music. C. Country music.三、语篇理解(每小题1分,共5分)本题你将听到一篇短文。
请你根据短文内容和所提出的5个问题,从每小题所给的A、B、C三个选项中,选出一个最佳选项。
()11. What happened to the young man?A. He lost his watch.B. He missed his father.C. He failed to get a gift.()12. Who did the young man ask for help?A. Some workers.B. A group of children.C. His parents.()13. When did the little boy ask for another chance?A. When the young man felt hopeless.B. After he got some candies.C. Before children searched the workshop.()14. How did the little boy succeed?A. By trying over and over again.B. By sitting silently on the ground.C. By finding the light of the watch.()15. What does the story tell us?A. More hands make lighter work.B. Confidence is the key to success.C. Good solutions lie in a peaceful mind.四、听力填空(每小题1分,共5分)本题你将听到一篇演讲词。
期末检测(三)2021-2022学年人教版八年级英语上册(word版 含答案)

人教版八年级上册--单元知识梳理和检测期末综合测试(三)一、选择题( ) 1. —Would you like to go shopping with me, mum?—If dad doesn’t go, .A. neither do IB. so do IC. neither will ID. so will I( ) 2. —Where is Kate? —Look, . She is at the school gate.A. there she isB. there is sheC. here you areD. here it is( ) 3. There seems a 1ot of money in his pocket.A. to haveB. havingC. to beD. being( ) 4. It was because I like you I speak out frankly.A. thatB. whyC. BecauseD. who( ) 5. Tom did all he could to get on well his classmates.A. which; withB. that; /C. that; withD. /; /( ) 6. I hear the tall girl wearing glasses is your new classmate. She’s from America, ?A. has sheB. isn’t sheC. hasn’t sheD. does she( ) 7. good advice you’ve told me! Thank you very much!A. WhatB. What aC. HowD. How a( ) 8 —you ever Dali?—Never. But I am going there this vacation.A. Do; go toB. Have; been toC. Have; gone toD. Will; go to( ) 9.—have you visited Nanjing? —Three times.A. How oftenB. How many timesC. How longD. How soon( ) 10. He’s never read this book before, .A. isn’t heB. does heC. has heD. won’t he( ) 11. How does this weather make him ?A. feelsB. feelC. feelingD. to feel( ) 12. Soft drinks to children for free in some restaurants on Children’s Day.A. offerB. have offeredC. are offeredD. will be offered( ) 13. When I was walking past the window, I noticed Wang Fei my homework. I really got .A. copying, annoyedB. copying, annoyingC. copy, annoyedD. copied, annoyed( ) 14. We should never till tomorrow what we can do today.A. put onB. put offC. give upD. give away( ) 15. It took her to cook the delicious food.A. three and a half hourB. three and a half hoursC. a half and three hourD. three hour and a half( ) 16.—Do you know the boy is sitting next to Peter?—Yes, he is Peter’s friend. They are celebrating his birthday.A. who; ninthB. who; ninethC. that; ninethD. which; ninth( ) 17. you have nothing important to do, why not come with me to the cinema?A. SinceB. WhenC. ForD. Because( ) 18. you say sorry to your uncle, he won’t forgive you.A. AlthoughB. UnlessC. IfD. Since( ) 19. It’s snowing heavily, so there is a lot of snow all the ground.A. AboveB. overC. onD. in( ) 20.—Where are you going your next vacation?—We decided Europe.A. on; forB. for; toC. on; toD. for; on二、完形填空Long long ago, a poor farmer had a dog and a cat. The dog and the cat 1 for the farmer and they got food from him. One night, the farmer said, “I will not get enough 2 for both of you to live in. If you work 3 than your partner, you will have the chance to live in the house.” Then they 4 good night to each other.The next morning, the dog and the cat got up early. The dog went to the field and worked hard; but the cat climbed up a tree and began to 5 . When the cat woke up, he went to the field and left a lot of footprints in the field.In the evening, they both went back home. The dog told the farmer that he finished all the 6 , but the cat also told the farmer that he finished all the work, the farmer decided to go and check in the 7 the next day.What did the farmer 8 ? There were all the cat's footprints in the field.From then on, the cat lived in the 9 and the dog lived out of it. So the dog was 10 whenever he met the cat. However, the farmer never knew why.( ) 1. A. worked B. lived C. played D. made( ) 2. A. halls B. stores C. rooms D. malls( ) 3. A. earlier B. harder C. more happily D. more slowly( ) 4. A. talked B. said C. spoke D. told( ) 5. A. laugh B. cry C. sleep D. walk( ) 6. A. work B. homework C. test D. food( ) 7. A. field B. village C. market D. hospital( ) 8. A. hear B. see C. feel D. taste( ) 9. A. school B. classroom C. house D. store .( ) 10. A. excited B. worried C. happy D. angry三、阅读理解Many teenagers(青少年) feel that the most important people in their lives are their friends. They believe that their family members, and in particular(尤其是) their parents, don't know them as well as their friends do. In large families, it is quite often for brothers and sisters to fight(打架) with each other and then they only go to their friends for getting ideas.It is very important for teenagers to have one good friend or a circle of friends. Even when they are not with their friends, they usually spend a lot of time talking among themselves on the phone. This communication(交际) is very important in children's growing up, because they can discuss something difficult to their family members.Parents often try to choose(选择) their children's friends for them. Some parents may even stop their children from meetin g their good friends. The question of“choice" is an interesting one. Have you ever thought of the following questions: Who choose your friends? Do you choose your friends or your friends choose you? Have you got a good friend your parents don't like? Your answers are welcome.( ) 1. Who know them better than their parents for the teenagers?A. Their friends.B. Their parents.C. Brothers and sisters.D. Family members.( ) 2. How do they communicate when the teenagers stay alone?A. Go to their friends.B. Talk with their parents.C. Have a discussion with their family by phone.D. Talk with their friends on the phone.( ) 3. Which of the following sentences is true?A. Parents should like everything their children enjoy.B. In all family children can choose everything they like.C. Parents should try their best to understand their children better.D. Teenagers can only go to their friends for help.( ) 4. What is the meaning for“Your answers are welcome."?A. You are welcomed to have a discussion with us.B. You have got an idea, so your answers are welcome.C. Your answers are always right.D. You can give us all the right answers.( ) 5. Which is the best title ( 标题) of the passage?A. Only parents can decide.B. Parents and children.C. Teenagers need friends.D. A strange question.四、短文填空Failure is a common thing in our life. Everything has (1) possible results: success or failure. People all over the world like (2) , but there is still failure in our life.What do you think of failure? (3) do you deal with the failure? Different people have different ( 4)on failure. Some people consider it as a good thing, because they can learn a lesson (5) it. Then they try their best to find the (6 ) of failure, and correct what is wrong. So they can do it better next time. But some people regard it (7) a bad thing. They lose their (8) . Also they are discouraged. Finally they give it up.Which opinion is right? How about the (9 ) one? Please remember: Failure is the (10) of success. When you have failure in your life, please find out the reason of failure and do your best to do it better next time.五、作文。
人教版部编版八年级下册数学期末试卷检测(提高,Word版含解析)

人教版部编版八年级下册数学期末试卷检测(提高,Word 版含解析) 一、选择题1.当x =0时,下列式子有意义的是( )A .0xB .xC .x D .1x -2.下列各组数中,能构成直角三角形的是( ) A .2,3,4B .4,5,6C .1,3,2D .5,11,133.如图,在△ABC 中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是( )A .∠B =∠FB .∠B =∠BCFC .AC =CFD .AD =CF4.小明和小兵两人参加了5次体育项目训练,其中小明5次训练测试的成绩分别为11、13、11、12、13;小兵5次训练测试成绩的平均分为12,方差为7.6.关于小明和小兵5次训练测试的成绩,则下列说法不正确的是( ) A .两人测试成绩的平均分相等 B .小兵测试成绩的方差大 C .小兵测试的成绩更稳定些 D .小明测试的成绩更稳定些 5.△ABC 中,AB=15,AC=13,高AD=12,则△ABC 的周长为( )A .42B .32C .42或32D .37或336.如图,菱形 ABCD 的顶点 C 在直线 MN 上,若∠1=50°,∠2=20°,则∠BDC 的度数为()A .20°B .30°C .35°D .40°7.如图,数轴上A 点表示的数为2-,B 点表示的数是1.过点B 作BC AB ⊥,且2BC =,以点A 为圆心,AC 的长为半径作弧,弧与数轴的交点D 表示的数为( )A 13B 132C 132D 1338.如图,在平面直角坐标系中,四边形11112222333,,OA B C A A B C A A B C ,…都是菱形,点123,,A A A …都在x 轴上,点123,,C C C ,…都在直线3333y x =+上,且11212323160,1C OA C A A C A A OA ∠=∠=∠==︒=,则点n C 的横坐标是( )A .2321n -⨯-B .2321n -⨯+C .1321n -⨯-D .1321n -⨯+二、填空题9.若1x -在实数范围内有意义,则x 的取值范围是____________. 10.菱形的周长是20,一条对角线的长为6,则它的面积为_____. 11.如图,每个方格都是边长为1的小正方形,则AB +BC =_____.12.如图,点E 是矩形纸片ABCD 的边BC 上的一动点,沿直线AE 折叠纸片,点B 落在点B '位置,连接C B '.若AB =3,BC =6,则线段C B '长度的最小值为 ________________.13.定义:对于一次函数y kx b =+,我们把点(),b k 称为这个一次函数的伴随点.已知一次函数4y x m =+-的伴随点在它的图象上,则=m __________.14.如图,在正方形ABCD 中,点E 、F 分别在对角线BD 上,请你添加一个条件____________,使四边形AECF 是菱形.15.甲从A 地出发以某一速度向B 地走去,同时乙从B 地出发以另一速度向A 地而行,如图中的线段1y 、2y 分别表示甲、乙离B 地的距离(km )与所用时间()h x 的关系.则A 、B两地之间的距离为______km,甲、乙两人相距4km时出发的时间为______h.16.如图,正方形ABCD的面积为144,点H是边DC上的一个动点,将正方形沿过点H的直线GH折叠(点G在边AB上),使顶点D的对应点E恰好落在BC边上的三等分点处,则线段DH的长是___.三、解答题17.计算:(1)23439 3415⨯(2)20511235--⨯18.位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D的位置,问此时游船移动的距离AD的长是多少?19.图①、图②均是44⨯的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,点A、B均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,所画图形不全等,不要求写画法.(1)在图①中以线段AB为边画一个正方形ABCD.(2)在图②中以线段AB为边画一个菱形ABEF.20.已知:如图,在ABC 中,AD 是BAC 的平分线,//,//DE AC DF AB . 求证:四边形AEDF 是菱形.21.先观察下列等式,再回答问题: 2211+2+()1 =1+1=2;2212+2+()212=2 12;2213+2+()3=3+13=313;…(1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.22.在乡村道路建设过程中,甲、乙两村之间需要修建水泥路,甲、乙两村合作完成.已知甲村需要水泥70吨,乙村需要水泥110吨,A 厂可提供100吨水泥,B 厂可提供80吨水泥,两厂到两村的运费如表:目的地运费/(元/吨)甲村乙村 A 厂 240 180 B 厂250160x (吨)之间的函数关系式,并写出自变量x 的取值范围;(2)请你设计出运费最低的运送方案,并求出最低运费.23.将两张宽度相等的纸片叠放在一起,得到如图的四边形ABCD .(1)求证:四边形ABCD 是菱形;(2)如图,联结AC ,过点A 、D 分别作BC 的垂线、DE ,垂足分别为点F 、E . ①设M 为AC 中点,联结、,求证:;②如果,P 是线段AC 上一点(不与点A 、C 重合),当为等腰三角形时,求的值.24.如图,在平面直角坐标系中,直线1l :1y kx b =+经过,两点,且a 、b满足,过点B 作轴,交直线2l :于点P ,连接.(1)求直线AB 的函数表达式; (2)在直线2l 上是否存在一点Q ,使得?若存在,求出点Q 的坐标;若不存在,请说明理由. (3)点是x 轴上的一个动点,点D 是y 轴上的一个动点,过点C 作x 轴的垂线交直线1l 、2l 于点M 、N ,若是等腰直角三角形,请直接写出符合条件的的值.25.如图1,在OAB 中,OAB 90∠=,30AOB ∠=,8OB =,以OB 为边,在OAB Λ外作等边OBC Λ,D 是OB 的中点,连接AD 并延长交OC 于E .(1)求证:四边形ABCE 是平行四边形;(2)连接AC ,BE 交于点P ,求AP 的长及AP 边上的高BH ;(3)在(2)的条件下,将四边形OABC 置于如图所示的平面直角坐标系中,以E 为坐标原点,其余条件不变,以AP 为边向右上方作正方形APMN : ①M 点的坐标为 .②直接写出正方形APMN 与四边形OABC 重叠部分的面积(图中阴影部分).26.如图所示,四边形ABCD 是正方形, M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点AB 、重合),另一直角边与CBM ∠的平分线BF 相交于点F . (1)求证: ADE FEM ∠=∠;(2)如图(1),当点E 在AB 边的中点位置时,猜想DE 与EF 的数量关系,并证明你的猜想; (3)如图(2),当点E 在AB 边(除两端点)上的任意位置时,猜想此时DE 与EF 有怎样的数量关系,并证明你的猜想.【参考答案】一、选择题 1.C 解析:C 【分析】根据零指数幂、分式有意义,二次根式有意义的条件进行判断即可; 【详解】解:当x =0时,0x 0x 当x =0=0x x当x =0时,x-1=-11x - 故选:C【点睛】本题考查了零指数幂、分式有意义,二次根式有意义的条件,熟练掌握相关知识是解题的关键2.C解析:C 【分析】根据勾股定理的逆定理对四组数据进行逐一判断即可. 【详解】解:A 、∵22 +32 ≠4 2 ,∴不能构成直角三角形; B 、∵42 +52 ≠62 ,∴不能构成直角三角形;C 、∵22212+= ,∴能构成直角三角形;D 、∵5 2 +11 2 ≠13 2 ,∴不能构成直角三角形. 故选C . 【点睛】本题考查了用勾股定理的逆定理判断三角形的形状,即只要三角形的三边满足a 2 +b 2 =c2,则此三角形是直角三角形.3.B解析:B 【解析】 【分析】根据已知条件可以得到//AC DE ,对选项判断即可求出解. 【详解】解:∵D ,E 分别是AB ,BC 的中点 ∴//AC DE ,12DE AC =A :根据∠B =∠F 得不出四边形ADFC 为平行四边形,选项不符合题意; B :∠B =∠BCF ,∴CF//AD ,∴四边形ADFC 为平行四边形,选项符合题意; C :根据AC =CF 得不出四边形ADFC 为平行四边形,选项不符合题意; D :根据AD =CF 得不出四边形ADFC 为平行四边形,选项不符合题意; 故答案为B . 【点睛】此题考查了中位线的性质以及平行四边形的判定,熟练掌握有关性质即判定方法是解题的关键.4.C解析:C 【解析】 【分析】先计算出小明5次训练测试成绩的平均分和方差,再与小兵5次训练测试成绩的平均分和方差进行比较即可得出结论. 【详解】解:小明5次训练测试成绩的平均分为1(1113111213)125++++=(分);小明5次训练测试成绩的方差为:2222221[(1112)(1312)(1112)(1212)(1312)]0.85S =-+-+-+-+-=(分2)∴22S S <小明小兵∴两人的平均成绩一样好,小兵的方差大, ∴小明测试的成绩更稳定些 故选:C . 【点睛】本题考查了方差的意义.方差它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.5.C解析:C 【分析】存在2种情况,△ABC 是锐角三角形和钝角三角形时,高AD 分别在△ABC 的内部和外部 【详解】情况一:如下图,△ABC 是锐角三角形∵AD 是高,∴AD ⊥BC ∵AB=15,AD=12 ∴在Rt △ABD 中,BD=9 ∵AC=13,AD=12 ∴在Rt △ACD 中,DC=5∴△ABC 的周长为:15+12+9+5=42 情况二:如下图,△ABC 是钝角三角形在Rt △ADC 中,AD=12,AC=13,∴DC=5 在Rt △ABD 中,AD=12,AB=15,∴DB=9∴BC=4∴△ABC 的周长为:15+13+4=32 故选:C 【点睛】本题考查勾股定理,解题关键是多解,注意当几何题型题干未提供图形时,往往存在多解情况.6.C解析:C 【解析】 【分析】先求出BCD ∠,根据菱形性质得出BC CD =,即得到CBD CDB ∠=∠,可得BDC ∠的度数. 【详解】∵∠1=50°,∠2=20° ∴18012110BCD ︒︒∠=-∠-∠= ∵四边形ABCD 为菱形 ∴BC BD =∴1(180)352BDC BCD ︒︒∠=-∠=故选:C . 【点睛】本题考查了菱形的性质求角度,熟知以上知识是解题的关键.7.C解析:C 【解析】 【分析】根据题意先求得AB 的长,根据勾股定理求得AC 的长,根据题意AC AD =,进而求得D 点表示的数. 【详解】依题意,数轴上A 点表示的数为2-,B 点表示的数是1,()123AB ∴=--=,BC AB ⊥,2BC =,AC ∴ AC AD =,AD ∴=数轴上A 点表示的数为2-,∴D 2.故选C .【点睛】本题考查了实数与数轴,勾股定理,勾股定理求得AC 是解题的关键.8.A解析:A 【分析】分别过点123,,,...C C C 作x 轴的垂线,交于123,,,...D D D ,再连接112233,,,...C D C D C D ,利用勾股定理及根据菱形的边长求得1A 、2A 、3A ⋯的坐标然后分别表示出1C 、2C 、3C ⋯的坐标找出规律进而求得n C 的坐标.【详解】解:分别过点123,,,...C C C 作x 轴的垂线,交于123,,,...D D D ,再连接112233,,,...C D C D C D 如下图:11OA =,11OC ∴=,1121232360C OA C A A C A A ∴∠=∠=∠=⋯=︒,在11Rt OC D 中,111122OD OC ==根据勾股定理得:2221111OD OC C D =-,即222111()2OD =-,解得:13OD =1C ∴312,11(2C ∴3),四边形111OA B C ,1222A A B C ,2333A A B C ,⋯都是菱形,122A C ∴=,234A C =,348A C =,⋯,2C ∴的纵坐标为:22122122413A C D D AC =--33y 2,23)C ∴,3C 的纵坐标为:33C D =y x =为5,3(5C ∴,,4(11C ∴,,5(23C ,,6(47C ∴,;,⋯,2(321n n C -⨯-,2n -则点n C 的横坐标是:2321n -⨯-,故选:A .【点睛】本题是对点的坐标变化规律的考查,主要利用了菱形的性质,解直角三角形,根据已知点的变化规律求出菱形的边长,得出系列C 点的坐标,找出规律是解题的关键.二、填空题9.1≥x 且3x ≠【解析】【分析】根据分母不等于0,且被开方数是非负数列式求解即可.【详解】由题意得10x -≥且30x -≠解得1≥x 且3x ≠故答案为:1≥x 且3x ≠【点睛】本题考查了代数式有意义时字母的取值范围,代数式有意义时字母的取值范围一般从几个方面考虑:①当代数式是整式时,字母可取全体实数;②当代数式是分式时,考虑分式的分母不能为0;③当代数式是二次根式时,被开方数为非负数.10.D解析:【解析】【分析】先画出图形,根据菱形的性质可得5AD =,DO =3,根据勾股定理可求得AO 的长,从而得到AC 的长,再根据菱形的面积公式即可求得结果.【详解】由题意得2045AD =÷=,6BD =∵菱形ABCD∴3DO =,AC ⊥BD ∴4AO ==∴28AC AO == ∴1242S AC BD =⋅=考点:本题考查的是菱形的性质【点睛】解答本题的关键是熟练掌握菱形的对角线互相垂直且平分,菱形的四条边相等;同时熟记菱形的面积等于对角线乘积的一半.11.A解析:25【解析】【分析】根据勾股定理可以求出AB 和BC 的长,进而可求出AB+BC 的值.【详解】解:∵每个方格都是边长为1的小正方形,∴22125AB =+=,22125BC =+=∴AB +BC =5525+=.故答案为25.【点睛】本题考查了勾股定理.熟练掌握勾股定理是解题的关键.12.A解析:35﹣3【分析】连接AC ,当A 、B '、C 共线时,C B '的值最小,进而解答即可.【详解】解:如图,连接AC .∵折叠,∴AB =A B '=3,∵四边形ABCD 是矩形,∴∠B =90°,∴AC=∵C B '≥AC ﹣A B ',∴当A 、B '、C 共线时,C B '的值最小为:3,故答案为:3.【点睛】本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是熟练掌握基本知识,作出正确的辅助线,属于中考常考题型.13.43【分析】先写出4y x m =+-的伴随点,再根据伴随点在它的图象上代入一次函数解析式,计算即可求得m .【详解】解:4y x m =+-的伴随点为(),4m -,因为4y x m =+-伴随点在它的图象上,则有44m m -=+- 解得43m =. 故答案为:43. 【点睛】本题考查一次函数图象上点的坐标特征. 一次函数图象上任意一点的坐标都满足函数关系式y=kx+b .14.B解析:BE=DF【分析】根据正方形的性质,可得正方形的四条边相等,对角线平分对角,根据 SAS ,可得△ABF 与△CBF 与△CDE 与△ADE 的关系,根据三角形全等,可得对应边相等,再根据四条边相等的四边形,可得证明结果.【详解】添加的条件为:BE=DF ,理由:正方形ABCD 中,对角线BD ,∴AB=BC=CD=DA ,∠ABE=∠CBE=∠CDF=∠ADF=45°.∵BE=DF ,∴△ABE ≌△CBE ≌△DCF ≌△DAF (SAS ).∴AE=CE=CF=AF ,∴四边形AECF 是菱形;故答案为:BE=DF .【点睛】本题考查了正方形的性质,菱形的判定,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.15.2或3【分析】①利用路程的函数图象解得的解析式,再求的值;②根据题意列方程解答即可.【详解】解:①设=kx +b ,∵经过点P (2.5,7.5),(4,0).∴ ,解得 ,∴=解析:2或3【分析】①利用路程1y 的函数图象解得1y 的解析式,再求的1y 值;②根据题意列方程解答即可.【详解】解:①设1y =kx +b ,∵1y 经过点P (2.5,7.5),(4,0).∴ 2.57.540k b k b ⎧⎨⎩+=+= , 解得520k b -⎧⎨⎩== , ∴1y =−5x +20,当x =0时,1y =20.答:AB 两地之间的距离为20km .②根据题意得:53204x x +=-或53204x x +=+,解得:2x =或3x =.即出发2小时或3小时,甲、乙两人相距4km【点睛】此题主要考查了根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.熟练掌握相遇问题的解答也很关键.16.或【分析】由已知可知CE =4或CE =8,由折叠可知DH =EH ,则CH =12﹣DH ,分两种情况求,在Rt △ECH 中,利用勾股定理求解.【详解】解:∵正方形ABCD 的面积为144,∴正方形的边解析:263或203【分析】由已知可知CE=4或CE=8,由折叠可知DH=EH,则CH=12﹣DH,分两种情况求,在Rt△ECH中,利用勾股定理求解.【详解】解:∵正方形ABCD的面积为144,∴正方形的边长为12,∵E为BC的三等分点,∴BE=4或BE=8,由折叠可知DH=EH,∴CH=12﹣DH,当CE=8时,在Rt△ECH中,EH2=EC2+CH2,∴DH2=64+(12﹣DH)2,∴DH=263;当CE=4时,在Rt△ECH中,EH2=EC2+CH2,∴DH2=16+(12﹣DH)2,∴DH=203;综上所述:DH的长为263或203,故答案为263或203.【点睛】本题考查了正方形的性质,折叠的性质,勾股定理,以及分类讨论的数学思想,分类讨论是解答本题的关键.三、解答题17.(1)6;(2)-1【分析】(1)将二次根式的系数相乘,将二次根式相乘,再化简即可得到答案;(2)根据除法法则和乘法法则计算二次根式的乘除法,再将结果相加减即可.【详解】(1)(2).解析:(1)6;(2)-1(1)将二次根式的系数相乘,将二次根式相乘,再化简即可得到答案;(2)根据除法法则和乘法法则计算二次根式的乘除法,再将结果相加减即可.【详解】(1263=⨯(22121=--=-. 【点睛】此题考查二次根式的计算,正确掌握二次根式的乘除法法则,二次根式混合运算法则,以及二次根式的性质化简二次根式是解题的关键.18.游船移动的距离AD 的长是9米【分析】根据条件先计算经过10秒拉回绳子的长,然后计算出绳子CD 的长,在中,在中,,即可求出最终结果.【详解】解:工作人员以0.7米/秒的速度拉绳子,经过10秒解析:游船移动的距离AD 的长是9米【分析】根据条件先计算经过10秒拉回绳子的长,然后计算出绳子CD 的长,在Rt BCD 中BD Rt ABC 中,AB =【详解】 解:工作人员以0.7米/秒的速度拉绳子,∴经过10秒拉回绳子100.7=7⨯米,开始时绳子AC 的长为17m ,∴拉了10秒后,绳子CD 的长为17-7=10米,∴在Rt BCD 中,6BD ===米,在Rt ABC 中,15AB =米,∴AD =15-6=9米,答:游船移动的距离AD 的长是9米.【点睛】本题主要考查勾股定理的运用,属于综合题,难度一般,熟练掌握勾股定理解三角形是解决本题的关键.19.(1)见解析;(2)见解析【分析】(1)根据正方形的判定进行画图即可;(2)根据菱形的判定进行画图即可.【详解】解:(1)如图所示:,,∴,∴∠ABC=90°,∴四边形AB解析:(1)见解析;(2)见解析【解析】【分析】(1)根据正方形的判定进行画图即可;(2)根据菱形的判定进行画图即可.【详解】解:(1)如图所示:22AC=+=,221310AB CD AD BC====+=,125∴222+=,AB BC AC∴∠ABC=90°,∴四边形ABCD是正方形;(2)如图所示22====+=,AB EF AF BE125∴四边形ABEF是菱形.【点睛】本题主要考查了菱形的判定,正方形的判定,勾股定理和勾股定理的逆定理,解题的关键在于能够熟练掌握相关知识进行求解.20.见解析.【分析】根据四边形是平行四边形,再证明有一组邻边相等即可.【详解】解:∵,∴四边形是平行四边形,∵平分,∴,∵,∴,∴,∴,∴平行四边形是菱形.【点睛】本题考查了解析:见解析.【分析】根据//,//DE AC DF AB 四边形AEDF 是平行四边形,再证明有一组邻边相等即可.【详解】解:∵//,//DE AC DF AB ,∴四边形AEDF 是平行四边形,∵AD 平分BAC ∠,∴12∠=∠,∵//DE AC ,∴23∠∠=,∴13∠=∠,∴AE DE =,∴平行四边形AEDF 是菱形.【点睛】本题考查了平行线的性质,菱形的判定,等腰三角形的判定,解题关键是熟练运用相关性质,准确进行推理证明.21.(1);(2),证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即可猜想出第四个等式为44;(2)根据等式的变化,找出变化规律“n解析:(1144+=144;(2211n n n n ++=,证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即=414+=414;(2)根据等式的变化,找出变化规律=n 211n n n ++=”,再利用222112n n n n++=+()()开方即可证出结论成立. 【详解】(1)∵1+1=2;=212+=212;=313+=313;里面的数字分别为1、2、3,∴ 144+= 144.(21+1=2,212+=212313+=313=414+=414,…,∴= 211n n n n ++=.证明:等式左边==n 211n n n++==右边.=n 211n n n ++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律n 211n n n ++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.22.(1)y =﹣30x+37100(0≤x≤70);(2)最低运送方案为A 厂运往甲村水泥70吨,运往乙村水泥30吨:B 厂运往甲村水泥0吨,B 厂运往乙村水泥80吨,最低运费为35000元.【分析】(1解析:(1)y=﹣30x+37100(0≤x≤70);(2)最低运送方案为A厂运往甲村水泥70吨,运往乙村水泥30吨:B厂运往甲村水泥0吨,B厂运往乙村水泥80吨,最低运费为35000元.【分析】(1)由从A厂运往甲村水泥x吨,根据题意首先求得从A厂运往乙村水泥(100-x)吨,B 厂运往甲村水泥(70-x)吨,B厂运往乙村水泥吨,然后根据表格求得总运费y(元)关于x(吨)的函数关系式;(2)根据(1)中的一次函数解析式的增减性,即可知当x=70时,总运费y最省,然后代入求解即可求得最低运费.【详解】(1)设从A厂运往甲村水泥x吨,则A厂运往乙村水泥(100﹣x)吨,B厂运往甲村水泥(70﹣x)吨,B厂运往乙村水泥110﹣(100﹣x)=(10+x)吨,∴y=240x+180(100﹣x)+250(70﹣x)+160(10+x)=﹣30x+37100,x的取值范围是0≤x≤70,∴y=﹣30x+37100(0≤x≤70);(2)∵y=﹣30x+37100(0≤x≤70),﹣30<0,∴y随x的增大而减小,∵0≤x≤70,∴当x=70时,总费用最低,最低运费为:﹣30×70+37100=35000 (元),∴最低运送方案为A厂运往甲村水泥70吨,运往乙村水泥30吨:B厂运往甲村水泥0吨,B厂运往乙村水泥80吨,最低运费为35000元.【点睛】本题主要考查了一次函数的实际应用问题,解决本题的关键是理解题意,读懂表格,求得一次函数解析式,然后根据一次函数的性质求解.23.(1)见解析;(2)①见解析;②或【分析】(1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.(2)①过点作于,连接,由,可得,再证明解析:(1)见解析;(2)①见解析;②或【分析】(1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.(2)①过点M作于G,连接BD,由,可得,再证明,利用三角形内角和定理即可得出答案;②设,则,设,则,根据勾股定理可得,即,从而得出,即可得到,根据P是线段AC上一点(不与点A、C重合),不存在,可得出当为等腰三角形时,仅有两种情形:或,分类讨论即可求得答案.【详解】解:(1)如图1,过点A作于E,于F,两条纸条宽度相同,.,//AD BC,∴四边形ABCD是平行四边形..,∴四边形ABCD是菱形;(2)①如图2,过点M作于G,连接BD,则,四边形ABCD是菱形,∴与BD互相垂直平分,AC经过点M,,,,,,,∴,,在和中,,,,,,,,,,,,,,,,,,;②,∴设,则,设,则,,,,,,,,,即,,,P是线段AC上一点(不与点A、C重合),不存在,∴当为等腰三角形时,仅有两种情形:或,Ⅰ.当时,则,如图3,,,,,,,∴;Ⅱ.当时,如图4,过点F作于点H,在中,,,,,∴;综上所述,当为等腰三角形时,的值为或.【点睛】本题是四边形综合题,考查了平行四边形的判定与性质,菱形的判定与性质,全等三角形判定和性质,三角形面积公式,菱形面积,等腰三角形性质,勾股定理等,运用分类讨论思想和方程思想思考解决问题是解题关键.24.(1);(2)存在点,点的纵坐标为0或4;(3)4或或47或.【解析】【分析】(1)根据非负性求出a、b的值,然后运用待定系数法解答即可;(2)根据平行和坐标以及SΔBPQ=SΔBPA确定Q解析:(1)122y x =-+;(2)存在点Q ,Q 点的纵坐标为0或4;(3)4或45或或4-.【解析】 【分析】(1)根据非负性求出a 、b 的值,然后运用待定系数法解答即可; (2)根据平行和坐标以及确定Q 坐标即可;(3)连接DM 、DN ,由题意可得M 、N 的坐标分别为(n ,),(n ,n ),MN=|32n-2|,然后再分MN=DM,MN=DN,DM=DN 三种情况解答即可.【详解】 解:(1)∵∴∴()4,0A ()0,2B把()4,0A 、()0,2B 代入1y kx b =+中,得:解得:∴122y x =-+ (2)存在点Q ,使.∵()0,2B ∴∴∵∴Q 点的纵坐标为0或4∴(3) ①当DM=MN 或DM=DN 时,如图:过M 做DM ∥x 轴交y 轴于D 点,连接DN∵C点坐标为(n,n),∴M、N的坐标分别为(n,),(n,n),D(0,n) MN=|32n-2|,∴|32n-2|=|n|,解得:n=4或n=45②当DM=DN或DM=DN时,如图∵C点坐标为(n,n),∴M、N的坐标分别为(n,),(n,n),D(0,n) MN=|32n-2|,又∵是等腰直角三角形∴D在MN的垂直平分线上,DF=12MN ∴,D(0, +1)F(n,|)∴|n| =12|32n-2|,解得:或4-综上,n的取值为4或45或或4-时,是等腰直角三角形.【点睛】本题属于一次函数综合题,考查了一次函数图像上点的坐标特点、一次函数的解析式、一次函数的动点问题以及等腰三角形等知识,考查知识点较多难度较大,解答的关键在于对所学知识的灵活应用以及较强的计算能力.25.(1)见解析;(2),;(3)①;②【分析】(1)利用直角三角形斜边中线的性质可得DO=DA,推出∠AEO=60°,进一步得出BC∥AE,CO∥AB,可得结论;(2)先计算出OA=,推出PB=解析:(1)见解析;(2)27PA=4217BH3)①(423,23)M+;2635【分析】(1)利用直角三角形斜边中线的性质可得DO=DA,推出∠AEO=60°,进一步得出BC∥AE,CO∥AB,可得结论;(2)先计算出OA=43PB=23AP=27BH即可;(3)①求出直线PM的解析式为3,再利用两点间的距离公式计算即可;②易得直线BC的解析式为y=3,联立直线BC和直线PM的解析式成方程组,求得点G的坐标,再利用三角形面积公式计算.【详解】(1)证明:∵Rt△OAB中,D为OB的中点,∴AD=12OB,OD=BD=12OB,∴DO=DA,∴∠DAO=∠DOA=30°,∠EOA=90°,∴∠AEO=60°,又∵△OBC为等边三角形,∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴CO ∥AB ,∴四边形ABCE 是平行四边形;(2)解:在Rt △AOB 中,∠AOB=30°,OB=8, ∴AB=4, ∴OA=∵四边形ABCE 是平行四边形, ∴PB=PE ,PC=PA , ∴PB=∴PC PA == ∴1122ABC S AC BH AB BE ∆=⋅⋅=⋅⋅,即11422BH ⨯=⨯⨯ ∴BH (3)①∵C (0,4), 设直线AC 的解析式为y=kx+4, ∵P (0),∴0=,解得,k=,∴y=, ∵∠APM=90°,∴直线PM 的解析式为, ∵P (0),∴, 解得,m=-3,∴直线PM 的解析式为,设M (x ), ∵AP=∴(x-2+)2=(2,化简得,x 2,解得,x 1=4,x 2=4(不合题意舍去),当x=234+时,y=3×(234+)-3=23,∴M(234+,23),故答案为:(234+,23);②∵(0,4),(43,0)C B∴直线BC的解析式为:34y x=-+,联立3334y xy x⎧=-⎪⎪⎨⎪=-+⎪⎩,解得143565xy⎧=⎪⎪⎨⎪=⎪⎩,∴146(3,)55G,16126=23234 3.2525PBG PBAS S S∆∆∴+=⨯⨯+⨯⨯=阴【点睛】本题考查的是平行四边形的判定,等边三角形的性质,两点间的距离,正方形的性质,矩形的性质,一次函数的图象和性质,掌握相关的判定定理和性质定理是解题的关键.26.(1)详见解析;(2),理由详见解析;(3),理由详见解析【分析】(1)根据,等量代换即可证明;(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案;(3)在解析:(1)详见解析;(2)DE EF=,理由详见解析;(3)DE EF=,理由详见解析【分析】(1)根据90,90AED FEB ADE AED∠+∠=︒∠+∠=︒,等量代换即可证明;(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案;(3)在DA边上截取DN EB=,连接NE,证出()DNE EBF ASA≌即可得出答案.【详解】(1)证明:∵90DAB DEF∠=∠=︒,∴90,90AED FEB ADE AED∠+∠=︒∠+∠=︒,∴ADE FEM∠=∠;(2) ;DE EF=理由如下:如图,取AD的中点N,连接NE,∵四边形ABCD 为正方形, ∴AD AB = ,∵,N E 分别为,AD AB 中点 ∴11,22AN DN AD AE EB AB ====, ∴,DN BE AN AE == 又∵90A ∠=︒ ∴45ANE ∠=︒∴180135DNE ANE ∠=︒-∠=︒, 又∵90CBM ∠=︒,BF 平分CBM ∠ ∴45,135CBF EBF ∠=︒∠=︒. ∴DNE EBF ∠=∠ 在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩()DNE EBF ASA ≌,∴DE EF =(3) DE EF =.理由如下:如图,在DA 边上截取DN EB =,连接NE ,∵四边形ABCD 是正方形, DN EB =, ∴AN AE =,∴AEN △为等腰直角三角形, ∵45ANE ∠=︒∴18045135DNE ∠=︒-︒=︒, ∵BF 平分CBM ∠, AN AE =, ∴9045135EBF ∠=︒+︒=︒, ∴DNE EBF ∠=∠, 在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴()DNE EBF ASA ≌,∴DE EF.【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE≌△EBF.。
人教版八年级期末试卷(Word版含解析)

人教版八年级期末试卷(Word 版含解析) 一、选择题 1.使式子2a -有意义的a 的取值范围是( )A .2a >B .2a ≥C .2a ≠D .2a ≤ 2.下列四组线段,能构成直角三角形的是( ) A .1,1,2 B .3,2,5 C .5,6,7 D .6,8,10 3.如图,四边形ABCD 中,对角线AC ,BD 相交于点O ,下列条件不能判定这个四边形是平行四边形的是( )A .//AB DC ,DAB BCD ∠=∠B .AB DC =,AD BC = C .AO CO =,BO DO = D .//AB DC ,AD BC =4.某校有甲、乙两个合唱队,两队队员的平均身高都为160cm ,标准差分别是S 甲、S 乙,且S S >甲乙,则两个队的队员的身高较整齐的是( )A .甲队B .两队一样整齐C .乙队D .不能确定 5.如图,四边形ABCD 中,E ,F 分别是边AD ,BC 的中点,G ,H 分别是对角线BD ,AC 的中点,若四边形EGFH 为矩形,则四边形ABCD 需满足的条件是( )A .AC =BDB .AC ⊥BD C .AB =DC D .AB ⊥DC6.如图,在Rt ACB ∆中,90ACB ︒∠=,25A ︒∠=,D 是AB 上一点,将Rt ABC ∆沿CD 折叠,使B 点落在AC 边上的E 处,则ADE ∠等于( )A .25︒B .30︒C .35︒D .40︒7.如图,在平行四边形纸片ABCD 中,对角线AC 与BD 相交于点E ,∠AEB =45°,BD =4,将纸片沿对角线AC 对折,使得点B 落在点B ′的位置,连接DB ',则DB '的长为( )A .22B .23C .42D .158.如图①,在矩形ABCD 中,AB < AD ,对角线AC 、BD 相交于点O ,动点P 从点A 出发,沿A →B →C →D 向点D 运动.设点P 的运动路程为x ,ΔAOP 的面积为y ,y 与x 的函数关系图象如图②所示,则下列结论错误的是( )A .四边形ABCD 的面积为12B .AD 边的长为4C .当x =2.5时,△AOP 是等边三角形D .ΔAO P 的面积为3时,x 的值为3或10二、填空题9.二次根式5x -中字母x 的取值范围是__________.10.已知菱形的边长为2cm ,一个内角为60︒,那么该菱形的面积为__________2cm . 11.已知ABC 中,90C =∠,3AC =,5AB =,则BC =______.12.如图,在矩形ABCD 中,∠BOC =120°,AB =10,则BD 的长为_______.13.已知一次函数y =kx ﹣b ,当自变量x 的取值范围是1≤x ≤3时,对应的因变量y 的取值范围是5≤y ≤10,那么k ﹣b 的值为_______.14.在矩形ABCD 中,由9个边长均为1的正方形组成的“L 型”模板如图放置,此时量得CF=3,则BC 边的长度为_____________.15.如图,在平面直角坐标系中,直线l :1y x =-与x 轴交于点1A ,如图所示依次作正方形111A B C O 、正方形2221A B C C 、…、正方形1n n n n A B C C -,使得点1A 、2A 、3A 、…在直线l 上,点1C 、2C 、3C 、…在y 轴正半轴上,则点2021B 的坐标是__________.16.将ABCD 纸片按如图的方式折叠成一个叠合矩形EFGH ,若5EF =,12EH =,则AD 的长为______.三、解答题17.计算:(111233 (250328⨯-2 (3)332)-327-π0|-(-13)-1; (4)2448318.如图,将长为2.5米的梯子AB 斜靠在墙AO 上,BO 长0.7米.如果将梯子的顶端A 沿墙下滑0.4米,即AM 等于0.4米,则梯脚B 外移(即BN 长)多少米?19.如图,在4×4的正方形网格中,每个小格的顶点叫做格点,以格点为顶点按下列要求画图.(1)在图①中画一条线段AB ,使AB =29,线段AB 的端点在格点上;(2)在图②中画一个斜边长为34的等腰直角三角形DCE ,其中∠DCE =90°,三角形的顶点在格点上.20.已知:如图,在ABC 中,AD 是BAC ∠的平分线,//,//DE AC DF AB . 求证:四边形AEDF 是菱形.21.观察下列等式: ()()2121212121-==++-; ()()3232323232-=++-;③()()14343434343-==-++-;······ 回答下列问题:(1)利用你观察到的规律,化简:165=+ . (2)11n n=++ .(n 为正整数) (3)利用上面所揭示的规律计算:11111 (1223342016201720172018)++++++++++ 22.小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:(1)放入一个小球量筒中水面升高 cm ;(2)求放入小球后量筒中水面的高度y (cm )与小球个数x (个)之间的一次函数关系式(不要求写出自变量的取值范围);(3)量筒中至少放入几个小球时有水溢出?23.在正方形ABCD 中,点E 、F 分别是边AD 和DC 上一点,且DE =DF ,连结CE 和AF ,点G 是射线CB 上一点,连结EG ,满足EG =EC ,AF 交EG 于点M ,交EC 于点N . (1)证明:∠DAF =∠DCE ;(2)求线段EG 与线段AF 的关系(位置与数量关系),并说明理由;(3)是否存在实数m ,当AM =mAF 时,BC =3BG ?若存在,请求出m 的值;若不存在,请说明理由.24.如图,在平面直角坐标系中,过点A 30)的两条直线分别交y 轴于B (0,m)、C (0,n)两点,且m 、n (m>n)满足方程组254m n m n +=⎧⎨-=⎩的解. (1)求证:AC ⊥AB ;(2)若点D在直线AC上,且DB=DC,求点D的坐标;(3)在(2)的条件下,在直线BD上寻找点P,使以A、B、P三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.25.(1)问题探究:如图①,在四边形ABCD中,AB∥CD,E是BC的中点,AE是∠BAD 的平分线,则线段AB,AD,DC之间的等量关系为;(2)方法迁移:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,AE是∠BAF的平分线,试探究线段AB,AF,CF之间的等量关系,并证明你的结论;(3)联想拓展:如图③,AB∥CF,E是BC的中点,点D在线段AE上,∠EDF=∠BAE,试探究线段AB,DF,CF之间的数量关系,并证明你的结论.26.如图,平行四边形ABCD中,连接对角线BD,∠ABD=30°,E为平行四边形外部一点,连接AE、BE、DE,若AE=BE,∠DAE=60°.(1)如图1,若∠C=45°,BC=2,求AB的长;(2)求证:DE=BC;(3)如图2,若∠BCD=15°,连接CE,延长CB与DE交于点F,连接AF,直接写出(AFBF)2的值.【参考答案】一、选择题1.B解析:B根据二次根式的性质,被开方数大于或等于0即可求解.【详解】解:根据题意得:a -2≥0,解得:a ≥2.故选B .【点睛】此题考查二次根式有意义的条件,明白被开方数的非负性是关键.2.D解析:D【分析】勾股定理的逆定理:一个三角形中,如果有两边的平方和等于第三边的平方,那么这个三角形是直角三角形,根据定理逐一判断即可.【详解】解:2221122,+=≠ 故A 不符合题意; ()222327,+=≠故B 不符合题意; 22256617,+=≠故C 不符合题意;2226810010,+==故D 符合题意;故选:.D【点睛】本题考查的是勾股定理的逆定理,掌握利用勾股定理的逆定理判断三角形是直角三角形是解题的关键.3.D解析:D【解析】【分析】分别利用平行四边形的判定方法判断得出即可.【详解】A 、∵AB ∥CD ,∴∠DAB +∠ADC =180°,而DAB BCD ∠=∠,∴∠ADC +∠BCD =180°,∴AD ∥BC ,∴四边形ABCD 是平行四边形,故此选项不合题意;B 、∵AB =DC ,AD =BC ,∴四边形ABCD 是平行四边形,故此选项不合题意;C 、∵AO =CO ,BO =DO ,∴四边形ABCD 是平行四边形,故此选项不合题意;D 、AB =DC ,AD ∥BC 无法得出四边形ABCD 是平行四边形,故此选项符合题意;【点睛】此题主要考查了平行四边形的判定,正确把握判定方法是解题关键.4.C解析:C【解析】【分析】根据标准差的定义:方差的算术平方根,因此标准差越小,代表方差越小,即越稳定,由此求解即可.【详解】解:∵S甲>S乙,∴S2甲>S2乙,∴乙队的队员的身高较整齐故选C.【点睛】本题主要考查了标准差,解题的关键在于能够熟练掌握标准差的定义.5.D解析:D【分析】由题意易得GF∥EH∥CD,GE∥FH∥AB,则有四边形EGFH为平行四边形,由矩形的性质可得∠GFH=90°,然后可得∠GFB+∠HFC=90°,最后问题可求解.【详解】解:∵E,F分别是边AD,BC的中点,G,H分别是对角线BD,AC的中点,∴GF∥EH∥CD,GE∥FH∥AB,∴四边形EGFH为平行四边形,∠GFB=∠DCB,∠HFC=∠ABC,若四边形EGFH为矩形,则有∠GFH=90°,∴∠GFB+∠HFC=90°,∴∠DCB+∠ABC=90°,∴AB⊥DC;故选D.【点睛】本题主要考查矩形的性质与判定及三角形中位线,熟练掌握矩形的性质与判定及三角形中位线是解题的关键.6.D解析:D【解析】【分析】先根据三角形内角和定理求出∠B的度数,再由图形翻折变换的性质得出∠CED的度数,再由三角形外角的性质即可得出结论.【详解】解:在Rt △ACB 中,∠ACB =90°,∠A =25°,∴∠B =90°-25°=65°,∵△CDE 由△CDB 折叠而成,∴∠CED =∠B =65°,∵∠CED 是△AED 的外角,∴∠ADE =∠CED -∠A =65°-25°=40°.故选:D .【点睛】本题考查了三角形内角和定理,翻折变换的性质,根据题意得出∠ADE =∠CED -∠A 是解题关键.7.A解析:A【解析】【分析】 先利用平行四边形的性质得到122BE DE BD ===,再由折叠的性质得到45BEA B EA '==∠∠,2B E BE '==,由此可得到90B ED '=∠,再利用勾股定理求解即可.【详解】解:∵四边形ABCD 是平行四边形,∴122BE DE BD ===, 由折叠的性质可知:45BEA B EA '==∠∠,2B E BE '==,∴90B EB BEA B EA ''∠=∠+∠=,∴18090B ED B EB ''==∠-∠,∴在直角三角形B ED '中2222B D B E ED ''=+=,故选A .【点睛】本题主要考查了平行四边形的性质,折叠的性质,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.8.C解析:C【分析】过点P作PE⊥AC于点E,根据ΔAOP的边OA是一个定值,OA边上的高PE最大时是点P 分别与点B和点D重合,因此根据这个规律可以对各个选项作出判断.【详解】A、过点P作PE⊥AC于点E,当点P在AB和BC边上运动时,PE逐渐增大,到点B时最大,然后又逐渐减小,到点C时为0,而y=12OA PE中,OA为定值,所以y是先增大后减小,在B点时面积最大,在C点时面积最小;观察图②知,当点P与点B重合时,ΔAOP 的的面积为3,此时矩形的面积为:4×3=12,故选项A正确;B、观察图②知,当运动路程为7时,y的值为0,此时点P与点C重合,所以有AB+BC=7,又AB∙BC=12,解得:AB=3,BC=4,或AB=4,BC=3,但AB<BC,所以AB=3,BC=4,根据四边形ABCD为矩形,所以AD=4,故选项B正确;C、当x=2.5时,即x<3,点P在边AB上由勾股定理,矩形的对角线为5,则OA=2.5,所以OA=AP,△AOP是等腰三角形,但△ABC是三边分别为3,4,5的直角三角形,故∠BAC不可能为60°,从而△AOP不是等边三角形,故选项C错误;D、当点P在AB和BC边上运动时,点P与点B重合时最大面积为3,此时x的值为3;当点P在边CD和DA上运动时,PE逐渐增大,到点D时最大,然后又逐渐减小,到点A时为0,而y=12OA PE也是先增大再减小,在D点时面积最大,在A点时面积最小;所以当点P与点D重合时,最大面积为3,此时点P运动的路程为AB+BC+CD=10,即x=10,所以当x=3或10时,ΔAOP的面积为3,故选项D正确.故选:C.【点睛】本题是动点问题的函数图象,考查了函数的图象、图形的面积、矩形的性质、解方程等知识,关键是确定点P到AC的距离的变化规律,从而可确定y的变化规律,同时善于从函数图象中抓住有用的信息,获得问题的突破口.二、填空题9.5x≥【解析】根据二次根式成立的条件可直接进行求解.【详解】解:由题意得:50x -≥,解得:5x ≥;故答案为5x ≥.【点睛】本题主要考查二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题的关键. 10.A 解析:23【解析】【分析】连接AC ,过点A 作AM ⊥BC 于点M ,根据菱形的面积公式即可求出答案.【详解】解:过点A 作AM ⊥BC 于点M ,∵菱形的边长为2cm ,∴AB =BC =2cm ,∵有一个内角是60°,∴∠ABC =60°,∴∠BAM =30°,∴112BM AB ==(cm ), ∴223AM AB BM -cm ),∴此菱形的面积为:233=cm 2).故答案为:23【点睛】本题主要考查了菱形的性质和30°直角三角形性质,解题的关键是熟练运用菱形的性质,本题属于基础题型. 11.A解析:4【解析】【分析】直接利用勾股定理计算即可.解:∵在Rt △ABC 中,∠C=90°,AB=5,AC=3,4BC ∴==故答案为:4【点睛】本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.即如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么a 2+b 2=c 2.熟记定理是解题的关键.12.B解析:20【分析】先根据矩形的性质和∠BOC =120∘,证明△AOB 是等边三角形,即可得到OB =AB =10,BD =2OB =20.【详解】解:∵四边形ABCD 是矩形,∴OA =12AC ,OB =12BD ,AC =BD ,∴OA =OB ,∵∠BOC =120∘,∴∠AOB =60∘,∴△AOB 是等边三角形,∴OB =AB =10,∴BD =2OB =20;故答案为:20.【点睛】本题主要考查了矩形的性质,等边三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.13.5或10【分析】本题分情况讨论①k >0时,x =1时对应y =5;②k >0时,x =1时对应y =10.【详解】解:①k >0时,由题意得:x =1时,y =5,∴k -b =5;②k <0时,由题意得:x =1时,y =10,∴k -b =10;综上,k -b 的值为5或10.故答案为:5或10.【点睛】本题考查了待定系数法求函数解析式,注意本题需分两种情况,不要漏解.14.A解析:7【分析】连接AF,作GH⊥AE于点H,则有AE=EF=HG=4,FG=2,AH=2,根据矩形的性质及勾股定理即可求得【详解】解:由图可知,AE=EF=5,根据勾股定理,易得CE=4,由题可知AE⊥EF,易得△ABE≌△ECF,即BE=CF=3,即BC=3+4=7,故答案为:7【点睛】本题考查了利用矩形的性质和勾股定理及全等三角形的性质求解.15.(22020,22021-1)【分析】根据一次函数图象上点的坐标特征结合正方形的性质,可得出点A1、B1的坐标,同理可得出A2、A3、A4、A5、…及B2、B3、B4、B5、…的坐标,根据点的坐解析:(22020,22021-1)【分析】根据一次函数图象上点的坐标特征结合正方形的性质,可得出点A1、B1的坐标,同理可得出A2、A3、A4、A5、…及B2、B3、B4、B5、…的坐标,根据点的坐标变化可找出变化规律:“B n(2n-1,2n-1)(n为正整数)”,依此规律即可得出结论.【详解】解:当y=0时,有x-1=0,解得:x=1,∴点A1的坐标为(1,0).∵四边形A1B1C1O为正方形,∴点B1的坐标为(1,1).同理,可得出:A2(2,1),A3(4,3),A4(8,7),A5(16,15),…,∴B2(2,3),B3(4,7),B4(8,15),B5(16,31),…,∴B n(2n-1,2n-1)(n为正整数),∴点B2021的坐标是(22020,22021-1).故答案为:(22020,22021-1).【点睛】本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型:点的坐标,根据点的坐标的变化找出变化规律“B n(2n-1,2n-1)(n为正整数)”是解题的关键.16.13【分析】根据折叠的性质可得,由已知条件,矩形的性质以及勾股定理即可求得,进而即可求得【详解】四边形是矩形,,,,,四边形是平行四边形,,折叠,,,,,故答案为:13【解析:13【分析】根据折叠的性质可得AD HE =,由已知条件,矩形的性质以及勾股定理即可求得HF ,进而即可求得AD【详解】四边形EFGH 是矩形,5EF =,12EH =,90EFH ∠=︒,13FH ∴=,四边形ABCD 是平行四边形,∴AD BC =,折叠,,,DH NH AH HM CF FN ∴===,,FB FM HD HN ==,,BF FC NF FM AH HD MH NH ∴+=++=+,2,2BF FC AH HD AD MH NH NF FM HF +++=+++=,∴13AD HF ==故答案为:13【点睛】本题考查了平行四边形的性质,折叠的性质,矩形的性质,勾股定理,证明AD HE =是解题的关键.三、解答题17.(1);(2)6;(3)-2;(4)4+2【分析】(1)将二次根式化为最简二次根式,然后进行加减运算即可.(2)将二次根式化为最简二次根式,利用二次根式的混合运算法则求解即可.(3)利用平方解析:(1;(2)3)-2;(4)4+【分析】(1)将二次根式化为最简二次根式,然后进行加减运算即可.(2)将二次根式化为最简二次根式,利用二次根式的混合运算法则求解即可.(3)利用平方差公式、绝对值性质、负指数幂进行化简,然后计算即可得到答案.(4)将二次根式化为最简二次根式,然后括号中的每一项分别除以除数,最后计算得到答案.【详解】解:(1)原式=(2)原式=-=-=(3)原式=3-4-|-3-1|-(-3)=-1-4+3=-2.(4)原式=+÷4=+【点睛】本题主要是考查了二次根式的混合运算,注意在进行二次根式的运算中,一定先要把二次根式化简成最简二次根式进行计算.18.梯脚外移0.8米.【分析】直角利用勾股定理求出AO,ON的长,再利用NB=ON-OB,即可求出答案.【详解】解:由题意得:AB=2.5米,BO=0.7米,在Rt△ABO中,由勾股定理得:解析:梯脚B外移0.8米.【分析】直角利用勾股定理求出AO,ON的长,再利用NB=ON-OB,即可求出答案.【详解】解:由题意得:AB=2.5米,BO=0.7米,在Rt△ABO中,由勾股定理得:2222AO AB BO=-=-==(米).2.50.7 5.76 2.4∴MO=AO-AM=2.4-0.4=2(米),在Rt△MNO中,由勾股定理得:22222=-=-=-==(米).2.52 6.254 2.25 1.5NO MN MO∴NB=ON-OB=1.5-0.7=0.8(米),∴梯脚B外移(即BN长)0.8米.【点睛】本题主要考查了勾股定理的应用,读懂题意,正确应用勾股定理是解题的关键.19.(1)见解析;(2)见解析【解析】【分析】(1)利用勾股定理求出AB=时的两条直角边,再在图中作出即可;(2)利用勾股定理求出斜边长DE=时的两条直角边,再在图中作出DE,再根据等腰直角三角解析:(1)见解析;(2)见解析【解析】【分析】(1)利用勾股定理求出AB=29时的两条直角边,再在图中作出即可;(2)利用勾股定理求出斜边长DE=34时的两条直角边,再在图中作出DE,再根据等腰直角三角形DCE,得到DC=CE=17,再在图中作出图形即可.【详解】解:(1)∵AB=29又222+5=29∴如图①所示,线段AB即为所求;(2)∵34DCE223+534∴如图②所示,斜边长DE34又∵=∴DC =CE∴如图②中,等腰直角三角形DCE 即为所求.【点睛】本题考查勾股定理.根据线段的长找出相对应直角三角形的两条直角边是本题的关键. 20.见解析.【分析】根据四边形是平行四边形,再证明有一组邻边相等即可.【详解】解:∵,∴四边形是平行四边形,∵平分,∴,∵,∴,∴,∴,∴平行四边形是菱形.【点睛】本题考查了解析:见解析.【分析】根据//,//DE AC DF AB 四边形AEDF 是平行四边形,再证明有一组邻边相等即可.【详解】解:∵//,//DE AC DF AB ,∴四边形AEDF 是平行四边形,∵AD 平分BAC ∠,∴12∠=∠,∵//DE AC ,∴23∠∠=,∴13∠=∠,∴AE DE =,∴平行四边形AEDF 是菱形.【点睛】本题考查了平行线的性质,菱形的判定,等腰三角形的判定,解题关键是熟练运用相关性质,准确进行推理证明.21.(1);(2);(3)【解析】【分析】(1)根据平方差公式分母有理化即可;(2)根据平方差公式分母有理化即可;(3)对每一个式子分母有理化,再进行合并计算即可;【详解】(1);故答案解析:(1231【解析】【分析】(1)根据平方差公式分母有理化即可;(2)根据平方差公式分母有理化即可;(3)对每一个式子分母有理化,再进行合并计算即可;【详解】==(1==(2,(3··=1?·=;1【点睛】本题主要考查了二次根式分母有理化,平方差公式,准确计算是解题的关键.22.(1)2;(2)y=2x+30;(3)10【分析】(1)比较第一、二两个量桶可知,放入三个球,水面上升6cm,由此可求放入一个小球量桶中水面升高的高度;(2)根据(1)的结论可知,放入小球x(解析:(1)2;(2)y=2x+30;(3)10【分析】(1)比较第一、二两个量桶可知,放入三个球,水面上升6cm,由此可求放入一个小球量桶中水面升高的高度;(2)根据(1)的结论可知,放入小球x(个)后,量桶中水面的高度,即可得到y与x 的一次函数关系式;(3)根据(2)可以得出y>49,再进行求解即可得出答案.【详解】解:(1)36-30=6(cm),6÷3=2(cm)故答案为:2;(2)设y=kx+b,把(0,30),(3,36),代入得:30336bk b=⎧⎨+=⎩,解得230kb=⎧⎨=⎩,即y=2x+30;(3)由2x+30>49,得x>9.5,即至少放入10个小球时有水溢出.【点睛】本题主要考查一次函数实际应用问题,综合考查同学们识图能力、处理信息能力、待定系数法以及函数所反映的对应与变化思想的应用.23.(1)见解析;(2),,见解析;(3)或【分析】(1)根据正方形的性质得到对应边相等,证明即可得到;(2)作,交于点,交于点,则,通过证明,得到,可推导出,从而证得结论;(3)存在,作于点,解析:(1)见解析;(2),,见解析;(3)或【分析】(1)根据正方形的性质得到对应边相等,证明即可得到;(2)作,交于点K,交AD于点H,则,通过证明,得到,可推导出,从而证得结论;(3)存在,作于点L,连结EF,分两种情况,即点G在BC边上、点G在CB 边的延长线上,分别设和,将AE、DE、DF用或表示出来,再将、AM用或表示出来,即可求出的值.【详解】解:(1)证明:如图1,四边形ABCD是正方形,,,,,.(2),,理由如下:如图2(或图3),作,交于点K,交AD于点H,,,四边形是平行四边形,;由(1)得,,,,,,,,,,,,,,,.(3)存在,作于点L,连结EF,,∴四边形是矩形,,,如图4,点G在边BC上,设,,,,,,,,,,,由得,,∴,,,,;如图5,点G在边CB的延长线上,设,则,,,,,由得,,,,,综上所述,或.【点睛】此题重点考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、勾股定理以及二次根式等知识,第(3)题要分类讨论,求出所有符合条件的值,此题难度较大,属于考试压轴题.24.(1)见解析;(2);(3)点P的坐标为:(﹣3,0),(﹣,2),(﹣3,3﹣),(3,3+)【解析】【分析】(1)先解方程组得出m和n的值,从而得到B,C两点坐标,结合A点坐标算出AB2,解析:(1)见解析;(2)()-231,;(3)点P的坐标为:(﹣303 2),(﹣3,333,3【解析】【分析】(1)先解方程组254m nm n+=⎧⎨-=⎩得出m和n的值,从而得到B,C两点坐标,结合A点坐标算出AB2,BC2,AC2,利用勾股定理的逆定理即可证明;(2)过D作DF⊥y轴于F,根据题意得到BF=FC,F(0,1),设直线AC:y=kx+b,利用A和C的坐标求出表达式,从而求出点D坐标;(3)分AB=AP,AB=BP,AP=BP三种情况,结合一次函数分别求解.【详解】解:(1)∵254m nm n+=⎧⎨-=⎩,得:31 mn=⎧⎨=-⎩,∴B(0,3),C(0,﹣1),∵A(﹣3,0),B(0,3),C(0,﹣1),∴OA=3,OB=3,OC=1,∴AB2=AO2+BO2=12,AC2=AO2+OC2=4,BC2=16∴AB2+AC2=BC2,∴∠BAC=90°,即AC⊥AB;(2)如图1中,过D作DF⊥y轴于F.∵DB=DC,△DBC是等腰三角形∴BF=FC,F(0,1),设直线AC:y=kx+b,将A(﹣3,0),C(0,﹣1)代入得:直线AC解析式为:y=33-x-1,将D点纵坐标y=1代入y=33-x-1,∴x=-23,∴D的坐标为(﹣23,1);(3)点P的坐标为:(﹣3032),(﹣3,333,3设直线BD的解析式为:y=mx+n,直线BD与x轴交于点E,把B(0,3)和D(﹣31)代入y=mx+n,∴313nm n=⎧⎪⎨=-+⎪⎩,解得333mn⎧=⎪⎨⎪=⎩,∴直线BD的解析式为:y=33x+3,令y=0,代入y=33x+3,可得:x=33-,∵OB=3,∴BE=()223336+=,∴∠BEO=30°,∠EBO=60°∵AB=23,OA=3,OB=3,∴∠ABO=30°,∠ABE=30°,当PA=AB时,如图2,此时,∠BEA=∠ABE=30°,∴EA=AB,∴P与E重合,∴P的坐标为(﹣33,0),当PA=PB时,如图3,此时,∠PAB=∠PBA=30°,∵∠ABE=∠ABO=30°,∴∠PAB=∠ABO,∴PA∥BC,∴∠PAO=90°,∴点P3令x=﹣3,代入y=33x+3,∴y=2,∴P(﹣3,2),当PB=AB时,如图4,∴由勾股定理可求得:3EB=6,若点P在y轴左侧时,记此时点P为P1,过点P1作P1F⊥x轴于点F,∴P13∴EP1=6﹣3∴FP1=33令y=333,∴x=﹣3,∴P1(﹣3,33若点P在y轴的右侧时,记此时点P为P2,过点P2作P2G⊥x轴于点G,∴P23∴EP23∴GP23令33,∴x=3,∴P2(3,3综上所述,当A、B、P三点为顶点的三角形是等腰三角形时,点P的坐标为(﹣3032),(﹣3,333,3【点睛】本题考查了解二元一次方程组,勾股定理的逆定理,含30°的直角三角形,等腰三角形的性质,一次函数的应用,知识点较多,难度较大,解题时要注意分类讨论.25.(1)AD=AB+DC;(2)AB=AF+CF,证明详见解析;(3)AB=DF+CF,证明详见解析.【分析】(1)结论:AD=AB+DC.延长AE,DC交于点F,证明△ABE≌△FEC(AAS)解析:(1)AD=AB+DC;(2)AB=AF+CF,证明详见解析;(3)AB=DF+CF,证明详见解析.【分析】(1)结论:AD=AB+DC.延长AE,DC交于点F,证明△ABE≌△FEC(AAS),即可推出AB=CF,再证明DA=DF,即可解决问题.(2)结论:AB=AF+CF,如图②,延长AE交DF的延长线于点G,证明方法类似(1).(3)结论;AB=DF+CF.如图③,延长AE交CF的延长线于点G,证明方法类似(1).【详解】解:(1)探究问题:结论:AD=AB+DC.理由:如图①中,延长AE,DC交于点F,∵AB∥CD,∴∠BAF=∠F,在△ABE和△FCE中,CE=BE,∠BAF=∠F,∠AEB=∠FEC,∴△ABE≌△FEC(AAS),∴CF=AB,∵AE是∠BAD的平分线,∴∠BAF=∠FAD,∴∠FAD=∠F,∴AD=DF,∵DC+CF=DF,∴DC+AB=AD.故答案为AD=AB+DC.(2)方法迁移:结论:AB=AF+CF.证明:如图②,延长AE交DF的延长线于点G,∵E 是BC 的中点,∴CE =BE ,∵AB ∥DC ,∴∠BAE =∠G .且BE =CE ,∠AEB =∠GEC∴△AEB ≌△GEC (AAS )∴AB =GC∵AE 是∠BAF 的平分线∴∠BAG =∠FAG ,∵∠BAG ∠G ,∴∠FAG =∠G ,∴FA =FG ,∵CG =CF+FG ,∴AB =AF+CF .(3)联想拓展:结论;AB =DF+CF .证明:如图③,延长AE 交CF 的延长线于点G ,∵E 是BC 的中点,∴CE =BE ,∵AB ∥CF ,∴∠BAE =∠G ,在△AEB 和△GEC 中,BAE G AEB GEC BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AEB ≌△GEC ,∴AB =GC ,∵∠EDF =∠BAE ,∴∠FDG =∠G ,∴FD =FG ,∴AB =DF+CF .【点睛】本题是四边形的综合问题,考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.26.(1);(2)证明见解析;(3)【分析】(1)过点D 作DF ⊥AB 于F ,有等腰直角三角形和含30度角的直角三角形的性质,利用勾股定理求出AF 和BF 的长即可求解.(2)过点E 作EF ⊥AB 于F ,过点解析:(1)62+;(2)证明见解析;(3)43-【分析】(1)过点D 作DF ⊥AB 于F ,有等腰直角三角形和含30度角的直角三角形的性质,利用勾股定理求出AF 和BF 的长即可求解. (2)过点E 作EF ⊥AB 于F ,过点A 作AG ⊥BD 交BD 延长线于G ,先证明△GAD ≌△FAE ,再证明三角形ADE 时等边三角形,即可得到答案;(3)过点A 作AP ⊥DE 于P ,过点D 作DN ⊥BF 于点N ,可证明∠BDN =∠DBN =45°,∠FDN =30°,以及EF =BF ,设FN =m ,根据勾股定理,用含m 的式子分别表示出2AF 和2BF ,即可得出结果.【详解】解:(1)如图,过点D 作DF ⊥AB 于F ,∴∠AFD =∠BFD =90°∵四边形ABCD 是平行四边形,∠C =45°,BC =2∴∠A =∠C =45°,AD =BC =2∴AF =DF ,∵∠DBA =30°,∴BD =2DF ,在直角三角形AFD 中,222AF DF AD +=,∴224AF =,∴2AF DF ==,∴222BD DF ==,在直角三角形DFB 中,226BF BD DF =-=,∴62AB AF BF =+=+;(2)过点E 作EF ⊥AB 于F ,过点A 作AG ⊥BD 交BD 延长线于G ,∵AE =BE ,∴12A FB A BF ==, ∵∠G =90°,∠DBA =30°,∴12AG AB =,∠DAB =60°∴AG AF =,∵∠DAE =60°,∴∠GAD =∠FAE =60°-∠DAF ,∵∠G =∠AFE =90°,∴△GAD ≌△FAE (ASA ),∴AD =AE ,∴三角形ADE 时等边三角形,∴AD =DE ,∴DE =BC ;(3)如图,过点A 作AP ⊥DE 于P ,过点D 作DN ⊥BF 于点N ,则∠APE =∠APF =∠DNF =∠DNB =90°,∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,∴∠ABF =∠C =15°,∠DFB =∠ADF =60°,∴∠DBN =∠ABF +∠ABD =45°,∠FDN =30°,∴∠BDN =∠DBN =45°,∴∠EBD =∠EDB =∠FDN +∠BDN =75°,∴∠FEB =180°-75°-75°=30°,∴∠FBE =∠DFB -∠FEB =60°-30°=30°=∠FEB ,∴EF =BF ,设FN =m ,DF =2m , ∴223BN DN DF FN m ==-=, ∴3EF BF m m ==+,33AE DE m m ==, ∴1332m m PE PD DE +=== ∴3332m m m m PF m +-== ∵2AE DE PE ==,∴22223AP AE PE PE =-=, ∴(22222231043AF AP PF PE PF m =+=+=+, ∵()(222343BF m m m ==+, ∴()22222104343423m AF AF BF BF m +⎛⎫=== ⎪⎝⎭+【点睛】本题主要考查了等腰三角形的性质,等腰直角三角形的性质与判定,含30度角的直角三角形的性质,勾股定理,平行四边形的性质,全等三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.。
八年级上册道德与法治期末试卷测试题(Word版含解析)

八年级上册道德与法治期末试卷测试题(Word版含解析)一、选择题1.亚力士多德说:“人是政治的存在者,必定要过共同的生活。
”这深刻阐述了个人和社会的关系。
对此理解正确的是()①个人是社会的有机组成部分,社会由个人组成②为了社会的发展,我们必须舍弃个人利益③每个人都从社会中获得物质支持和精神滋养④个人的生存、发展离不开社会A.①②③B.①②④C.①③④D.②③④2.作为为新时代的青少年,我们要学习做一个积极的社会人,养成亲社会行为。
下列行为符合上述要求的是()①当同学们知道小梅因家境贫寒面临辍学时,都踊跃捐款资助②小亮的好朋友被小平欺负了,他挺身而出,和好朋友一起揍了小平一顿③小明积极参加无偿献血活动④小强游览泰山时在石壁上刻下“小强到此一游”A.③④B.②④C.①③D.①②3.人民日报载文:“人非孤立存在,而是存在于一定的社会中。
因此,人的发展人的素质提高,需要社会发展为之提供必需的物质和文化条件。
”从个人和社会的关系看,上述材料表明()A.个人与社会相互区别,不能等同B.社会离不开个人,个人是组成社会的细胞C.个人的生存、发展离不开社会D.个人的存在和发展会对社会产生巨大影响4.在网络交往中,我们要学会“信息节食”,“信息节食”是指()①在无关信息面前不停留②坚决拒绝网络,从不上网③在无聊信息上不浪费精力④只要是自己感兴趣的信息就可以长时间关注A.①②B.③④C.①③D.②④5.第四届世界互联网大会·乌镇峰会于2017年12月3日—5日在浙江省乌镇举行。
会议主题为“发展数字经济,促进开放共享——携手共建网络空间命运共同体”。
来自全球1500多名嘉宾参加大会。
全球各界人士广泛关注互联网,是因为()①互联网可以满足人们各个方面的需要②互联网使世界变成了“鸡犬之声相闻”的地球村③互联网的积极作用取代了其消极作用④互联网为人们的生活和工作带来极大便利A.①②B.②③C.②④D.③④6.小林非常喜欢在微信晒朋友圈,晒作业、晒美食、晒玩具、晒与家人的生活片段……。
八年级数学下册期末试卷(Word版含解析)

八年级数学下册期末试卷(Word 版含解析) 一、选择题 1.二次根式2x -中x 的值不能是( )A .0B .1C .2D .32.下列条件:①222b c a =-;②C A B ∠=∠-∠;③111::::345a b c =;④::3:4:5A B C ∠∠∠=,能判定ABC 是直角三角形的有( )A .4个B .3个C .2个D .1个3.四边形的三个相邻内角的度数依次如下,那么其中是平行四边形的为( ) A .88︒,108︒,88︒ B .108︒,108︒,82︒ C .88︒,92︒,92︒D .108︒,72︒,108︒ 4.某单位招聘项目经理,考核项目为个人形象、专业知识、策划能力,三个项目权重之比为2:3:5,某应聘者三个项目的得分依次为80,90,80,则他最终得分为( ) A .79 B .83 C .85 D .875.如图,菱形ABCD 的边长为2,60BAD ∠=︒,点P 是边AD 的中点,点Q 是对角线AC 上一动点,则DPQ 周长的最小值是( )A .13+B .33+C .23+D .36.如图,将□ABCD 沿对角线AC 折叠,使点B 落在'B 处,若1240︒∠=∠=,则B =( )A .60︒B .100︒C .110︒D .120︒7.如图,已知AOBC 的顶点O (0,0),点B 在x 轴正半轴上,按以下步骤作图: ①以点O 为圆心,适当长度为半径作弧,分别交边OA ,OB 于点D ,E ;②分别以点D ,E 为圆心,大于12DE 的长为半径作弧,两弧在∠AOB 内交于点F ;③作射线OF ,交边AC 于点G .若G 的坐标为(2,4),则点A 的坐标是( )A .(﹣3,4)B .(﹣2,4)C .(225,4)-D .(54,4)- 8.如图,在平面直角坐标系中,OABC 的顶点A 在x 轴上,定点B 的坐标为(8,4),若直线经过点D (2,0),且将平行四边形OABC 分割成面积相等的两部分,则直线DE 的表达式是( )A .y=x-2B .y=2x-4C .y=x-1D .y=3x-6二、填空题9.若225b a a =-+--,则a b -=_______________________.10.菱形两条对角线长分别为2、6,则这个菱形的面积为_________.11.在Rt ABC ∆中,90C ∠=︒,30A ∠=︒,2AC =,斜边AB 的长为__________. 12.如图,在矩形ABCD 中,AD =10,AB =6,点E 为BC 上的点,ED 平分∠AEC ,则EC =___.13.已知一次函数y =kx ﹣b ,当自变量x 的取值范围是1≤x ≤3时,对应的因变量y 的取值范围是5≤y ≤10,那么k ﹣b 的值为_______.14.如图, 在矩形ABCD 中, 对角线AC , BD 交于点O , 已知∠AOD=120°, AB=1,则BC 的长为______15.如图1,在平面直角坐标系中,将平行四边形ABCD 放置在第一象限,且AB //x轴.直线y =﹣x 从原点出发沿x 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l 与直线在x 轴上平移的距离m 的函数图象如图2,那么AB 的长为___.16.如图所示,将矩形ABCD 沿直线AE 折叠(点E 在边CD 上),折叠后顶点D 恰好落在边BC 上的点F 处,若AD =5,AB =4,则EC 的长是_____.三、解答题17.(1)23317(2)21148--+--- (2)1(6215)36252-⨯-+- (3)148312242÷-⨯+ (4)205112(31)(31)35+-⨯++- 18.位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A 拉回点B 的位置(如图).在离水面高度为8m 的岸上点C ,工作人员用绳子拉船移动,开始时绳子AC 的长为17m ,工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D 的位置,问此时游船移动的距离AD 的长是多少?19.如图,在4×4的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形或四边形.(绘图要求:①所绘图形不得超出正方形网格;②必须用直尺和中性笔绘图,确保所绘图形的顶点必须在格点上)(1)在图①中,画一个直角三角形,使它的三边长都是有理数;(2)在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数; (3)在图③中,画一个直角三角形,使它的三边长都是无理数;(4)在图④中,画一个正方形,使它的面积为10.20.如图,ABCD 的对角线AC 的垂直平分线与AD 、BC 分别交于E 、F ,垂足为点O .(1)求证:四边形AFCE 是菱形.(2)若2AE ED =,6AC =,4EF =,则ABCD 的面积为 . 21.先阅读下列材料,再解决问题: 阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.例如:22232232121(2)212(12)+=+⨯⨯=++⨯⨯=+=|1+2|=1+2解决问题:①模仿上例的过程填空:146514235+=+⨯⨯=_________________=________________=_________________②根据上述思路,试将下列各式化简:(1)28103-; (2)312+. 22.某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y (元)与所用的水(自来水)量x (吨)之间的函数图象.根据下面图象提供的信息,解答下列问题:(1)当1730x ≤≤时,求y 与x 之间的函数关系式;(2)已知某户居民上月水费为91元,求这户居民上月的用水量;(3)当一户居民在某月用水为15吨时,求这户居民这个月的水费.23.如图1,四边形ACBD 中,AC =AD ,BC =BD .我们把这种两组邻边分别相等的四边形叫做“筝形”,如图2,在“筝形”ACBD 中,对角线AB =CD ,过点B 作BE ⊥AC 于E 点,F 为线段BE 上一点,连接FA 、FD ,FA =FB .(1)求证:△ABF ≌△CDA ;(2)如图3,FA 、FD 分别交CD 、AB 于点M 、N ,若AM =MF ,求证:BN =CM +MN .24.定义:对于平面直角坐标系xOy中的点P(a,b)和直线y=ax+b,我们称点P((a,b)是直线y=ax+b的关联点,直线y=ax+b是点P(a,b)的关联直线.特别地,当a=0时,直线y=b(b为常数)的关联点为P(0,b).如图,已知点A(-2,-2),B(4,-2),C(1,4).(1)点A的关联直线的解析式为______;直线AB的关联点的坐标为______;(2)设直线AC的关联点为点D,直线BC的关联点为点E,点P在y轴上,且S△DEP=2,求点P的坐标.(3)点M(m,n)是折线段AC→CB(包含端点A,B)上的一个动点.直线l是点M的关联直线,当直线l与△ABC恰有两个公共点时,直接写出m的取值范围.25.如图①,已知正方形ABCD的边长为3,点Q是AD边上的一个动点,点A关于直线BQ的对称点是点P,连接QP、DP、CP、BP,设AQ=x.(1)BP+DP的最小值是_______,此时x的值是_______;(2)如图②,若QP的延长线交CD边于点M,并且∠CPD=90°.①求证:点M是CD的中点;②求x的值.(3)若点Q是射线AD上的一个动点,请直接写出当△CDP为等腰三角形时x的值.【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件即可得出答案.【详解】 2x -∴20x -≥,解得:2x ≤,故选项中符合条件的x 的值有0,12,, ∴x 不能为3,故选:D .【点睛】本题考查了二次根式有意义的条件,熟知根号下为非负数是解本题的关键.2.C解析:C【分析】根据三角形的内角和定理以及勾股定理的逆定理即可得到结论.【详解】解:①222b c a =-即222+=a b c ,△ABC 是直角三角形,故①符合题意;②∵∠A +∠B +∠C =180°,∠C =∠A −∠B ,∴∠A +∠B +∠A −∠B =180°,即∠A =90°,∴△ABC 是直角三角形,故②符合题意;③∵111::::345a b c =, 设a =3k ,b =4k ,c =5k , 则222543k k k ⎛⎫⎛⎫⎛⎫+≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴△ABC 不是直角三角形,故③不合题意;④∵::3:4:5A B C ∠∠∠=,∴∠C =5345++×180°=75°,故不是直角三角形;故④不合题意. 综上,符合题意的有①②,共2个,故选:C .【点睛】本题主要考查了直角三角形的判定方法.①如果三角形中有一个角是直角,那么这个三角形是直角三角形;②如果一个三角形的三边a ,b ,c 满足a 2+b 2=c 2,那么这个三角形是直角三角形.3.D解析:D【解析】【分析】两组对角分别相等的四边形是平行四边形,根据所给的三个角的度数可以求出第四个角,然后根据平行四边形的判定方法验证即可.【详解】A 、第四个角是76°,有一组对角不相等,不是平行四边形;B 、第四个角是72°,两组对角都不相等,不是平行四边形;C 、第四个角是88°,而C 中相等的两个角不是对角,不是平行四边形;D 、第四个角是72°,满足两组对角分别相等,因而是平行四边形.故选:D .【点睛】本题主要考查平行四边形的判定:两组对角分别相等的四边形是平行四边形.注意角的对应的位置关系,并不是有两组角相等的四边形就是平行四边形.4.B解析:B【解析】【分析】根据加权平均数的定义列式计算即可.【详解】 解:他最终得分为802903805235⨯+⨯+⨯++=83(分). 故选:B .【点睛】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义. 5.A解析:A【分析】连接BQ ,BD ,当P ,Q ,B 在同一直线上时,DQ +PQ 的最小值等于线段BP 的长,依据勾股定理求得BP的长,即可得出DQ+PQ的最小值,进而得出△DPQ周长的最小值.【详解】解:如图所示,连接BQ,BD,∵点Q是菱形对角线AC上一动点,∴BQ=DQ,∴DQ+PQ=BQ+PQ,当P,Q,B在同一直线上时,BQ+PQ的最小值等于线段BP的长,∵四边形ABCD是菱形,∠BAD=60°,∴△BAD是等边三角形,又∵P是AD的中点,∴BP⊥AD,AP=DP=1,∴Rt△ABP中,∠ABP=30°,∴AP=1AB=1,2∴BP22413--AB AP∴DQ+PQ3又∵DP=1,∴△DPQ3+1,故选:A.【点睛】本题主要考查了菱形的性质以及最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.6.D解析:D【解析】【分析】由平行线的性质可得∠DAC=∠B'AB=40°,由折叠的性质可得∠BAC=∠B'AC=20°,由三角形内角和定理即可求解.【详解】解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠1=∠B'AB=40°,同理,∠2=∠DAC=40°,∵将□ABCD沿对角线AC折叠,∴∠BAC =∠B 'AC =20°,∴∠B =180°﹣∠2﹣∠BAC =120°,故选:D .【点睛】本题考查了翻折变换的性质、平行四边形的性质以及三角形内角和定理;熟练掌握折叠的性质是解题的关键.7.A解析:A【解析】【分析】首先证明AO AG =,设AO AG x ==,则2AT x =-,在Rt AOT △中,2224(2)x x =+-,求出x ,可得结论.【详解】解:如图,设AC 交y 轴于T .(2,4)G ,2TG ∴=.4OT =,四边形AOBC 是平行四边形,//AC OB ∴,AGO GOB ∴∠=∠,AOG GOB ∠=∠,AOG AGO ∴∠=∠,AO AG ∴=,设AO AG x ==,则2AT x =-,在Rt AOT △中,2224(2)x x =+-,5x ∴=,523AT ∴=-=,(3,4)A ∴-,故选:A .【点睛】本题考查作图-基本作图,平行四边形的性质,等腰三角形的判定和性质,勾股定理等知识,解题的关键是证明AO AG =,学会利用参数解决问题.8.A解析:A【分析】过平行四边形的对称中心的直线把平行四边形分成面积相等的两部分,先求出平行四边形对称中心的坐标,再利用待定系数法求一次函数解析式解答即可.【详解】解:∵点B 的坐标为(8,4),∴平行四边形的对称中心坐标为(4,2),设直线DE 的函数解析式为y=kx+b ,则4220k b k b +=⎧⎨+=⎩, 解得12k b =⎧⎨=-⎩, ∴直线DE 的解析式为y=x-2.故选:A .【点睛】本题考查了待定系数法求一次函数解析式,平行四边形的性质,熟练掌握过平行四边形的中心的直线把平行四边形分成面积相等的两部分是解题的关键.二、填空题9.7【解析】【分析】先由二次根式有意义可得20,20a a -≥⎧⎨-≥⎩从而依次求解,a b 的值,可得答案. 【详解】解: 5b =20,20a a -≥⎧∴⎨-≥⎩解得:2,a =5,b ∴=-()257.a b ∴-=--=故答案为:7.【点睛】本题考查的是二次根式有意义的条件,一元一次不等式组的解法,掌握二次根式有意义的条件是解题的关键.10【解析】【分析】根据菱形的面积等于两对角线乘积的一半求出其面积即可.【详解】解:∵一个菱形的两条对角线长分别为2和6, ∴这个菱形的面积12632=⨯⨯=, 故答案为:3.【点睛】本题考查的是菱形的面积计算,熟知菱形的面积等于两对角线乘积的一半是解题的关键. 11.B解析:433【解析】【分析】由90C ∠=︒,30A ∠=︒得到2,AB BC = 利用勾股定理可得答案.【详解】解:设BC ,x =90C ∠=︒,30A ∠=︒, 2,AB x ∴=2AC =,222(2)2,x x ∴=+122323,33x x ∴==-(舍去), 42 3.3AB x ∴==4 3.3【点睛】 本题考查的是含30角的直角三角形的性质与勾股定理的应用,掌握相关知识点是解题的关键.12.A解析:2【分析】根据平行线的性质以及角平分线的定义证明∠ADE=∠AED,根据等角对等边,即可求得AE 的长,在直角△ABE中,利用勾股定理求得BE的长,进而得出EC.【详解】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEC=∠ADE,又∵∠DEC=∠AED,∴∠ADE=∠AED,∴AE=AD=10,在直角△ABE中,BE8=.∴EC=BC-BE=10-8=2,故答案为:2.【点睛】本题考查了矩形的性质,勾股定理,等腰三角形的判定,解决本题的关键是灵活运用矩形的性质,等腰三角形的判定和勾股定理.13.5或10【分析】本题分情况讨论①k>0时,x=1时对应y=5;②k>0时,x=1时对应y=10.【详解】解:①k>0时,由题意得:x=1时,y=5,∴k-b=5;②k<0时,由题意得:x=1时,y=10,∴k-b=10;综上,k-b的值为5或10.故答案为:5或10.【点睛】本题考查了待定系数法求函数解析式,注意本题需分两种情况,不要漏解.14.A【分析】根据矩形的性质可得∠ACB的度数,从而利用勾股定理可求出BC的长度.【详解】解:由题意得:∠ACB=30°,∠ABC=90°,在Rt△ABC中,AC=2AB=2,由勾股定理得,【点睛】本题考查了矩形的性质,比较简单,解答本题的关键是求出∠ACB的度数.15.4【分析】由图1,当直线在DE 的左下方时,由图2可得AE 长度;由图1,当直线在DE 和BF 之间时,长度不变,由图2可得EB 的长度,从而AB=AE+EB ,即求得AB .【详解】如图1,当直线在DE解析:4【分析】由图1,当直线在DE 的左下方时,由图2可得AE 长度;由图1,当直线在DE 和BF 之间时,长度不变,由图2可得EB 的长度,从而AB =AE +EB ,即求得AB .【详解】如图1,当直线在DE 的左下方时,由图2得:AE =7-4=3;由图1,当直线在DE 和BF 之间时,由图2可得:EB=8-7=1,所以AB =AE +EB =3+1=4.故答案为:4.【点睛】本题考查一次函数的图象与图形的平移,平行四边形的性质,关键是明确题意,读懂函数图象,利用数形结合的思想.16.5【分析】由折叠可得,.再由矩形性质结合勾股定理即可求出BF 的长,从而求出CF 的长.设,则,在中,利用勾股定理列出关于x 的等式,解出x 即可.【详解】解:由折叠可知,,∵四边形ABCD 是矩形解析:5【分析】由折叠可得5AD AF ==,DE EF =.再由矩形性质结合勾股定理即可求出BF 的长,从而求出CF 的长.设EC x =,则4DE EF x ==-,在Rt CEF 中,利用勾股定理列出关于x 的等式,解出x 即可.【详解】解:由折叠可知5AD AF ==,DE EF =,∵四边形ABCD 是矩形,∴在Rt ABF 中,3BF ==,∴532CF BC BF =-=-=.设EC x =,则4DE EF x ==-,∴在Rt CEF 中,222+=CF CE EF ,即2222(4)x x +=-,解得: 1.5x =.故EC 的长为1.5.故答案为1.5.【点睛】本题考查折叠的性质,矩形的性质和勾股定理.利用数形结合的思想是解答本题的关键.三、解答题17.(1)1;(2);(3);(4).【分析】(1)直接利用二次根式的性质以及立方根的性质分别化简,再利用有理数的加减运算法则计算得出答案;(2)直接利用二次根式的乘法运算法则以及结合绝对值的性质解析:(1)1;(2)2-;(3)44)3.【分析】(1)直接利用二次根式的性质以及立方根的性质分别化简,再利用有理数的加减运算法则计算得出答案;(2)直接利用二次根式的乘法运算法则以及结合绝对值的性质化简,先算乘法,再化简二次根式,去绝对值,最后利用二次根式的加减运算法则计算得出答案;(3)直接利用二次根式的乘除运算法则化简,先算乘除,再利用二次根式的加减运算法则计算得出答案;(4)直接利用二次根式的乘法运算法则化简,先算乘除,再利用有理数的加减运算法则计算得出答案.【详解】解:(13212=- 312122=--+ =1;(2)2=62=2=2-;(3==4=4(41)=-13121231=+-+-=.3【点睛】本题主要考查了二次根式的混合运算以及实数运算,正确化简二次根式是解题关键.18.游船移动的距离AD的长是9米【分析】根据条件先计算经过10秒拉回绳子的长,然后计算出绳子CD的长,在中,在中,,即可求出最终结果.【详解】解:工作人员以0.7米/秒的速度拉绳子,经过10秒解析:游船移动的距离AD的长是9米【分析】根据条件先计算经过10秒拉回绳子的长,然后计算出绳子CD的长,在Rt BCD中BD Rt ABC中,AB=【详解】解:工作人员以0.7米/秒的速度拉绳子,∴经过10秒拉回绳子100.7=7⨯米,开始时绳子AC的长为17m,∴拉了10秒后,绳子CD的长为17-7=10米,∴在Rt BCD中,6BD===米,在Rt ABC中,222217815AB AC BC =-=-=米, ∴AD =15-6=9米,答:游船移动的距离AD 的长是9米.【点睛】本题主要考查勾股定理的运用,属于综合题,难度一般,熟练掌握勾股定理解三角形是解决本题的关键.19.(1)见解析;(2)见解析;(3)见解析;(4)见解析;【解析】【分析】根据勾股定理即可得.【详解】解:(1)如图①所示,三边分别为:3,4,5;(2)如图②所示,三边分别为:,,2或解析:(1)见解析;(2)见解析;(3)见解析;(4)见解析;【解析】【分析】根据勾股定理即可得.【详解】解:(1)如图①所示,三边分别为:3,4,5;(2)如图②所示,三边分别为:2,2,2或22,22,4 ;(3如图③所示,三边分别为:5,5,10或2,22,10或10,10,25;(4)如图④所示,正方形的边长为:10,则面积:(10)2=10.【点睛】本题考查了勾股定理,解题的关键是掌握勾股定理.20.(1)见解析;(2)18【分析】(1)由四边形ABCD 是平行四边形易证△AOE ≌△COF ,从而可得OE=OF ,所以四边形AFCE 是平行四边形,又EF ⊥AC ,根据菱形的判定定理即可得证; (2)由解析:(1)见解析;(2)18【分析】(1)由四边形ABCD 是平行四边形易证△AOE ≌△COF ,从而可得OE =OF ,所以四边形AFCE 是平行四边形,又EF ⊥AC ,根据菱形的判定定理即可得证;(2)由(1)可求三角形ACE 的面积,又2AE ED =,从而可得三角形CED 的面积,则ABCD 的面积即可求解.【详解】(1)∵四边形ABCD 是平行四边形,∴AE //FC .∴∠EAO =∠FCO ,∠AEO =∠CFO .∵EF 平分AC ,∴OA =OC .∴△AOE ≌△COF .∴OE =OF .∴四边形AFCE 是平行四边形.又∵EF ⊥AC ,∴四边形AFCE 是菱形(对角线互相垂直的平行四边形是菱形).(2)∵四边形AFCE 是菱形,6AC =,4EF =,∴三角形ACE 的面积为16262⨯⨯=, ∵2AE ED =,∴三角形CED 的面积等于三角形ACE 的面积的一半,即三角形CED 的面积为1632⨯=, ∴三角形ACD 的面积为639+=,∴ABCD 的面积等于三角形ACD 的面积的2倍,即ABCD 的面积为1892=⨯. 故答案为:18.【点睛】本题考查了菱形的判定及平行四边形面积的求法,解题的关键是熟练掌握菱形的判定定理.21.①,,3+;②(1)5-;(2) .【解析】【分析】①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】①===3+,故答案为,,3+;②(1)解析:3+②(1)5(2) 12 【解析】【分析】 ①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】3+3=5=12+=12. 【点睛】本题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.22.(1);(2)25吨;(3)45元【分析】(1)利用待定系数法求解函数关系式的方法即可;(2)将y=91代入(1)中解析式中求得x 值即可;(3)将x=17代入(1)中解析式中求得y 值,再求得解析:(1)534y x =-;(2)25吨;(3)45元【分析】(1)利用待定系数法求解函数关系式的方法即可;(2)将y =91代入(1)中解析式中求得x 值即可;(3)将x =17代入(1)中解析式中求得y 值,再求得当017x ≤<时,y 与x 之间的函数关系式,将x =15代入求解y 值即可.【详解】解:(1)设y 与x 之间的函数关系式为:y kx b =+,由题意得:116306620k b k b=+⎧⎨=+⎩,∴534k b =⎧⎨=-⎩, ∴y 与x 之间的函数关系式为:534y x =-.(2)∵91元66>元,∴由91534x =-得:25x =. 答:这户居民上月用水量25吨.(3)当17x =吨时,5173451y =⨯-=元,∴当017x ≤<时,y 与x 之间的函数关系式为:3y x =,当15x =时,45y =元,答:这户居民这个月的水费45元.【点睛】本题考查一次函数的应用,理解题意,能从函数图象中获取有效信息,会利用待定系数法求解函数关系式是解答的关键.23.(1)证明见解析;(2)证明见解析【分析】(1)根据已知条件可得△ABC ≌△ABD ,再根据∠AOC+∠AOD=180°,进而可证得AB ⊥CD ,进而得到∠ACO=∠ABE ,进而证得△ABF ≌△CD解析:(1)证明见解析;(2)证明见解析【分析】(1)根据已知条件可得△ABC ≌△ABD ,再根据∠AOC+∠AOD=180°,进而可证得AB ⊥CD ,进而得到∠ACO=∠ABE ,进而证得△ABF ≌△CDA ;(2)取AB 中点H ,根据已知条件可知MO 为△AFH 的中位线,进而可证得△AFH ≌△DAO ,进一步得到△AFD 为等腰直角三角形,然后过点F 作FI ⊥AF 交AB 于点I ,取CD 上点G 使MG=MN ,连接AG ,先证△AFI ≌△DAM ,而后△FMN ≌△FIN ,得到∠FIN =∠FMN ,进而可证△AMG ≌△FMN ,得到∠AGM=∠FNM ,进而证得△ACG ≌△FBN ,得到BN=CG ,再根据CG=CM+MG ,得到BN=CM+MG ,又MG=MN ,继而得到BN=CM+MN .【详解】证明:(1)∵AC=AD ,BC=BD ,AB=AB ,∴△ABC≌△ABD,∴∠CAO=∠DAO,又∵∠ACO=∠ADO,∴∠AOC=∠AOD,又∵∠AOC+∠AOD=180°,∴∠AOC=∠AOD=90°,∴AB⊥CD,在Rt△AOC中,∠ACO+∠CAO=90°,在Rt△AEB中,∠ABE+∠CAO=90°,∴∠ACO=∠ABE,又∵AC=AD,FA=FB,∴∠ACO=∠ADO=∠ABF=∠FAB,∵,∴△ABF≌△CDA;(2)如图,取AB中点H,∵△ABF是等腰三角形,∴FH⊥AB,∵AM=MF且MO⊥AB,∴MO为△AFH的中位线,∴AO=OH=,又∵AH===DO,由△ABF≌△CDA,可知:AF=BF=AC=AD,∴△AFH≌△DAO,∴∠AFH=∠DAO,∵∠FAH+∠AFH=90°,∴∠FAH+∠DAO=90°,∴∠FAD=90°,∴△AFD为等腰直角三角形,过点F作FI⊥AF交AB于点I,取CD上点G使MG=MN,连接AG,由△AFH≌△DAO可得∠FAI=∠ADM,又∵AD=AF,∴△AFI≌△DAM,∴FI=AM,又∵AM=MF,∴FI=MF,由FI⊥AF可知∠AFI=90°,∠AFN=45°,∴∠NFI=∠AFI-∠AFN=90°-45°=45°,∴∠MFN=∠NFI,又∵FI=FM,∴△FMN≌△FIN,∴∠FIN =∠FMN,又∵∠AMD=∠FIA,∴∠AMD=∠FMN,又∵AM=FM,MG=MN,∴△AMG≌△FMN,∴∠AGM=∠FNM,又∵∠FNM=∠FNB,∴∠AGM=∠FNB,又∵∠ACG=∠FBN,AC=FB,∴△ACG≌△FBN,∴BN=CG,又∵CG=CM++MG,∴BN=CM+MG,又∵MG=MN,∴BN=CM+MN.【点睛】本题考查全等三角形的判定与性质、等腰三角形的性质、中位线等知识,解题的关键是综合运用相关知识解题.24.(1)y=-2x-2,(0,-2);(2)P(0,5)或P(0,3);(3)-2≤m<,或2<m≤4【解析】【分析】(1)利用待定系数法求得直线AB的解析式,根据关联点和关联直线的定义可得结论解析:(1)y=-2x-2,(0,-2);(2)P (0,5)或P (0,3);(3)-2≤m <23,或2<m≤4【解析】【分析】 (1)利用待定系数法求得直线AB 的解析式,根据关联点和关联直线的定义可得结论; (2)先根据关联点求D 和E 的坐标,根据面积和列式可得P 的坐标;(3)点M 分别在线段AC→CB 上讨论,根据直线l 与△ABC 恰有两个公共点时,可得m 的取值范围.【详解】解:(1)设直线AB 的解析式为:y=kx+b ,把点A (-2,-2),B (4,-2)代入得:2242k b k b -+=-⎧⎨+=-⎩, 解得:02k b =⎧⎨=-⎩, ∴直线AB 的解析式为:y=-2,∴点A 的关联直线的解析式为y=-2x-2;直线AB 的关联点的坐标为:(0,-2);故答案为:y=-2x-2,(0,-2);(2)∵点A (-2,-2),B (4,-2),C (1,4).∴直线AC 的解析式为y=2x+2,直线BC 的解析式为y=-2x+6,∴D (2,2),E (-2,6).∴直线DE 的解析式为y=-x+4,∴直线DE 与y 轴交于点F (0,4),如图1,设点P (0,y ),∵S △DEP =2,∴S △DEP =S △EFP +S △DFP=142y ⨯-×|-2|+1422y ⨯-⨯=2,解得:y=5或y=3,∴P(0,5)或P(0,3).(3)①当M在线段AC上时,如图3,∵AC:y=2x+2,∴设M(m,2m+2)(-2≤m≤1),则关联直线l:y=mx+2m+2,把C(1,4)代入y=mx+2m+2得:m+2m+2=4,m=23,∴-2≤m<23;②当M在线段BC上时,如图3,∵BC:y=-2x+6,∴设M(m,-2m+6)(1≤m≤4),则关联直线l:y=mx-2m+6,把A(-2,-2)代入y=mx-2m+6得:-2m-2m+6=-2,m=2,∴2<m≤4;综合上述,-2≤m<23或2<m≤4.【点睛】本题是一次函数的综合题,也是有关关联点和关联直线的新定义问题,考查了一次函数图象上点的坐标特征、理解新定义、利用待定系数法求一次函数的解析式,本题中理解关联点和关联直线的定义,正确进行分类讨论是解题的关键.25.(1);;(2)①见详解;②x=1;(3)△CDP为等腰三角形时x的值为:或或.【分析】(1)BP+DP为点B到D两段折线的和.由两点间线段最短可知,连接DB,若P点落在BD上,此时和最短,且为解析:(1)32;323-;(2)①见详解;②x=1;(3)△CDP为等腰三角形时x的值为:633-或3或633+.【分析】(1)BP+DP为点B到D两段折线的和.由两点间线段最短可知,连接DB,若P点落在BD 上,此时和最短,且为32.考虑动点运动,这种情形是存在的,由AQ=x,则QD=3-x,PQ=x.又PDQ=45°,所以QD=2PQ,即3-x=2x.求解可得答案;(2)由已知条件对称分析,AB=BP=BC,则∠BCP=∠BPC,由∠BPM=∠BCM=90°,可得∠MPC=∠MCP.那么若有MP=MD,则结论可证.再分析新条件∠CPD=90°,易得①结论.②求x的值,通常都是考虑勾股定理,选择直角三角形QDM,发现QM,DM,QD都可用x来表示,进而易得方程,求解即可.(3)若△CDP为等腰三角形,则边CD比为改等腰三角形的一腰或者底边.又P点为A点关于QB的对称点,则AB=PB,以点B为圆心,以AB的长为半径画弧,则P点只能在弧AB上.若CD为腰,以点C为圆心,以CD的长为半径画弧,两弧交点即为使得△CDP为等腰三角形(CD为腰)的P点.若CD为底边,则作CD的垂直平分线,其与弧AC的交点即为使得△CDP为等腰三角形(CD为底)的P点.则如图所示共有三个P点,那么也共有3个Q点.作辅助线,利用直角三角形性质求之即可.【详解】解:(1)连接DB,若P点落在BD上,此时BP+DP最短,如图:由题意,∵正方形ABCD的边长为3,∴223332BD+=∴BP +DP 的最小值是32; 由折叠的性质,PQ AQ x ==,则3QD x =-,∵∠PDQ=45°,∠QPD=90°,∴△QPD 是等腰直角三角形,∴22QD QP x ==,∴32x x -=,解得:323x =-;故答案为:32;323-;(2)如图所示:①证明:在正方形ABCD 中,有AB=BC ,∠A=∠BCD=90°.∵P 点为A 点关于BQ 的对称点,∴AB=PB ,∠A=∠QPB=90°,∴PB=BC ,∠BPM=∠BCM , ∴∠BPC=∠BCP ,∴∠MPC=∠MPB-∠CPB=∠MCB-∠PCB=∠MCP ,∴MP=MC .在Rt △PDC 中,∵∠PDM=90°-∠PCM ,∠DPM=90°-∠MPC ,∴∠PDM=∠DPM ,∴MP=MD ,∴CM=MP=MD ,即M 为CD 的中点.②解:∵AQ=x ,AD=3,∴QD=3-x ,PQ=x ,CD=3.在Rt △DPC 中,∵M 为CD 的中点,∴DM=QM=CM=32, ∴QM=PQ+PM=x+32,∴(x+32)2=(3−x)2+(32)2,解得:x=1.(3)如图,以点B为圆心,以AB的长为半径画弧,以点C为圆心,以CD的长为半径画弧,两弧分别交于P1,P3.此时△CDP1,△CDP3都为以CD为腰的等腰三角形.作CD的垂直平分线交弧AC于点P2,此时△CDP2以CD为底的等腰三角形.;①讨论P1,如图作辅助线,连接BP1、CP1,作QP1⊥BP1交AD于Q,过点P1,作EF⊥AD 于E,交BC于F.∵△BCP1为等边三角形,正方形ABCD边长为3,∴P1F33P1E=333在四边形ABP1Q中,∵∠ABP1=30°,∴∠AQP1=150°,∴△QEP1为含30°的直角三角形,∴31=9332.∵AE=3,2∴x=AQ=AE-QE=39(33)633--=-.22②讨论P2,如图作辅助线,连接BP2,AP2,过点P2作QG⊥BP2,交AD于Q,连接BQ,过点P2作EF⊥CD于E,交AB于F.∵EF垂直平分CD,∴EF垂直平分AB,∴AP2=BP2.∵AB=BP2,∴△ABP2为等边三角形.在四边形ABP2Q中,∵∠BAD=∠BP2Q=90°,∠ABP2=60°,∴∠AQG=120°∴∠EP2G=∠DQG=180°-120°=60°,∴P2E=333∴EG=933,2∴DG=DE+GE=39+=,3333322∴QD=33∴3③对P3,如图作辅助线,连接BP1,CP1,BP3,CP3,过点P3作BP3⊥QP3,交AD的延长线于Q,连接BQ,过点P1,作EF⊥AD于E,此时P3在EF上,不妨记P3与F重合.∵△BCP1为等边三角形,△BCP3为等边三角形,BC=3,∴P1P3=33P1E=333∴EF=333+在四边形ABP3Q中∵∠ABF=∠ABC+∠CBP3=150°,∴∠EQF=30°,∴39332.∵AE=32,∴x=AQ=AE+QE=32+9333362=.综合上述,△CDP为等腰三角形时x的值为:633-3633+.【点睛】本题第一问非常基础,难度较低.第二问因为动点的原因,思路不易找到,这里就需要做题时充分分析已知条件,尤其是新给出的条件.其中求边长是勾股定理的重要应用,是很重要的考点.第三问是一个难度非常高的题目,可以利用尺规作图的思想将满足要求的点P找全.另外求解各个Q点也是考察三角函数及勾股定理的综合应用,有着极高的难度.。
安徽省芜湖市市区2021-2022学年八年级上学期期末教学质量测评英语试题(word版 含答案)

6. What book does Henry want to borrow? A. A book about music. B. A book about history.7. How many days can Henry keep the book?A. Seven days.B. Twenty-one days.8. What will Henry do in class? A. Give a talk.C. Abook C. Thirty days.C. Sing a song.B. Make a role-play.HI.短文理解(共4小题,每小题1分;共4分)你将听到一段短文,短文后有五个小题。
请在每小题所给的A 、B 、C 三个选项中选出一个最佳八年级英语试卷时间:100分钟;满分 100分)第一部分 听力部分(共四大题,满分 15 分)I.短对话理解(共5小题,每小题 1分;满分 5分)你将听到五段对话,每段对话后有一个小题。
请在每小题所给的 A 、B 、C 三个选项中选2021-2022学年度第一学期期末教学质量测评A. Boring.B. Tiring.C. Great. 2. When does the girl get up on Sundays?A. At six.B. Later than six.C. Earlier than six.3. Where is Mr. Jackson now?A. In the classroom.B. At home.C. In the office.4. Who is the tallest of the three?A. Nick.B. Jim.C. Sam.5. When will the meeting start?A. At 8:3().B. At 9:30.C. At 11:3().II.长对话理解(共3小题,每小题1分; 满分3分)出一个最佳选项,每段对话读两遍。
期末达标测试卷(B卷) 2022-2023学年统编版语文八年级下册(word版含答案)

2022-2023学年人教部编版八年级下学期语文期末达标测试卷(B卷)试卷满分120分,考试时间120分钟一、积累与运用(31分)1.下列加粗字的注音不完全正确的一项是()(2分)A.轻盈(yíng)矗立(chù)翡翠(fěi)B.眺望(tiào)犹豫(yù)苍劲(jìn)C.闸门(zhá)砚池(yàn)擦拭(shì)D.硕大(shuò)喧哗(xuān)驿道(yì)2.下列句中加粗词语使用不正确的一项是()(2分)A.红军曾在我们村安营扎寨。
B.人们正在散步时,突然天降大雨,真是大煞风景。
C.儿童时代的事至今仍历历在目,使我回味无穷。
D.这些人对个人利益斤斤计较,而对广大群众的疾苦却漫不经心。
3.下列句子中标点符号使用不正确的一项是()(2分)A.李白的“浮云游子意,落日故人情”(《送友人》)、“朝如青丝暮成雪”(《将进酒》)都是脍炙人口的名句。
B.不知不觉,三年的高中生活转瞬即逝。
李萍上了大学,张华当TIA,我进了部队:我们都有美好的前途。
C.材料是文章的血肉,结构是文章的骨骼。
骨骼完整匀称,人才能身姿挺拔;结构井然有序,文章才就立得起来。
D.据王璨的《英雄记抄》说,诸葛亮与徐庶、石广元、孟公威等人一道游学读书,“三人务于精熟,而亮独观其大略。
”4.下列关于文学常识表述,有误的一项是()(2分)A.顾拜旦是法国教育家、社会活动家,现代奥林匹克运动的创始人,他终生倡导奥林匹克精神,被誉为“现代奥林匹克之父”。
B.《在长江源头各拉丹冬》是美国著名作家马克·吐温创作的一篇游记,这篇文章以散文笔法,叙述奇人奇事、惊险的旅途、怪异的车夫,富有传奇色彩。
C.《礼记》又名《小戴礼记》,相传是西汉经学家戴圣编纂的,是中国古代重要的典章制度选集,是一部儒家思想的资料汇编。
D.《卖炭翁》的作者是唐代诗人白居易,通过卖炭翁的遭遇,深刻地揭露了“宫市”的腐败本质,表达了作者对下层劳动人民的深切同情。
八年级物理全册全套试卷达标检测卷(Word版 含解析)

八年级物理全册全套试卷达标检测卷(Word版含解析)一、初二物理声现象实验易错压轴题(难)1.如图所示,将塑料刻度尺的一端紧压在桌面上,另一端伸出桌面,拨动刻度尺使之振动,听塑料尺振动时发出的声音.(1)实验通过改变___________来改变声音的响度,通过改变_______来改变声音的音调.(2)换用钢尺做此实验,钢尺伸出桌面的长度、振动幅度和频率与塑料尺均相同时,听到声音的主要差异是________ (选填“响度”“音调”或“音色”)不同.(3)实验设计隐含的物理方法是比较法和_________法.(4)刻度尺振动产生的声音通过________传进耳朵,引起鼓膜______,人便听到声音.(5)实验中当刻度尺伸出桌面的部分超过一定长度时,无论如何用力拨动也听不到声音.原因是___.【答案】拨动塑料尺的力度塑料尺伸出桌面的长度音色控制变量空气振动刻度尺振动得太慢,产生的是次声波,人耳无法听到【解析】【详解】(1)响度与振幅有关,用不同大小的力拨动塑料尺,塑料尺的振幅不同,发出的声音响度不同;物体振动的快慢与物体的质量、粗细、长短等因素有关,实验要通过改变刻度尺伸出桌面的长度来改变音调.(2)钢尺和塑料尺的材料不同,当钢尺伸出桌面的长度、振动幅度和速度与塑料尺均相同时,听到声音的主要差异是音色的不同.(3)实验中研究响度与振幅关系时,应控制频率不变,而在研究音调与频率关系时,则要控制振幅相同,故实验设计隐含的物理方法除比较法外,还有控制变量法.(4)我们听到的声音,都是声波通过空气传入人耳,引起鼓膜的振动,再传给听小骨、耳蜗,传给听觉神经,引起听觉.(5) 实验中当刻度尺伸出桌面的部分超过一定长度时,无论如何用力拨动也听不到声音,原因是刻度尺振动得太慢,产生的是次声波,人耳无法听到.2.探究声音的特征:(1)为了探究音调与什么因素有关,小明设计了下面几个实验,如图所示,你认为能够完成探究目的是_____,通过探究可知:音调是由发声体振动的_____决定的.(2)如图所示,将一把钢尺紧按在桌面上,一端伸出桌面适当的长度,拨动钢尺,就可听到_____(选填“钢尺”或“桌面被拍打”)振动发出的声音,若改用更大的力拨动钢尺,则听到声音的_____(选填“音调”、“音色”或“响度”)变大;逐渐增加钢尺伸出桌面的长度,仔细聆听钢尺振动发出声音后,发现音调逐渐变_____(选填“高”或“低”)了,观察发现此时钢尺振动慢了,当钢尺伸出桌面超过一定长度时,虽然用同样的力拨动钢尺,却听不到声音了,这是由于_____.【答案】A、B、C 频率(快慢)钢尺响度低钢尺的振动频率低于20HZ【解析】(1)A、硬纸板接触齿数不同的齿轮,振动的频率不同,发出的声音的音调不同,符合题意;B. 改变钢尺伸出桌边的长度振动的频率不同,发出的声音的音调不同,符合题意;C. 用塑料尺子在梳子齿上快慢不同的滑动时,梳子齿振动的频率不同,发出的声音的音调不同,符合题意;D. 改变吹笔帽的力度,振幅不同,响度不同,研究响度跟振幅的关系,不符合题意;故选D.通过探究可知:音调是由发声体振动的频率决定的; (2)将一把钢尺紧紧按在桌面上,一端伸出桌面适当的长度,拨动钢尺,就可听到钢尺振动发出的声音;若改用更大的力拨动钢尺,钢尺的振幅变大,响度变大;改变钢尺伸出桌面的长度,用同样大小的力拨动其伸出桌面的一端,这样会导致钢尺振动的快慢不同,即发出声音的音调不同;钢尺伸出桌面超过一定长度,振动得很慢,即钢尺振动的频率小于20Hz,所以人耳听不到.3.在探究声音的产生与传播时,小明和小华一起做了下面的实验:(1)如图①所示,用悬挂着的乒乓球接触正在发声的音叉可观察到______,它说明了声音是由______产生的。
八年级下册数学期末试卷达标检测卷(Word版含解析)
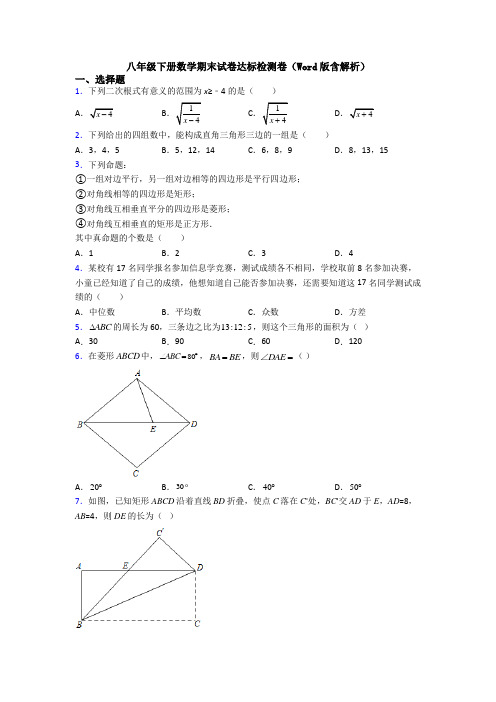
八年级下册数学期末试卷达标检测卷(Word 版含解析)一、选择题1.下列二次根式有意义的范围为x ≥﹣4的是( )A .4x -B .14x -C .14x +D .4x + 2.下列给出的四组数中,能构成直角三角形三边的一组是( )A .3,4,5B .5,12,14C .6,8,9D .8,13,153.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线相等的四边形是矩形;③对角线互相垂直平分的四边形是菱形;④对角线互相垂直的矩形是正方形.其中真命题的个数是( )A .1B .2C .3D .44.某校有17名同学报名参加信息学竞赛,测试成绩各不相同,学校取前8名参加决赛,小童已经知道了自己的成绩,他想知道自己能否参加决赛,还需要知道这17名同学测试成绩的( )A .中位数B .平均数C .众数D .方差 5.ABC ∆的周长为60,三条边之比为13:12:5,则这个三角形的面积为( )A .30B .90C .60D .120 6.在菱形ABCD 中,80ABC ∠=︒,BA BE =,则DAE =∠( )A .20︒B .30C .40︒D .50︒7.如图,已知矩形ABCD 沿着直线BD 折叠,使点C 落在C '处,BC '交AD 于E ,AD =8,AB =4,则DE 的长为( )A .3B .4C .5D .68.如图,在平面直角坐标系中,已知A (5,0)点P 为线段OA 上任意一点.在直线y =34x 上取点E ,使PO =PE ,延长PE 到点F ,使PA =PF ,分别取OE 、AF 中点M 、N ,连结MN ,则MN 的最小值是( )A .2.5B .2.4C .2.8D .3二、填空题9.函数01(1)2y x x =+-+中x 的取值范围是______. 10.已知菱形的两条对角线长分别为1和4,则菱形的面积为______.11.如图,每个小正方形的边长都为1,则ABC ∆的三边长a ,b ,c 的大小关系是________(用“>”连接).12.如图,点P 是矩形ABCD 的对角线AC 上一点,过点P 作EF ∥BC ,分别交AB ,CD 于点E 、F ,连接PB 、PD ,若AE =2,PF =9,则图中阴影面积为______;13.某一次函数的图象经过点(2,-3),且函数y 随x 的增大而增大,请你写出一个符合条件的函数解析式_____________________.14.在矩形ABCD 中,3AB =,ABC ∠的平分线BE 交AD 所在的直线于点E ,若2DE =,则AD 的长为__________.15.如图,在平面直角坐标系中,点A ,A 1,A 2,…在x 轴上,点P ,P 1,P 2,…在直线l :y=kx +34(k >0)上,∠OPA =90°,点P (1,1),A (2,0),且AP 1,A 1P 2,…均与OP 平行,A 1P 1,A 2P 2,…均与AP 平行,则有下列结论:①直线AP 1的函数解析式为y =x ﹣2;②点P 2的纵坐标是259;③点P 2021的纵坐标为(53)2021.其中正确的是_____(填序号).16.如图,在平面直角坐标系xOy 中,一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ,则正方形OABC 的面积为____.三、解答题17.计算: ①33118(3)2⨯+-; ②2(32)24-+.18.笔直的河流一侧有一旅游地C ,河边有两个漂流点A ,B .其中AB =AC ,由于某种原因,由C 到A 的路现在已经不通,为方便游客决定在河边新建一个漂流点H (A ,H ,B 在同一直线上),并新修一条路CH ,测得BC =5千米,CH =4千米,BH =3千米. (1)判断△BCH 的形状,并说明理由;(2)求原路线AC 的长.19.阅读理解:我们给出如下定义:若一个四边形中存在一组相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称:__________,__________.(2)如图,已知格点(小正方形的顶点)()0,0O ,()3,0A ,()0,4B ,请你画出以格点为顶点,OA ,OB 为勾股边且对角线相等的两个勾股四边形OAMB .20.如图,矩形ABCD 的对角线AC 与BD 交于点,作CF ∥BD ,DF ∥AC .求证:四边形DECF 为菱形.21.阅读材料:规定初中考试不能使用计算器后,小明是这样解决问题的:已知a 23+,求2281a a -+的值.他是这样分析与解的:∵a 23+2323(23)(23)-=+-, ∴23a -= ∴2(2)3,a -= 2443a a -+=∴241a a -=-, ∴2281a a -+=2(24)1a a -+=2(1)11⨯-+=-.请你根据小明的分析过程,解决如下问题:(1)若a 21-,直接写出2481a a -+的值是 . (21315375121119+++++ 22.某商场要印制商品宣传材料,甲印刷厂的收费标准是:每份材料收1元印制费,另收1500元制版费;乙印刷厂的收费标准是:每份材料收2.5元印制费,不收制版费. (1)分别写出两厂的收费y (元)与印制数量x (份)之间的关系式;(2)印制800份宣传材料时,选择哪一家印刷厂比较合算?商场计划花费3000元用于印刷上述宣传材料,选择哪一家印刷厂能多印制一些宣传材料?23.在正方形ABCD 中,点E 是CD 边上任意一点,连接过点B 作于F ,交AD 于.如图1,过点D 作于G .求证:;如图2,点E 为CD 的中点,连接DF ,试判断存在什么数量关系并说明理由;如图3,,连接,点为的中点,在点E 从点D 运动到点C 的过程中,点随之运动,请直接写出点运动的路径长.24.如图,已知点()4,0A 、()0,2B ,线段OA OC =且点C 在y 轴负半轴上,连接AC .(1)如图1,求直线AB 的解析式;(2)如图1,点P 是直线CA 上一点,若3ABC ABP SS =,求满足条件的点P 坐标; (3)如图2,点M 为直线5:2l x =上一点,将点M 水平向右平移6个单位至点N ,连接BM 、MN 、NC ,求BM MN NC ++的最小值及此时点N 的坐标.25.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.【参考答案】一、选择题1.D解析:D【分析】根据二次根式中的被开方数是非负数,分式的分母不为0列出不等式,分别计算即可.【详解】解:A 、x ﹣4≥0,解得x ≥4,故此选项不符合题意;B 、x ﹣4>0,解得x >4,故此选项不符合题意;C 、x +4>0,解得x >﹣4,故此选项不符合题意;D 、x +4≥0,解得x ≥﹣4,故此选项符合题意.故选:D .【点睛】本题考查了二次根式有意义的条件和分式有意义的条件,解题关键是熟记二次根式和分式有意义的条件,列出不等式求解.2.A解析:A【分析】分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形.【详解】解:A.∵32+42=52,∴能构成直角三角形三边;B.∵52+122≠142,∴不能构成直角三角形三边;C.∵62+82≠92,∴不能构成直角三角形三边;D.∵82+132≠152,∴不能构成直角三角形三边.故选A.【点睛】本题考查了利用勾股定理逆定理判定直角三角形的方法.在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.B解析:B【解析】【分析】根据平行四边形、矩形、菱形和正方形的判定直接进行判断即可.【详解】解:①一组对边平行且相等的四边形是平行四边形,原命题是假命题;②对角线相等的平行四边形是矩形,原命题是假命题;③对角线互相垂直平分的四边形是菱形,是真命题;④对角线互相垂直的矩形是正方形,是真命题;故选:B.【点睛】本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.4.A解析:A【解析】【分析】由于比赛取前8名参加决赛,共有17名选手参加,根据中位数的意义分析即可.【详解】解:由于总共有17个人,且他们的分数互不相同,第9名的成绩是中位数,要判断是否进入前8名,故应知道自己的成绩和中位数.故选:A.【点睛】本题考查了统计量的选择,以及中位数意义,解题的关键是正确的求出这组数据的中位数.5.D解析:D根据已知条件可求得三边的长,再判断这个三角形是直角三角形,即可求得面积.【详解】∵三条边之比为13:12:5,∴122+52=132,∴△ABC 是直角三角形,∵△ABC 的周长为60,∴三边长分别是:26,24,10,∴这个三角形的面积是:24×10÷2=120,故选D .【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.6.B解析:B【解析】【分析】利用菱形的性质和等腰三角形的性质即可求解.【详解】解:在菱形ABCD 中,80ABC ∠=︒,∴18080100BAD ∠=︒-︒=︒,40ABE ∠=︒,∵BA BE =, ∴18040702BAE BEA ︒-︒∠=∠==︒, ∴1007030DAE BAD BAE ∠=∠-∠=︒-︒=︒,故选:B .【点睛】本题考查了菱形的性质和等腰三角形的性质,运用知识准确计算是解题的关键. 7.C解析:C【解析】【分析】根据折叠前后角相等可知△ABE ≌△C'ED ,利用勾股定理可求出.【详解】解:∵四边形ABCD 是矩形,∴AB=CD ,∠C =∠A =90°由折叠的性质可得:C'D =CD =AB ;∠C'=∠C =∠A在△ABE 与△C'ED 中''C ED AEB C A ⎪∠=∠⎨⎪∠=∠⎩∴△ABE ≌△C'ED (AAS )∴DE=BE设DE =BE =x ,则AE =8-x ,AB =4,在直角三角形ABE 中,()22816x x =-+ 解得x =5故选C .【点睛】本题考查勾股定理在折叠问题中的应用,找到合适的直角三角形构建等量关系是本题关键.8.B解析:B【分析】如图,连接PM ,PN ,设AF 交EM 于J ,连接PJ .证明四边形PMJN 是矩形,推出MN=PJ ,求出PJ 的最小值即可解决问题.【详解】解:如图,连接PM ,PN ,设AF 交EM 于J ,连接PJ .∵PO=PE ,OM=ME ,∴PM ⊥OE ,∠OPM=∠EPM ,∵PF=PA ,NF=NA ,∴PN ⊥AF ,∠APN=∠FPN ,∴∠MPN=∠EPM+∠FPN=12(∠OPF+∠FPA )=90°,∠PMJ=∠PNJ=90°,∴四边形PMJN 是矩形,∴MN=PJ ,∴当JP ⊥OA 时,PJ 的值最小此时MN 的值最小, ∵AF ⊥OM ,A (5,0),直线OM 的解析式为y=34x ∴设直线AF 的解析式为y=4-3x+b ∵直线AF 过A (5,0), ∴4-5+b 3⨯=0,∴b=203, ∴y=420-x+33, 由3442033y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩,解得165125x y ⎧=⎪⎪⎨⎪=⎪⎩∴16(,)5125J ∴PJ 的最小值为125=2.4 即MN 的最小值为2.4故选:B .【点睛】本题考查一次函数的应用,矩形的判定和性质,垂线段最短等知识,解题的关键是学会用转化的思想思考问题,属于中考选择题中的压轴题.二、填空题9.x >﹣2且x ≠1.【解析】【分析】从二次根式,分式,零指数幂三个角度去思考求解即可.【详解】由题意得,x +2>0,且x ﹣1≠0,解得x >﹣2且x ≠1,所以x 的取值范围是x >﹣2且x ≠1.故答案为:x >﹣2且x ≠1.【点睛】本题考查了分式有意义的条件,二次根式有意义的条件,零指数幂有意义的条件,熟练上述基本条件是解题的关键.10.2【解析】【分析】利用菱形的面积等于对角线乘积的一半求解.【详解】解:菱形的面积=12×1×4=2. 故答案为2.【点睛】本题考查了菱形的性质:熟练掌握菱形的性质(菱形具有平行四边形的一切性质; 菱形的四条边都相等; 菱形的两条对角线互相垂直,并且每一条对角线平分一组对角). 记住菱形面积=12ab (a 、b 是两条对角线的长度). 11.c a b >>;【解析】【分析】观察图形根据勾股定理分别计算出a 、b 、c ,根据二次根式的性质即可比较a 、b 、c 的大小.【详解】解:在图中,每个小正方形的边长都为1,由勾股定理可得:22242025=+==a ,22331832=+==b ,221526=+=c ,∵262018>>,即262532>>,∴c a b >>,故答案为:c a b >>.【点睛】本题考查了勾股定理和比较二次根式的大小,本题中正确求出a 、b 、c 的值是解题的关键.12.A解析:18【分析】作PM ⊥AD 于M ,交BC 于N ,根据矩形的性质可得S △PEB =S △PFD 即可求解.【详解】解:作PM ⊥AD 于M ,交BC 于N .则有四边形AEPM ,四边形DFPM ,四边形CFPN ,四边形BEPN 都是矩形,,,,,ADC ABC AMP AEP PBE PBN PFD PDM PFC PCN S S S S S S S S S S ∴=====,∴DFPM BEPN S S 矩矩=,12442DFP PBE S S ∴==⨯⨯=, ∴S 阴=9+9=18,故答案为:18.【点睛】本题考查矩形的性质、三角形的面积等知识,解题的关键是证明DFP PBE S S =.13.5y x =-(答案不唯一)【分析】根据题意,写出一个0k >且经过(2,3)-的解析式即可【详解】函数y 随x 的增大而增大0k ∴>图象经过点(2,-3)例如:5y x =-(答案不唯一)【点睛】本题考查了一次函数的性质,一次函数的定义,理解一次函数的性质是解题的关键. 14.5或1【分析】当点E 在AD 上时,根据平行线的性质和角平分线的定义可得3AE AB ==,可得AD 的长;当点E 在AD 的延长线上时,同理可求出AD 的长.【详解】解:如图1,当点E 在AD 上时,四边形ABCD 是矩形,90A ∴∠=︒,//AD BC ,AEB CBE ∴∠=∠, BE 平分ABC ∠,ABE CBE ∴∠=∠,ABE AEB ∴∠=∠,3AE AB ∴==,2DE =,325AD AE DE ∴=+=+=;如图2,当点E 在AD 的延长线上时,同理3AE =,321AD AE DE ∴=-=-=.故答案为:5或1.【点睛】本题主要考查了矩形的性质,等腰直角三角形的性质等知识,解题的关键是正确画出两种图形.15.①②③【分析】由已知易求得直线的解析式为:,直线为:,进而根据待定系数法可求得 的解析式为:即可判断①;解析式联立构成方程组可求得 的坐标,同理求得 的坐标,即可判断②;由、的坐标得出规律即可得解析:①②③【分析】由已知易求得直线OP 的解析式为:y x =,直线l 为:1344y x =+,进而根据待定系数法可求得 1AP 的解析式为:2y x =-即可判断①;解析式联立构成方程组可求得 1P 的坐标,同理求得 2P 的坐标,即可判断②;由1P 、2P 的坐标得出规律即可得出点 2021P 的纵坐标为202153⎛⎫ ⎪⎝⎭,即可判断③.【详解】解:设1AP 的解析式为y kx b =+,∵P (1,1),∴直线OP 为y x =,∵AP 1∥OP ,∴k =1,即y x b =+,∵A (2,0),∴2+b =0,解得b =﹣2,∴AP 1的解析式为2y x =-,故①正确;∵点P ,P 1,P 2,…在直线l :34y kx =+(k >0)上, ∴1=k +34,解得k =14,∴直线l 为:1344y x =+, 解21344y x y x =-⎧⎪⎨=+⎪⎩得11353x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴115133P ⎛⎫ ⎪⎝⎭,, 设11A P 的解析式为y x b =-+, 代入111533P ⎛⎫ ⎪⎝⎭,可得,11A P 的解析式为:163y x =-+, ∴A 1的坐标为(163,0), 同理求得A 1P 2的解析式为:163y x =-, 解1631344y x y x ⎧=-⎪⎪⎨⎪=+⎪⎩得739259x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴P 2纵坐标为259,故②正确; ∵P 1纵坐标为53,P 2纵坐标为259=(53)2, 以此类推,点P 2021的纵坐标为(53)2021.故③正确. 故答案为:①②③.【点睛】本题考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,总结出点的纵坐标的规律是解题的关键.16.【分析】过点作轴于点,过点作轴于点,由正方形的性质就可以得出,就可以得出,,由一次函数的图象经过正方形的顶点和,设点,就可以得出代入解析式就可以求出的值,由正方形的面积等于就可以求出结论.【详 解析:325【分析】过点C 作CD x ⊥轴于点D ,过点A 作AE y ⊥轴于点E ,由正方形的性质就可以得出CDO AEO ∆≅∆,就可以得出CD AE =,OD OE =,由一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ,设点(,24)C a a -,就可以得出(24,)A a a --代入解析式就可以求出a 的值,由正方形的面积等于2OC 就可以求出结论.【详解】解:过点C 作CD x ⊥轴于点D ,过点A 作AE y ⊥轴于点E ,90CDO AEO ∴∠=∠=︒.四边形OABC 是正方形,90AOC ∴∠=︒,OC OA =.90DOE ∠=︒,AOC DOE ∴∠=∠,AOC AOD DOE AOD ∴∠-∠=∠-∠,COD AOE ∴∠=∠.在CDO ∆和AEO ∆中,CDO AEO COD AOE OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()CDO AEO AAS ∴∆≅∆CD AE ∴=,OD OE =.一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ,设点(,24)C a a -, OD a ∴=,24CD a =-,OE a ∴=,24AE a =-,(24,)A a a ∴--,2(24)4a a ∴-=--,125a ∴=. 125OD ∴=,45CD =, 在Rt CDO ∆中,由勾股定理,得2222212432555OC OD CD ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭. 2OABC S CO =正方形,325OABC S ∴=正方形. 故答案为:325. 【点睛】 本题考查了正方形的性质及面积公式的运用,垂直的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,一次函数图象上点的坐标的特征的运用,构造K 字形全等,得出AC 两点坐标关系是解题的关键.三、解答题17.①0;②5【分析】(1)先运用二次根式或立方根的性质化简各个根式,再计算即可;(2)先运用完全平方公式计算,再合并同类二次根式计算即可.【详解】解:①原式=0;②原式=5.【解析:①0;②5【分析】(1)先运用二次根式或立方根的性质化简各个根式,再计算即可;(2)先运用完全平方公式计算,再合并同类二次根式计算即可.【详解】解:原式3=-=-33=0;②2原式32=+-=5.【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的运算法则和运算顺序是解题的关键.18.(1)直角三角形,理由见解析;(2)原来的路线AC的长为千米.【分析】(1)根据勾股定理的逆定理解答即可;(2)根据勾股定理解答即可.【详解】解:(1)△HBC是直角三角形,理由是:在△解析:(1)直角三角形,理由见解析;(2)原来的路线AC的长为256千米.【分析】(1)根据勾股定理的逆定理解答即可;(2)根据勾股定理解答即可.【详解】解:(1)△HBC是直角三角形,理由是:在△CHB中,∵CH2+BH2=42+32=25,BC2=25,∴CH2+BH2=BC2,∴△HBC是直角三角形且∠CHB=90°;(2)设AC=AB=x千米,则AH=AB-BH=(x-3)千米,在Rt△ACH中,由已知得AC=x,AH=x-3,CH=4,由勾股定理得:AC2=AH2+CH2,∴x2=(x-3)2+42,解这个方程,得x=256,答:原来的路线AC的长为256千米.【点睛】本题考查勾股定理的应用,解决本题的关键是掌握勾股定理的逆定理和定理.19.(1)矩形,正方形;(2)见解析【解析】【分析】(1)根据勾股四边形的定义即可求解;(2)由勾股定理可知可知四边形对角线为5,据此即可作图.【详解】解:(1)由勾股四边形的定义矩形、正方解析:(1)矩形,正方形;(2)见解析【解析】【分析】(1)根据勾股四边形的定义即可求解;(2)由勾股定理可知可知四边形OAMB对角线为5,据此即可作图.【详解】解:(1)由勾股四边形的定义矩形、正方形都满足一组相邻两边的平方和等于一条对角线的平方,故答案为:矩形,正方形;(2)如图,证明:∵∠AOB=90°,∴222OA OB AB+=,∴四边形OAMB为勾股四边形,由勾股定理得,22345OM+∴AB=OM,∴四边形OAMB都是勾股四边形,符合题意.【点睛】本题为新定义问题,考查了勾股定理等知识,矩形、正方形的性质,熟知勾股定理,理解勾股四边形的定义是解题关键.20.见解析【分析】根据DF∥AC,CF∥BD,即可证出四边形EDFC是平行四边形,又知四边形ABCD是矩形,故可得ED=BD=AC=EC,即可证出四边形EDFC是菱形.【详解】证明:∵DF∥AC解析:见解析【分析】根据DF∥AC,CF∥BD,即可证出四边形EDFC是平行四边形,又知四边形ABCD是矩形,故可得ED=12BD=12AC=EC,即可证出四边形EDFC是菱形.【详解】证明:∵DF∥AC,CF∥BD∴四边形EDFC是平行四边形,∵四边形ABCD是矩形,∴ED=12BD=12AC=EC,∴四边形EDFC是菱形.【点睛】本题主要考查矩形性质和菱形的判定的知识点,解答本题的关键是熟练掌握菱形的判定定理,此题比较简单.21.(1)5;(2)5.【解析】【详解】试题分析: 根据平方差公式,可分母有理化,根据整体代入,可得答案.试题解析:(1)∵a=,∴4a2-8a+1=4×()2-8×()+1=5;(2)解析:(1)5;(2)5.【解析】【详解】试题分析: 根据平方差公式,可分母有理化,根据整体代入,可得答案.,试题解析:(1)∵∴4a2-8a+1)2-8×)+1=5;×(2)原式=12×)=12×10=12=5.点睛:本题主要考查了分母有理化,利用分母有理化化简是解答此题的关键.22.(1)y甲=x+1500,y乙=2.5x;(2)印制800份宣传材料时,选择乙厂比较合算;商场计划花费3000元用于印刷上述宣传材料,选择甲厂能多印制一些宣传材料【分析】(1)根据“甲印刷厂的收解析:(1)y甲=x+1500,y乙=2.5x;(2)印制800份宣传材料时,选择乙厂比较合算;商场计划花费3000元用于印刷上述宣传材料,选择甲厂能多印制一些宣传材料【分析】(1)根据“甲印刷厂的收费标准是:每份材料收1元印制费,另收1500元制版费”可得甲厂关系式,根据“乙印刷厂的收费标准是:每份材料收2.5元印制费,不收制版费”可得乙厂关系式;(2)把x=800代入两厂关系式进行计算即可得哪厂比较合算;把y=3000代入两厂关系式进行计算可得哪厂能多印制一些宣传材料.【详解】解:(1)根据题意得:y甲=x+1500,y乙=2.5x;(2)当x=800时,y甲=800+1500=2300,y乙=2.5×800=2000,∵2300>2000,∴印制800份宣传材料时,选择乙厂比较合算;当y=3000时,甲厂:3000=x+1500,解得x=1500,乙厂:3000=2.5x,解得x=1200,∵1500>1200,∴商场计划花费3000元用于印刷上述宣传材料,选择甲厂能多印制一些宣传材料.【点睛】本题考查了一次函数的应用,理解题意是解题的关键.23.(1)见解析;(2)FH+FE=DF,理由见解析;(3)【分析】(1)如图1中,证明△AFB≌△DGA(AAS)可得结论.(2)结论:FH+FE=DF.如图2中,过点D作DK⊥AE于K,DJ⊥解析:(1)见解析;(2),理由见解析;(3)【分析】(1)如图1中,证明△AFB≌△DGA(AAS)可得结论.(2)结论:.如图2中,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J,证明四边形DKFJ是正方形,可得结论.(3)如图3中,取AD的中点J,连接PJ,延长JP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K.设PT=b.证明△KPJ是等腰直角三角形,推出点P在线段JR上运动,求出JR即可解决问题.【详解】解:(1)如图1中,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵DG⊥AE,AE⊥BH,∴∠AFB=∠DGH=90°,∴∠FAB+∠DAG=90°,∠DAG+∠ADG=90°,∴∠BAF=∠ADG,∴△AFB≌△DGA(AAS),∴AF=DG,BF=AG,∴BF-DG=AG-AF=FG.(2)结论:FH+FE=2DF.理由:如图2中,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J,∵四边形ABCD是正方形,∴∠BAD=∠ADE=90°,AB=AD,∵AE⊥BH,∴∠AFB=90°,∴∠DAE+∠EAB=90°,∠EAB+∠ABH=90°,∴∠DAE=∠ABH,∴△ABH≌△DAE(ASA),∴AH=AE,∵DE=EC=1CD,CD=AD,2∴AH=DH,∴DE=DH,∵DJ⊥BJ,DK⊥AE,∴∠J=∠DKE=∠KFJ=90°,∴四边形DKFJ是矩形,∴∠JDK=∠ADC=90°,∴∠JDH=∠KDE,∵∠J=∠DKE=90°,∴△DJH≌△DKE(AAS),∴DJ=DK,JH=EK,∴四边形DKFJ是正方形,∴FK=FJ=DK=DJ,∴DF=2FJ,∴FH+FE=FJ-HJ+FK+KE=2FJ=2DF;(3)如图3中,取AD的中点J,连接PJ,延长JP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K.设PT=b.∵△ABH≌△DAE,∴AH=DE,∵∠EDH=90°,HP=PE,∴PD=PH=PE,∵PK⊥DH,PT⊥DE,∴∠PKD=∠KDT=∠PTD=90°,∴四边形PTDK是矩形,∴PT=DK=b,PK=DT,∵PH=PD=PE,PK⊥DH,PT⊥DE,∴DH=2DK=2b,DE=2DT,∴AH=DE=1-2b,∴PK=12DE=12-b,JK=DJ-DK=12-b,∴PK=KJ,∵∠PKJ=90°,∴∠KJP=45°,∴点P在线段JR上运动,∵2DJ=,∴点P 的运动轨迹的长为.【点睛】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,轨迹等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数解决问题,属于中考压轴题. 24.(1);(2)点P 的坐标为(,)或(,);(3)的最小值为;点N 的坐标为(,).【解析】【分析】(1)直接利用待定系数法,即可求出直线的解析式;(2)根据题意,先求出点C 的坐标,然后求出直线解析:(1)122y x =-+;(2)点P 的坐标为(163,43)或(83,43-);(3)BM MN NC ++的最小值为6N 的坐标为(172,711). 【解析】【分析】(1)直接利用待定系数法,即可求出直线的解析式;(2)根据题意,先求出点C 的坐标,然后求出直线AC 的解析式,由3ABC ABP S S =,得到3AC AP =,再分别求出AC 和AP 的长度,即可求出点P 的坐标;(3)根据题意,6MN =为定值,在图中找出一点B ',使得B N BM '=,即点B '、N 、C 三点共线时,使得BM MN NC ++有最小值,此时求出B C B N NC BM NC ''=+=+,即可得到答案.【详解】解:(1)设直线AB 为y kx b =+,把点()4,0A 、()0,2B ,代入,则402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩, ∴122y x =-+; (2)∵线段4OA OC ==,且点C 在y 轴负半轴上,∴点C 的坐标为(0,-4),∵点A 为(4,0),∴直线AC 的解析式为:4y x =-;∵点B 到直线AC 的距离就是△ABC 和△ABP 的高,∴△ABC 和△ABP 的高相同,∵3ABC ABP SS =, ∴11322AC h AP h ••=⨯••,∴3AC AP =, ∵224442AC =+=, ∴1424233AP =⨯=, ∵点P 在直线AC 上,则设点P 为(x ,x -4),∴2242(4)(4)243AP x x x =-+-=•-=, ∴443x -=, ∴163x =或83x =, ∴点P 的坐标为(163,43)或(83,43-); (3)根据题意,∵点B 与点M 的水平距离为52, ∴在点N 的右边水平距离为52处作直线11x =,如图:令点B '为(11,2),此时有B N BM '=,∵6MN =,∴66BM MN NC BM NC B N NC '++=++=++,∴当点B '、N 、C 三点共线时,使得BM MN NC ++有最小值,最小值为:66BM MN NC B N NC B C ''++=++=+;∵点B '(11,2),点C 为(0,-4),∴直线B C '的解析式为:6411y x =-,B C '∴BM MN NC ++有最小值为:66B C '+=+∵点N 的横坐标为:517622+=, ∴点N 的纵坐标为:6177411211y =⨯-=, ∴点N 的坐标为:(172,711). 【点睛】 本题考查了一次函数的性质,利用勾股定理求两点之间的距离,最短路径问题,坐标与图形,解题的关键是熟练掌握一次函数的图形和性质,正确找出使得线段之和最小时的临界点,注意运用数形结合的思想进行解题.25.(1)15,8;(2),见解析;(3);(4)4【分析】解决问题(1)只需运用面积法:,即可解决问题;(2)解法同(1);(3)连接、、,作于,由等边三角形的性质得出,由勾股定理得出,得出的解析:(1)15,8;(2)PE PF CG +=,见解析;(3)4)4【分析】解决问题(1)只需运用面积法:ABC ABP ACP S S S ∆∆∆=+,即可解决问题;(2)解法同(1);(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,由等边三角形的性质得出152BM BC ==,由勾股定理得出AM =ABC ∆的面积12BC AM =⨯=ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++= (4)过点E 作EQ BC ⊥,垂足为Q ,易证BE BF =,过点E 作EQ BF ⊥,垂足为Q ,由解决问题(1)可得PG PH EQ +=,易证EQ DC =,BF DF =,只需求出BF 即可.【详解】解:(1)∵PE AB ⊥,10AB =,3PE =,∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=, ∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴358CG PE PF =+=+=.故答案为:15,8.(2)∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴CG PE PF =+.(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,如图2所示:∵10AB AC BC ===,∴ABC ∆是等边三角形,∵AM BC ⊥, ∴152BM BC ==, ∴222210553AM AB BM =-=-=,∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯=, ∵PE BC ⊥,PF AC ⊥,PG AB ⊥,∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=,∴22535310PE PF PG ⨯++==. (4)过点E 作EQ BC ⊥,垂足为Q ,如图3所示:∵四边形ABCD 是矩形,∴AD BC =,90C ADC ∠=∠=︒,∵8AD =,3CF =,∴5BF BC CF AD CF =-=-=,由折叠可得:5DF BF ==,BEF DEF ∠=∠,∵90C ∠=︒, ∴4DC =,∵EQ BC ⊥,90C ADC ∠=∠=︒,∴90EQC C ADC ∠=︒=∠=∠,∴四边形EQCD 是矩形,∴4EQ DC ==,∵//AD BC ,∴DEF EFB ∠=∠,∵BEF DEF ∠=∠,∴BEF EFB ∠=∠,∴BE BF =,由解决问题(1)可得:PG PH EQ +=,∴4PG PH +=,即PG PH +的值为4.【点睛】本题是四边形综合题目,考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.。
人教版八年级期末试卷试卷(word版含答案)

人教版八年级期末试卷试卷(word 版含答案) 一、选择题 1.函数y =35x x --的自变量x 的取值范围是( ) A .x ≠5 B .x >3且x ≠5 C .x ≥3 D .x ≥3且x ≠5 2.下列四组数据中,不能作为直角三角形三边长的是( ) A .5,12,13B .1,2,3C .6,8,10D .3,4,5 3.下面条件中,能判定四边形是平行四边形的条件是( ) A .一组对角相等 B .对角线互相平分 C .一组对边相等 D .对角线互相垂直 4.一年级(1)班部分同学背诵课文《人之初》的时间(单位:s )26,42,30,40,29,29,27,29,28,30,设平均数为P ,众数为Z ,中位数为W ,则( )A .P= ZB .P=WC .Z=WD .P= Z=W 5.下列三角形中,是直角三角形的是( ).A .三角形的三边满足关系a +b =cB .三角形的三边为9,40,41C .三角形的一边等于另一边的一半D .三角形的三边比为1∶2∶36.如图,在△ABC 中,AC =22,∠ABC =45°,∠BAC =15°,将△ABC 沿直线AC 翻折至△ABC 所在的平面内,得△ADC .过点A 作AE ,使∠EAD =∠DAC ,与CD 的延长线交于点E ,则线段ED 的长为( )A .23﹣6B .26﹣23C .26﹣2D .32﹣6 7.如图,在Rt ABC △中,90ACB ∠=︒,30B ∠=︒,CD 是斜边AB 上的高,1cm AD =,则BC 的长度是( )A .3cmB 3cmC .23cmD .4cm8.如图,已知直线3:3l y x =,过点()0,1A 作y 轴的垂线交直线l 于点,B 过点B 作直线l 的垂线交y 轴于点1A ;过点1A 作y 轴的垂线交直线l 于点1B ,过点1B 作直线l 的垂线交y 轴于点2A ;······,按此作法继续下去,则点2020B 的坐标为( )A .()20203,2020B .()40403,4040C .()2020202043,4⋅D .()2020202023,2⋅ 二、填空题9.若y x a =+的取值范围是1≥x ,则a =__________.10.如图,在菱形ABCD 中,E ,F ,G 分别是AD ,AB ,CD 的中点,且10cm FG =,6cm EF =,则菱形ABCD 的面积是___2cm .11.如图,在△ABD 中,∠D =90°,CD =6,AD =8,∠ACD =2∠B ,BD 的长为_____.12.如图,长方形ABCD 中,3cm AB =,9cm AD =,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则ABE △的面积是__________.13.某生态体验园推出了甲、乙两种消费卡.甲、乙两卡所需费用y 甲,y 乙(单位:元)与入园次数x (单位:次)的函数关系如图所示.当x 满足________时,y y >甲乙.14.如图,下列条件之一能使平行四边形ABCD 是菱形的为_____________.①AC ⊥BD ;②∠BAD=90°;③AB=BC ;④AC=BD .15.如图所示,直线y =x +4与两坐标轴分别交于A ,B 两点,点C 是OB 的中点,D ,E 分别是直线AB 和y 轴上的动点,则CDE 周长的最小值是____________.16.如图所示,四边形ABCD 是长方形,把ACD △沿AC 折叠到ACD ',AD 与BC 交于点E ,若4,3AD DC ==,则BE 的长为________.三、解答题17.计算:(1)(1323(24536; (345335 (418328-+12. 18.一架长为10米的梯子AB ,顶端B 靠在墙上,梯子底端A 到墙的距离6AC =米.(1)求BC 的长;(2)如图梯子的顶端B 沿墙向下滑动3米,问梯子的底端A 向外移动了多少米? 19.如图,网格中的每个小正方形的边长为1,点、、A B C 均在格点上.(1)直接写出AC 的长为___________,ABC 的面积为_____;(2)请在所给的网格中,仅用无刻度的直尺作出AC 边上的高BD ,并保留作图痕迹. 20.如图所示,在矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交BC ,AD 于点E ,F ,垂足为O ,连接AE ,CF .(1)求证:四边形AFCE 为菱形;(2)求AF 的长.21.小明在解决问题:已知a 23+2a 2-8a +1的值,他是这样分析与解答的: 因为a 23+()()232323-+-=23 所以a -23所以(a -2)2=3,即a 2-4a +4=3.所以a 2-4a =-1.所以2a 2-8a +1=2(a 2-4a)+1=2×(-1)+1=-1.请你根据小明的分析过程,解决如下问题:(1)计算:2+1- .(2)计算:1112+13+24+3+++…+1100+99;(3)若a=121-,求4a2-8a+1的值.22.我国传统的计重工具——秤的应用,方便了人们的生活,如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤).如表中为若干次称重时所记录的一些数据.x(厘米)1247y(斤)0.75 1.00 1.50 2.25(1)在图2中将表x,y的数据通过描点的方法表示,观察判断x,y的函数关系,并求秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少斤?(2)已知秤砣到秤纽的最大水平距离为50厘米,这杆秤的可称物重范围是多少斤?23.图1,在正方形ABCD中,,P为线段BC上一点,连接,过点B作,交CD于点Q.将沿所在直线对折得到,延长交于点N.(1)求证:.(2)若,求AN的长.(3)如图2,延长交BA的延长线于点,若,记的面积为,求与x之间的函数关系式.24.在平面直角坐标系xOy 中,对于任意三点A ,B ,C 的“矩积”,给出如下定义:“横底”a :任意两点横坐标差的最大值;“纵高”h :任意两点纵坐标差的最大值;则“矩积”S =ah .例如:三点坐标分别为A (1,﹣2),B (2,2),C (﹣1,﹣3),则“横底”a =3,“纵高”h =5,“矩积”S =ah =15.已知点D (﹣2,3),E (1,﹣1).(1)若点F 在x 轴上.①当D ,E ,F 三点的“矩积”为24,则点F 的坐标为 ;②直接写出D ,E ,F 三点的“矩积”的最小值为 ;(2)若点F 在直线y =mx+4上,使得D ,E ,F 三点的“矩积”取到最小值,直接写出m 的取值范围是 .25.如图,菱形纸片ABCD 的边长为2,60,BAC ∠=︒翻折,,B D ∠∠使点,B D 两点重合在对角线BD 上一点,,P EF GH 分别是折痕.设()02AE x x =<<.(1)证明:AG BE =;(2)当02x <<时,六边形AEFCHG 周长的值是否会发生改变,请说明理由; (3)当02x <<时,六边形AEFCHG 的面积可能等于534吗?如果能,求此时x 的值;如果不能,请说明理由.26.如图,Rt △CEF 中,∠C =90°,∠CEF ,∠CFE 外角平分线交于点A ,过点A 分别作直线CE ,CF 的垂线,B ,D 为垂足.(1)∠EAF = °(直接写出结果不写解答过程);(2)①求证:四边形ABCD 是正方形.②若BE =EC =3,求DF 的长.(3)如图(2),在△PQR 中,∠QPR =45°,高PH =5,QH =2,则HR 的长度是 (直接写出结果不写解答过程).【参考答案】一、选择题1.D解析:D【分析】根据二次根式和分式有意义的条件列出不等式,求解不等式即可.【详解】根据题意得:x﹣3≥0且x﹣5≠0,解得x≥3且x≠5.∴自变量x的取值范围是x≥3且x≠5.故选:D.【点睛】本题考查了二次根式和分式由意义的条件,理解二次根式和分式由意义的条件是解题的关键.2.B解析:B【分析】利用勾股定理逆定理进行求解即可.【详解】解:A、222+,能构成直角三角形,故此选项不符合题意;512=13B、222+≠,不能构成直角三角形,故此选项符合题意;123C、222+,能构成直角三角形,故此选项不合题意;68=10D、222+,能构成直角三角形,故此选项不合题意;34=5故选B.【点睛】本题考查勾股定理的应用,熟练掌握勾股定理的逆定理是解题关键.主要看较短两边的平方和是否等于较长边的平方3.B解析:B【解析】【分析】根据平行四边形判定定理判断即可.【详解】∵一组对角相等的四边形不是平行四边形,∴A错误;∵对角线互相平分的四边形是平行四边形,∴B正确;∵一组对边相等的四边形不是平行四边形,∴C错误;∵对角线互相垂直的四边形不是平行四边形,∴D错误;故选B.【点睛】本题考查了平行四边形的判定定理,熟练掌握平行四边形的判定定理是解题的关键.4.C解析:C【解析】【分析】分别求出这组数据的平均数,中位数,众数进行判断即可.【详解】 解:由题意得:平均数264230402929272928303110P +++++++++== 把这组数据重新排列如下:26,27,28,29,29,29,30,30,40,42,∴处在最中间的两个数为29、29,∴中位数2929292W +==, ∵29出现了3次,出现的次数最多,∴众数29Z =,∴Z W =,故选C .【点睛】本题主要考查了求中位数,众数和平均数,解题的关键在于能够熟练掌握三者的定义. 5.B解析:B【详解】A. 不能构成三角形,此选项错误;B.由于9²+40²=41²,是直角三角形,此选项正确;C. 不能判定是直角三角形,此选项错误;D.不能构成三角形,此选项错误.故选B.6.D解析:D【解析】【分析】延长BC 交AE 于H ,由折叠的性质∠DAC=∠BAC=15°,∠ADC=∠ABC=45°,∠ACB=∠ACD=120°,由外角的性质可求∠AED=∠EAC ,可得AC=EC ,再求得∠ABC=∠BAH=45°,AH=BH ,利用等腰直角三角形的性质和直角三角形的性质可求解.【详解】解:如图,延长BC 交AE 于H ,∵∠ABC=45°,∠BAC=15°,∴∠ACB=120°,∵将△ACB沿直线AC翻折,∴∠DAC=∠BAC=15°,∠ADC=∠ABC=45°,∠ACB=∠ACD=120°,CB=CD,∵∠DAE=∠DAC,∴∠DAE=∠DAC=15°,∴∠CAE=30°,∵∠ADC=∠DAE+∠AED,∴∠AED=45°-15°=30°,∴∠AED=∠EAC,∴AC=EC2∵∠ABC=45°,∠BAH=45°,∴∠BHA=90°,BH=AH,在Rt△A CH中,∠CAH=30°,AC2∴CH2BH=AH226-=AC CH∴CB=CD=BH-CH62∴ED=EC-CD=(=2262326故选:D.【点睛】本题考查了轴对称的性质,等腰直角三角形的性质和直角三角形的性质等知识,灵活运用这些性质进行推理是本题的关键.7.C解析:C【解析】【分析】根据三角形的内角和求出∠A,根据余角的定义求出∠ACD,根据含30度角的直角三角形性质求出AC=2AD,AB=2AC,进而利用勾股定理求出BC即可.【详解】解:∵CD ⊥AB ,∠ACB =90°,∴∠ADC =90°=∠ACB ,∵∠B =30°,∴∠A =90°−∠B =60°,∴∠ACD =90°−∠A =30°,∵AD =1cm ,∴AC =2AD =2(cm ),∴AB =2AC =4(cm ),∴BC=cm ),故选:C .【点睛】本题主要考查的是勾股定理、含30度角的直角三角形性质和三角形内角和定理的应用,关键是求出AC =2AD ,AB =2AC .8.C解析:C【分析】先根据所给一次函数判断出直线与x 轴夹角是30°,在含有30°角的直角三角形中依次得到线段长度,表示出A 、A 1、A 2…及B 、B 1、B 2…的坐标,找到规律后求出A 2020的坐标,再根据A 2020的坐标与B 2020的纵坐标相同即可得出结论.【详解】解:∵直线l 的解析式为:y =, ∴直线l 与x 轴的夹角为30°,∵AB ∥x 轴,∴∠ABO =30°,∵OA =1,∴AB∵A 1B ⊥l ,∴∠ABA 1=60°,∴AA 1=3,∴A1(0,4),B 1(4),同理可得B 2(16),…∴A 2020纵坐标为:20204,∴A 2020(0,20204),∴B2020(2020420204),故选C .【点睛】本题考查了一次函数的综合题应用,从可求得的坐标中寻找规律,得出结论,解决本题的关键是判断出直线与x 轴的夹角.二、填空题9.-1【解析】【分析】根据二次根式的被开方数是非负数列出不等式,解不等式得到答案.【详解】解:由题意得:x +a ≥0,解得:x ≥−a ,则−a =1,解得:a =−1,故答案为:−1.【点睛】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键. 10.A解析:96【解析】【分析】连接AC ,BD ,交点为O ,EF 与AC 交于点M ,EG 与BD 交于点N ,由三角形中位线定理得出//EF BD ,12EF BD =,//EG AC ,12EG AC =,得出90FEG ∠=︒,由勾股定理求出EG 的长,根据菱形的面积公式可得出答案.【详解】解:如图,连接AC ,BD ,交点为O ,EF 与AC 交于点M ,EG 与BD 交于点N ,四边形ABCD 是菱形,AC BD ∴⊥,E ,F ,G 分别是AD ,AB ,CD 的中点,//EF BD ∴,12EF BD =,//EG AC ,12EG AC =, ∴四边形OMEN 是矩形,90FEG ∴∠=︒,10FG cm =,6EF cm =,22221068EG FG EF cm ∴=--=,16AC cm ∴=,12BD cm =,∴菱形ABCD 的面积是211161296()22AC BD cm ⋅=⨯⨯=. 故答案为96.【点睛】本题考查了菱形的性质,三角形中位线定理,勾股定理,菱形的面积,根据三角形的中位线定理求出AC 和BD 的长是解题的关键.11.A解析:【解析】【分析】根据勾股定理求出AC ,根据三角形的外角的性质得到∠B =∠CAB ,根据等腰三角形的性质求出BC ,计算即可.【详解】解:∵∠D =90°,CD =6,AD =8,∴AC10,∵∠ACD =2∠B ,∠ACD =∠B +∠CAB ,∴∠B =∠CAB ,∴BC =AC =10,∴BD =BC +CD =16,故答案:16.【点睛】本题考查勾股定理、三角形的外角的性质,直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么a 2+b 2=c 2.12.E解析:26cm【分析】首先翻折方法得到ED =BE ,再设出未知数,分别表示出线段AE ,ED ,BE 的长度,然后在Rt △ABE 中利用勾股定理求出AE 的长度,进而求出AE 的长度,就可以利用面积公式求得△ABE 的面积.【详解】解:∵长方形折叠,使点B 与点D 重合,∴ED =BE ,∠A 90=︒,设AE =xcm ,则ED =BE =(9﹣x )cm ,在Rt △ABE 中,222AB AE BE +=,∴2223(9)x x +=-,解得:x=4,∴△ABE 的面积为:3×4×12=6(2cm ),故答案为26cm .【点睛】本题考查了折叠的性质,长方形的性质,勾股定理的运用;解题的关键是熟练掌握折叠的性质,找准折叠前后相等的角和边.13.x >10【分析】运用待定系数法,即可求出y 与x 之间的函数表达式,联立方程组解答即可求出两直线的交点坐标,根据函数图象回答即可.【详解】解:设y 甲=k 1x ,根据题意得5k 1=100,解得k 1=20,∴y 甲=20x ;设y 乙=k 2x +100,根据题意得:20k 2+100=300,解得k 2=10,∴y 乙=10x +100;解方程组2010100y x y x =⎧⎨=+⎩,解得10200x y =⎧⎨=⎩, ∴两直线的交点坐标为(10,200);根据图象可知:当x >10时,y y >甲乙.故答案为:x >10.【点睛】本题主要考查了一次函数的应用、学会利用方程组求两个函数图象的解得交点坐标,正确由图象得出正确信息是解题关键.14.A解析:①③.【分析】根据菱形的判定定理判定即可.【详解】解:①ABCD 中,AC ⊥BD ,根据对角线互相垂直的平行四边形是菱形,即可判定ABCD 是菱形,故①正确; ②ABCD 中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,可判定ABCD 是矩形,而不能判定ABCD 是菱形,故②错误; ③ABCD 中,AB=BC ,根据一组邻边相等的平行四边形是菱形,即可判定ABCD 是菱形,故③正确; ④ABCD 中,AC=BD ,根据对角线相等的平行四边形是矩形,可判定ABCD 是矩形,而不能判定ABCD 是菱形,故④错误.故答案为①③.【点睛】本题主要考查了菱形的判定定理. ①一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形.15.【分析】作点关于的对称点,关于的对称点,连接,,FB ,FG ,由轴对称的性质,可得,,故当点,,,在同一直线上时,的周长,此时周长最小,依据勾股定理即可得到的长,进而得到周长的最小值.【详解】 解析:210 【分析】作点C 关于AB 的对称点F ,关于AO 的对称点G ,连接DF ,EG ,FB ,FG ,由轴对称的性质,可得DF DC =,EC EG =,故当点F ,D ,E ,G 在同一直线上时,DEC 的周长CD DE CE DF DE EG FG =++=++=,此时DEC 周长最小,依据勾股定理即可得到FG 的长,进而得到DEC 周长的最小值.【详解】解:如图,作点C 关于AB 的对称点F ,关于AO 的对称点G ,连接DF ,EG ,FB ,FG ,直线4y x =+与两坐标轴分别交于A 、B 两点,∴令x =0,则y =4;令y =0,则x =-4,)4(0,A ∴,(4,0)B -,∴4OA OB ==,又∵点C 是OB 的中点,∴122OC BC OB ===,∵点C 与点G 关于AO 对称,∴2OG OC ==,EC EG =,∴6BG OB OG =+=,∵OA OB =,90AOB ∠=︒,45ABC ACB ∴∠=∠=︒, 又∵点C 与点F 关于AB 对称,45ABC ABF ∴∠=∠=︒,2BC BF ==,DF DC =,90FBC ∴∠=︒,∵DF DC =,EC EG =,∴CDE △的周长CD DE CE DF DE EG FG =++=++≥,当点F ,D ,E ,G 在同一直线上时,CDE △的周长最小,为FG 的长,∵在Rt BFG △中,FG =CDE ∴周长的最小值是故答案为:【点睛】本题考查一次函数图象上点的坐标特征,轴对称-最短问题,等腰直角三角形的判定与性质,勾股定理等知识,解题的关键是利用轴对称的性质找到点D 、点E 位置,属于中考常考题型.16.【分析】根据矩形性质得AB =DC =3,BC =AD =4,AD ∥BC ,∠B =90°,再根据折叠性质得∠DAC =∠D′AC ,而∠DAC =∠ACB ,则∠D′AC =∠ACB ,所以AE =EC ,设BE =x ,则 解析:78【分析】根据矩形性质得AB =DC =3,BC =AD =4,AD ∥BC ,∠B =90°,再根据折叠性质得∠DAC =∠D ′AC ,而∠DAC =∠ACB ,则∠D ′AC =∠ACB ,所以AE =EC ,设BE =x ,则EC =4﹣x ,AE =4﹣x ,然后在Rt △ABE 中利用勾股定理可计算出BE .【详解】解:∵四边形ABCD 为矩形,∴AB =DC =3,BC =AD =4,AD ∥BC ,∠B =90°.∵△ACD 沿AC 折叠到△ACD ′,AD ′与BC 交于点E ,∴∠DAC =∠D ′AC ,∵AD ∥BC ,∴∠DAC =∠ACB ,∴∠D ′AC =∠ACB ,∴AE =EC .设BE =x ,则EC =4﹣x ,AE =4﹣x ,在Rt △ABE 中,∵AB 2+BE 2=AE 2,∴32+x 2=(4﹣x )2,解得x =78, 即BE 的长为78. 故答案为:78. 【点睛】本题考查了折叠的性质、矩形的性质和勾股定理,解题关键是设未知数,表示线段长,利用勾股定理列方程.三、解答题17.(1)-1+(2)(3)(4)0【分析】(1)利用多项式乘以多项式展开,然后合并即可;(2)把二次根式相乘化为最简二次根式即可;(3)把二次根式化为最简二次根式即可;(4)先把二次根式化为解析:(1)-23)5(4)0【分析】(1)利用多项式乘以多项式展开,然后合并即可;(2)把二次根式相乘化为最简二次根式即可;(3)把二次根式化为最简二次根式即可;(4)先把二次根式化为最简二次根式,然后合并即可.【详解】解:(1)(12,=-(2(3=(4122421222=11 22 -+=0【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的加减乘除运算,再合并即可.在二次根式的混合运算中,要结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径.18.(1)8米;(2)米【分析】(1)直接利用勾股定理得出BC 的长;(2)在△CED 中,再利用勾股定理计算出CE 的长,进而可得AE 的长.【详解】解:(1)一架长米的梯子,顶端靠在墙上,梯子底端解析:(1)8米;(2)()6米【分析】(1)直接利用勾股定理得出BC 的长;(2)在△CED 中,再利用勾股定理计算出CE 的长,进而可得AE 的长.【详解】解:(1)一架长10米的梯子AB ,顶端B 靠在墙上,梯子底端A 到墙的距离6AC =米,∠C =90°,8BC ∴.答:BC 的长为8米.(2)3BD =,8BC =,835CD BC BD ∴=-=-=,又∠C =90°,CE ∴=6AE CE AC ∴=-=.答:梯子的底端A 向外移动了()6米.【点睛】此题主要考查了勾股定理的应用,正确应用勾股定理是解题关键. 19.(1),;(2)见解析【解析】【分析】(1)根据勾股定理和三角形的面积公式即可得到结论;(2)根据无刻度直尺作图中作垂直的技巧画出线段BD 即可;【详解】解:(1),:(2)如图所示,解析:(1)AC =9ABC S =;(2)见解析【解析】【分析】(1)根据勾股定理和三角形的面积公式即可得到结论;(2)根据无刻度直尺作图中作垂直的技巧画出线段BD 即可;【详解】解:(1)222529,AC =+=,111452425149222ABC S =⨯-⨯⨯-⨯⨯-⨯⨯=: (2)如图所示,BD 即为所求.【点睛】本题考查了作图-应用与设计作图,三角形的面积的计算,勾股定理,正确的作出图形是解题的关键.20.(1)见解析;(2)AF=5【分析】(1)根据EF 是AC 的垂直平分线可以得到AF=CF ,AE=CE ,再只需证明△AFO ≌△CEO即可得到答案;(2)根据四边形AECF 是菱形可以得到AE=EC解析:(1)见解析;(2)AF =5【分析】(1)根据EF 是AC 的垂直平分线可以得到AF =CF ,AE =CE ,再只需证明△AFO ≌△CEO 即可得到答案;(2)根据四边形AECF 是菱形可以得到AE =EC =x ,则BE =8-x ,然后利用勾股定理求解即可.【详解】解:(1)∵EF 是AC 的垂直平分线,∴AF =CF ,AE =CE ,AO =CO∵四边形ABCD 是矩形,∴AF ∥EC∴∠FAO =∠ECO ,∠AFO =∠CEO ,在△AFO 和△CEO 中,AFO CEO AO COFAO ECO ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFO ≌△CEO (AAS ),∴AF =EC ,∴AF =FC =AE =EC ,∴四边形AECF 是菱形;(2)由(1)得AE =CE =AF ,设AE =CE =AF =x ,则BE =8-x ,∵四边形ABCD 是矩形,∴∠B =90°,在直角三角形ABE 中222AB BE AE +=,∴()22248x x +-=, 解得x =5,∴AF =5,21.(1) ,1;(2) 9;(3) 5【解析】【分析】(1);(2)根据例题可得:对每个式子的分子和分母中同时乘以与分母中的式子相乘符合平方差公式的根式,去掉分母,然后合并同类项二次根式即可求 解析:2,1;(2) 9;(3) 5【解析】【分析】(1()()2121212121-==++-;(2)根据例题可得:对每个式子的分子和分母中同时乘以与分母中的式子相乘符合平方差公式的根式,去掉分母,然后合并同类项二次根式即可求解;(3)首先化简a ,然后把所求的式子化成()2413a --代入求解即可.【详解】 (1)计算:2121=+; (2)原式)(213243...1009910011019=++++==-=;(3)()()12121212121a +===+--+,则原式()()224213413a a a =-+-=--,当21a =+时,原式()24235=⨯-=.【点睛】 本题考查了二次根式的化简求值,正确读懂例题,对根式进行化简是关键.22.(1),4.5斤;(2)最多13斤.【分析】(1)根据表中数据利用描点法在图二中画图,可得出x ,y 满足一次函数的变化关系,设函数关系式为,利用待定系数法求解即可;(2)根据秤砣到秤纽的最大水平解析:(1)1142y x =+,4.5斤;(2)最多13斤. 【分析】(1)根据表中数据利用描点法在图二中画图,可得出x ,y 满足一次函数的变化关系,设函数关系式为y kx b =+,利用待定系数法求解即可;(2)根据秤砣到秤纽的最大水平距离为50厘米可知50x ≤,求出y 的取值范围即可.【详解】解:(1)利用描点法画出图像如下,观察图象可知x ,y 满足一次函数的变化关系,设y kx b =+,把107521x y .x y ====,,,,代入可得:0.7512k b k b =+⎧⎨=+⎩, 解得1412k b ⎧=⎪⎪⎨⎪=⎪⎩, ∴1142y x =+, 当16x =时, 4.5y =,∴秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤;(2)由题意可得50x ≤ , 所以可得:311142x +≤, 即13y ≤,∴这杆秤的可称物重范围是13斤以内.【点睛】本题考查了一次函数的图象及应用,待定系数法,一元一次不等式等知识,利用数形结合的思想是解题的关键.23.(1)证明见解析;(2);(3).【分析】(1)先证,再据ASA 证明△ABP ≌△BCQ ,可证得BP=CQ ;(2)连接,先证,得到,设AN=x ,用x 表示出ND ;再求出DQ 和的值,再在RT △NDQ解析:(1)证明见解析;(2);(3). 【分析】(1)先证,再据ASA 证明△ABP ≌△BCQ ,可证得BP=CQ ; (2)连接,先证,得到,设AN=x ,用x 表示出ND ;再求出DQ 和的值,再在RT △NDQ 中用勾股定理列方程求解;(3)作QG ⊥AB 于G ,先证MB=MQ 并设其为y ,再在RT △MGQ 中用勾股定理列出关于x 、y 的方程,并用x 表示y ;用y 表示出△MBQ 的面积,用x 表示出△的面积.最后据用x 、y 表示出S ,并把其中的y 用x 代换即可.【详解】(1)在正方形ABCD 中,,,,,,,.(2)在正方形ABCD 中连接,如下图:由折叠知BC=,又AB=BC,∠BAN=90°∴,,,,,,,设,,,,,.(3)如下图,作,垂足为G,由(1)知∵∠MBQ=∠CQB=∠MQB∴BM=MQ设,则.,,,故.【点睛】此题综合考查了正方形性质、三角形全等,勾股定理等知识点,其关键是要熟练掌握相关知识,能灵活应用.24.(1)①(﹣5,0)或(4,0);②12;(2)或【解析】【分析】(1)①已知F在x轴上,故“纵高”=4,根据“矩积”的定义,可知“横底”=6,应分三种情况进行分类讨论,当a<-2时、当-2≤解析:(1)①(﹣5,0)或(4,0);②12;(2)12m≥或1m≤-【解析】【分析】(1)①已知F在x轴上,故“纵高”=4,根据“矩积”的定义,可知“横底”=6,应分三种情况进行分类讨论,当a<-2时、当-2≤a≤1时、当a>1时;②将F点的横坐标仍按照三类情况进行讨论,根据“矩积”的定义可求解;(2)使直线过点D(-2,3)或点H(1,3),求出该特殊位置时m的值,即可求解.【详解】解:(1)设点F坐标为(a,0),①∵D,E,F三点的“矩积”为24,“纵高”=4,∴“横底”=6,当a<-2时,则“横底”=1-a=6,∴a=-5;当-2≤a≤1时,则“横底”=3≠6,不合题意舍去;当a>1时,则“横底”=a-(-2)=6;∴a=4,∴点F(﹣5,0)或(4,0),故答案为:(﹣5,0)或(4,0);②当a<-2时,则1-a>3,∴S=4(1-a)>12,当﹣2≤a≤1时,S=3⨯4=12,当a>1时,则a-(-2)>3,∴S=4⨯[a-(-2)]>12,∴D,E,F三点的“矩积”的最小值为12,故答案为:12;(2)由(1)可知:设点F(a,0),当﹣2≤a≤1时,D,E,F三点的“矩积”能取到最小值,如图下图所示,直线y=mx+4恒过点(0,4),使该直线过点D(-2,3)或点H(1,3),当F 在点D或点H时,D,E,F三点的“矩积”的最小值为12,当直线y=mx+4过点D(-2,3)时,∴3=-2m+4,∴解得:1m=2,当直线y=mx+4过点H(1,3)时,∴3=m+4,∴m=-1,∴当m≥12或m≤-1时,D,E,F三点的“矩积”能取到最小值.【点睛】本题主要考察了一次函数的几何应用,提出了“矩积”这个全新的概念,解题的关键在于通过题目的描述,知道“矩积”的定义,同时要注意分类讨论.25.(1)见解析;(2)不变,见解析;(3)能,或【分析】(1)由折叠的性质得到BE=EP,BF=PF,得到BE=BF,根据菱形的性质得到AB∥CD∥FG,BC∥EH∥AD,于是得到结论;(2)由解析:(1)见解析;(2)不变,见解析;(3)能,212x=-21【分析】(1)由折叠的性质得到BE=EP ,BF=PF ,得到BE=BF ,根据菱形的性质得到AB ∥CD ∥FG ,BC ∥EH ∥AD ,于是得到结论;(2)由菱形的性质得到BE=BF ,AE=FC ,推出△ABC 是等边三角形,求得∠B=∠D=60°,得到∠B=∠D=60°,于是得到结论;(3)记AC 与BD 交于点O ,得到∠ABD=30°,解直角三角形得到AO=1,S 四边形ABCD AEFCHG 时,得到S △BEF +S △DGH GH 与BD 交于点M ,求得GM=12x ,根据三角形的面积列方程即可得到结论. 【详解】解:()1折叠后B 落在BD 上,,BE EP ∴=BF PF = BD 平分,ABC ∠BE BF ∴=,∴四边形BEPF 为菱形,同理四边形GDHP 为菱形,////,// //,AB CD FG BC EH AD ∴∴四边形AEPG 为平行四边形,AG EP BE ∴==.()2不变.理由如下:由()1得.AG BE =四边形BEPF 为菱形,,.BE BF AE FC ∴==60,BAC ABC ∠=︒为等边三角60B D ∴∠=∠=︒,,,EF BE GH DG ∴==36AEFCHG C AE EF FC CH GH AG AB ∴=+++++==六边形为定值.()3记AC 与BD 交于点O .2,60,AB BAC =∠=30,ABD ∴∠=1,AO ∴=3,BO12332ABC S ∴=⨯23ABCD S ∴=四边形当六边形AEFCHG 534 53233344DEF DGH S S +=由()1得BE AG =AE DG ∴=DG x =2BE x ∴=-记GH 与BD 交于点,M12GM x ∴=,3DM = 23DHGS x ∴= 同理)2233233BEF Sx x =-= 223333334x x +化简得22410,x x -+= 解得121x =221x = ∴当21x =21AEPCHG 534 【点睛】此题是四边形的综合题,主要考查了菱形的性质,等边三角形的判定和性质,三角形的面积公式,菱形的面积公式,解本题的关键是用x 表示出相关的线段,是一道基础题目. 26.(1)45;(2)①见解析;②DF 的长为2;(3)【分析】(1)根据平角的定义得到∠DFE+∠BEF =360°﹣90°=270°,根据角平分线的定义得到∠AFE =DFE ,∠AEF =BEF ,求得∠解析:(1)45;(2)①见解析;②DF 的长为2;(3)157【分析】(1)根据平角的定义得到∠DFE +∠BEF =360°﹣90°=270°,根据角平分线的定义得到∠AFE =12∠DFE ,∠AEF =12∠BEF ,求得∠AEF +∠AFE =12(∠DFE +∠BEF ),根据三角形的内角和定理即可得到结论;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,先证明四边形ABCD是矩形,再由角平分线的性质得出AB=AD,即可得出四边形ABCD是正方形;②设DF=x,根据已知条件得到BC=6,由①得四边形ABCD是正方形,求得BC=CD=6,根据全等三角形的性质得到BE=EG=3,同理,GF=DF=x,根据勾股定理列方程即可得到结论;(3)把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,得出MG=DG=MP=PH=6,GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR 中,由勾股定理得出方程,解方程即可.【详解】解:(1)∵∠C=90°,∴∠CFE+∠CEF=90°,∴∠DFE+∠BEF=360°﹣90°=270°,∵AF平分∠DFE,AE平分∠BEF,∴∠AFE=12∠DFE,∠AEF=12∠BEF,∴∠AEF+∠AFE=12(∠DFE+∠BEF)=12⨯270°=135°,∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,故答案为:45;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°=∠C,∴四边形ABCD是矩形,∵∠CEF,∠CFE外角平分线交于点A,∴AB=AG,AD=AG,∴AB=AD,∴四边形ABCD是正方形;②设DF=x,∵BE=EC=3,∴BC =6,由①得四边形ABCD 是正方形,∴BC =CD =6,在Rt △ABE 与Rt △AGE 中,AB AG AE AE =⎧⎨=⎩, ∴Rt △ABE ≌Rt △AGE (HL ),∴BE =EG =3,同理,GF =DF =x ,在Rt △CEF 中,EC 2+FC 2=EF 2,即32+(6﹣x )2=(x +3)2,解得:x =2,∴DF 的长为2;(3)解:如图2所示:把△PQH 沿PQ 翻折得△PQD ,把△PRH 沿PR 翻折得△PRM ,延长DQ 、MR 交于点G , 由(1)(2)得:四边形PMGD 是正方形,MR +DQ =QR ,MR =HR ,DQ =HQ =2, ∴MG =DG =MP =PH =5,∴GQ =3,设MR =HR =a ,则GR =5﹣a ,QR =a +2,在Rt △GQR 中,由勾股定理得:(5﹣a )2+32=(2+a )2,解得:a =157,即HR =157; 故答案为:157. 【点睛】本题考查了正方形的判定与性质、全等三角形的判定与性质、角平分线的性质、勾股定理、矩形的判定、翻折变换的性质等知识;本题综合性强,有一定难度.。
八年级上册大连物理期末试卷达标检测(Word版 含解析)

八年级上册大连物理期末试卷达标检测(Word版含解析)一、初二物理声现象实验易错压轴题(难)1.如图所示,某同学用尺子探究音调和响度分别与什么有关时,做了以下实验:(1)该同学把钢尺紧按在桌面上,一端伸出桌边,拨动钢尺,听它振动发出的声音,同时注意钢尺振动的快慢;改变钢尺伸出桌边的长度,再次拨动,使钢尺每次振动的幅度大致相同.实验发现:尺子伸出桌面的长度越长,振动越慢,发出声音的音调越________;由此可得出结论:音调的高低与发声体振动的________有关;(2)又把钢尺紧按在桌面上,一端伸出桌边,拨动钢尺,听它振动发出的声音,同时注意钢尺振动幅度;改变拨动钢尺的力度,再次拨动,使钢尺每次的振动快慢大致相同.实验发现拨动尺子的力度越大,尺子________越大,发出声音的________越大;(3)在实验中会发现:当尺子伸出桌面超过一定长度时,虽然用较大的力拨动钢尺,却听不到声音,这是由于________【答案】低频率振动的幅度响度尺子伸出桌面的长度越长时,振动频率越低,发出声音的音调越低,当尺子伸出桌面超过一定长度时,发出声音的音调低于20Hz,属于次声波,低于人类听觉的下限.【解析】【分析】(1)音调指声音的高低,是由发声体振动的频率决定,物体振动越快,音调就越高,物体振动越慢,音调就越低;(2)响度指声音的强弱,是由发声体振动的振幅决定,振幅越大,响度越大;(3)大多数人能够听到的频率范围从20Hz到20000Hz.【详解】(1)当尺子伸出桌面的长度越长时,振动越慢,发出声音的音调越低;当尺子伸出桌面的长度越短时,振动越快,发出声音的音调越高;由此可得出结论:音调的高低与发声物体的振动频率有关;(2)拨动尺子的力度越大尺子振动幅度越大,发出声音的响度越大;拨动尺子的力度越小尺子振动幅度越小,发出声音的响度越小;由此可得出结论:响度的大小与发声物体的振动幅度有关;(3)尺子伸出桌面的长度越长时,振动频率越低,发出声音的音调越低,所以当尺子伸出桌面超过一定长度时,虽然用较大的力拨动钢尺,但发出声音的频率低于20Hz,属于次声波,人听不到声音.2.在学习吉他演奏的过程中,小华发现琴弦发出的声音的音调高低是受各种因素影响的,他决定对此进行探究.经过和同学们讨论,提出了以下猜想:猜想一:琴弦发出的声音的音调高低,可能与琴弦的横截面积有关.猜想二:琴弦发出的声音的音调高低,可能与琴弦的长短有关.猜想三:琴弦发出的声音的音调高低,可能与琴弦的材料有关.为了验证上述猜想是否正确,他们找到了下表所列9种规格的琴弦,因为音调的高低取决于声源振动的频率,于是借来一个能够测量振动频率的仪器进行实验.(1)为了验证猜想一,应选用编号为_______、_______、_______的琴弦进行实验.为了验证猜想二,应选用编号为_______、_______、_______的琴弦进行实验.表中有的材料规格还没有填全,为了验证猜想三,必须知道该项内容,请你在表中填上所缺数据_________.(2)随着实验的进行,小华又觉得琴弦音调的高低,可能还与琴弦的松紧有关,为了验证这一猜想,必须进行的操作是:___________________________________.(3)探究过程通常采用下列一些步骤:①分析归纳②实验研究③提出问题④猜想假设⑤得出结论等.你认为小华要完成本探究的全过程,所采取步骤的合理顺序是__________.(4)在上述探究过程中,总要控制某些因素,使它们保持不变,进而寻找出另外一些因素间的关系,这种研究问题的方法叫做___________________________________.【答案】A B C A D F 80 1.02 一根琴弦,用一定大小的力拉紧琴弦,拨动琴弦,测出此时振动的频率;改用不同的力拉紧琴弦,拨动琴弦,分别测出相应的振动的频率,进行分析比较③④②①⑤控制变量法.【解析】(1)当研究琴弦发出声音的音调高低可能与琴弦的横截面积有关时,应控制材料和长度相同,改变琴弦的横截面积,故选A. B. C;当研究琴弦发出声音的音调高低可能与琴弦的长短有关时,应控制材料和横截面积相同,改变琴弦的长短,故选A. D. F;如果验证猜想三:琴弦发出声音的音调高低,可能与琴弦的材料有关,应控制长度和横截面积相同,改变琴弦的材料不同,故表格应该填入与G、H相同的数据,即80和1.02;(2)探究琴弦音调的高低与琴弦的松紧程度的关系时,需要使用同一根琴弦,且控制拨弦的力相同、弦的松紧程度不同,来研究音调高低和琴弦的松紧程度的关系;(3)探究实验的步骤是:提出问题、猜想假设、实验研究、分析归纳、得出结论,因此顺序为:③④②①⑤(4) 实验中用到的物理学研究方法是控制变量法.故答案为 (1)A、B. C;A、D. F(或H、J);80;1.02;(2)取任意编号的一种琴弦,调整其松紧程度,用相同的力拨动琴弦,比较音调的高低;(3)控制变量法.点睛:本题需要用好控制变量法:探究琴弦发出声音的音调高低与琴弦的横截面积的关系时,控制琴弦的长度和材料不变;探究琴弦发出声音的音调高低与琴弦的长短的关系时,控制横截面积和材料不变;琴弦发出声音的音调高低与琴弦的材料的关系时,控制横截面积和长度不变.3.现在大多数房屋的门窗玻璃是“双层中空(接近真空)”的,能起到“隔音保温”的作用.小明在敲玻璃时,感觉双层玻璃与单层玻璃的振动情况不一样,产生了探究“受敲击时,双层玻璃和单层玻璃的振动强弱情况”的想法.为此,进行了以下实验:①如图所示,将单层玻璃板固定在有一定倾角的斜面底端,把玻璃球A靠在玻璃板的右侧,把橡胶球B悬挂在支架上靠在玻璃板的左侧.②把橡胶球B向左拉开一定的高度,放手后让其撞击玻璃板,玻璃球A被弹开,在下表中记下玻璃球没斜面向上滚动的距离,共做3次.③换成双层玻璃板重复②的实验.⑴实验时,把橡胶球B向左拉开“一定的高度”,目的是为了保证橡胶球B与玻璃撞击时的________能保持不变;⑵受到橡胶球B的撞击后,玻璃板振动的强弱是通过__________来反映的;⑶分析表中的实验数据,可以得出的结论是__________;⑷中空双层玻璃具有“隔音和保温”作用,是因为①隔音:___________;②保暖:___________.【答案】速度玻璃球滚动的距离大小单层玻璃比双层玻璃的振动幅度大真空不能传播声音真空传导热量的能力比玻璃差【解析】解答:(1)根据控制变量法应保持橡胶球B与玻璃撞击时的动能相同,由于是同一个橡胶球,则应保持橡胶球B向左拉开“一定的高度”,从同一高度落下;(2)当玻璃板受到橡胶球的敲击时,玻璃板振动的强弱是通过玻璃球被弹开的距离来反映的,这是转换的研究方法;(3)同样的撞击下,单层玻璃后的玻璃球比双层玻璃后的玻璃球运动的距离远;所以结论是:受敲击时,单层玻璃比双层玻璃的振动强;(4)两层玻璃之间接近真空,中空双层玻璃具有“隔音和保温”作用,①由于声音的传播是需要介质的,而真空不能传声,所以这种窗户能起到较好的隔音效果;②由于真空传导热量的能力比玻璃差,所以这种窗户能起到较好的保温效果。
八年级上册全册全套试卷达标检测卷(Word版 含解析)

八年级上册全册全套试卷达标检测卷(Word 版 含解析)一、八年级数学全等三角形解答题压轴题(难)1.综合实践如图①,90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥,垂足分别为点D E 、,2.5, 1.7AD cm DE cm ==.(1)求BE 的长;(2)将CE 所在直线旋转到ABC ∆的外部,如图②,猜想AD DE BE 、、之间的数量关系,直接写出结论,不需证明;(3)如图③,将图①中的条件改为:在ABC ∆中,,AC BC D C E =、、三点在同一直线上,并且BEC ADC BCA α∠=∠=∠=,其中α为任意钝角.猜想AD DE BE 、、之间的数量关系,并证明你的结论.【答案】(1)0.8cm;(2)DE=AD+BE;(3)DE=AD+BE ,证明见解析.【解析】【分析】(1)本小题只要先证明ACD CBE ≅,得到AD CE =,CD BE =,再根据2.5, 1.7AD cm DE cm ==,CD CE DE =-,易求出BE 的值;(2)先证明ACD CBE ≅,得到AD CE =,CD BE =,由图②ED=EC+CD ,等量代换易得到AD DE BE 、、之间的关系;(3)本题先证明EBC DCA ∠=∠,然后运用“AAS”定理判定BEC CDA ≅,从而得到,BE CD EC AD ==,再结合图③中线段ED 的特点易找到AD DE BE 、、之间的数量关系.【详解】解:(1)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∵90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中,90ADC E ACD BCEAC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ 2.5, 1.7AD cm DE cm ==, 2.5 1.70.8()CD CE DE AD DE cm =-=-=-= ∴0.8BE cm =(2)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∴90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中,90ADC E ACD BCE AC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+(3)∵BEC ADC BCA α∠=∠=∠=∴180BCE ACD a ︒∠+∠=-180BCE BCE a ︒∠+∠=-∴ACD BCE ∠=∠在ACD 与CBE △中, ADC E a ACD BCE AC BC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+【点睛】本题考查的知识点是全等三角形的判定,确定一种判定定理,根据已知条件找到判定全等所需要的边相等或角相等的条件是解决这类题的关键.2.如图1,在ABC∆中,90ACB∠=,AC BC=,直线MN经过点C,且AD MN⊥于点D,BE MN⊥于点E.易得DE AD BE=+(不需要证明).(1)当直线MN绕点C旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE AD BE、、之间的数量关系,并说明理由;(2)当直线MN绕点C旋转到图3的位置时,其余条件不变,请直接写出此时DE AD BE、、之间的数量关系(不需要证明).【答案】(1) 不成立,DE=AD-BE,理由见解析;(2) DE=BE-AD【解析】【分析】(1)DE、AD、BE之间的数量关系是DE=AD-BE.由垂直的性质可得到∠CAD=∠BCE,证得△ACD≌△CBE,得到AD=CE,CD=BE,即有DE=AD-BE;(2)DE、AD、BE之间的关系是DE=BE-AD.证明的方法与(1)一样.【详解】(1)不成立.DE、AD、BE之间的数量关系是DE=AD-BE,理由如下:如图,∵∠ACB=90°,BE⊥CE,AD⊥CE,AC CB=,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ACD和△CBE中,90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△CBE(AAS),∴AD=CE,CD=BE,∴DE=CE-CD=AD-BE;(2)结论:DE=BE-AD.∵∠ACB=90°,BE⊥CE,AD⊥CE,AC CB=,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ACD和△CBE中,90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∴DE=CD-CE=BE-AD.【点睛】本题考查了旋转的性质、直角三角形全等的判定与性质,旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.3.(1)问题发现:如图(1),已知:在三角形ABC∆中,90BAC︒∠=,AB AC=,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点,D E,试写出线段,BD DE和CE之间的数量关系为_________________.(2)思考探究:如图(2),将图(1)中的条件改为:在ABC∆中, ,,,AB AC D A E=三点都在直线l上,并且BDA AEC BACα∠=∠=∠=,其中α为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图(3),,D E是,,D A E三点所在直线m上的两动点,(,,D A E三点互不重合),点F为BAC∠平分线上的一点,且ABF∆与ACF∆均为等边三角形,连接,BD CE,若BDA AEC BAC∠=∠=∠,试判断DEF∆的形状并说明理由.【答案】(1)DE=CE+BD;(2)成立,理由见解析;(3)△DEF为等边三角形,理由见解析.【解析】【分析】(1)利用已知得出∠CAE=∠ABD,进而根据AAS证明△ABD与△CAE全等,然后进一步求解即可;∠=∠=∠=,得出∠CAE=∠ABD,在△ADB与△CEA中,根(2)根据BDA AEC BACα据AAS证明二者全等从而得出AE=BD,AD=CE,然后进一步证明即可;(3)结合之前的结论可得△ADB与△CEA全等,从而得出BD=AE,∠DBA=∠CAE,再根据等边三角形性质得出∠ABF=∠CAF=60°,然后进一步证明△DBF与△EAF全等,在此基础上进一步证明求解即可.【详解】(1)∵BD⊥直线l,CE⊥直线l,∴∠BDA=∠AEC=90°,∴∠BAD+∠ABD=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∴∠CAE=∠ABD,在△ABD与△CAE中,∵∠ABD=∠CAE,∠BDA=∠AEC,AB=AC,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD,故答案为:DE=CE+BD;(2)(1)中结论还仍然成立,理由如下:∠=∠=∠=,∵BDA AEC BACα∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α,∴∠CAE=∠ABD,在△ADB与△CEA中,∵∠ABD=∠CAE,∠ADB=∠CEA,AB=AC,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE,即:DE=CE+BD ,(3)DEF ∆为等边三角形,理由如下:由(2)可知:△ADB ≌△CEA ,∴BD=EA ,∠DBA=∠CAE ,∵△ABF 与△ACF 均为等边三角形,∴∠ABF=∠CAF=60°,BF=AF ,∴∠DBA+∠ABF=∠CAE+CAF ,∴∠DBF=∠FAE ,在△DBF 与△EAF 中,∵FB=FA ,∠FDB=∠FAE ,BD=AE ,∴△DBF ≌△EAF(SAS),∴DF=EF ,∠BFD=∠AFE ,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF 为等边三角形.【点睛】本题主要考查了全等三角形性质与判定的综合运用,熟练掌握相关概念是解题关键.4.(1)如图(a )所示点D 是等边ABC 边BA 上一动点(点D 与点B 不重合),连接DC ,以DC 为边在BC 上方作等边DCF ,连接AF .你能发现线段AF 与BD 之间的数量关系吗?并证明.(2)如图(b )所示当动点D 运动至等边ABC 边BA 的延长线上时,其他作法与(1)相同,猜想AF 与BD 在(1)中的结论是否仍然成立?(直接写出结论)(3)①如图(c )所示,当动点D 在等边ABC 边BA 上运动时(点D 与点B 不重合),连接DC ,以DC 为边在BC 上方、下方分别作等边DCF 和等边DCF ',连接AF 、BF ',探究AF 、BF '与AB 有何数量关系?并证明.②如图(d )所示,当动点D 在等边ABC 边BA 的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.【答案】(1)AF=BD ,理由见解析;(2)AF=BD ,成立;(3)①AF BF AB '+=,证明见解析;②①中的结论不成立新的结论是AF AB BF '=+,理由见解析【解析】【分析】(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS 可证得BCD ACF △≌△,然后由全等三角形的对应边相等知AF BD = .(2)通过证明BCD ACF △≌△,即可证明AF BD =.(3)①'AF BF AB += ,利用全等三角形BCD ACF △≌△的对应边BD AF = ,同理'BCF ACD △≌△ ,则'BF AD = ,所以'AF BF AB +=;②①中的结论不成立,新的结论是'AF AB BF =+ ,通过证明BCF ACD △≌△,则'BF AD =(全等三角形的对应边相等),再结合(2)中的结论即可证得'AF AB BF =+ .【详解】(1)AF BD =证明如下:ABC 是等边三角形,BC AC ∴=,60BCA ︒∠=.同理可得:DC CF =,60DCF ︒∠=.BCA DCA DCF DCA ∴∠-∠=∠-∠.即BCD ACF ∠=∠.BCD ACF ∴△≌△.AF BD ∴=.(2)证明过程同(1),证得BCD ACF △≌△,则AF BD =(全等三角形的对应边相等),所以当动点D 运动至等边△ABC 边BA 的延长线上时,其他作法与(1)相同,AF BD =依然成立.(3)①AF BF AB '+=证明:由(1)知,BCD ACF △≌△.BD AF ∴=.同理BCF ACD '△≌△.BF AD '∴=.AF BF BD AD AB '∴+=+=.②①中的结论不成立新的结论是AF AB BF '=+;BC AC =,BCF ACD '∠=∠,F C DC '=,BCF ACD '∴△≌△.BF AD '∴=.又由(2)知,AF BD =.AF BD AB AD AB BF '∴==+=+.即AF AB BF '=+.【点睛】本题考查了三角形的综合问题,掌握等边三角形的三条边、三个内角都相等的性质、全等三角形的判定定理、全等三角形的对应边相等是解题的关键.5.如图,ABC∆是等边三角形,点D在边AC上(“点D不与,A C重合),点E是射线BC上的一个动点(点E不与点,B C重合),连接DE,以DE为边作作等边三角形DEF∆,连接CF.(1)如图1,当DE的延长线与AB的延长线相交,且,C F在直线DE的同侧时,过点D作//DG AB,DG交BC于点G,求证:CF EG=;(2)如图2,当DE反向延长线与AB的反向延长线相交,且,C F在直线DE的同侧时,求证:CD CE CF=+;(3)如图3,当DE反向延长线与线段AB相交,且,C F在直线DE的异侧时,猜想CD、CE、CF之间的等量关系,并说明理由.【答案】(1)证明见详解;(2)证明见详解;(3)CF=CD+CE,理由见详解.【解析】【分析】(1)由ABC∆是等边三角形,//DG AB,得∠CDG=∠A=60°,∠ACB=60°,CDG∆是等边三角形,易证∆ GDE≅∆ CDF(SAS),即可得到结论;(2)过点D作DG∥AB交BC于点G,易证∆ GDE≅∆ CDF(SAS),即可得到结论;(3)过点D作DG∥AB交BC于点G,易证∆ GDE≅∆ CDF(SAS),即可得到结论.【详解】(1)∵ABC∆是等边三角形,//DG AB,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG∆是等边三角形,∴DG=DC.∵DEF∆是等边三角形,∴DE=DF,∠EDF=60°,∴∠CDG-∠GDF=∠EDF-∠GDF,即:∠GDE=∠CDF,在∆ GDE和∆ CDF中,∵DE DFGDE CDFDG DC=⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE≅∆ CDF(SAS),∴CF EG=;(2)过点D作DG∥AB交BC于点G,如图2,∵ABC ∆是等边三角形,//DG AB ,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG ∆是等边三角形,∴DG=DC.∵DEF ∆是等边三角形,∴DE=DF ,∠EDF=60°,∴∠CDG-∠CDE=∠EDF-∠CDE ,即:∠GDE=∠CDF ,在∆ GDE 和∆ CDF 中,∵DE DF GDE CDF DG DC =⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE ≅ ∆ CDF(SAS),∴CF GE =,∴CD CG CE GE CE CF ==+=+(3)CF =CD +CE ,理由如下:过点D 作DG ∥AB 交BC 于点G ,如图3,∵ABC ∆是等边三角形,//DG AB ,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG ∆是等边三角形,∴DG=DC=GC.∵DEF ∆是等边三角形,∴DE=DF ,∠EDF=60°,∴∠CDG+∠CDE=∠EDF+∠CDE ,即:∠GDE=∠CDF ,在∆ GDE 和∆ CDF 中,∵DE DF GDE CDF DG DC =⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE ≅ ∆ CDF(SAS),∴CF GE ==GC+CE=CD+CE.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.二、八年级数学轴对称解答题压轴题(难)6.(1)如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边,在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;(2)如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?若成立,请证明;(3)Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.【答案】(1)AF=BD,理由见解析;(2)AF与BD在(1)中的结论成立,理由见解析;(3)Ⅰ. AF+BF′=AB,理由见解析,Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′,理由见解析.【解析】【分析】(1)由等边三角形的性质得BC=AC,∠BCA=60°,DC=CF,∠DCF=60°,从而得∠BCD=∠ACF,根据SAS证明△BCD≌△ACF,进而即可得到结论;(2)根据SAS证明△BCD≌△ACF,进而即可得到结论;(3)Ⅰ.易证△BCD≌△ACF(SAS),△BCF′≌△ACD(SAS),进而即可得到结论;Ⅱ.证明△BCF′≌△ACD,结合AF=BD,即可得到结论.【详解】(1)结论:AF=BD,理由如下:如图1中,∵△ABC是等边三角形,∴BC=AC,∠BCA=60°,同理知,DC=CF,∠DCF=60°,∴∠BCA-∠DCA=∠DCF-∠DCA,即:∠BCD=∠ACF,在△BCD和△ACF中,∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩,∴△BCD ≌△ACF (SAS ),∴BD =AF ;(2)AF 与BD 在(1)中的结论成立,理由如下:如图2中,∵△ABC 是等边三角形,∴BC =AC ,∠BCA =60°,同理知,DC =CF ,∠DCF =60°,∴∠BCA +∠DCA =∠DCF +∠DCA ,即∠BCD =∠ACF ,在△BCD 和△ACF 中,∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩,∴△BCD ≌△ACF (SAS ),∴BD =AF ;(3)Ⅰ.AF +BF ′=AB ,理由如下:由(1)知,△BCD ≌△ACF (SAS ),则BD =AF ;同理:△BCF ′≌△ACD (SAS ),则BF ′=AD ,∴AF +BF ′=BD +AD =AB ;Ⅱ.Ⅰ中的结论不成立,新的结论是AF =AB +BF ′,理由如下:同理可得:BCF ACD ∠=∠′,F C DC =′,在△BCF ′和△ACD 中,BC AC BCF ACD F C DC =∠⎧⎪=∠=⎪⎨⎩′′, ∴△BCF ′≌△ACD (SAS ),∴BF ′=AD ,又由(2)知,AF =BD ,∴AF =BD =AB +AD =AB +BF ′,即AF =AB +BF ′.【点睛】本题主要考查等边三角形的性质定理,三角形全等的判定和性质定理,熟练掌握三角形全等的判定和性质定理,是解题的关键.7.已知:三角形ABC 中,∠A=90°,AB=AC,D 为BC 的中点.(1)如图,E 、F 分别是AB 、AC 上的点,且BE=AF,求证:△DEF 为等腰直角三角形.(2)若E 、F 分别为AB,CA 延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF 是否仍为等腰直角三角形?画出图形,写出结论不证明.【答案】(1)见解析;(2)见解析【解析】【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解:(1)连结AD ,∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF(SAS),∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.(2)连结AD∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD=BD ,AD⊥BC ,∴∠DAC=∠ABD=45° ,∴∠DAF=∠DBE=135°,又∵AF=BE ,∴△DAF≌△DBE(SAS),∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.∴△DEF为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.8.在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).(1)求证:∠BAD=∠EDC;(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.【答案】(1)见解析;(2)见解析【解析】【分析】(1)根据等边三角形的性质,得出∠BAC=∠ACB=60°,然后根据三角形的内角和和外角性质,进行计算即可.(2)根据轴对称的性质,可得DM=DA,然后结合(1)可得∠MDC=∠BAD,然后根据三角形的内角和,求出∠ADM=60°即可.【详解】解:(1)如图1,∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∴∠BAD=60°﹣∠DAE,∠EDC=60°﹣∠E,又∵DE=DA,∴∠E=∠DAE,∴∠BAD=∠EDC.(2)由轴对称可得,DM=DE,∠EDC=∠MDC,∵DE=DA,∴DM=DA,由(1)可得,∠BAD=∠EDC,∴∠MDC=∠BAD,∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,∴∠MDC+∠ADB=120°,∴∠ADM=60°,∴△ADM是等边三角形,∴AD=AM.【点睛】本题主要考察了轴对称和等边三角形的性质,解题的关键是熟练掌握这些性质.9.如图,在等边△ABC中,线段AM为BC边上的高,D是AM上的点,以CD为一边,在CD的下方作等边△CDE,连结BE.(1)填空:∠ACB=____;∠CAM=____;(2)求证:△AOC≌△BEC;(3)延长BE交射线AM于点F,请把图形补充完整,并求∠BFM的度数;(4)当动点D在射线AM上,且在BC下方时,设直线BE与直线AM的交点为F.∠BFM 的大小是否发生变化?若不变,请在备用图中面出图形,井直接写出∠BFM的度数;若变化,请写出变化规律.【答案】(1)60°,30°;(2)答案见解析;(3)60°;(4)∠BFM=60°.【解析】【分析】(1)根据等边三角形的性质即可进行解答;(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;(3)补全图形,由△ADC≌△BEC得∠CAM=∠CBE=30°,由三角形内角和定理即可求得∠BFM的度数;(4)画出相应图形,可知当点D在线段AM的延长线上且在BC下方时,如图,可以得出△ACD≌△BCE,进而得到∠CBE=∠CAD=30°,据此得出结论.【详解】(1)∵△ABC是等边三角形,∴∠ACB=60°;∴线段AM为BC边上的高,∴∠CAM=12∠BAC=30°,故答案为60,30°;(2)∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD+∠DCB=∠DCB+∠BCE,∴∠ACD=∠BCE.在△ADC和△BEC中,AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE(SAS);(3)补全图形如下:由(1)(2)得∠CAM=30°,△ADC≌△BEC,∴∠CBE=∠CAM=30°,∵∠BMF=90°,∴∠BFM=60°;(4)当动点D在射线AM上,且在BC下方时,画出图形如下:∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠DCB=∠DCB+∠DCE,∴∠ACD=∠BCE,在△ACD和△BCE中,AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD=30°,又∵∠AMC=∠BMO,∴∠AOB=∠ACB=60°.即动点D在射线AM上时,∠AOB为定值60°.【点睛】本题考查了等边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.解题时注意:全等三角形的对应角相等,等边三角形的三个内角都相等,等边三角形的三个内角相等,且都等于60°.10.如图,在等边ABC∆中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边CDE∆,连结BE.(1)求CAM∠的度数;(2)若点D在线段AM上时,求证:ADC BEC∆≅∆;(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断AOB∠是否为定值?并说明理由.【答案】(1)30°;(2)证明见解析;(3)AOB∠是定值,60AOB∠=︒.【解析】【分析】(1)根据等边三角形的性质可以直接得出结论;(2)根据等边三角形的性质就可以得出AC AC=,DC EC=,,60ACB DCE∠=∠=︒,由等式的性质就可以BCE ACD∠=∠,根据SAS就可以得出ADC BEC∆≅∆;(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知ACD BCE≅∆∆,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出ACD BCE≅∆∆而有30CBE CAD∠=∠=︒而得出结论;当点D在线段MA的延长线上时,如图3,通过得出ACD BCE ≅∆∆同样可以得出结论.【详解】(1)ABC ∆是等边三角形,60BAC ∴∠=︒.线段AM 为BC 边上的中线,12CAM BAC ∴∠=∠, 30CAM ∴∠=︒.(2)ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACD DCB DCB BCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=.在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆;(3)AOB ∠是定值,60AOB ∠=︒,理由如下:①当点D 在线段AM 上时,如图1,由(2)可知ACD BCE ≅∆∆,则30CBE CAD ∠=∠=︒,又60ABC ∠=︒,603090CBE ABC ∴∠+∠=︒+︒=︒,ABC ∆是等边三角形,线段AM 为BC 边上的中线AM ∴平分BAC ∠,即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒.②当点D 在线段AM 的延长线上时,如图2,ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACB DCB DCB DCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=,在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆,30CBE CAD ∴∠=∠=︒,同理可得:30BAM ∠=︒,903060BOA ∴∠=︒-︒=︒.③当点D 在线段MA 的延长线上时,ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒,ACD BCE ∠∠∴=,在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆,CBE CAD ∴∠=∠,同理可得:30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒,∵30BAM ∠=︒,903060BOA ∴∠=︒-︒=︒.综上,当动点D 在直线AM 上时,AOB ∠是定值,60AOB ∠=︒.【点睛】此题考查等边三角形的性质,全等三角形的判定及性质,等边三角形三线合一的性质,解题中注意分类讨论的思想解题.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.(阅读材料)因式分解:()()221x y x y ++++.解:将“x y +”看成整体,令x y A +=,则原式()22211A A A =++=+.再将“A ”还原,原式()21x y =++.上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.(问题解决)(1)因式分解:()()2154x y x y +-+-;(2)因式分解:()()44a b a b ++-+;(3)证明:若n 为正整数,则代数式()()()21231n n n n ++++的值一定是某个整数的平方.【答案】(1)()()144x y x y +-+-1.(2)()22a b +-;(3)见解析. 【解析】【分析】(1)把(x-y )看作一个整体,直接利用十字相乘法因式分解即可;(2)把a+b 看作一个整体,去括号后利用完全平方公式即可将原式因式分解;(3)将原式转化为()()223231n n n n ++++,进一步整理为(n 2+3n+1)2,根据n 为正整数得到n 2+3n+1也为正整数,从而说明原式是整数的平方.【详解】(1)()()[][]21541()14()(1)(144)x y x y x y x y x y x y +-+-=+-+-=+-+-; (2)()()2244()4()4(2)a b a b a b a b a b ++-+=+-++=+-; (3)原式()()223231n n n n =++++()()2223231n n n n =++++ ()2231n n =++. ∵n 为正整数,∴231n n ++为正整数.∴代数()()()21231n n n n ++++的值一定是某个整数的平方. 【点睛】本题考查因式分解的应用,解题的关键是仔细读题,理解题意,掌握整体思想解决问题的方法.12.图①是一个长为2m 、宽为2n 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积: 方法1: 方法2:(2)观察图②请你写出下列三个代数式:(m+n )2,(m ﹣n )2,mn 之间的等量关系. ;(3)根据(2)题中的等量关系,解决:已知:a ﹣b=5,ab=﹣6,求:(a+b )2的值;【答案】(1)(m-n)2;(m+n)2-4mn;(2)(m-n)2=(m+n)2-4mn;(3)1.【解析】【分析】(1)方法1:表示出阴影部分的边长,然后利用正方形的面积公式列式;方法2:利用大正方形的面积减去四周四个矩形的面积列式;(2)根据不同方法表示的阴影部分的面积相同解答;(3)根据(2)的结论整体代入进行计算即可得解.【详解】解:(1)方法1:∵阴影部分的四条边长都是m-n,是正方形,∴阴影部分的面积=(m-n)2方法2:∵阴影部分的面积=大正方形的面积减去四周四个矩形的面积∴阴影部分的面积=(m+n)2-4mn;(2)根据(1)中两种计算阴影部分的面积方法可知(m-n)2=(m+n)2-4mn;(3)由(2)可知(a+b)2=(a-b)2+4ab,∵a-b=5,ab=-6,∴(a+b)2=(a-b)2+4ab=52+4×(-6)=25-24=1.【点睛】本题考查几何图形与完全平方公式,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.13.你会对多项式(x2+5x+2)(x2+5x+3)﹣12分解因式吗?对结构较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),能使复杂的问题简单化、明朗化.从换元的个数看,有一元代换、二元代换等.对于(x2+5x+2)(x2+5x+3)﹣12.解法一:设x2+5x=y,则原式=(y+2)(y+3)﹣12=y2+5y﹣6=(y+6)(y﹣1)=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).解法二:设x2+5x+2=y,则原式=y(y+1)﹣12=y2+y﹣12=(y+4)(y﹣3)=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).解法三:设x2+2=m,5x=n,则原式=(m+n)(m+n+1)﹣12=(m+n)2+(m+n)﹣12=(m+n+4)(m+n﹣3)=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).按照上面介绍的方法对下列多项式分解因式:(1)(x 2+x ﹣4)(x 2+x+3)+10;(2)(x+1)(x+2)(x+3)(x+6)+x 2;(3)(x+y ﹣2xy)(x+y ﹣2)+(xy ﹣1)2.【答案】(1) (x+2)(x-1) (2 x x ++1)(2)(266x x ++)2(3) (x+y-xy-1)2【解析】【分析】(1)令m=2x x +,原式=()()4m 310m -++因式分解即可;(2)()()()()21236x x x x x +++++=(276x x ++)(256x x ++)+2x ,令n=256x x ++,再将原式=(n+2)n+x 2进行因式分解即可;(3)令a=x+y,b=xy ,代入原式即可因式分解.【详解】(1)令m=2x x +,原式=()()4m 310m -++=m 2-m-2=(m-2)(m+1)= (2x x +-2)(2x x ++1)=(x+2)(x-1) (2x x ++1)(2)()()()()21236x x x x x +++++=(276x x ++)(256x x ++)+2x , 令n=256x x ++,原式=(n+2)n+x 2=n 2+2n+x 2=(n+x)2=(266x x ++)2(3) 令a=x+y,b=xy ,原式=()()()2221a b a b --+-=(a-b)2-2(a-b)+1=(a-b-1)2=(x+y-xy-1)2【点睛】此题主要考查复杂的因式分解,解题的关键是读懂材料学会材料中因式分解的方法.14.一个四位正整数m 各个数位上的数字互不相同且都不为0,四位数m 的前两位数字之和为5,后两位数字之和为11,称这样的四位数m 为“半期数”;把四位数m 的各位上的数字依次轮换后得到新的四位数m′,设m′=abcd ,在m′的所有可能的情况中,当|b+2c ﹣a ﹣d|最小时,称此时的m′是m 的“伴随数”,并规定F (m′)=a 2+c 2﹣2bd ;例如:m =2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F (5236)=52+32﹣2×2×6=10.(1)最大的四位“半期数”为;“半期数”3247的“伴随数”是.(2)已知四位数P=abcd是“半期数”,三位数Q=2ab,且441Q﹣4P=88991,求F(P')的最大值.【答案】(1)4192,7324;(2)42.【解析】【分析】(1)根据“半期数”的定义分析最大的四位“半期数”应该是千位最大,最大只能为4,所以百位是1,十位最大是9,个位是2,所以最大半期数为:4192,分析3247的所有可能为,2473,4732,7324.根据题意|b+2c﹣a﹣d|最小的数是7324,所以3247的“伴随数”是:7324.(2)根据定义可知a+b=5,c+d=11.再根据441Q﹣4P=88991,可以算出P的值,从而求出F(P')的最大值.【详解】解;(1)根据题意可得最大的四位“半期数”应该是千位最大,最大只能为4,所以百位是1,十位最大是9,个位是2,所以最大半期数为:4192.∵3247的所有可能为,2473,4732,7324.∵|4+14﹣2﹣3|=13,|7+6﹣4﹣2|=7,|3+4﹣7﹣4|=4, 4最小,所以7324为3247的“伴随数”.故答案为4192;7324.(2)∵P为“半期数”∴a+b=5,c+d=11,∴b=5﹣a,d=11﹣c,∴P=1000a+100(5﹣a)+10c+11﹣c=900a+9c+511.∵Q=200+10a+c,∴441Q﹣4P=88991,∴441(200+10a+c)﹣4(900a+9c+511)=88991化简得:2a+c=7①当a=1时,c=5,此时这个四位数为1456符合题意;②当a=2时,c=3,此时这个四位数为2338不符合题意,舍去;③当a=3时,c=1,不符合题意,舍去;综上所述:这个四位数只能是1456,则P'可能为4561,5614,6145.∵|5+12﹣4﹣1|=12,|6+2﹣5﹣4|=1,|1+8﹣6﹣5|=2,1最小,所以5614为P的“伴随数”,∴F(5614)=a2+c2﹣2bd=25+1﹣2×6×4=﹣22;F(4561)=a2+c2﹣2bd=16+36﹣2×5×1=42;F(6145)=a2+c2﹣2bd=36+16﹣2×1×5=42;∴F(P')的最大值为42.【点睛】解决本道题的关键是理解好半期数的定义:一个四位正整数m各个数位上的数字互不相同且都不为0,四位数m的前两位数字之和为5,后两位数字之和为11,称这样的四位数m 为“半期数”,然后根据当|b+2c﹣a﹣d|最小时,称此时的m'是m的“伴随数”来确定伴随数.15.下面是某同学对多项式()()22676114x x x x -+-++进行因式分解的过程.解:设26x x y -=,原式(7)(11)4y y =+++(第一步)21881y y =++(第二步)2(9)y =+(第三步)()2269x x =-+.(第四步) 请你回答下列问题:(1)该同学第二步到第三步运用了因式分解的_______;A .提公因式法B .平方差公式C .两数和的完全平方公式D .两数差的完全平方公式(2)该同学因式分解的结果不彻底,请直接写出因式分解的最后结果_______; (3)仿照以上方法因式分解:()()222221x x x x --++.【答案】(1)C ;(2)4(3)-x ;(3)4(1)x -【解析】【分析】(1)根据公式法分解因式可得答案;(2)先将269x x -+分解因式得2(3)x -,由此得到答案;(3)设22x x y -=,得到原式()21y =+,将22x x y -=代回得到()2221x x -+,再将括号内根据完全平方公式分解即可得到答案.【详解】解:(1)由21881y y ++2(9)y =+是运用了因式分解的两数和的完全平方公式,故选:C ;(2)∵269x x -+=2(3)x -,∴()2269x x -+=4(3)-x ,故答案为:4(3)-x ;(3)设22x x y -=, 原式()21y y =++,221y y =++,()21y =+, ()2221x x =-+, 4(1)x =-.【点睛】此题考查特殊方法分解因式,完全平方公式分解因式法,分解因式时注意应分解到不能再分解为止.四、八年级数学分式解答题压轴题(难)16.已知:12x M +=,21x N x =+. (1)当x >0时,判断M N -与0的关系,并说明理由;(2)设2y N M=+. ①当3y =时,求x 的值; ②若x 是整数,求y 的正整数值.【答案】(1)见解析;(2)①1;②4或3或1【解析】【分析】(1)作差后,根据分式方程的加减法法则计算即可;(2)①把M 、N 代入整理得到y ,解分式方程即可;②把y 变形为:221y x =++,由于x 为整数,y 为整数,则1x +可以取±1,±2,然后一一检验即可.【详解】(1)当0x >时,M -N ≥0.理由如下: M -N =()()21122121x x x x x -+-=++ . ∵x >0,∴(x -1)2≥0,2(x +1)>0,∴()()21021x x -≥+,∴M -N ≥0. (2)依题意,得:4224111x x y x x x +=+=+++. ①当3y =,即2431x x +=+时,解得:1x =.经检验,1x =是原分式方程的解,∴当y =3时,x 的值是1. ②2422222111x x y x x x +++===++++ . ∵x y ,是整数,∴21x +是整数,∴1x +可以取±1,±2. 当x +1=1,即0x =时,22401y =+=> ;当x +1=﹣1时,即2x =-时,2201y =-=(舍去); 当x +1=2时,即1x =时,22302y =+=> ; 当x +1=-2时,即3x =-时,22102y =+=>-() ; 综上所述:当x 为整数时,y 的正整数值是4或3或1.【点睛】本题考查了分式的加减法及解方式方程.确定x +1的取值是解答(2)②的关键.17.某市为了做好“全国文明城市”验收工作,计划对市区S 米长的道路进行改造,现安排甲、乙两个工程队进行施工.(1)已知甲工程队改造360米的道路与乙工程队改造300米的道路所用时间相同.若甲工程队每天比乙工程队多改造30米,求甲、乙两工程队每天改造道路的长度各是多少米.(2)若甲工程队每天可以改造a 米道路,乙工程队每天可以改造b 米道路,(其中a b ).现在有两种施工改造方案: 方案一:前12S 米的道路由甲工程队改造,后12S 米的道路由乙工程队改造; 方案二:完成整个道路改造前一半时间由甲工程队改造,后一半时间由乙工程队改造. 根据上述描述,请你判断哪种改造方案所用时间少?并说明理由.【答案】(1)甲工程队每天道路的长度为180米,乙工程队每天道路的长度为150米;(2)方案二所用的时间少【解析】【分析】(1)设乙工程队每天道路的长度为x 米,根据“甲工程队改造360米的道路与乙工程队改造300米的道路所用时间相同”,列出分式方程,即可求解;(2)根据题意,分别表示出两种方案所用的时间,再作差比较大小,即可得到结论.【详解】(1)设乙工程队每天道路的长度为x 米,则甲工程队每天道路的长度为()30x +米, 根据题意,得:36030030x x=+, 解得:150x =,检验,当150x =时,()300x x +≠,∴原分式方程的解为:150x =,30180x +=,答:甲工程队每天道路的长度为180米,乙工程队每天道路的长度为150米;(2)设方案一所用时间为:111()222s s a b s t a b ab+=+=,方案二所用时间为2t ,则221122t a t b s +=,22s t a b=+, ∴22()22()a b a b S S S ab a b ab a b +--=++, ∵a b ,00a b >>,,∴()20a b ->, ∴202a b S S ab a b+->+,即:12t t >, ∴方案二所用的时间少.【点睛】 本题主要考查分式方程的实际应用以及分式的减法法则,找出等量关系,列分式方程,掌握分式的通分,是解题的关键.18.某商场计划销售A ,B 两种型号的商品,经调查,用1500元采购A 型商品的件数是用600元采购B 型商品的件数的2倍,一件A 型商品的进价比一件B 型商品的进价多30元. (1)求一件A ,B 型商品的进价分别为多少元?(2)若该商场购进A ,B 型商品共100件进行试销,其中A 型商品的件数不大于B 型的件数,已知A 型商品的售价为200元/件,B 型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?【答案】(1) B 型商品的进价为120元, A 型商品的进价为150元;(2) 5500元.【解析】分析:(1)设一件B 型商品的进价为x 元,则一件A 型商品的进价为(x+30)元,根据“用1500元采购A 型商品的件数是用600元采购B 型商品的件数的2倍”,这一等量关系列分式方程求解即可;(2)根据题意中的不等关系求出A 商品的范围,然后根据利润=单价利润×减数函数关系式,根据函数的性质求出最值即可.详解:(1)设一件B 型商品的进价为x 元,则一件A 型商品的进价为(x+30)元. 由题意: =×2,解得x=120,经检验x=120是分式方程的解,答:一件B 型商品的进价为120元,则一件A 型商品的进价为150元.(2)因为客商购进A 型商品m 件,销售利润为w 元.m≤100﹣m ,m≤50,由题意:w=m (200﹣150)+(100﹣m )(180﹣120)=﹣10m+6000,∵﹣10<0,∴m=50时,w 有最小值=5500(元)点睛:此题主要考查了分式方程和一次函数的应用等知识,解题关键是理解题意,学会构建方程或一次函数解决问题,注意解方式方程时要检验.。
八年级上册武汉数学压轴题 期末复习试卷达标检测卷(Word版 含解析)

八年级上册武汉数学压轴题期末复习试卷达标检测卷(Word版含解析)一、压轴题1.如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=12x+b过点P.(1)求点P坐标和b的值;(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;②求出t为多少时,△APQ的面积小于3;③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.2.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).3.如图1.在△ABC中,∠ACB=90°,AC=BC=10,直线DE经过点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足分别为点D和E,AD=8,BE=6.(1)①求证:△ADC≌△CEB;②求DE的长;(2)如图2,点M以3个单位长度/秒的速度从点C出发沿着边CA运动,到终点A,点N 以8个单位长度/秒的速度从点B出发沿着线BC—CA运动,到终点A.M,N两点同时出发,运动时间为t秒(t>0),当点N到达终点时,两点同时停止运动,过点M作PM⊥DE 于点P,过点N作QN⊥DE于点Q;①当点N在线段CA上时,用含有t的代数式表示线段CN的长度;②当t为何值时,点M与点N重合;③当△PCM与△QCN全等时,则t=.4.已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.(1)如图1,①求证:点B,C,D在以点A为圆心,AB为半径的圆上;②直接写出∠BDC的度数(用含α的式子表示)为;(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转的过程中,在什么情况下线段BF的长取得最大值?若AC2a,试写出此时BF的值.∆中,线段AM为BC边上的中线.动点D在直线AM上时,以5.如图,在等边ABC∆,连结BE.CD为一边在CD的下方作等边CDE∠的度数;(1)求CAM∆≅∆;(2)若点D在线段AM上时,求证:ADC BEC∠是否(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断AOB为定值?并说明理由.6.问题情景:数学课上,老师布置了这样一道题目,如图1,△ABC是等边三角形,点D 是BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线于点E.试探究AD与DE 的数量关系.操作发现:(1)小明同学过点D作DF∥AC交AB于F,通过构造全等三角形经过推理论证就可以解决问题,请您按照小明同学的方法确定AD与DE的数量关系,并进行证明.类比探究:(2)如图2,当点D是线段BC上任意一点(除B、C外),其他条件不变,试猜想AD与DE之间的数量关系,并证明你的结论.拓展应用:(3)当点D在线段BC的延长线上,且满足CD=BC,在图3中补全图形,直接判断△ADE的形状(不要求证明).7.(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.8.如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.(1)求∠AFE的度数;(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=29CP,求PFAF的值.(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)9.如图,在平面直角坐标系中,直线AB经过点A 332)和B30),且与y轴交于点D,直线OC与AB交于点C,且点C3.(1)求直线AB的解析式;(2)连接OA,试判断△AOD的形状;(3)动点P从点C出发沿线段CO以每秒1个单位长度的速度向终点O运动,运动时间为t 秒,同时动点Q从点O出发沿y轴的正半轴以相同的速度运动,当点Q到达点D时,P,Q 同时停止运动.设PQ 与OA 交于点M ,当t 为何值时,△OPM 为等腰三角形?求出所有满足条件的t 值.10.如图,以ABC 的边AB 和AC ,向外作等腰直角三角形ABE △和ACF ,连接EF ,AD 是ABC 的高,延长DA 交EF 于点G ,过点F 作DG 的垂线交DG 于点H .(1)求证:FHA ADC ≌△△; (2)求证:点G 是EF 的中点.11.在等腰Rt △ABC 中,AB =AC ,∠BAC =90°(1)如图1,D ,E 是等腰Rt △ABC 斜边BC 上两动点,且∠DAE =45°,将△ABE 绕点A 逆时针旋转90后,得到△AFC ,连接DF ①求证:△AED ≌△AFD ;②当BE =3,CE =7时,求DE 的长;(2)如图2,点D 是等腰Rt △ABC 斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt △ADE ,当BD =3,BC =9时,求DE 的长.12.定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.(1)如图1,已知A (3,2),B (4,0),请在x 轴上找一个C ,使得△OAB 与△OAC 是偏差三角形.你找到的C 点的坐标是______,直接写出∠OBA 和∠OCA 的数量关系______.(2)如图2,在四边形ABCD 中,AC 平分∠BAD ,∠D+∠B=180°,问△ABC 与△ACD 是偏差三角形吗?请说明理由.(3)如图3,在四边形ABCD 中,AB=DC ,AC 与BD 交于点P ,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC <90°,且点C 到直线BD 的距离是3,求△ABC 与△BCD 的面积之和.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)b=72;(2)①△APQ 的面积S 与t 的函数关系式为S=﹣32t +272或S=32t ﹣272;②7<t <9或9<t <11,③存在,当t 的值为3或9+2或9﹣2或6时,△APQ 为等腰三角形. 【解析】分析:(1)把P (m ,3)的坐标代入直线1l 的解析式即可求得P 的坐标,然后根据待定系数法即可求得b ;(2)根据直线2l 的解析式得出C 的坐标,①根据题意得出9AQ t =-,然后根据12P S AQ y =⋅即可求得APQ 的面积S 与t 的函数关系式;②通过解不等式273322t -<或327 3.22t -<即可求得7<t <9或9<t <11.时,APQ 的面积小于3;③分三种情况:当PQ =PA 时,则()()()2222(71)032103,t -++-=++-当AQ =PA 时,则()()222(72)2103,t --=++-当PQ =AQ 时,则()222(71)03(72)t t -++-=--, 即可求得.详解:解;(1)∵点P (m ,3)为直线l 1上一点, ∴3=−m +2,解得m =−1, ∴点P 的坐标为(−1,3), 把点P 的坐标代入212y x b =+ 得,()1312b =⨯-+, 解得72b =; (2)∵72b =; ∴直线l 2的解析式为y =12x +72, ∴C 点的坐标为(−7,0),①由直线11:2l y x =-+可知A (2,0), ∴当Q 在A . C 之间时,AQ =2+7−t =9−t ,∴11273(9)32222S AQ yP t t =⋅=⨯-⨯=-; 当Q 在A 的右边时,AQ =t −9,∴11327(9)32222S AQ yP t t ;=⋅=⨯-⨯=- 即△APQ 的面积S 与t 的函数关系式为27322S t =-或327.22S t =- ②∵S <3,∴273322t -<或3273.22t -< 解得7<t <9或9<t <11.③存在; 设Q (t −7,0),当PQ =PA 时,则()()()2222(71)032103,t -++-=++-∴22(6)3t -=,解得t =3或t =9(舍去),当AQ =PA 时,则()()222(72)2103,t --=++-∴2(9)18,t -=解得9t =+9t =- 当PQ =AQ 时,则()222(71)03(72)t t -++-=--,∴22(6)9(9)t t -+=-,解得t =6.故当t 的值为3或9+9-6时,△APQ 为等腰三角形.点睛:属于一次函数综合题,考查了一次函数图象上点的坐标特征,待定系数法求函数解析式,等腰三角形的性质以及三角形的面积,分类讨论是解题的关键.2.(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE≌△CBD得到∠ACE=∠CBD,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF;②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA;(2)证明△AEC≌△CDB得到∠E=∠D,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.3.(1)①证明见解析;②DE=14;(2)①8t-10;②t=2;③t=10,2 11【解析】【分析】(1)①先证明∠DAC=∠ECB,由AAS即可得出△ADC≌△CEB;②由全等三角形的性质得出AD=CE=8,CD=BE=6,即可得出DE=CD+CE=14;(2)①当点N在线段CA上时,根据CN=CN−BC即可得出答案;②点M与点N重合时,CM=CN,即3t=8t−10,解得t=2即可;③分两种情况:当点N在线段BC上时,△PCM≌△QNC,则CM=CN,得3t=10−8t,解得t=1011;当点N在线段CA上时,△PCM≌△QCN,则3t=8t−10,解得t=2;即可得出答案.【详解】(1)①证明:∵AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∵∠ACB=90°,∴∠DAC+∠DCA=∠DCA+∠BCE=90°,∴∠DAC=∠ECB,在△ADC和△CEB中ADC CEBDAC ECBAC CB∠∠∠∠⎧⎪⎨⎪⎩===,∴△ADC≌△CEB(AAS);②由①得:△ADC≌△CEB,∴AD=CE=8,CD=BE=6,∴DE=CD+CE=6+8=14;(2)解:①当点N在线段CA上时,如图3所示:CN=CN−BC=8t−10;②点M与点N重合时,CM=CN,即3t=8t−10,解得:t=2,∴当t为2秒时,点M与点N重合;③分两种情况:当点N在线段BC上时,△PCM≌△QNC,∴CM=CN,∴3t=10−8t,解得:t=1011;当点N在线段CA上时,△PCM≌△QCN,点M与N重合,CM=CN,则3t=8t−10,解得:t=2;综上所述,当△PCM与△QCN全等时,则t等于1011s或2s,故答案为:1011s或2s.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识;本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键.4.(1)①详见解析;②12α;(2)详见解析;(3)当B、O、F三点共线时BF最长,(10+2)a【解析】【分析】(1)①由线段垂直平分线的性质可得AD=AC=AB ,即可证点B ,C ,D 在以点A 为圆心,AB 为半径的圆上;②由等腰三角形的性质可得∠BAC=2∠BDC ,可求∠BDC 的度数;(2)连接CE ,由题意可证△ABC ,△DCE 是等边三角形,可得AC=BC ,∠DCE=60°=∠ACB ,CD=CE ,根据“SAS”可证△BCD ≌△ACE ,可得AE=BD ;(3)取AC 的中点O ,连接OB ,OF ,BF ,由三角形的三边关系可得,当点O ,点B ,点F 三点共线时,BF 最长,根据等腰直角三角形的性质和勾股定理可求10BO a =,2OF OC a ==,即可求得BF【详解】(1)①连接AD ,如图1.∵点C 与点D 关于直线l 对称,∴AC = AD .∵AB = AC ,∴AB = AC = AD .∴点B ,C ,D 在以A 为圆心,AB 为半径的圆上.②∵AD=AB=AC ,∴∠ADB=∠ABD ,∠ADC=∠ACD ,∵∠BAM=∠ADB+∠ABD ,∠MAC=∠ADC+∠ACD ,∴∠BAM=2∠ADB ,∠MAC=2∠ADC ,∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α∴∠BDC=12α 故答案为:12α. (2连接CE ,如图2.∵∠BAC=60°,AB=AC,∴△ABC是等边三角形,∴BC=AC,∠ACB=60°,∵∠BDC=1α,2∴∠BDC=30°,∵BD⊥DE,∴∠CDE=60°,∵点C关于直线l的对称点为点D,∴DE=CE,且∠CDE=60°∴△CDE是等边三角形,∴CD=CE=DE,∠DCE=60°=∠ACB,∴∠BCD=∠ACE,且AC=BC,CD=CE,∴△BCD≌△ACE(SAS)∴BD=AE,(3)如图3,取AC的中点O,连接OB,OF,BF,,F是以AC为直径的圆上一点,设AC中点为O,∵在△BOF中,BO+OF≥BF,当B、O、F三点共线时BF最长;如图,过点O作OH⊥BC,∵∠BAC=90°,2a,∴24BC AC a==,∠ACB=45°,且OH⊥BC,∴∠COH=∠HCO=45°,∴OH=HC,∴2=,OC HC∵点O是AC中点,AC2a,∴2=,OC a==,∴OH HC a∴BH=3a,∴BO =,∵点C 关于直线l 的对称点为点D ,∴∠AFC=90°,∵点O 是AC 中点,∴OF OC ==,∴BF a =, ∴当B 、O 、F 三点共线时BF 最长;最大值为)a .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理,三角形的三边关系,灵活运用相关的性质定理、综合运用知识是解题的关键.5.(1)30°;(2)证明见解析;(3)AOB ∠是定值,60AOB ∠=︒.【解析】【分析】(1)根据等边三角形的性质可以直接得出结论;(2)根据等边三角形的性质就可以得出AC AC =,DC EC =,,60ACB DCE ∠=∠=︒,由等式的性质就可以BCE ACD ∠=∠,根据SAS 就可以得出ADC BEC ∆≅∆;(3)分情况讨论:当点D 在线段AM 上时,如图1,由(2)可知ACD BCE ≅∆∆,就可以求出结论;当点D 在线段AM 的延长线上时,如图2,可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论;当点D 在线段MA 的延长线上时,如图3,通过得出ACD BCE ≅∆∆同样可以得出结论.【详解】(1)ABC ∆是等边三角形,60BAC ∴∠=︒.线段AM 为BC 边上的中线,12CAM BAC ∴∠=∠, 30CAM ∴∠=︒.(2)ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACD DCB DCB BCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=.在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆;(3)AOB ∠是定值,60AOB ∠=︒,理由如下:①当点D 在线段AM 上时,如图1,由(2)可知ACD BCE ≅∆∆,则30CBE CAD ∠=∠=︒,又60ABC ∠=︒,603090CBE ABC ∴∠+∠=︒+︒=︒,ABC ∆是等边三角形,线段AM 为BC 边上的中线AM ∴平分BAC ∠,即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒.②当点D 在线段AM 的延长线上时,如图2,ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACB DCB DCB DCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=,在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆,30CBE CAD ∴∠=∠=︒,同理可得:30BAM ∠=︒,903060BOA ∴∠=︒-︒=︒.③当点D 在线段MA 的延长线上时,ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒,ACD BCE ∠∠∴=,在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆,CBE CAD ∴∠=∠,同理可得:30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒,∵30BAM ∠=︒,903060BOA ∴∠=︒-︒=︒.综上,当动点D 在直线AM 上时,AOB ∠是定值,60AOB ∠=︒.【点睛】此题考查等边三角形的性质,全等三角形的判定及性质,等边三角形三线合一的性质,解题中注意分类讨论的思想解题.6.(1)AD =DE ,见解析;(2)AD =DE ,见解析;(3)见解析,△ADE 是等边三角形,【解析】【分析】(1)根据题意,通过平行线的性质及等边三角形的性质证明ADF EDC ∆∆≌即可得解; (2)根据题意,通过平行线的性质及等边三角形的性质证明AFD DCE ∆∆≌即可得解; (3)根据垂直平分线的性质及等边三角形的判定定理进行证明即可.【详解】(1)如下图,数量关系:AD =DE .证明:∵ABC ∆是等边三角形∴AB =BC ,60B BAC BCA ∠∠∠︒===∵DF ∥AC∴BFD BAC ∠∠=,∠BDF =∠BCA∴60B BFD BDF ∠∠∠︒===∴BDF ∆是等边三角形,120AFD ∠︒=∴DF =BD∵点D 是BC 的中点∴BD =CD∴DF =CD∵CE是等边ABC∆的外角平分线∴120DCE AFD∠︒∠==∵ABC∆是等边三角形,点D是BC的中点∴AD⊥BC∴90ADC∠︒=∵60BDF ADE∠∠︒==∴30ADF EDC∠∠︒==在ADF∆与EDC∆中AFD ECDDF CDADF EDC∠∠⎧⎪⎨⎪∠∠⎩===∴()ADF EDC ASA∆∆≌∴AD=DE;(2)结论:AD=DE.证明:如下图,过点D作DF∥AC,交AB于F ∵ABC∆是等边三角形∴AB=BC,60B BAC BCA∠∠∠︒===∵DF∥AC∴BFD BAC BDF BCA∠∠∠∠=,=∴60B BFD BDF∠∠∠︒===∴BDF∆是等边三角形,120AFD∠︒=∴BF=BD∴AF=DC∵CE是等边ABC∆的外角平分线∴120DCE AFD∠︒∠==∵∠ADC是ABD∆的外角∴60ADC B FAD FAD∠∠∠︒∠=+=+∵60ADC ADE CDE CDE ∠∠∠︒∠=+=+∴∠FAD=∠CDE在AFD∆与DCE∆中AFD DCEAF CDFAD EDC∠∠⎧⎪⎨⎪∠∠⎩===∴()AFD DCE ASA∆∆≌∴AD=DE;(3)如下图,ADE∆是等边三角形.证明:∵BC CD=∴AC CD=∵CE平分ACD∠∴CE垂直平分AD∴AE=DE∵60ADE∠=︒∴ADE∆是等边三角形.【点睛】本题主要考查了等边三角形的性质及判定,三角形全等的判定及性质,平行线的性质,垂直平分线的性质等相关内容,熟练掌握三角形综合解决方法是解决本题的关键.7.(1)证明见解析;(2)①②③;(3)∠A+∠C=180°.【解析】【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;(2)同(1)的方法判断出△ABD≌△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF≌△ACO,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF<CF,进而判断出∠OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP (SAS),即可得出结论.【详解】(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE,在△ABD和△ACE中,AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩===,∴△ABD≌△ACE;(2)如图2,∵△ABC 和△ADE 是等边三角形,∴AB=AC ,AD=AE ,∠BAC=∠DAE=60°,∴∠BAD=∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== , ∴△ABD ≌△ACE ,∴BD=CE ,①正确,∠ADB=∠AEC ,记AD 与CE 的交点为G ,∵∠AGE=∠DGO ,∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE ,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB 上取一点F ,使OF=OC ,∴△OCF 是等边三角形,∴CF=OC ,∠OFC=∠OCF=60°=∠ACB ,∴∠BCF=∠ACO ,∵AB=AC ,∴△BCF ≌△ACO (SAS ),∴∠AOC=∠BFC=180°-∠OFC=120°,∴∠AOE=180°-∠AOC=60°,③正确,连接AF ,要使OC=OE ,则有OC=12CE , ∵BD=CE , ∴CF=OF=12BD , ∴OF=BF+OD ,∴BF <CF , ∴∠OBC >∠BCF ,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC >30°,而没办法判断∠OBC 大于30度,所以,④不一定正确,即:正确的有①②③,故答案为①②③;(3)如图3,延长DC 至P ,使DP=DB ,∵∠BDC=60°,∴△BDP 是等边三角形,∴BD=BP ,∠DBP=60°,∵∠BAC=60°=∠DBP ,∴∠ABD=∠CBP ,∵AB=CB ,∴△ABD ≌△CBP (SAS ),∴∠BCP=∠A ,∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°. 【点睛】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.8.(1)∠AFE =60°;(2)见解析;(3)75【解析】【分析】(1)通过证明 BCE CAD ≌ 得到对应角相等,等量代换推导出60AFE ∠=︒;(2)由(1)得到60AFE ∠=︒,CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF 上取一点K 使得KF =AF ,作辅助线证明ABK 和ACF 全等,利用对应边相等,等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC 为等边三角形,∴AC =BC ,∠BAC =∠ABC =∠ACB =60°, 在BCE 和CAD 中,60BE CD CBE ACD BC CA =⎧⎪∠=∠=︒⎨⎪=⎩,∴ BCE CAD ≌(SAS ),∴∠BCE =∠DAC ,∵∠BCE +∠ACE =60°,∴∠DAC +∠ACE =60°,∴∠AFE =60°.(2)证明:如图1中,∵AH ⊥EC ,∴∠AHF =90°,在Rt △AFH 中,∵∠AFH =60°,∴∠FAH =30°,∴AF =2FH ,∵ EBC DCA ≌,∴EC =AD ,∵AD =AF +DF =2FH +DF ,∴2FH +DF =EC .(3)解:在PF 上取一点K 使得KF =AF ,连接AK 、BK ,∵∠AFK =60°,AF =KF ,∴△AFK 为等边三角形,∴∠KAF =60°,∴∠KAB =∠FAC ,在ABK 和ACF 中,AB AC KAB ACF AK AF =⎧⎪∠=∠⎨⎪=⎩,∴ ABK ACF ≌(SAS ),BK CF =∴∠AKB =∠AFC =120°,∴∠BKE =120°﹣60°=60°,∵∠BPC =30°,∴∠PBK =30°, ∴29BK CF PK CP ===, ∴79PF CP CF CP =-=, ∵45()99AF KF CP CF PK CP CP CP ==-+=-= ∴779559CP PF AF CP == . 【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.9.(1)y+2;(2)△AOD 为直角三角形,理由见解析;(3)t =23. 【解析】【分析】(1)将点A 、B 的坐标代入一次函数表达式:y =kx +b ,即可求解;(2)由点A 、O 、D 的坐标得:AD 2=1,AO 2=3,DO 2=4,故DO 2=OA 2+AD 2,即可求解; (3)点C,1),∠DBO =30°,则∠ODA =60°,则∠DOA =30°,故点C1),则∠AOC =30°,∠DOC =60°,OQ =CP =t ,则OP =2﹣t .①当OP =OM 时,OQ =QH +OH,即2(2﹣t )+12(2﹣t )=t ,即可求解;②当MO =MP 时,∠OQP =90°,故OQ =12O P ,即可求解;③当PO =PM 时,故这种情况不存在. 【详解】 解:(1)将点A 、B 的坐标代入一次函数表达式:y =kx +b 得:3=220k b b ⎧+⎪⎨⎪=+⎩,解得:3=2kb⎧⎪⎨⎪=⎩-故直线AB的表达式为:y=﹣33x+2;(2)直线AB的表达式为:y=﹣3x+2,则点D(0,2),由点A、O、D的坐标得:AD2=1,AO2=3,DO2=4,故DO2=OA2+AD2,故△AOD为直角三角形;(3)直线AB的表达式为:y=﹣3x+2,故点C(3,1),则OC=2,则直线AB的倾斜角为30°,即∠DBO=30°,则∠ODA=60°,则∠DOA=30°故点C(3,1),则OC=2,则点C是AB的中点,故∠COB=∠DBO=30°,则∠AOC=30°,∠DOC=60°,OQ=CP=t,则OP=OC﹣PC=2﹣t,①当OP=OM时,如图1,则∠OMP=∠MPO=12(180°﹣∠AOC)=75°,故∠OQP=45°,过点P作PH⊥y轴于点H,则OH=12OP=12(2﹣t),由勾股定理得:PH32﹣t)=QH,OQ=QH+OH32﹣t)+12(2﹣t)=t,解得:t=33;②当MO =MP 时,如图2,则∠MPO =∠MOP =30°,而∠QOP =60°,∴∠OQP =90°,故OQ =12OP ,即t =12(2﹣t ), 解得:t =23; ③当PO =PM 时,则∠OMP =∠MOP =30°,而∠MOQ =30°,故这种情况不存在;综上,t =2323. 【点睛】本题考查等腰三角形的性质、一次函数解析式、勾股定理、含30°的角的直角三角形的性质等知识点,还利用了方程和分类讨论的思想,综合性较强,难度较大,解题的关键是学会综合运用性质进行推理和计算.10.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)先利用同角的余角相等得到一对角相等,再由一对直角相等,且AF AC =,利用AAS 得到AFH CAD ∆≅∆;(2)由(1)利用全等三角形对应边相等得到FH AD =,再EK AD ⊥,交DG 延长线于点K ,同理可得到AD EK =,等量代换得到FK EH =,再由一对直角相等且对顶角相等,利用AAS 得到FHG EKG ≅△△,利用全等三角形对应边相等即可得证.【详解】证明:(1) ∵FH AG ⊥,90AEH EAH ∴∠+∠=︒,90FAC ∠=︒,90FAH CAD ∴∠+∠=︒,AFH CAD ∴∠=∠,在AFH∆和CAD∆中,90AHF ADCAFH CADAF AC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AFH CAD AAS∴∆≅∆,(2)由(1)得AFH CAD∆≅∆,FH AD∴=,作FK AG⊥,交AG延长线于点K,如图;同理得到AEK ABD∆≅∆,EK AD∴=,FH EK∴=,在EKG∆和FHG∆中,90EKG FHGEGK FGHEK FH∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()EKG FHG AAS∴∆≅∆,EG FG∴=.即点G是EF的中点.【点睛】此题考查了全等三角形的判定与性质,熟练掌握K字形全等进行证明是解本题的关键.11.(1)①见解析;②DE=297;(2)DE的值为517【解析】【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,可得x2=(7﹣x)2+32,解方程即可;(2)分两种情形:①当点E在线段BC上时,如图2中,连接BE.由△EAD≌△ADC,推出∠ABE=∠C=∠ABC=45°,EB=CD=5,推出∠EBD=90°,推出DE2=BE2+BD2=62+32=45,即可解决问题;②当点D在CB的延长线上时,如图3中,同法可得DE2=153.【详解】(1)①如图1中,∵将△ABE绕点A逆时针旋转90°后,得到△AFC,∴△BAE≌△CAF,∴AE=AF,∠BAE=∠CAF,∵∠BAC=90°,∠EAD=45°,∴∠CAD+∠BAE=∠CAD+∠CAF=45°,∴∠DAE=∠DAF,∵DA=DA,AE=AF,∴△AED≌△AFD(SAS);②如图1中,设DE=x,则CD=7﹣x.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵∠ABE=∠ACF=45°,∴∠DCF=90°,∵△AED≌△AFD(SAS),∴DE=DF=x,∵在Rt△DCF中, DF2=CD2+CF2,CF=BE=3,∴x2=(7﹣x)2+32,∴x=297,∴DE=297;(2)∵BD=3,BC=9,∴分两种情况如下:①当点E在线段BC上时,如图2中,连接BE.∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=综上所述,DE的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.12.(1)(2,0),∠OBA+∠OCA=180°;(2)△ABC与△ACD是偏差三角形,理由见解析;(3)27 2【解析】【分析】(1)根据偏差三角形的定义,即可得到C的坐标,根据等腰三角形的性质和平角的定义,即可得到结论;(2)在AD上取一点H,使得AH=AB,易证△CAH≌△CAB,进而可得∠D=∠CHD,根据偏差三角形的定义,即可得到结论;(3)延长CA至点E,使AE=BD,连接BE,由SAS可证∆BDC≅∆EAB,得EA=BD,点B到直线EA的距离是3,根据三角形的面积公式,即可求解.【详解】(1)∵当AC=AB时,△OAB与△OAC是偏差三角形,A(3,2),B(4,0),∴点C的坐标为(2,0),如图1,∵AC=AB,∴∠ACB=∠ABC,∵∠OCA+∠ACB=180°,∴∠OBA+∠OCA=180°,故答案为:(2,0),∠OBA+∠OCA=180°;(2)△ABC与△ACD是偏差三角形,理由如下:如图2中,在AD上取一点H,使得AH=AB.∵AC平分∠BAD,∴∠CAH=∠CAB,又∵ AC=AC,∴△CAH≌△CAB(SAS),∴CH=CB,∠B=∠AHC,∵∠B+∠D=180°,∠AHC+∠CHD=180°,∴∠D=∠CHD,∴CH=CD,∴CB=CD,∵△ACD和△ABC中,AC=AC,∠CAD=∠CAB,BC=CD,△ADC与△ABC不全等,∴△ABC与△ACD是偏差三角形;(3)如图3中,延长CA至点E,使AE=BD,连接BE,∵∠BAC+∠BDC=180°,∠BAC+∠BAE=180°,∴∠BDC=∠BAE,又∵AB=CD,∴∆BDC≅∆EAB(SAS),∴EA=BD,∵点C到直线BD的距离是3,∴点B到直线EA的距离是3,∴S△ABC+S△BCD=S△ABC+S△EAB= S△BCE=12∙(AC+EA)×3 =12∙(AC+BD)×3 =12×9×3=272.【点睛】本题主要考查等腰三角形的性质,三角形全等的判定和性质,添加辅助线,构造全等三角形,是解题的关键.。
四川省遂宁市2019-2020学年八年级下学期期末教学水平监测语文试题(Word版含解析)

遂宁市初中2021届第二学年教学水平监测调考语文试题本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
总分150分。
考试时间120分钟。
第Ⅰ卷(选择题,满分21分)注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上,并检查条形码粘贴是否正确。
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题(每小题3分,共24分)1. 下列加点字的读音完全正确的一项是A. 缄.默(jiān)龟.裂(guī)追溯.(sù)强.词夺理(qiǎng)B. 骤.然(zhòu)裸.露(luǒ)寒噤.(jìn)气喘吁.吁(xū)C. 遗骸.(hài)蛮横.(hèng)驰骋.(chěng)名副.其实(fú)D. 翌.日(yì)狩.(shǒu)猎铸.成(zhù)风雪载.途(zǎi)2. 下列选项中有错别字的一项是A. 远不是秋高气爽时节的明媚,这一个风云变幻的季节里,气势磅礴的密云来去匆匆。
B. 所幸,奥林匹克主义并没有成为这场浩劫的牺牲品,而是无所畏惧、无可指摘地挺了过来。
C. 但见色彩斑斓,彩霞满天,白云缭绕,轻歌曼舞,那朵朵白云精美柔细,宛如游思蛛网一般。
D. 这腰鼓,使冰冷的空气立即变得燥热了,使恬静的阳光立即变得飞溅了,使困倦的世界立即变得亢奋了。
3. 下列加点成语运用正确的一项是A. 他不懂古文,面对图书馆里满架的中国历史资料,只能叹为观止....。
B. 晚上,我和妈妈悠闲地在花园里散步,明亮的路灯戛然而止....,四周一片漆黑,原来是停电了。
C. 遂宁观音湖湿地生态公园,既能让你饱览巧夺天工....的自然美景,又能让你领略多姿多彩的人文风情。
鲁教版八年级上册英语期末测试卷(word版,含答案解析)

鲁教版八年级上册英语期末测试卷一、单项选择(共20小题;共40分)从下面各题所给选项中,选择最佳选项。
1. (天津河西区期末) They need to raise school things in order to _____ the children in the mountains.A.helpsB.helpingC.helpD.helpful2. The U.K. _____ four parts. They are England, Scotland, Wales and Northern Ireland.A.includesB.catchesC.carriesD.touches3. In order _____ for school, Mary gets up very early every morning.A.not to be lateB.not being lateC.to be lateD.being late4. —Do you know anything about Canada?—Yes, it's a _____ country, but it has a small _____.A.small; peopleB.huge; peopleC.small; populationD.huge; population5.Alex is writing an email _____ John will know what he is doing.A.althoughB.so thatC.unlessD.because6. Mrs Smith lives next to us. She is really a good _____ because she is always ready to help people around her.A.visitorB.waiterC.neighbourD.manager7. He _____ until the meeting is over.A.leavesB.will leaveC.won't leaveD.didn't leave8. (2014辽宁沈阳铁西区月考)A lot of famous doctors gathered (聚集) in New York _____ save this old scientist.A.so thatB.in order toC.in order thatD.as a result9. The _____ of the fire is that a worker smoked in the workshop.A.reasonB.resultC.excuseD.cause10. _____ make our city more beautiful, we plant lots of trees every year.A.So thatB.ForC.In order toD.Because11. As we know, careless driving can _____ many accidents.A.keepB.causeC.watchD.change12. —Do his pets _____ the cat?—Yes. He has three pet cats _____ this one.A.include; includeB.include; includingC.including; includingD.including; include13. My family always go somewhere interesting _____ the holiday begins.A.as soon asB.unlessC.so thatD.though14. Mr. Green speaks very loudly _____ all the people can hear him clearly.A.so thatB.whenC.becauseD.in order to15. —I'm really tired because I studied until midnight last night.—_____A.No problem.B.Why don't you go to bed earlier tonight?C.You're welcome.D.You can study for a test by taking notes.16. I want to pick some apples, please get the and placeit _____ the tree.A.againstB.underC.onD.in17. We can see flags flying slightly when there is a _____.A.typhoonB.strong windC.gentle windD.hurricane18. He worked hard _____ go to the best university.A.in order thatB.in order toC.in order soD.so to根据语境,选出最佳选项。
八年级下册数学期末试卷综合测试卷(word含答案)(1)

八年级下册数学期末试卷综合测试卷(word含答案)(1) 一、选择题1.函数y=35xx--的自变量x的取值范围是()A.x≠5B.x>3且x≠5C.x≥3D.x≥3且x≠5 2.由下列线段组成的三角形不是直角三角形的是()A.7,24,25 B.4,5,41C.3,5,4 D.4,5,6 3.下列关于平行四边形的命题中,错误的是()A.两组对角分别相等的四边形是平行四边形B.一组对边相等,另一组对边平行的四边形是平行四边形C.一组对边平行,一组对角相等的四边形是平行四边形D.一组对边平行且相等的四边形是平行四边形4.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲乙丙丁平均数()cm183183183183方差 5.7 3.5 6.78.6要从中选择一名发挥稳定的运动员去参加比赛,应该选择()A.甲B.乙C.丙D.丁5.如图,已知矩形ABCD的对角线AC的长为10cm,连结矩形各边中点E、F、G、H得四边形EFGH,则四边形EFGH的周长为()cm.A.20 B.202C.203D.256.如图,已知E为邻边相等的平行四边形ABCD的边BC上一点,且∠DAE=∠B=80º,那么∠CDE的度数为()A.20º B.25º C.30º D.35º7.如图,在△ABC中,BC=2∠C=45°,若D是AC的三等分点(AD>CD),且AB =BD ,则AB 的长为( )A .2B .5C .3D .528.一条公路旁依次有A 、B 、C 三个村庄,甲、乙两人骑自行车分别从A 村、B 村同时出发前往C 村,甲、乙之间的距离()km s 与骑行时间()t h 之间的函数关系如图所示,下列结论:①A 、B 两村相距8km ;②甲出发2h 后到达C 村;③甲每小时比乙我骑行8km ;④相遇后,乙又骑行了15min 或45min 时两人相距2km .其中正确结论的个数是( )A .1B .2C .3D .4二、填空题9.若13x x --在实数范围内有意义,则x 的取值范围是____________. 10.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,已知4OA =,菱形ABCD 的面积为24,则BD 的长为______.11.如图,两个较大正方形的面积分别为225、289,则字母A 所代表的正方形的边长为_____12.如图,在矩形ABCD 中,点E 在AD 上,且EC 平分BED ∠,若1AB =,45EBC ∠=︒,则DE 的长为__________.13.已知一次函数y x b =-+的图象过点()8,2,那么此一次函数的解析式为__________. 14.若顺次连接四边形ABCD 四边中点所得的四边形是菱形,则原四边形的对角线AC 、BD 所满足的条件是________.15.在平面直角坐标系中,矩形OABC 的顶点O 为坐标原点,顶点A ,C 分别在x 轴和y 轴上,OA =4,OC =3,D 为AB 边的中点,E 是OA 边上的一个动点,当△CDE 的周长最小时,则点E 的坐标为_____.16.如图,∠ABD =∠BDC =90°,AB =12,BC =8,CD =10A 与点D 重合,折痕为HG ,则线段BH 的长为___.三、解答题17.计算:(1)218×12﹣24;(2)48÷3﹣12×12+24. 18.如图,在甲村到乙村的公路一旁有一块山地正在开发.现A 处需要爆破,已知点A 与公路上的停靠站B ,C 的距离分别为400 m 和300 m ,且AC ⊥AB .为了安全起见,如果爆破点A 周围半径260 m 的区域内不能有车辆和行人,问在进行爆破时,公路BC 段是否需要暂时封闭?为什么?19.如图,4×10长方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A ,B ,E ,F 都在格点上,按下列要求作图,使得所画图形的顶点均在格点上. (1)在图中画出以AB 为边的正方形ABCD ;(2)在图中画出以EF 为边的等腰三角形EFG ,且△EFG 的周长为1010+; (3)在(1)(2)的条件下,连接CG ,则线段CG 的长为 .20.如图,在ABCD 中,两条对角线AC 和BD 相交于点O ,并且6BD =,8AC =,5BC =.(1)AC 与BD 有什么位置关系?为什么?(2)四边形ABCD 是菱形吗?为什么?21.阅读材料:规定初中考试不能使用计算器后,小明是这样解决问题的:已知a 23+,求2281a a -+的值.他是这样分析与解的:∵a 23+2323(23)(23)-=+-, ∴23a -= ∴2(2)3,a -= 2443a a -+=∴241a a -=-, ∴2281a a -+=2(24)1a a -+=2(1)11⨯-+=-.请你根据小明的分析过程,解决如下问题:(1)若a 21-,直接写出2481a a -+的值是 . (21315375121119+++++ 22.为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买A 、B 两种不同型号的篮球共300个.已知购买3个A 型篮球和2个B 型篮球共需340元,购买2个A 型篮球和1个B 型篮球共需要210元.(1)求购买一个A 型篮球、一个B 型篮球各需多少元?(2)若该校计划投入资金W 元用于购买这两种篮球,设购进的A 型篮球为t 个,求W 关于t 的函数关系式;(3)学校在体育用品专卖店购买A 、B 两种型号篮球共300个,经协商,专卖店给出如下优惠:A 种球每个降价8元,B 种球打9折,计算下来,学校共付费16740元,学校购买A 、B 两种篮球各多少个?23.如图,矩形ABCD 中,AB=4,AD=3,∠A 的角平分线交边CD 于点E .点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动,Q 为AP 的中点,过点Q 作QH ⊥AB 于点H ,在射线AE 的下方作平行四边形PQHM (点M 在点H 的右侧),设P 点运动时间为秒.(1)直接写出的面积(用含的代数式表示).(2)当点M 落在BC 边上时,求的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的的值;若不存在请说明理由(不能添加辅助线). 24.如图,在平面直角坐标系中,直线28y x =+与x 轴交于点A,与y 轴交于点B,过点B 的直线x 轴于点C ,且AB=BC .(1)求直线BC 的表达式(2)点P 为线段AB 上一点,点Q 为线段BC 延长线上一点,且AP=CQ,PQ 交x 轴于点P ,设点Q 的横坐标为m ,求PBQ ∆的面积(用含m 的代数式表示)(3)在(2)的条件下,点M 在y 轴的负半轴上,且MP=MQ ,若45BQM ︒∠=求点P 的坐标.25.如图,Rt △CEF 中,∠C =90°,∠CEF ,∠CFE 外角平分线交于点A ,过点A 分别作直线CE ,CF 的垂线,B ,D 为垂足.(1)∠EAF = °(直接写出结果不写解答过程);(2)①求证:四边形ABCD 是正方形.②若BE =EC =3,求DF 的长.(3)如图(2),在△PQR 中,∠QPR =45°,高PH =5,QH =2,则HR 的长度是 (直接写出结果不写解答过程).【参考答案】一、选择题1.D解析:D【分析】根据二次根式和分式有意义的条件列出不等式,求解不等式即可.【详解】根据题意得:x﹣3≥0且x﹣5≠0,解得x≥3且x≠5.∴自变量x的取值范围是x≥3且x≠5.故选:D.【点睛】本题考查了二次根式和分式由意义的条件,理解二次根式和分式由意义的条件是解题的关键.2.D解析:D【分析】根据勾股定理的逆定理对各选项进行逐一判断即可.【详解】解:A、∵72+242=625=252,∴能够成直角三角形,故本选项不符合题意;B、∵42+52412,∴能够成直角三角形,故本选项不符合题意;C、∵32+42=52,∴能够成直角三角形,故本选项不符合题意;D、∵42+52≠62,∴不能够成直角三角形,故本选项符合题意.故选:D.【点睛】本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.3.B解析:B【解析】【分析】根据平行四边形的判定方法,一一判断即可.【详解】解:A. 两组对角分别相等的四边形是平行四边形,正确;根据平行四边形的判定方法,可得结论;B. 一组对边相等,另一组对边平行的四边形是平行四边形,错误;如:等腰梯形;C. 一组对边平行,一组对角相等的四边形是平行四边形正确,由题意可以证明两组对边分别平行,四边形是平行四边形;D. 一组对边平行且相等的四边形是平行四边形,正确,根据平行四边形的判定方法,可得结论.故选:B【点睛】本题考查平行四边形的判定,解题的关键是熟练掌握平行四边形的判定方法,属于中考基础题.4.B解析:B【解析】【分析】首先比较出甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的方差的大小关系,然后根据方差越大,波动性越大,判断出应该选择谁参加比赛即可.【详解】解:因为3.5<5.7<6.7<8.6,所以乙最近几次选拔赛成绩的方差最小,所以要从中选择一名发挥稳定的运动员去参加比赛,应该选择乙.故选:B.【点睛】此题主要考查了方差的含义和应用,要熟练掌握,解答此题的关键是要明确:方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.5.A解析:A【分析】连接BD,根据三角形中位线定理易得四边形EFGH的各边长等于矩形对角线的一半,而矩形对角线相等,从而算出周长即可.【详解】连接BD,∵H、G是AD与CD的中点,∴HG是△ACD的中位线,∴HG=1AC=5cm,同理EF=5cm,2∵四边形ABCD是矩形,∴根据矩形的对角线相等,即BD=AC=10cm,∵H、E是AD与AB的中点,∴EH是△ABD的中位线,∴EH=1BD=5cm,同理FG=5cm,2∴四边形EFGH的周长为20cm.故选A.【点睛】熟练掌握矩形对角线相等和三角形中位线等于第三边的一半的性质是解决本题的关键. 6.C解析:C【解析】【分析】依题意得出AE=AB=AD,∠ADE=50°,又因为∠B=80°故可推出∠ADC=80°,∠CDE=∠ADC-∠ADE,从而求解.【详解】∵AD∥BC,∴∠AEB=∠DAE=∠B=80°,∴AE=AB=AD,在三角形AED中,AE=AD,∠DAE=80°,∴∠ADE=50°,又∵∠B=80°,∴∠ADC=80°,∴∠CDE=∠ADC-∠ADE=30°.故选:C.【点睛】考查菱形的边的性质,同时综合利用三角形的内角和及等腰三角形的性质,解题关键是利用等腰三角形的性质求得∠ADE的度数.7.B解析:B【解析】【分析】作BE ⊥AC 于E ,根据等腰三角形三线合一性质可得AE =DE ,根据∠C =45°,得出∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°,可得BE =CE ,利用勾股定理求出CE =BE =2,根据D 是AC 的三等分点得出AE =DE =121233AC AC ⨯==CD ,求出CD =1,利用勾股定理2222215AB BE AE =+=+=即可.【详解】解:作BE ⊥AC 于E ,∵AB =BD ,∴AE =DE ,∵∠C =45°,∴∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°,∴BE =CE ,在Rt △BEC 中,∴()22222+222BE CE CE BC ===,∴CE =BE =2,∵D 是AC 的三等分点, ∴CD =13AC ,AD =AC -CD =1233AC AC AC -=, ∴AE =DE =121233AC AC ⨯==CD , ∴CE =CD +DE =2CD =2,∴CD =1,∴AE =1,在Rt △ABE 中,根据勾股定理2222215AB BE AE =+=+=.故选B .【点睛】本题考查等腰三角形的性质,等腰直角三角形判定与性质,勾股定理,三等分线段,掌握等腰三角形的性质,等腰直角三角形判定与性质,勾股定理,三等分线段是解题关键. 8.C解析:C【分析】由图像与纵轴的交点可得出A 、B 两地的距离;当s=0时,即为甲、乙相遇的时候,同理根据图像的拐点判断其他即可.【详解】解:由图像可知A 村、B 村相离8km ,故①正确;甲出发2h 后到达C 村,故②正确;当0≤t≤1时,易得一次函数的解析式为s=-8t+8,故甲的速度比乙的速度快8km/h ,故③正确;当1≤t≤1.5时,函数图象经过点(1,0)(1.5,4)设一次函数的解析式为s=kt+b则有:104 1.5k b k b =+⎧⎨=+⎩解得21k b =⎧⎨=⎩ ∴s=2t+1当s=2时,得2=2t+1,解得t=0.5<1,不符合题意,④错误.故答案为C.【点睛】本题考查了一次函数的应用和函数与方程的思想,解题的关键在于读懂图象,根据图像的信息进行解答.二、填空题9.1≥x 且3x ≠【解析】【分析】根据分母不等于0,且被开方数是非负数列式求解即可.【详解】由题意得10x -≥且30x -≠解得1≥x 且3x ≠故答案为:1≥x 且3x ≠【点睛】本题考查了代数式有意义时字母的取值范围,代数式有意义时字母的取值范围一般从几个方面考虑:①当代数式是整式时,字母可取全体实数;②当代数式是分式时,考虑分式的分母不能为0;③当代数式是二次根式时,被开方数为非负数.10.A解析:6【解析】【分析】根据菱形的性质得到AC =8,根据菱形的面积等于两条对角线乘积的一半,即可求解.【详解】解:∵四边形ABCD 为菱形;∴AC =2OA =8,12ABCD S AC BD =⋅菱形, ∴12482BD =⨯⨯, ∴BD =6,故答案为:6【点睛】本题考查了菱形的性质,解题的关键是熟记菱形面积的两种表示法:(1)底乘高,(2)对角线乘积的一半,本题运用的是第二种.11.E解析:8【解析】【分析】根据正方形的面积等于边长的平方,由正方形PQED 的面积和正方形PRQF 的面积分别表示出PR 的平方及PQ 的平方,又三角形PQR 为直角三角形,根据勾股定理求出QR 的平方,即可求小正方形的边长.【详解】如图,∵正方形PQED 的面积等于225,∴即PQ 2=225,∵正方形PRGF 的面积为289,∴PR 2=289,又△PQR 为直角三角形,根据勾股定理得:PR 2=PQ 2+QR 2,∴QR 2=PR 2−PQ 2=289−225=64,∴QR=8,即字母A 所代表的正方形的边长为8.【点睛】本题考查勾股定理,根据勾股定理求出小正方形的面积是关键.12.D21【分析】由矩形的性质和角平分线的定义得出∠DEC =∠ECB =∠BEC ,推出BE =BC ,求得 AE =AB =1,然后依据勾股定理可求得BC 的长;【详解】解:∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠DEC =∠BCE ,∵EC 平分∠DEB ,∴∠DEC =∠BEC ,∴∠BEC =∠ECB ,∴BE =BC ,∵四边形ABCD 是矩形,∴∠A =90°,AD BC =∵∠ABE =45°,∴∠ABE =∠AEB =45°,∴AB =AE =1,由勾股定理得:BE ==,∴BC =AD =BE, ∴1DE AD AE =-,1.【点睛】本题考查了矩形的性质,等腰三角形的性质与判定,勾股定理的应用;熟练掌握矩形的性质,证出BE =BC 是解题的关键.13.10y x =-+【分析】用待定系数法即可得到答案.【详解】解:把()8,2代入y x b =-+得82b -+=,解得10b =,所以一次函数解析式为10y x =-+.故答案为10y x =-+【点睛】本题考查求一次函数解析式,解题的关键是熟练掌握待定系数法.14.A解析:AC BD =【分析】如下图,根据三角形中位线的定理,可得AG=EF=12AC ,GF=AE=12BD ,再根据菱形四条边相等的性质,可得出AC 与BD 的关系.【详解】如下图,点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点∵点E、F是AB、BC的中点∴EF=12AC同理可得:AG=EF=12AC,GF=AE=12BD∵要使得四边形HEFG是菱形,则HE=EF=FG=GH ∴只需AC=BD即可故答案为:AC=BD【点睛】本题考查菱形的性质和三角形中位线的性质,解题关键是得出AG=EF=12 AC,GF=AE=12 BD.15.(,0)【分析】作点D关于x轴对称点F,根据题意求出D点的坐标,从而得到F点的坐标,同时连接CF,则CF与x轴的交点即为所求E点,此时满足△CDE的周长最小,利用CF的解析式求解即可.【详解】解析:(83,0)【分析】作点D关于x轴对称点F,根据题意求出D点的坐标,从而得到F点的坐标,同时连接CF,则CF与x轴的交点即为所求E点,此时满足△CDE的周长最小,利用CF的解析式求解即可.【详解】解:作点D关于x轴对称点F,如图,∵四边形OABC 是矩形,∴OC =BD =3,点C 的坐标为()0,3,∵D 为AB 边的中点,∴AD =32, ∵OA =4,∴D 点的坐标为34,2⎛⎫ ⎪⎝⎭,则F 点的坐标为34,2⎛⎫- ⎪⎝⎭, 根据轴对称的性质可得:EF =ED ,∴C △CDE =CD +CE +DE =CD +CE +EF ,其中CD 为定值,当CE +EF 值最小时,△CDE 周长最小,此时点C ,E ,F 三点共线,设直线CF 的解析式为:()0y kx b k =+≠,将()0,3和34,2⎛⎫- ⎪⎝⎭代入解析式得: 3342b k b =⎧⎪⎨+=-⎪⎩,解得:983k b ⎧=-⎪⎨⎪=⎩, ∴直线CF 的解析式为:938y x =-+, 令0y =,得:9308x -+=, 解得:83x =, ∴点E 坐标(83,0), 故答案为:803⎛⎫ ⎪⎝⎭,. 【点睛】本题考查一次函数与轴对称的综合运用,理解最短路径的求解方法,熟悉待定系数法求一次函数解析式是解题关键.16.5【分析】在Rt△BDC中由勾股定理可求出BD,根据翻折变换可得AH=HD,在Rt△BDH 中由勾股定理可得答案.【详解】解:在Rt△BDC中,∵BC=8,CD=2,∴BD=,由题意,得解析:5【分析】在Rt△BDC中由勾股定理可求出BD,根据翻折变换可得AH=HD,在Rt△BDH中由勾股定理可得答案.【详解】解:在Rt△BDC中,∵BC=8,CD=∴BD=由题意,得AH=HD,设BH=x,则AH=12﹣x=HD,在Rt△BDH中,由勾股定理得,HB2+BD2=HD2,即x2)2=(12﹣x)2,解得x=5,即HB=5,故答案为:5.【点睛】本题考查了翻折变换,勾股定理.掌握翻折变换的性质及勾股定理是解题的关键.三、解答题17.(1);(2)【分析】(1)先利用二次根式的性质化简,然后根据二次根式的混合计算法则求解即可;(2)先利用二次根式的性质化简,然后根据二次根式的混合计算法则求解即可.【详解】解:(1)解析:(1)2)4【分析】(1)先利用二次根式的性质化简,然后根据二次根式的混合计算法则求解即可;(2)先利用二次根式的性质化简,然后根据二次根式的混合计算法则求解即可.【详解】解:(1)===(22=4=4=【点睛】本题主要考查了利用二次根式的化简和二次根式的混合运算,熟练掌握相关计算法则是解题的关键.18.需要封闭,理由见解析【分析】过作于 先求解 再利用等面积法求解 再与260比较,可得答案.【详解】解:过作于所以进行爆破时,公路BC 段需要暂时封闭.【点睛】解析:需要封闭,理由见解析【分析】过A 作AK BC ⊥于,K 先求解,BC 再利用等面积法求解,AK 再与260比较,可得答案.【详解】解:过A 作AK BC ⊥于,K,400,300,AB AC AB AC22500,BC AB AC11,AB AC BC AK22AK300400500,240,AK240260,所以进行爆破时,公路BC段需要暂时封闭.【点睛】本题考查的是勾股定理的应用,利用等面积法求解直角三角形斜边上的高,掌握“等面积法求解直角三角形斜边上的高”是解题的关键.19.(1)见解析;(2)见解析;(3)【解析】【分析】(1)根据正方形的判定画出以AB为边的正方形ABCD即可;(2)画出以EF为边的等腰三角形EFG,且△EFG的周长为等腰三角形即可;(3)解析:(1)见解析;(2)见解析;(35【解析】【分析】(1)根据正方形的判定画出以AB为边的正方形ABCD即可;(2)画出以EF为边的等腰三角形EFG,且△EFG的周长为1010(3)由勾股定理求出CG即可.【详解】解:(1)如图,所作正方形ABCD即为以AB为边的正方形ABCD;(2)如图,所作△EFG即为以EF为边的等腰三角形EFG,且△EFG的周长为1010+(3)如图,CG22+512【点睛】本题考查作图-应用与设计,勾股定理,解题的关键是理解题意,根据GE=GF=5画出等腰三角形.20.(1)AC⊥BD,证明见解析;(2)四边形ABCD是菱形,见解析【分析】(1)首先根据平行四边形的性质得出OC, OB的长,再利用勾股定理逆定理求出∠BOC=90,可得AC与BD的位置关系;(解析:(1)AC⊥BD,证明见解析;(2)四边形ABCD是菱形,见解析【分析】(1)首先根据平行四边形的性质得出OC,OB的长,再利用勾股定理逆定理求出∠BOC=90︒,可得AC与BD的位置关系;(2)菱形的判定方法:对角线互相垂直平分的四边形是菱形,可得答案.【详解】解:(1)AC⊥BD;理由如下:在ABCD中,132==OB BD,142OC AC==∵22291625+=+==OB OC BC∴∠BOC=90︒∴AC⊥BD.(2)四边形ABCD是菱形∵四边形ABCD是平行四边形(已知),AC⊥BD(已证)∴四边形ABCD是菱形.【点睛】此题主要考查了菱形的判定,平行四边形的性质,以及勾股定理的逆定理的运用,解题的关键是根据条件证出BO2+CO2=CB2.21.(1)5;(2)5.【解析】【详解】试题分析: 根据平方差公式,可分母有理化,根据整体代入,可得答案.试题解析:(1)∵a=,∴4a2-8a+1=4×()2-8×()+1=5;(2)解析:(1)5;(2)5.【解析】【详解】试题分析: 根据平方差公式,可分母有理化,根据整体代入,可得答案.试题解析:(1)∵, ∴4a 2-8a+1)2-8×)+1=5;(2)原式=12×=12×) =12×10=5.点睛:本题主要考查了分母有理化,利用分母有理化化简是解答此题的关键. 22.(1)一个A 型篮球为80元,一个B 型篮球为50元;(2)函数解析式为:;(3)A 型篮球120个,则B 型篮球为180个.【分析】(1)设一个A 型篮球为x 元,一个B 型篮球为y 元,根据题意列出方程组求 解析:(1)一个A 型篮球为80元,一个B 型篮球为50元;(2)函数解析式为:()30150000300W t t =+≤≤;(3)A 型篮球120个,则B 型篮球为180个.【分析】(1)设一个A 型篮球为x 元,一个B 型篮球为y 元,根据题意列出方程组求解即可得; (2)A 型篮球t 个,则B 型篮球为()300t -个,根据单价、数量、总价的关系即可得; (3)根据A 型篮球与B 型篮球的优惠政策求出单价,然后代入(2)解析式中求解即可得.【详解】解:(1)设一个A 型篮球为x 元,一个B 型篮球为y 元,根据题意可得:323402210x y x y +=⎧⎨+=⎩, 解得:8050x y =⎧⎨=⎩,∴一个A 型篮球为80元,一个B 型篮球为50元;(2)A 型篮球t 个,则B 型篮球为()300t -个,根据题意可得:()()805030030150000300W t t t t =+-=+≤≤,∴函数解析式为:()30150000300W t t =+≤≤;(3)根据题意可得:A 型篮球单价为()808-元,B 型篮球单价为500.9⨯元,则()()16740808500.9300t t =-+⨯⨯-,解得:120t =,300180t -=,∴A 型篮球120个,则B 型篮球为180个. 【点睛】题目主要考查二元一次方程组及一次函数的应用,理解题意,列出相应方程是解题关键.23.(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,. 【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是解析:(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,.【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是等腰直角三角形,然后根据等腰直角三角形的性质可得AH 的长,最后根据等腰直角三角形的面积公式即可得; (2)先根据平行四边形的性质可得,从而可得,再根据三角形中位线定理可得是的中位线,从而可得,然后与(1)所求的建立等式求解即可得;(3)分①当点H 是AB 的中点时,;②当点Q 与点E 重合时,;③当时,三种情况,分别求解即可得.【详解】 (1)由题意得:,点Q 为AP 的中点,,四边形ABCD 是矩形,,是BAD的角平分线,,,是等腰直角三角形,,则的面积为;(2)如图1,四边形PQHM是平行四边形,,点M在BC边上,,点Q为AP的中点,是的中位线,,由(1)知,,则,解得;(3)由题意,有以下三种情况:①如图2,当点H是AB的中点时,则,四边形PQHM是平行四边形,,,在和中,,由(2)可知,此时;②如图3,当点Q与点E重合时,在和中,,,,则,解得;③如图4,当时,四边形ABCD是矩形,四边形PQHM是平行四边形,,,在和中,,,,在中,,是等腰直角三角形,,,在中,,是等腰直角三角形,,则由得:,解得;综上,如图2,当时,;如图3,当时,;如图4,当时,.【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点,较难的是题(3),依据题意,正确分三种情况讨论并画出图形是解题关键.24.(1)y=-2x+8;(2)S=16m-2m2;(3)(-2,4)【解析】【分析】(1)先求出点A,点B坐标,由等腰三角形的性质可求点C坐标,由待定系数法可求BC 的解析式;(2)过点P作PG解析:(1)y=-2x+8;(2)S=16m-2m2;(3)(-2,4)【解析】【分析】(1)先求出点A,点B坐标,由等腰三角形的性质可求点C坐标,由待定系数法可求BC 的解析式;(2)过点P作PG⊥AC,PE∥BC交AC于E,过点Q作HQ⊥AC,由“AAS”可证△AGP≌△CHQ,可得AG=HC=m-4,PG=HQ=2m-8,由“AAS”可证△PEF≌△QCF,可得S△PEF=S△QCF,即可求解;(3)如图2,连接AM,CM,过点P作PE⊥AC,由“SSS”可证△APM≌△CQM,△ABM≌△CBM,可得∠PAM=∠MCQ,∠BQM=∠APM=45°,∠BAM=∠BCM,由“AAS”可证△APE≌△MAO,可得AE=OM,PE=AO=4,可求m的值,可得点P的坐标.【详解】解:(1)∵直线y=2x+8与x轴交于点A,与y轴交于点B,∴点B(0,8),点A(-4,0)∴AO=4,BO=8,∵AB=BC,BO⊥AC,∴AO=CO=4,∴点C(4,0),设直线BC解析式为:y=kx+b,由题意可得:804bk b=⎧⎨=+⎩,解得:28kb=-⎧⎨=⎩,∴直线BC解析式为:y=-2x+8;(2)如图1,过点P作PG⊥AC,PE∥BC交AC于E,过点Q作HQ⊥AC,设△PBQ的面积为S,∵AB=CB,∴∠BAC=∠BCA,∵点Q横坐标为m,∴点Q(m,-2m+8)∴HQ=2m-8,CH=m-4,∵AP=CQ,∠BAC=∠BCA=∠QCH,∠AGP=∠QHC=90°,∴△AGP≌△CHQ(AAS),∴AG=HC=m-4,PG=HQ=2m-8,∵PE∥BC,∴∠PEA=∠ACB,∠EPF=∠CQF,∴∠PEA=∠PAE,∴AP=PE,且AP=CQ,∴PE=CQ,且∠EPF=∠CQF,∠PFE=∠CFQ,∴△PEF≌△QCF(AAS)∴S△PEF=S△QCF,∴△PBQ的面积=四边形BCFP的面积+△CFQ的面积=四边形BCFP的面积+△PEF的面积=四边形PECB的面积,∴S=S△ABC-S△PAE=12×8×8-12×(2m-8)×(2m-8)=16m-2m2;(3)如图2,连接AM,CM,过点P作PE⊥AC,∵AB=BC,BO⊥AC,∴BO是AC的垂直平分线,∴AM=CM,且AP=CQ,PM=MQ,∴△APM≌△CQM(SSS)∴∠PAM=∠MCQ,∠BQM=∠APM=45°,∵AM=CM,AB=BC,BM=BM,∴△ABM≌△CBM(SSS)∴∠BAM=∠BCM,∴∠BCM=∠MCQ,且∠BCM+∠MCQ=180°,∴∠BCM=∠MCQ=∠PAM=90°,且∠APM=45°,∴∠APM=∠AMP=45°,∴AP=AM,∵∠PAO+∠MAO=90°,∠MAO+∠AMO=90°,∴∠PAO=∠AMO,且∠PEA=∠AOM=90°,AM=AP,∴△APE≌△MAO(AAS)∴AE=OM,PE=AO=4,∴2m-8=4,∴m=6,∴P(-2,4).【点睛】本题是一次函数综合题,考查了待定系数法求解析式,全等三角形的判定和性质,等腰三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.25.(1)45;(2)①见解析;②DF的长为2;(3)【分析】(1)根据平角的定义得到∠DFE+∠BEF=360°﹣90°=270°,根据角平分线的定义得到∠AFE=DFE,∠AEF=BEF,求得∠解析:(1)45;(2)①见解析;②DF的长为2;(3)15 7【分析】(1)根据平角的定义得到∠DFE+∠BEF=360°﹣90°=270°,根据角平分线的定义得到∠AFE=12∠DFE,∠AEF=12∠BEF,求得∠AEF+∠AFE=12(∠DFE+∠BEF),根据三角形的内角和定理即可得到结论;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,先证明四边形ABCD是矩形,再由角平分线的性质得出AB=AD,即可得出四边形ABCD是正方形;②设DF=x,根据已知条件得到BC=6,由①得四边形ABCD是正方形,求得BC=CD=6,根据全等三角形的性质得到BE=EG=3,同理,GF=DF=x,根据勾股定理列方程即可得到结论;(3)把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,得出MG=DG=MP=PH=6,GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR 中,由勾股定理得出方程,解方程即可.【详解】解:(1)∵∠C=90°,∴∠CFE+∠CEF=90°,∴∠DFE+∠BEF=360°﹣90°=270°,∵AF平分∠DFE,AE平分∠BEF,∴∠AFE=12∠DFE,∠AEF=12∠BEF,∴∠AEF +∠AFE =12(∠DFE +∠BEF )=12⨯270°=135°,∴∠EAF =180°﹣∠AEF ﹣∠AFE =45°, 故答案为:45;(2)①作AG ⊥EF 于G ,如图1所示:则∠AGE =∠AGF =90°, ∵AB ⊥CE ,AD ⊥CF , ∴∠B =∠D =90°=∠C , ∴四边形ABCD 是矩形,∵∠CEF ,∠CFE 外角平分线交于点A , ∴AB =AG ,AD =AG , ∴AB =AD ,∴四边形ABCD 是正方形; ②设DF =x , ∵BE =EC =3, ∴BC =6,由①得四边形ABCD 是正方形, ∴BC =CD =6,在Rt △ABE 与Rt △AGE 中,AB AGAE AE=⎧⎨=⎩ , ∴Rt △ABE ≌Rt △AGE (HL ), ∴BE =EG =3, 同理,GF =DF =x ,在Rt △CEF 中,EC 2+FC 2=EF 2, 即32+(6﹣x )2=(x +3)2, 解得:x =2, ∴DF 的长为2; (3)解:如图2所示:把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,∴MG=DG=MP=PH=5,∴GQ=3,设MR=HR=a,则GR=5﹣a,QR=a+2,在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,解得:a=157,即HR=157;故答案为:157.【点睛】本题考查了正方形的判定与性质、全等三角形的判定与性质、角平分线的性质、勾股定理、矩形的判定、翻折变换的性质等知识;本题综合性强,有一定难度.。
八年级上册数学 全册全套试卷达标检测(Word版 含解析)

八年级上册数学 全册全套试卷达标检测(Word 版 含解析)一、八年级数学三角形填空题(难)1.直角三角形中,两锐角的角平分线所夹的锐角是_____度.【答案】45【解析】【分析】根据题意画出符合条件的图形,然后根据直角三角形的两锐角互余和角平分线的性质,以及三角形的外角的性质求解即可.【详解】如图所示△ACB 为Rt△,AD ,BE ,分别是∠CAB 和∠ABC 的角平分线,AD ,BE 相交于一点F . ∵∠ACB=90°,∴∠CAB+∠ABC=90°∵AD,BE ,分别是∠CAB 和∠ABC 的角平分线,∴∠FAB+∠FBA=12∠CAB+12∠ABC=45°. 故答案为45.【点睛】此题主要考查了直角三角形的两锐角互余和三角形的外角的性质,关键是根据题意画出相应的图形,利用三角形的相关性质求解.2.如图,在ABC ∆中,B 与C ∠的平分线交于点P .若130BPC ∠=︒,则A ∠=______.【答案】80°【解析】【分析】根据三角形内角和可以求得∠PBC+∠PCB 的度数,再根据角平分线的定义,求出∠ABC+∠ACB,最后利用三角形内角和定理解答即可.【详解】解:在△PBC中,∠BPC=130°,∴∠PBC+∠PCB=180°-130°=50°.∵PB、PC分别是∠ABC和∠ACB的角平分线,∴∠ABC+∠ACB=2(∠PBC+∠PCB)=2×50°=100°,在△ABC中,∠A=180°-(∠ABC+∠ACB)=180°-100°=80°.故答案为80°.【点睛】本题主要考查了三角形的内角和定理和角平分线的定义,掌握三角形的内角和定理和角平分线的定义是解题的关键.3.已知一个三角形的三边长为3、8、a,则a的取值范围是_____________.【答案】5<a<11【解析】【分析】根据三角形的三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边可得8-3<a<8+3,再解即可.【详解】解:根据三角形的三边关系可得:8-3<a<8+3,解得:5<a <11,故答案为:5<a<11.【点睛】此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.4.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB= .【答案】85°.【解析】试题分析:令A→南的方向为线段AE,B→北的方向为线段BD,根据题意可知,AE,DB 是正南,正北的方向BD//AE=45°+15°=60°又=180°-60°-35°=85°.考点:1、方向角. 2、三角形内角和.5.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC=______°.【答案】110【解析】已知∠A=50°,∠ABO=28°,∠ACO=32°,根据三角形外角的性质可得∠BDC=∠A+∠ABO=78°,∠BOC=∠BDC+∠ACO=110°.6.如图,直线a∥b,∠l=60°,∠2=40°,则∠3=______.【答案】80°.【解析】【分析】根据平行线的性质求出∠4,再根据三角形内角和定理计算即可.【详解】∵a∥b,∴∠4=∠l=60°,∴∠3=180°-∠4-∠2=80°,故答案为80°.【点睛】本题考查了平行线的性质、三角形内角和定理,掌握两直线平行,同位角相等是解题的关键.二、八年级数学三角形选择题(难)7.如图,CD 是ABC 的一条中线,E 为BC 边上一点且2,BE CE AE CD 、相交于,F 四边形BDFE 的面积为6,则ABC 的面积是( )A .14B .14.4C .13.6D .13.2【答案】B【解析】 【分析】 连结BF ,设S △BDF =x ,则S △BEF =6-x ,由CD 是中线可以得到S △ADF =S △BDF ,S △BDC =S △ADC ,由BE =2CE 可以得到S △CEF =12S △BEF ,S △ABE =23S △ABC ,进而可用两种方法表示△ABC 的面积,由此可得方程,进而得解.【详解】解:如图,连接BF ,设S △BDF =x ,则S △BEF =6-x ,∵CD 是中线,∴S △ADF =S △BDF =x ,S △BDC = S △ADC =12△ABC , ∵BE =2CE ,∴S △CEF =12S △BEF =12(6-x),S △ABE =23S △ABC , ∵S △BDC = S △ADC =12△ABC ,∴S △ABC =2S △BDC=2[x +32(6-x)] =18-x ,∵S △ABE =23S △ABC , ∴S △ABC =32S △ABE =32[2x + (6-x)] =1.5x +9,∴18-x =1.5x +9,解得:x =3.6,∴S △ABC =18-x ,=18-3.6=14.4,故选:B .【点睛】本题考查了三角形的中线能把三角形的面积平分,等高三角形的面积比等于底的比,熟练掌握这个结论记以及方程思想是解题的关键.8.适合下列条件的△ABC 中, 直角三角形的个数为 ①111345a b c ,,;===②6a =,∠A =45°;③∠A =32°, ∠B =58°; ④72425a b c ===,,;⑤22 4.a b c ===,,⑥::3:4:5a b c =⑦::12:13:15A B C ∠∠∠=⑹5a b c === A .2个B .3个C .4个D .5个【答案】C【解析】 根据勾股定理的逆定理,可分别求出各边的平方,然后计算判断:222111+345≠()()(),故①不能构成直角三角形;当a=6,∠A=45°时,②不足以判定该三角形是直角三角形;根据直角三角形的两锐角互余,可由∠A+∠B=90°,可知③是直角三角形;根据72=49,242=576,252=625,可知72+242=252,故④能够成直角三角形;由三角形的三边关系,2+2=4可知⑤不能构成三角形;令a=3x ,b=4x ,c=5x ,可知a 2+b 2=c 2,故⑥能够成直角三角形;根据三角形的内角和可知⑦不等构成直角三角形;由a 2=5,b 2=20,c 2=25,可知a 2+b 2=c 2,故⑧能够成直角三角形.点睛:此题主要考查了直角三角形的判定,解题关键是根据角的关系,两锐角互余,和边的关系,即勾股定理的逆定理,可直接求解判断即可,比较简单.9.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于215°,则∠BOD的度数为()A.20°B.35°C.40°D.45°【答案】B【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和,由五边形内角和可求得五边形OAGFE的内角和,则可求得∠BOD.【详解】解:∵∠1、∠2、∠3、∠4的外角的角度和为215°,∴∠1+∠2+∠3+∠4+215°=4×180°,∴∠1+∠2+∠3+∠4=505°,∵五边形OAGFE内角和=(5-2)×180°=540°,∴∠1+∠2+∠3+∠4+∠BOD=540°,∴∠BOD=540°-505°=35°,故选:B.【点睛】本题主要考查多边形的内角和,利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键.10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是()A.∠A=∠1+∠2 B.2∠A=∠1+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)【答案】B【分析】根据四边形的内角和为360°、平角的定义及翻折的性质,就可求出2∠A=∠1+∠2这一始终保持不变的性质.【详解】∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,则2∠A+(180°-∠2)+(180°-∠1)=360°,∴可得2∠A=∠1+∠2.故选:B【点睛】本题主要考查四边形的内角和及翻折的性质特点,解决本题的关键是熟记翻折的性质.的高的是()11.如下图,线段BE是ABCA.B.C.D.【答案】D【解析】【分析】根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高.【详解】解:由图可得,线段BE是△ABC的高的图是D选项;故选:D.【点睛】本题主要考查了三角形的高线的画法,掌握三角形的高的画法是解题的关键.12.已知三角形的两边分别为1和4,第三边长为整数,则该三角形的周长为()A.7 B.8 C.9 D.10【答案】C【解析】【分析】根据三角形的三边关系“第三边大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是整数,从而求得周长.【详解】设第三边为x,根据三角形的三边关系,得:4-1<x<4+1,即3<x<5,∵x为整数,∴x的值为4.三角形的周长为1+4+4=9.故选C.【点睛】此题考查了三角形的三边关系.关键是正确确定第三边的取值范围.三、八年级数学全等三角形填空题(难)13.在Rt△ABC中,∠BAC=90°AB=AC,分别过点B、C做经过点A的直线的垂线BD、CE,若BD=14cm,CE=3cm,则DE=_____【答案】11cm或17cm【解析】【分析】分两种情形画出图形,利用全等三角形的性质分别求解即可.【详解】解:如图,当D,E在BC的同侧时,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵BD⊥DE,∴∠BDA=90°,∴∠BAD+∠DBA=90°,∴∠DBA=∠CAE,∵CE⊥DE,∴∠E=90°,在△BDA和△AEC中,ABD CAED EAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDA≌△AEC(AAS),∴DA=CE=3,AE=DB=14,∴ED=DA+AE=17cm.如图,当D,E在BC的两侧时,同法可证:BD=CE+DE,可得DE=11cm,故答案为:11cm或17cm.【点睛】此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定定理与性质定理.14.如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.【答案】7【解析】试题解析:∵△ABC为等边三角形,∴AB=CA,∠BAE=∠ACD=60°;又∵AE=CD,在△ABE和△CAD中,AB CABAE ACDAE CD⎧⎪∠∠⎨⎪⎩===∴△ABE≌△CAD;∴BE=AD,∠CAD=∠ABE;∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°;∵BQ⊥AD,∴∠AQB=90°,则∠PBQ=90°-60°=30°;∵PQ=3,∴在Rt△BPQ中,BP=2PQ=6;又∵PE=1,∴AD=BE=BP+PE=7.故答案为7.15.如图,ABC ∆中,090,,102ACB AC BC AB ∠===,点G 为AC 中点,连接BG ,CE BG ⊥于F ,交AB 于E ,连接GE ,点H 为AB 中点,连接FH ,以下结论:①ACE ABG ∠=∠;②5CF =;③AGE CGB ∠=∠;④FH 平分BFE ∠。
八年级上册全册全套试卷达标检测(Word版 含解析)

八年级上册全册全套试卷达标检测(Word版含解析)一、初二物理机械运动实验易错压轴题(难)1.小明在“测小车的平均速度”的实验中,设计了如图所示的实验装置:小车从带刻度(分度值为1cm)的斜面顶端由静止下滑,图中的圆圈是小车到达A、B、C三处时电子表的显示:(1)该实验是根据公式_____ 进行测量的。
(2)实验中为了方便计时,应使斜面坡度较 _____ (填“大、小”)。
(3)请根据图中所给信息回答:s AB=_____ cm,t BC=_____ s,v AC=_____cm/s。
(4)实验前必须学会熟练使用电子表,如果让小车过了A点后才开始计时,则会使所测AC 段的平均速度v AC偏_____(填“大、小”)。
【来源】贵州省遵义市第十一中学2019-2020学年八年级(上)期中考试物理试题【答案】svt=;小; 40.0; 1; 30.0;大。
【解析】【分析】本题考查探究测量平均速度实验的原理和数据处理。
【详解】(1)[1]测量平均速度,所用的公式是svt=;(2)[2]为了方便计时,应让小车冲下斜面的运动较慢,所以应使斜面坡度较小;(3)[3][4]由图可知,从A到B的路程s AB=4.00dm=40.0cm;从B点到C点所用的时间t BC=1s;[5]从A到C的路程s AB=9.00dm=90.0cm,对应的时间t AB=3s,所以从A到C的平均速度90.0cm30.0cm/s3sACACACsvt===(4)[6]如果小车过A点后才开始计时,那么实际测得的从A到C的时间会偏小,但s AB保持不变,所以对应的平均速度v AC偏大。
2.小明在“测小车的平均速度”的实验中,设计了如图所示的实验装置:小车从带刻度的斜面顶端由静止下滑,图中的圆圈是小车到达A、B、C三处时电子表的显示:(1)该实验是根据公式_____进行测量的;(2)实验中为了方便计时,应使斜面坡度较_____(填“大、小”);(3)请根据图中所给信息回答:AC v =_____m/s (保留两位有效数字),BC v _____AC v (填“>”、“<”或“=”);(4)实验前必须学会熟练使用电子表,如果让小车过了A 点后才开始计时,则会使所测AC 段的平均速度AC v 偏_____(填“大、小”)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级期末试卷达标检测卷(Word版含解析)一、八年级数学全等三角形解答题压轴题(难)1.(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论是(直接写结论,不需证明);(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.【答案】(1)EF=BE+DF.(2)成立,理由见解析;(3)10.【解析】【分析】(1)如图1,延长FD到G,使得DG=DC,先证△ABE≌△ADG,得到AE=AG,∠BAE=∠DAG,进一步根据题意得∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可.(2)如图2,延长FD到点G.使DG=BE.连结AG,证得△ABE≌△ADG,得到AE=AG,∠BAE=∠DAG,再结合题意得到∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可.(3)如图3,延长DC到点G,截取CG=AE,连接BG,先证△AEB≌△CGB,得到BE=BG,∠ABE=∠CBG,结合已知条件得∴∠CBF+∠CBG=45°,再证明△EBF≌△GBF,得到EF=FG,最后求三角形的周长即可.【详解】解答:(1)解:如图1,延长FD到G,使得DG=DC在△ABE和△ADG中,∵DC DGB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=12∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△GAF中,∵AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;故答案为:EF=BE+DF.(2)解:结论EF=BE+DF仍然成立;理由:如图2,延长FD到点G.使DG=BE.连结AG在△ABE和△ADG中,∵DG BEB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=12∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△GAF中,∵AE AGEAF GAF AF AF=⎧⎪∠=∠⎨⎪=⎩,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,在△AEB与△CGB中,∵AE CGA BOG AF BF=⎧⎪∠=∠⎨⎪=⎩,∴△AEB≌△CGB(SAS),∴BE=BG,∠ABE=∠CBG.∵∠EBF=45°,∠ABC=90°,∴∠ABE+∠CBF=45°,∴∠CBF+∠CBG=45°.在△EBF与△GBF中,∵BE BGEBF GBF BF BF=⎧⎪∠=∠⎨⎪=⎩,∴△EBF≌△GBF(SAS),∴EF=GF,∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10.【点睛】本题主要考查了三角形全等的判定和性质,灵活运用全等三角形的性质和判定是解答本题的关键.但本题分为三问,难度不断增加,对提升思维能力大有好处.2.如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.(1)请你探究线段CE与FE之间的数量关系(直接写出结果,不需说明理由);(2)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由;(3)将图1中的△AED绕点A顺时针旋转任意的角度(如图3),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由.【答案】(1)线段CE与FE之间的数量关系是CE2FE;(2)(1)中的结论仍然成立.理由见解析;(3)(1)中的结论仍然成立.理由见解析【解析】【分析】(1)连接CF,直角△DEB中,EF是斜边BD上的中线,因此EF=DF=BF,∠FEB=∠FBE,同理可得出CF=DF=BF,∠FCB=∠FBC,因此CF=EF,由于∠DFE=∠FEB+∠FBE=2∠FBE,同理∠DFC=2∠FBC,因此∠EFC=∠EFD+∠DFC=2(∠EBF+∠CBF)=90°,因此△EFC是等腰直角三角形,2EF;(2)思路同(1)也要通过证明△EFC是等腰直角三角形来求解.连接CF,延长EF交CB 于点G,先证△EFC是等腰三角形,可通过证明CF是斜边上的中线来得出此结论,那么就要证明EF=FG,就需要证明△DEF和△FGB全等.这两个三角形中,已知的条件有一组对顶角,DF=FB,只要再得出一组对应角相等即可,我们发现DE∥BC,因此∠EDB=∠CBD,由此构成了两三角形全等的条件.EF=FG,那么也就能得出△CFE是个等腰三角形了,下面证明△CFE是个直角三角形.由上面的全等三角形可得出ED=BG=AD,又由AC=BC,因此CE=CG,∠CEF=45°,在等腰△CFE中,∠CEF=45°,那么这个三角形就是个等腰直角三角形,因此就能得出(1)中的结论了;(3)思路同(2)通过证明△CFE来得出结论,通过全等三角形来证得CF=FE,取AD的中点M,连接EM,MF,取AB的中点N,连接FN、CN、CF.那么关键就是证明△MEF和△CFN全等,利用三角形的中位线和直角三角形斜边上的中线,我们不难得出EM=PN=12AD,EC=MF=12AB,我们只要再证得两对应边的夹角相等即可得出全等的结论.我们知道PN是△ABD的中位线,那么我们不难得出四边形AMPN为平行四边形,那么对角就相等,于是90°+∠CNF=90°+∠MEF,因此∠CNF=∠MEF,那么两三角形就全等了.证明∠CFE是直角的过程与(1)完全相同.那么就能得出△CEF是个等腰直角三角形,于是得出的结论与(1)也相同.【详解】(1)如图1,连接CF,线段CE与FE之间的数量关系是CE=2FE;解法1:∵∠AED=∠ACB=90°∴B、C、D、E四点共圆且BD是该圆的直径,∵点F是BD的中点,∴点F是圆心,∴EF=CF=FD=FB,∴∠FCB=∠FBC,∠ECF=∠CEF,由圆周角定理得:∠DCE=∠DBE,∴∠FCB+∠DCE=∠FBC+∠DBE=45°∴∠ECF=45°=∠CEF,∴△CEF是等腰直角三角形,∴CE=2EF.解法2:易证∠BED=∠ACB=90°,∵点F是BD的中点,∴CF=EF=FB=FD,∵∠DFE=∠ABD+∠BEF,∠ABD=∠BEF,∴∠DFE=2∠ABD,同理∠CFD=2∠CBD,∴∠DFE+∠CFD=2(∠ABD+∠CBD)=90°,即∠CFE=90°,∴CE=2EF.(2)(1)中的结论仍然成立.解法1:如图2﹣1,连接CF,延长EF交CB于点G,∵∠ACB=∠AED=90°,∴DE∥BC,∴∠EDF=∠GBF,又∵∠EFD=∠GFB,DF=BF,∴△EDF≌△GBF,∴EF=GF,BG=DE=AE,∵AC=BC,∴CE=CG,∴∠EFC=90°,CF=EF,∴△CEF为等腰直角三角形,∴∠CEF=45°,∴CE=2FE;解法2:如图2﹣2,连结CF、AF,∵∠BAD=∠BAC+∠DAE=45°+45°=90°,又点F是BD的中点,∴FA=FB=FD,而AC=BC,CF=CF,∴△ACF≌△BCF,∴∠ACF=∠BCF=12∠ACB=45°,∵FA=FB,CA=CB,∴CF所在的直线垂直平分线段AB,同理,EF所在的直线垂直平分线段AD,又DA⊥BA,∴EF⊥CF,∴△CEF为等腰直角三角形,∴CE=2EF.(3)(1)中的结论仍然成立.解法1:如图3﹣1,取AD的中点M,连接EM,MF,取AB的中点N,连接FN、CN、CF,∵DF=BF,∴FM∥AB,且FM=12 AB,∵AE=DE,∠AED=90°,∴AM=EM,∠AME=90°,∵CA=CB,∠ACB=90°∴CN=AN=12AB,∠ANC=90°,∴MF∥AN,FM=AN=CN,∴四边形MFNA为平行四边形,∴FN=AM=EM,∠AMF=∠FNA,∴∠EMF=∠FNC,∴△EMF≌△FNC,∴FE=CF,∠EFM=∠FCN,由MF∥AN,∠ANC=90°,可得∠CPF=90°,∴∠FCN+∠PFC=90°,∴∠EFM+∠PFC=90°,∴∠EFC=90°,∴△CEF为等腰直角三角形,∴∠CEF=45°,∴CE=2FE.【点睛】本题解题的关键是通过全等三角形来得出线段的相等,如果没有全等三角形的要根据已知条件通过辅助线来构建.3.(1)已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A等于60°(如图①).求证:EB=AD;(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变(如图②),(1)的结论是否成立,并说明理由.【答案】(1)证明见解析(2)证明见解析【解析】试题分析:(1)作DF∥BC交AC于F,由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;(2)作DF∥BC交AC的延长线于F,同(1)证出△DBE≌△CFD,得出EB=DF,即可得出结论.试题解析:(1)证明:如图,作DF∥BC交AC于F,则△ADF为等边三角形∴AD=DF,又∵∠DEC=∠DCB,∠DEC+∠EDB=60°,∠DCB+∠DCF=60°,∴∠EDB=∠DCA ,DE=CD,在△DEB和△CDF中,120EBD DFCEDB DCFDE CD,,∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△DEB≌△CDF,∴BD=DF,∴BE=AD .(2).EB=AD成立;理由如下:作DF∥BC交AC的延长线于F,如图所示:同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,又∵∠DBE=∠DFC=60°,∴△DBE≌△CFD(AAS),∴EB=DF,∴EB=AD.点睛:此题主要考查了三角形的综合,考查等边三角形的判定与性质,全等三角形的判定与性质,等腰三角形的判定与性质,等腰直角三角形的判定与性质,平行线的性质等知识,综合性强,有一定的难度,证明三角形全等是解决问题的关键.4.如图,AB=12cm,AC⊥AB,BD⊥AB ,AC=BD=9cm,点P在线段AB上以3 cm/s的速度,由A向B运动,同时点Q在线段BD上由B向D运动.(1)若点Q的运动速度与点P的运动速度相等,当运动时间t=1(s),△ACP与△BPQ是否全等?说明理由,并直接判断此时线段PC和线段PQ的位置关系;(2)将“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变.若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能使△ACP与△BPQ全等.(3)在图2的基础上延长AC,BD交于点E,使C,D分别是AE,BE中点,若点Q以(2)中的运动速度从点B出发,点P以原来速度从点A同时出发,都逆时针沿△ABE三边运动,求出经过多长时间点P与点Q第一次相遇.【答案】(1)△ACP≌△BPQ,理由见解析;线段PC与线段PQ垂直(2)1或32(3)9s 【解析】【分析】(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.(3)因为V Q<V P,只能是点P追上点Q,即点P比点Q多走PB+BQ的路程,据此列出方程,解这个方程即可求得.【详解】(1)当t=1时,AP=BQ=3,BP=AC=9,又∵∠A=∠B=90°,在△ACP与△BPQ中,AP BQA BAC BP=⎧⎪∠=∠⎨⎪=⎩,∴△ACP≌△BPQ(SAS),∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°,∠CPQ=90°,则线段PC与线段PQ垂直.(2)设点Q的运动速度x,①若△ACP≌△BPQ,则AC=BP,AP=BQ,912tt xt=-⎧⎨=⎩,解得31t x =⎧⎨=⎩, ②若△ACP ≌△BPQ ,则AC=BQ ,AP=BP ,912xt t t=⎧⎨=-⎩ 解得632t x =⎧⎪⎨=⎪⎩, 综上所述,存在31t x =⎧⎨=⎩或632t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. (3)因为V Q <V P ,只能是点P 追上点Q ,即点P 比点Q 多走PB+BQ 的路程, 设经过x 秒后P 与Q 第一次相遇,∵AC=BD=9cm ,C ,D 分别是AE ,BD 的中点;∴EB=EA=18cm.当V Q =1时,依题意得3x=x+2×9,解得x=9;当V Q =32时, 依题意得3x=32x+2×9, 解得x=12.故经过9秒或12秒时P 与Q 第一次相遇.【点睛】本题考查了一元一次方程的应用,解题的关键是熟练的掌握一元一次方程的性质与运算.5.如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE ⊥AC ,连结 DF 交射线 AC 于点 G(1)当 DF ⊥AB 时,求 t 的值;(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
