重庆中考数学题一次函数行程问题

合集下载

一次函数行程问题及答案详解

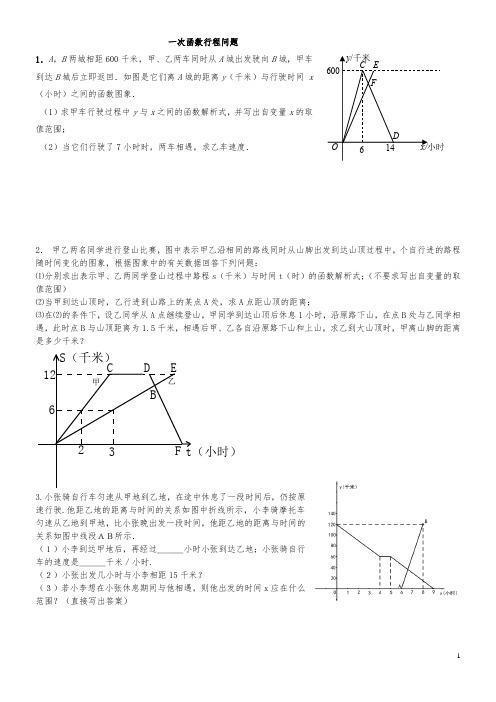
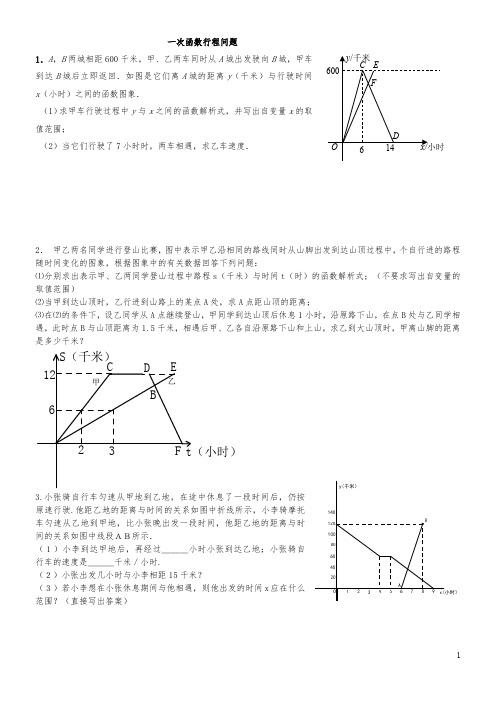
一次函数行程问题1．A ，B 两城相距600千米，甲、乙两车同时从A 城出发驶向B 城，甲车到达B 城后立即返回．如图是它们离A 城的距离y （千米）与行驶时间 x （小时）之间的函数图象．（1）求甲车行驶过程中y 与x 之间的函数解析式，并写出自变量x 的取值范围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s （千米）与时间t （时）的函数解析式；（不要求写出自变量的取值范围）⑵当甲到达山顶时，乙行进到山路上的某点A 处，求A 点距山顶的距离；⑶在⑵的条件下，设乙同学从A 点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B 处与乙同学相遇，此时点B 与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米？12623S（千米）t（小时）CD EF B甲乙3.小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行车的速度是＿＿＿千米／小时.（２）小张出发几小时与小李相距15千米？（３）若小李想在小张休息期间与他相遇，则他出发的时间x 应在什么范围？（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时； (2)求线段CD 所表示的函敛关系式；(3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，5．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y (千米)，图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系．（1）根据图中信息，求线段AB 所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t 时，求t 的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)6. 在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与．B ．港的距离．．．．分别为1y 、2y （km ），1y 、2y 与x 的函数关系如图所示．（1）填空：A 、C 两港口间的距离为 km ， a ；（2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．(第23题图)x （小时）7.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行，并以各自的速度匀速行驶，途径配货站C ，甲车先到达C 地，并在C 地用1小时配货，然后按原速度开往B 地，乙车从B 地直达A 地，图16是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像（1）A 、B 两地的距离是千米，甲车出发小时到达C 地；（2）求乙车出发2小时后直至到达A 地的过程中，与的函数关系式及的取值范围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米8．小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O －A －B －C 和线段OD 分别表示两人离学校的路程s （千米）与所经过的时间t （分钟）之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟。

初中数学《一次函数应用—行程问题》典型例题及答案解析

初中数学《一次函数应用—行程问题》典型例题及答案解析一、单选题1．一辆汽车和一辆摩托车分别从A，B两地去同一个城市，它们离A地的路程随时间变化的图象如图所示．则下列结论：①摩托车比汽车晚到1h；②A，B两地的路程为20km；③摩托车的速度为45km/h，汽车的速度为60km/h；④汽车出发1小时后与摩托车相遇，此时距B地40千米．其中正确结论的个数是()A．2个B．3个C．4个D．1个【答案】B【解析】试题解析：分析图象可知(1)4−3=1，摩托车比汽车晚到1h，正确；(2)因为汽车和摩托车分别从A，B两地去同一城市，从y轴上可看出A，B两地的路程为20km，正确；(3)摩托车的速度为(180−20)÷4=40km/h,汽车的速度为180÷3=60km/h,故(3)错误；(4)根据汽车出发1小时后行驶60km，摩托车1小时后行驶40km，加上20km，则两车行驶的距离相等，此时距B地40千米；故正确；故正确的有3个，故选B.2．小明的爷爷每天坚持锻炼身体，星期天爷爷从家里跑步到公园，打了一会儿太极拳，然后沿原路漫步走到家，下面能反映当天爷爷离家的距离y（米）与时间x（分钟）之间关系的大致图象的是（）.A．B．C．D．【答案】D【解析】爷爷从家里到公园这一过程，y随着x的增大而增大；打太极这一过程，y保持不变；沿原路漫步回家这一过程，y随着x的增大而减小.故选D.点睛：此题主要根据函数的增减性进行判断.3．已知汽车油箱内有油40L，每行驶100km耗油10L，则汽车行驶过程中油箱内剩余的油量Q（L）与行驶路程s（km）之间的函数表达式是（）A．Q＝40B．Q＝40C．Q＝40D．Q＝40【答案】C【解析】汽车油箱内有油40L，每行驶100km耗油10L，汽车行驶过程中油箱内剩余的油量与行驶路程之间的函数表达式为: Q＝40故选: C.4．甲从P地前往Q地,乙从Q地前往P地.设甲离开P地的时间为t( 小时),两人距离Q地的路程为S( 千米),图中的线段分别表示S与t之间的函数关系.根据图象的信息,下列说法正确的序号是( )①甲的速度是每小时80千米；②乙的速度是每小时50千米；③乙比甲晚出发1小时；④甲比乙少用2.25小时到达目的地；⑤图中a的值等于A．①②③④⑤B．①③④⑤C．①③⑤D．①③【答案】C【解析】①由图甲走了300千米，耗时3.75/小时.正确.②由图知乙走了300千米，耗时5/小时.错误.③乙在前一个小时路程没变，所以乙比甲晚出发1小时，正确.④由图知，5-3.75=1.25小时.错误.⑤由题意得，上下两个三角形相似，解得a 正确. 所以①③⑤正确.点睛：本题也可以根据图象信息，在直角坐标系下，看懂横纵坐标所表示的意义及其关系，把两个一次函数解析式求出来，函数的k 就是速度（可解决①②），函数的交点问题，只需要联立一次函数解析式（可解决⑤）.5．目前，全球淡水资源日益减少，提倡全社会节约用水.据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升.小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x 分后，水龙头滴出y 毫升的水，请写出y 与x 之间的函数关系式是（）A ． 0.05y x =B ． 5y x =C ． 100y x =D ． 0.05100y x =+【答案】B【解析】由题意得，一分钟滴水1000.055⨯=，所以5y x = 选B.6．在一条笔直的公路上，依次有A 、B 、C 三地．小军、小扬从A 地同时出发匀速运动，小军以2千米/分的速度到达B 地立即返回A 地，到达A 后小军原地休息，小扬途经B 地前往C 地．小军与小扬的距离s （单位：千米）和小扬所用的时间t （单位：分钟）之间的函数关系如图所示．下列说法：①小军用了4分钟到达B 地；②当t=4时，小军和小扬的距离为4千米；③C 地与A 地的距离为10千米；④小军、小扬在5分钟时相遇．其中正确的个数为（）A ． 1个B ． 2个C ． 3个D ． 4个【答案】C【解析】试题解析：由图可知，小军到达B 所用的时间为4分钟，故①正确；当小扬与小军相距8千米时，小军刚好返回A 地，则此时小军行驶的总的时间为8分钟，故小扬的速度为8÷8=1千米/分，∴当t=4时，小军和小扬的距离为：4×（2-1）=4千米，故②正确；∴C 地与A 地的距离为：1×10=10千米，故③正确；∴小军和小扬相遇的时间为：8×2÷（1+2）=分钟，故④错误；故选C ．7．甲乙两车分别从M 、N 两地相向而行，甲车出发1小时后，乙车出发，并以各自的速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的路程S （千米）与甲车所用时间t （小时）之间的函数图象，其中D 点表示甲车到达N 地停止运行，下列说法中正确的是（）A ． M 、N 两地的路程是1000千米；B ．甲到N 地的时间为4.6小时；C ．甲车的速度是120千米/小时；D ．甲乙两车相遇时乙车行驶了440千米.【答案】C【解析】试题解析： 0t =时， 560,S = ,M N ∴两地的路程560千米.A 错误. 甲车的速度为()5604401120km/h.-÷= C 正确. 设乙车的速度为km/h v ，则()()12031440.v +⨯-= 解得100.v =乙车行驶速度为100km/h. 甲车到达N 地的时间为.B 错误. ∵甲车出发1小时后乙车出发，∴乙车出发312-=小时后与甲车相遇. 甲乙两车相遇时乙车行驶了1002200⨯=千米.D 错误.故选：C.8．如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象．下列结论中，错误的是( )A ．轮船的速度为20 km /hB ．快艇的速度为40 km /hC ．轮船比快艇先出发2 hD ．快艇不能赶上轮船【答案】D【解析】试题解析：观察图象，该函数图象表示的是路程与之间的函数关系，可知轮船出发4小时后被快艇追上，在4小时时快艇和轮船行驶的路程相等，所以错误的是第四个结论．故选D ．9．汽车由A 地驶往相距120 km 的B 地，它的平均速度是30 km /h ，则汽车距B 地的路程s(km )与行驶时间t(h )的函数关系式及自变量t 的取值范围是( )A ． s ＝120－30t(0≤t≤4)B ． s ＝120－30t(t ＞0)C ． s ＝30t(0≤t≤4)D ． s ＝30t(t ＜4)【答案】A【解析】平均速度是30km/h ，∴t 小时行驶30tkm ，∴S=120-30t ，∵时间为非负数，汽车距B 地路程为非负数，∴t≥0，120-30t≥0，解得0≤t≤4．故选A ．10．小明和小亮在同一条笔直的道路上进行500米匀速跑步训练，他们从同一地点出发，先到达终点的人原地休息，已知小明先出发2秒，在跑步的过程中，小明和小亮的距离y （米）与小亮出发的时间t （秒）之间的函数关系如图所示，则下列结论错误的是（）．A ． 8a =B ． 92b =C ． 123c =D ．当20t =时， 10y =【答案】D【解析】根据题意， 0t =时，小明出发2秒行驶的路程为8米，所以，小明的速度824=÷=米/秒，∵先到终点的人原地休息，∴100秒时，小亮先到达终点， ∴小亮的速度5001005=÷=米/秒，∴a=8÷(5-4)=8(秒)，()51004100292b =⨯-⨯+=（米）， 100924123c =+÷=（秒）， ∴小明出发123秒时到达了终点，故A 、B 、C 均正确，小亮出发20秒，小亮走了205100⨯=米，小明走了22488⨯=米，1008812-=米， ∴小亮在小明前方12米，故D 错误．故选D.【点睛】本题主要考查一次函数的应用，能正确地识图，明确图中的拐点的含义是解题的关键.11．甲乙两辆车分别从A 、B 二地相对开出，2）。

专题06 一次函数中的行程问题(解析版)中考数学二轮专题复习之函数与实际问题真题满分过(全国通用)

专题06 一次函数中的行程问题（2）【真题讲解】例．（2019·吉林长春市·中考真题）已知A 、B 两地之间有一条270千米的公路，甲、乙两车同时出发，甲车以60千米/时的速度沿此公路从A 地匀速开往B 地，乙车从B 地沿此公路匀速开往A 地，两车分别到达目的地后停止．甲、乙两车相距的路程y （千米）与甲车的行驶时间x （时）之间的函数关系如图所示．（1）乙车的速度为千米/时，a = ，b = ．（2）求甲、乙两车相遇后y 与x 之间的函数关系式．（3）当甲车到达距B 地70千米处时，求甲、乙两车之间的路程．【答案】（1）75；3.6；4.5；（2）()()1352702 3.660 3.6 4.5x x y x x ⎧-<≤⎪=⎨<≤⎪⎩；（3）当甲车到达距B 地70千米处时，求甲、乙两车之间的路程为180千米．【分析】（1）根据图象可知两车2小时后相遇，根据路程和为270千米即可求出乙车的速度；然后根据“路程、速度、时间”的关系确定a b 、的值；（2）运用待定系数法解得即可；（3）求出甲车到达距B 地70千米处时行驶的时间，代入（2）的结论解答即可．【详解】解：（1）乙车的速度为：()270602275-⨯÷=千米/时，27075 3.6a =÷=，27060 4.5b =÷=．故答案为75；3.6；4.5；（2）60 3.6216⨯=（千米），当2 3.6x <≤时，设11y k x b =+，根据题意得：1111203.6216k b k b +=⎧⎨+=⎩，解得11135270k b =⎧⎨=-⎩， ∴()1352702 3.6y x x =-<≤；当3.6 4.5<≤x 时，设60y x =，∴()()1352702 3.660 3.6 4.5x x y x x ⎧-<≤⎪=⎨<≤⎪⎩；（3）甲车到达距B 地70千米处时行驶的时间为：()2027070606-÷=（小时），此时甲、乙两车之间的路程为：201352701806⨯-=（千米）．答：当甲车到达距B 地70千米处时，求甲、乙两车之间的路程为180千米．【点睛】考核知识点：一次函数的应用.把实际问题转化为函数问题是关键.【真题演练】一、单选题1．（2019·辽宁辽阳市·中考真题）一条公路旁依次有,,A B C 三个村庄，甲乙两人骑自行车分别从A 村、B 村同时出发前往C 村，甲乙之间的距离()s km 与骑行时间t(h)之间的函数关系如图所示，下列结论：①,A B 两村相距10km ；②出发1.25h 后两人相遇；③甲每小时比乙多骑行8km ；④相遇后，乙又骑行了15min 或65min 时两人相距2km ．其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个【答案】D【分析】根据题意结合一次函数的图像与性质即可一一判断.【详解】解：由图象可知A 村、B 村相离10km ，故①正确，当1.25h 时，甲、乙相距为0km ，故在此时相遇，故②正确，当0 1.25t ≤≤时，易得一次函数的解析式为810s t =-+，故甲的速度比乙的速度快8/km h ．故③正确当1.252t ≤≤时，函数图象经过点(1.25,0)(2,6)设一次函数的解析式为s kt b =+ 代入得0 1.2562k b k b =+⎧⎨=+⎩，解得k 8b 10=⎧⎨=-⎩ ∴810s t =+当2s =时．得2810t =-，解得 1.5t h =由1.5 1.250.2515min h -==同理当2 2.5t ≤≤时，设函数解析式为s kt b =+将点(2,6)(2.5,0)代入得0 2.5k b 62k b =+⎧⎨=+⎩，解得k 12b 30=-⎧⎨=⎩∴1230s t =-+当2s =时，得21230t =-+，解得73t =由7131.2565min 312h -== 故相遇后，乙又骑行了15min 或65min 时两人相距2km ，④正确．故选D ．【点睛】此题主要考查一次函数的应用，解题的关键是熟知一次函数的图像与应用.2．（2019·山东威海市·中考真题）甲、乙施工队分别从两端修一段长度为380米的公路．在施工过程中，乙队曾因技术改进而停工一天，之后加快了施工进度并与甲队共同按期完成了修路任务．下表是根据每天工程进度绘制而成的．下列说法错误的是( )A ．甲队每天修路20米B ．乙队第一天修路15米C ．乙队技术改进后每天修路35米D ．前七天甲，乙两队修路长度相等【答案】D【分析】根据题意和表格中的数据可以判断各个选项中的说法是否正确，本题得以解决．【详解】由题意可得，甲队每天修路：16014020-=(米)，故选项A 正确；乙队第一天修路：352015-=(米)，故选项B 正确；乙队技术改进后每天修路：2151602035--=(米)，故选项C 正确；前7天，甲队修路：207140⨯=米，乙队修路：270140130-=米，故选项D 错误；故选D ．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质解答．二、填空题3．（2019·重庆中考真题）一天，小明从家出发匀速步行去学校上学．几分钟后，在家休假的爸爸发现小明忘带数学书，于是爸爸立即匀速跑步去追小明，爸爸追上小明后以原速原路跑回家．小明拿到书后以原速的54快步赶往学校，并在从家出发后23分钟到校（小明被爸爸追上时交流时间忽略不计）．两人之间相距的路程y （米）与小明从家出发到学校的步行时间x （分钟）之间的函数关系如图所示，则小明家到学校的路程为________米．【答案】2080【分析】设小明原速度为x 米/分钟，则拿到书后的速度为1.25x 米/分钟，家校距离为11 (2311) 1.2526x x x -⨯=+．设爸爸行进速度为y 米/分钟，由题意及图形得：11(1611)(1611)(1.25)1380x y x y =-⎧⎨-⨯+=⎩，解得：80x =，176y =．据此即可解答．【详解】解：设小明原速度为x （米/分钟），则拿到书后的速度为1.25x （米/分钟），则家校距离为11 (2311) 1.2526x x x -⨯=+．设爸爸行进速度为y （米/分钟），由题意及图形得：11(1611)(1611)(1.25)1380x y x y =-⎧⎨-⨯+=⎩．解得：80x =，176y =．∴小明家到学校的路程为：80262080⨯=（米）．故答案为2080【点睛】本题考查一次函数的应用、速度、路程、时间之间的关系等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．4．（2019·辽宁大连市·中考真题）甲、乙两人沿同一条直路走步，如果两人分别从这条道路上的,A B 两处同时出发，都以不变的速度相向而行，图1是甲离开A 处后行走的路程y （单位：m ）与行走时x （单位：min ）的函数图象，图2是甲、乙两人之间的距离（单位：m ）与甲行走时间x （单位:min ）的函数图象，则a b -=_____．【答案】12【分析】从图1，可见甲的速度为120602=，从图2可以看出，当x=67 时，二人相遇，即：6607V +⨯乙（） =120，解得：乙的速度V 乙=80，已的速度快，从图2看出已用了b 分钟走完全程，甲用了a 分钟走完全程，即可求解．【详解】解：从图1，可见甲的速度为120602=，从图2可以看出，当67x =时，二人相遇，即：6601207V +⨯=乙，解得：乙的速度：80V =乙，∴乙的速度快，从图2看出已用了b 分钟走完全程，甲用了a 分钟走完全程， 120120160802a b -=-=. 故答案为12．【点睛】本题考查了一次函数的应用，把一次函数和行程问题结合在一起，关键是能正确利用待定系数法求一次函数的解析式，明确三个量的关系：路程=时间×速度．三、解答题5．（2019·江苏淮安市·中考真题）快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为x 小时，快车行驶的路程为1y 千米，慢车行驶的路程为2y 千米．如图中折线OAEC 表示1y 与x 之间的函数关系，线段OD 表示2y 与x 之间的函数关系．请解答下列问题：（1）求快车和慢车的速度；（2）求图中线段EC 所表示的1y 与x 之间的函数表达式；（3）线段OD 与线段EC 相交于点F ，直接写出点F 的坐标，并解释点F 的实际意义．【答案】（1）快车的速度为90千米/小时，慢车的速度为60千米/小时；（2）190135=-x y ；（3）点F 的坐标为(4.5,270)，点F 代表的实际意义是在4.5小时时，甲车与乙车行驶的路程相等．【分析】（1）根据函数图象中的数据可以求得快车和慢车的速度；（2）根据函数图象中的数据可以求得点E 和点C 的坐标，从而可以求得1y 与x 之间的函数表达式；（3）根据图象可知，点F 表示的是快车与慢车行驶的路程相等，从而以求得点F 的坐标，并写出点F 的实际意义．【详解】（1）快车的速度为：180290÷=千米/小时，慢车的速度为：180360÷=千米/小时，答：快车的速度为90千米/小时，慢车的速度为60千米/小时；（2）由题意可得，点E 的横坐标为：2 1.5 3.5+=，则点E 的坐标为(3.5,180)，快车从点E 到点C 用的时间为：(360180)902-÷=（小时），则点C 的坐标为(5.5,360)，设线段EC 所表示的1y 与x 之间的函数表达式是1y kx b =+，3.51805.5360k b k b +=⎧⎨+=⎩，得90135k b =⎧⎨=-⎩，即线段EC 所表示的1y 与x 之间的函数表达式是190135=-x y ；（3）设点F 的横坐标为a ，则6090135a a =-，解得， 4.5a =，则60 270a =，即点F 的坐标为(4.5,270)，点F 代表的实际意义是在4.5小时时，甲车与乙车行驶的路程相等．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，列出方程6．（2019·江苏徐州市·中考真题）如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点A ．甲从中山路上点B 出发，骑车向北匀速直行；与此同时，乙从点A 出发，沿北京路步行向东匀速直行．设出发min x 时，甲、乙两人与点A 的距离分别为1y m 、2y m ．已知1y 、2y 与x 之间的函数关系如图②所示．（1）求甲、乙两人的速度；（2）当x 取何值时，甲、乙两人之间的距离最短？【答案】（1）甲的速度为240/min m ，乙的速度为80/min m ．（2）当92x =时，甲、乙两人之间的距离最短．【分析】 (1)设甲、乙两人的速度，并依题意写出函数关系式，再根据图②中函数图象交点列方程组求解；(2)设甲、乙之间距离为d ，由勾股定理可得222(1200240)(80)d x x =-+=2964000()1440002x -+，根据二次函数最值即可得出结论．【详解】(1)设甲、乙两人的速度分别为/min am ，/min bm ，甲从B 到A 用时为p 分钟，则：11200(0)1200()ax x p y ax x p -≤≤⎧=⎨->⎩， 2y bx =，由图②知： 3.75x =或7.5时，12y y =，则有1200 3.75 3.757.512007.5a b a b -=⎧⎨-=⎩，解得： 24080a b =⎧⎨=⎩， p=1200÷240=5，答：甲的速度为240/min m ，乙的速度为80/min m ；(2)设甲、乙之间距离为d ，则222(1200240)(80)d x x =-+2964000()1440002x =-+， ∴当92x =时，2d 的最小值为144000，即d 的最小值为答：当92x =时，甲、乙两人之间的距离最短．【点睛】本题考查了函数图象的读图识图能力，正确理解图象交点的含义，从图象中发现和获取有用信息，提高分析问题、解决问题的能力．7．（2019·吉林中考真题）甲、乙两车分别从,A B 两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到B 地，乙车立即以原速原路返回到B 地，甲、乙两车距B 地的路程()y km 与各自行驶的时间()x h 之间的关系如图所示． ⑴m =________，n =________；⑴求乙车距B 地的路程y 关于x 的函数解析式，并写出自变量x 的取值范围； ⑴当甲车到达B 地时，求乙车距B 地的路程【答案】（1）4，120；（2）60240y x =-+；（3）乙车距B 地的路程为30km .【分析】（1）观察图象即可解决问题；（2）运用待定系数法解得即可；（3）把x=3代入（2）的结论即可．【详解】解：（1）根据题意可得m=2×2=4，n=280-280÷3.5=120；故答案为4；120；（2）设y 关于x 的函数解析式为()02y kx x =≤≤，因为图象过()2,120，所以2120k =，解得60k =，所以y 关于x 的函数解析式为60y x =，设y 关于x 的函数解析式为()124y k x b x =+≤≤，因为图象过()()2,120,4,0两点，所以11212040k b k b +=⎧⎨+=⎩，解得：160240k b =-⎧⎨=⎩，所以y 关于x 的函数解析式为60240y x =-+；（3）当 3.5x =时，60 3.524030y =-⨯+=，所以当甲车到达B 地时，乙车距B 地的路程为30km ．【点睛】此题考查的知识点是一次函数的应用，解题的关键是熟练掌握待定系数法确定函数的解析式． 8．（2019·宁夏中考真题）在综合与实践活动中，活动小组对学校400米的跑道进行规划设计，跑道由两段直道和两端是半圆弧的跑道组成．其中400米跑道最内圈为400米，两端半圆弧的半径为36米．（π取3.14）．（1）求400米跑道中一段直道的长度；（2）在活动中发现跑道周长（单位：米）随跑道宽度（距最内圈的距离，单位：米）的变化而变化．请完成下表：若设x 表示跑道宽度（单位：米），y 表示该跑道周长（单位：米），试写出y 与x 的函数关系式：（3）将446米的跑道周长作为400米跑道场地的最外沿，那么它与最内圈（跑道周长400米）形成的区域最多能铺设道宽为1.2米的跑道多少条？【答案】（1）400米跑道中一段直道的长度为86.96m ；（2） 6.28400y x =+；（3）最多能铺设道宽为1.2米的跑道6条．【分析】()1根据周长的意义：直道长度+弯道长度400=求出，()2跑道宽度增加，就是半圆的半径增加，依据圆的周长公式可求当跑道宽度为1、2、3、4、5、⋯⋯时，跑道的周长，填写表格.并求出函数关系式．()3依据关系式，可求当跑道周长为446米时，对应的跑道的宽度，再根据每道宽1.2米，求出可以设计几条跑道．【详解】解：（1）400米跑道中一段直道的长度(400236 3.14)286.96m =-⨯⨯÷= （2）表格如下：2400 6.28400y x x π=+=+；（3）当446y =时，即6.28400446x +=，解得：7.32x m ≈7.32 1.26÷≈ 条∴最多能铺设道宽为1.2米的跑道6条．【点睛】体会跑道周长怎样随着跑道宽度的变化而变化的关系，进而得出宽度周长y 与跑道宽度x 之间的函数关系式，其中圆的周长公式、一次函数性质是解决问题必需的知识．9．（2019·湖南永州市·中考真题）在一段长为1000的笔直道路AB 上，甲、乙两名运动员均从A 点出发进行往返跑训练．已知乙比甲先出发30秒钟，甲距A 点的距离y （米）与其出发的时间x （分钟）的函数图象如图所示，乙的速度是150米分钟，且当乙到达B 点后立即按原速返回．（1）当x 为何值时，两人第一次相遇？（2）当两人第二次相遇时，求甲的总路程．【答案】（1）当x为0.75分钟时，两人第一次相遇；（2）当两人第二次相遇时，甲行驶的总路程是1100米．【分析】（1）根据函数图象中的数据可以计算出当x为何值时，两人第一次相遇；（2）根据函数图象中的数据可以计算出当两人第二次相遇时，甲行驶的总路程．【详解】（1）甲的速度为：100÷4＝250米/分钟，令250x＝150（x3060 +），解得，x＝0.75，答：当x为0.75分钟时，两人第一次相遇；（2）当x＝5时，乙行驶的路程为：150×（53060+）＝825＜1000，∴甲乙第二次相遇的时间为：10008255 5.5100015010-5-+=+（分钟），则当两人第二次相遇时，甲行驶的总路程为：1000+（5.5-5）×200＝1100（米），答：当两人第二次相遇时，甲行驶的总路程是1100米．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．10．（2019·湖北咸宁市·中考真题）小慧家与文具店相距960m，小慧从家出发，沿笔直的公路匀速步行12min来到文具店买笔记本，停留3min，因家中有事，便沿着原路匀速跑步6min返回家中．()1小慧返回家中的速度比去文具店的速度快多少？()2请你画出这个过程中，小慧离家的距离y与时间x的函数图象；()3根据图象回答，小慧从家出发后多少分钟离家距离为720?m【答案】（1）小慧返回家中的速度比去文具店的速度快80(/)m min ；（2）作图见解析；（3）小慧从家出发后9分钟或16.5分钟离家距离为720m . 【解析】【分析】()1根据速度＝路程/时间的关系，列出等式96096080612-=即可求解； ()2根据题中已知，描点画出函数图象；()3根据图象可得小慧从家出发后9分钟或16.5分钟离家距离为720m .【详解】（1）由题意可得，96096080612-=/m min （）答：小慧返回家中的速度比去文具店的速度快80/m min （）； ()2如图所示：()3根据图象可得，小慧从家出发后9分钟或16.5分钟离家距离为720m【点睛】本题考查一次函数的应用；能够理解题意，准确画出函数图象，并从图象中获取信息是解题的关键．。

2024学年九年级中考数学专题复习：行程问题(一次函数的综合实际应用)(提升篇)(含答案)

2024学年九年级中考数学专题复习：行程问题（一次函数的综合实际应用）姓名：___________班级：___________考号：___________1．一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，图中的折线表示两车之间距离()kmy与慢车行驶时间()h x之间的函数关系图象，请根据图象提供的信息回答：（1）快车的速度是______km/h．（2）求线段BC所表示的函数关系式．（3）若在第一列快车与慢车相遇时，第二列快车从乙地出发驶往甲地，速度与第一列快车相同，直接写出第二列快车出发多长时间与慢车相距200km．2．A、B两地相距60km，甲从A地去B地，乙从B地去A地，图中12，分别表示甲、乙l l两人离B地的距离y（km）与甲出发时间x（h）的函数关系图象．（1）求点A的坐标，并说明其实际意义；（2）甲出发多少时间，两人之间的距离恰好相距5km；（3）若用y3（km）表示甲、乙两人之间的距离，请在坐标系（图3）中画出y3（km）关于时间x（h）的函数关系图象，注明关键点的数据．3．快车甲和慢车乙分别从A、B两站同时出发，相向而行．快车到达B站后，停留1小时，然后原路原速返回A站，慢车到达A站即停运休息．下图表示的是两车之间的距离y（千米）与行驶时间x（小时）的函数图象．请结合图象信息．解答下列问题：（1）直接写出快、慢两车的速度及A、B两站间的距离；（2）求快车从B返回A站时，y与x之间的函数关系式；（3）出发几小时，两车相距200千米？请直接写出答案．4．甲、乙两人从相距4千米的两地同时、同向出发，乙每小时走4千米，小狗随甲一起同向出发，小狗追上乙的时候它就往甲这边跑，遇到甲时又往乙这边跑，遇到乙的时候再往甲这边跑…就这样一直匀速跑下去．如图，折线A B C--，A D E--分别表示甲、小狗在行进过程中，y与甲行进时间x(h)之间的部分函数图象．离乙的路程()km(1)求AB所在直线的函数解析式；(2)小狗的速度为______km/h；求点E的坐标；(3) 小狗从出发到它折返后第一次与甲相遇的过程中，求x为何值时，它离乙的路程与离甲的路程相等？5．甲、乙两地高速铁路建设成功，一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车均匀速行驶并同时出发．设普通列车行驶的时间为x（小时），两车之间的距离为y（千米）．图中的折线表示y与x之间的函数关系图像．求：(1)甲、乙两地相距______千米；(2)求动车和普通列车的速度；(3)求C点坐标和直线CD解析式；(4)求普通列车行驶多少小时后，两车相距1000千米．6．甲、乙两车分别从A，B两地同时出发，匀速行驶，先相向而行．途中乙车因故停留1小时，然后以原速继续向A地行驶，甲车到达B地后，立即按原路原速返回A地（甲车掉头的时间忽略不计），到达A地后停止行驶，原地休息；甲、乙两车距B地的路程y（千米）与所用时间x （时）之间的函数图象如图，请结合图象信息解答下列问题：(1)乙车的速度为千米/时，在图中的（）内应填上的数是．(2)求甲车从B地返回A地的过程中，y与x的函数关系式．(3)两车出发后几小时相距120千米，请直接写出答案：时．7．甲、乙两人从A地前往B地，先到终点的人在原地休息．已知甲先出发30s后，乙才出发．在运动过程中，甲、乙两人离A地的距离分别为1y（单位：m）、2y（单位：m），都是甲出发时间x（单位：s）的函数，它们的图象如图①．设甲的速度为1v m/s，乙的速度为2v m/s．(1)12:v v=______，=a______；(2)求2y与x之间的函数表达式；(3)在图②中画出甲、乙两人之间的距离s（单位：m）与甲出发时间x（单位：s）之间的函数图象．8．小明从学校出发，匀速骑行前往距离学校2400米的图书馆，小明出发的同时，同学小阳以每分钟80米的速度从图书馆沿同一条道路步行回学校，两人距离学校的路程y（单位：米）与小明从学校出发的时间x（单位：分钟）的函数图象如图所示．(1)点C的坐标为_________；(2)求直线BC的表达式；(3)若小明在图书馆停留7分钟后沿原路按原速返回，请补全小明距离学校的路程y与x的函数图象；(4)在（3）的基础上，小明能否在返校途中追上小阳？若能，请计算此时两人与学校之间的距离；若不能，请说明理由．9．如图，已知：平面直角坐标系中，正比例函数y＝kx（k≠0）的图象经过点A（﹣2，﹣2），点B是第二象限内一点，且点B的横、纵坐标分别是一元二次方程x2﹣36＝0的两个根．过点B作BC⊥x轴于点C．（1）直接写出k的值和点B的坐标：k＝；B（，）；（2）点P从点C出发，以每秒1个单位长度的速度沿x轴向右运动，设运动时间为t，若△BPO 的面积是S，试求出S关于t的函数解析式（直接写出t的取值范围）（3）在（2）的条件下，当S＝6时，以PQ为一边向直线PQ下方作正方形PQRS，求点R 的坐标．10．甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶，乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．根据图像回答下列问题：（1）乙车行驶小时追上了甲车．（2）乙车的速度是；（3）m=；（4）点H的坐标是；（5）n=．11．已知矩形ABCD中，AB＝4米，BC＝6米，E为BC中点，动点P以2米/秒的速度从A 出发，沿着△AED的边，按照A→E→D→A顺序环行一周，设P从A出发经过x秒后，△ABP 的面积为y（平方米），求y与x间的函数关系式．12．某兴趣小组利用计算机进行电子虫运动实验．如图1，在相距100个单位长度的线段AB 上，电子虫甲从端点A出发，匀速往返于端点A、B之间，电子虫乙同时从端点B出发，设定不低于甲的速度匀速往返于端点B、A之间．他们到达端点后立即转身折返，用时忽略不计．兴趣小组成员重点探究了甲、乙迎面相遇的情况，这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种．设甲、乙第一次迎面相遇时，相遇地点与点A之间的距离为x个单位长度，他们第二次迎面相遇时，相遇地点与点A之间的距离为y个单位长度．(1)请直接写出：当x＝20时，y的值为_________；当x＝40时，y的值为________；(2)兴趣小组成员发现了y与x的函数关系，并画出了部分函数图像（如图2中的线段OM，但不包括点O，因此点O用空心画出）①请直接写出：a＝_______；②分别求出各部分图像对应的函数解析式，并在图2中补全函数图像，标出关键点的坐标；(2)小黄在距离学校多少米处遭遇堵车？从小黄遇到堵车到小吴追上小黄用了多少时间？(3)小吴和小黄何时相距520m？15．甲、乙两人计划8：00一起从学校出发，乘坐班车去博物馆参观，乙乘坐班车准时出发，但甲临时有事没赶上班车，8：45甲沿相同的路线自行驾车前往，结果比乙早1小时到达．甲、乙两人离学校的距离y（千米）与甲出发时间x（小时）的函数关系如图所示．（1）点A的实际意义是什么？（2）求甲、乙两人的速度；（3）求OC和BD的函数关系式；（4）求学校和博物馆之间的距离．16．甲乙两人沿相同的路线同时登山甲、乙两人距地面的高度y（米）与登山时间x（分钟）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：（1）甲距地面的高度y（米）与登山时间x（分）之间的函数关系式为：y 甲．（2）若乙提速后，乙的速度是甲登山速度的3倍，登山多长时间时，乙追上了甲?此时乙距A 地的高度为多少米？答案：21200 430v=15 6v∴=⨯30 a∴=⨯。

2021重庆年中考17题一次函数图形行程问题专题训练(3)

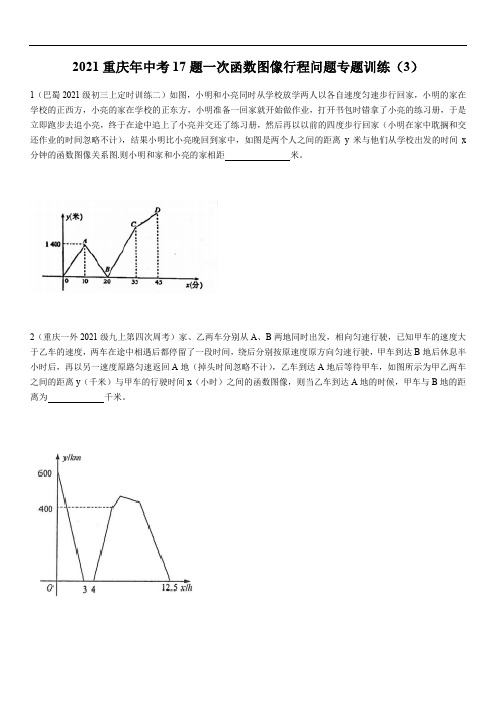
2021重庆年中考17题一次函数图像行程问题专题训练（3）1（巴蜀2021级初三上定时训练二）如图，小明和小亮同时从学校放学两人以各自速度匀速步行回家，小明的家在学校的正西方，小亮的家在学校的正东方，小明准备一回家就开始做作业，打开书包时错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以以前的四度步行回家（小明在家中耽搁和交还作业的时间忽略不计），结果小明比小亮晚回到家中，如图是两个人之间的距离y米与他们从学校出发的时间x 分钟的函数图像关系图.则小明和家和小亮的家相距米。

2（重庆一外2021级九上第四次周考）家、乙两车分别从A、B两地同时出发，相向匀速行驶，已知甲车的速度大于乙车的速度，两车在途中相遇后都停留了一段时间，绕后分别按原速度原方向匀速行驶，甲车到达B地后休息半小时后，再以另一速度原路匀速返回A地（掉头时间忽略不计），乙车到达A地后等待甲车，如图所示为甲乙两车之间的距离y（千米）与甲车的行驶时间x（小时）之间的函数图像，则当乙车到达A地的时候，甲车与B地的距离为千米。

3（重庆八中2021级九上第一次月考模拟)一艘轮船额一艘快艇分别从甲、乙两个港口出发（水流速度不计）相向而行，快艇匀速航行到达甲港后，立即原速返回乙港（掉头时间忽略不计）在返回途中追上轮船刚好到达一个景点，轮船靠岸一小时供游客观赏游玩，绕后继续以原速航行到乙港，两船到达乙港均停止航行，轮船和快艇之间的距离y（千米）与轮船出发时间x（小时）之间的函数图像如图所示，当快艇返回到乙港时，轮船距乙港还有千米4（重庆育才2021级九上第一次月考复习）一条笔直的公路上顺次有A、B、C三地，小明驾车从B地出发匀速行驶前往A地，到达A地后停止，在小明出发的同时，小李驾车从B地匀速出发行驶前往A地，到达A地停留2小时后，调头按原速向C行驶，若AB两地之间相距200千米，在行驶的过程中，两人之间的距离y（千米）与小李驾车时间x（小时）之间的函数图像如图所示，则在他们出发后经过小时相遇。

一次函数行程问题(附答案详细讲解)

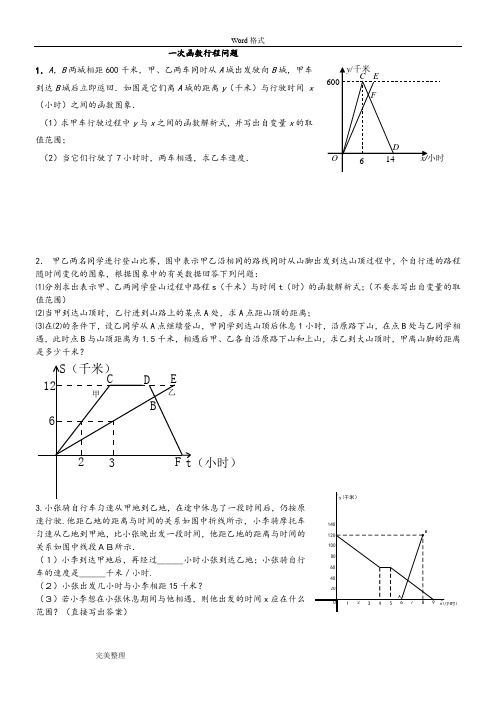
BA O80140120x(小时）1006040y(千米）20987654321一次函数行程问题1．A ，B 两城相距600千米，甲、乙两车同时从A 城出发驶向B 城，甲车到达B 城后立即返回．如图是它们离A 城的距离y （千米）与行驶时间 x （小时）之间的函数图象．（1）求甲车行驶过程中y 与x 之间的函数解析式，并写出自变量x 的取值范围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s （千米）与时间t （时）的函数解析式；（不要求写出自变量的取值范围）⑵当甲到达山顶时，乙行进到山路上的某点A 处，求A 点距山顶的距离；⑶在⑵的条件下，设乙同学从A 点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B 处与乙同学相遇，此时点B 与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米？12623S（千米）t（小时）CD EF B甲乙3.小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行车的速度是＿＿＿千米／小时.（２）小张出发几小时与小李相距15千米？（３）若小李想在小张休息期间与他相遇，则他出发的时间x 应在什么范围？（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

(完整word版)2019重庆中考17题-行程问题

中考专题17—行程问题【例1】（重庆巴蜀中学2017下期期中）一次越野赛跑中，当小明跑了1600米时，小刚跑了1450米,此后两人分别以另一速度跑完全程，两人到达终点时均停止跑步。

如图，折线图表示改变速度后两人之间的距离y（单位：米）与改变速度后跑步所用的时间x（秒)之间的关系，则这次越野赛跑的全程为米。

【变式1】（2017重庆八中4月一模）小兵早上从家匀速步行去学校，走到途中发现数学书忘在家里了，随即打电话给爸爸，爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店，此时还未遇到爸爸，小兵便在书店挑选了几支笔，刚付完款，爸爸正好赶到，将书交给了小兵,然后,小兵以原速继续上学，爸爸也以原速返回家,爸爸到家后，过一会小兵才到达学校。

两人之间的距离y（米)与小兵从家出发的时间x(分钟）的函数关系如图所示,则家与学校相距米。

【变式2】如图:小明和小亮同时从学校放学,两人以各自速度匀速步行回家，小明的家在学校的正西方向，小亮的家在学校的正东方向，小明准备一回家就开始做作业，打开书包时发现错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以先前的速度步行回家,（小明在家中耽搁和交还作业的时间忽略不计）结果小明比小亮晚回到家中。

如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图。

则小明的家和小亮的家相距米【变式3】一天早晨，小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车,沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离y（米)与小玲从家出发后步行的时间x（分）之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为米．【例2】（2017重庆一中月考）甲、乙两车分别从A，B两地同时相向匀速行驶，当乙车到达A地后,继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头,并保持原速与乙车同向行驶，经过15小时后两车同时到达距A地300千米的C地（中途休息时间忽略不计）。

一次函数行程问题(附答案详解)

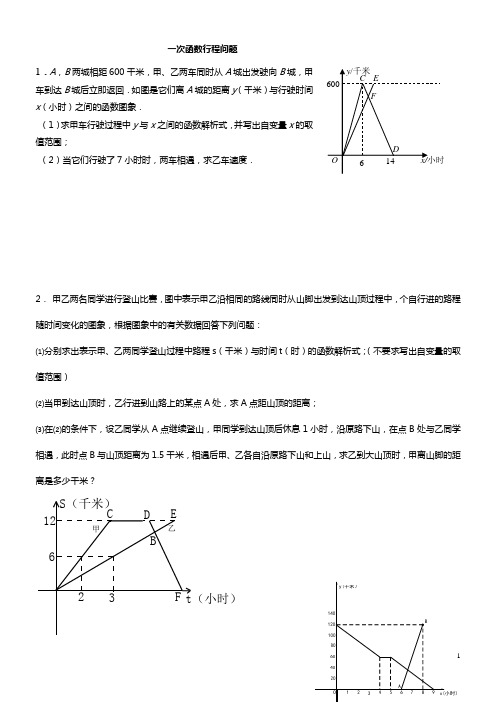
B80140120100y(千米）一次函数行程问题1．A ，B 两城相距600千米，甲、乙两车同时从A 城出发驶向B 城，甲车到达B 城后立即返回．如图是它们离A 城的距离y （千米）与行驶时间x （小时）之间的函数图象．（1）求甲车行驶过程中y 与x 之间的函数解析式，并写出自变量x 的取值范围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s （千米）与时间t （时）的函数解析式；（不要求写出自变量的取值范围）⑵当甲到达山顶时，乙行进到山路上的某点A 处，求A 点距山顶的距离；⑶在⑵的条件下，设乙同学从A 点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B 处与乙同学相遇，此时点B 与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米？12623S（千米）t（小时）CD EF B甲乙3.小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行车的速度是＿＿＿千米／小时. （２）小张出发几小时与小李相距15千米？（３）若小李想在小张休息期间与他相遇，则他出发的时间x 应在什么范围？（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时； (2)求线段CD 所表示的函敛关系式；(3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，(第23题图)x （小时）5．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y (千米)，图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系．（1）根据图中信息，求线段AB 所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t 时，求t 的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)6. 在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与．B ．港的距离．．．．分别为1y 、2y （km ），1y 、2y 与x 的函数关系如图所示．（1）填空：A 、C 两港口间的距离为 km ， a ；（2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．7.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行，并以各自的速度匀速行驶，途径配货站C ，甲车先到达C 地，并在C 地用1小时配货，然后按原速度开往B 地，乙车从B 地直达A 地，图16是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像O y/km9030 a3Px/h（1）A 、B 两地的距离是千米，甲车出发小时到达C 地；（2）求乙车出发2小时后直至到达A 地的过程中，与的函数关系式及的取值范围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米8．小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O －A －B －C 和线段OD 分别表示两人离学校的路程s （千米）与所经过的时间t （分钟）之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟。

(完整版)一次函数行程问题(附答案详解)(最新整理)

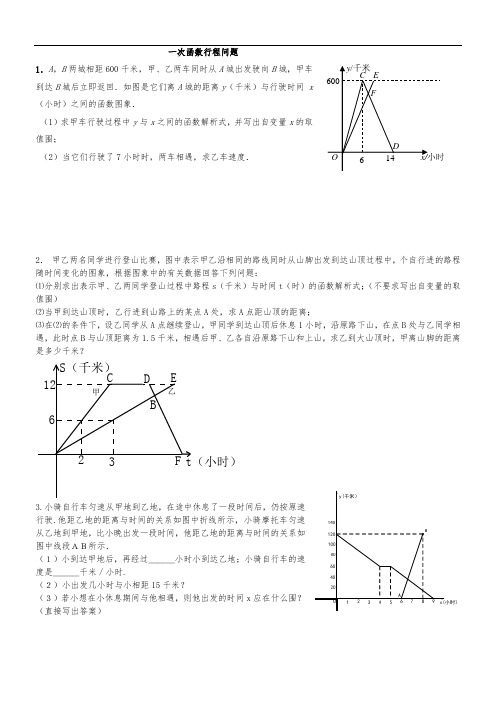
一次函数行程问题1．A ，B 两城相距600千米，甲、乙两车同时从A 城出发驶向B 城，甲车到达B 城后立即返回．如图是它们离A 城的距离y （千米）与行驶时间x （小时）之间的函数图象．（1）求甲车行驶过程中y 与x 之间的函数解析式，并写出自变量x 的取值范围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s （千米）与时间t （时）的函数解析式；（不要求写出自变量的取值范围）⑵当甲到达山顶时，乙行进到山路上的某点A 处，求A 点距山顶的距离；⑶在⑵的条件下，设乙同学从A 点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B 处与乙同学相遇，此时点B 与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米？12623S （千米）t （小时）CD EF B甲乙3.小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行车的速度是＿＿＿千米／小时.（２）小张出发几小时与小李相距15千米？（３）若小李想在小张休息期间与他相遇，则他出发的时间x 应在什么范围？（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时；(2)求线段CD 所表示的函敛关系式；(3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，(千23千千)千千5．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y (千米)，图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系．（1）根据图中信息，求线段AB 所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t 时，求t 的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)6. 在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与B 港的距离分别为、（km ），、与x 的函数关系如图所示．1y 2y 1y 2y （1）填空：A 、C 两港口间的距离为 km ，；a （2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．7.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行，并以各自的速度匀速行驶，途径配货站C ，甲车先到达C 地，并在C 地用1小时配货，然后按原速度开往B 地，乙车从B 地直达A 地，图16是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像（1）A 、B 两地的距离是千米，甲车出发小时到达C 地；（2）求乙车出发2小时后直至到达A 地的过程中，与的函数关系式及的取值范围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米8．小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O －A －B －C 和线段OD 分别表示两人离学校的路程（千米）与所经过的时间（分钟）之间的函数关系，请根据图象回答下列问题：s t （1）小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟。

一次函数行程问题及答案详解

一次函数行程问题 1． A， B两城相距 600 千米，甲、乙两车同时从 A 城出发驶向 B 城，甲车到达 B 城后立即返回．如图是它们离 A 城的距离 y（千米）与行驶时间 x （小时）之间的函数图象．
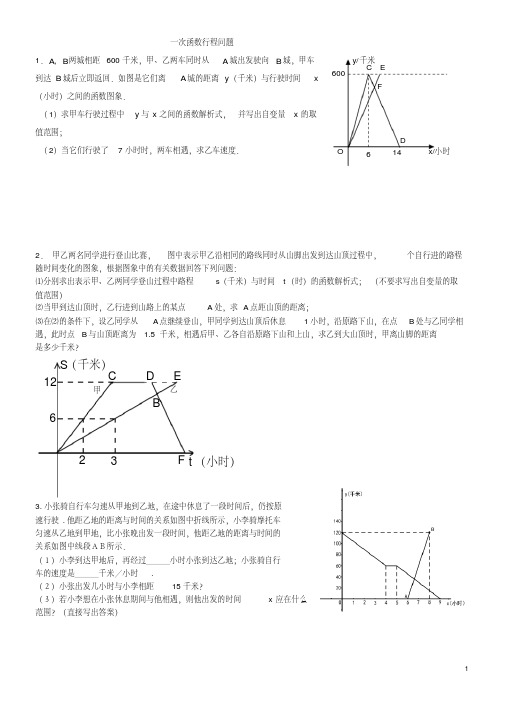
（ 1）求甲车行驶过程中 y 与 x 之间的函数解析式，并写出自变量 x 的取值范围；
（ 2）当它们行驶了 7 小时时，两车相遇，求乙车速度．
s（千米）
4
AB
小聪 D 小明
2
第 1题
C
O
15
30 45
t （分钟）
（ 1）小聪在天一阁查阅资料的时间为 ________分钟，小聪返回学校的速度为 _______千米 / 分钟。
（ 2）请你求出小明离开学校的路程 s （千米）与所经过的时间 t （分钟）之间的函数关系 ;
（ 3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
中 y 关于 x 的函数的大致图像 . ( 温馨提示：请画在答题卷相对应的图上 )
6. 在一条直线上依次有 A、B、C三个港口，甲、乙两船同时分别从 A、B港口出发，沿直线匀速驶向 C港，最终达到 C港．设甲、乙两船行驶 x（ h）后，与．B．港．的．距．离．分别为 y1 、 y2（ km）， y1 、 y2 与 x 的函数关系如图所示．
S（千米）
12
C
甲
6
DE
乙
B
23
F t （小时）
3. 小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原
速行驶 . 他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车
匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的
关系如图中线段ＡＢ所示．
（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行

初中数学《一次函数的应用-行程问题》典型例题及答案解析

由乙车刚到达货站的时间，可以得出甲车行驶的总路程，结合、两地的距离即可判断④也成立.
综上可知①②③④皆成立.
【详解】
线段代表乙车在途中的货站装货耗时半小时，
（小时），即①成立；
分钟小时，
甲车的速度为（千米/时），即②成立；
设乙车刚出发时的速度为千米/时，则装满货后的速度为千米/时，
根据题意可知：，
7．如图，一辆汽车和一辆摩托车分别从A，B两地去同一城市，l1，l2分别表示汽车、摩托车离A地的距离s（km）随时间t（h）变化的图象，则下列结论：①摩托车比汽车晚到1 h；②A，B两地的距离为20 km；③摩托车的速度为45 km/h，汽车的速度为60 km/h；④汽车出发1 h后与摩托车相遇，此时距离B地40 km；⑤相遇前摩托车的速度比汽车的速度快．其中正确的结论有（）
【答案】B
【解析】
【分析】
设同向行驶的相邻两车的距离及车、小林的速度为未知数，等量关系为：5×车速-5×小林的速度=同向行驶的相邻两车的距离；3×车速+3×小林的速度=同向行驶的相邻两车的距离；把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式，相除可得所求时间．
【详解】
设101路公交车的速度是x米/分，小林行走的速度是y米/分，同向行驶的相邻两车的间距为s米.
解得：，
乙车发车时，甲车行驶的路程为（千米），
乙车追上甲车的时间为（小时），
小时分钟，即③成立；
乙车刚到达货站时，甲车行驶的时间为小时，
此时甲车离地的距离为（千米），即④成立；
综上可知正确的有：①②③④.
故选： .
【点睛】
本题考查了一次函数的应用，解题的关键是知道各数量间的关系结显繁琐，解决该类题型的方法是掌握各数量间的关系结合行程得出结论.

2020年重庆中考行程类专题

y/米400012x/分O y/米x/分钟138********专题3一次函数行程专项训练类型一、单线型例1．某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落在公司，无法联系，于是乙匀速骑车去追赶甲．乙刚出发2分钟时，甲也发现自己手机落在公司，立刻按原路原速骑车回公司，2分钟后甲遇到乙，乙把手机给甲后立即原路原速返回公司，甲继续原路原速赶往某小区送物件，甲乙两人相距的路程y （米）与甲出发的时间x （分钟）之间的关系如图所示（乙给甲手机的时间忽略不计）．则乙回到公司时，甲距公司的路程是米．变式1.一天，小明从家出发匀速步行去学校上学.几分钟后，在家休假的爸爸发现小明忘带数学书，于是爸爸立即匀速跑步去追小明，爸爸追上小明后以原速原路跑回家.小明拿到书后以原速度的45快步赶往学校，并在从家出发后23分钟到校（小明被爸爸追上时交流时间忽略不计）.两人之间相距的路程y(米)与小明从家出发到学校的步行时间x （分钟）之间的函数关系如图所示，则小明家到学校的路程为米.变式2.甲、乙两人分别从各自家出发乘坐出租车前往智博会，由于堵车，两人同时选择就近下车，已知甲车在乙车前面200米的A地下车，然后分别以各自的速度匀速走向会场，3分钟后，乙发现有物品遗落在出租车上，于是立即以不变的速度返回寻找，找到出租车时，出租车恰好向会场方向行驶了100米，乙拿到物品后立即以原速返回继续走向会场，同时甲以先前速度的一半走向会场，又经过10分钟，乙在B地追上甲，两人随后一起以甲放慢后的速度行走1分钟到达会场，甲、乙两人相距的路程y（m）与甲行走的时间x（min）之间的关系如图所示，（乙拿物品的时间忽略不计），则A地距离智博会会场的距离为米变式3.张同学与王同学分别从A，B两地出发参加往直线往返运动，同时出发匀速相向而行；张同学的速度为120米/分，王同学的速度大于张同学：第一次相遇后，王同学在相遇处休息12分钟后以原速接着向A地运动，此时张同学未到达B地；两人分别到达后以原路原速返回，两人之间的距离y（米）与运动时间x（分）之间的关系如图所示，则第分钟时两人第二次相遇．类型二、双线型例1、快、慢两车分别从相距480km的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留了1小时，然后继续以原速驶向甲地，到达甲地后即停止行驶；快车到达乙地后，立即按原路原速返回甲地（调头时间忽略不计）．如图是快、慢两车距乙地路程y（km）与所用时间x（h）之间的函数图像，这当两车第一次相遇时，快车距离甲地路程是________千米变式1.牛牛和峰峰在同一直线跑道AB进行往返跑，牛牛从起点A出发，峰峰在牛牛前方C处与牛牛同时出发，当牛牛超越峰峰到达终点B处时，休息了100秒才又以原速返回A地，而峰峰到达终点B处后马上以原来速度的3.2倍往回跑，最后两人同时到达A地，两人距B地的路程记为y（米），峰峰跑步时间记为x(秒)，y和x的函数关系如图所示，则牛牛和峰峰第一次相遇时他们距A点____________米变式2.“渝黔高速铁路”即将在 2017 年底通车，通车后，重庆到贵阳、广州等地的时间将大大缩短。

2021年重庆年中考17题一次函数图像与行程问题综合专题(重庆育才试题集)

2021年重庆年中考17题一次函数图像与行程问题专题（重庆育才试题集）A、两地同时相向而行，并以各自的速度匀速行驶，途中1（育才2021级初三上定时训练二）小明和小亮分别从B会经过奶茶店C，小明先到达奶茶店C，并在C地休息了一小时，然后按原速度前往B地，小亮从B地直达A地，结果还是小明先到达目的地，下图是小明和小亮两人之间的距离y（千米）与小亮出发时间x（时）的函数的图像，请问当小明到达B地时，小亮距离A地千米.2（育才2020级初三下中考模拟5月份）一辆货车从A地匀速驶往相距350km的B地，当货车行驶1小时经过途中的C地时，一辆快递车恰好从C地出发以另一速度匀速驶往B地，当快递车到达B地后立即掉头以原来的速度匀速驶往A地．（货车到达B地，快递车到达A地后分别停止运动）行驶过程中两车与B地间的距离y（单位：km）与货车从出发所用的时间x（单位：h）间的函数关系如图所示．则货车到达B地后，快递车再行驶h到达A地．3（育才2020级初三下中考模拟二）快、慢车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早小时，慢车速度是快车速度的一半．快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示．在快车从乙地返回甲地的过程中，当慢车恰好在快车前，且与快车相距80千米的路程时，慢车行驶的总的时间是小时．4（育才2020级初三下中考模拟三））A、B两地之间路程为4500米，甲、乙两人骑车都从A地出发，已如甲先出发6分钟后，乙才出发，乙在A、B之间的C地追赶上甲，当乙追赶上甲后，乙立即返A地，甲继续向B地前行．甲到达B地后停止骑行．乙骑行到A地时也停止（假定乙在C地掉头的时间忽略不计），在整个骑行过程中，甲和乙均保持各自的速度匀速骑行，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与B地相距的路程是米．5（育才2019级初三下中考模拟一）甲乙沿着同一路线以各自的速度匀速从A地到B地，甲出发1分钟后乙随即出发，甲、乙到达B地后均立即按原路原速返回A地，甲、乙之间的距离y（米）与甲出发的时间x（分）之间的部分图象如图所示．当甲返回到A地时，乙距离B地米．6（育才2020级初三下中考模拟二练习）小刚从家出发匀速步行去学校上学．几分钟后发现忘带数学作业，于是掉头原速返回并立即打电话给爸爸，挂断电话后爸爸立即匀速跑步去追小刚，同时小刚以原速的两倍匀速跑步回家，爸爸追上小刚后以原速的倍原路步行回家．由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校，并在从家出发后23分钟到校（小刚被爸爸追上时交流时间忽略不计）．两人之间相距的路程y（米）与小刚从家出发到学校的步行时间x（分钟）之间的函数关系如图所示，则小刚家到学校的路程为米．7（双福育才2020级初三下中考模拟一）小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行,小宁先出发5分钟后,小强骑自行车匀速回家,小宁出发时跑步，中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟,两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示，下列选项正确的是()A.小强骑车的速度为250m/minB.小宁由跑步变为步行的时刻为15分钟C.小强到家的时刻为15分钟D.当小强到家时，小宁离图书馆的距离为1500m8（育才2020级初三下入学测试）一个阳光明媚的上午，小育和小才相约从学校沿相同的路线去学校旁边的公园写生，小育出发5分钟后小才出发，此时小育发现忘记带颜料，立即按原速原路回学校拿颜料，小育拿到颜料后，以比原速提高20%的速度赶去公园，结果还是比小才晚2分钟到公园（小育拿颜料的时间忽略不计）．在整个过程中，小才保持匀速运动，小育提速前后也分别保持匀速运动，如图所示是小育与小才之间的距离y（米）与小育出发的时间x（分钟）之间的函数图象，则学校到公园的距离为米．第17题图9（育才2020级初三上第二次月考）一条笔直的公路上顺次有A、B、C三地，甲车从B地出发往A地匀速行驶，到达A地后停止，在甲车出发的同时，乙车从B地出发往A地匀速行驶(乙车比甲上快），到达A地停留1小时后，调头按原速向C地行驶，甲乙两车相遇后，甲车速度提升至原速的1.5倍，乙车速变不变，若AB两地相距300千米，在两车行驶的过程中，甲，乙两车之间的距离y（千米）与乙车行驶时间x(时）之间的关系如图所示，则甲车到达A地后，经过时乙车到达C地.10（双福育才2020级初三下第二次诊断性测试）甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，中途与乙相遇后休息了一会儿，然后以原来的速度继续行驶直到A地．设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示，则乙车到达A地时甲车距B地的路程为千米．11（育才2020级初三下开学试卷）一条笔直的公路上顺次有A、B、C三地，甲车从B地出发往A地匀速行驶，到达A地后停止，在甲车出发的同时，乙车从B地出发往A地匀速行驶，到达A地停留1小时后，调头按原速向C地行驶，若AB两地相距300千米，在两车行驶的过程中，甲、乙两车之间的距离y（千米）与乙车行驶时间x （小时）之间的函数图象如图所示，则在他们出发后经过小时相遇．12（育才2020级初三上期末试卷）自行车远动员甲准备参加一项国际自行车赛事，为此特地骑自行车从A地出发，匀速前往168千米外的B地进行拉练．出发2小时后，乙发现他忘了带某训练用品，于是马上骑摩托车从A 地出发匀速去追甲送该用品．已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米，但摩托车行驶一小时后突遇故障，修理15分钟后，又上路追甲，但速度减小了，乙追上甲交接了训练用品（交接时间忽略不计），随后立即以修理后的速度原路返回，甲继续以原来的速度骑行直至B地．如图表示甲、乙两人之间的距离S（千米）与甲骑行的时间t（小时）之间的部分图象，则当甲达到B地时，乙距离A地千米．13（育才2020级初三上开学测试）国防教育和素质拓展期间，某天小明和小亮分别从校园某条路的A，B两端同时相向出发，当小明和小亮第一次相遇时，小明觉得自己的速度太慢便决定提速至原速的倍，当他到达B端后原地休息，小亮匀速到达A端后，立即按照原速返回B端（忽略掉头时间）．两人相距的路程y（米）与小亮出发时间t（秒）之间的关系如图所示，当小明到达B端后，经过秒，小亮回到B端．14（育才2020级初三上期中试卷）小蒲家与学校之间是一条笔直的公路，小蒲从家步行前往学校的途中发现忘带作业本，便向路人借了手机打给妈妈，妈妈接到电话后，带上作业本马上赶往学校，同时小蒲沿原路返回，两人相遇后，小蒲立即赶往学校，妈妈沿原路返回家，小蒲到达学校刚好比妈妈到家晩了2分钟．若小蒲步行的速度始终不变，打电话和交接作业本的时间忽略不计，小蒲和妈妈之间的距离y米与小蒲打完电话后步行的时间x分钟之间的函数关系如图所示；则相遇后妈妈返回家的速度是每分钟米．15（育才2020级初三下入学测试）国防教育和素质拓展期间，某天小明和小亮分别从校园某条路的A ，B 两端同时相向出发，当小明和小亮第一次相遇时，小明觉得自己的速度太慢便决定提速至原速的32倍，当他到达B 端后原地休息，小亮匀速到达A 端后，立即按照原速返回B 端（忽略掉头时间）．两人相距的路程y （米）与小亮出发时间t （秒）之间的关系如图所示，当小明到达B 端后，经过______秒，小亮回到B 端．16（育才2019级初三是哪个期末测试）甲、乙两车从A 地出发，沿同一路线驶向B 地。

一次函数行程问题(附问题详解详解)

BA O80140120x(小时）1006040y(千米）20987654321一次函数行程问题1．A ，B 两城相距600千米，甲、乙两车同时从A 城出发驶向B 城，甲车到达B 城后立即返回．如图是它们离A 城的距离y （千米）与行驶时间 x （小时）之间的函数图象．（1）求甲车行驶过程中y 与x 之间的函数解析式，并写出自变量x 的取值围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s （千米）与时间t （时）的函数解析式；（不要求写出自变量的取值围）⑵当甲到达山顶时，乙行进到山路上的某点A 处，求A 点距山顶的距离；⑶在⑵的条件下，设乙同学从A 点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B 处与乙同学相遇，此时点B 与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米？12623S（千米）t（小时）CD EF B甲乙3.小骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小骑摩托车匀速从乙地到甲地，比小晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小到达甲地后，再经过＿＿＿小时小到达乙地；小骑自行车的速度是＿＿＿千米／小时.（２）小出发几小时与小相距15千米？（３）若小想在小休息期间与他相遇，则他出发的时间x 应在什么围？（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时； (2)求线段CD 所表示的函敛关系式；(3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，(第23题图)x （小时）5．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y (千米)，图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系．（1）根据图息，求线段AB 所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t 时，求t 的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)6. 在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与．B ．港的距离．．．．分别为1y 、2y （km ），1y 、2y 与x 的函数关系如图所示．（1）填空：A 、C 两港口间的距离为 km ， a ；（2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值围．7.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行，并以各自的速度匀速行驶，途径配货站C ，甲车先到达C 地，并在C 地用1小时配货，然后按原速度开往B 地，乙车从B 地直达A 地，图16是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像（1）A 、B 两地的距离是千米，甲车出发小时到达C 地；（2）求乙车出发2小时后直至到达A地的过程中，与的函数关系式及的取值围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米8．小聪和小明沿同一条路同时从学校出发到天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O－A－B－C和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟。

一次函数行程问题(附答案详解)

一次函数行程问题1．A，B两城相距600千米，甲、乙两车同时从A城出Array发驶向B城，甲车到达B城后立即返回．如图是它们离A城的距离y（千米）与行驶时间x（小时）之间的函数图象．（1）求甲车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；（2）当它们行驶了7小时时，两车相遇，求乙车速度．2．甲乙两名同学进行登山比赛，图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中，个自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：⑴分别求出表示甲、乙两同学登山过程中路程s（千米）与时间t（时）的函数解析式；（不要求写出自变量的取值范围）⑵当甲到达山顶时，乙行进到山路上的某点A处，求A点距山顶的距离；⑶在⑵的条件下，设乙同学从A点继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B处与乙同学相遇，此时点B与山顶距离为1.5千米，相遇后甲、乙各自沿原路下山和上山，求乙到大山顶时，甲离山脚的距离是多少千米BAO80140120x(小时）1006040y(千米）2098765432112623S（千米）t（小时）CD EF B甲乙3.小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段ＡＢ所示．（１）小李到达甲地后，再经过＿＿＿小时小张到达乙地；小张骑自行车的速度是＿＿＿千米／小时.（２）小张出发几小时与小李相距15千米（３）若小李想在小张休息期间与他相遇，则他出发的时间x 应在什么范围（直接写出答案）4．周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。

接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，(1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时；(2)求线段CD 所表示的函敛关系式；(3)问小明能否在12：0 0前回到家若能，请说明理由：若不能，请算出12：00时他离家的路程，(第23题图)x （小时）5．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y (千米)，图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系．（1）根据图中信息，求线段AB 所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t 时，求t 的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)6. 在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与．B．港的距离．．．．分别为y、2y（km），1y、2y与x的函数关系如图所示．1（1）填空：A、C两港口间的距离为 km， a；（2）求图中点P的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．7.某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行，并以各自的速度匀速行驶，途径配货站C，甲车先到达C地，并在C地用1小时配货，然后按原速度开往B地，乙车从B地直达A地，图16是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像（1）A、B两地的距离是千米，甲车出发小时到达C地；（2）求乙车出发2小时后直至到达A地的过程中，与的函数关系式及的取值范围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米8．小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O－A－B－C和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟。

重庆中考数学 题一次函数行程问题

一次函数行程问题及答案详解

初中数学《一次函数应用—行程问题》典型例题及答案解析

专题06 一次函数中的行程问题(解析版)中考数学二轮专题复习之函数与实际问题真题满分过(全国通用)

2024学年九年级中考数学专题复习：行程问题(一次函数的综合实际应用)(提升篇)(含答案)

2021重庆年中考17题一次函数图形行程问题专题训练(3)

一次函数行程问题(附答案详细讲解)

(完整word版)2019重庆中考17题-行程问题

一次函数行程问题(附答案详解)

(完整版)一次函数行程问题(附答案详解)(最新整理)

一次函数行程问题及答案详解

初中数学《一次函数的应用-行程问题》典型例题及答案解析

2020年重庆中考行程类专题

2021年重庆年中考17题一次函数图像与行程问题综合专题(重庆育才试题集)

一次函数行程问题(附问题详解详解)

一次函数行程问题(附答案详解)

重庆中考数学题一次函数行程问题