二次函数专项练习
二次函数的定义专项练习30题(有答案)

二次函数的定义专项练习 30 题(有答案)1.下列函数中,是二次函数的有( )① y=1﹣ x 2② y= ③ y=x (1﹣x )④ y= ( 1﹣ 2x )( 1+2x )A 1 个B 2 个C 3 个D 4 个5.若 y=(m 2+m )是二次函数,则 m 的值是( )A m=1 ±2B m=2C m= ﹣ 1 或D m=3...m=3.6.下列函数 ,y=3x 2,,y=x (x ﹣2),y=(x ﹣ 1)2﹣ x 2 中,二次函数的个数为 (7.下列结论正确的是()二次函数中两个变量的值是非零实数二次函数中变量 x 的值是所有实数2形如 y=ax +bx+c 的函数叫二次函数2二次函数 y=ax +bx+c 中 a ,b ,c 的值均不能为零8.下列说法中一定正确的是()A . y=ax 2 是二次函数B . 二次函数自变量的取值范围是所有实数C . 二次方程是二次函数的特例D .二次函数自变量的取值范围是非零实数3.下列具有二次函数关系的是()A . 正方形的周长 y 与边长 xB . 速度一定时,路程 s 与时间 tC . 三角形的高一定时,面积 y 与底边长 xD .正方形的面积 y 与边长 x4.若 y=(2﹣ m )是二次函数,则 m 等于( )2.下列结论正确的是()D 不能确定 A C ﹣ 2 ±2B 2A .B .C .D .2A . 函数 y=ax 2+bx+c (其中 a ,b , c 为常数)一定是二次函数B . 圆的面积是关于圆的半径的二次函数C . 路程一定时,速度是关于时间的二次函数D .圆的周长是关于圆的半径的二次函数29.函数 y=( m ﹣ n )x 2+mx+n 是二次函数的条件是()A .m 、n 是常数,且 m ≠0 B . m 、 n 是常数,且 m ≠nC .m 、n 是常数,且 n ≠0D .m 、 n 可以为任何常数10.下列两个量之间的关系不属于二次函数的是()A .速度一定时,汽车行使的路程与时间的关系B . 质量一定时,物体具有的动能和速度的关系C .质量一定时,运动的物体所受到的阻力与运动速度的关系D .从高空自由降落的物体,下降的高度与下降的时间的关系11.下列函数中, y 是 x 二次函数的是( ) A y=x ﹣1B y=x 2+ ﹣ 10C2 y=x +2xD 2y =x ﹣ 1 ....12.下面给出了 6 个函数:其中是二次函数的有( )A 1 个B 2个C 3 个213.自由落体公式 h= gt 2(g 为常量),h 与 t 之间的关系是()A 正比例函数B 一次函数C 二次函数D 以上答案都不对14.如果函数 y= ( k ﹣ 3) +kx+1 是二次函数,那么 k 的值一定是 ___________ .15.二次函数 y= ( x ﹣2) 2﹣ 3 中,二次项系数为 __________ ,一次项系数为 ___________ 为 _________ .16.已知函数 y=(k+2) 是关于 x 的二次函数,则 k= __________ . 17.已知二次函数的图象是开口向下的抛物线, m= ___________ .2218.当 m __________ 时,关于 x 的函数 y= (m 2﹣1)x 2+(m ﹣1) x+3 是二次函数.2 2 219. y=(m 2﹣ 2m ﹣3)x 2+(m ﹣1)x+m 2是关于 x 的二次函数要满足的条件是 ___________ .① y=3x 2﹣1;② y=﹣ x 2﹣3x ; ③ y=;2④ y=x (x +x+1 );⑤y=⑥ y=,常数项220.二次函数 y=ax +bx+c ( a ≠0)中,当 b=0,c ≠0 时,函数表达式为 _______ ;当 b ≠0,c=0 时,函数表达式为 ________ .221.函数 y=2x +3x+7 中自变量的取值范围为 ___________ . 22.如果函数是关于 x 的二次函数,则 k= ___________ .23.如图所示,长方体的底面是边长为 xcm 的正方形,高为 6cm ,请你用含 x 的代数式表示这个长方体的 侧面展开图的面积 S= __________ ,长方体的体积为 V= ____________ ,各边长的和 L= ____________在上面的三个函数中, __________ 是关于 x 的二次函数.时,它的图象是抛物线.25.已知二次函数 ,当 x >0时,y 随 x 的增大而增大,则 m=27.已知是 x 的二次函数,求出它的解析式.28.用一根长为 800cm 的木条做一个长方形窗框,若宽为 x cm ,写出它的面积 y 与 x 之间的函数关系式, 并判断 y 是 x 的二次函数吗?2229.已知函数 y=(m ﹣m )x +(m ﹣1)x+m+1 . (1)若这个函数是一次函数,求 m 的值;(2)若这个函数是二次函数,则 m 的值应怎样? 30.已知 ,当 m 为何值时,是二次函数?26.已知 是 x 的二次函数,求 m 的值和二次函数的解析式. +3 ,当m=二次函数的定义 30 题参考答案:1. ① y=1﹣ x =﹣ x +1,是二次函数; ② y= ,分母中含有自变量,不是二次函数;22③ y=x (1﹣x ) =﹣x +x ,是二次函数; ④ y=( 1﹣2x )(1+2x ) =﹣4x +1,是二次函数. 二次函数共三个, 故选 C2. A 、应强调 a 是常数, a ≠0,错误; B 、二次函数解析式是整式,自变量可以取全体实数,正确; C 、二次方程不是二次函数,更不是二次函数的特例,错误;D 、二次函数的自变量取值有可能是零,如 y=x 2,当 x=0 时, y=0,错误. 故选 B . 3. A 、y=4x ,是一次函数,错误; B 、s=vt ,v 一定,是一次函数,错误; C 、y= hx ,h 一定,是一次函数,错误 D 、y=x 2,是二次函数,正确.故选 D .24.根据二次函数的定义,得: m 2﹣2=2 解得 m=2 或 m=﹣ 2又∵ 2﹣m ≠0∴m ≠2∴当 m=﹣2 时,这个函数是二次函数.故选 C5.根据题意的得:,解得: ,∴ m=3,故选 D .,y=x ( x ﹣ 2)都符合二次函数定义的条件,是二次函数;,y=(x ﹣1)2﹣x 2 整理后,都是一次函数.二次函数有三个.故选B .7.A 、例如 y=x 2,自变量取 0,函数值是 0,所以不对; B 、二次函数中变量 x 的值可以取所有实数,正确; C 、应强调当 a ≠0 时,是二次函数,错误; D 、要求 a ≠0,b 、c 可以为 0.故选 B28. A 、只有当 a ≠0才是二次函数,错误; B 、由已知得 S=πR 2, S 是 R 的二次函数,正确;9.根据二次函数的定义可得: m ﹣ n ≠0,即 m ≠n .故选 B .210. A 、s=vt , v 一定,是一次函数,错误; B 、 E=mv ,m 一定,是二次函数,正确;C 、 f=mv 2,v 一定,是二次函数,正确;D 、H=gt 2,g 一定,是二次函数,正确.故选 A .11. A 、一次函数,不是二次函数; B 、不是关于 x 的整式,不符合二次函数的定义; C 、符合二次函数的定义; D 、 y 的指数为 2,不符合二次函数的定义;故选 C .12. ① 符合二次函数的定义;② 符合二次函数的定义;③ 不是整式,不符合二次函数的定义;④ 整理后 x 的最高次数为 3,不符合二次函数的定义;⑤ 不是整式,不符合二次函数的定义;⑥ 不是整式,不符合二次函数的定义; 所以是二次函数的共有 2 个,故选 B .13.因为等号的右边是关于 t 的二次式,所以 h 是 t 的二次函数.214.根据二次函数的定义,得: k 2﹣ 3k+2=2,解得 k=0 或 k=3; 又∵ k ﹣ 3≠0,∴ k ≠3.∴当 k=0 时,这个函数是二次函数.2215. ∵y= (x ﹣2) 2﹣3= x 2﹣ 2x ﹣1,∴二次项系数为 ,一次项系数为﹣ 2,常数项为﹣ 1.216. ∵函数 y=(k+2) 是关于 x 的二次函数,∴ k +k ﹣4=2,解得 k=2 或﹣ 3,且 k+2 ≠0,k ≠﹣2.6. y=3x 2,C 、由已知得 v= ,s 一定,是反比例函数,错误;D 、由已知得 C=2πR ,是一次函数,错误.故选 B .故 k=2 或﹣ 317.∵二次函数的图象是开口向下的抛物线, ∴ ,解得 m= ﹣2. 故答案为:﹣ 2218.∵ y 是 x 的二次函数,∴ m 3﹣ 1≠0,∴ m ≠±1,故满足的条件是 m ≠±1.故答案为: ≠±1 219.由题意得: m 2﹣2m ﹣3≠0,(m ﹣3)(m+1)≠0,解得 m ≠﹣1且 m ≠3.220.当 b=0, c ≠0 时,二次函数表达式为 y=ax 2+c ;2当 b ≠0, c=0 时,二次函数表达式为 y=ax 2+bx . 故答案为: 22 y=ax +c ;y=ax +bx . 21.函数 y=2x +3x+7 中,自变量 x 的取值范围是全体实数.故答案为:全体实数.22. ∵函数 是关于 x 的二次函数, ∴k ﹣1≠0且 k 2﹣ k+2=2 ,解得 k=0 或 k=1 ,∴ k=0 . 故答案为 0. 23.长方体的侧面展开图的面积 S=4x ×6=24x ;22长方体的体积为 V=x 2×6=6x 2; 各边长的和 L=4x ×2+6×4=8x+24 ;其中, V=6x 2 是关于 x 的二次函数24. ∵二次函数的图象是抛物线,∴ m ﹣1=2,解得 m=3 .225.根据题意得 m ≠0 且 m ﹣2m ﹣ 6=2,解得 m 1=4,m 2=﹣2, ∵二次函数的对称轴为 y 轴,当 x >0 时, y随 x 的增大而增大, ∴二次函数的图象的开口向上,即 m > 0,∴ m=4.故答案为 4 26. ∵ 是 x 的二次函数, ∴,解得 m=3 或 m= ﹣ 1,22∴此二次函数的解析式为: y=6x 2+9 或 y=2x 2﹣ 4x+12 2 227.由二次函数的定义,可知 m +m ≠0,即 m ≠0, m ≠﹣1 又因为 m ﹣2m ﹣1=2,m ﹣2m ﹣3=0 2解得 m=3 或 m= ﹣1(不合题意,舍去)所以 m=3 故 y=12x 2+9 28.设宽为 xcm ,由题意得,矩形的周长为 800cm ,∴矩形的长为cm ,2∴y=x ×=﹣x +400x ( 0< x < 40). y 是 x 的二次函数.329.(1)根据一次函数的定义,得: m 2﹣ m=0 解得 m=0 或 m=1又∵ m ﹣ 1≠0 即 m ≠1;∴当 m=0 时,这个函数是一次函数; (2)根据二次函数的定义,得: m 2﹣ m ≠0 解得 m 1≠0, m 2≠1∴当 m 1≠0, m 2≠1 时,这个函数是二次函数.30.根据题意得:原函数为二次函数,则有解得: m=3 .。
二次函数专项练习完整版
2.下列函数中,其中是以 x 为自变量的二次函数是( A.y= x(x﹣3) B.y=(x+2) (x﹣2)﹣(x﹣1)2 C.y=x2+ D.y=
3.抛物线 y= x2,y=﹣3x2,y=﹣x2,y=2x2 的图象开口最大的是( A.y= x2 B.y=﹣3x2 C.y=﹣x2 D.y=2x2 )
A.先向左平移 2 个单位,再向上平移 1 个单位 B.先向左平移 2 个单位,再向下平移 1 个单位 C.先向右平移 2 个单位,再向上平移 1 个单位 D.先向右平移 2 个单位,再向下平移 1 个单位 18.抛物线 y=x2 向左平移 1 个单位,再向下平移 2 个单位,得到新的图象的二 次函数表达式是( A.y=(x+1)2+2 ) B.y=(x﹣1)2﹣2 C.y=(x+1)2﹣2 D.y=(x﹣1)2+2
12.抛物线 y=﹣x2+2x+6 在直线 y=﹣2 上截得的线段长度为( A.2 B.3 C.4 D.6
13.已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c <0;②a﹣b+c<0;③2a+b<0;④abc>0,其中所有正确结论的序号是( )
A.③④
B.②③
28.已知抛物线 y=ax2+bx+c(a<0)过 A(﹣2,0) 、O(0,0) 、B(﹣3,y1) 、 C(3,y2)四点,则 y1 与 y2 的大小关系是 .
29.如图,已知抛物线 y=ax2+bx+c 与 x 轴交于 A、B 两点,顶点 C 的纵坐标为﹣ 2,现将抛物线向右平移 2 个单位,得到抛物线 y=a1x2+b1x+c1,则下列结论正确 的是 ①b>0 ②a﹣b+c<0 . (写出所有正确结论的序号)
《二次函数》专项练习题

《二次函(Han)数》专项练习题一、精心(Xin)选一选1.下列函数(Shu)中,二次函数是( ) (A )(B )(C )(D )2.二次函(Han)数的(De)顶点坐标是( )(A )(3,0) (B )(-3,0) (C )(0,3) (D )(0,-3) 3.抛物(Wu)线的(De)对称轴是( ) (A ) (B ) (C ) (D )4.把抛(Pao)物线的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是,则有( )(A ) (B ) (C )(D )5. 已知h 关于t 的函数关系式为,(g 为正常数,t 为时间),则函数图象为( )(A ) (B ) (C ) (D ) 6.已知二次函数的图象上有,,(,)三个点,则,,3y 的大小关系为( )(A )(B ) (C )(D )7.关于二次函数的最大(小)值的叙述正确的是( ) (A )当2x =时,函数有最大值 (B )当2x =时,函数有最小值 (C )当2x =-时,函数有最大值 (D )当2x =-时,函数有最小值 8.已知二次函数的图象如右图所示,则a ,b ,c 满足( )(A)a <0,b <0,c >0 (B)a <0,b <0,c <0 (C)a <0,b >0,c >0 (D)a >0,b <0,c >0二、耐心填一填 1.用配方法把二次函数化为的形式,得__________.yO2.已知二次函数的图象开口向下,且(Qie)与轴的正半轴相交,请你写(Xie)出一个满足条件的二次函数的解析式:____________. 3. 已知抛(Pao)物线y =x 2+x +b 2经(Jing)过点(a ,)和(He)(-a ,y 1),则(Ze)y 1的(De)值是 .4.对于反比例函(Han)数与二次函数,请说出它们的两个相同点①__________,②____________;再说出它们的两个不同点①__________,②____________.5.某物体从上午7时至下午4时的温度M (℃)是时间t (小时)的函数:(其中表示中午12时,表示下午1时),则上午10时此物体的温度为__________.6. 如图,已知二次函数y =ax 2+bx +c 的图象与x 轴交于A (1,0),B (3,0)两点,与y 轴交于点C (0,3),则二次函数的图象的顶点坐标是 .三、用心想一想1.已知抛物线c bx ax y ++=2经过A (1,-4),B (1,0),C (-2,5)三点.(1)求抛物线的解析式并画出这条抛物线;(2)直角坐标系中点的横坐标与纵坐标均为整数的点称为整点.试结合图象,写出在第四象限内抛物线上的所有整点的坐标. 2.某广告公司设计一幅周长为20m 的矩形广告牌,设矩形一边长为米,广告牌的面积为平方米.(1)写出广告牌面积S 与边长x 的函数关系式; (2)画出这个函数的大致图象(其中);(3)根据图象观察当边长x 为何值时,广告牌的面积最大? 3.如图3—1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据: x /m 5 10 20 30 450 y /m 0.125 0.5 2 4.5 812.5(1)请你以上表中的各对数据(x ,y )作为点的坐标,尝试在图3—2所示的坐标系中画出y 关于x 的函数图象;(2)①填写下表:x 5 10 20 30 40 50②根据所填表中数据呈现的规律,猜想出用x 表示y的二次函数的表达式: .O 10 20 30 40 50 60 x /m 2 14 12 10 8 64 y /m 图3—2x x y(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?4.心理学家发现,学生对概念的(De)接受能力y 与提出概念所用的时(Shi)间x (单位:分)之间满(Man)足函数关系:y =-0.1x 2+2.6x +43 (0≤x ≤30).y 值越大,表示接(Jie)受能力越强.(1)x 在什么范围内,学生的接受能力(Li)逐步增强?x 在什么范围内(Nei),学生的接受能力逐步降低?(2)第(Di)10分时,学生的接受能力是多少? (3)第几分时,学生的接受(Shou)能力最强?参考答案:一、1~8 ADBAA DDA二、1.;2.等;3.;4.相同点:图象都是曲线;都经过点(-1,2)(或都经过点(2,-1);在第二象限,函数值都随自变量的增大而增大.不同点:图象的形状不同;自变量的取值范围不同;一个有最大值,一个没有最大值等; 5.102℃;6.(2,-1). 三、1.(1);(2)(1,4)、(2,3);2.(1);(2)略;(3);3.(1)图象如下图所示.(2)①填表正确如下: x 510 20 30 40 50 2x y 200 200200200200200②O 10 20 30 40 50 60 x /m 2 14 12 10 8 6 4 y /m(3)当水面宽度为36m时,相应的x=18,则,此时该河段的最大水深为1.62m.因为(Wei)货船吃水深为1.8m,而(Er)1.62<1.8,所以(Yi)当水面宽度为36m时,该货船不能通过这个河段.4.(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9.所以(Yi),当0≤x≤13时,学生的接受能力逐步增(Zeng)强,当(Dang)13≤x≤30时,学生的接受能力逐(Zhu)步下降.(2)当(Dang)x=10时,y=-0.1(10-13)2+59.9=59.第10分时,学生的接受能力为59.(3)x=13,y取得最大值,所以,在第13分时,学生的接受能力最强.。
中考数学专项练习二次函数的性质(含解析)

中考数学专项练习二次函数的性质(含解析)【一】单项选择题1.对于二次函数y=〔x﹣1〕2+2的图象,以下说法正确的选项是〔〕A.开口向下B.对称轴是x=﹣1 C.顶点坐标是〔1,2〕 D.与x轴有两个交点2.抛物线上部分点坐标如表所示,以下说法错误的选项是〔〕A.抛物线与y轴的交点为(0,6)B.抛物线的对称轴是在y轴的右侧;C.抛物线一定经过点(3 ,0)D.在对称轴左侧,y随x增大而减小.3.二次函数y=3x2+1和y=3〔x﹣1〕2 ,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点〔0,0〕;③当x>0时,它们的函数值y都是随着x的增大而增大;④它们的开口的大小是一样的.其中正确的说法有〔〕A.1个B.2个C.3个D.4个4.二次函数y=〔x﹣1〕2﹣2的顶点坐标是〔〕A.〔﹣1,﹣2〕B.〔﹣1,2〕C.〔1,﹣2〕D.〔1,2〕5.如图,从1×2的矩形ABCD的较短边AD上找一点E,过这点剪下两个正方形,它们的边长分别是AE、DE,当剪下的两个正方形的面积之和最小时,点E应选在〔〕A.AD的中点B.AE:ED=〔﹣1〕:2 C.AE:ED=:1 D.AE:ED=〔﹣1〕:26.二次函数y=3x2-6x+5的图象的顶点坐标是〔〕A.〔1,2〕 B.〔1, 8〕 C.〔﹣1,2〕 D.〔1,﹣4〕7.对于二次函数y=〔x﹣1〕2+2的图象,以下说法正确的选项是〔〕A.开口向下B.对称轴是x=﹣1 C.顶点坐标是〔1,2〕 D.与x轴有两个交点8.二次函数y=x2﹣2的图象的顶点是〔〕A.〔2,﹣2〕B.〔﹣1,0〕C.〔1,9〕D.〔0,﹣2〕9.抛物线y=2x2+1的顶点坐标是〔〕A.〔2,1〕 B.〔0,1〕 C.〔1,0〕 D.〔1,2〕10.二次函数y=ax2+bx+c〔a≠0〕的图象如下图,给出以下结论:①a >0;②该函数的图象关于直线x=1对称;③当x=-1或x=3时,函数y的值都等于0.其中正确结论的个数是〔〕A.3B.2C.1D.011.对于二次函数y=2〔x+1〕〔x﹣3〕,以下说法正确的选项是〔〕A.图象的开口向下B.当x>1时,y随x的增大而减小C.当x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣112.如图,抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为〔0,3〕,那么点B的坐标为〔)A.〔2,3〕 B.〔3,2〕 C.〔3,3〕 D.〔4,3〕13.在二次函数y=﹣x2+2x+1的图象中,假设y随x的增大而增大,那么x的取值范围是〔〕A.x>1B.x<1C.x>﹣1D.x<﹣114.抛物线y=〔x+1〕2的顶点坐标是〔〕A.〔﹣1,0〕B.〔﹣1,1〕C.〔0,﹣1〕D.〔1,0〕【二】填空题15.点A(x1 ,y1)、B(x2 ,y2)在二次函数y=(x-1)2+1的图像上,假设x1>x2>1,那么y1________y2 .(填〝>〞〝=〞或〝<〞)16.M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为〔a,b〕,那么y=﹣abx2+〔a+b〕x的顶点坐标为________17.二次函数y=x2+〔m﹣1〕x+1,当x>1时,y随x的增大而增大,那么m的取值范围是________.18.写出一个二次函数解析式,使它的图象的顶点在y轴上:________.19.抛物线〔<0〕过A〔,0〕、O〔0,0〕、B〔,〕、C〔3,〕四点.那么________ 〔用〝<〞,〝>〞或〝=〞填空〕.20.二次函数y=﹣3x2﹣6x+5的图像的顶点坐标是________.21.二次函数y=ax2+bx+c〔a≠0〕的图象如下图,有以下5个结论:①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④a m +bm+a>0〔m≠﹣1〕;⑤设A〔100,y〕,B〔﹣100,y 〕在该抛物线上,那么y>y .其中正确的结论有________ .〔写出所有正确结论的序号〕【三】解答题22.点A〔﹣2,n〕在抛物线y=x2+bx+c上.〔1〕假设b=1,c=3,求n的值;〔2〕假设此抛物线经过点B〔4,n〕,且二次函数y=x2+bx+c的最小值是﹣4,请画出点P〔x﹣1,x2+bx+c〕的纵坐标随横坐标变化的图象,并说明理由.23.二次函数y=ax2+bx+c〔a≠0〕的图象上部分点的横坐标x与纵坐标求:〔1〕这个二次函数的解析式;〔2〕这个二次函数图象的顶点坐标及上表中m的值.【四】综合题24.如图,抛物线l1经过原点与A点,其顶点是P〔﹣2,3〕,平行于y 轴的直线m与x轴交于点B〔b,0〕,与抛物线l1交于点M.〔1〕点A的坐标是________;抛物线l1的解析式是________;〔2〕当BM=3时,求b的值;〔3〕把抛物线l1绕点〔0,1〕旋转180°,得到抛物线l2 .①直接写出当两条抛物线对应的函数值y都随着x的增大而减小时,x的取值范围________;〔4〕②直线m与抛物线l2交于点N,设线段MN的长为n,求n与b 的关系式,并求出线段MN的最小值与此时b的值.25.二次函数y=mx2﹣5mx+1〔m为常数,m>0〕,设该函数的图象与y 轴交于点A,该图象上的一点B与点A关于该函数图象的对称轴对称.〔1〕求点A,B的坐标;〔2〕点O为坐标原点,点M为该函数图象的对称轴上一动点,求当M运动到何处时,△MAO的周长最小.【一】单项选择题1.对于二次函数y=〔x﹣1〕2+2的图象,以下说法正确的选项是〔〕A.开口向下B.对称轴是x=﹣1 C.顶点坐标是〔1,2〕 D.与x轴有两个交点【考点】二次函数的性质【解析】【解答】解:二次函数y=〔x﹣1〕2+2的图象开口向上,顶点坐标为〔1,2〕,对称轴为直线x=1,抛物线与x轴没有公共点.应选:C、【分析】根据抛物线的性质由a=1得到图象开口向上,根据顶点式得到顶点坐标为〔1,2〕,对称轴为直线x=1,从而可判断抛物线与x轴没有公共点.2.抛物线上部分点坐标如表所示,以下说法错误的选项是〔〕A.抛物线与y轴的交点为(0,6)B.抛物线的对称轴是在y轴的右侧;C.抛物线一定经过点(3 ,0)D.在对称轴左侧,y随x增大而减小.【考点】二次函数的性质3.二次函数y=3x2+1和y=3〔x﹣1〕2 ,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点〔0,0〕;③当x>0时,它们的函数值y都是随着x的增大而增大;④它们的开口的大小是一样的.其中正确的说法有〔〕A.1个B.2个C.3个D.4个【考点】二次函数的性质【解析】【解答】解:①因为a=3>0,它们的图象都是开口向上,此选项正确;②y=3x2+1对称轴是y轴,顶点坐标是〔0,1〕,y=3〔x﹣1〕2的对称轴是x=1,顶点坐标是〔1,0〕,此选项错误;③二次函数y=3x2+1当x>0时,y随着x的增大而增大;y=3〔x﹣1〕2当x10时,y随着x的增大而增大;④因为a=3,所以它们的开口的大小是一样的,此选项正确.综上所知,正确的有①④两个.应选:B、【分析】根据a的值可以判定开口方向和开口大小,利用顶点式直接找出对称轴和顶点坐标,利用对称轴和开口方向确定y随着x的增大而增大对应x的取值范围.4.二次函数y=〔x﹣1〕2﹣2的顶点坐标是〔〕A.〔﹣1,﹣2〕B.〔﹣1,2〕C.〔1,﹣2〕D.〔1,2〕【考点】二次函数的性质【解析】【解答】解:因为y=〔x﹣1〕2﹣2是抛物线的顶点式,根据顶点式的坐标特点,顶点坐标为〔1,﹣2〕.应选C、【分析】解析式为抛物线的顶点式,根据顶点式的坐标特点,直接写出顶点坐标.5.如图,从1×2的矩形ABCD的较短边AD上找一点E,过这点剪下两个正方形,它们的边长分别是AE、DE,当剪下的两个正方形的面积之和最小时,点E应选在〔〕A.AD的中点B.AE:ED=〔﹣1〕:2 C.AE:ED=:1 D.AE:ED=〔﹣1〕:2【考点】二次函数的性质【解析】【解答】解:设AE=x.那么DE=1﹣x.剪下的两个正方形的面积之和为y,那么y=AE2+DE2=x2+〔1﹣x〕2=2〔x﹣〕2+.当x=时,y取最小值.即点E是AD的中点.应选A、【分析】设AE=x.那么DE=1﹣x.剪下的两个正方形的面积之和为y,所以由正方形的面积公式得到y=AE2+DE2=2〔x﹣〕2+.当x=时,y取最小值.即点E是AD的中点.、6.二次函数y=3x2-6x+5的图象的顶点坐标是〔〕A.〔1,2〕 B.〔1, 8〕 C.〔﹣1,2〕 D.〔1,﹣4〕【考点】二次函数的性质【解析】【解答】∵a=3,b=-6,c=5,∴x=-=1,y==2,即顶点坐标是〔1,2〕.应选A.【点评】此题考查用公式法求二次函数的顶点坐标.做对此题的关键是记熟公式7.对于二次函数y=〔x﹣1〕2+2的图象,以下说法正确的选项是〔〕A.开口向下B.对称轴是x=﹣1 C.顶点坐标是〔1,2〕 D.与x轴有两个交点【考点】二次函数的性质【解析】【解答】解:二次函数y=〔x﹣1〕2+2的图象开口向上,顶点坐标为〔1,2〕,对称轴为直线x=1,抛物线与x轴没有公共点.应选:C、【分析】根据抛物线的性质由a=1得到图象开口向上,根据顶点式得到顶点坐标为〔1,2〕,对称轴为直线x=1,从而可判断抛物线与x轴没有公共点.8.二次函数y=x2﹣2的图象的顶点是〔〕A.〔2,﹣2〕B.〔﹣1,0〕C.〔1,9〕D.〔0,﹣2〕【考点】二次函数的性质【解析】【解答】解:二次函数y=x2﹣2的图象的顶点坐标是〔0,﹣2〕.应选D、【分析】根据顶点式解析式写出顶点坐标即可.9.抛物线y=2x2+1的顶点坐标是〔〕A.〔2,1〕 B.〔0,1〕 C.〔1,0〕 D.〔1,2〕【考点】二次函数的性质【解析】【解答】∵y=2x2+1=2〔x﹣0〕2+1,∴抛物线的顶点坐标为〔0,1〕,应选B、【分析】此题主要考查抛物线的顶点坐标,掌握顶点式方程y=a〔x﹣h〕2 +k的顶点坐标为〔h ,k〕是解题的关键.10.二次函数y=ax2+bx+c〔a≠0〕的图象如下图,给出以下结论:①a >0;②该函数的图象关于直线x=1对称;③当x=-1或x=3时,函数y的值都等于0.其中正确结论的个数是〔〕A.3B.2C.1D.0【考点】二次函数的性质【解析】【分析】根据抛物线的性质解题.【解答】①抛物线开口向下,a<0,所以①错误;②抛物线是关于对称轴对称的轴对称图形,所以②该函数的图象关于直线x =1对称,正确;③当x=-1或x=3时,函数y的值都等于0,也正确.应选B、【点评】此题考查了抛物线的开口方向,轴对称性和与x轴的交点等知识.11.对于二次函数y=2〔x+1〕〔x﹣3〕,以下说法正确的选项是〔〕A.图象的开口向下B.当x>1时,y随x的增大而减小C.当x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣1【考点】二次函数的性质【解析】【解答】解:二次函数y=2〔x+1〕〔x﹣3〕可化为y=2〔x﹣1〕2﹣8的形式,A、∵此二次函数中a=2>0,∴抛物线开口向上,故本选项错误;B、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x>1时,y随x的增大而增大,故本选项错误;C、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x<1时,y随x的增大而减小,故本选项正确;D、由二次函数的解析式可知抛物线对称轴为x=1,故本选项错误.应选C、【分析】先把二次函数化为顶点式的形式,再根据二次函数的性质进行解答.12.如图,抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为〔0,3〕,那么点B的坐标为〔)A.〔2,3〕 B.〔3,2〕 C.〔3,3〕 D.〔4,3〕【考点】二次函数的性质【解析】【分析】抛物线的对称轴为x=2,知道A的坐标为〔0,3),由函数的对称性知B点坐标.【解答】由题意可知抛物线的y=x2+bx+c的对称轴为x=2,∵点A的坐标为〔0,3),且AB与x轴平行,可知A、B两点为对称点,∴B点坐标为〔4,3)应选D、【点评】此题主要考查二次函数的对称性13.在二次函数y=﹣x2+2x+1的图象中,假设y随x的增大而增大,那么x的取值范围是〔〕A.x>1B.x<1C.x>﹣1D.x<﹣1【考点】二次函数的性质【解析】【解答】解:∵a=﹣1<0,∴二次函数图象开口向下,又∵对称轴是直线x=﹣=1,∴当x<1时,函数图象在对称轴的左边,y随x的增大而增大.应选B、【分析】抛物线y=﹣x2+2x+1中的对称轴是直线x=1,开口向下,x<1时,y随x的增大而增大.14.抛物线y=〔x+1〕2的顶点坐标是〔〕A.〔﹣1,0〕B.〔﹣1,1〕C.〔0,﹣1〕D.〔1,0〕【考点】二次函数的性质【解析】【解答】解:∵二次函数的解析式为y=〔x+1〕2 ,∴其顶点坐标为:〔﹣1,0〕.应选A、【分析】直接根据二次函数的顶点坐标式进行解答即可.【二】填空题15.点A(x1 ,y1)、B(x2 ,y2)在二次函数y=(x-1)2+1的图像上,假设x1>x2>1,那么y1________y2 .(填〝>〞〝=〞或〝<〞) 【考点】二次函数的性质16.M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为〔a,b〕,那么y=﹣abx2+〔a+b〕x的顶点坐标为________【考点】二次函数的性质17.二次函数y=x2+〔m﹣1〕x+1,当x>1时,y随x的增大而增大,那么m的取值范围是________.【考点】二次函数的性质18.写出一个二次函数解析式,使它的图象的顶点在y轴上:________.【考点】二次函数的性质19.抛物线〔<0〕过A〔,0〕、O〔0,0〕、B〔,〕、C〔3,〕四点.那么________ 〔用〝<〞,〝>〞或〝=〞填空〕.【考点】二次函数的性质【解析】【解答】∵抛物线与x轴交于A〔-2,0〕、O〔0,0〕两点,∴抛物线对称轴为x= =-1,∵B〔-3,y1〕、C〔3,y2〕,点B离对称轴较近,且抛物线开口向下,∴y1>y2 .【分析】根据可知点A、O关于抛物线的对称轴对称,因此可求出抛物线的对称轴为直线x=-1,再根据二次函数的性质即可求得结论。
二次函数专项练习

二次函数专项练习一.选择题(共7小题)1.在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是()A.B .C .D .2.二次函数y=x2﹣2x﹣3的图象如图所示.当y<0时,自变量x的取值范围是()A.﹣1<x<3B.x<﹣1C.x>3D.x<﹣3或x>33.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a<0②该函数的图象关于直线x=1对称③b2﹣4ac<0④4a﹣2b+c>0其中正确结论的个数是()A.1个B.2个C.3个D.4个4.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0B.当x=0时,y的值大于1C.当x=﹣1时,y的值大于1D.当x=﹣3时,y的值小于05.如图,抛物线y=﹣x2+x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为()A.3B.4C.5D.66.如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论正确的是()A.b2>4ac B.ac>0C.a﹣b+c>0D.4a+2b+c<07.二次函数y=﹣x2+bx+c的图象如图所示:若点A(x1,y1),B(x2,y2)在此函数图象上,x1<x2<1,y1与y2的大小关系是()A.y1≤y2B.y1<y2C.y1≥y2D.y1>y2二.填空题(共11小题)8.如图,在平面直角坐标系中,沿着两条坐标轴摆着两个相同的矩形,其长、宽分别为2,1,抛物线y=﹣x2+bx+c经过A、B两点,则b=,c=.9.如图,矩形PABC的顶点P在抛物线y=﹣(x﹣1)2﹣2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为.10.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是.(写出所有正确结论的序号)①b>0②a﹣b+c<0③阴影部分的面积为4④若c=﹣1,则b2=4a.11.如图,抛物线y=ax2+bx+c的对称轴为x=﹣2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,﹣2),则点B的坐标为.12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2),如图所示,则能使y1<y2成立的x的取值范围是.13.如图,点A (﹣,t)在抛物线y=a(x﹣1)2+k(a>0)上,过点A平行于x轴的直线交抛物线于另一点B,则线段AB的长是.14.二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是.15.二次函数y=a(x﹣1)2+k(a>0)中x、y的几组对应值如下表.x﹣215y m n p表中m、n、p的大小关系为(用“<”连接)16.在平面直角坐标系中,点A是抛物线y=a(x﹣3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为.17.如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为.18.抛物线y=a(x﹣2)2﹣2的图象如图所示,则它关于y轴对称的抛物线的解析式为.三.解答题(共7小题)19.如图,在平面直角坐标系xOy中,函数y=ax2+bx+1(a≠0)的图象与x轴的正半轴交于点A,与x轴的负半轴交于点B,与y轴交于点C、P(1,﹣1),在△PAC中,∠P=90°,PA=PC.(1)求点A的坐标;(2)将△PAC沿AC翻折,若点P的对应点Q恰好落在函数y=ax2+bx+1(a≠0)的图象上,求a与b的值.20.如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.21.如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.(1)求这条抛物线对应的函数关系式.(2)当四边形OMPN为正方形时,求m的值.(3)求四边形OMPN的周长的最大值.(4)若直线PN与这条抛物线的另一个交点为点Q ,直接写出≤QN≤1时m的取值范围.22.如图,一次函数y=﹣分别交y 轴、x 轴于A 、B 两点,抛物线y=﹣x 2+bx +c 过A 、B 两点.(1)求这个抛物线的解析式;(2)作垂直x 轴的直线x=t ,在第一象限交直线AB 于M ,交这个抛物线于N .求当t 取何值时,以A 、O 、M 、N为顶点的四边形是平行四边形?23.如图,有一个抛物线型拱桥,其最大高度为16m ,跨度为40m ,现把它的示意图放在平面直角坐标系中,求此抛物线的函数关系式.24.如图,已知抛物线经过点A (﹣1,0)、B (3,0)、C (0,3)三点.(1)求抛物线的解析式.(2)点M 是线段BC 上的点(不与B ,C 重合),过M 作MN ∥y 轴交抛物线于N ,若点M 的横坐标为m ,请用m 的代数式表示MN 的长.(3)在(2)的条件下,连接NB 、NC ,是否存在m ,使△BNC 的面积最大?若存在,求m 的值;若不存在,说明理由.25.如图,已知二次函数y=ax 2﹣4x +c 的图象经过点A 和点B .(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P (m ,m )与点Q 均在该函数图象上(其中m >0),且这两点关于抛物线的对称轴对称,求m 的值及点Q 到x轴的距离.二次函数专项练习参考答案与试题解析一.选择题(共7小题)1.在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是()A.B.C.D .【解答】解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,故选:D.2.二次函数y=x2﹣2x﹣3的图象如图所示.当y<0时,自变量x的取值范围是()A.﹣1<x<3B.x<﹣1C.x>3D.x<﹣3或x>3【解答】解:由图象可以看出:y<0时,自变量x的取值范围是﹣1<x<3;故选:A.3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a<0②该函数的图象关于直线x=1对称③b2﹣4ac<0④4a﹣2b+c>0其中正确结论的个数是()A.1个B.2个C.3个D.4个【解答】解:①∵抛物线开口向下,∴a<0;故本选项正确;②∵二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点坐标是(﹣3,0)、(1,0),∴对称轴为直线x==1,故本选项正确;③∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个不同的交点,∴b2﹣4ac>0;故本选项错误;④根据二次函数的图象知,当x=﹣2时,y<0,即4a﹣2b+c<0;故本选项错误;综上所述,以上说法正确的个数是2个;故选:B.4.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0B.当x=0时,y的值大于1C.当x=﹣1时,y的值大于1D.当x=﹣3时,y的值小于0【解答】解:A、由图象知,点(1,1)在图象的对称轴的左边,所以y的最大值大于1,不小于0;故本选项错误;B、由图象知,当x=0时,y的值就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左边,故y<1;故本选项错误;C、对称轴在(1,1)的右边,在对称轴的左边y随x的增大而增大,∵﹣1<1,∴x=﹣1时,y的值小于x=1时,y的值1,即当x=﹣1时,y的值小于1;故本选项错误;D、当x=﹣3时,函数图象上的点在点(﹣2,﹣1)的左边,所以y的值小于0;故本选项正确.故选:D.5.如图,抛物线y=﹣x2+x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为()A.3B.4C.5D.6【解答】解:作DE⊥OC于E,根据抛物线的对称性得到:S阴影=S矩形OADE.∵A(0,3),∴D的纵坐标为3,代入y=﹣x2+x得,3=﹣x2+x,解得x=1或6,∴AD=1,OA=3,∴S阴影=S矩形OADE=1×3=3.故选:A.6.如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论正确的是()A.b2>4ac B.ac>0C.a﹣b+c>0D.4a+2b+c<0【解答】解:∵抛物线与x轴有两个交点,∴b2﹣4ac>0,即b2>4ac,所以A选项正确;∵抛物线开口向下,∴a<0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴ac<0,所以B选项错误;∵抛物线过点A(3,0),二次函数图象的对称轴是x=1,∴抛物线与x轴的另一个交点为(﹣1,0),∴a﹣b+c=0,所以C选项错误;∵当x=2时,y>0,∴4a+2b+c>0,所以D选项错误.故选:A.7.二次函数y=﹣x2+bx+c的图象如图所示:若点A(x1,y1),B(x2,y2)在此函数图象上,x1<x2<1,y1与y2的大小关系是()A.y1≤y2B.y1<y2C.y1≥y2D.y1>y2【解答】解:∵a<0,x1<x2<1,∴y随x的增大而增大∴y1<y2.故选:B.二.填空题(共11小题)8.如图,在平面直角坐标系中,沿着两条坐标轴摆着两个相同的矩形,其长、宽分别为2,1,抛物线y=﹣x2+bx+c经过A、B两点,则b=﹣1,c=3.【解答】解:∵两个相同的矩形,其长、宽分别为2,1,∴A(﹣2,1),B(﹣1,3),∵抛物线y=﹣x2+bx+c经过A、B两点,∴,解得,故答案为﹣1,3.9.如图,矩形PABC的顶点P在抛物线y=﹣(x﹣1)2﹣2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.【解答】解:抛物线y=﹣(x﹣1)2﹣2的顶点坐标为(1,﹣2),当点P位于抛物线的顶点处时,PA=2,∵PC=2PA,∴PC=4,∴周长的最小值为2×(2+4)=12,故答案为:12.10.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是③④.(写出所有正确结论的序号)①b>0②a﹣b+c<0③阴影部分的面积为4④若c=﹣1,则b2=4a.【解答】解:∵抛物线开口向上,∴a>0,又∵对称轴为x=﹣>0,∴b<0,∴结论①不正确;∵x=﹣1时,y>0,∴a﹣b+c>0,∴结论②不正确;∵抛物线向右平移了2个单位,∴平行四边形的底是2,∵函数y=ax2+bx+c的最小值是y=﹣2,∴平行四边形的高是2,∴阴影部分的面积是:2×2=4,∴结论③正确;∵,c=﹣1,∴b2=4a,∴结论④正确.综上,结论正确的是:③④.故答案为:③④.11.如图,抛物线y=ax2+bx+c的对称轴为x=﹣2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,﹣2),则点B的坐标为(﹣4,﹣2).【解答】解:由题意可知抛物线的y=ax2+bx+c的对称轴为x=﹣2,∵点A的坐标为(0,﹣2),且AB与x轴平行,∴A、B两点为对称点,∴B点坐标为(﹣4,﹣2).故答案是:(﹣4,﹣2).12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2),如图所示,则能使y1<y2成立的x的取值范围是﹣2<x<8.【解答】解:由图形可得,当﹣2<x<8时,二次函数图象在一次函数图象下方,y1<y2,所以,使y1<y2成立的x的取值范围是﹣2<x<8.故答案为:﹣2<x<8.13.如图,点A (﹣,t)在抛物线y=a(x﹣1)2+k(a>0)上,过点A平行于x轴的直线交抛物线于另一点B,则线段AB的长是3.【解答】解:∵点A (﹣,t)在抛物线y=a(x﹣1)2+k(a>0)上,∴该抛物线的对称轴是直线x=1,∵过点A平行于x轴的直线交抛物线于另一点B,∴点B的横坐标是:1×2﹣(﹣)=,∴AB==3,故答案为:3.14.二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是﹣1<x<3.【解答】解:函数值y<0时,自变量x的取值范围是﹣1<x<3.故答案是:﹣1<x<3.15.二次函数y=a(x﹣1)2+k(a>0)中x、y的几组对应值如下表.x﹣215y m n p表中m、n、p的大小关系为n<m<p(用“<”连接)【解答】解:∵a>0,∴抛物线开口向上,∵对称轴为x=1,∴对称轴左侧y随x的增大而减小,∵﹣2<1,∴m>n,∵对称轴x=1右侧y随x的增大而增大,∴p>n,∵x=﹣2时与x=4时的函数值相等,∴p>m,∴p>m>n,故答案为n<m<p.16.在平面直角坐标系中,点A是抛物线y=a(x﹣3)2+k 与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为18.【解答】解:∵抛物线y=a(x﹣3)2+k的对称轴为x=3,且AB∥x轴,∴AB=2×3=6,∴等边△ABC的周长=3×6=18.故答案为:18.17.如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为12.【解答】解:连接AP,A′P′,过点A作AD⊥PP′于点D,由题意可得出:AP∥A′P′,AP=A′P′,∴四边形APP′A′是平行四边形,∵抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),∴PO==2,∠AOP=45°,又∵AD⊥OP,∴△ADO是等腰直角三角形,∴PP′=2×2=4,∴AD=DO=sin45°•OA=×3=,∴抛物线上PA段扫过的区域(阴影部分)的面积为:4×=12.故答案为:12.18.抛物线y=a(x﹣2)2﹣2的图象如图所示,则它关于y轴对称的抛物线的解析式为y=2(x+2)2﹣2.【解答】解:将点(1,0)代入y=a(x﹣2)2﹣2中,得a﹣2=0,解得a=2,又原抛物线顶点坐标为(2,﹣2),∴它关于y轴对称的抛物线顶点坐标为(﹣2,﹣2),∴新抛物线的解析式为y=2(x+2)2﹣2.故本题答案为:y=2(x+2)2﹣2.三.解答题(共7小题)19.如图,在平面直角坐标系xOy中,函数y=ax2+bx+1(a≠0)的图象与x轴的正半轴交于点A,与x轴的负半轴交于点B,与y轴交于点C、P(1,﹣1),在△PAC中,∠P=90°,PA=PC .(1)求点A的坐标;(2)将△PAC沿AC翻折,若点P的对应点Q恰好落在函数y=ax2+bx+1(a≠0)的图象上,求a与b的值.【解答】解:(1)如图1,过点P作x轴的平行线交y轴于D,作AE⊥PD于E,∴∠CDP=∠PEA=90°,∵∠P=90°,∴∠PCD=∠APE,在△PCD和△APE中,,∴△PCD≌△APE,∴PE=CD=2,∴DE=DP+PE=3,∴点A的坐标为(3,0);(2)如图2,作PG⊥y轴于G,作QF⊥y轴于F,∵∠P=90°,PA=PC,∴△APC为等腰直角三角形,∴∠PCA=45°,由翻折变换的性质可知,∠PCQ=90°,CP=CQ,∴△PCG≌△QCF,∴QF=CG=2,CF=GP=1,∴点Q的坐标为(2,2),则,解得,,答:a的值是﹣,b 的值是.20.如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.【解答】解:(1)将点A(1,0)代入y=(x﹣2)2+m得(1﹣2)2+m=0,解得m=﹣1,所以二次函数解析式为y=(x﹣2)2﹣1;当x=0时,y=4﹣1=3,所以C点坐标为(0,3),由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,所以B点坐标为(4,3),将A(1,0)、B(4,3)代入y=kx+b 得,解得,所以一次函数解析式为y=x﹣1;(2)当kx+b≥(x﹣2)2+m时,1≤x≤4.21.如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.(1)求这条抛物线对应的函数关系式.(2)当四边形OMPN为正方形时,求m的值.(3)求四边形OMPN的周长的最大值.(4)若直线PN与这条抛物线的另一个交点为点Q ,直接写出≤QN≤1时m的取值范围.【解答】解:(1)∵抛物线的顶点坐标为(2,6),∴设抛物线对应的函数关系式为y=a(x﹣2)2+6.∵抛物线经过点(4,2),∴a(4﹣2)2+6=2,解得a=﹣1.∴抛物线对应的函数关系式为y=﹣(x﹣2)2+6,即y=﹣x2+4x+2;(2)∵点P在抛物线y=﹣x2+4x+2上,且点P的横坐标为m,∴P点坐标为P(m,﹣m2+4m+2).当四边形OMPN为正方形时,PN=PM,∴m=﹣m2+4m+2.解得m1=,m2=(舍去).∵抛物线y=﹣x2+4x+2与x轴正半轴的交点为(2+,0),且2<<2+,∴m 的值为.(3)设四边形OMPN的周长为C,C=2m+2(﹣m2+4m+2)=﹣2m2+10m+4=﹣2(m﹣)2+.∵a=﹣2<0,2<<2+,∴当m=时,四边形OMPN 周长的最大值为.(4)如图,点Q与点P(m,﹣m2+4m+2)关于x=2对称,得Q(4﹣m,﹣m2+4m+2).①当m<4时,由≤QN≤1时,得≤4﹣m≤1,解得3≤m ≤;②当m>4时,由≤QN≤1时,得≤m﹣4≤1,解得,≤m<2+;综上所述,若直线PN与这条抛物线的另一个交点为点Q ,直接写出≤QN≤1时m的取值范围3≤m ≤或≤m<2+.22.如图,一次函数y=﹣分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,以A、O、M、N为顶点的四边形是平行四边形?【解答】解:(1)∵一次函数y=﹣分别交y轴、x轴于A、B两点,∴A、B点的坐标为:A(0,2),B(4,0),将其分别代入y=﹣x2+bx+c,得,解得b=,∴抛物线解析式为:y=﹣x2+x+2;(2)∵点M在直线y=﹣上,点N在抛物线y=﹣x2+bx+c上,∴M(t ,﹣t+2)(0<t<4),则N(t,﹣t2+t+2).又∵如图所示,以A、O、M、N为顶点的四边形是平行四边形,即四边形AOMN为平行四边形,∴AO=NM,即2=(﹣t2+t+2)﹣(﹣t+2),整理,得t2﹣4t+2=0,解得t==2±.即当t=2±时,以A、O、M、N为顶点的四边形是平行四边形.23.如图,有一个抛物线型拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中,求此抛物线的函数关系式.【解答】解:设y=a(x﹣20)2+16因为抛物线过(0,0)所以代入得:400a+16=0即a=﹣故此抛物线的函数关系式为:y=﹣(x﹣20)2+16.24.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.【解答】解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)设直线BC的解析式为:y=kx+b,则有:,解得;故直线BC的解析式:y=﹣x+3.已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).(3)如图;∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,∴S△BNC=(﹣m2+3m)•3=﹣(m ﹣)2+(0<m<3);∴当m=时,△BNC 的面积最大,最大值为.25.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.【解答】解:(1)将x=﹣1,y=﹣1;x=3,y=﹣9,分别代入y=ax2﹣4x+c得,解得,∴二次函数的表达式为y=x2﹣4x﹣6.(2)对称轴为直线x=2;顶点坐标为(2,﹣10).(3)将(m,m)代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解得m1=﹣1,m2=6.∵m>0,∴m1=﹣1不合题意,舍去.∴m=6,∵点P与点Q关于对称轴x=2对称,∴点Q到x轴的距离为6.。
中考数学总复习《二次函数》专项提升练习题(附答案)

中考数学总复习《二次函数》专项提升练习题(附答案) 学校:___________班级:___________姓名:___________考号:___________一、单选题1.已知二次函数2281y x x =-+,当11x -≤≤时,函数y 的最小值是( )A .1B .5-C .6-D .7-2.把一抛物线向上平移3个单位,再向左平移1个单位得到的解析式为22y x =,则原抛物线的解析式为( ) A .()2213y x =-+B .()2213y x =++C .()2213y x =+-D .()2213y x =--3.新定义:若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,如:()1,3A 与()2,6B --,()0,0C 等都是“三倍点”.若二次函数2y x x c =--+的图像在31x -<<的范围内,至少存在一个“三倍点”,则c 的取值范围是( )A .45c -≤<B .43c -≤<-C .164c -≤<D .114c -≤< 4.如图为2y x bx c =++的图象,则( )A .0b > 0c <B .0b > 0c >C .0b < 0c >D .0b < 0c < 5.把抛物线22y x =-先向右平移6个单位长度,再向下平移2个单位长度后,所得函数的表达式为( )A .22(6)2y x =-++B .22(6)2y x =-+-C .22(6)2y x =--+D .22(6)2y x =---6.如图,抛物线2y ax c =-经过正方形OACB 的三个顶点A ,B ,C ,点C 在y 轴上,则ac 的值为( )A .1B .2C .3D .47.如图,菱形ABCD 的边长为3cm ,=60B ∠︒动点P 从点B 出发以3cm /s 的速度沿着边BC CD DA --运动,到达点A 后停止运动;同时动点Q 从点B 出发,以1cm/s 的速度沿着边BA 向A 点运动,到达点A 后停止运动.设点P 的运动时间为(s)x ,BPQ 的面积为()2cm y ,则y 关于x 的函数图象为( )A .B .B .C .D .8.已知在平面直角坐标系中,抛物线1C 的图象如图所示,对称轴为直线2x =-,将抛物线1C 向右平移2个单位长度得到抛物线2C :2y ax bx c =++ (a 、b 、c 为常数,且0a ≠),则代数式b c a +-与0的大小关系是( )A .0b c a +-<B .0b c a +-=C .0b c a +->D .不能确定二、填空题9.若关于x 的二次函数2321y x x m =-+-的值恒为正数,则m 的取值范围为 . 10.将抛物线2(1)2y x =++先向右平移3个单位,再向下平移4个单位,则所得抛物线的解析式为 .11.小华酷爱足球运动一次训练时,他将足球从地面向上踢出,足球距地面的高度h (单位:m )与足球被踢出后经过的时间t (单位:s )之间的关系为:2412h t t =-+,则足球距离地面的最大高度为 m .12.如图是抛物线型拱桥,当拱顶离水面2m 时,水面宽4m ,若水面下降1m ,则水面宽度增加 m .(结果可保留根号)13.如图,抛物线()20y ax bx c a =++≠的对称轴是直线2x =-,且抛物线与x 轴交于A ,B两点,若5OA OB =,则下列结论中:①0abc >;①()220a c b +->;①50a c +=;①若m 为任意实数,则224am bm b a ++≥,正确的是 .(填序号)三、解答题 14.已知抛物线23y ax bx =++交x 轴于()()1030A B ,,,两点 (1)求抛物线的函数表达式;(2)当x 取何值时,y 随x 的增大而减小.15.如图,抛物线214y x bx c =++过点()0,0O ,()10,0E 矩形ABCD 的边AB 在线段OE 上(点B 在点A 的左侧),点C ,D 在抛物线上.设动点B 坐标为(),0t .(1)求抛物线的函数表达式及顶点坐标;(2)当t 为何值时矩形ABCD 的周长有最大值?最大值是多少?16.“潼南柠檬”获评国家地理标志商标,被认定为全国名特优新农产品,柠檬即食片是其加工产品中非常受欢迎的一款零食.一家超市销售了净重500g 一袋的柠檬即食片,进价为每袋10元.销售过程中发现,如果以单价14元销售,那么一个月内可售出200袋.根据销售经验,提高销售单价会导致销售量减少,即销售单价每提高1元,每月销售量相应减少20袋.根据物价部门规定,这种柠檬即食片的销售单价不得低于进价且不得高于18元.(1)求每月销售量y (件)与销售单价x (元)之间的函数关系式;(2)设超市每月销售柠檬即食片获得离利润为w (元),当销售单价定为多少元时,每月可获得最大利润?最大利润是多少?(3)若超市想每月销售柠檬即食片所得利润w 稳定在900元,销售单价应定为多少元?17.如图,一名同学推铅球,铅球出手后行进过程中离地面的高度y (单位:m )与水平距离x (单位:m )近似满足函数关系212123y x x c =-++.已知铅球落地时的水平距离为10m .(1)求铅球出手后水平距离与这名同学相距多远时,铅球离地面最高?(2)在铅球出手后的行进过程中,当它离地面的高度为5m 3时,此时铅球的水平距离是多少?18.我市某企业安排20名工人生产甲、乙两种产品,根据生产经验,每人每天生产2件甲产品或1件乙产品(每人每天只能生产一种产品).甲产品生产成本为每件10元;若安排1人生产一件乙产品,则成本为38元,以后每增加1人,平均每件乙产品成本降低2元.规x x≥人生产乙产品.定甲产品每天至少生产20件.设每天安排()1(1)根据信息填表:产品种类每天工人数(人)每天产量(件)每件产品生产成本(元)甲10-乙x402x(2)为了增加利润,企业须降低成本,该企业如何安排工人生产才能使得每天的生产总成本最低?最低成本是多少?参考答案:1.B2.D3.A4.D5.D6.B7.D8.C9.43m > 10.2(2)2y x =--11.912.()264-13.③④/④③14.(1)243y x x =-+(2)当2x <,y 随x 的增大而减小15.(1)抛物线的函数表达式为21542y x x =-,顶点坐标为2554⎛⎫- ⎪⎝⎭,; (2)当1t =时,矩形ABCD 的周长有最大值,最大值为412.16.(1)()480201018y x x =-≤≤; (2)当销售单价定为17元时,每月可获得最大利润;每月获得最大利润为980元.(3)当销售单价定为15元时,每月获得利润可稳定在900元.17.(1)铅球出手后水平距离与这名同学相距3m 远时,铅球离地面最高为3m(2)此时铅球的水平距离为8m18.安排10名工人生产甲产品,10名工人生产乙产品才能使得每天的生产总成本最低,最低成本是400元。
中考数学《二次函数》专项练习题-附带答案

中考数学《二次函数》专项练习题-附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列函数中,是二次函数的是()A.y=−8x B.y=8C.y=8x2D.y=8x−4x2.抛物线y=2x2﹣1的对称轴是()A.直线x=﹣1 B.直线x=1C.x轴D.y轴43.已知抛物线y=ax2(a≠0)的开口向下,则a的值可能为()A.-2 B.1C.1 D.√244.设函数y1=−(x−a1)2,y2=−(x−a2)2直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2)得()A.若1<a1<a2,则c1<c2B.若a1<1<a2,则c1<c2C.若a1<a2<1,则c1<c2D.若a1<a2<1,则c2<c15.若点M(0,5),N(2,5)在抛物线y=2(x−m)2+3上,则m的值为()A.2 B.1 C.0 D.-16.二次函数y=ax2+bx+c的图像经过点(−5,0),(3,0)则关于x的方程ax2+bx+c=0的根是()A.x1=0,x2=3B.x1=−5,x2=0C.x1=5,x2=−3D.x1=−5,x2=37.如图,抛物线y=ax2+bx+c的对称轴为直线x=1,经过点(3,0)下列结论:①abc>0;②b2−4ac>0;③3a+c=0;④抛物线经过点(−3,y1)和(4,y2),则y1>y2;⑤am2−b≤a−bm (m为任意实数).其中,正确结论的个数是()A.1 B.2 C.3 D.48.如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y=−112x2+23x+53,则该同学此次投掷实心球的成绩是()A.2m B.6m C.8m D.10m二、填空题9.抛物线y=2(x+1)2+2的顶点坐标是.10.已知函数y=mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点,则实数m的值为.11.把抛物线y=12x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为.12.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有实数根,则m的最小值为13.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的有关系如图所示,D为该水流的最高点DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m则该水流距水平面的最大高度AD的为m.三、解答题14.已知二次函数y=−2x2+bx+c的图像经过A(−1,0),B(3,0)求抛物线的解析式15.将二次函数y=2x2+4x−1的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.16.已知二次函数y=x2+bx+c经过(0,−2)和(1,−2).(1)求该二次函数的表达式和对称轴.(2)当−1≤x≤3时,求该二次函数的最大值和最小值.17.如图,二次函数y=x2+bx+c的图象与x轴分别交于点A,B(4,0)(点A在点B 的左侧),且经过点(−3,7),与y轴交于点C .(1)求b,c的值.(2)将线段OB平移,平移后对应点O′和B′都落在拋物线上,求点B′的坐标. 18.某某商店销售一种销售成本为 40 元/件的商品,销售一段时间后发现,每天的销量 y(件)与当天的销售单价 x (元/件)满足一次函数关系,并且当 x =20 时,y=1000,当 x =25 时,y=950.(1)求出y与x的函数关系式,并写出自变量的取值范围;(2)求出每件售价多少元时,商店销售该商品每天能获得最大利润,最大利润是多少元;(3)如果该商店要使每天的销售利润不低于 13750 元,且每天的总成本不超过 20000 元,那么销售单价应控制在什么范围内?参考答案1.C2.D3.A4.C5.B6.D7.C8.D9.(-1,2)10.1或﹣4511.y =12(x +1)2−212.-313.914.解:把(-1,0)、(3,0)代入y =−2x 2+bx +c 中得{−2−b +c =0−18+3b +c =0解得{b =4c =6∴二次函数的解析式为y =−2x 2+4x +6.15.解:y =2(x 2+2x)−1y =2(x 2+2x +1)−2−1y =2(x +1)2−3∴开口方向:向上,顶点坐标:(-1,-3),对称轴:直线x =−1.16.(1)解:将点(0,-2)与(1,-2)分别代入y=x 2+bx+c得{c =−21+b +c =−2解得:{b =−1c =−2所以所求的函数解析式为:y=x 2-x-2对称轴直线为:x =−b 2a =−−12=12;(2)解:∵函数y=x 2-x-2 中,二次项系数为1>0,对称轴直线是x=12 ∴抛物线的开口向上,当x=12时,函数有最小值y= −94又-1≤x ≤3,故当x=3时,有最大值y=4∴当-1≤x ≤3时,函数的最大值是4,最小值是−94.17.(1)解:将点 B(4,0) 、 (−3,7) 代入二次函数解析式 y =x 2+bx +c 得 {16+4b +c =09−3b +c =7解得 {b =−2c =−8; (2)解:由(1)得二次函数的解析式为 y =x 2−2x −8 ,由题意可得 OB =4 设平移后点 O ′ 和 B ′ 的坐标分别为 (x 1,m) , (x 2,m) 则 x 1,x 2 为一元二次方程 x 2−2x −8=m 的两个根( x 1<x 2 ),且 x 2−x 1=4∴x 2−2x −8−m =0由根与系数的关系可得: x 2+x 1=2 x 1x 2=−8−m∴{x 2+x 1=2x 2−x 1=4解得 {x 1=−1x 2=3∴x 1x 2=−1×3=−8−m∴m =5∴B ′(3,−5) .18.(1)解:设y 与x 的函数关系式为y =kx +b∵当x =20时y =1000,当x =25时∴{20k +b =100025k +b =950解得{k =−10b =120∴y 与x 的函数关系式为y =−10x +1200(40≤x ≤120);(2)解:设销售利润为w 元,则w =(x −40)(−10x +1200)=−10x 2+1600x −48000=−10(x −80)2+16000∵a =−10<0∴抛物线开口向下∴当x =80时答:当每件售价80元时,商店销售该商品每天可获得最大利润,最大利润是16000元.(3)解:当w=13750时解得:x1=65∵a=−10<0,抛物线开口向下∴w≥13750时的解集为:65≤x≤95又∵每天的总成本不超过20000元∴40(−10x+1200)≤20000解得:x≥70∴70≤x≤95答:销售单价应控制在70元至95元之间.。
求二次函数解析式专项练习60题(含解析)

文档从网络中收集,已重新整理排版.word版本可编辑.欢迎下载支持.求二次函数解析式专项练习60题(含解析)1.已知二次函数图象的顶点坐标是(1,﹣4),且与y轴交于点(0,﹣3),求此二次函数的解析式.2.已知二次函数y=x2+bx+c的图象经过点A(﹣1,12),B(2,﹣3).(1)求这个二次函数的解析式.(2)求这个图象的顶点坐标及与x轴的交点坐标.3.在平面直角坐标系xOy中,直线y=﹣x绕点O顺时针旋转90°得到直线l,直线l与二次函数y=x2+bx+2图象的一个交点为(m,3),试求二次函数的解析式.4.已知抛物线y=ax2+bx+c与抛物线形状相同,顶点坐标为(﹣2,4),求a,b,c的值.5.已知二次函数y=ax2+bx+c,其自变量x的部分取值及对应的函数值y如下表所示:(1)求这个二次函数的解析式;x …﹣2 0 2 …y …﹣1 1 11 …6.已知抛物线y=x+(m+1)x+m,根据下列条件分别求m的值.(1)若抛物线过原点;(2)若抛物线的顶点在x轴上;(3)若抛物线的对称轴为x=2.7.已知抛物线经过两点A(1,0)、B(0,3),且对称轴是直线x=2,求其解析式.8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)写出y>0时,x的取值范围_________;(2)写出y随x的增大而减小的自变量x的取值范围_________;(3)求函数y=ax2+bx+c的表达式.9.已知二次函数y=x2+bx+c的图象经过点A(﹣2,5),B(1,﹣4).(1)求这个二次函数解析式;(2)求这个图象的顶点坐标、对称轴、与坐标轴的交点坐标;(3)画出这个函数的图象.10.已知:抛物线经过点A(﹣1,7)、B(2,1)和点C(0,1).(1)求这条抛物线的解析式;(2)求该抛物线的顶点坐标.11.若二次函数y=ax2+bx+c的图象与y轴交于点A(0,3),且经过B(1,0)、C(2,﹣1)两点,求此二次函数的解析式.12.二次函数y=x2+bx+c的图象过A(2,3)和B(﹣1,0)两点,求此二次函数的解析式.13.已知:一抛物线y=ax2+bx﹣2(a≠0)经过点(3,4)和点(﹣1,0)求该抛物线的解析式,并用配方法求它的对称轴.14.二次函数y=2x2+bx+c的图象经过点(0,﹣6)、(3,0),求这个二次函数的解析式,并用配方法求它的图象的顶点坐标.15.如图,抛物线y=﹣x2+5x+m经过点A(1,0),与y轴交于点B,(1)求m的值;(2)若抛物线与x轴的另一交点为C,求△CAB的面积;(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.16.如图,抛物线y=﹣x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).(1)求这条抛物线对应函数的表达式;(2)若P点在该抛物线上,求当△PAB的面积为8时,点P的坐标.17.已知二次函数的图象经过点(0,﹣1)、(1,﹣3)、(﹣1,3),求这个二次函数的解析式.并用配方法求出图象的顶点坐标.18.已知:二次函数的顶点为A(﹣1,4),且过点B(2,﹣5),求该二次函数的解析式.19.已知一个二次函数y=x2+bx+c的图象经过(1,2)、(﹣1,6),求这个函数的解析式.20.已知二次函数y=x2+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)求该二次函数图象与x轴的另一个交点.21.已知抛物线最大值为3,其对称轴为直线x=﹣1,且过点(1,﹣5),求其解析式.22.已知二次函数图象顶点坐标为(﹣2,3),且过点(1,0),求此二次函数解析式.23.已知抛物线y=﹣x2+bx+c,它与x轴的两个交点分别为(﹣1,0),(3,0),求此抛物线的解析式.24.一个二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,求这个函数的关系式.25.已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(1,﹣4).(1)求这个函数的解析式;(2)求这个函数图象与x轴、y轴的交点坐标.26.已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).求二次函数的解析式.27.已知二次函数y=ax2+bx+c,当x=0时,函数值为5,当x=﹣1或﹣5时,函数值都为0,求这个二次函数的解析式.28.已知抛物线的图象经过点A(1,0),顶点P的坐标是.(l)求抛物线的解析式;(2)求此抛物线与两坐标轴的三个交点所围成的三角形的面积.29.如图为抛物线y=﹣x2+bx+c的一部分,它经过A(﹣1,0),B(0,3)两点.(1)求抛物线的解析式;(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.30.已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).(1)试求二次函数的解析式;(2)求y的最大值;(3)写出当y>0时,x的取值范围.31.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.32.抛物线y=﹣x2+bx+c的对称轴是x=l,它与x轴有两个交点,其中的一个为(3,0),求此抛物线的解析式.33.已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).(1)求该二次函数的解析式;(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.34.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(2,0),B(5,3).(1)求m的值和抛物线的解析式;(2)求不等式ax2+bx+c≤x+m的解集(直接写出答案);(3)若抛物线与y轴交于C,求△ABC的面积.35.二次函数的图象经过点(1,2)和(0,﹣1)且对称轴为x=2,求二次函数解析式.36.如图所示,二次函数y=﹣x2+bx+c的图象经过坐标原点O和A(4,0).(1)求出此二次函数的解析式;(2)若该图象的最高点为B,试求出△ABO的面积;(3)当1<x<4时,y的取值范围是_________.37.已知:一个二次函数的图象经过(﹣1,10),(1,4),(2,7)三点.(1)求出这个二次函数解析式;(2)利用配方法,把它化成y=a(x+h)2+k的形式,并写出顶点坐标和y随x变化情况.38.已知抛物线y=x2﹣2(k﹣2)x+1经过点A(﹣1,2)(1)求此抛物线的解析式;(2)求此抛物线的顶点坐标与对称轴.39.根据条件求下列抛物线的解析式:(1)二次函数的图象经过(0,1),(2,1)和(3,4);(2)抛物线的顶点坐标是(﹣2,1),且经过点(1,﹣2).40.已知二次函数的图象的顶点坐标为(3,﹣2)且与y轴交于(0,)(1)求函数的解析式;(2)当x为何值时,y随x增大而增大.41.已知二次函数的图象经过点(0,﹣2),且当x=1时函数有最小值﹣3.(1)求这个二次函数的解析式;(2)如果点(﹣2,y1),(1,y2)和(3,y3)都在该函数图象上,试比较y1,y2,y3的大小.42.已知二次函数y=x2+bx+c的图象经过点(0,3)、(4,3)(1)求二次函数的解析式,并在给定的坐标系中画出该函数的图象(不用列表);(2)直接写出x2+bx+c>3的解集.43.不论m取任何实数,y关于x的二次函数y=x2+2mx+m2+2m﹣1的图象的顶点都在一条直线上,求这条直线的函数解析式.44.抛物线y=ax2+bx+c过点A(﹣2,1),B(2,3),且与y轴负半轴交于点C,S△ABC=12,求其解析式.45.直线y=kx+b过x轴上的A(2,0)点,且与抛物线y=ax2相交于B、C两点,已知B点坐标为(1,1),求直线和抛物线所表示的函数解析式,并在同一坐标系中画出它们的图象.46.已知二次函数y=x2+bx+c的图象经过点P(2,7)、Q(0,﹣5).(1)试确定b、c的值;(2)若该二次函数的图象与x轴交于A、B两点(其中点A在点B的左侧),试求△PAB的面积.47.抛物线y=ax2﹣3ax+b经过A(﹣1,0),C(3,﹣2)两点.(1)求此抛物线的解析式;(2)求出这个二次函数的对称轴和顶点坐标.48.已知二次函数y=x2+bx+c的图象经过点A(0,4),且对称轴是直线x=﹣2,求这个二次函数的表达式.49.已知关于x的二次函数的图象的顶点坐标为(﹣4,3),且图象过点(l,﹣2).(1)求这个二次函数的关系式;(2)写出它的开口方向、对称轴.50.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.(1)求m的值和二次函数的解析式.(2)二次函数交y轴于C,求△ABC的面积.51.若二次函数的图象的对称轴是直线x=1.5,并且图象过A(0,﹣4)和B(4,0)(1)求此二次函数的解析式;(2)求此二次函数图象上点A关于对称轴对称的点A′的坐标.52.若二次函数y=ax2+bx+c中,c=3,图象的顶点坐标为(2,﹣1),求该二次函数的解析式.53.过点A(﹣1,4),B(﹣3,﹣8)的二次函数y1=ax2+bx+c与二次函数的图象的形状一样,开口方向相同,只是位置不同,求这个函数的解析式及顶点坐标.54.二次函数的图象与x轴的两交点的横坐标为1和﹣7,且经过点(﹣3,8).求:(1)这个二次函数的解析式;(2)试判断点A(﹣1,2)是否在此函数的图象上.55.已知二次函数y=ax2+bx+c的图象经过点(0,﹣9)、(1,﹣8),对称轴是y轴.(1)求这个二次函数的解析式;(2)将上述二次函数图象沿x轴向右平移2个单位,设平移后的图象与y轴的交点为C,顶点为P,求△POC的面积.56.如图,抛物线y=ax2+bx经过点A(4,0)、B(2,2),连接OB、AB.(1)求抛物线的解析式;(2)求证:△OAB是等腰直角三角形.57.如图,抛物线y=x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)若将上述抛物线先向下平移3个单位,再向右平移2个单位,请直接写出平移后的抛物线的解析式.58.已知二次函数y=﹣x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.59.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标.60.已知函数y=x2+bx+c过点A(2,2),B(5,2).(1)求b、c的值;(2)求这个函数的图象与x轴的交点C的坐标;(3)求S△ABC的值.二次函数解析式60题参考答案:1.∵顶点坐标是(1,﹣4)因此,设抛物线的解析式为:y=a(x﹣1)2﹣4,∵抛物线与y轴交于点(0,﹣3)把(0,﹣3)代入解析式:﹣3=a(0﹣1)2﹣4解之得:a=1(14分)∴抛物线的解析式为:y=x2﹣2x﹣3.2.(1)把点A(﹣1,12),B(2,﹣3)的坐标代入y=x2+bx+c 得得∴y=x2﹣6x+5.(2)y=x2﹣6x+5,y=(x﹣3)2﹣4,故顶点为(3,﹣4).令x2﹣6x+5=0解得x1=1,x2=5.与x轴的交点坐标为(1,0),(5,0).3.由题意,直线l的解析式为y=x,将(m,3)代入直线l的解析式中,解得m=3.将(3,3)代入二次函数的解析式,解得,∴二次函数的解析式为4.抛物线y=ax2+bx+c 与抛物线形状相同,则a=±.当a=时,解析式是:y=(x+2)2+4=x2+x+5.即a=,b=1,c=5;当a=﹣时,解析式是:y=﹣(x+2)2+4=﹣x2﹣x+3.即a=﹣,b=﹣1,c=3.5.(1)依题意,得,解得;∴二次函数的解析式为:y=x2+3x+1.(2)由(1)知:y=x2+3x+1=(x+)2﹣,故其顶点坐标为(﹣,﹣)6.(1)∵抛物线过原点,∴0=02+(m+1)×0+m.解得m=0;(2)∵抛物线的顶点在x轴上.∴△=(m+1)2﹣4m=0.解得:m=1;(3)∵抛物线的对称轴是x=2,∴﹣=2.解得m=﹣57.∵抛物线对称轴是直线x=2且经过点A(1,0)由抛物线的对称性可知:抛物线还经过点(3,0)设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0)即:y=a(x﹣1)(x﹣3)把B(0,3)代入得:3=3a∴a=1∴抛物线的解析式为:y=x2﹣4x+3.8.(1)抛物线开口向下,与x轴交于(1,0),(3,0),当y>0时,x的取值范围是:1<x<3;(2)抛物线对称轴为直线x=2,开口向下,y随x的增大而减小的自变量x的取值范围是x>2;(3)抛物线与x轴交于(1,0),(3,0),设解析式y=a(x﹣1)(x﹣3),把顶点(2,2)代入,得2=a(2﹣1)(2﹣3),解得a=﹣2,∴y=﹣2(x﹣1)(x﹣3),即y=﹣2x2+8x﹣6.9.(1)把A(﹣2,5),B(1,﹣4)代入y=x2+bx+c,得,解得b=﹣2,c=﹣3,∴二次函数解析式为y=x2﹣2x﹣3.(2)∵y=x2﹣2x﹣3,∴﹣=1,=﹣4,∴顶点坐标(1,﹣4),对称轴为直线x=1;又当x=0时,y=﹣3,∴与y轴交点坐标为(0,﹣3);y=0时,x=3或﹣1,∴与x轴交点坐标为(3,0),(﹣1,0).(3)图象如图.10.(1)设所求抛物线解析式为y=ax2+bx+c.根据题意,得,解得.故所求抛物线的解析式为y=2x2﹣4x+1.(2)∵,∴该抛物线的顶点坐标是(1,﹣1)11.∵二次函数y=ax2+bx+c的图象与y轴交于点A(0,3),∴c=3.又∵二次函数y=ax2+bx+c的图象经过B(1,0)、C(2,﹣1)两点,∴代入y=ax2+bx+c得:a+b+c=0,①4a+2b+c=﹣1,②由①②及c=3解得∴二次函数的解析式为y=x2﹣4x+312.由题意得解得,.此二次函数的解析式为y=x2﹣1.13.把点(3,4)、(﹣1,0)代入y=ax2+bx﹣2得:解得:则抛物线的解析式是y=x2﹣x﹣2=(x ﹣)2﹣则抛物线的对称轴是:x=14.由题意得,解得.∴这个二次函数的解析式是y=2x2﹣4x﹣6.y=2(x2﹣2x)﹣6=2(x2﹣2x+1)﹣2﹣6(1分)=2(x﹣1)2﹣8.(1分)∴它的图象的顶点坐标是(1,﹣8).15.(1)根据题意,把点A的坐标代入抛物线方程得:0=﹣1+5+m,即得m=﹣4;(2)根据题意得:令y=0,即﹣x2+5x﹣4=0,解得x1=1,x2=4,∴点C坐标为(4,0);令x=0,解得y=﹣4,∴点B的坐标为(0,﹣4);∴由图象可得,△CAB的面积S=×OB×AC=×4×3=6;(3)根据题意得:①当点O为PB的中点,设点P的坐标为(0,y),(y>0)则y﹣4=0,即得y=4,∴点P的坐标为(0,4).②当AB=BP时,AB=,∴OP 的长为:﹣4,∴P(0,﹣4),∴P(0,﹣4),或(0,4)16.(1)点(1,0),(3,0)在抛物线y=﹣x2+bx+c上.则有解得:则所求表达式为y=﹣x2+4x﹣3.(2)依题意,得AB=3﹣1=2.设P点坐标为(a,b)当b>0时,×2×b=8.则b=8.故﹣x2+4x﹣3=8即x2+4x+11=0△=(﹣4)2﹣4×1×11=16﹣44=﹣28<0,方程﹣x2+4x+11=0无实数根.当b<0时,×2×(﹣b)=8,则b=﹣8故﹣x2+4x﹣3=﹣8 即﹣x2+4x﹣5=0.解得x1=﹣1,x2=5所求点P坐标为(﹣1,﹣8),(5,﹣8)17.设二次函数的解析式为y=ax2+bx+c,由题意得,解得.故二次函数的解析式为y=x2﹣3x﹣1;y=x2﹣3x﹣1=x2﹣3x+()2﹣()2﹣1=(x ﹣)2﹣,所以抛物线的顶点坐标为(,﹣).18.设此二次函数的解析式为y=a(x+1)2+4.∵其图象经过点(2,﹣5),∴a(2+1)2+4=﹣5,∴a=﹣1,∴y=﹣(x+1)2+4=﹣x2﹣2x+3.故答案为:y=﹣x2﹣2x+319.∵二次函数y=x2+bx+c的图象经过(1,2)、(﹣1,6),∴,解得,∴所求的二次函数的解析式为y=x2﹣2x+3.20.(1)把A(2,0)、B(0,﹣6)代入y=x2+bx+c得,4+2b+c=0,c=﹣6,∴b=1,c=﹣6,∴这个二次函数的解析式y=x2+x﹣6;(2)令y=0,则x2+x﹣6=0,解方程得x1=2,x2=﹣3,∴二次函数图象与x轴的另一个交点为(﹣3,0).21.∵已知抛物线最大值为3,其对称轴为直线x=﹣1,∴抛物线的顶点坐标为(﹣1,3)设抛物线的解析式为:y=a(x+1)2+3,∵(1,﹣5)在抛物线y=a(x+1)2+3上,∴解得a=﹣2,∴此抛物线的解析式y=﹣2(x+1)2+322.设二次函数式为y=k(x+2)2+3.将(1,0)代入得9k+3=0,解得k=.∴所求的函数式为 y=(x+2)2+323.根据题意得,,解得,∴抛物线的解析式为y=﹣x2+2x+3;或:由已知得,﹣1、3为方程﹣x2+bx+c=0的两个解,∴﹣1+3=b,(﹣1)×3=c,解得b=2,c=3,∴抛物线的解析式为y=﹣x2+2x+3.24.设二次函数的关系式为y=ax2+bx+c(a≠0),∵二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,∴点(0,0),(﹣1,﹣1),(1,9)满足二次函数的关系式,∴,解得,所以这个函数关系式是:y=4x2+5x25.(1)由题意,将A与B 代入代入二次函数解析式得:,解得:,则二次函数解析式为y=x2﹣2x﹣3;(2)令y=0,则x2﹣2x﹣3=0,即(x+1)(x﹣3)=0,解得:x1=﹣1,x2=3,∴与x轴交点坐标为(﹣1,0),(3,0);令x=0,则y=﹣3,∴与y轴交点坐标为(0,﹣3)26.根据题意,得,解得,;∴该二次函数的解析式为:y=x2﹣2x﹣3.27.由题意得,二次函数y=ax2+bx+c,过(0,5)(﹣1,0)(﹣5,0)三点,∴,解得a=1,b=6,c=5,∴这个二次函数的解析式y=x2+6x+528.(1)由题意,可设抛物线解析式为y=a(x ﹣)2+,把点A(1,0)代入,得a(1﹣)2+=0,解之得a=﹣1,∴抛物线的解析式为y=﹣(x ﹣)2+,即y=﹣x2+5x﹣4;(2)令x=0,得y=﹣4,令y=0,解得x1=4,x2=1,S=×(4﹣1)×4=6.所以抛物线与两坐标轴的三个交点所围成的三角形的面积为6.29.(1)∵抛物线经过A(﹣1,0),B(0,3)两点∴解得∴抛物线的解析式为y=﹣x2+2x+3.(2)∵y=﹣x2+2x+3可化为y=﹣(x﹣1)2+4,∴抛物线y=﹣x2+2x+3的顶点坐标为(1,4),又∵此抛物线向左平移3个单位,再向下平移1个单位,∴平移后的抛物线的顶点坐标为(﹣2,3).∴平移后的抛物线的解析式为y=﹣(x+2)2+3=﹣x2﹣4x﹣1.30.(1)∵二次函数图象与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3),∴x=﹣1,y=0代入y=﹣x2+bx+c得:﹣1﹣b+c=0①,把x=0,y=3代入y=﹣x2+bx+c得:c=3,把c=3代入①,解得b=2,则二次函数解析式为y=﹣x2+2x+3;(2)∵二次函数y=﹣x2+2x+3的二次项系数a=﹣1<0,∴抛物线的开口向下,则当x=﹣=﹣=1时,y有最大值,最大值为=4;(3)令二次函数解析式中的y=0得:﹣x2+2x+3=0,可化为:(x﹣3)(x+1)=0,解得:x1=3,x2=﹣1,由函数图象可知:当﹣1<x<3时,y>031.∵函数的最大值是2,则此函数顶点的纵坐标是2,又顶点在y=x+1上,那么顶点的横坐标是1,设此函数的解析式是y=a(x﹣1)2+2,再把(2,1)代入函数中可得a(2﹣1)2+2=1,解得a=﹣1,故函数解析式是y=﹣x2+2x+1.32.∵﹣=﹣=1,∴b=2,又∵点(3,0)在函数上,∴﹣9+6+c=0,∴c=3,∴函数的解析式是y=﹣x2+2x+3.33.(1)设y=a(x+1)2﹣4,把点(0,﹣3)代入得:a=1,∴函数解析式y=(x+1)2﹣4或y=x2+2x﹣3;(2)∵x2+2x﹣3=0,解得x1=1,x2=﹣3,∴A(﹣3,0),B(1,0),C(0,﹣3),∴△ABC的面积=.34.(1)解:∵直线y=x+m经过A点,∴当x=2时,y=0,∴m+2=0,∴m=﹣2,∵抛物线y=x2+bx+c过A(2,0),B(5,3),∴,解得,∴抛物线的解析式为y=x2﹣6x+8;(2)由图可知,不等式ax2+bx+c≤x+m的解集为2≤x≤5;(3)解:设直线AB与y轴交于D,∵A(2,0)B(5,3),∴直线AB的解析式为y=x﹣2,∴点D(0,﹣2),由(1)知C(0,8),∴S△BCD =×10×5=25,∵S△ACD =×10×2=10,∴S△ABC=S△BCD﹣S△ACD=25﹣10=15.35.设二次函数的解析式为y=ax2+bx+c,由题意得,二次函数的图象对称轴为x=2且图象过点(1,2),(0,﹣1),故可得:,解得:.即可得二次函数的解析式为:y=﹣x2+4x﹣136.(1)由条件得解得所以解析式为y=﹣x2+4x,(2)∵该图象的最高点为B,∴点B的坐标为(2,4),∴△ABO的面积=×4×4=8,(3)∵当x=1时,y=3,∴当1<x<4时,y的取值范围是0<y<4.故答案为:0<y<4.37.(1)这个二次函数解析式y=ax2+bx+c(a≠0),把三点(﹣1,10),(1,4),(2,7)分别代入得:,解得:,故这个二次函数解析式为:y=2x2﹣3x+5;(2)y=2x2﹣3x+5=2(x2﹣x+﹣)+5=2(x ﹣)2﹣+5=2(x ﹣)2+,则抛物线的顶点坐标是(,),因为抛物线的开口向上,所以当x >时,y随x的增大而增大,当x时,y随x的增大而减小.38.(1)将A(﹣1,2)代入y=x2﹣2(k﹣2)x+1得:2=1﹣2(k ﹣2)+1,解得:k=2,则抛物线解析式为y=x2+1;(2)对于二次函数y=x2+1,a=1,b=0,c=1,∴﹣=0,=1,则顶点坐标(0,1);对称轴为直线x=0(y轴)39.(1)设抛物线的解析式是y=ax2+bx+c,把(0,1),(2,1),(3,4)代入得:,解得:,∴y=x2﹣2x+1.(2)设抛物线的解析式是:y=a(x+2)2+1,把(1,﹣2)代入得:﹣2=a(1+2)2+1,∴a=﹣,∴y=﹣(x+2)2+1,即y=﹣x2﹣x ﹣.40.(1)设函数的解析式是:y=a(x﹣3)2﹣2根据题意得:9a﹣2=,解得:a=;∴函数解析式是:y=﹣2;(2)∵a=>0 ∴二次函数开口向上又∵二次函数的对称轴是x=3.∴当x>3时,y随x增大而增大.41.(1)由题意知:抛物线的顶点坐标为(1,﹣3)设二次函数的解析式为y=a(x﹣1)2﹣3,由于抛物线过点(0,﹣2),则有:a(0﹣1)2﹣3=﹣2,解得a=1;因此抛物线的解析式为:y=(x﹣1)2﹣3.(2)∵a=1>0,∴故抛物线的开口向上;∵抛物线的对称轴为x=1,∴(1,y2)为抛物线的顶点坐标,∴y2最小.由于(﹣2,y1)和(4,y1)关于对称轴对称,可以通过比较(4,y1)和(3,y3)来比较y1,y3的大小,由于在y轴的右侧是增函数,所以y1>y3.于是y2<y3<y1.42.(1)由于二次函数y=x2+bx+c的图象经过点(0,3)、(4,3),则,解得:,∴此抛物线的解析式为:y=x2﹣4x+3.函数图象如下:(2)由函数图象可直接写出x2+bx+c>3的解集为:x<0或x>4.43.二次函数可以变形为y=(x+m)2+2m﹣1,抛物线的顶点坐标为(﹣m,2m﹣1).由,消去m,得y=﹣2x﹣1.所以这条直线的函数解析式为y=﹣2x﹣144.设直线AB的解析式为y=kx+b,∴,解得,直线AB的解析式为y=x+2,令x=0,则y=2,∴直线AB与y轴的交点坐标(0,2),∵S△ABC=12,∴C(0,﹣4),∵抛物线y=ax2+bx+c过点A(﹣2,1),B(2,3),且与y轴负半轴交于点C,∴,解得,∴抛物线的解析式为y=x2+x﹣445.∵直线y=kx+b过点A(2,0)和点B(1,1),∴,解得,∴直线AB所表示的函数解析式为y=﹣x+2,∵抛物线y=ax2过点B(1,1),∴a×12=1,解得a=1,∴抛物线所表示的函数解析式为y=x2.它们在同一坐标系中的图象如下所示:46.(1)∵二次函数y=x2+bx+c的图象经过点P(2,7)、Q(0,﹣5),,解得b=4,c=﹣5.∴b、c的值是4,5;(2)∵二次函数的图象与x轴交于A、B两点,(其中点A在点B 的左侧),∴A(1,0),B(﹣5,0),∴AB=6,∵P点的坐标是:(2,7),∴△PAB的面积=×6×7=2147.(1)根据题意得,解得,所以抛物线的解析式为y=﹣x﹣2;(2)y=﹣x﹣2=(x ﹣)2﹣,所以抛物线的对称轴为直线x=,顶点坐标为(,﹣)48.∵二次函数的图象过A(0,4),∴c=4,∵对称轴为x=﹣1,∴x=﹣=﹣2,解得b=4;∴二次函数的表达式为y=x2+4x+4.49.(1)∵关于x的二次函数的图象的顶点坐标为(﹣4,3),∴设该二次函数的关系式为:y=a(x+4)2+3(a≠0);又∵图象过点( l,﹣2),∴﹣2=a(1+4)2+3,解得,a=﹣;∴设该二次函数的关系式为:y=﹣(x+4)2+3;(2)由(1)知,该二次函数的关系式为:y=﹣(x+4)2+3,∴a=﹣<0,∴该抛物线的方向向下;∵关于x的二次函数的图象的顶点坐标为(﹣4,3),∴对称轴方程为:x=﹣4.50.(1)把A(﹣1,0)代入y1=﹣x+m得﹣(﹣1)+m=0,解得m=1,把A(﹣1,0)、B(2,﹣3)代入y2=ax2+bx﹣3得,解得.故二次函数的解析式为y2=x2﹣﹣2x﹣3;(2)因为C点坐标为(0,﹣3),B(2,﹣3),所以BC⊥y轴,所以S△ABC =×2×3=3.51.(1)设此二次函数的解析式为y=ax2+bx+c,把A(0,﹣4)和B(4,0),即对称轴x=1.5代入解析式得:,解得:故y=x2﹣3x﹣4;(2)∵A(0,﹣4),对称轴是x=1.5,∴A′(3,﹣4)52.∵二次函数y=ax2+bx+c的顶点坐标为(﹣,),二次函数y=ax2+bx+c中,c=3,图象的顶点坐标为(2,﹣1),∴﹣=2,=﹣1,解得a=1,b=﹣4,∴二次函数的解析式y=x2﹣4x+353.∵二次函数y1=ax2+bx+c 与二次函数的图象的形状一样,开口方向相同,∴a=﹣2,将点A(﹣1,4),B(﹣3,﹣8)代入y1=﹣2x2+bx+c,得,解得,∴y1=﹣2x2﹣2x+4;∵y1=﹣2x2﹣2x+4=﹣2(x2+x)+4=﹣2(x+)2+,∴顶点坐标为(﹣,).故这个函数的解析式为y1=﹣2x2﹣2x+4,顶点坐标为(﹣,).54.(1)∵二次函数的图象与x轴的两交点的横坐标为1和﹣7,且经过点(﹣3,8),∴两交点的横坐标为:(1,0),(﹣7,0),且经过点(﹣3,8),∴代入解析式:y=a(x﹣1)(x+7),8=a(﹣3﹣1)×(﹣3+7),解得:a=﹣,∴y=﹣(x﹣1)(x+7);(2)∵将点A(﹣1,2)此函数的解析式,∴左边=2,右边=﹣(﹣1﹣1)(﹣1+7)=6;∴左边≠右边,∴点A(﹣1,2)不在此函数的图象上.55.(1)∵二次函数的对称轴为y轴,即x=0,∴b=0,即二次函数解析式为y=ax2+c,又二次函数的图象经过点(0,﹣9)、(1,﹣8),∴,解得:,则二次函数的解析式为y=x2﹣9;(2)由平移规律得:二次函数向右平移2个单位的解析式为:y=(x﹣2)2﹣9,即y=x2﹣4x﹣5,令x=0,解得:y=﹣5,∴C(0,﹣5),即OC=5,又平移后抛物线的顶点P的坐标为(2,9),即P的横坐标为2,则S△POC =OC•x P的横坐标=×5×2=5.56.1)解:由题意得,解得;∴该抛物线的解析式为:y=﹣x2+2x;(2)证明:过点B作BC⊥x轴于点C,则OC=BC=AC=2;∴∠BOC=∠OBC=∠BAC=∠ABC=45°;∴∠OBA=90°,OB=AB;∴△OAB是等腰直角三角形;57.(1)将A(﹣1,0)代入抛物线y=x2+bx﹣2得,×(﹣1)2﹣b﹣2=0,解得,b=﹣,则函数解析式为y=x2﹣x﹣2.配方得,y=(x ﹣)2﹣,可见,顶点坐标为(,﹣).(2)将上述抛物线先向下平移3个单位,再向右平移2个单位,可得,y=(x ﹣﹣2)2﹣﹣3=(x ﹣)2﹣=x2﹣x.58.(1)把(2,0)、(0,﹣6)代入二次函数解析式,可得,解得,故解析式是y=﹣x2+4x﹣6;(2)∵对称轴x=﹣=4,∴C点的坐标是(4,0),∴AC=2,OB=6,AB=2,BC=2,∴S△ABC =AC•OB=×2×6=6,△ABC的周长=AC+AB+BC=2+2+2.59.(1)A坐标是(﹣1,﹣1),B点的坐标是(3,﹣9),代入y=ax2﹣4x+c 得:解得:a=1,c=﹣6.则二次函数表达式是:y=x2﹣4x﹣6(2)y=x2﹣4x﹣6=(x﹣2)2﹣10,因此对称轴为直线x=2,顶点坐标为(2,﹣10)60.(1)把A(2,2),B(5,2)分别代入y=x2+bx+c,文档从网络中收集,已重新整理排版.word版本可编辑.欢迎下载支持. 可得,解得;(2)由b=﹣7,c=12,知y=x2﹣7x+12令y=0,得x2﹣7x+12=0,∴x=3或x=4,∴C(3,0)或C(4,0);(3)∵A(2,2)B(5,2)∴AB=|2﹣5|=3,且△ABC的AB边上的高h=2,∴S△ABC =AB•h=×3×2=311word版本可编辑.欢迎下载支持.。
中考数学真题二次函数专项练习(带答案)

中考数学真题二次函数一、选择题1.已知点M(−4,a−2) N(−2,a) P(2,a)在同一个函数图象上.则这个函数图象可能是()A.B.C.D.2.抛物线y=ax2−a(a≠0)与直线y=kx交于A(x1,y1).B(x2,y2)两点.若x1+x2<0.则直线y= ax+k一定经过().A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限3.设二次函数y=a(x−m)(x−m−k)(a>0,m,k是实数).则()A.当k=2时.函数y的最小值为−a B.当k=2时.函数y的最小值为−2aC.当k=4时.函数y的最小值为−a D.当k=4时.函数y的最小值为−2a4.已知二次函数y=ax2−(3a+1)x+3(a≠0).下列说法正确的是()A.点(1,2)在该函数的图象上B.当a=1且−1≤x≤3时.0≤y≤8C.该函数的图象与x轴一定有交点D.当a>0时.该函数图象的对称轴一定在直线x=32的左侧5.一个球从地面竖直向上弹起时的速度为10米/秒.经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2.那么球弹起后又回到地面所花的时间t(秒)是()A.5B.10C.1D.2二、填空题6.在平面直角坐标系xOy中.一个图形上的点都在一边平行于x轴的矩形内部(包括边界).这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图.函数y=(x−2)2(0⩽x⩽3)的图象(抛物线中的实线部分).它的关联矩形为矩形OABC.若二次函数y=14x2+bx+c(0⩽x⩽3)图象的关联矩形恰好也是矩形OABC.则b=.三、解答题7.设二次函数y=ax2+bx+1.(a≠0.b是实数).已知函数值y和自变量x的部分对应取值如下表所示:(1)若m=4.求二次函数的表达式;(2)写出一个符合条件的x的取值范围.使得y随x的增大而减小.(3)若在m、n、p这三个实数中.只有一个是正数.求a的取值范围.8.如图.已知二次函数y=x2+bx+c图象经过点A(1,−2)和B(0,−5).(1)求该二次函数的表达式及图象的顶点坐标.(2)当y≤−2时.请根据图象直接写出x的取值范围.9.已知二次函数y=−x2+bx+c.(1)当b=4,c=3时.①求该函数图象的顶点坐标.②当−1⩽x⩽3时.求y的取值范围.(2)当x⩽0时.y的最大值为2;当x>0时.y的最大值为3.求二次函数的表达式.10.在二次函数y=x2−2tx+3(t>0)中.(1)若它的图象过点(2,1).则t的值为多少?(2)当0≤x≤3时.y的最小值为−2.求出t的值:(3)如果A(m−2,a),B(4,b),C(m,a)都在这个二次函数的图象上.且a<b<3.求m的取值范围。
中考数学《二次函数》专项练习(附答案解析)

中考数学《二次函数》专项练习(附答案解析)一、综合题1.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是()(填方案一,方案二,或方案三),则B点坐标是(),求出你所选方案中的抛物线的表达式;(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.2.如图,抛物线 y =-x2+3x +4 与x轴负半轴相交于A点,正半轴相交于B点,与 y 轴相交于C 点.(1)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线 BC 对称的点的坐标;(2)在(1)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.3.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.4.已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.(1)求点A的坐标;(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.5.如图,抛物线G:y=−x2+2mx−m2+m+3的顶点为P(x P,y P),抛物线G与直线l:x=3交于点Q.(1)x P=,y P=(分别用含m的式子表示);y P与x P的函数关系式为;(2)求点Q的纵坐标y Q(用含m的式子表示),并求y Q的最大值;(3)随m的变化,抛物线G会在直角坐标系中移动,求顶点P在y轴与l之间移动(含y轴与l)的路径的长.6.如图,抛物线的顶点D的坐标为(﹣1,4),抛物线与x轴相交于A.B两点(A在B的左侧),与y轴交于点C(0,3).(1)求抛物线的表达式;(2)如图1,已知点E(0,﹣3),在抛物线的对称轴上是否存在一点F,使得△CEF的周长最小,如果存在,求出点F的坐标;如果不存在,请说明理由;(3)如图2,连接AD,若点P是线段OC上的一动点,过点P作线段AD的垂线,在第二象限分别与抛物线、线段AD相交于点M、N,当MN最大时,求△POM的面积.7.已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).(1)求该抛物线的解析式;(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.8.如图,在平面直角坐标系xOy中,O为坐标原点,点A(4,0),点B(0,4),ΔABO的中线AC与y轴交于点C,且⊙M经过O,A,C三点.(1)求圆心M的坐标;(2)若直线AD与⊙M相切于点A,交y轴于点D,求直线AD的函数表达式;(3)在过点B且以圆心M为顶点的抛物线上有一动点P,过点P作PE∥y轴,交直线AD于点E.若以PE为半径的⊙P与直线AD相交于另一点F.当EF=4√5时,求点P的坐标.9.如图1所示,已知抛物线y=−x2+4x+5的顶点为D,与x轴交于A、B两点(A左B右),与y轴交于C点,E为抛物线上一点,且C、E关于抛物线的对称轴对称,作直线AE.(1)求直线AE的解析式;(2)在图2中,若将直线AE沿x轴翻折后交抛物线于点F,则点F的坐标为(直接填空);(3)点P为抛物线上一动点,过点P作直线PG与y轴平行,交直线AE于点G,设点P的横坐标为m,当S△PGE∶S△BGE=2∶3时,直接写出所有符合条件的m值,不必说明理由.10.综合与探究如图,直线y=−23x+4与x轴,y轴分别交于B,C两点,抛物线y=ax2+43x+c经过B,C两点,与x轴的另一个交点为A(点A在点B的左侧),抛物线的顶点为点D.抛物线的对称轴与x轴交于点E.(1)求抛物线的表达式及顶点D的坐标;(2)点M是线段BC上一动点,连接DM并延长交x轴交于点F,当FM:FD=1:4时,求点M的坐标;(3)点P是该抛物线上的一动点,设点P的横坐标为m,试判断是否存在这样的点P,使∠PAB+∠BCO=90°,若存在,请直接写出m的值;若不存在,请说明理由.11.如图,点A,B在函数y=14x2的图像上.已知A,B的横坐标分别为-2、4,直线AB与y轴交于点C,连接OA,OB.(1)求直线AB的函数表达式;(2)求ΔAOB的面积;(3)若函数y=14x2的图像上存在点P,使得ΔPAB的面积等于ΔAOB的面积的一半,则这样的点P共有个.12.如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y 轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.(1)求一次函数解析式;(2)求顶点P的坐标;,求点M (3)平移直线AB使其过点P,如果点M在平移后的直线上,且tan∠OAM=32坐标;(4)设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.13.如图,抛物线y=ax2+bx+4经过点A(−1,0),B(2,0)两点,与y轴交于点C,点D是拋物线在x轴上方,对称轴右侧上的一个动点,设点D的横坐标为m.连接AC,BC,DB,DC.(1)求抛物线的解析式;(2)当△BCD的面积与△AOC的面积和为7时,求m的值;2(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.(x+m)(x−3m)图象的顶点为M,图象交x轴于A、14.如图,y关于x的二次函数y=−√33mB两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(−3,0),连接ED.(m>0)(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.15.在图1中,抛物线y=ax2+2ax﹣8(a≠0)与x轴交于点A、B(点A在B左侧),与y轴负半轴交于点C,OC=4OB,连接AC,抛物线的对称轴交x轴于点E,交AC于点F.(1)AB的长为,a的值为;(2)图2中,直线ON分别交EF、抛物线于点M、N,OM=√17,连接NC.①求直线ON的解析式;②证明:NC∥AB;③第四象限存在点P使△BFP与△AOC相似,且BF为△BFP的直角边,请直接写出点P坐标.16.如图,直线AB的解析式为y=−43x+4,抛物线y=−13x2+bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.(1)求抛物线的解析式;(2)如图(1),当点P在第一象限内的抛物线上时,求△ABP面积的最大值,并求此时点P的坐标;(3)过点A作直线l//x轴,过点P作PH⊥l于点H,将△APH绕点A顺时针旋转,使点H的对应点恰好落在直线AB上,同时恰好落在坐标轴上,请直接写出点P的坐标.参考答案与解析1.【答案】(1)解:方案一:点B的坐标为(5,0),设抛物线的解析式为:y=a(x+5)(x−5).由题意可以得到抛物线的顶点为(0,5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15(x+5)(x−5)方案2:点B的坐标为(10,0).设抛物线的解析式为:y=ax(x−10).由题意可以得到抛物线的顶点为(5,5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15x(x−10);方案3:点B的坐标为(5,−5),由题意可以得到抛物线的顶点为(0,0).设抛物线的解析式为:y=ax2,把点B的坐标(5,−5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15x2;(2)解:方案一:由题意:把x=3代入y=−15(x+5)(x−5),解得:y=165=3.2,∴水面上涨的高度为3.2m方案二:由题意:把x=2代入y=−15x(x−10)解得:y=165=3.2,∴水面上涨的高度为3.2m.方案三:由题意:把x=3代入y=−15x2解得:y=−95= −1.8,∴水面上涨的高度为5−1.8= 3.2m.2.【答案】(1)解: 将点D( m,m+1 )代入y=−x2+3x+4中,得:m+1=−m2+3m+4,解得:m=−1或3,∵点D在第一象限,∴m=3,∴点D的坐标为(3,4);令y=0,则−x2+3x+4=0,解得:x1=−1,x2=4,令x=0,则y=4,由题意得A(-1,0),B(4,0),C(0,4),∴OC=OB=4,BC= 4√2,CD=3,∵点C、点D的纵坐标相等,∴CD∥AB,∠OCB=∠OBC=∠DCB=45°,∴点D关于直线BC的对称点E在y轴上.根据对称的性质知:CD=CE=3 ,∴OE=OC−CE=4−3=1,∴点D关于直线BC对称的点E的坐标为(0,1);(2)解: 作PF⊥AB于F,DG⊥BC于G,由(1)知OB=OC=4,∠OBC=45°.∵∠DBP=45°,∴∠CBD=∠PBF.∵CD=3,∠DCB=45°,∴CG=DG= 3√22,∵BC= 4√2,∴BG= 4√2−3√22=5√22∴tan∠PBF=tan∠CBD=DGBG =35.设PF=3t,则BF=5t,OF=5t−4.∴P(−5t+4,3t),∵P点在抛物线上,∴3t=−(−5t+4)2+3(−5t+4)+4解得:t=2225或t=0(舍去).∴点P的坐标为( −25,6625).3.【答案】(1)解:在Rt△AOB中,OA=1,tan∠BAO= OBOA=3,∴OB=3OA=3.∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).代入解析式为{a+b+c=09a−3b+c=0c=3,解得: {a =−1b =−2c =3.∴抛物线的解析式为y=﹣x 2﹣2x+3(2)解:①∵抛物线的解析式为y=﹣x 2﹣2x+3,∴对称轴l=﹣ b2a =﹣1,∴E 点的坐标为(﹣1,0).如图, 当∠CEF=90°时,△CEF ∽△COD .此时点P 在对称轴上,即点P 为抛物线的顶点,P (﹣1,4);当∠CFE=90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于点M ,则△EFC ∽△EMP . ∴EMMP =EFFC =DO OC=13 ,∴MP=3EM .∵P 的横坐标为t ,∴P (t ,﹣t 2﹣2t+3).∵P 在第二象限,∴PM=﹣t 2﹣2t+3,EM=﹣1﹣t ,∴﹣t 2﹣2t+3=﹣(t ﹣1)(t+3),解得:t 1=﹣2,t 2=﹣3(因为P 与C 重合,所以舍去),∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.∴P (﹣2,3).∴当△CEF 与△COD 相似时,P 点的坐标为:(﹣1,4)或(﹣2,3); ②设直线CD 的解析式为y=kx+b ,由题意,得{−3k +b =0b =1 ,解得: {k =13b =1,∴直线CD 的解析式为:y= 13 x+1.设PM 与CD 的交点为N ,则点N 的坐标为(t , 13 t+1),∴NM= 13 t+1.∴PN=PM ﹣NM=﹣t 2﹣2t+3﹣( 13 t+1)=﹣t 2﹣ 73t +2. ∵S △PCD =S △PCN +S △PDN ,∴S △PCD = 12 PN •CM+ 12 PN •OM= 12 PN (CM+OM )= 12 PN •OC= 12 ×3(﹣t 2﹣ 73t +2)=﹣ 32 (t+76)2+ 12124 ,∴当t=﹣ 76 时,S △PCD 的最大值为 12124 . 4.【答案】(1)解:∵抛物线C 1:y=ax 2+4ax+4a+b (a ≠0,b >0)经过原点O , ∴0=4a+b ,∴当ax 2+4ax+4a+b=0时,则ax 2+4ax=0, 解得:x=0或﹣4,∴抛物线与x 轴另一交点A 坐标是(﹣4,0)(2)解:∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1)∴顶点M坐标为(﹣2,b),∵△AMO为等腰直角三角形,∴b=2,∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,∴a(0+2)2+2=0,解得:a=﹣12,∴抛物线C1:y=﹣12x2﹣2x(3)解:∵b=1,抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,(如图2)∴a=﹣14,∴y=﹣14(x+2)2+1=﹣14x2﹣x,设N(n,﹣1),又因为点P(m,0),∴n﹣m=m+2,∴n=2m+2即点N的坐标是(2m+2,﹣1),∵顶点N在抛物线C1上,∴﹣1=﹣14(2m+2+2)2+1,解得:m=﹣2+ √2或﹣2﹣√2 5.【答案】(1)m;m+3;y P=x P+3(2)解:∵抛物线 G :y =−x 2+2mx −m 2+m +3 与直线 l :x =3 交于点 Q , ∴把 x =3 代入 y =−x 2+2mx −m 2+m +3 , 得 y Q =−m 2+7m −6 .∵y Q =−m 2+7m −6=−(m −72)2+254,∴当 m =72 时, y Q 的最大值为 254 .(3)解:∵点 P 在 y 轴与 l 之间沿直线 l 1:y =x +3 运动, 如图,设直线 l 1:y =x +3 与 y 轴和直线 l 分别交于点 B 和点 P 1 ,线段 BP 1 的长即为点 P 路径长.把 x B =0 , x P 1=3 代入 y =x +3 得点 B(0,3) ,点 P 1(3,6) , 过点 P 1 作 P 1M ⊥y 轴,垂足为M , 则 P 1M =3,BM =3 , 在 Rt △BMP 1 中, BP 1=√BM 2+MP 12=√32+32=3√2 ,∴点 P 路径长为 3√2 .6.【答案】(1)解:设抛物线的表达式为:y =a (x+1)2+4, 把x =0,y =3代入得:3=a (0+1)2+4,解得:a =﹣1 ∴抛物线的表达式为y =﹣(x+1)2+4=﹣x 2﹣2x+3(2)解:存在.如图1,作C 关于对称轴的对称点C ′,连接EC ′交对称轴于F ,此时CF+EF的值最小,则△CEF的周长最小.∵C(0,3),∴C′(﹣2,3),易得C′E的解析式为:y=﹣3x﹣3,当x=﹣1时,y=﹣3×(﹣1)﹣3=0,∴F(﹣1,0)(3)解:如图2,∵A(﹣3,0),D(﹣1,4),易得AD的解析式为:y=2x+6,过点D作DH⊥x轴于H,过点M作MG⊥x轴交AD于G,AH=﹣1﹣(﹣3)=2,DH=4,∴AD=√AH2+DH2=√22+42=2√5,设M(m,﹣m2﹣2m+3),则G(m,2m+6),(﹣3≤m≤﹣1),∴MG=(﹣m2﹣2m+3)﹣(2m+6)=﹣m2﹣4m﹣3,由题易知△MNG∽△AHD,∴MGMN =ADAH即MN=AH×MGAD =22√5=−√55(m+2)2+√55∵√55<0∴当m =﹣2时,MN 有最大值;此时M (﹣2,3),又∵C (0,3),连接MC ∴MC ⊥y 轴∵∠CPM =∠HAD ,∠MCP =∠DHA =90°, ∴△MCP ∽△DHA , ∴PCAH =MCDH 即 PC2=24 ∴PC =1∴OP =OC ﹣PG =3﹣1=2, ∴S △POM = 12×2×2 =2,7.【答案】(1)解:由题意,得 {0=16a −8a +c 4=c解得 {a =−12c =4∴所求抛物线的解析式为:y=﹣ 12 x 2+x+4(2)解:设点Q 的坐标为(m ,0),过点E 作EG ⊥x 轴于点G .由﹣ 12 x 2+x+4=0, 得x 1=﹣2,x 2=4∴点B 的坐标为(﹣2,0) ∴AB=6,BQ=m+2 ∵QE ∥AC ∴△BQE ∽△BAC∴EG CO =BQBA 即 EG4=m+26 ∴EG =2m+43∴S △CQE =S △CBQ ﹣S △EBQ = 12 BQ •CO ﹣ 12 BQ •EG = 12 (m+2)(4﹣2m+43)= −13m 2+23m +83 =﹣ 13 (m ﹣1)2+3 又∵﹣2≤m ≤4∴当m=1时,S △CQE 有最大值3,此时Q (1,0) (3)解:存在.在△ODF 中. (ⅰ)若DO=DF ∵A (4,0),D (2,0) ∴AD=OD=DF=2又在Rt △AOC 中,OA=OC=4 ∴∠OAC=45度 ∴∠DFA=∠OAC=45度∴∠ADF=90度.此时,点F 的坐标为(2,2) 由﹣ 12 x 2+x+4=2, 得x 1=1+ √5 ,x 2=1﹣ √5此时,点P 的坐标为:P (1+ √5 ,2)或P (1﹣ √5 ,2). (ⅱ)若FO=FD ,过点F 作FM ⊥x 轴于点M由等腰三角形的性质得:OM= 12OD=1∴AM=3∴在等腰直角△AMF中,MF=AM=3∴F(1,3)由﹣12x2+x+4=3,得x1=1+ √3,x2=1﹣√3此时,点P的坐标为:P(1+ √3,3)或P(1﹣√3,3).(ⅲ)若OD=OF∵OA=OC=4,且∠AOC=90°∴AC= 4√2∴点O到AC的距离为2√2,而OF=OD=2 <2√2,与OF≥2 √2矛盾,所以AC上不存在点使得OF=OD=2,此时,不存在这样的直线l,使得△ODF是等腰三角形综上所述,存在这样的直线l,使得△ODF是等腰三角形所求点P的坐标为:P(1+ √5,2)或P(1﹣√5,2)或P(1+ √3,3)或P(1﹣√3,3)8.【答案】(1)解:∵C为OB的中点,点B(0,4),∴点C(0,2),又∵M为AC中点,点A(4,0),0+4 2=2,2+02=1,∴点M(2,1)(2)解:∵⊙P与直线AD,则∠CAD=90°,设:∠CAO=α,则∠CAO=∠ODA=∠PEH=α,tan∠CAO=OCOA =12=tanα,则sinα=√5,cosα=√5,AC=√10,则CD=ACsin∠CDA =√10sinα=10,则点D(0,−8),设直线AD的解析式为:y=mx+n,将点A、D的坐标分别代入得:{0=4m+n−8=n,解得:{m=2n=−8,所以直线AD的表达式为:y=2x−8(3)解:设抛物线的表达式为:y=a(x−2)2+1,将点B坐标代入得:4=a(0-2)2+1,解得:a=34,故抛物线的表达式为:y=34x2−3x+4,过点P作PH⊥EF,则EH=12EF=2√5,cos∠PEH=EHPE =2√5PE=cosα=√5,解得:PE=5,设点P(x,34x2−3x+4),则点E(x,2x−8),则PE=34x2−3x+4−2x+8=5,解得x=143或2(舍去2),则点P(143,193) .9.【答案】(1)解:∵抛物线的解析式为y=−x2+4x+5,∴该抛物线的对称轴为:x=−42×(−1)=2,令y=−x2+4x+5中x=0,则y=5,∴点C的坐标为(0,5),∵C、E关于抛物线的对称轴对称,∴点E的坐标为(2×2−0,5),即(4,5),令y =−x 2+4x +5中y =0,则−x 2+4x +5=0, 解得:x 1=−1,x 2=5,∴点A 的坐标为(−1,0)、点B 的坐标为(5,0), 设直线AE 的解析式为y =kx +b ,将点A(−1,0)、E(4,5)代入y =kx +b 中, 得:{0=−k +b 5=4k +b ,解得:{k =1b =1,∴直线AE 的解析式为y =x +1; (2)(6,-7)(3)解:符合条件的m 值为0、3、3−√412和3+√412.10.【答案】(1)解:当x =0时,得y =4, ∴点C 的坐标为(0,4),当y =0时,得−23x +4=0,解得:x =6, ∴点B 的坐标为(6,0), 将B ,C 两点坐标代入,得{36a +43×6+c =0,c =4. 解,得{a =−13,c =4.∴抛物线线的表达式为y =−13x 2+43x +4.∵y =−13x 2+43x +4=−13(x 2−4x +4−4)+4=−13(x −2)2+163.∴顶点D 坐标为(2,163). (2)解:作MG ⊥x 轴于点G ,∵∠MFG =∠DFE ,∠MGF =∠DEF =90°, ∴ΔMGF ∽ΔDEF .∴FM FD =MG DE.∴14=MG163.∴MG =43当y =43时,43=−23x +4 ∴x =4.∴点M 的坐标为(4,43).(3)解:∵∠PAB +∠BCO =90°,∠CBO +∠BCO =90°, ∴∠PAB =∠CBO ,∵点B 的坐标为(6,0),点C 的坐标为(0,4), ∴tan ∠CBO =46=23, ∴tan ∠PAB =23, 过点P 作PQ ⊥AB , 当点P 在x 轴上方时,−13m 2+4m +12m +2=23解得m=4符合题意, 当点P 在x 轴下方时,13m 2−4m −12m +2=23解得m=8符合题意, ∴存在,m 的值为4或8.11.【答案】(1)解:∵A ,B 是抛物线 y =14x 2 上的两点,∴当 x =−2 时, y =14×(−2)2=1 ;当 x =4 时, y =14×42=4 ∴点A 的坐标为(-2,1),点B 的坐标为(4,4) 设直线AB 的解析式为 y =kx +b , 把A ,B 点坐标代入得 {−2k +b =14k +b =4解得, {k =12b =2所以,直线AB 的解析式为: y =12x +2 ; (2)解:对于直线AB : y =12x +2 当 x =0 时, y =2 ∴OC =2∴S ΔAOB =S ΔAOC +S ΔBOC = 12×2×2+12×2×4 =6 (3)412.【答案】(1)解:∵A (﹣1,0), ∴OA=1 ∵OB=3OA , ∴B (0,3)∴图象过A 、B 两点的一次函数的解析式为:y=3x+3(2)解:∵二次函数y=ax 2﹣2ax+c (a <0)的图象与x 轴负半轴交于点A (﹣1,0),与y 轴正半轴交于点B (0,3), ∴c=3,a=﹣1,∴二次函数的解析式为:y=﹣x 2+2x+3 ∴抛物线y=﹣x 2+2x+3的顶点P (1,4) (3)解:设平移后的直线的解析式为:y=3x+m ∵直线y=3x+m 过P (1,4), ∴m=1,∴平移后的直线为y=3x+1 ∵M 在直线y=3x+1,且 设M (x ,3x+1)①当点M 在x 轴上方时,有 3x+1x+1=32 ,∴x =13 , ∴M 1(13,2)②当点M 在x 轴下方时,有 −3x+1x+1=32 ,∴x =−59 , ∴M 2(−59 , −23)(4)解:作点D 关于直线x=1的对称点D ′,过点D ′作D ′N ⊥PD 于点N , 当﹣x 2+2x+3=0时,解得,x=﹣1或x=3, ∴A (﹣1,0), P 点坐标为(1,4),则可得PD 解析式为:y=2x+2, 根据ND ′⊥PD ,设ND ′解析式为y=kx+b , 则k=﹣ 12 ,将D ′(2,2)代入即可求出b 的值, 可得函数解析式为y=﹣ 12 x+3,将两函数解析式组成方程组得: {y =−12x +3y =2x +2 ,解得 {x =25y =145 ,故N ( 25 , 145 ),由两点间的距离公式:d= √(2−25)2+(2−145)2 = 4√55, ∴所求最小值为4√5513.【答案】(1)解:把A (-1,0),B (2,0)代入抛物线解析式得: {a −b +4=04a +2b +4=0,解得: {a =−2b =2∴抛物线的解析式为: y =−2x 2+2x +4 (2)解:如图,连接OD ,由 y =−2x 2+2x +4 可得: 对称轴为 x =−22×(−2)=12 ,C (0,4)∵D(m,−2m 2+2m +4)(12<m <2) ,A (-1,0),B (2,0) ∴∴S △BCD =S △OCD +S △BCD −S △OBC=12×4m +12×2·(−2m 2+4m +2)−12×2×4=−2m 2+4m S △AOC =12×1×4=2又∵S △BCD +S △AOC =72 ∴−2m 2+4m +2=72 ,∴4m 2−8m +3=0解得: m 1=12 , m 2=32 ,当 m 1=12 时,点在对称轴上,不合题意,舍去,所以取 m 2=32 , 综上, m =32(3)解: M 1(0,0) , M 2(4,0) , M 3(√142,0) , M 4(−√142,0)14.【答案】(1)解:令y =0,则−√33m (x +m)(x −3m)=0,解得x 1=−m ,x 2=3m ;令x =0,则y =−√33m (0+m)(0−3m)=√3m .故A(−m ,0),B(3m ,0),D(0,√3m).(2)解:设直线ED 的解析式为y =kx +b ,将E(−3,0),D(0,√3m)代入得:{−3k +b =0b =√3m解得,k =√33m ,b =√3m .∴直线ED 的解析式为y =√33mx +√3m .将y =−√33m (x +m)(x −3m)化为顶点式:y =−√33m (x −m)2+4√33m . ∴顶点M 的坐标为(m ,4√33m).代入y =√33mx +√3m 得:m 2=m∵m >0,∴m =1.所以,当m =1时,M 点在直线DE 上. 连接CD ,C 为AB 中点,C 点坐标为C(m ,0). ∵OD =√3,OC =1, ∴CD =2,D 点在圆上又∵OE =3,DE 2=OD 2+OE 2=12, EC 2=16,CD 2=4, ∴CD 2+DE 2=EC 2.∴∠EDC =90°∴直线ED 与⊙C 相切.(3)解:当0<m <3时,S △AED =12AE ⋅OD =√32m(3−m)S =−√32m 2+3√32m . 当m >3时,S ΔAED =12AE ⋅OD =√32m(m −3).即S =√32m 2_3√32m . S 关于m 的函数图象的示意图如右:15.【答案】(1)6;1(2)解:①由抛物线的表达式知,抛物线的对称轴为x=﹣1,故设点M的坐标为(﹣1,m),则OM=12+m2=(√17)2,解得m=4(舍去)或﹣4,故点M的坐标为(﹣1,﹣4),由点O、M的坐标得,直线OM(即ON)的表达式为y=4x②,故答案为y=4x;②联立①②并解得{x=−2y=−8,故点N(﹣2,﹣8),∵点C、N的纵坐标相同,故NC∥x轴,即NC∥AB;③当∠BFP为直角时,由A(﹣4,0),C(0,-8)可求AC解析式为y=-2x﹣8,把x=-1,代入y=-2x﹣8得,y=-6,点F的坐标为:(-1,-6),由点F、B的坐标得,直线BF的表达式为y=2x﹣4,当x=﹣2时,y=2x﹣4=﹣8,故点N在直线BF上,连接FN,过点F作FP⊥BF交NC的延长线于点K,由直线BF 的表达式知,tan ∠BNK =2,则tan ∠FKN = 12 , 故设直线PF 的表达式为y =﹣ 12 x+t , 将点F 的坐标代入上式并解得t =﹣ 132 ,则直线PF 的表达式为y =﹣ 12 x ﹣ 132 ,故设点P 的坐标为(m ,﹣ 12 m ﹣ 132 ), 在Rt △AOC 中,tan ∠ACO = AOCO = 12 ,则tan ∠OCA =2, ∵△BFP 与△AOC 相似, 故∠FBP =∠ACO 或∠OAC ,则tan ∠FBP =tan ∠ACO 或tan ∠OAC ,即tan ∠FBP = 12 或2, 由点B 、F 的坐标得:BF = √32+62=3√5 , 则PF =BFtan ∠FBP =3√52或6 √5 ,由点P 、F 的坐标得:PF 2=(m+1)2+(﹣ 12 m ﹣ 132 +6)2=( 3√52)2或(6 √5 )2, 解得m =2或﹣4(舍去)或11或﹣13(舍去), 故点P 的坐标为(11,﹣12)或(2,﹣ 152 ); 当∠PBF 为直角时,过点B 作BP ⊥BF ,同理可求直线PF 的表达式为y =﹣ 12 x+1,故设点P 的坐标为(m ,﹣ 12 m ﹣1),同理可得,PB =BFtan ∠FBP =3√52或6 √5 ,由点P 、B 的坐标得:PB 2=(m-2)2+(﹣ 12 m+1)2=(3√52)2或(6 √5 )2,解得m=-1(舍去)或5或14或﹣10(舍去),点P的坐标为(5,﹣32)或(14,-6);综上,点P的坐标为(11,﹣12)或(2,﹣152)或(5,﹣32)或(14,-6);16.【答案】(1)解:当x=0时,y=−43x+4=4,则A(0,4),把A(0,4),C(6,0)代入y=−13x2+bx+c得{−12+6b+c=0c=4,解得{b=43c=4,∴抛物线解析式为y=−13x2+43x+4;(2)连接OP,设P(m,−13m2+43m+4),当y=0时,−43x+4=0,解得x=3,则B(3,0),S△ABP=S△AOP+S△POB−S△AOB=12⋅4⋅m+12⋅3⋅(−13m2+43m+4)−12⋅3⋅4=−12m2+4m,=−12(m−4)2+8,当m=4时,△ABP面积有最大值,最大值为8,此时P点坐标为(4,4);(3)在Rt△OAB中,AB=√32+42=5,当点P′落在x轴上,如图2,∵△APH绕点A顺时针旋转,使点H的对应点恰好落在直线AB上,同时恰好落在x 轴上∴P′H′=PH=4−(−13m2+43m+4)=13m2−43m,AH′=AH=m,∠P′H′A=∠PHA=90∘,∵∠P′BH′=∠ABO,∴△BP ′H ′ ∽ △BAO ,∴P ′H ′ : OA =BH ′ :OB ,即 (13m 2−43m) : 4=BH ′ :3, ∴BH ′=14m 2−m , ∵AH ′+BH ′=AB ,∴m +14m 2−m =5 ,解得 m 1=2√5 , m 2=−2√5( 舍去 ) ,此时P 点坐标为 (2√5,−8+8√53) ; 当点 P ′ 落在y 轴上,如图3,同理可得 P ′H ′=PH =13m 2−43m , AH ′=AH =m , ∠P ′H ′A =∠PHA =90∘ , ∵∠P ′AH ′=∠BAO , ∴△AH ′P ′′ ∽ △AOB ,∴P ′H ′ : OB =AH ′ :AO ,即 (13m 2−43m) : 3=m :4, 整理得 4m 2−25m =0 ,解得 m 1=254, m 2=0( 舍去 ) ,此时P 点坐标为 (254,−4348) ; 综上所述,P 点坐标为 (2√5,−8+8√53) 或 (254,−4348) ;。
九年级数学二次函数专项训练含答案精选5篇

九年级上册数学二次函数同步练习一、单选题1.下列函数中,是二次函数的是( ) A .y =(2x ﹣1)2 B .y =(x +1)2﹣x 2 C .y =ax 2D .y =2x +32.若抛物线258(3)23m m y m x x -+=-+-是关于x 的二次函数,那么m 的值是( )A .3B .2-C .2D .2或33.若抛物线y =x 2-x -2经过点A (3,a ),则a 的值是( ) A .2B .4C .6D .84.已知二次函数2135y x x =-+,则其二次项系数a ,一次项系数b ,常数项c 分别是( ) A .1,3,5a b c ==-= B .1,3,5a b c ===C .5,3,1a b c ===D .5,3,1a b c ==-=5.如果函数2(2)25y a x x =-+-是二次函数,则a 的取值范围是( ) A .2a ≠ B .a≥0C .a=2D .a>06.下列函数中①31y x ;①243y x x =-;①1y x=;①225=-+y x ,是二次函数的有() A .①①B .①①C .①①D .①①7.若抛物线2y x bx c =-++经过点()2,3-,则247c b --的值是( ) A .6B .7C .8D .208.函数y=ax2+bx+c(a ,b ,c 是常数)是二次函数的条件是( ) A .a≠0,b≠0,c≠0 B .a<0,b≠0,c≠0 C .a>0,b≠0,c≠0 D .a≠0二、填空题 9.若()2321m m y m x --=+是二次函数,则m 的值为______.10.若22ay x -=是二次函数,则=a ________.11.在二次函数21y x =-+中,二次项系数、一次项系数、常数项的和为_____. 12.下列函数一定是二次函数的是__________.①2y ax bx c =++;①3y x =-;①2431y x x =-+;①2(1)y m x bx c =-++;①y =(x -3)2-x 213.当常数m ≠______时,函数y =(m 2﹣2m ﹣8)x 2+(m +2)x +2是二次函数;当常数m =___时,这个函数是一次函数. 14.已知函数2135m y x -=-① 当m = _________时,y 是关于x 的一次函数; ① 当m =_________时,y 是关于x 的二次函数 .15.二次函数()22339y m x x m =+++-的图象经过原点,则m =__________.16.已知二次函数2y x bx 3=-++,当x 2=时,y 3=.则这个二次函数的表达式是________. 三、解答题17.下列函数中(x ,t 是自变量),哪些是二次函数? 22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++.18.已知函数y =(m 2-2)x 2+(m x +8. (1)若这个函数是一次函数,求m 的值; (2)若这个函数是二次函数,求m 的取值范围.19.若函数y=(a -1)x b+1+x 2+1是二次函数,试讨论a 、b 的取值范围.20.篱笆墙长30m ,靠墙围成一个矩形花坛,写出花坛面积y(m 2)与长x 之间的函数关系式,并指出自变量的取值范围.参考答案:1.A 2.C 3.B 4.D 5.A 6.B 7.B 8.D 9.4 10.2± 11.0 12.①13. 4,-2 4 14. 1 3215.316.2y x 2x 3=-++17.2132y x =-+和215s t t =++是二次函数18.(1)m (2)m ≠m ≠19.①a≠0;①b=0或-1,a 取全体实数①当a=1,b 为全体实数时,y=x 2+1是二次函数 20.y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数单元综合测试卷一.选择题(共10小题)1.下列各式中,是y 关于x 的二次函数的是( ) A .y =4xB .y =3x ﹣5C .y =D .y =2x 2+12.已知:a >b >c ,且a +b +c =0,则二次函数y =ax 2+bx +c 的图象可能是下列图象中的( )A.B.C.D.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2 5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣66.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+17.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1 8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.49.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°二.填空题(共6小题)11.函数是二次函数,则m的值为.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?21.如图,抛物线与x轴交于A(﹣1,0)、B(4,0),与y轴交于C.(1)求抛物线的解析式;(2)如图1,已知线段DE与线段BC关于平面内某点成中心对称,其中DE的两端点刚好一个落在抛物线上,一个落在对称轴上,求落在对称轴上的点的坐标;(3)如图2,点M为第二象限抛物线上,作MN∥BC交抛物线于点N,直线NB、MC 交于点P,求P点的横坐标.22.在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y'),给出如下定义:若y'=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)点(﹣5,﹣2)的“可控变点”坐标为;(2)若点P在函数y=﹣x2+16的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;(3)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,求实数a的取值范围.23.在平面直角坐标系中,抛物线y=x2+bx+c经过A(﹣4,0),点M为抛物线的顶点,点B在y轴上,直线AB与抛物线在第一象限交于点C(2,6),如图①.(1)求抛物线解析式;(2)直线AB的函数解析式为,点M的坐标为.(3)在y轴上找一点Q,使得△AMQ的周长最小,具体作法如图②,作点A关于y轴的对称点A',连接MA′交y轴于点Q,连接AM,AQ,此时△AMQ的周长最小,请求出点Q的坐标;(4)在坐标平面内是否存在点N,使以点A,O,C,N为顶点的四边形是平行四边形?若存在请直接写出点N的坐标;若不存在,请说明理由.参考答案一.选择题(共10小题)1.下列各式中,是y关于x的二次函数的是()A.y=4x B.y=3x﹣5C.y=D.y=2x2+1解:A.根据二次函数的定义,y=4x是一次函数,不是二次函数,故A不符合题意.B.根据二次函数的定义,y=3x﹣5不是二次函数,是一次函数,故B不符合题意.C.根据二次函数的定义,y=是反比例函数,不是二次函数,故C不符合题意.D.根据二次函数的定义,y=2x2+1是二次函数,故D符合题意.故选:D.2.已知:a>b>c,且a+b+c=0,则二次函数y=ax2+bx+c的图象可能是下列图象中的()A.B.C.D.解:A、由图知a>0,﹣=1,c>0,即b<0,∵已知a>b>c,故本选项错误;B、由图知a<0,而已知a>b>c,且a+b+c=0,必须a>0,故本选项错误;C、图C中条件满足a>b>c,且a+b+c=0,故本选项正确;D、∵a+b+c=0,即当x=1时a+b+c=0,与图中与x轴的交点不符,故本选项错误.故选:C.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)解:∵二次函数可化为y=(x﹣3)2+5,∴二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是(3,5),故选:D.4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2解:y=x2+2x﹣1=(x2+2x+1)﹣2=(x+1)2﹣2,即y=(x+1)2﹣2.故选:D.5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣6解:y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2,∴当x<2时,y随着x增大而增大,∴当x=时有最大值y=﹣2(﹣2)2+2=﹣2.5,故选:C.6.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+1解:设所求的抛物线解析式为y=a(x﹣3)2+1,∵所求抛物线与函数y=的图象相同且开口方向相反,∴a=﹣,∴所求的抛物线解析式为y=﹣(x﹣3)2+1.故选:D.7.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1解:当x=﹣1时,y1=(x﹣1)2=(﹣1﹣1)2=4;当x=1时,y2=(x﹣1)2=(1﹣1)2=0;当x=2时,y3=(x﹣1)2=(2﹣1)2=1,所以y2<y3<y1.故选:C.8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.4解:根据表格数据可知:抛物线的对称轴是直线x==,∴③错误;∵抛物线与x轴的一个交点为(﹣2,0),∴抛物线与x轴的另一个交点为(3,0),∴方程ax2+bx+c=0有两根为x1=﹣2,x2=3;故①正确;从表格可知当x=0时,y=6,∴抛物线与y轴的交点为(0,6);∴②正确;从表格可知:当x<时,y随x的增大而增大,当x>时,y随x的增大而减小,∴抛物线开口向下,故④错误.故选:B.9.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对解:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∴∠OBE=∠OCF=45°,∵BE=CF,∴△BOE≌△COF,∴OE=OF,∠BOE=∠COF,∴∠BOE+∠COE=∠COF+∠COE,即∠EOF=∠BOC=90°,且S△COE+S△COF=S△COE+S△BOE,即S四边形OECF=S△BOC=S正方形ABCD=×4×4=4,由垂线段最短可得,当OE⊥BC时,OE=BC=×4=2,△OEF面积取最小值为×2×2=2,∴结论Ⅰ和Ⅱ都对,结论Ⅲ错,故选:A.10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°解:把(25,0.725),(50,0.06),(60,0.09)代入y=ax2+bx+c得:,解得,∴y=0.0001x2﹣0.008x+0.21=0.0001(x﹣40)2+0.05,∵0.0001>0,∴x=40时,y最小为0.05,∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°,故选:B.二.填空题(共6小题)11.函数是二次函数,则m的值为3.解:∵函数是二次函数,∴m2﹣7=2且m+3≠0,解得:m=3.则m的值为3.故答案为:3.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为5.解:∵y=x2﹣4x+c,∴抛物线开口向上,对称轴为直线x=﹣=2,∴点A,B关于直线x=2对称,∵点A横坐标为﹣1,∴点B横坐标为5,故答案为:5.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=5.解:∵|2﹣a|=3,∴2﹣a=±3,解得:a=﹣1或5,又二次函数y=ax2开口向上,则a>0,故a=5.故答案为:5.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是3.解:∵点A(m,n)在抛物线y=x2﹣3x+1上,∴n=m2﹣3m+1,∴m﹣n=﹣m2+4m﹣1=﹣(m﹣2)2+3,∴当m=2时,m﹣n有最大值为3,故答案为:3.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为﹣.解:设A(x1,0),B(x2,0),令y=0,则y=﹣x2+2x+c=0,由根与系数的关系得:x1+x2=2,x1•x2=﹣c,则AB=|x1﹣x2|===2,令x=0,则y=c,∴C(0,c),∵CD∥x轴,∴点D纵坐标为c,当y=c时,则﹣x2+2x+c=c,解得:x=2,或x=0,∴D(2,c),∴CD=2,∵AB+CD=3,∴2+2=3,解得:c=﹣,故答案为:﹣.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为142.解:连接AC,过B作BH⊥AC于H,以B为圆心,BG为半径作圆,交BH于G',如图:∵四边形ABCD是矩形,∴∠EBF=90°,∵EF=10,点G是EF的中点,∴BG=EF=10=5,∴G在以B为圆心,5为半径的弧上,当G运动到G'时,S△ACG最小,此时四边形AGCD 面积的最小值,最小值即为四边形AG'CD的面积,∵AB=12=CD,BC=16=AD,∴AC=20,S△ACD=×12×16=96,∴BH==,∴G'H=BH﹣5=﹣5=,∴S△ACG'=AC•G'H=×20×=46,∴S四边形AG'CD=S△ACD+S△ACG'=46+96=142,即四边形AGCD面积的最小值是142.故答案为:142.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.解:(1)由图象可知,抛物线经过点(﹣1,0),对称轴为直线x=1,∴抛物线与x轴的另一个交点为(3,0),∴当y=0时,x的值为﹣1和3;(2)∵抛物线经过点(﹣1,0),(3,0),(0,﹣3),∴设抛物线的解析式为y=a(x+1)(x﹣3),代入(0,﹣3)得,﹣3=﹣3a,解得a=1,∴抛物线的解析式为y=(x+1)(x﹣3),令y=5得5=(x+1)(x﹣3),解得x1=4,x2=﹣2,∴当y>5时,求x的范围是x>4或x<﹣2;(3)∵y=(x+1)(x﹣3)=(x﹣1)2+4,∴抛物线开口向上,顶点为(1,4),对称轴为直线x=1,∴y随x的增大而增大时,x的范围是x>1.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.解:(1)y=x2﹣6x+8=x2﹣6x+9﹣1=(x﹣3)2﹣1;(2)开口向上,对称轴是直线x=3,顶点坐标是(3,﹣1);(3)x>3时,y随x的增大而增大;x<3时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.解:∵h=﹣5t2+20t=﹣5(t﹣2)2+20,且﹣5<0,∴当t=2时,h取最大值20,答:小球飞行高度达到最高时的飞行时间为2s.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?解:(1)根据题意,降价2元则销售量为60+2×10=80(斤),销售利润为:(30﹣15﹣2)×80=1040(元),答:若降价2元,则每天的销售利润是1040元;(2)设每斤“阳光玫瑰葡萄”应降价x元,根据题意得:(30﹣15﹣x)(60+10x)=1100,整理得:x2﹣9x+20=0,解得x1=4,x2=5,∵为了尽快减少库存,∴x=5,此时30﹣x=25,答:每斤“阳光玫瑰葡萄”的售价应降至每斤25元;(3)设水果商每天获得的利润为y元,根据题意得:w=(30﹣x﹣15)(60+10x)=﹣10x2+90x+900=﹣10(x﹣)2+1102.5,∵﹣10<0,∴当x=时,y有最大值,最大值为1102.5,此时30﹣x=30﹣4.5=25.5,答:将商品的销售单价定为25.5元时,商场每天销售该商品获得的利润w最大,最大利润是1102.5元.21.如图,抛物线与x轴交于A(﹣1,0)、B(4,0),与y轴交于C.(1)求抛物线的解析式;(2)如图1,已知线段DE与线段BC关于平面内某点成中心对称,其中DE的两端点刚好一个落在抛物线上,一个落在对称轴上,求落在对称轴上的点的坐标;(3)如图2,点M为第二象限抛物线上,作MN∥BC交抛物线于点N,直线NB、MC 交于点P,求P点的横坐标.解:(1)把A(﹣1,0)、B(4,0)代入得:,解得,∴抛物线的解析式为y=x2﹣x﹣2;(2)∵y=x2﹣x﹣2=(x﹣)2﹣,∴抛物线的对称轴是直线x=,在y=x2﹣x﹣2中,令x=0得y=﹣2,∴C(0,﹣2),①若线段DE与线段BC关于点K成中心对称,C的对应点D在对称轴上,B的对应点在抛物线上,如图:设D(,m),E(n,n2﹣n﹣2),而B(4,0),C(0,﹣2),∵K是DC的中点,也是BE的中点,∴,解得,∴D(,);②若线段DE与线段BC关于点T成中心对称,B的对应点D在对称轴上,C的对应点在抛物线上,如图:设D(,m'),E(n',n'2﹣n'﹣2),而B(4,0),C(0,﹣2),∵T是EC的中点,也是BD的中点,∴,解得,∴D(,);综上所述,落在对称轴上的点的坐标为(,)或(,);(3)由B(4,0),C(0,﹣2)可得直线BC解析式为y=x﹣2,设M(t,t2﹣t﹣2),由M(t,t2﹣t﹣2),C(0,﹣2)可得直线MC解析式为:y=(t﹣)x﹣2,由MN∥BC设直线MN解析式为y=x+p,将M(t,t2﹣t﹣2)代入得:t2﹣t﹣2=t+p,∴p=t2﹣2t﹣2,∴直线MN解析式为y=x+t2﹣2t﹣2,由得或,∴N(﹣t+4,t2﹣t),由B(4,0),N(﹣t+4,t2﹣t)可得直线NB的解析式为y=(﹣t+)x+2t﹣10,解(﹣t+)x+2t﹣10=(t﹣)x﹣2得x=2,∴P的横坐标为2.22.在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y'),给出如下定义:若y'=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)点(﹣5,﹣2)的“可控变点”坐标为(﹣5,2);(2)若点P在函数y=﹣x2+16的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;(3)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,求实数a的取值范围.解:(1)∵﹣5<0,∴y'=﹣y=2,∴点(﹣5,﹣2)的“可控变点”坐标为(﹣5,2),故答案为:(﹣5,2);(2)依题意,y=﹣x2+16图象上的点P的“可控变点”必在函数的图象上.∵“可控变点”Q的纵坐标y′是7,∴当﹣x2+16=7时,解得x=3;当x2﹣16=7,解得x=﹣;综上所述“可控变点”Q的横坐标为或3;(3)依题意,y=﹣x2+16图象上的点P的“可控变点”必在函数的图象上,∵﹣16≤y'≤16,∴﹣16=﹣x2+16,∴x=,当x=﹣5时,x2﹣16=9,当y'=9时,x=,∴a的取值范围是.23.在平面直角坐标系中,抛物线y=x2+bx+c经过A(﹣4,0),点M为抛物线的顶点,点B在y轴上,直线AB与抛物线在第一象限交于点C(2,6),如图①.(1)求抛物线解析式;(2)直线AB的函数解析式为y=x+4,点M的坐标为(﹣2,﹣2).(3)在y轴上找一点Q,使得△AMQ的周长最小,具体作法如图②,作点A关于y轴的对称点A',连接MA′交y轴于点Q,连接AM,AQ,此时△AMQ的周长最小,请求出点Q的坐标;(4)在坐标平面内是否存在点N,使以点A,O,C,N为顶点的四边形是平行四边形?若存在请直接写出点N的坐标;若不存在,请说明理由.解:(1)把A(﹣4,0),C(2,6)代入y=x2+bx+c得:,解得,∴抛物线解析式为y=x2+2x;(2)设直线AB解析式为y=mx+n,把A(﹣4,0),C(2,6)代入得:,解得,∴直线AB解析式为y=x+4,∵y=x2+2x=(x+2)2﹣2,∴抛物线的顶点M坐标为(﹣2,﹣2);故答案为:y=x+4,(﹣2,﹣2);(3)∵A(﹣4,0),A,A'关于y轴对称,∴A'(4,0),设直线A'Q解析式为y=m'x+n',把A'(4,0),M(﹣2,﹣2)代入得:,解得,∴直线A'Q解析式为y=x﹣,令x=0得y=﹣,∴Q(0,﹣);(4)存在点N,使以点A,O,C,N为顶点的四边形是平行四边形,理由如下:设N(p,q),又A(﹣4,0),O(0,0),C(2,6),①若AN,OC为对角线,则AN,OC的中点重合,∴,解得,∴N(6,6);②若ON,AC为对角线,则ON,AC的中点重合,∴,解得,∴N(﹣2,6);③若CN,AO为对角线,则CN,AO的中点重合,∴,解得,∴N(﹣6,﹣6).综上所述,N的坐标为(6,6)或(﹣2,6)或(﹣6,﹣6).九年级数学上册《二次函数》专题测试题(附答案)一.选择题(共8小题,满分32分)1.若y=(a+1)x|a+3|﹣x+3是关于x的二次函数,则a的值是()A.1B.﹣5C.﹣1D.﹣5或﹣12.下列关于二次函数y=﹣(x﹣m)2+m2+1(m为常数)的结论错误的是()A.当x>0时,y随x的增大而减小B.该函数的图象一定经过点(0,1)C.该函数图象的顶点在函数y=x2+1的图象上D.该函数图象与函数y=﹣x2的图象形状相同3.已知:抛物线的解析式为y=﹣3(x﹣2)2+1,则抛物线的对称轴是直线()A.x=﹣1B.x=1C.x=2D.x=﹣24.将二次函数y=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为()A.y=2(x+5)2﹣3B.y=2(x+5)2+3C.y=2(x﹣5)2﹣3D.y=2(x﹣5)2+35.二次函数y=ax2+bx+c的图象如图所示,下列结论:(1)4ac<b2;(2)abc<0;(3)2a+b<0;(4)(a+c)2<b2其中正确的个数是()A.1B.2C.3D.46.已知抛物线y=ax2+4ax﹣8与直线y=n相交于A,B两点(点A在点B左侧),AB=4,且抛物线与x轴只有一个交点,则n的值为()A.﹣8B.﹣4C.4D.87.已知二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,关于x的方程ax2+bx+c+m =0(m>0)有两个整数根,其中一个根是3,则另一个根是()A.﹣5B.﹣3C.﹣1D.38.物理课上我们学习了竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是40m②小球抛出3s后,速度越来越快③小球抛出3s时速度为0④小球的高度h=30m时,t=1.5s其中正确的是()A.①②③B.①②C.②③④D.②③二.填空题(共8小题,满分32分)9.已知抛物线y=x2+bx+c关于直线x=2对称,设x=1,2,4时对应的函数值依次为y1,y2,y4,那么y1,y2,y4的大小关系是.(用“<”连接)10.已知抛物线y=ax2﹣2ax﹣1(a<0)(I)抛物线的对称轴为;(2)若当﹣2≤x≤2时,y的最大值是1,求当﹣2≤x≤2时,y的最小值是.11.已知二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),则关于x 的一元二次方程ax2﹣2ax+c=0的两根之积是.12.已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是.13.将抛物线y=﹣(x﹣3)2﹣1向右平移5个单位,再向上平移2个单位,所得的抛物线的解析式为.14.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,9),B(1,1),则方程ax2﹣bx﹣c=0的解是.15.抛物线y=ax2+bx+tc(a<0)交x轴于点A、B,交y轴于点C(0,3),其中点B坐标为(1,0),同时抛物线还经过点(2,﹣5).(1)抛物线的解析式为;(2)设抛物线的对称轴与抛物线交于点E,与x轴交于点H,连接EC、EO,将抛物线向下平移n(n>0)个单位,当EO平分∠CEH时,则n的值为.16.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y (个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额﹣总成本).三.解答题(共6小题,满分56分)17.已知二次函数y=x2+mx+m2﹣3(m为常数,m>0)的图象经过点P(2,4).(1)求m的值;(2)判断二次函数y=x2+mx+m2﹣3的图象与x轴交点的个数,并说明理由.18.对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:h=v0t﹣gt2(h是物体离起点的高度,v0是初速度,g是重力系数,取10m/s2,t是抛出后经过的时间).杂技演员抛球表演时,以10m/s的初速度把球向上抛出.(1)球抛出后经多少秒回到起点?(2)几秒后球离起点的高度达到1.8m?(3)球离起点的高度能达到6m吗?请说明理由.19.在平面直角坐标系中,已知二次函数y=ax2+(a﹣1)x﹣1.(1)若该函数的图象经过点(1,2),求该二次函数图象的顶点坐标.(2)若(x1,y1),(x1,y2)为此函数图象上两个不同点,当x1+x2=﹣2时,恒有y1=y2,试求此函数的最值.(3)当a<0且a≠﹣1时,判断该二次函数图象的顶点所在象限,并说明理由.20.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.(1)求y与x的函数关系式(不要求写出自变量x的取值范围);(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?21.如图,抛物线y=﹣x2+bx+c过点A(4,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点D、N.(1)求直线AB的表达式和抛物线的表达式;(2)若DN=3DM,求此时点N的坐标;(3)若点P为直线AB上方的抛物线上一个动点,当∠ABP=2∠BAC时,求点P的坐标.22.如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣2),点C(0,﹣5),顶点为点M,过点A作AB∥x轴,交y轴于点D,交二次函数y=x2+bx+c的图象于点B,连接BC.(1)求该二次函数的表达式及点M的坐标;(2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)若E为线段AB上一点,且BE:EA=3:1,P为直线AC上一点,在抛物线上是否存在一点Q,使以B、P、E、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的横坐标;若不存在,请说明理由.参考答案一.选择题(共8小题,满分32分)1.解:∵函数y=(a+1)x|a+3|﹣x+3是关于x的二次函数,∴|a+3|=2且a+1≠0,解得a=﹣5,故选:B.2.解:A.∵y=﹣(x﹣m)2+m2+1(m为常数),∴抛物线开口向下,对称轴为直线x=m,∴x>m时,y随x增大而减小,故A错误,符合题意;∵当x=0时,y=1,∴该函数的图象一定经过点(0,1),故B正确,不合题意;∵y=﹣(x﹣m)2+m2+1,∴抛物线顶点坐标为(m,m2+1),∴抛物线顶点在抛物线y=x2+1上,故C正确,不合题意;∵y=﹣(x﹣m)2+m2+1与y=﹣x2的二次项系数都为﹣1,∴两函数图象形状相同,故D正确,不合题意.故选:A.3.解:∵y=﹣3(x﹣2)2+1,∴抛物线对称轴为直线x=2.故选:C.4.解:将二次函数y=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为y=2(x+5)2+3,故选:B.5.解:根据图象知道抛物线与x轴有两个交点,∴b2﹣4ac>0,即4ac<b2,故(1)正确.∵抛物线开口朝下,∴a<0,∵对称轴在y轴右侧,∴b>0,∵抛物线与y轴的交点在x轴的上方,∴c>0,∴abc<0,故(2)正确;∵对称轴x=﹣>1,∴2a+b>0,故(3)错误;根据图象知道当x=1时,y=a+b+c>0,根据图象知道当x=﹣1时,y=a﹣b+c<0,∴(a+c)2﹣b2=(a+c+b)(a+c﹣b)<0,故(4)正确;故选:C.6.解:∵抛物线与x轴只有一个交点,∴a≠0且Δ=16a2﹣4a×(﹣8)=0,∴a=﹣2,∴抛物线解析式为y=﹣2x2﹣8x﹣8,∵抛物线的对称轴为直线x=﹣=﹣2,而AB平行x轴,AB=4,∴A点的横坐标为﹣4,B点的横坐标为0,当x=0时,y=﹣8,∴n的值为﹣8.故选:A.7.解:∵二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,∴函数y=ax2+bx+c的对称轴是直线x=﹣1,又∵关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3.∴二次函数y=ax2+bx+c的图象与直线y=﹣m的一个交点的横坐标为3,∵对称轴是直线x=﹣1,∴二次函数y=ax2+bx+c的图象与直线y=﹣m的另一个交点的横坐标为﹣5,∴关于x的方程ax2+bx+c+m=0(m>0)的另一个根是﹣5,故选:A.8.解:①由图象知小球在空中达到的最大高度是40m;故①错误;②小球抛出3秒后,速度越来越快;故②正确;③小球抛出3秒时达到最高点即速度为0;故③正确;④设函数解析式为:h=a(t﹣3)2+40,把O(0,0)代入得0=a(0﹣3)2+40,解得,∴函数解析式为,把h=30代入解析式得,,解得:t=4.5或t=1.5,∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;故选D.二.填空题(共8小题,满分32分)9.解:∵抛物线y=x2+bx+c的开口向上,对称轴是直线x=2,∴当x=2时取最小值,又|1﹣2|<|4﹣2|,∴y1<y4,故答案为:y2<y1<y4.10.解:(1)抛物线的对称轴为:直线x=﹣=1,故答案为:直线x=1;(2)∵抛物线y=ax2﹣2ax﹣1=a(x﹣1)2﹣a﹣1(a<0),∴该函数图象的开口向下,对称轴是直线x=1,当x=1时,取得最大值﹣a﹣1,∵当﹣2≤x≤2时,y的最大值是1,∴x=1时,y=﹣a﹣1=1,得a=﹣2,∴y=﹣2(x﹣1)2+1,∵﹣2≤x≤2,∴x=﹣2时,取得最小值,此时y=﹣2(﹣2﹣1)2+1=﹣17,故答案为:﹣17.11.解:∵二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),∴该函数的对称轴是直线x=﹣=1,∴该函数图象与x轴的另一个交点坐标为(3,0),∴关于x的一元二次方程ax2﹣2ax+c=0的两实数根是x1=﹣1,x2=3,∴两根之积为﹣3,故答案为:﹣3.12.解:如图,当y=0时,﹣x2+4x+5=0,解得x1=﹣1,x2=5,则A(﹣1,0),B(5,0),将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+1)(x﹣5),即y=x2﹣4x﹣5(﹣1≤x≤5),当直线y=﹣x+b经过点A(﹣1,0)时,1+b=0,解得b=﹣1;当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时,方程x2﹣4x﹣5=﹣x+b有相等的实数解,解得b=﹣,所以当直线y=﹣x+b与新图象有4个交点时,b的取值范围为﹣<b<﹣1.故答案为:﹣<b<﹣1.13.解:将抛物线y=﹣(x﹣3)2﹣1向右平移5个单位,再向上平移2个单位,所得的抛物线的解析式为y=﹣(x﹣3﹣5)2﹣1+2,即y=﹣(x﹣8)2+1,故答案为:y=﹣(x﹣8)2+1.14.解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,9),B(1,1),∴方程ax2=bx+c的解为x1=﹣3,x2=1,∴ax2﹣bx﹣c=0的解是x1=﹣3,x2=1,故答案为:x1=﹣3,x2=1.15.解:(1)将点C(0,3)、B(1,0)、(2,﹣5)代入抛物线y=ax2+bx+tc中,得:a+b+c=0,c=3,4a+2b+c=﹣5;解得:a=﹣1,b=﹣2,c=3,∴抛物线的解析式为y=﹣x2﹣2x+3.(2)抛物线向下平移n个单位后,E为(﹣1,4﹣n),C为(0,3﹣n),∴EC=,∵CO∥EH,∴当CO=CE=时,∠CEO=∠COE=∠OCH,∴3﹣n=或n﹣3=,即n=3﹣或3+.16.解:当10≤x≤20时,设y=kx+b,把(10,20),(20,10)代入可得:,解得,∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为y=﹣x+30,设该食品零售店每天销售这款冷饮产品的利润为w元,w=(x﹣8)y=(x﹣8)(﹣x+30)=﹣x2+38x﹣240=﹣(x﹣19)2+121,∵﹣1<0,∴当x=19时,w有最大值为121,故答案为:121.三.解答题(共6小题,满分56分)17.解:(1)将(2,4)代入y=x2+mx+m2﹣3得4=4+2m+m2﹣3,解得m1=1,m2=﹣3,又∵m>0,∴m=1.(2)∵m=1,∴y=x2+x﹣2,∵Δ=b2﹣4ac=12+8=9>0,∴二次函数图象与x轴有2个交点.18.解:∵初速度为10m/s,g取10m/s2,∴h=10t﹣×10t2=10t﹣5t2,(1)当h=0时,。
综合算式专项练习题二次函数运算

综合算式专项练习题二次函数运算在数学中,二次函数是一种常见的函数类型,它的形式为f(x) =ax^2 + bx + c,其中a、b、c为实数且a不等于零。
二次函数在数学建模、物理学、经济学等领域中有广泛的应用。
为了帮助学生巩固二次函数的运算技巧,本文将提供一些综合算式专项练习题。
一、填空题1. 设函数f(x) = 2x^2 + 3x - 4,求f(2)的值。
解析:将x = 2代入函数f(x)中,得到f(2) = 2(2)^2 + 3(2) - 4 = 12。
答案:12。
2. 已知函数g(x) = -x^2 + 5x + 2,求使得g(x) = 0的x的值。
解析:将g(x) = 0转化为方程-x^2 + 5x + 2 = 0,通过求根公式或配方法得到x = -1或x = 2。
答案:x = -1或x = 2。
3. 若函数h(x) = 3x^2 + 2kx + 5,在k的取值范围内,使得h(x)恰有两个实根,求k的取值范围。
解析:二次函数有两个实根当且仅当判别式大于零。
判别式为Δ = (2k)^2 - 4(3)(5) = 4k^2 - 60。
要使得Δ大于零,即4k^2 - 60 > 0,解得k < -√15或k > √15。
答案:k < -√15或k > √15。
二、计算题1. 已知函数f(x) = x^2 - 3x + 2和g(x) = 2x + 1,求f(g(x))。
解析:将g(x) = 2x + 1代入f(x)中,得到f(g(x)) = (2x + 1)^2 - 3(2x + 1) + 2 = 4x^2 + 4x + 1 - 6x - 3 + 2 = 4x^2 - 2x。
答案:f(g(x)) = 4x^2 - 2x。
2. 设函数f(x) = -x^2 + 4x - 3,求f(3x - 1)的值。
解析:将3x - 1代入f(x)中,得到f(3x - 1) = -(3x - 1)^2 + 4(3x - 1) -3 = -9x^2 + 18x - 10。
二次函数数学题目
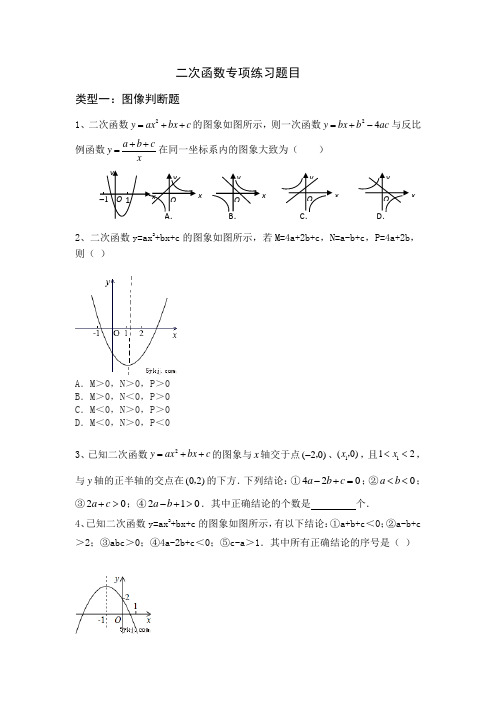
二次函数专项练习题目类型一:图像判断题1、二次函数2y ax bx c=++的图象如图所示,则一次函数24y bx b ac=+-与反比例函数a b cyx++=在同一坐标系内的图象大致为()2、二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a+2b,则()A.M>0,N>0,P>0B.M>0,N<0,P>0C.M<0,N>0,P>0D.M<0,N>0,P<03、已知二次函数2y ax bx c=++的图象与x轴交于点(20)-,、1(0)x,,且112x<<,与y轴的正半轴的交点在(02),的下方.下列结论:①420a b c-+=;②0a b<<;③20a c+>;④210a b-+>.其中正确结论的个数是个.4、已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c >2;③abc>0;④4a-2b+c<0;⑤c-a>1.其中所有正确结论的序号是()x xx xA.①②B.①③④C.①②③⑤D.①②③④⑤5、如图,已知二次函数y=ax2+bx+c的图象与x轴交于(x1,0)(x2,0)两点,且0<x1<1,1<x2<2,与y轴交于点(0,2).下列结论①2a+b>-1,②3a+b>0,③a+b<-2,④a>0,⑤a-b<0,其中结论正确的个数是()A.4 B.3 C.2 D.16、已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0;②b<a;③3a+c>0.其中正确结论的个数是()A.0 B.1 C.2 D.37、已知b>0时,二次函数y=ax2+bx+a2-1的图象如下列四个图之一所示:根据图象分析,a的值等于()A.-2 B.-1 C.1 D.28、二次函数2=-++的图象如何平移就褥到2y x x241=-的图像( )2y xA.向左平移1个单位,再向上平移3个单位.B.向右平移1个单位,再向上平移3个单位.C.向左平移1个单位,再向下平移3个单位D.向右平移1个单位,再向下平移3个单位。
