第二章 聚类分析
聚类分析数据

聚类分析数据聚类分析是一种数据挖掘方法,用于将相似的数据点分组成簇。
它能够匡助我们发现数据中的潜在模式和结构,从而提供洞察力和指导性的决策支持。
在本文中,我们将探讨聚类分析的基本概念、常用的聚类算法以及应用案例。
一、聚类分析的基本概念聚类分析是一种无监督学习方法,它不依赖于预先标记的训练数据。
其主要目标是通过将相似的数据点分组成簇,使得簇内的数据点相似度较高,而簇间的数据点相似度较低。
聚类分析通常用于探索性数据分析和数据预处理阶段,以匡助我们理解数据的内在结构和特征。
在聚类分析中,我们需要考虑以下几个关键概念:1. 数据相似度度量:聚类算法需要一种度量方法来衡量数据点之间的相似度或者距离。
常用的度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。
2. 聚类算法:聚类算法是用于将数据点分组成簇的数学模型或者算法。
常见的聚类算法包括K均值聚类、层次聚类、DBSCAN等。
3. 聚类评估指标:为了评估聚类结果的质量,我们需要一些指标来衡量聚类的密切度和分离度。
常用的评估指标有轮廓系数、Davies-Bouldin指数、Calinski-Harabasz指数等。
二、常用的聚类算法1. K均值聚类算法:K均值聚类是一种基于距离的聚类算法,它将数据点分配到K个簇中,使得簇内的数据点与簇中心的距离最小化。
它的基本思想是通过迭代优化来不断更新簇中心和数据点的分配,直到达到收敛条件。
2. 层次聚类算法:层次聚类是一种基于距离或者相似度的聚类算法,它通过逐步合并或者分割簇来构建聚类层次结构。
层次聚类可以分为凝结型层次聚类和分裂型层次聚类两种方法。
3. DBSCAN算法:DBSCAN是一种基于密度的聚类算法,它将数据点分为核心点、边界点和噪声点三类。
DBSCAN通过计算数据点的密度来确定核心点,并将密度可达的数据点分配到同一个簇中。
三、聚类分析的应用案例聚类分析在各个领域都有广泛的应用,下面是几个常见的应用案例:1. 市场细分:聚类分析可以匡助企业将客户细分为不同的市场群体,从而针对不同的群体制定个性化的营销策略。
聚类分析

聚类分析聚类分析又称群分析,它是研究(样品或指标)分类问题的一种多元统计方法,所谓类,通俗地说,就是指相似元素的集合。
聚类分析内容非常丰富,按照分类对象的不同可分为样品分类(Q-型聚类分析)和指标或变量分类(R-型聚类分析);按照分类方法可分为系统聚类法和快速聚类法。
1. 系统聚类分析先将n 个样品各自看成一类,然后规定样品之间的“距离”和类与类之间的距离。
选择距离最近的两类合并成一个新类,计算新类和其它类(各当前类)的距离,再将距离最近的两类合并。
这样,每次合并减少一类,直至所有的样品都归成一类为止。
系统聚类法直观易懂。
1.1系统聚类法的基本步骤:第一,计算n 个样品两两间的距离 ,记作D= 。
第二,构造n 个类,每个类只包含一个样品。
第三,合并距离最近的两类为一新类。
第四,计算新类与各当前类的距离。
第五,重复步骤3、4,合并距离最近的两类为新类,直到所有的类并为一类为止。
第六,画聚类谱系图。
第七,确定类的个数和类。
1.2 系统聚类方法:1.2.1最短距离法1.2.2最长距离法1.2.3中间距离法1.2.4重心法1.2.5类平均法1.2.6离差平方和法(Ward 法)上述6种方法归类的基本步骤一致,只是类与类之间的距离有不同的定义。
最常用的就是最短距离法。
1.3 最短距离法以下用ij d 表示样品i X 与j X 之间距离,用ij D 表示类i G 与j G 之间的距离。
定义类i G 与j G 之间的距离为两类最近样品的距离,即ij G G G G ij d D j J i i ∈∈=,min设类p G 与q G 合并成一个新类记为r G ,则任一类k G 与r G 的距离是:ij G X G X kr d D j j i i ∈∈=,min ⎭⎬⎫⎩⎨⎧=∈∈∈∈ij G X G X ij G X G X d d q j k i p j k i ,,min ,min min {}kq kp D D ,min = 最短距离法聚类的步骤如下:ij d {}ij d(1)定义样品之间距离,计算样品两两距离,得一距离阵记为)0(D ,开始每个样品自成一类,显然这时ij ij d D =。
第2章 聚类分析

第2章 聚类分析 章
2.1 距离聚类的概念 2.2 相似性测度和聚类准则 2.3 基于距离阈值的聚类算法 2.4 层次聚类法 2.5 动态聚类法 2.6 聚类结果的评价
n 1 汉明距离: Dh ( X i , X j ) = n − ∑ xik ⋅ x jk 2 k =1
式中, xik、xjk分别表示Xi和Xj的第k个分量。 两个模式向量的各分量取值均不同:Dh(Xi, Xj)=n; 全相同: Dh(Xi, Xj)=0 5.角度相似性函数 .
S(Xi , X j ) =
欧氏距离定义为:
X 2 = [ x 21 , x 22 ,...., x 2 n ]T
D( X 1 , X 2 ) = X 1 − X 2 = ( X 1 − X 2 ) T ( X 1 − X 2 )
= ( x11 − x21 ) 2 + LL + ( x1n − x2 n ) 2 ( D_Distance ) 距离越小,越相似。
x2
x2
ω1
M1
M1
ω1 ω2
M2
ω2
M2
O (a)
x1 O
(b)
x1
正确分类
错误分类
2.3 基于距离阈值的聚类算法
2.3.1 近邻聚类法 1. 问题:有N个待分类的模式 {X 1 , X 2 ,L, X N } ,要求按距离阈 问题: 值T分类到以 Z1 , Z 2 ,L 为聚类中心的模式类中。 (T_threshold ) 2. 算法描述 ① 任取样本Xi 作为第一个聚类中心的初始值,如令Z1 = X1 。 ② 计算样本X2 到Z1 的欧氏距离 D21 = X 2 − Z1 , 若 D21 > T ,定义一新的聚类中心Z2 = X2 ; 否则 X2 ∈以Z1为中心的聚类。
聚类分析方法

聚类分析方法聚类分析是一种常用的数据分析方法,它可以将数据集中的对象按照其相似性进行分组,形成若干个簇。
通过聚类分析,我们可以发现数据中的内在结构,帮助我们更好地理解数据集的特点和规律。
在实际应用中,聚类分析被广泛应用于市场分割、社交网络分析、图像处理等领域。
本文将介绍聚类分析的基本原理、常用方法和应用场景,希望能够帮助读者更好地理解和应用聚类分析。
聚类分析的基本原理是将数据集中的对象划分为若干个簇,使得同一簇内的对象相似度较高,不同簇之间的对象相似度较低。
在进行聚类分析时,我们需要选择合适的相似性度量方法和聚类算法。
常用的相似性度量方法包括欧氏距离、曼哈顿距离、余弦相似度等,而常用的聚类算法包括K均值聚类、层次聚类、DBSCAN等。
不同的相似性度量方法和聚类算法适用于不同的数据类型和应用场景,选择合适的方法对于聚类分析的效果至关重要。
K均值聚类是一种常用的聚类算法,它通过不断迭代更新簇中心的方式,将数据集中的对象划分为K个簇。
K均值聚类的优点是简单、易于理解和实现,但是它对初始簇中心的选择较为敏感,容易收敛到局部最优解。
层次聚类是另一种常用的聚类算法,它通过逐步合并或分裂簇的方式,构建一棵层次化的聚类树。
层次聚类的优点是不需要事先确定簇的个数,但是它对大数据集的处理效率较低。
DBSCAN是一种基于密度的聚类算法,它能够发现任意形状的簇,并且对噪声数据具有较强的鲁棒性。
不同的聚类算法适用于不同的数据特点和应用场景,我们需要根据具体情况选择合适的算法进行聚类分析。
聚类分析在实际应用中有着广泛的应用场景。
在市场分割中,我们可以利用聚类分析将顾客分为不同的群体,从而制定针对性的营销策略。
在社交网络分析中,我们可以利用聚类分析发现社交网络中的社区结构,从而发现潜在的影响力人物。
在图像处理中,我们可以利用聚类分析对图像进行分割和特征提取,从而实现图像内容的理解和识别。
聚类分析在各个领域都有着重要的应用,它为我们理解和利用数据提供了有力的工具。
第二章作业聚类分析

第二章作业1.画出给定迭代次数为n的系统聚类法的算法流程框图. 答:算法流程图如下:2.对如下5个6维模式样本,用最小距离准则进行系统聚类分析: x 1: 0, 1, 3, 1, 3, 4 x 2: 3, 3, 3, 1, 2, 1 x 3: 1, 0, 0, 0, 1, 1 x 4: 2, 1, 0, 2, 2, 1x 5: 0, 0, 1, 0, 1, 0解:将每一样本看成单独一类,得(0)11{}G x =, (0)22{}G x =,(0)33{}G x = (0)44{}G x =, (0)55{}G x =计算各类之间的欧式距离,可得距离矩阵(0)D (表1-1)。
表1-1① 矩阵(0)D,它是(0)3G 和(0)5G 之间的距离,将它们合并为一类,得到新的分类为(1)(0)11{}G G =,(1)(0)22{}G G =,(1)(0)(0)335{,}G G G = (1)(0)44{}G G =计算聚类后的距离矩阵(1)D 。
按最小距离准则,分别计算(0)3G 与(1)1G 、(1)2G 、(1)4G ,(0)5G 与(1)1G 、(1)2G 、 (1)4G 之间的两种距离,并选用最小距离。
如(1)(0)(1)(0)(1)133151min{D G G G G =与的距离,与的距离}}=5 由此可求得距离矩阵(1)D (表1-2)② 距离矩阵(1)D ,它是(1)3G 和(1)4G 之间的距离,于是合并(1)3G 和(1)4G ,得到新的分类为(2)(1)11{}G G =,(2)(1)22{}G G =,(2)(1)(1)334{,}G G G =按最小距离准则计算距离矩阵(2)D ,得表1-3表1-3选择距离阈值(2)D 则算法停止,得到聚类结果G 1(2)={X1} G 2(2) ={X2} G 3(2)={X3,X5, X4}。
3. 模式样本如下:{X1(0,0),X2(1,0),X3(0,1),X4(1,1),X5(2,1),X6(1,2),X7(2,2),X8(3,2),X9(6,6),X10(7,6),X11(8,6), X12(6,7), X13(7,7), X14(8,7), X15(9,7), X16(7,8), X17(8,8), X18(9,8), X19(8,9), X20(9,9). 选K=2,11210(1)=(00),(1)(76)ttz x z x ===,用K —均值算法进行分类。
聚类分析_精品文档

1聚类分析内涵1.1聚类分析定义聚类分析(Cluste.Analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术.也叫分类分析(classificatio.analysis)或数值分类(numerica.taxonomy), 它是研究(样品或指标)分类问题的一种多元统计方法, 所谓类, 通俗地说, 就是指相似元素的集合。
聚类分析有关变量类型:定类变量,定量(离散和连续)变量聚类分析的原则是同一类中的个体有较大的相似性, 不同类中的个体差异很大。
1.2聚类分析分类聚类分析的功能是建立一种分类方法, 它将一批样品或变量, 按照它们在性质上的亲疏、相似程度进行分类.聚类分析的内容十分丰富, 按其聚类的方法可分为以下几种:(1)系统聚类法: 开始每个对象自成一类, 然后每次将最相似的两类合并, 合并后重新计算新类与其他类的距离或相近性测度. 这一过程一直继续直到所有对象归为一类为止. 并类的过程可用一张谱系聚类图描述.(2)调优法(动态聚类法): 首先对n个对象初步分类, 然后根据分类的损失函数尽可能小的原则对其进行调整, 直到分类合理为止.(3)最优分割法(有序样品聚类法): 开始将所有样品看成一类, 然后根据某种最优准则将它们分割为二类、三类, 一直分割到所需的K类为止. 这种方法适用于有序样品的分类问题, 也称为有序样品的聚类法.(4)模糊聚类法: 利用模糊集理论来处理分类问题, 它对经济领域中具有模糊特征的两态数据或多态数据具有明显的分类效果.(5)图论聚类法: 利用图论中最小支撑树的概念来处理分类问题, 创造了独具风格的方法.(6)聚类预报法:利用聚类方法处理预报问题, 在多元统计分析中, 可用来作预报的方法很多, 如回归分析和判别分析. 但对一些异常数据, 如气象中的灾害性天气的预报, 使用回归分析或判别分析处理的效果都不好, 而聚类预报弥补了这一不足, 这是一个值得重视的方法。
聚类分析数据

聚类分析数据引言概述:聚类分析是一种数据分析方法,通过将数据分成不同的群组或者类别,匡助我们理解数据之间的关系和模式。
在各个领域,聚类分析都被广泛应用,例如市场营销、社交网络分析和医学研究等。
本文将详细介绍聚类分析的原理和应用,以及使用聚类分析来解决实际问题的方法。
一、聚类分析的原理1.1 聚类分析的定义和目标聚类分析是一种无监督学习方法,它通过将相似的数据点归为一类,将不相似的数据点分为不同的类别。
其目标是在数据中发现隐藏的模式和结构。
1.2 聚类算法的类型聚类算法有多种类型,常见的包括层次聚类、K均值聚类和密度聚类等。
层次聚类通过不断合并或者分割数据点来构建聚类树。
K均值聚类将数据点分为K个簇,通过最小化簇内的平方误差来优化聚类结果。
密度聚类根据数据点的密度来划分簇。
1.3 聚类分析的评估指标评估聚类结果的指标包括轮廓系数、Davies-Bouldin指数和互信息等。
轮廓系数衡量了数据点在自己所在簇和其他簇之间的距离。
Davies-Bouldin指数衡量了簇的密切度和分离度。
互信息衡量了聚类结果与真实类别之间的一致性。
二、聚类分析的应用2.1 市场营销中的聚类分析聚类分析可以匡助市场营销人员理解消费者的行为和需求。
通过将消费者分为不同的群组,可以定制个性化的营销策略。
例如,可以将消费者分为高价值客户、潜在客户和流失客户等,针对不同群组制定不同的促销活动。
2.2 社交网络分析中的聚类分析在社交网络中,聚类分析可以匡助我们发现社区结构和关键人物。
通过将用户分为不同的社区,可以了解社交网络中的群组和交互模式。
例如,可以将社交网络中的用户分为朋友圈、兴趣群体和影响力人物等,进一步分析他们之间的关系和行为。
2.3 医学研究中的聚类分析聚类分析在医学研究中被广泛应用,例如疾病分类和药物研发等。
通过将患者分为不同的簇,可以发现不同疾病的特征和治疗方法。
同时,聚类分析还可以匡助筛选候选药物和预测药物的疗效。
第二章距离分类器和聚类分析
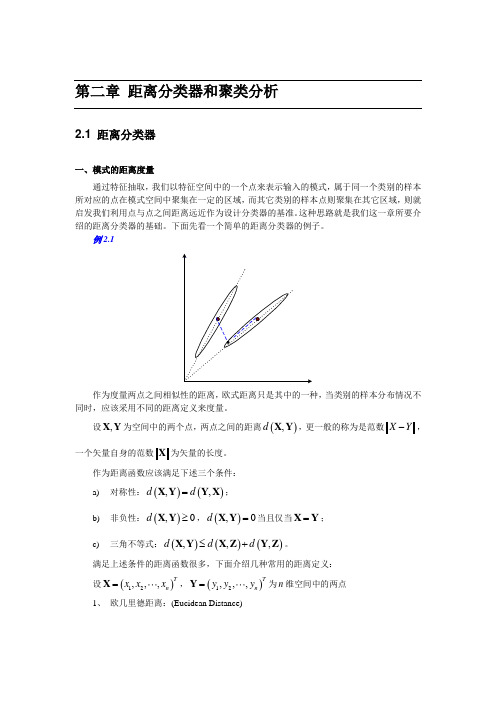
第二章 距离分类器和聚类分析2.1 距离分类器一、模式的距离度量通过特征抽取,我们以特征空间中的一个点来表示输入的模式,属于同一个类别的样本所对应的点在模式空间中聚集在一定的区域,而其它类别的样本点则聚集在其它区域,则就启发我们利用点与点之间距离远近作为设计分类器的基准。
这种思路就是我们这一章所要介绍的距离分类器的基础。
下面先看一个简单的距离分类器的例子。
例2.1作为度量两点之间相似性的距离,欧式距离只是其中的一种,当类别的样本分布情况不同时,应该采用不同的距离定义来度量。
设,X Y 为空间中的两个点,两点之间的距离(),d X Y ,更一般的称为是范数X Y -,一个矢量自身的范数X 为矢量的长度。
作为距离函数应该满足下述三个条件: a) 对称性:()(),,d d =X Y Y X ;b) 非负性:(),0d ≥X Y ,(),0d =X Y 当且仅当=X Y ; c) 三角不等式:()()(),,,d d d ≤+X Y X Z Y Z 。
满足上述条件的距离函数很多,下面介绍几种常用的距离定义: 设()12,,,Tn x x x =X ,()12,,,Tn y y y =Y 为n 维空间中的两点1、 欧几里德距离:(Eucidean Distance)()()1221,ni i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y2、 街市距离:(Manhattan Distance)()1,ni i i d x y ==-∑X Y3、 明氏距离:(Minkowski Distance)()11,mnm i i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y当2m =时为欧氏距离,当1m =时为街市距离。
4、 角度相似函数:(Angle Distance)(),T d ⋅=X YX Y X Y1nTi i i x y =⋅=∑X Y 为矢量X 和Y 之间的内积,(),d X Y 为矢量X 与Y 之间夹角的余弦。
模式识别 第二章 聚类分析

现金识别例子
100元A面第1个样本第10点和20点的距离 X: (75, 76,101, 83,102, 96, 91, 82) Y: (70, 74, 90, 76, 99, 96, 90, 86) X-Y: 5, 2, 11, 7, 3, 0, 1, -4
Eucliden=15.000000 Manhattan=33.000000 Chebyshev=11.000000 Minkowski=11.039449——m=8
其中马式矩阵为100圆A面的,上面是各面到 100圆A面的均值点的平均马式距离。
现金识别例子——100圆A面的传感器1 到其它各面传感器1的街坊距离
2.2 模式相似性测度
二、相似测度
测度基础:以两矢量的方向是否相近作为考虑的基 础,矢量长度并不不重要。设 1.角度相似系数(夹角余弦) (2-2-11)
变得很费力。因此可使用聚类分析的方法将数据分
成几组可判断的聚类m(m<<N)来处理,每一个
类可当作独立实体来对待。从这个角度看,数据被
压缩了。
17
第二章 聚类分析 聚类应用的四个基本方向
二、假说生成
在这种情况下,为了推导出数据性质的一些假
说,对数据集进行聚类分析。因此,这里使用聚类 作为建立假说的方法,然后用其他数据集验证这些 假说。
现金识别例子
SW的逆矩阵为: 0.3 -0.0 0.1 -0.1 -0.1 -0.1 -0.2 0.2 -0.0 0.3 -0.1 -0.1 0.1 -0.6 0.3 0.2 0.1 -0.1 0.3 -0.1 -0.0 -0.2 -0.3 0.4 -0.1 -0.1 -0.1 0.2 0.1 0.3 -0.1 -0.2 -0.1 0.1 -0.0 0.1 0.7 -0.7 -0.4 0.2 -0.1 -0.6 -0.2 0.3 -0.7 2.2 -0.0 -1.0 -0.2 0.3 -0.3 -0.1 -0.4 -0.0 1.2 -0.5 0.2 0.2 0.4 -0.2 0.2 -1.0 -0.5 1.0
聚类分析解析课件

类间距的度量
类:一个不严格的定义
定义9.1:距离小于给定阀值的点的集合 类的特征
◦ 重心:均值 ◦ 样本散布阵和协差阵 ◦ 直径
类间距的定义
最短距离法 最长距离法 重心法 类平均法 离差平方和法 等等
最小距离法(single linkage method)
极小异常值在实际中不多出现,避免极 大值的影响
类的重心之间的距离
对异常值不敏感,结果更稳定
离差平方和法(sum of squares
method或ward method)
W代表直径,D2=WM-WK-WL
即
DK2L
nL nk nM
XK XL XK XL
Cluster K
Cluster M
Cluster L
◦ 对异常值很敏感;对较大的类倾向产生较大的距 离,从而不易合并,较符合实际需要。
如表9.2所示,每个样品有p个指标,共 有n个样品
每个样品就构成p维空间中的一个点
:第i个样品的第k个指标对应的取值
◦ i=1……n; k=1……p
:第i个样品和第j个样品之间的距离
◦ i=1……n; j=1……n
点间距离测量问题
样品间距离与指标间距离 间隔尺度、有序尺度与名义尺度 数学距离与统计距离 相似性与距离:一个硬币的两面
类图上发现相同的类
饮料数据
16种饮料的热量、咖啡因、钠及价格四种变量
SPSS实现
选择Analyze-Classify-Hierarchical Cluster, 然 后 把 calorie ( 热 量 ) 、 caffeine ( 咖 啡
因)、sodium(钠)、price(价格)选入 Variables, 在Cluster选Cases(这是Q型聚类:对观测 值聚类),如果要对变量聚类(R型聚类) 则选Variables, 为 了 画 出 树 状 图 , 选 Plots , 再 点 Dendrogram等。 可以在Method中定义点间距离和类间距 离
聚类分析法

聚类分析法聚类分析是一种常用的数据分析方法,主要用于将相似的样本归类到同一类别中。
它是数据挖掘和机器学习领域中非常重要的一项技术,被广泛应用于各个领域,如市场研究、医学诊断、社交网络分析等。
本文将介绍聚类分析的基本概念、方法和应用,并分析其优势和局限性。
聚类分析是一种无监督学习方法,它不依赖于事先标定好的训练数据集。
通过对给定的数据进行聚类,我们可以发现数据中隐藏的模式、结构和规律。
聚类分析的基本思想是通过计算样本之间的相似度或距离,将相似的样本归为一类,从而实现对数据的分类。
在聚类分析中,相似度或距离的度量是一个关键问题,常用的度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。
聚类分析的方法主要有层次聚类和划分聚类两种。
层次聚类是将样本逐步合并或分割成不同的类别,形成层次化的分类结果。
划分聚类是将所有的样本划分为K个不相交的类别,每个类别之间是互不重叠的。
这两种方法各有优劣,选择何种方法取决于具体的问题和数据特点。
聚类分析的应用非常广泛。
在市场研究中,聚类分析可以将消费者按照其购买行为、兴趣偏好等特征划分为不同的群体,为企业提供有针对性的营销策略。
在医学诊断中,聚类分析可以将病人按照其病情特征进行分类,帮助医生进行准确的诊断和治疗。
在社交网络分析中,聚类分析可以将社交网络中的用户划分为不同的社区,研究社交网络的结构和特征。
然而,聚类分析也存在一些局限性和挑战。
首先,聚类算法的结果很大程度上依赖于选择的相似度或距离度量方法,不同的度量方法可能导致不同的聚类结果。
其次,聚类算法对初始的聚类中心的选择非常敏感,不同的初始选择可能会得到不同的聚类结果。
此外,聚类算法还面临维度灾难的问题,当数据的维度很大时,聚类算法的计算复杂度会急剧增加。
在实际应用中,我们还可以将聚类分析与其他数据挖掘方法相结合,以获得更好的分析结果。
比如,我们可以将聚类分析与关联规则挖掘结合起来,通过挖掘不同类别之间的关联规则,深入分析不同类别之间的关系。
聚类分析——精选推荐

聚类分析聚类分析简单说就是对数据进⾏分类,对于⼀个⾏列数据表来说,我们既可以对变量(通常是数据表中的列)进⾏分类,也可以对个案(通常是数据表中的⾏)进⾏分类。
对变量的聚类称为R型聚类,对个案的聚类称为Q型聚类,这两种聚类在数学上是对称的,并⽆不同。
聚类是⼀种探索性分析,事先并不知道有多少种分类,⽽是从数据本⾝出发,根据算法⾃⾏分类,算法不同,聚类的结果也不同。
但是原则都是统⼀的,那就是:类别内部的差异尽可能⼩,⽽类别间的差异尽可能⼤。
⼀、聚类分析的基本算法1.⾮层次聚类法⾸先根据经验或者专业确定⼀个最终的类别个数,在所有数据中选取⼀些作为初始类作为质⼼,通过计算剩余数据到质⼼之间的距离来判断归类,每归⼀类就重新计算质⼼,如此迭代直⾄达到标准。
整个计算过程都是针对数据本⾝,不会出现类与类之间的层次关系,因此速度较快。
缺点是只能对个案进⾏聚类,⽽不能对变量聚类,数据必须是连续型数据,并且要求多元正态性和⽅差齐性。
2.层次聚类法⾸先确定数据间的距离计算⽅式和类与类之间的距离计算⽅式,根据距离的远近进⾏归类,这种⽅法存在类与类之前的层次关系,因此成为层次聚类法,缺点是计算速度较慢,优点是既能对变量进⾏聚类,也能对个案进⾏聚类,并且数据可以为连续型数据和分类数据,提供的距离测量⽅法也很丰富。
3.智能聚类法⽆论是层次聚类法还是⾮层次聚类法,都属于传统聚类法,都有⼀定的局限,⽽随着数据挖掘⽽发展起来的智能聚类法,既继承了传统聚类⽅法的优点,也改进了诸如计算速度慢等缺点,同时还可以⾃动判断最佳类别数,越来越受到重视。
⼆、距离与相似系数既然聚类分析对数据进⾏分类的标准主要是距离和相似系数,那么就来介绍⼀下这两个指标在聚类分析中都有哪些计算⽅式。
聚类分析中的距离分为数据与数据间的距离和类与类之间的距离,类与类之间的距离只有层次聚类法和智能聚类法会⽤到。
数据与数据间的距离计算⽅式有1.欧式距离(Euclidean)两样本x,y之间的距离是各样本中变量之差的平⽅和的平⽅根。
市场研究——聚类分析法

市场研究——聚类分析法
聚类分析法在市场研究中有着广泛的应用。
通过对市场中消费者、产品、品牌等进行聚类分析,可以帮助市场研究人员更好地理解市场细分和
目标受众,并制定针对不同群体的市场营销策略。
下面将详细介绍聚类分
析法的原理、应用和步骤。
聚类分析的原理是将数据样本划分为不同的类别或群组,使得同类之
间的差异最小,而不同类之间的差异最大。
输入聚类分析的数据通常是多
维的,每个维度代表一个变量。
聚类分析的目标是找到一个最优的聚类方案,使得相同类别内的样本相似度最高,而不同类别的样本相似度最低。
聚类分析法的应用非常广泛。
在市场研究中,它可以用于客户细分、
产品定位、市场定位等方面。
通过对消费者进行聚类,可以发现隐藏在市
场中的不同消费者群体,并确定他们的特征、需求和偏好。
对产品和品牌
进行聚类分析,则可以帮助确定产品和品牌的差异化定位和市场竞争策略。
需要注意的是,聚类分析法只是一种分析工具,通过聚类分析得到的
结果并不一定代表真实的市场现象,仅供市场研究人员参考和决策。
在市场研究中,聚类分析法的应用是非常重要的。
它能够帮助市场研
究人员更好地理解市场细分和目标受众,并制定针对不同群体的市场营销
策略。
随着数据量的不断增加和分析技术的不断发展,聚类分析法在市场
研究中的应用前景将更加广阔。
聚类分析方法

聚类分析方法聚类分析是一种常用的数据分析方法,它可以帮助我们将数据集中的对象按照它们的相似性进行分组。
通过聚类分析,我们可以发现数据中的内在结构和规律,从而更好地理解数据。
在本文中,我们将介绍聚类分析的基本概念、常见的聚类方法以及聚类分析的应用场景。
首先,让我们来了解一下聚类分析的基本概念。
聚类分析是一种无监督学习方法,它不需要预先标记的训练数据,而是根据数据对象之间的相似性来进行分组。
在聚类分析中,我们通常会使用距离或相似度作为衡量对象之间关系的指标。
常见的距离指标包括欧氏距离、曼哈顿距离和余弦相似度等。
通过计算对象之间的距离或相似度,我们可以将它们划分到不同的类别中,从而实现数据的聚类。
接下来,让我们来介绍一些常见的聚类方法。
最常用的聚类方法包括层次聚类、K均值聚类和密度聚类。
层次聚类是一种基于对象之间相似性构建层次结构的方法,它可以分为凝聚式层次聚类和分裂式层次聚类。
K均值聚类是一种迭代的聚类方法,它将数据对象划分为K个类别,并通过迭代优化来找到最优的聚类中心。
密度聚类是一种基于数据密度的聚类方法,它可以发现任意形状的聚类簇,并对噪声数据具有较强的鲁棒性。
最后,让我们来看一些聚类分析的应用场景。
聚类分析可以应用于各个领域,例如市场营销、生物信息学、社交网络分析等。
在市场营销中,我们可以利用聚类分析来识别不同的消费群体,并针对不同群体制定个性化的营销策略。
在生物信息学中,聚类分析可以帮助我们发现基因表达数据中的基因模式,并识别相关的生物过程。
在社交网络分析中,我们可以利用聚类分析来发现社交网络中的社区结构,并识别影响力较大的节点。
总之,聚类分析是一种非常有用的数据分析方法,它可以帮助我们发现数据中的内在结构和规律。
通过本文的介绍,相信大家对聚类分析有了更深入的了解,希望能够在实际应用中发挥其价值,为各行各业的发展提供有力支持。
第二章聚类分析

一个DATA步后面可以跟几个PROC步, 也可以若干个DATA步后面跟几个PROC 步;或以PROC步打头,后面跟若干个 DATA步,再跟PROC步,程序中的每个
系统聚类分析方法
系统聚类分析也叫分层聚类分析,是目 前国内外使用得最多的一种方法,有关 它的研究极为丰富,聚类分析的方法也 最多。
系统聚类的步骤
(1)计算n个样品两两之间的距离记为矩阵D; (2) 首先构造n个类,每一类中只包含一个
样品;
(3) 合并距离最近的两类为新类; (4) 计算新类与当前类的距离,若类的个数
R型聚类分析的主要作用:
1. 可了解个别变量之间及变量组合之间的 亲疏程度;
2. 根据变量的分类结果以及它们之间的关 系,可以选择主要变量进行回归分析或Q 型聚类分析。
事物之间的相似性测度
聚类分析用于系统类群相似性的研 究,其实质上是寻找一种能客观反映样品 或变量之间亲疏关系的统计量,然后根 据这种统计量把样品或变量分成若干类。 常用的统计量有距离和相似系数。
所研究问题的特征人为的选择变量,这些变量 应该和分析的目标密切相关,反映分类对象的 特征,在不同研究对象上的值具有明显差异, 变量之间不应该高度相关。选变量时并不是加 入的变量越多,得到的结果越客观。有时,加 入一两个不合适的变量就会使分类结果大相径 庭。变量之间高度相关相当于加权,此时,有 两种处理方法:(1)首先进行变量聚类,从 每类中选一代表性变量,再进行样品聚类; (2)进行主成分分析或因子分析,降维,使 之成为不相关的新变量,再进行样品聚类。
1.可综合利用多个变量的信息对Fra bibliotek品进行 分类;
聚类分析课件

聚类分析课件聚类分析课件聚类分析是一种常用的数据分析方法,它可以将一组数据分成不同的类别或簇,每个簇内的数据点具有相似的特征,而不同簇之间的数据点具有较大的差异。
聚类分析在各个领域都有广泛的应用,如市场细分、社交网络分析、医学诊断等。
在本文中,我们将介绍聚类分析的基本概念、常用算法和实际应用案例。
一、聚类分析的基本概念聚类分析的目标是通过对数据进行分组,使得每个组内的数据点相似度较高,而不同组之间的相似度较低。
聚类分析的基本概念包括距离度量和聚类算法。
1. 距离度量距离度量是衡量数据点之间相似度或差异度的标准。
常用的距离度量方法包括欧氏距离、曼哈顿距离和闵可夫斯基距离等。
欧氏距离是最常用的距离度量方法,它计算数据点在多维空间中的直线距离。
曼哈顿距离则计算数据点在坐标轴上的绝对距离,而闵可夫斯基距离则是这两种距离的一种泛化形式。
2. 聚类算法常用的聚类算法包括K-means算法、层次聚类算法和DBSCAN算法等。
K-means算法是一种迭代的、基于距离的聚类算法,它将数据点分成K个簇,使得每个簇内的数据点与该簇的中心点的距离最小。
层次聚类算法则是一种自底向上的聚类算法,它通过计算数据点之间的相似度来构建一个层次结构。
DBSCAN算法是一种基于密度的聚类算法,它将数据点分为核心点、边界点和噪声点三类,具有较好的鲁棒性和灵活性。
二、常用的聚类分析算法1. K-means算法K-means算法是一种迭代的、基于距离的聚类算法。
它的基本思想是随机选择K个初始中心点,然后将每个数据点分配到距离其最近的中心点所对应的簇中。
接着,重新计算每个簇的中心点,并重复这个过程直到收敛。
K-means算法的优点是简单易实现,但它对初始中心点的选择敏感,并且需要预先指定簇的个数K。
2. 层次聚类算法层次聚类算法是一种自底向上的聚类算法。
它的基本思想是将每个数据点看作一个独立的簇,然后通过计算数据点之间的相似度来构建一个层次结构。
聚类分析讲义范文

聚类分析讲义范文一、聚类分析的基本原理聚类分析的基本原理是通过计算数据点之间的相似性度量,将相似性高的数据点归为一类,从而形成簇(cluster)。
相似性度量方法主要包括欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等。
欧几里得距离是最常用的相似性度量方法,其计算公式为:d(x, y) = sqrt((x1-y1)^2 + (x2-y2)^2 + ... + (xn-yn)^2)聚类分析的基本步骤包括:1.选择合适的相似性度量方法和聚类算法。
2.初始化聚类中心,将数据点分配到最近的聚类中心。
3.更新聚类中心,重新计算每个聚类中心的位置。
4.重复第2步和第3步,直到聚类中心的位置不再变化为止。
5.输出聚类结果。
二、聚类分析的常用算法1. K-means算法:K-means算法是最常用的聚类算法之一、其核心思想是在每次迭代中,计算每个数据点到所有聚类中心的距离,并将每个数据点分配到距离最近的聚类中心。
然后,重新计算每个聚类中心的位置。
重复执行这两个步骤,直到聚类中心的位置不再变化。
K-means算法的优势是简单快速,但对初始聚类中心的选择较为敏感。
2.层次聚类算法:层次聚类算法通过计算所有数据点之间的相似性,构建一个层次性的聚类结果。
这个结果可以表示为一个树状结构,其中每个节点代表一个聚类。
层次聚类算法的优势是不需要预先指定聚类个数,但计算复杂度较高。
3.密度聚类算法:密度聚类算法将聚类看作是在数据空间中找到高密度区域的过程。
该算法通过计算每个数据点在其邻域内的密度,将高密度区域作为簇的候选。
然后,通过在高密度区域之间构建连接来将簇进行合并。
密度聚类算法的优势在于可以发现任意形状和大小的簇,对于噪声和异常点具有较好的鲁棒性。
三、聚类分析的评估方法四、聚类分析的应用聚类分析在市场调研中可以帮助企业识别相似的顾客群体,从而定制合适的产品和推广策略。
在社交网络分析中,聚类分析可以用来发现具有相似兴趣和行为的用户群体,从而进行精准广告投放。
环境监测数据的聚类分析与挖掘

环境监测数据的聚类分析与挖掘第一章:绪论随着经济的快速发展和城市化进程的加快,环境监测越来越重要。
环境监测数据是环保部门和政府衡量和管理环境质量的重要指标。
然而,由于数据量庞大、复杂、分布不均等特点,传统的统计和分析方法难以处理环境监测数据。
因此,利用聚类分析和挖掘技术,提取环境监测数据的有用信息,对于环境保护和管理具有重要的意义。
本文将分别从环境监测数据聚类分析和挖掘两个方面,进行详细的讨论。
第二章:环境监测数据聚类分析2.1 聚类分析的定义和基本方法聚类分析是一种将对象归类成不同组别的方法。
其主要目的是通过对数据进行分析,将相似的样本聚为一类,不同的样本聚为另一类。
它具有以下几个基本步骤:1.定义距离度量方法:计算样本之间的相似度或者距离。
2.分类原则的选择:为样本分类选择一个准则。
3.聚类算法的选择:基于相似度和分类原则确定聚类算法。
4.研究型簇和确定最终研究组。
2.2 环境监测数据聚类分析的应用环境监测数据聚类分析是从大数据中提取有用信息的重要方法。
它可以应用于许多不同的领域,包括环境科学、天气和气候研究、医学、金融等。
在环境监测中,聚类分析可以用来识别不同的环境污染来源,区分不同的风险区域,和确定监测站点的数量和位置。
2.3 环境监测数据聚类分析的案例研究以北京市PM2.5的数据为例,对PM2.5进行聚类分析。
首先,确定距离度量方法使用欧氏距离,接着采用基于均值的聚类算法。
最后,对实验得到的簇进行分析,确定Pm2.5主要的污染来源。
通过分析得到的聚类结果可以发现,PM2.5主要的污染来源包括汽车尾气、建筑工地的灰尘、和农业废气等。
第三章:环境监测数据挖掘3.1 环境监测数据挖掘的概念和方法环境监测数据挖掘是一种将大数据转换为有用信息的技术。
它可以分为基于分类和基于关联的挖掘方法。
其中,分类分析可以用于预测环境的变化和分析各种环境污染物之间的关系。
关联分析可以发现不同环境因素之间的相互作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)D(0)中最小的元素是D12=D56=1,于是将G1和G2合 并成G7,G5和G6合并成G8,并利用(5.12)式计算新类与 其它类的距离D(1)
G7 0 3 5 7 G3 0 2 4 0 2 0 G4 G8
G7 G3 G4 G8
(3)在D(1)中最小值是D34=D48=2,由于G4与G3合并, 又与G8合并,因此G3、G4、G8合并成一个新类G9,其与其 它类的距离D(2)
4.距离选择的原则 (1)要考虑所选择的距离公式在实际应用中有明 确的意义。如欧氏距离就有非常明确的空间距离 概念。马氏距离有消除量纲影响的作用。 (2)要综合考虑对样本观测数据的预处理和将要 采用的聚类分析方法。如在进行聚类分析之前已 经对变量作了标准化处理,则通常就可采用欧氏 距离。 (3)要考虑研究对象的特点和计算量的大小。样 品间距离公式的选择是一个比较复杂且带有一定 主观性的问题,我们应根据研究对象的特点不同 做出具体分折。实际中,聚类分析前不妨试探性 地多选择几个距离公式分别进行聚类,然后对聚 类分析的结果进行对比分析,以确定最合适的距 离测度方法。
分别为变量i和j的均值 显然也有,∣rij∣ 1。
有了对单个样品和单个指标相似形的度量方
法后,如何根据类间距离大小和相关系数大小 来进行分类呢?会用到以下聚类方法:
系统聚类 模糊聚类 K均值聚类 有序样品聚类
第三节 系统聚类
一 系统聚类的基本思想 二 类间距离与系统聚类法 三 类间距离的统一性
有两个关键问题:
类与类间的距离如何衡量? 如何选择分几类呢?
二、类间距离
最短距离法、最长距离法、类平均法、重心法和
离差平方和法等。
它们的归类步骤基本上是一致的,主要差异是类
间距离的计算方法不同。
以下用dij表示样品(指标)Xi与Xj之间距离,用D表
示类Gi与Gj之间的距离。
1. 最短距离法 定义类与之间的距离为两类最近样品(指标)的距离,即为
G7 G7 G9 0 3
G9 0
(4)最后将G7和G9合并成G10,这时所有的六个样品聚为一 类,其过程终止。 上述聚类的可视化过程如下:
【例5.2】针对例5.1的数据,试用重心法将它们聚类。 (1)假设样品采用欧氏距离,样品间的平方距离阵D2(0)
G1 0 1 16 36 64 81 G2 0 9 25 49 64 0 4 16 25 0 4 9 0 1 0 G3 G4 G5 G6
2
Dp为p类的离差平方和 Dq为q类的离差平方和 Dpq为p和q组成总类的离差平方和
5.组间平均链接
该个体与小类中每个个体距离的平均
6.组内平均链接
该个体与小类中每个给体距离,以及小类内部每 个个体距离的平均
case 1 2 3 4 5 1 0 8.062 17.804 26.907 30.414 2 8.062 0 25.456 34.655 38.21
Dk ( p ,q ) min{d ij | i G p , j Gq }
. .
.
.
2. 最长距离法 定义类 Gi 与 G j 之间的距离为两类最远样品的距离,即 为
Dk ( p, q) max{dij | i GP , j Gq }
. .
.
.
3.类平均法 两类间距离为类中任意两样品(指标)距离的平均。
4.重新确定各类中心 。 利用分配过来的样本重新计算类均值. 5.判断是否满足终止聚类的条件. 跌代次数:SPSS默认为10
类中心点偏移程度:新确定的类中心点距离上个类中
心点的最大偏移量小于指定量.
系统聚类与K均值聚类的区别与联系
K均值法和系统聚类法一样,都是以距离的
远近亲疏为标准进行聚类的.
在经济学中,根据经济发展的不同阶段对世界各个国家进行 分类. 医学研究中,阑尾炎类型的划分:性单纯性阑尾炎,急性化脓性
阑尾炎,坏疽性及穿孔性阑尾炎。
在社会学研究中,需要构造人口生育分类模式、人口死亡分 类状况,以此来研究人口的生育和死亡规律。
聚类分析的核心思想就是根据具体的指标(变量)对
你所研究的样品进行分类.
二、变量相似性的度量
R型聚类分析中,常用相似系数表示变量间的相似性。 1、夹角余弦
cos ij
2 2 [( x ki )( x kj )]1/ 2
n
x ki x kj k
1
n
n
k 1
k 1
x ki
变量i的第k个取值 变量j的第k个取值
x kj
显然,∣cos ij∣ 1。
一、系统聚类的基本思想
系统聚类的基本思想是:距离相近的样品(或变量)
先聚成类,距离相远的后聚成类,过程一直进行下 去,每个样品(或变量)总能聚到合适的类中。 系统聚类过程是:假设总共有n个样品(或变量) 第一步:将每个样品(或变量)独自聚成一类,共有 n类; 第二步:根据所确定的样品(或变量)“距离”公式, 把距离较近的两个样品(或变量)聚合为一类,其 它的样品(或变量)仍各自聚为一类,共聚成n 1 类; 第三步:将“距离”最近的两个类进一步聚成一类, 共聚成n 2类;……,以上步骤一直进行下去,最 后将所有的样品(或变量)全聚成一类。
二氧化碳影响因素聚类
2.相关系数 相关系数经常用来度量变量间的相似性。变量Xi与Xj的相关 系数定义为
rij
(x ki k
1
n
X i )(x kj X j )
2 nΒιβλιοθήκη [ (x ki X i )
k 1
n
(x kj k
1
Xj) ]
2
1/2
X i 和X j
欧氏距离 3 4 17.804 26.907 25.456 34.655 0 9.22 12.806 9.22 0 3.606
5 30.414 38.21 12.806 3.606 0
三、分类数的确定
可以根据碎石图确定: X轴表示分几类 Y轴表示聚合系数
四、聚类分析步骤 以最短距离法步骤为例: (1)选择样品(指标)距离公式,计算样品的两两距 离,得距离阵记为D(0) ,开始每个样品自成一类, 这时Dij = dij。 (2)找出距离最小元素,设为Dpq,则将Gp和Gq合 并成一个 新类,记为Gr,即Gr = {Gp,Gq}。 (3)根据最短距离法计算新类与其它类的距离。 (4)重复(2)、(3)两步. 如果某一步距离最小的元素不止一个,则对应这些 最小元素的类同时合并。
系统聚类可以选择分类数, 而K—均值法只能 产生指定类数的聚类结果。所以有时也借助 系统聚类法以一部分样品为对象进行聚类,
其结果作为K—均值法确定类数的参考。
【例5.3】假定我们对A、B、C、D四个样品分别测量两个变 量,得到结果。
样品 变量
X1
A B C D 5 -1 1 -3
5. 离差平方和法 又称为Ward法。如果分类正确,同类样品的离差平方和应 当较小,类与类的离差平方和较大。 具体做法是先将n个样品各自成一类,然后每次缩小一类, 每缩小一类,离差平方和就要增大,选择使方差增加最小的 两类合并,直到所有的样品归为一类为止。
Dw D p q D p Dq
第二章 聚类分析
第一节 第二节 第三节 第四节 第五节 聚类分析核心思想 相似性的量度 系统聚类分析法 K均值聚类分析 实例分析与计算机实现
第一节 核心思想
“物以类聚,人以群分”。
“近朱者赤,近墨者黑” 在生物学中,为了研究生物的演变,生物学家需要根据各种 生物不同的特征对生物进行分类。
【例5.1】设有六个样品,每个只测量一个指标,分别是1,2, 5,7,9,10,试用最短距离法将它们分类。 (1)选择样品距离公式,绝对距离最简单,形成D(0)
G1 0 1 4 6 8 9 G2 0 3 5 7 8 0 2 4 5 0 2 3 0 1 0 G3 G4 G5 G6
G1 G2 G3 G4 G5 G6
dij ( q ) ( X ik X
k 1
dij () max X ik X jk
1 k p
p
q jk
)1/ q
明考夫斯基距离的缺陷:
容易受变量的量纲影响. 没有考虑变量间的相关性 两种改进措施: “马氏距离”法和变量标准化处理法(见书)
高校科研的样本
学校 1 2 3 参加科研人数 (人) 410 336 490 欧氏距离 元 (1,2) (1,3) (2,3) 265000 218000 47000 万元 81.6 193.7 254.8 投入经费(元) 4380000 1730000 220000 立项课题数() 19 21 8
指标是什么?书上的例子.
将居民户按户主收入状况进行分类,那么衡量 收入状况的指标有:标准工资收入\职工奖金…..
样品是什么?
你所研究的11户居民.
进一步解读指标:
间隔尺度
有序尺度
名义尺度 思考:能不能对指标进行聚类?
所以,聚类分析包括两种类型:
Q型聚类:根据指标(变量)对样品进行分类
G7 G9 G8
G7 0 20.25 64
G9 0 12.5
G8
0
(4)在中最小值是=12.5,那么与合并一个新类,其与与 其它类的距离
G7 G10
G7 0 39.0625
G10 0
(5)最后将G7和G10合并成G11,这时所有的六个样品聚为一 类,其过程终止。 上述重心法聚类的可视化过程见图5.3所示,横坐标的刻度表 示并类的距离。
R型聚类:对指标(变量)进行分类
问题:大家认为聚类的结果是什么呢?
第二节 相似性的量度
