湖南省株洲市2019届二模-答案

合集下载

株洲市2019年第二次模拟考试-高考模拟

株洲市2019年第二次模拟考试-高考模拟各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢第Ⅰ卷（选择题共45分）一、（18分，每小题3分）1．下列词语中，加点字的读音全都正确的一项是A．熟稔（rěn）押解（jiè）甲胄（zhòu）引吭高歌（kàng）B．荫庇（yīn）纰漏（pī）狙击（jū）亘古未有（gèn）c．勖勉（xù）麾下（huī）休憩（qì）奇葩异草（bā）D．广袤（mào）骁勇（xiāo）沉疴（kē）龇牙咧嘴（zī）2．下列词语中，没有错别字的一组是A．景仰削足试履赏赉生死攸关B．谙习越俎代疱定型变幻莫测c．安详功亏一篑诡秘晶莹剔透D．祛署循私舞弊拮据烜赫一时3．依次填入下列各句横线上的词语，恰当的一组是①人们要正确对待他人和自己，要正确处理人与人之间的关系，不要妒贤忌能，不要___________他人。

②课文被视为精确无误的典范，学生只有迷信的义务，很少有____________的权利，更谈不上去化解了。

③我们只有走教育的产业化道路，才能实现教育的规模生产和规模______________。

A．强求质疑效益B．苛求置疑效率c．苛求质疑效益D．强求置疑效率4．下列句子中，加点的成语使用正确的一句是A．日本的历史教科书，能够不惜笔墨地把子虚乌有的神话故事写进去，而对其野蛮的侵略史却“惜墨如金”。

B．环境污染造成的严重社会问题正深入人心，成为各国政府十分关注的问题。

c．当代诗坛颇不景气，想起唐诗宋词的成就，不禁令人产生今非昔比的感慨啊。

D．近几年，黄河、岷江的部分河段多次出现断流现象，面对这江河日下的情况，人们开始冷静地思考环保问题。

5．下列各句中，没有语病的一句是A．邮票的图案设计、边框的图案装饰、色彩的运用、文字说明和面值数字的安排，都凝结着美术工作者的辛勤劳动成果。

B．我们一贯主张，国与国之间的事端应通过和平谈判来解决，反对诉诸于武力或以武力相威胁。

湖南省株洲市名校2019年中考物理第二次练兵模拟试卷+(13套中考模拟试卷)

物理中考模拟试卷含答案注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、单项选择题（包括11题，每题2分，共22分。

每题给出的四个选项中，只有一个选项最符合题目的要求。

）12.人类对于宇宙的探索是在一次次挫折中不断向前发展的，比如俄罗斯“福布斯—土壤”火星探测器在地球近地轨道上因主发动机启动失败而无法变轨。

经查，是太空中的带电粒子对机载计算机系统产生影响导致程序出错。

下列粒子中，首先可以排除对计算机系统A电子B质子C中子D氦核13.如图是获取电能的几种途径，其中消耗不可再生能源的是（）14. 诗句“两岸猿声啼不住，轻舟已过万重山”中，描写轻舟运动时所选的参照物是A．轻舟B．两岸的山C．河中的水D．轻舟上的人15. 在操场上上体育课，体育老师发出的口令，近处的学生听到了，而远处的学生没有听清楚。

其原因是A.老师发的声音音色不好B.远处学生听到的声音响度小C.老师发出的声音频率较低D远处学生听到的声音振动幅度大16.为了进行光学实验，物理课外小组的同学在老师的指导下自制了一个平行光源，在硬圆纸筒的一端安装了一个可在筒内前后移动的灯泡。

为使筒内射出的灯光是平行光，在纸筒的另一端需要安装的光学器件和灯泡的位置应分别是，A.凸透镜焦点处B.凸透镜焦点以内C.凸透镜焦点与二倍焦距点之间D.凹透镜二倍焦距点之外17.2018年6月18日，执行我国首次载人交会对接任务的神舟九号飞船与“天宫一号太空舱”成功对接。

图为女航天员王亚平在太空授课，展示基础物理实验。

你认为我们做过的物理实验可在太空舱中进行的是（）①用天平测量物体的质量②探究平面镜成像特点③墨水的扩散实验④用托里拆利实验装置测量气压A.①②B. ①②③C. ②③D.②③④18.如图是家用煤气灶灶头的示意图。

Asin(wx+φ)的图象及应用(含解析)

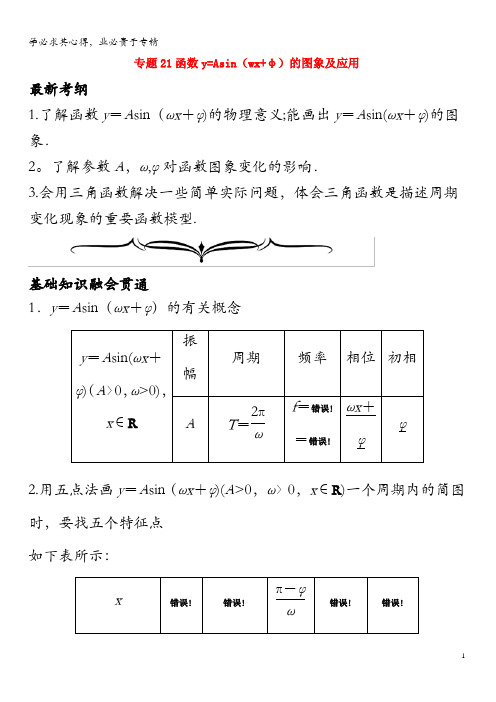
专题21函数y=Asin（wx+φ）的图象及应用最新考纲1.了解函数y＝A sin（ωx＋φ)的物理意义;能画出y＝A sin(ωx＋φ)的图象．2。

了解参数A，ω,φ对函数图象变化的影响．3.会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型.基础知识融会贯通1．y＝A sin（ωx＋φ）的有关概念y＝A sin(ωx＋φ)（A〉0，ω>0)，x∈R 振幅周期频率相位初相A T＝2πωf＝错误!＝错误!ωx＋φφ2.用五点法画y＝A sin（ωx＋φ)(A>0，ω〉0，x∈R)一个周期内的简图时，要找五个特征点如下表所示：x错误!错误!π－φω错误!错误!3.函数y＝sin x的图象经变换得到y＝A sin（ωx＋φ）（A>0,ω〉0)的图象的两种途径【知识拓展】1．函数y＝A sin(ωx＋φ)＋k图象平移的规律：“左加右减，上加下减”．2．由y＝sin ωx到y＝sin(ωx＋φ）(ω〉0，φ〉0)的变换：向左平移错误!个单位长度而非φ个单位长度．3．函数y＝A sin(ωx＋φ）的对称轴由ωx＋φ＝kπ＋π2，k∈Z确定；对称中心由ωx＋φ＝kπ，k∈Z确定其横坐标．重点难点突破【题型一】函数y＝A sin(ωx＋φ）的图象及变换【典型例题】已知向量（cos x ，)，（sin x，cos2x），x∈R，设函数f(x ）•．(1）求f（x）的表达式并完成下面的表格和画出f（x）在[0，π］范围内的大致图象；0πx0πf（x）（2)若方程f（x）﹣m＝0在[0，π］上有两个根α、β，求m的取值范围及α+β的值．【解答】解：（1）f（x )sin2x cos2x＝sin（2x），0πx0πf（x）010﹣1如图示:（2）由图可知m∈（﹣1，)∪(，1）,或，∴或．【再练一题】将函数y＝sin2x的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y＝f（x）的图象，则（）A．y＝f(x）的图象关于直线对称B．f(x）的最小正周期为C．y＝f（x）的图象关于点对称D．f（x）在单调递增【解答】解：函数y＝sin2x的图象上各点的横坐标伸长到原来的2倍,可得：y＝sin x,即f（x)＝sin x．根据正弦函数的图象及性质：可知：对称轴x，∴A不对．周期T＝2π，∴B不对．对称中心坐标为：(kπ，0），∴C不对．单调递增区间为［］，k∈Z，∴f（x）在单调递增．故选：D．思维升华(1）y＝A sin(ωx＋φ)的图象可用“五点法”作简图得到，可通过变量代换z＝ωx＋φ计算五点坐标．(2)由函数y＝sin x的图象通过变换得到y＝A sin(ωx＋φ）图象有两条途径：“先平移后伸缩"与“先伸缩后平移”．【题型二】由图象确定y＝A sin（ωx＋φ）的解析式【典型例题】函数y＝2sin(ωx+φ)（ω＞0,0＜φ＜π）的部分图象如图所示．则f（π）＝（）A．1 B．C．D．2【解答】解：根据函数y＝2sin（ωx+φ）（ω＞0，0＜φ＜π)的部分图象，可得：T•,解得:ω＝2，由于点（,2）在函数图象上，可得：2sin(2φ）＝2，可得:2φ＝2kπ，k∈Z，解得:φ＝2kπ，k∈Z,由于：0＜φ＜π,可得：φ，即y＝2sin（2x），可得:f（π)＝2sin（2π）＝1．故选：A．【再练一题】函数y＝2sin（ωx+φ)(ω＞0，0＜φ＜π）的部分图象如图所示．则函数f(x）的单调递增区间为（)A．B．C．D．【解答】解：根据函数y＝2sin（ωx+φ）（ω＞0,0＜φ＜π)的部分图象，可得：T•,解得：ω＝2,由于点(，2）在函数图象上，可得：2sin（2φ）＝2，可得：2φ＝2kπ,k∈Z，解得:φ＝2kπ,k∈Z，由于：0＜φ＜π，可得：φ，即y＝2sin(2x)，令2kπ2x2kπ，k∈Z，解得：kπx≤kπ，k∈Z，可得：则函数f(x)的单调递增区间为：［kπ，kπ]，k∈Z．故选:C．思维升华y＝A sin（ωx＋φ）中φ的确定方法（1)代入法：把图象上的一个已知点代入（此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入．（2）五点法：确定φ值时,往往以寻找“五点法"中的特殊点作为突破口．【题型三】三角函数图象性质的应用命题点1 三角函数模型【典型例题】如图，扇形OAB的半径为1,圆心角为,若P为弧上异于A，B的点，且PQ⊥OB交OB于Q点,当△POQ的面积大于时，∠POQ 的大小范围为．【解答】解：设∠POQ＝θ，则PQ＝sinθ，OQ＝cosθ，(0＜θ）．∴，由，得sin2θ，又2θ∈（0，π），∴2θ,则θ．∴∠POQ的大小范围为．故答案为：．【再练一题】海上一艘轮船以60nmile/h的速度向正东方向航行，在A处测得小岛C在北偏西30°的方向上，小岛D在北偏东30°的方向上，航行20min后到达B处测得小岛C在北偏西60°的方向上，小岛D在北偏西15°的方向上，则两个小岛间的距离CD＝nmile【解答】解：∵△ABC中，由题意可得：∠CAB＝120°，∠BAC＝30°,AB＝6020，∴由正弦定理，∴BC20，∵在△ABD中，由于∠DAB＝60°，∠ADB＝45°，由正弦定理可得：，可得：BD10，∴△BCD中，由余弦定理可得CD2＝（10）2+（20）2﹣2×1020cos45°，∴解得:CD＝10．即目标C、D之间的距离为10．故答案为:10．命题点2 函数零点(方程根)问题【典型例题】已知函数f（x）＝2sin(ωx）sin（ωx)(ω＞0)，若函数g（x)＝f（x）在[0，］上有且只有三个零点，则ω的取值范围为（）A．[2，）B．（2，）C．[）D．（)【解答】解：f（x）＝2sin（ωx）sin（ωx)＝2sin（ωx）sin(ωx）＝﹣2cos（ωx）sin（ωx）＝﹣sin（2ωx），由g(x）＝f（x）0得f(x），即﹣sin（2ωx）,得sin（2ωx)，∵0≤x，∴0≤2ωx≤πω，则2ωxπω，∵sin，∴要使sin（2ωx)，在0≤x上有三个根，∴2π≤ωπ4π,得2π≤ωπ，即2≤ω，即ω的取值范围是［2，)，故选:A．【再练一题】已知函数，若函数F（x）＝f（x）﹣3的所有零点依次记为x1,x2,x3，…，x n，且x1＜x2＜x3＜…＜x n，则x1+2x2+2x3+…+2x n﹣1+x n＝( ）A．B．445πC．455πD．【解答】解：函数，令2x kπ得x，k∈Z，即f（x）的对称轴方程为x，k∈Z．∵f（x）的最小正周期为T＝π,0≤x，当k＝0时,可得第一根对称轴x，当k＝30时,可得x，∴f（x）在［0，］上有30条对称轴，根据正弦函数的性质可知:函数与y＝3的交点有30个点，即x1，x2关于对称，x2,x3关于对称,…,即x1+x22，x2+x32，…，x30+x31＝2将以上各式相加得：x1+2x2+2x3+…+2x28+2x29+2x30+x31＝2(）＝(2+5+8+…+89）455π故选：C．命题点3 三角函数图象性质的综合【典型例题】已知函数（ω＞0)，且，当ω取最小值时，以下命题中假命题是( )A．函数f(x）的图象关于直线对称B．是函数f（x)的一个零点C．函数f（x）的图象可由的图象向左平移个单位得到D．函数f（x)在上是增函数【解答】解:f(x）sinωx cosωx+cosωx sinωx cosωx sin（ωx）,∵f（）sin(π）＝0，∴πkπ，∴ω＝3k﹣1,k∈Z．∵ω＞0,∴ω的最小值为2．此时f（x）sin（2x）．∵f（）sin，∴当x时,f（x）取得最大值,故A正确；∵f（)＝0，∴x是f（x)的零点，故B正确;∵f（x）sin[2（x）]，∴f（x)的图象由g(x)的图象向右平移个单位得到,故C错误；∵f（x）的周期为T＝π，区间长度为，且当x时，f（x）取得最大值，∴f（x)在上是增函数,故D正确．故选：C．【再练一题】函数，若,且函数f（x)的图象关于直线对称，则以下结论正确的是( ）A．函数f（x)的最小正周期为B．函数f（x）的图象关于点对称C．函数f（x)在区间上是增函数D．由y＝2cos2x的图象向右平移个单位长度可以得到函数f（x）的图象【解答】解：函数，∵，即2sinφ，∵φ∴φ又∵函数f（x）的图象关于直线对称,∴，k∈Z．可得ω＝12k﹣10，∵0＜ω＜12．∴ω＝2．∴f（x）的解析式为：f（x)＝2sin(2x)．最小正周期T,∴A不对．当x时，可得y≠0，∴B不对．令2x，可得，∴C不对．函数y＝2cos2x的图象向右平移个单位，可得2cos2（x）＝2cos（2x）＝2sin(2x)＝2sin(2x)．∴D项正确．故选：D．思维升华（1）三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题,利用三角函数的有关知识解决问题．（2)方程根的个数可转化为两个函数图象的交点个数．(3)研究y＝A sin（ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．基础知识训练1．【山东省日照市2019届高三5月校际联合考试】将函数的图象向右平移6π个单位长度得到()g x 图象，则函数的解析式是（ ) A ． B ． C ．D ．【答案】C 【解析】由题意，将函数的图象向右平移6π个单位长度，可得的图象.故选：C ．2．【辽宁省朝阳市重点高中2019届高三第四次模拟】已知函数的两个相邻的对称轴之间的距离为2π，为了得到函数的图象，只需将()y f x =的图象（）A ．向左平移6π个单位长度B ．向右平移6π个单位长度C ．向左平移12π个单位长度 D ．向右平移12π个单位长度【答案】D 【解析】因为函数的两个相邻的对称轴之间的距离为2π，所以()f x 的最小正周期为T π=，因此22Tπω==，所以，因此,为了得到函数的图象，只需将的图象向右平移12π个单位长度.故选D3．【安徽省合肥市2019届高三第三次教学质量检测】为了得到函数sin y x =的图像，只需将函数的图像（ )A ．横坐标伸长为原来的两倍,纵坐标不变，再向右平移6π个单位 B ．横坐标伸长为原来的两倍，纵坐标不变，再向左平移6π个单位C ．横坐标缩短为原来的12,纵坐标不变，再向右平移6π个单位D ．横坐标缩短为原来的12,纵坐标不变，再向左平移6π个单位【答案】A 【解析】把函数的图像上所有点的横坐标伸长为原来的两倍,纵坐标不变得到函数，再将函数的图像上所有点向右平移6π个单位得到函数sin y x =。

株洲市2019年第二次模拟考试-高考模拟

株洲市2019年第二次模拟考试-高考模拟本文从网络收集而来，上传到平台为了帮到更多的人，如果您需要使用本文档，请点击下载按钮下载本文档（有偿下载），另外祝您生活愉快，工作顺利，万事如意！第Ⅰ卷（选择题共45分）一、（18分，每小题3分）1．下列词语中，加点字的读音全都正确的一项是A．熟稔（rěn）押解（jiè）甲胄（zhòu）引吭高歌（kàng）B．荫庇（yīn）纰漏（pī）狙击（jū）亘古未有（gèn）c．勖勉（xù）麾下（huī）休憩（qì）奇葩异草（bā）D．广袤（mào）骁勇（xiāo）沉疴（kē）龇牙咧嘴（zī）2．下列词语中，没有错别字的一组是A．景仰削足试履赏赉生死攸关B．谙习越俎代疱定型变幻莫测c．安详功亏一篑诡秘晶莹剔透D．祛署循私舞弊拮据烜赫一时3．依次填入下列各句横线上的词语，恰当的一组是①人们要正确对待他人和自己，要正确处理人与人之间的关系，不要妒贤忌能，不要___________他人。

②课文被视为精确无误的典范，学生只有迷信的义务，很少有____________的权利，更谈不上去化解了。

③我们只有走教育的产业化道路，才能实现教育的规模生产和规模______________。

B．环境污染造成的严重社会问题正深入人心，成为各国政府十分关注的问题。

c．当代诗坛颇不景气，想起唐诗宋词的成就，不禁令人产生今非昔比的感慨啊。

D．近几年，黄河、岷江的部分河段多次出现断流现象，面对这江河日下的情况，人们开始冷静地思考环保问题。

湖南省株洲市2019届高三第二次教学质量检测(二模)文科数学试题(教师版)

株洲市 2019 届高三第二次教学质量统一检测
文科数学
一、选择题 . 在每小题给出的四个选项中，只有一项是符合题目要求的 .
1. 已知集合 M
1,0,1,2 , N x 1 x 3 ，则 M N （）
A. 1,0,1,2,3
B. 1,0,1
C. 1,2
D. 1,2,3
【答案】 C 【解析】【分析】根据交集的定义，找出集合 M,N 的公共元素即可。
的面积为 S，
∵由电脑随机从正方形中抽取 10000 个点，落在图形
3335,6665
S
,∴
3335
1
1
,S .
1 10000 3
3
故选 A.
内和图形外的点分别为
【点睛】本题主要考查几何概型的应用，利用面积比之间的关系是解决本题的关键，比较基础．
4. 已知向量 a 1,1 ,b 1,2 ,c k,1 ，且 2a b c ，则实数 k （）
利用复数代数形式的乘除运算，把复数化简为
z a bi 的形式，再求其共轭复数即可。
1 【详解】 z 2 =2-i ， z 2 i . 故选 B.
i
【点睛】对于复数的四则运算，要熟悉复数的相关基本概念，如复数 a bi a, b R 的实部为 a, 虚部为 b，
模为 a2 b2 ，对应点为 (a,b), 共轭复数为 a bi 。
到跳出循环时 x 的值是解题的关键．
7. 某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如
图所示 . 则该物质含量的众数和平均数分别为（
）
A. 83 和 84
B. 83和 85
C. 85 和 84

湖南省株洲市2019届高三第二次教学质量统一检查(二模)参考答案

株洲市2019届高三年级教学质量统一检测（二）语文参考答案一、现代文阅读（共36分）（一）论述类文本阅读（9分，每小题3分）1、C（A项，《朱子读书法》为“近世”士子读书方法指南；讨论的也不是《朱子读书法》能否成为指南。

B项，原文为“不仅仅”为了获取外在知识。

D项，《四书章句集注》为“从小学开始到科举求官”的教科书，选项时间有误。

）2、A（“传统中国的读书方法与意义”是本文的论题而非论点。

论题是提出的问题或涉及的内容和范围。

论点是针对论题发表的具体观点、看法、主张，是对论题的答复。

文章标题可以是论题或论点，本文是论题。

）3、D（应为儒家的“入世”思想）（二）实用类文本阅读（12分）4、B（句前缺少限制性，如“特朗普认为”）5、A（“其高端智能化制造业”，原文中没有“智能化”）6、①“材料一”侧重分析美国发动贸易战的原因；把收入分配（贫富）差距扩大的国内矛盾转嫁给其他国家。

（2分）②“材料二”侧重分析美国的贸易霸凌主义本质；拖慢甚至终止中国的经济发展，把中国引向“中等收入陷阱”。

（2分）③“材料三”侧重分析中国如何应对美国发动的贸易战；通过进一步改革开放，化解风险，转危为机。

（2分）（三）文学类文本阅读（15分）7、C（A项中“最具代表性”文中没有；B项“根本原因”是彻悟；D项强加因果。

）8、参考要点：（1）不同点：蒙娜丽莎微笑：神秘（1分），主要是快乐的微笑（1分）；佛菩萨：无限的喜悦（1分），“举身微笑”，弥漫全身（1分）。

共同点：根植于内心或有一颗喜乐的心灵（1分），常人难以仿效或企及（1分）。

（言之成理即可）（6分）9、参考示例：（1）微笑的真义是指“因心的喜乐而生发微笑，也会因微笑而永葆心的喜乐”，只有微笑要根植内心，超脱不执着，平常人也可以拥有最美的微笑。

（2）点题，与第②段相照应（呼应）。

（3）深化（升华）主旨，表明了作者对平常人发自内心、纯真善良微笑的期待和赞许。

（每点2分。

从内容解说、情感、结构、表达效果等角度结合文本分析作答，言之成理即可）（6分）二、古代诗文阅读（共34分）（一）文言文阅读（19分）10、A11、B（“辟召”包括中央政府和地方官聘请两方面，师爷由主官私人聘请）12、B（此时彭宠还没有“怨”）13、（1）恰逢上谷太守耿况派骑兵来救朱浮，朱浮才得逃走，仅（才）只身免于死（逃出了险境），（蓟）城向彭宠投降了。

株洲2019届高三二模文科综合答案

株洲市2019届高三年级教学质量统一检测（二）政治参考答案一、单项选择题（48分）12-17 DBCCB 18-23 DDCBD DC二、非选择题（52分）38.①创新是发展的第一动力，是建设社会主义经济体系的战略支撑，是发展的基点。

打造粤港澳大湾区经济有利于推动高科技产业、现代服务业的发展，加快培育发展新动能。

（3分）②打造粤港澳大湾区经济体现了开放发展理念，奉行互利共赢的开放战略，遵循共建共享原则，顺应了我国经济深度融入世界经济的趋势，有利于推动发展更高层次的开放型经济体系。

（3分）③打造粤港澳大湾区经济有利于实现区域经济协调发展、共享发展，满足人民日益增长的美好生活需要。

（2分）④粤港澳大湾区是我国高端制造业的承载区，打造粤港澳大湾区经济有利于建设现代化经济体系，大力发展实体经济，深化供给侧结构性改革，加快发展先进制造业，增强我国经济质量优势。

（3分）⑤现代经济的健康发展必须发挥市场对资源配置的决定性因素，实行科学的宏观调控。

打造粤港澳大湾区经济有利于将成熟的市场体制与较强的政府决策力和执行力相结合，推动经济的健康有序发展。

（3分）39.①中国共产党领导的多党合作与政治协商制度是中国特色社会主义政党制度，是我国的一项基本政治制度，实践证明，它适应我国基本的国情和生产力发展的要求，具有强大的生命力。

（4分）②中国共产党领导的多党合作与政治协商制度不是一党制，也根本区别于西方的多党制。

中国共产党是执政党，民主党派是参政党，中国共产党和民主党派是通力合作、共同致力于社会主义事业的亲密友党。

这有利于保持政治的稳定性和政策的连续性，推动决策的科学化与民主化。

（4分）③中国共产党领导的多党合作与政治协商制度是马克思主义政党理论同中国实际相结合的产物，它的首要前提和根本保证是坚持中国共产党的领导，能够真实、广泛、持久代表和实现最广大人民的根本利益、全国各族各界根本利益。

（4分）(本题从三个维度思考，一是从中国特色和中国实践角度，二是从政党关系角度，三是从代表利益和实现利益角度，每个角度4分)40.（1）①意识是指客观存在在人脑中的主观映象，党在十九大提出的乡村振兴战略是新时代农村现状的反映。

2019-2020学年株洲市第四中学高三英语二模试卷及答案

2019-2020学年株洲市第四中学高三英语二模试卷及答案第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项ALOI English—English Conversation ClassesTake English conversation classes with native English -speaking teachers from theUnited States,IrelandandAustralia, live, 1 - on - 1.This is by far the best way to improve your real spoken English and listening abilities and get to a level where you can use it in real - life situations. Our teachers mainly carry on conversations about work in different fields, such as business, finance, politics and travel. However, if you like, you can have normal day - to - day conversations about events, weather, etc. If you would like to learn some grammar during conversation, we can do that too!Our English Conversation classes：• Your conversations will always be with a native English speaker.• You can choose the time, day and teacher for each class.• The classes are made for each student individually. They will be at your level, studying what you need and what interests you.Packages10 Classes Package $ 229.90Interested in taking 10, 55 - minute conversation English classes?Schedule a first free class with LOI English and talk to the teacher about it. After that, you can arrange to take our 10 - class conversation English course.20 Classes Package $ 439,80Interested in taking 20, 55 - minute conversation English classes?Schedule a first free class with LOI English and talk to the teacher about it. After that, you can arrange to take our 20 - class conversation English course.1. What do the classes mainly focus on?A. Daily conversations.B. Work - related topics.C. Grammar rules.D. Area - based accents.2. Which is NOT offered to the students?A. Native English - speaking teachers.B. Personalized courses.C. Choice of class time and teacher.D. Offline learning materials.3. What should a student do first if he decides on either of the packages?A. Arrange a free class with LOI English.B. Bargain with LOI English for lower fees.C. Choose an experienced LOI English teacher.D. Make a promise to sit through each class.BThere are 195 countries in the world today but almost none of them have purple on their national flag. So what’s wrong with purple? It’s such a popular color1 today. Why would no country use it in their flag? The answer is really quite simple. Purple was just for too expensive.The color1 purple has been associated with royalty power and wealth for centuries. Queen Elizabeth I forbade anyone except close members of the royal family to wear it. Purple’s high status comes from the rarity and cost of the dye (染料)originally used to produce it. Fabric traders got the dye from a small sea snail (海螺)that was only found in the Tyre region of the Mediterranean. More than 10,000 snails were needed to create just one gram of purple; not to mention a lot of work went into producing the dye, which made purple dye so expensive.Since only wealthy rulers could afford to buy and wear the color1 , it became associated with the royal family. Sometimes, however, the dye was too expensive even for royalty. Third century Roman Emperor Aurelio famously wouldn’t allow his wife to buy a scarf made from purple silk because it cost three times its weight in gold. A single pound of dye cost three pounds of gold, which equals 56,000 dollars today. Therefore, even the richest countries couldn’t spend that much having purple on their flags.The dye became more accessible to lower-class about a century and a half ago. In 1856, 18-year-old English chemist William Henry Perkin accidentally created a man-made purple compound (化合物)while attemptingto produce an anti-malaria drug. He noticed that the compound could be used to dye fabrics, so he patented the dye, manufactured it and got rich. Purple dye was then mass-produced so everybody could afford it.Till now, a handful of new national flags have been designed and a few of them have chosen to use purple in their flag. So don’t be making any bets just yet.4. Why was color1 purple expensive in the past?A. Because only royal families were allowed to wear purple.B. Because it took a long time to get purple dye from gold.C. Because purple was worth as much as its weight in gold.D. Because purple dye used to be rare and hard to produce.5. Why did Roman Emperor Aurelio forbid his wife to buy a purple scarf?A. Because of poor quality.B. Because of long tradition.C. Because of bad taste.D. Because of high price.6. What is purple's situation now?A. Purple has been widely used on national flags.B. Purple dye is now affordable to ordinary people.C. Royal family stop using purple because it’s toocommon.D. Fewer snails are used to produce purple dye than before.7. Which of the following would be the best title for the passage?A. No Purple Flags?B. Purple vs GoldC. How to Produce Purple Dye?D. The Birth of Purple ColorCMark Bertram lost the tips of two fingers at work in 2018 when his hand became trapped in a fan belt. “It’s life-changing but it’s not life-ending,”he says.After two surgeries and occupational therapy, Bertram decided to ask Eric Catalano, a tattoo artist, to create fingernail tattoos. The idea made everyone in the studio laugh—until they saw the final result. “The mood changed,” Catalano recalls from his Eternal Ink Tattoo Studio in Hecker, Illinois. “Everything turned from funny to wow.”Catalano posted a photo of the tattoos, and it eventually was viewed by millions of people around the world. The viral photo pushed Catalano, 40, further into the world of paramedical tattooing. Now people who want to cover their life-altering scars come from as far away as Ireland to visit his shop.Leslie Pollan, a dog breeder, was bitten on the face by a puppy. She underwent countless surgeries but those gave her no hope. She ultimately traveled six hours for a session with Catalano. HecamouflagedPollan’s lip scar, giving her back confidence.Though he is now known for his talent with intricate fingernail, Catalano uses the techniques he picked up years ago while helping breast cancer survivors. Those tattoos are among the most common paramedical requests. His grandmother had breast cancer, and her battle with the disease is one reason Catalano is so dedicated to helping those with the diagnosis.Catalano performs up to eight reconstructive tattoos each “Wellness Wednesday”. While he charges $100 per regular tattoo, he doesn’t charge for paramedical tattoos: A GoFundMe page established last year brought in more than $16,000, allowing Catalano to donate his work.“Financially, it doesn’t make sense,” Catalano says. “But every time I see emotions from my customers, I am 100 percent sure this is something that I can’t stop doing.”8. How did people in the studio react to Bertram’s idea at first?A. They took it lightly.B. They found it creative.C. They were confused.D. They were impressed.9. What does the underlined word “camouflaged” in Paragraph 4 probably mean?A. Exposed.B. Hid.C. Ignored.D. Removed.10. What does Catalano say about his work with paramedical tattoos?A. It is flexible.B. It is demanding.C. It is profitable.D. It is rewarding.11. Which of the following can best describe Catalano?A. Humorous and experienced.B. Devoted and generous.C. Cooperative and grateful.D. Professional and tolerant.DThere will be more plastic than fish in the world’s oceans by 2050. That is what a new report from the World Economic Forum and Ellen MacArthur Foundation warns. If the current trend continues, the report said, oceans will contain one ton of plastic for every three tons of fish in 2025. By 2050, plastics will weigh more than fish. The problem is that each year at least 8 million tons of plastics end up in oceans around the world. This is the same as dumping the contents of one garbage truck into the ocean every minute.Not all plastic ends up in the ocean because someone throws a plastic bottle into the water. Plastic containers and other trash thrown onto streets and sidewalks often are swept into oceans. Unlike other types of trash in the ocean, the plastic never bio-degrades. There is a way to slow the amount of plastics going into the oceans — people can recycle more. Currently only about 14 percent of plastics are recycled. Research in Europe shows as much as 53 percent of plastic could be recycled using available technology. The report says that another solution is using less plastic for packaging products. But that is not likely to happen.“Given plastic packaging’s many benefits, both the possibility and desirability of an across-the-board dramatic reduction in the volume of plastic packaging used is clearly low, ”the report said. But the authors note reducingthe use of plastics should be tried“where possible. ”For decades, scientists warned that plastics are killing fish. Research shows that fish are dying from choking after eating plastics. Another cause of death is that plastics cause“intestinal blockage and starvation, ”the environmental group said.12. Why is the garbage truck mentioned in Paragraph 1 ?A. To explain how plastics end up in the ocean.B. To warn people against the ocean pollution.C. To clarify the seriousness of the problem.D. To point out some details of the report.13. Why is plastic more dangerous than other types of trash?A. There is too much of it.B. It poisons the ocean water.C. It is from different sources.D. It is hard to break down.14. What is the author’s attitude to the suggested solutions?A. Pessimistic.B. Curious.C. Unconcerned.D. Terrified.15. What can we infer from the text?A. People are not aware of the problem.B. Recycling is limited by lack of technology.C. Plastic packaging has become part of our life.D. Fish in the ocean will be replaced by plastics.第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

湖南省株洲市2019届高三数学第二次教学质量检测(二模)试题理(含解析)

株洲市2019届高三第二次教学质量统一检测理科数学一、选择题：本在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，则（）A. B. C. D.【答案】C【解析】【分析】根据交集的定义，找出集合M,N的公共元素即可。

【详解】因为集合，所以，故选C.【点睛】本题考查集合的表示方法，交集的定义与运算，属于基础题。

2.为虚数单位，复数的虚部是（）A. B. C. D.【答案】B【解析】【分析】根据复数的除法运算求出复数的代数形式后可得答案．【详解】由题意得，，所以复数的虚部是．故选B．【点睛】本题考查复数的运算和虚部的概念，解题时容易认为复数的虚部为，要强化对复数概念的理解，属于基础题．3.如图，在边长为的正方形内有不规则图形，由电脑随机从正方形中抽取个点，若落在图形内和图形外的点分别为，则图形面积的估计值为（）A. B. C. D.【答案】C【解析】【分析】根据面积型的几何概型概率公式进行估计计算可得答案．【详解】设图形的面积为，则由几何概型及题意得，所以，即图形面积的估计值为．故选C．【点睛】本题考查几何概型概率的应用，解题的关键是明确落在图形内的点的概率等于两图形的面积比，属于基础题．4.已知双曲线的一条渐近线的倾斜角为，且的一个焦点到的距离为，则双曲线的方程为（）A. B.C. D.【答案】D【解析】【分析】根据题意求出参数的值后可得双曲线的方程．【详解】由可得，即渐近线的方程为，又一条渐近线的倾斜角为，所以．因为双曲线的一个焦点到的距离为，所以，所以，所以双曲线的方程为．故选D．【点睛】本题考查双曲线方程的求法，解题的关键是根据题意求出参数的值，解题是要注意将条件中给出的数据进行适当的转化，属于基础题．5.已知等差数列单调递增且满足，则的取值范围是（）A. B. C. D.【答案】B【解析】试题分析：∵等差数列单调递增，∴，∵，即，即，∴．考点：等差数列的通项公式．6.在边长为的菱形中，为的中点，则的值为（）A. B. C. D.【答案】A【解析】【分析】选择向量为基底，根据向量数量积的定义求解即可．【详解】选择向量基底，则，所以．故选A．【点睛】求向量数量积的两种方法：一是根据数量积的定义求解，此时需要先选择基底，将所有向量都用该基底表示，然后按照定义求解；二是根据向量的坐标进行计算，此时需要建立直角坐标系，进而得到向量的坐标，最后转化为数的运算问题．7.已知命题，命题，则下列命题正确的是（）A. B.C. D.【答案】C【解析】【分析】利用导数和函数零点分别判断命题p,q的真假，从而判断出复合命题的真假即可。

【水印已去除】2019年湖南省株洲市高考数学二模试卷(理科)

2019年湖南省株洲市高考数学二模试卷（理科）一、选择题：本在每小题给出的四个选项中，只有一项是符合题目要求的.1．（3分）已知集合M＝{﹣1，0，1，2}，N＝{x|1≤x≤3}，则M∩N＝（）A．{﹣1，0，1，2，3}B．{﹣1，0，1}C．{1，2}D．{1，2，3}2．（3分）i为虚数单位，复数的虚部是（）A．﹣1B．1C．i D．﹣i3．（3分）如图，在边长为1的正方形内有不规则图形Ω，由电脑随机从正方形中抽取10000个点，若落在图形Ω内和图形Ω外的豆子分别为3335，6665，则图形Ω面积的估计值为（）A．B．C．D．4．（3分）已知双曲线C：﹣＝1的一条渐近线l的倾斜角为，且C的一个焦点到l的距离为，则双曲线C的方程为（）A．＝1B．＝1C．＝1D．x2﹣5．（3分）已知等差数列{a n}单调递增且满足a1+a10＝4，则a8的取值范围是（）A．（2，4）B．（﹣∞，2）C．（2，+∞）D．（4，+∞）6．（3分）如图，在边长为2的菱形ABCD中，∠BAD＝60°，E为CD的中点，则的值为（）A．1B ．C ．D ．7．（3分）已知命题p：∀x＞0，e x＞x+1，命题q：∃x∈（0，+∞），lnx≥x，则下列命题正确的是（）A．p∧q B．（￢p）∧q C．p∧（￢q）D．（￢p）∧（￢q）8．（3分）一个几何体的三视图如图所示，那么这个几何体的体积为（）A．96B．120C．144D．1809．（3分）高铁是一种快捷的交通工具，为我们的出行提供了极大的方便．某高铁换乘站设有编号为①，②，③，④，⑤的五个安全出口，若同时开放其中的两个安全出口，疏散1000名乘客所需的时间如下：则疏散乘客最快的一个安全出口的编号是（）A ．①B．②C．④D．⑤10．（3分）若函数f（x）＝cos（2x﹣）﹣a（x∈[0，]）恰有三个不同的零点x1，x2，x3，则x1+x2+x3的取值范围是（）A．[，）B．[，）C．（，]D．（，] 11．（3分）已知长方体ABCD﹣A1B1C1D1，AB＝AA1＝2，AD＝1，正方形CC1D1D所在平面记为α，若经过点A的直线l与长方体ABCD﹣A1B1C1D1所有的棱所成角相等，且l ∩α＝M，则线段AM的长为（）A．B．3C．D．12．（3分）设函数f（x）＝，其中a≤﹣2，则满足f（x）+f（x﹣1）＜3的x取值范围是（）A．（﹣1，+∞）B．（﹣，+∞）C．（﹣2，+∞）D．（0，+∞）二、填空题（将答案填在答题纸上）13．（3分）已知实数x，y满足条件，则y﹣2x的最大值为．14．（3分）在（1﹣）（1+x）5的展开式中，x2项的系数为（用数字作答）．15．（3分）已知数列{a n}的前n项和为S n，a1＝4，4S n＝a1+a2+……+a n+1（n≥1），则a n ＝．16．（3分）已知F1，F2是椭圆C：+＝1（a＞b＞0）的左右焦点，B是短轴的一个端点，线段BF2的延长线交椭圆C于点D，若△F1BD为等腰三角形，则椭圆C的离心率为．三、解答题（解答应写出文字说明、证明过程或演算步骤.）17．如图，在四边形ABCD中，∠ADC＝，AD＝3，sin∠BCD＝，连接BD，3BD＝4BC．（Ⅰ）求∠BDC的值；（Ⅱ）若BD＝，∠AEB＝，求△ABE的面积最大值．18．如图，已知四棱锥P﹣ABCD的底面为边长为2的菱形，∠BAD＝，P A＝PB，M为AB中点，连接MD．（Ⅰ）求证：平面PCD⊥平面PMD；（Ⅱ）若平面P AB⊥平面ABCD，且二面角B﹣AP﹣D的余弦值为，求四棱锥P﹣ABCD的体积．19．已知抛物线E：y2＝2px（p＞0）经过点A（1，2），过A作两条不同直线l1，l2，其中直线l1，l2关于直线x＝1对称．（Ⅰ）求抛物线E的方程及准线方程；（Ⅱ）设直线l1，l2分别交抛物线E于B、C两点（均不与A重合），若以线段BC为直径的圆与抛物线E的准线相切，求直线BC的方程．20．从某公司生产线生产的某种产品中抽取1000件，测量这些产品的一项质量指标，由检测结果得如图所示的频率分布直方图：（Ⅰ）求这1000件产品质量指标的样本平均数和样本方差s2（同一组中的数据用该组区间的中点值作代表）；（Ⅱ）由直方图可以认为，这种产品的质量指标值Z服从正态分布N（μ，σ2），其中μ近似为样本平均数，δ2近似为样本方差s2．（i）利用该正态分布，求P（175.6＜Z＜224.4）；（ii）已知每件该产品的生产成本为10元，每件合格品（质量指标值Z∈（175.6，224.4）的定价为16元；若为次品（质量指标值Z∉（175.6，224.4），除了全额退款外且每件次品还须赔付客户48元．若该公司卖出100件这种产品，记Y表示这件产品的利润，求E （Y）．附：≈12.2．若Z～N（μ，δ2），则P（μ﹣δ＜Z＜μ+δ）＝0.68，P（μ﹣2δ＜Z ＜μ+2δ）＝0.95．21．设函数f（x）＝e x（ax+2），g（x）＝x2+4x+2（Ⅰ）讨论y＝f（x）的极值；（Ⅱ）若曲线y＝f（x）和曲线y＝g（x）在点P（0，2）处有相同的切线，且当x≥﹣2时，mf（x）≥g（x），求m的取值范围．[选修4-4：坐标系与参数方程]22．在直角坐标系xoy中，圆C的参数方程为（φ为参数），现以原点O为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求圆C的极坐标方程；（Ⅱ）设P，Q是圆C上的两个动点，且∠POQ＝，求|OP|+|OQ|的最大值．[选修4-5：不等式选讲]23．已知函数f（x）＝|2x﹣a|+|x﹣1|，a∈R．（Ⅰ）若a＝﹣2，解不等式f（x）≤5；（Ⅱ）当a＜2时，函数f（x）的最小值为3，求实数a的值．2019年湖南省株洲市高考数学二模试卷（理科）参考答案与试题解析一、选择题：本在每小题给出的四个选项中，只有一项是符合题目要求的.1．【解答】解：∵M＝{﹣1，0，1，2}，N＝{x|1≤x≤3}；∴M∩N＝{1，2}．故选：C．2．【解答】解：∵＝，∴复数的虚部是1．故选：B．3．【解答】解：设图形Ω的面积为S，因为由电脑随机从正方形中抽取10000个点，落在Ω图形内和图形Ω外的豆子分别3335，6665，所以＝，故选：A．4．【解答】解：双曲线的渐近线方程为y＝±x，焦点坐标为（±c，0），∴，解得b＝，a＝1．∴双曲线的方程为：x2﹣＝1．故选：D．5．【解答】解：设公差为d，则∵a1+a10＝4，∴2a1+9d＝4，∴a1＝2﹣，∴a8＝a1+7d＝2+d，∴a8＝2+d＞2．故选：C．6．【解答】解：在菱形ABCD中，∠BAD＝60，∴△ABD为正三角形，由＜＞＝60°，可得＜＞＝180°﹣60°＝120°．∴＝（+）•＝+═2×2×cos60°+1×2×cos120°＝2﹣1＝1，故选：A．7．【解答】解：令f（x）＝e x﹣x﹣1，则f′（x）＝e x﹣1，当x＞0时，f′（x）＞0，所以f（x）在（0，+∞）单调递增，f（x）＞f（0）＝0，∴∀x＞0，e x＞x+1，p真；令g（x）＝lnx﹣x，g′（x）＝﹣1＝，当0＜x＜1时，g′（x）＞0，当x＞1时，g′（x）＜0，即当x＝1时，g（x）取得极大值，同时也是最大值g（1）＝﹣1＜0，所以g（x）≤0 在（0，+∞）恒成立，则q为假命题；则p∧（￢q）为真命题，故选：C．8．【解答】解：由已知中的三视图，可得该几何体是一个以侧视图为底面的柱体，柱体的底面由一个边长为4的正方形和一个底边长为4，高为2的三角形组成，故柱体的底面面积S＝4×4+×2×4＝20，柱体的高即为三视图的长，即h＝6．故柱体的体积V＝Sh＝120，故选：B．9．【解答】解：设某高铁换乘站设有编号为①，②，③，④，⑤的五个安全出口疏散乘客时间分别为a、b、c、d、e，则a+b＝120，b+c＝220，c+d＝160，d+e＝140，a+e＝200，解得：a＝60，b＝60，c＝160，d＝0，e＝140，则疏散乘客最快的一个安全出口的编号是④，10．【解答】解：设t＝2x﹣，因为x∈[0，]，所以t∈[﹣，2π]，则g（t）＝cos t，t∈[﹣，2π]，函数f（x）＝cos（2x﹣）﹣a（x∈[0，]）恰有三个不同的零点x1，x2，x3等价于y＝g（t）与直线y＝a有三个不同的交点，由图可知：t2+t3＝2π，t1∈[﹣，0），即2x2+2x3＝2π，2x1∈[﹣，0），即x2+x3＝，x1∈[0，），所以x1+x2+x3∈[，），故选：A．11．【解答】解：以D为原点建立空间坐标系D﹣xyz，如图所示，则＝（1，0，0），＝（0，2，0），＝（0，0，2），设M（0，x，y），则＝（﹣1，x，y），∴cos＜＞＝，cos＜＞＝，cos＜，＞＝，∵点A的直线l与长方体ABCD﹣A1B1C1D1所有的棱所成角相等，∴|x|＝|y|＝1，∴AM＝＝．故选：D．12．【解答】解：函数f（x）＝，其中a≤﹣2，若x＜a≤﹣2，则x﹣1＜a﹣1≤﹣3，f（x）的导数为f′（x）＝﹣3x2+3＝﹣3（x+1）（x﹣1）＜0，可得f（x）＞f（﹣2）＝2，f（x﹣1）＞f（﹣3）＝27﹣9＝18，即有f（x）+f（x﹣1）＞20，不符题意；则x≥a，若x﹣1≥a，f（x）+f（x﹣1）＜3，即为﹣x﹣x+1＜3，解得x＞﹣1；若a﹣1≤x﹣1＜a，f（x）+f（x﹣1）＜3，即为﹣x﹣（x﹣1）3+3（x﹣1）＜3，化为x3﹣3x2+x+5＞0，由于a≤﹣2，且a≤x＜a+1，可得g（x）＝x3﹣3x2+x+5的导数g′（x）＝3x2﹣6x+1＞0，即g（x）在[a，a+1）递增，g（a）取得最小值，且为a3﹣3a2+a+5，且a3﹣3a2+a+5，而在a≤﹣2时，a3﹣3a2+a+5递增，且为负值，不符题意．综上可得x的范围是（﹣1，+∞）．故选：A．二、填空题（将答案填在答题纸上）13．【解答】解：实数x，y满足条件的可行域如图：设z＝y﹣2x，则y＝2x+z，当y＝2x+z经过可行域的A（0，2）时，目标函数取得最大值：2．故答案为：2．14．【解答】解：∵（1﹣）（1+x）5＝（1﹣）（1+5x+10x2+10x3+5x4+x5），故x2项的系数为10﹣10＝0，故答案为：0．15．【解答】解：∵4S n＝a1+a2+……+a n+1（n≥1），∴4S n﹣1＝a1+a2+……+a n（n≥2），两式相减可得4a n＝a n+1，即＝4，当n＝1时，4S1＝a1+a2，∴a2＝3a1＝12，∵＝3≠4，∴数列{a n}从第二项开始，以12为首项，以4为公比的等比数列，∴a n＝12×4n﹣2＝3×4n﹣1，n≥2，综上所述a n＝，故答案为：．16．【解答】解：∵BF1+BF2＝2a，DF1+DF2＝2a，∴BD+DF1+BF1＝4a，∵△F1BD是等腰三角形，BF1＝BF2＝a，∴DF2＝BD﹣BF2＝a，不妨设B在x轴上方，作DM⊥x轴于M，则＝，∴MF2＝c，DM＝b，即D（，﹣b）．代入椭圆方程可得+＝1，故＝，解得e＝．故答案为：．三、解答题（解答应写出文字说明、证明过程或演算步骤.）17．【解答】解：（Ⅰ）在△BCD中，由正弦定理得＝，∴sin∠BDC＝＝．∵3BD＝4BC，∴BD＞BC，∴∠BDC为锐角，∴∠BDC＝．（Ⅱ）在△ABD中，AD＝3，BD＝，∠ADB＝﹣＝，∴AB＝＝2．在△ABE中，由余弦定理得AB2＝AE2+BE2﹣2AE•BE•cos，∴12＝AE2+BE2﹣AE•BE≥2AE•BE﹣AE•BE＝AE•BE，当且仅当AE＝BE时等号成立，∴AE•BE≤12，∴S△ABE＝AE•BE•sin≤＝3，即△ABE面积的最大值为3．18．【解答】（Ⅰ）证明：连接BD，∵菱形ABCD中，∠BAD＝，∴△ABD为等边三角形，又M为BC中点，∴DM⊥AB．∵P A＝PB，∴PM⊥AB，又DM∩PM＝M，∴AB⊥平面PMD，又AB∥CD，∴CD⊥平面PMD，又CD⊂平面PCD，∴平面PCD⊥平面PMD．（Ⅱ）解：∵平面P AB⊥平面ABCD，平面P AB∩平面ABCD＝AB，PM⊥AB，PM⊂平面P AB，∴PM⊥平面ABCD，以M为原点，MB，MD，MP所在直线分别为x轴，y轴，z轴建立空间直角坐标系M﹣xyz，设PM＝a，则P（0，0，a），A（﹣1，0，0），D（0，﹣，0），∴＝（1，，0），＝（1，0，a），设平面ADP的一个法向量为＝（x，y，z），则，即，令z＝﹣，可地＝（a，﹣a，﹣），又＝（0，1，0）为平面P AB的法向量，由题意得cos＜＞＝＝＝，解得a＝，即PM＝，又菱形ABCD的面积为AB×DM＝2，∴四棱锥P﹣ABCD的体积为V＝＝2．19．【解答】解：（Ⅰ）∵抛物线E过点A（1，2），∴2p＝4，解得p＝2，∴抛物线的方程为y2＝4x，准线方程为x＝﹣1．（Ⅱ）不妨设B在C的左边，从而可设直线AB的方程为x﹣1＝m（y﹣2）（m＞0），即x＝my﹣2m+1，联立抛物线方程，消去x整理得y2﹣4my+8m﹣4＝0．则2+y B＝4m，故y B＝4m﹣2，∴x B＝4m2﹣4m+1，∴点B（4m2﹣4m+1，4m﹣2）．又由条件得AB与AC的倾斜角互补，以﹣m代替点B坐标中的m，可得点C（4m2+4m+1，﹣4m﹣2）．∴|BC|＝＝8m，且BC中点的横坐标为＝1+4m2，∵以线段BC为直径的圆与抛物线E的准线相切，∴4m2+1+1＝＝4m，解得m＝∴B（3﹣2，2﹣2），C（3+2，﹣2﹣2），∴k BC＝﹣1，∴直线BC的方程为y﹣（2﹣2）＝﹣（x﹣3+2），即x+y﹣1＝0．20．【解答】解（Ⅰ）由题意得＝170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02＝200s2＝（170﹣200）2×0.02+（180﹣200）2×0.09+（190﹣200）2×0.22+（200﹣200）2×0.33+（210﹣200）2×0.24+（220﹣200）2×0.08+（230﹣200）2×0.02＝150∴，即样本平均数为200，样本方差为150．（Ⅱ）（i）由（Ⅰ）可知，μ＝200，σ＝≈12.2，∴Z～N（200，12.22），∴P（175.6＜Z＜224.4）＝P（μ﹣2σ＜μ+σ）≈0.95，（ii）设X表示100件产品的正品数，由题意得X～B（100，0.95）∴EX＝100×0.95＝95，∴EY＝16EX﹣48×5﹣100×10＝280．21．【解答】解：（Ⅰ）∵f（x）＝e x（ax+2），∴f′（x）＝e x（ax+a+2）．①当a＝0时，∴f′（x）＝2e x＞0恒成立，∴f（x）在R上单调递增，无极值．②当a＞0时，由f′（x）＝0，解得x＝﹣，可得函数f（x）在（﹣∞，﹣）上单调递减；函数f（x）在（﹣，+∞）上单调递增．所以当x＝﹣时，f（x）有极小值，且f（﹣）＝﹣a，无极大值．③当a＜0时，由f′（x）＝0，解得x＝﹣，可得函数f（x）在（﹣∞，﹣）上单调递增；函数f（x）在（﹣，+∞）上单调递减．所以当x＝﹣时，f（x）有极大值，且f（﹣）＝﹣a，无极小值．综上所述：当a＝0时，f（x）在R上无极值．当a＞0时，f（x）有极小值，且f（﹣）＝﹣a，无极大值．③当a＜0时，由f′（x）＝0，解得x＝﹣，f（x）有极大值，且f（﹣）＝﹣a，无极小值．（Ⅱ）由题意得：g′（x）＝2x+4，∵曲线y＝f（x）和曲线y＝g（x）在点P（0，2）处有相同的切线，∴f′（0）＝g′（0），即a+2＝4，解得a＝2，∴f（x）＝e x（2x+2）．令F（x）＝mf（x）﹣g（x）＝me x（2x+2）﹣（x2+4x+2），则F′（x）＝me x（2x+4）﹣（2x+4）＝（me x﹣1）（2x+4），由题意可得F（0）＝2m﹣2≥0，解得m≥1．由F′（x）＝0，解得x1＝﹣lnm，x2＝﹣2．①当﹣lnm＞﹣2，即1≤m＜e2时，则﹣2＜x1≤0，∴当x∈（﹣2，x1）时，F′（x）＜0，F（x）单调递减；当x∈（x1，+∞）时，F′（x）＞0，F（x）单调递增．∴F（x）在（﹣2，+∞）上的最小值为F（x1）＝2x1+2﹣﹣4x1﹣2＝﹣x1（x1+2）≥0．∴mf（x）≥g（x），恒成立．②当﹣lnm＝﹣2，即m＝e2时，则F′（x）＝（e x+2﹣1）（2x+4），∴当x≥﹣2时，F′（x）≥0，函数F（x）在（﹣2，+∞）上单调递增，又F（﹣2）＝0，∴当x≥﹣2时，F（x）≥0，即mf（x）≥g（x），恒成立．③当﹣lnm＜﹣2，即m＞e2时，则F（﹣2）＝﹣2me﹣2+2＝﹣2e﹣2（m﹣e2）＜0．从而当x≥﹣2时，F（x）≥0，即mf（x）≥g（x）不可能恒成立．综上所述m的取值范围为[1，e2]．[选修4-4：坐标系与参数方程]22．【解答】解（Ⅰ）圆C直角坐标方程为（x﹣1）2+y2＝1，x2+y2﹣2x＝0C：ρ2﹣2ρcosθ＝0，ρ＝2cosθP（ρ1，θ），Q（ρ2，）|OP|＝ρ1＝2cosθ，|OQ|＝ρ2＝2cos （θ+），|OP|+|OQ|＝2cosθ+2cos（θ+）＝3cosθ﹣sinθ＝2cos（θ+）∵，∴﹣＜θ＜∴θ＝﹣时，|OP|+|OQ|取得最大值2．[选修4-5：不等式选讲]23．【解答】解（Ⅰ）a＝﹣2时，不等式为|2x+2|+|x﹣1|≤5①当x≤﹣1 时，不等式化为﹣2x﹣2﹣x+1≤5，x≥﹣2，此时﹣2≤x≤﹣1②当﹣1＜x＜1 时，不等式化为2x+2﹣x+1≤5，x≤2时，﹣1≤x＜1；③当x≥1 时，不等式化为2x+2+x﹣1≤5，x≤，此时1综上所述，不等式的解集为{x|﹣2}（Ⅱ）法一：函数f（x）＝|2x﹣a|+|x﹣1|，当a＜2，即＜1时，f（x）＝所以f（x）min＝f（）＝﹣+1＝3，得a＝﹣4＜2（符合题意），故a＝﹣4．法二：f（x）＝|2x﹣a|+|x﹣1|＝|x﹣|+|x﹣|+|x﹣1|≥|x﹣|+|x﹣1|≥|（x﹣）﹣（x﹣1）|＝|﹣1|所以f（x）min＝|﹣1|＝3，又a＜2，所以a＝﹣4．。

2019届湖南省株洲市高三第二次教学质量检测(二模)数学(理科)试题(解析版)

【详解】因为集合，所以，故选C.【点睛】本题考查集合的表示方法，交集的定义与运算，属于基础题。

2.为虚数单位，复数的虚部是（）A. B. C. D.【答案】B【解析】【分析】根据复数的除法运算求出复数的代数形式后可得答案．【详解】由题意得，，所以复数的虚部是．故选B．【点睛】本题考查复数的运算和虚部的概念，解题时容易认为复数的虚部为，要强化对复数概念的理解，属于基础题．3.如图，在边长为的正方形内有不规则图形，由电脑随机从正方形中抽取个点，若落在图形内和图形外的点分别为，则图形面积的估计值为（）A. B. C. D.【答案】C【解析】【分析】根据面积型的几何概型概率公式进行估计计算可得答案．【详解】设图形的面积为，则由几何概型及题意得，所以，即图形面积的估计值为．故选C．【点睛】本题考查几何概型概率的应用，解题的关键是明确落在图形内的点的概率等于两图形的面积比，属于基础题．4.已知双曲线的一条渐近线的倾斜角为，且的一个焦点到的距离为，则双曲线的方程为（）A. B.C. D.【答案】D【解析】【分析】根据题意求出参数的值后可得双曲线的方程．【详解】由可得，即渐近线的方程为，又一条渐近线的倾斜角为，所以．因为双曲线的一个焦点到的距离为，所以，所以，所以双曲线的方程为．故选D．【点睛】本题考查双曲线方程的求法，解题的关键是根据题意求出参数的值，解题是要注意将条件中给出的数据进行适当的转化，属于基础题．5.已知等差数列单调递增且满足，则的取值范围是（）A. B. C. D.【答案】B【解析】试题分析：∵等差数列单调递增，∴，∵，即，即，∴．考点：等差数列的通项公式．6.在边长为的菱形中，为的中点，则的值为（）A. B. C. D.【答案】A【解析】【分析】选择向量为基底，根据向量数量积的定义求解即可．【详解】选择向量为基底，则，所以．故选A．【点睛】求向量数量积的两种方法：一是根据数量积的定义求解，此时需要先选择基底，将所有向量都用该基底表示，然后按照定义求解；二是根据向量的坐标进行计算，此时需要建立直角坐标系，进而得到向量的坐标，最后转化为数的运算问题．7.已知命题，命题，则下列命题正确的是（）A. B.C. D.【答案】C【解析】【分析】利用导数和函数零点分别判断命题p,q的真假，从而判断出复合命题的真假即可。

湖南省株洲市2019届高三第二次教学质量检测(二模)理科数学试题含答案

疏散乘客时间（s） 120
220
160
140
200
则疏散乘客最快的一个安全出口的编号是
A．①
B．②
C．④
D．⑤
10．若函数 f (x) cos(2x ) a 4
(
x

[0,
9 8
])
恰有三个不同的零点
x1,
x2
,
x3,
则
x1
x2
x3 的
取值范围是
A． [5π , 11π ) 48
B．
9 4
,
7 2

C． (5π , 11π ] 48
D．

9 4
，7 2

11．已知长方体 ABCD A1B1C1D1 ， AB AA1 2, AD 1，正方形 CC1D1D 所在平面记为，若
经过点 A 的直线 l 与长方体 ABCD A1B1C1D1 所有的棱所成角相等，且 l M , 则线段 AM
C．{1, 2}
D．{1, 2,3}
2． i 为虚数单位，复数 4 3i 的虚部是 3 4i
A． 1
B．1
C． i
D． i
3．如图，在边长为 1 的正方形内有不规则图形 Ω，由电脑随机从正方形中
抽取 10000 个点，若落在图形 Ω 内和图形 Ω 外的豆子数分别为 3335，

6665，则图形 Ω 面积的估计值为
A． 1 6
B． 1 4
C． 1 3
D． 1 2
（第 3 题图）
4．已知双曲线 C： x2 y2 1的一条渐近线 l 的倾斜角为，且 C 的一个焦点到 l 的距离为 3 ，