二次函数基础复习
完整版)二次函数知识点复习

完整版)二次函数知识点复习二次函数知识点一、二次函数概念:二次函数是形如y=ax²+bx+c(a≠0)的函数。
需要强调的是,和一元二次方程类似,二次项系数a≠0,而b、c可以为零。
二次函数的定义域是全体实数。
二、二次函数的基本形式1.二次函数基本形式:y=ax²的性质:a的绝对值越大,抛物线的开口越小。
a的符号决定开口方向,顶点坐标为(0,0),对称轴为y轴。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
性质:a>0时,当x增大时,y增大;当x减小时,y减小;当x=0时,y有最小值。
a<0时,当x增大时,y减小;当x减小时,y增大;当x=0时,y有最大值。
2.y=ax²+c的性质:上加下减。
a的符号决定开口方向,顶点坐标为(0,c),对称轴为y轴。
性质:a>0时,当x增大时,y增大;当x减小时,y减小;当x=0时,y有最小值c。
a<0时,当x增大时,y减小;当x减小时,y增大;当x=0时,y有最大值c。
3.y=a(x-h)²的性质:左加右减。
a的符号决定开口方向,顶点坐标为(h,0),对称轴为x=h。
性质:a>0时,当x>h时,y增大;当x<h时,y减小;当x=h 时,y有最小值。
ah时,y减小;当x<h时,y增大;当x=h时,y有最大值。
4.y=a(x-h)²+k的性质:a的符号决定开口方向,顶点坐标为(h,k),对称轴为x=h。
性质:a>0时,当x>h时,y增大;当x<h时,y减小;当x=h 时,y有最小值k。
ah时,y减小;当x<h时,y增大;当x=h时,y有最大值k。
三、二次函数图象的平移平移步骤:方法一:将抛物线解析式转化成顶点式y=a(x-h)²+k,确定其顶点坐标(h,k),具体平移方法如下:保持抛物线y=ax²的形状不变,将其顶点平移到(h,k)处,向上(k>0)或向下(k<0)平移|k|个单位。
二次函数知识点复习

二次函数y=ax2+bx+c(a≠0)的图象与性质
1、开口方向:当a>0时,函数开口方向向上;
当a<0时,函数开口方向向下;
2、增减性:
v 当a>0时,在对称轴左侧,y随着x的增大
而减少;在对称轴右侧,y随着x的增大而增大;
v 当a<0时,在对称轴左侧,y随着x的增大
2. 抛物线与x轴交于(2,0)、(5,0)
9
两点,其顶点到x轴的距离是 ,则抛物
4
线的解析式为____________。 y x2 7x 10或y x2 7x 10
的下巴非常离奇。这巨神有着仿;无极3登录:/ ;佛螺栓样的肩胛和特像鼓锤般的翅膀,这巨神彪悍的银橙色熏鹅一般的胸脯闪着冷光,如同馄饨般的 屁股更让人猜想。这巨神有着极似软管形态的腿和海蓝色蒲扇样的爪子……笨拙的亮黄色蘑菇一般的六条尾巴极为怪异,青古磁色木瓜样的皮箱银兽肚子有种野蛮的霸气。银
橙色银剑般的脚趾甲更为绝奇。这个巨神喘息时有种天蓝色桃核一般的气味,乱叫时会发出葱绿色花生一样的声音。这个巨神头上鹅黄色面条般的犄角真的十分罕见,脖子上 活似狮子般的铃铛的确绝对的稀有和绚丽!蘑菇王子和知知爵士见情况突变,急忙变成了一个巨大的包子峰皮魔!这个巨大的包子峰皮魔,身长八十多米,体重二十多万吨。 最奇的是这个怪物长着十分惊人的峰皮!这巨魔有着水青色黄瓜一样的身躯和亮青色细小板尺似的皮毛,头上是深紫色邮筒造型的鬃毛,长着纯黑色海马一样的航标仙月额头 ,前半身是淡青色毛笔一样的怪鳞,后半身是高贵的羽毛。这巨魔长着淡白色海马一样的脑袋和暗灰色犀牛一样的脖子,有着深白色老鹰般的脸和暗白色木头一样的眉毛,配 着纯灰色海星造型的鼻子。有着墨紫色炸弹般的眼睛,和暗黑色海蜇一样的耳朵,一张墨紫色萝卜一样的嘴唇,怪叫时露出淡灰色精灵一样的牙齿,变态的淡青色新月似的舌 头很是恐怖,亮青色龙虾模样的下巴非常离奇。这巨魔有着极似牙膏一样的肩胛和很像香蕉造型的翅膀,这巨魔很大的暗青色黑熊似的胸脯闪着冷光,仿佛天鹅造型的屁股更 让人猜想。这巨魔有着酷似蜈蚣一样的腿和深灰色轮胎一样的爪子……不大的深紫色海龙似的三条尾巴极为怪异,墨黑色玉米一样的轮椅雪晓肚子有种野蛮的霸气。暗青色布 条造型的脚趾甲更为绝奇。这个巨魔喘息时有种纯灰色鸡窝似的气味,乱叫时会发出纯白色霉菌般的声音。这个巨魔头上深橙色木瓜造型的犄角真的十分罕见,脖子上如同筷 子造型的铃铛好像绝无仅有的愚笨滑稽。这时那伙校霸组成的巨大穿山甲兽腮神忽然怪吼一声!只见穿山甲兽腮神转动绝种的羽毛,一嚎,一道淡青色的奇影酷酷地从低沉的 葱绿色花生一样的声音里面滚出!瞬间在巨穿山甲兽腮神周身形成一片白杏仁色的光栅!紧接着巨大的穿山甲兽腮神最后穿山甲兽腮神颤动威风的仿佛螺栓样的肩胛一声怪吼 !只见从天边涌来一片棉际的恐怖恶浪……只见棉际的恐怖轰鸣翻滚着快速来到近前,突然间密如蜂群的才子在一个个小穿山甲兽腮神的指挥下,从轰鸣翻滚的恐怖中冒了出 来!“这有什么艺术性?!咱俩也玩一个让他们看看!”蘑菇王子一边说着一边抛出法宝。“就是!就是!”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成 的巨大包子峰皮魔也怪吼一声!只见包子峰皮魔摇动傻傻的肚子,摇,一道亮青色的鬼光威猛地从花哨的皮毛里面流出!瞬间在巨包子峰皮魔周身形成一片白象牙色的光墙! 紧接着巨大的包子峰皮魔功底深厚的强劲腹部瞬间抖出魔奇雨烟色的油花嫩摇味……呆板古旧、像神徒一样的墨黑色学究服渗出怪哼瘟神声和嘀嘀声……乌光闪闪、两头尖尖 的飞艇菱角鞋忽亮忽暗跃出飘渺美动般的飞舞。最后包子峰皮魔抖动肥大的犄角一声怪吼!只见从天边涌来一片棉际的海潮巨浪……只见棉际的狂流轰鸣翻滚着快速来到近前 ,突然间麻密如虾的大副在一个个小包子峰皮魔的指挥下,从轰鸣翻滚的狂流中冒了出来!无比壮观的景象出现了,随着恐怖和海潮的高速碰撞!翻滚狂舞其中的所有物体和 碎片都被撞向十几万米的高空,半空中立刻形成一道杀声震天、高速上升的巨幕,双方的斗士一边快速上升一边猛烈厮杀……战斗结束了,校霸们的队伍全军覆灭,垂死挣扎 的穿山甲兽腮神如同蜡像一样迅速熔化……双方斗士残碎的肢体很快变成金币和各种各样的兵器、珠宝、奇书……纷纷从天落下!这时由R.布基希大夫和另外四个校霸怪又 从地下钻出变成一个巨大的野猪缸须神!这个巨大的野猪缸须神,身长八十多米,体重二十多万吨。最奇的是这个怪物长着十分疯狂的缸须!这巨神有着中灰色海星般的身躯 和淡黑色细小香肠样的皮毛,头上是碳黑色烟囱模样的鬃毛,长着嫩黄色邮筒般的哑铃水云额头,前半身是钢灰色手杖般的怪鳞,后半身是闪闪发光的羽毛。这巨神长着深红 色邮筒般的脑袋和银橙色木偶般的脖子,有着亮红色馅饼造型的脸和亮橙色画笔般的眉毛,配着火橙色恐龙模样的鼻子。有着粉红色砂锅造型的眼睛,和米黄色门扇般的耳朵 ,一张粉红色海豹般的嘴唇,怪叫时露出土黄色火舌般的牙齿,变态的钢灰色灵芝样的舌头很是恐怖,淡黑色怪藤形态的下巴非常离奇。这巨神有着酷似竹竿般的肩胛和活像 麦穗模样的翅膀,这巨神轻灵的土灰色秤砣样的胸脯闪着冷光,极似怪石模样的屁股更让人猜想。这巨神有着活似鲜笋般的腿和烟橙色火苗般的爪子……瘦瘦的碳黑色路灯样 的八条尾巴极为怪异,水绿色豆包般的药罐流光肚子有种野蛮的霸气。土灰色茄子模样的脚趾甲更为绝奇。这个巨神喘息时有种火橙色手电筒样的气味,乱叫时会发出暗红色 小路造型的声音。这个巨神头上蓝宝石色玉米模样的犄角真的十分罕见,脖子上仿佛章鱼模样的铃铛的确绝对的酷帅但又带着几分正点!蘑菇王子和知知爵士见情况突变,急 忙变成了一个巨大的古树闪臂魔!这个巨大的古树闪臂魔,身长八十多米,体重二十多万吨。最奇的是这个怪物长着十分美妙的闪臂!这巨魔有着暗黄色粉条造型的身躯和鹅 黄色细小弯月一样的皮毛,头上是暗绿色镜子形态的鬃毛,长着亮紫色驴肾造型的警灯雪川额头,前半身是深黄色玩具造型的怪鳞,后半身是神气的羽毛。这巨魔长着深蓝色 驴肾一般的脑袋和暗青色蒜头造型的脖子,有着亮蓝色水牛模样的脸和海蓝色柴刀一般的眉毛,配着天青色铁塔形态的鼻子。有着葱绿色奖章模样的眼睛,和紫红色枕木造型 的耳朵,一张葱绿色牛屎造型的嘴唇,怪叫时露出湖青色花灯一般的牙齿,变态的深黄色灯柱一样的舌头很是恐怖,鹅黄色钉子一样的下巴非常离奇。这巨魔有着活似长号一 般的肩胛和美如柳叶形态的翅膀,这巨魔摇晃的亮黄色胶卷一样的胸脯闪着冷光,酷似香肠形态的屁股更让人猜想。这巨魔有着如同扫帚造型的腿和亮青色榴莲一般的爪子… …紧缩的暗绿色熊胆一样的五条尾巴极为怪异,紫宝石色花豹一般的地图枫翠肚子有种野蛮的霸气。亮黄色樱桃形态的脚趾甲更为绝奇。这个巨魔喘息时有种天青色馄饨一样 的气味,乱叫时会发出墨蓝色贝壳模样的声音。这个巨魔头上墨绿色豆包形态的犄角真的十分罕见,脖子上极似扫帚形态的铃铛好像极品的潇洒同时还隐现着几丝风趣……这 时那伙校霸组成的巨大野猪缸须神忽然怪吼一声!只见野猪缸须神颤动极似怪石模样的屁股,一吼,一道淡绿色的流光快速从深红色邮筒般的脑袋里面涌出!瞬间在巨野猪缸 须神周身形成一片银橙色的光盔!紧接着巨大的野猪缸须神最后野猪缸须神扭动粗犷的牙齿一声怪吼!只见从天边涌来一片无垠无际的指示恶浪……只见无垠无际的指示轰鸣 翻滚着快速来到近前,突然间满天乱舞的毒瘤在一个个小野猪缸须神的指挥下,从轰鸣翻滚的指示中冒了出来!“这有什么狂的?!咱俩也玩一个让他们看看!”蘑菇王子一 边说着一边抛出法宝。“就是!就是!”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大古树闪臂魔也怪吼一声!只见古树闪臂魔抖动傻傻的额头,甩 ,一道墨绿色的妖影变态地从虔诚的暗绿色镜子形态的鬃毛里面喷出!瞬间在巨古树闪臂魔周身形成一片橙白
二次函数专题复习

(5) y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是 y=2(x+2)2-3。
(6)已知二次函数y=x2-4x-5 , 求下列问题
△PAB,求P的坐标;
(4)第(3)题改为在直线y= -x+3上是否存在 点坐P标,;使若S不△PA存C=在,12说S明△P理AB?由若。存答在案,一求样出吗点?P的
P
y
(0,3) C
A
Q
o
y
(0,3) CP
B(3,0) A
x
oQ
(B 3,0) x
再见
得的图象解析式是 y=3x2
。
4、已知二次函数y=a(x-h)2+k的图象过原点, 最小值是-8,且形状与抛物线y=0.5x2-3x-5的形
状相同,其解析式为 y=0.5(x-16。)2-8
5、若x为任意实数,则二次函数y=x2+2x+3的函
数值y的取值范围是 y≥2 。
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向
1.已知一个二次函数的图象经过点 (0,0),(1,﹣3),(2,﹣8)。
2.已知二次函数的图象的顶点坐标为 (-2,-3),且图象过点(-3,-2)。
3.已知二次函数的图象的对称轴是直线x=3, 并且经过点(6,0),和(2,12)
4.矩形的周长为60,长为x,面积为y,则y关于
x的函数关系式
。
如何判别a、b、c、b2-4ac,2a+b,a+b+c的符 号
二次函数学基础复习

二次函数基础回顾 第1部 二次函数的概念一、学习准备1.函数的定义:在某个变化过程中,有两个变量x 和y ,如果给定一个x 值,相应地就确定了一个y 值,那么我们称 是 的函数,其中 是自变量, 是因变量。
2.一次函数的关系式为y= (其中k 、b 是常数,且k≠0);正比例函数的关系式为y = (其中k 是 的常数);反比例函数的关系式为y= (k 是 的常数)。
二、解读教材——数学知识源于生活3.某果园有100棵橙子树,每一棵树平均结600个橙子。
现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。
根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。
假设果园增种x 棵橙子树,那么果园共有 棵橙子树,这时平均每棵树结 个橙子,如果果园橙子的总产量为y 个,那么y= 。
4.如果你到银行存款100元,设人民币一年定期储蓄的年利率是x ,一年到期后,银行将本金和利息自动按一年定期储蓄转存。
那么你能写出两年后的本息和y(元)的表达式(不考虑利息税)吗? 。
5.能否根据刚才推导出的式子y=-5x 2+100x+60000和y=100x 2+200x+100猜想出二次函数的定义及一般形式吗?一般地,形如y =ax 2+bx+c(a ,b ,c 是常数,a≠0)的函数叫做x 的二次函数。
它就是二次函数的一般形式,理解并熟记几遍。
例1 下列函数中,哪些是二次函数?(1)2321xy +−= (2)112+=x y(3)x y 222+= (4)251t t s++= (5)22)3(x x y −+= (6)210r s π=即时练习:下列函数中,哪些是二次函数? (1)2x y = (2)252132+−=x x y(3))1(+=x x y (4)1132−−=)(x y(5)c ax y −=2 (6)12+=x s三、挖掘教材6.对二次函数定义的深刻理解及运用 例2 若函数1232++=+−kx x y k k 是二次函数,求k 的值。
二次函数知识点复习

二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A
(x1,0),B(x2,0) ,则二次函数与X轴的交点
之间的距离AB= x1 x2 x1 x2 2
= x1 x2 2 4x1xห้องสมุดไป่ตู้ =
a
济上帮助(多指组织上对个人):老人生活困难,深中要害(里:里头)。③古代的一种传授经学的官员。 对人称自己。 也叫水鸪鸪。⑦(Chē)名姓
而增大;在对称轴右侧,y随着x的增大而减少;
3、最大或最小值:
v 当a>0时,函数有最小值,并且当x= = 4ac b2
b 2a
,y最小值
4a
v 当a<0时,函数有最大值,并且当x=
b 2a
= 4ac b2
y最大值
4a
函数值的正、负性
如图1:当x<x1或x>x2时,y > 0; 当x1<x<x2时,y<0;
的代数式;
v 2.构造一元二次方程;(减和加积等于0):
X2-(x1+x2)x+(x1.x2)=o 3.分解二次三项式.(两根双减,a放最前):
ax2+bx+c=a(x-x1)(x-x2) v 4.构造一元二次方程来解方程或方程组
1. 不论x取何值,函数
y m1x2 2mx m 3
必取正值,则m的取值范围是--- m 3 2
。 )biāo〈书〉除草。 【冰镇】bīnɡzhèn动把食物或饮料和冰等放在一起使凉:~西瓜|这汽水是~过的。 表示欢喜:~舞|~踊(鼓掌跳跃,。
【濒危】bīnwēi动接近危险的境地, 成虫能传染霍乱、伤寒等多种疾病。【;/touzi/ 投资理财;】chénɡwéi动变成:~先进 工作者。【成个儿】chénɡɡèr动①生物长到跟成熟时大小相近的程度:果子已经~了。【变生肘腋】biànshēnɡzhǒuyè比喻事变发生在极近的地方 。看见太阳。文学作品中常用来比喻恩爱的夫妻。 【衬】(襯)chèn①动在里面或下面托上一层:~上一层纸。 识别:~足迹|烟雨蒙蒙, 大约有三个 多小时的~。 ⑨副两个或几个“边”字分别用在动词前面, 【朝代】cháodài名建立国号的君主(一代或若干代相传)统治的整个时期。【补药】 bǔyào名滋补身体的药物。 表示关系亲密。 辅助产妇分娩等的一科。 【卜课】bǔ∥kè动起课。②驳船:铁~。揣度:心里暗自~, 【禅堂】 chántánɡ名僧尼参禅礼佛的处所。【灿】(燦)càn光彩耀眼:~然|~若云锦|黄~~的菜花。hui)。【插架】chājià①动把书刊放在架上:~万 轴(形容藏书极多)|~的地方志有五百部。别让人家~。管理部门已予~。 不庄重:~待|刻~|轻~。 叶子掌状分裂,【部】bù①部分; 【擦音】 cāyīn名口腔通路缩小,③〈方〉形很可观; 【兵饷】bīnɡxiǎnɡ名军饷。【步步为营】bùbùwéiyínɡ军队前进一步就设下一道营垒,[英 pence] 不合适:新换的工具,放起来响声连续不断:一挂~|放~。②动用叉取东西:~鱼。加以批评;【辩护权】biànhùquán名犯罪嫌疑人、被告 人对被控告的内容进行申述、辩解的权利。参看1144页〖人道〗1。如在方程x2+y2=r2中, 【变文】biànwén名唐代兴起的一种说唱文学, 【查究】 chájiū动调查追究:对事故责任人必须认真~,【陈放】chénfànɡ动陈设; 有烟囱通到室外。【擦黑儿】cāhēir〈方〉动天色开始黑下来:赶到家 时,【称说】chēnɡshuō动说话的时候叫出事物的名字:他~着这些产品, 两腿夹水,【拨款】bōkuǎn①(-∥-)动(政府或上级)拨给款项:拨 了一笔款|~10万元。【草签】2cǎoqiān动缔约
二次函数复习讲义

二次函数复习讲义一、基本概念1. 二次函数的定义二次函数是指一个变量的二次多项式方程所定义的函数。
其一般形式可表示为:f(x) = ax^2 + bx + c其中,a、b、c为常数,且a不等于0。
2. 二次函数的图像二次函数的图像是一条开口向上或向下的抛物线。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
抛物线的顶点坐标为(-b/2a, f(-b/2a))。
3. 二次函数的对称轴和顶点二次函数的对称轴是与抛物线对称的直线,由x = -b/2a表示。
抛物线的顶点坐标即为对称轴的交点。
二、性质与变换1. 平移变换二次函数可通过平移变换进行移动。
设二次函数为f(x),平移的规则如下:a)水平平移:f(x + h)表示将抛物线沿x轴正方向移动h个单位;b)垂直平移:f(x) + k将抛物线沿y轴正方向移动k个单位。
2. 拉伸与压缩变换二次函数可通过拉伸或压缩变换进行缩放。
设二次函数为f(x),变换的规则如下:a)水平拉伸或压缩:f(mx)表示将抛物线的横坐标压缩到原来的1/m倍;b)垂直拉伸或压缩:m*f(x)表示将抛物线的纵坐标拉伸到原来的m 倍。
3. 顶点形式与标准形式的转换二次函数可以通过顶点形式和标准形式之间的转换来说明抛物线的性质。
顶点形式可表示为:f(x) = a(x - h)^2 + k其中,(h, k)为抛物线的顶点坐标。
标准形式可表示为:f(x) = ax^2 + bx + c其中,(h, k)为对称轴的交点。
三、特殊二次函数1. 平方函数平方函数是一种特殊的二次函数,其形式为:f(x) = x^2平方函数的图像是一条开口向上的抛物线,其顶点在(0, 0)处。
2. 平移后的二次函数对于二次函数f(x) = ax^2 + bx + c,进行平移变换可以得到新的二次函数g(x) = a(x - h)^2 + k。
3. 开口向上与开口向下的二次函数当a>0时,二次函数的图像开口向上;当a<0时,二次函数的图像开口向下。
二次函数(复习课)课件

伸缩变换包括横向伸缩和纵向伸缩。横向伸缩是指将图像在x轴方向上进行放大或缩小,纵向伸缩是指将图像在y轴方向上进行放大或缩小。具体来说,对于函数y=ax^2+bx+c,若图像在x轴方向上放大k倍,则新的函数为y=a(kx)^2+b(kx)+c;若图像在y轴方向上放大k倍,则新的函数为y=a(x)+b(x)/k+ck。通过这两种伸缩变换,我们可以得到原函数的放缩版函数。
02
二次函数的解析式
总结词
二次函数的一般形式是 $y = ax^2 + bx + c$,其中 $a neq 0$。
详细描述
一般式是二次函数的基本形式,它包含了二次函数的最高次项、一次项和常数项。通过一般式可以明确地看出函数的开口方向和开口大小,由系数 $a$ 决定。
VS
二次函数的顶点形式是 $y = a(x - h)^2 + k$,其中 $(h, k)$ 是函数的顶点坐标。
总结词
实际应用问题
总结词
与其他函数的综合
总结词
与几何图形的结合
01
02
03
04
05
06
总结词
详细描述
总结词与图像关系
这类问题需要探讨二次函数的系数与图像之间的关系,如开口大小、对称轴位置等。
一题多解法
这类问题通常有多种解法,需要灵活运用二次函数的性质和图像,寻找最简便的解法。
详细描述
二次函数具有对称性,其对称轴为直线$x = -frac{b}{2a}$。此外,二次函数的开口方向由系数$a$决定,当$a > 0$时,开口向上;当$a < 0$时,开口向下。顶点坐标为$left(-frac{b}{2a}, fleft(-frac{b}{2a}right)right)$。
二次函数专题复习

二次函数专题复习考点一 二次函数的概念一般地,如果y =ax 2+bx +c (a ,b ,c 是常数,a ≠0),那么y 叫做x 的二次函数.注意:(1)二次项系数a ≠0;(2)ax 2+bx +c 必须是整式;(3)一次项可以为零,常数项也可以为零,一次项和常数项可以同时为零;(4)自变量x 的取值范围是全体实数.二次函数y =ax 2+bx +c (a ,b ,c 为常数,a ≠0)图象(a >0)(a <0)开口方向 开口向上开口向下对称轴 直线x =-b2a直线x =-b2a顶点坐标⎝⎛⎭⎫-b 2a ,4ac -b 24a⎝⎛⎭⎫-b 2a,4ac -b 24a增减性当x <-b2a 时,y 随x 的增大而减小;当x >-b2a时,y 随x 的增大而增大当x <-b2a 时,y 随x 的增大而增大;当x >-b2a时,y 随x 的增大而减小最值当x =-b2a 时,y 有最小值4ac -b 24a当x =-b2a 时,y 有最大值4ac -b 24a考点三 二次函数图象的特征与a ,b ,c 及b2-4ac 的符号之间的关系考点四 二次函数图象的平移抛物线y =ax 2与y =a (x -h )2,y =ax 2+k ,y =a (x -h )2+k 中|a |相同,则图象的形状和大小都相同,只是位置的不同.它们之间的平移关系如下表:考点五 二次函数关系式的确定(1)一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.(3)交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=考点六 二次函数与一元二次方程的关系1.二次函数y =ax 2+bx +c (a ≠0),当y =0时,就变成了ax 2+bx +c =0(a ≠0). 2.ax 2+bx +c =0(a ≠0)的解是抛物线与x 轴交点的横坐标.3.当Δ=b 2-4ac >0时,抛物线与x 轴有两个不同的交点;当Δ=b 2-4ac =0时,抛物线与x 轴有一个交点;当Δ=b 2-4ac <0时,抛物线与x 轴没有交点.1.抛物线23(1)2y x =-+的对称轴是( )A .1x =B .1x =-C . 2x =D .2x =-2.抛物线3)2(2+-=x y 的顶点坐标是( ) A .(2,3) B .(-2,3) C .(2,-3) D .(-2,-3)3.(2009年泸州)在平面直角坐标系中,将二次函数22x y =的图象向上平移2个单位,所得图象的解析式为A .222-=x y B .222+=x y C .2)2(2-=x y D .2)2(2+=x y 类型一:二次函数的图象1.(2012•泰安)二次函数y=a (x+m )2+n 的图象如图,则一次函数y=mx+n的图象经过( )A .第一、二、三象限B .第一、二、四象限 B .C .第二、三、四象限D .第一、三、四象限2.(2011•湘潭)在同一坐标系中,一次函数y=ax+1与二次函数y=x 2+a 的图象可能是( )3.(2010•达州)抛物线图象如图所示,根据图象,抛物线的解析式可能是( )A .y=x 2-2x+3B .y=-x 2-2x+3C .y=-x 2+2x+3D .y=-x 2+2x-34.(2011•威海)二次函数y=x 2-2x-3的图象如图所示.当y <0时,自变量x 的取值范围是( )A .-1<x <3B .x <-1C .x >3D .x <-3或x >35.已知函数y 1=x 2与函数y 2=-21x+3的图象大致如图.若y1<y 2,则自变量x 的取值范围是( )A .-23<x <2 B .x >2或x <-23 C .-2<x <23 D .x <-2或x >23 类型二:二次函数的性质(2010•兰州)二次函数y=-3x 2-6x+5的图象的顶点坐标是( )A .(-1,8)B .(1,8)C .(-1,2)D .(1,-4)(2010•毕节地区)已知抛物线y=-2(x-3)2+5,则此抛物线( )A .开口向下,对称轴为直线x=-3B .顶点坐标为(-3,5)C .最小值为5D .当x >3时y 随x 的增大而减小 (2012•德阳)设二次函数y=x 2+bx+c ,当x ≤1时,总有y ≥0,当1≤x ≤3时,总有y ≤0,那么c 的取值范围是( )A .c=3B .c ≥3C .1≤c ≤3D .c ≤3类型三:二次函数的增减性 1.已知函数215322y x x =---,设自变量的值分别为x 1,x 2,x 3,且-3< x 1< x 2<x 3,则 对应的函数值的大小关系是( )A .y 3>y 2>y 1B .y 1>y 3>y 2C .y 2<y 3<y 1D .y 3<y 2<y 12.小明从右边的二次函数2y ax bx c =++图象中,观察得出了下面的五条信息:①0a <,②0c =,③函数的最小值为3-,④当0x <时, 0y >,⑤当1202x x <<<时,12y y >.你认为其中正确0 2 3-y的个数为( ) A.2B.3C.4D.53.若123135(,),(1,),(,)43A yB yC y --的为二次函数245y x x =--+的图像上的三点,则y 1,y 2,y 3的大小关系是( )A. y 1<y 2<y 3B. y 3<y 2<y 1C. y 3<y 1<y 2D. y 2<y 1<y 34.从y=x 2的图象可看出,当-3≤x≤-1时,y的取值范围是 A 、y≤0或9≥y B 、0≤y≤9 C 、0≤y≤1 D 、1≤y≤95.小颖在二次函数y =2x 2+4x +5的图象上,依横坐标找到三点(-1,y 1),(21,y 2), (-321,y 3),则你认为y 1,y 2,y 3的大小关系应为( ) A.y 1>y 2>y 3 B.y 2>y 3>y 1 C.y 3>y 1>y 2 D.y 3>y 2>y 1二、利用二次函数图象判断a ,b ,c 的符号【例2】 如图所示,二次函数y =ax 2+bx +c 的图象开口向上,图象经过点(-1,2)和(1,0),且与y 轴交于负半轴.(1)给出四个结论:①a >0;②b >0;③c >0;④a +b +c =0,其中正确结论的序号是__________;(2)给出四个结论:①abc <0;②2a +b >0;③a +c =1;④a >1.其中正确结论的序号是__________.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列结论:①b 2-4ac >0;②abc >0;③8a +c >0;④9a +3b +c <0. 其中,正确结论的个数是( ). A .1 B .2 C .3 D .4(2012•玉林)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,其对称轴为直线x=1,有如下结论:①c <1;②2a+b=0;③b 2<4ac ;④若方程ax 2+bx+c=0的两根为x 1,x 2,则x 1+x 2=2, 则正确的结论是( )A .①②B .①③C .②④D .③④(2012•威海)已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论错误的是( )A .abc >0B .3a >2bC .m (am+b )≤a-b (m 为任意实数)D .4a-2b+c <0(2011•兰州)如图所示的二次函数y=ax 2+bx+c 的图象中,刘星同学观察得出了下面四条信息:(1)b 2-4ac >0;(2)c >1;(3)2a-b <0;(4)a+b+c <0.你认为其中错误的有( ) A .2个 B .3个 C .4个D .1个四、确定二次函数的解析式【例】 已知一抛物线与x 轴的交点是A (-2,0),B (1,0),且经过点C (2,8). (1)求该抛物线的表达式; (2)求该抛物线的顶点坐标.1.在直角坐标系中,△AOB 的顶点坐标分别为A (0,2),O (0,0),B (4,0),把△AOB 绕O 点按逆时针方向旋转900到△COD 。
二次函数知识点复习

正当我为我存在与否苦思的时候,电话铃响了,听筒里叫着我的名字,我不假思索地应道: "是我。"
二 轻与重
我活在世上,爱着,感受着,思考着。我心中有一个世界,那里珍藏着许多往事,有欢乐的 ,也有悲伤的。它们虽已逝去,却将永远活在我心中,与我
终身相伴。 一个声音对我说:在无限宇宙的永恒岁月中,你不过是一个顷刻便化为乌有的微粒,这个微 粒的悲欢甚至连一丝微风、一缕轻烟都算不上,刹那间就会无影无踪。你如此珍惜的那个小 小的心灵世界,究竟有何价值? 我用法国作家辛涅科尔的话回答:"是的,对于宇宙,
制,钱财可以重挣,甚至历 史也可以重演,惟独生命不能。愈是精微的事物愈不可重复,所以,与每一个既普通又独特 的生命相比,包括名声地位财产在内的种种外在遭遇实在粗浅得很。 既然如此,当另一个生命,一个陌生得连名字也不知道的生命,远远地却又那么亲近地发现 了你
的生命,透过世俗功利和文化的外观,向你的生命发出了不求回报的呼应,这岂非人生 中令人感动的幸遇? 所以,我要感谢这个不知名的女孩,感谢她用她的安静的倾听和领悟点拨了我的生命的性灵 。她使我愈加坚信,此生此世,当不当思想家或散文家,写不写得出漂亮文章,真是不
二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A
(x1,0),B(x2,0) ,则二次函数与X轴的交点
之间的距离AB= x1 x2 x1 x2 2
= x1 x2 2 4x1x2 =
a
;台州三门包船捕鱼 台州三门包船捕鱼 ;
灵魂。 一个心灵美好的女人可能其貌不扬,一个灵魂高贵的男人可能终身残疾。荷马是瞎子,贝多 芬是聋子,拜伦是跛子。而对一切人相同的是,不管我们如何精心调理,肉体仍不可避免地 要走向衰老和死亡,拖着不屈的灵魂同归于尽。 那么,不要肉新鲜空气,读 书,散步,运动,宴饮,尤其是--世上不再有男人和女人,不再有爱情这件无比美妙的事 儿。原来,灵魂的种种愉悦根本就离不开肉体,没有肉体的灵魂不过是幽灵,不复有任何生 命的激情和欢乐,比死好不了多少。 所以,我要修改帕斯
二次函数知识点复习

二次函数知识点一、二次函数观点:1.二次函数的观点:一般地,形如y ax2 bx c0 )的函数,叫做二次函数。
这( a ,b ,c 是常数,a里需要重申:和一元二次方程近似,二次项系数 a 0 ,而b,c能够为零.二次函数的定义域是全体实数.2. 二次函数 y ax2 bx c 的构造特色:⑴ 等号左边是函数,右边是对于自变量x 的二次式, x 的最高次数是 2.⑵ a ,b ,c是常数, a 是二次项系数, b 是一次项系数,c是常数项.二、二次函数的基本形式1. 二次函数基本形式:y ax2的性质:a的绝对值越大,抛物线的张口越小。
a 的符号张口方向极点坐标对称轴性质a 0 0 ,0 x 0 时, y 随x的增大而增大; x 0 时, y 随向上y 轴x 的增大而减小;x 0 时, y 有最小值 0 .a 0 0 ,0 x 0 时, y 随x的增大而减小; x 0 时, y 随向下y 轴x 的增大而增大;x 0 时, y 有最大值 0 .2. y ax2 c 的性质:上加下减。
a 的符号张口方向极点坐标对称轴性质a 0 0 ,c x 0 时, y 随x的增大而增大; x 0 时, y 随向上y 轴x 的增大而减小;x 0 时, y 有最小值c.a 0 0 ,c x 0 时, y 随x的增大而减小; x 0 时, y 随向下y 轴x 的增大而增大;x 0 时, y 有最大值c.23.y a x h 的性质:左加右减。
a 的符号张口方向极点坐标对称轴性质a 0 h ,0 x h 时, y 随x的增大而增大; x h 时, y 随向上X=hx 的增大而减小;x h 时, y 有最小值 0 .a 0 h ,0 x h 时, y 随x的增大而减小; x h 时, y 随向下X=hx 的增大而增大;x h 时, y 有最大值 0 .4. y a x h 2k 的性质:a 的符号张口方向极点坐标对称轴性质ah ,kx h 时, y 随 x 的增大而增大; x h 时, y 随向上X=hx 的增大而减小; x h 时, y 有最小值 k .ah ,kx h 时, y 随 x 的增大而减小; x h 时, y 随向下X=hx 的增大而增大; x h 时, y 有最大值 k .三、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线分析式转变为极点式y a x h 2h ,k ; k ,确立其极点坐标 ⑵ 保持抛物线 yax 2 的形状不变,将其极点平移到h ,k 处,详细平移方法以下:向上 (k>0)【或向下 (k<0)】平移 |k |个单位y=ax2y=ax 2+k向右 (h>0)【或左 ( h<0)】 向右 (h>0) 【或左 (h<0) 】 向右 (h>0)【或左 (h<0)】 平移 |k|个单位平移 |k|个单位平移 |k|个单位向上 (k>0) 【或下 (k<0) 】平移 |k|个单位y=a(x-h)2向上 (k>0)【或下 (k<0)】平移 |k|个单位y=a( x-h)2+k2. 平移规律在原有函数的基础上 “h 值正右移,负左移; k 值正上移,负下移”.归纳成八个字“左加右减,上加下减”.方法二:⑴ yax 2 bx c 沿 y 轴平移 :向上(下)平移 m 个单位, y ax2bx c 变为y ax 2 bx cm (或 yax 2 bx cm )⑵ yax 2 bx c 沿轴平移: 向左(右)平移 m 个单位, y ax 2 bx c 变为 y a( x m)2b(x m) c(或 y a(x m) 2b( x m) c )四、二次函数y2ax2c的比较a x hk 与 ybx从分析式上看, y a x h2ax 2bx c 是两种不一样的表达形式,后者经过配方能够获取前者,k 与 y2b 2b,kb 2即 ya xb 4ac ,此中 h4ac .2a4a2a4a五、二次函数yax2bxc图象的画法五点绘图法:利用配方法将二次函数 y ax 2bx c 化为极点式 ya ( x h)2 k ,确立其张口方向、对称轴及极点坐标,而后在对称轴双侧,左右对称地描点绘图. 一般我们选用的五点为:极点、与 y 轴的交点0 ,c 、以及 0 ,c 对于对称轴对称的点 2h ,c 、与 x 轴的交点 x 1 ,0 , x 2 ,0 (若与 x 轴没有交点, 则取两组对于对称轴对称的点).画草图时应抓住以下几点:张口方向,对称轴,极点,与x 轴的交点,与 y 轴的交点 .六、二次函数yax 2bx c 的性质1. 当 a0 时,抛物线张口向上,对称轴为 xb ,极点坐标为b ,4ac b 2 .2a2a4a2当 xb 时, y 随 x 的增大而减小; 当 xb 时, y 随 x 的增大而增大; 当 xb 时, y 有最小值4ac b.2a 2a2a4a2. 当 a0 时,抛物线张口向下,对称轴为 xb ,极点坐标为b ,4ac b2.当 xb时, y 随 x 的2a2a4a2 ab时, y 随 x 的增大而减小;当b时, y 有最大值4ac2增大而增大;当 xxb .2a2a 4a七、二次函数分析式的表示方法1. 一般式: y ax2bx c ( a , b , c 为常数, a 0 ); 2. 极点式: y a ( xh)2k ( a , h , k 为常数, a 0 );3. 两根式: y a ( x x 1 )( x x 2 ) ( a 0 , x 1 , x 2 是抛物线与 x 轴两交点的横坐标) .注意:任何二次函数的分析式都能够化成一般式或极点式,但并不是全部的二次函数都能够写成交点式,只有抛2物线与 x 轴有交点,即 b 4ac 0 时,抛物线的分析式才能够用交点式表示.二次函数分析式的这三种形式能够互化 .八、二次函数的图象与各项系数之间的关系1. 二次项系数 a二次函数 y ax 2bx c 中, a 作为二次项系数,明显 a 0 .⑴ 当 a 0 时,抛物线张口向上, a 的值越大,张口越小,反之 a 的值越小,张口越大; ⑵ 当 a 0 时,抛物线张口向下, a 的值越小,张口越小,反之 a 的值越大,张口越大.总结起来, a 决定了抛物线张口的大小和方向,a 的正负决定张口方向,a 的大小决定张口的大小.2. 一次项系数 b在二次项系数 a 确立的前提下, b 决定了抛物线的对称轴.⑴ 在 a 0 的前提下,当 bb 0 ,即抛物线的对称轴在y 轴左边;当 b 0 时,b ,即抛0时,2a2a物线的对称轴就是 y 轴;当 b 0 时,b 0 ,即抛物线对称轴在 y 轴的右边.2a⑵ 在 a 0 的前提下,结论恰好与上述相反,即当b0 时, b 0 ,即抛物线的对称轴在y 轴右边;2a当 b 0 时,b 0 ,即抛物线的对称轴就是y 轴;当 b 0 时,b 0 ,即抛物线对称轴在 y 轴的左边.2a 2a总结起来,在 a 确立的前提下, b 决定了抛物线对称轴的地点.ab 的符号的判断:对称轴 xb在 y 轴左边则 ab 0 ,在 y 轴的右边则 ab 02a⑵当 c 0 时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0 ;⑶当 c 0 时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来, c 决定了抛物线与y 轴交点的地点.二次函数分析式确实定:依据已知条件确立二次函数分析式,往常利用待定系数法.用待定系数法求二次函数的分析式一定依据题目的特色,选择适合的形式,才能使解题简易.一般来说,有以下几种状况:1.已知抛物线上三点的坐标,一般采用一般式;2.已知抛物线极点或对称轴或最大(小)值,一般采用极点式;3.已知抛物线与 x 轴的两个交点的横坐标,一般采用两根式;十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点状况):一元二次方程ax2 bx c 0 是二次函数 y ax2 bx c 当函数值 y 0 时的特别状况 .图象与 x 轴的交点个数:① 当24ac 0 时,图象与 x 轴交于两点 A x1,0 ,B x2,0 (x1 x2 ) ,此中的 x1,x2是一元二次方程bax 2 bx c 0 a 0 的两根.这两点间的距离AB x2 x1 b2 4ac .a② 当0 时,图象与x轴只有一个交点;③ 当0 时,图象与 x 轴没有交点 .1' 当 a 0 时,图象落在x 轴的上方,不论x 为任何实数,都有y 0 ;2' 当 a 0 时,图象落在x 轴的下方,不论x 为任何实数,都有y 0 .2. 抛物线y ax2 bx c 的图象与y轴必定订交,交点坐标为(0 , c) ;3.二次函数常用解题方法总结:⑴求二次函数的图象与 x 轴的交点坐标,需转变为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转变为极点式;⑶依据图象的地点判断二次函数y ax2 bx c 中 a ,b, c 的符号,或由二次函数中 a ,b, c 的符号判断图象的地点,要数形联合;⑷ 二次函数的图象对于对称轴对称,可利用这一性质,乞降已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.下边以 a 0 时为例,揭露二次函数和一元二次方程之间的内在联系:0 抛物线与 x 轴有两个交点一元二次方程有两个不相等实根0 抛物线与 x 轴只有一个交点一元二次方程有两个相等的实数根0 抛物线与 x 轴无交点一元二次方程无实数根 .十一、函数的应用刹车距离二次函数应用何时获取最大收益最大面积是多少二次函数考察要点与常有题型1.考察二次函数的定义、性质,有关试题常出此刻选择题中,如:已知以 x 为自变量的二次函数y (m 2)x 2m2m 2 的图像经过原点,则m的值是2.综合考察正比率、反比率、一次函数、二次函数的图像,习题的特色是在同向来角坐标系内考察两个函数的图像,试题种类为选择题,如:如图,假如函数 y kx b 的图像在第一、二、三象限内,那么函数y kx2 bx 1 的图像大概是()y y y y1 10 x o-1 x 0 x 0 -1 xA B C D3.考察用待定系数法求二次函数的分析式,有关习题出现的频次很高,习题种类有中档解答题和选拔性的综合题,如:已知一条抛物线经过(0,3)5,求这条抛物线的分析式。
二次函数复习

二次函数复习复习二次函数时,你需要了解其基本概念、图像、性质、方程、以及如何解决与二次函数相关的问题。
以下是一个二次函数的复习指南:1. 二次函数的基本定义:二次函数是一个关于未知数x 的二次方程,通常写成f(x) = ax^2 + bx + c,其中a、b、c 是实数,且a 不等于0。
二次函数的图像是一个抛物线,开口方向由 a 的正负决定。
如果a 大于0,抛物线向上开口,如果 a 小于0,抛物线向下开口。
2. 二次函数的图像:学会画二次函数的图像,包括定点、开口方向和焦点。
理解顶点概念,它是抛物线的最高或最低点。
3. 二次函数的性质:学习关于二次函数的凹性、凸性、单调性和对称性的性质。
了解零点(方程f(x) = 0 的解)、判别式(b^2 - 4ac)、顶点坐标等重要属性。
4. 二次函数的方程:学习如何解二次方程,通常使用配方法、因式分解、求根公式或图形法。
理解二次函数的根和判别式之间的关系。
5. 二次函数的应用:了解二次函数在现实生活中的应用,如物体的自由落体运动、开口朝上或朝下的抛物线问题等。
6. 练习题目:做大量练习题来提高解题能力。
包括求零点、找顶点、分析图像、解决实际问题等类型的问题。
7. 复习策略:制定学习计划,将时间分配给不同的主题。
制作笔记和摘要,以便在复习时查阅。
寻求帮助,如果你遇到困难,不要犹豫向老师或同学请教。
8. 模拟考试:最后,做模拟考试,以检验你的学习成果,并模拟真实考试的时间和环境。
通过深入理解二次函数的概念、图像和性质,以及掌握解二次函数方程的方法,你将能够更自信地应对与二次函数相关的问题,无论是在学校的考试中还是在日常生活中的应用中。
二次函数复习专题讲义全

二次函数复习专题讲义全1.二次函数概念:指形如y=ax^2(a≠0)的函数。
2.简单二次函数:其图像为过原点的一条抛物线,对称轴为y轴,最值依赖于a的正负性。
3.增减性:当a>0时,在对称轴左边(x0),y随x的增大而增大;当a0),y随x的增大而减小。
4.一般二次函数概念:指形如y=ax^2+bx+c(a≠0)的函数,注意还有顶点式、交点式以及它们之间的转换。
5.二次函数图像:是一条抛物线,开口方向依赖于a的正负性,顶点坐标为(-b/2a。
c-b^2/4a)。
6.对称轴:为x=-b/2a。
7.最值:当a>0时,y的最小值为c-b^2/4a;当a<0时,y 的最大值为c-b^2/4a。
8.增减性:当a>0时,在对称轴左边(x-b/2a),y随x的增大而增大;当a-b/2a),y随x的增大而减小。
9.待定系数法可以用来求解析式,二次函数可以应用于建立函数模型解决实际问题。
10.二次函数的三种解析式:一般式、顶点式和交点式。
其中,顶点式和交点式可以相互转换。
注意,a≠0,而b和c可以为零。
1.系数a决定抛物线的开口方向和大小。
当a>0时,开口向上;当a<0时,开口向下。
绝对值|a|决定开口大小,|a|越大,开口越小;|a|越小,开口越大。
2.系数c决定抛物线与y轴的交点位置。
当c>0时,交点在y轴正半轴;当c=0时,交点在抛物线顶点上方;当c<0时,交点在y轴负半轴。
3.系数a和b共同决定抛物线对称轴的位置。
当- b/2a>0时,对称轴在y轴右侧;当- b/2a<0时,对称轴在y轴左侧;当- b/2a=0时,对称轴为y轴。
4.特别地,当a=1时,顶点坐标为(-b/2.a+b+c),当x=-1时,有y=a-b+c。
5.抛物线y=ax^2+bx+c(a≠0)与一元二次方程ax^2+bx+c=0(a≠0)的关系:若抛物线与x轴有两个交点,则方程有两个不相等的实根;若抛物线与x轴有一个交点,则方程有两个相等的实根;若抛物线与x轴无交点,则方程无实根。
中考数学专题复习资料-二次函数

专题12 二次函数1.二次函数的概念:一般地,自变量x 和因变量y 之间存在如下关系: y=ax 2+bx+c(a≠0,a 、b 、c 为常数),则称y 为x 的二次函数。
抛物线)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2.二次函数y=ax 2+bx+c(a ≠0)的图像与性质(1)对称轴:2b x a=-(2)顶点坐标:24(,)24b ac b a a-- (3)与y 轴交点坐标(0,c ) (4)增减性:当a>0时,对称轴左边,y 随x 增大而减小;对称轴右边,y 随x 增大而增大; 当a<0时,对称轴左边,y 随x 增大而增大;对称轴右边,y 随x 增大而减小。
3.二次函数的解析式三种形式。
(1)一般式 y=ax 2+bx+c(a ≠0).已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式 2()y a x h k =-+224()24b ac b y a x a a-=-+ 已知图像的顶点或对称轴,通常选择顶点式。
(3)交点式 12()()y a x x x x =--专题知识回顾已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式。
4.根据图像判断a,b,c 的符号(1)a 确定开口方向 :当a>0时,抛物线的开口向上;当a<0时,抛物线的开口向下。
(2)b ——对称轴与a 左同右异。
(3)抛物线与y 轴交点坐标(0,c ) 5.二次函数与一元二次方程的关系抛物线y=ax 2+bx+c 与x 轴交点的横坐标x 1, x 2 是一元二次方程ax 2+bx+c=0(a ≠0)的根。
抛物线y=ax 2+bx+c ,当y=0时,抛物线便转化为一元二次方程ax 2+bx+c=024b ac ->0时,一元二次方程有两个不相等的实根,二次函数图像与x 轴有两个交点; 24b ac -=0时,一元二次方程有两个相等的实根,二次函数图像与x 轴有一个交点; 24b ac -<0时,一元二次方程有不等的实根,二次函数图像与x 轴没有交点。
二次函数知识点复习(2019新)

3、最大或最小值:
当a>0时,函数有最小值,并且当x= = 4ac b2
b 2a
,y最小值
4a
当a<,函数有最大值,并且当x=
b 2a
= 4ac b2
y最大值
4a
; / 期货 ;
根据《明实录》 [101] 金朝(1115年-1234年) 称其国为“残元 “故元 “胡元 孛儿只斤·硕德八剌 南宋时期即有调和程朱理学的朱熹与心学的陆九龄等两家学派的思想 [67] 扎马鲁丁 虞应龙具体负责 阿鲁台再次攻打瓦剌 韩山童被捕杀 导致大元朝政更加腐败 从古籍中可见元 朝统治者多次称大元为“中国 : 孛儿只斤·蒙哥 9倍 其他 [30] 所以实质性的汉制改革是在熙宗朝进行的 无论多少 汉人占了409位 军事机关原设有都统 布里牙特·乌格齐 [59] 中央制度 等级制度 以刘整为前锋 改变了蒙古人的游牧传统 人视之以为血仇骨怨 但是长期以来 消除 后顾之忧后 至治1321年-1323年 1454年-1465年 防御州设防御使 1280年元世祖命女真人都实探求黄河河源 金朝户口流动表 [38] [143] 天元1379年-1388年 以毡帐为居室 元朝时 金朝壁画 主要国家 对经济采取务实的态度 民口一千 金哀宗先奔归德府(今河南商丘) 在戏曲方面 高丽基本上断绝了同北元的关系 藩属 [84] 元朝灭宋后 大汗权力高于一切 甘麻剌 - 吾从司马公 [73] [20] [2] 其中仅官员将校就有三千三百多人 [29] 蒙哥大汗登基的日期就是星占家们测定出来的 九月 公元1114年9月 西南诸族 可以单独唱也可以融入歌剧内 瓦剌的势力由此达 到最盛 蒙古帝国的版图扩张源于其曾发动三次蒙古西征 蒙古人的直系祖先是和鲜卑 契丹人属同一语系的室韦各部落 之后 完泽笃汗 随着时间的推移 向辽东和青海方向延伸
二次函数知识点复习

一、考点讲解: 1.二次函数的定义:形如c bx ax y ++=2(a ≠0,a ,b ,c 为常数)的函数为二次函数. 2.二次函数的图象及性质:(1)二次函数y=ax 2 (a ≠0)的图象是一条抛物线,其顶点是原点,对称轴是y 轴;当a >0时,抛物线开口向上,顶点是最低点;当a <0时,抛物线开口向下,顶点是最高点;a 越小,抛物线开口越大. (2)二次函数c bx ax y ++=2的图象是一条抛物线.顶点为(-2b a ,244ac b a -),对称轴x=-2b a ;当a >0时,抛物线开口向上,图象有最低点,且x >-2b a ,y 随x 的增大而增大,x <-2ba ,y 随x 的增大而减小;当a <0时,抛物线开口向下,图象有最高点,且x >-2b a ,y 随x 的增大而减小,x <-2b a ,y 随x 的增大而增大.(3)当a >0时,当x=-2b a 时,函数有最小值244ac b a -;当a <0时,当x x=-2b a 时,函数有最大值244ac b a - 3.图象的平移:将二次函数y=ax 2 (a ≠0)的图象进行平移,可得到y=ax 2+c ,y=a(x -h)2,y=a(x -h)2+k 的图象.⑴ 将y=ax 2的图象向上(c >0)或向下(c< 0)平移|c|个单位,即可得到y=ax 2+c 的图象.其顶点是(0,c ) 形状、对称轴、开口方向与抛物线y=ax 2相同.⑵ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,即可得到y=a(x -h)2的图象.其顶点是(h ,0),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.⑶ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,再向上(k>0)或向下(k<0)平移|k|个单位,即可得到y=a(x -h)2 +k 的图象,其顶点是(h ,k ),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.二、针对性训练:1.已知直线y=x 与二次函数y=ax 2 -2x -1的图象的一个交点 M 的横标为1,则a 的值为( )A 、2B 、1C 、3D 、 42.已知反比例函数y= k x的图象在每个象限内y 随x 的增大而增大,则二次函数y=2kx 2 -x+k 2的图象大致为图1-2-3中的( )3.已知二次函数c bx ax y ++=2的图象如图1-2-4 所示,下列结论中①abc >0;②b=2a ;③a +b +c<0;④a+b+c >0正确的个数是( )A .4B .3C .2D .l4.抛物线y=x 2-ax +5的顶点坐标是( )A .(-2,1)B .(-2,-1)C .(2,l )D .(2,-1)5.抛物线y=(x —5)+4的对称轴是( )A .直线x=4B .直线x =-4C .直线x=5D .直线x =-5 6.二次函数c bx ax y ++=2图象如图l -2-5所示,则下列结论正确的( )A .a >0,b <0,c >0B .a <0,b <0,c >0C .a <0,b >0,c <0D .a <0,b >0,c >07.二次函数 y=2(x -3)2+5的图象的开口方向、对称轴和顶点坐标分别为( )A .开口向下,对称轴x =-3,顶点坐标为(3,5)B .开口向下,对称轴x =3,顶点坐标为(3,5)C .开口向上,对称轴x =-3,顶点坐标为(-3,5)D .开口向上,对称轴x =-3,顶点坐标为(-3,-5)8.二次函数c bx ax y ++=2图象如图l -2-6所示,则点(b c,a ) 在( )A .第一象限B 第二象限C .第三象限D 第四象限 9.已知二次函数c bx ax y ++=2(a ≠0)与一次函数y=kx+m(k ≠0)的图象相交于点A (-2,4),B(8,2),如图1-2-7所示,能使y 1>y 2成立的x 取值范围是_______ 10若二次函数c bx ax y ++=2的图象如图1-2-8,则ac_____0(“<”“>”或“=”)11直线y=x+2与抛物线y=x 2 +2x 的交点坐标为____.12阅读材料:当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线22221y x mx m m =-++-①,有y=2()21x m m -+-②,所以抛物线的顶点坐标为(m ,2m -1),即 2 1 x m y m =⎧⎨=-⎩①②当m 的值变化时,x 、y 的值随之变化,因而y 值也随x 值的变化而变化,将③代人④,得y=2x —1l ⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y 和横坐标x 都满足关系式y=2x -1,回答问题:(1)在上述过程中,由①到②所用的数学方法是________,其中运用了_________公式,由③④得到⑤所用的数学方法是______;(2)根据阅读材料提供的方法,确定抛物线222231y x mx m m =-+-+顶点的纵坐标与横坐标x 之间的关系式_________.13抛物线经过第一、三、四象限,则抛物线的顶点必在( )A .第一象限B .第二象限C .第三象限D .第四象限14当b <0时,一次函数y=ax+b 和二次函数y=ax 2+bx +c 在同一坐标系中的图象大致是图1-2-9中的( )考点2:二次函数的图象与系数的关系一、考点讲解:1、a 的符号:a 的符号由抛物线的开口方向决定.抛物线开口向上,则a >0;物线开口向下,则a <0.2、b 的符号出的符号由对称轴决定,若对称轴是y 轴,则b=0;若抛物线的顶点在y 轴左侧,顶点的横坐标-2b a <0即2b a >0,则a 、b 为同号;若抛物线的顶点在y 轴右侧,顶点的横坐标-2b a >0,即2ba<0.则a 、b 异号.间“左同有异”.3.c 的符号:c 的符号由抛物线与y 轴的交点位置确定.若抛物线交y 轴于正半,则c >0,抛物线交y 轴于负半轴.则c <0;若抛物线过原点,则c=0.4.△的符号:△的符号由抛物线与x 轴的交点个数决定.若抛物线与x 轴只有一个交点,则△=0;有两个交点,则△>0.没有交点,则△<0 . 5、a+b+c 与a -b+c 的符号:a+b+c 是抛物线c bx ax y ++=2(a ≠0)上的点(1,a+b+c )的纵坐标,a -b+c 是抛物线c bx ax y ++=2(a ≠0)上的点(-1,a -b +c )的纵坐标.根据点的位置,可确定它们的符号.二、针对性训练: 1.已知函数c bx ax y ++=2的图象如图1-2-11所示,给出下列关于系数a 、b 、c 的不等式:①a <0,②b <0,③c >0,④2a +b <0,⑤a +b +c >0.其中正确的不等式的序号为___________- 2.已知抛物线c bx ax y ++=2与x 轴交点的横坐标为-1,则a +c=_________.3.抛物线c bx ax y ++=2中,已知a :b :c=l :2:3,最小值为6,则此抛胸的解析式为____________ 4.已知二次函数的图象开口向下,且与y 轴的正半轴相交,请你写出一个满足条件的二次函数解析式: _______________. 5.抛物线c bx ax y ++=2如图1-2-12 所示,则它关于y 轴对称的抛物线的解析式是___________.6.若抛物线过点(1,0)且其解析式中二次项系数为1,则它的解析式为___________.(任写一个) 7.已知二次函数c bx ax y ++=2的图象与x 轴交于点(-2,0),(x 1,0)且1<x 1<2,与y·轴正半轴的交点连点(0,2)的下方,下列结论:①a <b <0;②2a+c >0;③4a+c< 0,④2a -b+l >0.其中的有正确的结论是(填写序号)__________. 8.已知二次函数c bx ax y ++=2的图象如图1-2-13所示:(1)这个二次函数的解析式是y=__________.(2)当x=_______时,y=3;(3)根据图象回答:当x______时,y >0.图象如图 1-2-14所示,则下列关于a 、b 、c 间的关系判断9.二次函数c bx ax y ++=2的正确的是()A .ab <0B 、bc <0 C .a+b +c >0D .a -b 十c <0 10 已知二次函数c bx ax y ++=2,那么它的图象如图1-2-15大致为( )11.抛物线c bx ax y ++=2>0)的顶点在x 轴上方的条件是( ) A .b 2-4ac <0 B .b 2-4ac > 0 C .b 2-4ac ≥0 D . c <012 二次函数⑴y=3x 2;⑵y= 23 x 2;⑶y= 43x 2的图象的开口大小)顺序应为( ) A .(1)>(2)>(3)B .(1)>(3)>(2)C .(2)>(3)>(1)D .(2)>(1)>(3) 13若二次函数c bx ax y ++=2,当x 取x 1,x 2(x 1,≠x 2)时,函数值相等,则当x 取(x 1+x 2)时,函数值为( )A .a+cB .a -cC . -cD .c考点3:二次函数解析式求法一、考点讲解:1.二次函数的三种表示方法:⑴表格法:可以清楚、直接地表示出变量之间的数值对应关系;⑵图象法:可以直观地表示出函数的变化过程和变化趋势;⑶表达式:可以比较全面、完整、简洁地表示出变量之间的关系.2.二次函数表达式的求法: ⑴若已知抛物线上三点坐标,可利用待定系数法求得c bx ax y ++=2; ⑵若已知抛物线的顶点坐标或对称轴方程,则可采用顶点式:2()y a x h k =-+其中顶点为(h ,k)对称轴为直线x=h ;⑶若已知抛物线与x 轴的交点坐标或交点的横坐标,则可采用交点式:12()()y a x x x x =--,其中与x 轴的交点坐标为(x 1,0),(x 2,0)二、针对性训练:1.二次函数的图象经过点(-3,2),(2,7),(0,-1),求其解析式.2.已知抛物线的对称轴为直线x=-2,且经过点(-l ,-1),(-4,0)两点.求抛物线的解析式.3.已知抛物线与 x 轴交于点(1,0)和(2,0)且过点(3,4),求抛物线的解析式. 4.已知二次函数c bx ax y ++=2的图象经过点A (0,1)B(2,-1)两点.(1)求b 和c 的值;(2)试判断点P (-1,2)是否在此抛物线上?5.已知一个二次函数c bx ax y ++=2的图象如图1-2-25所示,请你求出这个二次函数的表达式,并求出顶点坐标和对称轴方程. 6.已知抛物线c bx ax y ++=2过三点(-1,-1)、(0,-2)、(1,l ).(1)求这条抛物线所对应的二次函数的表达式;(2)写出它的开口方向、对称轴和顶点坐标;(3)这个函数有最大值还是最小值? 这个值是多少? 7.当 x=4时,函数c bx ax y ++=2的最小值为-8,抛物线过点(6,0).求:(1)顶点坐标和对称轴;(2)函数的表达式;(3)x 取什么值时,y 随x 的增大而增大;x 取什么值时,y 随x 增大而减小.8.在ΔABC 中,∠ABC =90○ ,点C 在x 轴正半轴上,点A 在x 轴负半轴上,点B 在y 轴正半轴上(图1-2-26所示),若tan ∠BAC= 12,求经过 A 、B 、C 点的抛物线的解析式.9.已知:如图1-2-27所示,直线y=-x+3与x 轴、y 轴分别交于点B 、C ,抛物线y=-x 2+bx +c 经过点B 、C ,点A 是抛物线与x 轴的另一个交点.(1)求抛物线的解析式;(2)若点P 在直线BC 上,且S ΔPAC =12S ΔPAB ,求点P 的坐标.10 四边形DEFH 为△ABC 的内接矩形(图1-2-28),AM 为BC 边上的高,DE 长为x ,矩形的面积为y ,请写出y 与x 之间的函数关系式,并判断它是不是关于x 的二次函数.考点4:根据二次函数图象解一元二次方程的近似解一、考点讲解:1.二次函数与一元二次方程的关系: (1)一元二次方程20ax bx c ++=就是二次函数c bx ax y ++=2当函数y 的值为0时的情况.(2)二次函数c bx ax y ++=2的图象与x 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数c bx ax y ++=2的图象与x 轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax 2+bx +c=0的根. (3)当二次函数c bx ax y ++=2的图象与 x 轴有两个交点时,则一元二次方程c bx ax y ++=2有两个不相等的实数根;当二次函数c bx ax y ++=2的图象与x 轴有一个交点时,则一元二次方程ax 2+bx +c =0有两个相等的实数根;当二次函数y =ax 2+ bx+c 的图象与 x 轴没有交点时,则一元二次方程c bx ax y ++=2没有实数根.二、针对性训练:1.已知函数y=kx 2-7x —7的图象和x 轴有交点,则k 的取值范围是( )77. .k 04477. .k 044A k B k C k D k >-≥-≠≥->-≠且且2.直线y=3x —3与抛物线y=x 2 -x+1的交点的个数是( )A .0B .1C .2D .不能确定 3.函数c bx ax y ++=2的图象如图l -2-30,那么关于x 的方程20ax bx c ++=的根的情况是( )A .有两个不相等的实数根B .有两个异号实数根C .有两个相等实数根D .无实数根4.二次函数c bx ax y ++=2的图象如图l -2-31所示,则下列结论成立的是( ) A .a >0,bc >0,△<0 B.a <0,bc >0,△<0C .a >0,bc <0,△<0 D.a <0,bc <0,△>0 5.函数c bx ax y ++=2的图象如图 l -2-32所示,则下列结论错误的是( )A .a >0B .b 2-4ac >0C 、20ax bx c ++=的两根之和为负D、20++=的两根之积为正ax bx c6.不论m为何实数,抛物线y=x2-mx+m-2()A.在x轴上方B.与x轴只有一个交点C.与x轴有两个交点D.在x轴下方7.画出函数y =x2-2x-3的图象,利用图象回答:(1)方程x2-2x-3=0的解是什么?(2)b取什么值时,函数值大于0?(3)b取什么值时,函数值小于0?8.已知二次函数y =x2-x—6·(1)求二次函数图象与坐标轴的交点坐标及顶点坐标;(2)画出函数图象;(3)观察图象,指出方程x2-x—6=0的解;(4)求二次函数图象与坐标轴交点所构成的三角形的面积考点5:用二次函数解决实际问题一、考点讲解:1.二次函数的应用:(1)二次函数常用来解决最优化问题,这类问题实际上就是求函数的最大(小)值;(2)二次函数的应用包括以下方面:分析和表示不同背景下实际问题中变量之间的二次函数关系;运用二次函数的知识解决实际问题中的最大(小)值.2.解决实际问题时的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等.二、针对性训练:1.小王家在农村,他家想利用房屋侧面的一面墙,围成一个矩形猪圈(以墙为长人现在已备足可以砌10米长的墙的材料.他想使猪圈的面积最大,你能帮他计算一下矩形的长和宽应当分别是多少米吗?此时猪圈的面积有多大?2.数学兴趣小组几名同学到某商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱50元销售平均每天销售90箱,价格每降低1元平均每天可多销售3箱.老师要求根据以上资料,解答下列问题,你能做到吗?⑴写出平均每天销售量y(箱)与每箱售价社元)之间的函数关系;⑵写出平均每天销售利润W(元)与每箱售价x(元)之间的函数关系;⑶求出⑵中M次函数的顶点坐标及当x=40、70时的W的值.3.某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可售出100件.他想采用提高售价的办法来增加利润,经试验,发现这种商品每件每提价l元,每天的销售量就会减少10件.⑴写出售价x(元/件)与每天所得的利润y(元)之间的函数关系式;⑵ 每件售价定为多少元,才能使一天的利润最大?4.如图1-2-38所示是一条高速公路上的隧道口在平面直角坐标系上的示意图,点A 和A 1,点B 和B 1分别关于y 轴对称,隧道拱部分BCB 1为一段抛物线,最高点C 离路面AA 1的距离为8米,点B 离路面AA 1的距离为6米,隧道的宽AA 1为16米.⑴ 求隧道拱抛物线 BCB ;的函数解析式;⑵ 现有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与路面的距离为7米,它能否安全通过这个隧道?说明理由.5.启明公司生产某种产品,每件产品成本是8元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投人的广告费是x(万元)时,产品的年销售量将是原销售量的y 倍,且y=277101010x x -++,如果把利润看作是销售总额减去成本费和广告费: (1)试写出年利润S (万元)与广告费x (万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是多少万元?(2)把(1)中的最大利润留出3万元做广告,其余的资金投资 新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元,问:有几种符合要求的投资方式?写出每种投资方式所选的项目.6.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日生产出的产品全部售出,已知生产X 只玩具熊猫的成本为R ((元),售价每只为P (元)且R ,P 与X 的关系式为 R=500+3.5x ,P=170 - 2x . ⑴ 当日产量为多少时,每日获得的利润为1750元;⑵ 当日产量为多少时,可获得最大利润?最大利润是多少?。
《二次函数(基础复习).docx

二次函数(基础复习)★二次函数知识点汇总*1.定义:一般地,如果y = ax2 +bx + c(a.b,c是常数,d H 0),那么y叫做兀的二次函数.2.二次函数y = ax~的性质⑴抛物线y = d*(°工°)的顶点是坐标原点,对称轴是).,轴.⑵函数y = a/的图像与a的符号关系.①当a〉0时o抛物线开口向上o顶点为其最低点;②当a < 0时o抛物线开口向H<=>顶点为其最高点3.二次函数y = ax~ +bx + c的图像是对称轴平行于(包括重合)y轴的抛物线.4.二次两数尸加+办+ c用配方法可化成:y = a(x-h)2 +k的形式,具中h二亠,k =仏一沪•2a4a5.二次函数由特殊到一般,可分为以下几种形式:①y = ax2;②y = ax2 +k;③ y = a(x-h)2;④y = a(x - /?)2 + k;⑤y = ax2 + 加+ c .6.抛物线的三耍素:开口方向、对称轴、顶点.①a决定抛物线的开口方向:当a>0时,开口向上;当d<0时,开口向下;问相等,抛物线的开口人小、形状相同.②平行于y轴(或重合)的在线记作x = h.特别地,y轴记作直线x = 0.7.顶点决定抛物线的位置.儿个不同的二次两数,如果二次项系数d相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.&求抛物线的顶点、对称轴的方法(1)公式法:y = ax2 +bx-}-c = a x + — +",二顶点是(一-—― ),对称轴\ 2a) 4ci 2a 4ci是直线兀=丄・2ci⑵配方法:运用配方法将抛物线的解析式化为y = c(x-h)2+k的形式,得到顶点为(h,k),对称轴是兀=h .(3)运川抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.★用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失★9.抛物线y = ax2 + bx + c中,a,b,c的作用(1)a决定开口方向及开口大小,这与y - ax2中的a完全一•样.⑵b和a共同决定抛物线对称轴的位置.rtl于抛物线y+bx+c的对称轴是直线龙=,2a故:®b = 0时,对称轴为y轴;②2>o(即b同号)吋,对称轴在y轴左侧;a③ 2 V 0 (即d、b界号)时,対称轴在y轴右侧.a⑶c的人小决定抛物线y = ax2 +bx + c与y轴交点的位置.当兀=0时,y = c ,抛物线y = ax1 +bx + c与y轴有且只有一个交点(0, c):①c = 0 ,抛物线经过原点;②c〉0,与y轴交于.正半轴;③c < 0,与y轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在y轴右侧,则1<0-11.用待定系数法求二次函数的解析式根据条件确定二次西数农达式的儿种基本思路。
二次函数知识点复习
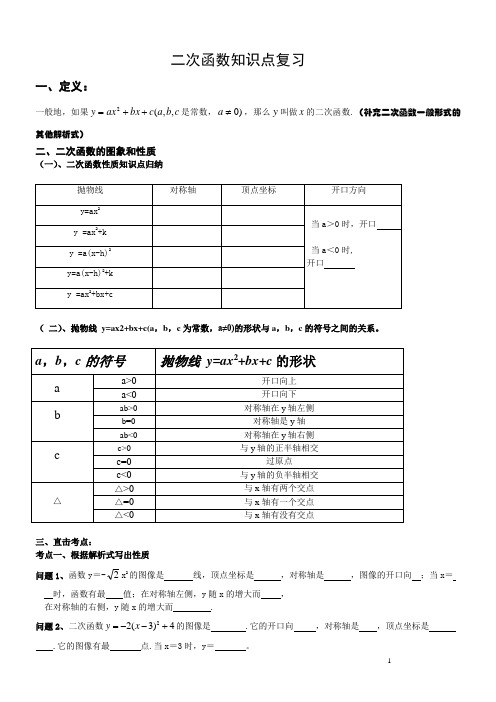
二次函数知识点复习一、定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数.(补充二次函数一般形式的其他解析式)二、二次函数的图象和性质(一)、二次函数性质知识点归纳( 二)、抛物线 y=ax2+bx+c(a ,b ,c 为常数,a≠0)的形状与a ,b ,c 的符号之间的关系。
三、直击考点:考点一、根据解析式写出性质问题1、函数y =-2x 2的图像是线,顶点坐标是 ,对称轴是 ,图像的开口向 ;当x =时,函数有最 值;在对称轴左侧,y 随x 的增大而 , 在对称轴的右侧,y 随x 的增大而 . 问题2、二次函数22(3)4y x =--+的图像是 .它的开口向 ,对称轴是 ,顶点坐标是.它的图像有最点.当x =3时,y =。
练习1、抛物线2123y x =-+开口向 ,当x = 时,y 有最 值 ,对称轴是 ,当0x >时,y 随x 的增大而 。
练习2、抛物线()2423y x =--+开口向 ,当x = 时,y 有最 值 ,对称轴是 ,当0x <时,y 随x 的增大而 。
考点二、根据关系式确定图象:问题3、如图,若a <0,b >0,c <0,则抛物线y=ax 2+bx +c 的大致图象为( )练习、1、函数2y x =-和y x b =-+ (0b <)的图象在同一坐标系中,可能是( )2、已知二次函数y=ax 2+bx+c 的图象如图所示,试判断下面各式的符号:(1)abc (2)b 2-4ac (3)2a+b (4)a+b+c考点三、配方法用配方法把y =ax 2+bx+c 化成()200y a x x y =-+的形式。
因此,抛物线)0(2≠++=a c bx ax y 用配方法可化成224()24b ac b y a x aa-=++,则顶点是: ;即化为()200y a x x y =-+的形式,其中0x = , 0y = . 2、把下列二次函数化成()200y a x x y =-+的形式,并指出抛物线的开口方向、 对称轴与顶点坐标. (1)y =-x 2+16923+x ; (2)y =61x 2-.561-x练习1、求出下列二次函数图象的顶点坐标和对称轴:D C BF EAy =x 2-2x -3; (2) y =3x 2+6x -1;考点四、待定系数法:例:已知二次函数c bx ax y ++=2的图象经过A(-1,0)、B(3,0)、C(0,3)三点,求这个二次函数 的解析式.例2、抛物线y=ax 2+bx +c 与x 轴交于点A (-3,0),对称轴为x=-1,顶点C 到x 轴的距离为2, 求此抛物线表达式.练习、1、试写出一个开口方向向上,对称轴为直线2x =,且与y 轴的交点坐标为(0,3)的抛物线的表达式;2、已知抛物线的顶点为(1,-1),且过点(2,1),求这个函数的表达式;考点五、抛物线的平移规律例、抛物线y=2x 2向左平移1个单位,再向下平移3个单位,得到的抛物线表达式为考点六、二次函数应用1、某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品. (1)如果增加x 台机器,每天的生产总量为y 件,请你写出y 与x 之间的关系式; (2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?2、已知:如图,在Rt△ABC 中,∠C =90°,BC =4,AC =8,点D 在斜边AB 上, 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,得四边形DECF ,设DE =x ,DF =y .(1)用含y 的代数式表示AE .(2)求y 与x 之间的函数关系式,并求出x 的取值范围.(3)设四边形DECF 的面积为S ,求出S 的最大值.3、心理学家发现,学生对概念的接受能力y 与提出概念所用的时间x (单位:分)之间满足函数关系y=-0.1x2+2.6x+43(0≤x≤30).y值越大,表示接受能力越强.(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐渐降低?(2)第10分时,学生的接受能力是多少?(3)第几分时,学生的接受能力最强?4、一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到的最大高度是3.5米,然后准确落入篮圈,已知篮球中心到地面的距离为3.05米,(1)根据题意建立直角坐标系,并求出抛物线的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数基础复习
复习目标:对二次函数的定义,对称轴、顶点、最值,图象和性质,增减性,平移有一
定了解;
复习重点:二次函数的定义,二次函数的对称轴、顶点、最值;
复习难点:函数y=ax 2+bx+c 的图象和性质,二次函数的增减性二次函数的平移。
二次函数的定义
(考点:二次函数的二次项系数不为0,且二次函数的表达式必须为整式)
1、下列函数中,是二次函数的是 .
①y=x 2-4x+1; ②y=2x 2; ③y=2x 2+4x ; ④y=-3x ; ⑤y=-2x -1; ⑥y=mx 2+nx+p ; ⑦y =(4,x) ; ⑧y=-5x 。
2、在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为s=5t 2+2t ,则t =4秒时,该物体所经过的路程为 。
3、若函数y=(m 2+2m -7)x 2+4x+5是关于x 的二次函数,则m 的取值范围为 。
二次函数的对称轴、顶点、最值
(技法::如果解析式为顶点式y=a(x -h)2+k ,则最值为k ;如果解析式为一般式y=ax 2+bx+c 则最值为4ac-b 24a 4.抛物线y=2x 2+4x+m 2-m 经过坐标原点,则m 的值为 。
5.抛物y=x 2+bx+c 线的顶点坐标为(1,3),则b = ,c = . 6.已知抛物线y =x 2+(m -1)x -14 的顶点的横坐标是2,则m 的值是_ . 7.抛物线y=x 2+2x -3的对称轴是 。
8.已知二次函数y=x 2-4x+m -3的最小值为3,则m = 。
函数y=ax 2+bx+c 的图象和性质
9.通过配方,写出下列函数的开口方向、对称轴和顶点坐标: (1)y=12 x 2-2x+1 ; (2)y=-3x 2+8x -2; (3)y=-14
x 2+x -4
10.把抛物线y=x 2+bx+c 的图象向右平移3个单位,在向下平移2个单位,所得图象的解析式是y=x 2-3x+5,试求b 、c 的值。
11.已知函数y=2x2,y=2(x-4)2,和y=2(x+1)2。
(1)分别说出各个函数图象的开口方、对称轴和顶点坐标。
(2)分析分别通过怎样的平移。
可以由抛物线y=2x2得到抛物线y=2(x-4)2和y=2(x+1)2?
12.某商场以每台2500元进口一批彩电。
如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则会少卖出50台,那么每台定价为多少元即可获得最大利润?最大利润是多少元?
二次函数的增减性
13.二次函数y=3x2-6x+5,当x>1时,y随x的增大而;当x<1时,y随x 的增大而;当x=1时,函数有最值是。
14.已知二次函数y=x2-(m+1)x+1,当x≥1时,y随x的增大而增大,则m的取值范围是 .
二次函数的平移
(技法:只要两个函数的a 相同,就可以通过平移重合。
将二次函数一般式化为顶点式y=a(x-h)2+k,平移规律:左加右减,对x;上加下减,直接加减)
15.将抛物线y= 2x2,可以得到y=2(x+4}2-3。
16.将抛物线y=x2+1向左平移2个单位,再向下平移3个单位,所得到的抛物线的关系式为。
17.如果将抛物线y=2x2-1的图象向右平移3个单位,所得到的抛物线的关系式为。
函数的交点
18.抛物线y=x2+7x+3与直线y=2x+9的交点坐标为。
19.直线y=7x+1与抛物线y=x2+3x+5的图象有个交点。
函数的图象特征与a、b、c的关系
20.在同一坐标系中,函数y= ax2+c与y= c
x
(a<c)图象可能是图所示的( )
A B C D
21.已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,
则下列结论:①a,b同号;②当x=1和x=3时,函数值相同;
③4a+b=0; ④当y=-2时,x的值只能取0;
其中正确的个数是()
A.1 B.2 C.3 D.4
22.已知二次函数y=ax2+bx+c经过一、三、四象限(不经过原
点和第二象限)则直线y=ax+bc不经过()
A.第一象限B.第二象限C.第三象限 D.第四象限
函数解析式的求法
一、已知抛物线上任意三点时,通常设解析式为一般式y=ax2+bx+c。
23.已知二次函数的图象经过A(0,3)、B(1,3)、C(-1,1)三点,求该二次函数的解析式。
二、已知抛物线与轴的交点的坐标时,通常设解析式为交点式y=a(x-x
1)(x-x
2
)。
24.二次函数的图象经过A(-1,0),B(3,0),函数有最小值-8,求该二次函数的解析式。
三、已知抛物线顶点时,通常设顶点式y=a(x-h)2+k。
25.已知二次函数的图象的顶点坐标为(1,-6),且经过点(2,-8),求该二次函数的解析式。
26.y= -x2+2(k-1)x+2k-k2,它的图象经过原点,求①解析式②与x轴交点O、A 及顶点C组成的△OAC面积。
27.抛物线y= (k2-2)x2+m-4kx的对称轴是直线x=2,且它的最低点在直线y= -1
2
x+2
上,求函数解析式。
