高中数学必修二导学案：第二章第三节平面与平面垂直的性质
人教版高中数学全套教案导学案高中数学 (2.3.2 平面与平面垂直的判定)示范教案 新人教A版必修2
2.3.2 平面与平面垂直的判定整体设计教学分析在空间平面与平面之间的位置关系中，垂直是一种非常重要的位置关系，它不仅应用较多，而且是空间问题平面化的典范.空间中平面与平面垂直的定义是通过二面角给出的，二面角是高考中的重点和难点.使学生掌握两个平面互相垂直的判定，提高学生空间想象能力，提高等价转化思想渗透的意识，进一步提高学生分析问题、解决问题的能力；使学生学会多角度分析、思考问题，培养学生的创新精神.三维目标1.探究平面与平面垂直的判定定理，二面角的定义及应用，培养学生的归纳能力.2.掌握平面与平面垂直的判定定理的应用，培养学生的空间想象能力.3.引导学生总结求二面角的方法,培养学生归纳问题的能力.重点难点教学重点:平面与平面垂直判定.教学难点:平面与平面垂直判定和求二面角.课时安排1课时教学过程复习两平面的位置关系：（1）如果两个平面没有公共点，则两平面平行⇔若α∩β=∅,则α∥β.（2）如果两个平面有一条公共直线，则两平面相交⇔若α∩β=AB,则α与β相交.两平面平行与相交的图形表示如图1.图1导入新课思路1.(情境导入)为了解决实际问题，人们需要研究两个平面所成的角.修筑水坝时，为了使水坝坚固耐用必须使水坝面与水平面成适当的角度；发射人造地球卫星时，使卫星轨道平面与地球赤道平面成一定的角度.为此，我们引入二面角的概念，研究两个平面所成的角.思路2.(直接导入)前边举过门和墙所在平面的关系，随着门的开启，其所在平面与墙所在平面的相交程度在变，怎样描述这种变化呢？今天我们一起来探究两个平面所成角问题.推进新课新知探究提出问题①二面角的有关概念、画法及表示方法.②二面角的平面角的概念.③两个平面垂直的定义.④用三种语言描述平面与平面垂直的判定定理，并给出证明.⑤应用面面垂直的判定定理难点在哪里？讨论结果：①二面角的有关概念.二面角的定义：从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫二面角的棱，这两个半平面叫二面角的面.二面角常用直立式和平卧式两种画法：如图2（教师和学生共同动手）.直立式：平卧式：(1) (2)图2二面角的表示方法：如图3中，棱为AB，面为α、β的二面角，记作二面角α-AB-β.有时为了方便也可在α、β内（棱以外的半平面部分）分别取点P、Q，将这个二面角记作二面角P-AB-Q.图3如果棱为l，则这个二面角记作αlβ或PlQ.②二面角的平面角的概念.如图4,在二面角αlβ的棱上任取点O，以O为垂足，在半平面α和β内分别作垂直于棱的射线OA和OB，则射线OA和OB组成∠AOB.图4再取棱上另一点O′，在α和β内分别作l的垂线O′A′和O′B′，则它们组成角∠A′O′B′.因为OA∥O′A′,OB∥O′B′，所以∠AOB及∠A′O′B′的两边分别平行且方向相同, 即∠AOB=∠A′O′B′.从上述结论说明了：按照上述方法作出的角的大小，与角的顶点在棱上的位置无关.由此结果引出二面角的平面角概念：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角.图中的∠AOB,∠A′O′B′都是二面角αlβ的平面角.③直二面角的定义.二面角的大小可以用它的平面角来度量，二面角的平面角是多少度，就说二面角是多少度.平面角是直角的二面角叫做直二面角.教室的墙面与地面，一个正方体中每相邻的两个面、课桌的侧面与地面都是互相垂直的.两个平面互相垂直的概念和平面几何里两条直线互相垂直的概念相类似，也是用它们所成的角为直角来定义，二面角既可以为锐角，也可以为钝角，特殊情形又可以为直角.两个平面互相垂直的定义可表述为：如果两个相交平面所成的二面角为直二面角，那么这两个平面互相垂直.直二面角的画法：如图5.图5④两个平面垂直的判定定理.如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直. 两个平面垂直的判定定理符表述为：⎭⎬⎫⊂⊥αβAB AB ⇒α⊥β.两个平面垂直的判定定理图形表述为：如图6.图6证明如下：已知AB⊥β，AB∩β=B ，AB ⊂α. 求证：α⊥β.分析：要证α⊥β,需证α和β构成的二面角是直二面角，而要证明一个二面角是直二面角，需找到其中一个平面角，并证明这个二面角的平面角是直角. 证明：设α∩β=CD ，则由AB ⊂α,知AB 、CD 共面. ∵AB⊥β，CD ⊂β,∴AB⊥CD，垂足为点B. 在平面β内过点B 作直线BE⊥CD, 则∠ABE 是二面角αCD β的平面角.又AB⊥BE，即二面角αCD β是直二面角, ∴α⊥β.⑤应用面面垂直的判定定理难点在于：在一个平面内找到另一个平面的垂线,即要证面面垂直转化为证线线垂直. 应用示例思路1例1 如图7,⊙O 在平面α内，AB 是⊙O 的直径，PA⊥α，C 为圆周上不同于A 、B 的任意一点.图7求证：平面PAC⊥平面PBC.证明：设⊙O 所在平面为α,由已知条件，PA⊥α,BC ⊂α,∴PA⊥BC. ∵C 为圆周上不同于A 、B 的任意一点,AB 是⊙O 的直径, ∴BC⊥AC.又∵PA 与AC 是△PAC 所在平面内的两条相交直线，∴BC⊥平面PAC.∵BC ⊂平面PB C,∴平面PAC⊥平面PBC. 变式训练如图8，把等腰Rt△ABC 沿斜边AB 旋转至△ABD 的位置，使CD=AC ，图8（1）求证：平面ABD⊥平面ABC ； （2）求二面角CBDA 的余弦值. （1）证明：由题设,知AD=CD=BD,作DO⊥平面ABC ，O 为垂足，则OA=OB=OC. ∴O 是△ABC 的外心，即AB 的中点. ∴O∈AB ，即O ∈平面ABD. ∴OD ⊂平面ABD.∴平面ABD⊥平面ABC.（2）解:取BD 的中点E ，连接CE 、OE 、OC, ∵△BCD 为正三角形，∴CE⊥BD.又△BOD 为等腰直角三角形,∴OE⊥BD. ∴∠OEC 为二面角CBDA 的平面角. 同（1）可证OC⊥平面ABD.∴OC⊥OE.∴△COE 为直角三角形. 设BC=a ，则CE=a 23，OE=a 21，∴cos∠OEC=33=CE OE . 点评：欲证面面垂直关键在于在一个平面内找到另一个平面的垂线.例2 如图9所示，河堤斜面与水平面所成二面角为60°，堤面上有一条直道CD ，它与堤角的水平线AB 的夹角为30°，沿这条直道从堤脚向上行走到10 m 时人升高了多少？（精确到0.1 m ）图9解：取CD 上一点E ，设CE=10 m ，过点E 作直线AB 所在的水平面的垂线EG ，垂足为G ，则线段EG 的长就是所求的高度.在河堤斜面内，作EF⊥AB，垂足为F ，并连接FG,则FG⊥AB,即∠EFG 就是河堤斜面与水平面ABG 所成二面角的平面角, ∠EFG=60°,由此,得EG=EFsin60°=CEsin30°sin60°=10×2352321=⨯≈4.3（m ）.答：沿直道行走到10 m 时人升高约4.3 m. 变式训练已知二面角αAB β等于45°，CD ⊂α，D ∈AB ，∠CDB=45°. 求CD 与平面β所成的角.解：如图10，作CO⊥β交β于点O ，连接DO ，则∠CDO 为DC 与β所成的角.图10过点O 作OE⊥AB 于E ，连接CE ，则CE⊥AB. ∴∠CEO 为二面角αAB β的平面角， 即∠CEO=45°. 设CD=a,则CE=a 22,∵CO⊥OE，OC=OE ， ∴CO=a 21.∵CO⊥DO,∴sin∠CDO=21=CD CO . ∴∠CDO=30°,即DC 与β成30°角.点评：二面角是本节的另一个重点，作二面角的平面角最常用的方法是：在一个半平面α内找一点C ，作另一个半平面β的垂线，垂足为O,然后通过垂足O 作棱AB 的垂线，垂足为E,连接AE,则∠CEO 为二面角α-AB-β的平面角.这一过程要求学生熟记.思路2例1 如图11，ABCD 是菱形，PA⊥平面ABCD ，PA=AD=2，∠BAD=60°.图11（1）求证：平面PBD⊥平面PAC ； （2）求点A 到平面PBD 的距离； （3）求二面角APBD 的余弦值.（1）证明：设AC 与BD 交于点O ，连接PO, ∵底面ABCD 是菱形,∴BD⊥AC.∵PA⊥底面ABCD,BD ⊂平面ABCD,∴的PA⊥BD. 又PA∩AC=A,∴BD⊥平面PAC.又∵BD ⊂平面PBD,∴平面PBD⊥平面PAC.(2)解：作AE⊥PO 于点E,∵平面P BD⊥平面PAC,∴AE⊥平面PBD. ∴AE 为点A 到平面PBD 的距离.在△PAO 中,PA=2,AO=2·cos30°=3,∠PAO=90°, ∵PO=722=+AO PA ,∴AE=7212732==∙PO AO PA .∴点A 到平面PBD 的距离为7212. （3）解：作AF⊥PB 于点F,连接EF, ∵AE⊥平面PBD,∴AE⊥PB. ∴PB⊥平面AEF,PB⊥EF.∴∠AFE 为二面角APBD 的平面角. 在Rt△AEF 中,AE=7212,AF=2, ∴sin∠AFE=742=AF AE ,cos∠AFE=77)742(12=-. ∴二面角APBD 的余弦值为77. 变式训练如图12，PA⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点. （1）求证：MN∥平面PAD ； （2）求证：MN⊥CD；（3）若二面角PDCA=45°，求证：MN⊥平面PDC.图12 图13证明：如图13所示,（1）取PD 的中点Q ，连接AQ 、NQ,则QN21DC,AM 21DC, ∴QN AM.∴四边形AMNQ 是平行四边形.∴MN∥AQ.又∵MN ⊄平面PAD,AQ ⊂平面PAD,∴MN∥平面PAD. （2）∵PA⊥平面ABCD ，∴PA⊥CD. 又∵CD⊥AD,PA∩AD=A,∴CD⊥平面PAD. 又∵AQ ⊂平面PAD,∴CD⊥AQ. 又∵AQ∥MN,∴MN⊥CD.（3）由（2）知，CD⊥平面PAD, ∴CD⊥AD,CD⊥PD.∴∠PDA 是二面角PDCA 的平面角.∴∠PDA=45°. 又∵PA⊥平面ABCD,∴PA⊥AD.∴AQ⊥PD. 又∵MN∥AQ,∴MN⊥CD.又∵MN⊥PD,∴MN⊥平面PDC.例2 如图14,已知直四棱柱ABCD —A 1B 1C 1D 1的底面是菱形，且∠DAB=60°,AD=AA 1，F 为棱BB 1的中点，M 为线段AC 1的中点.图14（1）求证：直线MF∥平面ABCD ； （2）求证：平面AFC 1⊥平面ACC 1A 1；（3）求平面AFC 1与平面ABCD 所成二面角的大小. （1）证明：延长C 1F 交CB 的延长线于点N ，连接AN. ∵F 是BB 1的中点，∴F 为C 1N 的中点，B 为CN 的中点. 又M 是线段AC 1的中点，故MF∥AN. 又∵MF ⊄平面ABCD,AN ⊂平面ABCD, ∴MF∥平面ABCD.（2）证明：连接BD ，由直四棱柱ABCD —A 1B 1C 1D 1,可知AA 1⊥平面ABCD, 又∵BD ⊂平面ABCD ，∴A 1A⊥BD. ∵四边形ABCD 为菱形，∴AC⊥BD. 又∵AC∩A 1A=A,AC 、A 1A ⊂平面ACC 1A 1, ∴BD⊥平面ACC 1A 1.在四边形DANB 中，DA∥BN 且DA=BN ， ∴四边形DANB 为平行四边形. 故NA∥BD，∴NA⊥平面ACC 1A 1. 又∵NA ⊂平面AFC 1,∴平面AFC 1⊥平面ACC 1A 1.（3）解：由（2）,知BD⊥平面ACC 1A 1，又AC 1⊂平面ACC 1A 1，∴BD⊥AC 1. ∵BD∥NA，∴AC 1⊥NA.又由BD⊥AC,可知NA⊥AC，∴∠C 1AC 就是平面AFC 1与平面ABCD 所成二面角的平面角或补角. 在Rt△C 1AC 中，tan∠C 1AC=311=CA C C ，故∠C 1AC=30°. ∴平面AFC 1与平面ABCD 所成二面角的大小为30°或150°.变式训练如图15所示，在四棱锥S —ABCD 中，底面ABCD 是矩形，侧面SDC⊥底面ABCD ，且AB=2，SC=SD=2.图15（1）求证：平面SAD⊥平面SBC ；（2）设BC=x ，BD 与平面SBC 所成的角为α，求sin α的取值范围. （1）证明：在△SDC 中，∵SC=SD=2，CD=AB=2,∴∠DSC=90°,即DS⊥SC.∵底面ABCD 是矩形,∴BC⊥CD.又∵平面SDC⊥平面ABCD,∴BC⊥面SDC. ∴DS⊥BC.∴DS⊥平面SBC.∵DS ⊂平面SAD,∴平面SAD⊥平面SBC.（2）解：由（1）,知DS⊥平面SBC,∴SB 是DB 在平面SBC 上的射影. ∴∠DBS 就是BD 与平面SBC 所成的角，即∠DBS=α. 那么sin α=DBDS. ∵BC=x,CD=2⇒DB=24x +,∴sin α=242x+.由0＜x ＜+∞,得0＜sin α＜22. 知能训练课本本节练习. 拓展提升如图16，在四棱锥P —ABCD 中，侧面PAD 是正三角形，且与底面ABCD 垂直，底面ABCD 是边长为2的菱形，∠BAD=60°，N 是PB 中点，过A 、D 、N 三点的平面交PC 于M ，E 为AD 的中点.图16（1）求证：EN∥平面PCD ；（2）求证：平面PBC⊥平面ADMN ；（3）求平面PAB 与平面ABCD 所成二面角的正切值. (1)证明：∵AD∥BC,BC ⊂面PBC,AD ⊄面PBC, ∴AD∥面PBC.又面ADN∩面PBC=MN, ∴AD∥MN.∴MN∥BC. ∴点M 为PC 的中点.∴MN21BC. 又E 为AD 的中点，∴四边形DENM 为平行四边形. ∴EN∥DM.∴EN∥面PDC.（2）证明：连接PE 、BE,∵四边形ABCD 为边长为2的菱形，且∠BAD=60°, ∴BE⊥AD.又∵PE⊥AD,∴AD⊥面PBE.∴AD⊥PB. 又∵PA=AB 且N 为PB 的中点, ∴AN⊥PB.∴PB⊥面ADMN.∴平面PBC⊥平面ADMN.（3）解：作EF⊥AB，连接PF ，∵PE⊥平面ABCD,∴AB⊥PF. ∴∠PFE 就是平面PAB 与平面ABCD 所成二面角的平面角. 又在Rt△AEB 中，BE=3，AE=1，AB=2,∴EF=23. 又∵PE=3,∴tan∠PFE=233 EFPE=2,即平面PAB 与平面ABCD 所成的二面角的正切值为2. 课堂小结知识总结：利用面面垂直的判定定理找出平面的垂线，然后解决证明垂直问题、平行问题、求角问题、求距离问题等.思想方法总结：转化思想，即把面面关系转化为线面关系，把空间问题转化为平面问题. 作业课本习题2.3 A 组1、2、3.设计感想线面关系是线线关系和面面关系的桥梁和纽带，空间中直线与平面垂直的性质定理不仅是由线面关系转化为线线关系，而且将垂直关系转化为平行关系，因此直线与平面垂直的性质定理在立体几何中有着特殊的地位和作用，因此它是高考考查的重点.本节不仅选用了大量经典好题，还选用了大量的2007高考模拟题，相信能够帮助大家解决立体几何中的重点难点问题.。
人教版高中数学必修二 导学案：第二章第三节平面与平面垂直的性质
第二章第三节平面与平面垂直的性质
三维目标
1.理解并能证明平面与平面垂直的性质定理；
2.会运用性质定理解决一些简单问题.
________________________________________________________________________________ 目标三导 学做思1
问题1. 如图所示，侧面与地面什么关系？
图1 图2
问题2. 证明面面垂直的性质定理, 并用符号语言、图形语言表示面面垂直的性质定理.
D 1 C 1
A
1C
问题3. 如何在黑板面上画一个面与地面垂直的直线？
【学做思2】
1.如图
2.3-22，已知α⊥β，a ⊥β,a ⊄α,试判断直线a 与平面α的位置关系.
图2.3-22
*2. 正方形ABCD 和四边形ACEF 所在的平面互相垂直，AC EF //，2=AB ，1==EF CE
求证：⊥CF 平面BDE
达标检测
*1.如图所示，在四棱锥ABCD S -中，底面ABCD 是矩形，侧面⊥SDC 底面ABCD . 求证：平面⊥SCD 平面SBC .
2.求证：三个两两垂直的平面的交线两两垂直.。
高中数学必修二 8 6 3 平面与平面垂直(第2课时)平面与平面垂直的性质 导学案新
【新教材】 8.6.3 平面与平面垂直（人教A 版）第2课时 平面与平面垂直的性质1．理解平面和平面垂直的性质定理并能运用其解决相关问题.2．通过对性质定理的理解和应用，培养学生的空间转化能力和逻辑推理能力．1.逻辑推理：探究归纳平面和平面垂直的性质定理，线线垂直、线面垂直、面面垂直之间的转化；2.直观想象：题中几何体的点、线、面的位置关系.重点：平面和平面垂直的性质定理.难点：平面和平面垂直的性质定理的应用.一、 预习导入阅读课本141-142页，填写。
1、平面与平面垂直的性质定理探究: (1)如果α⊥β,则α内的直线必垂直于β内的无数条直线吗?(2)如果α⊥β,过β内的任意一点作α与β交线的垂线,则这条直线必垂直于α吗?1.如图,在三棱锥P-ABC 中,平面PAB ⊥平面ABC,平面PAC ⊥平面ABC,则下列结论中错误的是( )A.AP ⊥ACB.AP ⊥ABC.AP ⊥平面ABCD.AP 与BC 所成的角为45°2.在正方体ABCD-A 1B 1C 1D 1中,直线l ⊥平面A 1C 1(l 与棱不重合),则( ) A.B 1B ⊥l B.B 1B ∥l C.B 1B 与l 异面 D.B 1B 与l 相交 3.已知m,n 是两条不同的直线,α,β是两个不同的平面,且m ∥α,n ⊂β,则下列叙述正确的是( )A.若α∥β,则m ∥nB.若m ∥n,则α∥βC.若n ⊥α,则m ⊥βD.若m ⊥β,则α⊥β4.如图所示,在三棱柱ABC-A 1B 1C 1中,∠BAC=90°, BC 1⊥AC,则C 1在平面ABC 上的射影H 必在直线 上.题型一平面与平面平行的性质定理的应用-中，PA⊥平面ABC，平面PAB⊥平面PBC.求证：BC⊥平面PAB.例1 在三棱锥P ABC跟踪训练一1.如图,P是四边形ABCD所在平面外一点,四边形ABCD是∠DAB= 60°,且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.题型二线面、面面垂直的的综合应用例2 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD= PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.跟踪训练二1、如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点, EP⊥平面ABCD.(1)求证:AQ∥平面CEP;(2)求证:平面AEQ⊥平面DEP.1.已知两个平面垂直,下列说法:①一个平面内的已知直线必垂直于另一个平面内的任意一条直线②一个平面内的已知直线必垂直于另一个平面的无数条直线③一个平面内的任一条直线必垂直于另一个平面④过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.其中正确说法个数是()A.3B.2C.1D.02.在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC是()A.直角三角形B.等腰三角形B.等边三角形D.等腰直角三角形3.如图,平行四边形ABCD中,AB⊥BD.沿BD将△ABD折起,使平面ABD⊥平面BCD,连接AC,则在四面体ABCD的四个面所在平面中,互相垂直的平面的对数为()A.1B.2C.3D.44.如图所示,三棱锥P ABC的底面在平面α上,且AC⊥PC,平面PAC⊥平面PBC,P,A,B是定点,则动点C运动形成的图形是.5.如图,在四棱柱ABCD A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=,AD=CD=1.(1)求证:BD⊥AA1;(2)若E为棱BC的中点,求证:AE∥平面DCC1D1.答案小试牛刀1．D.2．B.3．D.4. AB.自主探究例1 【答案】证明见解析⊥于点D. 【解析】证明：如图所示，在平面AB内作AD PB=，∵平面PAB⊥平面PBC，且平面PAB⋂平面PBC PB∴AD⊥平面PBC.⊥.又BC⊂平面PBC，∴AD BC∵PA⊥平面ABC，BC⊂平面ABC，⊥.∴PA BC⋂=，∴BC⊥平面P AB.∵PA AD A跟踪训练一1.【答案】证明见解析.【解析】(1)如图所示,连接BD.因为四边形ABCD是菱形,且∠DAB=60°,所以△ABD是正三角形,因为G是AD的中点,所以BG⊥AD.又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD.所以BG⊥平面PAD.(2)连接PG.因为△PAD为正三角形,G为AD的中点,所以PG⊥AD.由(1)知BG⊥AD,而PG∩BG=G,PG⊂平面PBG,BG⊂平面PBG.所以AD⊥平面PBG.又因为PB⊂平面PBG,所以AD⊥PB.例2 【答案】（1）见解析（2）见解析. (3) .【解析】(1)证明:因为长方形ABCD中,BC∥AD,又BC⊄平面PDA,AD⊂平面PDA,所以BC∥平面PDA.(2)证明:取CD的中点H,连接PH,因为PD=PC,所以PH⊥CD.又因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,所以PH ⊥平面ABCD.又因为BC ⊂平面ABCD,所以PH ⊥BC.又因为长方形ABCD 中,BC ⊥CD,PH∩CD=H,所以BC ⊥平面PDC.又因为PD ⊂平面PDC,所以BC ⊥PD.(3)解:连接AC.由(2)知PH 为三棱锥P-ADC 的高.因为△ADC =12·AD·CD=12×3×6=9,所以P ADC V -=13·S △ADC ·PH=13×由(2)知BC ⊥PD,又因为AD ∥BC,所以AD ⊥PD,所以S △PDA =12·PD·AD=12×4×3=6.设点C 到平面PDA 的距离为h.因为C PDA V -=P ADC V -,所以13·S △PDA ·所以3PDA S ∆⋅63⨯=. 跟踪训练二1、【答案】证明见解析【解析】证明:(1)在矩形ABCD 中,因为AP=PB,DQ=QC,所以AP CQ.所以AQCP 为平行四边形.所以CP ∥AQ. 因为CP ⊂平面CEP,AQ ⊄平面CEP,所以AQ ∥平面CEP.(2)因为EP ⊥平面ABCD,AQ ⊂平面ABCD,所以AQ ⊥EP.因为AB=2BC,P为AB的中点,所以AP=AD.连接PQ,则四边形ADQP为正方形. 所以AQ⊥DP.又EP∩DP=P,所以AQ⊥平面DEP.因为AQ⊂平面AEQ,所以平面AEQ⊥平面DEP.当堂检测1-3. CAC4.以AB为直径的圆(除去A,B两点).5．【答案】证明见解析.【解析】证明:(1)在四边形ABCD中,因为AB=BC,AD=DC,所以BD⊥AC,又平面AA1C1C⊥平面ABCD,且平面AA1C1C∩平面ABCD=AC,BD⊂平面ABCD,所以BD⊥平面AA1C1C,又因为AA1⊂平面AA1C1C,所以BD⊥AA1.(2)在三角形ABC中,因为AB=AC,且E为棱BC的中点,所以AE⊥BC,又因为在四边形ABCD中,AB=BC=CA=,AD=CD=1.所以∠ACB=60°,∠ACD=30°,所以DC⊥BC,所以AE∥CD.因为CD⊂平面DCC1D1,AE⊄平面DCC1D1,故得AE∥平面DCC1D1.。
高中数学必修二教案：2.3.4 平面与平面垂直的性质
集体备课电子教案高一年级数学备课组（总第课时）主备人：时间：年月日的底面是矩形，侧面VAB⊥底面ABCD中，底面ABCD是边长为a为正三角形，其所在的平面垂直于底面ABCD 的底面是直角梯形，∠ABC＝∠BCD＝90°精美句子1、善思则能“从无字句处读书”。
读沙漠，读出了它坦荡豪放的胸怀；读太阳，读出了它普照万物的无私；读春雨，读出了它润物无声的柔情。
读大海，读出了它气势磅礴的豪情。
读石灰，读出了它粉身碎骨不变色的清白。
2、幸福幸福是“临行密密缝，意恐迟迟归”的牵挂；幸福是“春种一粒粟，秋收千颗子”的收获. 幸福是“采菊东篱下，悠然见南山”的闲适；幸福是“奇闻共欣赏，疑义相与析”的愉悦。
幸福是“随风潜入夜，润物细无声”的奉献；幸福是“夜来风雨声，花落知多少”的恬淡。
幸福是“零落成泥碾作尘，只有香如故”的圣洁。
幸福是“壮志饥餐胡虏肉，笑谈渴饮匈奴血”的豪壮。
幸福是“先天下之忧而忧，后天下之乐而乐”的胸怀。
幸福是“人生自古谁无死，留取丹心照汗青”的气节。
3、大自然的语言丰富多彩：从秋叶的飘零中，我们读出了季节的变换；从归雁的行列中，我读出了集体的力量；从冰雪的消融中，我们读出了春天的脚步；从穿石的滴水中，我们读出了坚持的可贵；从蜂蜜的浓香中，我们读出了勤劳的甜美。
4、成功与失败种子，如果害怕埋没，那它永远不能发芽。
鲜花，如果害怕凋谢，那它永远不能开放。
矿石，如果害怕焚烧（熔炉），那它永远不能成钢（炼成金子）。
蜡烛，如果害怕熄灭（燃烧），那它永远不能发光。
航船，如果害怕风浪，那它永远不能到达彼岸。
5、墙角的花，当你孤芳自赏时，天地便小了。
井底的蛙，当你自我欢唱时，视野便窄了。
笼中的鸟，当你安于供养时，自由便没了。
山中的石！当你背靠群峰时，意志就坚了。
水中的萍！当你随波逐流后，根基就没了。
空中的鸟！当你展翅蓝天中，宇宙就大了。
空中的雁！当你离开队伍时，危险就大了。
地下的煤！你燃烧自己后，贡献就大了6、朋友是什么？朋友是快乐日子里的一把吉它，尽情地为你弹奏生活的愉悦；朋友是忧伤日子里的一股春风，轻轻地为你拂去心中的愁云。
高中数学 第二章2.3.2平面与平面垂直的判定导学案 新人教A版必修2
2.3.2 平面与平面垂直的判定问题导学一、面面垂直的判定活动与探究1在直三棱柱ABC－A1B1C1中，底面△ABC为等边三角形，E∈BB1，且BE＝EB1．求证：平面A1EC⊥平面ACC1A1(注：侧棱和底面垂直的棱柱叫直棱柱)．迁移与应用1．如图，已知AB⊥平面BCD，BC⊥CD，则图中互相垂直的平面共有__________对．2．在四棱锥P－ABCD中，若PA⊥平面ABCD，且四边形ABCD是菱形，求证：平面PAC⊥平面PBD．证明面面垂直有两种基本方法：①定义法：先作(或找)出二面角的平面角，再证明该角是90°；②判定定理法：在一个平面内找(或作)出一条直线，再证明该直线与另一个平面垂直．二、求二面角的大小活动与探究2四边形ABCD是正方形，PA⊥平面ABCD，且PA=AB．(1)求二面角A－PD－C平面角的度数；(2)求二面角B－PA－D平面角的度数；(3)求二面角B－PA－C平面角的度数．迁移与应用1．在正方体ABCD－A1B1C1D1中，O是BD的中点，二面角C1－AB－C的平面角是__________；二面角C1－BD－C的平面角是__________，其正切值为__________．2．在三棱锥S－ABC中，SA⊥平面ABC，BC⊥AC，则二面角S－BC－A的平面角是__________．求二面角的大小的方法为：一作，即先作出二面角的平面角；二证，即说明所作角是二面角的平面角；三求，即利用二面角的平面角所在的三角形算出角的三角函数值，再求出角的大小．三、线面垂直与面面垂直的综合应用活动与探究3如图，P是矩形ABCD所在平面外一点，PA⊥平面ABCD，E，F分别是AB，PD的中点，又二面角P－CD－B为45°．(1)求证：AF∥平面PEC；(2)求证：平面PEC⊥平面PCD．迁移与应用1．过一条直线和一个平面垂直的平面有( )A．一个B．无数个C．一个或无数个D．0个2．如图所示，在四棱锥S－ABCD中，底面四边形ABCD是平行四边形，SC⊥平面ABCD，E为SA的中点．求证：平面EBD⊥平面ABCD．证“面面垂直”转化为“线面垂直”，证“线面垂直”转化为“线线垂直”，即线线垂直→线面垂直→面面垂直．当堂检测1．下列命题中①两个相交平面组成的图形叫做二面角；②异面直线a，b分别和一个二面角的两个面垂直，则a，b组成的角与这个二面角的平面角相等或互补；③二面角的平面角是从棱上一点出发，分别在两个面内作射线所成角的最小角；④二面角的大小与其平面角的顶点在棱上的位置没有关系．其中正确的是( )A．①③ B．②④ C．③④ D．①②2．对于直线a，b，c和平面α，β，已知a⊂α，b⊂β，c⊂β，a⊥b，a⊥c，则α与β的位置关系是( )A．α⊥β B．α∥βC．α∩β＝l D．不确定3．以等腰直角三角形斜边上的高为棱，把它折成直二面角，则折后两条直角边的夹角为( )A．30° B．45° C．60° D．90°4．在正方体ABCD－A1B1C1D1中，平面AA1C1C与平面C1BD的位置关系是________．5．在四面体A－BCD中，BD＝2a，其余棱长均为a，则二面角A－BD－C的大小为__________．提示：用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记．答案：课前预习导学【预习导引】1．两个半平面二面角的棱二面角的面α－AB－βP－AB－Qα－l－βP－l －Q2．垂直于l射线OA和OB直二面角预习交流1(1)提示：0°≤θ＜180°(2)提示：二面角α－l－β的平面角∠AOB满足的条件是：①O∈l；②OA⊂α，OB⊂β；③OA⊥l，OB⊥l．(3)提示：根据等角定理，二面角的平面角的大小与在棱上选取的点的位置无关．3．直二面角预习交流2提示：90°4．垂线a⊥α，a⊂β，则α⊥β预习交流3 提示：要证明两个平面垂直，只需在一个平面内找(或作)一条直线与另一个平面垂直，并证明即可．课堂合作探究【问题导学】活动与探究1 思路分析：要证明平面A1EC⊥平面ACC1A1，只需在平面A1EC内找一条线与平面ACC1A1垂直．证明：取A1C的中点F，AC的中点G，连接EF，FG，BG，则GF 12AA1．又BE 12AA1，∴GF BE．∴EF∥GB．∵△ABC是等边三角形，∴BG⊥AC．∴EF⊥AC．又AA1⊥平面ABC，∴AA1⊥BG．∴EF⊥AA1．∵AC∩AA1＝A，∴EF⊥平面ACC1A1．∵EF⊂平面A1EC，∴平面A1EC⊥平面ACC1A1．迁移与应用1．32．证明：∵PA⊥平面ABCD，且BD⊂平面ABCD，∴PA ⊥BD ．∵四边形ABCD 是菱形， ∴AC ⊥BD ．∵PA ∩AC ＝A ，∴BD ⊥平面PAC ．∵BD ⊂平面PBD ，∴平面PAC ⊥平面PBD ．活动与探究2 思路分析：(1)证明面PAD ⊥面PCD ；(2)，(3)先找出二面角的平面角，再证明该角满足平面角的定义，最后在三角形中求角的大小．解：(1)∵PA ⊥平面ABCD ，∴PA ⊥CD ．又四边形ABCD 为正方形，∴CD ⊥AD ．PA ∩AD ＝A ，∴CD ⊥平面PAD ． 又CD ⊂平面PCD ，∴平面PAD ⊥平面PCD ．∴二面角A －PD －C 平面角的度数为90°． (2)∵PA ⊥平面ABCD ， ∴AB ⊥PA ，AD ⊥PA ．∴∠BAD 为二面角B －PA －D 的平面角．又由题意∠BAD ＝90°， ∴二面角B －PA －D 平面角的度数为90°． (3)∵PA ⊥平面ABCD ， ∴AB ⊥PA ，AC ⊥PA ．∴∠BAC 为二面角B －PA －C 的平面角．又四边形ABCD 为正方形，∴∠BAC ＝45°，即二面角B －PA －C 平面角的度数为45°．迁移与应用 1．∠C 1BC ∠C 1OC 2 2．∠SCA活动与探究3 思路分析：(1)取PC 中点G ，可证AF ∥EG ；(2)证明AF ⊥平面PCD ，则EG ⊥平面PCD ，可得平面PEC ⊥平面PCD ．证明：(1)取PC 的中点G ；连接EG ，FG ．∵F 是PD 的中点，∴FG12CD ．又AE 12CD ， ∴AE FG ．∴四边形AEGF 是平行四边形．∴AF ∥EG ． 又AF ⊄平面PEC ，EG ⊂平面PEC ，∴AF ∥平面PEC ． (2)∵PA ⊥平面ABCD ，∴PA ⊥CD ．又∵CD ⊥AD ，且PA ∩AD ＝A ， ∴CD ⊥平面PAD ． ∴CD ⊥AF ，CD ⊥PD ．∴∠PDA 是二面角P －CD －B 的平面角，即∠PDA ＝45°． 又∵PA ⊥AD ，F 是PD 中点，∴AF⊥PD．∵PD∩CD＝D，∴AF⊥平面PCD．∵AF∥EG，∴EG⊥平面PCD．∵EG⊂平面PEC，∴平面PEC⊥平面PCD．迁移与应用1．C2．证明：如图所示，连接AC，与BD交于点F，连接EF．因为F为ABCD对角线AC 与BD的交点，所以F为AC的中点．又E为SA的中点，所以EF为△SAC的中位线，所以EF∥SC．又SC⊥平面ABCD，所以EF⊥平面ABCD．又EF⊂平面EBD，所以平面EBD⊥平面ABCD．【当堂检测】1．B 2．D 3．C 4．垂直5．90°。
高中数学必修二导学案直线与平面、平面与平面垂直性质
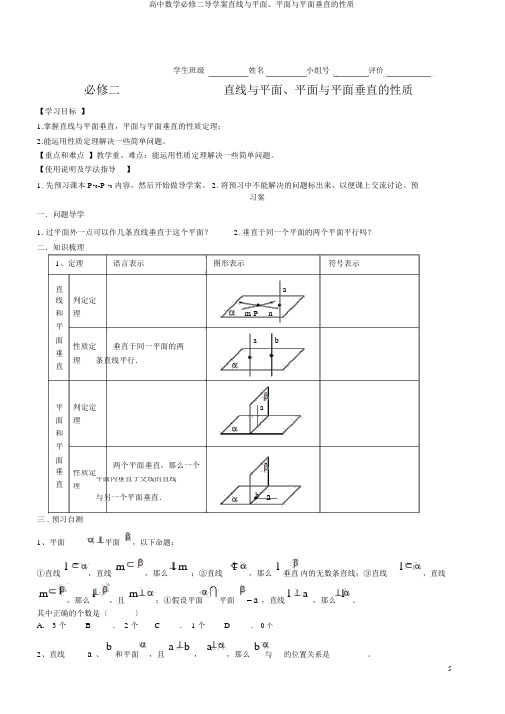
学生班级姓名 小组号 评价必修二直线与平面、平面与平面垂直的性质【学习目标 】1.掌握直线与平面垂直，平面与平面垂直的性质定理；2.能运用性质定理解决一些简单问题。
【重点和难点 】教学重、难点：能运用性质定理解决一些简单问题。
【使用说明及学法指导 】1. 先预习课本 P 70-P 73 内容，然后开始做导学案。
2. 将预习中不能解决的问题标出来，以便课上交流讨论。
预习案一．问题导学1. 过平面外一点可以作几条直线垂直于这个平面？2. 垂直于同一个平面的两个平面平行吗？二．知识梳理1、定理语言表示图形表示符号表示直 a线 判定定和 理 m P n平面 性质定 垂直于同一平面的两ab垂理条直线平行．直平 判定定 a面 理 和 平面两个平面垂直，那么一个垂性质定直 平面内垂直于交线的直线理b a与另一个平面垂直．三 . 预习自测 1、平面平面，以下命题：①直线l，直线m，那么lm；②直线l，那么 l 垂直 内的无数条直线；③直线 l，直线m，那么l，且m；④假设平面 平面= a ，直线la，那么l。
其中正确的个数是〔 〕A ． 3个B． 2个C． 1个D． 0个2、直线a 、b 和平面 ，且ab，a，那么 b与的位置关系是 _______。
5四 . 我的疑问：探究案一．合作探究探究 1.直线与平面垂直的性质定理的简单应用例 1：如图，在四棱锥P ABCD 中，PA 平面 ABCD ， AD AB ， AC CD ，ABC 60 0 ，AP AB BC ，点 E 是 PC 的中点，证明：〔1〕 AE CD ；〔 2〕 PD 平面 ABE 。
PEA DCB探究 2. 平面与平面垂直的性质定理的简单应用例 2：如图，在三棱锥 A BCD 中，AB平面BCD，平面ABC平面AC D，求证：BC CD 。
AB DC二、课堂小结：训练案一、课堂训练与检测1、以下命题：①a // b，a，那么b；② a，b，那么 a // b；③ a，a b ，那么 b //；④ a //，a b ，那么 b；其中正确命题的序号是_________________。
2高中数学必修2精品教案：2.3 平面与平面垂直的判定 教案2
《2.3.2平面与平面垂直的判定》教学设计教学内容人教版新教材高二数学第二册第二章第三节第2课教材分析直线与平面垂直问题是直线与平面的重要内容，也是高考考查的重点，求解的关键是根据线与面之间的互化关系，借助创设辅助线与面，找出符号语言与图形语言之间的关系把问题解决。
通过对有关概念和定理的概括、证明和应用，使学生体会“转化”的观点，提高学生的空间想象力和逻辑推理能力。
学情分析1.学生思维活跃，参与意识、自主探究能力较强，故采用启发、探究式教学。
2.学生的抽象概括能力和空间想象力有待提高，故采用多媒体辅助教学。
教学目标1.知识与技能（1）使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；（2）使学生掌握两个平面垂直的判定定理及其简单的应用；（3）使学生理会“类比归纳”思想在数学问题解决上的作用。
（4）通过实例让学生直观感知“二面角”概念的形成过程；（5）类比已学知识，归纳“二面角”的度量方法及两个平面垂直的判定定理。
2.情感态度与价值观（1）培养学生的几何直观能力，使他们在直观感知，操作确认的基础上学会归纳.（2）发展学生的合情推理能力和空间想象力，培养学生的质疑思辨、创新的精神.（3）让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣.教学重、难点1.重点：平面与平面垂直的判定。
2.难点：找出二面角的平面角。
教学理念学生是学习和发展的主体，教师是教学活动的组织者和引导者.设计思路：通过“直观感知、操作确认，推理证明”，培养学生空间概念、空间想象能力以及逻辑推理能力。
让学生在观察物体模型的基础上，进行操作确认，获得对性质定理正确性的认识；“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念认识；利用框图对本章知识进行系统的小结，直观、简明再现所学知识，化抽象学习为直观学习，易于识记；同时凸现数学知识的发展和联系。
通过揭示概念的形成、发展和应用过程，使学生理会教学存在于观实生活周围，从中激发学生积极思维，培养学生的观察、分析、解决问题能力。
高中数学必修2导学案 2.3.2平面与平面垂直的判定
§2.3.2 平面与平面垂直的判定学习目标：1. 理解二面角的有关概念，会作二面角的平面角，能求简单二面角平面角的大小；2. 理解面面垂直的定义，掌握面面垂直的判定定理，初步学会用定理证明垂直关系；3. 熟悉线线垂直、线面垂直的转化.学习重点: 平面与平面垂直的判定；学习难点: 如何度量二面角的大小。
课前预习（预习教材P 67~ P 69，找出疑惑之处）复习1：⑴若直线垂直于平面，则这条直线________平面内的任何直线；⑵直线与平面垂直的判定定理为_________________________________________________.复习2：⑴什么是直线与平面所成的角?⑵直线与平面所成的角的范围为_______________.课内探究探究1：二面角的有关概念图11-1问题：上图中，水坝面与水平面、卫星轨道平面与地球赤道平面都有一定的角度.这两个角度的共同特征是什么?新知1：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫二面角的棱，这两个半平面叫二面角的面.图11-2中的二面角可记作：二面角AB αβ--或l αβ--或P AB Q --.图11-2问题：二面角的大小怎么确定呢？新知2：如图11-3，在二面角lαβ--的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作垂直于棱l的射线,OA OB，则射线OA和OB构成的AOB∠叫做二面角的平面角.平面角是直角的二面角叫直二面角.反思：⑴两个平面相交，构成几个二面角?它们的平面角的大小有什么关系？⑵你觉的二面角的大小范围是多少？⑶二面角平面角的大小和O点的选择有关吗？除了以上的作法，二面角的平面角还能怎么作？探究2：平面与平面垂直的判定问题：教室的墙给人以垂直于地面的形象，想一想教室相邻的两个墙面与地面可以构成几个二面角？它们的大小是多少？新知3：两个平面所成二面角是直二面角，则这两个平面互相垂直.如图11-4，α垂直β，记作αβ⊥.图11-4问题：除了定义，你还能想出什么方法判定两个平面垂直呢？新知4：两个平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直.l反思：定理的实质是什么?例1 如图11-5，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于,A B的任意一点，求证：平面PAC⊥平面PBC.图11-5例2 如图11-6，在正方体中，求面A D CB''与面ABCD所成二面角的大小（取锐角）.图11-6小结：求二面角的关键是作出二面角的平面角.※动手试试练. 如图11-7，在空间四边形SABC中，ASC∠ =90°，60ASB BSC∠==°，SA SB SC==，B'C'A'DCBAD'⑴求证：平面ASC ⊥平面ABC .⑵求二面角S AB C --的平面角的正弦值.图11-7当堂检测1. 以下四个命题，正确的是（ ）.A.两个平面所成的二面角只有一个B.两个相交平面组成的图形叫做二面角C.二面角的平面角是这两个面中直线所成的角中最小的一个D.二面角的大小和其平面角的顶点在棱上的位置无关2. 对于直线,m n ,平面,αβ,能得出αβ⊥的一个条件是（ ）.A.,//,//m n m n αβ⊥B.,,m n m n αβα⊥=⊂C.//,,m n n m βα⊥⊂D.//,,m n m n αβ⊥⊥3. 在正方体1111ABCD A B C D -中，过,,A C D 的平面与过1,,D B B 的平面的位置关系是（ ）.A.相交不垂直B.相交成60°角C.互相垂直D.互相平行4. 二面角的大小范围是________________.5. 若平面内的一条直线和这个平面的一条斜线的射影垂直，则它和这条斜线的位置关系为_______.课后反思1. 二面角的有关概念，二面角的求法；2. 两个平面垂直的判定定理及应用.知识拓展二面角的平面角的一个常用作法：如图过平面α内一点A ，作AB β⊥于点B ，再作BO l ⊥于O ，连接OA ，则AOB ∠即为所求平面角.(为什么?)课后训练 1．过平面α外两点且垂直于平面α的平面 （ ）()A 有且只有一个 ()B 不是一个便是两个 ()C 有且仅有两个 ()D 一个或无数个2．若平面α⊥平面β，直线n ⊂α，m ⊂β,m n ⊥，则（ ）()A n ⊥β ()B n ⊥β且m ⊥α ()C m ⊥α ()D n ⊥β与m ⊥α中至少有一个成立3．对于直线,m n 和平面,αβ，α⊥β的一个充分条件是（ ）()A m n ⊥，//,//m n αβ ()B ,,m n m n αβα⊥=⊂ ()C //,,m n n m βα⊥⊄ ()D ,,m n m n αβ⊥⊥⊥4．设,,l m n 表示三条直线，,,αβγ表示三个平面，给出下列四个命题：①若,l m αα⊥⊥，则//l m ；②若,m n β⊂是l 在β内的射影，m l ⊥，则m n ⊥；③若,//m m n α⊂，则//n α； ④若,αγβγ⊥⊥，则//αβ． 其中真命题是（ ） ()A ①② ()B ②③ ()C ①③ ()D ③④5：已知平面α∩平面β=直线a ，α、β垂直于平面γ，又平行于直线b ，求证:(1) a ⊥γ；(2)b ⊥γ．6. 如图11-8，AC ⊥面BCD ，BD CD ⊥，设ABC ∠=1θ，2CBD θ∠=，3ABD θ∠=，求证：312cos cos cos θθθ=图11-87. 如图11-8，在正方体中，,E F 是棱A B ''与D C ''的中点，求面EFCB 与面ABCD 所成二面角的正切值.（取锐角）图11-8。
高中数学新人教版必修2教案2.3.4平面与平面垂直的性质(教案).doc
备课人
滕领涛
授课时间
12.14
课题
§2、3.4平面与平面垂直的性质
教
学
目
标
知识与技能
使学生掌握平面与平面垂直的性质定理；能运用性质定理解决一些简单问题
过程与方法
启发引导，充分发挥学生的主体作用
情感态度价值观
通过“直观感知、操作确认，推理证明”，培养学生空间概念、空间想象能力以及逻辑推理能力
重点
性质定理的证明
难点
性质定理的证明及应用
教
学
设
计
教学内容
教学环节与活动设计
（一）复习导入
问题：直线与平面垂直的性质定理，如何推导的？
（二）研探新知
类比上面定理：若在两个平面互相垂直的条件下，又会得出怎样的结论呢？
课本P71思考（1）（2）
例如：如何在黑板面上画一条与地面垂直的直线？
课本P72思考
结论：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内
（三）应用巩固
例子：课本P.74例4
做法：教师给出问题，学生思考探究、判断并说理由，教师最后评议。
课本P72探究
要注意判定定理和性质定理的交替运用，同时还要贯通三种垂直关系，即直线与直线垂直，直线与平面垂直，平面与平面垂直的相互转化
教师引导学生观察教室相邻两面墙的交线，容易发现该交线与地面垂直.
让学生发现只要在黑板上画出一条与这交线平行的直线，则所画直线必与地面垂直。然后师生互动，共同完成性质定理的确认与证明，并归纳性质定理：
两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
1
教
学设Βιβλιοθήκη 计教学内容教学环节与活动设计
[精品]新人教A版必修二高中数学2.3.2平面与平面垂直的判定导学案
![[精品]新人教A版必修二高中数学2.3.2平面与平面垂直的判定导学案](https://img.taocdn.com/s3/m/9fddadfcd15abe23482f4d84.png)
2. 3.2平面与平面垂直的判定【教学目标】（1）使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；（2）使学生掌握两个平面垂直的判定定理及其简单的应用；（3）使学生理会“类比归纳”思想在数学问题解决上的作用。
（4）通过实例让学生直观感知“二面角”概念的形成过程；（5）类比已学知识，归纳“二面角”的度量方法及两个平面垂直的判定定理。
【教学重难点】重点：平面与平面垂直的判定。
难点：找出二面角的平面角。
【教学过程】（一）创设情景，揭示课题问题1：平面几何中“角”是怎样定义的？问题2：在立体几何中，“异面直线所成的角”、“直线和平面所成的角”又是怎样定义的？它们有什么共同的特征？以上问题让学生自由发言，教师再作小结，并顺势抛出问题：在生产实践中，有许多问题要涉及到两个平面相交所成的角的情形，你能举出这个问题的一些例子吗？如修水坝、发射人造卫星等，而这样的角有何特点，该如何表示呢？下面我们先利用具体的实物来进行观察,研探。
（二）研探新知1、二面角的有关概念老师展示一张纸面，并对折让学生观察其状，然后引导学生用数学思维思考，并对以上问题类比，归纳出二面角的概念及记法表示（如下表所示）2、二面角的度量二面角定理地反映了两个平面相交的位置关系，如我们常说“把门开大一些”，是指二面角大一些，那我们应如何度量二两角的大小呢？师生活动：师生共同做一个小实验（预先准备好的二面角的模型）在其棱上位取一点为顶点，在两个半平面内各作一射线（如图2.3-3），通过实验操作，研探二面角大小的度量方法——二面角的平面角。
教师特别指出：（1）在表示二面角的平面角时，要求OA ⊥L ，OB⊥L ；（2）∠AOB的大小与点O在L上位置无关；（3）当二面角的平面角是直角时，这两个平面的位置关系怎样？承上启下，引导学生观察，类比、自主探究，获得两个平面互相垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。
高一数学必修二2.3.1直线与平面垂直的判定2.3.2平面与平面垂直的判定导学案(解析版)
2.3.1直线与平面垂直的判定 2.3.2平面与平面垂直的判定一、课标解读（1）使学生掌握直线和平面垂直的定义及判定定理； （2）使学生掌握直线和平面所成角的概念（3）使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；（4）使学生掌握两个平面垂直的判定定理及其简单的应用；（5）培养学生的几何直观能力，使他们在直观感知，操作确认的基础上学会归纳、概括结论。
二、自学导引问题1：（1）请同学们观察图片，说出旗杆与地面、树干与地面的位置有什么关系？（2）请把自己的数学书打开直立在桌面上，观察书脊与桌面的位置有什么关系？ （3）思考：一条直线与平面垂直时，这条直线与平面内的直线有什么样的位置关系？有什么生活实例能验证这一关系呢？直线与平面垂直的定义：用符号语言表示为：问题2：如图，请同学们拿出准备好的一块（任意）三角形的纸片，我们一起来做一个实验：过△ABC 的顶点A 翻折纸片，得到折痕AD ，将翻折后的纸片竖起放置在桌面上，（BD 、DC 与桌面接触）.观察并思考：①折痕AD 与桌面垂直吗？DCBA②如何翻折才能使折痕AD 与桌面所在的平面垂直？ 直线与平面垂直的判定定理：用符号语言表示为：问题3：直线与平面所成角的概念？问题4：怎样作出二面角的平面角？问题5：平面与平面垂直的定义？问题6：两个平面互相垂直的判定方法有哪些？ 三、典例精析例1 已知两两垂直所在平面外一点，是PC PB PA ABC P ,,∆,H 是ABC ∆ 的垂心.求证：⊥PH 平面ABC变式训练1 如图所示，ABC PA O C O AB 平面上的一点，为圆的直径，为圆⊥, F CP AF E BP AE 于于⊥⊥,.求证：AEF BP 平面⊥例2 如图所示,已知 60,90=∠=∠=∠CSA BSA BSC ,又SC SB SA ==. 求证:平面SBC ABC 平面⊥变式训练２ 如图所示,在四面体ABCD 中,AC CD CB AD AB a BD =====,2 =a ,求证:平面BCD ABD 平面⊥._ C例3 如图所示,已知的斜线，是平面内，在平面ααOA BOC ∠且AOCAOB ∠=∠=60,a OC OB OA ===,a BC 2=,求所成的角与平面αOA .变式训练3 如图所示，在矩形ABCD 中，3,33==BC AD ,沿着对角线BD 将BCD ∆折起，使点C 移到'C 点，且'C 点在平面ABD 上的射影O 恰在AB 上.（1）求证：D AC BC ''平面⊥（2）求直线AB 与平面D BC '所成角的正弦值四、自主反馈1. 如图BC 是Rt ⊿ABC 的斜边，过A 作⊿ABC 所在平面α 垂线AP ，连PB 、PC ，过A 作AD ⊥BC 于D ，连PD ，那么图中直角三角形的个数是 （ ）A ．4个B ．6个C ．7个D ．8个2.下列说法正确的是 ( ) A ．直线a 平行于平面M ，则a 平行于M 内的任意一条直线 B ．直线a 与平面M 相交，则a 不平行于M 内的任意一条直线C ．直线a 不垂直于平面M ，则a 不垂直于M 内的任意一条直线D ．直线a 不垂直于平面M ，则过a 的平面不垂直于M3.直三棱柱ABC —A 1B 1C 1中，∠ACB =90°，AC =AA 1=a ，则点A 到平面A 1BC 的距离是 ( )A.aB. 2aC.22a D. 3a 4.已知PA 、PB 、PC 是从点P 发出的三条射线，每两条射线的夹角都是60︒，则直线PC 与平面PAB 所成的角的余弦值为 。
高中人教版数学必修2《平面与平面垂直的性质》精品导学案
平面与平面垂直的性质【学习目标】1.探究平面与平面垂直的性质定理，进一步培养学生的空间想象能力.2.面面垂直的性质定理的应用，培养学生的推理能力.3.通过平面与平面垂直的性质定理的学习,培养学生转化的思想.【学习重点】平面与平面垂直的性质定理. 【学习难点】平面与平面性质定理的应用. 一、 教材导读1、长方体1111ABCD A B C D -中，平面11CDD C ⊥平面ABCD ，则平面11CDD C 中所有的直线都与平面ABCD 垂直吗？什么情况下平面11CDD C 里的直线与平面ABCD 垂直？2、平面与平面垂直的性质定理： 线面垂直性质定理：文字语言：简单概括： 符号语言：图形语言：反思：定理的实质是什么？__________________________________________作用：___________________________________________________________ 二、 定理应用例1 如图，已知α⊥β，a ⊥β,a ⊄α,试判断直线a 与平面α的位置关系.A C 1CB变式1 如图已知平面α交平面β于直线a.α、β同垂直于平面γ，又同平行于直线b.求证：(1)a⊥γ；(2)b⊥γ.例2 如图10，四棱锥P—ABCD的底面是AB=2，BC=2的矩形，侧面PAB 是等边三角形，且侧面PAB⊥底面ABCD.图10 图11（1）证明侧面PAB⊥侧面PBC；（2）求侧棱PC与底面ABCD所成的角；（3）求直线AB与平面PCD的距离.变式2 如图斜三棱柱ABC—A1B1C1的棱长都是a，侧棱与底面成60°角，侧B1⊥面ABC.求平面AB1C1与底面ABC所成二面角面BCC的大小.例3如图，把等腰直角三角形ABC沿斜边AB旋转至△ABD的位置，使CD=AC, （1）求证：平面ABD⊥平面ABC；（2）求二面角CBDA的余弦值.变式3如图14，在矩形ABCD中，AB=33,BC=3，沿对角线BD把△BCD折起，使C移到C′，且C′在面ABC内的射影O恰好落在AB上.（1）求证：AC′⊥BC′；（2）求AB与平面BC′D所成的角的正弦值；（3）求二面角C′BDA的正切值.例4 如图15,三棱柱ABC—A1B1C1中，∠BAC=90°，AB=BB1=1，直线B1C与平面ABC成30°角，求二面角BB1CA的正弦值.变式4如图边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=22，M为BC的中点.(1)证明：AM⊥PM；(2)求二面角P-AM-D的大小.四．当堂检测1、判断下列命题的真假①两个平面垂直，过其中一个平面内一点作与它们交线垂直的直线，必垂直于另一个平面.②两个平面垂直，分别在这两个平面内且互相垂直的两直线，一定分别与另一平面垂直.③两个平面垂直，分别在这两个平面内的两直线互相垂直。
高中数学必修2导学案 直线、平面垂直的判定及其性质
§2.3.4 直线、平面垂直的判定及其性质（练习）学习目标：1. 熟练掌握直线与平面、平面与平面垂直的判定和性质定理，能够灵活运用；2. 掌握垂直关系中线线垂直、线面垂直、面面垂直的互化，掌握“平行”与“垂直”关系的相互转换；3. 能求直线与平面所成的角及简单的二面角的平面角大小.课前预习（预习教材P 64~ P 72，找出疑惑之处）复习1：直线与平面垂直的有关结论⑴如果一条直线____________________________________________，则这条直线和这个平面垂直； ⑵线面垂直的判定定理是_______________________________________________________________； ⑶两条平行线中的一条垂直于一个平面，则____________________________________；⑷一条直线垂直于两个平行平面中的一个，则___________________________________________； ⑸面面垂直的性质定理是________________________________________________.复习2：平面与平面垂直的有关结论⑴两个平面垂直的定义是_______________________________________________________________； ⑵两个面垂直的判定定理是_____________________________________________________________. 复习3：⑴斜线和平面所成的角怎么作?直线和平面所成的角的范围是_____________；⑵二面角的定义是怎样的？它的平面角又是怎么作的?课内探究例1 如图14-1所示，在正方体中，P 、Q 、R 、S 分别为棱A D ''、A B ''、AB 、BB '的中点. 求证：平面PQS B RC '⊥图14-1小结：面面垂直通常转化为线面垂直(关键找到一个面内垂直于另一个面的线)，线面垂直又转化为线线垂直，线线垂直往往又用到线面垂直的定义.例2 如图14-2所示，设a 、b 为异面直线，AB 垂直于a 、b ，且与a 、b 分别交于A 、B 两点. ⑴α为平面，若a ∥α,b ∥α,求证：AB α⊥；⑵若a α⊥，b β⊥，c αβ=，求证：AB ∥c图14-（1） 图14-2（2）小结：“平行”与“垂直”的转化；线面垂直的判定和性质定理的灵活运用.例3 如图14-3，二面角l αβ--的平面角是个锐角，点P 到α、β和棱l的距离分别为4⑴分别求直线PC 与面α和面β所成的角;⑵求二面角l αβ--的大小.图14-3※ 动手试试练1. 在正方体ABCD A B C D''''-中，求证：平面ACC A''⊥平面A BD'.练2. 如图14-4，VO ABC⊥，O CD∈，VA VB=，AD BD=，求证：CD AB⊥，AC BC=.图14-4当堂检测1. a b⊥，且a∥α，则直线b和面α是（）.A.bα⊂ B.b与α相交或b∥α或bα⊂C.bα⊄ D.b∥α或bα⊂2. 过平面外一点P：①存在无数条直线与平面α平行②存在无数条直线与平面α垂直③仅有一条直线与平面α平行④仅有一条直线与平面α垂直；其中正确结论的个数是（）.A.1个B.2个C.3个D.4个3. 下列说法错误的是（）.A.过一点和一个平面垂直的平面有无数个B.过一个平面的一条垂线的所有平面都与此平面垂直C.过一个平面的一条斜线的平面与此平面不垂直D.二面角的任意一个平面角所在平面垂直于此二面角的两个面4. 两个长方形所在平面互相垂直，长宽如图所示，则cosα与cosβ的比值为________.5. 正方体ABCD A B C D''''-的棱长为1，P是AD的中点，则二面角A BD P'--的大小为________.课后反思1. 垂直关系的证明：根据题设条件，合理、灵活的运用各种判定和性质定理，注意条件的转化；βα2342. 求线面角和二面角的关键是利用垂直关系，作出角，然后利用三角形的知识加以解决.知识拓展论证垂直问题要注意垂直关系的转化，每一种垂直的判定就是从某一垂直开始转向另一垂直，最终达到目的，其转化关系为：线线垂直线面垂直面面垂直课后训练1. 如图14-5，2VA VB AC BC====，23AB=，1VC=，求二面角V AB C--大小.图14-52. S为ABC∆所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC.求证：AB BC⊥.性质定理判定定理性质定理判定定理。
人教版数学高一必修二导学案 2.3 直线、平面垂直的判定及其性质
2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定一、考纲要求 1线面垂直定义：如果一条直线和一个平面相交，并且和这个平面内的任意一条直线都垂直，我们就说这条直线和这个平面互相垂直其中直线叫做平面的垂线，平面叫做直线的垂面交点叫做垂足 直线与平面垂直简称线面垂直，记作：a ⊥α 2直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面 3.斜线: 斜足斜线在平面上的投影: 直线和平面所成的角:一条直线垂直于平面，我们说它们所成的角是直角；(判断直线与平面垂直的方法4) 一条直线和平面平行或在平面内，我们说它们所成的角是0°的角．二、自主学习问题1、结合对下列问题的思考，试着给出直线和平面垂直的定义．(1)阳光下，直立于地面的旗杆AB 与它在地面上的影子BC 所成的角度是多少？(2)随着太阳的移动,影子BC 的位置也会移动,而旗杆AB 与影子BC 所成的角度是否会发生改变? (3)旗杆AB 与地面上任意一条不过点B 的直线B 1C 1的位置关系如何?依据是什么？问题2、直线与平面垂直的定义如果直线l 与平面α内的任意一条直线都垂直，我们就说直线l 与平面α互相垂直，记作：l ⊥α. 直线l 叫做平面α的垂线，平面α叫做直线l 的垂面．直线与平面垂直时，它们唯一的公共点P 叫做垂足。
符号语言： 图形语言:a l l a αα⎫⇒⊥⎬⊥⎭是平面内任一直线思想: 直线与平面垂直 ⇒直线与平面垂直思考：（1）如果一条直线垂直于一个平面内的无数条直线，那么这条直线是否与这个平面垂直？（2）如果一条直线垂直于一个平面，那么这条直线是否垂直于这个平面内的所有直线？即若αα⊂⊥a l ,，则a l ⊥问题3、请同学们拿出一块三角形纸片，我们一起做一个试验：过三角形的顶点A 翻折纸片，得到折痕AD （如图1），将翻折后的纸片竖起放置在桌面上（BD 、DC 与桌面接触）（图1）（图2） （1）折痕AD 与桌面垂直吗？（2）如何翻折才能使折痕AD 与桌面所在的平面垂直？问题4、直线与平面垂直的判定定理。
高一数学必修2人教A导学案2.3.2平面与平面垂直的判定.doc
2. 3.2平面与平面垂直的判定【教学目标】（1）使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；（2）使学生掌握两个平面垂直的判定定理及其简单的应用； （3）使学生理会“类比归纳”思想在数学问题解决上的作用。
（4）通过实例让学生直观感知“二面角”概念的形成过程；（5）类比已学知识，归纳“二面角”的度量方法及两个平面垂直的判定定理。
【教学重难点】重点：平面与平面垂直的判定。
难点：找出二面角的平面角。
【教学过程】（一）创设情景，揭示课题问题1：平面几何中“角”是怎样定义的？ 问题2：在立体几何中，“异面直线所成的角”、“直线和平面所成的角”又是怎样定义的？它们有什么共同的特征？以上问题让学生自由发言，教师再作小结，并顺势抛出问题：在生产实践中，有许多问题要涉及到两个平面相交所成的角的情形，你能举出这个问题的一些例子吗？如修水坝、发射人造卫星等，而这样的角有何特点，该如何表示呢？下面我们先利用具体的实物来进行观察,研探。
（二）研探新知1、二面角的有关概念老师展示一张纸面，并对折让学生观察其状，然后引导学生用数学思维思考，并对以上问题类从二面角定理地反映了两个平面相交的位置关系，如我们常说“把门开大一些”，是指二面角大一些，那我们应如何度量二两角的大小呢？师生活动：师生共同做一个小实验（预先准备好的二面角的模型）在其棱上位取一点为顶点，在两个半平面内各作一射线（如图2.3-3），通过实验操作，研探二面角大小的度量方法——二面角的平面角。
教师特别指出：（1）在表示二面角的平面角时，要求OA ⊥L ，OB ⊥L ； （2）∠AOB 的大小与点O 在L 上位置无关； （3）当二面角的平面角是直角时，这两个平 面的位置关系怎样？承上启下，引导学生观察，类比、自主探究， 获得两个平面互相垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。
图2.3-3（三）实际应用,巩固深化 例1、（课本69页例3）设AB 是圆O 的直径，PA 垂直于圆O 所在平面，C 是圆周上的任意点，求证：面PAC ⊥面PBC.变式： 课本69P 的探究问题 例2、已知直线PA 垂直正方形ABCD 所在的平面，A 为垂足。
人教新课标版数学高一-必修二导学案 平面与平面垂直的性质
时间课时课题 2.3.4平面与平面垂直的性质主备人王建东学习目标使学生掌握直线与平面垂直，平面与平面垂直的性质定理；能运用性质定理解决一些简单问题；了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系。
学习重点难点重点：平面与平面垂直的性质及其应用。
难点：掌握两个平面垂直的性质及应用．学法与教具学习过程备注复习直线和平面垂直的性质定理:两个平面垂直的判定定理：二面角的定义：问题1：黑板所在平面与地面所在平面垂直，你能否在黑板上画一条直线与地面垂直？问题2：如图，长方体ABCD－A'B'C'D'中，平面A'ADD'与平面ABCD垂直，直线A'A垂直于其交线AD，平面A'ADD’内的直线A'A与平面ABCD垂直吗？探究1:如图，设α⊥β，α∩β＝CD，AB α，AB⊥CD，且AB∩CD＝B，我们看直线AB与平面β的位置关系。
归纳得到平面与平面垂直的性质定理:定理两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
想一想:用符号语言如何表述这个定理?可以通过直线与平面垂直判定平面与平面垂直，平面与平面垂直性质定理说明，由平面与平面垂直可以得到直线与平面垂直，这种直线与平面的的位置关系同平面与平面的位置关系的相互转化，是解决空间图形的重要思想方法。
探究2：1.若两个平面垂直，过其中一个平面内一点能否作另一个平面的垂线?这条直线与这个平面有何关系?可作多少条这样的垂线?2.练习：两个平面互相垂直，下列命题正确的是（）A、一个平面内的已知直线必垂直于另一个平面内的任意一条直线B、一个平面内的已知直线必垂直于另一个平面内的无数条直线C、一个平面内的任意一条直线必垂直于另一个平面D、过一个平面内任意点作交线的垂线，则此垂线必垂直于另一个平面.问题3：思考：设平面α⊥平面β，点P在平面α内，过点P作平面β的垂线a，直线a与平面α具有什么位置关系？例1:如图，已知平面α，β满足α⊥β，直线a满足a⊥β，a α，试判断直线a与平面α的位置关系。
高中数学必修二导学案 平面与平面垂直的判定
学生班级 姓名 小组号 评价必修二 2.3.2平面与平面垂直的判定【学习目标】1.正确理解和掌握“二面角”、“二面角的平面角”、“直二面角”及“两个平面互相垂直”等概念；2.掌握两个平面垂直的判定定理及其简单的应用，体会“类比归纳”思想在解决数学问题中的作用。
【重点和难点】教学重、难点：掌握两个平面垂直的判定定理及其简单的应用。
【使用说明及学法指导】1.先预习课本P 67-P 69内容，然后开始做导学案。
2.将预习中不能解决的问题标出来，以便课上交流讨论。
预习案一．问题导学1.两个平面垂直，则一个平面内的任何一条直线都垂直于另一个平面吗？2.利用判定定理证明面面垂直的关键是什么？二．知识梳理1、二面角：从一条直线出发的两个半平面所组成的图形叫做二面角。
如图一：记法：l αβ--或P l --Q 。
（图一）（图二）2、二面角的平面角：在二面角l αβ--的棱l 上任取一点O ，以点O 为垂足，在半平面α和β内分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的∠AOB 叫做 。
如图二， 为二面角l αβ--的平面角。
平面角是直角的二面角叫做直二面角。
注意：（1）二面角的平面角的取值范围： ；（2）∠AOB 的大小与点O 在l 上的位置 。
（“有关”或“无关”）3、说明：可以由直线与平面垂直证明平面与平面垂直。
三.预习自测1、若l 为一条直线，γβα,,为三个互不重合的平面，给出下列三个命题：①βαβγγα⊥⇒⊥⊥,；②βαγβγα⊥⇒⊥//,；③βαβα⊥⇒⊥l l ,//。
其中正确的命题是（ ）A.0个B.1个C.2个D.3个四.我的疑问：探究案一． 合作探究探究1.面面垂直的判定例1、 如图，AB 是⊙O 的直径，PA 垂直于⊙O 所在的平面，C 是圆周上不同于A ，B 的任意一点，（1） 你能发现哪些平面垂直；（2） 求证：平面PAC ⊥平面PBC 。
探究2.用定义求二面角的平面角的大小例2、已知S 是△ABC 所在平面外一点，∠ASC=90º，∠ASB=∠BSC=60º，且SA=SB=SC ，（1）求证：平面SAC⊥平面ABC ；（2）求二面角B —AS —C 的余弦值。
人教版高中数学必修二学案：2.3.2平面与平面垂直的判定2
百度文库- 让每个人平等地提升自我
1
平面与平面垂直的判定(2)
编制：于胜斌编制时间：10月14日使用班级：高二(9、10)班编号：16
学习目标: 了解两个平面互相垂直的定义;理解并掌握平面与平面垂直的判定定理并会利用定理证明面面垂直.
一、自主学习：
看教材P68下--P69例3之上部分，完成下面内容：
1．平面与平面垂直的定义：
2．两个平面互相垂直的画法：画两个互相垂直的平面
3．平面与平面垂直的判定定理：
(1)文字语言:
(2)图形语言:
(3)符号语言:
(4)数学思想:
二、合作探究：
例1.已知直线PA垂直于圆O所在的平面，A为垂足，AB为圆O的直径，C是圆周上异于A、B的一点。
求证：平面PAC 平面PBC。
探究1、四面体P-ABC的四个面的形状是怎样的?
探究2、有哪些直线和平面垂直？
探究3、有哪些平面相互垂直？
变式:如图P为ΔABC所在平面外一点，PA⊥平面ABC，∠ABC＝90°，AE⊥PC于E，AD⊥PB于D，求证：(1)平面ADE⊥平面PBC；
(2)平面ADE⊥平面PAC。
三、小结:。
精选人教版高中数学必修二导学案：第二章第三节平面与平面垂直的性质
第二章第三节平面与平面垂直的性质
三维目标
1.理解并能证明平面与平面垂直的性质定理；
2.会运用性质定理解决一些简单问题.
________________________________________________________________________________ 目标三导 学做思1
问题1. 如图所示，侧面与地面什么关系？
图1 图2
问题2. 证明面面垂直的性质定理, 并用符号语言、图形语言表示面面垂直的性质定理.
D 1 C 1
A 1C
问题3. 如何在黑板面上画一个面与地面垂直的直线？
【学做思2】
1.如图
2.3-22，已知α⊥β，a⊥β,a ⊄α,试判断直线a 与平面α的位置关系.
图2.3-22
*2. 正方形ABCD 和四边形ACEF 所在的平面互相垂直，AC EF //，2=
AB ，1==EF CE
求证：⊥CF 平面BDE
达标检测
*1.如图所示，在四棱锥ABCD S -中，底面ABCD 是矩形，侧面⊥SDC 底面ABCD . 求证：平面⊥SCD 平面SBC .
2.求证：三个两两垂直的平面的交线两两垂直.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章第三节平面与平面垂直的性质
三维目标
1.理解并能证明平面与平面垂直的性质定理；
2.会运用性质定理解决一些简单问题.
________________________________________________________________________________ 目标三导学做思 1
问题 1. 如图所示，侧面与地面什么关系？
图1 图2
问题 2. 证明面面垂直的性质定理, 并用符号语言、图形语言表示面面垂直的性质定理.
B
D 1C
1
A 1
A C
B 1D
问题 3. 如何在黑板面上画一个面与地面垂直的直线？
【学做思2】
1.如图
2.3-22，已知α⊥β，a⊥β,aα,试判断直线a与平面α的位置关系.
图2.3-22
*2. 正方形ABCD 和四边形ACEF 所在的平面互相垂直，
AC EF //，2AB ，1EF CE 求证：CF 平面BDE
达标检测
*1.如图所示，在四棱锥
ABCD S 中，底面ABCD 是矩形，侧面SDC 底面ABCD . 求证：平面SCD 平面SBC .
2.求证：三个两两垂直的平面的交线两两垂直.。