电磁场与电磁波-3
谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】

第3章 静态电磁场及其边值问题的解(一)思考题3.1 电位是如何定义的?中的负号的意义是什么?答:由静电场基本方程▽×E=0和矢量恒等式可知,电场强度E 可表示为标量函数φ的梯度,即式中的标量函数φ称为静电场的电位函数,简称电位;式中负号表示场强方向与该点电位梯度的方向相反。
3.2“如果空间某一点的电位为零,则该点的电场强度也为零”,这种说法正确吗?为什么?答:不正确。
因为电场强度大小是该点电位的变化率。
3.3“如果空间某一点的电场强度为零,则该点的电位为零”,这种说法正确吗?为什么?答:不正确。
此时该点电位可能是任一个不为零的常数。
3.4 求解电位函数的泊松方程或拉普拉斯方程时,边界条件有何意义?答:边界条件起到给方程定解的作用。
3.5 电容是如何定义的?写出计算电容的基本步骤。
答:两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比,即其基本计算步骤:①根据导体的几何形状,选取合适坐标系;②假定两导体上分别带电荷+q和-q;③根据假定电荷求出E;④由求得电位差;⑤求出比值3.6 多导体系统的部分电容是如何定义的?试以考虑地面影响时的平行双导线为例,说明部分电容与等效电容的含义。
答:多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下,与另一个导体构成的电容。
计及大地影响的平行双线传输线,如图3-1-1所示,它有三个部分电容C11、C12和C22,导线1、2间的等效电容为;导线1和大地间的等效电容为;导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系?在什么条件下二者是一致的?答:表示连续分布电荷系统的静电能量计算公式,虽然只有ρ≠0的区域才对积分有贡献,但不能认为静电场能量只存在于有电荷区域,它只适用静电场。
表示静电场能量存在于整个电场区域,所有E≠0区域对积分都有贡献,既适用于静电场,也用于时变电磁场,当电荷分布在有限区域内,闭合面S无限扩大时,有限区内的电荷可近似为点电荷时,二者是一致的。
电磁场与电磁波试题答案

《电磁场与电磁波》试题1一、填空题(每小题1分,共10分)1.在均匀各向同性线性媒质中,设媒质的导磁率为μ,则磁感应强度B 和磁场H满足的方程为: 。
2.设线性各向同性的均匀媒质中,02=∇φ称为 方程。
3.时变电磁场中,数学表达式H E S⨯=称为 。
4.在理想导体的表面, 的切向分量等于零。
5.矢量场)(r A穿过闭合曲面S 的通量的表达式为: 。
6.电磁波从一种媒质入射到理想 表面时,电磁波将发生全反射。
7.静电场是无旋场,故电场强度沿任一条闭合路径的积分等于 。
8.如果两个不等于零的矢量的 等于零,则此两个矢量必然相互垂直。
9.对平面电磁波而言,其电场、磁场和波的传播方向三者符合 关系。
10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 函数的旋度来表示。
二、简述题 (每小题5分,共20分)11.已知麦克斯韦第二方程为t B E ∂∂-=⨯∇ ,试说明其物理意义,并写出方程的积分形式。
12.试简述唯一性定理,并说明其意义。
13.什么是群速?试写出群速与相速之间的关系式。
14.写出位移电流的表达式,它的提出有何意义?三、计算题 (每小题10分,共30分)15.按要求完成下列题目 (1)判断矢量函数y x e xz ey B ˆˆ2+-=是否是某区域的磁通量密度?(2)如果是,求相应的电流分布。
16.矢量z y x e e eA ˆ3ˆˆ2-+=,z y x e e e B ˆˆ3ˆ5--=,求 (1)B A+ (2)B A⋅17.在无源的自由空间中,电场强度复矢量的表达式为()jkz y x e E e E eE --=004ˆ3ˆ(1) 试写出其时间表达式; (2) 说明电磁波的传播方向;四、应用题 (每小题10分,共30分)18.均匀带电导体球,半径为a ,带电量为Q 。
试求 (1) 球内任一点的电场强度(2) 球外任一点的电位移矢量。
19.设无限长直导线与矩形回路共面,(如图1所示), (1)判断通过矩形回路中的磁感应强度的方向(在图中标出); (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。
电磁场与电磁波:第三章作业答案
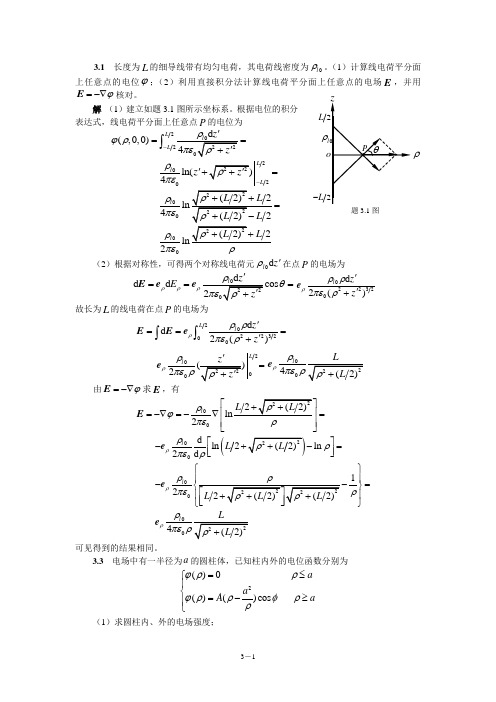
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
电磁场与电磁波实验报告

电磁场与电磁波实验报告电磁场与电磁波实验报告引言:电磁场和电磁波是物理学中非常重要的概念。
电磁场是由电荷产生的一种物理场,它的存在和变化会影响周围空间中的其他电荷。
而电磁波则是电磁场的一种传播形式,它以电磁场的振荡和传播为基础,具有波动性质。
本次实验旨在通过实际操作和测量,深入了解电磁场和电磁波的特性。
实验一:测量电磁场强度在实验一中,我们使用了一个电磁场强度计来测量不同位置的电磁场强度。
首先,我们将电磁场强度计放置在一个固定的位置,记录下此时的电磁场强度。
然后,我们将电磁场强度计移动到其他位置,重复测量过程。
通过这些数据,我们可以得出不同位置的电磁场强度的分布情况。
实验结果显示,电磁场强度随着距离的增加而逐渐减弱。
这符合电磁场的特性,即电荷产生的电磁场在空间中以一定的规律传播,而传播的强度会随着距离的增加而减弱。
这一实验结果验证了电磁场的存在和变化对周围环境的影响。
实验二:测量电磁波频率和波长在实验二中,我们使用了一个频率计和一个波长计来测量电磁波的频率和波长。
首先,我们将频率计和波长计设置好,并将它们与电磁波源连接。
然后,我们观察频率计和波长计的测量结果,并记录下来。
通过这些数据,我们可以得出电磁波的频率和波长的数值。
实验结果显示,不同频率的电磁波具有不同的波长。
频率越高的电磁波,波长越短;频率越低的电磁波,波长越长。
这符合电磁波的特性,即电磁波的振荡频率和波长之间存在一定的关系。
这一实验结果验证了电磁波的波动性质,以及频率和波长之间的关系。
实验三:观察电磁波的干涉和衍射现象在实验三中,我们使用了一块光栅和一个狭缝装置来观察电磁波的干涉和衍射现象。
首先,我们将光栅放置在光源前方,并调整光源的位置和光栅的角度。
然后,我们观察到在光栅后方的屏幕上出现了一系列明暗相间的条纹。
这些条纹是由电磁波的干涉和衍射效应引起的。
实验结果显示,当电磁波通过光栅时,会发生干涉和衍射现象。
干涉现象表现为明暗相间的条纹,而衍射现象表现为条纹的扩散和交替。
《电磁场与电磁波》课后习题解答(全)

(3)
【习题3.4】
解:(1)在区域中,传导电流密度为0,即J=0
将 表示为复数形式,有
由复数形式的麦克斯韦方程,可得电场的复数形式
所以,电场的瞬时值形式为
(2) 处的表面电流密度
(3) 处的表面电荷密度
(4) 处的位移电流密度
【习题3.5】
解:传导电流密度 (A/ )
位移电流密度
【习题3.6】
(2)内导体表面的电流密度
(3)
所以,在 中的位移电流
【习题2.13】
解:(1)将 表示为复数形式:
则由时谐形式的麦克斯韦方程可得:
而磁场的瞬时表达式为
(2)z=0处导体表面的电流密度为
z=d处导体表面的电流密度为
【习题2.14】
已知正弦电磁场的电场瞬时值为
式中
试求:(1)电场的复矢量;
(2)磁场的复矢量和瞬时值。
由安培环路定律: ,按照上图所示线路积分有
等式左边
等号右边为闭合回路穿过的总电流
所以
写成矢量式为
将 代入得
【习题3.18】
解:当 时, ,
当 时, ,
这表明 和 是理想导电壁得表面,不存在电场的切向分量 和磁场的法向分量 。
在 表面,法线
所以
在 表面,法线
所以
【习题3.19】
证明:考虑极化后的麦克斯韦第一方程
(1)
和 (2)
若采用库仑规范,即 (3)
对(1)式两边取散度,有
将(2)、(3)式代入,得
故电流连续性也是满足的。
【习题4.3】解:
【习题4.4】
证明:因为 即
故 满足连续性方程。
另外, 满足洛仑兹条件。
第三课时电磁场和电磁波讲课文档

典例剖析
【例2】 电磁波与声波比较( )
A.电磁波的传播不需要介质,声波的传播需要介质 B.由空气进入水中时,电磁波速度变小,声波速度变大 C.由空气进入水中时,电磁波波长变小,声波波长变大 D.电磁波和声波在介质中的传播速度,都是由介质决定,与频率无关
第29页,共43页。
[解析] 可以根据电磁波的特点和声波的特点进行分析选项A、B 均与事实相符,所以A、B项正确.根据λ= ,电磁波速v度变小, 频率不变,波长变小;声波速度变大,频率不变,波长变大,所f 以选项 C正确.电磁波在介质中的速度,与介质有关,也与频率有关,在同 一种介质中,频率越大,波速越小,所以选项D错误,故选ABC.
传播方 式 地波
地波和 天波 天波
主要用途
超远程无 线电 通信和导 航 调幅无线 电广播、电 报、通信
第12页,共43页。
微 米波 波
分米 波 厘米 波 毫米 波
10 m~1 m 30 MHz~300 MHz
近似 直线 传播
1 m~0.1 m 300 MHz~3000 直线
MHz
传播
10 cm~1 3000
(2)雷达用的是微波波段,因为电磁波波长越短,传播的直线性越好,反
射性越强.活学活用
第20页,共43页。
3.雷达是利用电磁波来测定物体的位置和速度的设备,它可以向一定 方向发射不连续的电磁波,当遇到障碍物时要发生反射.雷达在发射
和接收电磁波时,在荧光屏上分别呈现出一个尖形波.某型号防 空雷达发射相邻两次电磁波之间的时间间隔为5×10-4 s.现在
第31页,共43页。
典例剖析 【例3】 雷达向远处发射无线电波,每次发射的时间是1μs,两次发
3电磁场与电磁波-第三章new

对于体、 对于体、面、线电荷的电位,可用场源积分法分别求得: 线电荷的电位,可用场源积分法分别求得: 总结: 总结: 求解电场强度时, 求解电场强度时,可先求 电位函数, 电位函数,然后计算电 位函数的负梯度便得电 场强度E(r)。 场强度 。 可见电位的计算式简便得多(标 可见电位的计算式简便得多( 量积分) 再求场强时, 量积分),再求场强时,微分 总是可计算的 也简单。 总是可计算的,也简单。
∮E.dl l
= 0
3.2.2
无旋场, 静电场为无旋场 静电场为无旋场, 一定是保守场 一定是保守场
3.2.11
因上式积分路径及面元是任意的, 因上式积分路径及面元是任意的,有: x E = 0
总结真空中静电场的基本方程(微分形式 为 总结真空中静电场的基本方程 微分形式)为: 微分形式
在场源变量ρ已知的情况下,通过D 在场源变量ρ已知的情况下,通过D0=ε0E, 联立求解上述两个矢量方程就能求得E 联立求解上述两个矢量方程就能求得E。 据亥姆霍兹定理:场可由散度与旋度共同确定, 据亥姆霍兹定理:场可由散度与旋度共同确定, 只有在给定散度与旋度方程的条件下才能唯一的 只有在给定散度与旋度方程的条件下才能唯一的 的确定此矢量场。 的确定此矢量场。 当电荷对称分布时,适当选取坐标系,可使D 当电荷对称分布时,适当选取坐标系,可使D0 只有一个分量,且仅是坐标的函数, 或E只有一个分量,且仅是坐标的函数,则 E自动 =0,此时只要计算∮ ds=q即可得场解 即可得场解。 满足xE =0,此时只要计算∮D0.ds=q即可得场解。
R
3
4π
B(r ) =
0 I
4
∫ π
dl ′ X R
l
R3
> ε0 > 1/0 > 电荷 > 电流 > 标量源 > 矢量源 叉积
电磁场与电磁波课后思考题答案

电磁场与波课后思考题2-1 电场强度的定义是什么?如何用电场线描述电场强度的大小及方向?电场对某点单位正电荷的作用力称为该点的电场强度,以E 表示。
用曲线上各点的切线方向表示该点的电场强度方向,这种曲线称为电场线。
电场线的疏密程度可以显示电场强度的大小。
2-2给出电位与电场强度的关系式,说明电位的物理意义。
静电场中某点的电位,其物理意义是单位正电荷在电场力的作用下,自该点沿任一条路径移至无限远处过程中电场力作的功。
2-3什么是等位面?电位相等的曲面称为等位面。
2-5给出电流和电流密度的定义。
电流是电荷的有规则运动形成的。
单位时间内穿过某一截面的电荷量称为电流。
分为传导电流和运流电流两种。
传导电流是导体中的自由电子(或空穴)或者是电解液中的离子运动形成的电流。
运流电流是电子、离子或其它带电粒子在真空或气体中运动形成的电流。
电流密度:是一个矢量,以J 表示。
电流密度的方向为正电荷的运动方向,其大小为单位时间内垂直穿过单位面积的电荷量。
2-10运动电荷,电流元以及小电流环在恒定磁场中受到的影响有何不同?运动电荷受到的磁场力始终与电荷的运动方向垂直,磁场力只能改变其运动方向,磁场与运动电荷之间没有能量交换。
当电流元的电流方向与磁感应强度B 平行时,受力为零;当电流元的方向与B 垂直时,受力最大,电流元在磁场中的受力方向始终垂直于电流的流动方向。
当电流环的磁矩方向与磁感应强度B 的方向平行时,受到的力矩为零;当两者垂直时,受到的力矩最大2-11什么是安培环路定理?试述磁通连续性原理。
为真空磁导率,70 10π4-⨯=μ (H/m),I 为闭合曲线包围的电流。
安培环路定理表明:真空中恒定磁场的磁通密度沿任意闭合曲面的环量等于曲线包围的电流与真空磁导率的乘积。
真空中恒定磁场通过任意闭合面的磁通为0。
磁场线是处处闭合的,没有起点与终点,这种特性称为磁通连续性原理。
2-12什么是感应电动势和感应磁通? 感应电场强度沿线圈回路的闭合线积分等于线圈中的感应电动势,即 穿过闭合线圈中的磁通发生变化时,线圈中产生的感应电动势e 为ϕ-∇=E S J Id d ⋅=tqI d d =Bv q ⨯=F Bl I F⨯=d ISB B Il IlBl Fl T ====2)(B S I T ⨯=S I =m BT ⨯=m Il B l⎰=⋅ 0 d μ ⎰=⋅SS B 0d t l E ld d d Φ-=⋅⎰t e d d Φ-=线圈中感应电流产生的感应磁通方向总是阻碍原有刺磁通的变化,所以感应磁通又称反磁通。
电磁场与电磁波(第4版)第3章部分习题参考解答
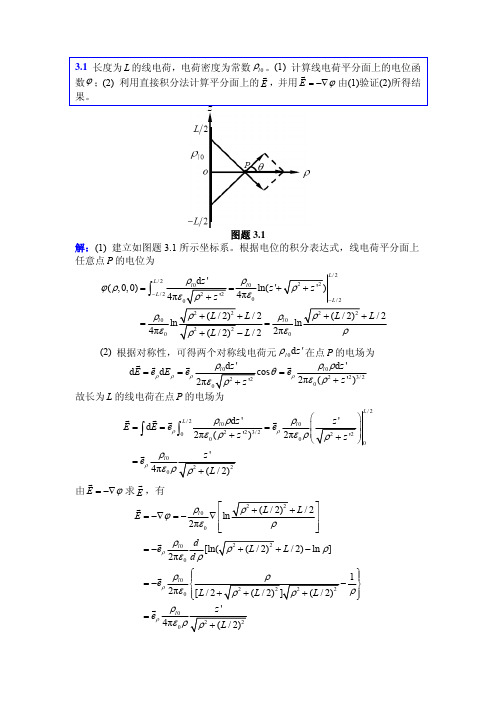
ρ ≥ a 时, E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷,试判断下列函数中哪些是可能的电位解? (1) e− y cosh x ;(2) e− y cos x ;(3) e− 2 sin x cos x ;(4) sin x sin y sin z 。 解:在电荷体密度 ρ = 0 的空间,电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解; ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解; ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ,另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ,则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2
电磁场与电磁波知识点总结

电磁场与电磁波知识点总结电磁场知识点总结篇一电磁场知识点总结电磁场与电磁波在高考物理中属于非主干知识点,多以选择题的形式出现,题目难度较低,属于必得分题目,重点考察考生对基本概念的理解和掌握情况。
下面为大家简单总结一下高中阶段需要大家掌握的电磁场与电磁波相关知识点。
电磁场知识点总结一、电磁场麦克斯韦的电磁场理论:变化的电场产生磁场,变化的磁场产生电场。
理解:* 均匀变化的电场产生恒定磁场,非均匀变化的电场产生变化的磁场,振荡电场产生同频率振荡磁场* 均匀变化的磁场产生恒定电场,非均匀变化的磁场产生变化的电场,振荡磁场产生同频率振荡电场* 电与磁是一个统一的整体,统称为电磁场(麦克斯韦最杰出的贡献在于将物理学中电与磁两个相对独立的部分,有机的统一为一个整体,并成功预言了电磁波的存在)二、电磁波1、概念:电磁场由近及远的传播就形成了电磁波。
(赫兹用实验证实了电磁波的存在,并测出电磁波的波速)2、性质:* 电磁波的传播不需要介质,在真空中也可以传播* 电磁波是横波* 电磁波在真空中的传播速度为光速* 电磁波的波长=波速*周期3、电磁振荡LC振荡电路:由电感线圈与电容组成,在振荡过程中,q、I、E、B 均随时间周期性变化振荡周期:T = 2πsqrt[LC]4、电磁波的发射* 条件:足够高的振荡频率;电磁场必须分散到尽可能大的'空间* 调制:把要传送的低频信号加到高频电磁波上,使高频电磁波随信号而改变。
调制分两类:调幅与调频# 调幅:使高频电磁波的振幅随低频信号的改变而改变# 调频:使高频电磁波的频率随低频信号的改变而改变(电磁波发射时为什么需要调制?通常情况下我们需要传输的信号为低频信号,如声音,但低频信号没有足够高的频率,不利于电磁波发射,所以才将低频信号耦合到高频信号中去,便于电磁波发射,所以高频信号又称为“载波”)5、电磁波的接收* 电谐振:当接收电路的固有频率跟收到的电磁波频率相同时,接受电路中振荡电流最强(类似机械振动中的“共振”)。
电磁场与电磁波课后习题及答案三章习题解答

(4)r cos'球坐标;
:;(2)利用直接积分法计算线电荷平分面上任意点的电场E,并用E中核对。
(1)建立如题3.8图所示坐标系。根据电位的积分表达式,线电荷平分面上任意点
3.8
点的电位 解 电位为
L2
(r,0)
X-24兀e0Jr2+z"2
'仝in(z、.r2z2)
4-;°
:?iodz'
_L2
,io I」2(L2)2L2in
a的圆柱体,
(r)=0
Ja-
「(r)二A(r)cos
Lr
(1)求圆柱内、外的电场强度;
(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解(1)由E,可得到r::a时,E0
2
r a时,E_--e^ — [ A(^ —)cos]-e^—[A(r_rrr /'
2 2oo
-erA(1RcoseA(12)sin
「EgS= 9,可求得大、小圆柱中的正、负电荷在点P产生
3.4半径为a的球中充满密度:(r)的体电荷,已知电位移分布为
Dr二亏Aa4
(r-a)
L
1
解:由
r d r
故在
r d r
54
在
r dr
3.5一个半径为a薄导体球壳内表面涂覆了一薄层绝缘膜,球内充满总电荷量为Q为的体
电荷,球壳上又另充有电荷量Q。已知球内部的电场为E=er(r.;:a)4,设球内介质为真空。计
解由于两圆柱面间的电荷不是轴对称分布,不能直接用高斯定律求解。但可把半径为a的
小圆柱面内看作同时具有体密度分别为二订的两种电荷分布,这样在半径为b的整个圆柱体内具
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+ 0202εερA -=Φ∇-= (2) ()x y z E A e yz e xz e xy Φ=-∇=-++ 020=Φ∇-=ερ (3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦20004sin sin 3sin BzBz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭ (4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为22001111100()()22S S d R d R d ρρΦεε=+-=- 下顶面在球心产生的电位为22002222200()()22S S d R d R d ρρΦεε=+-=- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
绪论-电磁场与电磁波(第3版)-邹澎-清华大学出版社

三、电磁场理论的重要性
3、电磁理论与电路的关系 我们专业的基础课和专业基础课可分为两大类:
与场有关的课程:电磁学、电磁场与电磁波、微波、天线、 电波传播、电磁兼容技术……
与路有关的课程:电路分析、模拟电路、数字电路、高频 电路,射频电路设计……
三、电磁场理论的重要性
这两类课程都是研究电磁现象的,所用的方法不同:
1、数学工具:微分、积分、矢量分析、微分方程、数学 物理方程。
①、显得理论性比较强*; ②、利用教学工具的能力在科研和工程设计中起着非常重 要的作用,希望同学们在学习电磁场课的过程中,提高利 用数学工具解决实际问题的能力。
四、学习方法
2、本书内容可分为几部分(把握重点)
①、复习性内容:大学物理中学过内容(在电磁场理论中也
公众应用 :机场监视、海上导航、气象 雷达、测量学、飞机着陆、夜间防盗、 速度测量(警戒雷达)、测绘等
科学应用:天文学、绘图和成像,精密 距离测量,自然资源遥感等
二、电磁场理论的广泛应用
5、微波炉
微波炉
微波炉的发明者是美国的斯本塞
三、电磁场理论的重要性
1、是一门重要的专业基础课
①、所有的信息都是通过电磁场和电磁波传递的*,因此必 须掌握电磁场和电磁波的基本规律。
是很重要的内容),在本课程中不作为重点,但作为预
备知识,要求熟悉,可参考大学物理教材复习* 。
②、基本内容:电磁场课程中的基本概念、基本方法。
③、阅读性内容:扩大知识面。
④、第7章在微波技术课中讲,其它章也有一些小节不讲。
以讲课内容为准(在书上作些批注)。
3、 评分方法
①、作业计入期末成绩(要求平时按时完成) 10%
②、是进一步学习一些后续课程的基础:微波技术、光纤 通信、天线、电波传播、电磁兼容技术、射频电路设 计……
电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)第3章

3-18证明无源区中电位分布函数不可能具有最大值或最小值。
证明以直角坐标系为例。已知无源区中电位满足拉普拉斯方程
该方程的通解为 。若此解在 点取得极值,那么在该点应有
若是一维空间,因 , ,可见 为常数,即电位函数没有极值。
若是二维空间, , ,显然 和 不可能同时大于零或同时小于零,因此不可能有极大值或极小值。
解根据镜像法可知,无限大的导体平面与无限长圆柱导线之间的场分布与两根无限长平行圆柱导线之间的一半空间的场分布完全相同。因此,圆柱导线与导体平面之间的单位长度内的电容是两根平行圆柱导线的单位长度内的电容一倍。由教材3-3节获知两根平行圆柱导线的单位长度内的电容为
式中D为两根圆柱导线轴线之间的距离,a为圆柱导线的半径。因此,对于本题的圆柱导线与导体平面之间的单位长度内的电容为
要使点电荷受力为零,则 应满足下列方程
求解此高次方程可用作图法。为此,先将上式化简为
再化为关于 的方程即
若 ,则上面的方程又可写为
令 , ,分别作图求得y1和y2的交点,即是所要求的解。根据题意可知 ,由下图可见 的解位于 =1.5~2之间。其值近似为 ,即 时,点电荷q受力为零。
3-14试证位于内半径为a的导体球形空腔中的点电荷q受到的电场力大小为
答根据镜像法,如果劈形导体的夹角不为 的整数分之一时,则镜像电荷不能最终和原电荷重合,这样将会产生无限多个镜像电荷,每个镜像电荷都会产生一定的电位,导致合成电位无限大,因而无解。
当点电荷位于两块无限大导体板之间时,可采用镜像法求解。此时虽然也会产生无限多个镜像电荷,但是远处的镜像电荷对于两板之间的场点贡献越来越小,因
若高度h>>a,上式还可进一步简化为
《电磁场和电磁波》 讲义

《电磁场和电磁波》讲义一、什么是电磁场在我们生活的世界中,电磁场是一种无处不在但又常常被我们忽略的存在。
简单来说,电磁场就是由带电粒子的运动所产生的一种物理场。
想象一下,当一个电子在空间中移动时,它的周围就会产生一个电场。
这个电场会对周围的其他带电粒子产生力的作用。
与此同时,如果这个电子在移动的过程中还在不断地改变速度,那么就会产生磁场。
电场和磁场就像是一对好兄弟,它们总是同时出现,相互关联,并且相互影响。
这种相互作用的结果就是我们所说的电磁场。
电磁场的强度和方向可以用数学上的向量来描述。
电场强度用 E 表示,磁场强度用 B 表示。
它们的大小和方向会随着带电粒子的运动状态以及空间位置的变化而变化。
二、电磁场的特性电磁场具有一些非常重要的特性。
首先,电磁场可以在空间中传播。
这就像我们扔一块石头到水里,会产生一圈圈的水波向外扩散一样,电磁场也能以电磁波的形式在空间中传播能量和信息。
其次,电磁场遵循一定的规律。
比如,库仑定律描述了两个静止点电荷之间的电场力作用;安培定律则描述了电流与磁场之间的关系。
再者,电磁场具有能量。
当电磁场发生变化时,能量会在电场和磁场之间相互转换。
这也是电磁波能够传播的一个重要原因。
三、电磁波的产生电磁波的产生通常需要一个源,比如一个加速运动的电荷或者一个变化的电流。
以天线为例,当电流在天线中快速变化时,就会产生迅速变化的电磁场,并向周围空间发射出去,形成电磁波。
另外,原子内部的电子在不同能级之间跃迁时,也会释放出电磁波。
这种电磁波的频率和能量与电子跃迁的能级差有关。
四、电磁波的性质电磁波具有波动性和粒子性双重性质。
从波动性的角度来看,电磁波和其他波一样,具有波长、频率、振幅等特征。
波长是相邻两个波峰或波谷之间的距离;频率则是单位时间内波振动的次数;振幅表示波的能量大小。
电磁波的频率范围非常广泛,从极低频率的无线电波到高频率的伽马射线。
不同频率的电磁波在性质和应用上有着很大的差异。
电磁场与电磁波(第四版)课后答案 第三章习题

3.23一电荷量为 q 质量为 m 的小带电体,放置在无限长导体 平面下方,与平面距离 h 。求 q 的值以使带电体上受到的 −3 静电力恰好与重力相平衡(设 m = 2 ×10 kg , h = 0.02m)。 解:小带电体可视为一点电荷 q ,它所受静电力,来自导体
' 平板的感应电荷,也就是镜像电荷 q(平面上方 h 处, q' =−q)对它的作用力。
a2 ϕ = A(r − ) cos ϕ r
r≥a
(1)求圆柱内、外的电场强度; (2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。 解: (1)电场
在
处 ur r ur a 2 uu a2 E = − er A cos ϕ (1 + 2 ) − eϕ A(1 − 2 sin ϕ ) r r 即 ur ur uu r a2 A a2 A E = er (− A − 2 ) cos ϕ + eϕ ( A − 2 sin ϕ ) ( r ≥ a ) r r
由安培环路定律有315无限长直线电流垂直于磁导率分别为的两种磁介质的交界面试求1两种媒质中的磁感应以z轴为中心为半径做一个圆形回路c由安培环路定律有16319同轴线内导体是半径为a的圆柱外导体是半径为b的薄圆柱面其厚度可忽略不计
第三章 习题
3.3 有一半径为 a 的圆柱体,已知柱内外的电位函数分别为 ϕ =0 r≤a
E1t = E2t = E
En = 0
所以此题仍可用高斯定理
∫
S
ur u r D dS = q
求解,即
D1S1 + D2 S2 = q
4π r 2 4π r 2 ε1 E + ε2E =q 2 2
所以
E=
谢处方《电磁场与电磁波》(第4版)章节习题-第3章 静态电磁场及其边值问题的解【圣才出品】

第3章 静态电磁场及其边值问题的解一、判断题1.为了简化空间电位分布的表达式,总可以将电位参考点选择在无穷远处。
()【答案】×2.焦耳定律只适用于传导电流,不适应于运流电流。
()【答案】√3.绝缘介质与导体分界面上,在静电情况下导体外的电力线总是垂直于导体表面的。
()【答案】√4.位移电流的假说就是变化的磁场产生电场的假说。
()【答案】×5.任意两个带电导体之间都存在电容,对电容有影响的因素包括导体几何形状,导体上的电荷量、两导体相对位置和空间介质。
()【答案】×6.恒定电场中理想导体内的电场强度为零。
()【答案】√7.空间体积中有电流时,该空间内表面上便有面电流。
()【答案】×8.应用分离变量法求解电、磁场问题时,要求整个场域内媒质必须是均匀、线性的。
()【答案】×9.一个点电荷Q放在球形高斯面中心处。
如果此电荷被移开原来的球心,但仍在球内,则通过这个球面的电通量将会改变。
()【答案】×台10.在线性磁介质中,由的关系可知,电感系数不仅与导线的几何尺寸、材料L Iψ=特性有关,还与通过线圈的电流有关。
( )【答案】×二、填空题1.镜像法是在所求场的区域之外,用_______来代替场问题的边界。
假想电荷和场区域原有的电荷一起产生的电场必须要满足_______。
【答案】一些假想电荷;原问题的边界条件。
2.磁介质中恒定磁场的基本方程为:_______。
【答案】,;,.d 0S B S =⎰v v Ñ0B ∇⋅=v d 0CH l ⋅=⎰v v ÑH J ∇⨯=v v 3.位移电流假说的实质是_______。
【答案】变化的电场可以产生磁场4.位移电流和真实电流(如传导电流和运流电流)的区别在于_______。
【答案】位移电流不对应任何带电质点的运动,只是电场随时间的变化率5.已知磁感应强度为,则m 的值为_______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 电导
习题13
• 厚度方向
E U / d J z E
I J dr 1 I Er dr U J r
U I (r22 r12 ) d
• 弧面
1 I r2 U ln( ) d r1
• 角向
ห้องสมุดไป่ตู้
E U / r
r2 I d ln r 1 U
边界条件
• 切向和法向
E1t E2t
D1n D2n
电位函数
(r )
1 4
i
qi r ri
E
泊松方程 拉普拉斯方程
2 - /
- /
2
0
2
边界条件
• 切向和法向
1 2
D1n D2n
1 2 1 2 n n
• • • • 高斯定理 镜像 分离变量 数值计算
• 电感 • 磁能 • 静磁力
电感
L / I
Wm I / 2 LI 2 / 2
电场能量
1 We J AdV 2
电场能量密度
1 1 we J A B H 2 2
静磁力
dWs Fi dgi dWm
Wm Fi gi
• 中心镜像电荷
q' F2 q 4d 2 Q F3 q 4d 2
• 球体电荷
习题26
• 介质 镜像 电荷
• 极化面电荷密度
习题27
习题28
习题30
习题31
习题11
• 恒定电场
J E
1 b V1 ln( ) 2r 1 a I 1 c V2 ln( ) 2r 2 b I 1
E1
I
2r 1
I 1 E2 2r 2
• 内导体表面电荷
1 1
I
1
2a 1
Q1 1
I
1
习题12
• 采用静电比拟法
电容
C Q /V
We QV / 2 CV 2 / 2
电场能量
电场能量密度
1 We dV 2 1 1 we D E 2 2
静电力
dWs Fi dgi dWe
电荷Q 不变 电压V不变
We Fi g i
We Fi gi
静磁场
H J
a3 E1 0 3r 2
a2 V1 0 3
r D2 3
r a2 E2 V2 r 0 3 r 0 6
a 2 a 2 a 2 1 V V1 V2 ( 1 ) 3 0 6 0 r 3 0 2 r
习题6
• 电位移矢量
• 电位 • 电容
q 1 1 1 1 ( ) 1 ( ) 2 4 R2 d R1 4 R1 d R2
q
q 4 C 1 2 1 1 1 1 R1 R2 d R1 d R2 I 4 G 1 2 1 1 1 1 R1 R2 d R1 d R2
磁通不变 电流不变
Wm Fi g i
静态场
• 镜像法
点电荷和导体平面
• 分离变量
通解同边界条件结合
习题1
• 电位函数
(r)
4 V r r 0
1
r0
dv
(r 0)dv dz0
r 0 ez z 0
习题5
• 电位移矢量
a3 D1 2 3r
Dds Q
1
1 2 2 n n 1 1 -3 0 E0 cos n
1 2 2 r n r r
3 0 2 2 -3 E0 cos n 0 2
0 - 3 3 0 E0 cos 1 3 0 E0 cos 0 2 0 2
习题10
• 静电力
习题15
H I 2r
B H
J M
M r 1H
Js n M 1 M 2
习题19
• 同轴线
H
I 2r
B H
• 储能密度
• 电感
1 wm H 2 1 2 W LI 2
习题20
• 磁能
H nI
wm
2 2
1 BH 2
Wm
• 电流恒定
0
2
n I S L x r x
Wm 0 2 2 Fx n I S r 1 x 2
习题22
• 镜像电荷
q F q 2 4 2d
习题24
• 球体镜像电荷
a q' q d
a2 d' d
q' F1 q 4 (d a 2 / d ) 2
静态电磁场
D
E 0
高斯定理
D d s dv
S V
E
B 0
H J
B A
H d l J d s
S
静电场
D
2
• • • •
高斯定理 镜像 分离变量 数值计算
• 电容 • 电能 • 静电力
