QPSK通信系统的MonteCarlo仿真实验报告报告

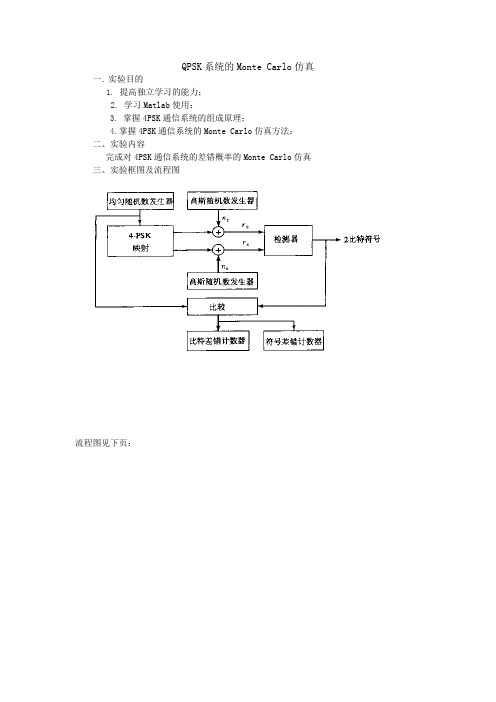
QPSK通信系统的Monte Carlo仿真实验报告2012级通信二班贾师师201200121052 一．【实验目的】1.1提高独立学习的能力1.2培养发现问题，解决问题，分析问题的能力1.3学习Matlab的使用1.4掌握4PSK通信系统的Monte Carlo仿真方法1.5掌握4PSK通信系统的组成原理1.6比较编码信号与未编码信号在随机信道中的传输，加深对纠错编码原理的理解。

二．【实验内容】完成对QPSK通信系统的差错概率的Monte Carlo仿真。

三．【实验原理】1.调制解调原理一组M载波相位调制信号波形的一般表示为：是发送滤波器的脉冲形状，A为信号的幅度。

将式中的余弦函数的相角看成两个相角的和，可以将上表示为将归一化，则函数能量、A可归一化到1。

这样一个相位调制信号可以看做两个正交载波，起始幅度取决于在每个信号区间内的相位，因此，数字相位调制信号在几何上可以用和的二维向量来表示，即同样，将加性噪声分解成两路，加入噪声后的二维向量为判决方法:1）最大投影法：最佳检测器将接收到的信号向量r投射到M个可能的传输信号向量之一上去，并选取对应于最大投影的向量。

我们在试验中用的是将r向量与作为标准的s向量作向量积后选取最大者的方法。

2）最小距离法：我们在实验中实现最小距离法判决的方法是求出r向量的终点与作为标准的s向量的终点后选取最小者的方法。

由于二相相位调制与二进制PAM 是相同的，所以差错概率为式中是每比特能量。

4PSK 可以看作是两个在正交载波上的二相相位调制系统，所以1个比特的差错概率与二相相位调制是一致的。

2.信道纠错编码在随机信道中，错码的出现是随机的，且错码之间是统计独立的。

由高斯白噪声引起的错码就具有这种性质。

当信道中加性干扰主要是这种噪声时，就称这种信道为随机信道。

由于信息码元序列是一种随机序列，接收端是无法预知的，也无法识别其中有无错码。

为了解决这个问题，可以由发送端的信道编码器在信息码元序列中增加一些监督码元。

这些监督码元和信源码元之间有一定的关系，使接收端可以利用这种关系由信道译码器来发现或纠正可能存在的错码。

在信息码元序列中加入监督码元就称为差错控制编码，有时也称为纠错编码。

汉明码是一种能够纠正一位错码且编码效率较高的线性分组码。

下面是汉明码的构造原理。

一般说来，若码长为n，信息位数为k，则监督位数r＝n−k。

如果希望用r 个监督位构造出r 个监督关系式来指示一位错码的n 种可能位置，则要求设分组码(n，k)中k＝4，为了纠正一位错码，由上式可知要求监督位数r≥3。

若取r=3，则n= k + r =7。

用α6α5…α0 表示这7 个码元，用S1 、S2 、S3 表示三个监督关系式中的校正子，则S1 S2 S3 的值与错码位置的对应关系可以规定如下表所列。

由表中规定可见，仅当一错码位置在α2 、α4 、α5 或α6 时，校正子S1 为1；否则S1 为0。

这就意味着α2 、α4 、α5 和α6 四个码元构成偶数监督关系同理，α1 、α3 、α5 和α6 构成偶数监督关系以及α0 、α3 、α4 和α6 构成偶数监督关系在发送端编码时，信息位α6 、α5 、α4 和α3 的值决定于输入信号，因此它们是随机的。

监督位α2 、α1 和α0 应根据信息位的取值按监督关系来确定，即监督位应使上三式中S1 、S2 和S3 的值为零（表示变成的码组中应无错码）由上式经移项运算，解出监督位给定信息位后，可直接按上式算出监督位，其结果如下表所列。

接收端接收到每个码组后，先计算出校正因子S1、S2、和S3，再按事先规定的对应关系判断误码情况并且纠正。

四．【系统框图】（一）未加信道纠错编码的QPSK 调制通信系统（二）信道纠错编码（7，4）汉明码+QPSK 调制的通信系统五．【实验内容】（一）未加信道纠错编码的QPSK 调制通信系统 1) 最大投影点准则进行判决a, 计算噪声方差2σ分别为0、0.1、0.5、1.0时的符号差错概率和比特差错概率；b, 画出在每种2σ时，在检测器输入端1000个接收到的信号加噪声的样本（星座图）；（1）N=1000，方差=0时：AWGN 信道输入数据信道编码 (汉明码)Q -PSK调制Q -PSK解调信道解码 (汉明码)输出数据（2）N=1000，方差=0.1时：符号差错概率：0.10%比特差错概率：0.05%（3）N=1000，方差=0.5时：符号差错概率：12.40%比特差错概率：6.40%。

（4）N=1000，方差=1时：符号差错概率：24.50%比特差错概率：12.90%结论：噪声的方差越大，星座图越分散，对信号影响越大。

附录：实验程序N=input('N=');%输入信源长度s=input('方差=');%输入噪声方差sgma=sqrt(s);%计算标准差[a,b]=signalsource(N);%信源信号m=source2(a,b,N);%转换成四进制sm=zhengjiaoyingshe(m,N);%将四进制信号映射成4PSK两路正交信号n=guass(N,sgma);%产生噪声r=sm+n;%加入噪声c=touyingzhunze(r,N); %利用投影准则判决，%若用最小欧氏距离法则，则改为c=julizhunze(r,N);y=rebuild(c,N);%还原信号[ps,pb]=error1(y,a,b,N)sprintf('符号差错概率：%2.2f%%',ps*100)sprintf('比特差错概率：%2.2f%%',pb*100)figure(1);rc=zeros(1,N);rs=zeros(1,N);%生成两路空信号for i=1:Nrc(i)=r(1,i);rs(i)=r(2,i);endplot(rc,rs,'*', 'color','green');%画星座图axis([-2 2 -2 2]);line([2,-2],[0,0],'linewidth',2,'color','red')line([0,0],[2,-2],'linewidth',2,'color','red')title('星座图');hold offc, 分别画出数据点为1000、5000、10000、100000时的Monte Carlo 仿真误比特率曲线和理论误比特率曲线，比较差别，分析数据点的数量对仿真结果的影响；（蓝色曲线表示理论误比特率曲线，红色表示仿真误比特率曲线）N=1000N=5000N=10000N=100000结论：由各点的Monte Carlo仿真误比特率曲线可以看出，仿真误比特率略大于理论误比特率，且仿真点数越多，曲线越平滑，越贴近理论曲线，即各信噪比下的误比特率越接近于理论值。

附录：实验程序N=input('N=');%输入信源长度SNR2=0:0.5:10;%理论图的信噪比范围Eb=1;snr=zeros(1,21); %产生空序列用来定义仿真图的snrsgma=zeros(1,21); %产生空序列用来定义仿真图的sgmapb1=zeros(1,21); %产生空序列用来定义仿真图的未加汉明码的误码率snr(1)=0;for i=2:21 %求出每点的snrsnr(i)=snr(i-1)+0.5;endfor i=1:21 %21个点循环21次[a,b]=signalsource(N); %生成要发送序列h=xulie(a,b,N);sgma(i)=sqrt((Eb/(10^(snr(i)/10)))/2); %由信噪比求噪声方差 pb1(i)=pbquxian(N,a,b,sgma(i)); %求未加汉明码误码率endfigure(2);semilogy(snr,pb1,'r'); %画出未加汉明码的仿真误比特率曲线hold on;for i=1:length(SNR2),%计算信噪比区间大小SNR=exp(SNR2(i)*log(10)/10); %信噪比pe(i) =1/2*erfc(sqrt(2*SNR)); %理论误比特率endsemilogy (SNR2,pe);gridxlabel('信噪比/dB')ylabel('误比特率')title('QPSK通信系统的蒙特卡洛仿真')hold off;（2）将检测器的判决准则改为最小距离法（星座图上符号间的距离），比较与上面结果的区别。

（1）N=1000，方差=0：符号差错概率：0.00%比特差错概率：0.00%（2）N=1000，方差=0.1：符号差错概率：0.10%比特差错概率：0.05%（3）N=1000，方差=0.5：符号差错概率：12.20%比特差错概率：6.15%（4）N=1000，方差=1：符号差错概率：29.20%比特差错概率：15.55%结论：在仿真中用最小距离法得到的星座图与用最大投影准则得到的星座图相同，差错概率不同。

附录：实验程序N=input('N=');%输入信源长度s=input('方差=');%输入噪声方差sgma=sqrt(s);%计算标准差[a,b]=signalsource(N);%信源信号m=source2(a,b,N);%转换成四进制sm=zhengjiaoyingshe(m,N);%将四进制信号映射成4PSK两路正交信号n=guass(N,sgma);%产生噪声r=sm+n;%加入噪声c=julizhunze(r,N); %利用最小欧氏距离判决，%若用最小欧氏距离法则，则改为c=julizhunze(r,N);y=rebuild(c,N);%还原信号[ps,pb]=error1(y,a,b,N)sprintf('符号差错概率：%2.2f%%',ps*100)sprintf('比特差错概率：%2.2f%%',pb*100)figure(1);rc=zeros(1,N);rs=zeros(1,N);%生成两路空信号for i=1:Nrc(i)=r(1,i);rs(i)=r(2,i);endplot(rc,rs,'*', 'color','green');%画星座图axis([-2 2 -2 2]);line([2,-2],[0,0],'linewidth',2,'color','red')line([0,0],[2,-2],'linewidth',2,'color','red')title('星座图');hold off（二）信道纠错编码（7，4）汉明码+QPSK调制的通信系统1）比较经过信道纠错编码的QPSK调制系统与未加信道编码的系统的传输性能。